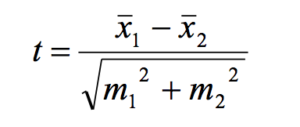Ошибки применения критерия стьюдента - Решение и исправление самых разных ошибок на TopOshibok.ru

Как видно из табл.1
наибольшей популярностью при проверке
гипотез о равенстве двух генеральных
средних (математических ожиданий)
пользуется t-критерий
Стьюдента. Частота применения данного
критерия в разных журналах отличается
друг от друга не очень значительно.
Например, в 11-ти выпусках БЭБМ за 1997г.
t-критерий использован в
114 статьях, тогда как корреляционный и
дисперсионный анализ применен всего
лишь в 15 публикациях, критерий
Колмогорова-Смирнова — в одной статье,
парная линейная регрессия — в трех
статьях, точный критерий Фишера — в трех
статьях и т.д. В 56 статьях этих выпусков,
в которых использовалось выражение «p
< 0,05», вообще не упоминался
использованный статистический критерий.
При чтении статей БЭБМ складывается
впечатление, что большинство авторов
данного журнала знают и используют лишь
единственный статистический критерий
— t-критерий Стьюдента.

Критерий Стьюдента был разработан
английским химиком У.Госсетом, когда
он работал на пивоваренном заводе
Гиннеса и по условиям контракта не имел
права открытой публикации своих
исследований. Поэтому публикации своих
статей по t-критерию
У.Госсет сделал в 1908г. в журнале
«Биометрика» под псевдонимом
«Student», что в переводе
означает «Студент». В отечественной
же литературе принято писать «Стьюдент».
Коварная простота вычисления t-критерия
Стьюдента, а также его наличие в
большинстве статистических пакетов и
программ привели к широкому использованию
этого критерия даже в тех условиях,
когда применять его нельзя. В течение
3-х лет нами был проведен опрос более
250 медиков и биологов, занятых научными
исследованиями. Им задавался единственный
вопрос: «Каковы достаточные и
необходимые условия использования
t-критерия Стьюдента при
сравнении групповых средних»? Ни один
из опрашиваемых не смог полностью и
правильно ответить на него. Примерно
50% говорили о нормальности распределения,
однако не могли при этом объяснить, как
реально проверить нормальность
распределения. Впрочем, очевидно и 250
статистиков не смогли бы внятно объяснить,
чем, например, эритроциты отличаются
от лейкоцитов. Этот пример иллюстрирует,
что прикладная статистика является не
менее узкоспециальной областью
профессиональной деятельности, нежели
медицина и биология.

Рассмотрим более подробно
особенности использования статистического
критерия t-Стьюдента.
Наиболее часто t-критерий
используется в двух случаях. В первом
случае его применяют для проверки
гипотезы о равенстве генеральных средних
двух независимых, несвязанных выборок
(так называемый двухвыборочный
t-критерий). В этом случае
есть контрольная группа и опытная
группа, состоящая из разных пациентов,
их количество в группах может быть
различно. Во втором же случае используется
так называемый парный t-критерий,
когда одна и та же группа объектов
порождает числовой материал для проверки
гипотез о средних. Поэтому эти выборки
называют зависимыми, связанными.
Например, измеряется содержание
лейкоцитов у здоровых животных, а затем
у тех же самых животных после облучения
определенной дозой излучения. В обоих
случаях должно выполняться требование
нормальности распределения исследуемого
признака в каждой из сравниваемых групп.
Из всех 877 проанализированных публикаций,
в которых был использован t-критерий
Стьюдента, упоминание о проверке
нормальности распределения исследуемых
признаков было только в 5 статьях. Более
того, лишь в единичных работах был
проведен достаточно детальный анализ
распределения вероятностей исследуемых
количественных признаков, и на этом
основании было принято аргументированное
решение о выборе статистического
критерия [17-18]. Наши личные исследования
показали, что 50-70% наиболее часто
упоминаемых в публикациях по кардиологии
и радиобиологии количественных
показателей не подчиняются нормальному
распределению. Для проверки гипотезы
о нормальности распределения (основной
гипотезы) может быть использован целый
набор так называемых критериев согласия:
критерий асимметрии и эксцесса,
Dn-критерий Колмогорова,
Хи-квадрат — критерий Пирсона, Омега-квадрат
критерий, критерий Шапиро-Уилки, и т.д.
Предположим, применив один из этих
критериев, мы установили, что исследуемый
признак подчиняется нормальному
распределению в каждой из групп сравнения.
Однако это требование является
необходимым, но не достаточным для
применения t-критерия
Стьюдента. Следующее требование, которое
должно выполняться, это равенство
генеральных дисперсий в сравниваемых
группах. Как известно из курса статистики,
для проверки гипотезы о равенстве двух
генеральных дисперсий нормально
распределенных совокупностей используются
такие критерии, как F-критерий
Фишера, критерий Кохрана, критерий
Вальда и т.д. Для многих статей, в которых
был использован двухвыборочный t-критерий
Стьюдента и приведены объемы выборок
и среднеквадратичные отклонения,
примерно в 50% случаев проверка равенства
генеральных дисперсий дала отрицательный
результат.

Проверка гипотезы о генеральных
средних двух групп с неравными дисперсиями
в математической статистике называется
проблемой Беренса-Фишера и имеет в
настоящее время только приближенные
решения. Подробное изложение проблемы
Беренса-Фишера можно найти в /19,с.258/,
/20,с.235/, /21,с.190/, /12,с.93/. Почему так важно
требование равенства дисперсий в
сравниваемых группах? Не вдаваясь в
детали этой проблемы, отметим, что чем
больше различаются между собой дисперсии
и объемы выборок, тем сильнее отличается
распределение «вычисляемого t-критерия»
от распределения истинного «t-критерия
Стьюдента». При этом различную величину
имеет как сам t-критерий,
так и такой параметр этих распределений,
как число степеней свободы. В свою
очередь число степеней свободы сказывается
на величине достигнутого (критического)
уровня значимости (р < …. ) определяемого
для вычисленной величины t-критерия.
Во многих статистических пакетах
величина t-критерия
вычисляется для двух случаев: 1) дисперсии
равны; 2) дисперсии неравны. При этом
предполагается, что в обоих случаях
требование нормальности распределения
выполняется. Для случая неравных
дисперсий существует несколько наиболее
популярных приближенных решений,
например критерии Кохрана-Кокса,
Саттерзвайта, Уэлча, Гронау и т.д.
Пренебрежение авторами публикаций,
приведенными выше условиями допустимости
использования t-критерия
Стьюдента, приводит к существенному
искажению результатов проверки гипотез
о равенстве средних. На рисунке приведены
графики зависимости величины t-критерия
Стьюдента для случая равных (t=)
и неравных генеральных дисперсий (t|=),
а также отвечающие им значения достигнутых
уровней значимости ( p <
) в зависимости от величины разности D
между генеральными средними.

Как
видно из этого рисунка, достигнутый
уровень значимости (p
< ) для случая неравных дисперсий ( Р
|= ) всегда выше, чем для случая равных
дисперсий (Р =). Величина ( Р |= ) определялась
с использованием аппроксимаций критерия
Беренса-Фишера по Уэлчу, Саттерзвайту,
Гронау и Кохрану-Коксу. Отличия значений
( Р |= ) для этих аппроксимаций наблюдались
в 3-4-ом знаках. Значения Рн/п были получены
для непараметрических критериев
Вилкоксона, Краскела-Валлиса и Манна-Уитни
с помощью статистических пакетов SGWIN
2.1, PRISM
2.01, SPSS
7.53, SAS
6.04 и STATISTICA
5.1. О том, сколь сильно могут отличаться
при этом как значения самого t-критерия,
так и достигнутого уровня значимости
р < , можно судить по результатам
выполненного нами анализа реальных
данных полученных в отделении ИБС НИИ
Кардиологии Томского отделения РАМН.
В табл. 2 приведены итоги проверки гипотез
о равенстве средних в двух группах с
помощью t-критерия
Стьюдента для случая равных дисперсий,
и для случая неравных дисперсий

Условные обозначения
к табл.2.

Х21
— отношение iR
(периода изометрического расслабления)
к длительности RR
при пробе с дипиридамолом (ПД) перед
началом лечения.

Z9
— толщина межжелудочковой перегородки
после лечения, мм.

Z14
— конечный систолический объем в покое
после лечения, мл.

Z15
— ударный объем в покое после лечения,
мл.

Z16
— фракция выброса в покое после лечения,
усл. ед.

А5
— наличие (отсутствие) депрессии сегмента
ST
при ВЭМ.

А6
— наличие (отсутствие) депрессии сегмента
ST
при ПД.

А7 — наличие (отсутствие)
обызвествления коронарных артерий.

А10 — наличие
(отсутствие) нарушений сердечного ритма.

А12 — наличие
(отсутствие) нарушений сердечного ритма
при ПД.

Таблица 2 Результаты
проверки гипотез о равенстве групповых
средних различными критериями.

Исследуемая количественная переменная	Z9	Z15	X21	Z14	Z16	X21	Z9
Группирующая переменная	A5	A7	A5	A12	A7	A10	A6
Значения групповых средних	10,17 8,21	141,7 107,9	0,14 0,11	37,4 19,9	0,77 0,72	1,24 1,04	8,10 9,15
Величина t-критерия Стьюдента для случая равных дисперсий	2,94	1,98	2,69	1,57	2,23	2,09	1,84
Величина t-критерия для случая неравных дисперсий	1,76	2,54	2,03	2,93	1,85	1,73	1,77
Величина достигнутого уровня значимости р < для t-критерия Стьюдента при равных дисперсиях	0,0048	0,0138	0,0107	0,1235	0,0297	0,0401	0,0714
Величина достигнутого уровня значимости р < для t-критерия по Саттерзвайту при неравных дисперсиях	0,1049	0,0665	0,0755	0,0307	0,0830	0,1229	0,0851
Величина достигнутого уровня значимости р < для t-критерия по Кохрану-Коксу при неравных дисперсиях	0,1059	0,0693	0,0797	0,0482	0,0866	0,1259	0,0879
Значение F-критерия Фишера при проверке гипотезы о равенстве дисперсий	9,29	2,57	2,71	4,55	2,00	1,59	5,23
Величина достигнутого уровня значимости р < для F-критерия Фишера при проверке гипотезы о равенстве дисперсий	0,0000	0,023	0,055	0,24	0,10	0,30	0,0000

Таким образом, для исследованных
нами переменных принятие или отклонение
гипотезы о равенстве генеральных средних
в группах во многом определяется
результатом проверки гипотезы о равенстве
генеральных дисперсий. Предположим,
что проверка основной гипотезы подтвердила
нормальность исследуемых нами переменных
в обеих сравниваемых группах. Далее,
зададимся уровнем значимости равным
0,05 , т.е. для критериев с достигнутым
уровнем значимости р<0,05 нулевую
гипотезу о равенстве будем отклонять,
а при р>0,05 гипотезу о равенстве будем
принимать. В этом случае, для толщины
межжелудочковой перегородки Z9
мы должны принять гипотезу о равенстве
средних в подгруппах по А5 для неравных
дисперсий, и отклонить эту гипотезу при
равных дисперсиях. Аналогичные
неоднозначные выводы получены и для
других пар признаков. Только для пары
Z9 — А6 нулевая гипотеза о
равенстве средних принимается для всех
трех случаев. Проведенная нами проверка
еще для 50 аналогичных пар признаков
показала, что для 43 пар принятие или
отклонение гипотезы о равенстве групповых
средних непосредственно зависело от
результата проверки гипотезы о дисперсиях.
Напомним, что мы предположили нормальность
распределения количественной переменной
в обеих группах. Дальнейшая проверка
50 исследуемых кардиологических признаков
показала, что нормальность распределения
наблюдалась в обеих группах у 8 признаков,
в одной из групп — у 19, и отсутствовала
в обеих группах у 31 признака. В таких
ситуациях допустимо применение только
непараметрических критериев, таких как
Ван дер Вардена, Краскела-Валлиса,
Манна-Уитни, Вилкоксона, критерия знаков
и т.д.
В табл.3 приведены результаты
проверки гипотезы о равенстве групповых
средних для признака Х21 (группирующий
признак А5) с помощью нескольких
непараметрических критериев. Проверка
гипотез производилась с помощью пакетов
SGWIN 2.1, PRISM
2.01, SPSS 7.53, SAS
6.04 и STATISTICA 5.1 .

Таблица 3. Результаты
проверки гипотез о равенстве групповых
средних непараметрическими критериями.

	Критерий Вилкоксона	Критерий Краскела-Валлиса	Критерий Ван-дер Вардена	Критерий Манна-Уитни
Достигнутый уровень значимости р <	0,0321	0,0307	0,0224	0,0307

В проанализированных нами статьях
непараметрические критерии, такие как
критерий Вилкоксона, Манна-Уитни,
Сиджела-Тьюки, медианный критерий,
критерий знаков и т.д. были использованы
примерно в 1% статей. Отметим, что в
большинстве это были статьи по
радиобиологии и радиоэкологии.

Итак, корректное применение
t-критерия Стьюдента для
двух групп требует обязательной
нормальности распределения исследуемой
количественной переменной в обеих
группах и столь же обязательного
равенства дисперсий в сравниваемых
совокупностях. Поэтому в тех статьях,
где проверка гипотез о равенстве двух
средних производилась с помощью
t-критерия Стьюдента, и
нет упоминания критериев проверки
нормальности распределения и равенства
дисперсий, можно достаточно основательно
предполагать некорректное использование
авторами публикации данного критерия,
а стало быть, и сомнительность декларируемых
ими выводов.

Достаточно часто встречается
и такая ошибка, как использование
t-критерия Стьюдента при
сравнении двух долей (пропорций). Другая
частая ошибка — применение t-критерия
Стьюдента для проверки гипотез о
равенстве трех и более групповых средних.
Например, для случая трех групп попарно
сравнивают группы 1-2, 1-3 и 2-3 с одним и
тем же уровнем значимости, например
р=0,05. Такой прием недопустим, поскольку
в этом случае принимаемый критический
уровень значимости, равный, например
5% , неравномерно распределяется между
тремя парами групп. В результате этого
авторы также получают ложные выводы о
равенстве либо неравенстве средних
значений в сравниваемых группах. В том
случае, когда необходимо осуществить
проверку статистической гипотезы о
равенстве генеральных средних для трех
и более групп, необходимо применять так
называемую общую линейную модель,
реализованную в процедуре однофакторного
дисперсионного анализа с фиксированными
эффектами. Часто этот метод называют
сокращенно ANOVA (Analysis
of Variance —
анализ отклонений, вариаций). Теория
метода, разработанная английским
статистиком Р.Фишером, с многочисленными
примерами его приложения дана в
/12,19-22/. Если в результате применения
процедуры ANOVA гипотеза о
равенстве всех трех (или более) генеральных
средних отклоняется, то вполне возможно,
что часть групповых средних равна между
собой, а другие средние не равны. Для
такого более тонкого анализа используют
методы линейных контрастов, называемые
также методами множественных сравнений.
Такие методы сравнения позволяют
проверить гипотезы о равенстве между
собой отдельных пар групповых средних.
Наиболее часто для этой цели используют
методы сравнения Шеффе, Тьюки, Бонферони,
Дункана, Габриеля, REGWF,
SNK, LSD и т.д.
/12,19-22/. Отметим, что дисперсионный анализ
для подобной цели был использован всего
лишь в 4% работ. Примеры использования
дисперсионного анализа с применением
методов множественных сравнений имеются
в [12,19-22]. О малоизвестности данного
метода в среде кардиологов говорит не
только мизерная частота его упоминания
в публикациях, но и следующий известный
авторам реальный факт. Два исследователя
одного из НИИ Томского отделения РАМН
направили в английский журнал статью,
которая была возвращена на доработку,
с предложением применить метод ANOVA.
Полгода авторы статьи потратили на то,
чтобы установить, что ANOVA
— это дисперсионный анализ, которому
уже более 60 лет.

Источник

Т-критерий Стьюдента (t-тест) простым языком

Сегодня мы говорим о t-критерии. Т-критерий наиболее популярный статистический тест в биомедицинских исследованиях. Также его называют парный Т-критерий Стьюдента, t-test, two-sample unpaired t-test. Однако, при использовании этого статистического инструмента допускается достаточно много ошибок. Сегодня в этой статье мы постараемся разобраться, как избежать ошибок применения t-критерия Стьюдента, как интерпретировать его результаты и как рассчитывать t-критерий самостоятельно. Об этом обо всем читайте далее.

При описании любого статистического критерия, будь то t-критерий Стьюдента, либо какой-либо еще, нужно вспомнить о том, как же вообще используются статистические критерии. Для того, чтобы понять, как используется любой критерий, нужно перейти к нескольким достаточно логичным для понимания этапам:

Этапы статистического вывода (statistic inference)

Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.

Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.

Видео-версия статьи

Пример использования т-критерия Стьюдента

А пример будет достаточно простой: мне интересно, стали ли люди выше за последние 100 лет. Для этого нужно подобрать некоторые данные. Я обнаружил интересную информацию в достаточно известной статье The Guardian (Tall story’s men and women have grown taller over last century, Study Shows (The Guardian, July 2016), которая сравнивает средний возраст человека в разных странах в 1914 году и в аналогичных странах в 2014 году.

Там приведены данные практически по всем государствам. Однако, я взял лишь 5 стран для простоты вычислений: это Россия, Германия, Китай, США и ЮАР, соответственно 1914 год и 2014 год.

Общее количество наблюдений – 5 в 1914 году в группе 1914 года и общее значение также 5 в 2014 году. Будем думать опять же для простоты, что эти данные сопоставимы, и с ними можно работать.

Дальше нужно выбрать критерии – критерии, по которым мы будем давать ответ. Равны ли средние по росту в 1914 году x̅₁₉₁₄ и в 2014 году x̅₂₀₁₄. Я считаю, что нет. Поэтому моя гипотеза это то, что они не равны (x̅₁₉₁₄≠x̅₂₀₁₄). Соответственно альтернативная гипотеза моему предположению, так называемая нулевая гипотеза (нулевая гипотеза консервативна, обратная вашей, часто говорит об отсутствии статистически значимых связей/зависимостей) будет говорить о том, что они между собой на самом деле равны (x̅₁₉₁₄=x̅₂₀₁₄), то есть о том, что все эти находки случайны, и я, по сути, не прав.

Теперь нужно дать какой-то аргументированный ответ. Даем его с помощью статистического критерия. Соответственно теперь наступает самое важное: как выбрать статистический критерий? Я думаю, это будет темой отдельной статьи. Для корректности использования t-критерия Стьюдента лишь скажу, что нужно, чтобы:

Условия применения статистического критерия т-теста (критерия Стьюдента)

— данные распределялись по закону нормального распределения;

— данные были количественными;

— и это две независимые между собой выборки (независимые это значит, что в этих группах разные люди, а никак, например, до и после применения препарата у одной группы, люди должны быть разными, тогда группы являются несвязанными, либо независимыми), этот аспект стоит учитывать для выбора вида т-критерия Стьюдента, так как для парных выборок существует свой парный т-критерий (paired t-test).

В итоге Мы определились с тем, что это будет t-критерий Стьюдента.

Формула t-критерия Стьюдента достаточно простая. Она гласит о том, что в числителе у нас разница средних, в знаменателе у нас корень квадратный суммы ошибок репрезентативности по этим группам:

Ошибки репрезентативности были подробно объяснены мною в статье по доверительным интервалам. Поэтому я рекомендую вам ознакомиться с ней, чтобы лучше разобраться, что такое ошибки репрезентативности, что такое выборка, как она соотносится с генеральной совокупностью.

Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (m^r).

Давайте остановимся на том, что же значат эти значения:

— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;

— если совсем упрощать значение стандартного отклонения (SD), то можно сказать, что оно представляет собой обобщенную среднюю отклонения каждого значения от среднего (стандартное отклонение показывает, насколько широко значения рассеяны (разбросаны) относительно средней). И дальше мы находим нечто среднее отклонений каждого варианта в группе от среднего;

— и ошибка репрезентативности она тоже находится достаточно просто: это как раз наше отклонение от средней некоторое стандартизованное, поэтому стандартное отклонение на размер выборки (m_r=).

Итак, продолжаем. В ходе подстановки каждого значения в нашу формулу, мы находим, что t-критерий Стьюдента равен 3,78. Однако, я думаю, пока тем, кто не знаком со статистическими критериями, это мало о чем говорит.

Итак, теперь настает четвертый этап вопрос интерпретации. Ранее мы получили значение t-критерия в 3,78. Однако, что же это значит? Стоит отметить, что результаты статистических критериев и вообще их интерпретация не говорит о точном «да», либо «нет» в выводе, то есть рост отличается, либо рост не отличается. Всегда это вопрос определенной доли вероятности – доли вероятности ошибиться при констатации положительного результата (речь об ошибке первого рода (I type error, Alpha)). То есть, например, если мы скажем, что средний рост в начале ХХ и в начале XXI века отличаются с долей ошибкой меньше 5 %. Как раз эта величина в 5 % и фиксируется как достаточная для большинства биомедицинских исследований, помните, р больше, либо меньше 0,05.

Итак, как нам перейти от нашей t к р вероятности? Это сделать достаточно просто, стоит лишь воспользоваться табличными значениями t для определенных степеней свободы. Теперь вопрос: как найти эти степени свободы? Но это сделать достаточно просто. Для того, чтобы обнаружить степени свободы для наших групп, нужно лишь сложить количество наблюдений 5 и 5 в нашем случае и вычесть 2. В нашем случае степень свободы равна 8.

Итак, t=3,78, степень свободы равна 8. Переходим в табличное значение и получаем р вероятность – вероятность равна 0,005. То есть вероятность того, что мы ошибаемся при констатации факта различия роста ранее и сейчас, крайне мала – это 0,005 %, не 5 %, а 0,005 %. То есть мы можем говорить с высокой долей достоверности того, что наш рост сейчас в XXI веке и 100 лет назад отличаются.

Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.

На этом наш разговор о t-критерии Стьюдента закончен. Спасибо, что ознакомились с этой статьей. Я очень надеюсь на вашу обратную связь. Пожалуйста, подписывайтесь на наш сайте, ставьте лайки, предлагайте свои темы для следующих выпусков. Спасибо большое за поддержку. С вами был Кирилл Мильчаков. Пока, до новых встреч!

Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях:

Источник

Лабораторная работа №4

Сравнение групп Критерий Стьюдента Краткие сведения из теории

Результатом исследования обычно является
утверждение, имеющее важное значение,
например, какой метод лучше для лечения
болезни, каковы самые распространенные
побочные эффекты определенного вида
хирургического вмешательства, каков
коэффициент выживаемости после
определенного лечения и действительно
ли новое экспериментальное лекарство
улучшает состояние организма.

Однако, прежде чем получить результат
(утверждение или вывод), необходимо
правильно cпланировать
ход исследования, одним из важных этаповявляется формулировка исходного
утверждения, правильность которого
и проверяется в ходе исследования.
Такое утверждение называетсягипотезой.

Гипотеза —
утверждение, предполагающее доказательство

Проверка гипотезы— это статистическая
процедура, предназначенная для проверки
утверждения. Обычно утверждение касается
исследуемогопараметрасовокупности (т.е. некой величины, которая
характеризует какую-то интересующую
нас сторону объекта).

К примеру, среднее
время госпитализации у первой исследуемой
группы составило 4,5 суток, у второй –
6,3 суток (переменная– время
госпитализации,параметр–
среднее значение дней госпитализации).
В этом примере под гипотезой может
выступать утверждение: различие между
средними значениями статистически
значимо

После того как исследователь определил
переменную и параметр, влияние, на
которые того или иного фактора проверяется
в исследовании, он формулирует нулевую
гипотезу.

Например, при лечении
пациентов согласно официальным схемам
лечения (первая группа) и лечение той
же болезни, но не согласующееся полностью
с официальными схемами (вторая группа)
среднее время госпитализации составило:
у первой исследуемой группы 4,5 суток, у
второй – 6,3 суток. В этом случае влияющий
фактор – лечение согласно официальным
схемам лечения. Анулевая гипотеза:
различие между группами является
случайным и статистически незначимо

Нулевая гипотеза— это предположение,что исследуемые факторы не оказывают
никакого влияния на измеряемый признак
и полученные различия (исследуемых
параметров, средних значений
количества суток госпитализации у двух
групп выше) случайны.

Например, сравнивая
различающиеся средние значения
артериального давления при применении
двух разных анестетиков, мы выдвигаем
нулевую гипотезу о том, что полученные
различия случайны и значимой разницы
между двумя анестетиками нет

Статистическая
значимость результатов. Уровень
значимости

Получив результат, исследователь делает
вывод о том, значим ли полученный
результат с точки зрения статистического
анализа. Другими словами он делает вывод
о статистической значимостиполученного результата.

Для того, чтобы сделать вывод о наличии
или отсутствии статистической значимости
используется так называемый критерий
значимости.

Полученное числовое
значение критерия значимости указывает
на то, принимается или отвергается
нулевая гипотеза. Однако, выводво многомзависити от того с
какой вероятностью мы можем получить
наблюдаемые результаты при верности
нулевой гипотезы

Статистическое исследование всегда
допускает возможное наличие ошибки, и
необходимо учитывать максимальную
вероятность ее возникновения. Если эта
вероятность мала, то нулевая
гипотезаотвергаетсяи делаетсязаключение о значимостиполученного
результата (например, различие средних
значений двух групп статистически
значимо и не обусловлено случайностью)

Максимальную приемлемую
вероятность отвергнуть верную нулевую
гипотезу называют уровнем значимостии обозначаютα (альфа).

Обычно принимают α = 0,05 (5%). Однако
эта величина может быть и другой: 0,01
(1%), 0,1(10%) и т.д. в зависимости от строгости
исследования.

Если в ходе исследования мы получили
результат, который отвергает нулевую
гипотезу, при уровне значимости 5%, то
можно сказать следующее: если бы
нулевая гипотеза была справедлива, то
вероятность получить наблюдаемые
результаты была бы меньше 5%. В принятой
системе обозначений это записывается
как Р < 0,05.Р есть вероятность ошибочно
отвергнуть нулевую гипотезу. Это еще
не означает что влияние изучаемых
факторов доказано (это вопрос тесно
связан с планированием эксперимента),
но, в тоже время, маловероятно, что
результат обусловлен случайностью.

Стандартное заключение
может выглядеть следующим образом:
нулевая гипотеза об отсутствиивлияния исследуемого препарата, например,
на давление, вряд ли справедлива, иразличия между группами статистически
значимы при 5% уровне значимости.
Разумеется, этот вывод по сути своей
носит вероятностный характер. Не
исключено, что ошибочно признается
неэффективный препарат эффективным,
то есть находятся различия там, где их
нет. Однако можно утверждать, что
вероятность подобной ошибкине
превышает 5%

Критерий
Стьюдента

Критерий Стьюдента используется для
сравнения только двух групп. Это частный
случай дисперсионного анализа. Критерий
Стьюдента чрезвычайно популярен, он
используется более чем в половине
медицинских публикаций.

Следует помнить,
что критерий Стьюдента предназначен
для сравнения только двухгрупп, а
не нескольких групп попарно

Ошибочное использование критерия
Стьюдента увеличивает вероятность
«выявить» не существующие различия.

Например, вместо того
чтобы признать несколькометодов
лечения равно эффективными (или
неэффективными), один из них объявляют
«лучшим».

Общая формула для вычисления критерия
Стьюдента:

Для двух случайных выборок извлеченных
из одной нормально распределенной
совокупности это отношение, как правило,
будет близко к нулю.Чем меньше (по
абсолютной величине, по модулю) t, тем
больше вероятность справедливости
нулевой гипотезы. Чем больше t, тем больше
оснований отвергнуть нулевую гипотезу
и считать, что различия статистически
значимы.Величина критерия Стьюдента,
начиная с которойотвергаетсянулевая гипотеза, называетсякритическим
значениемкритерия Стьюдента (t_кр).

Если значение tкритерия Стьюдента по модулюбольшечемкритическое значение критерия
Стьюдента(найденное по таблице
критических значений или рассчитанное
при помощи программного обеспечения)
длязаданного уровня значимости,
то нулевая гипотезаотвергается,
и различия считаютсястатистически
значимыми

Это означает, что если бы группы
представляли собой две случайные выборки
из одной и той же совокупности, то
вероятность получить наблюдаемые
различия (или более сильные) равна 0,05
(или другому значению выбранного уровня
значимости).Следовательно, ошибочный
вывод о существовании различий мы будем
делать в 5% случаев.Застраховаться
от подобных ошибок можно приняв уровень
значимости не 0,05, а к примеру 0,01. Однако
даже в этом случае ошибочные выводы о
существовании различий все же не
исключены — их вероятность снижается
до 1% и в тоже время вероятность не найти
различии там где они есть теперь
повысилась.

Ошибки
в использовании критерия Стьюдента

Критерий Стьюдента предназначен для
сравнения двух групп. Однако на практике
он широко используется для оценки
различий большего числа групп посредством
попарного их сравнения. При этом вступает
в силу эффект множественных сравнений.

Пример

Исследуется
влияние препаратов А и Б на уровень
глюкозы плазмы. Исследование проводят
на трех группах — получавших препарат
А, получавших препарат Б и получавших
плацебо В. С помощью критерия Стьюдента
проводят 3 парных сравнения: группу А
сравнивают с группой В, группу Б — с
группой В и наконец А с Б. Получив
достаточно высокое значение t в каком
либо из трех сравнении сообщают что «P
< 0,05». Это означает, что вероятность
ошибочного заключения о существовании
различии не превышает 5%. Но это неверно:
вероятность ошибки значительно превышает
5%. Разберемся подробнее. В исследовании
был принят 5% уровень значимости. Значит,
вероятность ошибиться при сравнении
групп А и В — 5%. Казалось бы все правильно.
Но точно также мы ошибемся в 5% случаев
при сравнении групп Б и В. И наконец при
сравнении групп А и Б ошибка возможна
также в 5% случаев. Следовательно,
вероятность ошибиться хотя бы в одном
из трех сравнении составит не 5%, а
значительно больше. Итак, в нашем
исследовании вероятность ошибиться
хотя бы в одном из сравнений составляет
примерно 15%. При сравнении четырех групп
число пар и соответственно возможных
попарных сравнений равно 6. Поэтому при
уровне значимости в каждом из сравнений
0,05 вероятность ошибочно обнаружить
различие хотя бы в одном равна уже не
0,05, а примерно 6 × 0,05 = 0,30. И когда
исследователь, выявив таким способом
«эффективный» препарат будет говорить
про 5% вероятность ошибки, на самом деле
эта вероятность равна 30%.

Правила использования
критерия Стьюдента:

• Критерий Стьюдента
может быть использован только в случае
выборок с нормально распределеннымизначениями признака;

• Критерий Стьюдента
может быть использован для проверки
гипотезы о различии средних только
для двух групп;

• Если схема
эксперимента предполагает большее
число групп, необходимо воспользоваться
дисперсионным анализом;

• Если критерии
Стьюдента был использован для проверки
различий между несколькими группами,
то истинный уровень значимости можно
получить, умножив уровень значимости,
приводимый авторами на число возможных
сравнений

Общая последовательность
действий при использовании критерия
Стьюдента:

Формирование таблиц результатов
измерения (записываются и организуются
в таблицу исследуемые показатели первой
группы и показатели второй группы)
Выполняется анализ полученных данных
(описательная статистика)
Проверка соответствия распределения
данных нормальному закону распределения
Выбирается значение уровня значимости
(в зависимости от строгости исследования:
0,1 или 0,05 или 0,01)
Формулируется нулевая гипотеза (различие
между группами незначимо или является
следствием случайности)
Рассчитывается значение критерия
Стьюдента t(значение
критерия, начиная с которого мы отвергаем
нулевую гипотезу) и вероятность
ошибочного результатаP(вероятность ошибочно отвергнуть верную
нулевую гипотезу, то есть найти различия
там, где их нет)
На основании значения уровня значимости
и количества элементов выборки
определяется величина критического
значения критерия t_кр(значение критерия, начиная с которого
мы отвергаем нулевую гипотезу).
Сравниваются между собой tиt_кр, а такжеPи α, еслиt>t_криP< α, то нулевая
гипотеза отвергается и различия между
группами статистически значимы, в
противном случае различия – случайны
или незначимы. Следует учитывать, что
даже при обнаруженной статистической
значимости различий исследователь
может ошибаться, но допустимая вероятность
равна уровню значимости.

Задача

Обновлено: 22.06.2023

В группу параметрических критериев методов математической статистики входят методы для вычисления описательных статистик, построения графиков на нормальность распределения, проверка гипотез о принадлежности двух выборок одной совокупности. Эти методы основываются на предположении о том, что распределение выборок подчиняется нормальному (гауссовому) закону распределения. Среди параметрических критериев статистики нами будут рассмотрены критерий Стьюдента и Фишера.

Чтобы определить, имеем ли мы дело с нормальным распределением, можно применять следующие методы:

1) в пределах осей можно нарисовать полигон частоты (эмпирическую функцию распределения) и кривую нормального распределения на основе данных исследования. Исследуя формы кривой нормального распределения и графика эмпирической функции распределения, можно выяснить те параметры, которыми последняя кривая отличается от первой;

2) вычисляется среднее, медиана и мода и на основе этого определяется отклонение от нормального распределения. Если мода, медиана и среднее арифметическое друг от друга значительно не отличаются, мы имеем дело с нормальным распределением. Если медиана значительно отличается от среднего, то мы имеем дело с асимметричной выборкой.

3) эксцесс кривой распределения должен быть равен 0. Кривые с положительным эксцессом значительно вертикальнее кривой нормального распределения. Кривые с отрицательным эксцессом являются более покатистыми по сравнению с кривой нормального распределения;

4) после определения среднего значения распределения частоты и стандартного oтклонения находят следующие четыре интервала распределения сравнивают их с действительными данными ряда:

а) — к интервалу должно относиться около 25% частоты совокупности,

б) — к интервалу должно относиться около 50% частоты совокупности,

в) — к интервалу должно относиться около 75% частоты совокупности,

г) — к интервалу должно относиться около 100% частоты совокупности.

При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.

Статистика критерия для случая несвязанных, независимых выборок равна:

где , — средние арифметические в экспериментальной и контрольной группах,

— стандартная ошибка разности средних арифметических. Находится из формулы:

где n ₁ и n ₂ соответственно величины первой и второй выборки.

Если n ₁= n ₂, то стандартная ошибка разности средних арифметических будет считаться по формуле:

где n величина выборки.

Подсчет числа степеней свободы осуществляется по формуле:

При численном равенстве выборок k = 2 n — 2.

Далее необходимо сравнить полученное значение t _эмп с теоретическим значением t—распределения Стьюдента (см. приложение к учебникам статистики). Если t _эмп t _крит, то гипотеза H ₀ принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза.

Рассмотрим пример использования t -критерия Стьюдента для несвязных и неравных по численности выборок.

Пример 1 . В двух группах учащихся — экспериментальной и контрольной — получены следующие результаты по учебному предмету (тестовые баллы; см. табл. 1). [1]

Таблица 1. Результаты эксперимента

Первая группа (экспериментальная) N ₁=11 человек

Вторая группа (контрольная)

12 14 13 16 11 9 13 15 15 18 14

13 9 11 10 7 6 8 10 11

Общее количество членов выборки: n ₁=11, n ₂=9.

Расчет средних арифметических: Х_ср=13,636; Y _ср=9,444

Стандартное отклонение: s _x=2,460; s _y =2,186

По формуле (2) рассчитываем стандартную ошибку разности арифметических средних:

Считаем статистику критерия:

Сравниваем полученное в эксперименте значение t с табличным значением с учетом степеней свободы, равных по формуле (4) числу испытуемых минус два (18).

Табличное значение t_крит равняется 2,1 при допущении возможности риска сделать ошибочное суждение в пяти случаях из ста (уровень значимости=5 % или 0,05).

Если полученное в эксперименте эмпирическое значение t превышает табличное, то есть основания принять альтернативную гипотезу (H₁) о том, что учащиеся экспериментальной группы показывают в среднем более высокий уровень знаний. В эксперименте t=3,981, табличное t=2,10, 3,981>2,10, откуда следует вывод о преимуществе экспериментального обучения.

Здесь могут возникнуть такие вопросы:

1. Что если полученное в опыте значение t окажется меньше табличного? Тогда надо принять нулевую гипотезу.

2. Доказано ли преимущество экспериментального метода? Не столько доказано, сколько показано, потому что с самого начала допускается риск ошибиться в пяти случаях из ста (р=0,05). Наш эксперимент мог быть одним из этих пяти случаев. Но 95% возможных случаев говорит в пользу альтернативной гипотезы, а это достаточно убедительный аргумент в статистическом доказательстве.

3. Что если в контрольной группе результаты окажутся выше, чем в экспериментальной? Поменяем, например, местами, сделав средней арифметической экспериментальной группы, a — контрольной:

Отсюда следует вывод, что новый метод пока не проявил себя с хорошей стороны по разным, возможно, причинам. Поскольку абсолютное значение 3,9811>2,1, принимается вторая альтернативная гипотеза (Н₂) о преимуществе традиционного метода.

В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле:

где — разности между соответствующими значениями переменной X и переменной У, а d — среднее этих разностей;

Sd вычисляется по следующей формуле:

Число степеней свободы k определяется по формуле k= n -1. Рассмотрим пример использования t -критерия Стьюдента для связных и, очевидно, равных по численности выборок.

Если t _эмп t _крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Пример 2. Изучался уровень ориентации учащихся на художественно-эстетические ценности. С целью активизации формирования этой ориентации в экспериментальной группе проводились беседы, выставки детских рисунков, были организованы посещения музеев и картинных галерей, проведены встречи с музыкантами, художниками и др. Закономерно встает вопрос: какова эффективность проведенной работы? С целью проверки эффективности этой работы до начала эксперимента и после давался тест. Из методических соображений в таблице 2 приводятся результаты небольшого числа испытуемых. [2]

Таблица 2. Результаты эксперимента

Вспомогательные расчеты

до начала эксперимента (Х)

эксперимента (У)

Вначале произведем расчет по формуле:

Затем применим формулу (6), получим:

И, наконец, следует применить формулу (5). Получим:

Число степеней свободы: k =10-1=9 и по таблице Приложения 1 находим t_крит =2.262, экспериментальное t=6,678, откуда следует возможность принятия альтернативной гипотезы (H₁) о достоверных различиях средних арифметических, т. е. делается вывод об эффективности экспериментального воздействия.

В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза Н₀ отклоняется и принимается гипотеза Н₁ .

Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления F_эмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:

где — дисперсии первой и второй выборки соответственно.

Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение F_эмп всегда будет больше или равно единице.

Число степеней свободы определяется также просто:

k ₁=n_l — 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k ₂= n ₂ — 1 для второй выборки.

В Приложении 1 критические значения критерия Фишера находятся по величинам k ₁ (верхняя строчка таблицы) и k ₂ (левый столбец таблицы).

Если t _эмп> t _крит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.

Пример 3. В двух третьих классах проводилось тестирование умственного развития по тесту ТУРМШ десяти учащихся. [3] Полученные значения величин средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.

Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:

Рассчитав дисперсии для переменных X и Y, получаем:

Тогда по формуле (8) для расчета по F критерию Фишера находим:

По таблице из Приложения 1 для F критерия при степенях свободы в обоих случаях равных k =10 — 1 = 9 находим F _крит=3,18 ( c следователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.

Сравнивая на глазок (по процентным соотношениям) результаты до и после какого-либо воздействия, исследователь приходит к заключению, что если наблюдаются различия, то имеет место различие в сравниваемых выборках. Подобный подход категорически неприемлем, так как для процентов нельзя определить уровень достоверности в различиях. Проценты, взятые сами по себе, не дают возможности делать статистически достоверные выводы. Чтобы доказать эффективность какого-либо воздействия, необходимо выявить статистически значимую тенденцию в смещении (сдвиге) показателей. Для решения подобных задач исследователь может использовать ряд критериев различия. Ниже будет рассмотрены непараметрические критерии: критерий знаков и критерий хи-квадрат.

Критерий предназначен для сравнения состояния некоторого свойства у членов двух зависимых выборок на основе измерений, сделанных по шкале не ниже ранговой.

Имеется две серии наблюдений над случайными переменными X и У, полученные при рассмотрении двух зависимых выборок. На их основе составлено N пар вида (х _i , у _i ), где х _i , у _i — результаты двукратного измерения одного и того же свойства у одного и того же объекта.

В педагогических исследованиях объектами изучения могут служить учащиеся, учителя, администрация школ. При этом х _i , у _i могут быть, например, балловыми оценками, выставленными учителем за двукратное выполнение одной и той же или различных работ одной и той же группой учащихся до и после применения некоторого педагогическою средства.

Нулевая гипотеза формулируются следующим образом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно различны в одной и той же совокупности при первичном и вторичном измерениях этого свойства.

Статистика критерия (Т) определяется следующим образом:

Нулевая гипотеза принимается на уровне значимости 0,05, если наблюдаемое значение T n — t_a , где значение n — t_a определяется из статистических таблиц для критерия знаков Приложения 2.

Пример 4. Учащиеся выполняли контрольную работу, направленную на проверку усвоения некоторого понятия. Пятнадцати учащимся затем предложили электронное пособие, составленное с целью формирования данного понятия у учащихся с низким уровнем обучаемости. После изучения пособия учащиеся снова выполняли ту же контрольного работу, которая оценивалась по пятибалльной системе.

Результаты двукратного выполнения работы представляют измерения по шкале порядка (пятибалльная шкала). В этих условиях возможно применение знакового критерия для выявления тенденции изменения состояния знаний учащихся после изучения пособия, так как выполняются все допущения этого критерия.

Результаты двукратного выполнения работы (в баллах) 15 учащимися запишем в форме таблицы (см. табл. 1). [4]

Этапы статистического вывода (statistic inference)

Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.

Предлагаю долго не ходить вокруг да около и посмотреть применение t-критерия Стьюдента на реальном примере.

Видео-версия статьи

Пример использования т-критерия Стьюдента

Условия применения статистического критерия т-теста (критерия Стьюдента)

— данные распределялись по закону нормального распределения;

— данные были количественными;

В итоге Мы определились с тем, что это будет t-критерий Стьюдента.

Для того, чтобы не тратить время, я в принципе все уже рассчитал по каждой из групп: средняя (x̅) ,стандартное отклонение (SD) и ошибка репрезентативности (m r ).

Давайте остановимся на том, что же значат эти значения:

— средняя (x̅) это среднеарифметическое по 5 наблюдениям в каждой группе;

Вот то, что касается расчета t-критерия Стьюдента и его интерпретации.

Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).

Распределение Стьюдента

Общий подход в проверке гипотез описан здесь, поэтому сразу к делу. Предположим для начала, что выборка извлечена из нормальной совокупности случайных величин X с генеральной средней μ и дисперсией σ 2 . Средняя арифметическая из этой выборки, очевидно, сама является случайной величиной. Если извлечь много таких выборок и посчитать по ним средние, то они также будут иметь нормальное распределение с математическим ожиданием μ и дисперсией

Тогда случайная величина

имеет стандартное нормальное распределение со всеми вытекающими отсюда последствиями. Например, с вероятностью 95% ее значение не выйдет за пределы ±1,96.

Однако такой подход будет корректным, если известна генеральная дисперсия. В реальности, как правило, она не известна. Вместо нее берут оценку – несмещенную выборочную дисперсию:

Возникает вопрос: будет ли генеральная средняя c вероятностью 95% находиться в пределах ±1,96s_x̅. Другими словами, являются ли распределения случайных величин

Впервые этот вопрос был поставлен (и решен) одним химиком, который трудился на пивной фабрике Гиннесса в г. Дублин (Ирландия). Химика звали Уильям Сили Госсет и он брал пробы пива для проведения химического анализа. В какой-то момент, видимо, Уильяма стали терзать смутные сомнения на счет распределения средних. Оно получалось немного более размазанным, чем должно быть у нормального распределения.

Посмотрим, что же мог увидеть У. Госсет. Сгенерируем 20 тысяч нормальных выборок из 6-ти наблюдений со средней (X̅) 50 и среднеквадратичным отклонением (σ) 10. Затем нормируем выборочные средние, используя генеральную дисперсию:

Получившиеся 20 тысяч средних сгруппируем в интервалы длинной 0,1 и подсчитаем частоты. Изобразим на диаграмме фактическое (Norm) и теоретическое (ENorm) распределение частот выборочных средних.

Точки (наблюдаемые частоты) практически совпадают с линией (теоретическими частотами). Оно и понятно, ведь данные взяты из одной и то же генеральной совокупности, а отличия – это лишь ошибки выборки.

Проведем новый эксперимент. Нормируем средние, используя выборочную дисперсию.

Снова подсчитаем частоты и нанесем их на диаграмму в виде точек, оставив для сравнения линию стандартного нормального распределения. Обозначим эмпирическое частоты средних, скажем, через букву t.

У Госсета-Стьюдента не было последней версии MS Excel, но именно этот эффект он и заметил. Почему так получается? Объяснение заключается в том, что случайная величина

зависит не только от ошибки выборки (числителя), но и от стандартной ошибки средней (знаменателя), которая также является случайной величиной.

Давайте немного разберемся, какое распределение должно быть у такой случайной величины. Вначале придется кое-что вспомнить (или узнать) из математической статистики. Есть такая теорема Фишера, которая гласит, что в выборке из нормального распределения:

1. средняя X̅ и выборочная дисперсия s 2 являются независимыми величинами;

2. соотношение выборочной и генеральной дисперсии, умноженное на количество степеней свободы, имеет распределение χ 2 (хи-квадрат) с таким же количеством степеней свободы, т.е.

где k – количество степеней свободы (на английском degrees of freedom (d.f.))

Вернемся к распределению средней. Разделим числитель и знаменатель выражения

Числитель – это стандартная нормальная случайная величина (обозначим ξ (кси)). Знаменатель выразим из теоремы Фишера.

Тогда исходное выражение примет вид

Это и есть t-критерий Стьюдента в общем виде (стьюдентово отношение). Вывести функцию его распределения можно уже непосредственно, т.к. распределения обеих случайных величин в данном выражении известны. Оставим это удовольствие математикам.

Функция t-распределения Стьюдента имеет довольно сложную для понимания формулу, поэтому не имеет смысла ее разбирать. Вероятности и квантили t-критерия приведены в специальных таблицах распределения Стьюдента и забиты в функции разных ПО вроде Excel.

Итак, вооружившись новыми знаниями, вы сможете понять официальное определение распределения Стьюдента.
Случайной величиной, подчиняющейся распределению Стьюдента с k степенями свободы, называется отношение независимых случайных величин

где ξ распределена по стандартному нормальному закону, а χ 2 _k подчиняется распределению χ 2 c k степенями свободы.

Таким образом, формула критерия Стьюдента для средней арифметической

есть частный случай стьюдентова отношения

Из формулы и определения следует, что распределение т-критерия Стьюдента зависит лишь от количества степеней свободы.

При k > 30 t-критерий практически не отличается от стандартного нормального распределения.

В отличие от хи-квадрат, t-критерий может быть одно- и двусторонним. Обычно пользуются двусторонним, предполагая, что отклонение может происходить в обе стороны от средней. Но если условие задачи допускает отклонение только в одну сторону, то разумно применять односторонний критерий. От этого немного увеличивается мощность критерия.

Условия применения t-критерия Стьюдента

Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.

Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.

Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.

Пример проверки гипотезы о математическом ожидании с помощью t- критерия Стьюдента в MS Excel

В Excel есть несколько функций, связанных с t-распределением. Рассмотрим их.

СТЬЮДЕНТ.РАСП.2Х – двухсторонне распределение. В качестве аргумента подается абсолютное значение (по модулю) t-критерия и количество степеней свободы. На выходе получаем вероятность получить такое или еще больше значение t-критерия (по модулю), т.е. фактический уровень значимости (p-value).

СТЬЮДЕНТ.РАСП.ПХ – правостороннее t-распределение. Так, 1-СТЬЮДЕНТ.РАСП(2;5;1) = СТЬЮДЕНТ.РАСП.ПХ(2;5) = 0,05097. Если t-критерий положительный, то полученная вероятность – это p-value.

СТЬЮДЕНТ.ОБР – используется для расчета левостороннего обратного значения t-распределения. В качестве аргумента подается вероятность и количество степеней свободы. На выходе получаем соответствующее этой вероятности значение t-критерия. Отсчет вероятности идет слева. Поэтому для левого хвоста нужен сам уровень значимости α, а для правого 1 — α.

СТЬЮДЕНТ.ОБР.2Х – обратное значение для двухстороннего распределения Стьюдента, т.е. значение t-критерия (по модулю). Также на вход подается уровень значимости α. Только на этот раз отсчет ведется с двух сторон одновременно, поэтому вероятность распределяется на два хвоста. Так, СТЬЮДЕНТ.ОБР(1-0,025;5) = СТЬЮДЕНТ.ОБР.2Х(0,05;5) = 2,57058

СТЬЮДЕНТ.ТЕСТ – функция для проверки гипотезы о равенстве математических ожиданий в двух выборках. Заменяет кучу расчетов, т.к. достаточно указать лишь два диапазона с данными и еще пару параметров. На выходе получим p-value.

ДОВЕРИТ.СТЬЮДЕНТ – расчет доверительного интервала средней с учетом t-распределения.

Рассмотрим такой учебный пример. На предприятии фасуют цемент в мешки по 50кг. В силу случайности в отдельно взятом мешке допускается некоторое отклонение от ожидаемой массы, но генеральная средняя должна оставаться 50кг. В отделе контроля качества случайным образом взвесили 9 мешков и получили следующие результаты: средняя масса (X̅) составила 50,3кг, среднеквадратичное отклонение (s) – 0,5кг.

Согласуется ли полученный результат с нулевой гипотезой о том, что генеральная средняя равна 50кг? Другими словами, можно ли получить такой результат по чистой случайности, если оборудование работает исправно и выдает среднее наполнение 50 кг? Если гипотеза не будет отклонена, то полученное различие вписывается в диапазон случайных колебаний, если же гипотеза будет отклонена, то, скорее всего, в настройках аппарата, заполняющего мешки, произошел сбой. Требуется его проверка и настройка.

Краткое условие в обще принятых обозначениях выглядит так.

Есть основания предположить, что распределение заполняемости мешков подчиняются нормальному распределению (или не сильно от него отличается). Значит, для проверки гипотезы о математическом ожидании можно использовать t-критерий Стьюдента. Случайные отклонения могут происходить в любую сторону, значит нужен двусторонний t-критерий.

Вначале применим допотопные средства: ручной расчет t-критерия и сравнение его с критическим табличным значением. Расчетный t-критерий:

Теперь определим, выходит ли полученное число за критический уровень при уровне значимости α = 0,05. Воспользуемся таблицей для критерия Стьюдента (есть в любом учебнике по статистике).

По столбцам идет вероятность правой части распределения, по строкам – число степеней свободы. Нас интересует двусторонний t-критерий с уровнем значимости 0,05, что равносильно t-значению для половины уровня значимости справа: 1 — 0,05/2 = 0,975. Количество степеней свободы – это объем выборки минус 1, т.е. 9 — 1 = 8. На пересечении находим табличное значение t-критерия – 2,306. Если бы мы использовали стандартное нормальное распределение, то критической точкой было бы значение 1,96, а тут она больше, т.к. t-распределение на небольших выборках имеет более приплюснутый вид.

Сравниваем фактическое (1,8) и табличное значение (2.306). Расчетный критерий оказался меньше табличного. Следовательно, имеющиеся данные не противоречат гипотезе H₀ о том, что генеральная средняя равна 50 кг (но и не доказывают ее). Это все, что мы можем узнать, используя таблицы. Можно, конечно, еще p-value попробовать найти, но он будет приближенным. А, как правило, именно p-value используется для проверки гипотез. Поэтому далее переходим в Excel.

Готовой функции для расчета t-критерия в Excel нет. Но это и не страшно, ведь формула t-критерия Стьюдента довольно проста и ее можно легко соорудить прямо в ячейке Excel.

Получили те же 1,8. Найдем вначале критическое значение. Альфа берем 0,05, критерий двусторонний. Нужна функция обратного значения t-распределения для двухсторонней гипотезы СТЬЮДЕНТ.ОБР.2Х.

Полученное значение отсекает критическую область. Наблюдаемый t-критерий в нее не попадает, поэтому гипотеза не отклоняется.

Однако это тот же способ проверки гипотезы с помощью табличного значения. Более информативно будет рассчитать p-value, т.е. вероятность получить наблюдаемое или еще большее отклонение от средней 50кг, если эта гипотеза верна. Потребуется функция распределения Стьюдента для двухсторонней гипотезы СТЬЮДЕНТ.РАСП.2Х.

P-value равен 0,1096, что больше допустимого уровня значимости 0,05 – гипотезу не отклоняем. Но теперь можно судить о степени доказательства. P-value оказался довольно близок к тому уровню, когда гипотеза отклоняется, а это наводит на разные мысли. Например, что выборка оказалась слишком мала для обнаружения значимого отклонения.

Пусть через некоторое время отдел контроля снова решил проверить, как выдерживается стандарт заполняемости мешков. На этот раз для большей надежности было отобрано не 9, а 25 мешков. Интуитивно понятно, что разброс средней уменьшится, а, значит, и шансов найти сбой в системе становится больше.

Допустим, были получены те же значения средней и стандартного отклонения по выборке, что и в первый раз (50,3 и 0,5 соответственно). Рассчитаем t-критерий.

Критическое значение для 24-х степеней свободы и α = 0,05 составляет 2,064. На картинке ниже видно, что t-критерий попадает в область отклонения гипотезы.

Можно сделать вывод о том, что с доверительной вероятностью более 95% генеральная средняя отличается от 50кг. Для большей убедительности посмотрим на p-value (последняя строка в таблице). Вероятность получить среднюю с таким или еще большим отклонением от 50, если гипотеза верна, составляет 0,0062, или 0,62%, что при однократном измерении практически невозможно. В общем, гипотезу отклоняем, как маловероятную.

Расчет доверительного интервала для математического ожидания с помощью t-распределения Стьюдента в Excel

С проверкой гипотез тесно связан еще один статистический метод – расчет доверительных интервалов. Если в полученный интервал попадает значение, соответствующее нулевой гипотезе, то это равносильно тому, что нулевая гипотеза не отклоняется. В противном случае, гипотеза отклоняется с соответствующей доверительной вероятностью. В некоторых случаях аналитики вообще не проверяют гипотез в классическом виде, а рассчитывают только доверительные интервалы. Такой подход позволяет извлечь еще больше полезной информации.

Рассчитаем доверительные интервалы для средней при 9 и 25 наблюдениях. Для этого воспользуемся функцией Excel ДОВЕРИТ.СТЬЮДЕНТ. Здесь, как ни странно, все довольно просто. В аргументах функции нужно указать только уровень значимости α, стандартное отклонение по выборке и размер выборки. На выходе получим полуширину доверительного интервала, то есть значение которое нужно отложить по обе стороны от средней. Проведя расчеты и нарисовав наглядную диаграмму, получим следующее.

Как видно, при выборке в 9 наблюдений значение 50 попадает в доверительный интервал (гипотеза не отклоняется), а при 25-ти наблюдениях не попадает (гипотеза отклоняется). При этом в эксперименте с 25-ю мешками можно утверждать, что с вероятностью 97,5% генеральная средняя превышает 50,1 кг (нижняя граница доверительного интервала равна 50,094кг). А это довольно ценная информация.

Таким образом, мы решили одну и ту же задачу тремя способами:

1. Древним подходом, сравнивая расчетное и табличное значение t-критерия
2. Более современным, рассчитав p-value, добавив степень уверенности при отклонении гипотезы.
3. Еще более информативным, рассчитав доверительный интервал и получив минимальное значение генеральной средней.

Важно помнить, что t-критерий относится к параметрическим методам, т.к. основан на нормальном распределении (у него два параметра: среднее и дисперсия). Поэтому для его успешного применения важна хотя бы приблизительная нормальность исходных данных и отсутствие выбросов.

Напоследок предлагаю видеоролик о том, как рассчитать критерий Стьюдента и проверить гипотезу о генеральной средней в Excel.

Иногда просят объяснить, как делаются такие наглядные диаграммы с распределением. Ниже можно скачать файл, где проводились расчеты для этой статьи.

Наступила осень, а значит, настало время для запуска нового тематического проекта «Статистический анализ с R». В нем мы рассмотрим статистические методы с точки зрения их применения на практике: узнаем какие методы существуют, в каких случаях и каким образом их проводить в среде R. На мой взгляд, Критерий Стьюдента или t-тест (от англ. t-test) идеально подходит в качестве введения в мир статистического анализа. Тест Стьюдента достаточно прост и показателен, а также требует минимум базовых знаний в статистике, с которыми читатель может ознакомиться в ходе прочтения этой статьи.

Примечание_1: здесь и в других статьях Вы не увидите формул и математических объяснений, т.к. информация рассчитана на студентов естественных и гуманитарных специальностей, которые делают лишь первые шаги в стат. анализе.

Примечание_2: перед прочтением, я рекомендую ознакомиться с этой статьей, чтобы вспомнить базовые понятия описательной статистики, такие как медиана, стандартное отклонение, квантили и прочее.

Что такое t-тест и в каких случаях его стоит применять

В начале следует сказать, что в статистике зачастую действует принцип бритвы Оккамы, который гласит, что нет смысла проводить сложный статистический анализ, если можно применить более простой (не стоит резать хлеб бензопилой, если есть нож). Именно поэтому, несмотря на свою простоту, t-тест является серьезным инструментом, если знать что он из себя представляет и в каких случаях его стоит применять.

Любопытно, что создал этот метод Уильямом Госсет — химик, приглашенный работать на фабрику Guinness. Разработанный им тест служил изначально для оценки качества пива. Однако, химикам фабрики запрещалось независимо публиковать научные работы под своим именем. Поэтому в 1908 году Уильям опубликовал свою статью в журнале «Biometrika» под псевдонимом «Стьюдент». Позже, выдающийся математик и статистик Рональд Фишер доработал метод, который затем получил массовое распространение под названием Student’s t-test.

Критерий Стьюдента (t-тест) — это статистический метод, который позволяет сравнивать средние значения двух выборок и на основе результатов теста делать заключение о том, различаются ли они друг от друга статистически или нет. Если Вы хотите узнать, отличается ли средний уровень продолжительности жизни в Вашем регионе от среднего уровня по стране; сравнить урожайность картофеля в разных районах; или изменяется ли кровяное давление до и после употребления нового лекарства, то t-тест может быть Вам полезен. Почему может быть? Потому что для его проведения, необходимо, чтобы данные выборок имели распределение близкое к нормальному. Для этого существуют методы оценки, которые позволяют сказать, допустимо ли в данном случае полагать, что данные распределены нормально или нет. Поговорим об этом подробнее.

Нормальное распределение данных и методы его оценки qqplot и shapiro.test

Нормальное распределение данных характерно для количественных данных, на распределение которых влияет множество факторов, либо оно случайно. Нормальное распределение характеризуется несколькими особенностями:

Оно всегда симметрично и имеет форму колокола.
Значения среднего и медианы совпадают.
В пределах одного стандартного отклонения в обе стороны лежат 68.2% всех данных, в пределах двух — 95,5%, в пределах трех — 99,7%

Давайте создадим случайную выборку с нормальным распределением на языке программирования R, где общее количество измерений = 100, среднее арифметическое = 5, а стандартное отклонение = 1. Затем отобразим его на графике в виде гистограммы:

Ваш график может слегка отличаться от моего, так как числа сгенерированы случайным образом. Как Вы видите, данные не идеально симметричны, но кажется сохраняют форму нормального распределения. Однако, мы воспользуемся более объективными методами определения нормальности данных.

Одним из наиболее простых тестов нормальности является график квантилей (qqplot). Суть теста проста: если данные имеют нормальное распределение, то они не должны сильно отклоняться от линии теоретических квантилей и выходить за пределы доверительных интервалов. Давайте проделаем этот тест в R.

Как видно из графика, наши данные не имеют серьезных отклонений от теоретического нормального распределения. Но порой при помощи qqplot невозможно дать однозначный ответ. В этом случае следует использовать тест Шапиро-Уилка, который основан на нулевой гипотезе, что наши данные распределены нормально. Если же P-значение менее 0.05 (p-value

Провести тест Шапиро-Уилка в R не составит труда. Для этого нужно всего лишь вызвать функцию shapiro.test, и в скобках вставить имя ваших данных. В нашем случае p-value должен быть значительно больше 0.05, что не позволяет отвергнуть нулевую гипотезу о том, что наши данные распределены нормально.

Запускаем t-тест Стьюдента в среде R

Итак, если данные из выборок имеют нормальное распределение, можно смело приступать к сравнению средних этих выборок. Существует три основных типа t-теста, которые применяются в различных ситуациях. Рассмотрим каждый из них с использованием наглядных примеров.

Одновыборочный критерий Стьюдента (one-sample t-test)

Одновыборочный t-тест следует выбирать, если Вы сравниваете выборку с общеизвестным средним. Например, отличается ли средний возраст жителей Северо-Кавказского Федерального округа от общего по России. Существует мнение, что климат Кавказа и культурные особенности населяющих его народов способствуют продлению жизни. Для того, чтобы проверить эту гипотезу, мы возьмем данные РосСтата (таблицы среднего ожидаемого продолжительности жизни по регионам России) и применим одновыборочный критерий Стьюдента. Так как критерий Стьюдента основан на проверке статистических гипотез, то за нулевую гипотезу будем принимать то, что различий между средним ожидаемым уровнем продолжительности по России и республикам Северного Кавказа нет. Если различия существуют, то для того, чтобы считать их статистически значимыми p-value должно быть менее 0.05 (логика та же, что и в вышеописанном тесте Шапиро-Уилка).

Загрузим данные в R. Для этого, создадим вектор со средними значениями по республикам Кавказа (включая Адыгею). Затем, запустим одновыборочный t-тест, указав в параметре mu среднее значение ожидаемого возраста жизни по России равное 70.93.

Несмотря на то, что у нас всего 7 точек в выборке, в целом они проходят тесты нормальности и мы можем на них полагаться, так как эти данные уже были усреднены по региону.

Результаты t-теста говорят о том, что средняя ожидаемая продолжительность жизни у жителей Северного Кавказа (74.6 лет) действительно выше, чем в среднем по России (70.93 лет), а результаты теста являются статистически значимыми (p когда Вы сравниваете две независимые выборки . Допустим, мы хотим узнать, отличается ли урожайность картофеля на севере и на юге какого-либо региона. Для этого, мы собрали данные с 40 фермерских хозяйств: 20 из которых располагались на севере и сформировали выборку «North», а остальные 20 — на юге, сформировав выборку «South».

Загрузим данные в среду R. Кроме проверки нормальности данных, будет полезно построить «график с усами», на котором можно видеть медианы и разброс данных для обеих выборок.

Как видно из графика, медианы выборок не сильно отличаются друг от друга, однако разброс данных гораздо сильнее на севере. Проверим отличаются ли статистически средние значения при помощи функции t.test. Однако в этот раз на место параметра mu мы ставим имя второй выборки. Результаты теста, которые Вы видите на рисунке снизу, говорят о том, что средняя урожайность картофеля на севере статистически не отличается от урожайности на юге (p = 0.6339).

Двувыборочный для зависимых выборок ( dependent two-sample t-test )

Третий вид t-теста используется в том случае, если элементы выборок зависят друг от друга . Он идеально подходит для проверки повторяемости результатов эксперимента: если данные повтора статистически не отличаются от оригинала, то повторяемость данных высокая. Также двувыборочный критерий Стьюдента для зависимых выборок широко применяется в медицинских исследованиях при изучении эффекта лекарства на организм до и после приема.

Для того, чтобы запустить его в R, следует ввести все ту же функцию t.test . Однако, в скобках, после таблиц данных, следует ввести дополнительный аргумент paired = TRUE . Этот аргумент говорит о том, что Ваши данные зависят друг от друга. Например:

Также в функции t.test существует два дополнительных аргумента, которые могут улучшить качество результатов теста: var.equal и alternative . Если вы знаете, что вариация между выборками равна, вставьте аргумент var.equal = TRUE . Если же вы хотите проверить гипотезу о том, что разница между средними в выборках значительно меньше или больше 0, то введите аргумент alternative=»less» или alternative=»greater» (по умолчанию альтернативная гипотеза говорит о том, что выборки просто отличаются друг от друга: alternative=»two.sided» ).

Заключение

Статья получилась довольно длинной, зато теперь Вы знаете: что такое критерий Стьюдента и нормальное распределение; как при помощи функций qqplot и shapiro.test проверять нормальность данных в R; а также разобрали три типа t-тестов и провели их в среде R.

Тема для тех, кто только начинает знакомиться со статистическим анализом — непростая. Поэтому не стесняйтесь, задавайте вопросы, я с удовольствием на них отвечу. Гуру статистики, пожалуйста поправьте меня, если где-нибудь допустил ошибку. В общем, пишите Ваши комментарии, друзья!

t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез ( статистических критериев ), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках .

Здравствуйте! Благодарю за подробное пояснение по теме t-критерия. Пытаюсь провести сравнительный анализ в своей магистерской диссертации по двум независимым выборкам. Шкал у меня несколько. В результате анализа с помощью программы SPSS какие-то значения по критерию равенства дисперсий Ливиня оказались меньше 0,05. Насколько я понимаю, использование t-критерия в этом случае будет неправомерным. Что посоветуете в этом случае?

Здравствуйте! Спасибо за Ваш комментарий. К сожалению, ни с SPSS, ни с критерием Ливиня мне не доводилось работать, поэтому помочь не в силах.

Добрый день, извините, что не по теме. Пишу дипломную работу и мне нужно оценить 2 уравнения методом максимального правдоподобия в R. Нигде не могу найти про это в интернете.Вы не знаете как это можно сделать?

Читайте также:

Портретная живопись серова кратко
Горбачев и его окружение кратко
Проблема человека в социологии кратко
Всеобщая история 18 век 8 класс кратко
Итоги реформ китая во второй половине xx века кратко

Источник