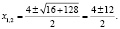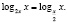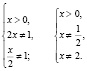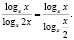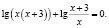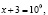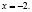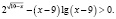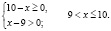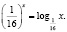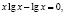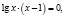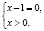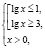По теме: методические разработки, презентации и конспекты
Урок — семинар в 11 классе «Решение показательных и логарифмических уравнений с модулем»
Данный урок — семинар рекомендуется для работы в профильном классе, а также материал этого занятия можно использовать на факультативном занятии. Здесь предложен конспект урока, презентация, разадаточн…
Применение нестандартных способов при решении показательных и логарифмических уравнений и неравенств.
Разработка урока по теме «Применение нестандартных способов при решении
показательных и логарифмических уравнений …
Решение показательных и логарифмических уравнений и неравенств
— Урок с использованием ИКТ (используется авторский мультимедийный продукт)9-11 кл. .-Тема. Решение логарифмических и показательных неравенств. 11 класс.Тип. Урок повторения, систематизации и обобщени…
Решение показательных и логарифмических уравнений
Представлены графики показательной и логарифмической функций. В примерах видны основные методы решения уравнений. Самостоятельная работа направлена на дифференцированный подход….
Урок алгебры в 11 классе с углубленным изучением математики по теме: «Решение показательных и логарифмических уравнений с переменным основанием. Введение сложной экспоненты».
Форма: урок-практикум.Задачи: путем введения сложной экспоненты научить решать показательные и логарифмические уравнения с переменным основанием.Цели урока:Образовательные: -…
Обобщающий урок по теме:»Решение показательных и логарифмических уравнений и неравенств» в 10 — 11 классе
Ребятам нравится практичесое приложение данного материала, спор двух очень сложных для решения и понимания функций (показательной и логарифмической).Решение большого количества различных заданий дает …
Крупноблочное изучение тем : «Показательная логарифмическая функция», «Решение показательных и логарифмических уравнений и неравенств»
Данная методическая разработка поможеть учителю в планировании учебной деятельности…
Как избежать типичных ошибок, возникающих при выполнении заданий ЕГЭ по математике
Дземяшкевич Е.В., преподаватель математики
(Факультет довузовской подготовки ТулГУ)
Чтобы подготовиться к ЕГЭ по математике, необходимо уже сегодня перестать комплексовать и паниковать перед предстоящим единым экзаменом. Уже сейчас можно сказать, что на ЕГЭ можно получить вполне приличное количество баллов: время для форсированной подготовки еще не потеряно. Конечно, ЕГЭ — это не легко и просто, но и не безнадежно. Важно, чтобы школьник сам честно сформулировал для себя планируемый результат обучения. Это вовсе не означает, что выпускник, наметивший себе «3», может получить только «3» и не более, напротив, ориентируясь на намеченный результат, может и должен получить на один балл выше. Ученики, ориентированные на получение «4», должны помнить, что если постараться, то можно получить и «5».
Но не всегда так получается. Возможны ошибки при решении заданий, недостатки при подготовке, которые приводят к низким результатам ЕГЭ.
Для устранения недостатков в подготовке учеников к ЕГЭ по математике, необходимо совершенствовать процесс преподавания: активнее включать в учебный процесс идеи дифференцированного обучения; использовать практические разработки по индивидуализации обучения (создание индивидуальных модулей обучения), учитывать рекомендации психологов по организации усвоения и пр.).
Поговорим подробнее об ошибках, которые возможны при выполнении заданий ЕГЭ. Рассмотрим важные темы, встречающиеся на экзамене по математике.
| Тема | Ошибки | Рекомендации |
|---|---|---|
| преобразование иррациональных выражений | При кажущейся простоте этого задания, решаемость его далека от 100%. Сложно заставить себя при выполнении этих заданий сделать проверку. Казалось бы, все свойства действий с корнями просты. Вроде всё просто. Только не все выпускники могут вычислить или, не обращая внимания на степень корня, извлекают корень квадратный. | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения). |
| преобразование показательных выражений | Выполнить проверку показательного выражения сложно | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения); можно составить аналогичное задание и попытаться найти закономерность. |
| преобразование логарифмических выражений | Особенность темы заключается в том, что большинство одиннадцатиклассников узнают о логарифмах только в ноябре-декабре. Времени на «присвоение знаний» нет. Многие выпускники бояться решать задания с логарифмами, несмотря на то, что все свойства логарифмов они знают. Самое сложное при выполнении этих заданий – выполнить проверку. | Не торопясь, выполнить все действия на черновике (обязательно записать все этапы решения). |
| линейные уравнения | Решают все, правда, если a 0. Как только уравнение решается автоматически, возможны ошибки. Например, . Что это? Невнимательность? Досадная ошибка? | При решении линейных уравнений никто не застрахован от ошибок. Обязательно выполняем проверку. |
| квадратные уравнения | Очень большой процент ошибок приходится на квадратные уравнения. Ошибки начинаются с вычисления дискриминанта. В формулах для вычисления корней есть ошибки для –b и 2a. Не стоит упоминать про формулу «четного коэффициента» — много ошибок, особенно у сильных учеников. Важно повторить теорему Виета. | Не стоит пренебрегать проверкой корней с помощью теоремы Виета или подстановкой: она занимает меньше времени, чем полная проверка всего решения сложного задания. |
| дробно-рациональные уравнения | Школьники решают очень тяжело. Серьезные проблемы возникают при решении такого уравнения: даже записывая такое формальное условие- знаменатель не равен нулю – они о нем тут же забывают. | Чтобы избежать многих ошибок, проверка нужна обязательно: подстановка и удовлетворение условию «знаменатель не равен нулю». Обязательно включать в каждую домашнюю работу хотя бы одно задание на решение дробно рационального уравнения |
| рациональные неравенства | Линейные: чаще всего при делении на отрицательное число, неравенство вида: |
© Факультет довузовской подготовки Тульского государственного университета
300012, город Тула, проспект Ленина, 84, кор. 8, 3-й учебный корпус ТулГУ
(4872) 25-46-83, 25-46-84, 717-535
Тульский государственный университет
300012, город Тула, проспект Ленина, 92
(4872) 33-24-10, 35-34-44
Приемная комиссия ТулГУ: (4872) 332-332
Для того, чтобы мы могли качественно предоставить Вам услуги, мы используем cookies, которые сохраняются на Вашем компьютере (сведения о местоположении; ip-адрес; источник, откуда пришел на сайт пользователь, эта же информация используется для обработки статистических данных использования сайта посредством интернет-сервисов Google Analytics и Яндекс.Метрика). Продолжая использовать сайт, Вы соглашаетесь на использовании cookies. Отключить cookies Вы можете в настройках своего браузера.
math4school.ru
Ошибки в уравнениях
При выполнении контрольных, тестовых и экзаменационных работ по математике учащиеся решают самые разнообразные уравнения, отличающиеся по тематике и по сложности. Разобрать все ошибки, которые при этом допускаются, не представляется возможным. Ниже предлагаются примеры лишь наиболее распространенных ошибок и анализ ситуаций, в которых эти ошибки допускаются.
Потеря корней
При решении уравнений из-за выполнения нетождественных преобразований может произойти либо потеря корней , либо появление посторонних корней .
При выполнении нетождественных преобразований в процессе решения уравнения может произойти сужение области допустимых значений неизвестного , а значит, корни могут оказаться потерянными.
K Упражнение. Решить уравнение lg (x – 10) 2 + lg x 2 = 2lg 24 .
L Неправильное решение.
2lg (x – 10) + 2lg x = 2lg 24,
Произвели проверку и убедились, что все корни удовлетворяют данному уравнению.
Комментарий . Из-за неправильного применения формул произошло сужение области допустимых значений неизвестного.
J Правильное решение.
Ответ: –2; 4; 6 и 12.
При делении обеих частей уравнения на выражение, содержащее неизвестное , могут быть потеряны корни, которые обращают эти выражения в ноль.
K Упражнение 1. Решить уравнение 3 х ( х 2 – 2 х – 3) = 9 ( х 2 – 2 х – 3) .
L Неправильное решение.
Разделим обе части уравнения на квадратный трехчлен, записанный в скобках, и получим:
J Правильное решение.
Перенесем правую часть исходного уравнения влево и вынесем общий множитель за скобки:
K Упражнение 2. Решить уравнение lg 2 x – lg x = 0 .
L Неправильное решение.
Разделим обе части уравнения на lg x и получим:
J Правильное решение.
Необходимо помнить, что обычно легче исключить посторонний корень, чем найти потерянный.
Посторонние корни
При решении уравнений существуют два диаметрально противоположных мнения относительно полученного результата. Одни считают, что проверка должна производиться всегда, другие считают ее необязательной. На самом деле проверка полученных корней в одних случаях является обязательной и является частью решения уравнения, а в других случаях в проверке необходимости нет.
Проверка полученного решения уравнения обычно делается с целью исключения посторонних корней, которые чаще всего появляются в результате нетождественных преобразований, приводящих к расширению области допустимых значений переменного. Рассмотрим далее некоторые случаи появления посторонних корней.
Это может случиться при умножении обеих частей дробного уравнения на выражение, содержащее неизвестную величину .
K Упражнение. Решить уравнение
| 5 – x | – | 5 + 3х | = 0 . |
| x – 1 | x 2 – 1 |
L Неправильное решение.
Умножим все члены уравнения на х 2 – 1 и получим:
Комментарий . Был приобретен посторонний корень х = 1, в чем можно убедиться с помощью проверки .
J Правильный ответ: х = 0.
Появление посторонних корней может быть вызвано сокращением дроби на множитель, содержащий неизвестную величину .
K Упражнение. Решить уравнение
L Неправильное решение.
Заметим, что х 2 – 81 = (x – 9) (x + 9) и произведем сокращение дроби на x – 9 . Имеем:
Комментарий . Был приобретен посторонний корень х = 9 .
J Правильный ответ: решений нет.
Приведение подобных слагаемых с неизвестным в знаменателе, в том случае, если они взаимно уничтожаются, также может привести к приобретению постороннего корня.
K Упражнение. Решить уравнение
| 2 | + х 2 – | 2 | – 4х = 0 . |
| 3х 2 | 3х 2 |
L Неправильное решение.
После приведения подобных слагаемых получим:
Комментарий . Был приобретен посторонний корень х = 0 .
J Правильный ответ: 4 .
Заметим, что аналогичная ситуация может сложиться и для слагаемых, содержащих переменную под знаком корня или под знаком логарифма.
Очень часто посторонние корни появляются при возведении в четную степень обеих частей уравнения . Рассмотрим следующее иррациональное уравнение и на его примере – процесс появления посторонних корней.
K Упражнение. Решить уравнение √ х + 3 + √ 7 – х = 2 .
L Неправильное решение.
И число –2 , и число 6 содержатся в области допустимых значений переменной х , значит, являются решениями исходного уравнения.
Комментарий . Оба корня посторонние и были приобретены в процессе решения. Как же это произошло? Дело вот в чем. В процессе решения с помощью возведения в квадрат и элементарных преобразований мы перешли от уравнения
Последнему уравнению число –2 удовлетворяет, после подстановки получаем верное равенство 1 = 1 . Предыдущее же уравнение при подстановке –2 дает ложное равенство 1 = –1 , которое стало верным именно в результате возведения в квадрат, ведь 1 2 = (–1) 2 . Число –2 является корнем второго уравнения, для первого – посторонний корень. А вот число 6 не является корнем ни одного из них.
Шестерка выходит на арену при переходе от уравнения
которое уже имеет один корень –2 , к уравнению
Теперь возведение в квадрат превращает ложное равенство 2 = –2 в истинное равенство 4 = 4 , которые соответствуют этим уравнениям для случая х = 6 . Для последнего уравнения 6 – истинный корень, а для предпоследнего – ложный. И вот, путем преобразований мы получаем уравнение
для которого числа –2 и 6 — самые настоящие корни, а для исходного — посторонние. Два раза мы применяли возведение в квадрат и каждый раз приобретали посторонний корень, каждый из которых благополучно преодолел фильтр ОДЗ. В данном случае проверка обязательна.
J Правильный ответ: решений нет.
Необходимо помнить, что если область допустимых значений неизвестного найдена и при решении уравнения получены корни, принадлежащие ей, то проверка корней не нужна, только если при этом в процессе решения все преобразования были тождественными.
Если при решении уравнения используется тот факт, что произведение равно нулю, когда хотя бы один из множителей равен нулю , прежде чем писать ответ, необходимо убедиться, что все найденные корни удовлетворяют условию.
K Упражнение. Решить уравнение ( x – 5) (х + 2) √ х – 3 = 0 .
L Неправильное решение.
Перейдем от данного уравнения у совокупности уравнений:
Комментарий . Число –2 обращает подкоренное выражение х – 3 в отрицательное число, а значит не может быть корнем уравнения.
J Правильный ответ: 5 и 3 .
Часто причиной изменения множества корней уравнения во время его преобразования является применение равенств, правая и левая части которых имеют разные области определения . Таких равенств много, вот некоторые из них:
| tg ( x + y ) = | tg x + tg y |
| 1 – tg x · tg y |
| sin 2 x = | 2 tg x |
| 1 + tg 2 x |
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области выражения, стоящего в левой части. Поэтому использование этих равенств слева направо может привести к потере корней, а справа налево – к появлению посторонних корней .
L Неправильное решение.
так как х ≥ 3 , то |х – 1| = х – 1 и
Комментарий . Применение формулы √ х · y = √ х · √ y привело к потере корня x = 1 . И вот почему. Исходное уравнение имеет область допустимых значений <1>∪[3; +∞) , а вот уже ОДЗ уравнения (left| x-1right|cdot sqrt=x-1) – только [3; +∞) , что и привело к потере 1 .
Можем порекомендовать возвести обе части исходного уравнения в квадрат. Это может привести к появлению посторонних корней, избавиться от которых проверкой, как правило, проще, чем заниматься поисками потерянных корней.
J Правильное решение.
(left(x-1 right)^2cdot left(x-3 right)=left(x-1 right)^2;)
(left(x-1 right)^2cdot left(x-3 right)-left(x-1 right)^2=0;)
(left(x-1 right)^2cdot left(x-4 right)=0;)
Проверкой убеждаемся, что оба корня действительные.
Ошибки, связанные с заменой переменной
При решении некоторых уравнений достаточно удачным является метод замены переменной . Но применение этого метода учащиеся осуществляют не всегда правильно.
Так необходимо помнить, что при наличии нескольких степеней заменять новой переменной надо ту, у которой показатель наименьший .
K Упражнение. Решить уравнение (5 left(x-3 right)^<1/4>-6=left(x-3 right)^<1/2>.)
L Неправильное решение.
Сделав замену ( left(x-3 right)^<1/2>=t), считают, что ( left(x-3 right)^<1/4>=t^2) и уравнение переписывают в виде 5t 2 – t – 6 = 0 , после чего, конечно, верный результат уже не получить.
J Правильное решение.
Верный результат можно получить, сделав замену ( left(x-3 right)^<1/4>=t), тогда ( left(x-3 right)^<1/2>=t^2) с продолжением:
Правильно сделав замену и верно найдя значение вспомогательной переменной, учащиеся часто допускают ошибку, используя не то равенство, которым вспомогательная переменная вводилась .
K Упражнение. Решить уравнение х + 4 √ x – 5 = 0 .
L Неправильное решение.
Комментарий . После нахождения значений вспомогательной переменной t для нахождения х следовало использовать подстановку √ x = t , а не x = t 2 .
J Правильное решение.
При решении иррациональных уравнений учащиеся чаще всего применяют метод возведения в соответствующую степень. В результате этого решения иррациональных уравнений получаются громоздкими и не всегда доводятся до конца .
K Упражнение. Решить уравнение (x^2-4x-sqrt<2x^2-8x+12>=6.)
L Неправильное (нерациональное) решение.
Чаще всего данное уравнение начинают решать так:
Нередко продолжения решения не следует, так как с полученным уравнением четвертой степени справится не каждый.
Комментарий . В качестве альтернативы можно предложить способ введения новой переменной.
J Правильное решение.
и исходное уравнение принимает вид:
А дальше все просто:
Комментарий . Числа –2 и 6 не подвергались проверке осознанно. В данном случае после возведения в квадрат не могли появиться посторонние корни, так как и квадратный корень, и подкоренное выражение после возведения в квадрат заведомо равны положительным числам.
Ошибки, связанные с использованием модуля
При решении уравнений, в тех случаях, когда необходимо использовать понятия модуля и арифметического корня , допускаются серьезные ошибки, связанные либо с незнанием, либо с непониманием этих понятий.
K Упражнение 1. Решить уравнение (sqrt=9.)
L Неправильное решение.
J Правильное решение.
K Упражнение 2. Решить уравнение (sqrt<(x+3)^2>=x+3.)
L Неправильное решение.
Ответ: корнем данного уравнения является любое действительное число.
J Правильное решение.
Учитывая, что решение уравнений, содержащих модуль, часто вызывает затруднения, приведем полное и развернутое решение одного из таких уравнений.
K Упражнение. Решить уравнение |x – 3| + |x –4| = 1 .
J Правильное решение.
Находим нули модулей, для |х – 3| это 3 , для |x – 4| это 4 , и разбиваем ими область допустимых значений неизвестного на числовые промежутки:
На каждом из этих промежутков исходное уравнение принимает свой вид.
1) при х ∈ (–∞; 3) исходное уравнение принимает вид:
так как 3 ∉ (–∞; 3 ) , то на этом промежутке решений нет;
2) при х ∈ [3; 4) исходное уравнение принимает вид:
что является истинным тождеством; значит, каждое число рассматриваемого промежутка [3; 4) является решением уравнения;
3) при х ∈ [4; +∞) исходное уравнение принимает вид:
так как 4 ∈ [4; +∞) , то 4 – корень уравнения.
Так как [3; 4)∪ <4>= [3; 4] , то корнями исходного уравнения являются все числа числового промежутка [3; 4] .
Подбор корней без обоснования
К ошибочным решениям можно отнести и верный подбор корня заданного уравнения, иногда просто угадывание, без доказательства его единственности .
K Упражнение. Решить уравнение х (х + 1) (х + 2) (х + 3) = 24 .
L Неправильное решение.
Подбором находят корень х = 1 из разложения 24 = 1 · 2 · 3 · 4.
Комментарий . Был подобран корень х = 1 , но не обнаружен еще один корень х = –4 , который соответствует разложению 24 = –4 · (–3) · (–2) · (–1) . Но даже если и второй корень успешно подобран, но не обосновано отсутствие других корней, то считать такое решение уравнения правильным нельзя.
J Правильное решение.
введем новую переменную x 2 + 3х + 1 = t , тогда
1) x 2 + 3х + 1 = –5, x 2 + 3х + 6 = 0, решений нет;
Наиболее распространенным методом доказательства единственности корня нестандартного уравнения является использование свойства монотонности входящих в уравнение функций . Часто при этом используется производная.
K Упражнение. Решить уравнение x 11 + 5х – 6 = 0 .
L Неправильное решение.
Методом подбора находим корень уравнения х = 1 .
Комментарий . Не приведено обоснование единственности подобранного корня уравнения.
J Правильное решение.
Корень х = 1 легко угадывается, а производная левой части равна 11x 10 + 5 и положительна на всей числовой оси. Отсюда следует монотонность функции у = x 11 + 5х – 6 , что и доказывает единственность подобранного корня.
Ошибки в логарифмических и показательных уравнениях
Для решения логарифмических и показательных уравнений используются специальные приемы, основанные на свойствах логарифмов и степеней. Рассмотрим связанные с применением этих приемов ошибки.
При решении уравнений, которые можно свести к равенству степеней с одинаковыми основаниями или с одинаковыми показателями , не всегда делаются правильные выводы.
K Упражнение 1. Решить уравнение (log7 x) 1 /3 = 1 .
L Неправильное решение.
Так как при одинаковых основаниях показатели не равны, то равенство степеней невозможно, а, значит, корней нет.
Ответ: корней нет.
J Правильное решение.
Возведем в куб обе части уравнения, тогда
K Упражнение 2. Решить уравнение (х + 5) х 2 + х – 2 = 1 .
L Неправильное решение.
Комментарий . Потерян корень х = –4 . Избежать этого можно было и при данном способе решения уравнения, если учесть, что степень равна 1 не только в случае нулевого показателя, но и в случае основания равного 1 при произвольном показателе. И тогда в дополнение к приведенному решению имеем:
J Правильное решение.
Прологарифмируем обе части уравнения по некоторому основанию, например 10, при условии х > 5 , тогда
Необходимо помнить, что:
из равенства степеней, основания которых равны единице, не следует обязательное равенство показателей этих степеней;
степенно–показательное уравнение предпочтительно решать путем логарифмирования.
При решении логарифмических уравнений часто приходится применять свойства логарифмов с одинаковыми основаниями . При применении этих свойств учащиеся часто допускают ошибки.
L Неправильное решение.
Комментарий . В решении допущены две серьезные ошибки: во-первых, произведение логарифмов двух чисел заменено логарифмом произведения этих чисел; во-вторых, при решении уравнения 3х 2 = 81x потерян корень х = 0 (этот корень, конечно, не является корнем исходного уравнения, что не оправдывает его потерю).
J Правильное решение.
K Упражнение 2. Решить уравнение lg x 2 = 4 .
L Неправильное решение.
J Правильное решение 1.
2lg |x| = 4; lg | x| = 2; |x| = 100; x = ±100.
J Правильное решение 2.
lg x 2 = lg 10000; x 2 = 10000; x = ±100.
Большие затруднения у многих учащихся возникают при выполнении действий над логарифмами с разными основаниями , так как учащиеся либо не умеют пользоваться соответствующими формулами, либо не знают их.
Следует помнить, что переход к логарифму с другим основанием может привести как к приобретению посторонних корней, так и к потере корней .
K Упражнение 1. Решить уравнение (left(log_5 +2 right)<log _<5>>^2 ;x=0.)
L Неправильное решение.
(left(1 +2 log _<5>xright)log _<5>x=0;)
Комментарий . Преобразование логарифма с основание х в логарифм с основанием 5 привело к появлению постороннего корня, так как произошло расширение ОДЗ.
J Правильное решение.
Приведенное выше решение следует дополнить указанием области допустимых значений неизвестного в исходном уравнении. Это объединение числовых промежутков (0; 1)∪(1; +∞) . И указанием того факта, что 1 ∉ (0; 1)∪(1; +∞) , а, значит, не является корнем.
K Упражнение 2. Решить уравнение (20log_<4x>sqrt+ 7log_<16x>x^3-3log _x^2=0.)
L Неправильное решение.
Комментарий . В приведенном решении потерян корень, и вот почему. Был выполнен переход к логарифму с основанием х . Это вызвало изменения в ОДЗ неизвестного. Одно из таких изменений – это х ≠ 1 . Поэтому число 1 , как возможный корень исходного уравнения, следует рассмотреть отдельно.
J Правильное решение.
Приведенное выше решение нужно дополнить лишь проверкой того, не является ли 1 корнем уравнения. Подставляем 1 в исходное уравнение и убеждаемся, что 1 – корень.
Ошибки в тригонометрических уравнениях
Выделение в отдельный подраздел тригонометрических уравнений связано стем, что при их решении применяются не только алгебраические методы. Рассмотрим наиболее типичные ошибки, которые допускают учащиеся при решении тригонометрических уравнений.
Часто можно встретить неправильную запись решения тригонометрического уравнения или лишь частное решение .
Статья. Проблемы, типичные ошибки учащихся, допускаемые при решении уравнений и неравенств.
Задание «Проблемы, типичные ошибки учащихся»
Вспоминается расхожая истина – умные люди учатся на чужих ошибках. В математике приходится учиться, в основном, на собственных ошибках. Если ученик не ошибается, то он не учится. Ошибка – вещь необходимая и полезная. Нужно лишь правильно относиться к ошибке, правильно ее использовать.
Обидно получать плохие оценки из-за ошибок «на ровном месте». Глупые ошибки – проблема многих учеников: случайная потеря знака, скобки, необоснованное изменение чисел, пропуски переменных и всевозможные ляпы. Сами ученики порой не могут объяснить, чем вызваны эти ошибки.
Решая уравнения и неравенства учащиеся допускают типичные ошибки:
· Незнание правил, определений, формул.
· Непонимание правил, определений, формул.
· Неумение применять правила, определения, формулы.
· Неверное применение формул.
· Невнимательное чтение условия и вопроса задания.
· Раскрытие скобок и применение формул сокращенного умножения.
Какие же проблемы, трудности общего характера возникают у учащихся при изучении математики ( их несомненно можно отнести и к трудностям, которые возникают у уч-ся при изучении темы «Уравнения и неравенства»):
· Пропуски занятий приводят к незнанию материала, пробелам в знаниях.
· Поверхностное, невдумчивое восприятие нового материала приводят к непониманию его.
· Недостаточная мозговая деятельность приводит к неумению применять правила, определения и формулы .
· Неряшливый, неаккуратный почерк ученика приводит к досадным ошибкам . Учащиеся не всегда сами понимают, что именно они написали.
· Усталость . Чрезмерная нагрузка и недостаточный сон приводит к снижению внимания, скорости мышления и, как следствие, к многочисленным ошибкам.
· Кратковременное или полное переключение внимания с одной деятельности на другую (учебную или внеучебную) приводит к утрате только что воспринятого материала, приходится все начинать сначала.
· Скорость работы. Низкая скорость выполнения мыслительных операций часто мешает ученику контролировать себя и это может стать еще одной причиной ошибки. «Зависание» с какой-нибудь одной частью задания удаляет из «оперативной памяти» информацию о другой, в которой допускается не вынужденная ошибка. Скорость работы определяется физиологией конкретного школьника и навыками выполнения тех или иных операций.
· Мотивация. Следствие низкой мотивации – потеря внимания и ошибка.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
Предлагаю на конкретных примерах рассмотреть ошибки подобного рода и определить способы их предупреждения и исправления, но прежде всего хочу обратить внимание на следующую мысль: не надо бояться приобрести посторонние корни, их можно отбросить путем проверки ,надо бояться потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение
Область определения исходного уравнения задается системой
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Хочу подтвердить сказанное следующим примером.
Ученик предлагает следующее ошибочное решение этого уравнения:
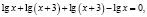
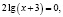
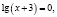
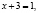
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Предлагаю проанализировать, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 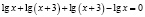
Чтобы избежать потери корня, можно поступить следующим образом: перейти в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Предлагаю рассмотреть это на следующем примере.
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
Для всех x из промежутка (9;10] выражение 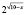
Для всех x из промежутка (9;10] выражение ( x – 9) имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение
– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x ∈ (9;10]. Хочу заметить, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Некоторые учащиеся, решая это уравнение графически (хочу отметить, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
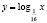
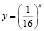
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 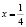
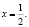
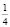
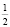
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции «разномонотонны» (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Остановлюсь на типичных ошибки такого рода.
а) Решить уравнение x х = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
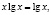
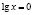
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее произошла потеря двух корней уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
7. При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше.Этого делать не следует.
8.Хочу привести пример еще одной ошибки, связанной с решением неравенств.
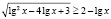
Привожу ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
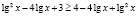
откуда получаем неверное числовое неравенство 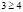
Однако полученный вывод неверен, например, при х = 1000 имеем
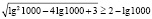
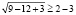
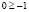
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Привожу правильное решение. Найдем область определения исходного неравенства. Она задается системой
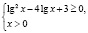
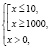
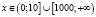
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 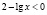
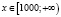
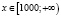
б) 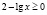
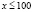
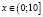
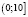
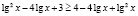
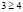
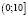
Ответ: 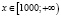
9. Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Большинство ошибок напрямую не связаны с наличием или отсутствием знаний, хотя доведение некоторых вычислительных операций до автоматизма несколько снижает вероятность их появления.
Необходимо осуществлять процесс обучения правилам с помощью специальной модели с использованием приема, активизирующего рефлексивную деятельность учащихся по предупреждению и исправлению ошибок, которые возникают в результате формального усвоения правил.
Самостоятельная работа учащихся над ошибками обеспечивает более осознанный их анализ и анализ собственных действий по решению конкретной задачи, что оказывает благоприятное влияние на качество получаемых знаний и стимулирует развитие логического мышления.
Пример неосознанного применения алгоритма: получив уравнение sin x = 1,2, ученик автоматически ищет его корни по хорошо известной формуле, не обращая внимания на недопустимые значения sin x .
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Выработке навыков самоконтроля помогает и приём приближённой оценки ожидаемого результата.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок.
Систематические проверки чужих записей формируют у ученика привычку критически относиться к своему решению. Для этого подходят задания типа «найди ошибку в решении». Процесс отыскания и исправления ошибок самими учащимися под руководством учителя можно сделать поучительным для учащихся.
Для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля. Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
· проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
· проверка правильности решения задач путём составления и решения задач, обратных к данной;
· оценка результата решения задачи с точки зрения здравого смысла;
· проверка аналитического решения графическим способом.
Способы исправления и предупреждения ошибок
Свести ошибки к минимуму способствуют следующие профилактические меры:
- Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
- Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
- При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентировать внимание на каждом элементе формулы, выполнение разнотипных заданий позволит свести ошибочность к минимуму.
- Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
- Прочному усвоению (а значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее.
источники:
http://math4school.ru/oshibki_v_uravnenijah.html
http://znanio.ru/media/statya_problemy_tipichnye_oshibki_uchaschihsya_dopuskaemye_pri_reshenii_uravnenij_i_neravenstv-173622
УДК 372.8:51
Ю.А. Афоничева
НЕКОТОРЫЕ АСПЕКТЫ ИЗУЧЕНИЯ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ В СРЕДНЕЙ ШКОЛЕ
В статье рассматриваются вопросы, связанные с изучением темы «Показательные уравнения и неравенства» в средней школе; выявлены типичные ошибки учащихся; установлены причины их возникновения; определены возможные пути их устранения.
Ключевые слова: показательные уравнения, показательные неравенства, типичные ошибки учащихся, решение показательных уравнений и неравенств.
Стремительные процессы технологизации общества, информатизации всех отраслей экономики требуют высокого качества математических знаний и более широкого и интенсивного использования математических методов. Применение математических методов тесно связано с изучением показательных уравнений и неравенств, так как эта тема является своего рода обобщением и систематизацией линии уравнений и неравенств в средней школе.
В данной статье рассмотрим некоторые аспекты, связанные с темой «Показательные уравнения и неравенства», проанализируем возможные затруднения учащихся при изучении этой темы, определим пути повышения уровня знаний по данной теме. Целью данной работы является выявление данных ошибок учащихся, установление причин возникновения типичных ошибок, нахождение возможных путей их устранения.
Данный вид уравнений и неравенств является довольно сложным для понимания и усвоения учащимися. Проблемы, связанные с низким уровнем усвоения данной темы отражаются на результатах государственной итоговой аттестации и снижают общий уровень подготовки будущих абитуриентов.
Первая группа типичных ошибок: учащиеся не знают четкого алгоритма решения показательных уравнений и неравенств, делают неравносильные преобразования, вводят новые переменные и забывают возвращаться к обратной замене и т.д.
Вторая группа ошибок возникает из-за отсутствия обобщения и понимания межпредметных связей. Множество процессов и явлений в природе описываются показательной функцией, поэтому с решением показательных уравнений и неравенств учащиеся сталкиваются не только при изучении математики. Учащиеся часто не могут применить уже имеющиеся знания для решения задач из смежных областей. Они решают показательные уравнения и неравенства в контексте конкретных тем курса математики и не понимают, как можно использовать данные методы для решения задач из других областей.
К третьей группе ошибок можно отнести ошибки смешанного типа. При изучении данной темы учащиеся сталкиваются с большим количеством задач, которые в свою очередь, включают в себя операции со степенями, логарифмами. Данные задачи требуют от ученика не только знаний о показательных уравнениях и неравенствах, в них необходимо классифицировать уравнения и неравенства, применять соответствующие методы. Смешанные задания рассматриваются только в учебниках профильного уровня, поэтому ученики не могут успешно применять алгоритмы и методы решения, что влечет за собой ухудшение результатов ЕГЭ и общих знаний.
Проанализировав учебники «Алгебра и начала анализа» Ш.А. Алимова, Ю.М. Колягина, М.В. Ткачевой, Н. Е. Федоровой, М.И. Шабунина [1,2], Г.К. Муравина, О.В. Муравиной [4,5,6,7] базового и углубленного уровней с целью нахождения возможных типичных ошибок, мы констатируем следующее: причин возникновения ошибок при решении задач по теме «Показательные уравнения и неравенства» несколько. Выделим их:
— недостаточность примеров и задач, методов их решения по теме «Показательные уравнения и неравенства» в учебниках базового уровня;
— изложение теоретического материала в большей части идет в словесно-символьной форме, низкий процент использования графических схем, иллюстраций, алгоритмов;
— недостаточность в обобщении и систематизации знаний, которые будут использоваться учащимися для решения разных типов задач [8].
К сожалению, того объёма часов, выделенных на изучение данной темы, явно недостаточно для формирования целостных знаний и умений [3]. Как результат, проверка знаний итоговой аттестации по
© Афоничева Ю.А., 2019.
ISSN 2223-4047
Вестник магистратуры. 2019. № 2-1(89)
заданиям, включающим в себя решение уравнений, неравенств и их систем, показывает, что результаты овладения этими знаниями в большинстве случаев низкие. Данные задачи наиболее успешно решаются учащимися, изучающими математику на профильном уровне.
Для систематизации знаний учащихся необходимо составить типологию задач. В результате анализа соответствующей литературы, собственного педагогического опыта мы получили следующие типы задач.
Первый тип задач связан к простейшим операциям со степенью. Например, 4 = 1; 3х’+хЧ2 = 1;
1
*+— ?
3 2 • 3 = 1. Для решения таких задач необходимо систематизировать знания о свойствах степени.
Второй тип задач решается сведением к квадратному уравнению путем замены. Например, 25* + 6 • 5х + 5 = 0. В данном случае учащимся необходимы знания для решения квадратных уравнений.
Третий тип предполагает усложнение самой структуры уравнения или неравенства, включения в выражение иррациональностей и модулей. Примеры таких уравнений: 3= 3х; 3|х+1′ = 32 |х|. Здесь учащимся необходимы знания об области определения функции, а также знания методов, основанных на разбиении координатной прямой на интервалы, решении задачи с учетом изменения значений функции на каждом из интервалов.
Четвертый тип задач требует доказательства и связан с использованием изученных свойств показательной функции. Пример таких заданий: Доказать, что при любом х верно 2х+2-х>2.
Выделенные типы задач по данной теме можно систематизировать и обобщить приемы их решения, использовать различные алгоритмы, схемы действий, планы решений. Таким планом решения может быть следующий алгоритм действий:
1. Необходимо добиться того, чтобы слева и справа в уравнении стояли одинаковые числа-основания, после чего можно приравнять показатели степеней и работать уже с новым, более простым уравнением. Это необходимо сделать с помощью тождественных преобразований. Убрать одинаковые основания можно только тогда, когда основания стоят без других множителей и слагаемых. Например: 6 6х-5 = 62х+1 ■ Шестерки убрать нельзя! Преобразование будет эквивалентным, убрать одинаковые основания мы можем только тогда, когда наше уравнение имеет канонический вид: а'<х) = а8<х)
2. Необходимо повторить и систематизировать правила действия со степенями, корнями. Данные знания понадобятся при решении такого вида уравнений: 32х — 27х+2 = 0. Правила действий со степенями с отрицательным показателем понадобятся в уравнениях: 5*2-6ж+5 = 0,004х-1. В таких уравнениях важно помнить, что в десятичной дроби тяжело распознать степень числа, поэтому всегда преобразовываем их к
обыкновенным. Правила действия с корнями будут необходимы в уравнениях вида: 0,25 • 45х-16 = (—) . В таких уравнениях важно помнить, что любой корень всегда можно преобразовать в степень с дробным показателем.
3. Любое положительное число в любой степени дает только положительное число, на данном элементарном преобразовании делается большое количество ошибок. Например, уравнения такого вида: 7017х
+ 50,3х+1 + з0,23х+2 = _ 5
4. Если представлено уравнение в виде суммы или разности одного и того же числа в разных степенях, то можно применить метод разложения на множители. Например, 5х+2 _ 5х+1 + 5х = 105.
5. Необходимо повторить и систематизировать знания по следующим темам: квадратные уравнения, дробно-рациональные уравнения, логарифмы. Например, уравнение 3х + 731-х = 10, используя ряд
21
преобразований, необходимо свести к дробно-рациональному: t + — = 10. Умножив обе части на t не равное 0, получим квадратное уравнение: ^ _ 10t + 21 = 0. При нахождении второго корня приходим к решению уравнения 3х = 7, где появляется необходимость использовать логарифм: х2 = log37.
6. Если мы видим, что в уравнении стоят одинаковые выражения с неизвестной, то можно воспользоваться методом замены переменной. Это будет полезно для следующего уравнения: 52х — 4 5х + 5 = 0.
7. В задачах повышенного уровня сложности часто применяется метод разложения на множители с использованием группировки. Например, 6х _ 92х _ 83х + 72 = 0.
8. Если перед нами представлено уравнение повышенного уровня сложности, где присутствуют одинаковые показатели и разные основания, то можно использовать почленное деление на показательное выражение. Например: 5 32х + 3 52х = 8 15х .
1
9. Не забывать про существование ОДЗ, например, в уравнении 2*-3 = 0,5х-1 необходимо учитывать то, что делить на 0 нельзя!
Для устранения ошибок, перечисленных выше, необходимо провести исследование и выяснить какая из причин возникновения ошибок является ключевой. Необходимо найти причинно-следственную связь между существующей ошибкой и соответствующей темой школьного курса математики.
Таким образом, в данной работе были выявлены типичные ошибки учащихся, установлены причины возникновения типичных ошибок, определены возможные пути их устранения.
Библиографический список
1.Алгебра и начала математического анализа. 10 класс: учеб. для общеобр. учреждений: базовый и проф. уровни / Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин / под ред .А.Б. Жижченко — 4-е изд.- М.: Просвещение, 2011. — 368 с.
2.Алгебра и начала математического анализа. 10-11 классы: учебник для общеобр. учреждений: базовый и углубл. уровень / Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева и др. — 3-е изд. — М.: Просвещение, 2016. — 464 с.
3.Бурмистрова Т.А. Программы общеобр. учреждений. Алгебра и начала математического анализа. 10-11 класс. — М.: Просвещение, 2009. — 159 с.
4.Муравин Г.К. Алгебра и начала математического анализа. 10 класс : учеб. для общеобр. учреждений / Г.К. Муравин. — М. : Дрофа, 2013. — 287 с.
5.Муравин Г.К. Алгебра и начала математического анализа. 11 класс : учеб. для общеобр. учреждений / Г.К. Муравин, О.В. Муравина. — М. : Дрофа, 2013. — 253 с.
6.Муравин Г.К. Алгебра и начала математического анализа. Углубл. уровень. 10 класс / Г.К. Муравин, О.В. Муравина — М. : Дрофа, 2013. — 318 с.
7.Муравин Г.К. Алгебра и начала математического анализа. Углубл. уровень. 11 класс / Г.К. Муравин, О.В. Муравина — М. : ДРОФА, 2014. — 318 с.
8.Кара-Сал Н.М. Использование системы заданий по теме «Показательные уравнения» для обобщения и систематизации знаний школьников //Вестник тувинского государственного университета — 2015. [Электронный ресурс]. URL: https://elibrary.ru/item.asp?id=26021082
Что такое показательные уравнения
Если ты забыл следующие темы, то для получения наилучшего результата, пожалуйста, повтори:
- Свойства степени и корня
- Решение линейных и квадратных уравнений
- Разложение на множители
Повторил? Замечательно!
Тогда тебе не составит труда заметить, что корнем уравнения ( 3x+5=2{x} -1) является число ( x=-6).
Ты точно понял, как я это сделал? Правда? Тогда продолжаем. Теперь ответь мне на вопрос, чему равно ( 5) в третьей степени? Ты абсолютно прав:
( {{5}^{3}}=5cdot 5cdot 5=125).
А восьмерка – это какая степень двойки? Правильно – третья! Потому что:
( 2cdot 2cdot 2={{2}^{3}}=8).
Ну вот, теперь давай попробуем решить следующую задачку: Пусть я ( x) раз умножаю само на себя число ( 2) и получаю в результате ( 16).
Спрашивается, сколько раз я умножил ( 2) само на себя? Ты, конечно, можешь проверить это непосредственно:
( begin{align} & 2=2 \ & 2cdot 2=4 \ & 2cdot 2cdot 2=8 \ & 2cdot 2cdot 2cdot 2=16 \ end{align} )
Тогда ты можешь сделать вывод, что ( 2) само на себя я умножал ( displaystyle 4) раза.
Как еще это можно проверить?
А вот как: непосредственно по определению степени: ( displaystyle {{2}^{4}}=16).
Но, согласись, если бы я спрашивал, сколько раз два нужно умножить само на себя, чтобы получить, скажем ( displaystyle 1024), ты бы сказал мне: я не буду морочить себе голову и умножать ( displaystyle 2) само на себя до посинения.
И был бы абсолютно прав. Потому как ты можешь записать все действия кратко (а краткость – сестра таланта)
( displaystyle {{2}^{x}}=1024),
где ( displaystyle x) – это и есть те самые «разы», когда ты умножаешь ( displaystyle 2) само на себя.
Я думаю, что ты знаешь ( а если не знаешь, срочно, очень срочно повторяй степени!), что ( displaystyle 1024={{2}^{10}}), тогда моя задачка запишется в виде:
( displaystyle {{2}^{x}}={{2}^{10}}), откуда ты можешь сделать вполне оправданный вывод, что:
( x=10).
Вот так вот незаметно я записал простейшее показательное уравнение:
( {{2}^{x}}={{2}^{10}})
И даже нашел его корень ( x=10). Тебе не кажется, что все совсем тривиально? Вот и я думаю именно так же.
Вот тебе еще один пример:
( {{1000}^{x}}=100).
Но что же делать?
Ведь ( 100) нельзя записать в виде степени (разумной) числа ( 1000).
Давай не будем отчаиваться и заметим, что оба этих числа прекрасно выражаются через степень одного и того же числа.
Какого?
Верно: ( 100={{10}^{2}},~1000={{10}^{3}}).
Тогда исходное уравнение преобразуется к виду:
( {{10}^{3x}}={{10}^{2}}),
откуда, как ты уже понял, ( 3x=2,~x=frac{2}{3}).
Давай более не будем тянуть и запишем определение:
Пример 1 (меркантильный)
Пусть у тебя есть ( displaystyle 1000000) рублей, а тебе хочется превратить его в ( displaystyle 1500000) рублей.
Банк предлагает тебе взять у тебя эти деньги под ( displaystyle 12%) годовых с ежемесячной капитализацией процентов (ежемесячным начислением).
Спрашивается, на сколько месяцев нужно открыть вклад, чтобы набрать нужную конечную сумму?
Вполне приземленная задача, не так ли?
Тем не менее ее решение связано с построением соответствующего показательного уравнения:
Пусть ( Sn) – начальная сумма, ( Sk) – конечная сумма, ( i) – процентная ставка за период, ( x) – количество периодов.
Тогда:
( Sk=Sn{{left( 1+frac{i}{100} right)}^{x}})
В нашем случае ( displaystyle Sn=1000000={{10}^{6}},~Sk=1500000=1.5cdot {{10}^{6}},~i=1) (если ставка ( 12%) годовых, то за месяц начисляют ( 1%)).
А почему ( i) делится на ( 100)? Если не знаешь ответ на этот вопрос, вспоминай тему «Проценты»!
Тогда мы получим вот такое уравнение:
( 1.5cdot {{10}^{6}}={{10}^{6}}{{left( 1+0.01 right)}^{x}})
( 1.5={{1.01}^{x}})
Данное показательное уравнение уже можно решить только при помощи калькулятора (его внешний вид на это намекает, причем для этого требуется знание логарифмов, с которыми мы познакомимся чуть позже), что я и сделаю: ( xtilde{ }40.7489)…
Таким образом, для получения ( 1.5) млн. нам потребуется сделать вклад на ( 41) месяц (не очень быстро, не правда ли?)
Пример 1. Метод простой замены
( {{4}^{x}}+{{2}^{x+1}}-3=0)
Решение:
Это уравнение решается при помощи «простой замены», как ее пренебрежительно называют математики.
В самом деле, замена здесь – самая очевидная. Стоит лишь увидеть, что
( {{4}^{x}}={{2}^{2x}}={{({{2}^{x}})}^{2}})
Тогда исходное уравнение превратится вот в такое:
( {{({{2}^{x}})}^{2}}+{{2}^{x+1}}-3=0)
Если же дополнительно представить ( {{2}^{x+1}}) как ( 2cdot {{2}^{x}}), то совершенно ясно, что надо заменять: конечно же, ( t={{2}^{x}}). Во что тогда превратится исходное уравнение? А вот во что:
( {{t}^{2}}+2t-3=0)
Ты без проблем самостоятельно отыщешь его корни: ( {{t}_{1}}=-3,~{{t}_{2}}=1).
Что нам делать теперь?
Пришло время возвращаться к исходной переменной ( displaystyle x).
А что я забыл указать? Именно: при замене некоторой степени на новую переменную (то есть при замене вида ( t={{a}^{x}})), меня будут интересовать только положительные корни!
Ты и сам без труда ответишь, почему.
Таким образом, ( {{t}_{1}}=-3) нас с тобой не интересует, а вот второй корень нам вполне подходит:
( {{t}_{2}}=1), тогда ( {{2}^{x}}=1), откуда ( x=0).
Ответ: ( x=0)
Как видишь, в предыдущем примере, замена так и просилась к нам в руки. К сожалению, так бывает далеко не всегда.
Однако давай не будем переходить сразу к грустному, а потренируемся еще на одном примере с достаточно простой заменой.
Пример 2. Метод простой замены
( {{3}^{3x+1}}-4cdot {{9}^{x}}=17cdot {{3}^{x}}-6)
Решение:
Ясно, что скорее всего заменять придется ( {{3}^{x}}) (это наименьшая из степеней, входящая в наше уравнение).
Однако прежде чем вводить замену, наше уравнение нужно к ней «подготовить», а именно:
( {{3}^{3x+1}}=3cdot {{left( {{3}^{x}} right)}^{3}}), ( {{9}^{x}}={{({{3}^{x}})}^{2}}).
Тогда можно заменять ( t={{3}^{x}}), в результате я получу следующее выражение:
( 3{{t}^{3}}-4{{t}^{2}}=17t-6)
( 3{{t}^{3}}-4{{t}^{2}}-17t+6=0)
О ужас: кубическое уравнение с совершенно жуткими формулами его решения (ну если говорить в общем виде). Но давай не будем сразу отчаиваться, а подумаем, что нам делать.
Я предложу смошенничать: мы знаем, что для получения «красивого» ответа, нам нужно получить ( t) в виде некоторой степени тройки (с чего бы это, а?).
А давай попробуем угадать хотя бы один корень нашего уравнения (я начну гадать со степеней тройки).
Первое предположение ( displaystyle t=1). Не является корнем. Увы и ах! Хорошо, а теперь возьмем…
Как видишь, отбор корней показательных уравнений требует достаточно глубокого знания свойств логарифмов, так что я советую тебе быть как можно внимательнее, когда решаешь показательные уравнения.
Как ты понимаешь, в математике все взаимосвязано! Как говорила моя учительница по математике, математику, как историю, за ночь не прочитаешь.
Как правило, всю сложность при решении задач повышенной сложности составляет именно отбор корней уравнения.
Еще один пример для тренировки
( {{9}^{x+1}}-2cdot {{3}^{x+2}}+5=0,~) при ( ~xin (lo{{g}_{3}}frac{3}{2};sqrt{5}))
Решение:
Ясно, что само уравнение решается довольно просто. Сделав замену ( t={{3}^{x}}) мы сведем наше исходное уравнение к следующему:
( {{t}^{2}}-18t+5=0)
( {{t}_{1}}=frac{1}{3},~{{t}_{2}}=frac{5~}{3})
Тогда ( {{x}_{1}}=-1,~{{x}_{2}}=mathbf{lo}{{mathbf{g}}_{3}}left( frac{5}{3} right)~~~)
Вначале давай рассмотрим первый корень.
Сравним ( -1) и ( lo{{g}_{3}}left( frac{3}{2} right)):
так как ( frac{3}{2}>1), то ( lo{{g}_{3}}left( frac{3}{2} right)>0). (свойство логарифмической функции ( y=lo{{g}_{a}}x) при ( a>1)).
Тогда ясно, что( lo{{g}_{3}}left( frac{3}{2} right)>-1) и первый корень не принадлежит нашему промежутку.
Теперь второй корень:
Пример уравнения с нестандартной заменой!
( displaystyle 4sqrt[x]{81}-12sqrt[x]{36}+9sqrt[x]{16}=0)
Решение:
Давай сразу начнем с того, что делать можно, а что – в принципе можно, но лучше не делать.
Можно – представить все через степени тройки, двойки и шестерки. К чему это приведет?
Да ни к чему и не приведет: мешанина степеней, причем от некоторых будет довольно сложно избавиться.
А что же тогда нужно?
Давай заметим, что ( 81={{9}^{2}},~16={{4}^{2}},~) а ( 36=4cdot 9.)
И что нам это даст? А то, что мы можем свести решение данного примера к решению достаточно простого показательного уравнения!
Вначале давай перепишем наше уравнение в виде:
( displaystyle 4cdot {{9}^{frac{2}{x}}}~-12cdot {{4}^{frac{1}{x}}}{{9}^{frac{1}{x}}}+9cdot {{4}^{frac{2}{x}}}=0)
Такие уравнения называются однородными (подробнее читай в теме «Однородные уравнения»).
Теперь разделим обе части получившегося уравнения на ( {{4}^{frac{2}{x}}}):
Например, уравнение вида:
( {{a}^{F(x)}}=b(x)), причем ( b(x)ne {{a}^{i}}), ( i)( in R/Q)
В общем случае можно решить только логарифмированием обеих частей (например по основанию ( a)), при котором исходное уравнение превратится в следующее:
( F(x)=lo{{g}_{a}}b(x))
Давай рассмотрим следующий пример:
( {{x}^{1+lgx}}=10x)
Ясно, что по ОДЗ логарифмической функции, нас интересуют только ( x>0). Однако, это следует не только из ОДЗ логарифма, а еще по одной причине. Я думаю, что тебе не будет трудно угадать, по какой же именно.
Давай прологарифмируем обе части нашего уравнения по основанию ( 10):
( lg({{x}^{1+lgx}})=lg(10x))
( (1+lg(x))cdot lg(x)=1+lg(x))
( (1+lg(x))(lg(x)-1)=0)
( lg(x)=1,~lg(x)=-1)
( {{x}_{1}}=10,~{{x}_{2}}=0,1)
Как видишь, логарифмирование нашего исходного уравнения достаточно быстро привело нас к правильному (и красивому!) ответу.
Давай потренируемся еще на одном примере:
( {{x}^{lo{{g}_{4}}x-2}}={{2}^{2(lo{{g}_{4}}x-1)}})
Здесь тоже нет ничего страшного: прологарифмируем обе стороны уравнения по основанию ( 4), тогда получим:
( lo{{g}_{4}}({{x}^{lo{{g}_{4}}x-2}})=lo{{g}_{4}}({{2}^{2(lo{{g}_{4}}x-1)}});)
( left( lo{{g}_{4}}x-2 right)text{lo}{{text{g}}_{4}}x=2left( text{lo}{{text{g}}_{4}}x-1 right)text{lo}{{text{g}}_{4}}2;)
( (lo{{g}_{4}}x-2)lo{{g}_{4}}x=(lo{{g}_{4}}x-1);)
Сделаем замену: ( t=lo{{g}_{4}}x)
( {{t}_{1}}=frac{3+sqrt{5}}{2},~{{t}_{2}}=frac{3-sqrt{5}}{2})
Тогда ( {{x}_{1}}=lo{{g}_{4}}left( frac{3+sqrt{5}}{2} right),~{{x}_{2}}=lo{{g}_{4}}left( frac{3-sqrt{5}}{2} right),~)
Однако мы кое-что упустили! Ты заметил, где я сделал промах?
Ведь ( frac{3-sqrt{5}}{2}<1,~) тогда:
( {{x}_{2}}=lo{{g}_{4}}left( frac{3-sqrt{5}}{2} right)<0,~~) что не удовлетворяет требованию ( x>0) (подумай откуда оно взялось!)
Ответ: ( lo{{g}_{4}}left( frac{3+sqrt{5}}{2} right))
Попробуй самостоятельно записать решение показательных уравнений, приведенных ниже
- ( {{x}^{2l{{g}^{3}}x-1.5lgx}}=sqrt{10})
- ( {{(x+5)}^{lo{{g}_{7}}(x+5)}}=7)
А теперь сверь свое решение с этим:
1. Логарифмируем обе части по основанию ( 10), учитывая, что ( x>0):
( lg left( {{x}^{2l{{g}^{3}}x-1.5lgx}} right)=lgsqrt{10})
( left( 2l{{g}^{3}}x-1.5lgx right)lgx=frac{1}{2},~), замена ( ~t=l{{g}^{2}}xge 0)
( 4{{t}^{2}}-3t-1=0)
( 4{{t}^{2}}-3t-1=0) (второй корень нам не подходит ввиду замены)
( l{{g}^{2}}x=1,~{{x}_{1}}=1,~{{x}_{2}}=0.1~)
2. Логарифмируем по основанию ( displaystyle 7):
( displaystyle lo{{g}_{7}}{{left( x+5 right)}^{lo{{g}_{7}}left( x+5 right)}}=lo{{g}_{7}}7)
Преобразуем полученное выражение к следующему виду:
( displaystyle left( lo{{g}_{7}}left( x+5 right)+1 right)left( lo{{g}_{7}}left( x+5 right)-1 right)=0)
( displaystyle {{x}_{1}}=2,~{{x}_{2}}=-frac{34}{7})
Простейшие показательные уравнения
Давайте начнем с простейших степенных уравнений и разберем несколько примеров:
Пример 1
$$ 2^x=8;$$
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (x,) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Это несложно:
$$ 2^3=2*2*2=8; $$
Если (x=3), то мы получим верное равенство, а значит, мы решили уравнение.
Решим что-нибудь посложнее.
Пример 2
$$ 3^{4x-1}=frac{1}{9};$$
Попробуем преобразовать правую часть уравнения:
$$frac{1}{9}=frac{1}{3^2}=3^{-2};$$
Мы применили свойство отрицательной степени по формуле:
$$ a^{-n}=frac{1}{a^n};$$
Теперь наше уравнение будет выглядеть так:
$$ 3^{4x-1}=3^{-2};$$
Заметим, что слева и справа стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные: слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
$$ 4x-1=-2;$$
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
$$4х=-2+1;$$
$$4x=-1;$$
$$x=-frac{1}{4}.$$
Поздравляю, мы нашли корень нашего показательного уравнения.
Пример 3
$$125^x=25;$$
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую части, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
$$ (5^3)^x=5^2;$$
Воспользуемся одним из свойств степени ((a^n)^m=a^{n*m}):
$$ 5^{3*x}=5^2;$$
И опять мы получили две показательные функции, у которых одинаковые основания, и для того, чтобы равенство выполнялось, необходимо приравнять их степени:
$$ 3*x=2;$$
$$ x=frac{2}{3};$$
И еще один пример:
Пример 4
$$2^x=-4;$$
Те, кто хорошо знаком со свойствами степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры наподобие примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Алгоритм решения показательных уравнений
Пусть у нас есть вот такой пример:
$$ a^x=b;$$
где (a,b) какие-то положительные числа ((a gt 0, ; b gt 0)).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
$$ a^x=a^m;$$
Раз основания одинаковые, то мы можем просто приравнять степени:
$$x=m.$$
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени, и сложное показательное уравнение решено. Осталось только понять, как делать такие преобразования. Опять разберем на примерах:
Пример 5
$$2^x=16;$$
Замечаем, что (16=2*2*2*2=2^4:)
$$2^x=2^4;$$
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6
$$5^{-x}=125;$$
$$Downarrow$$
$$5^{-x}=5*5*5;$$
$$Downarrow$$
$$5^{-x}=5^3;$$
$$Downarrow$$
$$–x=3;$$
$$Downarrow$$
$$x=-3.$$
Пример 7
$$27^{4x}=81;$$
$$Downarrow$$
$$(3*3*3)^{4x}=3*3*3*3;$$
$$Downarrow$$
$$(3^3)^{4x}=3^4;$$
$$Downarrow$$
$$3^{12x}=3^4;$$
$$Downarrow$$
$$12x=4;$$
$$Downarrow$$
$$x=frac{4}{12}=frac{1}{3}.$$
Здесь мы заметили, что (27=3^3) и (81=3^4.)
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается? Например:
Пример 8
$$ 3^x=2;$$
(3) и (2) привести к одинаковому основанию затруднительно. Но, тем не менее, мы должны это сделать. Оказывается, произвольное положительное число (b) ((b>0)) можно представить в виде степени любого, нужного вам, положительного числа (a) ((a>0, ; a neq 1)) по формуле с использованием логарифма:
$$ b=a^{log_{a}(b)};$$
Эта очень важная формула, рекомендую ее выучить. Вернемся к нашему примеру и по этой формуле представим (2ку) в виде (3ки) в какой-то степени, где (a=3), а (b=2:)
$$ 2=3^{log_{3}(2)};$$
Подставим данное преобразование в наш пример:
$$3^x=3^{log_{3}(2)};$$
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
$$x=log_{3}(2).$$
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Рассмотрим еще несколько аналогичных примеров.
Пример 9
$$ 7^{2x}=5;$$
$$ 7^{2x}=7^{log_{7}(5)};$$
$$2x=log_{7}(5);$$
$$x=frac{1}{2}*log_{7}(5).$$
Те, кто хорошо знают свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
$${small x=frac{1}{2}*log_{7}(5)=log_{7}(5^{frac{1}{2}})=log_{7}(sqrt{5});}$$
Все эти варианты ответа верные, их можно смело писать в ответ.
Итак, мы с вами научились решать любые показательные уравнения вот такого вида:
$$a^x=b,$$
где (a gt 0; ; b gt 0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложные. Например, в ЕГЭ по профильной математике №14 из 2й части. Но бояться тут не нужно, все, на первый взгляд, сложные уравнения при помощи, обычно, не самых сложных преобразований сводятся к уравнениям вида: (a^x=b), где (a gt 0; ; b gt 0). Рассмотрим теперь сложные показательные уравнения:
Решение показательных уравнений при помощи замены
Рассмотрим уравнение:
Пример 10
$$ 9^x-5*3^x+6=0;$$
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^{2x}=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^{n*m}).
Подставим в исходное уравнение:
$$(3^x)^2-5*3^x+6=0;$$
Обратим внимание, что во всем уравнении все (x) «входят» в одинаковую функцию: (3^x). Сделаем замену (t=3^x.) Напоминаю, что (t=3^x gt 0,) так как показательная функция всегда положительна по определению.
$$t^2-5t+6=0;$$
Квадратное уравнение, которое решается через дискриминант:
$$D=5^2-4*6=25-24=1;$$
$$t_{1}=frac{5+sqrt{1}}{2}=3;$$
$$t_{2}=frac{5-sqrt{1}}{2}=2;$$
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену, и уравнение сводится к решению двух простых показательных уравнений:
$$ 3^x=3;$$
$$3^x=3^1;$$
$$x=1.$$
И второй корень:
$$ 3^x=2;$$
$$3^x=3^{log_{3}(2)};$$
$$x=log_{3}(2).$$
Ответ: (x_{1}=1; ; x_{2}=log_{3}(2).)
И еще один пример на замену:
Пример 11
$$3^{4x^2-6x+3}-10*3^{2x^2-3x+1}+3=0;$$
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания одинаковые, а вот степени отличаются. Преобразуем первое слагаемое. Если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
$${ small 3^{4x^2-6x+3}=3^{4x^2-6x+2+1}=}$$
$${ small=3^{2(2x^2-3x+1)+1}=3^{2*(2x^2-3x+1)}*3^1=}$$
$${ small=3*(3^{2x^2-3x+1})^2;}$$
Подставим в исходное уравнение:
$${small 3*(3^{2x^2-3x+1})^2-10*3^{2x^2-3x+1}+3=0;}$$
Теперь показательные функции одинаковые, и можно сделать замену:
$$t=3^{2x^2-3x+1}, quad t gt 0;$$
$$3*t^2-10t+3=0;$$
$$D=100-36=64;$$
$$t_{1}=frac{-(-10)+sqrt{64}}{2*3}=3;$$
$$t_{2}=frac{-(-10)-sqrt{64}}{2*3}=frac{1}{3};$$
Обратная замена, и наше уравнение сводится к простейшему:
$$ 3^{2x^2-3x+1}=3;$$
$$ 2x^2-3x+1=1;$$
$$x(2x-3)=0;$$
$$x_1=0; quad x_2=frac{3}{2}.$$
И второе значение (t):
$$3^{2x^2-3x+1}=frac{1}{3};$$
$$3^{2x^2-3x+1}=3^{-1};$$
$$2x^2-3x+1=-1;$$
$$2x^2-3x+2=0;$$
$$D=9-16=-7 lt 0;$$
Раз дискриминант получился меньше нуля, то вторая ветка решений нам корней не дает.
Ответ: (x_{1}=0; ; x_{2}=frac{3}{2}.)
Однородные показательные уравнения
Иногда встречаются такие показательные уравнения, в которых не сразу видно, как сделать одинаковые функции, а именно, одинаковые основания, чтобы произвести замену. Посмотрим на такой пример:
Пример 12
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x};$$
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наше уравнение на (3^x):
$$ {small 7^{x+1}+3*7^{x}=3^{x+2}+3^{x} qquad |:3^x}$$
$$ { small frac{7^{x+1}}{3^x}+frac{3*7^{x}}{3^x}=frac{3^{x+2}}{3^x}+frac{3^{x}}{3^x};}$$
Здесь нам придется воспользоваться свойствами степеней:
$$frac{a^n}{a^m}=a^{n-m};$$
$$ a^n*a^m=a^{n+m};$$
$$ frac{a^n}{b^n}=left(frac{a}{b}right)^n;$$
Разберем каждое слагаемое:
$$ {small frac{7^{x+1}}{3^x}=frac{7*7^x}{3^x}=7*frac{7^x}{3^x}=7*left(frac{7}{3}right)^x;}$$
$$ frac{3*7^{x}}{3^x}=3*frac{7^x}{3^x}=3*left(frac{7}{3}right)^x;$$
$$ frac{3^{x+2}}{3^x}=3^2*frac{3^x}{3^x}=3^2*1=9;$$
$$ frac{3^{x}}{3^x}=1;$$
Теперь подставим получившееся преобразование в исходное уравнение:
$$ 7*left(frac{7}{3}right)^x+3*left(frac{7}{3}right)^x=9+1;$$
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену. Пусть (t=(frac{7}{3})^x):
$$7t+3t=10;$$
$$10t=10;$$
$$t=1;$$
Сделаем обратную замену:
$$left(frac{7}{3}right)^x=1;$$
Вспоминаем, что (1=left(frac{7}{3}right)^0):
$$left(frac{7}{3}right)^x=left(frac{7}{3}right)^0;$$
$$x=0.$$
Ответ: (x=0).
Пример 13
$$2^{x+2}+0,5^{-x-1}+4*2^{x+1}=28;$$
Первым делом, нужно сделать так, чтобы все показательные функции были с одинаковым основанием и, в идеале, с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
$$ a^n*a^m=a^{n+m};$$
$$a^{-n}=frac{1}{a^n};$$
$${(a^n)}^m=a^{n*m};$$
Разберем каждое слагаемое нашего уравнения:
$$2^{x+2}=2^x*2^2=4*2^x;$$
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
$${ small 0,5^{-x-1}=0,5^{-(x+1)}={left(frac{1}{2}right)}^{-(x+1)}=}$$
$${ small ={(2^{-1})}^{-(x+1)}=2^{x+1}=2^x*2^1=2*2^x;}$$
И последнее слагаемое со степенью:
$$ 4*2^{x+1}=4*2^x*2^1=8*2^x;$$
Подставим все наши преобразования в исходное уравнение:
$$4*2^x+2*2^x+8*2^x=28;$$
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
$$2^x*(4+2+8)=28;$$
$$14*2^x=28;$$
$$2^x=frac{28}{14}=2;$$
$$2^x=2^1;$$
$$x=1.$$
Ответ: (x=1.)
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера.
Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И рассмотрим другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше.
Пример 14
$$2^{x+1}*5^x=10^{x+1}*5^{x+2};$$
Вот такое уравнение, в котором у нас, во-первых, показательные функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2ка), (5ка) и (10ка). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
$$2^{x+1}*5^x=(2*5)^{x+1}*5^{x+2};$$
Воспользуемся формулой ((a*b)^n=a^n*b^n):
$$ 2^{x+1}*5^x=2^{x+1}*5^{x+1}*5^{x+2};$$
И перекинем с помощью деления все показательные функции с основанием (2) влево, а с основанием (5) вправо:
$$frac{2^{x+1}}{2^{x+1}}=frac{5^{x+1}*5^{x+2}}{5^x};$$
Сокращаем и воспользуемся формулами (a^n*a^m=a^{n+m}) и (frac{a^n}{a^m}=a^{n-m}):
$$1=frac{5^{x+1+x+2}}{5^x};$$
$$1=frac{5^{2x+3}}{5^x};$$
$$1=5^{2x+3-x};$$
$$1=5^{x+3};$$
$$5^0=5^{x+3};$$
$$x+3=0;$$
$$x=-3.$$
Ответ: (x=-3).
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше, и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом. Чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Что такое показательные уравнения
Если ты забыл следующие темы, то для получения наилучшего результата, пожалуйста, повтори:
- Свойства степени и корня
- Решение линейных и квадратных уравнений
- Разложение на множители
Повторил? Замечательно!
Тогда тебе не составит труда заметить, что корнем уравнения \( 3x+5=2{x} -1\) является число \( x=-6\).
Ты точно понял, как я это сделал? Правда? Тогда продолжаем. Теперь ответь мне на вопрос, чему равно \( 5\) в третьей степени? Ты абсолютно прав:
\( {{5}^{3}}=5\cdot 5\cdot 5=125\).
А восьмерка – это какая степень двойки? Правильно – третья! Потому что:
\( 2\cdot 2\cdot 2={{2}^{3}}=8\).
Ну вот, теперь давай попробуем решить следующую задачку: Пусть я \( x\) раз умножаю само на себя число \( 2\) и получаю в результате \( 16\).
Спрашивается, сколько раз я умножил \( 2\) само на себя? Ты, конечно, можешь проверить это непосредственно:
\( \begin{align} & 2=2 \\ & 2\cdot 2=4 \\ & 2\cdot 2\cdot 2=8 \\ & 2\cdot 2\cdot 2\cdot 2=16 \\ \end{align} \)
Тогда ты можешь сделать вывод, что \( 2\) само на себя я умножал \( \displaystyle 4\) раза.
Как еще это можно проверить?
А вот как: непосредственно по определению степени: \( \displaystyle {{2}^{4}}=16\).
Но, согласись, если бы я спрашивал, сколько раз два нужно умножить само на себя, чтобы получить, скажем \( \displaystyle 1024\), ты бы сказал мне: я не буду морочить себе голову и умножать \( \displaystyle 2\) само на себя до посинения.
И был бы абсолютно прав. Потому как ты можешь записать все действия кратко (а краткость – сестра таланта)
\( \displaystyle {{2}^{x}}=1024\),
где \( \displaystyle x\) – это и есть те самые «разы», когда ты умножаешь \( \displaystyle 2\) само на себя.
Я думаю, что ты знаешь ( а если не знаешь, срочно, очень срочно повторяй степени!), что \( \displaystyle 1024={{2}^{10}}\), тогда моя задачка запишется в виде:
\( \displaystyle {{2}^{x}}={{2}^{10}}\), откуда ты можешь сделать вполне оправданный вывод, что:
\( x=10\).
Вот так вот незаметно я записал простейшее показательное уравнение:
\( {{2}^{x}}={{2}^{10}}\)
И даже нашел его корень \( x=10\). Тебе не кажется, что все совсем тривиально? Вот и я думаю именно так же.
Вот тебе еще один пример:
\( {{1000}^{x}}=100\).
Но что же делать?
Ведь \( 100\) нельзя записать в виде степени (разумной) числа \( 1000\).
Давай не будем отчаиваться и заметим, что оба этих числа прекрасно выражаются через степень одного и того же числа.
Какого?
Верно: \( 100={{10}^{2}},~1000={{10}^{3}}\).
Тогда исходное уравнение преобразуется к виду:
\( {{10}^{3x}}={{10}^{2}}\),
откуда, как ты уже понял, \( 3x=2,~x=\frac{2}{3}\).
Давай более не будем тянуть и запишем определение:
Пример 1 (меркантильный)
Пусть у тебя есть \( \displaystyle 1000000\) рублей, а тебе хочется превратить его в \( \displaystyle 1500000\) рублей.
Банк предлагает тебе взять у тебя эти деньги под \( \displaystyle 12\%\) годовых с ежемесячной капитализацией процентов (ежемесячным начислением).
Спрашивается, на сколько месяцев нужно открыть вклад, чтобы набрать нужную конечную сумму?
Вполне приземленная задача, не так ли?
Тем не менее ее решение связано с построением соответствующего показательного уравнения:
Пусть \( Sn\) – начальная сумма, \( Sk\) – конечная сумма, \( i\) – процентная ставка за период, \( x\) – количество периодов.
Тогда:
\( Sk=Sn{{\left( 1+\frac{i}{100} \right)}^{x}}\)
В нашем случае \( \displaystyle Sn=1000000={{10}^{6}},~Sk=1500000=1.5\cdot {{10}^{6}},~i=1\) (если ставка \( 12\%\) годовых, то за месяц начисляют \( 1\%\)).
А почему \( i\) делится на \( 100\)? Если не знаешь ответ на этот вопрос, вспоминай тему «Проценты»!
Тогда мы получим вот такое уравнение:
\( 1.5\cdot {{10}^{6}}={{10}^{6}}{{\left( 1+0.01 \right)}^{x}}\)
\( 1.5={{1.01}^{x}}\)
Данное показательное уравнение уже можно решить только при помощи калькулятора (его внешний вид на это намекает, причем для этого требуется знание логарифмов, с которыми мы познакомимся чуть позже), что я и сделаю: \( x\tilde{\ }40.7489\)…
Таким образом, для получения \( 1.5\) млн. нам потребуется сделать вклад на \( 41\) месяц (не очень быстро, не правда ли?)
Пример 1. Метод простой замены
\( {{4}^{x}}+{{2}^{x+1}}-3=0\)
Решение:
Это уравнение решается при помощи «простой замены», как ее пренебрежительно называют математики.
В самом деле, замена здесь – самая очевидная. Стоит лишь увидеть, что
\( {{4}^{x}}={{2}^{2x}}={{({{2}^{x}})}^{2}}\)
Тогда исходное уравнение превратится вот в такое:
\( {{({{2}^{x}})}^{2}}+{{2}^{x+1}}-3=0\)
Если же дополнительно представить \( {{2}^{x+1}}\) как \( 2\cdot {{2}^{x}}\), то совершенно ясно, что надо заменять: конечно же, \( t={{2}^{x}}\). Во что тогда превратится исходное уравнение? А вот во что:
\( {{t}^{2}}+2t-3=0\)
Ты без проблем самостоятельно отыщешь его корни: \( {{t}_{1}}=-3,~{{t}_{2}}=1\).
Что нам делать теперь?
Пришло время возвращаться к исходной переменной \( \displaystyle x\).
А что я забыл указать? Именно: при замене некоторой степени на новую переменную (то есть при замене вида \( t={{a}^{x}}\)), меня будут интересовать только положительные корни!
Ты и сам без труда ответишь, почему.
Таким образом, \( {{t}_{1}}=-3\) нас с тобой не интересует, а вот второй корень нам вполне подходит:
\( {{t}_{2}}=1\), тогда \( {{2}^{x}}=1\), откуда \( x=0\).
Ответ: \( x=0\)
Как видишь, в предыдущем примере, замена так и просилась к нам в руки. К сожалению, так бывает далеко не всегда.
Однако давай не будем переходить сразу к грустному, а потренируемся еще на одном примере с достаточно простой заменой.
Пример 2. Метод простой замены
\( {{3}^{3x+1}}-4\cdot {{9}^{x}}=17\cdot {{3}^{x}}-6\)
Решение:
Ясно, что скорее всего заменять придется \( {{3}^{x}}\) (это наименьшая из степеней, входящая в наше уравнение).
Однако прежде чем вводить замену, наше уравнение нужно к ней «подготовить», а именно:
\( {{3}^{3x+1}}=3\cdot {{\left( {{3}^{x}} \right)}^{3}}\), \( {{9}^{x}}={{({{3}^{x}})}^{2}}\).
Тогда можно заменять \( t={{3}^{x}}\), в результате я получу следующее выражение:
\( 3{{t}^{3}}-4{{t}^{2}}=17t-6\)
\( 3{{t}^{3}}-4{{t}^{2}}-17t+6=0\)
О ужас: кубическое уравнение с совершенно жуткими формулами его решения (ну если говорить в общем виде). Но давай не будем сразу отчаиваться, а подумаем, что нам делать.
Я предложу смошенничать: мы знаем, что для получения «красивого» ответа, нам нужно получить \( t\) в виде некоторой степени тройки (с чего бы это, а?).
А давай попробуем угадать хотя бы один корень нашего уравнения (я начну гадать со степеней тройки).
Первое предположение \( \displaystyle t=1\). Не является корнем. Увы и ах! Хорошо, а теперь возьмем…
Как видишь, отбор корней показательных уравнений требует достаточно глубокого знания свойств логарифмов, так что я советую тебе быть как можно внимательнее, когда решаешь показательные уравнения.
Как ты понимаешь, в математике все взаимосвязано! Как говорила моя учительница по математике, математику, как историю, за ночь не прочитаешь.
Как правило, всю сложность при решении задач повышенной сложности составляет именно отбор корней уравнения.
Еще один пример для тренировки
\( {{9}^{x+1}}-2\cdot {{3}^{x+2}}+5=0,~\) при \( ~x\in (lo{{g}_{3}}\frac{3}{2};\sqrt{5})\)
Решение:
Ясно, что само уравнение решается довольно просто. Сделав замену \( t={{3}^{x}}\) мы сведем наше исходное уравнение к следующему:
\( {{t}^{2}}-18t+5=0\)
\( {{t}_{1}}=\frac{1}{3},~{{t}_{2}}=\frac{5~}{3}\)
Тогда \( {{x}_{1}}=-1,~{{x}_{2}}=\mathbf{lo}{{\mathbf{g}}_{3}}\left( \frac{5}{3} \right)~~~\)
Вначале давай рассмотрим первый корень.
Сравним \( -1\) и \( lo{{g}_{3}}\left( \frac{3}{2} \right)\):
так как \( \frac{3}{2}>1\), то \( lo{{g}_{3}}\left( \frac{3}{2} \right)>0\). (свойство логарифмической функции \( y=lo{{g}_{a}}x\) при \( a>1\)).
Тогда ясно, что\( lo{{g}_{3}}\left( \frac{3}{2} \right)>-1\) и первый корень не принадлежит нашему промежутку.
Теперь второй корень:
Пример уравнения с нестандартной заменой!
\( \displaystyle 4\sqrt[x]{81}-12\sqrt[x]{36}+9\sqrt[x]{16}=0\)
Решение:
Давай сразу начнем с того, что делать можно, а что – в принципе можно, но лучше не делать.
Можно – представить все через степени тройки, двойки и шестерки. К чему это приведет?
Да ни к чему и не приведет: мешанина степеней, причем от некоторых будет довольно сложно избавиться.
А что же тогда нужно?
Давай заметим, что \( 81={{9}^{2}},~16={{4}^{2}},~\) а \( 36=4\cdot 9.\)
И что нам это даст? А то, что мы можем свести решение данного примера к решению достаточно простого показательного уравнения!
Вначале давай перепишем наше уравнение в виде:
\( \displaystyle 4\cdot {{9}^{\frac{2}{x}}}~-12\cdot {{4}^{\frac{1}{x}}}{{9}^{\frac{1}{x}}}+9\cdot {{4}^{\frac{2}{x}}}=0\)
Такие уравнения называются однородными (подробнее читай в теме «Однородные уравнения»).
Теперь разделим обе части получившегося уравнения на \( {{4}^{\frac{2}{x}}}\):
Например, уравнение вида:
\( {{a}^{F(x)}}=b(x)\), причем \( b(x)\ne {{a}^{i}}\), \( i\)\( \in R/Q\)
В общем случае можно решить только логарифмированием обеих частей (например по основанию \( a\)), при котором исходное уравнение превратится в следующее:
\( F(x)=lo{{g}_{a}}b(x)\)
Давай рассмотрим следующий пример:
\( {{x}^{1+lgx}}=10x\)
Ясно, что по ОДЗ логарифмической функции, нас интересуют только \( x>0\). Однако, это следует не только из ОДЗ логарифма, а еще по одной причине. Я думаю, что тебе не будет трудно угадать, по какой же именно.
Давай прологарифмируем обе части нашего уравнения по основанию \( 10\):
\( lg({{x}^{1+lgx}})=lg(10x)\)
\( (1+lg(x))\cdot lg(x)=1+lg(x)\)
\( (1+lg(x))(lg(x)-1)=0\)
\( lg(x)=1,~lg(x)=-1\)
\( {{x}_{1}}=10,~{{x}_{2}}=0,1\)
Как видишь, логарифмирование нашего исходного уравнения достаточно быстро привело нас к правильному (и красивому!) ответу.
Давай потренируемся еще на одном примере:
\( {{x}^{lo{{g}_{4}}x-2}}={{2}^{2(lo{{g}_{4}}x-1)}}\)
Здесь тоже нет ничего страшного: прологарифмируем обе стороны уравнения по основанию \( 4\), тогда получим:
\( lo{{g}_{4}}({{x}^{lo{{g}_{4}}x-2}})=lo{{g}_{4}}({{2}^{2(lo{{g}_{4}}x-1)}});\)
\( \left( lo{{g}_{4}}x-2 \right)\text{lo}{{\text{g}}_{4}}x=2\left( \text{lo}{{\text{g}}_{4}}x-1 \right)\text{lo}{{\text{g}}_{4}}2;\)
\( (lo{{g}_{4}}x-2)lo{{g}_{4}}x=(lo{{g}_{4}}x-1);\)
Сделаем замену: \( t=lo{{g}_{4}}x\)
\( {{t}_{1}}=\frac{3+\sqrt{5}}{2},~{{t}_{2}}=\frac{3-\sqrt{5}}{2}\)
Тогда \( {{x}_{1}}=lo{{g}_{4}}\left( \frac{3+\sqrt{5}}{2} \right),~{{x}_{2}}=lo{{g}_{4}}\left( \frac{3-\sqrt{5}}{2} \right),~\)
Однако мы кое-что упустили! Ты заметил, где я сделал промах?
Ведь \( \frac{3-\sqrt{5}}{2}<1,~\) тогда:
\( {{x}_{2}}=lo{{g}_{4}}\left( \frac{3-\sqrt{5}}{2} \right)<0,~~\) что не удовлетворяет требованию \( x>0\) (подумай откуда оно взялось!)
Ответ: \( lo{{g}_{4}}\left( \frac{3+\sqrt{5}}{2} \right)\)
Попробуй самостоятельно записать решение показательных уравнений, приведенных ниже
- \( {{x}^{2l{{g}^{3}}x-1.5lgx}}=\sqrt{10}\)
- \( {{(x+5)}^{lo{{g}_{7}}(x+5)}}=7\)
А теперь сверь свое решение с этим:
1. Логарифмируем обе части по основанию \( 10\), учитывая, что \( x>0\):
\( \lg \left( {{x}^{2l{{g}^{3}}x-1.5lgx}} \right)=lg\sqrt{10}\)
\( \left( 2l{{g}^{3}}x-1.5lgx \right)lgx=\frac{1}{2},~\), замена \( ~t=l{{g}^{2}}x\ge 0\)
\( 4{{t}^{2}}-3t-1=0\)
\( 4{{t}^{2}}-3t-1=0\) (второй корень нам не подходит ввиду замены)
\( l{{g}^{2}}x=1,~{{x}_{1}}=1,~{{x}_{2}}=0.1~\)
2. Логарифмируем по основанию \( \displaystyle 7\):
\( \displaystyle lo{{g}_{7}}{{\left( x+5 \right)}^{lo{{g}_{7}}\left( x+5 \right)}}=lo{{g}_{7}}7\)
Преобразуем полученное выражение к следующему виду:
\( \displaystyle \left( lo{{g}_{7}}\left( x+5 \right)+1 \right)\left( lo{{g}_{7}}\left( x+5 \right)-1 \right)=0\)
\( \displaystyle {{x}_{1}}=2,~{{x}_{2}}=-\frac{34}{7}\)
Артамонова
А.Е.
Тип урока: урок повторения и обобщения
знаний, закрепления умений.
1) образовательные – сформировать у
учащихся умение различать показательные уравнения по способам решения,
отработать навыки решения всех видов показательных уравнений;
2) развивающие – развивать умения
работать с книгой, самостоятельно добывать знания; развивать и совершенствовать
умения применять имеющиеся у учащихся знания в изменённой ситуации; развивать
логическое мышление, умение сравнивать, анализировать, делать выводы и обобщать;
3) воспитательные – воспитывать
трудолюбие, умение общаться со своими сверстниками в процессе работы в парах,
культуру поведения, чувство ответственности.
Оборудование урока: презентация, магнитная
доска, карточки; чистые листы для самостоятельной работы; основные формулы свойств
степеней;
1.
Математика:
алгебра и начала математического анализа, геометрия. : Алгебра и начала
математического анализа. 10 класс: учеб. для общеобразоват. организаций:
базовый и углубл. уровни /С.М. Никольский, М. К. Потапов, Н. Н. Решетников и
др. — 3-е изд. -М.: Просвещение, 2016.
2.
М.И.
Башмаков Алгебра и начала анализа: Учебник для 10-11 кл сред. шк..
3.
Решение
задач по математике. М. И. Сканави / Авт.- сост. Мардыко Е.Н. – Мн.:
«современное слово» 1999.
4.
Математика.
Задачи М. И. Сканави с решениями. М.34. Сост. С. М. Марач, П. В. Полуносик. –
Мн.: изд. В. М. Скакун,1998.
· Мотивация.
· Подведение итогов. Рефлексия.
|
Учебный элемент |
Учебный |
Руководство |
||||||||||||||
|
УЭ0 2 мин |
ОРГАНИЗАЦИОННЫЙ Задача: подготовить учащихся к работе на уроке. Знания, не Леонардо да Винчи Сегодня на уроке мы Напомнить учащимся, 1 уровень – 2 уровень – 3 уровень – 1 уровень – самый общий, т.е. знаниями этого уровня должны 2 уровень включает 3 уровень – все, |
Внимательно ознакомьтесь УЭ1-УЭ4 соответствуют УЭ5 обеспечивает 2 УЭ7 – 3 уровень подготовки. Вся работа над данным |
||||||||||||||
|
УЭ 1 7мин |
Показательные 1. Решите уравнения
4.Найти ошибки в решениях показательных
|
|||||||||||||||
|
УЭ 2 10 мин |
Цель: закрепить Решите
|
Вспомните основные правила решения показательных Выполните письменно самостоятельную работу. Проверьте правильность решения с учителем. Проставьте |
||||||||||||||
|
УЭ 3 10 мин |
Цель: закрепить Метод разложения на множители состоит в Пример. Решить Воспользуемся основными свойствами Вынесем общий множитель х=1 Ответ: 1.
|
Работая в парах, прочитайте Выполните самостоятельные Проверьте свою работу Если набрано 4 баллов, |
||||||||||||||
|
УЭ4 (8 мин) |
Цель: закрепить Метод сведения к квадратному уравнению Пример. Решить Решение: Если ввести y = Оно имеет корни у=1 и у = 3. Значит,
Уравнение Уравнение
|
Работая в парах, прочитайте Выполните самостоятельные Проверьте свою работу Если набрано 5 баллов, |
||||||||||||||
|
УЭ5 (8 мин) |
Цель: закрепить навык решения Покажем как решать однородное уравнение Пример 1. Решить уравнение Поделим обе части уравнения на Получим уравнение Решение однородных уравнений вида к Пример 2. Решение. Данное
Обозначим Учитывая, что у Ответ: 0. Самостоятельная
|
Работая в парах, Если набрано 5 баллов, |
||||||||||||||
|
УЭ 6 (2 м) |
Физкультминутка. Примите удобную позу сидя на стуле. В положении |
|||||||||||||||
|
УЭ 7 (20 мин) |
Вы освоили решение уравнений 2 уровня Самостоятельная (задания 1. 2. 3. 4. 5. 6. Проверьте и оцените |
Можно воспользоваться 1.Воспользуйтесь основными 2. Воспользуйтесь основными 3. Воспользуйтесь основными 4. Воспользуйтесь основными 5.Преобразуйте левую 6.Воспользуйтесь |
||||||||||||||
|
УЭ 8 |
Дифференцированная На “3”. Решите уравнения: 1) 2) 3) На “4”. Решите уравнение: 1) 2) 3) На “ 5”. Решите уравнение: 1) 2) 3) |
Дети выбирают сами. |
||||||||||||||
|
3 мин |
Подведение Оценка за весь Рефлексия. 1.Прочитайте ещё — Достигли ли Вы 2. Вопрос классу: |
Хочется закончить урок словами
Я.А.Коменского: “ Считай несчастным тот день или тот час, в который ты не
усвоил ничего нового и ничего не прибавил к своему образованию ”.
Приложение 1.
Оценочный лист учащегося.
|
Фамилия |
|||
|
Имя |
|||
|
УЭ |
К-во баллов за |
Корректирующие |
Общее к-во баллов |
|
№ 1 |
|||
|
№ 2 |
|||
|
№ 3 |
|||
|
№ 4 |
|||
|
№ 5 |
|||
|
№7 |
|||
|
Итоговое количество |
|||
|
Оценка |
|
УЭ 2 10 мин |
Цель: закрепить Решите
|
Вспомните основные правила решения показательных Выполните письменно самостоятельную работу. Проверьте правильность решения с учителем. |
||||||||||||||
|
УЭ 3 10 мин |
Цель: закрепить Метод разложения на множители состоит в Пример. Решить Воспользуемся основными свойствами Вынесем общий множитель х=1 Ответ: 1.
|
Работая в парах, Выполните самостоятельные Проверьте свою работу Если набрано 4 баллов, |
||||||||||||||
|
УЭ4 (8 мин) |
Цель: закрепить Метод сведения к квадратному уравнению Пример. Решить Решение: Если ввести y = Оно имеет корни у=1 и у = 3. Значит,
Уравнение Уравнение
|
Работая в парах, Выполните самостоятельные Проверьте свою работу Если набрано 5 баллов, |
||||||||||||||
|
УЭ5 (8 мин) |
Цель: закрепить навык решения Покажем как решать однородное уравнение Пример 1. Решить уравнение Поделим обе части уравнения на Получим уравнение Решение однородных уравнений вида к Пример 2. Решение. Данное
Обозначим Учитывая, что у Ответ: 0. Самостоятельная
|
Работая в парах, Если набрано 5 баллов, |
||||||||||||||
|
УЭ 7 (20 мин) |
Вы освоили решение уравнений 2 уровня Самостоятельная (задания 7. 8. 9. 10. 11. 12. Проверьте и оцените |
Можно воспользоваться 1.Воспользуйтесь основными 2. Воспользуйтесь основными 3. Воспользуйтесь основными 4. Воспользуйтесь основными 5.Преобразуйте 6.Воспользуйтесь формулой |
||||||||||||||
|
УЭ 8 |
Дифференцированная На “3”. Решите уравнения: 1) 2) 3) На “4”. Решите уравнение: 1) 2) 3) На “ 5”. Решите уравнение: 1) 2) 3) |
Дети выбирают сами. |