- Авторы
- Файлы
- Литература
Далингер В.А.
1
1 Омский государственный педагогический университет
1. Васин А.П., Лебедев А.К. Решение показательных и логарифмических уравнений и неравенств (методы решения конкурсных задач). – М.: Изд-во Центра заочного обучения «Пифагор», 1994.
2. Далингер В.А. Типичные ошибки по математике на вступительных экзаменах и как их не допускать. – Омск: Изд-во Омского ИУУ, 1991.
3. Далингер В.А. Все для обеспечения успеха на выпускных и вступительных экзаменах по математике. Выпуск 5. Показательные, логарифмические уравнения, неравенства и их системы: Учебное пособие. – Омск: Изд-во ОмГПУ, 1996.
4. Далингер В.А. Начала математического анализа: Типичные ошибки, их причины и пути предупреждения: Учебное пособие. – Омск: «Издатель-Полиграфист», 2002.
5. Далингер В.А., Зубков А.Н. Пособие для сдачи экзамена по математике: Анализ ошибок абитуриентов по математике и пути их предупреждения. – Омск: Изд-во ОмГПУ, 1991.
6. Кутасов А.Д. Показательные и логарифмические уравнения, неравенства, системы: Учебно-методическое пособие N7. – Изд-во Российского открытого университета, 1992.
Ошибки, допускаемые обучающимися при решении логарифмических уравнений и неравенств, самые разнообразные: от неверного оформления решения до ошибок логического характера. об этих и других ошибках пойдет речь в этой статье.
1. Самая типичная ошибка состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних коней.
Рассмотрим на конкретных примерах ошибки подобного рода, но прежде обращаем внимание читателя на следующую мысль: не бойтесь приобрести посторонние корни, их можно отбросить путем проверки, бойтесь потерять корни.
а) Решить уравнение:
log3(5 – x) = 3 – log3(–1 – x).
Это уравнение учащиеся очень часто решают следующим образом.
log3(5 – x) = 3 – log3(–1 – x), log3(5 – x) + log3(–1 – x) = 3, log3((5 – x)( –1 – x)) = 3, (5 – x)( –1 – x) = 33, x2 – 4x – 32 = 0,
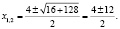
x1 = –4; x2 = 8.
Учащиеся часто, не проводя дополнительных рассуждений, записывают оба числа в ответ. Но как показывает проверка, число x = 8 не является корнем исходного уравнения, так как при x = 8 левая и правая части уравнения теряют смысл. Проверка показывает, что число x = –4 является корнем заданного уравнения.
б) Решить уравнение 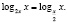
Область определения исходного уравнения задается системой
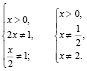
Для решения заданного уравнения перейдем к логарифму по основанию x, получим
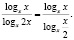
Мы видим, что левая и правая части этого последнего уравнения при x = 1 не определены, но это число является корнем исходного уравнения (убедиться в этом можно путем непосредственной подстановки). Таким образом, формальный переход к новому основанию привел к потере корня. Чтобы избежать потери корня x = 1, следует указать, что новое основание должно быть положительным числом, отличным от единицы, и рассмотреть отдельно случай x = 1.
2. Целая группа ошибок, вернее сказать недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению. Остановимся в связи с этим на примере.
Решить уравнение
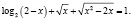
Найдем область определения этого уравнения, для чего решим систему неравенств:
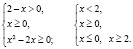
Откуда имеем x = 0. Проверим непосредственной подстановкой, является ли число x = 0 корнем исходного уравнения
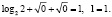
Ответ: x = 0.
3. Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами. Подтвердим сказанное следующим примером.
Решить уравнение
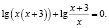
Приведем ошибочное решение этого уравнения:
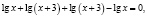
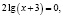
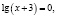
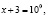
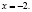
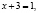
Поверка показывает, что х = –2 не является корнем исходного уравнения.
Напрашивается вывод, что заданное уравнение корней не имеет.
Однако это не так. Выполнив подстановку х = –4 в заданное уравнение, мы можем убедиться, что это корень.
Проанализируем, почему произошла потеря корня.
В исходном уравнении выражения х и х + 3 могут быть одновременно оба отрицательными или оба положительными, но при переходе к уравнению 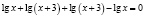
Чтобы избежать потери корня, можно поступить следующим образом: перейдем в исходном уравнении от логарифма суммы к логарифму произведения. Возможно в этом случае появление посторонних корней, но от них, путем подстановки, можно освободиться.
4. Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, то есть привычным путем. Покажем это на примере.
Решить неравенство
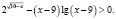
Попытка решать это неравенство привычными алгоритмическими способами не приведет к ответу. Решение здесь должно состоять в оценке значений каждого слагаемого левой части неравенства на области определения неравенства.
Найдем область определения неравенства:
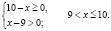
Для всех x из промежутка (9;10] выражение 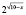
Для всех x из промежутка (9;10] выражение x – 9 имеет положительные значения, а выражение lg(x – 9) имеет значения отрицательные или ноль, тогда выражение (– (x – 9) lg(x – 9) положительно или равно нулю.
Окончательно имеем x∈ (9;10]. Заметим, что при таких значениях переменной каждое слагаемое, стоящее в левой части неравенства, положительно (второе слагаемое может быть равно нулю), а значит их сумма всегда больше нуля. Следовательно, решением исходного неравенства является промежуток (9;10].
5. Одна из ошибок связана с графическим решением уравнений.
Решить уравнение
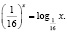
Наш опыт показывает, что учащиеся, решая это уравнение графически (заметим, что его другими элементарными способами решить нельзя), получают лишь один корень (он является абсциссой точки, лежащей на прямой y = x), ибо графики функций
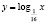
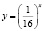
это графики взаимно обратных функций.
На самом деле исходное уравнение имеет три корня: один из них является абсциссой точки, лежащей на биссектрисе первого координатного угла y = x, другой корень 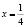
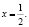
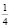
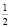
Заметим, что уравнения вида logax = ax при 0 < a < e-e 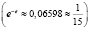
Этот пример удачно иллюстрирует следующий вывод: графическое решение уравнения f(x) = g(x) “безупречно”, если обе функции разномонотонны (одна из них возрастает, а другая – убывает), и недостаточно математически корректно в случае одномонотонных функций (обе либо одновременно убывают, либо одновременно возрастают).
6. Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода. Покажем типичные ошибки такого рода.
а) Решить уравнение xx = x.
Функция, стоящая в левой части уравнения, – показательно-степенная и раз так, то на основание степени следует наложить такие ограничения: x > 0, x ≠ 1. Прологарифмируем обе части заданного уравнения:
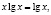
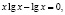
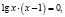
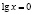
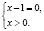
Откуда имеем x = 1.
Логарифмирование не привело к сужению области определения исходного уравнения. Но тем не менее мы потеряли два корня уравнения; непосредственным усмотрением мы находим, что x = 1 и x = –1 являются корнями исходного уравнения.
б) Решить уравнение 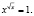
Как и в предыдущем случае, мы имеем показательно-степенную функцию, а значит x > 0, x ≠ 1.
Для решения исходного уравнения прологарифмируем его обе части по любому основанию, например, по основанию 10: 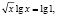
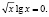
Учитывая, что произведение двух множителей равно нулю тогда, когда хотя бы один из них равен нулю, а другой при этом имеет смысл, мы имеем совокупность двух систем:
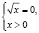
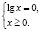
Первая система не имеет решения; из второй системы мы получаем x = 1. Учитывая наложенные ранее ограничения, число x = 1 не должно являться корнем исходного уравнения, хотя непосредственной подстановкой мы убеждаемся в том, что это не так.
7. Рассмотрим некоторые ошибки, связанные с понятием сложной функции вида 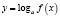
Определить вид монотонности функции 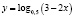
Наша практика показывает, что абсолютное большинство учащихся определяют монотонность в данном случае лишь по основанию логарифма, а так как 0 < 0,5 < 1, то отсюда следует ошибочный вывод – функция 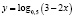
Нет! Эта функция возрастающая.
Условно для функции вида 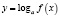
– Возрастающая (Убывающая) = Убывающая;
– Возрастающая (Возрастающая) = Возрастающая;
– Убывающая (Убывающая) = Возрастающая;
– Убывающая (Возрастающая) = Убывающая;
8. Решите уравнение
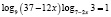
Это задание взято из третьей части ЕГЭ, которое оценивается баллами (максимальный балл – 4).
Приведем решение, которое содержит ошибки, а значит за него не будет выставлен максимальный балл.
Сводим логарифмы к основанию 3. Уравнение примет вид
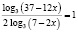
Отсюда
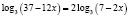
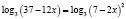
Потенцируя, получаем
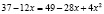
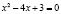
х1 = 1, х2 = 3.
Выполним проверку, чтобы выявить посторонние корни
x = 1:
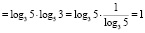
значит х = 1 – корень исходного уравнения.
х = 3:
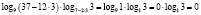
значит х = 3 корнем исходного уравнения не является.
Поясним, почему это решение содержит ошибки. Суть ошибки в том, что запись 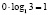
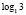
9. Вернемся к уже прокомментированной выше ошибке, но при этом приведем и новые рассуждения.
При решении логарифмических уравнений 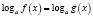
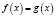
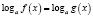
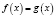
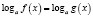
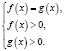
Если при решении логарифмического уравнения выражения
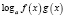
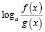
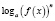
где n – четное число, преобразовываются соответственно по формулам 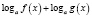
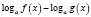
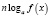
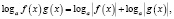
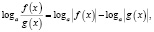
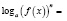
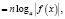
n – четное число.
Обратно, если при решении логарифмического уравнения выражения 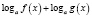
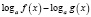
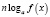
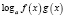
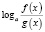
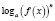
то область определения уравнения может расшириться, в силу чего возможно приобретение посторонних корней. Помня об этом, в подобных ситуациях необходимо следить за равносильностью преобразований и, если область определения уравнения расширяется, делать проверку получаемых корней.
10. При решении логарифмических неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной.
Школьники очень часто ошибочно делают обратный переход раньше, на стадии нахождения корней рациональной функции, получившейся в левой части неравенства. Этого делать не следует.
11. Приведем пример еще одной ошибки, связанной с решением неравенств.
Решите неравенство
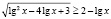
Приведем ошибочное решение, которое очень часто предлагают учащиеся.
Возведем обе части исходного неравенства в квадрат. Будем иметь:
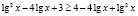
откуда получаем неверное числовое неравенство 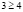
Однако полученный вывод неверен, например, при х = 1000 имеем
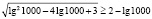
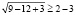
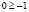
Полученное числовое неравенство верно, а значит х = 1000 является решением.
Значит, заданное неравенство имеет решение, и, следовательно, приведенное выше решение ошибочно.
Приведем правильное решение. Найдем область определения исходного неравенства. Она задается системой
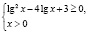
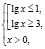
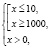
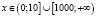
Ясно, что на интервале (10;1000) нет решений, ибо левая часть заданного неравенства при любом х из этого интервала не имеет смысла.
Рассмотрим два случая.
а) 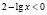
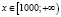
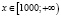
б) 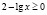
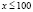
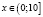
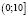
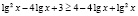
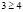
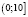
Ответ: 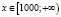
12. Типичная ошибка при решении логарифмических уравнений, неравенств и их систем состоит в том, что неверно преобразовываются логарифмические выражения, входящие в них.
13. Часто допускаются ошибки при решении систем уравнений, в том числе и систем логарифмических уравнений, методом деления одного уравнения системы на другое.
Приведем пример такой ошибки, для чего указанным методом решим систему
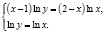
Разделив первое уравнение системы на второе, будем иметь
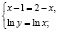
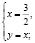
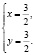
Но легко видеть, что и пара (1;1), которая удовлетворяет области определения системы уравнений 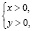
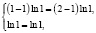
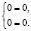
Поясним, почему произошла потеря решения системы.
Если задана система двух уравнений с двумя неизвестными
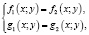
из которой мы получаем
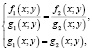
то вторая система уравнений будет следствием первой системы уравнений (значит содержит все решения первой системы) в том и только в том случае, когда нет ни одной пары (х; у), при которой бы функции 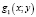
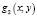
Как мы видим, такая пара (1; 1) в данном случае нашлась, потому-то и произошла потеря решения.
Более глубокий анализ этих и других ошибок читатель найдет в наших работах [2, 3, 4, 5].
Библиографическая ссылка
Далингер В.А. ТИПИЧНЫЕ ОШИБКИ УЧАЩИХСЯ ПРИ РЕШЕНИИ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ, НЕРАВЕНСТВ И ИХ СИСТЕМ И ПУТИ ИХ ПРЕДУПРЕЖДЕНИЯ // Международный журнал экспериментального образования. – 2015. – № 4-2.
– С. 445-450;
URL: https://expeducation.ru/ru/article/view?id=7437 (дата обращения: 22.09.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Тема: Решение логарифмических неравенств. Методы отбора корней. Типичные ошибки обучающихся.
Добрый день. Предлагаю рассмотреть способы решения и ошибки в решениях задания профильного уровня математики ЕГЭ этого года №15. Данное здание входит в число тех, к которым учащиеся приступают чаще всего. Поэтому, применяя различные методы решения данного задания мы можем предупредить те ошибки, которые ученики допускают на экзамене и тем самым позволить учащимся быть более успешными. Текст задания вы видите на экране.
Решить неравенство: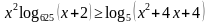
Рассмотрим, как можно было бы решать данное неравенство разными подходами. Заметим, что 625 это 54, следующее, что можно заметить, что выражение 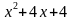
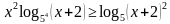
Далее приводим множители в левой и правой части к такому виду, чтобы они стали одинаковыми:
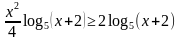
В правой части выносим 2 очень аккуратно, не забываем, что появляется модуль, но за счет того, что выражение (х+2) есть в левой части, используя свойства логарифмической функции модуль опускаем, но не забываем, что х-2. Исходное неравенство мы преобразовали в неравенство вида: 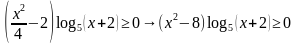
Далее рассмотрим несколько способов решения данного неравенства.
Способ 1. Левая часть неравенства — это произведение двух множителей, значит есть две возможности, когда оба выражения принимают неотрицательные или неположительные значения.
Первая возможность: 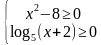
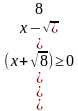
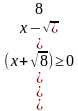










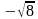
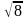
-1
Зафиксируем этот момент: [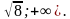
Рассмотрим вторую возможность, когда оба множителя принимают неположительные значения. Аналогично повторим все для 2 случая: 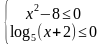
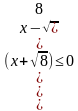
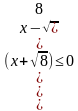








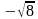
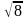
-1
-2
Отметим все на числовой прямой:
Получаем: ( .
Объединяем решения и получаем ответ: ( ]
Способ 2. (Метод рационализации, композиции, метод замены множителей).
Заметим, что в произведении, стоящем в левой части мы можем заменить логарифм на следующее выражение: -2)(5-1)(х+2-1)≥0

умножаем обе части на 4, получаем
-8)(5-1)(х+2-1)≥0, далее разделим обе части на 4:
. Но еще мы должны учитывать, что х-2. Используя метод интервалов, проставляем знаки на числовой прямой








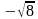
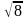
-1
-2
Получаем ответ: ( ]
.
Способ 3. (Классический метод интервалов)
Рассмотрим функцию После введения функции определяем ее область определения Df=(-2 При таком способе явно выписываем область определения.
Далее решаем уравнение f(x)=0
=8 x+2=1
=-
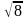
=
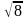
Замечаем, что корень =- .
Отмечаем нули функции только на области определения, это важно. На каждом из промежутков находим знаки функции.







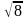
-1
-2
+ — +
Решением неравенства будет объединение промежутков ( ]
.
Способ 4. Он основан на выяснении знака одного из множителей.
У нас есть три варианта:
х+21
х-1









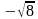
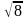
-1
Получаем промежуток .
0
-2






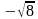
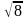
-1

-2
Получаем промежуток ( ).
х+2=1
х=-1
Объединяя все решения, получаем ответ: ( ]
.
Далее рассмотрим типичные ошибки, которые допускают ученики при решении данного неравенства
1.Деление обеих частей неравенства на выражение, которое может принимать отрицательное значение.
В неравенстве 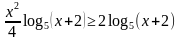
и получают неравенство
, не учитывая, что данное выражение может быть отрицательным.
2. Сокращение логарифмов в обеих частях неравенства при том, что в неравенстве остались другие элементы:
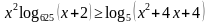
Ошибка от того, что при решении логарифмических неравенств мы учим детей «отбрасывать» логарифмы, забывая о том, что это работает только в том случае, когда в уравнении нет других элементов.
3. Этот случай похож на второй: 
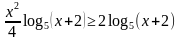
4. Некорректное применение свойств разности логарифмов в случаях, когда при логарифмах стоят коэффициенты:
5. Использование того, что показательная функция возрастает, хотя она может и убывать:
Ученики убирают основания степени забывая, что здесь рассматриваются 2 возможности, идущие от свойств показательной функции.
Спасибо за внимание!
План-конспект урока на тему «О типичных ошибках при решении логарифмических уравнений и неравенств».
Автор: Семёнов Илья Владимирович,
учитель ГАОУ РМЭ «Лицей Бауманский».
Цель урока: показать стандартные ошибки при решении логарифмических уравнений и неравенств с целью их предотвращения.
Задачи урок:
— образовательная: научить учащихся решать сложные логарифмические уравнения и неравенства рациональным способом, при этом правильно применять свойства логарифма;
— развивающая: развитие умения составлять алгоритмические предписания и умение действовать в соответствии с предложенным алгоритмом, развить навык рационального способа решения задач, развивать творческое мышление;
— воспитательная: воспитать культуру оформления сложных логарифмических уравнений и неравенств, культуру графической иллюстрации, самостоятельность, внимательность, умение работать в коллективе, умение вести диспут.
Тип урока: комбинированный урок.
Метод преподавания: словесный, объяснительно-иллюстративный.
Требования к учащимся:
- учащиеся должны знать: определение логарифма, его свойства; формулу перехода к новому основанию; особенности решения логарифмических неравенств по разному основанию; метод рационализации;
- учащиеся должны уметь: решать дробно-рациональные неравенства, использовать метод интервалов.
Оборудование: мел, доска.
Формы работы: фронтальная, индивидуальна, групповая.
Структура урока:
- Организационная часть урока.
Проверка учащихся и класса к уроку: наличие учебников и тетрадей, тишина в классе, чистота доски и влажность губки. Приветствие учащихся.
- Основная часть. Первичное закрепление.
Данный урок проводится после проведения входного контрольной работы. На основе проанализированных результатов (ошибок учащихся), а так же научных статей мы постарались выявить основные ошибки при решении логарифмических уравнений и неравенств.
Опишем основные из них:
А) Игнорирование модуля при вынесении четной степени из подлогарифмического выражения;
Б) Вынесение степени из подлогарифмического выражения, когда логарифм в какой-либо степени (;
В) Переменное основание (учащиеся решают логарифмические уравнения и неравенства по алгоритму, шаблонно, при этом имея скудный багаж решенных задач. По этой причине допускаются ошибки при решении логарифмического неравенства по основанию );
Г) Забывают сделать отбор корней через О.Д.З.;
Д) Хоть и не относится к логарифмическим уравнениям и неравенствам, но является частым следствием их решения решение дробно-рациональных неравенств, т.е. полное игнорирование знаменателя дроби при их решении;
Е) Нет четкой картины при использование метода интервалов;
Ж) Нет знаний элементарных функций, а в следствии и не могут верно накладывать ограничения при решении логарифмических уравнений и неравенств;
З) Неверное разложение логарифмических выражений:
—
—
И) Решая логарифмические неравенства методом замены не могут верно вернуться к введенной замене;
Й) Не видят разницы между системой и совокупностью, а в следствии не могут верно использовать равносильный переход и переход к введенной замене.
Постараемся учесть все замечания, изложенные выше и акцентировать на них внимание при решении данных проблем.
Учащимся предлагается решить логарифмические неравенства:
Начнем с первого неравенства:
О.Д.З.:
Разложив первое неравенство системы на линейные множители получаем: . Данные неравенство равносильны друг другу. Решением данной системы является промежуток
Переходим к решению логарифмического неравенства6
Разложив подлогарифмическое выражение на линейные множители получаем: .
С данного шага надо дать возможность учащимся самим выбрать путь решения:
1 способ.
С данного шага стоит уточнить порядок действий
А) можно использовать определение логарифма и перейти к выражению . В итоге мы получили сложное выражение, с которым сложно справиться.
Б) можно вынести четную степени из подлогарифмического выражения и получится выражение: . Главное в данном шаге это то, что при вынесении четной степени из подлогарифмичесокго выражения влечет то, что появляется модуль. На этом надо сделать акцент при объяснении материала.
Продолжаем решение: .
Используя определение логарифма получаем: .
По определению модуля получаем двойное неравенство:
Осталось найти пересечение множеств решения логарифмического неравенства с О.Д.З.: Решением данной системы является промежуток:
Ответ:
2 способ. Через разложение логарифма.
Приведем лишь рекомендации к решению. Используя формулы:
—
—
получаем следующее выражение:
.
Далее, решение логарифмического неравенства аналогично первому способу.
3 способ. Метод рационализации.
Объяснение по усмотрению учителя и в зависимости от профиля обучения. Так же в зависимости от доступного времени.
Переходим к решению второго неравенства.
Учащимся предлагается решать данное неравенство самостоятельно, а учитель указывает только ответ. Ответ: . На решение выделяется около 5-7 минут.
Вероятнее всего учащиеся не придут к верному ответу. Учащиеся зададутся, верен ли ответ, данный учителем. И вывод заключается в следующем – учащиеся, что то не учли. Может быть, кто-то дойдет до проблемы, если нет, то учитель объяснит сам.
Решение.
О.Д.З.: Решение системы:
Решим неравенство:
Проблема заключается в следующем – не учитывается то, что логарифм находится в квадрате (и не забываем что выносим четную степень), т.е.
Так как неравенство определено на множестве положительных чисел (по О.Д.З.), то модуль можно раскрывать с положительным значением.
Данное логарифмическое неравенство не сложно решить методом замены. Введем замену: .
Стоит спросить учащихся, а стоит ли накладывать ограничения на
Часто учащиеся не могут верно ответить на данный вопрос, потому что не имеют четкого представления о элементарных функция.
Как стоит поступить в данном случае? Стоит спросить учащихся, чем является ? А
это то, в какую степень возводят основание логарифма и получают подлогарифмическое выражение, а степень определена на множестве действительных чисел.
Продолжаем решать:
Разложив данное квадратное выражение на линейные множители получаем:
Главная проблема заключается в следующем: учащиеся находят корни квадратного выражения и бездумно возвращаются к подстановке не дорешав неравенство с введенной заменой. Стоит акцентировать внимание, что надо дорешать наше неравенство относительно .
Следующая проблема — учащиеся не могут перейти к введенной замене.
Стоит сделать следующее – спросить учащихся как представить промежуток через двойное неравенство. Ответ:
Далее задать вопрос – как данное двойное неравенство представить через систему или совокупность: И только с данного шага можно вернуться к подстановке:
Стоит спросить учащихся, какие условия есть для решения логарифмического неравенства по определению. Речь идет о том, что если , то знак неравенства сохраняется без изменений, если же
то необходимо поменять знак на противоположный.
Продолжаем решение:
Решением данной системы является промежуток: .
Осталось объединить решение логарифмического неравенства с О.Д.З.:. Решением данной системы является промежуток:
.
Ответ: .
Так же данное неравенство можно решить методом рационализации.
- Информация о домашнем задании.
На усмотрение учителя.
- Подведение итогов урока.
На данном уроке мы постарались уделить внимание основным ошибкам при решении логарифмических уравнений и неравенств.
Учитель спрашивает, полезна ли была данная информация для учащихся, весь ли материл был доступен и понятен. Есть ли у учащихся вопросы?
Учитель прощается. Урок окончен.
Решение сложных логарифмических неравенств: частые ошибки и способы их избежать
Логарифмические неравенства – это неравенства, которые включают логарифмические выражения. Решение таких неравенств может быть сложным и приводит к множеству ошибок, которые нужно избежать.
Типы логарифмических неравенств
Существует несколько типов логарифмических неравенств:
- Неравенство с единицей в логарифме: log(x) < 1.
- Неравенство с переменной в логарифме: log(x) < log(y).
- Неравенство с константой в логарифме: log(x) < c.
Частые ошибки при решении логарифмических неравенств
Рассмотрим типичные ошибки, с которыми сталкиваются при решении логарифмических неравенств:
- Ошибочное применение правил логарифмов: иногда люди стараются упростить логарифмические выражения, не понимая, что они делают. Например, они могут умножить логарифм, не понимая, что это приведет к изменению знака неравенства.
- Изменение знака неравенства: при изменении знака неравенства нужно помнить, что некоторые правила меняют направление неравенства. Например, при делении обеих сторон неравенства на отрицательное число.
- Избыточное упрощение: при упрощении логарифмических выражений люди часто отбрасывают некоторые члены, что может привести к образованию неверных уравнений.
Способы избежать ошибок
Чтобы избежать ошибок при решении логарифмических неравенств, нужно применять следующие методы:
- Правильно применять правила логарифмов, особенно когда дело касается умножения и деления логарифмов.
- Проверять знак неравенства на каждом этапе решения.
- Не избыточно упрощать логарифмические выражения, сохраняя все члены.
Вывод
Решение логарифмических неравенств – это сложный процесс, который может привести к множеству ошибок. Однако, чтобы избежать ошибок, нужно понимать типы логарифмических неравенств и использовать правильно правила логарифмов. В противном случае, решение может быть неверным.
СТРУКТУРА
РЕШЕНИЙ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ В ХОДЕ ЗАДАНИЙ
ЕГЭ
Аннотация
С
целью повышения уровня математической подготовки будущих студентов
математических и технических специальностей необходимо особое внимание уделять
тем вопросам математики, без прочного знания которых невозможно успешное
обучение в высшем учебном заведении. Формирование и развитие навыков применения
традиционного метода, основанного на монотонности логарифмической функции, и
метода рационализации к решению логарифмических неравенств является важной
составляющей процесса подготовки старшеклассников к сдаче Единого
государственного экзамена по математике профильного уровня. Содержание статьи
представляет интерес для учителей, старшеклассников, готовящихся к поступлению
в вузы на специальности технического или математического направления.
Логарифмические уравнения – уравнения, содержащие неизвестное под знаком логарифма. Обычно решение логарифмических
уравнений начинается с определения ОДЗ. В логарифмических
уравнениях рекомендуется все логарифмы преобразовать так, чтобы их основания
были равны. Затем уравнения либо выражают через один какой – либо логарифм,
который обозначается новой переменной, либо уравнение преобразовывают к виду,
удобному для потенцирования.
Чем раньше школьник
начинает подготовку, тем успешнее он сдает экзамены. Одно из экзаменационных
заданий заключается в решении логарифмических неравенств, и, соответственно,
даёт возможность получить дополнительный балл. Данная информация,
представленная ниже, может быть использована для урока обобщения и для
подготовки к ЕГЭ.
Краткие теоретические сведения и решения задач позволяют учащимся
самостоятельно развивать умения и навыки решения логарифмических уравнений.
Стоит отметить,
что при решении сложных неравенств часто применяют метод рационализации, т.е.
приведение неравенства к более простому виду, а именно, к рациональному
неравенству. Это позволяет использовать для его решения
метод интервалов. Этот метод применяют к решению логарифмических, показательных и иррациональных
неравенств.
Рассмотрим
понятие логарифма.
Пример.
log₃81=4. Почему именно 4? В такую степень нужно возвести число 3,
чтобы получилось 81. Когда вам понятен данный принцип, можно приступать и к
более сложным вычислениям.
Пример самого
простого логарифмического неравенства: log ₐf(x)> log ₐg(x)
Простейшие
логарифмические неравенства не ограничиваются данным примером, есть еще три,
только с другими знаками. Это нужно для полного понимания, как решать
неравенство с логарифмами. Теперь приведем более применимый пример, все
еще достаточно простой. log2 (2x+4)> log2 3
Решить данное
неравенство можно с помощью области допустимых значений (ОДЗ). В заданиях для
ЕГЭ нередко всплывает данная формулировка. Область допустимых значений может
пригодиться не только в случае логарифмических неравенств. ОДЗ будем
рассматривать, исходя из вышеприведённого примера, чтобы понять принцип
структуры самого решения. Из определения логарифма следует что, 2х+4
должно быть больше нуля. В нашем случае это означает следующее: 2х+4>0. Это
число по определению должно быть положительным. Решение неравенства,
представленного выше, и будет определением области допустимых значений, здесь
явно, что X не может быть меньше 2.
Теперь перейдем к решению простейшего логарифмического неравенства: log2 (2x+4)> log2 3. Отбрасываем из обеих
частей неравенства сами логарифмы. В результате у нас остается простое
неравенство: 2x + 4>3. Решить
его несложно. X должен быть больше -0,5. Теперь совмещаем два полученных
значения в систему. Таким образом, x>-2, х>-0,5. Это и будет область допустимых
значений для рассматриваемого логарифмического неравенства.
Зачем вообще
нужно ОДЗ? Это возможность отсеять неверные и невозможные ответы. Если ответ не
входит в область допустимых значений, значит, ответ попросту не имеет смысла.
Это стоит запомнить надолго, так как в ЕГЭ часто встречается необходимость
поиска ОДЗ, и касается она не только логарифмических неравенств.
Решение состоит из
нескольких этапов. Во-первых, необходимо найти область допустимых значений. В
ОДЗ будет два значения, это мы рассмотрели выше. Далее нужно решить само
неравенство. Методы решения бывают следующими:
·
метод замены множителей;
·
декомпозиции;
·
метод рационализации.
В зависимости от ситуации стоит применять один из
вышеперечисленных методов. Перейдем непосредственно к решению. Раскроем
наиболее популярный метод, который подходит для решения заданий ЕГЭ практически
во всех случаях. Далее мы рассмотрим метод декомпозиции. Он может помочь, если
попалось особенно «заковыристое» неравенство. Итак, алгоритм решения
логарифмического неравенства.
Примеры
решения: log0,2 (x²+6x + 
основание, если оно больше единицы, знак остается прежним при нахождении
области допустимых значений; в противном случае нужно изменить знак
неравенства.
В результате
получается неравенство: x²+6x+8˂5х+10. Теперь приводим левую часть к виду уравнения, равному
нулю. Вместо знака «меньше» ставим «равно», решаем уравнение. Таким образом, мы
найдем ОДЗ. Ответы -4 и -2. Нужно отобразить эти точки на графике, расставить
«+» и «-». Что нужно для этого сделать? Подставить в выражение числа из
интервалов. Где значения положительны, там ставим «+».
Ответ: х не может быть
больше -4 и меньше -2.
Мы нашли область
допустимых значений только для левой части, теперь нужно найти область
допустимых значений правой части. Это не в пример легче. Ответ: -2. Пересекаем
обе полученные области.
И только теперь начинаем
решать само неравенство x²+6x + 8˂5х+10. Упростим его, насколько возможно, чтобы решать было
легче: x²+ x -2˂0.
Снова применяем
метод интервалов в решении. Опустим выкладки, с ним уже и так все понятно по
предыдущему примеру. Ответ: х €(-2,1).
Но этот метод
подходит, если логарифмическое неравенство имеет одинаковые основания.
Решение
логарифмических уравнений и неравенств с разными основаниями предполагает
изначальное приведение к одному основанию. Далее стоит применять вышеописанный
метод. Но есть и более сложный случай. Рассмотрим один из самых сложных видов
логарифмических неравенств.
Ими являются логарифмические
неравенства с переменным основанием и они могут
встретиться в ЕГЭ. Чтобы решать логарифмические неравенства, достаточно однажды
ознакомиться с примером.
log х2+3х (x+ 3) ˂ 1
Чтобы
решить логарифмическое неравенство представленного вида, необходимо привести
правую часть к логарифму с тем же основанием. Принцип напоминает равносильные
переходы. В итоге неравенство будет выглядеть следующим образом.
log х2+3х (x+ 3) ˂ log х2+3х (x²+ 3х)
Собственно,
остается создать систему неравенств без логарифмов. Используя метод
рационализации, переходим к равносильной системе неравенств. Понимание самого
правила придёт, когда получится подставить соответствующие значения и
проследить их изменения. В системе будут следующие неравенства.
(x²+3х-1)((х+3)-( x²+3х)) ˂0
х+3>0
x²+ 3х>0
x²+ 3х≠0
Воспользовавшись
методом рационализации при решении неравенств нужно помнить следующее: из
основания необходимо вычесть единицу, х по определению логарифма из обеих
частей неравенства вычитается (правое из левого), два выражения перемножаются и
выставляются под исходным знаком по отношению к нулю.
Дальнейшее
решение осуществляется методом интервалов и важно понять отличия в методах
решения, тогда все начнет легко получаться.
Рассмотрим
подробнее решение логарифмических неравенств при помощи метода рационализации.
При изучении в школьном
курсе математики всего многообразия логарифмических неравенств особое место
отводится неравенствам с переменным основанием. Хочется также отметить, что
последнее время эта
тема стала достаточно актуальной при включении в состав заданий
части «С» контрольных измерительных материалов для проведения Единого Государственного
Экзамена по математике.
Так, неравенство вида log ₐ ‹ₓ› f‹ ₓ› > log ₐ ‹ₓ ›g (x) является стандартным школьным
неравенством. Как правило, его решение предполагает сведение
к равносильной совокупности двух систем неравенств, а именно:
В качестве замечания стоит
заметить, что для решения полученной совокупности, отдельно находить область
определения неравенства не следует. Но нельзя также не отметить и недостаток
этого метода. Как правило, такие неравенства являются заданиями типа C в ЕГЭ. А это значит, что в качестве аргумента
логарифма может быть выбран, скажем, квадратный трёхчлен, что значительно
усложнит работу и без того состоящей в решении семи неравенств, не включая двух
систем и совокупности. Такая ситуация, в условиях ограниченности времени
проведения экзамена, а также преобладающего цейтнота, может показаться учащимся
вовсе не перспективной. На наш взгляд, в этом и есть причина низкого процента
решения выпускниками задач подобного типа. Мы предлагаем при решении неравенств
с переменным основанием пользоваться методом рационализации (декомпозиции). Он
заключается в сведении неравенства к наиболее простому, равносильному данному.
К сожалению, этот метод не попал в поле зрения авторов школьных учебников по
алгебре, поэтому даже для самых подготовленных учеников он становится зачастую
полным откровением. Так, проведением несложных рассуждений можно доказать, что
для неравенства
logₐ‹ₓ›f ‹ₓ›- logₐ‹ₓ›g(х)˅0
неравенство (а(х)-1)(f(х)- g(х)) ˅0 является равносильным при одновременном выполнении
условий f(х)>0,
g(х)>0, а(х) >0, а(х)≠1.
Вместо знака «∨» можно поставить любой знак
неравенства, например ,«≤», «≥». Главное, чтобы в обоих неравенствах знаки были
одинаковыми. Следуя заявленной теореме, мы избавляемся от логарифмов и сводим задачу
к рациональному неравенству, что экономит учащемуся не только время на
экзамене, но и позволяет потенциально сделать меньше арифметических ошибок и
ошибок “по невнимательности”.
Задача №1 (Диагностическая работа)
Решите неравенство: (х+1)
Решение: (х+1)
(х+1)
х
Ответ: х
Задача №2 (Диагностическая работа)
Решите неравенство:
Решение:
Х
Ответ. Х
В ЕГЭ входит 9 заданий с
логарифмами: 3 задания базового уровня и 6 заданий профильного уровня.
В логарифмических
неравенствах много нюансов. Простейшие из них решать достаточно легко.
Обязательно стоит постоянно практиковаться в решении самых разных задач в
рамках экзамена и тогда вероятно получить наивысший балл в ходе ЕГЭ.
КИМ ЕГЭ по математике
профильного уровня в 2017 г. по сравнению с 2016 г. не претерпели изменений в
содержательном плане. Были изменены подходы к разработке заданий 15 (неравенство)
с целью исключения искусственных выражений с логарифмами по переменному
основанию.
По данным анализа типичных
ошибок участников ЕГЭ 2017 (http://www.fipi.ru/sites/default/files/document/1509023556/matematika_2017_.pdf) в задании 5 базового уровня
проверялось умение решать простейшее логарифмическое, показательное уравнение,
его выполнили 93% участников, почти 2% участников ошиблись в свойствах степеней.
Задание 15 проверяло умение решать неравенства. Ненулевые баллы за это задание
получили около 15% участников экзамена; максимальный балл – около 11%. Типичные
ошибки связаны с невнимательным чтением математической записи неравенства,
непониманием алгоритма решения совокупностей и систем логарифмических
неравенств. Очень много ошибок допущено участниками экзамена при решении
дробно-рационального неравенства (забыт знаменатель). Следует отметить
небрежность, которая была во многих работах, при изображении множеств на
координатной прямой.
Список
литературы
1.
КоряновА.Г., ПрокофьевА.А., Математика ЕГЭ – 2017. Типовые задания С3. Методы
решения неравенств с одной переменной.
2.
Материалы для подготовки к ЕГЭ. — URL: http://alexlarin.net.
3.
Математика. Подготовка к ЕГЭ – 2018. Решаем задание С3 методом рационализации:
учебно-методическое пособие/ Под ред. Ф.Ф. Лысенко , С.Ю., Кулабухова –
Ростов-на-Дону: Легион, 2018.
4.
Ященко
И. В., Семенов А. В., Высоцкий И. Р. Методические рекомендации по некоторым
аспектам совершенствования преподавания математики. — URL: http://www.fipi.ru.