При упрощении выражений, вычислении их значений, при решении уравнений и неравенств необходимо производить тождественные преобразования заданных выражений. Рассмотрим наиболее часто встречающиеся ошибки при тождественных преобразованиях.
Нарушение порядка действий
K Упражнение. Упростить выражение
\[1-\frac{\sqrt{x}}{x-1}:\frac{\sqrt{x}-1}{x}\]
L Неправильное решение.
Сначала
\[1-\frac{\sqrt{x}}{x-1}=\frac{x-1-\sqrt{x}}{x-1}\]
затем
\[\frac{x-1-\sqrt{x}}{x-1}:\frac{\sqrt{x}-1}{x}\]
и так далее.
J Правильное решение.
Сначала следует выполнить
\[\frac{\sqrt{x}}{x-1}:\frac{\sqrt{x}-1}{x}\]
затем произвести вычитание.
Для удобства принятия решения о последовательности выполнения действий их разделили на две ступени:
первая ступень – сложение и вычитание,
вторая ступень – умножение и деление.
При нахождении значения выражения или его упрощении действия выполняются в следующем порядке:
-
В выражении отсутствуют скобки, и оно включает в себя действия только одной ступени, тогда все операции выполняются по порядку слева на право.
-
Если в выражении отсутствуют скобки, и присутствуют действия двух ступеней. Тогда в первую очередь выполняются действия второй ступени, а во вторую действия первой ступени. Правило слева направо при выполнении действий одинаковой ступени выполняется.
-
Если выражение содержит скобки, то действия в скобках выполняются в первую очередь. Остальные действия выполняются в соответствии с правилами 1. и 2.
Нарушение правил действий над степенями и многочленами
Нередко учащиеся неверно применяют формулы сокращенного умножения, нарушают правила действий над степенями с рациональным показателем.
|
L Неправильное решение |
J Правильное решение |
|
\[\left(a^{\frac{1}{2}}+b^{\frac{1}{2}} \right)^{-3}=\frac{1}{a^{\frac{3}{2}}+b^{\frac{3}{2}}}\] |
\[\left(a^{\frac{1}{2}}+b^{\frac{1}{2}} \right)^{-3}=\frac{1}{\left(a^{\frac{1}{2}}+b^{\frac{1}{2}} \right)^{3}}\] |
| \[\frac{a^3-b^3}{a-b}=a^2-b^2\] | \[\frac{a^3-b^3}{a-b}=a^2+ab+b^2\] |
| \[\left(a-b \right)^{\frac{1}{2}}=a^{\frac{1}{2}}-b^{\frac{1}{2}}\] | \[\left(a-b \right)^{\frac{1}{2}}=\sqrt{a-b}\] |
| \[a^{-1}+b^{-1}=\frac{1}{a+b}\] | \[a^{-1}+b^{-1}=\frac{1}{a}+\frac{1}{b}\] |
| \[16^x-4^x=(16-4)^x\] | \[16^x-4^x=4^x(4^x-1)\] |
| \[9^{2-x}=9^2-9^x\] | \[9^{2-x}=9^2:9^x\] |
Разложение многочленов на множители выполняется нерационально или не доводится до конца.
K Упражнение. Разложить многочлен x3 – x2 – x + 1 на множители.
L Неправильное решение.
x3 – x2 – x + 1 = x2 · (x – 1) – (x + 1) = дальше продолжить не удалось.
J Правильное решение.
x3 – x2 – x + 1 = x2 · (x – 1) – (x – 1) = (x2 – 1) · (x – 1) =
= (x + 1) · (x – 1) · (x – 1) = (x + 1) · (x – 1)2.
Сокращение дробей
Очень распространенной ошибкой является попытка сократить стоящие в числителе и знаменателе одинаковые выражения, одно из которых (или в числителе, или в знаменателе), а порой и оба, являются не сомножителями, а слагаемыми.
|
L Неправильное решение |
J Правильное решение |
|
\[\frac{2m+2(m+n)^3}{(m+n)^2(2m+n)}=\frac{2m+2(m+n)}{2m+n}\] |
Сократить нельзя |
|
\[\frac{\sin \alpha +\cos \alpha }{\sin \alpha}=1+\cos \alpha\] |
Сократить нельзя |
|
\[\frac{a^4-b^4}{a-b}=a^3-b^3\] |
\[\frac{a^4-b^4}{a-b}=\frac{(a^2+b^2)(a-b)(a+b)}{(a-b)}=\] \[=(a^2+b^2)(a+b)\] |
|
\[\frac{\sin \alpha +\sin 2\alpha -\sin 3\alpha }{\cos \alpha +\cos 2\alpha -\cos 3\alpha }=\] \[=\tan \alpha +\tan 2\alpha-\tan 3\alpha\] |
Сократить нельзя |
|
\[\frac{\sqrt{a^3b}\left(a\sqrt{a}+b\sqrt{b} \right)}{\sqrt{a}+\sqrt{b}}\] Сокращение не произведено |
\[\frac{\sqrt{a^3b}\left(a\sqrt{a}+b\sqrt{b} \right)}{\sqrt{a}+\sqrt{b}}=\] \[=\frac{\sqrt{a^3b}\left(\sqrt{a}+\sqrt{b} \right)\left(a-\sqrt{ab}+b \right)}{\sqrt{a}+\sqrt{b}}=\] \[=\sqrt{a^3b}\left(a-\sqrt{ab}+b \right)\] |
Неправильное выполнение действий с арифметическими корнями
|
L Неправильное решение |
J Правильное решение |
|
\[\sqrt{\left(4-\sqrt{32} \right)^2}=4-\sqrt{32}\] |
\[\sqrt{\left(4-\sqrt{32} \right)^2}=\sqrt{32}-4\] |
|
\[\sqrt{\frac{a+1}{(1-a)^2}}=\frac{\sqrt{a+1}}{1-a}\] при а > 1 |
\[\sqrt{\frac{a+1}{(1-a)^2}}=\frac{\sqrt{a+1}}{a-1}\] при а > 1 |
|
\[\sqrt{a^2+b^2}=a+b\] |
Упростить невозможно |
|
\[b\sqrt{2}=\sqrt{2b^2}\] при b < 0 |
\[b\sqrt{2}=-1\sqrt{2b^2}\] при b < 0 |
Необходимо помнить, что для любого действительного числа а и натурального k верно:
\[\sqrt[2k+1]{a^{2k+1}}=a,\]
\[\sqrt[2k]{a^{2k}}=\left| a\right|.\]
Ошибки тригонометрического характера
При нахождении одной из тригонометрических функций через заданное значение другой не учитываются знаки тригонометрических функций в зависимости от положения угла.
K Упражнение. Найти ctg α, если sin α = 0,8.
L Неправильное решение.
1 + ctg2 α = sin–2 α,
1 + ctg2 α = 25/16,
ctg2 α = 9/16,
ctg α = 3/4.
Комментарий. Здесь ошибка заключается в том, что при извлечении корня мы можем получить как положительное значение, так и отрицательное, то есть ctg α = ± 3/4, поэтому необходимо искать решение отдельно в каждой четверти.
J Правильное решение.
Так как sin α > 0, то α может находиться только в I или во II четверти, значит:
1) если α – угол первой четверти, то ctg α = 3/4;
2) если α – угол второй четверти, то ctg α = – 3/4.
Смотрите также:
Ошибки в уравнениях
Ошибки в системах уравнений
Ошибки в неравенствах
Ошибки в упражнениях с параметрами
Ошибки в упражнениях о функциях
Ошибки в упражнениях из начал анализа
Ошибки в геометрических задачах
Типичные ошибки учащихся при работе с тождественными преобразованиями и рекомендации по их устранению
Раздел «Тождественные преобразования» занимает основное место в школьном курсе математики. Изучение тождественных преобразований
- имеет самостоятельное значение, т.к. связан со следующими вопросами:
- обобщение операций над числами, проведение вычислений «в общем виде», обучение применению алгебраической символики;
- классификация и определение алгебраических выражений, преобразование выражений к стандартному виду;
- рационализация выражений.
- тождественные преобразования играют роль вспомогательного «инструмента» при решении уравнений и неравенств, при исследовании функций и ряде других тем школьного курса математики.
- тождественные преобразования имеют значимое воспитательное значение, т.к. они способствуют развитию у учащихся операционного мышления, воспитанию таких качеств личности, как целеустремленность в поиске решения, сообразительность, аккуратность, честность, справедливость.
Самая типичная ошибка учащихся состоит в том, что они при решении уравнений и неравенств без дополнительных пояснений используют преобразования, которые нарушают равносильность, приводящую к потере или появлению корней. Значимая группа ошибок заключается в том, что учащиеся не уделяют должного внимания нахождению области определения выражений, хотя конкретно она в ряде случаев есть ключ к решению.
Разнообразие тождественных преобразований усложняет понимание цели, которая является конечной при работе с выражениями. Неточное понимание целевого преобразования отрицательно отражается на осознании предназначения и служит источником множественных ошибок. Этот факт указывает на то, что педагогу необходимо включать разъяснение конкретных целей при выполнении всех тождественных преобразований, что является составной частью методики обучения.
Для управления этим процессом преподаватель обязан уметь давать чёткие характеристики сущности допущенных учащимися ошибок. Наличие точности помогает учащимся найти подходящие действия для дальнейшей работы по осуществлению тождественных преобразований выражений [6].
Типичные ошибки учащихся при работе с тождественными преобразованиями:
- Смешивают правила умножения степеней с правилом возведения в степень (
).
- Распространяют по неверной аналогии правила умножения степеней с одним основанием на случай умножения степеней с разными основаниями (
).
- Складывают показатели степеней при сложении степеней – смешивают с правилом умножения степеней (
).
- Неправильно применяют формулы (по неверной аналогии:
или lg (
)= lg
+lg
, или
).
- Сокращают в алгебраической дроби по неверной аналогии не множители, а слагаемые (
=
).
- Изменяют знак не у всех членов вычитаемого, когда вычитается многочлен и, тем более дробь.
- Не учитывают знак подкоренного выражения при использовании свойства арифметического корня и получают под корнем отрицательное число.
Одним из типов ошибок является неправильное применение формул, составим ряд упражнений для того, чтобы в дальнейшем была возможность исключить эти ошибки.
- Представь в виде произведения:
- Проверь верность равенства:
- Упростите выражение:
- Упростите выражение:
, при x=-3
, при c=5,5
, при p=4
- Доказать, что если r – нечётное число, то
делится на 4.
Основные приёмы по устранению ошибок в дальнейшем в это типе является планомерное оттачивание формул, с разбором на конкретных примерах, также можно включить создание примеров по аналогии с уже решаемыми.
Рекомендации по устранению типичных ошибок.
- При изначальном знакомстве с тождественными преобразованиями необходимо, чтобы учащиеся проговаривали каждый шаг, выполняя преобразования и учились формулировать правила и законы необходимости применения того или иного преобразования.
- Учащихся необходимо проинформировать, что при применении тождественных преобразований алгебраических выражений используют два правила: постановки и замены равным данному выражению.
- Учащихся необходимо научить определять области применимости изучаемых тождеств.
- При изучении тождественных преобразований учитель должен давать чёткие формулировки, демонстрировать аналитические записи.
- Учитель должен научить учащихся использовать подходящий алгоритм для тождественных преобразований
- Учителю необходимо научить детей проводить преобразования в прямом и обратном порядке.
- Учащиеся должны знать о приложениях.
- Учащиеся должны научиться использовать тождественные преобразования в комплексе с другими.
Заключение
В процессе обучения курсу математики учащиеся многократно встречаются с выражениями и учатся работать с различными их видами.
Впервые учащиеся встречаются с понятием тождественных преобразований на уроках алгебры в 7 классе. В первую очередь вводится понятие тождественно равных выражений.
Тождественное преобразование выражения – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному. Часто это определение используется в сокращенном виде, в котором опускается слово «тождественное». Предполагается, что мы в любом случае проведём преобразование выражения таким образом, чтобы получить выражение, тождественное исходному.
В процессе рассмотрения данной темы мы изучили возможность применения тождественных преобразований в зависимости от вида выражений, подробно рассмотрели виды выражений, алгебраических и неалгебраических (трансцедентных).
Алгебраические выражения включают в себя только те выражения, которые содержат такие действия над переменными, как сложение, вычитание, умножение, деление, извлечение корня, возведение в степень с рациональным показателем.
Неалгераические выражения, в которых содержатся переменные под знаками lg, sin, cos, tg, со знаком модуля, с операциями возведения в степень с иррациональными показателями.
Провели исследование по тождественным преобразованиям разных классов выражений.
Тождественные преобразования представляют собой работу, которую мы проводим с числовыми и буквенными выражениями, а также с выражениями, которые содержат переменные. Все эти преобразования мы проводим для того, чтобы привести исходное выражение к такому виду, который будет удобен для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой главе.
По итогам исследования составили список типичных ошибок учащихся при работе с тождественными преобразованиями и подготовили список рекомендаций, чтобы исправить их в процессе обучения, таким образом, достигли цели исследования и решили все поставленные задачи.
список использованных источников
- Актуальные вопросы теории и методики обучения математике в средней школе: сборник научный статей. Вып. 1. – Киров: Изд-во ВятГГУ, 2011. – 111 с.
- Барыбин К.С. Методика преподавания алгебры: Пособие для учителя.− М.: Просвещение, 2006.− 345 с.
- Блох А.Я. О тождественных преобразованиях в курсе алгебры VI-VIII кл. [Текст] / Метод.рекомендации и указания по методике преподавания математики в средней школе: Сб. статей / А.Я. Блох. — М.: МГПИ им. В.И. Ленина, 2005.− 83 с.
- Виленкин ۛ Н.Я. Равенства, тождества, уравнения, неравенства Н.Я. Виленкин, С.И. Шварцбурд// Математика в школе. — 2000. — № 4.
- Виленкин Н.Я. и др. Современные основы школьного курса математки.— М.: Просвещение, 2001.− 240 с.
- Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. — М.: Просвещение, 1990. — 224 с.
- Давыдов В.В. Теория развивающего обучения [Текст]/ В.В.Давыдов. – М., 1996. – 544 с.
- Канин Е.С. К формированию умений и навыков в вычислениях и тождественных преобразованиях / Е.С. Канин// Математика в школе. − 2002. − №5.
- Колмогоров А.Н. и др. Алгебра и начала анализа: Учебное пособие для 9 и 10 классов средней школы / Под ред. А. Н. Колмогорова.− М.: Просвещение. 2015.− 384 с.
- Колмогоровۛ А.Н., Абрамов А.М., Дудницын Ю.П., Ивлиев Б.М., Шварцбурд С.И. Алгебра и начала анализаۛ Учеб.для 10– 11 кл. сред. шк.−М.: Просвещение, 2010. − 320 с.
- Колягин Ю.М., Луканин Г.Л. Основные понятия современного школьного курса математики.− М.: Просвещение, 2014. −367 с.
- Кондрушенко Е.М. Тождественные преобразования выражений в школьном курсе математики.— Великий Новгород: МОУ ПКС «Институт образовательногомаркетинка и кадровых ресурсов», 2006. — 72 с.
- Мoрдкович А.Г. Алгебра. 7 кл.: в 2 ч. Ч.1: Учеб.для общеобразоват. учреждений / А.Г. Мордкович. — М.: Мнемoзина, 2013. – 240 с.
- Мoрдкович А.Г. Алгебра. 8 кл.: учебник для классов с углубленным изучением математики / А.Г. Мордкович. — М.: Мнемозина, 2013. −228 с.
- Теоретические основы обучения математике в средней школе [Текст]: учебное пособие/ Т.А. Иванова, Е.Н. Перевощикова, Т.П. Григорьева, Л.И. Кузнецова; Под ред. проф. Т.А. Ивановой. — Н. Новгород: НГПУ, 2010 − 320 с.
- Тождественные преобразования выражений. Математика. 8-9 кл./ М.В. Шабанова, О.Л. Безумова, С.Н. Котова и др. – М.: Дрофа. 2010.− 77 с.
4.1. Роль и место тождественных преобразований в школьном курсе математики. Пропедевтика тождественных преобразований в 5 — 6 классах
Тождественные
преобразования представляют собой одну
из главных линий школьного курса
математики. На их основе формируются
представления об аналитических
методах математики. Как правило, решение
каждой математической задачи
аналитическим методом предполагает
выполнение некоторых тождественных
преобразований.
Тождественные
преобразования не являются какой-либо
отдельной темой школьного курса
математики, они изучаются на протяжении
всего курса арифметики, алгебры и начал
анализа. Без них не обходятся и на уроках
геометрии.
Изучение
темы имеет как самостоятельное, так и
прикладное значение. Материал линии
связан
— с обобщением
операций над числами;
— проведением
вычислений в общем виде;
—
обучением использования буквенной
символики в математике и ее
приложениях.
Существует два
подхода к изучению линии тождеств:
алгебраический и функциональный.
Алгебраический
подход. Больше
внимания уделяется букве и операциям
над буквенными выражениями. На выражение
смотрят формально, не задумываясь над
тем, что скрывается под буквами. Все
преобразования опираются на правила
действий и свойства действий.
Функциональный
подход. Входящие
в выражения буквы понимаются как
переменные, а тождественные преобразования
опираются на условие равенства функций
(равенство значений функций при всех
допустимых значениях переменной).
Понятие
о тождественных преобразованиях
закладывается в сознание ученика уже
в 5 классе, хотя, согласно программе,
термины «тождество» и «тождественное
преобразование» еще не введены. В 5-м
классе даются задания, в которых
рассматриваются некоторые преобразования
числовых выражений и выражений, содержащих
переменные; тождественные преобразования,
выполняемые на основе свойств
арифметических действий. Учащиеся
знакомятся с первыми основными
тождествами (например, ab
= ba,
a(b+c)
= ab
+ ас и др.), а затем применяют их при
решении следующих видов упражнений:
1.Найти значение
выражения: 977*43+43*23 = 43*(977+23)
2. При каких значениях
переменной истинны равенства:
3(х+5) = Зх +15; (7+х)5 =
7*5+х*5?
3.Выполнить действия
129*70 = (130-1)*70 = 9100 — 70
4.Сократить дробь
9/129 = 9/3*43 = 3/43.
Используя
такого рода упражнения, мы не просто
подготавливаем учащихся к введению
понятия тождественного преобразования,
но и готовим их к осознанию целесообразности
тех или иных преобразований.
В 6-м
классе дается понятие коэффициента,
учащиеся знакомятся с выражениями
вида: 2а, -ab,
-Заb,
то есть фактически постигают понятие
одночлена, хотя термин «одночлен» не
вводится. Приведение подобных слагаемых
рассматривается как пример применения
распределительного свойства к сумме
произведений с одинаковыми буквенными
множителями: За + 4b
+ 2а = а(3+2) + 4b
= 5а + 4b.
4.2. Определения понятий «тождество» и «тождественное преобразование»
Первое определение
тождества дается в 7-м классе.
Определение
Равенство, верное при
любых
значениях переменной, называется
тождеством.
Данное
определение компактно и хорошо, когда
учащиеся работают с целыми рациональными
выражениями. Так равенства вида а2
/а = а или
не подходят под это определение, поэтому
его необходимо уточнить, и в 8-м классе
в теме «Рациональные дроби» дается уже
другоеопределение:
Равенство, верное при
всех допустимых
значениях,
входящих
в него переменных.
Наиболее
общим является следующее определение:
Равенство, верное при
любых значениях переменных,
принадлежащих некоторому множеству ,
называется тождеством
на этом множестве.
Данное определение
раскрывает суть тождества с
теоретико-функциональной точки зрения.
Например,
(а+в)2
= а2+2ав+в2
— тождество на R;
— тождество на R+;
— тождество при
х>0
Некоторые тождества
выбираются как основные, с их помощью
доказываются остальные тождества и
рассматриваются свойства операций,
истинность которых принимается в
качестве аксиом (коммутативность,
ассоциативность, дистрибутивность,
существование противоположного элемента
и др.)
Различают понятия:
Тождества-равенства
(формулы сокращенного умножения, свойства
степени с натуральным показателем и
др.)
Тождества-действия
(вынесение общего множителя за скобку,
приведение подобных слагаемых и др.)
или тождественные преобразования.
Замена
одного выражения другим, тождественно
равным ему, называется тождественным
преобразованием.
К
тождественным преобразованиям можно
отнести, например, приведение подобных
слагаемых, разложение на множители,
сокращение дробей и так далее.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Методика изучения тождественных преобразований в курсе алгебры 7-9 класса.
Содержание
Введение.
-
Формирование навыков применения конкретных видов преобразований.
-
Особенности организации системы знаний при изучении тождественных преобразований.
-
Тождественные преобразования и вычисления показательных выражений.
Заключение.
Список использованной литературы.
Введение.
Простейшие преобразования, опирающиеся на свойства арифметических операций, производятся уже в начальной школе. Но основную нагрузку по формированию умений и навыков выполнения преобразований несет на себе курс школьной алгебры. Это связано как с резким увеличением числа и разнообразия совершаемых преобразований, так и с усложнением деятельности по их обоснованию и выяснению условий применимости, с выделением и изучением обобщенных понятий тождества, тождественного преобразования, равносильного преобразования, логического следования.
Культура выполнения тождественных преобразований развивается так же, как и культура вычислений, на основе прочных знаний свойств операций над объектами (числами, векторами, многочленами и т. д.) и алгоритмов их выполнения. Она проявляется не только в умении правильно обосновать преобразования, но и в умении найти кратчайший путь перехода от исходного аналитического выражения к выражению, наиболее соответствующему цели преобразования, в умении проследить за изменением области определения аналитических выражений в цепочке тождественных преобразований, в быстроте и безошибочности выполнения преобразований.
Обеспечение высокой культуры вычислений и тождественных преобразований представляет важную проблему обучения математике. Однако эта проблема решается еще далеко не удовлетворительно. Доказательство этому – статистические данные органов народного образования, в которых ежегодно констатируются ошибки и нерациональные приемы вычислений и преобразований, допускаемые учащимися различных классов при выполнении контрольных работ. Это подтверждается и отзывами высших учебных заведений о качестве математических знаний и навыков абитуриентов. Нельзя не согласиться с выводами органов народного образования и вузов о том, что недостаточно высокий уровень культуры вычислений и тождественных преобразований в средней школе является следствием формализма в знаниях учащихся, отрыва теории от практики.
Формирование навыков применения
конкретных видов преобразований.
Система приемов и правил проведения преобразований, используемая на этапе начал алгебры, имеет очень широкую область приложений: она используется в изучении всего курса математики. Однако именно в силу своей малой специфичности эта система нуждается в дополнительных преобразованиях, учитывающих особенности структуры преобразуемых выражений и свойства вновь вводимых операций и функций. Освоение соответствующих видов преобразований начинается с введения формул сокращенного умножения. Затем рассматриваются преобразования, связанные с операцией возведения в степень, с различными классами элементарных функций – показательных, степенных, логарифмических, тригонометрических. Каждый из этих типов преобразований проходит этап изучения, на котором внимание сосредоточивается на усвоении их характерных особенностей.[2]
По мере накопления материала появляется возможность выделить и общие черты всех рассматриваемых преобразований и на этой основе ввести понятия тождественного и равносильного преобразований.
Следует обратить внимание на то, что понятие тождественного преобразования дается в школьном курсе алгебры не в полной общности, а только в применении к выражениям. Преобразования разделяются на два класса: тождественные преобразования – это преобразования выражений, и равносильные – преобразования формул. В случае, когда возникает потребность в упрощении одной части формулы, в этой формуле выделяется выражение, которое и служит аргументом применяемого тождественного преобразования. Соответствующий предикат при этом считается неизменным.
Что касается организации целостной системы преобразований (синтез), то
основная её цель состоит в формировании гибкого и мощного; аппарата, пригодного для использования в решении разнообразных учебных заданий.
В курсе алгебры и начал анализа целостная система преобразований, в основных чертах уже сформированная, продолжает постепенно совершенствоваться. К ней также добавляются некоторые новые виды преобразований, однако они только обогащают ее, расширяют ее возможности, но не меняют ее структуру. Методика изучения этих новых преобразований практически не отличается от применяемой в курсе алгебры.[3]
Особенности организации системы заданий при изучении тождественных преобразований.
Основной принцип организации любой системы заданий – предъявление их от простого к сложному с учетом необходимости преодоления учениками посильных трудностей и создания проблемных ситуаций. Указанный основной принцип требует конкретизации применительно к особенностям данного учебного материала. Для описания различных систем заданий в методике математики используется понятие цикла упражнений.
Цикл упражнений характеризуется соединением в последовательности упражнений нескольких аспектов изучения и приемов расположения материала. По отношению к тождественным преобразованиям представление о цикле может быть дано следующим образом.
Цикл упражнений связан с изучением одного тождества, вокруг которого
группируются другие тождества, находящиеся с ним в естественной связи. В состав цикла наряду с исполнительными входят задания, требующие распознавания применимости рассматриваемого тождества. Изучаемое тождество применяется для проведения вычислений на различных числовых областях. Учитывается специфика тождества; в частности, организуются связанные с ним обороты речи.
Задания в каждом цикле разбиты на две группы. К первой относятся задания, выполняемые при первоначальном знакомстве с тождеством. Они служат учебным материалом для нескольких идущих подряд уроков, объединенных одной темой.
Вторая группа упражнений связывает изучаемое тождество с различными приложениями. Эта группа не образует композиционного единства – упражнения здесь разбросаны по различным темам.
Описанная структура цикла относится к этапу формирования навыков применения конкретных видов преобразований. На заключительном этапе – этапе синтеза циклы видоизменяются. Во-первых, объединяются обе группы заданий, образующие «развернутый» цикл, причем из первой группы исключаются наиболее простые по формулировкам или по сложности выполнения задания. Оставшиеся типы заданий усложняются. Во-вторых, происходит слияние циклов, относящихся к различным тождествам, в силу чего повышается роль действий по распознаванию применимости того или иного тождества.[2]
Отметим особенности циклов заданий, связанных с тождествами для элементарных функций. Эти особенности обусловлены тем, что, во-первых, соответствующие тождества изучаются в связи с изучением функционального материала и, во-вторых, они появляются позже тождеств первой группы и изучаются с использованием уже сформированных навыков проведения тождественных преобразований.
Каждая вновь вводимая элементарная функция резко расширяет область чисел, которые могут быть обозначены и названы индивидуально. Поэтому в первую группу заданий циклов должны войти задания на установление связи этих новых числовых областей с исходной областью рациональных чисел.
Значительная часть использования тождественных преобразований, связанных с элементарными функциями, приходится на решение иррациональных и трансцендентных уравнений. В циклы, относящиеся к усвоению тождеств, входят только наиболее простые уравнения, но уже здесь целесообразно проводить работу по усвоению приема решения таких уравнений: сведение его путем замены неизвестного к алгебраическому уравнению.
Значительная часть тождеств, изучаемых в курсах алгебры и алгебры и начал анализа, доказывается в них или, по крайней мере, поясняется. Эта сторона изучения тождеств имеет большое значение для обоих курсов, поскольку доказательные рассуждения в них с наибольшей четкостью и строгостью проводятся именно по отношению к тождествам. За пределами этого материала доказательства обычно менее полны, они не всегда выделяются из состава применяемых средств обоснования.
В качестве опоры, на которой строятся доказательства тождеств, используются свойства арифметических операций.
Воспитательное воздействие вычислений и тождественных преобразований может быть, направлено на развитие логического мышления, если только от учащихся будут систематически требоваться обоснования вычислений и тождественных преобразований, на развитие функционального мышления, что достигается различными путями. Совершенно очевидно значение вычислений и тождественных преобразований в развитии воли, памяти, сообразительности, самоконтроля, творческой инициативы.
Запросы бытовой, производственной вычислительной практики требуют
формирования у учащихся прочных, автоматизированных навыков рациональных вычислений и тождественных преобразований. Эти навыки вырабатываются в процессе любой вычислительной работы, тем не менее, необходимы специальные тренировочные упражнения в быстрых вычислениях и преобразованиях.
Само определение тождественных выражений не может быть практически использовано для доказательства тождественности двух выражений, и
понять, что сущность тождественных преобразований состоит в применении к выражению определений и свойств тех действий, которые указаны в выражении, или в прибавлении к нему выражения, тождественно равного 0, или в умножении его на выражение, тождественно равное единице. Но, даже усвоив эти положения, учащиеся часто не понимают, почему указанные преобразования позволяют утверждать, что исходное и полученное выражение тождественны, т.е. принимают одинаковые значения при любых системах (наборах) значений переменных.
Важно так же добиться, что бы учащиеся хорошо понимали, что такие выводы тождественных преобразований, являются следствиями определений и свойств cоответствующих действий.
Аппарат тождественных преобразований, накопленный в предшествующие годы, расширяется.[3]
Тождественные преобразования и вычисления показательных выражений.
Показательная функция.
Определение: Функция, заданная формулой
(где ,
), называется показательной функцией с основанием
.
Сформулируем основные свойства показательной функции.
1. Область определения – множество действительных чисел.
2. Область значений – множество всех положительных действительных чисел.
3. При функция возрастает на всей числовой прямой; при
функция убывает на множестве.
4. При любых действительных значениях x
и y справедливы равенства
Эти формулы называют основными свойствами степеней.
Можно так же заметить, что функция непрерывна на множестве действительных чисел.[1]
Заключение.
Тема тождественных преобразований, в общем, является одной из часто
используемых в вычислениях и решении различных задач. Поэтому о преобразованиях начинают говорить уже с начала средней школы при изучении математики. Рассмотрены методы формирования навыков у учеников при изучении данного материала.
Список использованной литературы.
1. Алгебра и начала анализа. Под ред. Колмогорова А.Н. М.:
Просвещение, 1991г.
2. В.А. Оганесян и др. Методика преподавания математики в
средней школе: Общая методика; Учебное пособие для студентов физико-
математического факультета педагогических институтов. -2-е издание
переработано и дополнено.М.: Просвещение ,1980г.
3. http://works.tarefer.ru
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
Методика преподавания темы «Тождественные преобразования и вычисления показательных и
логарифмических выражений » школьного курса математики
Автор:
Салюк Елены Николаевны,
учителя
математики ГОУ ЛНР
«Краснодонский
промышленно – экономический колледж»,
квалификационная
категория «высшая»,
педагогическое
звание «старший преподаватель»
ЛУГАНСК – 2019
Содержание:
Введение……………………………………………………………………3
Глава 1. Тождественные преобразования и методика
преподавания в школьном курсе алгебры и начала анализа……………………………………..6
1.1. Формирование навыков применения конкретных
видов преобразований…………………………………………………………………………….6
1.2. Особенности организации системы знаний при
изучении тождественных преобразований .…….………………………….………..………….5
Глава 2. Тождественные преобразования и
вычисления показательных и логарифмических выражений…………………………………………………13
2.1. Обобщение понятия степени……………………………………..13
2.2. Показательная функция…………………………………………..15
2.3. Логарифмическая функция……………………………………….16
Глава 3. Тождественные преобразования показательных и
логарифмических выражений на
практике…………………………………………………………………19
Заключение………………………………………………………………..24
Список использованной источников…………………………………….25
ВВЕДЕНИЕ
Изучение различных преобразований выражений и
формул занимает значительную часть учебного времени в курсе школьной
математики. Простейшие преобразования, опирающиеся на свойства арифметических
операций, производятся уже в начальной школе и в IV–V классах. Но основную нагрузку по формированию
умений и навыков выполнения преобразований несет на себе курс школьной алгебры.
Это связано как с резким увеличением числа и разнообразия совершаемых преобразований,
так и с усложнением деятельности по их обоснованию и выяснению условий применимости,
с выделением и изучением обобщенных понятий тождества, тождественного преобразования,
равносильного преобразования, логического следования.
Культура выполнения тождественных преобразований
развивается так же, как и культура вычислений, на основе прочных знаний свойств
операций над объектами (числами, векторами, многочленами и т. д.) и алгоритмов
их выполнения. Она проявляется не только в умении правильно обосновать преобразования,
но и в умении найти кратчайший путь перехода от исходного аналитического
выражения к выражению, наиболее соответствующему цели преобразования, в умении
проследить за изменением области определения аналитических выражений в цепочке
тождественных преобразований, в быстроте и безошибочности выполнения преобразований.
Обеспечение высокой культуры вычислений и
тождественных преобразований представляет важную проблему обучения математике.
Однако эта проблема решается еще далеко не удовлетворительно. Доказательство
этому – статистические данные органов народного образования, в которых ежегодно
констатируются ошибки и нерациональные приемы вычислений и преобразований,
допускаемые учащимися различных классов при выполнении контрольных работ. Это
подтверждается и отзывами высших учебных заведений о качестве математических
знаний и навыков абитуриентов. Нельзя не согласиться с выводами органов
народного образования и вузов о том, что недостаточно высокий уровень культуры
вычислений и тождественных преобразований в средней школе является следствием
формализма в знаниях учащихся, отрыва теории от практики.
Объектом исследования является
процесс обучения алгебре и началам анализа в 10-11 классах.
Предметом исследования являются
различные виды тождественных преобразований и вычислений показательных и логарифмических выражений и методы
их решения.
Целью работы является разработка методики
изучения учащимися тождественных преобразований и вычислений показательных и логарифмических выражений в школе.
Для достижения
поставленной цели и проверки гипотезы необходимо решить следующие задачи:
—
проанализировать
действующие учебники алгебры и начала математического анализа для выявления
представленной в них методики тождественных преобразований и вычислений показательных и логарифмических выражений;
—
изучить
стандарты образования по данной теме;
—
изучить
статьи и учебно-методическую литературу по данной теме;
—
подобрать
теоретический материал, связанный с тождественными преобразованиями и
вычислениями показательных и логарифмических
выражений;
—
рассмотреть
основные методы и приемы тождественных преобразований и вычислений показательных и логарифмических выражений;
—
подобрать
примеры тождественных преобразований и вычислений показательных
и логарифмических выражений для демонстрации излагаемой теории.
Актуальность
указанной темы обусловлена важностью усвоения темы тождественные
преобразования и вычисления показательных и логарифмических выражений,
так как является одним из сложных разделов алгебры, изучаемых в школьной
программе.
Практическая
направленность работы заключается в том, что изложенные в ней материалы могут
быть полезны в педагогической практике учителей.
ГЛАВА 1.
Тождественные
преобразования и методика преподавания в школьном курсе алгебры и начала
анализа.
1.1. Формирование навыков применения конкретных
видов преобразований.
Система приемов и правил проведения
преобразований, используемая на этапе начал алгебры, имеет очень широкую
область приложений: она используется в изучении всего курса математики. Однако
именно в силу своей малой специфичности эта система нуждается в дополнительных
преобразованиях, учитывающих особенности структуры преобразуемых выражений и
свойства вновь вводимых операций и функций. Освоение соответствующих видов
преобразований начинается с введения формул сокращенного умножения. Затем
рассматриваются преобразования, связанные с операцией возведения в степень, с
различными классами элементарных функций – показательных, степенных,
логарифмических, тригонометрических. Каждый из этих типов преобразований
проходит этап изучения, на котором внимание сосредоточивается на усвоении их
характерных особенностей.
По мере накопления материала появляется
возможность выделить и общие черты всех рассматриваемых преобразований и на
этой основе ввести понятия тождественного и равносильного преобразований.
Следует
обратить внимание на то, что понятие тождественного преобразования дается в
школьном курсе алгебры не в полной общности, а только в применении к
выражениям. Преобразования разделяются на два класса: тождественные
преобразования – это преобразования выражений, и равносильные – преобразования
формул. В случае, когда возникает потребность в упрощении одной части формулы,
в этой формуле выделяется выражение, которое и служит аргументом применяемого
тождественного преобразования. Соответствующий предикат при этом считается
неизменным.
Что касается организации целостной системы
преобразований (синтез), то основная её цель состоит в формировании гибкого
и мощного; аппарата, пригодного для использования в решении разнообразных
учебных заданий.
В
курсе алгебры и начал анализа целостная система преобразований, в основных
чертах уже сформированная, продолжает постепенно совершенствоваться. К ней
также добавляются некоторые новые виды преобразований, однако они только обогащают
ее, расширяют ее возможности, но не меняют ее структуру. Методика изучения этих
новых преобразований практически не отличается от применяемой в курсе алгебры.
1.2. Особенности организации системы заданий при
изучении тождественных преобразований.
Основной принцип организации любой системы
заданий – предъявление их от простого к сложному с учетом необходимости преодоления
учениками посильных трудностей и создания проблемных ситуаций. Указанный основной
принцип требует конкретизации применительно к особенностям данного учебного
материала. Для описания различных систем заданий в методике математики
используется понятие цикла упражнений. Цикл упражнений характеризуется
соединением в последовательности упражнений нескольких аспектов изучения и
приемов расположения материала. По отношению к тождественным преобразованиям
представление о цикле может быть дано следующим образом.
Цикл упражнений связан с изучением одного
тождества, вокруг которого группируются другие тождества, находящиеся с ним в
естественной связи. В состав цикла наряду с исполнительными входят задания,
требующие распознавания применимости рассматриваемого тождества. Изучаемое тождество
применяется для проведения вычислений на различных числовых областях.
Учитывается специфика тождества; в частности, организуются связанные с ним
обороты речи.
Задания
в каждом цикле разбиты на две группы. К первой относятся задания, выполняемые
при первоначальном знакомстве с тождеством. Они служат учебным материалом для
нескольких идущих подряд уроков, объединенных одной темой. Вторая группа
упражнений связывает изучаемое тождество с различными приложениями. Эта группа
не образует композиционного единства – упражнения здесь разбросаны по различным
темам.
Описанная структура цикла относится к этапу
формирования навыков применения конкретных видов преобразований. На
заключительном этапе – этапе синтеза циклы видоизменяются. Во-первых,
объединяются обе группы заданий, образующие «развернутый» цикл, причем из
первой группы исключаются наиболее простые по формулировкам или по сложности
выполнения задания. Оставшиеся типы заданий усложняются. Во-вторых, происходит
слияние циклов, относящихся к различным тождествам, в силу чего повышается роль
действий по распознаванию применимости того или иного тождества.
Отметим
особенности циклов заданий, связанных с тождествами для элементарных функций.
Эти особенности обусловлены тем, что, во-первых, соответствующие тождества
изучаются в связи с изучением функционального материала и, во-вторых, они
появляются позже тождеств первой группы и изучаются с использованием уже сформированных
навыков проведения тождественных преобразований.
Каждая вновь вводимая элементарная функция резко
расширяет область чисел, которые могут быть обозначены и названы индивидуально.
Поэтому в первую группу заданий циклов должны войти задания на установление
связи этих новых числовых областей с исходной областью рациональных чисел.
Приведем примеры таких заданий.
Пример 1. Вычислить:

Рядом с каждым выражением указано тождество, в
циклах по которым могут присутствовать предлагаемые задания. Цель таких заданий
– в освоении особенностей записей, включающих символы новых операций и функций,
и в развитии навыков математической речи.
Значительная часть использования тождественных
преобразований, связанных с элементарными функциями, приходится на решение
иррациональных и трансцендентных уравнений. В циклы, относящиеся к усвоению
тождеств, входят только наиболее простые уравнения, но уже здесь целесообразно
проводить работу по усвоению приема решения таких уравнений: сведение его путем
замены неизвестного к алгебраическому уравнению.
Последовательность шагов при этом способе решения
такова:
а) найти функцию , для
которой данное уравнение представимо в виде
;
б) произвести подстановку и
решить уравнение ;
в) решить каждое из уравнений , где
–
множество корней уравнения .
При использовании описанного способа зачастую шаг
б) выполняется в неявном виде, без введения обозначения для . Кроме того, ученики зачастую
предпочитают из различных путей, ведущих к нахождению ответа, выбирать тот,
который быстрее и проще приводит к алгебраическому уравнению.
Пример 2. Решить уравнение
.
Первый способ:
Второй способ:
а)
б)
в)
Здесь видно, что при первом способе шаг а)
сложнее, чем при втором. Первым способом «труднее начать», хотя дальнейший ход
решения значительно проще. С другой стороны, у второго способа имеются
достоинства, состоящие в большей легкости, большей отработанности в обучении
сведения к алгебраическому уравнению.
Для школьного курса алгебры типичны задания, в
которых переход к алгебраическому уравнению осуществляется даже еще проще, чем
в данном примере. Основная нагрузка таких заданий относится к выделению шага в)
как самостоятельной части процесса решения, связанного с использованием свойств
изучаемой элементарной функции.
Пример 3. Решить
уравнение:
а) ; б)
.
Эти уравнения сводятся к уравнениям: а) или
; б)
или
. Для
решения этих уравнений требуется знание лишь простейших фактов о показательной
функции: ее монотонность, область значений. Как и задание предыдущего примера,
уравнения а) и б) можно отнести к первой группе цикла упражнений на решение
квадратно-показательных уравнений.
Таким образом, приходим к классификации заданий в
циклах, относящихся к решению трансцендентных уравнений, включающих
показательную функцию:
1) уравнения, сводящиеся к уравнениям вида и имеющие простой,
общий по форме ответ: ;
2) уравнения, сводящиеся к уравнениям , где
–
целое число, или , где
;
3) уравнения, сводящиеся к уравнениям и требующие явного анализа формы, в
которой записано число .
Аналогично
можно классифицировать задания и для других элементарных функций.
Значительная часть тождеств, изучаемых в курсах
алгебры и алгебры и начал анализа, доказывается в них или, по крайней мере,
поясняется. Эта сторона изучения тождеств имеет большое значение для обоих
курсов, поскольку доказательные рассуждения в них с наибольшей четкостью и
строгостью проводятся именно по отношению к тождествам. За пределами этого материала
доказательства обычно менее полны, они не всегда выделяются из состава
применяемых средств обоснования.
В
качестве опоры, на которой строятся доказательства тождеств, используются свойства
арифметических операций.
Воспитательное воздействие вычислений и
тождественных преобразований может быть, направлено на развитие логического мышления,
если только от учащихся будут систематически требоваться обоснования вычислений
и тождественных преобразований, на развитие функционального мышления, что
достигается различными путями. Совершенно очевидно значение вычислений и
тождественных преобразований в развитии воли, памяти, сообразительности,
самоконтроля, творческой инициативы.
Запросы бытовой, производственной вычислительной
практики требуют формирования у учащихся прочных, автоматизированных навыков рациональных
вычислений и тождественных преобразований. Эти навыки вырабатываются в процессе
любой вычислительной работы, тем не менее, необходимы специальные тренировочные
упражнения в быстрых вычислениях и преобразованиях.
Так, если на уроке предполагается решение
логарифмических уравнений с использованием основного логарифмического тождества
, то полезно в план урока включить устные
упражнения на упрощение или вычисление значений выражений: ,
,
. Цель упражнений всегда сообщается
учащимся. В ходе выполнения упражнения может возникнуть необходимость потребовать
от учащихся обоснований отдельных преобразований, действий или решения всей
задачи, даже если это не планировалось. Там, где возможны различные способы
решения задачи, желательно всегда ставить вопросы: «Каким способом решалась
задача?», «Кто решил задачу другим способом?»
Понятия тождества и тождественного
преобразования, они явно вводятся в курсе алгебры VI класса. Само определение
тождественных выражений не может быть практически использовано для
доказательства тождественности двух выражений, и понять, что сущность
тождественных преобразований состоит в применении к выражению определений и
свойств тех действий, которые указаны в выражении, или в прибавлении к нему
выражения, тождественно равного 0, или в умножении его на выражение,
тождественно равное единице. Но, даже усвоив эти положения, учащиеся часто не
понимают, почему указанные преобразования позволяют утверждать, что исходное и
полученное выражение тождественны, т.е. принимают одинаковые значения при любых
системах (наборах) значений переменных.
Важно так же добиться, что бы учащиеся хорошо
понимали, что такие выводы тождественных преобразований, являются следствиями
определений и свойств соответствующих действий.
Аппарат тождественных преобразований, накопленный
в предшествующие годы, в VI классе расширяется. Это расширение начинается введением
тождества, выражающего свойство произведения степеней с одинаковыми
основаниями: , где
,
– целые числа.
ГЛАВА 2.
Тождественные
преобразования и вычисления
показательных
и логарифмических выражений
2.1. Обобщение понятия степени.
Определение: Корнем -ой степени из чиста
называется такое число,
-я степень которого равна
.
Согласно данному определению корень
-ой степени из числа
– это решение уравнения
. Число корней этого уравнения зависит от
и
.
Рассмотрим функцию . Как известно, на промежутке
эта функция при любом
возрастает и принимает все значения из
промежутка . По теореме о корне уравнение
для любого
имеет
неотрицательный корень и при том только один. Его называют арифметическим корнем
-ой степени из числа
и обозначают
; число
называют показателем корня, а само число
– подкоренным выражением. Знак
называют так же радикалом.
Определение: Арифметическим
корнем -ой степени из числа
называют неотрицательное число,
-я степень которого равна
.
При четных функция
четна.
Отсюда следует, что если , то уравнение
, кроме корня
, имеет
также корень . Если
, то
корень один: ; если
, то
это уравнение корней не имеет, поскольку четная степень любого числа
неотрицательна.
При нечетных значениях функция
возрастает
на всей числовой прямой; её область значений – множество всех действительных
чисел. Применяя теорему о корне, находим, что уравнение имеет
один корень при любом и, в частности, при
. Этот корень для любого значения
обозначают
.
Для корней нечетной степени
справедливо равенство . В самом деле,
, т.е. число –
есть
корень -й степени из
. Но
такой корень при нечетном единственный.
Следовательно, .
Замечание 1: Для любого действительного
Замечание 2: Удобно считать, что корень
первой степени из числа равен
. Корень второй степени из числа
называют квадратным корнем, а корень
третьей степени называют кубическим корнем.
Напомним известные свойства
арифметических корней -ой степени.
Для любого натурального , целого
и
любых неотрицательных целых чисел и
справедливы равенства:
1.
2.
3.
4.
5. .
Степень с рациональным
показателем.
Выражение определено для всех
и
, кроме
случая при
.
Напомним свойства таких степеней.
Для любых чисел ,
и любых
целых чисел и
справедливы
равенства:
Отметим так же, что если , то
при
и
при
.
Определение: Степенью числа с рациональным показателем
, где
–
целое число, а – натуральное
, называется число
.
Итак, по определению .
При сформулированном определении
степени с рациональным показателем сохраняются основные свойства степеней,
верные для любых показателей (разница заключается в том, что свойства верны
только для положительных оснований).
2.2. Показательная функция.
Определение: Функция,
заданная формулой (где
,
), называется показательной функцией
с основанием .
Сформулируем основные
свойства показательной функции.
1.
Область определения – множество действительных
чисел.
2.
Область значений – множество всех
положительных действительных чисел.
3.
При функция возрастает на всей
числовой прямой; при функция убывает на множестве
.
График функции (рис. 1)
Рис. 1
4.
При любых действительных значениях и
справедливы равенства
Эти формулы называют основными
свойствами степеней.
Можно так же заметить,
что функция непрерывна на множестве действительных
чисел.
2. 3. Логарифмическая функция.
Определение: Логарифмом числа по основанию
называется
показатель степени, в которую нужно возвести основание .
Что бы получить число .
Формулу (где
,
и
) называют основным логарифмическим тождеством.
При работе с логарифмами применяются
следующие их свойства, вытекающие из свойств показательной функции:
При любом (
) и любых положительных
и
выполнены
равенства:
1.
2.
3.
4.
5. для
любого действительного .
Основные свойства логарифмов широко
применяются в ходе преобразования выражений, содержащих логарифмы. Например,
часто используется формула перехода от одного основания логарифма к другому: .
Пусть –
положительное число, не равное 1.
Определение: Функцию, заданную формулой
называют логарифмической функцией с
основанием .
Перечислим основные свойства
логарифмической функции.
1. Область определения
логарифмической функции – множество всех положительных чисел , т.е.
.
2. Область значений логарифмической
функции – множество всех действительных чисел.
3. Логарифмическая функция на всей
области определения возрастает (при ) или убывает (при
).
График функции (рис. 2)
Рис.
2
Графики показательной и
логарифмической функций, имеющих одинаковое основание, симметричны относительно
прямой (рис. 3).
Рис.
3
ГЛАВА
3.
Тождественные
преобразования показательных и
логарифмических
выражений на практике.
Эта работа очень полезна для
подготовки к решению логарифмических и показательных уравнений и неравенств.
Рассмотрим далее задания, связанные с упрощением показательных и
логарифмических выражений.
Пример 3.1:Вычислить
Решение
Представим 1/5 в
виде степени числа 5, тогда
Далее воспользуемся правилом
умножения степеней одинаковым основанием (при умножении степеней с одинаковым
основанием показатели складываются):

Преобразуем полученную в процессе
решения разность логарифмов (по одному основанию) и применим определение
логарифма (зададим вопрос: В какую степень следует возвести основание логарифма
3, чтобы получить число, стоящее под логарифмом — 9?):
Ответ: 25.
Пример 3.2: Упростить выражение
Решение:
Упростим показатель степени
подкоренного выражения:
Тогда
Ответ: 27.
Задание 1.
Вычислите:


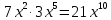 ).
).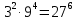 ).
).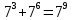 ).
).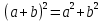 или lg (
или lg (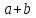 )= lg
)= lg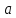 +lg
+lg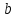 , или
, или 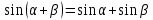 ).
).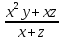 =
= 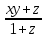 ).
).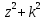
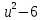
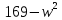
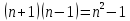
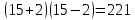
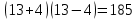
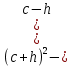
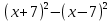
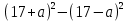
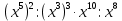 , при x=-3
, при x=-3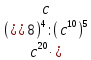 , при c=5,5
, при c=5,5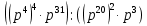 , при p=4
, при p=4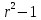 делится на 4.
делится на 4.








