Фотобанк StylishBag
МЕНЮ
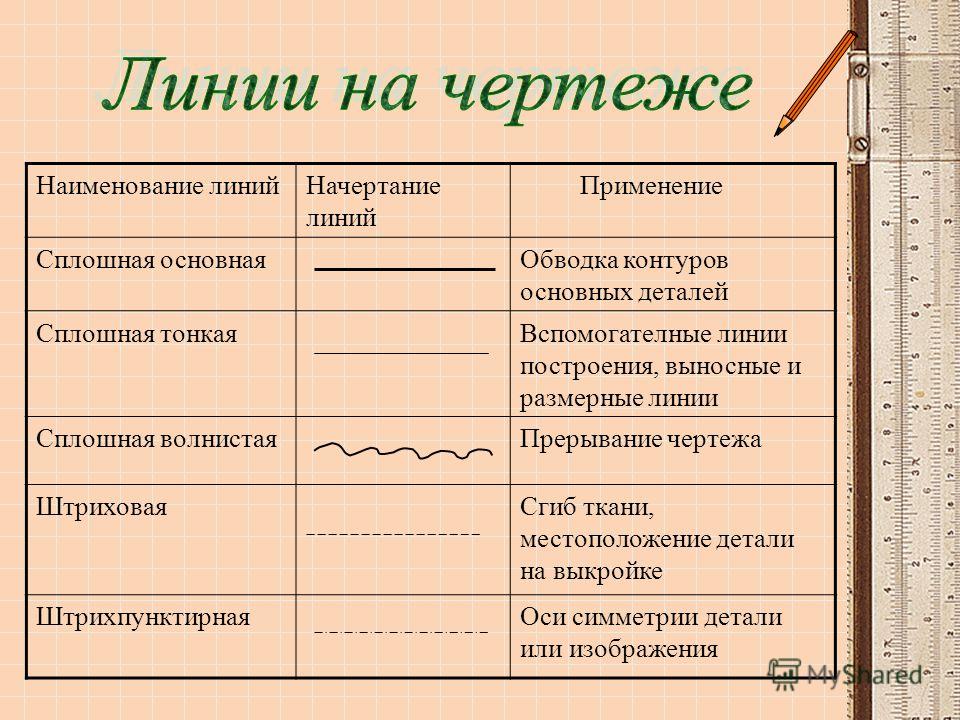
Ошибки определения и построения линий на плане
Обновлено: 21.09.2023
Читайте также:
- Новая дорога м4 в обход аксая план
- Схема подключения радиаторов отопления при двухтрубной системе
- Средообразующая деятельность живого вещества 9 класс презентация
2.3.1
Реальная ошибка ( С.К.О.) положения
контурной точки на карте принимается
равной 0.5 мм в масштабе карты :
мм,
предельная
мм
2.3.2
Ошибка в длине линии
,
измеренной по карте в
раз
больше ошибки определения планового
положения точки.
мм,
2.3.3
Для ломаных линий :
,
где
—
число звеньев ломаной линии.
2. Точность определения расстояний и направлений между контурными точками плана
При
подготовке исходных данных для
перенесения проекта в натуру и решении
других задач приходится измерять
расстояния и направления между контурными
точками.
-
Точность
определения расстояний (горизонтальных,
проложений)
между близлежащими контурными точками.
Съемка их проведена
с одной точки съемочного обоснования.
Горизонтальное
проложение
между контурными точками:
,
где
— соответственно координаты концов
линий, определяемые
графически.
С.
к. п.
линии
при условии, что с.к.
п. положения концов линий
.
где
—
коэффициент автокорреляции координат
контурной точки.
Коэффициент
автокорреляции координат для близлежащих
точек :
,
где
и
и
соответственно с.к.п. положения
исходного пункта и контурной точки.
Для
близлежащих контурных точек можно
принять
= 0,4 -0,6.
Погрешность
расстояния
равна
погрешности
положения
контурной
точки лишь при
=
0. Корреляцией
координат контурных точек можно
пренебречь, если
концы линии находятся на значительном
расстоянии
друг от друга или их съемка выполнена
с разных точек съемочной сети.
Таким
образом, при некоррелированных
координатах, (когда
=
0 ) :
Пример
1
При
съемке застроенных территорий с
капитальной застройкой
0,3 мм на плане . При
=
0,6, для близлежащих контурных точек
получим:
на
плане.
С
вероятностью, близкой к 1.0 предельная
погрешность
расстояния между близлежащими точками
капитальных зданий и сооружений
не превысит 0,4 мм на плане.
Пример 2
Для
плана
на незастроенной территории с четкими
очертаниями контуров, погрешность тг
= 0,5мм на
плане; положение точек независимо, так
как их съемка выполнена
с разных точек съемочного обоснования
тогда
мм
на плане.Следовательно,
предельная погрешность расстояния
мм
на
плане.
3.
Средняя квадратическая погрешность
определения направления (дирекционного
угла)
3.1
Дирекционный
угол линии между точками с координатами
,
определяется
по формуле :
.
СКП
определения величины дирекционного
угла
линии
длиной S
между контурными точками, положение
которых некоррелировано, определится
по формуле
Для
близлежащих контурных точек СКП
дирекционного угла:
Формулы
(1.1), (1.2) показывают, что СКП
дирекционного угла уменьшается с
увеличением
расстояния между точками. Поэтому при
привязке проекта
автомобильной дороги к пунктам
геодезического обоснования
за исходное направление принимают
имеющее
большую длину.
Например,
при
8 см
на плане и
мм
на плане,
найдем
Предельная
погрешность определения дирекционного
угла
3.2
СКП измерения дирекционного угла
линии
длиной S
между контурными точками, положение
которых некоррелировано,
определится по формуле
4.
Точность определения высотных параметров
НА плане.
Точность
топографических планов в высотном
отношении
характеризуется
средней квадратической
или
средней
погрешностью
определения по
горизонталям плана высот точек
относительно ближайших пунктов
съемочного
обоснования. Погрешности
и
связаны следующей зависимостью:
=
1,25
,
что следует
учитывать при расчетах точности
крупномасштабных топографических
съемок.
Основным
видом наземных топографических съемок
является тахеометрическая , обладающая
рядом несомненных преимуществ.
Тахеометрическая
съемка производятся
путем набора пикетов, интерполирования
и проведения горизонталей.
Полнота и детальность изображения
рельефа зависят от высоты сечения,
густоты
пикетов и пр. Но
до мельчайших подробностей рельеф
изобразить нельзя,
какой бы ни была высота сечения рельефа,.
Это не позволит
сделать масштаб плана. При съемках
приходится обобщать рельеф, выделяя
главное и отбрасывая второстепенное.
Погрешности,
влияющие на точность положения
горизонталей:.
Первая
группа — погрешности,
влияющие на точность положения
горизонтали по высоте и не
зависящие
от угла наклона топографической
поверхности:
1)
построения съемочного обоснования;
2)
«топографической шероховатости»
поверхности земли (мелкие неровности
земной поверхности); 3) определения
высот пикетов;
4)
обобщения рельефа,
возникающие из-за неоднородности ската
между пикетами;
5)
несовершенства
средств вычисления отметок точек.
Вторая
группа —
погрешности, вызывающие плановое
смещение горизонтали.
Точность высотного положения горизонтали
в этом случае зависит
от угла наклона топографической
поверхности:
1)
построения планового обоснования;
2)
нанесения пикетов на план;
3)
интерполирования и проведения
горизонталей;
4)
вычерчивания горизонталей;.
Точность
положения горизонтали по высоте
зависит
главным образом от погрешностей
обобщения рельефа при съемке. Горизонтали
получают на плане путем линейного
интерполирования
между высотами пикетов. Однако в
результате интерполирования мы
имеем точку
высотой
,
а не точку земной поверхности с высотой
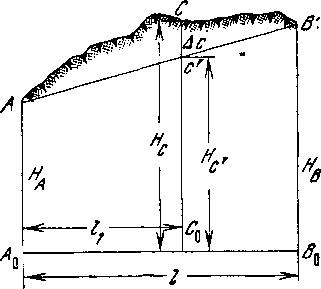
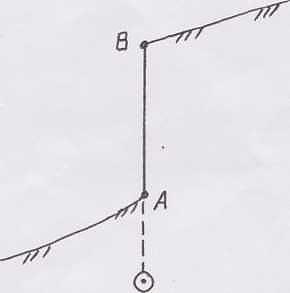
(рис.1).
Разность
назовается
истинной
погрешностью обобщения рельефа
при производстве съемки.
Рис.
1. Обобщение рельефа при съемке
Средняя
квадратическая погрешность
при
съемке вследствие
обобщения рельефа, вычисляется по
формуле
,
где
— коэффициент случайного влияния
обобщения рельефа при съемке,
приведенный к длине в 1
м;
—
расстояние между пикетами,
выраженное в метрах.Величина
коэффициента
зависит
от характера рельефа и колеблется
в пределах 0,01—0,02. Для
промышленно-гражанского
строительства принято
= 0,012.
Из
расчета численных значении
погрешностей, влияющих на точность
положения горизонталей получены
многочисленные
формулы для оценки точности положения
горизонталей по высоте
и определения отметок точек
по плану.
1.
Формула
проф. Н. Г. Видуева
для вычисления средней
квадратической
погрешности ( С.К.П.) положения
горизонтали по высоте:
где
— высота сечения рельефа,
— знаменатель масштаба плана,
— средний уклон
местности.
2.
Формула проф.
В. Д. Большакова
для вычисления (
С.К.П.)
определения
высоты точки по горизонталям плана:
где
—
высота
сечения рельефа,
—
коэффициент случайного влияния обобщения
рельефа при съемке,
—
расстояние между пикетами при съемке
рельефа,
=0,03м;
= 0,7 мм на плане,
—
знаменатель численного
масштаба плана;
— коэффициент, колеблющийся
в пределах 0,010—0,015 для местности с углом
наклона
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема 1.2. Масштабы
1. Понятие о масштабах.
При измерении линий на местности измеряется их наклонная длина. На план или карту наносят проекции этих линий на горизонтальную плоскость уменьшенные в несколько сотен или тысяч раз..
Линия не имеет наклона – ее проекция будет равна измеренной длине.
d = D (при ν =0).
d — проекция линий ( горизонтальное проложение).
ν – угол наклона линии.
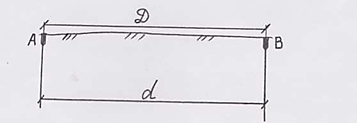
Линия имеет наклон 900 – в этом случае проекция линии превращается в точку.
d = 0 ( при ν = 900).
Линия имеет угол наклона от 00 до 900
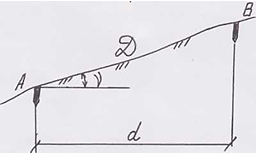
d = D* cos ν ( при 00ν 0)
Проекция линии на горизонтальной плоскости называется ее горизонтальным проложением.
В соответствии с основными целями геодезии и ее задачами в землеустройстве, снимаемая территория наносится на план или карту всегда с определенной степенью уменьшения.
В геодезии применяются следующие виды масштабов:
1. численный ( применяется всегда)
2. именованный (словесный) масштаб
3.линейный ( применяются для удобства и повышения скорости обработки материалов съемок).
4. поперечный
5. масштаб шагов ( применяется при глазомерных съемках).
6. масштаб времени
МАСШТАБ – это степень уменьшения, выраженная отношением длины отрезка линии на плане (профиле) к соответствующей ей проекции на местности.
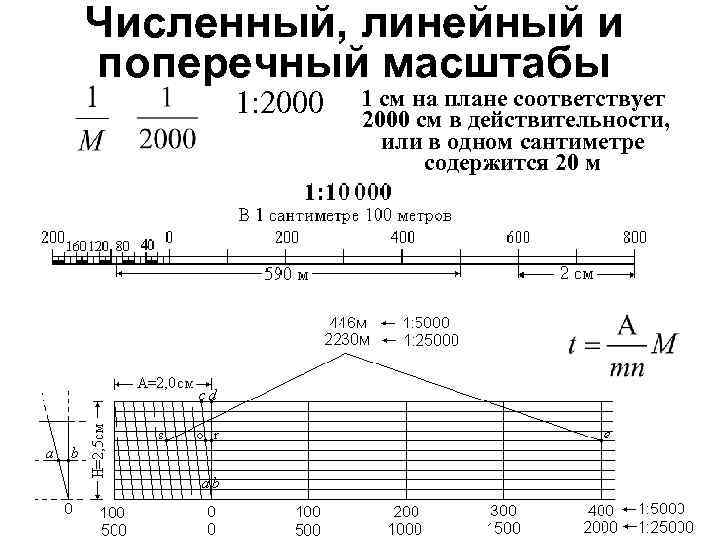
Численный масштаб – это дробь, у которой числитель, равный единице, показывает длину отрезка на плане (профиле), а знаменатель – соответствующую ей длину проекции отрезка на местности.
— 1:1000 – в 1 см -10м; в 1 мм – 1 м
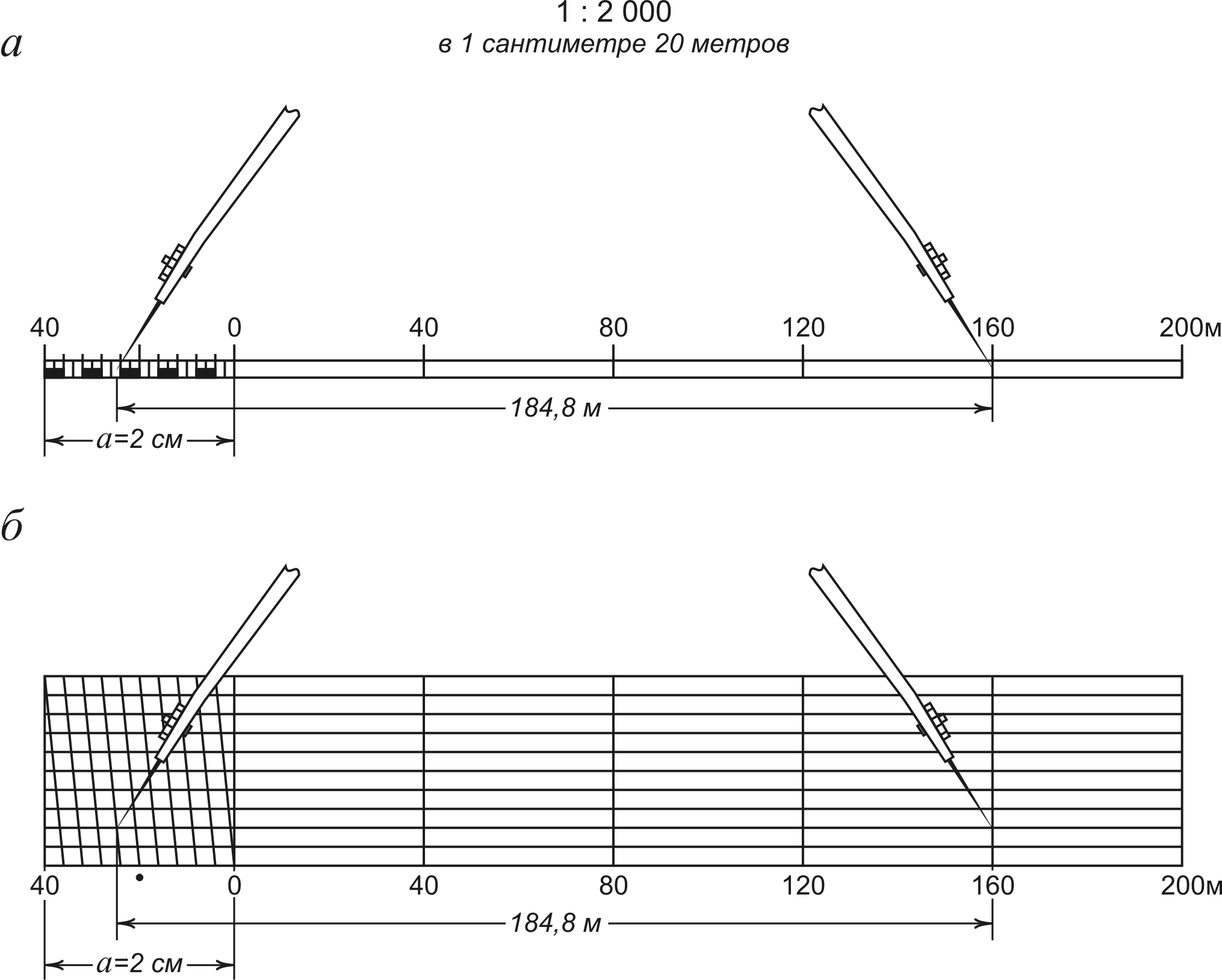
— 1: 2000 — в 1 см – 20 м; в 1 мм — 2 м.
В зависимости от величины знаменателя различают мелкие и крупные масштабы, чем больше знаменатель, тем мельче масштаб и наоборот.
Именованный (словесный) масштаб — вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.
Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.
— в 1 сантиметре 5 километров (в 1 см 5 км).
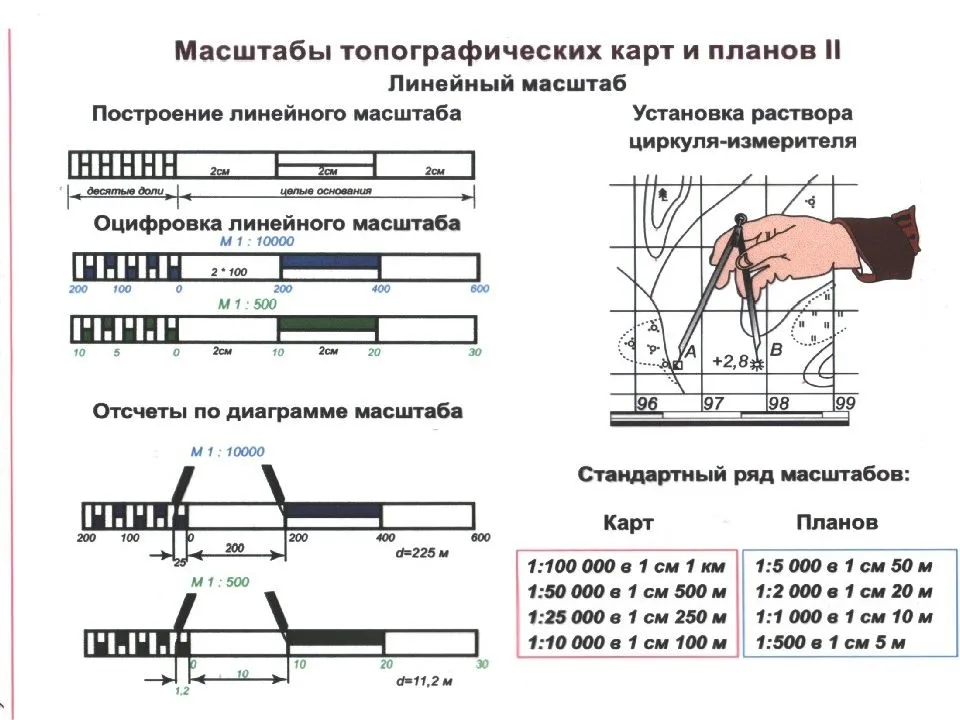
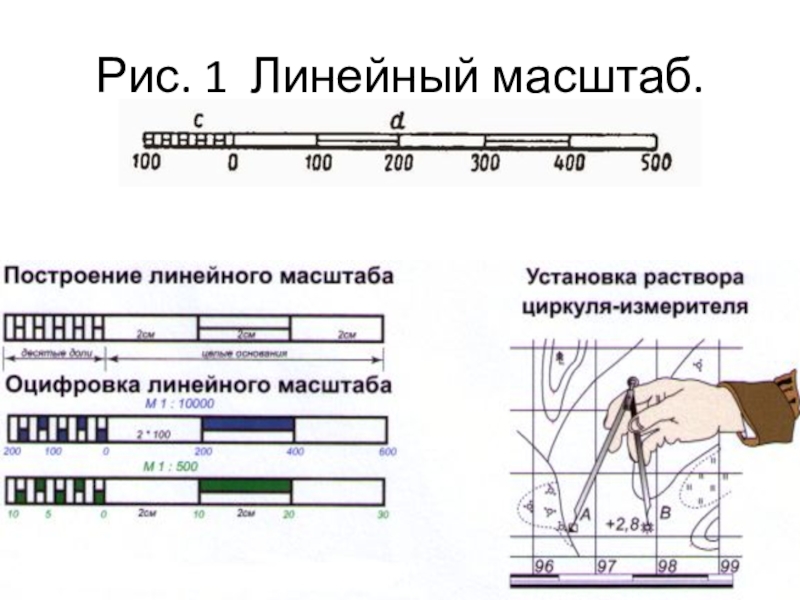
Линейный масштаб – это график, построенный для работы с данной картой по ее численному масштабу.
График имеет вид прямой, разделенной на равные отрезки ( основания). Слева от нуля графика оставляют один отрезок и делят его 10 частей.
Вправо от нуля в конце каждого отрезка надписывают числа метров местности соответствующие расстояниям концов от нуля.
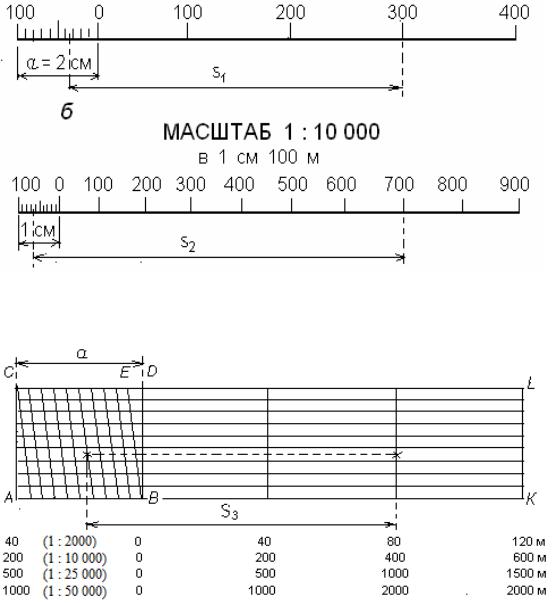
Рис.4 Линейный масштаб
Длина отрезка, который откладывают по линии при построении масштаба, называется его основанием.
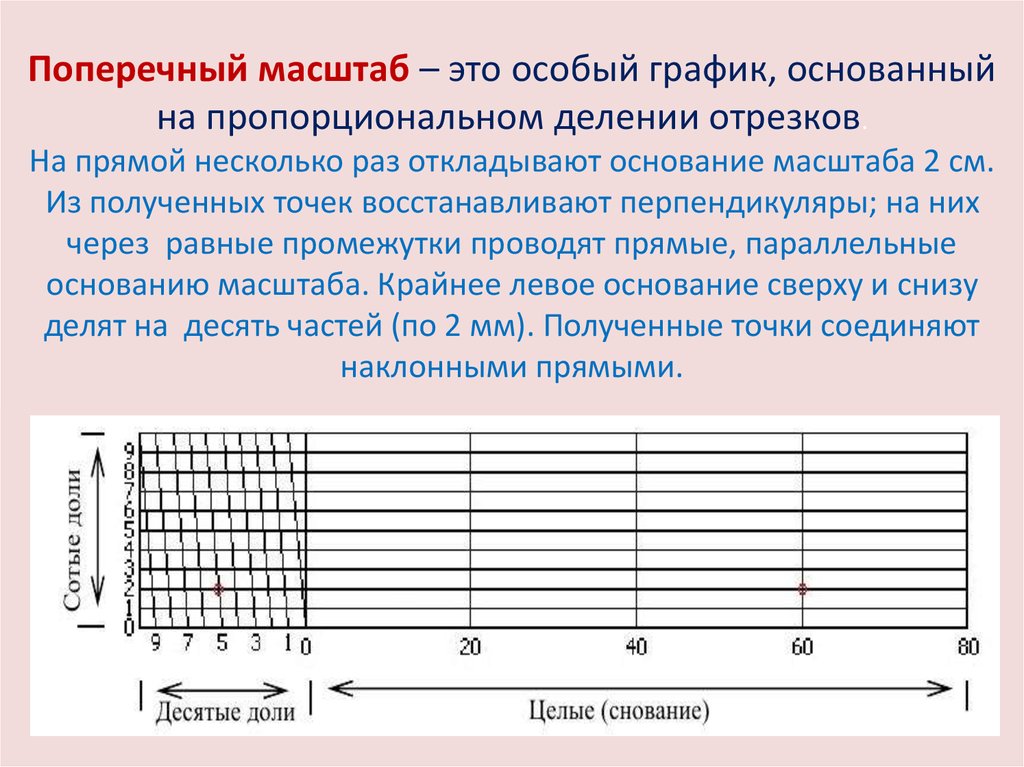
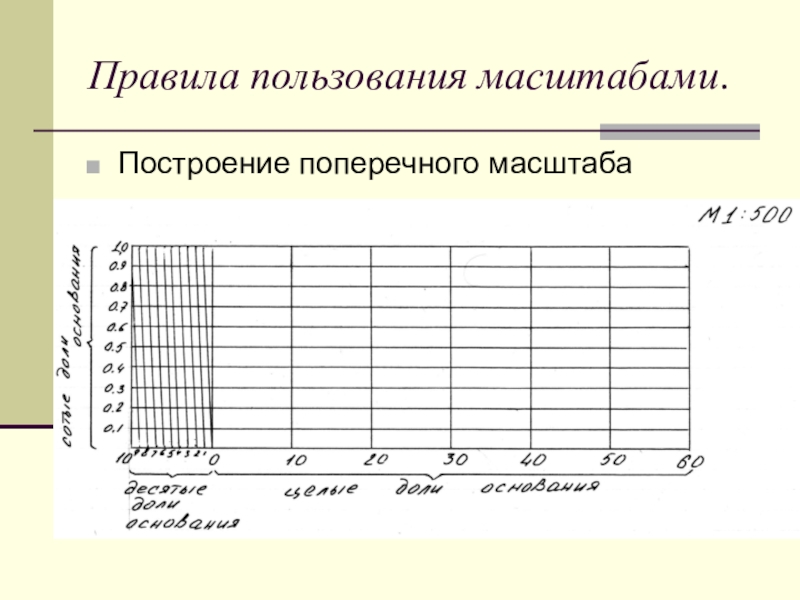
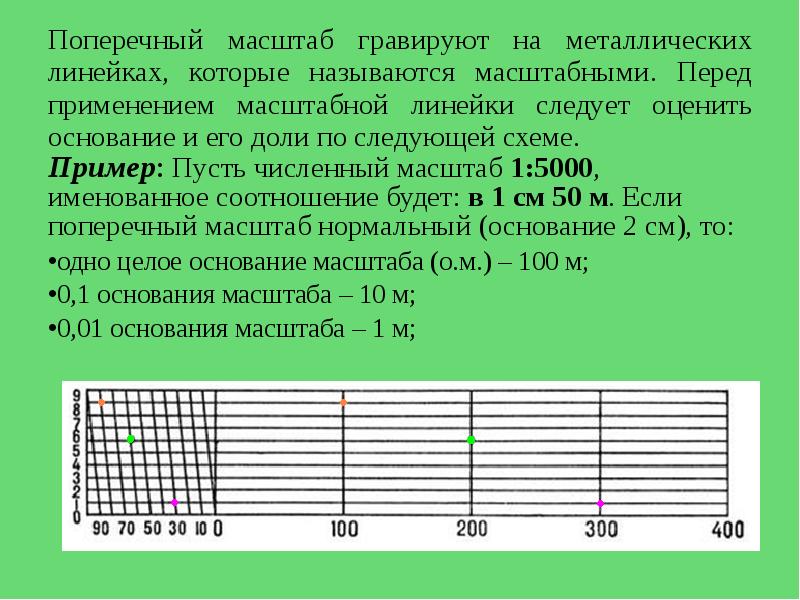
Поперечный масштаб строится для точности работы с планом или картой, при чем график является универсальным, т.е. имея этот график можно работать с любой картой или планом.
Наименьшее деление поперечного масштаба t = 0,01 основания.
Невооруженным глазом при нормальном зрении можно различать точки, удаленные друг от друга на 0,01 см или 0,1мм. Расстояние на местности, которое соответствует 0,01 см на плане, называется точностью масштаба.
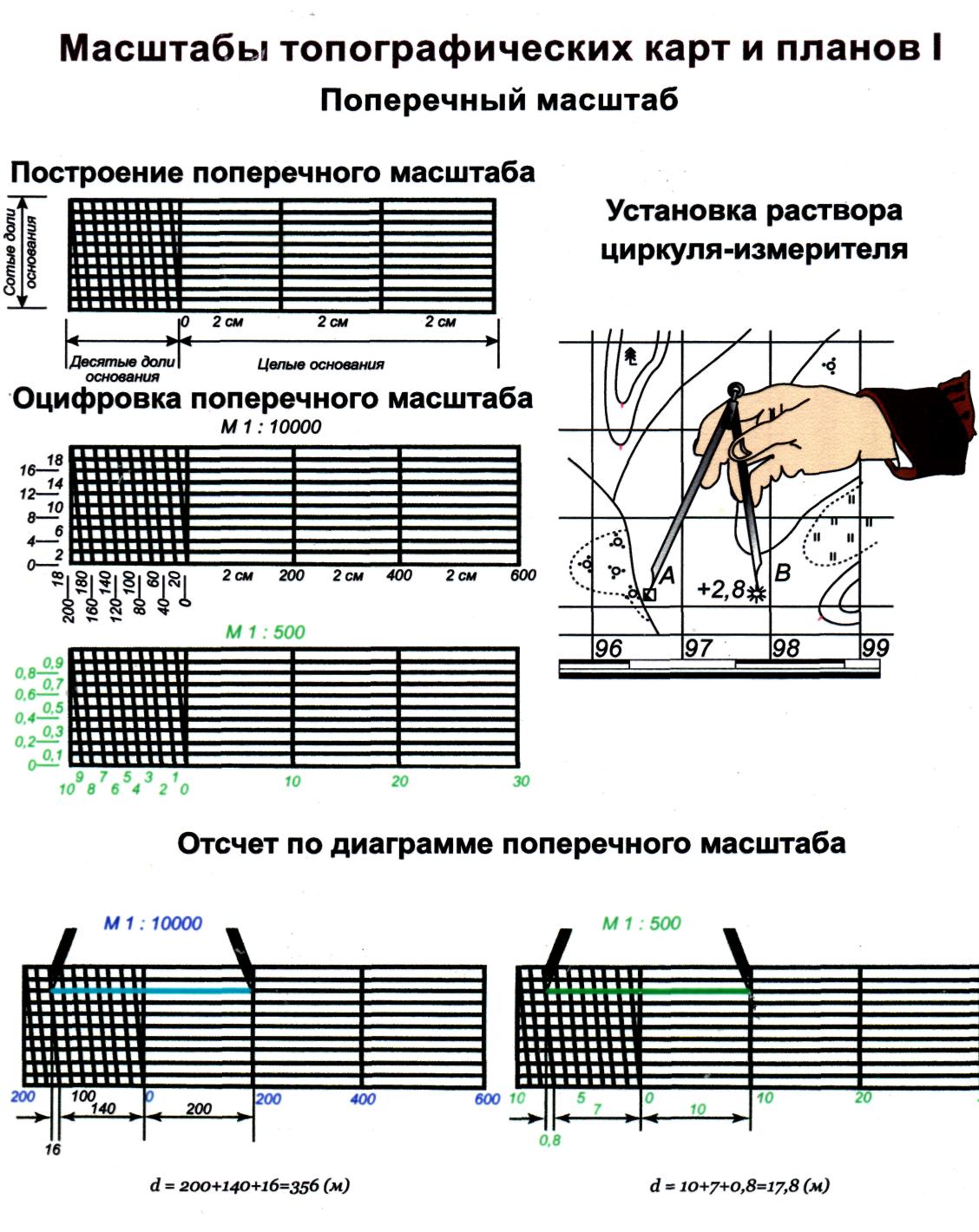
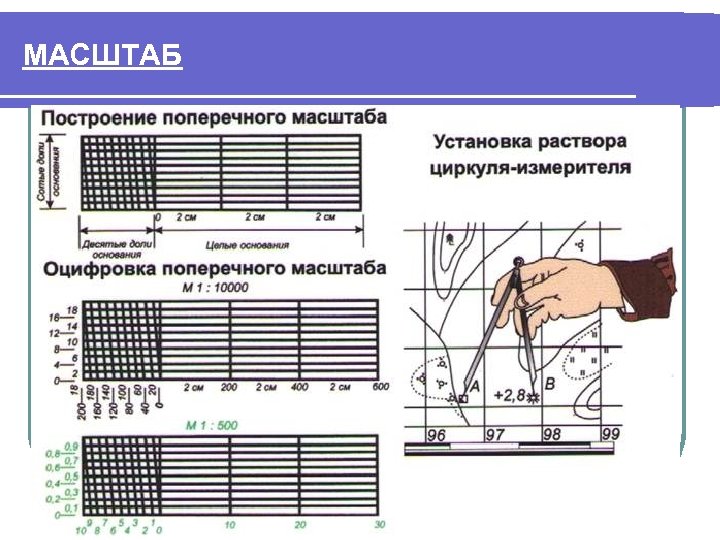
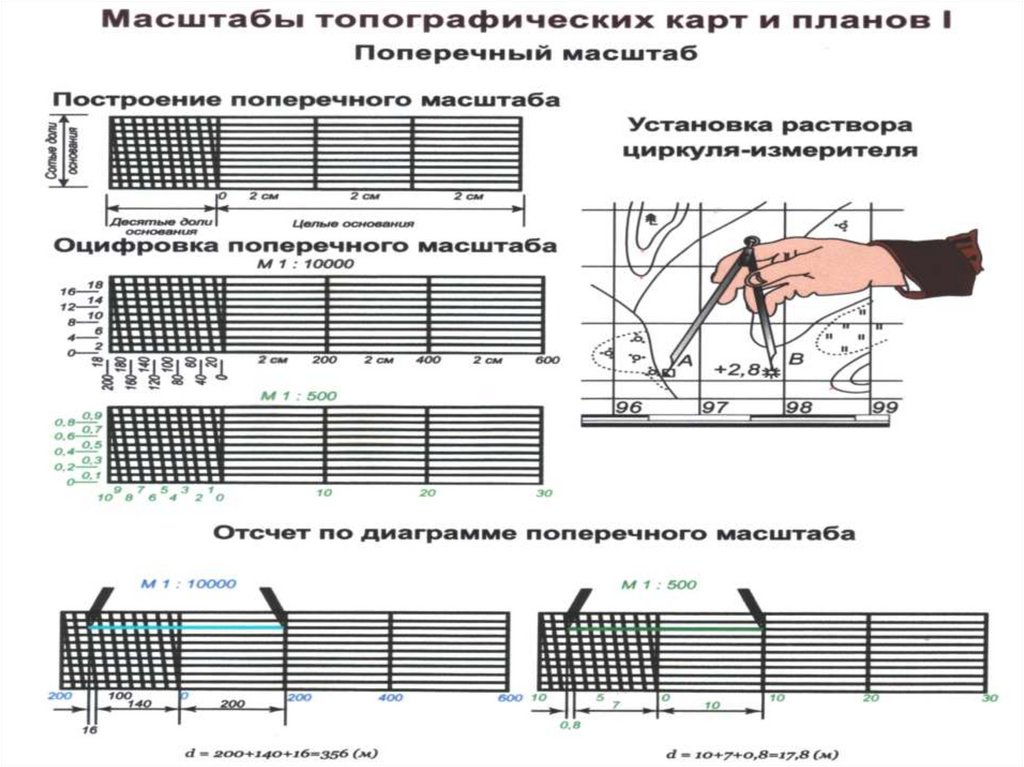
2. Теория и построение поперечного масштаба, его точность.
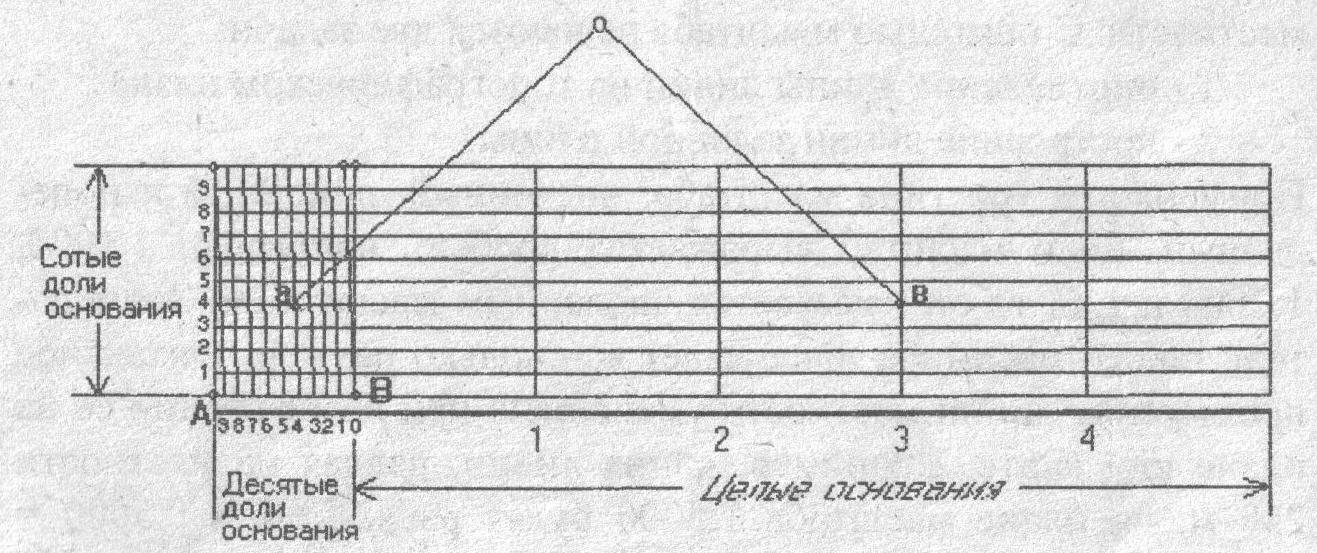
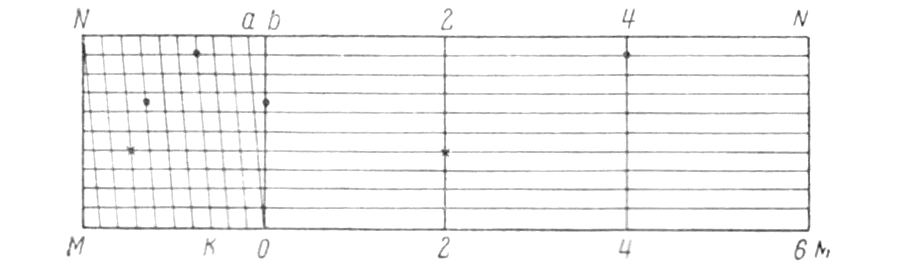
2.1 Построение поперечного масштаба. При пользовании простым линейным масштабом приходится мелкие доли в крайнем левом основании отсчитывать на глаз. Чтобы эти отсчеты были более точными и надежными, употребляют особых вид линейного масштаба, который называется поперечным. Для получения поперечного масштаба сначала выполняют на горизонтальной линии ММ построение простого линейного масштаба. Затем из концов отложенных оснований восстанавливают вверх от линии ММ перпендикуляры МN, ob, 2—2 и т. д.
Левые нижние и верхние основания Мо и Nb делят на 10 равных частей и точки деления соединяют, как показано на рисунке, косыми линиями, называемыми-трансверсалями.
Рис. 5 Поперечный масштаб
Полученный чертеж и называется поперечным масштабом. Из построения его следует, что расстояния между соседними трансверсалями по параллелям равны 0.1 ℓ. Расстояния же от перпендикуляра ob до первой трансверсали оа при переходе от параллели к параллели изменяются.
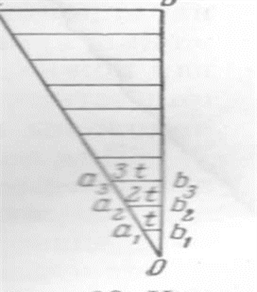
Изобразим треугольник abo в увеличенном виде (рис. 6) и обратим в нем внимание на расстояние a1b1=t , которое является наименьшим.
Из подобия прямоугольных треугольников a1b1 с1 и abo имеем:
t : ab = ob1: ob; t = ab*ob1/ob .
Здесь по построению ab =0,1 ℓ и оb1: оb=0,1; следовательно.
t =0,01ℓ,
Рис.6
т. е. наименьшее деление поперечного масштаба составляет 0,01 основания масштаба.
Из подобия треугольников a2b2о и abо, затем a3b3о и abо и т.д. аналогично получим:
a2b2=0.02l=2t a3b3=0.03l=3t
и т. д., т. е. при переходе вверх с параллели на соседнюю параллель расстояния от перпендикуляра оb до первой трансверсали увеличиваются на величину наименьшего деления. Очевидно, что точки пересечения любой трансверсали с параллелями при переходе с параллели на параллель вверх сдвигаются влево от перпендикулярного положения на ту же величину. Описанный поперечный масштаб называется сотенным или нормальным.
Теоретически при построении поперечного масштаба можно как первое левое основание, так и расстояние вверх по перпендикулярам делить не обязательно на 10, а на какое угодно другое число равных частей. Разница будет только в том, что наименьшее деление его будет составлять другую долю от основания. Обозначим в общем виде число частей основания буквой т и число частей, отложенных по перпендикуляру вверх, буквой п. В таком случае наименьшее деление выразится формулой:
t=l/mn
2.2 Пользование поперечным масштабом.
Для практического использования на заводах изготовляют специальные металлические масштабные линейки, на которых с помощью особых делительных машин гравируют нормальные поперечные масштабы с основанием 2 см. Подписи на них дают в сантиметрах. На рисунке 5 изображена левая часть такого масштаба. В конце правой части гравируют также пятидесятенный масштаб, у которого основание разделено на 5 равных частей, так что по нему можно непосредственно учитывать 0,02 основания, т. е. 0,04 см.
Пользование поперечным масштабом непосредственно вытекает из его теории. Пусть, например, требуется взять в раствор измерителя 4,78 см. На нижней горизонтальной линии ММ непосредственно можно взять расстояние 4.60 см (расстояние 4 — к). Для заданного отсчета это расстояние нужно увеличить на 0,18 см, для чего левая ножка измерителя должна быть передвинута по трансверсали к вверх на девятую параллель (так как 0,18 =0,02*9). На этой параллели ножки измерителя устанавливают в точки, отмеченные на рисунке кружками. Крестиками на 4-й параллели отмечено расстояние 3,48 см. Практически ножки измерителя можно устанавливать на глаз посредине между параллелями и таким образом учитывать сотые доли сантиметра. Например, если ножки поставить посредине между 6-й и 7-й параллелями, как отмечено на рисунке точками, то взятое расстояние будет 1.33 см.
Для измерения линии, начерченной на бумаге, ее берут в раствор измерителя и прикладывают его к масштабу так, чтобы левая ножка находилась в пределах крайнего левого основания, а правая все время точно совмещалась с каким-либо перпендикуляром правее нуля. Передвигая в этом положении измеритель вверх, добиваются, чтобы левая ножка точно совместилась с пересечением ближайшей левой от нее трансверсали с некоторой параллелью, на которой должна находиться и правая ножка. В этом положении производят отсчеты: по перпендикуляру, с которым совмещена правая ножка, целые сантиметры, по нижним делениям крайнего левого основания четные десятые доли сантиметра и по номеру параллели, на которой расположены ножки измерителя, четные сотые доли сантиметра.
Для перехода от длин линий на местности к длинам их на плане и обратно поперечные масштабы подписываются, как было указано для простых линейных масштабов. Если при переходах пользоваться масштабной линейкой, то предварительно следует установить значения его делений в соответствии с численным масштабом. Например, для масштаба 1 : 25 000 основание составит 500 м, деления крайнего левого основания будут по 50м и наименьшее деление масштаба — 5 м.
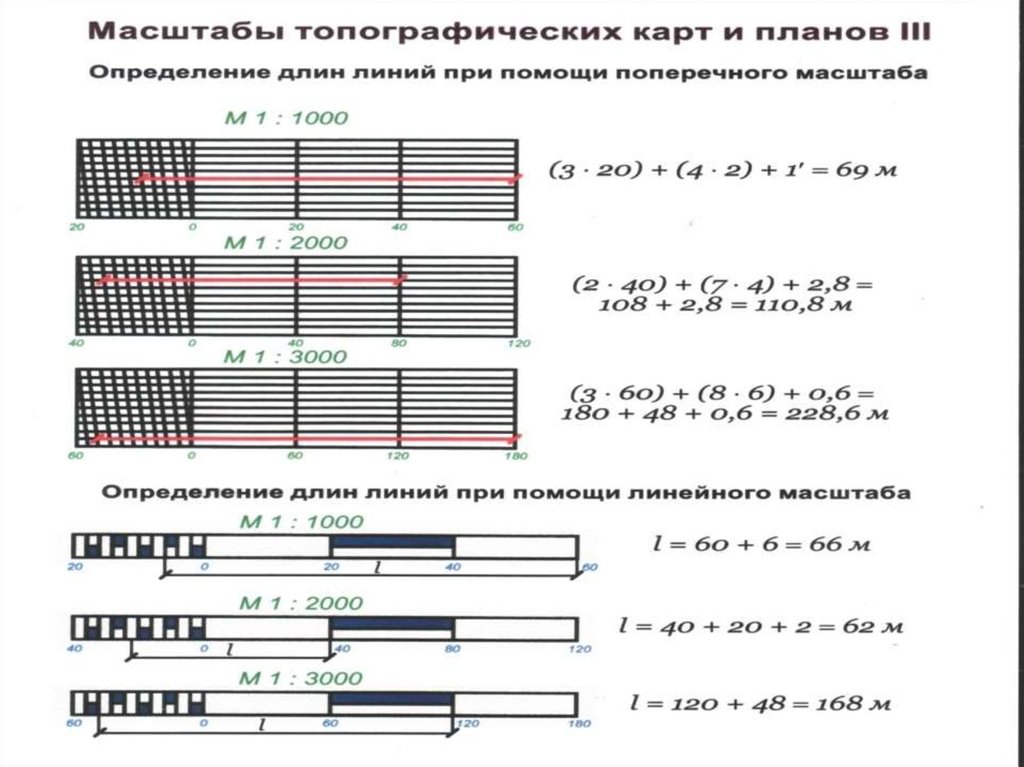
3. Способы определения длин линий, измеренных на плане
Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.
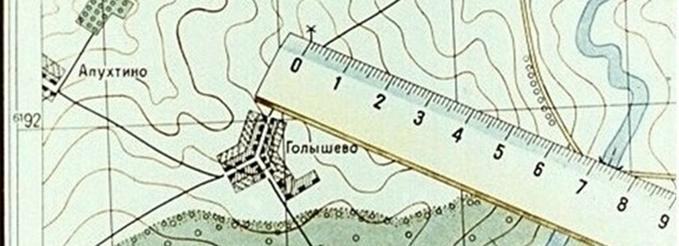
Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 7); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).
Рис. 7. Определение по карте расстояние между точками местности с помощью линейки.
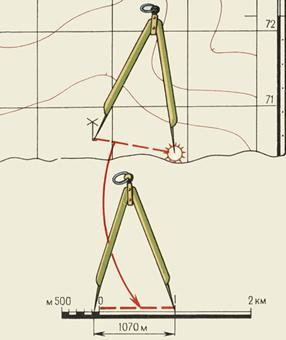
Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 8). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.
Рис. 8. Измерение на карте расстояний циркулем-измерителем по линейному масштабу
Рис. 9. Измерение на карте расстояний циркулем-измерителем по извилистым линиям
Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя.
В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 7).
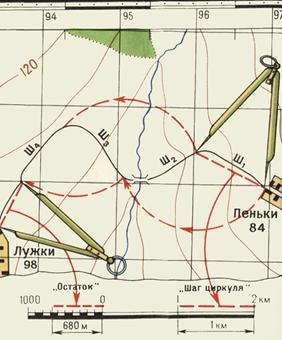
Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.
Таким же способом измеряют расстояния по извилистым линиям (рис. 9). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.
Рис. 10. Измерения расстояния курвиметром
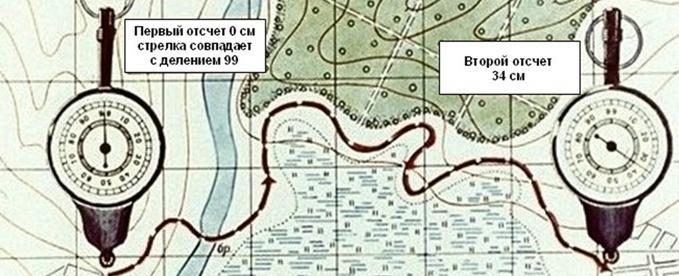
Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 10), который особенно удобен для измерения извилистых и длинных линий.
В приборе имеется колесико, которое соединено системой передач со стрелкой.
При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)
Точность измерения расстояний по карте. Поправки на расстояние за наклон и извилистость линий.
Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.
Наиболее точно определить расстояние по карте можно по прямой линии.
При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0,7-1 мм в масштабе карты, что составляет для карты масштаба 1:25000 — 17,5-25 м, масштаба 1:50000 – 35-50 м, масштаба 1:100000 – 70-100 м.
В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость.
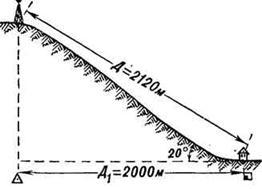
Например, При крутизне ската 20° (рис. 11) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше.
Подсчитано, что при угле наклона (крутизне ската) 20° полученный результат измерения расстояния по карте следует увеличивать на 6% (на 100 м прибавлять 6 м), при угле наклона 30° — на 15%, а при угле 40° — на 23%.
Рис. 11. Проекция длины ската на плоскость (карту)
При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний.
Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах.
Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице.
Простейшие способы измерения площадей по карте.
Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки, имеющейся на карте. Каждому квадрату сетки карт масштабов 1:10000 — 1:50000 на местности соответствует 1 км2 , квадрату сетки карт масштаба 1:100000 — 4 км2, квадрату сетки карт масштаба 1:200000 — 16 км2.
Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений).
Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта.
По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников {в гектарах ) указаны на линейке для каждого масштаба карты.
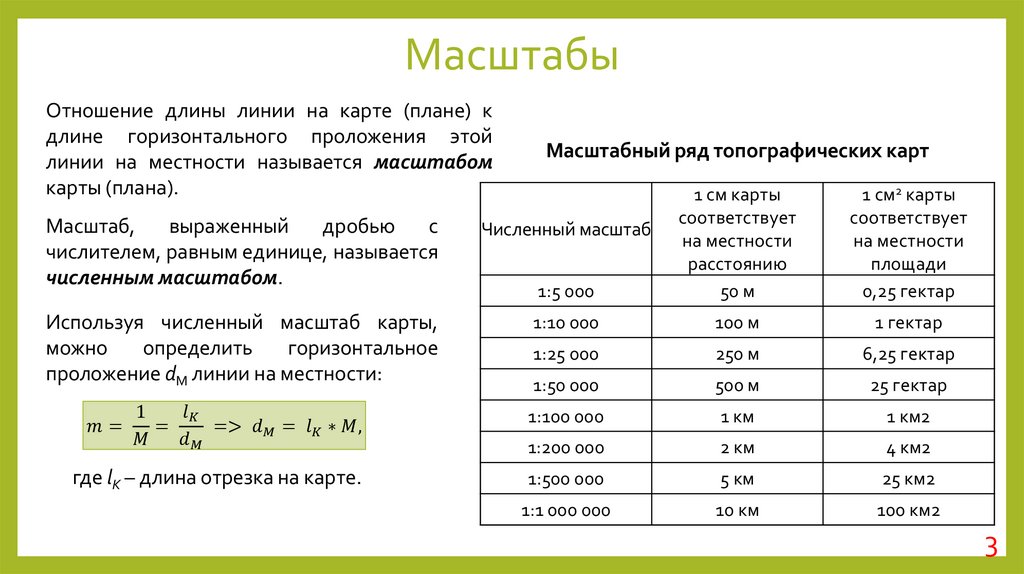
Масштабы топографических карт
|
Численный масштаб карты |
Название карты |
1 см на карте соответствует на местности расстоянию |
1 см2на карте соответствует на местности площади |
|
1:5 000 1:10 000 1:25 000 1:50 000 1:1100 000 1:200 000 1:500 000 1:1 000 000 |
Пятитысячная Десятитысячная Двадцатипятитысячная Пятидесятитысячная Стотысячная Двухсоттысячная Пятисоттысячная, или полумиллионная Миллионная |
50 м 100 м 250 м 500 м 1 км 2 км 5 км 10 км |
0,25 га 1 га 6,25 га 25 га 1 км2 4 км2 25 км2 100 км2 |
Ниже приведены численые маштабы карт и соответствующие им именованые масштабы:
-
Масштаб 1: 100 000
1 мм на карте — 100 м (0,1 км) на местности
1 см на карте — 1000 м (1 км) на местности
10 см на карте — 10000 м (10 км) на местности
-
Масштаб 1:10000
1 мм на карте – 10 м (0,01 км) на местности
1 см на карте — 100 м (0,1 км) на местности
10 см на карте — 1000м (1 км) на местности
-
Масштаб 1:5000
1 мм на карте – 5 м (0,005 км) на местности
1 см на карте — 50 м (0,05 км) на местности
10 см на карте – 500 м (0,5 км) на местности
-
Масштаб 1:2000
1 мм на карте – 2 м (0,002 км) на местности
1 см на карте – 20 м (0,02 км) на местности
10 см на карте – 200 м (0,2 км) на местности
-
Масштаб 1:1000
1 мм на карте – 100 см (1 м) на местности
1 см на карте – 1000см (10 м) на местности
10 см на карте – 100 м на местности
-
Масштаб 1:500
1 мм на карте – 50 см (0,5 метра) на местности
1 см на карте – 5 м на местности
10 см на карте – 50 м на местности
-
Масштаб 1:200
1 мм на карте –0,2 м (20 см) на местности
1 см на карте – 2 м (200 см) на местности
10 см на карте – 20 м (0,2 км) на местности
-
Масштаб 1:100
1 мм на карте – 0,1 м (10 см) на местности
1 см на карте – 1 м (100 см) на местности
10 см на карте – 10м (0,01 км) на местности
Пример 1.
Переведите численный масштаб карты в именованный:
а) 1 : 200 000
б) 1 : 10 000 000
в) 1 : 25 000
Решение:
Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.
Например, в масштабе 1 : 500 000 в знаменателе после цифры 5 находится пять нулей.
Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.
Пример для масштаба 1 : 500 000
В знаменателе после цифры — пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.
Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.
Если, например, в знаменателе масштаба 1 : 10 000 закроем два нуля, получим:
в 1 см — 100 м.
Ответы:
а) в 1 см — 2 км;
б) в 1 см — 100 км;
в) в 1 см — 250 м.
Используйте линейку, накладывайте на карты для облегчения измерения расстояний.
Пример 2.
Переведите именованный масштаб в численный:
а) в 1 см — 500 м
б) в 1 см — 10 км
в) в 1 см — 250 км
Решение:
Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.
Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.
Например, для именованного масштаба в 1 см — 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1 : 10 000.
Для масштаба в 1 см — 5 км приписываем к пятерке пять нулей и получаем: 1 : 500 000.
Ответы:
а) 1 : 50 000;
б) 1 : 1 000 000;
в) 1 : 25 000 000.
Карты в зависимости от масштабов условно подразделяют на следующие типы:
▪ топографические планы — 1:400 — 1:5 000;
▪ крупномасштабные топографические карты — 1:10 000 — 1:100 000;
▪ среднемасштабные топографические карты — от 1:200 000 — 1:1 000 000;
▪ мелкомасштабные топографические карты — менее 1:1 000 000.
Библиографическое описание:
Гакаев, Р. А. Точность и погрешность измерений на картах при выполнении практических работ по топографии / Р. А. Гакаев. — Текст : непосредственный // Педагогика высшей школы. — 2016. — № 1 (4). — С. 48-53. — URL: https://moluch.ru/th/3/archive/21/817/ (дата обращения: 22.09.2023).
Суть практических работ по топографии заключается в том, что студенты, изучив теоретический материал, выполняют практические задания по формированию соответствующих умений и навыков работы с топографической картой. Часть практических работ выполняются индивидуальными заданиями: ориентирование, определение направлений движения по заданным азимутам, составление плана местности, определение относительной высоты холма, скорости течения реки, измерение длин линий по прямой и кривой и др. Практические работы с топографическими картами формируют навыки сложного чтения карты, позволяют, в будущем, анализировать географические явления, составлять физико-географические и экономико-географические характеристики отдельных участков или районов, давать оценку территории по заданным критериям.
Топографические карты являются общегосударственными, предназначаются для детального изучения и оценки местности, ориентирования на ней, для измерений и расчетов при разработке и проведении мероприятий различного значения, обучения, а также для других видов научно-исследовательских работ, требующих использования точных данных об объектах местности. На них с математической точностью и одинаковой полнотой изображаются все видимые объекты территории с четким сохранением их планового положения. Географическое содержание карты ограничено внутренней рамкой, которая является элементом ее математической основы. Все, что расположено за ней на ее полях, называется зарамочным содержанием. Зарамочное содержание топографических карт всех масштабов стандартно. Оно способствует быстрому выполнению по карте различных измерений и вычислений, повышающих ценность ее использования. На топографических картах местные предметы изображаются условными общепринятыми знаками, а рельеф — горизонталями.
По топографическим картам изучают и оценивают местность, решают различные расчетные задачи, связанные с определением расстояний, углов и площадей, высот, превышений и взаимной видимости точек местности, крутизны и видов скатов и т. п.
Целью практических занятий по топографии — освоение главных положений теории и возможность формирования у студентов навыков и умений работы с топографическими картами. Задания сопровождаются подробными указаниями по его выполнению, а наиболее сложные вопросы рассматриваются на однотипных с заданием примерах. При работе с топографической картой у студентов формируется картографический образ — основа картографической информации, которая предназначена для восприятия в виде образных картографических представлений о географических объектах, рельефе, речной сети, пространственных моделей изучаемых территорий. Картографический образ изучаемых территорий создается всем многообразием условных знаков: их сочетанием и формой, величиной, ориентировкой, цветом, оттенком цвета, внутренней структурой. Для его формирования важным является пространственная комбинация условных знаков, их взаимное расположение, положение относительно пространственных координат, взаимная упорядоченность, объединение или совмещение и другие их отношения. [1, 2].
Определяя расстояние по карте между точками местности (предметами, объектами), пользуясь численным масштабом, измеряют расстояние между этими объектами в сантиметрах и умножают полученное число на величину масштаба. Для примера, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 1); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).
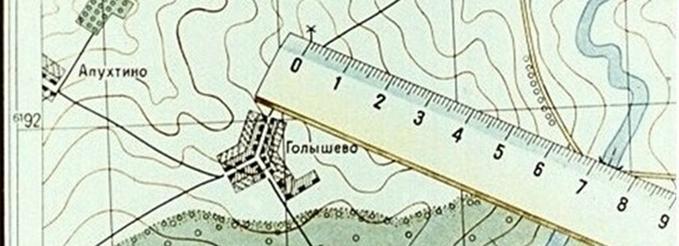
Рис. 1. Определение расстояние между точками местности с помощью линейки
Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 2, 3). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах.
Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя. В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом. Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.
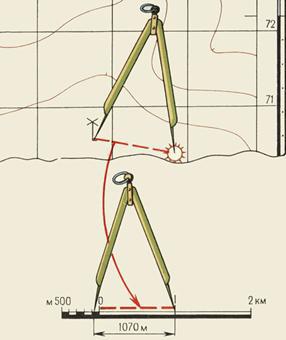
Рис. 2. Измерение на карте расстояний циркулем-измерителем по линейному масштабу
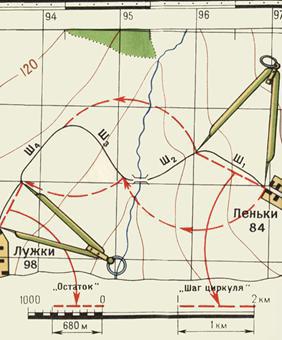
Рис. 3. Измерение на карте расстояний циркулем-измерителем по извилистым линиям
Таким же способом измеряют расстояния по извилистым линиям. В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.
Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 4), который особенно удобен для измерения извилистых и длинных линий. В приборе имеется колесико, которое соединено системой передач со стрелкой [2].
При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба.
Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов. Наиболее точно определить расстояние по карте можно по прямой линии.
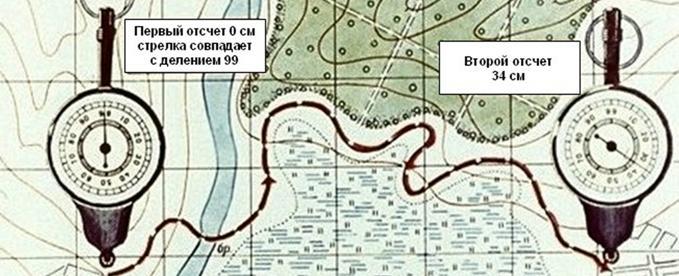
Рис. 4. Измерения расстояния при помощи курвиметра
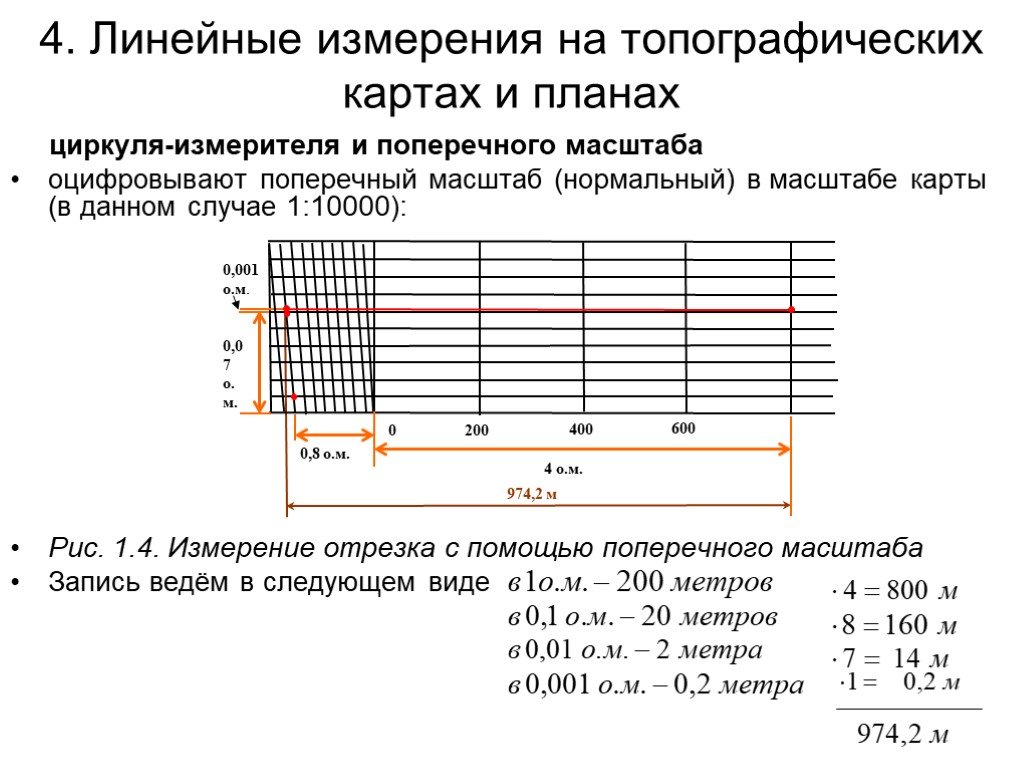
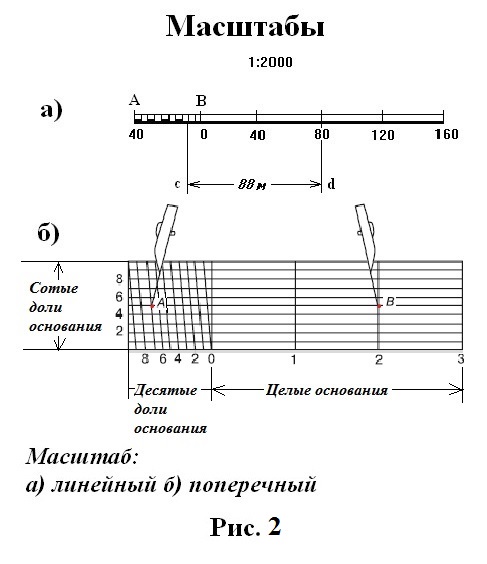
Для более точного построения и измерения отрезков пользуются поперечными масштабами. Поперечный масштаб позволяет существенно повысить точность графических работ на планах и картах. Достигается это за счет разделения коротких отрезков линейного масштаба на несколько (обычно на 10) более мелких частей с помощью простых геометрических построений (рис. 5).
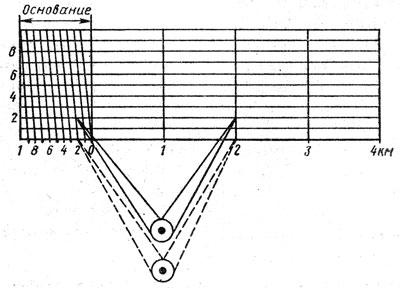
Рис. 5. Определение расстояния с помощью поперечного масштаба
Каждая такая часть называется основанием масштаба. Крайнее левое основание в верхней и нижней частях поперечного масштаба делится на десять равных частей. Концы этих десятых долей основания соединяются между собой прямыми, отсекающими на горизонтальных линиях сотые доли основания. Таким образом, на поперечном масштабе измеряемое расстояние может быть выражено в целых, десятых и сотых долях основания масштаба. А поскольку известна величина основания масштаба (2 см), то можно легко определить «цену» основания в метрах. Так, для масштаба 1:25000 «цена» основания поперечного масштаба составит 500 м, его десятая доля — 50 м, а одна сотая часть — 5 м. Кроме того, на глаз можно взять еще и половину «сотни» — 2,5 м. Циркулем измеряют расстояние между двумя предметами на карте. Затем прикладывают циркуль к нижней линии поперечного масштаба и отсчитывают расстояние, которое получается — 2200 м с излишком. Для определения величины этого излишка циркуль передвигают параллельно нижней линии вверх До пересечения с диагональю и считывают окончательную величину расстояния — 2220 м. [3].
При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0,7–1 мм в масштабе карты, что составляет для карты масштаба 1:25000–17,5–25 м, масштаба 1:50000–35–50 м, масштаба 1:100000–70–100 м. В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость. Например, при крутизне ската 20° (рис. 6) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше.
Подсчитано, что при угле наклона (крутизне ската) 20° полученный результат измерения расстояния по карте следует увеличивать на 6 % (на 100 м прибавлять 6 м), при угле наклона 30° — на 15 %, а при угле 40° — на 23 %.
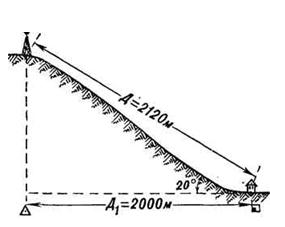
Рис. 6. Проецирование длины ската на карту
При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний. Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах. Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице.
Таблица 1
|
Характер местности |
Коэффициент увеличения длины маршрута, измеренного по карте масштаба |
||
|
1: 50000 |
1: 100000 |
1: 200000 |
|
|
Горная (сильнопересеченная) |
1,15 |
1,20 |
1,25 |
|
Холмистая (среднепересеченная) |
1,05 |
1,10 |
1,15 |
|
Равнинная (слабопересеченная) |
1,00 |
1,00 |
1,05 |
Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки, имеющейся на карте. Каждому квадрату сетки карт масштабов 1:10000–1:50000 на местности соответствует 1 км2, квадрату сетки карт масштаба 1:100000–4 км2, квадрату сетки карт масштаба 1:200000–16 км2. Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика, с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений).
Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта. По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.
В процессе измерительных работ на топографических картах формируются умения читать план местности, простого и сложного чтения топографической карты, с большой точностью определять азимут на заданный объект, переходить од одних координат к другим, с высокой точностью проводить измерения расстояний различными способами и др.
Литература:
- Гакаев Р. А., Хадаев Т. Ш. Формирование географических и исторических знаний учащихся комбинированным использованием картографического материала [Текст] // Педагогическое мастерство: материалы VI междунар. науч. конф. (г. Москва, июнь 2015 г.). — М.: Буки-Веди, 2015. — с. 5–8.
- Николаев А. С. Военная топография. Москва. Воениздат. 1977.
- Сычугова О. В. и др. Масштабы карт и планов. Решение задач по топографической карте. Екатеринбург. 2008 г.
Основные термины (генерируются автоматически): расстояние, поперечный масштаб, линейный масштаб, масштаб карты, карт масштаба, линия, топографическая карта, численный масштаб, зарамочное содержание, картографический образ.
Похожие статьи
Визуальный анализ топографических карт различных…
карт масштаба, визуальный анализ, земная поверхность, топографическая карта, инженерное оборудование местности, оценка местности, масштаб, географическая среда, географический ландшафт, дорожная сеть.
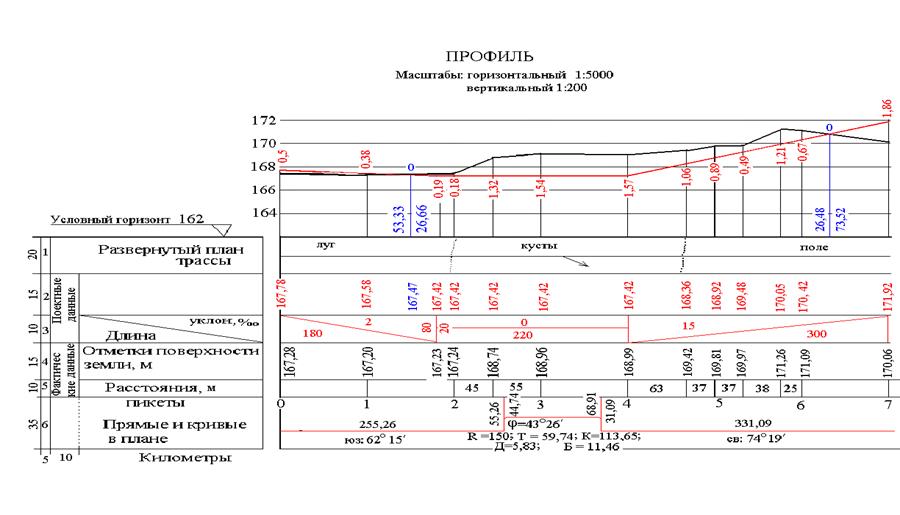
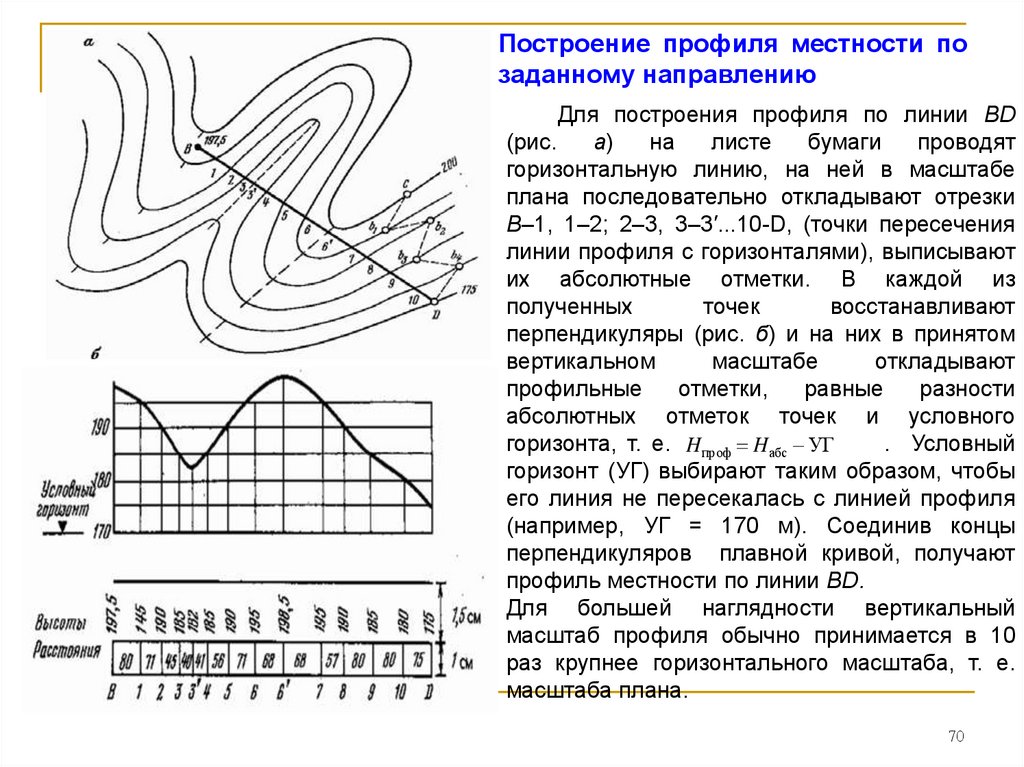
Изображение рельефа горизонталями и построение профиля по…
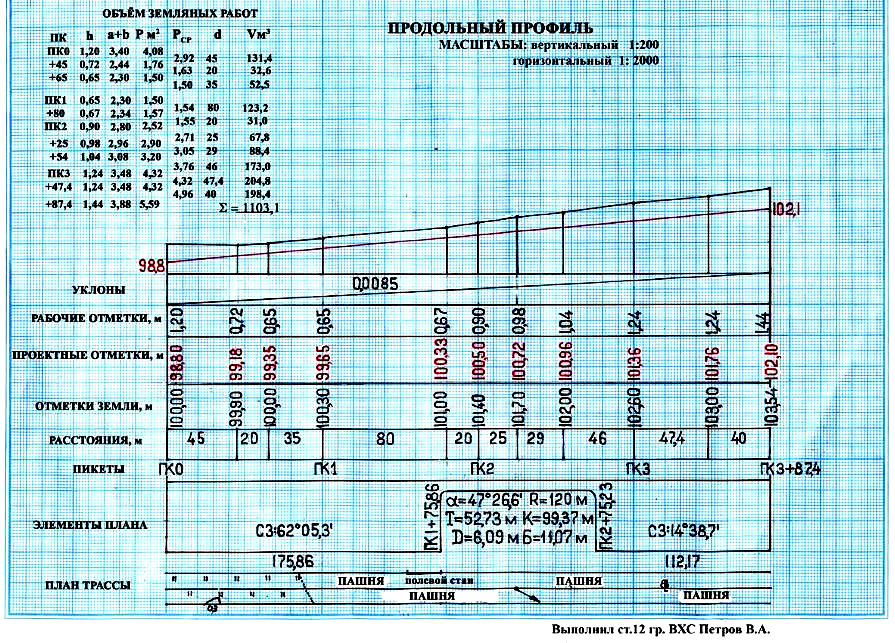
Обычно горизонтальный масштаб профиля равен масштабу топографической карты, по которой он строится, а вертикальный масштаб принимают в 10 раз крупнее горизонтального. Например, масштаб карты 1:50 000.
Составление условных обозначений для карт при выполнении…
Объекты, очертания которых могут быть изображены в масштабе карты с сохранением истинных пропорций, изображают контурными или масштабными знаками. Масштабный условный знак состоит из внешней границы объекта…
Визуальный язык картографии: эволюция графического образа…
Визуальный анализ топографических карт различных масштабов…
Электронная карта — эта цифровая картографическая модель; визуализированная или подготовленная к визуализации на экране средства отображения информации в специальной системе условных…
Снижение погрешности гамма-спектрометрических измерений…
Зарамочное содержание топографических карт всех масштабов стандартно. Рис. 1. Определение расстояние между точками местности с помощью линейки.
Изменение ширины координатной зоны проекции Гаусса…
Рис. 1. График масштаба длин линий.
Таким образом, использование системы координат Гаусса — Крюгера не ограничивается традиционной разбивкой земного эллипсоида на 3-х, или 6-градусные зоны.
Методы картографического исследования и этапы их…
На картах крупных и средних масштабов длины прямых и ломаных линий измеряется с помощью циркуля-измерителя и поперечного масштаба с точностью, близкой к предельной для данной карты.
Современные геодезические работы при строительстве дорог
горизонталь, вертикальный масштаб, высота сечения, топографическая карта, высота, линия, изображение рельефа, условный горизонт, земная…
Этапы и проблемы создания электронной карты
Электронная карта — эта цифровая картографическая модель; визуализированная или подготовленная к визуализации на экране средства отображения информации в специальной системе условных знаков, содержание которой соответствует содержанию карты…