From Wikipedia, the free encyclopedia
A faulty generalization is an informal fallacy wherein a conclusion is drawn about all or many instances of a phenomenon on the basis of one or a few instances of that phenomenon. It is similar to a proof by example in mathematics.[1] It is an example of jumping to conclusions.[2] For example, one may generalize about all people or all members of a group from what one knows about just one or a few people:
- If one meets a rude person from a given country X, one may suspect that most people in country X are rude.
- If one sees only white swans, one may suspect that all swans are white.
Expressed in more precise philosophical language, a fallacy of defective induction is a conclusion that has been made on the basis of weak premises, or one which is not justified by sufficient or unbiased evidence.[3] Unlike fallacies of relevance, in fallacies of defective induction, the premises are related to the conclusions, yet only weakly buttress the conclusions, hence a faulty generalization is produced. The essence of this inductive fallacy lies on the overestimation of an argument based on insufficiently-large samples under an implied margin or error.[2]
Logic[edit]
A faulty generalization often follows the following format:
- The proportion Q of the sample has attribute A.
- Therefore, the proportion Q of the population has attribute A.
Such a generalization proceeds from a premise about a sample (often unrepresentative or biased), to a conclusion about the population itself.[3]
Faulty generalization is also a mode of thinking that takes the experiences of one person or one group, and incorrectly extends it to another.
Inductive fallacies[edit]
- Hasty generalization is the fallacy of examining just one or very few examples or studying a single case and generalizing that to be representative of the whole class of objects or phenomena.
- The opposite, slothful induction, is the fallacy of denying the logical conclusion of an inductive argument, dismissing an effect as «just a coincidence» when it is very likely not.
- The overwhelming exception is related to the hasty generalization but works from the other end. It is a generalization that is accurate, but tags on a qualification that eliminates enough cases (as exceptions); that what remains is much less impressive than what the original statement might have led one to assume.
- Fallacy of unrepresentative samples is a fallacy where a conclusion is drawn using samples that are unrepresentative or biased.[4]
- Misleading vividness is a kind of hasty generalization that appeals to the senses.
- Statistical special pleading occurs when the interpretation of the relevant statistic is «massaged» by looking for ways to reclassify or requantify data from one portion of results, but not applying the same scrutiny to other categories.[5]
- This can be considered a special case of the fallacy of composition, where the item under discussion is a group, and the fallacy is what can be derived from knowledge of part of the item.
Hasty generalization[edit]
«Over-extension» redirects here. For the error common in language-learning, see Errors in early word use.
Hasty generalization is an informal fallacy of faulty generalization, which involves reaching an inductive generalization based on insufficient evidence[3]—essentially making a rushed conclusion without considering all of the variables or enough evidence. In statistics, it may involve basing broad conclusions regarding a statistical survey from a small sample group that fails to sufficiently represent an entire population.[1][6][7] Its opposite fallacy is called slothful induction, which consists of denying a reasonable conclusion of an inductive argument (e.g. «it was just a coincidence»).
Examples[edit]
Hasty generalization usually follows the pattern:
- X is true for A.
- X is true for B.
- Therefore, X is true for C, D, E, etc.
For example, if a person travels through a town for the first time and sees 10 people, all of them children, they may erroneously conclude that there are no adult residents in the town.
Alternatively, a person might look at a number line, and notice that the number 1 is a square number; 3 is a prime number, 5 is a prime number, and 7 is a prime number; 9 is a square number; 11 is a prime number, and 13 is a prime number. From these observations, the person might claim that all odd numbers are either prime or square, while in reality, 15 is an example that disproves the claim.
Alternative names[edit]
The fallacy is also known as:
- Black Swan fallacy
- Illicit generalization
- Fallacy of insufficient sample
- Generalization from the particular
- Leaping to a conclusion
- Blanket statement
- Hasty induction
- Law of small numbers
- Unrepresentative sample
- Secundum quid
When referring to a generalization made from a single example, the terms «fallacy of the lonely fact»,[8] or the «fallacy of proof by example», might be used.[9]
When evidence is intentionally excluded to bias the result, the fallacy of exclusion—a form of selection bias—is said to be involved.[10]
See also[edit]
- Accident (fallacy) – Informal fallacy
- Association fallacy – Informal inductive fallacy
- Availability bias – Heuristic bias that if something can be recalled, it must be important
- Blind men and an elephant – Parable illustrating ontologic reasoning
- Cherry picking (fallacy) – Fallacy of incomplete evidence
- Cognitive distortion – Exaggerated or irrational thought pattern
- Confirmation bias – Bias confirming existing attitudes
- Converse accident – Informal fallacy
- Fallacy of composition – Fallacy of inferring on the whole from a part
- Fallacy of the single cause – Assumption of a single cause where multiple factors may be necessary
- Generalization (logic) – rule in predicate logic
- Generalization error – Measure of algorithm accuracy
- Hypercorrection – Non-standard language usage from the over-application of a perceived prescriptive rule
- Package-deal fallacy – Logical fallacy
- Pooh-pooh – Fallacy in informal logic
- Problem of induction – Question of whether inductive reasoning leads to definitive knowledge
- Statistical significance – Concept in inferential statistics
- Stereotype – Generalized but fixed and oversimplified image or idea of a particular type of person or thing
- Straw man – Form of argument and informal fallacy
- Syllogism – Type of logical argument that applies deductive reasoning
References[edit]
- ^ a b Bennett, Bo. «Hasty Generalization». logicallyfallacious.com. Retrieved 2019-12-05.
- ^ a b Dowden, Bradley. «Hasty Generalization». Internet Encyclopedia of Philosophy. Retrieved 2019-12-05.
- ^ a b c Nordquist, Richard. «Logical Fallacies: Examples of Hasty Generalizations». ThoughtCo. Retrieved 2019-12-05.
- ^ Dowden, Bradley. «Fallacies — Unrepresentative Sample». Internet Encyclopedia of Philosophy. Retrieved 2019-12-05.
- ^ Fischer, D. H. (1970), Historians’ Fallacies: Toward A Logic of Historical Thought, Harper torchbooks (first ed.), New York: HarperCollins, pp. 110–113, ISBN 978-0-06-131545-9, OCLC 185446787
- ^ «Fallacy: Hasty Generalization (Nizkor Project)». Archived from the original on 2008-12-17. Retrieved 2008-10-01.
- ^ «Fallacy». www.ditext.com. Retrieved 2019-12-05.
- ^ Fischer, David Hackett (1970). Historians’ Fallacies: Toward a Logic of Historical Thought. HarperCollins. pp. 109–110. ISBN 978-0-06-131545-9.
- ^ Marchant, Jamie. «Logical Fallacies». Archived from the original on 2012-06-30. Retrieved 2011-04-26.
- ^ «Unrepresentative Sample». Archived from the original on 2008-04-15. Retrieved 2008-09-01.
Видовые
и родовые понятия тесно связаны между
собой логическими операциями ограничения
и обобщения.
Ограничение
понятия
– это логическая операция перехода от
родового понятия к видовому с помощью
прибавления к его содержанию какого-либо
признака (или нескольких признаков).
Вспомним
об обратном отношении между объёмом и
содержанием понятия: чем больше объём,
тем меньше содержание, и наоборот.
Ограничение понятия, или переход от
родового понятия к видовому – это
уменьшение его объёма, а значит –
увеличение содержания. Вот почему при
добавлении каких-либо признаков к
содержанию понятия автоматически
уменьшается его объём. Например, если
к содержанию понятия «физический
прибор»
(Ф. п.) прибавить признак «измерять
напряжение электрического тока»,
то оно превратится в понятие «вольтметр»
(В), которое будет видовым по отношению
к исходному родовому понятию «физический
прибор»
(рис. 10).
Так
же, если к содержанию понятия «геометрическая
фигура»
(Г. ф.) прибавить признак «иметь
равные стороны и прямые углы»,
то оно превратится в понятие «квадрат»
(К), которое будет видовым по отношению
к исходному родовому понятию «геометрическая
фигура»
(рис. 11).
Обобщение
понятия
– это логическая операция перехода от
видового понятия к родовому с помощью
исключения из его содержания какого-либо
признака (или нескольких признаков).
Содержание понятия, лишённое каких-то
признаков, уменьшается, но при этом
автоматически увеличивается объём
понятия, которое из видового становится
родовым или обобщается. Например, если
от содержания понятия «биология»
(Б) отбросить признак «изучать
различные формы жизни»,
то оно превратится в понятие «наука»
(Н), которое будет родовым по отношению
к исходному видовому понятию «биология»
(рис. 12).
Так
же, если от содержания понятия «атом
водорода»
(А. в.) отбросить признак «иметь
один электрон»,
то оно превратится в понятие «атом
химического элемента»
(А. х. э.), которое будет родовым по
отношению к исходному видовому понятию
«атом
водорода»
(рис. 13).
Ограничения
и обобщения понятий складываются в
логические цепочки, в которых каждое
понятие (за исключением начального и
конечного) является видовым по отношению
к одному соседнему понятию и родовым
по отношению к другому. Например, если
последовательно обобщать понятие
«Солнце»,
то получится следующая цепочка: Солнце
→ звезда
→ небесное
тело→
→ физическое
тело
→ форма
материи.
В этой цепочке понятие «звезда»
является родовым по отношению к понятию
«Солнце»,
но видовым по отношению к понятию
«небесное
тело»;
так же понятие «небесное
тело»
является родовым по отношению к понятию
«звезда»,
но видовым по отношению к понятию
«физическое
тело»
и т. д. Движение по нашей цепочке от
понятия «Солнце» к понятию «форма
материи»
представляет собой серию последовательных
обобщений, а движение в обратном
направлении – серию ограничений. Если
изобразить отношения между понятиями
из указанной цепочки на схеме Эйлера,
то получатся круги, последовательно
располагающиеся один в другом: самый
маленький будет обозначать понятие
«Солнце»,
а самый большой – «форма
материи».
Пределом
цепочки ограничения любого понятия
всегда будет какое-либо единичное
понятие (см. раздел 1.1.), а пределом цепочки
обобщения, как правило, будет какое-либо
широкое, философское понятие, например:
объект
мироздания, форма материи
или форма
бытия.
Наиболее
частые ошибки, которые допускают при
ограничении и обобщении понятий,
заключаются в том, что вместо вида для
какого-то рода называют часть из некого
целого, и вместо рода для какого-то вида
называют целое по отношению к какой-либо
части. Например, в качестве ограничения
понятия «цветок»
предлагают понятие «стебель».
Действительно, стебель – это часть
цветка, но ограничить понятие – значит
подобрать не часть для целого, а вид для
рода. Следовательно, правильным
ограничением понятия «цветок»
будет понятие «ромашка»,
или «тюльпан»,
или «хризантема»
и т. п. В качестве обобщения понятия
«дерево»
нередко предлагают понятие «лес».
Конечно же, лес является неким целым по
отношению к деревьям, из которых он
состоит, но обобщить понятие – значит
подобрать не целое для части, а род для
вида. Следовательно, правильным обобщением
понятия «дерево»
будет понятие «растение»,
или «объект
флоры»,
или «живой
организм»
и т. п.
Итак,
почти любое понятие (за исключением
единичных и широких, философских) можно
как ограничить, так и обобщить. Другими
словами, подобрать для него как видовое
понятие, так и родовое. Например,
ограничением понятия «человек»
(Ч) будет понятие «спортсмен»
(С) или «писатель»,
или «мужчина»,
или «молодой
человек»
и т. п., а его обобщением будет понятие
«живое
существо»
(Ж. с.) (рис. 14).
Операции
обобщения и ограничения понятий следует
отличать от отношений целого к части
(и наоборот). Например, неправильно
обобщать понятие “городская улица”
до понятия “город” или ограничивать
понятие “педагогический институт” до
понятия “факультет педагогического
института”, так как в обоих случаях
речь идет не об отношении рода и вида,
а об отношении части и целого.
Обобщение
и ограничение понятий схематически
можно изобразить так:
При
обобщении отбрасываются признаки, при
этом содержание уменьшается, а объем
увеличивается. При ограничении, наоборот,
к родовому понятию А
добавляются все новые и новые видовые
признаки (а,
b, с
и т. д.), поэтому объем уменьшается, а
содержание увеличивается.
Произведем
обобщение и ограничение понятий: “волк”
и “река”
Волк
|
Обобщение |
Ограничение |
|
1. |
1. |
|
2. |
2. |
|
3. |
3. |
|
4. |
|
|
5. |
|
|
б. |
Река
|
Ограничение |
Обобщение |
|
1. |
1. |
|
2. |
2. |
|
3. |
3. |
|
4. |
4. |
|
5. |
Проверьте
себя:
1.
Что такое ограничение понятия?
2.
Что представляет собой логическая
операция обобщения понятия?
3.
Каким образом ограничения и обобщения
понятий складываются в логические
цепочки? Каковы пределы цепочек
ограничений и обобщений?
4.
Какие ошибки часто допускают при
ограничении и обобщении понятий?
Продемонстрируйте на самостоятельно
подобранных примерах, что целое и часть
нельзя путать с видом и родом.
5.
Всякое ли понятие можно подвергнуть
ограничению или обобщению? Какие понятия
не поддаются этим логическим операциям?
6.
Правильно ли проведены ограничения:
Строение
— комната;
строение
— беседка;
населенный
пункт — столица — центр столицы — центр
современной столицы?
Степная
птица — редкая степная птица — редкая
степная птица высотой около метра
(дрофа).
7.
Правильно ли проведены обобщения:
а)
береза — лиственное дерево — смешанный
лес — лес;
б)
улица — квартал — поселок городского
типа — город — населенный пункт.
в)
верблюд — самое выносливое и неприхотливое
домашнее животное пустыни — выносливое
и неприхотливое домашнее животное
пустыни — домашнее животное пустыни —
домашнее животное — животное.
г)
соболь — ценный пушной зверек — пушной
зверь — зверь.
8.
Подберите пять любых понятий и проделайте
с ними ограничение и обобщение, т. е.
подберите для каждого как видовое, так
и родовое понятие, иллюстрируя эти
операции схемами Эйлера.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1.8. Цепочки ограничений и обобщений понятий
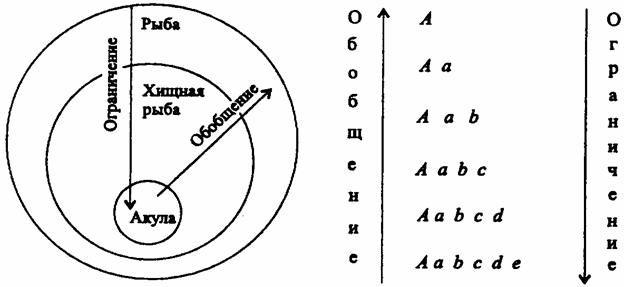
Ограничения и обобщения понятий складываются в логические цепочки, в которых каждое понятие (за исключением начального и конечного) является видовым по отношению к одному соседнему понятию и родовым по отношению к другому. Например, если последовательно обобщать понятие Солнце, то получится следующая цепочка:
Солнце ? звезда ? небесное тело ? физическое тело ? форма материи
В этой цепочке, как видим, понятие звезда является родовым по отношению к понятию Солнце, но видовым по отношению к понятию небесное тело; так же понятие небесное тело является родовым по отношению к понятию звезда, но видовым по отношению к понятию физическое тело и т. д. Понятно, что движение по нашей цепочке от понятия Солнце к понятию форма материи представляет собой серию последовательных обобщений, а движение в обратном направлении – ограничений. (Если изобразить отношения между понятиями из указанной цепочки на схеме Эйлера, то получатся круги, последовательно располагающиеся один в другом: самый маленький обозначает понятие Солнце, а самый большой – форма материи).
Пределом цепочки ограничения любого понятия всегда будет какое-либо единичное понятие, а пределом цепочки обобщения, как правило, будет какое-либо широкое, философское понятие (например, объект мироздания, форма материи или форма бытия).
Наиболее частые ошибки, которые допускают при ограничении и обобщении понятий, заключаются в том, что вместо вида для какого-то рода называют часть из некого целого, и вместо рода для какого-то вида называют целое по отношению к какой-либо части. Например, в качестве ограничения понятия цветок предлагают понятие стебель. Стебель, конечно же, является частью цветка, но ограничить понятие – это значит подобрать не часть для целого, а вид для рода, т. е. правильным ограничением понятия цветок будет понятие ромашка или тюльпан, или хризантема и т. п. Так же, например, в качестве обобщения понятия дерево нередко предлагают понятие лес. Конечно же, лес является неким целым по отношению к деревьям, из которых он состоит, но обобщить понятие – это значит подобрать не целое для части, а род для вида, т. е. правильным обобщением понятия дерево будет понятие растение или объект флоры, или живой организм и т. п.
Итак, почти любое понятие можно как ограничить, так и обобщить. Это значит подобрать для него как видовое понятие, так и родовое. Например, ограничением понятия человек будет понятие спортсмен (или писатель, или мужчина, или молодой человек и т. п.), а его обобщением будет понятие живое существо:
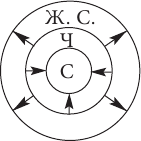
Выше было сказано, что ограничить и обобщить можно почти любое понятие. Правильнее было бы утверждать, что подавляющее большинство понятий можно подвергнуть логическим операциям ограничения и обобщения. Какие же понятия невозможно ограничить или обобщить? Мы их уже упоминали – это единичные понятия или широкие, философские понятия, на которых заканчивается любая логическая цепочка ограничения или обобщения. Единичные понятия невозможно ограничить (однако их можно последовательно, поэтапно обобщать вплоть до какого-то широкого, философского понятия), а философские, предельно широкие по объему понятия невозможно обобщить (но их можно последовательно ограничивать вплоть до какого-то единичного понятия).
Данный текст является ознакомительным фрагментом.
Читайте также
§ 4. ВИДЫ ПОНЯТИЙ
§ 4. ВИДЫ ПОНЯТИЙ
Понятия делятся на виды по: (1) количественным характеристикам объемов понятий; (2) типу обобщаемых предметов; (3) характеру признаков, на основе которых обобщаются и выделяются предметы. Большей частью эта классификация относится к простым понятиям
§ 4. Виды понятий
§ 4. Виды понятий
В зависимости от специфики объема и содержания все понятия делятся на определенные виды. Дадим характеристику видов понятий по объему.Единичным называется понятие, в котором мыслится один предмет. Например, «русский адвокат Федор Никифорович Плевако
§ 4. ВИДЫ ПОНЯТИЙ
§ 4. ВИДЫ ПОНЯТИЙ
Понятия (классы) делятся на пустые и непустые. О них шла речь в предыдущем параграфе. Рассмотрим виды непустых понятий. По объему они делятся на: 1) единичные и общие, (последние — на регистрирующие и нерегистрирующие); по типу обобщаемых предметов — на 2)
§ 4. ВИДЫ ПОНЯТИЙ
§ 4. ВИДЫ ПОНЯТИЙ
Понятия делятся на виды по: (1) количественным характеристикам объемов понятий; (2) типу обобщаемых предметов; (3) характеру признаков, на основе которых обобщаются и выделяются предметы. Большей частью эта классификация относится к простым понятиям
НОВЫЕ ЦЕПОЧКИ
НОВЫЕ ЦЕПОЧКИ
Когда стали появляться первые фабрики, начал свое существование совершенно иной рабочий режим, поначалу воздействующий на крошечную часть популяции, а затем распространявшийся по мере того, как сельскохозяйственный труд приходил в упадок, а работа
2. Виды понятий
2. Виды понятий
В современной логике принято делить понятия на: ясные и размытые; единичные и общие; собирательные и несобирательные; конкретные и абстрактные; положительные и отрицательные; безотносительные и соотносительные. Перейдем к рассмотрению каждого вида
ЭКСПЛИКАЦИЯ ПОНЯТИЙ
ЭКСПЛИКАЦИЯ ПОНЯТИЙ
Одно из требований логики и методологии науки — определенность и однозначность терминологии. А если вы обратитесь к сочинениям на социальные темы, то первое, что вы заметите, это игнорирование этого требования. Все основные понятия (без исключения!)
В плену ограничений
В плену ограничений
Здесь Гайавата в своей пироге уже не по реке плывет, он достиг моря и бросает вызов осетру Мише-Наме – царю всех рыб, дремлющему на дне. Даже пребывая в море – неограниченном пространстве широты души и свободы мысли, объемлющей бесконечность, можно
Смешение понятий
Смешение понятий
Понятие духа было известно и раньше. Книги Ветхого Завета сообщают о существовании «духов плотских существ». Древнеиндийские Веды свидетельствуют о наличии внутри человека атмана, то есть того же духа. По представлениям древних египтян, внутри
Ты можешь стать частью цепочки. Ты можешь создавать будущее
Ты можешь стать частью цепочки. Ты можешь создавать будущее
Наша задача – понять. Наше понимание должно стать мостом. Наша задача – захотеть узнать, понять больше; наша задача – узнать истину, нашу собственную истину и истину других людей. Понять, что представляют из себя
§ 43. Разделение понятий
§ 43. Разделение понятий
Различию простых признаков и зависящему от этого различию сложных понятий противостоит различие того, в чем понятие мыслится. Различные понятия, которые мыслятся в том же самом объекте, следовательно, могут быть относительно него предицированы,
Аналитики понятий глава первая О способе открытия всех чистых рассудочных понятий
Аналитики понятий глава первая
О способе открытия всех чистых рассудочных понятий
Когда начинают применять познавательную способность, то в различных случаях возникают различные понятия, дающие возможность познать эту способность; если наблюдение их производилось
Дедукции чистых рассудочных понятий раздел второй Трансцендентальная дедукция чистых рассудочных понятий
Дедукции чистых рассудочных понятий раздел второй
Трансцендентальная дедукция чистых рассудочных понятий
§ 15. О возможности связи вообще
Многообразное [содержание] представлений может быть дано только в чувственном созерцании, т. е. в созерцании, которое есть не что
Обыкновенно принято логические ошибки делить на две группы: на ошибки логические в собственном смысле и ошибки, происходящие вследствие неправильности в словесном выражении мысли. В первом случае ошибка заключается в неправильности логического процесса, во втором случае – в неправильности выражения. Из ошибок по словесному выражению заметим следующую:
Homonymia – ошибка, которая происходит вследствие того, что одно и то же слово служит для обозначения различных понятий, т.е. употребляется в различных значениях. Например, многие думают, что «материализм» философский есть то же самое, что и «материализм» практический, жизненный. В этом случае происходит смешение понятий вследствие смешения слов. Другие ошибки, происходящие вследствие неправильностей в словесном выражении мысли, указываются в грамматике.
Для того чтобы понять, благодаря чему логические ошибки получают то или иное обозначение, вспомним обозначение частей доказательства. В доказательстве мы различаем: тезис, аргументы и форму доказательства. Ошибки могут быть по отношению к каждой части доказательства. Из предыдущего ясно, что если взять ложные аргументы, то получится ошибка; но ошибка может быть и в том случае, если форма умозаключения будет неправильная.
Ошибки дедукции. Логические ошибки могут быть по отношению к тезису.
Если доказывается не то, что требовалось доказать, то такая подмена тезиса называется ignoratio elenchi (elenchus означает опровержение какого-либо аргумента, а ignoratio elenchi означает незнание того силлогизма, которым можно опровергнуть противника). Например, если нужно доказать, что что-либо несправедливо в моральном смысле, а кто-нибудь стал бы доказывать, что это несправедливо в юридическом смысле, то он вместо одного доказывал бы совсем иное, хотя и сходное. Если доказывается что-либо отличное по роду от того, что нужно доказать; это будет ошибкой μετάβασις είσ άλλο γένοζ или «переходом в другой род». Например, когда кто-нибудь хочет доказывать невиновность обвиняемого тем, что другие совершили то же самое преступление, но избегли наказания.
Уклонение от тезиса может происходить ещё и в том смысле, что доказывается слишком, мало, так что тезис частью остаётся недоказанным, или доказывается слишком много, так что из данных оснований следует не только тезис, но и какое-нибудь ложное положение. Такое ошибочное доказательство называют: qui nimium probat, nihil probat («кто доказывает чересчур, тот ничего не доказывает»). Например, для доказательства положения, что сумма углов треугольника равняется двум прямым, недостаточно было бы доказывать, что эта сумма будет не больше 180° (здесь доказывается слишком мало). Если бы мы хотели доказать, что кто-нибудь добродетелен, и при этом стали бы доказывать, что о нём ничего не известно дурного, то этим доказывалось бы слишком мало. Если бы кто-нибудь стал доказывать недозволительность самоубийства на том основании, что человек не может у себя отнимать того, что он сам себе не дал, то доказывал бы слишком много, потому что из его доказательства выходило бы, что он не может резать ногти, волосы, что он не может продавать унаследованное или полученное в подарок и т.п. Поэтому он тезиса, собственно, не доказывает. Как легко видеть, такое ошибочное доказательство получается в том случае, когда приводятся положения, которые оказываются ложными при данной степени общности, но которые могли бы быть истинными при меньшей степени общности.
К этой же группе ошибок следует отнести ошибку, происходящую вследствие пользования приёмом, который называется argumentum ad hominem («аргумент к человеку», т.е. личный, а не объективный аргумент) и который употребляется в том случае, когда, вместо того чтобы доказывать ложность какого-либо мнения, подвергают рассмотрению личность того, кто высказал это мнение. Если, например, кто-нибудь желает доказать несостоятельность научной теории какого-либо писателя и вместо того, чтобы подвергать критическому разбору именно теорию автора, раскрывает принадлежность автора к несимпатичному для читателей политическому направлению, то он пользуется аргументом ad hominem. Это доказательство, логически самое слабое, фактически пользуется большим успехом.
По отношению к основаниям доказательства, или аргументам, могут быть следующие ошибки.
Основная ошибка, error fundamentalis, – ложное основное положение, на котором строится какое-либо доказательство и из которого могут делаться различные выводы. Например, основной ошибкой в астрономических рассуждениях до Коперника был аргумент, что Солнце и звёзды вращаются вокруг Земли.
Ошибка petitio principii («предрешение; предвосхищение основания») бывает тогда, когда для доказательства какого-либо положения мы кладём в основу доказательства такое положение, которое предполагает истинным доказываемое положение. Положим, кто-нибудь хочет доказать тезис:
«Все частички материи имеют один и тот же вес».
На вопрос, почему он так думает, он мог бы привести следующее основание доказательства:
«Если мы возьмём два тела с одинаковым объёмом, то окажется, что то тело, которое тяжелее, имеет большее число частичек, т.е. больший вес зависит от количества частичек».
На вопрос, откуда же известно, что больший вес тела с одинаковым объёмом зависит именно от количества частичек, он ответит:
«Если принять в соображение, что все частички материи имеют одинаковый вес, то сделается вполне очевидным, что чем тело тяжелее, тем большее число частичек в нём содержится при одинаковом объёме».
В этом примере тезис доказывается при помощи положения, которое само может быть доказано при допущении истинности тезиса. Таким образом, в ошибке petitio principii мы принимаем за истинное то положение, которое должно быть доказано.
Родственными с petitio principii являются ошибки: idem per idem («то же через то же») и circulus in demonstrando («круг в доказательстве»). Ошибка idem per idem – когда какое-либо положение доказывается посредством этого самого положения. Например, на вопрос, почему мы видим сквозь стекло, иногда отвечают: потому, что оно прозрачно; но очевидно, что назвать вещество прозрачным – значит, другими словами, сказать, что сквозь него можно видеть.
Ошибкой circulus in demonstrando называется тот случай, когда тезис A доказывается посредством аргумента B, который в свою очередь доказывается посредством аргумента A. Например, мы утверждаем, что сочинение того или иного писателя заслуживает доверия, потому что он правдив. Нас спрашивают:
«Откуда вам известно, что этот писатель правдив?», и мы отвечаем: «Это доказывается содержанием его сочинений». В этом случае мы делаем круг в доказательстве.
Особняком стоят следующие ошибки.
Ошибка a dicto secundum quid ad dictum simpliciter («от сказанного в относительном смысле к сказанному безотносительно») возникает в том случае, когда выражение, взятое в условном, относительном смысле, принимается затем в смысле безусловном. Например, мышьяк, стрихнин, синильная кислота, будучи введены в организм в значительном количестве, причиняют смерть. Мы в данном случае об этих веществах говорим в условном смысле, т.е. говорим об их ядовитости, когда они введены в организм «в значительном количестве». Но если бы мы сказали, что они всегда причиняют смерть, то мы допустили бы указанную ошибку, потому что в очень малых дозах они не смертельны и, как известно, употребляются в качестве лекарств. Во втором случае мы отбросили то условие, которое указывали в первом случае.
Ошибка fallacia a sensu composite ad sensum divisum («ошибка от собирательного смысла к смыслу разделительному») происходит вследствие смешения термина собирательного с термином общим. Когда мы употребляем общий термин, того, что справедливо относительно целого класса, обозначаемого общим термином, справедливо и относительно каждого индивидуума, входящего в этот класс; но когда мы употребляем собирательный термин, то это может быть несправедливо. То, что справедливо относительно целого, обозначаемого собирательным термином, то может быть несправедливо относительно частей, входящих в это целое. Например, какое-нибудь общество, в котором я состою членом, приняло решение, заслуживающее порицания. Если бы кто-нибудь стал и меня упрекать за это решение, то он допустил бы ошибку fallacia a sensu composite ad sensum divisum, ибо это утверждение, справедливое относительно общества, взятого в целом, может быть совершенно несправедливо относительно отдельных членов этого общества, которые могли подавать свой голос против указанного решения.
Fallacia a sensu diviso ad sensum compositum («ошибка от смысла разделительного к смыслу собирательному») получается в том случае, когда мы о собирательном целом утверждаем то, что справедливо только относительно частей этого целого. Здесь происходит также смешение между термином общим и собирательным. В общих понятиях то, чего мы не можем сказать относительно индивидуума того или другого класса, мы не можем утверждать и о самом классе. В собирательных понятиях, наоборот, мы о частях собирательного целого можем утверждать много такого, чего не можем утверждать относительно целого. Например, кто-нибудь, рассуждая о своих расходах, может сказать: «Этот расход меня не разорит», и о другом расходе скажет: «И этот расход меня не разорит». Если он будет рассуждать таким образом и обо всех остальных расходах, то он должен будет признать, что все расходы его не разорят, что будет ошибочно: то, что справедливо относительно каждого расхода, взятого в отдельности, может быть совсем несправедливо относительно всех расходов, взятых вместе. Другой пример. Больной хочет определить, смертельна ли его болезнь или нет. Рассмотрев каждый симптом в отдельности, он находит, что каждый симптом в отдельности не смертелен; отсюда он делает вывод, что его болезнь не смертельна. Но это рассуждение может оказаться неправильным, потому что каждый симптом в отдельности может быть не смертельным, а все в целом могут быть смертельны.
Ошибки индукции. К ошибкам, связанным с индукцией, относятся прежде всего поспешные обобщения (fallacia fictae universalitatis). Когда путешественники после поверхностного знакомства с каким-либо народом делают попытки характеризовать его, например когда они произносят: «греки лживы», «турки жестоки» и т.п., то они впадают именно в ошибку поспешного обобщения. Ошибка post hoc ergo propter hoc («после этого значит по причине этого») называется также ошибкой): non causa pro causa («от того, что не является причиной, к причине»). Если кто-нибудь заметил, что после какого-либо события возникает какое-либо действие, то он считает первое событие причиной, хотя в действительности, может быть, есть события, от которых данное событие находится в большей зависимости и которое собственно является истинной причиной данного действия. Когда после появления кометы возникали какие-либо несчастья, то обыкновенно комету считали причиной несчастий. Когда в трубке возникала пустота и вода в ней поднималась, то думали, что пустота есть причина поднятия воды. Если после введения какой-нибудь формы правления возникают какие-нибудь события, то обыкновенно эти формы правления считаются причиной их, между тем как истинные причины, может быть, заключаются в чём-нибудь другом, например в определённой степени умственного или нравственного развития общества.
Есть случаи, которые особенно предрасполагают к тем или иным выводам. Это бывает обыкновенно тогда, когда у нас бывает почему-либо интерес помнить случаи, подтверждающие одно положение, и забывать случаи, опровергающие это положение, если предсказание какого-нибудь календаря один раз сбывается, то необразованные люди склонны в этом случае черпать для себя уверенность в правдивости предсказания этого календаря, совсем упуская из виду тысячу случаев, в которых его предсказания не сбывались. На этом основана вера в различных предсказателей, шарлатанов и т.п.
Следует привести несколько примеров ошибок индукции по простому перечислению. Некоторые часто рассуждают так: «большинство женщин в прошлом не равнялось мужчинам по энергии и уму; поэтому следует признать, что женщина вообще ниже мужчины». Но то положение, что в прошлом женщины в умственной жизни не равнялись мужчинам, есть положение эмпирическое, справедливое лишь для известного времени и при известных условиях. В другое время и при других условиях может быть совсем иначе. Ошибкой по простому перечислению нужно считать утверждение, что война всегда будет между народами, потому что до сих пор она всегда была.
Ошибка аналогии. В качестве примера ложной аналогии можно привести то умозаключение, по которому политические тела, подобно телам органическим, переживают юный и зрелый возрасты, старость и подвергаются смерти. Ошибкой аналогии нужно считать утверждение, будто у муравьёв есть рабы, воины, домашние животные и т.п.
Софизмы. Те ошибки, которые совершаются непреднамеренно, называются паралогизмами, а те, которые совершаются преднамеренно, для того чтобы ввести кого-либо в заблуждение, называются софизмами. Приведём несколько примеров софизмов, идущих к нам из древности.
1. Софизм «лгун». Вполне возможно, что лгун сознается в том, что он лгун. В таком случае он скажет правду. Но тот, который говорит правду, не есть лгун. Следовательно, возможно, что лгун не есть лгун. (Какая ошибка?)
2. Софизм «рогатый». То, чего ты не потерял, ты имеешь; ты не потерял рогов. Следовательно, ты имеешь рога. (Какая ошибка?)
3. Софизм «куча». Будет ли куча песку, из которой мы взяли одну песчинку, считаться кучей? Да, будет. А если взять ещё одну песчинку? Будет. Так как при последовательном отнятии по одной песчинке куча не перестаёт быть кучей, то одна песчинка должна называться кучей. (Какая ошибка?)
4. Софизм Эватла. Эватл брал уроки софистики у софиста Протагора под тем условием, что гонорар он уплатит только в том случае, если выиграет первый процесс. Ученик после обучения не взял на себя ведения какого-либо процесса и потому считал себя вправе не платить гонорара. Учитель грозил подать жалобу в суд, говоря ему следующее: «Судьи или присудят тебя к уплате гонорара или не присудят. В обоих случаях ты должен будешь уплатить. В первом случае в силу приговора судьи, во втором случае в силу нашего договора». На это Эватл отвечал: «Ни в том, ни в другом случае я не заплачу. Если меня присудят к уплате, то я, проиграв первый процесс, не заплачу в силу нашего договора, если же меня не присудят к уплате гонорара, то я не заплачу в силу приговора суда». (Ошибка становится ясной, если мы раздельно поставим два вопроса: 1) должен ли Эватл платить или нет и 2) выполнены ли условия договора или нет.)
Вопросы для повторения
На какие два класса делятся логические ошибки? Что такое homonymia? Что такое ignoratio elenchi? Что такое qui nimium probat nihil probat? Что называется доказательством ad hominem? Что называется основной ошибкой? Что такое petitio principii? Что такое idem per idem? Что называется circulus in demonstrando? Какая ошибка называется fallacia a dicto secundum quid ad dictum simpliciter? Какая ошибка называется fallacia a sensu composite ad sensum divisum? Какая ошибка называется fallacia a sensu diviso ad sensum compositum? Перечислите, какие существуют ошибки индукции, и объясните их. Какое различие между софизмами и паралогизмами?
Государственное
автономное
профессиональное
образовательное учреждение
«Бузулукский
лесхоз-техникум»
Статья по логике
на
тему : «Ограничение
и обобщение понятий. Энтимема. Полисиллогизм. Сорит.»
Выполнил преподаватель
дисциплины ОГСЭ. 01
Основы философии
Щербакова Н.Ю.
Бузулук, 2018
План
I.
Введение.
История возникновения науки логики.
II.
Содержание
2.1.
Ограничение
и обобщение понятий.
2.2.
Энтимема.
Полисиллогизм. Сорит.
III.
Заключение
IV.
Библиография
Введение.
История возникновения науки логики.
Логика в
Китае появилась в период появления большого количества школ, конкуренции и
дискуссий между ними. Современник Конфуция Мо-цзы («Учитель Мо»,
«Мудрец Мо»; V—IV вв. до н. э) был известен как основатель моизма (школы мо цзя), представители
которой занимались поиском источников достоверного рассуждения и условий его
правильности. В области аргументации они предпочитали разработку рассуждения по
аналогии разработке
дедукции. В процессе анализа семантики языка моисты разработали метод
классификации имён по степени их общности и деления вещей по видам (метод «трёх
правил», «трёх фа»). Одно из ответвлений моизма, логики (мин цзя, школа имён,
V—III вв. до н. э), приступило к исследованию собственно формальной логики (её
представители подошли к открытию категорического
силлогизма ранее или одновременно с её формулировкой
Аристотелем). Позднее, при династии Цинь, эта
линия исследований исчезла в Китае, поскольку тогда философия легизма жестоко подавляла
все остальные философские школы. Вновь логика в Китае появилась только с
проникновением туда индийской логики буддистов и далее
сильно отстала от развития европейской и ближневосточной логики.
Истоки
логики в Индии можно проследить в грамматических текстах V века до н. э. Две из
шести ортодоксально-индуистских
(ведийских) школ индийской философии — ньяя и вайшешика —
занимались методологией познания, из этого проблемного поля и выделилась
логика. Само название школы «ньяя» значит «логика». Главным её
достижением и была разработка логики и методологии, ставших впоследствии общим
достоянием (ср. аристотелевская логика в Европе). Основным текстом школы были Ньяя-сутры Акшапады Гаутамы (II век н. э.).
Поскольку ньяики считали единственным путём освобождения от страданий
достижение надёжного знания, они разрабатывали тонкие методы отличения надёжных
источников знания от ложных мнений. Есть только четыре источника знания (четыре
праманы): восприятие, умозаключение, сравнение и свидетельство. Строгая
пятичленная схема умозаключения включала в себя: начальную посылку, основание,
пример, приложение и вывод.
Буддийская философия (не
входившая в число шести ортодоксальных школ) была главным оппонентом ньяиков в
логике. Нагарджуна,
основатель мадхьямики
(«срединного пути»), развил рассуждение, известное как «катускоти», или
тетралемма. Этот четырёхсторонний аргумент систематически проверял и отклонял
утверждение высказывания, его отрицание, соединение утверждения и отрицания и,
наконец, отклонение и его утверждения, и его отрицания. У Дигнаги и его
последователя Дхармакирти
буддийская логика достигла вершины. Центральным пунктом их анализа было
установление (определение) необходимой логической присущности (включённости в
определение), «вьяпти», также известное как «неизменное следование» или
«убеждение». Для этой цели они развили учение об «апоха» или различении, о
правилах включения признаков в определение или исключения их из него. Школа навья-ньяя («новая
ньяя», «новая логика») была основана в XIII веке Ганешей
Упадхьяей из Митилы, автора «Таттвачинтамами» («Сокровище мысли о
реальности»). Впрочем, и он опирался на работы своих предшественников X века.
В истории
европейской логики можно выделить этапы: аристотелевский (традиционный)
продолжался сотни лет, в течение которых логика развивалась очень медленно; схоластический
этап развития, пик которого приходится на XIV век; нововременной этап.
Основателем
логики в древнегреческой философии считается
древнегреческий философ Аристотель, так как
полагается, что он вывел первую логическую теорию. Предшественниками Аристотеля в
развитии логической науки в Древней Греции были Парменид, Зенон Элейский, Сократ и Платон. Аристотель же
впервые систематизировал доступные знания о логике, обосновал формы и правила
логического мышления. Его цикл сочинений «Органон» состоит из шести
работ, посвящённых логике: «Категории», «Об истолковании», «Топика», «Первая аналитика» и
«Вторая аналитика», «Софистические опровержения». После Аристотеля в Древней Греции логика
также разрабатывалась представителями школы стоиков. Большой вклад в
развитие этой науки внесли оратор Цицерон и древнеримский
теоретик ораторского искусства Квинтилиан.
По мере
приближения к Средним векам логика
получала более широкое распространение. Её начали разрабатывать арабоязычные
исследователи, например, Аль-Фараби (ок. 870—950 гг.).
Средневековая логика называется схоластической, а её расцвет в XIV веке связывают с
именами учёных Уильяма Оккама, Альберта Саксонского и Уолтера Берли.
В эпоху
Возрождения и в Новое время отмечается появлением множества крайне
значимых для науки публикаций. Френсис Бэкон в 1620 году
опубликовывает свой «Новый органон»,
содержащий основы индуктивных методов,
усовершенствованных позднее Джоном Стюартом Миллем и
получивших название методов установления причинных связей между явлениями
Бэкона-Милля. Суть индукции (обобщения) — в восхождении (в процессе
познания) от частных случаев к общим правилам. Также необходимо искать причины
своих ошибок. В 1662 году в Париже издан учебник «Логика
Пор-Рояля», авторами которого являются П. Николь и А. Арно, создавшие
логическое учение на основе методологических принципов Рене Декарта.
В конце XIX — начале XX веков были заложены
основы т. н. математической, или символической, логики. Её суть
заключается в том, что для обнаружения истинностного значения выражений
естественного языка можно применять математические методы. Именно использование
символической логики отличает современную логическую науку от традиционной.
Огромный
вклад в развитие символической логики внесли такие учёные, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др. В XX веке математическая логика
оформилась в качестве самостоятельной дисциплины в рамках логической науки.
Начало XX века ознаменовалось
становлением идей неклассической логики, многие важные положения которой были
предвосхищены и/или заложены Н. А. Васильевым и И. Е. Орловым.
В середине
XX века развитие вычислительной техники привело к появлению логических
элементов, логических блоков и устройств вычислительной техники, что было
связано с дополнительной разработкой таких областей логики, как проблемы
логического синтеза, логическое проектирование и проблемы логического
моделирования логических устройств и средств вычислительной техники.
В 80-х
годах XX века начались исследования в области искусственного интеллекта на базе
языков и систем логического программирования. Началось и создание экспертных
систем с использованием и развитием автоматического доказательства теорем, а
также методов доказательного программирования для верификации алгоритмов и
программ для ЭВМ.
В 80-е годы
начались также изменения в образовании. Появление персональных компьютеров в
средних школах привело к созданию учебников информатики с изучением элементов
математической логики для объяснения логических принципов работы логических
схем и устройств вычислительной техники, а также принципов логического
программирования для компьютеров пятого поколения, и разработке учебников
информатики с изучением языка исчисления предикатов для проектирования баз
знаний.
Раскроем
предложенные вопросы по логике – это ограничение и
обобщение понятий, а также энтимема и полисиллогизм, сорит.
2.1 Ограничение и обобщение понятий.
Среди различных
видов отношений между понятиями следует обратить особенное внимание на
отношение подчинения. Как уже говорилось, понятия с меньшим объемом называются
видовыми, а понятия с большим объемом — родовыми, причем объем видового понятия
всегда полностью включается в объем родового. Видовые и родовые понятия тесно
связаны между собой логическими операциями ограничения и обобщения.
Ограничение понятия — это
логическая операция перехода от родового понятия к видовому с помощью прибавления
к его содержанию какого-либо признака. Вспомним об обратном отношении между
объемом и содержанием понятия: чем больше объем, тем меньше содержание и
наоборот. Ограничение понятия или переход от родового понятия к видовому — это
уменьшение его объема, а значит — увеличение содержания. Вот почему при
добавлении каких-то признаков к содержанию понятия автоматически уменьшается
его объем. Например, если к содержанию понятия физический прибор прибавить признак «измерять напряжение
электрического тока», то оно превратится в понятие вольтметр, которое
будет видовым по отношению к исходному родовому понятию физический прибор:
родовое
Так же, если к
содержанию понятия геометрическая
фигура прибавить признак «иметь равные стороны и прямые
углы», то оно превратится
в понятие квадрат, которое будет видовым по отношению к
исходному родовому понятию геометрическая фигура:
родовое

Обобщение
понятия — это логическая
операция, которая противоположна ограничению и представляет собой переход от
видового понятия к родовому с помощью отбрасывания от его содержания
какого-либо признака. (Понятно, что содержание понятия, лишенное каких-то
признаков, уменьшается, но при этом автоматически увеличивается объем понятия,
которое из видового становится родовым или обобщается). Например, если от содержания
понятия биология отбросить признак «изучать различные формы жизни», то оно превратится в понятие наука, которое будет родовым по отношению к
исходному видовому понятию биология:
родовое
Так же, если от
содержания понятия атом водорода отбросить признак «иметь один
электрон»,
то оно превратится в понятие атом химического элемента, которое будет родовым по
отношению к исходному видовому понятию атом водорода:
родовое

Цепочки ограничений и обобщений понятий
Ограничения
и обобщения понятий складываются в логические цепочки, в которых каждое
понятие (за исключением начального и конечного) является видовым по отношению к
одному соседнему понятию и родовым по отношению к другому. Например, если
последовательно обобщать понятие Солнце, то получится следующая цепочка:
Солнце звезда небесное
тело физическое тело форма материи
В
этой цепочке, как видим, понятие звезда является родовым по
отношению к понятию Солнце, но видовым по отношению к понятию небесное тело; так же понятие небесное тело является родовым по
отношению к понятию звезда, но видовым по отношению к понятию физическое
тело и
т. д. Понятно, что движение по нашей цепочке от понятия Солнце к понятию форма материи представляет собой серию
последовательных обобщений, а движение в обратном направлении — ограничений.
(Если изобразить отношения между понятиями из указанной цепочки на схеме
Эйлера, то получатся круги, последовательно располагающиеся один в другом:
самый маленький обозначает понятие Солнце, а самый большой — форма
материи).
Пределом
цепочки ограничения любого понятия всегда будет какое-либо единичное понятие,
а пределом цепочки обобщения, как правило, будет какое-либо широкое,
философское понятие
(например, объект
мироздания, форма материи или форма бытия).
Наиболее частые
ошибки, которые допускают при ограничении и обобщении понятий, заключаются в
том, что вместо вида для какого-то рода называют часть из некого целого, и
вместо рода для какого-то вида называют целое по отношению к какой-либо части.
Например, в качестве ограничения понятия цветок предлагают понятие стебель. Стебель, конечно же, является частью цветка, но ограничить понятие —
это значит подобрать не часть для целого, а вид для рода, т. е. правильным
ограничением понятия цветок будет понятие ромашка или тюльпан, или хризантема и т. п. Так же, например, в качестве
обобщения понятия дерево нередко предлагают понятие лес. Конечно же, лес является неким целым по
отношению к деревьям, из которых он состоит, но обобщить понятие — это значит
подобрать не целое для части, а род для вида, т. е. правильным обобщением
понятия дерево будет понятие растение или объект флоры, или живой организм и т. п.
Итак, почти
любое понятие можно как ограничить, так и обобщить. Это значит подобрать для
него как видовое понятие, так и родовое. Например, ограничением понятия человек будет понятие спортсмен (или писатель, или мужчина, или молодой человек и т. п.), а его обобщением будет понятие живое существо:
Выше было
сказано, что ограничить и обобщить можно почти любое понятие. Правильнее было
бы утверждать, что подавляющее большинство понятий можно подвергнуть логическим
операциям ограничения и обобщения. Какие же понятия невозможно ограничить или
обобщить? Мы их уже упоминали — это единичные понятия или широкие, философские понятия, на которых заканчивается любая
логическая цепочка ограничения или обобщения. Единичные понятия невозможно
ограничить (однако их можно последовательно, поэтапно обобщать вплоть до
какого-то широкого, философского понятия), а философские, предельно широкие по
объему понятия невозможно обобщить (но их можно последовательно ограничивать
вплоть до какого-то единичного понятия).
2.1 Энтимема.
Полисиллогизм. Сорит.
Поскольку простой силлогизм — это одна
из широко распространенных разновидностей умозаключения, он часто используется
в повседневном и научном мышлении.
Однако, при его употреблении, мы, как
правило, не соблюдаем его жесткую логическую структуру (в которой отчетливо
прослеживаются две посылки и вытекающий из них вывод).
Например, вместо того, чтобы сказать:
Все рыбы не являются
млекопитающими.
Все киты являются
млекопитающими.
_________________________________________
Следовательно, все киты не
являются рыбами.
мы, скорее всего,
скажем: Все киты не рыбы, так как они — млекопитающие, или: Все киты не
рыбы, потому что рыбы — не млекопитающие. Нетрудно увидеть, что эти
два умозаключения представляют собой сокращенную форму вышеприведенного
простого силлогизма.
Таким образом, в мышлении и
речи обычно используется не простой силлогизм, а его различные сокращенные
разновидности, которые и будут рассмотрены далее.
Энтимема
— это
простой силлогизм, в котором пропущена одна из посылок или вывод. Понятно, что
из любого силлогизма можно вывести три энтимемы. Например, из силлогизма:
Все металлы
электропроводны.
Железо — это металл.
____________________________
Железо электропроводно.
следуют три энтимемы.
1. Железо электропроводно, так
как оно является металлом (пропущена большая
посылка).
2. Железо электропроводно,
потому что все металлы электропроводы (пропущена
меньшая посылка).
3. Все металлы электропроводны,
а железо — это металл (пропущен
вывод).
Эпихейрема
— это
простой силлогизм, в котором обе посылки являются энтимемами. Возьмем, два
силлогизма и выведем из них энтимемы.
1 силлогизм
Все, что приводит общество
к бедствиям, есть зло.
Социальная несправедливость
приводит общество к бедствиям.
_____________________________________
Социальная несправедливость — это зло.
Пропуская в этом силлогизме большую посылку, получаем энтимему: Социальная несправедливость — это зло, так как она
приводит общество к бедствиям.
2 силлогизм
Все, что способствует обогащению одних за счет
обнищания других, — это социальная несправедливость.
Частная собственность способствует обогащению
одних за счет обнищания других.
_____________________________________
Частная собственность — это социальная несправедливость.
Пропуская
в этом силлогизме большую посылку, получаем энтимему: Частная собственность — это социальная несправедливость,
так как она способствует обогащению одних за счет обнищания других.
Если расположить
эти две энтимемы друг за другом, то они станут посылками нового, третьего
силлогизма, который и будет эпихейремой:
Социальная несправедливость — это зло, так как
оно приводит общество к бедствиям.
Частная собственность — это социальная
несправедливость, так как она способствует обогащению одних за счет обнищания
других.
____________________________________________________
Частная собственность — это зло.
Как видим, в
составе эпихейремы можно выделить три силлогизма: два из них являются
посылочными, а один строится из выводов посылочных силлогизмов. Этот последний
силлогизм представляет собой основу для окончательного вывода.
Полисиллогизмы и сориты
Помимо энтимемы
и образуемой из нее (т. е. из двух энтимем) эпихейремы существуют еще две
разновидности сокращенного простого силлогизма. Это полисиллогизм и образуемый
из него сорит.
Полисиллогизм, также часто называемый сложным силлогизмом, —
это два или несколько простых силлогизмов, связанных между собой таким
образом, что вывод одного из них является посылкой следующего. Например:
Все, что развивает мышление, полезно.
Все интеллектуальные игры развивают мышление.
__________________________________________
Все
интеллектуальные игры полезны.
Шахматы — это интеллектуальная игра.
__________________________________________
Шахматы полезны.
Фигурными скобками выделены два
силлогизма, объединенные в полисиллогизм. Обратим внимание на то, что вывод
предыдущего силлогизма стал большей посылкой последующего. В этом случае
получившийся полисиллогизм называется прогрессивным. Если же вывод предыдущего силлогизма становится
меньшей посылкой последующего, то полисиллогизм называется регрессивным. Например:
Все звезды — это небесные тела.
Солнце — это звезда.
_____________________________
Солнце — это небесное тело.
Все небесные тела участвуют в гравитационных
взаимодействиях.
Солнце — это небесное тело.
______________________________
Солнце участвует в гравитационных
взаимодействиях.
Вывод
предыдущего силлогизма является меньшей посылкой следующего. Можно заметить,
что в этом случае два силлогизма невозможно графически соединить в
последовательную цепочку, как в случае прогрессивного полисиллогизма.
Полисиллогизм
может состоять не только из двух, но и из большего количества простых силлогизмов.
Приведем пример полисиллогизма (прогрессивного), который состоит из трех
простых силлогизмов.
Все материальное имеет физические свойства.
Все
объекты Вселенной материальны.
______________________________________________
Все объекты Вселенной имеют физические свойства.
Кванты — это объекты Вселенной.
______________________________________________
Кванты
имеют физические свойства.
Фотоны — это кванты электромагнитного поля.
______________________________________________
Фотоны имеют физические свойства.
Сорит, также часто называемый сложносокращенным силлогизмом,
— это полисиллогизм, в котором пропущена посылка последующего силлогизма,
являющаяся выводом предыдущего. Вернемся к рассмотренному выше примеру
прогрессивного полисиллогизма и пропустим в нем большую посылку второго
силлогизма, которая представляет собой вывод первого силлогизма. Получится
прогрессивный сорит:
Все, что развивает мышление, полезно.
Все интеллектуальные игры развивают мышление.
Шахматы — это интеллектуальная игра.
_____________________________________________
Шахматы полезны.
Теперь обратимся к рассмотренному выше
примеру регрессивного поли-силлогизма и пропустим в нем меньшую посылку
второго силлогизма, кото-рая является выводом первого силлогизма. Получится
регрессивный сорит:
Все звезды — это небесные тела.
Солнце — это звезда.
Все небесные тела участвуют в гравитационных
взаимодействиях.
______________________________________________
Солнце участвует в гравитационных
взаимодействиях.
Сделаем прогрессивный сорит из
вышеприведенного прогрессивного полисиллогизма, состоящего из трех простых
силлогизмов:
Все материальное имеет физические свойства.
Все объекты Вселенной материальны.
Кванты — это объекты Вселенной.
Фотоны — это кванты электромагнитного поля.
_____________________________________________
Фотоны имеют физические свойства.
Итак, на практике, т. е. в повседневном
мышлении обычно используется не простой, категорический силлогизм, а его
различные сокращенные формы: энтимемы, эпихейремы, полисиллогизмы и сориты.
Заключение
Логикой владеют все люди, независимо от
того, изучали они ее или нет. Такая логика обычно называется интуитивной и
формируется в процессе жизненного опыта с детства: ничего не зная из области
теоретической логики, мы, тем не менее, мыслим в целом правильно, при этом
соблюдая логические правила и законы стихийно, или бессознательно.
Подкрепив и обогатив свою логическую
интуицию теоретическими знаниями, которые помогут в дальнейшем использовать
логику не только интуитивно, но и осознанно, а значит, — более эффективно.
Логика появилась около 25 веков назад,
однако, несмотря на столь «почтенный возраст», она до сих пор сохраняет свою
актуальность, т. е. и сегодня находит повсеместное практическое применение.
Поскольку логика является инструментом правильного мышления, она представляет
собой универсальную науку: ее освоение одинаково полезно и даже необходимо
каждому ученику или студенту, независимо от того, на какие предметы он
ориентирован — социально-гуманитарные или естественно-математические. Знание логики требуется любому человеку,
ведь разнообразные логические ошибки засоряют не только научное, но и
повседневное мышление, мешают нам думать, общаться, понимать друг друга и самих
себя, создавая серьезные коммуникативные затруднения. Неясность и
неопределенность мышления, его непоследовательность и сумбурность,
противоречивость и необоснованность является прямым результатом отсутствия
должного уровня логической культуры.
Мышление,
соответствующее требованиям логики, подобно прозрачному ручью, сквозь воды
которого виден каждый камушек и песчинка его дна; ручью, к которому хочется припасть
в знойный день, чтобы утолить жажду освежающей и приятной прохладой. Мышление,
построенное на нарушениях логических законов, подобно мутному потоку, в
котором ничего не видно, и вода совершенно непригодна для питья. Правда,
некоторые говорят, что в мутной воде удобнее «ловить рыбу», т. е. строить
такие высказывания и создавать такие тексты, — сложные и малопонятные для
адресата, — в которых внешняя солидность, глубокомысленность и наукообразность
маскирует внутреннюю запутанность, непоследовательность и бессодержательность.
Иначе говоря, «ловить рыбу в мутной воде» — это значит создавать видимость
мысли и дела там, где нет ни того, ни другого. Добросовестный человек не может
быть сторонником такой «рыбалки».
Библиография
1. Гусев Д.А.
Логика – М.: Прометей, 2015. – 300 с.
2. Ивин А.А.
Логика: Учебник для гуманитарных факультетов. – М.: ФАИР-ПРЕСС, 1999. – 320 с.
3. Ивлев Ю.В.
Логика: учеб. – 4-е изд., перераб. и доп. – М.:ТК Велби, Проспект, 2008. – 304
с.
4. Ивин А.А.,
Никифоров А.Л. Словарь по логике. М.: Владос, 1997
5. Краткий
словарь по логике. М., 1991.