Ошибки наблюдения первого и второго рода - Решение и исправление самых разных ошибок на TopOshibok.ru

Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.

Определения

Пусть дана выборка $tex:{\mathbf {X}}=(X_{1},\ldots ,X_{n})^{{\top }}$ из неизвестного совместного распределения $tex:{\mathbb {P}}^{{{\mathbf {X}}}}$ , и поставлена бинарная задача проверки статистических гипотез:

$tex:{\begin{matrix}H_{0}\\H_{1},\end{matrix}}$

где $tex:H_{0}$ — нулевая гипотеза, а tex:H_1 — альтернативная гипотеза. Предположим, что задан статистический критерий

$tex:f:{\mathbb {R}}^{n}\to \{H_{0},H_{1}\}$ ,

сопоставляющий каждой реализации выборки $tex:\mathbf {X}=\mathbf {x}$ одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации:

Распределение $tex:{\mathbb {P}}^{{{\mathbf {X}}}}$ выборки $tex:\mathbf {X}$ соответствует гипотезе $tex:H_{0}$ , и она точно определена статистическим критерием, то есть $tex:f({\mathbf {x}})=H_{0}$ .
Распределение $tex:{\mathbb {P}}^{{{\mathbf {X}}}}$ выборки $tex:\mathbf {X}$ соответствует гипотезе $tex:H_{0}$ , но она неверно отвергнута статистическим критерием, то есть $tex:f({\mathbf {x}})=H_{1}$ .
Распределение $tex:{\mathbb {P}}^{{{\mathbf {X}}}}$ выборки $tex:\mathbf {X}$ соответствует гипотезе , и она точно определена статистическим критерием, то есть $tex:f({\mathbf {x}})=H_{1}$ .
Распределение $tex:{\mathbb {P}}^{{{\mathbf {X}}}}$ выборки $tex:\mathbf {X}$ соответствует гипотезе , но она неверно отвергнута статистическим критерием, то есть $tex:f({\mathbf {x}})=H_{0}$ .

Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно. ¹⁾²⁾

	Верная гипотеза
$tex:H_{0}$
Результат применения критерия	$tex:H_{0}$	$tex:H_{0}$ верно принята	$tex:H_{0}$ неверно принята (Ошибка второго рода)
	$tex:H_{0}$ неверно отвергнута (Ошибка первого рода)	$tex:H_{0}$ верно отвергнута

Верная гипотеза

$tex:H_{0}$

Результат

применения

критерия

$tex:H_{0}$

верно принята

$tex:H_{0}$

неверно принята

(Ошибка второго рода)

$tex:H_{0}$

неверно отвергнута

(Ошибка первого рода)

$tex:H_{0}$

верно отвергнута

О смысле ошибок первого и второго рода

Из определения выше видно, что ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы $tex:H_{0}$ и tex:H_1 , то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза $tex:H_{0}$ соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследуемый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза tex:H_1 обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.

С учётом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня. Слово «положительный» в данном случае не имеет отношения к желательности или нежелательности самого события.

Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают положительный результат (т.е. показывают наличие заболевания у пациента), когда на самом деле пациент этим заболеванием не страдает. Такой результат называется ложноположительным.

В других областях обычно используют словосочетания со схожим смыслом, например, «ложное срабатывание», «ложная тревога» и т.п. В информационных технологиях часто используют английский термин false positive без перевода.

Из-за возможности ложных срабатываний не удаётся полностью автоматизировать борьбу со многими видами угроз. Как правило, вероятность ложного срабатывания коррелирует с вероятностью пропуска события (ошибки второго рода). То есть: чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система защиты может выродиться в свою противоположность и привести к тому, что побочный вред от неё будет превышать пользу.

Соответственно, ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).

Слово «отрицательный» в данном случае не имеет отношения к желательности или нежелательности самого события.

Термин широко используется в медицине. Например, тесты, предназначенные для диагностики заболеваний, иногда дают отрицательный результат (т.е. показывают отсутствие заболевания у пациента), когда на самом деле пациент страдает этим заболеванием. Такой результат называется ложноотрицательным.

В других областях обычно используют словосочетания со схожим смыслом, например, «пропуск события», и т.п. В информационных технологиях часто используют английский термин false negative без перевода.

Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок.

Вероятности ошибок (уровень значимости и мощность)

Вероятность ошибки первого рода при проверке статистических гипотез называют уровнем значимости и обычно обозначают греческой буквой $tex:\alpha$ (отсюда название $tex:\alpha$ -errors).

Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой $tex:\beta$ (отсюда $tex:\beta$ -errors). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле $tex:(1-\beta )$ . Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.

Обе эти характеристики обычно вычисляются с помощью так называемой функции мощности критерия. В частности, вероятность ошибки первого рода есть функция мощности, вычисленная при нулевой гипотезе. Для критериев, основанных на выборке фиксированного объема, вероятность ошибки второго рода есть единица минус функция мощности, вычисленная в предположении, что распределение наблюдений соответствует альтернативной гипотезе. Для последовательных критериев это также верно, если критерий останавливается с вероятностью единица (при данном распределении из альтернативы).

В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).

Примеры использования

Радиолокация

В задаче радиолокационного обнаружения воздушных целей, прежде всего, в системе ПВО ошибки первого и второго рода, с формулировкой «ложная тревога» и «пропуск цели» являются одним из основных элементов как теории, так и практики построения радиолокационных станций. Вероятно, это первый пример последовательного применения статистических методов в целой технической области.

Компьютеры

Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.

Компьютерная безопасность

Наличие уязвимостей в вычислительных системах приводит к тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:

когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)

Фильтрация спама

Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «антиспам»-алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).

Ошибка второго рода происходит, когда антиспам-система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности антиспам-алгоритма.

Пока не удалось создать антиспамовую систему без корреляции между вероятностью ошибок первого и второго рода. Вероятность пропустить спам у современных систем колеблется в пределах от 1% до 30%. Вероятность ошибочно отвергнуть валидное сообщение — от 0,001 % до 3 %. Выбор системы и её настроек зависит от условий конкретного получателя: для одних получателей риск потерять 1% хорошей почты оценивается как незначительный, для других же потеря даже 0,1% является недопустимой.

Вредоносное программное обеспечение

Понятие ошибки первого рода также используется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с антитроянскими и антишпионскими программами.

Поиск в компьютерных базах данных

При поиске в базе данных к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.

Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.

Оптическое распознавание текстов (OCR)

Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек.

Досмотр пассажиров и багажа

Ошибки первого рода регулярно встречаются каждый день в компьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т.п. (см. обнаружение взрывчатых веществ, металлодетекторы).

Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как правонарушителя) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.

Биометрия

Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т.д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т.п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.³⁾

Массовая медицинская диагностика (скрининг)

В медицинской практике есть существенное различие между скринингом и тестированием:

Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые, в основном, применяются для подтверждения предполагаемого диагноза.

К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.⁴⁾)

Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.

Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15%, это самый высокий показатель в мире.⁵⁾ Самый низкий уровень наблюдается в Нидерландах, 1%.⁶⁾

Медицинское тестирование

Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.

Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70%, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).

Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.⁷⁾

Исследования сверхъестественных явлений

Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиасвидетельство» (изображение, видеозапись, аудиозапись и т.д.), которое имеет обычное объяснение.

См. также

Источник

Ошибки первого и второго рода

Как было указано выше, при статистическом анализе гипотеза никогда не может быть доказана как истинная или ложная, она только принимается или отвергается на основании статистических критериев. Это решение ассоциируется с двумя типами ошибки: нулевая гипотеза отвергается, будучи истинной (ошибка первого рода или альфа-ошибка), или принимается, будучи ложной (ошибка второго рода или бета-ошибка). Вероятность совершения ошибки первого рода представляет собой уровень значимости статистического критерия, который всегда должен указываться при представлении • результатов.
Например, рандомизированные клинические испытания лекарственных средств могут привести к ошибкам обоих типов. На основании полученных результатов может быть сделан вывод об эффективности нового препарата, когда на самомделе он не имеет преимуществ перед стандартным лечением. В этом случае ошибка, которая ведет к ложному положительному выводу об эффективности препарата, является ошибкой первого рода. И наоборот, может быть сделано заключение о неэффективности нового лекарственного средства, когда в действительности оно является эффективным. Такой ложный отрицательный вывод свидетельствует об ошибке второго рода.
Вероятность отказа от нулевой гипотезы, когда она является ложной, называется мощностью статистического критерия. Она равна единице минус вероятность ошибки второго рода. Мощность статистического критерия зависит от объема выборки: чем больше выборка, тем больше мощность критерия при всех других одинаковых параметрах. Мощность критерия также зависит от выбранного уровня значимости. При любом данном объеме выборки чем выше уровень значимости (т.е. чем ниже вероятность ошибки первого рода), тем меньше мощность критерия (тем выше вероятность ошибки второго рода). Во многих исследованиях ставится задача достичь мощности критерия, равной 0,8 при уровне значимости 0,05. Это означает, что вероятность ошибки второго рода (0,2) в 4 раза превышает вероятность ошибки первого рода (0,05), а это в свою очередь отражает тот факт, что в большинстве исследований ошибка первого рода считается более серьезной, чем ошибка второго рода. Мощность критерия должна указываться при получении отрицательного результата.
Мощность статистического критерия должна обязательно приниматься во внимание в процессе планирования эпидемиологического исследования, поскольку она показывает, будет ли данная проверка иметь статистически значимый результат при различных обстоятельствах.

Источник: Бигпхоп Р., «Основы эпидемиологии» 1993

А так же в разделе «Ошибки первого и второго рода »

Наблюдения и эксперименты
Эпидемиологические исследования, проводимые путем наблюдений Описательные исследования
Экологические исследования
Поперечные исследования
Исследования типа случай — контроль
Когортные исследования
Экспериментальные эпидемиологические исследования
Рандомизированные контролируемые испытания
Полевые испытания
Испытания на коммунальном уровне
Потенциальные ошибки в эпидемиологических исследованиях
Случайная ошибка
Систематическая ошибка
Достоверность
Вопросы этики
Глава 4 Основные статистические аспекты,
Распределения и основные критерии Распределения
Характеристика положения
Нормальное и логарифмически нормальное распределения
Оценка Популяции и выборки
Доверительные интервалы
Статистические выводы Проверка гипотез
Различия между статистической значимостью, значимостью в клиническом отношении и значимостью с точки зрения общественного здравоохранения
Взаимосвязь двух переменных
Критерий хи-квадрат
Регрессия
Глава 5 Причинная обусловленность болезней в эпидемиологии
Единичные и множественные причины
Взаимодействие причин
Временная связь
Убедительность ассоциации
Последовательность выявления ассоциации
Степень выраженности ассоциации
Зависимость доза — ответ
Организация исследования
Вынесение суждений

Источник

Ошибки первого и второго рода

Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.

Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.

Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.

Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.

Замечание 1.
Правильное решение может быть принято
также в двух случаях:

гипотеза принимается,
причём и в действительности она
правильная;
гипотеза отвергается,
причём и в действительности она неверна.

Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).

Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия

Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.

Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.

Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:.

Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.

Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.

Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии,
то наблюдаемое значение критерия.

Критическая
область. Область принятия гипотезы.
Критические точки

После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.

Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.

Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.

Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.

Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.

Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.

Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.

Правосторонней
называют критическую область, определяемую
неравенством
>,
где— положительное число.

Левосторонней
называют критическую область, определяемую
неравенством
<,
где— отрицательное число.

Односторонней
называют правостороннюю или левостороннюю
критическую область.

Двусторонней
называют критическую область, определяемую
неравенствами
где.

В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):

,
или равносильным неравенством
.

Отыскание
правосторонней критической области

Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?

Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее,
была равна принятому уровню значимости:
Р(>)=.

Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.

Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>,
то нулевую гипотезу отвергают; если же<,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.

Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение

Р(>)=?
(*)

Поскольку вероятность
события
>мала (— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.

Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.

Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».

На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.

Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.

Отыскание
левосторонней и двусторонней критических
областей***

Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<(<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<)=.

Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее,
была равна принятому уровню значимости:

.
(*)

Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и(>0),
то

Учитывая (*), получим
.

Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.

Дополнительные
сведения о выборе критической области.
Мощность критерия

Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.

Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.

Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.

Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.

Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.

Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.

Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
иневозможно; если уменьшить,
тобудет возрастать. Например, если принять=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.

Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.

Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.

Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.

Соседние файлы в папке Лекции 2 семестр

Источник

Ошибки, встроенные в систему: их роль в статистике

Время на прочтение
6 мин

Количество просмотров 14K

В прошлой статье я указал, как распространена проблема неправильного использования t-критерия в научных публикациях (и это возможно сделать только благодаря их открытости, а какой трэш творится при его использовании во всяких курсовых, отчетах, обучающих задачах и т.д. — неизвестно). Чтобы обсудить это, я рассказал об основах дисперсионного анализа и задаваемом самим исследователем уровне значимости α. Но для полного понимания всей картины статистического анализа необходимо подчеркнуть ряд важных вещей. И самая основная из них — понятие ошибки.

Ошибка и некорректное применение: в чем разница?

В любой физической системе содержится какая-либо ошибка, неточность. В самой разнообразной форме: так называемый допуск — отличие в размерах разных однотипных изделий; нелинейная характеристика — когда прибор или метод измеряют что-то по строго известному закону в определенных пределах, а дальше становятся неприменимыми; дискретность — когда мы чисто технически не можем обеспечить плавность выходной характеристики.

И в то же время существует чисто человеческая ошибка — некорректное использование устройств, приборов, математических законов. Между ошибкой, присущей системе, и ошибкой применения этой системы есть принципиальная разница. Важно различать и не путать между собой эти два понятия, называемые одним и тем же словом «ошибка». Я в данной статье предпочитаю использовать слово «ошибка» для обозначения свойства системы, а «некорректное применение» — для ошибочного ее использования.

То есть, ошибка линейки равна допуску оборудования, наносящего штрихи на ее полотно. А ошибкой в смысле некорректного применения было бы использовать ее при измерении деталей наручных часов. Ошибка безмена написана на нем и составляет что-то около 50 граммов, а неправильным использованием безмена было бы взвешивание на нем мешка в 25 кг, который растягивает пружину из области закона Гука в область пластических деформаций. Ошибка атомно-силового микроскопа происходит из его дискретности — нельзя «пощупать» его зондом предметы мельче, чем диаметром в один атом. Но способов неправильно использовать его или неправильно интерпретировать данные существует множество. И так далее.

Так, а что же за ошибка имеет место в статистических методах? А этой ошибкой как раз и является пресловутый уровень значимости α.

Ошибки первого и второго рода

Ошибкой в математическом аппарате статистики является сама ее Байесовская вероятностная сущность. В прошлой статье я уже упоминал, на чем стоят статистические методы: определение уровня значимости α как наибольшей допустимой вероятности неправомерно отвергнуть нулевую гипотезу, и самостоятельное задание исследователем этой величины перед исследователем.
Вы уже видите эту условность? На самом деле, в критериальных методах нету привычной математической строгости. Математика здесь оперирует вероятностными характеристиками.
И тут наступает еще один момент, где возможна неправильная трактовка одного слова в разном контексте. Необходимо различать само понятие вероятности и фактическую реализацию события, выражающуюся в распределении вероятности. Например, перед началом любого нашего эксперимента мы не знаем, какую именно величину мы получим в результате. Есть два возможных исхода: загадав некоторое значение результата, мы либо действительно его получим, либо не получим. Логично, что вероятность и того, и другого события равна 1/2. Но показанная в предыдущей статье Гауссова кривая показывает распределение вероятности того, что мы правильно угадаем совпадение.

Наглядно можно проиллюстрировать это примером. Пусть мы 600 раз бросаем два игральных кубика — обычный и шулерский. Получим следующие результаты:

До эксперимента для обоих кубиков выпадение любой грани будет равновероятно — 1/6. Однако после эксперимента проявляется сущность шулерского кубика, и мы можем сказать, что плотность вероятности выпадения на нем шестерки — 90%.

Другой пример, который знают химики, физики и все, кто интересуется квантовыми эффектами — атомные орбитали. Теоретически электрон может быть «размазан» в пространстве и находиться практически где угодно. Но на практике есть области, где он будет находиться в 90 и более процентах случаев. Эти области пространства, образованные поверхностью с плотностью вероятности нахождения там электрона 90%, и есть классические атомные орбитали, в виде сфер, гантелей и т.д.

Так вот, самостоятельно задавая уровень значимости, мы заведомо соглашаемся на описанную в его названии ошибку. Из-за этого ни один результат нельзя считать «стопроцентно достоверным» — всегда наши статистические выводы будут содержать некоторую вероятность сбоя.

Ошибка, формулируемая определением уровня значимости α, называется ошибкой первого рода. Ее можно определить, как «ложная тревога», или, более корректно, ложноположительный результат. В самом деле, что означают слова «ошибочно отвергнуть нулевую гипотезу»? Это значит, по ошибке принять наблюдаемые данные за значимые различия двух групп. Поставить ложный диагноз о наличии болезни, поспешить явить миру новое открытие, которого на самом деле нет — вот примеры ошибок первого рода.

Но ведь тогда должны быть и ложноотрицательные результаты? Совершенно верно, и они называются ошибками второго рода. Примеры — не поставленный вовремя диагноз или же разочарование в результате исследования, хотя на самом деле в нем есть важные данные. Ошибки второго рода обозначаются буквой, как ни странно, β. Но само это понятие не так важно для статистики, как число 1-β. Число 1-β называется мощностью критерия, и как нетрудно догадаться, оно характеризует способность критерия не упустить значимое событие.
Однако содержание в статистических методах ошибок первого и второго рода не является только лишь их ограничением. Само понятие этих ошибок может использоваться непосредственным образом в статистическом анализе. Как?

ROC-анализ

ROC-анализ (от receiver operating characteristic, рабочая характеристика приёмника) — это метод количественного определения применимости некоторого признака к бинарной классификации объектов. Говоря проще, мы можем придумать некоторый способ, как отличить больных людей от здоровых, кошек от собак, черное от белого, а затем проверить правомерность такого способа. Давайте снова обратимся к примеру.

Пусть вы — подающий надежды криминалист, и разрабатываете новый способ скрытно и однозначно определять, является ли человек преступником. Вы придумали количественный признак: оценивать преступные наклонности людей по частоте прослушивания ими Михаила Круга. Но будет ли давать адекватные результаты ваш признак? Давайте разбираться.
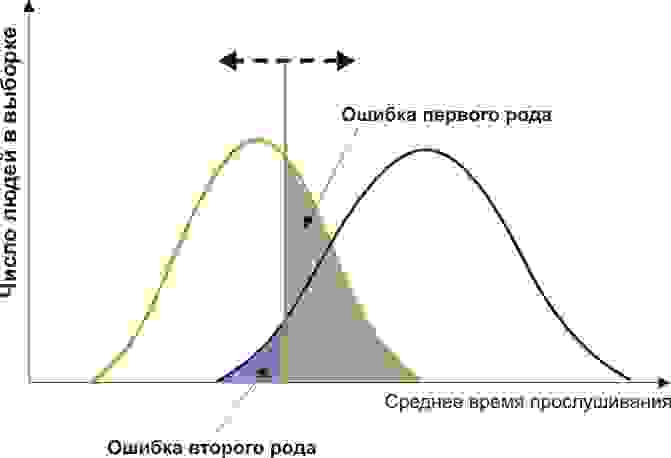
Вам понадобится две группы людей для валидации вашего критерия: обычные граждане и преступники. Положим, действительно, среднегодовое время прослушивания ими Михаила Круга различается (см. рисунок):

Здесь мы видим, что по количественному признаку времени прослушивания наши выборки пересекаются. Кто-то слушает Круга спонтанно по радио, не совершая преступлений, а кто-то нарушает закон, слушая другую музыку или даже будучи глухим. Какие у нас есть граничные условия? ROC-анализ вводит понятия селективности (чувствительности) и специфичности. Чувствительность определяется как способность выявлять все-все интересующие нас точки (в данном примере — преступников), а специфичность — не захватывать ничего ложноположительного (не ставить под подозрение простых обывателей). Мы можем задать некоторую критическую количественную черту, отделяющую одних от других (оранжевая), в пределах от максимальной чувствительности (зеленая) до максимальной специфичности (красная).
Посмотрим на следующую схему:

Смещая значение нашего признака, мы меняем соотношения ложноположительного и ложноотрицательного результатов (площади под кривыми). Точно так же мы можем дать определения Чувствительность = Полож. рез-т/(Полож. рез-т + ложноотриц. рез-т) и Специфичность = Отриц. рез-т/(Отриц. рез-т + ложноположит. рез-т).

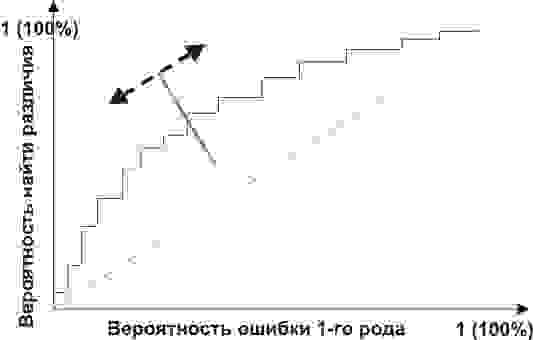
Но главное, мы можем оценить соотношение положительных результатов к ложноположительным на всем отрезке значений нашего количественного признака, что и есть наша искомая ROC-кривая (см. рисунок):

А как нам понять из этого графика, насколько хорош наш признак? Очень просто, посчитать площадь под кривой (AUC, area under curve). Пунктирная линия (0,0; 1,1) означает полное совпадение двух выборок и совершенно бессмысленный критерий (площадь под кривой равна 0,5 от всего квадрата). А вот выпуклость ROC кривой как раз и говорит о совершенстве критерия. Если же нам удастся найти такой критерий, что выборки вообще не будут пересекаться, то площадь под кривой займет весь график. В целом же признак считается хорошим, позволяющим надежно отделить одну выборку от другой, если AUC > 0,75-0,8.

С помощью такого анализа вы можете решать самые разные задачи. Решив, что слишком много домохозяек оказались под подозрением из-за Михаила Круга, а кроме того упущены опасные рецидивисты, слушающие Ноггано, вы можете отвергнуть этот критерий и разработать другой.

Возникнув, как способ обработки радиосигналов и идентификации «свой-чужой» после атаки на Перл-Харбор (отсюда и пошло такое странное название про характеристику приемника), ROC-анализ нашел широкое применение в биомедицинской статистике для анализа, валидации, создания и характеристики панелей биомаркеров и т.д. Он гибок в использовании, если оно основано на грамотной логике. Например, вы можете разработать показания для медицинской диспансеризации пенсионеров-сердечников, применив высокоспецифичный критерий, повысив эффективность выявления болезней сердца и не перегружая врачей лишними пациентами. А во время опасной эпидемии ранее неизвестного вируса вы наоборот, можете придумать высокоселективный критерий, чтобы от вакцинации в прямом смысле не ускользнул ни один чих.

С ошибками обоих родов и их наглядностью в описании валидируемых критериев мы познакомились. Теперь же, двигаясь от этих логических основ, можно разрушить ряд ложных стереотипных описаний результатов. Некоторые неправильные формулировки захватывают наши умы, часто путаясь своими схожими словами и понятиями, а также из-за очень малого внимания, уделяемого неверной интерпретации. Об этом, пожалуй, нужно будет написать отдельно.

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Методика проверки статистических гипотез
2 Альтернативная методика на основе достигаемого уровня значимости
3 Типы критической области
4 Ошибки первого и второго рода
5 Свойства статистических критериев
6 Типы статистических гипотез
7 Типы статистических критериев
- 7.1 Критерии согласия
- 7.2 Критерии сдвига
- 7.3 Критерии нормальности
- 7.4 Критерии однородности
- 7.5 Критерии симметричности
- 7.6 Критерии тренда, стационарности и случайности
- 7.7 Критерии выбросов
- 7.8 Критерии дисперсионного анализа
- 7.9 Критерии корреляционного анализа
- 7.10 Критерии регрессионного анализа
8 Литература
9 Ссылки

Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.

Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.

Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза.

Методика проверки статистических гипотез

Пусть задана случайная выборка $x^m = (x_1,\ldots,x_m)$ — последовательность объектов из множества .
Предполагается, что на множестве существует некоторая неизвестная вероятностная мера $\mathbb{P}$ .

Методика состоит в следующем.

Формулируется нулевая гипотеза о распределении вероятностей на множестве . Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая и альтернативная . Иногда альтернатива не формулируется в явном виде; тогда предполагается, что означает «не ». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.
Задаётся некоторая статистика (функция выборки) $T:\: X^m \to \mathbb{R}$ , для которой в условиях справедливости гипотезы выводится функция распределения и/или плотность распределения . Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика . Вывод функции распределения при заданных и является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для ; в статистических пакетах имеются готовые вычислительные процедуры.
Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число $\alpha \in [0,1]$ . На практике часто полагают $\alpha=0.05$ .
На множестве допустимых значений статистики выделяется критическое множество $\Omega_\alpha$ наименее вероятных значений статистики , такое, что $\mathbb{P}\{T\in\Omega_\alpha\left|H_0\right.\} = \alpha$ . Вычисление границ критического множества как функции от уровня значимости $\alpha$ является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.
Собственно статистический тест (статистический критерий) заключается в проверке условия:

Итак, статистический критерий определяется статистикой
и критическим множеством $\Omega_\alpha$ , которое зависит от уровня значимости $\alpha$ .

Замечание.
Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна.
Тому есть две причины.

Альтернативная методика на основе достигаемого уровня значимости

Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в докомпьютерную эпоху. Чаще всего использовались таблицы, в которых для некоторых априорных уровней значимости были выписаны критические значения. В настоящее время результаты проверки гипотез чаще представляют с помощью достигаемого уровня значимости.

Достигаемый уровень значимости (пи-величина, англ. p-value) — это наименьшая величина уровня значимости,
при которой нулевая гипотеза отвергается для данного значения статистики критерия

$p(T) = \min \{ \alpha:\: T\in\Omega_\alpha \},$

где
$\Omega_\alpha$ — критическая область критерия.

Другая интерпретация:
достигаемый уровень значимости p(T) — это вероятность при справедливости нулевой гипотезы получить значение статистики, такое же или ещё более экстремальное, чем

Если достигаемый уровень значимости достаточно мал (близок к нулю), то нулевая гипотеза отвергается.
В частности, его можно сравнивать с фиксированным уровнем значимости;
тогда альтернативная методика будет эквивалентна классической.

Типы критической области

Обозначим через $t_\alpha$ значение, которое находится из уравнения $F(t_\alpha) = \alpha$ , где $F(t) = \mathbb{P}\left\{ T<t \right\}$ — функция распределения статистики .
Если функция распределения непрерывная строго монотонная,
то $t_\alpha$ есть обратная к ней функция:

$t_\alpha = F^{-1}(\alpha)$

Значение $t_\alpha$ называется также $\alpha$ —квантилем распределения F(t) .

На практике, как правило, используются статистики с унимодальной (имеющей форму пика) плотностью распределения.
Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения.
Поэтому чаще всего возникают критические области одного из трёх типов:

Левосторонняя критическая область:

определяется интервалом $\Omega_\alpha = (-\infty,\, t_\alpha)$

пи-величина:

Правосторонняя критическая область:

определяется интервалом $\Omega_\alpha = (t_{1-\alpha},\,+\infty)$

пи-величина:

Двусторонняя критическая область:

определяется двумя интервалами $\Omega_\alpha = (-\infty,\, t_{\alpha/2}) \cup (t_{1-\alpha/2},\,+\infty);$

пи-величина: $p(T) = \min \left\{ 2F(T),\; 2(1-F(T)) \right\}.$

Ошибки первого и второго рода

Ошибка первого рода или «ложная тревога» (англ. type I error, $\alpha$ error, false positive) — когда нулевая гипотеза отвергается, хотя на самом деле она верна. Вероятность ошибки первого рода:

$\alpha = \mathbb{P}\left\{ T\in\Omega_\alpha | H_0 \right\}.$

Ошибка второго рода или «пропуск цели» (англ. type II error, $\beta$ error, false negative) — когда нулевая гипотеза принимается, хотя на самом деле она не верна. Вероятность ошибки второго рода:

$\beta(H_1) = \mathbb{P}\left\{ T\notin\Omega_\alpha | H_1 \right\}.$

	Верная гипотеза

Результат применения критерия		верно принята	неверно принята (Ошибка второго рода)
	неверно отвергнута (Ошибка первого рода)	верно отвергнута

Свойства статистических критериев

Мощность критерия:
$1 - \beta(H) = \mathbb{P}\left\{ T\in\Omega_\alpha | H \right\}$ — вероятность отклонить гипотезу H_0 , если на самом деле верна альтернативная гипотеза .
Мощность критерия является числовой функцией от альтернативной гипотезы .

Несмещённый критерий:
$1-\beta(H) \geq \alpha$
для всех альтернатив
или, что то же самое,
$\mathbb{P}\left\{ T\in\Omega_\alpha | H \right\} \geq \mathbb{P}\left\{ T\in\Omega_\alpha | H_0 \right\}$
для всех альтернатив .

Состоятельный критерий:
$\beta(H) \to 0$ при $m\to\infty$ для всех альтернатив .

Равномерно более мощный критерий.
Говорят, что критерий с мощностью $1-\beta(H)$ является равномерно более мощным, чем критерий с мощностью $1-\beta'(H)$ , если выполняются два условия:

$\beta(H_0) = \beta'(H_0)$ ;
$\beta(H_1) \leq \beta'(H_1)$ для всех рассматриваемых альтернатив $H_1\neq H_0$ , причём хотя бы для одной альтернативы неравенство строгое.

Типы статистических гипотез

Простая гипотеза однозначно определяет функцию распределения на множестве . Простые гипотезы имеют узкую область применения, ограниченную критериями согласия (см. ниже). Для простых гипотез известен общий вид равномерно более мощного критерия (Теорема Неймана-Пирсона).

Сложная гипотеза утверждает принадлежность распределения к некоторому множеству распределений на . Для сложных гипотез вывести равномерно более мощный критерий удаётся лишь в некоторых специальных случаях.

Типы статистических критериев

В зависимости от проверяемой нулевой гипотезы статистические критерии делятся на группы, перечисленные ниже по разделам.

Наряду с нулевой гипотезой, которая принимается или отвергается по результату анализа выборки, статистические критерии могут опираться на дополнительные предположения, которые априори предпологаются выполненными.

Параметрические критерии предполагают, что выборка порождена распределением из заданного параметрического семейства. В частности, существует много критериев, предназначенных для анализа выборок из нормального распределения. Преимущество этих критериев в том, что они более мощные. Если выборка действительно удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. Однако если выборка им не удовлетворяет, то вероятность ошибок (как I, так и II рода) может резко возрасти. Прежде чем применять такие критерии, необходимо убедиться, что выборка удовлетворяет дополнительным предположениям. Гипотезы о виде распределения проверяются с помощью критериев согласия.

Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев.

Критерии согласия

Критерии согласия проверяют, согласуется ли заданная выборка с заданным фиксированным распределением, с заданным параметрическим семейством распределений, или с другой выборкой.

Критерий Колмогорова-Смирнова
Критерий хи-квадрат (Пирсона)
Критерий омега-квадрат (фон Мизеса)

Критерии сдвига

Специальный случай двухвыборочных критериев согласия.
Проверяется гипотеза сдвига, согласно которой распределения двух выборок имеют одинаковую форму и отличаются только сдвигом на константу.

Критерий Стьюдента
Критерий Уилкоксона-Манна-Уитни

Критерии нормальности

Критерии нормальности — это выделенный частный случай критериев согласия.
Нормально распределённые величины часто встречаются в прикладных задачах, что обусловлено действием закона больших чисел.
Если про выборки заранее известно, что они подчиняются нормальному распределению, то к ним становится возможно применять более мощные параметрические критерии.
Проверка нормальность часто выполняется на первом шаге анализа выборки, чтобы решить, использовать далее параметрические методы или непараметрические.
В справочнике А. И. Кобзаря приведена сравнительная таблица мощности для 21 критерия нормальности.

Критерий Шапиро-Уилка
Критерий асимметрии и эксцесса

Критерии однородности

Критерии однородности предназначены для проверки нулевой гипотезы о том, что
две выборки (или несколько) взяты из одного распределения,
либо их распределения имеют одинаковые значения математического ожидания, дисперсии, или других параметров.

Критерии симметричности

Критерии симметричности позволяют проверить симметричность распределения.

Одновыборочный критерий Уилкоксона и его модификации: критерий Антилла-Кёрстинга-Цуккини, критерий Бхаттачария-Гаствирса-Райта
Критерий знаков
Коэффициент асимметрии

Критерии тренда, стационарности и случайности

Критерии тренда и случайности предназначены для проверки нулевой гипотезы об
отсутствии зависимости между выборочными данными и номером наблюдения в выборке.
Они часто применяются в анализе временных рядов, в частности, при анализе регрессионных остатков.

Критерии выбросов

Критерии дисперсионного анализа

Критерии корреляционного анализа

Критерии регрессионного анализа

Литература

Вероятность и математическая статистика: Энциклопедия / Под ред. Ю.В.Прохорова. — М.: Большая российская энциклопедия, 2003. — 912 с.
Кобзарь А. И. Прикладная математическая статистика. Справочник для инженеров и научных работников. — М.: Физматлит, 2006. — 816 с.

Ссылки

Statistical hypothesis testing — статья в англоязычной Википедии.

Источник