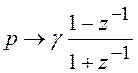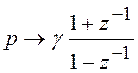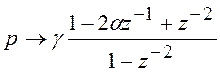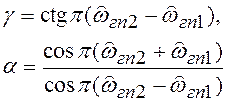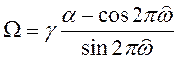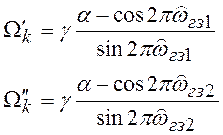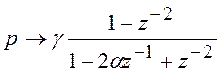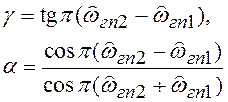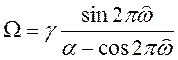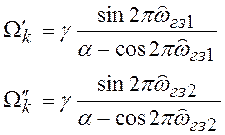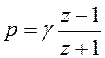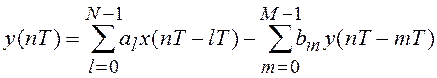Поскольку для значения a11=0 множители знаменателя равны соответственно (z + 0.5 + j1. 658) и (z + 0.5 — j1. 658), корни находятся снаружи единичной окружности и равны Z = -0.5 ± j1.658. Следовательно, система неустойчива для маленьких значений a11, но становится устойчивой для средних значений a11, и снова неустойчивой для больших величин a11.
Корни находятся снаружи единичной окружности z = -0.5 ± j1.658 для a11 = 0 и двигаются в сторону действительной оси. Бесконечная чувствительность будет тогда, когда корни совпадают в z = 0.732 ± j0.
Пределы устойчивости для a11, когда 2.0 < a11 < 2.5. Для a11 < 2.0 тип
увеличения неустойчивости – синусоидальный, в то время как для a11 > 2.5 тип увеличения неустойчивости – линейный. Обратите внимание на то, что чувствительность корня изменяется очень сильно, когда a11 располагается в определенных пределах, и интересным является второй пример точки годографа с бесконечной чувствительностью, расположенной на действительной оси, где корни совпадают z = 0.732 ± j0.
Вто время как в предыдущем разделе рассматривались эффекты квантования коэффициентов передаточной функции, в этом разделе рассматриваются эффекты квантования на входе системы, промежуточных переменных ЦОС и выходного сигнала. Существуют соответствующие методы для оценки максимальной величины ошибки квантования в цифровых системах.
Есть три источника квантования – на входе ЦОС, внутри ЦОС, и на выходе ЦОС, которые возникают потому, что:
•Входной сигнал для дискретной системы является непрерывным и необходимо его аналого-цифровое преобразование прежде, чем любые вычисления будут выполняться.
•Цифровой процессор отбрасывает часть вычисленных результатов при выполнении умножения и деления. Отбрасывание необходимо потому, что число битов, требуемых для точного представления результата, увеличивается по сравнению с числом битов, необходимых для представле-
ния коэффициентов матриц aij, bi, Ci, d. Без усечения или округления разрядность данных при умножении или делении увеличивается неограниченно.
•На выходе дискретного процессора обычно необходим непрерывный аналоговый сигнал, а используемый цифро-аналоговый преобразователь обычно имеет меньшее разрешение по сравнению с цифровым процессором. При этом отбрасывание самых младших битов дает ошибку квантования.
Все эти ошибки можно описать как шумоподобные ошибки квантования.
Ошибка квантования с округлением ε есть разница между точным значением величины и значением самого близкого из набора уровней, которые отличаются
друг от друга на q. И альтернативная ей, ошибка квантования с усечением ε –
|
Лекции по ППО ВС РВ © Клюс В.Б. |
36 |
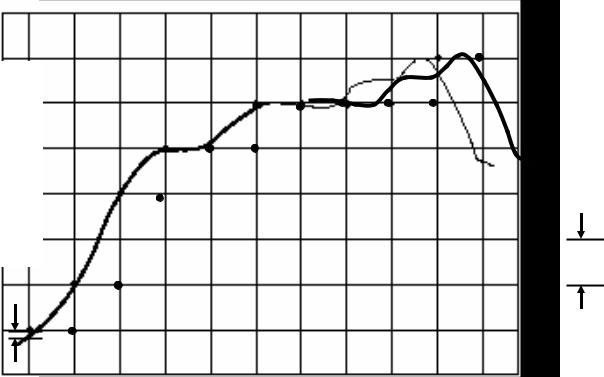
разница между точным значением величины и значением самого близкого снизу из набора уровней. Ошибка с округлением показана на рис.21 .15, на котором точная величина наложена на сетку квантованных уровней и интервалы дис-
кретизации. Ошибка квантования с округлением ε в моменты дискретизации k = 1, 2,… является интервалом между непрерывным сигналом и самым близким уровнем квантования.
Уровни квантования
q
ε
k k+1 k+2 k+3 k+4 k+5 k+6 k+7 k+8 k+9 k+10
Интервал дискретизации
Рисунок2.15. Непрерывный сигнал, наложенный на сетку интервалов дискретизации и уровней квантования, расположенных через q
Так как различие в уровнях квантования – q, ошибка округления ε между непрерывным сигналом и каждым из квантованных уровней не превышает ±q/2. Если предположить, что колебание сигнала является большим, чем q от одной
выборки к следующей, то ошибка ε для одной выборки будет статистически независимой от ошибки ε для любой другой выборки и будет иметь равную вероятность в диапазоне ±q/2.
Противоположный случай – постоянный или медленно изменяющийся сигнал. Для систем управления с обратной связью статистическая зависимость между выборками из-за квантования вызывает предельные циклы. Если там преобладает только одна такая нелинейность в контуре обратной связи, то возможно использование метода функции описания, чтобы приблизительно определить поведение предельного цикла. Однако добавление подходящего высокочастотного возмущающего сигнала ко входу системы сделает и ошибку квантования, и ошибку округления однородно распределенной, белой, и взаимно
|
некоррелированной. |
|
|
Лекции по ППО ВС РВ © Клюс В.Б. |
37 |
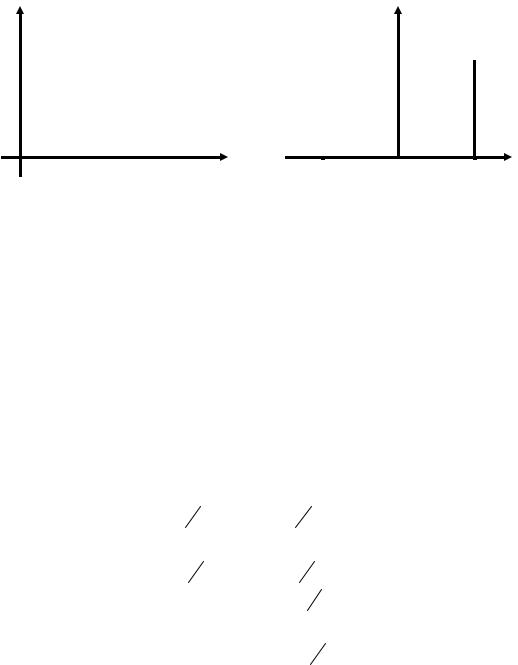
Три источника ошибки квантования эквивалентны добавлению шумоподобного воздействия ко входу, вычисленным результатам и выходу, соответственно. Результирующая функция плотности вероятности ошибки показана на рис.21 .16,a или рис.21 .16,б, в зависимости от того, усечение, или округление происходит при квантовании. Усечение – простое отбрасывание самых младших битов, при округлении используется наименьший значащий бит квантования, чтобы минимизировать абсолютную величину ошибки.
|
ε |
q/2 ε |
|||||
|
q |
q/2 |
|||||
|
а |
б |
Рисунок2.16. Функции плотности вероятности ошибки квантования для усечения (a) и округления (б)
Среднее или матожидание μ и дисперсия σ2 шума определяются как пер-
вый и второй моменты Ε{ξ}, Ε{ξ2} из соответствующих функций плотности вероятности.
Квантование с усечением:
|
q |
q |
1 |
q |
|||||
|
∫ |
∫ |
|||||||
|
μ = Ε{ε} = |
εf (ε)dε = |
ε |
dε = |
(2.32) |
||||
|
0 |
0 |
q |
2 |
|
σ |
2 |
= Ε{(ε − μ) |
2 |
}= Ε{ε |
2 |
2 |
q |
2 |
1 |
q |
2 |
= |
q |
2 |
. |
(2.33) |
||||||||||
|
}− Ε{ε} |
= ∫ε |
dε − |
12 |
|||||||||||||||||||||||
|
0 |
q |
2 |
||||||||||||||||||||||||
|
Квантование с округлением: |
||||||||||||||||||||||||||
|
q |
2 |
q 2 |
1 |
(2.34) |
||||||||||||||||||||||
|
μ = Ε{ε} = ∫εf (ε)dε = |
∫ |
ε |
dε = 0 |
|||||||||||||||||||||||
|
−q |
−q |
q |
||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||
|
σ |
2 |
= Ε{(ε − μ) |
2 |
}= Ε{ε |
2 |
2 |
q |
2 |
2 |
1 |
2 |
= |
q2 |
. |
(2.35) |
|||||||||||
|
}− Ε{ε} |
= ∫ε |
dε − 0 |
12 |
|||||||||||||||||||||||
|
−q |
2 |
q |
||||||||||||||||||||||||
|
Результаты (21 .32)-(21 .35) показывают, что дисперсия для усечения такая же, |
как и для округления, и только матожидание является различным. Модель для шумовых источников при каждой выборке в момент k определяется как
|
ε (k,•)= w(k,•)+ με |
(2.36) |
|
Лекции по ППО ВС РВ © Клюс В.Б. |
38 |
где запись ε(k, •) и w(k,•) описывает реальные значения стохастических про-
цессов такие, что ε(k, •) и w(k,•) являются произвольными переменными для любого фиксированного k, k = 1,… .
Случайная переменная w(k,•) имеет нулевое матожидание и дисперсию
q2/12, в то время как με определяется как με = 0 или με = q/2 в зависимости от того, используется округление или усечение соответственно. Описание шумовых источников как переменной и постоянной части позволяет рассматривать
отдельно их влияние – w(k,•) исключительно на дисперсию и με как производную от смещения АЦП.
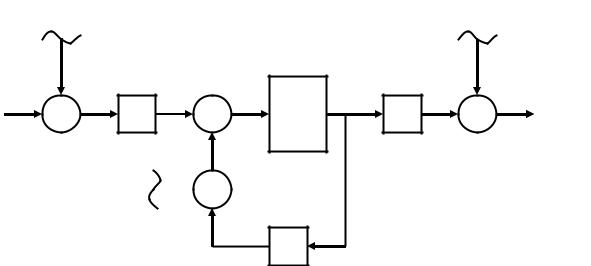
Источники ошибки показаны на диаграмме состояния (рис.21 .17) как шум аналого-цифрового преобразования на входе εi(k,w), шум вычисления εc(k,w) и шум цифро-аналогового преобразования на выходе εo(k,w).
|
εi(k,•) |
εo(k,•) |
||||||
|
Z-1 |
u(k) |
||||||
|
x(k) |
+ |
b |
+ |
c |
+ |
Y(k) |
εc(k,•) 
Рисунок2.17. Диаграмма состояния, показывающая скалярную входную ошибку квантования εi(k,•), векторный шум вычисления εc(k,•) и скаляр εo(k,•)
Соответствующее уравнение состояния
u(k+1) = A u(k) + b [ x(k) + εi(k) ] + εc(k) ,
(2.37)
y(k) = c u(k) + εo(k) .
Вычисление выходной дисперсии σ y2 требует нахождения значения вто-
|
рого момента y(k). |
|
|
σy2 = Ε{y(k)yT (k)}= Ε{[cu(k) +εo (k,•)][cu(k) +εo (k,•)]T }= |
|
|
= Ε{[cu(k) +εo (k,•)][uT (k)cT +εoT (k,•)]}= |
(2.38 |
= Ε{cu(k)uT (k)cT +εo (k,•)uT (k)cT + cu(k)εoT (k,•) +εo (k,•)εoT (k,• )
Поскольку εo(k,•) имеет нулевое матожидание и некоррелировано с x(k)
|
Лекции по ППО ВС РВ © Клюс В.Б. |
39 |
|
Ε{y(k) yT (k)}= cΕ{u(k)uT (k)cT }+Ε{εo (k,•)εoT (k,•)}= |
(2.39) |
||
|
= cP |
(k)cT + R (0) , |
||
|
uu |
o |
где Ro(τ), τ = 0, является автокорреляционной функцией выходного шума. Уравнение (21 .39) показывает, что выходная дисперсия является суммой
выходной ковариации шума и уровня ковариации Puu(k) взвешенного выход-
ным вектором с. Вычисление уровня ковариации Puu(k) требует рекуррентной формулы, которая находится из ожидаемой величины второго момента u(k+1).
Из (21 .37),
PUU (k +1) = Ε{u(k +1)uT (k +1)}=
= Ε{[Au(k) + bwi (k,•) + wc (k,•)][Au(k) + bwi (k,•) + wc (k,•)]T }=
= Ε{[Au(k) + bwi (k,•) + wc (k,•)][uT (k)AT + wiT (k,•)bT + wcT (k,•)]}= (2.40) = Ε{Au(k)uT (k)AT + Au(k)wiT (k,•)bT + Au(k)wcT (k,•) +
+bwi (k,•)uT (k)AT +bwi (k,•)wiT (k,•)bT +bwi (k,•)wcT (k,•) + + wc (k,•)uT (k)AT + wc (k,•)wiT (k,•)bT + wc (k,•)wcT (k,•)} .
Так как шумовые источники wi(k,•), wc(k,•) статистически независимы друг от друга и от u(k), ожидаемое значение их перекрестных произведений нулевое. Уравнение (21 .40) приводится к виду
|
PUU (k +1) = Au(k)uT (k)AT + bwi (k,•)wiT (k,•)bT + wc (k,•)wcT (k,•) , |
(2.41) |
|||
|
или |
(k)AT +bR (0)bT + R (0) , |
|||
|
P |
(k +1) = AP |
(2.42) |
||
|
UU |
UU |
i |
c |
где Ri(τ) и Rc(τ), τ = 0, являются автокорреляционными функциями входного шума и шума вычисления, соответственно.
Уравнение (21 .42) говорит, что значение ковариации при выборке k+1 получается из ковариации для предыдущей выборки плюс компоненты входного шума и шума вычислений. Если состояние u(k) было точно известно из началь-
ного состояния и при допущении Puu(0)=0, тогда для каждого следующего отсчета k=1, 2, … представленного как u(k), получается как дано в (21 .42). Так как матрица А устойчива с собственными значениями внутри единичного круга,
|
lim PUU (k) → PUU (k +1) , |
(2.43) |
|
k →∞ |
и вычисление выражения (21 .42) – простая рекурсивная задача с доступными инструментальными средствами работы с матрицами. Обратите внимание, что результирующий шум имеет не равномерный закон распределения, а скорее гауссовский в соответствии с центральной предельной теоремой.
Пример 3.
Рассмотрим динамическую систему из примера 1, но со значением a11=2.4, дающую фильтр нижних частот. Предположим, что входной сигнал
|
Лекции по ППО ВС РВ © Клюс В.Б. |
40 |
продискретизирован 10-разрядным А/Ц преобразователем с диапазоном от -1 до +1 В и самый младший бит соответствует приблизительно 20 мВ. Предпо-
ложим также, что в ЦПС переменные u1(k) и u2(k) представлены 16разрядными словами в дополнительном коде с динамическим диапазоном от -1 (8000h) до (+1-1/215) (7FFFh), где суффикс «h» обозначает шестнадцатеричное число. При вычислениях ЦПС усекает результаты, то есть при умножении в качестве результата берутся 16-разрядные слова и результаты выдаются в диапазоне от -1 до +1 В на 9-разрядный Ц/А преобразователь с весом младшего разряда приблизительно равным 40 мВ. Определим, какой величины будет выходной шум.
Результирующая диаграмма состояния для данного случая показана на рис.21 .18 с источниками шума ei, ec1, ec2, eo. Заметим, что не имеется никакого
источника шума, связанного коэффициентом С22, равным -1, так как при этом фактически умножения нет, а есть только вычитание.
εi (k,•)
|
X(k) |
+ |
εo (k,•) |
|
|
+ |
Z-1 |
U1(k) |
||
|
) |
||||
|
εc1 |
(k, |
|||
|
a11 |
• |
2.4
+
|
Z-1 |
U2(k) |
|||||||
|
+ |
+ |
Y(k) |
||||||
|
-1 |
||||||||
εc2 (k,•)
-3
+
Рисунок2.18. Диаграмма состояния для примера 3, показывающая шумовые источники из-за эффектов квантования
Матожидания и дисперсии различных источников представлены далее. Входной шум:
|
μi |
= 0 ; |
||||||
|
1 |
2 |
||||||
|
σ 2 |
= |
29 |
= 3.18 ×10−7 B2 |
R = 3.18 ×10−7 |
B2 . |
(2.44) |
|
|
i |
12 |
i |
|||||
Шум вычисления:
1
μc1,c2 = 2215 =1.53×10−5 ;
|
Лекции по ППО ВС РВ © Клюс В.Б. |
41 |
|
1 |
2 |
||||||||||
|
7.76 |
×10−11 |
0 |
. |
||||||||
|
215 |
|||||||||||
|
σ 2 |
= |
= 7.76 ×10−11 |
R |
= |
|||||||
|
c1,c2 |
12 |
c |
0 |
7.76 ×10−11 |
|||||||
Выходной шум:
|
1 |
|||||||||||||||||||||
|
μo |
= |
28 |
=1.95×10−3 ; |
||||||||||||||||||
|
2 |
|||||||||||||||||||||
|
1 |
2 |
||||||||||||||||||||
|
σ 2 |
= |
28 |
=1.27 ×10−6 |
R =1.27 ×10−6 . |
|||||||||||||||||
|
o |
12 |
o |
|||||||||||||||||||
|
Используя значения (21 .44), уровень ковариации согласно (21 .42) равен |
|||||||||||||||||||||
|
P |
(k +1) |
= |
2.4 |
− 3 P |
(k ) |
2.4 |
− 3 T |
+ 0 |
3.18 ×10 −7 |
0 |
T |
+ |
|||||||||
|
UU |
1 |
UU |
1 |
||||||||||||||||||
|
−1 |
−1 |
1 |
1 |
(2.45) |
|||||||||||||||||
|
7.76 ×10 −11 |
0 |
||||||||||||||||||||
|
+ |
|||||||||||||||||||||
|
0 |
7.76 ×10 −11 |
. |
|||||||||||||||||||
Рис.21 .19 показывает рекурсивное решение для k = 0, 1, … учитывая, что начальное состояние известно и равно
|
0 |
0 |
(2.46) |
|
PUU (0) = |
. |
|
|
0 |
0 |
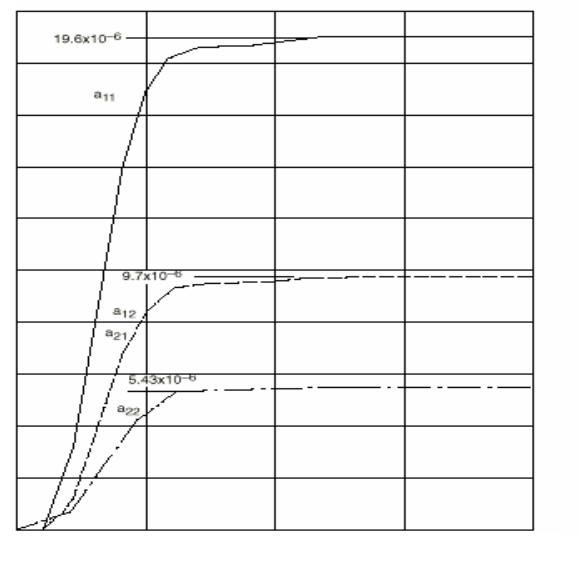
Значение ковариации увеличивается по траектории от ноля до величины установившегося значения. Динамика состояния определяет скорость увеличения траектории. Окончательная величина матрицы значений ковариации равна
|
×10 |
−6 |
9.70×10 |
−6 |
|||||
|
lim |
P |
19.6 |
. |
(2.47) |
||||
|
(k) = |
×10−6 |
5.43×10−6 |
||||||
|
k →∞ |
UU |
9.70 |
||||||
Значения дисперсии находятся на основной диагонали матрицы ковариа-
ций (21 .47) и, следовательно, σu12=19.6×10-6 и σu22=5.43×10-6 . Обратите внимание, что начальное предположение, сделанное, чтобы исключить первоначальную неопределенность PUU(0) не оказывает воздействия на конечный результат (21 .47). Если, например, PUU(0) первоначально большое относительно установившейся величины состояние ковариации, PUU(k) уменьшалось бы до ранее полученного результата (21 .47).
Если известно состояние ковариации PUU(k), то выходная дисперсия может
|
быть найдена из (21 .39): |
||||||||||
|
Ε{y(k) yT (k)}= cP |
(k)cT + R |
(0) = |
||||||||
|
uu |
o |
|||||||||
|
×10 |
−6 |
9.70×10 |
−6 |
[0 1]T +1.27 |
×10−6 |
= |
(2.48) |
|||
|
= [0 1] 19.6 |
||||||||||
|
9.70×10−6 |
5.43×10 |
−6 |
||||||||
= 5.43×10−6 +1.27×10−6 = 6.70×10−6 .
|
Лекции по ППО ВС РВ © Клюс В.Б. |
42 |
Значение ковариации
|
20 |
||||
|
18 |
||||
|
16 |
||||
|
14 |
||||
|
12 |
||||
|
10 |
||||
|
8 |
||||
|
6 |
||||
|
4 |
||||
|
2 |
||||
|
0 |
5 |
10 |
15 |
20 |
|
0 |
Номер выборки
Рисунок2.19. Решение уравнения для матрицы ковариации. Асимптотическое приближение при k → ∞
Одно из назначений вычисления ковариации – способность различить видимые источники неопределенности для полной оптимизации системы. В этом случае имеется незначительный вклад ошибок вычисления, и более существенный вклад выхода Ц/A преобразователя. Если при полной оптимизация системы исходить из стоимости, то, учитывая вклад Ц/A преобразователя можно обойтись меньшим разрешением и менее дорогим 8-разрядным ЦАП.
Чтобы учесть эффекты усечения и округления, как видно из рис.21 .15 и (21 .32), дисперсии для любого случая должна быть та же самая, но усечение дает
среднее отличное от нуля μc1 = μc2 = q/2 = 1.53×10-5, которое представляет смещение состояния от u(k) до u(k+1). Эффект моделируется выражениями
(21 .44) и
|
μi = 0, |
×10 |
−5 |
, |
μo =1.95 ×10−3 . |
(2.49) |
||
|
μc = 1.53 |
−5 |
||||||
|
1.53 |
×10 |
||||||
|
Лекции по ППО ВС РВ © Клюс В.Б. |
43 |
При использовании этих средних в качестве входных, уравнение состояния (21 .37) преобразуется в
|
u1 |
(k +1) |
2.4 |
−3 |
u1(k) |
0 |
0 |
1.53 |
×10 |
−5 |
; |
|||||
|
= |
1 |
+ 0 + |
0 + |
×10 |
|||||||||||
|
u2 |
(k +1) |
−1 |
u2 (k) |
1 |
1 |
1.53 |
−5 |
||||||||
|
(2.50) |
|||||||||||||||
|
y(k) = [0 |
u (k) |
||||||||||||||
|
1] |
1 |
+1.95×10−3 , |
|||||||||||||
|
u2 (k) |
|||||||||||||||
|
рекурсивное решение, которого дает |
−5 |
||||||||||||||
|
lim |
u (k) |
×10 |
, |
(2.51) |
|||||||||||
|
1 |
= |
−7.65 |
|||||||||||||
|
k →∞ u2 (k) |
−3.06×10−5 |
||||||||||||||
|
и выход |
|||||||||||||||
|
lim y(k) |
= cu(k) + Ro = |
||||||||||||||
|
k →∞ |
|||||||||||||||
|
= [0 |
7.65×10 |
−5 |
+1.95 |
×10−3 |
=1.92×10−3 |
B . |
(2.52) |
||||||||
|
1] − |
|||||||||||||||
|
−3.06×10−5 |
|||||||||||||||
2.4.3. Минимизация эффектов квантования в ЦПС семейства TMS320 Чтобы увидеть, как в ЦПС семейства TMS320 уменьшить эффекты кван-
тования, необходимо вначале рассмотреть, как представляются десятичные числа и как выполняются арифметические операции в ЦПС.
Центральное арифметическо-логическое устройство процессоров семейства TMS320C5х имеет входное 16-разрядное сдвигающее устройство, 17×17разрядный параллельный умножитель, 40-разрядное арифметическо-логическое устройство (АЛУ), два 40-разрядных аккумулятора, и дополнительные сдвигающие устройства на выходах аккумулятора и умножителя. Типичная операция умножения двух чисел А×B требует команду «LD» для загрузки регистра «T» значением A, команду «MPY» указывающую второй операнд в памяти данных B и команду «STH», чтобы сохранить в память данных 16 старших битов 32-разрядного результата, который находится в аккумуляторе. Таким образом, одиночное умножение двух чисел требует трех команд, и если используется внутренняя память на кристалле, не требующая циклов ожидания, как например, для медленной памяти вне кристалла, то время умножения для TMS320VC5402 со временем выполнения команды 10 наносекунд, будет равно времени для трех команд или 30 наносекунд. При использовании 2-х операндных команд умножения время умножения сокращается до 20 наносекунд, но адреса операндов должны быть предварительно загружены в два вспомогательных регистра. Если умножение объединяется с добавлением затем к АЛУ, то выборка данных, умножение и накопление могут выполняться в одном цикле команды «MACD», которая значительно повышает эффективность вычислений.
Десятичные числа представляются в виде 16-разрядных (одинарной точности) вычисленных дробей. Цифровые слова имеют форму
|
Лекции по ППО ВС РВ © Клюс В.Б. |
44 |

|
СР |
МР |
|||||
|
Номер разряда |
15 |
14 |
13 |
12 11 |
… |
0 |
|
Величина |
-S |
S/2 |
S/4 |
S/8 S/16 |
… |
S/215 , |
где бит 15 – знаковый разряд. Подразумеваемая точка основания системы счисления расположена между битами 15 и 14, а биты от 0 до 14 задают 15 разрядов величины числа. S – положительное число из диапазона от 0 до ∞, которое является коэффициентом пересчета цифрового слова. Коэффициент пересчета S позволяет цифровому слову представлять любое число из интервала [ -S, +S(1- 1/215) ] для цифрового диапазона слова от 8000h до 7FFFh, где суффикс «h» указывает шестнадцатеричную величину.
Общие специальные случаи – для S=215=32768, который смещает деся-
|
тичную точку вправо, чтобы представлять |
целые числа в |
интервале |
|
[-32768, 32767], и для S=1, который выравнивает десятичную точку так, чтобы |
||
|
десятичное число, представляемое цифровым |
словом, имело |
интервал |
[-1, 0.9999695]. Особенность этого второго представления – предотвращение переполнения АЛУ, так как произведение любых чисел из данного интервала будет всегда давать другое число, содержащееся внутри интервала [-1, 0.9999695].
Поскольку каждое цифровое слово имеет заданный масштабный множитель, соблюдаются два правила при выполнении арифметических операций:
Правило 1. Сложение
Если две переменных x и y с соответствующими масштабными множителями Sx и Sy складываются, x + y, то оба масштабных множителя должны быть
одинаковыми, Sx = Sy. Правило 2. Умножение
Если константа C умножается на переменную x с масштабным множителем Sx, чтобы получить переменную y: y = Cx, то масштабный множитель Sy с учетом масштаба C получается согласно правилу
CЦПС = C Sx .Sy
Применение этого правила переводит десятичную константу C к десятичной дроби СЦПС с интервалом [ -1, (1-1/215) ]. СЦПС представляется внутри ЦПС как цифровое слово в интервале [8000h, 7FFFh].
Правило 1 относится к механизму масштабирования при сложении и дает ошибку квантования в младшем разряде, если сдвигаемая переменная отбрасывается после добавления ко второй переменной. Приведенный далее пример иллюстрирует эту ситуацию.
Правило 2 относится к умножению и, следовательно, воздействует на квантование как было описано ранее. Рассмотрим применение правила 2.
Предположим, что необходимо вычислить выражение y = 5x, где x находится в интервале [-1.8, +1.6], и это желательно привести к шкале используемого ЦПС. Так как максимум абсолютной величины x равен 1.8, масштабный
|
Лекции по ППО ВС РВ © Клюс В.Б. |
45 |
множитель Sx должен быть некоторым числом ≥ 1.8, и чтобы минимизировать эффекты квантования, выбираем Sx так, чтобы Sx=1.8 точно. При таком выборе Sx получим почти симметричный интервал [-1.8, 1.8(1-1/215)] с цифровым интервалом слова [8000h, 7FFFh], что перекрывает интервал x настолько близко, насколько возможно. Так как Sx=1.8, произведение y = 5x попадает в интервал [-5×1.8, +5×1.8(1-1/215)], или [-9, ≈ 8.999725]. Соответствующий интервал Sy должен быть ≥ 9. Поскольку максимальная положительная величина СЦПС (1-1/215) ≈0.9999695, а не 1, то Sy должно быть немного большим, чем 9 и, например, выберем Sy=10.
Учитывая заданное значение Sx и выбранное значение Sy для СЦОС, полу-
чим
CЦПС = 5 1.8 = 0.90000 = 7333h .
10
Применение этих двух правил для масштабирования и уменьшение эффектов квантования в цифровых процессорах сигналов семейства TMS320 включает следующие особенности для арифметики с фиксированной точкой:
1.Наиболее очевидная и важная особенность уменьшения эффектов квантования – ширина АЛУ, аккумулятора и 17×17 разрядного умножителя. 40-разрядная ширина позволяет выполнять накопление любых 32разрядных слов повышенной точности или 16-разрядных слов без переполнения. При умножении 32-разрядное произведение соответствует 32разрядной ширине аккумулятора, и любой полный результат умножения знаковых чисел помещается в АЛУ, или умножение расширенной точности 32×32 бита возможно для беззнаковых чисел.
2.Вторая особенность – на входе АЛУ имеется сдвигающее устройство, чей 16-разрядный вход соединяется с шиной данных, а 40-разрядный выход соединяется со входом АЛУ. Сдвигающее устройство выполняет левый сдвиг от 0 до 16 бит над входными данными, где выходные младшие разряды заполняются нолями, а старшие заполняются нолями или расширением знака, в зависимости от «SXM» (режим расширения знака) бита. Если прибавление
x с масштабным множителем Sx выполняется к содержимому аккумулятора y с масштабным множителем Sy, и если Sx и Sy отличаются как степени 2, то сдвигающее устройство может пересчитать масштаб x к Sy перед сложением. Эта вторая особенность позволяет просто реализовать правило 1, но не касается проблемы квантования, потому что это применимо только к сложению.
3.Третья особенность, которая касается квантования– возможность исключения режима переполнения аккумулятора для операций сложения и вычитания по модулю. Модульная арифметика выгодна там, где несколько чисел, обычно переменного знака, складывают вместе и результат всегда меньше, чем сумма их абсолютных величин. Общий пример такого вычисления– суммирование значений с ответвлений КИХ-фильтра, чтобы сформировать сигнал на его выходе.
|
Лекции по ППО ВС РВ © Клюс В.Б. |
46 |
Для модульной арифметики аккумулятор ориентируется на максимальный числовой диапазон конечных результатов вместо максимального диапазона промежуточных данных. После настройки на конечный результат изначально предполагается, что число положительных и отрицательных переполнений будет примерно одинаковым, переполнения игнорируются в промежуточных результатах накопления, поскольку числа добавляются или вычитаются. Таким образом, биты, которые в другом случае предотвратили бы переполнение, дают дополнительные значащие биты в представлении конечной суммы в аккумуляторе. Модульное сложение уменьшает шум квантования, позволяя уменьшить масштабный множитель аккумулятора, что позволяет накапливать полные 31-разрядные результаты умножения без усечения. Наличие 8 защитных разрядов еще более расширяет диапазон представления чисел.
4.Четвертая особенность уменьшает квантование передаточной функции, позволяя сдвинуть результат умножения прежде, чем он будет добавлен к аккумулятору. В произведении y = Cx этот общий выходной масштаб Sy мо-
жет быть заметно большим, чем константа C и входной масштаб Sx. Из правила 2, однако следует, что если масштаб Sy большой, то СЦПС будет ма-
леньким, и число значащих битов, определяющих сомножитель СЦПС уменьшается, чтобы получить более квантованную передаточную функцию. Более привлекательное решение для квантования коэффициентов состоит в том, чтобы уменьшить масштабный множитель аккумулятора в два раза при
вычислении СЦПС, и применить правый сдвиг произведения в регистре «P» прежде, чем оно будет добавлено к аккумулятору. Таким образом, это кван-
тование коэффициентов дает дополнительные значащие биты для СЦПС, чтобы представить C.
Обычно левый сдвиг на +1 требуется для знакового умножения дробных чисел, потому что произведение на выходе умножителя имеет двойной знаковый разряд. Если не делать никакого сдвига перед сложением, то эффект эквивалентен правому сдвигу для более низкого масштабного множителя. Бо-
лее низкий масштабный множитель Sacc/2 для выхода умножителя функционирует, согласно правилу 2, и дает левый сдвиг СЦПС и дополнительный значащий бит результата. Таким образом, сдвиг результата умножения дает компромисс между квантованием передаточной функции и шумом
квантования. Шум квантования очень маленький и не увеличивается с числом сдвигов. Он всегда равен Sacc/231, где Sacc – масштабный коэффициент аккумулятора.
5.Пятая особенность– сдвигающее устройство на выходе аккумулятора. Команда «STH» копирует весь аккумулятор в сдвигающее устройство, где всё это 40-разрядное число сдвигается на какое-нибудь число разрядов от 0 до 15, и затем копирует старшие (младшие для команды «STL») 16 битов сдвинутой величины в память данных. Сам аккумулятор при этом не изменяется. Выходной сдвигатель, таким образом, позволяет иметь большой масштабный множитель аккумулятора с несколькими старшими битами, чтобы предотвратить переполнение при циклическом сложении, но позволяет полно-
|
Лекции по ППО ВС РВ © Клюс В.Б. |
47 |
стью сохранить 15 значащих битов (одинарная точность) из 31 бита аккумулятора. Без этого сдвигателя любое различие между аккумулятором и выходными масштабными множителями давало бы результат, который имел бы меньшее количество значащих битов и большую ошибку квантования.
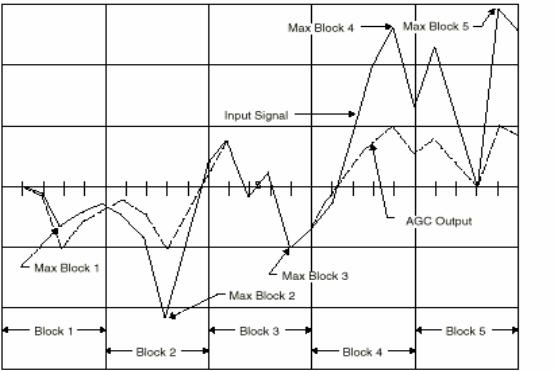
6.Шестая особенность– простая реализация функции автоматической регулировки усиления (АРУ). Функция АРУ позволяет динамически масштабировать входные данные, чьи входная амплитуда значительно изменяется через какое-то время. Для некоторых приложений, например передача данных, данные организованы в виде блоков, в то время как для других приложений входные данные предусматривают изменяемый формат. Входной сигнал организован в виде цифровых слов внутри блоков данных, но значительно изменяется во времени с каждым блоком данных в пределах цифрового слова большей величины. Самая большая величина внутри каждого блока используется для масштабирования входного сигнала. Рис.21 .20 показывает структуру данных и блоков данных для телекоммуникации. Для этих приложений обычное используемое масштабирование в ЦПС, чтобы приспособить сигнал самой большой амплитуды, неизменно приводит для сигналов с мень-
шей амплитудой к ошибке усечения или округления.
Значение слова данных
3
2
1
0
-1
-2
|
-3 |
0 |
5 |
10 |
15 |
20 |
25 |
|
Слово данных |
Рисунок2.20. Структура данных и блоков данных для телекоммуникации
С другой стороны, функция АРУ автоматически корректирует входной сигнал, как показано на рис.21 .20 до амплитуды, необходимой для соответствующего масштаба и минимальной ошибки.
Чтобы применить функцию АРУ к блоку отсчетов данных, первое слово блока данных загружается в первый аккумулятор. Команда «MAX» затем проверяет каждое следующее слово данных блока загружаемое во второй аккумулятор, чтобы найти большее слово данных. Если большее значение
|
Лекции по ППО ВС РВ © Клюс В.Б. |
48 |
найдено, то эта команда сохраняет большее число из второго аккумулятора в первый аккумулятор. После того как проверка закончится, максимальное слово данных для данного блока данных всегда будет находиться в первом аккумуляторе.
По этому максимальному известному значению обратная величина может быть найдена делением или по таблице. Обратная величина затем загружается в регистр «T», и все слова блока данных затем умножаются на нее, то есть, масштабируются путем деления на максимум. В качестве альтернативы, выбором из таблицы можно определить максимально возможный левый сдвиг (умножение на степень 2) для уменьшения максимального значения в блоке. Левые сдвиги можно выполнять автоматически, загружая в «T» величину сдвига и затем использовать команду «LD TS», чтобы загрузить аккумулятор с левым сдвигом на число разрядов, задаваемых с помощью «T».
7.И, в заключение, перечислим ряд дополнительных особенностей. Рассмотренные выше особенности составляют минимальное подмножество математических возможностей, которые любой ЦПС должен иметь, но которые могут отсутствовать в микроконтроллерах. Одна из них– способность сохранить содержимое аккумулятора со сдвигом вправо, в то время как само содержимое аккумулятора не изменяется и не появляется ни какой ошибки усечения. Вторая– наличие флага переноса и заема для повышенной точности 64-разрядного сложения и вычитания. И третья– возможность знакового и беззнакового умножения, которая позволяет выполнять умножение с повышенной точностью.
|
Лекции по ППО ВС РВ © Клюс В.Б. |
49 |
Соседние файлы в папке 28-12-2014_12-52-57
- #
- #
- #
В современных технических системах широко используются локальные системы автоматического контроля и управления. Локализация таких систем непосредственно на объекте управления ставит задачу миниатюризации аппаратной части системы при обеспечении высокой точности контроля и управления. Важной особенностью таких систем является обработка сигналов в темпе их поступления, чтобы исключить информационные потери. Такой режим работы, режим реального времени, предъявляет жесткие ограничения как на время решения задач приема, преобразования, фильтрации, обработки и принятия решения, так и на скорости информационного обмена [1].
Применение микропроцессорной техники позволяет решить задачу миниатюризации аппаратной части системы, однако режим реального времени требует высокого быстродействия используемых устройств, что обуславливает применение устройств с фиксированной точкой и ограниченной разрядной сеткой. Переход к цифровым методам обработки и схемотехнике приводит к появлению специфических ошибок – ошибок квантования [2]. При этом нецелесообразно использовать алгоритмы фильтрации и обработки сигналов высоких порядков из-за накопления вычислительных ошибок.
Квантование усложняет характер протекания динамических процессов и в первом приближении цифровые системы, рассматриваются как импульсные с последующим учетом влияния квантования по уровню, в виде дополнительных шумов квантования [2].
Анализ и получение оценки верхней границы ошибок квантования в микропроцессорных системах фильтрации и обработки сигналов с фиксированной точкой и ограниченной разрядной сеткой позволит учесть вес ошибок при анализе точности системы контроля и управления.
Цифровая фильтрация и обработка сигналов выполняется обычно цифровыми фильтрами. Основными источниками ошибок квантования могут быть:
— квантование входного сигнала в устройствах преобразования из аналогового вида в цифровой;
— квантование коэффициентов процедуры фильтрации и обработки сигналов;
— квантование арифметических операций в устройстве, выполняющем процедуру фильтрации и обработки сигналов.
Преобразование аналогового сигнала в цифровой осуществляется в аналого-цифровом преобразователе. Теоретически установлено, что квантование с линейной шкалой приводит к возникновению методической погрешности, называемой шумом квантования. Максимальное значение этой погрешности равно единицы младшего разряда, а дисперсия
при работе со случайными процессами равна приближенно [3]
,
где — шаг квантования;
— среднеквадратическое отклонение.
Однако этот результат относится к идеальным АЦП, у которых характеристика квантования, представляющая собой зависимость выходного кода от , при числе разрядов
имеет
ступеней, а шаг квантования
постоянен по всей характеристике.
Характеристики квантования реальных АЦП отличаются от идеальных из-за наличия неизбежных аппаратурных погрешностей, обусловленных несовершенством отдельных элементов преобразователей, уходом параметров в зависимости от времени, температуры, нестабильности источников питания и т.п. Общее число источников, вызывающих аппаратурные погрешности, всегда велико и зависит лишь от того, насколько малую погрешность должен обеспечивать АЦП, т.е. от класса точности данного АЦП.
Поэтому для анализа ошибок квантования может быть построена нелинейная модель квантования конкретного АЦП, учитывающая нелинейные процессы квантования и влияния дестабилизирующих факторов схемы конкретного АЦП, и линейная модель квантования, которая приближенно, но с достаточной достоверностью, описывает процесс квантования [2, 4, 5].
Воспользуемся линейной моделью формирования выходного сигнала АЦП, состоящей из дискретизатора, который с периодом дискретизации из аналогового сигнала
формирует дискретный сигнал
, и сумматора, который добавляет ошибку квантования по уровню
для формирования выходного цифрового сигнала
[6].
Для сопряжения АЦП с компьютерной системой применяются прямой (CSB) и дополнительный (CTC) двоичные коды: прямой — для униполярных сигналов и дополнительный — для биполярных сигналов. При разрядности в прямом двоичном коде используются все разряды для кодирования входного сигнала
, а в дополнительном коде один разряд выделяется для знака и
разрядов для кодирования величины сигнала, т.е.
.
При анализе ошибок квантования делается допущение, что ошибка равновероятна в пределах шага квантования и тогда ошибку квантования рассматривают как случайную величину с равномерной плотностью распределения [2]. Квантование может выполняться двумя способа – округлением и усечением. Среднее значение шума квантования при округлении центрировано
, а при усечении смещено
, где
. Дисперсия шума квантования
для обоих способов равна
. (1)
Для удобства использования дисперсии шума квантования ее выражают в логарифмическом масштабе [4]
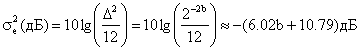
Анализ отечественных и зарубежных АЦП фирм Texas Instruments, Motorola, National Semiconductor, Linear Technology, Philips, Analog Devices, Maxim Integrated Products, Burr—Brown Corporation показал, что типовая разрядность АЦП составляет 8-, 10- и 12-разрядов, а также 14-, 16-, 18- и 24-разрядные [7, 8, 9]. Тогда оценку дисперсии ошибки квантования при различной разрядности АЦП можно рассчитать по формулам (1) и (2) для униполярных и биполярных сигналов, таблица 1.
Таблица 1
Оценка дисперсии шума квантования преобразователей
|
Оценка дисперсии ( |
Разрядность кода преобразователя ( |
||||||
|
8 |
10 |
12 |
14 |
16 |
18 |
24 |
|
|
Униполярные сигналы |
-59 |
-71 |
-83 |
-95 |
-107 |
-119 |
-155 |
|
Биполярные сигналы |
-53 |
-65 |
-77 |
-89 |
-101 |
-113 |
-149 |
Обратное преобразование цифрового сигнала в аналоговый выполняется после управляющего устройства и поэтому для оценки ошибки квантования устройства фильтрации и обработки это преобразование можно опустить.
Однако ошибка квантования возникает, если число разрядов ЦАП меньше числа разрядов управляющего устройства . Выпускаются ЦАП с разрядностью 8-, 10- и 12-разрядов, однако встречаются и 14-, 16-, 18- и 20-разрядные [8, 9].
Линейная модель ошибки квантования в этом случае представляется в виде ошибки (1) или (2) при равном разрядности ЦАП, таблица 1.
При реализации цифрового фильтра коэффициенты и
его передаточной функции
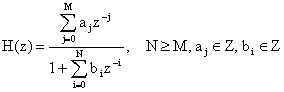
должны быть представлены в двоичном коде. Для этого их нормализуют так, чтобы и
, а затем квантуют. При этом возникает ошибка квантования представления коэффициентов, которая влияет на точность реализации частотных характеристик в виде дополнительной погрешности аппроксимации.
В зависимости от вида аппроксимирующей функции известны четыре типа фильтров – Баттерворта (B), Чебышева (T), инверсный Чебышева (I) эллиптический (C). По виду АЧХ в полосе пропускания (ПП) их можно разделить на две группы
— с монотонной АЧХ – фильтры Баттерворта и инверсный Чебышева;
— с равноволновой АЧХ – фильтры Чебышева и эллиптический.
Для оценки влияния разрядности представления коэффициентов фильтра на погрешность АЧХ исследована относительная погрешность АЧХ
на уровне 1%
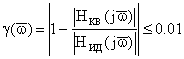
где — нормированная цифровая частота,
,
— текущая угловая частота,
— период дискретизации,
,
— соответственно АЧХ с квантованными и идеальными коэффициентами.
Результаты исследования приведены в таблице 2, где указана разрядность дробной части коэффициентов и
и соответствующий ей диапазон нормированных частот среза
для фильтров нижних (ФНЧ) и верхних (ФВЧ) частот, а также ширина полосы пропускания и полосы задержания
для полосовых (ПФ) и режекторных (РФ) фильтров. Для обеспечения минимальной разрядности коэффициентов фильтра их частоты среза для ФНЧ и ФВЧ, а также полосы пропускания и задержания для ПФ и РФ должны находиться в диапазоне
.
Таблица 2
Разрядность коэффициентов фильтра
|
Вид АЧХ в ПП |
Класс фильтра |
Тип фильтра |
Порядок фильтра N |
||
|
2 |
4 |
6 |
|||
|
Монотонный |
ФНЧ |
B |
8, 10, |
10, 12, |
12, 14, |
|
I |
10, 12, |
12, 14, |
14, 16, |
||
|
ФВЧ |
B |
8, 10, |
10, 12, |
12, 14, |
|
|
I |
10, 12, |
12, 14, |
14, 16, |
||
|
ПФ |
B |
8, 10, |
10, 12, |
12, 14, |
|
|
I |
10, 12, |
12, 14, |
14, 16, |
||
|
РФ |
B |
8, 10, |
10, 12, |
12, 14, |
|
|
I |
10, 12, |
12, 14, |
14, 16, |
||
|
Равноволновой |
ФНЧ |
T |
8, 10, |
10, 12, |
12, 14, |
|
C |
8, 10, |
12, 14, |
18, 20, |
||
|
ФВЧ |
T |
8, 10, |
10, 12, |
12, 14, |
|
|
C |
8, 10, |
12, 14, |
18, 20, |
||
|
ПФ |
T |
8, 10, |
10, 12, |
12, 14, |
|
|
C |
8, 10, |
12, 14, |
18, 20, |
||
|
РФ |
T |
8, 10, |
10, 12, |
12, 14, |
|
|
C |
8, 10, |
12, 14, |
18, 20, |
В исследовании уровень колебательности АЧХ в полосе пропускания для фильтров Чебышева и эллиптического задавался равным 1дБ, а в полосе задержания для фильтров инверсного Чебышева и эллиптического —20дБ. Следует также отметить, что порядок фильтров ПФ и РФ в два раза выше .
Поскольку фильтры высокого порядка обычно строят на фильтрах низкого порядка, то целесообразно ориентироваться на фильтры второго порядка. Однако при каскадном соединении фильтров низкого порядка разрядность их коэффициентов на один-два разряда выше.
Ошибки квантования арифметических операций возникают в местах суммирования и умножения. Если разрядная сетка устройства выбрана правильно и при суммировании переполнения не возникают, то источниками шума можно считать операции умножения. Однако при анализе промежуточных результатов алгоритма обработки возникают переполнения и при операции суммирования [10]. Поэтому источниками ошибки квантования следует рассматривать и суммирование и умножение.
Если к -му узлу подключены
источников шума и каждый из них создает белый шум с дисперсией (1), то в соответствии с моделью Джексона дисперсия выходного шума
будет определяться как [2]
, (3)
где — количество узлов в устройстве,
— количество источников шума в
-м узле,
— комплексный коэффициент передачи от
-го узла до выхода устройства. Коэффициент
, входящий в формулу (1), в данном случае соответствует разрядности дробной части коэффициента.
Из выражения (3) выделяют квадрат коэффициента усиления шума [11]
,
который зависит от коэффициентов передаточной функции и
, а также структурной организации устройства, т.е. этот шум присущ структуре устройства и его называют структурным шумом [12].
Поскольку коэффициент усиления шума частотно-зависимый, то его определяют в полосе пропускания полезного сигнала, чтобы при минимизации его уменьшить долю дополнительного шума в полезном сигнале на выходе устройства [13]. Тогда для удобства пользования вводится усредненный в полосе пропускания коэффициент усиления шума
,
где — ширина полосы пропускания.
В этом случае дисперсия выходного шума квантования равна
(4)
или в логарифмическом масштабе, таблица 3
Поскольку , то
. В таблице 3, например, выходной шум арифметических операций приведен для канонической структуры цифрового фильтра второго порядка (ФНЧ, ФВЧ) и каскадного соединения двух фильтров второго порядка (ПФ, РФ) минимальной размерности с сосредоточенными источниками шума [14]. Разрядность дробной части коэффициентов передаточной функции
взята минимальной, чтобы обеспечить
для ФНЧ и ФВЧ и
— для ПФ и РФ. Значения дисперсии шума
рассчитана для биполярных сигналов при условии, что разрядность дробных частей входного сигнала и коэффициентов равны. Значение дисперсии шума для униполярных сигналов на 6 дБ меньше.
В результате на выходе цифрового фильтра будет формироваться дискретный сигнал ошибки от прохождения шума квантования входного сигнала через цифровой фильтр в полосе пропускания, дисперсия которого равна [2]
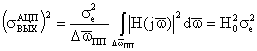
и от структурного шума цифрового фильтра, дисперсия которого определяется по формуле (4).
Таблица 3
Оценка дисперсии выходного шума (дБ)
|
Вид АЧХ в ПП |
Класс фильтра |
Тип фильтра и разрядн. коэфф. |
|
|
|
|
|
|
Монотонный |
ФНЧ |
B-8 |
8.255 |
—44.681 |
—0.472 |
—53.408 |
—44.135 |
|
I-10 |
7.467 |
—57.510 |
—2.783 |
—67.760 |
—57.118 |
||
|
ФВЧ |
B-8 |
8.261 |
—44.675 |
—0.498 |
—53.434 |
—44.132 |
|
|
I-10 |
7.477 |
—57.501 |
—2.820 |
—67.797 |
—57.113 |
||
|
ПФ |
B-9 |
14.918 |
—44.038 |
—0.423 |
—59.380 |
—43.913 |
|
|
I-10 |
14.854 |
—50.124 |
—2.548 |
—67.526 |
—50.045 |
||
|
РФ |
B-9 |
14.709 |
—44.247 |
—6.383 |
—65.340 |
—44.214 |
|
|
I-10 |
32.053 |
—32.925 |
+0.080 |
—64.897 |
—32.922 |
||
|
Равноволновой |
ФНЧ |
T-8 |
8.217 |
—44.719 |
—0.568 |
—53.504 |
—44.180 |
|
C-8 |
8.223 |
—44.713 |
—0.552 |
—53.488 |
—44.172 |
||
|
ФВЧ |
T-8 |
8.255 |
—44.681 |
—0.514 |
—53.450 |
—44.140 |
|
|
C-8 |
8.255 |
—44.681 |
—0.514 |
—53.450 |
—44.140 |
||
|
ПФ |
T-9 |
15.764 |
—43.193 |
—0.519 |
—59.476 |
—43.092 |
|
|
C-9 |
23.851 |
—35.105 |
—0.561 |
—59.518 |
—35.090 |
||
|
РФ |
T-10 |
18.280 |
—46.697 |
+2.512 |
—62.465 |
—46.584 |
|
|
C-9 |
21.966 |
—36.991 |
+2.484 |
—56.473 |
—36.942 |
При некоррелированности шума выходной шум цифрового фильтра будет равен
.
Подставляя формулы (4) и (5) получим
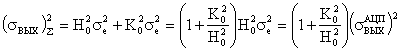
Из (6) следует, что минимальное значение суммарного шума зависит от соотношения усредненных в полосе пропускания коэффициентов и
. В таблице 3 для сравнения приведены значения
,
и
. Тогда можно отметить, что:
— усредненный в полосе пропускания коэффициент усиления шума значительно больше усредненного в полосе пропускания коэффициента усиления фильтра — ;
— дисперсия прохождения шума квантования входного сигнала через цифровой фильтр на порядок меньше дисперсии выходного шума квантования арифметических операций
;
— дисперсия выходного шума цифрового фильтра можно оценить по величине дисперсии выходного шума квантования арифметических операций
, т.е.
.
Таким образом, верхняя граница ошибок квантования определяется ошибками квантования арифметических операций. При заданных коэффициентах процедуры фильтрации и обработки сигналов и
и их разрядности
ошибки квантования арифметических операций определяется коэффициентом усиления шума
и зависит от структурной организации процедуры обработки.
Quantization errors of an input signal, coefficients of the fixed-point digital filter and output of arithmetic operations are analyzed. Limits of quantization error in a passband are received and dependence of a output noise dispersion from digital filter structural organization is shown.
1. Ситников В.С., Кисель А.Г. Аппаратное и программное обеспечение натурного эксперимента при проведении гидрофизических исследований. // Акустика и ультразвуковая техника: Сб. научн. тр. – Київ: Техніка, 1992. – Вып. 27. – С. 46–50.
2. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. – М.: Мир. 1978. – 848 с.
3. Бахтиаров Г.Д., Малинин В.В., Школин В.П. Аналого-цифровые преобразователи. – М.: Сов. Радио, 1980. – 280 с.
4. Бесекерский В.А., Изранцев В.В. Системы автоматического управления с микро-ЭВМ. – М.: Наука, 1987. – 320 с.
5. Бойко Н.П., Стеклов В.К. Системы автоматического управления на базе микро-ЭВМ. – К.: Техніка, 1989. – 182 с.
6. Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. – СПб.: Политехника, 1999. – 592 с.
7. Интегральные микросхемы: Микросхемы для аналого-цифрового преобразования и средств мультимедиа. Выпуск 1.– М.: ДОДЭКА, 1996. – 384 с.
8. Силовые и аналоговые электронные компоненты: Краткий справочник. – Киев: ООО “БИС-электроник”, 2000. – 60 с.
9. Каталог VD MAIS 2001-2002: Микросхемы Analog Devices. – Киев: VD MAIS, 2001. – 92 с.
10. Сергиенко А.Б. Цифрова обработка сигналов.- СПб.: Питер, 2002. – 608 с.
11. Ситников В.С. Выбор наилучшей структуры цифровой системы. // Тр. Одесск. политехн. ун-та. – Одесса, 2001. – Вып. 3(15). – С. 131–133.
12. Ситников В.С. Количественная оценка структуры цифровой системы. // Міжнар. конф. “Кораблебудування: освіта, наука, виробництво”: матер. конф. (м. Миколаїв, 24-25 вересня 2002р.) – Т. ІІ. – Миколаїв, 2002. – С. 223–226.
13. Малахов В.П., Ситников В.С., Ступень П.В., Ульяшин С.В. Выбор структуры цифрового фильтра по уровню выходного шума округления. // Технология и конструирование в электронной аппаратуре. – 2001. – № 2. – С.17–22.
14. Ситников В.С., Шумейко К.П. Применение цифровых фильтров в системах защиты речевых сообщений. // Праці УНДІРТ. – Одеса, 2003. – №1(33). – С. 62–65.
Рассмотренное билинейное
преобразование вида (6.21) позволило получить передаточную функцию цифрового
ФНЧ. Существует более общее преобразование, позволяющее преобразовать
аналоговый ФНЧ в избирательный БИХ-фильтр любого типа (ФНЧ, ФВЧ, ПФ, РФ). Не
рассматривая вывода соответствующих формул, приводим их в таблице 6.1.
Здесь последовательно указаны
нормированные значения граничных частот цифрового фильтра, формулы замены
переменной в , формулы для расчета параметра
, позволяющие
получить по заданным и
нормированный
аналоговый прототип с частотами среза и,
наконец, формула для расчета граничной частоты полосы задерживания (
определять
не надо, т.к. она всегда равна 1). Для ПФ и РФ расчет выполняется по двум формулам и
из двух значений и
выбирается то,
модуль которого наименьший.
Пример 5.1 Рассчитать дискретный фильтр НЧ с параметрами: кГц;
кГц;
кГц;
дБ;
дБ.
По формуле (6.24) находим
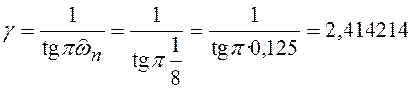
Далее находим нормированную частоту
задерживания аналогового ФНЧ-прототипа
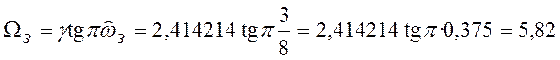
Тем самым произведен перерасчет
требований, предъявленных к дискретному фильтру в требования к аналоговому
прототипу.
Таблица 6.1
|
Цифровой фильтр |
Граничные “цифровые” частоты |
Формула замены |
Параметр |
Связь “аналоговых” частот с “цифровыми” |
Граничные “аналоговые” частоты |
|
Нижних частот |
|
|
|
|
|
|
Верхних частот |
|
|
|
|
|
|
Полосовой |
|
|
|
|
|
|
Режекторный |
|
|
|
|
|
Как рассчитать аналоговый
фильтр-прототип? Исходными требованиями для расчета являются требования к
НЧ-прототипу (рисунок 6.10,б). По ним, пользуясь любым справочником по расчету
аналоговых фильтров, рассчитывают передаточную функцию аналогового
фильтра-прототипа.
Пример 6.2 Для ,
дБ,
дБ (параметры ФНЧ-прототипа,
взятые из предыдущего примера), пользуясь справочником, находим, что
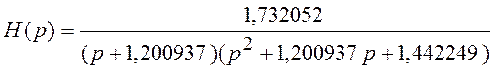
Как осуществить переход к дискретному
фильтру? Для перехода от к
воспользуемся билинейным преобразованием
Для
рассмотренного выше примера , поэтому
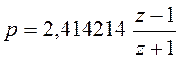
выражение . Получим
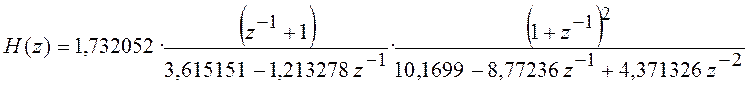
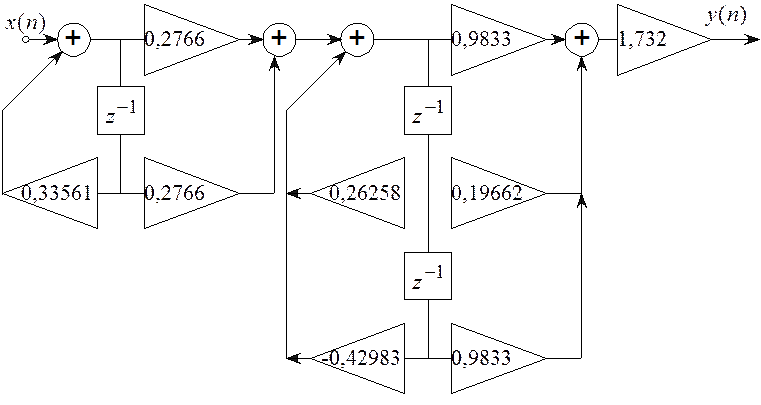
Дискретный фильтр с такой передаточной
функцией легко реализовать в виде
каскадного соединения типовых звеньев 1-го и 2 порядка. Для этого функцию перепишем в виде
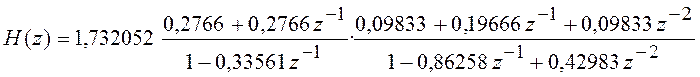
Схема фильтра, имеющего такую
передаточную функцию приведена на рисунке 6.11.
7 Эффекты квантования в цифровых
системах
7.1 Основные понятия
В разделе “Аналоговые, дискретные и
цифровые сигналы” главы 1 мы обсуждали разницу между дискретными и цифровыми
сигналами. До сих пор, строго говоря, речь шла о дискретных сигналах и
системах, поскольку отсчеты сигналов и коэффициентов фильтров считались
представленными точно (без погрешностей). Сигналы на входе и выходе
ЦФ являются цифровыми, т.е.
последовательностями чисел. Каждое из этих чисел представляется в виде
двоичного кода, и в ЦФ в соответствии с алгоритмом
выполняются
операции пересылки, сложения и умножения кодов. Представить числа точно
конечным числом разрядов кода невозможно. При этом алгоритм функционирования
реализуется неточно. Ошибки цифровой фильтрации обусловлены следующими
факторами:
—
ошибки квантования входных и выходных сигналов;
—
квантованием коэффициентов фильтра и
;
—
конечной разрядностью операционных устройств;
—
округлением промежуточных результатов вычислений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Поскольку для значения a11=0 множители знаменателя равны соответственно (z + 0.5 + j1. 658) и (z + 0.5 — j1. 658), корни находятся снаружи единичной окружности и равны Z = -0.5 ± j1.658. Следовательно, система неустойчива для маленьких значений a11, но становится устойчивой для средних значений a11, и снова неустойчивой для больших величин a11.
Корни находятся снаружи единичной окружности z = -0.5 ± j1.658 для a11 = 0 и двигаются в сторону действительной оси. Бесконечная чувствительность будет тогда, когда корни совпадают в z = 0.732 ± j0.
Пределы устойчивости для a11, когда 2.0 < a11 < 2.5. Для a11 < 2.0 тип
увеличения неустойчивости – синусоидальный, в то время как для a11 > 2.5 тип увеличения неустойчивости – линейный. Обратите внимание на то, что чувствительность корня изменяется очень сильно, когда a11 располагается в определенных пределах, и интересным является второй пример точки годографа с бесконечной чувствительностью, расположенной на действительной оси, где корни совпадают z = 0.732 ± j0.
Вто время как в предыдущем разделе рассматривались эффекты квантования коэффициентов передаточной функции, в этом разделе рассматриваются эффекты квантования на входе системы, промежуточных переменных ЦОС и выходного сигнала. Существуют соответствующие методы для оценки максимальной величины ошибки квантования в цифровых системах.
Есть три источника квантования – на входе ЦОС, внутри ЦОС, и на выходе ЦОС, которые возникают потому, что:
•Входной сигнал для дискретной системы является непрерывным и необходимо его аналого-цифровое преобразование прежде, чем любые вычисления будут выполняться.
•Цифровой процессор отбрасывает часть вычисленных результатов при выполнении умножения и деления. Отбрасывание необходимо потому, что число битов, требуемых для точного представления результата, увеличивается по сравнению с числом битов, необходимых для представле-
ния коэффициентов матриц aij, bi, Ci, d. Без усечения или округления разрядность данных при умножении или делении увеличивается неограниченно.
•На выходе дискретного процессора обычно необходим непрерывный аналоговый сигнал, а используемый цифро-аналоговый преобразователь обычно имеет меньшее разрешение по сравнению с цифровым процессором. При этом отбрасывание самых младших битов дает ошибку квантования.
Все эти ошибки можно описать как шумоподобные ошибки квантования.
Ошибка квантования с округлением ε есть разница между точным значением величины и значением самого близкого из набора уровней, которые отличаются
друг от друга на q. И альтернативная ей, ошибка квантования с усечением ε –
|
Лекции по ППО ВС РВ © Клюс В.Б. |
36 |

разница между точным значением величины и значением самого близкого снизу из набора уровней. Ошибка с округлением показана на рис.21 .15, на котором точная величина наложена на сетку квантованных уровней и интервалы дис-
кретизации. Ошибка квантования с округлением ε в моменты дискретизации k = 1, 2,… является интервалом между непрерывным сигналом и самым близким уровнем квантования.
Уровни квантования
q
ε
k k+1 k+2 k+3 k+4 k+5 k+6 k+7 k+8 k+9 k+10
Интервал дискретизации
Рисунок2.15. Непрерывный сигнал, наложенный на сетку интервалов дискретизации и уровней квантования, расположенных через q
Так как различие в уровнях квантования – q, ошибка округления ε между непрерывным сигналом и каждым из квантованных уровней не превышает ±q/2. Если предположить, что колебание сигнала является большим, чем q от одной
выборки к следующей, то ошибка ε для одной выборки будет статистически независимой от ошибки ε для любой другой выборки и будет иметь равную вероятность в диапазоне ±q/2.
Противоположный случай – постоянный или медленно изменяющийся сигнал. Для систем управления с обратной связью статистическая зависимость между выборками из-за квантования вызывает предельные циклы. Если там преобладает только одна такая нелинейность в контуре обратной связи, то возможно использование метода функции описания, чтобы приблизительно определить поведение предельного цикла. Однако добавление подходящего высокочастотного возмущающего сигнала ко входу системы сделает и ошибку квантования, и ошибку округления однородно распределенной, белой, и взаимно
|
некоррелированной. |
|
|
Лекции по ППО ВС РВ © Клюс В.Б. |
37 |

Три источника ошибки квантования эквивалентны добавлению шумоподобного воздействия ко входу, вычисленным результатам и выходу, соответственно. Результирующая функция плотности вероятности ошибки показана на рис.21 .16,a или рис.21 .16,б, в зависимости от того, усечение, или округление происходит при квантовании. Усечение – простое отбрасывание самых младших битов, при округлении используется наименьший значащий бит квантования, чтобы минимизировать абсолютную величину ошибки.
|
ε |
q/2 ε |
|||||
|
q |
q/2 |
|||||
|
а |
б |
Рисунок2.16. Функции плотности вероятности ошибки квантования для усечения (a) и округления (б)
Среднее или матожидание μ и дисперсия σ2 шума определяются как пер-
вый и второй моменты Ε{ξ}, Ε{ξ2} из соответствующих функций плотности вероятности.
Квантование с усечением:
|
q |
q |
1 |
q |
|||||
|
∫ |
∫ |
|||||||
|
μ = Ε{ε} = |
εf (ε)dε = |
ε |
dε = |
(2.32) |
||||
|
0 |
0 |
q |
2 |
|
σ |
2 |
= Ε{(ε − μ) |
2 |
}= Ε{ε |
2 |
2 |
q |
2 |
1 |
q |
2 |
= |
q |
2 |
. |
(2.33) |
||||||||||
|
}− Ε{ε} |
= ∫ε |
dε − |
12 |
|||||||||||||||||||||||
|
0 |
q |
2 |
||||||||||||||||||||||||
|
Квантование с округлением: |
||||||||||||||||||||||||||
|
q |
2 |
q 2 |
1 |
(2.34) |
||||||||||||||||||||||
|
μ = Ε{ε} = ∫εf (ε)dε = |
∫ |
ε |
dε = 0 |
|||||||||||||||||||||||
|
−q |
−q |
q |
||||||||||||||||||||||||
|
2 |
2 |
|||||||||||||||||||||||||
|
σ |
2 |
= Ε{(ε − μ) |
2 |
}= Ε{ε |
2 |
2 |
q |
2 |
2 |
1 |
2 |
= |
q2 |
. |
(2.35) |
|||||||||||
|
}− Ε{ε} |
= ∫ε |
dε − 0 |
12 |
|||||||||||||||||||||||
|
−q |
2 |
q |
||||||||||||||||||||||||
|
Результаты (21 .32)-(21 .35) показывают, что дисперсия для усечения такая же, |
как и для округления, и только матожидание является различным. Модель для шумовых источников при каждой выборке в момент k определяется как
|
ε (k,•)= w(k,•)+ με |
(2.36) |
|
Лекции по ППО ВС РВ © Клюс В.Б. |
38 |

где запись ε(k, •) и w(k,•) описывает реальные значения стохастических про-
цессов такие, что ε(k, •) и w(k,•) являются произвольными переменными для любого фиксированного k, k = 1,… .
Случайная переменная w(k,•) имеет нулевое матожидание и дисперсию
q2/12, в то время как με определяется как με = 0 или με = q/2 в зависимости от того, используется округление или усечение соответственно. Описание шумовых источников как переменной и постоянной части позволяет рассматривать
отдельно их влияние – w(k,•) исключительно на дисперсию и με как производную от смещения АЦП.
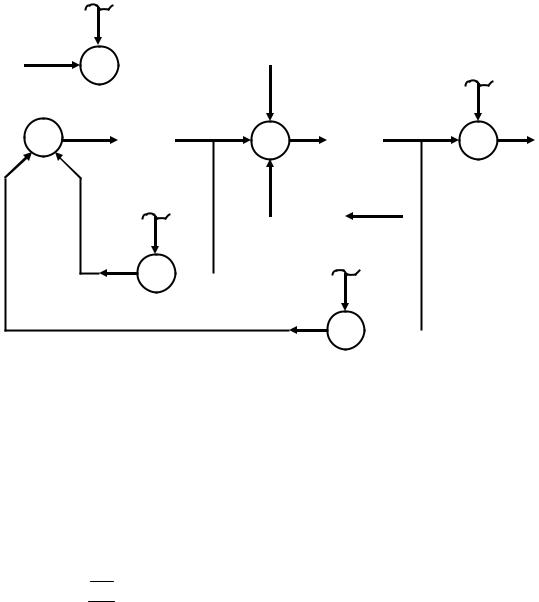
Источники ошибки показаны на диаграмме состояния (рис.21 .17) как шум аналого-цифрового преобразования на входе εi(k,w), шум вычисления εc(k,w) и шум цифро-аналогового преобразования на выходе εo(k,w).
|
εi(k,•) |
εo(k,•) |
||||||
|
Z-1 |
u(k) |
||||||
|
x(k) |
+ |
b |
+ |
c |
+ |
Y(k) |
εc(k,•) 
Рисунок2.17. Диаграмма состояния, показывающая скалярную входную ошибку квантования εi(k,•), векторный шум вычисления εc(k,•) и скаляр εo(k,•)
Соответствующее уравнение состояния
u(k+1) = A u(k) + b [ x(k) + εi(k) ] + εc(k) ,
(2.37)
y(k) = c u(k) + εo(k) .
Вычисление выходной дисперсии σ y2 требует нахождения значения вто-
|
рого момента y(k). |
|
|
σy2 = Ε{y(k)yT (k)}= Ε{[cu(k) +εo (k,•)][cu(k) +εo (k,•)]T }= |
|
|
= Ε{[cu(k) +εo (k,•)][uT (k)cT +εoT (k,•)]}= |
(2.38 |
= Ε{cu(k)uT (k)cT +εo (k,•)uT (k)cT + cu(k)εoT (k,•) +εo (k,•)εoT (k,• )
Поскольку εo(k,•) имеет нулевое матожидание и некоррелировано с x(k)
|
Лекции по ППО ВС РВ © Клюс В.Б. |
39 |
|
Ε{y(k) yT (k)}= cΕ{u(k)uT (k)cT }+Ε{εo (k,•)εoT (k,•)}= |
(2.39) |
||
|
= cP |
(k)cT + R (0) , |
||
|
uu |
o |
где Ro(τ), τ = 0, является автокорреляционной функцией выходного шума. Уравнение (21 .39) показывает, что выходная дисперсия является суммой
выходной ковариации шума и уровня ковариации Puu(k) взвешенного выход-
ным вектором с. Вычисление уровня ковариации Puu(k) требует рекуррентной формулы, которая находится из ожидаемой величины второго момента u(k+1).
Из (21 .37),
PUU (k +1) = Ε{u(k +1)uT (k +1)}=
= Ε{[Au(k) + bwi (k,•) + wc (k,•)][Au(k) + bwi (k,•) + wc (k,•)]T }=
= Ε{[Au(k) + bwi (k,•) + wc (k,•)][uT (k)AT + wiT (k,•)bT + wcT (k,•)]}= (2.40) = Ε{Au(k)uT (k)AT + Au(k)wiT (k,•)bT + Au(k)wcT (k,•) +
+bwi (k,•)uT (k)AT +bwi (k,•)wiT (k,•)bT +bwi (k,•)wcT (k,•) + + wc (k,•)uT (k)AT + wc (k,•)wiT (k,•)bT + wc (k,•)wcT (k,•)} .
Так как шумовые источники wi(k,•), wc(k,•) статистически независимы друг от друга и от u(k), ожидаемое значение их перекрестных произведений нулевое. Уравнение (21 .40) приводится к виду
|
PUU (k +1) = Au(k)uT (k)AT + bwi (k,•)wiT (k,•)bT + wc (k,•)wcT (k,•) , |
(2.41) |
|||
|
или |
(k)AT +bR (0)bT + R (0) , |
|||
|
P |
(k +1) = AP |
(2.42) |
||
|
UU |
UU |
i |
c |
где Ri(τ) и Rc(τ), τ = 0, являются автокорреляционными функциями входного шума и шума вычисления, соответственно.
Уравнение (21 .42) говорит, что значение ковариации при выборке k+1 получается из ковариации для предыдущей выборки плюс компоненты входного шума и шума вычислений. Если состояние u(k) было точно известно из началь-
ного состояния и при допущении Puu(0)=0, тогда для каждого следующего отсчета k=1, 2, … представленного как u(k), получается как дано в (21 .42). Так как матрица А устойчива с собственными значениями внутри единичного круга,
|
lim PUU (k) → PUU (k +1) , |
(2.43) |
|
k →∞ |
и вычисление выражения (21 .42) – простая рекурсивная задача с доступными инструментальными средствами работы с матрицами. Обратите внимание, что результирующий шум имеет не равномерный закон распределения, а скорее гауссовский в соответствии с центральной предельной теоремой.
Пример 3.
Рассмотрим динамическую систему из примера 1, но со значением a11=2.4, дающую фильтр нижних частот. Предположим, что входной сигнал
|
Лекции по ППО ВС РВ © Клюс В.Б. |
40 |

продискретизирован 10-разрядным А/Ц преобразователем с диапазоном от -1 до +1 В и самый младший бит соответствует приблизительно 20 мВ. Предпо-
ложим также, что в ЦПС переменные u1(k) и u2(k) представлены 16разрядными словами в дополнительном коде с динамическим диапазоном от -1 (8000h) до (+1-1/215) (7FFFh), где суффикс «h» обозначает шестнадцатеричное число. При вычислениях ЦПС усекает результаты, то есть при умножении в качестве результата берутся 16-разрядные слова и результаты выдаются в диапазоне от -1 до +1 В на 9-разрядный Ц/А преобразователь с весом младшего разряда приблизительно равным 40 мВ. Определим, какой величины будет выходной шум.
Результирующая диаграмма состояния для данного случая показана на рис.21 .18 с источниками шума ei, ec1, ec2, eo. Заметим, что не имеется никакого
источника шума, связанного коэффициентом С22, равным -1, так как при этом фактически умножения нет, а есть только вычитание.
εi (k,•)
|
X(k) |
+ |
εo (k,•) |
|
|
+ |
Z-1 |
U1(k) |
||
|
) |
||||
|
εc1 |
(k, |
|||
|
a11 |
• |
2.4
+
|
Z-1 |
U2(k) |
|||||||
|
+ |
+ |
Y(k) |
||||||
|
-1 |
||||||||
εc2 (k,•)
-3
+
Рисунок2.18. Диаграмма состояния для примера 3, показывающая шумовые источники из-за эффектов квантования
Матожидания и дисперсии различных источников представлены далее. Входной шум:
|
μi |
= 0 ; |
||||||
|
1 |
2 |
||||||
|
σ 2 |
= |
29 |
= 3.18 ×10−7 B2 |
R = 3.18 ×10−7 |
B2 . |
(2.44) |
|
|
i |
12 |
i |
|||||
Шум вычисления:
1
μc1,c2 = 2215 =1.53×10−5 ;
|
Лекции по ППО ВС РВ © Клюс В.Б. |
41 |
|
1 |
2 |
||||||||||
|
7.76 |
×10−11 |
0 |
. |
||||||||
|
215 |
|||||||||||
|
σ 2 |
= |
= 7.76 ×10−11 |
R |
= |
|||||||
|
c1,c2 |
12 |
c |
0 |
7.76 ×10−11 |
|||||||
Выходной шум:
|
1 |
|||||||||||||||||||||
|
μo |
= |
28 |
=1.95×10−3 ; |
||||||||||||||||||
|
2 |
|||||||||||||||||||||
|
1 |
2 |
||||||||||||||||||||
|
σ 2 |
= |
28 |
=1.27 ×10−6 |
R =1.27 ×10−6 . |
|||||||||||||||||
|
o |
12 |
o |
|||||||||||||||||||
|
Используя значения (21 .44), уровень ковариации согласно (21 .42) равен |
|||||||||||||||||||||
|
P |
(k +1) |
= |
2.4 |
− 3 P |
(k ) |
2.4 |
− 3 T |
+ 0 |
3.18 ×10 −7 |
0 |
T |
+ |
|||||||||
|
UU |
1 |
UU |
1 |
||||||||||||||||||
|
−1 |
−1 |
1 |
1 |
(2.45) |
|||||||||||||||||
|
7.76 ×10 −11 |
0 |
||||||||||||||||||||
|
+ |
|||||||||||||||||||||
|
0 |
7.76 ×10 −11 |
. |
|||||||||||||||||||
Рис.21 .19 показывает рекурсивное решение для k = 0, 1, … учитывая, что начальное состояние известно и равно
|
0 |
0 |
(2.46) |
|
PUU (0) = |
. |
|
|
0 |
0 |
Значение ковариации увеличивается по траектории от ноля до величины установившегося значения. Динамика состояния определяет скорость увеличения траектории. Окончательная величина матрицы значений ковариации равна
|
×10 |
−6 |
9.70×10 |
−6 |
|||||
|
lim |
P |
19.6 |
. |
(2.47) |
||||
|
(k) = |
×10−6 |
5.43×10−6 |
||||||
|
k →∞ |
UU |
9.70 |
||||||
Значения дисперсии находятся на основной диагонали матрицы ковариа-
ций (21 .47) и, следовательно, σu12=19.6×10-6 и σu22=5.43×10-6 . Обратите внимание, что начальное предположение, сделанное, чтобы исключить первоначальную неопределенность PUU(0) не оказывает воздействия на конечный результат (21 .47). Если, например, PUU(0) первоначально большое относительно установившейся величины состояние ковариации, PUU(k) уменьшалось бы до ранее полученного результата (21 .47).
Если известно состояние ковариации PUU(k), то выходная дисперсия может
|
быть найдена из (21 .39): |
||||||||||
|
Ε{y(k) yT (k)}= cP |
(k)cT + R |
(0) = |
||||||||
|
uu |
o |
|||||||||
|
×10 |
−6 |
9.70×10 |
−6 |
[0 1]T +1.27 |
×10−6 |
= |
(2.48) |
|||
|
= [0 1] 19.6 |
||||||||||
|
9.70×10−6 |
5.43×10 |
−6 |
||||||||
= 5.43×10−6 +1.27×10−6 = 6.70×10−6 .
|
Лекции по ППО ВС РВ © Клюс В.Б. |
42 |

Значение ковариации
|
20 |
||||
|
18 |
||||
|
16 |
||||
|
14 |
||||
|
12 |
||||
|
10 |
||||
|
8 |
||||
|
6 |
||||
|
4 |
||||
|
2 |
||||
|
0 |
5 |
10 |
15 |
20 |
|
0 |
Номер выборки
Рисунок2.19. Решение уравнения для матрицы ковариации. Асимптотическое приближение при k → ∞
Одно из назначений вычисления ковариации – способность различить видимые источники неопределенности для полной оптимизации системы. В этом случае имеется незначительный вклад ошибок вычисления, и более существенный вклад выхода Ц/A преобразователя. Если при полной оптимизация системы исходить из стоимости, то, учитывая вклад Ц/A преобразователя можно обойтись меньшим разрешением и менее дорогим 8-разрядным ЦАП.
Чтобы учесть эффекты усечения и округления, как видно из рис.21 .15 и (21 .32), дисперсии для любого случая должна быть та же самая, но усечение дает
среднее отличное от нуля μc1 = μc2 = q/2 = 1.53×10-5, которое представляет смещение состояния от u(k) до u(k+1). Эффект моделируется выражениями
(21 .44) и
|
μi = 0, |
×10 |
−5 |
, |
μo =1.95 ×10−3 . |
(2.49) |
||
|
μc = 1.53 |
−5 |
||||||
|
1.53 |
×10 |
||||||
|
Лекции по ППО ВС РВ © Клюс В.Б. |
43 |
При использовании этих средних в качестве входных, уравнение состояния (21 .37) преобразуется в
|
u1 |
(k +1) |
2.4 |
−3 |
u1(k) |
0 |
0 |
1.53 |
×10 |
−5 |
; |
|||||
|
= |
1 |
+ 0 + |
0 + |
×10 |
|||||||||||
|
u2 |
(k +1) |
−1 |
u2 (k) |
1 |
1 |
1.53 |
−5 |
||||||||
|
(2.50) |
|||||||||||||||
|
y(k) = [0 |
u (k) |
||||||||||||||
|
1] |
1 |
+1.95×10−3 , |
|||||||||||||
|
u2 (k) |
|||||||||||||||
|
рекурсивное решение, которого дает |
−5 |
||||||||||||||
|
lim |
u (k) |
×10 |
, |
(2.51) |
|||||||||||
|
1 |
= |
−7.65 |
|||||||||||||
|
k →∞ u2 (k) |
−3.06×10−5 |
||||||||||||||
|
и выход |
|||||||||||||||
|
lim y(k) |
= cu(k) + Ro = |
||||||||||||||
|
k →∞ |
|||||||||||||||
|
= [0 |
7.65×10 |
−5 |
+1.95 |
×10−3 |
=1.92×10−3 |
B . |
(2.52) |
||||||||
|
1] − |
|||||||||||||||
|
−3.06×10−5 |
|||||||||||||||
2.4.3. Минимизация эффектов квантования в ЦПС семейства TMS320 Чтобы увидеть, как в ЦПС семейства TMS320 уменьшить эффекты кван-
тования, необходимо вначале рассмотреть, как представляются десятичные числа и как выполняются арифметические операции в ЦПС.
Центральное арифметическо-логическое устройство процессоров семейства TMS320C5х имеет входное 16-разрядное сдвигающее устройство, 17×17разрядный параллельный умножитель, 40-разрядное арифметическо-логическое устройство (АЛУ), два 40-разрядных аккумулятора, и дополнительные сдвигающие устройства на выходах аккумулятора и умножителя. Типичная операция умножения двух чисел А×B требует команду «LD» для загрузки регистра «T» значением A, команду «MPY» указывающую второй операнд в памяти данных B и команду «STH», чтобы сохранить в память данных 16 старших битов 32-разрядного результата, который находится в аккумуляторе. Таким образом, одиночное умножение двух чисел требует трех команд, и если используется внутренняя память на кристалле, не требующая циклов ожидания, как например, для медленной памяти вне кристалла, то время умножения для TMS320VC5402 со временем выполнения команды 10 наносекунд, будет равно времени для трех команд или 30 наносекунд. При использовании 2-х операндных команд умножения время умножения сокращается до 20 наносекунд, но адреса операндов должны быть предварительно загружены в два вспомогательных регистра. Если умножение объединяется с добавлением затем к АЛУ, то выборка данных, умножение и накопление могут выполняться в одном цикле команды «MACD», которая значительно повышает эффективность вычислений.
Десятичные числа представляются в виде 16-разрядных (одинарной точности) вычисленных дробей. Цифровые слова имеют форму
|
Лекции по ППО ВС РВ © Клюс В.Б. |
44 |

|
СР |
МР |
|||||
|
Номер разряда |
15 |
14 |
13 |
12 11 |
… |
0 |
|
Величина |
-S |
S/2 |
S/4 |
S/8 S/16 |
… |
S/215 , |
где бит 15 – знаковый разряд. Подразумеваемая точка основания системы счисления расположена между битами 15 и 14, а биты от 0 до 14 задают 15 разрядов величины числа. S – положительное число из диапазона от 0 до ∞, которое является коэффициентом пересчета цифрового слова. Коэффициент пересчета S позволяет цифровому слову представлять любое число из интервала [ -S, +S(1- 1/215) ] для цифрового диапазона слова от 8000h до 7FFFh, где суффикс «h» указывает шестнадцатеричную величину.
Общие специальные случаи – для S=215=32768, который смещает деся-
|
тичную точку вправо, чтобы представлять |
целые числа в |
интервале |
|
[-32768, 32767], и для S=1, который выравнивает десятичную точку так, чтобы |
||
|
десятичное число, представляемое цифровым |
словом, имело |
интервал |
[-1, 0.9999695]. Особенность этого второго представления – предотвращение переполнения АЛУ, так как произведение любых чисел из данного интервала будет всегда давать другое число, содержащееся внутри интервала [-1, 0.9999695].
Поскольку каждое цифровое слово имеет заданный масштабный множитель, соблюдаются два правила при выполнении арифметических операций:
Правило 1. Сложение
Если две переменных x и y с соответствующими масштабными множителями Sx и Sy складываются, x + y, то оба масштабных множителя должны быть
одинаковыми, Sx = Sy. Правило 2. Умножение
Если константа C умножается на переменную x с масштабным множителем Sx, чтобы получить переменную y: y = Cx, то масштабный множитель Sy с учетом масштаба C получается согласно правилу
CЦПС = C Sx .Sy
Применение этого правила переводит десятичную константу C к десятичной дроби СЦПС с интервалом [ -1, (1-1/215) ]. СЦПС представляется внутри ЦПС как цифровое слово в интервале [8000h, 7FFFh].
Правило 1 относится к механизму масштабирования при сложении и дает ошибку квантования в младшем разряде, если сдвигаемая переменная отбрасывается после добавления ко второй переменной. Приведенный далее пример иллюстрирует эту ситуацию.
Правило 2 относится к умножению и, следовательно, воздействует на квантование как было описано ранее. Рассмотрим применение правила 2.
Предположим, что необходимо вычислить выражение y = 5x, где x находится в интервале [-1.8, +1.6], и это желательно привести к шкале используемого ЦПС. Так как максимум абсолютной величины x равен 1.8, масштабный
|
Лекции по ППО ВС РВ © Клюс В.Б. |
45 |
множитель Sx должен быть некоторым числом ≥ 1.8, и чтобы минимизировать эффекты квантования, выбираем Sx так, чтобы Sx=1.8 точно. При таком выборе Sx получим почти симметричный интервал [-1.8, 1.8(1-1/215)] с цифровым интервалом слова [8000h, 7FFFh], что перекрывает интервал x настолько близко, насколько возможно. Так как Sx=1.8, произведение y = 5x попадает в интервал [-5×1.8, +5×1.8(1-1/215)], или [-9, ≈ 8.999725]. Соответствующий интервал Sy должен быть ≥ 9. Поскольку максимальная положительная величина СЦПС (1-1/215) ≈0.9999695, а не 1, то Sy должно быть немного большим, чем 9 и, например, выберем Sy=10.
Учитывая заданное значение Sx и выбранное значение Sy для СЦОС, полу-
чим
CЦПС = 5 1.8 = 0.90000 = 7333h .
10
Применение этих двух правил для масштабирования и уменьшение эффектов квантования в цифровых процессорах сигналов семейства TMS320 включает следующие особенности для арифметики с фиксированной точкой:
1.Наиболее очевидная и важная особенность уменьшения эффектов квантования – ширина АЛУ, аккумулятора и 17×17 разрядного умножителя. 40-разрядная ширина позволяет выполнять накопление любых 32разрядных слов повышенной точности или 16-разрядных слов без переполнения. При умножении 32-разрядное произведение соответствует 32разрядной ширине аккумулятора, и любой полный результат умножения знаковых чисел помещается в АЛУ, или умножение расширенной точности 32×32 бита возможно для беззнаковых чисел.
2.Вторая особенность – на входе АЛУ имеется сдвигающее устройство, чей 16-разрядный вход соединяется с шиной данных, а 40-разрядный выход соединяется со входом АЛУ. Сдвигающее устройство выполняет левый сдвиг от 0 до 16 бит над входными данными, где выходные младшие разряды заполняются нолями, а старшие заполняются нолями или расширением знака, в зависимости от «SXM» (режим расширения знака) бита. Если прибавление
x с масштабным множителем Sx выполняется к содержимому аккумулятора y с масштабным множителем Sy, и если Sx и Sy отличаются как степени 2, то сдвигающее устройство может пересчитать масштаб x к Sy перед сложением. Эта вторая особенность позволяет просто реализовать правило 1, но не касается проблемы квантования, потому что это применимо только к сложению.
3.Третья особенность, которая касается квантования– возможность исключения режима переполнения аккумулятора для операций сложения и вычитания по модулю. Модульная арифметика выгодна там, где несколько чисел, обычно переменного знака, складывают вместе и результат всегда меньше, чем сумма их абсолютных величин. Общий пример такого вычисления– суммирование значений с ответвлений КИХ-фильтра, чтобы сформировать сигнал на его выходе.
|
Лекции по ППО ВС РВ © Клюс В.Б. |
46 |
Для модульной арифметики аккумулятор ориентируется на максимальный числовой диапазон конечных результатов вместо максимального диапазона промежуточных данных. После настройки на конечный результат изначально предполагается, что число положительных и отрицательных переполнений будет примерно одинаковым, переполнения игнорируются в промежуточных результатах накопления, поскольку числа добавляются или вычитаются. Таким образом, биты, которые в другом случае предотвратили бы переполнение, дают дополнительные значащие биты в представлении конечной суммы в аккумуляторе. Модульное сложение уменьшает шум квантования, позволяя уменьшить масштабный множитель аккумулятора, что позволяет накапливать полные 31-разрядные результаты умножения без усечения. Наличие 8 защитных разрядов еще более расширяет диапазон представления чисел.
4.Четвертая особенность уменьшает квантование передаточной функции, позволяя сдвинуть результат умножения прежде, чем он будет добавлен к аккумулятору. В произведении y = Cx этот общий выходной масштаб Sy мо-
жет быть заметно большим, чем константа C и входной масштаб Sx. Из правила 2, однако следует, что если масштаб Sy большой, то СЦПС будет ма-
леньким, и число значащих битов, определяющих сомножитель СЦПС уменьшается, чтобы получить более квантованную передаточную функцию. Более привлекательное решение для квантования коэффициентов состоит в том, чтобы уменьшить масштабный множитель аккумулятора в два раза при
вычислении СЦПС, и применить правый сдвиг произведения в регистре «P» прежде, чем оно будет добавлено к аккумулятору. Таким образом, это кван-
тование коэффициентов дает дополнительные значащие биты для СЦПС, чтобы представить C.
Обычно левый сдвиг на +1 требуется для знакового умножения дробных чисел, потому что произведение на выходе умножителя имеет двойной знаковый разряд. Если не делать никакого сдвига перед сложением, то эффект эквивалентен правому сдвигу для более низкого масштабного множителя. Бо-
лее низкий масштабный множитель Sacc/2 для выхода умножителя функционирует, согласно правилу 2, и дает левый сдвиг СЦПС и дополнительный значащий бит результата. Таким образом, сдвиг результата умножения дает компромисс между квантованием передаточной функции и шумом
квантования. Шум квантования очень маленький и не увеличивается с числом сдвигов. Он всегда равен Sacc/231, где Sacc – масштабный коэффициент аккумулятора.
5.Пятая особенность– сдвигающее устройство на выходе аккумулятора. Команда «STH» копирует весь аккумулятор в сдвигающее устройство, где всё это 40-разрядное число сдвигается на какое-нибудь число разрядов от 0 до 15, и затем копирует старшие (младшие для команды «STL») 16 битов сдвинутой величины в память данных. Сам аккумулятор при этом не изменяется. Выходной сдвигатель, таким образом, позволяет иметь большой масштабный множитель аккумулятора с несколькими старшими битами, чтобы предотвратить переполнение при циклическом сложении, но позволяет полно-
|
Лекции по ППО ВС РВ © Клюс В.Б. |
47 |

стью сохранить 15 значащих битов (одинарная точность) из 31 бита аккумулятора. Без этого сдвигателя любое различие между аккумулятором и выходными масштабными множителями давало бы результат, который имел бы меньшее количество значащих битов и большую ошибку квантования.
6.Шестая особенность– простая реализация функции автоматической регулировки усиления (АРУ). Функция АРУ позволяет динамически масштабировать входные данные, чьи входная амплитуда значительно изменяется через какое-то время. Для некоторых приложений, например передача данных, данные организованы в виде блоков, в то время как для других приложений входные данные предусматривают изменяемый формат. Входной сигнал организован в виде цифровых слов внутри блоков данных, но значительно изменяется во времени с каждым блоком данных в пределах цифрового слова большей величины. Самая большая величина внутри каждого блока используется для масштабирования входного сигнала. Рис.21 .20 показывает структуру данных и блоков данных для телекоммуникации. Для этих приложений обычное используемое масштабирование в ЦПС, чтобы приспособить сигнал самой большой амплитуды, неизменно приводит для сигналов с мень-
шей амплитудой к ошибке усечения или округления.
Значение слова данных
3
2
1
0
-1
-2
|
-3 |
0 |
5 |
10 |
15 |
20 |
25 |
|
Слово данных |
Рисунок2.20. Структура данных и блоков данных для телекоммуникации
С другой стороны, функция АРУ автоматически корректирует входной сигнал, как показано на рис.21 .20 до амплитуды, необходимой для соответствующего масштаба и минимальной ошибки.
Чтобы применить функцию АРУ к блоку отсчетов данных, первое слово блока данных загружается в первый аккумулятор. Команда «MAX» затем проверяет каждое следующее слово данных блока загружаемое во второй аккумулятор, чтобы найти большее слово данных. Если большее значение
|
Лекции по ППО ВС РВ © Клюс В.Б. |
48 |
найдено, то эта команда сохраняет большее число из второго аккумулятора в первый аккумулятор. После того как проверка закончится, максимальное слово данных для данного блока данных всегда будет находиться в первом аккумуляторе.
По этому максимальному известному значению обратная величина может быть найдена делением или по таблице. Обратная величина затем загружается в регистр «T», и все слова блока данных затем умножаются на нее, то есть, масштабируются путем деления на максимум. В качестве альтернативы, выбором из таблицы можно определить максимально возможный левый сдвиг (умножение на степень 2) для уменьшения максимального значения в блоке. Левые сдвиги можно выполнять автоматически, загружая в «T» величину сдвига и затем использовать команду «LD TS», чтобы загрузить аккумулятор с левым сдвигом на число разрядов, задаваемых с помощью «T».
7.И, в заключение, перечислим ряд дополнительных особенностей. Рассмотренные выше особенности составляют минимальное подмножество математических возможностей, которые любой ЦПС должен иметь, но которые могут отсутствовать в микроконтроллерах. Одна из них– способность сохранить содержимое аккумулятора со сдвигом вправо, в то время как само содержимое аккумулятора не изменяется и не появляется ни какой ошибки усечения. Вторая– наличие флага переноса и заема для повышенной точности 64-разрядного сложения и вычитания. И третья– возможность знакового и беззнакового умножения, которая позволяет выполнять умножение с повышенной точностью.
|
Лекции по ППО ВС РВ © Клюс В.Б. |
49 |
Соседние файлы в папке 28-12-2014_12-52-57
- #
- #
- #
Sensors
Andrea Colagrossi, … Matteo Battilana, in Modern Spacecraft Guidance, Navigation, and Control, 2023
Quantization errors
Quantization error is a systematic error resulting from the difference between the continuous input value and its quantized output, and it is like round-off and truncation errors. This error is intrinsically associated with the AD conversion that maps the input values from a continuous set to the output values in a countable set, often with a finite number of elements. The quantization error is linked to the resolution of the sensor. Namely, a high-resolution sensor has a small quantization error. Indeed, the maximum quantization error is smaller than the resolution interval of the output, which is associated to the least significant bit representing the smallest variation that can be represented digitally:
LSB=FSR2NBIT
where FSR is the full-scale range of the sensor, and NBIT is the number of bits (i.e., the resolution) used in the AD converter to represent the sensor’s output. Quantization errors are typically not corrected, and the discrete values of the output are directly elaborated by the GNC system, which is designed to operate on digital values.
Fig. 6.9 shows a convenient model block to simulate quantization errors.
Figure 6.9. Quantization error model.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323909167000068
Digital Filters
Marcio G. Siqueira, Paulo S.R. Diniz, in The Electrical Engineering Handbook, 2005
2.11 Quantization in Digital Filters
Quantization errors in digital filters can be classified as:
- •
-
Round-off errors derived from internal signals that are quantized before or after more down additions;
- •
-
Deviations in the filter response due to finite word length representation of multiplier coefficients; and
- •
-
Errors due to representation of the input signal with a set of discrete levels.
A general, digital filter structure with quantizers before delay elements can be represented as in Figure 2.23, with the quantizers implementing rounding for the granular quantization and saturation arithmetic for the overflow nonlinearity.
FIGURE 2.23. Digital Filter Including Quantizers at the Delay Inputs
The criterion to choose a digital filter structure for a given application entails evaluating known structures with respect to the effects of finite word length arithmetic and choosing the most suitable one.
2.11.1 Coefficient Quantization
Approximations are known to generate digital filter coefficients with high accuracy. After coefficient quantization, the frequency response of the realized digital filter will deviate from the ideal response and eventually fail to meet the prescribed specifications. Because the sensitivity of the filter response to coefficient quantization varies with the structure, the development of low-sensitivity digital filter realizations has raised significant interest (Antoniou, 1993; Diniz et al., 2002).
A common procedure is to design the digital filter with infinite coefficient word length satisfying tighter specifications than required, to quantize the coefficients, and to check if the prescribed specifications are still met.
2.11.2 Quantization Noise
In fixed-point arithmetic, a number with a modulus less than one can be represented as follows:
(2.84)x=b0b1b2b3…bb,
where b0 is the sign bit and where b1b2b3 … bb represent the modulus using a binary code. For digital filtering, the most widely used binary code is the two’s complement representation, where for positive numbers b0 = 0 and for negative numbers b0 = 1. The fractionary part of the number, called x2 here, is represented as:
(2.85)x2={xif b0=0.2−|x|if b0=1.
The discussion here concentrates in the fixed-point implementation.
A finite word length multiplier can be modeled in terms of an ideal multiplier followed by a single noise source e(n) as shown in Figure 2.24.
FIGURE 2.24. Model for the Noise Generated after a Multiplication
For product quantization performed by rounding and for signal levels throughout the filter much larger than the quantization step q = 2−b, it can be shown that the power spectral density of the noise source ei(n) is given by:
(2.86)Pei(z)=q212=2−2b12.
In this case, ei(n) represents a zero mean white noise process. We can consider that in practice, ei(n) and ek(n + l) are statistically independent for any value of n or l (for i ≠ k). As a result, the contributions of different noise sources can be taken into consideration separately by using the principle of superposition.
The power spectral density of the output noise, in a fixed-point digital-filter implementation, is given by:
(2.87)Py(z)=σe2Σi=1KGi(z)Gi(z−1),
where Pei(ejw)=σe2, for all i, and each Gi(z) is a transfer function from multiplier output (gi(n)) to the output of the filter as shown in Figure 2.25. The word length, including sign, is b + 1 bits, and K is the number of multipliers of the filter.
FIGURE 2.25. Digital Filter Including Scaling and Noise Transfer Functions.
2.11.3 Overflow Limit Cycles
Overflow nonlinearities influence the most significant bits of the signal and cause severe distortion. An overflow can give rise to self-sustained, high-amplitude oscillations known as overflow limit cycles. Digital filters, which are free of zero-input limit cycles, are also free of overflow oscillations if the overflow nonlinearities are implemented with saturation arithmetic, that is, by replacing the number in overflow by a number with the same sign and with maximum magnitude that fits the available wordlength.
When there is an input signal applied to a digital filter, overflow might occur. As a result, input signal scaling is required to reduce the probability of overflow to an acceptable level. Ideally, signal scaling should be applied to ensure that the probability of overflow is the same at each internal node of the digital filter. This way, the signal-to-noise ratio is maximized in fixed-point implementations.
In two’s complement arithmetic, the addition of more than two numbers will be correct independently of the order in which they are added even if overflow occurs in a partial summation as long as the overall sum is within the available range to represent the numbers. As a result, a simplified scaling technique can be used where only the multiplier inputs require scaling. To perform scaling, a multiplier is used at the input of the filter section as illustrated in Figure 2.25.
It is possible to show that the signal at the multiplier input is given by:
(2.88)xi(n)=12πj∮cXi(z)zn−1dz=12π∫02πFi(ejω)X(ejω)ejωndω,
where c is the convergence region common to Fi(z) and X(z).
The constant λ is usually calculated by using Lp norm of the transfer function from the filter input to the multiplier input Fi(z), depending on the known properties of the input signal. The Lp norm of Fi(z) is defined as:
(2.89)‖Fi(ejω)‖p=[12π∫02π|Fi(ejω)|pdω]1p,
for each p ≥ 1, such that ∫02π|Fi(ejω)|pdω≤∞. In general, the following inequality is valid:
(2.90)|xi(n)| ≤ ‖Fi‖p‖X‖q, (1p+1q=1),
for p, q = 1, 2 and ∞.
The scaling guarantees that the magnitudes of multiplier inputs are bounded by a number Mmax when |x(n)| ≤ Mmax. Then, to ensure that all multiplier inputs are bounded by Mmax we must choose λ as follows:
(2.91)λ=1Max{‖F1‖p,…,‖F1‖p,…, ‖FK‖p},
which means that:
(2.92)‖F′i(ejω)‖p≤1, for‖X(ejω)‖q ≤ Mmax.
The K is the number of multipliers in the filter.
The norm p is usually chosen to be infinity or 2. The L∞ norm is used for input signals that have some dominating frequency component, whereas the L2 norm is more suitable for a random input signal. Scaling coefficients can be implemented by simple shift operations provided they satisfy the overflow constraints.
In case of modular realizations, such as cascade or parallel realizations of digital filters, optimum scaling is accomplished by applying one scaling multiplier per section.
As an illustration, we present the equation to compute the scaling factor for the cascade realization with direct-form second-order sections:
(2.93)λi=1‖∏j=1i−1Hj(z)Fi(z)‖p,
where:
Fi(z)=1z2+m1iz+m2i.
The noise power spectral density is computed as:
(2.94)Py(z)=σe2[3+3λ12∏i=1mHi(z)Hi(z−1)+5Σj=2m1λj2∏i=jmHi(z)Hi(z−1)],
whereas the output noise variance is given by:
(2.95)σo2=σe2[3+3λ12||∏i=1mHi(ejω)||22+5Σj=2m1λj2||∏i=jmHi(ejω)||22].
As a design rule, the pairing of poles and zeros is performed as explained here: poles closer to the unit circle pair with closer zeros to themselves, such that ||Hi(z)||p is minimized for p = 2 or p = ∞.
For ordering, we define the following:
(2.96)Pi=| |Hi(z)| |∞| |Hi(z)| |2.
For L2 scaling, we order the section such that Pi is decreasing. For L∞ scaling, Pi should be increasing.
2.11.4 Granularity Limit Cycles
The quantization noise signals become highly correlated from sample to sample and from source to source when signal levels in a digital filter become constant or very low, at least for short periods of time. This correlation can cause autonomous oscillations called granularity limit cycles.
In recursive digital filters implemented with rounding, magnitude truncation,72 and other types of quantization, limitcycles oscillations might occur.
In many applications, the presence of limit cycles can be harmful. Therefore, it is desirable to eliminate limit cycles or to keep their amplitude bounds low.
If magnitude truncation is used to quantize particular signals in some filter structures, it can be shown that it is possible to eliminate zero-input limit cycles. As a consequence, these digital filters are free of overflow limit cycles when overflow nonlinearities, such as saturation arithmetic, are used.
In general, the referred methodology can be applied to the following class of structures:
- •
-
State-space structures: Cascade and parallel realization of second-order state-space structures includes design constraints to control nonlinear oscillations (Diniz and Antoniou, 1986).
- •
-
Wave digital filters: These filters emulate doubly terminated lossless filters and have inherent stability under linear conditions as well as in the nonlinear case where the signals are subjected to quantization (Fettweis, 1986).
- •
-
Lattice realization: Modular structures allowing easy limit cycles elimination (Gray and Markel, 1975).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500621
Biomedical signals and systems
Sri Krishnan, in Biomedical Signal Analysis for Connected Healthcare, 2021
2.2.1 Noise power
The quantization error (e) or noise tends to have a random behavior, and they could be mathematically represented using statistical variables. Power of a random variable with a probability density function of p(e) could be obtained by computing the second-order statistics of variance, and it is denoted by
σ2=∫−q/2q/2e2p(e)de
A good assumption for p(e) is a uniform probability density function which will have a value of 1/q over the range of −q/2 to q/2.
=∫−q/2q/2e2·1qde=q212
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128130865000049
Measurement of high voltages
E. Kuffel, … J. Kuffel, in High Voltage Engineering Fundamentals (Second Edition), 2000
Static errors
The quantization error is present because the analogue value of each sample is transformed into a digital word. This A-to-D conversion entails a quantization of the recorder’s measuring range into a number of bands or code bins, each represented by its central value which corresponds to a particular digital code or level. The number of bands is given by 2N, where N is the resolution of the A-to-D converter. The digital output to analogue input relationship of an ideal digitizer is shown diagrammatically in Fig. 3.49. For any input in the range (iΔVav – 0.5 * ΔVav to iΔVav + 0.5 * ΔVav), where iΔVav is the voltage corresponding to the width of each code bin, or one least significant bit (LSB), and iΔVav is the centre voltage corresponding to the i th code, an ideal digitizer will return a value of Ii. Therefore, the response of an ideal digitizer to a slowly increasing linear ramp would be a stairway such as that shown in Fig. 3.50. A quick study of these figures reveals the character of the quantization error associated with the ideal A-to-D conversion process. The maximum error possible is equivalent to a voltage corresponding to ±(½) of an LSB. For an ideal digital recorder, this quantization would be the only source of error in the recorded samples. For a real digital recorder, this error sets the absolute upper limit on the accuracy of the readings. In the case of an 8-bit machine, this upper limit would be 0.39 per cent of the recorder’s full-scale deflection. The corresponding maximum accuracy (lowest uncertainty) of a 10-bit recorder is 0.10 per cent of its full-scale deflection.
Figure 3.49. Analogue input to digital output relation of an ideal A/D converter
Figure 3.50. Response of an ideal A/D converter to a slowly rising ramp
The error caused by discrete time sampling is most easily demonstrated with reference to the recording of sinusoidal signals. As an example we can look at the discrete time sampling error introduced in the measurement of a single cycle of a pure sine wave of frequency f, which is sampled at a rate of four times its frequency. When the sinusoid and the sampling clock are in phase, as shown in Fig. 3.51, a sample will fall on the peak value of both positive and negative half-cycles. The next closest samples will lie at π/2 radians from the peaks. As the phase of the clock is advanced relative to the input sinusoid the sample points which used to lie at the peak values will move to lower amplitude values giving an error (Δ) in the measurement of the amplitude (A) of
Figure 3.51. Sample points with sinusoid and sampling clock in phase. (Error in peak amplitude = 0)
Δ = A(1 − cos ϕ)
where ϕ is the phase shift in the sample points. This error will increase until ϕ – π/4 (Fig. 3.52). For ϕ > π/4 the point behind the peak value will now be closer to the peak and the error will decrease for a ϕ in the range of π/4 to π/2. The maximum per unit value of the discrete time sampling error is given by eqn 3.93,
Figure 3.52. Sample points with sampling clock phase advanced to π/4 with respect to the sinusoid. Error in peak amplitude (Δ) is at a maximum
(3.93)Δmax=I−cos(πfts)
where ts is the recorder’s sampling interval and f the sinewave frequency.
The maximum errors obtained through quantization and sampling when recording a sinusoidal waveform are shown in Fig. 3.53. The plotted quantities were calculated for an 8-bit 200-MHz digitizer.
Figure 3.53. Sampling and quantization errors of an ideal recorder
In a real digital recorder, an additional two categories of errors are introduced. The first includes the instrument’s systematic errors. These are generally due to the digitizer’s analogue input circuitry, and are present to some degree in all recording instruments. They include such errors as gain drift, linearity errors, offset errors, etc. They can be compensated by regular calibration without any net loss in accuracy. The second category contains the digitizer’s dynamic errors. These become important when recording high-frequency or fast transient signals. The dynamic errors are often random in nature, and cannot be dealt with as simply as their systematic counterparts and are discussed below.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750636346500046
Remaining useful life prediction
Yaguo Lei, in Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery, 2017
6.3.4.3 RUL Prediction
The constructed indicator WMQE is further input into the RUL prediction module. In this module, a PF-based prediction algorithm is utilized to predict RUL of the rotating machinery whose degradation processes are described using a variant of Paris–Erdogan model. The Paris–Erdogan model is formulated as
(6.96)dxdt=c(Δδ)γ, Δδ=mx
where x represents the semicrack length, t is the number of stress cycles (i.e., the fatigue life), c, γ, and m are material constants which are determined by tests, and Δδ is amplitude of stress intensity factor roughly proportional to the square root of x.
It is seen from Eq. (6.96) that there are several model parameters in the Paris–Erdogan model, that is, c, γ, and m, which are difficult to measure during the operation process of the rotating machinery. For convenient application, the Paris–Erdogan model is transformed into the following format with α=cmγ and β = γ/2.
(6.97)dxdt=αxβ.
Then, the above function is rewritten into the following state space model.
(6.98)xk=xk−1+αk−1xk−1βΔtkαk=αk−1zk=xk+νk,
where αk−1 is a random variable following a normal distribution of Nμα,σα2, β is a constant parameter, Δtk=tk−tk−1, zk is the measured WMQE value at tk and νk is the measurement noise following the normal distribution of N0,σν2. With the transformation of the Paris–Erdogan model, the model parameters are more convenient to estimate according to the measurements. In addition, the state space model inherits the superiority of the Paris–Erdogan model in describing the general degradation processes. Therefore, it is supposed to be a good model for a general degradation process.
After the transformation, the unknown model parameters are changed to be Θ=μα,σα2,β,σν2′, where (·)′ denotes the vector transposition. Then, the measured WMQE values constructed from vibration signals are input into the model, and the model parameters are initialized using MLE. It is assumed that there are a series of measurements z0:M=z0,…,zM′ at ordered times t0,…,tM. According to Eq. (6.98), zk is formulated as follows:
(6.99)zk=xk−1+αkxk−1βΔtk+νk.
The degradation state xk−1 has the following relationship with the measurement zk−1.
(6.100)xk−1=zk−1−νk−1.
The degradation state xk−1 is hard to be acquired in real applications. If the measurement noise νk−1 is small enough compared with the measurement itself, it is negligible and xk−1 is approximated by zk−1. Let T=z0βΔt1,…,zM−1βΔtM′. z1:M=z1,…,zM′ is multivariate normally distributed, which is denoted as follows:
(6.101)z1:M∼Nz0:M−1+μαT,σα2TT′+σν2IM,
where IM is an identity matrix of order M.
Let Δz1:M=z1−z0,…,zM−zM−1′, and the log-likelihood function of the unknown parameters based on the measurements is expressed as
(6.102)ℓΘ|z0:M=−M2ln2π−12lnσα2TT′+σν2IM −12Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT =−M2ln2π−M2lnσα2−12lnTT′+σ˜ν2IM −12σα2Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT,
with σ~ν2=σν2/σα2. The first partial derivatives of ℓΘ|z0:M with respect to μα and σα2 are calculated and formulated with
(6.103)∂ℓΘ|z0:M∂μα=1σα2T′TT′+σ~ν2IM-1Δz1:M−μαT,
(6.104)∂ℓΘ|z0:M∂σα2=−M2σα2+12σα4Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαT.
Let ∂ℓΘ|z0:M/∂μα=0 and ∂ℓΘ|z0:M/∂σα2=0. The MLE results of μα and σα2 are
(6.105)μα=T′TT′+σ~ν2IM−1Δz1:MT′TT′+σ~ν2IM−1T,
(6.106)σα2=Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαTM.
With Eqs. (6.105) and (6.106) substituted into Eq. (6.102), the log-likelihood function is reduced into a two-variable function about β and σ~ν2, which is denoted by
(6.107)ℓΘ|z0:M=−M2ln2π−M2lnσα2−12lnTT′+σ~ν2IM−M2.
The MLE values of β and σ~ν2 are obtained by maximizing the log-likelihood function (6.107) through two-dimensional optimizing. Then the MLE values of β and σ~ν2 are substituted into Eqs. (6.105) and (6.106), and the MLE values of μα and σα2 are acquired. The value of σν2 is calculated with σ~ν2 multiplied by σα2. Finally, all of the unknown parameters Θ=μα,σα2,β,σν2′ are initialized.
After parameter initialization, the model parameters are further updated and the RUL is predicted using a PF-based prediction algorithm. Based on the initialized parameters, a series of initial particles y0nn=1:Ns are sampled from the initial PDF of the system state p(y0n|Θ0)∼N(y0,Q0) with
(6.108)y0=x0μα and Q0=000σα2.
Ns is the number of particles and the weight of each particle is set to be 1/Ns. Then new particles ykni=1:Ns are obtained following
(6.109)ykn=xknμαn=xk−1n+μαnxk−1nβΔtkμαn.
When the new measurement zk at tk is available, each particle weight is updated and normalized by
(6.110)wkn=wk−1npzk|ykn, w~kn=wkn∑n=1Nswkn,
where
(6.111)pzk|ykn=12πσνexp−12zk−xknσν2.
The particles are resampled according to the particle weights and their weights are reset to be 1/Ns. After that, the RUL is predicted based on the resampled particles. The RUL lk at tk is defined as
(6.112)lk=inflk:xlk+tk≥λ|x1:k,
where λ is a prespecified failure threshold. Each particle is transmitted following the transition function of Eq. (6.98) from current state until the state value exceeds the failure threshold, and the RUL lknn=1:Ns predicted using each particle is acquired. Then the PDF of the RUL is approximated by
(6.113)plk|z0:k=∑n=1Nsw~knδlk−lkn.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128115343000068
Orbit and Attitude Sensors
Enrico Canuto, … Carlos Perez Montenegro, in Spacecraft Dynamics and Control, 2018
Exercise 1
Prove that the quantization error defined by Eq. (8.6) is bounded by |n˜y(i)|≤ρy/2 and under the random assumption has zero mean and variance equal to ρy2/12. □
A typical model of the random error d˜ in Eq. (8.4), which includes quantization errors, is the linear continuous-time stochastic state equation
(8.7)x˜˙(t)=A˜x˜+G˜w˜d˜(t)=C˜x˜+D˜w˜E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=S˜w2δ(τ)E{x˜(0)}=x˜0,E{(x˜(0)−x˜0)(x˜(0)−x˜0)T}=P˜0≥0E{(x˜(0)−x˜0)w˜T(0)}=0,
which is similar to the DT Eq. (4.159) of Section 4.8.1. Eq. (8.7) being continuous-time, the eigenvalues of the state matrix A˜ are assumed to lie on the imaginary axis and when equal to zero may be multiple. The statistics in Eq. (8.7) assumes that w˜ is a zero-mean second-order stationary white noise with constant spectral density S˜w2, and impulsive covariance, where δ(τ) denotes a Dirac delta (see Sections 13.2.1 and 13.7.3Section 13.2.1Section 13.7.3). The initial state may be modeled as a random vector with mean value x˜0 and covariance matrix P˜0, but is uncorrelated from any simultaneous white noise as expressed by the last identity in Eq. (8.7). This uncorrelation has been already referred to as the causality constraint. In principle, Eq. (8.7) may be unobservable from the output d˜ and uncontrollable by the noise w˜, because the output d˜ may include polynomial and trigonometric components (deterministic signals) just driven by the initial state x˜0. For instance, a trigonometric component tuned to the angular frequency ω˜ corresponds to a second-order subsystem with eigenvalues ±jω˜. A first-order polynomial corresponds to a second-order subsystem with a pair of zero eigenvalues and a single eigenvector. The mixed case of stochastic processes and deterministic signals can be simplified by assuming that trigonometric and polynomial components are the free response of the equations driven by w˜, and that Eq. (8.7) is observable and controllable.
The simplest model of the class in Eq. (8.7), which is common to inertial sensors (accelerometers in Section 8.4 and gyroscopes in Section 8.5), is the scalar first-order random drift [32]:
(8.8)x˜˙(t)=w˜x,x˜(0)=x˜0d˜(t)=x˜+w˜dE{x˜(0)}=x˜0,var{x˜}=σ02,E{(x˜−x˜0)w˜T(0)}=0w˜=[w˜xw˜d],E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=[S˜wx200S˜wd2]δ(τ),
where, if [unit] denotes the unit of measurement of x˜, we find S˜wx2 in [(unit/s)2Hz−1] and S˜wd2 in [unit2Hz−1]. The initial state x˜0 accounts for a constant bias and is uncorrelated with any simultaneous noise; the scalar input noise w˜x and the output noise w˜d in Eq. (8.8) are uncorrelated with each other. The output process d˜ is nonstationary and the autocorrelation is given by
(8.9)R˜d(t,t+τ)=S˜wx2min(t,t+τ)+S˜wd2δ(τ).
Although x˜ is nonstationary, the spectral density S˜x2(f) can be defined through the AS equation x˜˙=−εx˜+w˜x, where ε > 0 must be sufficiently smaller than the cutoff frequency f0 to be defined in the next paragraph. We can write the following identities:
(8.10)S˜d2(f)=S˜x2(f)+S˜wd2=S˜wx2(2πf)2+S˜wd2,f>ε2π=fεσ˜x2=limf→∞∫0fS˜x2νdν<∞,
where if, for f < ε, S˜x2(f) is bounded, also the variance σ˜x2 is bounded. The Bode plot of S˜d(f) is approximately flat for f>f0=2π−1S˜wx/S˜wd>fε and has a −20 dB/decade slope for fε < f < f0. The first PSD in the first row of Eq. (8.10) is a first-order random walk, which is known, in the realm of inertial sensors, as the (long-term) bias instability of the sensor. The name is appropriate because it describes the long-term fluctuations—bounded because of ε—around the mean sensor bias x˜0. The square root of the second term S˜wd corresponds to the minimum-valued profile of the overall spectral density. Let us call it, as already anticipated, noise floor, although the name sometimes refers to the whole instrument noise (here referred to as the background noise). In the realm of inertial sensors, it is known as the velocity random walk in the case of linear accelerometers, the unit being [m/(s2Hz)], and the angular random walk (ARW) in the case of gyroscopes, the unit being[rad/(sHz)]. The name, which may cause same confusion, is justified by the fact that when either of the two measurements (linear acceleration and angular rate) is time integrated for generating either velocity or attitude measurements, the integrated noise floor becomes a random walk. By restricting to gyroscopes, the ARW unit [rad/(sHz)] is usually simplified to [rad/s], de facto to the non-SI unit [degree/hour]. Indeed, the simplified unit is at the same time the unit of S˜wd and the unit of the root mean square (RMS) σ¯w(t,Δt) of the random walk increment w¯d(t,Δt)=∫tt+Δtw˜d(τ)dτ, namely:
(8.11)σ¯w(t,Δt)=E{1Δt(∫tt+Δtw˜d(τ)dτ)2}=S˜wd.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081007006000088
Sampling Theory
Luis Chaparro, in Signals and Systems Using MATLAB (Second Edition), 2015
8.3.2 Quantization and Coding
Amplitude discretization of the sampled signal xs(t) is accomplished by a quantizer consisting of a number of fixed amplitude levels against which the sample amplitudes {x(nTs)} are compared. The output of the quantizer is one of the fixed amplitude levels that best represents {x(nTs)} according to some approximation scheme. The quantizer is a non-linear system.
Independent of how many levels or, equivalently, of how many bits are allocated to represent each level of the quantizer, in general there is a possible error in the representation of each sample. This is called the quantization error. To illustrate this, consider the 2-bit or four-level quantizer shown in Figure 8.12. The input of the quantizer are the samples {x(nTs)}, which are compared with the values in the bins [-2Δ,-Δ],[-Δ,0],[0,Δ], and [Δ,2Δ]. Depending on which of these bins the sample falls in it is replaced by the corresponding levels -2Δ,-Δ,0, or Δ, respectively. The value of the quantization step Δ for the four-level quantizer is
Figure 8.12. Four-level quantizer and coder.
(8.23)Δ=dynamic range of signal2b=2max|x(t)|22
where b = 2 is number of bits of the code assigned to each level. The bits assigned to each of the levels uniquely represents the different levels [-2Δ,-Δ,0,Δ]. As to how to approximate the given sample to one of these levels, it can be done by rounding or by truncating. The quantizer shown in Figure 8.12 approximates by truncation, i.e., if the sample kΔ≤x(nTs)<(k+1)Δ, for k = −2, −1,0,1, then it is approximated by the level kΔ.
To see how quantization and coding are done, and how to obtain the quantization error, let the sampled signal be
x(nTs)=x(t)|t=nTS
The given four-level quantizer is such that if the sample x(nTs) is such that
(8.24)kΔ≤x(nTs)<(k+1)Δ⇒xˆ(nTs)=kΔk=-2,-1,0,1
The sampled signal x(nTs) is the input of the quantizer and the quantized signal xˆ(nTs) is its output. So that whenever
-2Δ≤x(nTs)<-Δ⇒xˆ(nTs)=-2Δ-Δ≤x(nTs)<0⇒xˆ(nTs)=-Δ0≤x(nTs)<Δ⇒xˆ(nTs)=0Δ≤x(nTs)<2Δ⇒xˆ(nTs)=Δ
To transform the quantized values into unique binary 2-bit values, one could use a code such as
xˆ(nTs)⇒binary code-2Δ10-Δ110Δ00Δ01
which assigns a unique 2 bit binary number to each of the 4 quantization levels. Notice that the first bit of this code can be considered a sign bit, “1” for negative levels and “0” for positive levels.
If we define the quantization error as
ε(nTs)=x(nTs)-xˆ(nTs)
and use the characterization of the quantizer given by Equation (8.24) as
xˆ(nTs)≤x(nTs)≤xˆ(nTs)+Δ
by subtracting xˆ(nTs) from each of the terms gives that the quantization error is bounded as follows
(8.25)0≤ε(nTs)≤Δ
i.e., the quantization error for the four-level quantizer being considered is between 0 and Δ. This expression for the quantization error indicates that one way to decrease the quantization error is to make the quantization step Δsmaller. Increasing the number of bits of the A/D converter makes Δ smaller (see Equation (8.23) where the denominator is 2 raised to the number of bits) which in turn makes smaller the quantization error, and improves the quality of the A/D converter.
In practice, the quantization error is random and so it needs to be characterized probabilistically. This characterization becomes meaningful when the number of bits is large, and when the input signal is not a deterministic signal. Otherwise, the error is predictable and thus not random. Comparing the energy of the input signal to the energy of the error, by means of the so-called signal to noise ratio (SNR), it is possible to determine the number of bits that are needed in a quantizer to get a reasonable quantization error.
Example 8.5
Suppose we are trying to decide between an 8 and a 9 bit A/D converter for a certain application where the signals in this application are known to have frequencies that do not exceed 5 kHz. The dynamic range of the signals is 10 volts, so that the signal is bounded as −5 ≤ x(t) ≤ 5. Determine an appropriate sampling period and compare the percentage of error for the two A/Ds of interest.
Solution
The first consideration in choosing the A/D converter is the sampling period, so we need to get an A/D converter capable of sampling at fs = 1/Ts > 2 fmax samples/second. Choosing fs = 4 fmax = 20 k samples/second then Ts = 1/20 msec/sample or 50 microseconds/sample. Suppose then we look at the 8-bit A/D converter, the quantizer has 28 = 256 levels so that the quantization step is Δ=10/256 volts and if we use a truncation quantizer the quantization error would be
0≤ε(nTs)≤10/256
If we find that objectionable we can then consider the 9-bit A/D converter, with a quantizer of 29 = 512 levels and the quantization step Δ=10/512 or half that of the 8-bit A/D converter, and
0≤ε(nTs)≤10/512
So that by increasing one bit we cut the quantization error in half from the previous quantizer. Inputting a signal of constant amplitude 5 into the 9-bit A/D gives a quantization error of [(10/512)/5] × 100% = (100/256)% ≈ 0.4% in representing the input signal. For the 8-bit A/D it would correspond to 0.8% error. ▪
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123948120000085
Compression
StéphaneMallat , in A Wavelet Tour of Signal Processing (Third Edition), 2009
Weighted Quantization and Regions of Interest
Visual distortions introduced by quantization errors of wavelet coefficients depend on the scale 2j. Errors at large scales are more visible than at fine scales [481]. This can be taken into account by quantizing the wavelet coefficients with intervals Δj=Δwj that depend on the scale 2j. For R¯≤1 bit/pixel, wj = 2−j is appropriate for the three finest scales. The distortion in (10.34) shows that choosing such weights is equivalent to minimizing a weighted mean-square error.
Such a weighted quantization is implemented like in (10.35) by quantizing weighted wavelet coefficients fB[m]/wj with a uniform quantizer. The weights are inverted during the decoding process. JPEG-2000 supports a general weighting scheme that codes weighted coefficients w[m]fB[m] where w[m] can be designed to emphasize some region of interest Ω ⊂ [0, 1]2 in the image. The weights are set to w[m] = w > 1 for the wavelet coefficients fB[m]=〈f,ψj,p,q1〉 where the support of ψj,p,q1 intersects Ω. As a result, the wavelet coefficients inside Ω are given a higher priority during the coding stage, and the region Ω is coded first within the compressed stream. This provides a mechanism to more precisely code regions of interest in images—for example, a face in a crowd.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123743701000148
Signal and Image Representation in Combined Spaces
Zoran. Cvetković, Martin. Vetterli, in Wavelet Analysis and Its Applications, 1998
6.1 Two lemmas on frames of complex exponentials
Estimates of bounds on the quantization error in Subsection 4.3 are derived from the next two lemmas [5].
Lemma 1
Letejλnωbe a frame in L2[− σ, σ]. If M is any constant and {μn} is a sequence satisfying |μn − λn| ≤ M, for all n, then there is a number C = C(M, σ, {λn}) such that
(6.1.1)∑n|fμn|2∑n|fλn|2≤C
for every cr-bandlimited signal f(x).
Lemma 2
Letejλnωbe a frame in L2[− σ, σ], with bounds 0 < A ≤ B < ∞ and δ a given positive number. If a sequence { μn } satisfies | λn − μn \ < δ for all n, then for every σ-bandlimited signal f(x)
(6.1.2)A1−C2||f||2≤∑n|fμn|2≤B(1+C)2||f||2,
where
(6.1.3)C=BAeγδ−12
Remark 1
If δ in the statement of Lemma 2 is chosen small enough, so that C is less then 1, then ejμnω is also a frame in L2[− σ, σ]. Moreover, there exists some δ 1/4 ({λn},σ), such that whenever δ < δ 1/4 ({λn }, σ), ejμnω is a frame with frame bounds A/A and 9B/4.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1874608X98800125
Live HDR Video Broadcast Production
I.G. Olaizola, … J. Gorostegui, in High Dynamic Range Video, 2017
1.4.1 Banding
Banding effects are directly related to quantization errors. As the dynamic range increases, the quantization effects become more noticeable and banding artifacts arise. To avoid this, smaller quantization steps must be taken, but this requires a higher bitdepth (from 8 to 10 or 12 in order to have backwards compatibility with existing infrastructures, and ideally 14 or 16 bits) and nonlinear transform functions based on the HVS that minimize the observable banding effects. Nowadays, this is partially solved by the electro-optical transfer function (EOTF) and opto-electronic transfer function (OETF) mapping curves that will be introduced in a further section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012809477800008X
Рассмотренное билинейное
преобразование вида (6.21) позволило получить передаточную функцию цифрового
ФНЧ. Существует более общее преобразование, позволяющее преобразовать
аналоговый ФНЧ в избирательный БИХ-фильтр любого типа (ФНЧ, ФВЧ, ПФ, РФ). Не
рассматривая вывода соответствующих формул, приводим их в таблице 6.1.
Здесь последовательно указаны
нормированные значения граничных частот цифрового фильтра, формулы замены
переменной в , формулы для расчета параметра
, позволяющие
получить по заданным и
нормированный
аналоговый прототип с частотами среза и,
наконец, формула для расчета граничной частоты полосы задерживания (
определять
не надо, т.к. она всегда равна 1). Для ПФ и РФ расчет выполняется по двум формулам и
из двух значений и
выбирается то,
модуль которого наименьший.
Пример 5.1 Рассчитать дискретный фильтр НЧ с параметрами: кГц;
кГц;
кГц;
дБ;
дБ.
По формуле (6.24) находим
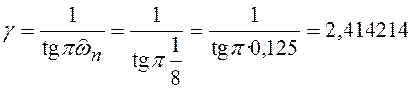
Далее находим нормированную частоту
задерживания аналогового ФНЧ-прототипа
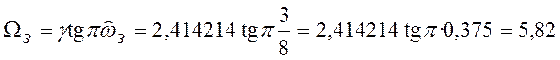
Тем самым произведен перерасчет
требований, предъявленных к дискретному фильтру в требования к аналоговому
прототипу.
Таблица 6.1
|
Цифровой фильтр |
Граничные “цифровые” частоты |
Формула замены |
Параметр |
Связь “аналоговых” частот с “цифровыми” |
Граничные “аналоговые” частоты |
|
Нижних частот |
|
|
|
|
|
|
Верхних частот |
|
|
|
|
|
|
Полосовой |
|
|
|
|
|
|
Режекторный |
|
|
|
|
|
Как рассчитать аналоговый
фильтр-прототип? Исходными требованиями для расчета являются требования к
НЧ-прототипу (рисунок 6.10,б). По ним, пользуясь любым справочником по расчету
аналоговых фильтров, рассчитывают передаточную функцию аналогового
фильтра-прототипа.
Пример 6.2 Для ,
дБ,
дБ (параметры ФНЧ-прототипа,
взятые из предыдущего примера), пользуясь справочником, находим, что
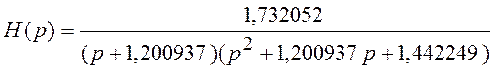
Как осуществить переход к дискретному
фильтру? Для перехода от к
воспользуемся билинейным преобразованием
Для
рассмотренного выше примера , поэтому
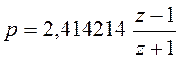
выражение . Получим
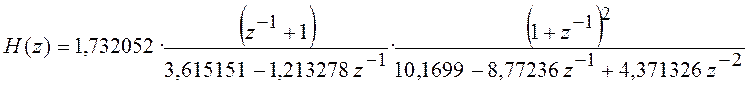
Дискретный фильтр с такой передаточной
функцией легко реализовать в виде
каскадного соединения типовых звеньев 1-го и 2 порядка. Для этого функцию перепишем в виде
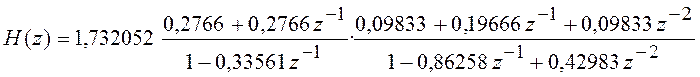
Схема фильтра, имеющего такую
передаточную функцию приведена на рисунке 6.11.
7 Эффекты квантования в цифровых
системах
7.1 Основные понятия
В разделе “Аналоговые, дискретные и
цифровые сигналы” главы 1 мы обсуждали разницу между дискретными и цифровыми
сигналами. До сих пор, строго говоря, речь шла о дискретных сигналах и
системах, поскольку отсчеты сигналов и коэффициентов фильтров считались
представленными точно (без погрешностей). Сигналы на входе и выходе
ЦФ являются цифровыми, т.е.
последовательностями чисел. Каждое из этих чисел представляется в виде
двоичного кода, и в ЦФ в соответствии с алгоритмом
выполняются
операции пересылки, сложения и умножения кодов. Представить числа точно
конечным числом разрядов кода невозможно. При этом алгоритм функционирования
реализуется неточно. Ошибки цифровой фильтрации обусловлены следующими
факторами:
—
ошибки квантования входных и выходных сигналов;
—
квантованием коэффициентов фильтра и
;
—
конечной разрядностью операционных устройств;
—
округлением промежуточных результатов вычислений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.