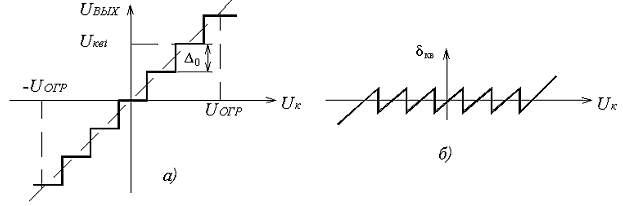Ошибки квантования и округления - Решение и исправление самых разных ошибок на TopOshibok.ru

средства ЦОС [5]. Принцип стробоскопического преобразования или когерентной выборки заключается в жесткой связи между частотой дискретизации и частотой сигнала или их гармониками и субгармониками. Он легко иллюстрируется во временной и частотной области на примере простого гармонического колебания, частота fс которого в результате преобразования на гармониках частоты дискретизации переносится на низкую частоту Fпр = |kfд − fc|, заключенную в пределах 0− fд/2. Стробоскопическое преобразование применяется в цифровой осциллографии, при цифровом измерении параметров сигналов и характеристик объектов [10]. Такие измерители, реализуемые на базе персональных компьютеров со встроенными или внешними средствами аналогового ввода — вывода, называются модульными виртуальными приборами или инструментами [41]. Вопросы дискретизации и цифровой оценки параметров сигналов для них рассмотрены в [42, 43].

1.8.1.ОПРЕДЕЛЕНИЕ И СПОСОБЫ

При квантовании по уровню бесконечное множество возможных значений дискретного сигнала x(n) в заданном максимальном диапазоне его изменения Dxmax= (xmax − xmin) замещается конечным числом уровней квантования m дискретного квантованного сигнала xкв(n). С одним из них в соответствии с определенным правилом или алгоритмом и отождествляется точное мгновенное значение дисретного сигнала x(n) (рис. 1.13). Интервал между уровнями квантования называется шагом квантования по уровню Q = Dxmax /m.

i	xmax	Xкв(n)
m /2

		e(n)
3
2		Q	nTд
1

0	Tд 2Tд 3Tд
-1
-2
-3

Рис.1.13. Иллюстрация квантования сигнала по уровню

Квантование возможно с усечением и с округлением. Квантованный дискретный сигнал хкв(n) определяется при этом как

хкв(n) = [x(n)/Q]ц.ч.Q = iQ	(1.9)
при усечении и
хкв(n) = [(x(n)/Q)+0,5]ц.ч.Q = iQ	(1.9′)

при округлении, где i = [ ]ц.ч. − это целая часть отношения, заключенного в прямые скобки и соответствующая номеру уровня квантования, с которым отождествляется точное значение квантуемого дискретного сигнала с ближайшим меньшим − при усечении и ближайшим – при округлении. Для однополярного сигнала 0 ≤ i ≤ (m − 1), двухполярного (− m/2) ≤ i ≤ (m/2) − 1.

1.8.2. ПОГРЕШНОСТЬ КВАНТОВАНИЯ

Разность между квантованным и точным значениями дискретного сигнала: e(n) = хкв(n) − x(n) определяет погрешность, возникающую при квантовании сигнала по уровню. В соответствии с амплитудной характеристикой квантователя она принимает значения − Q < e(n) ≤ 0 —

при усечении (рис.1.14, а, б) и − Q/2 < e(n) ≤ Q/2 − при округлении (рис.1.15, а, б). Предельные значения погрешности квантования Em= e(n) max = ηQ, где η = 1 при усечении и ½ при округлении.

хкв(n)

х(n)

-3Q2Q

Q 2Q 3Q…

-2Q

-3Q

e(n)

х(n)

б)

-Q

Рис. 1.14. Амплитудная характеристика квантования с усечением (а) и соответствующая ему погрешность квантования (б)

x кв(n )

2 Q

x (n )

…

-(5 /2 )Q -(3 /2 )Q – Q /2

Q /2 (3/2 )Q (5 /2)Q …

-Q

-2 Q

e(n )

Q /2

x (n )

б)

-Q /2

Рис. 1.15. Амплитудная характеристика квантования с округлением (а) и соответствующая ему погрешность квантования (б)

Вследствие априорной неизвестности значений сигнала и погрешности квантования ее рассматривают как случайный дискретный процесс или шум квантования, накладывающийся на квантуемый дискретный сигнал: хкв(n) = x(n) + e(n) и с равной вероятностью принимающий любые значения в

вышеуказанных пределах.	На графиках законов распределения шума
квантования рис.1.16, а, б	обоим способам квантования соответствует

одинаковая плотность вероятностей p(e)=1/Q, отвечающая условию нормировки.

Р(е)

1/Q

-Q

-Q/2

Q/2

Рис. 1.16. Плотности вероятностей шума квантования при усечении (а) и округлении (б)

Шум квантования характеризуется следующими параметрами:

математическим ожиданием M[e] =	0∫ e p( e )de =	− Q / 2 − при усечении и
			− Q
Q / 2	=	0 −	при округлении;
M[e] = ∫ e p( e )de
− Q / 2
		D[e]	Q / 2	Q2 / 12 −
дисперсией		= ∫ e2 p( e )de =	для обоих способов

− Q / 2

квантования;

среднеквадратическим значением σe = Q/ 12 . Спектрально-корреляционные свойства шума квантования существенно

зависят от вида и параметров преобразуемого сигнала. В общем случае значения отсчетов шума квантования коррелированы со значениями входного сигнала и между собой. Наиболее высокая степень корреляции наблюдается при детерминированных сигналах и наименьшая − случайных. К последним относятся реальные речевые, музыкальные сигналы, выходные сигналы измерительных датчиков, а также любые сигналы на входе системы ЦОС с наложенными на них шумами или случайными помехами. Наложение внешнего шума или помехи с приведенным ко входу АЦП уровнем, превышающим значение единицы младшего разряда Q, существенно декоррелирует или рандомизирует шум квантования [44]. Это позволяет рассматривать шум квантования, возникающий при преобразовании случайного сигнала, как дискретный случайный процесс типа белый шум с равномерной спектральной плотностью: Pкв = σ2кв/fд. Повышение частоты

дискретизации fд уменьшает спектральную плотность шума квантования в основной полосе, позволяя при определенных условиях уменьшить необходимое значение разрядности АЦП, т. е. обменять разрядность сигнала на скорость его обработки [44].

Модель шума квантования с вышеприведенными характеристиками широко используется в теории ЦОС.

Соседние файлы в предмете Электроника

#
13.09.201320.9 Mб14Бараночников М.Л. Микромагнитоэлектроника. Т.2. — М., ДМК Пр.pdf
#
#
#
13.09.20137.25 Mб24Вишневский В.М. и др. — Широкополосные беспроводные сети пер.djv
#
13.09.201317.1 Mб28Герасимов В.Г. (ред). — Электрические измерения и основы эле.pdf
#
#
#
13.09.20134.01 Mб30Долуханов М.П. — Распространение радиоволн (1972).djvu
#
#
#

Источник

Цифровое представление аналогового аудиосигнала. Краткий ликбез

Время на прочтение
7 мин

Количество просмотров 43K

Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.

Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.

Чем отличается цифровой аудиосигнал от аналогового?

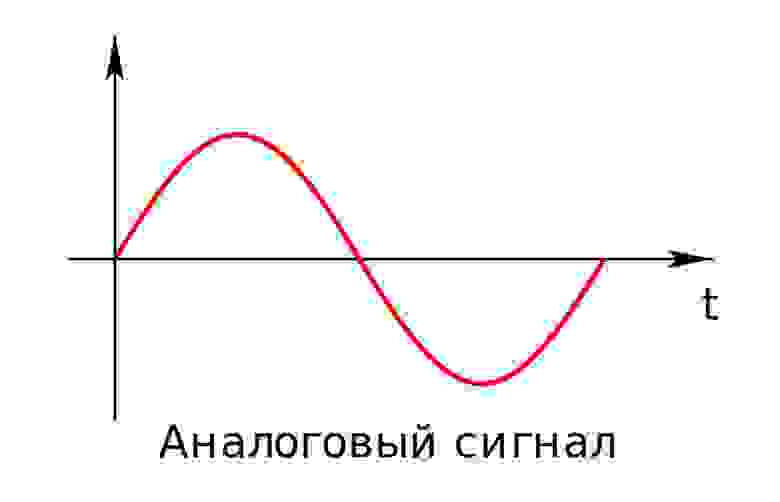
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).

рис. 1

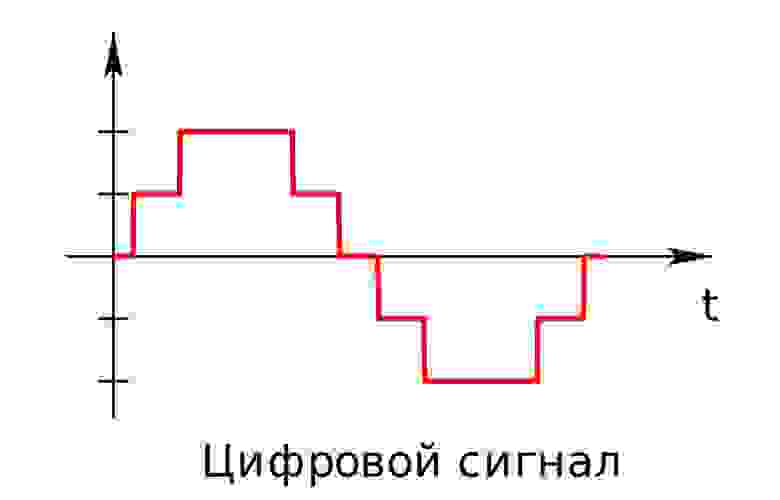
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).

рис. 2

Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.

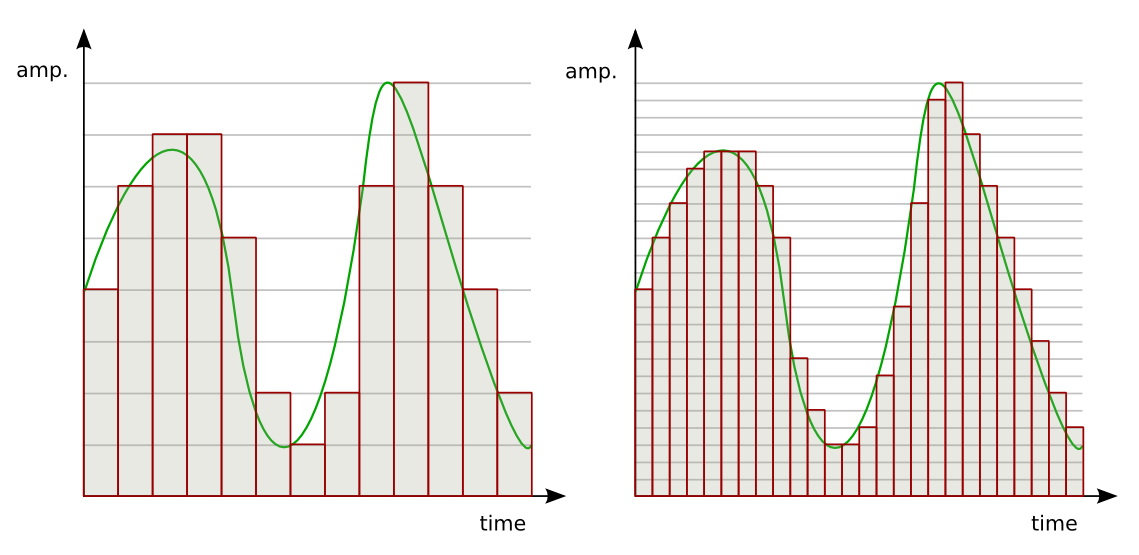
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).

рис. 3

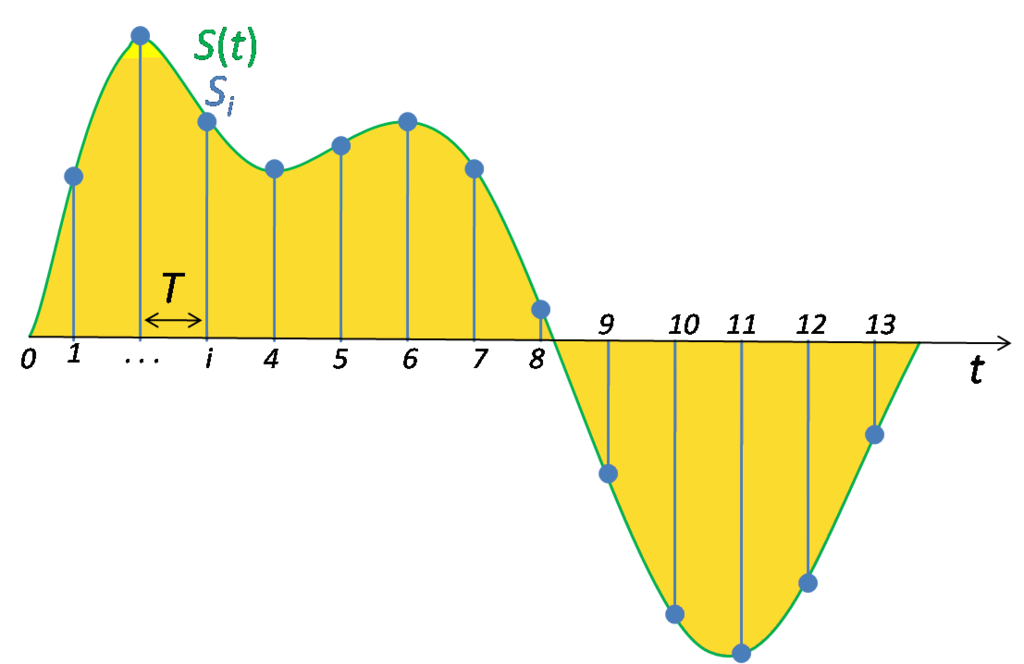
Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).

рис. 4

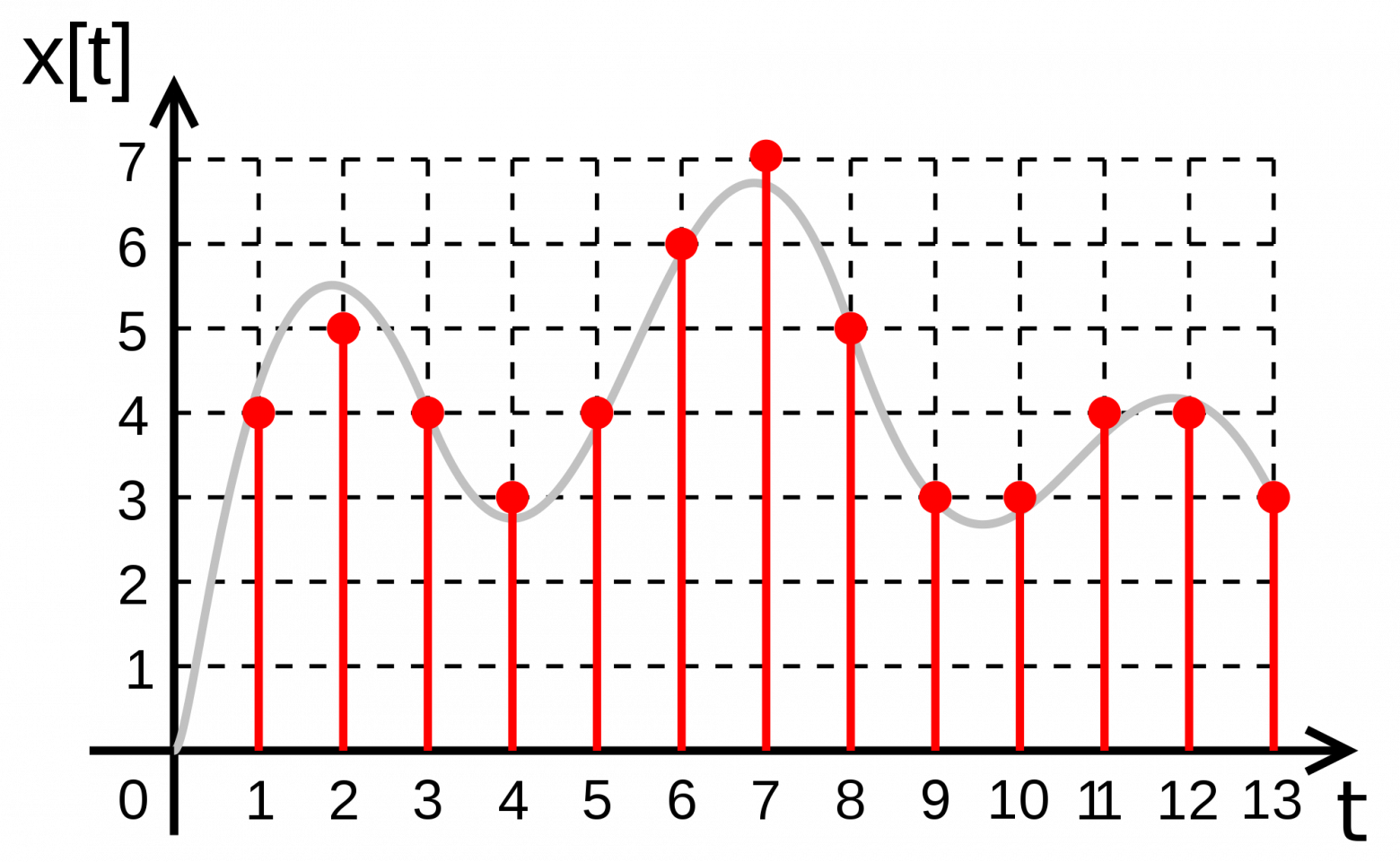
Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).

рис. 5

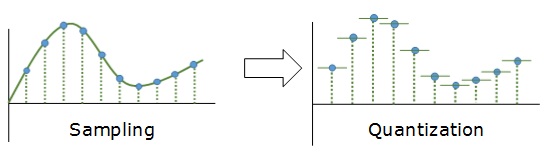
Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).

рис. 6

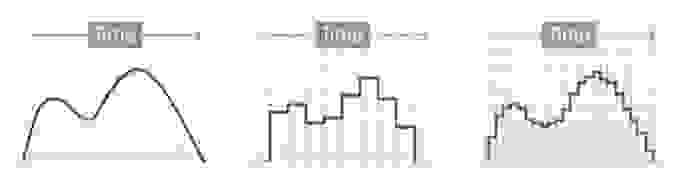
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)

рис. 7

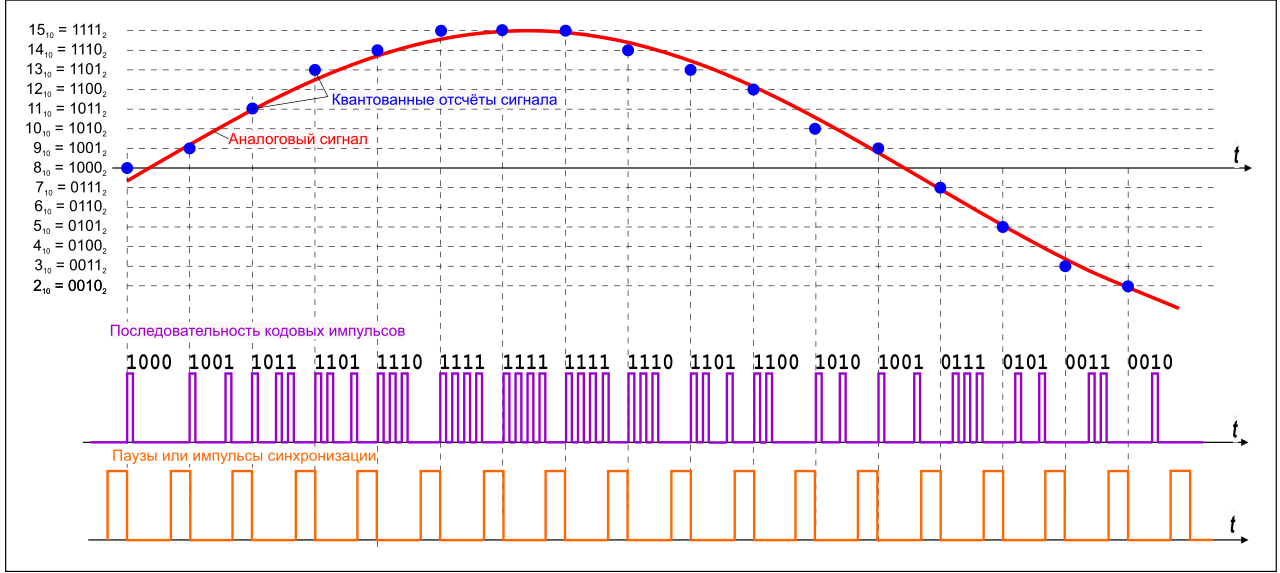
Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).

рис. 8.

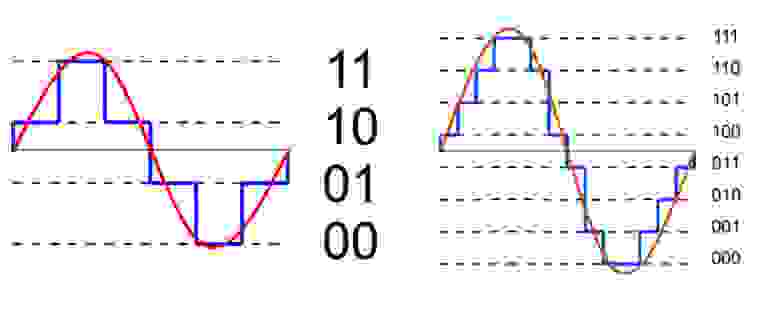
Данная формула позволяет вычислить количество уровней квантования:

Если N — количество уровней квантования,
n — разрядность, то

Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.

При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.

Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением $X$ и квантованным значением $X'$ ( $X-X'$ )

Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).

Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).

рис. 9

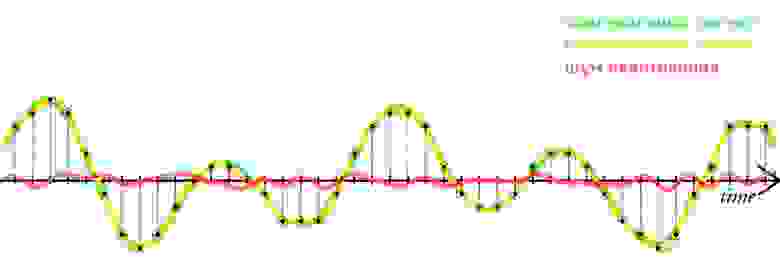
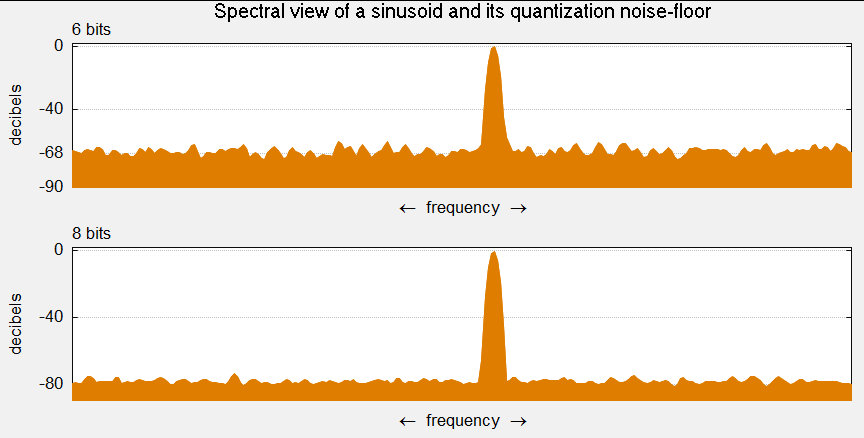
Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).

рис. 10. Интенсивность шумов при разрядности 6 бит и 8 бит

Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.

шум квантования

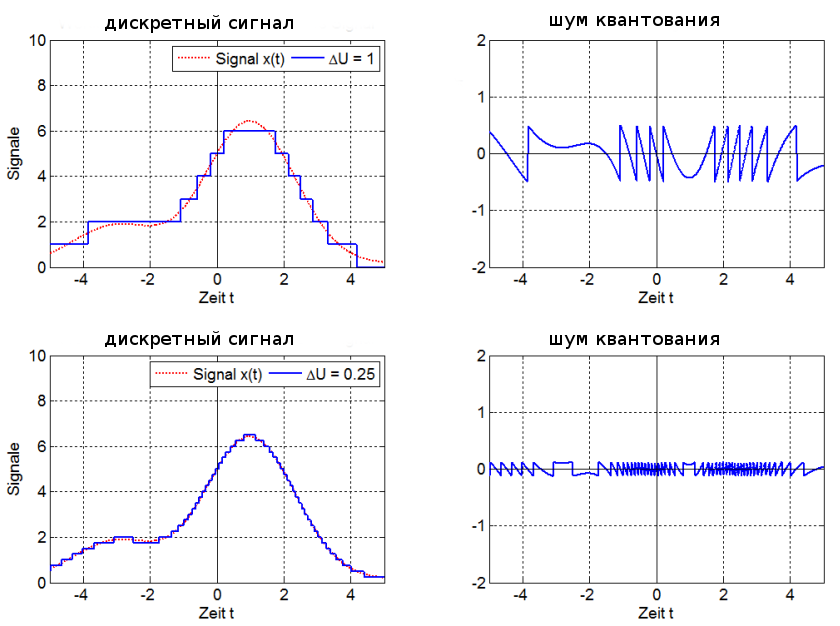
амплитуда сигнала при разрядности 1 бит (сверху) и 4 бит

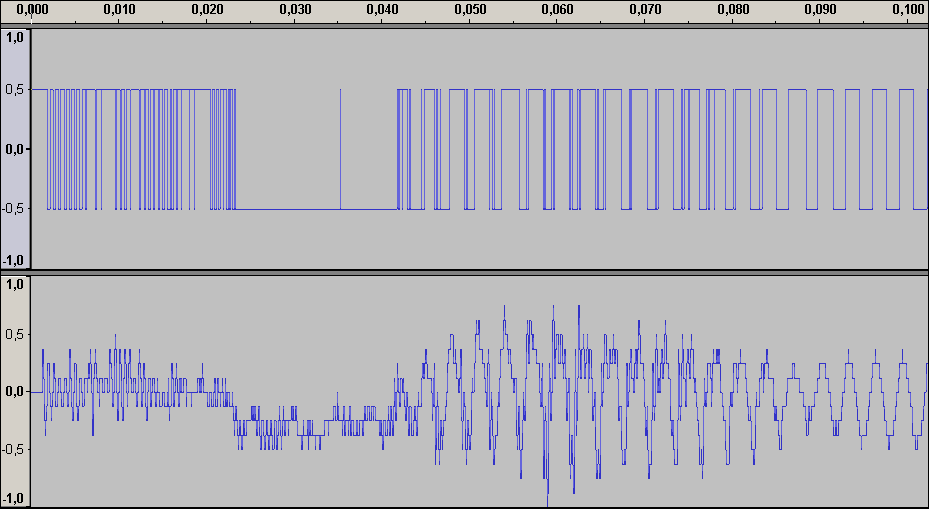
Аудиопример 1: 8bit/44.1kHz, ~50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.

Аудиопример 1

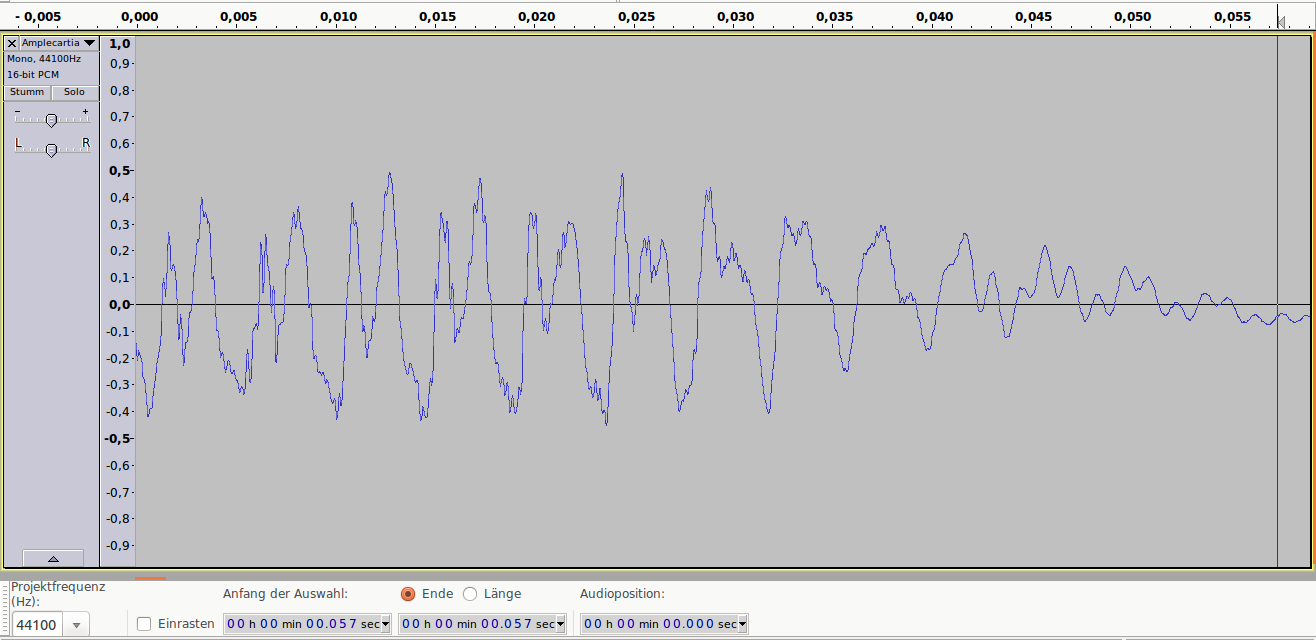
Аудиопример 2: 4bit/48kHz, ~25dB SNR

Аудиопример 2

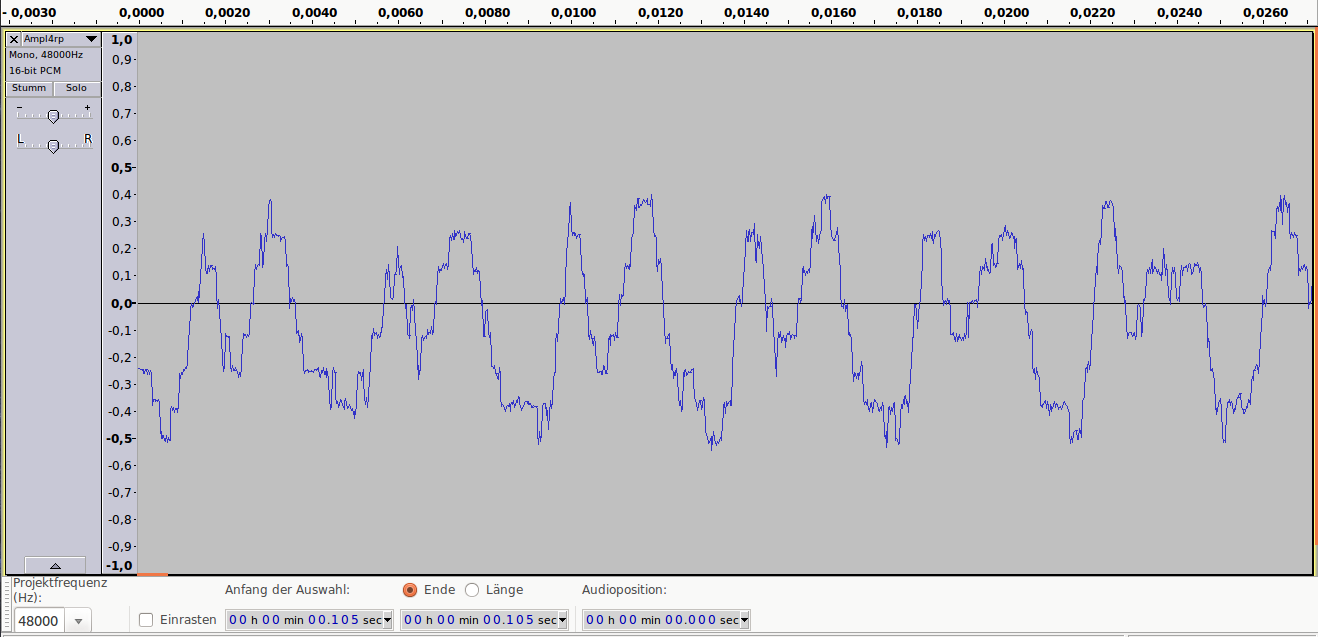
Аудиопример 3: 1bit/48kHz, ~8dB SNR

Аудиопример 3

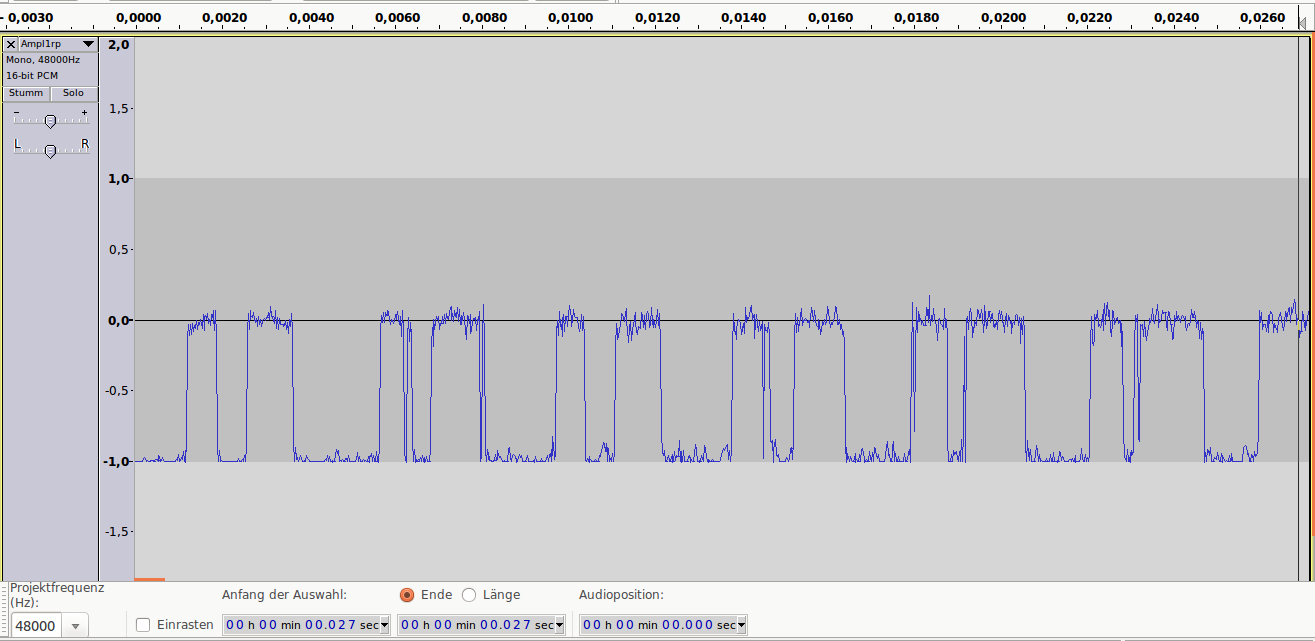
Теперь о дискретизации.

Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то
$F=1/T$

Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).

Теорема Котельникова гласит:

Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.

Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.

Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?

Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.

Алиасинг

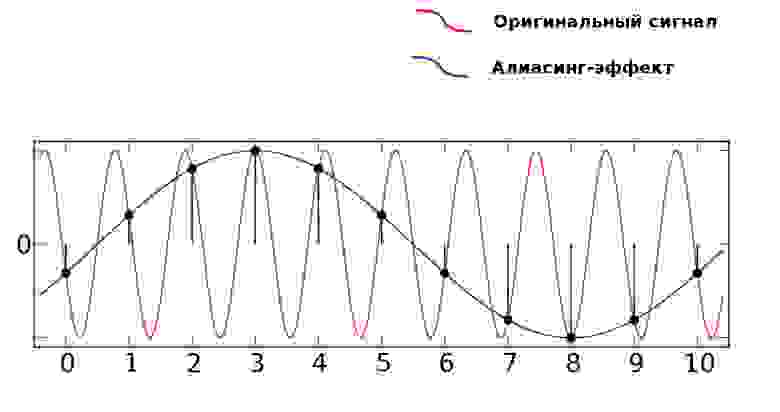
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.

Аудиопример 4: Линейно возрастающая частота от ~100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.

Спектральный анализ

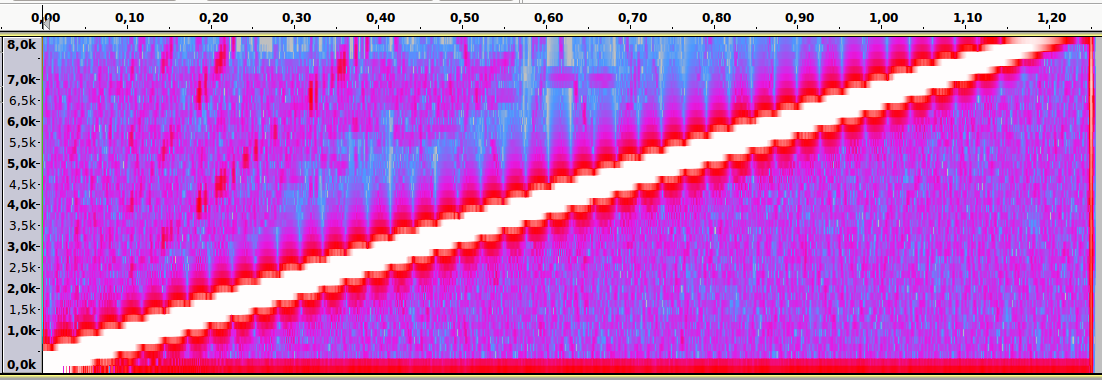
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг

Спектральный анализ

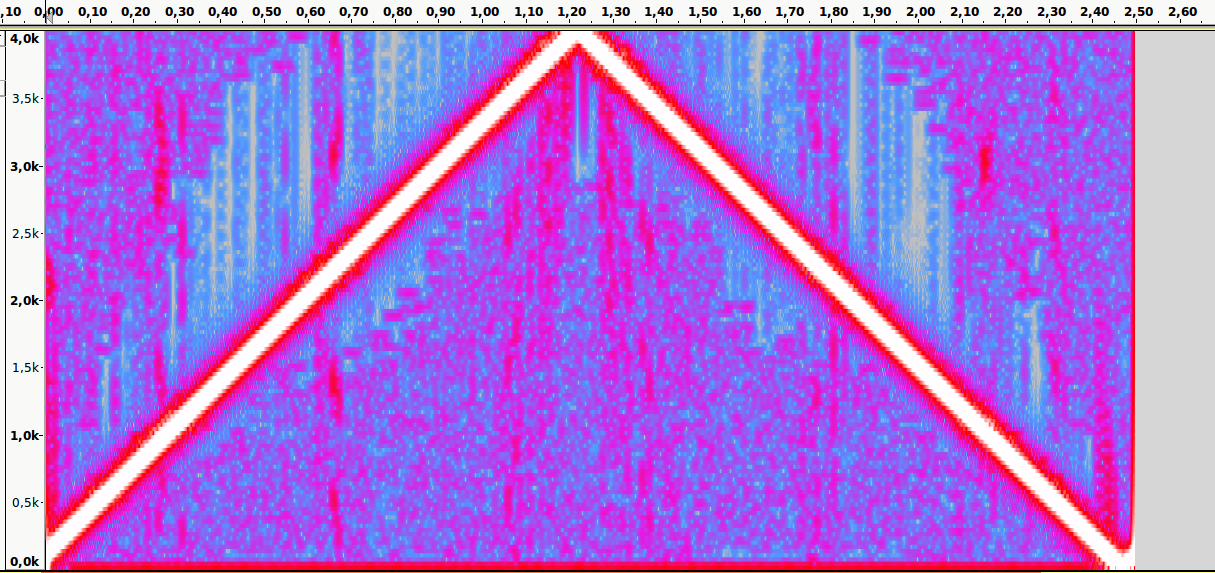
Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.

Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.

Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):

Битрейт = Частота дискретизации * Разрядность * Количество каналов

Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s

При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.

При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.

Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.

При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.

ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.

Существуют 3 метода хранения цифрового аудиоматериала:

Несжатые («сырые») данные
Данные, сжатые без потерь
Данные, сжатые с потерями

Несжатый (RAW) формат данных

содержит просто последовательность бинарных значений.
Именно в таком формате хранится аудиоматериал в Аудио-CD. Несжатый аудиофайл можно открыть, например, в программе Audacity. Они имеют расширение .raw, .pcm, .sam, или же вообще не имеют расширения. RAW не содержит заголовка файла (метаданных).

Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.

Аудиоформаты с сжатием без потерь

Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.

Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.

Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).

рис. 11

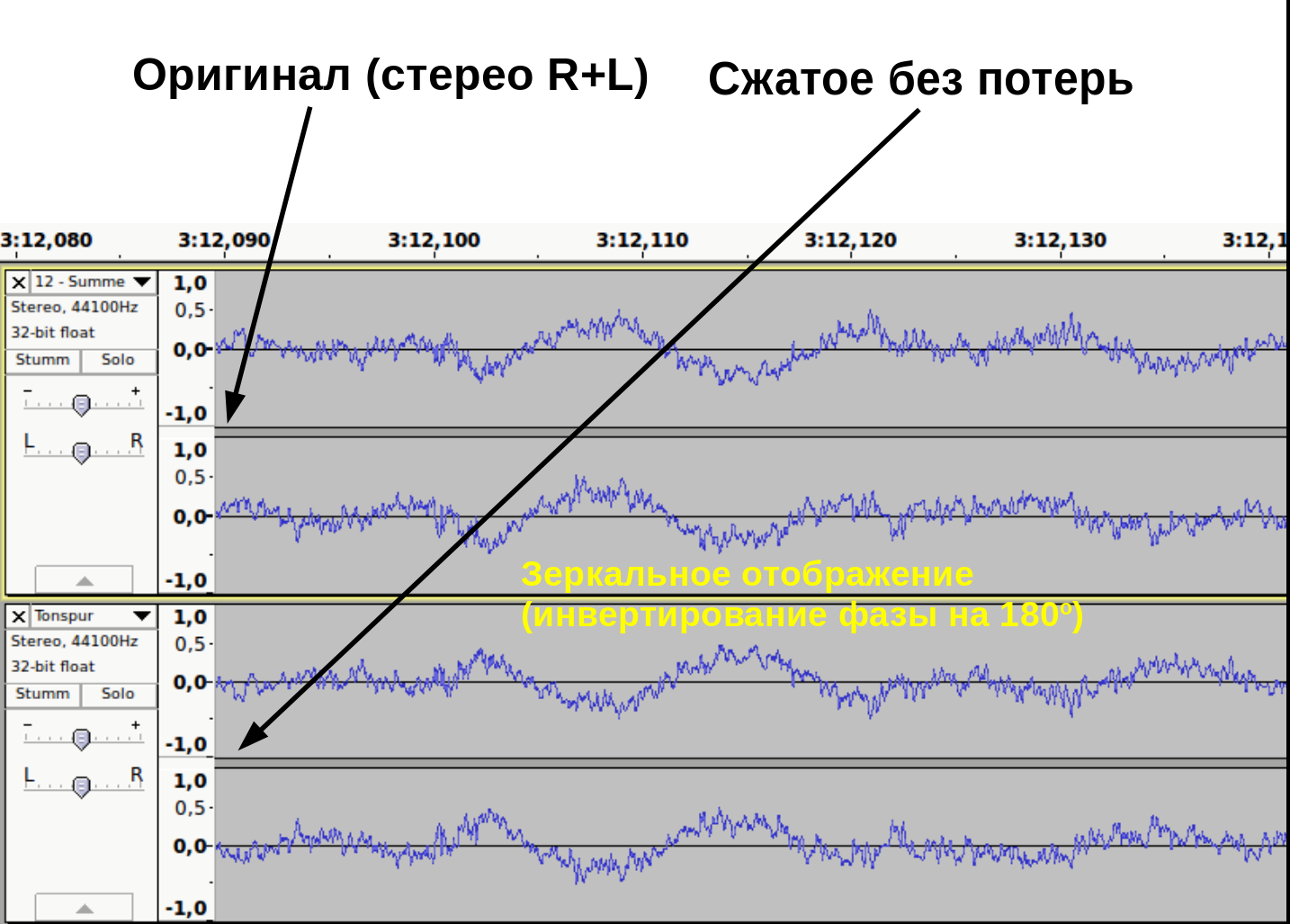
Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…

При сжатии с потерями

акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».

Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.

Этим и пользуется кодек: 2kHz-звук можно убрать.

Спектральный анализ кодека mp3 с разными уровнями компрессии

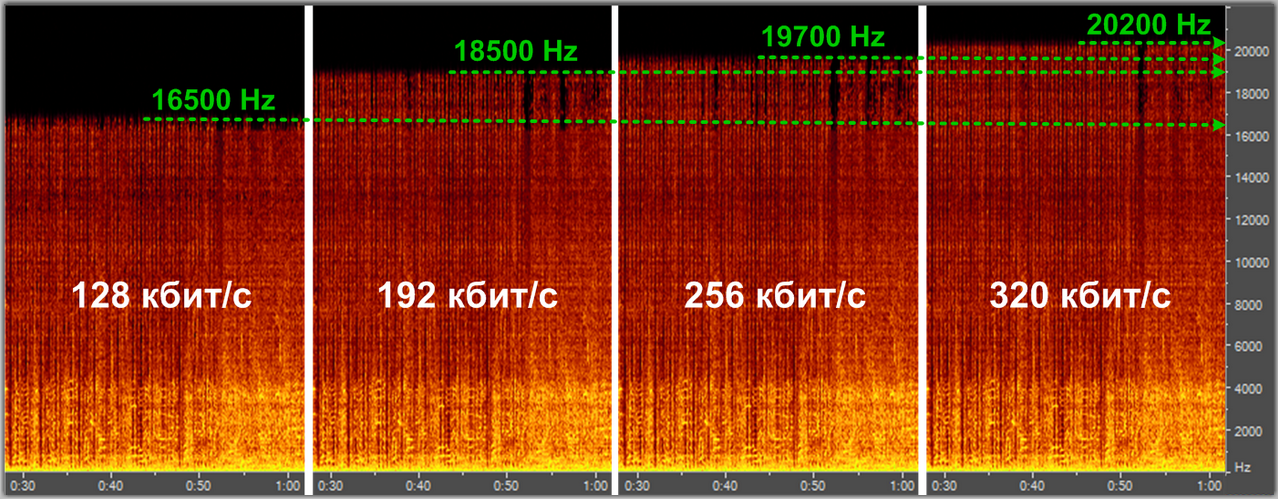
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…

Спасибо за внимание.

UPD:
Если по каким-либо причинам аудиофайлы не загружаются, можете их скачать здесь: cloud.mail.ru/public/HbzU/YEsT34i4c

Источник

Sensors

Andrea Colagrossi, … Matteo Battilana, in Modern Spacecraft Guidance, Navigation, and Control, 2023

Quantization errors

Quantization error is a systematic error resulting from the difference between the continuous input value and its quantized output, and it is like round-off and truncation errors. This error is intrinsically associated with the AD conversion that maps the input values from a continuous set to the output values in a countable set, often with a finite number of elements. The quantization error is linked to the resolution of the sensor. Namely, a high-resolution sensor has a small quantization error. Indeed, the maximum quantization error is smaller than the resolution interval of the output, which is associated to the least significant bit representing the smallest variation that can be represented digitally:

LSB=FSR2NBIT

where FSR is the full-scale range of the sensor, and NBIT is the number of bits (i.e., the resolution) used in the AD converter to represent the sensor’s output. Quantization errors are typically not corrected, and the discrete values of the output are directly elaborated by the GNC system, which is designed to operate on digital values.

Fig. 6.9 shows a convenient model block to simulate quantization errors.

Figure 6.9. Quantization error model.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780323909167000068

Digital Filters

Marcio G. Siqueira, Paulo S.R. Diniz, in The Electrical Engineering Handbook, 2005

2.11 Quantization in Digital Filters

Quantization errors in digital filters can be classified as:

•: Round-off errors derived from internal signals that are quantized before or after more down additions;
•: Deviations in the filter response due to finite word length representation of multiplier coefficients; and
•: Errors due to representation of the input signal with a set of discrete levels.

A general, digital filter structure with quantizers before delay elements can be represented as in Figure 2.23, with the quantizers implementing rounding for the granular quantization and saturation arithmetic for the overflow nonlinearity.

FIGURE 2.23. Digital Filter Including Quantizers at the Delay Inputs

The criterion to choose a digital filter structure for a given application entails evaluating known structures with respect to the effects of finite word length arithmetic and choosing the most suitable one.

2.11.1 Coefficient Quantization

Approximations are known to generate digital filter coefficients with high accuracy. After coefficient quantization, the frequency response of the realized digital filter will deviate from the ideal response and eventually fail to meet the prescribed specifications. Because the sensitivity of the filter response to coefficient quantization varies with the structure, the development of low-sensitivity digital filter realizations has raised significant interest (Antoniou, 1993; Diniz et al., 2002).

A common procedure is to design the digital filter with infinite coefficient word length satisfying tighter specifications than required, to quantize the coefficients, and to check if the prescribed specifications are still met.

2.11.2 Quantization Noise

In fixed-point arithmetic, a number with a modulus less than one can be represented as follows:

(2.84)x=b0b1b2b3…bb,

where b₀ is the sign bit and where b₁b₂b₃ … b_b represent the modulus using a binary code. For digital filtering, the most widely used binary code is the two’s complement representation, where for positive numbers b₀ = 0 and for negative numbers b₀ = 1. The fractionary part of the number, called x₂ here, is represented as:

(2.85)x2={xif b0=0.2−|x|if b0=1.

The discussion here concentrates in the fixed-point implementation.

A finite word length multiplier can be modeled in terms of an ideal multiplier followed by a single noise source e(n) as shown in Figure 2.24.

FIGURE 2.24. Model for the Noise Generated after a Multiplication

For product quantization performed by rounding and for signal levels throughout the filter much larger than the quantization step q = 2^−b, it can be shown that the power spectral density of the noise source e_i(n) is given by:

(2.86)Pei(z)=q212=2−2b12.

In this case, e_i(n) represents a zero mean white noise process. We can consider that in practice, e_i(n) and e_k(n + l) are statistically independent for any value of n or l (for i ≠ k). As a result, the contributions of different noise sources can be taken into consideration separately by using the principle of superposition.

The power spectral density of the output noise, in a fixed-point digital-filter implementation, is given by:

(2.87)Py(z)=σe2Σi=1KGi(z)Gi(z−1),

where Pei(ejw)=σe2, for all i, and each G_i(z) is a transfer function from multiplier output (g_i(n)) to the output of the filter as shown in Figure 2.25. The word length, including sign, is b + 1 bits, and K is the number of multipliers of the filter.

FIGURE 2.25. Digital Filter Including Scaling and Noise Transfer Functions.

2.11.3 Overflow Limit Cycles

Overflow nonlinearities influence the most significant bits of the signal and cause severe distortion. An overflow can give rise to self-sustained, high-amplitude oscillations known as overflow limit cycles. Digital filters, which are free of zero-input limit cycles, are also free of overflow oscillations if the overflow nonlinearities are implemented with saturation arithmetic, that is, by replacing the number in overflow by a number with the same sign and with maximum magnitude that fits the available wordlength.

When there is an input signal applied to a digital filter, overflow might occur. As a result, input signal scaling is required to reduce the probability of overflow to an acceptable level. Ideally, signal scaling should be applied to ensure that the probability of overflow is the same at each internal node of the digital filter. This way, the signal-to-noise ratio is maximized in fixed-point implementations.

In two’s complement arithmetic, the addition of more than two numbers will be correct independently of the order in which they are added even if overflow occurs in a partial summation as long as the overall sum is within the available range to represent the numbers. As a result, a simplified scaling technique can be used where only the multiplier inputs require scaling. To perform scaling, a multiplier is used at the input of the filter section as illustrated in Figure 2.25.

It is possible to show that the signal at the multiplier input is given by:

(2.88)xi(n)=12πj∮cXi(z)zn−1dz=12π∫02πFi(ejω)X(ejω)ejωndω,

where c is the convergence region common to F_i(z) and X(z).

The constant λ is usually calculated by using L_p norm of the transfer function from the filter input to the multiplier input F_i(z), depending on the known properties of the input signal. The L_p norm of F_i(z) is defined as:

(2.89)‖Fi(ejω)‖p=[12π∫02π|Fi(ejω)|pdω]1p,

for each p ≥ 1, such that ∫02π|Fi(ejω)|pdω≤∞. In general, the following inequality is valid:

(2.90)|xi(n)| ≤ ‖Fi‖p‖X‖q, (1p+1q=1),

for p, q = 1, 2 and ∞.

The scaling guarantees that the magnitudes of multiplier inputs are bounded by a number M_max when |x(n)| ≤ M_max. Then, to ensure that all multiplier inputs are bounded by M_max we must choose λ as follows:

(2.91)λ=1Max{‖F1‖p,…,‖F1‖p,…, ‖FK‖p},

which means that:

(2.92)‖F′i(ejω)‖p≤1, for‖X(ejω)‖q ≤ Mmax.

The K is the number of multipliers in the filter.

The norm p is usually chosen to be infinity or 2. The L_∞ norm is used for input signals that have some dominating frequency component, whereas the L₂ norm is more suitable for a random input signal. Scaling coefficients can be implemented by simple shift operations provided they satisfy the overflow constraints.

In case of modular realizations, such as cascade or parallel realizations of digital filters, optimum scaling is accomplished by applying one scaling multiplier per section.

As an illustration, we present the equation to compute the scaling factor for the cascade realization with direct-form second-order sections:

(2.93)λi=1‖∏j=1i−1Hj(z)Fi(z)‖p,

where:

Fi(z)=1z2+m1iz+m2i.

The noise power spectral density is computed as:

(2.94)Py(z)=σe2[3+3λ12∏i=1mHi(z)Hi(z−1)+5Σj=2m1λj2∏i=jmHi(z)Hi(z−1)],

whereas the output noise variance is given by:

(2.95)σo2=σe2[3+3λ12||∏i=1mHi(ejω)||22+5Σj=2m1λj2||∏i=jmHi(ejω)||22].

As a design rule, the pairing of poles and zeros is performed as explained here: poles closer to the unit circle pair with closer zeros to themselves, such that ||H_i(z)||_p is minimized for p = 2 or p = ∞.

For ordering, we define the following:

(2.96)Pi=| |Hi(z)| |∞| |Hi(z)| |2.

For L₂ scaling, we order the section such that P_i is decreasing. For L_∞ scaling, P_i should be increasing.

2.11.4 Granularity Limit Cycles

The quantization noise signals become highly correlated from sample to sample and from source to source when signal levels in a digital filter become constant or very low, at least for short periods of time. This correlation can cause autonomous oscillations called granularity limit cycles.

In recursive digital filters implemented with rounding, magnitude truncation,⁷² and other types of quantization, limitcycles oscillations might occur.

In many applications, the presence of limit cycles can be harmful. Therefore, it is desirable to eliminate limit cycles or to keep their amplitude bounds low.

If magnitude truncation is used to quantize particular signals in some filter structures, it can be shown that it is possible to eliminate zero-input limit cycles. As a consequence, these digital filters are free of overflow limit cycles when overflow nonlinearities, such as saturation arithmetic, are used.

In general, the referred methodology can be applied to the following class of structures:

•: State-space structures: Cascade and parallel realization of second-order state-space structures includes design constraints to control nonlinear oscillations (Diniz and Antoniou, 1986).
•: Wave digital filters: These filters emulate doubly terminated lossless filters and have inherent stability under linear conditions as well as in the nonlinear case where the signals are subjected to quantization (Fettweis, 1986).
•: Lattice realization: Modular structures allowing easy limit cycles elimination (Gray and Markel, 1975).

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780121709600500621

Biomedical signals and systems

Sri Krishnan, in Biomedical Signal Analysis for Connected Healthcare, 2021

2.2.1 Noise power

The quantization error (e) or noise tends to have a random behavior, and they could be mathematically represented using statistical variables. Power of a random variable with a probability density function of p(e) could be obtained by computing the second-order statistics of variance, and it is denoted by

σ2=∫−q/2q/2e2p(e)de

A good assumption for p(e) is a uniform probability density function which will have a value of 1/q over the range of −q/2 to q/2.

=∫−q/2q/2e2·1qde=q212

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128130865000049

Measurement of high voltages

E. Kuffel, … J. Kuffel, in High Voltage Engineering Fundamentals (Second Edition), 2000

Static errors

The quantization error is present because the analogue value of each sample is transformed into a digital word. This A-to-D conversion entails a quantization of the recorder’s measuring range into a number of bands or code bins, each represented by its central value which corresponds to a particular digital code or level. The number of bands is given by 2^N, where N is the resolution of the A-to-D converter. The digital output to analogue input relationship of an ideal digitizer is shown diagrammatically in Fig. 3.49. For any input in the range (iΔV_av – 0.5 * ΔV_av to iΔV_av + 0.5 * ΔV_av), where iΔV_av is the voltage corresponding to the width of each code bin, or one least significant bit (LSB), and iΔV_av is the centre voltage corresponding to the i th code, an ideal digitizer will return a value of I_i. Therefore, the response of an ideal digitizer to a slowly increasing linear ramp would be a stairway such as that shown in Fig. 3.50. A quick study of these figures reveals the character of the quantization error associated with the ideal A-to-D conversion process. The maximum error possible is equivalent to a voltage corresponding to ±(½) of an LSB. For an ideal digital recorder, this quantization would be the only source of error in the recorded samples. For a real digital recorder, this error sets the absolute upper limit on the accuracy of the readings. In the case of an 8-bit machine, this upper limit would be 0.39 per cent of the recorder’s full-scale deflection. The corresponding maximum accuracy (lowest uncertainty) of a 10-bit recorder is 0.10 per cent of its full-scale deflection.

Figure 3.49. Analogue input to digital output relation of an ideal A/D converter

Figure 3.50. Response of an ideal A/D converter to a slowly rising ramp

The error caused by discrete time sampling is most easily demonstrated with reference to the recording of sinusoidal signals. As an example we can look at the discrete time sampling error introduced in the measurement of a single cycle of a pure sine wave of frequency f, which is sampled at a rate of four times its frequency. When the sinusoid and the sampling clock are in phase, as shown in Fig. 3.51, a sample will fall on the peak value of both positive and negative half-cycles. The next closest samples will lie at π/2 radians from the peaks. As the phase of the clock is advanced relative to the input sinusoid the sample points which used to lie at the peak values will move to lower amplitude values giving an error (Δ) in the measurement of the amplitude (A) of

Figure 3.51. Sample points with sinusoid and sampling clock in phase. (Error in peak amplitude = 0)

Δ = A(1 − cos ϕ)

where ϕ is the phase shift in the sample points. This error will increase until ϕ – π/4 (Fig. 3.52). For ϕ > π/4 the point behind the peak value will now be closer to the peak and the error will decrease for a ϕ in the range of π/4 to π/2. The maximum per unit value of the discrete time sampling error is given by eqn 3.93,

Figure 3.52. Sample points with sampling clock phase advanced to π/4 with respect to the sinusoid. Error in peak amplitude (Δ) is at a maximum

(3.93)Δmax=I−cos(πfts)

where t_s is the recorder’s sampling interval and f the sinewave frequency.

The maximum errors obtained through quantization and sampling when recording a sinusoidal waveform are shown in Fig. 3.53. The plotted quantities were calculated for an 8-bit 200-MHz digitizer.

Figure 3.53. Sampling and quantization errors of an ideal recorder

In a real digital recorder, an additional two categories of errors are introduced. The first includes the instrument’s systematic errors. These are generally due to the digitizer’s analogue input circuitry, and are present to some degree in all recording instruments. They include such errors as gain drift, linearity errors, offset errors, etc. They can be compensated by regular calibration without any net loss in accuracy. The second category contains the digitizer’s dynamic errors. These become important when recording high-frequency or fast transient signals. The dynamic errors are often random in nature, and cannot be dealt with as simply as their systematic counterparts and are discussed below.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780750636346500046

Remaining useful life prediction

Yaguo Lei, in Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery, 2017

6.3.4.3 RUL Prediction

The constructed indicator WMQE is further input into the RUL prediction module. In this module, a PF-based prediction algorithm is utilized to predict RUL of the rotating machinery whose degradation processes are described using a variant of Paris–Erdogan model. The Paris–Erdogan model is formulated as

(6.96)dxdt=c(Δδ)γ, Δδ=mx

where x represents the semicrack length, t is the number of stress cycles (i.e., the fatigue life), c, γ, and m are material constants which are determined by tests, and Δδ is amplitude of stress intensity factor roughly proportional to the square root of x.

It is seen from Eq. (6.96) that there are several model parameters in the Paris–Erdogan model, that is, c, γ, and m, which are difficult to measure during the operation process of the rotating machinery. For convenient application, the Paris–Erdogan model is transformed into the following format with α=cmγ and β = γ/2.

(6.97)dxdt=αxβ.

Then, the above function is rewritten into the following state space model.

(6.98)xk=xk−1+αk−1xk−1βΔtkαk=αk−1zk=xk+νk,

where α_k−1 is a random variable following a normal distribution of Nμα,σα2, β is a constant parameter, Δtk=tk−tk−1, z_k is the measured WMQE value at t_k and ν_k is the measurement noise following the normal distribution of N0,σν2. With the transformation of the Paris–Erdogan model, the model parameters are more convenient to estimate according to the measurements. In addition, the state space model inherits the superiority of the Paris–Erdogan model in describing the general degradation processes. Therefore, it is supposed to be a good model for a general degradation process.

After the transformation, the unknown model parameters are changed to be Θ=μα,σα2,β,σν2′, where (·)′ denotes the vector transposition. Then, the measured WMQE values constructed from vibration signals are input into the model, and the model parameters are initialized using MLE. It is assumed that there are a series of measurements z0:M=z0,…,zM′ at ordered times t₀,…,t_M. According to Eq. (6.98), z_k is formulated as follows:

(6.99)zk=xk−1+αkxk−1βΔtk+νk.

The degradation state x_k−1 has the following relationship with the measurement z_k−1.

(6.100)xk−1=zk−1−νk−1.

The degradation state x_k−1 is hard to be acquired in real applications. If the measurement noise ν_k−1 is small enough compared with the measurement itself, it is negligible and x_k−1 is approximated by z_k−1. Let T=z0βΔt1,…,zM−1βΔtM′. z1:M=z1,…,zM′ is multivariate normally distributed, which is denoted as follows:

(6.101)z1:M∼Nz0:M−1+μαT,σα2TT′+σν2IM,

where I_M is an identity matrix of order M.

Let Δz1:M=z1−z0,…,zM−zM−1′, and the log-likelihood function of the unknown parameters based on the measurements is expressed as

(6.102)ℓΘ|z0:M=−M2ln2π−12lnσα2TT′+σν2IM −12Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT =−M2ln2π−M2lnσα2−12lnTT′+σ˜ν2IM −12σα2Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT,

with σ~ν2=σν2/σα2. The first partial derivatives of ℓΘ|z0:M with respect to μ_α and σα2 are calculated and formulated with

(6.103)∂ℓΘ|z0:M∂μα=1σα2T′TT′+σ~ν2IM-1Δz1:M−μαT,

(6.104)∂ℓΘ|z0:M∂σα2=−M2σα2+12σα4Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαT.

Let ∂ℓΘ|z0:M/∂μα=0 and ∂ℓΘ|z0:M/∂σα2=0. The MLE results of μ_α and σα2 are

(6.105)μα=T′TT′+σ~ν2IM−1Δz1:MT′TT′+σ~ν2IM−1T,

(6.106)σα2=Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαTM.

With Eqs. (6.105) and (6.106) substituted into Eq. (6.102), the log-likelihood function is reduced into a two-variable function about β and σ~ν2, which is denoted by

(6.107)ℓΘ|z0:M=−M2ln2π−M2lnσα2−12lnTT′+σ~ν2IM−M2.

The MLE values of β and σ~ν2 are obtained by maximizing the log-likelihood function (6.107) through two-dimensional optimizing. Then the MLE values of β and σ~ν2 are substituted into Eqs. (6.105) and (6.106), and the MLE values of μ_α and σα2 are acquired. The value of σν2 is calculated with σ~ν2 multiplied by σα2. Finally, all of the unknown parameters Θ=μα,σα2,β,σν2′ are initialized.

After parameter initialization, the model parameters are further updated and the RUL is predicted using a PF-based prediction algorithm. Based on the initialized parameters, a series of initial particles y0nn=1:Ns are sampled from the initial PDF of the system state p(y0n|Θ0)∼N(y0,Q0) with

(6.108)y0=x0μα and Q0=000σα2.

Ns is the number of particles and the weight of each particle is set to be 1/Ns. Then new particles ykni=1:Ns are obtained following

(6.109)ykn=xknμαn=xk−1n+μαnxk−1nβΔtkμαn.

When the new measurement z_k at t_k is available, each particle weight is updated and normalized by

(6.110)wkn=wk−1npzk|ykn, w~kn=wkn∑n=1Nswkn,

where

(6.111)pzk|ykn=12πσνexp−12zk−xknσν2.

The particles are resampled according to the particle weights and their weights are reset to be 1/Ns. After that, the RUL is predicted based on the resampled particles. The RUL l_k at t_k is defined as

(6.112)lk=inflk:xlk+tk≥λ|x1:k,

where λ is a prespecified failure threshold. Each particle is transmitted following the transition function of Eq. (6.98) from current state until the state value exceeds the failure threshold, and the RUL lknn=1:Ns predicted using each particle is acquired. Then the PDF of the RUL is approximated by

(6.113)plk|z0:k=∑n=1Nsw~knδlk−lkn.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128115343000068

Orbit and Attitude Sensors

Enrico Canuto, … Carlos Perez Montenegro, in Spacecraft Dynamics and Control, 2018

Exercise 1

Prove that the quantization error defined by Eq. (8.6) is bounded by |n˜y(i)|≤ρy/2 and under the random assumption has zero mean and variance equal to ρy2/12. □

A typical model of the random error d˜ in Eq. (8.4), which includes quantization errors, is the linear continuous-time stochastic state equation

(8.7)x˜˙(t)=A˜x˜+G˜w˜d˜(t)=C˜x˜+D˜w˜E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=S˜w2δ(τ)E{x˜(0)}=x˜0,E{(x˜(0)−x˜0)(x˜(0)−x˜0)T}=P˜0≥0E{(x˜(0)−x˜0)w˜T(0)}=0,

which is similar to the DT Eq. (4.159) of Section 4.8.1. Eq. (8.7) being continuous-time, the eigenvalues of the state matrix A˜ are assumed to lie on the imaginary axis and when equal to zero may be multiple. The statistics in Eq. (8.7) assumes that w˜ is a zero-mean second-order stationary white noise with constant spectral density S˜w2, and impulsive covariance, where δ(τ) denotes a Dirac delta (see Sections 13.2.1 and 13.7.3Section 13.2.1Section 13.7.3). The initial state may be modeled as a random vector with mean value x˜0 and covariance matrix P˜0, but is uncorrelated from any simultaneous white noise as expressed by the last identity in Eq. (8.7). This uncorrelation has been already referred to as the causality constraint. In principle, Eq. (8.7) may be unobservable from the output d˜ and uncontrollable by the noise w˜, because the output d˜ may include polynomial and trigonometric components (deterministic signals) just driven by the initial state x˜0. For instance, a trigonometric component tuned to the angular frequency ω˜ corresponds to a second-order subsystem with eigenvalues ±jω˜. A first-order polynomial corresponds to a second-order subsystem with a pair of zero eigenvalues and a single eigenvector. The mixed case of stochastic processes and deterministic signals can be simplified by assuming that trigonometric and polynomial components are the free response of the equations driven by w˜, and that Eq. (8.7) is observable and controllable.

The simplest model of the class in Eq. (8.7), which is common to inertial sensors (accelerometers in Section 8.4 and gyroscopes in Section 8.5), is the scalar first-order random drift [32]:

(8.8)x˜˙(t)=w˜x,x˜(0)=x˜0d˜(t)=x˜+w˜dE{x˜(0)}=x˜0,var{x˜}=σ02,E{(x˜−x˜0)w˜T(0)}=0w˜=[w˜xw˜d],E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=[S˜wx200S˜wd2]δ(τ),

where, if [unit] denotes the unit of measurement of x˜, we find S˜wx2 in [(unit/s)2Hz−1] and S˜wd2 in [unit2Hz−1]. The initial state x˜0 accounts for a constant bias and is uncorrelated with any simultaneous noise; the scalar input noise w˜x and the output noise w˜d in Eq. (8.8) are uncorrelated with each other. The output process d˜ is nonstationary and the autocorrelation is given by

(8.9)R˜d(t,t+τ)=S˜wx2min(t,t+τ)+S˜wd2δ(τ).

Although x˜ is nonstationary, the spectral density S˜x2(f) can be defined through the AS equation x˜˙=−εx˜+w˜x, where ε > 0 must be sufficiently smaller than the cutoff frequency f₀ to be defined in the next paragraph. We can write the following identities:

(8.10)S˜d2(f)=S˜x2(f)+S˜wd2=S˜wx2(2πf)2+S˜wd2,f>ε2π=fεσ˜x2=limf→∞∫0fS˜x2νdν<∞,

where if, for f < ε, S˜x2(f) is bounded, also the variance σ˜x2 is bounded. The Bode plot of S˜d(f) is approximately flat for f>f0=2π−1S˜wx/S˜wd>fε and has a −20 dB/decade slope for f_ε < f < f₀. The first PSD in the first row of Eq. (8.10) is a first-order random walk, which is known, in the realm of inertial sensors, as the (long-term) bias instability of the sensor. The name is appropriate because it describes the long-term fluctuations—bounded because of ε—around the mean sensor bias x˜0. The square root of the second term S˜wd corresponds to the minimum-valued profile of the overall spectral density. Let us call it, as already anticipated, noise floor, although the name sometimes refers to the whole instrument noise (here referred to as the background noise). In the realm of inertial sensors, it is known as the velocity random walk in the case of linear accelerometers, the unit being [m/(s2Hz)], and the angular random walk (ARW) in the case of gyroscopes, the unit being[rad/(sHz)]. The name, which may cause same confusion, is justified by the fact that when either of the two measurements (linear acceleration and angular rate) is time integrated for generating either velocity or attitude measurements, the integrated noise floor becomes a random walk. By restricting to gyroscopes, the ARW unit [rad/(sHz)] is usually simplified to [rad/s], de facto to the non-SI unit [degree/hour]. Indeed, the simplified unit is at the same time the unit of S˜wd and the unit of the root mean square (RMS) σ¯w(t,Δt) of the random walk increment w¯d(t,Δt)=∫tt+Δtw˜d(τ)dτ, namely:

(8.11)σ¯w(t,Δt)=E{1Δt(∫tt+Δtw˜d(τ)dτ)2}=S˜wd.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780081007006000088

Sampling Theory

Luis Chaparro, in Signals and Systems Using MATLAB (Second Edition), 2015

8.3.2 Quantization and Coding

Amplitude discretization of the sampled signal x_s(t) is accomplished by a quantizer consisting of a number of fixed amplitude levels against which the sample amplitudes {x(nT_s)} are compared. The output of the quantizer is one of the fixed amplitude levels that best represents {x(nT_s)} according to some approximation scheme. The quantizer is a non-linear system.

Independent of how many levels or, equivalently, of how many bits are allocated to represent each level of the quantizer, in general there is a possible error in the representation of each sample. This is called the quantization error. To illustrate this, consider the 2-bit or four-level quantizer shown in Figure 8.12. The input of the quantizer are the samples {x(nT_s)}, which are compared with the values in the bins [-2Δ,-Δ],[-Δ,0],[0,Δ], and [Δ,2Δ]. Depending on which of these bins the sample falls in it is replaced by the corresponding levels -2Δ,-Δ,0, or Δ, respectively. The value of the quantization step Δ for the four-level quantizer is

Figure 8.12. Four-level quantizer and coder.

(8.23)Δ=dynamic range of signal2b=2max|x(t)|22

where b = 2 is number of bits of the code assigned to each level. The bits assigned to each of the levels uniquely represents the different levels [-2Δ,-Δ,0,Δ]. As to how to approximate the given sample to one of these levels, it can be done by rounding or by truncating. The quantizer shown in Figure 8.12 approximates by truncation, i.e., if the sample kΔ≤x(nTs)<(k+1)Δ, for k = −2, −1,0,1, then it is approximated by the level kΔ.

To see how quantization and coding are done, and how to obtain the quantization error, let the sampled signal be

x(nTs)=x(t)|t=nTS

The given four-level quantizer is such that if the sample x(nT_s) is such that

(8.24)kΔ≤x(nTs)<(k+1)Δ⇒xˆ(nTs)=kΔk=-2,-1,0,1

The sampled signal x(nT_s) is the input of the quantizer and the quantized signal xˆ(nTs) is its output. So that whenever

-2Δ≤x(nTs)<-Δ⇒xˆ(nTs)=-2Δ-Δ≤x(nTs)<0⇒xˆ(nTs)=-Δ0≤x(nTs)<Δ⇒xˆ(nTs)=0Δ≤x(nTs)<2Δ⇒xˆ(nTs)=Δ

To transform the quantized values into unique binary 2-bit values, one could use a code such as

xˆ(nTs)⇒binary code-2Δ10-Δ110Δ00Δ01

which assigns a unique 2 bit binary number to each of the 4 quantization levels. Notice that the first bit of this code can be considered a sign bit, “1” for negative levels and “0” for positive levels.

If we define the quantization error as

ε(nTs)=x(nTs)-xˆ(nTs)

and use the characterization of the quantizer given by Equation (8.24) as

xˆ(nTs)≤x(nTs)≤xˆ(nTs)+Δ

by subtracting xˆ(nTs) from each of the terms gives that the quantization error is bounded as follows

(8.25)0≤ε(nTs)≤Δ

i.e., the quantization error for the four-level quantizer being considered is between 0 and Δ. This expression for the quantization error indicates that one way to decrease the quantization error is to make the quantization step Δsmaller. Increasing the number of bits of the A/D converter makes Δ smaller (see Equation (8.23) where the denominator is 2 raised to the number of bits) which in turn makes smaller the quantization error, and improves the quality of the A/D converter.

In practice, the quantization error is random and so it needs to be characterized probabilistically. This characterization becomes meaningful when the number of bits is large, and when the input signal is not a deterministic signal. Otherwise, the error is predictable and thus not random. Comparing the energy of the input signal to the energy of the error, by means of the so-called signal to noise ratio (SNR), it is possible to determine the number of bits that are needed in a quantizer to get a reasonable quantization error.

Example 8.5

Suppose we are trying to decide between an 8 and a 9 bit A/D converter for a certain application where the signals in this application are known to have frequencies that do not exceed 5 kHz. The dynamic range of the signals is 10 volts, so that the signal is bounded as −5 ≤ x(t) ≤ 5. Determine an appropriate sampling period and compare the percentage of error for the two A/Ds of interest.

Solution

The first consideration in choosing the A/D converter is the sampling period, so we need to get an A/D converter capable of sampling at f_s = 1/T_s > 2 f_max samples/second. Choosing f_s = 4 f_max = 20 k samples/second then T_s = 1/20 msec/sample or 50 microseconds/sample. Suppose then we look at the 8-bit A/D converter, the quantizer has 2⁸ = 256 levels so that the quantization step is Δ=10/256 volts and if we use a truncation quantizer the quantization error would be

0≤ε(nTs)≤10/256

If we find that objectionable we can then consider the 9-bit A/D converter, with a quantizer of 2⁹ = 512 levels and the quantization step Δ=10/512 or half that of the 8-bit A/D converter, and

0≤ε(nTs)≤10/512

So that by increasing one bit we cut the quantization error in half from the previous quantizer. Inputting a signal of constant amplitude 5 into the 9-bit A/D gives a quantization error of [(10/512)/5] × 100% = (100/256)% ≈ 0.4% in representing the input signal. For the 8-bit A/D it would correspond to 0.8% error. ▪

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123948120000085

Compression

StéphaneMallat , in A Wavelet Tour of Signal Processing (Third Edition), 2009

Weighted Quantization and Regions of Interest

Visual distortions introduced by quantization errors of wavelet coefficients depend on the scale 2^j. Errors at large scales are more visible than at fine scales [481]. This can be taken into account by quantizing the wavelet coefficients with intervals Δj=Δwj that depend on the scale 2^j. For R¯≤1 bit/pixel, w_j = 2^−j is appropriate for the three finest scales. The distortion in (10.34) shows that choosing such weights is equivalent to minimizing a weighted mean-square error.

Such a weighted quantization is implemented like in (10.35) by quantizing weighted wavelet coefficients f_B[m]/w_j with a uniform quantizer. The weights are inverted during the decoding process. JPEG-2000 supports a general weighting scheme that codes weighted coefficients w[m]f_B[m] where w[m] can be designed to emphasize some region of interest Ω ⊂ [0, 1]² in the image. The weights are set to w[m] = w > 1 for the wavelet coefficients fB[m]=〈f,ψj,p,q1〉 where the support of ψj,p,q1 intersects Ω. As a result, the wavelet coefficients inside Ω are given a higher priority during the coding stage, and the region Ω is coded first within the compressed stream. This provides a mechanism to more precisely code regions of interest in images—for example, a face in a crowd.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123743701000148

Signal and Image Representation in Combined Spaces

Zoran. Cvetković, Martin. Vetterli, in Wavelet Analysis and Its Applications, 1998

6.1 Two lemmas on frames of complex exponentials

Estimates of bounds on the quantization error in Subsection 4.3 are derived from the next two lemmas [5].

Lemma 1

Letejλnωbe a frame in L²[− σ, σ]. If M is any constant and {μ_n} is a sequence satisfying |μ_n − λ_n| ≤ M, for all n, then there is a number C = C(M, σ, {λ_n}) such that

(6.1.1)∑n|fμn|2∑n|fλn|2≤C

for every cr-bandlimited signal f(x).

Lemma 2

Letejλnωbe a frame in L²[− σ, σ], with bounds 0 < A ≤ B < ∞ and δ a given positive number. If a sequence { μ_n } satisfies | λ_n − μ_n \ < δ for all n, then for every σ-bandlimited signal f(x)

(6.1.2)A1−C2||f||2≤∑n|fμn|2≤B(1+C)2||f||2,

where

(6.1.3)C=BAeγδ−12

Remark 1

If δ in the statement of Lemma 2 is chosen small enough, so that C is less then 1, then ejμnω is also a frame in L²[− σ, σ]. Moreover, there exists some δ _1/4 ({λ_n},σ), such that whenever δ < δ _1/4 ({λ_n }, σ), ejμnω is a frame with frame bounds A/A and 9B/4.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1874608X98800125

Live HDR Video Broadcast Production

I.G. Olaizola, … J. Gorostegui, in High Dynamic Range Video, 2017

1.4.1 Banding

Banding effects are directly related to quantization errors. As the dynamic range increases, the quantization effects become more noticeable and banding artifacts arise. To avoid this, smaller quantization steps must be taken, but this requires a higher bitdepth (from 8 to 10 or 12 in order to have backwards compatibility with existing infrastructures, and ideally 14 or 16 bits) and nonlinear transform functions based on the HVS that minimize the observable banding effects. Nowadays, this is partially solved by the electro-optical transfer function (EOTF) and opto-electronic transfer function (OETF) mapping curves that will be introduced in a further section.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B978012809477800008X

Источник

Ошибки квантования

В реальных
устройствах цифровой обработки сигналов
необходимо учитывать
эффекты, обусловленные квантованием
входных сигналов
и конечной разрядностью всех регистров.
Источниками ошибок
в процессах обработки сигналов являются
округление (усечение)
результатов арифметических операций,
шум аналого-цифрового квантования
входных аналоговых сигналов, неточность
реализации характеристик цифровых
фильтров из-за округления их коэффициентов
(параметров). В дальнейшем с целью
упрощения анализа предполагается, что
вес источники ошибок независимы и не
коррелируют с входным сигналом (хотя
мы и рассмотрим явление предельных
циклов, обусловленных коррелированным
шумом округления).

Эффект квантования
приводят в конечном итоге к погрешностями выходных сигналах цифровых фильтров
(ЦФ), а в некоторыхслучаяхи к неустойчивым
режимам. Выходную ошибку ЦФ будем
рассчитыватькаксуперпозицию ошибок, обусловленных
каждым независимымисточником.

Квантование
чисел– нелинейная операция;m-разрядное
двоичное числоА
представляетсяb-разрядным
двоичнымчислом
B=F(A),
причем b
< m. В
результате квантования число А
представляется
с ошибкой

е
=B–А= F(А)
–А.

Шаг квантования
Q
=
2^–^b
определяется весом младшего
числовогоразряда.
При квантовании
используется усечение или округление.

Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
e_ус=
F_ус(А) –А.

Оценим величину
ошибки в предположении m
» b.
Для положительных чисел при любом
способе кодирования –2^–^b
<е_ус0. Для
отрицательных чисел при использовании
прямого и обратного кодов ошибка усечения
неотрицательна: 0е_ус< 2^–^b,
а в дополнительном коде эта ошибка
неположительна: 0е_ус> –2^–^b.
Таким образом, во всех случаях
абсолютное значение ошибки усечения
не превосходит шага квантования:maxe_ус
< 2^–^b
=Q.

Округление
m-разрядного
числаA
доb
разрядов (b «
m)b-й
разряд остается неизменным или
увеличивается на единицув
зависимости от соотношения (больше –
меньше) между отбрасываемой дробью
0,а_b+₁…а_т
и величиной
,
гдеа_i–i-й
разряд числаA;
i =
b+1,
…,m.
Округление можно практически выполнить
путемприбавления
единицы к (b+1)-му
разряду и усечения полученного числа
до b разрядов.
В таком случае ошибка округления е_oк
=
f_ок(А)–
А
при всех способах кодирования лежит в
пределах

–2^–⁽^b⁺¹⁾
<
е_o_к
< 2^–⁽^b⁺¹⁾
(1.11)

и, следовательно,
max<2^–^b
= Q/2.
(1.12)

В задачах ЦОС
ошибки квантования чисел рассматриваются
как стационарный
шумоподобный процесс с равномерным
распределением
вероятности по диапазону распределения
ошибок квантования.



(nT)

x(nT)

e(nT)

Рис. 3. Линейная модель квантования
сигналов:

(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);

x(nT) —квантованный
b-разрядный
цифровой сигнал;

e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.

Квантование
дискретных сигналов состоит в
представлении отсчета
(выборки сигнала) числамиx(nT),
содержащими b
числовых разрядов. Квантование сигналов,
как и квантование
чисел – нелинейная операция. Однако
при анализе процессов в ЦФ целесообразно
использовать линейную модель квантования
сигналов – рис. 3.

Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).

Вероятностные
оценки ошибок квантования основаны на
предположениях о том, что
последовательностье(пТ)являетсястационарным
случайным процессом с равномерным
распределением вероятности по
диапазону ошибок квантования ие(пТ)
не коррелирован
с f(nT).
Математическое
ожидание (среднее значение) _e
и дисперсия
ошибки квантованияе
определяются
по формулам:

=E(е)
=,

===E(е²)
–,

где р_е
— плотность вероятности ошибки. По
этим формуламвычисляются
математическое ожидание и дисперсия
для ошибок
округления и усечения:

В логарифмическоммасштабе

Лекция 2

В настоящее время во всём мире развивается цифровая форма передачи сигналов: цифровая телефония, цифровое кабельное телевидение, цифровые системы коммутации и системы передачи, цифровые сети связи. Качество цифровой связи значительно выше, чем аналоговой, так как цифровые сигналы гораздо более помехоустойчивы: нет накопления шумов, легко обрабатываются, цифровые сигналы можно «сжимать», что позволяет в одной полосе частот организовать больше каналов с высокой скоростью передачи и отличным качеством.

Цифровой сигнал – это последовательность импульсов. Общепринято импульсную последовательность представлять как чередование двух символов: 0 и 1. «Binary Digit» – «двоичная цифра». Отсюда и пошло понятие бит, то есть одна позиция в цифровом сигнале есть 1 бит; это может быть либо 0, либо 1. Восемь позиций в цифровом сигнале определяется понятием байт [1].

При передаче цифровых сигналов вводится понятие скорости передачи – это количество бит, передаваемых в единицу времени (в секунду).

Для передачи непрерывных сообщений цифровыми методами необходимо произвести преобразование этих сообщений в дискретные, которое осуществляется путём дискретизации непрерывных сигналов во времени и квантования их по уровню, и преобразования квантованных отсчётов в цифровой сигнал [6].

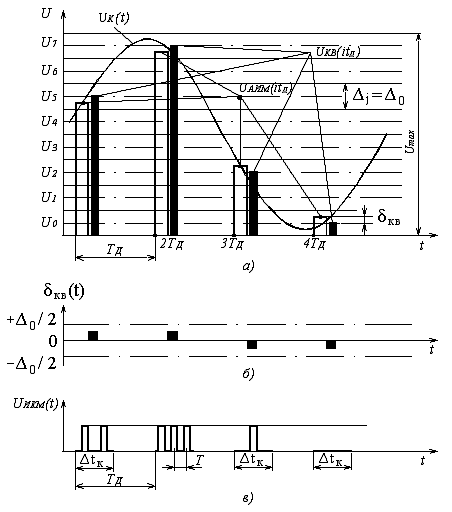
Дискретизация сигналов заключается в замене непрерывного сообщения u_к(t) последовательностью его отсчётов, то есть последовательностью импульсов, модулированных по амплитуде (смотри рисунок 5.1, а). Частота дискретизации F_д выбирается из условия (4.4.1). Полученный аналоговый АИМ сигнал u_АИМ(iT_д), где i = 1, 2, 3 …, приведённый на рисунке 5.1, а, затем подвергается операции квантования, которая состоит в замене отсчётов мгновенных значений сигнала u_АИМ(iT_д) дискретными значениями u₀, u₁, u₂ … u₇ разрешённых уровней u_кв(iT_д). В процессе квантования мгновенные значения АИМ сигнала уровней u_АИМ(iT_д) заменяются ближайшими разрешёнными уровнями сигнала u_кв(iT_д) (смотри рисунок 5.1, а).

Рисунок 5.1. Принцип ИКМ: а – дискретизация; б – ошибка квантования; в – цифровой сигнал с ИКМ

Такое преобразование первичных сигналов можно называть квантованной амплитудно-импульсной модуляцией (КАИМ). Особенностью такого сигнала является то, что все его уровни можно пронумеровать и тем самым свести передачу КАИМ-сигнала к передаче последовательностей номеров уровней, которые этот сигнал принимает в моменты i∙t_д.

Расстояние между ближайшими разрешёнными уровнями квантования (u₀ … u₇ на рисунке 5.1, а) ∆ называется шагом квантования. Шкала квантования называется равномерной, если все шаги квантования равны между собой ∆_j= ∆₀[5].

Если в момент взятия i-го отсчёта мгновенное значение непрерывного сообщения u_к(t_i) удовлетворяет условию

u_j – ∆_j/2 ≤ u_АИМ(iT_д) ≤ u_j + ∆_j/2, (5.1)

то квантованному импульсу u_кв(iT_д) присваивается амплитуда разрешённого u_j уровня квантования (смотри рисунок 5.1, а). При этом возникает ошибка квантования δ_кв, представляющая разность между передаваемой квантованной величиной u_кв(iT_д) и истинным значением непрерывного сигнала в данный момент времени u_АИМ(iT_д) (смотри рисунок 5.1, б):

δ_кв(iT_д) = u_кв(iT_д) – u_АИМ(iT_д). (5.2)

Как следует из рисунков 5.1, б и (5.1), ошибка квантования лежит в пределах

–∆₀/2 ≤ δ_кв ≤ ∆₀/2. (5.3)

Амплитудная характеристика квантующего устройства при равномерной шкале квантования приведена на рисунке 5.2, а. Она имеет ступенчатую форму, и при изменении непрерывного сообщения u_к(t) и соответствующего ему АИМ сигнала u_АИМ(iT_д) в пределах одной ступени выходной сигнал остаётся постоянным, а при достижении границы этой ступени изменяется скачком на величину шага квантования. При этом ошибка квантования зависит от u_к(t) и имеет вид, изображённый на рисунке 5.2, б.

Рисунок 5.2. Амплитудная характеристика квантователя (а) и зависимость ошибки квантования от амплитуды импульсов (б)

Как следует из рисунка 5.2, б, из-за нелинейности амплитудной характеристики квантователя ошибка квантования δ_квпредставляет собой функцию с большим числом резких скачков, частота следования которых существенно выше частоты исходного сообщения u_к(t), то есть при квантовании происходит расширение спектра сигнала. При этом соседние боковые полосы будут накладываться друг на друга и в полосу пропускания ФНЧ на выходе канала попадут составляющие спектра искажений от квантования, распределение которых в полосе ФНЧ считается равномерным. Поскольку практически все дискретные значения непрерывного сообщения находятся в пределах зоны квантования от –u_огр до +u_огр, то при равномерной шкале квантования ∆_j= ∆₀и тогда:

Ркв = (1/12) ∆²₀. (5.4)

Из выражения (5.4) видно, что при равномерной шкале квантования мощность шума квантования не зависит от уровня квантуемого сигнала и определяется только шагом квантования ∆₀.

Рассмотрим теперь кодирование и декодирование сигналов. Следующий шаг в преобразовании сигнала состоит в переводе квантованного АИМ-сигнала в цифровой. Эта операция называется кодированием АИМ-сигнала. Кодом называется закон, устанавливающий соответствие между квантованной амплитудой и структурой кодовой группы [8].

Различают равномерный и неравномерный коды. Если все кодовые группы состоят из равного числа символов, то код называется равномерным. Если же кодовые группы состоят из различного числа символов, то код называется неравномерным. В системах передачи с импульсно-кодовой модуляцией, как правило, используется равномерный двоичный код.

Для определения структуры двоичной кодовой комбинации на выходе кодера в простейшем случае необходимо в двоичном коде записать амплитуду АИМ отсчётов, выраженную в шагах квантования

, (5.5)

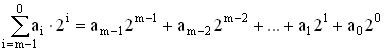
где a_i= {0,1} – состояние соответствующего разряда комбинации; 2ⁱ – вес соответствующего разряда в шагах квантования.

Если в десятичной системе «вес» каждой позиции числа равен числу десять в некоторой степени, то в двоичной системе вместо числа десять используют число два. «Веса» первых тринадцати позиций двоичного числа имеют следующие значения:

Таблица – 5.1

2¹²	2¹¹	2¹⁰	2⁹	2⁸	2⁷	2⁶	2⁵	2⁴	2³	2²	2¹	2⁰
4096	2048	1024	512	256	128	64	32	16	8	4	2	1

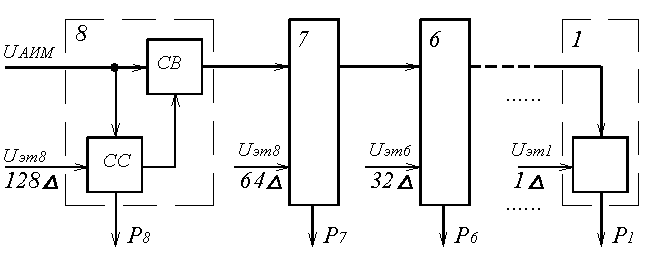
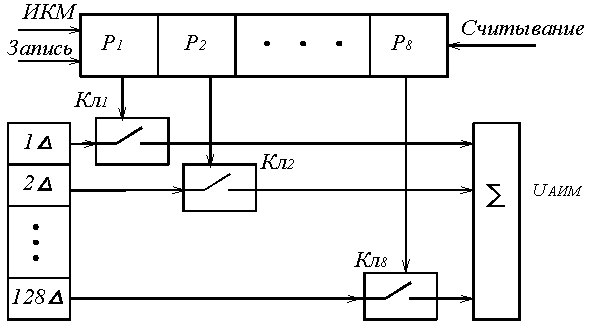
По принципу действия кодеры делятся на кодеры счётного типа, матричные, взвешивающего типа и другие. Наиболее часто используются кодеры взвешивающего типа, простейшим из которых является кодер поразрядного взвешивания (рисунок 5.3), реализующий функцию (5.5) с формирования натурального двоичного кода [5]. Принцип работы такого кодера заключается в уравновешивании кодируемых АИМ отсчётов суммой эталонных напряжений. Схема линейного кодера поразрядного взвешивания содержит восемь ячеек (при m = 8), обеспечивающих формирование значения коэффициента а_i соответствующего разряда (5.5). В состав каждой ячейки (за исключением последней, соответствующей младшему по весу разряду) входит схема сравнения СС и схема вычитания СВ.

Схема сравнения обеспечивает сравнение амплитуды поступающего АИМ сигнала с эталонными сигналами, амплитуды которых равны весам соответствующих разрядов

U_эт8 = 2⁷∆ = 128∆; U_эт7 = 2⁶∆ = 64∆; … U_эт1 = 2⁰∆ = 1∆.

Если на входе СС_i амплитуда поступающего АИМ сигнала равна или превышает U_этi, то на выходе схемы сравнения формируется «1», а в СВ_i из входного сигнала вычитается U_этi, после чего он поступает на вход следующей ячейки. Если же амплитуда АИМ сигнала на входе СС_i меньше U_этi, то на выходе СС_i формируется «0» и АИМ сигнал проходит через СВ_i без изменений. После окончания процесса кодирования текущего отсчёта на выходе кодера получается восьмиразрядный параллельный код, кодер устанавливается в исходное состояние и начинается кодирование следующего отсчёта.

Рисунок 5.3. Линейный кодер поразрядного действия

Если, например, на вход кодера поступил АИМ отсчёт с амплитудой U_АИМ = 185∆, то СС₈ формирует Р₈ = 1 и на вход седьмой ячейки поступил сигнал с амплитудой U_АИМ= 185∆ – 128∆ = 57∆. На выходе СС₇ сформируется Р₇ = 0 и на вход шестой ячейки кодера поступит сигнал с той же амплитудой U_АИМ = 57∆. На выходе СС₆ сформируется Р₆ = 1 и на вход следующей ячейки поступит сигнал с амплитудой U_АИМ= 57∆ – 32∆ = 25∆ и так далее. В результате будет сформирована кодовая комбинация 10111001.

В процессе декодирования сигнала m – разрядные кодовые комбинации преобразуются в АИМ отсчёты соответствующей амплитуды [4]. Сигнал на выходе декодера получается в результате суммирования эталонных сигналов U_этi тех разрядов кодовой комбинации, значения которых равно 1 (рисунок 5.4). Так, если на вход декодера поступила кодовая комбинация 10111001, то амплитуда АИМ отсчёта на его выходе будет равна U_АИМ= 128∆ + 32∆ + 16∆ + 8∆ + 1∆ = 185∆.

В линейном декодере (рисунок 5.4) под воздействием управляющих сигналов, поступающих от генераторного оборудования, в регистр сдвига записывается очередная восьмиразрядная кодовая комбинация. В момент прихода импульса считывания замыкаются только те ключи Кл₁ … Кл₈, которые соответствуют разрядам, имеющим значения «1». В результате в сумматоре объединяются соответствующие эталонные напряжения и на его выходе получается соответствующая амплитуда АИМ отсчёта.

Рисунок 5.4. Линейный декодер взвешивающего типа

Рассмотренная схема кодера (рисунок 5.3) поразрядного взвешивания содержит большое число схем сравнения, которые являются относительно сложными устройствами. На практике чаще используется кодер взвешивающего типа с одной схемой сравнения и цепью обратной связи, содержащей декодер. Как следует из выражения (5.4), мощность шума квантования при линейном кодировании будет равной при различных амплитудах квантованных сигналов. Для синусоидальных сигналов отношение сигнал/шум квантования, рассчитывается по формуле:

, (5.6)

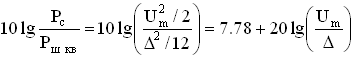
где U_m – амплитуда квантуемого сигнала.

Из формулы видно, что для слабых входных сигналов это отношение гораздо хуже, чем для сигналов большой амплитуды. Для устранения этого недостатка было предложено использовать неравномерное квантование, то есть изменять шаг квантования пропорционально изменению амплитуды входного сигнала.

Для кодирования с неравномерной шкалой квантования могут быть использованы:

прямое нелинейное кодирование, при котором кодер сочетает в себе функции аналого-цифрового преобразования (АЦП) и компрессора;
аналоговое компандирование, при котором компрессирование сигнала осуществляется перед линейным кодером и экспандирование сигнала после линейного декодера;
преобразование на основе линейного кодирования, при котором кодирование сигнала осуществляется в линейном кодере с большим числом разрядов с последующим цифровым компандированием [5].

Переменную величину шага квантования можно получить с помощью устройства с нелинейной амплитудной характеристикой (рисунок 5.5) (которая называется компрессором, поскольку сжимает динамический диапазон входного сигнала) и равномерного квантователя (смотри рисунок 5.2). На приёмной стороне осуществляется расширение динамического диапазона экспандером, имеющим характеристику, противоположную компрессору, что обеспечивает линейность системы передачи. Совокупность операций сжатия динамического диапазона компрессором и расширение его экспандером называется компадированием сигнала.

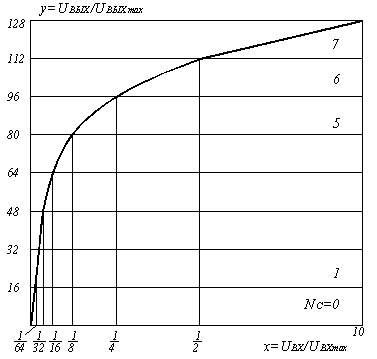
В настоящее время в системах ВРК с ИКМ применяется характеристика компадирования типа А (рисунок 5.5).

Рисунок 5.5. Характеристика компрессирования типа А

На этом рисунке сегментированная характеристика компрессии типа А для положительных сигналов (для отрицательных сигналов характеристика имеет аналогичный вид). Общее число сегментов характеристики N_с = 16, однако четыре центральных сегмента (по два в положительной и отрицательной областях) имеют одинаковый шаг квантования и фактически образуют один сегмент, вследствие чего число сегментов равно N_с = 13. Поэтому такая характеристика получила название типа А = 87.16/13. В центральном сегменте (N_с =1 или 2) значение ∆₀ минимально (то есть равно ∆₀) и соответствует равномерной двенадцатиразрядной шкале (m = 12), а в каждом последующем сегменте к краям характеристики шаг квантования увеличивается вдвое.

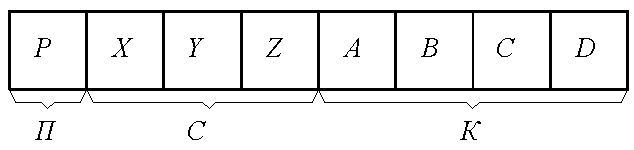
Представление ИКМ сигнала восьмиразрядными кодовыми комбинациями использует формат «знак – абсолютное значение», где один разряд отображает полярность АИМ сигнала П, а остальные – определяют его абсолютное значение. Семь разрядов, отображающих абсолютное значение, подразделяются на определитель номера сегмента С из трёх разрядов и определитель шага квантования К из четырёх разрядов (рисунок 5.6).

Рисунок 5.6. Формат восьмиразрядной ИКМ комбинации

Для реализации такого кодера необходимо задать величины эталонных напряжений для нижней границы каждого сегмента и при кодировании внутри сегмента (таблица 5.2).

Схемы и принцип действия нелинейных кодеков взвешивающего типа в основном те же, что и у линейных кодеков. Отличие заключается в последовательности включения эталонных напряжений в процессе кодирования исходного сигнала [5].

Таблица 5.2. Эталонные напряжения для нелинейного кодека

Номер сегмента N_с	Эталонное напряжение нижней границы сегмента	Эталонные напряжения при кодировании в пределах сегмента
8∆_i(A)	4∆_i(B)	2∆_iI(С)	∆_i(D)
0	0	8∆₀	4∆₀	2∆₀	1∆₀
1	16∆₀	8∆₀	4∆₀	2∆₀	1∆₀
2	32∆₀	16∆₀	8∆₀	4∆₀	2∆₀
3	64∆₀	32∆₀	16∆₀	8∆₀	4∆₀
4	128∆₀	64∆₀	32∆₀	16∆₀	8∆₀
5	256∆₀	128∆₀	64∆₀	32∆₀	16∆₀
6	512∆₀	256∆₀	128∆₀	64∆₀	32∆₀
7	1024∆₀	512∆₀	256∆₀	128∆₀	64∆₀

Таким образом, максимальный шаг квантования (в седьмом сегменте) в 64 раза превышает минимальный шаг квантования, а отношение сигнал/шум квантования (для максимального значения синусоидального сигнала) может быть определено по выражению (5.6) и составит: для второго сегмента

Р_с – Р_ш _кв = 7.78 + 20lg(А/∆) = 7.78 + 20 lg(32∆₀/∆₀) = 37.88 дБ;

Для седьмого сегмента

Р_с – Р_ш _кв = 7.78 + 20 lg(2048∆₀/64∆₀) = 37.88 дБ.

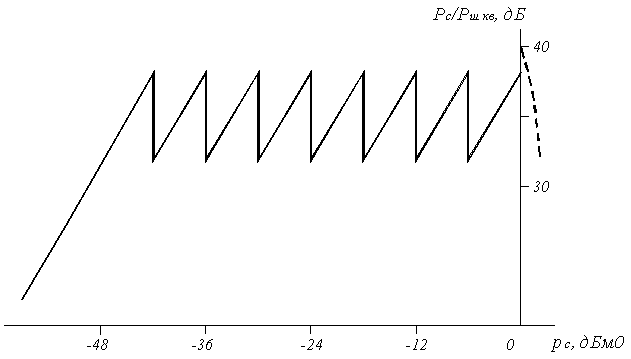
Зависимость отношения сигнал/шум квантования от уровня входного сигнала при компадировании по закону А = 87.6/13 приведена на рисунке 5.7. Для сигналов в пределах нулевого и первого сегментов осуществляется равномерное квантование с шагом ∆₀, поэтому Р_с – Р_ш _кв увеличивается с ростом р_с. При переходе ко второму сегменту шаг квантования увеличивается в два раза, вследствие чего Р_с – Р_ш _кв резко уменьшается на 6 дБ, а затем в пределах данного сегмента возрастает с ростом р_с, поскольку внутри сегмента осуществляется равномерное квантование. После попадания сигнала в зону ограничения отношение сигнал/шум резко уменьшается за счёт перегрузки кодера.

Рисунок 5.7. Зависимость Р_с/Р_{ш кв} = f(р_с)

На рисунке 5.8 представлена упрощённая схема нелинейного кодера взвешивающего типа, реализующего прямое кодирование АИМ сигнала.

Рисунок 5.8. Нелинейный кодер взвешивающего типа

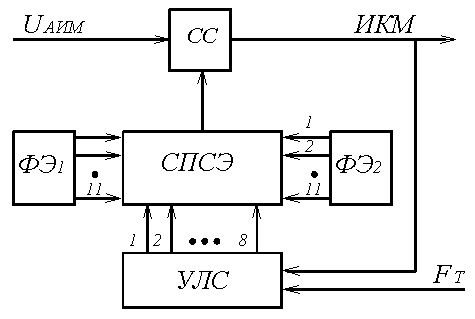
Кодирование осуществляется за восемь тактовых интервалов, в каждом из которых формируется один из символов кодовой комбинации (рисунок 5.6). В первом такте определяется знак поступившего на вход кодера отсчёта. Если отсчёт положительный, то в знаковом разряде формируется «1» и к схеме переключения и суммирования эталонов СПСЭ подключается формирователь положительных эталонных напряжений ФЭ₁, в противном случае формируется «0» и к схеме подключается ФЭ₂. Затем происходит формирование кода номера сегмента методом деления их числа пополам (рисунок 5.9).

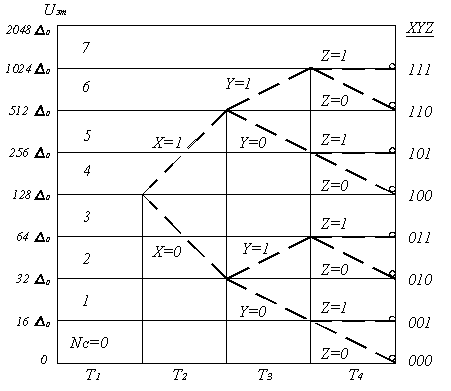
Рисунок 5.9. Алгоритм формирования кода номера сегмента

Во втором такте управляющая логическая схема УЛС и СПСЭ обеспечивают подачу на вход схемы сравнения эталонного сигнала U_эт= 128 ∆₀, соответствующего нижней границе четвёртого (среднего) сегмента. Если амплитуда отсчёта U_АИМ ≥ U_эт = 128 ∆₀, то принимается решение, что амплитуда отсчёта попадёт в один из четырёх вышележащих сегментов и формируется очередной символ X = 1, который по цепи обратной связи поступает на вход УЛС. В противном случае принимается решение, что амплитуда отсчёта попадает в один из нижележащих сегментов и формируется X = 0.

В третьем такте в зависимости от значения предыдущего символа X уточняется номер сегмента, в который попадает амплитуда кодируемого отсчёта. Если X = 1, то УЛС и СПСЭ подают на вход СС эталонное напряжение U_эт= 512 ∆₀, соответствующего нижней границе шестого сегмента. При этом, если U_АИМ ≥ U_эт = 512 ∆₀ то принимается решение, что отсчёт попадает в один из двух вышележащих сегментов и формируется очередной символ Y = 1. В противном случае, если U_АИМ ≤ U_эт = 512 ∆₀, принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.

Если же X = 0, то УЛС с помощью СПСЭ обеспечивает подачу на вход СС эталонного напряжения U_эт= 32 ∆₀, соответствующего нижней границе второго сегмента. Если U_АИМ ≥ U_эт = 32 ∆₀, то принимается решение, что отсчёт попадает во второй и третий сегменты и формируется Y = 1. Если U_АИМ ≤ U_эт = 32 ∆₀, то принимается решение, что отсчёт попадает в два нижележащих сегмента и формируется Y = 0.

В четвёртом такте аналогичным образом формируется символ Z и окончательно формируется код номера сегмента. В результате, после четырёх тактов кодирования, сформируется четыре символа восьмиразрядной кодовой комбинации PXYZ (рисунок 5.6) и к СС подключается одно из восьми эталонных напряжений, соответствующих нижней границе сегмента, в котором находится кодируемый отсчёт.

В оставшихся четырёх тактах последовательно формируются символы ABCD кодовой комбинации, значения которых зависят от номера шага квантования внутри сегмента, соответствующего амплитуде кодируемого отсчёта. Поскольку внутри любого сегмента осуществляется равномерное квантование, то процесс кодирования реализуется, как и в линейных кодерах взвешивающего типа, путём последовательного включения эталонных напряжений соответствующих данному сегменту (таблица 5.2).

Практикум на применение нелинейного кодера при компадировании по закону А = 87.6/13:

Например, если на вход кодера поступил положительный отсчёт с амплитудой U_АИМ = 889 ∆₀, то после первых четырёх тактов сформируются символы PXYZ = 1110 и к СС подключится эталонное напряжение U_эт= 512 ∆₀, соответствующее нижней границе шестого сегмента, поскольку кодируемый сигнал находится в этом сегменте. В пятом такте к этому эталонному сигналу добавляется максимальное эталонное напряжение U_эт= 256 ∆₀, соответствующее символу А в определителе шага квантования К (рисунок 5.6) шестого сегмента (таблица 5.2). Так как U_АИМ > U_эт = (512 +256) ∆₀, то формируется символ А = 1 и это эталонное напряжение остаётся включенным. В шестом такте подключается эталонное напряжение соответствующее символу В в определителе шага квантования U_эт = 128 ∆₀ и так как U_АИМ > U_эт = (512 +256 + 128) ∆₀, то на выходе СС формируется символ В = 1 и это эталонное напряжение остаётся включенным. В седьмом такте подключается эталонное напряжение соответствующее символу С в определителе шага квантования U_эт = 64 ∆₀ и так как U_АИМ < U_эт = (512 +256 + 128 + 64) ∆₀, то на выходе СС формируется символ С = 0. В восьмом такте вместо U_эт = 64 ∆₀ подключается эталонное напряжение соответствующее символу D в определителе шага квантования U_эт = 32 ∆₀ и так как U_АИМ < U_эт = (512 +256 + 128 + 32) ∆₀, то на выходе СС формируется символ D = 0 и это эталонное напряжение отключается и на этом процесс кодирования очередного отсчёта заканчивается. При этом на выходе кодера сформирована кодовая комбинация PXYZABCD = 11101100, соответствующая амплитуде уравновешивающего АИМ сигнала на входе СС U_АИМ = 896 ∆₀. Разница между входным и уравновешивающим АИМ сигналами на входах СС представляет ошибку квантования δ_кв = U_АИМ – U_АИМ = 7∆₀.

Источник