Ошибки квантования и дискретизации

Теорема
Котельникова точно справедлива только
для сигналов с финитным (конечным)
спектром. На рис. 4.15 показаны некоторые
варианты финитных спектров.

Однако
спектры реальных информационных сигналов
бесконечны (рис. 4.16). В этом случае теорема
Котельникова справедлива с погрешностью.

Погрешность
дискретизации определяется энергией
спектральных составляющих сигнала,
лежащих за пределами частоты
(рис. 4.16).

.

Вторая причина
возникновения погрешностей — неидеальность
восстанавливающего ФНЧ.

Таким
образом? погрешность дискретизации и
восстановления непрерывного сигнала
определяется следующими причинами:

1. Спектры реальных
   сигналов не финитны.

2. АЧХ реальных ФНЧ
   неидеальны.

Рис.4.17.
Структурная схема RC-фильтра

Например,
если в качестве ФНЧ использовать
RC-фильтр
(рис.4.17), то восстановленный сигнал на
его выходе будет иметь вид, представленный
на рис.4.18.

Импульсная
реакция RC-фильтра
равна:

.

Вывод:
чем выше
и чем ближе характеристики ФНЧ к
идеальным, тем ближе восстановленный
сигнал к исходному.

4.6. Квантование сообщений. Ошибки квантования

Итак
показано, что передачу практически
любых сообщений
можно свести к передаче их отсчетов,
или чисел,
следующих друг за другом с интервалом
дискретности.
Тем самым непрерывное (бесконечное)
множество возможных значений сообщения
заменяетсяконечным
числом его дискретных значений
.
Однако сами эти числа имеют непрерывную
шкалу уровней (значений), то есть
принадлежат опять же континуальному
множеству. Дляабсолютно
точного
представления таких чисел, к примеру,
в десятичной (или двоичной) форме,
необходимо теоретически бесконечное
число разрядов. Вместе с тем, на практике
нет необходимости в абсолютно точном
представлении значений
,
как и любых чисел вообще.

Во-первых,
сами источники сообщений обладают
ограниченным динамическим диапазоном
и вырабатывают исходные сообщения с
определенным уровнем искажений и ошибок.
Этот уровень может быть большим или
меньшим, но абсолютной точности
воспроизведения достичь невозможно.

Во-вторых,
передача сообщений по каналам связи
всегда производится в присутствии
различного рода помех. Поэтому, принятое
(воспроизведенное) сообщение (оценка
сообщения
)
всегда в определенной степени отличается
от переданного, то есть на практикеневозможна
абсолютно точная передача сообщений
при наличии помех в канале связи.

Наконец,
сообщения передаются для их восприятия
и использования получателем. Получатели
же информации — органы чувств человека,
исполнительные механизмы и т.д. — также
обладают конечной разрешающей
способностью, то есть не замечают
незначительной разницы между абсолютно
точным и
приближенным
значениями
воспроизводимого сообщения. Порог
чувствительности к искажениям также
может быть различным, но он всегда есть.

С
учетом этих замечаний процедуру
дискретизации сообщений можно продолжить,
а именно подвергнуть отсчеты

квантованию.

Процесс
квантования состоит в замене непрерывного
множества значений отсчетов
дискретным
множеством
.
Тем самым точные значения чиселзаменяются их приблизительными
(округленными до ближайшего разрешенного
уровня) значениями. Интервал между
соседними разрешенными уровнями,
или уровнями квантования,называетсяшагом
квантования.

Различают
равномерное и неравномерное квантование.
В большинстве случаев применяется и
далее подробно рассматривается
равномерное квантование (рис. 4.19), при
котором шаг квантования постоянный:
;
однако иногда определенное преимущество
дает неравномерное квантование, при
котором шаг квантования
разный
для различных
(рис. 4.20).

Квантование
приводит к искажению сообщений. Если
квантованное сообщение, полученное в
результате квантования отсчета
,
обозначить как
,
то

где

— разность между истинным значением
элементарного сообщения

и
квантованным
сообщением (ближайшим разрешенным
уровнем)
,
называемая ошибкой
квантования, или шумом
квантования.
Шум квантования оказывает на процесс
передачи информации по существу такое
же влияние, как и помехи в канале связи.
Помехи, так же как и квантование, приводят
к тому, что оценки
,
получаемые на приемной стороне системы
связи, отличаются на некоторую величину
от истинного значения.

Поскольку
квантование сообщений приводит к
появлению ошибок и потере некоторой
части информации, можно определить
цену таких потерь
и среднюю величину ошибки, обусловленной
квантованием:

Чаще
всего в качестве функции потерь (цены
потерь) используется квадратичная
функция вида

В
этом случае мерой ошибок квантования
служит дисперсия этих ошибок. Для
равномерного
-уровневого
квантования с шагом

дисперсия ошибок квантования определяется
следующим образом:

.
(4.9)

Абсолютное
значение ошибки квантования не превосходит
половины шага квантования
,
и
тогда при
достаточно большом числе уровней
квантования
и малой величине
плотность
распределения вероятностей ошибок
квантования

можно
считать равномерной на интервале +
… —:

В
результате величина ошибки квантования
определится соотношением

(4.10)

и
соответствующим выбором шага квантования

может быть сделана сколь угодно малой
или сведена к любой наперед заданной
величине.

Относительно
требуемой точности передачи отсчетов
сообщений можно высказать те же
соображения, что и для ошибок временной
дискретизации: шумы квантования или
искажения, обусловленные квантованием,
не имеют существенного значения, если
эти искажения меньше ошибок, обусловленных
помехами и допустимых техническими
условиями.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Московский государственный университет приборостроении и информатики (МГУПИ) Реферат По дисциплине «Информатика» Тема: иск етиза ия и квантование сигналов по ешности иск етиза иииквантования. Выполнил: студент первого курса очной формы обучения, направление 230100 Васильев мит ий Олегович Ст. преп. Каф. ИТ-4 Москва 2011 Министерство Образования и Науки Российской Федерации Проверил: Кукин М.А. 1.Введение В первой половине ХХ века при регистрации и обработке информации использовались, в основном, измерительные приборы и устройства аналогового типа, работающие в реальном масштабе времени, при этом даже для величин, дискретных в силу своей природы, применялось преобразование дискретных сигналов в аналоговую форму. Положение изменилось с распространением микропроцессорной техники и ЭВМ.

Цифровая регистрация и обработка информации оказалась более совершенной и точной, более универсальной, многофункциональной и гибкой. Мощь и простота цифровой обработки сигналов настолько преобладают над аналоговой, что преобразование аналоговых по природе сигналов в цифровую форму стало производственным стандартом. ~2,с.31 2.Види информиции Информация может быть двух видов: дискретная (цифровая) и не- информация прерывная (аналоговая).

Дискретная ~1,с.71 характеризуется последовательными точными значениями некоторой величины, а непрерывная — непрерывным процессом изменения некоторой величины. Непрерывную информацию может, например, выдавать датчик атмосферного давления или датчик скорости автомашины. Дискретную информацию можно получить от любого цифрового индикатора: электронных часов, счетчика магнитофона и т. и.

Дискретная информация удобнее для обработки человеком, но непрерывная информация часто встречается в практической работе, поэтому необходимо уметь переводить непрерывную информацию в дискретную (дискретизация) и наоборот. Модем (это слово происходит от слов модуляция и демодуляция) представляет собой устройство для такого перевода: он переводит цифровые данные от компьютера в звук или электромагнитные колебания-копии звука и наоборот. 3. Способы представления информации Непрерывный (аналоговый) способ представления информации- представление информации, в котором сигнал на выходе датчика будет меняться вслед за изменениями соответствующей физической величины.

Примером непрерывного сообщения служит человеческая речь, передаваемая модулированной звуковой волной; параметром сигнала в этом случае является давление, создаваемое этой волной в точке нахождения приемника — человеческого уха. Аналоговый способ представления информации имеет недостатки: Точность представления информации определяется точностью измерительного прибора (например, точность числа отображающего напряжение в электрической цепи, зависит от точности вольтметра).

Наличие помех может сильно исказить представляемую информацию. Дискретность (от лат. Йзсгегцзразделенный, прерывистый) — прерывность; противопоставляется непрерывности. Дискретное изменение величины во времени — это изменение, происходящее через определенные промежутки времени (скачками); система целых (в противоположность системе действительных чисел) является дискретной. Дискретный сигнал- сигнал, параметр которого принимает последовательное во времени конечное число значений (при этом все они могут быть пронумерованы). Сообщение, передаваемое с помощью таких сигналов — дискретным сообщением.

Информация передаваемая источником, в этом случае также называется дискретной информацией. 4.Дискретизация Дискретизация — преобразование непрерывной функции в дискретную. Используется в гибридных вычислительных системах и цифровых устройствах при импульсно-кодовой модуляции сигналов в системах передачи данных. При дискретизации только по времени, непрерывный аналоговый сигнал заменяется последовательностью отсчетов, величина которых может быть равна значению сигнала в данный момент времени.

Возможность точного воспроизведения такого представления зависит от интервала времени между отсчетами ЛГ. Согласно теореме Котельникова: 1 Х1 <— где гп«и: — наибольшая частота спектра сигнала. 12,с.51 При переводе непрерывной информации в дискретную важна так называемая частота дискретизации ч, определяющая период (Т=1/ч) определения значения непрерывной величины .

11,с.71 Чем выше частота дискретизации, тем точнее происходит перевод непрерывной информации в дискретную. Но с ростом этой частоты растет и размер дискретных данных, получаемых при таком переводе, и, следовательно, сложность их обработки, передачи и хранения. Однако для повышения точности дискретизации необязательно безграничное увеличение ее частоты. Эту частоту разумно увеличивать только до предела, определяемого теоремой Котельникова. Примером использования этой теоремы являются лазерные компакт-диски, звуковая информация на которых хранится в цифровой форме.

11,с.81 Согласно теореме Котельникова частоту дискретизации нужно выбрать не меньшей 40 КГц (в промышленном стандарте на компакт-диске используется частота 44.1 КГц). При преобразовании дискретной информации в непрерывную, определяющей является скорость этого преобразования: чем она выше, с тем более высокочастотными гармониками получится непрерывная величина. Но чем большие частоты встречаются в этой величине, тем сложнее с ней работать.

Например, обычные телефонные линии предназначены для передачи звуков частотой до 3 КГц. 11,с.8~ Устройства для преобразования непрерывной информации в дискретную обобщающе называются АЦП (аналого-цифровой преобразователь) или АОС (Апа1о8 1о Ирта1 Сопчег~ог, АЛ)), а устройства для преобразования дискретной информации в аналоговую — ЦАП (цифро-аналоговый преобразователь) или ПАС (Иф1а1 1о Апа!о8 Сопчеггог, Р/А).

11,с.81 5. Э ТА ПБТ ДИСКРЕ ТИЗА ЦИИ Область определения функции разбивается точками х1, х2,, хп на отрезки равной длины и на каждом из этих отрезков значение функции принимается постоянным и равным, например, среднему значению на этом отрезке; полученная на этом этапе функция называется ступенчатой. Следующий шаг — проецирование значений «ступенек» на ось значений функции (ось ординат).

11олученная таким образом последовательность значений функции у1, у2,, уп является дискретным представлением непрерывной функции, точность которого можно неограниченно улучшать путем уменьшения длин отрезков разбиения области значений аргумента.[2,с.14~ У1 У» ~ а; ~~.1~,1 Х Рисунок 4 — Дискретизация Ось значений функции можно разбить на отрезки с заданным шагом и отобразить каждый из выделенных отрезков из области определения функции в соответствующий отрезок из множества значений.

В итоге получим конечное множество чисел, определяемых, например, по середине или одной из границ таких отрезков. Таким образом, любое сообщение может быть представлено как дискретное, иначе говоря, последовательностью знаков некоторого алфавита. Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер — цифровая машина, т.е. внутреннее представление информации в нем дискретно.

Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки. Существуют и другие вычислительные машины аналоговые ЭВМ. Они используются обычно для решения задач специального характера и широкой публике практически не известны. Эти ЭВМ в принципе не нуждаются в дискретизации входной информации, так как ее внутренне представление у них непрерывно. В этом случае все наоборот — если внешняя информация дискретна, то ее перед использованием необходимо преобразовать в непрерывную.~2,с.151 б. Квантпвание ~2,с. б-8~ Квантование (англ.

с1папйкайоп) — в информатике разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей. Квантование часто используется при обработке сигналов, в том числе при сжатии звука и изображений. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования. Рисунок 1 — Квантованный сигнал Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации).

При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике — по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть, разбивает по уровню сигнала (на графике — по вертикали). Сигнал, к которому применены дискретизация и квантование, называется цифровым.

Рисунок 3 — Цифровой сигнал При оцифровке сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит = 6 дБ). 7.Погрешность квантования Начальный сигнал, приобретенный при амплитудной модуляции, состоит из импульсов, у каких амплитуда может лежать в границах некого ограниченного спектра значений. По данной причине для подготовки такового сигнала к шагу кодировки, когда каждый импульс в потоке преобразовывается в последовательность нулей и единиц, нужно применять ограниченную шкалу значений.

Нельзя 9 ждать, что каждый начальный импульс будет в точности совпадать с одним из значений в избранной шкале. Это значит, что некие импульсы должны быть скорректированы, и при всем этом для их не будет никакой сопровождающей информации, с помощью которой они могли бы в предстоящем быть восстановлены в начальное состояние. Такое несоответствие именуют ошибкой, либо погрешностью квантования.

1. Сигналы

• Сигнал – физический процесс, несущий в себе
информацию. Параметры процесса изменяются в
соответствии с сообщением, которое необходимо
передать.
• Понятие «сигнал» – абстракция конкретных
физических процессов (сила тока, напряжение и
пр.)
• Математическая модель сигнала – функция от
времени, тип которой зависит от типа сигнала.

2. Сигналы

• Периодические – непериодические
• Непрерывные — дискретные

3. Периодический сигнал

Периодический сигнал – сигнал, форма которого
регулярно повторяется через некоторый
временной интервал (называемый периодом)

4. Математическое определение

Сигнал x(t) называется периодическим с
периодом Т, если
x(t + T) = x(t) для всех t

5. Свойства

• Если Т – период колебания, то 2T, 3T,
4T, …, а также -T, -2T, -3T, -4T, …
являются периодами данного колебания
• Всякое периодическое колебание
является бесконечно длинным (от минус
бесконечности до плюс бесконечности)

6. Вывод

• Строго говоря, периодическое
колебание – абстракция, которой в
реальности нет (хотя бы потому, что в
реальном мире бесконечно длинных
сигналов нет)
• Кроме того, в реальности сигналы
повторяют себя не точно
• Однако периодический сигнал – это
очень полезная абстракция

7. Частота

• Если Т – период колебания, то
частотой колебания называется
величина F = 1/T
• Частота измеряется в Герцах (Гц)
• Чем больше Герц, тем выше частота
(и тем больше колебаний
совершается за единицу времени)

8. Круговая частота

• Если F – частота колебания, то
круговой частотой того же
колебания называют
= 2 F ( — число «пи», 3,14…)
• Круговая частота измеряется в
радианах в секунду

9. Гармоническое колебание

10. Физические примеры гармонических колебаний

• Маятник
• Грузик на пружинке

11. Общая запись

• x(t) = A*sin(2* *F + )
A – амплитуда гармонического колебания
F – частота гармонического колебания
— фаза гармонического колебания

12. Колебания с разными амплитудами

• Физический смысл – размах красного
маятника в два раза больше, чем размах
черного

13. Колебания с разными частотами

• Физический смысл – красный маятник
колеблется в два раза чаще, чем черный

14. Колебания с разными фазами

Физический смысл – красный маятник начал
колебаться раньше, чем черный маятник

15. Можно собирать периодические колебания, суммируя гармонические с разными частотами, амплитудами и фазами

16. Пример

• Суммируются 3 гармонических колебания с
частотами 100 Гц, 200 Гц, 300 Гц

17. Функция

• sum_3harmonics – суммирует и
рисует 3 гармоники с частотами 100
Гц, 200 Гц, 300 Гц
• Амплитуды и фазы подбираются
пользователем произвольно

18. Пример

sum_3harmonics([3,2,1],[0,0,0])

19. Можно ли произвольное периодическое колебание разложить на сумму гармонических?

20. Теорема Фурье

Всякое периодическое колебание частоты F можно
получить в результате суммирования бесконечного числа
гармоник с частотами F, 2F, 3F, 4F, …, и специально
подобранными амплитудами и фазами
x(t) = A0 + A1sin(2 Ft + 1) + A2sin(2 2Ft + 2) +
A3sin(2 3Ft + 3) + … (и т.д.) ИЛИ
x(t ) A0 Ak sin( 2 kFt k )
k 1

21. Терминология

• Гармоника с частотой F называется
основной гармоникой
• Гармоники с частотами 2F, 3F, 4F, …,
называются высшими гармониками (или
обертонами)
• Постоянная A0 называется постоянной
составляющей
• В англояз. лит-ре постоянная
составляющая обозначается как DC (от
direct current), а все гармоники – как AC (от
alternating current)

22. Пример: возьмем следующий сигнал

23. 1 гармоника

fourier_demo1(1)

24. 4 гармоники

fourier_demo1(4)

25. Явление Гиббса

26. Пример

27. 5 гармоник

fourier_demo2(5)

28. 20 гармоник

fourier_demo2(20)

29. 100 гармоник

fourier_demo2(100)

30. Явление Гиббса

• Явление Гиббса – появление
пульсаций значительной амплитуды в
окрестности скачкообразного
изменения сигнала
• При этом эти пульсации не исчезают
при увеличении количества гармоник

31. Явление Гиббса

Таким образом, если в сигнале есть
скачки, то в окрестности этих скачков
разложение Фурье описывает этот
сигнал с большой погрешностью

32. В чем опасность явления Гиббса?

33. Явление Гиббса

34. Аналого-цифровое преобразование

Передача голоса через цифровую сеть
Для преобразования используется КОДЕК (кодер-декодер)
Аналоговый
сигнал
Цифровой
сигнал

35. Процесс преобразования

ИКМ передатчик
АЦП
АС
Схема
стробирования
Выборка аналогового
сигнала с помощью
амплитудно-импульсной
модуляции (АИМ или PAM)
Квантование
Присваивание
определенных целых
значений полученным
выборкам (отсчетам)
Рисунок 13
Двоичное
кодирование
Аналоговый сигнал
преобразуется в
цифровой сигнал
(каждой выборке
сопоставляется
двоичный код)
ЦС
Кодер
Кодовые
комбинации
преобразуются в
цифровой сигнал

36. Непрерывные и дискретные сигналы

Аналоговый сигнал непрерывен по времени и состоянию (в любой момент
времени t t0 ; t1 может принимать любое значение x xmin ; xmax ). Описывается
непрерывной или кусочно-непрерывной функцией x(t ) .
Синусоидальный сигнал
1
Непрерывный сигнал y(t)
y (t ) = A sin 2: f t
0.5
0
-0.5
-1
0
10
20
Непрерывное время ( с )
30

37. Непрерывные и дискретные сигналы

Дискретный сигнал дискретен по времени и непрерывен по состоянию.
Описывается решетчатой функцией (последовательностью) x nT , n 0,1, 2, , которая
определена только в дискретные моменты времени nT , и может принимать любые
значения x xmin ; xmax .
Синусоидальный сигнал
1
Непрерывный сигнал y(t)
y (t ) = A sin 2: f t
0.5
0
-0.5
-1
0
10
20
Непрерывное время ( с )
30

38. Непрерывные и дискретные сигналы

39. Дискретизация и квантование

• При вводе непрерывного сигнала в компьютер
сигнал дискретизируется и квантуется
• Фонетист всегда имеет дело с дискретными
квантованными сигналами
• Методы цифровой обработки сигналов (например,
Быстрое Преобразование Фурье) существенно
используют свойства дискретных сигналов
Цифровой сигнал – дискретный по времени и квантованный по состоянию
сигнал. Описывается квантованной решетчатой функцией xq nT , отсчеты которой
принимают дискретные значения уровней квантования из интервала x xmin ; xmax .

40. Дискретизация

41. Шаг дискретизации

Чем выше частота дискретизации, тем ближе форма восстановленного сигнала
приближается к оригиналу
На практике частота дискретизации выбирается исходя из теоремы Котельникова
и составляет 8 кГц для речевого сигнала

42. Дискретные сигналы и системы

Дискретизация по времени
Квантование по уровню
A
6
5
4
3
2
1
0
B
C
D
0
1
2
3
4
5
6
7
8
9
10
2
2
3
5
4
1
0
1
2
1
3
0
Рис 13а. Дискретизация по времени и квантование по уровню
B – полученная последовательность цифр
C – полученная последовательность двоичных кодовых групп
D – ошибки квантования

43. Частота дискретизации

Интервал T называют периодом дискретизации, а обратную величину –
частотой дискретизации
fd
1
T
Значения дискретной последовательности x nT в моменты nT
отсчетами.
Дискретный синусоидальный сигнал
x nT x n A sin 2 fnT A sin nT
T – период дискретизации
А – амплитуда
– круговая частота
f – частота сигнала
2 f
называют

44. Представление сигналов во временной и частотной области

1
x (t) = A sin 2: f t
0.5
0
-0.5
Амплитуда
-1
0
5
0
0.02
10
15
20
25
30
1
0.5
0
0.04
0.06
Частота ( Гц )
0.08
0.1
Один дискретный гармонический сигнал во временной (вверху) области и в
частотной (внизу) области.

45. Представление сигналов во временной и частотной области

1
0.5
0
-0.5
-1
0
5
10
15
20
25
30
Амплитуда
x (t) = A 1 sin 2: f 1 t + A 2 sin 2: f 2 t
1
0.5
0
0
0.02
0.04
0.06
0.08
Частота ( Гц )
0.1
0.12
Сумма двух дискретных гармонических сигналов во временной и частотной
областях.

46. Частота дискретизации

• Интервал дискретизации (sampling
period) t – интервал времени между
двумя соседними временными
отсчетами
• Частота дискретизации (sampling
frequency, sampling rate) Fs = 1/ t
• Частота дискретизации определяет
количество отсчетов в секунду

47. Пример

• Если частота дискретизации сигнала
= 16 кГц, то это означает, что за 1
секунду запоминаются 16000
отсчетов сигнала
• Это также означает, что временной
интервал между двумя соседними
отсчетами равен 0.0000625 секунд
(0.0625 миллисекунд)

48. Насколько часто нужно запоминать отсчеты непрерывного сигнала?

Частота дискретизации или скорость выборки (sampling rate). Ключевой вопрос:
сколько требуется выборок для полного описания сигнала?
При дискретизации с частотой f s отсчетов в секунду мы не можем различить
дискретизированные значения синусоиды частотой f0 Гц и синусоиды частотой f0 k· f s
Гц, где k – любое положительное или отрицательное число.

49. Теорема Котельникова

Если спектр непрерывного сигнала не
содержит информации выше частоты
F, то частота дискретизации должна
быть не менее 2F
(Частоту F называют частотой Найквиста – Nyquist
frequency)
Теорема Котельникова (теорема Найквиста – Шеннона):
если аналоговый сигнал x(t ) имеет конечный (ограниченный по ширине) спектр, то он
может быть восстановлен однозначно и без потерь по своим отсчётам, взятым с
частотой, большей или равной удвоенной верхней частоте fc : f 2 fc

50. Применительно к речи

• Считается, что спектральные
компоненты выше 3400 Гц не влияют
на разборчивость речи
• Поэтому можно приблизительно
считать, что выше 4000 Гц
информация, нужная для слухового
восприятия речи, отсутствует
• Следовательно, минимальная
частота дискретизации для речи = 8
кГц

51. Проблема выбора частоты

Частотная неоднозначность
1
Отсчеты
Cигнал f = 0.05 Гц
Сигнал f = 0.30 Гц
Сигнал f = 0.55 Гц
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
5
10
15
Время ( с )
20
25
При дискретизации с частотой f s отсчетов в секунду мы не можем различить
дискретизированные значения синусоиды частотой f0 Гц и синусоиды частотой f0 k· f s
Гц, где k – любое положительное или отрицательное число.
Вопрос: Когда я сложил два числа, я получил сумму четыре. Какие два числа я сложил?
Ответ: Существует бесконечное число двух чисел, которые в сумме дают четыре.
Проблема состоит в том, что никакой алгоритм обработки не может определить,
является ли данная последовательность дискретных отсчетов, значения которых
показаны точками, результатом дискретизации синусоиды частотой 7 кГц или
синусоиды частотой 1 кГц.
30

52. Примеры дискретизации

а) Дискретизация синусоиды частотой 7 кГц с частотой 6 кГц
б) Дискретизация синусоиды частотой 4 кГц с частотой 6 кГц
с) Спектральные соотношения, демонстрирующие наложение синусоид с частотами 4
кГц и 7 кГц

53. Примеры дискретизации

Рассмотрим дискретизацию непрерывного действительного сигнала, спектр которого
показан на рисунке (а).
Спектр симметричен относительно частоты 0 Гц и его значения равны 0 для частот
выше +В Гц и ниже -В Гц, т. е. это сигнал с ограниченным спектром. Термин «сигнал с
ограниченным спектром» означает, что энергия сигнала за пределами диапазона ±В Гц
ниже чувствительности системы.
Задавшись частотой дискретизации fs отсчетов в секунду, можно увидеть эффект
размножения спектра при дискретизации на рисунке (b), на котором показаны исходный
спектр, а также бесконечное количество копий, повторяющихся с периодом f s Гц.

54. Примеры дискретизации

а) Спектр исходного непрерывного сигнала
b) Размножение спектра дискретного сигнала при f s / 2 B
c) Наложение частот при слишком низкой частоте дискретизации, т.к. f s / 2 B

55. Примеры дискретизации

Если сигнал представляется последовательностью дискретных значений, его спектр
принимает размноженную форму.
Размноженные спектры реально существуют
В практических схемах АЦП f s всегда берется больше 2В, чтобы оставить
разделительный промежуток в районе частот заворота f s / 2 .
Понизим частоту дискретизации до величины f s / 2 = 1.5В Гц. Спектральный результат
такой дискретизации показан на рисунке (с). Копии спектра теперь перекрывают
исходный спектр с центром на частоте 0 Гц.
Во-первых, нижняя и верхняя границы копий спектра с центральными частотами f s и
f s теперь лежат в интересующей нас полосе частот. Дискретные отсчеты, связанные
со спектром, показанным на рисунке (с), больше не представляют корректно исходный
сигнал. Спектральная информация в полосах частот от -В до -В/2 и от В/2 до В Гц
искажена.
Второй эффект, иллюстрируемый рисунком (с), состоит в том, что весь спектр
исходного непрерывного сигнала сосредоточен в полосе частот между -fs/2 и + fs/2.
Это ключевое свойство показано на рисунке (b). Любая энергия, расположенная
выше +В Гц и ниже -В Гц в спектре исходного непрерывного сигнала, показанного на
рисунке (а), всегда после дискретизации окажется в интересующей нас полосе частот,
независимо от частоты дискретизации. По этой причине на практике необходимы
непрерывные (аналоговые) фильтры нижних частот.

56. Примеры дискретизации

Размножение спектра:
а) Спектр смеси сигнала с шумом
b) Спектр дискретного сигнала, в котором шум искажает полезный сигнал

57. Примеры дискретизации

Низкочастотная фильтрация перед дискретизацией с частотой f s Гц

58. Ресэмплирование

• Ресэмплирование (resampling) –
переход от одной частоты
дискретизации к другой

59. Квантование

60. Квантование

q
Дискретный по времени x(t) и квантованный по уровню x (t)
Квантование
Дискретный по времени и квантованный по уровню сигнал
1
Дискретный сигнал
Квантованный по значению сигнал
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
0
5
10
Период дискретизации T 1 c,
Частота дискретизации f d 1 Гц,
Шаг квантования 0,125
Интервалов квантования N 16
15
Время ( с )
20
25
30

61. Квантование

• Исходно имеется дискретный набор
возможных значений амплитуд
(уровней квантования)
• Квантование сводится к тому, что
значение амплитуды каждого отсчета
сигнала округляется до ближайшего
дискретного уровня
• В память записываются не исходные
значения амплитуды, а округленные

62. Квантование

• Чем больше уровней квантования,
тем меньше ошибка, возникающая
из-за округления (т.наз. шум
квантования)
• Количество уровней квантования
обычно определяется количеством
бит на амплитуду
• Если количество бит на амплитуду =
n, то общее количество уровней
n
квантования = 2

63. Пример

• Пусть используется квантование 16
бит / отсчет (16 бит на отсчет)
• Это означает, что общее количество
16
уровней квантования = 2 = 65536
уровней
• Из этого числа половина уровней
используется для округления
положительных значений амплитуд, а
другая половина – отрицательных
значений

64. Квантование сигнала по уровню

i
m/2
xmax
xкв (n)
e(n)
3
2
1
0
-1
-2
-3
Q
nTд
Tд 2Tд 3Tд
-m/2 xmin
Рисунок 14
Погрешность квантования eкв(n) = хкв(n) x(n)
64

65. Квантование

16 уровней квантования требуют 4-х разрядный АЦП
Число уровней = 2 n
Рисунок 15

66. ИКМ

Исходный сигнал
АИМ отсчеты
ИКМ отсчеты с ошибкой
квантования
Сигнал на выходе ИКМ
Рисунок 16

67. Ошибки квантования

Преобразование непрерывного по уровню сигнала в цифровой — это
операция квантования (quantization). Термин «квантование»
происходит от латинского слова «quantum», что означает
«сколько». Квантование – это преобразование непрерывного по уровню
сигнала в цифровой сигнал с конечным количеством числовых
разрядов.
Разность между выходным сигналом квантователя и аналоговым
входным сигналом представляет собой неустранимую погрешность
(ошибку, шум) квантования по уровню
e( t ) y(t ) x( t )
.
При квантовании округлением ошибка
q
q
e( t )
2
2
q
e
(
t
)
Максимальное значение погрешности квантования равно max
.
2
Кроме квантования округлением (rounding) применяется также
квантование усечением (truncation). Оно более простое. Ненужные
разряды (цифры) при этом просто отбрасываются, но максимальная
погрешность квантования удваивается 0 e( t ) q , e ( t ) q .
max

68. Дискретные сигналы и системы

Квантование по уровню
Digital
0
1
2
3
4
3
2
1
4
5
6
7
111
110
101
Analog
-4
-3
-2
-1
0 100
-1
-2
-3
-4
1
2
3
011
010
001
000
Рис 17 — Получение двоичных кодовых групп
4

69. Ошибка квантования

1
0.5
0
-0.5
Модуль ошибки квантования
-1
0
5
10
15
20
25
30
0
5
10
15
Время (с)
20
25
30
0.2
0.15
0.1
0.05
0

70. Теорема Фурье

Всякое периодическое колебание частоты F можно получить в результате
суммирования бесконечного числа гармоник с частотами F, 2F, 3F, 4F, …,
и специально подобранными амплитудами и фазами
x(t) = A0 + A1sin(2 Ft + 1) + A2sin(2 2Ft + 2) + A3sin(2 3Ft + 3) + … (и
т.д.) ИЛИ
x(t ) A0 Ak sin( 2 kFt k )
k 1

71. Амплитудно-частотный спектр

72. Спектр мощности

73. Логарифмический спектр

74. Перевод в децибеллы

• Имеем дискретный набор гармоник
• Для каждой гармоники считаем
десятичный логарифм от амплитуды
данной гармоники
• Умножаем результат на 10
• Получаем логарифмический спектр в
децибеллах (дБ)

75. Огибающая спектра (spectral envelope)

76. Периодическое продолжение

С точки зрения спектрального анализа
дискретных сигналов, ЛЮБОЙ
дискретный сигнал считается
периодически продолженным

77. Пример – исходный и периодически продолженный сигналы

78. Периодическое продолжение

• Любой сигнал (вне зависимости от
того, является ли он физически
периодически или нет)
рассматривается как периодически
продолженный (= периодический)
• Для БПФ и участок гласного, и
участок фрикативного будут равно
периодическими

79. Теорема Фурье

• Раз любой дискретный сигнал
рассматривается как периодический
(с периодом Т, равным длительности
сигнала), то к нему можно применить
теорему Фурье
• Следовательно, любой дискретный
сигнал может быть представлен как
сумма гармоник с частотами (1/T),
(2/T), (3/T), (4/T) и т.д.

80. Пример

• Пусть длительность Т
анализируемого сигнала = 20
миллисекунд (0.02 секунд). Тогда
сигнал может быть представлен в
виде суммы гармоник с частотами 50
Гц (1 / 0.02), 100 Гц (2 / 0.02), и т.д.

81. Пример

Вычислим амплитуды разложения в ряд Фурье и построим линейчатый график
амплитудного спектра

82. Пример

Вычислим амплитуды разложения в ряд Фурье и построим линейчатый график
амплитудного спектра

83. Пример

По амплитудам разложения ak , bk восстановим исходный сигнал, используя ряд
Фурье и построим графики

84. Пример

По амплитудам разложения ak , bk восстановим исходный сигнал, используя ряд
Фурье и построим графики

85. Дискретное преобразование Фурье

• Дискретное преобразование Фурье
(ДПФ) (Discrete Fourier Transform, DFT) –
результат применения теоремы Фурье к
дискретному сигналу
• ДПФ позволяет вычислить спектр сигнала
по самому сигналу
• Обратное дискретное преобразование
Фурье (ОДПФ) (Inverse Discrete Fourier
Transform, IDFT) позволяет вычислить
сигнал по его спектру

86. Дискретное преобразование Фурье (discrete Fourier transform, DFT)

• Имеем исходную последовательность N комплексных
чисел (например, значения сигнала в N точках выборки)
x0, x1, … xN-1 . Последовательность N комплексных чисел
X0, X1, … XN-1, вычисляемых из исходной по формулам:
(21)
называется дискретным преобразованием Фурье (DFT)
исходной последовательности.
Обратное дискретное преобразование Фурье (Inverse
discrete Fourier transform, IDFT) дается формулой:
(22)

87. Дискретное преобразование Фурье (discrete Fourier transform, DFT)

• Нормировочный множитель 1/N и знаки экспонент в DFT
и IDFT—это соглашения, различающиеся в разных
реализациях. Единственное требование – знаки должны
быть противоположны, а произведение нормировочных
множителей должно быть 1/N.

88.

89.

90.

91. Пример ДПФ

Пример: На интервале Т= [0,99], N=100, задан дискретный сигнал
s(k) = δ(k-i) — прямоугольный импульс с единичными значениями на
точках k от 3 до 8. Форма сигнала и модуль его спектра в главном
частотном диапазоне, вычисленного по формуле
S(n) = s(k)× exp(-i2πkn/100) с нумерацией по n от -50 до +50 с шагом
по частоте, соответственно, Δω=2π /100, приведены на рисунке ниже.

92. Быстрое преобразование Фурье

• Быстрое преобразование Фурье (БПФ) (Fast
Fourier Transform, FFT) – способ «быстрого»
вычисления ДПФ за счет одного математического
трюка
• Обратное быстрое преобразование Фурье
(ОБПФ) (Inverse Fast Fourier Transform, IFFT) способ «быстрого» вычисления ОДПФ за счет
одного математического трюка
• Общее количество операций в БПФ – примерно
• Например, для 256 отсчетов имеем количество
операций 2048 операций (вместо 65536 для ДПФ)
N log 2 N

93. Быстрое преобразование Фурье (БПФ)

БПФ есть математически эквивалентный, но более
быстрый алгоритм вычисления ДПФ. Основная идея –
можно достичь экономии в расчетах, если сначала разбить
исходный ряд на два более коротких, выполнить ДПФ для
них, а потом определенным образом собрать полное ДПФ.
Соответственно можно получить еще большую экономию,
если при расчете ДПФ от половинок исходного сигнала,
тоже разделить каждую половинку на две части. И т.д.
Особенность БПФ – требования к длине реализации N.
Для достижения максимальной эффективности требуется
чтобы N было степенью двойки, т.е. 32,64,128,256,512, и
т.д. Если в исходном сигнале число отсчетов N не кратно
степени 2, то сигнал следует искусственно дополнить до
ближайшей степени 2 нулями либо средним значением по
имеющейся части.

94. В чем трюк?

Если длина сигнала в отсчетах есть
степень двойки (например, 256 отсчетов
8
9
= 2 , 512 отсчетов = 2 ), то количество
операций можно существенно сократить

95. БПФ

• Таким образом, для эффективного
использования БПФ длина сигнала в
отсчетах должна быть 64 или 128 или
256 или 512 или 1024 или 2048 и т.д.
• Как этого добиться в
действительности?

96. Дополнение нулями (zero-padding)

97. MATLAB

• Y = fft(x) — без дополнения нулями
(может вычислять ОЧЕНЬ медленно,
если длина сигнала x в отсчетах не
равна степени двойки)
• Y = fft(x, N) – с дополнением нулями
до N (где N – число, равное степени
двойки, и большее, чем исходная
длина сигнала x в отсчетах)
• X = ifft(Y) – ОБПФ

98. Пример

99. 512-БПФ (амплитудный спектр)

100. 512-БПФ (логарифмический спектр)

101. Свойство 3

• БПФ-спектр симметричен относительно
срединной гармоники (например, 256-й
гармоники для 512-точечного БПФ)
• Соответствующая частота = половине
частоты дискретизации
• Например, для частоты дискретизации 16
кГц БПФ-спектр симметричен
относительно частоты 8 кГц
• Необходимо вычислять спектр только до
половины частоты дискретизации

102. 512-БПФ, физический спектр

103. 512-БПФ

104. ОБПФ

105. Что нужно помнить

• Если длина сигнала в отсчетах = N, в секундах =
Т, то сигнал можно представить суммой из N
гармоник с частотами 1/T, 2/T, 3/T, …, N/T
• БПФ-спектр нужно вычислять до гармоники с
частотой N/(2T)
• Если частота дискретизации сигнала = Fs, то
БПФ-спектр вычисляется до частоты Fs/2
• Если N – не степень двойки, то необходимо
дополнить нулями сигнал до ближайшего числа,
являющегося степенью двойки (в MATLAB это
делается автоматически)

106. Фурье-изображение прямоугольного импульса

Процесс из одиночного прямоугольного импульса
0.8
Y(t)
0.6
0.4
0.2
0
0
0.2
0.4
0.6
Время (с)
0.8
1
Сформируем процесс, состоящий из одиночного прямоугольного импульса. Зададим
шаг дискретизации Ts=0.01с, длительность процесса Т=100с, амплитуду импульса
А=0.75 и его ширину w=0.5с:

107. Фурье-изображение прямоугольного импульса

Модуль Фурье-изображения прямоугольного импульса
20
Модуль
15
10
5
0
-50
0
Частота (Гц)
50
Сформируем процесс, состоящий из одиночного прямоугольного импульса. Зададим
шаг дискретизации Ts=0.01с, длительность процесса Т=100с, амплитуду импульса
А=0.75 и его ширину w=0.5с:

108. Фурье-изображение полигармонического процесса

Рассмотрим пример трехчастотных гармонических колебаний — с частотою 1/π, 1 и 3
Гц и амплитудами соответственно 0.6, 0.3 та 0.7:
y (t ) 0.6·cos(2t ) 0.3sin(2 t ) 0.7 cos(6 t / 4).
Найдем Фурье-изображение этого процесса и выведем графики самого процесса,
модуля его Фурье-изображения, а также действительную и мнимую части:
Трехчастотный полигармонический процесс
2
Y(t)
1
0
-1
-2
0
10
20
30
40
50
Время (с)
60
70
80
90
100

109. Фурье-изображение полигармонического процесса

Модуль Фурье-изображения полигармонического процесса
3500
3000
Модуль
2500
2000
1500
1000
500
0
-4
-2
0
Частота (Гц)
2
4
Результат Фурье-преобразования мало что говорит об амплитудах гармонических
составляющих. Это обусловлено различием между определениями Фурье-изображения
и комплексного спектра. Поэтому для незатухающих (установившихся, стационарных)
колебаний любого вида намного удобнее находить не Фурье-изображение, а его
величину, деленную на число точек в реализации.

110. Фурье-изображение полигармонического процесса

Действит. часть
3000
Комплексный спектр полигармонических колебаний
2000
1000
0
-1000
-4
-3
-2
-1
-3
-2
-1
0
1
2
3
4
0
1
Частота (Гц)
2
3
4
Мнимая часть
4000
2000
0
-2000
-4000
-4
Результат Фурье-преобразования мало что говорит об амплитудах гармонических
составляющих. Это обусловлено различием между определениями Фурье-изображения
и комплексного спектра. Поэтому для незатухающих (установившихся, стационарных)
колебаний любого вида намного удобнее находить не Фурье-изображение, а его
величину, деленную на число точек в реализации.

3.1. Анализ причин формирования погрешностей цифрового моделирования

При преобразовании аналогового сигнала в цифровой выполняются две основные операции: временная дискретизация и квантование по уровню. При выполнении этих операций возникают погрешности и поэтому для разработки методики использования методов цифрового моделирования необходимо выявление источников формирование погрешностей и их анализ. Как указывалось выше, структура рекурсивного алгоритма полностью совпадает со структурой цифрового фильтра, реализующего этот алгоритм [87]. Следовательно, анализ погрешностей рекурсивного алгоритма можно проводить теоретически и экспериментально на цифровом фильтре.

Погрешности дискретизации. Теоретически процесс дискретизации аналогового сигнала приведен при выводе теоремы Котельникова, согласно которой для передачи информации без искажений частота дискретизации должна быть в два раза больше высшей частотной составляющей аналогового сигнала. Однако эта теорема применима для идеализированного случая, а именно частотный спектр аналогового сигнала должен быть ограничен, а временной соответственно неограничен, а при восстановлении сигнала должен быть использован идеальный фильтр с прямоугольной частотной характеристикой и использован ряд Котельникова. Таким образом, теорема Котельникова имеет фундаментальное значение. На практике в цифровых системах управления при восстановлении сигнала используется устройство выборки и хранения, представляющее собой экстраполятор нулевого порядка. Поэтому выбор частоты дискретизации в цифровых системах управления по теореме Котельникова может не обеспечить требуемой точности или даже нормальной работы. Из анализа проведенных исследований [16] следует, что при восстановлении гармонической функции с помощью экстраполятора нулевого порядка с погрешностью не более 1 % частота дискретизации должна быть больше основной частоты в 22 раза. Выбор частоты дискретизации должен выполняться из условия компромисса между точностью преобразования и объемом выполняемых операций в единицу времени, то есть быстродействием цифровой системы. Погрешность и быстродействие цифровой системы зависит от алгоритма обработки информации погрешностей квантования по уровню. Поэтому для разработки методик обоснованного выбора частоты дискретизации необходимы экспериментальные исследования погрешностей типовых динамических звеньев.

Погрешности квантования в цифровых системах. При анализе точности цифровых систем обычно выделяются три источника погрешностей: квантование входного сигнала, квантование коэффициентов фильтра (передач и передач с задержкой) и округление результатов арифметических операций. Из этих трех источников погрешности округления является наиболее существенной. Погрешность квантования коэффициентов цифрового фильтра вызывает искажение его частотной характеристики в сравнении с частотной характеристикой аналоговой модели, а также может привести к неустойчивости фильтра [5, 19, 20].

Погрешность квантования входного сигнала. Квантование входного сигнала осуществляется аналого-цифровым преобразователем. При этом входной сигнал периодически дискретизируется и каждая выборка кодируется в цифровое слово длиной В бит. Погрешность квантования входного сигнала ограничивается половиной шага квантования. Для большинства входных сигналов последовательность {e(n)} может рассматриваться как белый шум, статистически не зависящий от исходной последовательности, и поэтому ее называют шумом квантования. Белый шум – это абсолютно случайный процесс, обладающий равномерным спектром в очень широком диапазоне частот [4]. Понятие белого шума – это удобная абстракция, поскольку средний квадрат такого процесса равен бесконечности вследствие того, что площадь, ограниченная функцией спектральной плотности, бесконечна. Понятие белого шума оказывается полезным при анализе линейных систем, особенно в тех случаях, когда ширина спектральной плотности сигнала на входе системы значительно шире полосы пропускания этой системы или время корреляции шума много меньше всех существующих постоянных времени системы, на которую воздействует шум. Таким образом, предположение, что входной сигнал является белым шумом, значительно упрощает решение задачи.

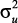
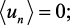
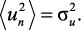
В линейной системе с передаточной функцией W(z) и стационарным входным сигналом {un} выходной сигнал {υn} тоже будет стационарным [4]. Обычно предполагается, что входная последовательность является белым шумом, имеет нулевое среднее и дисперсию , то есть

(3.1)

Стационарный случайный процесс принято описывать двумя характеристиками – спектральной плотностью G(z) и автокорреляционной функцией В(τ). Для белого шума эти характеристики соответственно равны 1(z) и δ(τ). Спектральные плотности входной и выходной последовательностей для стационарного случайного процесса связаны соотношением:

(3.2)

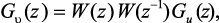
где W(z–1) величина комплексно-сопряженная W(z), z = ejλ и λ = 2πf/F, f, F – частоты аналогового сигнала и дискретизации.

Автокорреляционная функция вычисляется по формуле Винера-Хинчина

(3.3)

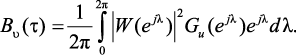
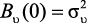
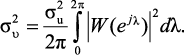
При τ = 0 имеем , и тогда значение спектральной плотности для белого шума 1(ejλ) определяется выражением

(3.4)

В общем случае, когда {un} не является белым шумом, но сохраняет стационарность и имеет нулевое среднее значение и спектральную плотность мощности Φuu(z), его дисперсия

(3.5)

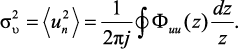
Выходной сигнал в этом случае также является стационарным случайным процессом с нулевым средним, спектральной плотностью мощности и дисперсией соответственно

(3.6)

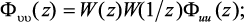
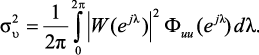
В соответствии с этим входной сигнал представляется в виде двух аддитивных составляющих: исходной {x(n)} и шум квантования {e(n)}. В соответствии с принципом суперпозиции для линейного цифрового фильтра выходной сигнал также состоит из двух аддитивных составляющих: идеального выходного сигнала {y(n)} и сигнала погрешности, вызванной входным шумом {e(n)}.

Сигнал погрешности определяется выражением:

(3.7)

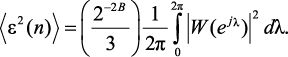
Погрешность квантования коэффициентов. При практической реализации фильтра с передаточной функцией

(3.8)

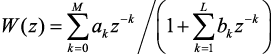
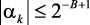
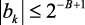
коэффициенты всегда квантуются. Если αk и βk – погрешности квантования коэффициентов, удовлетворяющие условиям: и ,
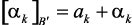
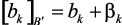
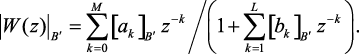
то реальные коэффициенты имеют вид , , где B’ число бит для представления коэффициентов. В результате передаточная функция принимает следующий вид

(3.9)

Смещение полюсов и нулей передаточной функции вследствие квантования коэффициентов можно определить по формуле:

(3.10)

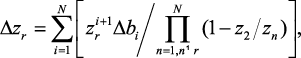
где Δbi – изменение коэффициента bi, z1 z2 … zr – положение полюсов идеального фильтра. Доказано, что чувствительность смещения полюсов к коэффициентам увеличивается с ростом порядка фильтра при прямой форме реализации. Таким образом, реализация фильтра выше второго порядка в прямой форме нежелательна. В этом случае предпочтительнее параллельная или каскадная форма. Если полюсы близко расположены к единичной окружности в z-плоскости, то в результате их смещения фильтр может стать неустойчивым.

Погрешность округления. Как указывалось выше, основной погрешностью в цифровых в рекурсивных фильтрах является погрешность округления [4], которая накапливается за счет перехода из предыдущих состояний в последующие. Точное значение отсчета сигнала в двоичной форме определяется выражением

(3.11)

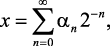
где αn = 0 или 1.

При округлении длины x некоторым количеством разрядов N вместо точного значения получается его округленное (машинное) представление. Существуют два способа выполнения этой операции: усечение или округление. При усечении сохраняются старшие N бит, а все младшие разряды усекаются, а при округлении выполняется операция согласно формуле

(3.12)

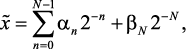
причем коэффициент βN равен αn или αn + 1 в зависимости от того, нуль или единица содержится в (N + 1)-м разряде.

Округление является более точным, чем усечение, но аппаратно реализуется сложнее и требует больших затрат времени. По этой причине чаще применяется первый способ.