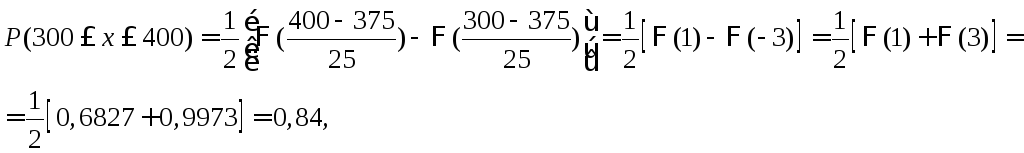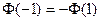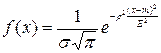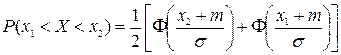Ошибки измерений подчиняются нормальному закону прибор имеет систематическую

Решение типовых задач. Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками

Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением =100 м. Найти:

1) вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м,

2) вероятность того, что измеренная дальность не превзойдет истинной.

Обозначим через X суммарную ошибку измерения дальности. Ее систематическая составляющая — 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид

.

1) Согласно общей формуле имеем

.

Интеграл вероятности является функцией нечетной, поэтому

.

;

.

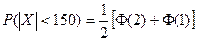
2) Вероятность того, что измеренная дальность не превзойдет истинной,

.

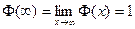
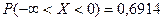
Так как , а из таблицы находим , то

.

Пример 12.2. Определить срединную ошибку прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ± 20 м.

Из условия задачи следует, что

.

Неизвестное значение срединной ошибки находим как решение уравнения

.

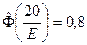
С помощью таблицы получим

,

м.

Дата добавления: 2014-12-23 ; просмотров: 177 ; Нарушение авторских прав

Источник

Занятие 12. Закон нормального распределения.

Краткая теоретическая часть

Плотность вероятности нормально распределенной случайной величины имеет вид

,

где — среднее квадратическое отклонение, — срединное отклонение (иногда называемое и «вероятным отклонением»),

Вероятность попадания нормально распределенной случайной величины X в интервал вычисляется по одной из следующих формул:

1) ,

где — функция Лапласа (интеграл вероятности);

2) ,

где — приведенная функция Лапласа.

Значения функций и даны в специальных таблицах.

Во всех задачах данного параграфа ошибки измерения считаются нормальными величинами.

1. Нормальное распределение играет достаточно важную роль в теории вероятностей и среди законов занимает особое положение. Укажите причины, по которым, на Ваш взгляд, это происходит:

а) Это наиболее часто употребляемый во многих приложениях закон распределения

б) Нормальный закон распределения применим как для дискретных, так и для непрерывных случайных величин

в) Нормальный закон распределения является предельным законом, к которому сходятся другие при весьма типичных часто встречающихся условиях

г) Нормальный закон распределения таков, что позволяет характеризовать сравнительную крутость других законов относительно него

2. Плотность вероятности нормально распределенной случайной величины имеет вид:

а)

б)

в) или

г)

д)

е) или

3. Параметры и закона нормального распределения совпадают с математическим ожиданием и среднеквадратическим отклонением нормально распределенной случайной величины соответственно. Следовательно, они определенным образом характеризуют случайную величину. А как? Выберите наиболее точный, на Ваш взгляд, вариант ответа.

а) Характеризуют форму кривой распределения и положение распределения случайной величины на оси абсцисс соответственно

б) Характеризуют положение распределения случайной величины на оси абсцисс и форму кривой распределения соответственно

в) Определяют центр рассеянья и центр симметрии случайной величины соответственно

г) Определяют центр симметрии и центр рассеянья случайной величины соответственно

4. Какой особенностью обладают моменты нормального распределения?

а) Все четные центральные моменты равны нулю.

б) Все нечетные центральные моменты равны нулю.

в) Все центральные моменты равны нулю

5. Одной из формул, по которым можно вычислить вероятность попадания нормально распределенной случайной величины в заданный интервал является (здесь — функция Лапласа (интеграл вероятности)):

а)

б)

в)

г)

6. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, обладают следующим свойством:

в) равны параметру Пуассона

Решение типовых задач

Пример 12.1. Измерение дальности до объекта сопровождается систематическими и случайными ошибками. Систематическая ошибка равна 50 м в сторону занижения дальности. Случайные ошибки подчиняются нормальному закону со средним квадратическим отклонением =100 м. Найти:

1) вероятность измерения дальности с ошибкой, не превосходящей по абсолютной величине 150 м,

2) вероятность того, что измеренная дальность не превзойдет истинной.

Обозначим через X суммарную ошибку измерения дальности. Ее систематическая составляющая — 50 м. Следовательно, плотность вероятности суммарной ошибки имеет вид

.

1) Согласно общей формуле имеем

.

Интеграл вероятности является функцией нечетной, поэтому

.

;

.

2) Вероятность того, что измеренная дальность не превзойдет истинной,

.

Так как , а из таблицы находим , то

.

Пример 12.2. Определить срединную ошибку прибора, если систематических ошибок он не имеет, а случайные распределены по нормальному закону и с вероятностью 0,8 не выходят за пределы ± 20 м.

Из условия задачи следует, что

.

Неизвестное значение срединной ошибки находим как решение уравнения

.

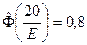
С помощью таблицы получим

,

м.

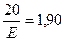
12.4. Задачи для самостоятельной работы

12.1. Измерительный прибор имеет систематическую ошибку 5 м и среднюю квадратическую ошибку 75 м, Какова вероятность того, что ошибка измерения не превзойдет по абсолютной величине 5 м?

(Ответ: )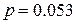

12.2. Систематическая ошибка удержания высоты самолетом +20 м, а случайная ошибка имеет среднее квадратическое отклонение 75 м. Для полета самолета отведен коридор высотой 100 м. Какова вероятность, что самолет будет лететь ниже, внутри и выше коридора, если самолету задана высота, соответствующая середине коридора?

12.3. Срединная ошибка измерения дальности радиолокатором равна 25 м, а систематическая ошибка отсутствует. Определить:

а) дисперсию ошибок измерения дальности;

б) вероятность получения ошибки измерения дальности, по абсолютной величине не превосходящей 20 м.

12.4. Случайное отклонение размера детали от номинала при изготовлении ее на данном станке имеет нулевое математическое ожидание и среднее квадратическое отклонение, равное 5 мк. Сколько необходимо изготовить деталей, чтобы с вероятностью не менее 0,9 среди них была хотя бы одна годная, если для годной детали допустимо отклонение размера от номинала не более, чем на 2 мк?

(Ответ: )

12.5. Даны две случайные величины X и Y, имеющие одинаковые дисперсии, но первая распределена нормально,а вторая равномерно. Определить соотношение между их срединными отклонениями.

(Ответ: )

12.6. Нормально распределенная случайная величина X имеет математическое ожидание м и срединное отклонение 10 м. Вычислить таблицу функции распределения для значений аргумента через каждые 10 м и построить график.

12.7. Систематическая ошибка высотомера равна +20 м, а случайные ошибки распределены по нормальному закону. Какую среднюю квадратическую ошибку должен иметь высотомер, чтобы с вероятностью 0,9 ошибка измерения высоты по абсолютной величине была меньше 100 м?

(Ответ: . Получающееся трансцендентное уравнение проще решить графически)

12.8. Найти связь между средним арифметическим отклонением

нормально распределенной случайной величины и ее средним квадратическим отклонением.

(Ответ: )

12.9. Определить для нормально распределенной случайной величины X, имеющей М [X] = 0,

1)

2) (при

(Ответ: 1) 0,1587; 0,0228; 0,00135; 2) 0,3173; 0,0455; 0,0027)

12.10. Заряд охотничьего пороха отвешивается на весах, имеющих среднюю квадратическую ошибку взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить вероятность повреждения ружья, если максимально допустимый вес порохового заряда 2,5 г.

(Ответ: )

12.11. Производятся два независимых измерения прибором, имеющим среднюю квадратическую ошибку 30м и систематическую ошибку +10м. Какова вероятность того, что обе ошибки измерений, имея разные знаки, по абсолютной величине превзойдут 10 м?

(Ответ: )

12.12. На плоскости проведены две параллельные прямые, расстояние между ними L. На эту же плоскость бросается круг радиуса R. Центр рассеивания расположен на расстоянии b от одной из линий во внешнюю сторону. Срединное отклонение центра круга в направлении, перпендикулярном линии, равно Е.

Определить при одном бросании:

а) вероятность накрытия кругом хотя бы одной прямой;

б) вероятность накрытия обеих прямых, если L= 10м, R = 8м, b=5м, E=10м.

12.13. Изделие считается высшего качества, если отклонение его размеров от номинала не превосходит по абсолютной величине 3,45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону со средним квадратическим отклонением, равным 3 мм, а систематические отклонения отсутствуют. Определить среднее число изделий высшего сорта, если изготовляются четыре изделия.

(Ответ: изделия)

12.14. Какой ширины должно быть поле допуска, чтобы с вероятностью не более 0,0027 получалась деталь с контролируемым размером вне поля допуска, если случайные отклонения размера от середины поля допуска подчиняются закону нормального распределения с параметрами = 0 и = 5 мк

12.15. Какое наибольшее расстояние допустимо между двумя рыболовецкими судами, идущими параллельными курсами, чтобы вероятность обнаружения косяка рыбы, находящегося посередине между ними, была не менее 0,5, если дальность обнаружения косяка для каждого из судов является независимой нормально распределенной случайной величиной с км и средним квадратическим отклонением =1,1 км?

12.16. При большом числе измерений установлено, что 75% ошибок

б) не превосходят по абсолютной величине 1,25 мм.

Заменяя частоты появления ошибок их вероятностями, определить в обоих случаях среднее квадратическое отклонение ошибок измерения, считая их нормально распределенными с нулевым математическим ожиданием.

12.17. Случайное отклонение X размера детали от номинала распределено по нормальному закону с математическим ожиданием и средним квадратическим отклонением . Годными деталями являются те, для которых а b.

а) функцию распределения случайных отклонений размеров деталей, подлежащих переделке;

б) функцию распределения случайных отклонений размеров годных деталей.

(Ответ: а) ) для ; б) для )

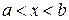
12.18. Нормально распределенная случайная величина X имеет нулевое математическое ожидание. Определить среднее квадратическое отклонение , при котором вероятность была бы наибольшей ( ).

(Ответ: )

1. Б.В. Гнеденко. Курс теории вероятностей, Изд. «Наука», 1969.

2. Е.С. Вентцель. Теория вероятностей, Изд. «Наука», 1969.

3. И.В. Дунин – Барковский, Н.В. Смирнов, Теория вероятностей и математическая статистика, ГТТИ, 1965.

4. И.Н. Коваленко, А.А. Филиппова, Теория вероятностей и математическая статистика, «Высшая школа», 1973.

5. Ю.В. Кожевников, Теория вероятностей и математическая статистика, Изд. «Машиностроение», 2002.

6. Сборник задач по теории вероятностей, математической статистике и теории случайных функций. Под редакцией А.А Свешникова, «Наука», 1970.

7. Л.Д. Мешалкин, Сборник задач по теории вероятностей, Изд. «МГУ». М., 1963.

8. Г.В. Емильянов , В.П. Скитович, Задачи по теории вероятностей и математической статистике, Изд. «ЛГУ». Ленинград, 1967.

9. В.В. Скворцов, Теория вероятностей, Изд. «Мир». М., 1993.

10. Руководство для инженеров по решнию задач теории вероятностей. Под редакцией А.А Свешникова, «Судпромгиз». Ленинград, 1962.

Источник

Тема. Законы распределения случайных величин

1. Нормальное распределение

Пример 1.Вес вылавливаемых в пруду
рыб подчиняется нормальному закону с
математическим ожиданием, равным 375 г,
и средним квадратическим отклонением
25 г. Определить вероятность того, что
вес одной пойманной рыбы будет заключен
в пределах от 300 до 400г.

Решение.

Дано: М(Х)=а=375 г.,
г.,
с=300г.,d=400г.

Найдем искомую вероятность.

где функции Лапласа Ф(1) = 0,6827, Ф(3) = 0,9973.

Пример 2. Ошибка измерения прибора
подчиняется нормальному распределению.
С вероятностью 0,92 ошибка измерения не
превосходит 4. Найти среднее квадратическое
отклонение ошибки прибора. Систематическая
ошибка отсутствует.

Решение.

Дано:
,

Воспользовавшись второй теоремой о
нормальной случайной величине, найдем
величину
.

Из таблицы Лапласа, зная
, найдемt=1,75.

Тогда
или

Ответ:
.

2. Равномерное распределение

Пример 3. Цена деления шкалы
прибора 0,5 вольт. При измерениях показания
округляются до ближайшего целого
деления. Найти вероятность того, что
при считывании показаний будет сделана
ошибка, не превышающая 0,01 вольт.

Решение.

Дано: Случайная величина Х — истинное
показание прибора имен равномерное
распределение с параметрами а=0 ,в=0,5. Тогда.
Искомая вероятность – это вероятность
показания х либо на,
либо на.

Задания для самостоятельной работы

1) Размер детали подчиняется
нормальному закону распределения со
средней арифметической 15 мм и дисперсией
0,25. Определить ожидаемый процент брака,
если допустимые размеры находятся в
пределах от 14 мм до 17 мм. Найти выражение
интегральной и дифференциальной функции.

2) Изготовленные цехом детали по
размерам диаметра распределяются по
нормальному закону с математическим
ожиданием, равным 4,5 см, и средним
квадратическим отклонением 0,5 см.
Определить вероятность того, что размер
диаметра наудачу взятой детали отклонится
от математического ожидания не более,
чем на 1 см.

3) Математическое ожидание нормально
распределенной случайной величины
равно 15, среднее квадратическое отклонение
равно 5. Определить вероятность того,
что абсолютная величина отклонения
Х-М(Х) будет меньше 10.

4) Ошибка измерения – нормально
распределенная случайная величина с
дисперсией, равной 100. Систематическая
ошибка отсутствует. Найти вероятность
того, что ошибка измерения окажется в
интервале (3;6).

5) Ошибка взвешивания – случайная
нормально распределенная величина с
дисперсией 400. Весы заранее настроены
на обвес 50 г. Найти вероятность того,
что ошибка взвешивания находится в
пределах от 30 до 70 г.

6) Автобус некоторого маршрута идет
с интервалом в десять минут. Пассажир
в какой-то момент подходит к остановке.
Время, в течении которого пассажир
ожидает автобус, представляет случайную
величину, имеющую равномерное
распределение. Определить дифференциальную
функцию распределения этой случайной
величины, ее математическое ожидание
и дисперсию.

7) По данным задачи 6 определить
вероятность того, что пассажир подошедший
к остановке, будет ждать автобус менее
4 минут.

Цена деления шкалы измерительного
прибора равна 0,2. Показания прибора
округляют до ближайшего целого деления.
Найти вероятность того, что при отсчете
будет сделана ошибка:

а) меньшая 0,04;

б) большая 0,05.

9) Минутная стрелка электрических
часов перемещается скачком в конце
каждой минуты. Найти вероятность того,
что в данное мгновение часы покажут
время, которое отличается от истинного
не более чем на 20 сек.

Форма контроля:
Проверка
решений задач и заданий

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Фрагмент работы:

Ошибки измерений прибора подчиняются нормальному закону распределе…

К.Р. №1.

№1.

В урне тысяча лотерейных билетов с номерами от 1 до 1000. Найти вероятность того, что номер наудачу вынутого билета: а) четный; б) нечетный; в)  1000; г)  1000.

РЕШЕНИЕ:

…

№2.

Три фирмы выполняют один и тот же заказ. Вероятность того, что первая фирма выполнит заказ в срок 0.75, вторая — 0.8, третья — 0.9, по отдельности. Определить вероятность того, что: а) одновременно первая и вторая выполнят заказ, а третья не успеет; 6) все три одновременно не выполнят заказ в срок.

РЕШЕНИЕ:

…

№3.

В клетке 30 попугаев: 20 говорящих и 10 неговорящих. Наудачу выбирают 4 попугая. Какова вероятность того, что среды них трое будут говорящих?

РЕШЕНИЕ:

…

№4.

На экспертизу под скрытыми девизами поступают проекты от трех конкурирующих фирм. Вероятность того, что проект первой фирмы пройдет экспертизу с положительной оценкой равна 0.8, второй — 0.6, третий — 0.9. Для экспертизы выбрали наудачу только один проект. Он ее прошел с хорошей оценкой. Какова вероятность того, что это был проект первой фирмы?

РЕШЕНИЕ:

…

К.Р. №2.

№1.

Производится ряд выстрелов по мишени с вероятностью попадания 0.7 при каждом выстреле; стрельба ведется до первого попадания в мишень, но не свыше 5 выстрелов. Найти закон распределения, математическое ожидание и дисперсию числа произведенных выстрелов. Построить функцию распределения, определить вероятность того, что число выстрелов до первого попадания будет не меньше трех.

РЕШЕНИЕ:

…

№2.

Для непрерывной случайной величины задана плотность распределения

-x+

Требуется построить графики плотности распределения и функции распределения, определив предварительно параметр А. Найти математическое ожидание, дисперсию, среднеквадратическое отклонение. Найти вероятность того, что отклонение случайной величины от математического ожидания будет не более среднеквадратического отклонения.

РЕШЕНИЕ:

…

№3.

Ошибки измерений прибора подчиняются нормальному закону распределения. Прибор имеет систематическую ошибку a и среднеквадратическую ошибку :

a= 5 м =75 м n=3 =0 м =80 м

Какова вероятность того, что n ошибок измерений попадают в интервал (;)?

РЕШЕНИЕ:

…

Список файлов
33531.docx	97 КБ

Информация по контрольной
код работы (ID)	33531
просмотров	1613
страниц	7
таблиц	2
формул	> 36
изображений	3
оформление по ГОСТу	ДА
были доработки	НЕТ
проверено преподавателем Сибстрин	ДА

Его решение имеет вид ш Ьг аг 2(1пЬ вЂ” 1па) 158 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Нетрудно проверить, что при фиксированных значениях а и Ь, в силу условия О < а < Ь < +со справедливы соотношения Р(а < Х < Ь) = Фо( ) Фо(-) — +О Ь а Р1а <Х <Ь) =Фо( — ) Фо( ) — + О. Позтому вероятность Р(а < Х < Ь) при (Ь2 2) 2(1п Ь вЂ” 1па) принимает максимальное значение. Вопросы и задачи 4.1. Дайте определение случайной величины. 4.2. Что называют законом распределения (вероятностей) случайной величины? 4.3.

Дайте определение функции распределения (вероятностей). Перечислите и докажите свойства функции распределе- 4.4. Как, зная функцию распределения, найти вероятность попадания случайной величины в заданный интервал? 4.5. Какие свойства должна иметь некоторая функция для того, чтобы она могла быть функцией распределения? 4.6. Какую случайную величину называют дискретной? Приведите примеры дискретных случайных величин.

4.7. Что называют рядом распределения дискретной случайной величины? Как еще можно задать закон распределения дискретной случайной величины? Волросм иэалачя 159 4.8. Какой вид имеет функция распределения дискретной случайной величины? 4.9. Какое распределение называют биномиальным? 4.10. Какое распределение называют распределением Пуассона? 4.11.

Какое распределение называют геометрическим распределением? 4.12. Какую случайную величину называют непрерывной? Приведите примеры непрерывный случайных величин. 4.13. Дайте определение плотности распределения (вероятностей). Перечислите и докажите свойства плотности распределения. Существует ли плотность распределения у дискретной случайной величины? 4.14. Как, зная плотность распределения, найти вероятность попадания случайной величины в заданный интервал? 4.15. Чем различаются графики функций распределения дискретной и непрерывной случайных величин? 4.18. Какое распределение называют равномерным? 4.17.

Какое распределение называют экспоненциальным (показательным)? 4.18. Какое распределение называют нормальным? 4.19. Как выглядит график плотности нормального распределения? 4.20. Что называют интегралом Лапласа? Как, пользуясь таблицей значений интеграла Лапласа, вычислить вероятность попадания нормально распределенной случайной величины в некоторый интервал? 4.21. Какое распределение называют распределением Вейбулла? 160 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 4.22.

Какое распределение называют гамма-распределением? 4.23. Из партии в 10 деталей, среди которых две бракованные, наудачу выбирают три детали. Найдите закон распределения числа бракованных деталей среди выбранных. Постройте функцию распределения. Ответ: 4.24. Вероятность приема самолетом радиосигнала при каждой передаче равна 0,7. Найдите ряд распределения и функцию распределения числа Х принятых сигналов при шестикратной передаче. Ответ: Ряд распределения и функцию распределения случайной величины Х легко построить, зная, что Р(Х = з) = =Со1(0,7)'(0,3)о ‘, 4 =0,6. 4.25.

Найдите закон распределения случайной величины Х вЂ” числа таких бросаний трех игральных костей, в каждом из которых ровно на двух костях появится по 2 очка, если общее число бросаний равно 15. Ответ: Р(Х=з)=С11зр’Чы ‘, 4=0,15, где р=Сз(1/6)~(5/6) = = 5/72 я~ 0,0694. 4.26. В течение часа на станцию скорой помощи поступает случайное число Х вызовов, распределенное по закону Пуассона с параметром Л = 5. Найдите вероятность того, что в течение часа поступит: а) ровно два вызова; б) не более двух вызовов; в) не менее двух вызовов. О, С.Сз-с 7/15 Р(Х з) зз 4=0,1,2; Р(х) = С1зо 14/15 1, х<0; х Е (О, 1]; х Е (1, 2]; х > 2.

161 Вопросы и задачи Ответ: а) Р1Х =2) =5эе ~/2! 0,086; б) Р(Х < 2) = (5о/О! + 51/1! + 5э/2!)е а — 0,127; в) Р1Х ) 2) = 1 — Р1Х < 2) = 1 — (5е/О!+ 51/1!)е ~ 0,041. 4.27. Число вызовов, поступающих на АТС (автоматическая телефонная ставция) каждую минуту, распределено по закону Пуассона с параметром Л = 1,5. Найдите вероятность того, что за минуту поступит: а) ровно три вызова; б) хотя бы один вызов; в) менее пяти вызовов. Ответ: а) 0,12551; б) 0,77687; в) 0,98143.

4.28. В приборный отсек космического корабля за время полета попадает случайное число частиц, распределенное по закону Пуассона с параметром Л, причем вероятность попасть в блок управления, расположенный в отсеке космического корабля, для каждой иэ этих частиц равна р. Определите вероятность попадания в блок: а) ровно й частиц; б) хотя бы одной частицы. Ответ: а) (Лр)»е «и/й!; 6) 1 — е ~’з. 4.29. По цели производят серию независимых выстрелов до первого попадания.

Даны вероятность р попадания в цель при одном выстреле и запас патронов и. Найдите ряд распределения и функцию распределения числа Х израсходованньп~ патронов. рд’ ‘, з’=б;и:Т (9=1-р); Ответ: Р1Х =з) = ! 9 ~ Ф=п. 4.30. Летательный аппарат, по которому ведется стрельба, состоит из двух различных по уязвимости частей. Аппарат выходит из строя при одном попадании в первую часть или трех попаданиях во вторую.

Стрельба ведется до поражения летательного аппарата. Постройте ряд распределения и функцию 6 — той 162 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ распределения числа попаданий Х в летательный аппарат, которое понадобится для его поражения, если каждый попаюпий в аппарат снаряд с вероятностью 0,3 поражает первую часть и с вероятностью 0,7 — вторую. О т в е т: Р(Х = 1) = 0,3; Р [Х = 21 = 0,21; Р(Х = 3) = 0,49.

4.31. Непрерывная случайная величина Х распределена по экспоненцизльному закону с параметром А = 0,2. Найдите вероятность попадания этой случайной величины в интервал (О, 2). Ответ: 1 — е е4 я~ 0 33. 4.32. Длительность времени Х безотказной работы элемента имеет экспоненцизльное распределение с параметром Л = = 0,02 ч 1. Вычислите вероятность того, что за время $ = 100 ч элемент: а) выйдет из строя; б) будет исправно работать. Ответ: а) 1 — е з ж0,865; б) е з 0,135. 4.33. Случайная величина Х имеет нормальное распределение с параметрами гп = 2 и и = 1. Определите вероятность попадания случайной величины в интервал (1, 5).

Ответ: 0,83999. 4.34. Случайная величина Х распределена по нормальному закону с параметрами т = 4 и и = 1. Определите вероятность попадания случайной величины Х в интервал (6, 8). Ответ: 0,0227. 4.35. Случайная величина Х имеет нормальное распределение с параметрами т и и. Вычислите вероятность попадания случайной величины в интервал (пз — 4о’, т). Ответ: 0,499971. 4.36.

Случайная величина Х подчинена нормальному закону распределения с тп = О. Вероятность попадания случайной величины в интервал (-0,3, 0,3) равна 0,5. Найдите среднее квадратичное отклонение и. Ответ: о 0,44. 153 Воиросьг и задачи 4.3Т. Измерительный прибор имеет систематическую погрешность 5 м. Случайные погрепности подчиняются нормальному закону со средним квадратическим отклонением, равным 10 м. Какова вероятность того, что погрешность измерения не превзойдет по абсолютному значению 5 м? Ответ: 0,3413.

4.38. Измерение дальности до объекта сопровождается случайными погрешностями, подчиняющимися нормальному закону со средним квадратичным отклонением, равным 50 м. Систематическая погрешность отсутствует. Найдите: а) вероятность измерения дальности с погрешностью, не превосходящей по абсолютному значению 100 м; б) вероятность того, что измеренная дальность не превзойдет истинной. Ответ: а) 0,9545; б) 0,5. 4.39.

Высотомер имеет случайную и систематическую погрешности. Систематическы погрешность равна 20 м. Случайная погрешность распределена по нормальному закону. Какую среднюю квадратичную погрешность должен иметь прибор, чтобы с вероятностью 0,9452 погр~пность измерения высоты бь|ла меньше 10 му Ответ: 50 м. 4.40. Случайны величина Х распределена по нормальному закону с математическим ожиданием пз и средним квадратичным отклонением о. Определите абсциссы и ординаты точек перегиба кривой плотности распределения. Ответ: шло; е 1~з/(а~(2~г). 4.41. Нормально распределенная случайная величина Х имеет математическое ожидание, равное нулю.

Найдите среднее квадратичное отклонение а,при котором вероятность попадания случайной величины в интервал (5, 10) была бы наибольшей. О: = ~/75Д2) 2). 164 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ 4.42. Время Х (в часах) безотказной работы электрической лампочки имеет распределение Вейбулла с параматрами а = = 0,02 и ~3 = 0,5. Определите вероятность того, что лампочка проработает не менее 10000 ч. Ответ: Р(Х ) 100001 =е ~Ли~сесе -0,14. 4.43. Время Х (в месяцах) безотказной работы некоторой системы, состоящей из одного основного и двух резервных элементов, имеет гамма-распределение с параматрами у = 3 и А = 0,05. Найдите вероятность того, что система проработает не менее 5 лет.

О т в е т: Р 1Х ) 60) = е з(1+ 3 = Зз/2) и 0,42, 5. МНОГОМЕРНЫЕ СЛ’У ЧАЙНЫЕ ВЕЛИЧИНЫ В прикладных задачах обычно приходится рассматривать не одну случайную величину, а несколько случайных величин, одновременно измеряемых (наблюдаемых) в эксперименте. При этом с каждым элементпарным всходом ат е Й бывает связан набор числовых значений некоторых количественных параметров. В этой главе мы обобщим ранее полученные результаты на совокупность из нескольких случайных величин, задзвных на одном и том же веролптностпном простпранстпве. 5.1. Многомерная случайная величина.

Совместная функция распределения Определение 5.1. Совокупность случайныя величин Хт = Хт(от), …, Х„= Х„(ы), заданных на одном и том же веролтпностпном простпранстпве (Й,З,Р), называют многомерной (и-мерной) случайной величиной или тт-мерным случайным еектпором. При этом сами случайные величины Хт, Хт,, Х„называют коордннатптьнн случайного вектпора. В частности, при и = 1 говорят об одномерной, при и = 2 — двумерной с.аучайной еелнчнне (или двумерном случайном вектпоре). Для и-мерного случайного вектора воспользуемся обозначе. пнями (Хм …, Х„) и Х = (Хт, …, Х„). В случае двумерных и трехмерных случайных векторов наряду с обозначениями (Хм Хз) и (Хы Хг, Хз) будем испольэовать также обозначения (Х, У) и (Х, У, Я).