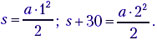Ошибки допускаемые при решении задач на движение - Решение и исправление самых разных ошибок на TopOshibok.ru

В методической литературе обычно выделяют следующие виды текстовых задач на движение:

— задачи на встречное движение;

— задачи на движение в одном направлении;

— задачи на движение в разных направлениях;

— задачи на движение по водоему (в стоячей воде, по течению реки, против течения реки).

Задачи на движение включает три величины: скорость, время, расстояние, которые связаны пропорциональной зависимостью.

Рассматривая классификацию задач на движение, необходимо отметить следующее: различают простые и составные задачи на движение.

Составные задачи на движение подразделяют на:

-задачи на движение в одном направлении

-задачи на сближение объектов,

-задачи на удаление объектов,

-задачи на движение по реке.

Кроме того, некоторые задачи на движение могут рассматриваться как:

— задачи на нахождение четвертого пропорционального;

-задачи на нахождение неизвестного по двум разностям;

-задачи на пропорциональное деление.

Типичные ошибки, возникающие у учащихся при решении задач на движение:

1) неумение строить модель условия задачи (в виде таблиц, схем,

рисунков или уравнений), где даны значения некоторых взаимосвязанных величин ;

2) определять этапы решения задачи;

3 ) представлять вычислительные результаты в задаче;

4) производить исследование полученного решения задачи;

5)знать в задачах движения по водоему различия скорости объекта в стоячей воде, по течению реки и против течения;

6) использовать краткие записи как модели текстов сложных задач и задач повышенной сложности для создания поисковой схемы и решения задач, выбирать модель текста задачи, оптимальную для предложенной в задаче ситуации;

7) уметь выбирать наиболее удачный метод решения задачи и понимать выбор метода, предусматривать различные методы, находить различные решения задачи, если это реально

Задача на движение в противоположных направлениях

При решении задач такого типа суммарная скорость имеет другое название. Расстояние, на которое удаляются движущиеся предметы за единицу времени, называют скоростью удаления. При движении в противоположных направлениях скорость удаления равна сумме скоростей движущихся объектов, т.е. Vуд V1  V2.

Задача. Из двух пунктов V и X выехали навстречу друг другу одновременно два автобуса. Один приехал в X через 1 часа 15 минут после встречи, а другой — в V 48 минут после встречи. Расстояние между пунктами равно 90 км. Найдите с какой скоростью двигались автобусы .

Решение:

Пусть х и у скорости первого и второго автобусов соответственно. z – время до встречи автобус.

Скорость

Расстояние

Время

I автобус

х км\ч

1  х

1 ч.

II автобус

у км\ч

 у

ч.

450 360

  90

5 4z 4  5z

450(45z) 360(5 4z)  90(45z)(5 4z)

1800 2250z 18001440z  90(2016z  25z  20z2)

36003690z 18003690z 1800z2

1800z2 1800 z2 1 z 1

x ; x  40

1

y  ; y  50

1

Ответ: 40км/ч и 50км/ч

Задачи на движение по водоему

При решении задач на движение по реке помогают знания из жизненного опыта Vкатера Vсобств.

Задачи на движение по озеру.

Озеро – стоячая вода, поэтому при движении она не помогает, но и не препятствует движению катера (или другого объекта). Очевидно, что катер движется с той скоростью, которая называется собственной скоростью катера (скоростью, обусловленной мощностью его двигателя).

Задача. Сколько времени понадобится моторной лодке, чтобы пересечь озеро, если собственная скорость лодки 15 км/ч, а длина озера 6 км?

Решение:

Задача на применение формулы движения в одном направлении в одно действие:

1) 15:6  2 (ч) – время которое понадобиться лодке, что бы пересечь озеро.

Ответ: 2ч30мин

Задачи на движение по течению реки (часто говорят – «вниз» по реке) скорость катера увеличивается, т.к. движущаяся вода как бы «подталкивает», т.е. увеличивает его движение. В этом случае к собственной скорости катера необходимо прибавить скорость течения реки:

Vкатера Vсобств. Vтеч.реки .

Задачи на движение против течения реки («вверх» по реке) скорость катера уменьшается, т.к. река замедляет его движение, «сносит» катер. В этом случае от собственной скорости катера следует вычесть скорость

течения реки Vкатера Vсобств. Vтеч.реки

Задача. Найдите собственную скорость байдарки, если известно, что скорость течения реки 4 км/ч. Она прошла по течению 35 км и, обратно прошла ещё 25 км, затратив на весь путь 6 часов. [14].

Решение:

Пусть х км/ч – собственная скорость байдарки. Следовательно скорость по течению реки х+4 км/ч, а против х-4 км/ч. По условию по течению она прошла 35 км., а против 25. Время в пути 6 ч. Составим уравнение:

35 35

 6 х  4 х  4

Решив уравнение, получим: х 10.

Ответ: 10 км/ч

Источник

ВВЕДЕНИЕ

Математика проникает почти во все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В связи с этим стало жизненно необходимым усовершенствовать математическую подготовку подрастающего поколения.

Действующая программа начальной школы требует развития самостоятельности детей. Самостоятельность тем более необходима при решении текстовых задач. В ряду текстовых задач по математике задачи на движения занимают особое место. Ученик начальной школы должен уметь кратко записать условие задачи, проиллюстрировать его с помощью рисунка, схемы или чертежа, обосновать каждый шаг в анализе задачи и ее решении, проверить правильность решения. Однако на практике эти требования выполняются далеко не всеми учащимися, что приводит к серьезным проблемам в знаниях и навыках детей, создает препятствия в дальнейшем математическом образовании.

Почему же учащиеся допускают так много ошибок при решении задач?
Наблюдения показывают, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного и графического моделирования. Как правило, в процессе анализа используются лишь различные виды краткой записи условия задачи или готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется крайне редко. К тому же при фронтальном анализе и решении задачи учителя нередко ограничиваются правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания.
Для устранения отмеченных недостатков необходимо, прежде всего, улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися.
Многие учащиеся не только не хотят решать задачи на движение, но и не умеют. Как показывает практика обучения, умение решать задачи на движение у учащихся сформировано недостаточно.

Как обучать детей нахождению способа решения задачи на движение? Этот вопрос – центральный в методике обучению решения задач. Для ответа на него в литературе предложено немало практических приемов, облегчающих поиск способа решения задачи. Однако теоретические положения относительного нахождения пути решения задачи остаются мало разработанными.

Первоначальные математические знания усваиваются детьми в определенной, приспособленной к их пониманию системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в доступном для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает математическое мышление учащихся. Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания.

К сожалению, в настоящее время из-за желания учителей включить в урок различные виды работы, несколько ослаблено внимание к выработке у учащихся навыков и умений решения задач. А ведь регулярное включение в работу с классом задач развивающего характера, повышенной трудности способствуют развитию интереса и интеллектуальных способностей детей, активизирует их познавательную деятельность. Так же для повышения интереса к решению задач на движение следует использовать разнообразные чертежи и схемы. Они позволяют наглядно представить ситуацию, способствуют осознанному приобретению знаний, умений и навыков, развивать память, речь, мышление. Учитель начальных классов должен выработать навык решения как простых, так и составных задач на движение, на основании которого учащиеся смогут решать более сложные задачи по алгебре и физике в старших классах. Вот почему очень важно сформировать навык решения задач на движение в начальных классах. Именно поэтому тема нашего исследования «Решение задач на движение в 4 классе».

Проблема исследования: каковы наиболее эффективные пути в обучении решению задач на движение в начальной школе.
Объектом исследования является обучение решению задач на движение на уроках математики в 4 классе.

Предметом исследования является процесс решения задач на движение младшими школьниками.

Цель – исследовать работу над задачей, выявить новые подходы к решению задач на движение.

В соответствии с проблемой, целью, предметом исследования нами были поставлены следующие задачи:
1. Изучить психолого-педагогическую и методическую литературу по исследуемой проблеме;
2. Изучить опыт учителей по работе над задачами на движение;

3. Выявить роль задач на движение в процессе обучения;

4. Провести анализ нетрадиционных подходов в методике работы над задачей на движение;

В нашем исследовании использовались следующие методы:
• теоретический анализ научно-методической литературы;
• наблюдение;
• анализ результатов деятельности;
Структура исследования: Работа состоит из введения, двух глав, заключения, список литературы и приложения.
База исследования: НОУ РО «Православная гимназия г. Дзержинска».

1. АНАЛИЗ ТЕОРЕТИЧЕСКОГО МАТЕРИАЛА ПО ОЗНАКОМЛЕНИЮ МЛАДШИХ ШКОЛЬНИКОВ С ЗАДАЧАМИ НА ДВИЖЕНИЕ

1.1. Развитие младших школьников на уроке математике

Развитие младшего школьника — важная составная часть педагогического процесса. Помочь учащимся в полной мере проявить свои способности, развить инициативу, самостоятельность, творческий потенциал — одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов[2].

В развитии познавательной деятельности младшего школьника особую роль играет мышление. П.П. Блонский [1] подчеркивал: «Мышление – та функция, интенсивнейшее развитие которой является одной из самых характерных особенностей школьного возраста. Ни в ощущении, ни мнемических способностях нет такой огромной разницы между ребенком 6 – 7 лет и юношей 17 – 18 лет, какая существует в их мышлении»,.

В тесной связи с мышлением развиваются все познавательные процессы. Именно с развитием мышления складываются такие важные новообразования школьного возраста, как внутренний план действий (действий «в уме») и рефлексия (умение рассматривать и оценивать свои собственные действия) [20].

Математика даёт реальные предпосылки для развития мышления, задача учителя — полнее использовать эти возможности при обучении детей математике. Однако, конкретной программы приемов мышления, которые должны быть сформулированы при изучении данного предмета, нет. В результате работа над развитием мышления идёт без знания системы необходимых приёмов, без знания их содержания и последовательности формирования.

Нуралиева Г.В. [17] отмечает, что первоначальные математические знания усваиваются детьми в определённой, приспособленной к их пониманию, системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в достигнутом для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает мышление учащихся. Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания.

Познавая предметы и явления окружающей действительности, мы можем мысленно расчленять предмет или явление на составные части и мысленно же соединять части в одно целое. Операция мышления, направленная на расчленение целого на составляющие его части, называется анализом. Операция мышления, направленная на установление связи между предметами или явлениями, называется синтезом. Эти операции мышления взаимно связаны.

Ф. Энгельс [19] отменяет, что «…мышление состоит столько же в разложении предметов создания на их элементы, сколько в объединении связанных друг с другом элементов в некоторое единство. Без анализа нет синтеза».

Анализ и синтез, взаимно связанные операции мышления, находят постоянное применение, как при изучении элементов арифметической теории, так и при решении примеров и задач.

Уже на первых шагах обучения при изучении чисел первого десятка учащиеся пользуются наглядно-действенным анализом (разложением) предметных множеств на составляющие их элементы и наглядно-действенным синтезом (соединением), группируя элементы во множества.

Наглядный анализ и синтез сменяется затем анализом и синтезом по представлению: ребёнок может выполнить разложение чисел или их соединение, оперируя со зрительными образами, которые сохраняются в его памяти и могут быть воспроизведены в его сознании.

Более высокой ступенью является умственный анализ и синтез, выполняемый мысленно при помощи внутренней речи.

При обучении любому разделу математики приходится опираться на анализ и синтез.

Анализ и синтез, как взаимосвязанные мыслительные операции находят своё применение при решении текстовых задач.

Ученик под руководством учителя, прежде всего, анализирует содержание задачи, расчленяя его на числовые данные, условия и вопрос.

При решении составных арифметических задач требуется применить более сложный и более тонкий анализ и синтез. Анализ содержания составной задачи, так же как и простой, сводится к расчленению его на числовые данные, условия и вопрос. Однако сами данные, условие и искомое должны подвергнуться дополнительно анализу, расчленению на составляющие их элементы.

В процессе начального обучения математике находит своё применение приём сравнения, то есть выделение сходных и различных признаков у рассматриваемых чисел, арифметических примеров, арифметических задач[13].

После решения задач учащиеся сравнивают, каким действием решается та или другая задача: одна сложением, другая умножением, а затем сопоставляют способы решения с различиями в условиях задач. Такое сопоставление помогает учащимся лучше осознать смысл выражений «больше на несколько единиц» и «больше в несколько раз» и прочнее установить связь между условием каждой задачи и способом её решения.

Сравнение основано на анализе и синтезе: необходимо расчленить каждую задачу на составляющие её элементы, а затем мысленно соединить сходные элементы, выделив при этом существенные различия.

При объяснении учащимся новой для них по способам решения задачи с многозначными числами часто используется приём аналогии: учитель предлагает решить аналогичную задачу с небольшими числами, вычисления над которыми можно выполнить устно.

Используя в начальном обучении математике различные методы, учитель применяет их так, чтобы они содействовали активизации мышления учащихся, и тем самым способствовали его развитию.

1.2. Виды задач на движение. Этапы разбора

Рассмотрим несколько видов задач на движение: решение простых задач на движение в одном направлении, решение составных задач на встречное и противоположное движение, составные задачи, в том числе задачи на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разностям с величинами S, t, V.

Важным результатом ознакомления учащихся 4 класса является усвоение простейших формул, связывающих такие величины, как скорость, время и расстояние (V, t, S).

Рассмотрим основные пути усвоения зависимости между этими величинами, характеризующими равномерное движение.

На рассмотрение связи между скоростью, временем и расстоянием выделяется 4-5 уроков в начале изучения умножения и деления многозначных чисел. Полученные сведения систематически используются в дальнейшем при решении задач «на движение» в течение всего учебного года[11].

В результате рассмотрения этих вопросов ученик должен получить представление о новой величине – скорости, которая характеризуется расстоянием, проходимым в единицу времени (c понятием – скорость, учащиеся познакомились в 3 классе). Подчеркивается, что речь идет о таком движении, при котором скорость не изменяется. Раскрывается связь между скоростью, расстоянием и временем (при равномерном движении) в виде формулы V= S: t, где S – пройденное расстояние, V – скорость движения, t – затраченное время. Дети учатся решать задачи, в которых по времени и скорости находится путь; по времени и пути находится скорость; по скорости и пути находится время.

В ходе решения этих задач у учащихся формируются представления о некоторых средних скоростях (пешехода, велосипедиста, автомобиля, теплохода, самолета), представления о встречном движении и о движении в одном и том же направлении. На этой основе дети должны уметь решать простые и несложные составные задачи.

На первом из уроков необходимо, опираясь на жизненный опыт и наблюдения учащихся обратить внимание детей на то, что некоторые предметы могут двигаться быстрее и медленнее. Например, велосипедист может обогнать пешехода, автомобиль – велосипедиста, самолет – автомобиль и т.д. Предметы могут двигаться равномерно. Так, например, пешеход может проходить за каждый час по 3 км; автомобиль может проезжать за каждый час по 100 км; бегун может пробегать за каждую секунду по 8 м и т.д. В этом случае говорят, что скорость (соответственно) пешехода – 3 км в час (записывают 3км/ч), автомобиля 100 км/ч, бегуна – 8 м/с.

Таким образом, скорость движения – это расстояние, которое проходит движущийся предмет за единицу времени. Затем рассматриваются простые задачи, на основании которых делается вывод, что для того, чтобы найти скорость движения предмета, нужно расстояние, которое прошел предмет, разделить на затраченное для этого время. Коротко этот вывод можно сформулировать так: скорость равна расстоянию, деленному на время. Если скорость обозначить буквой V, путь S, а время буквой t, то можно записать этот вывод в виде формулы: V= S: t.

На последующих уроках с помощью соответствующих простых задач устанавливается, что расстояние равно скорости, умноженной на время: S =V*t.

Можно обратить внимание учащихся на связь между этими тремя формулами (например, последняя формула может быть выведена из первой: t= S: V) на основе правила нахождения неизвестного делителя V, когда известно частное t и делимое S.

Тоом А.Л. [19] отмечает, что основной методический аппарат, с помощью которого происходит ознакомление учащихся с взаимосвязью между величинами, представляет собой подбор задач и примеров, которые их раскрывают. Для определения соответствующей методики следует также иметь в виду указания, что «первоначальное ознакомление детей с разного рода зависимостями очень важно для установления причинной связи между явлениями окружающей действительности и имеет большое значение для подведения детей к идее функциональной зависимости». Заметим, что в этом случае речь идет о зависимости между двумя (а не тремя) величинами, например, между путем, пройденным телом, и временем, затраченным на прохождение этого пути (здесь скорость – величина постоянная). В этом случае мы имеем дело с тремя множествами: 1) множество значений такой величины, как время движения; 2) множеством значений длины (пути, пройденного за различные промежутки времени) и 3) множеством пар, в которых на первом месте стоит значение времени, а на втором соответствующее одно значение пути. В таком случае, действительно, формируются определенные функциональные представления. Причем эта функция может быть задана, например, таблицей:

Время в

секундах

Расстояние в метрах

Из этой таблицы можно сделать вывод, что тело двигалось неравномерно, что, в частности, в течение одной секунды (пятой) оно было неподвижно, что формулой эту зависимость выразить нельзя. Иногда в более простых случаях зависимость между временем движения и пройденным за это время можно выразить и с помощью формулы.

Например, наблюдая изменения расстояния S в зависимости от времени t по таблице:

Время в

часах

Расстояние в километрах

нетрудно заметить, что V= S: t.

На основании полученной закономерности можно, например, выяснить, какое расстояние S пройдет тело за 10ч (50 км), за какое время t тело пройдет расстояние в 100 км (20ч) и т.д.

Для ознакомления детей с примерами зависимости между величинами следует брать такие примеры, которые достаточно часто встречаются детьми в жизни, понятны им.

Рассмотрим решение задач на встречное и противоположное движение.

Методика обучения решения задач «на встречное движение» основывается на четких представлениях учащихся о скорости равномерного движения, которые уточняются и обобщаются на специально отведенных этому вопросу уроках[19]. На основе жизненных наблюдений выясняется и иллюстрируется смысл слов «двигаться навстречу друг другу», «в противоположных направлениях», «выехали одновременно из двух пунктов и встретились через…» и т.п.

После наглядной инсценировки каждого из случаев с помощью учащихся целесообразно с постепенным усложнением научить детей изображать схему таких задач «в отрезках». Причем стараться соблюдать отношения их длины в зависимости от скоростей и пройденных (в частности «до встречи») расстояний. Если, например, скорость одного поезда была 60 км в час, а другого – 45 км/ч, то первая стрелка должна быть длиннее второй и т.п. Если в распоряжении учителя имеется диафильм «Задачи на движение», то его можно использовать на этом уроке. Только после такой подготовительной работы последовательно, под руководством учителя рассматривается задача ей подобная. Прежде чем разбирать эту задачу на уроке, следует повторить и восстановить в памяти следующие сведения: связь между скоростью, расстоянием и временем (как одна из трех величин выражается через две другие?), ситуацию, при которой «два пешехода одновременно вышли навстречу…» Затем учащийся под руководством учителя и при его участии вчитывается в задачу :

Два пешехода вышли одновременно навстречу друг другу из двух сел и встретились через 3 часа. Первый пешеход шел со скоростью 4 км/ч, второй – 5км/ч. Найди расстояние между селами.

По схеме, дублированной на доске, вызываемые учащиеся рассказывают содержание задачи. При этом выясняется: откуда начал движение каждый пешеход? С какой скоростью двигался каждый? Почему их место встречи на схеме обозначено ближе к месту выхода одного из пешеходов? Кого из них? Можно спросить при этом: «В каком случае флажок окажется точно на полпути? Что означает деление слева от флажка, справа от флажка? Почему они различны по длине? Что означают числа под стрелками?

Такое подробное рассмотрение учит детей «читать» схему. Затем учитель может спросить у класса: «Как решить задачу?»

Возможно, один из учеников приведет примерно такое рассуждение: «Один пешеход до встречи прошел 4*3=12 (км), а другой – 5*3=15 (км). Расстояние между селами будет 12+15=27 (км).

Если такого ученика не нашлось и предложения детей неполны или неверны, то учитель проводит, пользуясь наводящими вопросами, эту работу с классом, постепенно подводя его к составлению по задаче выражения:

4*3 + 5*3 (км)

Найдя значение этого выражения, получим ответ: расстояние между селами равно 27 км.

В связи с нашей задачей учитель должен провести специальную работу, на основе которой будет выявлен смысл понятия «скорость сближения».

Для этого по схеме выясняется, что за каждый час пешеходы сближаются на (4+5) км в час. «На сколько километров сблизятся пешеходы за 3ч?» Это дает нам второй путь решения задачи: (4+5)*3.

Затем, пользуясь схемами, подробно рассматривают задачу. Из двух сел, находящихся на расстоянии 27 км, вышли одновременно навстречу друг другу два пешехода и встретились через 3ч. Первый пешеход шел со скоростью 4 км/ч. С какой скоростью шел второй пешеход?

Задачу, как более сложную и опирающуюся на понятие «скорость сближения», можно рассмотреть в заключение урока, когда дети уже приобретут некоторый опыт решения подобных задач.

4*3= 12 (км) прошел до встречи первый пешеход;

27-12=15 (км) прошел до встречи второй пешеход;

15:3=5 (км/ч) скорость, с которой шел второй пешеход, и только теперь целесообразно составить выражение к этой задаче:

(27- 4*3): 3

На следующих уроках продолжается работа по формированию и совершенствованию навыков решения задач «на встречное движение».

Эти задачи получают некоторое развитие для случая, когда предметы начинают движение из одной точки и в противоположных направлениях. Перед решением таких задач следует проиллюстрировать на схеме и в инсценировке, что «встречное движение» – тоже движение в «противоположных направлениях», что после встречи, если скорости тел не изменились, они будут «удаляться» друг от друга с той же скоростью, с какой «сближались». Поэтому скорость удаления тоже равна сумме скоростей движущихся тел.

В результате решения соответствующих простых задач ученики должны усвоить такие связи: 1. если известны расстояния и время движения, то можно найти скорость действием деления; 2. если известна скорость и время движения, можно узнать расстояние действием умножения; 3. если известны расстояние и скорость, можно найти время движения действием деления.

Далее, опираясь на эти знания, дети будут решать составные задачи, в том числе задачи на нахождение четвертого пропорционального, на пропорциональное деление, на нахождение неизвестного по двум разностям с величинами S, t, V.

При работе с этими задачами надо чаще использовать иллюстрации в виде чертежа, так как чертеж помогает правильно использовать, определять и представлять жизненную ситуацию, отраженную в задаче.

Задачи на пропорциональное деление вводятся по-разному: можно предложить для решения готовую задачу, а можно сначала составить ее, преобразовать задачу на нахождение четвертого пропорционального, в задачу на пропорциональное деление, и после их решения сравнить как сами задачи, так и их решения.

Прежде чем ввести задачи на встречное движение очень важно сформировать правильные понятия об одновременном движении двух тел. Важно, чтобы дети уяснили, что если два тела вышли одновременно навстречу друг другу, то до встречи они будут в пути одинаковое время и пройдут все расстояние.

Чтобы дети осознали это, следует включать задачи-вопросы, аналогичные следующим.

Из двух городов одновременно отплыли навстречу друг другу два теплохода и встретились через 3 часа. Сколько времени был в пути каждый теплоход?

Из деревни в город вышел пешеход и в это же время из города навстречу ему выехал велосипедист, который встретил пешехода через 40 минут. Сколько времени был в пути до встречи пешеход?

Теперь можно ознакомить детей с решением задач на встречное движение. Целесообразно на одном уроке ввести все 3 вида, получая новые задачи путем преобразования данных в обратные. Такой прием позволяет детям самостоятельно найти решение, поскольку задача нового вида будет получена из задачи, уже решенной детьми.

Итак, учитель читает задачу.

Из двух поселков одновременно навстречу друг другу выехали 2 велосипедиста и встретились через 2 часа. Один ехал со скоростью 15 км/ч, а второй – 18 км/ч. Найти расстояние между поселками.

Что известно о движении велосипедистов? Что надо узнать?

Пусть это будет поселок, из которого вышел 1 велосипедист (Учитель выставляет в наборное полотно карточку с римской цифрой «I»). А это поселок из которого выехал 2 велосипедист (Выставляет карточку «II»). Двое из вас будут велосипедистами. (Выходят два ученика). С какой скоростью ехал 1 велосипедист? (15 км/ч). Это твоя скорость. (Учитель дает карточку, на которой написано число 15). Это твоя скорость. (Дает второму ученику карточку с числом 18). Сколько времени они будут двигаться до встречи? (» часа). Начинайте двигаться. Прошел час (Дети вставляют одновременно свои карточки в наборное полотно). Прошел второй час. (Дети вставляют карточки). Встретились ли велосипедисты? (Встретились). Почему? (Шли до встречи 2 часа. Обозначим место встречи. (Вставляет ). Что надо узнать? (Все расстояние). Обозначу вопросительным знаком.

После такого разбора учащиеся сами находят два способа решения. Решение надо записать с пояснением сначала определенными действиями, а позднее можно записать выражением .

1 способ

15*2=30 (км) проехал первый велосипедист

18*2=36 (км) проехал второй велосипедист

30 + 36=66 (км) расстояние между поселками

2 способ

15 + 18=33 (км) сблизились велосипедисты в 1 час

33*2 = 66 (км) расстояние между поселками

Если дети затрудняются в решении II способом, надо вновь проиллюстрировать движение: прошел час – сблизились на 33 км, то есть велосипедисты 2 раза проехали по 33 км. То есть по 33 взять сколько раз? (» раза).

Учитель на доске, а дети в тетрадях выполняют чертеж к решенной задаче.

15км/ч2 ч18 км/ч

I . ______________________________________. II

Выясняется, какой из велосипедистов прошел до встречи большее расстояние и почему.

Учитель изменяет условие задачи, используя тот же чертеж.

15км/ч?18 км/ч

I . ______________________________________. II

66 км

Дети составляют задачу по этому чертежу, затем коллективно разбирается, после чего записывается решение с пояснением. Условие задачи еще раз меняется.

? 2 ч 18 км/ч

I . ______________________________________. II

66 км

Ученики составляют задачу, после чего коллективно разбирают 2 способа решения.

1 способ.

18*2=36 (км) проехал до встречи II велосипедист

66-36=30 (км) проехал до встречи I велосипедист

30:2=15 (км/ч) скорость I велосипедиста

2 способ

66:2=33 (км) сближались велосипедисты в час

33-18=15 (км/ч) скорость I велосипедиста

На последующих уроках проводится работа по закреплению умения решать задачи рассмотренных видов.

Здесь так же, как и при решении других задач, полезно предлагать различные упражнения творческого характера. В частности, ставится вопрос вида: «Могли ли велосипедисты (теплоходы, пешеходы и т.п.) встретиться на середине пути? При каких условиях? Если велосипедисты после встречи будут продолжать движение, то какой их них придет раньше к месту выхода другого велосипедиста, если будет двигаться с той же скоростью и др.?

Зайцев В.В [7 ]отмечает, что ознакомление с задачами на движение в противоположных направлениях может быть проведено аналогично введению задач на встречное движение. Проведя подготовительную работу, надо, чтобы ученики пронаблюдали движение двух тел (пешеходов, автомашин, катеров и т.д.) при одновременном выходе их одного пункта. Ученики должны заметить, что при таком движении расстояние между движущимися телами увеличивается. При этом надо показать, как выполняется чертеж. При ознакомлении с решением задач этого вида тоже может на одном уроке решать три взаимообратные задачи, после чего выполнить сначала сравнение задач, а затем их решений.

На этапе закрепления умения решать такие задачи ученики выполняют различные упражнения, как и в других случаях, в том числе проводят сравнение соответствующих задач на встречное движение в противоположных направлениях, а также сравнение решений этих задач.

Эффективны на этом этапе упражнения на составление различных задач на движение по данным в таблице значениям величин и соответствующим выражениям.

Например, дается таблица:

Скорость	60 км/ч	75 км/ч
Время	4 ч	4 ч

Предлагается, используя данные таблицы, составить задачи, которые решаются так:

60*4

75*4

(60+75):4

(75-60)*4

По двум последним выражениям ученики могут составить задачи на встречное движение и на движение в противоположных направлениях. Естественно, в таблице могут быть даны и другие величины.

1.3. Трудности при решении задач на движение.

Анализ работы психологов [ 18] позволил нам выделить уровни умения решать задачи младшими школьниками. Охарактеризуем их.

Низкий уровень. Восприятие задачи осуществляется учеником поверхностно, неполно. При этом ученик вычленяет разрозненные данные, зачастую несущественные элементы задачи. Ученик не может и не пытается предвидеть ход ее решения.

Средний уровень. Восприятие задачи сопровождается ее анализом. Ученик стремится понять задачу, выделить данные и искомое, но способен установить между ними лишь отдельные связи.

Высокий уровень. Ученик выделяет целостную систему взаимосвязей между данными и искомым. Ученик способен самостоятельно увидеть разные способы решения и выделить наиболее рациональный из возможных[11].

Для того чтобы организовать разноуровневую работу над задачей в одно и то же время, мы используем индивидуальные карточки-задания, которые готовим заранее в трех вариантах. Карточки содержат системы заданий, связанные с анализом и решением одной и той же задачи, но на разных уровнях. В размноженном виде они предлагаются учащимся в виде печатной основы. Ученики выполняют задание письменно в специально отведенном для этого месте. Предлагая ученику вариант оптимального для ученика уровня сложности, мы осуществляем дифференциацию поисковой деятельности при решении задач.

Приведем примеры таких карточек.

Решать такие задачи можно с 3 класс. От двух пристаней, расстояние между которыми 117км, отправились одновременно навстречу друг другу по реке два катера. Один шел со скоростью 17 км/ч, другой – 24 км/ч.

Какое расстояние будет между катерами через 2 ч после начала движения?

1-й уровень

Рассмотри чертеж к задаче и выполни задания:

_____________________________

а) обведи синим карандашом отрезок, обозначающий расстояние, пройденное первым катером за 2 часа. Вычисли это расстояние;

б) обведи красным карандашом отрезок, обозначающий расстояние, пройденное вторым катером за 2 часа. Вычисли это расстояние.

в) рассмотри отрезки, обозначающие расстояние, пройденное двумя катерами за это время. Вычисли это расстояние.

г) прочитай вопрос задачи и обозначь дугой на чертеже отрезок, соответствующий искомому. Вычисли это расстояние.

Если задача решена, то запиши ответ.

Ответ:

Рассмотри еще раз задание (1) и запиши план решения этой задачи (без вычислений).

Проверь себя! Ответ: 35 км.

У данной задачи есть более рациональный способ решения. Но он, как правило, более труден для слабых учащихся, так как предусматривает оперирование менее конкретным понятием «скорость сближения». Поэтому предлагаем рассмотреть этот способ решения и объяснить его. Это задание обозначим в карточке как дополнительное.

Дополнительное задание.

Рассмотри другой способ решения данной задачи. Запиши пояснения к каждому действию и вычисли ответ:

17+24=

…*2=…

117-…=…

Ответ:

2 уровень

Закончи чертеж к задаче. Обозначь на нем данные и искомое:

_____________________________

Рассмотри «дерево рассуждений» от данных к вопросу. Укажи на нем последовательность действий и арифметические знаки каждого действия.

17 км/ч 24 км/ч

скорость сближения2ч

расстояние, пройденное 117км

двумя катерами

расстояние между

двумя катерами

Пользуясь «деревом рассуждений», запиши план решения задачи.

Запиши решение задачи:

по действиям;

выражением.

Ответ:

Дополнительное задание:

Пользуясь чертежом, найди другой способ решения задачи и запиши его:

по действиям с пояснением;

выражением.

Ответ:

Проверь себя! Сопоставь ответы, полученные разными способами.

3 уровень

Выполни чертеж.

Пользуясь чертежом, найди более рациональный способ решения. Составь к этому способу «дерево рассуждений».

Запиши план решения задачи в соответствии с «деревом рассуждений».

Пользуясь планом, запиши решение задачи:

по действиям;

выражением.

Ответ.

Проверь себя! Ответ задачи 35 км.

Дополнительное задание.

Узнай, какое расстояние будет между катерами при той же скорости и направлении движения через 3ч? 4ч?

В задачах мы намеренно как бы изолируем план решения от вычислительных действий. Это сделано с целью формирования умения осуществлять целостное планирование решения задачи. Преимущество его перед «пошаговым» видим в том, что при этом внимание учащихся концентрируется на поиске обобщенного способа решения задачи вне зависимости от конкретных числовых данных, отвлекаясь от них.

Важным является вопрос об организации такой работы на уроке. Благодаря тому, что варианты заданий приспособлены к возможностям учащихся, а печатная форма предъявления задания снимает сложности, связанные с оформлением, на уроке может быть организована самостоятельная работа учащихся. Во время этой работы учитель имеет возможность оказать индивидуальную помощь отдельным учащимся.

Но возможны и другие варианты.

Например, по мере надобности учитель может руководить работой учащихся одного из уровней, в то время как другие работают самостоятельно.

Может быть организована и групповая работа учащихся на уроке. При этом дети каждой группы обсуждают и выполняют задания совместно. Состав таких групп может быть как одноуровневым, так и разноуровневым, в зависимости от целей, которые ставит учитель в этой работе. В конце урока работы учащихся собираются учителем для проверки[9].

Работа над задачей на уроке с помощью описанных нами карточек-заданий органично вписывается в ход урока, удобна в организации, повышает самостоятельность учащихся, позволяет формировать у них умения решать текстовые математические задачи на доступном уровне сложности, — это совершенствует обучение решению задач учащихся начальных классов.

1.4. Анализ работы над задачей по методике Истоминой Н.Б.

Учебно-методический комплект «Гармония» для четырехлетней начальной школы, создан на кафедре методики начального обучения Московского Государственного Открытого Педагогического Университета им. М.А. Шолохова.

Входящие в комплект «Гармония» учебники, учебники- тетради с печатной основой являются результатом многолетнего научно- методического поиска путей совершенствования начального образования, который осуществлялся авторами комплекта.

В связи с этим первой особенностью комплекта «Гармония» является его направленность на преодоление объективно сложившегося разделения традиционной и развивающих систем обучения на основе органичного соединения подтвердивших свою жизненность положений традиционной методики и новых подходов к решению методических проблем.

Вторая особенность комплекта находит выражение в методе воплощения в нем основных направлений модернизации школьного образования (гуманизации, гуманитаризации, дифференциации, деятельностного и личностно- ориентированного подхода к процессу обучения)[3].

Комплекта «Гармония» предусматривает новый методический подход к обучению младших школьников решению текстовых задач, в соответствии с которым дети знакомятся с текстовой задачей только после того, как у них сформированы те знания, умения и навыки: а) навыков чтения; б) приемов умственной деятельности (анализ и синтез, сравнение, обобщение); в) представлений о смысле арифметических действий, на которые они смогут опираться, осуществляя поиск решения задачи. Только после этого переходят к решению задач, причем дети чертят схемы к задачам, что так же развивает мышление у младших школьников в процессе решения задач [9 ].

Методическая интерпретация современных тенденций развития начального образования и их реализация в учебниках позволяет рассматривать учебно-методический комплект по математике Н.Б. Истоминой как источник интеллектуального и эмоционального развития ребёнка, его познавательных интересов, умения общаться со взрослыми и сверстниками, как возможность полнее выражать свои мысли и чувства. Реализованные в учебниках методические подходы к организации учебной деятельности школьников создают условия для понимания ребёнком изучаемых вопросов, для гармоничных отношений учителя с учеником и детей друг с другом, обеспечивают ситуации успеха за счёт мер по целенаправленному преодолению трудностей обучения.

Истомина Н.Б. [9] делит методику работы над задачей на два этапа: I этап – подготовительный. На нем младшие школьники овладевают навыками чтения; приемами умственной деятельности (анализа и синтеза, сравнения, классификации, аналогии, обобщения); усваивают смысл основных математических понятий: «сложение», «увеличить на», «вычитание», «уменьшить на», «разностное сравнение»; учатся использовать отрезки как средство моделирования этих понятий, овладевают умением складывать и вычитать отрезки, знакомятся со схемой.

II этап – основной. На нем учащиеся знакомятся со структурой задачи (условие, вопрос, известные, неизвестные), учатся анализировать ее текст (здесь уже не имеет значения, простая это задача или составная), переводить словесную модель в схематическую и (или) в символическую и овладевают умением записывать решение и ответ задачи.

Наталья Борисовна отмечает [9 ] , что большую роль в формировании представлений о величинах играет выполнение практических заданий. Практическая направленность курса в изучении величин создает благоприятные условия для совершенствования вычислительных навыков.

Истомина Н.Б. [8] в 4 классе сначала знакомит учащихся с понятием «скорость движения». На первом уроке преследуются следующие цели: познакомить учащихся с понятием «скорость», рассматриваются единицы измерения величины «скорость»; так же дети учатся решать задачи на нахождение скорости и расстояния. Для того что бы дети пришли самостоятельно к понятию включается коллективная работа. Дети вспоминают такие величины, как расстояние, время, единицы их измерения. Учитель сообщает, что на данном уроке класс познакомиться с новой величиной, которая называется скоростью, и узнают, как связаны между собой скорость, время и расстояние. Перед тем, как ввести понятие «скорость движения» предлагается решить несколько простых задач (см. Приложение № 1) В ходе решения дети отвечают на вопросы учителя. Отвечая на поставленные вопросы учащиеся узнают скорость движения. Делается вывод, что это то же величина и у неё есть единицы измерения. Наталья Борисовна [8] даёт следующее определение: Скорость – это расстояние, пройденное за единицу времени. Единицы скорости: км\ч, м\мин, км\с. Затем учащимся предлагается выполнить задания учебника и сравнить свои ответы с рассуждениями Маши и Миши. Затем учащиеся сами приходят к выводу, чтобы узнать скорость движения, нужно расстояние разделить на время.

В продолжении темы дети решают задачу (№ 382), данные которой заносятся в таблицу с помощью учителя.

Машина	Скорость (км\ч)	Время (ч)	Расстояние (км)
«Жигули»	?	2	180
«Запорожец»	?	3	180
«Жигули»	одинаковая	6	?

Решение задачи осуществляется по вопросам:

Чему равна скорость «Жигулей»?

180: 2 = 90 (км\ч).

2)Чему равна скорость «Запорожца»?

180:3=60 (км\ч).

Какое расстояние пройдут «Жигули» за 6 часов?

90 * 6 = 540 (км).

Затем дети делают самостоятельно вывод: чтобы узнать расстояние, нужно скорость умножить на время.

Далее учащиеся решают аналогичные задачи, заполняя таблицы.

На последующих уроках Истомина Н.Б. знакомит детей с взаимосвязью величин: скорость, время, расстояние; зависимостью между величинами: скорость, время, расстояние (См. Приложение № 2 ).

Наталья Борисовна [ 9 ] отмечает, что «Наглядность задач необходима для их лучшего понимания, ощущения действительности и необходимости математики в повседневной жизни».

Учебно-методический комплект по математике для четырехлетней начальной школы (автор Н.Б. Истомина) удостоен премии правительства РФ в области образования за 1999 год [3].

2. РАЗРАБОТКА И АПРОБАЦИЯ МЕТОДИКИ РЕШЕНИЯ ЗАДАЧ НА ДВИЖЕНИЕ В 4 КЛАССЕ

2.1. Диагностика сформированности умения решения задач на движение по УМК «Гармония»

Практическая часть данной работы проводилась в НОУ РО «Православная гимназия г. Дзержинска» 4 «Б» классе. Данный класс работает по программе «Гармония». Предоставим сведения о классе. Полную характеристику класса (см. Приложение № 3).

Количество учащихся в классе 17, возраст 10 -11 лет. Дети обучаются в НОУРО «Православная гимназия г. Дзержинска». Подавляющее большинство детей воспитываются в полных семьях, в доброжелательной атмосфере. Состав класса: мальчиков – 10 человек, девочек – 7 человек.

Ребята активно участвуют в жизни гимназии, в различных межшкольных мероприятиях. Это всё благодаря активности, сплочённости коллектива. Мотивация учения в классе: ученики стараются запоминать новый материал, накапливать знания, применять их в своей практической деятельности. Успеваемость: в классе большинство учеников «хорошисты», но есть ученики, которые вот-вот станут отличниками, если уделят внимание некоторым предметам. Есть ученики, их трое, которые имеют по одной тройке.

Отношение к учению: Ребята с интересом слушают и принимают новую информацию. Некоторые ученики требуют особого внимания со стороны учителя. Есть ребята, которые сочиняют стихи. Иногда даже объединяются в группы, чтобы сочинить отдельное произведение. Мальчики занимаются конструированием. Почти все родители следят за успехами детей.

Цель практической части: Выявить наличие сформированности практических знаний по решению задач на движение.

Данная контрольная работа проводилась в рамках тематического планирования. Для учащихся было подготовлено два варианта контрольной работы. Каждая из которой содержала одну задачу на движение. Материал для контрольной работы составлен по пособию Истоминой Н.Б., Шмырёва Г.Г. [10] «Контрольные работы. 4 класс». Ознакомиться с контрольными работами можно в (Приложении № 4 ).

Представим варианты контрольной работы.

1 вариант.

1. Решите равенство:

350 * 270 =

902 * 497 =

17052 : 28 =

14274 : 549 =

2. Решите равенство:

(9298-5398):100+503*71=

3. Решите выражение:

5 км 6м*4 =

64 т 720 кг : 8 =

6 ч – 38 мин =

4. Решите задачу:

Из двух городов, расстояние между которыми 5250 км, вылетели в 8 ч утра навстречу друг другу два самолёта. Через 3 ч они встретились в пути. Один самолёт летел со скоростью 850 км\ч. С какой скоростью летел другой самолёт?

2 вариант.

1. Решите равенство:

730 * 240 =

403 * 592 =

22848 : 34 =

18447 : 473 =

Решите равенство:

(3685 — 2785): 100 + 502 * 68 =

3. Решите выражение:

7 км 5 м * 3 =

48 т 540 кг : 6 =

2 ч – 36 мин =

4. Решите задачу:

Два велосипедиста выехали одновременно навстречу друг другу. Первый ехал со скоростью 15 км\ч. Второй проехал до встречи на 6 км больше, чем первый. С какой скоростью ехал второй велосипедист, если он встретился с первым через 3 ч?

На выполнение данной контрольной работы учащимся отводилось 40 мин. Перед выполнением работы ребятам проводилась инструкция по выполнению.

Данная контрольная работа выполнялась на двойных листах в клетку. Отметка выставляется в соответствии с нормами оценок. Представим отметки за контрольную работу.

№	Ф.И.	Результаты контрольной работы
1	Баринова Д.	5 (отл.)
2	Беззубова Ел.	5 (отл.)
3	Борисенко Ив.	3 (уд.)
4	Буланов Ар.	4 (хор.)
5	Кумбрасьев М.	Отсутствовал по болезни
6	Лушникова Ал.	3 (уд.)
7	Наумов М.	4 (хор.)
8	Николаева М.	5 (отл.)
9	Ошмарин Ил.	3 (уд.)
10	Поляшова Н.	5 (отл.)
11	Пушкина М.	5 (отл.)
12	Россиев М.	4 (хор.)
13	Россиев Н.	4 (хор.)
14	Солдатенков Вл.	4 (отл.)
15	Трофимов Ар.	4 (хор.)
16	Трошин Дм.	4 (хор.)
17	Шашкова Ан.	5 (отл.)

Работу выполнили на :

На «5» — 6 чел. (37 %)

На «4» — 7 чел. (44%)

На «3» — 3 чел. (19%)

Выразим полученные данные в процентах и изобразим с помощью диаграммы.

Проанализируем данную работу. Три человека (Борисенко Ив., Ошмарин Ил., Лушникова Ал.) выполнили работу на «3». Эти ребята в течении года имеет по математике стабильную тройку.

С задачей справились: 14 человек, 2 человека допустили ошибки в вычислениях (2 вариант).

Выразим данные показатели в процентах и изобразим с помощью диаграммы.

Выполнили правильно: 14 чел. – 87.5 %

Допустили ошибки: 2 чел. – 12.5%

Если проанализировать всю работу, то большее количество ошибок было допущено в первом задании (решить равенство). Пять человек допустили ошибки в вычислениях в столбик (действие умножение).

Выразим полученные даны в процентах и изобразим в виде диаграммы.

Выполнили правильно:11 чел.- 69 %

Допустили ошибки: 5 чел. – 31 %

Пять человек допустили ошибки во втором задании (решить выражение). Все учащиеся расставили правильно порядок действий, но сделали ошибку в вычислениях в столбик.

Выразим полученные даны в процентах и изобразим в виде диаграммы.

Выполнили правильно: 11 чел.- 69 %

Допустили ошибки: 5 чел. – 31 %

Третье задание правильно выполнили 14 человек, а двое допустили ошибки.

Выполнили правильно: 14 чел. – 87.5 %

Допустили ошибки: 2 чел. – 12.5%

Полученные данные занесём в сводную таблицу.

	1	2	3	4 (задача)
Выполнили правильно	69%	69%	87.5%	87.5%
Допустили ошибки	31%	31%	12.5%	12.5%

Можно сделать вывод, что тема по решению задач на движение классом усвоена. С ребятами, которые допустили ошибки планируется провести дополнительные занятия и поупражняться в решении задач данного типа.

С нашей точки зрения, усвоить решение задач на движение ребятам помогают схемы. С помощью схематического изображения учащиеся легко находят неизвестное.

Следует иметь в виду, что деятельность детей в процессе обучения решению задач направлена не на отработку умения решать задачи определённых типов, а на формирование общих умений: читать текст задачи, устанавливать взаимосвязь между условием и вопросом, данными и искомыми, выбирать арифметическое действие для её решения.

Мы с огромным удовольствием вот уже четвёртый год работаем по учебникам Наталии Борисовны Истоминой и в тетрадях с печатной основой. Мы считаем, что работа в тетрадях «Учимся решать задачи» обеспечивает хороший результат. Ребята хорошо справляются с решением задач и с контрольными работами, многие любят решать задачи потрудней, а урок математики стал для них одним из самых любимых. И в этом огромная заслуга учебно-методического комплекта, созданного Н.Б. Истоминой, который отражает содержательную логику процесса обучения и те методические приёмы и подходы, которые помогают учителю сделать процесс обучения развивающим, помогают учителю при построении урока.

Всем сердцем принимаю высказывание Натальи Борисовны [9] относительно того, «что критериями оценки развивающего уроков математики должны является — логика их построения, направленная на решение учебной задачи, вариативность предлагаемых заданий и взаимосвязь между ними, которая обеспечивается различными методическими приёмами; продуктивная мыслительная деятельность учащихся, активное высказывание детьми самостоятельных суждений и способов их обоснования».

2.2. Методические рекомендации по теме»Простые задачи на движение»

Многие учителя, знакомы с трудностями, связанными с организацией на уроке фронтальной работы над текстовой задачей. Ведь в то время, когда большая часть учащихся класса только приступает к осмыслению содержания задач вместе с учителем, другая пусть меньшая часть, уже знает, как их решать. Одни учащиеся способны видеть разные решения, другим необходима значительная помощь для того, чтобы просто задачу решить. Да и потребность в мере помощи различна у разных учеников. При этом определенная часть учащихся класса так и остается недогруженной, так как предлагаемые задачи слишком для них просты. В связи с этим мы задались вопросом: «Как же организовать на уроке работу над задачей, чтобы она соответствовала возможностям учащихся?» [ 14].

Лавриненко Т.А[12]. считает, что первоначальные математические знания усваиваются детьми в определенной, приспособленной к их пониманию системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в доступном для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает математическое мышление учащихся. Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания

Таким образом, при ознакомлении учащихся со скоростью движения и изучения связи между величинами скорость, время, расстояние, необходимо использовать схемы, чертежи, занимательные задачи и задачи развивающего характера, которые повышают интерес у учащихся, способствуют осознанному приобретению знаний, умений и навыков, развивают память, речь, мышление. После ознакомления со скоростью движения и изучения связи между величинами, скорость, время, расстояние , необходимо сформировать у детей умения и навыки решения задач на встречное движение различных видов, а также умение решать и составлять задачи по чертежам и таблицам. Ученики должны научиться сравнивать задачи и выявлять сходное и различное, составлять задачи по выражениям.

Анализ работы психологов [ 5 ] позволил нам выделить уровни умения решать задачи младшими школьниками. Охарактеризуем их.

Для того, чтобы организовать разноуровневую работу над задачей в одно и то же время, мы используем индивидуальные карточки-задания, которые готовим заранее в трех вариантах. Карточки содержат системы заданий, связанные с анализом и решением одной и той же задачи, но на разных уровнях. В размноженном виде они предлагаются учащимся в виде печатной основы. Ученики выполняют задание письменно в специально отведенном для этого месте. Предлагая ученику вариант оптимального для ученика уровня сложности, мы осуществляем дифференциацию поисковой деятельности при решении задач. При изучении темы «Простые задачи на движение» для организации коллективных занятий используются 6 типов доводящих карточек для ознакомления с различными видами движения, нахождения скорости, времени, расстояния. К каждой доводящей карточке прилагается карточка-задание (ЗД), которая помогает закрепить навык решения задач доводящей карточки. Знания учеников проверяются через дополнительные карточки: «Проверь себя!», «Проверочная работа» и «Контрольная работа».Как происходит запуск карточки ученику? Используя для образца доводящую карточку, учитель объясняет ученику, как решить первую задачу его карточки-задания, и записывает в его тетрадь подробные решения. Ученик самостоятельно по этому образцу решает вторую задачу. После того, как учитель проверил решение, карточка считается «запущенной». Для слабых учеников в начале занятия можно ввести дополнительное устное проговаривание вслух решения своей задачи.Затем ученики работают в парах. Каждый по очереди исполняет роль учителя и объясняет напарнику задачу своей карточки (ЗД) по плану, изложенному в доводящей карточке. После этого выполняется работа по карточкам «Проверь себя!», «Проверочная работа» и «Контрольная работа», которые оцениваются учителем.

Все эти карточки могут быть использованы и в традиционной школе: доводящие — как методические рекомендации при объяснении темы «Простые задачи на движение», а все остальные — как задачи для работы на уроках. Приведём примеры таких карточек.

Доводящая карточка №1

Читаю задачу: «По шоссе едет автомобиль. От Ульяновска до Инзы он прошел 170 км, от Инзы до Пензы 40 км, от Пензы до Шарыпова — 140 км. Какое расстояние прошел автомобиль?» [4].

Что известно в задаче?

Эта задача на движение в одном направлении, т.е. автомобиль проходит расстояние между всеми городами, которые встречаются на пути.

Чтобы легче было выполнить задание, надо выполнить чертеж.

В этой задаче на чертеже отрезок обозначает расстояние од одного города до другого. И чем дальше едет автомобиль, тем большее расстояние он проходит.

К 170 км А 40 кмН140 км Ш

__________________________________________________________

Что требуется узнать в задаче?

По условию задачи известно, что расстояние от Ульяновска до Инзы 170 км, от Инзы до Пензы 40 км, от Пензы до Шарыпова 140 км. Значит, все расстояние будет равно сумме расстояний от Ульяновска через каждый город до Шарыпова, поэтому все расстояния нужно сложить.

Оформляем задачу так:

170 + 40 + 140 = 350 (км)

Ответ: 350 км прошел автомобиль.

Задание: Придумай подобную задачу, выполни чертеж к задаче и реши ее.

Доводящая карточка №2

Читаю задачу: «Из Ульяновска и Инзы навстречу друг другу выехали два автомобиля. Один автомобиль проехал 80 км до встречи с другим. Сколько километров проехал второй автомобиль, если известно, что расстояние между городами 170 км?» [15].

Что известно в задаче?

Эта задача на встречное движение, то есть автомобили одновременно выезжают навстречу друг другу и едут до встречи одинаковое время. При этом автомобили пройдут все расстояние между пунктами, из которых они выехали.

Чтобы решить задачу надо выполнить чертеж.

80 км ?

К_____________________________А

_____________________________

170 км

В этой задаче отрезок обозначает расстояние, которое должны пройти оба автомобиля до встречи; точки К, А — это пункты выхода автомобилей, флажок — место встречи, стрелки — направление движения.

Что требуется узнать в задаче? Что надо делать, чтобы ответить на вопрос задачи?

По условию расстояние от Ульяновска до Инзы равно 170 км, один автомобиль проехал 80 км. Находим расстояние, которое проехал второй автомобиль. Для этого мы должны от всего расстояния отнять известную часть пройденного пути, то есть 170-80=90 (км)

Оформляй задачу так: 170 — 80 = 90 (км)

Ответ: 90 км проехал второй автомобиль.

Задание: Придумай подобную задачу и реши ее.

Доводящая карточка №3

Читаю задачу: «Из Ульяновска одновременно отправились в противоположные стороны два автомобиля. Первый поехал в Инзу и проехал 170 км, второй — в Николаево и проехал 225 км. На каком расстоянии друг от друга оказались автомобили?»

Что известно в задаче?

Эта задача на движение в противоположных направлениях. Поэтому с увеличением времени движения расстояние между автомобилями будет увеличиваться.

Чтобы было легче решить задачу, выполним чертеж.

К225 км 170 км А

__________________________________________

Что требуется узнать в задаче? Что надо знать, чтобы ответить на вопрос?

По условию задачи известно, что от Ульяновска до Инзы 170 км, а от Ульяновска до Канска 225 км. Значит, мы должны узнать расстояние от одной конечной точки до другой действием сложения. Все расстояние будет равно сумме расстояний от Ульяновска до каждого города, то есть 170+225.

Оформляй задачу так:

170 + 225 = 395 (км)

Ответ: на расстоянии 395 км оказались автомобили.

Задание: Придумай подобную задачу, выполни чертеж к задаче и реши ее.

Карточки-задания

Задание №1.

1. С работы мама шла в магазин, в аптеку, а потом пошла домой. Какое расстояние прошла мама, если от работы до магазина 500м, от магазина до аптеки 100м, а от аптеки до дома 350м?

2. Мальчик из школы прошел до дома 50 м, а потом пошел в библиотеку. Какое расстояние прошел мальчик от школы до библиотеки, если от дома мальчика до библиотеки 450м?

Задание №2.

1. Витя и Петя бежали навстречу друг другу по беговой дорожке, длина которой 100м. Сколько метров пробежал Витя, если Петя пробежал 60м?

2. Расстояние между городами 560 км. Одновременно навстречу друг другу выехали два поезда. Первый проехал до встречи 300 км. Какое расстояние до встречи проехал второй?

Задание №3

1. Из города одновременно вышли в противоположном направлении два пешехода. Первый пешеход прошел 10 км, а второй — 15км. На каком расстоянии друг от друга оказались пешеходы?

2. После уроков Ира и Вася пошли домой, но в разные стороны. Ира до дома шла 150м, а Вася — 200м. На каком расстоянии оказались Ира и Вася друг от друга?

Проверь себя

1. Теплоход плыл 2ч со скоростью 18 км/ч. Какое расстояние проплыл теплоход?

2. Поезд прошел 210 км за 3ч. С какой скоростью шел поезд?

3. Велосипедист проехал 54км со скоростью 18 км/ч. Сколько времени велосипедист был в пути?

4. Пешеход был в пути 3ч и прошел 15км. С какой скоростью шел пешеход?

5. Расстояние в 120 км мотоциклист проехал со скоростью 40 км/ч. За сколько часов мотоциклист проехал это расстояние?

Проверочная работа. Материал взят из книги Нешкова Н.И. [ 16].

Мальчик пробежал 100 м за 10с. С какой скоростью бежал мальчик?

Теплоход проплыл 48км со скоростью 16 км/ч. За какое время проплыл это расстояние теплоход?

Турист за 4 ч прошел 20 км. С какой скоростью шел турист?

Катер плыл 3ч со скоростью 15 км/ч. Какое расстояние проплыл катер.

За сколько времени лыжник пройдет расстояние 18 км, если он будет идти со скоростью 6 км/ч.

Контрольная работа

1. Лыжник прошел с одинаковой скоростью 42км за 3ч. Найти скорость лыжника.

Всадник, двигаясь со скоростью 12 км/ч, проехал 36 км. Сколько времени затратил всадник на этот путь?

Автомобиль ехал со скоростью 80 км/ч и проехал 240 км. Сколько времени был в пути автомобиль?

Туристы проехали 6 ч на лодке со скоростью 15 км/ч. Какое расстояние они проплывут.

Расстояние в 360 км скорый поезд проехал за 4ч. С какой скоростью ехал поезд.

ЗАКЛЮЧЕНИЕ

Как научить детей решать задачи? С психолого-методической точки зрения, по всей вероятности, необходимо организовать обучение с опорой на опыт дошкольников, на их предметно-действенное и наглядно-образное мышление, необходимо формировать и развивать у учеников математические понятия на основе содержательного обобщения уже известных фактов.

Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащихся. Поэтому важно, что бы учитель имел глубокие представления о текстовой задаче, о ее структуре, умел решать такие задачи различными способами.

Задачи на движение служат также одним из важнейших средств ознакомления детей с математическими отношениями, выражаемыми словами «быть на столько-то больше (меньше)», «быть на столько-то раз больше (меньше)». Они используются и в целях уяснения понятия доли (задачи на нахождение доли величины и искомого значения величины по доле), помогают и при формировании ряда геометрических понятий, а также при рассмотрении элементов алгебры.

Через решение задач дети знакомятся с важными в познавательном и воспитательном отношении фактами. Так, содержание многих задач, решаемых в начальных классах, отражает труд детей и взрослых, достижения нашей страны в области народного хозяйства, техники, науки, культуры.

Сам процесс решения задач при определенной методике оказывает весьма положительное влияние на умственное развитие школьников, поскольку он требует выполнения умственных операций: анализа и синтеза, конкретизации и абстрагирования, сравнения, обобщения. Так, при решении любой задачи ученик выполняет анализ: отделяет вопрос от условия, выделяет данные и искомые числа; намечая план решения, он выполняет синтез, пользуясь при этом конкретизацией (мысленно рисует условие задачи), а затем абстрагированием (отвлекаясь от конкретной ситуации, выбирает арифметические действия); в результате многократного решения задач какого-либо вида ученик обобщает знания связей между данными и искомым в задачах этого вида, в результате чего обобщается способ решения задач этого вида [2].

После ознакомления со скоростью движения и изучения связи между величинами, скорость, время, расстояние, необходимо сформировать у детей умения и навыки решения задач на встречное движение различных видов, а также умение решать и составлять задачи по чертежам и таблицам. Ученики должны научиться сравнивать задачи и выявлять сходное и различное, составлять задачи по выражениям.

Решение задач — упражнения, развивающие мышление. Мало того, решение задач способствует воспитанию терпения, настойчивости, воли, способствует пробуждению интереса к самому процессу поиска решения, дает возможность испытать глубокое удовлетворение, связанное с удачным решением.

Леонтьев А.И. [ 15] считает, что наглядность задач необходима для их лучшего понимания, ощущения действительности и необходимости математики в повседневной жизни.

Наталья Борисовна отмечает [9 ], что большую роль в формировании представлений о величинах играет выполнение практических заданий. Практическая направленность курса в изучении величин создает благоприятные условия для совершенствования вычислительных навыков (схемы, чертежи).

Кроме графических моделей для лучшего усвоения учебного материала необходимо в уроки математики вводить элементы истории, и чем раньше дети узнают что такое математика, как появилось число, отрезок, деньги и т.д., тем быстрее будет происходить расширение умственного кругозора учащихся и повышение их общей культуры, повысится интерес к изучению математики, углубится понимание изучаемого фактического материала.

Нельзя забывать, что решение задач воспитывает у детей многие положительные качества характера и развивает их эстетически.

Изучена методика работы над задачей на движение: понятие и виды задач, способы ее решения, этапы, задачи, общие вопросы методики обучения решению задач, разработаны планы-конспекты уроков.

Проведена работа по диагностике сформированности умения решать задачи на движение.

ОГЛАВЛЕНИЕ

Стр.

ВВЕДЕНИЕ……………………………………………………………………… 3

Глава1. АНАЛИЗ ТЕОРИТИЧЕСКОГО МАТЕРИАЛА ПО ОЗНАКОМЛЕНИЮ МЛАДШИХ ШКОЛЬНИКОВ С ЗАДАЧАМИ НА ДВИЖЕНИЕ………………………………………………………………………6

Развитие младших школьников на уроке математике…………………..6
Виды задач на движение. Этапы разбора…………………………………9
Трудности при решении задач на движение……………………………19
Анализ работы над задачей по методике Истоминой Н.Б……………..23

Глава 2. РАЗРАБОТКА И АПРОБАЦИЯ МЕТОДИКИ РЕШЕНИЯ ЗАДАЧ НА ДВИЖЕНИЕ В 4 КЛАССЕ…………………………………………………28

2.1. Диагностика сформированности умения решения задач на движение по УМК «Гармония»………………………………………………………………..28

2.2. Методические рекомендации по теме «Простые задачи на движение»………………………………………………………………………..34

ЗАКЛЮЧЕНИЕ………………………………………………………………….44

ЛИТЕРАТУРА……………………………………………………………………47

ПРИЛОЖЕНИЕ 1. Психолого-педагогическая характеристика 4 «Б»класса НОУРО «Православная гимназия г. Дзержинска»……………………………48

ПРИЛОЖЕНИЕ 2.Простые задачи на движение………………………………..49

ПРИЛОЖЕНИЕ 3.Конспекты уроков по УМК «Гармония»…………………50

ПРИЛОЖЕНИЕ 4.Контрольные работы (детские работы)…………………..51

Источник

Задачи, тесты

проф. П. Ф.
Севрюков,
< sevryukovpf@yandex.ru >, Ставропольский КрИПКРО, г. Ставрополь

Серьёзные ошибки в несерьёзных задачах

Нередко при решении простых, на первый взгляд, физических задач встречаются досадные небрежности, которые оказываются существенными даже при анализе условия задачи. Особенно часто это имеет место в задачах по механике, в которых, казалось бы, всё достаточно понятно и можно даже «потрогать руками». Рассмотрим несколько стандартных простых случаев.

Начнём с задач, в которых необходимо чётко уяснить смысл условия, а уже потом пытаться их решить. Это, скорее, задачи логические. Самое интересное, что они могут быть заданы и учителями математики.

• Задача 1. Крокодил Гена с Чебурашкой плыли вверх по течению реки. Гена сидел на вёслах, а Чебурашка, сидя на корме, ел апельсины. В момент, когда лодка проплывала под мостом, а Гена был поглощён движением, Чебурашка заснул и нечаянно столкнул ящик с апельсинами в воду. Через полчаса Гена обнаружил пропажу ящика с апельсинами, развернул лодку по течению реки и стал догонять уплывающий ящик; ещё через полчаса выловил его на расстоянии двух километров ниже моста по течению реки. Какова скорость течения реки?

Решение. Ясно, что нужно просто внимательно прочитать условие задачи. За час ящик проплыл 2 км, следовательно, скорость течения реки 2 км/ч.

Следующая задача хорошо известна, она встречается в книге «Живая математика» Я.И.Перельмана [1].

• Задача 2. Охотник, войдя в лес, видит на дереве белку. Белка выглядывает из-за ствола, смотрит на охотника, а сама охотнику не показывается. Охотник начинает медленно обходить дерево вокруг. Белка, цепляясь коготками за кору дерева, перемещается по стволу так, что всё время, выглядывая из-за ствола, смотрит на охотника, но свою спинку и хвостик охотнику не показывает. Охотник три раза обошёл вокруг дерева, сколько раз он обошёл вокруг белки?

Решение. Решая задачи подобного типа (а именно такие задачи появляются на олимпиадах 7–8-го классов), нужно чётко понимать, что в задачу нельзя добавлять «от себя» ни одного слова, поскольку при этом мы невольно производим подмену условия. Обратим внимание на то, что из условия задачи нельзя понять, что означает фраза «обойти вокруг белки». Эта задача допускает два варианта подхода.

Если мы будем считать, что «обойти вокруг белки», – это увидеть спинку белки, то охотник не обошёл вокруг белки ни разу. Если же «обойти вокруг белки» – обойти вокруг того места, где сидит белка (дерево), то охотник обошёл вокруг белки три раза. Полный ответ на вопрос, поставленный в задаче, состоит в разборе двух рассмотренных вариантов.

Рассмотрим задачу статики.

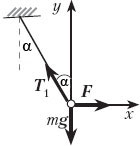
• Задача 3. На упругой нерастяжимой нити висит шарик массой m, имеющий заряд q. Где нужно расположить шарик, имеющий заряд Q, чтобы натяжение нити уменьшилось в три раза?

Решение. Ясно, что при отсутствии кулоновской силы натяжение нити Т по величине равно силе тяжести mg. Кажется, что сила натяжения нити уменьшится, если сила Кулона F будет направлена вертикально вверх. Её можно найти из соотношения T₁ + F – mg = 0 (это видно из рисунка).

T₁ = 1/3 mg ; F = mg — 1/3mg = 2/3mg.

Сила Кулона 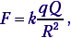где R – расстояние от заряда q до заряда Q, k – постоянная Кулона. При этом в случае, если заряды q и Q одноимённы, заряд Q нужно расположить под зарядом q, а в случае, если они разноимённы, – на нити подвеса. Расстояние до заряда Q находится из соотношения

Примечание. Это «правильное» решение требует дополнительного обоснования. Не совсем понятно, почему заряд Q не может находиться в стороне от вертикали. Предположим, что это возможно. Покажем приложенные к заряду на нити силы на рисунке. Сила натяжения T₁, равная по модулю 1/3mg, сила тяжести mg и сила Кулона F должны в сумме давать нуль: F + mg + T₁ = 0. В проекции на ось Y:

T₁cosα – mg = 0; · cosα – mg = 0,

откуда cosα = 3, что не может быть, поскольку |cosα| ≤ 1.

Теперь при решении задачи совершенно строго показано, что заряд Q должен быть расположен на одной вертикали с нитью подвеса. (К сожалению, доказано нестрого. Судя по рисунку, автор расположил заряд Q на одной высоте с шариком m. Это лишь частный случай. – Ред.)

Рассмотрим несколько несложных задач кинематики точки. Обратим внимание на то, что в многочисленных тестах часто используются величины, не относящиеся к системе СИ, причём переходить к системным единицам не всегда целесообразно.

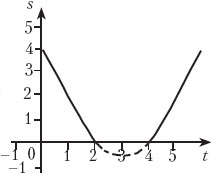
• Задача 4. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 30 см от начального положения шарик побывал дважды: через 1 с и через 3 с после начала движения. Найдите максимальное расстояние, на которое шарик смог откатиться вверх. Считать движение шарика прямолинейным и равноускоренным.

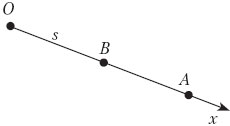
Решение. Обратим внимание на то, что трение в задаче не упоминается. В реальности шарик, вкатываясь на наклонную плоскость, замедляет своё движение, двигаясь до верхней точки 2 с, останавливается, а потом катится вниз по наклонной плоскости. Ясно, что при движении вверх и вниз шарик проходит расстояние от начала наклонной плоскости (точка А) до верхней точки (точка О) и обратно за одно и то же время. Воспользуемся обратимостью движения.

Рассмотрим движение шарика сверху вниз. В точке О шарик начинает движение без начальной скорости и проходит расстояние ОВ = s за 1 c, а расстояние ОА = s + 30 за 2 с, имея одно и то же ускорение а.

Запишем два уравнения движения для отрезков ОВ и ОА (в тестах нет смысла подробно расписывать решение):

Исключая из них а (например, разделив второе уравнение на первое), получаем s = 10 cм. Окончательно ОА = s + 30 = 40 (см).

Примечание. Выбор противоположного направления движения (снизу вверх) приводит к необходимости учитывать начальную скорость, с которой шарик вкатывается на наклонную плоскость. Решение простой задачи при этом сильно усложняется.

• Задача 5. Мяч бросили с начальной скоростью 20 м/с под углом 60° к горизонту. На какой высоте скорость мяча будет направлена под углом 45° к горизонту? Ускорение свободного падения g считать равным 10 м/с.

Решение (1-й способ). Будем считать, что мяч в момент броска находится в начале координат (x₀ = 0; y₀ = 0) и имеет проекции скорости υ_0x = υ₀cos60°; υ_0y = υ₀sin60°. Ясно, что горизонтальная составляющая скорости остаётся постоянной, поскольку за счёт вертикально направленного ускорения свободного падения будет изменяться только вертикальная составляющая скорости:

υ_x = υ_0x = υ₀cos60° = 10;

υ_y = υ_0y – gt = υ₀sin60° – gt = 10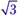– 10t.

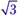
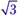
Из условия задачи следует, что требуется найти высоту, на которой горизонтальная и вертикальная составляющие скорости равны, т.е. справедливы соотношения υ_x = υ_y= 10; 10 = 10– 10t, откуда находим момент времени t =— 1, когда мяч находится на заданной высоте.

Далее определим саму высоту, записав уравнение движения мяча вдоль вертикали в этот момент:

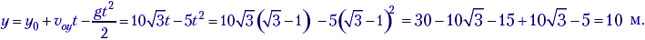
Примечание (2-й способ). Хорошо известная формула связи скоростей, ускорения движения точки и дуговой координаты υ² — υ₀² = 2a_τs является следствием теоремы об изменении кинетической энергии материальной точки, и формулой кинематики может считаться с большой натяжкой.

Для рассмотренной задачи эта формула даёт решение с учётом постоянства горизонтальной составляющей скорости, следовательно, и равенства проходимых по горизонтали расстояний за равные промежутки времени, а также равенства составляющих скорости в искомой точке:

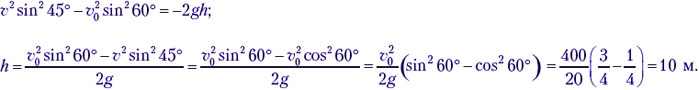
Без подробных комментариев второй способ решения не может считаться обоснованным.

Обратим внимание на некорректность некоторых обоснований при использовании законов сохранения и общих теорем механики.

• Задача 6. Снаряд массой 25 кг, имеющий скорость 300 км/ч, находясь в верхней точке траектории, разрывается на две части. Часть массой 15 кг после взрыва летит по направлению полёта снаряда со скоростью 400 км/ч. Определите скорость второй части снаряда в момент взрыва.

Решение. Достаточно часто в решебниках встречается ремарка: «Будем считать систему замкнутой, тогда…» Но, по условию задачи, система замкнутой не является: и на снаряд, и на оба осколка действуют нескомпенсированные силы тяжести, являющиеся внешними! При этом закон сохранения импульса выполняется, только причина сохранения объясняется по-другому.

Примечание. Импульс системы сохраняется при равенстве нулю правой части уравнения закона изменения импульса системы. При постоянстве внешних сил в нашей задаче изменение импульса системы происходит за время t: (mυ₁ + mυ₂) – mυ = F_внешt, где F_внеш = mg –
равнодействующая всех действующих внешних сил – сила тяжести, действующая на снаряд или оба осколка.

Закон сохранения импульса выполняется либо в замкнутой системе (F_внеш = 0, не действуют внешние силы), либо при кратковременном ударе, взрыве (t = 0).

В нашем случае закон сохранения импульса mυ = mυ₁ + mυ₂ в проекциях на горизонтальную ось даёт при направлении векторов скорости осколков вдоль оси, совпадающей по направлению с вектором скорости снаряда в момент взрыва: 25 · 300 = 15 · 400 + 10υ₂; υ₂ = 150 км/ч (по направлению движения снаряда).

Рассмотрим задачу динамики, две части которой принципиально отличаются.

• Задача 7. На горизонтальной плоскости лежат связанные тела массами m и 2m. Коэффициент трения между каждым из тел и плоскостью равен f. Какую силу нужно приложить к телу меньшей массы, чтобы оба тела сдвинулись с места? Рассмотрите случаи, когда тела связаны нерастяжимой нитью и пружиной.

Решение 1. Рассмотрим случай, когда два тела связаны нерастяжимой нитью.

Этот тривиальный случай (длина нити не изменяется, следовательно, система тел вместе с нитью может рассматриваться в данной задаче как единое недеформируемое целое) рассматривается в статике при рассмотрении равновесия при наличии трения. Ясно, что силы тяжести mg и 2mg и нормальные реакции N₁ и N₂, приложенные к каждому из тел, перпендикулярны линии действия силы F и влияют только на величины сил трения: F₁= fmg и F₂ = 2fmg (силы трения F₁ и F₂, очевидно, должны быть направлены в сторону, противоположную направлению силы F). Силы натяжения нити T₁ и T₂, приложенные к двум телам и направленные вдоль нити, являются внутренними для системы тел, и при нерастяжимости нити друг друга компенсируют.

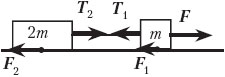
Тогда при величине силы F > 3fmg оба тела одновременно будут сдвинуты с места.

Решение 2. Случай, когда два тела связаны между собой пружиной жёсткостью k, качественно отличается от ранее рассмотренного случая с нитью. Обратим внимание на то, что сначала, увеличивая величину силы F, мы сдвигаем с места тело массой m (при этом сила упругости возрастает пропорционально удлинению пружины), а только при равенстве силы упругости силе трения, действующей на тело массой 2m, большее тело будет сдвинуто с места и выполнится условие, поставленное в задаче.

Итак, если F_упр > F_тр2, то

2fmg < kx, (1)

и тело массой 2m будет сдвинуто с места.

Поскольку сила упругости не является постоянной, рассмотрим, какую работу совершат все приложенные к телу массой m силы при растяжении пружины на величину х. Такой подход при малом х в классической механике называется методом возможных перемещений.

Итак (с учётом направления векторов сил), работа внешней силы должна быть равна сумме работ силы трения и силы упругости: 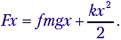Поскольку х ≠ 0, получаем а с учётом соотношения (1) F > 2fmg.

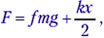
Примечание 1. В решении подобных задач встречается «усреднение» силы упругости, изменяющейся от 0 до значения kx, как kx/2, при этом подгонка под ответ при помощи усреднения никак не обосновывается.

Примечание 2. Мы получили почти парадоксальный результат. Вспомним, сколько раз мы видели пружины в сцепках между вагонами на железнодорожных вокзалах!

Задачи на движение встречаются и в школьном курсе математики. Эти задачи (особенно в разделе «Производная») требуют очень внимательного отношения. Для примера рассмотрим задание № 5 варианта 96 из [2, изд-е 3-е]. Не секрет, что учителя математики обращаются при решении таких задач за помощью к физикам и не всегда получают квалифицированный ответ [3].

• Задача 8. Тело движется по прямой так, что расстояние до него от некоторой точки А этой прямой изменяется по закону s = 0,5t² – 3t + 4 (м), где t – время движения в секундах. Найдите минимальное расстояние, на которое тело приблизится к точке А.

Решение. Ясно, что речь идёт о движении точки, а не тела, поскольку имеющее размеры тело не может двигаться по прямой. Простим эту некорректность математикам. Попытаемся решить задачу как классическую задачу «на экстремум»:

s′= t – 3 ⇒ s′= 0 ⇒ t = 3.

Далее: s (3) = –0,5 м. «Расстояние» отрицательно, что противоречит физическому смыслу понятия «расстояние».

Ясно, что, когда тело находится в точке А, расстояние между точкой и телом минимально (равно 0). Решение квадратного уравнения 0,5t² – 3t + 4 = 0 даёт моменты времени 2 с и 4 с.

Примечание 1. Несложно проверить, что в интервале времени от 2 до 4 с «расстояние» отрицательно. Задача имеет реальный физический смысл только первые 2 (!) секунды движения. Данное задание во всех знакомых мне решебниках выполнено с ошибками: или берётся модуль полученного расстояния, или указывается, что расстояние равно нулю при t = 2 и t = 4 (мне пришлось держать в руках более десятка «опусов»).

Напомню, что расстояние есть функция неотрицательная, непрерывная. Дадим иллюстрацию к рассмотренной задаче.

Функция s терпит разрыв – становится отрицательной при 2 < t < 4!

В 5-м издании Г.В.Дорофеев исправил ошибку условия: s = 0,5t² – 3t + 8 (м). При таких условиях задача решается как экстремальная и получается ответ 3,5 м.

Примечание 2. Обратим внимание на то, что, по условию задачи, не требуется указать момент времени, когда искомое расстояние минимально. Отвечая именно на поставленный вопрос (без указания моментов времени), мы избегаем лишних ошибок.

Достаточно часто в задачах по механике понятия «перемещение», «расстояние» и «координата» путаются [4]. Обратим внимание при решении следующей задачи на то, что при движении по прямой пройденный путь и перемещение совпадают только в том случае, когда вектор скорости не изменяет направления!

• Задача 9. Точка движется по прямой так, что её координата изменяется по закону x = t² – 4t + 10 (м), где t – время движения в секундах. Для момента времени t = 5 c найдите координату точки. Найдите перемещение точки, совершённое за первые 5 с движения, и расстояние, пройденное за это время.

Решение. Координата точки при t = 5 c равна x(5) = 25 – 20 + 10 = 15 м.

Начальная координата точки при t₀ = 0 c равна х(0) = 10 м.

Перемещение найдём как разность конечной и начальной координат точки: х = х(5) – х(0) = 15 – 10 = 5 м.

Найдём закон изменения скорости со временем: υ = x′= 2t – 4 м/с. Это можно сделать и без использования производной, записав в явном виде закон движения по прямой как x =x₀ + υ₀t + at²/2 = 10 – 4t + t² ⇒ υ = υ₀ + at = –4 + 2t.

Очевидно, что первые 2 с точка движется в сторону, противоположную направлению оси X (υ < 0), останавливается (υ (2) = 0 м/с), а потом движется в направлении, совпадающем с направлением координатной оси.

Найдём координату остановки (поворота):

х(2) = 4 – 8 + 10 = 6 м.

В первые 2 с был пройден путь |х(2) – х(0)| = 4 м при уменьшении координаты точки. В последующие 3 с был пройден путь |х(5) – х(2)| = 9 м. За 5 с пройдено расстояние s = 4 + 9 = 13 м.

Литература

Перельман Я.И. Живая математика. – М.: Учпедгиз, 1953.
Дорофеев Г.В. Сборник заданий для проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 класс. Изд. 3-е. – М.: Дрофа, 2002.
Севрюков П.Ф. Задачи на движение: простые и не очень. – Математика в школе, 2008, № 10.
Севрюков П.Ф. О некоторых понятиях и определениях школьного курса механики. – «Физика-ПС», 2008, № 19.

Источник

Подготовка к ОГЭ по математике

Решение текстовых задач.

Ильина Л.Я. – учитель математики

МБОУ «СОШ№1 им.Н.Н.Яковлева» г.Олекминска РС(Я)

Типичные ошибки при решении текстовых задач:

Невнимательное чтение условия и вопроса задания.
Неверное применение формул.
Логические ошибки при решении текстовых задач.
Вычислительные ошибки.

Задание №22

Задачи на движение.

Бродский И.Л., Видус А.М., Коротаев А.Б. Сборник текстовых задач по математике ля профильных классов. 7-11 классы/ Под ред. И.Л. Бродского. М.: АРКТИ, 2004. – 140с.

Задачи на движение содержат величины:

– время,

– скорость,

– расстояние.

Уравнения, связывающее эти три величины:

Повторение. 5 класс. Устно.

Собственная скорость теплохода 40,5 км/ч, а скорость течения реки 5,3 км/ч. Найдите скорость теплохода по течению и против течения.

Повторение. 6 класс

Путешественник проплыл по реке на плоту 75 км за 25 ч. Обратно он вернулся на моторной лодке, собственная скорость которой 28км/ч. Сколько времени затратил путешественник на обратный путь?

Повторение. 7 класс

Лодка шла против течения реки 4,5ч и по течению 2,1ч. Найти скорость лодки в стоячей воде, если она прошла всего 52,2 км, а скорость течения реки равна 3км/ч.

Задание № 22 ОГЭ

Баржа прошла по течению 56км и, повернув обратно, прошла еще 54 км, затратив на весь путь 5 часов. Найдите собственную скорость баржи, если скорость течения реки равна 5км/ч.

Задание № 22 ОГЭ вариант 30, стр.183

Расстояние между пристанями А и В равно 60км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 30 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.

Желаю плодотворной подготовки к экзаменам!!!

Источник

С начала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснить различные стороны взаимосвязей в окружающей его жизни, даёт возможность применять изучаемые теоретические положения. Состояние математического развития учащихся наиболее ярко характеризуется их умением решать задачи. Задачи – это основное средство оттачивания мысли каждого школьника. Задачи на движение являются одной из самых трудных тем в курсе математики начальной школы. Трудность этих задач для ребенка методически обусловлена двумя причинами.

В первую очередь, это содержательная трудность. «Скорость» — это физическая величина, связывающая две величины, которые ребенок уже привык за период предыдущего обучения воспринимать каждую «саму по себе»: время и расстояние (длина). Для осознания каждой из них имеется либо визуальная опора (у длины, которую можно непосредственно «оценить глазом»), либо уже привычный инструмент измерения — линейка, часы. «Скорость» — это абстракция, которую ребенок не может ни увидеть, ни непосредственно измерить (т. е. «оценить» хотя бы, как время). Сама запись «скорости»: км/ч, м/мин. тоже не всегда понятна младшим школьникам.

Второй причиной является технологическая трудность — составление чертежа. Ученик начальной школы должен уметь кратко записать условие задачи, проиллюстрировать его с помощью таблицы, рисунка, схемы или чертежа, обосновать каждый шаг в анализе задачи и её решении, проверить правильность решения.

Рассматривая классификацию задач на движение, необходимо отметить следующее. Различают простые и составные задачи на движение. Составные задачи на движение подразделяют на задачи на движение в одном направлении, задачи на сближение объектов, задачи на удаление объектов, задачи на движение по реке. Кроме того, некоторые задачи на движение могут рассматриваться как задачи на нахождение четвертого пропорционального, задачи на нахождение неизвестного по двум разностям, задачи на пропорциональное деление.

Как научить детей решать задачи? С психолого-методической точки зрениянеобходимо организовать обучение с опорой на опыт детей, на их предметно-действенное и наглядно-образное мышление, необходимо формировать и развивать у учеников математические понятия на основе содержательного обобщения уже известных фактов.

Наглядность задач необходима для их лучшего понимания, ощущения действительности и необходимости математики в повседневной жизни.

Замечено, что учителя старших классов делают упор на логическое мышление учащихся, на оперирование знаковыми системами без необходимой опоры на образные компоненты. Но уже доказано, что до 80% информации человек получает через зрительный канал. Именно этот факт является важнейшим при обучении математике в начальной школе.

Прежде чем приступить к решению задач, содержащих такие величины, как «скорость», «время» и «расстояние», необходимо разъяснить учащимся само понятие скорости. При этом следует опираться на опыт детей, широко использовать практический и наглядный методы. Подготовительная работа к решению простых задач на движение предусматривает обобщение представлений детей о движении, знакомство с новой величиной «скорость», раскрытие связей между величинами: скоростью, временем, расстоянием. С целью обобщения представлений о движении полезно провести специальную экскурсию по наблюдению за движением транспорта, после чего провести наблюдения в условиях класса, где движения будут демонстрировать сами дети. На экскурсии и во время работы в классе пронаблюдать за движением одного тела и двух тел относительно друг друга. Так, одно тело может двигаться быстрее, медленнее, может остановиться, может двигаться по прямой или кривой. Два тела могут двигаться в одном направлении, а могут в противоположных, либо приближаясь одно к другому. Дети часто употребляют в своей речи слова «быстрее», «медленнее», не отдавая себе отчета в том, что эти слова связаны со скоростью (дети больше связывают их со временем). Для разъяснения понятия скорости можно задавать детям такие вопросы:

Кто быстрее преодолеет данное расстояние: автомобилист или велосипедист, велосипедист или пешеход?
Как вы понимаете слова «быстрее пройдет данное расстояние?»

Чаще всего ответ учащихся связан со временем: «Пройдет за меньшее время». А почему он пройдет за меньшее время? (Он проходит в час расстояние большее.) Значит, его скорость больше.

Наблюдая указанные ситуации в условиях класса, надо показать детям, как выполняются чертежи: расстояние принято обозначать отрезком, место (пункт отправления, встречи, прибытия) обозначают либо точкой на отрезке и соответствующей буквой, либо чёрточкой, либо флажком; направление движения указывают стрелками.

Понятие о скорости конкретизируется в процессе решения задач, например, таких:

Пешеход за 3 ч прошел 15 км. В каждый час он проходил одинаковое расстояние. Сколько километров пешеход проходил в час?

Разбор задачи следует сопровождать графической моделью, на которой обозначаются данные задачи: обозначим все расстояние отрезком и отметим, что это расстояние он прошел за 3 часа:

Поскольку главная трудность при решении таких задач состоит в том, что неподвижная картинка является моделью равномерного непрерывного процесса (движения), в рисунок принято вводить стрелку, символизирующую это движение и его направление.

Можно ли найти на чертеже точку, в которой окажется пешеход через 1 час? Через 2 часа?
Покажите, откуда он вышел? Где пешеход окажется через три часа?

Что можно сказать о длинах трех отрезков? (Они равные, так как за час пешеход проходил одинаковое расстояние.)
Как найти это расстояние? (15:3.)
А можно ли узнать, сколько километров пройдет пешеход за 4 ч (за 5 ч, за 6 ч) двигаясь с той же скоростью?
За какое время он может пройти расстояние в 35 км (40 км), если будет двигаться с той же скоростью?

Поиск ответов на такие вопросы поможет ученикам глубже осознать пропорциональную зависимость между скоростью, временем и расстоянием.

Для того чтобы учащиеся осознали зависимость между скоростью, временем и расстоянием, целесообразно рассматривать сразу по три взаимообратные задачи, оформляя их в таблицу. Вводятся буквенные обозначения: S- пройденное расстояние, V – скорость движения, t- затраченное время. Целесообразно ввести формулы, отражающие взаимосвязь этих величин. В процессе работы над текстовыми задачами я стараюсь добиться у учащихся умения чётко представлять ситуацию, о которой говорится в задаче, анализировать, сопоставлять, устанавливать зависимость между величинами, участвующими в данной задаче, например, между скоростью, временем и расстоянием, а не просто механически пользоваться готовыми формулами.

Почему же учащиеся допускают так много ошибок при решении задач?
Наблюдения показывают, что одна из основных причин допускаемых детьми ошибок в решении текстовых задач – неправильная организация первичного восприятия учащимися условия задачи и ее анализа которые проводятся без должной опоры на жизненную ситуацию, отраженную в задаче, без ее предметного и графического моделирования. Как правило, в процессе анализа для экономии времени используются готовые схемы, а создание модели на глазах у детей или самими детьми в процессе разбора задачи применяется редко. К тому же при фронтальном анализе и решении задачи учителя нередко ограничиваются правильными ответами двух-трех учеников, а остальные записывают за ними готовые решения без глубокого их понимания. Для устранения отмеченных недостатков необходимо, прежде всего, улучшить методику организации первичного восприятия и анализа задачи, чтобы обеспечить осознанный и доказательный выбор арифметического действия всеми учащимися. На этапе обучения анализировать условие задачи можно применять следующие задания:

1.Впиши

V t S

ч – t

км – S

м/мин — V

км/с

сут.

м/с

дм

мин

дм/ч

Прочитай задачи и подчеркни в них цифру обозначающую скорость – зелёной чертой, время – красной чертой, расстояние (путь) – синей.

Лыжник прошел дистанцию 24 км за три часа. С какой скоростью он шел?
Мотоциклист ехал 4 часа со скоростью 80 км/ч. Какое расстояние он проехал?
Лодка проплыла 28 км со скоростью 7 км/ч. Какое время она была в пути?

Как обучать детей нахождению способа решения задачи на движение? Этот вопрос – центральный в методике обучению решения задач. С точки зрения математической структуры эти задачи не являются новым видом — это задачи на пропорциональную зависимость: расстояние (длина) прямо пропорционально скорости и времени движения; и обратно: скорость движения обратно пропорциональна времени движения при постоянном значении расстояния. Та же зависимость наблюдается в задачах «на куплю-продажу», «на площадь», «на работу». Однако многие учителя полагают, что задачи «на движение» представляют собой особую группу задач нового вида, и при обучении их решению нужны какие-то новые приемы. Покажем, что заранее сформированное у ребенка умение переводить словесно заданный текст задачи на язык графики (в схему в отрезках) является универсальным приемом самостоятельной деятельности ребенка при решении задачи на движение. Задачи «на движение», содержащие пропорциональные величины, позволяют использовать как таблицы, так и схематические чертежи, причем последние являются, безусловно, более наглядной моделью.

Когда простые задачи усвоены, вводятся составные задачи на встречное движение, движение в противоположных направлениях.

Методика обучения решения задач «на встречное движение» основывается на четких представлениях учащихся о скорости равномерного движения, которые уточняются и обобщаются на специально отведенных этому вопросу уроках. На основе жизненных наблюдений выясняется и иллюстрируется смысл слов «двигаться навстречу друг другу», «в противоположных направлениях», «выехали одновременно из двух пунктов и встретились через…» и т.п.

Необходимо познакомить детей с понятием «общей скорости» (скорость сближения или удаления) и пояснить, что использование понятия «общая скорость» упрощает решение задач.

Перед решением таких задач следует проиллюстрировать на схеме и в инсценировке, что «встречное движение» – тоже движение в «противоположных направлениях», что после встречи, если скорости тел не изменились, они будут «удаляться» друг от друга с той же скоростью, с какой «сближались». Поэтому скорость удаления тоже равна сумме скоростей движущихся тел.

Здесь так же, как и при решении других задач, полезно предлагать различные упражнения творческого характера. В частности, ставится вопрос вида: «Могли ли поезда встретиться на середине пути? При каких условиях? Если поезда после встречи будут продолжать движение, то какой из них придёт раньше к месту выхода другого поезда, если будет двигаться с той же скоростью и др? Подводим детей к выводу. При решении задач на встречное движение используют понятие « скорость сближения».

При решении задач на движение в противоположных направлениях применяют понятие «скорость удаления».

Скорость сближения и скорость удаления в этих задачах находится сложением скоростей движущихся объектов.

Vсбл. = V1 + V2

Vуд. = V1 + V2

Можно пользоваться общим алгоритмом решения задач на движение.

Обобщению умения решать задачи рассмотренного вида помогают упражнения творческого характера.

Полезны упражнения на составление задач учащимися с последующим их решением, а также упражнения по преобразованию задач. Это прежде всего составление задач аналогичных решению. Или составление и решение задач по их краткой схематической записи.

Для того чтобы организовать разноуровневую работу над задачей в одно и то же время, можно использовать индивидуальные карточки-задания, которые готовим заранее в трех вариантах. Карточки содержат системы заданий, связанные с анализом и решением одной и той же задачи, но на разных уровнях.

Процесс решения задач при определенной методике оказывает весьма положительное влияние на умственное развитие школьников, поскольку он требует выполнения умственных операций: анализа и синтеза, конкретизации и абстрагирования, сравнения, обобщения.

Задача на движение в противоположных направлениях

Задачи на движение по водоему

Задачи, тесты

проф. П. Ф. Севрюков,< sevryukovpf@yandex.ru >, Ставропольский КрИПКРО, г. Ставрополь

Серьёзные ошибки в несерьёзных задачах

Источник

проф. П. Ф.
Севрюков,
< sevryukovpf@yandex.ru >, Ставропольский КрИПКРО, г. Ставрополь