Ошибки дискретизации это - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

In numerical analysis, computational physics, and simulation, discretization error is the error resulting from the fact that a function of a continuous variable is represented in the computer by a finite number of evaluations, for example, on a lattice. Discretization error can usually be reduced by using a more finely spaced lattice, with an increased computational cost.

Examples[edit]

Discretization error is the principal source of error in methods of finite differences and the pseudo-spectral method of computational physics.

When we define the derivative of $\,\!f(x)$ as $f'(x)=\lim _{{h\rightarrow 0}}{{\frac {f(x+h)-f(x)}{h}}}$ or $f'(x)\approx {\frac {f(x+h)-f(x)}{h}}$ , where $\,\!h$ is a finitely small number, the difference between the first formula and this approximation is known as discretization error.

[edit]

In signal processing, the analog of discretization is sampling, and results in no loss if the conditions of the sampling theorem are satisfied, otherwise the resulting error is called aliasing.

Discretization error, which arises from finite resolution in the domain, should not be confused with quantization error, which is finite resolution in the range (values), nor in round-off error arising from floating-point arithmetic. Discretization error would occur even if it were possible to represent the values exactly and use exact arithmetic – it is the error from representing a function by its values at a discrete set of points, not an error in these values.^[1]

References[edit]

^ Higham, Nicholas (2002). Accuracy and Stability of Numerical Algorithms (PDF). Other Titles in Applied Mathematics (2 ed.). SIAM. p. 5. doi:10.1137/1.9780898718027. ISBN 978-0-89871-521-7.

Преобразование аналоговых сигналов

Большинство DSP
приложений имеют дело с аналоговыми
сигналами, поэтому аналоговый сигнал
должен быть преобразован в цифровую
форму.
Аналоговый сигнал, являющийся
непрерывным и определенным с бесконечной
точностью, преобразуется в дискретную
последовательность, составляющими
которой являются значения, представляемые
в цифровой форме.

При преобразовании
сигнала из аналоговой формы в дискретную
часть информации теряется из-за:

погрешностей в
измерениях
неточностей в
синхронизации
ограничений на
продолжительность измерений

Эти явления
называются ошибками
дискретизации.

Перед выборкой
непрерывный аналоговый сигнал должен
быть предварительно сохранен. С другой
стороны, при измерении сигнала будет
происходить его изменение.

Только после того,
как сигнал был предварительно сохранен
можно произвести его измерение, а
измеренные значения преобразовать в
цифровую форму.

Дискретные выборки
сигнала, представляющие собой цифрованные
измеренные значения аналогового сигнала,
производятся обычно через равные
промежутки времени.

Важно отметить,
что выборка сигнала производится только
тогда, когда весь сигнал был предварительно
сохранен. Это означает возможность
использования более медленных АЦП
(ADC). Но схема, отвечающая за предварительное
сохранение сигнала должна функционировать
достаточно быстро, чтобы сигнал не
успевал существенно измениться. После
сохранения сигнала АЛУ не требуется
высокое быстродействие для преобразования
его в цифровую форму.

При измерении
аналогового сигнала неизвестно, что
действительно измеряется. В процессе
измерения сигнала часть информации
теряется.
Иногда можно обладать
некоторыми предварительными сведениями
о сигнале или сделать предположения о
возможном его поведении, которые позволят
частично восстановить потерянную при
дискретизации информацию.

Ошибки дискретизации

При преобразовании
аналогового сигнала в цифровую форму
его точность ограничивается числом
доступных разрядов для представления
данных.
На диаграмме представлен
аналоговый сигнал, который преобразуется
в цифровую форму при 8-разрядной точности
выборки.
Плавно изменяющийся аналоговый
сигнал в дискретном представлении будет
иметь ступенчатую форму благодаря
ограничению, накладываемому на точность
его представления.

Ошибки, появляющиеся
в результате оцифровывания аналогового
сигнала являются нелинейными
и зависящими
от сигнала.

Нелинейность
ошибок означает невозможность их расчета
с помощью обычной математики.
Зависимость
от сигнала
означает когерентность ошибок
невозможность их уменьшения с помощью
обычных приемов.

Проблема, связанная
с возникновением ошибок, является общей
для цифровой обработки сигналов. Эти
ошибки появляются из-за ограниченной
точности (т.е. длины слова), являются
нелинейными (следовательно их невозможно
просчитать) и зависящими от сигнала
(следовательно когерентными). Возникновение
ошибок приводит к невозможности точного
расчета DSP алгоритма при ограничении
на точность представления данных.
Поэтому единственным выходом из такой
ситуации является тестирование работы
алгоритма при различных входных сигналах.
Нелинейность ошибок также приводит к
нестабильности работы, особенно при
применении IIR (БИХ) фильтров.

Длина машинного
слова, используемого в цифровой обработке
сигналов определяет точность и
динамический диапазон. Неточность в
синхронизации приводит к появлению
ошибок в выбранном дискретном сигнале.

Ошибки вносимые
синхронизацией также являются нелинейными
и зависят от сигнала.

Реальные DSP системы
подвержены воздействию от трех источников
ошибок:

ограничение при
цифровом преобразовании сигнала его
точности конечной длиной машинного
слова
ограниченная
точность арифметических вычислений,
выполняемых процессором
ограничение
точности сигнала длиной машинного
слова при его преобразовании из
дискретной формы обратно в аналоговую

В совокупности
эти ошибки составляют понятие ошибок
дискретизации.
Ошибки являются нелинейными и зависящими
от сигнала. Нелинейность ошибок означает
невозможность их расчета c помощью
обычной математики. Зависимость от
сигнала определяет необходимость
расчета эффекта от ошибок, свойственных
каждому отдельно взятому сигналу.
Простым решением для уменьшения ошибок,
накладываемых ограниченной длиной
машинного слова, является создание
моделей для каждого источника ошибок,
которые представляют искажения при
дискретизации как случайные шумы.

Модель дискретизации
с влиянием случайных шумов является
наглядной при понимании сути эффекта.
Но в действительности эта модель не
является абсолютно правильной, особенно
для систем с обратной связью, таких,
например, как IIR (БИХ) фильтры.
Эффект,
связанный с появлением ошибок, похож
на наличие в системе случайных шумов.

Источник

Адаптивное построение сетки состоит в том, что после создания расчетной модели и задания граничных условий генерируется конечно-элементная сетка, затем выполняется анализ, оценивается ошибка дискретизации сетки, после чего меняется размер сетки. Процесс протекает до тех пор, пока значение погрешности не станет меньше заданного, или число итераций не достигнет допустимого значения. [c.67]

Ошибки дискретизации являются результатом замены реальной теплопроводящей среды дискретными электрическими ячейками. При этом следует иметь в виду, что ошибки в основном возникают в результате ири-менения сосредоточенных емкостей и индуктивностей. Ошибки, связанные с дискретизацией области, определяются шагом сетки и зависят от характера температурного поля. Это может быть легко продемонстрировано с помощью разложения в ряд Тейлора температуры в некоторой точке области. Ошибка дискретизации координат определяется зависимостью [c.359]

Шаг сетки Ах явно входит в выражение для ошибки. Если его уменьшить, то ошибка также уменьшится. При Дл —>»0 ошибка также стремится к нулю. Полагая, что члены, включающие производные выше четвертого порядка, пренебрежимо малы, определим ошибку дискретизации области [c.359]

Эксперименты показывают, что для многих теплотехнических задач разбиение области в направлении одной координаты иа 8—10 элементарных слоев приводит к существенному уменьшению ошибки дискретизации. Это значит, что если (Д л /б) s O,l, то ошибка дискретизации оказывается настолько малой, что ее в ряде случаев можно не учитывать, так как она стремится к нулю. [c.359]

Ошибки дискретизации могут быть уменьшены использованием более мелких элементов или расположением криволинейных элементов около границ и, во всяком случае, стремятся к нулю по мере стремления к нулю размера элемента. Ошибки пробной функции не обязательно уменьшаются по мере уменьшения размера элементов и могут поэтому мешать сходимости к точному решению нли даже приводить к расходимости, [c.169]

Мы хотим предложить объяснение этого чуда, основанное на нашем наблюдении, что обычное измерение числа обусловленности для этих матриц неестественно. В вычислительных целях мы будем рассматривать эти матрицы как преобразования евклидова пространства (дискретного Ж°) в себя и потому возьмем одну и ту же норму для невязки уравнения и для результирующей ошибки в решении. Это целиком противоположно тому, что делается в дифференциальной задаче, или тому, что происходит при оценке ошибки дискретизации / измеряется в норме пространства Л1 и ее ошибка — в ш и ее ошибка — в Ж. (В вариационной задаче соответственно и Ж .) В самом деле, оператор I = с каким-либо обычным краевым условием вполне обусловлен как преобразование из Ж в Ж°. Ограниченность операторов I и была существенным моментом в разд. 1.2. Можно показать, что это верно и для разностного оператора б , а также для любого приемлемого аналога в методе конечных элементов, если только эти естественные нормы сохраняются. Следовательно, должен быть алгоритм решения уравнения КО, = Р, отражающий это свойство, и тогда чудо развеялось бы ошибки в Л1 и ш соответствовали бы их положению. [c.147]

Важный вывод ошибка округления не зависит сильно от степени полиномиального элемента. Главным образом она зависит от h, от порядка рассматриваемой задачи и от основного собственного значения непрерывной задачи. Поэтому при наличии ошибок округления достичь численную точность можно, увеличивая степень пробных функций. Число обусловленности для кубических элементов лишь немного хуже, чем для линейных, так что ошибки округления в этих случаях для заданного значения h сравнимы. Однако ошибка дискретизации для кубических элементов на порядок меньше. Поэтому в переходный момент, когда округления не позволяют получать более точные результаты за счет уменьшения h, с помощью кубического элемента этого можно достичь. Особенно это относится к вычислению напряжений, где дифференцирование (или взятие разностей) перемещений вводит в численную ошибку дополнительный множитель Л». Даже в задачах второго порядка ошибка округления становится значительной и наилучший выход из положения — увеличить степень пробных функций. [c.250]

Ошибки дискретизации возникают прн замене реальной конструкции ограниченны числом конечных элементов (с учетом их формы и размеров). [c.28]

В (15.3.1-8) не дается никаких оценок ошибки аппроксимации. Для неравномерной сетки (х. Фх , yj Фу 1) ошибка дискретизации уменьшается почти линейно с уменьшением шага. Некоторые идеи, касающиеся выбора подходящего шага с целью существенного ограничения этой ошибки, даются в п. 15.3.1.4. Кроме того, более полно этот вопрос рассмотрен в классической математической литературе [15.58, 15.47]. [c.406]

Построение разностной сетки. Для того чтобы затраты времени счета и памяти ЭВМ оставались в разумных пределах, необходимо ограничить число узлов сетки. Соответствующий компромисс между точностью и стоимостью вычислительных ресурсов можно найти, оценив ошибки аппроксимации. В критических областях, с большими ошибками дискретизации, шаг сетки должен быть мелким, в то время как в областях, где ошибки невелики, его можно увеличить. Из этих соображений очевидно, что равномерная сетка непригодна, поскольку в этом случае шаг сетки должен был бы подстраиваться под критические области, и число узлов стало бы очень большим. [c.409]

Так как ошибки дискретизации зависят от распределения величин ф, п, р, то прием- [c.409]

Как уже обсуждалось ранее, скорость ионизации очень чувствительна к напряженности электрического поля. Следовательно, скорость генерации будет иметь в области отсечки канала сильный пик, который можно правильно рассчитать лишь используя очень мелкую сетку. Интеграл от генерационного члена по всей области дает ток через поверхность, и, следовательно, ошибка дискретизации пропорциональна ошибке в вычислении этого тока. Если мы рассмотрим лишь первую производную электрического поля [c.411]

Для снижения методической погрешности при использовании моделей средних значений важно осуществить рациональное условное деление конструкции ЭМУ на отдельные элементы, либо увеличить число таких разбиений. Но в последнем случае метод приближается к методу сеток и становится громоздким, в то время как практически важно получение высокой точности расчетов при ограниченной дискретизации. При умелом применении схем замещения методическая ошибка в сравнении с методом сеток составляет обычно не более 5 % даже при ограниченной степени дискретизации. По крайней мере, это заметно меньше, чем погрешности от неточности задания входной информации. При выборе числа разбиений важен и характер решаемой задачи. При грубой оценке показателей поля возможна упрощенная схема замещения с пятью-шестью укрупненными телами (ротора в целом, объединенных обмотки и пакета статора и т.д.). Если необходим анализ изменения осевой нагрузки на подшипники, то особо подробно должны быть представлены тела, входящие в замкнутую размерную цепь их установки, а остальные элементы могут рассматриваться укрупненно. При анализе относительных температурных деформаций требуется наиболее детальная дискретизация ЭМУ, особенно для элементов, имеющих различные коэффициенты линейного расширения. Здесь ТС, например, должна содержать не менее 15—20 тел. [c.127]

При получении совмеш,енных изображений в соответствии с уровнем обработки S остаточная среднеквадратическая ошибка регистрации не должна превышать 50% шага дискретизации. Значение этого параметра зависит главным образом от точности работы системы ориентации спутника. [c.98]

Поверхность тела представляется при помощи четырехугольных и треугольных элементов с квадратичным изменением формы и линейным, квадратичным или кубическим изменением перемещения и вектора напряжений относительно внутренней системы координат. Тело разбивается на подобласти производится дискретизация интегрального уравнения для каждой подобласти, и получается система уравнений ленточного типа. Для вычисления интегралов используется квадратурная формула Гаусса, число узлов в которой выбирается на основании верхней оценки для ошибки, определенной по значениям производных от подынтегральных выражений. Масштаб коэффициентов в уравнениях выбирается таким образом, чтобы получить устойчивую при счете систему, разрешимую методом исключения без итерации остатков. Поблочное решение уравнений позволяет рассматривать большие задачи. В программе используется большое число процедур, осуществляющих контроль и автоматическое формирование данных. Результаты решения задачи о фланце трубопровода и характеристики выполнения программы сравниваются с результатами, полученными методом конечных элементов, и экспериментальными результатами. [c.111]

Здесь штрихом обозначены измеряемые величины, символом 5 — ошибки измерений. Функции Wf t), Wh t) — импульсные переходные функции стационарных линейных фильтров, применяемых при формировании измерений СНС и гравиметра, — оператор свертки фильтра (указанные фильтры необходимы, в частности, для подавления сигнала вне интервала частот Найквиста, с целью исключения явления маскировки частот при дискретизации измерений). Заметим, что в общем случае измерения в (5) проводятся с разной частотой дискретизации. [c.136]

При этом следует соблюдать определенную осторожность. Если нестационарные конечно-разностные уравнения сходятся к устойчивому стационарному решению, то еше нельзя считать, что соответствующие дифференциальные уравнения в частных производных имеют устойчивое стационарное решение. Как мы уже видели, дискретизация иногда приводит к появлению схемной вязкости. Эта и другие ошибки аппроксимации могут привести к тому, что конечно-разностные уравнения окажутся более устойчивыми, чем дифференциальные уравнения в частных производных. Выяснение отличия гидродинамической устойчивости от завышенной численной устойчивости представляет трудную задачу (см. разд. 6.5). [c.165]

Заметим, что ошибка в г з, обусловленная дискретизацией, приводит к возникновению ошибки при вычислении толщины вытеснения б (Шлихтинг [1968]), если последнюю определять по формуле [c.236]

Вычислить локальную ошибку отсеченИя , или дискретизации, с помощью разложения в ряд Тейлора. [c.28]

Исследуем ошибки округления двумя способами. Рассмотрим свободно опертую балку с и и М, равными нулю на обоих концах. Тогда уравнения М» = / и гю» = М можно решить отдельно, сначала для М, а затем для ш, применяя для этого либо конечные разности, либо конечные элементы. Предположим, что приближенное решение задачи М» = / содержит ошибку округления еь обычно порядка для ЭВМ с длиной слова 1. Тогда приближенное решение задачи т» = —/ будет прежде всего содержать свою собственную ошибку округления е2 того же порядка и, кроме того, унаследованную ошибку ез. Последняя удовлетворяет равенству ез = Ъх, или, скорее, точно удовлетворяет используемой дискретизации этого уравнения, и потому порядок ошибки ез также равен Ошибки округления не объединяются в [c.146]

При втором способе получаются правильные величины скоростей, но в результате дискретизации вносится ошибка в величины г )1,/. Очевидно, что оба эти способа сходятся при Ау- 0. Поскольку наибольшее влияние на динамику течения оказывает и, а не г1), второй способ, заключающийся в задании во входном сечении потока профиля для и при допущении ошибок в величинах г , кажется предпочтительнее. [c.236]

Требования к отношению сигнал-помеха в канале передачи ИКМ сигнала (канала записи — воспроизведения) невысоки, поскольку необходимо передать лишь два уровня сигнала — О и 1. Нелинейные искажения, возникающие в этом канале, практически не оказывают существенного влияния на восстановленный сигнал. Точность передачи сигналов с ИКМ зависит от параметров аналого-цифрового преобразования (АЦП)— частоты дискретизации и шага квантования. Для неискаженной передачи частота дискретизации /д в соответствии с теоремой Котельникова должна по крайней мере вдвое превышать высшую частоту Fb передаваемого аналогового сигнала. Шаг квантования определяет максимальную погрешность восстановленного сигнала и характеризует ошибки квантования, которые проявляются как шум квантования . Шаг квантования связан с числом уровней [c.21]

Ошибки могут возникать на различных стадиях конечно-элементного анализа пр постановке задачи, дискретизации (построении модели), численном решении. [c.28]

Адаптивное построение сетки. Адаптивное построение сетки состоит в том, что после создания модели и задания граничных условий программа генерирует конечноэлементную сетку, выполняет расчет, оценивает ошибку за счет сеточной дискретизации и меняет размер сетки от решения к решению до тех пор, пока расчетная погрешность не станет меньше некоторой наперед заданной величины (или пока не будет достигнуто установленное число итераций). [c.92]

Для каналов первого класса принята частота дискретизации 21 1/3 кГц, второго класса — 14 2/9 кГц, высшего класса — 32 кГц. В каналах высшего класса применено 10-разрядное кодирование с мгновенным компандированием, в каналах первого и второго классов — 9-разрядное. Таким образом, скорость цифрового потока при организации канала высшего класса составляет 320 Кбит/с, первого класса — 192 Кбит/с и второго класса — 128 Кбит/с. В первичном цифровом потоке 2048 Кбит/с в системе Орбита-Рв передаются 10 каналов первого класса, либо 15 каналов второго класса, либо 6 каналов высшего класса. Всего для сигналов ЗВ выделяются два потока по 2048 Кбит/с. В системе использовано помехоустойчивое кодирование, обеспечивающее допустимую при цифровой передаче вероятность ошибки poш=10- . [c.314]

При применении прямых методов получение достаточно точных решений связано с решением больших систем уравнений, решение которых затруднено из-за ограниченных возможностей вычислительных машин (память, быстродействие, ошибки округления). Поэтому при составлении программ решения больших систем линейных алгебраических уравнений, полученных при дискретизации вариационных задач, стремятся учесть особый вид магриц таких систем например, их малую заполненность, ленточную структуру и т. д. Такие системы можно решать на ЭВМ точными методами (Гаусса, Жордана), если использовать внешние запоминающие устройства и применять специальные приемы, направленные на экономию памяти и времени счета, например блочный метод Гаусса. [c.180]

Штриховая кривая 1 на жс. 4.6 соответствует интегрированию уравнений продолжения модифицированным методом Эйлера с шагом АХ по параметру X, который на начальном участке деформирования при малых Р соответствовал приращению относительного прогиба w(0)/i = 0,005. Штрихпунктирная кривая 2 совтветствует тому же методу, но с шагом w(0)/R = 0/)( 5. Сплошная кривая 3 получена прт комбинировании двух шагов w 0)fR = 0,005 модифицированного метода Эйлера с одним шагом по неявной схеме дискретного продолжения, описанной в ЗА. Эта кривая практически соответствует точному решению задачи (4.3.2), (4.3.3) (конечно, в пределах принятой дискретизации). Как видно из жс. 4.6, модифицированный метод Эйлера дает накопление ошибки, особенно существенное в тех областях параметра, где решение претерпевает значительные изменения. В то же время расход машинного времени при получении кривых 2 и 3 практически одинаков (даже для кривой 5 он был несколько меньшим). Поэтому для всех дальнейших расчетов бьша использована именно такая комбинация непрерывного и дискретного продолжения. [c.120]

Для вычисления ДПФР, кроме матрицы bi k, I), определяющей комплексную амплитуду поля на объекте, необходимо еще задаться и величинами и и v, характеризующими относительные размеры объекта, наблюдаемого из воображаемой точки регистрации голограммы. При их выборе следует руководствоваться условиями (1.46) малости ошибки при дискретизации фазовых множителей. [c.21]

Численные эксперименты показали, что скорость сходимости итерационного процесса в смешанных задачах слабо зависит от степени дискретизации. Рассматривалась, например, следующа краевая задача [121] для единичного куба на центральной части граней куба, размером 0,8X0,8, задавались перемещения, а на остальной части куба — усилия, соответствующие гидростатическому сжатию. Граничная поверхность разбивалась на 96, 216 н 600 граничных элементов. Исследовался стационарный итерационный процесс (4,2) для дискретного уравнения (2,31) при р=1 и Р = 2, Для первой дискретизации при р=1 отклонение искомы поверхностных сил от точного решения на первой итерации составило 65%, на шестой — 7,5%, на одиннадцатой — 0,9%, Для остальных дискретизаций (216 и 600 граничных элементов) ошибка в 1 % была достигнута соответственно на тринадцатой и четырнадцатой итерациях. При р = 2 итерационный процесс (4,2) сходился значительно быстрее для первой дискретизации (96 гра ничных элементов) отклонение искомых поверхностных сил от точного решения на первой итерации составило 31, %, на второй-— 9%, на третьей —2,6 %, на четвертой — 0,86 % для остальньис дискретизаций (216 и 600 граничных элементов) ошибка в 1 % была достигнута соответственно на пятой и шестой итерациях. [c.239]

Базис Каруиепа — Лоэва не отвечает требованиям универсальности (т. е. применимости для достаточно широкого класса сигналов), устойчивости к ошибкам задания статистических характеристик сигнала и требует больших вычислительных затрат при реализации. Поэтому имеет смысл ставить задачу выбора не формально оптимального, а рационального базиса в (1.21), (1.22), удовлетворяющего указанным требованиям. Однако удовлетворить всем требованиям одновременно невозможно. На практике используются различные виды дискретизации [12]. Из них рассмотрим наиболее часто используемые при обработке сигналов аналитических приборов. [c.20]

Максимум ошибки всегда достигается на конце большой полуоси эллипса. Поэтому возникла гипотеза, что большая часть ошибки описывается геометрическими причинами — тем, что последовательность точек дискретизации, равномерная в стандартной координате на эллипсе, описывает эллипс неточно (с точки зрения вычислительного метода). Была найдена геометрическая характеристика, с которой ошибка хорошо коррел-лировала. Это отношение кривизны эллипса в вершине к кривизне окружности, проведенной через нее и еще две соседние точки дискретизации. Так, при отношении, близком к двум, ошибка достигала 16%, к трем — 19%. Наличие геометрического описания ошибок позволяет надеяться, что при более удачной расстановке точек на контуре трещины можно ожидать значительного уменьшения ошибок. Действительно, удалось найти геометрический критерий расстановки точек на контурах, позволяющий минимизировать ошибки вычислений (точнее максимум ошибки в точках контура трещины). Точнее, если расстановка точек удовлетворяла этому критерию, то соответствующая ошибка не более чем в 1,5 раза превышала минимально возможную. Опишем здесь результат оптимизации метода. [c.195]

Погрешности реконструкции в основном обусловлены неидеальностью используемых аппроксимаций алгоритма реконструкции. Среди наиболее существенных источников пофешностей реконструкции следует указать ошибки, возникающие из-за недостаточно малого интервала дискретизации по углу, пофешности неоптимальной интерполяции и двумерной дискретизации томофаммы, чрезмерный уровень низкочастотной фильтрации реконструированных структур из-за попытки компенсации отмеченных пофешностей снижением высокочастотных компонент ядра свертки или двумерной фильтрацией реконструированных томофамм. [c.150]

Общая идея постановки граничных условий, отвечающих бесконечности на наиболее удаленной границе разностной сетки, была предложена Ричардсоном [1910]. Кавагути [1965], Фридман [1970], а также Ли и Фын [1970] в выходном сечении брали, например, профиль Пуазейля. Заметим, что асимптотическое решение, используемое в качестве граничного условия, должно рассматриваться в переменных задачи-, например, если конечно-разностные уравнения записаны в переменных г]) и то и решение Пуазейля должно быть записано для ф и Если и задается по имеющемуся решению дифференциальных уравнений, а ф находится при помощи квадратур, то при этом возникает ошибка в результатах, обусловленная дискретизацией (аналогичная ситуация возникает и в случае постановки условий на входной границе потока см. предыдущий раздел). Для течений более общего вида, например таких, как асимптотическое течение в пограничном слое, решение дифференциальных уравнений будет отличаться от асимптотического конечно-разностного решения по всем переменным. На выходной границе предпочтительнее брать конечно-разностное решение асимптотического обыкновенного дифференциального уравнения (Кавагути [1965]). [c.237]

Заметим, что вычисление аппроксимации Ритца предполагалось непрерывньш по времени-, до сих пор лишь дискретизация заменяла все допустимое пространство его подпространством 5 . Это соответствует изложению задачи Коши в гл. 7, где ошибки метода» Ритца отделены от ошибок метода конечных. разностей (или другого метода) по временному направлению. Для нелинейной задачи большие дискуссии вызвал наилучший метод приращений , но мы полагаем, что все основные возможности сходятся в одном. Они просто вносят новую ошибку, пропорциональную степени приращения в случае разностного уравнения. [c.138]

В практических задачах времт тоже должно быть дискретизировано, что предполагает применение метода конечных разностей. Например, схема- Кранка — Николсона симметрична относительно п+1/2 при вычислении uf tn+ ) через и потому имеет точность порядка At . Таким образом, окончательно вычисленное приближение содержит эту ошибку, как и ошибку метода Галёркина, вызванную дискретизацией по х. Последнюю из них мы проанализируем подробно и покажем, что при к 2т ее оптимальный порядок для 5-й производной тоже р -вен Этот результат применяется к уравнениям параболического типа, например к уравнению теплопроводности Ь — эллиптический оператор того же типа, что и в стационарных задачах. В случае гиперболических уравнений, не содержащих диссипативных членов, возможности метода конечных элементов несколько меньше трудности в сравнении с явными разностными методами- могут оказаться слишком большими. Тем не менее даже в этом случае достигнуты значительные результаты исследование границ можно проводить почти автоматически в гл. 7 включен набросок теории метода конечных элементов для гиперболического случая. [c.139]

Естественно спросить почему конечные элементы не используются также и по временной переменной Конечно, можно было бы попытаться применить их, но это не даст особого успеха. С математической точки зрения вполне разумно изучить дискретизацию в два этапа сначала исследовать ошибку метода конечных элементов и(х, i) —u (x, t], а затем ошибку в возникающую при решении обыкновенных дифференциальных уравнений. По временной переменной геометрия области не вызывает трудностей, которые надо было бы преодолевать с помощью метода конечных элементов, и на самом деле непосредственное применение принципа Галёркина может связать все временные слои и уничтожить главное свойство распространения вперед по. времени. Мы не видим причин отказываться от этой дополнительной гибкости конечных разностей. [c.282]

Моделирование позволило отметить некоторые особенности аналогового вычисления суммарного изображения Это, прежде всего, отсутствие регистрации проекций, которое позволяет избежать погрешностей их съема и ввода в ЭВМ, т. е в этом случае восстанов тение искомого распределения осуществляется в отсутствие шумов При моделировании указанная особенность томографической Интерферометрии учитывалась Однако при реализации некоторых математических операций в оптических системах с преобразованием волнового фронта возможно их неточное выполнение из-за аберраций оптических элементов и погрешности юстировки. В томографическом интерферометре искажения, обусловленные аберрациями, устранялись голографической регистрацией волнового фронта. Возможная ошибка ( 30 ) из-за неточности согласования углов зондирования и поворота волнового фронта была равна погрешности из-за дискретизации проекций при цифровом вычислении суммарного изображения на сетке 51X51 отсчетов [c.138]

Форматы кодов у устройств разного назначения существенно различны, поскольку у них не совпадают законы кодирования, способы защиты от ощибок, число звуковых каналов, характер и объем дополнительной информации. Так, у студийной аппаратуры определяющими факторами являются высокое качество передачи и возможность введения дополнительной служебной информации (адресно-временного кода для монтажа программ, режиссерских комментариев и т. д.). Результирующая скорость цифрового потока больщой роли не играет, поскольку специфика работы студийной аппаратуры не связана с передачей этих потоков по каналам связи. Поэтому в таких устройствах применяют равномерное квантование с числом разрядов не менее 16 (в пультах и устройствах шумоподавления число разрядов на отсчет доходит до 24) и высокую частоту дискретизации (48 кГц). Избыточность, вводимая для борьбы с ошибками, достигает 33%, а управляющие сигналы, осуществляющие перестройку системы обработки сигнала, и адресно-временной код передаются совместно со звуковыми. [c.238]

Источник

Основной
причиной преобразования аналоговой
информации в дискретную форму стало
невозможность улучшения качества
передачи данных в аналоговой форме.
Поэтому на смену аналоговой техники
передачи пришла цифровая техника. В
этой технике используется дискретная
модуляция исходных, непрерывных во
времени аналоговых процессов.
Рассматриваемый принцип импульсно
кодовой модуляции применяют в телефонии.
В этом случае дискретизация происходит
как по времени, так и по амплитуде.
Амплитуда исходной непрерывной функции
измеряется через заданный период
времени, за счёт этого происходит
дискретизация по времени, затем каждый
замер представляется в виде двоичного
числа, определённой разрядности, что
означает дискретизацию по значению.
Устройство, которое выполняет эту
функцию, называется АЦП. После чего
замеры передаются по линиям связи в
виде 0 и 1. При этом применяется те же
методы кодирования, что и при изначально
дискретной информации. На принимающей
стороне коды преобразуются в исходный
последовательности, а ЦАП производит
декодирование в аналоговый сигнал.

Дискретная
модуляция основана на теории отображения
Найквиста. В соответствии с этой теорией
аналоговая непрерывная функция,
переданная в виде последовательности
ей дискретных значений, может быть точно
восстановлена, если частота её
дискретизации была в 2 и более раз выше
частоты самой высокой гармоники спектра
её функции. В том случае, если это условие
не выполняется, то восстановленная
функция будет существенно отличаться
от исходной.

Ошибка
интерполяции равна разности исходного
задержанного процесса и восстановленного
процесса, причем задержка выбирается
такой, чтобы ошибка была минимальной.

∆_инт(t)
= x(t — t_опт)
— x_в(t).

В
системах с обратной связью задержка
восстановленного сигнала нежелательна.
Она может привести не только к увеличению
ошибок моделирования, но и к потере
устойчивости модели. В этом случае
ошибка определяется как:

∆_полн(t)
= x(t) — x_в(t)

и
называется полной ошибкой.

Так
как ошибки зависят от времени, то для
их числовой оценки используется
среднеквадратическая ошибка, усредненная
за время Т, в течение которого измеряется
ошибка.

5. Эффективное кодирование, назначения, способы реализации, основные ограничения.

Этот
вид кодирования используется для
уменьшения объемов информации на
носителе — сигнале.

Для
кодирования символов исходного алфавита
используют двоичные коды переменной
длины: чем больше частота символа, тем
короче его код. Эффективность кода
определяется средним числом двоичных
разрядов для кодирования одного символа
– l_ср
по формуле

где
k – число символов исходного алфавита;

n_s
– число двоичных разрядов для кодирования
символа s;

f_s
– частота символа s; причем

При
эффективном кодировании существует
предел сжатия, ниже которого не
«спускается» ни один метод эффективного
кодирования — иначе будет потеряна
информация. Этот параметр определяется
предельным значением двоичных разрядов
возможного эффективного кода – l_пр:

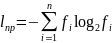
где
n – мощность кодируемого алфавита,

f_i
– частота i-го символа кодируемого
алфавита.

Существуют
два классических метода эффективного
кодирования: метод Шеннона-Фано и метод
Хаффмена. Входными данными для обоих
методов является заданное множество
исходных символов для кодирования с их
частотами; результат — эффективные коды.

Метод
Хаффмена построения эффективного кода
реализуется в два этапа: сворачивание
кода и разворачивание кода.

1.
Сворачивание кода.

Формируют
начальную последовательность символов
источника информации путём упорядочивания
по неубыванию вероятностей их появления
на выходе источника. Последние два
символа последовательности объединяют
в один с вероятностью появления на
выходе источника информации, равной
сумме вероятностей появления каждого
из этих символов. Эту операцию повторяют
итеративно до тех пор, пока в
последовательности не останется только
лишь два символа.

2.
Разворачивание кода.

Одному
символу приписываем код 0, а другому 1.
Каждый символ разбивается на две
последовательности в порядке, обратном
порядку сворачивания кода. Эту операцию
повторяют итеративно для каждой из
полученных двух последовательностей
до тех пор, пока имеется последовательность,
состоящая более чем из одного символа.
При этом кодовая комбинация каждой
дочерней последовательности получается
путём приписывания к кодовой комбинации
родительской последовательности символа
0 или 1 справа.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

CFD Solution Analysis: Essentials

Jiyuan Tu, … Chaoqun Liu, in Computational Fluid Dynamics (Third Edition), 2018

Discretisation Error

These errors are due to the difference between the exact solution of the modelled equations and a numerical solution with a limited time and space resolution. They arise because an exact solution to the equation being solved is not obtained but numerically approximated. For a consistent discretization of the algebraic equations, the computed results are expected to become closer to the exact solution of the modelled equations as the number of grid cells is increased. However, the results are strongly affected by the density of the mesh and distribution of the grid nodal points.

We identify two types of discretization errors: local and global (or accumulated). To have an idea about the local error and global error, consider the finite-difference formulation of the derivatives for the transport variable ϕ in space and time at a specified grid nodal point expressed through the Taylor series expansion:

(6.5)∂ϕ∂x=ϕi+1,j−ϕi,jΔx+OΔx︸Truncation errorSpatial derivative

(6.6)∂ϕ∂t=ϕi,jn+1−ϕi,jnΔt+OΔt︸Truncateion errorTime derivative

Termination of the Taylor series expansion in Eqs (6.5) and (6.6) results in the so-called truncation errors involved in the approximation.

The local error is the formulation associated with a single step and provides an idea about the accuracy of the method used. For this error, the accuracy of the numerical solution concerns mainly on the approximation of the spatial derivative. The solution accuracy for a transient problem, however, focuses on the advancement of the transport variable ϕ through time usually characterized by the global error. The representations of the local error and global error are best illustrated in Fig. 6.1. We can observe that the smaller the mesh size or time step in transient problems, the smaller the error, and thus the more accurate the approximation.

Fig. 6.1. The local and global discretization errors resulting from the finite-difference method at a specified grid nodal point.

We shall illustrate the significance of the discretization error through a worked example below.

Example 6.8

Consider the transient one-dimensional convection-type equation to further illustrate the aspect of discretization error. A fourth-order central difference is employed for the spatial derivative to attain higher accuracy. Using the Euler explicit method, demonstrate the discretization error that is associated with the numerical solution obtained through the first- and second-order approximations to the time derivative at a fixed time step size of Δt = 1/128 accompanied by the variation of two different grid step sizes of Δx = 1 and Δx = 1/2.

Solution: Through the consideration of additional grid nodal points along the spatial direction x and applying the Taylor series expansion, the fourth-order finite-difference approximation can be obtained as

∂ϕ∂x=−ϕi+2+8ϕi+1−8ϕi−1+ϕi−212Δx+OΔx4︸Truncationerror

Substituting the above approximation along with the first-order forward difference to the time derivative yields the following algebraic equation:

ϕin+1−ϕinΔt−u−ϕi+2+8ϕi+1−8ϕi−1+ϕi−212Δx=0

For the second-order approximation of the time derivative, the central difference is employed, in other words,

ϕin+1−ϕin−12Δt−u−ϕi+2+8ϕi+1−8ϕi−1+ϕi−212Δx=0

This newly developed formula is similar to the well-known leapfrog method.

The computed results compared with the exact solution for the first-order and second-order time approximations against two different grid sizes are illustrated in Figs 6.8.1 and 6.8.2.

Fig. 6.8.1. Fourth order grid and first order time approximations of convection-type equation for the variable ϕ with a fixed time step of Δt = 1/128 and two grid sizes of Δx = 1 and Δx = 1/2.

Fig. 6.8.2. Fourth order grid and second order time approximations of convection-type equation for the variable ϕ with a fixed time step of Δt = 1/128 and two grid sizes of Δx = 1 and Δx = 1/2.

Discussion: By increasing the approximation of the time derivative from first order to second order, the numerical simulation for the higher-order time approximation at a grid size of Δx = 1 is shown to be less sensitive to the time step changes with the suppression of wiggles through time (compare the solutions between Figs 6.8.1 and 6.8.2). By halving the grid size to Δx = 1/2, the numerical simulation is stabilized. The solution for the second-order time derivatives converges to the exact solution profile, but the first-order solution retains some oscillatory wiggles around the exact solution profile and is still far from its converged state. In this example, the systematic reduction of the grid step sizes and the use of higher approximation for the time derivative characterize the diminishing contribution of the respective local and global discretization errors.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780081011270000064

Introduction

J. Blazek, in Computational Fluid Dynamics: Principles and Applications (Second Edition), 2005

Each discretisation of the governing equations introduces a certain error – the discretisation error. Several consistency requirements have to be fulfilled by the discretisation scheme in order to ensure that the solution of the discretised equations closely approximates the solution of the original equations. This problem is addressed in the first two parts of Chapter 10. Before a particular numerical solution method is implemented, it is important to know, at least approximately, how the method will influence the stability and the convergence behaviour of the CFD code. It was frequently confirmed that the Von Neumann stability analysis can provide a good assessment of the properties of a numerical scheme. Therefore, the third part of Chapter 10 deals with stability analysis for various model equations.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780080445069500035

Numerical Field Calculation for Charged Particle Optics

Erwin Kasper, in Advances in Imaging and Electron Physics, 2001

5.4.2 Error Analysis and Improvements

In the case of arbitrary triangular meshes, it is difficult to analyse the discretization errors of the approximation (5.66) with (5.72) and (5.75). However, for meshes that are obtained by subdividing along diagonals, as shown in Fig. 5.22 such an analysis is feasible.

Figure 5.22. Different triangulations of a square-shaped mesh. The points in diagonal directions always have vanishing coefficients. In the traditional form of the FEM only configuration (c) gives the correct results.

According to Eq. (5.72a), the L-coefficients vanish for all neighbors in diagonal directions, regardless of how the bisections into triangles were made, and consequently a five-point formula is found. However, this depends on the mode of subdivision, because the material coefficient s is evaluated at different centroids of triangles. This inconsistency already causes a discretization error of second order, which can easily be removed.

It is favorable to introduce the coefficients

(5.76a)εk±:=εu0+pk/2∓ηqk,v0+qk/2±ηpk,k=1,…,M,η≪1,

if ε(u, v) is discontinuous and

(5.76b)εk′=εk+=εk−=εu0+pk/2,v0+qk/2

for a continuous function. This means that the coefficient is determined not at a centroid but at the midpoint (k′) on the line from point (0) to point (k), as shown in Fig. 5.21. Equation (5.72a) is now replaced by

(5.77)−L0k=εk−γk−+εk+γk+/2,k=1,…,M,

whereupon the second and more general form of Eq. (5.72b) has still to be satisfied. After a corresponding change of notation and some elementary calculations, it is now possible to show that for the homogeneous PDE with A = B = ε and D ≡ Q ≡ 0 the five-point formula (4.60) is obtained, as it should be.

Another source of errors of second order is Eq. 5.75. This is most easily seen for a constant function Q(u, v) = Q₀, Eq. 5.75 then simplifying to

(5.78)S0=16Q0∑i=1MDi=Q0ac/3,

a_c being the total area of the carrier. For the configurations shown in Fig. 5.22, this takes different values, whereas the L-coefficients remain the same. This is certainly a severe error that must be eliminated by suitable modifications.

A fairly easy way is found by imposing the condition that a function with some free parameters shall become a particular integral of the inhomogenous PDE. An example of such a function is

(5.79a)ϕuv=ϕ0+p2+q2C0+pC1+qC2/4,

where C₀, C₁, and C₂ being the free parameters. We must assume here a linear function ε(u, v), and we write

(5.79b)ε0:=εu0v0,ε′:=εu0+p/2,v0+q/2.

The source function corresponding to Eq. (5.79a) is then found by differentiation

(5.79c)Quv:=Δ⋅ε∇ϕ=ε′3C0+2pC1+2qC2−2ε0C0+R,

where R is the remainder. The latter consists of quadrupole terms with derivatives of ε as coefficients; such terms can be ignored within the framework of the FOFEM. The source at the center, Q₀ = ε₀C₀, can now be used to eliminate the free parameters, the result being

(5.79d)ε′ϕ−ϕ0=p2+q2Q+2−ε′/ε0Q0/8.

Considering Eqs. (5.76b) and (5.77), the total source term becomes

(5.80a)−∑k=1ML0kϕk−ϕ0=S0=∑k=0MC0kQk,

with the source coefficients

(5.80b)C0k=pk2+qk2γk−+γk+/16k=1,…,M,

(5.80c)C00=∑k=1Mpk2+qk2γk−+γk+2−εk′/ε0/16.

If the source function Q(u, v) is discontinuous, like the current density at the surface of a coil, for example, then the following replacements should be made:

(5.81)γk−+γk+Qj→γk−+Qj−+γk++Qj+j=0ork.

All the deficiencies described earlier now vanish, because only those nodes that contribute also to the potential term contribute to the source term. In orthogonal structures the final formulas become independent of the mode of bisection into triangles. Moreover, it can be shown that the mesh formula is now consistent with (Eq. 4.60) in its inhomogeneous form, as it should be.

In spite of these improvements, which can easily be incorporated in FOFEM programs, this method is still not exact in second order, if tilted meshes are taken into account, as must be done in realistic applications. The error can then be reduced only by suitable choice of the meshes. Apart from orthogonal ones, there is a second class of configurations that are obtained by smooth and locally affine deformations of regular hexagonal elements, as is shown in Fig. 5.23. In such a case, the deformations should be small enough such that obtuse angles never appear, as the latter would cause negative potential coefficients. The optimum consists of completely regular elements, whose construction was dealt with in Section 5.1. If abrupt alterations of the mesh sizes cannot be avoided because of unfortunate geometric constraints, then discretization errors of second order must be taken into account.

Figure 5.23. Appropriate mesh construction for the application of the FOFEM by affine distortion of regular hexagonal structures. The hatched area is an example for one of the hexagonal carriers.

All these arguments demonstrate that the FOFEM is not very favorable. The only reason for its frequent use in practice is its simplicity when compared with other methods.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1076567001800690

Computational Electromagnetics: The Finite-Difference Time-Domain Method

Allen Taflove, … Melinda Piket-May, in The Electrical Engineering Handbook, 2005

Discretization Error

The design of an effective PML requires balancing the theoretical reflection error R(θ) and the numerical discretization error. For example, equation 9.128 provides σ_{x, max} for a polynomial-graded conductivity given a predetermined R(0) and m. If σ_{x, max} is too small, the primary reflection from the PML is due to its PEC backing, and equation 9.125 provides a fairly accurate approximation of the reflection error. However, if σ_{x, max} is too large, the discretization error due to the FDTD approximation dominates, and the actual reflection error is potentially much higher than what equation 9.125 predicts. Consequently, there is an optimal choice for σ_{x, max} that balances reflection from the PEC outer boundary and discretization error.

Through extensive numerical experimentation, Gedney (1996) and He (1997) found that, for a broad range of applications, an optimal choice for a 10-cell-thick, polynomial-graded PML is R(0) ≈ e⁻¹⁶. For a 5-cell-thick PML, R(0) ≈ e⁻⁸ is optimal. From equation 9.128, this leads to an optimal σ_{x, max} for polynomial grading:

(9.129)σx, opt≈−(m+1)⋅(−16)(2η)⋅(10Δ).=0.8(m+1)ηΔ.

This expression has proven to be adequate for many applications. Its value, however, may be too large when the PML terminates highly elongated resonant structures or sources with a very long time duration. For detailed discussions and examples of PML performance over a wide range of possible loss profiles, see Gedney (1998) and Gedney and Taflove (2000).

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780121709600500463

11th International Symposium on Process Systems Engineering

Sen Huang, … Lorenz T. Biegler, in Computer Aided Chemical Engineering, 2012

Element Mesh Generation:

For the given initial mesh h¯ , initialize the placement of mesh points hopt←h¯, discretization error ε^rd←+∞; give the amplitude of mesh point disturbance d, tolerence on discretization error ε_c.

Upper-level: Generate an element mesh for dynamic optimization:

Disturb placement of mesh points by uniform distribution h_i^opt ← U[h_i^opt — d, h_i^opt + d].

Adjust the mesh to match the given time horizon hiopt←tf⋅hiopt/∑i=1Nmaxhiopt

Lower-level: Solve problem (2) using mesh h^opt .

Check error estimate (3) at the solution:

If e ≤ ε_c, save mesh h^opt, and the algorithm can stop while enough meshes, say 50 meshes, are obtained; otherwise, if e < ε^rd, update ε^rd← e.

Go to step 1.

Note that different from the MFE strategy, which solves problem (2) together with the following error estimate:

(4){z˙ti,nonc-hifzti,nonc,yti,nonc,uti,nonc,p≤εc∑i=1NEhi=tf,hi≥0

the simplified MFE does not involve solving such a more constrained and difficult NLP. Instead, the simplified MFE exploits a derivative-free method to look for meshes for accurate discretization.

Let M denote the set of the obtained meshes. The online phase takes advantage of M to generate at low cost the discretization mesh for the current power change demand p. A straightforward way is to use regression methods. A profile can then be obtained, which represents the configuration of the newly generated element mesh. Let config denote the configuration, the placement of the mesh points can be calculated by config(index), where index = 1..NE is the index of mesh points and config(NE) = t_f.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780444595065500912

Parallel Efficiency of the Lattice Boltzmann Method for Compressible Flows

Andrew. T. Hsu, … Akin Ecer, in Parallel Computational Fluid Dynamics 2000, 2001

3 NUMERICAL SIMULATION

If we regard the viscous terms and the diffusion terms of the right hand sides of Eqs. (4) and (5) as the discretization error the equations (3-5) become an inviscid Euler system. In fact, the viscosity and diffusivity are of order [τ − (1/2)] l²/∆t, where l is the length of the lattice and ∆t is the unit time. In two previous papers [5,6] we simulated Sod shock-tube problem and two-dimensional shock reflection. The numerical results agree well with exact solutions. In the following, we simulate two more complex flows with strong shocks under the condition τ = l and γ = 1.4.

A double Mach reflection of a strong shock (an normal shock passing a wedge) [14] is calculated on a 360 × 140 hexagonal lattice. Figure 1 shows the density contours at t = 200^th iteration. Complex features, such as oblique shocks, contact discontinuity and triple points are well captured and are in good agreement with results obtained by a upwind method [14] and a gas kinetic method [13].

Figure 1. Density distribution for Mach 10 reflection shock on lattice 360 × 140 at 200^th iteration.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780444506733501147

Numerical Field Calculation for Charged Particle Optics

Erwin Kasper, in Advances in Imaging and Electron Physics, 2001

4.5.4 Evaluation of Series Expansions

If the configuration round a mesh point is irregular as in Fig. 4.12, the analytic derivation of mesh formulas of higher than the second order becomes very tedious. Only very few attempts have been made to overcome this obstacle therefore [8], and usually a discretization error of third order, resulting from irregular boundaries is tolerated as an unsurmountable limit.

A possibility for further development is the series expansion of the potential in terms of suitable trial functions with initially unknown coefficients. These trial functions T_n(r), (n = 1, …, N) should satisfy exactly (or at least very accurately) the PDE to be solved. The expansion coefficients are then found from the condition that the given potentials are assumed at the surrounding points (1, …, N). The potential at the central point is subsequently obtained by evaluation of the now known expansion at this position. Because this concept is rather general, we shall present it here in a form that could also be used in three dimension though this would become laborious.

Let D be a homogeneously linear partial differential operator of second order and DΦ(r) = 0 the PDE to be solved. Then a suitable set of trial functions must be chosen, which are linearly independent and satisfy DT_n(r) = 0. The series expansion in question is now

(4.213)Φr=∑n=1NcnTnr.

The condition that the prescribed values ϕ_j := Φ(r_j) (j = 1, …, N) are assumed by this expression requires the solution of a linear system of equations

(4.214)∑n=1NAjncn:=∑n=1NTnrjcn=ϕjj=1,…,N.

We must assume here that the matrix A is nonsingular. Then we can write

(4.215)cn=∑k=1NAnk−1ϕkn=1,…,N,

and introduce this into Eq. (4.213), whereupon our problem is solved. For the central mesh point r₀, the condition

(4.216)ϕ0=Φr0=∑k=1N∑n=1NTnr0Ank−1ϕk

is obtained. This is none other than the required mesh formula

(4.217a)ϕ0=∑k=1Nμkϕk

with the coefficients

(4.217b)μk=∑n=1NTnr0Ank−1k=1,…,N.

Apart from this systematic derivation of mesh formulas, this method also offers a way of calculating derivatives

(4.218)∇Φr=∑n=1Ncn∇Tnr

and even derivatives of higher orders, if necessary. These could be used for purposes of field calculation and interpolation. Another essential task is the derivation of mesh formulas for positions at material boundaries, as dealt with in the preceding section.

The situation is shown in Fig. 4.17: we have a surface with normal n and different material coefficients ε₁ and ε₂ on either side. The numbers N₁ and N₂of surrounding points may be different and surface points can be used twice. The set of trial functions here will be different, as a constant for the lowest order is unacceptable here. Instead of Eq. (4.213), there are now two series expansions

Figure 4.17. Arbitrary configuration of nodes and corresponding space vectors in the vicinity of a material boundary. Here the numbers N₁ = 4 and N₂ = 5 were chosen. The vector n is the surface normal at point 0.

(4.219)Φr=ϕ0+∑n=1NkcnkTnrk=1,2

to be used in the two separate domains. We have to calculate two inverse matrices and express the coefficients in terms of potential differences:

(4.220)cnk=∑j=1NkAk−1njϕj−ϕ0k=1,2.

It is now straightforward to write down the continuity condition for the position r₀

(4.221)ε1n⋅∇Φ1=ε2n⋅∇Φ2,

leading to

(4.222)ε1∑i=1N1ci1n⋅∇Tir0=ε2∑i=1N2ci2n⋅∇Tir0.

On introducing the coefficients (4.220) into this equation, we obtain a linear relation of the general form

(4.223a)ε1∑j=1N1Fj1ϕj′−ϕ0=ε2∑j=1N2Fj2ϕj−ϕ0

with coefficients

(4.223b)Fjk=∑i=1NkAk−1ijn⋅∇Tir0k=1,2.

It remains to find the discretization of an inhomogeneous linear PDE

(4.224)DΨr=Sr,

S(r) being a given source function. This problem can be reduced to the task of finding any convenient particular solution Ψ_p(r) of this PDE. When this is found, we can use the above outlined relations because Φ(r) = Ψ(r) − Ψ_p(r) solves DΦ = 0. This implies that for instance

(4.225)Ψr0=Ψpr0+∑k=1NμkΨrk−Ψprk

follows from Eq. (4.217a), and also Eq. (4.223a) must be modified accordingly. From a purely theoretical standpoint, therefore, all the problems have been solved in principle, but in practice there are numerous obstacles to be overcome.

There are two essential difficulties: the first is that the rank N of the matrix is rather high, and the number of neighbor points is correspondingly large if a certain polynomial order M of the approximation is to be reached: in two dimensions we have N = 2 M + 1, whereas in three dimensions this number is N = (M + l)². For a large number N, it might become difficult to find suitable neighbor points. The other, more serious problem arises from ill-conditioned or even singular matrices, which may result from an unsuitable choice of configurations. Here we shall outline briefly a method, which has been tested by the author and which gave good results. This method will also exhibit some interesting physical relations.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1076567001800689

29th European Symposium on Computer Aided Process Engineering

Hojae Lee, Christos T. Maravelias, in Computer Aided Chemical Engineering, 2019

3 Determining the key model parameter, δ

As mentioned earlier, DCA requires the user to select the discretization step length, δ, in the first stage model. If chosen carefully, the speed and accuracy of DCA can be improved significantly. However, selecting δ’s that bring such results is non trivial.

In order to find the best performing δ, we introduce an error evaluation function denoted as ε(δ). For a given instance, ε(δ) measures the amount of discretization error introduced by the chosen δ, considering how much the shortage of each unit is constraining the objective value.

(10)εδ=1δ∑i∑j∈Jiωijτij−δτ¯ij,ωij=Nij∑iNijDj∑jDj

(11)Dj=∑nλjn∗∀j

(12)Nij=∑nXijn∗∀i,j∈Ji

where, X_ijn^⁎ is the solution of the LP relaxed model of the first stage, and λ_jn^⁎ is the dual variable associated with the allocation constraints (Eq. 9 in Shah et al. (1993)) in the LP relaxed model.

As shown in Figure 1, ε(δ) is an accurate metric to quantify the amount of discretization error introduced. Specifically, DCA obtains high quality first and third stage solutions, whenever δ’s that lead to low values of ε(δ) are used. Although only shown for two instances, we observed similar results for all other instances tested.

Figure 1. Using the error evaluation function, ε(δ), as a metric to determine δ’s, illustrated for (a) instance 1, and (b) instance 2

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B978012818634350196X

Structured Finite Volume Schemes

J. Blazek, in Computational Fluid Dynamics: Principles and Applications (Second Edition), 2005

4.2.4 Cell-Centred versus Cell-Vertex Schemes

In the preceding three subsections, both the cell-centred and the cell-vertex discretisation methodologies were outlined. The following paragraphs compare the three schemes and give an overview of the, at times controversial, debate about their relative merits.

First, let us consider the accuracy of the discretisations. It follows from the discussion in [4], [21] that the cell-vertex scheme (either with overlapping or dual control volumes) can be made first-order accurate on distorted grids. On Cartesian or on smooth grids (i.e., where the volumes between adjacent cells vary only moderately and which are only slightly skewed), the cell-vertex scheme is second- or higher-order accurate [22], depending on the flux evaluation scheme. In the opposite, the discretisation error of a cell-centred scheme depends strongly on the smoothness of the grid. For example, for an arrangement of the cells sketched in Fig. 4.7, an averaging does not provide the correct value at the midpoint of a face even for a linearly varying function. The consequence is that on a grid with slope discontinuity the discretisation error will not be reduced even when the grid is infinitely refined. As demonstrated in [4], such zero-order errors manifest themselves as oscillations or kinks in isolines, whereas a cell-vertex scheme experiences no problems in the same situation. Nevertheless, on Cartesian or on sufficiently smooth grids, the cell-centred scheme can also reach second- or higher-order accuracy. A further analysis of the discretisation errors were presented in [23]–[26].

Figure 4.7. Cell-centred flux balance on a skewed grid; cross denotes the midpoint of the cell face.

Second, let us compare the three methods and their characteristics at boundaries. It is mainly at the solid wall boundary where the cell-vertex scheme with dual control volumes faces difficulties. Recalling Fig. 4.6 again, it is apparent that only about one half of the control volume is left at the boundary. The integration of fluxes around the faces results in a residual located inside — ideally in the centroid — of the control volume. But, the residual is associated with the node residing directly at the wall. This mismatch leads to increased discretisation error in comparison to the cell-centred scheme. The definition of the dual control volume causes also problems at sharp corners (like trailing edges), which show up as unphysical peaks in pressure or density. Further complications arise, e.g., at coordinate cuts or at periodic boundaries (see Chapter 8), where the fluxes from both parts of the control volume have to be summed up correctly. All cell-vertex schemes also require additional logic, in order to assure a consistent solution at boundary points shared by multiple grid blocks. No such problems appear for cell-centred schemes.

The cell-vertex scheme with overlapping control volumes has an advantage over the dual volume scheme in the treatment of wall boundaries, but it cannot be combined with the popular upwind discretisation methods like TVD, AUSM, or CUSP. The discretisation involves more points than those of the cell-centred and the dual control-volume schemes (27 instead of 7 in 3D), which leads to smearing of discontinuities and memory overhead in the case of an implicit time discretisation.

The last main difference between the cell-centred and the cell-vertex schemes appears for unsteady flow problems. As mentioned earlier in Section 3.2, the cell-vertex schemes require at least an approximate treatment of the mass matrix [27], [28]. On the contrary, the mass matrix can be completely discarded in the case of a cell-centred scheme, because the residual is naturally associated with the centroid of the control volume.

In summary, the cell-vertex scheme with dual control volumes and the cell-centred scheme are numerically very similar in the interior of a stationary flow field. The main differences occur on distorted grids, in the boundary treatment and for unsteady flows. In the last two cases, the cell-centred approach shows advantages over the cell-vertex schemes, which result in a more straightforward implementation in a flow solver.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780080445069500060

Handbook of Numerical Methods for Hyperbolic Problems

A. Chertock, in Handbook of Numerical Analysis, 2017

2.3.1 Accuracy

The two terms in the error estimate (23) may be balanced by choosing an appropriate size of ɛ. Intuitively, it is clear that if the smoothing parameter ɛ is too small in comparison to the minimal distance between particles, the approximate solution defined by (19) will vanish away from the ɛ-neighbourhood of the particles and is thus irrelevant. On the other hand, large values of ɛ will generate unacceptable smoothing errors. Theoretically ɛ is chosen so that the smoothing error and the discretization error are of the same order and it is common to take ɛ∼h (see, e.g., Chertock and Kurganov, 2006, 2009; Hald, 1987; Raviart, 1985). It should be noted, however, that it is not clear what the optimal proportionality constant is. That strongly depends on both the smoothness of the flow and the cut-off function and its value at the origin. It has been also observed in various numerical experiments that the overall accuracy of the particle method can deteriorate over long-time integrations, see, e.g., the discussion in Beale and Majda (1985), Hald (1987), Hald and del Prete (1978), Nordmark (1991), Koumoutsakos (2005), Perlman (1985) and in references therein.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/S1570865916300448

Макеты страниц

Высокая степень развития рационального интеллекта у человека привела к значительной и печальной потере возможностей его интуиции, которая так необходима сегодня для дальнейшего развития. (Жак Моно, Случайность и необходимость)

Тот, кто не допускает ошибок, не способен познать истину.

Рабиндранат Тагор

В гл. 9 предполагалось, что необходимые для вычислений математические операции реализуются идеально. Когда мы записывали выражение

то молчаливо предполагали, что операции умножения (идеального аналогового умножения) и интегрирования осуществляются без ошибок. Однако известно, что на практике все чаще и чаще аналоговые операции умножения и интегрирования заменяются численным умножением и интегрированием (после аналого-цифрового преобразования). При огромном количестве исходных данных (когда величина ВТ равна и более) для вычисления корреляции необходимо найти способ уменьшения числа символов для записи каждого слова, т. е. осуществлять кодирование с минимальным общим числом символов. Следовательно, очень важно изучить влияние дискретизации.

10.1. Статистическое изучение влияния дискретизаций

Постановка проблемы.

Прежде всего мы изучим влияние дискретизации на корреляционную функцию, а затем покажем, что некоторые полученные результаты применимы и в более

общем случае. Общая структура дискретного коррелометра может быть представлена в виде блок-схемы, приведенной на рис. 10.1. Это устройство осуществляет оценку истинной автокорреляционной функции

Рис. 10.1.

Оценка отлична в общем случае от истинного значения по двум причинам:

1. Поскольку сигнал x(t) по предположению стационарен и эргодичен, то

Однако при вычислении оценки интервал интегрирования Т не может быть бесконечным, и, следовательно, мы получаем . Ошибка, порожденная такой заменой, была изучена в гл. 9.

2. Очень трудно реализовать запаздывание для непрерывных сигналов и очень легко — для дискретизованных сигналов. Поэтому наиболее часто рассматриваются дискретные сигналы. В этой главе мы изучим ошибку, обусловленную дискретизацией сигналов.

Дискретизация случайной величины.

Определение. Пусть х — случайная величина. Дискретизацией величины х называется шаг дискретизации и — натуральное число.

Плотность вероятности дискретизованной случайной величины. Пусть — плотность вероятности величины х. Изучим влияние дискретизации на

По определению величины х имеем

Но

где

Отсюда

Следовательно, плотность вероятности дискретизованной случайной величины х записывается в виде

Отсюда

Из последнего выражения следуют два эффекта (рис. 10.2) влияния дискретизации на :

1) эффект фильтрации с помощью фильтра-интегратора на интервале импульсный отклик которого равен

2) эффект дискретизации с шагом т. е. влияние дискретизации с помощью дискретизатора-интегратора.

Характеристическая функция дискретизованной случайной величины.

Напомним, что характеристическая функция случайной величины х определяется равенством

Из этого равенства следует соотношение между фурье-образом плотности вероятности и характеристической функции

Рис. 10.2.

. Используя формулу (10.2), вычислим характеристическую функцию дискретизованной случайной величины. Запишем выражение (10.2) в виде

Используя теорему Парсеваля и фурье-образ гребневой функции Дирака, получим

Перейдем в равенстве (10.3) к фурье-образам:

Положив , получаем искомое выражение

Выражение (10.4) позволяет обнаружить по спектру плотности вероятности два эффекта влияния дискретизации, о которых говорилось выше в связи с дискретизацией плотности вероятности:

• эффект фильтрации (рис. 10.3), соответствующий умножению функции на величину ;

• эффект дискретизации, соответствующий суммированию спектра после фильтрации с периодичностью

Очевидно, что дискретизация не изменяет существенно в окрестности точки кроме случая, когда для т. е. когда повторяемый таким образом спектр не восстанавливается через промежуток, длина которого больше половины периода (рис. 10.4). Это замечание будет нами использовано в дальнейшем, когда мы распространим его на случай двух случайных величин.

Рис. 10.3.

Рис. 10.4.

Дискретизация двух случайных величин.

Обобщения. Для того чтобы получить сведения о влиянии дискретизации на момент второго порядка (с целью использования их для корреляционной функции), мы изучим статистические воздействия дискретизации на двумерную случайную величину Необходимые выкладки аналогичны выкладкам предыдущего раздела. Поэтому мы даем лишь окончательные формулы и обращаем внимание на интересующие нас результаты.

Совместная плотность вероятности и характеристическая функция двух дискретизованных случайных величин. Используя предыдущие обозначения для двух случайных величин дискретизованных с шагами получаем формулы

Влияние дискретизации на момент второго порядка и на корреляцию двух случайных величин. Воздействие фильтрации и дискретизации. Поскольку выражение (10.6) аналогично выражению (10.4), то справедливы все предыдущие заключения о

воздействии фильтрации и дискретизации на характеристическую функцию.

Достаточное условие равенства нулю ошибки дискретизации для момента второго порядка. Согласно известной формуле теории вероятности, имеем

Из выражений (10.6) и (10.7) следует, что выполнение условия

для любых и любых достаточно для выполнения равенства

Связь между корреляционными функциями двух дискретизованных и недискретизованных сигналов. Если равенства (10.8) не выполнены, то между существует более сложная связь. Рассмотрим два случайных стационарных процесса Для нахождения соотношения между истинной корреляционной функцией

и корреляционной функцией дискретизованных сигналов можно использовать полученные выше формулы (10.6) и (для сокращения записи иногда обозначают если такое обозначение не может вызвать неоднозначного толкования).

Бонне, используя формулы (10.6) и (10.7), провел соответствующие вычисления и получил равенства

где

В большинстве случаев коэффициентом а можно пренебречь, и предыдущая формула для принимает вид

с точностью до бесконечно малых величин более высокого порядка.

Этот важный результат можно интерпретировать следующим образом. В любом коррелометре с двумя входами дискретизация с шагом эквивалентна последовательному умножению на и добавлению двух независимых шумов с дисперсией и корреляционной функцией на каждом входе.

Итак, схемы, представленные на рис. 10.1 и 10.5, эквивалентны.

Рис. 10.5.

Данный результат согласуется с результатом, полученным Блан-Лапьером: добавление к сигналу шума с точки зрения статистики эквивалентно некоторой дискретизации сигнала.

Из формулы (10.9) следует, что ошибка дискретизации входных сигналов зависит от отношения Приведем в качестве примера результаты по дискретизации, полученные Бонне [6]:

Дискретизация с помощью конечного числа разбиений.

При всех предыдущих вычислениях предполагалось, что число дискретных значений бесконечно. В действительности такое предположение нереализуемо и максимальный уровень дискретизации ограничен сверху конечным числом А. Последнее означает, что каждый раз, когда величина сигнала превосходит А, ему приписывается значение, равное А. Эта процедура эквивалентна усечению плотности вероятности на интервале . Совокупности вероятностей, содержащиеся на интервалах , -«проектируются» в точки —А и А. Ошибка, порожденная процедурой усечения, будет мала, если «проектируемые» совокупности вероятностей «малы». Порядок величины, характеризующей «проектируемые» совокупности вероятно

стей, может быть оценен с помощью неравенства Чебышева из которого следует, что ошибка, обусловленная заменой бесконечного числа дискретных значений конечным числом, зависит от отношения Согласно Бонне [6], этой ошибкой можно пренебречь, если

Итак, мы показали, что ошибка, порожденная дискретизацией, уменьшается с уменьшением отношения Кроме того, ошибка, порожденная конечностью числа дискретных значений, уменьшается с возрастанием отношения Следовательно, уменьшение полной ошибки всегда соответствует увеличению отношения которое равно общему числу уровней дискретизации.

Частный случай.

Коррелометр с двумя уровнями дискретизации (коррелометр с совпадением полярности, коррелометр с подрезанием, коррелометр Фарана и Хилла). В этом частном случае предыдущие формулы принимают относительно простой вид [8]:

где — нормированная корреляционная функция:

В тех случаях (они довольно многочисленны), когда достаточно вычислить нормированные корреляционные функции, переход от осуществляется с помощью простого соотношения

Оглавление

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
ВВЕДЕНИЕ
Глава 1. ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ О ШУМАХ КАК О СЛУЧАЙНЫХ ПРОЦЕССАХ
Глава 2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
2.2. Преобразование Фурье непериодических функций
2.3. Преобразование Фурье физических функций
2.4. Физический смысл преобразования Фурье
2.5. Условия существования преобразования Фурье
2.6. Некоторые свойства преобразования Фурье
2.7. Несколько функций и их фурье-образы
2.8. Частный случай вещественных сигналов
2.9. Отрицательные частоты
2.10. Аналитический сигнал
2.11. Почему выбрано преобразование Фурье?
2.12 Физическая реализация фурье-образа. Преобразование Фурье в оптике
2.13. Свойства функции sin х/х
2.14. Лямбда-функция
Глава 3. МОЩНОСТЬ И ЭНЕРГИЯ СИГНАЛОВ
3.2. Частотная мощность. Спектральная плотность мощности. Спектр мощности
3.3. Общее определение спектральной плотности
3.4. Теорема Парсеваля
3.5. Понятие скалярного произведения и нормы
Глава 4. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
4.2. Связь между фурье-образом и изображением Лапласа
Глава 5. СВЕРТКА
5.2. Уравнение свертки
5.3. Несколько замечаний относительно свертки
5.4. Физическая интерпретация свертки
5.5. Прямая и обратная задачи, связанные с операцией свертки
5.6. Свертка и преобразование Фурье. Теорема Планшереля
Глава 6. ФИЛЬТРАЦИЯ
6.2. Временная фильтрация
6.3. Частотная фильтрация («линейная фильтрация» в смысле Блан-Лапьера)
6.4. Связь между фильтрацией и сверткой
6.5. Физически реализуемые линейные фильтры частоты
6.6. Идеальный фильтр
6.7. Реализуемые непрерывные аналоговые фильтры [3]
6.8. Фильтры с линейным сдвигом фаз
6.9. Узкополосные фильтры
6.10. Обобщение понятия фильтрации
Глава 7. ДИСКРЕТИЗАЦИЯ
7.2. Теоремы дискретизации
7.3. Дискретизация сигналов конечной длительности
7.4. Дискретизация фурье-образов
7.5. Выбор частоты дискретизации на практике
7.6. Противомаскировочный фильтр
7.7. Физическая дискретизация. Комбинированная дискретизация
7.8. Субдискретизация. Обобщение теоремы Шеннона [9]
7.9. Заключение
Глава 8. КОРРЕЛЯЦИЯ И НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ СТАТИСТИКИ
8.2. Величина, характеризующая «связь» между двумя физическими процессами. Случай, когда известна одна реализация физического процесса, наблюдаемая в течение большого интервала времени
8.3. Эргодичность
8.4. Коэффициент корреляции и теория информации
8.5. Практические замечания
8.6. Характеристические функции
8.7. Спектральная плотность случайного сигнала
8.8. Связь между временными представлениями сигналов и спектральными плотностями. Теорема Винера — Хинчина
8.9. Функция связи
8.10. Распределение Гаусса, или нормальное распределение
8.11. Спектральная плотность и центрирование сигналов
Глава 9. ОЦЕНКА ОШИБОК ИЗМЕРЕНИЙ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
9.2. Оценка корреляционных функций
9.3. Оценка спектральных плотностей
9.4. Оценка одномерной плотности вероятности
9.5. Последовательное вычисление среднего значения и дисперсии
9.6. Физическая интерпретация дисперсии
9.7. Идеальный интегратор и низкочастотный фильтр
9.8. Дискретные сигналы
Глава 10. ОШИБКИ ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ ПРИ ДИСКРЕТИЗАЦИИ СИГНАЛОВ
10.2. Коррелометры с вспомогательными шумами
10.3. Условия на вспомогательные шумы, при которых отсутствует смещение оценки корреляционной функции
10.4. Вычисление дисперсии. Состоятельность оценки
10.5. Практические приложения
10.6. Важное замечание
10.7. Замечание относительно генераторов вспомогательных шумов
Глава 11. ОСНОВНЫЕ СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
11.2. Периодические функции
11.3. Переходные функции
11.4. Дистрибутивность операций вычисления корреляции и спектральной плотности
11.5. Связь между входным и выходным сигналами линейной однородной во времени системы при условии, что входной сигнал является случайным и стационарным 2-го порядка
Глава 12. ОСНОВНЫЕ ПРИЛОЖЕНИЯ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ И СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
12.2. Обнаружение периодического сигнала с известным периодом на фоне шума
12.3. Выделение сигнала на фоне шума. Усреднение
12.4. Обнаружение скрытых периодичностей
12.5. Получение спектральных плотностей по корреляционным функциям
12.6. Измерение динамических характеристик (переходных функций, импульсных характеристик) линейных систем. Идентификация процессов
12.7. Измерение когерентности
12.8. Применение когерентности к измерению передаточных функций линейных и однородных во времени систем. Спектральная лупа
12.9. Измерение временного сдвига двух сигналов
Глава 13. СПЕКТРАЛЬНЫЙ АНАЛИЗ. ИЗМЕРЕНИЕ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
13.2. Влияние фильтрации, обусловленной дискретизацией спектральной плотности
13.3. Дискретизация спектральной плотности, реализуемая на практике
13.4. Систематическая ошибка при измерении спектральной плотности
13.5. Измерение спектральной плотности
13.6. Спектральный анализ методом фильтрации
13.7. Измерение спектральной плотности методом фильтрации
13.8. Дискретное преобразование Фурье и измерение спектральных плотностей [2, 6, 7]
13.9. Вычисление автокорреляционных функций и взаимных корреляционных функций по спектральной плотности
13.10. Явление Гиббса
13.11. Корреляционный метод спектрального анализа
13.12. Корреляционный анализатор спектра
13.13. Точность определения спектральной плотности, полученной преобразованием Фурье корреляционной функции [1]
13.14. Замечания по поводу применения спектральных анализаторов. Определение оптимальной частоты дискретизации
Глава 14. ВЕСОВЫЕ ОКНА
14.2. Окна, связанные с преобразованием Фурье
14.3. Окна, используемые в методе коррелограмм
14.4. Окна, применяемые в методе периодограмм
14.5. Окна, применяемые в методе фильтрации с возведением в квадрат и усреднением
14.6. Основные характеристики временных и спектральных окон
14.7. Первое семейство временных весовых окон
14.8. Второе семейство временных весовых окон (Метод периодограмм)
14.9. Исследование спектра в простом случае
14.10. Выбор весовой функции

Источник

В численном анализе , вычислительной физики и моделирования , ошибка дискретизации есть ошибка в результате того факта , что функция из непрерывной переменной представляется в компьютере с помощью конечного числа оценок, например, на решетке . Ошибка дискретизации обычно может быть уменьшена за счет использования решетки с более мелкими интервалами, что увеличивает вычислительные затраты .

Примеры

Ошибка дискретизации является основным источником ошибок в методах конечных разностей и псевдоспектральном методе вычислительной физики.

Когда мы определяем производную как или , где — конечно малое число, разница между первой формулой и этим приближением называется ошибкой дискретизации.
$\, \! f (х)$ $f '(x) = \ lim _ {{h \ rightarrow 0}} {{\ frac {f (x + h) -f (x)} {h}}}$ $f '(x) \ приблизительно {\ frac {f (x + h) -f (x)} {h}}$ $\,\!час$

При обработке сигналов аналогом дискретизации является дискретизация , и она не приводит к потерям, если выполняются условия теоремы дискретизации , в противном случае результирующая ошибка называется наложением .

Ошибка дискретизации, которая возникает из-за конечного разрешения в области, не следует путать с ошибкой квантования , которая представляет собой конечное разрешение в диапазоне (значениях), ни с ошибкой округления, возникающей из арифметики с плавающей запятой . Ошибка дискретизации возникла бы, даже если бы можно было точно представить значения и использовать точную арифметику — это ошибка представления функции ее значениями в дискретном наборе точек, а не ошибка в этих значениях.

Ссылки

Смотрите также

Дискретность
Линейный многоступенчатый метод
Ошибка квантования

Источник

Examples[edit]

[edit]

References[edit]

See also[edit]

Преобразование аналоговых сигналов

Ошибки дискретизации

5. Эффективное кодирование, назначения, способы реализации, основные ограничения.

CFD Solution Analysis: Essentials

Discretisation Error

Introduction

Numerical Field Calculation for Charged Particle Optics

5.4.2 Error Analysis and Improvements

Computational Electromagnetics: The Finite-Difference Time-Domain Method

Discretization Error

11th International Symposium on Process Systems Engineering

Element Mesh Generation:

Parallel Efficiency of the Lattice Boltzmann Method for Compressible Flows

3 NUMERICAL SIMULATION

Numerical Field Calculation for Charged Particle Optics

4.5.4 Evaluation of Series Expansions

29th European Symposium on Computer Aided Process Engineering

3 Determining the key model parameter, δ

Structured Finite Volume Schemes

4.2.4 Cell-Centred versus Cell-Vertex Schemes

Handbook of Numerical Methods for Hyperbolic Problems

2.3.1 Accuracy

10.1. Статистическое изучение влияния дискретизаций

Постановка проблемы.

Дискретизация случайной величины.

Характеристическая функция дискретизованной случайной величины.

Дискретизация двух случайных величин.

Дискретизация с помощью конечного числа разбиений.

Частный случай.

Примеры

Ссылки

Смотрите также