Рассмотрим
ошибки редукции и центрирования более
подробно.
Пусть
теодолит установлен в точке В – вершине
измеряемого угла безошибочно, а визирная
марка в точке А установлена не точно,
т.е. ось вращения визирной марки проходит
через точку А´
Н
рисунке
е1
— линейный элемент редукции;
Θ
— угловой элемент редукции.
Визирная
марка относительно истинного положения
– точки А — может занимать любое другое
положение. От этого будет меняться
величина ошибки α или элементы редукции.
Рассмотрим вариант, когда линейный
элемент неизменен, а меняется лишь
угловой элемент редукции. Тогда точка
А´ движется по окружности, т.е. число
перемещений
n
= 2·π/d Θ (17.6)
Выразим
α из треугольника АВ А´.
(е1
/
sin α)
= (S/ sin Θ)
(17.7)
Длина
визирного луча S
много больше линейного элемента редукции,
а величина ошибки α мала в сравнении с
величиной измеряемого угла. По этой
причине можно считать , что стороны
треугольника ВА и В А´ равны. Следовательно,
α
= (е1/
S)
· ρ · sin
Θ (17.8)
Таких
значений α будет бесконечно много.
Средняя квадратическая ошибка редукции
для одного направления может быть
найдена по формуле Гаусса.
mредА
2
= [α²] /n
(17.9)
С
учетом выражения (17.8) будем иметь:
mредА
2
= [((е1/
S) · ρ
· sin Θ
)²] /n (17.10)
Приняв
во внимание (17.6), получим:
mредА
2
= (е1²/2·π
S2)
· ρ2
· Σsin2
Θ d Θ (17.11)
Заменим
знак суммы интегралом с пределами от 0
до 2·π.
mредА
2
= (е1²/2·π
S2)
· ρ2
· ∫sin2
Θ d Θ (17.12)
Выполнив
интегрирование, получим
mредА
= (е1/√(2·π)
S)
· ρ
(17.13)
Для
измеренного угла β
в случае неточной установки двух визирных
марок ошибка составит:
mред
2
=
mредА
2
+
mредС
2
(17.14)
mред
2
=
(е1²/2
S12)
· ρ2
+ (е1²/2
S22)
· ρ2
=
( е1²·
ρ2)
/2·(1/ S12
+
1/ S22)
(17.15)
Ошибка
редукции не зависит от величины
измеряемого угла. Чем больше разница в
длинах визирных лучей (сторон измеряемого
угла), тем больше ошибка редукции. Чем
короче сторона хода, тем больше ошибка
редукции при приблизительно равных
сторонах. Необходимо соблюдать требования
Инструкции к минимальной длине стороны.
Значение
линейного элемента редукции позволяет
выбрать средство центрирования визирных
марок. Это значение будет зависеть от
значения ошибки редукции.
Ошибка
центрирования будет рассмотрена с
помощью следующего рисунка.
П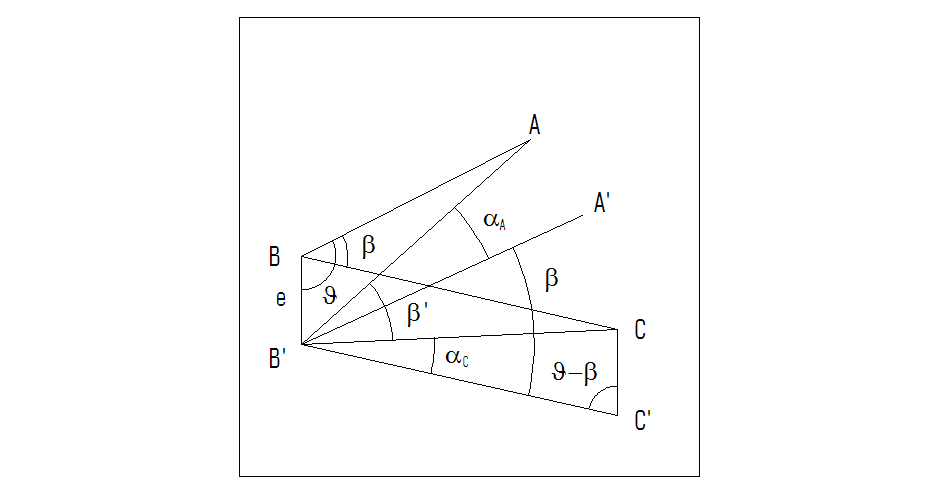
визирные цели установлены в точках А и
С безошибочно, а ось вращения прибора
проходит через точку В´. Тогда фактически
будет измеряться угол А В´С. Его значение
будет отличаться от истинного (угла
АВС) на величину α — ошибки измерения
угла. Построим из точки В´ линии,
параллельные истинному положению
визирных лучей.
Отрезок
В В´ — линейный элемент центрирования
– обозначим е , а угол АВ В´ — угловой
элемент центрирования – обозначим Θ.
Рассуждая
по аналогии с предыдущим выводом, можно
записать выражение (17.16) для возможного
количества установок прибора относительного
верного положения – точки В.
n
= 2·π/d Θ
(17.16)
Из
рисунка и по построению следует, что
β
+ αА
= β´
+ αС
(17.17)
β´
= β
+ αА
— αС
(17.18)
Исходя
из структуры результата измерения, αА
— αС
есть ошибка в измерении горизонтального
угла, вызванная неточным центрированием
теодолита, т.е. ошибкой центрирования.
Получим выражение для этой ошибки,
рассмотрев два треугольника:
ΔА
В´ А´ (αА)
и ΔСВ´С´ (αС).
е
/
sin αА
= S1
/
sin Θ
(17.19)
αА
= (е/
S1)
· ρ
· sin Θ
(17.20)
е
/
sinαС
= S2/
sin( Θ-
β) (17.21)
αС
= (е/
S2)
· ρ
· sin ( Θ-
β) (17.22)
αА
— αС
=
(е/
S1)
· ρ
· sin Θ
— (е/
S2)
· ρ
· sin ( Θ-
β) (17.23)
При
бесконечно большом числе установок
теодолита таких разностей будет n.
Тогда
средняя квадратическая ошибка
центрирования может быть вычислена по
формуле Гаусса.
mцентр
2
= [(αА
— αС)
²]
/n (17.24)
С
учетом(17.16) получим
mцентр
2
= [((е/ S1)
· ρ · sin
Θ — (е/ S2)
· ρ · sin
( Θ- β))
²]
d Θ/2·π (17.25)
Вынесем
из-под знака суммы общие множители и
получим
mцентр
2
= (е2
· ρ2
)/ 2·π
· [(1/ S1)
2
· sin2
Θ
+ (1/ S2)
2
· sin2
( Θ-
β) –
—
(2/ S1S2)
· sin2
Θ
· sin2
( Θ-
β)] d Θ
(17.26)
Заменим
знак суммы интегралом и проинтегрируем
полученное выражение. Приняв следующие
условия. Пределы интегрирования от 0 до
2·π, длины визирных лучей одинаковы и
равны S.
В
итоге получим
mцентр
2
= (е2
/
S2)
· ρ2
· (1- cos β)] (17.27)
Ошибка
центрирования будет зависеть от величины
измеряемого угла β.
Чем ближе будет значение угла к 180 ̊,
тем ошибка будет больше. Поэтому при
вытянутом ходе следует особо тщательно
центрировать теодолит на пунктах хода.
Кроме этого. На величину этой ошибки
оказывают влияние длины визирных лучей.
Чем короче сторона хода, тем ошибка
центрирования больше. Из формулы (17.27)
можно выразить линейный элемент
центрирования и определиться с методикой
установки прибора на пункте.
Для
уменьшения влияния ошибок центрирования
и редукции при производстве измерений
в полигонометрических ходах используют
трехштативную систему.
Суть
ее заключается в том, что на трех смежных
пунктах штативы центрируются один раз,
а затем последовательно переставляются
в подставках прибор и визирные марки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
08.11.2019212.12 Кб11.docx
- #
- #
Ошибка — центрирование
Cтраница 1
Ошибка центрирования представляет собой смещение оптической оси относительно геометрической оси линзы, закрепленной в оправе. Ошибка выражается в миллиметрах.
[1]
Ошибка центрирования и ошибка наведения на веху тем больше влияют на результат, чем короче стороны измеряемого угла. При работе тридцатисекундным теодолитом ошибка отсчета оказывается наиболее крупной из всех остальных, вследствие чего повышение точности достигается применением способа повторений.
[2]
Ошибка центрирования теодолита и визирных марок не должна быть более 1 мм.
[3]
Для уменьшения влияния ошибки центрирования в подземных выработках применяют косвенный способ примыкания к отвесам.
[4]
Для ослабления вредного влияния ошибки центрирования инструмента на триангуляционном пункте примычный угол со рекомендуется измерять через вспомогательные направления.
[5]
Для того чтобы определить ошибку центрирования, исследуемую линзу закрепляют на вращающемся шпинделе так, чтобы ее оптическая ось совпала с осью вращения. Изображение какого-либо предмета ( окна, лампы) отражается от обеих поверхностей линзы. Линза вращается на станке, а ее ось смещают до тех пор, пока оба зеркальных изображения перестанут перемещаться одно относительно другого. Затем устанавливают на краю линзы наконечник индикатора или рычажной головки и определяют ее наибольшее и наименьшее биение при полном обороте. Половина этой разности представляет собой ошибку центрирования.
[6]
При внецентренном способе измерения угла ошибка центрирования является результатом действия ошибок определения линейного и углового элементов центрировки.
[7]
Угол в 45 измерен с ошибкой центрирования / И 10 мм и ошибкой редукции / иь2 мм.
[8]
При рекогносцировке важно помнить, что ошибки центрирования и редукции сильно снижают точность измерения углов с короткими сторонами.
[9]
При построении заданного створа сюда добавляются ошибки центрирования теодолита и визирной марки.
[10]
Расчеты показывают, что средняя величина ошибки центрирования инструмента при измерении углов в ходах полигонометрии 1 разряда не должна выходить за пределы 0 7 мм. Такую точность центрирования инструмента обеспечить нитяным отвесом невозможно, поэтому в городской полигонометрии для измерения углов необходимо применять инструменты, снабженные оптическими центрирами.
[11]
В подземных выработках первая линия подземной полигономе-трии бывает короткой, поэтому ошибка центрирования угломерного инструмента над точкой А1 существенная.
[12]
В ходах подходной полигонометрии на участках с короткими линиями для исключения ошибки центрирования при измерении углов на концах коротких линий одновременно устанавливают два инструмента. Так, при измерении угла ABC ( рис. 107) в точке А устанавливают визирное приспособление обычного типа, а визируя на точку С крест нитей сетки трубы инструмента, установленного в точке В, наводят на центрировочный штифт угломерного инструмента, центрированного над точкой С. Трубу инструмента в точке С при этом устанавливают горизонтально и перпендикулярно направлению линии СВ.
[13]
Двух — или трехкратное независимое центрирование инструмента и визирных приспособлений в процессе измерения угла ослабляет влияние ошибок центрирования и редукции на результаты угловых измерений.
[14]
Описанный способ позволяет непосредственно измерять углы между направлениями на оси вращения инструментов, которыми измеряют углы на соседних пунктах, и тем самым уменьшить влияние ошибок центрирования и редукции.
[15]
Страницы:
1
2
Здесь не учтены ошибки деления. Приведенные числа показывают, следовательно, только точность отсчета они относятся главным образом к геодезическим и астрономическим инструментам, имеющим шкалы наиболее часто применяемого диаметра. Ошибки центрирования часто бывают большими. Поэтому хорошие геодезические и астрономические инструменты имеют две шкалы, поворачиваемые на 180°. За результат измерения принимается среднее из двух отсчетов. [c.340]
Средняя погрешность Е угла АВС полигона (фиг. 2), вызываемая ошибками центрирования (эксцентриситетом) теодолита и сигналов,, определяется следующей ф-лой [c.239]
Частой ошибкой начинающих конструкторов является введение центрирования там, где оно не требуется условиями работы. В узле установки подшипника (И, 12) центрирование боковых щек не продиктовано необходимостью. Достаточно ограничиться фиксацией щек в радиальном направлении крепежными болтами (13). В конструкции упорного подшипника (14, 15) можно обойтись без центрирования упорной шайбы т, зафиксировав ее установочными штифтами п (16), так или иначе необходимыми для предупреждения поворота шайбы. [c.499]
Грубую ошибку представляет установка дистанционных втулок без центрирования или с недостаточно уверенным центрированием (малая величина 5). Вследствие наличия заходных фасок на центрирующих поверхностях втулок, а также неточностей длины посадочных поясов на валу и в корпусе возможна потеря центрирования и смещение втулок в радиальном направлении. [c.483]
Конечная суммарная ошибка второй ветви, вызываемая погрешностями центрирования деталей, которые входят в систему, а также погрешностями размеров поверхностей, ограничивающих замыкающее звено, при работе насоса меняет направление. [c.664]
Типичные ошибки установки прокладок представлены на рис. 307. В конструкции на рис. 307,7 прокладка не зафиксирована в радиальном направлении и может быть сдвинута при установке и выдавлена при затяжке. Центрирование прокладки по стержню стяжного болта (рис. 307, II) не дает эффекта, так как центрирование осуществляется вслепую после установки прокладки и крышки .значительная часть прокладки находится навесу и не зажимается уплотняемыми поверхностями. [c.137]
Увеличение напряжения, вызванное небольшими ошибками в центрировании контуров. [c.276]
Первый член представляет собою в соответствии с хорошо известной формулой напряжение на внутренней поверхности вполне концентрической трубы, а второй член представляет собой добавочное напряжение, вызванное небольшой ошибкой при центрировании контуров. Если плохо центрированную трубу сравнить с концентрической трубой того же внутреннего радиуса, с внешним радиусом, соответствующим наименьшей толщине стенок, так что = — d, то наибольшее напряжение в этой второй трубе выразится формулой [c.276]
Нужно отметить, что монтажный персонал нередко совершает ошибку, вращая при центрировании один какой-либо вал, а другой оставляя неподвижным. При этом используют только одну из скоб, показанных на рис. 127, которую устанавливают на вращаемую полумуфту. [c.251]
Следует отметить, что ремонтный персонал нередко совершает ошибку, вращая при центрировании один какой-либо вал, а другой оставляя неподвижным. При этом используют только одну из скоб. [c.175]
Если конструкция обрабатываемой детали не позволяет приблизить планшайбу к растачиваемому отверстию, то для уменьшения вылета оправки можно устанавливать специальные башмаки на планшайбу (люнеты перед обрабатываемой деталью) или же люнетные втулки в уже расточенное в передней стенке детали отверстие. Эти способы повышают жесткость упругой системы, просты в исполнении и не требуют значительных затрат вспомогательного времени. Однако ошибки в центрировании передней опоры относительно оси оправки приводят к искривлению оси растачиваемых отверстий. [c.249]
Для определения так называемой комплексной ошибки расположения профиля элементов и смещения плоскости симметрии зуба от оси поверхности центрирования для прямобочных соединений в работе [26] приводится аналитическое выражение [c.38]
Из приведенных зависимостей следует, что неравномерность распределения нагрузки в соединении, нагруженном поперечной силой, зависит от трех основных параметров коэффициента нагрузки, являющегося, в сущности, конструктивной характеристикой узла, в который входит соединение зазора между центрирующими диаметрами соединения отношения жесткости центрирования к жесткости зубьев. Боковой зазор и поперечная сила на распределение нагрузки не влияют. Число зубьев соединения влияет на распределение нагрузки весьма незначительно в соединении с шестью зубьями неравномерность распределения нагрузки примерно на 5—12 % выше, чем в соединении с десятью зубьями при прочих равных условиях. Поэтому приведенную на рис. 3.8 зависимость вр(Ч ) и W можно использовать для любого числа зубьев без существенной ошибки. [c.122]
При т = 0,01 м, а = Ь = 00 л, у = (Р и 71 = 180° получим, что К — 0,7. Отсюда можно сделать вывод, что чем точнее требуется измерить угол, тем меньше должна быть ошибка в центрировании. [c.693]
Установка зажимного приспособления и заготовки. Посредством зажимного приспособления образуется соединение стола станка с заготовкой, при этом ось нарезаемого колеса должна точно совпадать с осью вращения стола. Низкая стойкость фрезы, повышенное радиальное биение, ошибки шага и другие погрешности нарезаемого колеса обычно являются результатом неточной установки зажимного приспособления. Точность установки зажимного приспособления оценивается по поверхностям, которые служат базами при установке зубчатого колеса в приспособлении. Этими поверхностями обычно являются оправка или втулка для центрирования заготовки и торец, на который устанавливается заготовка. Биение указанных поверхностей после закрепления приспособления на столе станка не должна превышать 0,01— 0,015 мм. Следует избегать зажима заготовки в приспособлении гайкой. Затяжка гайки, особенно с применением удара, нарушает точность делительного колеса в столе станка. [c.173]
Контролируемое кольцо центрируется в измерительном устройстве конической оправкой 2, которая перемещается по центральному штоку 1, жестко закрепленному на корпусе измерительной станции. С оправкой 2 жестко связана обойма 3, несущая пневматические сопла. Такая система центрирования детали исключает ошибки измерения от неравномерности зазоров между контролируемой поверхностью и соплами (рабочий зазор устанавливается регулировкой компенсационных колец между фланцами сопел и обоймой). Во избежание излишнего давления на контролируемое кольцо коническая оправка вместе с обоймой разгружается пружинами. [c.47]
При установке заготовок в патроны и оправки, кроме погрешностей, возникающих в осевом направлении, которые создают ошибки линейных размеров, возникают погрешности от различных биений. Такие погрешности возникают вследствие неправильного центрирования заготовки в приспособлении. Величины этих отклонений приведены в табл. 4. [c.25]
Если давление постоянное, то любого нарушения равновесия из-за начального отклонения золотника относительно пружин можно избежать путем регулировки системы или изменения тока электромеханического преобразователя, так что эффект открытия золотника действует подобно тому, как отрицательная гидравлическая пружина постоянной жесткости действует на плоский золотник. Если же давление изменяется, например, в результате изменения давления источника питания, то сила открытия также будет изменяться и появляющаяся в результате этого ошибка положения поршня будет пропорциональна изменению давления. Обеспечить устойчивое положение рабочего поршня, при котором он был бы нечувствителен к изменению давления питания, можно только при помощи начальной регулировки центрированного плоского золотника относительно подвесных пружин. [c.309]
Частой ошибкой начинающих конструкторов является введение центрирования там, где по условиям работы деталей можно обойтись без него. Например, в случае промежуточной установки подшипника качения центрирование боковых щек (рис. 362, а—г) не продиктовано необходимостью. В данном случае можно ограничиться фиксацией щек в радиальном направлении крепежными болтами (рис. 362, г), что значительно облегчает изготовление. [c.461]
Грубые ошибки, подобные изображенным на рис. 446, а, в, допускают только начинающие конструкторы. Чаще встречаются ошибки, заключающиеся во введении излишней подгонки, излишнего центрирования и т. п. Например, подгонка призматической закладной шпонки к шпоночной канавке по всему контуру (рис. 446, е) намного и притом совершенно напрасно осложняет производство. Правильно подгонять шпонку только по рабочим граням, оставляя зазоры по торцам шпонки и между верхней плоскостью шпонки и днищем шпоночной канавки (рис. 446, ж, з). [c.533]
Бесцентровое шлифование как процесс, сочетающий высокую производительность и точность обработки деталей, находит широкое применение на заводах. Точность обеспечивается хорошей поддержкой изделия без люнетов, вдвое меньшим влиянием износа шлифовального круга (ошибка от износа круга переносится не на радиус, а на диаметр обрабатываемого изделия), отсутствием ошибок центрирования и простотой конструкции станка. Вместе с тем бесцентровое шлифование не обеспечивает повышение соосности наружной и внутренней поверхностей ступенчатых валов, в меньшей степени выправляет некруглость, чем шлифование в центрах, приводит к увеличению некруглости после обработки деталей со шпоночными канавками и другим изменениям круглого профиля изделия. [c.11]
Для проверки центрирования роторов применяют, как правило, новый щуп (№ 3 или 5). Работа изношенным щупом не рекомендуется, так как это может привести к ошибкам при измерениях. При замере щупом торцевых зазоров следует заводить щуп всегда на одну и ту же глубину — порядка 40—50 мм и с одинаковым усилием. Измерение зазора считается законченным, если увеличение набора на 0,01 мм вызывает значительное возрастание усилия, нео(бходимого для введения щупа в зазор. [c.70]
Основное понятие. Ошибка центрирования представляет собой смещение оптической оси относительно гео.четрической оси линзы, закрепленной в оправе. Ошибка выражается в миллиметрах. [c.773]
При первом способе условия обработки оказываются наиболее благоприятными, так как исключаются ошибки, неизбежные прп каждой новой устаповке заготовки. Прп втором и третьем способах точность центрирования будет целиком зависеть от точности приспособления. [c.381]
Соединение циферблата с механизмом имеет большое значение, поскольку оно обеспечивает его устойчивость и центрирование. Эксцентричность циферблата является недостатко.м, влияющим на отсчет времени, особенно в точных часах и хронометрах. Если ось секундной стрелки находится не в центре соответствующего отверстия циферблата, то при отсчете может быть допущена ошибка в несколько секунд. [c.138]
Новязка общая, по оси х, по оси у, угловая Неточность центрирования теодолита. . Ошибка визирования, измерения угла, [c.466]
Фиксирующие пальцы служат в первую очередь для точной и воспроизводимой установки образцов, но одновременно они до определенного предела предотвращают проскальзывание образцов в захватах. Конструктивное выполнение узлов крепления образцов может быть разным. Наиболее простым является способ, при котором фиксирующие пальцы опираются в У-образных пазах захватов (рис. 2.3.1). В работе [205] описана более сложная, но, судя по результатам опытов, удачная конструкция зажимного приспособления (рис. 2.3.2). Образцы с размерами концевой части (вместе с накладками) 57×13 хЗ,9 мм вставляются в пазы клиновых захватов зажимного приспособления пазы имеют размеры 57 х16 хЗ,8 мм. Это — первый этап центрирования, исключающий грубые ошибки. Захваты удерживаются в полуоткрытом состоянии при помощи двух винтов 6. Затем вставляются фиксирующие пальцы 4, и образец нагружается небольшой силой (напряжение в рабочей части образца при этом составляет 40 МН/м ), которая уравновешивается пружиной 2. После этого винты 6 вывинчиваются, и пружина 3 прижимает клиновые захваты к образцу. При дальнейшем нагружении клиновые [c.70]
Однако такие образцы имеют существенные недостатки. Так, радиальные переходы не всегда могут быть выполнены с необходимой тщательностью обработки и с одинаковой точностью относительно всех осей симметрии образцов. Определение прочности стеклопластмасс на образцах с разной шириной рабочей части (15 мм, если материалы толщиной 4—6 мм, и 10 мм — если их толщина 3—4 мм), как этого требует ГОСТ 11262—65, не позволяет получить сопоставимые данные и вносит в расчетные показатели большие погрешности. Немалые систематические, в том числе субъективные, ошибки в оценке прочностных характеристик стеклопластиков возможны также вследствие того, что трудно надежно проверить центрирование на машине каждого из образцов и, тем более, предупредить появление их скольжения и перекосов в процессе испытаний. Без использования сложных дополнительных устройств на образцах принятой формы нельзя исследо- [c.5]
Для уменьшения трения применяются конструкции направляющих с оливированными подшипниками (рис. 66,в). Однако в такой конструкции снижается точность передачи за счет увеличения по грешности центрирования, зависящей от ошибки формы цапфы и подшипника, от зазора между цапфой и подшипником. Если осевое усилие передается на подпятник, то момент трения [c.106]
Содержание:
- Недостатки изготовления и сборки
- Третье геометрическое условие
- Вывод:
| Предмет: | Геодезия |
| Тип работы: | Курсовая работа |
| Язык: | Русский |
| Дата добавления: | 06.03.2019 |
- Данный тип работы не является научным трудом, не является готовой выпускной квалификационной работой!
- Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.
Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!
По этой ссылке вы сможете найти много готовых курсовых работ по геодезии:
Посмотрите похожие темы возможно они вам могут быть полезны:
Введение:
Как и при любом другом измерении, основными источниками угловых ошибок измерения являются:
- Инструментальные ошибки;
- Тематические ошибки (личные ошибки);
- Ошибки из-за влияния внешней среды;
- Ошибки, связанные с процедурой измерения.
Данная классификация погрешностей измерений в значительной степени условна. При анализе ошибок измерений рекомендуется учитывать их в соответствии с технологией процесса измерения, которую можно условно разделить на три этапа.
На первом этапе они изучают:
- Неточность нанесения штрихов на конечности;
- Отклонение формы внутренней поверхности уровня ампулы от сферической;
- Качество изготовления оптики телескопа, в том числе прямолинейность фокусирующей линзы;
- Несоответствие между центрами конечности и алидады (эксцентриситет алидады);
- Отклонение фактической точности считывающих устройств от точности, заданной конструктивно, определяют с помощью микроскопа;
- Качество работы крепежных и ходовых винтов;
- Поворот подъемных винтов и осевых шарниров.
Недостатки изготовления и сборки
Перечисленные недостатки изготовления и сборки устройства вносят существенные ошибки в измерение горизонтальных углов. Они относятся к инструментальным ошибкам. Они не могут быть устранены во время работы устройства наблюдателем. Поэтому их следует идентифицировать на этапе подготовки устройства к измерениям, а по результатам исследования определяется возможность использования устройства для измерения углов. Исправление этих недостатков возможно, как правило, только на заводе или в специализированных мастерских. В то же время влияние некоторых источников таких ошибок может быть ослаблено или устранено путем использования соответствующих методов работы с инструментами. Примером этого является ослабление влияния эксцентриситета алидады горизонтального круга, принимая показания на двух противоположных сторонах конечности, если это предусмотрено теодолитной конструкцией, или путем изменения положения конечности с помощью около 1800 между полу-приемами.
На этом же этапе исследуется соответствие относительного положения основных геометрических осей их проектным требованиям. Этот тип исследования называется проверкой. Если относительное положение отдельных осей не соответствует их проектным требованиям, они корректируются (корректируются). Однако в любом случае сохраняется частичное несоответствие относительного положения геометрических осей, что, безусловно, повлияет на точность измерений. Задача пользователя — оценить прогнозируемую ошибку и принять решение о возможности и необходимости ее ослабления или игнорировать ее. Критерием здесь является требование заказчика к точности конечных результатов измерения угла.
Так что невыполнение первого геометрического условия, — перпендикулярность оси цилиндрического уровня оси вращения теодолита, приводит к наклону циферблата под углом его.
Погрешность измерения горизонтального угла ηi от наклона конечности имеет функциональную зависимость:
- ηiт = (tgν1 — tgν2) это, (6)
- где ν1 и ν2 — углы наклона сторон измеряемого угла.
Это показывает, что если углы наклона линий визирования примерно одинаковы (ν1≈ν2), то наклон конечности в небольших пределах не окажет существенного влияния на точность измеренного угла. Поэтому во многих руководствах по эксплуатации теодолита написано, что пузырь уровня при отклонении от горизонтального угла может отклоняться от нулевой точки до двух делений, или угол поворота для теодолитов технической точности составляет 1,5 ‘.
В то же время при использовании этого теодолита для монтажа строительных конструкций в вертикальном положении всегда ν1 ≠ ν2, и их разность может достигать 45 °. А это значит, что ηiТ — это. Это значение является значительным, поскольку наклон оси вращения теодолита будет вызывать наклон оси вращения телескопа под тем же углом, и, следовательно, наклон конструкции здания. Если мы примем допуск отклонения пузырька уровня от нулевой точки деления 2, то верхняя головка колонны отклонится от вертикали только из-за этого источника ошибки на величину порядка 5 мм в конструкции. высота 10 м. Во многих случаях это значение превышает допуск для установки такого рода конструкции в вертикальном положении. Поэтому при корректировке этого состояния теодолита, используемого на строительной площадке, необходимо выполнять его с максимально возможной точностью (не ниже 0,5 деления шкалы уровня).
Невыполнение второго геометрического условия, перпендикулярности оси вращения телескопа и визирной оси, приводит к ошибке ηc при измерении горизонтального угла.
Аналитическое выражение которого имеет вид:
- ηc = c0 (1 / cos ν1 — 1 / cos ν2), (7)
- где c0 — значение коллимационной ошибки в горизонтальном положении оси визирования телескопа (ν = 0);
- ν1 и ν2 — углы наклона сторон измеряемого угла.
Это показывает, что влияние коллимационной ошибки на точность измерения горизонтального угла в одном положении вертикального круга тем меньше, чем меньше разница между углами наклона лучей-мишеней и при тех же углах наклона его это ноль. При измерении горизонтального угла в двух положениях вертикального круга (KL и KP) влияние коллимационной ошибки равно нулю независимо от разности углов наклона сторон OA и OV.
На строительной площадке установка конструкций в вертикальном положении выполняется, как правило, в одном положении вертикального круга, а разница в углах наклона может достигать 450. Поэтому наличие коллимационной ошибки будет иметь значительное влияние на точность установки конструкции в вертикальном положении.
Таким образом, если теодолит предназначен для полного измерения горизонтальных углов, то ошибка коллимации не может быть скорректирована. И, наоборот, при использовании теодолита для установки или выравнивания вертикальности конструкций, корректировка коллимационной ошибки должна выполняться со всей осторожностью. В то же время следует помнить, что довести его до нуля невозможно, и остаточная стоимость всегда будет оказывать определенное влияние на точность установки в вертикальном положении. Важно предварительно рассчитать его стоимость и оценить влияние на конечный результат.
Третье геометрическое условие
Невыполнение третьего геометрического условия, то есть перпендикулярности оси вращения телескопа к оси вращения теодолита, не оказывает существенного влияния на точность измерения горизонтального угла. Это верно, если угол измеряется в KL и KP, и стороны имеют приблизительно одинаковые углы наклона.
Функциональная зависимость между погрешностью измерения горизонтального угла от угла наклона оси вращения трубы и углами наклона линий визирования составляет:
- ηiт = (tgν1 — tgν2) qт, (8)
- где qt — угол наклона оси вращения телескопа, вызванный неравенством опор.
Если в результате проверки этого условия установлено, что угол qt превышает значение, указанное для этого класса работ, то не рекомендуется устанавливать конструкции в вертикальном положении с таким теодолитом. Геодезические и топографические работы могут быть выполнены, если измерения производятся в двух положениях круга.
Следующая группа ошибок напрямую связана с процессом приведения теодолита в рабочее положение. Прежде всего, это ошибка при центрировании теодолита и прицельных целей (ошибка при сокращении). Эти ошибки оказывают наиболее существенное влияние на точность измерения горизонтальных углов.
В идеале невозможно центрировать теодолит, поэтому в любом случае центр конечности будет находиться над точкой O, а над точкой O ′ на расстоянии e (линейный центрирующий элемент) от точки O). Так, при центрировании с отвесом значение е достигает 5 мм., А при оптическом отвесе 2 мм.
Вторым элементом ошибки центрирования является угол Θ (угловой центрирующий элемент). Оба элемента (e и θ) являются случайными величинами и подчиняются закону нормального распределения при условии, что центрирующее устройство хорошо откалибровано и выровнено.
Таким образом, вместо угла AOB (β) мы всегда измеряем угол AO’B (β ‘). разница ηc.t. = β’– β — погрешность измерения горизонтального угла, которая зависит от точности центрирования теодолита. Формула (9) может быть записана как ηc.t. = xB — xА .
В формуле (10) xB и xA являются значениями ошибок в направлениях OB и OA, вызванных ошибкой центрирования. Они зависят от величины линейного центрирующего элемента e; длина сторон SB и SA; угол ориентации линейного элемента θ, а также значение угла β.
Их аналитические выражения применительно имеют вид:
- xА = (е / SA) ρ sinβ (11)
- xB = (e / SB) ρ sin (θ + β), (12)
- где ρ — количество секунд в радианах (206265 ″).
Если взять SC = SA = S, то окончательное выражение ошибки измерения угла из-за ошибки центровки примет вид: ηc.t = (e / S) ρ (sin (θ + β) — sinβ)).
Анализ этого выражения для экстремальных значений позволяет сделать вывод: ηc.t → 0 при S →; ηc.t → max = (е / SC) ρ при β = 1800 и θ = 900.
Таким образом, всегда следует стремиться к увеличению длины сторон, если позволяют условия. При измерении углов с помощью теодолитов технической точности длина сторон менее 40 м не допускается, поскольку погрешность ηc.t становится сопоставимой с точностью этого устройства.
Точность измерения горизонтальных углов также зависит от погрешности уменьшения, то есть от погрешности центрирования цели. Геометрический смысл этой ошибки полностью аналогичен ошибке центрирования теодолита. Как и при центрировании теодолита, линейные l и угловые Θ центрирующие элементы являются случайными
Таким образом, вместо точки A цель центрируется над точкой A ′, и поэтому измеренный угол будет содержать ошибку y. Величина этой ошибки зависит от величины линейного элемента l; SOA расстояние и угол Θ1. Аналитически зависимость y от этих факторов можно выразить формулой y = l ρ sinΘ1 ⁄ SOA.
Анализ этой формулы показывает, что независимо от значения l для угла Θ = 00 или 1800 ошибка y = 0. При При = 900 или 2700 ошибка y максимальна.
Отсюда рекомендация: при измерении углов на практике рекомендуется, чтобы полюс был установлен непосредственно в центре точки и удерживался в вертикальном положении во время измерения. Если по какой-либо причине это не может быть сделано, то разрешено устанавливать веху вне точки, но обязательно выровняйте измеренную линию. Кроме того, при создании обоснования стрельбы не рекомендуется выбирать длины сторон теодолитного хода короче 40 метров. Наиболее эффективный метод ослабления эффектов ошибок центрирования и уменьшения — это повторное центрирование устройства и цели между отдельными методами измерения (в случаях, когда измерения угла выполняются несколькими методами).
После приведения теодолита в рабочее положение он направлен на цель.
Ошибка этого процесса зависит от многих факторов:
- Увеличить телескоп;
- Прозрачность атмосферы;
- Фон, на который проецируется цель;
- Геометрические размеры цели;
- Расстояния от теодолита до цели;
- Острота зрения наблюдателя;
- Шаг резьбы направляющих винтов и т. д.
Невозможно выразить зависимость ошибки зрения от этих факторов в виде математической зависимости. В учебной литературе он представлен в виде формулы ηв = 60 ″ / v, то есть в зависимости только от одного фактора увеличение телескопа v.
Рекомендации по смягчению влияния ошибок наведения на точность измеренного угла следующие:
- Измерения должны выполняться в часы спокойной атмосферы;
- Видимость между вершиной угла и целью должна быть с земли;
- Указать на самое дно вехи;
- Установить веху или другую цель непосредственно в фиксированной точке;
- Управление должно осуществляться только с помощью свинцового винта Alidade;
- Цель для ввода в биссектрису сетки нитей в центре поля зрения трубы.
После наведения на цель считываются показания по шкале алидады горизонтального круга. Здесь основной является ошибка в оценке доли шкалы алидады на глаз. Поскольку теодолиты технической точности имеют шкалу алидады с ценой деления t = 5 ′, при подсчете на глаз ошибка будет ηо = 0.1t, т.е. = 30 ″. Это одна из самых значительных ошибок из всей серии ошибок при измерении горизонтальных углов. Определяет класс точности устройства. Они руководствуются этим при определении значимости других ошибок. Таким образом, считается, что любая другая ошибка не окажет существенного влияния на конечный результат измерения, если его значение меньше или равно 0,3 ηо.
На точность измерения горизонтальных углов существенно влияют внешние условия: температура и давление воздуха; влажность и прозрачность атмосферы; колебание воздушных масс. Наиболее существенное влияние на точность измерений оказывает боковая составляющая рефракции. Это является следствием прохождения целевого пучка через слои атмосферы с различной плотностью. Распределение плотности слоев воздуха связано с распределением температуры.
Поэтому преломляющее поле обычно отождествляют с температурным полем и значением парциального угла преломления, которое можно определить по формуле:
- δ ″ = 10,9
- где Р — давление воздуха, мм;
- Т — абсолютная температура;
- S — расстояние между устройством и целью;
- dt / dy — горизонтальный градиент температуры.
Вывод:
Несмотря на простоту функциональной взаимосвязи между параметрами атмосферы, невозможно учесть влияние рефракции при измерении горизонтальных углов. Поэтому главная рекомендация ослаблять влияние преломления на точность измерения горизонтальных углов состоит в том, что измерения должны проводиться в спокойной атмосфере, а стороны угла не должны располагаться близко к стенам зданий или других сооружений с локальное температурное поле.
На этапе вычислительной обработки результатов измерений основной ошибкой является ошибка округления и сохранение правильного количества значащих цифр при записи окончательного результата.
Основные методы и способы разбивочных работ
Разбивка отдельных элементов сооружения ведется с хорошо закрепленных на местности точек и линий опорной сети или с точек главных разбивочных осей сооружения.
В разбивке могут быть использованы способы прямоугольных координат (перпендикуляров), полярных координат, биполярных координат (угловых, линейных, комбинированных и створных засечек), створов и промеров.
Разбивка и перенесение проектов сооружений в натуру по своим действиям обратным геодезическим съемочным работам.
Способ угловой засечки применяют для разбивки недоступных точек, находящихся на значительном расстоянии от исходных пунктов.
Различают прямую и обратную угловые засечки.
В способе прямой угловой засечки положение на местности проектной точки С (рисунок 6) находят отложением на исходных пунктах А и В проектных углов β1 и β2. Базисом засечки служит или специально измеренная сторона, или сторона разбивочной сети. Проектные углы β1 и β2 вычисляют как разность дирекционных углов сторон. Дирекционные углы находят из решения обратной геодезической задачи по проектным координатам определяемой точки и известным координатам исходных пунктов.
Рекомендуемые материалы
Рисунок 6 — Схема разбивки способами прямой угловой и линейной засечек
На точность разбивки способом прямой угловой засечки оказывают влияние ошибки собственно прямой засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки, т.е.

Средняя квадратическая ошибка собственно засечки равна

или

где mβ — средняя квадратическая ошибка отложения углов β1 и β2.
Для приближенных расчетов принимают S1 = S2 = S. Тогда формула (16) будет иметь вид:

При разбивочных работах центрирование теодолита и визирных целей с помощью оптических отвесов, фиксация выносимой точки могут быть выполнены сравнительно точно. Поэтому основными ошибками, определяющими точность способа прямой угловой засечки, являются ошибки собственно засечки и исходных данных. Суммарная величина этих ошибок составит:

На принципе редуцирования основано и применение для разбивки способа обратной угловой засечки. На местности находят приближенно положение О’ разбиваемой проектной точки О (рисунок 7). В этой точке устанавливают теодолит и с требуемой точностью измеряют углы не менее чем на три исходных пункта с известными координатами. По формулам обратной засечки вычисляют координаты приближенно определенной точки и сравнивают их с проектными значениями. По разности координат вычисляют величины редукции (угловой и линейный элементы) и смещают точку в проектное положение. Для контроля на этой точке измеряют углы, вновь вычисляют ее координаты и сравнивают их с проектным. В случае недопустимых расхождений все действия повторяют.
Для вычисления координат точки О’ можно использовать формулы Деламбера и Гаусса. Применительно к (рисунок 7), они будут иметь вид:



На точность разбивки способом обратной угловой засечки оказывают влияние ошибки собственно засечки, исходных данных, центрирования теодолита и визирных целей, фиксации разбивочной точки и редуцирования. Очевидно, что при сравнительно больших расстояниях от определяемого до опорных пунктов влияние первых двух источников будет наиболее существенным; остальными ошибками можно пренебречь.
Рисунок 7 — Схема способа обратной угловой засечки
Ошибка собственно обратной засечки может быть подсчитана по приближенной формуле:

где S — расстояние от определяемого до соответствующих опорных пунктов;
b — расстояние между соответствующими опорными пунктами;
ωbac — угол между исходными сторонами.
Ошибки исходных данных учитывают по формуле:

где тА = тв = тс= тАВС – ошибка в положении исходного пункта;
τ = β1 + β2 + ωВАС – 1800.
В способе линейной засечки положение выносимой в натуру точки С (рисунок 6) определяют в пересечении проектных расстояний S1 и S2, отложенных от исходных точек А и В. Этот способ обычно применяют для разбивки осей строительных конструкций в случае, когда проектные расстояния не превышают длины мерного прибора.
Наиболее удобно разбивку производить при помощи двух рулеток. От точки А по рулетке откладывают расстояние S1, а от точки В по второй рулетке – S2. Перемещая обе рулетки при совмещенных нулях с центрами пунктов А и В, на пересечении концов отрезков S1 и S2 находят положение определяемой точки С.
Ошибка собственно линейной засечки при одинаковой точности ms отложения расстояний S1 и S2 может быть подсчитана по формуле:

Минимальной ошибка собственно линейной засечки будет при угле γ = 90°. В этом случае

Влияние ошибок исходных данных в линейной засечке выражается формулой:

При mА = mВ = mАВ

Для засечки при γ = 90° mисх = mАВ.
В случае применения мерных приборов ошибки центрирования отсутствуют. Тогда общая ошибка в определении положения разбиваемой точки С будет в основном зависеть от суммарной ошибки собственно засечки и исходных данных и выражаться формулой:

Для приближенных расчетов, приняв γ = 90°, будем иметь

В случае, если для линейной засечки применяются дальномерные комплекты, которые центрируются при помощи штативов, то влияние ошибок центрирования можно определить по формуле:

Способ полярных координат широко применяют при разбивке осей зданий, сооружений и конструкций с пунктов теодолитных или полигонометрических ходов, когда эти пункты расположены сравнительно недалеко от выносимых в натуру точек.
В этом способе положение определяемой точки С (рисунок 
Средняя квадратическая ошибка выноса в натуру точки С определяется формулой

Рисунок 8 — Схема разбивки способом полярных координат
Ошибка собственно разбивки полярным способом зависит от ошибки тβ построения угла β и ошибки ms отложения проектного расстояния S

Влияние ошибок исходных данных при тА = тв = тАВ выражается формулой:

а ошибок центрирования

Формулы (32) и (33) аналогичны. Из них следует, что для уменьшения влияния ошибок исходных данных и центрирования необходимо, чтобы угол β и отношение S/b были минимальны, полярный угол был бы меньше прямого, а проектное расстояние – меньше базиса разбивки, т. е. β 

Для приближенных расчетов, приняв β = 90° и S = b, получим


а для суммарной ошибки в положении точки, разбиваемой способом полярных координат,

Если разбиваемая точка находится на значительном расстоянии от исходного пункта, то приходится несколько раз откладывать полярным способом проектные углы и расстояния, прокладывая проектный ход (рисунок 9). При наличии прямой видимости с точки С на точку В для контроля измеряют примычные углы γ1 и γ2, образуя замкнутый угловой полигон. Поэтому такой способ называют способом проектного полигона. При точных разбивочных работах углы полигона уравнивают, вычисляют по ним и проектным расстояниям координаты точки С, сравнивают их с проектными и при необходимости редуцируют в проектное положение.
Рисунок 9 — Схема разбивки способом проектного полигона
При редкой разбивочной основе способ проектного полигона может быть использован для разбивки всех точек пересечения основных осей сооружения от одного исходного пункта. В этом случае проектный ход с проектными углами и расстояниями прокладывают полностью.
Способы створной и створно-линейной засечек широко применяют для выноса в натуру разбивочных осей зданий и сооружений, а также монтажных осей конструкций и технологического оборудования.
Положение проектной точки С в способе створной засечки определяют на пересечении двух створов, задаваемых между исходными точками 1-1′ и 2-2′ (рисунок 10). Створ задают обычно теодолитом, который центрируют над исходным пунктом (например, 1), а зрительную трубу ориентируют по визирной цели, отцентрированной на другом исходном пункте (в данном случае — 1′). Положение точки С фиксируют в заданном створе.
Средняя квадратическая ошибка створной засечки зависит от ошибок построения первого mс1, и второго mc2 створов, а также ошибки фиксации

Рисунок 10 — Схемы разбивки способами створной (а) и
створно-линейной (б) засечек
Основными ошибками при построении каждого из створов являются ошибки положения исходных точек, ошибки центрирования теодолита и визирных целей, ошибка визирования и перемены фокусировки зрительной трубы при наведении на визирную цель и на определяемую точку, т.е.

Ошибки положения исходных точек для задания створа имеют значения только в направлении, перпендикулярном створу, т. е. для каждого створа по одной из координат х или у. Их влияние определяется формулой:

где d — расстояние от точки установки теодолита до определяемой точки;
S — расстояние между исходными точками (длина створа).
Совместное влияние ошибок центрирования теодолита и визирной цели выражается формулой:

Анализируя формулы (38) и (39), можно сделать вывод, что наименьшее влияние ошибки исходных данных и центрирования оказывают на положение определяемой точки в середине створа. По мере приближения ее к исходным пунктам эти ошибки возрастают.
При построении створа приходится визировать дважды: вначале на визирную цель, установленную на исходной точке, затем на цель, фиксирующую положение разбиваемой точки в створе. В обоих случаях линейная величина ошибки визирования для определяемой точки будет пропорциональна расстоянию d от теодолита до этой точки. Следовательно, для створных построений ошибка визирования (в мм) будет равна

При построении створа приходится визировать на точки, расположенные от теодолита на разных расстояниях, что приводит к необходимости менять фокусировку трубы. Изменение хода фокусирующей линзы вызывает смещение визирной оси трубы и приводит к ошибке, которую необходимо учитывать при точных работах.
В современных высокоточных теодолитах ошибка из-за перефокусировки трубы примерно равна ошибке визирования. Поэтому для приближенных расчетов можно принять тфок = твиз. С учетом этого совместное влияние ошибок визирования и фокусирования при створных построениях может быть выражено формулой:

Створно-линейный способ позволяет определить проектное положение выносимой в натуру точки С (рисунок 10) путем отложения проектного расстояния d по створу АВ.
Способ прямоугольных координат применяют в основном при наличии на площадке или в цехе промышленного предприятия строительной сетки, в системе координат которой задано положение всех главных точек и осей проекта.
Разбивку проектной точки С (рисунок 11) производят по вычисленным значениям приращений ее координат ∆х и ∆у от ближайшего пункта сетки. Большее приращение (на рисунке – ∆у) откладывают по створу пунктов сетки АВ. В полученной точке D устанавливают теодолит и строят от стороны сетки прямой угол. По перпендикуляру откладывают меньшее приращение и закрепляют полученную точку С. Для контроля положение точки С можно определить от другого пункта строительной сетки.
Схема способа прямоугольных координат по существу сочетает в себе схему створно-линейного и полярного способов.
Рисунок 11 — Схема разбивки способом прямоугольных координат
Средняя квадратическая ошибка в положении точки С, определенной способом прямоугольных координат, может быть выражена формулой:

где m∆x, и т∆у — ошибки отложения приращения координат.
Вместе с этой лекцией читают «12. Истолкование уравнения Д. Бернулли».
Если по перпендикуляру откладывается ордината, то в формуле (42) величина ∆х заменяется на ∆у.
Влияние ошибок в положении исходных пунктов при условии тA = тB = mAB выражается формулой:

а ошибок центрирования

где b — длина стороны строительной сетки.








