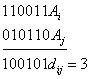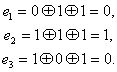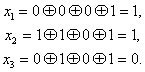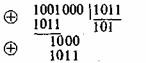Ошибки число искаженных символов кодовой комбинации

11

1. Общие принципы использования избыточности для обеспечения помехоустойчивости кодов.

Для
обеспечения высокой достоверности
передачи информации по каналу с помехами
применяют помехоустойчивое кодирование.

Помехоустойчивые
коды должны обеспечивать как обнаружение,
так и исправление ошибок (корректирующие
коды), т.е. кодирование должно осуществляться
так, чтобы сигнал, соответствующий
последовательности символов, после
воздействия на него предполагаемой в
канале помехи оставался ближе к сигналу,
соответствующему конкретной переданной
последовательности символов, чем к
сигналам, соответствующим другим
возможным последовательностям. Степень
близости обычно определяется по числу
разрядов, в которых последовательности
отличаются друг от друга.

Это
достигается ценой введения при кодировании
избыточности
(избыточных, дополнительных символов),
которая позволяет так выбрать передаваемые
последовательности символов, чтобы они
удовлетворяли дополнительным условиям,
проверка которых на приемной стороне
дает возможность обнаружить и исправить
ошибки.

Начнем
эту серьезную тему со старого анекдота.
Беседуют два пенсионера:

-Вы
не могли бы сказать номер вашего телефона?
– говорит один.

-Вы
знаете, признается другой, — я, к сожалению,
точно его не помню.

-Какая
жалость, сокрушается первый, — ну скажите
хотя бы приблизительно…

Действительно,
просьба поражает своей нелепостью.
Совершенно очевидно, что в 6-значном
наборе цифр достаточно ошибиться в
одном символе, чтобы остальная информация
стала абсолютно бесполезной. Однако
представим себе, что тот же самый телефон
написан словами русского языка и, скажем,
при передаче этого текста часть букв
потеряна.

Рассмотрим
например телефонный номер 34-33-44.
Соответственно запись «трицть четре
трцать три сорк чтре», в которой имеется
не один, а несколько пропущенных символов,
по-прежнему легко читается. Это связано
с тем, наш язык имеет определенную
избыточность, которая с одной стороны,
увеличивает длину записи, а с другой –
повышает надежность ее передачи. Это
же свойство обеспечивает надежное
общение людей даже при наличии у них
дефектов речи. Объясняется это тем, что
вероятность появления каждого последующего
символа в цифровой записи телефона
одинакова, в то время как в тексте,
записанном словами русского языка, это
не так. Очевидно, например, что твёрдый
знак в русском языке появляется
значительно реже, чем, например, буква
«а». (Наиболее вероятно появление в
русском языке буквы «о» p=0,096,
наименее вероятно – буква «ф» p=0,002)
Более того, некоторые сочетания букв
более вероятны, чем другие, а такие, как
два твердых знака подряд, невозможны в
принципе, и т.д. Зная, какова вероятность
появления какой-либо буквы в тексте, и
сравнив её с максимальной, можно
установить, насколько экономичен или
избыточен данный способ кодирования
(в нашем случае русский язык).

Мы
уже знаем, что количество информации в
сообщении тем больше, чем больше его
неопределенность (энтропия). Для любой
системы кодирования можно оценить её
максимально возможную энтропию
(информационную ёмкость) H_max
, которая соответствует случаю
равновероятности появления символов
в коде и равна, как вы уже знаете,
,
гдеN
– объём алфавита символов кода. Для
русского языка H_max
= 5 (если буквы е и ё неразличимы). Также
можно определить действительную
энтропию H.
Для русского языка H

1,5 бит. Случай H
< H_max
означает, что каждый символ (в русском
языке буква) несет меньше информации,
чем максимально возможно. Это явление
называют избыточностью R
(или редунданцией — redundancy)
и вычисляют как отношение:

Измерение
избыточности естественных языков дает
потрясающие результаты: она составляет
80%,
а это свидетельствует о том, что
практически 80% передаваемой с помощью
языка информации является избыточной,
т.е. лишней. Любопытен и тот факт, что
показатели избыточности разных языков
очень близки. Данная цифра примерно
определяет теоретический предел сжатия
текстовых файлов.

Факт
избыточности свидетельствует с одной
стороны о возможности перехода к системе
кодирования, которая уменьшила бы
избыточность передаваемого сообщения,
что в свою очередь уменьшит размер
сообщения и длительность его передачи
(коды сжатия, эффективные коды). С другой
стороны использование избыточных
сообщений, т.е. сообщений подчиняющихся
априорно известным ограничениям
(условиям, правилам) позволяет обнаружить
и исправить ошибки передачи, которые
приводят к нарушению этих ограничений.
Следовательно наличие избыточности
способствует повышению помехоустойчивости
сообщений.

Все
помехоустойчивые коды можно разделить
на два типа:

• обнаруживающие
  (проверочные EDC
  – Error
  Detection
  Code);

• корректирующие
  (ECC – Error Correction Code).

У
подавляющего большинства существующих
в настоящее время помехоустойчивых
кодов избыточность является следствием
их алгебраической структуры. В связи с
этим их называют алгебраическими кодами.
Алгебраические коды можно подразделить
на два больших класса: блоковые и
непрерывные.

В
случае блоковых кодов процедура
кодирования заключается в сопоставлении
каждой букве сообщения (или, что чаще,
последовательности из k двоичных
символов, соответствующих этой букве)
блока из n двоичных символов. Блоковый
код называют равномерным, если n остается
постоянным для всех букв сообщения.
Отношение k/n определяют как относительную
скорость кода.

Различают
разделимые и неразделимые блоковые
коды. При кодировании разделимыми кодами
выходные последовательности состоят
из символов, роль которых может быть
четко разграничена. Это, во-первых, k
информационных символов, совпадающих
с символами последовательности,
поступающей на вход кодера, во-вторых,
(n-k) избыточных (проверочных) символов,
вводимых в исходную последовательность
кодером, и служащих для обнаружения и
исправления ошибок.

При
кодировании неразделимыми кодами
разделить символы выходной последовательности
на информационные и проверочные
невозможно.

Непрерывными
(древовидными) называют такие коды, в
которых введение избыточных символов
в кодируемую последовательность
информационных символов осуществляется
непрерывно, без разделения ее на
независимые блоки.

Рассмотрим
принципы использования избыточности
для обнаружения ошибок. Пусть на вход
кодера поступает последовательность
из k информационных двоичных символов.
На выходе ей соответствует последовательность
из n двоичных символов, причем n>k.

Всего
может быть 2^k
различных входных и 2ⁿ
различных выходных последовательностей.
Из общего числа 2ⁿ
выходных последовательностей только
2^k
последовательностей соответствуют
входным. Назовем их разрешенными кодовыми
комбинациями. Остальные 2ⁿ-2^k
возможные выходные последовательности
для передачи не используются. Они могут
возникнуть лишь в результате ошибки
передачи. Назовем их запрещенными
комбинациями.

Каждая
из 2^k
разрешенных комбинаций в результате
действия помех может трансформироваться
в любую другую, всего имеется 2^k2ⁿ
возможных случаев передачи. В это число
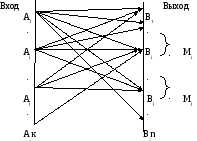
входят (рис. 6.1.):

• 2^k
  случаев безошибочной передачи (
  );

• 2^k(2^k-1)
  случаев перехода в другие разрешенные
  комбинации, что соответствует
  необнаруживаемым ошибкам ( );

• 2^k(2ⁿ-2^k)
  случаев перехода в неразрешенные
  комбинации, которые могут быть обнаружены
  ( ).

Следовательно,
часть обнаруживаемых ошибочных кодовых
комбинаций от общего числа возможных
случаев передачи составляет:

Рис.
6.1.
Трансформация
передаваемых кодовых комбинаций.

Рассмотрим
теперь случай исправления ошибок.

Любой
метод помехоустойчивого кодирования
можно рассматривать как правило разбиения
всего множества запрещенных кодовых
комбинаций на 2^k
непересекающихся подмножеств M_i,
каждое из которых ставится в соответствие
одной из разрешенных комбинаций. При
получении запрещенной комбинации,
принадлежащей подмножеству M_i,
принимается решение, что передавалась
разрешенная комбинация A_i.
Ошибка будет исправлена в тех случаях,
когда полученная комбинация действительно
образовалась из A_i,
т.е. в (2ⁿ-2^k)
случаях. Т.е. отношение числа исправляемых
кодом ошибочных кодовых комбинаций к
числу обнаруживаемых ошибочных комбинаций
равно:

Способ
разбиения на подмножества зависит от
того, какие ошибки должны исправляться
данным конкретным кодом.

Большинство
разработанных до настоящего времени
кодов предназначено для корректирования
взаимно-независимых
ошибок определенной
кратности и
пачек (пакетов) ошибок.

Взаимно-независимыми
ошибками будем
называть такие искажения в передаваемой
последовательности символов, при которых
вероятность появления любой комбинации
искаженных символов зависит только от
числа искаженных символов r и вероятности
искажения одного символа p. Эти ошибки
чаще всего вызываются флуктуационными
помехами.

Кратностью
ошибки называют
количество искаженных символов в кодовой
комбинации. Наиболее вероятны ошибки
меньшей кратности. Их и следует
обнаруживать и исправлять в первую
очередь.

При
взаимно-независимых ошибках вероятность
искажения любых r символов в n-разрядной
кодовой комбинации

где
количество способов, которыми можно
выбрать из n элементов r (число сочетаний
из n по r)

Соседние файлы в папке Лекции по информатике

• #
• #
• #
• #
• #
• #
• #

7.1. Классификация корректирующих кодов

7.2. Принципы помехоустойчивого кодирования

7.3. Систематические коды

7.4. Код с четным числом единиц. Инверсионный код

7.5. Коды Хэмминга

7.6. Циклические коды

7.7. Коды с постоянным весом

7.8. Непрерывные коды

7.1. Классификация корректирующих кодов

В каналах с помехами эффективным средством повышения достоверности передачи сообщений является помехоустойчивое кодирование. Оно основано на применении специальных кодов, которые корректируют ошибки, вызванные действием помех. Код называется корректирующим, если он позволяет обнаруживать или обнаруживать и исправлять ошибки при приеме сообщений. Код, посредством которого только обнаруживаются ошибки, носит название обнаруживающего кода. Исправление ошибки при таком кодировании обычно производится путем повторения искаженных сообщений. Запрос о повторении передается по каналу обратной связи. Код, исправляющий обнаруженные ошибки, называется исправляющим, кодом. В этом случае фиксируется не только сам факт наличия ошибок, но и устанавливается, какие кодовые символы приняты ошибочно, что позволяет их исправить без повторной передачи. Известны также коды, в которых исправляется только часть обнаруженных ошибок, а остальные ошибочные комбинации передаются повторно.

Для того чтобы «од обладал корректирующими способностями, в кодовой последовательности должны содержаться дополнительные (избыточные) символы, предназначенные для корректирования ошибок. Чем больше избыточность кода, тем выше его корректирующая способность.

Помехоустойчивые коды могут быть построены с любым основанием. Ниже рассматриваются только двоичные коды, теория которых разработана наиболее полно.

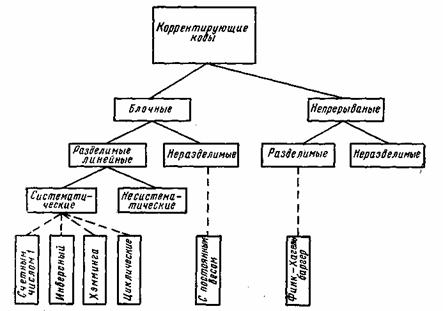
В настоящее время известно большое количество корректирующих кодов, отличающихся как принципами построения, так и основными характеристиками. Рассмотрим их простейшую классификацию, дающую представление об основных группах, к которым принадлежит большая часть известных кодов [12]. На рис. 7.1 показана схема, поясняющая классификацию, проведенную по способам построения корректирующих кодов.

Все известные в настоящее время коды могут быть разделены

на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки операции кодирования и декодирования в каждом блоке производятся отдельно. Отличительной особенностью непрерывных кодов является то, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. Здесь процессы кодирования и декодирования не требуют деления кодовых символов на блоки.

Рис. 7.1. Классификация корректирующих кодов

Разновидностями как блочных, так и непрерывных кодов являются разделимые и неразделимые коды. В разделимых кодах всегда можно выделить информационные символы, содержащие передаваемую информацию, и контрольные (проверочные) символы, которые являются избыточными и служат ‘исключительно для коррекции ошибок. В неразделимых кодах такое разделение символов провести невозможно.

Наиболее многочисленный класс разделимых кодов составляют линейные коды. Основная их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов.

В свою очередь, линейные коды могут быть |разбиты на два подкласса: систематические и несистематические. Все двоичные систематические коды являются групповыми. Последние характеризуются принадлежностью кодовых комбинаций к группе, обладающей тем свойством, что сумма по модулю два любой пары комбинаций снова дает комбинацию, принадлежащую этой группе. Линейные коды, которые не могут быть отнесены к подклассу систематических, называются несистематическими. Вертикальными прямоугольниками на схеме рис. 7.1 представлены некоторые конкретные коды, описанные в последующих параграфах.

7.2. Принципы помехоустойчивого кодирования

В теории помехоустойчивого кодирования важным является  вопрос об использовании  избыточности для корректирования возникающих при  передаче ошибок. Здесь   удобно   рассмотреть блочные моды, в которых всегда имеется возможность выделить отдельные кодовые комбинации. Напомним, что для равномерных кодов, которые в дальнейшем только и будут изучаться, число возможных комбинаций равно M=2ⁿ, где п — значность кода. В обычном некорректирующем коде без избыточности, например в коде Бодо, число комбинаций М выбирается равным числу сообщений алфавита источника М0и все комбинации используются для передачи информации. Корректирующие коды строятся так, чтобы число комбинаций М превышало число сообщений источника М0. Однако в.этом случае лишь М0комбинаций из общего числа  используется для передачи  информации.  Эти  комбинации называются разрешенными, а остальные М—М0комбинаций носят название запрещенных. На приемном конце в декодирующем устройстве известно, какие комбинации являются разрешенными и какие запрещенными. Поэтому если переданная разрешенная комбинация в результате ошибки преобразуется в некоторую запрещенную комбинацию, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Естественно, что ошибки, приводящие к образованию другой разрешенной комбинации, не обнаруживаются.

Различие между комбинациями равномерного кода принято характеризовать расстоянием, равным числу символов, которыми отличаются комбинации одна от другой. Расстояние d между двумя комбинациями  и  определяется количеством единиц в сумме этих комбинаций по модулю два. Например,

Для любого кода d. Минимальное расстояние между разрешенными комбинациями ,в данном коде называется кодовым расстоянием d.

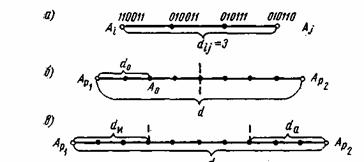
Расстояние между комбинациями  и  условно обозначено на рис. 7.2а, где показаны промежуточные комбинации, отличающиеся друг от друга одним символом. B общем случае некоторая пара разрешенных комбинаций  и , разделенных кодовым расстоянием d, изображается на прямой рис. 7.2б, где точками указаны запрещенные комбинации. Для того чтобы в результате ошибки комбинация  преобразовалась в другую разрешенную комбинацию , должно исказиться d символов.

Рис. 7.2.  Геометрическое представление разрешенных и запрещенных кодовых комбинаций

При искажении меньшего числа символов комбинация  перейдет в запрещенную комбинацию и ошибка будет обнаружена. Отсюда следует, что ошибка всегда обнаруживается, если ее кратность, т. е. число искаженных символов в кодовой комбинации,

                                                                                                              (7.1)

Если g>d, то некоторые ошибки также обнаруживаются. Однако полной гарантии обнаружения ошибок здесь нет, так как ошибочная комбинация ib этом случае может совпасть с какой-либо разрешенной комбинацией. Минимальное кодовое расстояние, при котором обнаруживаются любые одиночные ошибки, d=2.

Процедура исправления ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна:

                                                                                                         (7.2)

где — вероятность искажения одного символа. Так как обычно <<1, то вероятность многократных ошибок уменьшается с увеличением их кратности, при этом более вероятны меньшие расстояния d0. В этих условиях исправление ошибок может производиться по следующему правилу. Если принята запрещенная комбинация, то считается переданной ближайшая разрешенная комбинация. Например, пусть образовалась запрещенная комбинация  (см.рис.7.2б), тогда принимается решение, что была передана комбинация . Это .правило декодирования для указанного распределения ошибок является оптимальным, так как оно обеспечивает исправление максимального числа ошибок. Напомним, что аналогичное правило используется в теории потенциальной помехоустойчивости при оптимальном приеме дискретных сигналов, когда решение сводится к выбору того переданного сигнала, который ib наименьшей степени отличается от принятого. Нетрудно определить, что при таком правиле декодирования будут исправлены все ошибки кратности

                                                                                                             (7.3)

Минимальное значение d, при котором еще возможно исправление любых одиночных ошибок, равно 3.

Возможно также построение таких кодов, в которых часть ошибок исправляется, а часть только обнаруживается. Так, в соответствии с рис. 7.2в ошибки кратности  исправляются, а ошибки, кратность которых лежит в пределах только обнаруживаются. Что касается ошибок, кратность которых сосредоточена в пределах , то они обнаруживаются, однако при их исправлении принимается ошибочное решение — считается переданной комбинация А вместо Aили наоборот.

Существуют двоичные системы связи, в которых решающее устройство выдает, кроме обычных символов 0 и 1, еще так называемый символ стирания . Этот символ соответствует приему сомнительных сигналов, когда затруднительно принять определенное решение в отношении того, какой из символов 0 или 1 был передан. Принятый символ в этом случае стирается. Однако при использовании корректирующего кода возможно восстановление стертых символов. Если в кодовой комбинации число символов  оказалось равным gc, причем

                                                                                                            (7.4)

а остальные символы приняты без ошибок, то такая комбинация полностью восстанавливается. Действительно, для восстановления всех символов  необходимо перебрать всевозможные сочетания из gc символов типа 0 и 1. Естественно, что все эти сочетания, за исключением одного, будут неверными. Но так как в неправильных сочетаниях кратность ошибок , то согласно неравенству (7.1) такие ошибки обнаруживаются. Другими словами, в этом случае неправильно восстановленные сочетания из gc символов совместно с правильно принятыми символами образуют запрещенные комбинации и только одно- сочетание стертых символов даст разрешенную комбинацию, которую и следует считать как правильно восстановленную.

Если , то при восстановлении окажется несколько разрешенных комбинаций, что не позволит принять однозначное решение.

Таким образом, при фиксированном кодовом расстоянии максимально возможная кратность корректируемых ошибок достигается в кодах, которые обнаруживают ошибки или .восстанавливают стертые символы. Исправление ошибок представляет собой более трудную задачу, практическое решение которой сопряжено с усложнением кодирующих и декодирующих устройств. Поэтому исправляющие «оды обычно используются для корректирования ошибок малой кратности.

Корректирующая способность кода возрастает с увеличением d. При фиксированном числе разрешенных комбинаций Мувеличение d возможно лишь за счет роста количества запрещенных комбинаций:

                                                                                                  (7.5)

что, в свою очередь, требует избыточного числа символов r=n—k, где k — количество символов в комбинации кода без избыточности. Можно ввести понятие избыточности кода и количественно определить ее по аналогии с (6.12) как

                                                                                          (7.6)

При независимых ошибках вероятность определенного сочетания g ошибочных символов в n-значной кодовой комбинации выражается ф-лой ((7.2), а количество всевозможных сочетаний g ошибочных символов в комбинации зависит от ее длины и определяется известной формулой числа сочетаний

Отсюда полная вероятность ошибки кратности g, учитывающая все сочетания ошибочных символов, равняется:

                                                                                              (7.7)

Используя (7.7), можно записать формулы, определяющие вероятность отсутствия ошибок в кодовой комбинации, т. е. вероятность правильного приема

и вероятность правильного корректирования ошибок

Здесь суммирование ‘Производится по всем значениям кратности ошибок g, которые обнаруживаются и исправляются. Таким образом, вероятность некорректируемых ошибок равна:

                                                  (7.8)

Анализ ф-лы (7.8) показывает, что при малой величине Р0и сравнительно небольших значениях п наиболее вероятны ошибки малой кратности, которые и необходимо корректировать в первую очередь.

Вероятность Р, избыточность  и число символов n являются основными характеристиками корректирующего кода, определяющими, насколько удается повысить помехоустойчивость передачи дискретных сообщений и какой ценой это достигается.

Общая задача, которая ставится при создании кода, заключается, в достижении наименьших значений Р и . Целесообразность применения того или иного кода зависит также от сложности кодирующих и декодирующих устройств, которая, в свою очередь, зависит от п. Во многих практических случаях эта сторона вопроса является решающей. Часто, например, используются коды с большой избыточностью, но обладающие простыми правилами кодирования и декодирования.

В соответствии с общим принципом корректирования ошибок, основанным на использовании разрешенных и запрещенных комбинаций, необходимо сравнивать принятую комбинацию со всеми комбинациями данного кода. В результате М сопоставлений и принимается решение о переданной комбинации. Этот способ декодирования логически является наиболее простым, однако он требует сложных устройств, так как в них должны запоминаться все М комбинаций кода. Поэтому на практике чаще всего используются коды, которые позволяют с помощью ограниченного числа преобразований принятых кодовых символов извлечь из них всю информацию о корректируемых ошибках. Изучению таких кодов и посвящены последующие разделы.

7.3. Систематические коды

Изучение конкретных способов помехоустойчивого кодирования начнем с систематических кодов, которые в соответствии с классификацией (рис. 7.1) относятся к блочным разделимым кодам, т. е. к кодам, где операции кодирования осуществляются независимо в пределах каждой комбинации, состоящей из информационных и контрольных символов.

Остановимся кратко на общих принципах построения систематических кодов. Если обозначить информационные символы буквами с, а контрольные — буквами е, то любую кодовую комбинацию, содержащую k информационных и r контрольных символов, можно представить последовательностью:, где с и е в двоичном коде принимают значения 0 или 1.

Процесс кодирования на передающем конце сводится к образованию контрольных символов, которые выражаются в виде линейной функции информационных символов:

                                                                       (7.9)

Здесь  — коэффициенты, равные 0 или 1, а  и  — знаки суммирования по модулю два. Значения  выбираются по определенным правилам, установленным для данного вида кода. Иными словами, символы е представляют собой суммы по модулю два информационных символов в различных сочетаниях. Процедура декодирования принятых комбинаций может осуществляться различными» методами. Один из них, так называемый метод контрольных чисел, состоит в следующем. Из информационных символов принятой кодовой комбинации  образуется по правилу (7.9) вторая группа контрольных символов

Затем производится сравнение обеих групп контрольных символов путем их суммирования по модулю два:

                                                                                                (7.10)

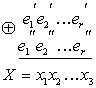
Полученное число X называется контрольным числом или синдромом. С его помощью можно обнаружить или исправить часть ошибок. Если ошибки в принятой комбинации отсутствуют, то все суммы, а следовательно, и контрольное число X будут равны .нулю. При появлении ошибок некоторые значения х могут оказаться равным 1. В этом случае , что и позволяет обнаружить ошибки. Таким образом, контрольное число Х определяется путем r проверок на четность.

Для исправления ошибок знание одного факта их возникновения является недостаточным. Необходимо указать номер ошибочно принятых символов. С этой целью каждому сочетанию исправляемых ошибок в комбинации присваивается одно из контрольных чисел, что позволяет по известному контрольному числу определить место положения ошибок и исправить их.

Контрольное число X записывается в двоичной системе, поэтому общее количество различных контрольных чисел, отличающихся от нуля, равно. Очевидно, это количество должно быть не меньше числа различных сочетаний ошибочных символов, подлежащих исправлению. Например, если код предназначен для исправления одиночных ошибок, то число различных вариантов таких ошибок равно . В этом случае должно выполняться условие

                                                                                                        (7.11)

Формула (7.11) позволяет при заданном количестве информационных символов k определить необходимое число контрольных символов r, с помощью которых исправляются все одиночные ошибки.

7.4. Код с чётным числом единиц. Инверсионный код

Рассмотрим некоторые простейшие систематические коды, применяемые только для обнаружения ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит, помимо информационных символов, один контрольный символ, выбираемый равным 0 или 1 так, чтобы сумма единиц в комбинации всегда была четной. Примером могут служить пятизначные комбинации кода Бодо, к которым добавляется шестой контрольный символ: 10101,1 и 01100,0. Правило вычисления контрольного символа можно выразить на

основании (7.9) в следующей форме: . Отсюда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю (— суммирование по модулю):

                                                                                                       (7.12)

Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем, случае ошибок нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы (7.12), поэтому такие ошибки не обнаруживаются. На основании ,(7.8) вероятность необнаруженной ошибки равна:

К достоинствам кода следует отнести простоту кодирующих и декодирующих устройств, а также малую .избыточность , однако последнее определяет и его основной недостаток — сравнительно низкую корректирующую способность.

Значительно лучшими корректирующими способностями обладает инверсный код, который также применяется только для обнаружения ошибок. С принципом построения такого кода удобно ознакомиться на примере двух комбинаций: 11000, 11000 и 01101, 10010. В каждой комбинации символы до запятой являются информационными, а последующие — контрольными.   Если   количество единиц в информационных символах четное, т. е. сумма этих

символов

                                                                                                                 (7.13)

равна нулю, то контрольные символы представляют собой простое повторение информационных. В противном случае, когда число единиц нечетное и сумма (7.13) равна 1, контрольные символы получаются из информационных посредством инвертирования, т. е. путем замены всех 0 на 1, а 1 на 0. Математическая форма записи образования контрольных символов имеет вид . При декодировании происходит сравнение принятых информационных и контрольных символов. Если сумма единиц в принятых информационных символах четная, т. е. , то соответствующие друг другу информационные и контрольные символы суммируются по модулю два. В противном случае, когда c‘=1, происходит такое же суммирование, но с инвертированными контрольными символами. Другими словами, в соответствии с (7.10) производится r проверок на четность: . Ошибка обнаруживается, если хотя бы одна проверка на четность дает 1.

Анализ показывает, что при  наименьшая кратность необнаруживаемой ошибки g=4. Причем не обнаруживаются только те ошибки четвертой кратности, которые искажают одинаковые номера информационных и контрольных символов. Например, если передана комбинация 10100, 10100, а принята 10111, 10111, то такая четырехкратная ошибка обнаружена не будет, так как здесь все значения  равны 0. Вероятность необнаружения ошибок четвертой кратности определяется выражением

Для g>4 вероятность необнаруженных ошибок еще меньше. Поэтому при достаточно малых вероятностях ошибочных символов ро можно полагать, что полная вероятность необнаруженных ошибок

Инверсный код обладает высокой обнаруживающей способностью, однако она достигается ценой сравнительно большой избыточности, которая, как нетрудно определить, составляет величину =0,5.

7.5. Коды Хэмминга

К этому типу кодов обычно относят систематические коды с расстоянием d=3, которые позволяют исправить все одиночные ошибки (7.3).

Рассмотрим построение семизначного кода Хэмминга, каждая комбинация которого содержит четыре  информационных и триконтрольных символа. Такой код, условно обозначаемый (7.4), удовлетворяет неравенству (7.11)    и   имеет   избыточность

Если информационные символы с занимают в комбинация первые четыре места, то последующие три контрольных символа образуются по общему правилу (7.9) как суммы:

                                                                              (7.14)

Декодирование осуществляется путем трех проверок на четность (7.10):

                                                                                  (7.15)

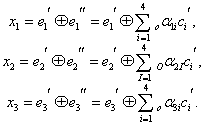
Так как х равно 0 или 1, то всего может быть восемь контрольных чисел Х=х1х2х3: 000, 100, 010, 001, 011, 101, 110 и 111. Первое из них имеет место в случае правильного приема, а остальные семь появляются при наличии искажений и должны использоваться для определения местоположения одиночной ошибки в семизначной комбинации. Выясним, каким образом устанавливается взаимосвязь между контрольными числами я искаженными символами. Если искажен один из контрольных символов:  или , то, как следует из (7.15), контрольное число примет соответственно одно из трех значений: 100, 010 или 001. Остальные четыре контрольных числа используются для выявления ошибок в информационных символах.

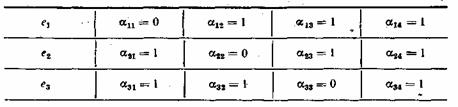
Таблица 7.1

Порядок присвоения контрольных чисел ошибочным информационным символам может устанавливаться любой, например, как показано в табл. 7.1. Нетрудно показать, что этому распределению контрольных чисел соответствуют коэффициенты , приведенные в табл. 7.2.

Таблица 7.2

Если подставить коэффициенты  в выражение (7.15), то получим:

                                                                                  (7.16)

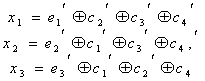
При искажении одного из информационных символов становятся равными единице те суммы х, в которые входит этот символ. Легко проверить, что получающееся в этом случае контрольное число согласуется с табл. 7.1.Нетрудно заметить, что первые четыре контрольные числа табл. 7.1 совпадают со столбцами табл. 7.2. Это свойство дает возможность при выбранном распределении контрольных чисел составить таблицу коэффициентов . Таким образом, при одиночной ошибке можно вычислить контрольное число, позволяющее по табл. 7.1 определить тот символ кодовой комбинации, который претерпел искажения. Исправление искаженного символа двоичной системы состоит в простой замене 0 на 1 или 1 на 0. B качестве примера рассмотрим передачу комбинации, в которой информационными символами являются , Используя ф-лу (7.14) и табл. 7.2, вычислим контрольные символы:

Передаваемая комбинация при этом будет . Предположим, что принята комбинация — 1001, 010 (искажен символ ). Подставляя соответствующие значения в (7.16), получим:

Вычисленное таким образом контрольное число  110 позволяет согласно табл. 7.1 исправить ошибку в символе.

Здесь был рассмотрен простейший способ построения и декодирования кодовых комбинаций, в которых первые места отводились информационным символам, а соответствие между контрольными числами и ошибками определялось таблице. Вместе с тем существует более изящный метод отыскания одиночных ошибок, предложенный впервые самим Хэммингом. При этом методе код строится так, что контрольное число в двоичной системе счисления сразу указывает номер искаженного символа. Правда, в этом случае контрольные символы необходимо располагать среди информационных, что усложняет процесс кодирования. Для кода (7.4) символы в комбинации должны размещаться в следующем порядке: , а контрольное число вычисляться по формулам:

                                                                                         (7.17)

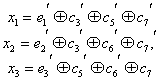
Так, если произошла ошибка в информационном символе с’5 то контрольное  число , что соответствует  числу 5 в двоичной системе.

В заключение отметим, что в коде (7.4) при появлении многократных ошибок контрольное число также может отличаться от нуля. Однако декодирование в этом случае будет проведено неправильно, так как оно рассчитано на исправление лишь одиночных ошибок.

7.6. Циклические коды

Важное место среди систематических кодов занимают циклические коды. Свойство цикличности состоит в том, что циклическая перестановка всех символов кодовой комбинации  дает другую комбинацию  также принадлежащую этому коду. При такой перестановке символы кодовой комбинации перемещаются слева направо на одну позицию, причем крайний правый символ переносится на место крайнего левого символа. Например, .

Комбинации циклического кода, выражаемые двоичными числами, для удобства преобразований обычно определяют в виде полиномов, коэффициенты которых равны 0 или 1. Примером этому может служить следующая запись:

Помимо цикличности, кодовые комбинации обладают другим важным свойством. Если их представить в виде полиномов, то все они делятся без остатка на так называемый порождающий полином G(z) степени , где k—значность первичного кода без избыточности, а п-значность циклического кода

Построение комбинаций циклических кодов возможно путем умножения комбинации первичного кода A*(z) ,на порождающий полином G(z):

A(z)=A*(z)G(z).

Умножение производится по модулю zⁿ и в данном случае сводится к умножению по обычным правилам с приведением подобных членов по модулю два.

В полученной таким способом комбинации A(z) в явном виде не содержатся информационные символы, однако они всегда могут быть выделены в результате обратной операции: деления A(z) на G(z).

Другой способ кодирования, позволяющий представить кодовую комбинацию в виде информационных и контрольных символов, заключается в следующем. К комбинации первичного кода дописывается справа г нулей, что эквивалентно повышению полинома A*(z) на ,г разрядов, т. е. умножению его на гг. Затем произведение z^rA*(z) делится на порождающий полином. B общем случае результат деления состоит из целого числа Q(z) и остатка R(z). Отсюда

Вычисленный остаток К(г) я используется для образования комбинации циклического кода в виде суммы

A(z)=z^rA*(z)@R(z).

Так как сложение и вычитание по модулю два дают один и тот же результат, то нетрудно заметить, что A(z) = Q(z)G(z), т. е. полученная комбинация удовлетворяет требованию делимости на порождающий полином. Степень полинома R{z) не превышает r—1, поэтому он замещает нули в комбинации zA*(z).

Для примера рассмотрим циклический код c n = 7, k=4, r=3 и G(z)=z³-z+1=1011. Необходимо закодировать комбинацию A*(z)=z*+1 = 1001. Тогда zA*(z)=z+z= 1001000. Для определения остатка делим z³A*(z) на G(z):

Окончательно получаем

В А(z) высшие четыре разряда занимают информационные символы, а остальные при — контрольные.

Контрольные символы в циклическом коде могут быть вычислены по общим ф-лам (7.9), однако здесь определение коэффициентов  затрудняется необходимостью выполнять требования делимости А(z) на порождающий полином G(z).

Процедура декодирования принятых комбинаций также основана на использовании полиномов G(z). Если ошибок в процессе передачи не было, то деление принятой комбинации A(z) на G(z) дает целое число. При наличии корректируемых ошибок в результате деления образуется остаток, который и позволяет обнаружить или исправить ошибки.

Кодирующие и декодирующие устройства циклических кодов в большинстве случаев обладают сравнительной простотой, что следует считать одним из основных их преимуществ. Другим важным достоинством этих кодов является их способность корректировать пачки ошибок, возникающие в реальных каналах, где действуют импульсные и сосредоточенные помехи или наблюдаются замирания сигнала.

В теории кодирования весом кодовых комбинаций принято называть .количество единиц, которое они содержат. Если все комбинации кода имеют одинаковый вес, то такой код называется кодом с постоянным весом. Коды с постоянным весом относятся к классу блочных неразделимых кодов, так как здесь не представляется возможным выделить информационные и контрольные символы. Из кодов этого типа наибольшее распространение получил обнаруживающий семизначный код 3/4, каждая разрешенная комбинация которого имеет три единицы и четыре нуля. Известен также код 2/5. Примером комбинаций кода 3/4 могут служить следующие семизначные последовательности: 1011000, 0101010, 0001110 и т. д.

Декодирование принятых комбинаций сводится к определению их веса. Если он отличается от заданного, то комбинация принята с ошибкой. Этот код обнаруживает все ошибки нечетной краткости и часть ошибок четной кратности. Не обнаруживаются только так называемые ошибки смещения, сохраняющие неизменным вес комбинации. Ошибки смещения характеризуются тем, что число искаженных единиц всегда равно числу искаженных нулей. Можно показать, что вероятность необнаруженной ошибки для кода 3/4 равна:

 при                                                                                (7.18)

В этом коде из общего числа комбинаций М = 2⁷=128 разрешенными являются лишь , поэтому в соответствии с (7.6) коэффициент избыточности

Код 3/4 находит применение при частотной манипуляции в каналах с селективными замираниями, где вероятность ошибок смещения невелика.

7.8. Непрерывные коды

Из непрерывных кодов, исправляющих ошибки, наиболее известны коды Финка—Хагельбаргера, в которых контрольные символы образуются путем линейной операции над двумя или более информационными символами. Принцип построения этих кодов рассмотрим на примере простейшего цепного кода. Контрольные символы в цепном коде формируются путем суммирования двух информационных символов, расположенных один относительно другого на определенном расстоянии:

;                                                                             (7.19)

Расстояние между информационными символами l=k—i определяет основные свойства кода и называется шагом сложения. Число контрольных символов при таком способе кодирования равно числу информационных символов, поэтому избыточность кода =0,5. Процесс образования последовательности контрольных символов показан на рис.7. символы разметаются  между информационными символами с задержкой на два шага сложения.

Рис. 7.3. Образование и размещение контрольных символов в цепном коде Финка—Хагельбаргера

При декодировании из принятых информационных символов по тому же правилу (7.19) формируется вспомогательная последовательность контрольных символов е», которая сравнивается с принятой последовательностью контрольных символов е’ (рис. 7.36). Если произошла ошибка в информационном символе, например, c‘k, то это вызовет искажения сразу двух символов e«k и e«km, что и обнаружится в результате их сравнения с  и e‘km. Отсюда по общему индексу k легко определить и исправить ошибочно принятый информационный символ с’Ошибка в принятом контрольном символе, например, e‘k приводит к несовпадению контрольных последовательностей лишь в одном месте. Исправление  такой ошибки не требуется.

Важное преимущество непрерывных кодов состоит в их способности исправлять не только одиночные ошибки, но я группы (пакеты) ошибок. Если задержка контрольных символов выбрана равной 2l, то можно показать, что максимальная длина исправляемого пакета ошибок также равна 2l при интервале между пакетами не менее 6l+1. Таким образом, возможность исправления длинных пакетов связана с увеличением шага сложения, а следовательно, и с усложнением кодирующих и декодирующих устройств.

Вопросы для повторения

1. Как могут быть  классифицированы  корректирующие коды?

2. Каким образом исправляются ошибки в кодах, которые только их обнаруживают?

3. В чем состоят основные принципы корректирования ошибок?

4. Дайте определение кодового расстояния.

5. При каких условиях код может обнаруживать или исправлять ошибки?

6. Как используется корректирующий код в системах со стиранием?

7. Какие характеристики определяют корректирующие способности кода?

8. Как осуществляется построение кодовых комбинаций в систематических кодах?

9. На чем  основан  принцип  корректирования  ошибок  с использованием  контрольного числа?

10. Объясните метод построения кода с четным числом единиц.

11. Как осуществляется процедура кодирования в семизначном коде Хэмминга?

12. Почему семизначный код 3/4 не обнаруживает ошибки смещения?

13. Каким образом производится непрерывное кодирование?

14. От чего зависит длина пакета исправляемых ошибок в коде Финка—Хагельбаргера?

Оценка корректирующей способности блокового (n, k) кода

Кодовое (хемминговое) расстояние  — число несовпадающих разрядов двух кодовых комбинаций.

Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.

Кратность ошибки (r) —  число искаженных символов кодовой комбинации.

Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.

Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.

Доля обнаруживаемых ошибок  2^k(2ⁿ-2^k)/(2^k2ⁿ) = 1 — 2^k—n

Число кодовых комбинаций: любых 2ⁿ , разрешенных 2^к, запрещенных  2ⁿ — 2^k .

Число вариантов передачи кода  2^к 2ⁿ. Ошибка обнаруживается, если при передаче разрешенной комбинации получена запрещенная комбинация. Число таких вариантов 2^k(2ⁿ-2^k).

Рекомендуемые материалы

Доля исправляемых ошибок среди обнаруживаемых 2^k(2^n—k-1)/2^k(2ⁿ-2^k)=2^—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2^n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к  переданной разрешенной комбинации. Число таких случаев  2^k(2^n-k-1).

Установим связь кодового расстояния d и кратности обнаруживаемых и исправляемых ошибок. Все возможные кодовые комбинации можно представить точками или векторами в многомерном пространстве.   Точки подмножества запрещенных комбинаций, соответствующих разрешенной комбинации, можно считать расположенными на сферах радиусов 1, 2, и т.д., равных кодовому расстоянию до разрешенной комбинации. Как видно из рисунка, где кодовое расстояние      d =6, можно обнаружить ошибки кратности r =5 и исправить ошибки кратности s =2. В общем случае должны выполняться условия:

Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».

d ³ r + 1   для обнаружения ошибки кратности r,

d ³ 2s + 1 для исправления  ошибки кратности s,

d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности  r и s.

Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний С_n^r .   При  s = 1 (исправление ошибки кратности 1) должно выполняться условие 2^n—k-1 > C_n¹  = n, при  s = 2 — условие  2^n—k-1 > C_n¹+ C_n², в общем случае – условие

Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.

Назначение помехоустойчивого кодирования – защита информации от помех и ошибок при передаче и хранении информации. Помехоустойчивое кодирование необходимо для устранения ошибок, которые возникают в процессе передачи, хранения информации. При передачи информации по каналу связи возникают помехи, ошибки и небольшая часть информации теряется. 

Без использования помехоустойчивого кодирования было бы невозможно передавать большие объемы информации (файлы), т.к. в любой системе передачи и хранении информации неизбежно возникают ошибки.

Рассмотрим пример CD диска. Там информация хранится прямо на поверхности диска, в углублениях, из-за того, что все дорожки на поверхности, часто диск хватаем пальцами, елозим по столу и из-за этого без помехоустойчивого кодирования, информацию извлечь не получится.

Использование кодирования позволяет извлекать информацию без потерь даже с поврежденного CD/DVD диска, когда какая либо область становится недоступной для считывания.

В зависимости от того, используется в системе обнаружение или исправление ошибок с помощью помехоустойчивого кода, различают следующие варианты:

• запрос повторной передачи (Automatic Repeat reQuest, ARQ): с помощью помехоустойчивого кода выполняется только обнаружение ошибок, при их наличии производится запрос на повторную передачу пакета данных;
• прямое исправление ошибок (Forward Error Correction, FEC): производится декодирование помехоустойчивого кода, т. е. исправление ошибок с его помощью.

Возможен также гибридный вариант, чтобы лишний раз не гонять информацию по каналу связи, например получили пакет информации, попробовали его исправить, и если не смогли исправить, тогда отправляется запрос на повторную передачу. 

Исправление ошибок в помехоустойчивом кодировании

Любое помехоустойчивое кодирование добавляет избыточность, за счет чего и появляется возможность восстановить информацию при частичной потере данных в канале связи (носителе информации при хранении). В случае эффективного кодирования убирали избыточность, а в помехоустойчивом кодировании добавляется контролируемая избыточность. 

Простейший пример – мажоритарный метод, он же многократная передача, в котором один символ передается многократно, а на приемной стороне принимается решение о том символе, количество которых больше.

Допустим есть 4 символа информации, А, B, С,D, и эту информацию повторяем несколько раз. В процессе передачи информации по каналу связи, где-то возникла ошибка. Есть три пакета (A1B1C1D1|A2B2C2D2|A3B3C3D3), которые должны нести одну и ту же информацию. 

Но из картинки справа, видно, что второй символ (B1 и C1) они отличаются друг от друга, хотя должны были быть одинаковыми. То что они отличаются, говорит о том, что есть ошибка. 

Необходимо найти ошибку с помощью голосования, каких символов больше, символов В или символов С? Явно символов В больше, чем символов С, соответственно принимаем решение, что передавался символ В, а символ С ошибочный. 

Для исправления ошибок нужно, как минимум 3 пакета информации, для обнаружения, как минимум 2 пакета информации.

Параметры помехоустойчивого кодирования

Первый параметр, скорость кода R характеризует долю информационных («полезных») данных в сообщении и определяется выражением: R=k/n=k/m+k

• где n – количество символов закодированного сообщения (результата кодирования);
•   m – количество проверочных символов, добавляемых при кодировании;
•   k – количество информационных символов.

Параметры n и k часто приводят вместе с наименованием кода для его однозначной идентификации. Например, код Хэмминга (7,4) значит, что на вход кодера приходит 4 символа, на выходе 7 символов,  Рида-Соломона (15, 11) и т.д. 

Второй параметр, кратность обнаруживаемых ошибок – количество ошибочных символов, которые код может обнаружить.

Третий параметр, кратность исправляемых ошибок – количество ошибочных символов, которые код может исправить (обозначается буквой t).

Контроль чётности

Самый простой метод помехоустойчивого кодирования это добавление одного бита четности. Есть некое информационное сообщение, состоящее из 8 бит, добавим девятый бит. 

Если нечетное количество единиц, добавляем 0.

1 0 1 0 0 1 0 0 | 0

Если четное количество единиц, добавляем 1.

1 1 0 1 0 1 0 0 | 1

Если принятый бит чётности не совпадает с рассчитанным битом чётности, то считается, что произошла ошибка.

1 1 0 0 0 1 0 0 | 1 

Под кратностью понимается, всевозможные ошибки, которые можно обнаружить. В этом случае, кратность исправляемых ошибок 0, так как мы не можем исправить ошибки, а кратность обнаруживаемых 1. 

Есть последовательность 0 и 1, и из этой последовательности составим прямоугольную матрицу размера 4 на 4. Затем для каждой строки и столбца посчитаем бит четности. 

Прямоугольный код – код с контролем четности, позволяющий исправить одну ошибку:

И если в процессе передачи информации допустим ошибку (ошибка нолик вместо единицы, желтым цветом), начинаем делать проверку. Нашли ошибку во втором столбце, третьей строке по координатам. Чтобы исправить ошибку, просто инвертируем 1 в 0, тем самым ошибка исправляется. 

Этот прямоугольный код исправляет все одно-битные ошибки, но не все двух-битные и трех-битные. 

Рассчитаем скорость кода для: 

• 1 1 0 0 0 1 0 0 | 1 

Здесь R=8/9=0,88

• И для прямоугольного кода:

Здесь R=16/24=0,66 (картинка выше, двадцать пятую единичку (бит четности) не учитываем)

Более эффективный с точки зрения скорости является первый вариант, но зато мы не можем с помощью него исправлять ошибки, а с помощью прямоугольного кода можно. Сейчас на практике прямоугольный код не используется, но логика работы многих помехоустойчивых кодов основана именно на прямоугольном коде. 

Классификация помехоустойчивых кодов

• Непрерывные — процесс кодирования и декодирования носит непрерывный характер. Сверточный код является частным случаем непрерывного кода. На вход кодера поступил один символ, соответственно, появилось несколько на выходе, т.е. на каждый входной символ формируется несколько выходных, так как добавляется избыточность.
• Блочные (Блоковые) — процесс кодирования и декодирования осуществляется по блокам. С точки зрения понимания работы, блочный код проще, разбиваем код на блоки и каждый блок кодируется в отдельности. 

По используемому алфавиту:

• Двоичные. Оперируют битами.
• Не двоичные (код Рида-Соломона). Оперируют более размерными символами. Если изначально информация двоичная, нужно эти биты превратить в символы. Например, есть последовательность 110 110 010 100 и нужно их преобразовать из двоичных символов в не двоичные, берем группы по 3 бита — это будет один символ, 6, 6, 2, 4 — с этими не двоичными символами работают не двоичные помехоустойчивые коды. 

Блочные коды делятся на

• Систематические  — отдельно не измененные информационные символы, отдельно проверочные символы. Если на входе кодера присутствует блок из k символов, и в процессе кодирования сформировали еще какое-то количество проверочных символов и проверочные символы ставим рядом к информационным в конец или в начало. Выходной блок на выходе кодера будет состоять из информационных символов и проверочных. 
• Несистематические — символы исходного сообщения в явном виде не присутствуют. На вход пришел блок k, на выходе получили блок размером n, блок на выходе кодера не будет содержать в себе исходных данных. 

В случае систематических кодов, выходной блок в явном виде содержит в себе, то что пришло на вход, а в случае несистематического кода, глядя на выходной блок нельзя понять что было на входе. 

Смотря на картинку выше, код 1 1 0 0 0 1 0 0 | 1 является систематическим, на вход поступило 8 бит, а на выходе кодера 9 бит, которые в явном виде содержат в себе 8 бит информационных и один проверочный.  

Код Хэмминга

Код Хэмминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Позволяет устранить одну ошибку и находить двойную. 

Код Хэмминга (7,4) — 4 бита на входе кодера и 7 на выходе, следовательно 3 проверочных бита. С 1 по 4 информационные биты, с 6 по 7 проверочные (см. табл. выше). Пятый проверочный бит y5, это сумма по модулю два 1-3 информационных бит. Сумма по модулю 2 это вычисление бита чётности. 

Декодирование кода Хэмминга

Декодирование происходит через вычисление синдрома по выражениям:

Синдром это сложение бит по модулю два. Если синдром не нулевой, то исправление ошибки происходит по таблице декодирования:

Расстояние Хэмминга

Расстояние Хэмминга — число позиций, в которых соответствующие символы двух кодовых слов одинаковой длины различны. Если рассматривать два кодовых слова, (пример на картинке ниже, 1 0 1 1 0 0 1 и 1 0 0 1 1 0 1) видно что они отличаются друг от друга на два символа, соответственно расстояние Хэмминга равно 2.

Кратность исправляемых ошибок и обнаруживаемых, связано минимальным расстоянием Хэмминга. Любой помехоустойчивый код добавляет избыточность с целью увеличить минимальное расстояние Хэмминга. Именно минимальное расстояние Хэмминга определяет помехоустойчивость. 

Помехоустойчивые коды

Современные коды более эффективны по сравнению с рассматриваемыми примерами. В таблице ниже приведены Коды Боуза-Чоудхури-Хоквингема (БЧХ)

Из таблицы видим, что там один класс кода БЧХ, но разные параметры n и k. 

• n — количество символов на входе. 
• k — количество символов на выходе. 
• t — кратность исправляемых ошибок. 
• Отношение k/n — скорость кода. 
• G (энергетический выигрыш) — величина, показывающая на сколько можно уменьшить отношение сигнал/шум (Eb/No) для обеспечения заданной вероятности ошибки.

Несмотря на то, что скорость кода близка, количество исправляемых ошибок может быть разное. Количество исправляемых ошибок зависит от той избыточности, которую добавим и от размера блока. Чем больше блок, тем больше ошибок он исправляет, даже при той же самой избыточности. 

Пример: помехоустойчивые коды и двоичная фазовая манипуляция (2-ФМн). На графике зависимость отношения сигнал шум (Eb/No) от вероятности ошибки. За счет применения помехоустойчивых кодов улучшается помехоустойчивость. 

Из графика видим, код Хэмминга (7,4) на сколько увеличилась помехоустойчивость? Всего на пол Дб это мало, если применить код БЧХ (127, 64) выиграем порядка 4 дБ, это хороший показатель. 

Компромиссы при использовании помехоустойчивых кодов

Чем расплачиваемся за помехоустойчивые коды? Добавили избыточность, соответственно эту избыточность тоже нужно передавать. Нужно: увеличивать пропускную способность канала связи, либо увеличивать длительность передачи. 

Компромисс:

1. Достоверность vs полоса пропускания.
2. Мощность vs полоса пропускания.
3. Скорость передачи данных vs полоса пропускания

Необходимость чередования (перемежения)

Все помехоустойчивые коды могут исправлять только ограниченное количество ошибок t. Однако в реальных системах связи часто возникают ситуации сгруппированных ошибок, когда в течение непродолжительного времени количество ошибок превышает t.

Например, в канале связи шумов мало, все передается хорошо, ошибки возникают редко, но вдруг возникла импульсная помеха или замирания, которые повредили на некоторое время процесс передачи, и потерялся большой кусок информации. В среднем на блок приходится одна, две ошибки, а в нашем примере потерялся целый блок, включая информационные и проверочные биты. Сможет ли помехоустойчивый код исправить такую ошибку? Эта проблема решаема за счет перемежения. 

Пример блочного перемежения:

На картинке, всего 5 блоков (с 1 по 25). Код работает исправляя ошибки в рамках одного блока (если в одном блоке 1 ошибка, код его исправит, а если две то нет). В канал связи отдается информация не последовательно, а в перемешку. На выходе кодера сформировались 5 блоков и эти 5 блоков будем отдавать не по очереди а в перемешку. Записали всё по строкам, но считывать будем, чтобы отправлять в канал связи, по столбцам. Информация в блоках перемешалась. В канале связи возникла ошибка и мы потеряли большой кусок. В процессе приема, мы опять составляем таблицу, записываем по столбцам, но считываем по строкам. За счет того, что мы перемешали большое количество блоков между собой, групповая ошибка равномерно распределится по блокам. 

Для того чтобы в принятом сообщении можно было обнаружить ошибку, это сообщение должно обладать некоторой избыточной информацией, позволяющей отличать ошибочный код от правильного. Например, если переданное сообщение состоит из трёх абсолютно одинаковых частей, то в принятом сообщении отделение правильных символов от ошибочных может быть осуществлено по результатам накопления посылок одного вида, например 0 или 1. Для двоичных кодов этот метод можно проиллюстрировать следующим примером:

10110 – переданная кодовая комбинация;

10010 – 1-я принятая комбинация;

10100 – 2-я принятая комбинация;

00110 – 3-я принятая комбинация;

10110 — накопленная комбинация . Как видим, несмотря на то, что во всех трёх принятых комбинациях были ошибки накопленная не содержит ошибок1.

Принятое сообщение может также состоять из кода и его инверсии. Код инверсии посылается в канал связи как одно целое. Ошибка на приёмном конце выделяется при сопоставлении кода и его инверсии (подробнее см. тема 7).

Для того чтобы искажение любого из символов сообщения привело к запрещенной комбинации. Необходимо в коде выделить комбинации, отличающиеся друг от друга в ряде символов, часть из этих комбинаций запретить и тем самым ввести в код избыточность. Например, в равномерном блочном коде считать разрешенными кодовые комбинации с постоянным соотношением нулей и единиц в каждой кодовой комбинации. Такие коды получили название кодов с постоянным весом. Для двоичных кодов число кодовых комбинаций с постоянным весом длиной в n символов равно

, (55)

где l – число единиц в кодовом слове. Если бы не существовало условие постоянного веса, то число комбинаций кода могло бы быть гораздо большим, а именно 2ⁿ. Примером кода с постоянным весом может служить стандартный телеграфный код №3 (см. приложение 4). Комбинации этого кода построены таким образом, что на 7 тактов, в течении которых должна быть принята одна комбинация, всегда приходятся три токовые и четыре без токовые посылки. Увеличение или уменьшение количества токовых посылок говорит о наличии ошибок.

Еще одним примером ведения избыточности в код является метод суть которого состоит в том, что к исходным кодам добавляются нули либо единицы таким образом, чтобы сумма их была всегда четной или нечетной. Сбой любого одного символа всегда нарушит условия четности(нечетности), и ошибка будет обнаружена. В этом случае комбинации друг от друга должны отличаться минимум в двух символах (см. задачу 6.9), то есть ровно половина комбинаций кода является запрещенной (запрещенными являются все нечетные комбинации при проверке на четность или наоборот).

Во всех упомянутых выше случаях сообщения обладают избыточной информацией. Избыточность сообщения говорит о том, что оно могло бы содержать большее количество информации, если бы не многократное повторение одного и того же кода не добавления коду его инверсии, не несущей никакой информации, если бы не искусственное запрещение части комбинаций кода и т. д. Но все перечисленные виды избыточности приходиться вводить для того, что бы можно было отличить ошибочную комбинацию от правильной.

Коды без избыточности обнаруживать, а тем более исправлять ошибки не могут1. минимальное количество символов, в которых любые две комбинации кода отличаются друг от друга называются кодовым расстоянием. Минимальное количество символов, в которых все комбинации кода отличаются друг от друга, называются минимальным кодовым расстоянием. Минимальное кодовое расстояние – параметр, определяющий помехоустойчивость кода и заложенную в коде избыточности. Минимальным кодовым расстоянием определяются корректирующие свойства кода.

В общем случае для обнаружения r ошибок минимальное кодовое расстояние

. (56)

Минимальное кодовое расстояние, необходимое для одновременного обнаружения и исправления ошибок,

, (57)

где s – число исправляемых ошибок.

Для кодов, только исправляющих ошибки, . (58)

Для того чтобы определить кодовое расстояние между двумя комбинациями двоичного кода, достаточно просуммировать эти комбинации по модулю 2 и посчитать число единиц в полученной комбинации (см. задачу 6.21).

Понятие кодового расстояния хорошо усваиваются на примере построения геометрических моделей кодов. На геометрических моделях вершинах n – угольников, где n – значность кода, расположены кодовые комбинации, а количества рёбер n угольника, отделяющих одну комбинацию от другой равно кодовому расстоянию (см. задачу 6.19).

Если кодовая комбинация двоичного кода A отстоит от кодовой комбинации B на расстоянии d, то это значит, что в коде A нужно d символов заменить на обратные, чтобы получить код B, но это не означает, что нужно d добавочных символов, чтобы код

обладал данными корректирующими свойствами. В двоичных кодах для обнаружения одиночной ошибки достаточно иметь 1 дополнительный символ независимо от числа информационных разрядов кода, а минимально кодовое расстояние d₀=2.

Для обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов и числом корректирующих разрядов должно удовлетворять следующим условиям:

, (59)

, (60)

при этом подразумевается, что общая длина кодовой комбинации

. (61)

Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d₀ = 3 удобно пользоваться выражениями

, (62)

если известна длина полной кодовой комбинации n, и

, (63)

если при расчетах удобней исходить из заданного числа информационных символов 1.

Для кодов, обнаруживающих трёхкратные ошибки (d₀=4),

(64)

или

. (65)

Для кодов длиной в n символов, исправляющих одну или две ошибки (d₀=5),

. (66)

Для практических расчетов можно пользоваться выражением

. (67)

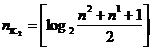
Для кодов, исправляющих 3 ошибки (d₀=7),

. (68)

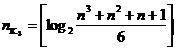
Для кодов, исправляющих s ошибок (d₀=2s+1),

. (69)

Выражение слева известно как нижняя граница Хэмминга [16], а выражение справа – как верхняя граница Варшамова – Гильбета [3]1.

Для приближенных расчетов можно пользоваться выражением

. (70)

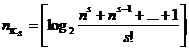
Можно предположить, что значение будет приближаться к верхней или нижней границе в зависимости от того, на сколько выражены выражения под знаком логарифма (см. страницу 7) приближается к целой степени двух.

Линейные групповые коды

Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.

Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.

Правила сложения по модулю 2 определяются следующими равенствами:

Последовательность нулей и единиц, принадлежащих данному коду, будем называть кодовым вектором.

Свойства линейных кодов: сумма (разность) кодовых векторов линейного кода даёт вектор, принадлежащий данному коду.

Линейные коды образуют алгебраическую группу по отношению к операции сложению по модулю 2. в этом смысле они являются групповыми кодами.

Свойства группового кода: минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.

Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов (см. задачу 6.42).

Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2 (см. задачу 6.44). Таким образом, для данного группового кода.

Групповые коды удобно задавать матрицам, размерность которых определяется параметрами кода и . Число строк в матрице равно , число столбцов матрицы равно :

. (71)

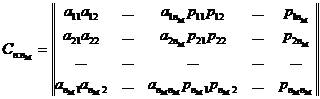
Коды, порождаемые этими матрицами, известны как (n;k) – коды, где k = , а соответствующие им матрицы называются порождающими, производящими, образующими.

Порождающая матрица С может быть представлена двумя матрицами И и П (информационная и проверочная). Число столбцов матрицы П равно n_K, число столбцов матрицы И равно n_M:

. (72)

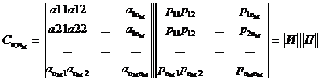
Теорией и практикой установлено [8,9,13], что в качестве матрицы удобно брать единичную матрицу в канонической формуле:

.

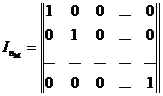
При выборе матрицы П исходят из следующих соображений: чем больше единиц в разрядах проверочной матрицы П, тем ближе соответствующий порождаемый код к оптимальному код к оптимальному1, с другой стороны, число единиц матрицы П определяет число сумматоров по модулю 2 в шифраторе и дешифратор, т. е. Чем больше единиц в матрице П, тем сложнее аппаратура. Вес каждой строки матрицы П должен быть не менее , гдеW_И – вес соответствующей строки матрицы И. Если матрица И – единичная, то W_И = 1 (удобство выбора в количестве матрицы И единичной матрицы очевидно: при WИ > 1 усложнилась бы как построение кодов, так и их технологическая реализация).

При соблюдении перечисленных условий любую порождающую матрицу группового кода можно привести к следующему виду:

… …

,

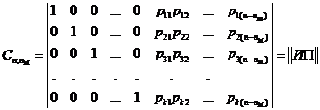
называемому левой канонической формой порождающей матрицы.

Для кодов с производящая матрица С имеет вид:

.

Во всех комбинациях кода, построенного при помощи такой матрицы, четное число единиц.

Для кодов с порождающая матрица не может быть представлена в форме, общей для всех видов с данными . Вид матрицы зависит от конкретных требований к порождаемому коду (в качестве примера построения некоторого абстрактного группового кода с может быть предложена задача 6.48). Этим требованиям могут быть либо минимум корректирующих разрядов, либо максимальная простата аппаратуры.

Корректирующие коды с минимальным количеством избыточных разрядов называют плотно упакованными или совершенными кодами.

Для кодов с соотношения n и n₀ следующее: (3;1), (7;4), (15;11), (31;26), (63;57) и т. д. (см., например, задачу 6.52).

Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью , и имеющие и , были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь

комбинации с максимальным весом. Для этого при построении кодов с последовательно используются векторы длиной , весом , , …, (см. задачи 6.50; 6.65). Тем же Слепяном в работе[11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность. Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы. При построении кодов с максимально простыми шифраторами и дешифраторами последовательно выбираются векторы весом (см. задачи 6.55; 6.65). если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяют условию , больше , то в первом случае не используют наборы с наименьшим весом, а во втором – с наибольшим.

Строчки образующей матрицы С представляют собой комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки в информационной части кода, находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй , третьей и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита (см. задачу 6.57).

Алгоритм образования проверочных символов по известной информационной части кода может быть записан следующим образом:

. . . . . . . . . . . . . . . . . . . . . . . . . . . .

или (73)

В процессе декодирования осуществляются проверки, идея которых в общем виде может быть представлена следующим образом:

, j = 1, 2, …, . (74) Для каждой конкретной матрицы существует своя, одна-единственная система проверок. Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом p₁ входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд p₂ и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода (см. задачу 6.60).

В результате осуществления проверок образуется проверочный вектор,, …, , который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производится по виду синдрома, так как каждому ошибочному разряду соответствует один-единственный проверочный вектор (см. задачи 6.60; 6.62).

Вид синдрома для каждой конкретной матрицы может быть определен при помощи проверочной матрицы Н, которая представляет собой транспонированную матрицу П, дополненную единичной матрицей , число столбцов которой равно числу проверочных разрядов кода:.

Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н (см. задачи 6.60; 6.62).

Процедура исправления ошибок в процессе декодирования групповых кодов сводится к следующему.

Строится кодовая таблица. В первой строке таблицы располагаются все кодовые векторы . В первом столбце второй строки размещается вектор , вес которого равен 1.

Остальные позиции второй строки заполняются векторами, по лученными в результате суммирования по модулю 2 вектора с вектором расположенными в соответствующем столбце первой строки. В первом столбце третьей строки записывается вектор , вес которого также равен 1, однако, если вектор содержит единицу в первом разряде, то — во втором. В остальные позиции третьей строки записывают суммы и .

Аналогично поступают до тех пор, пока не будут просуммированы с векторами все векторы , весом 1, с единицами в каждом из n разрядов. Затем суммируются по модулю 2 векторы , с весом 2, с последовательным перекрытием всех возможных разрядов. Все вектора определяет число исправляемых ошибок. Число векторов определяется возможным числом неповторяющихся синдромов и равно (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определить один-единственный соответствующий ему вектор . Векторы есть векторы ошибок, которые могут быть исправлены данным групповым кодом.

По виду синдрома принятая комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинацией с вектором ошибки , т. е. к определенной строке кодовой табл. 6.1.

Таблица 6.1.

A r			…
			…
			…
…	…	…	…	…
			…

Принятая кодовая комбинация сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы (см. задачу 6.68). процесс исправления ошибки заключается в замене на обратное значение разрядов., соответствующих единицам в векторе ошибок .

Векторы , , …, не должны быть равны ни одному из векторов , , …, в противном случае в таблице появились бы нулевые векторы.

Тривиальные систематические коды. Код Хэмминга.

Систематические коды представляют собой такие коды, в которых информационные и корректирующие разряды расположены по строго определенной системе и всегда занимают строго определенные места в кодовых комбинациях. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину. Групповые коды также являются систематическими, но не все систематические коды могут быть отнесены к групповым.

Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, число столбцов которой определяется числом контрольных разрядов кода. Каждая строка добавочной матрицы должна содержать не менее единиц, а сумма по модулю для любых строк не менее единиц (где минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю для строк производящей матрицы во всех возможных сочетаниях (см. например, задачу 6.74).

Код Хэмминга является типичным примером систематического кода. Однако при его построении к матрицам обычно не прибегают. Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных символов, либо количество информационных комбинаций . При помощи (59) и (60) вычисляются и . Соотношения между n, , и для Хэмминга предоставлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону , где 0, 1, 2 и т. д. — натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т.д.

Затем определяется значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной. Если эта сумма четна, то значение контрольного коэффициента — 0, в противно случае — 1.

Проверочные позиции выбираются следующим образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы:

.

Первой строке соответствует проверочный коэффициент , второй и т. д., как показано в табл. 2 приложения 8. Затем выявляют проверочные позиции, выписывая коэффициенты по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т. е. , , , , , и т. д.; во вторую — коэффициенты, содержащие 1 во втором разряде, т. е. , , , , , и т. д.; в третью проверку — коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствует номерам проверочных позиций, что позволяет составить общую таблицу проверок (табл. 3, приложение 8). Старшинство разрядов считается слева направо, а при проверке сверху вниз. Порядок проверок показывает также и порядок следования разрядов в получения разрядов в полученном двоичном коде.

Если в принятом коде есть ошибка, то результат проверок по контрольным позициям образует двоичное число, указывающее номер ошибочной позиции. Исправляют ошибку, изменяя символ ошибочной позиции а обратный (см. задачу 6.78).

Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одиночной ошибки проверки по позициям укажут на наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки (см. задачу 6.82).

Циклические коды.

Циклические коды [4, 6, 7, 9, 12, 13] названы так потому, что в них часть комбинаций кода либо все комбинации могут быть получены путем циклического сдвига одной или нескольких комбинацикода. Циклический сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Циклические коды, практически1, все относятся к систематическим кодам, в них контрольные и информационные разряды расположены на строго определенных местах. Кроме того, циклические коды относятся к числу блочных кодов. Каждый блок (одна буква является частным случаем блока) кодируется самостоятельно.

Идея построения циклических кодов базируется на использовании неприводимых в поле[1] двоичных чисел многочленов. Неприводимыми называются многочлены, которые не могут быть представлены в виде произведения многочленов низших степеней с коэффициентами из того же поля, так же, как простые числа не могут быть представлены произведением других чисел. Иными словами, неприводимые многочлены делятся без остатка только на себя или на единицу.

Неприводимые многочлены в теории циклических кодов играют роль образующих (генераторных, производящих) многочленов. Если заданную кодовую комбинацию умножить на выбранный неприводимый многочлен, то получим циклический код, корректирующие способности которого определяются неприводимым многочленом.

Предположим, требуется закодировать одну из комбинаций четырехзначного двоичного кода. Предположим также, что эта комбинация . Пока не обосновывая свой выбор, берем из таблицы неприводимых многочленов (табл. 2, приложение 9) в качестве образующего многочлен . Затем умножим на одночлен той же степени, что и образующий многочлен. От умножения многочлена на одночлен степени n степень каждого члена многочлена повысится на n, что эквивалентно приписыванию n нулей со стороны младших разрядов многочлена. Так как степень выбранного неприводимого многочлена равна трем, то исходная информационная комбинация умножается на одночлен третьей степени:

Это делается для того, чтобы впоследствии на мест этих нулей можно было бы записать корректирующие разряды.

Значение корректирующих разрядов находят по результату от деления на :

или

1101000	1011
1011		1111+
	1100
	1011
	1110
	1011
	1010
	1011
	001

Таким образом,

,

или в общем виде

, (75)

где частное, а остаток от деления на .

Так как в двоичной арифметике , а значит, , то можно при сложении двоичных чисел переносить слагаемые из одной части равенства в другую без изменения знака (если это удобно), поэтому равенство вида можно записать и как , и как . Все три равенства данном случае означают, что либо a и b равны 0, либо a и b равны 1, т. е. имеют одинаковую четность.

Таким образом, выражение (75) можно записать как

, (76)

что в случае нашего примера даст

или

1 1 1 1 1 0 1 1 = 1 1 0 1 0 0 0 + 0 0 1 =

=1 1 0 1 0 0 1

Многочлен 1101001 и есть искомая комбинация, где 1101 – информационная часть, а 001 – контрольные символы. Заметим, что искомую комбинацию мы получили бы и как в результате умножения одной из комбинаций полного четырехзначного двоичного кода (в двоичном случае 1111) на образующий многочлен, так и умножением заданной комбинации на одночлен, имеющий ту же степень, что и выбранный образующий многочлен (в нашем случае таким образом была получена комбинация 1101000) с последующим добавлением к полученному произведению остатка от деления этого произведения на образующий многочлен (в нашем примере остаток имел вид 001).

Таким образом, мы уже знаем два способа образования комбинаций линейных систематических кодов, к которым относятся и интересующие нас циклические коды. Эти способы явились теоретическим основанием для построения кодирующих и декодирующих устройств.

Шифраторы циклических кодов, в том или ином виде, построены по принципу умножения двоичных многочленов. Кодовые комбинации получаются в результате сложения соседних комбинаций по модулю два, что, как мы увидим ниже, эквивалентно умножению первой комбинации на двучлен .

Итак, комбинации циклических кодов можно представить в виде многочлена, у которых показатели степени x соответствуют номером разрядов, коэффициенты при x равны 0 или 1 в зависимости от того, стоит 0 или 1 в разряде кодовой комбинации , которую представляет данный многочлен. Например,

000101;

001010;

010100;

101000.

Циклический сдвиг кодовой комбинации аналогичен умножению соответствующего многочлена на x:

;

;

.Если степень многочлена достигает разрядности кода, то происходит «перенос» в нулевую степень при x. В шифраторах циклических кодов эта операция осуществляется путем соединения выхода ячейки старшего разряда со входом ячейки нулевого разряда.

Сложение по модулю 2 любых двух соседних комбинаций циклического кода эквивалентного операции умножения многочлена соответствующего комбинации первого слагаемого на многочлен , если приведение подобных членов осуществляется по модулю 2:

0 0 0 1 0 1			0 0 0 1 0 1
	0 0 1 0 1 0
	0 0 1 1 1 1
			0 0 1 0 1 0
			0 0 1 1 1 1

т. е. существует принципиальная возможность получения любой кодовой комбинации циклического кода путем умножения соответствующим образом подобного образующего многочлена на некоторый другой многочлен.

Однако мало построить циклический код. Надо уметь выделить из него возможные ошибочные разряды, т. е. ввести некоторые опознаватели ошибок, которые выделяли бы ошибочный блок из всех других. Так, как циклические коды – блочные, то каждый блок должен иметь свой опознаватель. И тут решающую роль играют свойства образующего многочлена . Методика построения циклического кода такова, что образующий многочлен принимает участие в образовании каждой кодовой комбинации, поэтому любой многочлен циклического кода делится на образующий без остатка. Но без остатка делятся только те многочлены, которые принадлежат данному коду, т. е. образующий многочлен позволяет выбрать разрешенные комбинации из всех возможных. Если же при делении циклического кода на образующий многочлен будет получен остаток, то значит либо в коде произошла ошибка, либо это комбинация какого-то другого кода (запрещенная комбинация), что для декодирующего устройства не имеет принципиальной разницы. По остатку и обнаруживается наличие запрещенной комбинации, т. е. обнаруживается ошибка. Остатки от деления многочленов являются опознавателями ошибок циклического кодов.

С другой стороны, остатки от деления единицы с нулями на образующий многочлен используются для построения циклических кодов (возможность этого видна из выражения (76)).

При делении единицы с нулями образующих многочлен следует помнить, что длина остатка должна быть не меньше числа контрольных разрядов, поэтому в случае нехватки разрядов в остатке к остатку приписывают справа необходимое число нулейНапример,

1 0 0 0 0 0 0 0 0 0 0	1 0 1 1
1 0 1 1		1 1 1 1 1 +
	0 1 1 0 0
	1 0 1 1		Остатки
	1 1 1 0		0 1 1
	1 0 1 1			1 1 0
	1 0 1 0		1 1 1
	1 0 1 1			1 0 1
	1 0 0 0		0 0 1
	1 0 1 1			0 1 0
	1 1		1 0 0
	0 1 1
	1 1 0
	и т. д.,

начиная с восьмого, остатки будут повторятся.

Остатки от деления используют для построения образующих матриц, которые, благодоря вой наглядности и удобству получения производных комбинаций, получили широкое распространение для построения циклических кодов. Построение образующей матицы сводится к составлению единичной транспонированной и дополнительной матрицы, элементы которой представляют собой остатки от деления единицы с нулями на образующий многочлен 1. Напомним, что единичная транспонированная матрица представляет собой квадратную матрицу, все элементы которой – нули, кроме элементов, расположенных по диагонали справа на лево сверху вниз (в нетранспонированной матрице диагональ с единичными элементами расположена слева на права сверху вниз). Элементы дополнительной матрицы приписываются справа от единичной транспонированной матрицы.

Однако не все остатки от деления единицы с нулями на образующий многочлен могут быть использованы в качестве элементов дополнительной матрицы. Использоваться могут лишь те остатки вес которых , где минимальное кодовое расстояние длина остатков должна быть не менее количества контрольных разрядов, а число остатков должно равняться числу информационных разрядов.

Строки образующие матрицы представляют собой первые комбинации искомого кода. Остальные комбинации кода получаются в результате суммирования по модулю 2 всевозможных сочетаний строк образующей матрицы (см. задачу 6.108)1.

Описанный выше метод построения образующих матриц не является единственным. Образующая матрица может быть построена в результате непосредственного умножения элементов единичной матрицы на образующий многочлен. Это часто бывает удобнее чем нахождение остатков от деления. Полученные коды ничем не отличаются от кодов, построенных по образующим матрицам, а которых дополнительная матрица состоит из остатков от деления единицы с нулями на образующий многочлен ( см. задачи 6.103; 6.108; 6.110).

Образующая матрица может быть построена таким путем циклического сдвига комбинации, полученной в результате умножения строки единичной матрицы ранга на образующий многочлен (см. задачу 6.126).

В заключение предлагаем еще один метод построения циклических кодов. Достоинством этого метода является исключительная простота схемных реализаций кодирующих и декодирующих устройств.

Для получения комбинаций циклического кода в этом случае достаточно произвести циклический сдвиг строки образующей матрицы и комбинации, являющейся ее зеркальным отображением (см. задача 6.112). При построении кодов с число комбинаций, получаемых суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы, равно числу комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации (см. задачи 6.103; 6.112). Однако этот способ используется для получения кодов с малым числом информационных разрядов. Уже при число комбинаций, получаемых в результате циклического сдвига, будет меньше, чем число комбинаций, получаемых в результате суммирования всевозможных сочетаний строк образующей матрицы (см., например, задачи 6.123 и 6.128).

Число ненулевых комбинаций, получаемых в результате суммирования по модулю 2 всевозможных два строк образующей матрицы,

, (77)

где число информационных разрядов кода2.

Число ненулевых комбинаций, получаемых в результате циклического сдвига любой строки образующей матрицы и зеркальной ей комбинации,

, (78)

где n – длина кодовой комбинации.

При числе информационных разрядов число комбинаций от суммирования строк образующей матрицы растет гораздо быстрее, чем число комбинаций, получаемых в результате циклического сдвига строки образующей матрицы и зеркальной ей комбинации. В последнем случае коды получаются избыточными (так как при той же длине кода можно иным способом передать большее количество сообщений), соответственно, падает относительная скорость передачи информации. В таких случаях целесообразность применения того или иного метода кодирования может быть определена из конкретных технических условий.

Ошибки в циклических кодах обнаруживаются и исправляются при помощи остатков от деления полученной комбинации на образующий многочлен. Остатки от деления являются опознавателями ошибок, но не указывают непосредственно на место ошибки в циклическом коде.

Идея исправления ошибок базируется на том, что ошибочная комбинация после определенного числа циклических сдвигов «подгоняется»под остаток таким образом, что в сумме с остатком она дает исправленную комбинацию. Остаток при этом представляет собой не что иное, как разницу между искаженными и правильными символами, единицы в остатке стоят как раз на местах искаженных разрядов в подогнанной циклическими сдвигами комбинации. Подгоняют искаженную комбинацию до тех пор, пока число единиц в остатке не будет равно числу ошибок в коде. При этом, естественно, число единиц может быть либо равно числу ошибок s; исправляемых данным кодом (код исправляют 3 ошибки и в искаженной комбинации 3 ошибки), либо меньше s (код исправляет 3 ошибки, а в принятой комбинации – 1 ошибка).

Место ошибки в кодовой комбинации не имеет значения. Если , то после определенного количества сдвигов все ошибки окажутся в зоне «разового» действия образующего многочлена, т. е. достаточно получить один остаток, вес которого , и этого уже будет достаточно для исправления искажаемой комбинации. В смысле коды БЧХ (о них мы будем говорить ниже) могут исправлять пачки ошибок, лишь бы длина пачки не превышала s.

Подробно процесс исправления ошибок рассматривается ниже на примере построения конкретных кодов.

Построение и декодирование конкретных циклических кодов.

I. Коды исправляющие одиночную ошибку, .

1. Расчет соотношения между контрольными и информационными символами кода производятся на основании выражений (59) — (69).

Если задано число информационных разрядов , то число контрольных разрядов находим из выражения

.

Общее число символов кода

.

Если задана длина кода n, то число контрольных разрядов

.

Соотношение числа контрольных и информационных символов для кодов с приведены в табл. 3 приложения 9.

2. Выбор образующего многочлена производится по таблицам неприводимых двоичных многочленов.

Образующий многочлен следует выбирать как можно более коротким, но степень его должна быть не меньше числа контрольных разрядов , а число ненулевых членов – не меньше минимального кодового расстояния .

Выбор параметров единичной транспонированной матрицы происходит из условия, что число столбцов (строк) матрицы определяется числом информационных разрядов, т. е. ранг единичной матрицы равен .

3. Определение элементов дополнительной матрицы производится по остаткам от деления последней строки транспонированной матрицы (единицы с нулями) на образующий многочлен. Полученные остатки должны удовлетворять следующим требованиям:

а) число разрядов каждого остатка должно быть равно числу контрольных символов , следовательно, число разрядов дополнительной матрицы должно быть равно степени образующего многочлена;

б) число остатков должно быть не меньше числа строк единичной транспонированной матрицы, т. е. должно быть равно числу информационных разрядов ;

в) число единиц каждого остатка, т. е . его вес должно быть не менее величены , где минимальное кодовое расстояние, не меньше числа обнаруженных ошибок;

г) количество нулей, приписанных к единице с нулями в делении ее на выбранный неприводимый многочлен, должно быть таким, чтобы соблюдались условия а), б), в).

4. Образующая матрица составляется дописыванием элементов дополнительной матрицы справа от единичной транспонированной матрицы либо умножением элементов единичной матрицы на образующий многочлен.

5. Комбинациями искомого кода являются строки образующий матрицы и все возможные суммы по модулю 2 различных сочетаний строк образующей матрицы (см. задачу 6.108).

Как видно из решения задач 6.103 и 6.108, коды, получены при использовании неприводимых многочленов и , подобны друг другу и обладают равноценными корректирующими способностями. Сами же многочлены 1101 и 1011 называют обратными, или двойственными, многочленам. Если данный многочлен неприводимый, то неприводимый будет и двойственный ему многочлен.

6. Обнаружение и исправление ошибок производится по остатку от деления принятой комбинации на образующий многочлен . Если принятая комбинация делится на образующий многочлен без остатка, то код принят без ошибочно. Остаток от деления свидетельствует о наличии ошибки, но не указывает, какой именно. Для того чтобы найти ошибочный разряд и исправить его в циклических кодах, осуществляют следующие операции:

а) принятую комбинацию делят на образующий многочлен;

б) подсчитывают количество единиц в остатке (вес остатка). Если , где s – допустимое число исправляемых данным кодом ошибок, то принятую комбинацию складывают по модулю 2 с полученным остатком. Сумма даст исправленную комбинацию. Если , то

в) производят циклический сдвиг принятой комбинация влево на один разряд. Комбинацию, полученную в результате этого повторного деления , то делимое суммируют с остатком, затем

г) производят циклический сдвиг вправо на один разряд комбинации, полученной в результате суммирования последнего делим, с последним остатком. Полученная в результате комбинация уже не содержит ошибок. Если после первого циклического сдвига последующего деления остаток получается таким, что его вес ,

д) повторяют операцию пункта в) до тех пор, пока не будет . В этом случае комбинацию, полученную в результате последнего циклического сдвига, суммируют с остатка от деления этой комбинации на образующий многочлен, а затем

е) производят циклический сдвиг вправо ровно на столько разрядов, на сколько была сдвинута суммируемая с последним остатком

комбинации относительно принятой комбинации. В результате получим исправленную комбинацию (см. задачи 6.113 – 6.116)1.

II. Коды обнаруживающие трехкратные ошибки. .

1. Выбор числа корректирующих разрядов производится из соотношения

,

или

.

2. Выбор образующего многочлена производят, исходя из следующих соображений: для обнаружения трехкратной ошибки

,

Поэтому степень образующего многочлена не может быть меньше четырех; многочлен третьей степени, имеющий число ненулевых членов больше или равное трем, позволяет обнаруживать все двойные ошибки (см. задачи 6.121; 6.122), многочлен первой степени (х+1) обнаруживает любое количество нечетных ошибок (см. задачи 6.119; 6.120), следовательно, многочлен четвертой степени, получаемый в результате умножения этих многочленов, обладает их корректирующими свойствами: может обнаруживать две ошибки а также одну и три, т. е. все трехкратные ошибки (см. задачу 6.117).

3. Построение образующей матрицы производят либо нахождением остатков от деления единицы с нулями на образующий многочлен, либо умножением строк единичной матрицы на образующий многочлен (си. задачу 6.121).

4. Остальные комбинации корректирующего кода находят суммированием по модулю 2 всевозможных сочетаний строк образующей матрицы.

5. Обнаружение ошибок производится по остаткам от деления принятой комбинации на образующий многочлен . Если остатка нет, то контрольные разряды отбрасываются и информационная часть кода используется по назначению. Если в результате деления получается остаток, то комбинация бракуется. Заметим, что такие коды могут обнаруживать 75% любого количества ошибок, так как кроме двойной ошибки обнаруживаются все нечетные ошибки, но гарантированное количество ошибок, которое код никогда не пропустит, равно 3.П р и м е р. Исходная кодовая комбинация – 0101111000, принятая – 0001011001 (т. е. произошел тройной сбой). Показать процесс обнаружения ошибки если известно, что комбинации кода были образованы при помощи многочлена 101111.

Р е ш е н и е.	0 0 0 1 0 1 1 0 0 1	1 0 1 1 1 1
	1 0 1 1 1 1
	0 0 0 0 1 1 1

Остаток ненулевой, комбинация бракуется. Указать ошибочные разряды при трехкратных искажениях такие коды не могут.

III. Циклические коды, исправляющие две и большее количество ошибок, .

Методика построения циклических кодов с отличается от методики построения циклических кодов только в выборе образующего многочлена. В литературе эти коды известны как коды БЧХ (первые буквы фамилий Боуз, Чоудхури, Хоквинхем – авторов методики построения циклических кодов с ).

Построение образующего многочлена зависит в основном, от двух параметров: от длины кодового слова n и от числа исправляемых ошибок s. Остальные параметры, участвующие в построении образующего многочлена в зависимости от заданных n и s могут быть определены при помощи таблиц и вспомогательных соотношений, о которых будет сказано ниже.

Для исправления числа ошибок еще недостаточно условие, что бы между комбинациями кода минимальное кодовое расстояние , необходимо также чтобы длина кода n удовлетворяла условию

, (79)

при этом n всегда будет нечетным числом. Величина h определяет выбор числа контрольных символов и связанна с и s следующим соотношением:

. (80)

C другой стороны, число контрольных символов определяется образующим много членом и равно его степени (к этому вопросу мы еще вернемся). При больших значениях h длина кода n становиться очень большой, что вызывает вполне определенные трудности при технической реализации кодирующих и декодирующих устройств. При этом часть информационных разрядов порой остается неиспользованной. В таких случаях для определения h удобно пользоваться выражением

, (81)

где С является одним из сомножителей на которое разлагается число n.

Соотношение между n, С и h могут быть сведены в следующую таблицу:

№ п/п	h		C
1	3	7	1
2	4	15	5; 3
3	5	31	1
4	6	63	7; 3; 3
5	7	127	1
6	8	255	17; 5; 3
7	9	511	7; 3; 7
8	10	1023	31; 11; 3
9	11	2047	89; 23
10	12	4095	3; 3; 5; 7; 13

Например, при h=10 длина кодовой комбинации может быть равна и 1023 (C=1) и 341 (С=3), и 33 (С=31), и 31 (С=33), понятно, что n не может быть меньше. Величина С влияет выбор порядковых номеров минимальных многочленов, так как индексы первоначально выбранных многочленов умножаются С. сказанное выше хорошо усваивается на конкретном примере (см. задачу 6.132).

Построение образующего многочлена производится при помощи так называемых минимальных многочленов , которые являются простыми неприводимыми многочленами (см. табл. 2, приложение 9). Образующий многочлен представляет собой произведение нечетных минимальных многочленов и является их наименьшим общим кратным (НОК). Максимальный порядок определяет номер последнего из выбираемых табличных минимальных многочленов

, (82)

Порядок многочлена используется при определении числа сомножителей . Например, если s=6, то . Так как для построения используются только нечетные многочлены, то ими будут: ; ; ; ;; , старший из них имеет порядок . Как видим число сомножителей равно 6, т. е. числу исправляемых ошибок. Таким образом, число минимальных многочленов, участвующих в построении образующего многочлена,

, (83)

а старшая степень

(84)

(l указывает колонку в таблице минимальных многочленов, из которой обычно выбирается многочлен для построения ).

Степень образующего многочлена полученного в результате перемножения выбранных минимальных многочленов,

. (85)

В общем виде

, (86)

Декодирование кодов БЧХ производится по той же методике, что и декодирование циклических кодов с . Однако в связи с тем, что практически все коды БЧХ представлены комбинациями с n15, могут возникнуть весьма сложные варианты, когда для обнаружения и исправления ошибок необходимо производить большое число циклических сдвигов. В этом случае для облегчения можно комбинацию полученную после k-кратного сдвига и суммирования с остатком, сдвигать не вправо, а влево на n – k циклических сдвигов. Это целесообразно делать только при (см. задачу 6.134).

Оценка корректирующей способности блокового (n, k) кода

Кодовое (хемминговое) расстояние  — число несовпадающих разрядов двух кодовых комбинаций.

Минимальное кодовое расстояние (d) — минимальное расстояние, взятое по всем парам разрешенных кодовых комбинаций.

Кратность ошибки (r) —  число искаженных символов кодовой комбинации.

Вес кодовой комбинации — число единиц в двоичной кодовой комбинации.

Вектор ошибки — двоичный код, содержащий 1 в искаженных и 0 в остальных разрядах.

Доля обнаруживаемых ошибок  2^k(2ⁿ-2^k)/(2^k2ⁿ) = 1 — 2^k—n

Число кодовых комбинаций: любых 2ⁿ , разрешенных 2^к, запрещенных  2ⁿ — 2^k .

Число вариантов передачи кода  2^к 2ⁿ. Ошибка обнаруживается, если при передаче разрешенной комбинации получена запрещенная комбинация. Число таких вариантов 2^k(2ⁿ-2^k).

Рекомендуемые материалы

Доля исправляемых ошибок среди обнаруживаемых 2^k(2^n—k-1)/2^k(2ⁿ-2^k)=2^—k. Запрещенную кодовую комбинацию заменяют ближайшей разрешенной комбинацией. Ближайшими к разрешенной комбинации являются 2^n-k-1 запрещенных кодовых комбинаций. Ошибка будет исправлена, если принятая запрещенная комбинация окажется «ближайшей» к  переданной разрешенной комбинации. Число таких случаев  2^k(2^n-k-1).

Установим связь кодового расстояния d и кратности обнаруживаемых и исправляемых ошибок. Все возможные кодовые комбинации можно представить точками или векторами в многомерном пространстве.   Точки подмножества запрещенных комбинаций, соответствующих разрешенной комбинации, можно считать расположенными на сферах радиусов 1, 2, и т.д., равных кодовому расстоянию до разрешенной комбинации. Как видно из рисунка, где кодовое расстояние      d =6, можно обнаружить ошибки кратности r =5 и исправить ошибки кратности s =2. В общем случае должны выполняться условия:

Вместе с этой лекцией читают «3.6 Точечные случайные процессы. Формула Ито для считающих процессов. Компенсаторы».

d ³ r + 1   для обнаружения ошибки кратности r,

d ³ 2s + 1 для исправления  ошибки кратности s,

d ³ r + s + 1 (r ³ s) для обнаружения и одновременного исправления ошибок кратности  r и s.

Для исправления ошибки контрольная кодовая комбинация должна указывать место ошибки. Следовательно, число различных контрольных кодовых комбинаций должно быть не менее количества различных ошибок.. Число ошибок кратности r равно числу сочетаний С_n^r .   При  s = 1 (исправление ошибки кратности 1) должно выполняться условие 2^n—k-1 > C_n¹  = n, при  s = 2 — условие  2^n—k-1 > C_n¹+ C_n², в общем случае – условие

Эта оценка Хемминга определяет минимальную избыточность, необходимую для исправления ошибок. Коды с минимальной избыточностью, для которых неравенство превращается в равенство, называются совершенными.