Ошибки часов спутника и приемника

19.02.2021

Глава 4 — Источники ошибок ГНСС

В главе 2 мы представили концепцию источников ошибок ГНСС. Это факторы, которые затрудняют определение точного положения ГНСС приемника. В этой главе мы более подробно рассмотрим источники этих ошибок.

Таблица 13: Источники ошибок ГНСС

Источники ошибок

Спутниковые часы

Атомные часы на спутниках ГНСС очень точны, но они немного дрейфуют. К сожалению, небольшая неточность спутниковых часов приводит к значительной ошибке в определении приемником своего местоположения. Например, ошибка часов в 10(−6) сек приводит к ошибке положения в 3 м.

Часы на спутнике контролируются наземной системой управления ГНСС и сравниваются с еще более точными часами, используемыми в ней. В данных, передаваемых спутником пользователю, содержится оценка смещения бортовых часов. Обычно передаваемая точность составляет ± 2 м, хотя она может варьироваться в зависимости от разных систем ГНСС. Чтобы получить свое более точное местоположение, ГНСС приемник должен компенсировать ошибку часов.

Одним из способов компенсации погрешности часов является загрузка точной информации о часах спутника из систем дифференциальной коррекции (SBAS) или систем точного позиционирования (PPP). В передаваемой информации содержатся поправки за ошибки бортовых часов, которые были рассчитаны системами SBAS или PPP. Более подробные сведения о системах SBAS и PPP представлены в главе 5. 

Другой способ компенсации погрешности часов — настроить приемник для работы в режиме дифференциальной коррекции или кинематики реального времени (RTK). В главе 5 также подробно рассматриваются дифференциальные методы ГНСС и RTK.

Ошибки эфемерид

Спутники ГНСС движутся по очень точным, хорошо известным орбитам. Однако, параметры орбиты немного меняются. Также, как и в случае с часами спутника, небольшое изменение орбиты приводит к значительной ошибке в вычисленном положении приемника.

Наземная система управления ГНСС постоянно отслеживает орбиты спутников. Когда орбита спутника изменяется, наземная система управления отправляет поправку на спутники, и эфемериды спутников обновляются. Даже с поправками, внесенными наземной системой управления ГНСС, все еще есть небольшие ошибки в параметрах орбиты, которые могут привести к ошибке местоположения до ± 2.5 м. 

Одним из способов компенсации ошибок спутниковых орбит является загрузка точной эфемеридной информации из систем SBAS или PPP, которые будут более подробно рассматриваться в главе 5.

Другой способ компенсации ошибок спутниковой орбиты — использование приемника в режиме дифференциальной коррекции или RTK. Более подробная эта информация также представлена в главе 5. 

Ионосферные задержки

Ионосфера — это слой атмосферы на высоте от 80 до 600 км над Землей. Этот слой содержит электрически заряженные частицы, называемые ионами. Эти ионы задерживают прохождение спутниковых сигналов и могут вызвать значительную ошибку определения местоположения спутника (обычно ± 5 м, но эта ошибка может возрастать в периоды высокой ионосферной активности, вызванной влиянием Солнца).

Ионосферная задержка зависит от солнечной активности, времени года, сезона, времени суток и места. В результате очень трудно предсказать, насколько ионосферная задержка повлияет на расчетное местоположение.

Ионосферная задержка также изменяется в зависимости от частоты радиосигнала, проходящего через ионосферу. ГНСС приемники, которые принимают более одной частоты, например L1 и L2, могут использовать это для повышения точности. Сравнивая измерения на L1 с измерениями на L2, приемник может определить величину ионосферной задержки и удалить эту ошибку из рассчитанных координат.

Для приемников, которые могут отслеживать только одну частоту ГНСС, используются модели ионосферы для уменьшения влияния ошибок, вызванных влиянием ионосферы. Из-за различного характера ионосферной задержки модели не так эффективны, как использование нескольких частот для их устранения.

Ионосферные условия очень похожи в пределах отдельной области, поэтому спутниковые сигналы, поступающие на приемники базовой станции и подвижные приемники, имеют очень похожую задержку. Это позволяет компенсировать ионосферную задержку дифференциальными методами ГНСС и RTK.

Тропосферные задержки

Тропосфера — это ближайший к поверхности Земли слой атмосферы.

Вариации задержки в тропосфере вызываются изменением влажности, температуры и атмосферного давления.

Поскольку тропосферные условия в пределах отдельной зоны очень похожи, то базовая станция и приемники подвижного приемника испытывают очень похожее влияние тропосферы. Это позволяет дифференциальным методам ГНСС и RTK компенсировать тропосферную задержку.

Приемники ГНСС также могут использовать тропосферные модели для оценки количества ошибок, вызванных тропосферной задержкой. 

Собственные шумы приемника

Шум приемника добавляет к ошибке положения величины, вызванные аппаратным и программным обеспечением. Приемники ГНСС высшего класса, как правило, имеют меньшие ошибки из-за собственного шума, чем более дешевые приемники.

Влияние многолучевости

Как показано на рис. 38 многолучевое распространение происходит, когда сигнал от спутника ГНСС отражается от объекта, например, стены здания, а затем приходит к антенне приемника. Поскольку отраженный сигнал распространяется дольше, то он поступает в приемник с небольшой задержкой. Этот задержанный сигнал может привести к тому, что приемник вычислит неправильное положение.

Самый простой способ уменьшить ошибки из-за многолучевого распространения это разместить ГНСС антенну в месте, удаленном от отражающих поверхностей. Когда это невозможно, приемник и антенна ГНСС должны уметь обрабатывать многолучевые сигналы.

Ошибки многолучевого распространения с большой задержкой обычно обрабатываются ГНСС приемником, а ошибки сигнала с короткой задержкой отрабатываются антенной. Благодаря применению дополнительных технологий, высокопроизводительные приемники и ГНСС антенны, как правило, лучше устраняют ошибки многолучевости. 

Заключение

В этой главе описаны источники ошибок, которые вызывают погрешности при расчете позиции. В главе 5 мы опишем методы, которые используют приемники ГНСС для уменьшения этих ошибок и получения более точного местоположения.

Материалы взяты с сайта компании NovAtel. Ссылка на первоисточник: https://novatel.com/an-introduction-to-gnss

Кодовые
измерения.
Приемник спутниковых сигналов, как и
спутник, имеет датчик частоты и времени,
вырабатывающий частоты L1
и L2
(в одночастотном приемнике 
только L1).
Частота L1
модулируется копиями кодов С/А и Р,
частота L2

только кодом Р.

Интервал
времени между появлением на приемнике
собственного кода и аналогичного кода,
пришедшего от спутника, измеряют.

Если
бы часы приемника были точно синхронизированы
с часами спутника, то формирование кодов
на спутнике и в приемнике происходило
бы одновременно. В этом случае измеренный
интервал времени между появлениями на
приемнике собственного кода и кода,
пришедшего от спутника, был бы равен
времени прохождения сигнала от спутника
до приемника. Это позволило бы вычислить
расстояние до спутника. Однако показания
часов спутника и приемника расходятся
на величину, равную δ^s
– δ_p,
где δ^s
– ошибка часов спутника, δ_p
– ошибка часов приемника. Поэтому
измеренное расстояние R
– псевдорасстояние
отличается от верного.

Допустим,
что ионосферная и тропосферная задержки
сигнала учтены путем введения поправок.
Тогда измеренное псевдорасстояние

от пункта p
до
спутника s
в
эпоху t
может
быть представлено уравнением


,

где
X^s(t),
Y^s(t),
Z^s(t)
– координаты спутника в эпоху t;
X_p,
Y_p,
Z_p
– определяемые координаты приемника;
c
– скорость
света.

По
данным навигационного сообщения
определим и учтем ошибку часов спутника
,
после чего получим уравнение

.
(9.1)

Здесь
неизвестными являются X_p,
Y_p,
Z_p,
δ_p(t).
Для их определения необходимо иметь не
менее четырех уравнений, то есть измерить
в одну эпоху псевдорасстояния не менее,
чем до четырех спутников.

Определение
координат по результатам кодовых
измерений выполняется с точностью около
3 м.

Для
повышения точности пользуются
дифференциальным
методом. На
контрольном пункте с известными
координатами устанавливают приемник
спутниковых сигналов и, определив его
координаты по спутникам, вычисляют
расстояния до спутников. Сравнив эти
расстояния с вычисленными по известным
координатам, определяют поправки и по
радио сообщают их потребителям. Поправками
исправляют псевдорасстояния, измеряемые
потребителями. При этом ошибки определения
места относительно контрольного пункта
не превышают 1 м.

Кодовые
измерения применяются при решении задач
навигации. В геодезических работах
кодовые измерения играют вспомогательную
роль – определение приближенных
координат пунктов сети.

Фазовые
измерения.
Точные геодезические измерения выполняют
на несущих частотах L1
и L2
(в одночастотных приемниках – только
на частоте L1).
Измеряют разность фаз между колебаниями,
принятыми от спутника, и колебаниями
такой же частоты, выработанными в
приемнике.

Обозначим:
^s(t)
– фазу частоты f,
поступившей на приемник в эпоху t
от спутника s;
_p(t)
– фазу собственной частоты приемника
в ту же эпоху. Для указанных фаз справедливы
уравнения:

^s(t)
= f
t






,

_p
(t)
= f
t


.

В
этих уравнениях f
= L1
или f
= L2;

– расстояние от спутника до приемника;
с –
скорость света;

—
время, затраченное на путь сигнала от
спутника до приемника; ^s
и _p

ошибки часов спутника и приемника.

Отсюда,
для измеряемой разности фаз имеем
уравнение

=
^s(t)

_p
(t)
=



+

=





.

Умножим
это уравнение на длину волны 
и учтя, что 
= cT
= с
/ f
, где T
– период колебаний, получим

 =


+
с
(

).
(9.2)

Представим
разность фаз

в виде суммы двух частей:

=
N
+ ,
(9.3)

где
N
– целое число циклов, а 
– дробь.

Подставляя
выражение (9.3) в (9.2) напишем

+
с
(

).
(9.4)

Отметим,
что фазоизмерительные устройства
измеряют разность фаз только в пределах
одного периода, то есть дробную часть
.
А целую часть N
измерить невозможно.

Расстояние
между спутником и приемником непрерывно
изменяется, отчего изменяется и сдвиг
по фазе N+.
В приемнике спутниковых сигналов
предусмотрено измерение непрерывно
изменяющейся разности фаз 
и подсчет числа переходов ее через ноль.
Это число прибавляется к измеряемой
величине

,
отчего суммарный сдвиг по фазе оказывается
неправильной дробью, а неизвестное
число N
остается постоянным для всех расстояний
от пункта p
до спутника s.

Учитывая
изложенное, напишем уравнение измеренного
сдвига по фазе сигнала,
принятого от
спутника s
на пункте p
в эпоху t:

(9.5)

где

.

Разности
фаз измеряют с высокой точностью,
соответствующей долям миллиметра.
Однако вычислить решением системы
уравнений (9.5) координаты приемника с
указанной точностью не удается из-за
ошибок орбиты, влияния ионосферы и
других причин.

Точность
фазовых измерений реализуют, применяя
метод относительного
определения
положения пунктов. Результаты одновременных
наблюдений одного и того же спутника в
двух пунктах содержат значительные, но
общие, близкие по величине погрешности.
Поэтому разности результатов измерений
от них практически свободны, что позволяет
с высокой точностью определять разности
координат X,
Y,
Z
двух пунктов, то есть вектор X,
Y,
Z,
их соединяющий. Зная координаты
X,
Y,
Z
одного
пункта, определяют разности координат
X,
Y,
Z
до другого и вычисляют его координаты.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

The error analysis for the Global Positioning System is important for understanding how GPS works, and for knowing what magnitude of error should be expected. The GPS makes corrections for receiver clock errors and other effects but there are still residual errors which are not corrected. GPS receiver position is computed based on data received from the satellites. Errors depend on geometric dilution of precision and the sources listed in the table below.

Overview[edit]

Sources of User Equivalent Range Errors (UERE)

Source	Effect (m)
Signal arrival C/A	±3
Signal arrival P(Y)	±0.3
Ionospheric effects	±5
Ephemeris errors	±2.5
Satellite clock errors	±2
Multipath distortion	±1
Tropospheric effects	±0.5
C/A	±6.7
P(Y)	±6.0

User equivalent range errors (UERE) are shown in the table. There is also a numerical error with an estimated value, , of about 1 meter (3 ft 3 in). The standard deviations, , for the coarse/acquisition (C/A) and precise codes are also shown in the table. These standard deviations are computed by taking the square root of the sum of the squares of the individual components (i.e., RSS for root sum squares). To get the standard deviation of receiver position estimate, these range errors must be multiplied by the appropriate dilution of precision terms and then RSS’ed with the numerical error. Electronics errors are one of several accuracy-degrading effects outlined in the table above. When taken together, autonomous civilian GPS horizontal position fixes are typically accurate to about 15 meters (50 ft). These effects also reduce the more precise P(Y) code’s accuracy. However, the advancement of technology means that in the present, civilian GPS fixes under a clear view of the sky are on average accurate to about 5 meters (16 ft) horizontally.

The term user equivalent range error (UERE) refers to the error of a component in the distance from receiver to a satellite. These UERE errors are given as ± errors thereby implying that they are unbiased or zero mean errors. These UERE errors are therefore used in computing standard deviations. The standard deviation of the error in receiver position,
, is computed by multiplying PDOP (Position Dilution Of Precision) by
, the standard deviation of the user equivalent range errors.
is computed by taking the square root of the sum of the squares of the individual component standard deviations.

PDOP is computed as a function of receiver and satellite positions. A detailed description of how to calculate PDOP is given in the section Geometric dilution of precision computation (GDOP).

for the C/A code is given by:

The standard deviation of the error in estimated receiver position , again for the C/A code is given by:

The error diagram on the left shows the inter relationship of indicated receiver position, true receiver position, and the intersection of the four sphere surfaces.

Signal arrival time measurement[edit]

The position calculated by a GPS receiver requires the current time, the position of the satellite and the measured delay of the received signal. The position accuracy is primarily dependent on the satellite position and signal delay.

To measure the delay, the receiver compares the bit sequence received from the satellite with an internally generated version. By comparing the rising and trailing edges of the bit transitions, modern electronics can measure signal offset to within about one percent of a bit pulse width, , or approximately 10 nanoseconds for the C/A code. Since GPS signals propagate at the speed of light, this represents an error of about 3 meters.

This component of position accuracy can be improved by a factor of 10 using the higher-chiprate P(Y) signal. Assuming the same one percent of bit pulse width accuracy, the high-frequency P(Y) signal results in an accuracy of or about 30 centimeters.

Atmospheric effects[edit]

Inconsistencies of atmospheric conditions affect the speed of the GPS signals as they pass through the Earth’s atmosphere, especially the ionosphere. Correcting these errors is a significant challenge to improving GPS position accuracy. These effects are smallest when the satellite is directly overhead and become greater for satellites nearer the horizon since the path through the atmosphere is longer (see airmass). Once the receiver’s approximate location is known, a mathematical model can be used to estimate and compensate for these errors.

Ionospheric delay of a microwave signal depends on its frequency. It arises from ionized atmosphere (see Total electron content). This phenomenon is known as dispersion and can be calculated from measurements of delays for two or more frequency bands, allowing delays at other frequencies to be estimated.^[1] Some military and expensive survey-grade civilian receivers calculate atmospheric dispersion from the different delays in the L1 and L2 frequencies, and apply a more precise correction. This can be done in civilian receivers without decrypting the P(Y) signal carried on L2, by tracking the carrier wave instead of the modulated code. To facilitate this on lower cost receivers, a new civilian code signal on L2, called L2C, was added to the Block IIR-M satellites, which was first launched in 2005. It allows a direct comparison of the L1 and L2 signals using the coded signal instead of the carrier wave.

The effects of the ionosphere generally change slowly, and can be averaged over time. Those for any particular geographical area can be easily calculated by comparing the GPS-measured position to a known surveyed location. This correction is also valid for other receivers in the same general location. Several systems send this information over radio or other links to allow L1-only receivers to make ionospheric corrections. The ionospheric data are transmitted via satellite in Satellite Based Augmentation Systems (SBAS) such as Wide Area Augmentation System (WAAS) (available in North America and Hawaii), EGNOS (Europe and Asia), Multi-functional Satellite Augmentation System (MSAS) (Japan), and GPS Aided Geo Augmented Navigation (GAGAN) (India) which transmits it on the GPS frequency using a special pseudo-random noise sequence (PRN), so only one receiver and antenna are required.

Humidity also causes a variable delay, resulting in errors similar to ionospheric delay, but occurring in the troposphere. This effect is more localized than ionospheric effects, changes more quickly and is not frequency dependent. These traits make precise measurement and compensation of humidity errors more difficult than ionospheric effects.^[2]

The Atmospheric pressure can also change the signals reception delay, due to the dry gases present at the troposphere (78% N2, 21% O2, 0.9% Ar…). Its effect varies with local temperature and atmospheric pressure in quite a predictable manner using the laws of the ideal gases.^[3]

Multipath effects[edit]

GPS signals can also be affected by multipath issues, where the radio signals reflect off surrounding terrain; buildings, canyon walls, hard ground, etc. These delayed signals cause measurement errors that are different for each type of GPS signal due to its dependency on the wavelength.^[4]

A variety of techniques, most notably narrow correlator spacing, have been developed to mitigate multipath errors. For long delay multipath, the receiver itself can recognize the wayward signal and discard it. To address shorter delay multipath from the signal reflecting off the ground, specialized antennas (e.g., a choke ring antenna) may be used to reduce the signal power as received by the antenna. Short delay reflections are harder to filter out because they interfere with the true signal, causing effects almost indistinguishable from routine fluctuations in atmospheric delay.

Multipath effects are much less severe in moving vehicles. When the GPS antenna is moving, the false solutions using reflected signals quickly fail to converge and only the direct signals result in stable solutions.

Ephemeris and clock errors[edit]

While the ephemeris data is transmitted every 30 seconds, the information itself may be up to two hours old. Variability in solar radiation pressure^[5] has an indirect effect on GPS accuracy due to its effect on ephemeris errors. If a fast time to first fix (TTFF) is needed, it is possible to upload a valid ephemeris to a receiver, and in addition to setting the time, a position fix can be obtained in under ten seconds. It is feasible to put such ephemeris data on the web so it can be loaded into mobile GPS devices.^[6] See also Assisted GPS.

The satellites’ atomic clocks experience noise and clock drift errors. The navigation message contains corrections for these errors and estimates of the accuracy of the atomic clock. However, they are based on observations and may not indicate the clock’s current state.

These problems tend to be very small, but may add up to a few meters (tens of feet) of inaccuracy.^[7]

For very precise positioning (e.g., in geodesy), these effects can be eliminated by differential GPS: the simultaneous use of two or more receivers at several survey points. In the 1990s when receivers were quite expensive, some methods of quasi-differential GPS were developed, using only one receiver but reoccupation of measuring points. At the TU Vienna the method was named qGPS and post processing software was developed.^{[citation needed]}

Dilution of precision [edit]

Selective Availability[edit]

GPS formerly included a feature called Selective Availability (SA) that added intentional, time varying errors of up to 100 meters (328 ft) to the publicly available navigation signals. This was intended to deny an enemy the use of civilian GPS receivers for precision weapon guidance.

SA errors are actually pseudorandom, generated by a cryptographic algorithm from a classified seed key available only to authorized users (the U.S. military, its allies and a few other users, mostly government) with a special military GPS receiver. Mere possession of the receiver is insufficient; it still needs the tightly controlled daily key.

Before it was turned off on May 2, 2000, typical SA errors were about 50 m (164 ft) horizontally and about 100 m (328 ft) vertically.^[8] Because SA affects every GPS receiver in a given area almost equally, a fixed station with an accurately known position can measure the SA error values and transmit them to the local GPS receivers so they may correct their position fixes. This is called Differential GPS or DGPS. DGPS also corrects for several other important sources of GPS errors, particularly ionospheric delay, so it continues to be widely used even though SA has been turned off. The ineffectiveness of SA in the face of widely available DGPS was a common argument for turning off SA, and this was finally done by order of President Clinton in 2000.^[9]

DGPS services are widely available from both commercial and government sources. The latter include WAAS and the U.S. Coast Guard’s network of LF marine navigation beacons. The accuracy of the corrections depends on the distance between the user and the DGPS receiver. As the distance increases, the errors at the two sites will not correlate as well, resulting in less precise differential corrections.

During the 1990–91 Gulf War, the shortage of military GPS units caused many troops and their families to buy readily available civilian units. Selective Availability significantly impeded the U.S. military’s own battlefield use of these GPS, so the military made the decision to turn it off for the duration of the war.

In the 1990s, the FAA started pressuring the military to turn off SA permanently. This would save the FAA millions of dollars every year in maintenance of their own radio navigation systems. The amount of error added was «set to zero»^[10] at midnight on May 1, 2000 following an announcement by U.S. President Bill Clinton, allowing users access to the error-free L1 signal. Per the directive, the induced error of SA was changed to add no error to the public signals (C/A code). Clinton’s executive order required SA to be set to zero by 2006; it happened in 2000 once the U.S. military developed a new system that provides the ability to deny GPS (and other navigation services) to hostile forces in a specific area of crisis without affecting the rest of the world or its own military systems.^[10]

On 19 September 2007, the United States Department of Defense announced that future GPS III satellites will not be capable of implementing SA,^[11] eventually making the policy permanent.^[12]

Anti-spoofing[edit]

Another restriction on GPS, antispoofing, remains on. This encrypts the P-code so that it cannot be mimicked by a transmitter sending false information. Few civilian receivers have ever used the P-code, and the accuracy attainable with the public C/A code was much better than originally expected (especially with DGPS), so much so that the antispoof policy has relatively little effect on most civilian users. Turning off antispoof would primarily benefit surveyors and some scientists who need extremely precise positions for experiments such as tracking tectonic plate motion.

Relativity[edit]

The theory of relativity introduces several effects that need to be taken into account when dealing with precise time measurements. According to special relativity, time passes differently for objects in relative motion. That is known as kinetic time dilation: in an inertial reference frame, the faster an object moves, the slower its time appears to pass
(as measured by the frame’s clocks). General relativity takes into account also the effects that gravity has on the passage of time. In the context of GPS the most prominent correction introduced by general relativity is gravitational time dilation: the clocks located deeper in the gravitational potential well (i.e. closer to the attracting body) appear to tick slower.

Special relativity[edit]

Special relativity predicts that as the velocity of an object increases (in a given frame), its time slows down (as measured in that frame). For instance, the frequency of the atomic clocks moving at GPS orbital speeds will tick more slowly than stationary clocks by a factor of where the orbital velocity is v = 4 km/s and c = the speed of light. The result is an error of about -7.2 μs/day in the satellite. The special relativistic effect is due to the constant movement of GPS clocks relative to the Earth-centered, non-rotating approximately inertial reference frame. In short, the clocks on the satellites are slowed down by the velocity of the satellite. This time dilation effect has been measured and verified using the GPS.

General relativity[edit]

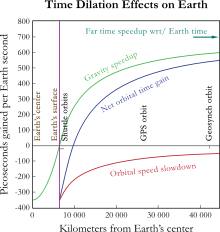
Special relativity allows the comparison of clocks only in a flat spacetime, which neglects gravitational effects on the passage of time. According to general relativity, the presence of gravitating bodies (like Earth) curves spacetime, which makes comparing clocks not as straightforward as in special relativity. However, one can often account for most of the discrepancy by the introduction of gravitational time dilation, the slowing down of time near gravitating bodies. In case of the GPS, the receivers are closer to Earth than the satellites, causing the clocks at the altitude of the satellite to be faster by a factor of 5×10⁻¹⁰, or about +45.8 μs/day. This gravitational frequency shift is measurable. During early development some believed that GPS would not be affected by general relativistic effects, but the Hafele–Keating experiment showed that it would be.

Combined kinetic and gravitational time dilations[edit]

Combined, these sources of time dilation cause the clocks on the satellites to gain 38.6 microseconds per day relative to the clocks on the ground. This is a difference of 4.465 parts in 10¹⁰.^[13] Without correction, errors of roughly 11.4 km/day would accumulate in the position.^[14] This initial pseudorange error is corrected in the process of solving the navigation equations. In addition, the elliptical, rather than perfectly circular, satellite orbits cause the time dilation and gravitational frequency shift effects to vary with time. This eccentricity effect causes the clock rate difference between a GPS satellite and a receiver to increase or decrease depending on the altitude of the satellite.

To compensate for the discrepancy, the frequency standard on board each satellite is given a rate offset prior to launch, making it run slightly slower than the desired frequency on Earth; specifically, at 10.22999999543 MHz instead of 10.23 MHz.^[15] Since the atomic clocks on board the GPS satellites are precisely tuned, it makes the system a practical engineering application of the scientific theory of relativity in a real-world environment.^[16] Placing atomic clocks on artificial satellites to test Einstein’s general theory was proposed by Friedwardt Winterberg in 1955.^[17]

Calculations[edit]

To calculate the amount of daily time dilation experienced by GPS satellites relative to Earth we need to separately determine the amounts due to the satellite’s velocity and altitude, and add them together.

Kinetic time dilation[edit]

The amount due to velocity is determined using the Lorentz transformation. The time measured by an object moving with velocity changes by (the inverse of) the Lorentz factor:

For small values of v/c this approximates to:

The GPS satellites move at 3874 m/s relative to Earth’s center.^[15] We thus determine:

This difference of 8.349×10⁻¹¹ represents the fraction by which the satellites’ clocks tick slower than the stationary clocks. It is then multiplied by the number of nanoseconds in a day:

That is the satellites’ clocks are slower than Earth’s clocks by 7214 nanoseconds a day due to their velocity.

Note that this speed of 3874 m/s is measured relative to Earth’s center rather than its surface where the GPS receivers (and users) are. This is because Earth’s equipotential makes net time dilation equal across its geodesic surface.^[18] That is, the combination of Special and General effects make the net time dilation at the equator equal to that of the poles, which in turn are at rest relative to the center. Hence we use the center as a reference point to represent the entire surface.

Gravitational time dilation[edit]

The amount of dilation due to gravity is determined using the gravitational time dilation equation:

where is the time passed at a distance from the center of the Earth and is the time passed for a far away observer.

For small values of this approximates to:

Determine the difference between the satellite’s time and Earth time :

Earth has a radius of 6,357 km (at the poles) making = 6,357,000 m and the satellites have an altitude of 20,184 km^[15] making their orbit radius = 26,541,000 m. Substituting these in the above equation, with Earth mass M = 5.974×10²⁴, G = 6.674×10⁻¹¹, and c = 2.998×10⁸ (all in SI units), gives:

This represents the fraction by which the clocks at satellites’ altitude tick faster than on the surface of the Earth. It is then multiplied by the number of nanoseconds in a day:

That is the satellites’ clocks gain 45850 nanoseconds a day due to gravitational time dilation.

Combined time dilation effects[edit]

These effects are added together to give (rounded to 10 ns):

45850 – 7210 = 38640 ns

Hence the satellites’ clocks gain approximately 38,640 nanoseconds a day or 38.6 μs per day due to relativistic effects in total.

In order to compensate for this gain, a GPS clock’s frequency needs to be slowed by the fraction:

5.307×10⁻¹⁰ –  8.349×10⁻¹¹ = 4.472×10⁻¹⁰

This fraction is subtracted from 1 and multiplied by the pre-adjusted clock frequency of 10.23 MHz:

(1 –  4.472×10⁻¹⁰) × 10.23 = 10.22999999543

That is we need to slow the clocks down from 10.23 MHz to 10.22999999543 MHz in order to negate both time dilation effects.

Sagnac distortion[edit]

GPS observation processing must also compensate for the Sagnac effect. The GPS time scale is defined in an inertial system but observations are processed in an Earth-centered, Earth-fixed (co-rotating) system. A coordinate transformation is thus applied to convert from the inertial system to the ECEF system. The resulting signal run time correction has opposite algebraic signs for satellites in the Eastern and Western celestial hemispheres. Ignoring this effect will produce an east–west error on the order of hundreds of nanoseconds, or tens of meters in position.^[19]

Natural sources of interference[edit]

Since GPS signals at terrestrial receivers tend to be relatively weak, natural radio signals or scattering of the GPS signals can desensitize the receiver, making acquiring and tracking the satellite signals difficult or impossible.

Space weather degrades GPS operation in two ways, direct interference by solar radio burst noise in the same frequency band^[20] or by scattering of the GPS radio signal in ionospheric irregularities referred to as scintillation.^[21] Both forms of degradation follow the 11 year solar cycle and are a maximum at sunspot maximum although they can occur at any time. Solar radio bursts are associated with solar flares and coronal mass ejections (CMEs)^[22] and their impact can affect reception over the half of the Earth facing the sun. Scintillation occurs most frequently at tropical latitudes where it is a night time phenomenon. It occurs less frequently at high latitudes or mid-latitudes where magnetic storms can lead to scintillation.^[23] In addition to producing scintillation, magnetic storms can produce strong ionospheric gradients that degrade the accuracy of SBAS systems.^[24]

Artificial sources of interference[edit]

In automotive GPS receivers, metallic features in windshields,^[25] such as defrosters, or car window tinting films^[26] can act as a Faraday cage, degrading reception just inside the car.

Man-made EMI (electromagnetic interference) can also disrupt or jam GPS signals. In one well-documented case it was impossible to receive GPS signals in the entire harbor of Moss Landing, California due to unintentional jamming caused by malfunctioning TV antenna preamplifiers.^[27][28] Intentional jamming is also possible. Generally, stronger signals can interfere with GPS receivers when they are within radio range or line of sight. In 2002 a detailed description of how to build a short-range GPS L1 C/A jammer was published in the online magazine Phrack.^[29]

The U.S. government reported that such jammers were used occasionally during the War in Afghanistan, and the U.S. military destroyed six GPS jammers during the Iraq War, including one that was destroyed with a GPS-guided bomb, noting the ineffectiveness of the jammers used in that situation.^[30] A GPS jammer is relatively easy to detect and locate, making it an attractive target for anti-radiation missiles. The UK Ministry of Defence tested a jamming system in the UK’s West Country on 7 and 8 June 2007.^{[citation needed]}

Some countries allow the use of GPS repeaters to allow the reception of GPS signals indoors and in obscured locations; while in other countries these are prohibited as the retransmitted signals can cause multi-path interference to other GPS receivers that receive data from both GPS satellites and the repeater. In the UK Ofcom now permits the use of GPS/GNSS Repeaters^[31] under a ‘light licensing’ regime.

Due to the potential for both natural and man-made noise, numerous techniques continue to be developed to deal with the interference. The first is to not rely on GPS as a sole source. According to John Ruley, «IFR pilots should have a fallback plan in case of a GPS malfunction».^[32] Receiver Autonomous Integrity Monitoring (RAIM) is a feature included in some receivers, designed to provide a warning to the user if jamming or another problem is detected. The U.S. military has also deployed since 2004 their Selective Availability / Anti-Spoofing Module (SAASM) in the Defense Advanced GPS Receiver (DAGR).^[33] In demonstration videos the DAGR was shown to detect jamming and maintain its lock on the encrypted GPS signals during interference which caused civilian receivers to lose lock.

See also[edit]

• GPS augmentation

Notes[edit]

References[edit]

• Grewal, Mohinder S.; Weill, Lawrence Randolph; Andrews, Angus P. (2001). Global positioning systems, inertial navigation, and integration. John Wiley and Sons. ISBN 978-0-471-35032-3.
• Parkinson; Spilker (1996). The global positioning system. American Institute of Aeronautics & Astronomy. ISBN 978-1-56347-106-3.
• Webb, Stephen (2004). Out of this world: colliding universes, branes, strings, and other wild ideas of modern physics. Springer. ISBN 0-387-02930-3. Retrieved 2013-08-16.

External links[edit]

• GPS.gov—General public education website created by the U.S. Government
• GPS SPS Performance Standard—The official Standard Positioning Service specification (2008 version).
• GPS SPS Performance Standard—The official Standard Positioning Service specification (2001 version).

     GNSS (глобальные навигационные спутниковые системы) для пользователя. Сегмент пользователя включает любого, использующего специальный GNSS-приемник для приема сигналов со спутников и определения собственного местоположения (координат). Девиз системы – «всегда и везде». То есть в любой точке на земной поверхности, в любой момент времени с использованием системы GNSS пользователь имеет возможность определить собственные координаты. На спутнике формируется бинарная последовательность, называемая кодом (двух типов C/A и P). На несущую частоту сигнала, излучаемого спутником, накладывается код и модулирует ее. Антенна приемника принимает код, который приходит с задержкой во времени Δτ. Эта задержка пропорционально пройденному сигналом расстоянию (Δτ’=Δτ+Δτ0), где Δτ’ – измеряемая временная задержка, Δτ0 – поправка за синхронизацию часов. Краткий обзор методов определения координат с помощью системы GNSS Существует несколько методов получения координат с использованием GNSS, которые можно разделить на три группы. Автономный режим. Используется единственный (автономный) приемник. Такой способ определения местоположения применяется туристами, автомобилистами, штурманами для навигации судов, находящихся вдали от берега, и военными. Точность определения координат порядка 10 м. Дифференциальные фазовые измерения. Позволяет получить точность 0,5 — 20 мм. Используется для геодезических измерений, сбора ГИС-данных, управления строительной техникой и т. д. Здесь измерения выполняют на 2 точках А и В. Тогда приращения координат АВ определяются с гораздо более высокой точностью. Повышение точности достигается за счет того, что расстояние АВ намного меньше, чем расстояния до спутников, и в приращениях компенсируются многие ошибки (приборные, влияние атмосферы и ионосферы). Дифференциальное координирование. Более известно, как DGPS, позволяет получать координаты с точностью 0,5 — 5 м. Используется для прибрежного кораблевождения, сбора данных для ГИС, в сельском хозяйстве и т. д. Принцип пространственной линейной засечки Принцип работы системы – динамическая пространственная линейная засечка. Если на какой-то момент времени t известны координаты 3 спутников и измерены расстояния от точки А на поверхности Земли до этих спутников, то можно определить координаты точки А. Как измерить расстояние до спутника? Если со спутника излучается электромагнитный сигнал, который принимается приемником в точке А, то, измерив время прохождения сигнала от спутника до приемника, можно вычислить расстояние, т. е. S=сt, где с – это скорость прохождения радиосигнала. Радиоволны распространяются со скоростью света, равной 290 000 км в секунду (186 000 миль в секунду). Сложность состоит в том, чтобы синхронизировать часы на спутнике и приемнике. Для этого нужен 4 спутник. Таким образом, каждый спутник системы в каждый момент времени «знает» собственные координаты. В результате в околоземном космическом пространстве создается динамическая сеть точек-спутников с известными координатами. Каждый спутник передает закодированную информацию о себе и об остальных спутниках системы, в том числе и информацию о собственных координатах. Следовательно, если удастся измерить расстояние между видимыми спутниками и определяемым объектом, то его координаты можно определить из решения пространственной линейной засечки. То есть из точек-спутников следует построить сферы радиусом, равным этим расстояниям, тогда эти сферы пересекутся в определяемой точке. Эта задача решается средствами третьего сегмента системы — приемниками пользователей. Их задачей является прием сигналов видимых спутников (не менее четырех), вычисление расстояний до спутников и собственных координат.
    В состав приемной аппаратуры входят не только антенны и собственно приемники спутниковых сигналов, но и компьютерные средства. Поэтому приемником (GPS или ГЛОНАСС) будем называть устройство, способное решать перечисленные выше задачи. Известно, что для вычисления трех координат объекта из классической пространственной линейной засечки достаточно измерить три расстояния до точек с известными координатами. Однако необходимым условием функционирования системы является наличие «видимости» на четыре спутника. Это объясняется тем, что в динамической сети время становится четвертой координатой. И если на спутниках можно смонтировать дорогостоящие атомные часы, то на многочисленных приемниках пользователей обходятся относительно дешевыми кварцевыми часами. Для определения поправок часов пользователей необходима дополнительная информация, которая и получается по результатам наблюдения четвертого спутника. Значит, для успешной работы приемник должен иметь не менее четырех частотных каналов для приема сигналов от спутников. Реально «видимыми» могут оказаться более четырех спутников. Если приемник имеет ровно четыре канала, то часть полезной информации не может быть принята и обработана. Поэтому обычно современные приемники имеют 12 каналов и более.
    Источники ошибок До сих пор мы принимали, что координаты, полученные с помощью системы GNSS, очень точны и свободны от ошибок, но это далеко не так. Существуют несколько источников ошибок, которые снижают точность координат. Источники ошибок можно разделить на следующие классы: • ионосферные и атмосферные задержки; • ошибки часов спутника и приёмника; • переотражение сигналов; • геометрическое снижение точности. Ионосферные и атмосферные задержки Поскольку спутниковый сигнал проходит через ионосферу, его прохождение может быть замедленно — эффект, подобный преломлению луча света, проходящего через стекло (рис. 13). Эти задержки воздействуют на скорость сигнала. Свет имеет постоянную скорость только в вакууме. Есть несколько факторов, которые оказывают влияние на величину задержки, вызванной ионосферой. К ним относятся: • Возвышение спутника – задержка сигналов от спутников, находящихся низко над горизонтом, будет больше, чем расположенных высоко, поскольку увеличивается расстояние, которое сигнал проходит через атмосферу. • Плотность ионосферы, на которую влияет солнечная энергии. Ночью влияние ионосферы весьма низкое, а днем ионосфера значительно больше замедляет сигнал. • Воздействие на сигнал водяных паров. Оно может быть компенсировано с помощью моделей атмосферы. Ошибки часов спутников и приемника. Даже при том, что часы на спутнике очень точны (ошибка хода составляет приблизительно 3 наносекунды), они иногда слегка спешат или отстают, что влияет на точность определения координат. Обнаруженные ошибки устраняются сегментом управления системой. Ошибки из-за переотражения сигнала Переотражение сигнала происходит, когда антенна приемника установлена рядом с большой отражающей поверхностью (здание, озеро и пр.). Сигнал достигает антенны не сразу, а сначала попадает на близлежащий объект. В результате антенна принимает отраженный сигнал. Влияние переотражения может быть ослаблено, если использовать специальные антенны. Геометрическое снижение точности Геометрическое снижение точности (DOP) – мера строгости спутниковой геометрии, и связано с расположением спутников на небесной сфере. DOP может усилить воздействие ошибок определения координат. На определение дальности до спутника воздействуют все вышеописанные ошибки. В случае, когда спутники расположены на небесной сфере достаточно широко, границы возможной ошибки малы. Когда спутники расположены близко друг к другу, увеличивается неопределенность положения. В зависимости от типа измерений могут быть вычислены различные типы геометрического снижения точности или DOP: VDOP — снижение точности по высоте. Дает снижение точности в вертикальном направлении. HDOP — снижение точности в плане. Дает снижение точности в горизонтальном направлении. PDOP — снижение точности положения. Дает снижение точности трехмерного положения. GDOP — геометрическое снижение точности. Дает снижение точности трёхмерного положения и времени. Наиболее комплексный показатель – GDOP, так как это комбинация всех коэффициентов. Некоторые приемники, однако, вычисляют PDOP или HDOP, которые не включают временную составляющую. Лучший путь уменьшения GDOP – это наблюдение как можно большего количества спутников. Помните, однако, что на сигналы от низко расположенных спутников ошибки воздействуют в большей степени. Общее правило при геодезических GPS измерениях — лучше наблюдать спутники с углами возвышения 15° и выше. Наиболее точные координаты будут вычисляться в случае низкого GDOP (обычно 8 или меньше). (По материалам «Формирование пространственно-привязанных локальных ГИС для целей картографирования: Учеб. пособие. – М.: РУДН, 2008. Елисеев В.М., Гаврилова О.В.»)

ГОСТ Р 53607- 2009
п. 6.2 «При удалении пункта наблюдения (ПН) от определяемого пункта (ОП) на расстояния до 200 км обслуживание обработки кодовых псевдодальностей выполняет локальная дифференциальная подсистема, в которой работает одна опорная станция. При удалении ПН от ОП на расстояниях от 200 до 2000 км обслуживание обработки кодовых псевдодальностей выполняет региональная дифференциальная подсистема. Она строит пространственно-временную модель поправок, то есть учитываются изменения в поправках по мере удаления НП от опорного пункта. В широкозонной дифференциальной подсистеме размер обслуживаемой области может достигать 5000 км. Если дифференциальный метод по наблюдениям фазы несущей обслуживается единственным базовым пунктом, то расстояния должны быть в пределах 10 км и редко до 30 км. При использовании метода множественных опорных пунктов размер области может достигать нескольких сотен километров.»
  Для информации: Сеть дифференциальных геодезических станций Тюменской области состоит из 25 равномерно распределённых по территории региона опорных станций и программное обеспечение Сети строит пространственно-временную модель поправок, то есть учитываются изменения в поправках по мере удаления НП от опорного пункта.