Если вы только начинаете изучать программирование, то можете столкнуться с «неочевидным» поведением ваших программ, особенно при работе с вещественными числами.
Самый популярный пример, иллюстрирующий эту проблему — сравнение 0.1 + 0.2 с 0.3. Для большинства людей очевидно, что 0.1 + 0.2 равно 0.3, поэтому ожидается, что это выражение вернет истину. Однако, если вы запустите его в Java, то результат может вас удивить:
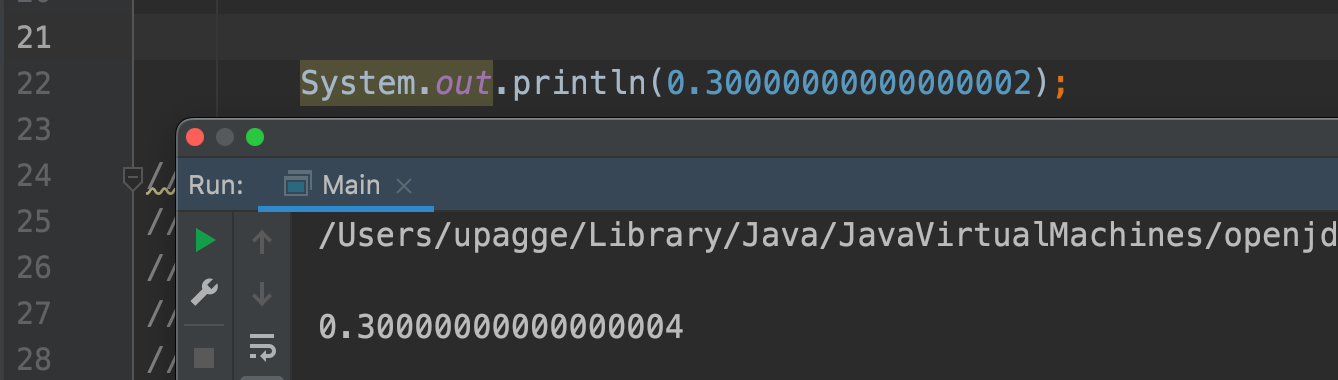
System.out.println(0.1 + 0.2 == 0.3); // falseЭто выражение выводит false! Но почему? Если мы выведем на консоль результат выражения 0.1 + 0.2, то увидим следующее:
System.out.println(0.1 + 0.2); // 0.30000000000000004Вместо ожидаемых 0.3 мы получили 0.30000000000000004. Но не спешите отказываться от Java: эта проблема будет присутствовать во многих языках программирования. Дело не в языке программирования, а в том, как компьютер работает с данными и хранит их.
Как компьютер хранит данные
А почему так произошло? Для начала следует понять, как данные хранятся в памяти компьютера. Это происходит в формате двоичного кода.
Давайте в качестве примера возьмем число 6.25 и переведем его в двоичный код. Для этого нужно целую часть делить на 2, записывая остаток от деления, а дробную часть умножать на 2, после чего записываем целую часть, а дробную продолжаем умножать на 2.
0:00
/
Таким образом, 6.25 в двоичном виде становится 110.01. Однако здесь появляется проблема: в мире нулей и единиц не существует представления для десятичной запятой, поэтому компьютер не сможет сохранить такое число в памяти в том виде, в котором мы привыкли его видеть.
Спонсор поста
Стандарт IEEE-754
Для представления вещественных чисел в формате, который позволит преобразовывать их в простую последовательность нулей и единиц без всяких дополнительных знаков, ученые разработали систему чисел с плавающей запятой. Этот стандарт получил название IEEE-754 (wiki).
Согласно этому стандарту, двоичное число представляется в виде формулы:
(-1)s × M × BE,
где s — знак числа, M — мантисса, B — основание, E — экспонента. Поскольку мы работаем в двоичном коде, основание равно двум, и формула принимает следующий вид:
(-1)s × M × 2E.
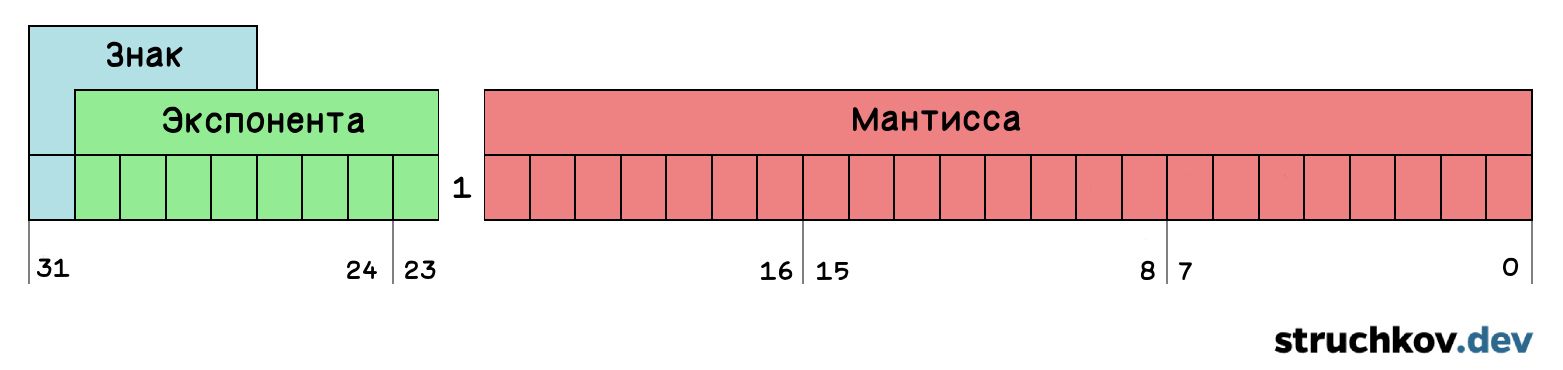
Разбираемся на пальцах 🖐
Может показаться, что все эти формулы сложны, но на самом деле принцип довольно прост. Вещественное число мы должны сохранить как три отдельных числа: знак, экспоненту и мантиссу. Количество бит для хранения всегда ограничено форматом. Рассмотрим формат, в котором доступно 32 бита: 1 бит знака, 8 битов для экспоненты и 23 бита для мантиссы. Этот формат называется «одинарной точностью».
Чтобы привести наше число 110.01 к формуле, нам нужно сдвинуть запятую влево настолько, чтобы в целой части была единица. При этом каждый сдвиг увеличивает степень основания. Именно поэтому эти числа называются числами с плавающей запятой 🙃
0:00
/
Почему основание 10, а не 2?
Несмотря на то, что основание равно 10, это на самом деле представление 2 в двоичной системе счисления. Для удобства восприятия я не стал переводить степень этой двойки в двоичную систему счисления.
Если бы у нас было число 0.011, мы бы сдвигали запятую вправо, пока в целой части не появилась бы единица. В этом случае степень основания уменьшалась бы.
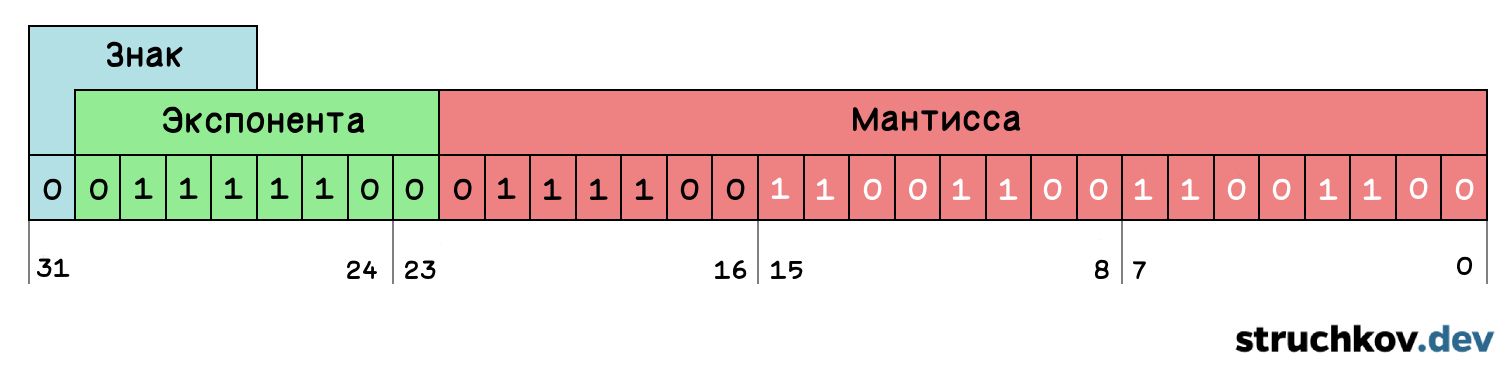
В итоге мы получаем 1.1001 x 22. Здесь 1.1001 — это наша мантисса, а поскольку наше число положительное, бит знака будет равен 0.
Уже в первых машинах использовались прием, который позволял не сохранять целую часть числа, так как она всегда равна единице. Такое представление называется «нормализованным». Оно позволяет экономить целый бит памяти, увеличивая точность представления числа. Кстати, основание всегда равно 10, поэтому его тоже не нужно сохранять.
Таким образом, нормализованное число имеет следующий вид:
(-1)s × 1.M × 2E
Полученную дробную часть мы записываем в мантиссу, при этом целую часть мы не записываем, поскольку она всегда равна единице.
0:00
/
Чтобы получить экспоненту, к степени двойки прибавляют 127, и полученное число преобразуют в двоичный код.
Почему нужно прибавить 127?
Под экспоненту в нашем представлении чисел с плавающей запятой выделено 8 бит, что позволяет сохранить 256 различных значений. Экспонента может быть как положительной, так и отрицательной, и нам нужно сохранить ее знак. Однако в этом представлении не предусмотрено отдельного бита для знака экспоненты.
Возможно, вы знакомы с понятием дополнительного кода, который позволяет представлять отрицательные числа в двоичной системе. Однако, в данном контексте его использование затруднило бы быстрое сравнение чисел по старшему биту.
Решение этой проблемы состоит в хранении экспоненты относительно «середины» доступного диапазона значений. Для 8-битного диапазона этой «серединой» будет число 127. Если количество бит для экспоненты увеличится, «середина» будет соответствовать половине доступного диапазона значений.
Таким образом, все отрицательные степени будут располагаться левее числа 127, а все положительные — правее.
Итак, к нашей изначальной степени прибавляем 127 и получаем 129. Преобразуем 129 в двоичную систему счисления, и вот — мы получили экспоненту.
0:00
/
Также мы записываем бит знака. Напомню, что для положительных чисел этот бит равен 0, а для отрицательных — 1.
0:00
/
Таким образом, мы перевели вещественное число в двоичное представление. Казалось бы, нет никаких проблем. Однако, проблемы не возникли только потому, что в качестве примера было выбрано «удачное» число.
Неконвертируемые числа
Теперь попробуем преобразовать число 5.9 в двоичное представление. Это задача оказывается аналогичной попытке записать результат деления 1 на 3 в десятичной системе счисления. В обоих случаях мы столкнемся с периодической дробью: 5.9 в двоичной системе становится 101.11100(1100).
Однако, нам все равно нужно каким-то образом записать это число в память компьютера, которая, напомним, ограничена 32 битами. Это возможно сделать только путем отсечения той части числа, которая не помещается в 32 бита.
Попытаемся записать как можно больше повторений периода и затем восстановить из этой записи десятичное число.
5.89999961
Этот результат отличается от исходного числа 5.9. Такова особенность работы компьютеров: они могут оперировать вещественными числами только до определенной точности. И эта точность – единственное, чем мы можем манипулировать. Но как мы можем это сделать?
Ранее мы рассмотрели пример, когда у нас было 32 бита для записи числа, что соответствует одинарной точности (float в Java). Мы можем увеличить этот размер в два раза до 64 бит, что уже соответствует двойной точности (double в Java). Чем больше бит у нас будет для записи, тем более точное число мы сможем сохранить. Однако восстановить исходное число с абсолютной точностью все равно не удастся.
В математике между числами 1.0 и 2.0 существует бесконечное количество вещественных чисел. Однако, используя одинарную точность (float), компьютерная память способна точно сохранить лишь 8 388 609 чисел, находящихся между 1.0 и 2.0.
Неточности при вычислениях
Вернемся к нашему примеру с числами 0.1 и 0.2. Если попробуем преобразовать эти числа в двоичную систему счисления, то обнаружим, что они также не могут быть точно переведены. Используя специализированный точный калькулятор, можно получить максимально приближенные значения этих чисел в двоичной системе, представленные здесь в десятичной форме:
0.1 = 0.1000000000000000055511151231257827021181583404541015625
0.2 = 0.200000000000000011102230246251565404236316680908203125
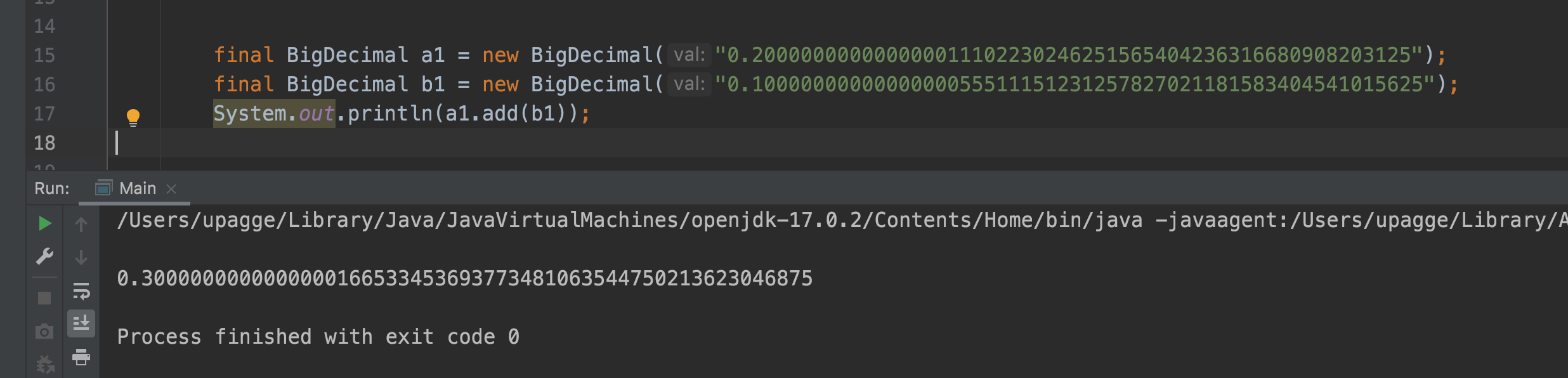
Это максимально точные значения, которые может хранить компьютер. Если сложить эти числа, мы получим:
0.3000000000000000166533453693773481063544750213623046875
Это значение близко к нашему результату 0.30…04, но, если применить правила математического округления, мы должны были получить 0.30…02. Давайте посмотрим, что получится, если мы попытаемся вывести на консоль 0.30…02.
То число, которое мы получили в результате сложения, также не может быть точно сохранено. Ближайшее значение, которое может сохранить компьютер, равно
0.3000000000000000444089209850062616169452667236328125.
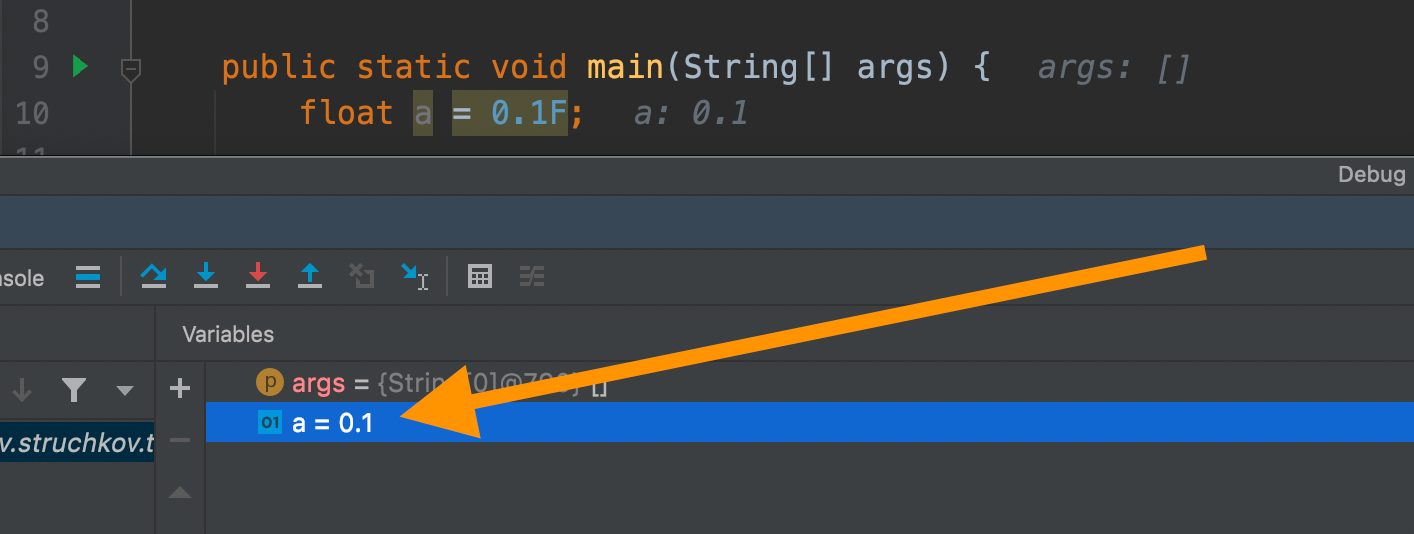
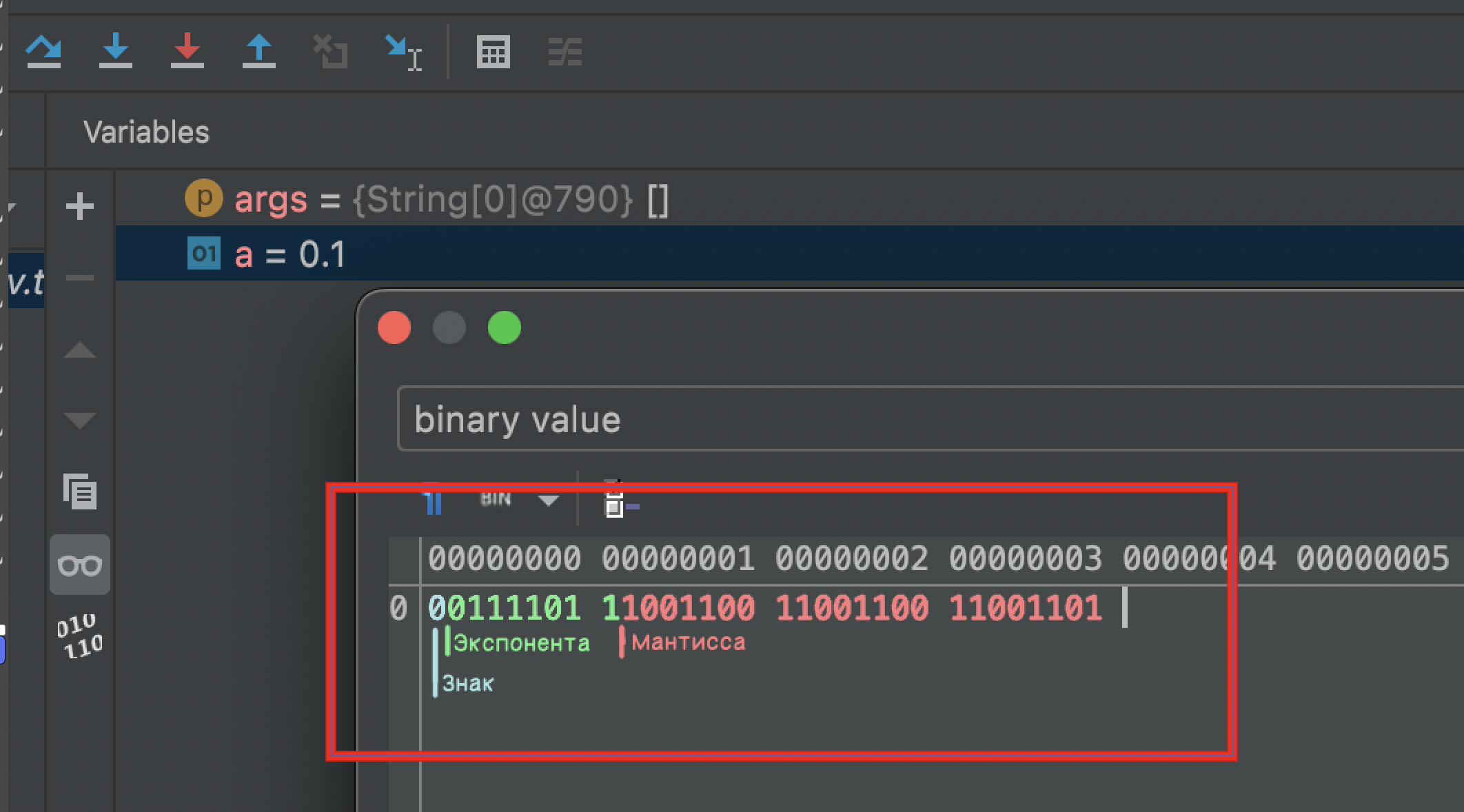
Вы могли заметить, что во время отладки значение переменной отображается как 0.1, а не 0.10…55.
Однако это лишь способ визуализации данных. Если посмотреть, что на самом деле хранится в памяти этой переменной, то мы обнаружим обычную структуру с знаком, экспонентой и мантиссой.
Преобразуя эту структуру обратно в десятичную систему, получим 0.10000000149012, хотя IDEA дополнительно округляет это значение до 0.1.
Проведем еще один небольшой эксперимент: найдем минимальное число, которое не будет округляться до 0.1.
Выводы
программирование — это не всегда математика
Из этой статьи вы узнали, как вещественные числа хранятся в памяти компьютера, и почему это создает проблемы.
Возможно, у вас возник вопрос: «Как мы запускаем ракеты в космос с такими неточными расчетами? Или как проходят финансовые операции?» Для выполнения вычислений без потери точности используются специальные классы, такие как BigDecimal. Этот класс позволяет складывать числа произвольной длины без потери точности, но за это приходится платить уменьшением производительности.
В заключении хочется сказать: таков удивительный мир программирования.
Время на прочтение
9 мин
Количество просмотров 40K

К старту курса по Fullstack-разработке на Python делимся решениями классической проблемы неточности чисел с плавающей точкой. В материале вы найдёте примеры работы с функциями и классами, предназначенными специально для решения проблем чисел с плавающей точкой.
Числа с плавающей точкой — быстрый и эффективный способ хранения чисел и работы с ними. Но он связан с рядом трудностей для начинающих и опытных программистов! Вот классический пример:
>>> 0.1 + 0.2 == 0.3
FalseВпервые увидев такое, можно растеряться. Такое поведение корректно! Поговорим о том, почему ошибки при операциях над числами с плавающей точкой так распространены, почему они возникают и как с ними справиться в Python.
Компьютер обманывает вас
Вы видели, что 0.1 + 0.2 не равно 0.3, но безумие на этом не заканчивается. Вот ещё пара примеров, сбивающих с толку:
>>> 0.2 + 0.2 + 0.2 == 0.6
False
>>> 1.3 + 2.0 == 3.3
False
>>> 1.2 + 2.4 + 3.6 == 7.2
FalseПроблема касается и сравнения:
>>> 0.1 + 0.2 <= 0.3
False
>>> 10.4 + 20.8 > 31.2
True
>>> 0.8 - 0.1 > 0.7
TrueЧто происходит? Когда вы вводите в интерпретатор Python число 0.1, оно сохраняется в памяти как число с плавающей точкой и происходит преобразование. 0.1 — это десятичное число с основанием 10, но числа с плавающей точкой хранятся в двоичной записи. То есть основание 0.1 преобразуется из 10 в 2.
Получающееся двоичное число может недостаточно точно представлять исходное число с основанием 10. 0.1 — один из примеров. Двоичным представлением будет 0.0(0011). То есть 0.1 — это бесконечно повторяющееся десятичное число, записанное с основанием 2. То же происходит, когда в виде десятичного числа с основанием 10 записывается дробь ⅓. Получается бесконечно повторяющееся десятичное число 0.3(3).
Память компьютера конечна, поэтому бесконечно повторяющееся представление двоичной дроби 0.1 округляется до конечной дроби. Её значение зависит от архитектуры компьютера (32- или 64-разрядная).
Увидеть значение с плавающей точкой, которое сохраняется для 0.1, можно с помощью метода .as_integer_ratio(). Представление с плавающей точкой состоит из числителя и знаменателя:
>>> numerator, denominator = (0.1).as_integer_ratio()
>>> f"0.1 ≈ {numerator} / {denominator}"
'0.1 ≈ 3602879701896397 / 36028797018963968'Чтобы отобразить дробь с точностью до 55 знаков после запятой, используем format():
>>> format(numerator / denominator, ".55f")
'0.1000000000000000055511151231257827021181583404541015625'Так 0.1 округляется до числа чуть больше, чем его истинное значение.
Узнайте больше о числовых методах, подобных .as_integer_ratio(), в моей статье 3 Things You Might Not Know About Numbers in Python («3 факта о числах в Python, которые вы могли не знать»).
Эта ошибка представления чисел с плавающей точкой встречается куда чаще, чем может показаться.
Ошибка представления числа очень типична
Существуют три причины, почему число округляется при его представлении в виде числа с плавающей точкой:
-
В числе больше значащих разрядов, чем позволяет плавающая точка.
-
Это иррациональное число.
-
Число рациональное, но без конечного двоичного представления.
64-разрядные числа с плавающей точкой имеют 16 или 17 значащих разрядов. Любое число, у которого значащих разрядов больше, округляется. Иррациональные числа, такие как π и e, нельзя представить конечной дробью с целочисленным основанием. И, опять же, иррациональные числа в любом случае округляются при сохранении в виде чисел с плавающей точкой.
В этих двух ситуациях создаётся бесконечный набор чисел, которые нельзя точно представить в виде числа с плавающей точкой. Но вы вряд ли столкнётесь с этими проблемами, не будучи химиком, имеющим дело с крошечными числами, или физиком — с астрономически большими числами.
А как на счёт бесконечных рациональных чисел, например 0.1 с основанием 2? Именно здесь вам встретится большинство связанных с плавающей точкой трудностей и благодаря математике — позволяющей определять, конечная дробь или нет, — вы будете сталкиваться с ошибками представления чаще, чем думаете.
С основанием 10 дробь можно представить как конечную, если её знаменатель — произведение степеней простых множителей 10. Два простых множителя 10 — это 2 и 5, поэтому дроби ½, ¼, ⅕, ⅛ и ⅒ — конечные, а ⅓, ⅐ и ⅑ — нет. У основания 2 только один простой множитель — 2.
Конечные дроби здесь только те, знаменатель которых равен степени числа 2. В результате дроби ⅓, ⅕, ⅙, ⅐, ⅑ и ⅒ — бесконечные, когда представлены в двоичной записи.
Теперь наш первый пример должен стать понятнее. 0.1, 0.2 и 0.3 при преобразовании в числа с плавающей точкой округляются:
>>> # -----------vvvv Display with 17 significant digits
>>> format(0.1, ".17g")
'0.10000000000000001'
>>> format(0.2, ".17g")
'0.20000000000000001'
>>> format(0.3, ".17g")
'0.29999999999999999'При сложении 0.1 и 0.2 получается число чуть больше 0.3:
>>> 0.1 + 0.2
0.30000000000000004А поскольку 0.1 + 0.2 чуть больше, чем 0.3, и 0.3 представлено числом, которое чуть меньше 0.3, выражение 0.1 + 0.2 == 0.3 оказывается False.
Об ошибке представления чисел с плавающей точкой должен знать каждый программист на любом языке — и уметь с ней справляться. Она характерна не только для Python. Результат вывода 0.1 + 0.2 на разных языках можно увидеть на сайте с подходящим названием 0.30000000000000004.com.
Как сравнивать числа с плавающей точкой в Python
Как же справляться с ошибками представления чисел с плавающей точкой при сравнении таких чисел в Python? Хитрость заключается в том, чтобы избегать проверки на равенство. Вместо ==, >= или <= всегда используйте с числами с плавающей точкой функцию math.isclose():
>>> import math
>>> math.isclose(0.1 + 0.2, 0.3)
TrueВ math.isclose() проверяется, достаточно ли близок первый аргумент ко второму. То есть проверяется расстояние между двумя аргументами. Оно равно абсолютной величине разницы обоих значений:
>>> a = 0.1 + 0.2
>>> b = 0.3
>>> abs(a - b)
5.551115123125783e-17Если abs(a — b) меньше некоего процента от большего значения a или b, то a считается достаточно близким к b, чтобы считаться «равным» b. Этот процент называется относительной погрешностью и указывается именованным аргументом rel_tol функции math.isclose(), который по умолчанию равен 1e-9.
То есть если abs(a — b) меньше 0.00000001 * max(abs(a), abs(b)), то a и b считаются «близкими» друг к другу. Это гарантирует, что a и b будут приблизительно с девятью знаками после запятой.
Если нужно, можно изменить относительную погрешность:
>>> math.isclose(0.1 + 0.2, 0.3, rel_tol=1e-20)
FalseКонечно, относительная погрешность зависит от ограничений задачи, но для большинства повседневных приложений стандартной относительной погрешности должно быть достаточно. Проблема возникает, если a или b равно нулю, а rel_tol меньше единицы. Тогда, как бы ни было близко ненулевое значение к нулю, относительной погрешностью гарантируется, что проверка на близость будет неудачной. В качестве запасного варианта здесь применяется абсолютная погрешность:
>>> # Relative check fails!
>>> # ---------------vvvv Relative tolerance
>>> # ----------------------vvvvv max(0, 1e-10)
>>> abs(0 - 1e-10) < 1e-9 * 1e-10
False
>>> # Absolute check works!
>>> # ---------------vvvv Absolute tolerance
>>> abs(0 - 1e-10) < 1e-9
TrueВ math.isclose() эта проверка выполняется автоматически. Абсолютная погрешность определяется с помощью именованного аргумента abs_tol. Но abs_tol по умолчанию равен 0.0, поэтому придётся задать его вручную, если нужно проверить близость значения к нулю.
В итоге в функции math.isclose() возвращается результат следующего сравнения — с относительными и абсолютными проверками в одном выражении:
abs(a - b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)math.isclose() появилась в PEP 485 и доступна с Python 3.5.
Когда стоит использовать math.isclose()?
В целом math.isclose() следует применять, сравнивая значения с плавающей точкой. Заменим == на math.isclose():
>>> # Don't do this:
>>> 0.1 + 0.2 == 0.3
False
>>> # Do this instead:
>>> math.isclose(0.1 + 0.2, 0.3)
TrueСо сравнениями >= и <= нужно быть осторожным. Обработаем равенство отдельно, используя math.isclose(), а затем проверим строгое сравнение:
>>> a, b, c = 0.1, 0.2, 0.3
>>> # Don't do this:
>>> a + b <= c
False
>>> # Do this instead:
>>> math.isclose(a + b, c) or (a + b < c)
TrueЕсть альтернативы math.isclose(). Если вы работаете с NumPy, можете использовать numpy.allclose() и numpy.isclose():
>>> import numpy as np
>>> # Use numpy.allclose() to check if two arrays are equal
>>> # to each other within a tolerance.
>>> np.allclose([1e10, 1e-7], [1.00001e10, 1e-8])
False
>>> np.allclose([1e10, 1e-8], [1.00001e10, 1e-9])
True
>>> # Use numpy.isclose() to check if the elements of two arrays
>>> # are equal to each other within a tolerance
>>> np.isclose([1e10, 1e-7], [1.00001e10, 1e-8])
array([ True, False])
>>> np.isclose([1e10, 1e-8], [1.00001e10, 1e-9])
array([ True, True])Имейте в виду: стандартные относительные и абсолютные погрешности — не то же самое, что math.isclose(). Стандартная относительная погрешность для numpy.allclose() и numpy.isclose() равна 1e-05, а стандартная абсолютная погрешность — 1e-08.
math.isclose() особенно удобна для модульных тестов, хотя и здесь имеются альтернативы. Во встроенном модуле unittest в Python есть метод unittest.TestCase.assertAlmostEqual().
Но в нём применяется только проверка абсолютной разницы. А это ещё и утверждение, то есть при сбоях возникает ошибка AssertionError, из-за которой оно непригодно для сравнений в бизнес-логике.
Отличная альтернатива math.isclose() для модульного тестирования — это функция pytest.approx() из pytest pytest. Как и в math.isclose(), здесь принимаются два аргумента и возвращается, равны они или нет в пределах некой погрешности:
>>> import pytest
>>> 0.1 + 0.2 == pytest.approx(0.3)
TrueКак и в math.isclose(), в pytest.approx() для задания относительной и абсолютной погрешностей есть именованные аргументы rel_tol и abs_tol. Но стандартные значения различаются. У rel_tol оно 1e-6, а у abs_tol — 1e-12.
Если первые переданные в pytest.approx() два аргумента подобны массиву (то есть это итерируемый объект Python, такой же, как список или кортеж или даже массив NumPy), тогда в pytest.approx() поведение подобно numpy.allclose() и возвращается то, равны эти два массива или нет в пределах погрешностей:
>>> import numpy as np
>>> np.array([0.1, 0.2]) + np.array([0.2, 0.4]) == pytest.approx(np.array([0.3, 0.6]))
TrueДля pytest.approx() сгодятся даже значения словаря:
>>> {'a': 0.1 + 0.2, 'b': 0.2 + 0.4} == pytest.approx({'a': 0.3, 'b': 0.6})
TrueЧисла с плавающей точкой отлично подходят для работы с числами, когда абсолютная точность не требуется. Они быстры и эффективны с точки зрения потребления памяти. Но, если точность нужна, стоит рассмотреть ряд альтернатив числам с плавающей точкой.
Точные альтернативы числам с плавающей точкой
В Python есть два встроенных числовых типа, которые обеспечивают полную точность в ситуациях, когда числа с плавающей точкой не подходят: Decimal и Fraction.
Тип Decimal
В типе Decimal могут храниться десятичные значения именно с той точностью, какая нужна. По умолчанию в нём сохраняются 28 значащих цифр (это число можно изменить согласно конкретной решаемой задаче):
>>> # Import the Decimal type from the decimal module
>>> from decimal import Decimal
>>> # Values are represented exactly so no rounding error occurs
>>> Decimal("0.1") + Decimal("0.2") == Decimal("0.3")
True
>>> # By default 28 significant figures are preserved
>>> Decimal(1) / Decimal(7)
Decimal('0.1428571428571428571428571429')
>>> # You can change the significant figures if needed
>>> from decimal import getcontext
>>> getcontext().prec = 6 # Use 6 significant figures
>>> Decimal(1) / Decimal(7)
Decimal('0.142857')Больше узнать о типе Decimal можно в документации Python.
Тип Fraction
Альтернатива числам с плавающей точкой — тип Fraction. В нём могут точно сохраняться рациональные числа. При этом устраняются проблемы с ошибками представления, возникающие в числах с плавающей точкой:
>>> # import the Fraction type from the fractions module
>>> from fractions import Fraction
>>> # Instantiate a Fraction with a numerator and denominator
>>> Fraction(1, 10)
Fraction(1, 10)
>>> # Values are represented exactly so no rounding error occurs
>>> Fraction(1, 10) + Fraction(2, 10) == Fraction(3, 10)
TrueУ типов Fraction и Decimal много преимуществ по сравнению со стандартными значениями с плавающей точкой. Но есть и недостатки: меньшая скорость и повышенное потребление памяти.
Если абсолютная точность не нужна, лучше оставаться с числами с плавающей точкой. А вот в случае с финансовыми и критически важными приложениями эти недостатки типов Fraction и Decimal могут оказаться неприемлемыми.
Заключение
Значения с плавающей точкой — это и благо, и проклятие одновременно. Они обеспечивают быстрые арифметические операции и эффективное потребление памяти за счёт неточного представления. Из этой статьи вы узнали:
-
Почему числа с плавающей точкой неточны.
-
Почему ошибка представления с плавающей точкой типична.
-
Как корректно сравнивать значения с плавающей точкой.
-
Как точно представлять числа, используя типы Fraction и Decimal.
Узнайте о числах в Python ещё больше. Например, знаете ли вы, что int — не единственный целочисленный тип в Python? Узнайте, какой есть ещё, а также о других малоизвестных фактах о числах в моей статье.
А мы поможем вам прокачать скиллы или с самого начала освоить профессию, востребованную в любое время:
-
Профессия Fullstack-разработчик на Python
-
Профессия Data Analyst
Выбрать другую востребованную профессию.
Получилось долго, но надеюсь интересно. А то писать ответы в две строки уже надоело:)
Старая история
Когда я учился в ВУЗе, у нас была большая расчётная задача, которая рассчитывалась двумя способами. А в конце два ответа должны были сойтись. Преподаватель допускал расхождение в 20%. Но проблема в том, что одна ветка вычислений — это около пол сотни только умножений. А ещё там была тригонометрия и логарифмы. И сам расчет занимал около часа, при условии, что человек понимает, что он делает.
И анализ расчетов не показывал ошибку. Если такой же расчет делал сосед, то у него получалась своя пара чисел. Когда у меня было 3 пары чисел, я понял, что так дело не пойдет.
математики раскрывают глаза
Но потом выяснилась причина — делая расчёты на калькуляторе, почти всегда на автомате округлял до 2-3 цифр после запятой (лень же 10-12 цифр переписывать). Преподаватель по математике, посмотрев на это, сказал, что легко получить разброс в полтора-два раза (что собственно и наблюдалось).
Поэтому, я вооружился Delfi и написал свой расчет. И в конце сошлось с точностью в сотые процента. Сравнивая с моими ручными расчетами, обнаружилось, что ошибка постепенно накапливалась. Но вот преподаватель, которая принимала работу, была немного в шоке (она не видела, что бы так сходились цифры и с калькулятором пыталась найти, где же именно я «подогнал»).
физики также в курсе
Поэтому, когда на физике (к примеру, на лабораторной работе или докторской диссертации) пишутся результаты расчетов, без указания погрешности они «не имеют никакого физического смысла».
Потом я сделал ещё расчет с расчетом погрешности на каждом шаге и все сошлось, но об этом ниже.
Теперь ближе к вопросу.
Посмотрим на такие варианты получения числа 10 (да, этот код на плюсах, но это ничего не меняет)
#include <string>
#include <iostream>
#include <cmath>
#include <iomanip>
void print(float f)
{
std::cout
// точность вывода по умолчанию
<< std::setprecision(6) << f << " = "
// максимальная точность вывода
<< std::setprecision(std::numeric_limits<long double>::digits10 + 1)
<< f << '\n';
}
int main()
{
float f1 = 10.0;
print(f1);
//
float f2 = 1.0 / 3.0 * 30;
print(f2);
//
float f3 = 0;
for (int i = 0; i < 100; i++) { f3+=0.1;}
print(f3);
//
float f4 = 0;
for (int i = 0; i < 1000; i++) { f4+=0.01;}
print(f4);
//
float f5 = exp(log(2)+log(5));
print(f5);
}
вывод
10 = 10
10 = 10
10 = 10.00000190734863281
10.0001 = 10.00013351440429688
10 = 10
Хотя эти все способы и дают 10, но это все немного «разные 10». В втором и пятом случае компилятор оптимизировал и там «честная 10.0» (да, компиляторы они такие. Иногда могут творить чудеса и скрывать пользовательские ошибки.
Теперь нужно понять, что оператор == для двух вещественных чисел делает просто побитовое сравнение (если типы не совпадают, то их вначале нужно «подогнать», а это ещё дополнительные ошибки).
Также, сразу видно, что в четвертом случае при выводе похоже что там 10, но по факту нет.
как же такое могло произойти?
Теперь пойдем ещё ближе. В своем коде похоже Вы делаете какие то расчеты, которые должны давать идентичные результаты. Но получаете их немного по разному (к примеру, это могут быть расчеты площади фигуры методом Монте-Карло).
игры также в курсе
В играх бывает похожий случай. Допустим у нас есть бродилка и главный герой может перемещается только шагами определенного размера. Естественно, к его текущим координатам мы добавляем/вычитаем размер шага. И ходя по комнате и вернувшись на начальную точку, можем обнаружить, что мы немного сместились. Это иногда бывает «очень неожиданным». В тех же шуттерах пуля может пролететь «рядом», хотя мы и целились очень точно.
Ищем решение
Что же делать? Нужно учитывать вот ту погрешность результатов. Иногда предлагают использовать ту же EPS, но это не совсем верный способ. Нужно сравнить два результата не как точечный результаты, а как два отрезка.
простые сложные примеры
Давайте посмотрим на такие сравнения 10±3 и 9±2. Если перевести их в «отрезки», это будет [7;13] и [7;11]. Скорее всего большинство людей будет считать первое больше второго. Но, учитывая погрешность, они могут быть равными. А могут и не быть. Поэтому, правильный ответ: 10±3 ≊ 9±2 (это знак равно или почти равно)
Новый вариант 10±3 и 5±2 -> [7;13] и [3;7]. И хотя на первый взгляд кажется, что второе число однозначно меньше, но это не так. При определенных обстоятельствах они могут быть равны 7. Да, вероятность этого достаточно низкая, но все же она существует. Поэтому здесь правильный знак 10±3 ≥ 5±2, как бы это и не было странно.
Но многие об этом забывают. А потом получаются странные результаты… А потом вдруг, «а есть ли о погрешности погрешность?»
как быть?
Как же сравнивать, учитывая все это? А тут всегда нужно смотреть на целевую задачу. Если это к примеру координаты человечка на карте, то лучше координаты округлять до кратности шага или вообще хранить в целых числах. Если это координаты корабля, то двойной размер корабля будет хороших мерилом точности. Если это расчет атомной бомбы, то тут похоже ошиблись форумом.
подбираемся к решению
Перейдем к коду. Я бы делал так сравнение на больше
abs(a-b) > eps && a>b
что в принципе можно переписать и как
a > b + eps
где eps либо выбирается методом «тыка» с подходящего справочника, либо просто сумма погрешности измерения для двух переменных.
а это уже формально ответ на вопрос
Посмотрим, что с Вашим способом сравнения не так
Debug.Log((p > 10 + Mathf.Epsilon));
выглядит он как мой. Но если посмотреть, что такое Mathf.Epsilon, то оказывается это
Представляет наименьшее положительное значение Double больше нуля. Это поле является константой.
Скажем так, это «атомарное» (то есть, неделимое, минимальное) положительное число. Разделить попалам его уже нельзя. Если немного подумать, то станет очевидно, что сравнение с ним немного бессмысленно — уж слишком маленькое это число
public const double Epsilon = 4.94065645841247E-324;
В любом случае, по ссылке выше об этом же и написано
При создании пользовательского алгоритма, который определяет, считаются ли два числа с плавающей запятой равными, мы не рекомендуем основывать свой алгоритм на значении Epsilon константы, чтобы добиться приемлемого абсолютного поля разности для двух значений, которые будут считаться равными
(это какой то машинный перевод, но вроде понятно).
P.S.
Оставлю эту игрушку здесь https://evanw.github.io/float-toy/ — очень помогает понять, как там все внутри крутится.
In most programming languages, floating point numbers are represented a lot like scientific notation: with an exponent and a mantissa (also called the significand). A very simple number, say 9.2, is actually this fraction:
5179139571476070 * 2 -49
Where the exponent is -49 and the mantissa is 5179139571476070. The reason it is impossible to represent some decimal numbers this way is that both the exponent and the mantissa must be integers. In other words, all floats must be an integer multiplied by an integer power of 2.
9.2 may be simply 92/10, but 10 cannot be expressed as 2n if n is limited to integer values.
Seeing the Data
First, a few functions to see the components that make a 32- and 64-bit float. Gloss over these if you only care about the output (example in Python):
def float_to_bin_parts(number, bits=64):
if bits == 32: # single precision
int_pack = 'I'
float_pack = 'f'
exponent_bits = 8
mantissa_bits = 23
exponent_bias = 127
elif bits == 64: # double precision. all python floats are this
int_pack = 'Q'
float_pack = 'd'
exponent_bits = 11
mantissa_bits = 52
exponent_bias = 1023
else:
raise ValueError, 'bits argument must be 32 or 64'
bin_iter = iter(bin(struct.unpack(int_pack, struct.pack(float_pack, number))[0])[2:].rjust(bits, '0'))
return [''.join(islice(bin_iter, x)) for x in (1, exponent_bits, mantissa_bits)]
There’s a lot of complexity behind that function, and it’d be quite the tangent to explain, but if you’re interested, the important resource for our purposes is the struct module.
Python’s float is a 64-bit, double-precision number. In other languages such as C, C++, Java and C#, double-precision has a separate type double, which is often implemented as 64 bits.
When we call that function with our example, 9.2, here’s what we get:
>>> float_to_bin_parts(9.2)
['0', '10000000010', '0010011001100110011001100110011001100110011001100110']
Interpreting the Data
You’ll see I’ve split the return value into three components. These components are:
- Sign
- Exponent
- Mantissa (also called Significand, or Fraction)
Sign
The sign is stored in the first component as a single bit. It’s easy to explain: 0 means the float is a positive number; 1 means it’s negative. Because 9.2 is positive, our sign value is 0.
Exponent
The exponent is stored in the middle component as 11 bits. In our case, 0b10000000010. In decimal, that represents the value 1026. A quirk of this component is that you must subtract a number equal to 2(# of bits) — 1 — 1 to get the true exponent; in our case, that means subtracting 0b1111111111 (decimal number 1023) to get the true exponent, 0b00000000011 (decimal number 3).
Mantissa
The mantissa is stored in the third component as 52 bits. However, there’s a quirk to this component as well. To understand this quirk, consider a number in scientific notation, like this:
6.0221413×1023
The mantissa would be the 6.0221413. Recall that the mantissa in scientific notation always begins with a single non-zero digit. The same holds true for binary, except that binary only has two digits: 0 and 1. So the binary mantissa always starts with 1! When a float is stored, the 1 at the front of the binary mantissa is omitted to save space; we have to place it back at the front of our third element to get the true mantissa:
1.0010011001100110011001100110011001100110011001100110
This involves more than just a simple addition, because the bits stored in our third component actually represent the fractional part of the mantissa, to the right of the radix point.
When dealing with decimal numbers, we «move the decimal point» by multiplying or dividing by powers of 10. In binary, we can do the same thing by multiplying or dividing by powers of 2. Since our third element has 52 bits, we divide it by 252 to move it 52 places to the right:
0.0010011001100110011001100110011001100110011001100110
In decimal notation, that’s the same as dividing 675539944105574 by 4503599627370496 to get 0.1499999999999999. (This is one example of a ratio that can be expressed exactly in decimal, but only approximately in binary; for more detail, see: 675539944105574 / 4503599627370496.)
Now that we’ve transformed the third component into a fractional number, adding 1 gives the true mantissa.
Recapping the Components
- Sign (first component):
0for positive,1for negative - Exponent (middle component): Subtract 2(# of bits) — 1 — 1 to get the true exponent
- Mantissa (last component): Divide by 2(# of bits) and add
1to get the true mantissa
Calculating the Number
Putting all three parts together, we’re given this binary number:
1.0010011001100110011001100110011001100110011001100110 x 1011
Which we can then convert from binary to decimal:
1.1499999999999999 x 23 (inexact!)
And multiply to reveal the final representation of the number we started with (9.2) after being stored as a floating point value:
9.1999999999999993
Representing as a Fraction
9.2
Now that we’ve built the number, it’s possible to reconstruct it into a simple fraction:
1.0010011001100110011001100110011001100110011001100110 x 1011
Shift mantissa to a whole number:
10010011001100110011001100110011001100110011001100110 x 1011-110100
Convert to decimal:
5179139571476070 x 23-52
Subtract the exponent:
5179139571476070 x 2-49
Turn negative exponent into division:
5179139571476070 / 249
Multiply exponent:
5179139571476070 / 562949953421312
Which equals:
9.1999999999999993
9.5
>>> float_to_bin_parts(9.5)
['0', '10000000010', '0011000000000000000000000000000000000000000000000000']
Already you can see the mantissa is only 4 digits followed by a whole lot of zeroes. But let’s go through the paces.
Assemble the binary scientific notation:
1.0011 x 1011
Shift the decimal point:
10011 x 1011-100
Subtract the exponent:
10011 x 10-1
Binary to decimal:
19 x 2-1
Negative exponent to division:
19 / 21
Multiply exponent:
19 / 2
Equals:
9.5
Further reading
- The Floating-Point Guide: What Every Programmer Should Know About Floating-Point Arithmetic, or, Why don’t my numbers add up? (floating-point-gui.de)
- What Every Computer Scientist Should Know About Floating-Point Arithmetic (Goldberg 1991)
- IEEE Double-precision floating-point format (Wikipedia)
- Floating Point Arithmetic: Issues and Limitations (docs.python.org)
- Floating Point Binary
What seems to have not been mentioned so far are the concepts of an unstable algorithm and an ill-conditioned problem. I’ll address the former first, as that seems to be a more frequent pitfall for novice numericists.
Consider the computation of the powers of the (reciprocal) golden ratio φ=0.61803… ; one possible way to go about it is to use the recursion formula φ^n=φ^(n-2)-φ^(n-1), starting with φ^0=1 and φ^1=φ. If you run this recursion in your favorite computing environment and compare the results with accurately evaluated powers, you’ll find a slow erosion of significant figures. Here’s what happens for instance in Mathematica:
ph = N[1/GoldenRatio];
Nest[Append[#1, #1[[-2]] - #1[[-1]]] & , {1, ph}, 50] - ph^Range[0, 51]
{0., 0., 1.1102230246251565*^-16, -5.551115123125783*^-17, 2.220446049250313*^-16,
-2.3592239273284576*^-16, 4.85722573273506*^-16, -7.147060721024445*^-16,
1.2073675392798577*^-15, -1.916869440954372*^-15, 3.1259717037102064*^-15,
-5.0411064211886014*^-15, 8.16837916750579*^-15, -1.3209051907825398*^-14,
2.1377864756200182*^-14, -3.458669982359108*^-14, 5.596472721011714*^-14,
-9.055131861349097*^-14, 1.465160458236081*^-13, -2.370673237795176*^-13,
3.835834102607072*^-13, -6.206507137114341*^-13, 1.004234127360273*^-12,
-1.6248848342954435*^-12, 2.6291189633497825*^-12, -4.254003796798193*^-12,
6.883122762265558*^-12, -1.1137126558640235*^-11, 1.8020249321541067*^-11,
-2.9157375879969544*^-11, 4.717762520172237*^-11, -7.633500108148015*^-11,
1.23512626283229*^-10, -1.9984762736468268*^-10, 3.233602536479646*^-10,
-5.232078810126407*^-10, 8.465681346606119*^-10, -1.3697760156732426*^-9,
2.216344150333856*^-9, -3.5861201660070964*^-9, 5.802464316340953*^-9,
-9.388584482348049*^-9, 1.5191048798689004*^-8, -2.457963328103705*^-8,
3.9770682079726053*^-8, -6.43503153607631*^-8, 1.0412099744048916*^-7,
-1.6847131280125227*^-7, 2.725923102417414*^-7, -4.4106362304299367*^-7,
7.136559332847351*^-7, -1.1547195563277288*^-6}
The purported result for φ^41 has the wrong sign, and even earlier, the computed and actual values for φ^39 share no digits in common (3.484899258054952*^-9for the computed version against the true value7.071019424062048*^-9). The algorithm is thus unstable, and one should not use this recursion formula in inexact arithmetic. This is due to the inherent nature of the recursion formula: there is a «decaying» and «growing» solution to this recursion, and trying to compute the «decaying» solution by forward solution when there is an alternative «growing» solution is begging for numerical grief. One should thus ensure that his/her numerical algorithms are stable.
Now, on to the concept of an ill-conditioned problem: even though there may be a stable way to do something numerically, it may very well be that the problem you have just cannot be solved by your algorithm. This is the fault of the problem itself, and not the solution method. The canonical example in numerics is the solution of linear equations involving the so-called «Hilbert matrix»:
The matrix is the canonical example of an ill-conditioned matrix: trying to solve a system with a large Hilbert matrix might return an inaccurate solution.
Here’s a Mathematica demonstration: compare the results of exact arithmetic
Table[LinearSolve[HilbertMatrix[n], HilbertMatrix[n].ConstantArray[1, n]], {n, 2, 12}]
{{1, 1}, {1, 1, 1}, {1, 1, 1, 1}, {1, 1, 1, 1, 1}, {1, 1, 1, 1, 1,
1}, {1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1,
1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}
and inexact arithmetic
Table[LinearSolve[N[HilbertMatrix[n]], N[HilbertMatrix[n].ConstantArray[1, n]]], {n, 2, 12}]
{{1., 1.}, {1., 1., 1.}, {1., 1., 1., 1.}, {1., 1., 1., 1., 1.},
{1., 1., 1., 1., 1., 1.}, {1., 1., 1., 1., 1., 1., 1.},
{1., 1., 1., 1., 1., 1., 1., 1.}, {1., 1., 1., 1., 1., 1., 1., 1., 1.},
{1., 1., 1., 0.99997, 1.00014, 0.999618, 1.00062, 0.9994, 1.00031,
0.999931}, {1., 1., 0.999995, 1.00006, 0.999658, 1.00122, 0.997327,
1.00367, 0.996932, 1.00143, 0.999717}, {1., 1., 0.999986, 1.00022,
0.998241, 1.00831, 0.975462, 1.0466, 0.94311, 1.04312, 0.981529,
1.00342}}
(If you did try it out in Mathematica, you’ll note a few error messages warning of the ill-conditioning appearing.)
In both cases, simply increasing the precision is no cure; it will only delay the inevitable erosion of figures.
This is what you might be faced with. The solutions might be difficult: for the first, either you go back to the drawing board, or wade through journals/books/whatever to find if somebody else has come up with a better solution than you have; for the second, you either give up, or reformulate your problem to something more tractable.
I’ll leave you with a quote from Dianne O’Leary:
Life may toss us some ill-conditioned problems, but there is no good reason to settle for an unstable algorithm.