Время на прочтение
9 мин
Количество просмотров 40K

К старту курса по Fullstack-разработке на Python делимся решениями классической проблемы неточности чисел с плавающей точкой. В материале вы найдёте примеры работы с функциями и классами, предназначенными специально для решения проблем чисел с плавающей точкой.
Числа с плавающей точкой — быстрый и эффективный способ хранения чисел и работы с ними. Но он связан с рядом трудностей для начинающих и опытных программистов! Вот классический пример:
>>> 0.1 + 0.2 == 0.3
FalseВпервые увидев такое, можно растеряться. Такое поведение корректно! Поговорим о том, почему ошибки при операциях над числами с плавающей точкой так распространены, почему они возникают и как с ними справиться в Python.
Компьютер обманывает вас
Вы видели, что 0.1 + 0.2 не равно 0.3, но безумие на этом не заканчивается. Вот ещё пара примеров, сбивающих с толку:
>>> 0.2 + 0.2 + 0.2 == 0.6
False
>>> 1.3 + 2.0 == 3.3
False
>>> 1.2 + 2.4 + 3.6 == 7.2
FalseПроблема касается и сравнения:
>>> 0.1 + 0.2 <= 0.3
False
>>> 10.4 + 20.8 > 31.2
True
>>> 0.8 - 0.1 > 0.7
TrueЧто происходит? Когда вы вводите в интерпретатор Python число 0.1, оно сохраняется в памяти как число с плавающей точкой и происходит преобразование. 0.1 — это десятичное число с основанием 10, но числа с плавающей точкой хранятся в двоичной записи. То есть основание 0.1 преобразуется из 10 в 2.
Получающееся двоичное число может недостаточно точно представлять исходное число с основанием 10. 0.1 — один из примеров. Двоичным представлением будет 0.0(0011). То есть 0.1 — это бесконечно повторяющееся десятичное число, записанное с основанием 2. То же происходит, когда в виде десятичного числа с основанием 10 записывается дробь ⅓. Получается бесконечно повторяющееся десятичное число 0.3(3).
Память компьютера конечна, поэтому бесконечно повторяющееся представление двоичной дроби 0.1 округляется до конечной дроби. Её значение зависит от архитектуры компьютера (32- или 64-разрядная).
Увидеть значение с плавающей точкой, которое сохраняется для 0.1, можно с помощью метода .as_integer_ratio(). Представление с плавающей точкой состоит из числителя и знаменателя:
>>> numerator, denominator = (0.1).as_integer_ratio()
>>> f"0.1 ≈ {numerator} / {denominator}"
'0.1 ≈ 3602879701896397 / 36028797018963968'Чтобы отобразить дробь с точностью до 55 знаков после запятой, используем format():
>>> format(numerator / denominator, ".55f")
'0.1000000000000000055511151231257827021181583404541015625'Так 0.1 округляется до числа чуть больше, чем его истинное значение.
Узнайте больше о числовых методах, подобных .as_integer_ratio(), в моей статье 3 Things You Might Not Know About Numbers in Python («3 факта о числах в Python, которые вы могли не знать»).
Эта ошибка представления чисел с плавающей точкой встречается куда чаще, чем может показаться.
Ошибка представления числа очень типична
Существуют три причины, почему число округляется при его представлении в виде числа с плавающей точкой:
-
В числе больше значащих разрядов, чем позволяет плавающая точка.
-
Это иррациональное число.
-
Число рациональное, но без конечного двоичного представления.
64-разрядные числа с плавающей точкой имеют 16 или 17 значащих разрядов. Любое число, у которого значащих разрядов больше, округляется. Иррациональные числа, такие как π и e, нельзя представить конечной дробью с целочисленным основанием. И, опять же, иррациональные числа в любом случае округляются при сохранении в виде чисел с плавающей точкой.
В этих двух ситуациях создаётся бесконечный набор чисел, которые нельзя точно представить в виде числа с плавающей точкой. Но вы вряд ли столкнётесь с этими проблемами, не будучи химиком, имеющим дело с крошечными числами, или физиком — с астрономически большими числами.
А как на счёт бесконечных рациональных чисел, например 0.1 с основанием 2? Именно здесь вам встретится большинство связанных с плавающей точкой трудностей и благодаря математике — позволяющей определять, конечная дробь или нет, — вы будете сталкиваться с ошибками представления чаще, чем думаете.
С основанием 10 дробь можно представить как конечную, если её знаменатель — произведение степеней простых множителей 10. Два простых множителя 10 — это 2 и 5, поэтому дроби ½, ¼, ⅕, ⅛ и ⅒ — конечные, а ⅓, ⅐ и ⅑ — нет. У основания 2 только один простой множитель — 2.
Конечные дроби здесь только те, знаменатель которых равен степени числа 2. В результате дроби ⅓, ⅕, ⅙, ⅐, ⅑ и ⅒ — бесконечные, когда представлены в двоичной записи.
Теперь наш первый пример должен стать понятнее. 0.1, 0.2 и 0.3 при преобразовании в числа с плавающей точкой округляются:
>>> # -----------vvvv Display with 17 significant digits
>>> format(0.1, ".17g")
'0.10000000000000001'
>>> format(0.2, ".17g")
'0.20000000000000001'
>>> format(0.3, ".17g")
'0.29999999999999999'При сложении 0.1 и 0.2 получается число чуть больше 0.3:
>>> 0.1 + 0.2
0.30000000000000004А поскольку 0.1 + 0.2 чуть больше, чем 0.3, и 0.3 представлено числом, которое чуть меньше 0.3, выражение 0.1 + 0.2 == 0.3 оказывается False.
Об ошибке представления чисел с плавающей точкой должен знать каждый программист на любом языке — и уметь с ней справляться. Она характерна не только для Python. Результат вывода 0.1 + 0.2 на разных языках можно увидеть на сайте с подходящим названием 0.30000000000000004.com.
Как сравнивать числа с плавающей точкой в Python
Как же справляться с ошибками представления чисел с плавающей точкой при сравнении таких чисел в Python? Хитрость заключается в том, чтобы избегать проверки на равенство. Вместо ==, >= или <= всегда используйте с числами с плавающей точкой функцию math.isclose():
>>> import math
>>> math.isclose(0.1 + 0.2, 0.3)
TrueВ math.isclose() проверяется, достаточно ли близок первый аргумент ко второму. То есть проверяется расстояние между двумя аргументами. Оно равно абсолютной величине разницы обоих значений:
>>> a = 0.1 + 0.2
>>> b = 0.3
>>> abs(a - b)
5.551115123125783e-17Если abs(a — b) меньше некоего процента от большего значения a или b, то a считается достаточно близким к b, чтобы считаться «равным» b. Этот процент называется относительной погрешностью и указывается именованным аргументом rel_tol функции math.isclose(), который по умолчанию равен 1e-9.
То есть если abs(a — b) меньше 0.00000001 * max(abs(a), abs(b)), то a и b считаются «близкими» друг к другу. Это гарантирует, что a и b будут приблизительно с девятью знаками после запятой.
Если нужно, можно изменить относительную погрешность:
>>> math.isclose(0.1 + 0.2, 0.3, rel_tol=1e-20)
FalseКонечно, относительная погрешность зависит от ограничений задачи, но для большинства повседневных приложений стандартной относительной погрешности должно быть достаточно. Проблема возникает, если a или b равно нулю, а rel_tol меньше единицы. Тогда, как бы ни было близко ненулевое значение к нулю, относительной погрешностью гарантируется, что проверка на близость будет неудачной. В качестве запасного варианта здесь применяется абсолютная погрешность:
>>> # Relative check fails!
>>> # ---------------vvvv Relative tolerance
>>> # ----------------------vvvvv max(0, 1e-10)
>>> abs(0 - 1e-10) < 1e-9 * 1e-10
False
>>> # Absolute check works!
>>> # ---------------vvvv Absolute tolerance
>>> abs(0 - 1e-10) < 1e-9
TrueВ math.isclose() эта проверка выполняется автоматически. Абсолютная погрешность определяется с помощью именованного аргумента abs_tol. Но abs_tol по умолчанию равен 0.0, поэтому придётся задать его вручную, если нужно проверить близость значения к нулю.
В итоге в функции math.isclose() возвращается результат следующего сравнения — с относительными и абсолютными проверками в одном выражении:
abs(a - b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)math.isclose() появилась в PEP 485 и доступна с Python 3.5.
Когда стоит использовать math.isclose()?
В целом math.isclose() следует применять, сравнивая значения с плавающей точкой. Заменим == на math.isclose():
>>> # Don't do this:
>>> 0.1 + 0.2 == 0.3
False
>>> # Do this instead:
>>> math.isclose(0.1 + 0.2, 0.3)
TrueСо сравнениями >= и <= нужно быть осторожным. Обработаем равенство отдельно, используя math.isclose(), а затем проверим строгое сравнение:
>>> a, b, c = 0.1, 0.2, 0.3
>>> # Don't do this:
>>> a + b <= c
False
>>> # Do this instead:
>>> math.isclose(a + b, c) or (a + b < c)
TrueЕсть альтернативы math.isclose(). Если вы работаете с NumPy, можете использовать numpy.allclose() и numpy.isclose():
>>> import numpy as np
>>> # Use numpy.allclose() to check if two arrays are equal
>>> # to each other within a tolerance.
>>> np.allclose([1e10, 1e-7], [1.00001e10, 1e-8])
False
>>> np.allclose([1e10, 1e-8], [1.00001e10, 1e-9])
True
>>> # Use numpy.isclose() to check if the elements of two arrays
>>> # are equal to each other within a tolerance
>>> np.isclose([1e10, 1e-7], [1.00001e10, 1e-8])
array([ True, False])
>>> np.isclose([1e10, 1e-8], [1.00001e10, 1e-9])
array([ True, True])Имейте в виду: стандартные относительные и абсолютные погрешности — не то же самое, что math.isclose(). Стандартная относительная погрешность для numpy.allclose() и numpy.isclose() равна 1e-05, а стандартная абсолютная погрешность — 1e-08.
math.isclose() особенно удобна для модульных тестов, хотя и здесь имеются альтернативы. Во встроенном модуле unittest в Python есть метод unittest.TestCase.assertAlmostEqual().
Но в нём применяется только проверка абсолютной разницы. А это ещё и утверждение, то есть при сбоях возникает ошибка AssertionError, из-за которой оно непригодно для сравнений в бизнес-логике.
Отличная альтернатива math.isclose() для модульного тестирования — это функция pytest.approx() из pytest pytest. Как и в math.isclose(), здесь принимаются два аргумента и возвращается, равны они или нет в пределах некой погрешности:
>>> import pytest
>>> 0.1 + 0.2 == pytest.approx(0.3)
TrueКак и в math.isclose(), в pytest.approx() для задания относительной и абсолютной погрешностей есть именованные аргументы rel_tol и abs_tol. Но стандартные значения различаются. У rel_tol оно 1e-6, а у abs_tol — 1e-12.
Если первые переданные в pytest.approx() два аргумента подобны массиву (то есть это итерируемый объект Python, такой же, как список или кортеж или даже массив NumPy), тогда в pytest.approx() поведение подобно numpy.allclose() и возвращается то, равны эти два массива или нет в пределах погрешностей:
>>> import numpy as np
>>> np.array([0.1, 0.2]) + np.array([0.2, 0.4]) == pytest.approx(np.array([0.3, 0.6]))
TrueДля pytest.approx() сгодятся даже значения словаря:
>>> {'a': 0.1 + 0.2, 'b': 0.2 + 0.4} == pytest.approx({'a': 0.3, 'b': 0.6})
TrueЧисла с плавающей точкой отлично подходят для работы с числами, когда абсолютная точность не требуется. Они быстры и эффективны с точки зрения потребления памяти. Но, если точность нужна, стоит рассмотреть ряд альтернатив числам с плавающей точкой.
Точные альтернативы числам с плавающей точкой
В Python есть два встроенных числовых типа, которые обеспечивают полную точность в ситуациях, когда числа с плавающей точкой не подходят: Decimal и Fraction.
Тип Decimal
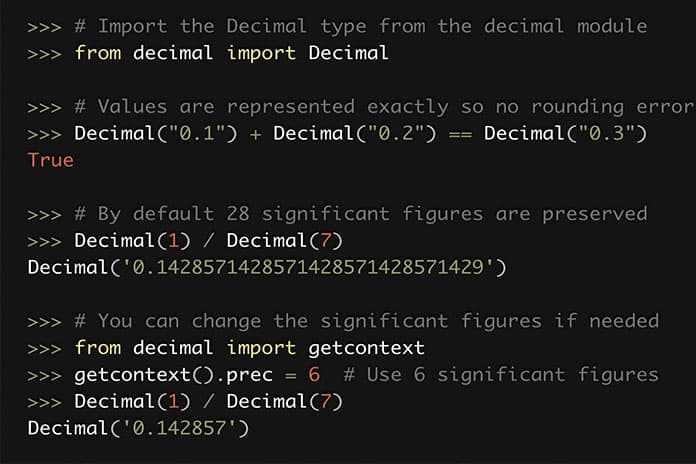
В типе Decimal могут храниться десятичные значения именно с той точностью, какая нужна. По умолчанию в нём сохраняются 28 значащих цифр (это число можно изменить согласно конкретной решаемой задаче):
>>> # Import the Decimal type from the decimal module
>>> from decimal import Decimal
>>> # Values are represented exactly so no rounding error occurs
>>> Decimal("0.1") + Decimal("0.2") == Decimal("0.3")
True
>>> # By default 28 significant figures are preserved
>>> Decimal(1) / Decimal(7)
Decimal('0.1428571428571428571428571429')
>>> # You can change the significant figures if needed
>>> from decimal import getcontext
>>> getcontext().prec = 6 # Use 6 significant figures
>>> Decimal(1) / Decimal(7)
Decimal('0.142857')Больше узнать о типе Decimal можно в документации Python.
Тип Fraction
Альтернатива числам с плавающей точкой — тип Fraction. В нём могут точно сохраняться рациональные числа. При этом устраняются проблемы с ошибками представления, возникающие в числах с плавающей точкой:
>>> # import the Fraction type from the fractions module
>>> from fractions import Fraction
>>> # Instantiate a Fraction with a numerator and denominator
>>> Fraction(1, 10)
Fraction(1, 10)
>>> # Values are represented exactly so no rounding error occurs
>>> Fraction(1, 10) + Fraction(2, 10) == Fraction(3, 10)
TrueУ типов Fraction и Decimal много преимуществ по сравнению со стандартными значениями с плавающей точкой. Но есть и недостатки: меньшая скорость и повышенное потребление памяти.
Если абсолютная точность не нужна, лучше оставаться с числами с плавающей точкой. А вот в случае с финансовыми и критически важными приложениями эти недостатки типов Fraction и Decimal могут оказаться неприемлемыми.
Заключение
Значения с плавающей точкой — это и благо, и проклятие одновременно. Они обеспечивают быстрые арифметические операции и эффективное потребление памяти за счёт неточного представления. Из этой статьи вы узнали:
-
Почему числа с плавающей точкой неточны.
-
Почему ошибка представления с плавающей точкой типична.
-
Как корректно сравнивать значения с плавающей точкой.
-
Как точно представлять числа, используя типы Fraction и Decimal.
Узнайте о числах в Python ещё больше. Например, знаете ли вы, что int — не единственный целочисленный тип в Python? Узнайте, какой есть ещё, а также о других малоизвестных фактах о числах в моей статье.
А мы поможем вам прокачать скиллы или с самого начала освоить профессию, востребованную в любое время:
-
Профессия Fullstack-разработчик на Python
-
Профессия Data Analyst
Выбрать другую востребованную профессию.
Числа с плавающей точкой представлены в компьютерах в виде двоичных дробей. Например, десятичная дробь 0.125 имеет значение 1/10 + 2/100 + 5/1000, и таким же образом двоичная дробь 0.001 имеет значение 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковые значения, единственное реальное отличие состоит в том, что первая записана в дробной записи с основанием 10, а вторая — с основанием 2.
К сожалению, большинство десятичных дробей не могут быть представлены точно как двоичные дроби. Следствием этого является то, что, как правило, вводимые десятичные числа с плавающей запятой аппроксимируются только двоичными числами с плавающей запятой, фактически сохраненными в машине.
Сначала проблему легче понять из базы 10. Рассмотрим дробь 1/3. Вы можете приблизить это как основную 10 фракцию: 0.3 или лучше, 0.33или лучше, 0.333 и так далее. Независимо от того, сколько цифр вы хотите записать, результат никогда не будет ровно 1/3, но будет все более приближенным к 1/3.
Таким же образом, независимо от того, сколько цифр из 2-х оснований вы хотите использовать, десятичное значение 0,1 не может быть представлено в точности как дробь из 2-х оснований. В базе 2 1/10 — бесконечно повторяющаяся дробь 0.0001100110011001100110011...
Остановитесь на любом конечном количестве битов, и вы получите приближение. На большинстве современных машин числа с плавающей запятой аппроксимируются с использованием двоичной дроби, а числитель использует первые 53 бита, начиная с самого старшего бита, а знаменатель — как степень двух. В случае 1/10 двоичная дробь равна 3602879701896397/2 ** 55, что близко, но не точно равно истинному значению 1/10.
Многие пользователи не знают о приближении из-за способа отображения значений. Python печатает только десятичное приближение к истинному десятичному значению двоичного приближения, хранящегося на машине. На большинстве машин, если бы Python должен был печатать истинное десятичное значение двоичного приближения, хранящегося для 0.1, он должен был бы отображать
>>> 0.1 # 0.1000000000000000055511151231257827021181583404541015625
Это больше цифр, чем большинство людей считают полезным, поэтому Python сохраняет количество цифр управляемым, отображая округленное значение вместо
Просто помните, что хотя напечатанный результат выглядит как точное значение 1/10, фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Интересно, что существует много разных десятичных чисел, которые имеют одну и ту же ближайшую приблизительную двоичную дробь. Например, числа 0.1 и 0.10000000000000001 и 0.1000000000000000055511151231... все приблизительно равны 3602879701896397/2 ** 55. Поскольку все эти десятичные значения имеют одинаковую аппроксимацию, любое из них может отображаться при сохранении инварианта eval(repr(x)) == x.
Исторически Python и встроенная функция repr() выбирали функцию с 17 значащими цифрами, 0.10000000000000001. Начиная с Python 3.1 в большинстве систем теперь может выбирать самый короткий из них и просто отображать 0.1.
Обратите внимание, что это по своей природе двоичное число с плавающей точкой: это не ошибка в Python и не ошибка в вашем коде. Вы увидите то же самое на всех языках, которые поддерживают арифметику с плавающей запятой.
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного числа значащих цифр:
>>> import math >>> format(math.pi, '.12g') # '3.14159265359' >>> format(math.pi, '.2f') # '3.14' >>> repr(math.pi) # '3.141592653589793'
Важно понимать, что в действительности это иллюзия: вы просто округляете отображение истинного значения.
Одна иллюзия может породить другую. Например, поскольку 0,1 не является точно 1/10, суммирование трех значений 0,1 может также не дать точно 0,3:
>>> 0.1 + 0.1 + 0.1 == 0.3 # False
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10, а 0,3 не может приблизиться к точному значению 3/10, предварительное округление функцией round() может не помочь:
>>> round(0.1, 1) + round(0.1, 1) + round(0.1, 1) == round(0.3, 1) # False
Двоичная арифметика с плавающей точкой содержит много сюрпризов, подобных этому. Проблема с 0.1 подробно объясняется в разделе «Ошибка представления». Смотрите также «Опасности с плавающей точкой» для более полного описания других распространенных сюрпризов.
Как говорится, «простых ответов нет». Тем не менее, не следует чрезмерно опасаться чисел с плавающей запятой! Ошибки в операциях с плавающей запятой Python наследуются от аппаратного обеспечения чисел с плавающей запятой, и на большинстве машин они имеют порядок не более одной части в 2 ** 53 на операцию. Это более чем достаточно для большинства задач, но вам нужно помнить, что это не десятичная арифметика и что каждая операция с плавающей запятой может подвергаться новой ошибке округления.
Несмотря на то, что патологические случаи существуют, для наиболее случайного использования арифметики с плавающей запятой вы увидите ожидаемый результат в конце, если просто округлите отображение окончательных результатов до ожидаемого количества десятичных цифр. str() обычно достаточно, и для более точного управления смотрите спецификаторы формата метода str.format().
Для случаев использования, которые требуют точного десятичного представления, попробуйте использовать модуль decimal, который реализует десятичную арифметику, подходящую для приложений бухгалтерского учета и высокоточных приложений.
Другая форма точной арифметики поддерживается модулем fractions, который реализует арифметику, основанную на рациональных числах, поэтому числа, такие как 1/3 могут быть представлены точно.
Если вы большой пользователь операций с плавающей запятой, вам следует взглянуть на пакет Numeric Python и многие другие пакеты для математических и статистических операций, предоставляемых проектом SciPy.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно хотите узнать точное значение числа с плавающей точкой. Метод float.as_integer_ratio() выражает значение типа float в виде дроби:
>>> x = 3.14159 >>> x.as_integer_ratio() # (3537115888337719, 1125899906842624)
Поскольку отношение является точным, оно может быть использовано для воссоздания исходного значения без потерь:
>>> x == 3537115888337719 / 1125899906842624 # True
Метод float.hex() выражает число с плавающей запятой в шестнадцатеричном формате (основание 16), снова давая точное значение, сохраненное компьютером:
>>> x.hex() # '0x1.921f9f01b866ep+1'
Это точное шестнадцатеричное представление может быть использовано для точного восстановления значения с плавающей точкой:
>>> x == float.fromhex('0x1.921f9f01b866ep+1') True
Поскольку представление является точным, оно полезно для надежного переноса значений между различными версиями Python и обмена данными с другими языками, поддерживающими тот же формат, например Java.
Другим полезным инструментом является функция math.fsum(), которая помогает уменьшить потерю точности во время суммирования. Она отслеживает «потерянные цифры», когда значения добавляются в промежуточный итог. Это может повлиять на общую точность, так что ошибки не накапливаются до такой степени, что бы влиять на итоговую сумму:
>>> import math >>> sum([0.1] * 10) == 1.0 False >>> math.fsum([0.1] * 10) == 1.0 True
Ошибка представления.
В этом разделе подробно объясняется пример 0.1 и показано, как вы можете выполнить точный анализ подобных случаев самостоятельно. Предполагается базовое знакомство с двоичным представлением чисел с плавающей точкой.
Ошибка представления относится к тому факту, что фактически большинство десятичных дробей не могут быть представлены точно как двоичные дроби (основание 2) . Это главная причина, почему Python или Perl, C, C++, Java, Fortran и многие другие языки часто не будут отображать точное десятичное число, которое ожидаете.
Это почему? 1/10 не совсем представимо в виде двоичной дроби. Почти все машины сегодня используют арифметику IEEE-754 с плавающей точкой, и почти все платформы отображают плавающие значения Python в IEEE-754 с «двойной точностью». При вводе, компьютер стремится преобразовать 0,1 в ближайшую дробь по форме J / 2 ** N, где J — целое число, содержащее ровно 53 бита.
Перепишем 1 / 10 ~= J / (2**N) как J ~= 2**N / 10 и напоминая, что J имеет ровно 53 бита, это >= 2**52, но < 2**53, наилучшее значение для N равно 56:
>>> 2**52 <= 2**56 // 10 < 2**53 # True
То есть 56 — единственное значение для N, которое оставляет J точно с 53 битами. Наилучшее возможное значение для J тогда будет округлено:
>>> q, r = divmod(2**56, 10) >>> r # 6
Поскольку остаток больше половины от 10, наилучшее приближение получается округлением вверх:
>>> q+1 # 7205759403792794
Поэтому наилучшее возможное приближение к 1/10 при двойной точности 754: 7205759403792794 / 2 ** 56. Деление числителя и знаменателя на два уменьшает дробь до: 3602879701896397 / 2 ** 55
Обратите внимание, поскольку мы округлили вверх, то значение на самом деле немного больше, чем 1/10. Если бы мы не округлили, то значение был бы немного меньше 1/10. Но ни в коем случае это не может быть ровно 1/10!
Таким образом, компьютер никогда не «видит» 1/10: то, что он видит, это точная дробь, указанная выше, наилучшее двоичное приближение 754, которое он может получить:
>>> 0.1 * 2 ** 55 # 3602879701896397.0
Если мы умножим эту дробь на 10 ** 55, мы увидим значение до 55 десятичных цифр:
>>> 3602879701896397 * 10 ** 55 // 2 ** 55 # 1000000000000000055511151231257827021181583404541015625
Это означает, что точное число, хранящееся в компьютере, равно десятичному значению полученному выше. Вместо отображения полного десятичного значения многие языки, включая более старые версии Python округляют результат до 17 значащих цифр:
>>> format(0.1, '.17f') '0.10000000000000001'
Модули fractions and decimal упрощают эти вычисления:
>>> from decimal import Decimal >>> from fractions import Fraction >>> Fraction.from_float(0.1) # Fraction(3602879701896397, 36028797018963968) >>> (0.1).as_integer_ratio() # (3602879701896397, 36028797018963968) >>> Decimal.from_float(0.1) # Decimal('0.1000000000000000055511151231257827021181583404541015625') >>> format(Decimal.from_float(0.1), '.17') # '0.10000000000000001'
Числа с плавающей точкой — это быстрый и эффективный способ хранения и работы с числами, но они имеют ряд подводных камней, которые наверняка ставят в тупик многих начинающих программистов, а возможно, и опытных! Классический пример, демонстрирующий подводные камни плавающих чисел, выглядит следующим образом:
>>> 0.1 + 0.2 == 0.3 False
Увидев это в первый раз, вы можете быть дезориентированы. Но не выбрасывайте свой компьютер в мусорную корзину. Это правильное поведение!
В этой статье вы узнаете, почему ошибки с плавающей точкой, подобные приведенной выше, встречаются часто, почему они имеют смысл, и что можно сделать, чтобы справиться с ними в Python.
Ваш компьютер — лжец (вроде того)
Вы видели, что 0,1 + 0,2 не равно 0,3, но на этом безумие не заканчивается. Вот еще несколько сбивающих с толку примеров:
>>> 0.2 + 0.2 + 0.2 == 0.6 False >>> 1.3 + 2.0 == 3.3 False >>> 1.2 + 2.4 + 3.6 == 7.2 False
Проблема также не ограничивается сравнением равенства:
>>> 0.1 + 0.2 <= 0.3 False >>> 10.4 + 20.8 > 31.2 True >>> 0.8 - 0.1 > 0.7 True
Так что же происходит? Ваш компьютер обманывает вас? Похоже на то, но под поверхностью происходит нечто большее.
Когда вы вводите число 0.1 в интерпретатор Python, оно сохраняется в памяти как число с плавающей точкой. При этом происходит преобразование. 0,1 — это десятичная дробь по основанию 10, но числа с плавающей точкой хранятся в двоичном формате. Другими словами, 0,1 преобразуется из основания 10 в основание 2.
Полученное двоичное число может не точно представлять исходное число по основанию 10. 0,1 — один из примеров. Двоичное представление 0.000111. То есть, 0,1 является бесконечно повторяющейся десятичной дробью при записи по основанию 2. То же самое происходит, когда вы записываете дробь ⅓ в виде десятичной дроби по основанию 10. В итоге вы получаете бесконечно повторяющуюся десятичную дробь 0.33.
Память компьютера ограничена, поэтому бесконечно повторяющееся двоичное дробное представление 0,1 округляется до конечной дроби. Значение этого числа зависит от архитектуры вашего компьютера (32-битная или 64-битная). Один из способов увидеть значение с плавающей точкой, которое хранится для 0,1, — использовать метод .as_integer_ratio() для плавающих чисел, чтобы получить числитель и знаменатель представления с плавающей точкой:
>>> numerator, denominator = (0.1).as_integer_ratio()
>>> f"0.1 ≈ {numerator} / {denominator}"
'0.1 ≈ 3602879701896397 / 36028797018963968'
Теперь используйте format(), чтобы показать дробь с точностью до 55 знаков после запятой:
>>> format(numerator / denominator, ".55f") '0.1000000000000000055511151231257827021181583404541015625'
Поэтому 0,1 округляется до числа, которое немного больше его истинного значения.
Эта ошибка, известная как ошибка представления с плавающей точкой (floating-point representation error), случается гораздо чаще, чем вы можете себе представить.
Ошибка репрезентативности действительно распространена
Существует три причины, по которым число округляется при представлении в виде числа с плавающей точкой:
- Число имеет больше значащих цифр, чем позволяет плавающая точка.
- Число иррационально.
- Число рационально, но имеет нетерминированное двоичное представление.
64-битные числа с плавающей точкой имеют 16 или 17 значащих цифр. Любое число с большим количеством значащих цифр округляется. Иррациональные числа, такие как π и e, не могут быть представлены ни одной конечной дробью ни в одной целочисленной базе. Поэтому, опять же, несмотря ни на что, иррациональные числа будут округляться при хранении в виде плавающих чисел.
Эти две ситуации создают бесконечное множество чисел, которые нельзя точно представить в виде числа с плавающей запятой. Но если вы не химик, имеющий дело с крошечными числами, или физик, имеющий дело с астрономически большими числами, вы вряд ли столкнетесь с этими проблемами.
А как насчет рациональных чисел без конца, например, 0,1 в основании 2? Именно здесь вы столкнетесь с большинством проблем с плавающей запятой, а благодаря математике, определяющей, заканчивается ли дробь, вы столкнетесь с ошибкой представления чаще, чем вы думаете.
В основании 10 дробь конечна, если ее знаменатель является произведением степеней простых множителей 10.
Два простых множителя 10 это 2 и 5, поэтому дроби ½, ¼, ⅕, ⅛ и ⅒ все конечны, а ⅓, ⅐ и ⅑ — нет. Однако в основании 2 есть только один простой множитель — 2. Поэтому только дроби, знаменатель которых равен степени 2, имеют конечный результат. В результате дроби типа ⅓, ⅕, ⅙, ⅐, ⅑ и ⅒, выраженные в двоичной форме, являются непересекающимися.
Теперь вы можете понять исходный пример в этой статье. 0.1, 0.2 и 0.3 округляются при преобразовании в числа с плавающей точкой:
>>> # -----------vvvv Display with 17 significant digits >>> format(0.1, ".17g") '0.10000000000000001' >>> format(0.2, ".17g") '0.20000000000000001' >>> format(0.3, ".17g") '0.29999999999999999'
При сложении 0,1 и 0,2 получается число, немного большее, чем 0,3:
>>> 0.1 + 0.2 0.30000000000000004
Поскольку 0,1 + 0,2 немного больше, чем 0,3, а 0,3 представляется числом, которое немного меньше его самого, выражение 0,1 + 0,2 == 0,3 имеет значение False.
Как сравнивать плавающие числа в Python
Как же бороться с ошибками представления с плавающей точкой при сравнении плавающих чисел в Python? Хитрость заключается в том, чтобы избежать проверки равенства. Никогда не используйте ==, >= или <= с плавающей точкой. Вместо этого используйте функцию math.isclose():
>>> import math >>> math.isclose(0.1 + 0.2, 0.3) True
math.isclose() проверяет, близок ли первый аргумент ко второму. Но что именно это значит? Основная идея заключается в том, чтобы проверить расстояние между первым и вторым аргументом, которое эквивалентно абсолютному значению разности этих величин:
>>> a = 0.1 + 0.2 >>> b = 0.3 >>> abs(a - b) 5.551115123125783e-17
Если abs(a — b) меньше некоторого процента от большего из a или b, то a считается достаточно близким к b, чтобы быть «равным» b. Этот процент называется относительным допуском.
Вы можете указать относительный допуск с помощью аргумента rel_tol ключевого слова math.isclose(), который по умолчанию равен 1e-9. Другими словами, если abs(a — b) меньше 1e-9 * max(abs(a), abs(b)), то a и b считаются «близкими» друг к другу. Это гарантирует, что a и b равны примерно до девяти знаков после запятой.
При необходимости вы можете изменить относительный допуск:
>>> math.isclose(0.1 + 0.2, 0.3, rel_tol=1e-20) False
Конечно, относительный допуск зависит от ограничений, установленных решаемой вами задачей. Однако для большинства повседневных приложений достаточно относительного допуска по умолчанию.
Однако существует проблема, если одно из a или b равно нулю, а rel_tol меньше единицы. В этом случае, как бы близко ненулевое значение ни было к нулю, относительный допуск гарантирует, что проверка на близость всегда будет неудачной. В этом случае использование абсолютного допуска работает как запасной вариант:
>>> # Relative check fails! >>> # ---------------vvvv Relative tolerance >>> # ----------------------vvvvv max(0, 1e-10) >>> abs(0 - 1e-10) < 1e-9 * 1e-10 False >>> # Absolute check works! >>> # ---------------vvvv Absolute tolerance >>> abs(0 - 1e-10) < 1e-9 True
math.isclose() выполнит эту проверку автоматически. Аргумент ключевого слова abs_tol определяет абсолютный допуск. Однако по умолчанию abs_tol равен 0.0, поэтому вам придется задать его вручную, если вам нужно проверить, насколько близко значение к нулю.
В целом, math.isclose() возвращает результат следующего сравнения, которое объединяет относительный и абсолютный тесты в одно выражение:
abs(a - b) <= max(rel_tol * max(abs(a), abs(b)), abs_tol)
math.isclose() была введена в PEP 485 и доступна с Python 3.5.
Когда следует использовать math.isclose()?
В целом, следует использовать math.isclose() всякий раз, когда вам нужно сравнить значения с плавающей точкой. Замените == на math.isclose():
>>> # Don't do this: >>> 0.1 + 0.2 == 0.3 False >>> # Do this instead: >>> math.isclose(0.1 + 0.2, 0.3) True
Также нужно быть осторожным со сравнениями >= и <=. Обработайте равенство отдельно с помощью math.isclose(), а затем проверьте строгое сравнение:
>>> a, b, c = 0.1, 0.2, 0.3 >>> # Don't do this: >>> a + b <= c False >>> # Do this instead: >>> math.isclose(a + b, c) or (a + b < c) True
Существуют различные альтернативы math.isclose(). Если вы используете NumPy, вы можете использовать numpy.allclose() и numpy.isclose():
>>> import numpy as np >>> # Use numpy.allclose() to check if two arrays are equal >>> # to each other within a tolerance. >>> np.allclose([1e10, 1e-7], [1.00001e10, 1e-8]) False >>> np.allclose([1e10, 1e-8], [1.00001e10, 1e-9]) True >>> # Use numpy.isclose() to check if the elements of two arrays >>> # are equal to each other within a tolerance >>> np.isclose([1e10, 1e-7], [1.00001e10, 1e-8]) array([ True, False]) >>> np.isclose([1e10, 1e-8], [1.00001e10, 1e-9]) array([ True, True])
Имейте в виду, что относительные и абсолютные допуски по умолчанию не совпадают с math.isclose(). Относительный допуск по умолчанию для numpy.allclose() и numpy.isclose() равен 1e-05, а абсолютный допуск по умолчанию для обоих вариантов равен 1e-08.
Метод math.isclose() особенно полезен для модульных тестов, хотя есть и альтернативы. Встроенный в Python модуль unittest имеет метод unittest.TestCase.assertAlmostEqual(). Однако этот метод использует только тест на абсолютное различие. Кроме того, это утверждение, а значит, при сбоях возникает ошибка AssertionError, что делает его непригодным для сравнений в вашей бизнес-логике.
Отличной альтернативой math.isclose() для модульного тестирования является функция pytest.approx() из пакета pytest. В отличие от math.isclose(), pytest.approx() принимает только один аргумент — ожидаемое значение:
>>> import pytest >>> 0.1 + 0.2 == pytest.approx(0.3) True
pytest.approx() имеет ключевые аргументы rel_tol и abs_tol для установки относительных и абсолютных допусков. Однако значения по умолчанию отличаются от math.isclose(). rel_tol по умолчанию имеет значение 1e-6, а abs_tol по умолчанию имеет значение 1e-12.
Если аргумент, переданный в pytest.approx(), является массивоподобным, то есть это итерабельность Python, например, список или кортеж, или даже массив NumPy, то pytest.approx() ведет себя аналогично numpy.allclose() и возвращает, равны ли два массива в пределах допусков:
>>> import numpy as np >>> np.array([0.1, 0.2]) + np.array([0.2, 0.4]) == pytest.approx(np.array([0.3, 0.6])) True
pytest.approx() будет работать даже со словарными значениями:
>>> {'a': 0.1 + 0.2, 'b': 0.2 + 0.4} == pytest.approx({'a': 0.3, 'b': 0.6})
True
Числа с плавающей точкой отлично подходят для работы с числами, когда не требуется абсолютная точность. Они быстрые и занимают мало памяти. Но если вам нужна точность, то следует рассмотреть некоторые альтернативы плавающим числам.
Точные альтернативы с плавающей точкой
В Python есть два встроенных числовых типа, которые обеспечивают полную точность в ситуациях, когда плавающие числа не подходят: Decimal и Fraction.
Тип Decimal может хранить десятичные значения с той точностью, которая вам необходима. По умолчанию Decimal сохраняет 28 значащих цифр, но вы можете изменить это значение на любое необходимое для решения конкретной задачи:
>>> # Import the Decimal type from the decimal module
>>> from decimal import Decimal
>>> # Values are represented exactly so no rounding error occurs
>>> Decimal("0.1") + Decimal("0.2") == Decimal("0.3")
True
>>> # By default 28 significant figures are preserved
>>> Decimal(1) / Decimal(7)
Decimal('0.1428571428571428571428571429')
>>> # You can change the significant figures if needed
>>> from decimal import getcontext
>>> getcontext().prec = 6 # Use 6 significant figures
>>> Decimal(1) / Decimal(7)
Decimal('0.142857')
Подробнее о типе Decimal можно прочитать в документации Python.
Тип дроби
Другой альтернативой числам с плавающей точкой является тип Fraction. Дробь может точно хранить рациональные числа и преодолевает проблемы ошибок представления, с которыми сталкиваются числа с плавающей точкой:
>>> # import the Fraction type from the fractions module >>> from fractions import Fraction >>> # Instantiate a Fraction with a numerator and denominator >>> Fraction(1, 10) Fraction(1, 10) >>> # Values are represented exactly so no rounding error occurs >>> Fraction(1, 10) + Fraction(2, 10) == Fraction(3, 10) True
Дробные и десятичные числа обладают многочисленными преимуществами по сравнению со стандартными значениями с плавающей точкой. Однако за эти преимущества приходится платить: снижение скорости и увеличение потребления памяти. Если вам не нужна абсолютная точность, лучше остановиться на плавающей точке. Но для таких задач, как финансовые и критически важные приложения, компромисс между дробью и десятичной дробью может оказаться оправданным.
Заключение
Значения с плавающей точкой — это одновременно и преимущество, и недостаток. Они обеспечивают быстрое выполнение арифметических операций и эффективное использование памяти ценой неточного представления. В этой статье вы узнали:
- Почему числа с плавающей точкой являются неточными
- Почему часто встречаются ошибки представления чисел с плавающей точкой
- Как правильно сравнивать значения с плавающей точкой в Python
- Как точно представлять числа с помощью типов Python Fraction и Decimal
Возможно вам будет интересно:
Алгоритмы сортировки 26 видов
Алгоритмы и структуры данных на Python
100+ сложных упражнений по программированию на Python
Пытаюсь решать задачку на python, 9 тестов на ОК но на 10м тесте выдает PE (Presentation Error). Какая может быть ошибка здесь?
У Саши и Даши есть карточки с цифрами. На каждой карточке написана ровно одна цифра. При этом у каждого из ребят может быть несколько карточек с одной и той же цифрой. Также может быть, что у кого-то нет ни одной карточки с какой-то цифрой.
Ребята хотят показать одно и то же число с помощью своих карточек (без ведущих нулей). Из всех чисел, которые они могут показать вместе, они хотят показать максимальное. Какое число покажут Саша и Даша?
Формат входных данных
В первой строке вводится набор цифр на карточках Саши без пробелов.
Во второй строке вводится набор цифр на карточках Даши без пробелов.
Гарантируется, что количество карточек у Саши и Даши по отдельности не превосходит 100000.
Формат выходных данных
Выведите максимальное число, которые могут показать Саша и Даша вместе с помощью своих карточек, без ведущих нулей. Если они не могут одновременно показать одно и то же число, то выведите −1.
входные данные
выходные данные
1)
280138
798081
8810
2)
123
456
-1
a = int(input())
b = int(input())
maxx = list(str(max(a, b)))
minn = list(str(min(a, b)))
lst = []
lst1 = []
for i in maxx:
if i in minn:
lst.append(i)
minn.remove(i)
lst1= sorted(lst, key=int, reverse=True)
if lst1:
print(*lst1, sep='',end="\n")
else:
print(-1)
Числа с плавающей точкой представлены в компьютерах в виде двоичных дробей. Например, десятичная дробь 0.125 имеет значение 1/10 + 2/100 + 5/1000, и таким же образом двоичная дробь 0.001 имеет значение 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковые значения, единственное реальное отличие состоит в том, что первая записана в дробной записи с основанием 10, а вторая — с основанием 2.
Сначала проблему легче понять из базы 10. Рассмотрим дробь 1/3. Вы можете приблизить это как основную 10 фракцию: 0.3 или лучше, 0.33или лучше, 0.333 и так далее. Независимо от того, сколько цифр вы хотите записать, результат никогда не будет ровно 1/3, но будет все более приближенным к 1/3.
Таким же образом, независимо от того, сколько цифр из 2-х оснований вы хотите использовать, десятичное значение 0,1 не может быть представлено в точности как дробь из 2-х оснований. В базе 2 1/10 — бесконечно повторяющаяся дробь 0.0001100110011001100110011...
Остановитесь на любом конечном количестве битов, и вы получите приближение. На большинстве современных машин числа с плавающей запятой аппроксимируются с использованием двоичной дроби, а числитель использует первые 53 бита, начиная с самого старшего бита, а знаменатель — как степень двух. В случае 1/10 двоичная дробь равна 3602879701896397/2 ** 55, что близко, но не точно равно истинному значению 1/10.
Многие пользователи не знают о приближении из-за способа отображения значений. Python печатает только десятичное приближение к истинному десятичному значению двоичного приближения, хранящегося на машине. На большинстве машин, если бы Python должен был печатать истинное десятичное значение двоичного приближения, хранящегося для 0.1, он должен был бы отображать
>>> 0.1 # 0.1000000000000000055511151231257827021181583404541015625
Это больше цифр, чем большинство людей считают полезным, поэтому Python сохраняет количество цифр управляемым, отображая округленное значение вместо
Просто помните, что хотя напечатанный результат выглядит как точное значение 1/10, фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Интересно, что существует много разных десятичных чисел, которые имеют одну и ту же ближайшую приблизительную двоичную дробь. Например, числа 0.1 и 0.10000000000000001 и 0.1000000000000000055511151231... все приблизительно равны 3602879701896397/2 ** 55. Поскольку все эти десятичные значения имеют одинаковую аппроксимацию, любое из них может отображаться при сохранении инварианта eval(repr(x)) == x.
Исторически Python и встроенная функция repr() выбирали функцию с 17 значащими цифрами, 0.10000000000000001. Начиная с Python 3.1 в большинстве систем теперь может выбирать самый короткий из них и просто отображать 0.1.
Обратите внимание, что это по своей природе двоичное число с плавающей точкой: это не ошибка в Python и не ошибка в вашем коде. Вы увидите то же самое на всех языках, которые поддерживают арифметику с плавающей запятой.
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного числа значащих цифр:
>>> import math >>> format(math.pi, '.12g') # '3.14159265359' >>> format(math.pi, '.2f') # '3.14' >>> repr(math.pi) # '3.141592653589793'
Важно понимать, что в действительности это иллюзия: вы просто округляете отображение истинного значения.
Одна иллюзия может породить другую. Например, поскольку 0,1 не является точно 1/10, суммирование трех значений 0,1 может также не дать точно 0,3:
>>> 0.1 + 0.1 + 0.1 == 0.3 # False
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10, а 0,3 не может приблизиться к точному значению 3/10, предварительное округление функцией round() может не помочь:
>>> round(0.1, 1) + round(0.1, 1) + round(0.1, 1) == round(0.3, 1) # False
Двоичная арифметика с плавающей точкой содержит много сюрпризов, подобных этому. Проблема с 0.1 подробно объясняется в разделе «Ошибка представления». Смотрите также «Опасности с плавающей точкой» для более полного описания других распространенных сюрпризов.
Как говорится, «простых ответов нет». Тем не менее, не следует чрезмерно опасаться чисел с плавающей запятой! Ошибки в операциях с плавающей запятой Python наследуются от аппаратного обеспечения чисел с плавающей запятой, и на большинстве машин они имеют порядок не более одной части в 2 ** 53 на операцию. Это более чем достаточно для большинства задач, но вам нужно помнить, что это не десятичная арифметика и что каждая операция с плавающей запятой может подвергаться новой ошибке округления.
Несмотря на то, что патологические случаи существуют, для наиболее случайного использования арифметики с плавающей запятой вы увидите ожидаемый результат в конце, если просто округлите отображение окончательных результатов до ожидаемого количества десятичных цифр. str() обычно достаточно, и для более точного управления смотрите спецификаторы формата метода str.format().
Для случаев использования, которые требуют точного десятичного представления, попробуйте использовать модуль decimal, который реализует десятичную арифметику, подходящую для приложений бухгалтерского учета и высокоточных приложений.
Другая форма точной арифметики поддерживается модулем fractions, который реализует арифметику, основанную на рациональных числах, поэтому числа, такие как 1/3 могут быть представлены точно.
Если вы большой пользователь операций с плавающей запятой, вам следует взглянуть на пакет Numeric Python и многие другие пакеты для математических и статистических операций, предоставляемых проектом SciPy.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно хотите узнать точное значение числа с плавающей точкой. Метод float.as_integer_ratio() выражает значение типа float в виде дроби:
>>> x = 3.14159 >>> x.as_integer_ratio() # (3537115888337719, 1125899906842624)
Поскольку отношение является точным, оно может быть использовано для воссоздания исходного значения без потерь:
>>> x == 3537115888337719 / 1125899906842624 # True
Метод float.hex() выражает число с плавающей запятой в шестнадцатеричном формате (основание 16), снова давая точное значение, сохраненное компьютером:
>>> x.hex() # '0x1.921f9f01b866ep+1'
Это точное шестнадцатеричное представление может быть использовано для точного восстановления значения с плавающей точкой:
>>> x == float.fromhex('0x1.921f9f01b866ep+1') True
Поскольку представление является точным, оно полезно для надежного переноса значений между различными версиями Python и обмена данными с другими языками, поддерживающими тот же формат, например Java.
Другим полезным инструментом является функция math.fsum(), которая помогает уменьшить потерю точности во время суммирования. Она отслеживает «потерянные цифры», когда значения добавляются в промежуточный итог. Это может повлиять на общую точность, так что ошибки не накапливаются до такой степени, что бы влиять на итоговую сумму:
>>> import math >>> sum([0.1] * 10) == 1.0 False >>> math.fsum([0.1] * 10) == 1.0 True
Ошибка представления.
В этом разделе подробно объясняется пример 0.1 и показано, как вы можете выполнить точный анализ подобных случаев самостоятельно. Предполагается базовое знакомство с двоичным представлением чисел с плавающей точкой.
Ошибка представления относится к тому факту, что фактически большинство десятичных дробей не могут быть представлены точно как двоичные дроби (основание 2) . Это главная причина, почему Python или Perl, C, C++, Java, Fortran и многие другие языки часто не будут отображать точное десятичное число, которое ожидаете.
Это почему? 1/10 не совсем представимо в виде двоичной дроби. Почти все машины сегодня используют арифметику IEEE-754 с плавающей точкой, и почти все платформы отображают плавающие значения Python в IEEE-754 с «двойной точностью». При вводе, компьютер стремится преобразовать 0,1 в ближайшую дробь по форме J / 2 ** N, где J — целое число, содержащее ровно 53 бита.
Перепишем 1 / 10 ~= J / (2**N) как J ~= 2**N / 10 и напоминая, что J имеет ровно 53 бита, это >= 2**52, но < 2**53, наилучшее значение для N равно 56:
>>> 2**52 <= 2**56 // 10 < 2**53 # True
То есть 56 — единственное значение для N, которое оставляет J точно с 53 битами. Наилучшее возможное значение для J тогда будет округлено:
>>> q, r = divmod(2**56, 10) >>> r # 6
Поскольку остаток больше половины от 10, наилучшее приближение получается округлением вверх:
>>> q+1 # 7205759403792794
Поэтому наилучшее возможное приближение к 1/10 при двойной точности 754: 7205759403792794 / 2 ** 56. Деление числителя и знаменателя на два уменьшает дробь до: 3602879701896397 / 2 ** 55
Обратите внимание, поскольку мы округлили вверх, то значение на самом деле немного больше, чем 1/10. Если бы мы не округлили, то значение был бы немного меньше 1/10. Но ни в коем случае это не может быть ровно 1/10!
Таким образом, компьютер никогда не «видит» 1/10: то, что он видит, это точная дробь, указанная выше, наилучшее двоичное приближение 754, которое он может получить:
>>> 0.1 * 2 ** 55 # 3602879701896397.0
Если мы умножим эту дробь на 10 ** 55, мы увидим значение до 55 десятичных цифр:
>>> 3602879701896397 * 10 ** 55 // 2 ** 55 # 1000000000000000055511151231257827021181583404541015625
Это означает, что точное число, хранящееся в компьютере, равно десятичному значению полученному выше. Вместо отображения полного десятичного значения многие языки, включая более старые версии Python округляют результат до 17 значащих цифр:
>>> format(0.1, '.17f') '0.10000000000000001'
>>> from decimal import Decimal >>> from fractions import Fraction >>> Fraction.from_float(0.1) # Fraction(3602879701896397, 36028797018963968) >>> (0.1).as_integer_ratio() # (3602879701896397, 36028797018963968) >>> Decimal.from_float(0.1) # Decimal('0.1000000000000000055511151231257827021181583404541015625') >>> format(Decimal.from_float(0.1), '.17') # '0.10000000000000001'
Содержание
- 1 Общий принцип
- 2 Ввод и вывод данных
- 3 Тестирование решений
- 3.1 CE — Ошибка компиляции (Compilation Error)
- 3.2 TLE — Нарушен предел времени (Time Limit Exceeded)
- 3.3 ILE — Нарушен предел ожидания (Idleness Limit Exceeded)
- 3.4 MLE — Нарушен предел памяти (Memory Limit Exceeded)
- 3.5 RTE — Ошибка во время выполнения (Run-time Error)
- 3.6 PE — Ошибка представления (Presentation Error)
- 3.7 WA — Неправильный ответ (Wrong Answer)
- 3.8 OK — Принято (Accepted)
- 3.9 CF — Ошибка тестирования (Check Failed)
- 3.10 SV — Нарушение безопасности (Security Violation)
- 4 Особенности языков программирования
- 4.1 Выбор языка программирования
- 5 Конфигурация тестирующего сервера
- 6 Языки программирования
Общий принцип
В систему посылаются только файлы с исходным кодом, а сама посылаемая программа должна состоять только из одного файла: *.dpr, *.cpp, *.java, *.pas и т. д. Нельзя отправить в систему скомпилированный exe-файл, файл проекта Visual Studio и т. п.
В решениях запрещается:
- осуществлять доступ к сети;
- выполнять любые операции ввода/вывода, кроме открывания, закрывания, чтения и записи стандартных потоков stdin, stdout, stderr и файлов с именами, явно прописанными в условии задачи;
- сознательно «ломать» тестирующую систему;
- выполнять другие программы и порождать новые процессы;
- изменять права доступа к файловой системе;
- работать с поддиректориями;
- создавать и манипулировать ресурсами GUI (окна, диалоговые сообщения и т. д.);
- работать со внешними устройствами (звук, принтер и т. д.);
- выполнять прочие действия, призванные нарушить ход учебного процесса.
Решения выполняются в специальном окружении, обеспечивающем безопасный запуск, и попытка выполнить какие-либо из указанных действий закончится, скорее всего, получением вердикта «Ошибка во время выполнения».
Ввод и вывод данных
Во всех задачах необходимо считывать входные данные из текстового файла и выводить результат в текстовый файл. Имена файлов указаны в условии задачи. Предполагается, что файлы располагаются в текущем каталоге программы, поэтому в решениях можно и нужно использовать только их имена без абсолютных путей в файловой системе тестирующего сервера.
Можно считать, что изначально при запуске решения выходной файл будет отсутствовать, и решение должно его создать и записать туда ответ.
Внимательно проверяйте имена файлов в решениях на соответствие условию задачи.
Если в коде решения имена файлов указаны неверно, это может приводить к непредсказуемым последствиям. Так, если имя выходного файла указано неверно и требуемый по условию файл не создаётся, система, скорее всего, выдаст вердикт «Ошибка представления».
В случае, когда в решении на Java перепутано имя входного файла и делается попытка открыть несуществующий файл, выбрасывается исключение. Если автор решения не перехватывает его, программа завершается с вердиктом «Ошибка во время выполнения». Если же исключение обрабатывается, то вполне возможны и другие вердикты в зависимости от того, отработает ли программа и что окажется в выходном файле. Если в решении на C++ неправильно указан входной файл и ошибки специально не обрабатываются, чтение из файла может приводить к чтению произвольных данных («мусора»). Если в программе вместо чтения из файла делается попытка считать данные со стандартного ввода (stdin, который обычно связан с клавиатурой консоли), программа заблокируется («повиснет») в ожидании ввода и будет завершена с вердиктом «Превышен предел времени».
Решение может выводить произвольные данные «в консоль», то есть в стандартные потоки stdout, stderr, которые обычно связаны с консольным окном (например для отладки). Это не запрещается и не влияет на результат. Проверяется только содержимое выходного файла. Следует помнить, что на вывод тратится дополнительное время, поэтому большой объём отладочной информации может критически замедлить вашу программу. Вывод в stderr медленнее, чем в stdout, поскольку не буферизируется.
Тестирование решений
Каждое отправленное решение проходит на сервере проверку на нескольких тестах. Задача считается решённой только в случае прохождения всех тестов. Решение запускается на всех тестах, которые есть по задаче, и процесс тестирования не прерывается на первом непройденном тесте, как это делается в соревнованиях типа ACM.
Тестирование осуществляется автоматически, поэтому решения должны строго следовать формату входных и выходных данных, который описан в условии. В случае неясности можно задавать вопросы преподавателям. Если не сказано явно, все входные данные можно считать корректными и удовлетворяющими ограничениям из условия. Например, если сказано, что на входе целое число от 1 до 100 включительно, то можно считать, что это так и есть, и проверять неравенства и выводить ошибку в случае, если это не так, в коде решения нет необходимости.
Тесты по каждой задаче не упорядочены по сложности, по размеру входных данных, по какому-то иному критерию, а следуют в исторически сложившемся порядке их добавления в систему.
Не гарантируется, что первый тест в системе будет совпадать с тестом из условия (зачастую это не так).
Результатом проверки является итоговое сообщение системы и, возможно, в скобках номер первого теста, вызвавшего ошибку (если таковая имела место). Например, вердикт «Неправильный ответ (43)» означает, что решение успешно скомпилировалось и прошло без ошибок первые 42 теста по задаче, но на тесте под номером 43 выдало неверный ответ.
Далее опишем все допустимые сообщения тестирующей системы и укажем возможные причины их появления.
CE — Ошибка компиляции (Compilation Error)
Не удалось скомпилировать решение и получить исполняемый файл для запуска. Решение в таком случае, очевидно, не может быть проверено ни на одном тесте.
Посмотреть вывод компилятора и понять, почему код не удаётся скомпилировать, можно путём нажатия на иконку в таблице с вашими решениями. Наиболее частые причины ошибки компиляции: выбран неверный компилятор (для другого языка программирования или же несовместимая версия, например Java v7 вместо Java v8), отправляется не тот файл (файл проекта IDE вместо файла с исходным кодом).
Время работы компилятора ограничено 30 секундами. Если он не успел отработать по каким-либо причинам, также будет выставлен вердикт «Ошибка компиляции».
TLE — Нарушен предел времени (Time Limit Exceeded)
Для каждого теста установлено своё ограничение по времени (Time Limit) в секундах. Для разных тестов по одной задаче ограничение по времени может быть разным.
Тестирующая система учитывает так называемое процессорное время (CPU Time) выполнения процесса в операционной системе. Нет смысла делать решение задачи многопоточным, потому что распараллеливание хоть и позволяет сократить реальное время работы (Wall Time), но не уменьшает процессорное время.
Процесс-решение запускается на тесте, и если процесс не успевает завершиться в течение отведённого времени, он принудительно завершается и выставляется вердикт «Нарушен предел времени». В качестве времени работы решения на тесте указывается то время, которое процесс фактически проработал до того, как был приостановлен. Нет возможности узнать, сколько бы программа проработала, если бы не была снята по времени. Если при ограничении по времени на тест в 1 секунду вы видите, что решение получает вердикт «Нарушен предел времени» и работает 1015 мс, то нельзя это понимать как «решение чуть-чуть не успевает, надо ускорить его на 15 мс». Если решение останавливается по времени, то вывод программы никак не проверяется на предмет его правильности.
Возможные причины появления ошибки «Нарушен предел времени»:
- неэффективный алгоритм (например, в решении реализован алгоритм с временной сложностью Ω(n2), хотя задача предполагает решение за O(n log n));
- недостаточно эффективная программная реализация (идея и алгоритм правильные, но код написан не очень хорошо: например, ввод данных из файла осуществляется медленно, чрезмерно часто выделяется и освобождается память);
- попытка чтения данных с консоли (
std::cin,scanf(),getchar()в C++,System.inв Java), тогда как нужно читать входные данные из файла (в этом случае программа блокируется в ожидании ввода и зависает, не расходуя при этом CPU Time, поэтому такой случай тестирующая система обрабатывает отдельно); - ошибка в программе (например, программа входит в бесконечный цикл).
Не рекомендуется «пропихивать» медленное решение, отправляя его многократно, пока система не «согласится» его принять. Решение в любой момент может быть перетестировано и, соответственно, может перестать быть принятым из-за нарушения предела времени.
ILE — Нарушен предел ожидания (Idleness Limit Exceeded)
Программа зависла в ожидании, не потребляя при этом ресурсы процессора.
Такое может быть, например, если согласно условию чтение входных данных осуществляется из файла, а решение выполняет ввод с консоли. В этом случае процесс решения заблокируется в ожидании нажатия клавиш на клавиатуре. Через некоторое время система тестирования принудительно завершит этот процесс и выставит вердикт ILE.
MLE — Нарушен предел памяти (Memory Limit Exceeded)
Программа использует слишком много оперативной памяти, стоит проанализировать использование памяти и оптимизировать его.
Также причиной чрезмерного использования памяти может быть ошибка в программе, например, вечный цикл в теле которого на каждой или некоторых итерациях выделяется дополнительная память. К используемой памяти относится не только память с данными, но также память с кодом и программным стеком.
Ограничение по памяти есть не для всех задач. Гарантируется, что для всех тестов в рамках одной задачи ограничение по памяти одинаково.
Как и в случае нарушения ограничения по времени, программа при нарушении ограничения по памяти аварийно завершается тестирующей системой, её вывод не проверяется на правильность. Точно так же не следует воспринимать размер памяти, использованной до момента аварийного завершения, как объём, которого решению хватило бы для успешной работы. Более точно, вердикт MLE, полученный с использованием 257 МБ памяти, говорит о том, что приложение успело использовать 257 МБ памяти и было принудительно остановлено, но ничего не говорит о том, сколько памяти использовало бы приложение, не будучи принудительно остановленным.
В некоторых случаях при разовом выделении чрезмерно большого блока в памяти, этот запрос может быть не выполнен операционной системой, что в результате может привести к ошибке во время выполнения или (значительно реже) другому результату неопределённого поведения в случае с языком C++.
RTE — Ошибка во время выполнения (Run-time Error)
В операционной системе есть такое понятие, как код завершения процесса (Exit Code). Этот подход используется как в Windows, так и в ОС семейства UNIX. Это целое число, которое остаётся после прекращения выполнения программы. Общепринятое соглашение гласит, что нулевой код завершения свидетельствует о нормальном завершении процесса без ошибок, любой другой — об ошибке. Тестирующая система проверяет код завершения вашего решения, и если он не равен нулю, выставляет вердикт «Ошибка во время выполнения». При этом никак не проверяется то, что решение успело вывести в выходной файл.
Укажем типичные причины ошибок во время выполнения.
- Использована директива
packageв коде программы на Java.- В результате программа на Java находится не в пакете по умолчанию. Компилятор Java сгенерировал класс в некотором пакете (ошибки компиляции нет), а при запуске виртуальная машина Java не смогла найти этот класс, потому что искала в пакете по умолчанию (возникло исключение
ClassNotFoundExceptionс сообщением Could not find or load main class).
- В результате программа на Java находится не в пакете по умолчанию. Компилятор Java сгенерировал класс в некотором пакете (ошибки компиляции нет), а при запуске виртуальная машина Java не смогла найти этот класс, потому что искала в пакете по умолчанию (возникло исключение
- Выход за границы допустимой области памяти в программе на C++.
- Выход за границы массива, разыменование неправильного указателя, обращение к нулевому указателю.
- Переполнение системного стека.
- Эта причина является частой в случае рекурсии. Вообще, системный стек используется для размещения параметров функций, локальных переменных. Его размер, как правило, невелик и по умолчанию равен 1 МБ. При вызове функции стековая структура позволяет естественным образом сохранить текущие состояния всех локальных переменных и вернуться к ним, когда вызов завершится и управление вернётся в исходную точку. Если в алгоритме используется глубокая рекурсия, то размера стека может не хватить для хранения контекстов всех вызовов. Решений этой проблемы два:
- переписать алгоритм нерекурсивно (например с использованием своего стека, а не системного);
- увеличить размер системного стека, что делается по-разному для разных языков программирования (см. примеры для C++ (Visual Studio) и Java).
- Эта причина является частой в случае рекурсии. Вообще, системный стек используется для размещения параметров функций, локальных переменных. Его размер, как правило, невелик и по умолчанию равен 1 МБ. При вызове функции стековая структура позволяет естественным образом сохранить текущие состояния всех локальных переменных и вернуться к ним, когда вызов завершится и управление вернётся в исходную точку. Если в алгоритме используется глубокая рекурсия, то размера стека может не хватить для хранения контекстов всех вызовов. Решений этой проблемы два:
- Ошибка ввода-вывода (попытка открыть несуществующий входной файл).
- Нужно проверить правильность имени входного файла.
- Программа целенаправленно была завершена с ненулевым кодом выхода.
- В программе на C++ это может быть, если функция
main()в C++ вернула ненулевой код (return (non-zero)в функцииmain()). Рекомендуется завершать функциюmain()операторомreturn 0(в старых компиляторах C++ это обязательно, современные компиляторы же подразумевают возврат нулевого кода автоматически). Также программу на C++ с произвольным кодом завершает вызовexit(). - В программе на Java можно завершить процесс с произвольным кодом с помощью
System.exit().
- В программе на C++ это может быть, если функция
- Необработанное исключение.
- Причин возникновения исключений может быть масса. Например, если в Java функции
Integer.parseInt()/Double.parseDouble()была передана строка, содержащая пробельные символы (ASCII-коды 9, 10, 13, 32), выбрасывается исключениеNumberFormatException.
- Причин возникновения исключений может быть масса. Например, если в Java функции
- Целочисленное деление на ноль.
- При выполнении деления нужно всегда думать, а не может ли делитель оказаться равным нулю. В то же время стоит отметить, что вещественное деление на ноль (в типах с плавающей точкой
double,float) по умолчанию не приводит к завершению программы, а даёт специальные значения+Inf,-InfилиNaN.
- При выполнении деления нужно всегда думать, а не может ли делитель оказаться равным нулю. В то же время стоит отметить, что вещественное деление на ноль (в типах с плавающей точкой
PE — Ошибка представления (Presentation Error)
Наиболее частая причина возникновения этой ошибки — не найден выходной файл. Возможно, вы забыли создать выходной файл и выводите ответ в консоль (он в таком случае игнорируется). Проверьте имена входного и выходного файла в вашей программе на соответствие условию задачи. Исторически сложилось, что в разных задачах входной и выходной файл именуются по разным правилам: input.txt и output.txt, in.txt и out.txt, input.in и output.out (обратите внимание, что нет расширения txt), [задача].in и [задача].out…
Для некоторых задач программа проверки (checker) дополнительно удостоверяется, что ваш вывод соответствует определённому формату, и выдаёт ошибку представления в случае, если это не так. Например, если в задаче нужно вывести число, а вы выводите строку. Или если в задаче нужно вывести сначала число k, затем k чисел, а ваше решение выводит число k и далее (k + 1) чисел (то есть решение выводит в файл лишние данные).
Также имейте в виду, что отлавливание исключений и других ошибок не должно быть самоцелью. Если исключение не обрабатывается каким-либо образом, обычно нет смысла его ловить по следующей причине. Аварийное завершение работы программы в результате ошибки во время выполнения приводит к вердикту «Ошибка во время выполнения», только если соответствующее исключение было «проброшено» наружу, а не «заглушено» на каком-то этапе. Если исключение отлавливается, но никак не обрабатывается, то в результате возникновения соответствующей ошибки следует ожидать вердикт «Ошибка представления» или же «Неправильный ответ» (реже).
WA — Неправильный ответ (Wrong Answer)
Для многих задач ответ однозначен, и проверяется просто побайтовое совпадение вашего выходного файла и сохранённого правильного ответа. Такая проверка требует строгого соблюдения формата файла, не допускает незначащих пробелов и пустых строк. Например, если правильный ответ имеет вид (пробелы обозначены символом ␣)
5 1␣2␣3␣4␣5
и решение вывело
5 1␣2␣3␣4␣5␣
(лишний пробел в конце второй строки), то будет получен вердикт «Неправильный ответ». Для некоторых задач написаны проверяющие программы (checker), которые к таким различиям лояльны и засчитывают ответы с лишними пробелами как правильные. Всегда точно следуйте формату файла и не выводите лишних пробелов, и проблем не будет.
После последней строки файла можно выводить или не выводить перевод строки — не важно. Есть две точки зрения в зависимости от того, с какой стороны смотреть на символ перевода строки:
- каждая строка завершается переводом строки, поэтому
nв конце файла нужен; - перевод строки является разделителем между соседними строками, поэтому
nв конце файла не нужен.
Первая точка зрения является общепринятой. Так, компилятор gcc, система контроля версий git и многие другие программы выдают предупреждение no newline at the end of file, если в самом конце файла нет символов новой строки. Обсуждение вопроса можно почитать на stackoverflow.
Поэтому рекомендуется придерживаться первого подхода и завершать все строки переводами строк.
Другие очевидные причины получения неправильного ответа:
- неверный алгоритм;
- ошибка в программе.
Бывает такое, что решение от запуска к запуску даёт разные ответы, или же правильно работает на одном компьютере и неправильно на другом. Такие случаи, как правило, связаны с ошибками в решениях.
OK — Принято (Accepted)
Программа работает правильно и прошла все тесты с соблюдением всех ограничений.
Если решение принято системой, это ещё не означает, что в его основе лежит правильный алгоритм. В любой момент могут появиться новые наборы входных данных, на которых будут заново протестированы все решения по задаче. Если ваше решение на самом деле не полностью верно и прошло только из-за недостаточно сильного набора тестов, оно может в будущем потерять статус «Принято».
CF — Ошибка тестирования (Check Failed)
Если указан номер теста, то программа успешно завершается на предложенном тесте (укладывается в отведённые время и память и не совершает ошибок во время выполнения), но результат не удаётся проверить из-за ошибок в программе проверки. Вашей ошибки в этом случае, возможно, никакой нет и после исправления программы проверки будет получен вердикт OK. Не исключены ещё два варианта: WA, PE.
Имейте в виду, что если ошибка тестирования возникает на первом же тесте, то на остальных Ваше решение не запускается вовсе. Соответственно, в этом случае после устранения ошибок программы проверки вердикты TLE, MLE, RTE также могут возникнуть в любом тесте, кроме первого.
Если же номер теста, на котором возникает ошибка тестирования, не указан, значит, программа проверки не была скомпилирована, а Ваше решение не запускалось вовсе. В этом случае правильным может быть любой вердикт, отличный от CF.
Если у Вас возникла ошибка тестирования, мы, скорее всего, это заметим достаточно быстро. Тем не менее, имеет смысл задать вопрос через пункт «Сообщения» в меню курса. Не забывайте выбрать задачу, которой касается этот вопрос.
SV — Нарушение безопасности (Security Violation)
Ошибка означает, что программа попыталась выполнить запрещённые действия.
К их числу относится попытка создания новых процессов. Вашим решениям запрещено запускать на выполнение другие программы. Например, в коде
порождается новый процесс командной оболочки cmd.exe и в нём выполняется команда pause. Пожалуйста, не пишите так, для достижения аналогичного эффекта можно использовать другие приёмы.
Особенности языков программирования
У каждого конкретного языка программирования есть свои особенности, о которых полезно знать. Далее рассмотрены отдельные особенности написания решений на разных языках программирования:
- C++;
- Java;
- C#;
- Python.
Выбор языка программирования
Разные задачи можно решать на разных языках. Часто для конкретной задачи тот или иной язык оказывается предпочтительным. Например, если в задаче требуются тяжёлые вычисления, то её может быть проще сдать на C++, чем на Java, за счёт более быстрой работы программы на C++ (для кода на Java могут потребоваться более изощрённые оптимизации, чтобы он прошёл по времени). С другой стороны, если задача требует проведения вычислений с большими целыми числами, выходящими за пределы диапазона 64-битных переменных, то есть «длинной арифметики», то решение существенно проще написать на Java, воспользовавшись готовым качественно написанным классом BigInteger для операций с числами произвольной длины.
Конфигурация тестирующего сервера
Сервер, на котором осуществляется запуск решений, является виртуальной машиной, выполняющейся внутри Microsoft Hyper-V Server 2012 R2. Виртуальный компьютер работает под управлением Windows 7 Professional x64, оснащён процессором Intel® Core™ i3-4130 (Haswell, кэш 3 МБ, 3,40 ГГц, доступно только одно ядро) и 4 ГБ оперативной памяти. Для хранения входных и выходных файлов используется RAM-диск, чтобы обеспечить максимальную производительность ввода-вывода.
Языки программирования
На странице учебного курса в системе на вкладке «Компиляторы» можно ознакомиться с актуальным списком доступных языков программирования, версиями компиляторов и параметрами командной строки их вызова.
Размер системного стека явно не задаётся (используется размер по умолчанию). При компиляции кода на C++ включен режим оптимизации O2.
Обработка ошибок увеличивает отказоустойчивость кода, защищая его от потенциальных сбоев, которые могут привести к преждевременному завершению работы.
Прежде чем переходить к обсуждению того, почему обработка исключений так важна, и рассматривать встроенные в Python исключения, важно понять, что есть тонкая грань между понятиями ошибки и исключения.
Ошибку нельзя обработать, а исключения Python обрабатываются при выполнении программы. Ошибка может быть синтаксической, но существует и много видов исключений, которые возникают при выполнении и не останавливают программу сразу же. Ошибка может указывать на критические проблемы, которые приложение и не должно перехватывать, а исключения — состояния, которые стоит попробовать перехватить. Ошибки — вид непроверяемых и невозвратимых ошибок, таких как OutOfMemoryError, которые не стоит пытаться обработать.
Обработка исключений делает код более отказоустойчивым и помогает предотвращать потенциальные проблемы, которые могут привести к преждевременной остановке выполнения. Представьте код, который готов к развертыванию, но все равно прекращает работу из-за исключения. Клиент такой не примет, поэтому стоит заранее обработать конкретные исключения, чтобы избежать неразберихи.
Ошибки могут быть разных видов:
- Синтаксические
- Недостаточно памяти
- Ошибки рекурсии
- Исключения
Разберем их по очереди.
Синтаксические ошибки (SyntaxError)
Синтаксические ошибки часто называют ошибками разбора. Они возникают, когда интерпретатор обнаруживает синтаксическую проблему в коде.
Рассмотрим на примере.
a = 8
b = 10
c = a b
File "", line 3
c = a b
^
SyntaxError: invalid syntax
Стрелка вверху указывает на место, где интерпретатор получил ошибку при попытке исполнения. Знак перед стрелкой указывает на причину проблемы. Для устранения таких фундаментальных ошибок Python будет делать большую часть работы за программиста, выводя название файла и номер строки, где была обнаружена ошибка.
Недостаточно памяти (OutofMemoryError)
Ошибки памяти чаще всего связаны с оперативной памятью компьютера и относятся к структуре данных под названием “Куча” (heap). Если есть крупные объекты (или) ссылки на подобные, то с большой долей вероятности возникнет ошибка OutofMemory. Она может появиться по нескольким причинам:
- Использование 32-битной архитектуры Python (максимальный объем выделенной памяти невысокий, между 2 и 4 ГБ);
- Загрузка файла большого размера;
- Запуск модели машинного обучения/глубокого обучения и много другое;
Обработать ошибку памяти можно с помощью обработки исключений — резервного исключения. Оно используется, когда у интерпретатора заканчивается память и он должен немедленно остановить текущее исполнение. В редких случаях Python вызывает OutofMemoryError, позволяя скрипту каким-то образом перехватить самого себя, остановить ошибку памяти и восстановиться.
Но поскольку Python использует архитектуру управления памятью из языка C (функция malloc()), не факт, что все процессы восстановятся — в некоторых случаях MemoryError приведет к остановке. Следовательно, обрабатывать такие ошибки не рекомендуется, и это не считается хорошей практикой.
Ошибка рекурсии (RecursionError)
Эта ошибка связана со стеком и происходит при вызове функций. Как и предполагает название, ошибка рекурсии возникает, когда внутри друг друга исполняется много методов (один из которых — с бесконечной рекурсией), но это ограничено размером стека.
Все локальные переменные и методы размещаются в стеке. Для каждого вызова метода создается стековый кадр (фрейм), внутрь которого помещаются данные переменной или результат вызова метода. Когда исполнение метода завершается, его элемент удаляется.
Чтобы воспроизвести эту ошибку, определим функцию recursion, которая будет рекурсивной — вызывать сама себя в бесконечном цикле. В результате появится ошибка StackOverflow или ошибка рекурсии, потому что стековый кадр будет заполняться данными метода из каждого вызова, но они не будут освобождаться.
def recursion():
return recursion()
recursion()
---------------------------------------------------------------------------
RecursionError Traceback (most recent call last)
in
----> 1 recursion()
in recursion()
1 def recursion():
----> 2 return recursion()
... last 1 frames repeated, from the frame below ...
in recursion()
1 def recursion():
----> 2 return recursion()
RecursionError: maximum recursion depth exceeded
Ошибка отступа (IndentationError)
Эта ошибка похожа по духу на синтаксическую и является ее подвидом. Тем не менее она возникает только в случае проблем с отступами.
Пример:
for i in range(10):
print('Привет Мир!')
File "", line 2
print('Привет Мир!')
^
IndentationError: expected an indented block
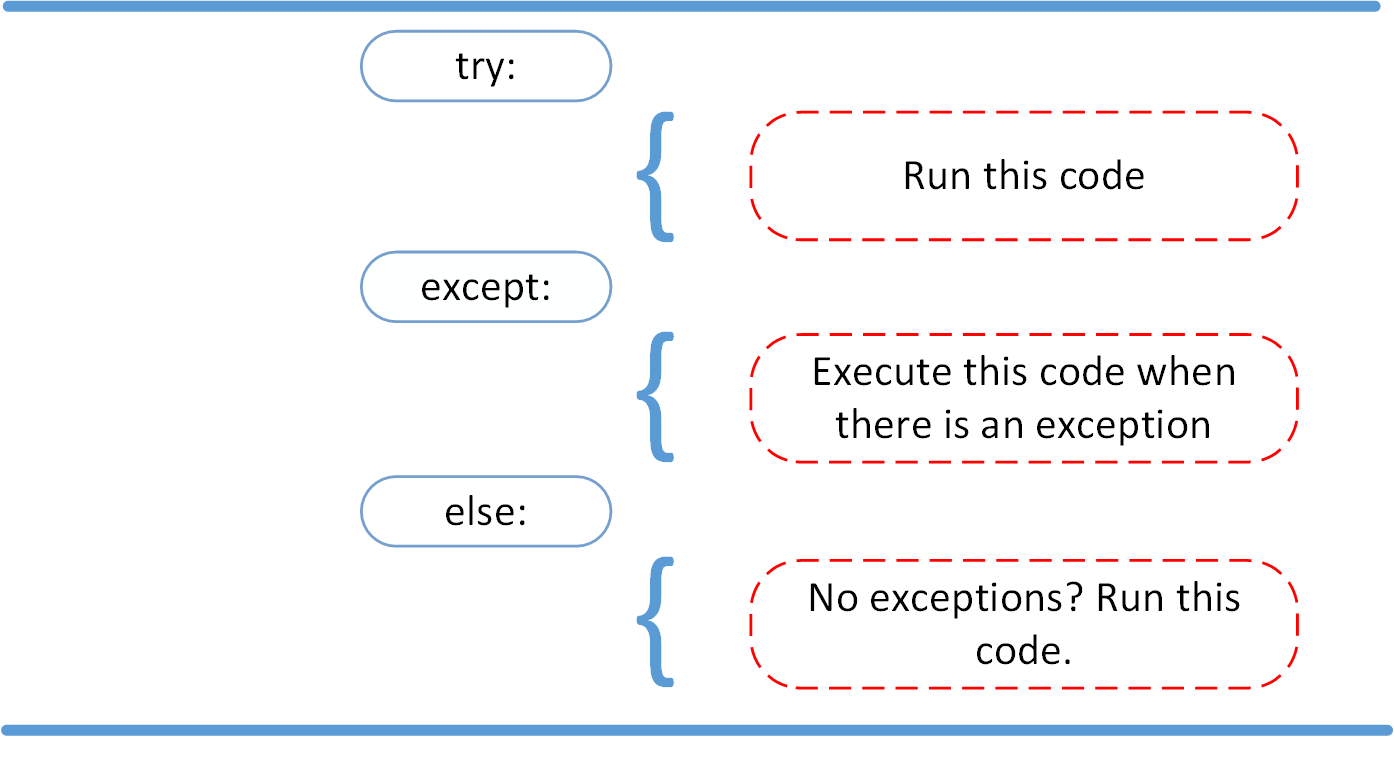
Исключения
Даже если синтаксис в инструкции или само выражение верны, они все равно могут вызывать ошибки при исполнении. Исключения Python — это ошибки, обнаруживаемые при исполнении, но не являющиеся критическими. Скоро вы узнаете, как справляться с ними в программах Python. Объект исключения создается при вызове исключения Python. Если скрипт не обрабатывает исключение явно, программа будет остановлена принудительно.
Программы обычно не обрабатывают исключения, что приводит к подобным сообщениям об ошибке:
Ошибка типа (TypeError)
a = 2
b = 'PythonRu'
a + b
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
in
1 a = 2
2 b = 'PythonRu'
----> 3 a + b
TypeError: unsupported operand type(s) for +: 'int' and 'str'
Ошибка деления на ноль (ZeroDivisionError)
10 / 0
---------------------------------------------------------------------------
ZeroDivisionError Traceback (most recent call last)
in
----> 1 10 / 0
ZeroDivisionError: division by zero
Есть разные типы исключений в Python и их тип выводится в сообщении: вверху примеры TypeError и ZeroDivisionError. Обе строки в сообщениях об ошибке представляют собой имена встроенных исключений Python.
Оставшаяся часть строки с ошибкой предлагает подробности о причине ошибки на основе ее типа.
Теперь рассмотрим встроенные исключения Python.
Встроенные исключения
BaseException
+-- SystemExit
+-- KeyboardInterrupt
+-- GeneratorExit
+-- Exception
+-- StopIteration
+-- StopAsyncIteration
+-- ArithmeticError
| +-- FloatingPointError
| +-- OverflowError
| +-- ZeroDivisionError
+-- AssertionError
+-- AttributeError
+-- BufferError
+-- EOFError
+-- ImportError
| +-- ModuleNotFoundError
+-- LookupError
| +-- IndexError
| +-- KeyError
+-- MemoryError
+-- NameError
| +-- UnboundLocalError
+-- OSError
| +-- BlockingIOError
| +-- ChildProcessError
| +-- ConnectionError
| | +-- BrokenPipeError
| | +-- ConnectionAbortedError
| | +-- ConnectionRefusedError
| | +-- ConnectionResetError
| +-- FileExistsError
| +-- FileNotFoundError
| +-- InterruptedError
| +-- IsADirectoryError
| +-- NotADirectoryError
| +-- PermissionError
| +-- ProcessLookupError
| +-- TimeoutError
+-- ReferenceError
+-- RuntimeError
| +-- NotImplementedError
| +-- RecursionError
+-- SyntaxError
| +-- IndentationError
| +-- TabError
+-- SystemError
+-- TypeError
+-- ValueError
| +-- UnicodeError
| +-- UnicodeDecodeError
| +-- UnicodeEncodeError
| +-- UnicodeTranslateError
+-- Warning
+-- DeprecationWarning
+-- PendingDeprecationWarning
+-- RuntimeWarning
+-- SyntaxWarning
+-- UserWarning
+-- FutureWarning
+-- ImportWarning
+-- UnicodeWarning
+-- BytesWarning
+-- ResourceWarning
Прежде чем переходить к разбору встроенных исключений быстро вспомним 4 основных компонента обработки исключения, как показано на этой схеме.
Try: он запускает блок кода, в котором ожидается ошибка.Except: здесь определяется тип исключения, который ожидается в блокеtry(встроенный или созданный).Else: если исключений нет, тогда исполняется этот блок (его можно воспринимать как средство для запуска кода в том случае, если ожидается, что часть кода приведет к исключению).Finally: вне зависимости от того, будет ли исключение или нет, этот блок кода исполняется всегда.
В следующем разделе руководства больше узнаете об общих типах исключений и научитесь обрабатывать их с помощью инструмента обработки исключения.
Ошибка прерывания с клавиатуры (KeyboardInterrupt)
Исключение KeyboardInterrupt вызывается при попытке остановить программу с помощью сочетания Ctrl + C или Ctrl + Z в командной строке или ядре в Jupyter Notebook. Иногда это происходит неумышленно и подобная обработка поможет избежать подобных ситуаций.
В примере ниже если запустить ячейку и прервать ядро, программа вызовет исключение KeyboardInterrupt. Теперь обработаем исключение KeyboardInterrupt.
try:
inp = input()
print('Нажмите Ctrl+C и прервите Kernel:')
except KeyboardInterrupt:
print('Исключение KeyboardInterrupt')
else:
print('Исключений не произошло')
Исключение KeyboardInterrupt
Стандартные ошибки (StandardError)
Рассмотрим некоторые базовые ошибки в программировании.
Арифметические ошибки (ArithmeticError)
- Ошибка деления на ноль (Zero Division);
- Ошибка переполнения (OverFlow);
- Ошибка плавающей точки (Floating Point);
Все перечисленные выше исключения относятся к классу Arithmetic и вызываются при ошибках в арифметических операциях.
Деление на ноль (ZeroDivisionError)
Когда делитель (второй аргумент операции деления) или знаменатель равны нулю, тогда результатом будет ошибка деления на ноль.
try:
a = 100 / 0
print(a)
except ZeroDivisionError:
print("Исключение ZeroDivisionError." )
else:
print("Успех, нет ошибок!")
Исключение ZeroDivisionError.
Переполнение (OverflowError)
Ошибка переполнение вызывается, когда результат операции выходил за пределы диапазона. Она характерна для целых чисел вне диапазона.
try:
import math
print(math.exp(1000))
except OverflowError:
print("Исключение OverFlow.")
else:
print("Успех, нет ошибок!")
Исключение OverFlow.
Ошибка утверждения (AssertionError)
Когда инструкция утверждения не верна, вызывается ошибка утверждения.
Рассмотрим пример. Предположим, есть две переменные: a и b. Их нужно сравнить. Чтобы проверить, равны ли они, необходимо использовать ключевое слово assert, что приведет к вызову исключения Assertion в том случае, если выражение будет ложным.
try:
a = 100
b = "PythonRu"
assert a == b
except AssertionError:
print("Исключение AssertionError.")
else:
print("Успех, нет ошибок!")
Исключение AssertionError.
Ошибка атрибута (AttributeError)
При попытке сослаться на несуществующий атрибут программа вернет ошибку атрибута. В следующем примере можно увидеть, что у объекта класса Attributes нет атрибута с именем attribute.
class Attributes(obj):
a = 2
print(a)
try:
obj = Attributes()
print(obj.attribute)
except AttributeError:
print("Исключение AttributeError.")
2
Исключение AttributeError.
Ошибка импорта (ModuleNotFoundError)
Ошибка импорта вызывается при попытке импортировать несуществующий (или неспособный загрузиться) модуль в стандартном пути или даже при допущенной ошибке в имени.
import nibabel
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
in
----> 1 import nibabel
ModuleNotFoundError: No module named 'nibabel'
Ошибка поиска (LookupError)
LockupError выступает базовым классом для исключений, которые происходят, когда key или index используются для связывания или последовательность списка/словаря неверна или не существует.
Здесь есть два вида исключений:
- Ошибка индекса (
IndexError); - Ошибка ключа (
KeyError);
Ошибка ключа
Если ключа, к которому нужно получить доступ, не оказывается в словаре, вызывается исключение KeyError.
try:
a = {1:'a', 2:'b', 3:'c'}
print(a[4])
except LookupError:
print("Исключение KeyError.")
else:
print("Успех, нет ошибок!")
Исключение KeyError.
Ошибка индекса
Если пытаться получить доступ к индексу (последовательности) списка, которого не существует в этом списке или находится вне его диапазона, будет вызвана ошибка индекса (IndexError: list index out of range python).
try:
a = ['a', 'b', 'c']
print(a[4])
except LookupError:
print("Исключение IndexError, индекс списка вне диапазона.")
else:
print("Успех, нет ошибок!")
Исключение IndexError, индекс списка вне диапазона.
Ошибка памяти (MemoryError)
Как уже упоминалось, ошибка памяти вызывается, когда операции не хватает памяти для выполнения.
Ошибка имени (NameError)
Ошибка имени возникает, когда локальное или глобальное имя не находится.
В следующем примере переменная ans не определена. Результатом будет ошибка NameError.
try:
print(ans)
except NameError:
print("NameError: переменная 'ans' не определена")
else:
print("Успех, нет ошибок!")
NameError: переменная 'ans' не определена
Ошибка выполнения (Runtime Error)
Ошибка «NotImplementedError»
Ошибка выполнения служит базовым классом для ошибки NotImplemented. Абстрактные методы определенного пользователем класса вызывают это исключение, когда производные методы перезаписывают оригинальный.
class BaseClass(object):
"""Опередляем класс"""
def __init__(self):
super(BaseClass, self).__init__()
def do_something(self):
# функция ничего не делает
raise NotImplementedError(self.__class__.__name__ + '.do_something')
class SubClass(BaseClass):
"""Реализует функцию"""
def do_something(self):
# действительно что-то делает
print(self.__class__.__name__ + ' что-то делает!')
SubClass().do_something()
BaseClass().do_something()
SubClass что-то делает!
---------------------------------------------------------------------------
NotImplementedError Traceback (most recent call last)
in
14
15 SubClass().do_something()
---> 16 BaseClass().do_something()
in do_something(self)
5 def do_something(self):
6 # функция ничего не делает
----> 7 raise NotImplementedError(self.__class__.__name__ + '.do_something')
8
9 class SubClass(BaseClass):
NotImplementedError: BaseClass.do_something
Ошибка типа (TypeError)
Ошибка типа вызывается при попытке объединить два несовместимых операнда или объекта.
В примере ниже целое число пытаются добавить к строке, что приводит к ошибке типа.
try:
a = 5
b = "PythonRu"
c = a + b
except TypeError:
print('Исключение TypeError')
else:
print('Успех, нет ошибок!')
Исключение TypeError
Ошибка значения (ValueError)
Ошибка значения вызывается, когда встроенная операция или функция получают аргумент с корректным типом, но недопустимым значением.
В этом примере встроенная операция float получат аргумент, представляющий собой последовательность символов (значение), что является недопустимым значением для типа: число с плавающей точкой.
try:
print(float('PythonRu'))
except ValueError:
print('ValueError: не удалось преобразовать строку в float: 'PythonRu'')
else:
print('Успех, нет ошибок!')
ValueError: не удалось преобразовать строку в float: 'PythonRu'
Пользовательские исключения в Python
В Python есть много встроенных исключений для использования в программе. Но иногда нужно создавать собственные со своими сообщениями для конкретных целей.
Это можно сделать, создав новый класс, который будет наследовать из класса Exception в Python.
class UnAcceptedValueError(Exception):
def __init__(self, data):
self.data = data
def __str__(self):
return repr(self.data)
Total_Marks = int(input("Введите общее количество баллов: "))
try:
Num_of_Sections = int(input("Введите количество разделов: "))
if(Num_of_Sections < 1):
raise UnAcceptedValueError("Количество секций не может быть меньше 1")
except UnAcceptedValueError as e:
print("Полученная ошибка:", e.data)
Введите общее количество баллов: 10
Введите количество разделов: 0
Полученная ошибка: Количество секций не может быть меньше 1
В предыдущем примере если ввести что-либо меньше 1, будет вызвано исключение. Многие стандартные исключения имеют собственные исключения, которые вызываются при возникновении проблем в работе их функций.
Недостатки обработки исключений в Python
У использования исключений есть свои побочные эффекты, как, например, то, что программы с блоками try-except работают медленнее, а количество кода возрастает.
Дальше пример, где модуль Python timeit используется для проверки времени исполнения 2 разных инструкций. В stmt1 для обработки ZeroDivisionError используется try-except, а в stmt2 — if. Затем они выполняются 10000 раз с переменной a=0. Суть в том, чтобы показать разницу во времени исполнения инструкций. Так, stmt1 с обработкой исключений занимает больше времени чем stmt2, который просто проверяет значение и не делает ничего, если условие не выполнено.
Поэтому стоит ограничить использование обработки исключений в Python и применять его в редких случаях. Например, когда вы не уверены, что будет вводом: целое или число с плавающей точкой, или не уверены, существует ли файл, который нужно открыть.
import timeit
setup="a=0"
stmt1 = '''
try:
b=10/a
except ZeroDivisionError:
pass'''
stmt2 = '''
if a!=0:
b=10/a'''
print("time=",timeit.timeit(stmt1,setup,number=10000))
print("time=",timeit.timeit(stmt2,setup,number=10000))
time= 0.003897680000136461
time= 0.0002797570000439009
Выводы!
Как вы могли увидеть, обработка исключений помогает прервать типичный поток программы с помощью специального механизма, который делает код более отказоустойчивым.
Обработка исключений — один из основных факторов, который делает код готовым к развертыванию. Это простая концепция, построенная всего на 4 блоках: try выискивает исключения, а except их обрабатывает.
Очень важно поупражняться в их использовании, чтобы сделать свой код более отказоустойчивым.
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Raising and Handling Python Exceptions
A Python program terminates as soon as it encounters an error. In Python, an error can be a syntax error or an exception. In this article, you will see what an exception is and how it differs from a syntax error. After that, you will learn about raising exceptions and making assertions. Then, you’ll finish with a demonstration of the try and except block.
Exceptions versus Syntax Errors
Syntax errors occur when the parser detects an incorrect statement. Observe the following example:
>>> print( 0 / 0 ))
File "<stdin>", line 1
print( 0 / 0 ))
^
SyntaxError: invalid syntax
The arrow indicates where the parser ran into the syntax error. In this example, there was one bracket too many. Remove it and run your code again:
>>> print( 0 / 0)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ZeroDivisionError: integer division or modulo by zero
This time, you ran into an exception error. This type of error occurs whenever syntactically correct Python code results in an error. The last line of the message indicated what type of exception error you ran into.
Instead of showing the message exception error, Python details what type of exception error was encountered. In this case, it was a ZeroDivisionError. Python comes with various built-in exceptions as well as the possibility to create self-defined exceptions.
Raising an Exception
We can use raise to throw an exception if a condition occurs. The statement can be complemented with a custom exception.
If you want to throw an error when a certain condition occurs using raise, you could go about it like this:
x = 10
if x > 5:
raise Exception('x should not exceed 5. The value of x was: {}'.format(x))
When you run this code, the output will be the following:
Traceback (most recent call last):
File "<input>", line 4, in <module>
Exception: x should not exceed 5. The value of x was: 10
The program comes to a halt and displays our exception to screen, offering clues about what went wrong.
The AssertionError Exception
Instead of waiting for a program to crash midway, you can also start by making an assertion in Python. We assert that a certain condition is met. If this condition turns out to be True, then that is excellent! The program can continue. If the condition turns out to be False, you can have the program throw an AssertionError exception.
Have a look at the following example, where it is asserted that the code will be executed on a Linux system:
import sys
assert ('linux' in sys.platform), "This code runs on Linux only."
If you run this code on a Linux machine, the assertion passes. If you were to run this code on a Windows machine, the outcome of the assertion would be False and the result would be the following:
Traceback (most recent call last):
File "<input>", line 2, in <module>
AssertionError: This code runs on Linux only.
In this example, throwing an AssertionError exception is the last thing that the program will do. The program will come to halt and will not continue. What if that is not what you want?
The try and except Block: Handling Exceptions
The try and except block in Python is used to catch and handle exceptions. Python executes code following the try statement as a “normal” part of the program. The code that follows the except statement is the program’s response to any exceptions in the preceding try clause.
As you saw earlier, when syntactically correct code runs into an error, Python will throw an exception error. This exception error will crash the program if it is unhandled. The except clause determines how your program responds to exceptions.
The following function can help you understand the try and except block:
def linux_interaction():
assert ('linux' in sys.platform), "Function can only run on Linux systems."
print('Doing something.')
The linux_interaction() can only run on a Linux system. The assert in this function will throw an AssertionError exception if you call it on an operating system other then Linux.
You can give the function a try using the following code:
try:
linux_interaction()
except:
pass
The way you handled the error here is by handing out a pass. If you were to run this code on a Windows machine, you would get the following output:
You got nothing. The good thing here is that the program did not crash. But it would be nice to see if some type of exception occurred whenever you ran your code. To this end, you can change the pass into something that would generate an informative message, like so:
try:
linux_interaction()
except:
print('Linux function was not executed')
Execute this code on a Windows machine:
Linux function was not executed
When an exception occurs in a program running this function, the program will continue as well as inform you about the fact that the function call was not successful.
What you did not get to see was the type of error that was thrown as a result of the function call. In order to see exactly what went wrong, you would need to catch the error that the function threw.
The following code is an example where you capture the AssertionError and output that message to screen:
try:
linux_interaction()
except AssertionError as error:
print(error)
print('The linux_interaction() function was not executed')
Running this function on a Windows machine outputs the following:
Function can only run on Linux systems.
The linux_interaction() function was not executed
The first message is the AssertionError, informing you that the function can only be executed on a Linux machine. The second message tells you which function was not executed.
In the previous example, you called a function that you wrote yourself. When you executed the function, you caught the AssertionError exception and printed it to screen.
Here’s another example where you open a file and use a built-in exception:
try:
with open('file.log') as file:
read_data = file.read()
except:
print('Could not open file.log')
If file.log does not exist, this block of code will output the following:
This is an informative message, and our program will still continue to run. In the Python docs, you can see that there are a lot of built-in exceptions that you can use here. One exception described on that page is the following:
Exception
FileNotFoundErrorRaised when a file or directory is requested but doesn’t exist. Corresponds to errno ENOENT.
To catch this type of exception and print it to screen, you could use the following code:
try:
with open('file.log') as file:
read_data = file.read()
except FileNotFoundError as fnf_error:
print(fnf_error)
In this case, if file.log does not exist, the output will be the following:
[Errno 2] No such file or directory: 'file.log'
You can have more than one function call in your try clause and anticipate catching various exceptions. A thing to note here is that the code in the try clause will stop as soon as an exception is encountered.
Look at the following code. Here, you first call the linux_interaction() function and then try to open a file:
try:
linux_interaction()
with open('file.log') as file:
read_data = file.read()
except FileNotFoundError as fnf_error:
print(fnf_error)
except AssertionError as error:
print(error)
print('Linux linux_interaction() function was not executed')
If the file does not exist, running this code on a Windows machine will output the following:
Function can only run on Linux systems.
Linux linux_interaction() function was not executed
Inside the try clause, you ran into an exception immediately and did not get to the part where you attempt to open file.log. Now look at what happens when you run the code on a Linux machine:
[Errno 2] No such file or directory: 'file.log'
Here are the key takeaways:
- A
tryclause is executed up until the point where the first exception is encountered. - Inside the
exceptclause, or the exception handler, you determine how the program responds to the exception. - You can anticipate multiple exceptions and differentiate how the program should respond to them.
- Avoid using bare
exceptclauses.
The else Clause
In Python, using the else statement, you can instruct a program to execute a certain block of code only in the absence of exceptions.
Look at the following example:
try:
linux_interaction()
except AssertionError as error:
print(error)
else:
print('Executing the else clause.')
If you were to run this code on a Linux system, the output would be the following:
Doing something.
Executing the else clause.
Because the program did not run into any exceptions, the else clause was executed.
You can also try to run code inside the else clause and catch possible exceptions there as well:
try:
linux_interaction()
except AssertionError as error:
print(error)
else:
try:
with open('file.log') as file:
read_data = file.read()
except FileNotFoundError as fnf_error:
print(fnf_error)
If you were to execute this code on a Linux machine, you would get the following result:
Doing something.
[Errno 2] No such file or directory: 'file.log'
From the output, you can see that the linux_interaction() function ran. Because no exceptions were encountered, an attempt to open file.log was made. That file did not exist, and instead of opening the file, you caught the FileNotFoundError exception.
Cleaning Up After Using finally
Imagine that you always had to implement some sort of action to clean up after executing your code. Python enables you to do so using the finally clause.
Have a look at the following example:
try:
linux_interaction()
except AssertionError as error:
print(error)
else:
try:
with open('file.log') as file:
read_data = file.read()
except FileNotFoundError as fnf_error:
print(fnf_error)
finally:
print('Cleaning up, irrespective of any exceptions.')
In the previous code, everything in the finally clause will be executed. It does not matter if you encounter an exception somewhere in the try or else clauses. Running the previous code on a Windows machine would output the following:
Function can only run on Linux systems.
Cleaning up, irrespective of any exceptions.
Summing Up
After seeing the difference between syntax errors and exceptions, you learned about various ways to raise, catch, and handle exceptions in Python. In this article, you saw the following options:
raiseallows you to throw an exception at any time.assertenables you to verify if a certain condition is met and throw an exception if it isn’t.- In the
tryclause, all statements are executed until an exception is encountered. exceptis used to catch and handle the exception(s) that are encountered in the try clause.elselets you code sections that should run only when no exceptions are encountered in the try clause.finallyenables you to execute sections of code that should always run, with or without any previously encountered exceptions.
Hopefully, this article helped you understand the basic tools that Python has to offer when dealing with exceptions.
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Raising and Handling Python Exceptions
Содержание:развернуть
- Как устроен механизм исключений
- Как обрабатывать исключения в Python (try except)
-
As — сохраняет ошибку в переменную
-
Finally — выполняется всегда
-
Else — выполняется когда исключение не было вызвано
-
Несколько блоков except
-
Несколько типов исключений в одном блоке except
-
Raise — самостоятельный вызов исключений
-
Как пропустить ошибку
- Исключения в lambda функциях
- 20 типов встроенных исключений в Python
- Как создать свой тип Exception
Программа, написанная на языке Python, останавливается сразу как обнаружит ошибку. Ошибки могут быть (как минимум) двух типов:
- Синтаксические ошибки — возникают, когда написанное выражение не соответствует правилам языка (например, написана лишняя скобка);
- Исключения — возникают во время выполнения программы (например, при делении на ноль).
Синтаксические ошибки исправить просто (если вы используете IDE, он их подсветит). А вот с исключениями всё немного сложнее — не всегда при написании программы можно сказать возникнет или нет в данном месте исключение. Чтобы приложение продолжило работу при возникновении проблем, такие ошибки нужно перехватывать и обрабатывать с помощью блока try/except.
Как устроен механизм исключений
В Python есть встроенные исключения, которые появляются после того как приложение находит ошибку. В этом случае текущий процесс временно приостанавливается и передает ошибку на уровень вверх до тех пор, пока она не будет обработано. Если ошибка не будет обработана, программа прекратит свою работу (а в консоли мы увидим Traceback с подробным описанием ошибки).
💁♂️ Пример: напишем скрипт, в котором функция ожидает число, а мы передаём сроку (это вызовет исключение «TypeError»):
def b(value):
print("-> b")
print(value + 1) # ошибка тут
def a(value):
print("-> a")
b(value)
a("10")
> -> a
> -> b
> Traceback (most recent call last):
> File "test.py", line 11, in <module>
> a("10")
> File "test.py", line 8, in a
> b(value)
> File "test.py", line 3, in b
> print(value + 1)
> TypeError: can only concatenate str (not "int") to str
В данном примере мы запускаем файл «test.py» (через консоль). Вызывается функция «a«, внутри которой вызывается функция «b«. Все работает хорошо до сточки print(value + 1). Тут интерпретатор понимает, что нельзя конкатенировать строку с числом, останавливает выполнение программы и вызывает исключение «TypeError».
Далее ошибка передается по цепочке в обратном направлении: «b» → «a» → «test.py«. Так как в данном примере мы не позаботились обработать эту ошибку, вся информация по ошибке отобразится в консоли в виде Traceback.
Traceback (трассировка) — это отчёт, содержащий вызовы функций, выполненные в определенный момент. Трассировка помогает узнать, что пошло не так и в каком месте это произошло.
Traceback лучше читать снизу вверх ↑
В нашем примере Traceback содержится следующую информацию (читаем снизу вверх):
TypeError— тип ошибки (означает, что операция не может быть выполнена с переменной этого типа);can only concatenate str (not "int") to str— подробное описание ошибки (конкатенировать можно только строку со строкой);- Стек вызова функций (1-я линия — место, 2-я линия — код). В нашем примере видно, что в файле «test.py» на 11-й линии был вызов функции «a» со строковым аргументом «10». Далее был вызов функции «b».
print(value + 1)это последнее, что было выполнено — тут и произошла ошибка. most recent call last— означает, что самый последний вызов будет отображаться последним в стеке (в нашем примере последним выполнилсяprint(value + 1)).
В Python ошибку можно перехватить, обработать, и продолжить выполнение программы — для этого используется конструкция try ... except ....
Как обрабатывать исключения в Python (try except)
В Python исключения обрабатываются с помощью блоков try/except. Для этого операция, которая может вызвать исключение, помещается внутрь блока try. А код, который должен быть выполнен при возникновении ошибки, находится внутри except.
Например, вот как можно обработать ошибку деления на ноль:
try:
a = 7 / 0
except:
print('Ошибка! Деление на 0')
Здесь в блоке try находится код a = 7 / 0 — при попытке его выполнить возникнет исключение и выполнится код в блоке except (то есть будет выведено сообщение «Ошибка! Деление на 0»). После этого программа продолжит свое выполнение.
💭 PEP 8 рекомендует, по возможности, указывать конкретный тип исключения после ключевого слова except (чтобы перехватывать и обрабатывать конкретные исключения):
try:
a = 7 / 0
except ZeroDivisionError:
print('Ошибка! Деление на 0')
Однако если вы хотите перехватывать все исключения, которые сигнализируют об ошибках программы, используйте тип исключения Exception:
try:
a = 7 / 0
except Exception:
print('Любая ошибка!')
As — сохраняет ошибку в переменную
Перехваченная ошибка представляет собой объект класса, унаследованного от «BaseException». С помощью ключевого слова as можно записать этот объект в переменную, чтобы обратиться к нему внутри блока except:
try:
file = open('ok123.txt', 'r')
except FileNotFoundError as e:
print(e)
> [Errno 2] No such file or directory: 'ok123.txt'
В примере выше мы обращаемся к объекту класса «FileNotFoundError» (при выводе на экран через print отобразится строка с полным описанием ошибки).
У каждого объекта есть поля, к которым можно обращаться (например если нужно логировать ошибку в собственном формате):
import datetime
now = datetime.datetime.now().strftime("%d-%m-%Y %H:%M:%S")
try:
file = open('ok123.txt', 'r')
except FileNotFoundError as e:
print(f"{now} [FileNotFoundError]: {e.strerror}, filename: {e.filename}")
> 20-11-2021 18:42:01 [FileNotFoundError]: No such file or directory, filename: ok123.txt
Finally — выполняется всегда
При обработке исключений можно после блока try использовать блок finally. Он похож на блок except, но команды, написанные внутри него, выполняются обязательно. Если в блоке try не возникнет исключения, то блок finally выполнится так же, как и при наличии ошибки, и программа возобновит свою работу.
Обычно try/except используется для перехвата исключений и восстановления нормальной работы приложения, а try/finally для того, чтобы гарантировать выполнение определенных действий (например, для закрытия внешних ресурсов, таких как ранее открытые файлы).
В следующем примере откроем файл и обратимся к несуществующей строке:
file = open('ok.txt', 'r')
try:
lines = file.readlines()
print(lines[5])
finally:
file.close()
if file.closed:
print("файл закрыт!")
> файл закрыт!
> Traceback (most recent call last):
> File "test.py", line 5, in <module>
> print(lines[5])
> IndexError: list index out of range
Даже после исключения «IndexError», сработал код в секции finally, который закрыл файл.
p.s. данный пример создан для демонстрации, в реальном проекте для работы с файлами лучше использовать менеджер контекста with.
Также можно использовать одновременно три блока try/except/finally. В этом случае:
- в
try— код, который может вызвать исключения; - в
except— код, который должен выполниться при возникновении исключения; - в
finally— код, который должен выполниться в любом случае.
def sum(a, b):
res = 0
try:
res = a + b
except TypeError:
res = int(a) + int(b)
finally:
print(f"a = {a}, b = {b}, res = {res}")
sum(1, "2")
> a = 1, b = 2, res = 3
Else — выполняется когда исключение не было вызвано
Иногда нужно выполнить определенные действия, когда код внутри блока try не вызвал исключения. Для этого используется блок else.
Допустим нужно вывести результат деления двух чисел и обработать исключения в случае попытки деления на ноль:
b = int(input('b = '))
c = int(input('c = '))
try:
a = b / c
except ZeroDivisionError:
print('Ошибка! Деление на 0')
else:
print(f"a = {a}")
> b = 10
> c = 1
> a = 10.0
В этом случае, если пользователь присвоит переменной «с» ноль, то появится исключение и будет выведено сообщение «‘Ошибка! Деление на 0′», а код внутри блока else выполняться не будет. Если ошибки не будет, то на экране появятся результаты деления.
Несколько блоков except
В программе может возникнуть несколько исключений, например:
- Ошибка преобразования введенных значений к типу
float(«ValueError»); - Деление на ноль («ZeroDivisionError»).
В Python, чтобы по-разному обрабатывать разные типы ошибок, создают несколько блоков except:
try:
b = float(input('b = '))
c = float(input('c = '))
a = b / c
except ZeroDivisionError:
print('Ошибка! Деление на 0')
except ValueError:
print('Число введено неверно')
else:
print(f"a = {a}")
> b = 10
> c = 0
> Ошибка! Деление на 0
> b = 10
> c = питон
> Число введено неверно
Теперь для разных типов ошибок есть свой обработчик.
Несколько типов исключений в одном блоке except
Можно также обрабатывать в одном блоке except сразу несколько исключений. Для этого они записываются в круглых скобках, через запятую сразу после ключевого слова except. Чтобы обработать сообщения «ZeroDivisionError» и «ValueError» в одном блоке записываем их следующим образом:
try:
b = float(input('b = '))
c = float(input('c = '))
a = b / c
except (ZeroDivisionError, ValueError) as er:
print(er)
else:
print('a = ', a)
При этом переменной er присваивается объект того исключения, которое было вызвано. В результате на экран выводятся сведения о конкретной ошибке.
Raise — самостоятельный вызов исключений
Исключения можно генерировать самостоятельно — для этого нужно запустить оператор raise.
min = 100
if min > 10:
raise Exception('min must be less than 10')
> Traceback (most recent call last):
> File "test.py", line 3, in <module>
> raise Exception('min value must be less than 10')
> Exception: min must be less than 10
Перехватываются такие сообщения точно так же, как и остальные:
min = 100
try:
if min > 10:
raise Exception('min must be less than 10')
except Exception:
print('Моя ошибка')
> Моя ошибка
Кроме того, ошибку можно обработать в блоке except и пробросить дальше (вверх по стеку) с помощью raise:
min = 100
try:
if min > 10:
raise Exception('min must be less than 10')
except Exception:
print('Моя ошибка')
raise
> Моя ошибка
> Traceback (most recent call last):
> File "test.py", line 5, in <module>
> raise Exception('min must be less than 10')
> Exception: min must be less than 10
Как пропустить ошибку
Иногда ошибку обрабатывать не нужно. В этом случае ее можно пропустить с помощью pass:
try:
a = 7 / 0
except ZeroDivisionError:
pass
Исключения в lambda функциях
Обрабатывать исключения внутри lambda функций нельзя (так как lambda записывается в виде одного выражения). В этом случае нужно использовать именованную функцию.
Иерархия классов для встроенных исключений в Python выглядит так:
BaseException
SystemExit
KeyboardInterrupt
GeneratorExit
Exception
ArithmeticError
AssertionError
...
...
...
ValueError
Warning
Все исключения в Python наследуются от базового BaseException:
SystemExit— системное исключение, вызываемое функциейsys.exit()во время выхода из приложения;KeyboardInterrupt— возникает при завершении программы пользователем (чаще всего при нажатии клавиш Ctrl+C);GeneratorExit— вызывается методомcloseобъектаgenerator;Exception— исключения, которые можно и нужно обрабатывать (предыдущие были системными и их трогать не рекомендуется).
От Exception наследуются:
1 StopIteration — вызывается функцией next в том случае если в итераторе закончились элементы;
2 ArithmeticError — ошибки, возникающие при вычислении, бывают следующие типы:
FloatingPointError— ошибки при выполнении вычислений с плавающей точкой (встречаются редко);OverflowError— результат вычислений большой для текущего представления (не появляется при операциях с целыми числами, но может появиться в некоторых других случаях);ZeroDivisionError— возникает при попытке деления на ноль.
3 AssertionError — выражение, используемое в функции assert неверно;
4 AttributeError — у объекта отсутствует нужный атрибут;
5 BufferError — операция, для выполнения которой требуется буфер, не выполнена;
6 EOFError — ошибка чтения из файла;
7 ImportError — ошибка импортирования модуля;
8 LookupError — неверный индекс, делится на два типа:
IndexError— индекс выходит за пределы диапазона элементов;KeyError— индекс отсутствует (для словарей, множеств и подобных объектов);
9 MemoryError — память переполнена;
10 NameError — отсутствует переменная с данным именем;
11 OSError — исключения, генерируемые операционной системой:
ChildProcessError— ошибки, связанные с выполнением дочернего процесса;ConnectionError— исключения связанные с подключениями (BrokenPipeError, ConnectionResetError, ConnectionRefusedError, ConnectionAbortedError);FileExistsError— возникает при попытке создания уже существующего файла или директории;FileNotFoundError— генерируется при попытке обращения к несуществующему файлу;InterruptedError— возникает в том случае если системный вызов был прерван внешним сигналом;IsADirectoryError— программа обращается к файлу, а это директория;NotADirectoryError— приложение обращается к директории, а это файл;PermissionError— прав доступа недостаточно для выполнения операции;ProcessLookupError— процесс, к которому обращается приложение не запущен или отсутствует;TimeoutError— время ожидания истекло;
12 ReferenceError — попытка доступа к объекту с помощью слабой ссылки, когда объект не существует;
13 RuntimeError — генерируется в случае, когда исключение не может быть классифицировано или не подпадает под любую другую категорию;
14 NotImplementedError — абстрактные методы класса нуждаются в переопределении;
15 SyntaxError — ошибка синтаксиса;
16 SystemError — сигнализирует о внутренне ошибке;
17 TypeError — операция не может быть выполнена с переменной этого типа;
18 ValueError — возникает когда в функцию передается объект правильного типа, но имеющий некорректное значение;
19 UnicodeError — исключение связанное с кодирование текста в unicode, бывает трех видов:
UnicodeEncodeError— ошибка кодирования;UnicodeDecodeError— ошибка декодирования;UnicodeTranslateError— ошибка переводаunicode.
20 Warning — предупреждение, некритическая ошибка.
💭 Посмотреть всю цепочку наследования конкретного типа исключения можно с помощью модуля inspect:
import inspect
print(inspect.getmro(TimeoutError))
> (<class 'TimeoutError'>, <class 'OSError'>, <class 'Exception'>, <class 'BaseException'>, <class 'object'>)
📄 Подробное описание всех классов встроенных исключений в Python смотрите в официальной документации.
Как создать свой тип Exception
В Python можно создавать свои исключения. При этом есть одно обязательное условие: они должны быть потомками класса Exception:
class MyError(Exception):
def __init__(self, text):
self.txt = text
try:
raise MyError('Моя ошибка')
except MyError as er:
print(er)
> Моя ошибка
С помощью try/except контролируются и обрабатываются ошибки в приложении. Это особенно актуально для критически важных частей программы, где любые «падения» недопустимы (или могут привести к негативным последствиям). Например, если программа работает как «демон», падение приведет к полной остановке её работы. Или, например, при временном сбое соединения с базой данных, программа также прервёт своё выполнение (хотя можно было отловить ошибку и попробовать соединиться в БД заново).
Вместе с try/except можно использовать дополнительные блоки. Если использовать все блоки описанные в статье, то код будет выглядеть так:
try:
# попробуем что-то сделать
except (ZeroDivisionError, ValueError) as e:
# обрабатываем исключения типа ZeroDivisionError или ValueError
except Exception as e:
# исключение не ZeroDivisionError и не ValueError
# поэтому обрабатываем исключение общего типа (унаследованное от Exception)
# сюда не сходят исключения типа GeneratorExit, KeyboardInterrupt, SystemExit
else:
# этот блок выполняется, если нет исключений
# если в этом блоке сделать return, он не будет вызван, пока не выполнился блок finally
finally:
# этот блок выполняется всегда, даже если нет исключений else будет проигнорирован
# если в этом блоке сделать return, то return в блоке
Подробнее о работе с исключениями в Python можно ознакомиться в официальной документации.