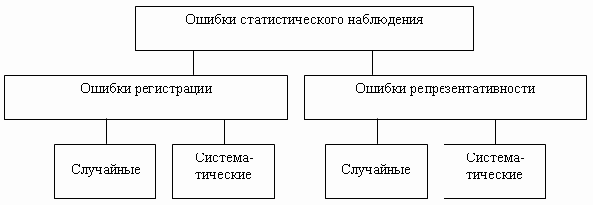
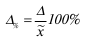Ошибка
репрезентативности –
это отклонение значения показателя
обследований совокупности от его
величины по исходной совокупности.
Такие ошибки характерны только для не
сплошного наблюдения. Возникают потому,
что отобранная и обследованная
совокупность недостаточно точно
воспроизводит (репрезентирует) всю
исходную совокупность в целом. Также
бывают случайными и систематическими.
Систематическими
называются ошибки репрезентативности,
которые возникают из-за нарушения
научного принципа отбора единиц в
выборочную совокупность. Они возникают
в тех случаях, когда в результате
неправильной организации отбора в
выборочную совокупность попали
преимущественно наилучшие или наихудшие
в отношении того или иного признака
единицы.
Случайные
ошибки репрезентативности –
это неточности, которые возникают из-за
того, что выборочная совокупность не
совсем правильно воспроизводит структуру
генеральной совокупности.
Ошибки
репрезентативности свойственны только
выборочному наблюдению. Они не могут
быть полностью устранены, но они могут
быть доведены до незначительных размеров.
Так как случайная ошибка выборки
возникает в результате случайных
различий между единицами выборочной и
генеральной совокупности, то при
достаточно большом объеме выборки она
будет сколь угодно мала. Предельные
теоремы теории вероятностей позволяют
определять размер случайных ошибок
выборки. Различают среднюю (стандартную)
ошибку выборки и предельную ошибку
выборки. Под средней ошибкой выборки
понимают такое расхождение между средней
выборочной и средней генеральной
совокупностями ,
которое не превышает.
Измерения
рассматриваются с двух точек
зрения: количественной,
выражающей числовое значение измеренной
физической величины и качественной,
характеризующей точность измерения.
Результаты измерений не являются точным
значением измеряемой величины, а
несколько отличаются (отклоняются) от
него. Отклонение измеренной величины
ℓ от ее истинного (точного) значения Х
называется истинной
ошибкой
или погрешностью измерения и обозначается
D. Ошибки всегда имеют величину и знак
плюс или минус. Величина ошибки показывает
на сколько измеренное значение отклонилось
от истинного; знак — в какую сторону
произошло отклонение. Ошибки характеризуют
точность измерения, т.е. степень близости
измеренной величины к ее истинному
значению. Чем меньше ошибка, тем точнее
измерение. На результат измерения
оказывают влияние многие факторы и
каждый из них порождает свою часть общей
ошибки. Ошибки, происходящие от отдельных
факторов, называют элементарными. Х
— ℓ = D или ℓ — Х = D (1) Ошибка (погрешность
) результата измерения является
алгебраической суммой элементарных
ошибок: [D] = D1 +
D2 +
D3 +
… + Dn (2)
Квадратные скобки означают знак суммы
( ввел Гаусс). Ошибки различают по двум
признакам: по источнику возникновения
(происхождения) и по характеру действия. По
источнику возникновения ошибки
подразделяют на приборные (инструментальные),
методические, личные и внешние. Приборные или
инструментальные ошибки обусловлены
неточным изготовлением и сборкой
отдельных деталей и узлов приборов,
неточной установкой их во время измерений
и др. причинами. Методические ошибки
возникают из-за несоблюдения методики
измерений. Личные ошибки связаны
с особенностями органов зрения человека
выполняющего измерения (наведение
зрительной трубы на удаленный предмет,
оценку доли наименьшего деления шкалы
«на глаз»каждый человек делает по-
разному). Внешние ошибки возникают
из-за воздействия внешней среды в которой
производятся измерения: температура,
давление и влажность воздуха; неравномерное
нагревание солнцем отдельных частей
приборов; степень освещенности; ветер,
турбулентность воздуха и др. По
характеру действия ошибки разделяют
на систематические и случайные.
Кроме того, результаты измерений могут
содержать грубые
ошибки. Грубыми
считают ошибки, превосходящие по
абсолютной величине некоторый
установленный предел. Они появляются
главным образом в результате промахов
и просчетов из-за невнимательности или
недостаточной квалификации (опытности)
исполнителя. Их выявляют путем повторных
(контрольных) измерений. Измерения,
содержащие грубые ошибки, не берут в
дальнейшую обработку, бракуют и заменяют
новыми. С целью выявления грубых ошибок
все геодезические измерения выполняют
с контролем, не менее двух раз: углы
измеряют при двух положениях теодолита;
длины линий — в прямом и обратном
направлениях; превышения — по двум
сторонам рейки и в прямом и обратном
ходах. Систематическими называют
ошибки, которые по знаку или величине
однообразно повторяются в многократных
измерениях какой-либо величины. Для их
выявления считают число положительных
и отрицательных ошибок и их сумму. При
отсутствии систематической части общей
ошибки число ошибок с разными знаками
примерно одинаковое и суммы их также
примерно равны между собой. Они возникают
из-за приборных, методических, личных
и внешних факторов. Например, несоответствие
фактической длины мерного прибора
указанному на нем. Систематические
ошибки различают по характеру проявления.
Они могут быть: а) переменные, прогрессивного
типа; б) односторонне действующие; в)
периодические; г) постоянные; д) смешанные.
Систематические ошибки прогрессивно
типа в процессе измерений возрастают
или убывают. Такого рода ошибки возникают,
например , при измерении линий стальной
лентой, длина которой больше или меньше
номинальной. Если ряд ошибок с переменными
абсолютными значениями искажен в одном
и том же направлении, то такой ряд ошибок
называется систематическим и
односторонним по знаку. Систематические
ошибки периодического характера
соответственно изменяют знак и величину.
Подобные ошибки возникают, например,
при измерении углов теодолитом, в котором
имеется эксцентриситет алидады. Если
при многократных измерениях ошибки
остаются неизменными как по абсолютному
значению, так и по знаку, то такие ошибки
называютсяпостоянными.
Так при многократном измерении угла
теодолитом имеет место одна и та же
ошибка за центрировку. При измерении
линий больше длины мерной ленты возникает
постоянная ошибка одинаковая на каждом
уложении ленты. Постоянная ошибка
является частным выражением систематической
ошибки.Знание причин возникновения
систематических ошибок позволяет
заранее принять меры по исключению их
из результатов измерений или уменьшению.
Систематические ошибки характерны тем,
что поддаются учету. Они могут быть
исключены или сведены к минимуму путем
тщательной проверки измерительных
приборов, изменением методики измерений,
предупреждением влияния внешних
факторов. Но несмотря на это общая ошибка
всегда содержит остаточную часть
систематической ошибки, хотя она и мала
по сравнению со случайной ошибкой. В
ряду измерений всегда имеется остаточная
часть ошибки. Случайными называют
ошибки, размер и влияние которых на
результат измерения неизвестны, величину
и знак их заранее определить нельзя.
Случайная величина – это переменная
величина, конкретное значение которой
зависит от случая, она может быть, а
может и не быть. Случайными ошибки
называют потому, что в ряду измерений
каждая последующая ошибка по абсолютной
величине может быть больше или меньше
предыдущей, иметь знак плюс или минус
и по предыдущим членам такого ряда
нельзя установить, какой именно будет
следующий за ним член ряда. Тем не менее,
случайные ошибки подчинены статистическим
закономерностям, называемых свойствами.
Чем больше число измерений войдет в ряд
их, тем резче выявится статистическая
закономерность. Знание свойств дает
возможность получить наиболее надежный
результат из ряда (нескольких) измерений,
а также оценить его точность.
33.
По данным распределения начертить
вариационную кривую. Предположим, нами
просчитано число зацепок на левом заднем
крыле у 100 экземпляров рабочих пчел
данного улья. Получены такие цифры: 21,
20, 18, 19, 24, 22 и так далее. Можно подсчитать,
сколько же раз попались пчелы с числом
зацепок 18, сколько с 19 зацепками и т. д.
Сделав это для всех 100 пчел.
Число
зацепок в крыле-18 19 20 21 22 23 24 25
Число
пчел с данным числом зацепок- 2 5 10 22 24
17 12 8
Число
зацепок в крыле-18 19 20 21 22 23 24 25, а число
пчел с данным числом зацепок- 2 5 10 22 24
17 12 8. Видно, что пчел с 18 зацепками была
две, с 19 — пять и т. д. Вариационный ряд
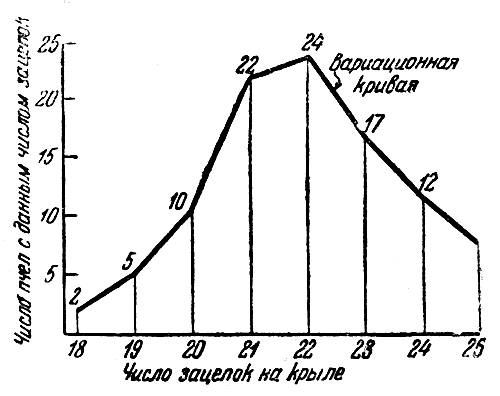
можно изобразить графически. На
горизонтальной оси помечено число
зацепок, а над соответственным числом
зацепок в виде вертикальной черты
изображено приходящееся сюда число
случаев. Если соединить вершины
вертикальных линий друг с другом, то
получится ломаная линия, которая носит
название вариационной кривой (см. рис.
2).
Рис.
2. Вариационная кривая числа зацепок на
заднем крыле рабочих пчел.
Первой
и основной характеристикой вариационного
ряда является среднее арифметическое.
Чтобы его получить, надо сложить все
100 чисел, характеризующих зацепки крыльев
вышеприведенной семьи пчел — +21 +20 +18 и
т. д., и сумму разделить на 100. Если наш
материал уже классифицирован в
вариационный ряд, для быстроты можно
заменить сложение умножением каждой
цифры, показывающей число случаев, на
стояющую над ней величину. Все эти
произведения надо просуммировать и
разделить на 100.
Среднее
арифметическое условно принято обозначать
буквой М.
В
нашем примере вычисление дает следующее:
М
= (2,18 + 5,19 + 10,20 + 22,21 + 24,22 + 17,23 + 12,24 +
8,25)/100=22,00
Кроме
вопроса о среднем арифметическом ряде,
его типе, ибо свойство М таково, что оно
является центром, вокруг которого налево
и направо распределяется одинаковое
количество отдельных случаев (При
так называемом «нормальном» распределении ),
может возникнуть вопрос, насколько
сильно рассеиваются вокруг типа отдельные
случаи. Раньше для учета этого явления
пользовались указанием размеров самого
мелкого и самого крупного экземпляра
вариационного ряда. В нашем примере
указали бы границы 18—25.
Теперь
же по ряду соображений принято пользоваться
так называемым стандартным отклонением
и коэффициентом изменчивости или
вариации.
Получаются
эти величины так. Возьмем в нашем примере
пчел с 18 зацепками. Каждая отклоняется
от М на 4 зацепки. Квадрат четырех 16. Так
как таких пчел две, то для них имеем
16х2=32.
Хотя
отклонение было с отрицательным знаком,
но вследствие возведения в квадрат
отрицательные знаки уничтожаются. Для
пчел с 19 зацепками имеем 3х3х5 = 45. Суммируя
все таким образом найденные произведения,
деля сумму на число всех случаев — 100,
получаем среднее квадратическое
уклонение, а извлекши из него квадратный
корень, получаем стандартное отклонение
(стандарт по-английски — тип), обозначаемое
греческой буквой σ (сигма). Для нашего
примера имеем:
σ
= ± √ (16,2 + 9,5 + 4,10 + 1,22 + 1,17 + 4,12 + 9,8)/100 = ±
√2,76 = ± 1,661 зацепок.
Сигма
— величина именованная и выражается в
тех же единицах как изучаемый признак.
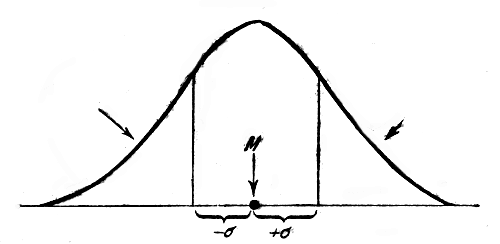
Геометрический смысл сигмы таков. Если
взять много материала (например 1000 пчел)
и по вышеизложенному начертить
вариационную кривую, то она будет весьма
плавно подниматься и перегибаться над
М. Если отложить налево и направо от М
по отсеку, равному сигме, то место
перехода каждой ветви кривой из вогнутой
в выпуклую будет как раз приходиться
над наружными точками сигм (см. рис. 3).
Рис.
3. Схема, поясняющая положение перелома
ветвей нормальной кривой над точками,
лежащими на расстоянии одной сигмы от
среднего арифметического.
Ясно,
что чем больше сигма, тем дальше будут
эти точки находиться от М, тем уплощеннее
будет кривая, тем больше будет рассеянность
отдельных особей вокруг типа.
Для
возможности сравнивать изменчивость
признаков, выражаемых разными единицами
измерений и дающих ряды с различной
величиной М, придумали характеристику
отвлеченную. Ее находят, выражая сигму
ряда в процентах среднего арифметического
данного ряда по формуле
С%
= (σ•100)/М = (1,661•100)/22 = 7,54%.
Это
— коэффициент вариации или коэффициент
изменчивости.
Так
вычисляют средние арифметические и
стандартные отклонения для признаков
счетных (число зацепок, число яйцевых
трубочек и т. д.). Несколько иначе
поступают, когда приходится иметь дело
с признаками, получаемыми путем измерений,
взвешиваний и т. д. При этом признаки
особей пчел или целых семей выражаются
не целыми числами, а числами с дробями
(например 25,1 кг меда с семьи и т. д.). В
этом случае при составлении вариационного
ряда: и вариационной кривой составляют
шкалу классов и разносят по классам
измерения особей или семей. Возьмем в
качестве примера определения, времени
остановки движения 15 особей пчел,
помещенных в атмосферу паров серного
эфира. Цифры в минутах и долях минуты
таковы: 6,25; 8,5; 5,0; 8,0; 6,25; 6,5; 3,5;, 6,5; 4,25; 4,4;
4,8; 7,8; 5,25; 5,75 и 6,7. Сперва надо наметить
пределы вариации: 3,5 до 8,5 минут.
Предположим, что мы хотим создать классы
величиной в 2 минуты. Toгда шкала классов
будет такова: 3—5—7—9. Всего у нас будет
три класса. Для того чтобы на границу
класса не попал ни один случай, припишем
к каждой границе 0,01. Границы будут
обозначаться; 3,01—5,01—7,01—9,01, а весь
вариационный ряд после распределения
показателей всех 15 пчел будет таков:
|
Шкала |
3,01 |
|
Число |
5 |
Вычисление
среднего арифметического и стандартного
отклонения можно вести как для вариационных
рядов счетных признаков (см. выше пример
с зацепками), только надо принимать, что
частоты — число пчел в классе — относятся
как бы к середине класса, например пять
пчел в первом классе падают на 4,01 минуты,
7 —на 6,01.
В
биометрических сочинениях приведенная
нами характеристика типа — среднее
арифметическое — и характеристики
разбросанности отклонений вокруг типа
— стандартное отклонение и коэфициент
вариации, сопровождаются так называемыми
средними и вероятными ошибками. Значение
этих ошибок в биометрии необычайно
велико. Дело в том, что когда мы определяем
среднее число зацепок у ста пчел одной
семьи, нас не интересуют именно эти 100
пчел, а интересует среднее число зацепок
на крыльях всех пчел этой семьи, из
которой в качестве пробной группы взято
100 штук. Оказывается, что о действительной
средней величине нашего признака можно
сделать заключение на основе пробы,
причем характеристики, носящие название
средних и вероятных ошибок, дают нам
возможность сделать это заключение с
такой точностью и уверенностью, с какой
мы это пожелаем. Здесь не место выводить
применяемые формулы; укажем, что формула
для средней ошибки среднего арифметического
такова: m = σ/√N , а для вероятной — РЕ=
6,6745(σ/√N) (m есть сокращенное условное
обозначение средней ошибки, а РЕ —
вероятной), где N — число случаев пробы.
Для
нашего примера с зацепками m = 1,661/√100 =
1,661/10 = 0,17 Теория вероятности отрасль
математики, которая лежит в основе
математической статистики, учит, что
если к среднему арифметическому прибавить
тройную среднюю ошибку: 22,0 + 3х0,17 = 22,51 и
вычесть ее из него 22—3х0,17 = 21,49, то мы
получаем такие пределы: 21,49 — 22,51. В этих
пределах с уверенностью, которую
практически можно считать достоверностью
(998 шансов против 2 в пользу нашего
утверждения), лежит среднее арифметическое
всего материала, из которого мы взяли
пробу и который нас собственно и
интересует. Если пользоваться вероятной
ошибкой, т. е. величиной, равной
приблизительно семи десятым средней
ошибки (множитель 0,6745), то для получения
той же степени достоверности надо брать
не утроенную среднюю ошибку, а вероятную
ошибку, помноженную на 4,5. Наконец, ошибки
имеют большое применение, когда нам
надо сравнить две характеристики двух
пробных групп и сделать заключение о
том, отличаются ли средние тех исходных
групп, из которых мы взяли пробу.
Предположим, у нас промерены пробы пчел
из Москвы и Харькова в отношений длины
их хоботка. Первые дали среднюю длину
в 6,115±0,003 мм, а вторые 6,549±0,003 мм. Насколько
достоверны эти отличия? Находят разницу
6,549 — 6,115 = 0,434 и ее вероятную ошибку по
следующей формуле: РЕ=± PE12+PE22
которая гласит, что вероятная ошибка
разницы средних равна корню квадратному
из суммы квадратов ошибок сравниваемых
средних. Если разница превышает свою
ошибку в 4, 5 или больше раз, мы вправе
говорить о статистической достоверности
различия всех харьковских и московских
пчел. В нашем примере это так и есть, ибо
0,434 в 108 раз больше, чем РЕ = ± √0,0032+0,0032 =
0,004.
Соседние файлы в предмете Ветеринарная генетика
- #
- #
- #
Содержание курса лекций “Статистика”
Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов
Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.
Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.
К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.
Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.
Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.
Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.
Отбор единиц в выборочную совокупность может быть повторным или бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.
Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.
На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.
Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.
При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).
Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.
Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.
Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.
При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:
N ‑ объем (число единиц) генеральной совокупности;
n ‑ объем (число единиц) выборочной совокупности;
‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);
‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;
М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);
р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как
m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,
определяется как ;
‑ средняя ошибка выборки;
‑ предельная ошибка выборки;
‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.
Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.
Таким образом среднюю ошибку выборки можно представить как
(10.1)
При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:
(10.2)
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.
Учитывая, что при достаточно большом объеме выборки отношение 
(10.3)
Где ‑ дисперсия изучаемого признака по выборочной совокупности.
При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.
Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.
Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.
При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:
Таблица 10.1 ‑ !!!Некоторые значения t
| Вероятность, рi. | 0,683 | 0,866 | 0,954 | 0,988 | 0,997 | 0,999 |
| Значение t | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 |
Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.
Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.
Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:
- Определение цели обследования.
- Установление границ генеральной совокупности.
- Составление программы наблюдения и программы разработки данных
- Определение вида выборки, процента отбора и метода отбора
- Отбор и регистрация наблюдаемых признаков у отобранных единиц.
- Насчет выборочных характеристик и их ошибок.
- Распространение полученных результатов на генеральную совокупность.
В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.
К наиболее распространенным на практике видам относятся:
- собственно-случайная (простая случайная) выборка;
- механическая (систематическая) выборка;
- типическая (стратифицированная, расслоенная) выборка;
- серийная (гнездовая) выборка.
Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.
Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.
Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.
Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.
Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.
Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:
(10.4)
Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.
Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:
(10.5)
а при расчете средней ошибки собственно-случайной бесповторной выборки:
(10.6)
Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.
Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:
(10.7)
где и
‑ генеральная и выборочная средняя соответственно;
‑ предельная ошибка выборочной средней.
Пример.
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:
Определим пределы генеральной средней:

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.
Пример 2.
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:
Таблица 10.2 ‑ Распределение семей по числу детей в городе N
| Число детей в семье | 0 | 1 | 2 | 3 | 4 | 5 |
| Количество
семей |
1000 | 2000 | 1200 | 400 | 200 | 200 |
С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:
Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей
|
Число детей в семье, х; |
Количество семей, f | ||||
|
0 1 2 3 4 5 |
1000 2000 1200 400 200 200 |
0
2000 2400 1200 800 1000 |
-1,5
-0,5 0,5 1,5 2,5 3,5 |
2,25
0,25 0,25 2,25 6,25 12,25 |
2250 500 300 900 1250 2450 |
|
Итого |
5000 | 7400 | – | – | 7650 |
Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).
Следовательно, пределы генеральной средней:
Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.
Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.
В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:
(10.8)
где ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.
Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:
(10.9)
Соответственно, при бесповторном отборе:
(10.10)
Пределы доли признака в генеральной совокупности p выглядят следующим образом:
(10.11)
Рассмотрим пример.
С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности:
n= 480 х 0,25 = 120 чел.
Выборочная доля w равна по условию 10%.
Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:
Пределы доли признака в генеральной совокупности:
Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:
(10.12)
Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.
С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:
Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:
Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:
(10.13)
Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.
Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.
Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.
Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит
Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.
Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.
Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.
Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.
Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.
Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.
При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.
Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).
С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.
Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.
Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).
Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.
Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.
Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.
При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
(10.14)
Где Ni – объем i-ой группы. а ni ‑ объем выборки из i-ой группы.
Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:
Средняя ошибка типической выборки определяется по формулам:
(10.15)

где – средняя из внутригрупповых дисперсий.
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:
(10.17)
Где ‑ среднее отклонение признака в i-ой группе.
Cредняя ошибка такого отбора определяется следующим образом:
(10.18)
(10.19)
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Таблица 10.4 ‑ Результаты обследования рабочих предприятия
| Цех | Всего рабочих, человек | Обследовано, человек | Число дней временной нетрудоспособности за год | |
| средняя | дисперсия | |||
| I
II III |
1000
1400 800 |
100
140 80 |
18
12 15 |
49
25 16 |
Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)
Рассчитаем среднюю из внутригрупповых дисперсий:
Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):
Рассчитаем выборочную среднюю:
С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:
Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:
С учетом полученных значений рассчитаем среднюю ошибку выборки:
В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
(10.20)
(10.21)
Где r ‑ число отобранных серий; R ‑ общее число серий.
Межгрупповую дисперсию вычисляют следующим образом:

где ‑ средняя i-й серии;
‑ общая средняя по всей выборочной совокупности.
Пример.
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.
Решение. Рассчитаем общую среднюю:
Межгрупповая (межсерийная) дисперсия равна:
Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):
Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:
Определение необходимого объема выборки
При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.
Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:
– собственно-случайная и механическая выборка:
(10.23)
(10.24)
– типическая выборка:
(10.25)
(10.26)
– серийная выборка:
(10.27)
(10.28)
При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.
Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.
Пример.
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.
Решение. Рассчитаем необходимый объем выборки:
Пример.
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Решение. Рассчитаем общую численность типической выборки:
Вычислим теперь объем отдельных типических групп:
Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.
Пример.
В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:
Содержание курса лекций “Статистика”
Контрольные задания
Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.
|
При использовании (IX.75) и (IX.76) |
21 и Ь должны быть заданы в кило- |
||
|
метрах. |
|||
|
О ш и б к и |
т р и а н г у л я ц и и . |
Эти ошибки являются |
наиболее |
|
опасными с точки зрения их накопления. |
Их удобно представить в |
виде «про- |
дольного» Р и «поперечного» (2 сдвига.
Л. П. Пеллиненом получена формула, которая позволяет определить суммарное действие ошибок триангуляции и «собственно астрономо-гравиметриче- ского нивелирования» на превышение квазигеоида, т. е. величину т^. Если через ар обозначить сферическое расстояние от начальной точки ряда до конечной, через Е — средний радиус Земли в км, [о.р и — продольный и радиаль-
ный случайные километровые сдвиги, то формула Л. П. Пеллинена будет иметь вид
|
= |
1 ^ |
( 1 т — 5 ^ ) . |
(IX.77) |
В табл. 13 приведены ожидаемые величины ошибок определения превышений квазигеоида для различных расстояний гр. При расчетах использованы
|
значения |
километровых ошибок: |яр = |
±5,3 см; щ = |
± 3 см. |
|||
|
Таблица 13 |
||||||
|
Ошибки определения превышений квазигеоида в ряде триангуляции, |
||||||
|
вытянутом по дуге большого круга |
||||||
|
1|>° |
||||||
|
Составляющие ошибки |
20 |
40 |
60 |
80 |
100 |
|
|
Влияние ошибок приращений высот квази- |
1.4 |
1,8 |
2,0 |
2,1 |
2,1 |
|
|
геоида по звеньям, м |
0,5 |
1,4 |
2,3 |
3,3 |
4,1 |
|
|
Косвенное влияние продольных сдвигов по |
||||||
|
звеньям, м |
1.5 |
2,3 |
3,1 |
3,9 |
.4,6 |
|
|
Суммарная ошибка, м |
||||||
|
На основании данных, приведенных в табл. 13, |
можно |
сделать |
вывод, |
|||
|
что при гр |
20° косвенное влияние продольных сдвигов на высоты квазигеоида |
|||||
|
становится существенным. |
||||||
|
О ш и б к и а с т р о н о м и ч е с к и х |
о п р е д е л е н и й . Если звено |
|||||
|
триангуляции расположено в меридианальном направлении, |
то |
П1Ъа = Ща = тЧч
где т,р — средняя квадратическая ошибка определения астрономической широты.
Если же звено расположено вдоль параллели, то
т$а = тг\а — тХ сое <р.
Ошибки определения астрономических координат в настоящее время составляют ±0,3—0,4″.
При Ь — Е, по формуле (IX.73) получим, что ошибки определения астро-
номических координат дают в превышении квазигеоида ошибку порядка 1 м. О ш и б к и г р а в и м е т р и ч е с к о й с ъ е м к и могут быть систе-
матическими и случайными.
280‘
Следует считать доказанным, что гравиметрические определения не могут быть источником существенных систематических ошибок при астрономо-гра- виметрическом нивелировании, если гравиметрические поправки вычислены правильно, т. е. с учетом аномалий в полосе достаточной ширины.
Верхний предел накопления систематических ошибок за счет ограничения области интегрирования расстоянием В = р1 от середипы звена определен формулой (IX.68)
где под (§ — у) можно понимать половину систематической части изменения поля аномалий от начала к концу ходовой линии нивелирования, выраженную в миллигалах.
Величина этой ошибки не зависит от длины ходовой линии и даже при
— у) ~ 50 мгл н р = 2 остается менее 5 • 10~6. Большие случайные погрешности в определении гравиметрической поправки входят в последующие высоты квазигеоида. Это обстоятельство может иметь место при пересечении горных районов, где ошибка интерполирования аномалий примерно в 2—3 раза больше, нежели в равнинных местах.
Случайная часть ошибки гравиметрической поправки для отдельного звена обусловлена двумя обстоятельствами: ограничением области интегрирования и ошибками интерполирования аномалий силы тяжести. Ограничение области интегрирования вызывает случайную ошибку в определении среднего наклона поверхности квазигеоида, предельная величина которой согласно IX,67 менее
О 4 А» — V ) / и
рз—1 ‘
эту ошибку можно сделать малой, соответственно выбрав величину р. Выполним некоторые расчеты. Ошибка в определении среднего наклона
квазигеоида на участке одного звена, равная 0,2″, приводит к ошибке в определении превышения (при расстоянии между пунктами А и В 21 = 100 км), равной 0,1 м. Ошибка же в определении превышения в конце ходовой линии в этом случае будет
Если Ь — длина ходовой линии —равна радиусу Земли В, то = 1 м. Таким образом, можно считать, что ошибка гравиметрического вывода уклонения отвеса (т^) обусловлена в основном ошибками интерполяции ано-
малий силы тяжести.
Существующая гравиметрическая съемка, выполняемая в интересах разведки полезных ископаемых, обеспечивает вывод гравиметрических уклонений
|
отвеса с точностью ±0,5″ и выше. |
||
|
Принимая т&е = ±0,5″, при Ь = В на основании формулы |
(IX.73) |
|
|
получим |
± 1,5 м. |
|
|
= |
||
|
При проектировании линий астрономо-гравиметрического нивелирования |
||
|
ставилось условие, чтобы ошибка на |
1 км хода нивелирования |
была не |
больше соответствующих ошибок плановых координат, с тем чтобы астрономогеодезическая сеть представляла собой пространственное построение, в котором вертикальные координаты определены не менее надежно, нежели плановые. Было принято см на 1 км.
281′
Величину т& определяют по колебаниям разностей астрономо-геодезиче- ских и гравиметрических уклонений отвеса на соседних астрономических пунктах. Так, обозначая через А | и Ат) — разности составляющих астроно- мо-геодезических и гравиметрических уклонений отвеса в меридиане и первом вертикале, по формуле для разностей двойных измерений находят средние квадратические ошибки
|
7Пд| = } |
п |
|
|
2 |
(Д6/-Д&-1)2 |
|
|
; |
||
|
2п |
||
|
тАт1 = |
2п |
|
где п — число звеньев в линии астрономо-гравиметрического нивелирования. Исходя из заданного значения ц,^, по формуле (IX.76) подбирали соответ-
|
ствующие |
и 21. Для достижения требуемой точности в зависимости от мест- |
||
|
ных условий |
иногда приходилось либо сгущать астропункты |
по |
сравнению |
|
с их нормальной плотностью в астрономо-геодезической сети |
(21 |
^ 100 км), |
либо проводить специальные гравиметрические съемки сгущения вокруг некоторых астропунктов (уменьшать т&). Однако, как правило, вдоль линий астрономо-гравиметрического нивелирования имеется равномерная гравиметрическая съемка, созданная для геофизических целей, которая обеспечивает требуемую точность нивелирования при обычной густоте астропунктов.
Как показало сопоставление (примерно для 1100 астропунктов) гравиметрических и астрономо-геодезических уклонений отвеса, на большей части территории СССР величина близка к ±0,5″, однако в горных и слабо изученных в гравиметрическом отношении районах она достигает величипы ±1,2″.
Уравнивание полигонов астрономо-гравиметрического нивелирования проводилось аналогично уравниванию полигонов геометрического нивелирования.
|
Вес каждого превышения |
полагали |
равным |
||||
|
1 |
||||||
|
Р* ~ |
(202 |
‘ |
||||
|
В результате уравнивания были получены превышения квазигеоида между |
||||||
|
астропунктами, а также |
средняя |
квадратическая |
ошибка единицы веса |
|||
|
и средняя квадратическая |
ошибка на |
1 км |
хода нивелирования, характери- |
|||
|
зующие систему полигонов в целом. Найденные величины |
лежат в пределах |
|||||
|
1,5—4,8 см на 1 км; среднее значение |
= |
± 3 см по всей сети. |
||||
|
Ожидаемые невязки полигонов подсчитывались |
по формуле (IX.74). До- |
пустимая невязка принималась равной удвоенной ожидаемой. Фактически полученные невязки в абсолютном большинстве случаев оказались меньше допустимых. Были получены также средние квадратические ошибки высот квазигеоида в различных точках сети полигонов относительно исходного пункта с учетом как ошибок собственно нивелирования, так и косвенного влияния ошибок плановых геодезических координат. Для большей части территории СССР
полученные ошибки не превышают ± 2 м, в самых отдаленных районах они достигают ±6м, в основном из-за косвенного влияния ошибок плановых координат.
Глава X
ПРОЕКТИРОВАНИЕ ГРАВИМЕТРИЧЕСКИХ СЪЕМОК. ПАЛЕТКИ
§ 59. ОШИБКИ ОПРЕДЕЛЕНИЯ АНОМАЛИЙ СИЛЫ ТЯЖЕСТИ
Точность определения аномалий силы тяжести зависит от точности измеренных значений силы тяжести § и точности вычисления нормальной силы тяжести у. Однако можно полагать, что они значительно меньше ошибок, обусловленных дискретностью гравиметрической съемки.
Расстояния между гравиметрическими пунктами могут изменяться в значительном диапазоне от десятков и сотен метров до нескольких тысяч километров. Если разбить всю изучаемую территорию на квадраты (или трапеции) со сторонами, равными среднему расстоянию между гравиметрическими пунктами, то на каждый квадрат (трапецию) будет в среднем приходиться один гравиметрический пункт. Следовательно, при решении практических задач аномалию силы тяжести, вычисляемую для конкретного гравиметрического пункта, относят не только к этому пункту, но и используют для представления гравитационного поля на некоторой площади (большей или меньшей, в зависимости от плотности гравиметрической съемки). Это приводит к ошибкам получившим название ошибок представительства.
Назовем среднюю квадратическую разность между наблюденным значением аномалии силы тяжести Ад в каждой точке внутри данного участка и сред-
|
ним значением аномалии |
Д^ср для этого участка полной ошибкой представи- |
||
|
тельства |
‘ |
||
|
б е = У — ^ — 4 = 1 |
‘ |
(Х.1) |
где п — число гравиметрических пунктов, расположенных в пределах участка.
|
Поскольку |
||
|
Д^ср = |
> п Д&р = 2 |
2 Д ^ Р = « |
то
[2 V —
или окончательно
283′
Эта формула удобнее (Х.1) в том отношении, что не требует вычислений для каждого участка величины Д#ср.
Развитием формулы (Х.2) является формула Хирвонена
где 6, О — соответственно среднее квадратическое значение точечной аномалии
и аномалии по участку. Если на участке несколько гравиметрических пунктов, под О понимается среднее квадратическое значение средней аномалии, получаемой по этим пунктам. Величины С ж & легко получить по данным статисти-
ческого анализа силы тяжести, в связи с чем формула Хирвонена ныне получила очень широкое распространение.
Величина полной ошибки представительства §§ включает в себя и ошибку измерения силы тяжести т. Если исключить из ошибку измерения т, то по-
лучится «чистая» ошибка представительства
6 * 8 = 1 / V — » » 2 .
При расчетах, связанных с проектированием гравиметрических съемок, необходимо знать зависимость между величиной «чистой» ошибки представительства и площадью участка, которой она соответствует.
Де Грааф Хентер [8] получил выражение, определяющее величину «чистой» ошибки представительства, как функцию размеров участка, который она «представляет».
Вид этой функции определялся эмпирически. Для различных прямоугольников со сторонами х и у по измеренным аномалиям силы тяжести вычислялись
|
соответствующие значения |
||||
|
Для определения вида функциональной зависимости |
= |
/ (х, |
у) подби- |
|
|
ралась такая функция / (х, у), чтобы |
отношение |
у) |
было |
примерно |
|
одинаковым для различных значений х |
и у. В результате получено |
|||
|
бев = с № + У у ) , |
(Х.З) |
где стороны прямоугольника х и у задаются в километрах; С — постоянный
коэффициент.
Коэффициент С определяется для каждого исследуемого района. В районах
|
средней аномальности (например, в равнинных районах СССР) |
С = |
|
= 0,54 мгл/км,/г. В районах повышенной аномальности (например, |
в гор- |
ных районах) коэффициент С может быть в 2—3 раза больше. Если участки,
на которые разбивается исследуемый район, имеют форму квадратов, можно пользоваться формулой
В зависимости от степени аномальности района и принятой плотности гравиметрической съемки определяется точность измерений силы тяжести.
Чтобы можно было пренебречь влиянием ошибки измерений на величину полной ошибки представительства, поставим условие, чтобы ошибка измерений т была в три раза меньше «чистой» ошибки представительства. Действительно, если
т = 4
284′
|
то |
|||
|
в* = | / ( б Ы 2 + { ( б Ы а |
= ± |
вив |
= Ьев. |
|
Определим, какова примерная точность измерений при различной плот- |
|||
|
ности гравиметрической съемки, считая, |
что |
С = |
0,54 мгл/км,/г. В этом слу- |
|
чае |
|||
|
= 1,08 Ух, |
т = |
0,36 |
Ух. |
Значения необходимой точности измерений при различной плотности гравиметрической съемки приведены в табл. 14.
Из таблицы следует, что при редкой гравиметрической съемке, когда один
|
пункт приходится на трапецию 10 X 10° (х |
1112 км) |
имеет смысл определять |
||||||||
|
силу |
тяжести |
с |
точностью |
поряд- |
Т а б л и ц а 14 |
|||||
|
ка ± 1 0 мгл; при увеличении плотности |
||||||||||
|
гравиметрической |
съемки точность на- |
Расстояние |
меж- |
|||||||
|
блюдений соответственно должна повы- |
Ье, мгл |
т , мгл |
||||||||
|
ду пунктами |
(ж), |
|||||||||
|
шаться. |
км |
|||||||||
|
Вычисление ошибок представитель- |
1112,0 |
36,0 |
12,0 |
|||||||
|
ства |
производилось неоднократно как |
|||||||||
|
114,2 |
11,4 |
3,8 |
||||||||
|
за границей, так и в СССР. |
||||||||||
|
31,6 |
6,0 |
2,0 |
||||||||
|
Так, |
по |
данным |
ЦНИИГАиК |
|||||||
|
(1943 |
г.) |
в равнинных |
районах |
СССР |
при расстояниях между гравиметрическими пунктами порядка 30 км. «чистая» ошибка представительства, вычисленная как по аномалиям в свободном воз-
|
духе, |
так и по аномалиям Буге, оказалась равной |
±7,1 мгл. |
|
В |
горных районах величина «чистой» ошибки |
представительства значи- |
тельно больше. Так, например, по тем же данным ЦНИИГАиК, в горах «чистая» ошибка представительства при расстояниях между пунктами —30 км оказалась по аномалиям в свободном воздухе ± 2 5 мгл, а по аномалиям Буге ±12,8 мгл.
При гравиметрических съемках большой плотности, когда расстояния
.между пунктами меньше 20 км, следует учитывать, что изменение аномалий от пункта к пункту носит в общем линейный характер, поэтому в промежуточных точках, находящихся между пунктами наблюдений, становится возможным определять значения аномалий методом линейной интерполяции.
В этом случае на гравиметрических картах следует проводить так называемые изоаномалы, т. е. линиий соединяющие точки с равными аномалиями. Определенное при помощи изоаномал значение аномалии называется интерполированным. Конечно, интерполированное значение аномалии отличается от действительного, полученного в данной точке измерением силы тяжести. Средняя квадратическая разность между действительными значениями аномалий и снятыми с карты называется полной ошибкой интерполяции аномалий силы тяжести В нее входят ошибка измерений т и погрешность, обусловленная
предположением о линейном изменении аномалий силы тяжести между пунктами 8дв (последняя величина называется «чистой» ошибкой интерполяции).
Таким образом,
б§з=У{8ёУ-т\
Определим полную ошибку интерполяции. В районе, где выполнена гравиметрическая съемка, исключается половина всех пунктов, т. е. густота еети
285′
разрежается вдвое, и по оставшимся пунктам строится карта изоаномал. Зате: по этой карте интерполированием между изолиниями определяют аномалии
вместах исключенных пунктов и сравнивают их с наблюденными аномалиям:
вэтих пунктах. Аналогично определяется ошибка интерполяции для съемк;. разреженной в 4, 8, 16 раз относительно первоначальной.
«Чистая» ошибка интерполяции может быть выражена эмпирической з; висимостью
б= кх,
где к — постоянный коэффициент; х — расстояние между пунктами. Значение коэффициента к, как и значение коэффициента С формулы (Х.З)
|
зависит |
от степени |
аномальности |
гравитационного поля в данном районе ь |
||||||||
|
должно |
определяться |
из |
специаль- |
||||||||
|
Т а б л и ц а |
15 |
ных исследований. Если |
гравитацион- |
||||||||
|
ное поле средней аномальности, можн< |
|||||||||||
|
бе’, мгл |
Л, мгл |
т , мгл |
X, км |
принять |
к — 0,11 мгл/км. |
||||||
|
Обычно при проектировании грави- |
|||||||||||
|
метрической съемки со средним расстоя- |
|||||||||||
|
0 , 2 |
0 , 5 |
0 , 0 7 |
1,7 |
нием между пунктами < 2 0 км исходя: |
|||||||
|
0 , 4 |
1 ,0 |
0 , 1 3 |
, 3 , 3 |
из величины полной ошибки |
интерпо- |
||||||
|
0 , 8 |
2 , 0 |
0 , 2 5 |
6 , 7 |
ляции, |
которая |
устанавливается длг |
|||||
|
1 , 2 |
3 , 0 |
0 , 3 8 |
10,0 |
||||||||
|
данной |
площади |
путем |
теоретических |
||||||||
|
1,6 |
4 , 0 |
0,51 |
13,3 |
||||||||
|
2,0 |
5 , 0 |
0 , 6 3 |
16,7 |
расчетов. Эта ошибка, очевидно, пол- |
|||||||
|
ностью характеризует точность грави- |
|||||||||||
|
метрической |
карты. |
||||||||||
|
По |
величине полной ошибки |
интерполяции |
устанавливается сечент |
||||||||
|
изоаномал к, |
необходимая точность наблюдений т. и плотность |
гравиметриче- |
|||||||||
|
ской съемки, |
т. е. среднее |
расстояние |
между пунктами х. Если принять, чт< |
ошибка наблюдения должна быть в три раза меньше «чистой» ошибки интерполяции, т. е. = 3 т, то т = б^-‘/|/Т0, х — 8§’/0,12. Примем также к =
=2,5 6*’.
Втабл. 15 приведены сечения изоаномал, ошибки наблюдений и требуемое расстояние между пунктам при различных величинах полной ошибки интерполяции.
На основании многочисленных исследований, выполненных различным авторами, можно сделать вывод, что при расстояниях между пунктами < 20 ку
ошибка интерполяции примерно в два раза меньше ошибки представительства. Это означает, что линейное интерполирование аномалий дает вполне ощутимый выигрыш в точности.
Напротив, при расстояниях порядка 30 км даже в равнинных районах средней аномальности ошибка интерполяции оказывается равной ошибке представительства ±7,0 мгл. Это обстоятельство означает, что при указанных
расстояниях (а тем более больших 30 км) аномалии силы тяжести от пункта к пункту изменяются не по линейному закону и потому производить линейное интерполирование аномалий не следует.
Интересно отметить, что в горных районах величина «чистой» ошибки интерполяции при расстояниях между пунктами порядка 30 км, определенная
|
по аномалиям Буге, |
оказывается значительно меньшей ошибки интерполяции, |
|
|
определенной по аномалиям в свободном воздухе (по аномалиям Буге |
— |
|
|
= ±10,6 мгл, а по |
аномалиям в свободном воздухе 6$’8 — ±28,2 мгл). |
Это |
266′
означает, что в горах аномалии Буге изменяются более плавно, нежели аномалии в свободном воздухе и линейная интерполяция аномалий Буге предпочтительнее линейной интерполяции аномалий в свободном воздухе.
§ 60. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ГРАВИМЕТРИЧЕСКИХ УКЛОНЕНИЙ ОТВЕСА
Для оценки влияния погрешностей аномалий силы тяжести на точность вычисления гравиметрических уклонений отвеса будем исходить из нулевого приближения к формулам (VIII. 108), совпадающего с формулами Венинг-Мей- неса (VIII.59), поскольку точность вычисления уклонений отвеса определяется в основном точностью формул нулевого приближения. Более того, можно воспользоваться соответствующими выражениями для плоскости (IX.56) и (IX.57).
|
Все расчеты будем делать лишь для составляющей |
так как формулы для |
||
|
получаются аналогично после замены соз А |
на з т А. |
||
|
Учитывая, что элемент поверхности в полярных координатах йа = г йг д.А |
|||
|
формулу (IX.56) перепишем |
в виде |
||
|
| = — |
— |
АйгАА. |
(Х.5) |
Довольно просто можно оценить ошибку той части уклонения отвеса, которая получается от учета аномалий в области, лежащей за пределами центральной зоны., принимаемой за окружность радиуса г0 = 21 (21 — среднее расстояние
между гравиметрическими пунктами в условиях равномерной, съемки).
Для вычисления интеграла (Х.5) методом численного интегрирования разобьем всю область интегрирования на достаточно малые ячейки, имеющие форму трапеций, внутри которых можно было бы считать (% — у) = сопз!..
В этом случае формулу (Х.5) можно представить в виде
где суммирование распространяется на все трапеции, число которых обозначим г, кроме центральной зоны радиуса г0.
Выполняя интегрирование в указанных пределах, получим
|
1 |
|||
|
соз АЛА — 1п |
(зш Аь — зш Ак_т) = |
||
|
гт~1 |
Ак-1 |
||
|
= |
21п Гы-* |
СОЗ |
Ак+Аь-1 |
|
2 |
Введя обозначения
Ак + Ак-1 _ л
2 СР
Ак — Ак-1
2 2
287
л полагая по малости угла з т АЛ/2 = А4/2, получим
п=1
|
? = — |
2 |
ОТ — ?>»1п |
008 |
|
п= |
О |
||
|
Обозначив коэффициенты |
при |
аномалиях |
— у)„ через /,„ будем иметь |
2лу 51П 1″
п=0
Поскольку в каждой ячейке, на которые разбита область интегрирования, имеется лишь один гравиметрический пункт, среднюю квадратическую ошибку определения аномалии положим равной полной ошибке представительства 6г (см. § 59).
Тогда для расчета средней квадратической ошибки составляющей уклоне-
|
ния отвеса получим формулу |
|
|
^ = |
(х-*» |
|
Подставив значения постоянных, будем иметь |
|
|
т\ = 0,0335″ Щ |
(Х.Т) |
Коэффициенты /„ определяют степень влияния соответствующей аномалии на величину уклонения отвеса.
Рассмотрим несколько схем для подсчета средней квадратической ошибки составляющей уклонения отвеса.
С х е м а А
Разбивка зоны интегрирования на элементарные площадки и расположение гравиметрических пунктов показано на рис. 59. Радиусы окружностей равны (2т ± 1) I, где т — номер зоны. Число трапеций в зоне г равно 8т.
Заметим, что для каждой зоны с номером т отношение гт/гт-г = (2т + 1)/(2т — 1) является величиной
|
постоянной. |
|||||||
|
Поэтому в |
соответствии |
с |
формулой (Х.6) |
||||
|
и принятыми обозначениями средняя квадратпче- |
|||||||
|
ская |
ошибка, |
вносимая зоной |
с |
номером т . |
|||
|
будет |
7. |
||||||
|
с » |
1 |
1 2»»-|-1 |
соз2 Аер |
(А4) |
|||
|
= |
2яу 81111А» |
2т—1 |
|||||
|
так как число трапеций г в зоне равно 8т, то |
|||||||
|
Рис. 59 |
АА |
2л |
п |
||||
|
8т ‘ |
4 т |
||||||
Очевидно, что
соз2 Ас р (ДЛ)^*’1 = АА у 2 соз2 Аср.
Так как
соз А 1 + соаЛ
288′
то
|
/ |
2 |
2 л |
= |
л / 1 + С08 2Л1 |
1 + |
СОВ2Л» |
1 + соз |
|||||
|
соз Аср |
УI/ |
I |
22 _| |
I |
2Е-4- |
|||||||
|
= |
У |
(С03 |
2А°Р |
+ |
008 |
2А°*> |
+ • • • + |
008 |
2лср). |
|||
|
Поскольку сумма косинусов, стоящих в скобке, |
равна нулю, то |
|||||||||||
|
, соз2 Аср=== |
«2», |
|||||||||||
|
при г = |
8т |
ТП |
||||||||||
|
1 / 2 |
СОЗ |
|||||||||||
|
Г |
(-878т |
|||||||||||
|
Л |
. / |
1 |
соз2 Аср = |
-^-т~1/к |
||||||||
|
Окончательно |
||||||||||||
|
бта? — |
:—77 |
|||||||||||
|
5 |
4у 81П 1 |
Это выражение используют для подсчета средних квадратических ошибок от каждой зоны, кроме нулевой (центральной). Результаты вычислений приведены в табл. 16.
|
Т а б л и ц а 16 |
||||||||
|
Средняя квадратическая ошибка, вносимая |
||||||||
|
№ зоны |
Зона |
зоной, « |
зоной и всеми предыдущи- |
|||||
|
ми зонами, « |
||||||||
|
1 |
1—31 |
±0,0588? |
±0,0586? |
|||||
|
2 |
31—51 |
0,0196? |
0,0616? |
|||||
|
3 |
51—71 |
0,0106? |
0,0626? |
|||||
|
4 |
11—91 |
0,0076? |
0,0626? |
|||||
|
5 |
Ш—Ш |
0,0046? |
0,0626? |
|||||
|
Схема В |
||||||||
|
Радиусы окружностей, ограничивающие |
зону |
с |
номером т, равны 2 тп1 |
|||||
|
и 2 (т + 1) |
Число трапеций в зоне равно 4 (2т |
+ |
1); (рис. 60). Имеем |
|||||
|
АА |
2я |
л |
||||||
|
4 ( 2 т + 1 ) |
2 ( 2 т + 1 ) ‘ |
|||||||
|
гт |
_ |
2(го+1) |
I _ |
го+1 |
||||
|
гт-х |
2тп1 |
тп |
||||||
|
Так как АА для зоны с номером т есть величина постоянная, то |
||||||||
|
соз2 Аср |
(АЛ)2 |
= Ал | / » 2 соз2 А, |
||||||
|
я |
т /~ 4(2/ге+1) |
я |
||||||
|
2(27/1+1) |
V |
2 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.
Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
Ошибки смещения бывают преднамеренными и непреднамеренными. Причиной возникновения преднамеренной ошибки является тенденциозный подход к выбору единиц из генеральной совокупности. Чтобы не допустить появления такой ошибки, необходимо соблюдать принцип случайности отбора единиц.
Непреднамеренные ошибки могут возникать на стадии подготовки выборочного наблюдения, формирования выборочной совокупности и анализа ее данных. Чтобы не допустить появления таких ошибок, необходима хорошая основа выборки, т. е. та генеральная совокупность, из которой предполагается производить отбор, например список единиц отбора. Основа выборки должна быть достоверной, полной и соответствовать цели исследования, а единицы отбора и их характеристики должны соответствовать действительному их состоянию на момент подготовки выборочного наблюдения. Нередки случаи, когда в отношении некоторых единиц, попавших в выборку, трудно собрать сведения из-за их отсутствия на момент наблюдения, нежелания дать сведения и т. п. В таких случаях эти единицы приходится заменять другими. Необходимо следить, чтобы замена осуществлялась равноценными единицами.
Случайная ошибка выборки возникает в результате случайных различий между единицами, попавшими в выборку, и единицами генеральной совокупности, т. е. она связана со случайным отбором. Теоретическим обоснованием появления случайных ошибок выборки являются теория вероятностей и ее предельные теоремы.
Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей и обобщающих характеристик будет сколь угодно малой величиной или практически не зависит от случая. Так как случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.
Предельные теоремы теории вероятностей позволяют определять размер случайных ошибок выборки. Различают среднюю (стандартную) и предельную ошибку выборки. Под средней (стандартной) ошибкой выборки понимают расхождение между средней выборочной и генеральной совокупностей. Предельной ошибкой выборки принято считать максимально возможное расхождение, т. е. максимум ошибки при заданной вероятности ее появления.
В математической теории выборочного метода сравниваются средние характеристики признаков выборочной и генеральной совокупностей и доказывается, что с увеличением объема выборки вероятность появления больших ошибок и пределы максимально возможной ошибки уменьшаются. Чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик. На основании теоремы, доказанной П. Л. Чебышевым, величину стандартной ошибки простой случайной выборки при достаточно большом объеме выборки (n) можно определить по формуле:
где µx– стандартная ошибка.
Из этой формулы средней (стандартной) ошибки простой случайной выборки видно, что величина µx зависит от изменчивости признака в генеральной совокупности (чем больше вариация признака, тем больше ошибка выборки) и от объема выборки n чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик).
Академик А. М. Ляпунов доказал, что вероятность появления случайной ошибки выборки при достаточно большом ее объеме подчиняется закону нормального распределения. Эта вероятность определяется по формуле:
В математической статистике употребляют коэффициент доверия t, и значения функции F(t) табулированы при разных его значениях, при этом получают соответствующие уровни доверительной вероятности.
Коэффициент доверия позволяет вычислить предельную ошибку выборки, вычисляемую по формуле:
Из формулы вытекает, что предельная ошибка выборки равна -кратному числу средних ошибок выборки.
Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности x и величину предельной ошибки этой средней ?x, которая показывает с определенной вероятностью), насколько выборочная может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна
Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю.
Наряду с абсолютной величиной предельной ошибки выборки рассчитывается и относительная ошибка выборки, которая определяется как процентное отношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности:
Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки. Средняя (стандартная) ошибка выборки зависит от объема выборки и степени вариации признака в генеральной совокупности.
Данный текст является ознакомительным фрагментом.
Читайте также
Наблюдения за объемом
Наблюдения за объемом
Имеет значение не сам объем, а его соотношения в различные периоды рыночного движения. Соотношения объемов – очень важный, но и наименее объективный из технических инструментов, так как здесь нет никаких непреложных правил. Вместо этого есть набор
Закономерности и наблюдения
Закономерности и наблюдения
Я верю в существование закономерностей на рынке и считаю, что отношусь к числу людей, которые способны их улавливать. Но я также хорошо помню и о том, что все закономерности нечеткие. Нечеткие они потому, что в них присутствует фактор
Ошибки в инвестициях – это ошибки инвесторов
Ошибки в инвестициях – это ошибки инвесторов
Сейчас я больше, чем когда бы то ни было, убежден в том, что все ошибки в инвестициях на самом деле ошибки инвесторов.Инвестиции не совершают ошибок. В отличие от инвесторов.Инвестирование – это выбор. Именно об этой
8. Способы статистического наблюдения
8. Способы статистического наблюдения
Способами получения статистической информа–ции являются документальный способ наблюдения; способ непосредственного наблюдения: опрос.Документальное наблюдение основано на исполь–зовании в качестве источника информации данных
9. Формы статистического наблюдения
9. Формы статистического наблюдения
В теории статистики рассматриваются и формы статистического наблюдения: отчетность; специально организованное статистическое наблюдение; реги–стры.Статистическая отчетность – основная форма статистического наблюдения, которая
2. Ошибки выборочного наблюдения
2. Ошибки выборочного наблюдения
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но
19. Наблюдения
19. Наблюдения
Наблюдение представляет собой сбор первичной информации об объекте наблюдения для построения гипотез, проверки исходных данных и т. д.К способам проведения наблюдения относят:1) прямой, который предполагает непосредственное наблюдение за объектом
6. Организация статистического наблюдения
6. Организация статистического наблюдения
Начальным этапом статистического исследования является статистическое наблюдение.В процессе статистического наблюдения формируется оснавная информация, которая является основной для статистического
11. Ошибки статистического наблюдения и контроль материалов наблюдения
11. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Любое статистическое наблюдение предполагает получение данных, которые будут
34. Определение выборочного наблюдения
34. Определение выборочного наблюдения
Так как сплошное наблюдение дорого и трудоемко, то его заменили выборочным.Выборочное наблюдение – это способ несплошного наблюдения, при котором лишь часть совокупности, отобранная по определенным правилам выборки и
Часть 5 Наблюдения
Часть 5
Наблюдения
За свою тридцатипятилетнюю карьеру в бизнесе я смотрел на мир с разных точек зрения. Я был свидетелем взлетов и падений в экономике и отрасли, появления на рынке новых продуктов и их исчезновения. Я представлял новые товары, возрождал старые, закрывал
Введение процедуры наблюдения
Введение процедуры наблюдения
Наблюдение вводится с целью сохранения активов должника, проведения оценки его финансового состояния, изучения объективной возможности восстановления платежеспособности и продолжения функционирования организации.С момента введения
1. Организация статистического наблюдения
1. Организация статистического наблюдения
Статистическое наблюдение – это организованная работа по сбору первичных сведений об изучаемых массовых явлениях и процессах общественной жизни. Статистическое наблюдение проводится организованно и по заранее разработанным
5. Ошибки статистического наблюдения и контроль материалов наблюдения
5. Ошибки статистического наблюдения и контроль материалов наблюдения
Важнейшей задачей статистического наблюдения является достоверность и точность собираемой статистической информации.Точность – это уровень соответствия значения какого–либо признака или
1. Определение выборочного наблюдения
1. Определение выборочного наблюдения
Статистические исследования очень трудоемки и дороги, поэтому возникла мысль о замене сплошного наблюдения выборочным.Основная цель несплошного наблюдения состоит в получении характеристик изучаемой статистической совокупности
Общие наблюдения и впечатления
Общие наблюдения и впечатления
Члены команды систематически выполняли требования восьми этапов цикла кайдзен и обнаружили, что с их помощью смогли построить процесс решения проблем в правильной последовательности. Использование таких инструментов, как «рыбий скелет»
а) Виды ошибок
В процессе исследования явлений может
возникать отклонение исчисленных
показателей от их действительной
величины, то есть могут возникать ошибки
статистического наблюдения.
По источникам происхождения ошибки
наблюдения можно подразделить на
следующие:
-
преднамеренные;
-
непреднамеренные,
которые в свою очередь делятся на:
-
случайные;
-
систематические;
-
репрезентативности
(представительности).
Преднамеренные(сознательные, злостные) получаются в
результате того, что сознательно
сообщаются неправильные данные. Например,
сокрытие фирмами прибыли от налогообложения,
искажение сведений об объеме выпускаемой
продукции, приписки и т. д.
Законом
предусматривается применение экономических
и административных мер к предприятиям
и лицам за злостные ошибки (иногда и
уголовная ответственность).
Непреднамеренные
случайныеошибки чаще связаны с
невнимательностью регистратора,
небрежностью в заполнении документов,
неточностью измерительных приборов,
ошибками в ответах опрашиваемых.
Непреднамеренные
систематическиеошибки возникают
при округлении признака в большую или
меньшую сторону, при использовании ЭВМ.
Ошибки
репрезентативности(представительности)
свойственны несплошному наблюдению,
они возникают вследствие неправильного
выбора единиц для обследования, нарушен
принцип случайного отбора, и выборочная
совокупность не полно характеризует
генеральную.
Б) Способы предотвращения ошибок статистического наблюдения
Чтобы
предупредить возникновение ошибок или
уменьшить их размеры необходимо:
-
обеспечивать
правильный подбор и подготовку кадров; -
вести широкую
разъяснительную работу, применять меры
взыскания за искажение фактов; -
проводить
систематический контроль.
Контроль может
быть: счетным и логическим.
Счетный контроль
заключается в проверке точности
арифметических расчетов.
Логический
контроль проводится путем сопоставления
полученных данных с известными признаками,
логическое осмысление, сопоставление
с данными за прошлый период.
Например, о
заработной плате работников предприятия
можно судить по отчету, по труду и по
отчету о себестоимости продукции.
Сведения о заработной плате должны быть
одинаковыми, сопоставимыми (приведите
примеры).
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
«Систематическая предвзятость» перенаправляется сюда. Эта статья посвящена метрологии и статистике. О социологическом и организационном феномене см. системная предвзятость.
|
|
Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. |
Ошибка наблюдения (или же погрешность измерения) — разница между измеренный значение количества и его истинное значение.[1] В статистика, ошибка не является «ошибкой». Вариабельность является неотъемлемой частью результатов измерений и процесса измерения.
Погрешности измерения можно разделить на две составляющие: случайная ошибка и систематическая ошибка.[2]
Случайные ошибки ошибки в измерениях, которые приводят к несогласованности измеряемых значений при повторных измерениях постоянный атрибут или количество принимаются. Систематические ошибки — это ошибки, которые не определяются случайно, но вносятся неточность (включая процесс наблюдения или измерения), присущий система.[3] Систематическая ошибка может также относиться к ошибке с ненулевым иметь в виду, то эффект из которых не уменьшается, когда наблюдения находятся усредненный.[нужна цитата ]
Наука и эксперименты
Когда либо случайность или неопределенность, смоделированная теория вероятности связано с такими ошибками, они являются «ошибками» в том смысле, в котором этот термин используется в статистика; видеть ошибки и остатки в статистике.
Каждый раз, когда мы повторяем измерение чувствительным прибором, мы получаем несколько разные результаты. Общее статистическая модель Используется в том, что ошибка состоит из двух дополнительных частей:
- Систематическая ошибка что всегда происходит с одним и тем же значением, когда мы используем инструмент одинаково и в одном и том же случае
- Случайная ошибка которые могут отличаться от наблюдения к другому.
Систематическая ошибка иногда называется статистическая погрешность. Его часто можно уменьшить с помощью стандартных процедур. Часть учебного процесса в различных науки учится использовать стандартные инструменты и протоколы, чтобы минимизировать систематические ошибки.
Случайная ошибка (или случайное изменение ) происходит из-за факторов, которые нельзя или не будут контролировать. Возможная причина отказа от контроля этих случайных ошибок заключается в том, что контролировать их каждый раз, когда проводится эксперимент или измерения, может быть слишком дорого. Другие причины могут заключаться в том, что все, что мы пытаемся измерить, изменяется во времени (см. динамические модели ) или фундаментально вероятностный (как в случае с квантовой механикой — см. Измерение в квантовой механике ). Случайная ошибка часто возникает, когда инструменты работают на пределе своих рабочих пределов. Например, цифровые весы часто показывают случайную ошибку в младшем разряде. Три измерения одного объекта могут показывать что-то вроде 0,9111 г, 0,9110 г и 0,9112 г.
Случайные ошибки против систематических ошибок
Ошибки измерения можно разделить на две составляющие: случайная ошибка и систематическая ошибка.[2]
Случайная ошибка всегда присутствует в измерении. Это вызвано непредсказуемыми по своей природе колебаниями в показаниях измерительного прибора или в интерпретации экспериментатором показаний прибора. Случайные ошибки проявляются как разные результаты якобы одного и того же повторного измерения. Их можно оценить путем сравнения нескольких измерений и уменьшить путем усреднения нескольких измерений.
Систематическая ошибка является предсказуемым и обычно постоянным или пропорциональным истинному значению. Если причину систематической ошибки можно определить, то обычно ее можно устранить. Систематические ошибки вызваны несовершенной калибровкой средств измерений или несовершенными методами измерения. наблюдение или вмешательство среда с процессом измерения и всегда влияют на результаты эксперимент в предсказуемом направлении. Неправильная установка нуля прибора, приводящая к ошибке нуля, является примером систематической ошибки прибора.
Стандарт испытаний производительности PTC 19.1-2005 «Неопределенность испытаний», опубликованный Американским обществом инженеров-механиков (ASME), детально описывает систематические и случайные ошибки. Фактически, он концептуализирует свои основные категории неопределенности в этих терминах. Случайная ошибка может быть вызвана непредсказуемыми флуктуациями в показаниях измерительного прибора или в интерпретации экспериментатором показаний прибора; эти колебания могут быть частично вызваны вмешательством окружающей среды в процесс измерения. Концепция случайной ошибки тесно связана с концепцией точность. Чем выше точность измерительного прибора, тем меньше вариабельность (стандартное отклонение ) колебаний его показаний.
Источники систематической ошибки
Несовершенная калибровка
Источниками систематической погрешности могут быть несовершенная калибровка средств измерений (погрешность нуля), изменение среда которые мешают процессу измерения и иногда несовершенные методы наблюдение может быть либо нулевой ошибкой, либо процентной ошибкой. Если вы представите экспериментатора, который измеряет период времени маятника, который проходит мимо реперный маркер: Если их секундомер или таймер запускаются с 1 секундой на часах, то все их результаты будут отключены на 1 секунду (нулевая ошибка). Если экспериментатор повторит этот эксперимент двадцать раз (начиная с 1 секунды каждый раз), то будет процентная ошибка в рассчитанном среднем их результатах; конечный результат будет немного больше истинного периода.
Расстояние измеряется радар будет систематически переоцениваться, если не учитывать небольшое замедление волн в воздухе. Неправильная установка нуля прибора, приводящая к ошибке нуля, является примером систематической ошибки прибора.
Систематические ошибки также могут присутствовать в результате оценивать на основе математическая модель или же физический закон. Например, оценочная частота колебаний из маятник будет систематически ошибаться, если не учтено небольшое движение поддержки.
Количество
Систематические ошибки могут быть постоянными или связаны (например, пропорциональными или процентными) с фактическим значением измеренной величины или даже со значением другой величины (показание линейка может зависеть от температуры окружающей среды). Если он постоянный, это просто из-за неправильного обнуления прибора. Когда он непостоянен, он может менять знак. Например, если на термометр действует пропорциональная систематическая ошибка, равная 2% от фактической температуры, а фактическая температура составляет 200 °, 0 ° или −100 °, измеренная температура будет 204 ° (систематическая ошибка = + 4 °), 0 ° (нулевая систематическая ошибка) или −102 ° (систематическая ошибка = −2 °) соответственно. Таким образом, температура будет завышена, когда она будет выше нуля, и занижена, когда она будет ниже нуля.
Дрейф
Систематические ошибки, изменяющиеся в процессе эксперимента (дрейф ) легче обнаружить. Измерения указывают на тенденции во времени, а не на случайные колебания иметь в виду. Дрейф очевиден, если измерение постоянный количество повторяется несколько раз, и во время эксперимента измерения смещаются в одну сторону. Если следующее измерение выше, чем предыдущее, что может произойти, если прибор нагревается во время эксперимента, тогда измеряемая величина является переменной, и можно обнаружить дрейф, проверяя нулевое показание во время эксперимента, а также в начале эксперимент (действительно, нулевое показание является мерой постоянной величины). Если нулевое показание постоянно выше или ниже нуля, имеется систематическая ошибка. Если это не может быть устранено, потенциально путем сброса прибора непосредственно перед экспериментом, тогда это необходимо разрешить, вычтя его (возможно, изменяющееся во времени) значение из показаний и приняв его во внимание при оценке точности измерения.
Если закономерностей в серии повторных измерений не наблюдается, наличие фиксированных систематических ошибок может быть обнаружено только в том случае, если измерения проверены либо путем измерения известной величины, либо путем сравнения показаний с показаниями, полученными с помощью другого устройства, известного как более точным. Например, если вы думаете о времени маятника, используя точный секундомер несколько раз вам будут представлены значения, распределенные случайным образом относительно среднего значения. Систематическая ошибка Hopings присутствует, если секундомер сравнивается с ‘говорящие часы ‘телефонной системы и оказалось, что она работает медленно или быстро. Очевидно, что время маятника необходимо корректировать в соответствии с тем, насколько быстро или медленно работает секундомер.
Измерительные инструменты, такие как амперметры и вольтметры необходимо периодически проверять соответствие известным стандартам.
Систематические ошибки также можно обнаружить путем измерения уже известных величин. Например, спектрометр оснащен дифракционная решетка можно проверить, используя его для измерения длина волны D-линий натрий электромагнитный спектр которые находятся на 600 нм и 589,6 нм. Измерения могут использоваться для определения количества линий на миллиметр дифракционной решетки, которые затем могут использоваться для измерения длины волны любой другой спектральной линии.
Постоянные систематические ошибки очень трудно устранить, поскольку их влияние можно наблюдать только в том случае, если их можно устранить. Такие ошибки невозможно устранить повторением измерений или усреднением большого количества результатов. Распространенный метод устранения систематической ошибки — это калибровка измерительного прибора.
Источники случайной ошибки
Случайная или стохастическая ошибка в измерении — это ошибка, которая является случайной от одного измерения к другому. Стохастические ошибки обычно нормально распределенный когда стохастическая ошибка является суммой многих независимых случайных ошибок из-за Центральная предельная теорема. Стохастические ошибки, добавленные в уравнение регрессии, учитывают изменение Y что не может быть объяснено включенным Иксс.
Обзоры
Термин «ошибка наблюдения» также иногда используется для обозначения ошибок ответа и некоторых других типов ошибка, не связанная с выборкой.[1] В ситуациях типа опроса эти ошибки могут быть ошибками при сборе данных, включая как неправильную запись ответа, так и правильную запись неточного ответа респондента. Эти источники ошибок, не связанных с выборкой, обсуждаются у Саланта и Диллмана (1994) и Бланда и Альтмана (1996).[4][5]
Эти ошибки могут быть случайными или систематическими. Случайные ошибки вызваны непреднамеренными ошибками респондентов, интервьюеров и / или кодировщиков. Систематическая ошибка может возникать при систематической реакции респондентов на метод, использованный при формулировке вопроса опроса. Таким образом, точная формулировка вопроса обследования имеет решающее значение, поскольку она влияет на уровень ошибки измерения.[6] Исследователям доступны различные инструменты, которые помогут им решить эту точную формулировку вопросов, например, оценка качества вопроса с помощью MTMM эксперименты. Эта информация о качестве также может быть использована для исправить ошибку измерения.[7][8]
Влияние на регрессионный анализ
Если зависимая переменная в регрессии измеряется с ошибкой, регрессионный анализ и соответствующая проверка гипотез не затрагиваются, за исключением того, что р2 будет ниже, чем при идеальном измерении.
Однако, если один или несколько независимые переменные измеряется с ошибкой, то коэффициенты регрессии и стандартные проверка гипотез недействительны.[9]:п. 187
Смотрите также
- Смещение (статистика)
- Когнитивное искажение
- Поправка на ошибку измерения (для корреляций Пирсона)
- Ошибки и неточности в статистике
- Ошибка
- Репликация (статистика)
- Статистическая теория
- Метрология
- Разбавление регрессии
- Метод испытания
- Распространение неопределенности
- Ошибка прибора
- Погрешность измерения
- Модели с ошибками в переменных
- Системная предвзятость
Рекомендации
- ^ а б Додж, Ю. (2003) Оксфордский словарь статистических терминов, ОУП. ISBN 978-0-19-920613-1
- ^ а б Джон Роберт Тейлор (1999). Введение в анализ ошибок: исследование неопределенностей в физических измерениях. Книги университетских наук. п. 94, §4.1. ISBN 978-0-935702-75-0.
- ^ «Систематическая ошибка». Merriam-webster.com. Получено 2016-09-10.
- ^ Salant, P .; Диллман, Д. А. (1994). Как провести опрос. Нью-Йорк: Джон Вили и сыновья. ISBN 0-471-01273-4.
- ^ Блэнд, Дж. Мартин; Альтман, Дуглас Г. (1996). «Статистические заметки: ошибка измерения». BMJ. 313 (7059): 744. Дои:10.1136 / bmj.313.7059.744. ЧВК 2352101. PMID 8819450.
- ^ Saris, W. E .; Галльхофер, И. Н. (2014). Разработка, оценка и анализ анкет для опросных исследований (Второе изд.). Хобокен: Вайли. ISBN 978-1-118-63461-5.
- ^ ДеКастелларнау А. и Сарис В. Э. (2014). Простая процедура для исправления ошибок измерения в опросном исследовании. Европейская образовательная сеть социальных исследований (ESS EduNet). Доступны на: http://essedunet.nsd.uib.no/cms/topics/measurement
- ^ Saris, W. E .; Ревилла, М. (2015). «Исправление ошибок измерений в обзорных исследованиях: необходимо и возможно» (PDF). Исследование социальных показателей. 127 (3): 1005–1020. Дои:10.1007 / с11205-015-1002-х. HDL:10230/28341.
- ^ Хаяси, Фумио (2000). Эконометрика. Издательство Принстонского университета. ISBN 978-0-691-01018-2.CS1 maint: ref = harv (связь)
дальнейшее чтение
- Кокран, У. Г. (1968). «Ошибки измерения в статистике». Технометрика. 10 (4): 637–666. Дои:10.2307/1267450. JSTOR 1267450.
2.4. Точность статистического наблюдения
Под точностью статистического наблюдения понимают степень соответствия значения наблюдаемого показателя, вычисленного по материалам обследования, его действительной величине. Расхождение, или разница, между ними называется ошибкой статистического наблюдения.
Различают две группы ошибок:
- ошибки регистрации;
- ошибки репрезентативности.
Ошибки регистрации присущи любому статистическому наблюдению, как сплошному, так и несплошному. Они делятся на случайные ошибки регистрации и систематические ошибки регистрации.
Случайными ошибками регистрации называют ошибки, возникающие вследствие действия случайных факторов. К ним можно отнести различного рода непреднамеренные описки: например, вместо возраста человека «15 лет» указано «5 лет», у Ивановой Марии Петровны в графе пол отмечен «Мужской» и т. п. Такие ошибки легко выявляются методом логического анализа, например, если человеку 8 лет, но имеется высшее образование, а в графе «Семейное положение» указано «Состоит в браке», то, естественно, следует исправить возраст. Если объем исследуемой совокупности велик или велика доля отбора при выборочном наблюдении, случайные ошибки регистрации имеют тенденцию взаимопогашаться вследствие действия закона больших чисел, поскольку ошибки, как правило, разнонаправлены и искажают статистический показатель как в большую, так и в меньшую сторону. При небольшом объеме наблюдения требуется тщательная выверка его результатов — логический анализ данных.
Систематические ошибки регистрации чаще всего имеют однонаправленные искажения: они либо увеличивают, либо уменьшают статистический показатель, и, что характерно, подобная ситуация повторяется от обследования к обследованию. Так, по результатам переписей (практически всех!) число замужних женщин превышает число женатых мужчин — мужчинам приятнее ощущать себя неженатыми, а для женщины как бы «стыдно» быть не замужем. Другой пример, когда человек округляет свой возраст — вместо 32 лет говорит 30, вместо 79-80 и т. п. (это явление широко известно и даже получило свое название — «аккумуляция возрастов»). Систематические ошибки регистрации могут возникать и из-за неточностей измерительных приборов, если сбор информации проводят путем непосредственного наблюдения.
Ошибки репрезентативности присущи только несплошному обследованию. Они также делятся на случайные и систематические ошибки.
Случайные ошибки репрезентативности возникают из-за того, что обследованию подвергается не вся совокупность в целом, а только ее часть, и, следовательно, при несплошном наблюдении они присутствуют всегда. В теории статистики разработаны специальные методы для оценки величин таких ошибок, на их основе для наблюдаемых показателей строят доверительные интервалы, т.д. эти ошибки вычисляются и находятся как бы «под контролем».
Хуже обстоит дело, если наряду со случайными ошибками имеются и ошибки систематические.
Систематические ошибки репрезентативности возникают, если при несплошном наблюдении кардинально нарушаются технологии отбора единиц из генеральной совокупности объектов, но чаще — если в ходе обследования не удается получить информацию обо всех отобранных для наблюдения единицах, например, вследствие отказа отвечать на вопросы анкеты, или если человека не удалось застать дома и т. п.
Ошибки статистического наблюдения для наглядности можно изобразить в виде схемы (рис. 2.1).
Рис.
2.1.
Виды ошибок статистического наблюдения
Для повышения точности наблюдения необходимо:
- правильно разработать формуляр статистического наблюдения: вопросы должны быть четкими, однозначными, не допускающими двойного толкования;
- иметь хорошо обученный персонал для проведения обследования;
- строго придерживаться выбранной технологии обследования (если проводится несплошное наблюдение) и помнить, что если не удается опросить какую-то конкретную единицу, отобранную для наблюдения, замена ее на другую единицу может привести к возникновению систематической ошибки репрезентативности;
- провести логический анализ данных, основанный на логических взаимосвязях показателей, после сбора всей совокупности анкет или формуляров;
- целесообразно провести и арифметический контроль данных, т.д. заново пересчитать расчетные величины, если какие-либо показатели получаются в результате определенных арифметических действий;
- предпринять определенные меры по восстановлению данных при наличии незаполненных анкет или формуляров либо при получении результатов обследования сделать поправку на неответы респондентов.
Ошибки выборочной совокупности
Статистическая оценка, полученная по данным выборки, отличается от генеральной характеристики на величину ошибки наблюдения (регистрации) и величину ошибки репрезентативности (выборки). Понятие репрезентативности (представительства) отобранной совокупности следует понимать как ее представительство по наиболее существенным признакам, т.е. признакам, которые оказывают наиболее значимое влияние на изучаемые характеристики.
Ошибкой репрезентативности называют расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности. Различают случайные и систематические ошибки выборки (рис.1).
Ошибки выборочной совокупности
Случайные
Ошибки
регистрации
Ошибки
репрезентативности
Систематические
Средняя
Ошибка выборки
(репрезентативности)
Предельная
Рис.1. Ошибки выборочной совокупности
Систематические ошибки могут быть связаны с нарушением правил отбора или условий реализации выборки.
Случайные ошибки репрезентативности называются ошибкой выборки – отклонения, возникающие от недостаточно равномерного представления в выборочной совокупности различных единиц генеральной совокупности.
Различают:
-
Среднюю ошибку выборки – характеризует меру отклонений выборочных показателей от аналогичных показателей генеральной совокупности. Формулы расчета средней ошибку выборки зависят от способа формирования выборочной совокупности. Для простой случайной выборки формулы представлены на рис.2.
-
П
редельную ошибку выборки – это максимально возможная при данной вероятности ошибка выборки. Определяется предельная ошибка выборки по формуле:
, (1)
где – средняя ошибка выборки;
– коэффициент доверия, определяемый по таблице в зависимости от уровня надежности (вероятности).
Коэффициент доверия t 1,0 2,0 3,0
Вероятность Ф(t) 0,683 0,954 0,997
Простая случайная
выборка
Повторная случайная
выборка
Бесповторная случайная
выборка
Средняя ошибка Средняя ошибка
для средней для средней
для доли для доли
Рис.2. Формулы расчета средней ошибки для простой случайной выборки
02 – дисперсия признака х в выборочной совокупности
w – доля единиц, обладающих исследуемым признаком
n – объем выборочной совокупности
N – объем генеральной совокупности
– выборочная средняя
– генеральная средняя.