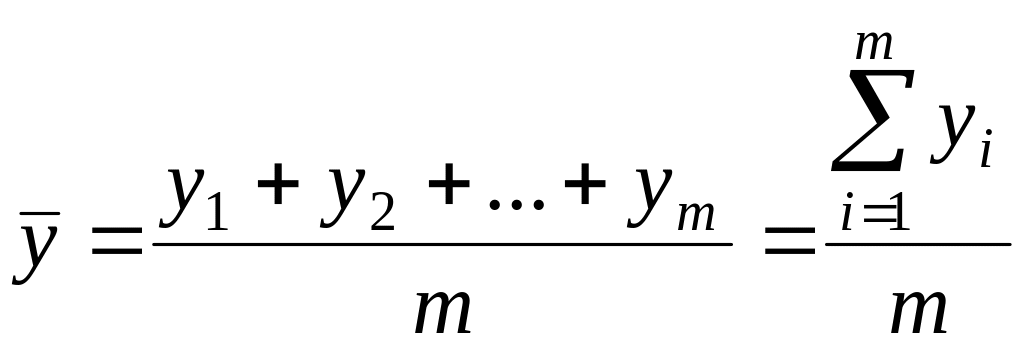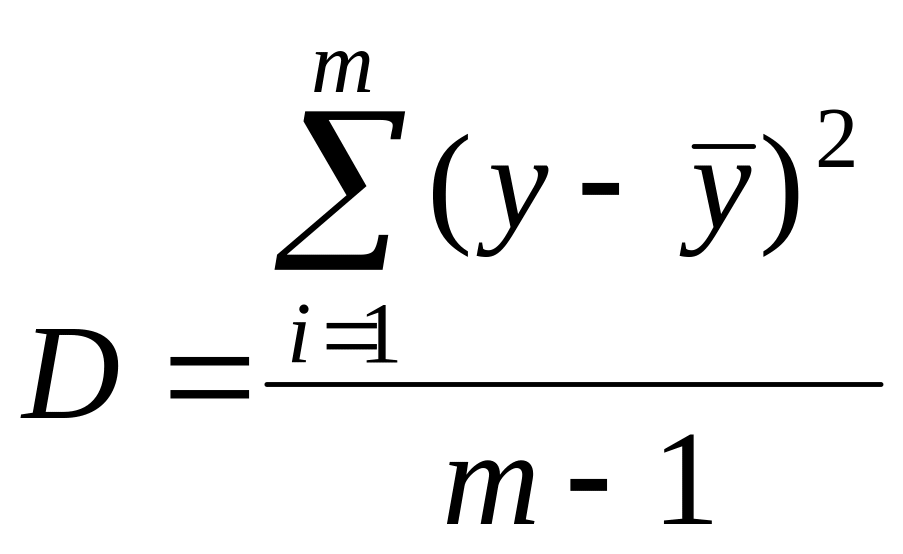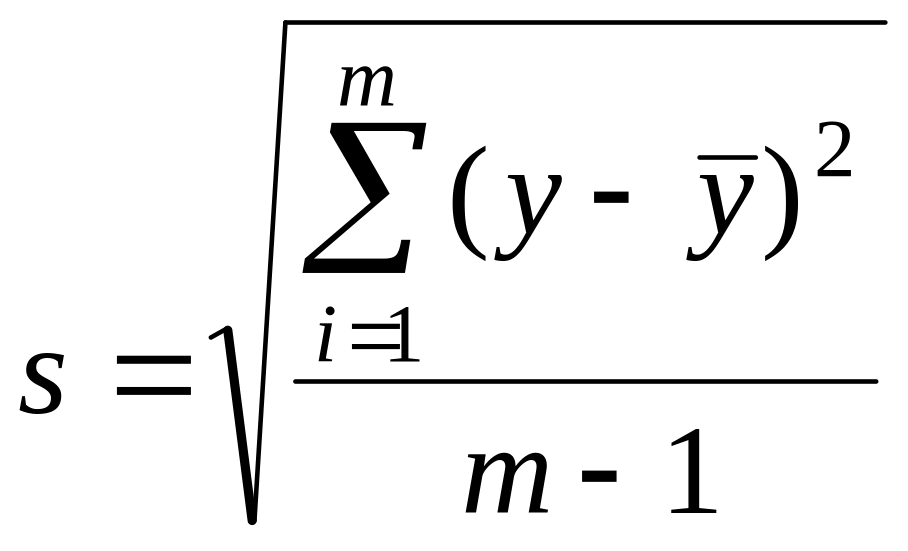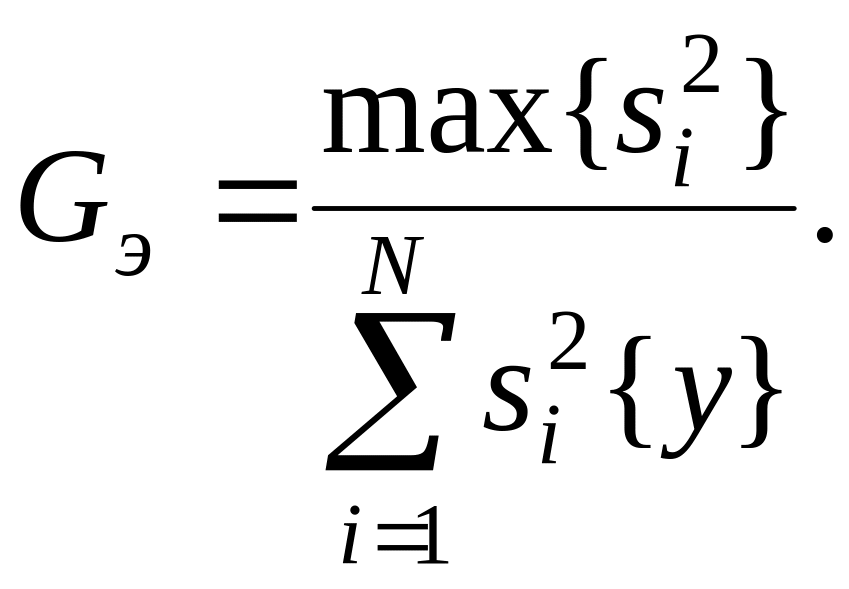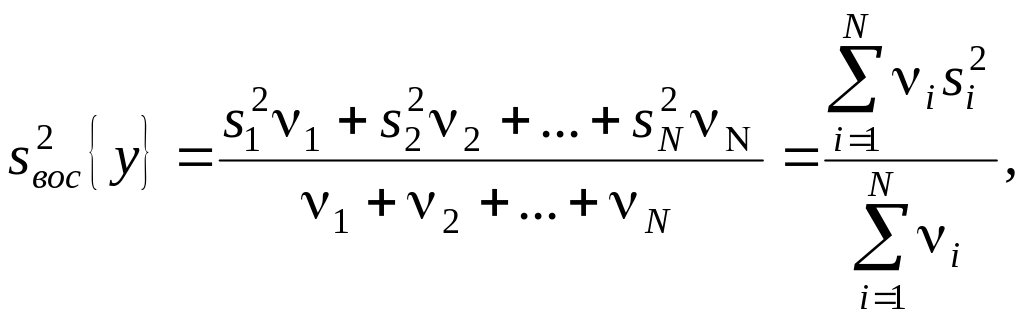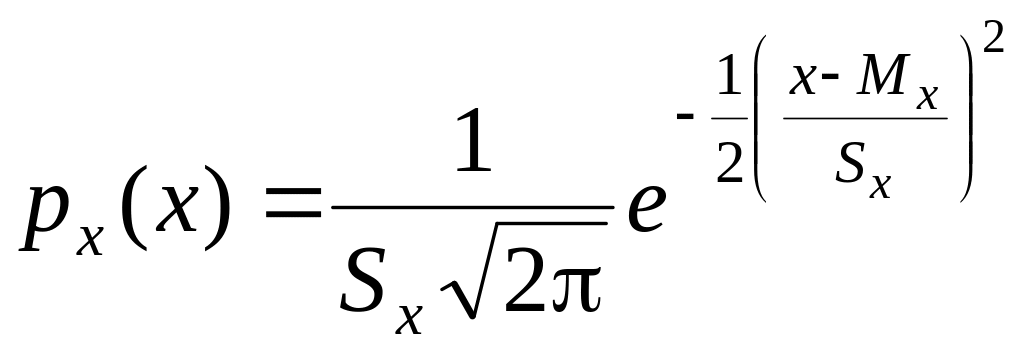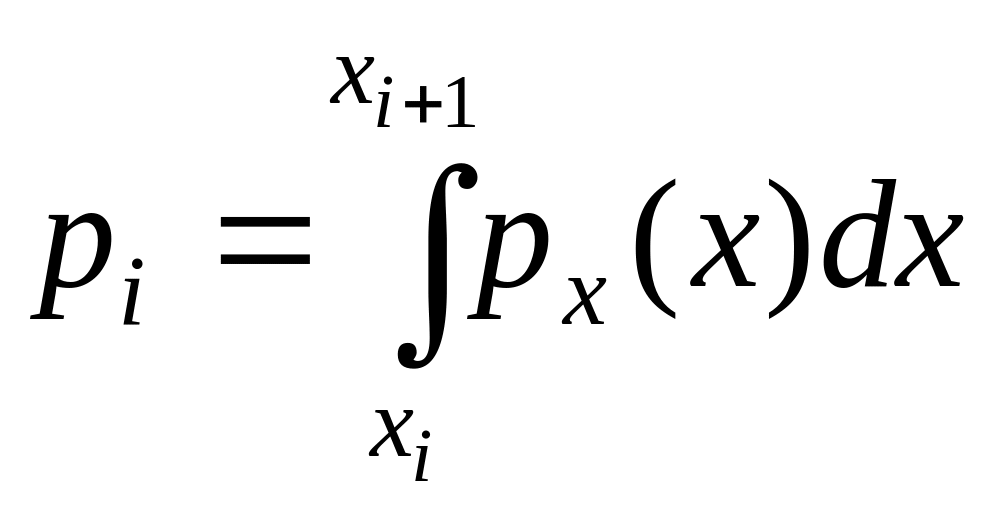Ошибка повторяемости формула

Для
определения вероятностных характеристик
погрешностей используются исходные
данные, полученные предварительно
опытным путем, посредством физического
эксперимента. Результаты эксперимента
в виде выборки некоторого объема n
обрабатывают методами математической
статистики и таким образом получают
оценочные характеристики погрешностей.

Познакомимся с
вычислением ошибки опыта, или, как ее
часто называют, ошибки воспроизводимости.

Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое

равно сумме всех m
отдельных результатов, деленной на
количество параллельных опытов


(7.1)

Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность

–
у,
где у
– результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.
Дисперсией называется среднее значение
квадрата отклонений величины от ее
среднего значения. Дисперсия обозначается
D
и выражается формулой


(7.2)

где
(m
– 1) – число
степеней свободы, равное количеству
опытов минус единица. Одна степень
свободы использована для вычисления
среднего.

Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой


. (7.3)

Стандарт
имеет размерность той величины, для
которой он вычислен. Дисперсия и стандарт
– это меры рассеяния, изменчивости. Чем
больше дисперсия и стандарт, тем больше
рассеяны значения параллельных опытов
около среднего значения.

Критерии
исключения грубых ошибок.
Ошибка опыта является суммарной
величиной, результатом многих ошибок:
ошибок измерений факторов, ошибок
измерения функции отклика и др. Каждую
из этих ошибок можно, в свою очередь,
разделить на составляющие.

Все
ошибки принято разделять на случайные,
систематические и промахи. Систематические
ошибки
находят, калибруя измерительные приборы
и сопоставляя опытные данные с
изменяющимися внешними условиями, при
сравнении с эталонным прибором. Если
систематические ошибки вызываются
внешними условиями (переменной
температуры, и т. д.), следует компенсировать
их влияние. Случайными
ошибками
называются те, которые появляются
нерегулярно, причины возникновения
которых неизвестны и которые невозможно
учесть заранее. При повторении опытов
такие ошибки могут вызвать большой
разброс экспериментальных результатов.

Очень важно
исключить из экспериментальных данных
грубые ошибки. Грубая погрешность,
или промах, – это погрешность результата
отдельного измерения, входящего в ряд
измерений, которая для данных условий
резко отличается от остальных результатов
этого ряда. Источником грубых погрешностей
нередко бывают резкие изменения условий
измерения и ошибки, допущенные оператором.
К ним можно отнести:

  • неправильный
    отсчет по шкале измерительного прибора,
    происходящий из-за неверного учета
    цены малых делений шкалы;

  • неправильная
    запись результата наблюдений, значений
    отдельных мер использованного набора,
    например гирь;

  • хаотические
    изменения параметров питающего средства
    измерений (СИ) напряжения, например его
    амплитуды или частоты.

Причинами
грубых погрешностей могут быть внезапные
и кратковременные изменения условий
измерения и оставшиеся незамеченными
неисправности в аппаратуре. Если промахи
обнаруживают в процессе измерений, то
результаты их содержащие отбрасывают.
Однако чаще всего промахи выявляют при
статистической обработке результатов
измерений с помощью специальных
критериев.

Корректная
статистическая обработка выборки
возможна только при ее однородности,
т.е. в том случае, когда все ее члены
принадлежат к одной и той же генеральной
совокупности. В противном случае
обработка данных бесмысленна. “Чужие”
отсчеты по своим значениям могут
существенно не отличаться от “своих”
отсчетов. Их можно обнаружить только
по виду гистограмм или дифференциальных
законов распределения. Наличие таких
аномальных отсчетов принято называть
загрязнениями
выборки, однако выделить члены выборки,
принадлежащие каждой из генеральных
совокупностей, практически невозможно.

Если
“свои” и “чужие” отсчеты различаются
по значениям, то их исключают из выборки.
Особую неприятность доставляют отсчеты,
которые хотя и не входят в компактную
группу основной массы отсчетов выборки,
но и не удалены от нее на значительное
расстояние, – так называемые предполагаемые
промахи. Отбрасывание “слишком”
удаленных от центра выборки отсчетов
называется “цензурированием” выборки.
Это осуществляется с помощью специальных
критериев.

При
однократных измерениях обнаружить
промах не представляется возможным.
Для уменьшения вероятности появления
промахов измерения проводят два-три
раза и за результат принимают среднее
арифметическое полученных отсчетов.
При многократных измерениях для
обнаружения промахов используют
статистические критерии, предварительно
определив, какому виду распределения
соответствует результат измерений.

Вопрос
о том, содержит ли результат наблюдений
грубую погрешность, решается общими
методами проверки статистических
гипотез. Проверяемая гипотеза состоит
в утверждении, что результат наблюдения
xi
не содержит грубой погрешности, т.е.
является одним из значений измеряемой
величины. Пользуясь определенными
статистическими критериями, пытаются
опровергнуть выдвинутую гипотезу. Если
это удается, то результат наблюдений
рассматривают как содержащий грубую
погрешность и его исключают.

Для
выявления грубых погрешностей задаются
вероятностью q
(уровнем значимости) того, что сомнительный
результат действительно мог иметь место
в данной совокупности результатов
измерений.

Критерий
“трех сигм”
применяется для результатов измерений,
распределенных по нормальному закону.
По этому критерию считается, что
результат, возникающий с вероятностью
q

0,003, маловероятен и его можно считать
промахом, если

,
где Sy
– оценка СКО измерений. Величины

и Sy
вычисляют без учета экстремальных
значений yi.
Данный критерий надежен при числе
измерений n

20… 50.

Это
правило обычно считается слишком
жестким, поэтому рекомендуется [5]
назначать границу цензурирования в
зависимости от объема выборки: при 6 <
n

100 она равна 4Sy;
при 100 < n

1000 – 4,5Sy;
при 1000 < n

10000 – 5Sy.
Данное правило применимо только для
нормального закона.

Вариационный
критерий Диксона.
Этот критерий очень удобен и достаточно
мощен (с малыми вероятностями ошибок).
При его применении полученные результаты
наблюдений записывают в вариационный
возрастающий ряд y1,
y2,
…, yn
(y1<
y2
< …< yn).
Критерий Диксона определяется как
KD=(yn–
yn—1)/
(yn–
y1).
Критическая область для этого критерия
P(KD>Zq)
= q.
Значения Zq
приведены в таблице 6.

Таблица 6. Значения критерия Диксона.

n

Zq
при q,
равном

0,10

0,05

0,02

0,01

4

6

8

10

14

16

18

20

30

0,68

0,48

0,40

0,35

0,29

0,28

0,26

0,26

0,22

0,76

0,56

0,47

0,41

0,35

0,33

0,31

0,30

0,26

0,85

0,64

0,54

0,48

0,41

0,39

0,37

0,36

0,31

0,89

0,70

0,59

0,53

0,45

0,43

0,41

0,39

0,34

Существуют и другие
критерии исключения грубых ошибок [5],
например, критерии Граббса, Шовене,
Шарлье, Романовского.

Дисперсия
воспроизводимости параллельных опытов.
При планировании физического эксперимента
определяются точки xi
(
)
в факторном пространстве, в которых
определяется экспериментальное значение
функции отклика. Так как функция отклика
y
имеет случайный характер, то в каждой
точке xi
проводятся m
повторных опытов, и дисперсия всего
эксперимента получается в результате
усреднения дисперсий всех опытов. По
терминологии, принятой в планировании
эксперимента, речь идет о подсчете
дисперсии воспроизводимости эксперимента.

В
каждой точке результаты наблюдений

,


,
… ,


усредняются:


. (7.5)

С
целью оценки ошибки воспроизводимости
в каждом опыте, состоящем из m
повторных наблюдений, подсчитываются
дисперсия

и стандарт

по формулам:


; (7.6)


,
(7.7)

где
(m–1)
– число степеней свободы, равное
количеству повторных опытов, минус
единица;

–
среднее арифметическое, определяемое
по формуле (7.5).

Если дисперсии
Di
(
),
вычисленные по формулам (7.6) однородны,
то можно вычислить средневзвешенную
дисперсию с суммарным числом степеней
свободы. Такая дисперсия является
значительно более надежной оценкой
дисперсии воспроизводимости, чем
отдельные выборочные дисперсии.
Однородность дисперсий означает, что
среди всех суммируемых дисперсий нет
таких, которые бы значительно превышали
все остальные.

Для проверки
однородности дисперсий

,
полученных по выборкам одинакового
объема m, используется
критерий Кохрэна, который определяется
отношением максимальной дисперсии к
сумме всех дисперсий


. (7.8)

С
критерием Кохрэна связаны числа степеней
свободы 1=m
– 1 и 2
= N.
Гипотеза об однородности дисперсией
подтверждается, если экспериментальное
значение критерия Кохрэна не превышает
табличного значения (Приложение 2).

В
случае однородности дисперсий можно
усреднять дисперсии и для подсчета
дисперсии воспроизводимости эксперимента
с числом степеней свободы вос=N
(m
– 1) пользоваться формулой


(7.9)

Такой формулой можно
пользоваться в случаях, когда число
повторных опытов одинаково во всей
матрице.

На
практике часто приходится сталкиваться
со случаями, когда число повторных
опытов различно. Это происходит вследствие
отброса грубых наблюдений, неуверенности
экспериментатора в правильности
некоторых результатов (в таких случаях
возникает желание еще и еще раз повторить
опыт) и т. п.

Тогда
при усреднении дисперсий приходится
пользоваться средним взвешенным
значением дисперсий, взятым с учетом
числа степеней свободы


(7.10)

где



– дисперсия первого опыта,


– дисперсия второго опыта и т. д., ν1
– число степеней свободы в первом опыте,
равное числу параллельных опытов m
минус 1, т. е. ν1=
m1–1;
ν2
– число степеней свободы во втором
опыте и т. д. Число степеней свободы
средней дисперсии принимается равным
сумме чисел степеней свободы дисперсий,
из которых она вычислена.

После исключения
из повторных опытов грубых ошибок во
всех опытах необходимо снова проверить
однородность дисперсий

.

Отметим, что
повторные опыты нельзя путать с повторными
измерениями в одном опыте. Такие измерения
часто делаются и являются полезными,
но не могут заменить повторных опытов.

Определение
закона распределения результатов
измерений или случайных погрешностей
измерений.
При определении закона распределения
случайных погрешностей измерений
переходят от выборки результатов
измерений y1,
y2,
y3,
…, yn
к выборке отклонений от среднего
арифметического результатов измерений
Δy1,
Δy2,
Δy3,
…, Δyn,
где Δ yi
= yi
–

.

Первым
шагом при идентификации закона
распределения является построение по
результатам измерения yi,
i=1,
2, …, n,
вариационного
ряда
(упорядоченной выборки). В вариационном
ряду результаты измерения располагают
в порядке возрастания. Далее этот ряд
разбивают на оптимальное число r,
как правило одинаковых интервалов
длиной

.

Далее
определяют число попаданий mi
(частоты) результатов измерений в
интервалы группирования. В рассматриваемом
интервале отношение частоты mi
к общему числу n
измерений определяет частность


(7.11)

или
оценочную вероятность появления
соответствующего результата измерения.
Частоту появления результата измерения
можно графически представить в виде
гистограммы, т.е. ступенчатой диаграммы
оценки p*
плотности вероятности распределения
результатов измерения по размеру.
Частота pi
соответствует площади i-го
прямоугольника, а оценку плотности
вероятности получают делением частости
(площади) на интервал h
(основание):


(7.12)

При
увеличении числа интервалов и
соответственно уменьшении их длины
гистограмма все более приближается к
гладкой кривой – графику плотности
распределения вероятности.

По
виду построенной гистограммы может
быть оценен закон распределения
результатов измерений.

Принято
считать, что в большинстве тщательно
поставленных экспериментов ошибки с
хорошим приближением подчинены
нормальному закону распределения


, (7.13)

где
е
– основание натурального логарифма,
px(x)
– плотность распределения вероятности.
Теоретически это утверждение обосновывается
исходя из центральной предельной теоремы
теории вероятностей, которая утверждает,
что сумма многих независимых источников
погрешностей с произвольными функциями
распределения асимптотически имеет
нормальное распределение, если только
ни одна из этих погрешностей не является
превалирующей.

В
результате получим следующий график:

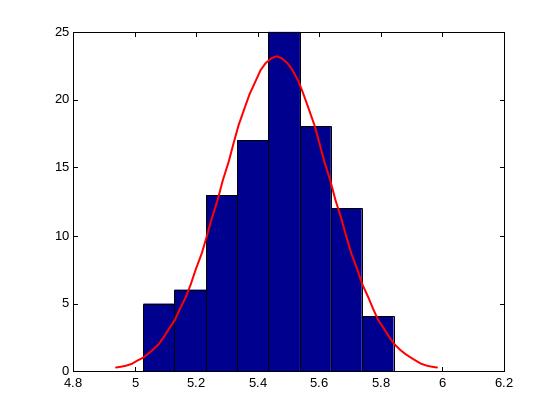
При
числе наблюдений n
> 50 для проверки гипотезы о нормальности
закона распределения случайной величины
часто используют критерий согласия 2.
Идея этого метода состоит в контроле
отклонений гистограммы экспериментальных
данных от гистограммы с таким же числом
интервалов, построенных на основе
нормального закона распределения.

Для
этого критерия мерой отклонения
статистического распределения случайной
величины от нормального закона служит
величина

2
=

, (7.14)

где
mi
– экспериментальные значения частот
в интервалах разбиения [xi,
xi+1];
n
– число интервалов разбиения;

– теоретические вероятности попадания
результатов наблюдения в интервалы
разбиения.

Величина
k2
подчиняется 2
распределению с k
степенями свободы. Для нормального
распределения число степеней свободы
определяют по формуле k = m – 3.

Методика проверки
соответствия принятого и экспериментального
законов распределения заключается в
следующем:

  • определяются
    среднее арифметическое значение

    измеряемой величины по формуле (7.1) и
    среднеквадратическое отклонение
    результата измерения sy
    по формуле (7.3);

  • группируются
    результаты наблюдений по интервалам
    длиной h,
    число которых определяется так же, как
    и при построении гистограммы;

  • вычисляется
    число наблюдений для каждого из
    интервалов, теоретически соответствующее
    нормальному закону распределения. Для
    этого сначала от реальных середин
    интервалов yi0
    переходят к нормированным серединам

    .
    Затем для каждого значения zi
    с помощью аналитической модели находят
    функции плотности вероятности по
    формуле

По
найденному значению f(zi)
определяют ту часть Ni
имеющихся наблюдений, которая теоретически
должна быть в каждом из интервалов

,
где n
– общее число наблюдений.

  • если
    в какой-либо интервал теоретически
    попадает меньше пяти наблюдений, то в
    обеих гистограммах его соединяют с
    соседним интервалом. После этого
    определяют число степеней свободы ν
    = m
    – 3, где m
    – общее число интервалов. Если было
    произведено укрупнение интервалов, то
    m
    – общее число интервалов после
    укрупнения;

  • по
    формуле (7.14) определяют эмпирическое
    значение величины χ2;

  • выбирают
    уровень значимости критерия q.
    Он должен быть небольшим, чтобы была
    мала вероятность совершить ошибку
    первого рода. При заданном уровне
    значимости q
    и числу степеней свободы ν
    находят границу критической области

    ,
    такую что

    =
    q.
    Вероятность того, что полученное
    значение χ2
    превышает

    ,
    равна q
    и мала. Поэтому, если оказывается

    ,
    то гипотеза о нормальности закона
    распределения опытных данных принимается,
    т.е. она правдоподобна и не противоречит
    опытным данным с доверительной
    вероятностью p
    =1– q.
    В противном случае гипотеза отвергается,
    как противоречащая опытным данным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Каждый исследователь, который проводит эксперимент и получает конкретный результат, должен задать вопрос: «Могу ли я сделать это снова?» Повторяемость является мерой вероятности того, что ответ будет положительным. Чтобы рассчитать повторяемость, вы проводите один и тот же эксперимент несколько раз и выполняете статистический анализ результатов. Повторяемость связана со стандартным отклонением, и некоторые статистики считают два эквивалента. Однако вы можете пойти еще дальше и приравнять повторяемость к стандартному отклонению от среднего, которое вы получите, поделив стандартное отклонение на квадратный корень из числа выборок в наборе выборок.

TL; DR (слишком долго; не читал)

Стандартное отклонение серии экспериментальных результатов является мерой повторяемости эксперимента, который дал результаты. Вы также можете пойти еще дальше и приравнять повторяемость к стандартному отклонению от среднего.

Расчет повторяемости

Чтобы получить надежные результаты для повторяемости, вы должны быть в состоянии выполнить одну и ту же процедуру несколько раз. В идеале один и тот же исследователь проводит одну и ту же процедуру с использованием одних и тех же материалов и измерительных приборов в одинаковых условиях окружающей среды и проводит все испытания в течение короткого периода времени. После того, как все эксперименты завершены и результаты записаны, исследователь вычисляет следующие статистические величины:

Среднее значение: среднее значение в основном является средним арифметическим. Чтобы найти его, вы суммируете все результаты и делите их на количество результатов.

Стандартное отклонение: чтобы найти стандартное отклонение, вычтите каждый результат из среднего значения и возведите в квадрат разницу, чтобы убедиться, что у вас есть только положительные числа. Суммируйте эти квадратные различия и разделите на число результатов минус один, а затем возьмите квадратный корень из этого коэффициента.

Стандартное отклонение от среднего: стандартное отклонение от среднего — это стандартное отклонение, деленное на квадратный корень из числа результатов.

Независимо от того, принимаете ли вы повторяемость за стандартное отклонение или стандартное отклонение от среднего, верно, что чем меньше число, тем выше повторяемость и тем выше достоверность результатов.

пример

Компания хочет продать устройство, которое запускает шары для боулинга, утверждая, что устройство точно запускает шары с количеством футов, выбранных на циферблате. Исследователи установили циферблат на 250 футов и проводят повторные тесты, отбирая мяч после каждого испытания и перезапуская его, чтобы устранить изменчивость веса. Они также проверяют скорость ветра перед каждым испытанием, чтобы убедиться, что она одинакова для каждого запуска. Результаты в ногах:

250, 254, 249, 253, 245, 251, 250, 248.

Чтобы проанализировать результаты, они решили использовать стандартное отклонение от среднего в качестве меры повторяемости. Они используют следующую процедуру для его расчета:

  1. Найти среднее

    2. Среднее значение — это сумма всех результатов, деленная на количество результатов = 250 футов.

  2. Рассчитать сумму квадратов

    3. Чтобы вычислить сумму квадратов, они вычитают каждый результат из среднего значения, возводят в квадрат разницу и складывают результаты:

    (0) 2 + (4) 2 + (-1) 2 + (3) 2 + (-5) 2 + (1) 2 + (0) 2 + (-2) 2 = 56

  3. Найти стандартное отклонение (SD)

    4. Они находят SD, деля сумму квадратов на количество испытаний минус один и беря квадратный корень из результата:

    SD = квадратный корень из (56 ÷ 7) = 2, 83.

  4. Рассчитать стандартное отклонение от среднего значения (SDM)

    5. Они делят стандартное отклонение на квадратный корень из числа испытаний (n), чтобы найти стандартное отклонение среднего значения:

    SDM = SD ÷ корень (n) = 2, 83 ÷ 2, 83 = 1.

    SD или SDM 0 идеально. Это означает, что между результатами нет различий. В этом случае SDM больше 0. Несмотря на то, что среднее значение всех испытаний совпадает с показаниями набора номера, результаты различаются, и компания должна решить, достаточно ли низкая дисперсия для соответствия его стандарты.

Источник

Результат любого измерения не определён однозначно и имеет случайную составляющую.
Поэтому адекватным языком для описания погрешностей является язык вероятностей.
Тот факт, что значение некоторой величины «случайно», не означает, что
она может принимать совершенно произвольные значения. Ясно, что частоты, с которыми
возникает те или иные значения, различны. Вероятностные законы, которым
подчиняются случайные величины, называют распределениями.

2.1 Случайная величина

Случайной будем называть величину, значение которой не может быть достоверно определено экспериментатором. Чаще всего подразумевается, что случайная величина будет изменяться при многократном повторении одного и того же эксперимента. При интерпретации результатов измерений в физических экспериментах, обычно случайными также считаются величины, значение которых является фиксированным, но не известно экспериментатору. Например смещение нуля шкалы прибора. Для формализации работы со случайными величинами используют понятие вероятности. Численное значение вероятности того, что какая-то величина примет то или иное значение определяется либо как относительная частота наблюдения того или иного значения при повторении опыта большое количество раз, либо как оценка на основе данных других экспериментов.

Замечание. 
Хотя понятия вероятности и случайной величины являются основополагающими, в литературе нет единства в их определении. Обсуждение формальных тонкостей или построение строгой теории лежит за пределами данного пособия. Поэтому на начальном этапе лучше использовать «интуитивное» понимание этих сущностей. Заинтересованным читателям рекомендуем обратиться к специальной литературе: [5].

Рассмотрим случайную физическую величину x, которая при измерениях может
принимать непрерывный набор значений. Пусть
P[x0,x0+δ⁢x] — вероятность того, что результат окажется вблизи
некоторой точки x0 в пределах интервала δ⁢x: x∈[x0,x0+δ⁢x].
Устремим интервал
δ⁢x к нулю. Нетрудно понять, что вероятность попасть в этот интервал
также будет стремиться к нулю. Однако отношение
w⁢(x0)=P[x0,x0+δ⁢x]δ⁢x будет оставаться конечным.
Функцию w⁢(x) называют плотностью распределения вероятности или кратко
распределением непрерывной случайной величины x.

Замечание. В математической литературе распределением часто называют не функцию
w⁢(x), а её интеграл W⁢(x)=∫w⁢(x)⁢𝑑x. Такую функцию в физике принято
называть интегральным или кумулятивным распределением. В англоязычной литературе
для этих функций принято использовать сокращения:
pdf (probability distribution function) и
cdf (cumulative distribution function)
соответственно.

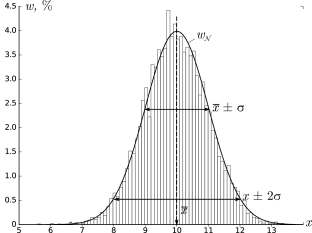
Гистограммы.

Проиллюстрируем наглядно понятие плотности распределения. Результат
большого числа измерений случайной величины удобно представить с помощью
специального типа графика — гистограммы.
Для этого область значений x, размещённую на оси абсцисс, разобьём на
равные малые интервалы — «корзины» или «бины» (англ. bins)
некоторого размера h. По оси ординат будем откладывать долю измерений w,
результаты которых попадают в соответствующую корзину. А именно,
пусть k — номер корзины; nk — число измерений, попавших
в диапазон x∈[k⁢h,(k+1)⁢h]. Тогда на графике изобразим «столбик»
шириной h и высотой wk=nk/n.
В результате получим картину, подобную изображённой на рис. 2.1.

Рис. 2.1: Пример гистограммы для нормального распределения (x¯=10,
σ=1,0, h=0,1, n=104)

Высоты построенных столбиков будут приближённо соответствовать значению
плотности распределения w⁢(x) вблизи соответствующей точки x.
Если устремить число измерений к бесконечности (n→∞), а ширину корзин
к нулю (h→0), то огибающая гистограммы будет стремиться к некоторой
непрерывной функции w⁢(x).

Самые высокие столбики гистограммы будут группироваться вблизи максимума
функции w⁢(x) — это наиболее вероятное значение случайной величины.
Если отклонения в положительную и отрицательную стороны равновероятны,
то гистограмма будет симметрична — в таком случае среднее значение ⟨x⟩
также будет лежать вблизи этого максимума. Ширина гистограммы будет характеризовать разброс
значений случайной величины — по порядку величины
она, как правило, близка к среднеквадратичному отклонению sx.

Свойства распределений.

Из определения функции w⁢(x) следует, что вероятность получить в результате
эксперимента величину x в диапазоне от a до b
можно найти, вычислив интеграл:

Px∈[a,b]=∫abw⁢(x)⁢𝑑x. (2.1)

Согласно определению вероятности, сумма вероятностей для всех возможных случаев
всегда равна единице. Поэтому интеграл распределения w⁢(x) по всей области
значений x (то есть суммарная площадь под графиком w⁢(x)) равен единице:

Это соотношение называют условием нормировки.

Среднее и дисперсия.

Вычислим среднее по построенной гистограмме. Если размер корзин
h достаточно мал, все измерения в пределах одной корзины можно считать примерно
одинаковыми. Тогда среднее арифметическое всех результатов можно вычислить как

Переходя к пределу, получим следующее определение среднего значения
случайной величины:

где интегрирование ведётся по всей области значений x.
В теории вероятностей x¯ также называют математическим ожиданием
распределения.
Величину

σ2=(x-x¯)2¯=∫(x-x¯)2⁢w⁢𝑑x (2.3)

называют дисперсией распределения. Значение σ есть
срекднеквадратичное отклонение в пределе n→∞. Оно имеет ту
же размерность, что и сама величина x и характеризует разброс распределения.
Именно эту величину, как правило, приводят как характеристику погрешности
измерения x.

Доверительный интервал.

Обозначим как P|Δ⁢x|<δ вероятность
того, что отклонение от среднего Δ⁢x=x-x¯ составит величину,
не превосходящую по модулю значение δ:

P|Δ⁢x|<δ=∫x¯-δx¯+δw⁢(x)⁢𝑑x. (2.4)

Эту величину называют доверительной вероятностью для
доверительного интервала |x-x¯|≤δ.

2.2 Нормальное распределение

Одним из наиболее примечательных результатов теории вероятностей является
так называемая центральная предельная теорема. Она утверждает,
что сумма большого количества независимых случайных слагаемых, каждое
из которых вносит в эту сумму относительно малый вклад, подчиняется
универсальному закону, не зависимо от того, каким вероятностным законам
подчиняются её составляющие, — так называемому нормальному
распределению (или распределению Гаусса).

Доказательство теоремы довольно громоздко и мы его не приводим (его можно найти
в любом учебнике по теории вероятностей). Остановимся
кратко на том, что такое нормальное распределение и его основных свойствах.

Плотность нормального распределения выражается следующей формулой:

w𝒩⁢(x)=12⁢π⁢σ⁢e-(x-x¯)22⁢σ2. (2.5)

Здесь x¯ и σ
— параметры нормального распределения: x¯ равно
среднему значению x, a σ —
среднеквадратичному отклонению, вычисленным в пределе n→∞.

Как видно из рис. 2.1, распределение представляет собой
симметричный
«колокол», положение вершины которого
соответствует x¯ (ввиду симметрии оно же
совпадает с наиболее вероятным значением — максимумом
функции w𝒩⁢(x)).

При значительном отклонении x от среднего величина
w𝒩⁢(x)
очень быстро убывает. Это означает, что вероятность встретить отклонения,
существенно большие, чем σ, оказывается пренебрежимо
мала. Ширина «колокола» по порядку величины
равна σ — она характеризует «разброс»
экспериментальных данных относительно среднего значения.

Замечание. Точки x=x¯±σ являются точками
перегиба графика w⁢(x) (в них вторая производная по x
обращается в нуль, w′′=0), а их положение по высоте составляет
w⁢(x¯±σ)/w⁢(x¯)=e-1/2≈0,61
от высоты вершины.

Универсальный характер центральной предельной теоремы позволяет широко
применять на практике нормальное (гауссово) распределение для обработки
результатов измерений, поскольку часто случайные погрешности складываются из
множества случайных независимых факторов. Заметим, что на практике
для приближённой оценки параметров нормального распределения
случайной величины используются выборочные значения среднего
и дисперсии: x¯≈⟨x⟩, sx≈σx.

x-x0σ2=2w⁢(x)σ1=1

Рис. 2.2: Плотность нормального распределения

Доверительные вероятности.

Вычислим некоторые доверительные вероятности (2.4) для нормально
распределённых случайных величин.

Замечание. Значение интеграла вида ∫e-x2/2⁢𝑑x
(его называют интегралом ошибок) в элементарных функциях не выражается,
но легко находится численно.

Вероятность того, что результат отдельного измерения x окажется
в пределах x¯±σ оказывается равна

P|Δ⁢x|<σ=∫x¯-σx¯+σw𝒩⁢𝑑x≈0,68.

Вероятность отклонения в пределах x¯±2⁢σ:

а в пределах x¯±3⁢σ:

Иными словами, при большом числе измерений нормально распределённой
величины можно ожидать, что лишь треть измерений выпадут за пределы интервала
[x¯-σ,x¯+σ]. При этом около 5%
измерений выпадут за пределы [x¯-2⁢σ;x¯+2⁢σ],
и лишь 0,27% окажутся за пределами
[x¯-3⁢σ;x¯+3⁢σ].

Пример. В сообщениях об открытии бозона Хиггса на Большом адронном коллайдере
говорилось о том, что исследователи ждали подтверждение результатов
с точностью «5 сигма». Используя нормальное распределение (2.5)
нетрудно посчитать, что они использовали доверительную вероятность
P≈1-5,7⋅10-7=0,99999943. Такую точность можно назвать фантастической.

Полученные значения доверительных вероятностей используются при
стандартной записи результатов измерений. В физических измерениях
(в частности, в учебной лаборатории), как правило, используется P=0,68,
то есть, запись

означает, что измеренное значение лежит в диапазоне (доверительном
интервале) x∈[x¯-δ⁢x;x¯+δ⁢x] с
вероятностью 68%. Таким образом погрешность ±δ⁢x считается
равной одному среднеквадратичному отклонению: δ⁢x=σ.
В технических измерениях чаще используется P=0,95, то есть под
абсолютной погрешностью имеется в виду удвоенное среднеквадратичное
отклонение, δ⁢x=2⁢σ. Во избежание разночтений доверительную
вероятность следует указывать отдельно.

Замечание. Хотя нормальный закон распределения встречается на практике довольно
часто, стоит помнить, что он реализуется далеко не всегда.
Полученные выше соотношения для вероятностей попадания значений в
доверительные интервалы можно использовать в качестве простейшего
признака нормальности распределения: в частности, если количество попадающих
в интервал ±σ результатов существенно отличается от 2/3 — это повод
для более детального исследования закона распределения ошибок.

Сравнение результатов измерений.

Теперь мы можем дать количественный критерий для сравнения двух измеренных
величин или двух результатов измерения одной и той же величины.

Пусть x1 и x2 (x1≠x2) измерены с
погрешностями σ1 и σ2 соответственно.
Ясно, что если различие результатов |x2-x1| невелико,
его можно объяснить просто случайными отклонениями.
Если же теория предсказывает, что вероятность обнаружить такое отклонение
слишком мала, различие результатов следует признать значимым.
Предварительно необходимо договориться о соответствующем граничном значении
вероятности. Универсального значения здесь быть не может,
поэтому приходится полагаться на субъективный выбор исследователя. Часто
в качестве «разумной» границы выбирают вероятность 5%,
что, как видно из изложенного выше, для нормального распределения
соответствует отклонению более, чем на 2⁢σ.

Допустим, одна из величин известна с существенно большей точностью:
σ2≪σ1 (например, x1 — результат, полученный
студентом в лаборатории, x2 — справочное значение).
Поскольку σ2 мало, x2 можно принять за «истинное»:
x2≈x¯. Предполагая, что погрешность измерения
x1 подчиняется нормальному закону с и дисперсией σ12,
можно утверждать, что
различие считают будет значимы, если

Пусть погрешности измерений сравнимы по порядку величины:
σ1∼σ2. В теории вероятностей показывается, что
линейная комбинация нормально распределённых величин также имеет нормальное
распределение с дисперсией σ2=σ12+σ22
(см. также правила сложения погрешностей (2.7)). Тогда
для проверки гипотезы о том, что x1 и x2 являются измерениями
одной и той же величины, нужно вычислить, является ли значимым отклонение
|x1-x2| от нуля при σ=σ12+σ22.


Пример. Два студента получили следующие значения для теплоты испарения
некоторой жидкости: x1=40,3±0,2 кДж/моль и
x2=41,0±0,3 кДж/моль, где погрешность соответствует
одному стандартному отклонению. Можно ли утверждать, что они исследовали
одну и ту же жидкость?
Имеем наблюдаемую разность |x1-x2|=0,7 кДж/моль,
среднеквадратичное отклонение для разности
σ=0,22+0,32=0,36 кДж/моль.
Их отношение |x2-x1|σ≈2. Из
свойств нормального распределения находим вероятность того, что измерялась
одна и та же величина, а различия в ответах возникли из-за случайных
ошибок: P≈5%. Ответ на вопрос, «достаточно»
ли мала или велика эта вероятность, остаётся на усмотрение исследователя.

Замечание. Изложенные здесь соображения применимы, только если x¯ и
его стандартное отклонение σ получены на основании достаточно
большой выборки n≫1 (или заданы точно). При небольшом числе измерений
(n≲10) выборочные средние ⟨x⟩ и среднеквадратичное отклонение
sx сами имеют довольно большую ошибку, а
их распределение будет описываться не нормальным законом, а так
называемым t-распределением Стъюдента. В частности, в зависимости от
значения n интервал ⟨x⟩±sx будет соответствовать несколько
меньшей доверительной вероятности, чем P=0,68. Особенно резко различия
проявляются при высоких уровнях доверительных вероятностей P→1.

2.3 Независимые величины

Величины x и y называют независимыми если результат измерения одной
из них никак не влияет на результат измерения другой. Для таких величин вероятность того, что x окажется в некоторой области X, и одновременно y — в области Y,
равна произведению соответствующих вероятностей:

Обозначим отклонения величин от их средних как Δ⁢x=x-x¯ и
Δ⁢y=y-y¯.
Средние значения этих отклонений равны, очевидно, нулю: Δ⁢x¯=x¯-x¯=0,
Δ⁢y¯=0. Из независимости величин x и y следует,
что среднее значение от произведения Δ⁢x⋅Δ⁢y¯
равно произведению средних Δ⁢x¯⋅Δ⁢y¯
и, следовательно, равно нулю:

Δ⁢x⋅Δ⁢y¯=Δ⁢x¯⋅Δ⁢y¯=0. (2.6)

Пусть измеряемая величина z=x+y складывается из двух независимых
случайных слагаемых x и y, для которых известны средние
x¯ и y¯, и их среднеквадратичные погрешности
σx и σy. Непосредственно из определения (1.1)
следует, что среднее суммы равно сумме средних:

Найдём дисперсию σz2. В силу независимости имеем

Δ⁢z2¯=Δ⁢x2¯+Δ⁢y2¯+2⁢Δ⁢x⋅Δ⁢y¯≈Δ⁢x2¯+Δ⁢y2¯,

то есть:

Таким образом, при сложении независимых величин их погрешности
складываются среднеквадратичным образом.

Подчеркнём, что для справедливости соотношения (2.7)
величины x и y не обязаны быть нормально распределёнными —
достаточно существования конечных значений их дисперсий. Однако можно
показать, что если x и y распределены нормально, нормальным
будет и распределение их суммы.

Замечание. Требование независимости
слагаемых является принципиальным. Например, положим y=x. Тогда
z=2⁢x. Здесь y и x, очевидно, зависят друг от друга. Используя
(2.7), находим σ2⁢x=2⁢σx,
что, конечно, неверно — непосредственно из определения
следует, что σ2⁢x=2⁢σx.

Отдельно стоит обсудить математическую структуру формулы (2.7).
Если одна из погрешностей много больше другой, например,
σx≫σy,
то меньшей погрешностью можно пренебречь, σx+y≈σx.
С другой стороны, если два источника погрешностей имеют один порядок
σx∼σy, то и σx+y∼σx∼σy.

Эти обстоятельства важны при планирования эксперимента: как правило,
величина, измеренная наименее точно, вносит наибольший вклад в погрешность
конечного результата. При этом, пока не устранены наиболее существенные
ошибки, бессмысленно гнаться за повышением точности измерения остальных
величин.

Пример. Пусть σy=σx/3,
тогда σz=σx⁢1+19≈1,05⁢σx,
то есть при различии двух погрешностей более, чем в 3 раза, поправка
к погрешности составляет менее 5%, и уже нет особого смысла в учёте
меньшей погрешности: σz≈σx. Это утверждение
касается сложения любых независимых источников погрешностей в эксперименте.

2.4 Погрешность среднего

Выборочное среднее арифметическое значение ⟨x⟩, найденное
по результатам n измерений, само является случайной величиной.
Действительно, если поставить серию одинаковых опытов по n измерений,
то в каждом опыте получится своё среднее значение, отличающееся от
предельного среднего x¯.

Вычислим среднеквадратичную погрешность среднего арифметического
σ⟨x⟩.
Рассмотрим вспомогательную сумму n слагаемых

Если {xi} есть набор независимых измерений
одной и той же физической величины, то мы можем, применяя результат
(2.7) предыдущего параграфа, записать

σZ=σx12+σx22+…+σxn2=n⁢σx,

поскольку под корнем находится n одинаковых слагаемых. Отсюда с
учётом ⟨x⟩=Z/n получаем

Таким образом, погрешность среднего значения x по результатам
n независимых измерений оказывается в n раз меньше погрешности
отдельного измерения. Это один из важнейших результатов, позволяющий
уменьшать случайные погрешности эксперимента за счёт многократного
повторения измерений.

Подчеркнём отличия между σx и σ⟨x⟩:

величина σx — погрешность отдельного
измерения — является характеристикой разброса значений
в совокупности измерений {xi}, i=1..n. При
нормальном законе распределения примерно 68% измерений попадают в
интервал ⟨x⟩±σx;

величина σ⟨x⟩ — погрешность
среднего — характеризует точность, с которой определено
среднее значение измеряемой физической величины ⟨x⟩ относительно
предельного («истинного») среднего x¯;
при этом с доверительной вероятностью P=68% искомая величина x¯
лежит в интервале
⟨x⟩-σ⟨x⟩<x¯<⟨x⟩+σ⟨x⟩.

2.5 Результирующая погрешность опыта

Пусть для некоторого результата измерения известна оценка его максимальной
систематической погрешности Δсист и случайная
среднеквадратичная
погрешность σслуч. Какова «полная»
погрешность измерения?

Предположим для простоты, что измеряемая величина в принципе
может быть определена сколь угодно точно, так что можно говорить о
некотором её «истинном» значении xист
(иными словами, погрешность результата связана в основном именно с
процессом измерения). Назовём полной погрешностью измерения
среднеквадратичное значения отклонения от результата измерения от
«истинного»:

Отклонение x-xист можно представить как сумму случайного
отклонения от среднего δ⁢xслуч=x-x¯
и постоянной (но, вообще говоря, неизвестной) систематической составляющей
δ⁢xсист=x¯-xист=const:

Причём случайную составляющую можно считать независимой от систематической.
В таком случае из (2.7) находим:

σполн2=⟨δ⁢xсист2⟩+⟨δ⁢xслуч2⟩≤Δсист2+σслуч2. (2.9)

Таким образом, для получения максимального значения полной
погрешности некоторого измерения нужно квадратично сложить максимальную
систематическую и случайную погрешности.

Если измерения проводятся многократно, то согласно (2.8)
случайная составляющая погрешности может быть уменьшена, а систематическая
составляющая при этом остаётся неизменной:

Отсюда следует важное практическое правило
(см. также обсуждение в п. 2.3): если случайная погрешность измерений
в 2–3 раза меньше предполагаемой систематической, то
нет смысла проводить многократные измерения в попытке уменьшить погрешность
всего эксперимента. В такой ситуации измерения достаточно повторить
2–3 раза — чтобы убедиться в повторяемости результата, исключить промахи
и проверить, что случайная ошибка действительно мала.
В противном случае повторение измерений может иметь смысл до
тех пор, пока погрешность среднего
σ⟨x⟩=σxn
не станет меньше систематической.


Замечание. Поскольку конкретная
величина систематической погрешности, как правило, не известна, её
можно в некотором смысле рассматривать наравне со случайной —
предположить, что её величина была определена по некоторому случайному
закону перед началом измерений (например, при изготовлении линейки
на заводе произошло некоторое случайное искажение шкалы). При такой
трактовке формулу (2.9) можно рассматривать просто
как частный случай формулы сложения погрешностей независимых величин
(2.7).
Подчеркнем, что вероятностный закон, которому подчиняется
систематическая ошибка, зачастую неизвестен. Поэтому неизвестно и
распределение итогового результата. Из этого, в частности, следует,
что мы не можем приписать интервалу x±Δсист какую-либо
определённую доверительную вероятность — она равна 0,68
только если систематическая ошибка имеет нормальное распределение.
Можно, конечно, предположить,
— и так часто делают — что, к примеру, ошибки
при изготовлении линеек на заводе имеют гауссов характер. Также часто
предполагают, что систематическая ошибка имеет равномерное
распределение (то есть «истинное» значение может с равной вероятностью
принять любое значение в пределах интервала ±Δсист).
Строго говоря, для этих предположений нет достаточных оснований.


Пример. В результате измерения диаметра проволоки микрометрическим винтом,
имеющим цену деления h=0,01 мм, получен следующий набор из n=8 значений:

Вычисляем среднее значение: ⟨d⟩≈386,3 мкм.
Среднеквадратичное отклонение:
σd≈9,2 мкм. Случайная погрешность среднего согласно
(2.8):
σ⟨d⟩=σd8≈3,2
мкм. Все результаты лежат в пределах ±2⁢σd, поэтому нет
причин сомневаться в нормальности распределения. Максимальную погрешность
микрометра оценим как половину цены деления, Δ=h2=5 мкм.
Результирующая полная погрешность
σ≤Δ2+σd28≈6,0 мкм.
Видно, что σслуч≈Δсист и проводить дополнительные измерения
особого смысла нет. Окончательно результат измерений может быть представлен
в виде (см. также правила округления
результатов измерений в п. 4.3.2)



d=386±6⁢мкм,εd=1,5%.


Заметим, что поскольку случайная погрешность и погрешность
прибора здесь имеют один порядок величины, наблюдаемый случайный разброс
данных может быть связан как с неоднородностью сечения проволоки,
так и с дефектами микрометра (например, с неровностями зажимов, люфтом
винта, сухим трением, деформацией проволоки под действием микрометра
и т. п.). Для ответа на вопрос, что именно вызвало разброс, требуются
дополнительные исследования, желательно с использованием более точных
приборов.


Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=±1 м/c.
Результаты измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=162,0⁢м/с,
среднеквадратичное отклонение σv=13,8⁢м/c, случайная
ошибка для средней скорости
σv¯=σv/6=5,6⁢м/с.
Поскольку разброс экспериментальных данных существенно превышает погрешность
каждого измерения, σv≫δ⁢v, он почти наверняка связан
с реальным различием скоростей пули в разных выстрелах, а не с ошибками
измерений. В качестве результата эксперимента представляют интерес
как среднее значение скоростей ⟨v⟩=162±6⁢м/с
(ε≈4%), так и значение σv≈14⁢м/с,
характеризующее разброс значений скоростей от выстрела к выстрелу.
Малая инструментальная погрешность в принципе позволяет более точно
измерить среднее и дисперсию, и исследовать закон распределения выстрелов
по скоростям более детально — для этого требуется набрать
бо́льшую статистику по выстрелам.


Пример. Измерение скорости
полёта пули было осуществлено с погрешностью δ⁢v=10 м/c. Результаты
измерений для n=6 выстрелов представлены в таблице:

Усреднённый результат ⟨v⟩=163,3⁢м/с,
σv=12,1⁢м/c, σ⟨v⟩=5⁢м/с,
σполн≈11,2⁢м/с. Инструментальная
погрешность каждого измерения превышает разброс данных, поэтому в
этом опыте затруднительно сделать вывод о различии скоростей от выстрела
к выстрелу. Результат измерений скорости пули:
⟨v⟩=163±11⁢м/с,
ε≈7%. Проводить дополнительные выстрелы при такой
большой инструментальной погрешности особого смысла нет —
лучше поработать над точностью приборов и методикой измерений.

2.6 Обработка косвенных измерений

Косвенными называют измерения, полученные в результате расчётов,
использующих результаты прямых (то есть «непосредственных»)
измерений физических величин. Сформулируем основные правила пересчёта
погрешностей при косвенных измерениях.

2.6.1 Случай одной переменной

Пусть в эксперименте измеряется величина x, а её «наилучшее»
(в некотором смысле) значение равно x⋆ и оно известно с
погрешностью σx. После чего с помощью известной функции
вычисляется величина y=f⁢(x).

В качестве «наилучшего» приближения для y используем значение функции
при «наилучшем» x:

Найдём величину погрешности σy. Обозначая отклонение измеряемой
величины как Δ⁢x=x-x⋆, и пользуясь определением производной,
при условии, что функция y⁢(x) — гладкая
вблизи x≈x⋆, запишем

где f′≡d⁢yd⁢x — производная фукнции f⁢(x), взятая в точке
x⋆. Возведём полученное в квадрат, проведём усреднение
(σy2=⟨Δ⁢y2⟩,
σx2=⟨Δ⁢x2⟩), и затем снова извлечём
корень. В результате получим


Пример. Для степенной функции
y=A⁢xn имеем σy=n⁢A⁢xn-1⁢σx, откуда



σyy=n⁢σxx,или  εy=n⁢εx,


то есть относительная погрешность степенной функции возрастает пропорционально
показателю степени n.

Пример. Для y=1/x имеем ε1/x=εx
— при обращении величины сохраняется её относительная
погрешность.

Упражнение. Найдите погрешность логарифма y=ln⁡x, если известны x
и σx.

Упражнение. Найдите погрешность показательной функции y=ax,
если известны x и σx. Коэффициент a задан точно.

2.6.2 Случай многих переменных

Пусть величина u вычисляется по измеренным значениям нескольких
различных независимых физических величин x, y, …
на основе известного закона u=f⁢(x,y,…). В качестве
наилучшего значения можно по-прежнему взять значение функции f
при наилучших значениях измеряемых параметров:

Для нахождения погрешности σu воспользуемся свойством,
известным из математического анализа, — малые приращения гладких
функции многих переменных складываются линейно, то есть справедлив
принцип суперпозиции малых приращений:

где символом fx′≡∂⁡f∂⁡x обозначена
частная производная функции f по переменной x —
то есть обычная производная f по x, взятая при условии, что
все остальные аргументы (кроме x) считаются постоянными параметрами.
Тогда пользуясь формулой для нахождения дисперсии суммы независимых
величин (2.7), получим соотношение, позволяющее вычислять
погрешности косвенных измерений для произвольной функции
u=f⁢(x,y,…):

σu2=fx′⁣2⁢σx2+fy′⁣2⁢σy2+… (2.11)

Это и есть искомая общая формула пересчёта погрешностей при косвенных
измерениях.

Отметим, что формулы (2.10) и (2.11) применимы
только если относительные отклонения всех величин малы
(εx,εy,…≪1),
а измерения проводятся вдали от особых точек функции f (производные
fx′, fy′ … не должны обращаться в бесконечность).
Также подчеркнём, что все полученные здесь формулы справедливы только
для независимых переменных x, y, …

Остановимся на некоторых важных частных случаях формулы
(2.11).


Пример. Для суммы (или разности) u=∑i=1nai⁢xi имеем



σu2=∑i=1nai2⁢σxi2.

(2.12)


Пример. Найдём погрешность степенной функции:
u=xα⋅yβ⋅…. Тогда нетрудно получить,
что



σu2u2=α2⁢σx2x2+β2⁢σy2y2+…


или через относительные погрешности



εu2=α2⁢εx2+β2⁢εy2+…

(2.13)


Пример. Вычислим погрешность произведения и частного: u=x⁢y или u=x/y.
Тогда в обоих случаях имеем



εu2=εx2+εy2,

(2.14)

то есть при умножении или делении относительные погрешности складываются
квадратично.


Пример. Рассмотрим несколько более сложный случай: нахождение угла по его тангенсу



u=arctgyx.


В таком случае, пользуясь тем, что (arctgz)′=11+z2,
где z=y/x, и используя производную сложной функции, находим
ux′=uz′⁢zx′=-yx2+y2,
uy′=uz′⁢zy′=xx2+y2, и наконец



σu2=y2⁢σx2+x2⁢σy2(x2+y2)2.


Упражнение. Найти погрешность вычисления гипотенузы z=x2+y2
прямоугольного треугольника по измеренным катетам x и y.

По итогам данного раздела можно дать следующие практические рекомендации.

  • •

    Как правило, нет смысла увеличивать точность измерения какой-то одной
    величины, если другие величины, используемые в расчётах, остаются
    измеренными относительно грубо — всё равно итоговая погрешность
    скорее всего будет определяться самым неточным измерением. Поэтому
    все измерения имеет смысл проводить примерно с одной и той же
    относительной погрешностью    .

  • •

    При этом, как следует из (2.13), особое внимание
    следует уделять измерению величин, возводимых при расчётах в степени
    с большими показателями. А при сложных функциональных зависимостях
    имеет смысл детально проанализировать структуру формулы
    (2.11):
    если вклад от некоторой величины в общую погрешность мал, нет смысла
    гнаться за высокой точностью её измерения, и наоборот, точность некоторых
    измерений может оказаться критически важной.

  • •

    Следует избегать измерения малых величин как разности двух близких
    значений (например, толщины стенки цилиндра как разности внутреннего
    и внешнего радиусов): если u=x-y, то абсолютная погрешность
    σu=σx2+σy2
    меняется мало, однако относительная погрешность
    εu=σux-y
    может оказаться неприемлемо большой, если x≈y.

Источник

Понравилась статья? Поделить с друзьями:
  • Ошибка печати ddst
  • Ошибка повторного получения лицензии параметры владельца
  • Ошибка повторного получения лицензии 1с параметры пользователя отличаются
  • Ошибка печати canon mf410
  • Ошибка повторно подключите диск