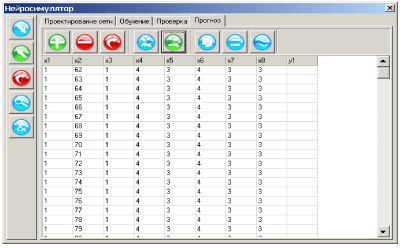
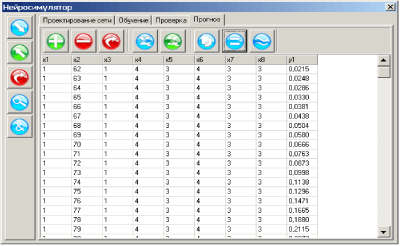
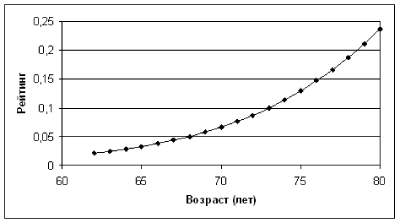
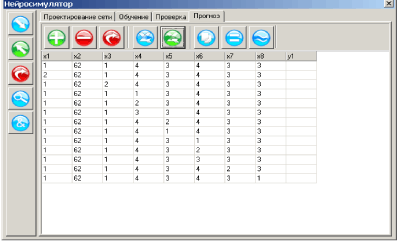
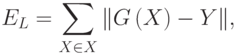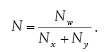Ошибка обобщения нейросети - TopOshibok.ru - решение и исправление самых разных ошибок

Характер приближений в информационных моделях

Специфичность информационных моделей проявляется не только в способах их синтеза, но и характере делаемых приближений (и связанных с ними ошибок). Отличия в поведении системы и ее информационной модели возникают вследствие свойств экспериментальных данных.

Информационные модели ab initio являются неполными. Пространства входных и выходных переменных не могут, в общем случае, содержать все параметры, существенные для описания поведения системы. Это связано как с техническими ограничениями, так и с ограниченностью наших представлений о моделируемой системе. Кроме того, при увеличении числа переменных ужесточаются требования на объем необходимых экспериментальных данных для построения модели (об этом см. ниже). Эффект опущенных (скрытых) входных параметров может нарушать однозначность моделируемой системной функции F.
База экспериментальных данных, на которых основывается модель G рассматривается, как внешняя данность. При этом, в данных всегда присутствуют ошибки разной природы, шум, а также противоречия отдельных измерений друг другу. За исключением простых случаев, искажения в данных не могут быть устранены полностью.
Экспериментальные данные, как правило, имеют произвольное распределение в пространстве переменных задачи. Как следствие, получаемые модели будут обладать неодинаковой достоверностью и точностью в различных областях изменения параметров.
Экспериментальные данные могут содержать пропущенные значения (например, вследствие потери информации, отказа измеряющих датчиков, невозможности проведения полного набора анализов и т.п.). Произвольность в интерпретации этих значений, опять-таки, ухудшает свойства модели.

Такие особенности в данных и в постановке задач требуют особого отношения к ошибкам информационных моделей.

Ошибка обучения и ошибка обобщения

Итак, при информационном подходе требуемая модель G системы F не может быть полностью основана на явных правилах и формальных законах. Процесс получения G из имеющихся отрывочных экспериментальных сведений о системе F может рассматриваться, как обучение модели G поведению F в соответствии с заданным критерием, настолько близко, насколько возможно. Алгоритмически, обучение означает подстройку внутренних параметров модели (весов синаптических связей в случае нейронной сети) с целью минимизации ошибки модели 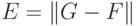$E = \left\| {G - F}\right\|$ .

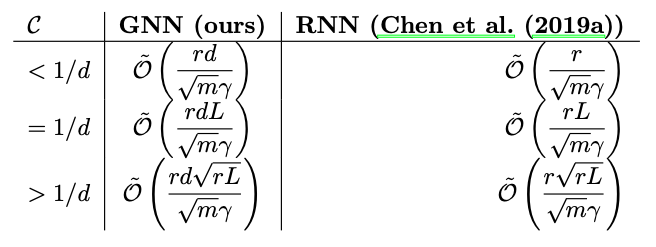
Прямое измерение указанной ошибки модели на практике не достижимо, поскольку системная функция F при произвольных значениях аргумента не известна. Однако возможно получение ее оценки:

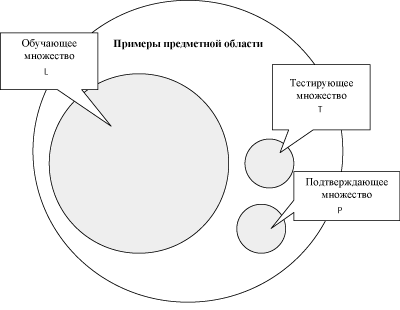
$E_L = \sum\limits_{X \in X}{\left\| {G\left( X \right) - Y}\right\|},$

где суммирование по X проводится по некоторому конечному набору параметров X, называемому обучающим множеством. При использовании базы данных наблюдений за системой, для обучения может отводиться некоторая ее часть, называемая в этом случае обучающей выборкой. Для обучающих примеров X отклики системы Y известны^{7С учетом описанных выше особенностей экспериментальных данных.}. Норма невязки модельной функции G и системной функции Y на множестве X играет важную роль в информационном моделировании и называется ошибкой обучения модели.

Для случая точных измерений (например, в некоторых задачах классификации, когда отношение образца к классу не вызывает сомнений) однозначность системной функции для достаточно широкого класса G моделей гарантирует возможность достижения произвольно малого значения ошибки обучения E_L. Нарушение однозначности системной функции в присутствии экспериментальных ошибок и неполноты признаковых пространств приводит в общем случае к ненулевым ошибкам обучения. В этом случае предельная достижимая ошибка обучения может служить мерой корректности постановки задачи и качества класса моделей G.

В приложениях пользователя обычно интересуют предсказательные свойства модели. При этом главным является вопрос, каковым будет отклик системы на новое воздействие, пример которого отсутствует в базе данных наблюдений. Наиболее общий ответ на этот вопрос дает (по-прежнему недоступная) ошибка модели E. Неизвестная ошибка, допускаемая моделью G на данных, не использовавшихся при обучении, называется ошибкой обобщения модели E_G.

Основной целью при построении информационной модели является уменьшение именно ошибки обобщения, поскольку малая ошибка обучения гарантирует адекватность модели лишь в заранее выбранных точках (а в них значения отклика системы известны и без всякой модели!). Проводя аналогии с обучением в биологии, можно сказать, что малая ошибка обучения соответствует прямому запоминанию обучающей информации, а малая ошибка обобщения — формированию понятий и навыков, позволяющих распространить ограниченный опыт обучения на новые условия. Последнее значительно более ценно при проектировании нейросетевых систем, так как для непосредственного запоминания информации лучше приспособлены не нейронные устройства компьютерной памяти.

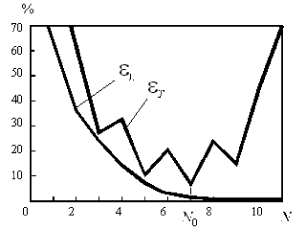
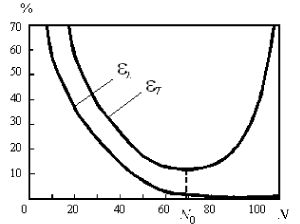
Важно отметить, что малость ошибки обучения не гарантирует малость ошибки обобщения. Классическим примером является построение модели функции (аппроксимация функции) по нескольким заданным точкам полиномом высокого порядка. Значения полинома (модели) при достаточно высокой его степени являются точными в обучающих точках, т.е. ошибка обучения равна нулю. Однако значения в промежуточных точках могут значительно отличаться от аппроксимируемой функции, следовательно ошибка обобщения такой модели может быть неприемлемо большой.

Поскольку истинное значение ошибки обобщения не доступно, в практике используется ее оценка. Для ее получения анализируется часть примеров из имеющейся базы данных, для которых известны отклики системы, но которые не использовались при обучении. Эта выборка примеров называется тестовой выборкой. Ошибка обобщения оценивается, как норма уклонения модели на множестве примеров из тестовой выборки.

Оценка ошибки обобщения является принципиальным моментом при построении информационной модели. На первый взгляд может показаться, что сознательное не использование части примеров при обучении может только ухудшить итоговую модель. Однако без этапа тестирования единственной оценкой качества модели будет лишь ошибка обучения, которая, как уже отмечалось, мало связана с предсказательными способностями модели. В профессиональных исследованиях могут использоваться несколько независимых тестовых выборок, этапы обучения и тестирования повторяются многократно с вариацией начального распределения весов нейросети, ее топологии и параметров обучения. Окончательный выбор «наилучшей» нейросети выполняется с учетом имеющегося объема и качества данных, специфики задачи, с целью минимизации риска большой ошибки обобщения при эксплуатации модели.

Источник

Ограничения репрезентативной способности и оценка ошибки обобщения для графовых нейронных сетей

Время на прочтение
5 мин

Количество просмотров 2.1K

В настоящее время, одним из трендов в исследовании графовых нейронных сетей является анализ работы таких архитектур, сравнение с ядерными методами, оценка сложности и обобщающей способности. Все это помогает понять слабые места существующих моделей и создает пространство для новых.

Работа направлена на исследование двух проблем, связанных с графовыми нейронными сетями. Во-первых, авторы приводят примеры различных по структуре графов, но неразличимых и для простых, и для более мощных GNN. Во-вторых, они ограничивают ошибку обобщения для графовых нейронных сетей точнее, чем VC-границы.

Введение

Графовые нейронные сети — это модели, которые работают напрямую с графами. Они позволяют учитывать информацию о структуре. Типичная GNN включает в себя небольшое число слоев, которые применяются последовательно, обновляя представления вершин на каждой итерации. Примеры популярных архитектур: GCN, GraphSAGE, GAT, GIN.

Процесс обновления эмбеддингов вершин для любой GNN-архитектуры можно обобщить двумя формулами:

$a_v^{t+1} = AGG \left(h_w^t: w \in \mathcal{N}\left(v\right)\right) \\ h_v^{t+1} = COMBINE \left(h_v^t, a_v^{t+1}\right),$

где AGG — обычно функция, инвариантная к перестановкам (sum, mean, max etc.), COMBINE — функция объединяющая представление вершины и ее соседей.

Дерево вычислений для двухслойной GNN на примере узла A. Источник: https://eng.uber.com/uber-eats-graph-learning/

Более продвинутые архитектуры могут учитывать дополнительную информацию, например, фичи ребер, углы между ребрами и т.д.

В статье рассматривается класс GNN для задачи graph classification. Эти модели устроены так:

Сначала производятся эмбеддинги вершин с помощью L шагов графовых сверток
Из эмбеддингов вершин получают представление графа с помощью инвариантной к перестановкам функций (например, sum, mean, max)
Классификатор предсказывает бинарную метку по представлению графа

Ограничения графовых нейронных сетей

В статье авторы рассматривают ограничения для трех классов GNN:

Локально инвариантные графовые нейронные сети (LU-GNN). Сюда входят вышеупомянутые GCN, GraphSAGE, GAT, GIN и другие
CPNGNN, которая вводит локальный порядок, нумеруя соседние вершины от 1 до d, где d — степень вершины (в оригинальной работе это называют port numbering)
DimeNet, которая оперирует 3D-графами, учитывая расстояния между вершинами и углы между ребрами

Ограничения LU-GNN

Графы G и G неразличимы LU-GNN, так как деревья вычислений будут совпадать для узлов одного цвета, следовательно эмбеддинги, полученные с помощью инвариантной к перестановкам readout-функции, будут одинаковыми. CPNGNN с введением подходящего порядка сможет различать как одноцветные вершины в G и G, так и сами графы.

Ограничения CPNGNN

Однако, существует “плохой” порядок, при котором и CPNGNN произведет одинаковые эмбеддинги для вершин одного цвета.

Граф S₈ и две копии S₄ различаются в таких характеристиках, как обхват, окружность (длина наименьшего и наибольшего циклов соответственно), радиус, диаметр и количество циклов, но CPNGNN с таким порядком портов и readout-ом, инвариантным к перестановкам, произведет для одинаковые эмбеддинги. А значит, по ним невозможно будет восстановить правильные характеристики для обоих графов.

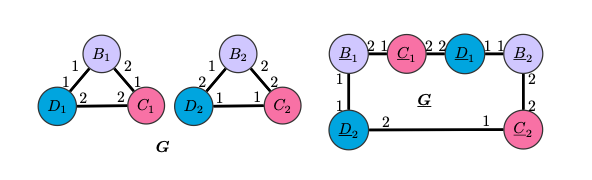
Здесь CPNGNN с такими же условиями не сможет восстановить характеристики из предыдущего примера для графа G₂и двух копий G₁. Однако, DimeNet сможет это сделать, так как она учитывает углы, которые не везде совпадают в случае этих графов, например, $\angle A_1B_1C_1$ и $\angle \underline{A}_1\underline{B}_1\underline{C}_1$ .

Ограничения DimeNet

DimeNet не сможет различить G₄ и граф, составленный из двух копий G₃, так как расстояния и углы в этих графах будут идентичны. Значит, она так же не вычислит характеристики обоих графов. Можно заметить, что G₄ и G₃ являются графами S₄ и S₈, натянутыми на куб, а значит, даже усовершенствованная версия DimeNet с нумерацией портов из S₄ и S₈ не будет справляться с этой задачей.

Шаг в сторону более мощных GNN

Авторы предлагают объединить идеи вышеупомянутых подходов и добавить больше геометрической информации. Например, включить углы и расстояния между плоскостями, которые будут заданы тройкой ребер.

GNN, предложенная авторами работает так:

Шаг DimeNet
Дополнение message-эмбеддинга ребра $m_{uv}^{\left(l\right)}$ геометрической информацией $\Phi_{uv}$ по формуле $\underline{m}_{uv}^{\left(l\right)} = \underline{f}\left(m_{uv}^{\left(l\right)}, \Phi_{uv}\right)$
Получение эмбеддинга вершины с учетом введенного локального порядка $\left(c_v\left(i\right), t_{i, v}\right)$ , где c — i-ый сосед вершины v, t — эмбеддинг порядка.

Формула обновления представления вершины:

$h_{v}^{\left( l + 1 \right)} = f \left( h_{v}^{\left( l \right)}, \underline{m}_{c_v\left( 1 \right)v}^{\left( l \right )}, t_{1, v}, ..., \underline{m}_{c_v\left( d \left( v \right ) \right)v}^{\left( l \right )}, t_{ d \left( v \right ), v} \right )$
Шаг инвариантного к перестановкам readout-а
Классификатор или регрессор в зависимости от задачи

Такая модель позволит различать графы во всех вышеприведенных примерах.

Оценка ошибки обобщения

Авторы рассматривают конкретный класс моделей: LU-GNN, в которой обновление представления вершины происходит согласно

$h_v^{l + 1} = \phi \left( W_1x_v + W_2 \rho \left( \sum_{u \in \mathcal{N} \left( v \right)} g\left( h_u^l \right)\right) \right),$

где $\phi,\ g,\ \rho$ — нелинейные функции активации, x_v — вектор признаков для вершины v, такие, что $\rho \left(0\right) = 0,\ \forall v: \lVert x_v \rVert_2 \le B_x,\ \forall x \in \mathbb{R}^r: \lVert \phi \left( x \right ) \rVert_{\infty} \le b < \infty,\ \phi\left( 0 \right ) = 0,\ g\left( 0 \right ) = 0$ . Также, $\phi,\ g,\ \rho$ липшицевы с константами $C_{\phi},\ C_{g},\ C_{\rho}$ соответственно, а $\lVert W_1 \rVert_2 \le B_1,\ \lVert W_2 \rVert_2 \le B_2$ . $W_1,\ W_2,\ \phi,\ g,\ \rho$ одинаковы на всех слоях GNN.
Далее бинарный классификатор применяется к представлению каждой вершины отдельно и полученные метки усредняются. Параметр $\beta$ бинарного классификатора обладает свойством $\lVert \beta \rVert_2 \le B_{\beta}$ .

Пусть $f\left(G\right)$ — результат применения GNN к графу с меткой $y \in \{0, 1\}$ , $p\left( f \left( G \right ), y \right ) = y \left( 2f \left( G \right ) - 1 \right ) + \left( 1 - y \right ) \left( 1 - 2 f \left( G \right ) \right )$ — разница между вероятностями правильного и неправильного лейбла, $p\left( f \left( G \right ), y \right ) < 0$ только в случае ошибки классификации.

Фукнция потерь, где $a = -p\left( f \left( G \right ), y \right )$ , — индикаторная функция:

$loss_{\gamma}\left( a \right ) = \mathbb{I}\left[ a > 0\right ] + (1 + \frac{a}{\gamma})\mathbb{I}\left[ a \in \left[ \gamma, 0 \right ] \right].$

Тогда эмпирическая сложность Радемахера для класса функций предсказания GNN на тренировочном множестве $\{G_j, y_j\}_{j=1}^m$ :

$\hat{\mathcal{R}}\left( f \right) = \frac{1}{m} \sum_{j = 1}^m loss_{\gamma} \left( -p\left( f \left(G_j\right), y_j \right) \right)$

Авторы строят доказательство, пользуясь леммой, в которой утверждается, что с большой вероятностью, ошибку предсказания для GNN можно ограничить суммой ошибки на тренировочной выборке и способностью модели предсказывать класс по эмбеддингу графа. Для класса, рассматриваемого авторами (GNN, которые предсказывают метку графа по меткам большинства вершин), второе слагаемое можно заменить на способность предсказывать класс по вершинам, то есть деревьям вычислений, следовательно можно анализировать эти деревья.

Все вышеописанное было проделано для того, чтобы можно было использовать два факта:

Так как исследуется дерево, можно выразить эмбеддинг вершины рекурсивно через поддеревья
Малые изменения в весах модели так же вносят малый вклад в изменение класса (доказательство приведено в статье)

Это позволяет вывести границы ошибки обобщения по аналогии с RNN

Cравнение с RNN, видно сходство

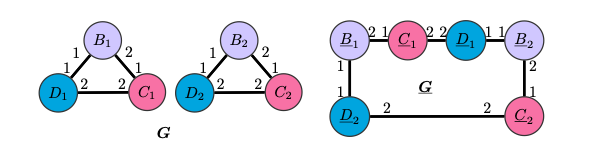
В таблице $\mathcal{C}$ — “сложность перколяции”: $\mathcal{C} = C_{\phi}C_gC_{\rho}B_2$ , r — размер эмбеддинга, d — максимальная степень вершины, m — размер тренировочной выборки, L — количество слоев, $\gamma$ — зазор, зависящий от данных

Эти оценки позволяют существенно более точно оценить ошибку обобщения, по сравнению с работой, где получили оценку $\tilde{\mathcal{O}} \left(r^3N / \sqrt{m} \right)$

Важной частью этой статьи является использование локальной инвариантности к перестановкам внутри GNN, а не только глобальной (в readout-е), как в этой и этой статьях. Это позволяет более точно оценить ошибку обобщения, так как не приходится учитывать каждый порядок, в котором могут быть расположены вершины графа.

Выводы

Важна как мощность модели (способность различать всевозможные пары графов), так и ее обобщающая способность. Однако, более сложные модели склонны к переобучению, поэтому нужно выбирать модели, которые находят баланс, например, исходя из размера датасета, вычислительных ресурсов и других факторов.

С доказательствами и более подробной информацией можно ознакомиться, прочитав оригинальную статью или посмотрев доклад от одного из авторов.

Источник

Во многих популярных курсах машинного и глубокого обучения вас научат классифицировать собак и кошек, предсказывать цены на недвижимость, покажут еще десятки задач, в которых машинное обучение вроде как отлично работает. Но вам расскажут намного меньше (или вообще ничего) о тех случаях, когда ML-модели не работают так, как ожидалось.

Частой проблемой в машинном обучении является неспособность ML-моделей корректно работать на большем разнообразии примеров, чем те, что встречались при обучении. Здесь идет речь не просто о других примерах (например, тестовых), а о других типах примеров. Например, сеть обучалась на изображениях коровы, в которых чаще всего корова был на фоне травы, а при тестировании требуется корректное распознавание коровы на любом фоне. Почему ML-модели часто не справляются с такой задачей и что с этим делать – мы рассмотрим далее. Работа над этой проблемой важна не только для решения практических задач, но и в целом для дальнейшего развития ИИ.

Конечно, этим проблемы машинного обучения не ограничиваются, существуют также сложности с интерпретацией моделей, проблемы предвзятости и этики, ресурсоемкости обучения и прочие. В данном обзоре рассмотрим только проблемы обобщения.

Содержание

Проблемы обобщения
    Задача обобщения в машинном обучении
    Утечка данных
    Shortcut learning: «right for the wrong reasons»
    Shortcut learning в языковых моделях
    Уровни обобщения моделей машинного обобщения
    Состязательные атаки
    Проблема неконкретизации в ML-задачах
    Выводы
Способы решения проблем обобщения
    Стресс-тесты для диагностики работы модели
    Доменная адаптация
    Еще больше данных?
    Более крупные или более эффективные модели?
    Модификации способов обучения языковых моделей
    Архитектура моделей и структура данных
    Направления исследований
    Общий искусственный интеллект
Заключение

Проблемы обобщения

Задача обобщения в машинном обучении

Задача машинного обучения заключается в написании алгоритмов, которые автоматически выводят общие закономерности из частных случаев (обучающих примеров). Этот процесс называется обобщением (generalization), или индукцией. Часто требуется найти зависимость между исходными данными и целевыми данными в виде функции .

Например, требуется определить по фотографии тип или положение изображенного объекта. Для решения этой задачи можно собрать большое количество размеченных данных (supervised learning), можно также использовать ненадежно размеченные данные (weakly-supervised learning), например фотографии из Instagram c хештегами, или даже неразмеченные данные (self-supervised learning). Но в любом случае мы используем некий набор конкретных примеров.

Понятно, что чем больше доступно примеров, тем выше будет качество полученного решения (при прочих равных условиях). Больше данных – выше точность. Все логично?

Существуют даже теоремы, доказывающие для различных ML-алгоритмов стремление получаемого решения к идеалу при неограниченном увеличении количества обучающих данных и размера модели (это свойство называется universal consistency; например, для нейронных сетей см. Faragó and Lugosi, 1993). При доказательстве подобных теорем считается, что данные X, y берутся из некоего фиксированного, но неизвестного распределения P(X, y) . Такой подход называется statistical learning framework, он излагается почти в любой книге по машинному обучению (например, см. Deep Learning book, раздел 5.2, есть также русское издание).

С развитием технологий стали доступны дешевые вычисления и огромные объемы данных, что позволило эффективно решать очень сложные задачи. Например, языковая модель GPT-3 (Brown et al., 2020) от компании OpenAI обучалась на 570 Гб текстов и имеет 175 миллиардов параметров, по приблизительным подсчетам обучение стоило миллионы долларов. Примеры текстов, которые генерирует GPT-3, можно найти здесь, здесь, здесь и здесь. В Google обучили сеть с 1.6 триллиона параметров (Fedus et al., 2021), в Китае – сеть с 1.75 триллиона параметров, и это далеко не предел: уже делаются попытки обучать сеть со 120 триллионами параметров, что примерно равно количеству синапсов в человеческом мозге. Более крупные модели и больше обучающих данных — выше точность.

Казалось бы, что может пойти не так?

Рассмотрим несколько примеров, когда простого увеличения объема обучающих данных может оказаться недостаточно. Начнем с проблемы утечки данных, и затем рассмотрим более общую проблему ограниченного разнообразия обучающих данных и ситуации, когда модель лишь «делает вид», что обучается.

Утечка данных

Утечкой данных называется ситуация, когда существует некий признак, который при обучении содержал больше информации о целевой переменной, чем при последующем применении модели на практике. Утечка данных может возникать в самых разных формах.

Пример 1. При диагностике заболеваний по рентгеновским снимкам модель обучается и тестируется на данных, собранных с разных больниц. Рентгеновские аппараты в разных больницах выдают снимки с немного разной тональностью, при этом различия могут быть даже незаметны человеческим глазом. Модель может обучиться определять больницу на основе тональности снимка, а значит и вероятный диагноз (в разных больницах лежат люди с разными диагнозами), при этом вообще не анализируя изображение на снимке. Такая модель покажет отличную точность при тестировании, так как тестовые снимки взяты из той же выборки данных.

Пример 2. В задаче диагностики реальных и фейковых вакансий почти все фейковые вакансии относились к Европе. Обученная на этих данных модель может не считать подозрительными любые вакансии из других регионов. При применении на практике такая модель станет бесполезна, как только фейковые вакансии станут размещаться в других регионах. Конечно можно удалить регион из признаков, но тогда модель будет пытаться предсказать регион по другим признакам (скажем, по отдельным словам в описании и требованиях), и проблема сохранится.

Пример 3. В той же задаче есть признак «имя компании», и у компаний может быть по нескольку вакансий. Если компания фейковая, то все ее вакансии фейковые. Если мы разделим данные на обучающую и тестовую часть (или на фолды) таким образом, что вакансии одной и той же компании попадут и в обучающую, и в тестовую часть, то модели достаточно будет запомнить имена фейковых компаний для предсказания на тестовой выборке, в результате на тесте мы получим сильно завышенную точность.

Все описанные проблемы нельзя решить просто увеличением количества обучающих данных без изменения подхода к обучению. Здесь можно возразить, что утечка данных не является проблемой самих ML-алгоритмов, поскольку алгоритм и не может знать о том, какой признак нужно учитывать, а какой нет. Но давайте посмотрим на другие похожие примеры.

Shortcut learning: «right for the wrong reasons»

В начале XX века жила лошадь по имени Умный Ганс, которая якобы умела решать сложные арифметические задачи, постукивая копытом нужное число раз. В итоге оказалось, что лошадь определяет момент, когда нужно прекращать стучать копытом, по выражению лица того, кто задает вопрос. С тех пор имя «умного Ганса» стало нарицательным (1, 2) – оно означает получение решения обходным путем, не решая при этом саму задачу в том смысле, какой мы хотим. Такое обходное «решение» внезапно перестает работать, если меняются условия (например, человек, задающий вопрос лошади, сам не знает ответа на него).

Исследователи давно заметили, что многие современные модели глубокого обучения похожи на «умного Ганса». Вспомним хотя бы легендарную статью на Хабре про «леопардовый диван»:

… Где-то в этот момент в мозг начинает прокрадываться ужасная догадка — а что если вот это различие в текстуре пятен и есть главный критерий, по которому алгоритм отличает три возможных класса распознавания [леопарда, ягуара, гепарда] друг от друга? То есть на самом деле сверточная сеть не обращает внимания на форму изображенного объекта, количество лап, толщину челюсти, особенности позы и все вот эти тонкие различия, которые, как мы было предположили, она умеет понимать — и просто сравнивает картинки как два куска текстуры?

Это предположение необходимо проверить. Давайте возьмем для проверки простую, бесхитростную картинку, без каких-либо шумов, искажений и прочих факторов, осложняющих жизнь распознаванию. Уверен, эту картинку с первого взгляда легко опознает любой человек.

… Похоже, что наша догадка насчет текстуры близка к истине. … Я сделал еще пару проверок (Microsoft, Google) — некоторые из них ведут себя лучше, не подсовывая ягуара, но победить повернутый набок диван не смог никто. Неплохой результат в мире, где уже мелькают заголовки в духе «{Somebody}’s Deep Learning Project Outperforms Humans In Image Recognition».

В самом деле, зачем модели, решающей задачу классификации, выучивать форму и другие комплексные свойства объекта, называемого «леопард», если простое присутствие нужной текстуры на изображении дает почти 100%-ю точность выявления леопарда в обучающей (и тестовой) выборке из ImageNet?

То же самое касается предсказания объекта с учетом фона. Мы не закладывали при обучении никакой информации о том, на основании чего мы хотим получать предсказание: на основании объекта или окружающего его фона. Было даже обнаружено (Zhu et al., 2016), что нейронные сети способны с хорошей точностью предсказывать класс объекта, если сам объект вырезан и оставлен только фон.

Shortcut learning — явление, когда модели получают верный ответ с помощью неверных в общем случае рассуждений («right for the wrong reasons»), которые хорошо работают только для обучающего распределения данных. Поскольку обучающая и тестовая выборка обычно берутся из одного распределения, то такие модели могут давать хорошую точность и при тестировании.

Shortcuts are decision rules that perform well on standard benchmarks but fail to transfer to more challenging testing conditions, such as real-world scenarios.

Другие примеры можно найти в замечательной статье Shortcut Learning in Deep Neural Networks (Geirhos et al., 2020), опубликованной в журнале Nature и основанной на обобщении информации из более чем 140 источников.

Смена угла поворота объекта, появление его в необычном (с точки зрения обучающей выборки) окружении, добавление необычного шума может полностью испортить работу модели. На иллюстрации ниже слева показаны пары изображений, одинаково классифицируемые с точки зрения человека, но совершенно разные с точки зрения сверточной нейронной сети. Справа показаны, наоборот, изображения, имеющие одинаковый класс для нейронной сети и разный для человека.

В целом исследователями был сделан вывод о том, что многие современные сверточные нейронные сети предпочитают ориентироваться на локальные участки текстур (Jo and Bengio, 2017; Geirhos et al., 2018), которые могут относиться как к объекту, так и к фону, и не классифицируют объект на основании его общей формы (Baker et al., 2018).

Сейчас нейронные сети начинают решать очень сложные задачи, такие как работа с трехмерными сценами, анимация объектов и прочее. Казалось бы, задача классификации собак и кошек уже давно решена? Оказывается, что нет. Как показано на примерах ниже, одна из самых современных нейронных сетей для детектирования объектов YOLOv5 может быть легко обманута необычными деталями, не относящимися к самому объекту, либо может принимать несколько объектов за один. Предсказания получены с помощью интерактивной версии YOLOv5, интерпретация выполнена с помощью Grad-CAM (Selvaraju et al., 2016; репозиторий). Оригиналы изображений можно найти по ссылкам: 1, 2, 3, 4.

Добавление собачьего корма в последнем изображении существенно повышает уверенность в распознавании собаки, хотя сам корм сеть распознает как «книгу». При этом на GradCAM зависимость ответа от наличия собачьего корма в кадре не видна, так как рамка ограничена рамкой объекта. В целом даже небольшие изменения, такие как кадрирование с обрезкой 5% фона или пересохранение в jpeg сильно меняет предсказание модели в сложных для нее случаях.

Сверточные сети для классификации, даже самые современные, часто классифицируют черных котов как породу собак схипперке (которые тоже имеют черную шерсть), даже если по морде и форме тела видно, что это кот. Имеются в виду, конечно, сети общего назначения, которые не дообучались специально для точного распознавания пород собак и кошек, хотя и в этом случае нет гарантии точного распознавания.

Jo and Bengio, 2017 используют фильтрацию, основанную на преобразовании Фурье, для внесения в изображения помех, которые не мешают распознаванию их человеком, но сильно снижают качество работы сверточных нейронных сетей. Увеличение глубины сетей не избавляет от этой проблемы. Более того, если добавить в обучающий датасет один из типов Фурье-искажений, то это не делает сеть устойчивее к другим типам Фурье-искажений (которых может быть очень много).

The current incarnation of deep neural networks exhibit a tendency to learn surface statistical regularities as opposed to higher level abstractions in the dataset. For tasks such as object recognition, … [this is] sufficient for high performance generalization, but in a narrow distributional sense.

To this end, we draw an analogy to adversarial training: augmenting the training set with a specific subset of adversarial examples does not make the network immune to adversarial examples in general. …we do not believe that this sort of data augmentation is sufficient for learning higher level abstractions in the dataset.

Shortcut learning в языковых моделях

Та же проблема есть и в языковых моделях. Например, модель BERT (Devlin et al., 2018) обучена на таком объеме текстов, который человек не прочитает за всю жизнь, но при этом она в основном выучивает поверхностные, стереотипные ассоциации слов друг с другом (word co-occurence), и вряд ли хорошо понимает смысл текста.

Some of BERT’s world knowledge success comes from learning stereotypical associations, e. g. a person with an Italian-sounding name is predicted to be Italian, even when it is incorrect. (Rogers et al., 2020)

Попробуем протестировать некоторые из наиболее популярных на сегодняшний день языковых моделей: RoBERTa (Liu et al., 2019), ALBERT (Lan et al., 2019) и mT5 (Xue et al., 2020), взяв для тестирования их крупные варианты из репозитория HuggingFace: roberta-large, albert-xxlarge-v2 и mt5-xl. Эти модели обучались на разных задачах, в числе которых была задача предсказания закрытых маской слов в тексте, называемая masked language model objective, или cloze task. Проверим их работу на различных примерах.

Примечание. Вы можете сами повторить эксперимент, используя окно «Hosted inference API» по приведенным выше ссылкам; для mT5 можно использовать этот ноутбук, требуется GPU с большим объемом памяти.

Как видим, модели иногда неплохо запоминают простые факты, но при этом все рассмотренные модели часто делают ошибки там, где нужно понимать логику повествования. Если логика повествования противоречит статистике совместной встречаемости слов, то модели обычно предпочитают статистику. Например, в последних двух примерах модель ALBERT вероятно работает так: если «approaches», то «discuss», если «approach», то «propose» – потому при обучении часто встречались такие сочетания. Слово «existing» при этом ее не смущает.

Здесь можно возразить, что слова, вставленные моделью, могут быть не цельными предложениями, а их частями, например «those who are eaten by whales are tiny animals», но этим нельзя объяснить все случаи в таблице.

Также можно возразить, что эти модели не обучались генерировать тексты без логических ошибок, они обучались воспроизводить реальные тексты, даже если в них есть ошибки. Но даже с учетом этого, те варианты слов, которые выбирают модели, часто оказываются абсурдны и практически не могли встретиться в написанных человеком текстах.

Вполне вероятно, что будь модели еще в 100 раз крупнее, обучаясь в 100 раз дольше и на большем объеме данных – они не совершили бы таких очевидных ошибок. Но даже эти модели очень большие (3.7 миллиарда параметров в mT5-XL) и обучались на сотнях гигабайт текстов, чему качество их работы на нетипичных примерах явно не соответствует – это наводит на мысль о неоптимальности подхода в целом.

Проблема shortcut learning присутствует и в тех моделях, которые специально дообучались для лидербордов GLUE (Wang et al., 2018) и SuperGLUE (Wang et al., 2019). Эти бенчмарки нацелены на измерение уровня «понимания естественного языка» моделями машинного обучения. SuperGLUE содержит 8 задач, на некоторых из которых уже побит уровень человека (имеется в виду средний уровень человека, отличающегося от разметчика, т. к. разметка тоже делалась людьми).

Но действительно ли уровень человека побит? Как выясняется, высокая метрика качества в SuperGLUE достигается в основном с помощью shortcut learning, при этом модели эксплуатируют систематические проблемы в разметке датасета для предсказания ответа «обходным путем» (Gururangan et al., 2018; Du et al., 2021), и мнение многих исследователей (1, 2, 3, 4 и др.) сходится в том, что на текущий момент языковые модели-трансформеры далеки от понимания смысла текстов в том смысле, в каком их понимает человек. Во введении мы рассматривали языковую модель GPT-3, имеющую огромный размер и генерирующую реалистичные тексты. Вот, что о ней думает Ян Лекун:

Some people have completely unrealistic expectations about what large-scale language models such as GPT-3 can do. … GPT-3 doesn’t have any knowledge of how the world actually works. It only appears to have some level of background knowledge, to the extent that this knowledge is present in the statistics of text. But this knowledge is very shallow and disconnected from the underlying reality. …trying to build intelligent machines by scaling up language models is like building a high-altitude airplanes to go to the moon. You might beat altitude records, but going to the moon will require a completely different approach.

Cовременные языковые модели вроде GPT-3 (а также Gohper, InstructGPT, Wu Dao и другие) не стоит переоценивать, но, как мне кажется, не стоит и недооценивать. Со многими задачами они действительно очень хорошо справляются. Поскольку данный обзор посвящен проблемам машинного обучения, то в нем делается акцент на недостатках текущих ML-моделей (а значит и путях дальнейших исследований), но и преимуществ у них тоже много.

Уровни обобщения моделей машинного обобщения

Почти любой датасет имеет ограниченное разнообразие и не покрывает всех ситуаций, в которых желательна корректная работа модели. Особенно это проявляется в случае сложных данных, таких как изображения, тексты и звукозаписи. В данных могут существовать «паразитные корреляции» (spurious correlations), позволяющие с хорошей точностью предсказывать ответ только на данной выборке без «комплексного» понимания изображения или текста.

Это как раз и есть рассмотренные выше предсказания на основе фона, отдельных текстурных пятен или отдельных рядом стоящих слов. Датасеты, в которых паразитные корреляции явно выражены, называются biased (предвзятыми). Пожалуй, что все датасеты в задачах CV и NLP в той или иной степени предвзяты.

В статье о shortcut learning (Geirhos et al., 2020) авторы рассматривают несколько уровней обобщения, которые могут достигать модели машинного обучения:

Uninformative features. Сеть использует признаки, которые не позволяют эффективно предсказывать ответ даже на обучающей выборке, например, нейронная сеть со случайно инициализированным выходным слоем.

Overfitting features. Сеть использует признаки, которые позволяют эффективно предсказывать ответ на обучающей выборке, но не на всем распределении, из которого получена эта выборка. Под «распределением» здесь понимается вероятностное совместное распределение P(x, y) , из которого взяты данные (более подробно см. также этот обзор, раздел «распределение данных»).

Shortcut features. Сеть использует признаки, которые позволяют эффективно предсказывать ответ на распределении данных P(x, y) , из которого взята обучающая (и, как правило, тестовая) выборка. Поскольку выборка является набором независимых примеров, используется термин independent and identically distributed (i. i. d.). Способность алгоритма с хорошей точностью работать на некоем фиксированном распределении данных авторы называют i. i. d. обобщением. Как мы видели выше, для этого вовсе не обязательно уметь решать саму поставленную задачу в общем виде, часто можно использовать «обходные пути» или утечки данных.

Intended features. Сеть использует признаки, которые позволяют эффективно предсказывать ответ в общем случае. Такие признаки будут хорошо работать и вне обучающего распределения данных, когда «обходные пути» закрыты (например, объект находится на необычном фоне, в необычной позиции, имеет необычную текстуру и пр.).

Ситуация, когда распределение данных отличается при обучении и применении называется сдвигом распределения данных (distributional shift). Иными словами, данные, на которых модель будет применяться, среднестатистически отличаются от тех, на которых модель обучалась и тестировалась. В частности, может идти речь о появлении новых типов примеров или изменении соотношения количества примеров разных типов. Это происходит из-за того, что обучающие данные часто недостаточно разнообразны и не покрывают все те типы примеров, на которых желательна корректная работа модели (либо покрывают их в неправильном соотношении).

Хорошая работа модели в условиях сдвига данных называется out-of-distribution обобщением (OOD generalization), она также известна под названием domain generalization (Zhou et al., 2021; Wang et al., 2021; см. также на paperswithcode.com), очевидна ее связь с преодолением проблемы shortcut learning.

If an image classifier was trained on photo images, would it work on sketch images? What if a car detector trained using urban images is tested in rural environments? Is it possible to deploy a semantic segmentation model trained using sunny images under rainy or snowy weather conditions? Can a health status classifier trained using one patient’s electrocardiogram data be used to diagnose another patient’s health status? … Indeed, without access to target domain data, training a generalizable model that can work effectively in any unseen target domain is arguably one of the hardest problems in machine learning. (Zhou et al., 2021)

Еще один типичный пример – системы распознавания лиц. В обучающем датасете, даже очень большом, может ни быть ни одного изображения человеческого лица, на которое нанесен некий рисунок. Модель, обученная на таком датасете, научится быть инвариантной к положению лица в кадре и его выражению, и почти безошибочно идентифицировать человека. Однако модель может перестать корректно работать в случае, если надеты необычные очки или на лицо нанесен рисунок, потому что изображений такого типа не встречалось при обучении (либо они встречались чрезвычайно редко и практически не оказали влияния на обучение).

В результате люди придумывают все новые и новые способы обманывать системы распознавания лиц, не пряча при этом полностью лицо. Модель не встречалась с такими изображениями при обучении и распознает лица неправильно, даже если человек на месте модели легко опознал бы знакомое лицо.

Конечно, распознавание лиц может не всегда использоваться во благо обществу, но здесь речь идет об общей проблеме систем машинного обучения. Эффективное out-of-distribution обобщение остается открытой проблемой, которую необходимо решать, если мы хотим дальнейшего развития ИИ. В целом, ее можно описать так:

Generalizing beyond one’s experiences – a hallmark of human intelligence from infancy – remains a formidable challenge for modern AI. (Battaglia et al., 2018)

Состязательные атаки

С работы Szegedy et al., 2013 начались исследования в области так называемых состязательных атак на нейронные сети (adversarial attacks). Авторы показали, что наложением на изображение незначительного шума можно заставить нейронные сети ошибаться в задаче классификации, предсказывая совсем другой класс. Конечно, для этого подходит не любой шум, а специальный паттерн шума, найти который можно с помощью оптимизации.

Еще более неожиданным оказалось то, что в точности тот же паттерн шума заставлял ошибаться на том же изображении и другие сети, обученные с другими гиперпараметрами и на других подвыборках обучающих данных. Кроме этого, авторы работы исследовали интерпретируемость фильтров промежуточных слоев сверточных сетей.

В дальнейшем было обнаружено (Kurakin et al., 2016), что «обманывать» модель с помощью зашумленных изображений можно даже в том случае, когда зашумленное изображение фотографируется камерой (см. видео). При этом разные модели удается обманывать одним и тем же паттерном шума, что позволяет осуществлять подобные атаки (с переменным успехом) даже тогда, когда используемая модель неизвестна.

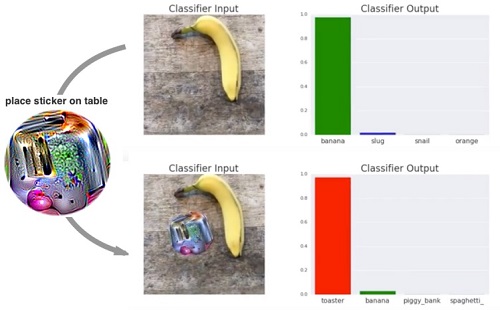
В 2017 году изобрели совсем простой способ «обмануть» сверточную нейронную сеть: достаточно наклеить на объект стикер со специальным рисунком, и сеть перестанет правильно классифицировать объект (Brown et al., 2017). Впрочем, такой стикер не универсален и будет работать только для определенных сетей, против которых он создавался.

Обзор других многочисленных работ по состязательным атакам можно найти в Akhtar and Mian, 2018 и Akhtar et al., 2021. Проблемы состязательных атак и недостаточного out-of-distribution обобщения в компьютерном зрении, вероятно, связаны между собой. Человеческое зрение тоже подвержено такому типу атак, что доказывают оптические иллюзии.

Проблема неконкретизации в ML-задачах

Рассмотрим еще одну работу, изучающую поведение ML-моделей за пределами обучающего распределения данных.

Для каждой задачи может существовать бесконечное количество разных обученных моделей с разными весами и вычислительными архитектурами, дающих примерно одинаковую точность на обучающей выборке. Это известная и центральная проблема машинного обучения (Mitchell, 1980). Но эта же проблема существует и в другом варианте: для каждой задачи может существовать бесконечное количество разных обученных моделей, дающих примерно одинаковую точность на обучающем распределении данных, из которого взята тестовая выборка.

В работе D’Amour et al., 2020 эту проблему называют проблемой неконкретизации ML-задачи (underspecification of ML-pipeline). Например, если задачей является обучить систему распознавания изображений с помощью сверточной сети, то может существовать огромное множество разных сверточных сетей с разной архитектурой и инициализацией весов, дающих примерно одинаковую точность на тестовой выборке. При смене условий (выходе за пределы обучающего распределения) эти модели могут начать работать сильно по-разному.

В одном из экспериментов авторы обучили на ImageNet 50 сверточных нейронных сетей ResNet-50 (He et al., 2015). На валидационной части ImageNet все сети давали примерно одинаковую точность 75.9% ± 0.1% (указано одно стандартное отклонение). Затем авторы протестировали сети на датасете ImageNet-С (Hendrycks and Dietterich, 2019), содержащем изображения с различными шумами и искажениями (out-of-distrubiton данные с точки зрения ImageNet). В результате на изображениях с пикселизацией сети давали точность 19.7% ± 2.4%, на изображениях с уменьшенной или увеличенной контрастностью сети давали точность 9.1% ± 0.8% и так далее. Аналогичная ситуация наблюдалась на сетях ResNet-101×3 BiT (Kolesnikov et al., 2019).

Видно, что точность моделей не только стала намного хуже, но и увеличился разброс значений точности среди моделей (2.4% против 0.1%). Более того, отклонения от средней точности на разных типах искажений почти не коррелируют. Это означает, что если модель справляется лучше модели на изображениях с пикселизацией, то это не означает, что она будет лучше справляться на изображениях с измененной контрастностью.

Подобный эксперимент авторы повторили и с другими данными: на медицинских изображениях, где использовались изображения и 5 камер (первые 4 камеры – обучающее распределение, 5-я камера — out-of-distrubiton данные), и получили аналогичный результат. Таким образом, поведение моделей, имеющих одинаковую точность на тестовой выборке из обучающего распределения, может быть существенно разным за пределами этого распределения.

А ведь в описанных выше экспериментах речь шла о моделях лишь с разной инициализацией весов, что уж говорить о моделях с разной архитектурой? Авторы предполагают, что не только архитектура, но и, скажем, оптимизатор и стратегия управления learning rate может сильно влиять на свойства модели (помимо общей точности на обучающем распределении) и точность работы полученной модели на тех или иных примерах за пределами обучающего распределения.

Выводы

ML-модели часто полагаются на «обходные» способы получения ответа (shortcuts), вызванные недостаточным разнообразием обучающего распределения данных и наличия в нем паразитных корреляций (это напоминает утечку данных). Такая модель лишь имитирует решение задачи, и поэтому может перестать корректно работать, если условия изменятся.
Следовательно, модели часто показывают низкую точность работы на таких данных, вероятность встретить которые в обучающем датасете была невелика: например, диван леопардовой расцветки, лицо с нанесенной краской, объекты в необычном окружении или текст, в котором используются нестереотипные словосочетания. Например, исходная цель обучения CV-систем обычно такова: мы хотим, чтобы система распознавала интересующие нас объекты в тех случаях, когда это может сделать человек. Но проблема в том, что мы не достигаем этой цели.
Модели, показывающие одинаковую среднюю точность при тестировании, могут работать существенно по-разному, что особенно проявляется за пределами распределения данных, на котором модели обучались и тестировались.
Системы компьютерного зрения (и не только) подвержены состязательным атакам, при которых внесение различных помех или добавление незначительных деталей может испортить работу модели. Человеческое зрение намного устойчивее к таким атакам.

Здесь еще можно вспомнить платформу Kaggle для проведения ML-соревнований. Часто считают, что рейтинг на Kaggle не полностью отражает уровень ML-специалиста из-за того, что реальный процесс ML-разработки содержит намного больше шагов, чем просто обучения модели. Однако при этом считается, что Kaggle хорошо развивает умение обучать качественные ML-модели. Исходя из рассмотренного выше можно усомниться и в этом факте. На Kaggle качество моделей как правило оценивается на том же распределении, из которого взята обучающая выборка, поэтому проблемы shortcut learning и устойчивость модели к сдвигу данных не играет особой роли. Кроме того, утечки данных (как разновидность сдвига данных) в реальной работе вредны, а на Kaggle скорее полезны.

Способы решения проблем обобщения

Закончив раздел «кто виноват», перейдем к разделу «что делать». Вопрос в том, как изгнать «умного Ганса» из ML-моделей и обучить их в полной мере решать поставленную задачу. Рассмотрим сначала наиболее прямолинейные способы, и закончим исследовательскими гипотезами и обзором работ, посвященных разработкам новых архитектур и методов обучения.

Стресс-тесты для диагностики работы модели

Авторы статей о shortcut learning (Geirhos et al., 2020) и неконкретизации (D’Amour et al., 2020) сходятся в том, что необходимо не только оценивать общую точность модели на тестовой выборке, но и оценивать точность на отдельных типах примеров. В частности, авторы предлагают следующие типы тестов:

Stratified evaluations. Разбиение тестовой выборки на типы (например, по значению какого-то признака, по классу) и оценка точности модели отдельно на каждом типе примеров. Процитирую пример из другого обзора:

Пусть модель тестировалась на датасете, в котором 80% изображений были высокого качества (HQ), а применяться будет в условиях, когда, наоборот, 80% изображений будут низкого качества (LQ). Пусть мы сравниваем две модели: на HQ-изображениях точность первой модели лучше, чем второй, а на LQ-изображениях, наоборот, точность второй модели лучше, чем первой. Если при тестировании большая часть изображений были HQ, то мы сделаем вывод, что первая модель лучше, тогда как на самом деле лучше была бы вторая.

Shifted evaluations. Тестирование модели на всех типах данных, на которых желательна ее хорошая работа. Например, на зашумленных данных, на фотографиях с разных времен года и так далее.
Contrastive evaluations. Вместо расчета средней метрики качества модели по какой-либо выборке, мы изучаем изменение метрики качества при изменении выборки (или одного примера). Например, поворачиваем фотографии на один и тот же угол и сравниваем метрику качества.

В задачах обработки естественного языка Ribeiro et al., 2020 предлагают целый ряд проверок, которые стоит проделать на обученных моделях.

Доменная адаптация

Перечисленные способы помогут вывить проблемы в функционировании модели. После этого соответствующие примеры можно добавить в обучающие данные (или увеличить их процентное соотношение). Обучая модель на недостающих типах данных, мы превращаем out-of-distribution данные в in-distribution данные и повышаем качество работы модели на этих данных. Это наиболее прямолинейное решение проблемы сдвига данных называется доменной адаптацией (см. на paperswithcode.com). Для дообучения можно использовать и неразмеченные данные (см. обзор на Хабре: часть 1, часть 2). Но такой способ не универсален. Мы можем не знать заранее всех свойств данных, с которыми будет работать модель, и не иметь возможности собрать обучающие данные.

Существует так называемая «проблема черного лебедя» (black swan), когда ошибка на очень редком типе примеров может привести к значительным последствиям: например, автоматически управляемый автомобиль попадет в ДТП из-за сбоя в работе его систем компьютерного зрения. Есть много примеров, когда электромобили Tesla неправильно распознавали происходящее вокруг, например, принимали луну за светофор. Насколько бы разнообразным ни был датасет, все равно может оставаться шанс, что мы что-то не учли и не добавили в него какой-то тип примеров.

Если задачей является обучение модели общего назначения для дальнейшего файн-тюнинга, например, предобучение языковой модели, сети для распознавания изображений, сети для распознавания речи или же мультимодальной сети, наподобие CLIP (Radford et al., 2021), то скрытых bias’ов в данных и возможностей для shortcut learning неисчислимое множество, и невозможно устранить их все.

В целом, система с низким out-of-distribution обобщением производит впечатление не слишком «интеллектуальной», а доменная адаптация часто напоминает подстановку «костылей» под модель, не способную хорошо обобщаться. Это напоминает ученика, который научился решать уравнения вида , но не может решить уравнения , потому что буква стала другой и незнакомой. Дообучив его решать уравнения с , мы выясняем, что теперь он не умеет решать уравнения с , и так далее, при этом логика его действий сильно зависит от того, какой буквой обозначена неизвестная переменная. Нужно ли искать новые архитектуры и способы обучения, способные лучше обобщаться и более устойчивые к сдвигу данных?

Еще больше данных?

От себя могу предположить, что, как ни странно, еще большее увеличение объема обучающих данных может помочь. С увеличением объема данных почти всегда растет разнообразие данных (умозрительно можно предположить, что если объем растет линейно, то разнообразие растет логарифмически). А ведь разнообразие данных — это именно то, что нужно? Возможно, с какого-то момента, когда loss уже нельзя будет еще сильнее понизить простым запоминанием поверхностной статистики (т. е. с помощью shortcut’ов), процесс оптимизации будет стагнировать и будет вынужден начать искать другие пути понижения loss, в том числе через систематическое обобщение.

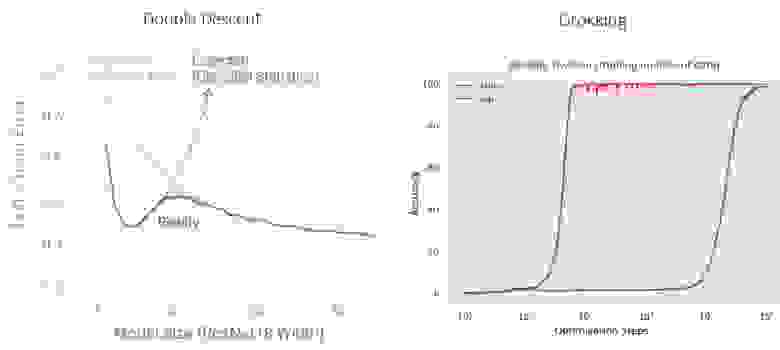
Конечно эта лишь гипотеза, и вероятно неверная. Но на мой взгляд важно иметь в виду, что зависимость качества обучения от размера модели и объема данных может быть необычной и непредсказуемой. Например, в Nakkiran et al., 2019 (double descent) была показана необычная зависимость точности на валидации от размера модели, а в Power et al., 2022 (grokking) от длительности обучения.

Более крупные или более эффективные модели?

Сейчас глубокое обучение в основном идет по пути экстенсивного развития, при котором улучшения достигаются увеличением объема обучающих данных и размера моделей («stack more layers»). Разработке принципиально иных архитектур и способов обучения уделяется мало внимания и финансирования, что и понятно: в таких исследованиях нет никакой гарантии успеха и получения работающего решения в обозримые сроки. Но как мы увидели выше, простое увеличение объема данных не всегда дает решение, обладающее желаемым уровнем обобщения. Об этом говорят авторы работы, посвященной графовым сетям (Battaglia et al., 2018):

The question of how to build artificial systems which exhibit combinatorial generalization has been at the heart of AI since its origins, and was central to many structured approaches, including logic, grammars, classic planning, graphical models, causal reasoning, Bayesian nonparametrics, and probabilistic programming (Chomsky, 1957; Nilsson and Fikes, 1970; Pearl, 1986, 2009; Russell and Norvig, 2009; Hjort et al., 2010; Goodman et al., 2012; Ghahramani, 2015). … A key reason why structured approaches were so vital to machine learning in previous eras was, in part, because data and computing resources were expensive, and the improved sample complexity afforded by structured approaches’ strong inductive biases was very valuable.

In contrast with past approaches in AI, modern deep learning methods (LeCun et al., 2015; Schmidhuber, 2015; Goodfellow et al., 2016) often follow an «end-to-end» design philosophy which emphasizes minimal a priori representational and computational assumptions, and seeks to avoid explicit structure and «hand-engineering». This emphasis has fit well with — and has perhaps been affirmed by — the current abundance of cheap data and cheap computing resources, which make trading off sample efficiency for more flexible learning a rational choice. …

Despite deep learning’s successes, however, important critiques (Marcus, 2001; Shalev-Shwartz et al., 2017; Lake et al., 2017; Lake and Baroni, 2018; Marcus, 2018a, 2018b; Pearl, 2018; Yuille and Liu, 2018) have highlighted key challenges it faces in complex language and scene understanding, reasoning about structured data, transferring learning beyond the training conditions, and learning from small amounts of experience. These challenges demand combinatorial generalization, and so it is perhaps not surprising that an approach which eschews compositionality and explicit structure struggles to meet them.

Авторы работы, посвященной системам компьютерного зрения (Yuille and Liu, 2018), также делают вывод о том, что больших данных может быть недостаточно, и нужно искать новые подходы к обучению и оценке качества моделей.

We argue that Deep Nets in their current form are unlikely to be able to overcome the fundamental problem of computer vision, namely how to deal with the combinatorial explosion, caused by the enormous complexity of natural images, and obtain the rich understanding of visual scenes that the human visual achieves. We argue that this combinatorial explosion takes us into a regime where «big data is not enough» and where we need to rethink our methods for benchmarking performance and evaluating vision algorithms. … We question whether Deep Nets will be sufficient to address these challenges and argue that methods that are compositional, generative, and combine signal and symbolic processing will be needed.

Рост результатов на различных бенчмарках, например SuperGLUE, тоже в основном обусловлен ростом размера моделей и количества обучающих данных. Но обучающие данные все же не бесконечны. Современные языковые модели и так обучаются почти на всех данных, какие удалось собрать со всего интернета.

В какой-то момент, скорее всего, потребуется прекратить рост размера моделей, объема датасетов и сосредоточиться на разработке совершенно иных подходов, стандартизировав наборы обучающих данных (как предлагает Linzen, 2020) для лучшего сравнения эффективности подходов.

Модификации способов обучения языковых моделей

Современные языковые модели предобучаются, например, на следующих задачах:

Предсказание токенов (т. е. слов или их частей), закрытых маской (masked language modeling, BERT, Devlin et al., 2018). Иногда используют модификацию этой задачи, в которой закрываются маской словосочетания, представляющие собой целостные сущности (knowledge masking, ERNIE, Sun et al., 2019).
Предсказания следующего токена в тексте (generative pre-training, GPT, Radford et al., 2018). При этом на архитектуру модели накладывается ограничение: -й входной токен не должен влиять на выходные токены с индексами меньше .
Предсказание отдельных токенов в тексте, полученном конкатенацией предложения из энциклопедии и информации из графа знаний (universal knowledge-text prediction, ERNIE 3.0, Sun et al., 2021). Кроме этой задачи, модель ERNIE 3.0 также обучается на задачах generative pre-training и knowledge masked language modeling.
Наборы sequence-to-sequence задач, генерируемых в self-supervised режиме, в том числе аналоги задачи masked language modeling (T5, Raffel et al., 2019, см. figure 2, table 3).

Чтобы лучше понять свойства этих задач, можно попробовать порешать их самостоятельно. Я сделал Colab-ноутбук для генерации случайных обучающих примеров в задаче masked language modeling (MLM). Из примеров можно видеть следующее:

Существенная часть замаскированных токенов определяется тривиально
Во многих случаях предсказать замаскированные токены исходя из контекста невозможно, а значит для решения задачи на большом корпусе текста нужно запоминать множество различных фактов: сюжеты литературных произведений, историю, политику и так далее, а также множество статистики совместной встречаемости слов в тексте (shortcuts). Даже выучив множество фактов и статистики, решить задачу MLM можно далеко не всегда.
Лишь изредка возможно предсказать замаскированный токен на основании контекста и логики, и чаще всего эта логика достаточно простая. Исчезающе редки примеры, где для предсказания нужна нетривиальная логика, которую нельзя имитировать запоминанием фактов и статистики.

Следовательно, приоритетом для снижения loss на задаче MLM является запоминание фактов и статистики. Способность рассуждать и делать выводы (отображая слова в некую модель мира и обратно, как это делает человек) для снижения loss является лишь второстепенным фактором, при этом выучить эту способность должно быть намного сложнее, чем запомнить факты.

Получается, что мы обучаем сеть на такой задаче, которую нельзя хорошо решить, обладая одной лишь логикой и пониманием смысла общеупотребимых слов, но можно неплохо решить с помощью запоминания огромного объема фактов и shortcut’ов. Обученная таким способом модель действительно может оказаться способной генерировать правдоподобные тексты, но лишь «вспоминая», что когда-то видела что-то похожее. Таким образом, модель долго и старательно обучается, но вовсе не тому, чего мы от нее хотим.

Отсюда можно сделать вывод о том, что обучение сетей, которые действительно понимают смысл текста в том смысле, в каком его понимает человек (вместо использования shortcut’ов для имитации понимания текста) будет затруднительным, если принципиально не менять задачу предобучения или архитектуру модели.

Архитектура моделей и структура данных

Модель эффективно обобщается, если ее структура соответствует структуре моделируемых данных. По этой причине на выборке, сгенерированной случайно инициализированной нейронной сетью, хорошо обобщается другая нейронная сеть (Gorishniy et al., 2021), на выборке, сгенерированной случайным решающим деревом, хорошо обобщаются другие деревья, сверточные сети хорошо обобщаются на текстурах и составленных из них изображениях (Ulyanov et al., 2017), а AlphaFold 2 за счет структурного модуля хорошо обобщается на трехмерных структурах белков (Jumper et al., 2021). Какова же структура текстов и изображений? Можно назвать два основных уровня:

Уровень 1. Низкоуровневая локальная структура. В изображениях это набор локальных признаков (текстуры и границы), в текстах это буквы и морфология слов. Также сюда можно отнести уровень звукового/визуального восприятия текста и интонацию.

Уровень 2. Высокоуровневая иерархическая разреженная структура. В текстах эта структура начинается с синтаксиса, следующим уровнем является связь между предложениями, абзацами и более крупными частями текста. В изображениях обычно тоже есть некая иерархическая структура, соответствующая объектам и их частям в трехмерном пространстве на разном расстоянии. При этом между элементами иерархической структуры имеется разреженный граф смысловых и причинно-следственных взаимосвязей. Например, рассуждая о человеке на фотографии, мы никак не будем учитывать цвет стоящего неподалеку автомобиля. Разреженность помогает не обращать внимание на паразитные корреляции и избегать shortcut learning’а.

Кроме того, когда человек воспринимает фотографию, иерархическая структура изображения отображается в модель мира, и человек сознательно или подсознательно выводы о том, логично ли изображенное на фотографии, в каком контексте и зачем оно сделано и каково развитие событий в момент съемки. С текстом все в целом аналогично.

Судя по всему, для исправления проблемы shortcut learning модель должна реализовывать именно такой способ обработки изображения или текста, то есть уметь представлять входные данные (изображение или текст) как иерархическую комбинацию составляющих частей с разреженными взаимосвязями, что соответствует уровню 2, и быть способной корректно интерпретировать те же части в необычных комбинациях. По сравнению с абстрактным свойством out-of-distribution обобщения, это более конкретное желаемое свойство называют систематическим, композиционным, или комбинаторным обобщением (Bahdanau et al., 2018; Furrer et al., 2020). Достижение такого уровня обобщения остается открытой проблемой машинного обучения.

If you think about child learning, for example, their world is changing over time, their body is changing over time, and so we need systems that are going to be able to handle those changes and do things like continual learning, life-long learning and so on. This has been a long-standing goal for machine learning, but I think we haven’t yet built the solutions to this. And one of the crucial elements in order to be successful in this … is introducing more forms of compositionality. It means being able to learn from some finite sets of combinations about a much larger set of combinations. (Yoshua Bengio, NeurIPS 2019)

Здесь часто вспоминают символьные подходы, с которых и начинались исследования ИИ в XX веке. По структуре такие системы, кажется, обладают всем необходимым: они могут работать с объектами и их частями, то есть с интерпретируемыми промежуточными данными, работать иерархически, реализовывать сложные цепочки рассужедний, а вычисления внутри них могут затрагивать лишь немногие объекты и взаимосвязи, что означает разреженность. Непонятно лишь одно: как их обучать, чтобы они могли быть сложными и достаточно гибкими одновременно.

Например, пусть некая подсистема решает, какую из операций из набора ${F_1, F_2, F_3}$ применить к данным . Для этого она выдает вероятности и выбирает операцию с наибольшей вероятностью. Допустим, на текущем примере мы выбрали операцию $A = text{argmax}_i P(F_i)$ , и в итоге получили значение функции потерь . Производные равны нулю, поэтому такую систему не получится обучить обычным градиентным спуском. Можно попробовать рассчитать ответ, используя по очереди все F_i , и снизить вероятности P(F_i) для тех F_i , на которых loss получился выше, чем на других. Но если граф принятия решений содержит не одну, а много операций принятия решения (), тогда придется перебирать очень много разных вариантов последовательностей решений. Аналогичная проблема возникает, если мы выбираем не операцию, а один или несколько элементов среди доступных данных (hard attention).

Направления исследований

В машинном обучении каждый день публикуется множество научных статей. Что-то модно, что-то вышло из моды, какие-то работы еще ждут признания, а какие-то так и остались незамеченными. Приведенный ниже список статей не претендует на полноту и описывает лишь некоторые из современных направлений исследований.

В перечисленных ниже работах изучаются проблемы современных систем компьютерного зрения. В некоторых из них также предлагаются различные модификации процесса обучения и способа оценки качества моделей, в том числе с помощью meta-learning.

Szegedy et al., 2013. Intriguing properties of neural networks.
Peng et al., 2017. Zero-Shot Deep Domain Adaptation.
Yuille and Liu, 2018 Deep Nets: What have they ever done for Vision?
Li et al., 2017. Learning to Generalize: Meta-Learning for Domain Generalization.
Beery et al., 2018. Recognition in Terra Incognita.
Baker et al., 2018. Deep convolutional networks do not classify based on global object shape.
Balaji et al., 2018. MetaReg: Towards Domain Generalization using Meta-Regularization.
Hendrycks et al., 2019. Natural Adversarial Examples.
Brendel and Bethge, 2019. Approximating CNNs with Bag-of-local-Features models works surprisingly well on ImageNet.
Lapuschkin et al., 2019. Unmasking Clever Hans Predictors and Assessing What Machines Really Learn.
Wang et al., 2019. High Frequency Component Helps Explain the Generalization of CNN.
Ilyas et al., 2019. Adversarial Examples Are Not Bugs, They Are Features.
Bucher et al., 2019. Zero-Shot Semantic Segmentation.
Taori et al., 2020. Measuring Robustness to Natural Distribution Shifts in Image Classification.
Djolonga et al., 2020. On Robustness and Transferability of Convolutional Neural Networks.
Mahajan et al., 2020. Domain Generalization using Causal Matching.
Zhou et al., 2020. Deep Domain-Adversarial Image Generation for Domain Generalisation.
Fabbrizzi et al., 2021. A Survey on Bias in Visual Datasets.
Shu et al., 2021. Open Domain Generalization with Domain-Augmented Meta-Learning.
Zhou et al., 2021. MixStyle Neural Networks for Domain Generalization and Adaptation.

Проблемы современных языковых моделей, проблемы данных, на которых они обучаются, и некоторые способы улучшения данных и способов обучения описаны в следующих работах:

Gururangan et al., 2018. Annotation Artifacts in Natural Language Inference Data.
Kaushik and Lipton, 2018. How Much Reading Does Reading Comprehension Require? A Critical Investigation of Popular Benchmarks.
Jawahar et al., 2019. What does BERT learn about the structure of language?
Goldberg, 2019. Assessing BERT’s Syntactic Abilities.
McCoy et al., 2019. Right for the Wrong Reasons: Diagnosing Syntactic Heuristics in NLI.
Zellers et al., 2019. HellaSwag: Can a Machine Really Finish Your Sentence?
Lin et al., 2019. Open Sesame: Getting Inside BERT’s Linguistic Knowledge.
Kovaleva et al., 2019. Revealing the Dark Secrets of BERT.
Kavumba et al., 2019. When Choosing Plausible Alternatives, Clever Hans can be Clever.
McCoy et al., 2019. BERTs of a feather do not generalize together: Large variability in generalization across models with similar test set performance.
Keysers et al., 2019. Measuring Compositional Generalization: A Comprehensive Method on Realistic Data.
Rogers, 2020. A Primer in BERTology: What we know about how BERT works.
Goodwin et al., 2020. Probing Linguistic Systematicity.
Ribeiro et al., 2020. Beyond Accuracy: Behavioral Testing of NLP models with CheckList.
Linzen, 2020. How Can We Accelerate Progress Towards Human-like Linguistic Generalization?
Bender and Koller, 2020. Climbing towards NLU: On Meaning, Form, and Understanding in the Age of Data.
Yu and Ettinger, 2020. Assessing Phrasal Representation and Composition in Transformers.
Liu et al., 2021. GPT Understands, Too.
Du et al., 2021. Towards Interpreting and Mitigating Shortcut Learning Behavior of NLU Models.
Shin et al., 2021. Constrained Language Models Yield Few-Shot Semantic Parsers.
Yanaka et al., 2021. SyGNS: A Systematic Generalization Testbed Based on Natural Language Semantics.
Sanh et al., 2021. Multitask Prompted Training Enables Zero-Shot Task Generalization.
Shavrina and Malykh, 2021. How not to Lie with a Benchmark: Rearranging NLP Leaderboards.
Veres, 2021. Language Models are not Models of Language.
Wei et al., 2021. Finetuned Language Models Are Zero-Shot Learners.
Ouyang et al., 2022. Training language models to follow instructions with human feedback.

В том числе, с помощью языковых моделей успешно решаются задачи генерации программного кода и решения математических задач, что само по себе интересно и может помочь лучше понять свойства такого типа моделей:

Cobbe et al., 2021. Training Verifiers to Solve Math Word Problems.
Polu et al., 2022. Formal Mathematics Statement Curriculum Learning.

Исследователи давно ищут возможность обучить модели систематическому обобщению, пониманию понятий части и целого и оперированию абстрактными концепциями. Некоторые из последних работ по этой теме:

Lake et al., 2015. Human-level concept learning through probabilistic program induction.
Bengio, 2017. The Consciousness Prior.
Sabour et al., 2017 Dynamic Routing Between Capsules.
Evans and Grefenstette, 2017. Learning Explanatory Rules from Noisy Data.
Bahdanau et al., 2018. Systematic Generalization: What Is Required and Can It Be Learned?
Battaglia et al., 2018. Relational inductive biases, deep learning, and graph networks.
Vlastelica et al., 2021. Neuro-algorithmic Policies enable Fast Combinatorial Generalization.
Hinton, 2021. How to represent part-whole hierarchies in a neural network.

Высокая способность к обобщению также требуется при обучении агентов, так как окружение может быть очень разнообразным и меняться от действий самих агентов, а значит важным является способность агентов корректно функционировать в новых условиях, не встречавшихся раньше.

Gupta et al., 2021. Embodied Intelligence via Learning and Evolution.
Hazra et al., 2021. Zero-Shot Generalization using Intrinsically Motivated Compositional Emergent Protocols.
Jang et al., 2021. BC-Z: Zero-Shot Task Generalization with Robotic Imitation Learning.

Мнение многих исследователей сходится в том, что для создания ML-систем следующего поколения, способных исправить важные недостатки текущих систем, нужно пробовать объединять нейронные сети и символьные вычисления:

Besold et al., 2017. Neural-Symbolic Learning and Reasoning: A Survey and Interpretation.
Mao et al., 2019. The Neuro-Symbolic Concept Learner: Interpreting Scenes, Words, and Sentences From Natural Supervision.
Vankov and Bowers, 2019. Training neural networks to encode symbols enables combinatorial generalization.
Latapie et al., 2021. Neurosymbolic Systems of Perception & Cognition: The Role of Attention.
Niepert et al., 2021. Implicit MLE: Backpropagating Through Discrete Exponential Family Distributions.

Одним из многообещающих подходов к повышению обобщающей способности моделей считается meta-learning («learning-to-learn»):

Hospedales et al., 2020. Meta-Learning in Neural Networks: A Survey.

Много работ посвящено попыткам улучшения трансформера (Vaswani et al., 2017), а также попыткам перенести его обобщающие свойства (inductive biases) на другие архитектуры или найти более простые альтернативы. Трансформер можно рассматривать как графовую нейронную сеть, в которой вершины хранят информацию, а ребра не хранят информации. Однако недавно были опубликованы работы, в которых предлагаются модификации трансформера с хранением информации в ребрах (подобный подход уже использовался, например, в AlphaFold 2). Также была обнаружена интересная взаимосвязь трансформера с сетями Хопфилда.

Kerg et al., 2019. Untangling tradeoffs between recurrence and self-attention in neural networks.
Gao et al., 2020. Systematic Generalization on gSCAN with Language Conditioned Embedding.
Ramsauer et al., 2020. Hopfield Networks is All You Need.
Tay et al., 2020. Efficient Transformers: A Survey.
Dosovitskiy et al., 2020. An Image is Worth 16×16 Words: Transformers for Image Recognition at Scale.
Bello, 2021. LambdaNetworks: Modeling Long-Range Interactions Without Attention.
Lu et al., 2021. Pretrained Transformers as Universal Computation Engines.
Jaegle et al., 2021. Perceiver: General Perception with Iterative Attention.
Pan et al., 2021. On the Integration of Self-Attention and Convolution.
Liu et al., 2021. Pay Attention to MLPs.
Lee-Thorp et al., 2021. FNet: Mixing Tokens with Fourier Transforms.
Peng et al., 2021. Random Feature Attention.
Nguyen et al., 2021. FMMformer: Efficient and Flexible Transformer via Decomposed Near-field and Far-field Attention.
Xu et al., 2021. CDTrans: Cross-domain Transformer for Unsupervised Domain Adaptation.
Nawrot et al., 2021. Hierarchical Transformers Are More Efficient Language Models.
Bergen et al., 2021. Systematic Generalization with Edge Transformers.
Hussain et al., 2021. Edge-augmented Graph Transformers: Global Self-attention is Enough for Graphs.
Wang et al., 2022. When Shift Operation Meets Vision Transformer: An Extremely Simple Alternative to Attention Mechanism.

Если модель встречается с необычным примером и не может выдать на нем корректный ответ, то можно по крайней мере научить модель сомневаться, то есть оценивать уверенность в предсказании. Это может помочь не только в случае сдвига данных, но и на тех примерах, на которых точечная оценка условного распределения P(Y|X) даст высокую ожидаемую ошибку (то есть ответ нельзя с уверенностью предсказать из исходных данных). В этом контексте часто упоминают байесовские методы, ансамблирование и генеративные модели. Некоторые из работ по теме байесовских методов и оценки уверенности в предсказаниях:

Wang and Vasconcelos, 2018. Towards Realistic Predictors.
Maddox et al., 2019. A Simple Baseline for Bayesian Uncertainty in Deep Learning.
Nalisnick et al., 2019. Detecting Out-of-Distribution Inputs to Deep Generative Models Using Typicality.
Ren et al., 2019. Likelihood Ratios for Out-of-Distribution Detection.
Jospin et al., 2020. Hands-on Bayesian Neural Networks — a Tutorial for Deep Learning Users.
Lakshminarayanan, 2020. Uncertainty & Out-of-Distribution Robustness in Deep Learning.
Yang et al., 2021. Generalized Out-of-Distribution Detection: A Survey.
Henning et al., 2021. Are Bayesian neural networks intrinsically good at out-of-distribution detection?
Huyen, 2022. Data Distribution Shifts and Monitoring.

Еще несколько общих статей о проблемах современного машинного обучения, паразитных корреляциях в данных и подходах к повышению обобщающей способности (некоторые из них подробно разбирались в этом обзоре):

Tommasi et al., 2015. A Deeper Look at Dataset Bias.
Ross et al., 2017. Right for the Right Reasons: Training Differentiable Models by Constraining their Explanations.
Shalev-Shwartz et al., 2017. Failures of Gradient-Based Deep Learning.
Marcus, 2018. Deep Learning: A Critical Appraisal.
Mehrabi et al., 2019. A Survey on Bias and Fairness in Machine Learning.
Geirhos et al., 2020. Shortcut Learning in Deep Neural Networks.
D’Amour et al., 2020. Underspecification Presents Challenges for Credibility in Modern Machine Learning.
Xu et al., 2020. How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks.
Pezeshki et al., 2021. Gradient Starvation: A Learning Proclivity in Neural Networks.
Balestriero et al., 2021. Learning in High Dimension Always Amounts to Extrapolation.
Shen et al., 2021. Towards Out-Of-Distribution Generalization: A Survey.

Многие исследователи считают, что важно не только обучить модели выявлять статистические зависимости, но и находить в данных причинно-следственные связи. Имея лишь выборку из распределения данных, это не всегда можно сделать. Например, пусть мы имеем набор фотографий с неизвестной планеты, и на некоторых фотографиях есть огонь и есть неопознанные существа, при этом появление существ и огня на фотографиях сильно коррелирует. Что является причиной, а что следствием? Разводят ли существа огонь сами, приходят ли к уже появившемуся огню, или же оба явления имеют общую причину (прилетает звездолет, высаживает существ и оставляет на земле огонь после взлета)? Это практически невозможно определить из фотографий (или же очень сложно, по косвенным признакам). Поиска причинно-следственных связей является более сложной задачей, чем поиск статистических зависимостей. Следующие книги и статьи посвящены именно этой теме:

Pearl, 2009. Causality: Models, Reasoning and Inference, 2nd edition.
Guo et al., 2018. A Survey of Learning Causality with Data: Problems and Methods
Pearl, 2018. Theoretical Impediments to Machine Learning With Seven Sparks from the Causal Revolution.
Pearl, 2018. The Seven Tools of Causal Inference with Reflections on Machine Learning.
Schölkopf, 2019. Causality for Machine Learning.
Arjovsky et al., 2019. Invariant Risk Minimization.
Träuble et al., 2020. On Disentangled Representations Learned From Correlated Data

Отдельно можно отметить работу группы Йошуа Бенжио в институте MILA (Канада):

Bengio et al., 2019. A Meta-Transfer Objective for Learning to Disentangle Causal Mechanisms.
Goyal et al., 2019. Recurrent Independent Mechanisms.
Ke et al., 2019. Learning Neural Causal Models from Unknown Interventions.
Ahmed et al., 2020. Systematic generalisation with group invariant predictions.
Goyal and Bengio, 2020. Inductive Biases for Deep Learning of Higher-Level Cognition.
Krueger et al., 2020. Out-of-Distribution Generalization via Risk Extrapolation (REx).
Goyal et al., 2021. Neural Production Systems.
Schölkopf et al., 2021. Towards Causal Representation Learning.
Xia et al., 2021. The Causal-Neural Connection: Expressiveness, Learnability, and Inference.
Zhao et al., 2021. A Consciousness-Inspired Planning Agent for Model-Based Reinforcement Learning.
Ahuja et al., 2021. Invariance Principle Meets Information Bottleneck for OOD Generalization.
Liu et al., 2021. Discrete-Valued Neural Communication.
Rahaman et al., 2021. Dynamic Inference with Neural Interpreters.

Различные модальности (изображения, текст и др.) могут дополнять друг друга и формировать более целостную картину мира, чем каждая модальность по отдельности, поэтому мультимодальное обучение кажется многообещающим. В последние пару лет в этой области были достигнуты впечатляющие результаты.

Su et al., 2019. VL-BERT: Pre-training of Generic Visual-Linguistic Representations.
Ramesh et al., 2021. Zero-Shot Text-to-Image Generation.
Radford et al., 2021. Learning Transferable Visual Models From Natural Language Supervision.
Goh et al., 2021. Multimodal Neurons in Artificial Neural Networks.
Singh et al., 2021. Illiterate DALL-E Learns to Compose.
Lin et al., 2021. M6: A Chinese Multimodal Pretrainer.
Wang et al., 2022. Unifying Architectures, Tasks, and Modalities Through a Simple Sequence-to-Sequence Learning Framework.

Одним из возможных путей к созданию ML-систем следующего поколения может стать обучение систем, способных анализировать видео и предсказывать следующие события (далее чем несколько кадров), в том числе в текстовом виде. Такие системы могут быть способы отличать статистические зависимости от причинно-следственных связей, а также соотносить текст с происходящими событиями. Похожая задача возникает при обучении агентов, которым необходимо предсказывать последствия своих и чужих действий. Агента может заменить на наблюдателя, задача которого — лишь предсказывать последствия чужих действий. Можно искать и другие способы создания самообучающейся модели мира, какая существует, например, в сознании человека.

Ha and Schmidhuber, 2018. World Models.
Lotter et al., 2018. A neural network trained to predict future video frames mimics critical properties of biological neuronal responses and perception.
Zhang and Tao, 2019. Slow Feature Analysis for Human Action Recognition.
Xu et al., 2020. Video Prediction via Example Guidance.
Apostolidis et al., 2021. Video Summarization Using Deep Neural Networks: A Survey.
Lee et al., 2021. Revisiting Hierarchical Approach for Persistent Long-Term Video Prediction.
Wu et al., 2021. Generative Video Transformer: Can Objects be the Words?

Общий искусственный интеллект

Исследователей всегда интересовала тема общего искусственного интеллекта и создания систем, которые мыслят как люди. Проблема здесь начинается с того, что разные люди по-разному определяют, что же конкретно это означает. Как мне кажется, здесь может помочь введение более узких терминов с более конкретными определениями, вместо расплывчатых и спорных понятий «общего ИИ» и «сильного ИИ». Если разные люди хотят предложить разные определения, то пусть придумают для них разные термины.

Например, можно предложить такое определение: полнофункциональный искусственный интеллект — это система, способная решать все задачи, которые может решать человек. Если больше не останется таких типов задач, которые может решить практически любой человек, но не может решить ИИ (качество решения оценивается голосованием людей), то тогда можно будет считать, что создан полнофункциональный ИИ, согласно его определению. Конечно, не обязательно требовать от ИИ выполнения механических движений или, скажем, мимики лица. Поэтому можно предложить более узкое понятие: полнофункциональный текстовый искусственный интеллект — это система, способная решать все задачи, которые может решать человек в текстовом виде, будь он по ту сторону монитора и имея достаточно времени. Конечно, и такое определение может породить споры, но все же оно несколько более конкретно.

Я никоим образом не являюсь специалистом по вопросу общего ИИ, но как автор обзора выскажу мнение по поводу его достижения. Меня привлекает идея постепенного улучшения, когда на каждом шаге ищутся недостатки систем текущего поколения и находятся способы их преодоления для создания систем следующего поколения. Можно провести аналогию с градиентным спуском или методом отжига: мы постепенно улучшаем решение, не пытаясь все выбросить и начать с нуля, и периодически пробуем внедрить какие-то принципиальные изменения. Тогда на текущем этапе развития машинного обучения нужно сосредоточиться на решении проблем обобщения, которым и был посвящен этот обзор.

Приведу также несколько работ, в которых рассматривается вопрос общего искусственного интеллекта и сопоставления биологического интеллекта с текущими ML-системами.

Marcus, 2001. The Algebraic Mind: Integrating Connectionism and Cognitive Science.
Marcus, 2004. The Birth of the Mind: How a Tiny Number of Genes Creates The Complexities of Human Thought.
Griffiths et al., 2010. Probabilistic models of cognition: exploring representations and inductive biases.
Goertzel, 2014. Artificial General Intelligence: Concept, State of the Art, and Future Prospects.
Lake et al., 2016. Building machines that learn and think like people.
Hassabis, 2017. Neuroscience-Inspired Artificial Intelligence.
Goertzel, 2018. From Here to Human-Level AGI in 4 Simple Steps.
Chollet, 2019. On the Measure of Intelligence.
Wang, 2019. On Defining Artificial Intelligence.
Wang et al., 2020. On Defining Artificial Intelligence – Commentaries and Author’s Response.
Marcus, 2020. The Next Decade in AI: Four Steps Towards Robust Artificial Intelligence.
Fjelland, 2020. Why general artificial intelligence will not be realized.
Chollet, 2020. A Definition of Intelligence for the Real World?
Stoop, 2021. Note on the Reliability of Biological vs. Artificial Neural Networks.
Goertzel, 2021. The General Theory of General Intelligence: A Pragmatic Patternist Perspective.

Интересны работы с участием нейробиолога Карла Фристона, который исследует принципы работы человеческого мозга и их возможную связь с вариационными байесовскими методами в математической статистике:

Friston, 2010. The free-energy principle: a unified brain theory?
Isomura et al., 2022. Canonical neural networks perform active inference.
Friston et al., 2022. The free energy principle made simpler but not too simple.
Parr et al., 2022. Active Inference: The Free Energy Principle in Mind, Brain, and Behavior.

Заключение

Как мне кажется, проблемы содержатся не только в алгоритмах, но и в человеческом сознании. Людям неинтересно изучать и исследовать. Чтение статей, изучение информации воспринимается лишь как скучная необходимость, сложные вопросы и исследовательские задачи не занимают людей, а интересует в основном лишь заработок.

Еще одна сложность в том что количество научных статей и книг в области исследовательского ML стремительно растет. На конференции NeurIPS 2021 было опубликовано более 2300 статей (больше, чем за 2010-2015 годы вместе взятые): одни только аннотации заняли бы целый том. Возникает острая потребность в систематизации информации. Читать статьи в оригинале долго и тяжело по нескольким причинам.

Каждая статья содержит обзор других работ, и если вы читаете, скажем, 20 статей по одной и той же области, то эти обзоры во многом дублируют друг друга и отбивают интерес к чтению.
Материал статьи может быть изложен не лучшим образом, непонятно или с повторениями. Сейчас не принято, как раньше, публиковать короткие статьи, хотя содержание многих статей можно было бы изложить на одной странице.
Раздел про гиперпараметры, датасеты и детали эксперимента может быть важен тем, кто будет имплементировать это на практике через месяц после выхода статьи, но через 5 лет станет не особенно интересен, хотя предложенный в статье метод может сохранить свою актуальность. Если же совсем не читать экспериментальный раздел, то можно упустить что-то важное.
При чтении статьи восприятие происходит однобоко. Непонятно, был ли предложенный в статье метод признан эффективным на практике, получил ли широкое распространение, или же вскоре был предложен более эффективный подход? Актуален ли метод по сей день, или если нет то почему? Часто не хватает взгляда со стороны от компетентного специалиста, желательно от нескольких.

Исходя из всего этого, систематизация и изложение статей в сокращенном варианте, как мне кажется, могло бы принести огромную пользу для сообщества. Конечно, многими прилагаются усилия в этом направлении, но этого пока недостаточно. Краткие изложения статей остаются бесплатной работой для энтузиастов, тогда как пользу они приносят вполне реальную.

На мой взгляд, будь эта практика более широко распространена, и будь у людей больше интереса к исследованиям, мы могли бы уже создавать такие системы искусственного интеллекта, которую бы приносили огромную пользу человечеству (в медицине, физике, интернет-технологиях, оптимизации работы людей и, стало быть, сокращении рабочей недели) и которые пока что остаются лишь в области фантастики.

Данный обзор первоначально размещен на сайте generalized.ru, где вы можете найти и другие обзоры.

Источник

Искусственный интеллект: популярное введение для учителей и школьников

Проектирование персептронов

Теорема существования

Итак, мы убедились в том, что:

1. Подавляющее большинство всех
прикладных задач, решаемых методом
математического моделирования, сводится к
нахождению некоторой сложной функции,
осуществляющей многомерное преобразование
вектора входных параметров X в вектор
выходных параметров Y.

2. Универсальным инструментом
построения такой функции являются нейросетевые
технологии.

Естественно, возникает вопрос: всегда
ли можно построить нейросеть, выполняющую
преобразование, заданное любым множеством
обучающих примеров, и каким требованиям эта
нейросеть должна удовлетворять?

Чтобы ответить на эти вопросы, надо
вспомнить, что каждый нейрон нейронной сети
выполняет суммирование сигналов, поступающих от
других нейронов, которые в тех, других нейронах
прошли через нелинейное (например, сигмоидное)
преобразование. Другими словами, персептрон
аппроксимирует зависимости предметной области,
которые в общем случае являются функциями многих
аргументов, причем эту аппроксимацию персептрон
выполняет с помощью суммы функций, каждая из
которых является функцией только
одного-единственного аргумента.

Вопрос о том, всегда ли можно любую
функцию многих переменных представить в виде
суммы функций меньшего количества переменных,
интересовал математиков на протяжении
нескольких веков. Так, в 1900 г. на Всемирном
математическом конгрессе в Париже знаменитым
немецким математиком Давидом Гильбертом были
сформулированы 23 проблемы, которые он предложил
решать математикам начинающегося XX в. Одна из
этих проблем, под номером тринадцать,
декларировала невозможность такого
представления. Таким образом, получалось, что
персептрон, сколько бы он нейронов не имел, не
всегда мог построить аппроксимацию любой
функции нескольких переменных.

Сомнения относительно возможностей
персептронов развеяли советские математики —
академик А.Н. Колмогоров (1903–1987) и академик В.И.
Арнольд (род. в 1937). Им удалось доказать, что любая
непрерывная функция n переменных f(x₁,
x₂, … x_n) всегда может быть
представлена в виде суммы непрерывных функций
одного переменного f₁(x₁) + f₂(x₁)
+ … + f_n(x_n), гипотеза Гильберта
была опровергнута, и нейроинформатике, таким
образом, был открыт “зеленый свет”.

В 1987–1991 гг. профессором
Калифорнийского университета (США) Р.Хехт-Нильсеном
теоремы Арнольда – Колмогорова были
переработаны применительно к нейронным сетям.
Было доказано, что для любого множества
непротиворечивых между собой пар произвольной
размерности (X_q, D_q),
q = 1, …, Q, существует двухслойный персептрон
с сигмоидными активационными функциями и с
конечным числом нейронов, который для каждого
входного вектора X_q формирует
соответствующий ему выходной вектор D_q.

Таким образом, была доказана
принципиальная возможность построения
нейронной сети, выполняющей преобразование,
заданное любым множеством различающихся между
собой обучающих примеров, и установлено, что
такой универсальной нейронной сетью является
двухслойный персептрон, т.е. персептрон с одним
скрытым слоем, причем активационные функции его
нейронов должны быть сигмоидными.

Необходимое количество нейронов в
скрытых слоях персептрона можно определить по
формуле, являющейся следствием из теорем
Арнольда – Колмогорова – Хехт-Нильсена:

,

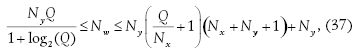
(37)

— где N_y — размерность
выходного сигнала;

Q — число элементов множества
обучающих примеров;

N_w — необходимое число
синаптических связей;

N_x — размерность входного
сигнала.

Оценив с помощью этой формулы
необходимое число синаптических связей N_w,
можно рассчитать необходимое число нейронов в
скрытых слоях. Например, число нейронов скрытого
слоя двухслойного персептрона будет равно

(38)

Последняя формула становится
очевидной, если ее левую и правую части умножить
на и нарисовать схему двухслойного (т.е. с одним
скрытым слоем) персептрона.

Рекомендации по проведению урока

До сих пор материал элективного
курса “Искусственный интеллект” в большей
части носил позитивный рекламный характер. Много
говорилось о преимуществах и широких
возможностях метода нейросетевого
моделирования, и почти ничего — о его
недостатках. Не говорилось о трудностях и
проблемах, связанных с применением нового
метода. Но освоить метод можно только
познакомившись со всеми его проблемами, изучив
способы их преодоления, изучив и поняв
теоретическую базу.

С одной из таких трудностей,
называемой “Проблемой исключающего ИЛИ”,
школьники уже столкнулись на 1-й лабораторной
работе.

Задайте школьникам два вопроса для
размышлений:

1. Всегда ли можно подобрать и обучить
персептрон, обеспечивающий решение любой задачи?

2. Каким образом лучше задавать
количество внутренних нейронных слоев и
количество нейронов в них? Может быть, как в мозге
— 10¹¹ нейронов? Может быть, чем больше, тем
лучше?

Ответы на эти вопросы выясняются в
результате освоения теоретического материала
этого урока.

Важнейшее место в теории нейронных
сетей занимает теорема Арнольда – Колмогорова –
Хехт-Нильсена, доказательство которой
достаточно сложно и здесь не приводится. Тем не
менее весьма интересной и поучительной
представляется история этой теоремы.

Как мы уже не раз отмечали, с
физической точки зрения персептрон
(нейрокомпьютер) — это устройство, моделирующее
человеческий мозг на структурном уровне. Однако
с математической точки зрения персептрон — это
всего лишь аппроксиматор, заменяющий функцию
многих аргументов суммой функций, каждая из
которых зависит только от одного аргумента.
Вопрос о том, всегда ли можно любую функцию
многих переменных представить в виде суммы
функций меньшего количества переменных,
интересовал математиков на протяжении
нескольких последних веков.

Так, в 1900 г. на Всемирном
математическом конгрессе в Париже знаменитым
немецким математиком Давидом Гильбертом были
сформулированы 23 проблемы, которые он предложил
решать математикам начинающегося XX в. Одна из
этих проблем, под номером 13, декларировала
невозможность такого представления. Таким
образом, приговор новой области искусственного
интеллекта был вынесен за полвека до ее
появления.

Многие проблемы Гильберта были решены.
Его утверждения-гипотезы подтверждались одна за
другой. Но с тринадцатой возникли проблемы.
Сенсационной была работа известного советского
математика академика А.Н. Колмогорова,
опубликованная в 1956 г. В ней он доказал, что
всякая непрерывная функция n переменных
представима в виде суперпозиции непрерывных
функций трех переменных. В следующем, 1957 году его
ученик В.И. Арнольд, будучи студентом третьего
курса МГУ, доказал, что всякая непрерывная
функция трех переменных представима в виде
суперпозиций непрерывных функций двух
переменных.

Таким образом, по мнению многих
авторитетных математиков, 13-я проблема Гильберта
была решена. Она была решена студентом 3-го курса
МГУ, причем решена с точностью до наоборот.

В 1987 и 1991 гг. профессором
Калифорнийского университета (США)
Р.Хехт-Нильсеном были опубликованы еще две
статьи, в которых теоремы Арнольда –
Колмогорова были переработаны применительно к
нейронным сетям. В результате была доказана
принципиальная возможность построения
нейронной сети, выполняющей преобразование,
заданное любым обучающим множеством
различающихся между собой примеров. И
установлено, что такой универсальной нейросетью
является двухслойный персептрон, т.е. персептрон
с одним скрытым слоем с сигмоидными
активационными функциями.

Теорема Арнольда – Колмогорова –
Хехт-Нильсена имеет очень важное для практики
следствие в виде формулы (37), с помощью которой
можно определять необходимое количество
синаптических весов нейронной сети. Оценив с
помощью этой формулы необходимое число
синаптических весов, можно рассчитать
необходимое число нейронов в скрытых слоях. Для
этого служит формула (38), но прежде чем выписывать
ее на доске, озадачьте школьников — нарисуйте
персептрон с одним скрытым слоем и предложите
школьникам самим придумать формулу для
вычисления числа скрытых нейронов N, если
известны N_x, N_y и N_w.
Тех, кто справится и напишет формулу (38), не
забудьте поощрить хорошей оценкой.

А теперь зададимся вопросом. Что было
бы, если бы гипотеза 13-й проблемы Гильберта
оказалась верной?

Тогда бы у нейроинформатики не было
теоретического фундамента. Ее прикладные
возможности были бы серьезно ограничены, если не
сказать сильнее — правомерность ее
существования, как области науки, была бы под
вопросом. Кому нужен нейрокомпьютер, который в
принципе не может решать ряд задач, для решения
которых он предназначен! Не было бы у
нейроинформатики ее многочисленных
практических приложений.

Но они есть. В настоящее время
нейроинформатику можно заносить в Книгу
рекордов Гиннесса — она побила все рекорды по
количеству приложений в самых разнообразных
областях. Жизнь блестяще подтвердила теоремы и
доказательства, выполненные в 1956–57 гг. Андреем
Николаевичем Колмогоровым и его учеником
Владимиром Игоревичем Арнольдом.

Здесь можно дать школьникам домашнее
задание: подготовить материал и сделать
сообщение о жизни и заслугах этих двух
замечательных ученых. Информацию о них школьники
могут самостоятельно получить из сети Интернет.

Проблемы и методы проектирования

Как следует из теорем Арнольда –
Колмогорова – Хехт-Нильсена, для построения
нейросетевой модели любого сколь угодно
сложного объекта достаточно использовать
персептрон с одним скрытым слоем сигмоидных
нейронов, число которых определяется формулами
(37), (38). Однако в практических реализациях
персептронов как количество слоев, так и число
нейронов в каждом из них часто отличаются от
теоретических. Иногда целесообразно
использовать персептроны с большим количеством
скрытых слоев. Такие персептроны могут иметь
меньшие размерности матриц синаптических весов,
чем двухслойные персептроны, реализующие то же
самое преобразование.

Строгой теории выбора оптимального
количества скрытых слоев и нейронов в скрытых
слоях пока не существует. На практике чаще всего
используются персептроны, имеющие один или два
скрытых слоя, причем количество нейронов в
скрытых слоях обычно колеблется от до N_x
/ 2 до 3N_x.

При проектировании персептронов
необходимо понимать, что персептрон должен не
только правильно реагировать на примеры, на
которых он обучен, но и уметь обобщать
приобретенные знания, т.е. правильно реагировать
на примеры, которых в обучающем множестве
примеров не было. Чтобы оценить способность сети
к обобщению, помимо обучающего множества
примеров L (см. рис. 18), в рассмотрение
вводят некоторое количество тестовых примеров,
образующих тестирующее множество T.
Примеры тестирующего множества относятся к той
же самой предметной области, но в процессе
обучения не участвуют. После обучения вычисляют
среднеквадратичную (или максимальную) ошибку
между прогнозом сети Y и желаемым выходом
сети D. Причем ошибку, вычисленную на
обучающем множестве L, называют ошибкой
обучения и обозначают e_L, а
вычисленную на тестирующем множестве T — ошибкой
обобщения или тестирования и обозначают e_T.

Рис. 18. Деление примеров предметной
области на обучающее множество L,
тестирующее множество T и подтверждающее
множество P

Обратим внимание, что ошибка
обучения вычисляется на тех примерах предметной
области, на которых сеть обучалась. Ошибка же
обобщения вычисляется на примерах той же
предметной области, но которые сеть никогда “не
видела”. Поэтому ошибки e_T и e_L имеют разную природу и,
соответственно, разный характер поведения. При
увеличении числа нейронов скрытых слоев
персептрона N ошибка обучения e_L
обычно падает, тогда как ошибка обобщения e_T сначала падает, а затем,
начиная с некоторого оптимального значения N
= N₀, возрастает. Характерные кривые
зависимости ошибок обучения и обобщения от числа
нейронов скрытых слоев персептрона приведены на рис.
19.

Рис. 19. Характерные зависимости
ошибки обучения e_Lи
ошибки обобщения (тестирования) e_T
от количества нейронов скрытых слоев
персептрона N

В газетной статье мы не будем
объяснять причины такого поведения, а только
укажем, что свойство нейронных сетей терять
способности к обобщению при чрезмерном
увеличении числа нейронов скрытых слоев в
научной литературе называется переобучением,
или гиперразмерностью. Студенты этот эффект
называют “горем от ума”.

С эффектом гиперразмерности нам еще
придется бороться. А пока, вооружившись
приобретенными теоретическими знаниями,
приведем некоторые практические рекомендации по
проектированию персептронов, т.е. по выбору числа
входов, числа выходов, количества скрытых слоев,
количества нейронов в скрытых слоях, виду
активационных функций.

1. Число входов персептрона должно
совпадать с размерностью вектора входных
параметров X, который определен условиями
решаемой задачи.

2. Число нейронов выходного слоя должно
совпадать с размерностью выходного вектора D,
что также определено условиями задачи.

3. Число скрытых слоев персептрона
согласно теоремам Арнольда – Колмогорова –
Хехт-Нильсена должно быть не менее одного, причем
нейроны в скрытых слоях должны иметь сигмоидную
активационную функцию.

4. Число нейронов в скрытых слоях может
быть приближенно оценено по формулам (37), (38),
однако его желательно оптимизировать для каждой
конкретной задачи либо путем экспериментального
построения кривых (рис. 19). При построении
кривых рис. 19 используются примеры
тестирующего множества T.

В наиболее ответственных случаях
наряду с обучающим множеством L и
тестирующим множеством T в рассмотрение
вводят еще одно множество примеров, называемое
подтверждающим, и обозначают его буквой P (см.
рис. 18). Примеры этого множества также
относятся к рассматриваемой предметной области,
однако ни в обучении, ни в тестировании сети они
не участвуют. Поэтому ошибка прогнозирования ,
вычисленная на примерах подтверждающего
множества P, является наиболее
объективной оценкой качества нейросетевой
математической модели.

Вопросы с ответами

1. К какому нежелательному
последствию может привести чрезмерное
уменьшение количества нейронов в скрытых слоях
персептрона?

Ответ: Как видно из рис. 19,
это может привести к тому, что персептрон не
удастся достаточно хорошо обучить, т.е. не
удастся снизить ошибку обучения до приемлемо
малой величины.

2. К какому нежелательному последствию
может привести чрезмерное увеличение нейронов в
скрытых слоях персептрона?

Ответ: Это может привести к явлению
гиперразмерности (или переобучения), т.е. к тому,
что хорошо обучившийся персептрон не будет
проявлять обобщающих свойств, т.е. ошибка
обобщения окажется чрезмерно большой.

Лабораторная
работа № 8: “Моделирование таблицы
умножения”¹

В этой и во всех последующих
лабораторных работах используется программа
“Нейросимулятор”, позволяющая создавать и
применять нейронные сети персептронного типа.
Освоение этой программы мы начнем на примере
моделирования таблицы умножения.

Запустите лабораторную работу № 8. На
экране компьютера появится рабочее окно
программы “Нейросимулятор” (см. рис. 20).

Программа “Нейросимулятор” может
работать в четырех режимах: “Проектирование
сети”, “Обучение”, “Проверка” и “Прогноз”.
Переход из одного режима в другой осуществляется
путем нажатия соответствующих закладок,
расположенных в верхней части рабочего окна.

Вы сейчас находитесь в режиме
“Проектирование сети”. Задайте школьникам
вопрос: Что понимается под проектированием сети?

Ответ: Проектирование персептрона
включает определение числа входов, числа
выходов, числа скрытых слоев, числа нейронов в
скрытых слоях (число скрытых нейронов), а также
задание активационных функций нейронов.

Задайте следующий вопрос: Сколько
входов и сколько выходов должен иметь
персептрон, моделирующий таблицу умножения?

Ответ: Он должен иметь два входа: —
для первого множителя, — для второго множителя, и
один выход: — для результата умножения.

Вопрос: Сколько скрытых слоев и
сколько нейронов в скрытых слоях должен иметь
персептрон? Какие там должны быть активационные
функции?

Ответ: Согласно теореме Арнольда –
Колмогорова – Хехт-Нильсена, персептрон должен
иметь хотя бы один скрытый слой нейронов с
сигмоидными активационными функциями. Их
количество предварительно может быть оценено с
помощью формул (37)–(38), однако потом его
желательно уточнить с целью минимизации ошибки
обобщения.

На открытом рабочем окне программы
“Нейросимулятор” (рис. 20) изображен
персептрон, имеющий два входа и один выход — как
раз то, что нам нужно для моделирования таблицы
умножения. Кроме того, персептрон имеет один
скрытый слой, состоящий из трех нейронов с
сигмоидными активационными функциями.

Находясь в режиме “Проектирование
сети”, школьникам следует научиться изменять
количество входных и выходных нейронов,
количество скрытых слоев, количество нейронов в
скрытых слоях, виды и параметры активационных
функций. Сделать это несложно, поскольку всякое
изменение структуры сети тут же отражается на ее
графическом представлении.

Попросите школьников поменять
структуру персептрона — добавить один или два
нейрона в скрытый слой. Сообщите им, что
уточнением числа скрытых слоев и количества
нейронов в них, а также выбором типа
активационных функций они будут заниматься
позже, а пока пусть сохранят свой проект
(выбранную структуру и параметры персептрона)
путем нажатия кнопки “Сохранить проект”. В
качестве имени файла, в котором будет сохранен
проект, рекомендуйте использовать уникальное
имя, например — номер класса (группы), в котором
они учатся, и фамилию школьника.

Еще раз убедившись, что ваш персептрон
имеет два входа и один выход, переведите
программу в режим “Обучение”, нажав
соответствующую закладку в верхней части
рабочего окна. Теперь ваша цель состоит в том,
чтобы создать множество обучающих примеров. В
нашем случае это таблица умножения, которой
школьники должны обучить персептрон. Нажимая
несколько раз кнопку “Добавить обучающий
пример” (на кнопке изображен знак “+”), введите
цифры, как показано на рис. 21. Это и есть
множество обучающих примеров, в данном
случае — таблица умножения на 2 и на 3.

Обратите внимание, что в вашей таблице
умножения не хватает одного примера: 2 х 5 = 10. Этот
пример “забыт” специально. После того как
нейросеть будет обучена, мы спросим ее, сколько
будет 2 х 5, и проверим ее способность к обобщению.

Проследите, чтобы школьники ввели
таблицу умножения на 2 и на 3 (“забыв” ввести 2 х 5 =
10), как показано на рис. 21, и, прежде чем
приступать к обучению персептрона, задайте
следующие вопросы:

1. Какие процессы происходят в
нейронной сети во время ее обучения?

Ответ: Во время обучения сети
происходит корректировка сил синаптических
связей между нейронами.

2. В чем состоит цель обучения
нейронной сети?

Ответ: Цель обучения нейронной
сети — подобрать силы синаптических связей
такими, чтобы сеть могла правильно реагировать
на примеры обучающего множества. Например, чтобы
при вводе вопроса, сколько будет дважды два, сеть
отвечала — четыре.

3. Как задаются силы синаптических
связей до того, как сеть начали обучать?

Ответ: Датчиком случайных чисел.

4. Назовите известные вам способы
обучения персептронов.

Ответ: Правила Хебба,
дельта-правило, обобщенное дельта-правило,
алгоритм обратного распространения ошибки.

5. Каким из этих способов можно обучать
созданный нами персептрон?

Ответ: Методом обратного
распространения ошибки.

6. Почему именно им?

Ответ: Потому что персептрон имеет
скрытый слой нейронов.

Рис. 21. Введено обучающее множество
примеров — таблица умножения
на 2 и на 3

7. Какие параметры требуется задать для
работы алгоритма обратного распространения
ошибки?

Ответ: Коэффициент скорости
обучения, количество эпох обучения.

Теперь обратите внимание школьников
на то, что “по умолчанию” в программе
“Нейросимулятор” (см. рис. 21) выбран алгоритм
обратного распространения ошибки, что
коэффициент скорости обучения установлен 0,08, а
количество эпох обучения — 300, что начальные
значения синаптических весов (инициализация
весов) заданы случайно по стандартному закону
распределения.

Нажав клавишу “Обучить сеть”, вы
запустите процесс обучения персептрона методом
обратного распространения ошибки, который будет
отображаться в виде графика зависимости
максимальной (синий цвет) и среднеквадратичной
(красный цвет) ошибок от числа эпох обучения (см. рис.
22).

Рис. 22. Графическое отображение
процесса обучения сети

После выполнения 300 эпох обучение
прекращается, однако вы его можете продолжить,
нажимая клавишу “Учимся”, причем при каждом
нажатии этой клавиши процесс обучения
продляется еще на 300 эпох. Обратите внимание, что
нужное количество эпох обучения (например, 1000
вместо 300) можно задать до начала процесса
обучения.

Если ошибка обучения не будет
снижаться, нажмите кнопку “Закрыть” и начните
процесс обучения заново. Добившись снижения
максимальной ошибки обучения, например, до 0,01,
закройте графическое изображение (нажатием
клавиши “Закрыть”) и переведите программу в
режим “Проверка”. Нажмите кнопку “Скопировать
из обучающих примеров”, а затем — кнопку
“Вычислить”. В появившемся окне (рис. 23) вы
можете сравнить желаемые выходы се-
ти d1 с тем, что насчитал обученный вами
персептрон: y1. Например, как видно из первой
строки, вместо того чтобы выдать 2 x 2 = 2,
персептрон ответил: 2 x 1 = 2,0901. Ошибка
обучения e_L на этом примере
составила: |2,0902 — 2| = 0,0902, что в
процентах (относительно максимального значения
выхода сети max(d1) = 27) составляет: .

Аналогично можно подсчитать ошибку
обучения на втором примере:

затем на третьем и т.д., а затем выбрать
максимальную по всем примерам относительную
ошибку обучения персептрона. Значение этой
ошибки можно увидеть в нижней части рабочего
окна: 1,05%.

Рис. 23. В режиме «Проверка»
можно сравнить желаемые выходы сети d1 с тем,
что насчитал персептрон y1

После того как вы нашли максимальную
ошибку обучения персептрона, нажмите клавишу
“Сбросить примеры”, а затем — клавишу
“Добавить строку”, введите пример, которого не
было в обучающем множестве: 2 x 5 = 10, после чего
нажмите кнопку “Вычислить”.

Ответ изображен на рис. 24. Ошибка
обобщения составила: 0,93%.

Рис. 24. Сеть ответила, что дважды
пять будет примерно 9,9074

А теперь попробуем добиться более
хороших результатов, воспользовавшись
следствием из теоремы Арнольда – Колмогорова –
Хехт-Нильсена (формулы (37), (38)). Подставляя в
формулу (37) число входных нейронов N_x = 2,
число выходных нейронов N_y = 1 и
количество обучающих примеров Q = 18, получим
оценку необходимого количества синаптических
связей нейросети:

Применение формулы (38) дает оценку
необходимого количества скрытых нейронов:

Как видим, интервал допустимых
значений N получился весьма широким. Выберем
значение N посередине полученного интервала:

Вернувшись в режим “Проектирование
сети”, увеличим количество нейронов скрытого
слоя до 7 (рис. 25). Затем, выполняя обучение
сети и проверку ее прогнозирующих свойств,
получаем значительно более хороший результат,
приведенный на рис. 26 и 27, из которых видно,
что ошибка обучения сети e_L
снизилась до 0,33%, а ошибка обобщения снизилась до
0,11%.

Рис. 25. Структура сети с семью
нейронами скрытого слоя

Рис. 26. Результат работы сети с
семью нейронами скрытого слоя. Ошибка обучения
составила: e_L= 0,33%

И в заключение попросите школьников
нажать кнопку “Вычислить и округлить”.
Результат будет следующим: 2 x 5 = 10,0.

Рис. 27. Результат работы сети с
семью нейронами скрытого слоя. Ошибка обобщения
составила: e_T= 0,11%

А теперь спросите школьников:

— Сколько времени они сами потратили
для того, чтобы научиться таблице умножения?

— Может ли ребенок, которого обучили
всей таблице умножения за исключением 2 x 5 = 10,
самостоятельно догадаться, сколько будет дважды
пять?

— Можно ли утверждать, что интеллект
программы “Нейросимулятор” оказался сильнее
интеллекта ребенка, усваивающего таблицу
умножения?

Ответ предполагается положительным,
хотя у школьников может оказаться и иное мнение,
которое тоже следует уважать. В случае
возникновения спора сошлитесь на то, что мнения
специалистов здесь расходятся, и потому вопрос
является дискуссионным.

Попросите школьников сохранить свои
проекты, путем нажатия клавиши “Сохранить
проект”. Приучайте их и в дальнейшем не забывать
это делать.

Итак, применение формул, являющихся
следствием теоремы Арнольда – Колмогорова –
Хехт-Нильсена, позволило существенно улучшить
качество нейронной сети. Однако, как мы только
что видели, эти формулы дают очень грубую оценку
— довольно широкий интервал, внутри которого
должно находиться оптимальное число нейронов.
Поэтому это число желательно каждый раз
уточнять, выполняя оптимизацию сети.

Дайте задание школьникам
оптимизировать персептрон, т.е. найти
оптимальное количество нейронов скрытого слоя
путем построения графика зависимости
максимальной ошибки обобщения (тестирования) e_T от числа нейронов скрытых
слоев (см. рис. 19). Объявите
конкурс-соревнование среди школьников: кто
добьется самой наименьшей ошибки обобщения, тот
получит отличную оценку.

Обратите внимание школьников, что
качество нейросетевой модели определяется в
первую очередь ее прогностическими свойствами.
Это значит, что сейчас и впредь бороться надо
главным образом за снижение ошибки обобщения e_T (а не ошибки обучения e_L).

Подведение итогов конкурса можно
продолжить на следующем уроке, совместив с
выполнением следующей лабораторной работы.
Сообщите школьникам, что проектированием и
оптимизацией нейросетей им придется заниматься
каждый раз при решении других, более серьезных
задач, чем моделирование таблицы умножения.

Оптимизацию нейронных сетей удобно
выполнять с использованием приложения Microsoft Excel.
Для обмена данными с Microsoft Excel в режимах
“Обучение”, “Проверка” и “Прогноз”²
имеются кнопки “Загрузить из Excel-файла” и
“Отправить в Excel-файл”. Кроме того, в режимах
“Проверка” и “Прогноз” имеется кнопка
“Скопировать из обучающих примеров”, нажатие
которой позволяет скопировать в рабочее окно
входные векторы (X_q) обучающих
примеров, которые уже были введены в режиме
“Обучение”.

Использование указанных кнопок
позволяет частично автоматизировать ручной
труд, что является полезным и даже необходимым
при выполнении последующих лабораторных работ, в
которых объемы входной и выходной информации
весьма значительны.

Лабораторная работа № 9:
«Моделирование таблиц умножения и сложения»

Задание лабораторной работы состоит в
том, чтобы создать персептрон, моделирующий
одновременно две таблицы: таблицу умножения и
таблицу сложения на два и на три.

Сформулируйте это задание школьникам
и спросите, сколько, по их мнению, персептрон
должен иметь входов и выходов. В ответ логично
услышать, что персептрон должен иметь два
входных и два выходных нейрона. Первый выходной
нейрон предназначен для вывода произведения
двух вводимых чисел, а второй нейрон — для вывода
их суммы.

Теперь школьникам можно предложить
запустить нейросимулятор (открыв лабораторную
работу № и самостоятельно спроектировать и
обучить необходимый для выполнения задания
персептрон.

В краткой газетной статье мы
воздержимся от изложения подробной инструкции
по выполнению этой лабораторной работы,
порекомендовав в случае затруднений обратиться
к материалу описания предыдущей лабораторной
работы.

Пожалуйста, учтите, что школьники
могут проявить инициативу и выполнить задание
лабораторной работы как-то по-другому. Они могут
создать еще один входной нейрон и подавать на
него признак действия: например, единичку, если
требуется сложить два числа, и ноль, если
требуется их умножить. В этом случае персептрону
нужен только один выход, на котором, в
зависимости от введенного признака, будет
формироваться результат сложения либо
умножения.

В любом случае следует ознакомиться с
результатами работы школьников и поощрить тех,
кто добился минимальной ошибки обобщения e_T.

Лабораторная работа № 10:
«Прогнозирование выборов президента
страны»

На предыдущих
лабораторных работах школьники освоили
программу “Нейросимулятор”, позволяющую
создавать и применять нейронные сети
персептронного типа. Освоение программы они
выполнили на примере моделирования таблиц
умножения и сложения.

Цель этой и последующих лабораторных
работ состоит в демонстрации возможностей
программы “Нейросимулятор” и самого метода
нейросетевого математического моделирования.
Цель лабораторных работ состоит также в
приобретении навыков применения метода
нейросетевого математического моделирования
для решения широкого круга разнообразных задач,
имеющих практическое значение.

Ранее упоминалось о том, что с помощью
нейронной сети пермскими студентами была
предсказана победа на выборах 2008 года Президента
России Д.Медведева, причем для обучения
нейронной сети они использовали зарубежный опыт.
В то время, а это было начало 2007 года, результат
президентских выборов был далеко не очевиден, и
правильный прогноз нейросети, опубликованный
более чем за год до выборов, был серьезным
успехом.

Теперь школьникам предлагается
аналогичное задание — создать нейросетевую
прогностическую систему и повторить прогноз
результата президентских выборов 2008 года, однако
для обучения нейросети предлагается
использовать не зарубежный, а отечественный опыт
президентских выборов России за период с 1991 по 2004
гг.

При составлении обучающего и
тестирующего множеств мы рекомендуем
использовать следующую информацию:

x₁ — пол претендента в
президенты России, который будем кодировать с
помощью цифр: 1 — мужской, 2 — женский;

x₂— возраст претендента;

x₃ — от какой партии
баллотируется: 1 — от правящей, т.е. от партии,
набравшей более 5% голосов; 2 — от всех остальных
партий;

x₄ — место рождения: 1 —
Москва, Санкт-Петербург; 2 — прочие города России;
3 — российские села, деревни; 4 — зарубежье;

x₅ — статус: 1 — действующий
президент; 2 — преемник президента; 3 — остальные;

x₆ — сфера деятельности: 1 —
спорт, культура, медицина; 2 — военная
деятельность; 3 — экономика; 4 — политика;

x₇— семейное положение: 1 —
не женат/не замужем; 2 — разведен/разведена; 3 —
женат/замужем;

x₈ — известность: 1 —
неизвестный; 2 — известный; 3 — очень известный;

d — результат голосований: 1 —
победа; 0 — поражение.

Таблица 1

Школьникам можно дать задание собрать
необходимую для обучения персептрона информацию
о президентских выборах в России из сети
Интернет (например, с сайтов www.wikipedia.ru
и www.peoples.ru) и выполнить все
задания лабораторной работы самостоятельно.

Здесь мы приведем пример выполнения
этого задания, который можно использовать, если у
школьников возникнут трудности.

В табл. 11 приведены данные о
претендентах и результаты президентских выборов
в России за период с 1991 по 2004 гг., а в табл. 12 —
аналогичные данные по выборам 2008 г. Примеры табл.
11 мы будем использовать как обучающее множество,
а табл. 12 — как тестирующее.

Теперь задайте школьникам вопрос: Что
понимается под проектированием нейронной сети?

Ответ: Спроектировать нейронную
сеть — это значит определить количество входов,
количество выходов, число скрытых слоев, число
нейронов в скрытых слоях, типы активационных
функций.

Следующий вопрос: Сколько входов и
выходов должна иметь нейронная сеть,
предназначенная для прогнозирования
результатов выборов российского президента?

Ответ: В табл. 11 и 12 подобраны
примеры обучающего и тестирующего множества, в
которых параметры x₁, x₂, …, x₈
характеризуют претендента, и от них зависит
исход голосований, задаваемый параметром d.
Поэтому параметры x₁, x₂, …, x₈
являются входными, а параметр d — выходным.
Следовательно, нейронная сеть должна иметь 8
входов и 1 выход.

Вопрос: Сколько в проектируемой
нейронной сети должно быть скрытых слоев,
сколько нейронов в скрытых слоях и какими должны
быть активационные функции нейронов?

Ответ: Согласно теореме Арнольда –
Колмогорова – Хехт-Нильсена, персептрон должен
иметь хотя бы один скрытый слой нейронов с
сигмоидными активационными функциями.
Количество нейронов в скрытом слое оценивается с
помощью формул (37), (38). Учитывая, что в нашем
случае число входов N_x = 8, число выходов N_y
= 1, количество примеров обучающего множества Q = 33,
согласно первой из этих двух формул количество
сил синаптических связей нейросети должно
лежать в интервале:

Применяя вторую формулу, получаем
оценку количества нейронов в скрытом слое:

Для начала работы берем среднее
значение из этого интервала:

Теперь попросите школьников открыть
лабораторную работу № 8 и, запустив программу
“Нейросимулятор”, в режиме “Проектирование
сети” создать нейронную сеть требуемой
структуры, как показано на рис. 28.

Рис. 28. Структура нейросети,
предназначенной для прогнозирования
результатов выборов Президента России

Переключив “Нейросимулятор” в режим
“Обучение”, попросите школьников ввести
примеры обучающего множества из табл. 11. Это
можно сделать вручную, многократно используя
кнопку “Добавить строку”, либо с помощью кнопки
“Загрузить из Excel-файла” считать информацию из
предварительно подготовленного Excel-файла.

Нажав кнопку “Обучить сеть” и
убедившись, что процесс обучения сходится, т.е.
ошибка обучения уменьшается, переведите
“Нейросимулятор” в режим “Проверка”, нажмите
последовательно кнопку “Скопировать из
обучающих примеров” (введенное вами множество
обучающих примеров скопируется из режима
“Обучение” в режим “Проверка”) и кнопку
“Вычислить” (обученный вами персептрон
произведет вычисления для всех представленных
примеров). Сравнивая содержимое столбцов d1
(желаемый выход персептрона, т.е. тот, который был
задан в обучающем множестве примеров) и y1
(прогнозный выход персептрона), убедитесь, что
персептрон обучился с приемлемой степенью
точности.

Таблица 12

Теперь нажмите кнопку “Сбросить
примеры” и попросите школьников ввести
тестирующее множество примеров из табл. 12.
Сделать это можно вручную, многократно используя
кнопку “Добавить строку”, либо с помощью кнопки
“Загрузить из Excel-файла” считать информацию из
предварительно подготовленного Excel-файла. Нажав
после этого кнопку “Вычислить”, сравните
желаемые выходы сети d1 с прогнозными y1.

Рис. 29. Проверка на тестирующем
множестве:: прогноз президентских выборов 2008
года

Глядя на рис. 29, где приведены
результаты вычислений, и вспоминая, что первые
три строки в тестирующем множестве
соответствуют параметрам политических деятелей:
А.Богданова, В.Жириновского и Г.Зюганова, — а
последняя строка соответствует параметрам
Д.Медведева, и учитывая, что цифрой “1” мы
кодировали победу, а цифрой “0” — поражение,
можно заключить, что созданная нами
нейросетевая прогностическая система
предсказывает победу Д.Медведеву и поражение
А.Богданову, В.Жириновскому и Г.Зюганову, что и
произошло в действительности на президентских
выборах 2008 г. Отметим, что, как видно из рис.
29, погрешность e обобщения сети
составила 11,95%.

Нажав кнопку “Отправить в Excel-файл” и
выполнив в Excel-редакторе необходимые
манипуляции, полученный результат изобразим в
виде гистограммы, как показано на рис. 30.

Рис. 30. Значения рейтингов
претендентов на президентских выборах 2008 г.:

1 — А. Богданов,

2 — В.Жириновский,

3 — Г.Зюганов,

4 — Д.Медведев

Теперь, после того как мы убедились в
том, что нейронная сеть правильно выполнила
прогноз, а значит, выявила и усвоила
закономерности предметной области, попробуем
использовать нашу модель в практических целях.
Выберем кого-нибудь из политиков, например
В.Жириновского, и узнаем, как будет изменяться
его рейтинг в зависимости от возраста. Для этого
переведем программу “Нейросимулятор” в режим
“Прогноз” и введем параметры интересующего нас
политика. Причем сделаем это несколько раз,
создав несколько строк. В первой строке оставим
возраст В.Жириновского таким, каким он был на
момент выборов 2008 года, а в каждой последующей
строке увеличим его возраст на 1 год, как показано
на рис. 31. Напомним, что выполнить эту
операцию можно путем нажатия кнопки “Добавить
пример” или с помощью загрузки из заранее
приготовленного Excel-файла.

Рис. 31. Программа
«Нейросимулятор» в режиме «Прогноз» с
введенныит параметрами В.Жириновского. Его
возраст (x2) увеличивается в каждой новой строке
на 1 год

Нажав кнопку “Вычислить”, в столбце y1
получаем прогноз сети — зависимость
политического рейтинга В.Жириновского от его
возраста (рис. 32).

Полученную зависимость полезно
отобразить графически, как показано на рис. 33.
Сделать это можно, нажав кнопку “Отправить в
Excel-файл” и выполнив необходимые манипуляции в
Excel-редакторе.

Глядя на графическое изображение рис.
33, можно сделать вывод, что В.Жириновскому ни в
коем случае не следует уходить с политической
арены, так как с возрастом его рейтинг будет
увеличиваться.

Выясним, как можно повлиять на рейтинг
В.Жириновского путем изменения его параметров.
Для этого в режиме “Прогнозирование” введем
строки, содержащие параметры В.Жириновского.
Первую строку оставим без изменения. Начиная со
второй строки, будем поочередно изменять
параметры, оставляя неизменным лишь возраст. Как
показано на рис. 34, во второй строке изменен
параметр x1, в третьей строке изменен параметр
x3, в четвертой, пятой и шестой строках изменен
параметр x4 и т.д.

Нажимая кнопку “Вычислить”, получаем
прогноз (см. рис. 35), результаты которого
представлены в виде гистограммы на рис. 36.

Рис. 32. Прогноз сети: рейтинг
В.Жириновского в зависимости от его возраста

Рис. 33. Зависимость рейтинга
В,Жириновского от его возраста

Рис. 34. Нейросимулятор,
подготовленный для прогнозирования рейтинга
В.Жириновского при варьировании его параметров

Рис. 35. Прогноз рейтинга
В.Жириновского при варьировании его параметров

Рис. 36. Прогноз рейтинга
В.Жириновского при варьировании его параметров

1 — исходное состояние: фактический
рейтинг,

2 — такой рейтинг был бы у
В.Жириновского, если бы он был женщиной,

3 — если бы он баллотировался от
партии, не имеющей места в парламенте,

4 — если бы он родился не за рубежов, а в
Москве или Санкт-Петербурге,

5 — если бы он родился в других городах
России,

6 — если бы он родился в российском
селе или деревне,

7 — если бы он был преемником
Президента России,

8 — если бы он был Президентом России,

9 — если бы он сменил деятельность на
спорт, культуру или медицину,

10 — если бы он сменил деятельность на
военную,

11 — если бы он сменил деятельность на
экономическую,

12 — если бы он развелся,

13 — если бы он не имел известности

Итак, анализируя полученную картину,
можно сделать заключение, что серьезнейшим
фактором, снижающим рейтинг В.Жириновского,
является то, что он родился за рубежом.
Единственный шанс победить на выборах — это
стать преемником президента или самим
президентом, что нереально. Смена партии, вида
деятельности и семейного положения не приведут к
заметному изменению его рейтинга. Однако не
будем забывать, что, согласно данным рис. 33,
с каждым годом рейтинг В.Жириновского будет
повышаться, поэтому шансы стать Президентом
России в будущем у него все-таки есть.

Зададимся теперь вопросом: Насколько
надежны полученные в результате нейропрогноза
выводы?

Отвечая на этот вопрос, заметим, что
практически всякая математическая модель имеет
свою погрешность, и доверять результатам
математического моделирования можно только в
пределах этой погрешности. Погрешность модели
определяется при ее тестировании на примерах,
ответы на которые известны. Величина погрешности
зависит от многих причин, в том числе от того,
насколько полно модель учитывает свойства
предметной области.

В нашей математической модели учтены 8
входных параметров, и она проверена на четырех
тестовых примерах (см. рис. 29 и 30): на выборах
2008 года она правильно (с максимальной
погрешностью 11,95%) предсказала победу Д.Медведеву
и поражение А.Богданову, В.Жириновскому и
Г.Зюганову. Таким образом, мы убедились, что наша
модель правильно усвоила закономерности
предметной области и у нас, казалось бы, нет
причин не доверять результатам ее
прогнозирования. Тем не менее надо отдавать себе
отчет в том, что на самом деле результат
голосований зависит от гораздо большего
количества различных факторов, что для более
ответственных прогнозов следует увеличить
объемы обучающего и тестирующего множества
примеров.

Посоветуйте заинтересовавшимся
школьникам взять разработку систем
прогнозирования президентских выборов в
качестве темы курсовой работы. Пусть они
попробуют учитывать другие входные параметры и в
других количествах, а на выходе сети кодировать
не победу и поражение в виде единицы и нуля, а
процент проголосовавших “за”. Пусть сопоставят
свои результаты с графиками рис. 16 и пусть не
удивляются, если они будут отличаться. Причины
возникновения погрешностей нейросетевого
прогнозирования мы только что обсудили.

Посоветуйте школьникам не замыкаться
только на президентских выборах, а охватить еще и
выборы в местные законодательные собрания и
другие органы управления краев и областей.

В заключение обратите внимание на то, что
методы нейросетевого моделирования пока еще не
освоены профессиональными политтехнологами, и
вашим школьникам предоставляется шанс первыми
попробовать применить эти методы на практике.

Уважемые коллеги! Напоминаем, что
скачать лабораторные работы можно с сайта http://www.LbAI.ru

1 Напомним, что скачать
лабораторные работы можно с сайта http://www.LbAI.ru

2 Режим работы
нейросимулятора, задаваемый закладкой
“Прогноз”, понадобится в дальнейшем в тех
случаях, когда результат работы нейронной сети
заранее неизвестен.

Л.. Н.. Ясницкий

Источник

6.6.Анализ данных методом нейросетевого моделирования 141

6.6.АЛГОРИТМ ИНТЕЛЛЕКТУАЛЬНОГО АНАЛИЗА ДАННЫХ МЕТОДОМ НЕЙРОСЕТЕВОГО

МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Завершая изучение метода математического моделирования на основе персептронов, в качестве итога приведем примерный алгоритм его применения (рис. 6.17).

Рис. 6.17. Рекомендуемая схема применения метода нейросетевого математического моделирования

142 Глава 6. Оптимальное проектирование и обучение нейронных сетей

Этап 1. Постановка задачи

На этом этапе определяются цели моделирования, устанавливаются входные и выходные параметры модели, а также структура (состав

идлина) входного вектора X , и выходного вектора D.

Вкачестве компонент входного вектора X важно выбрать значимые параметры — те, которые оказывают существенное влияние на результат. Если же имеются сомнения в значимости того или иного входного параметра, то его лучше включить во входной вектор, рассчитывая, что в последующем с помощью создаваемой нейросети можно будет оценить степень влияния этого параметра на результат. Если его влияние окажется слабым, то в последующей работе исключить этот параметр.

Выходной вектор D формируется таким, чтобы его компоненты давали возможность получить ответы на все поставленные вопросы.

Компоненты входного вектора X и выходного вектора D представляют собой числа. Это могут быть значения каких-либо величин, например температуры тела, артериального давления, частоты пульса

идр. Это могут быть также числа, кодирующие наличие или отсутствие каких-либо признаков, например единица, если пол мужской,

идвойка, если пол женский. В некоторых случаях, если данные нечеткие и есть сомнение в их правильности, полезно кодировать оценку их вероятности. Например, если у врача есть сомнения в правильности выставляемого диагноза, то он может закодировать не сам диагноз, а его вероятность или степень развития болезни, применяя десятиили стобалльную систему оценки.

Этап 2. Формирование примеров

На этом этапе формируется содержимое входных и выходных векторов. В результате создается множество пар X q–Dq (q = 1, . . ., Q), где такая пара составляет пример, характеризующий предметную область. Значения компонент векторов X q и Dq могут быть сформированы различными способами: получены путем проведения социологических опросов, экспертных оценок, анкетирования, специальных экспериментов над предметной областью, взяты из средств массовой информации, из архивных материалов организаций, социальных сетей, интернет-форумов и из других источников.

Числовую информацию, приготовленную для ввода в нейросеть, желательно нормировать — привести к диапазону [0, 1] или [−1, 1].

Все множество примеров разбивают на обучающее L и тестирующее T (см. рис. 6.1). Обычно объем тестирующего множества выбирают не менее 10–15% от обучающего. Необходимый минимальный объем обучающего множества зависит от задачи. Ранее для расчета минимально допустимого объема обучающего множества рекомендовалась

6.6. Анализ данных методом нейросетевого моделирования 143

формула: Q = 7 · Nx + 15 [19], в которой Nx — количество входных

параметров нейросетевой модели. Однако в практике применения нейросетевых технологий встречаются случаи, когда для решения задач хватает значительно меньшего количества обучающих примеров.

Помимо обучающего множества L и тестирующего множества T , формируется еще и подтверждающее множество P из примеров, принадлежащих той же самой предметной области, но не пересекающееся ни с множеством L, ни с множеством P (см. рис. 6.1). Объем множества P обычно рекомендуется не более 10% от объема множества L.

Этап 3. Первоначальное проектирование сети

Структура персептрона выбирается из следующих соображений:

1.количество входных нейронов Nx должно быть равно размерности входного вектора X ;

2.количество выходных нейронов Ny должно быть равно размерности выходного вектора D;

3.количество скрытых слоев, согласно теореме Арнольда — Колмогорова — Хехт-Нильсена (см. § 6.1), должно быть не менее одного; на последующих этапах количество скрытых слоев может корректироваться, если это позволит улучшить качество работы сети;

4.количество нейронов в скрытых слоях первоначально рассчитывается с помощью формул (6.1), (6.2); на последующих этапах количество нейронов в скрытых слоях также может корректироваться, если это позволит улучшить качество работы сети;

5.активационные функции скрытых нейронов, согласно теореме Арнольда — Колмогорова — Хехт-Нильсена, рекомендуется задать сигмоидными, однако в дальнейшем, их вид может быть изменен, если это позволит улучшить качество работы сети.

При корректировке структуры персептрона следует иметь в виду, что увеличение количества скрытых нейронов обычно позволяет добиться меньшей ошибки обучения. Однако чрезмерное его увеличение приводит к эффекту гиперразмерности — потере обобщающих свойств сети, выражающейся в возрастании ошибки обобщения (тестирования).

Этап 4. Обучение сети

Обучение сети — очень важный, но не окончательный этап создания нейросетевой математической модели. Цель обучения — подобрать синаптические веса wij так, чтобы на каждый входной вектор X q множества обучающих примеров сеть выдавала вектор Y q, минимально отличающийся от заданного выходного вектора Dq. Эта цель достигается путем использования алгоритмов обучения нейронной сети.

144 Глава 6. Оптимальное проектирование и обучение нейронных сетей

Рис. 6.18. Характерные кривые зависимости ошибки обучения εL от чис-

ла эпох t в случае, когда сеть обучается успешно (а) и когда процесс обучения не дает желаемого результата (б)

Характерная кривая обучения — зависимость ошибок обучения от количества эпох обучения — приведена на рис. 6.18, а. Однако может случиться, что сеть «не захочет» обучаться: ошибка обучения с увеличением количества эпох не будет стремиться к нулю (см. рис. 6.18, б). Причинами этого нежелательного явления могут быть следующими.

1-я причина. Недостаточное количество скрытых слоев и скрытых нейронов — тогда рекомендуется увеличить их количество.

2-я причина. Наличие в обучающем множестве противоречащих друг другу (конфликтных) примеров, когда одним и тем же наборам входных параметров соответствуют разные наборы выходных параметров. Например — одним и тем же симптомам соответствуют разные диагнозы заболеваний. Обнаружить такие примеры в обучающем множестве можно путем его визуального анализа, или путем применения специальных программ. Затем следует разобраться в причинах возникновения конфликтных примеров: некоторые из них могут просто оказаться ошибочными, и их нужно удалить. Другая причина может быть связана с тем, что в самой структуре входного вектора отсутствуют какие-то параметры (например, возраст больного, рост, вес, цвет его глаз и др.), также оказывающие влияние на диагноз. В этом случае рекомендуется вернуться на этап 1 алгоритма (см. рис. 6.17) и пересмотреть постановку задачи, увеличить размерность входного вектора X , добавив дополнительные параметры, которые своими значениями обеспечат непротиворечивость примеров обучающего множества.

3-я причина. Попадание в локальный минимум. Эта проблема связана с тем, что поверхность функции-ошибки персептрона, схематично изображенная на рис. 6.6, имеет достаточно сложный характер со множеством мелких «ямочек», называемых локальными минимумами. Процесс обучения персептрона состоит в движении по этой поверх-

6.6. Анализ данных методом нейросетевого моделирования 145

ности небольшими шагами в сторону антиградиента, т. е. в сторону наибольшего наклона поверхности функции-ошибки. Естественно, что опускаясь таким образом по поверхности функции-ошибки, можно «застрять» в каком-либо мелком локальном минимуме, не достигнув самого глубокого минимума, называемого глобальным. В этом случае рекомендуется попробовать заново начать процесс обучения из другой начальной точки или сменить алгоритм обучения нейросети.

4-я причина. Наличие в множестве примеров поведения предметной области посторонних выбросов — примеров, которые не подчиняются закономерностям предметной области и значительно отличаются по своим параметрам от другой статистической информации, например, вследствие закравшихся ошибок. Рекомендуется выявить такие примеры, например, с помощью методики [57] (см. § 6.5), проанализировать их на предмет наличия ошибок и, если таковые обнаружатся — исправить ошибки или удалить выбросы.

5-я причина. Паралич сети. В этом случае процесс обучения «замирает» в результате неуправляемого возрастания синаптических весов и соответствующего возрастания аргументов активационных функций. Следствием является попадание в область насыщения, где производные от сигмоидных функций близки к нулю. Рекомендуется использовать активационные функции, которые не имеют горизонтальных асимптот, например логарифмические (см. § 6.5). Другой вариант — попробовать провести нормализацию чисел, формирующих примеры предметной области.

6-я причина. При слишком большой скорости обучения может потеряться устойчивость итерационного процесса — тогда рекомендуется уменьшить ее.

Заметим, что в практике нейросетевого моделирования обычно случается так, что не удается установить точную причину отсутствия сходимости процесса обучения нейронных сетей. Остается только предполагать эти причины и поочередно принимать меры по устранению возникших нежелательных явлений, т. е. выполнять рекомендации, указанные в приведенных выше шести пунктах.

Этап 5. Проверка и оптимизация сети

Проверка обобщающих свойств сети (иногда данный этап называют тестированием сети) производится на тестирующем множестве примеров, т. е. на тех примерах, которые не были использованы при обучении сети. Результаты тестирования полезно представить графически в виде гистограммы, на которой значения желаемых выходов персептрона Dq сопоставлены с действительными (прогнозными) Yq — теми, которые вычислил персептрон. Пример такой гистограммы приведен на рис. 6.19.

146	Глава 6. Оптимальное проектирование и обучение нейронных сетей
Рис. 6.19. Пример гистограммы, показывающей соотношение желаемых
	выходов сети с действительными (прогнозными)

Если разница между компонентами желаемого выходного вектора Dq и действительного выходного вектора Y q окажется незначительной, то можно переходить к следующему, этапу 6, не выполняя оптимизацию сети. Однако, чтобы лишний раз убедиться в адекватности разрабатываемой нейросетевой математической модели, полезно вернуться на этап 2 и те примеры, которые были тестирующими, (либо часть тестирующих примеров) включить в обучающее множества, а часть примеров, бывших обучающими, сделать тестирующими. После этого снова повторить этапы 3, 4 и 5.

Если же погрешность обобщения сети окажется неприемлемо большой, то надо попытаться оптимизировать сеть. Эта операция состоит в подборе наиболее подходящей для данной задачи структуры сети — количества скрытых слоев, количества скрытых нейронов, количества синаптических связей, а также вида и параметров активационных функций нейронов. В некоторых нейропакетах предусмотрена автоматическая оптимизация сети, но бывает полезно выполнить такую оптимизацию вручную, построив график зависимости погрешности обобщения εT

от числа скрытых нейронов (см. рис. 6.2) и от других параметров персептрона, а затем с помощью этих графиков выбрать структуру сети, обеспечивающую минимальную погрешность обобщения.

При выборе оптимальной структуры сети следует помнить, что цель оптимизации сети состоит в минимизации погрешности обоб-

6.6. Анализ данных методом нейросетевого моделирования 147

щения εT , но не погрешности обучения εL. Именно по величине

погрешности обобщения судят о качестве сети, о ее обобщающих и, следовательно, прогностических свойствах. Погрешность же обучения — это всего лишь промежуточный результат. Желательно, чтобы она была небольшой, но добиваться самого минимального ее значения вовсе не обязательно и даже вредно, поскольку, как видно из графиков рис. 6.2, это приводит к эффекту переобучения, т. е. росту погрешности обобщения.

Понятно, что оптимизация нейронной сети подразумевает многократные возвраты назад на этапы 4, 3, 2 или даже на этап 1. На этапе 1 заново выполняется постановка задачи, включающая переоценку значимости входных параметров с последующим их сокращением, или, наоборот, добавлением. Напомним, что малозначимые входные параметры, могут быть выявлены с помощью разрабатываемой нейросети путем поочередного исключения входных параметров и наблюдением за погрешностью обобщения. Если при исключении какого-либо входного параметра погрешность обобщения нейронной сети возрастет, то этот параметр является значимым для данной математической модели. В противном случае, параметр не является значимым, и его не следует учитывать при постановке задачи.

После оптимизации сети ее обобщающие свойства рекомендуется проверить на примерах подтверждающего множества P. Дело в том, что в процессе оптимизации сеть может «приспособиться» к примерам тестирующего множества. Если эти примеры по каким-либо причинам не характерны для всей предметной области, то на других примерах, которых не было ни в тестирующем, ни в обучающем множествах, она может дать неожиданно большую ошибку. Для исключения такого явления, а также чтобы окончательно убедиться в адекватности разрабатываемой математической модели, вычисляют ошибку прогнозирования сети εP на подтверждающем множестве, т. е. на тех

примерах, которые не участвовали ни в обучении, ни в тестировании. Результатом оптимизации и проверки сети является готовая к использованию нейросетевая математическая модель предметной об-

ласти — интеллектуальная информационная система (ИИС).

Этап 6. Исследование предметной области — интеллектуальный анализ данных

Путем проведения вычислительных экспериментов над математической нейросетевой моделью достигаются цели моделирования и находятся ответы на поставленные вопросы. Например, могут быть решены такие задачи, как оптимизация моделируемого объекта, прогнозирование его будущих свойств, выявление закономерностей предметной области и др.

148 Глава 6. Оптимальное проектирование и обучение нейронных сетей

Нейросетевая математическая модель, если она правильно спроектирована и обучена, «впитала в себя» закономерности моделируемой предметной области. Она реагирует на изменение входных параметров и ведет себя точно так же, как вела бы себя сама предметная область. Поэтому над такой моделью надо поставить как можно больше экспериментов. Можно попробовать поменять некоторые из входных параметров и посмотреть, как при этом меняются значения выходного вектора Y . Например, меняя возраст кандидата в президенты, можно пронаблюдать за изменением его рейтинга, как это было сделано в § 5.6. Надо постараться извлечь из этих виртуальных экспериментов как можно больше полезной информации.

Часто бывает полезно графически изображать зависимости выходных параметров модели от входных. Например на рис. 5.6 были

построены зависимости	рейтингов Д. Медведева и В. Жириновско-
го от их возраста, а на	рис. 5.7 — гистограмма, позволяющая давать

практические рекомендации по повышению политического рейтинга И. Хакамады. Эти интересные результаты и выводы были получены путем исследования предметной области (политического процесса — выборов президента страны) с помощью нейросетевой математической модели. Результаты моделирования полезно представлять в виде объемных фигур, как например на рис. 5.8.

Выполняя исследования предметной области с помощью нейросетевой математической модели, следует понимать, что во многих задачах входные параметры обычно коррелированны между собой. Например, при прогнозировании здоровья пациента на будущие периоды времени (см. § 5.2) недостаточно изменять только один входной параметр, отвечающий за его возраст, поскольку с возрастом обязательно изменяются другие его параметры — содержание холестерина и сахара в крови, артериальное давление и др.

Кроме того, следует помнить, что нейронные сети часто выявляют так называемые «ложные корреляционные зависимости». По этому поводу уместно привести классический пример. Однажды методом интеллектуального анализа статистической информации было установлено, что люди, злоупотребляющие кофе, чаще других болеют онкологическими заболеваниями. С другой стороны, известно, что кофе не содержит канцерогенных веществ. Объяснение этого парадокса нашлось, когда обнаружили, что за чашкой кофе часто следовала выкуренная сигарета. Она-то и явилась причиной онкозаболеваний.

В заключение укажем, что алгоритм создания интеллектуальной системы и ее применения для интеллектуального анализа данных, приведенный на рис. 6.17, апробирован при решении многих практических задач и представляется вполне эффективным. Однако в каждом конкретном случае, а также в зависимости от опыта, навыков и предпочтений разработчика интеллектуальной системы возможны

6.6. Анализ данных методом нейросетевого моделирования 149

отклонения от этого алгоритма. Например, если у разработчика хорошо развита интуиция или наработаны собственные алгоритмы для определения количества нейронов в скрытых слоях, то совсем не обязательным является использование формулы Арнольда — Колмогорова — Хехт-Нильсена.

Контрольные вопросы и задания

1.Перечислите этапы создания нейросетевой математической модели предметной области.

2.Как формируется структура входного вектора X , и выходного вектора D?

3.Перечислите способы формирования содержимого пар векторов

X q–Dq.

4.Как выполняется проектирование сети?

5.В чем состоит цель обучения сети, и как она достигается?

6.Назовите шесть причин, по которым сеть может не поддаваться обучению.

7.В чем состоит цель тестирования сети?

8.В чем состоит цель оптимизации сети?

9.В каких случаях используется подтверждающее множество примеров, и можно ли без него обойтись?

10.Приведите примеры ложных корреляционных зависимостей.

11.Зайдите на сайт www.LbAi.ru, скачайте и выполните все лабораторные работы. При выполнении лабораторных работ полезно использовать книги [73, 88].

12.Придумайте тему своего собственного проекта, лежащую в области ваших личных интересов. Выполните проект, следуя пунктам алгоритма рис. 6.17 (см. § 6.6) и используя программный инструментарий для работы с нейронными сетями, скачанный с сайта www.LbAi.ru (Лабораторная работа № 8). При выполнении задании полезно использовать книги [73, 88].

13.Перечислите свойства, которые нейросети и нейрокомпьютеры унаследовали от своего прототипа — человеческого мозга. Проявились ли некоторые из этих свойств при выполнении вашего проекта?

Глава 7

НЕКЛАССИЧЕСКИЕ НЕЙРОННЫЕ СЕТИ

Нейронные сети персептронного типа с сигмоидными активационными функциями, предложенные, исследованные и развитые в классических работах У. Мак-Каллока и В. Питтса [100], Ф. Розенбатта [101, 102], Б. Уидроу и М. Е. Хоффа [107], А. И. Галушкина с соавторами [6–11] и др., являются в настоящее время наиболее изученными и наиболее применяемыми из всего множества разновидностей известных нейронных сетей. Однако развитие нейроинформатики на этой нейросетевой парадигме не остановилось. Новейшие исследования мозга фиксируют все новые и новые данные, которые выходят за рамки классических гипотез нейроинформатики. Соответственно, появляются новые (неклассические) нейросетевые парадигмы, некоторые из которых рассматриваются в настоящей главе.

7.1.СЕТЬ КАСКАДНОЙ КОРРЕЛЯЦИИ ФАЛЬМАНА—ЛИБЬЕРА

В работе С. Е. Фальмана и К. Либьера [91] предложен оригинальный способ постепенного наращивания структуры нейронной сети в процессе ее обучения. Идея авторов состоит в следующем. Сначала создается простейший однослойный персептрон, затем, после попытки его обучения, следует серия этапов, состоящих в том, что в сеть добавляется по одному скрытому нейрону, каждый из которых своими синапсами подключается ко всем входным нейронам сети и ко всем ранее добавленным скрытым нейронам. Синаптические веса каждого скрытого нейрона подбираются так, чтобы обеспечивался максимальный коэффициент корреляции между его активностью (т. е. силой выходного сигнала) и ошибкой обучения сети, вычисляемой с помощью формулы:

y(q) −		εi(q) −	,	(7.1)
y	εi

где I — количество выходных нейронов; Q — количество обучающих примеров; y(q) — выходной сигнал нейрона-кандидата на q-м обучающем примере; ε(iq) = di(q) − y(iq) — погрешность i-го выходного нейрона

Источник

Характер приближений в информационных моделях

Ошибка обучения и ошибка обобщения

Ограничения репрезентативной способности и оценка ошибки обобщения для графовых нейронных сетей

Введение

Ограничения графовых нейронных сетей

Ограничения LU-GNN

Ограничения CPNGNN

Ограничения DimeNet

Шаг в сторону более мощных GNN

Оценка ошибки обобщения

Выводы

Содержание

Проблемы обобщения

Задача обобщения в машинном обучении

Утечка данных

Shortcut learning: «right for the wrong reasons»

Shortcut learning в языковых моделях

Уровни обобщения моделей машинного обобщения

Состязательные атаки

Проблема неконкретизации в ML-задачах

Выводы

Способы решения проблем обобщения

Стресс-тесты для диагностики работы модели

Доменная адаптация

Еще больше данных?

Более крупные или более эффективные модели?

Модификации способов обучения языковых моделей

Архитектура моделей и структура данных

Направления исследований

Общий искусственный интеллект

Заключение

Искусственный интеллект: популярное введение для учителей и школьников

Проектирование персептронов

Теорема существования

Проблемы и методы проектирования

Лабораторная работа № 9: «Моделирование таблиц умножения и сложения»

Л.. Н.. Ясницкий

Интересное по теме:

Лабораторная работа № 9:
«Моделирование таблиц умножения и сложения»