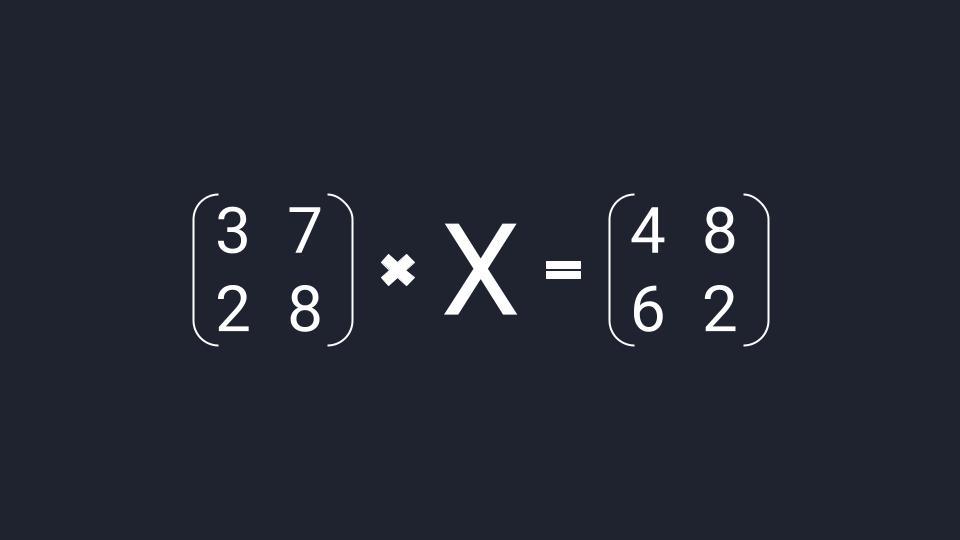Ошибка матрица делитель не квадратная - Решение и исправление самых разных ошибок на TopOshibok.ru

Garri	#1 Оставлено : 27 апреля 2010 г. 22:49:31(UTC)
Статус: Member Группы: Registered Зарегистрирован: 21.06.2009(UTC) Сообщений: 12 Откуда: МО г. Мытищи	При деление числа на матрицу, скажем, 3х1 появляется надпись — Матрица-делитель не квадратная. Возможно ли решение? http://letitbit.net/download/20470.2031b48dfe0c52768f71fa7c2/zz.jpeg.html

smath	#2 Оставлено : 27 апреля 2010 г. 23:35:54(UTC)
Статус: Administration Группы: Developers, Registered, Knovel Developers, Administrators, Advanced Member Зарегистрирован: 11.07.2008(UTC) Сообщений: 912 Сказал «Спасибо»: 639 раз Поблагодарили: 262 раз в 102 постах	Зависит от того, что Вы хотите получить… В контексте математики программа абсолютно законно сообщает, что данная операция незаконна, т.к. нельзя найти обратную матрицу от неквадратной.
	WWW

Garri	#3 Оставлено : 28 апреля 2010 г. 0:02:19(UTC)
Статус: Member Группы: Registered Зарегистрирован: 21.06.2009(UTC) Сообщений: 12 Откуда: МО г. Мытищи	тут имеется ввиду столбец из 3-х чисел. Число делится на каждое значение из этого столбеца, в результате получается 3 др. числа. Если так нельзя использовать матрицу то что можно использовать таким образом?

smath	#4 Оставлено : 28 апреля 2010 г. 0:53:16(UTC)
Статус: Administration Группы: Developers, Registered, Knovel Developers, Administrators, Advanced Member Зарегистрирован: 11.07.2008(UTC) Сообщений: 912 Сказал «Спасибо»: 639 раз Поблагодарили: 262 раз в 102 постах	Много раз писал как работать с подобным классом задач. Посмотрите например тут: http://ru.smath.info/forum/default.aspx?g=posts&t=401 Предлагаю сделать так: (скачать файл расчёта) С уважением.
	WWW

Garri	#5 Оставлено : 28 апреля 2010 г. 1:14:00(UTC)
Статус: Member Группы: Registered Зарегистрирован: 21.06.2009(UTC) Сообщений: 12 Откуда: МО г. Мытищи	Спасибо, будем разбираться.

Пользователи, просматривающие эту тему

Guest (2)

Быстрый переход

Вы не можете создавать новые темы в этом форуме.

Вы не можете отвечать в этом форуме.

Вы не можете удалять Ваши сообщения в этом форуме.

Вы не можете редактировать Ваши сообщения в этом форуме.

Вы не можете создавать опросы в этом форуме.

Вы не можете голосовать в этом форуме.

Источник

Решение матричных уравнений

Финальная глава саги.

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано.

Краткое содержание прошлых частей:

Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности.
Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел.
Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше).
Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми.
Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный.

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

Шаг 1. Упрощаем уравнение

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

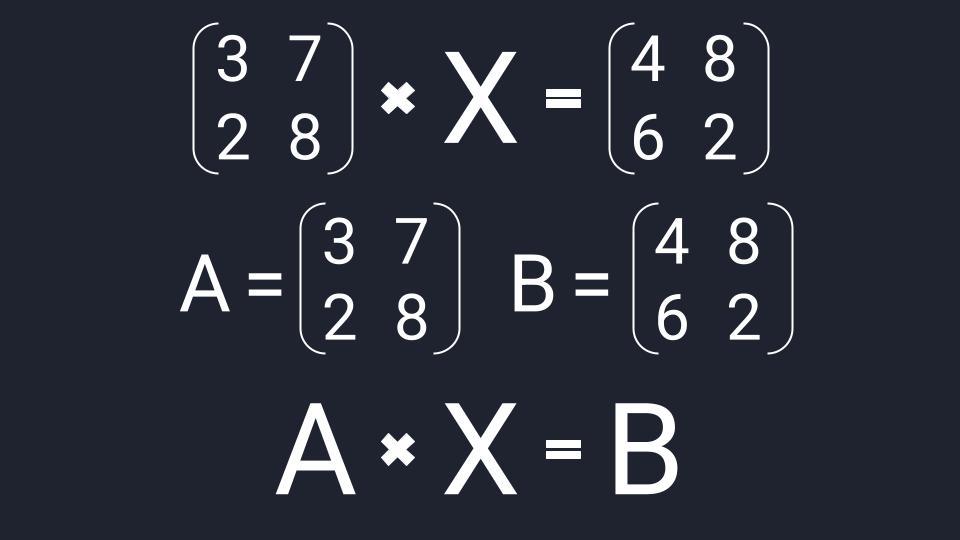
Приводим матричное уравнение к упрощённому виду

Шаг 2. Вводим единичную матрицу

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу.

Можно представить, что есть число 100 — это «сто в первой степени», 100 1

И есть число 0,01 — это «сто в минус первой степени», 100 -1

При перемножении этих двух чисел получится единица:
100 1 × 100 -1 = 100 × 0,01 = 1.

Вот такое, только в мире матриц.

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А -1 . Неизвестную матрицу Х оставляем без изменений и переписываем уравнение:

А -1 × А × Х = А -1 × В

Добавляем единичную матрицу и упрощаем запись:

А -1 × А = E — единичная матрица

E × Х = А -1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А -1 × В — новая запись уравнения

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B.

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A -1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто.

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы:

Делим единицу на определитель матрицы A.
Считаем транспонированную матрицу алгебраических дополнений.
Перемножаем значения и получаем нужную матрицу.

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Третье действие: получаем обратную матрицу

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А -1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Проверяем ответ и получаем матрицу B — наши расчёты верны

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Решение матричных уравнений: теория и примеры

Решение матричных уравнений: как это делается

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :

Как решить матричное уравнение во втором случае? Если дано уравнение

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

Решение матричных уравнений: примеры

Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :

Наконец, находим неизвестную матрицу:

Пример 2. Решить матричное уравнение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .

Сначала найдём определитель матрицы A :

Найдём алгебраические дополнения матрицы A :

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :

Находим матрицу, обратную матрице A :

Найдём матрицу, обратную матрице B .

Сначала найдём определитель матрицы B :

Найдём алгебраические дополнения матрицы B :

Составим матрицу алгебраических дополнений матрицы B :

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :

Находим матрицу, обратную матрице B :

источники:

http://function-x.ru/matrix_equations.html

Источник

Xcode на маке. Компилирует, но выдает ошибку (Threat 1: signal SIGABRT), если матрица не квадратная.

#include <iostream>

using namespace std;

const int N=3;
const int M=10;

int main(int argc, const char * argv[]) {
    int a[N][M];

    for(int i=0;i<M;i++){
        for(int j=0;j<N;j++){
            a[i][j]=rand()%2;
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }

    return 0;
}

post_zeew

22k3 золотых знака26 серебряных знаков37 бронзовых знаков

задан 29 окт 2016 в 20:04

Поменяйте местами M и N в циклах.

Вы объявляете Ваш массив как int a[N][M];, где N = 3 и M = 10.

Вы обращаетесь к массиву с помощью двух индексов a[i][j].

Индекс i должен быть в пределах от 0 и до N, а j – от 0 и до M.

В Вашем же варианте Вы выходите за пределы массива.

ответ дан 29 окт 2016 в 20:15

post_zeewpost_zeew

22k3 золотых знака26 серебряных знаков37 бронзовых знаков

Как уже было замечено в комментариях, у вас неправильно заданы верхние границы для циклов.

int a[N][M];

for(int i=0;i<M;i++){
            ^^^^
    for(int j=0;j<N;j++){
                ^^^^
        a[i][j]=rand()%2;
        cout<<a[i][j]<<" ";
    }
    cout<<endl;
}

Должно быть

int a[N][M];

for(int i=0;i<N;i++){
            ^^^
    for(int j=0;j<M;j++){
                ^^^
        a[i][j]=rand()%2;
        cout<<a[i][j]<<" ";
    }
    cout<<endl;
}

Чтобы избежать подобного рода ошибок вы можете в C++ инициализировать и вывести на консоль массив следующим образом, используя цикл на основе диапазон.

for ( autp &row : a )
{
    for ( auto &x : row )
    {
        x = rand() % 2;
        cout << x << " ";
    }
    cout << endl;
}

Имейте в виду, что функция rand определена в заголовке <cstdlib>, который следует включить в программу

#include <cstdlib>

ответ дан 29 окт 2016 в 20:20

Vlad from MoscowVlad from Moscow

44.7k3 золотых знака38 серебряных знаков89 бронзовых знаков

Источник

Download Article

If you know how to multiply two matrices together, you’re well on your way to «dividing» one matrix by another. That word is in quotes because matrices technically cannot be divided. Instead, we multiply one matrix by the inverse of another matrix.^[1] These calculations are commonly used to solve systems of linear equations.^[2]

1

Understand matrix «division.« Technically, there is no such thing as matrix division. Dividing a matrix by another matrix is an undefined function.^[3] The closest equivalent is multiplying by the inverse of another matrix. In other words, while [A] ÷ [B] is undefined, you can solve the problem [A] * [B]^-1. Since these two equations would be equivalent for scalar quantities, this «feels» like matrix division, but it’s important to use the correct terminology.
2
Confirm the «divisor matrix» is square. To take the inverse of a matrix, it must be a square matrix, with the same number of rows and columns. If the matrix you’re planning to inverse is non-square, there is no unique solution to the problem.^[4]
- The term «divisor matrix» is a little loose, since this is not technically a division problem. For [A] * [B]^-1, this refers to matrix [B]. In our example problem, this is ${\begin{pmatrix}7&4\\2&3\end{pmatrix}}$ .
- A matrix that has an inverse is called «invertible» or «non-singular.» Matrices without an inverse are «singular.»
Advertisement
3
Check that the two matrices can be multiplied together. To multiply two matrices together, the number of columns in the first matrix must equal the number of rows in the second matrix.^[5] If this does not work in either arrangement ([A] * [B]^-1 or [B]^-1 * [A]), there is no solution to the problem.
- For example, if [A] is a 4 x 3 matrix (4 rows, 3 columns) and [B] is a 2 x 2 matrix (2 rows, 2 columns), there is no solution. [A] * [B]^-1 does not work since 3 ≠ 2, and [B]^-1 * [A] does not work since 2 ≠ 4.
- Note that the inverse [B]^-1 always has the same number of rows and columns as the original matrix [B]. There’s no need to calculate the inverse to complete this step.
- In our example problem, both matrices are 2 x 2s, so they can be multiplied in either order.
4

Find the determinant of a 2 x 2 matrix. There’s one more requirement to check before you can take the inverse of a matrix. The determinant of the matrix must be nonzero. If the determinant is zero, the matrix does not have an inverse. Here’s how to find the determinant in the simplest case, the 2 x 2 matrix:^[6]
5
Find the determinant of a larger matrix. If your matrix is 3 x 3 or larger, finding the determinant takes a bit more work:^[8]
- 3 x 3 matrix: Choose any element and cross out the row and column it belongs to. Find the determinant of the remaining 2 x 2 matrix, multiply by the chosen element, and refer to a matrix sign chart to determine the sign. Repeat this for the other two elements in the same row or column as the first one you chose, then sum all three determinants. Read this article for step-by-step instructions and tips to speed this up.
- Larger matrices: Using a graphing calculator or software is recommended. The method is similar to the 3 x 3 matrix method, but is tedious by hand.^[9] For example, to find the determinant of a 4 x 4 matrix, you need to find the determinants of four 3 x 3 matrices.
6

Continue on. If your matrix is not square, or if its determinant is zero, write «no unique solution.» The problem is complete. If the matrix is square and its determinant is non-zero, continue to the next section for the next step: finding the inverse.

1

Switch the positions of the elements on the main 2 x 2 diagonal. If your matrix is 2 x 2, you can use a shortcut to make this calculation much easier.^[10] The first step in this shortcut involves switching the top left element with the bottom right element. For example:
2

Take the opposite of the other two elements, but leave them in position. In other words, multiply the top right and bottom left elements by -1:^[11]
3
Take the reciprocal of the determinant. You found the determinant of this matrix in the section above, so there’s no need to calculate it a second time. Just write down the reciprocal 1 / (determinant):^[12]
- In our example, the determinant is 13. The reciprocal of this is ${\frac {1}{13}}$ .
4

Multiply the new matrix by the reciprocal of the determinant. Multiply each element of the new matrix by the reciprocal you just found. The resulting matrix is the inverse of the 2 x 2 matrix:^[13]
5
Confirm the inverse is correct. To check your work, multiply the inverse by the original matrix. If the inverse is correct, their product will always be the identity matrix, ${\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ If the math checks out, continue on to the next section to complete your problem.
- For the example problem, multiply ${\begin{pmatrix}7&4\\2&3\end{pmatrix}}*{\begin{pmatrix}{\frac {3}{13}}&{\frac {-4}{13}}\\{\frac {-2}{13}}&{\frac {7}{13}}\end{pmatrix}}={\begin{pmatrix}1&0\\0&1\end{pmatrix}}$ .
- Here’s a refresher on how to multiply matrices.
- Note: Matrix multiplication is not commutative: the order of the factors matters. However, when multiplying a matrix by its inverse, both options will result in the identity matrix.^[14]
6
Review matrix inversion for 3 x 3 matrices or larger. Unless you are learning this process for the first time, save yourself time by using a graphing calculator or math software for larger matrices. If you do need to calculate it by hand, here’s a quick summary of one method:^[15]^[16]
- Adjoin the identity matrix I to the right side of your matrix. For example, [B] → [B | I ]. The identity matrix has «1» elements along the main diagonal, and «0» elements in all other positions.
- Perform row operations to reduce the matrix until the left side is in row-echelon form, then continue reducing until the left side is the identity matrix.
- Once the operation is complete, your matrix will be in the form [I | B^-1]. In other words, the right side will be the inverse of the original matrix.

1
Write both possible equations. In «ordinary math» with scalar quantities, multiplication is commutative; 2 x 6 = 6 x 2. This is not true for matrices, so you may need to solve two problems:^[17]
- [A] * [B]^-1 is the solution x for the problem x[B] = [A].
- [B]^-1 * [A] is the solution x for the problem [B]x = [A].
- If this is part of an equation, make sure you are performing the same operation on both sides. If [A] = [C], then [B]^-1[A] does not equal [C][B]^-1, because the [B]^-1 is on the left side of [A] but the right side of [C].^[18]
2

Find the dimensions of your answer. The dimensions of the final matrix are the outer dimensions of the two factors. It has the same number of rows as the first matrix, and the same number of columns as the second matrix.^[19]
3
4

Repeat the dot product process for each position in your matrix. For example, the element at position 2,1 is the dot product of [A] row 2 and [B]^-1 column 1. Try to complete the example on your own. You should get the following answers:^[21]

Add New Question

Question

If matrix AB is given, as well as A, how do I find B?

Well, first determine if A is invertible (i.e. has a nonzero determinant). If A is invertible, left multiply AB by A^-1. This produces: IB=B. There really is no such thing as matrix division. If A is singular (noninvertible), then B could be many different things. You could actually solve systems of equations to find possible entries for B. But if A is invertible, B is unique.
Question

How do I divide a matrix by a scalar number?

Just divide each individual number inside the matrix by the scalar number.
Question

What is the importance of matrix division?

Matrix division is very useful in solving systems of linear equations.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

You can divide a matrix by a scalar by dividing each element of the matrix by the scalar.

Calculators are not always 100% accurate when it involves matrix calculations. For instance, if your calculator tells you an element is a very small number (2E^-8, for example), the value is most likely zero.^[22]

About This Article

Article SummaryX

1. Find the determinant of matrix [B] by calculating ad-bc, where [a b] is the top row and [c d] is the bottom row.

Did this summary help you?

Thanks to all authors for creating a page that has been read 455,728 times.

Did this article help you?

Источник

[math]BadCatss,[/math]
У неквадратных матриц нет определитель(детерминант), но у каждая матрица [math]m \times n[/math] (m — ряда и n- столбца) независимо от того [math]m = n[/math] или [math]m \ne n[/math] есть ПЕРМАНЕНТ.
Eсли [math]A = \begin{pmatrix} a_{11} & … & a_{1n} \\ … & … & … \\ a_{m1} & … & a_{mn} \end{pmatrix}[/math]

и [math]m\leqslant n[/math] , то [math]per(A)= \sum a_{1i_{1} }a_{2i_{2} } \cdot \cdot \cdot a_{mi_{m} }[/math]

где суммирование производиться по всем [math]m[/math] перестановком [math](i_{1 }, i_{2}, \cdot \cdot \cdot i_{m} )[/math] целых чисeл [math]= 1, 2, …, n[/math]
Так что в Вашем случае
[math]per\begin{pmatrix} 1 & -5 & 2 & 2 \end{pmatrix} = 1 +(- 5) + 2 + 2 = 0[/math]

P.S. Я не знаю уровен Вашим знаниям, но судя по вопрос, каторы задаете — он очень недостающий, поетому скажу в дополнение, что перманент (per) используется в комбинаторной математике, смотрите например Г.Дж. Райзер «Комбинаторная математика».

Источник