Загрузить PDF
Загрузить PDF
При измерении чего-либо можно предположить, что есть некоторое «истинное значение», которое лежит в пределах диапазона значений, которые вы нашли. Для расчета более точной величины нужно взять результат измерения и оценить его при прибавлении или вычитании погрешности. Если вы хотите научиться находить такую погрешность, выполните следующие действия.
-
1
Выражайте погрешность правильно. Допустим, при измерении палки ее длина равна 4,2 см плюс-минус один миллиметр. Это означает, что палка примерно равна 4,2 см, но на самом деле может быть немного меньше или больше этого значения — с погрешностью до одного миллиметра.
- Запишите погрешность как: 4,2 см ± 0,1 см. Вы также можете переписать это как 4,2 см ± 1 мм, так как 0,1 см = 1 мм.
-
2
Всегда округляйте значения измерений до того же знака после запятой, что и в погрешности. Результаты измерений, которые учитывают погрешность, как правило, округляются до одной или двух значащих цифр. Наиболее важным моментом является то, что нужно округлить результаты до того же знака после запятой, что и в погрешности, чтобы сохранить соответствие.
- Если результат измерения 60 см, то и погрешность следует округлять до целого числа. Например, погрешность этого измерения может быть 60 см ± 2 см, но не 60 см ± 2,2 см.
- Если результат измерения 3,4 см, то погрешность округляется до 0,1 см. Например, погрешность этого измерения может быть 3,4 см ± 0,7 см, но не 3,4 см ± 1 см.
-
3
Найдите погрешность. Допустим, вы измеряете линейкой диаметр круглого шара. Это сложно, так как из-за кривизны шара будет трудно померить расстояние между двумя противоположными точками на его поверхности. Скажем, линейка может дать результат с точностью до 0,1 см, но это не значит, что вы можете измерить диаметр с той же точностью.[1]
- Изучите шар и линейку, чтобы получить представление о том, с какой точностью вы можете измерить диаметр. У стандартной линейки четко видна разметка по 0,5 см, но, возможно, вы сможете измерить диаметр с большей точностью, чем эта. Если вы думаете, что сможете измерить диаметр с точностью до 0,3 см, то погрешность в этом случае равна 0,3 см.
- Измерим диаметр шара. Допустим, вы получили результат около 7,6 см. Просто укажите результат измерения вместе с погрешностью. Диаметр шара составляет 7,6 см ± 0,3 см.
-
4
Рассчитайте погрешность измерения одного предмета из нескольких. Скажем, вам даны 10 компакт-дисков (CD), при этом размеры каждого одинаковы. Допустим, вы хотите найти толщину всего одного CD. Эта величина настолько мала, что погрешность практически невозможно вычислить. Тем не менее, чтобы вычислить толщину (и ее погрешность) одного CD, вы можете просто разделить результат измерения (и его погрешность) толщины всех 10 CD, сложенных вместе (один на другого), на общее количество CD.[2]
- Допустим, что точность измерения стопки CD с помощью линейки 0,2 см. Итак, ваша погрешность ± 0,2 см.
- Допустим, толщина всех CD равна 22 см.
- Теперь разделим результат измерения и погрешность на 10 (число всех CD). 22 см/10 = 2,2 см и 0,2 см/10 = 0,02 см. Это означает, что толщина одного компакт-диска 2,20 см ± 0,02 см.
-
5
Измерьте несколько раз. Для повышения точности измерений, будь то измерение длины или времени, замерьте искомую величину несколько раз. Вычисление среднего значения из полученных значений увеличит точность измерения и расчета погрешности.
Реклама
-
1
Проведите несколько измерений. Допустим, вы хотите найти, сколько времени падает мяч с высоты стола. Чтобы получить наилучшие результаты, измерьте время падения насколько раз, например, пять. Потом нужно найти среднее значение из пяти полученных значений измерений времени, а затем для наилучшего результата добавить или вычесть среднеквадратичное отклонение.[3]
- Допустим, в результате пяти измерений получены результаты: 0,43 с, 0,52 с, 0,35 с, 0,29 с и 0,49 с .
-
2
Найдите среднее арифметическое. Теперь найдите среднее арифметическое путем суммирования пяти различных результатов измерений и разделив результат на 5 (количество измерений). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 с. 2,08 / 5 = 0,42 с. Среднее время 0,42 с.
-
3
Найдите дисперсию полученных значений. Для этого, во-первых, найдите разницу между каждой из пяти величин и средним арифметическим. Чтобы сделать это, вычтите из каждого результата 0,42 с.[4]
-
- 0,43 с — 0,42 с = 0,01 с
- 0,52 с — 0,42 с = 0,1 с
- 0,35 с — 0,42 с = -0,07 с
- 0,29 с — 0,42 с = -0,13 с
- 0,49 с — 0,42 с = 0,07 с
- Теперь сложите квадраты этих разниц: (0,01) 2 + (0,1) 2 + (-0,07) 2 + (-0,13) 2 + (0,07) 2 = 0,037 с.
- Найти среднее арифметическое этой суммы можно, разделив ее на 5: 0,037 / 5 = 0,0074 с.
-
-
4
Найдите среднеквадратичное отклонение. Чтобы найти среднеквадратичное отклонение, просто возьмите квадратный корень из среднего арифметического суммы квадратов. Квадратный корень из 0,0074 = 0,09 с, так что среднеквадратичное отклонение равно 0,09 с.[5]
-
5
Запишите окончательный ответ. Чтобы сделать это, запишите среднее значение всех измерений плюс-минус среднеквадратичное отклонение. Поскольку среднее значение всех измерений равно 0,42 с, а среднеквадратичное отклонение 0,09 с, то окончательный ответ 0,42 с ± 0,09 с.
Реклама
-
1
Сложение. Чтобы сложить величины с погрешностями, сложите отдельно величины и отдельно погрешности.[6]
- (5 см ± 0,2 см) + (3 см ± 0,1 см) =
- (5 см + 3 см) ± (0,2 см + 0,1 см) =
- 8 см ± 0,3 см
-
2
Вычитание. Чтобы вычесть величины с погрешностями, вычтите величины и сложите погрешности.[7]
- (10 см ± 0,4 см) — (3 см ± 0,2 см) =
- (10 см — 3 см) ± (0,4 см + 0,2 см) =
- 7 см ± 0,6 см
-
3
Умножение. Чтобы умножить величины с погрешностями, перемножьте величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности (в процентах).[8]
Рассчитать можно только относительную погрешность, а не абсолютную, как и в случае со сложением и вычитанием. Чтобы узнать относительную погрешность, разделите абсолютную погрешность на измеренное значение, затем умножьте на 100, чтобы выразить результат в процентах. Например:- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
Следовательно: - (6 см ± 0,2 см) х (4 см ± 0,3 см) = (6 см ± 3,3 % ) x (4 см ± 7,5 %)
- (6 см x 4 см) ± (3,3 + 7,5) =
- 24 см ± 10,8 % = 24 см ± 2,6 см
- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
-
4
Деление. Чтобы разделить величины с погрешностями, разделите величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности.[9]
- (10 см ± 0,6 см) ÷ (5 см ± 0,2 см) = (10 см ± 6 %) ÷ (5 см ± 4 %)
- (10 см ÷ 5 см) ± (6 % + 4 %) =
- 2 см ± 10 % = 2 см ± 0,2 см
-
5
Возведение в степень. Для того, чтобы возвести в степень величину с погрешностью, возведите величину в степень, а относительную погрешность умножьте на степень.[10]
- (2,0 см ± 1,0 см)3 =
- (2,0 см)3 ± (50 %) x 3 =
- 8,0 см3 ± 150 % или 8,0 см3 ±12 см3
Реклама
Советы
- Вы можете дать погрешность как для общего результата всех измерений, так и для каждого результата одного измерения в отдельности. Как правило, данные, полученные из нескольких измерений, менее достоверны, чем данные, полученные непосредственно из отдельных измерений.
Реклама
Предупреждения
- Точные науки никогда не работают с «истинными» величинами. Хотя правильное измерение, скорее всего, даст величину в пределах погрешности, нет никакой гарантии, что это будет так. Научные измерения допускают возможность ошибок.
- Погрешности, описанные здесь, применимы только для случаев нормального распределения (распределения Гаусса). Другие распределения вероятностей требуют других решений.
Реклама
Об этой статье
Эту страницу просматривали 107 472 раза.
Была ли эта статья полезной?
Расчет погрешностей прямых измерений
Систематические
погрешности.
Систематические ошибки закономерным
образом изменяют значения измеряемой
величины. Наиболее просто поддаются
оценке погрешности, вносимые в
измерения
приборами, если они связаны с конструктивными
особенностями самих приборов. Эти
погрешности указываются в паспортах к
приборам. Погрешности некоторых приборов
можно оценить и не обращаясь к паспорту.
Для многих электроизмерительных приборов
непосредственно на шкале указан
их класс
точности.
Класс
точности прибора
– это отношение абсолютной погрешности
прибора
к максимальному значению измеряемой
величины
,
которое можно определить с помощью
данного прибора (это систематическая
относительная погрешность данного
прибора, выраженная в процентах от
номинала шкалы
).
.
Тогда
абсолютная погрешность
такого прибора определяется соотношением:
.
Для
электроизмерительных приборов введено
8 классов точности: 0,05; 0,1; 0,5; 1,0; 1,5; 2,0;
2,5; 4.
Чем
ближе измеряемая величина к номиналу,
тем более точным будет результат
измерения. Максимальная точность (т.е.
наименьшая относительная ошибка),
которую может обеспечить данный прибор,
равна классу точности. Это обстоятельство
необходимо учитывать при использовании
многошкальных приборов. Шкалу надо
выбирать с таким расчетом, чтобы
измеряемая величина, оставаясь в пределах
шкалы, была как можно ближе к номиналу.
Если
класс точности для прибора не указан,
то необходимо руководствоваться
следующими правилами:
-
Абсолютная
погрешность приборов с нониусом равна
точности нониуса. -
Абсолютная
погрешность приборов с фиксированным
шагом стрелки равна цене деления1. -
Абсолютная
погрешность цифровых приборов равна
единице минимального разряда. -
Для
всех остальных приборов абсолютная
погрешность принимается равной половине
цены деления.
Случайные
погрешности.
Эти погрешности имеют статистический
характер и описываются теорией
вероятности. Установлено, что при очень
большом количестве измерений вероятность
получить тот или иной результат в каждом
отдельном измерении можно определить
при помощи нормального распределения
Гаусса. При малом числе измерений
математическое описание вероятности
получения того или иного результата
измерения называется распределением
Стьюдента (более подробно об этом можно
прочитать в пособии Скворцовой И.Л.
«Ошибки измерений физических величин»).
Как
же оценить истинное значение измеряемой
величины?
Пусть
при измерении некоторой величины
мы получили N
результатов:
.
Среднее арифметическое серии измерений
ближе к истинному значению измеряемой
величины, чем большинство отдельных
измерений. Для получения результата
измерения некоторой величины
используется следующий алгоритм.
1).
Вычисляется
среднее арифметическое
серии из N
прямых измерений:
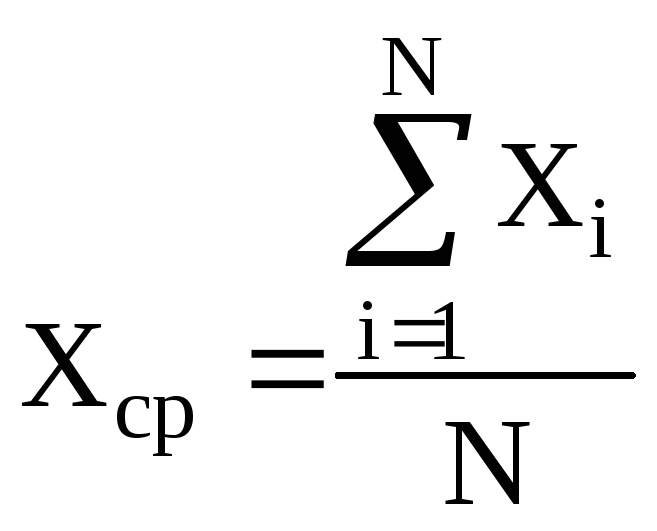
2).
Вычисляется абсолютная
случайная погрешность каждого измерения
– это разность между средним арифметическим
серии из N
прямых измерений и данным измерением:
.
3).
Вычисляется
средняя квадратичная абсолютная
погрешность
:
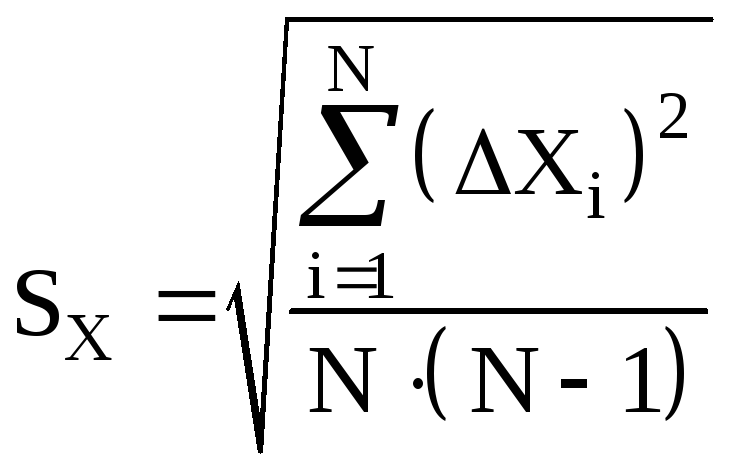
4).
Вычисляется
абсолютная
случайная погрешность
.
При
небольшом числе измерений абсолютную
случайную погрешность можно рассчитать
через среднюю квадратичную погрешность
и некоторый коэффициент
,
называемый коэффициентом Стъюдента:
,
Коэффициент
Стьюдента зависит от числа измерений
N
и коэффициента надежности
(в таблице 1 отражена зависимость
коэффициента Стьюдента от числа измерений
при фиксированном значении коэффициента
надежности
).
Коэффициент
надежности
– это вероятность, с которой истинное
значение
измеряемой величины попадает в
доверительный интервал.
Доверительный
интервал
– это числовой интервал, в который с
определенной вероятностью попадает
истинное значение измеряемой величины.
Таким
образом, коэффициент Стъюдента – это
число, на которое нужно умножить среднюю
квадратичную погрешность, чтобы при
данном числе измерений обеспечить
заданную надежность результата.
Чем
большую надежность необходимо обеспечить
для данного числа измерений, тем больше
коэффициент Стъюдента. С другой стороны,
чем больше число измерений, тем меньше
коэффициент Стъюдента при данной
надежности. В лабораторных работах
нашего практикума будем считать
надежность заданной и равной 0,9. Числовые
значения коэффициентов Стъюдента при
этой надежности для разного числа
измерений приведены в таблице 1.
Таблица
1
|
Число |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
… |
|
Коэффициент |
6,3 |
2,9 |
2,4 |
2,1 |
2,0 |
1,9 |
1,9 |
1,9 |
1,8 |
1,8 |
1,8 |
1,8 |
5).
Вычисляется
полная абсолютная погрешность.
При любых измерениях существуют и
случайные и систематические погрешности.
Расчет общей (полной) абсолютной
погрешности измерения дело непростое,
так как эти погрешности разной природы.
Для
инженерных измерений имеет смысл
суммировать систематическую и случайную
абсолютные погрешности
.
Для
простоты расчетов принято оценивать
полную абсолютную погрешность как сумму
абсолютной случайной и абсолютной
систематической (приборной) погрешностей,
если погрешности одного порядка величины,
и пренебрегать одной из погрешностей,
если она более
чем
на порядок (в 10 раз) меньше другой.
6).
Округляется погрешность и результат.
Поскольку результат измерений
представляется в виде интервала значений,
величину которого определяет полная
абсолютная погрешность, важное значение
имеет правильное округление результата
и погрешности.
Округление
начинают с абсолютной погрешности!!!
Число значащих цифр, которое оставляют
в значении погрешности, вообще говоря,
зависит от коэффициента надежности и
числа измерений. Однако даже для очень
точных измерений (например, астрономических),
в которых точное значение погрешности
важно, не оставляют более двух значащих
цифр. Бóльшее число цифр не имеет смысла,
так как определение погрешности само
имеет свою погрешность. В
нашем практикуме сравнительно небольшой
коэффициент надежности
и малое число измерений. Поэтому при
округлении (с избытком) полной абсолютной
погрешности оставляют одну значащую
цифру.
Разряд
значащей цифры абсолоютной погрешности
определяет разряд первой сомнительной
цифры в
значении
результата. Следовательно, само значение
результата нужно округлять (с поправкой)
до той значащей цифры, разряд которой
совпадает с разрядом значащей цифры
погрешности.
Сформулированное правило следует
применять и в тех случаях, когда некоторые
из цифр являются нулями.
Пример.
Если
при измерении массы тела получен
результат
,
то писать нули в конце числа 0,900 необходимо.
Запись
означала бы, что о следующих значащих
цифрах ничего не известно, в то время
как измерения показали, что они равны
нулю.
7).
Вычисляется
относительная
погрешность
.
.
При
округлении относительной погрешности
достаточно оставить две значащие цифры.
результат
серии измерений некоторой физической
величины представляют в виде интервала
значений с указанием вероятности
попадания истинного значения в данный
интервал, то
есть результат необходимо записать в
виде:
;
;
.
Здесь
– полная, округленная до первой значащей
цифры, абсолютная погрешность и
– округленное с учетом уже округленной
погрешности среднее значение измеряемой
величины. При
записи результата измерений обязательно
нужно указать единицу измерения величины.
Рассмотрим
несколько примеров:
-
Пусть
при измерении длины отрезка мы получили
следующий результат:
см и
см. Как грамотно записать результат
измерений длины отрезка? Сначала
округляем с избытком абсолютную
погрешность, оставляя одну значащую
цифру
см. Значащая цифра погрешности в разряде
сотых. Затем округляем с поправкой
среднее значение с точностью до сотых,
т.е. до той значащей цифры, разряд которой
совпадает с разрядом значащей цифры
погрешности
см. Вычисляем относительную погрешность
.
Результат
измерений записываем так:
см;
;
.
-
Пусть
при расчете сопротивления проводника
мы получили следующий результат:
и
.
Сначала округляем абсолютную погрешность,
оставляя одну значащую цифру
.
Затем округляем среднее значение с
точностью до целых
.
Вычисляем относительную погрешность
.
Результат
измерений записываем так:
;
;
.
-
Пусть
при расчете массы груза мы получили
следующий результат:
кг и
кг. Сначала округляем абсолютную
погрешность, оставляя одну значащую
цифру
кг. Затем округляем среднее значение
с точностью до десятков
кг. Вычисляем относительную погрешность
.
Результат
измерений массы груза записываем так:
кг; ;
.
Из
приведенных примеров видно, что округление
абсолютной погрешности производится
до первой значащей цифры в сторону
увеличения (с избытком). Среднее значение
измеряемой величины округляется с
поправкой до той значащей цифры, разряд
которой совпадает с разрядом значащей
цифры погрешности. При округлении
относительной погрешности оставляем
две значащие цифры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
А какая ваша оценка?
Вычисление погрешностей измерений
Выполнение лабораторных работ связано с измерением физических величин, т. е. определением значений величин опытным путём с помощью измерительных приборов (средств измерения), и обработкой результатов измерений.
Различают прямые и косвенные измерения. При этом результат любого измерения является приблизительным, т. е. содержит погрешность измерения. Точность измерения физической величины характеризуют абсолютная и относительная погрешности.
Прямое измерение — определение значения физической величины непосредственно с помощью измерительного прибора.
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δиx + Δоx при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Абсолютная инструментальная погрешность Δиx связана с классом точности прибора. Абсолютные инструментальные погрешности некоторых средств измерений представлены в таблице 1.
| Средства измерений | Диапазон измерений | Абсолютная инструментальная погрешность |
| Линейки: металлические деревянные пластмассовые |
150, 300, 500 мм 400, 500, 750 мм 200, 250, 300 мм |
0,1 мм 0,5 мм 1 мм |
| Лента измерительная | 150 см | 0,5 см |
| Мензурки 2-го класса | 100, 200, 250 см3 | 5 см3 |
| Амперметр школьный | 2 А | 0,05 А |
| Миллиамперметр | от 0 до Imax | 4 % максимального предела измерений Imax |
| Вольтметр школьный | 6 В | 0,15 В |
| Термометр лабораторный | 100 °С | 1 °С |
| Барометр-анероид | 720–780 мм рт. ст. | 3 мм рт. ст. |
| Штангенциркули с ценой деления 0,1; 0,05 мм | 155, 250, 350 мм | 0,1; 0,05 мм в соответствии с ценой деления нониуса |
| Микрометры с ценой деления 0,01 мм | 0–25, 25–50, 50–75 мм | 0,004 мм |
Абсолютная погрешность отсчёта Δоx связана с дискретностью шкалы прибора. Если величину измеряют с точностью до целого деления шкалы прибора, то погрешность отсчёта принимают равной цене деления. Если при измерении значение величины округляют до половины деления шкалы, то погрешность отсчёта принимают равной половине цены деления.
Абсолютная погрешность определяет значение интервала, в котором лежит истинное значение измеренной величины:
Относительную погрешность прямого измерения определяют отношением абсолютной погрешности к значению измеряемой величины:
Относительная погрешность характеризует точность измерения: чем она меньше, тем точность измерения выше.
Косвенное измерение — определение значения физической величины с использованием формулы, связывающей её с другими величинами, измеренными непосредственно с помощью приборов.
Одним из методов определения погрешности косвенных измерений является метод границ погрешностей. Формулы для вычисления абсолютных и относительных погрешностей косвенных измерений методом границ погрешностей представлены в таблице 2.
| Вид функции y | Абсолютная погрешность Δy | Относительная погрешность |
| x1 + x2 | Δx1 + Δx2 | |
| x1 − x2 | Δx1 + Δx2 | |
| Cx | CΔx | |
| x1x2 | |x1| Δx2 + |x2| Δx1 | |
| xn | |n||x|n−1Δx | |
| lnx | ||
| sinx | |cosx| Δx | |
| cosx | |sinx| Δx | |tgx| Δx |
| tgx |
Абсолютную погрешность табличных величин и фундаментальных физических постоянных определяют как половину единицы последнего разряда значения величины.
Статья обновлена 10.07.2022
Что такое погрешность измерения
Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.
- Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
- Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.
Математическая погрешность: формула для каждого типа
Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?
Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.
Формулы погрешностей вычисляются следующим образом.
Абсолютная погрешность измерений: формула
Формула дает разницу между измеренным и реальным значением.

Относительная погрешность: формула
Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Приведенная погрешность: формула
Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

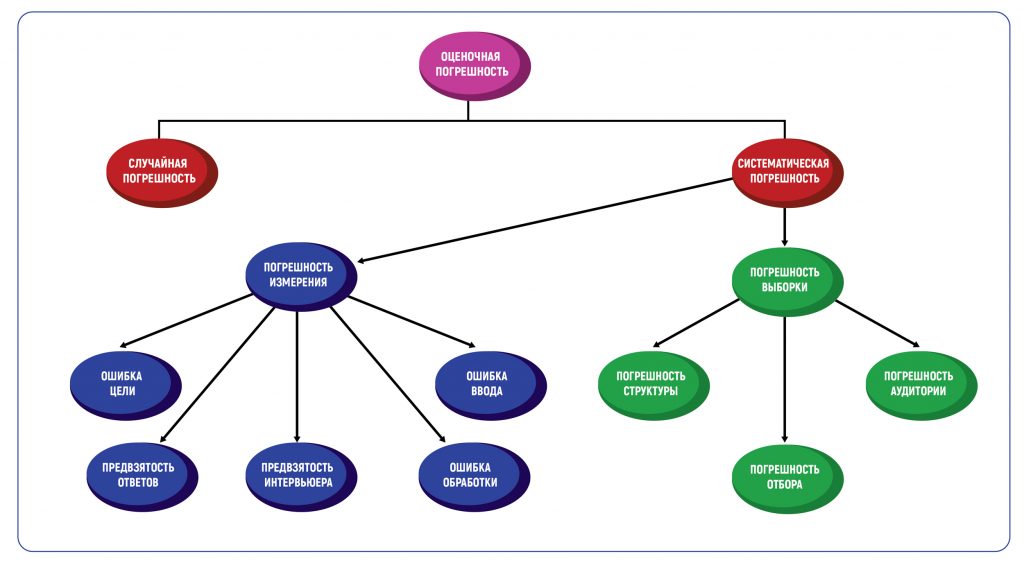
Классификация оценочной погрешности
Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.
Что такое случайная погрешность
Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.
Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.
Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.
Что такое систематическая погрешность
Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.
В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.
Погрешность выборки
Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.
Погрешность структуры
Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.
Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.
Погрешность аудитории
Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.
Погрешность отбора
Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.
Как минимизировать погрешность выборки
- Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам. - Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию. - Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.
Погрешность измерения
Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.
К погрешностям измерения приводят следующие виды ошибок.
Ошибка цели
Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.
Предвзятость ответов
Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.
Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.
Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.
Предвзятость интервьюера
Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.
Ошибка обработки
Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.
Ошибка ввода
Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.
Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.
Как минимизировать погрешность измерения
- Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью. - Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка. - Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования. - Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.
Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.
















