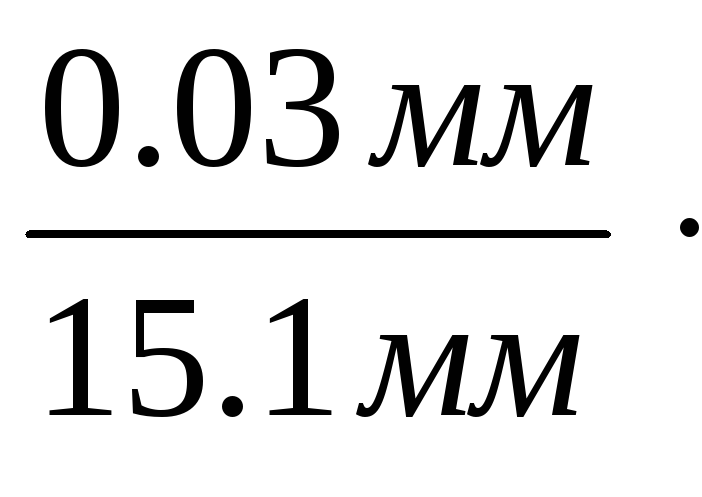Загрузить PDF
Загрузить PDF
При измерении чего-либо можно предположить, что есть некоторое «истинное значение», которое лежит в пределах диапазона значений, которые вы нашли. Для расчета более точной величины нужно взять результат измерения и оценить его при прибавлении или вычитании погрешности. Если вы хотите научиться находить такую погрешность, выполните следующие действия.
-
1
Выражайте погрешность правильно. Допустим, при измерении палки ее длина равна 4,2 см плюс-минус один миллиметр. Это означает, что палка примерно равна 4,2 см, но на самом деле может быть немного меньше или больше этого значения — с погрешностью до одного миллиметра.
- Запишите погрешность как: 4,2 см ± 0,1 см. Вы также можете переписать это как 4,2 см ± 1 мм, так как 0,1 см = 1 мм.
-
2
Всегда округляйте значения измерений до того же знака после запятой, что и в погрешности. Результаты измерений, которые учитывают погрешность, как правило, округляются до одной или двух значащих цифр. Наиболее важным моментом является то, что нужно округлить результаты до того же знака после запятой, что и в погрешности, чтобы сохранить соответствие.
- Если результат измерения 60 см, то и погрешность следует округлять до целого числа. Например, погрешность этого измерения может быть 60 см ± 2 см, но не 60 см ± 2,2 см.
- Если результат измерения 3,4 см, то погрешность округляется до 0,1 см. Например, погрешность этого измерения может быть 3,4 см ± 0,7 см, но не 3,4 см ± 1 см.
-
3
Найдите погрешность. Допустим, вы измеряете линейкой диаметр круглого шара. Это сложно, так как из-за кривизны шара будет трудно померить расстояние между двумя противоположными точками на его поверхности. Скажем, линейка может дать результат с точностью до 0,1 см, но это не значит, что вы можете измерить диаметр с той же точностью.[1]
- Изучите шар и линейку, чтобы получить представление о том, с какой точностью вы можете измерить диаметр. У стандартной линейки четко видна разметка по 0,5 см, но, возможно, вы сможете измерить диаметр с большей точностью, чем эта. Если вы думаете, что сможете измерить диаметр с точностью до 0,3 см, то погрешность в этом случае равна 0,3 см.
- Измерим диаметр шара. Допустим, вы получили результат около 7,6 см. Просто укажите результат измерения вместе с погрешностью. Диаметр шара составляет 7,6 см ± 0,3 см.
-
4
Рассчитайте погрешность измерения одного предмета из нескольких. Скажем, вам даны 10 компакт-дисков (CD), при этом размеры каждого одинаковы. Допустим, вы хотите найти толщину всего одного CD. Эта величина настолько мала, что погрешность практически невозможно вычислить. Тем не менее, чтобы вычислить толщину (и ее погрешность) одного CD, вы можете просто разделить результат измерения (и его погрешность) толщины всех 10 CD, сложенных вместе (один на другого), на общее количество CD.[2]
- Допустим, что точность измерения стопки CD с помощью линейки 0,2 см. Итак, ваша погрешность ± 0,2 см.
- Допустим, толщина всех CD равна 22 см.
- Теперь разделим результат измерения и погрешность на 10 (число всех CD). 22 см/10 = 2,2 см и 0,2 см/10 = 0,02 см. Это означает, что толщина одного компакт-диска 2,20 см ± 0,02 см.
-
5
Измерьте несколько раз. Для повышения точности измерений, будь то измерение длины или времени, замерьте искомую величину несколько раз. Вычисление среднего значения из полученных значений увеличит точность измерения и расчета погрешности.
Реклама
-
1
Проведите несколько измерений. Допустим, вы хотите найти, сколько времени падает мяч с высоты стола. Чтобы получить наилучшие результаты, измерьте время падения насколько раз, например, пять. Потом нужно найти среднее значение из пяти полученных значений измерений времени, а затем для наилучшего результата добавить или вычесть среднеквадратичное отклонение.[3]
- Допустим, в результате пяти измерений получены результаты: 0,43 с, 0,52 с, 0,35 с, 0,29 с и 0,49 с .
-
2
Найдите среднее арифметическое. Теперь найдите среднее арифметическое путем суммирования пяти различных результатов измерений и разделив результат на 5 (количество измерений). 0,43 + 0,52 + 0,35 + 0,29 + 0,49 = 2,08 с. 2,08 / 5 = 0,42 с. Среднее время 0,42 с.
-
3
Найдите дисперсию полученных значений. Для этого, во-первых, найдите разницу между каждой из пяти величин и средним арифметическим. Чтобы сделать это, вычтите из каждого результата 0,42 с.[4]
-
- 0,43 с — 0,42 с = 0,01 с
- 0,52 с — 0,42 с = 0,1 с
- 0,35 с — 0,42 с = -0,07 с
- 0,29 с — 0,42 с = -0,13 с
- 0,49 с — 0,42 с = 0,07 с
- Теперь сложите квадраты этих разниц: (0,01) 2 + (0,1) 2 + (-0,07) 2 + (-0,13) 2 + (0,07) 2 = 0,037 с.
- Найти среднее арифметическое этой суммы можно, разделив ее на 5: 0,037 / 5 = 0,0074 с.
-
-
4
Найдите среднеквадратичное отклонение. Чтобы найти среднеквадратичное отклонение, просто возьмите квадратный корень из среднего арифметического суммы квадратов. Квадратный корень из 0,0074 = 0,09 с, так что среднеквадратичное отклонение равно 0,09 с.[5]
-
5
Запишите окончательный ответ. Чтобы сделать это, запишите среднее значение всех измерений плюс-минус среднеквадратичное отклонение. Поскольку среднее значение всех измерений равно 0,42 с, а среднеквадратичное отклонение 0,09 с, то окончательный ответ 0,42 с ± 0,09 с.
Реклама
-
1
Сложение. Чтобы сложить величины с погрешностями, сложите отдельно величины и отдельно погрешности.[6]
- (5 см ± 0,2 см) + (3 см ± 0,1 см) =
- (5 см + 3 см) ± (0,2 см + 0,1 см) =
- 8 см ± 0,3 см
-
2
Вычитание. Чтобы вычесть величины с погрешностями, вычтите величины и сложите погрешности.[7]
- (10 см ± 0,4 см) — (3 см ± 0,2 см) =
- (10 см — 3 см) ± (0,4 см + 0,2 см) =
- 7 см ± 0,6 см
-
3
Умножение. Чтобы умножить величины с погрешностями, перемножьте величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности (в процентах).[8]
Рассчитать можно только относительную погрешность, а не абсолютную, как и в случае со сложением и вычитанием. Чтобы узнать относительную погрешность, разделите абсолютную погрешность на измеренное значение, затем умножьте на 100, чтобы выразить результат в процентах. Например:- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
Следовательно: - (6 см ± 0,2 см) х (4 см ± 0,3 см) = (6 см ± 3,3 % ) x (4 см ± 7,5 %)
- (6 см x 4 см) ± (3,3 + 7,5) =
- 24 см ± 10,8 % = 24 см ± 2,6 см
- (6 см ± 0,2 см) = (0,2 / 6) x 100 — добавив знак процента, получаем 3,3 %.
-
4
Деление. Чтобы разделить величины с погрешностями, разделите величины и сложите ОТНОСИТЕЛЬНЫЕ погрешности.[9]
- (10 см ± 0,6 см) ÷ (5 см ± 0,2 см) = (10 см ± 6 %) ÷ (5 см ± 4 %)
- (10 см ÷ 5 см) ± (6 % + 4 %) =
- 2 см ± 10 % = 2 см ± 0,2 см
-
5
Возведение в степень. Для того, чтобы возвести в степень величину с погрешностью, возведите величину в степень, а относительную погрешность умножьте на степень.[10]
- (2,0 см ± 1,0 см)3 =
- (2,0 см)3 ± (50 %) x 3 =
- 8,0 см3 ± 150 % или 8,0 см3 ±12 см3
Реклама
Советы
- Вы можете дать погрешность как для общего результата всех измерений, так и для каждого результата одного измерения в отдельности. Как правило, данные, полученные из нескольких измерений, менее достоверны, чем данные, полученные непосредственно из отдельных измерений.
Реклама
Предупреждения
- Точные науки никогда не работают с «истинными» величинами. Хотя правильное измерение, скорее всего, даст величину в пределах погрешности, нет никакой гарантии, что это будет так. Научные измерения допускают возможность ошибок.
- Погрешности, описанные здесь, применимы только для случаев нормального распределения (распределения Гаусса). Другие распределения вероятностей требуют других решений.
Реклама
Об этой статье
Эту страницу просматривали 107 472 раза.
Была ли эта статья полезной?
Вычисление абсолютной и относительной погрешностей измерений при прямых измерениях
1. Абсолютная погрешность
Оценить отклонение
каждого из результатов измерения от
истинной величины можно лишь при наличии
данных большого числа измерений с
использованием теории вероятности.
Однако на практике, в лабораторных
условиях проводят 3-5 измерений. В этом
случае абсолютная погрешность отдельного
i-го
измерения будет следующей:
|DАi|
= |АСР
— Аi|,
где
АСР
— средняя величина размера А. Средняя
арифметическая величина всех ½DАi½
значений
называется
абсолютной погрешностью опыта.
Окончательный результат измерения
может быть записан в виде
А = АСР
±
DАСР,
где
А — искомая величина, которая лежит
внутри интервала
АСР
±
DАСР.
Н
14
апример, если сделаем несколько
измерений длины заготовки в столярной
мастерской и получим среднее значение
lСР
= 75.5 см, а среднее
арифметическое абсолютной погрешности
lСР
= 0.3 см, то результат
запишется в виде
l
= (75.5 ± 0.3) см.
Это
означает, что истинное значение длины
заготовки лежит в интервале от 75.2 см до
75.8 см. При этом не имеет смысла вычислять
среднее значение с большим числом знаков
после запятой, так как от этого точность
не увеличивается.
2. Относительная погрешность
Абсолютная
погрешность измерения не характеризует
точности проведенных измерений. Поэтому
для того, чтобы сравнить точность
различных измерений и величин разной
размерности, находят среднюю относительную
погрешность результата (ЕА).
Относительная погрешность определяется
отношением абсолютной погрешности к
среднему арифметическому значению
измеряемой величины, которая определяется
в процентах:
ЕА=
100%.
Относительная
погрешность показывает, какая часть
абсолютной погрешности приходится на
каждую единицу измеренной величины.
Это дает возможность оценить точность
проведенных измерений, качество работы.
Так,
например, пусть при измерении бруска
длиной l
= 1.51 см была допущена абсолютная
погрешность 0.03 мм, а при измерении
расстояния от Земли до Луны L
= 3.64.105
км абсолютная погрешность составила
100 км. Может показаться, что первое
измерение выполнено намного точнее
второго. Однако о точности измерения
можно судить по относительной погрешности,
а она показывает, что второе измерение
было выполнено в семь раз точнее первого:
El
=
100% = 0.2%
и
ЕL
=
100%
= 0.03%.
Вычисление абсолютных и относительных погрешностей при косвенных2 измерениях
В
большинстве случаев при выполнении
физических экспериментов исследуемая
величина не может быть измерена
непосредственно, а является функцией
одной или нескольких переменных,
измеренных непосредственно. При косвенных
измерениях абсолютная и относительная
погрешности результатов измерений
находятся вычислением через абсолютные
и относительные погрешности непосредственно
измеренных величин.
Использование формул дифференцирования
Для
определения абсолютных и относительных
погрешностей искомой величины при
косвенных измерениях можно воспользоваться
формулами дифференцирования, потому
что абсолютная ошибка функции равна
абсолютной ошибке аргумента, умноженной
на производную этой функции, то есть
полному дифференциалу функции.
Рассмотрим
это более подробно. Допустим, что
физическая величина А является функцией
многих переменных:
A
= f
(x,
y,
z
…).
Правило
I. Вначале
находят абсолютную погрешность величины
А, а затем относительную погрешность.
Для этого необходимо:
1) Найти полный
дифференциал функции
.
2
16
) Заменить бесконечно малые dx, dу,
dz, … соответствующими абсолютными
ошибками аргументовDx,
Dy,
Dz,
… (при этом знаки «минус» в абсолютных
ошибках аргументов заменяют знаками
«плюс», так чтобы величина ошибки
была максимальной):
.
Применяя
это правило к частным случаям, получим:
—
абсолютная погрешность суммы равна
сумме абсолютных погрешностей слагаемых.
Если X
= a
+ b,
то DX
= Da
+ Db;
—
абсолютная погрешность разности равна
сумме абсолютных погрешностей
уменьшаемого и вычитаемого. Если X
= a
— b,
то DX
= Da
+ Db;
—
абсолютная погрешность произведения
двух сомножителей равна сумме произведений
среднего значения первого множителя
(aCP)
на абсолютную погрешность второго и
среднего значения второго множителя
(bCP)
на абсолютную погрешность первого. Если
X
= а
b,
то DX
= aCP
Db
+ bCP
Dа.
Если X
= a n
, то DX
= n
аCPn-1
Dа;
—
абсолютная погрешность дроби равна
сумме произведения знаменателя на
абсолютную погрешность числителя и
числителя на абсолютную погрешность
знаменателя, деленной на квадрат
знаменателя. Если X
=
,
то DX=
.
3) По определению
найдем относительную погрешность
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
12.02.2015183.3 Кб27Пример работы по теме ПЕРЕСКАЗ.doc
- #
Абсолютная и относительная погрешность
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
А какая ваша оценка?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе.
Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована (эталоны).
Обрати внимание!
Процесс измерения физической величины состоит из:
1) поиска её значения с помощью опытов и средств измерения;
2) вычисления достоверности (точности измерений) полученного значения.
Точность измерений зависит от многих причин:
- расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;
- деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;
- несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;
- физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой.
Рис. \(1\). Линейка и брусок
Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет \(1\) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между \(9\) и \(10\) метками.
У нас есть два варианта определения длины этого бруска.
\(1\). Если мы заявим, что длина бруска — \(9\) сантиметров, то недостаток длины от истинной составит более половины сантиметра (\(0,5\) см \(= 5\) мм).
\(2\). Если мы заявим, что длина бруска — \(10\) сантиметров, то избыток длины от истинной составит менее половины сантиметра (\(0,5\) см \(= 5\) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного.
Погрешность измерительного прибора равна цене деления прибора.
Для первой линейки цена деления составляет \(1\) сантиметр. Значит, погрешность этой линейки \(1\) см.
Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. В этом случае цена деления будет равна \(1\) мм, а длина бруска — \(9,8\) см.
Рис. \(2\). Деревянная линейка
Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления \(0,1\) мм и \(0,05\) мм.
Рис. \(3\). Штангенциркуль
На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений.
Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
Результаты измерения записывают в виде
A=a±Δa
, где \(A\) — измеряемая величина, \(a\) — средний результат полученных измерений,
Δa
— абсолютная погрешность измерений.
Источники:
Рис. 1. Линейка и брусок. © ЯКласс.