Ошибка экстраполяции формула - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

In mathematics, extrapolation is a type of estimation, beyond the original observation range, of the value of a variable on the basis of its relationship with another variable. It is similar to interpolation, which produces estimates between known observations, but extrapolation is subject to greater uncertainty and a higher risk of producing meaningless results. Extrapolation may also mean extension of a method, assuming similar methods will be applicable. Extrapolation may also apply to human experience to project, extend, or expand known experience into an area not known or previously experienced so as to arrive at a (usually conjectural) knowledge of the unknown^[1] (e.g. a driver extrapolates road conditions beyond his sight while driving). The extrapolation method can be applied in the interior reconstruction problem.

Example illustration of the extrapolation problem, consisting of assigning a meaningful value at the blue box, at x=7

, given the red data points

Methods[edit]

A sound choice of which extrapolation method to apply relies on a priori knowledge of the process that created the existing data points. Some experts have proposed the use of causal forces in the evaluation of extrapolation methods.^[2] Crucial questions are, for example, if the data can be assumed to be continuous, smooth, possibly periodic, etc.

Linear[edit]

Linear extrapolation means creating a tangent line at the end of the known data and extending it beyond that limit. Linear extrapolation will only provide good results when used to extend the graph of an approximately linear function or not too far beyond the known data.

If the two data points nearest the point x_* to be extrapolated are $(x_{{k-1}},y_{{k-1}})$ and $(x_{k},y_{k})$ , linear extrapolation gives the function:

$y(x_{*})=y_{{k-1}}+{\frac {x_{*}-x_{{k-1}}}{x_{{k}}-x_{{k-1}}}}(y_{{k}}-y_{{k-1}}).$

(which is identical to linear interpolation if $x_{{k-1}}<x_{*}<x_{k}$ ). It is possible to include more than two points, and averaging the slope of the linear interpolant, by regression-like techniques, on the data points chosen to be included. This is similar to linear prediction.

Polynomial[edit]

Lagrange extrapolations of the sequence 1,2,3. Extrapolating by 4 leads to a polynomial of minimal degree (cyan line).

A polynomial curve can be created through the entire known data or just near the end (two points for linear extrapolation, three points for quadratic extrapolation, etc.). The resulting curve can then be extended beyond the end of the known data. Polynomial extrapolation is typically done by means of Lagrange interpolation or using Newton’s method of finite differences to create a Newton series that fits the data. The resulting polynomial may be used to extrapolate the data.

High-order polynomial extrapolation must be used with due care. For the example data set and problem in the figure above, anything above order 1 (linear extrapolation) will possibly yield unusable values; an error estimate of the extrapolated value will grow with the degree of the polynomial extrapolation. This is related to Runge’s phenomenon.

Conic[edit]

A conic section can be created using five points near the end of the known data. If the conic section created is an ellipse or circle, when extrapolated it will loop back and rejoin itself. An extrapolated parabola or hyperbola will not rejoin itself, but may curve back relative to the X-axis. This type of extrapolation could be done with a conic sections template (on paper) or with a computer.

French curve[edit]

French curve extrapolation is a method suitable for any distribution that has a tendency to be exponential, but with accelerating or decelerating factors.^[3] This method has been used successfully in providing forecast projections of the growth of HIV/AIDS in the UK since 1987 and variant CJD in the UK for a number of years. Another study has shown that extrapolation can produce the same quality of forecasting results as more complex forecasting strategies.^[4]

[edit]

Can be created with 3 points of a sequence and the «moment» or «index», this type of extrapolation have 100% accuracy in predictions in a big percentage of known series database (OEIS).^[5]

Example of extrapolation with error prediction :

sequence = [1,2,3,5]

f1(x,y) = (x) / y

d1 = f1 (3,2)

d2 = f1 (5,3)

m = last sequence (5)

n = last $ last sequence

fnos (m,n,d1,d2) = round ( ( ( n * d1 ) — m ) + ( m * d2 ) )

round $ ((3*1.66)-5) + (5*1.6) = 8

Quality[edit]

Typically, the quality of a particular method of extrapolation is limited by the assumptions about the function made by the method. If the method assumes the data are smooth, then a non-smooth function will be poorly extrapolated.

In terms of complex time series, some experts have discovered that extrapolation is more accurate when performed through the decomposition of causal forces.^[6]

Even for proper assumptions about the function, the extrapolation can diverge severely from the function. The classic example is truncated power series representations of sin(x) and related trigonometric functions. For instance, taking only data from near the x = 0, we may estimate that the function behaves as sin(x) ~ x. In the neighborhood of x = 0, this is an excellent estimate. Away from x = 0 however, the extrapolation moves arbitrarily away from the x-axis while sin(x) remains in the interval [−1, 1]. I.e., the error increases without bound.

Taking more terms in the power series of sin(x) around x = 0 will produce better agreement over a larger interval near x = 0, but will produce extrapolations that eventually diverge away from the x-axis even faster than the linear approximation.

This divergence is a specific property of extrapolation methods and is only circumvented when the functional forms assumed by the extrapolation method (inadvertently or intentionally due to additional information) accurately represent the nature of the function being extrapolated. For particular problems, this additional information may be available, but in the general case, it is impossible to satisfy all possible function behaviors with a workably small set of potential behavior.

In the complex plane[edit]

In complex analysis, a problem of extrapolation may be converted into an interpolation problem by the change of variable ${\hat {z}}=1/z$ . This transform exchanges the part of the complex plane inside the unit circle with the part of the complex plane outside of the unit circle. In particular, the compactification point at infinity is mapped to the origin and vice versa. Care must be taken with this transform however, since the original function may have had «features», for example poles and other singularities, at infinity that were not evident from the sampled data.

Another problem of extrapolation is loosely related to the problem of analytic continuation, where (typically) a power series representation of a function is expanded at one of its points of convergence to produce a power series with a larger radius of convergence. In effect, a set of data from a small region is used to extrapolate a function onto a larger region.

Again, analytic continuation can be thwarted by function features that were not evident from the initial data.

Also, one may use sequence transformations like Padé approximants and Levin-type sequence transformations as extrapolation methods that lead to a summation of power series that are divergent outside the original radius of convergence. In this case, one often obtains
rational approximants.

Fast[edit]

The extrapolated data often convolute to a kernel function. After data is extrapolated, the size of data is increased N times, here N is approximately 2–3. If this data needs to be convoluted to a known kernel function, the numerical calculations will increase N log(N) times even with fast Fourier transform (FFT). There exists an algorithm, it analytically calculates the contribution from the part of the extrapolated data. The calculation time can be omitted compared with the original convolution calculation. Hence with this algorithm the calculations of a convolution using the extrapolated data is nearly not increased. This is referred as the fast extrapolation. The fast extrapolation has been applied to CT image reconstruction.^[7]

[edit]

Extrapolation arguments are informal and unquantified arguments which assert that something is probably true beyond the range of values for which it is known to be true. For example, we believe in the reality of what we see through magnifying glasses because it agrees with what we see with the naked eye but extends beyond it; we believe in what we see through light microscopes because it agrees with what we see through magnifying glasses but extends beyond it; and similarly for electron microscopes. Such arguments are widely used in biology in extrapolating from animal studies to humans and from pilot studies to a broader population.^[8]

Like slippery slope arguments, extrapolation arguments may be strong or weak depending on such factors as how far the extrapolation goes beyond the known range.^[9]

Notes[edit]

^ Extrapolation, entry at Merriam–Webster
^ J. Scott Armstrong; Fred Collopy (1993). «Causal Forces: Structuring Knowledge for Time-series Extrapolation». Journal of Forecasting. 12 (2): 103–115. CiteSeerX 10.1.1.42.40. doi:10.1002/for.3980120205. S2CID 3233162. Retrieved 2012-01-10.
^ AIDSCJDUK.info Main Index
^ J. Scott Armstrong (1984). «Forecasting by Extrapolation: Conclusions from Twenty-Five Years of Research». Interfaces. 14 (6): 52–66. CiteSeerX 10.1.1.715.6481. doi:10.1287/inte.14.6.52. S2CID 5805521. Retrieved 2012-01-10.
^ V. Nos (2021). «Probnet: Geometric Extrapolation of Integer Sequences with error prediction». Retrieved 2023-03-14.
^ J. Scott Armstrong; Fred Collopy; J. Thomas Yokum (2004). «Decomposition by Causal Forces: A Procedure for Forecasting Complex Time Series».
^ Shuangren Zhao; Kang Yang; Xintie Yang (2011). «Reconstruction from truncated projections using mixed extrapolations of exponential and quadratic functions» (PDF). Journal of X-Ray Science and Technology. 19 (2): 155–72. doi:10.3233/XST-2011-0284. PMID 21606580. Archived from the original (PDF) on 2017-09-29. Retrieved 2014-06-03.
^ Steel, Daniel (2007). Across the Boundaries: Extrapolation in Biology and Social Science. Oxford: Oxford University Press. ISBN 9780195331448.
^ Franklin, James (2013). «Arguments whose strength depends on continuous variation». Journal of Informal Logic. 33 (1): 33–56. doi:10.22329/il.v33i1.3610. Retrieved 29 June 2021.

References[edit]

Extrapolation Methods. Theory and Practice by C. Brezinski and M. Redivo Zaglia, North-Holland, 1991.
Avram Sidi: «Practical Extrapolation Methods: Theory and Applications», Cambridge University Press, ISBN 0-521-66159-5 (2003).
Claude Brezinski and Michela Redivo-Zaglia : «Extrapolation and Rational Approximation», Springer Nature, Switzerland, ISBN 9783030584177, (2020).

Источник

Определение формулы экстраполяции

Формула экстраполяции — это формула, используемая для оценки значения зависимой переменной относительно независимой переменной, которая должна лежать в диапазоне за пределами данного набора данных. Например, точно известен расчет линейного исследования с использованием двух конечных точек (x1, y1) и (x2, y2) на линейном графике, когда значение экстраполируемой точки равно «x», формула, которую можно использовать представляется как y1+ [(x−x1) / (x2−x1)] *(у2-у1).

Оглавление

Определение формулы экстраполяции
- Расчет линейной экстраполяции (шаг за шагом)
- Примеры
  - Пример №1
  - Пример #2
  - Пример №3
- Актуальность и использование
- Рекомендуемые статьи

Y(x) = Y(1)+ (x-x(1)/x(2)-x(1)) * (Y(2) – Y(1))

Формула экстраполяции

Формулу линейной экстраполяции можно разделить на следующие шаги:

Во-первых, необходимо проанализировать данные, чтобы определить, следуют ли данные за тенденцией и можно ли прогнозировать то же самое.
Должно быть две переменные: одна должна быть зависимой переменной, а вторая должна быть независимой переменной.
Числитель формулы начинается с предыдущего значения зависимой переменной. Затем нужно добавить долю независимой переменной при расчете среднего значения для интервалов классов.
Наконец, умножьте значение, полученное на шаге 3, на разницу непосредственно заданных зависимых значений. Добавление шага 4 к значению зависимой переменной даст экстраполированное значение.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы экстраполяции Excel здесь – Формула экстраполяции Шаблон Excel

Пример №1

Предположим, что значение некоторых переменных приведено ниже в виде (X, Y):

(4, 5)
(5, 6)

Основываясь на приведенной выше информации, вы должны найти значение Y(6), используя метод экстраполяции.

Решение

Используйте приведенные ниже данные для расчета.

Х1: 4,00
Y2: 6.00
Y1: 5,00
Х2: 5,00

Расчет Y(6) по формуле экстраполяции выглядит следующим образом:

Формула экстраполяции Пример 1.1

Экстраполяция Y(x) = Y(1) + (x) – (x1) / (x2) – (x1) x {Y(2) – Y(1)}

Y(6) = 5 + 6 – 4 / 5 – 4 х (6 – 5)

Ответ будет –

Формула экстраполяции Пример 1.2

Y3 = 7

Следовательно, значение для Y, когда значение X равно 6, будет равно 7.

Пример #2

Г-н М и г-н Н являются учащимися 5-го стандарта, и в настоящее время они анализируют данные, предоставленные им их учителем математики. Учитель попросил их вычислить вес учеников, чей рост будет 5,90, и сообщил им, что приведенный ниже набор данных следует линейной экстраполяции.

ИксВысотаДМассаX15.00Y150X25.10Y252X35.20Y353X45.30Y455X55.40Y556X65.50Y657X75.60Y758X85.70Y859X95.80Y962

Предполагая, что эти данные следуют линейному ряду, вы должны рассчитать вес, который будет зависимой переменной Y в этом примере, когда независимая переменная x (рост) равна 5,90.

Решение

В этом примере нам теперь нужно узнать значение, или, другими словами, нам нужно спрогнозировать значение учащихся, чей рост равен 5,90, на основе тенденции, указанной в примере. Затем мы можем использовать приведенную ниже формулу экстраполяции в Excel для расчета веса, который является зависимой переменной для заданного роста и независимой переменной.

Расчет Y (5,90) выглядит следующим образом:

Пример 2.1

Экстраполяция Y(5.90) = Y(8) + (x) – (x8) /(x9) – (x8) x [Y(9) – Y(8)]
Y(5,90) = 59 + 5,90 – 5,70 / 5,80 – 5,70 х (62 – 59)

Ответ будет –

Пример 2.2

= 65

Следовательно, значение Y, когда значение X равно 5,90, будет равно 65.

Пример №3

Г-н В. является исполнительным директором компании ABC. Он был обеспокоен продажами компании после тенденции к снижению. Поэтому он попросил свой исследовательский отдел произвести новый продукт, который будет соответствовать растущему спросу по мере увеличения производства. Через 2 года они разработали продукт, спрос на который рос.

Ниже приведены подробности за последние несколько месяцев:

Х (Производство)Произведено (единиц)Y (спрос)Спрос (единиц)X110.0Y120.00X220.00Y230.00X330.00Y340.00X440.00Y450.00X550.00Y560.00X660.00Y670.00X770.00Y780.00X880.00Y890.00X990.00Y9100.00

Они заметили, что, поскольку изначально это был новый и дешевый продукт, спрос на него будет линейным до определенного момента.

Следовательно, продвигаясь вперед, они сначала прогнозируют спрос, а затем сравнивают его с фактическим и производят соответственно, поскольку это потребовало от них огромных затрат.

Менеджер по маркетингу хочет знать, что будет требоваться, если они произведут 100 единиц. Основываясь на приведенной выше информации, вы должны рассчитать спрос в единицах, когда они производят 100 единиц.

Решение

Мы можем использовать приведенную ниже формулу для расчета потребности в единицах, которая является зависимой переменной для данных произведенных единиц, которая является независимой переменной.

Расчет Y(100) выглядит следующим образом:

Пример 3.1

Экстраполяция Y(100) = Y(8) + (x) – (x8) / (x9) – (x8) x [ Y(9) – Y(8)]
Y(100) = 90 + 100 – 80 / 90 – 80 х (100 – 90)

Ответ будет –

Пример 3.2

= 110

Следовательно, значение для Y, когда значение X равно 100, будет равно 110.

Актуальность и использование

В основном используется для прогнозирования данных, выходящих за пределы текущего диапазона данных. В этом случае предполагается, что тенденция будет продолжаться для данных данных и даже за пределами этого диапазона, что не всегда так. Следовательно, следует осторожно использовать экстраполяцию. Вместо этого interpolationInterpolationInterpolation представляет собой математическую процедуру, применяемую для получения значения между двумя точками, имеющими заданное значение. Он аппроксимирует значение данной функции в заданном наборе дискретных точек. Его можно применять для оценки различных концепций стоимости, математики, статистики. Этот метод лучше подходит для того, чтобы сделать то же самое.

5.1. Критерий качества оценки погрешности

При использовании
перечисленных методов оценки погрешности
возникает вопрос о допустимости
отбрасывания малых (n).

Какой критерий
можно для этого применить? Если может
быть найдена оценка погрешности
оценки погрешности
,
то отношение этих оценок по модулю
должно быть существенно меньше единицы:

. (2.16)

Это означает, что
относительная размытостьоценки
мала, и такой оценкеможно доверять.
Если же
,
то ширина области размытости сравнима
с
и такую оценку следуетотвергнуть.

Поскольку величина

получается в виде разностиz_nz,
то оценкой погрешности величины
является оценка погрешности
экстраполированного значенияz(с обратным знаком).

Какая информация
может быть использована для получения
такой оценки? Мы рассматриваем задачу
о нахождении оценок погрешности в
условиях, когда известны только численные
значения z_n.

Применим следующий
подход. Обозначим
экстраполированное числоz,
полученное с помощью какого-нибудь из
изложенных методов при конкретномn.
Тогда, увеличиваяn(вQ,Q²,
и т.д. вQ^mраз) мы можем получить последовательность
уточненных значений
.
Теперь представим
в виде (2.4)

(2.17)

и
получим дважды экстраполированное
значение
,
повторив экстраполяцию по Ричардсону
по формуле (2.6), (где вместо
используем
),
или методом Ромберга увеличивL.
Разность
является искомой оценкой погрешности
экстраполированного значения
.

Отметим, что в
результате указанных действий получаются
дважды экстраполированные значения
,
погрешность которых также может быть
оценена путем повторной (третьей по
счету) экстраполяции. Если эта оценка
мала по сравнению с
,
то экстраполированные величины
могут быть использованы как уточненные
значения с известной оценкой погрешности
и мерой ее размытости.

Процесс экстраполяции
может повторяться до тех пор, пока
очередное отношение ширины области
размытости к величине самой оценки не
приблизится к 1 или не превысит единицу.

Примечание. Идея
повторной экстраполяции не полностью
совпадает с идеей ускорения сходимости
последовательностей. В результате
повторной экстраполяции получается
несколько последовательностей, а в
результате ускорения – только одна
(«ускоренная»). Наличие нескольких
последовательностей позволяет провести
оценку скорости сходимости каждой из
них и сформулировать критерий размытости
оценок, без проверки выполнения которого
проведение экстраполяции может привести
не к уточнению, а к огрублению результатов.

5.2. Оценка погрешности методов повторной экстраполяции

Чтобы оценить
качество различных методов экстраполяции,
проанализируем ошибку, возникающую при
применении этих методов. При этом
ограничимся двумя экстраполяциями.

Представим z_iв виде

. (2.18)

Будем считать k₁иk₂известными.

Применим формулу
(2.6) для первой экстраполяции. Получим
два значения

,
, (2.19)

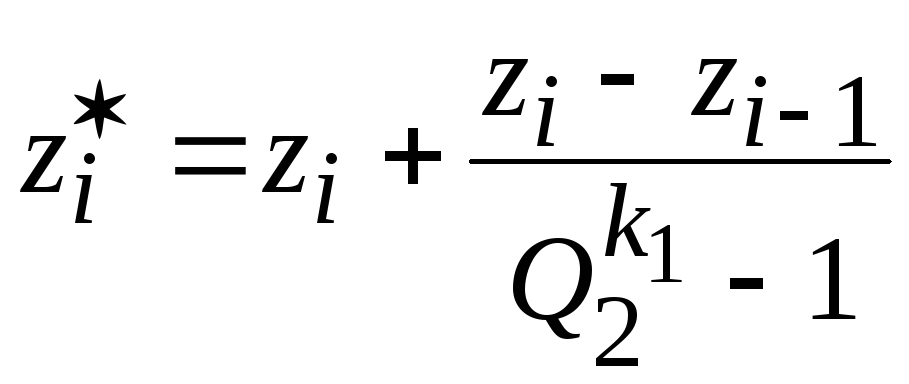
Найдем погрешность
экстраполированных значений. Для этого
подставим в (2.19) разложение (2.18)

, (2.20)

. (2.21)

Сравнивая (2.20) и
(2.21) нетрудно видеть, что при Q₁=Q₂=Qвеличины
представляются в виде

,
где

и
для следующей экстраполяции может быть
опять использована формула (2.6), которая
даст точное значение z.

Разность

(2.22)

представляет
собой погрешность, вносимую экстраполяцией.

При Q₁Q₂зависимость погрешности отnимеет вид более сложный, чемcn^—^k.
Игнорирование этого факта (что имеет
место при повторном применении формулы
(2.6)) может привести к ухудшению оценки.

При применении
точной интерполяционной формулы значение
zвычисляется в виде
суммы

причем
выбирается так,
чтобы суммарная погрешность оказалась
равной нулю. Это условие приводит к
равенству

откуда
получим

. (2.23)

В этом заключается
разница между повторной экстраполяцией
по формуле (2.6) и применением интерполяционной
формулы (2.10). Эта разница исчезает, если
Q₁=Q₂,
так как (2.23) приобретает вид

,
, (2.24)

что
совпадает с (2.6).

Примечание.
Величина ₂(n)
в (2.17) может оказаться суммой регулярной
составляющей, имеющей вид c_jn^—^k,
и нерегулярной составляющей, обусловленной,
например, погрешностью округления,
которая связана с ограниченной
разрядностью чисел в машинном преставлении.
Тогда исходная нерегулярная часть
погрешности, содержащаяся в вычисленных
значениях z_i,
при каждой экстраполяции умножается
на коэффициент, равный

Это ограничивает
число возможных экстраполяций.

Источник

2.4 Методы прогнозной экстраполяции

При формировании прогнозов с помощью экстраполяции обычно исходят из статистически складывающихся тенденций изменения тех или иных количественных характеристик объекта. Экстраполируются оценочные функциональные системные и структурные характеристики. Экстраполяционные методы являются одними из самых распространенных и наиболее разработанных среди всей совокупности методов прогнозирования.

С помощью этих методов экстраполируются количественные параметры больших систем, количественные характеристики экономического, научного, производственного потенциала, данные о результативности научно-технического прогресса, характеристики соотношения отдельных подсистем, блоков, элементов в системе показателей сложных систем и др.

Однако степень реальности такого рода прогнозов и соответственно мера доверия к ним в значительной мере обусловливаются аргументированностью выбора пределов экстраполяции и стабильностью соответствия «измерителей» по отношению к сущности рассматриваемого явления. Следует обратить внимание на то, что сложные объекты, как правило, не могут быть охарактеризованы одним параметром. В связи с этим можно сделать некоторое представление о последовательности действий при статистическом анализе тенденций и экстраполировании, которое состоит в следующем:

— во-первых, должно быть четкое определение задачи, выдвижение гипотез о возможном развитии прогнозируемого объекта, обсуждение факторов, стимулирующих и препятствующих развитию данного объекта, определение необходимой экстраполяции и её допустимой дальности;

— во-вторых, выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;

— в-третьих, сбор и систематизация данных. Перед сведением их в соответствующие таблицы еще раз проверяется однородность данных и их сопоставимость: одни данные относятся к серийным изделиям, а другие могут характеризовать лишь конструируемые объекты;

— в-четвертых, когда вышеперечисленные требования выполнены, задача состоит в том, чтобы в ходе статистического анализа и непосредственной экстраполяции данных выявить тенденции или симптомы изменения изучаемых величин. В экстраполяционных прогнозах особо важным является не столько предсказание конкретных значений изучаемого объекта или параметра в таком-то году, сколько своевременное фиксирование объективно намечающихся сдвигов, лежащих в зародыше назревающих тенденций.

Для повышения точности экстраполяции используются различные приемы. Один из них состоит, например, в том, чтобы экстраполируемую часть общей кривой развития (тренда) корректировать с учетом реального опыта развития отрасли-аналога исследований или объекта, опережающих в своем развитии прогнозируемый объект.

Под трендом понимается характеристика основной закономерности движения во времени, в некоторой мере свободной от случайных воздействий. Тренд — это длительная тенденция изменения экономических показателей. При разработке моделей прогнозирования тренд оказывается основной составляющей прогнозируемого временного ряда, на которую уже накладываются другие составляющие. Результат при этом связывается исключительно с ходом времени. Предполагается, что через время можно выразить влияние всех основных факторов.

Под тенденцией развития понимают некоторое его общее направление, долговременную эволюцию. Обычно тенденцию стремятся представить в виде более или менее гладкой траектории.

Анализ показывает, что ни один из существующих методов не может дать достаточной точности прогнозов на 20-25 лет. Применяемый в прогнозировании метод экстраполяции не дает точных результатов на длительный срок прогноза, потому что данный метод исходит из прошлого и настоящего, и тем самым погрешность накапливается. Этот метод дает положительные результаты на ближайшую перспективу прогнозирования тех или иных объектов не более 5 лет.

Для нахождения параметров приближенных зависимостей между двумя или несколькими прогнозируемыми величинами по их эмпирическим значениям применяется метод наименьших квадратов. Его сущность состоит в минимизации суммы квадратов отклонений между наблюдаемыми (фактическими) величинами и соответствующими оценками (расчетными величинами), вычисленными по подобранному уравнению связи.

Этот метод лучше других соответствует идее усреднения как единичного влияния учтенных факторов, так и общего влияния неучтенных.

Рассмотрим простейшие приемы экстраполяции. Операцию экстраполяции в общем виде можно представить в виде определения значения функции:

, (2.7)

где — экстраполируемое значение уровня; L – период упреждения; У_t – уровень, принятый за базу экстраполяции.

Под периодом упреждения при прогнозировании понимается отрезок времени от момента, для которого имеются последние статистические данные об изучаемом объекте, до момента, к которому относится прогноз.

Экстраполяция на основе среднего значения временного ряда. В самом простом случае при предположении о том, что средний уровень ряда не имеет тенденции к изменению или если это изменение незначительно, можно принятьт.е. прогнозируемый уровень равен среднему значению уровней в прошлом.

Доверительные границы для средней при небольшом числе наблюдений определяются следующим образом:

(2.8)

где t_a – табличное значение t – статистики Стьюдента с n-1 степенями и уровнем вероятности p;— средняя квадратическая ошибка средней величины. Значение ее определяется по формуле . В свою очередь, среднее квадратическое отклонение для выборки равно:

(2.9)

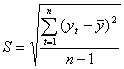
где y_t – фактические значения показателя.

Доверительный интервал, полученный как t_a_, учитывает неопределенность, которая связана с оценкой средней величины.

Общая дисперсия, связанная как с колеблемостью выборочной средней, так и с варьированием ндивидуальных значений вокруг средней, составит величину S²+S²/n. Таким образом, доверительные интервалы для прогностической оценки равны:

(2.10)

Экстраполяция по скользящей и экспоненциальной средней. Для краткосрочного прогнозирования наряду с другими приемами могут быть применены адаптивная или экспоненциальная скользящие средние. Если прогнозирование ведется на один шаг вперед, то или , где М_t — адаптивная скользящая средняя; N_t — экспоненциальная средняя. Здесь доверительный интервал для скользящей средней можно определить по формуле (2.10), в которой число наблюдений обозначено символом n. Поскольку при расчете скользящей средней через m обозначалось число членов ряда, участвующих в расчете средней, то заменим в этой формуле n на m, равным нечетным числам.

При экспоненциальном сглаживании дисперсия экспоненциальной средней равна , где S -среднее квадратическое отклонение, вместо величины в формуле (2.10) при исчислении доверительного интервала прогноза следует взять величину или . Здесь a— коэффициент экспоненциального сглаживания, изменяется от 0 до 1. Если 0<a<0,5, то при расчете прогноза учитываются прошлые значения временного ряда, а при 0,5<a<1 – значения, близкие к периоду упреждения. Примерное значение коэффициента сглаживания определяют по формуле Р.Брауна:

(2.11)

где m – число уровней временного ряда, входящих в интервал сглаживания.

Экстраполяция на основе среднего темпа. Если в основу прогностического расчета положен средний темп роста, то экстраполируемое значение уровня можно получить с помощью формулы: , где — средний темп роста, У_t — уровень, принятый за базу для экстраполяции. Здесь принят только один путь развития — развитие по геометрической прогрессии, или по экспонентной кривой. Во многих же случаях фактическое развитие явления следует иному закону, и экстраполяция по среднему темпу нарушает основное допущение, принимаемое при экстраполяции, — допущение о том, что развитие будет следовать основной тенденции — тренду, наблюдавшемуся в прошлом. Чем больше фактический тренд отличается от экспоненты, тем больше данные, получаемые при экстраполяции тренда, будут отличаться от экстраполяции на основе среднего темпа.

Средний темп или определяется на основе изучения прошлого, или оценивается каким-либо другим путем (например, подбор вариантов для различных ситуаций). В качестве исходного (базового) уровня для экстраполяции представляется естественным взять последний уровень ряда, поскольку будущее развитие начинается именно с этого уровня.

Статистическая надежность вышеприведенных методов оценивается с помощью коэффициента вариации:

(2.12)

где— среднее квадратическое отклонение;

— среднее значение временного ряда.

Метод считается статистически надежным и может быть использован для прогнозирования, если значение коэффициента вариации не превышает 10%.

Однофакторные прогнозирующие функции

Это такие функции, в которых прогнозируемый показатель зависит только от одного факториального признака.

В научно-техническом и экономическом прогнозировании в качестве главного фактора аргумента обычно используют время. Вполне очевидно, что не ход времени определяет величины прогнозируемого показателя, а действие многочисленных влияющих на него факторов. Однако каждому моменту времени соответствуют определенные характеристики всех этих факториальных признаков, которые со временем в той или иной мере изменяются. Таким образом, время можно рассматривать как интегральный показатель суммарного воздействия всех факториальных признаков.

В качестве фактора-аргумента в однофакторной прогнозирующей функции можно использовать не только время, но и другие факторы, если известна их количественная оценка на перспективу.

Наиболее простым из методов прогнозирования является экстраполяция тренда явления (процесса) за истекший период. Тренд (или вековая тенденция) характеризует процесс изменения показателя за длительное время, исключая случайные колебания. Тренд явления находят путем аппроксимации фактических уровней временного ряда на основе выбранной функции. Наиболее часто применяемые при прогнозировании функции показаны в табл. 2.3. В них фактор-аргумент обозначен символом t.

Таблица 2.3 Однофакторные прогнозирующие функции

Наименования функции	Вид функции
Степенной полином	y = a₀ + a₁t + a₂t²+…a_ntⁿ
Парабола	y=a₀+a₁t+a₂t²
Линейная функция	у = а₀+а₁t
Экспоненциальная (показательная)	,
Степенная
Логарифмическая	у = а₀+а₁lnt
Комбинация линейной и логарифмической функций	у = а₀+a₁t+а₂lnt
Функция Конюса
Функция Торнквиста
Логистическая (сигмоидальная)
Частный случай логистической функции
Гипербола	,
Комбинация линейной функции и гиперболы	у = а₀+а₁t +

При прогнозировании колебательных (циклических) процессов применяют тригонометрические функции, ряды Фурье.

Степенной полином может описать любые процессы изменения показателя y в зависимости от значений t. Корреляционное отношение для степенного полинома, служащее мерой тесноты корреляционной связи в нелинейных моделях, приближается к единице по мере увеличения числа степеней полинома до числа уровней временного ряда. Одновременно линия регрессии приближается к фактическим уровням показателя за прошедшее время, что не позволяет установить его тренд и экстраполировать его на перспективу. Поэтому для прогнозирования обычно не применяют полином выше третьей степени. Таким образом, в качестве прогнозирующей функции целесообразно использовать лишь три частных случая степенного полинома: линейную модель, параболу и полином третьего порядка.

Однофакторная линейная модель отражает постоянный ежегодный абсолютный прирост в размере a₁, т.е. арифметическую прогрессию. Парабола (степенной полином) второго порядка описывает случаи увеличения абсолютного ежегодного прироста на постоянную величину 2a₂, а третьего порядка – S – образную кривую с двумя точками изгибов.

Экспонента первого порядка (показательная функция) предусматривает постоянный ежегодный темп роста, равный процентов (т.е. геометрическую прогрессию), а второго порядка – постоянное увеличение ежегодных темпов роста в раз. Степенная функция соответствует случаю ускоряющегося при а1>1 или замедляющегося при а1<1 роста абсолютного ежегодного прироста. Логарифмическая функция выражает случай сокращения абсолютного ежегодного прироста, а функции Торнквиста и Конюса, комбинация линейной функции с логарифмической – затухающий рост абсолютного ежегодного прироста. Логистическая (сигмоидальная) кривая представляет собой модифицированную геометрическую прогрессию, в которой возрастание затухает по мере приближения к определенному пределу. Наконец, гиперболы характерны для тех случаев, когда в начальной стадии абсолютные уровни показателя резко сокращаются, а на последующих этапах этот процесс сокращения постепенно затухает

Коэффициенты в однофакторных прогнозирующих функциях а₀ и а₁ определяются с помощью метода наименьших квадратов, сущность которого заключается в минимизации суммы квадратов отклонений фактических значений от расчетных:

(2.13)

где— вид исследуемой функции (см. табл.2.3)

Пусть временной ряд может быть описан линейной функцией:

Подставим это выражение в формулу (2.13), получим:

Возьмем частные производные по а₀ и а₁:

В результате алгебраических преобразований данной системы: (сокращений, раскрытия скобок, переноса известных величин вправо, а неизвестных влево) — получим систему нормальных уравнений:

Из первого уравнения найдем а₀, из второго – а₁.

Формулы расчета а₀ и а₁ имею вид:

(2.14)

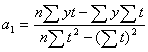
или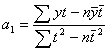

Прогнозируемые значения показателя у определяется по формуле:

=а₀+а₁(t+L), где L=1,2,…,(2.15)

если фактором-аргументом является время t. В случае, когда фактор-аргумент – независимая переменная (любой показатель х) то необходимо найти его прогнозируемые значения. Тогда:

=а₀+а₁х_t₊_L, где L=1,2,… (2.16)

Для оценки качества и надежности анализа регрессии используются следующие показатели: корреляционное отношение (η), коэффициент парной корреляции (r), коэффициент детерминации (r²), средняя ошибка предвидения (S_с), средняя ошибка коэффициента регрессии (S_а_j, j=0, 1,2, …).

Корреляционное отношение (η) указывает на степень взаимозависимости между у и х. Принимает значения между 0 и 1:

(2.17)

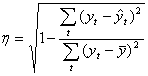
Коэффициент парной корреляции может быть определен по формуле:

(2.18)

где S₁₁, S₂₂, S₁₂ – соответственно остаточные дисперсии для функции, фактора-аргумента и их произведения: определяются по формулам:

;

Коэффициент корреляции, рассчитывается по формуле (2.18) и принимает значения от -1 до +1. Чем ближе значения коэффициента к единице, тем большая связь существует между функцией и аргументом.

Для проверки гипотезы о наличии связи определим критерий Стьюдента:

(2.19)

Если t_r>t_табл, то принимаем гипотезу о наличии связи, в противном случае – она отсутствует.

Коэффициент детерминации (r²) показывает, насколько уравнение регрессии подходит к значениям временного ряда или какой процент составляют учтенные факторы в уравнении регрессии.

Точность регрессионной модели определяется с помощью средней ошибки предвидения или среднего отклонения по формуле:

(2.20)

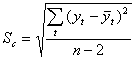
Средняя ошибка коэффициентов регрессии определяется по формуле:

(2.21)

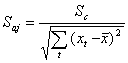
или ,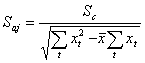

где j=1, 2, … , m; m – число факторов;

t=1, 2, … , n; n – число данных.

Оценка Стьюдента (t_а_j) показывает удельный вес фактора-аргумента х при объяснении у. Она вычисляется делением коэффициентов a_j на их средние ошибки S_aj:

(2.22)

Оценка Стьюдента показывает, во сколько раз значения j-го коэффициента превосходят его среднюю ошибку. Любое значение t_aj больше 2 или меньше -2 считается приемлемым. Чем больше величина t_aj, тем больше значимость коэффициентов регрессии, тем надежнее уравнение регрессии.

Статистическая надежность аппроксимирующей функции или коэффициента парной корреляции устанавливается также с помощью критерия Стьюдента (2.19).

С вероятностью ошибки р и с (n-2) степенями свободы выбранная функция признается статистически надежной, если рассчитанное значение критерия t_r превышает табличное.

Ошибкой прогноза называется отклонение предсказанного значения от наблюдаемого (фактического). Для оценки совокупной ошибки прогноза используются два показателя: средняя абсолютная ошибка ( ) и средняя относительная ошибка ( ), которые определяются по формулам:

(2.23)

(2.24)

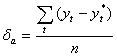
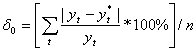
С помощью метода наименьших квадратов могут быть определены а₀ и а₁ во всех однофакторных прогнозирующих функциях, если эти функции предварительно линеаризовать, т.е. преобразовать в линейную модель. Линеаризация достигается логарифмированием или получением обратных значений функции, а также заменой переменных, представляющих собой преобразованные значения показателей у и t.

Многофакторные прогнозирующие функции

Каждый прогнозируемый показатель у_t (t=1,2…,n) можно рассматривать не только как функцию одного фактора-аргумента, но и от нескольких:

— в виде линейной многофакторной модели:

у_t=а₀+а₁х₁_t+а₂х₂_t+…+а_jх_jt+…+а_mх_mt(2.25)

где а₀, а_j – коэффициенты модели при j=1, 2, … , k;

х_jt – факторы-аргументы, влияющие на прогнозируемый показатель у_t, при j=1, 2, … , m; t=1,2,…, n;

— в виде нелинейной многофакторной модели (степенного типа):

(2.26)

которая путем логарифмирования преобразуется в линейную. Более сложные виды нелинейных многофакторных моделей редко используются в практике прогнозирования и планирования.

Коэффициенты а₀, а_j в моделях типа (2.25) и (2.26) определяются с помощью метода наименьших квадратов (2.13) из системы нормальных уравнений, представляющих собой частные производные по а₀, а_j равные нулю:

В результате решения данной системы уравнений находятся такие а₀ и а_j, при которых (2.13) стремится к нулю.

Факторы-аргументы должны отвечать следующим условиям: во-первых, иметь количественное измерение и отражаться в отчетах или, по крайней мере, определяться на основе специального анализа отчетных данных; во-вторых, иметь перспективные оценки значений на прогнозируемый период; в-третьих, число включаемых в модель факторов должно быть меньше числа данных ряда в три раза; в-четвертых, быть линейно независимыми.

Факторы считаются зависимыми (мультиколлинеарными), если линейный (парный) коэффициент корреляции (см. формулу 2.18) двух факторов более 0,8. Из них в модели оставляют тот, который имеет больший коэффициент корреляции с функцией у.

Оптимальное количество факторов-аргументов можно установить с помощью так называемого метода исключений. Сущность его заключается в следующем.

В модель типа (2.25) включают все возможные факторы, удовлетворяющие указанным выше условиям и строят эту модель. Для каждого j-го фактора-аргумента по формуле (2.22) находят оценки Стьюдента. Выбирают наименьшую величину оценки min t_a₁ и сравнивают с табличным значением – t_p при (n-k-1) – степенях свободы и выбранном уровне значимости р (обычно принимают р=0,05 или 5%). Если минимальная из рассчитанных оценок t_a>t_p, то модель оставляют в полученном виде. Если же t_ap, то фактор а₁ исключается из модели как незначимый. Затем с оставшимися факторами строят новую модель, определяют новое значение оценок Стьюдента, находят минимальную из них и т.д. до тех пор, пока в модели останутся все значимые факторы.

Тесноту связей между функцией и факторами-аргументами можно установить с помощью квадрата коэффициента множественной корреляции:

(2.27)

где

Квадрат коэффициента множественной корреляции показывает, какая часть общего рассеяния зависимой переменной может быть объяснена функцией вида (2.25) или вида (2.26).

Статистическая надежность многофакторной регрессионной модели (или коэффициента детерминации) устанавливается с помощью критерия Фишера:

(2.28)

где n – число данных;

m – число факторов-аргументов в модели;

R² – квадрат коэффициента множественной корреляции.

Если расчетное значение критерия Фишера превышает табличное при (n-m) и (m-1) степенях свободы и принятом р – уровне значимости то модель признается статистически надежной и значимой. Многофакторная регрессионная модель может быть использована для прогнозирования не более трехлетнего периода упреждения. Ошибки прогноза определяются по формулам (2.23-2.24).

Метод экспоненциального сглаживания

Сущность этого метода заключается в том, что прогноз ожидаемых величин (объемов, продаж и т.д.) определяется путем взвешенных средних величин текущего периода и сглаженных значений, сделанных в предшествующий. Такой процесс продолжается назад к началу временного ряда и представляет собой простую экспоненциальную модель для временных рядов с устойчивым трендом и малыми (независимыми) периодическими колебаниями.

Для многих временных рядов (показателей) наблюдается очевидная картина периодичности и случайности. Поэтому простая экспоненциальная модель расширяется с включением в нее двух последних компонент.

а) С устойчивым трендом

Пусть глаженное значение в момент времени t определяется по рекуррентной формуле:

(2.29)

где у_t – фактическое значение в момент времени t; ;

а – параметр сглаживания, определяется по формуле (2.11)

Тогда сглаженное значение в момент времени (t-1) равно:

(2.30)

Подставив в выражение (2.29), получим:

(2.31)

Продолжая этот процесс, прогноз может быть выражен в величинах прошлых значений временного ряда, т.е.:

, (2.32)

где L – период предсказания, но не более трех-пяти лет.

При t=1,2,…, n сглаженные значения в момент времени t определяются по формуле (2.29). Для этого же периода времени определяется среднее квадратическое отклонение (см. формулу 2.9) и коэффициент вариации (см. формулу 2.12), чтобы оценить точность выбранного параметра сглаживания. При t=1

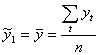
В случае если коэффициент вариации превышает 10%, то необходимо изменить интервал сглаживания, а следовательно, и параметр сглаживания .

При ,…, n прогнозы в момент времени t определяются по формуле (2.32) для оценки точности предсказания по среднему квадратическому отклонению и коэффициенту вариации.

При t=n+1, n+2, … определяются соответственно прогнозы данного показателя, в предположении, что текущее значение в момент времени t=n+1 совпадает с прогнозным в момент времени t=n.

б) С периодической компонентой

Пусть — сглаженное значение в момент времени t с учетом периодической компоненты. Периодичность совпадает с периодом предсказания. На практике обычно рассматриваются годовые или месячные изменения. Тогда оценка сглаженного значения запишется так:

(2.33)

где f_t_—_T – оценка периодической компоненты в предшествующем периоде; Т – длина периода.

В момент времени t периодическая компонента определяется по формуле:

(2.34)

Весовые параметры α и β подбираются либо с учетом текущих значений , либо с учетом прошлых значений . Оптимальные их значения устанавливаются по минимуму среднего квадратического отклонения.

Прогноз ожидаемых значений для оценки выбранных параметров α и β может быть определен мультипликативным образом по формуле:

(2.35)

где .

При t=n+1, n+2,…, N определяются собственно прогнозы по формуле:

(2.36)

где — прогноз сглаженного значения определяемый по формуле (2.32).

в) С периодической и случайной компонентами

Пусть оценка сглаженного значения с учетом периодической и случайной компоненты имеет вид:

(2.37)

где ε_t_-1 – оценка случайной компоненты в момент времени (t-1), текущее значение ε_t определяется по формуле:

(2.38)

где γ – параметр сглаживания для случайной компоненты, .

Прогноз ожидаемых значений для оценки выбранных параметров α, β и γ может быть получен по формуле:

(2.39)

где Т – период предсказания, Т=1, 2, …, 5;

,…, n.

При t=n+1, n+2, …, N определяются собственно прогнозы по формуле:

(2.40)

где — прогноз сглаженного значения, определяется по формуле (2.32).

Метод авторегрессионного преобразования

Сущность его заключается в построении модели по отклонениям значений временного ряда от выравненных по тренду значений. Пусть эти отклонения представляют собой случайные колебания временного ряда в каждый момент времени t:

(2.41)

Тогда для случайной величины ε_t можно построить модель авторегрессии, т.е. регрессионную модель линейного вида для остатков значений временного ряда. Эти случайные переменные распределены со средним значением 0 и конечным рассеиванием (дисперсией) и подчиняются закону стохастического линейного разностного уровня 1-го порядка с постоянными коэффициентами (процесс Маркова), то есть:

(2.42)

где ε_t_-1 – временной ряд случайной компоненты, сдвинутый на один шаг, t=1, 2, …, n.

По формулам вида (2.14) определим b₀ и b₁, получим:

;

(2.43)

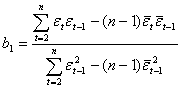
гдеи — соответственно средние значения по данному временному ряду и сдвинутому на один шаг.

Прогнозируемые значения случайной компоненты определяются по формуле:

(2.44)

где L=1, 2, …

При L=1 , при L=2, 3, … справедлива формула (2.44).

Определяем коэффициент автокорреляции r² по формуле парного коэффициента корреляции (см. формулу 2.18). Тогда коэффициент автокорреляции для авторегрессионной модели 1-го порядка равен:

(2.45)

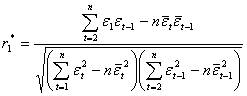
Затем строим авторегрессионную модель 2-го порядка:

(2.46)

где ε_t_-2 – временный ряд случайной компоненты, сдвинутой на два шага, при t=1, 2, …, n.

Коэффициенты b₀, b₁, b₂ находятся с помощью метода наименьших квадратов из системы нормальных уравнений.

Находим:

(2.47)

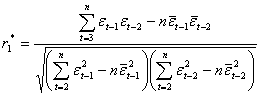
Если , то случайная компонента следует закону линейного разностного уравнения 1-го порядка (2.42), а прогнозы определяются по формуле (2.44). Если же , то строится линейное разностное уравнение 3-го порядка рассчитывается и т.д. Эти расчеты продолжаются до тех пор, пока , при τ=1,2,…, n/2. Выбирается авторегрессионная модель (τ-1) порядка. Оценка точности и надежности авторегрессионной модели определяется по среднему квадратическому отклонению (см. формулу 2.9) и коэффициенту вариации (см. формулу 2.12).

Источник

Уважаемые Коллеги!

Помогите мне, пожалуйста, в моих рассуждениях.

Есть некоторый, полученный экспериментально, временной ряд. Ряд аппроксимируется полиномом по методу наименьших квадратов и далее экстраполируется на несколько шагов вперед.
Необходимо оценить погрешность этой экстраполяции.

Сейчас я делаю следующим образом: определяю среднюю погрешность по всем точкам ряда, то есть:
1/n * Сумма (ABS(Эксперимент – Аппроксимация))
где: n – число точек ряда, Эксперимент и Аппроксимация – соответственно экспериментальное и аппроксимированное значения, ABS() – абсолютная величина, Сумма() – сумма по всем точкам ряда

И принимаю это значение за погрешность для экстраполированных точек.

Это не есть правильно, так как при таком подходе не учитывается динамика погрешности.

1. Например, предположим, что аппроксимируемый ряд имеет характер затухающих колебаний, ну то есть: Y =[10, -10, 8, -8, 6, -6, 4, -4]. Пусть мы аппроксимируем его прямой Y=0. Тогда, очевидно, что при экстраполяции вправо погрешность должна быть затухающей, и она не будет равна ни среднему значению экспериментальных точек, ни даже наименьшему их значению.

Я пробовал решить эту проблему, построив аппроксимирующую функцию для погрешности и экстраполировав ее. Но часто аппроксимация погрешности оказывается во много раз более сложной, чем аппроксимация самих экспериментальных данных, что, на мой взгляд, не есть хорошо.

2. С другой стороны, для хаотических временных рядов (не таких как приведенный выше), в которых аппроксимация отражает не столько конкретные значения сколько общий тренд выборки, правильным было бы, что чем дальше экстраполированная точка отстоит от известных экспериментальных значений, тем выше будет погрешность. Построение аппроксимирующей функции для погрешности в этом случае не дает положительного эффекта (ввиду хаотического разброса этой погрешности). Не корректный пример приведу, и не из технической области, но все же понятный, например, курс доллара можно предсказать относительно точно на завтра-послезавтра, а при попытке предсказать его на год-два вперед, оценить можно только общий тренд и чем дальше от сегодня будет искомая точка тем выше будет погрешность (вплоть до бесконечности).

Я пробовал решить эту проблему, введением некоего корректирующего коэффициента для погрешности на каждом шаге экстраполяции. Однако столкнулся с проблемой обоснованного выбора величины этого коэффициента.

Подскажите, пожалуйста, кто что сможет, по этому поводу.
Большое спасибо.

С уважением,
Никита

Источник

Methods[edit]

Linear[edit]

Polynomial[edit]

Conic[edit]

French curve[edit]

[edit]

Quality[edit]

In the complex plane[edit]

Fast[edit]

[edit]

See also[edit]

Notes[edit]

References[edit]

Определение формулы экстраполяции

Примеры

Актуальность и использование

Рекомендуемые статьи

5.1. Критерий качества оценки погрешности

5.2. Оценка погрешности методов повторной экстраполяции

2.4 Методы прогнозной экстраполяции