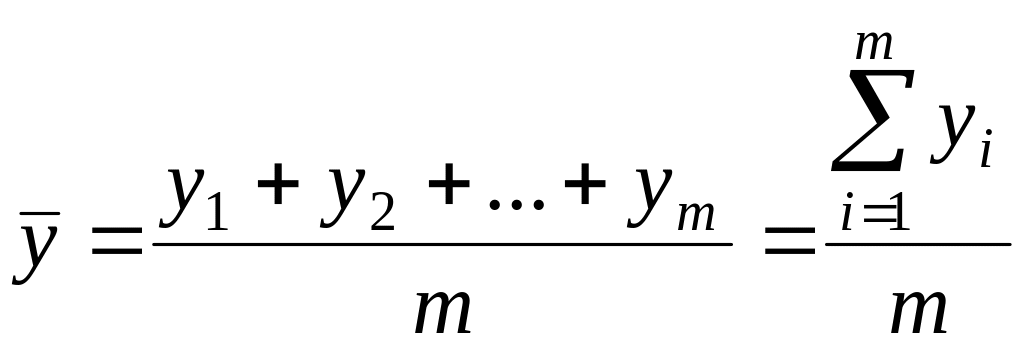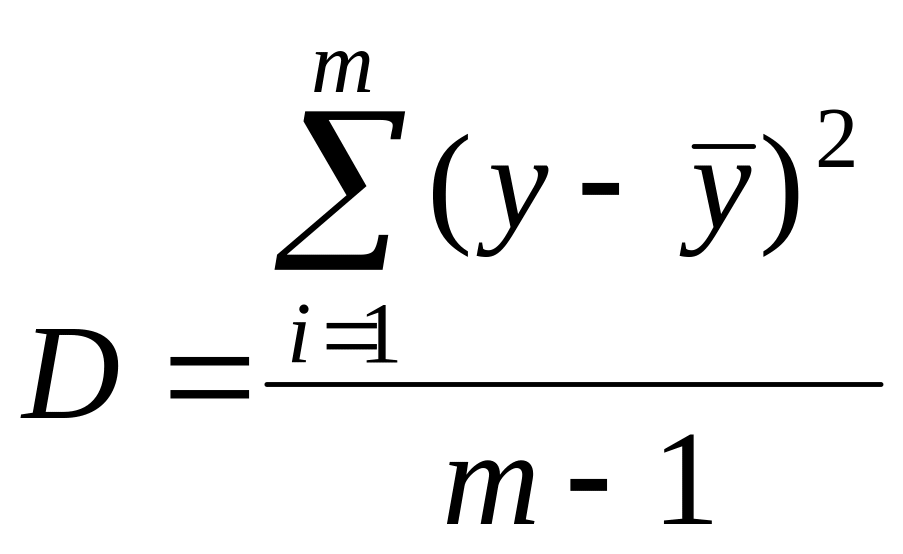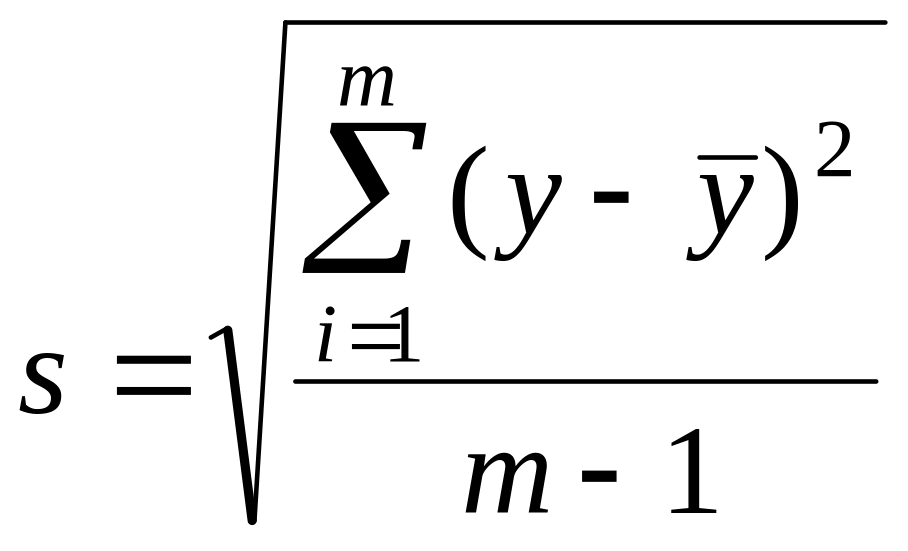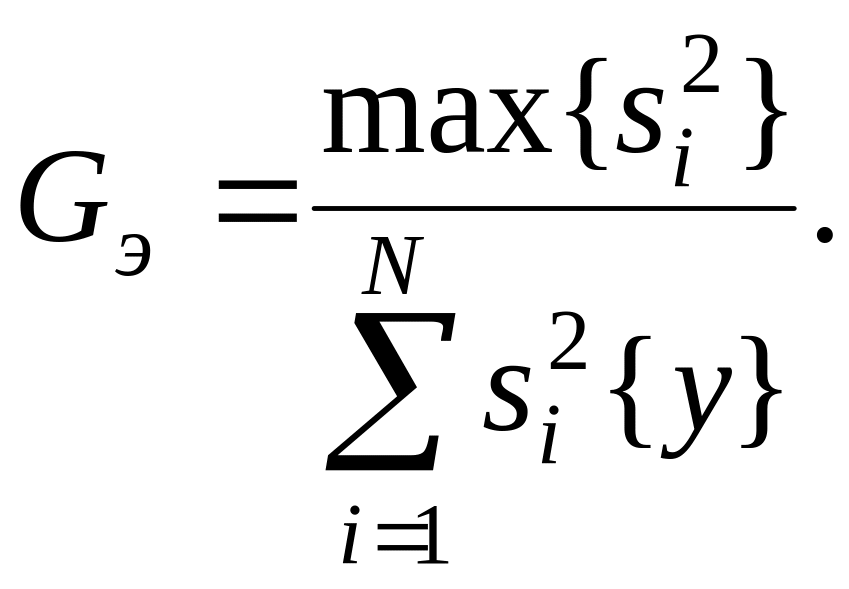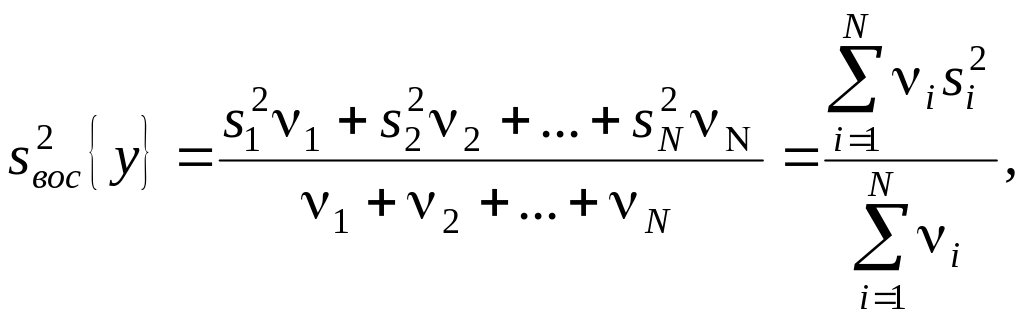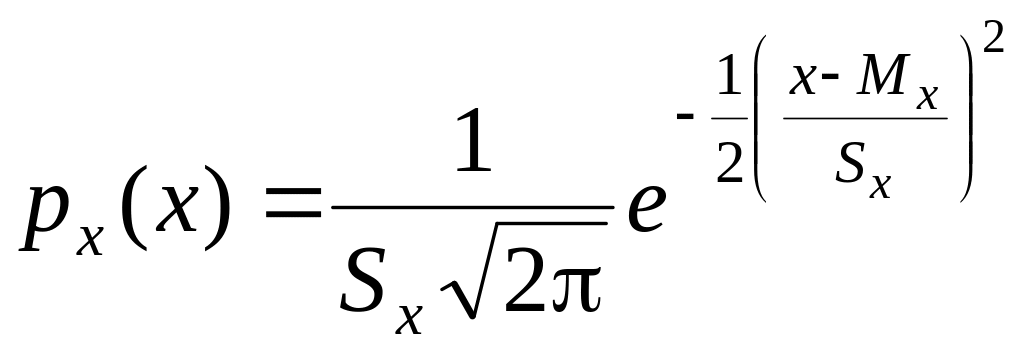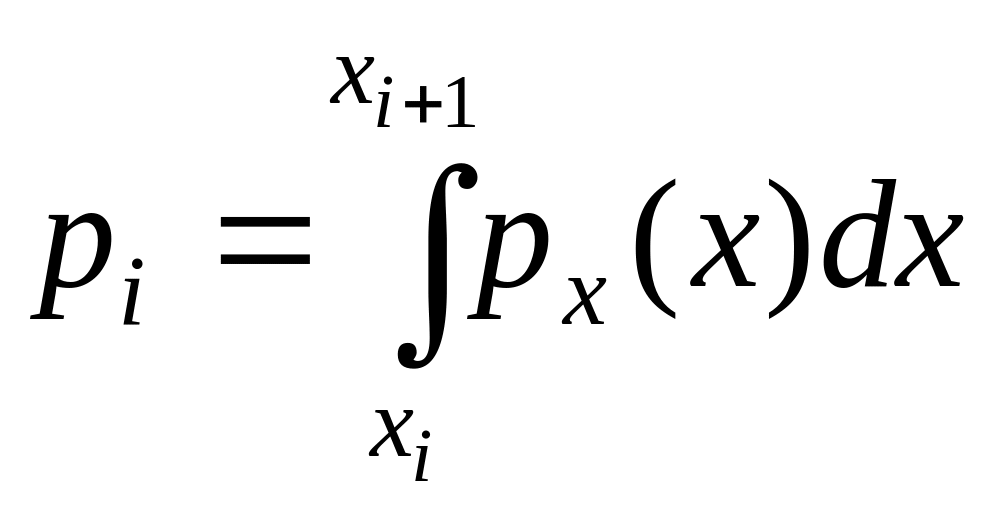Ошибка эксперимента формула

Абсолютная и относительная погрешности (ошибки).

Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x₁,
x₂,
x₃,
…, x_n

Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:

Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.

Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:

(13)

Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.

Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):

(14)

Отношения

называются относительными погрешностями
(ошибками) отдельных измерений.

Отношение средней
абсолютной погрешности результата

к среднему арифметическому значению

измеряемой величины называют относительной
ошибкой результата и выражают в процентах:

Относительная
ошибка характеризует точность измерения.

Законы распределения случайных величин.

Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.

Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.

Непрерывная
случайная величина принимает любые
значения в данном интервале.

Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.

Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.

Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.

Два события,
одновременное появление которых
невозможно, называются несовместными.

Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:

называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:

При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:

Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.

Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений х_i
на вероятность этих значений р_i:

Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:

,

где m_i
— число дискретных случайных величин,
имеющих значение х_i.

Для непрерывной
случайной величины математическим
ожиданием служит интеграл:

,

где р(х) — плотность
вероятности.

Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:

(15)

(16)

Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:

(17)

Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».

Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:

а) ряд распределения
(для дискретных величин);

б) функция
распределения;

в) кривая распределения
(для непрерывных величин).

Существует
относительно много законов распределения
случайных величин.

Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина

распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:

(18),

где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);

—
среднее квадратичное отклонение;

—
основание натурального логарифма
(неперово число);

f
(x)
– плотность вероятности (функция
распределения вероятностей).

Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.

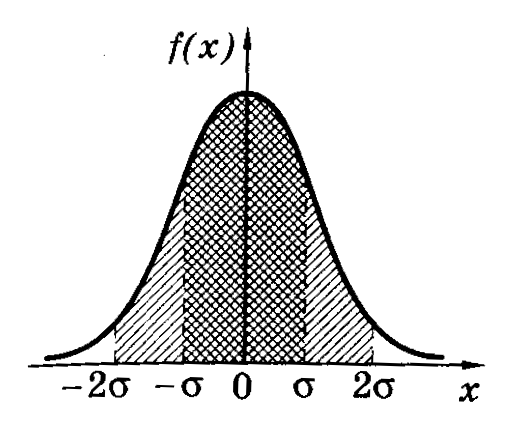
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).

Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:

(19)

Таким образом,
максимальное значение функции f_max(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом ₂>₁.
(При увеличении 
кривая распределения становится более
пологой, а при уменьшении 
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и ₃
= ₂.

Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал

теоретически была определена в 1860 году
английским физиком Максвеллом

. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т₁
< Т₂).
Закон распределения Максвелла определяется
формулой:

(20),

где m_о
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.

Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:

(21)

Где n(h)
– концентрация молекул газа на высоте
h,
n₀
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.

Распределение
Больцмана.

Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному

статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).

n

1. h

Гистограмма
распределения Больцмана.

Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов x_i
одинаковой ширины. Для каждого интервала
подсчитывают число m_i
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины

для каждого интервала x_i
и среднее значение случайной величины
<x_i
> в каждом интервале.

Затем по оси абсцисс
откладывают интервалы x_i,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой

– плотностью относительной частоты
).

Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).

Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:

(22)

Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:

(23)

Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.

Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.

Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.

Доверительной
вероятностью
(надежностью)

результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность 
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.

Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t_,n<>,
<x>
+ t_,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .

Коэффициент t_,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).

Значении коэффициента
Стьюдента t_,n
зависит от доверительной вероятности

и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.

Таблица 1

n	
0,6	0,7	0,8	0,9	0,95	0,98	0,99
2	1,38	2,0	3,1	6,3	12,7	31,8	63,7
3	1,06	1,3	1,9	2,9	4,3	7,0	9,9
4	0,98	1,3	1,6	2,4	3,2	4,5	5,8
5	0,94	1,2	1,5	2,1	2,8	3,7	4,6
6	0,92	1,2	1,5	2,0	2,6	3,4	4,0
7	0,90	1,1	1,4	1,9	2,4	3,1	3,7
8	0,90	1,1	1,4	1,9	2,4	3,0	3,5
9	0,90	1,1	1,4	1,9	2,3	2,9	3,4
10	0,88	1,1	1,4	1,9	2,3	2,8	3,3

В таблице 1 в верхней
строке заданы значения доверительной
вероятности 
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.

Окончательный
результат измерений записывается в
виде:

(25)

Где

– полуширина доверительного интервала.

Результат серии
измерений оценивается относительной
погрешностью:

(26)

How to Calculate Experimental Error in Chemistry

Updated on September 08, 2019

Error is a measure of accuracy of the values in your experiment. It is important to be able to calculate experimental error, but there is more than one way to calculate and express it. Here are the most common ways to calculate experimental error:

Error Formula

In general, error is the difference between an accepted or theoretical value and an experimental value.

Error = Experimental Value — Known Value

Relative Error Formula

Relative Error = Error / Known Value

Percent Error Formula

% Error = Relative Error x 100%

Example Error Calculations

Let’s say a researcher measures the mass of a sample to be 5.51 grams. The actual mass of the sample is known to be 5.80 grams. Calculate the error of the measurement.

Experimental Value = 5.51 grams
Known Value = 5.80 grams

Error = Experimental Value — Known Value
Error = 5.51 g — 5.80 grams
Error = — 0.29 grams

Relative Error = Error / Known Value
Relative Error = — 0.29 g / 5.80 grams
Relative Error = — 0.050

% Error = Relative Error x 100%
% Error = — 0.050 x 100%
% Error = — 5.0%

Как рассчитать экспериментальную ошибку в химии

На чтение 1 мин Просмотров 426 Опубликовано 05.06.2021

Ошибка – это мера точности значений в вашем эксперименте. Важно уметь вычислить экспериментальную ошибку, но есть несколько способов ее вычислить и выразить. Вот наиболее распространенные способы вычисления экспериментальной ошибки:

Содержание

1. Формула ошибки
2. Формула относительной ошибки
3. Формула процента ошибки
4. Пример расчета ошибки

Формула ошибки

В общем, ошибка – это разница между принятым или теоретическое значение и экспериментальное значение.

Ошибка = экспериментальное значение – известное значение

Формула относительной ошибки

Относительная ошибка = ошибка/известное значение

Формула процента ошибки

% Error = относительная ошибка x 100%

Пример расчета ошибки

Допустим, исследователь измеряет массу образца, который должен быть 5,51 грамм. Известно, что фактическая масса образца составляет 5,80 грамма. Рассчитайте погрешность измерения.

Экспериментальное значение = 5,51 грамма
Известное значение = 5,80 грамма

Ошибка = экспериментальное значение – известное значение
Ошибка = 5,51 г – 5,80 грамма
Ошибка = – 0,29 грамма

Относительная ошибка = ошибка/известное значение
Относительная ошибка = – 0,29 г/5,80 г
Относительная ошибка = – 0,050

% Error = относительная ошибка x 100%
% Error = – 0,050 x 100%
% Error = – 5,0%

Для
определения вероятностных характеристик
погрешностей используются исходные
данные, полученные предварительно
опытным путем, посредством физического
эксперимента. Результаты эксперимента
в виде выборки некоторого объема n
обрабатывают методами математической
статистики и таким образом получают
оценочные характеристики погрешностей.

Познакомимся с
вычислением ошибки опыта, или, как ее
часто называют, ошибки воспроизводимости.

Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое

равно сумме всех m
отдельных результатов, деленной на
количество параллельных опытов

(7.1)

Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность

–
у,
где у
– результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.
Дисперсией называется среднее значение
квадрата отклонений величины от ее
среднего значения. Дисперсия обозначается
D
и выражается формулой

(7.2)

где
(m
– 1) – число
степеней свободы, равное количеству
опытов минус единица. Одна степень
свободы использована для вычисления
среднего.

Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой

. (7.3)

Стандарт
имеет размерность той величины, для
которой он вычислен. Дисперсия и стандарт
– это меры рассеяния, изменчивости. Чем
больше дисперсия и стандарт, тем больше
рассеяны значения параллельных опытов
около среднего значения.

Критерии
исключения грубых ошибок.
Ошибка опыта является суммарной
величиной, результатом многих ошибок:
ошибок измерений факторов, ошибок
измерения функции отклика и др. Каждую
из этих ошибок можно, в свою очередь,
разделить на составляющие.

Все
ошибки принято разделять на случайные,
систематические и промахи. Систематические
ошибки
находят, калибруя измерительные приборы
и сопоставляя опытные данные с
изменяющимися внешними условиями, при
сравнении с эталонным прибором. Если
систематические ошибки вызываются
внешними условиями (переменной
температуры, и т. д.), следует компенсировать
их влияние. Случайными
ошибками
называются те, которые появляются
нерегулярно, причины возникновения
которых неизвестны и которые невозможно
учесть заранее. При повторении опытов
такие ошибки могут вызвать большой
разброс экспериментальных результатов.

Очень важно
исключить из экспериментальных данных
грубые ошибки. Грубая погрешность,
или промах, – это погрешность результата
отдельного измерения, входящего в ряд
измерений, которая для данных условий
резко отличается от остальных результатов
этого ряда. Источником грубых погрешностей
нередко бывают резкие изменения условий
измерения и ошибки, допущенные оператором.
К ним можно отнести:

• неправильный
  отсчет по шкале измерительного прибора,
  происходящий из-за неверного учета
  цены малых делений шкалы;

• неправильная
  запись результата наблюдений, значений
  отдельных мер использованного набора,
  например гирь;

• хаотические
  изменения параметров питающего средства
  измерений (СИ) напряжения, например его
  амплитуды или частоты.

Причинами
грубых погрешностей могут быть внезапные
и кратковременные изменения условий
измерения и оставшиеся незамеченными
неисправности в аппаратуре. Если промахи
обнаруживают в процессе измерений, то
результаты их содержащие отбрасывают.
Однако чаще всего промахи выявляют при
статистической обработке результатов
измерений с помощью специальных
критериев.

Корректная
статистическая обработка выборки
возможна только при ее однородности,
т.е. в том случае, когда все ее члены
принадлежат к одной и той же генеральной
совокупности. В противном случае
обработка данных бесмысленна. “Чужие”
отсчеты по своим значениям могут
существенно не отличаться от “своих”
отсчетов. Их можно обнаружить только
по виду гистограмм или дифференциальных
законов распределения. Наличие таких
аномальных отсчетов принято называть
загрязнениями
выборки, однако выделить члены выборки,
принадлежащие каждой из генеральных
совокупностей, практически невозможно.

Если
“свои” и “чужие” отсчеты различаются
по значениям, то их исключают из выборки.
Особую неприятность доставляют отсчеты,
которые хотя и не входят в компактную
группу основной массы отсчетов выборки,
но и не удалены от нее на значительное
расстояние, – так называемые предполагаемые
промахи. Отбрасывание “слишком”
удаленных от центра выборки отсчетов
называется “цензурированием” выборки.
Это осуществляется с помощью специальных
критериев.

При
однократных измерениях обнаружить
промах не представляется возможным.
Для уменьшения вероятности появления
промахов измерения проводят два-три
раза и за результат принимают среднее
арифметическое полученных отсчетов.
При многократных измерениях для
обнаружения промахов используют
статистические критерии, предварительно
определив, какому виду распределения
соответствует результат измерений.

Вопрос
о том, содержит ли результат наблюдений
грубую погрешность, решается общими
методами проверки статистических
гипотез. Проверяемая гипотеза состоит
в утверждении, что результат наблюдения
x_i
не содержит грубой погрешности, т.е.
является одним из значений измеряемой
величины. Пользуясь определенными
статистическими критериями, пытаются
опровергнуть выдвинутую гипотезу. Если
это удается, то результат наблюдений
рассматривают как содержащий грубую
погрешность и его исключают.

Для
выявления грубых погрешностей задаются
вероятностью q
(уровнем значимости) того, что сомнительный
результат действительно мог иметь место
в данной совокупности результатов
измерений.

Критерий
“трех сигм”
применяется для результатов измерений,
распределенных по нормальному закону.
По этому критерию считается, что
результат, возникающий с вероятностью
q

0,003, маловероятен и его можно считать
промахом, если

,
где S_y
– оценка СКО измерений. Величины

и S_y
вычисляют без учета экстремальных
значений y_i.
Данный критерий надежен при числе
измерений n

20… 50.

Это
правило обычно считается слишком
жестким, поэтому рекомендуется [5]
назначать границу цензурирования в
зависимости от объема выборки: при 6 <
n

100 она равна 4S_y;
при 100 < n

1000 – 4,5S_y;
при 1000 < n

10000 – 5S_y.
Данное правило применимо только для
нормального закона.

Вариационный
критерий Диксона.
Этот критерий очень удобен и достаточно
мощен (с малыми вероятностями ошибок).
При его применении полученные результаты
наблюдений записывают в вариационный
возрастающий ряд y₁,
y₂,
…, y_n
(y₁<
y₂
< …< y_n).
Критерий Диксона определяется как
K_D=(y_n–
y_n—1)/
(y_n–
y₁).
Критическая область для этого критерия
P(K_D>Z_q)
= q.
Значения Z_q
приведены в таблице 6.

Таблица 6. Значения критерия Диксона.

n	Zq при q, равном
0,10	0,05	0,02	0,01
4 6 8 10 14 16 18 20 30	0,68 0,48 0,40 0,35 0,29 0,28 0,26 0,26 0,22	0,76 0,56 0,47 0,41 0,35 0,33 0,31 0,30 0,26	0,85 0,64 0,54 0,48 0,41 0,39 0,37 0,36 0,31	0,89 0,70 0,59 0,53 0,45 0,43 0,41 0,39 0,34

Существуют и другие
критерии исключения грубых ошибок [5],
например, критерии Граббса, Шовене,
Шарлье, Романовского.

Дисперсия
воспроизводимости параллельных опытов.
При планировании физического эксперимента
определяются точки xⁱ
(
)
в факторном пространстве, в которых
определяется экспериментальное значение
функции отклика. Так как функция отклика
y
имеет случайный характер, то в каждой
точке xⁱ
проводятся m
повторных опытов, и дисперсия всего
эксперимента получается в результате
усреднения дисперсий всех опытов. По
терминологии, принятой в планировании
эксперимента, речь идет о подсчете
дисперсии воспроизводимости эксперимента.

В
каждой точке результаты наблюдений

,


,
… ,


усредняются:

. (7.5)

С
целью оценки ошибки воспроизводимости
в каждом опыте, состоящем из m
повторных наблюдений, подсчитываются
дисперсия

и стандарт

по формулам:

; (7.6)

,
(7.7)

где
(m–1)
– число степеней свободы, равное
количеству повторных опытов, минус
единица;

–
среднее арифметическое, определяемое
по формуле (7.5).

Если дисперсии
D_i
(
),
вычисленные по формулам (7.6) однородны,
то можно вычислить средневзвешенную
дисперсию с суммарным числом степеней
свободы. Такая дисперсия является
значительно более надежной оценкой
дисперсии воспроизводимости, чем
отдельные выборочные дисперсии.
Однородность дисперсий означает, что
среди всех суммируемых дисперсий нет
таких, которые бы значительно превышали
все остальные.

Для проверки
однородности дисперсий

,
полученных по выборкам одинакового
объема m, используется
критерий Кохрэна, который определяется
отношением максимальной дисперсии к
сумме всех дисперсий

. (7.8)

С
критерием Кохрэна связаны числа степеней
свободы ₁=m
– 1 и ₂
= N.
Гипотеза об однородности дисперсией
подтверждается, если экспериментальное
значение критерия Кохрэна не превышает
табличного значения (Приложение 2).

В
случае однородности дисперсий можно
усреднять дисперсии и для подсчета
дисперсии воспроизводимости эксперимента
с числом степеней свободы _вос=N
(m
– 1) пользоваться формулой

(7.9)

Такой формулой можно
пользоваться в случаях, когда число
повторных опытов одинаково во всей
матрице.

На
практике часто приходится сталкиваться
со случаями, когда число повторных
опытов различно. Это происходит вследствие
отброса грубых наблюдений, неуверенности
экспериментатора в правильности
некоторых результатов (в таких случаях
возникает желание еще и еще раз повторить
опыт) и т. п.

Тогда
при усреднении дисперсий приходится
пользоваться средним взвешенным
значением дисперсий, взятым с учетом
числа степеней свободы

(7.10)

где



– дисперсия первого опыта,


– дисперсия второго опыта и т. д., ν₁
– число степеней свободы в первом опыте,
равное числу параллельных опытов m
минус 1, т. е. ν₁=
m₁–1;
ν₂
– число степеней свободы во втором
опыте и т. д. Число степеней свободы
средней дисперсии принимается равным
сумме чисел степеней свободы дисперсий,
из которых она вычислена.

После исключения
из повторных опытов грубых ошибок во
всех опытах необходимо снова проверить
однородность дисперсий

.

Отметим, что
повторные опыты нельзя путать с повторными
измерениями в одном опыте. Такие измерения
часто делаются и являются полезными,
но не могут заменить повторных опытов.

Определение
закона распределения результатов
измерений или случайных погрешностей
измерений.
При определении закона распределения
случайных погрешностей измерений
переходят от выборки результатов
измерений y₁,
y₂,
y₃,
…, y_n
к выборке отклонений от среднего
арифметического результатов измерений
Δy₁,
Δy₂,
Δy₃,
…, Δy_n,
где Δ y_i
= y_i
–

.

Первым
шагом при идентификации закона
распределения является построение по
результатам измерения y_i,
i=1,
2, …, n,
вариационного
ряда
(упорядоченной выборки). В вариационном
ряду результаты измерения располагают
в порядке возрастания. Далее этот ряд
разбивают на оптимальное число r,
как правило одинаковых интервалов
длиной

.

Далее
определяют число попаданий m_i
(частоты) результатов измерений в
интервалы группирования. В рассматриваемом
интервале отношение частоты m_i
к общему числу n
измерений определяет частность

(7.11)

или
оценочную вероятность появления
соответствующего результата измерения.
Частоту появления результата измерения
можно графически представить в виде
гистограммы, т.е. ступенчатой диаграммы
оценки p^*
плотности вероятности распределения
результатов измерения по размеру.
Частота p_i
соответствует площади i-го
прямоугольника, а оценку плотности
вероятности получают делением частости
(площади) на интервал h
(основание):

(7.12)

При
увеличении числа интервалов и
соответственно уменьшении их длины
гистограмма все более приближается к
гладкой кривой – графику плотности
распределения вероятности.

По
виду построенной гистограммы может
быть оценен закон распределения
результатов измерений.

Принято
считать, что в большинстве тщательно
поставленных экспериментов ошибки с
хорошим приближением подчинены
нормальному закону распределения

, (7.13)

где
е
– основание натурального логарифма,
p_x(x)
– плотность распределения вероятности.
Теоретически это утверждение обосновывается
исходя из центральной предельной теоремы
теории вероятностей, которая утверждает,
что сумма многих независимых источников
погрешностей с произвольными функциями
распределения асимптотически имеет
нормальное распределение, если только
ни одна из этих погрешностей не является
превалирующей.

В
результате получим следующий график:

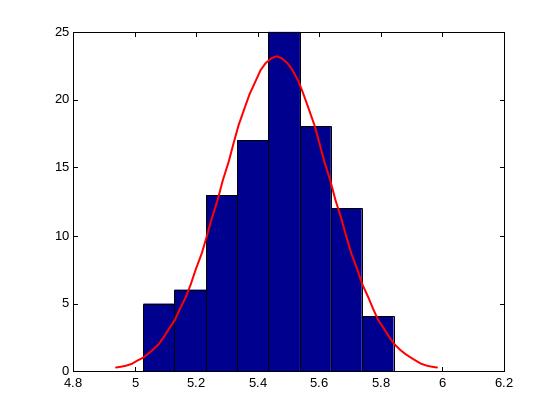
При
числе наблюдений n
> 50 для проверки гипотезы о нормальности
закона распределения случайной величины
часто используют критерий согласия ².
Идея этого метода состоит в контроле
отклонений гистограммы экспериментальных
данных от гистограммы с таким же числом
интервалов, построенных на основе
нормального закона распределения.

Для
этого критерия мерой отклонения
статистического распределения случайной
величины от нормального закона служит
величина

²
=

, (7.14)

где
m_i
– экспериментальные значения частот
в интервалах разбиения [x_i,
x_i+1];
n
– число интервалов разбиения;

– теоретические вероятности попадания
результатов наблюдения в интервалы
разбиения.

Величина
_k²
подчиняется ²
распределению с k
степенями свободы. Для нормального
распределения число степеней свободы
определяют по формуле k = m – 3.

Методика проверки
соответствия принятого и экспериментального
законов распределения заключается в
следующем:

• определяются
  среднее арифметическое значение

  измеряемой величины по формуле (7.1) и
  среднеквадратическое отклонение
  результата измерения s_y
  по формуле (7.3);

• группируются
  результаты наблюдений по интервалам
  длиной h,
  число которых определяется так же, как
  и при построении гистограммы;

• вычисляется
  число наблюдений для каждого из
  интервалов, теоретически соответствующее
  нормальному закону распределения. Для
  этого сначала от реальных середин
  интервалов y_i0
  переходят к нормированным серединам
  
  .
  Затем для каждого значения z_i
  с помощью аналитической модели находят
  функции плотности вероятности по
  формуле

По
найденному значению f(z_i)
определяют ту часть N_i
имеющихся наблюдений, которая теоретически
должна быть в каждом из интервалов

,
где n
– общее число наблюдений.

• если
  в какой-либо интервал теоретически
  попадает меньше пяти наблюдений, то в
  обеих гистограммах его соединяют с
  соседним интервалом. После этого
  определяют число степеней свободы ν
  = m
  – 3, где m
  – общее число интервалов. Если было
  произведено укрупнение интервалов, то
  m
  – общее число интервалов после
  укрупнения;

• по
  формуле (7.14) определяют эмпирическое
  значение величины χ²;

• выбирают
  уровень значимости критерия q.
  Он должен быть небольшим, чтобы была
  мала вероятность совершить ошибку
  первого рода. При заданном уровне
  значимости q
  и числу степеней свободы ν
  находят границу критической области
  
  ,
  такую что
  
  =
  q.
  Вероятность того, что полученное
  значение χ²
  превышает

  ,
  равна q
  и мала. Поэтому, если оказывается
  
  ,
  то гипотеза о нормальности закона
  распределения опытных данных принимается,
  т.е. она правдоподобна и не противоречит
  опытным данным с доверительной
  вероятностью p
  =1– q.
  В противном случае гипотеза отвергается,
  как противоречащая опытным данным.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #