Ошибка даламбера монету бросают два раза

Ошибка Даламбера

Пример 1.  Правильная монета подбрасывается 2 раза.

Событие A:  Выпадение хотя бы одного “орла”.

Решение. Число возможных исходов в серии из двух испытаний равно 4:

ОО,  ОР,  РО,  РР.

Число исходов, благоприятствующих событию A, равно 3:

ОО,  ОР,  РО.

Следовательно,

.

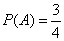
Пример 2.  В семье имеется 2 ребенка.

Событие A:  Хотя бы один из детей – мальчик.

Решение. Задача по своей сути не отличается от предыдущей. Только под испытанием теперь следует понимать рождение ребенка. Если рождение мальчика или девочки в одном испытании представляют собой случайные события, то число равно­вероятных исходов равно 4:

ММ,  МД,  ДМ,  ДД.

Только первые 3 исхода благоприятствуют событию A. Поэтому

.

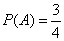
Ошибочное решение. Число возможных вариантов в серии из двух испытаний равно 3:

ММ,  МД,  ДД.

Первые два исхода благоприятствуют событию A. Поэтому

.

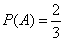
Анализ. Три события:

          “2 мальчика”,

         “1 мальчик и одна девочка”  и

         “2 девочки”

не являются равно­возможными, поскольку ММ и ДД представляют собой элементарные события, тогда как событие “1 мальчик и одна девочка” – составное событие, которое разлагается на 2 исхода: МД и ДМ.

Любопытно, что подобную ошибку в рассуждениях допустил в свое время великий математик Даламбер, рассматривая задачу о подбрасывании монеты (см. Пример 1).

Задачи Даламбера.
а) Монета бросается два раза. Какова вероятность того, что хотя бы один раз выпадет герб?
б) Монета бросается три раза. Какова вероятность того, что герб выпадет по крайней мере один раз?

Каждый год учителя жалуются на то, что падает
интерес у учеников к учебе, и каждый год
усложняются задания ГИА и ЕГЭ. Вот уже и элементы
теории вероятностей стали полноправными
заданиями в тестах. Этой теме в школьном курсе не
уделялось должного внимания и казалось, что
сложно будет побороть страх учеников перед этими
задачами. Но мы, учителя, поняли, что т.к. изменить
ситуацию невозможно, под нее надо
подстраиваться.

Проанализировав демонстрационные варианты,
убедилась, что для успешного решения указанных
задач необходимо повторить (а может быть выучить)
основные положения теории вероятностей.

Прежде всего, напомним учащимся, что же изучает
этот раздел математики?

Наблюдая со стороны за различными явлениями
или участвуя в проведении опытов, мы замечаем,
что некоторое явление может произойти, а может и
нет. Те события, исход которых предсказать
нельзя, назовем случайным.

Например, нельзя заранее предсказать будет ли
цифра «6» в номере машины, проезжающей сейчас
мимо вас, будет ли вынут именно красный шар из
коробки, в которой 4 шара разного цвета?
Предсказать исход одного испытания мы не можем, а
вот подсчитать вероятность его наступления при
большом количестве произведенных однородных
испытаний – это под силу теории вероятностей.

Основная формула классической вероятности
всего одна: , где n
– число благоприятных исходов, m – общее число
исходов.

При этом надо подчеркивать, что общее число
исходов конечно и все исходы равнозначны (в
противном случае применение этой формулы
невозможно, т.к. получим неверный результат).

Ученики школы среднего и старшего звена
знакомятся только со случайными событиями.
Причем, это знакомство в основном опирается на их
жизненный опыт, интуицию.

В своей повседневной жизни мы часто повторяем:
«с достаточной долей вероятности…», «мне
кажется невероятно, что это произойдет», «почти
со 100% вероятностью можно утверждать…». Этими
фразами мы, опираясь на знания предыдущих лет (а
иногда и на интуицию) прогнозируем исход
какого-то события. Однако, не смотря на наш
прогноз, указанное событие может произойти, а
может и нет. Так, купив лотерейный билет, мы
рассчитываем, конечно, на выигрыш. Подбрасывая
монету, скажем, 4 раза, предполагаем, что «орел» и
«решка» выпадут по 2 раза. Но проделав этот
нехитрый опыт, убеждаемся, что это совсем не так в
реальности. Вот тогда и возникает вопрос: а
сколько раз надо бросить монету, что б
вероятность выпадения нужной стороны её была
почти 50%?

На все эти вопросы и отвечает теория
вероятностей. Она дает возможность численно
характеризовать возможность наступления того
или иного события.

Еще очень важным моментом в подсчете
вероятности наступления события, является то,
что все испытания и их исход договорились
считать равновозможными (равновероятными).
Что это значит?

Рассмотрим, например, опыт, с однократным
подбрасыванием монеты. В реальной жизни может
быть несколько исходов: выпадет «орел», выпадет
«решка», монета встанет на ребро, укатится
куда-нибудь. Кроме того, при многократном
подбрасывании, может оказаться, что выпадение,
скажем, «орла» намного чаще, чем «решки».При
детальном исследовании монеты оказалось, что на
сторону «герба»ушло больше металла(при отливке
монеты) и эта сторона тяжелее. Может сказаться и
неоднородность металла при плавке, порыв ветра
при бросании монеты, неровность поверхности, на
которую падает монета и т.д. Чтоб исход испытания
не зависел от этих частностей, договорились
считать монету «правильной» или «симметричной»,
т.е. одинаковой по весу с обеих сторон, падающей
на одну и ту же плоскость в безветренную погоду.
Аналогично надо считать симметричными игральный
кубик и игральные кости при бросании их во время
эксперимента.

Следует предостеречь учеников от неверного
способа решения задач рассуждением, без учета
всех возможностей исходов. Приведу пример.

Задача. Бросают два игральных кубика.
Найти вероятность того, что сумма выпавших очков
будет равна пяти.

Ошибочное решение. В данной ситуации
возможны два исхода: либо сумма будет равна пяти,
либо не будет. Значит, общее число исходов – два,
а из них благоприятных – один (т.е. сумма равна
пяти). Значит, по формуле вероятности:

В чем ошибка ученика? Как мы знаем, каждый кубик
имеет 6 граней, на которых расположены точки от
одной до шести. Бросая оба кубика одновременно,
число очков, выпавших на первом кубике, не
зависит от того, какое число очков в это время
выпадет на втором. Т.е. шесть исходов первого
кубика сочетаются с шестью исходами второго. И
общее число равновозможных исходов: 6 • 6 = 36.
Тогда, благоприятных исходов, т.е. сумма равна
пяти будет 4 : 3+2; 2+3; 1+4; 4+1. Следовательно, ответ на
вопрос задачи: 

Очень уместно здесь познакомить учеников со
знаменитой ошибкой Даламбера.

Пример. Ошибка Даламбера. Какова
вероятность, что подброшенные, вверх две
правильные монеты упадут на одну и ту же сторону?

Решение, предложенное Даламбером. Опыт
имеет три равновозможных исхода:

1) обе монеты упали на «орла»;
2) обе монеты упали на «решку»;
3) одна из монет упала на «орла», другая на
«решку».

Из них благоприятными для нашего событиями
будут два исхода, поэтому искомая вероятность
равна .

Правильное решение. Опыт имеет четыре
равновозможных исхода:

1) первая монета упала на «орла», вторая тоже на
«орла»;
2) первая монета упала на «решку», вторая тоже на
«решку»;
3) первая монета упала на «орла», вторая – на
«решку»;
5) первая монета упала на «решку», вторая – на
«орла».

Из них благоприятными для нашего события будут
два исхода, поэтому искомая вероятность равна 

Даламбер совершил одну из самых
распространенных ошибок, допускаемую при
вычислении вероятности: он объединил два
принципиально разных исхода в один. Чтобы не
повторить эту ошибку, помните, что природа
различает все предметы, даже если внешне
они для нас неотличимы.

Надо напоминать учащимся, что нужно
анализировать полученный результат: найденная
вероятность не может быть больше 1, как не может,
например, упасть на землю яблок больше, чем их
находится на дереве. Что при бросании монеты,
вероятность выпадения «орла» или «решки» почти
одинакова, а вот вероятность, скажем, отказа
тормозов у автомобиля добросовестного водителя,
крайне мала. Поэтому учащиеся должны помнить, что
p є [0;1].

Крайне редко, но бывают задания, где
вероятность оказывается равной нулю (нулевая
вероятность). События, вероятность которых равна
нулю называются невозможными. Например,
сумма выпавших очков на двух костях равна 13 (мы
знаем, что максимальное число очков одной грани
– 6, значит для двух граней – 12).

Если же вероятность равна 1 (иногда говорят
«стопроцентная вероятность»), то событие
называем достоверным. Примером может служить
опыт с игральным кубиком и утверждение, что при
подбрасывании выпало не более 6 очков.

Все остальные события, вероятность которых
находится в интервале (0;1), будем называть случайными.
Они и составляют основную часть задач в теории
вероятностей. Их-то и решают по уже упомянутой
формуле.

Хочется еще раз напомнить, что половина успеха
в решении той или иной задачи (совсем
необязательно по теории вероятностей) заложена
во внимательном чтении условия. Очень много
ошибок допускают ученики торопясь сделать
задание, которое, как кажется, им знакомо и, не
вникнув в исходные данные, допускают
непростительные ошибки.

Приведу пример двух похожих, но абсолютно
разных по смыслу (и, естественно, по способу
решения) задач.

Задача №1. Фабрика выпускает сумки. В
среднем, на 100 сумок, приходится 8 сумок со
скрытыми дефектами. Найдите вероятность того,
что купленная сумка окажется качественной. (Если
необходимо, результат округлите до сотых).

Решение.  Вероятность найдем по
формуле:  .
Здесь из 100 сумок 8 некачественных, следовательно,
остальные качественные, т.е.   100 – 8 = 92 сумки.
m = 100,
n = 92

Ответ: 0,92

Задача №2. Фабрика выпускает сумки. В
среднем, на каждые 100 качественных сумок
приходится 8 сумок со скрытыми дефектами. Найдите
вероятность того, что купленная сумка окажется
качественной. (Если необходимо, результат
округлите до сотых).

Решение. Вероятность найдем по формуле: . В этой задаче, в
отличие от предыдущей общее количество сумок
складывается из качественных ( 100 штук) и
некачественных (8 штук), т.е.  m = 100 + 8 = 108 .

Среди этих 108 сумок, качественных было 100 штук, n
= 100

Ответ: 0,93

Литература.

1. Бунимович Е.А., Булычев В.А. «Вероятность и
   статистика» .М «Дрофа». 2002г.
2. Колмогоров А.Н.и др. Введение в теорию
   вероятностей.. М. «Наука» 1982г.
3. Скопец З.А. «Дополнительные главы по курсу
   математики». М. «Просвещение» .1974г.
4. Чистяков В.П. «Курс теории вероятностей». М.
   «Наука» 1982г.

Соседние файлы в папке Пз 1

• #
• #
• #
• #