Загрузить PDF
Загрузить PDF
Абсолютная ошибка – это разность между измеренным значением и фактическим значением.[1]
Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.[2]
Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.
-
1
Запишите формулу для вычисления абсолютной ошибки. Формула:
, где
– абсолютная ошибка (разность между измеренным и фактическим значениями),
– измеренное значение,
– фактическое значение.[3]
-
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
.
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м:
-
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
.
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м:
-
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[4]
Так вы вычислите абсолютную ошибку.- В нашем примере:
, то есть абсолютная ошибка измерения равна 1 м.
Реклама
- В нашем примере:
-
1
Запишите формулу для вычисления относительной ошибки. Формула:
, где
– относительная ошибка (отношение абсолютной ошибки к фактическому значению),
– измеренное значение,
– фактическое значение.[5]
-
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
.
- Например, если относительная ошибка равна 0,02, формула запишется так:
-
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо
.
- Например, если фактическое значение равно 105 м, формула запишется так:
.
- Например, если фактическое значение равно 105 м, формула запишется так:
-
4
Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
-
5
Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете
, то есть измеренное значение.
-
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[6]
Так вы вычислите абсолютную ошибку.- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
. Таким образом, абсолютная ошибка равна 2,1 м.
Реклама
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так:
-
1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
-
2
-
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.[9]
Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».[10]
Так вы вычислите абсолютную ошибку.- Например, если измеренная длина поля равна
м, то есть абсолютная ошибка равна 0,5 м.
Реклама
- Например, если измеренная длина поля равна
Советы
- Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.
Реклама
Об этой статье
Эту страницу просматривали 26 271 раз.
Была ли эта статья полезной?
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2248.
А какая ваша оценка?
•обучение проведению моделирования процессов и систем;
•повышение способности оценивания качества и надежности функционирования объекта проектирования.
При решении практических задач очень часто нет необходимости производить точные вычисления, поэтому используют приближенные вычисления и приближенные числа. Но при любых приближенных вычислениях очень важна точность, с которой производятся данные вычисления и точность, которая необходима для округления различных величин. Встает вопрос о погрешности величин и вычислений. Погрешности бывают двух видов: устранимые и неустранимые.
Источниками погрешностей могут служить различные причины. Вопервых, очень часто исходные данные получаются из эксперимента, а это само по себе влечет достаточно сильный разброс данных и ограниченную их точность, погрешности дают также и физические приборы, используемые во время эксперимента. Во-вторых, математическая модель, которая используется для формализации данного физического или химического процесса сама по себе является достаточно приблизительной, что тоже влечет за собой погрешности. В-третьих, иррациональные числа и физические константы в процессе вычисления берутся тоже с определенной точностью. Кроме того, потеря точности возможна и при выполнении арифметических операций, использовании бесконечных последовательностей и т.д. Влияние погрешностей на результат может быть достаточно велико, поэтому необходимо очень аккуратно обращаться с приближением чисел.
1.1. Абсолютная и относительная погрешности
Обозначим A точное значение некоторого числа, а a его приближенное значение. Записывается это следующим образом A ≈ a . Если A > a , то это
— 4 —
приближение по недостатку, а если A < a , то это приближение по избытку. Например, 3,14 <π < 3,15, поэтому приближение по недостатку 3,14, а по избытку 3,15.
Определение. Абсолютной погрешностью приближенного числа а
называют абсолютную величину разности между точным и приближенным значением числа:
|
∆ = |
A − a |
. |
(1.1) |
||
В практике возможны два случая:
1.Если точное значение известно тогда легко можно использовать формулу (1.1),
2.Если точное значение не известно, как чаще всего и бывает, то тогда используют понятие предельной абсолютной погрешности.
Определение. Предельной абсолютной погрешностью приближенного числа а называется погрешность, которая не меньше абсолютной погрешности этого числа.
|
∆a ≥ ∆ = |
A − a |
. |
(1.2) |
||
Таким образом, точное значение числа заключено в границах: a − ∆a ≤ A ≤ a + ∆a ,
A = a ± ∆a ,
где a − ∆a — приближение по недостатку, а a + ∆a — приближение по избытку. Пример. Определить предельную абсолютную погрешность числа
е=2,71828…с точностью до тысячных. Число е можно оценить следующим образом 2,7181<e< 2,7183. Тогда предельная абсолютная погрешность: ∆e = 0,0001. Отметим, что этот вариант не единственный, возможны и другие значения предельной абсолютной погрешности.
Ответ: ∆e = 0,0001.
Таким образом, предельной абсолютной погрешностью может являться любой представитель бесконечного множества неотрицательных чисел,
— 5 —

которые удовлетворяют неравенству (1.2). Но из разумных соображений выбирают наименьшее из этих чисел. Абсолютная погрешность характеризует ошибку, приходящуюся на единицу измерения той или иной величины.
Пример. Необходимо измерить длину некоторого расстояния. Измерения
|
были проведены с |
некоторой точностью:456,25 ≤ l ≤ 456,35м. Погрешность |
|
∆l = 0,05м. Запись |
результата в этом случае имеет следующий вид: |
l = 456,3 ± 0,05 м, где 456,3 – длина отрезка, а 0,05 – точность измерения.
Ответ: l = 456,3 ± 0,05 м.
Определение. Относительной погрешностью приближенного числа а
называют отношение абсолютной погрешности приближенного числа к точному значению этого числа:
|
δ = |
∆ |
= |
A − a |
. |
(1.3) |
||||
|
A |
|||||||||
|
A |
Здесь надо отметить, что, во-первых, A ≠ 0 , а во-вторых, очень редко бывает известно точное значение A. Тогда вместо A берут приближенное значение а.
Так же как и в предыдущем случае введем понятие предельной относительной
|
погрешности. |
||||
|
Определение. |
Предельной |
относительной |
погрешностью |
|
|
приближенного числа а |
называется |
погрешность, которая не меньше |
||
|
относительной погрешности этого числа: |
||||
|
δa ≥δ . |
(1.5) |
Отсюда следует, что ∆ = Aδ ≤ Aδa . На практике A ≈ a , поэтому считают ∆ = a δa . Границы точного числа А: A = a(1±δa ).
Пример. Вычислить предельную относительную погрешность при округлении числа е = 2,71828.… В одном из предыдущих примеров было
— 6 —

получено, что число e = 2,7182 ± 0,0001. Тогда предельная относительная погрешность δe = 2,718280,0001 ≈ 3,7 10−5 ≤ 4 10−5 .
Ответ: δe = 4 10−5
Докажем следующую формулу, связывающую предельную абсолютную и предельную относительную погрешности:
|
∆a = |
aδa |
. |
(1.6) |
|
1−δa |
Для определенности будем считать, что A > 0,a > 0,∆a < a .
По определению относительной и предельной относительной
|
погрешностей |
получаем δ = |
∆ |
≤ |
∆ |
, а |
δa = |
∆a |
. |
Тогда |
абсолютную |
|||||
|
A |
a + ∆ |
||||||||||||||
|
a + ∆a |
|||||||||||||||
|
погрешность |
можем представить |
∆ = |
A |
δ ≤ (a + ∆)δa . |
Выделив из этого |
||||||||||
|
неравенства |
∆, получаем |
∆ ≤ |
aδa |
. |
Тогда |
предельная |
абсолютная |
||||||||
|
1−δa |
|
погрешность равна ∆a = |
aδa |
. |
||
|
1−δa |
||||
|
На практике стараются, чтобы ∆a << a , а δ <<1; тогда можно принять |
||||
|
δ ≈ |
∆a , а ∆a ≈ aδa . |
(1.7) |
||
|
a |
Достаточно часто относительную погрешность измеряют в процентном отношении к приближенной величине. Относительная погрешность показывает, насколько велика абсолютная погрешность по отношению к самой величине.
1.2. Десятичная запись приближенных чисел. Значащие цифры
Любое положительное число А можно представить в виде бесконечной десятичной дроби
|
A =α |
m |
10m +α |
10m−1 |
+α |
m−2 |
10m−2 |
+… +α |
10m−n+1 |
+…, |
(1.8) |
|
m−1 |
m−n+1 |
— 7 —

|
где αi цифры (αi =0,1,2,…,9), |
i=m, m-1,…, причем |
αi ≠ 0 , m— |
старший |
|
десятичный разряд числа а. |
|||
|
Пример. Число 7654,7683… |
можно представить |
следующим |
образом: |
7654,7683… = 7 103 + 6 102 + 5 101 + 4 100 + 7 10−1 + 6 10−2 + 8 10−3 +…
Но работать с бесконечными числами не очень удобно, поэтому берут числа приближенные:
|
a ≈α |
m |
10m +α |
10m−1 +α |
m−2 |
10m−2 +… +α |
10m−N +1. |
|||
|
m−1 |
m−N +1 |
||||||||
|
Число (1.8) сохранено до m-N+1 разряда. |
|||||||||
|
Определение. Пусть |
αN |
первая ненулевая цифра в десятичной записи |
|||||||
|
приближенного |
числа а, |
считая слева. Тогда сама |
цифра |
αN и |
все, |
||||
|
последующие за ней, называются значащими цифрами. |
|||||||||
|
Пример. Рассмотрим |
приближенное число а=0,00234. Это число имеет |
||||||||
|
три значащие цифры 2,3,4. А приближенное число |
а=1,1030 |
имеет |
пять |
||||||
|
значащих цифр 1,1,0,3,0. |
Определение. N первых значащих цифр αm ,αm−1,…,αm−N +1 приближенного числа а называют верными, если выполняется следующее
неравенство: ∆ = A − a ≤ 12 10m−N +1 , то есть абсолютная погрешность этого
числа не более чем половина единицы разряда, выражаемого N-й значащей цифрой, считая слева направо.
Пример. Рассмотрим точное и приближенное числа А=78,98 и а=79,00. Определим количество верных цифр у приближенного числа при данном округлении.
Приближенное число будет иметь три верных цифры, так как
∆= A − a = 0,02 ≤ 12 10−1, а m − N +1 = −1 и m=1. Следовательно, N = 3 .
Ответ: приближенное число имеет три верные цифры.
—8 —
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Введение
- 1.1 Постановка вопроса. Виды погрешностей
- 2 Виды мер точности
- 3 Предельные погрешности
- 4 Погрешности округлений при представлении чисел в компьютере
- 5 Погрешности арифметических операций
- 6 Погрешности вычисления функций
- 7 Числовые примеры
- 8 Список литературы
- 9 См. также
Введение
Постановка вопроса. Виды погрешностей
Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.
При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления.
При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации.
Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.
Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10−6, если коэффициенты исходных уравнений задаются с точностью 10−2.
Виды мер точности
Мерой точности вычислений являются абсолютные и относительные погрешности. Абсолютная погрешность определяется формулой
где – приближение к точному значению
.
Относительная погрешность определяется формулой
Относительная погрешность часто выражается в процентах. Абсолютная и относительная погрешности тесно связаны с понятием верных значащих цифр. Значащими цифрами числа называют все цифры в его записи, начиная с первой ненулевой цифры слева. Например, число 0,000129 имеет три значащих цифры. Значащая цифра называется верной, если абсолютная погрешность числа не превышает половины веса разряда, соответствующего этой цифре. Например, , абсолютная погрешность
. Записывая число в виде
имеем , следовательно, число имеет две верных значащих цифр (9 и 3).
В общем случае абсолютная погрешность должна удовлетворять следующему неравенству:
где — порядок (вес) старшей цифры,
— количество верных значащих цифр.
В рассматриваемом примере .
Относительная погрешность связана с количеством верных цифр приближенного числа соотношением:
где — старшая значащая цифра числа.
Для двоичного представления чисел имеем .
Тот факт, что число является приближенным значением числа
с абсолютной погрешностью
, записывают в виде
причем числа и
записываются с одинаковым количеством знаков после запятой, например,
или
.
Запись вида
означает, что число является приближенным значение числа
с относительной погрешностью
.
Так как точное решение задачи как правило неизвестно, то погрешности приходится оценивать через исходные данные и особенности алгоритма. Если оценка может быть вычислена до решения задачи, то она называется априорной. Если оценка вычисляется после получения приближенного решения задачи, то она называется апостериорной.
Очень часто степень точности решения задачи характеризуется некоторыми косвенными вспомогательными величинами. Например точность решения системы алгебраических уравнений
характеризуется невязкой
где — приближенное решение системы.
Причём невязка достаточно сложным образом связана с погрешностью решения , причём если невязка мала, то погрешность может быть значительной.
Предельные погрешности
Пусть искомая величина является функцией параметров
— приближенное значение
. Тогда предельной абсолютной погрешностью называется величина
Предельной относительной погрешностью называется величина .
Пусть — приближенное значение
. Предполагаем, что
— непрерывно дифференцируемая функция своих аргументов. Тогда, по формуле Лагранжа,
где .
Отсюда
где .
Можно показать, что при малых эта оценка не может быть существенно улучшена. На практике иногда пользуются грубой (линейной) оценкой
где .
Несложно показать, что:
— предельная погрешность суммы или разности равна сумме предельных погрешностей.
— предельная относительная погрешность произведения или частного приближенного равна сумме предельных относительных погрешностей.
Погрешности округлений при представлении чисел в компьютере
Одним из основных источников вычислительных погрешностей является приближенное представление чисел в компьютере, обусловленное конечностью разрядной сетки (см. Международный стандарт представления чисел с плавающей точкой в ЭВМ). Число , не представимое в компьютере, подвергается округлению, т. е. заменяется близким числом
, представимым в компьютере точно.
Найдем границу относительной погрешности представления числа с плавающей точкой. Допустим, что применяется простейшее округление – отбрасывание всех разрядов числа, выходящих за пределы разрядной сетки. Система счисления – двоичная. Пусть надо записать число, представляющее бесконечную двоичную дробь
где ,
— цифры мантиссы.
Пусть под запись мантиссы отводится t двоичных разрядов. Отбрасывая лишние разряды, получим округлённое число
Абсолютная погрешность округления в этом случае равна
Наибольшая погрешность будет в случае , тогда
Т.к. , где
— мантисса числа
, то всегда
. Тогда
и относительная погрешность равна
. Практически применяют более точные методы округления и погрешность представления чисел равна
( 1 )
т.е. точность представления чисел определяется разрядностью мантиссы .
Тогда приближенно представленное в компьютере число можно записать в виде , где
– «машинный эпсилон» – относительная погрешность представления чисел.
Погрешности арифметических операций
При вычислениях с плавающей точкой операция округления может потребоваться после выполнения любой из арифметических операций. Так умножение или деление двух чисел сводится к умножению или делению мантисс. Так как в общем случае количество разрядов мантисс произведений и частных больше допустимой разрядности мантиссы, то требуется округление мантиссы результатов. При сложении или вычитании чисел с плавающей точкой операнды должны быть предварительно приведены к одному порядку, что осуществляется сдвигом вправо мантиссы числа, имеющего меньший порядок, и увеличением в соответствующее число раз порядка этого числа. Сдвиг мантиссы вправо может привести к потере младших разрядов мантиссы, т.е. появляется погрешность округления.
Округленное в системе с плавающей точкой число, соответствующее точному числу , обозначается через
(от англ. floating – плавающий). Выполнение каждой арифметической операции вносит относительную погрешность, не большую, чем погрешность представления чисел с плавающей точкой (1). Верна следующая запись:
где — любая из арифметических операций,
.
Рассмотрим трансформированные погрешности арифметических операций. Арифметические операции проводятся над приближенными числами, ошибка арифметических операций не учитывается (эту ошибку легко учесть, прибавив ошибку округления соответствующей операции к вычисленной ошибке).
Рассмотрим сложение и вычитание приближенных чисел. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме абсолютных погрешностей слагаемых.
Если сумма точных чисел равна
сумма приближенных чисел равна
где — абсолютные погрешности представления чисел.
Тогда абсолютная погрешность суммы равна
Относительная погрешность суммы нескольких чисел равна
( 2 )
где — относительные погрешности представления чисел.
Из (2) следует, что относительная погрешность суммы нескольких чисел одного и того же знака заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
При сложении чисел разного знака или вычитании чисел одного знака относительная погрешность может быть очень большой (если числа близки между собой). Так как даже при малых величина
может быть очень малой. Поэтому вычислительные алгоритмы необходимо строить таким образом, чтобы избегать вычитания близких чисел.
Необходимо отметить, что погрешности вычислений зависят от порядка вычислений. Далее будет рассмотрен пример сложения трех чисел.
( 3 )
При другой последовательности действий погрешность будет другой:
Из (3) видно, что результат выполнения некоторого алгоритма, искаженный погрешностями округлений, совпадает с результатом выполнения того же алгоритма, но с неточными исходными данными. Т.е. можно применять обратный анализ: свести влияние погрешностей округления к возмущению исходных данных. Тогда вместо (3) будет следующая запись:
где
При умножении и делении приближенных чисел складываются и вычитаются их относительные погрешности.
-
≅
с точностью величин второго порядка малости относительно .
Тогда .
Если , то
≅
При большом числе n арифметических операций можно пользоваться приближенной статистической оценкой погрешности арифметических операций, учитывающей частичную компенсацию погрешностей разных знаков:
где – суммарная погрешность,
– погрешность выполнения операций с плавающей точкой,
– погрешность представления чисел с плавающей точкой.
Погрешности вычисления функций
Рассмотрим трансформированную погрешность вычисления значений функций.
Абсолютная трансформированная погрешность дифференцируемой функции , вызываемая достаточно малой погрешностью аргумента
, оценивается величиной
.
Если , то
.
Абсолютная погрешность дифференцируемой функции многих аргументов , вызываемая достаточно малыми погрешностями
аргументов
оценивается величиной:
-
.
Если , то
.
Практически важно определить допустимую погрешность аргументов и допустимую погрешность функции (обратная задача). Эта задача имеет однозначное решение только для функций одной переменной , если
дифференцируема и
:
-
.
Для функций многих переменных задача не имеет однозначного решения, необходимо ввести дополнительные ограничения. Например, если функция наиболее критична к погрешности
, то:
-
(погрешностью других аргументов пренебрегаем).
Если вклад погрешностей всех аргументов примерно одинаков, то применяют принцип равных влияний:
Числовые примеры
Специфику машинных вычислений можно пояснить на нескольких элементарных примерах.
ПРИМЕР 1. Вычислить все корни уравнения
Точное решение задачи легко найти:
Если компьютер работает при , то свободный член в исходном уравнении будет округлен до
и, с точки зрения представления чисел с плавающей точкой, будет решаться уравнение
, т.е.
, что, очевидно, неверно. В данном случае малые погрешности в задании свободного члена
привели, независимо от метода решения, к погрешности в решении
.
ПРИМЕР 2. Решается задача Коши для обыкновенного дифференциального уравнения 2-го порядка:
Общее решение имеет вид:
При заданных начальных данных точное решение задачи: , однако малая погрешность
в их задании приведет к появлению члена
, который при больших значениях аргумента может существенно исказить решение.
ПРИМЕР 3. Пусть необходимо найти решение обыкновенного дифференциального уравнения:
Его решение: , однако значение
известно лишь приближенно:
, и на самом деле
.
Соответственно, разность будет:
Предположим, что необходимо гарантировать некоторую заданную точность вычислений всюду на отрезке
. Тогда должно выполняться условие:
Очевидно, что:
Отсюда можно получить требования к точности задания начальных данных при
.
Таким образом, требование к заданию точности начальных данных оказываются в раз выше необходимой точности результата решения задачи. Это требование, скорее всего, окажется нереальным.
Решение оказывается очень чувствительным к заданию начальных данных. Такого рода задачи называются плохо обусловленными.
ПРИМЕР 4. Решением системы линейных алгебраических уравнений (СЛАУ):
является пара чисел .
Изменив правую часть системы на , получим возмущенную систему:
с решением , сильно отличающимся от решения невозмущенной системы. Эта система также плохо обусловлена.
ПРИМЕР 5. Рассмотрим методический пример вычислений на модельном компьютере, обеспечивающем точность . Проанализируем причину происхождения ошибки, например, при вычитании двух чисел, взятых с точностью до третьей цифры после десятичной точки
, разность которых составляет
.
В памяти машины эти же числа представляются в виде:
-
, причем
и
Тогда:
Относительная ошибка при вычислении разности будет равна:
Очевидно, что , т.е. все значащие цифры могут оказаться неверными.
ПРИМЕР 6. Рассмотрим рекуррентное соотношение
Пусть при выполнении реальных вычислений с конечной длиной мантиссы на -м шаге возникла погрешность округления, и вычисления проводятся с возмущенным значением
, тогда вместо
получим
, т.е.
.
Следовательно, если , то в процессе вычислений погрешность, связанная с возникшей ошибкой округления, будет возрастать (алгоритм неустойчив). В случае
погрешность не возрастает и численный алгоритм устойчив.
Список литературы
- А.А.Самарский, А.В.Гулин. Численные методы. Москва «Наука», 1989.
- http://www.mgopu.ru/PVU/2.1/nummethods/Chapter1.htm
- http://www.intuit.ru/department/calculate/calcmathbase/1/4.html
См. также
- Практикум ММП ВМК, 4й курс, осень 2008
Абсолютная и относительная погрешности
Абсолютная погрешность приближения
Имея дело в вычислениях с бесконечными десятичными дробями, приходится для удобства выполнять приближение этих чисел, т. е. округлять их. Приблизительные числа получаются также при различных измерениях.
Бывает полезно узнать, как сильно приближенное значение числа отличается от его точного значения. Понятно, что чем это различие меньше, тем лучше, тем точнее выполнено измерение или вычисление.
Для определения точности измерений (вычислений) вводят такое понятие как погрешность приближения. По-другому его называют абсолютной погрешностью.
Абсолютной погрешностью приближения называется модуль разности между точным значением числа и его приближенным значением.
где х — это точное значение числа, а — его приближенное значение.
Например, в результате измерений было получено число 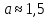
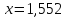
В случае с бесконечными дробями погрешность приближения определяется по той же формуле. На месте точного числа записывается сама бесконечная дробь. Например, 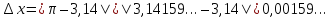
Приближение может выполняться как по недостатку, так и по избытку.
То же число π при приближении по недостатку с точностью до 0,01 равно 3,14, а при приближении по избытку с точностью до 0,01 равно 3,15.
Правило округления: если первая отбрасываемая цифра равна пяти или больше пяти, то выполняется приближение по избытку; если же меньше пяти, то по недостатку.
Например, т.к. третьей цифрой после запятой у числа π является 1, то при приближении с точностью до 0,01 оно выполняется по недостатку.
Вычислим абсолютные погрешности приближения до 0,01 числа π по недостатку и по избытку:
Как видим, абсолютная погрешность приближения по недостатку меньше, чем по избытку. Значит, приближение по недостатку в этом случае обладает более высокой точностью.
Относительная погрешность приближения
Абсолютная погрешность обладает одним важным недостатком – оно не позволяет оценить степень важности ошибки.
Например, покупаем мы на рынке 5 кг картофеля, а недобросовестный продавец при измерении веса ошибся на 50 г в свою пользу. Т.е. абсолютная погрешность составила 50 г. Для нас такая оплошность будет сущей мелочью и мы даже не обратим на неё внимания. А если при приготовлении лекарства произойдёт подобная ошибка? Тут уже всё будет намного серьёзней. А при загрузке товарного вагона наверняка возникают отклонения намного больше данного значения.
Поэтому сама по себе абсолютная погрешность малоинформативная. Кроме неё очень часто дополнительно рассчитывают относительное отклонение.
Относительной погрешностью приближения называется отношение абсолютной погрешности к точному значению числа.
Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
Приведём несколько примеров.
Пример 1. На предприятии 1284 рабочих и служащих. Округлить количество работающих до целых с избытком и с недостатком. Найти их абсолютные и относительные погрешности (в процентах). Сделать вывод.
Итак, 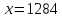
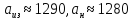
Абсолютная погрешность:
Относительная погрешность:
Значит, точность приближения с недостатком выше, чем точность приближения с избытком.
Пример 2. В школе 197 учащихся. Округлить количество учащихся до целых с избытком и с недостатком. Найти их абсолютные и относительные погрешности (в процентах). Сделать вывод.
Итак, 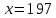
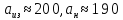
Абсолютная погрешность:
Относительная погрешность:
Значит, точность приближения с избытком выше, чем точность приближения с недостатком.
-
Найдите абсолютную погрешность приближения:
-
числа 2,87 числом 2,9; числом 2,8;
-
числа 0,6595 числом 0,7; числом 0,6;
-
числа
числом
;
-
числа
числом 0,3;
-
числа 4,63 числом 4,6; числом 4,7;
-
числа 0,8535 числом 0,8; числом 0,9;
-
число
числом
;
-
число
числом 0,2.
-
Приближённое значение числа х равно а. Найдите абсолютную погрешность приближения, если:
|
|
|
|
|
|
|
|
|
|
|
|
-
Запишите в виде двойного неравенства:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Найдите приближённое значение числа х, равное среднему арифметическому приближений с недостатком и избытком, если:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Докажите, что среднее арифметическое чисел а и b является приближённым значением каждого из этих чисел с точностью до
.
-
Округлите числа:
|
|
|
|
|
|
|
|
|
|
|
|
-
Представьте обыкновенную дробь в виде десятичной и округлите её до тысячных и найдите абсолютную погрешность:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
Докажите, что каждое из чисел 0,368 и 0,369 является приближённым значением числа
с точностью до 0,001. Какое из них является приближённым значением числа
с точностью до 0,0005?
-
Докажите, что каждое из чисел 0,38 и 0,39 является приближённым значением числа
с точностью до 0,01. Какое из них является приближённым значением числа
с точностью до 0,005?
-
Округлите число до единиц и найдите относительную погрешность округления:
|
|
|
|
|
|
|
|
-
Представьте каждое из чисел
и
в виде десятичной дроби. Округлив полученные дроби до десятых, найдите абсолютную и относительную погрешности приближений.
-
Представьте каждое из чисел
и
в виде десятичной дроби. Округлив полученные дроби до десятых, найдите абсолютную и относительную погрешности приближений.
-
Радиус Земли равен 6380 км с точностью до 10 км. Оцените относительную погрешность приближённого значения.
-
Наименьшее расстояние от Земли до Луны равно 356400 км с точностью до 100 км. Оцените относительную погрешность приближения.
-
Сравните качества измерения массы М электровоза и массы т таблетки лекарства, если
т (с точностью до 0,5 т), а
г (с точностью до 0,01 г).
-
Сравните качества измерения длины
реки Волги и диаметра
мячика для настольного тенниса, если
км (с точностью до 5 км) и
мм (с точностью до 1 мм).
3




























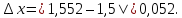
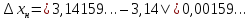
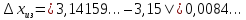
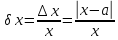
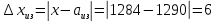
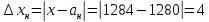
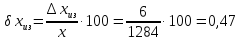
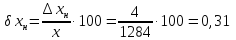
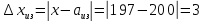
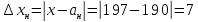
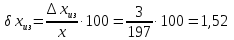
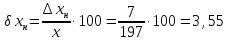
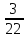 числом
числом 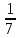 ;
;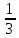 числом 0,3;
числом 0,3;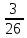 числом
числом 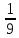 ;
;