Частные коэффициенты регрессии
Ошибки относительно линейной регрессии
Соотношения между дисперсиями, регрессиями и корреляциями различных порядков
Приближенные частные линейные регрессии
Частные коэффициенты регрессии
8. Обобщим теперь соотношения линейной регрессии на случай p величин. Для p совместно нормальных величин xi с нулевым средним и дисперсиями математическое ожидание величины x1 при условии, что x2, …, xp фиксированы, как видно из выражения в экспоненте распределения, равно
. (17)
Коэффициент регрессии x1 по xj при фиксированных остальных p-2 величинах будем обозначать или, короче
, где q символизирует совокупность величин, отличных от указанных первичными индексами, а индекс у q служит для различения этих совокупностей. Коэффициенты
называются частными коэффициентами регрессии.
Следовательно, мы имеем
. (18)
Сравнивая (18) с (17), получаем для многомерного нормального случая

Аналогично, коэффициент регрессии xj по x1 при фиксированных остальных переменных есть

Таким образом, поскольку C1j=Cj1, то из (6), (19) и (20) получаем

— очевидное обобщение соотношения (17). Соотношения (19) и (20) показывают, что коэффициент не симметричен относительно x1 и xj, как и следовало ожидать от коэ ффициента зависимости. Подобно(5) и (6), (19) и (20) являются определениями частных коэффициентов регрессии в общем случае.
Ошибки относительно линейной регрессии
9. Назовем ошибкой (эту величину часто называют «остатком» (residual) но мы будем проводить различие между ошибками (errors) относительно линейных регрессий в генеральной совокупности и остатками, возникающими при подгонке регрессий к выборочным данным) порядка (p-1) величину
.
Ее среднее равно нулю, а дисперсия равна
.
так что является дисперсией ошибки величины x1 относительно регрессии. Из (18) немедленно получаем


Если брать математическое ожидание в два этапа, фиксируя вначале x2, …, xp, то условное математическое ожидание от второго члена в (23) будет равно, согласно (18), нулю. Таким образом,

Дисперсия ошибки (24) не зависит от фиксируемых значений x3, …, xp, если только от них не зависят коэффициенты .
В этом случае условное распределение величины x1 называется гомоскедастическим (homoscedastic) (или гетероскедастическим (heteroscedastic) в противном случае). Это постоянство дисперсии ошибок делает интерпретацию регрессий и корреляций более простой.
Например, в нормальном случае условные дисперсии и ковариации, полученные при фиксировании множества величин, не зависят от значений, в которых последние фиксированы (см. (14)).
В других случаях при интерпретациях мы должны надлежащим образом учитывать обнаруженную гетероскедастичность, тогда, возможно, частные коэффициенты регрессии лучше всего рассматривать как показатели зависимости, усредненные по всевозможным значениям фиксированных величин.
Соотношения между дисперсиями, регрессиями и корреляциями различных порядков
Если даны p величин, то мы можем изучать корреляцию между любыми двумя из них, когда среди оставшихся зафиксированы значения произвольного подмножества величин. Аналогично, можно интересоваться регрессией произвольной величины относительно любого подмножества из оставшихся величин. С возрастанием p число всевозможных коэффициентов становится очень большим.
Если некоторый коэффициент содержит k вторичных индексов, то говорят, что он имеет порядок k. Так, порядок p12.34 равен 2, порядок p12.3 — единице, порядок p12 — нулю, тогда как β12.678 имеет порядок 3, а — порядок 4. В наших нынешних обозначениях коэффициенты линейной регрессии β1 и β2 должны быть записаны в виде β12 и β21 соответственно. Они имеют порядок нуль, как и обычная дисперсия σ2.
В 4 и 7 мы уже видели, как любой коэффициент корреляции первого порядка может быть выражен через коэффициенты нулевого порядка. Теперь будут получены более общие результаты такого сорта для коэффициентов всех типов.
11. Из (24) и (19) имеем

откуда
.
Пользуясь символом q, введенным в 8, получаем
, (26)
и аналогично, если 1 заменить любым другим индексом.
Точно таким же путем можно получить более общий результат

который сводится к (26) при l=m. Соотношение (27) применимо в случае, когда вторичные индексы одной величины включают в себя первичные индексы другой.
Если, с другой стороны, оба множества вторичных индексов не содержат l и m, то обозначим через r общее множество вторичных индексов. Ковариация двух ошибок xl.r, xm.r связана с их корреляцией и дисперсиями соотношениями:

что согласуется с уже найденным соотношением (21). Присоединяя множество индексов r к обеим величинам xl, xm, мы попросту должны сделать то же самое со всеми их коэффициентами.
12. Теперь можно использовать (26) для получения соотношения между дисперсиями ошибок различных порядков. Обозначая |D| корреляционный определитель всех величин, кроме x2. Тогда, имеем из (26)
(где индекс q-2 обозначает множество q без x2) и
,
откуда
. (29)
По определению |D|=C22, а согласно обобщенной теореме Якоби об определителях
, (30)
так как D11 является дополнительным минором для в C. Таким образом, используя (30), получаем из (29)

или, учитывая (6), находим
. (32)
Соотношение (32) является обобщением двумерного результата, который может быть представлен в виде
.
13. Соотношение (32) дает нам возможность выразить дисперсию ошибки порядка (p-1) через дисперсию ошибки и коэффициент корреляции порядка (p-2). Если мы теперь вновь воспользуемся (32) для того, чтобы выразить , то тем же путем найдем, что
.
Применяя последовательно (32) и записывая более полно индексы, получаем
. (33)
В (33), очевидно, не играет роли порядок вторичных индексов у σ1.23…p; мы их можем переставить так, как пожелаем. Например, для простоты в силу (26) можно написать
. (34)
В (34) индексы, отличные от 1, допускают перестановку. Соотношение (34) позволяет нам выразить дисперсию ошибки порядка s через дисперсию ошибки нулевого порядка и s коэффициентов корреляции, порядок которых принимает значения от нуля до (s-1).
14. Перейдем теперь к коэффициентам регрессии. Перепишем (15) для ковариации между x1 и x2 при фиксированном xp:
.
Присоединяя повсюду индексы 3, …, (p-1), имеем
. (35)
Используя определение (28) коэффициента регрессии как отношения ковариации к дисперсии, т.е.
,
и обозначим через r множество 3, …, (p-1), находим из (35)
,
или
. (36)
Если в (36) положить x1≡x2, то получим
, (37)
другую форму соотношения (32). Таким образом, из (36) и (37) имеем
. (38)
Это и есть требуемая формула для выражения коэффициента регрессии через некоторые коэффициенты следующего более низкого порядка. Повторно применяя (38), найдем представление любого коэффициента регрессии в терминах коэффициентов нулевого порядка.
Наконец, используя (21), из (38) получаем соотношение
, (39)
обобщающее (5) путем присоединения множества индексов r.
Приближенные частные линейные регрессии
15. В нашем изложении, начиная с 8, мы занимались точно линейными регрессионными зависимостями типа (18). Рассмотрим теперь вопрос подгонки регрессионных соотношений этого типа к наблюденным совокупностям, регрессии которых почти никогда не бывают точно линейными.
С помощью тех же рассуждений мы приходим к методу наименьших квадратов. Мы выбираем поэтому так, чтобы минимизировать сумму квадратов уклонений n наблюдений от подгоняемой регрессии:

где «иксы» измеряются от своих средних значений и предполагается n>p. Решение имеет вид
, (41)
где матрица X составлена из наблюдений над p-1 величинами x2, …, xp, а x1 — вектор наблюдений величины x1. Соотношение (41) можно переписать в виде
, (42)
где Vp-1 — матрица рассеяния для x2, …, xp, а M — вектор ковариаций между x1 и xj (j=2, …, p). Таким образом,
. (43)
Поскольку |Vp-1| есть минор V11 матрицы рассеяния V всех p величин, то (Vp-1)jl представляет собой дополнительный минор для
в V, так что сумма в правой части (43) является алгебраическим дополнением для (-σ1j) в V. Поэтому (43) представляется в виде
. (44)
Соотношение (44) совпадает с (19). Таким образом, мы приходим к заключению, что аппроксимация по методу наименьших квадратов дает те же коэффициенты регрессии, что и в случае точной линейной регрессии.
Из этого следует, что все результаты данной главы остаются в силе, когда для наблюденных совокупностей мы подгоняем регрессии по методу наименьших квадратов.
Связанные определения:
Выборочный коэффициент корреляции
Корреляционный анализ
Корреляция
Коэффициент корреляции
Линейная регрессия
Логистическая регрессия
Матрица плана
Метод наименьших квадратов
Независимый признак
Некоррелированный
Общая линейная модель
Регрессия
В начало
Содержание портала
-
Расчёт частных коэффициентов корреляции. Сравнение частных и парных коэффициентов корреляции
Частные коэффициенты
корреляции характеризуют взаимосвязь
между двумя выбранными переменными при
исключении влияния остальных показателей
(т.е. характеризуют «чистую» связь только
между этими признаками) и важны для
понимания взаимодействия всего комплекса
показателей, т.к. позволяют определить
механизмы усиления-ослабления влияния
переменных друг на друга.
Частный коэффициент
(k-2)-го
порядка между переменными, например,
между Y
и X1,
равен:
,
где Rij
– алгебраическое дополнение элемента
rij
корреляционной матрицы R
, равное Rij
=(-1)i+j
· Mij
Mij
– минор элемента rij
корреляционной матрицы R,
т.е. определитель матрицы на 1 меньшего
порядка, полученной из R
путём вычёркивания i-й
строки и j-го
столбца.
Н
алгебраическое дополнение
R12
рассчитывается следующим образом:
|
j |
1 |
2 |
3 |
4 |
5 |
|
|
i |
|
|||||
|
1 |
1 |
-0,3728125 |
0,47519037 |
-0,2997998 |
-0,384825 |
|
|
2 |
-0,372813 |
1 |
0,198409 |
-0,233376 |
0,021751 |
|
|
3 |
R= |
0,47519 |
0,198409 |
1 |
-0,656779 |
-0,073867 |
|
4 |
-0,2998 |
-0,233376 |
-0,656779 |
1 |
0,027049 |
|
|
5 |
-0,384825 |
0,021751 |
-0,073867 |
0,027049 |
1 |
Аналогично


Таким образом, для
расчёта частных коэффициентов корреляции
нужно сформировать в Excel
соответствующие матрицы размерности
(k-1)×(k-1)
(в нашем случае 4×4).
Чтобы найти
определители этих матриц, воспользуемся
встроенной функцией Excel:
ВСТАВКА (Office
2003) или
ФОРМУЛЫ (Office
2007)
Функция
МОПРЕД ,
указав в качестве
массива соответствующую матрицу
переменных.
Воспользовавшись
этой функцией, получаем:
R12=(-1)1+2·M12=
-(-0,2562274);
R11=(-1)1+1·M11=
0,5316755;
R22=(-1)2+2·M22=
0,3679652.
Аналогично
проводятся расчёты для всех остальных
частных коэффициентов корреляции.
R13=(-1)1+3·M13=
-0,2629254;
R14=(-1)1+4·M14=
-(-0,0416817);
R15=(-1)1+5·M15=
0,1784797;
R23=(-1)2+3·M23=
— 0,1469039;
R24=(-1)2+4·M24=
0,0640974;
R25=(-1)2+5·M25=
— (-0,0780138);
R34=(-1)3+4·M34=
— (-0,2423004);
R35=(-1)3+5·M35=
-0,0647635;
R45=(-1)4+5·M45=
— (-0,0212902);
R33=(-1)3+3·M33=
0,5384722;
R44=(-1)4+4·M44=
0,4160485;
R55=(-1)5+5·M55=
0,2916582;
Выборочные
частные коэффициенты корреляции:
;
;
;
и
т.д.
Таким образом,
получаем матрицу следующего вида.
Таблица 5
Матрица выборочных
частных коэффициентов корреляции
исследуемых экономических показателей
|
Y |
X1 |
X2 |
X3 |
X4 |
|
|
Y |
1,000000 |
-0,579294 |
0,491391 |
-0,088624 |
-0,453240 |
|
X1 |
-0,579294 |
1,000000 |
0,330026 |
-0,163819 |
-0,238139 |
|
X2 |
0,491391 |
0,330026 |
1,000000 |
-0,511918 |
0,163422 |
|
X3 |
-0,088624 |
-0,163819 |
-0,511918 |
1,000000 |
-0,061118 |
|
X4 |
-0,453240 |
-0,238139 |
0,163422 |
-0,061118 |
1,000000 |
Теперь необходимо
проверить значимость полученных частных
коэффициентов корреляции, т.е. гипотезу
H0:
ρij/{..}
= 0.
Для этого рассчитаем
наблюдаемые значения t-статистик
для всех коэффициентов по формуле:
г
– порядок частного коэффициента
корреляции, совпадающий с количеством
фиксируемых переменных случайных
величин (в нашем случае l=3,
например),
а n
– количество наблюдений.
l
Построим матрицу
наблюдаемыx
значений t-статистик
для всех коэффициентов rij/{..}
(таб.6).
Таблица 6
Матрица наблюдаемыx
значений t-статистик
частных
коэффициентов корреляции исследуемых
экономических показателей
|
tнабл |
Y |
X1 |
X2 |
X3 |
X4 |
|
Y |
-3,553431 |
2,8210443 |
-0,4448696 |
-2,5423262 |
|
|
X1 |
-3,553431 |
1,74807151 |
-0,8303141 |
-1,2259651 |
|
|
X2 |
2,8210443 |
1,74807151 |
-2,9796146 |
0,82824632 |
|
|
X3 |
-0,4448696 |
-0,8303141 |
-2,97961463 |
-0,3061634 |
|
|
X4 |
-2,5423262 |
-1,2259651 |
0,82824632 |
-0,3061634 |
Наблюдаемые значения
t-статистик
необходимо сравнить с критическим
значением tкр,
найденным для уровня значимости α=0,05
и числа степеней свободы ν=n
– l
— 2.
Для этого используем
встроенную статистическую функцию
Excel СТЬЮДРАСПОБР,
введя в
предложенное меню вероятность α=0,05 и
число степеней свободы ν=n–l–2=30-3-2=25.
(Можно найти значения tкр
по таблицам математической статистики
(см. Приложение, таб. П.2.2)).
Получаем
tкр=2,05953854.
По результатам,
представленным в таблице 6, наблюдаемое
значение t-статистики больше критического
tкр=2,05953854
по модулю для частных коэффициентов
корреляции
Следовательно,
гипотеза о равенстве нулю этих
коэффициентов отвергается с вероятностью
ошибки, равной 0,05, т.е. соответствующие
коэффициенты значимы.
Для остальных
коэффициентов наблюдаемое значение
t-статистики
меньше критического значения по модулю,
следовательно, гипотеза H0
не отвергается, т.е.
—
незначимы.
Для проверки
значимости частных коэффициентов
корреляции можно также воспользоваться
таблицами Фишера-Иейтса (см. Приложение,
таб. П.2.4) для нахождения критического
значения rкр
с учётом уровня значимости α=0,05
и числа степеней свободы ν=n-l-2=30-3-2=25.
По таб. rкр
(α=0,05; ν=25)=0,381.
Если соответствующий коэффициент |r|>
rкр,
то он считается значимым.
Отметим в матрице
частных коэффициентов корреляции
значимые.
Таблица 7
Матрица частных
коэффициентов корреляции исследуемых
показателей с выделением значимых
коэффициентов (при α=0,05)
|
Y |
X1 |
X2 |
X3 |
X4 |
|
|
Y |
1,000000 |
-0,579294 |
0,491391 |
-0,088624 |
-0,453240 |
|
X1 |
-0,579294 |
1,000000 |
0,330026 |
-0,163819 |
-0,238139 |
|
X2 |
0,491391 |
0,330026 |
1,000000 |
-0,511918 |
0,163422 |
|
X3 |
-0,088624 |
-0,163819 |
-0,511918 |
1,000000 |
-0,061118 |
|
X4 |
-0,453240 |
-0,238139 |
0,163422 |
-0,061118 |
1,000000 |
Для значимых
частных коэффициентов корреляции можно
построить с заданной надёжностью γ
интервальную оценку ρmin
≤ ρ
≤ ρmax
с
помощью Z-преобразования
Фишера:
Алгоритм построения
интервальной оценки для частного
генерального коэффициента корреляции
такой же, как и для парного; единственное
отличие заключается в расчёте ΔZ
:
,
где l
– порядок частного коэффициента
корреляции, совпадающий с количеством
фиксируемых переменных случайных
величин (в нашем случае l=3),
а n
– количество наблюдений.
Построим с
надёжностью
γ=0,95
и с учётом найденного
доверительные интервалы для всех
значимых частных коэффициентов
корреляции, полученных нами. Расчёты
представим в виде таблицы 8.
Таблица 8
Расчёт доверительных
интервалов для частных генеральных
коэффициентов корреляции исследуемых
экономических показателей с надёжностью
γ=0,95
|
r |
Zr |
Zmin |
Zmax |
ρmin |
ρmax |
|
|
Y X1 |
-0,57929 |
-0,66140 |
-1,06148 |
-0,26132 |
-0,78623 |
-0,25553 |
|
Y X2 |
0,491391 |
0,537893 |
0,137817 |
0,937969 |
0,136951 |
0,734288 |
|
Y |
-0,45324 |
-0,48877 |
-0,88885 |
-0,08870 |
-0,71082 |
-0,08846 |
|
X2 |
-0,51192 |
-0,56533 |
-0,9654 |
-0,16525 |
-0,74668 |
-0,16376 |
Таким образом,
доверительные интервалы с надёжностью
γ=0,95
для всех значимых частных генеральных
коэффициентов корреляции выглядят
следующим образом:
P(-0,78623≤
≤
-0,25553)=0,95
P(0,136951≤
≤ 0,734288)=0,95
P(-0,71082≤
≤
-0,08846)=0,95
P(-0,74668≤
≤ -0,16376)=0,95
Теперь построим
таблицу сравнения выборочных парных
и частных коэффициентов корреляции
для всех переменных.
Сравнение парных
и частных коэффициентов играет важную
роль в выявлении механизмов воздействия
переменных друг на друга.
Напомним, что
парный
коэффициент корреляции показывает
тесноту связи между двумя признаками
на фоне действия остальных переменных,
а частный
характеризует взаимосвязь этих двух
признаков при исключении влияния
остальных переменных, т.е. их «личную»
взаимосвязь.
Таким образом,
если оказывается, что парный коэффициент
корреляции между двумя переменными по
модулю больше
соответствующего частного, то остальные
переменные усиливают
связь между этими двумя признаками.
Соответственно, если парный коэффициент
корреляции между двумя переменными по
абсолютной величине меньше частного,
то остальные признаки ослабляют связь
между рассматриваемыми двумя.
Таблица 9
Таблица сравнения
выборочных оценок парных и частных
коэффициентов корреляции пар исследуемых
показателей с выделением значимых
коэффициентов (при α=0,05)
|
Между переменными |
Коэффициент |
|
|
парный |
частный |
|
|
Y X1 |
-0,3728125 |
-0,579294 |
|
Y X2 |
0,475190 |
0,491391 |
|
Y X3 |
-0,299800 |
-0,088624 |
|
Y X4 |
-0,384825 |
-0,453240 |
|
X1 |
0,19840901 |
0,330026 |
|
X1 |
-0,2333758 |
-0,163819 |
|
X1 |
0,02175139 |
-0,238139 |
|
X2 |
-0,6567793 |
-0,511918 |
|
X2 |
-0,07386735 |
0,163422 |
|
X3 |
0,02704939 |
-0,061118 |
По полученным
данным можно сделать следующие выводы.
Значимые
корреляционные зависимости, полученные
на этапе расчёта парных коэффициентов
корреляции, подтвердились и при
вычислении частных коэффициентов
корреляции. При этом выявлены следующие
механизмы воздействия переменных друг
на друга:
-
Наиболее тесная
связь наблюдается изучаемым признаком
Y
– рентабельностью и факторными
признаками X1
– оборачиваемость ненормируемых
средств и X4
– оборачиваемость нормируемых средств
(обратные зависимости) и
фондоотдачей
X2
(прямая
зависимость). -
Воздействие
других переменных (фондоотдачи X2,
фондовооруженности
труда X3
и оборачиваемости нормируемых оборотных
средств X4)
ослабляет отрицательную взаимосвязь
между рентабельностью (Y)
и оборачиваемостью ненормируемых
оборотных средств (X1),
т.к. абсолютная величина частного
коэффициент корреляции=— 0,579 превышает
абсолютное значение парного коэффициента
корреляции=— 0,373
-
Аналогичная
ситуация наблюдается и для значимой
обратной связи между рентабельностью
(Y)
и оборачиваемостью нормируемых
оборотных средств (X4)
— при исключении воздействия других
переменных абсолютная величина частного
коэффициент корреляции превышает
абсолютное значение парного коэффициента
корреляции. -
Влияние прочих
переменных немного ослабляет и значимую
положительную связь между рентабельностью
(Y)
и фондоотдачей (X2). -
Для связи между
рентабельностью (Y)
и фондовооруженностью труда (X3)
характерна обратная ситуация: воздействие
других переменных значительно усиливает
эту взаимосвязь (частный коэффициент
корреляции по абсолютной величине
меньше соответствующего парного
коэффициента), хотя оба коэффициента
корреляции являются незначимыми. -
Наиболее
сильная связь, выявленная на этапе
расчёта парных коэффициентов корреляции,
между
факторными
признаками фондоотдачей (X2)
и фондовооруженностью
труда (X3),
является весьма сильной и значимой,
хотя частный коэффициент по модулю
несколько меньше парного. Таким образом,
можно сделать вывод, что остальные
переменные, включённые в корреляционную
модель (Y
– рентабельность, X1
– оборачиваемость ненормируемых
средств и X4
– оборачиваемость нормируемых средств)
усиливают взаимосвязь между указанными
факторными признаками.
-
Расчёт
множественных коэффициентов корреляции
Множественные
коэффициенты корреляции служат мерой
связи одной переменной с совместным
действием всех остальных показателей.
Вычислим точечные
оценки множественных коэффициентов
корреляции. Множественный коэффициент
корреляции, например, для 1-го показателя
Y
вычисляется по формуле:
где |R|
— определитель корреляционной матрицы
R;
Rii
– алгебраическое дополнение элемента
rii
корреляционной
матрицы R.
Все алгебраические
дополнения Rii
были найдены в п.2.2 на этапе расчёта
частных коэффициентов корреляции,
поэтому осталось вычислить только
определитель самой корреляционной
матрицы.
R11=(-1)1+1·M11=
0,5316755;
R22=(-1)2+2·M22=
0,3679652.
R33=(-1)3+3·M33=
0,5384722;
R44=(-1)4+4·M44=
0,4160485;
R55=(-1)5+5·M55=
0,2916582;
Чтобы найти
определитель корреляционной матрицы,
воспользуемся встроенной математической
функцией Excel
МОПРЕД.
Получим
|R|
= 0,230032.
Таким образом,
получаем:
;
Множественный
коэффициент детерминации R2i/{..})
(и
его выборочная оценка r2i/{..})
показывает долю дисперсии рассматриваемой
случайной величины, обусловленную
влиянием остальных переменных, включённых
в корреляционную модель.
Соответственно
(1- R2i/{..})
показывает долю остаточной дисперсии
данной случайной величины, обусловленную
влиянием других, не включённых в
исследуемую модель факторов.
Множественные
коэффициенты детерминации получаются
возведением соответствующих множественных
коэффициентов корреляции в квадрат
(таб. 10).
Проверим значимость
полученных множественных коэффициентов
корреляции и детерминации.
Проверка значимости,
т.е. гипотезы о равенстве нулю
соответствующего множественного
коэффициента корреляции, осуществляется
с помощью статистики:
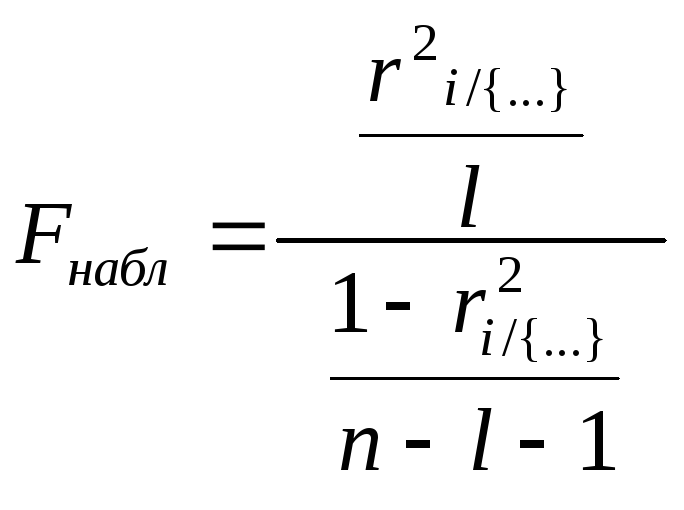
где l
– порядок множественного коэффициента
корреляции, совпадающий с количеством
фиксируемых переменных случайных
величин (в нашем случае l=4,
например,
),
аn
– количество наблюдений.
Произведя расчёты,
получим (таб.10).
Для определения
значимости множественных коэффициентов
корреляции и детерминации нужно найти
критическое значение F-распределения
для заданного уровня значимости α
и числа степеней свободы числителя
ν1=l
и знаменателя ν2=n—l-1.
Для определения
Fкр
можно
воспользоваться встроенной функцией
Excel:
ВСТАВКА (Office
2003) или
ФОРМУЛЫ (Office
2007)
Функция
FРАСПОБР,
введя в предложенное
меню вероятность α=0,05
и число степеней свободы ν1=l=4
и ν2=n—l—1=30-4-1=25.
Можно найти
значения Fкр
по таблицам математической статистики
(см. Приложение, таб. П.2.4).
Получаем Fкр(0,05;
4; 25)=2,75871047.
Таблица 10
Множественные
коэффициенты корреляции и детерминации
исследуемых показателей с выделением
значимых коэффициентов
(на уровне
значимости α=0,05)
-
Множественный
коэффициент корреляцииМножественный
коэффициент детерминации
r2Значение
статистикиF набл
rY
/{..}0,75322378
0,56734606
8,195736612
rX1/{..}
0,61225427
0,3748553
3,747694856
rX2/{..}
0,75684018
0,57280705
8,380375865
rX3/{..}
0,66865841
0,44710407
5,054112587
rX4/{..}
0,45967138
0,21129778
1,67441489
Если наблюдаемое
значение F-статистики
превосходит ее критическое значение
Fкр=2,75871047,
то гипотеза о равенстве нулю
соответствующего множественного
коэффициента корреляции отвергается
с вероятностью ошибки, равной 0,05.
Следовательно, у нас все коэффициенты,
кроме последнего, для переменной Х4,
значимо отличаются от нуля.
Полученные данные
позволяют сделать следующие выводы.
Множественный
коэффициент корреляции
=0,753
значим и имеет достаточно высокое
значение, что говорит о том, показательY
– рентабельность имеет тесную связь
с многомерным массивом факторных
признаков X1
– оборачиваемость ненормируемых
средств, X2
– фондоотдача,
X3
—
фондовооруженность труда и X4
– оборачиваемость нормируемых средств.
Это даёт основание для проведения
дальнейшего регрессионного анализа.
Множественный
коэффициент детерминации r2Y/{..})=0,5673
показывает, что 56,73% доли дисперсии Y
– объёма промышленной продукции,
обусловлены изменениями факторных
признаков.
Факторные признаки
тоже имеют достаточно высокие значения
множественных коэффициентов корреляции
и детерминации, что говорит об их сильной
взаимосвязанности, за исключением
переменной X4
– её множественный коэффициент не
значим, и это подтверждается тем фактом,
что только 21,13 % доли её дисперсии
обусловлены изменениями переменных,
включённых в рассматриваемую модель,
а, соответственно 78,87% дисперсии
обусловлены влиянием других, не
включённых в корреляционную модель
остаточных факторов.
Итак, полученные
результаты корреляционного анализа,
показавшие, что показатель Y
– рентабельность имеет тесную связь
с многомерным массивом факторных
признаков, позволяют перейти ко второму
этапу статистического исследования –
построению регрессионной модели.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
До этого момента мы рассматривали только отдельные переменные и их характерики, однако в практике мы редко работаем только с одной переменной. Как правило, у нас есть многомерное пространство признаков, и нас интересуют взаимосвязи между ними.
Ковариация
Мы хотим описать имеющиеся взаимосвязи как можно проще и опираясь на то, что у нас уже есть. Мы говорили, что дисперсия, или вариация, заключает в себе информацию об изменчивости признака. Если мы хотим исследовать взаимосвязь между признаками, то логично будет посмотреть, как изменяется один из признаков при изменении другого — иначе говоря, рассчитать совместную изменчивость признаков, или ко-вариацию (covariance).
Как мы её будем считать? Подумаем графически. Расположим две переменные на осях и сопоставим каждому имеющемуся наблюдению точку на плоскости.
КАРТИНКА
Отметим средние значения по обеим переменным.
КАРТИНКА
Заметим, что если наши наблюдения по переменной \(x_1\) отклоняются в большую сторону, то они отклоняются в большую сторону и по переменной \(x_2\). Аналогично, если они будут отклоняться в меньшую сторону по \(x_1\), то в меньшую же сторону они будут отклоняться и по \(x_2\).
КАРТИНКА
Получается, мы можем на основании согласованности отклонений уже заключить о направлении связи. Произведение отклонений по обеим величинам будет положительно, если отклонения сонаправленны. Запишем это математически.
\[
(\bar x_1 — x_{i1}) (\bar x_2 — x_{i2}) > 0 \Leftarrow \big( (\bar x_1 — x_{i1}) > 0 \wedge (\bar x_2 — x_{i2}) > 0 \big) \vee \big( (\bar x_1 — x_{i1}) < 0 \wedge (\bar x_2 — x_{i2}) < 0 \big)
\]
Соответственно, если отклонения будут направлены в разные стороны, из произведение будет отрицательным. Ну, осталось только понять, как совместные отклонения организованы в среднем — это и будет ковариацией двух величин:
\[
\mathrm{cov}(X_1, X_2) = \frac{1}{n-1} \sum_{i=1}^n (\bar x_1 — x_{i1}) (\bar x_2 — x_{i2})
\]
Что такое ковариация величины самой с собой (\(\mathrm{cov}(X_1, X_1)\))? Докажите через выведение формулы.
Важно отметить, что ковариация улавливается только линейную составляющую взаимосвязи между признаками, поэтому если \(\mathrm{cov}(X_1,X_2) = 0\), то мы можем сказать, что между переменными нет линейной взаимосвязи, однако это не значит, что между этими переменными нет никакой другой зависимости.
У ковариации есть два важных недостатка:
- это размерная величина, поэтому её значение зависит от единиц измерения признаков,
- она зависит от дисперсий признаков, поэтому по её значению можно определить только направление связи (прямая или обратная), однако ничего нельзая сказать о силе связи.
Поэтому нам нужно как-то модицифировать эту статистику, чтобы мы могли больше вытащить из её значения.
Корреляция
Раз ковариация зависит от дисперсии, то можно сделать некоторые математические преобразования, чтобы привести эмпирические распределения к какому-то одному виду — сделать так, чтобы они имели одинакое математическое ожидание (среднее) и одинаковую дисперсию. С этой задачей прекрасно справляется стандартизация. Напоминаю формулу:
\[
x_i^* = \frac{x_i — \bar x}{s}
\]
После такого преобразования математическое ожидание нашего распределения будет равно нуля, а стандартное отклонение — единице. Это избавит нас от влияния дисперсии на значение ковариации. Ковариация двух стандартно нормально распределенных величин называется корреляцией (correlation).
\[
\mathrm{cov}(X_1^*, X_2^*) = \frac{1}{n-1} \sum_{i=1}^n x_{i1}^* x_{i2}^* = \mathrm{corr}(X_1, X_2),
\]
где \(X_1^*\) и \(X_2^*\) — стандартизированные величины \(X_1\) и \(X_2\) соответственно.
Корреляцию можно выразить через ковариацию:
\[
\mathrm{corr}(X_1, X_2) = \frac{1}{n-1} \sum_{i=1}^n \Big( \frac{\bar x_1 — x_{i1}}{s_1} \Big) \Big( \frac{\bar x_2 — x_{i2}}{s_2} \Big) =
\frac{1}{s_1 s_2} \Big( \frac{1}{n-1} \sum_{i=1}^n (\bar x_1 — x_{i1})(\bar x_2 — x_{i2}) \Big) = \frac{\mathrm{cov}(X_1, X_2)}{s_1 s_2}
\]
Если внимательно всмотреться в формуле, то можно обнаружить, что корреляция это не что иное, как стандартизированное значение ковариации.
Коэффициент корреляции имеет четкие пределы изменения: \([-1; \,1]\). Крайнее левое значение говорит о том, что присутствует полная обратная линейная взаимосвязь, крайнее правое — что присутствует полная прямая линейная взаимосвязь. Как и ковариация, корреляция ловит только линейную составляющую связи, поэтому нулевое значение корреляци показывает, что между переменными отсутствует линейная взаимосвязь. Это всё еще не значит, что связи нет вовсе.
Тестирование статистической значимости коэффициента корреляции
Оценку коэффициента корреляции мы получаем методом моментов, заменяя истинный момент \(\rho_{ij}\) выборочным \(r_{ij}\):
\[
\hat \rho_{ij} = \overline{\big( (X_{ki} — \bar X_i) (X_{kj} — \bar X_j) \big)} = r_{ij}
\]
Если в генеральной совокупности связь между признаками отсутствует, то есть \(\rho_{ij} = 0\), будет ли равен нулю \(r_{ij}\)? Можно с уверенностью сказать, что не будет, так как выборочный коэффициент корреляции — случайная величина. А мы помним, что вероятность принятия случайной величиной своего конкретного значения равна нулю.
Тогда необходимо протестировать статистическую гипотезу:
\[
H_0: \rho_{ij} = 0 \; \text{(линейной связи нет)} \\
H_1: \rho_{ij} \neq 0 \text{(наиболее частый вариант альтернативы)}
\]
Для проверки нулевой гипотезы используется следующая статистика:
\[
t = \frac{r_{ij}}{\sqrt{\frac{1 — r^2_{ij}}{n-2}}} \overset{H_0}{\thicksim} t(\nu = n-2)
\]
Вывод о статистической значимости коэффициента корреляции делается согласно алгоритму тестировния статистических гипотез.
Доверительный интервал для коэффициента корреляции
С построением интервальной оценки коэффциента корреляции возникают некоторые сложности. Наша задача состоит в том, чтобы определить в каких границах будет лежать значение истинного коэффициента корреляции с заданной вероятностью:
\[
\mathrm{P} (\rho_{ij,\min} < \rho_{ij} < \rho_{ij,\max}) = \gamma
\]
Нам необходимо найти статистику, закон распределения корой известен, однако ранее упомянутся статистика не подходит, так как она имеет распределение Стьюдента, когда верна нулевая гипотеза об отсутствии связи. Если же мы строим интервальную оценку, нас интересует случай наличия связи.
Такую статистику искали долго, и её удалось найти, когда ввели определённое преобразование выборочного критерия корреяции — z-преобразования Фишера:
\[
z(r_{ij}) = \frac{1}{2} \ln \frac{1 + r_{ij}}{1 — r_{ij}} \thicksim \mathrm{N}(\bar z_{ij}, \tfrac{1}{n-3}),
\]
где \(n\) — объём выборки, а \(\bar z_{ij}\) получается расчётом по указанной формуле после подставления точечной оценки коэффициента корреляции.
Тогда интервальная оценка для величины \(z_{ij, \mathrm{true}}\) приобретает такой вид:
\[
\mathrm{P} \Big( \bar z_{ij} — t_\gamma \sqrt{\tfrac{1}{n-3}} < z_{ij, \mathrm{true}} < \bar z_{ij} + t_\gamma \sqrt{\tfrac{1}{n-3}} \Big) = \gamma = \Phi(t_\gamma)
\]
Далее путём обратного преобразования получаются значения границ интервала \((\rho_{ij,\min}, \; \rho_{ij,\max})\).
Ковариация и корреляция в R
Запасёмся данными. По ссылке скачается экселька.
dehum <- readxl::read_xlsx('data/clean_dannye_norm.xlsx')
str(dehum)## tibble [906 × 39] (S3: tbl_df/tbl/data.frame)
## $ SEX : num [1:906] 1 2 2 2 2 2 2 1 2 2 ...
## $ AGE : chr [1:906] "32" "22" "21" "15" ...
## $ MCA : num [1:906] NA NA 1 NA NA NA NA NA NA 1 ...
## $ MMA : num [1:906] NA NA NA NA NA NA NA NA NA NA ...
## $ MCI : num [1:906] NA NA NA NA NA NA NA NA NA NA ...
## $ MMI : num [1:906] NA NA NA 1 NA NA NA NA NA NA ...
## $ WCA : num [1:906] NA NA NA NA 1 NA NA NA NA NA ...
## $ WMA : num [1:906] 1 NA NA NA NA 1 NA NA NA NA ...
## $ WCI : num [1:906] NA NA NA NA NA NA NA NA NA NA ...
## $ WMI : num [1:906] NA NA NA NA NA NA 1 NA NA NA ...
## $ MX : num [1:906] NA NA NA NA NA NA NA 1 NA NA ...
## $ WX : num [1:906] NA 1 NA NA NA NA NA NA 1 NA ...
## $ sex_k : num [1:906] 2 2 1 1 2 2 2 2 2 1 ...
## $ intention : num [1:906] 2 2 2 1 2 2 1 2 2 2 ...
## $ victim : num [1:906] 2 2 1 2 1 2 2 2 2 1 ...
## $ CG : num [1:906] 0 2 0 0 0 0 0 1 2 0 ...
## $ DP : num [1:906] 2 1 5 3 1 1 3 1 1 2 ...
## $ GRa : num [1:906] 1 3 5 1 1 5 2 1 4 5 ...
## $ GRb : num [1:906] 1 3 5 2 1 4 1 1 3 6 ...
## $ GRc : num [1:906] 1 3 2 3 1 2 1 1 2 1 ...
## $ GR_average : num [1:906] 1 3 4 2 1 ...
## $ ARa : num [1:906] 1 2 3 1 2 4 4 1 2 3 ...
## $ ARb : num [1:906] 1 2 2 3 1 1 1 1 2 1 ...
## $ ARc : num [1:906] 1 2 1 4 1 1 1 1 2 1 ...
## $ AR_average : num [1:906] 1 2 2 2.67 1.33 ...
## $ SRa : num [1:906] 1 5 5 1 2 4 2 1 3 2 ...
## $ SRb : num [1:906] 1 4 4 1 2 5 1 1 3 3 ...
## $ SRc : num [1:906] 1 4 5 2 2 2 1 1 4 4 ...
## $ SR_average : num [1:906] 1 4.33 4.67 1.33 2 ...
## $ DHa : num [1:906] 3 1 5 3 1 5 1 1 3 2 ...
## $ DHb : num [1:906] 1 1 2 2 1 2 1 1 2 2 ...
## $ DHc : num [1:906] 1 1 5 4 1 2 3 1 4 2 ...
## $ DHd : num [1:906] 1 1 1 2 1 1 1 1 1 2 ...
## $ DHe : num [1:906] 2 4 5 2 2 1 2 1 3 1 ...
## $ DHf : num [1:906] 1 1 1 2 1 1 3 1 3 1 ...
## $ DHg : num [1:906] 1 1 2 4 1 4 5 1 1 1 ...
## $ DHh : num [1:906] 1 4 7 5 4 4 6 1 4 5 ...
## $ animal_average : num [1:906] 1.75 2.5 5.5 3.5 2 3 3 1 3.5 2.5 ...
## $ machine_average: num [1:906] 1 1 1.5 2.5 1 2 2.5 1 1.75 1.5 ...Это данные исследования на тему дегуманизации убийц. Нас будут интересовать следующие шкалы:
- DPa — шкала «одобрения казни»
- Шкала морального возмущения:
- GR_average — подшкала отвращения
- AR_average — подшкала гнева
- SR_average — подшкала презрения
- Шкала дегуманизации:
- animal_average — анималистическая дегуманизация
- machine_average — механистическая дегуманизация
Ковариация считается так:
cov(dehum$GR_average, dehum$AR_average)## [1] 1.567469А корреляция так:
cor(dehum$GR_average, dehum$AR_average)## [1] 0.7363325Ещё мы можем построить соответствующий график, чтобы отобразить закономерность — диаграмма рассеяния с линией тренда:
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.0 ──## ✓ ggplot2 3.3.2 ✓ purrr 0.3.4
## ✓ tibble 3.0.4 ✓ dplyr 1.0.2
## ✓ tidyr 1.1.2 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.0## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()dehum %>% ggplot(aes(GR_average, AR_average)) +
geom_point() +
geom_smooth(method = 'lm') # мы заинтересованы в отображении линейного компонента связи## `geom_smooth()` using formula 'y ~ x'Но это мы всё получали выборочные оценки коэффициентов. А как же тестировать гипотезы?
Легко и непринужденно! Просто дописать test в название функции:
cor.test(dehum$GR_average, dehum$AR_average)##
## Pearson's product-moment correlation
##
## data: dehum$GR_average and dehum$AR_average
## t = 32.72, df = 904, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7050124 0.7647859
## sample estimates:
## cor
## 0.7363325Что мы наблюдаем в аутпуте? Значение t-статистики, число степеней свободы, p-value для значения t-статистики, а также 95% доверительный интервал для коэффициента корреляции. Всё, что мы и хотели — за одну команду!
Коэффициенты корреляции для разных шкал
Дла разных шкал разработаны разные коэффициенты корреляции. Оценки коэффициентов будут рассчитываться по-разному, но логика тестирования статистических гипотез остаётся одинаковой.
| Переменная \(X\) | Переменная \(Y\) | Мера связи |
|---|---|---|
| Интервальная или отношений | Интервальная или отношений | Коэффициент Пирсона |
| Ранговая, интервальная или отношений | Ранговая, интервальная или отношений | Коэффициент Спирмена |
| Ранговая | Ранговая | Коэффициент Кенделла |
В функциях cor() и cor.test() требуемый коэффициент задаётся черед аргумент method:
cor.test(dehum$DP, dehum$animal_average, method = 'kendall')##
## Kendall's rank correlation tau
##
## data: dehum$DP and dehum$animal_average
## z = 9.5138, p-value < 2.2e-16
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
## tau
## 0.24636Частный и множественный коэффициент корреляции
Если у нас два признака, то с ними всё достаточно понятно. А если признаком много? Тогда у нас могут быть сложные взаимосвязи, и возможен такой случай, что некоторый признак оказывает связан как с одним, так и с другим из интересующих нас. Таким образом, мы можем наблюдать ложную корреляцию. Чтобы избавиться от влияния сторонних признаков, используюся частные коэффициенты корреляции.
Функция cor() может возвращать не только оценку одного коэффициента корреляции, но и корреляционную матрицу, отобрадающую связи всех признаков со всеми. Например, продолжим работать со шкалой морального возмущения и изучим взаимосвязи внутри неё:
dehum %>%
select(GR_average, AR_average, SR_average) %>%
cor()## GR_average AR_average SR_average
## GR_average 1.0000000 0.7363325 0.607245
## AR_average 0.7363325 1.0000000 0.630688
## SR_average 0.6072450 0.6306880 1.000000В корреляционной матрице на главной диагонали стоят единицы, отражающай связь переменной в самой собой — разумеется, она будет абсолютно линейная.
А как посчитать ковариационную матрицу?
В общем виде корреляционная матрица имеет следующий вид:
\[
R =
\begin{pmatrix}
1 & r_{12} & \dots & r_{1p} \\
r_{12} & 1 & \dots & r_{2p} \\
\vdots & \vdots & \ddots & \vdots \\
r_{p1} & r_{p2} & \dots & 1
\end{pmatrix}
\]
Матрица, как можно заметить, симметрична относительно главной диагонали, так как \(r_{ij} = r_{ji}\).
Её можно визуализироать, например, так:
dehum %>%
select(GR_average, AR_average, SR_average) %>%
cor() %>%
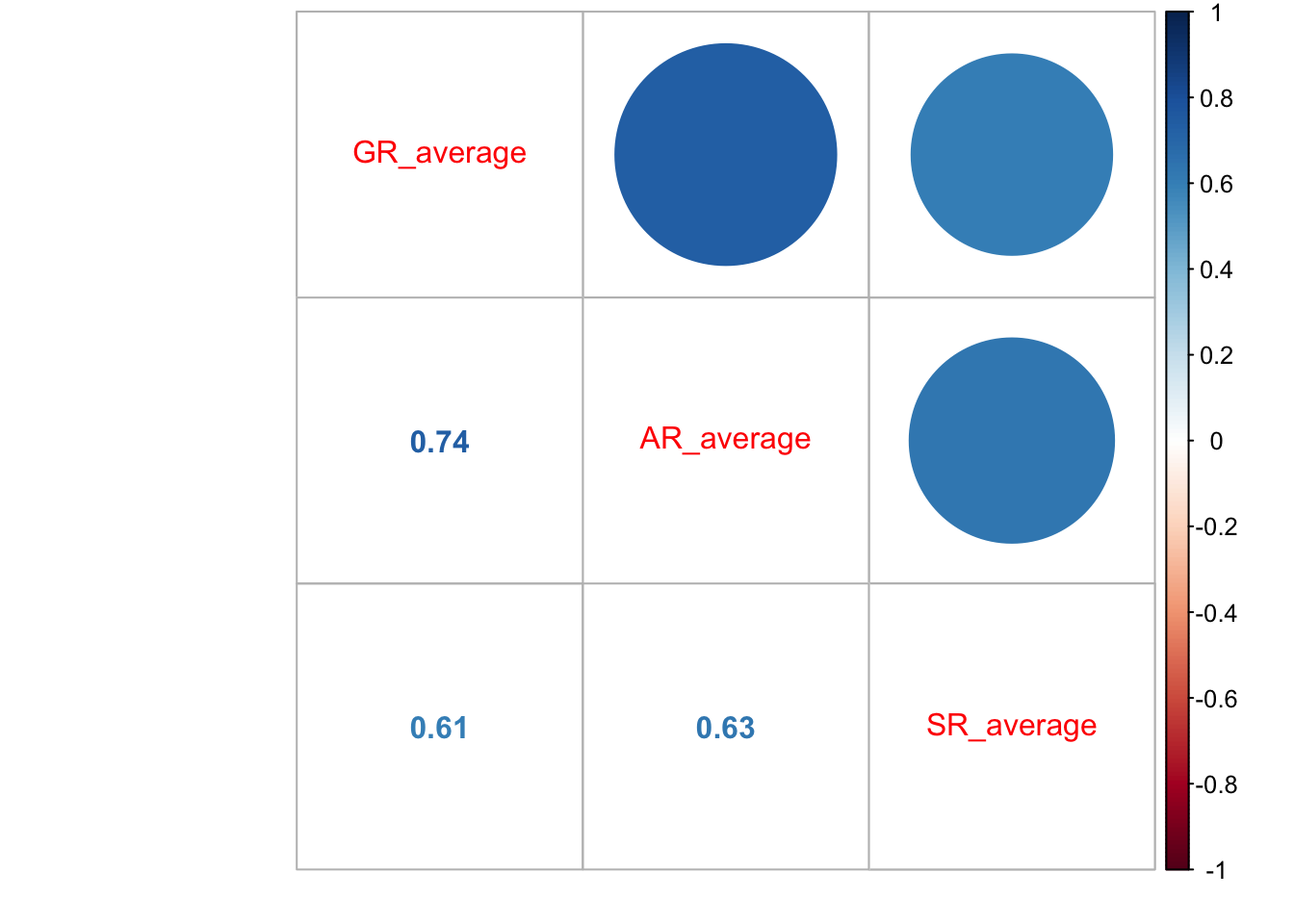
corrplot::corrplot()Но можно и усовершенствовать визуализацию, отобразив сами значения:
dehum %>%
select(GR_average, AR_average, SR_average) %>%
cor() %>%
corrplot::corrplot.mixed()На основе этой матрицы мы можем протестировать статистическую значимость каждого из коэффициентов (не забыв про поправки на множественные сравнения!):
cor_tests <- correlation::correlation(
dehum %>%
select(GR_average, AR_average, SR_average),
method = "spearman", # указываем, какой коэффициент нам нужен
adjust = "holm" # и какую поправку будем использовать
)
cor_tests## # Correlation table (spearman-method)
##
## Parameter1 | Parameter2 | rho | 95% CI | S | p
## --------------------------------------------------------------------
## GR_average | AR_average | 0.71 | [0.67, 0.74] | 3.65e+07 | < .001***
## GR_average | SR_average | 0.60 | [0.55, 0.64] | 4.99e+07 | < .001***
## AR_average | SR_average | 0.67 | [0.63, 0.70] | 4.13e+07 | < .001***
##
## p-value adjustment method: Holm (1979)
## Observations: 906Чтобы перенести их на график, нам нужно получить матрицу из p-значений:
p_values <- corrplot::cor.mtest(dehum %>%
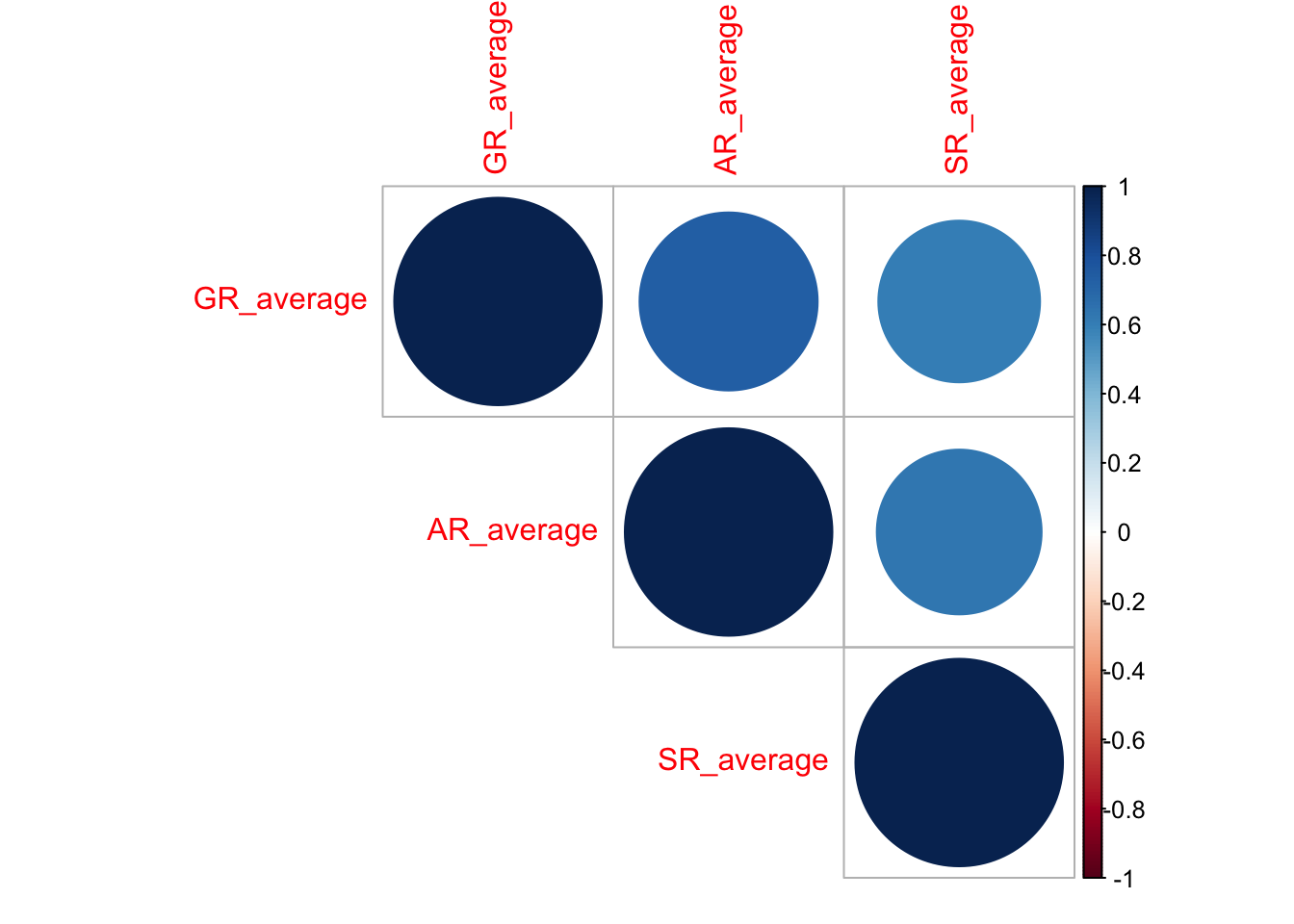
select(GR_average, AR_average, SR_average), adjust = 'holm')$pdehum %>%
select(GR_average, AR_average, SR_average) %>%
cor() %>%
corrplot::corrplot(type = 'upper',
p.mat = p_values,
sig.level = 0.05)Ну, у нас ничего не поменялось, так как коэффициенты все оказались значимы. Эх…
Но вот для примера на одно из встроенных датасетов:
corrplot::corrplot(
cor(mtcars),
type = "upper",
p.mat = corrplot::cor.mtest(mtcars)$p,
sig.level = 0.01
)Итак, возвращается к частному коэффициенту корреляции. Он определяется так:
\[
r_{ij, J(i,j)} = — \frac{A_{ij}}{\sqrt{A_{ii} A_{jj}}},
\]
где \(A\) — алгебраическое дополнение.
В общем виде это осознать сложно, поэтому давайте на примере трёх признаков.
\[
R =
\begin{pmatrix}
1 & r_{12} & r_{13} \\
r_{21} & 1 & r_{23} \\
r_{31} & r_{32} & 1
\end{pmatrix}
\]
\[
r_{12,3} = \frac{r_{12} — r_{13} \cdot r_{23}}{\sqrt{(1 — r^2_{23})(1-r^2{13})}}
\]
\[
H_0: \rho_{12,3} = 0 \\
H_1: \rho_{12,3} \neq 0 \\
t = \frac{r_{12,3} \sqrt{n-3}}{\sqrt{1 — r^2_{12,3}}} \overset{H_0}{\thicksim} t(\nu = n-3)
\]
Но слава богу, что в R это все делается в одну строку:
ppcor::pcor(
dehum %>%
select(GR_average, AR_average, SR_average)
)## $estimate
## GR_average AR_average SR_average
## GR_average 1.0000000 0.5730882 0.2720509
## AR_average 0.5730882 1.0000000 0.3414418
## SR_average 0.2720509 0.3414418 1.0000000
##
## $p.value
## GR_average AR_average SR_average
## GR_average 0.000000e+00 3.948903e-80 8.051918e-17
## AR_average 3.948903e-80 0.000000e+00 3.811050e-26
## SR_average 8.051918e-17 3.811050e-26 0.000000e+00
##
## $statistic
## GR_average AR_average SR_average
## GR_average 0.000000 21.01453 8.495546
## AR_average 21.014531 0.00000 10.916353
## SR_average 8.495546 10.91635 0.000000
##
## $n
## [1] 906
##
## $gp
## [1] 1
##
## $method
## [1] "pearson"ppcor::pcor.test(dehum$GR_average,
dehum$AR_average,
dehum$SR_average)## estimate p.value statistic n gp Method
## 1 0.5730882 3.948903e-80 21.01453 906 1 pearsonХорошо, а если нас интересует связь одного признака с несколькими сразу? Тогда нам нужен множественный коэффициент корреляции. Он также вычисляется на основе корреляционной матрицы и определяется следующим образом. Пусть нас интересует связь первого признака со всеми остальными:
\[
R_1 = \sqrt{1 — \frac{\det R}{A_{11}}}
\]
Квадрат множественонго коэффициента корреляции называется коэффициентом детерминации1. Он показывает, во-первых, степень тесноты связи данного признака со всеми остальными, но, кроме того, ещё и долю дисперсии данного признака, определяемую вариацией все остальных признаков, включенных в данную корреляционную модель.
Мы подробнее его изучим в следуюшей теме, а также увидим, где нам его найти, чтобы не считать руками.
Другие корреляции
Можно коррелировать не только количественные и ранговые шкалы между собой, но и качественные тоже:
| Переменная \(X\) | Переменная \(Y\) | Мера связи |
|---|---|---|
| Дихотомическая | Дихотомическая | \(\phi\)-коэффициент |
| Дихотомическая | Ранговая | Рангово-бисериальный коэффициент |
| Дихотомическая | Интервальная или отношений | Бисериальный коэффициент |
\(\phi\)-коэффициент
Этот коэффициент позволяет рассчитать корреляцию между двумы дихотомическими шкалами. Он основан на расчёте статистики \(\chi^2\).
По двум дихотомическим переменным можно построить таблицу сопряженности. Разберемся на котиках и пёсиках:
cats_n_dogs <- read_csv('https://raw.githubusercontent.com/angelgardt/hseuxlab-wlm2021/master/book/wlm2021-book/data/cats_n_dogs.csv')##
## ── Column specification ────────────────────────────────────────────────────────
## cols(
## id = col_double(),
## species = col_character(),
## size = col_character()
## )table(cats_n_dogs$species, cats_n_dogs$size)##
## big small
## cat 17 8
## dog 16 9По данной таблице можно рассчитать критерий согласия Пирсона (\(\chi^2\)):
chisq.test(table(cats_n_dogs$species, cats_n_dogs$size))##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: table(cats_n_dogs$species, cats_n_dogs$size)
## X-squared = 0, df = 1, p-value = 1Сам хи-квадрат тестирует гипотезу о том, что между двумя категориальными переменными нет связи. Он это делает путём сравнения теоретической и эмпирической таблицы частот.
Эмпирическую таблицу частот мы получаем по результатам наблюдений (то, что мы делаем с помощью функции table()):
| \(X_1\) | \(X_2\) | |
|---|---|---|
| \(Y_1\) | \(p_{X_1,Y_1} = a\) | \(p_{X_2,Y_1} = b\) |
| \(Y_2\) | \(p_{X_1,Y_2} = c\) | \(p_{X_2,Y_2} = d\) |
Далее вычисляются теоретические частоты:
| \(X_1^*\) | \(X_2^*\) | |
|---|---|---|
| \(Y_1^*\) | \(\frac{(a+b) \times (a+c)}{N}\) | \(\frac{(b+a) \times (b+d)}{N}\) |
| \(Y_2^*\) | \(\frac{(c+d) \times (a+c)}{N}\) | \(\frac{(d+c) \times (b + d)}{N}\) |
где \(N = a + b + c + d\).
Затем считаются расхождения частот, которые суммируются и получается статистика \(\chi^2\):
\[
\chi^2 = \sum_{i,j} \frac{p_{X_i,Y_j} — p_{X_i^*,Y_j^*}}{p_{X_i^*,Y_j^*}}
\]
Статистика подчиняется распределению \(\chi^2\), и чем больше значение этой статистики, тем сильнее связаны признаки. В нашем случае мы получили значение 0, что говорит о абсолютном отсутствии связи между видом животного и его размером.
Но по значению \(\chi^2\) сложно что-то сказать о силе связи, поэтому его нормируют следующим образом, чтобы получить значения от 0 до 1, которые можно интерпретироват аналогично коэффициенту корреляции:
\[
\phi = \sqrt{\frac{\chi^2}{N}}
\]
sqrt(
chisq.test(table(cats_n_dogs$species, cats_n_dogs$size))$statistic /
nrow(cats_n_dogs)
)## X-squared
## 0Так как в нашем случае значение \(\chi^2\) было 0, то и коэффициент \(\phi\) мы получили 0.
Бисериальный коэффициент корреляции
Этот коэффициент используется для вычисления корреляции между количественной (\(y\)) и категориальной (\(x\)) шкалой и рассчитывается следующим образом:
\[
r = \frac{\bar x_1 — \bar x_2}{s_y} \sqrt{\frac{n_1 n_2}{N(N-1)}},
\]
где \(\bar x_1\) — среднее по элементам переменной \(y\) из группы \(x_1\), \(\bar x_2\) — среднее по элементам \(y\) из группы \(x_2\), \(s_y\) — стандартное отклонение по переменной \(y\), \(n_1\) — число элементов в группе \(x_1\), \(n_2\) — число элементов в группе \(x_2\), \(N\) — общее число элементов.
Важно отметить, что несмотря на то, что значение коэффициента может быть как положительным, так и отрицательным, это не влияет на интерпретацию. Это одно из исключений из общего правила.
В R его можно вычислить так:
ltm::biserial.cor(dehum$GR_average, dehum$SEX)## [1] -0.01406144Рангово-бисериальный коэффициент корреляции
Если у нас не количественная, а ранговая шкала, то применяется рангово-бисериальный коэффициент:
\[
r = \frac{2(\bar x_1 — \bar x_2)}{N},
\]
где \(\bar x_1\) — средний ранг в группе \(x_1\), \(\bar x_2\) — средний ранг в группе \(x_2\), \(N\) — общее количество наблюдений.
polycor::polyserial(dehum$DP, dehum$SEX)## [1] 0.0530944