Обучение с
учителем
При
обучении нейронных сетей с учителем
важную роль играет выбор меры ошибки,
которая соответствует сути задачи.
Удачный
выбор меры погрешности упрощает задачу
обучения нейронной сети, так как обычно
приводит к более гладкой поверхности
невязки. Часта, в качестве меры погрешности
берётся средняя квадратичная ошибка.
Она определяется как сумма квадратов
разности между желаемой величиной
выхода “dk”
и реально полученными на нейронной сети
значениями “yk”
для каждого примера K.
Где
N-
количество примеров в обучаемом
множестве.
В
качестве меры погрешности также широко
используется расстояние Кульбака
–Лейблера, которое связанно с критерием
максимального правдоподобия.
Обучение
без учителя
Альтернативная
парадигма обучения без учителя, своим
название говорит об отсутвии вмешательства
внешнего учителя или корректора, который
контролирует процесс обучения. Блочная
диаграмма обучения без учителя имеет
вид:
Обучение
без учителя является более правдоподобной
моделью обучения в биологической
системе.
Искусственные
нейронные сети, обучающиеся без учителя,
служат средством для классификации,
кластеризации, организации и визуального
представления данных.
Процесс
обучения без учителя, как и в случае
обучения с учителем заключается в
корректировки синоптических весов.
Некоторые преобразования предусматривают
изменения структуры нейронной сети, то
есть количество нейронов и их связей.
Такие преобразования называются более
широким термином – самоорганизации.
Подстройка
синоптических весов может проводиться
только на основании информации доступной
в нейроне, то есть его состояние уже
имеющихся весовых коэффициентов.
Существует
лишь независимые от задачи мера качества
представления, которому должна научиться
нейронная сеть. При этом свободные
параметры сети оптимизируются по
отношению к этой мере.
При
обучении без учителя можно использовать
правила конкурентного обучения.
Например:
Если нейронная сеть состоит из 2 слоёв
входного и выходного, то входной слой
получает доступные данные, выходной
слой состоит из нейронов, которые
конкурирую друг с другом за право отклика
на признаки, содержащиеся во входных
данных. В каждый момент времени может
быть активным только один нейрон. В
простейшем случае нейронная сеть
действует по принципу “Победитель
получает всё”. При такой стратегии
нейрон с наибольшим суммарным входным
сигналом побеждает в соревновании и
переходит в активное состояние. Такой
нейрон называют нейроном-победителем,
при этом все остальные нейроны отключаются.
Обучение
без учителя является более чувствительным
к выбору оптимальных параметров по
отношению к обучению с учителем. Качества
обучения без учителя сильно зависит от
начальных значение синоптических
коэффициентов. Обучение без учителя
критично к выбору радиуса обучения и
скорости его обучения. Важным является
характер изменения коэффициента
обучения.
Модели
обучения нейронных сетей.
При
создании нейронных сетей используют
различные модели обучения. Существует
5 различных моделей обучения:
-
Обучение на основе
коррекции ошибок; -
Обучение с
использование памяти; -
Метод Хебба;
-
Конкурентное
обучение; -
Метод Больцмана.
Рассмотрим
более подробно конкурентное обучение
и обучение на основе ошибок.
1.
(Хайки С. Нейронные сети. Полный курс;)
2.
(Оссовский С.)
Обучение
на основе коррекции ошибок
Рассмотрим
нейронную сеть прямого распространения
с одним или несколькими скрытыми слоями
нейронов и единственным выходным
нейроном “k”.
Нейрон
“k”
работает под управление вектора сигнала

одним или несколькими слоями нейронов,
где “m”
дискретное время (номер шага итерационного
процесса настройки синоптических весов
нейрона “k”)
Скрытые
слои в свою очередь получают информацию
из входного вектора (возбуждения),
передаваемого
входному слою нейронной сети.
Выходной
нейрона “k”
обозначим
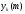
Этот сигнал является единственным
выходом нейронной сети. Он будет
сравниваться с желаемым выходом, который
обозначим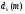
В
результате получаем сигнал ошибки
Сигнал
ошибки инициализирует механизм управления
целью, которого является применение
последовательности корректировок к
синоптическим весам нейрона “k”.
Эти
изменения нацелены на пошаговое
приближение выходного сигнала
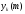
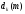
Эта
цель достигается за счёт минимизации
невязки (или функции стоимости или
индекса производительности ) E(m),
которая определяется в терминах сигнала
об ошибке по формуле:
E(m)
— это текущее значение энергии ошибки.
Пошаговая корректировка синоптических
весов нейрона “k”
продолжается до тех пор, пока система
не достигнет устойчивого состояния,
при котором синоптические веса практически
стабилизируются, в этой точке процесс
обучения останавливается.
Процесс
обучения, который мы описали, называется
обучением, основанным на коррекции
ошибок.
Минимизации
функции стоимости E(m)
выполняется по дельта правилу, которое
также называется Видроу – Хоффа.
Обозначим
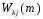
нейрона “k”
соответствующего элементу
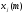
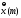
Согласно дельта правилу изменение,
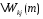
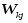
задаётся ворожением:
Где,
ЭТТА(знак)- некоторая положительная
константа называемая параметром скорости
обучения.
Ошибка
ek(m)
вычисляется через множители из последующих
слоёв и передается в обратном направлении.
Вычислив
изменения синоптического веса по формуле
(5) можно определить его новое значение
на следующем шаге дискредитации:
Граф
прохождения сигнала в процессе обучения
на основе коррекции ошибок для нейрона
“k”
имеет вид: (Рис 5)
Описание
рисунка: Входной сигнал
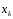
представляются в виде предсинаптического
и постсинаптического сигнала j-го
сигнала нейрона “N”.
Из
рисунка (5) следует обучение на основе
коррекции ошибок — это пример замкнутой
системы обратной связи.
Устойчивость
такой системы определяется параметрами
обратной связи. В данном случае существует
всего 1 обратная связь и единственный
параметр – коэффициент скорости обучения
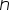
Выбор
параметра ЭТТА, влияет на точность
процесса обучения, ему отводится ключевая
роль в обеспечении производительности
процесса обучения на практике.
Таким
образом алгоритм обучения по дельта
правилу состоит из 6 шагов. (Они рассмотрены
в тетради по практике).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сразу хочу сказать, что здесь никакой воды про обучение с учителем, и только нужная информация. Для того чтобы лучше понимать что такое
обучение с учителем, метод коррекции ошибки, метод обратного распространения ошибки , настоятельно рекомендую прочитать все из категории Машинное обучение.
обучение с учителем (англ. Supervised learning) — один из способов машинного обучения, в ходе которого испытуемая система принудительно обучается с помощью примеров «стимул-реакция». С точки зрения кибернетики, является одним из видов кибернетического эксперимента. Между входами и эталонными выходами (стимул-реакция) может существовать некоторая зависимость, но она не известна. Известна только конечная совокупность прецедентов — пар «стимул-реакция», называемая обучающей выборкой. На основе этих данных требуется восстановить зависимость (построить модель отношений стимул-реакция, пригодных для прогнозирования), то есть построить алгоритм, способный для любого объекта выдать достаточно точный ответ. Для измерения точности ответов, так же как и в обучении на примерах, может вводиться функционал качества.
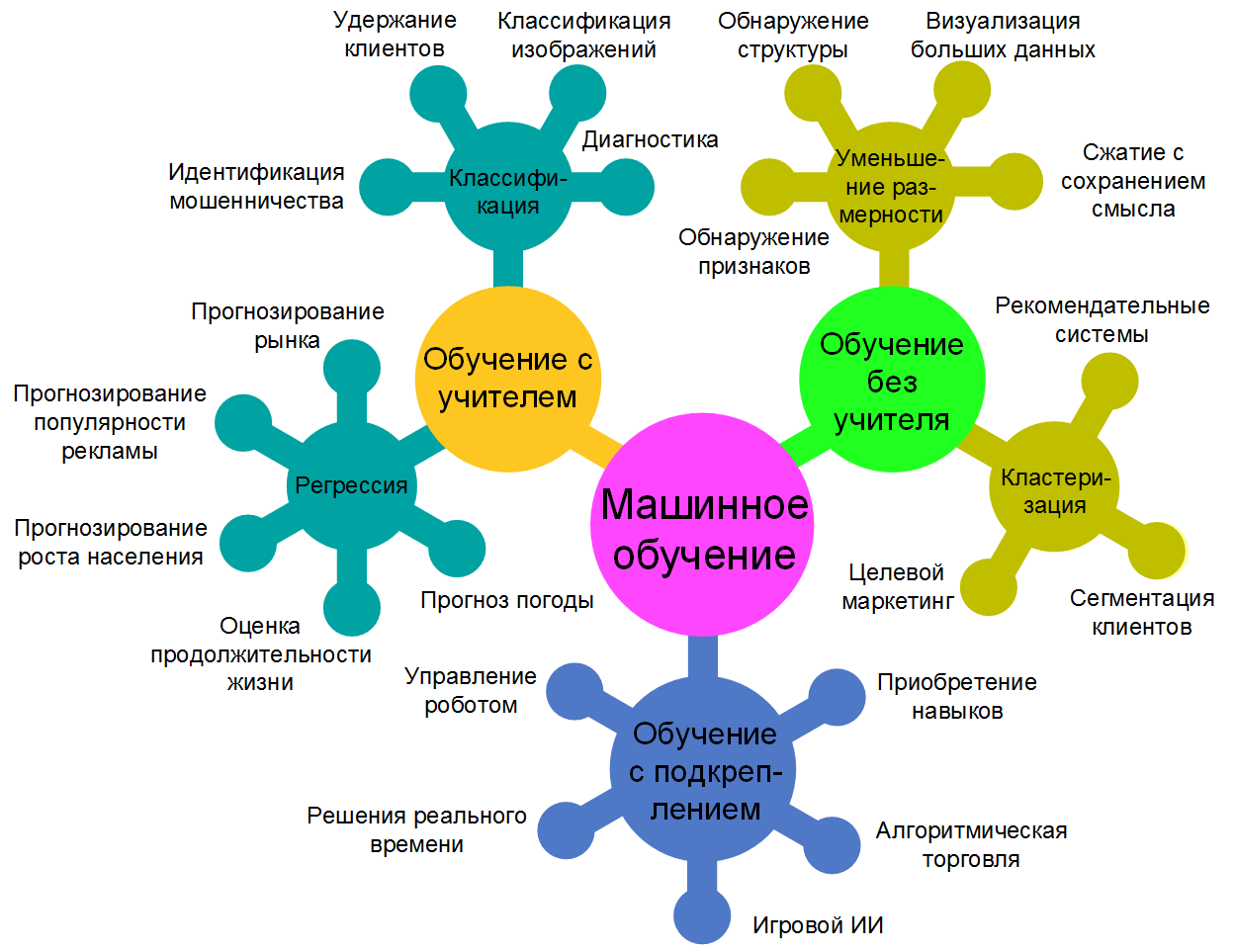
Виды машинного обучения
Классическое обучение
Принцип постановки данного эксперимента
Данный эксперимент представляет собой частный случай кибернетического эксперимента с обратной связью. Постановка данного эксперимента предполагает наличие экспериментальной системы, метода обучения и метода испытания системы или измерения характеристик.
Экспериментальная система в свою очередь состоит из испытываемой (используемой) системы, пространства стимулов получаемых из внешней среды и системы управления подкреплением (регулятора внутренних параметров). В качестве системы управления подкреплением может быть использовано автоматическое регулирующие устройство (например, термостат) или человек-оператор (учитель), способный реагировать на реакции испытываемой системы и стимулы внешней среды путем применения особых правил подкрепления, изменяющих состояние памяти системы.
Различают два варианта: (1) когда реакция испытываемой системы не изменяет состояние внешней среды, и (2) когда реакция системы изменяет стимулы внешней среды. Эти схемы указывают принципиальное сходство такой системы общего вида с биологической нервной системой.
Типология задач обучения с учителем
Типы входных данных
- Признаковое описание — наиболее распространенный случай. Каждый объект описывается набором своих характеристик, называемых признаками. Признаки могут быть числовыми или нечисловыми.
- Матрица расстояний между объектами. Каждый объект описывается расстояниями до всех остальных объектов обучающей выборки. С этим типом входных данных работают немногие методы, в частности, метод ближайших соседей, метод парзеновского окна, метод потенциальных функций.
- Временной ряд или сигнал представляет собой последовательность измерений во времени. Каждое измерение может представляться числом, вектором, а в общем случае — признаковым описанием исследуемого объекта в данный момент времени.
- Изображение или видеоряд.
- Встречаются и более сложные случаи, когда входные данные представляются в виде графов, текстов, результатов запросов к базе данных, и т. д. Как правило, они приводятся к первому или второму случаю путем предварительной обработки данных и извлечения признаков.
Типы откликов
- Когда множество возможных ответов бесконечно (ответы являются действительными числами или векторами), говорят о задачах регрессии и аппроксимации ;
- Когда множество возможных ответов конечно, говорят о задачах классификации и распознавания образов;
- Когда ответы характеризуют будущие поведение процесса или явления, говорят о задачах прогнозирования.
Вырожденные виды систем управления подкреплением («учителей»)
- Система подкрепления с управлением по реакции (R — управляемая система) — характеризуется тем, что информационный канал от внешней среды к системе подкрепления не функционирует. Данная система несмотря на наличие системы управления относится к спонтанному обучению, так как испытуемая система обучается автономно, под действием лишь своих выходных сигналов независимо от их «правильности». При таком методе обучения для управления изменением состояния памяти не требуется никакой внешней информации;
- Система подкрепления с управлением по стимулам (S — управляемая система) — характеризуется тем, что информационный канал от испытываемой системы к системе подкрепления не функционирует. Несмотря на не функционирующий канал от выходов испытываемой системы относится к обучению с учителем, так как в этом случае система подкрепления (учитель) заставляет испытываемую систему вырабатывать реакции согласно определенному правилу, хотя и не принимается во внимание наличие истиных реакций испытываемой системы.
Данное различие позволяет более глубоко взглянуть на различия между различными способами обучения, так как грань между обучением с учителем и обучением без учителя более тонка. Кроме этого, такое различие позволило показать дляискусственных нейронных сетей определенные ограничения для S и R — управляемых систем (см. Теорема сходимости перцептрона).
Обучение с учителем
Обучение с учителем (supervised learning) предполагает наличие полного набора размеченных данных для тренировки модели на всех этапах ее построения.
Наличие полностью размеченного датасета означает, что каждому примеру в обучающем наборе соответствует ответ, который алгоритм и должен получить. Таким образом, размеченный датасет из фотографий цветов обучит нейронную сеть, где изображены розы, ромашки или нарциссы. Когда сеть получит новое фото, она сравнит его с примерами из обучающего датасета, чтобы предсказать ответ.
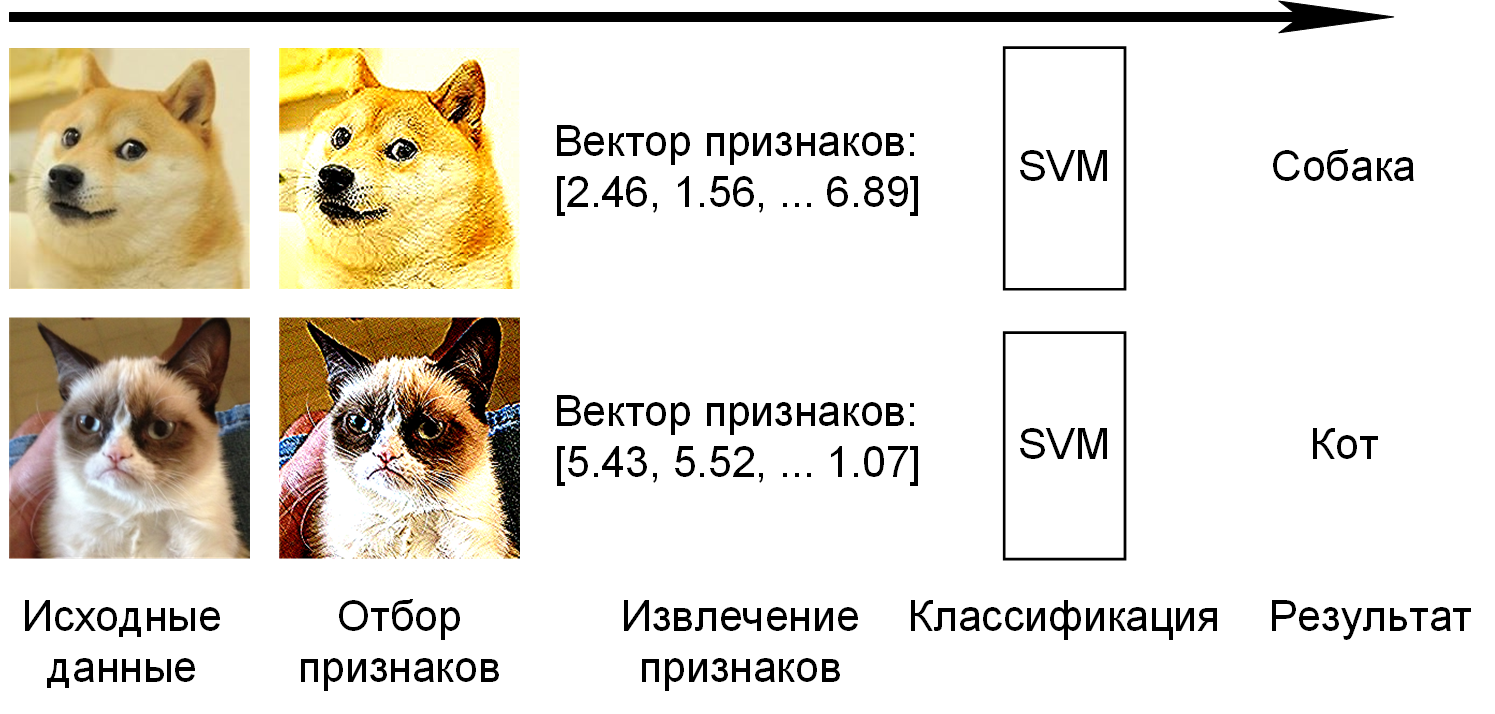
Пример обучения с учителем — классификация (слева), и дальнейшее ее использование для сегментации и распознавания объектов
В основном обучение с учителем применяется для решения двух типов задач: классификации и регрессии.
В задачах классификации алгоритм предсказывает дискретные значения, соответствующие номерам классов, к которым принадлежат объекты. В обучающем датасете с фотографиями животных каждое изображение будет иметь соответствующую метку — «кошка», «коала» или «черепаха». Качество алгоритма оценивается тем, насколько точно он может правильно классифицировать новые фото с коалами и черепахами.
А вот задачи регрессии связаны с непрерывными данными. Один из примеров, линейная регрессия, вычисляет ожидаемое значение переменной y, учитывая конкретные значения x.
Более утилитарные задачи машинного обучения задействуют большое число переменных. Как пример, нейронная сеть, предсказывающая цену квартиры в Сан-Франциско на основе ее площади, местоположения и доступности общественного транспорта. Алгоритм выполняет работу эксперта, который рассчитывает цену квартиры исходя из тех же данных.
Таким образом, обучение с учителем больше всего подходит для задач, когда имеется внушительный набор достоверных данных для обучения алгоритма. Но так бывает далеко не всегда. Недостаток данных — наиболее часто встречающаяся проблема в машинном обучении .
Классическое обучение любят делить на две категории — с учителем и без. Часто можно встретить их английские наименования — Supervised и Unsupervised Learning.
В первом случае у машины есть некий учитель, который говорит ей как правильно. Рассказывает, что на этой картинке кошка, а на этой собака. То есть учитель уже заранее разделил (разметил) все данные на кошек и собак, а машина учится на конкретных примерах.
В обучении без учителя, машине просто вываливают кучу фотографий животных на стол и говорят «разберись, кто здесь на кого похож». Данные не размечены, у машины нет учителя, и она пытается сама найти любые закономерности. Об этих методах поговорим ниже.
Очевидно, что с учителем машина обучится быстрее и точнее, потому в боевых задачах его используют намного чаще. Эти задачи делятся на два типа: классификация — предсказание категории объекта, и регрессия — предсказание места на числовой прямой.
4 комментария
Классификация
«Разделяет объекты по заранее известному признаку. Носки по цветам, документы по языкам, музыку по жанрам»
Сегодня используют для:
- Спам-фильтры
- Определение языка
- Поиск похожих документов
- Анализ тональности
- Распознавание рукописных букв и цифр
- Определение подозрительных транзакций
Популярные алгоритмы: Наивный Байес, Деревья Решений, Логистическая Регрессия, K-ближайших соседей, Машины Опорных Векторов
Здесь и далее в комментах можно дополнять эти блоки. Приводите свои примеры задач, областей и алгоритмов, потому что описанные мной взяты из субъективного опыта.
6 комментариев
Классификация вещей — самая популярная задача во всем машинном обучении. Машина в ней как ребенок, который учится раскладывать игрушки: роботов в один ящик, танки в другой. Опа, а если это робот-танк? Штош, время расплакаться и выпасть в ошибку.
Старый доклад Бобука про повышение конверсии лендингов с помощью SVM
Для классификации всегда нужен учитель — размеченные данные с признаками и категориями, которые машина будет учиться определять по этим признакам. Дальше классифицировать можно что угодно: пользователей по интересам — так делают алгоритмические ленты, статьи по языкам и тематикам — важно для поисковиков, музыку по жанрам — вспомните плейлисты Спотифая и Яндекс.Музыки, даже письма в вашем почтовом ящике.
Раньше все спам-фильтры работали на алгоритме Наивного Байеса. Машина считала сколько раз слово «виагра» встречается в спаме, а сколько раз в нормальных письмах. Перемножала эти две вероятности по формуле Байеса, складывала результаты всех слов и бац, всем лежать, у нас машинное обучение!
Позже спамеры научились обходить фильтр Байеса, просто вставляя в конец письма много слов с «хорошими» рейтингами. Метод получил ироничное название Отравление Байеса, а фильтровать спам стали другими алгоритмами. Но метод навсегда остался в учебниках как самый простой, красивый и один из первых практически полезных.
Возьмем другой пример полезной классификации. Вот берете вы кредит в банке . Об этом говорит сайт https://intellect.icu . Как банку удостовериться, вернете вы его или нет? Точно никак, но у банка есть тысячи профилей других людей, которые уже брали кредит до вас. Там указан их возраст, образование, должность, уровень зарплаты и главное — кто из них вернул кредит, а с кем возникли проблемы.
Да, все догадались, где здесь данные и какой надо предсказать результат. Обучим машину, найдем закономерности, получим ответ — вопрос не в этом. Проблема в том, что банк не может слепо доверять ответу машины, без объяснений. Вдруг сбой, злые хакеры или бухой админ решил скриптик исправить.
Для этой задачи придумали Деревья Решений. Машина автоматически разделяет все данные по вопросам, ответы на которые «да» или «нет». Вопросы могут быть не совсем адекватными с точки зрения человека, например «зарплата заемщика больше, чем 25934 рубля?», но машина придумывает их так, чтобы на каждом шаге разбиение было самым точным.
Так получается дерево вопросов. Чем выше уровень, тем более общий вопрос. Потом даже можно загнать их аналитикам, и они навыдумывают почему так.
Деревья нашли свою нишу в областях с высокой ответственностью: диагностике, медицине, финансах.
Два самых популярных алгоритма построения деревьев — CART и C4.5.
В чистом виде деревья сегодня используют редко, но вот их ансамбли (о которых будет ниже) лежат в основе крупных систем и зачастую уделывают даже нейросети. Например, когда вы задаете вопрос Яндексу, именно толпа глупых деревьев бежит ранжировать вам результаты.
Но самым популярным методом классической классификации заслуженно является Метод Опорных Векторов (SVM). Им классифицировали уже все: виды растений, лица на фотографиях, документы по тематикам, даже странных Playboy-моделей. Много лет он был главным ответом на вопрос «какой бы мне взять классификатор».
Идея SVM по своей сути проста — он ищет, как так провести две прямые между категориями, чтобы между ними образовался наибольший зазор. На картинке видно нагляднее:
У классификации есть полезная обратная сторона — поиск аномалий. Когда какой-то признак объекта сильно не вписывается в наши классы, мы ярко подсвечиваем его на экране. Сейчас так делают в медицине: компьютер подсвечивает врачу все подозрительные области МРТ или выделяет отклонения в анализах. На биржах таким же образом определяют нестандартных игроков, которые скорее всего являются инсайдерами. Научив компьютер «как правильно», мы автоматически получаем и обратный классификатор — как неправильно.
Сегодня для классификации все чаще используют нейросети, ведь по сути их для этого и изобрели.
Правило буравчика такое: сложнее данные — сложнее алгоритм. Для текста, цифр, табличек я бы начинал с классики. Там модели меньше, обучаются быстрее и работают понятнее. Для картинок, видео и другой непонятной бигдаты — сразу смотрел бы в сторону нейросетей.
Лет пять назад еще можно было встретить классификатор лиц на SVM, но сегодня под эту задачу сотня готовых сеток по интернету валяются, чо бы их не взять. А вот спам-фильтры как на SVM писали, так и не вижу смысла останавливаться.
Регрессия
«Нарисуй линию вдоль моих точек. Да, это машинное обучение»
Сегодня используют для:
- Прогноз стоимости ценных бумаг
- Анализ спроса, объема продаж
- Медицинские диагнозы
- Любые зависимости числа от времени
Популярные алгоритмы: Линейная или Полиномиальная Регрессия
Регрессия — та же классификация, только вместо категории мы предсказываем число. Стоимость автомобиля по его пробегу, количество пробок по времени суток, объем спроса на товар от роста компании и.т.д. На регрессию идеально ложатся любые задачи, где есть зависимость от времени.
Регрессию очень любят финансисты и аналитики, она встроена даже в Excel. Внутри все работает, опять же, банально: машина тупо пытается нарисовать линию, которая в среднем отражает зависимость. Правда, в отличии от человека с фломастером и вайтбордом, делает она это математически точно — считая среднее расстояние до каждой точки и пытаясь всем угодить.
Когда регрессия рисует прямую линию, ее называют линейной, когда кривую — полиномиальной. Это два основных вида регрессии, дальше уже начинаются редкоземельные методы. Но так как в семье не без урода, есть Логистическая Регрессия, которая на самом деле не регрессия, а метод классификации, от чего у всех постоянно путаница. Не делайте так.
Схожесть регрессии и классификации подтверждается еще и тем, что многие классификаторы, после небольшого тюнинга, превращаются в регрессоры. Например, мы можем не просто смотреть к какому классу принадлежит объект, а запоминать, насколько он близок — и вот, у нас регрессия.
Для желающих понять это глубже, но тоже простыми словами, рекомендую цикл статей Machine Learning for Humans
метод коррекции ошибки
Эта статья о нейросетях; о коррекции ошибок в информатике см.: обнаружение и исправление ошибок.
Метод коррекции ошибки — метод обучения перцептрона, предложенный Фрэнком Розенблаттом. Представляет собой такой метод обучения, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.
Модификации метода
В теореме сходимости перцептрона различаются различные виды этого метода, доказано, что любой из них позволяет получить схождение при решении любой задачи классификации.
Метод коррекции ошибок без квантования
Если реакция на стимул 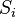
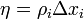
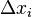
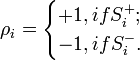
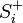
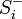
Метод коррекции ошибок с квантованием
Отличается от метода коррекции ошибок без квантования только тем, что 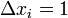
Этот метод и метод коррекции ошибок без квантованиея являются одинаковыми по скорости достижения решения в общем случае, и более эффективными по сравнению с методами коррекции ошибок со случайным знаком или случайными возмущениями.
Метод коррекции ошибок со случайным знаком подкрепления
Отличается тем, что знак подкрепления 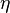
Метод коррекции ошибок со случайными возмущениями
Отличается тем, что величина и знак 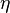
метод обратного распространения ошибки .
Метод обратного распространения ошибки (англ. backpropagation)— метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. А.И. Галушкиным , а также независимо и одновременно Полом Дж. Вербосом . Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно С.И. Барцевым и В.А. Охониным (Красноярская группа) .. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределенные системы, и т. п.
Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.
Сигмоидальные функции активации
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):
Рациональная сигмоида:
Гиперболический тангенс:
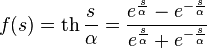
где s — выход сумматора нейрона, 
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активации, то сигмоиды рассчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации нужно рассчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции рассчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленнее пороговой функции активации как 1:4.
Функция оценки работы сети
В тех случаях, когда удается оценить работу сети, обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно, хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:
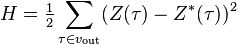
где 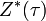
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок повысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе .
Описание алгоритма
Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть множество входов 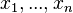


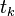
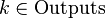
Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого обучающего примера и, таким образом, «двигаться» в многомерном пространстве весов. Чтобы «добраться» до минимума ошибки, нам нужно «двигаться» в сторону, противоположную градиенту, то есть, на основании каждой группы правильных ответов, добавлять к каждому весу

где 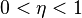
Производная считается следующим образом. Пусть сначала 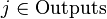

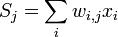
Аналогично, 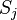
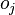
где 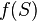
Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае
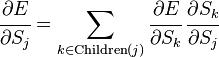
и
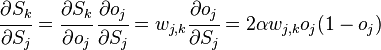
Ну а 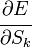
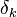
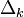

- для узла последнего уровня
- для внутреннего узла сети
- для всех узлов
, где 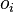
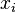
Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм
Алгоритм: BackPropagation
- Инициализировать
маленькими случайными значениями,
- Повторить NUMBER_OF_STEPS раз:
Для всех d от 1 до m:
- Подать
на вход сети и подсчитать выходы
каждого узла.
- Для всех
.
- Для каждого уровня l, начиная с предпоследнего:
Для каждого узла j уровня l вычислить
.
- Для каждого ребра сети {i, j}
.
.
- Подать
- Выдать значения
.
где 
Математическая интерпретация обучения нейронной сети
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющими обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Недостатки алгоритма
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Паралич сети
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Основную трудность при обучении нейронных сетей составляют как раз методы выхода из локальных минимумов: каждый раз выходя из локального минимума снова ищется следующий локальный минимум тем же методом обратного распространения ошибки до тех пор, пока найти из него выход уже не удается.
Размер шага
Внимательный разбор доказательства сходимости показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным. Если размер шага фиксирован и очень мал, то сходимость слишком медленная, если же он фиксирован и слишком велик, то может возникнуть паралич или постоянная неустойчивость. Эффективно увеличивать шаг до тех пор, пока не прекратится улучшение оценки в данном направлении антиградиента и уменьшать, если такого улучшения не происходит. П. Д. Вассерман описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня предложена разветвленная технология оптимизации обучения.
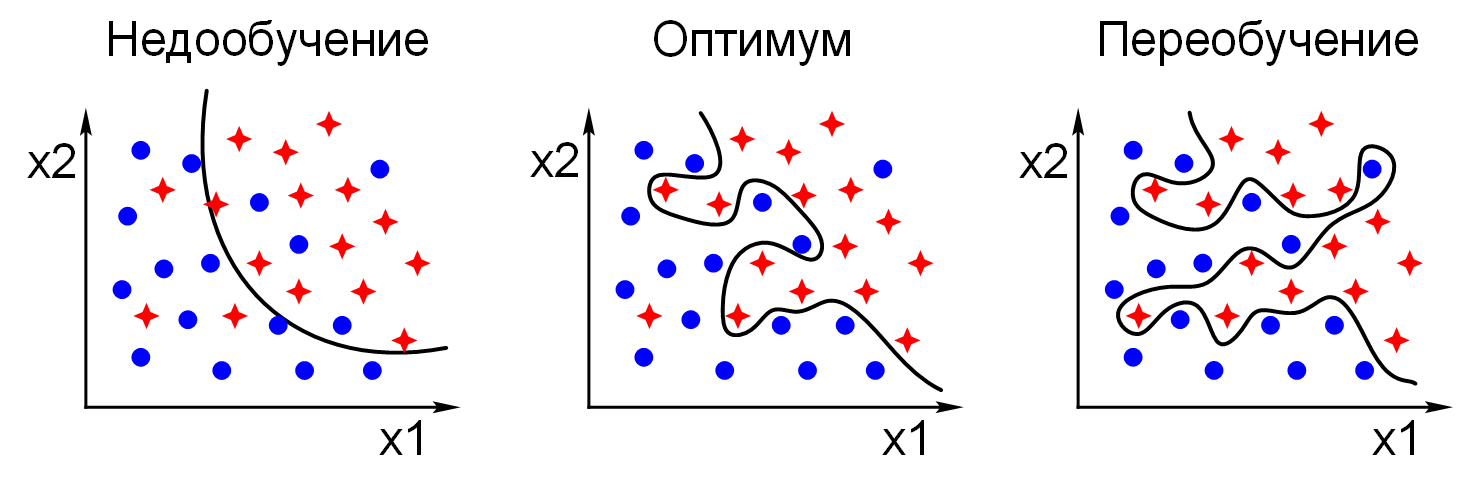
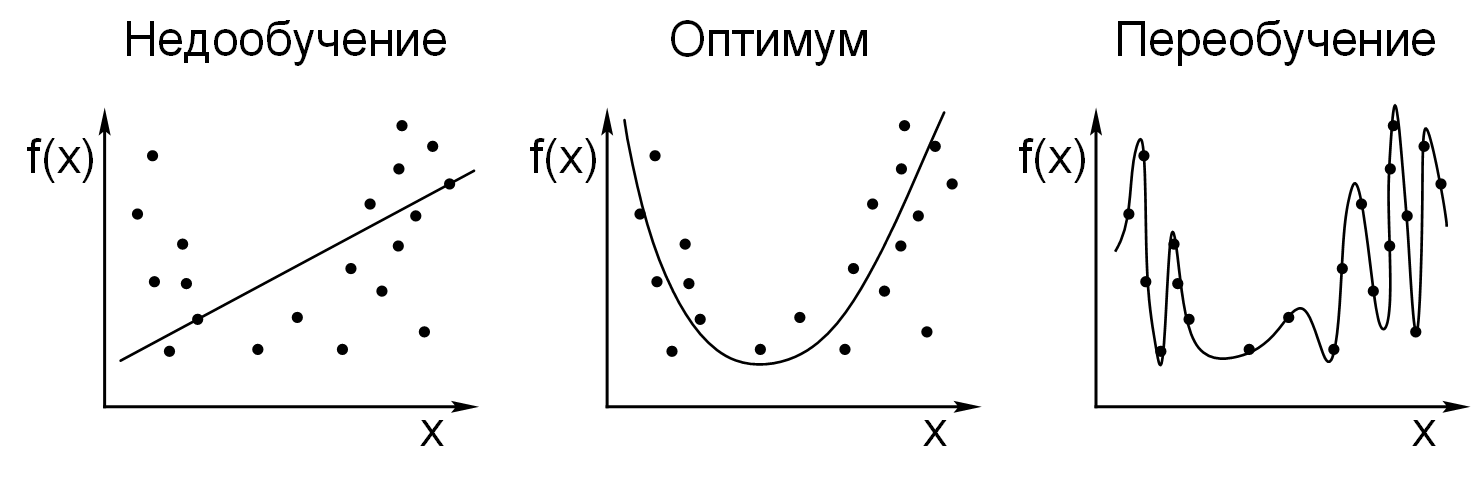
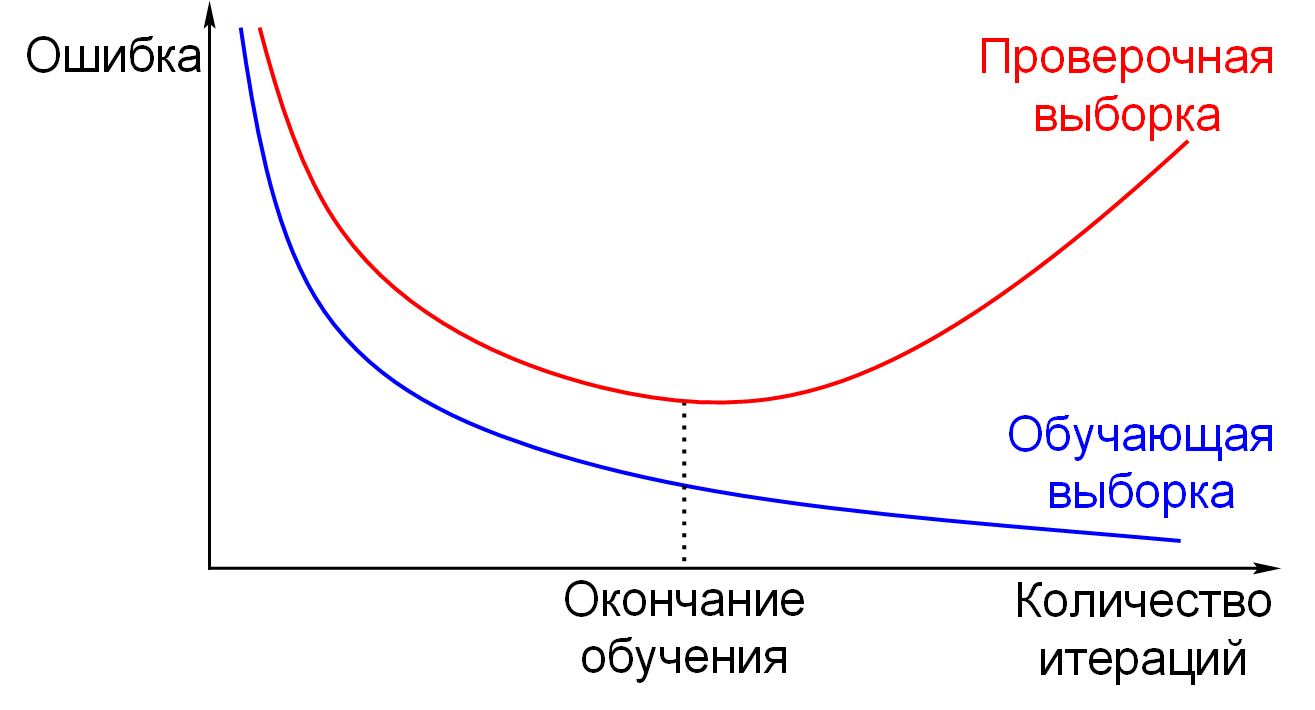
Следует также отметить возможность переобучения сети, что является скорее результатом ошибочного проектирования ее топологии. При слишком большом количестве нейронов теряется свойство сети обобщать информацию. Весь набор образов, предоставленных к обучению, будет выучен сетью, но любые другие образы, даже очень похожие, могут быть классифицированы неверно.
См. также
- Обучение без учителя
- Обучение с подкреплением
- Обучение на примерах
- Задачи прогнозирования
- обучение без учителя , алгоритм k-means , обучение с частичным привлечением учителя ,
А как ты думаешь, при улучшении обучение с учителем, будет лучше нам? Надеюсь, что теперь ты понял что такое обучение с учителем, метод коррекции ошибки, метод обратного распространения ошибки
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Машинное обучение
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
-
Методы коррекции ошибок
Техника
кодирования,
которая
позволяет
приемнику
не только
понять,
что
присланные
данные
содержат
ошибки, но
и исправить
их, называется
прямой
коррекцией
ошибок (Forward Error Correction, FEC).
Коды,
которые
обеспечивают
прямую
коррекцию
ошибок,
требуют
введения
большей
избыточности
в
передаваемые
данные,
чем
коды,
которые
только
обнаруживают
ошибки.
При
применении
любого
избыточного
кода не
все
комбинации
кодов являются разрешенными.
Например,
контроль по паритету
делает
разрешенными
только
половину кодов. Если мы
контролируем
три
информационных
бита,
то разрешенными 4-битными кодами
с дополнением
до нечетного
количества
единиц
будут:
000
1,
001
0,
010
0,
011
1,
100
0,
101
1,
110
1,
111
0,
то
есть
всего
8
кодов
из
16
возможных.
Для
того
чтобы
оценить
количество
дополнительных
битов,
требуемых
для
исправления
ошибок,
нужно
знать так
называемое
расстояние
Хемминга
между
разрешенными
комбинациями
кода.
Расстоянием
Хемминга
называется
минимальное
число
битовых
разрядов,
в
которых
отличается
любая
пара
разрешенных
кодов.
Для схем
контроля
по паритету
расстояние
Хемминга
равно
2.
Можно
доказать,
что
если мы
сконструировали
избыточный
код
с
расстоянием
Хемминга,
равным
n,
то
такой
код
будет
в
состоянии
распознавать
(n-
1)-кратные
ошибки и
исправлять (n-1)/2-кратные
ошибки.
Так
как коды
с
контролем
по паритету
имеют
расстояние
Хемминга,
равное
2,
то
они
могут
только
обнаруживать
однократные
ошибки и
не могут
исправлять
ошибки.
Коды
Хемминга
эффективно
обнаруживают
и
исправляют
изолированные
ошибки,
то есть отдельные
искаженные
биты,
которые
разделены
большим
количеством
корректных битов. Однако при появлении
длинной последовательности искаженных
битов (пульсации
ошибок)
коды Хемминга
не
работают.
Наиболее
часто
в современных
системах
связи применяется тип кодирования,
реализуемый
сверточным
кодирующим
устройством
(Сonvolutional
coder),
потому
что такое
кодирование
может быть
довольно
просто
реализовано
аппаратно
с
использованием
линий задержки
(delay)
и сумматоров.
В
отличие
от
рассмотренного
выше
кода,
который относится
к
блочным
кодам
без памяти,
сверточпый
код
относится
к
кодам
с
конечной
памятью (Finite memory
code);
это
означает,
что выходная
последовательность кодера является
функцией
не только
текущего
входного
сигнала,
но также
нескольких
из числа
последних предшествующих
битов.
Длина
кодового
ограничения
(Constraint
length of a code) показывает,
как
много
выходных
элементов
выходит
из системы
в пересчете
на
один
входной.
Коды
часто
характеризуются
их
эффективной
степенью
(или
коэффициентом)
кодирования (Code rate).
Вам
может встретиться
сверточный
код с коэффициентом кодирования
1/2.
Этот
коэффициент
указывает,
что
на
каждый
входной
бит
приходятся
два
выходных.
При
сравнении
кодов
обращайте
внимание
на
то,
что,
хотя
коды
с
более
высокой
эффективной
степенью
кодирования
позволяют
передавать
данные
с более высокой
скоростью,
они
соответственно
более
чувствительны
к
шуму.
В беспроводных
системах
с блочными
кодами
широко
используется
метод
чередования
блоков.
Преимущество
чередования
состоит
в том,
что приемник
распределяет
пакет ошибок, исказивший некоторую
последовательность
битов, по большому
числу
блоков,
благодаря
чему
становится
возможным
исправление
ошибок.
Чередование
выполняется
с
помощью
чтения
и
записи
данных
в
различном
порядке.
Если
во
время
передачи
пакет
помех
воздействует
на
некоторую
последовательность
битов,
то все
эти
биты
оказываются
разнесенными
по
различным
блокам.
Следовательно,
от
любой
контрольной
последовательности
требуется
возможность
исправления
лишь
небольшой
части
от
общего
количества
инвертированных
битов.
Соседние файлы в папке Методические материалы
- #
- #
- #
- #
16.03.2016785.94 Кб14305 — Презентации лекций(Беспроводные технологии)_часть 2.1.1_СОС.ppsx
- #
16.03.2016842.38 Кб11305 — Презентации лекций(Беспроводные технологии)_часть 2.1.2_СОС.ppsx
- #
16.03.2016244.08 Кб9805 — Презентации лекций(Беспроводные технологии)_часть 2.1.3_СОС.ppsx
- #
16.03.2016237.31 Кб8905 — Презентации лекций(Беспроводные технологии)_часть 2.2.1_СОС.ppsx
- #
16.03.2016297.49 Кб8905 — Презентации лекций(Беспроводные технологии)_часть 2.2.2_СОС.ppsx
«Цель этого курса — подготовить вас к вашему техническому будущему.»

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.
Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»
Мы уже перевели 26 (из 30) глав. И ведем работу над изданием «в бумаге».
Глава 12. Коды с коррекцией ошибок
(За перевод спасибо Mikhail Sheblaev, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru
В этой главе затронуты две темы: первая, очевидно, коды с коррекцией ошибок, а вторая — то, как иногда происходит процесс открытия. Как Вы все знаете, я официальный первооткрыватель кодов Хэмминга с коррекцией ошибок. Таким образом я, по-видимому, имею возможность описать, как они были найдены. Но вам необходимо остерегаться любых рассказов подобного типа. По правде говоря, в то время я уже очень интересовался процессом открытия, полагая во многих случаях, что метод открытия более важен, чем то, что открыто. Я знал достаточно, чтобы не думать о процессе во время исследований, так же, как спортсмены не думают о технике, когда выступают на соревнованиях, но отрабатывают её до автоматизма. Я также выработал привычку возвращаться назад после больших или малых открытий и пытаться отследить шаги, которые к ним привели. Но не обманывайтесь; в лучшем случае я могу описать сознательную часть и малую верхушку подсознательной части, но мы просто не знаем магии работы подсознания.
Я использовал релейный вычислитель Model 5 в Нью-Йорке, подготавливая его к отправке в Aberdeen Proving Grounds вместе с некоторым требуемым программным обеспечинием (главным образом математические программы). Если с помощью 2-из-5 блочных кодов обнаруживалась ошибка, машина, оставленная без присмотра, могла до трёх раз подряд повторять ошибочный цикл, прежде чем отбросить его и взять новую задачу, надеясь, что проблемное оборудование не будет задействовано в новом решении. Я был в то время, как говорится, старшим помощником младшего дворника, свободное машинное время я получал только на выходных — с 17-00 пятницы до 8-00 понедельника — это была уйма времени! Так я мог бы загрузить входную ленту с большим количеством задач и пообещать моим друзьям, вернувшись в Мюррей Хилл, Нью-Джерси, где находился исследовательский департамент, что я подготовлю ответы ко вторнику. Ну, в одни выходные, как только мы уехали вечером пятницы, машина полностью сломалась и у меня совершенно ничего не было к понедельнику. Я должен был принести извинения моим друзьям и пообещать им ответы к следующему вторнику. Увы! Та же ситуация случилась снова! Я был мягко говоря разгневан и воскликнул: «Если машина может определить, что ошибка существует, почему же она не определит где ошибка и не исправит её, просто изменив бит на противоположный?» (На самом деле, использованные выражения были чуть крепче!).
Заметим первым делом, что этот существенный сдвиг произошёл только потому, что я испытывал огромное эмоциональное напряжение в тот момент и это характерно для большинства великих открытий. Спокойная работа позволит вам улучшить и подробнее разработать идеи, но прорыв обычно приходит только после большого стресса и эмоциональной вовлечёности. Спокойный, холодный, не вовлечённый исследователь редко делает действительно большие новые шаги.
Вернёмся к рассказу. Я знал из предыдущих обсуждений, что конечно можно было бы соорудить три экземляра вычислителя, включая сравнивающие схемы, и использовать исправление ошибок методом голосования большинства. Но чего бы это стоило! Конечно, были и лучшие методы. Я также знал, как обсуждалось в предыдущей главе, о классной штуке с контролем чётности. Я разобрался в их строении очень внимательно.
С другой стороны, Пастер сказал: «Удача любит подготовленных». Как видите, я был подготовлен моей предыдущей работой. Я более чем хорошо знал кодирование «2-из-5», я понимал их фундаментально и работал и понимал общие последствия контроля чётности.
Рис. 12.I
После некоторых размышлений я понял, что если я расположу биты любого символа сообщения в виде прямоугольника и запишу чётность каждого столбца и каждой строки, то две непрошедшие проверки чётности покажут мне координаты одной ошибки и это будет включать угловой добавленный бит чётности (который мог быть установлен соответственно, если я имел нечётные значения) Рис. 12.I. Избыточность, отношение того, что Вы используете, к минимально необходимому количеству, есть
Любому, ко изучал матанализ, очевидно, что чем ближе прямоугольник к квадрату, тем меньше избыточность для сообщения того же размера. И, конечно, большие значения m и n были бы лучше, чем малые, но тогда риск двойной ошибки был бы велик с инженерной точки зрения. Заметим, что если две ошибки случаются, то Вы имеете: (1) если они не в одной строке или столбце, то просто две строки и два столбца содержат ошибки и мы не знаем, какая диагональная пара вызвала их; (2) если две ошибки случились в одной строке (или столбце), то у вас есть только один столбец (строка) и ни одной строки (столбца).
Перенесёмся сейчас на несколько недель позднее. Чтобы попасть в Нью-Йорк, я должен был добраться чуть раньше в Мюррей Хилл, Нью-Джерси, где я работал, и прокатиться на машине, доставляющей почту для компании. Ну да, поездка через северный Нью-Джерси ранним утром не очень живописна, поэтому я завёл привычку пересматривать свои достижения, так что перо вертелось в руках автоматически. В частности я крутил в голове прямоугольные коды. Внезапно, и я не знаю причин для этого, я обнаружил, что если я возьму треугольник и размещу биты контроля чётности на диагонали с тем, чтобы каждый бит проверял столбец и строку одновременно, то я получу более приемлемую избыточность, Рис 12.II.
Моя самодовольность вмиг исчезла! Получил ли я на сей раз лучший код? Спустя несколько миль размышления по этому поводу (помните, ничего не отвлекает в пейзаже северного Нью-Джерси) я понял, что куб информационных битов с контролем чётности по каждой плоскости и проверкой чётности по осям, по всем трём осям, даст мне три координаты для ошибки ценой всего 3n-2 проверок чётности для целого кодированого сообщения длины n^3. Лучше! Но было ли это самым лучшим решением? Нет! Будучи математиком, я быстро понял, что 4-х мерный куб (я не должен был размещать биты так, только обозначить внутренние связи) будет ещё лучше. Таким образом, даже более высокая размерность была бы ещё лучше. Вскоре стало ясно (скажем, миль через 5), что куб размерности 2х2х2х… х2 с n+1 проверкой чётности был бы лучше — очевидно!
Но однажды обожегши пальцы, я не собирался соглашаться с тем, что выглядело хорошо — я уже сделал эту ошибку прежде! Мог бы я доказать, что это было лучшим решением? Как это доказать? Один очевидный подход был в том, чтобы попробовать подсчитать параметры, у меня был n+1 контрольный бит, отображаемый в строку из n+1 битов, т.е. двоичное число длины n+1 разрядов, и это могло представить произвольный объект длины 2^{n+1}. Но мне был нужен только 2^n+1 разряд, 2^n точек в кубе плюс один бит, подтверждающий, что сообщение корректно. Я не учёл в рассмотрении почти что половину битов. Увы! Я прибыл к двери компании, зарегистрировался и пошёл на конференцию, дав идее вылежаться.
Когда я возвратился к идее после нескольких дней отвлекающих событий (в конце концов, предполагалось, что я способствовал командным усилиям компании), я наконец решил, что хороший подход должен будет использовать синдром ошибки как двоичное число, указывающее место ошибки, с, конечно, всеми нулевыми битами в случае корректного результата (более лёгкий тест, чем для всех единиц на большинстве компьютеров). Заметьте, знакомство с двоичной системой, которая не была тогда распространена (1947-1948) неоднократно играло заметную роль в моих построениях. Это плата за знание большего, чем нужно сиюминутно!
Как Вы сконструируете этот частный случай кода, исправляющего ошибки? Легко! Запишите позиции в двоичном коде:
Теперь очевидно, что проверка чётности в правой половине синдрома должна включать все позиции, имеющие 1 в правом столбце; вторая цифра справа должна включить числа, имеющие 1 во втором столбце и т.д. Поэтому Вы имеете:
Таким образом, если ошибка происходит в некотором разряде, соответствующие проверки чётности (и только эти) провалятся и дадут 1 в синдроме, это составит в точности двоичное представление позиции ошибки. Это просто!
Чтобы увидеть код в действии, мы ограничимся 4 битами для сообщениями и 3 контрольными позициями. Эти числа удовлетворяют условию
которое очевидно является необходимым условием, а равенство — достаточным. Выберем для положения битов проверки (так, чтобы контроль чётности был проще ) контрольные разряды 1, 2 и 4. Позиции для сообщения — 3, 5, 6 7. Пусть сообщение будет
1001
Мы (1) запишем сообщение в верхней строке, (2) закодируем следующую строку, (3) вставим ошибку в позиции 6 на следующей строке и (4) на следующих трёх строках вычислим три проверки чётности.
Применим проверки чётности к полученному сообщению:
Двоичное число 110 -> 6, следовательно измените в позиции 6, отбросьте контрольные разряды 1, 2 и 4 и Вы получите оригинальное сообщение, 1001.
Если это кажется волшебством, подумайте о сообщении из всех 0, которое будет иметь контрольные позиции в 0, а после представьте изменение одного бита и Вы увидите как позиция ошибки перемещается, а следом двоичное число синдрома соответственно изменится и будет точно соответствовать положению ошибки. Затем обратите внимание, что сумма любых двух корректных сообщений является всё ещё корректным сообщением (проверки чётности являются аддитивными по модулю 2, следовательно корректные сообщения образуют аддитивную группу по модулю 2). Корректное сообщение даст все нули, следовательно сумма корректных сообщений плюс ошибка одном разряде даст положение ошибки независимо от отправляемого сообщения. Проверки чётности концентрируются на ошибке и игнорируют сообщение.
Теперь сразу очевидно, что любой обмен любыми двумя или больше из столбцов, однажды согласованных на каждом конце канала, не будет иметь никакого существенного эффекта; код будет эквивалентен. Точно так же перестановка 0 и 1 в любом столбце не даст существенно различных кодов. В частности, (так называемый) Код Хемминга является просто красивым переупорядочиванием, и на практике Вы могли бы проверять контрольные биты в конце сообщения, вместо того, чтобы рассеивать их посреди сообщения.
Как насчёт двойной ошибки? Если мы хотим поймать (но не исправить) двойную ошибку, мы просто добавляем единственную новую проверку чётности к целому сообщению, которое мы отправляем. Давайте посмотрим то, что тогда произойдёт на Вашем конце канала.
Исправление одиночных ошибок плюс обнаружение двойных ошибок часто является хорошим балансом. Конечно, избыточность в коротком сообщении из 4 битов, теперь с 4 битами проверки, плоха, но число проверочных битов растёт (грубо ) как логарифм от длины сообщения. Слишком длинное сообщение — и Вы рискуете получить двойную неисправляемую ошибку (которую при помощи кода с исправлением одной ошибки Вы «исправите» в третью ошибку), слишком короткое сообщение — и стоимость избыточности слишком высока. Снова инженерные рассуждения в зависимости от конкретного случая…
Из аналитической геометрии Вы усвоили значимость использования дополняющих алгебраических и геометрических представлений. Естественное представление строки битов должно использовать n-мерный куб, каждая строка которого является вершиной куба. Используя эту картинку и наконец заметив, что любая одна ошибка в сообщении перемещает сообщение вдоль одного ребра, две ошибки — вдоль двух ребер и т.д., я медленно понял, что я должен был действовать в пространстве $L_1$. Расстояние между элементами есть количество разрядов, в которых они различаются. Таким образом у нас есть метрика на пространстве и она удовлетворяет трём стандартным условиям для расстояния (см Главу 10 где определяется стандартное расстояние в L_1).
Таким образом я должен был отнестись серьёзно к тому, что я знал как абстракцию Пифагоровой функции расстояния.
Имея понятие расстояние, мы можем определить сферу как все точки (вершины, поскольку всё рассматривается в множестве вершин), на фиксированном расстоянии от центра. Например, в 3-мерном кубе, который может быть легко нарисован, Рис. 12.III, точки (0,0,1), (0,1,0), и (1,0,0) находятся на единичном расстоянии от (0,0,0), в то время как точки (1,1,0), (1,0,1), и (0,1,1) находятся на расстоянии 2 далее, и наконец точка (1,1,1) находится на расстоянии 3 от начала координат.
Перейдём теперь в пространство с n измерениями и нарисуем сферу единичного радиуса вокруг каждой точки и предположим, что сферы не пересекаются. Очевидно, что центры сфер есть элементы кода и только эти точки, тогда результатом получения любой единичной ошибки в сообщении будет «не-кодовая» точка и Вы сможете понять откуда эта ошибка пришла. Она будет внутри сферы вокруг точки кода, которую я вам послал, что эквивалентно сфере радиуса 1 вокруг точки кода, которую Вы получили. Следовательно, у нас есть код с коррекцией ошибок. Минимальное расстояние между кодовыми точками равно 3. Если мы используем не пересекающиеся сферы радиуса 2, тогда двойная ошибка может быть исправлена, потому что полученная точка будет ближе к оригинальной кодовой точке, чем к любой другой точке; минимальное расстояние для двойной коррекции равно 5. Следующая таблица показывает эквивалентность расстояния между кодовыми точками и «исправимостью» ошибок:
Таким образом построение кода с коррекцией ошибок в точности то же, что построение множества кодовых точек в n-мерном пространстве
которое имеет необходимое минимальное расстояние между легальными сообщениями, так как условия, приведенные выше, необходимы и достаточны. Также должно быть понятно, что мы можем обменять исправление ошибок на их обнаружение — откажитесь от исправления одной ошибки и Вы получите обнаружение ещё двух вместо.
Ранее я показал как разработать коды, удовлетворяющие условиям в случае, когда минимальное расстояние равно 1,2, 3 или 4. Коды с большими минимальными расстояниями не так легко описываются и мы не пойдем далее в этом направлении. Легко найти верхнюю оценку того, насколько велики могут быть кодовые расстояния. Очевидно, что количество точек в сфере радиуса k есть (C(n, k) — биномиальный коэффициент)
Следовательно, если мы разделим объём всего пространства, 2^n, на объём сферы, то частное будет оценкой сверху числа не пересекающихся сфер, т.е. точек кода, в соответствующем пространстве. Чтобы получить дополнительное обнаружение ошибок, мы как и прежде добавим полную проверку чётности, таким образом увеличив минимальное расстояние, которое было 2k+1, до 2k+2 (так как любые две точки на минимальном расстоянии будут иметь одинаковую чётность, увеличим минимальное расстояние на 1).
Давайте подведём итог, где мы теперь. Мы видим, что надлежащим построением кода мы можем создать систему из ненадёжных частей и получить гораздо более надёжную машину, и мы видим сколько мы должны заплатить за это оборудование, хотя мы не исследовали стоимость скорости вычисления, если мы создаём компьютер с таким уровнем коррекции ошибок. Но я ранее упомянул другую выгоду, а именно обслуживание при эксплуатации, и я хотел бы напомнить о нём снова. Чем более изощрённое оборудование, а мы очевидно движемся в этом направлении, тем более насущным является эксплуатационное обслуживание, коды с исправлением ошибок означают, что оборудование не только будет давать (возможно) верные ответы, но и может быть успешно обслужено низкоквалифицированным персоналом.
Использование кодов с обнаружением ошибок и кодов с коррекцией ошибок постоянно растёт в нашем обществе. Отправляя сообщения с космических кораблей, посланных к дальним планетам, мы часто располагаем 20 ваттами мощности или менее (возможно даже 5 ваттами) и используем коды, которые корректируют сотни ошибок в одном блоке сообщения — коррекция производится на Земле, конечно же. Когда Вы не готовы преодолеть шум как в вышеописанной ситуации или в случае «преднамеренного затора», то такие коды — единственный известный выход в этой ситуации.
В конце лета 1961 года во время профессорского отпуска я рулил через всю страну от Стэнфорда, Калифорния к Лаборатории Белл Телефоун в Нью-Джерси. Я запланировал остановку в Моррисе, Иллинойс, где телефонная компания устанавливала первую электронную телефонную станцию, которая была уже не экспериментальной. Я знал, что станция активно использовала коды Хэмминга и, конечно, я был приглашён. Мне сказали, что никогда установка не проходила так легко, как эта. Я сказал себе: «Конечно, именно это я проповедовал в течение прошлых 10 лет». Когда во время начальной наладки все модули установлены и работают должным образом (и Вы в каком-то смысле знаете, что это из-за самопроверок и корректировки), и Вы поворачиваетесь, чтобы перейти к следующим шагам, если что-то пойдёт не так, оборудование вам просто скажет об этом! Лёгкость начальной установки, а также последующего обслуживания, просто была видна невооружённым глазом! Я могу не преувеличивать, исправление ошибок не только приводило к верным результатам во время работы, но и будучи применено правильно, значительно способствовало установке и обслуживанию на месте. И чем более изощрённо оборудование, тем более важны эти вещи!
Я хочу обратиться к другой части этой главы. Я аккуратно рассказал Вам многое из того, с чем я столкнулся на каждом этапе в обнаружении кодов с коррекцией ошибок, и что я сделал. Я сделал это по двум причинам. Во-первых, я хотел быть честным с Вами и показать Вам, как легко, следуя правилу Пастера «Удача улыбнётся подготовленным», преуспеть, просто готовя себя к успеху. Да, были элементы удачи в открытии; но в почти такой же ситуации было много других людей, и они не делали этого! Почему я? Удача, что и говорить, но также я подготовил себя к пониманию того, что происходило — больше, чем другие люди вокруг, просто реагировавшие на явления, когда они происходили, и не думающие глубоко относительно того, что было скрыто под поверхностью.
Я теперь бросаю вызов Вам. То, что я записал на нескольких страницах, было сделано в течение в общей сложности приблизительно трёх — шести месяцев, главным образом рабочих, в моменты обычного исполнения моих рабочих обязанностей в компании. (Патентование отсрочило публикацию более чем на год). Может ли кто-либо сказать, что он, на моём месте, возможно, не сделал бы это? Да, Вы так же способны, как и я, были сделать это — если бы Вы были там, и Вы подготовились также!
Конечно, проживая свою жизнь, Вы не знаете к чему готовиться — Вы хотите совершить нечто значительное и не потратить всю Вашу жизнь, являясь «швейцаром науки» или чем Вы ещё занимаетесь. Конечно, удача играет видную роль. Но насколько я вижу, жизнь дарит Вам многие, многие возможности для того, чтобы сделать нечто большое (определите это как хотите сами) и подготовленный человек обычно достигает успеха один или несколько раз, а неподготовленный человек будет проваливаться почти каждый раз.
Вышеупомянутое мнение не основано на этом опыте, или просто на моих собственных событиях, это — результат изучения жизней многих великих учёных. Я хотел быть учёным, следовательно я изучил их, и я изучил открытия, произошедшие там, где я был, я задавал вопросы тем, кто сделал это. Это мнение также основано на здравом смысле. Вы растите в себе стиль выполнения больших свершений, и затем, когда возможность находится, Вы почти автоматически реагируете с максимальной крутизной в своих действиях. Вы обучили себя думать и действовать надлежащим способам.
Существует один противный тезис, который надо упомянуть, однако, что быть великим в эпоху — это не то, что нужно в последующие годы уточнить. Таким образом Вы, готовя себя к будущим великим свершениям (а их возможность более распространена и их легче достигнуть, чем Вы думаете, так как не часто распознают большие свершения, когда это происходит под носом), необходимо думать о природе будущего, в котором Вы будете жить. Прошлое является частичным руководством, и единственное, что Вы имеете помимо истории, есть постоянное использование Вашего собственного воображения. Снова, случайный перебор случайных решений не приведёт Вас куда либо так далеко, как решения, принятые с Вашим собственным видением того, каким Ваше будущее должно быть.
Я и рассказал и показал Вам, как быть великим; теперь у Вас нет оправдания того, что Вы не делаете этого!
Продолжение следует…
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)
Содержание книги и переведенные главы
Предисловие
- Intro to The Art of Doing Science and Engineering: Learning to Learn (March 28, 1995) Перевод: Глава 1
- «Foundations of the Digital (Discrete) Revolution» (March 30, 1995) Глава 2. Основы цифровой (дискретной) революции
- «History of Computers — Hardware» (March 31, 1995) Глава 3. История компьютеров — железо
- «History of Computers — Software» (April 4, 1995) Глава 4. История компьютеров — Софт
- «History of Computers — Applications» (April 6, 1995) Глава 5. История компьютеров — практическое применение
- «Artificial Intelligence — Part I» (April 7, 1995) Глава 6. Искусственный интеллект — 1
- «Artificial Intelligence — Part II» (April 11, 1995) (готово)
- «Artificial Intelligence III» (April 13, 1995) Глава 8. Искуственный интеллект-III
- «n-Dimensional Space» (April 14, 1995) Глава 9. N-мерное пространство
- «Coding Theory — The Representation of Information, Part I» (April 18, 1995) (пропал переводчик :((( )
- «Coding Theory — The Representation of Information, Part II» (April 20, 1995) Глава 11. Теория кодирования — II
- «Error-Correcting Codes» (April 21, 1995) Глава 12. Коды с коррекцией ошибок
- «Information Theory» (April 25, 1995) (пропал переводчик :((( )
- «Digital Filters, Part I» (April 27, 1995) Глава 14. Цифровые фильтры — 1
- «Digital Filters, Part II» (April 28, 1995) Глава 15. Цифровые фильтры — 2
- «Digital Filters, Part III» (May 2, 1995) Глава 16. Цифровые фильтры — 3
- «Digital Filters, Part IV» (May 4, 1995) Глава 17. Цифровые фильтры — IV
- «Simulation, Part I» (May 5, 1995) (в работе)
- «Simulation, Part II» (May 9, 1995) Глава 19. Моделирование — II
- «Simulation, Part III» (May 11, 1995)
- «Fiber Optics» (May 12, 1995) Глава 21. Волоконная оптика
- «Computer Aided Instruction» (May 16, 1995) (пропал переводчик :((( )
- «Mathematics» (May 18, 1995) Глава 23. Математика
- «Quantum Mechanics» (May 19, 1995) Глава 24. Квантовая механика
- «Creativity» (May 23, 1995). Перевод: Глава 25. Креативность
- «Experts» (May 25, 1995) Глава 26. Эксперты
- «Unreliable Data» (May 26, 1995) Глава 27. Недостоверные данные
- «Systems Engineering» (May 30, 1995) Глава 28. Системная Инженерия
- «You Get What You Measure» (June 1, 1995) Глава 29. Вы получаете то, что вы измеряете
- «How Do We Know What We Know» (June 2, 1995) пропал переводчик :(((
- Hamming, «You and Your Research» (June 6, 1995). Перевод: Вы и ваша работа
Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code, (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complex function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
References[edit]
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
In computing, telecommunication, information theory, and coding theory, forward error correction (FEC) or channel coding[1][2][3] is a technique used for controlling errors in data transmission over unreliable or noisy communication channels.
The central idea is that the sender encodes the message in a redundant way, most often by using an error correction code or error correcting code, (ECC).[4][5] The redundancy allows the receiver not only to detect errors that may occur anywhere in the message, but often to correct a limited number of errors. Therefore a reverse channel to request re-transmission may not be needed. The cost is a fixed, higher forward channel bandwidth.
The American mathematician Richard Hamming pioneered this field in the 1940s and invented the first error-correcting code in 1950: the Hamming (7,4) code.[5]
FEC can be applied in situations where re-transmissions are costly or impossible, such as one-way communication links or when transmitting to multiple receivers in multicast.
Long-latency connections also benefit; in the case of a satellite orbiting Uranus, retransmission due to errors can create a delay of five hours. FEC is widely used in modems and in cellular networks, as well.
FEC processing in a receiver may be applied to a digital bit stream or in the demodulation of a digitally modulated carrier. For the latter, FEC is an integral part of the initial analog-to-digital conversion in the receiver. The Viterbi decoder implements a soft-decision algorithm to demodulate digital data from an analog signal corrupted by noise. Many FEC decoders can also generate a bit-error rate (BER) signal which can be used as feedback to fine-tune the analog receiving electronics.
FEC information is added to mass storage (magnetic, optical and solid state/flash based) devices to enable recovery of corrupted data, and is used as ECC computer memory on systems that require special provisions for reliability.
The maximum proportion of errors or missing bits that can be corrected is determined by the design of the ECC, so different forward error correcting codes are suitable for different conditions. In general, a stronger code induces more redundancy that needs to be transmitted using the available bandwidth, which reduces the effective bit-rate while improving the received effective signal-to-noise ratio. The noisy-channel coding theorem of Claude Shannon can be used to compute the maximum achievable communication bandwidth for a given maximum acceptable error probability. This establishes bounds on the theoretical maximum information transfer rate of a channel with some given base noise level. However, the proof is not constructive, and hence gives no insight of how to build a capacity achieving code. After years of research, some advanced FEC systems like polar code[3] come very close to the theoretical maximum given by the Shannon channel capacity under the hypothesis of an infinite length frame.
How it works[edit]
ECC is accomplished by adding redundancy to the transmitted information using an algorithm. A redundant bit may be a complex function of many original information bits. The original information may or may not appear literally in the encoded output; codes that include the unmodified input in the output are systematic, while those that do not are non-systematic.
A simplistic example of ECC is to transmit each data bit 3 times, which is known as a (3,1) repetition code. Through a noisy channel, a receiver might see 8 versions of the output, see table below.
| Triplet received | Interpreted as |
|---|---|
| 000 | 0 (error-free) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (error-free) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
This allows an error in any one of the three samples to be corrected by «majority vote», or «democratic voting». The correcting ability of this ECC is:
- Up to 1 bit of triplet in error, or
- up to 2 bits of triplet omitted (cases not shown in table).
Though simple to implement and widely used, this triple modular redundancy is a relatively inefficient ECC. Better ECC codes typically examine the last several tens or even the last several hundreds of previously received bits to determine how to decode the current small handful of bits (typically in groups of 2 to 8 bits).
Averaging noise to reduce errors[edit]
ECC could be said to work by «averaging noise»; since each data bit affects many transmitted symbols, the corruption of some symbols by noise usually allows the original user data to be extracted from the other, uncorrupted received symbols that also depend on the same user data.
- Because of this «risk-pooling» effect, digital communication systems that use ECC tend to work well above a certain minimum signal-to-noise ratio and not at all below it.
- This all-or-nothing tendency – the cliff effect – becomes more pronounced as stronger codes are used that more closely approach the theoretical Shannon limit.
- Interleaving ECC coded data can reduce the all or nothing properties of transmitted ECC codes when the channel errors tend to occur in bursts. However, this method has limits; it is best used on narrowband data.
Most telecommunication systems use a fixed channel code designed to tolerate the expected worst-case bit error rate, and then fail to work at all if the bit error rate is ever worse.
However, some systems adapt to the given channel error conditions: some instances of hybrid automatic repeat-request use a fixed ECC method as long as the ECC can handle the error rate, then switch to ARQ when the error rate gets too high;
adaptive modulation and coding uses a variety of ECC rates, adding more error-correction bits per packet when there are higher error rates in the channel, or taking them out when they are not needed.
Types of ECC[edit]
A block code (specifically a Hamming code) where redundant bits are added as a block to the end of the initial message
A continuous code convolutional code where redundant bits are added continuously into the structure of the code word
The two main categories of ECC codes are block codes and convolutional codes.
- Block codes work on fixed-size blocks (packets) of bits or symbols of predetermined size. Practical block codes can generally be hard-decoded in polynomial time to their block length.
- Convolutional codes work on bit or symbol streams of arbitrary length. They are most often soft decoded with the Viterbi algorithm, though other algorithms are sometimes used. Viterbi decoding allows asymptotically optimal decoding efficiency with increasing constraint length of the convolutional code, but at the expense of exponentially increasing complexity. A convolutional code that is terminated is also a ‘block code’ in that it encodes a block of input data, but the block size of a convolutional code is generally arbitrary, while block codes have a fixed size dictated by their algebraic characteristics. Types of termination for convolutional codes include «tail-biting» and «bit-flushing».
There are many types of block codes; Reed–Solomon coding is noteworthy for its widespread use in compact discs, DVDs, and hard disk drives. Other examples of classical block codes include Golay, BCH, Multidimensional parity, and Hamming codes.
Hamming ECC is commonly used to correct NAND flash memory errors.[6]
This provides single-bit error correction and 2-bit error detection.
Hamming codes are only suitable for more reliable single-level cell (SLC) NAND.
Denser multi-level cell (MLC) NAND may use multi-bit correcting ECC such as BCH or Reed–Solomon.[7][8] NOR Flash typically does not use any error correction.[7]
Classical block codes are usually decoded using hard-decision algorithms,[9] which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. In contrast, convolutional codes are typically decoded using soft-decision algorithms like the Viterbi, MAP or BCJR algorithms, which process (discretized) analog signals, and which allow for much higher error-correction performance than hard-decision decoding.
Nearly all classical block codes apply the algebraic properties of finite fields. Hence classical block codes are often referred to as algebraic codes.
In contrast to classical block codes that often specify an error-detecting or error-correcting ability, many modern block codes such as LDPC codes lack such guarantees. Instead, modern codes are evaluated in terms of their bit error rates.
Most forward error correction codes correct only bit-flips, but not bit-insertions or bit-deletions.
In this setting, the Hamming distance is the appropriate way to measure the bit error rate.
A few forward error correction codes are designed to correct bit-insertions and bit-deletions, such as Marker Codes and Watermark Codes.
The Levenshtein distance is a more appropriate way to measure the bit error rate when using such codes.
[10]
Code-rate and the tradeoff between reliability and data rate[edit]
The fundamental principle of ECC is to add redundant bits in order to help the decoder to find out the true message that was encoded by the transmitter. The code-rate of a given ECC system is defined as the ratio between the number of information bits and the total number of bits (i.e., information plus redundancy bits) in a given communication package. The code-rate is hence a real number. A low code-rate close to zero implies a strong code that uses many redundant bits to achieve a good performance, while a large code-rate close to 1 implies a weak code.
The redundant bits that protect the information have to be transferred using the same communication resources that they are trying to protect. This causes a fundamental tradeoff between reliability and data rate.[11] In one extreme, a strong code (with low code-rate) can induce an important increase in the receiver SNR (signal-to-noise-ratio) decreasing the bit error rate, at the cost of reducing the effective data rate. On the other extreme, not using any ECC (i.e., a code-rate equal to 1) uses the full channel for information transfer purposes, at the cost of leaving the bits without any additional protection.
One interesting question is the following: how efficient in terms of information transfer can an ECC be that has a negligible decoding error rate? This question was answered by Claude Shannon with his second theorem, which says that the channel capacity is the maximum bit rate achievable by any ECC whose error rate tends to zero:[12] His proof relies on Gaussian random coding, which is not suitable to real-world applications. The upper bound given by Shannon’s work inspired a long journey in designing ECCs that can come close to the ultimate performance boundary. Various codes today can attain almost the Shannon limit. However, capacity achieving ECCs are usually extremely complex to implement.
The most popular ECCs have a trade-off between performance and computational complexity. Usually, their parameters give a range of possible code rates, which can be optimized depending on the scenario. Usually, this optimization is done in order to achieve a low decoding error probability while minimizing the impact to the data rate. Another criterion for optimizing the code rate is to balance low error rate and retransmissions number in order to the energy cost of the communication.[13]
Concatenated ECC codes for improved performance[edit]
Classical (algebraic) block codes and convolutional codes are frequently combined in concatenated coding schemes in which a short constraint-length Viterbi-decoded convolutional code does most of the work and a block code (usually Reed–Solomon) with larger symbol size and block length «mops up» any errors made by the convolutional decoder. Single pass decoding with this family of error correction codes can yield very low error rates, but for long range transmission conditions (like deep space) iterative decoding is recommended.
Concatenated codes have been standard practice in satellite and deep space communications since Voyager 2 first used the technique in its 1986 encounter with Uranus. The Galileo craft used iterative concatenated codes to compensate for the very high error rate conditions caused by having a failed antenna.
Low-density parity-check (LDPC)[edit]
Low-density parity-check (LDPC) codes are a class of highly efficient linear block
codes made from many single parity check (SPC) codes. They can provide performance very close to the channel capacity (the theoretical maximum) using an iterated soft-decision decoding approach, at linear time complexity in terms of their block length. Practical implementations rely heavily on decoding the constituent SPC codes in parallel.
LDPC codes were first introduced by Robert G. Gallager in his PhD thesis in 1960,
but due to the computational effort in implementing encoder and decoder and the introduction of Reed–Solomon codes,
they were mostly ignored until the 1990s.
LDPC codes are now used in many recent high-speed communication standards, such as DVB-S2 (Digital Video Broadcasting – Satellite – Second Generation), WiMAX (IEEE 802.16e standard for microwave communications), High-Speed Wireless LAN (IEEE 802.11n),[14] 10GBase-T Ethernet (802.3an) and G.hn/G.9960 (ITU-T Standard for networking over power lines, phone lines and coaxial cable). Other LDPC codes are standardized for wireless communication standards within 3GPP MBMS (see fountain codes).
Turbo codes[edit]
Turbo coding is an iterated soft-decoding scheme that combines two or more relatively simple convolutional codes and an interleaver to produce a block code that can perform to within a fraction of a decibel of the Shannon limit. Predating LDPC codes in terms of practical application, they now provide similar performance.
One of the earliest commercial applications of turbo coding was the CDMA2000 1x (TIA IS-2000) digital cellular technology developed by Qualcomm and sold by Verizon Wireless, Sprint, and other carriers. It is also used for the evolution of CDMA2000 1x specifically for Internet access, 1xEV-DO (TIA IS-856). Like 1x, EV-DO was developed by Qualcomm, and is sold by Verizon Wireless, Sprint, and other carriers (Verizon’s marketing name for 1xEV-DO is Broadband Access, Sprint’s consumer and business marketing names for 1xEV-DO are Power Vision and Mobile Broadband, respectively).
Local decoding and testing of codes[edit]
Sometimes it is only necessary to decode single bits of the message, or to check whether a given signal is a codeword, and do so without looking at the entire signal. This can make sense in a streaming setting, where codewords are too large to be classically decoded fast enough and where only a few bits of the message are of interest for now. Also such codes have become an important tool in computational complexity theory, e.g., for the design of probabilistically checkable proofs.
Locally decodable codes are error-correcting codes for which single bits of the message can be probabilistically recovered by only looking at a small (say constant) number of positions of a codeword, even after the codeword has been corrupted at some constant fraction of positions. Locally testable codes are error-correcting codes for which it can be checked probabilistically whether a signal is close to a codeword by only looking at a small number of positions of the signal.
Interleaving[edit]
«Interleaver» redirects here. For the fiber-optic device, see optical interleaver.
A short illustration of interleaving idea
Interleaving is frequently used in digital communication and storage systems to improve the performance of forward error correcting codes. Many communication channels are not memoryless: errors typically occur in bursts rather than independently. If the number of errors within a code word exceeds the error-correcting code’s capability, it fails to recover the original code word. Interleaving alleviates this problem by shuffling source symbols across several code words, thereby creating a more uniform distribution of errors.[15] Therefore, interleaving is widely used for burst error-correction.
The analysis of modern iterated codes, like turbo codes and LDPC codes, typically assumes an independent distribution of errors.[16] Systems using LDPC codes therefore typically employ additional interleaving across the symbols within a code word.[17]
For turbo codes, an interleaver is an integral component and its proper design is crucial for good performance.[15][18] The iterative decoding algorithm works best when there are not short cycles in the factor graph that represents the decoder; the interleaver is chosen to avoid short cycles.
Interleaver designs include:
- rectangular (or uniform) interleavers (similar to the method using skip factors described above)
- convolutional interleavers
- random interleavers (where the interleaver is a known random permutation)
- S-random interleaver (where the interleaver is a known random permutation with the constraint that no input symbols within distance S appear within a distance of S in the output).[19]
- a contention-free quadratic permutation polynomial (QPP).[20] An example of use is in the 3GPP Long Term Evolution mobile telecommunication standard.[21]
In multi-carrier communication systems, interleaving across carriers may be employed to provide frequency diversity, e.g., to mitigate frequency-selective fading or narrowband interference.[22]
Example[edit]
Transmission without interleaving:
Error-free message: aaaabbbbccccddddeeeeffffgggg Transmission with a burst error: aaaabbbbccc____deeeeffffgggg
Here, each group of the same letter represents a 4-bit one-bit error-correcting codeword. The codeword cccc is altered in one bit and can be corrected, but the codeword dddd is altered in three bits, so either it cannot be decoded at all or it might be decoded incorrectly.
With interleaving:
Error-free code words: aaaabbbbccccddddeeeeffffgggg Interleaved: abcdefgabcdefgabcdefgabcdefg Transmission with a burst error: abcdefgabcd____bcdefgabcdefg Received code words after deinterleaving: aa_abbbbccccdddde_eef_ffg_gg
In each of the codewords «aaaa», «eeee», «ffff», and «gggg», only one bit is altered, so one-bit error-correcting code will decode everything correctly.
Transmission without interleaving:
Original transmitted sentence: ThisIsAnExampleOfInterleaving Received sentence with a burst error: ThisIs______pleOfInterleaving
The term «AnExample» ends up mostly unintelligible and difficult to correct.
With interleaving:
Transmitted sentence: ThisIsAnExampleOfInterleaving... Error-free transmission: TIEpfeaghsxlIrv.iAaenli.snmOten. Received sentence with a burst error: TIEpfe______Irv.iAaenli.snmOten. Received sentence after deinterleaving: T_isI_AnE_amp_eOfInterle_vin_...
No word is completely lost and the missing letters can be recovered with minimal guesswork.
Disadvantages of interleaving[edit]
Use of interleaving techniques increases total delay. This is because the entire interleaved block must be received before the packets can be decoded.[23] Also interleavers hide the structure of errors; without an interleaver, more advanced decoding algorithms can take advantage of the error structure and achieve more reliable communication than a simpler decoder combined with an interleaver[citation needed]. An example of such an algorithm is based on neural network[24] structures.
Software for error-correcting codes[edit]
Simulating the behaviour of error-correcting codes (ECCs) in software is a common practice to design, validate and improve ECCs. The upcoming wireless 5G standard raises a new range of applications for the software ECCs: the Cloud Radio Access Networks (C-RAN) in a Software-defined radio (SDR) context. The idea is to directly use software ECCs in the communications. For instance in the 5G, the software ECCs could be located in the cloud and the antennas connected to this computing resources: improving this way the flexibility of the communication network and eventually increasing the energy efficiency of the system.
In this context, there are various available Open-source software listed below (non exhaustive).
- AFF3CT(A Fast Forward Error Correction Toolbox): a full communication chain in C++ (many supported codes like Turbo, LDPC, Polar codes, etc.), very fast and specialized on channel coding (can be used as a program for simulations or as a library for the SDR).
- IT++: a C++ library of classes and functions for linear algebra, numerical optimization, signal processing, communications, and statistics.
- OpenAir: implementation (in C) of the 3GPP specifications concerning the Evolved Packet Core Networks.
List of error-correcting codes[edit]
| Distance | Code |
|---|---|
| 2 (single-error detecting) | Parity |
| 3 (single-error correcting) | Triple modular redundancy |
| 3 (single-error correcting) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (double-error correcting) | |
| 6 (double-error correct-/triple error detect) | Nordstrom-Robinson code |
| 7 (three-error correcting) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- BCH code, which can be designed to correct any arbitrary number of errors per code block.
- Barker code used for radar, telemetry, ultra sound, Wifi, DSSS mobile phone networks, GPS etc.
- Berger code
- Constant-weight code
- Convolutional code
- Expander codes
- Group codes
- Golay codes, of which the Binary Golay code is of practical interest
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- Hamming code
- Latin square based code for non-white noise (prevalent for example in broadband over powerlines)
- Lexicographic code
- Linear Network Coding, a type of erasure correcting code across networks instead of point-to-point links
- Long code
- Low-density parity-check code, also known as Gallager code, as the archetype for sparse graph codes
- LT code, which is a near-optimal rateless erasure correcting code (Fountain code)
- m of n codes
- Nordstrom-Robinson code, used in Geometry and Group Theory[25]
- Online code, a near-optimal rateless erasure correcting code
- Polar code (coding theory)
- Raptor code, a near-optimal rateless erasure correcting code
- Reed–Solomon error correction
- Reed–Muller code
- Repeat-accumulate code
- Repetition codes, such as Triple modular redundancy
- Spinal code, a rateless, nonlinear code based on pseudo-random hash functions[26]
- Tornado code, a near-optimal erasure correcting code, and the precursor to Fountain codes
- Turbo code
- Walsh–Hadamard code
- Cyclic redundancy checks (CRCs) can correct 1-bit errors for messages at most
bits long for optimal generator polynomials of degree
, see Mathematics of cyclic redundancy checks#Bitfilters
See also[edit]
- Code rate
- Erasure codes
- Soft-decision decoder
- Burst error-correcting code
- Error detection and correction
- Error-correcting codes with feedback
References[edit]
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
- ^ Charles Wang; Dean Sklar; Diana Johnson (Winter 2001–2002). «Forward Error-Correction Coding». Crosslink. The Aerospace Corporation. 3 (1). Archived from the original on 14 March 2012. Retrieved 5 March 2006.
How Forward Error-Correcting Codes Work]
- ^ a b Maunder, Robert (2016). «Overview of Channel Coding».
- ^ Glover, Neal; Dudley, Trent (1990). Practical Error Correction Design For Engineers (Revision 1.1, 2nd ed.). CO, USA: Cirrus Logic. ISBN 0-927239-00-0.
- ^ a b Hamming, Richard Wesley (April 1950). «Error Detecting and Error Correcting Codes». Bell System Technical Journal. USA: AT&T. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773.
- ^ «Hamming codes for NAND flash memory devices» Archived 21 August 2016 at the Wayback Machine. EE Times-Asia. Apparently based on «Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices». 2005. Both say: «The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications.»
- ^ a b «What Types of ECC Should Be Used on Flash Memory?» (Application note). Spansion. 2011.
Both Reed–Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. … Hamming based block codes are the most commonly used ECC for SLC…. both Reed–Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
- ^ Jim Cooke (August 2007). «The Inconvenient Truths of NAND Flash Memory» (PDF). p. 28.
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required … for MLC.
- ^ Baldi, M.; Chiaraluce, F. (2008). «A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions». International Journal of Digital Multimedia Broadcasting. 2008: 1–12. doi:10.1155/2008/957846.
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt (2006). «Keyboards and covert channels». USENIX. Retrieved 20 December 2018.
- ^ Tse, David; Viswanath, Pramod (2005), Fundamentals of Wireless Communication, Cambridge University Press, UK
- ^ Shannon, C. E. (1948). «A mathematical theory of communication» (PDF). Bell System Technical Journal. 27 (3–4): 379–423 & 623–656. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2.
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. (2014). «Optimizing the code rate for achieving energy-efficient wireless communications». Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). pp. 775–780. doi:10.1109/WCNC.2014.6952166. ISBN 978-1-4799-3083-8.
- ^ IEEE Standard, section 20.3.11.6 «802.11n-2009» Archived 3 February 2013 at the Wayback Machine, IEEE, 29 October 2009, accessed 21 March 2011.
- ^ a b Vucetic, B.; Yuan, J. (2000). Turbo codes: principles and applications. Springer Verlag. ISBN 978-0-7923-7868-6.
- ^ Luby, Michael; Mitzenmacher, M.; Shokrollahi, A.; Spielman, D.; Stemann, V. (1997). «Practical Loss-Resilient Codes». Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation.
- ^ «Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2)». En 302 307. ETSI (V1.2.1). April 2009.
- ^ Andrews, K. S.; Divsalar, D.; Dolinar, S.; Hamkins, J.; Jones, C. R.; Pollara, F. (November 2007). «The Development of Turbo and LDPC Codes for Deep-Space Applications». Proceedings of the IEEE. 95 (11): 2142–2156. doi:10.1109/JPROC.2007.905132. S2CID 9289140.
- ^ Dolinar, S.; Divsalar, D. (15 August 1995). «Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations». TDA Progress Report. 122: 42–122. Bibcode:1995TDAPR.122…56D. CiteSeerX 10.1.1.105.6640.
- ^ Takeshita, Oscar (2006). «Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective». IEEE Transactions on Information Theory. 53 (6): 2116–2132. arXiv:cs/0601048. Bibcode:2006cs……..1048T. doi:10.1109/TIT.2007.896870. S2CID 660.
- ^ 3GPP TS 36.212, version 8.8.0, page 14
- ^ «Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2)». En 302 755. ETSI (V1.1.1). September 2009.
- ^ Techie (3 June 2010). «Explaining Interleaving». W3 Techie Blog. Retrieved 3 June 2010.
- ^ Krastanov, Stefan; Jiang, Liang (8 September 2017). «Deep Neural Network Probabilistic Decoder for Stabilizer Codes». Scientific Reports. 7 (1): 11003. arXiv:1705.09334. Bibcode:2017NatSR…711003K. doi:10.1038/s41598-017-11266-1. PMC 5591216. PMID 28887480.
- ^ Nordstrom, A.W.; Robinson, J.P. (1967), «An optimum nonlinear code», Information and Control, 11 (5–6): 613–616, doi:10.1016/S0019-9958(67)90835-2
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat (2011). «Rateless Spinal Codes». Proceedings of the 10th ACM Workshop on Hot Topics in Networks. pp. 1–6. doi:10.1145/2070562.2070568. hdl:1721.1/79676. ISBN 9781450310598.
Further reading[edit]
- MacWilliams, Florence Jessiem; Sloane, Neil James Alexander (2007) [1977]. Written at AT&T Shannon Labs, Florham Park, New Jersey, USA. The Theory of Error-Correcting Codes. North-Holland Mathematical Library. Vol. 16 (digital print of 12th impression, 1st ed.). Amsterdam / London / New York / Tokyo: North-Holland / Elsevier BV. ISBN 978-0-444-85193-2. LCCN 76-41296. (xxii+762+6 pages)
- Clark, Jr., George C.; Cain, J. Bibb (1981). Error-Correction Coding for Digital Communications. New York, USA: Plenum Press. ISBN 0-306-40615-2.
- Arazi, Benjamin (1987). Swetman, Herb (ed.). A Commonsense Approach to the Theory of Error Correcting Codes. MIT Press Series in Computer Systems. Vol. 10 (1 ed.). Cambridge, Massachusetts, USA / London, UK: Massachusetts Institute of Technology. ISBN 0-262-01098-4. LCCN 87-21889. (x+2+208+4 pages)
- Wicker, Stephen B. (1995). Error Control Systems for Digital Communication and Storage. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-200809-2.
- Wilson, Stephen G. (1996). Digital Modulation and Coding. Englewood Cliffs, New Jersey, USA: Prentice-Hall. ISBN 0-13-210071-1.
- «Error Correction Code in Single Level Cell NAND Flash memories» 2007-02-16
- «Error Correction Code in NAND Flash memories» 2004-11-29
- Observations on Errors, Corrections, & Trust of Dependent Systems, by James Hamilton, 2012-02-26
- Sphere Packings, Lattices and Groups, By J. H. Conway, Neil James Alexander Sloane, Springer Science & Business Media, 2013-03-09 – Mathematics – 682 pages.
External links[edit]
- Morelos-Zaragoza, Robert (2004). «The Correcting Codes (ECC) Page». Retrieved 5 March 2006.
- lpdec: library for LP decoding and related things (Python)
Метод коррекции ошибки — метод обучения перцептрона, предложенный Ф.Розенблаттом. Представляет собой такой метод обучения, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.
Модификации метода
В теореме сходимости перцептрона различаются различные виды этого метода, доказано, что любой из них позволяет получить схождение при решении любой задачи классификации.
Метод коррекции ошибок без квантования
Если реакция на стимул 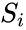

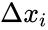
а 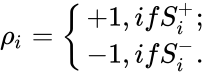
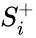

Метод коррекции ошибок с квантованием
Отличается от метода коррекции ошибок без квантованиея только тем, что 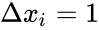
Это метод и метод коррекции ошибок без квантованиея являются одинаковыми по скорости достяжения решения в общем случае, и более эффективными по сравнению с методами коррекции ошибок со случайным знаком или случайными возмущениями.
Метод коррекции ошибок со случайным знаком подкрепления
Отличается тем, что знак подкрепления 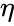
Метод коррекции ошибок со случайными возмущениями
Отличается тем, что величина и знак 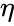
См. также
- Теорема сходимости Перцептрона
- Дельта-правило
- Перцептрон
Литература
- Фрэнк Розенблатт Принципы нейродинамики: перцептроны и теория механизмов мозга = Principles of Neurodynamic: perceptrons and the theory of brain mechanisms. — М.: «Мир», 1965.
Это основополагающая версия, написанная участниками этого проекта. Но содержимое этой страницы очень близкое по содержанию предоставлено для раздела Википедии на русском языке. Так же, как и в этом проекте, текст этой статьи, размещённый в Википедии, доступен на условиях CC-BY-SA . Статью, размещенную в Википедии можно найти по адресу: Метод коррекции ошибки.
Чтобы устранить ошибки передачи, вносимые атмосферой Земли (слева), ученые Годдарда применили исправление ошибок Рида – Соломона (справа), которое обычно используется на компакт-дисках и DVD. Типичные ошибки включают отсутствие пикселей (белые) и ложные сигналы (черные). Белая полоса указывает на короткий период, когда передача была приостановлена.
В теория информации и теория кодирования с приложениями в Информатика и телекоммуникации, обнаружение и исправление ошибок или же контроль ошибок методы, которые обеспечивают надежную доставку цифровые данные чрезмерно ненадежный каналы связи. Многие каналы связи подлежат канальный шум, и, таким образом, ошибки могут быть внесены во время передачи от источника к приемнику. Методы обнаружения ошибок позволяют обнаруживать такие ошибки, а исправление ошибок во многих случаях позволяет восстановить исходные данные.
Определения
Обнаружение ошибок это обнаружение ошибок, вызванных шумом или другими помехами во время передачи от передатчика к приемнику. Исправление ошибки это обнаружение ошибок и восстановление исходных безошибочных данных.
История
Современное развитие коды исправления ошибок зачисляется на Ричард Хэмминг в 1947 г.[1] Описание Код Хэмминга появился в Клод Шеннон с Математическая теория коммуникации[2] и был быстро обобщен Марсель Дж. Э. Голей.[3]
Вступление
Все схемы обнаружения и исправления ошибок добавляют избыточность (т.е. некоторые дополнительные данные) к сообщению, которые получатели могут использовать для проверки согласованности доставленного сообщения и для восстановления данных, которые были определены как поврежденные. Схемы обнаружения и исправления ошибок могут быть либо систематический или несистематический. В систематической схеме передатчик отправляет исходные данные и прикрепляет фиксированное количество проверить биты (или же данные о четности), которые получены из битов данных некоторыми детерминированный алгоритм. Если требуется только обнаружение ошибок, приемник может просто применить тот же алгоритм к полученным битам данных и сравнить свой вывод с полученными контрольными битами; если значения не совпадают, в какой-то момент во время передачи произошла ошибка. В системе, которая использует несистематический код, исходное сообщение преобразуется в закодированное сообщение, несущее ту же информацию и имеющее по крайней мере такое же количество битов, как и исходное сообщение.
Хорошая эффективность контроля ошибок требует, чтобы схема была выбрана на основе характеристик канала связи. Общий модели каналов включают без памяти модели, в которых ошибки возникают случайно и с определенной вероятностью, и динамические модели, в которых ошибки возникают в основном в всплески. Следовательно, коды обнаружения и исправления ошибок можно в целом различать между обнаружение / исправление случайных ошибок и обнаружение / исправление пакетных ошибок. Некоторые коды также могут подходить для сочетания случайных ошибок и пакетных ошибок.
Если характеристики канала не могут быть определены или сильно варьируются, схему обнаружения ошибок можно комбинировать с системой для повторных передач ошибочных данных. Это известно как автоматический повторный запрос (ARQ), и наиболее часто используется в Интернете. Альтернативный подход к контролю ошибок: гибридный автоматический запрос на повторение (HARQ), который представляет собой комбинацию ARQ и кодирования с исправлением ошибок.
Виды исправления ошибок
Есть три основных типа исправления ошибок.[4]
Автоматический повторный запрос (ARQ)
Автоматический повторный запрос (ARQ) — это метод контроля ошибок для передачи данных, который использует коды обнаружения ошибок, сообщения подтверждения и / или отрицательного подтверждения, и таймауты для достижения надежной передачи данных. An подтверждение это сообщение, отправленное получателем, чтобы указать, что он правильно получил кадр данных.
Обычно, когда передатчик не получает подтверждения до истечения тайм-аута (т. Е. В течение разумного промежутка времени после отправки кадра данных), он повторно передает кадр до тех пор, пока он не будет либо правильно принят, либо ошибка сохранится сверх заранее определенного количества повторных передач. .
Есть три типа протоколов ARQ. Остановка и ожидание ARQ, Go-Back-N ARQ, и Селективный повторный ARQ.
ARQ подходит, если канал связи имеет изменяющийся или неизвестный емкость, например, в Интернете. Однако ARQ требует наличия задний канал, приводит к возможному увеличению задержка из-за повторных передач и требует обслуживания буферов и таймеров для повторных передач, что в случае перегрузка сети может вызвать нагрузку на сервер и общую пропускную способность сети.[5]
Например, ARQ используется на коротковолновых радиоканалах в виде ARQ-E, или в сочетании с мультиплексированием как ARQ-M.
Прямое исправление ошибок
Прямое исправление ошибок (FEC) — это процесс добавления избыточный данные, такие как код исправления ошибок (ECC) в сообщение, чтобы оно могло быть восстановлено получателем, даже если было внесено несколько ошибок (в зависимости от возможностей используемого кода) либо в процессе передачи, либо при хранении. Поскольку получатель не должен запрашивать у отправителя повторную передачу данных, обратный канал не требуется при упреждающем исправлении ошибок и поэтому подходит для симплексная связь Такие как вещание. Коды с исправлением ошибок часто используются в нижний слой коммуникации, а также для надежного хранения на таких носителях, как Компакт-диски, DVD, жесткие диски, и баран.
Коды с исправлением ошибок обычно различают между сверточные коды и блочные коды:
- Сверточные коды обрабатываются побитно. Они особенно подходят для аппаратной реализации, а Декодер Витерби позволяет оптимальное декодирование.
- Коды блокировки обрабатываются на блок за блоком основание. Ранние примеры блочных кодов: коды повторения, Коды Хэмминга и многомерные коды проверки на четность. За ними последовал ряд эффективных кодов, Коды Рида – Соломона являются наиболее заметными из-за их широкого распространения в настоящее время. Турбо коды и коды с низкой плотностью проверки четности (LDPC) — относительно новые конструкции, которые могут обеспечить почти оптимальная эффективность.
Теорема Шеннона является важной теоремой для прямого исправления ошибок и описывает максимальную скорость передачи информации при котором возможна надежная связь по каналу с определенной вероятностью ошибки или соотношение сигнал шум (SNR). Этот строгий верхний предел выражается в терминах пропускная способность канала. В частности, теорема утверждает, что существуют такие коды, что с увеличением длины кодирования вероятность ошибки на дискретный канал без памяти можно сделать сколь угодно малым при условии, что кодовая скорость меньше пропускной способности канала. Кодовая скорость определяется как доля к / п из k исходные символы и п закодированные символы.
Фактическая максимальная допустимая кодовая скорость зависит от используемого кода исправления ошибок и может быть ниже. Это связано с тем, что доказательство Шеннона носило исключительно экзистенциальный характер и не показало, как построить коды, которые одновременно являются оптимальными и имеют эффективный алгоритмы кодирования и декодирования.
Гибридные схемы
Гибридный ARQ представляет собой комбинацию ARQ и прямого исправления ошибок. Есть два основных подхода:[5]
- Сообщения всегда передаются с данными четности FEC (и избыточностью обнаружения ошибок). Приемник декодирует сообщение, используя информацию о четности, и запрашивает повторную передачу с использованием ARQ только в том случае, если данных четности было недостаточно для успешного декодирования (идентифицированного посредством неудачной проверки целостности).
- Сообщения передаются без данных четности (только с информацией об обнаружении ошибок). Если приемник обнаруживает ошибку, он запрашивает информацию FEC от передатчика с помощью ARQ и использует ее для восстановления исходного сообщения.
Последний подход особенно привлекателен на канал стирания при использовании код бесскоростного стирания.
Схемы обнаружения ошибок
Обнаружение ошибок чаще всего осуществляется с помощью подходящего хеш-функция (или, в частности, контрольная сумма, циклическая проверка избыточности или другой алгоритм). Хеш-функция добавляет фиксированную длину тег в сообщение, что позволяет получателям проверять доставленное сообщение путем пересчета тега и сравнения его с предоставленным.
Существует огромное количество различных конструкций хеш-функций. Однако некоторые из них особенно широко используются из-за их простоты или их пригодности для обнаружения определенных видов ошибок (например, производительность циклического контроля избыточности при обнаружении пакетные ошибки ).
Кодирование минимального расстояния
Код с исправлением случайных ошибок, основанный на кодирование минимального расстояния может предоставить строгую гарантию количества обнаруживаемых ошибок, но не может защитить от атака на прообраз.
Коды повторения
А код повторения представляет собой схему кодирования, которая повторяет биты по каналу для достижения безошибочной связи. Учитывая поток данных, которые необходимо передать, данные разделяются на блоки битов. Каждый блок передается определенное количество раз. Например, чтобы отправить битовую комбинацию «1011», четырехбитовый блок можно повторить три раза, таким образом получая «1011 1011 1011». Если этот двенадцатибитовый шаблон был получен как «1010 1011 1011» — где первый блок не похож на два других, — произошла ошибка.
Код повторения очень неэффективен и может быть подвержен проблемам, если ошибка возникает в одном и том же месте для каждой группы (например, «1010 1010 1010» в предыдущем примере будет обнаружено как правильное). Преимущество кодов повторения состоит в том, что они чрезвычайно просты и фактически используются в некоторых передачах номера станций.[6][7]
Бит четности
А бит четности — это бит, который добавляется к группе исходных битов, чтобы гарантировать, что количество установленных битов (то есть битов со значением 1) в результате будет четным или нечетным. Это очень простая схема, которую можно использовать для обнаружения одного или любого другого нечетного числа (т. Е. Трех, пяти и т. Д.) Ошибок в выводе. Четное число перевернутых битов сделает бит четности правильным, даже если данные ошибочны.
Расширения и варианты механизма битов четности продольный контроль избыточности, поперечный контроль избыточности и аналогичные методы группировки битов.
Контрольная сумма
А контрольная сумма сообщения — это модульная арифметика сумма кодовых слов сообщения фиксированной длины слова (например, байтовых значений). Сумма может быть отменена с помощью дополнение операция перед передачей для обнаружения непреднамеренных сообщений с нулевым значением.
Схемы контрольной суммы включают биты четности, проверить цифры, и продольный контроль избыточности. Некоторые схемы контрольных сумм, такие как Алгоритм дамма, то Алгоритм Луна, а Алгоритм Верхоффа, специально разработаны для обнаружения ошибок, обычно вносимых людьми при записи или запоминании идентификационных номеров.
Циклическая проверка избыточности
А циклическая проверка избыточности (CRC) небезопасный хеш-функция предназначен для обнаружения случайных изменений цифровых данных в компьютерных сетях. Он не подходит для обнаружения злонамеренно внесенных ошибок. Характеризуется спецификацией порождающий полином, который используется как делитель в полиномиальное деление в столбик через конечное поле, принимая входные данные как дивиденд. В остаток становится результатом.
CRC имеет свойства, которые делают его хорошо подходящим для обнаружения пакетные ошибки. CRC особенно легко реализовать на оборудовании и поэтому обычно используются в компьютерная сеть и устройства хранения, такие как жесткие диски.
Бит четности можно рассматривать как 1-битную CRC особого случая.
Криптографическая хеш-функция
Выход криптографическая хеш-функция, также известный как Дайджест сообщения, может дать твердую уверенность в целостность данных независимо от того, являются ли изменения данных случайными (например, из-за ошибок передачи) или намеренно внесены. Любая модификация данных, скорее всего, будет обнаружена по несоответствию хеш-значения. Кроме того, с учетом некоторого хэш-значения, как правило, невозможно найти некоторые входные данные (кроме заданных), которые дадут такое же хеш-значение. Если злоумышленник может изменить не только сообщение, но и значение хеш-функции, то ключевой хеш или же код аутентификации сообщения (MAC) можно использовать для дополнительной безопасности. Не зная ключа, злоумышленник не может легко или удобно вычислить правильное ключевое значение хеш-функции для измененного сообщения.
Код исправления ошибок
Для обнаружения ошибок можно использовать любой код исправления ошибок. Код с минимум Расстояние Хэмминга, d, может обнаруживать до d — 1 ошибка в кодовом слове. Использование кодов с коррекцией ошибок на основе минимального расстояния для обнаружения ошибок может быть подходящим, если требуется строгое ограничение на минимальное количество обнаруживаемых ошибок.
Коды с минимальным расстоянием Хэмминга d = 2 являются вырожденными случаями кодов с исправлением ошибок и могут использоваться для обнаружения одиночных ошибок. Бит четности является примером кода обнаружения одиночной ошибки.
Приложения
Приложения, требующие малой задержки (например, телефонные разговоры), не могут использовать автоматический повторный запрос (ARQ); они должны использовать упреждающее исправление ошибок (FEC). К тому времени, когда система ARQ обнаружит ошибку и повторно передаст ее, повторно отправленные данные прибудут слишком поздно, чтобы их можно было использовать.
Приложения, в которых передатчик сразу же забывает информацию, как только она отправляется (например, большинство телекамер), не могут использовать ARQ; они должны использовать FEC, потому что при возникновении ошибки исходные данные больше не доступны.
Приложения, использующие ARQ, должны иметь обратный канал; приложения, не имеющие обратного канала, не могут использовать ARQ.
Приложения, требующие крайне низкого уровня ошибок (например, цифровые денежные переводы), должны использовать ARQ из-за возможности неисправимых ошибок с помощью FEC.
Техника обеспечения надежности и контроля также использует теорию кодов с исправлением ошибок.[8]
Интернет
В типичном TCP / IP стек, контроль ошибок выполняется на нескольких уровнях:
- Каждый Кадр Ethernet использует CRC-32 обнаружение ошибок. Кадры с обнаруженными ошибками отбрасываются аппаратурой приемника.
- В IPv4 заголовок содержит контрольная сумма защита содержимого заголовка. Пакеты с неверными контрольными суммами сбрасываются в сети или на приемнике.
- Контрольная сумма не указана в IPv6 заголовок, чтобы минимизировать затраты на обработку в сетевая маршрутизация и потому что текущий уровень связи предполагается, что технология обеспечивает достаточное обнаружение ошибок (см. также RFC 3819 ).
- UDP имеет необязательную контрольную сумму, покрывающую полезную нагрузку и адресную информацию в заголовках UDP и IP. Пакеты с неверными контрольными суммами отбрасываются Сетевой стек. Контрольная сумма не является обязательной для IPv4 и требуется для IPv6. Если этот параметр опущен, предполагается, что уровень канала передачи данных обеспечивает желаемый уровень защиты от ошибок.
- TCP предоставляет контрольную сумму для защиты полезной нагрузки и адресной информации в заголовках TCP и IP. Пакеты с неверными контрольными суммами отбрасываются сетевым стеком и в конечном итоге повторно передаются с использованием ARQ либо явно (например, через тройной удар ) или неявно из-за тайм-аут.
Телекоммуникации в дальнем космосе
Разработка кодов исправления ошибок была тесно связана с историей полетов в дальний космос из-за чрезмерного ослабления мощности сигнала на межпланетных расстояниях и ограниченной доступной мощности на борту космических зондов. В то время как ранние миссии отправляли свои данные в незашифрованном виде, начиная с 1968 года, цифровое исправление ошибок было реализовано в форме (субоптимально декодированные) сверточные коды и Коды Рида – Маллера.[9] Код Рида-Мюллера хорошо подходил к шуму, которому подвергался космический корабль (приблизительно соответствуя кривая колокола ), и был реализован для космического корабля Mariner и использовался в миссиях с 1969 по 1977 год.
В Вояджер 1 и Вояджер 2 миссии, начатые в 1977 году, были предназначены для доставки цветных изображений и научной информации из Юпитер и Сатурн.[10] Это привело к повышенным требованиям к кодированию, и, таким образом, космический аппарат поддерживался (оптимально Витерби-декодированный ) сверточные коды, которые могут быть соединенный с внешним Код Голая (24,12,8). Корабль «Вояджер-2» дополнительно поддерживал реализацию Код Рида – Соломона. Конкатенированный код Рида – Соломона – Витерби (RSV) позволил произвести очень мощную коррекцию ошибок и позволил космическому аппарату совершить длительный путь к Уран и Нептун. После модернизации системы ECC в 1989 году оба корабля использовали кодирование V2 RSV.
В Консультативный комитет по системам космических данных в настоящее время рекомендует использовать коды исправления ошибок с производительностью, как минимум, аналогичной коду Voyager 2 RSV. Составные коды все больше теряют популярность в космических миссиях и заменяются более мощными кодами, такими как Турбо коды или же Коды LDPC.
Различные виды дальних космических и орбитальных миссий предполагают, что попытка найти универсальную систему исправления ошибок будет постоянной проблемой. Для миссий, близких к Земле, характер шум в канал связи отличается от того, что испытывает космический корабль в межпланетной миссии. Кроме того, по мере того как космический корабль удаляется от Земли, проблема коррекции шума становится все более сложной.
Спутниковое вещание
Спрос на спутник транспондер пропускная способность продолжает расти, чему способствует желание предоставлять телевидение (включая новые каналы и телевидение высокой четкости ) и данные IP. Доступность транспондеров и ограничения полосы пропускания ограничили этот рост. Емкость транспондера определяется выбранным модуляция схема и доля мощности, потребляемой ТЭК.
Хранилище данных
Коды обнаружения и исправления ошибок часто используются для повышения надежности носителей данных.[11] «Трек паритета» присутствовал на первом хранение данных на магнитной ленте в 1951 г. «Оптимальный прямоугольный код», использованный в групповая кодированная запись ленты не только обнаруживают, но и исправляют однобитовые ошибки. Немного форматы файлов, особенно форматы архивов, включить контрольную сумму (чаще всего CRC32 ) для обнаружения повреждения и усечения и может использовать избыточность и / или файлы четности для восстановления частей поврежденных данных. Коды Рида-Соломона используются в компакт-диски для исправления ошибок, вызванных царапинами.
Современные жесткие диски используют коды CRC для обнаружения и коды Рида – Соломона для исправления незначительных ошибок при чтении секторов, а также для восстановления данных из «испорченных» секторов и сохранения этих данных в резервных секторах.[12] RAID системы используют различные методы исправления ошибок для исправления ошибок, когда жесткий диск полностью выходит из строя. Файловые системы, такие как ZFS или же Btrfs, а также некоторые RAID внедрения, поддержка очистка данных и повторное обновление, которое позволяет обнаруживать и (надеюсь) восстанавливать плохие блоки перед их использованием.[13] Восстановленные данные могут быть перезаписаны точно в том же физическом месте, чтобы освободить блоки в другом месте на том же оборудовании, или данные могут быть перезаписаны на заменяющее оборудование.
Память с исправлением ошибок
DRAM память может обеспечить более надежную защиту от мягкие ошибки полагаясь на коды исправления ошибок.[14] Такой исправляющая память, известный как ECC или же EDAC-защищенный память, особенно желательна для критически важных приложений, таких как научные вычисления, финансы, медицина и т. д., а также для приложений дальнего космоса из-за увеличения радиация в космосе.
Контроллеры памяти с исправлением ошибок традиционно используют Коды Хэмминга, хотя некоторые используют тройное модульное резервирование.
Чередование позволяет распределить эффект одного космического луча, потенциально нарушающего несколько физически соседних битов по множеству слов, путем связывания соседних битов с разными словами. Пока одно событие расстроено (SEU) не превышает порог ошибки (например, одиночная ошибка) в любом конкретном слове между обращениями, это может быть исправлено (например, с помощью однобитового кода исправления ошибок), и иллюзия безошибочной системы памяти может быть сохранен.[15]
Помимо оборудования, обеспечивающего функции, необходимые для работы памяти ECC, операционные системы обычно содержат соответствующие средства отчетности, которые используются для предоставления уведомлений о прозрачном восстановлении мягких ошибок. Увеличение количества мягких ошибок может указывать на то, что DIMM модуль нуждается в замене, и такая обратная связь не была бы легко доступна без соответствующих возможностей отчетности. Одним из примеров является Ядро Linux с EDAC подсистема (ранее известная как Bluesmoke), который собирает данные от компонентов компьютерной системы с включенной функцией проверки ошибок; Помимо сбора и отправки отчетов о событиях, связанных с памятью ECC, он также поддерживает другие ошибки контрольной суммы, в том числе обнаруженные на Шина PCI.[16][17][18]
Некоторые системы также поддерживают очистка памяти.
Смотрите также
- Код Бергера
- Пакетный код исправления ошибок
- Плевать будильник
- Память ECC, тип компьютерного хранилища данных
- Запрещенный ввод
- Адаптация ссылки
- Список алгоритмов обнаружения и исправления ошибок
- Список кодов исправления ошибок
- Список хеш-функций
- Надежность (компьютерные сети)
Рекомендации
- ^ Томпсон, Томас М. (1983), От кодов с исправлением ошибок до сферических упаковок и простых групп, Математические монографии Каруса (№ 21), Математическая ассоциация Америки, стр. vii, ISBN 0-88385-023-0
- ^ Шеннон, C.E. (1948), «Математическая теория коммуникации», Технический журнал Bell System, п. 418, г. 27 (3): 379–423, Дои:10.1002 / j.1538-7305.1948.tb01338.x, HDL:10338.dmlcz / 101429, PMID 9230594CS1 maint: location (связь)
- ^ Голей, Марсель Дж. Э. (1949), «Заметки о цифровом кодировании», Proc.I.R.E. (I.E.E.E.), п. 657, г. 37CS1 maint: location (связь)
- ^ Гупта, Викас; Верма, Чандеркант (ноябрь 2012 г.). «Обнаружение и исправление ошибок: Введение». Международный журнал перспективных исследований в области компьютерных наук и программной инженерии. 2 (11). S2CID 17499858.
- ^ а б А. Дж. Маколи, Надежная широкополосная связь с использованием кода коррекции стирания пакетов, ACM SIGCOMM, 1990.
- ^ Франк ван Гервен. «Номера (и другие загадочные) станции». Получено 12 марта 2012.
- ^ Гэри Катлак (25 августа 2010 г.). «Таинственная русская» цифровая станция «изменила вещание через 20 лет». Gizmodo. Получено 12 марта 2012.
- ^ Бен-Гал I .; Herer Y .; Раз Т. (2003). «Самокорректирующаяся процедура проверки при ошибках проверки» (PDF). IIE Сделки по качеству и надежности, 34 (6), стр. 529-540. Архивировано из оригинал (PDF) на 2013-10-13. Получено 2014-01-10.
- ^ К. Эндрюс и др., Разработка кодов Turbo и LDPC для приложений дальнего космоса, Труды IEEE, Vol. 95, № 11, ноябрь 2007 г.
- ^ Хаффман, Уильям Кэри; Плесс, Вера С. (2003). Основы кодов с исправлением ошибок. Издательство Кембриджского университета. ISBN 978-0-521-78280-7.
- ^ Куртас, Эрозан М .; Васич, Бэйн (2018-10-03). Расширенные методы контроля ошибок для систем хранения данных. CRC Press. ISBN 978-1-4200-3649-7.[постоянная мертвая ссылка ]
- ^ Мой жесткий диск умер. Скотт А. Моултон
- ^ Цяо, Чжи; Фу, песня; Чен, Синь-Бунг; Сеттлмайер, Брэдли (2019). «Создание надежных высокопроизводительных систем хранения: эмпирическое и аналитическое исследование». Международная конференция IEEE 2019 по кластерным вычислениям (CLUSTER): 1–10. Дои:10.1109 / CLUSTER.2019.8891006. ISBN 978-1-7281-4734-5. S2CID 207951690.
- ^ «Обзор методов повышения устойчивости DRAM к ошибкам «, Журнал системной архитектуры, 2018
- ^ «Использование StrongArm SA-1110 в бортовом компьютере наноспутника». Космический центр Цинхуа, Университет Цинхуа, Пекин. Архивировано из оригинал на 2011-10-02. Получено 2009-02-16.
- ^ Джефф Лейтон. «Обнаружение и исправление ошибок». Журнал Linux. Получено 2014-08-12.
- ^ «Проект EDAC». bluesmoke.sourceforge.net. Получено 2014-08-12.
- ^ «Документация / edac.txt». Документация ядра Linux. kernel.org. 2014-06-16. Архивировано из оригинал на 2009-09-05. Получено 2014-08-12.
дальнейшее чтение
- Шу Линь; Дэниел Дж. Костелло-младший (1983). Кодирование с контролем ошибок: основы и приложения. Prentice Hall. ISBN 0-13-283796-X.
внешняя ссылка
- Он-лайн учебник: теория информации, выводы и алгоритмы обучения, к Дэвид Дж. К. Маккей, содержит главы, посвященные элементарным кодам, исправляющим ошибки; о теоретических пределах исправления ошибок; и на последних современных кодах исправления ошибок, в том числе коды с низкой плотностью проверки четности, турбокоды, и коды фонтанов.
- Вычислить параметры линейных кодов — интерактивный интерфейс для генерации и вычисления параметров (например, минимальное расстояние, радиус покрытия ) из линейные коды исправления ошибок.
- Страница ECC
- SoftECC: система проверки целостности программной памяти
- Настраиваемая программная библиотека обнаружения и исправления ошибок DRAM для HPC
- Обнаружение и исправление скрытых искажений данных для крупномасштабных высокопроизводительных вычислений
Введение в машинное обучение и искусственные нейронные сети
Оглавление
Глава1. Введение в машинное обучение
Глава 2. Введение в искусственные нейронные сети
Глава1. Введение в машинное обучение
«По сути, все модели ошибочны, но некоторые из них полезны», –
Джордж Бокс, статистик [1.1]
Что такое машинное обучение
Машинное обучение (machine learning, ML) – это раздел информатики, который занимается
разработкой и анализом алгоритмов, позволяющих компьютерам меняться под воздействием внешних
факторов (обучаться). Алгоритмы обучения (learning algorithms) делают предсказания или принимают
решения не на основе строго статических программных команд, а на основе обучающей выборки
(т.е. обучающих данных), с помощью которой происходит настройка параметров модели. Для процесса
настройки (fitting) модели по выборке данных применяются различные разделы математики:
математическая статистика, методы оптимизации, численные методы, теория вероятностей, линейная
алгебра, математический анализ, дискретная математика, теория графов, различные техники работы
с цифровыми данными и др. Результатом работы алгоритма обучения является функция, которая
аппроксимирует (восстанавливает) неизвестную зависимость в обрабатываемых данных.
Машинное обучение является не только математической, но и прикладной, инженерной дисциплиной.
Практически ни одно исследование в области машинного обучения не обходится без последующего
тестирования на реальных данных для проверки практической работоспособности разрабатываемого метода.
Когда говорят о машинном обучении, то часто имеют ввиду вновь ставшие популярными искусственные
нейронные сети (ИНС) и глубокое обучение, которые являются моделями машинного обучения
(рисунок 1.1), т.е. частными случаями методов распознавания образов, дискриминантного анализа,
методов кластеризации и т. п.
Рис. 1.1 – Вложенность категорий
Типы обучения
Есть три типа методов машинного обучения: дедуктивное, индуктивное и трансдуктивное.
Дедуктивное обучение или обучение «сверху-вниз», от общего к частному предполагает
формализацию знаний экспертов и их перенос в компьютер в виде базы знаний. Дедуктивное обучение
принято относить к области экспертных систем. Имеются знания, сформулированные экспертом и
каким-либо образом формализованные через уравнения, теоремы, зависимости и т.д. Программа,
экспертная система, выводит из этих правил конкретные факты и новые правила.
Индуктивное обучение или обучение «снизу-вверх», от частного к общему, обучение на примерах,
обучение по прецедентам, основано на выявлении закономерностей в эмпирических данных,
т.е. данных полученных путём наблюдения или эксперимента. Индуктивное обучение компьютеров принято
относить к машинному обучению. Многие методы индуктивного обучения разрабатывались как альтернатива
классическим статистическим подходам и тесно связаны с извлечением информации (information extraction)
и интеллектуальным анализом данных (data mining). На основе эмпирических данных программа строит
общее правило. Эмпирические данные могут быть получены самой программой в предыдущие сеансы её
работы или просто предъявлены ей.
Трансдуктивное обучение [1.2] или обучение от частного к частному, позволяет на основе
эмпирических данных без выявления общих закономерностей и формализации знаний сделать выводы
о других эмпирических данных. Понятие трансдукции было предложено
Владимиром Вапником
в 1990 году: «При решении интересующей проблемы не решайте более общую проблему как промежуточный шаг.
Постарайтесь получить ответ, который вам действительно нужен, но не более общий». Например, если
не учитывать объекты без метки (рисунок 1.2), тогда невозможно правильно сегментировать множество,
потому что слишком мало размеченных объектов.
Рис. 1.2 – Пример трансдуктивного обучения
При решении задачи методом индукции, когда ищется общий ответ для всех возможных случаев,
неразмеченные объекты не учитываются, их как бы нет для решающего задачу, потому что с точки
зрения индуктивного обучения могут быть и другие неразмеченные объекты кроме имеющихся.
Учёт присутствующих неразмеченных данных может кардинально изменить качество решения, но если
появятся новые неразмеченные данные, то их появление может полностью изменить ответ.
Трансдуктивное обучение применяется в некоторых методах машинного обучения с частичным
привлечением учителя (semi-supervised learning). Взаимосвязь между тремя типами обучения
можно увидеть на рисунке 1.3.
Рис. 1.3 – Три типа обучения
Будем считать задачу обучения экзаменом, размеченные объекты – как решённые учителем примеры,
а неразмеченные объекты – как предоставленные учителем нерешённые примеры. С точки зрения
дедуктивного обучения у вас уже есть формула, показанная вам учителем, с помощью которой вы
можете решить все нерешённые задачи на экзамене, поэтому нет смысла решать предоставленные
учителем нерешённые примеры. С точки зрения индуктивного обучения нерешённые примеры являются
подобными тем, которые будут на экзамене. С точки зрения трансдуктивного обучения данные
учителем нерешённые примеры и есть экзамен, т.е. эти же примеры будут на экзамене.
Способы обучения
Методы машинного обучения обычно разделяются на две обширные категории, в зависимости от наличия
обучающего «сигнала» или «обратной связи» для алгоритма обучения: обучение с учителем
(supervised learning) и обучение без учителя (unsupervised learning).
При обучении с учителем система обучается на примерах с заранее известными правильными ответами.
На основе этих входных примеров и известных правильных ответов требуется восстановить
зависимость между множеством примеров и множеством ответов, т.е. построить алгоритм, который
будет выдавать достаточно точный ответ для любого примера. Совокупность примеров
(входных объектов) и соответствующих им правильных ответов называется обучающей выборкой.
Пусть обучающая выборка описывается парой значений 〈x, y〉,
где x=〈x1,x2,…,xn〉 – это данные
(многомерный вектор признаков), y – это целевое значение
(метка или правильный ответ). Надо найти функцию ƒ(x)=y.
Обучение без учителя, самообучение, происходит на примерах без заранее известных правильных ответов.
Система сама находит внутренние взаимосвязи, зависимости, закономерности, существующие между
объектами без вмешательства внешнего учителя, экспериментатора, человека. Пусть каждый объект описан
вектором признаков x=〈x1,x2,…,xn〉.
Надо найти механизм, который описывает структуру этих данных, которая заранее не известна.
Комбинированные виды обучения применяют различные сочетания обоих типов обучения
в одной программе. Например, обучение с частичным привлечением учителя,
обучение с подкреплением и некоторые другие.
При обучении с подкреплением учителем является сама окружающая среда, модель среды или
неявный учитель, например, одновременная активность нескольких нейронов
в искусственной нейронной сети.
Не всегда удаётся найти хорошую обучающую выборку. Часто данные размечены не полностью, т.е.
не для всех данных есть правильный ответ (метка). Разметка данных для машинного обучения является
однообразным и долгим трудом. Обычно имеется небольшое количество размеченных данных и большое
количество неразмеченных данных. В этом случае применяется обучение с частичным привлечением учителя.
Его ещё называют полуавтоматическим обучением (semi-supervised learning). Многие исследователи
машинного обучения обнаружили, что неразмеченные данные, при использовании в сочетании с небольшим
количеством размеченных данных, могут значительно улучшить точность обучения.
Обучение с частичным привлечением учителя является частным случаем трансдуктивного обучения.
Решаемые задачи
Методы машинного обучения разделяются по типам решаемых задач: классификация, кластеризация,
регрессия, прогнозирование, идентификация, восстановление плотности распределения вероятности
по набору данных, понижение размерности, одноклассовая классификация и выявление новизны,
построение ранговых зависимостей и т.д. Продолжают возникать новые типы задач и даже целые новые
дисциплины машинного обучения, например, добыча данных (data mining).
Классификация – разделение множества объектов или ситуаций на классы с помощью обучения
с учителем. Классифицировать объект – значит, указать номер, имя или метку класса, к которому
относится данный объект. Иногда требуется указать вероятность отношения объекта к классу. Например,
по обучающей выборке фотографий котов и собак научиться различать изображения котов и собак.
Кластеризация (сегментация) – разделение множества объектов или ситуаций на кластеры
с помощью обучения без учителя. Кластеризация (обучение без учителя) отличается от классификации
(обучения с учителем) тем, что перечень групп четко не задан и определяется в процессе работы
алгоритма, т.е. нет заранее определённых «правильных» ответов. Иногда указывается общее
количество кластеров, но часто алгоритм сам выбирает оптимальное количество кластеров.
Похожесть или близость объектов в кластере определяется через расстояние в многомерном
пространстве признаков. Для этого нужно определить само пространство признаков (какие свойства
измеряются) и метрику близости (как считается расстояние). Результаты кластеризации применяются
при нахождении новых, ранее неизвестных знаний и зависимостей в данных (добыча данных или
data mining). Например, задача нахождения целевой аудитории определённого товара путём анализа
потребительских корзин покупателей с учётом пола, возраста, социального статуса,
семейного положения и т.д.
Регрессия – нахождение зависимости выходной переменной от одной или нескольких
независимых входных переменных с помощью обучения с учителем. В отличие он задач классификации,
которые разделяют объекты на дискретное количество классов, задачи регрессии находят зависимости
между непрерывными величинами. Например, нахождение зависимости между количеством съеденной пищи
и весом тела.
Прогнозирование – это предсказание во времени. Прогнозирование похоже либо на регрессию,
либо на классификацию в зависимости от данных задачи (непрерывные или дискретные данные),
но в отличие от регрессии и классификации всегда направлено в будущее. В прогнозировании данные
упорядочиваются по времени, которое является явным и ключевым параметром, а найденная зависимость
экстраполируется в будущее. В прогнозировании применяются модели временных рядов.
Идентификация. Идентификация и классификация многими ошибочно понимаются как синонимы.
Задача идентификации исторически возникла из задачи классификации, когда вместо определения класса
объекта потребовалось уметь определять, обладает объект требуемым свойством или нет.
Особенностью задачи идентификации является то, что все объекты принадлежат одному классу,
и не существует возможности разделить класс на подклассы, т.е. сделать состоятельную выборку
из класса, которая не будет обладать требуемым свойством. Если требуется определить человека по
фотографии его лица, причём множество запомненных в базе людей постоянно меняется и появляются люди,
которых не было в обучающем множестве, то это задача идентификации, которая не сводится к задаче
классификации. В случае определения объекта по фотографии функция идентификации
ƒ(x1,x2) принимает в качестве аргументов
два вектора признаков фотографий, а на выходе равна либо 1 в случае фотографий одного и того же
объекта либо 0 в случае фотографий разных объектов одного и того же класса.
Восстановление плотности распределения вероятности по набору данных (kernel density estimate).
Данная задача является центральной проблемой математической статистики. Математическая статистика
решает обратные задачи: по результату эксперимента определяет свойства закона распределения.
Исчерпывающей характеристикой закона распределения является плотность распределения вероятностей.
Например, известен возраст людей, берущих кредит в банке, требуется найти плотность распределения
вероятности возрастов заёмщиков.
Понижение размерности данных и их визуализация. Является частным случаем кластеризации.
Каждый объект может быть представлен в виде многомерного вектора признаков
〈x1,x2,…,xn〉,
нужно получить более компактное признаковое описание объекта
〈x1,x2,…,xk〉, где
k < n. Понижение размерности может помочь другим методам путём
устранения избыточных данных. Используется при разведочном анализе и для устранения
«проклятия размерности», когда данные быстро становятся разреженными при увеличении размерности
пространства признаков. Например, дан список документов на человеческом языке,
требуется найти документы с похожими темами.
Одноклассовая классификация и выявление новизны. Или задача поиска аномалий, выбросов,
которые не относятся ни к одному кластеру. Нахождение объектов, которые отличаются по своим
свойствам от объектов обучающей выборки. Является задачей обучения без учителя. Например,
обнаружение инородных предметов (кости, камни, кусочки упаковки) в продуктах питания при их
сканировании рентгеновским сканером при неразрушающем контроле качества продукции, обнаружение
подозрительных банковских операций, обнаружение хакерской атаки, медицинская диагностика и т.д.
Построение ранговых зависимостей. Ранжирование – это процедура упорядочения объектов
по степени выраженности какого-либо качества в порядке убывания этого качества.
Задачами ранжирования являются: сортировка веб-страниц согласно заданному поисковому запросу,
персонализация новостной ленты, рекомендации товаров (видео, музыки), адресная реклама.
Добыча данных (data mining) или интеллектуальный анализ данных [1.3] – совокупность
методов обнаружения в данных ранее неизвестных, нетривиальных, практически полезных и доступных
интерпретации знаний, необходимых для принятия решений в различных сферах человеческой
деятельности. В данный момент добыча данных отделяется от машинного обучения в отдельную
дисциплину. Интеллектуальный анализ данных и машинное обучение имеют различные цели:
машинное обучение прогнозирует на основе известных свойств, полученных от обучающей выборки,
а интеллектуальный анализ данных фокусируется на добыче новых ранее неизвестных зависимостей
в данных. Однако обе дисциплины используют одинаковые методы.
Различные типы задач схематически представлены на рисунке 1.4.
Рис. 1.4 – Схематическое представление типов задач:
1) классификация; 2) кластеризация; 3) регрессия; 4) прогнозирование; 5) идентификация;
6) восстановление плотности распределения вероятности по набору данных;
7) понижение размерности; 
9) построение ранговых зависимостей; 10) добыча данных.
Сферы применения
Целью машинного обучения является частичная или полная автоматизация
человеческой деятельности в самых разных областях.
Распознавание речи – преобразование голосового сигнала в цифровую информацию, например,
текст или запрос для поискового сервера. Обратной задачей является синтез речи.
Распознавание жестов – преобразование жестов в цифровую информацию: текст,
клавиатурные команды. Распознавание эмоций и мимики.
Распознавание рукописных текстов – преобразование рукописного текста в цифровую информацию.
Распознавание образов и, в частности, компьютерное зрение – классификация и идентификация
объектов по характерным конечным наборам свойств и признаков.
Техническая диагностика – определение технического состояния объектов.
Медицинская диагностика – процесс установления диагноза, т.е. заключения о сущности болезни
и состоянии пациента. Анализ данных с сенсоров.
Прогнозирование временных рядов – предсказание будущих значений временного ряда
по настоящим и прошлым значениям.
Биоинформатика – междисциплинарная наука, использующая методы прикладной математики,
статистики и информатики в биохимии, биофизике, экологии, геномике и в других областях.
Обнаружение мошенничества – автоматическое обнаружение противоправных действий.
Обнаружение спама – обнаружение массовой рассылки корреспонденции рекламного или иного характера
лицам, не выражавшим желания её получать.
Категоризация документов – отнесении документа к одной из нескольких категорий
на основании содержания документа.
Биржевой технический анализ – прогнозирование вероятного изменения цен на основе закономерностей
изменений цен в прошлом в аналогичных обстоятельствах.
Финансовый надзор – это деятельность уполномоченных органов, направленная на исполнение требований
законодательства органами государственной власти, органами местного самоуправления,
их должностными лицами, юридическими лицами и гражданами с целью выявления, пресечения и
предупреждения правонарушений, обеспечения законности и финансовой дисциплины.
Кредитный скоринг – система оценки кредитоспособности (кредитных рисков) лиц,
основанная на численных статистических методах.
Прогнозирование ухода клиентов – прогнозирование потери клиентов, выраженное в отсутствии покупок
или платежей в течение определенного периода времени для компаний с подписной и транзакционной
моделью бизнеса (банки, операторы связи, SaaS-сервисы), подразумевающих регулярные платежи
в сторону компании.
Хемоинформатика (химическая информатика, молекулярная информатика) – применение методов
информатики для решения задач химии и синтеза новых соединений.
Обучение ранжированию в информационном поиске – увеличение качества поиска, создание
рекомендательных систем, оценка качества найденной информации.
Навигация и контроль действий – помощь водителям транспортных средств, а также беспилотные
транспортные средства, автоматический контроль транспортных потоков.
Домашняя автоматизация – система домашних устройств, способных выполнять действия и решать
определенные повседневные задачи без участия человека.
Машинное обучение бурно развивается, поэтому постоянно появляются новые
не перечисленные здесь сферы применения.
Краткая история
Термин «машинное обучение» в 1959 году ввёл исследователь в области компьютерных игр
Артур Самуэль в своей работе «Некоторые исследования в области Машинного Обучения
с использованием игры в шашки» [1.4] и определил его как «процесс, в результате которого
машина (компьютер) способна показывать поведение, которое в неё не было явно заложено
(запрограммировано)». Игру в шашки, изобретенную Самуэлем в 1952 году, принято считать
первой программой, способной самообучаться. Самуэль выбрал шашки, потому что правила игры
относительно просты, но имеют развитую стратегию.
Эффективность машинного обучения в решении задач была продемонстрирована достаточно давно:
еще в 1936 году знаменитый английский статистик Рональд Фишер сумел научить компьютер
определять вид ириса по ширине цветка и чашелистика.
В тридцатые годы 20 века Карел Чапек изобрел термин «робот», в сороковые годы Айзек Азимов
сформулировал законы робототехники, но первым, кто перевёл проблему «интеллектуальных машин»
из научной фантастики в разряд прикладных проблем был математик Алан Тьюринг. В 1950 году
в своей работе «Вычислительные машины и разум» [1.5] он рассмотрел вопрос
«Могут ли машины думать?», но так как термины «машины» и «думать» не могут быть определены
однозначно, Тьюринг предложил заменить вопрос на другой, тесно связанный с первым, но выраженный
не такими двусмысленными понятиями: может ли машина совершать действия, неотличимые от
обдуманных действий. С помощью такой постановки вопроса можно избежать сложных философских
проблем по определению терминов «думать», «мышление» и сосредоточить внимание
на решении практических задач.
Заменив философский вопрос на прикладной, Тьюринг предложил для проверки возможностей компьютерной
программы свой знаменитый Тест Тьюринга. Стандартная интерпретация этого теста звучит
следующим образом: «Человек взаимодействует с одним компьютером и одним человеком.
На основании ответов на вопросы он должен определить, с кем он разговаривает: с человеком
или компьютерной программой. Задача компьютерной программы – ввести человека в заблуждение,
заставив сделать неверный выбор». Однако Тьюринг говорит не об одурачивании людей,
а о воспроизведении когнитивных способностей человека [1.6]. Хотя бы внешне.
Тест Тьюринга имеет недостатки:
- чрезмерный антропоморфизм (рисунок 1.5);
- непрактичность – самолёты не машут крыльями, как птицы, чтобы летать, а машины не обязаны
имитировать поведение людей, чтобы решать прикладные задачи; - возможность имитации «мышления» по неким механическим правилам, например, как в мысленном
эксперименте «Китайская комната» Джона Сёрля (John Searle, 1980).
Рис. 1.5 – Поведение человека и разумное поведение
Несмотря на обоснованную критику, тест Тьюринга задаёт правильное направление мысли, а именно:
не важно, думает машина или нет, потому что нет однозначного определения слов «думать» или «интеллект»,
главное, что машина может справляться с поставленными перед ней сложными задачами, например,
имитировать поведение человека.
Современный интерес к машинному обучению возрос после того, как искусственные нейронные сети
вновь стали популярными. Искусственная нейронная сеть (ИНС) – это математическая модель,
а также её программное или аппаратное воплощение, построенная по принципу организации и
функционирования биологических нейронных сетей, т.е. сетей нервных клеток живого организма.
Необязательно, чтобы строение ИНС и мозга совпадали. В ИНС воплощены идеи коннекционизма,
т.е. моделирования мыслительных или поведенческих явлений в сетях
из связанных между собой простых элементов.
Первой попыткой построить ИНС по принципу функционирования мозга были нейронные сети
Уоррена Мак-Каллока и Уолтера Питтса, описанные в статье 1943 года «Логическое исчисление идей,
относящихся к нервной активности» [1.7, 1.8]. По примеру классических философов Греции они
попытались математически смоделировать работу мозга. Это была яркая идея, учитывая то,
что электрическая природа сигналов нейронов будет продемонстрирована только спустя семь лет
в конце 1950-х годов. Математическая модель сети Мак-Каллока и Питтса из искусственных нейронов
(рисунок 1.6) теоретически могла выполнять числовые или логические операции любой сложности.
Рис. 1.6 – Схема искусственного нейрона:
1) нейроны, выходные сигналы которых поступают на вход данному;
2) ωi – веса входных сигналов; 3) сумматор входных сигналов;
4) вычислитель передаточной (активационной) функции;
5) нейроны, на входы которых подаётся выходной сигнал данного
На вход искусственного нейрона поступают импульсы от произвольного числа других нейронов сети.
Связи, по которым выходные сигналы одних нейронов поступают на входы других, часто называют
синапсами по аналогии со связями между биологическими нейронами.
Каждая связь характеризуется своим весом. Связи с положительным весом называются возбуждающими,
а с отрицательным – тормозящими. Нейрон имеет один выход, часто называемый аксоном
по аналогии с биологическим прототипом. С единственного выхода нейрона сигнал может поступать
на произвольное число входов других нейронов. Если на выходе нейрона есть ненулевой сигнал
(положительный или отрицательный), то говорят, что нейрон активен или возбуждён.
В сумматоре поступающие импульсы на вход нейрона умножаются на веса входов и слаживаются:
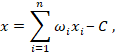 |
(1.1) |
где n – количество входящих синапсов;
ωi – веса входов (положительные возбуждающие
или отрицательные тормозящие); xi – сигналы на входах;
C – константа для формирования порога чувствительности нейрона,
которая называется сдвиг (bias). Функция x называется индуцированным
локальным полем нейрона или взвешенной суммой. Возможные значения сигналов на входах
нейрона xi считают заданными в интервале
[0,1]. Сигналы на входах, в зависимости от архитектуры сети,
могут быть либо дискретными (только 0 или только 1), либо аналоговыми
(непрерывными в интервале от 0 до 1 включительно).
Затем к индуцированному локальному полю нейрона x
(см. формулу 1.1) применяется функция, называемая передаточной
функцией ƒ(x) или функцией активации, функцией срабатывания,
которая определяет зависимость сигнала на выходе нейрона от взвешенной суммы сигналов на его
входах. Использование различных передаточных функций позволяет вносить нелинейность в работу
нейрона и в целом нейронной сети. Без этой нелинейности нейронная сеть вырождается в задачу
линейной алгебры, т.е. в обычное перемножение матриц и векторов.
Существует множество различных передаточных функций. Самой известной передаточной функцией
является функция Хевисайда (рисунок 1.7), которая представляет собой перепад (ступеньку)
и записывается формулой:
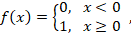 |
(1.2) |
где переменная x является индуцированным локальным полем
(взвешенной суммой с порогом) и вычисляется по формуле (1.1).
Рис. 1.7 – График функции Хевисайда, одной из передаточных функций
Построения Мак-Каллока и Питтса были теоретическими, а в 1951 году Марвин Минский и Дин Эдмондс
создают первую машину на нейронной сети: стохастический нейронный аналоговый калькулятор
с подкреплением (Stochastic Neural Analog Reinforcement Calculator, SNARC).
Машина состояла из 40 искусственных нейронов, соединённых в случайном порядке, была размером
с рояль и с помощью обучения с подкреплением моделировала поведение крысы в лабиринте
в поисках пищи. С помощью SNARC Марвин Минский проверял теорию Хебба о нейропластичности.
В 1957 году Фрэнк Розенблатт изобретает перцептрон (от лат. perсeptio – восприятие) –
математическую и компьютерную модель восприятия информации мозгом
(кибернетическую модель мозга) [1.9]. Изучая нейронные сети типа перцептрона, Розенблатт хотел
«понять фундаментальные законы организации, общие для всех систем обработки информации,
включая как машины, так и человеческий разум». Перцептрон и, в частности, элементарный перцептрон
состоит из трёх типов элементов и связей между ними (рисунок 1.8):
Рис. 1.8 – 1) схема перцептрона с тремя выходами;
2) элементарный перцептрон имеет только один выход
Сигналы на перцептрон поступают от S-элементов («S» от англ. «Sensor» – сенсор).
S-элементы выдают дискретный сигнал: либо 1, либо 0. S-элементы не являются нейронами,
потому что не обучаются, т.е. не меняют веса связей с нейронами. Внутри S-элементов есть датчик,
сенсор или рецептор. От воздействия какого-либо из видов энергии (например, свет, звук,
давление, тепло и т.п.) датчик внутри S-элемента вырабатывает сигнал. Если сигнал от датчика
превышает некоторый порог, то на выходе S-элемента получается сигнал +1, иначе – 0 (нет сигнала).
Поведение S-элемента описывается функцией Хевисайда (1.2) с некоторым порогом срабатывания
C (см. формулу 1.1).
S-элементы соединяются синапсами, S–A связями, с A-элементами. Веса S–A связей могут иметь три
дискретных значения: (–1) (тормозящий синапс), (+1) (возбуждающий синапс) и 0 (отсутствие синапса,
когда нет физической связи между сенсором S и нейроном A). S–A связи выбираются случайным,
но фиксированным образом, т.е. не меняются во время обучения и работы сети.
A-элементы («A» от англ. «Associative» – ассоциативный) называются ассоциативными, потому что
каждому такому элементу, как правило, соответствует целый набор (ассоциация) S-элементов.
A-элементы являются искусственными нейронами (см. рисунок 1.6).
Передаточной функцией (функцией активации) нейрона для A-элементов является функция
Хевисайда (1.2). Таким образом, A-элемент активизируется, как только взвешенная сумма
сигналов от S-элементов на его входе превысит некоторую пороговую величину
C (см. формулу 1.1),
и индуцированное локальное поле нейрона станет больше либо равным нулю:
x ≥ 0. В соответствии с функцией Хевисайда, выходной сигнал
ассоциативных нейронов является дискретным: либо 0 (нет сигнала), либо 1 (есть сигнал).
A-элементы соединяются синапсами (A–R связями) с R-элементами. Сигнал от
i-того ассоциативного элемента передаётся в
j-тый реагирующий элемент с коэффициентом
Wi,j. Этот коэффициент называется весом A–R связи.
Веса A–R связей Wi,j могут быть любыми
(являются вещественными числами). A–R связи выбираются случайным, но фиксированным образом,
т.е. не меняются во время обучения и работы сети. Обучение перцептрона состоит в изменении
весовых коэффициентов Wi,j.
R-элементы («R» от англ. «Reacting» – реагирующий) называются реагирующими,
потому что эти нейроны выдают результат, реагируют на входные импульсы от сенсоров.
R-элементы являются искусственными нейронами (см. рисунок 1.6). Реагирующий элемент выдаёт
выходной дискретный сигнал: (+1), если сумма значений входных сигналов, помноженных на веса,
является строго положительной; (–1), если сумма значений входных сигналов, помноженных на веса,
является строго отрицательной. Если сумма значений входных сигналов, помноженных на веса,
равна нулю, то выход можно считать либо равным нулю, либо неопределённым.
Таким образом, передаточной функцией (функцией активации) нейрона для R-элементов является
сигнум функция (сигнум, от лат. «signum» – знак):
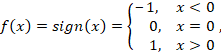 |
(1.3) |
где x является индуцированным локальным полем нейрона и вычисляется
по формуле (1.1). График сигнум функции изображён на рисунке 1.9.
Рис. 1.9 – График сигнум функции sign(x)
Согласно современной терминологии классический перцептрон является искусственной нейронной сетью:
- с одним скрытым слоем, трёхслойный по классификации Розенблатта и двухслойный по современной
системе обозначений с той особенностью, что первый слой не обучаемый; - с пороговой функцией активации Хевисайда (1.2) для ассоциативных нейронов
и сигнум функцией активации (1.3) для реагирующих нейронов; - с прямым распространением сигнала (без обратной связи).
Классический метод обучения перцептрона – это обучение с коррекцией ошибки, специальный
итерационный метод обучения проб и ошибок, который напоминает процесс обучения человека.
Представляет собой такой метод обучения с учителем, при котором вес
Wi,j связи A–R не изменяется до тех пор, пока текущая
реакция перцептрона остаётся правильной. При появлении неправильной реакции вес изменяется на
единицу, а знак изменения (+1 или –1) определяется противоположным от знака ошибки. Например,
мы хотим обучить элементарный перцептрон (см. рисунок 1.8.2)
разделять два класса объектов, круги и квадраты, так, чтобы при предъявлении объектов первого
класса (круги) выход перцептрона был положителен (+1), а при предъявлении объектов второго
класса (квадраты) – отрицательным (−1). Для этого выполним следующий алгоритм:
- Случайным образом выбираем пороги C
(см. формулу 1.1) для A-элементов. Случайным образом
устанавливаем связи S–A. Далее пороги и связи не изменяются. Все A-элементы элементарного
перцептрона соединены одной A–R связью с единственным выходным R-элемента
(см. рисунок 1.8.2). - Начальные коэффициенты Wi полагаем равными нулю.
- Предъявляем обучающую выборку: круги и квадраты с указанием класса, к которым они принадлежат.
- Если предъявили круг и выход перцептрона положительный – ничего не делаем.
- Если предъявили квадрат и выход перцептрона отрицательный – ничего не делаем.
- Если предъявили круг и выход перцептрона отрицательный – к весу
Wi каждого активного А-элемента
прибавляется единица. Активный элемент тот, который выдаёт единицу на выходе.
Если элемент не активный (ноль на выходе), то единица к весу этого элемента
не прибавляется. - Если предъявили квадрат и выход перцептрона положительный – от веса
Wi каждого активного A-элемента
отнимается единица.
- Шаг 3 выполним для всей обучающей выборки. В результате обучения сформируются значения
весов A–R связей Wi.
В книге 1962 года «Принципы нейродинамики: Перцептроны и теория механизмов мозга» [1.10]
Розенблатт сформулировал и доказал теорему о сходимости перцептрона: элементарный перцептрон,
обучаемый по методу коррекции ошибки (с квантованием или без него), независимо от начального
состояния весовых коэффициентов и порядка показа образцов из обучающей выборки всегда научится
различать два класса объектов за конечное число шагов, если только существует такая классификация.
Также в книге рассматриваются:
- многослойные перцептроны с дополнительными слоями A-элементов;
- перцептроны с перекрёстными связями, т.е. со связями между элементами одного слоя;
- перцептроны с обратными связями, которые согласно современной классификации
относится к рекуррентным нейронным сетям (RNN); - обучение без учителя или альфа-система подкрепления – это система подкрепления,
при которой веса всех активных связей Wi,j,
которые ведут к элементу uj, изменяются
на одинаковую величину, а веса неактивных связей за это время не изменяются.
Сначала перцептрон был реализован, как компьютерная программа, а впоследствии в 1960 году,
как электронное устройство – нейрокомпьютер Марк-1. Классификатор визуальных образов Марк-1
имел входной (сенсорный) слой из 400 светочувствительных S-элементов в сетке 20х20 (400 пикселей),
моделирующий небольшую сетчатку, как светочувствительные клетки сетчатки глаза или фоторезисторы
матрицы камеры. Далее был слой ассоциации из 512 A-элементов, сделанных с применением шаговых
двигателей. Каждый из A-элементов мог принимать несколько возбуждающих и тормозящих входов от
S-элементов. После слоя ассоциации располагался выходной (ответный) слой из восьми R-элементов.
Сенсорный слой случайным образом соединялся с ассоциативным слоем с помощью S–A связей на
специальной приборной доске, но после установки соединения все S–A связи оставались неизменными
до конца эксперимента. A–R связи между ассоциативным и выходным слоями имели переменные веса
(потенциометры с двигателем). Переменные веса корректировались с помощью метода коррекции ошибки.
Нейрокомпьютер Марк-1 состоял из шести стоек электронного оборудования и занимал примерно
3,4 м2 площади. Марк-1 был способен распознавать некоторые буквы
английского алфавита, написанные на карточках, которые подносили к его «глазам»
из 400 фотосенсоров.
В 1969 году вышла книга Марвина Минского (того самого, который сделал первый нейрокомпьютер SNARC)
и Сеймура Паперта «Перцептроны» [1.11], в которой были математически доказаны ограничения перцептронов.
Было показано, что перцептроны принципиально не в состоянии выполнять многие из тех функций,
которые хотели от них получить. Минский показал преимущество последовательных вычислений перед
параллельными в определённых классах задач. В то время была слабо развита теория о параллельных
вычислениях, а перцептрон полностью соответствовал принципам параллельных вычислений.
Некоторые ограничения перцептрона показаны на рисунке 1.10.
Рис. 1.10 – Ограничения перцептрона:
1) Это одна и та же буква? 2) Это один и тот же текст?
3) Из какого количества частей состоит фигура?
4) Внутри какого объекта нет другой фигуры?
5) Какая фигура внутри объектов повторяется два раза?
Основными недостатками классического перцептрона являются:
- трудности с распознаванием объекта, над которым провели операции переноса, поворота,
растяжения-сжатия (рисунки 1.10.1 и 1.10.2); - неспособность решать задачи на определение «связности» фигур
(рисунки 1.10.3, 1.10.4 и 1.10.5).
В начале 60-х годов многими математиками в рамках теории управления были заложены основы метода
обратного распространения ошибки (backpropagation), который необходим для глубокого обучения
(Deep Learning) [1.12]. Однако метод обратного распространения ошибки не применялся
непосредственно к нейронным сетям до 80-х годов.
В процессе своего развития машинное обучение пережило две «зимы искусственного интеллекта».
Зимой искусственного интеллекта называется период сниженного общественного интереса и
существенного уменьшения финансирования исследований в этой области со стороны бизнеса и
государственных организаций. Различают две зимы 1974–1980 и 1987–1993 годов, а также несколько
меньших периодов, связанных с провалами крупных проектов в этой области. Несмотря на
низкое финансирование, исследования в области машинного обучения продолжались.
Часто под другими названиями.
Модели машинного обучения
В машинном обучении существует огромное количество различных моделей,
самыми популярными из которых являются:
- метод опорных векторов (support vector machine, SVM);
- метод k-ближайших соседей (k-nearest neighbors, k-NN);
- дерево принятия решений (decision tree) и случайный лес (random forest);
- гауссовский процесс (Gaussian process);
- байесовская теория классификации;
- эволюционные алгоритмы, которые моделируют процессы естественного отбора;
- алгоритмы усиления (бустинга): AdaBoost, BrownBoost, CoBoost и т.д.;
- ансамблевое обучение (ensemble learning);
- марковские процессы;
- мешок слов;
- метод главных компонент (principal component analysis, PCA);
- искусственные нейронные сети;
- линейная и логистическая регрессии;
- метод k-средних (k-means);
- и др.
Список литературы
1.1. Box G.E.P., Hunter W.G., Hunter J.S., ″Statistics for Experimenters: Design, Innovation,
and Discovery,″ John Wiley & Sons, Hoboken, 2 ed., 2005, p. 664. ISBN: 978-0471718130.
1.2. O. Duchenne, J. Y. Audibert, R. Keriven, J. Ponce and F. Segonne, ″Segmentation by
transduction,″ 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage,
AK, 2008, pp. 1-8, doi: 10.1109/CVPR.2008.4587419
1.3. Дюк В.А., Флегонтов А.В., Фомина И.К. Применение технологий интеллектуального анализа данных
в естественнонаучных, технических и гуманитарных областях // Известия Российского государственного
педагогического университета им. А.И. Герцена. 2011. No 138. С. 77-84.
1.4. Samuel A.L., ″Some Studies in Machine Learning Using the Game of Checkers,″ in IBM Journal
of Research and Development, Vol. 3, No. 3, July 1959, pp. 210-229, doi: 10.1147/rd.33.0210.
1.5. Turing A.M., ″Computing machinery and intelligence,″ Oxford University Press on behalf
of the Mind Association, Mind, New Series, Vol. 59, No. 236, Oct., 1950, pp. 433–460.
1.6. Harnad S., ″The Turing Test Is Not A Trick: Turing Indistinguishability Is A Scientific
Criterion,″ SIGART Bulletin, No. 3(4), October, 1992, pp. 9–10.
1.7. McCalloch W.S., Pitts W., ″A Logical Calculus of Ideas Immanent in Nervous Activity,″
Bulletin of Mathematical Biophysics, Vol. 5, 1943, pp. 115–133, doi: 10.1007/BF02478259
1.8. Мак-Каллок У.С., Питтс В. Логическое исчисление идей, относящихся к нервной активности //
В сб. «Автоматы» под ред. К.Э. Шеннона и Дж. Маккарти. – М.: Изд-во иностр. лит.,
1956. – С. 363–384. (Перевод английской статьи 1943 г.)
1.9. Rosenblatt F., ″The perceptron: A probabilistic model for information storage and
organization in the brain,″ Psychological Review, Vol. 65, No. 6, 1958,
pp. 386–408, doi: 10.1037/h0042519
1.10. Rosenblatt F., ″Principles of neurodynamics: Perceptions and the theory of brain mechanism,″
Spartan Books, Washington, DC, 1962, p. 616.
1.11. Marvin L. Minsky, Seymour A. Papert, ″Perceptrons: expanded edition,″ MIT Press Cambridge,
MA, USA, 1988, p. 292. ISBN: 0-262-63111-3.
1.12. Schmidhuber J., ″Deep learning in neural networks: An overview,″ Neural Networks,
Vol. 61, 2015, pp. 85–117, doi: 10.1016/j.neunet.2014.09.003
Глава 2. Введение в искусственные нейронные сети
«Искусственный интеллект – это всё то, что ещё не сделано», –
Дуглас Хофштадтер, физик и информатик
Принципы работы искусственных нейронных сетей
Обзор основных архитектур ИНС
Одной из моделей машинного обучения являются искусственные нейронные сети (ИНС).
В настоящее время происходит возрождение ИНС под новым брендом «глубокое обучение»
(Deep Learning). ИНС являются иерархическими классификаторами, которые способны самостоятельно
выделять признаки в исходном сигнале. Общим показателем ИНС является количество скрытых слоёв.
Некоторые современные сети имеют сотни и даже тысячи скрытых слоёв. Выделяют большое множество
(зоопарк) архитектур ИНС. Перечислим самые популярные из них.
Сети без обратных связей или сети прямого распространения сигнала, в которых сигнал
переходит от выходов нейронов i-того слоя ко входам нейронов
(i+1)-го слоя и не возвращается на предыдущие слои:
- перцептроны (однослойные, многослойные с перекрёстными связями и т.д.), кроме перцептронов с обратными связями;
- байесовская нейронная сеть;
- экстремальная обучающаяся машина (extreme learning machine);
- фактически, любая ИНС, которая является направленным ациклическим (без циклов) графом.
Свёрточные нейронные сети (Convolutional Neural Networks, CNN, ConvNets),
отличительной особенностью которых является операция свёртки (конволюция):
- AlexNet [2.1];
- LeNet-5 [2.2];
- свёрточные сети с выделением области (Region Based CNNs, R-CNN) [2.3];
- развёртывающие нейронные сети (deconvolutional networks, DN, DeConvNet)
или обратные графические сети, свёрточные сети наоборот [2.4].
Генеративные состязательные сети (Generative adversarial networks, GAN) [2.5],
которые состоят из двух конкурирующих ИНС: генеративной модели, генерирующей образцы,
и дискриминативной модели, пытающейся отличить правильные («подлинные») образцы от неправильных.
GAN достаточно сложно обучить, потому что задачей является не просто обучение двух сетей,
но и соблюдение баланса, равновесия между ними. Если одна из сетей (генератор или дискриминатор)
станет намного лучше другой, то GAN не будет сходиться (обучаться).
Рекуррентные нейронные сети (Recurrent Neural Networks, RNN) [2.6, 2.7, 2.8]
или сети с памятью. Содержат нейроны, которые в процессе работы могут сохранять информацию
о своих предыдущих состояниях, такие нейроны получают информацию не только от предыдущего слоя,
но и от самих себя в результате предыдущего прохода. Рекуррентные сети являются нейросетевым
воплощением цепей Маркова. Различают множество архитектур рекуррентных ИНС:
- сеть с долговременной и кратковременной памятью (Long Short Term Memory, LSTM);
- полностью рекуррентная сеть;
- рекурсивная сеть;
- нейронная сеть Хопфилда, один из видов полносвязных ИНС;
- машина Больцмана и ограниченная машина Больцмана;
- нейронная сеть Хэмминга;
- двунаправленная ассоциативная память (BAM) или нейронная сеть Коско;
- двунаправленные рекуррентные ИНС (bidirectional recurrent neural networks);
- сети Элмана и Джордана;
- эхо-сети и импульсные (спайковые) нейронные сети;
- машины неустойчивых состояний (liquid state machines, LSM);
- нейронный компрессор истории;
- рекуррентные сети второго порядка;
- управляемые рекуррентные нейроны (Gated Recurrent Units, GRU);
- нейронные машины Тьюринга (Neural Turing machines, NTM) и т.д.
Автокодировщики, задачей которых является получение на выходном слое отклика,
наиболее близкого к входному. По этой причине выходной слой автокодировщика должен содержать
столько же нейронов, сколько и входной слой. Сеть напоминает по форме песочные часы,
так как скрытые слои автокодировщиков меньше, чем входной и выходной слои.
Различают следующие автокодировщики:
- ванильный автокодировщик (Vanilla autoencoder);
- многослойный автокодировщик;
- свёрточный автокодировщик;
- упорядоченный автокодировщик (regularized autoencoder);
- разреженный автокодировщик;
- шумоподавляющий (помехоустойчивый) автокодировщик (denoising autoencoder, DAE).
Глубокие нейронные сети, которые отличаются от просто нейронных сетей
наличием большого количества скрытых слоёв:
- глубокие сети доверия (Deep Belief Networks, DBN),
которые являются первыми глубокими сетями; - глубокая остаточная нейронная сеть (Residual neural network, ResNet) [2.9],
которая является попыткой смоделировать пирамидальные нейроны в коре больших полушарий; - глубокая машина Больцмана (Deep Boltzmann Machine, DBM);
- размещённые друг над другом автокодировщики (Stacked Auto-Encoders);
- глубокие свёрточные нейронные сети (Deep Convolutional Neural Networks, DCNN),
глубокие свёрточные обратные глубинные сети (Deep Convolutional Inverse Graphics Networks,
DCIGN) [2.10], VGG Net [2.11] и т.д.
Нейронные сети Кохонена, у которых основным элементом является слой Кохонена.
В этом слое выходные сигналы обрабатываются по правилу «победитель получает всё»,
т.е. наибольший сигнал превращается в единичный, а остальные обращаются в ноль:
- сети векторного квантования (learning vector quantization);
- самоорганизующиеся карты Кохонена;
- упругие карты.
Сети радиально-базисных функций (radial basis function networks),
которые использует радиальные базисные функции в качестве функций активации.
Смешанные нейронные сети, которые совмещают в себе различные архитектуры
для большей эффективности:
- GoogLeNet;
- AlphaGo и т.д.
Этот список не является исчерпывающим. Постоянно появляются новые архитектуры.
Более того, вышеизложенное разделение ИНС на архитектуры является условным,
так как нет чётких границ. Например, свёрточная ИНС одновременно является сетью
без обратных связей, она же глубокая нейронная сеть, а также она может являться
автокодировщиком или частью более сложной архитектуры. К сожалению, в этой главе
нет возможности подробно описать архитектуру каждой сети. Однако все ИНС используют
общие принципы работы и имеют схожие проблемы обучения, кратко рассмотренные ниже.
Существует множество программных библиотек для машинного обучения и обучения ИНС: TensorFlow,
Theano, Keras, Torch, Caffe, MXNet, Matlab Neural Networks Toolbox, Wolfram Mathematica и др.
Функции активации нейрона
В предыдущей главе были рассмотрены две ступенчатые функции активации перцептрона:
функция Хевисайда (1.2) и сигнум-функция (1.3). В современных ИНС широко применяется метод
обратного распространения ошибки (backpropagation), в котором используется производная
от функции активации. Но ступенчатые функции не дифференцируемы, т.е. не имеют производной
на ступеньке. Поэтому при использовании метода обратного распространения ошибки применяются
другие функции активации. В таблице 2.1 показаны несколько самых широко применяемых
в ИНС функций активации.
| № | Название | Формула | Изображение |
|---|---|---|---|
| 1 | Rectified linear unit (ReLU) | 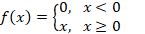 |
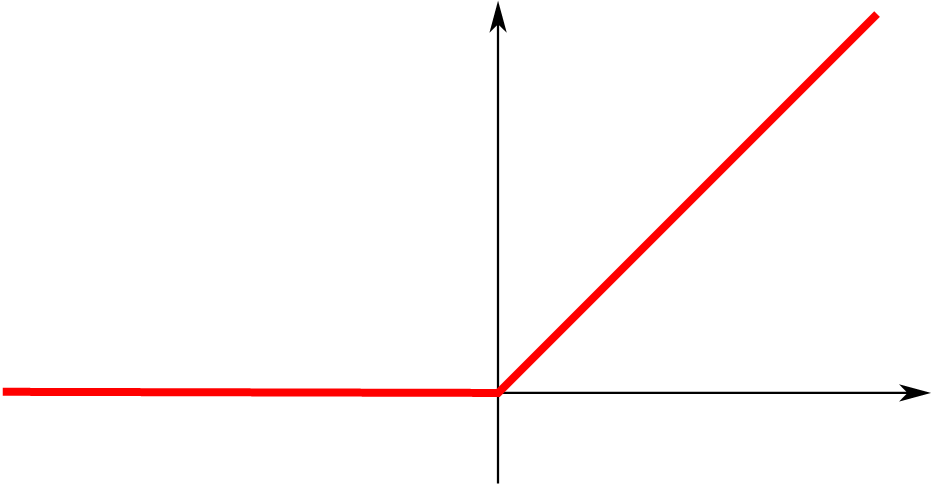 |
| 2 | Параметрический rectified linear unit (PReLU) | 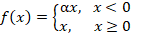 |
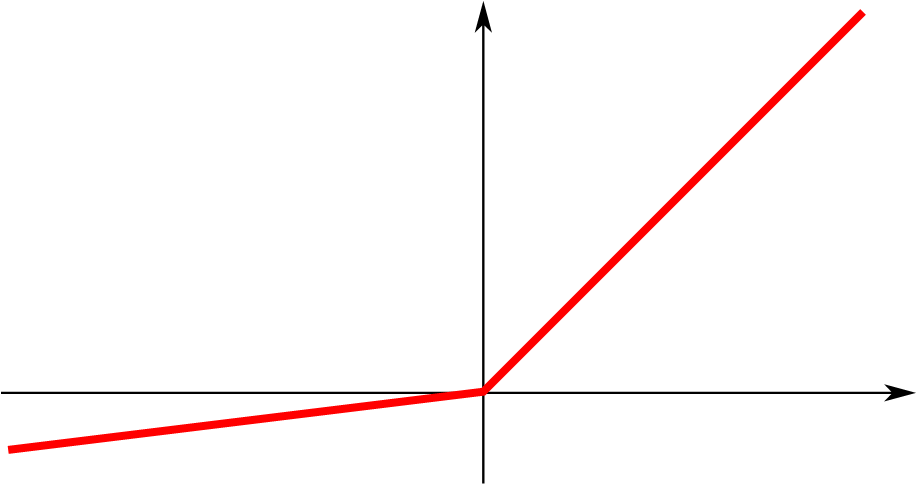 |
| 3 | Логистическая функция или сигмоида | 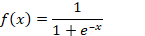 |
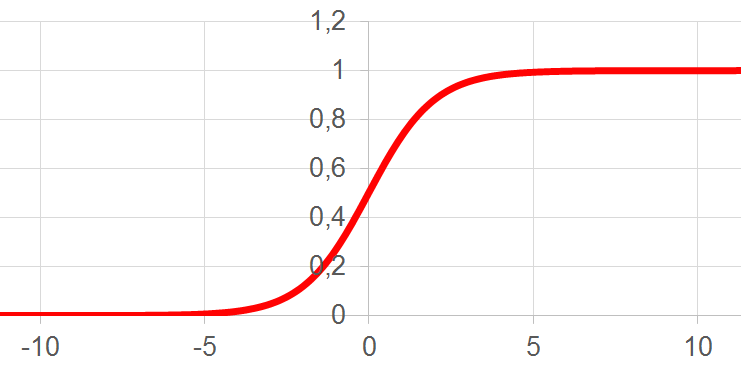 |
| 4 | Гиперболический тангенс (TanH) | 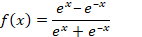 |
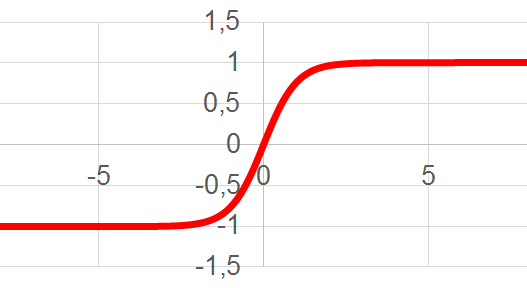 |
| 5 | Арктангенс (ArcTan) | 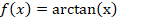 |
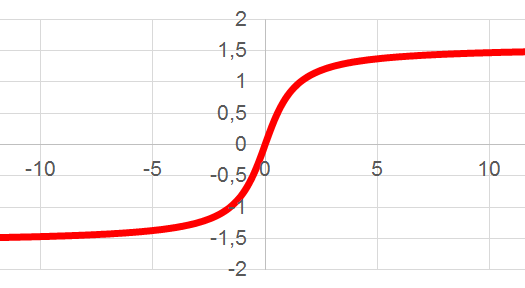 |
Здесь аргумент активационной функции x – это взвешенная сумма (1.1)
или индуцированное локальное поле; α во второй строке таблицы 2.1 –
это малый коэффициент, обычно равный α = 0,01. Малый коэффициент
α нужен, чтобы производная функции ReLU не была равна нулю при
x < 0. Однако наличие малого коэффициента α
некритично, как может показаться, так как вероятность того, что активационные функции всех
нейронов ИНС станут равными нулю крайне мала. Например, в одномерном случае невозможно
преодолеть гору, в двумерном случае гору можно обойти слева или справа, а в многомерном
N-мерном пространстве существует множество путей обхода препятствий,
и чем больше измерений, тем меньше вероятность попасть в локальный минимум.
Функция ReLU (строка 1 таблицы 2.1) была впервые применена в свёрточных ИНС для устранения
проблемы исчезающего градиента и доказала свою эффективность. В отличие от сигмоиды и
гиперболического тангенса, операция ReLU гораздо быстрее, при этом качество обучения снижается
незначительно. Поэтому ReLU на данный момент является самой популярной активационной функцией
в свёрточных ИНС.
Функция активации необходима для внесения нелинейности в систему. Без нелинейности ИНС будет
вырождаться в обычное перемножение матриц и векторов, т.е. в линейную алгебру. В данном контексте
уместно напомнить общеизвестный факт о том, что никакие линейные преобразования пространства
признаков не позволяют улучшить качество классификации, т.е. линейная разделимость объектов
в пространстве признаков является неэффективной. С помощью линейных преобразований невозможно
решить нетривиальные задачи, например, разделить пересекающиеся множества.
Свёрточные ИНС
Для анализа изображений чаще всего используются свёрточные ИНС. Свёрточная ИНС была предложена
и популяризована Яном Лекуном в 1988 году для распознавания изображений.
Отличительной чертой свёрточных ИНС является операция свёртки.
Как известно, цветные RGB изображения 256 на 256 пикселей, можно представить, как матрицу
256×256×3 из 256 строк, 256 столбцов и толщиной 3 слоя. При операции свёртки каждый пиксель
такого изображения умножается на матрицу (ядро или фильтр) свёртки, а результат суммируется
и записывается в аналогичную позицию выходного изображения. По сути операция свёртки – это
всё та же взвешенная сумма нейрона ∑ на рисунке 1.6, только выполняемая особым образом
(рисунок 2.1), где значения матрицы свёртки – это веса синапсов
wi, значения пикселей изображения – это значения
входящих сигналов нейрона xi, а результатом является
один пиксель нового изображения, в котором пиксели будут являться взвешенными суммами
∑wi*xi‒C
(см. формулу 1.1).
Рис. 2.1 – Операция свёртки для одного пикселя
нового изображения с нулевым порогом
На рисунке 2.1 показана операция свёртки одного ядра размером 3×3 с нулевым порогом
C (bias) с кусочком чёрно-белого изображения,
т.е. изображения с глубиной один слой, в результате чего получается один пиксель нового
обработанного изображения. Как правило, ядро свёртки передвигают на малое расстояние
при движении по изображению. Например, ядро свёртки 3×3 обычно передвигают всего на один
нейрон (пиксель), а ядро свёртки 5×5 передвигают на один–два нейрона (пикселя).
Глубина ядра свёртки всегда равна глубине обработанного изображения. Для исходного
чёрно-белого изображения глубина равна 1, а для цветного RGB изображения глубина равна 3.
Соответственно, на более глубоких свёрточных слоях глубина ядра свёртки увеличивается,
потому что увеличивается глубина обработанного изображения. Таким образом для исходного
цветного изображения матрица свёртки имеет глубину 3 и может быть равной: 3×3×3, либо 5×5×3,
либо 7×7×3 и т.д. Обычно берут нечётное число для величины ядра свёртки, т.к. считается,
что свёртка происходит вокруг центра, однако иногда встречаются свёрточные ИНС и с чётным
размером ядер.
Результатом свёртки ядра 3×3×3 с шагом один со всем RGB изображением 256×256×3 будет
новое изображение с матрицей 254×254×1, в котором значения пикселей будут являться взвешенными
суммами. Если ядро свёртки размером 3×3×3, то нейрон имеет 27 синапсов (3*3*3=27),
соединяющих его с 27 пикселями исходного изображения. Всего такой нейрон имеет 28 параметров,
т.к. двадцать восьмой параметр – это порог C (bias).
Новая матрица имеет меньшее количество строк и столбцов 254, а не 256, из-за того, что ядро 3×3
не может выходить за пределы изображения. В общем случае длина и ширина матрицы уменьшаются на
(k‒1) пиксель после каждой свёртки с единичным шагом, где k – это размер ядра. Иногда, для того,
чтобы матрица не уменьшалась в размерах, вокруг изображения добавляют фаску (прокладку,
zero padding) из нулей. Для ядра 3×3 с единичным шагом толщина фаски из нулей равна 1.
Для ядра 5×5 с единичным шагом толщина фаски из нулей равна 2.
Несколько десятков таких ядер свёртки (фильтров) называют свёрточным слоем
(convolutional layer). Свёрточный слой из N ядер превращает цветное RGB изображение 256×256×3
в матрицу 254×254×N значений. Такая матрица (или обработанное изображение) имеет глубину N,
равную количеству ядер свёртки (количеству фильтров).
Веса ядер, т.е. значения матриц свёртки в свёрточном слое, не закладываются исследователем
заранее, а вычисляются автоматически с помощью операции обратного распространения ошибки
(backpropagation), которая будет рассмотрена далее.
Для улучшения работы ИНС применяется метод исключений (dropout), при котором проводится обучение
ИНС с выбрасыванием случайных одиночных нейронов. Также для улучшения качества может применяться
сеть в сети (network in network layer) – это ядро свёртки размером 1×1×N, где N – это количество
ядер свёртки на предыдущем свёрточном слое, т.е. глубина матрицы. Сеть в сети была
впервые применена в GoogLeNet.
Как и во всяком искусственном нейроне (см. рисунок 1.6),
за взвешенной суммой ∑ следует функция активации. Для свёрточных ИНС функцией активации
является функция ReLU (строки 1 и 2 таблицы 2.1) и её модификации (Noisy ReLU, Leaky ReLU и др.).
Функция ReLU применяется к каждому значению матрицы 254×254×N.
Затем, как правило, применяется второй свёрточный слой из M ядер свёртки, который превратит
матрицу 254×254×N в матрицу 252×252×M. При этом глубина ядер на втором свёрточном слое будет
равна N и может быть равной: 3×3×N, либо 5×5×N, либо 7×7×N и т.д.
За вторым свёрточным слоем следует слой активации ReLU, т.е. функция ReLU применяется к каждому
значению матрицы 252×252×M. Слой активации обычно логически объединяют со слоем свёртки
(считают, что функция активации встроена в слой свёртки). На рисунке 2.2 показаны несколько
слоёв свёртки и активации цветного изображения.
Рис. 2.2 – Несколько слоёв свёртки и активации цветного изображения
Другим важным аспектом свёрточных ИНС является операция пулинга (pooling) или
субдискретизации, которая представляет собой нелинейное уплотнение карты признаков
(рисунок 2.3).
Рис. 2.3 – Пулинг с функцией максимума, фильтром 2×2 и шагом 2
Операция пулинга позволяет существенно уменьшить пространственный объём изображения,
сократить количество параметров и ускорить вычисления в сети и, как следствие,
предотвратить переобучение. Считается, что если на предыдущем свёрточном слое уже были выявлены
некоторые признаки, то для дальнейшей обработки такое подробное изображение уже не нужно,
и оно уплотняется. При пулинге наличие признака важнее, чем его точная позиция на изображении.
Слой пулинга вставляется между свёртками. Практика доказала преимущество пулинга с функцией
максимума (maxpooling). При пулинге глубина матрицы остаётся неизменной, меняется только
её длина и ширина. Ещё одним эффектом от пулинга является инвариантность (нечувствительность)
распознавания к изменению размера изображения. Иногда исследователи полностью отказываются
от пулинга, потому что утрачивается информация о точном местоположении признака.
Можно заметить, что функция ReLU неубывающая, а значит можно поменять местами слой активации
и слой пулинга с функцией максимума, тем самым ускорив вычисления,
но это уже вопрос оптимизации кода.
В самом конце свёрточная ИНС имеет полносвязные нейронные слои (fully connected layers).
Полносвязная ИНС по своим свойствам является линейным классификатором. После нескольких
прохождений свёртки и уплотнения изображение преобразуется в вектор признаков
(дескриптор), который уникальным образом характеризует это изображение.
Этот дескриптор подаётся на вход классификатора, где ему ставится в соответствие
некий класс объектов, например, «кот» или «собака». Полносвязная ИНС может быть заменена
на любой другой линейный классификатор (SVM, k-NN, логистическую регрессию,
наивный байесовский классификатор и т.д.).
Классическая архитектура свёрточной ИНС выглядит так:
Изображение → Свёртка → ReLU → Свёртка → ReLU → Пулинг →
→ Свёртка → ReLU → Свёртка → ReLU → Пулинг →
→ Свёртка → ReLU → Свёртка → ReLU → Пулинг →
→ Полносвязная ИНС или линейный классификатор → Результат
Свёрточная ИНС самонастраивается с помощью метода обратного распространения ошибки, автоматически
меняет свои фильтры, и сама вырабатывает необходимую иерархию абстрактных признаков
(последовательность карт признаков), фильтруя маловажные детали и выделяя существенное.
Больше о том, что такое признаки (features), и как с ними работать, можно узнать в следующем разделе.
Однако не пытайтесь понять и тем более изменить вырабатываемые автоматически признаки.
При работе с ИНС разработчик должен сосредоточится на общей архитектуре сети и обучающих данных,
чтобы улучшить результаты.
Исследователи заметили, что от слоя к слою признаки усложняются. Если на первом свёрточном слое
сеть учится распознавать углы, линии, оттенки и особые точки, то на втором свёрточном слое это
уже части объектов, например, части лиц. На третьем уровне уже можно выделить целые объекты:
лица, предметы, текст. На более высоких уровнях появляются комбинации объектов и их зависимости,
такие как книжная полка с книгами, группы лиц каких-нибудь музыкальных групп и т.д.
(см. рисунок 2.4).
Рис. 2.4 – Автоматическое усложнение признаков в свёрточной ИНС [2.12]
Недостатком свёрточной ИНС является большое количество варьируемых параметров: число слоёв,
размер ядра свёртки для каждого из слоёв, величина порога для взвешенной суммы свёртки,
количество ядер в каждом слое, шаг сдвига ядра, необходимость субдискретизации, параметры
полносвязной сети на выходе свёрточной и т.д. Все эти параметры выбираются исследователями
эмпирически (через практику). Не хватает теоретических исследований, точных расчётов и
рекомендаций для построения новых архитектур свёрточных ИНС.
Метод обратного распространения ошибки (backpropagation)
Метод обратного распространения ошибки (backpropagation) – это метод вычисления градиента,
который используется при автоматическом обновлении весов многослойного перцептрона.
Метод был исследован математиками в теории управления в начале 60-х годов двадцатого века,
но впервые применён к ИНС лишь спустя 20 лет в 80-х годах. Метод является частным случаем
более общей техники автоматического дифференцирования (automatic differentiation)
и модификацией классического метода градиентного спуска (gradient descent).
Для метода обратного распространения ошибки прежде всего требуется построить функцию потерь
или функцию оценки работы сети H. Простейшим и самым распространённым примером функции потерь
является квадратичное отклонение:
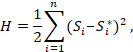 |
(2.1) |
где H – функция потерь;
Si – сигнал на i-том
выходном нейроне ИНС; Si* – ожидаемый
сигнал при правильном ответе на i-том выходном нейроне ИНС.
Сумма берётся по всем выходным нейронам сети от 1 до n. Таким образом при квадратичном
отклонении метод обратного распространения ошибки сводится к методу наименьших квадратов.
Т.е. веса синапсов wj,k,l и порог активации каждого
нейрона Cj,k в ИНС должны быть такими,
чтобы сумма (2.1) была минимальной, желательно, нулевой или близкой к нулю.
Здесь j – номер нейронного слоя,
k – номер нейрона в слое,
l – номер связи в нейроне.
Метод наименьших квадратов не всегда является наилучшим выбором функции потерь.
Умение конструировать оптимальную функцию потерь может существенно улучшить качество
распознавания и на порядок ускорить обучение ИНС.
Теоретически можно подобрать оптимальные веса синапсов и порогов активации нейронов с помощью
простого перебора, через прямое вычисление без применения эффективных приёмов (brute force
computation). Однако на практике для многослойных глубоких сетей время такого прямого вычисления
будет намного порядков превышать время жизни Вселенной.
Каждый синапс и каждый порог нейрона можно считать отдельным измерением некоего многомерного
пространства. В глубокой ИНС таких синапсов и порогов тысячи, а иногда и десятки миллионов.
При увеличении количества синапсов пространство становится многомерным и появляется проблема
под названием «проклятие размерности», которая связанна с экспоненциальным возрастанием
данных из-за увеличения размерности пространства. Например, чтобы покрыть единичный отрезок
[0, 1] точками с частотой 0,01, требуется 100 точек. Чтобы покрыть квадрат с такой же частотой,
требуется 104 точек. Для десятимерного куба требуется уже
102*10=1020 точек, что в 1018 раз больше,
чем в одномерном пространстве. Таким образом использование переборных (brute force) алгоритмов
становится неэффективным при возрастании размерности системы.
Ещё в 1961 году Ричард Беллман исследовал алгоритмы, которые хорошо работают в низких
размерностях, но становятся неразрешимыми в высоких размерностях. Он назвал этот эффект
«проклятие размерности». При увеличении размерности данные быстро становятся разреженными.
Методы удаления избыточных и сильно скоррелированных данных позволяют уменьшить размерность.
Одним из таких методов является метод обратного распространения ошибки.
Алгоритм обратного распространения ошибки состоит из пяти шагов.
Шаг 1. Конструируется функция потерь H,
которая совсем не обязательно должна быть квадратичным отклонением (2.1).
Шаг 2. Высчитывается величина ошибки.
Шаг 3. Проверяется, достигла ли функция потерь минимума.
Шаг 4. Если функция потерь не достигла минимума, тогда параметры ИНС,
т.е. веса синапсов и пороги активации, обновляются по итеративной формуле (2.2).
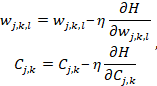 |
(2.2) |
где wj,k,l – вес синапса;
Cj,k – порог активации нейрона;
H – функция потерь;
0 < η < 1 – множитель, задающий скорость обучения;
j – номер нейронного слоя;
k – номер нейрона в слое;
l – номер связи в нейроне.
Для обновления параметров ИНС нужно двигаться в обратном направлении от выходов ко входам сети
и вычислять градиенты от функции потерь для каждого веса и порога. Обновлённые веса и пороги
участвуют в обновлении следующих в обратном порядке слоёв ИНС.
Шаг 5. Повторять шаги 2–4 пока функция потерь не достигнет своего минимума. Когда функция
потерь достигла минимума, ИНС считается обученной и готова к работе с новыми данными.
Величина шага коррекции ошибки задаётся с помощью множителя
0 < η < 1 (см. формулу 2.2).
Шаг коррекции ошибки не должен быть слишком маленьким, иначе обучение будет долгим.
Шаг коррекции ошибки не должен быть слишком большим, иначе можно «перешагнуть» через минимум,
из-за чего в сети может возникнуть паралич (слишком большие веса) или неустойчивость
(невозможность найти минимум функции потерь). Обычно множитель η не является константой и
выбирается автоматически по следующему принципу: если градиент большой – множитель η маленький;
если градиент маленький – множитель η большой.
При вычислении градиентов на шаге 4 алгоритма применяется цепное правило
дифференцирования сложной функции (chain rule):
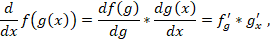 |
(2.3) |
где ƒ и g – функции переменной x.
Также применяется уравнение частной производной:
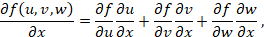 |
(2.4) |
где ƒ – функция трёх переменных u, v, w;
и где x – четвёртая переменная,
по которой производится дифференцирование.
К сожалению, пример с подробным вычислением минимума функции потерь не проводится в данной
главе из-за её ограниченного объёма. Однако вы можете легко найти такие примеры в Интернете.
Например, маленький и понятный курс видео лекций
«Neural Networks Demystified» и соответствующие
упражнения на GitHub.
Используя формулы (2.3) и (2.4) сначала корректируются веса и пороги для последнего нейронного
слоя по формуле (2.2). Затем, используя скорректированные веса и пороги последнего слоя,
корректируются веса и пороги предпоследнего слоя и т.д. Корректируются веса и пороги слоёв
в обратном порядке, т.е. в направлении от выхода ко входу сети. При этом для коррекции следующего
(в обратном порядке) слоя используются уже скорректированные параметры из предыдущих слоёв.
Таким образом выполняется шаг 4 алгоритма.
При нахождении минимума функции потерь есть вероятность попасть в локальный минимум вместо
глобального минимума. В этом случае применяются методы выхода из локальных минимумов.
При корректировке весов и порогов по формуле (2.2) градиент может стать слишком маленьким,
что приведёт к замедлению или даже полной остановке обучения. До 2006 года
проблема исчезающего градиента (the vanishing gradient problem) была основной причиной,
из-за которой было невозможно обучать глубокие сети с множеством слоёв, потому что от слоя к слою
градиент уменьшался при применении метода обратного распространения ошибки. Проблема исчезающего
градиента вынуждала исследователей использовать неглубокие сети с небольшим количеством слоёв.
Проблема исчезающего градиента возникает из-за того, что градиент некоторого слоя является
произведением градиентов всех предыдущих слоёв. Если градиенты на предыдущих слоях меньше
единицы и лежат на отрезке [0, 1], тогда их произведение будет давать меньшее число.
Например, 0,5*0,5=0,25, а при многократном умножении чисел, меньших единицы, их произведение
будет стремиться к нулю и становиться исчезающе малым: 0,510 ≈ 0,00098.
В 2006 году вышли три статьи Яна Лекуна (Yann LeCun), Джошуа Бенджио (Yoshua Bengio) и
Джеффри Хинтона (Geoffrey Hinton), в которых они предложили новую архитектуру ИНС,
способную преодолеть проблему исчезающего градиента: глубокую сеть доверия (deep belief network),
которая может быть представлена, как последовательность автокодировщиков под названием
ограниченные машины Больцмана (restricted Boltzmann machine). Сейчас глубокая сеть доверия
не является единственной архитектурой и техникой для преодоления проблемы исчезающего градиента,
но в то время глубокие сети доверия произвели революцию в ИНС. Например, выбор активационной
функции ReLU позволяет частично устранить эту проблему. На данный момент самой популярной
архитектурой ИНС для преодоления проблемы исчезающего градиента является глубокая остаточная
нейронная сеть (Residual Network, ResNet). Преодоление проблемы исчезающего градиента привело
к повышению интереса к ИНС и развитию глубокого обучения (Deep Learning).
Кроме проблемы исчезающего градиента существует проблема взрывного градиента,
которая является обратной к исчезающему, но результат у них один – прекращение обучения.
В глубоких и/или рекуррентных ИНС градиенты ошибок могут накапливаться во время обновления,
в результате чего градиент может становиться очень большим. Большие градиенты приводят к
нестабильной работе сети. Если вес синапса станет слишком большим из-за больших обновлений,
то это приведёт к параличу сети. Также большой вес может привести к численному переполнению,
выходу за пределы максимально возможного числа для компьютерной программы.
Известно, что полезная информация хранится в весах синапсов, а не в состояниях нейронов.
Поэтому, если разница между весами становится слишком маленькой, то в системе начинают
доминировать шумы. Если разница между весами становится слишком большой, то эта синаптическая
связь начинает подавлять другие связи.
Градиенты в глубоких ИНС являются нестабильными и стремятся либо к нулю, либо к бесконечности
при продвижении к первым слоям многослойной сети. Эта нестабильность является фундаментальной
проблемой для методов обучения глубоких ИНС с помощью градиентов.
Переобучение и недообучение
Переобучение (overfitting) – явление, при котором ошибка модели на объектах,
не участвовавших в обучении, оказывается существенно выше, чем ошибка на объектах,
участвовавших в обучении. Переобучение возникает при использовании слишком сложных моделей,
как правило, с большим количеством нейронов и синапсов, либо при слишком долгом процессе
обучения, либо при неудачной обучающей выборке.
Недообучение (underfitting) – явление, при котором ошибка обученной модели оказывается
слишком большой. Недообучение возникает при использовании слишком простых моделей, как правило,
с малым количеством нейронов и синапсов, либо при прекращении процесса обучения до достижения
состояния с достаточно малой ошибкой, либо при неудачной обучающей выборке.
На рисунке 2.5 приведены примеры недообученной, обученной и переобученной модели
в задаче классификации.
Рис. 2.5 – Недообучение, оптимум и переобучение в классификации
На рисунке 2.6 приведены примеры недообученной, обученной и переобученной модели
в задаче регрессии.
Рис. 2.6 – Недообучение, оптимум и переобучение в регрессии
Причины переобучения разнообразные:
- слишком мало данных для обучения либо слишком много нейронов и синапсов в ИНС – модель
запомнила все варианты из обучающей выборки и, таким образом, утратила возможность
обобщения, выдавая запомненные варианты вместо предсказаний; - слишком долгое обучение – модель находит закономерности в шуме (галлюцинирует);
- плохо подготовленные данные в обучающей выборке могут привести к тому, что модель будет
давать большую ошибку на новых данных, которые не участвовали в обучении.
Если модель запомнила все варианты в обучающей выборке, то новые примеры она может не угадать
просто потому, что они отличаются от тех, что были в выборке. Эта проблема возникает,
когда обучающая выборка слишком маленькая либо модель ИНС слишком сложная.
Если модель находит закономерности в шуме, то новые данные будут обладать другим шумом,
который всегда есть в данных, тогда ответ модели будет ошибочным. Эта проблема возникает,
когда обучение было слишком долгим и модель просто подогнана под шум в обучающей выборке
(рисунок 2.7).
Рис. 2.7 – Окончание обучения, дальше модель переобучается
Для того, чтобы контролировать модель на переобучение,
нужно использовать отдельные наборы данных для обучения и оценки.
Данные, на которых происходит оценка качества, не должны участвовать в обучении.
Рекомендации по созданию обучающей выборки
Важность правильной подготовки данных
Важность правильной подготовки данных для алгоритмов машинного обучения трудно переоценить:
примерно 80% времени тратится на работу с данными и менее 20% – на создание модели.
Плохо подготовленные данные дадут плохие результаты или результатов не будет.
У специалистов по работе с данными есть принцип «Мусор на входе – мусор на выходе»
(Garbage In, Garbage Out), который означает, что при плохих входящих данных будут получены
плохие результаты, даже если сам алгоритм правильный. Качество данных – это многоаспектное
понятие. Данные должны быть: точными, непротиворечивыми, полными, достоверными, объективными,
актуальными, репрезентативными и др. Провал в каком-либо из аспектов качества может сделать
данные малопригодными или бесполезными. Самое худшее, если данные выглядят пригодными,
но ведут к ложным результатам.
Разберём несколько ошибок при создании обучающей выборки.
Предположим, что в городе Минск есть поликлиника, где граждане каждый год проходят флюорографию.
Для простоты мысленного эксперимента будем считать, что городская поликлиника только одна.
Кроме поликлиники «для всех» в посёлке Боровляны около Минска есть онкологический центр,
куда направляются граждане с подозрением на раковые заболевания. В городской поликлинике есть
бюджетный цифровой флюорограф, а для онкоцентра был куплен дорогой цифровой флюорограф последней
модели, потому что люди с подозрением на рак должны обследоваться тщательнее. Все флюорограммы
грудной клетки из поликлиники и онкоцентра сохраняются в единую базу данных медицинских снимков.
Перед исследователем стоит задача: используя нейронные сети, научиться определять здоров человек
или нет по флюорограмме его лёгких.
Первая ошибка: взять все флюорограммы из базы данных и подать их на вход нейронной сети
в качестве обучающей выборки. Ошибка в том, что подавляющее большинство людей в обучающей выборке
будут здоровы, поэтому для достижения высокой точности правильных ответов достаточно всегда
выдавать один и тот же ответ «здоров». Предположим, из 10 000 человек только 10 будут больны.
Значит количество больных составляет: (10/10 000)*100% = 0,1%,
а количество здоровых равно: 100% ‒ 0,1% = 99,9%.
Если всегда выдавать ответ «здоров», то точность правильных ответов составит 99,9%,
а ошибка такого «предсказания» окажется очень маленькой: всего одна ошибка на тысячу
правильных ответов или 0,1%.
ИНС тренируется по принципу «чем больше правильных ответов, тем лучше»,
но для людей необходимо выявлять больных людей, а не считать правильные ответы.
Математически это можно выразить через статистические показатели эффективности теста
бинарной классификации – чувствительность и специфичность:
 |
(2.5) |
Чувствительность (true positive rate, TPR) равна доле правильно идентифицированных
положительных результатов, т.е. вероятности того, что больной будет классифицирован как больной.
Специфичность (true negative rate, SPC) равна доле правильно идентифицированных
отрицательных результатов, т.е. вероятности того, что здоровый будет классифицирован как здоровый.
Здесь «положительный результат» – это синоним болезни, а «отрицательный результат» – это
синоним здоровья. Такие термины приняты в медицинской практике.
Бинарный классификатор разделяет всё множество (людей) на два класса: больные и здоровые.
Всего есть четыре типа ответов бинарного классификатора
(рисунок 2.8):
- Истинно положительный (true positive, TP): больные правильно идентифицируются как больные.
- Ложно положительный (false positive, FP): здоровые неверно идентифицируются как больные.
- Ложно отрицательный (false negative, FN): больные неверно идентифицируются как здоровые.
- Истинно отрицательный (true negative, TN): здоровые правильно идентифицируются как здоровые.
Рис. 2.8 – Четыре вида ответов бинарного классификатора:
TP – true positive (правильно);
TN – true negative (правильно);
FP – false positive (ошибка первого рода);
FN – false negative (ошибка второго рода).
Когда классификатор всегда выдаёт ответ «здоров», то, в соответствии с формулой (2.5),
его чувствительность равна нулю, а специфичность равна единице:
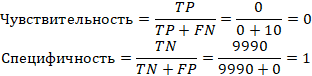 |
(2.6) |
Для того, чтобы исправить ошибку с несбалансированными данными, нужно сбалансировать обучающую
выборку по больным и здоровым, т.е. взять одинаковое количество больных и здоровых.
Например, десять тысяч флюорограмм здоровых людей должны «уравновешиваться» каким же количеством
флюорограмм больных людей, иначе обучающая выборка будет несбалансированной и получится
вышеописанная ошибка обучения.
Вторая ошибка: взяли 10 000 флюорограмм здоровых людей и
10 000 флюорограмм больных людей из общей базы и подали их на вход
ИНС в качестве обучающей выборки. Ошибка в том, что здесь не учтено равновесие обучающей
выборки по моделям цифровых флюорографов. Очевидно, что каждая модель и даже каждый отдельный
экземпляр одной и той же модели делает различные снимки. Снимки различаются оттенками,
цветовой гаммой, резкостью, градиентами и даже тем, что у одного флюорографа подставочка будет
немного выше, чем у другого, из-за чего снимки грудных клеток в онкоцентре будут чуть выше,
чем снимки грудных клеток в поликлинике.
В условии задачи сказано, что в онкоцентр направляются люди с подозрением на заболевание,
там их тщательно обследуют, делают множество снимков их грудной клетки. Как результат,
в базе данных будет преобладающее количество снимков больных из онкоцентра, которое будет
превышать количество снимков больных из поликлиники в разы. Также соотношение между снимками
больных и здоровых в онкоцентре будет гораздо выше, чем соотношение между снимками больных и
здоровых в поликлинике, потому что больных в онкоцентре больше.
Допустим, снимки из онкоцентра имеют синеватый оттенок по сравнению со снимками из поликлиники.
Таким образом нейронная сеть вместо определения реальных больных будет искать синеву на снимках,
потому что большинство снимков больных были сделаны в онкоцентре. Если снимок имеет синеву – это
больной, а если не имеет синевы – это здоровый. В результате на выходе ИНС будут высокие
показатели правильных ответов, а исследователь не будет знать, что допустил ошибку,
пока не опробует свою обученную модель на третьей модели флюорографа и увидит,
как резко упала точность классификации.
Конечно, можно нормировать все снимки по цвету, но оттенок – это только одно из многих различий
между изображениями с разных моделей приборов. Самым лучшим решением будет уравновесить снимки
по различным моделям цифровых флюорографов. Например, взять 5 000
флюорограмм больных и 5 000 флюорограмм здоровых из онкоцентра, затем
взять 5 000 флюорограмм больных и 5 000
флюорограмм здоровых из поликлиники. Таким образом обучающая выборка станет сбалансированной
по различным моделям флюорографов. После этого желательно ещё и нормировать все отобранные
снимки по цвету, резкости, отцентрировать их и т.д.
Внимательно и осознанно выбирайте метрику под ваш набор данных.
В случае сильно несбалансированных признаков можно получить бесполезную метрику.
Аугментация данных (data augmentation)
Аугментация данных (data augmentation) – это методика создания дополнительных
обучающих данных из имеющихся данных. Целей у аугментации несколько:
- «раздуть» обучающую выборку;
- повысить точность работы нейронной сети и её устойчивость к шумам;
- облегчить работу по созданию базы данных для обучения.
Для обучения глубокой ИНС нужно много данных: десятки и сотни тысяч изображений.
Не всегда получается найти достаточное количество данных. На многие изображения распространяются
лицензионные соглашения их обладателей, а также право на неприкосновенность частной жизни,
врачебная тайна для медицинских изображений и т.д. Базы данных часто являются платными,
потому что проделана огромная работа для создания таких баз. Если вы станете фотографировать
людей и/или их собственность на улице, то это может вызвать обоснованные претензии и даже
агрессию. В уголовных кодексах разных стран предусмотрена ответственность за «незаконные
собирание либо распространение информации о частной жизни». Генерация искусственных изображений
позволяет избежать проблем с законом и получить множество изображений бесплатно.
Создание дополнительных изображений с различными искажениями позволяет повысить точность
работы нейронной сети и её устойчивость к шумам. Например, повороты позволят получать правильные
ответы даже если изображение повёрнуто на некоторый угол.
Чтобы создать хорошую базу данных изображений, их нужно: собрать, обработать (кадрировать,
фильтровать и т.д.), разметить (выделить области интереса, regions of interest, ROI,
и присвоить им метку, название объекта на изображении). К тому же требуется собрать разнообразные
данные и сбалансировать их по различным моделям фотокамер, при различном освещении, с различных
ракурсов и т.д. Эти операции требуют значительных затрат рабочего времени, которые можно
уменьшить путём аугментации данных.
Для аугментации берутся несколько шаблонов, «идеальных» примеров, и с помощью различных
искажений создаются дополнительные примеры для обучения. Можно сгенерировать новые изображения
с использованием естественных. Применяются следующие искажения и их различные комбинации:
- геометрические (повороты, сдвиги, растяжения, сжатия, зеркальные отражения,
случайное кадрирование, random crop, афинные, проективные и т.д.); - яркостные и цветовые (изменения яркости, цветовой гаммы, color jitter,
изменения тона, насыщенности и значения цветового пространства HSV и т.д.); - замена фона;
- характерные искажения для решаемой задачи (шумы, блики, дополнительные линии,
размытие, разфокусировка и т.д.).
Генерировать изображения можно с помощью библиотек для работы с изображениями или
специальных программ. Наилучший результат получается, если комбинировать естественные
(реальные) и искусственные (сгенерированные) изображения, например, аугментировать
естественные изображения.
Отбор признаков (feature selection)
Каждый объект характеризуется набором признаков (features, «фичей», параметров).
Например, объект «сообщение электронной почты» характеризуется следующим набором признаков:
набор слов, длина сообщения, дата, отправитель, получатель, язык, частота сообщений
от данного адресата и т.д. Признаком объекта (изображения, текста, звука) может быть
любая количественная характеристика, главное, чтобы эта характеристика была уникальной
именно для данного типа объектов: расположение особых точек на изображении, вычисляемых
через алгоритм SURF; спектр сигнала; гистограмма; частота встречаемости пар точек
на изображении; градиенты (перепады) яркости на изображении и т.д.
Чем больше признаков, тем дольше работа алгоритма. Это очевидно.
На первый взгляд кажется, чем больше признаков, тем больше полезной информации в результате
получится. Это неочевидно, но далеко не всегда увеличение количества признаков даёт
положительные результаты. Например, если при составлении прогноза продаж, учитывать в качестве
дополнительного параметра фазу Луны, то предсказание только ухудшится. Поэтому прогнозы улучшают,
отбрасывая ненужные признаки и оставляя нужные, проводят отбор признаков.
Отбор признаков (feature selection) требует от исследователя интуиции, хорошего знания предмета
изучения, умения отделять главное от второстепенного. Отбор признаков для изображений
заключается в их предварительной обработке: увеличение контрастности, отсекание фона,
подавление шумов и т.д. Отбор признаков помогает решить следующие задачи:
- упростить модель с целью лучшего понимания её работы;
- уменьшить время обучения;
- избежать «проклятия размерности»;
- сократить переобучение.
Стоит отличать отбор признаков (feature selection) от извлечения признаков
(feature extraction). Отбор признаков – это выбор подмножества признаков из имеющихся
без преобразования объекта, например, изображение остаётся изображением.
Извлечение признаков – это преобразование объекта, т.е. преобразование отобранных признаков
в пространство более низкой размерности. Например, при извлечении признаков изображение
преобразуется в вектор признаков и фактически перестаёт быть изображением.
При преобразовании объекта, при извлечении признаков, такие измеряемые величины, как длина,
время, вес, цвет, как правило, теряются. Извлечение признаков трансформирует набор первоначально
отобранных признаков в другой набор, более подходящий для машинного обучения.
Хотя отбор признаков формально является частным случаем извлечения признаков,
для отбора признаков применяются собственные уникальные алгоритмы и методы.
Техники отбора признаков можно разделить на три категории: обёртки (wrapper methods),
фильтры (filter methods) и встроенные методы (embedded methods).
Также автоматический отбор признаков заложен в таких ИНС, как автокодировщики.
Часто применяют цепочки методов машинного обучения, когда признаки,
полученные с выхода предыдущего метода, подаются на вход следующего метода.
Самая распространённая ошибка – это провести отбор признаков у всей базы данных до обучения.
Отбор признаков – это неотъемлемая часть процесса обучения, поэтому нужно делать отбор
признаков независимо для обучающей и для проверочной выборок. Если этого не сделать и
провести отбор признаков у всей базы данных, то в данные непреднамеренно будет внесено
искажение, что приведёт к переобучению. Например, если сделать отбор признаков до проведения
k-кратной перекрёстной проверки (смотрите следующий раздел «Обучение модели»), тогда информация
из проверочной (validation) и из тестовой (test) выборок будет использована при обучении в
обучающей (train) выборке.
В этом случае проверочная и тестовая выборки будут участвовать в отборе признаков
для обучающей выборки, а обучающая выборка будет участвовать в отборе признаков для проверочной
и тестовой выборок. Но проверочная, тестовая и обучающая выборки должны быть независимыми,
иначе данные станут искажёнными. Значит отбор признаков должен проводиться независимо
для обучающей и проверочной выборок на каждой итерации k-кратной перекрёстной проверки,
а также независимо для обучающей и тестовой выборок на этапе разделения данных на две части.
Например, такой признак, как отклонение от средней площади квартиры, должен определяться
независимо для обучающей, проверочной и тестовой выборок, а не для всей базы данных квартир
целиком.
Извлечение признаков (feature extraction)
Извлечение признаков связано с уменьшением размерности пространства признаков.
Признаки могут быть извлечены из данных «как есть»: вес, рост, возраст, число покупок,
RGB пиксели на изображении и т.д.
Признаки могут быть спроектированы исходя из опыта и интуиции. Например, уход клиента
может быть связан с количеством обращений в техподдержку, значит, можно выделить признак
«число обращений в техподдержку».
Признаки могут быть извлечены автоматически с помощью интеллектуального анализа данных
(data mining). Часто автоматически извлечённые признаки бывают лучше,
чем разработанные вручную.
Для сложных объектов уже есть готовые «классические» техники извлечения признаков:
SVM, SIFT, HoG, преобразование Хафа, PCA, MFCC и т.д.
ИНС умеют автоматически извлекать признаки. Результатом работы свёрточной ИНС является
вектор признаков (descriptor, «дескриптор»), который представляет собой набор чисел,
характерный для данного класса объектов. Найденные вектора признаков подаются на классификатор
для разбиения их на классы. Классификатором часто является другая ИНС, например, полносвязные
слои нейронов (fully connected layers), а также любые алгоритмы классификации, например, SVM,
k-NN, логистическая регрессия, наивный байесовский классификатор и т.д.
Процесс отбора и извлечения признаков для изображений представлен на рисунке 2.9:
Рис. 2.9 – Отбор и извлечение признаков
Проектирование признаков (feature engineering)
Существует множество техник, которые позволяют заметно увеличить качество разрабатываемых
алгоритмов. Одна из таких техник – это проектирование (создание, разработка) признаков
(feature engineering). В то время, как методы отбора признаков хорошо изучены и уже существует
большое количество алгоритмов для этого, задача создания признаков является своего рода
искусством и часто является самым сложным этапом машинного обучения.
Например, с помощью линейной регрессии можно прогнозировать цену дома, как линейную комбинацию
длины и ширины дома. Но цена дома в первую очередь зависит от его площади, которая никак
не выражается через линейную комбинацию длины и ширины. Качество алгоритма увеличится,
если длину и ширину заменить на их произведение. Тем самым получается новый признак,
который заметно влияет на цену, а пространство признаков сокращается: вместо двух признаков
длины и ширины теперь один признак – площадь.
Сложно придумать метод, который для любой задачи давал бы технику построения признаков.
Автоматизация построения признаков стала новой темой исследований.
Например, Deep Feature Synthesis алгоритм по автоматическому построению признаков
от исследователей Массачусетского технологического института, который распространяется
как библиотека с открытым исходным кодом под названием Featuretools.
В качестве признака можно взять результат работы других алгоритмов.
Например, при решении задачи классификации можно сначала решить задачу кластеризации
и в качестве признака взять кластер объекта.
Оценка потенциальной пригодности признаков (созданных или отобранных) проводится
последовательным независимым тестированием каждого признака с помощью
t-теста или z-теста,
где определяется статистическая значимость признака. Данная оценка может быть выполнена
с помощью программного обеспечения Statistica или на языках программирования
R, Python, Delphi, C++ и т.д. с дополнительными библиотеками статистического анализа.
Следует помнить, что корректность t-теста обеспечивается
только в случае Гауссовского распределения значений признака. Поэтому желательно
провести предварительный тест на нормальность распределения значений признака.
Наглядным способом оценки информативности признаков является визуализация объектов (изображений)
как точек в N-мерном пространстве признаков путём редуцирования
размерности до двух методом многомерного масштабирования (Multi-Dimensional Scaling, MDS)
с последующим анализом получаемых диаграмм рассеяния (scatterplots) при варьировании признаков.
Визуализация позволяет оценить степень пересечения классов, идентифицировать резко выделяющиеся
объекты, сделать предварительную оценку и т.д.
Другое семейство способов отбора основано на непосредственном использовании признаков
для классификации объектов и вычисления важности (веса) каждого признака с точки зрения степени
полезности для классификации (метод случайных лесов, генетические алгоритмы, ИНС и др.).
Желательно, чтобы набор признаков был взаимно не коррелируемым,
т.е. чтобы признаки не зависели друг от друга.
Часто, чтобы эффективно решить задачу, необходимо быть экспертом в этой области и понимать,
какие параметры влияют на конкретную целевую переменную. Каждый знает,
что цена квартиры зависит в первую очередь от площади, однако в других предметных областях
такие заключения делать достаточно сложно.
Также стоит помнить теоремы об отсутствии бесплатных обедов: «No free lunch theorems».
Смысл этих двух математических теорем в том, что не существует алгоритма поиска, алгоритма
оптимизации или алгоритма обучения с учителем, который «работает» лучше других
на всём множестве задач. Если некоторый алгоритм работает лучше (быстрее, точнее)
на одних задачах, значит, на других задачах он будет хуже.
Т.е. способ решения задачи неотделим от данных, применяемых в этой задаче.
Преобразования признаков (feature transformations)
В машинном обучении существует большое количество преобразований признаков:
монотонное преобразование, изменение распределения, центрирование, регуляризация,
выделение главных компонент, объединение (bundling), дискретизация, масштабирование,
нормализация и т.д. [2.13]. Примеры преобразования признаков изображены на рисунке 2.10.
Рис. 2.10 – Примеры преобразования признаков
Целей у преобразований признаков много и все они разные для разных преобразований:
исследование данных, подготовка данных для конкретного метода машинного обучения,
устойчивость к шумам и выбросам, создание новых признаков, повышение точности и т.д.
Монотонное преобразование признаков критично для одних алгоритмов и не оказывает влияния
на другие. Нечувствительность к монотонному преобразованию признаков является одной из причин
популярности деревьев решений (decision trees) и всех производных алгоритмов (случайный лес,
градиентный бустинг и т.д.), потому что не все исследователи умеют и хотят работать
с преобразованиями признаков, а алгоритмы на основе деревьев решений устойчивы к необычным
распределениям.
Например, нужно предсказать стоимость квартиры по двум признакам – удалённости от центра
и количеству комнат. Количество комнат редко превосходит 5, а расстояние от центра
в больших городах измеряется десятками тысяч метров. В результате метод ближайших соседей (kNN)
не будет работать, потому что квартиры не будут группироваться по комнатам,
а только по расстоянию до центра города. В этом случае необходимо использовать одну и ту же
метрику, т.е. преобразовать метры и комнаты в безразмерные величины с одной и той же плотностью
распределения значений. Но это не всегда возможно, так как по некоторым метрикам нельзя
или трудно провести оптимизацию (AUC, NDCG).
ИНС получили такую большую популярность, потому что они проектируют, извлекают и преобразуют
признаки автоматически. Однако нужно помнить про правило «Мусор на входе – мусор на выходе»,
когда даже самая лучшая ИНС не сможет работать с плохо подготовленными данными.
Обучение модели
Разбиение данных для обучения и оценки
Когда данные подготовлены, они разбиваются случайным образом на две части:
для обучения (обучающая выборка, train set) и для оценки качества (тестовая выборка, test set).
Данные для оценки качества не участвуют в обучении. Это необходимо по двум причинам.
Во-первых, если оценивать качество на той же выборке, на которой обучалась модель,
то результаты всегда будут завышенными. При использовании обученной модели на реальных данных
её точность снизится. Чтобы узнать насколько снизится точность на реальных данных,
используются данные для тестирования, которые не участвовали в обучении.
Во-вторых, модель может переобучиться и, чтобы вовремя заметить переобучение, периодически
проводят оценку качества на данных для тестирования, которые не участвуют в обучении.
Метод разбиения данных на обучающую и тестовую выборки называется
методом удержания (holdout method).
Как правило, данных для обучения ИНС не бывает слишком много. Не помогает даже «раздутие»
данных с помощью аугментации. Часто не хватает нужных данных в каком-либо классе.
Например, количество здоровых обычно значительно превышает количество больных.
На сегодня задача сокращения данных для качественного обучения является
главной проблемой развития ИНС.
Чтобы увеличить обучающую выборку применяют способ, который называется
k-кратная перекрёстная проверка (k-fold cross-validation, «кросс-валидация»,
метод перекрёстного или скользящего контроля), который состоит из четырёх шагов.
- Исходная обучающая выборка случайным образом разбивается на
k непересекающихся (разных) примерно равных по размеру
частей. - (k-1) частей применяются для обучения, а оставшаяся одна часть
используется для проверки (валидации или контроля). Данная процедура повторяется
k раз, т.е. происходит k итераций.
Таким образом все данные для обучения используются в проверке. На практике чаще всего
выбирается k = 10, т.е. модель обучается на 9/10 данных
и проверяется на 1/10. - После k итераций строятся k
моделей и соответственно k оценок для ошибки предсказания. - В качестве окончательной оценки ошибки берётся их среднее взвешенное значение.
Когда одна k-кратная перекрёстная проверка завершена, то говорят,
что пройдена одна эпоха. Эпох может быть много. Для этого данные снова случайным образом
разбиваются на k частей, и перекрёстная проверка повторяется
(рисунок 2.11).
Рис. 2.11 – Разбиение данных при обучении:
метод удержания и методы k-кратной перекрёстной проверки (эпохи)
Проверку на переобучение с помощью тестовой выборки желательно совершать после каждой эпохи.
Частным случаем метода перекрёстной проверки является метод перекрёстной проверки с одним
отделяемым элементом (leave-one-out cross-validation, LOOCV), при котором величина проверочной
выборки равна одному элементу. Метод с одним отделяемым элементом является самым точным,
но требует много времени и компьютерных ресурсов.
Кроме методов удержания и k-кратной перекрёстной проверки существует множество методов
повторного взятия выборки (resampling methods), рассмотрение которых выходит за рамки
этой главы. Однако цель всех этих методов одна – увеличить объём данных для обучения,
не ухудшая качества обучения.
Будьте внимательны: отбор, извлечение и преобразование признаков для обучающей, проверочной
и тестовой выборок должны быть независимыми. Например, нахождение среднего роста для обучающей
выборки должно быть независимым от нахождения среднего роста для проверочной выборки.
Если находить средний рост по всем данным и использовать его в преобразовании параметров,
а потом уже разделять данные на обучающую и проверочную выборки, то информация из проверочной
выборки будет участвовать в обучении, и, таким образом, результаты обучения будут искажены.
Процесс обучения
Обучение происходит на тренировочных данных (train set). Обучение может означать подстройку
каких-то численных параметров модели без изменения её структуры (чаще) или изменение структуры
самой модели (реже).
Во всех ИНС есть гиперпараметры – это значения, которые нужно подбирать вручную,
эмпирически, методом проб и ошибок. На данный момент никто не может дать точный математический
ответ для всевозможных задач машинного обучения:
- сколько данных нужно для обучающей выборки;
- сколько времени будет проходить обучение;
- на сколько частей разбивать тренировочную выборку;
- оптимальное количество скрытых слоёв;
- количество нейронов в каждом слое;
- количество синапсов в каждом нейроне;
- размер ядер свёртки и шаг свёртки для свёрточных ИНС;
- какую метрику взять для оценки качества обучения и т.д.;
потому что не существует теории и математического аппарата для вычисления точных значений
гиперпараметров. Существуют лишь общие рекомендации, например, не стоит делать ИНС
с 1000 нейронов для решения простых задач. Обычно для достижения успеха требуется испытать
разные варианты одной модели или даже модели различных типов. Экспериментируйте!
Как правило, подобранные значения гиперпараметров не меняются во время обучения и
использования ИНС. Каждая архитектура ИНС имеет свой уникальный набор гиперпараметров,
который требуется подобрать и настроить вручную, если требуется сделать новую ИНС.
Чем больше гиперпараметров, тем труднее настроить ИНС.
Оценка качества обучения
Оценка качества является прикладной задачей анализа данных. Точность и качество работы
алгоритма в машинном обучении измеряется метрикой качества. Метрика – это правило
определения расстояния между любыми двумя точками. Каждый объект может быть представлен,
как точка в некотором многомерном (метрическом) пространстве. В общем, основная задача
машинного обучения как раз и заключается в представлении объектов в виде точек
в многомерном пространстве и определении метрики, т.е. расстояния между этими точками.
Разные задачи подразумевают различные метрики качества. Условно выделяют четыре класса метрик,
которые применяются в машинном обучении и на практике редко соответствуют друг другу:
бизнес-метрики, онлайн-метрики, офлайн-метрики, метрики обучения ИНС. Желательно использовать
одну и ту же метрику для обучения и оценки качества, но это не всегда возможно.
Бизнес-метрики важны для рынка, финансового планирования, построения бизнес-модели и направлены
на измерение доходов и потерь: ключевые показатели эффективности (key performance indicators,
KPI), лояльность и удержание клиентов, стоимость получения клиента, скорость оттока клиентов,
коэффициенты производительности и т.д.
Онлайн-метрики доступны в работающей системе в реальном времени. Например, среднее время
просмотра сайта пользователем, количество просмотров страницы, самые популярные товары
в данный момент, котировки акций на бирже, курсы валют, поисковые запросы и т.д.
Офлайн-метрики – это метрики, которые можно посчитать на исторических данных, т.е. данных,
которые были измерены в прошлом и хранятся отдельно от работающей системы в логах, записях,
базах данных и т.д.: среднеквадратичное отклонение (root-mean-square error, RMSE),
среднее абсолютное отклонение (mean absolute error, MAE), средняя абсолютная процентная
погрешность (MAPE), средняя процентная ошибка (MPE), коэффициент детерминации
(R2, R-квадрат) и т.д. К офлайн-метрикам также относятся различные метрики качества
бинарной классификации: чувствительность, специфичность
(см. формулу 2.5), аккуратность (accuracy),
площадь под ROC-кривой (ROC AUC), F-мера (представляет собой гармоническое среднее
между точностью и полнотой) и др.
Метрики обучения ИНС – это различные функции потерь искусственных нейронных сетей:
логарифмическая потеря (Log Loss, Cross Entropy Loss), минимакс (MinMax Rule),
ошибка перекрестной проверки (CV error), матрицы неточностей и т.д.
В случае многоклассовой классификации обычно применяется категорийная кросс-энтропия
(categorical cross-entropy).
Выбросы (аномальные значения) могут сильно исказить метрику. Поэтому желательно использовать
устойчивую к выбросам метрику либо отсеивать выбросы. Например, медиана устойчивее к выбросам,
чем арифметическое среднее. Более того, каждый сигнал имеет в себе шум даже самый «чистый».
Одним из критериев хорошего алгоритма является его устойчивость к шумам.
Регуляризация (regularization) – это один из способов сделать алгоритм устойчивым
к шумам и выбросам.
Регуляризация является основным методом из категории встроенных методов (embedded methods)
отбора признаков (смотрите подраздел «Отбор признаков»). Существуют различные её разновидности,
но основная идея в том, чтобы добавлять некоторую дополнительную информацию к условию с целью
решить некорректно поставленную задачу или предотвратить переобучение. Эта информация
часто имеет вид штрафа за сложность модели. Например, это могут быть ограничения гладкости
результирующей функции или ограничения по норме векторного пространства
(рисунок 2.12).
Рис. 2.12 – Пример регуляризации
Если классификатор бинарный, т.е. имеет только два класса, тогда для оценки качества его работы
можно применить таблицу неточностей (table of confusion):
| Категория класса i | Экспертная оценка | ||
| Положительная | Отрицательная | ||
| Оценка системы | Положительная | TP | FP |
| Отрицательная | FN | TN |
Таблица неточностей 2.2 фактически отображает рисунок 2.8 в виде матрицы размером 2×2.
Значения, которые расположены на диагонали матрицы, являются правильными ответами модели.
Все недиагональные значения – это неправильные ответы.
Если количество классов классификатора больше двух, тогда метрикой качества классификации
может быть матрица неточностей (confusion matrix), также известная как матрица ошибок
(error matrix), которая представляет собой таблицу визуализации производительности алгоритма
классификации при обучении с учителем. При обучении без учителя эту матрицу обычно называют
матрицей соответствия (matching matrix). В таблице 2.3 показаны результаты классификации
по трём классам.
| Классификация трёх классов | Реальность | |||
| Кот | Собака | Кролик | ||
| Оценка системы | Кот | 5 | 2 | 1 |
| Собака | 3 | 3 | 2 | |
| Кролик | 1 | 1 | 11 |
Каждая строка матрицы неточностей представляет экземпляры в прогнозируемом классе,
т.е. результат работы классификатора, в то время как каждый столбец представляет экземпляры
в реальном классе, т.е. реальность либо некую экспертную оценку. Диагональные элементы матрицы
неточностей являются правильными ответами классификатора. Все недиагональные элементы матрицы
неточностей – это ошибки классификатора. Так классификатор выдал ответ, что обнаружено восемь
картинок котов (сумма значений первой строки матрицы), однако в реальности из восьми картинок
только пять являются правильными ответами, две картинки являются собаками и одна картинка – это
кролик. Всего имеются девять изображений котов (сумма значений первого столбца матрицы).
Три из этих девяти картинок были ложно классифицированы, как собаки, и одно изображение кота
было ложно классифицирована, как кролик.
Матрицу неточностей для каждого конкретного класса можно преобразовать в таблицу неточностей
для бинарного классификатора, например, таблица 2.4.
| Категория класса «Кот» | Реальность | ||
| Кот | НЕ-Кот | ||
| Оценка системы | Кот | TP=5 | FP=2+1=3 |
| НЕ-Кот | FN=3+1=4 | TN=3+2+1+11=17 |
У бинарного классификатора часто есть порог, который можно регулировать, чтобы изменять ошибки
первого (FP) и второго (FN) рода (рисунок 2.13).
Рисунок 2.13 – Порог бинарного классификатора может меняться
Если порог метода на рисунке 2.13 сдвинуть вправо, тогда метод будет правильно определять
больше больных, но одновременно с этим в категорию больных будет попадать больше здоровых людей:
ошибка первого рода увеличивается (FP), ошибка второго рода уменьшается (FN). Если порог метода
сдвинуть влево, тогда метод будет правильно определять больше здоровых, но в категорию здоровых
будет попадать больше больных людей: ошибка первого рода уменьшается (FP), ошибка второго рода
увеличивается (FN).
Где выставить порог, чтобы получить оптимальный результат? Всё зависит от цены ошибки,
которая различна для разных задач. Если важно найти всех больных, то можно пренебречь
небольшим количеством ложных диагнозов для здоровых людей. Вместе с тем большое количество
ложных срабатываний спам-фильтра может привести к потере важных писем.
По матрице неточностей, особенно для большого количества классов, трудно оценить модель в целом.
Оценить модель в целом желательно одним числом. Одним из способов оценить модель в целом
является AUC-ROC (или ROC AUC) – площадь (area under curve, AUC) под кривой ошибок
(receiver operating characteristic curve, ROC-curve). Данная кривая представляет из себя линию
от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR)
и является зависимостью верно классифицированных положительных примеров от неверно
классифицированных отрицательных примеров (рисунок 2.14).
Рис. 2.14 – AUC-ROC-кривая и колоколообразные кривые для
плохого, хорошего и отличного методов классификации
Качество разных методов можно сравнивать по площади под кривой ошибок (ROC AUC).
Если площадь равна 0,5 (площадь прямоугольного треугольника), тогда метод является бесполезным,
потому что его прогнозы ничем не отличаются от случайного угадывания или подбрасывания монеты.
Площадь, равная 1,0 – это площадь идеального метода, который никогда не выдаёт ошибочных
прогнозов. Качество реальных методов лежит в пределах отрезка [0,5; 1,0).
Оценка качества обучения зависит от выбранной метрики. Методы машинного обучения разделяются
по типам решаемых задач. Каждый тип решаемых задач имеет свои собственные уникальные метрики:
метрики качества кластеризации, метрики качества классификации, метрики качества ранжирования,
метрики качества регрессии и т.д.
Так, например, метриками качества кластеризации являются похожесть и расстояние, которые
выбираются в зависимости от условий задачи. Похожесть обычно обратная мера к расстоянию.
Средняя похожесть в кластере выше, чем похожесть между элементами разных кластеров.
Среднее расстояние в кластере меньше, чем расстояние между элементами разных кластеров.
Метрики качества ранжирования (Mean Reciprocal Rank, Normalized Discounted Cumulative Gain,
Precision@K, Recall@K и др.) необходимы для решения задач ранжирования и рекомендаций.
Для метрик ранжирования важно учитывать порядок объектов и их позицию в списке.
После оценки качества обучения гиперпараметры ИНС изменяются и процесс обучения повторяется
до достижения удовлетворительного результата.
Процесс решения задачи в машинном обучении
Процесс решения задачи в машинном обучении можно условно разделить на несколько шагов.
-
Изучить задачу, понять, как она может быть сведена к одной из типовых задач
машинного обучения. Например, машинное обучение → обучение с подкреплением → управление
роботом (рисунок 2.15).
Рис. 2.15 – Некоторые типовые задачи машинного обучения
- Определить метод решения задачи средствами машинного обучения.
- Получить данные для обучения. Аугментировать данные.
- Отобрать, извлечь, спроектировать, преобразовать признаки.
- Провести обучение модели.
- Оценить результат с помощью различных метрик (в зависимости от задачи).
- Повторить шаги 1–6 для других методов и параметров.
Существуют общие рекомендации для обучения ИНС [2.14, 2.15, 2.16, 2.17].
Кратко перечислим некоторые из них.
Машинное обучение – это не волшебство, оно не даёт что-то из ничего,
но даёт большее из меньшего. В этом смысле машинное обучение похоже на сельское хозяйство.
Как фермер комбинирует семена с питательными веществами, чтобы вырастить урожай,
так знания комбинируются с данными, а дальше Природа делает за нас основную часть работы.
Прежде, чем обучать машину, разберитесь в задаче сами.
Способ решения задачи неотделим от данных, которые используются в задаче:
«No free lunch theorems».
Сбалансируйте ваши данные, подготовьте их, сделайте данные ценными:
«Мусор на входе – мусор на выходе».
Больше данных лучше, чем более «умный» алгоритм.
Выбросы могут исказить метрику. Фильтруйте их или используйте регуляризацию.
Старайтесь использовать одну и ту же метрику для обучения и оценки качества.
Учитывайте цену ошибки, когда выставляете порог чувствительности метода.
Используйте тестовые данные только для проверки и не используйте их в обучении.
Если на обучающих данных точность ≈ 99%, а на тестовых данных
точность ≈ 50%, то это переобучение.
Корреляция не доказывает причинную связь («Correlation is no proof of causation!»).
Если есть корреляция между утонувшими в бассейне и фильмами с участием Николаса Кейджа,
то этот факт не является поводом для обвинения актёра. Зачем же тогда искать корреляции?
Прогнозные модели используются в качестве руководства к действию, для дальнейшего изучения.
Если мы обнаружим, что пиво и подгузники в супермаркете часто покупаются вместе, возможно,
стоит поместить пиво рядом с секцией подгузников для увеличения продаж.
Экспериментируйте. Комбинация методов лучше, чем выбор одного лучшего метода.
Пробуйте разные методы обучения и способы получения признаков, а особенно их комбинации.
Нет универсального метода для всех задач («There’s no silver bullet»).
Здесь интуиция и творчество так же важны, как и технические навыки, но само
машинное обучение – контринтуитивная дисциплина.
Машинное обучение – это междисциплинарная наука, которая требует от исследователя
широких знаний во многих дисциплинах.
Машинное обучение молодая и активно развивающаяся дисциплина,
поэтому многие материалы есть только на английском языке.
Список литературы
2.1. Krizhevsky A., Sutskever I., Hinton G., ″ImageNet Classification with Deep Convolutional
Neural Networks,″ NIPS’12 Proceedings of the 25th International Conference on
Neural Information Processing Systems, Vol. 1, 2012, pp. 1097–1105.
2.2. Lecun Y., Bottou L., Bengio Y., Haffner P., ″Gradient-based learning applied to document
recognition,″ Proceedings of the IEEE, Vol. 86, No. 11, Nov. 1998, pp. 2278–2324,
doi: 10.1109/5.726791
2.3. He K., Gkioxari G., Dollár P., Girshick R., ″Mask R-CNN,″ IEEE International Conference
on Computer Vision (ICCV), 2017, pp. 2980–2988, arXiv:1703.06870, doi: 10.1109/ICCV.2017.322
2.4. Zeiler M., Krishnan D., Taylor G., Fergus R., ″Deconvolutional networks,″
IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR),
Jun. 2010, pp. 2528–2535, doi: 10.1109/CVPR.2010.5539957
2.5. Goodfellow I., et al., ″Generative adversarial nets,″ NIPS’14 Proceedings
of the 27th International Conference on Neural Information Processing Systems,
Vol. 2, 2014, pp. 2672–2680.
2.6. Elman J., ″Finding structure in time,″ Cognitive Science, Vol. 14, No. 2., 1990,
pp. 179–211, doi: 10.1016/0364-0213(90)90002-E
2.7. Jozefowicz R., Zaremba W., Sutskever I., ″An Empirical Exploration of Recurrent
Network Architectures,″ ICML’15 Proceedings of the 32nd International Conference on
Machine Learning, Vol. 37, Jul. 2015, pp. 2342–2350.
2.8. Greff K., Srivastava K., Koutník J., Steunebrink R., Schmidhuber J., ″LSTM: A search space
odyssey,″ IEEE Transactions on Neural Networks and Learning Systems, Vol. 28, No. 10,
Oct. 2017, pp. 2222–2232, doi: 10.1109/TNNLS.2016.2582924
2.9. He K., Zhang X., Ren S., Sun J., ″Deep residual learning for image recognition,″
IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, 2016,
pp. 770–778, doi: 10.1109/CVPR.2016.90
2.10. Kulkarni T., Whitney W., Kohli P., Tenenbaum J., ″Deep convolutional inverse
graphics network,″ NIPS’15 Proceedings of the 28th International Conference on
Neural Information Processing Systems, Vol. 2, 2015, pp. 2539–2547.
2.11. Simonyan K., Zisserman A., ″Very Deep Convolutional Networks for Large-Scale
Image Recognition,″ arXiv preprint, 2014. arXiv:1409.1556
2.12. Lee H., Grosse R., Ranganath R., Ng A., ″Convolutional Deep Belief Networks
for Scalable Unsupervised Learning of Hierarchical Representations,″ ICML ’09 Proceedings
of the 26th Annual International Conference on Machine Learning, 2009, pp. 609–616,
ISBN: 978-1-60558-516-1, doi: 10.1145/1553374.1553453
2.13. LeCun Y., Bottou L., Orr G., Müller K., ″Efficient BackProp″, ″Neural Networks:
Tricks of the Trade″, chapter 2, Springer-Verlag Berlin Heidelberg, 1998, pp. 9–50,
ISBN: 3-540-65311-2
2.14. Domingos P., ″A Few Useful Things to Know about Machine Learning,″ Communications
of the ACM, Vol. 55, No. 10, Oct. 2012, pp. 78–87, doi: 10.1145/2347736.2347755
2.15. Domingos P., ″The Master Algorithm: How the Quest for the Ultimate Learning Machine
Will Remake Our World,″ Basic Books, New York, NY, 2015, p. 352. ISBN: 978-0465065707
2.16. Bostrom N., ″Superintelligence: Paths, Dangers, Strategies,″ Oxford University Press,
2014, p. 328. ISBN: 978-0199678112
2.17. Herbert A. Simon, ″Spurious Correlation: A Causal Interpretation,″ Journal
of the American Statistical Association, Vol. 49, No. 267, Sep., 1954, pp. 467–479,
doi: 10.1080/01621459.1954.10483515
Он лежит в основе работы иммунной системы [276) — наиболее понятной биологичесюй системы распознавания. Модель селективного обучения Дарвина основана на теории отбора групп нейронов (йзеогу оТ пента! йгопр зе!есйоп). В ней предполагается, что нервная система работает по принципу естественного отбора, с тем отличием от эволюционного процесса, что все действие разворачивается в мозге и только на протяжении жизни организма. Согласно этой теории, основной операционной единицей нервной системы является отнюдь не отдельный нейрон, а локальная группа жестко связанных клеток. Принадлежность отдельных нейронов к различным группам определяется изменениями синаптических весов.
Локальная конкуренция и кооперация клеток обеспечивают локальный порядок сети. Коллекция групп нейронов называется полем или репертуараи (герег!о(ге). Ввиду случайной природы развития нейронной сети группы одного поля хорошо подходят для описания перекрывающихся, но подобных входных образов. За каждый входной образ отвечает одна или несколько групп неюторого поля. Тем самым обеспечивается отклик на неизвестные входные образы, который может оказаться очень важным.
Селекгивное обучение Дарвина отличается от всех других алгоритмов, обычно используемых в нейронных сетях, поскольку в структуре нейронной сети предполагается наличие множества подсетей, из которых в процессе обучения отбираются только те, выходной сигнал которых ближе всего к ожидаемому отклику.
Задачи 163 Это обсуждение можно завершить несколькими замечаниями, касающимися статистического и вероятностного аспектов обучения. ЧС-измерение зарекомендовало себя как основной параметр теории статистического обучения. На нем основаны принцип минимизации структурного риска и вероятностно-корректная в смысле аппроксимации модель обучения (РАС). ЧС-измерение является составной частью теории так называемых машин опорных векторов, которые рассматриваются в главе 6.
По мере ознакомления с материалом настоящей книги читателю еще не раз придется возвращаться к настоящей главе, посвященной основам процессов обучения. Задачи Правила обучения 2.1. Дельта-правило, описанное в формуле (2.3), и правило Хебба, описываемое соотношением (2,9), представляют собой два различных метода обучения.
Укажите различия между этими двумя правилами. 2.2. Правило обучения на основе коррекции ошибок можно реализовать с помощью запрета вычитания желаемого отклика (целевого значения) из фактического выходного сигнала с последующим применением антихеббовского правила ~748). Прокомментируйте зту интерпретацию обучения на основе коррекции ошибок. 2.3.
На рис. 2.27 показано двумерное множество точек. Часть этих точек принадлежит классу С,, остальные — классу Сз. Постройте границу решений, применив правило ближайшего соседа. 2.4. Рассмотрим группу людей, коллективное мнение которых по некоторому интересующему нас вопросу определяется как взвешенное среднее мнений отдельных членов группы. Предположим, что при изменении мнения члена группы в сторону коллективной точки зрения оно приобретает больший вес. С другой стороны, если отдельные члены группы встают в открытую оппозицию коллективной точке зрения, их мнение теряет вес. Эта форма взвешивания эквивалентна управлению с положительной обратной связью, конечным результатом которого является достижение общего консенсуса среди членов группы ~653]. Проведите аналогию между этой ситуацией и постулатом обучения Хебба.
164 Глава 2. Процессы обучения Рис. 2.27. Пример обучающею множества 2.5. Обобщенная форма правила Хебба описывается соотношением Ьшьт(п) = а Г(уь(п))С(х (и)) — ~5 шь;(п)Р(у„(п)), где х,(п) и уь(п) — предсииаптический и постсинаптический сигналы соответственно; г ( ) и С( ) — некоторые функции своих аргументов; Ьшь,(п) — изменение синаптического веса шьу в момент времени п, вызванное сигналамих (п) и уь(п). Найдите точку равновесия и максимальное значение спуска, определяемое этим правилом. 2.6.
Входной сигнал с единичной амплитудой многократно передается через синаптическую связь, начальное значение которой также равно единице. Вычислите изменение значений синаптического веса со временем с помощью следующих правил: а) простой формы правила Хебба (2.9), в предположении, что параметр ско- рости обучения т) = О, 1; б) правила ковариации (2.10) для значений предсинаптической х = 0 и пост- синаптической у = 1.0 активности. 2.7. Синапс Хебба, описываемый соотношением (2.9), предполагает использова- ние положительной обратной связи.
Докажите истинность этого утверждения. Задачи 166 2.8. Рассмотрим гипотезу коварнации для обучения на основе самоорганизации, описываемого выражением (2.10). В предположении эргодичности системы (когда среднее по времени может быть заменено средним по множеству) покажите, что ожидаемое значение Ьтоьз в (2.10) можно представить соотношением Е10аиь,~ = В (Е~уьх,1 — ух). Как можно интерпретировать этот результат? 2.9.
Согласно 1656), постулат Хебба формулируется следующим образом; Ьи ы = з1 (Уь — У,Кх; — х,) + а„ где х; и уь — предсинаптический и постсинаптический сигналы соответственно; а„з1, х, — константы. Предположим, что нейрон и — линейный, т.е. уь — — ~~~ шь х, +аз, где аз — еще одна константа. Предположим, что все входные сигналы имеют одинаковое распределение, т.е. Е 1х,’1 = Е[х ] = и. Пусть С вЂ” матрица коварнацин входного сигнала, элемент у’ которой определяется соотношением с; = Е~(х, — цИхт — 1г)). Найдите Е[Ьюь,).
2.10. Напишите выражение для описания выходного сигнала у, нейрона т’ в сети, показанной на рнс. 2.4. При этом можно использовать следующие переменные: х; — г-й входной сигнал; ш, — синаптический вес связи входа г с нейроном т; сь — вес латеральной связи нейрона Й с нейроном з; с, — индуцированное локальное поле нейрона з; ут = ‘р(пз). Какому условию должен удовлетворять нейрон з, чтобы выйти победителем? 2.11. Решите задачу 2.10 при условии, что каждый выходной нейрон имеет обратную связь с самим собой. 166 Глава 2. Процессы обучения Рис. 2.26.
Блочная диаграмма адаптивной системы изучения естественного языка на уровне семантики 2.12. Принцип латерального торможения сводится к следующему: «близкие нейроны возбуждаются, а дальние — тормозятся». Его можно промоделировать с помощью разности между двумя гауссовыми кривыми. Эти две кривые имеют общую область определения, но положительная кривая возбуждения имеет более крутой и высокий пик, чем отрицательная кривая торможения. Это значит, что модель такого соединения можно описать соотношением И/г ) -а’/ за~ -в’/ за,’ ~/2кгт, т/2пгт, где х — расстояние до нейрона, отвечающего за латеральное торможение. Шаблон Иг(х) используется для сканирования страницы, одна половина которой белая, а другая — черная.
Граница между двумя половинками перпендикулярна оси х. Постройте график изменения выхода процесса сканирования для гг, =5; гта =8 игг, = 1, гт, =2. Парадигмы обучения 2.13. На рис. 2.28 показана блочная диаграмма адаптивной системы изучения естественного языка (адарг)тге 1апйпайе-асс)шз)г)оп зузгеш) [371]. Синаптические связи в нейронной сети, входящей в состав этой системы, усиливаются и ослабляются в зависимости от значения обратной связи, полученной в результате реакции системы на входное возбуждение.
Этот принцип можно рассматривать как пример обучения с подкреплением. Обоснуйте правиль- ность этого утверждения. 2.14. К какой из двух парадигм (обучение с учителем и без него) можно отнести следующие алгоритмы: а) правило ближайшего соседа; б) правило /с ближайших соседей; Задачи 1Б7 в) обучение Хебба; г) правило обучения Больцмана. Обоснуйте свой ответ. 2.15. Обучение без учителя может быть реализовано в кумулятивном и интерак- тивном режимах. Опишите физический смысл этих двух возможностей. 2.16.
Рассмотрим сложности, с которыми сталкивается обучаемая машина при назначении коэффициентов доверия результату игры в шахматы (победа, поражение, ничья). Обьясните понятия временной и структурной задач присваивания коэффициентов доверия в контексте этой игры. 2.17. Задачу обучения с учителем можно рассматривать как задачу обучения с подкреплением, использующую в качестве подкрепления некоторую меру близости фактического отклика системы с желаемым. Опишите взаимосвязь между обучением с учителем и обучением с подкреплением. Память 2.18. Рассмотрим следующее ортонормальное множество ключевых образов, применяемых для построения корреляционной матрицы памяти: х, = [1, О, О, 0] т, хз = [О, 1, О, О] т, хз —— [0,0,1,0] н соответствующее множество запомненных образов: у, = [5,1 0]т = [ — 2,1,0]т, у, = [-2,4,8]т.
а) Вычислите матрицу памяти М. б) Покажите, что эта память обладает хорошими ассоциативными способностями. 2.19. Вернемся к предыдущей задаче построения корреляционной матрицы памяти. Предположим, что применяемый к этой памяти стимул представляет собой зашумленную версию ключевого образа х, вида х = [О, 8; — О, 15; О, 15; — О, 20] т. 168 Глава 2. Процессы обучения а) Вычислите отклик памяти у.
flashcard
в нервной сети есть входные сигналы есть один или несколько скрытых слоев
❮ prev
next ❯
и эти нейроны скрытых слоев воспроизводят Вектор сигнала x(n) и есть только один выходной Yk(n), n это дискретное время или же номер шага итеративного процесса настройки синаптических весов нейрона. и есть желаемый сигнал dk(n)
❮ prev
next ❯
terms list
в нервной сети есть входные сигналы есть один или несколько скрытых слоев
и эти нейроны скрытых слоев воспроизводят Вектор сигнала x(n) и есть только один выходной Yk(n), n это дискретное время или же номер шага итеративного процесса настройки синаптических весов нейрона. и есть желаемый сигнал dk(n)
ek(n) = dk(n) — Yk(n)
он инициализирует механизм управления цель которого применять корректировки к синтетическим Весам. эти изменения нацелены на приближение выходного сигнала Ук(n) к сигналу желаемому dk(n) . и эта цель достигается за счет МИНИМИЗАЦИИ функции стоимости или же индекса производительности E(n)
функция стоимости или же индекс производительности
E(n) = 1/2 * e²k(n)
E(n) — это текущее значение энергии ошибки.
и вот такие корректировки продолжается до тех пор пока система не достигнет устойчивого состояния
и в этой точке процесс обучения останавливается
минимизация функции стоимости E(n)
выполняется по Дельта правилу (видроу хофа) : а есть связь wkj(n) принадлежащая нейрону k, соответствующая элементу xj(n) вектора x(n) на шаге дискретизации n
Дельта правила к синаптическому весу wkj(n)
∆wkj(n) = ñek(n) xj(n)
ñ — это некоторая положительная Константа определяющая скорость обучения и она используется при переходе от шага процесса к другому.
эта корректировка применяемая к синаптическому весу нейрона пропорциональна произведению сигнала ошибки на входной сигнал его вызываний
новое значение для следующего шага дискретизации веса ∆wkj(n)
wkj(n+1) = wkj (n) + ∆wkj(n)
То есть можно рассматривать синаптические веса на на одном шаге wkj (n)и следующем wkj(n+1) как старые и новые значение веса wkj
wkj(n) = z^-1 [wkj(n+1) ]
z^-1 это уже известно оператор единичной задержки другими словами он представляет собой элемент памяти
принципе обучение на основе коррекции ошибок
Это пример замкнутой системы с обратной связью, устойчивость экосистемы определяется параметрами обратной связи, в данном случае нас интересует только коэффициент скорости обучения n. он играет ключевую роль в обеспечении производительности обучения.
логическое умозаключение от общих положений , законов и тому подобного к частному конкретному выводу, то есть выведение одной мысли другой делаемое на основании логических законов
создание, активация, подготовка к работе, определение параметров. приведение программы или устройства в состояние готовности к использованию
это представление непрерывной функции дискретной совокупности её значение при разных наборах аргументов

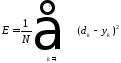
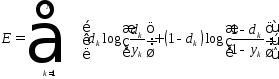

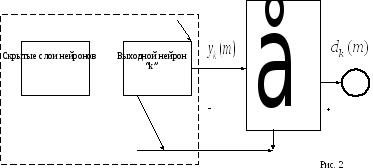
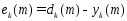
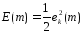
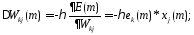
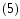
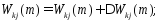

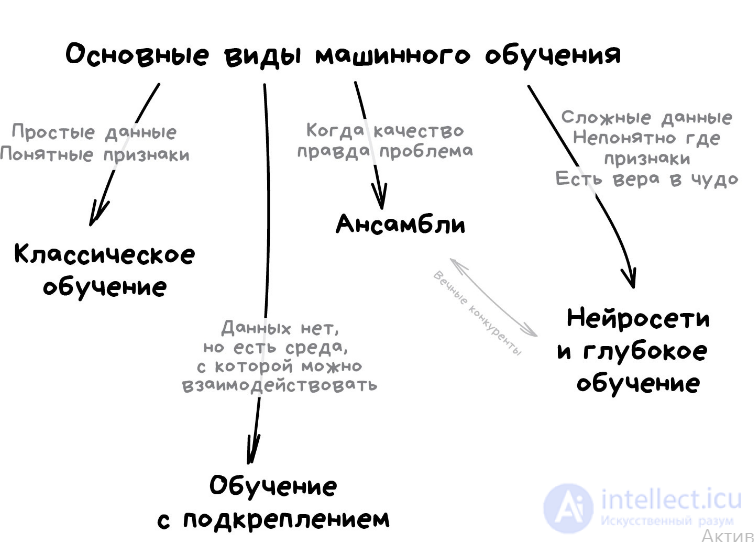
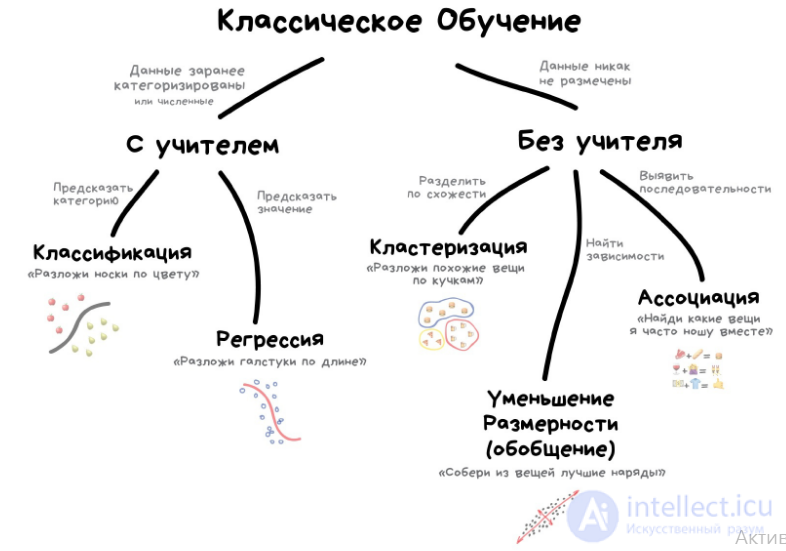
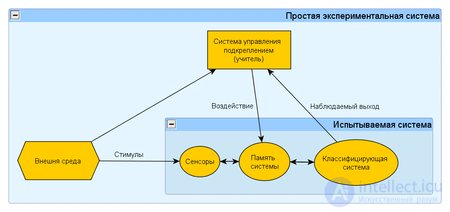
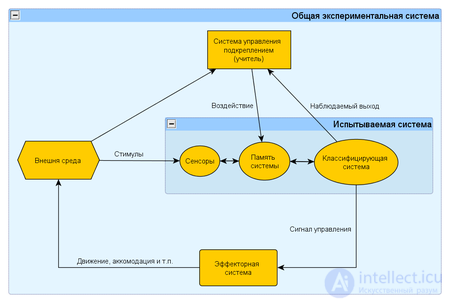
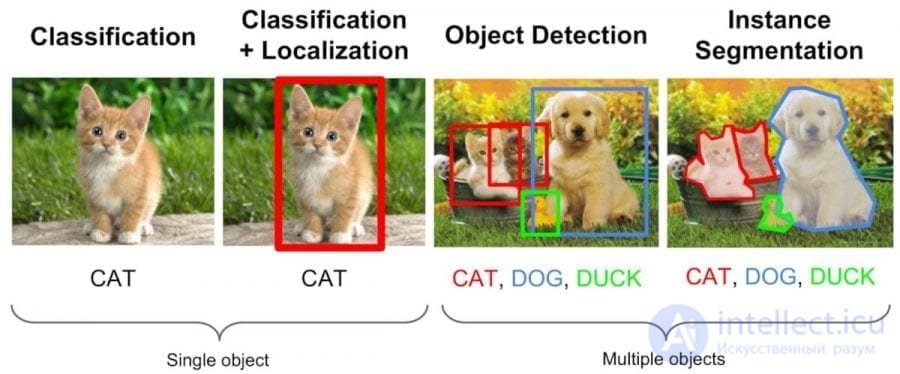
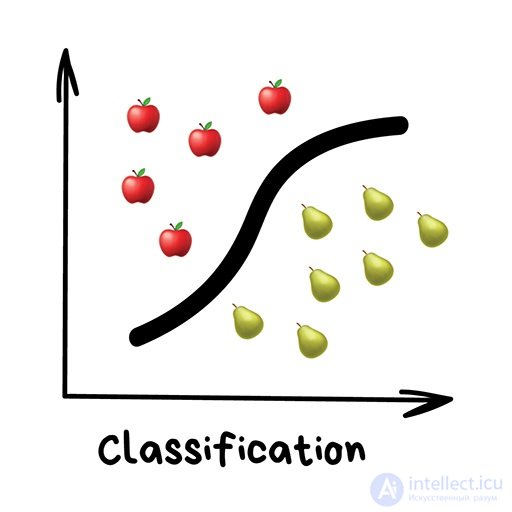
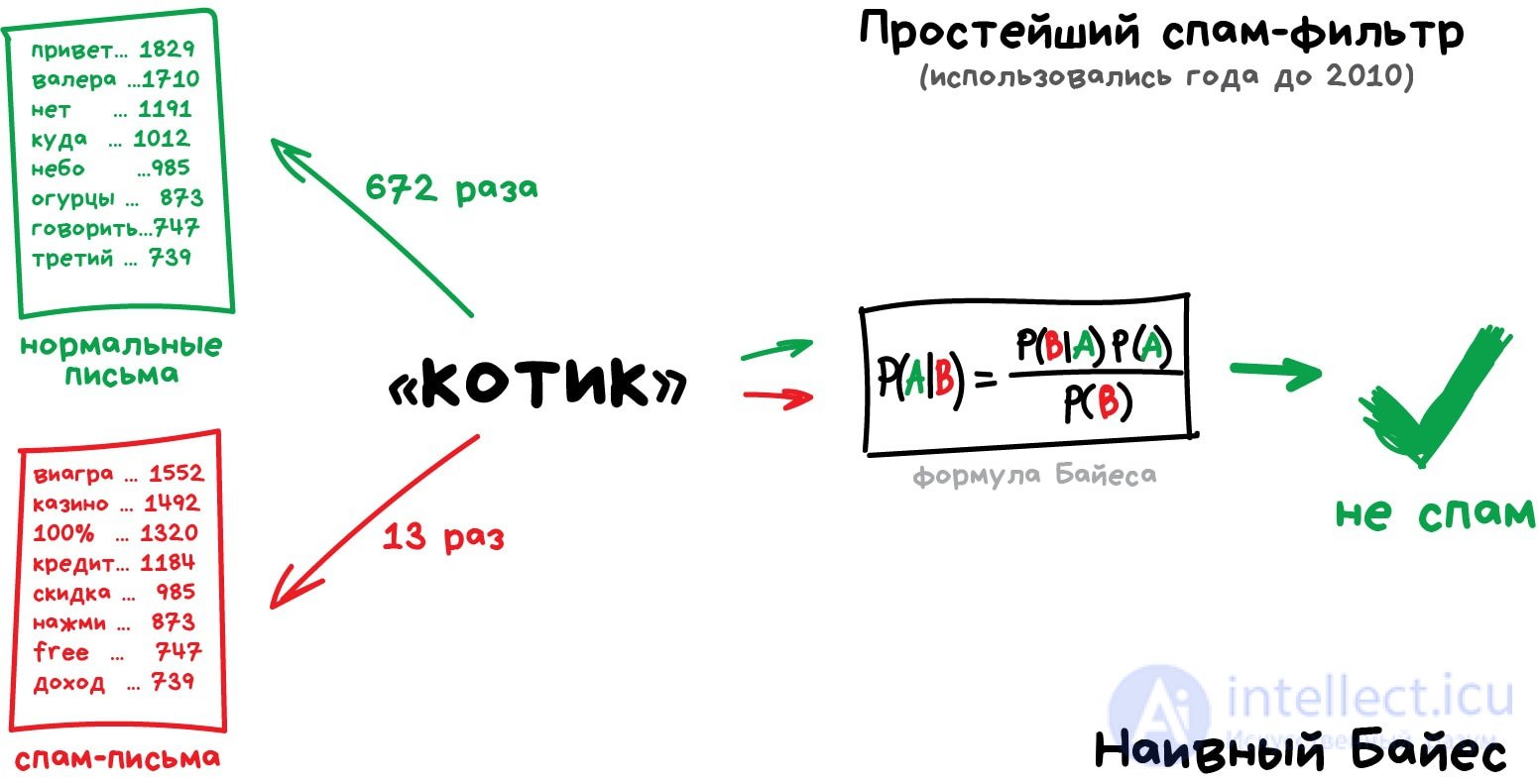

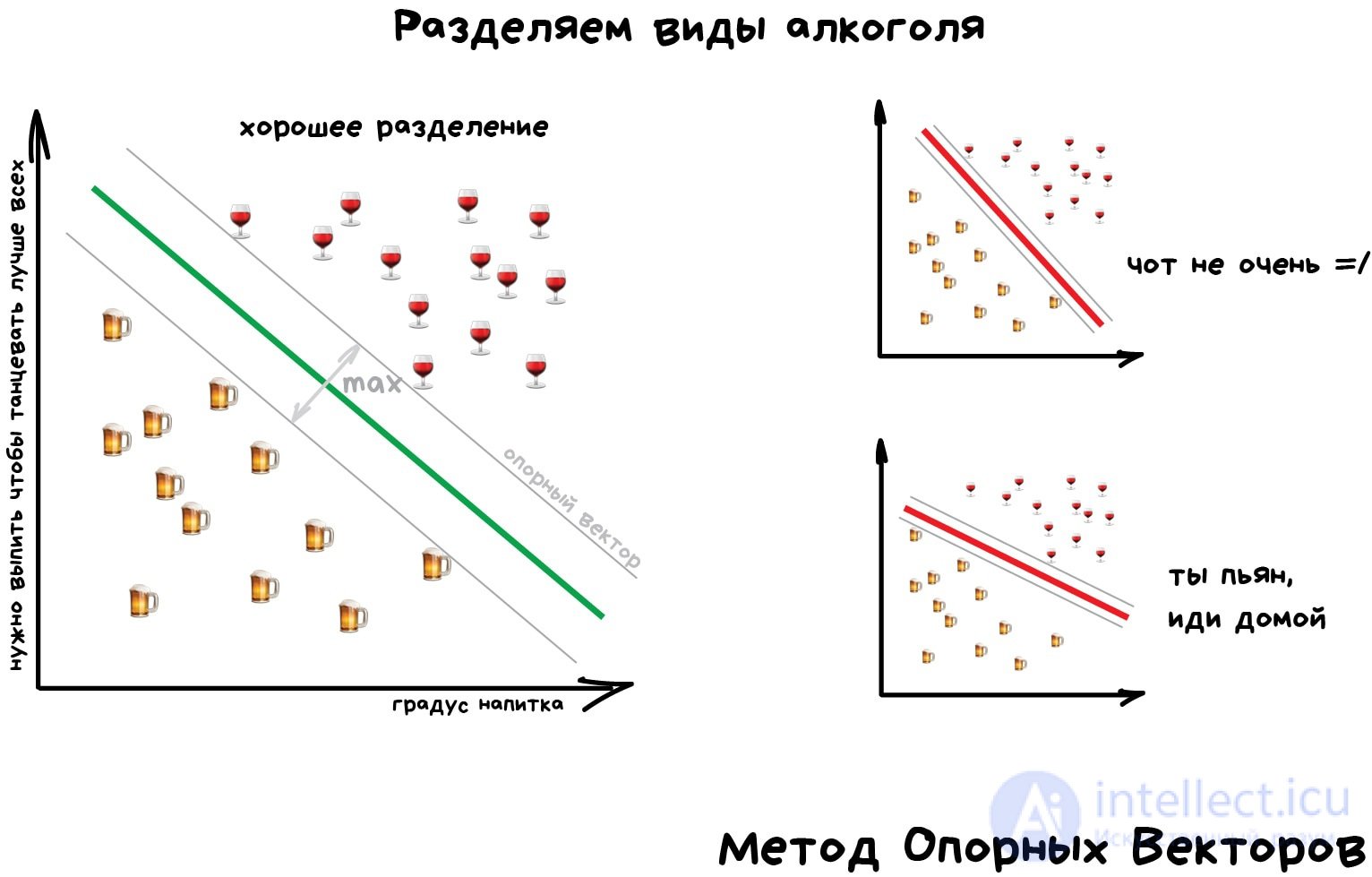
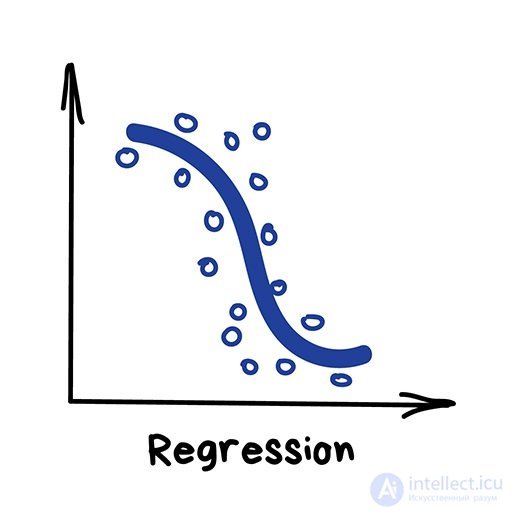


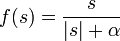
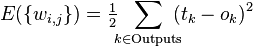
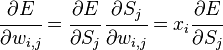
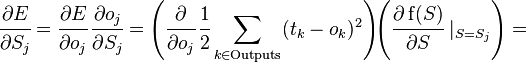
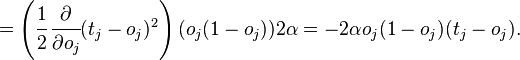

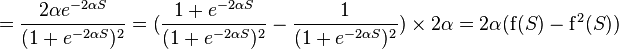
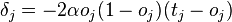
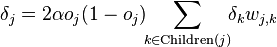

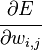

 маленькими случайными значениями,
маленькими случайными значениями, 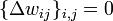
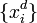 на вход сети и подсчитать выходы
на вход сети и подсчитать выходы 
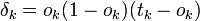 .
. .
.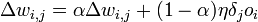 .
.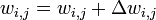 .
. .
.
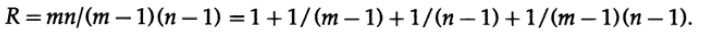
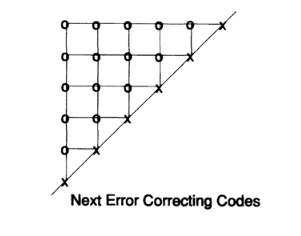








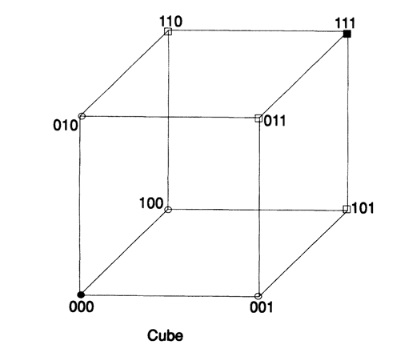


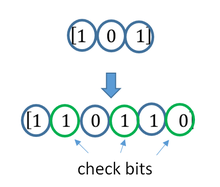




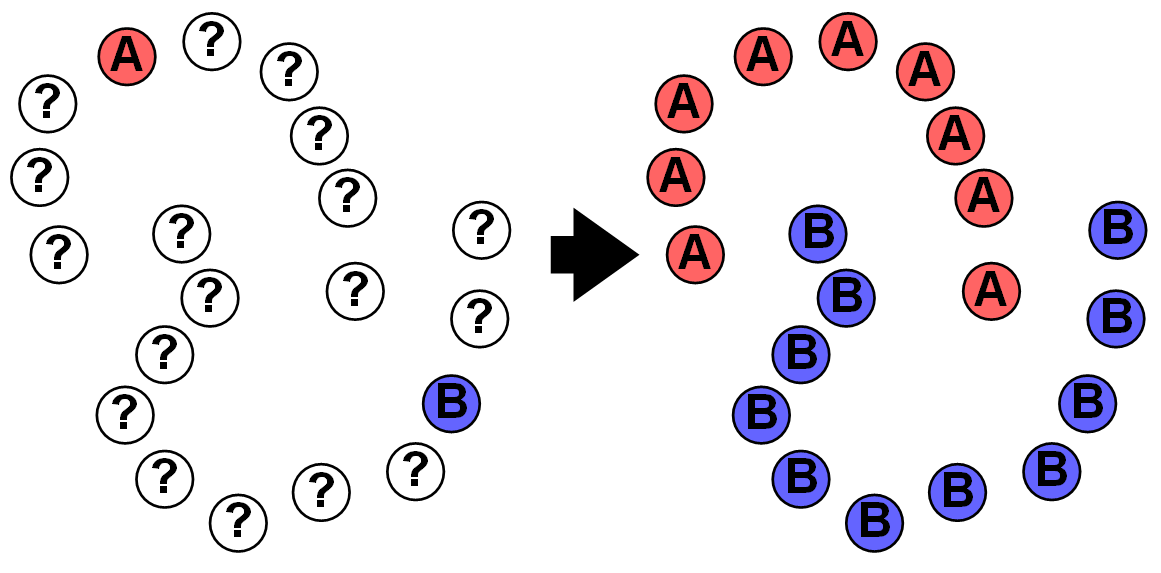
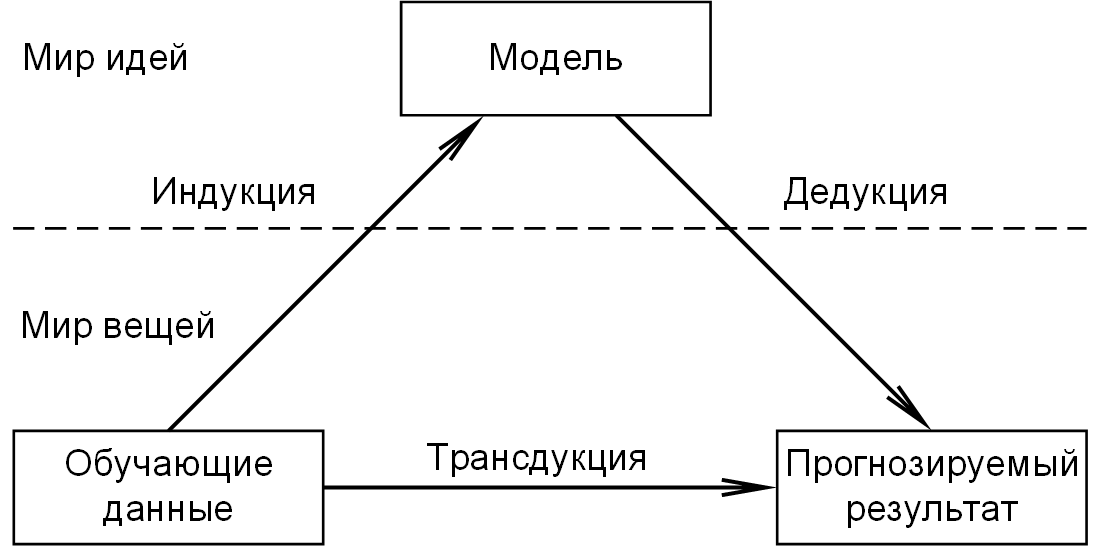
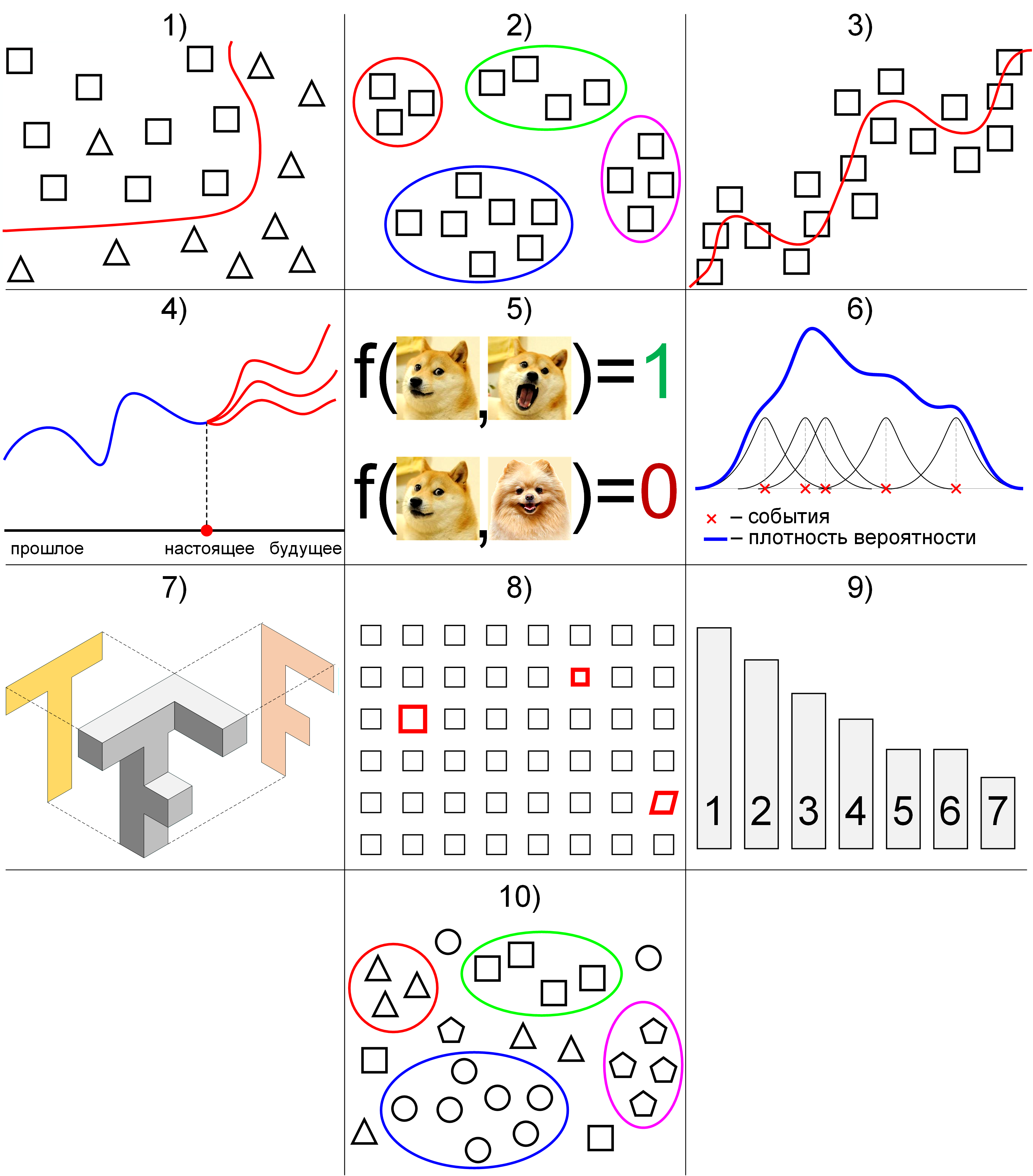
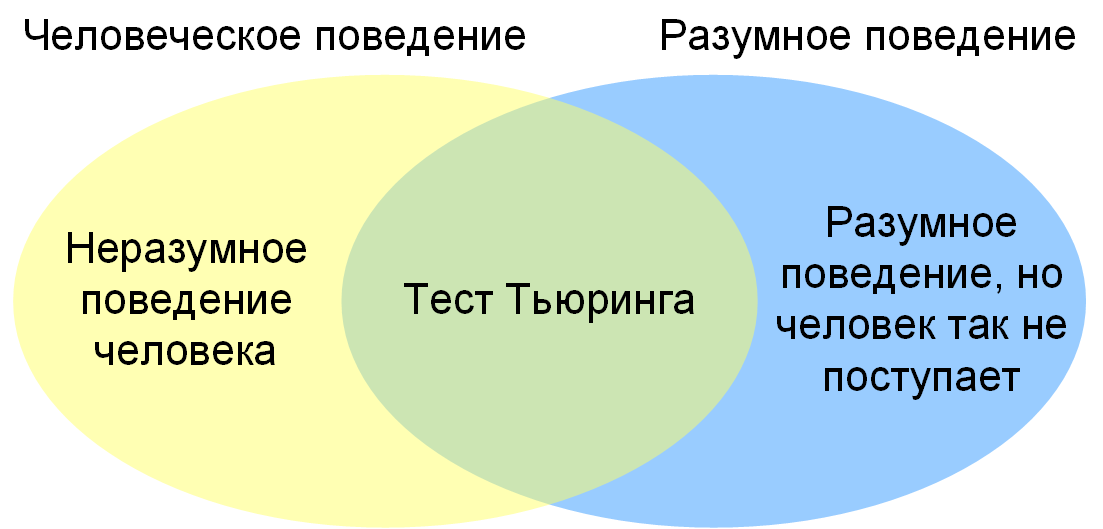
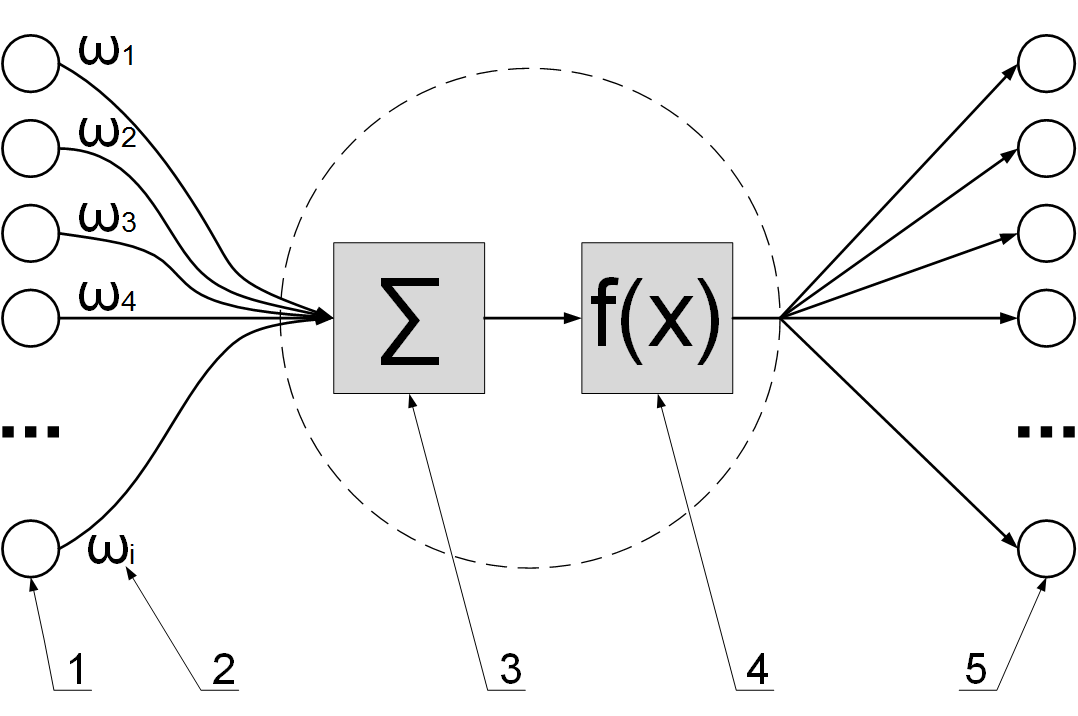
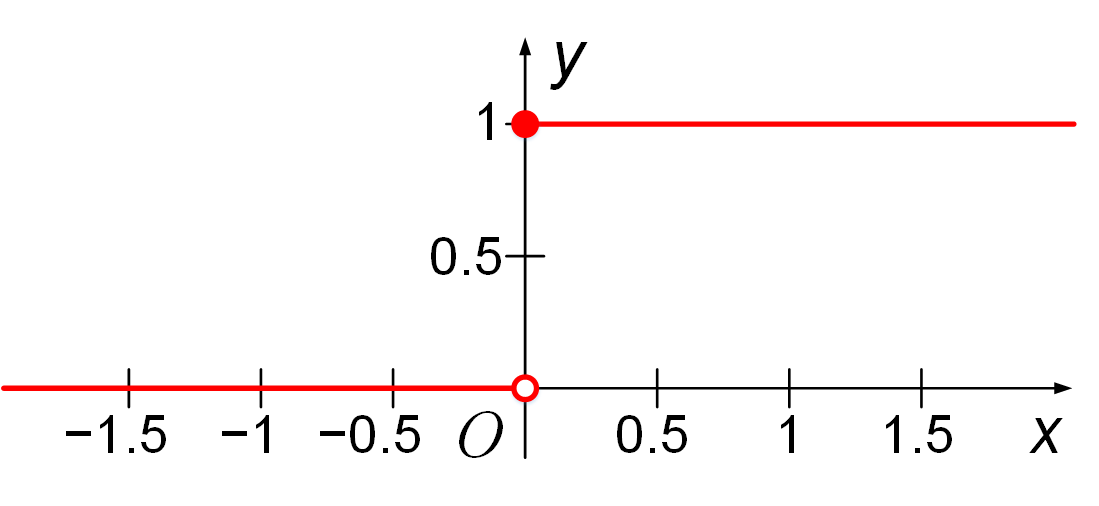

.png)
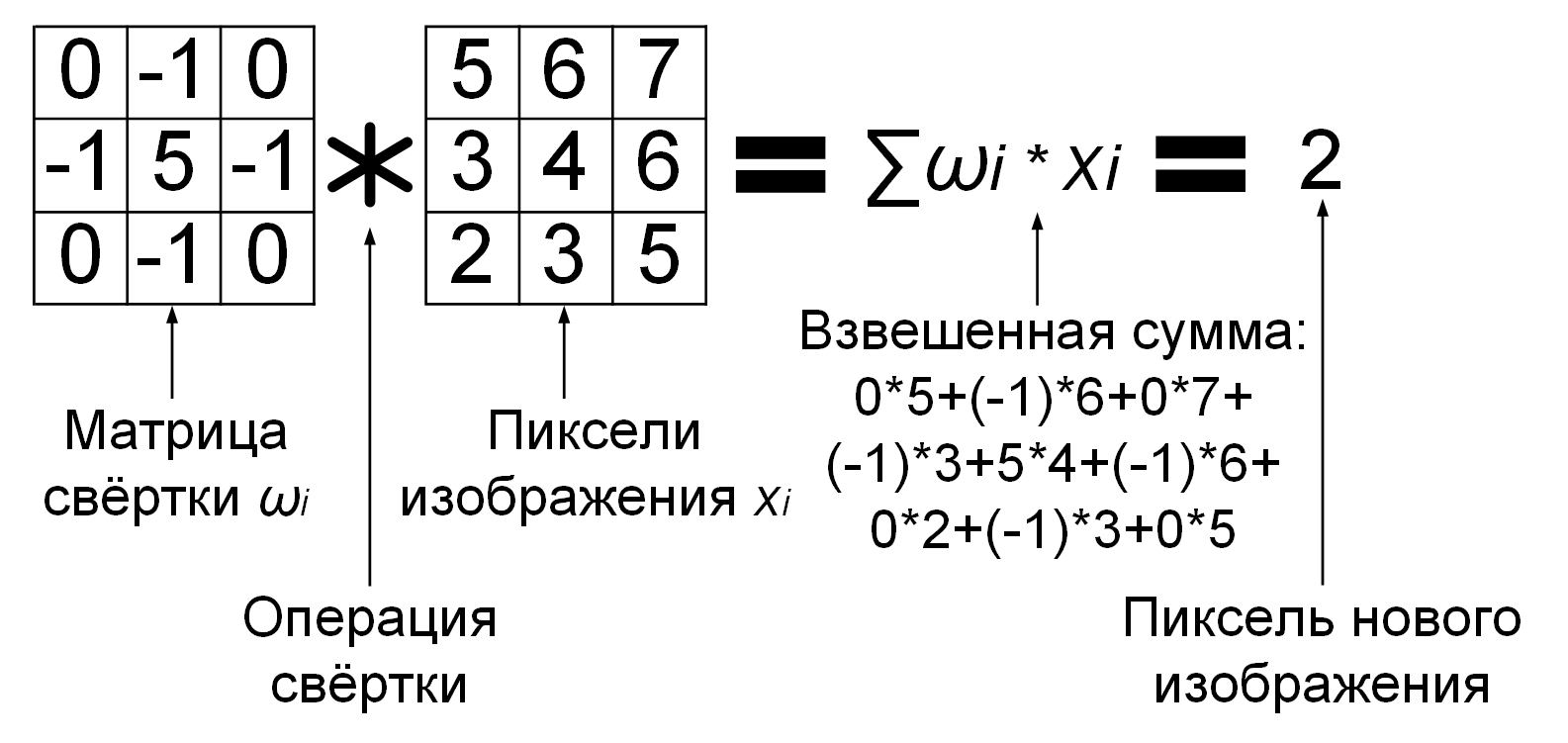
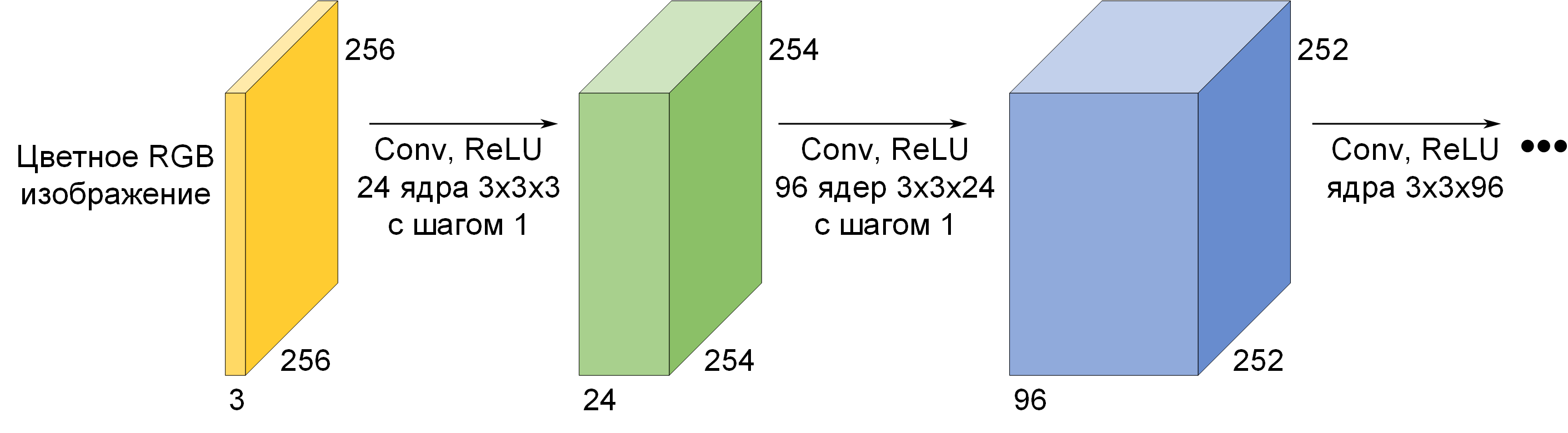
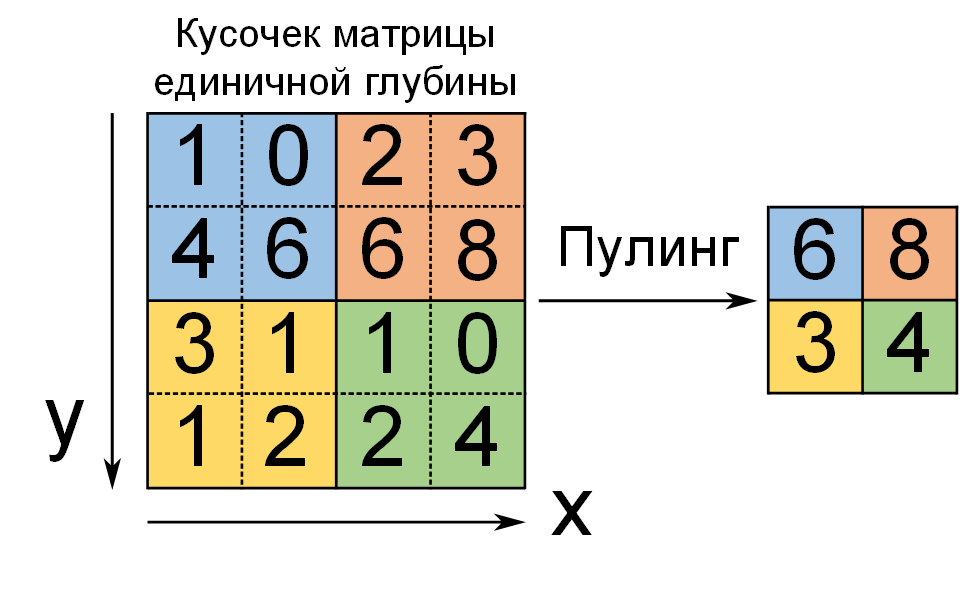
![Автоматическое усложнение признаков в свёрточной ИНС [2.12] Автоматическое усложнение признаков в свёрточной ИНС [2.12]](https://raw.githubusercontent.com/foobar167/articles/master/Machine_Learning/Brochure/data/Ris2.4-Avtomaticheskoye-uslozhneniye-priznakov-v-svortochnoy-NN.png)