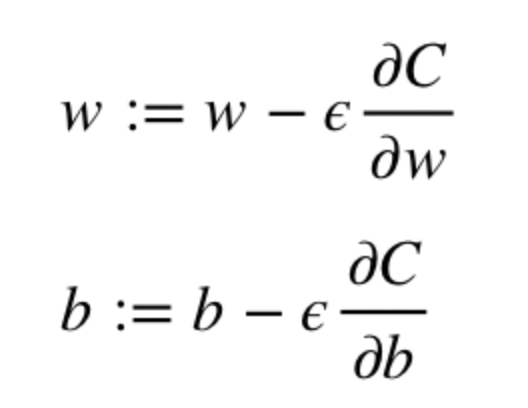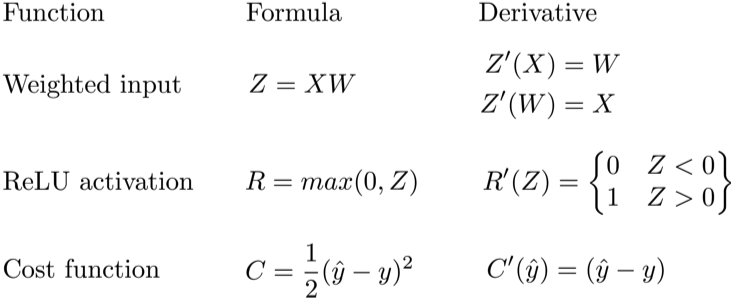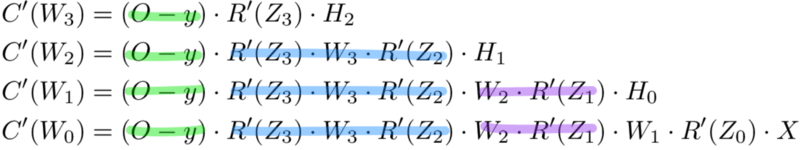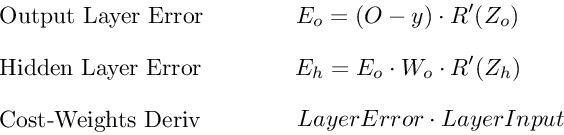Знакомимся с методом обратного распространения ошибки
Время на прочтение
6 мин
Количество просмотров 50K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!
Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.
Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.
Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:
Для l = 3:
W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.
Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.
b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.
Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:
Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:
И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:
Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.
Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:
(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:
(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:
«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:
Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z3)2 и (a3)2:
Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(\ldots (g_1(x)) \ldots))$, то $\frac{\partial f}{\partial x} = \frac{\partial g_m}{\partial g_{m-1}}\frac{\partial g_{m-1}}{\partial g_{m-2}}\ldots \frac{\partial g_2}{\partial g_1}\frac{\partial g_1}{\partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $\frac{\partial g_m}{\partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(\ldots g_1(w_0)\ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(\ldots g_1(w_0)\ldots))\cdot g’_{m-1}(g_{m-2}(\ldots g_1(w_0)\ldots))\cdot\ldots \cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),\ldots,g_{m-1}(\ldots g_1(w_0)\ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(\ldots g_1(w_0)\ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(\ldots g_1(w_0)\ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
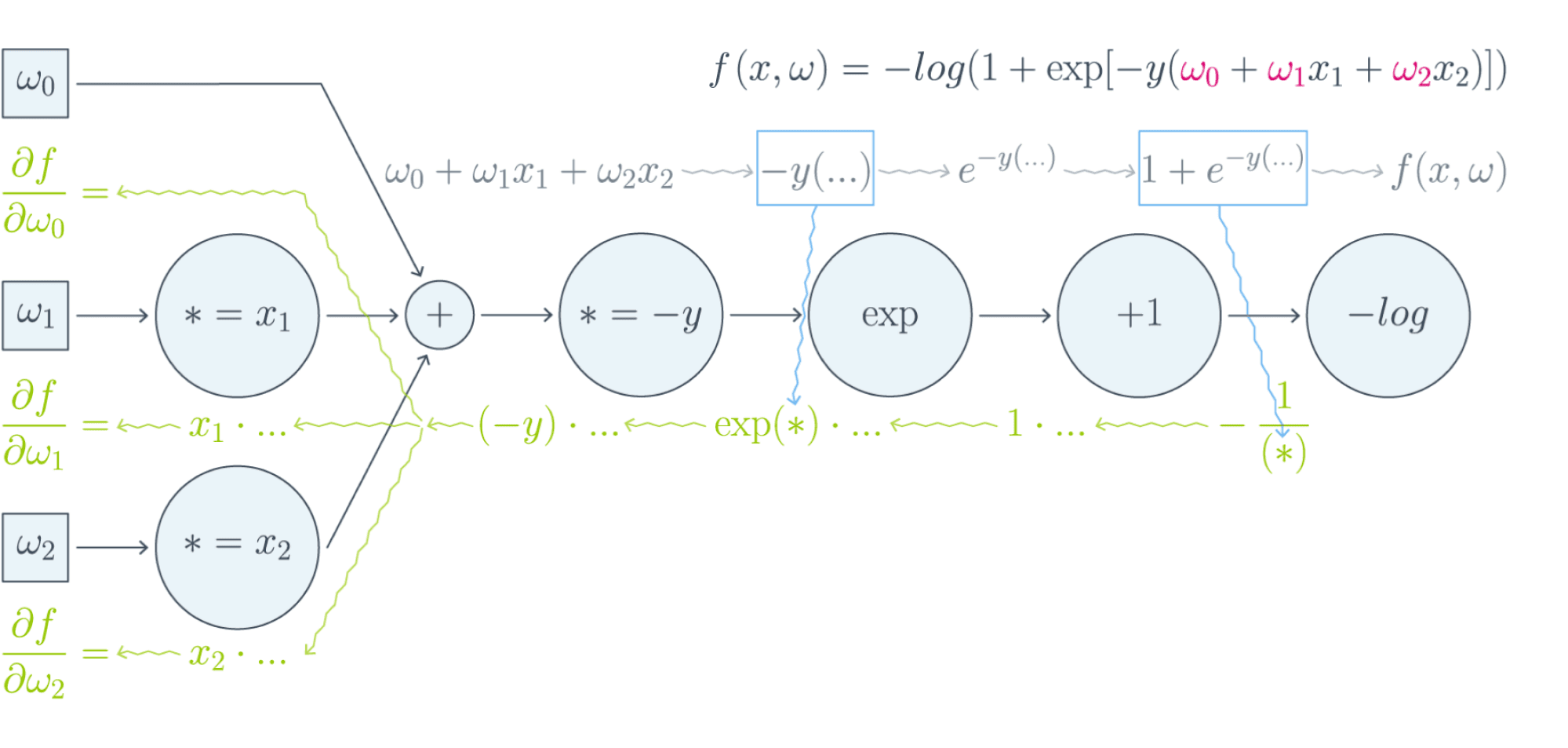
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$\frac{\partial f}{\partial w_0} = (-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$\frac{\partial f}{\partial w_1} = x_1\cdot(-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$\frac{\partial f}{\partial w_2} = x_2\cdot(-y)\cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}\cdot\frac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $N\times M$ и $N\times K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $\frac{\partial\mathcal{L}}{\partial X^{r+1}_{ij}}$ функции потерь $\mathcal{L}$, тогда
$$\frac{\partial\mathcal{L}}{\partial X^{r}_{st}} = \sum_{i,j}\frac{\partial f^{r+1}_{ij}}{\partial X^{r}_{st}}\frac{\partial\mathcal{L}}{\partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $\frac{\partial\mathcal{L}}{\partial X_{ij}^{r+1}}$ и $\frac{\partial\mathcal{L}}{\partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $\frac{\partial f_{ij}^{r+1}}{\partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $\frac{\partial f^{r+1}}{\partial X^{r}}$ рассматривать не как вычисляемые объекты $\frac{\partial f_{ij}^{r+1}}{\partial X_{st}^{r}}$, а как преобразования, которые превращают $\frac{\partial\mathcal{L}}{\partial X_{ij}^{r+1}}$ в $\frac{\partial\mathcal{L}}{\partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx,\ A\in Mat_{n}{\mathbb{R}}\text{ — матрица размера }n\times n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$\left[D_{x_0} (\color{#5002A7}{u} \circ \color{#4CB9C0}{v}) \right](h) = \color{#5002A7}{\left[D_{v(x_0)} u \right]} \left( \color{#4CB9C0}{\left[D_{x_0} v\right]} (h)\right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$\left[D_{x_0} f \right] (x-x_0) = \langle\nabla_{x_0} f, x-x_0\rangle.$$
С другой стороны,
$$\left[D_{h(x_0)} g \right] \left(\left[D_{x_0}h \right] (x-x_0)\right) = \langle\nabla_{h_{x_0}} g, \left[D_{x_0} h\right] (x-x_0)\rangle = \langle\left[D_{x_0} h\right]^* \nabla_{h(x_0)} g, x-x_0\rangle.$$
То есть $\color{#FFC100}{\nabla_{x_0} f} = \color{#348FEA}{\left[D_{x_0} h \right]}^* \color{#FFC100}{\nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $\nabla_{h(x_0)} g$.
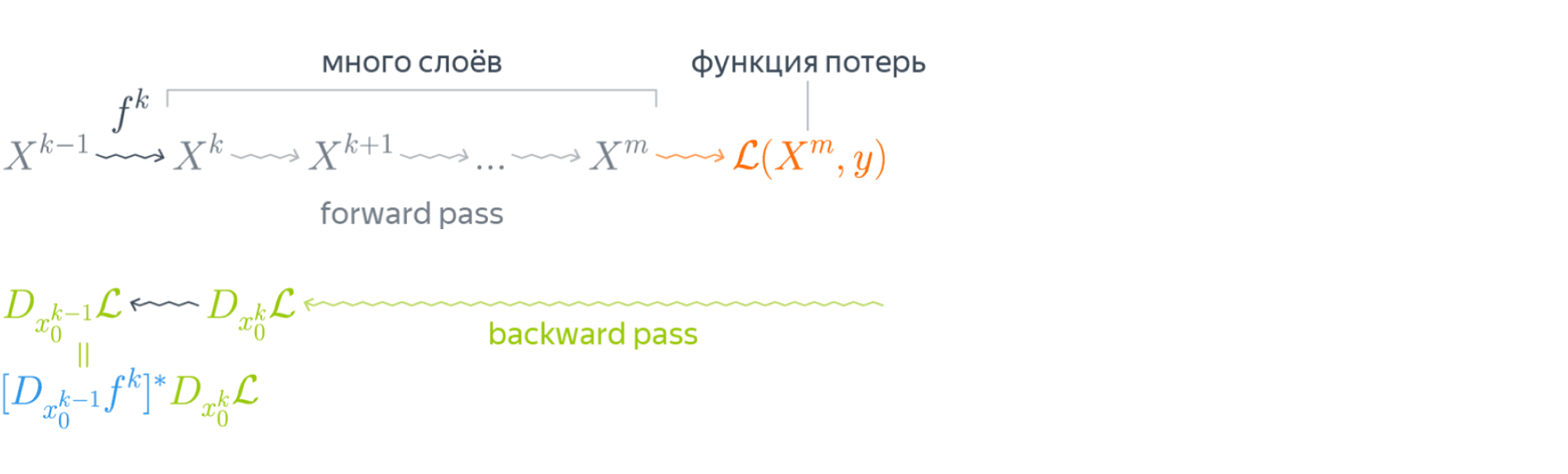
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$v\begin{pmatrix}
x_1 \\
\vdots\\
x_N
\end{pmatrix}
= \begin{pmatrix}
v(x_1)\\
\vdots\\
v(x_N)
\end{pmatrix}$$Тогда, как мы знаем,
$$\left[D_{x_0} f\right] (h) = \langle\nabla_{x_0} f, h\rangle = \left[\nabla_{x_0} f\right]^T h.$$
Следовательно,
$$
\left[D_{v(x_0)} u\right] \left( \left[ D_{x_0} v\right] (h)\right) = \left[\nabla_{v(x_0)} u\right]^T \left(v'(x_0) \odot h\right) =\\
$$$$
= \sum\limits_i \left[\nabla_{v(x_0)} u\right]_i v'(x_{0i})h_i
= \langle\left[\nabla_{v(x_0)} u\right] \odot v'(x_0), h\rangle.
,$$где $\odot$ означает поэлементное перемножение. Окончательно получаем
$$\color{#348FEA}{\nabla_{x_0} f = \left[\nabla_{v(x_0)}u\right] \odot v'(x_0) = v'(x_0) \odot \left[\nabla_{v(x_0)} u\right]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $\frac{\partial f}{\partial x_i} = \sum_j\big(\frac{\partial z_j}{\partial x_i}\big)\cdot\big(\frac{\partial h}{\partial z_j}\big)$. В этом случае матрица $\big(\frac{\partial z_j}{\partial x_i}\big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $\big(\frac{\partial z_j}{\partial x_i}\big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$\left[D_{X_0} f \right] (X-X_0) = \text{tr}, \left(\left[\nabla_{X_0} f\right]^T (X-X_0)\right).$$
Тогда
$$
\left[ D_{X_0W} g \right] \left(\left[D_{X_0} \left( \ast W\right)\right] (H)\right) =
\left[ D_{X_0W} g \right] \left(HW\right)=\\
$$ $$
= \text{tr}\, \left( \left[\nabla_{X_0W} g \right]^T \cdot (H) W \right) =\\
$$ $$
=
\text{tr} \, \left(W \left[\nabla_{X_0W} (g) \right]^T \cdot (H)\right) = \text{tr} \, \left( \left[\left[\nabla_{X_0W} g\right] W^T\right]^T (H)\right)
$$Здесь через $\ast W$ мы обозначили отображение $Y \hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
\text{tr} , (A B C) = \text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$\color{#348FEA}{\nabla_{X_0} f = \left[\nabla_{X_0W} (g) \right] \cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
\left[D_{W_0} f \right] (H) = \text{tr} , \left( \left[\nabla_{W_0} f \right]^T (H)\right)
$$Тогда
$$
\left[D_{XW_0} g \right] \left( \left[D_{W_0} \left(X \ast\right) \right] (H)\right) = \left[D_{XW_0} g \right] \left( XH \right) = \
$$ $$
= \text{tr} , \left( \left[\nabla_{XW_0} g \right]^T \cdot X (H)\right) =
\text{tr}, \left(\left[X^T \left[\nabla_{XW_0} g \right] \right]^T (H)\right)
$$Здесь через $X \ast$ обозначено отображение $Y \hookrightarrow XY$. Значит,
$$\color{#348FEA}{\nabla_{X_0} f = X^T \cdot \left[\nabla_{XW_0} (g)\right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $N\times K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = \left(\frac{e^{x_1}}{\sum_te^{x_t}},\ldots,\frac{e^{x_K}}{\sum_te^{x_t}}\right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $\frac{\partial s_l}{\partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = \frac{e^{x_l}} {\sum_te^{x_t}}$. Нетрудно проверить, что
$$\frac{\partial s_l}{\partial x_j} = \begin{cases}
s_j(1 — s_j),\ & j = l,\
-s_ls_j,\ & j\ne l
\end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$\frac{\partial s_{rl}}{\partial x_{ij}} = \begin{cases}
s_{ij}(1 — s_{ij}),\ & r=i, j = l,\
-s_{il}s_{ij},\ & r = i, j\ne l,\
0,\ & r\ne i
\end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $\nabla_{rl} = \nabla g = \frac{\partial\mathcal{L}}{\partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$\frac{\partial\mathcal{L}}{\partial x_{ij}} = \sum_{r,l}\frac{\partial s_{rl}}{\partial x_{ij}} \nabla_{rl}$$
Так как $\frac{\partial s_{rl}}{\partial x_{ij}} = 0$ при $r\ne i$, мы можем убрать суммирование по $r$:
$$\ldots = \sum_{l}\frac{\partial s_{il}}{\partial x_{ij}} \nabla_{il} = -s_{i1}s_{ij}\nabla_{i1} — \ldots + s_{ij}(1 — s_{ij})\nabla_{ij}-\ldots — s_{iK}s_{ij}\nabla_{iK} =$$
$$= -s_{ij}\sum_t s_{it}\nabla_{it} + s_{ij}\nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$\begin{multline*}
\color{#348FEA}{\nabla_{X_0}f =}\\
\color{#348FEA}{= -softmax(X_0) \odot \text{sum}\left(
softmax(X_0)\odot\nabla_{softmax(X_0)}g, \text{ axis = 1}
\right) +}\\
\color{#348FEA}{softmax(X_0)\odot \nabla_{softmax(X_0)}g}
\end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, \ldots, X^m = \widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
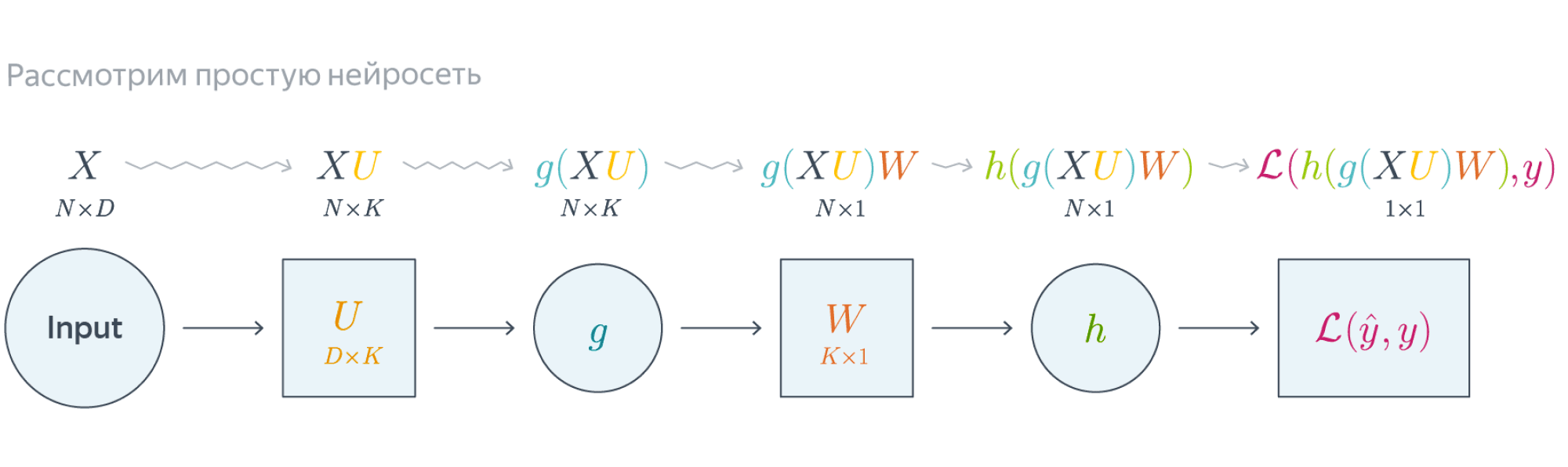
$$\nabla_{W_0}\mathcal{L} = \nabla_{W_0}{\left({\vphantom{\frac12}\mathcal{L}\circ h\circ\left[W\mapsto g(XU_0)W\right]}\right)}=$$
$$=g(XU_0)^T\nabla_{g(XU_0)W_0}(\mathcal{L}\circ h) = \underbrace{g(XU_0)^T}_{k\times N}\cdot
\left[\vphantom{\frac12}\underbrace{h’\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}_{N\times 1}\odot
\underbrace{\nabla_{h\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}\mathcal{L}}_{N\times 1}\right]$$
Итого матрица $k\times 1$, как и $W_0$
$$\nabla_{U_0}\mathcal{L} = \nabla_{U_0}\left(\vphantom{\frac12}
\mathcal{L}\circ h\circ\left[Y\mapsto YW_0\right]\circ g\circ\left[ U\mapsto XU\right]
\right)=$$
$$=X^T\cdot\nabla_{XU^0}\left(\vphantom{\frac12}\mathcal{L}\circ h\circ [Y\mapsto YW_0]\circ g\right) =$$
$$=X^T\cdot\left(\vphantom{\frac12}g'(XU_0)\odot
\nabla_{g(XU_0)}\left[\vphantom{\in_0^1}\mathcal{L}\circ h\circ[Y\mapsto YW_0\right]
\right)$$
$$=\ldots = \underset{D\times N}{X^T}\cdot\left(\vphantom{\frac12}
\underbrace{g'(XU_0)}_{N\times K}\odot
\underbrace{\left[\vphantom{\int_0^1}\left(
\underbrace{h’\left(\vphantom{\int_0^1}g(XU_0)W_0\right)}_{N\times1}\odot\underbrace{\nabla_{h(\vphantom{\int_0^1}g\left(XU_0\right)W_0)}\mathcal{L}}_{N\times 1}
\right)\cdot \underbrace{W^T}_{1\times K}\right]}_{N\times K}
\right)$$
Итого $D\times K$, как и $U_0$
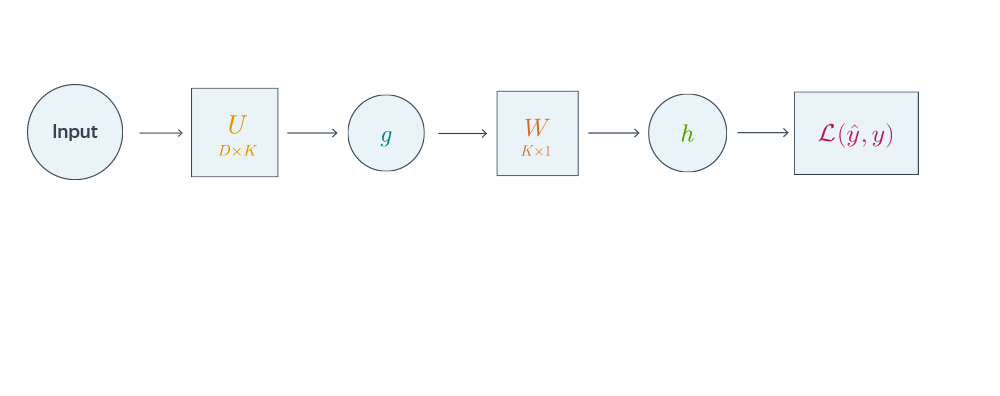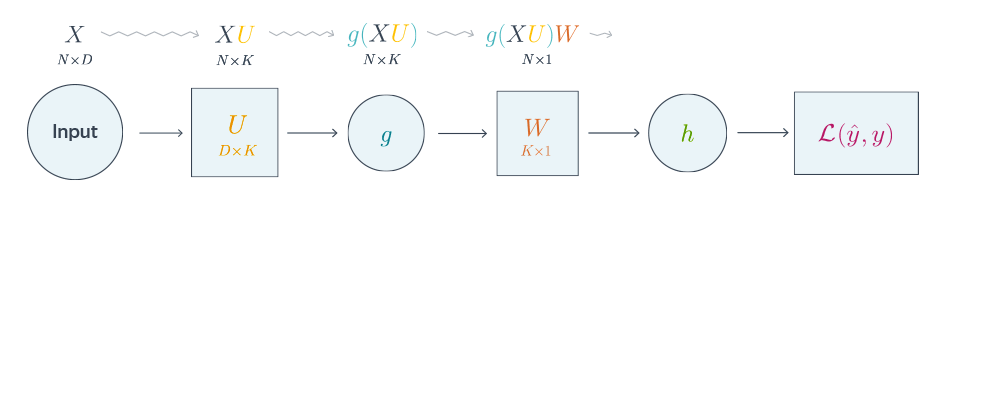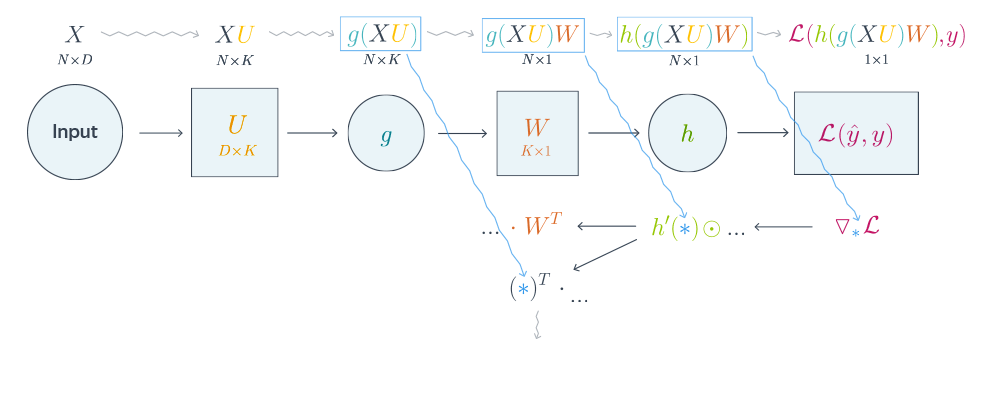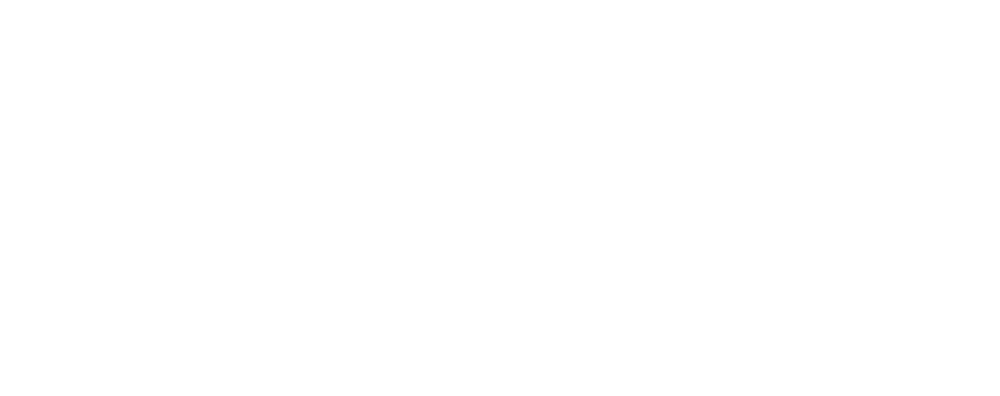
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = \sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
\widehat{y} = \sigma(X^1 W^2) = \sigma\Big(\big(\sigma(X^0 W^1 )\big) W^2 \Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = \sigma(X^0 W^1_0)$, $X^3 = \sigma(X^0 W^1_0) W^2_0$, $X^4 = \sigma(\sigma(X^0 W^1_0) W^2_0) = \widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = \mathcal{L}(y, \widehat{y}) = y \log(\widehat{y}) + (1-y) \log(1-\widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $\mathcal{L}$ по предсказаниям имеет вид
$$
\nabla_{\widehat{y}}l = \frac{y}{\widehat{y}} — \frac{1 — y}{1 — \widehat{y}} = \frac{y — \widehat{y}}{\widehat{y} (1 — \widehat{y})},
$$где, напомним, $ \widehat{y} = \sigma(X^3) = \sigma\Big(\big(\sigma(X^0 W^1_0 )\big) W^2_0 \Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $\sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $\sigma$, в которую подставлено предыдущее промежуточное представление:
$$
\nabla_{X^3}l = \sigma'(X^3)\odot\nabla_{\widehat{y}}l = \sigma(X^3)\left( 1 — \sigma(X^3) \right) \odot \frac{y — \widehat{y}}{\widehat{y} (1 — \widehat{y})} =
$$$$
= \sigma(X^3)\left( 1 — \sigma(X^3) \right) \odot \frac{y — \sigma(X^3)}{\sigma(X^3) (1 — \sigma(X^3))} =
y — \sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
\color{blue}{\nabla_{W^2_0}l} = (X^2)^T\cdot \nabla_{X^3}l = (X^2)^T\cdot(y — \sigma(X^3)) =
$$$$
= \color{blue}{\left( \sigma(X^0W^1_0) \right)^T \cdot (y — \sigma(\sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
\nabla_{X^2}l = \nabla_{X^3}l\cdot (W^2_0)^T = (y — \sigma(X^3))\cdot (W^2_0)^T =
$$$$
= (y — \sigma(X^2W_0^2))\cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $\sigma$.
$$
\nabla_{X^1}l = \sigma'(X^1)\odot\nabla_{X^2}l = \sigma(X^1)\left( 1 — \sigma(X^1) \right) \odot \left( (y — \sigma(X^2W_0^2))\cdot (W^2_0)^T \right) =
$$$$
= \sigma(X^1)\left( 1 — \sigma(X^1) \right) \odot\left( (y — \sigma(\sigma(X^1)W_0^2))\cdot (W^2_0)^T \right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
\color{blue}{\nabla_{W^1_0}l} = (X^0)^T\cdot \nabla_{X^1}l = (X^0)^T\cdot \big( \sigma(X^1) \left( 1 — \sigma(X^1) \right) \odot (y — \sigma(\sigma(X^1)W_0^2))\cdot (W^2_0)^T\big) =
$$$$
= \color{blue}{(X^0)^T\cdot\big(\sigma(X^0W^1_0)\left( 1 — \sigma(X^0W^1_0) \right) \odot (y — \sigma(\sigma(X^0W^1_0)W_0^2))\cdot (W^2_0)^T\big) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}\mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $\nabla_{X^k_0}\mathcal{L}$ в $\nabla_{X^{k-1}_0}\mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $\nabla_{W^k_0}\mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Нежное введение в обратное распространение во времени
Перевод
Ссылка на автора
Обратное распространение через время (BPTT) — это алгоритм обучения, используемый для обновления весов в повторяющихся нейронных сетях, таких как LSTM.
Чтобы эффективно сформулировать проблемы предсказания последовательности для повторяющихся нейронных сетей, вы должны иметь четкое концептуальное понимание того, что делает Backpropagation Through Time, и как настраиваемые вариации, такие как Truncated Backpropagation Through Time, влияют на навыки, стабильность и скорость при обучении вашей сети. В этом пост, вы получите нежное введение в Backpropagation Through Time, предназначенное для практикующего (без уравнений!).
В этом посте вы получите краткое введение в Backpropagation Through Time, предназначенное для практикующего (без уравнений!).
Прочитав этот пост, вы узнаете:
- Что такое обратное распространение во времени и как оно связано с алгоритмом обучения обратного распространения, используемым в многослойных сетях Perceptron.
- Мотивации, которые приводят к необходимости усеченного обратного распространения через время, наиболее широко используемый вариант глубокого обучения для обучения LSTM.
- Нотация для размышлений о том, как настроить усеченное обратное распространение через время, и о канонических конфигурациях, используемых в исследованиях и библиотеках глубокого изучения.
Давайте начнем.
Тренировочный алгоритм обратного распространения
Обратное распространение относится к двум вещам:
- Математический метод, используемый для вычисления производных и применения правила цепочки производных.
- Обучающий алгоритм обновления весов сети для минимизации ошибок.
Именно это последнее понимание обратного распространения мы используем здесь.
Целью алгоритма обучения обратного распространения является изменение весов нейронной сети, чтобы минимизировать ошибку выходных данных сети по сравнению с некоторыми ожидаемыми выходными данными в ответ на соответствующие входные данные.
Это контролируемый алгоритм обучения, который позволяет корректировать сеть с учетом конкретных ошибок.
Общий алгоритм выглядит следующим образом:
- Представьте обучающий шаблон ввода и распространите его по сети, чтобы получить вывод.
- Сравните прогнозируемые результаты с ожидаемыми и рассчитайте ошибку.
- Вычислить производные ошибки по весам сети.
- Отрегулируйте веса, чтобы минимизировать ошибку.
- Повторение.
Подробнее о Backpropagation читайте в посте:
- Как реализовать алгоритм обратного распространения с нуля в Python
Алгоритм обучения обратного распространения подходит для обучения нейронных сетей прямой связи на парах ввода-вывода фиксированного размера, но как насчет данных последовательности, которые могут быть упорядочены по времени?
Нужна помощь с LSTM для прогнозирования последовательности?
Пройдите мой бесплатный 7-дневный курс по электронной почте и откройте для себя 6 различных архитектур LSTM (с кодом).
Нажмите, чтобы зарегистрироваться, а также получите бесплатную PDF-версию курса Ebook.
Начни свой БЕСПЛАТНЫЙ мини-курс сейчас!
Обратное распространение во времени
Backpropagation Through Time, или BPTT, представляет собой применение алгоритма обучения Backpropagation к повторяющейся нейронной сети, применяемой к данным последовательности, таким как временной ряд.
Рекуррентная нейронная сеть показана по одному входу на каждом временном шаге и предсказывает один выход.
Концептуально, BPTT работает, развернув все входные временные шаги. Каждый временной шаг имеет один входной временной шаг, одну копию сети и один выходной. Затем ошибки рассчитываются и накапливаются для каждого временного шага. Сеть откатывается и весы обновляются.
Пространственно, каждый временной шаг развернутой рекуррентной нейронной сети может рассматриваться как дополнительный уровень, учитывая зависимость проблемы от порядка, и внутреннее состояние от предыдущего временного шага принимается в качестве входных данных для последующего временного шага.
Мы можем суммировать алгоритм следующим образом:
- Представить последовательность временных шагов входных и выходных пар в сеть.
- Разверните сеть, затем вычисляйте и накапливайте ошибки на каждом временном шаге.
- Сверните сеть и обновите вес.
- Повторение.
BPTT может быть вычислительно дорогим, так как количество временных шагов увеличивается.
Если входные последовательности состоят из тысяч временных шагов, то это будет количество производных, необходимых для одного обновления веса обновления. Это может привести к исчезновению или взрыву весов (к нулю или переполнению), а также к медленному обучению и умению моделировать шум.
Усеченное обратное распространение во времени
Усеченное обратное распространение через время, или TBPTT, является модифицированной версией обучающего алгоритма BPTT для рекуррентных нейронных сетей, где последовательность обрабатывается один шаг за раз и периодически (k1 временной шаг), обновление BPTT выполняется назад для фиксированного количества временных шагов ( k2 временные шаги).
Илья Суцкевер разъясняет это в своей диссертации:
Усеченное обратное распространение, пожалуй, самый практичный метод для обучения РНН
…
Одной из основных проблем BPTT является высокая стоимость обновления одного параметра, что делает невозможным использование большого количества итераций.
…
Стоимость может быть уменьшена с помощью наивного метода, который разбивает последовательность длиной 1000 на 50 последовательностей (скажем) каждая длиной 20 и обрабатывает каждую последовательность длины 20 как отдельный обучающий случай. Это разумный подход, который может хорошо работать на практике, но он не учитывает временные зависимости, которые охватывают более 20 временных шагов.
…
Усеченный BPTT является тесно связанным методом. Он обрабатывает последовательность по одному временному шагу за раз, и при каждом k1 временном шаге он запускает BPTT для k2 временных шагов, поэтому обновление параметра может быть дешевым, если k2 мало. Следовательно, его скрытые состояния были подвержены многим временным шагам и поэтому могут содержать полезную информацию о далеком прошлом, которая могла бы быть использована оппортунистически.
— Илья Суцкевер, Обучающие рекуррентные нейронные сети, Дипломная работа, 2013
Мы можем суммировать алгоритм следующим образом:
- Представить последовательность k1 временных шагов входных и выходных пар в сеть.
- Разверните сеть, затем вычислите и накапливайте ошибки в k2 временных шагах.
- Сверните сеть и обновите вес.
- Повторение
Алгоритм TBPTT требует рассмотрения двух параметров:
- k1: Число временных шагов прямого прохода между обновлениями. Как правило, это влияет на то, насколько медленными или быстрыми будут тренировки, учитывая частоту обновления веса.
- k2: Количество временных шагов, к которым применяется BPTT. Как правило, он должен быть достаточно большим, чтобы охватить временную структуру проблемы для изучения сетью. Слишком большое значение приводит к исчезновению градиентов.
Чтобы сделать это более понятным:
… Можно использовать приближение к ограниченной истории, в котором релевантная информация сохраняется для фиксированного числа временных шагов h, а любая информация, более старая, чем эта, забыта. В общем, это следует рассматривать как эвристический метод для упрощения вычислений, хотя, как обсуждается ниже, иногда он может служить адекватным приближением к истинному градиенту и может также быть более подходящим в тех ситуациях, когда веса корректируются как сеть пробеги. Давайте назовем этот алгоритм усеченным обратным распространением во времени. Если h представляет количество сохраненных предыдущих временных шагов, этот алгоритм будет обозначаться как BPTT (h).
…
Обратите внимание, что в BPTT (h) обратный проход по самым последним h временным шагам выполняется заново каждый раз, когда сеть проходит дополнительный временной шаг. Чтобы обобщить это, можно рассмотреть возможность прохождения через h0 дополнительных временных шагов перед выполнением следующего вычисления BPTT, где h0 & lt; = h.
…
Ключевой особенностью этого алгоритма является то, что следующий обратный проход не выполняется до момента времени t + h0; за прошедшее время история сетевого ввода, состояние сети и целевые значения сохраняются в буфере истории, но обработка этих данных не выполняется. Обозначим этот алгоритм BPTT (h; h0). Очевидно, что BPTT (h) — это то же самое, что BPTT (h; 1), а BPTT (h; h) — это поэтапный алгоритм BPTT.
— Рональд Дж. Уильямс и Цзин Пэн, Эффективный градиентный алгоритм для онлайнового обучения рекуррентных сетевых траекторий 1990
Мы можем позаимствовать нотацию у Уильямса и Пэна и обозначить различные конфигурации TBPTT как TBPTT (k1, k2).
Используя эту запись, мы можем определить некоторые стандартные или общие подходы:
Обратите внимание, что здесь n относится к общему количеству временных шагов в последовательности:
- TBPTT (п, п): Обновления выполняются в конце последовательности по всем временным шагам в последовательности (например, классический BPTT).
- TBPTT (1, п): временные шаги обрабатываются по одному за раз, за которым следует обновление, которое охватывает все временные шаги, замеченные до сих пор (например, классический TBPTT от Williams и Peng).
- TBPTT (k1,1): Сеть, вероятно, не имеет достаточного временного контекста для обучения, в значительной степени полагаясь на внутреннее состояние и входные данные.
- TBPTT (k1, k2), где k1 & lt; k2 & lt; n: Несколько обновлений выполняются для каждой последовательности, что может ускорить обучение.
- TBPTT (k1, k2), где k1 = k2: Обычная конфигурация, в которой фиксированное количество временных шагов используется как для прямого, так и для обратного временных шагов (например, от 10 до 100 с).
Мы можем видеть, что все конфигурации представляют собой вариацию TBPTT (n, n), которая, по сути, пытается аппроксимировать тот же эффект с возможно более быстрым обучением и более стабильными результатами.
Канонический TBPTT, о котором сообщается в статьях, может рассматриваться как TBPTT (k1, k2), где k1 = k2 = h и h & lt; = n, и где выбранный параметр невелик (от десятков до сотен шагов).
В библиотеках, таких как TensorFlow и Keras, все выглядит одинаково, и h определяет фиксированную векторизованную длину временных шагов подготовленных данных.
Дальнейшее чтение
Этот раздел предоставляет некоторые ресурсы для дальнейшего чтения
книги
- Neural Smithing: контролируемое обучение в искусственных нейронных сетях с прямой связью 1999
- Глубокое обучение, 2016
документы
- Изучение представлений по обратному распространению ошибок 1986
- Обратное распространение во времени: что это делает и как это сделать 1990
- Эффективный градиентный алгоритм для онлайнового обучения рекуррентных сетевых траекторий 1990
- Обучающие рекуррентные нейронные сети, Дипломная работа, 2013
- Градиентные алгоритмы обучения для рекуррентных сетей и их вычислительная сложность 1995
статьи
- обратное распространение в Википедии
- Обратное распространение во времени в Википедии
- Стили усеченного обратного распространения
- Ответ на вопрос «RNN: когда применять BPTT и / или обновлять веса?» на CrossValidated
Резюме
В этом посте вы открыли Backpropagation Through Time для обучения повторяющихся нейронных сетей.
В частности, вы узнали:
- Что такое обратное распространение во времени и как оно связано с алгоритмом обучения обратного распространения, используемым в многослойных сетях Perceptron.
- Мотивации, которые приводят к необходимости усеченного обратного распространения через время, наиболее широко используемый вариант глубокого обучения для обучения LSTM.
- Нотация для размышлений о том, как настроить усеченное обратное распространение через время, и о канонических конфигурациях, используемых в исследованиях и библиотеках глубокого изучения.
Есть ли у вас какие-либо вопросы о Backpropagation Through Time?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
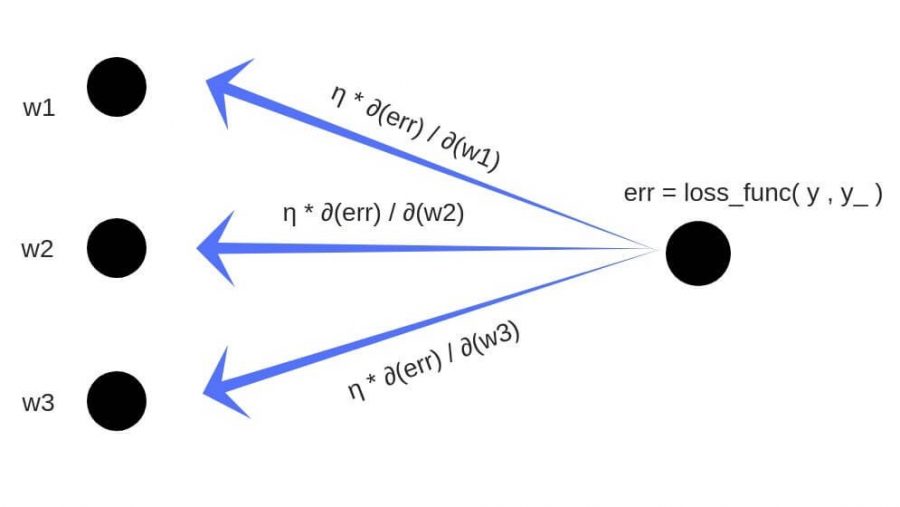
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь \Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
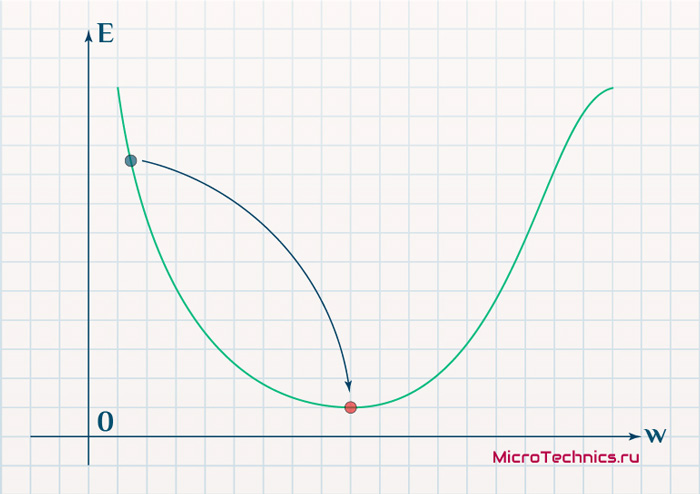
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
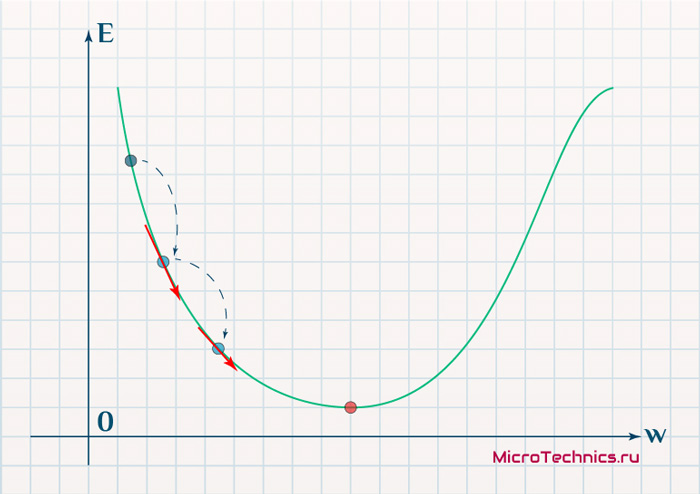
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
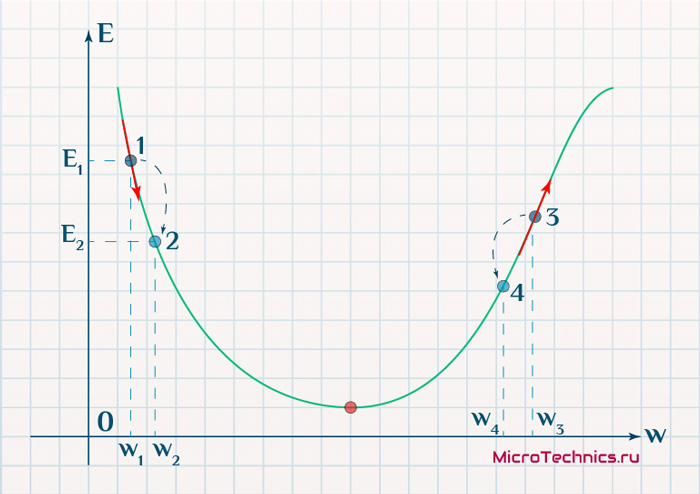
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение \Delta w (\Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: \Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | \bold{\Delta w} | Знак \bold{\Delta w} | Градиент |
|---|---|---|---|
| 1 \rArr 2 | w_2 — w_1 | + | — |
| 3 \rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
\Delta w = -\alpha \cdot \frac{dE}{dw}
Имеем в наличии:
- \Delta w — величина, на которую необходимо изменить значение w.
- \frac{dE}{dw} — градиент в этой точке.
- \alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина \frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
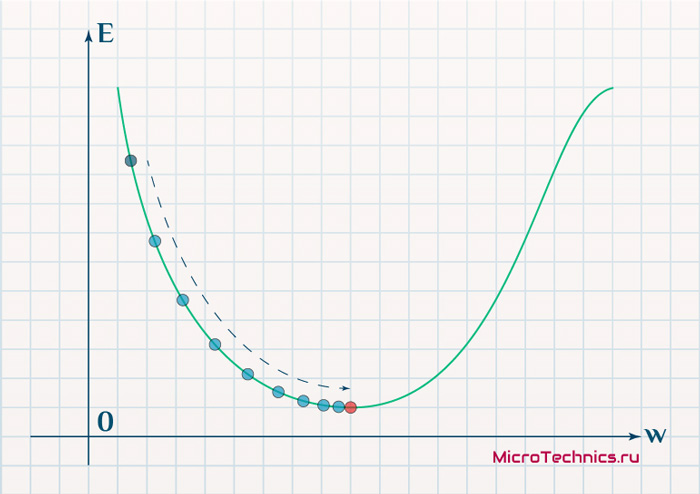
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
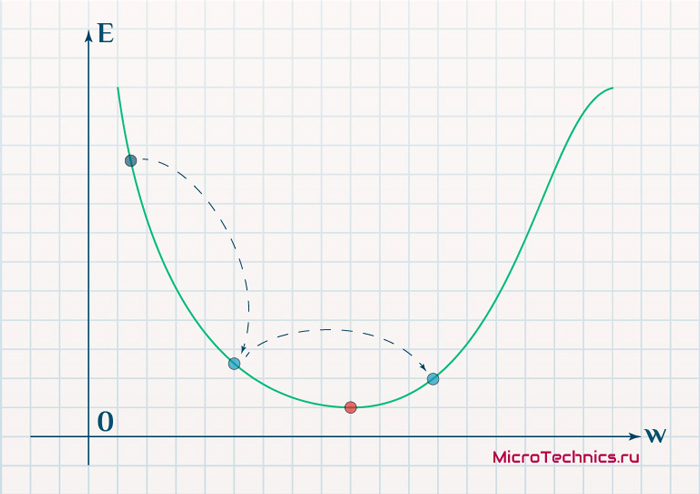
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
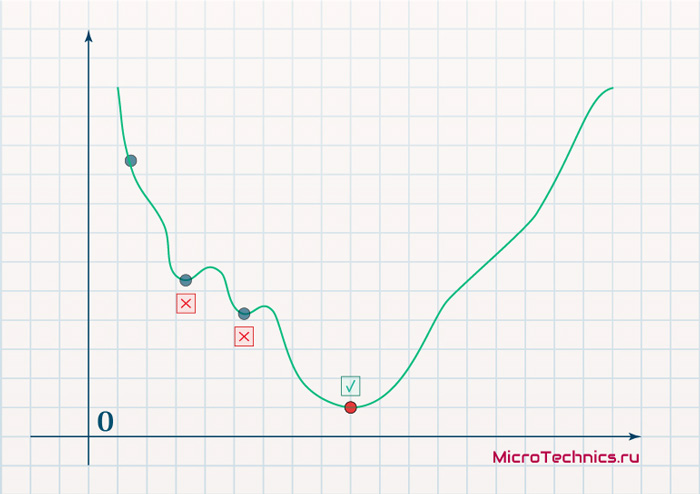
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
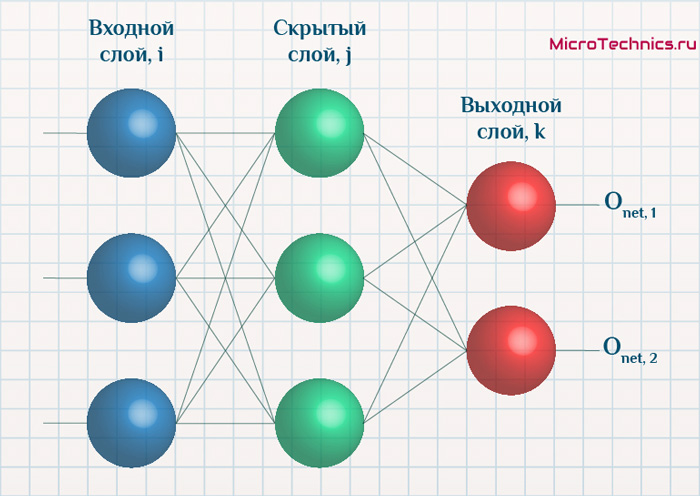
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины \Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (\frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | \bold{O_{net}} | \bold{O_{correct}} | \bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
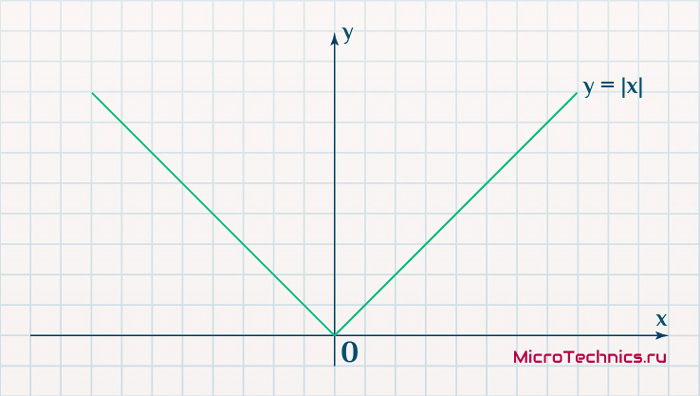
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: \frac{dE}{dw_{jk}} = \frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: \Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
\frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) \cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
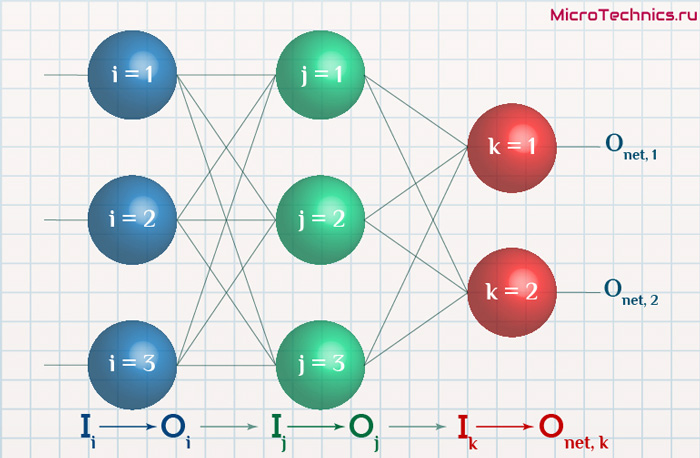
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что \sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k).
Итог: \frac{dE}{d w_{jk}} = -\delta_k \cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
\frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
Который примет следующий вид:
\delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
\frac{dE}{d w_{ij}} = -(\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j) \cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- скрытые слои: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Градиент: \frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
- Корректировка весовых коэффициентов: \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
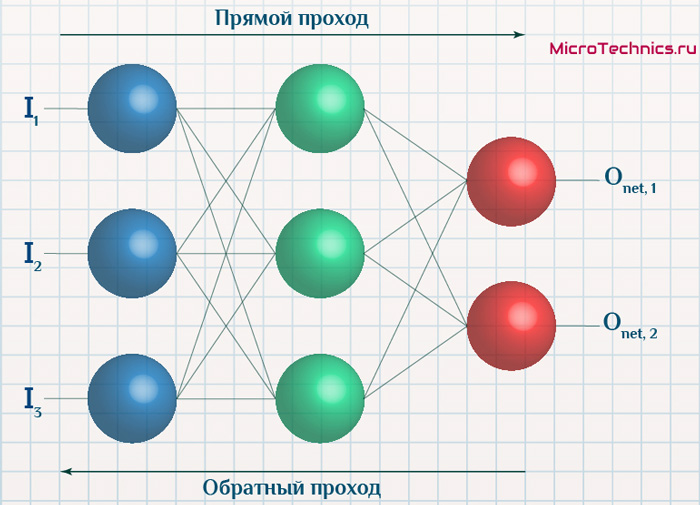
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- для скрытых: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Далее используем полученные значения для расчета \Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij \medspace new} = w_{ij} + \Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
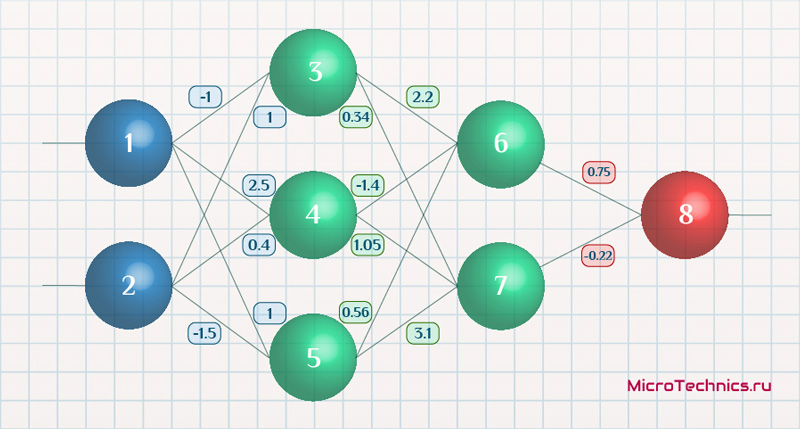
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = \frac{1}{1 + e^{-x}}
И ее производная:
f{\Large{\prime}}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения \alpha пусть будет равна 0.3, момент — \gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \\ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 \cdot w_{13} + O_2 \cdot w_{23} = 0.6 \cdot (-1\medspace) + 0.7 \cdot 1 = 0.1 \\
I_4 = 0.6 \cdot 2.5 + 0.7 \cdot 0.4 = 1.78 \\
I_5 = 0.6 \cdot 1 + 0.7 \cdot (-1.5\medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3\medspace) = 0.52 \\ O_4 = 0.86\\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 \cdot w_{36} + O_4 \cdot w_{46} + O_5 \cdot w_{56} = 0.52 \cdot 2.2 + 0.86 \cdot (-1.4\medspace) + 0.39 \cdot 0.56 = 0.158 \\
I_7 = 0.52 \cdot 0.34 + 0.86 \cdot 1.05 + 0.39 \cdot 3.1 = 2.288 \\
O_6 = f(I_6) = 0.54 \\
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 \cdot w_{68} + O_7 \cdot w_{78} = 0.54 \cdot 0.75 + 0.908 \cdot (-0.22\medspace) = 0.205 \\
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
\delta_8 = (O_{correct} - O_{net}) \cdot f{\Large{\prime}}(I_8) = (O_{correct} - O_{net}) \cdot f(I_8) \cdot (1-f(I_8)) = (0.9 - 0.551\medspace) \cdot 0.551 \cdot (1-0.551\medspace) = 0.0863 \\
\delta_7 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_7) = (\delta_8 \cdot w_{78}) \cdot f{\Large{\prime}}(I_7) = 0.0863 \cdot (-0.22\medspace) \cdot 0.908 \cdot (1 - 0.908\medspace) = -0.0016 \\
\delta_6 = 0.086 \cdot 0.75 \cdot 0.54 \cdot (1 - 0.54\medspace) = 0.016 \\
\delta_5 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_5) = (\delta_7 \cdot w_{57} + \delta_6 \cdot w_{56}) \cdot f{\Large{\prime}}(I_7) = (-0.0016 \cdot 3.1 + 0.016 \cdot 0.56) \cdot 0.39 \cdot (1 - 0.39\medspace) = 0.001 \\
\delta_4 = (-0.0016 \cdot 1.05 + 0.016 \cdot (-1.4)) \cdot 0.86 \cdot (1 - 0.86\medspace) = -0.003 \\
\delta_3 = (-0.0016 \cdot 0.34 + 0.016 \cdot 2.2) \cdot 0.52 \cdot (1 - 0.52\medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Как вы помните, \Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
\Delta w_{78} = \alpha \cdot \delta_8 \cdot O_7 = 0.3 \cdot 0.0863 \cdot 0.908 = 0.0235 \\
\Delta w_{68} = 0.3 \cdot 0.0863 \cdot 0.54= 0.014 \\
\Delta w_{57} = \alpha \cdot \delta_7 \cdot O_5 = 0.3 \cdot (−0.0016\medspace) \cdot 0.39= -0.00019 \\
\Delta w_{47} = 0.3 \cdot (−0.0016\medspace) \cdot 0.86= -0.0004 \\
\Delta w_{37} = 0.3 \cdot (−0.0016\medspace) \cdot 0.52= -0.00025 \\
\Delta w_{56} = \alpha \cdot \delta_6 \cdot O_5 = 0.3 \cdot 0.016 \cdot 0.39= 0.0019 \\
\Delta w_{46} = 0.3 \cdot 0.016 \cdot 0.86= 0.0041 \\
\Delta w_{36} = 0.3 \cdot 0.016 \cdot 0.52= 0.0025 \\
\Delta w_{25} = \alpha \cdot \delta_5 \cdot O_2 = 0.3 \cdot 0.001 \cdot 0.7= 0.00021 \\
\Delta w_{15} = 0.3 \cdot 0.001 \cdot 0.6= 0.00018 \\
\Delta w_{24} = \alpha \cdot \delta_4 \cdot O_2 = 0.3 \cdot (-0.003\medspace) \cdot 0.7= -0.00063 \\
\Delta w_{14} = 0.3 \cdot (-0.003\medspace) \cdot 0.6= -0.00054 \\
\Delta w_{23} = \alpha \cdot \delta_3 \cdot O_2 = 0.3 \cdot (−0.0087\medspace) \cdot 0.7= -0.00183 \\
\Delta w_{13} = 0.3 \cdot (−0.0087\medspace) \cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 \medspace new} = w_{78} + \Delta w_{78} = -0.22 + 0.0235 = -0.1965 \\
w_{68 \medspace new} = 0.75+ 0.014 = 0.764 \\
w_{57 \medspace new} = 3.1 + (−0.00019\medspace) = 3.0998\\
w_{47 \medspace new} = 1.05 + (−0.0004\medspace) = 1.0496\\
w_{37 \medspace new} = 0.34 + (−0.00025\medspace) = 0.3398\\
w_{56 \medspace new} = 0.56 + 0.0019 = 0.5619 \\
w_{46 \medspace new} = -1.4 + 0.0041 = -1.3959 \\
w_{36 \medspace new} = 2.2 + 0.0025 = 2.2025 \\
w_{25 \medspace new} = -1.5 + 0.00021 = -1.4998 \\
w_{15 \medspace new} = 1 + 0.00018 = 1.00018 \\
w_{24 \medspace new} = 0.4 + (−0.00063\medspace) = 0.39937 \\
w_{14 \medspace new} = 2.5 + (−0.00054\medspace) = 2.49946 \\
w_{23 \medspace new} = 1 + (−0.00183\medspace) = 0.99817 \\
w_{13 \medspace new} = -1 + (−0.00157\medspace) = -1.00157\\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Обратное распространение ошибки — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.
Обновление правила цепочки
Прямое распространение можно рассматривать как длинный ряд вложенных уравнений. Если вы так думаете о прямом распространении, то обратное распространение — это просто приложение правила цепочки (дифференцирования сложной функции) для поиска производных потерь по любой переменной во вложенном уравнении. С учётом функции прямого распространения:
f(x)=A(B(C(x)))
A, B, и C — функции активации на различных слоях. Пользуясь правилом цепочки, мы легко вычисляем производную f(x) по x:
f′(x)=f′(A)⋅A′(B)⋅B′(C)⋅C′(x)
Что насчёт производной относительно B? Чтобы найти производную по B, вы можете сделать вид, что B (C(x)) является константой, заменить ее переменной-заполнителем B, и продолжить поиск производной по B стандартно.
f′(B)=f′(A)⋅A′(B)
Этот простой метод распространяется на любую переменную внутри функции, и позволяет нам в точности определить влияние каждой переменной на общий результат.
Применение правила цепочки
Давайте используем правило цепочки для вычисления производной потерь по любому весу в сети. Правило цепочки поможет нам определить, какой вклад каждый вес вносит в нашу общую ошибку и направление обновления каждого веса, чтобы уменьшить ошибку. Вот уравнения, которые нужны, чтобы сделать прогноз и рассчитать общую ошибку или потерю:
Учитывая сеть, состоящую из одного нейрона, общая потеря нейросети может быть рассчитана как:
Cost=C(R(Z(XW)))
Используя правило цепочки, мы легко можем найти производную потери относительно веса W.
C′(W)=C′(R)⋅R′(Z)⋅Z′(W)=(y^−y)⋅R′(Z)⋅X
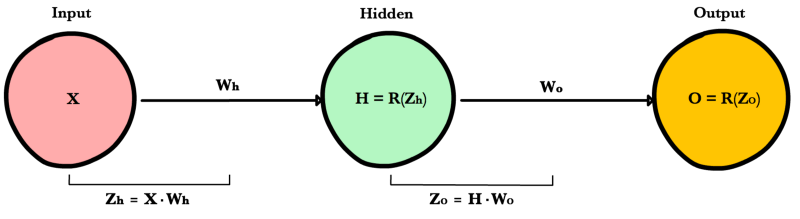
Теперь, когда у нас есть уравнение для вычисления производной потери по любому весу, давайте обратимся к примеру с нейронной сетью:
Какова производная от потери по Wo?
C′(WO)=C′(y^)⋅y^′(ZO)⋅Z′O(WO)=(y^−y)⋅R′(ZO)⋅H
А что насчет Wh? Чтобы узнать это, мы просто продолжаем возвращаться в нашу функцию, рекурсивно применяя правило цепочки, пока не доберемся до функции, которая имеет элемент Wh.
C′(Wh)=C′(y^)⋅O′(Zo)⋅Z′o(H)⋅H′(Zh)⋅Z′h(Wh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)⋅X
И просто забавы ради, что, если в нашей сети было бы 10 скрытых слоев. Что такое производная потери для первого веса w1?
C(w1)=(dC/dy^)⋅(dy^/dZ11)⋅(dZ11/dH10)⋅(dH10/dZ10)⋅(dZ10/dH9)⋅(dH9/dZ9)⋅(dZ9/dH8)⋅(dH8/dZ8)⋅(dZ8/dH7)⋅(dH7/dZ7)⋅(dZ7/dH6)⋅(dH6/dZ6)⋅(dZ6/dH5)⋅(dH5/dZ5)⋅(dZ5/dH4)⋅(dH4/dZ4)⋅(dZ4/dH3)⋅(dH3/dZ3)⋅(dZ3/dH2)⋅(dH2/dZ2)⋅(dZ2/dH1)⋅(dH1/dZ1)⋅(dZ1/dW1)
Заметили закономерность? Количество вычислений, необходимых для расчёта производных потерь, увеличивается по мере углубления нашей сети. Также обратите внимание на избыточность в наших расчетах производных. Производная потерь каждого слоя добавляет два новых элемента к элементам, которые уже были вычислены слоями над ним. Что, если бы был какой-то способ сохранить нашу работу и избежать этих повторяющихся вычислений?
Сохранение работы с мемоизацией
Мемоизация — это термин в информатике, имеющий простое значение: не пересчитывать одно и то же снова и снова. В мемоизации мы сохраняем ранее вычисленные результаты, чтобы избежать пересчета одной и той же функции. Это удобно для ускорения рекурсивных функций, одной из которых является обратное распространение. Обратите внимание на закономерность в уравнениях производных приведённых ниже.
Каждый из этих слоев пересчитывает одни и те же производные! Вместо того, чтобы выписывать длинные уравнения производных для каждого веса, можно использовать мемоизацию, чтобы сохранить нашу работу, так как мы возвращаем ошибку через сеть. Для этого мы определяем 3 уравнения (ниже), которые вместе выражают в краткой форме все вычисления, необходимые для обратного распространения. Математика та же, но уравнения дают хорошее сокращение, которое мы можем использовать, чтобы отслеживать те вычисления, которые мы уже выполнили, и сохранять нашу работу по мере продвижения назад по сети.
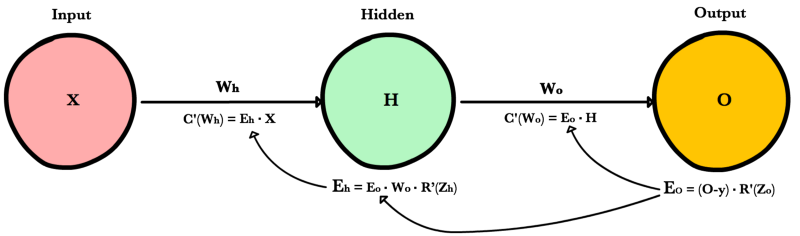
Для начала мы вычисляем ошибку выходного слоя и передаем результат на скрытый слой перед ним. После вычисления ошибки скрытого слоя мы передаем ее значение обратно на предыдущий скрытый слой. И так далее и тому подобное. Возвращаясь назад по сети, мы применяем 3-ю формулу на каждом слое, чтобы вычислить производную потерь по весам этого слоя. Эта производная говорит нам, в каком направлении регулировать наши веса, чтобы уменьшить общие потери.
Примечание: термин ошибка слоя относится к производной потерь по входу в слой. Он отвечает на вопрос: как изменяется выход функции потерь при изменении входа в этот слой?
Ошибка выходного слоя
Для расчета ошибки выходного слоя необходимо найти производную потерь по входу выходному слою, Zo. Это отвечает на вопрос: как веса последнего слоя влияют на общую ошибку в сети? Тогда производная такова:
C′(Zo)=(y^−y)⋅R′(Zo)
Чтобы упростить запись, практикующие МО обычно заменяют последовательность (y^−y)∗R'(Zo) термином Eo. Итак, наша формула для ошибки выходного слоя равна:
Eo=(y^−y)⋅R′(Zo)
Ошибка скрытого слоя
Для вычисления ошибки скрытого слоя нужно найти производную потерь по входу скрытого слоя, Zh.
C′(Zh)=(y^−y)⋅R′(Zo)⋅Wo⋅R′(Zh)
Далее мы можем поменять местами элемент Eo выше, чтобы избежать дублирования и создать новое упрощенное уравнение для ошибки скрытого слоя:
Eh=Eo⋅Wo⋅R′(Zh)
Эта формула лежит в основе обратного распространения. Мы вычисляем ошибку текущего слоя и передаем взвешенную ошибку обратно на предыдущий слой, продолжая процесс, пока не достигнем нашего первого скрытого слоя. Попутно мы обновляем веса, используя производную потерь по каждому весу.
Производная потерь по любому весу
Вернемся к нашей формуле для производной потерь по весу выходного слоя Wo.
C′(WO)=(y^−y)⋅R′(ZO)⋅H
Мы знаем, что можем заменить первую часть уравнением для ошибки выходного слоя Eh. H представляет собой активацию скрытого слоя.
C′(Wo)=Eo⋅H
Таким образом, чтобы найти производную потерь по любому весу в нашей сети, мы просто умножаем ошибку соответствующего слоя на его вход (выход предыдущего слоя).
C′(w)=CurrentLayerError⋅CurrentLayerInput
Примечание: вход относится к активации с предыдущего слоя, а не к взвешенному входу, Z.
Подводя итог
Вот последние 3 уравнения, которые вместе образуют основу обратного распространения.
Вот процесс, визуализированный с использованием нашего примера нейронной сети выше:
Обратное распространение: пример кода
def relu_prime(z): if z > 0: return 1 return 0 def cost(yHat, y): return 0.5 * (yHat - y)**2 def cost_prime(yHat, y): return yHat - y def backprop(x, y, Wh, Wo, lr): yHat = feed_forward(x, Wh, Wo) # Layer Error Eo = (yHat - y) * relu_prime(Zo) Eh = Eo * Wo * relu_prime(Zh) # Cost derivative for weights dWo = Eo * H dWh = Eh * x # Update weights Wh -= lr * dWh Wo -= lr * dWo