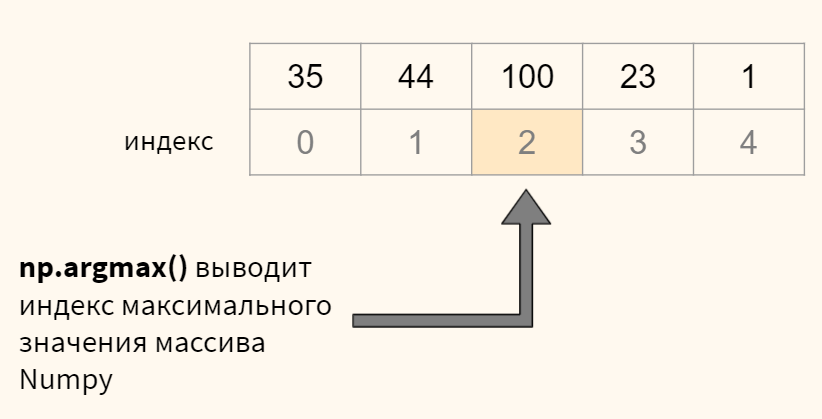
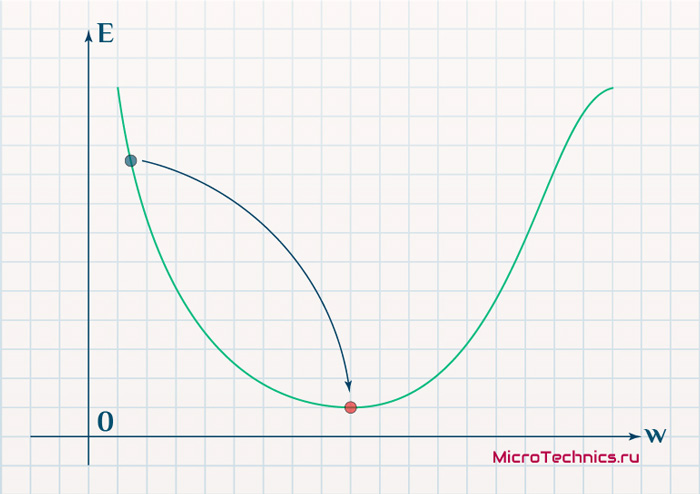
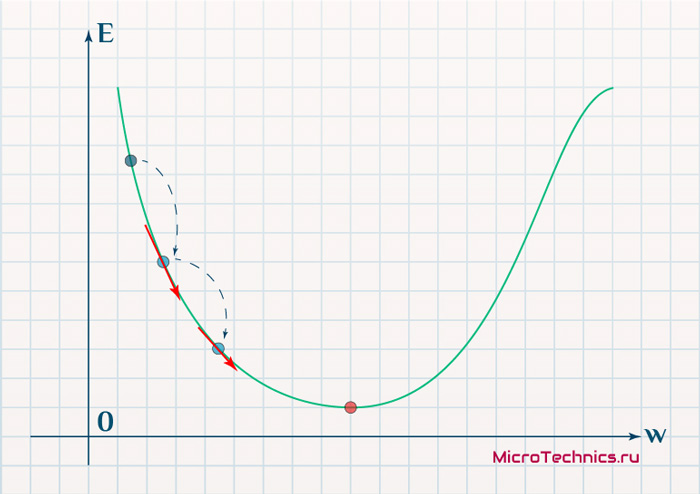
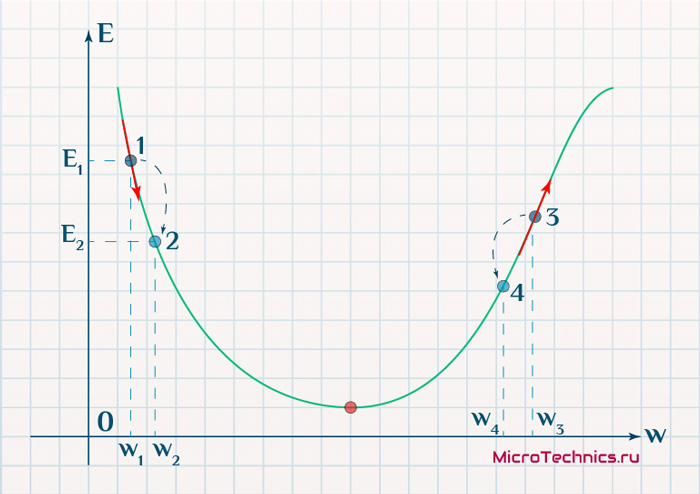
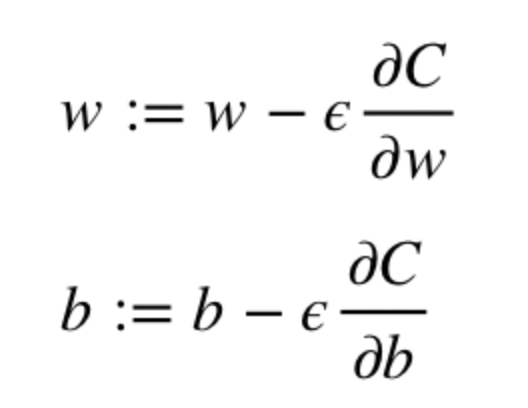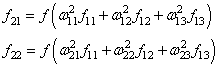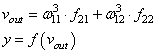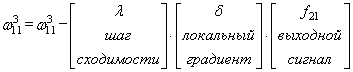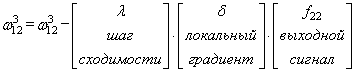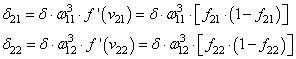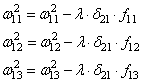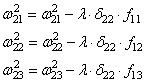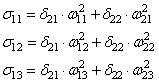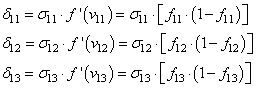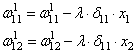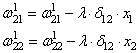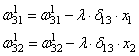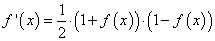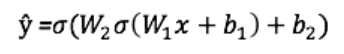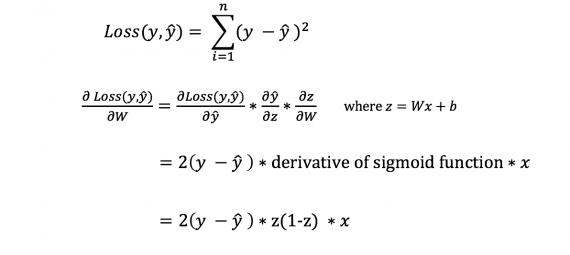Знакомимся с методом обратного распространения ошибки
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!
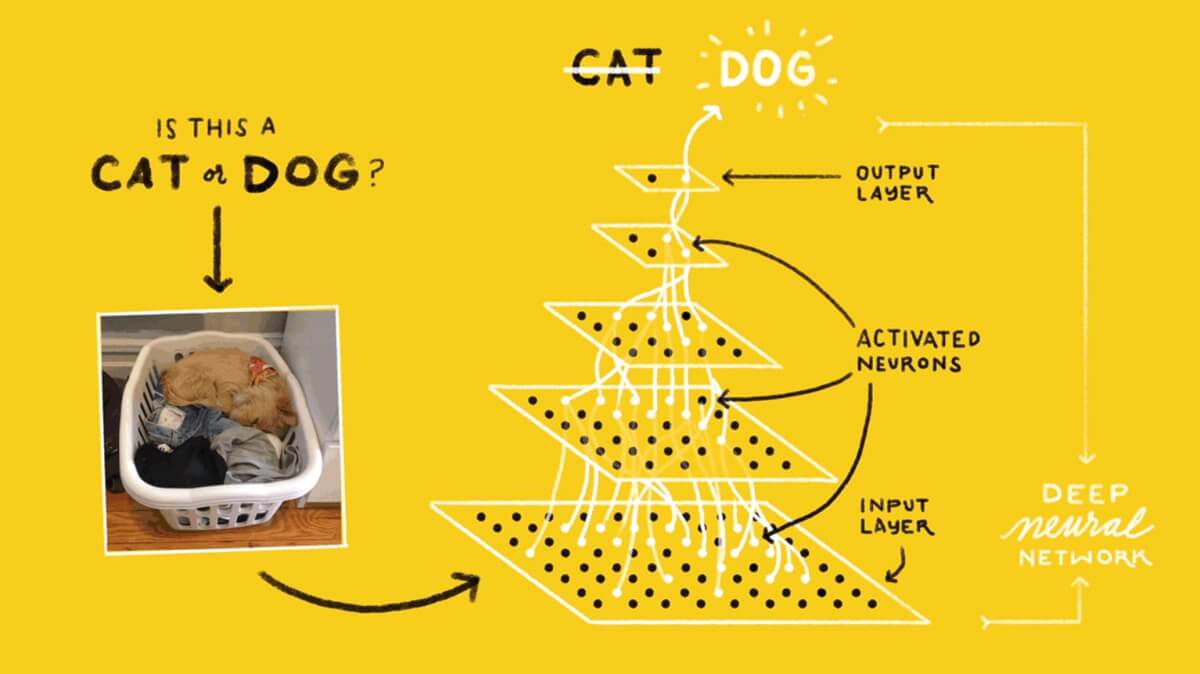
Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
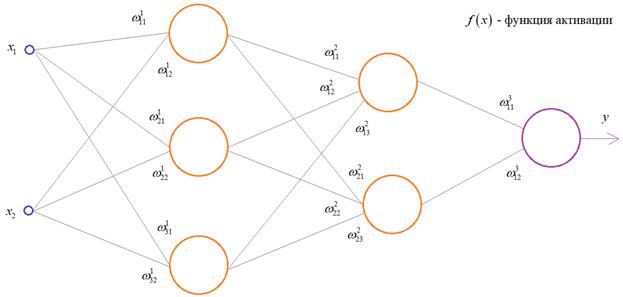
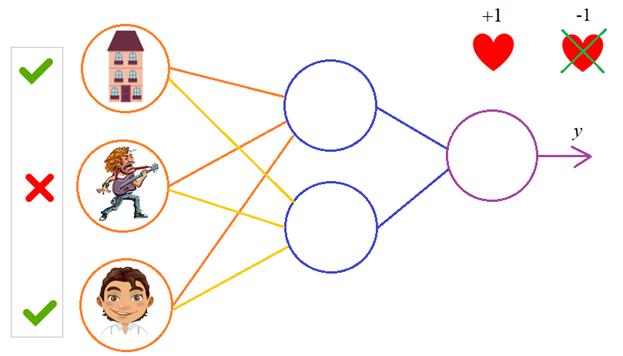
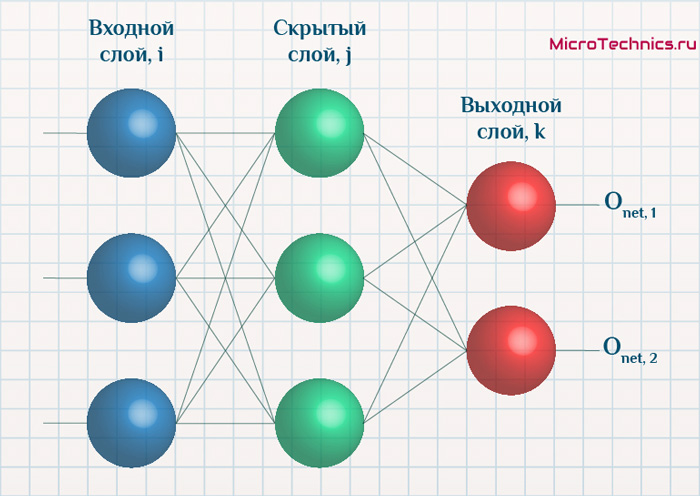
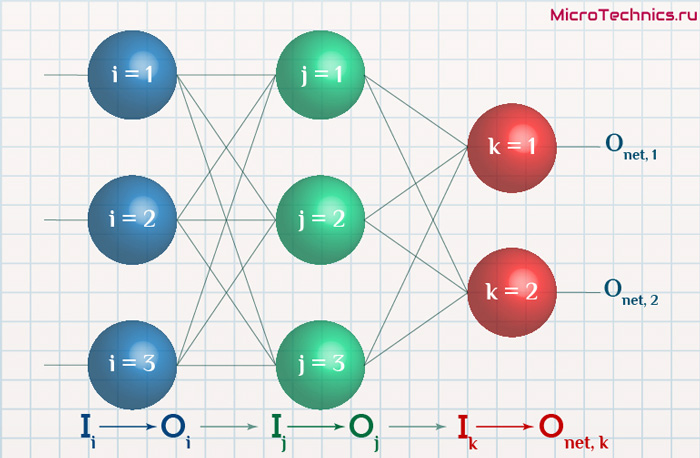
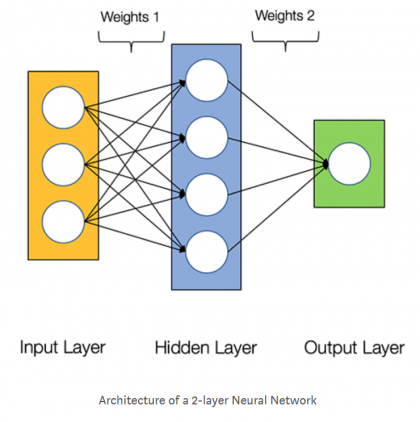
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.
Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.
Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:
Для l = 3:
W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
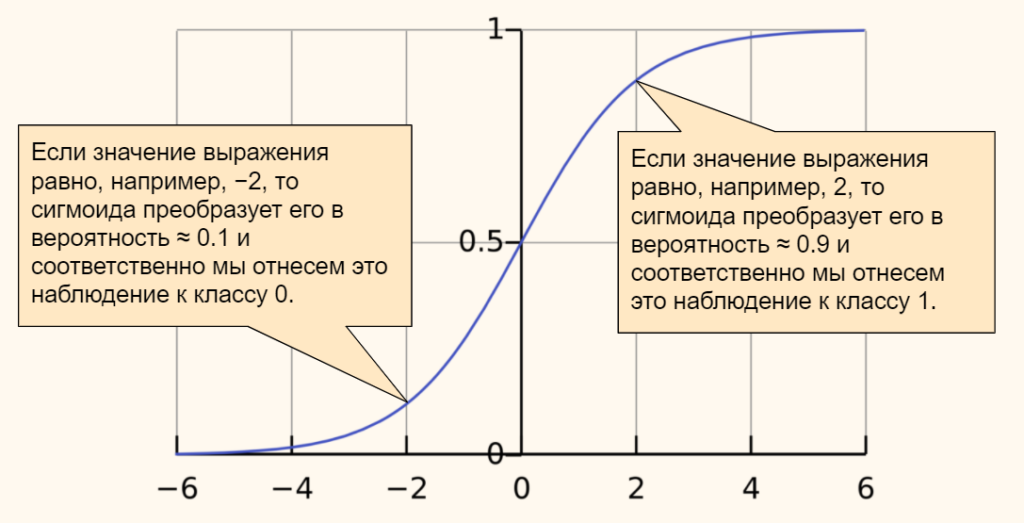
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.
Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.
b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.
Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:
Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:
И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
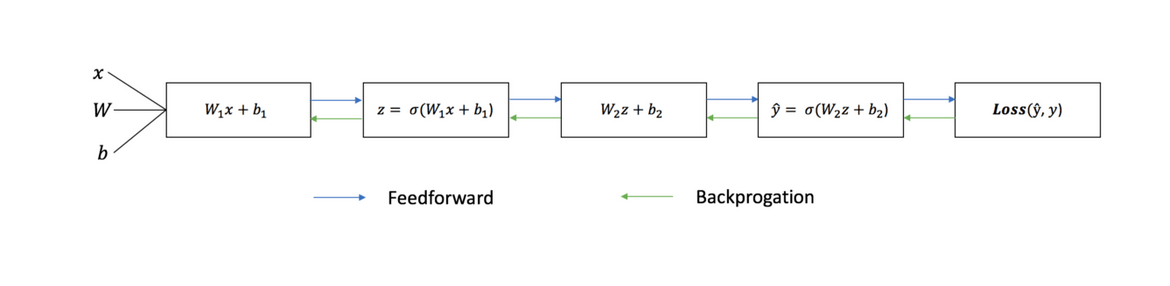
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
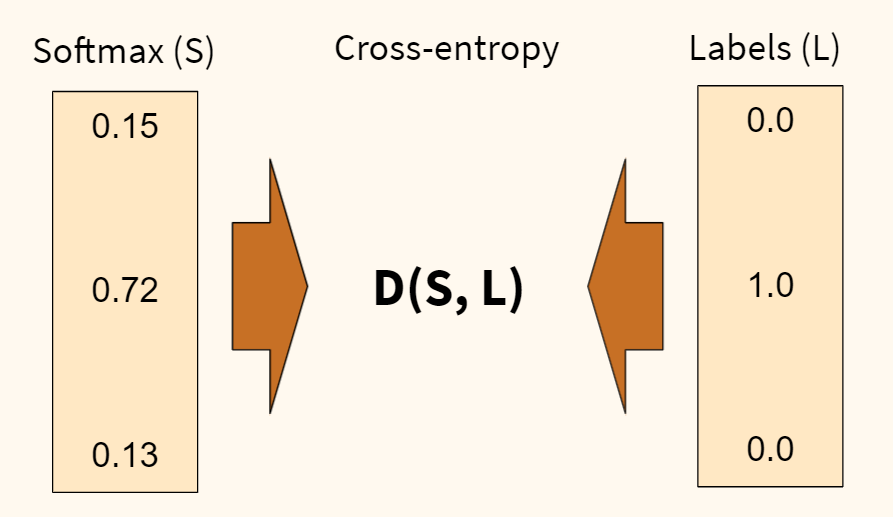
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:
Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.
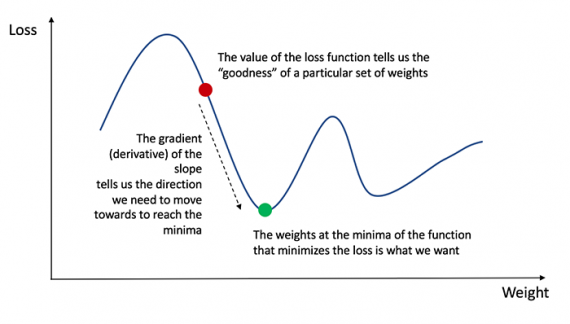
Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:
(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:
(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:
«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:
Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z2)3 и (a2)3:
Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
На предыдущих
занятиях мы с вами рассматривали НС с выбранными весами, либо устанавливали их,
исходя из определенных математических соображений. Это можно сделать, когда
сеть относительно небольшая. Но при увеличении числа нейронов и связей, ручной
подбор становится попросту невозможным и возникает задача нахождения весовых
коэффициентов связей НС. Этот процесс и называют обучением нейронной сети.
Один из
распространенных подходов к обучению заключается в последовательном
предъявлении НС векторов наблюдений и последующей корректировки весовых
коэффициентов так, чтобы выходное значение совпадало с требуемым:
Это называется обучение
с учителем, так как для каждого вектора мы знаем нужный ответ и именно его
требуем от нашей НС.
Теперь, главный
вопрос: как построить алгоритм, который бы наилучшим образом находил весовые
коэффициенты. Наилучший – это значит, максимально быстро и с максимально
близкими выходными значениями для требуемых откликов. В общем случае эта задача
не решена. Нет универсального алгоритма обучения. Поэтому, лучшее, что мы можем
сделать – это выбрать тот алгоритм, который хорошо себя зарекомендовал в
прошлом. Основной «рабочей лошадкой» здесь является алгоритм back propagation (обратного
распространения ошибки), который, в свою очередь, базируется на алгоритме градиентного
спуска.
Сначала, я думал
рассказать о нем со всеми математическими выкладками, но потом решил этого не
делать, а просто показать принцип работы и рассмотреть реализацию конкретного
примера на Python.
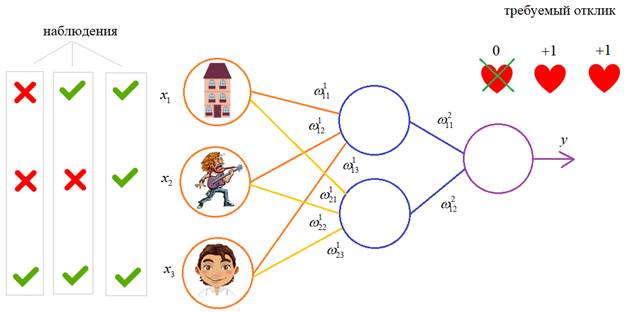
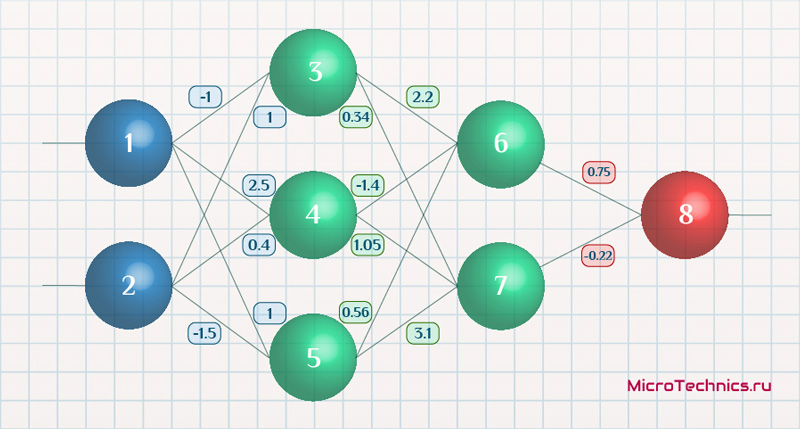
Чтобы все лучше
понять, предположим, что у нас имеется вот такая полносвязная НС прямого
распространения с весами связей, выбранными произвольным образом в диапазоне от
[-0.5; 0,5]. Здесь верхний индекс показывает принадлежность к тому или иному слою
сети. Также, каждый нейрон имеет некоторую активационную функцию :
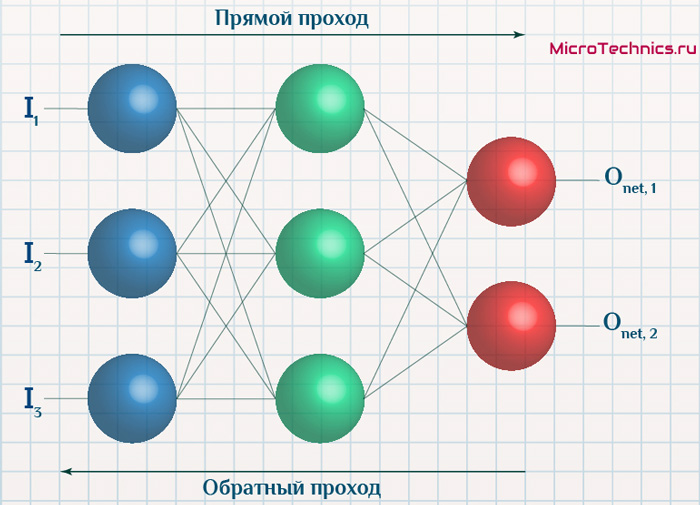
На первом шаге
делается прямой проход по сети. Мы пропускаем вектор наблюдения через
эту сеть, и запоминаем все выходные значения нейронов скрытых слоев:
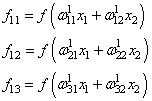
и последнее
выходное значение y:
Далее, мы знаем
требуемый отклик d для текущего вектора ,
значит для него можно вычислить ошибку работы НС. Она будет равна:
На данный момент
все должно быть понятно. Мы на первом занятии подробно рассматривали процесс
распространения сигнала по НС. И вы это уже хорошо себе представляете. А вот
дальше начинается самое главное – корректировка весов. Для этого делается
обратный проход по НС: от последнего слоя – к первому.
Итак, у нас есть
ошибка e и некая функция
активации нейронов .
Первое, что нам нужно – это вычислить локальный градиент для выходного нейрона.
Это делается по формуле:
Этот момент
требует пояснения. Смотрите, ранее используемая пороговая функция:
нам уже не
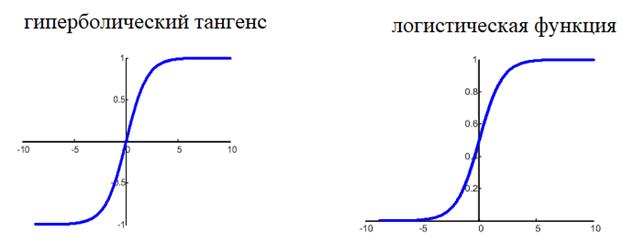
подходит, т.к. она не дифференцируема на всем диапазоне значений x. Вместо этого
для сетей с небольшим числом слоев, часто применяют или гиперболический
тангенс:
или логистическую
функцию:
Фактически, они
отличаются только тем, что первая дает выходной интервал [-1; 1], а вторая – [0;
1]. И мы уже берем ту, которая нас больше устраивает в данной конкретной
ситуации. Например, выберем логистическую функцию.
Ее производная
функции по аргументу x дает очень простое выражение:
Именно его мы и
запишем в нашу формулу вычисления локального градиента:
Но, так как
то локальный
градиент последнего нейрона, равен:
Отлично, это
сделали. Теперь у нас есть все, чтобы выполнить коррекцию весов. Начнем со
связи ,
формула будет такой:
Для второй связи
все то же самое, только входной сигнал берется от второго нейрона:
Здесь у вас
может возникнуть вопрос: что такое параметр λ и где его брать? Он
подбирается самостоятельно, вручную самим разработчиком. В самом простом случае
можно попробовать следующие значения:
(Мы подробно о
нем говорили на занятии по алгоритму градиентного спуска):
Итак, мы с вами
скорректировали связи последнего слоя. Если вам все это понятно, значит, вы уже
практически поняли весь алгоритм обучения, потому что дальше действуем подобным
образом. Переходим к нейрону следующего с конца слоя и для его входящих связей
повторим ту же саму процедуру. Но для этого, нужно знать значение его
локального градиента. Определяется он просто. Локальный градиент последнего
нейрона взвешивается весами входящих в него связей. Полученные значения на
каждом нейроне умножаются на производную функции активации, взятую в точках
входной суммы:
А дальше
действуем по такой же самой схеме, корректируем входные связи по той же
формуле:
И для второго
нейрона:
Осталось
скорректировать веса первого слоя. Снова вычисляем локальные градиенты для
нейронов первого слоя, но так как каждый из них имеет два выхода, то сначала
вычисляем сумму от каждого выхода:
А затем,
значения локальных градиентов на нейронах первого скрытого слоя:
Ну и осталось
выполнить коррекцию весов первого слоя все по той же формуле:
В результате, мы
выполнили одну итерацию алгоритма обучения НС. На следующей итерации мы должны
взять другой входной вектор из нашего обучающего множества. Лучше всего это
сделать случайным образом, чтобы не формировались возможные ложные
закономерности в последовательности данных при обучении НС. Повторяя много раз
этот процесс, весовые связи будут все точнее описывать обучающую выборку.
Отлично, процесс
обучения в целом мы рассмотрели. Но какой критерий качества минимизировался
алгоритмом градиентного спуска? В действительности, мы стремились получить
минимум суммы квадратов ошибок для обучающей выборки:
То есть, с
помощью алгоритма градиентного спуска веса корректируются так, чтобы
минимизировать этот критерий качества работы НС. Позже мы еще увидим, что на
практике используется не только такой, но и другие критерии.
Вот так, в целом
выглядит идея работы алгоритма обучения по методу обратного распространения
ошибки. Давайте теперь в качестве примера обучим следующую НС:
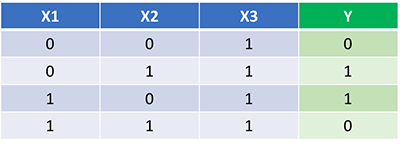
В качестве
обучающего множества выберем все возможные варианты (здесь 1 – это да, -1 – это
нет):
|
Вектор |
Требуемый |
|
[-1, -1, -1] |
-1 |
|
[-1, -1, |
1 |
|
[-1, 1, -1] |
-1 |
|
[-1, 1, 1] |
1 |
|
[1, -1, -1] |
-1 |
|
[1, -1, 1] |
1 |
|
[1, 1, -1] |
-1 |
|
[1, 1, 1] |
-1 |
На каждой
итерации работы алгоритма, мы будем подавать случайно выбранный вектор и
корректировать веса, чтобы приблизиться к значению требуемого отклика.
В качестве
активационной функции выберем гиперболический тангенс:
со значением
производной:
Программа на Python будет такой:
lesson 3. Back propagation.py
Ну, конечно, это
довольно простой, примитивный пример, частный случай, когда мы можем обучить НС
так, чтобы она вообще не выдавала никаких ошибок. Часто, в задачах обучения встречаются
варианты, когда мы этого сделать не можем и, конечно, какой-то процент ошибок
всегда остается. И наша задача сделать так, чтобы этих ошибок было как можно
меньше. Но более подробно как происходит обучение, какие нюансы существуют, как
создавать обучающую выборку, как ее проверять и так далее, мы об этом подробнее
будем говорить уже на следующем занятии.
Видео по теме
Deep Learning with Keras — Introduction
Deep Learning has become a buzzword in recent days in the field of Artificial Intelligence (AI). For many years, we used Machine Learning (ML) for imparting intelligence to machines. In recent days, deep learning has become more popular due to its supremacy in predictions as compared to traditional ML techniques.
Deep Learning essentially means training an Artificial Neural Network (ANN) with a huge amount of data. In deep learning, the network learns by itself and thus requires humongous data for learning. While traditional machine learning is essentially a set of algorithms that parse data and learn from it. They then used this learning for making intelligent decisions.
Now, coming to Keras, it is a high-level neural networks API that runs on top of TensorFlow — an end-to-end open source machine learning platform. Using Keras, you easily define complex ANN architectures to experiment on your big data. Keras also supports GPU, which becomes essential for processing huge amount of data and developing machine learning models.
In this tutorial, you will learn the use of Keras in building deep neural networks. We shall look at the practical examples for teaching. The problem at hand is recognizing handwritten digits using a neural network that is trained with deep learning.
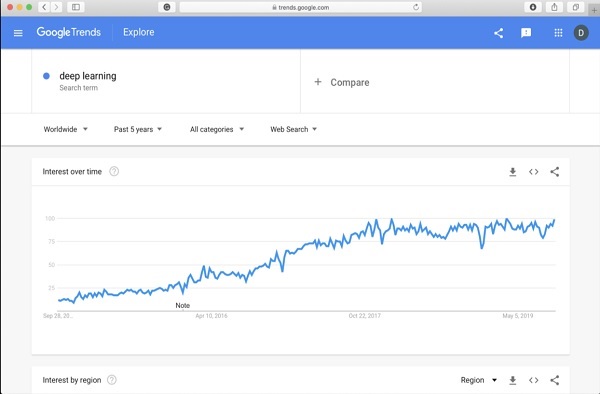
Just to get you more excited in deep learning, below is a screenshot of Google trends on deep learning here −
As you can see from the diagram, the interest in deep learning is steadily growing over the last several years. There are many areas such as computer vision, natural language processing, speech recognition, bioinformatics, drug design, and so on, where the deep learning has been successfully applied. This tutorial will get you quickly started on deep learning.
So keep reading!
Deep Learning with Keras — Deep Learning
As said in the introduction, deep learning is a process of training an artificial neural network with a huge amount of data. Once trained, the network will be able to give us the predictions on unseen data. Before I go further in explaining what deep learning is, let us quickly go through some terms used in training a neural network.
Neural Networks
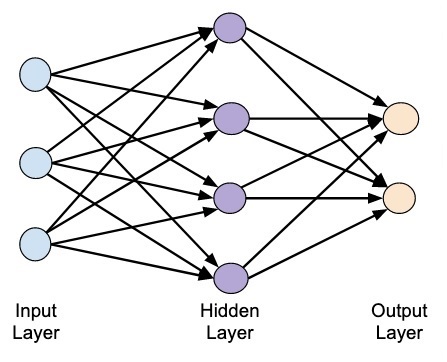
The idea of artificial neural network was derived from neural networks in our brain. A typical neural network consists of three layers — input, output and hidden layer as shown in the picture below.
This is also called a shallow neural network, as it contains only one hidden layer. You add more hidden layers in the above architecture to create a more complex architecture.
Deep Networks
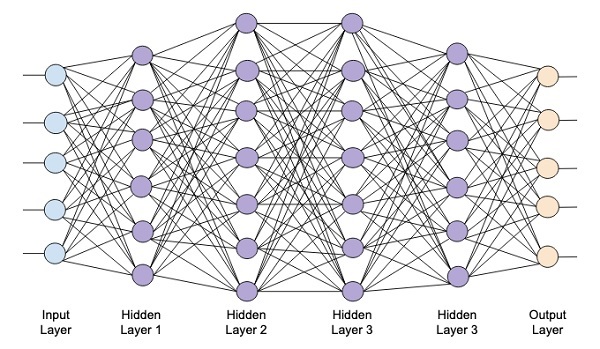
The following diagram shows a deep network consisting of four hidden layers, an input layer and an output layer.
As the number of hidden layers are added to the network, its training becomes more complex in terms of required resources and the time it takes to fully train the network.
Network Training
After you define the network architecture, you train it for doing certain kinds of predictions. Training a network is a process of finding the proper weights for each link in the network. During training, the data flows from Input to Output layers through various hidden layers. As the data always moves in one direction from input to output, we call this network as Feed-forward Network and we call the data propagation as Forward Propagation.
Activation Function
At each layer, we calculate the weighted sum of inputs and feed it to an Activation function. The activation function brings nonlinearity to the network. It is simply some mathematical function that discretizes the output. Some of the most commonly used activations functions are sigmoid, hyperbolic, tangent (tanh), ReLU and Softmax.
Backpropagation
Backpropagation is an algorithm for supervised learning. In Backpropagation, the errors propagate backwards from the output to the input layer. Given an error function, we calculate the gradient of the error function with respect to the weights assigned at each connection. The calculation of the gradient proceeds backwards through the network. The gradient of the final layer of weights is calculated first and the gradient of the first layer of weights is calculated last.
At each layer, the partial computations of the gradient are reused in the computation of the gradient for the previous layer. This is called Gradient Descent.
In this project-based tutorial you will define a feed-forward deep neural network and train it with backpropagation and gradient descent techniques. Luckily, Keras provides us all high level APIs for defining network architecture and training it using gradient descent. Next, you will learn how to do this in Keras.
Handwritten Digit Recognition System
In this mini project, you will apply the techniques described earlier. You will create a deep learning neural network that will be trained for recognizing handwritten digits. In any machine learning project, the first challenge is collecting the data. Especially, for deep learning networks, you need humongous data. Fortunately, for the problem that we are trying to solve, somebody has already created a dataset for training. This is called mnist, which is available as a part of Keras libraries. The dataset consists of several 28×28 pixel images of handwritten digits. You will train your model on the major portion of this dataset and the rest of the data would be used for validating your trained model.
Project Description
The mnist dataset consists of 70000 images of handwritten digits. A few sample images are reproduced here for your reference
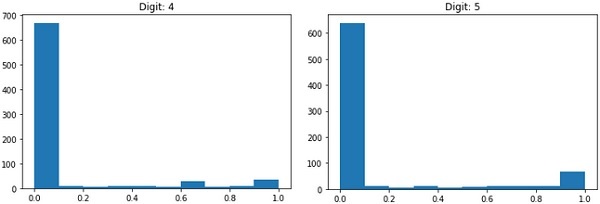
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Clearly, you can see that the distribution of the pixels (especially those tending towards white tone) differ, this distinguishes the digits they represent. We will feed this distribution of 784 pixels to our network as its input. The output of the network will consist of 10 categories representing a digit between 0 and 9.
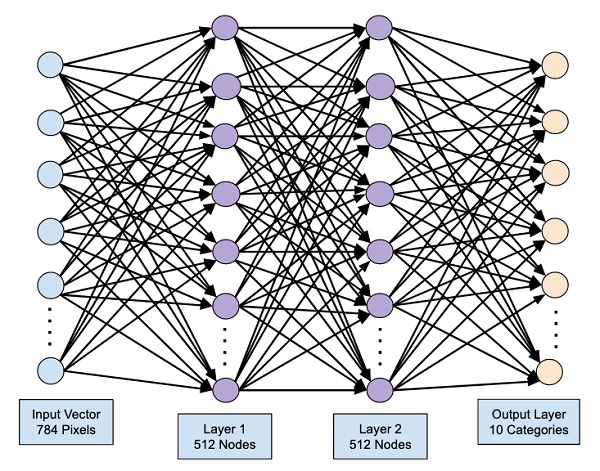
Our network will consist of 4 layers — one input layer, one output layer and two hidden layers. Each hidden layer will contain 512 nodes. Each layer is fully connected to the next layer. When we train the network, we will be computing the weights for each connection. We train the network by applying backpropagation and gradient descent that we discussed earlier.
Deep Learning with Keras — Setting up Project
With this background, let us now start creating the project.
Setting Up Project
We will use Jupyter through Anaconda navigator for our project. As our project uses TensorFlow and Keras, you will need to install those in Anaconda setup. To install Tensorflow, run the following command in your console window:
>conda install -c anaconda tensorflow
To install Keras, use the following command −
>conda install -c anaconda keras
You are now ready to start Jupyter.
Starting Jupyter
When you start the Anaconda navigator, you would see the following opening screen.
Click ‘Jupyter’ to start it. The screen will show up the existing projects, if any, on your drive.
Starting a New Project
Start a new Python 3 project in Anaconda by selecting the following menu option −
File | New Notebook | Python 3
The screenshot of the menu selection is shown for your quick reference −
A new blank project will show up on your screen as shown below −
Change the project name to DeepLearningDigitRecognition by clicking and editing on the default name “UntitledXX”.
Deep Learning with Keras — Importing Libraries
We first import the various libraries required by the code in our project.
Array Handling and Plotting
As typical, we use numpy for array handling and matplotlib for plotting. These libraries are imported in our project using the following import statements
import numpy as np import matplotlib import matplotlib.pyplot as plot
Suppressing Warnings
As both Tensorflow and Keras keep on revising, if you do not sync their appropriate versions in the project, at runtime you would see plenty of warning errors. As they distract your attention from learning, we shall be suppressing all the warnings in this project. This is done with the following lines of code −
# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False
We use Keras libraries to import dataset. We will use the mnist dataset for handwritten digits. We import the required package using the following statement
from keras.datasets import mnist
We will be defining our deep learning neural network using Keras packages. We import the Sequential, Dense, Dropout and Activation packages for defining the network architecture. We use load_model package for saving and retrieving our model. We also use np_utils for a few utilities that we need in our project. These imports are done with the following program statements −
from keras.models import Sequential, load_model from keras.layers.core import Dense, Dropout, Activation from keras.utils import np_utils
When you run this code, you will see a message on the console that says that Keras uses TensorFlow at the backend. The screenshot at this stage is shown here −
Now, as we have all the imports required by our project, we will proceed to define the architecture for our Deep Learning network.
Creating Deep Learning Model
Our neural network model will consist of a linear stack of layers. To define such a model, we call the Sequential function −
model = Sequential()
Input Layer
We define the input layer, which is the first layer in our network using the following program statement −
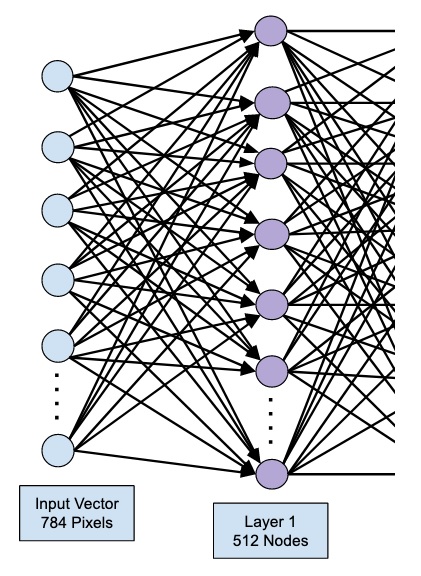
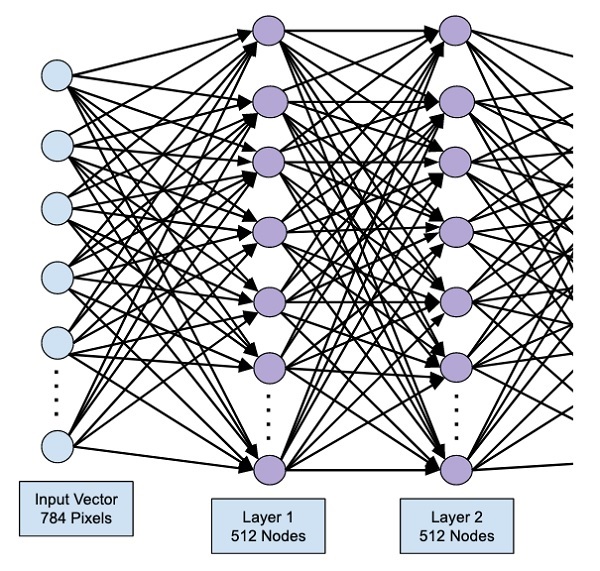
model.add(Dense(512, input_shape=(784,)))
This creates a layer with 512 nodes (neurons) with 784 input nodes. This is depicted in the figure below −
Note that all the input nodes are fully connected to the Layer 1, that is each input node is connected to all 512 nodes of Layer 1.
Next, we need to add the activation function for the output of Layer 1. We will use ReLU as our activation. The activation function is added using the following program statement −
model.add(Activation('relu'))
Next, we add Dropout of 20% using the statement below. Dropout is a technique used to prevent model from overfitting.
model.add(Dropout(0.2))
At this point, our input layer is fully defined. Next, we will add a hidden layer.
Hidden Layer
Our hidden layer will consist of 512 nodes. The input to the hidden layer comes from our previously defined input layer. All the nodes are fully connected as in the earlier case. The output of the hidden layer will go to the next layer in the network, which is going to be our final and output layer. We will use the same ReLU activation as for the previous layer and a dropout of 20%. The code for adding this layer is given here −
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
The network at this stage can be visualized as follows −
Next, we will add the final layer to our network, which is the output layer. Note that you may add any number of hidden layers using the code similar to the one which you have used here. Adding more layers would make the network complex for training; however, giving a definite advantage of better results in many cases though not all.
Output Layer
The output layer consists of just 10 nodes as we want to classify the given images in 10 distinct digits. We add this layer, using the following statement −
model.add(Dense(10))
As we want to classify the output in 10 distinct units, we use the softmax activation. In case of ReLU, the output is binary. We add the activation using the following statement −
model.add(Activation('softmax'))
At this point, our network can be visualized as shown in the below diagram −
At this point, our network model is fully defined in the software. Run the code cell and if there are no errors, you will get a confirmation message on the screen as shown in the screenshot below −
Next, we need to compile the model.
Deep Learning with Keras — Compiling the Model
The compilation is performed using one single method call called compile.
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
The compile method requires several parameters. The loss parameter is specified to have type ‘categorical_crossentropy’. The metrics parameter is set to ‘accuracy’ and finally we use the adam optimizer for training the network. The output at this stage is shown below −
Now, we are ready to feed in the data to our network.
Loading Data
As said earlier, we will use the mnist dataset provided by Keras. When we load the data into our system, we will split it in the training and test data. The data is loaded by calling the load_data method as follows −
(X_train, y_train), (X_test, y_test) = mnist.load_data()
The output at this stage looks like the following −
Now, we shall learn the structure of the loaded dataset.
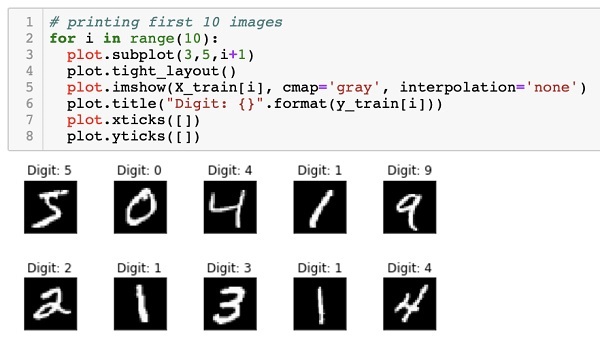
The data that is provided to us are the graphic images of size 28 x 28 pixels, each containing a single digit between 0 and 9. We will display the first ten images on the console. The code for doing so is given below −
# printing first 10 images
for i in range(10):
plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])
In an iterative loop of 10 counts, we create a subplot on each iteration and show an image from X_train vector in it. We title each image from the corresponding y_train vector. Note that the y_train vector contains the actual values for the corresponding image in X_train vector. We remove the x and y axes markings by calling the two methods xticks and yticks with null argument. When you run the code, you would see the following output −
Next, we will prepare data for feeding it into our network.
Deep Learning with Keras — Preparing Data
Before we feed the data to our network, it must be converted into the format required by the network. This is called preparing data for the network. It generally consists of converting a multi-dimensional input to a single-dimension vector and normalizing the data points.
Reshaping Input Vector
The images in our dataset consist of 28 x 28 pixels. This must be converted into a single dimensional vector of size 28 * 28 = 784 for feeding it into our network. We do so by calling the reshape method on the vector.
X_train = X_train.reshape(60000, 784) X_test = X_test.reshape(10000, 784)
Now, our training vector will consist of 60000 data points, each consisting of a single dimension vector of size 784. Similarly, our test vector will consist of 10000 data points of a single-dimension vector of size 784.
Normalizing Data
The data that the input vector contains currently has a discrete value between 0 and 255 — the gray scale levels. Normalizing these pixel values between 0 and 1 helps in speeding up the training. As we are going to use stochastic gradient descent, normalizing data will also help in reducing the chance of getting stuck in local optima.
To normalize the data, we represent it as float type and divide it by 255 as shown in the following code snippet −
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Let us now look at how the normalized data looks like.
Examining Normalized Data
To view the normalized data, we will call the histogram function as shown here −
plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))
Here, we plot the histogram of the first element of the X_train vector. We also print the digit represented by this data point. The output of running the above code is shown here −
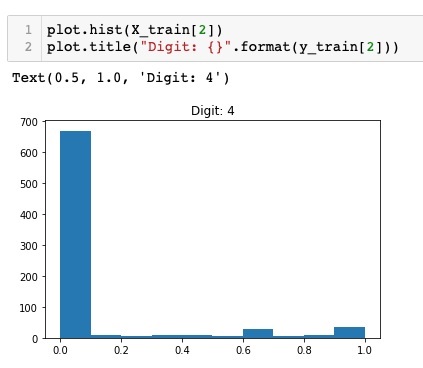
You will notice a thick density of points having value close to zero. These are the black dot points in the image, which obviously is the major portion of the image. The rest of the gray scale points, which are close to white color, represent the digit. You may check out the distribution of pixels for another digit. The code below prints the histogram of a digit at index of 2 in the training dataset.
plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])
The output of running the above code is shown below −
Comparing the above two figures, you will notice that the distribution of the white pixels in two images differ indicating a representation of a different digit — “5” and “4” in the above two pictures.
Next, we will examine the distribution of data in our full training dataset.
Examining Data Distribution
Before we train our machine learning model on our dataset, we should know the distribution of unique digits in our dataset. Our images represent 10 distinct digits ranging from 0 to 9. We would like to know the number of digits 0, 1, etc., in our dataset. We can get this information by using the unique method of Numpy.
Use the following command to print the number of unique values and the number of occurrences of each one
print(np.unique(y_train, return_counts=True))
When you run the above command, you will see the following output −
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))
It shows that there are 10 distinct values — 0 through 9. There are 5923 occurrences of digit 0, 6742 occurrences of digit 1, and so on. The screenshot of the output is shown here −
As a final step in data preparation, we need to encode our data.
Encoding Data
We have ten categories in our dataset. We will thus encode our output in these ten categories using one-hot encoding. We use to_categorial method of Numpy utilities to perform encoding. After the output data is encoded, each data point would be converted into a single dimensional vector of size 10. For example, digit 5 will now be represented as [0,0,0,0,0,1,0,0,0,0].
Encode the data using the following piece of code −
n_classes = 10 Y_train = np_utils.to_categorical(y_train, n_classes)
You may check out the result of encoding by printing the first 5 elements of the categorized Y_train vector.
Use the following code to print the first 5 vectors −
for i in range(5): print (Y_train[i])
You will see the following output −
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
The first element represents digit 5, the second represents digit 0, and so on.
Finally, you will have to categorize the test data too, which is done using the following statement −
Y_test = np_utils.to_categorical(y_test, n_classes)
At this stage, your data is fully prepared for feeding into the network.
Next, comes the most important part and that is training our network model.
Deep Learning with Keras — Training the Model
The model training is done in one single method call called fit that takes few parameters as seen in the code below −
history = model.fit(X_train, Y_train, batch_size=128, epochs=20, verbose=2, validation_data=(X_test, Y_test)))
The first two parameters to the fit method specify the features and the output of the training dataset.
The epochs is set to 20; we assume that the training will converge in max 20 epochs — the iterations. The trained model is validated on the test data as specified in the last parameter.
The partial output of running the above command is shown here −
Train on 60000 samples, validate on 10000 samples Epoch 1/20 - 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665 Epoch 2/20 - 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715 Epoch 3/20 - 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765 Epoch 4/20 - 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795 Epoch 5/20 - 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792
The screenshot of the output is given below for your quick reference −
Now, as the model is trained on our training data, we will evaluate its performance.
Evaluating Model Performance
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
We will print the loss and accuracy using the following two statements −
print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])
When you run the above statements, you would see the following output −
Test Loss 0.08041584826191042 Test Accuracy 0.9837
This shows a test accuracy of 98%, which should be acceptable to us. What it means to us that in 2% of the cases, the handwritten digits would not be classified correctly. We will also plot accuracy and loss metrics to see how the model performs on the test data.
Plotting Accuracy Metrics
We use the recorded history during our training to get a plot of accuracy metrics. The following code will plot the accuracy on each epoch. We pick up the training data accuracy (“acc”) and the validation data accuracy (“val_acc”) for plotting.
plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')
The output plot is shown below −
As you can see in the diagram, the accuracy increases rapidly in the first two epochs, indicating that the network is learning fast. Afterwards, the curve flattens indicating that not too many epochs are required to train the model further. Generally, if the training data accuracy (“acc”) keeps improving while the validation data accuracy (“val_acc”) gets worse, you are encountering overfitting. It indicates that the model is starting to memorize the data.
We will also plot the loss metrics to check our model’s performance.
Plotting Loss Metrics
Again, we plot the loss on both the training (“loss”) and test (“val_loss”) data. This is done using the following code −
plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')
The output of this code is shown below −
As you can see in the diagram, the loss on the training set decreases rapidly for the first two epochs. For the test set, the loss does not decrease at the same rate as the training set, but remains almost flat for multiple epochs. This means our model is generalizing well to unseen data.
Now, we will use our trained model to predict the digits in our test data.
Predicting on Test Data
To predict the digits in an unseen data is very easy. You simply need to call the predict_classes method of the model by passing it to a vector consisting of your unknown data points.
predictions = model.predict_classes(X_test)
The method call returns the predictions in a vector that can be tested for 0’s and 1’s against the actual values. This is done using the following two statements −
correct_predictions = np.nonzero(predictions == y_test)[0] incorrect_predictions = np.nonzero(predictions != y_test)[0]
Finally, we will print the count of correct and incorrect predictions using the following two program statements −
print(len(correct_predictions)," classified correctly") print(len(incorrect_predictions)," classified incorrectly")
When you run the code, you will get the following output −
9837 classified correctly 163 classified incorrectly
Now, as you have satisfactorily trained the model, we will save it for future use.
Deep Learning with Keras — Saving Model
We will save the trained model in our local drive in the models folder in our current working directory. To save the model, run the following code −
directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)
The output after running the code is shown below −
Now, as you have saved a trained model, you may use it later on for processing your unknown data.
Loading Model for Predictions
To predict the unseen data, you first need to load the trained model into the memory. This is done using the following command −
model = load_model ('./models/handwrittendigitrecognition.h5')
Note that we are simply loading the .h5 file into memory. This sets up the entire neural network in memory along with the weights assigned to each layer.
Now, to do your predictions on unseen data, load the data, let it be one or more items, into the memory. Preprocess the data to meet the input requirements of our model as what you did on your training and test data above. After preprocessing, feed it to your network. The model will output its prediction.
Deep Learning with Keras — Conclusion
Keras provides a high level API for creating deep neural network. In this tutorial, you learned to create a deep neural network that was trained for finding the digits in handwritten text. A multi-layer network was created for this purpose. Keras allows you to define an activation function of your choice at each layer. Using gradient descent, the network was trained on the training data. The accuracy of the trained network in predicting the unseen data was tested on the test data. You learned to plot the accuracy and error metrics. After the network is fully trained, you saved the network model for future use.
Deep Learning with Keras — Introduction
Deep Learning has become a buzzword in recent days in the field of Artificial Intelligence (AI). For many years, we used Machine Learning (ML) for imparting intelligence to machines. In recent days, deep learning has become more popular due to its supremacy in predictions as compared to traditional ML techniques.
Deep Learning essentially means training an Artificial Neural Network (ANN) with a huge amount of data. In deep learning, the network learns by itself and thus requires humongous data for learning. While traditional machine learning is essentially a set of algorithms that parse data and learn from it. They then used this learning for making intelligent decisions.
Now, coming to Keras, it is a high-level neural networks API that runs on top of TensorFlow — an end-to-end open source machine learning platform. Using Keras, you easily define complex ANN architectures to experiment on your big data. Keras also supports GPU, which becomes essential for processing huge amount of data and developing machine learning models.
In this tutorial, you will learn the use of Keras in building deep neural networks. We shall look at the practical examples for teaching. The problem at hand is recognizing handwritten digits using a neural network that is trained with deep learning.
Just to get you more excited in deep learning, below is a screenshot of Google trends on deep learning here −
As you can see from the diagram, the interest in deep learning is steadily growing over the last several years. There are many areas such as computer vision, natural language processing, speech recognition, bioinformatics, drug design, and so on, where the deep learning has been successfully applied. This tutorial will get you quickly started on deep learning.
So keep reading!
Deep Learning with Keras — Deep Learning
As said in the introduction, deep learning is a process of training an artificial neural network with a huge amount of data. Once trained, the network will be able to give us the predictions on unseen data. Before I go further in explaining what deep learning is, let us quickly go through some terms used in training a neural network.
Neural Networks
The idea of artificial neural network was derived from neural networks in our brain. A typical neural network consists of three layers — input, output and hidden layer as shown in the picture below.
This is also called a shallow neural network, as it contains only one hidden layer. You add more hidden layers in the above architecture to create a more complex architecture.
Deep Networks
The following diagram shows a deep network consisting of four hidden layers, an input layer and an output layer.
As the number of hidden layers are added to the network, its training becomes more complex in terms of required resources and the time it takes to fully train the network.
Network Training
After you define the network architecture, you train it for doing certain kinds of predictions. Training a network is a process of finding the proper weights for each link in the network. During training, the data flows from Input to Output layers through various hidden layers. As the data always moves in one direction from input to output, we call this network as Feed-forward Network and we call the data propagation as Forward Propagation.
Activation Function
At each layer, we calculate the weighted sum of inputs and feed it to an Activation function. The activation function brings nonlinearity to the network. It is simply some mathematical function that discretizes the output. Some of the most commonly used activations functions are sigmoid, hyperbolic, tangent (tanh), ReLU and Softmax.
Backpropagation
Backpropagation is an algorithm for supervised learning. In Backpropagation, the errors propagate backwards from the output to the input layer. Given an error function, we calculate the gradient of the error function with respect to the weights assigned at each connection. The calculation of the gradient proceeds backwards through the network. The gradient of the final layer of weights is calculated first and the gradient of the first layer of weights is calculated last.
At each layer, the partial computations of the gradient are reused in the computation of the gradient for the previous layer. This is called Gradient Descent.
In this project-based tutorial you will define a feed-forward deep neural network and train it with backpropagation and gradient descent techniques. Luckily, Keras provides us all high level APIs for defining network architecture and training it using gradient descent. Next, you will learn how to do this in Keras.
Handwritten Digit Recognition System
In this mini project, you will apply the techniques described earlier. You will create a deep learning neural network that will be trained for recognizing handwritten digits. In any machine learning project, the first challenge is collecting the data. Especially, for deep learning networks, you need humongous data. Fortunately, for the problem that we are trying to solve, somebody has already created a dataset for training. This is called mnist, which is available as a part of Keras libraries. The dataset consists of several 28×28 pixel images of handwritten digits. You will train your model on the major portion of this dataset and the rest of the data would be used for validating your trained model.
Project Description
The mnist dataset consists of 70000 images of handwritten digits. A few sample images are reproduced here for your reference
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Clearly, you can see that the distribution of the pixels (especially those tending towards white tone) differ, this distinguishes the digits they represent. We will feed this distribution of 784 pixels to our network as its input. The output of the network will consist of 10 categories representing a digit between 0 and 9.
Our network will consist of 4 layers — one input layer, one output layer and two hidden layers. Each hidden layer will contain 512 nodes. Each layer is fully connected to the next layer. When we train the network, we will be computing the weights for each connection. We train the network by applying backpropagation and gradient descent that we discussed earlier.
Deep Learning with Keras — Setting up Project
With this background, let us now start creating the project.
Setting Up Project
We will use Jupyter through Anaconda navigator for our project. As our project uses TensorFlow and Keras, you will need to install those in Anaconda setup. To install Tensorflow, run the following command in your console window:
>conda install -c anaconda tensorflow
To install Keras, use the following command −
>conda install -c anaconda keras
You are now ready to start Jupyter.
Starting Jupyter
When you start the Anaconda navigator, you would see the following opening screen.
Click ‘Jupyter’ to start it. The screen will show up the existing projects, if any, on your drive.
Starting a New Project
Start a new Python 3 project in Anaconda by selecting the following menu option −
File | New Notebook | Python 3
The screenshot of the menu selection is shown for your quick reference −
A new blank project will show up on your screen as shown below −
Change the project name to DeepLearningDigitRecognition by clicking and editing on the default name “UntitledXX”.
Deep Learning with Keras — Importing Libraries
We first import the various libraries required by the code in our project.
Array Handling and Plotting
As typical, we use numpy for array handling and matplotlib for plotting. These libraries are imported in our project using the following import statements
import numpy as np import matplotlib import matplotlib.pyplot as plot
Suppressing Warnings
As both Tensorflow and Keras keep on revising, if you do not sync their appropriate versions in the project, at runtime you would see plenty of warning errors. As they distract your attention from learning, we shall be suppressing all the warnings in this project. This is done with the following lines of code −
# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False
We use Keras libraries to import dataset. We will use the mnist dataset for handwritten digits. We import the required package using the following statement
from keras.datasets import mnist
We will be defining our deep learning neural network using Keras packages. We import the Sequential, Dense, Dropout and Activation packages for defining the network architecture. We use load_model package for saving and retrieving our model. We also use np_utils for a few utilities that we need in our project. These imports are done with the following program statements −
from keras.models import Sequential, load_model from keras.layers.core import Dense, Dropout, Activation from keras.utils import np_utils
When you run this code, you will see a message on the console that says that Keras uses TensorFlow at the backend. The screenshot at this stage is shown here −
Now, as we have all the imports required by our project, we will proceed to define the architecture for our Deep Learning network.
Creating Deep Learning Model
Our neural network model will consist of a linear stack of layers. To define such a model, we call the Sequential function −
model = Sequential()
Input Layer
We define the input layer, which is the first layer in our network using the following program statement −
model.add(Dense(512, input_shape=(784,)))
This creates a layer with 512 nodes (neurons) with 784 input nodes. This is depicted in the figure below −
Note that all the input nodes are fully connected to the Layer 1, that is each input node is connected to all 512 nodes of Layer 1.
Next, we need to add the activation function for the output of Layer 1. We will use ReLU as our activation. The activation function is added using the following program statement −
model.add(Activation('relu'))
Next, we add Dropout of 20% using the statement below. Dropout is a technique used to prevent model from overfitting.
model.add(Dropout(0.2))
At this point, our input layer is fully defined. Next, we will add a hidden layer.
Hidden Layer
Our hidden layer will consist of 512 nodes. The input to the hidden layer comes from our previously defined input layer. All the nodes are fully connected as in the earlier case. The output of the hidden layer will go to the next layer in the network, which is going to be our final and output layer. We will use the same ReLU activation as for the previous layer and a dropout of 20%. The code for adding this layer is given here −
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
The network at this stage can be visualized as follows −
Next, we will add the final layer to our network, which is the output layer. Note that you may add any number of hidden layers using the code similar to the one which you have used here. Adding more layers would make the network complex for training; however, giving a definite advantage of better results in many cases though not all.
Output Layer
The output layer consists of just 10 nodes as we want to classify the given images in 10 distinct digits. We add this layer, using the following statement −
model.add(Dense(10))
As we want to classify the output in 10 distinct units, we use the softmax activation. In case of ReLU, the output is binary. We add the activation using the following statement −
model.add(Activation('softmax'))
At this point, our network can be visualized as shown in the below diagram −
At this point, our network model is fully defined in the software. Run the code cell and if there are no errors, you will get a confirmation message on the screen as shown in the screenshot below −
Next, we need to compile the model.
Deep Learning with Keras — Compiling the Model
The compilation is performed using one single method call called compile.
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
The compile method requires several parameters. The loss parameter is specified to have type ‘categorical_crossentropy’. The metrics parameter is set to ‘accuracy’ and finally we use the adam optimizer for training the network. The output at this stage is shown below −
Now, we are ready to feed in the data to our network.
Loading Data
As said earlier, we will use the mnist dataset provided by Keras. When we load the data into our system, we will split it in the training and test data. The data is loaded by calling the load_data method as follows −
(X_train, y_train), (X_test, y_test) = mnist.load_data()
The output at this stage looks like the following −
Now, we shall learn the structure of the loaded dataset.
The data that is provided to us are the graphic images of size 28 x 28 pixels, each containing a single digit between 0 and 9. We will display the first ten images on the console. The code for doing so is given below −
# printing first 10 images
for i in range(10):
plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])
In an iterative loop of 10 counts, we create a subplot on each iteration and show an image from X_train vector in it. We title each image from the corresponding y_train vector. Note that the y_train vector contains the actual values for the corresponding image in X_train vector. We remove the x and y axes markings by calling the two methods xticks and yticks with null argument. When you run the code, you would see the following output −
Next, we will prepare data for feeding it into our network.
Deep Learning with Keras — Preparing Data
Before we feed the data to our network, it must be converted into the format required by the network. This is called preparing data for the network. It generally consists of converting a multi-dimensional input to a single-dimension vector and normalizing the data points.
Reshaping Input Vector
The images in our dataset consist of 28 x 28 pixels. This must be converted into a single dimensional vector of size 28 * 28 = 784 for feeding it into our network. We do so by calling the reshape method on the vector.
X_train = X_train.reshape(60000, 784) X_test = X_test.reshape(10000, 784)
Now, our training vector will consist of 60000 data points, each consisting of a single dimension vector of size 784. Similarly, our test vector will consist of 10000 data points of a single-dimension vector of size 784.
Normalizing Data
The data that the input vector contains currently has a discrete value between 0 and 255 — the gray scale levels. Normalizing these pixel values between 0 and 1 helps in speeding up the training. As we are going to use stochastic gradient descent, normalizing data will also help in reducing the chance of getting stuck in local optima.
To normalize the data, we represent it as float type and divide it by 255 as shown in the following code snippet −
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Let us now look at how the normalized data looks like.
Examining Normalized Data
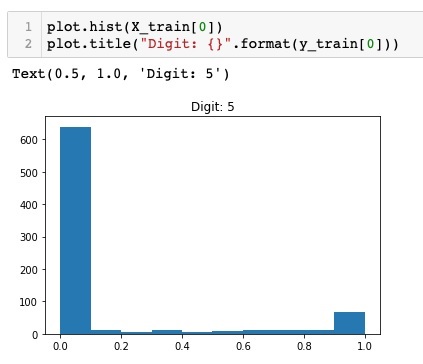
To view the normalized data, we will call the histogram function as shown here −
plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))
Here, we plot the histogram of the first element of the X_train vector. We also print the digit represented by this data point. The output of running the above code is shown here −
You will notice a thick density of points having value close to zero. These are the black dot points in the image, which obviously is the major portion of the image. The rest of the gray scale points, which are close to white color, represent the digit. You may check out the distribution of pixels for another digit. The code below prints the histogram of a digit at index of 2 in the training dataset.
plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])
The output of running the above code is shown below −
Comparing the above two figures, you will notice that the distribution of the white pixels in two images differ indicating a representation of a different digit — “5” and “4” in the above two pictures.
Next, we will examine the distribution of data in our full training dataset.
Examining Data Distribution
Before we train our machine learning model on our dataset, we should know the distribution of unique digits in our dataset. Our images represent 10 distinct digits ranging from 0 to 9. We would like to know the number of digits 0, 1, etc., in our dataset. We can get this information by using the unique method of Numpy.
Use the following command to print the number of unique values and the number of occurrences of each one
print(np.unique(y_train, return_counts=True))
When you run the above command, you will see the following output −
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))
It shows that there are 10 distinct values — 0 through 9. There are 5923 occurrences of digit 0, 6742 occurrences of digit 1, and so on. The screenshot of the output is shown here −
As a final step in data preparation, we need to encode our data.
Encoding Data
We have ten categories in our dataset. We will thus encode our output in these ten categories using one-hot encoding. We use to_categorial method of Numpy utilities to perform encoding. After the output data is encoded, each data point would be converted into a single dimensional vector of size 10. For example, digit 5 will now be represented as [0,0,0,0,0,1,0,0,0,0].
Encode the data using the following piece of code −
n_classes = 10 Y_train = np_utils.to_categorical(y_train, n_classes)
You may check out the result of encoding by printing the first 5 elements of the categorized Y_train vector.
Use the following code to print the first 5 vectors −
for i in range(5): print (Y_train[i])
You will see the following output −
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
The first element represents digit 5, the second represents digit 0, and so on.
Finally, you will have to categorize the test data too, which is done using the following statement −
Y_test = np_utils.to_categorical(y_test, n_classes)
At this stage, your data is fully prepared for feeding into the network.
Next, comes the most important part and that is training our network model.
Deep Learning with Keras — Training the Model
The model training is done in one single method call called fit that takes few parameters as seen in the code below −
history = model.fit(X_train, Y_train, batch_size=128, epochs=20, verbose=2, validation_data=(X_test, Y_test)))
The first two parameters to the fit method specify the features and the output of the training dataset.
The epochs is set to 20; we assume that the training will converge in max 20 epochs — the iterations. The trained model is validated on the test data as specified in the last parameter.
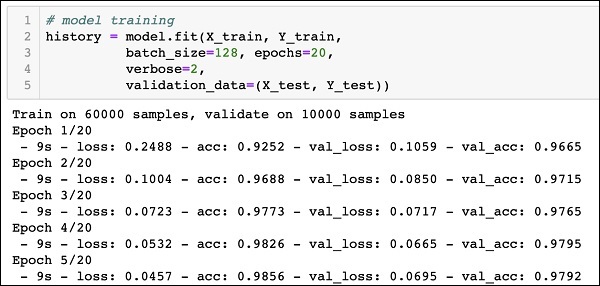
The partial output of running the above command is shown here −
Train on 60000 samples, validate on 10000 samples Epoch 1/20 - 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665 Epoch 2/20 - 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715 Epoch 3/20 - 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765 Epoch 4/20 - 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795 Epoch 5/20 - 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792
The screenshot of the output is given below for your quick reference −
Now, as the model is trained on our training data, we will evaluate its performance.
Evaluating Model Performance
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
We will print the loss and accuracy using the following two statements −
print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])
When you run the above statements, you would see the following output −
Test Loss 0.08041584826191042 Test Accuracy 0.9837
This shows a test accuracy of 98%, which should be acceptable to us. What it means to us that in 2% of the cases, the handwritten digits would not be classified correctly. We will also plot accuracy and loss metrics to see how the model performs on the test data.
Plotting Accuracy Metrics
We use the recorded history during our training to get a plot of accuracy metrics. The following code will plot the accuracy on each epoch. We pick up the training data accuracy (“acc”) and the validation data accuracy (“val_acc”) for plotting.
plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')
The output plot is shown below −
As you can see in the diagram, the accuracy increases rapidly in the first two epochs, indicating that the network is learning fast. Afterwards, the curve flattens indicating that not too many epochs are required to train the model further. Generally, if the training data accuracy (“acc”) keeps improving while the validation data accuracy (“val_acc”) gets worse, you are encountering overfitting. It indicates that the model is starting to memorize the data.
We will also plot the loss metrics to check our model’s performance.
Plotting Loss Metrics
Again, we plot the loss on both the training (“loss”) and test (“val_loss”) data. This is done using the following code −
plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')
The output of this code is shown below −
As you can see in the diagram, the loss on the training set decreases rapidly for the first two epochs. For the test set, the loss does not decrease at the same rate as the training set, but remains almost flat for multiple epochs. This means our model is generalizing well to unseen data.
Now, we will use our trained model to predict the digits in our test data.
Predicting on Test Data
To predict the digits in an unseen data is very easy. You simply need to call the predict_classes method of the model by passing it to a vector consisting of your unknown data points.
predictions = model.predict_classes(X_test)
The method call returns the predictions in a vector that can be tested for 0’s and 1’s against the actual values. This is done using the following two statements −
correct_predictions = np.nonzero(predictions == y_test)[0] incorrect_predictions = np.nonzero(predictions != y_test)[0]
Finally, we will print the count of correct and incorrect predictions using the following two program statements −
print(len(correct_predictions)," classified correctly") print(len(incorrect_predictions)," classified incorrectly")
When you run the code, you will get the following output −
9837 classified correctly 163 classified incorrectly
Now, as you have satisfactorily trained the model, we will save it for future use.
Deep Learning with Keras — Saving Model
We will save the trained model in our local drive in the models folder in our current working directory. To save the model, run the following code −
directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)
The output after running the code is shown below −
Now, as you have saved a trained model, you may use it later on for processing your unknown data.
Loading Model for Predictions
To predict the unseen data, you first need to load the trained model into the memory. This is done using the following command −
model = load_model ('./models/handwrittendigitrecognition.h5')
Note that we are simply loading the .h5 file into memory. This sets up the entire neural network in memory along with the weights assigned to each layer.
Now, to do your predictions on unseen data, load the data, let it be one or more items, into the memory. Preprocess the data to meet the input requirements of our model as what you did on your training and test data above. After preprocessing, feed it to your network. The model will output its prediction.
Deep Learning with Keras — Conclusion
Keras provides a high level API for creating deep neural network. In this tutorial, you learned to create a deep neural network that was trained for finding the digits in handwritten text. A multi-layer network was created for this purpose. Keras allows you to define an activation function of your choice at each layer. Using gradient descent, the network was trained on the training data. The accuracy of the trained network in predicting the unseen data was tested on the test data. You learned to plot the accuracy and error metrics. After the network is fully trained, you saved the network model for future use.
Введение
В предыдущей статье мы увидели, как создать простой нейрон (перцептрон), и изучили, как выполняются вычисления градиентного спуска, как строится сеть (MLP), состоящая из взаимосвязанных перцептронов, и как выполняется обучение этого типа сети.
В этой статье я хочу продемонстрировать, насколько просто реализовать этот тип алгоритма с помощью языка Python.
Python был внедрен в набор инструментов MQL5 и открывает двери для многих возможностей, таких как изучение данных, создание и использование моделей машинного обучения.
Эта встроенная интеграция MQL5 в Python открывает для нас много возможностей, которые позволяют построить от простой линейной регрессии до моделей глубокого обучения. Поскольку это язык для профессионального использования, существует множество библиотек, которые берут на себя всю тяжелую работу, связанную с вычислениями.
В нашем примере мы построим сеть вручную, но, как было сказано в предыдущей статье, это всего лишь шаг, чтобы понять, что на самом деле происходит в процессе обучения и прогнозирования, а затем я покажу более сложный пример с использованием TensorFlow и Keras.
Что такое TensorFlow?
TensorFlow — это библиотека с открытым кодом для быстрой числовой обработки.
Он был создан, поддержан и выпущен Google под лицензией Apache 2.0 с открытым кодом. API виртуально предназначен для языка программирования Python, хотя есть доступ к базовому C++ API.
В отличие от других числовых библиотек, предназначенных для использования в глубоком обучении, таких как Theano, TensorFlow предназначен для использования как в научно-исследовательских, так и в системах разработки и производства, особенно RankBrain в поисковой системе Google и в интересном проекте DeepDream.
Он может работать в системах на одном процессоре, на графическом процессоре, а также на мобильных устройствах и на крупномасштабных системах, распределенных на сотни машин.
Что такое Keras?
Keras — это мощная библиотека Python с открытым кодом, которую легко использовать при разработке и оценке моделей глубокого обучения.
Он охватывает эффективные библиотеки вычислений Theano и TensorFlow и позволяет определять и обучать модели нейронных сетей всего за несколько строк кода.
Руководство
Это руководство разделено на 4 части:
- Установка и подготовка среды Python в MetaEditor.
- Первые шаги и реконструкция модели (перцептрон и MLP).
- Создание простой модели с использованием Keras и TensorFlow.
- Как интегрировать MQL5 в Python.
1. Установка и подготовка среды Python.
Начнем с загрузки Python с официального сайта www.python.org/downloads/
Чтобы работать с TensorFlow необходимо установить версию выше 3.3 и ниже 3.8; я использую версию 3.7.
После загрузки и начала процесса установки мы активируем опцию «Добавить Python 3.7 в PATH», это гарантирует, что некоторые вещи будут работать без необходимости дополнительной настройки в будущем.
Чтобы запустить скрипт Python прямо из нашего терминала MetaTrader 5, нам нужно только выполнить предыдущую настройку.
- Установить путь исполняемого файла Python (среда)
- Установите необходимые зависимости для проекта
Нам нужно открыть MetaEditor и перейти в Инструменты>Параметры.
В данном этапе нам нужно определить путь, на котором находится наш исполняемый файл Python, и иметь в виду, что после установки он, вероятно, будет содержать путь Python по умолчанию, если по какой-то причине это не так, то введите полный путь к исполняемому файлу, чтобы вы могли запустить скрипты прямо из вашего терминала MetaTrader 5.
В моем случае я использую полностью отдельную библиотечную среду, называемую виртуальной средой, это способ получить «чистую» установку и собрать только библиотеки, необходимые для проекта.
Для получения дополнительной информации о пакете venv перейдите по ссылке.
Как только это будет готово, мы сможем запускать скрипты Python прямо из терминала. Для нашего эксперимента нам потребуется установить библиотеки:
Если у вас есть вопросы о том, как установить библиотеки, смотрите руководство по установке модуля.
- MetaTrader 5
- TensorFlow
- Matplotlib
- Pandas
- Sklearn
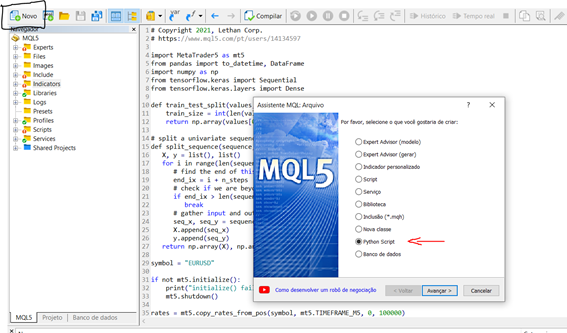
Теперь, когда мы установили и настроили среду, давайте проведем небольшой тест, чтобы понять, как создать и запустить скрипт в нашем терминале. Чтобы запустить новый скрипт прямо из MetaEditor, мы можем выполнить следующие шаги:
Новый > Python script
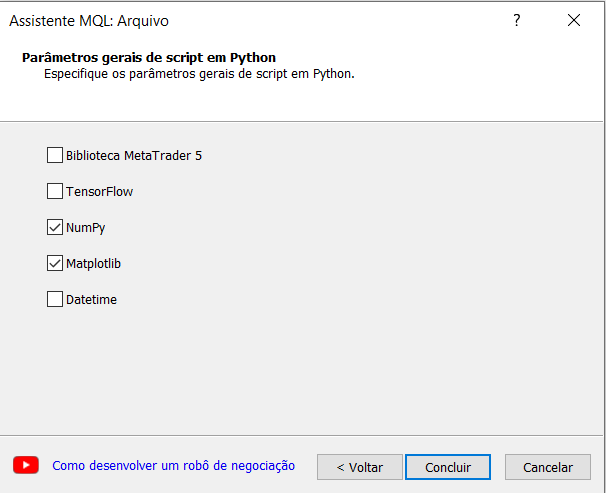
Определите имя для вашего скрипта, мастер создания MetaEditor подсказывает нам автоматически импортировать некоторые библиотеки, это очень интересно и для нашего эксперимента мы выберем вариант numpy.
Теперь давайте создадим простой скрипт, который генерирует синусоидальный график.
# Copyright 2021, Lethan Corp. # https: import numpy as np import matplotlib.pyplot as plt data = np.linspace(-np.pi, np.pi, 201) plt.plot(data, np.sin(data)) plt.xlabel('Angle [rad]') plt.ylabel('sin(data)') plt.axis('tight') plt.show()
Чтобы запустить скрипт, просто нажмите на компилировать (F7) или откройте терминал MetaTrader 5 и прикрепите скрипт к графику. После этого результаты будут отображаться во вкладке экспертов в случае, если есть распечатки, как при разработке алгоритма MQL5, в нашем случае откроется окно с графиком функции, которую мы создали выше.
2 — Первые шаги и реконструкция модели (перцептрон и MLP).
Мы будем использовать тот же набор данных, что и пример в MQL5, чтобы было проще.
Затем мы увидим функцию под названием predict(), которая прогнозирует выходное значение для строки с заданным набором весов, в этом случае первым весом всегда будет смещение. А также функция активации.
# Transfer neuron activation def activation(activation): return 1.0 if activation >= 0.0 else 0.0 # Make a prediction with weights def predict(row, weights): z = weights[0] for i in range(len(row) - 1): z += weights[i + 1] * row[i] return activation(z)
Как мы уже знаем, для обучения сети нам необходимо выполнить процесс градиентного спуска, который подробно обсуждался в предыдущей статье, а в продолжение я покажу обучающую функцию «train_weights()».
# Estimate Perceptron weights using stochastic gradient descent def train_weights(train, l_rate, n_epoch): weights = [0.0 for i in range(len(train[0]))] #random.random() for epoch in range(n_epoch): sum_error = 0.0 for row in train: y = predict(row, weights) error = row[-1] - y sum_error += error**2 weights[0] = weights[0] + l_rate * error for i in range(len(row) - 1): weights[i + 1] = weights[i + 1] + l_rate * error * row[i] print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error)) return weights
Применение модели MLP:
Это руководство разделено на 5 частей:
- Запуск сети
- Распространение (FeedForward)
- Обратное распространение (BackPropagation)
- Обучение
- Прогноз
Запуск сети:
Начнем с чего-нибудь простого, для этого создадим новую сеть, готовую к обучению.
У каждого нейрона есть набор весов, которые необходимо поддерживать. Один вес для каждого входного соединения и один дополнительный вес для смещения. Нам нужно будет сохранить дополнительные свойства нейрона во время обучения, поэтому мы будем использовать словарь для отображения каждого нейрона и чтобы хранить свойства по именам, например, как «веса» для весов.
from random import seed from random import random # Initialize a network def initialize_network(n_inputs, n_hidden, n_outputs): network = list() hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)] network.append(hidden_layer) output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)] network.append(output_layer) return network seed(1) network = initialize_network(2, 1, 2) for layer in network: print(layer)
Теперь, когда мы знаем, как создать и запустить сеть, давайте посмотрим, как мы можем использовать ее для расчета выходных данных.
Распространение (FeedForward)
from math import exp # Calculate neuron activation for an input def activate(weights, inputs): activation = weights[-1] for i in range(len(weights)-1): activation += weights[i] * inputs[i] return activation # Transfer neuron activation def transfer(activation): return 1.0 / (1.0 + exp(-activation)) # Forward propagate input to a network output def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron['weights'], inputs) neuron['output'] = transfer(activation) new_inputs.append(neuron['output']) inputs = new_inputs return inputs # test forward propagation network = [[{'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}], [{'weights': [0.2550690257394217, 0.49543508709194095]}, {'weights': [0.4494910647887381, 0.651592972722763]}]] row = [1, 0, None] output = forward_propagate(network, row) print(output)
При выполнении приведенного выше скрипта мы получим результат:
[0.6629970129852887, 0.7253160725279748]
Фактические выходные значения пока просто абсурдны, но скоро мы узнаем, как сделать так, чтобы веса в нейронах были более полезными.
Обратное распространение
# Calculate the derivative of an neuron output def transfer_derivative(output): return output * (1.0 - output) # Backpropagate error and store in neurons def backward_propagate_error(network, expected): for i in reversed(range(len(network))): layer = network[i] errors = list() if i != len(network)-1: for j in range(len(layer)): error = 0.0 for neuron in network[i + 1]: error += (neuron['weights'][j] * neuron['delta']) errors.append(error) else: for j in range(len(layer)): neuron = layer[j] errors.append(expected[j] - neuron['output']) for j in range(len(layer)): neuron = layer[j] neuron['delta'] = errors[j] * transfer_derivative(neuron['output']) # test backpropagation of error network = [[{'output': 0.7105668883115941, 'weights': [0.13436424411240122, 0.8474337369372327, 0.763774618976614]}], [{'output': 0.6213859615555266, 'weights': [0.2550690257394217, 0.49543508709194095]}, {'output': 0.6573693455986976, 'weights': [0.4494910647887381, 0.651592972722763]}]] expected = [0, 1] backward_propagate_error(network, expected) for layer in network: print(layer)
Образец выполнения распечатывает сеть после завершения проверки ошибок. Как мы видим, значения ошибок вычисляются и сохраняются в нейронах для выходного слоя и скрытого слоя.
[{‘output’: 0.7105668883115941, ‘weights’: [0.13436424411240122, 0.8474337369372327, 0.763774618976614], ‘delta’: -0.0005348048046610517}]
[{‘output’: 0.6213859615555266, ‘weights’: [0.2550690257394217, 0.49543508709194095], ‘delta’: -0.14619064683582808}, {‘output’: 0.6573693455986976, ‘weights’: [0.4494910647887381, 0.651592972722763], ‘delta’: 0.0771723774346327}]
Обучение сети
from math import exp from random import seed from random import random # Initialize a network def initialize_network(n_inputs, n_hidden, n_outputs): network = list() hidden_layer = [{'weights':[random() for i in range(n_inputs + 1)]} for i in range(n_hidden)] network.append(hidden_layer) output_layer = [{'weights':[random() for i in range(n_hidden + 1)]} for i in range(n_outputs)] network.append(output_layer) return network # Calculate neuron activation for an input def activate(weights, inputs): activation = weights[-1] for i in range(len(weights)-1): activation += weights[i] * inputs[i] return activation # Transfer neuron activation def transfer(activation): return 1.0 / (1.0 + exp(-activation)) # Forward propagate input to a network output def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron['weights'], inputs) neuron['output'] = transfer(activation) new_inputs.append(neuron['output']) inputs = new_inputs return inputs # Calculate the derivative of an neuron output def transfer_derivative(output): return output * (1.0 - output) # Backpropagate error and store in neurons def backward_propagate_error(network, expected): for i in reversed(range(len(network))): layer = network[i] errors = list() if i != len(network)-1: for j in range(len(layer)): error = 0.0 for neuron in network[i + 1]: error += (neuron['weights'][j] * neuron['delta']) errors.append(error) else: for j in range(len(layer)): neuron = layer[j] errors.append(expected[j] - neuron['output']) for j in range(len(layer)): neuron = layer[j] neuron['delta'] = errors[j] * transfer_derivative(neuron['output']) # Update network weights with error def update_weights(network, row, l_rate): for i in range(len(network)): inputs = row[:-1] if i != 0: inputs = [neuron['output'] for neuron in network[i - 1]] for neuron in network[i]: for j in range(len(inputs)): neuron['weights'][j] += l_rate * neuron['delta'] * inputs[j] neuron['weights'][-1] += l_rate * neuron['delta'] # Train a network for a fixed number of epochs def train_network(network, train, l_rate, n_epoch, n_outputs): for epoch in range(n_epoch): sum_error = 0 for row in train: outputs = forward_propagate(network, row) expected = [0 for i in range(n_outputs)] expected[row[-1]] = 1 sum_error += sum([(expected[i]-outputs[i])**2 for i in range(len(expected))]) backward_propagate_error(network, expected) update_weights(network, row, l_rate) print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error)) # Test training backprop algorithm seed(1) dataset = [[2.7810836,2.550537003,0], [1.465489372,2.362125076,0], [3.396561688,4.400293529,0], [1.38807019,1.850220317,0], [3.06407232,3.005305973,0], [7.627531214,2.759262235,1], [5.332441248,2.088626775,1], [6.922596716,1.77106367,1], [8.675418651,-0.242068655,1], [7.673756466,3.508563011,1]] n_inputs = len(dataset[0]) - 1 n_outputs = len(set([row[-1] for row in dataset])) network = initialize_network(n_inputs, 2, n_outputs) train_network(network, dataset, 0.5, 20, n_outputs) for layer in network: print(layer)
После обучения сеть распечатывается и отображаются выученные веса. Также в сети еще остаются выходные значения и значения дельты, которые можно игнорировать. Мы могли бы обновить нашу функцию обучения, чтобы удалить эти данные, если бы захотели.
>epoch=13, lrate=0.500, error=1.953
>epoch=14, lrate=0.500, error=1.774
>epoch=15, lrate=0.500, error=1.614
>epoch=16, lrate=0.500, error=1.472
>epoch=17, lrate=0.500, error=1.346
>epoch=18, lrate=0.500, error=1.233
>epoch=19, lrate=0.500, error=1.132
[{‘weights’: [-1.4688375095432327, 1.850887325439514, 1.0858178629550297], ‘output’: 0.029980305604426185, ‘delta’: -0.0059546604162323625}, {‘weights’: [0.37711098142462157, -0.0625909894552989, 0.2765123702642716], ‘output’: 0.9456229000211323, ‘delta’: 0.0026279652850863837}]
[{‘weights’: [2.515394649397849, -0.3391927502445985, -0.9671565426390275], ‘output’: 0.23648794202357587, ‘delta’: -0.04270059278364587}, {‘weights’: [-2.5584149848484263, 1.0036422106209202, 0.42383086467582715], ‘output’: 0.7790535202438367, ‘delta’: 0.03803132596437354}]
Чтобы сделать прогноз, мы можем использовать уже настроенный в предыдущем примере набор весов.
Прогнозирование
from math import exp # Calculate neuron activation for an input def activate(weights, inputs): activation = weights[-1] for i in range(len(weights)-1): activation += weights[i] * inputs[i] return activation # Transfer neuron activation def transfer(activation): return 1.0 / (1.0 + exp(-activation)) # Forward propagate input to a network output def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron['weights'], inputs) neuron['output'] = transfer(activation) new_inputs.append(neuron['output']) inputs = new_inputs return inputs # Make a prediction with a network def predict(network, row): outputs = forward_propagate(network, row) return outputs.index(max(outputs)) # Test making predictions with the network dataset = [[2.7810836,2.550537003,0], [1.465489372,2.362125076,0], [3.396561688,4.400293529,0], [1.38807019,1.850220317,0], [3.06407232,3.005305973,0], [7.627531214,2.759262235,1], [5.332441248,2.088626775,1], [6.922596716,1.77106367,1], [8.675418651,-0.242068655,1], [7.673756466,3.508563011,1]] network = [[{'weights': [-1.482313569067226, 1.8308790073202204, 1.078381922048799]}, {'weights': [0.23244990332399884, 0.3621998343835864, 0.40289821191094327]}], [{'weights': [2.5001872433501404, 0.7887233511355132, -1.1026649757805829]}, {'weights': [-2.429350576245497, 0.8357651039198697, 1.0699217181280656]}]] for row in dataset: prediction = predict(network, row) print('Expected=%d, Got=%d' % (row[-1], prediction))
При выполнении примера распечатывается ожидаемый результат для каждой записи в наборе обучающих данных, после чего следует четкий прогноз, сделанный сетью.
Это показывает, что сеть достигает 100% точности на этом небольшом наборе данных.
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=0, Got=0
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
Expected=1, Got=1
3. Создание простой модели с использованием Keras и TensorFlow.
Для сбора данных мы будем использовать пакет MetaTrader 5. Запускаем наш скрипт путем импорта библиотек, необходимых для извлечения, преобразования и прогнозирования цен. Обратите внимание, что мы не будем детально рассматривать часть подготовки данных, но не забывайте, что это очень важный шаг для модели.
Начнем с краткого предварительного просмотра данных. Набор данных (dataset) состоит из последних 1000 баров актива EURUSD. Для этого нам понадобятся несколько шагов, например:
- Импорт библиотек
- Подключение к MetaTrader
- Сбор данных
- Преобразование данных, установка даты
- Графические данные
import MetaTrader5 as mt5 from pandas import to_datetime, DataFrame import matplotlib.pyplot as plt symbol = "EURUSD" if not mt5.initialize(): print("initialize() failed") mt5.shutdown() rates = mt5.copy_rates_from_pos(symbol, mt5.TIMEFRAME_D1, 0, 1000) mt5.shutdown() rates = DataFrame(rates) rates['time'] = to_datetime(rates['time'], unit='s') rates = rates.set_index(['time']) plt.figure(figsize = (15,10)) plt.plot(rates.close) plt.show()
После запуска кода мы визуализируем данные закрытия на графике с линиями, как показано ниже.
Давайте использовать регрессионный подход, в котором будет предсказано значение закрытия следующего периода.
В этом примере мы будем использовать одномерный подход и, как указано выше, не обращая внимания на передовые методы подготовки данных.
Одномерный временной ряд — это набор данных, состоящий из одной серии наблюдений с временным порядком, и ему необходима модель, чтобы учиться на серии прошлых наблюдений, чтобы предсказать следующее значение в последовательности.
Первый шаг — разделить загруженную серию на набор для обучения и тестирования. Для этого создадим функцию, которая разделит такую серию на две части; мы будем использовать процентное значение от общего размера серии для отсечения, например, 70% для обучения и 30% для тестов. Для валидации (backtest) у нас есть другие подходы, такие как разделение серии на обучение, тестирование и валидацию. Поскольку мы говорим о финансовых сериях, нам надо будет особо стараться избегать переобучения.
В нашей функции мы ожидаем получить массив numpy и значение отсечения, и мы вернем две подобранные серии.
Первый возврат — это весь набор от первой позиции 0 до размера, который представляет размер фактора, а второй ряд — все остальное.
def train_test_split(values, fator): train_size = int(len(values) * fator) return values[0:train_size], values[train_size:len(values)]
Модели на Keras можно определить как последовательность слоев.
Мы создаем последовательную модель и добавляем слои — по одному за раз — до тех пор, пока мы не будем довольны нашей сетевой архитектурой.
Первое, что нужно сделать правильно, это убедиться, что входной слой имеет правильное количество входных ресурсов. Это можно указать при создании первого слоя с аргументом input_dim.
Как узнать количество слоев и их типы?
Это очень сложный вопрос. Есть эвристики, которые мы можем использовать, и зачастую лучшая сетевая структура находится в процессе экспериментов методом проб и ошибок. Как правило, требуется достаточно большая сеть, чтобы охватить структуру проблемы.
В этом примере мы будем использовать полносвязную однослойную сетевую структуру.
Полносвязные слои определяются с помощью класса Dense. Мы можем указать количество нейронов или узлов в слое в качестве первого аргумента и указать функцию активации с помощью аргумента активации.
В первом слое, мы будем использовать функцию активации выпрямленного линейного блока, называемого ReLU.
Прежде чем можно будет предсказать одномерный ряд, его необходимо подготовить.
Модель MLP будет обучаться с помощью функции, которая назначает последовательность прошлых наблюдений в качестве входных данных для выходных наблюдений. Таким образом, последовательность наблюдений должна быть преобразована в множество примеров, на которых модель смогла бы учиться.
Рассмотрим одномерную последовательность:
[10, 20, 30, 40, 50, 60, 70, 80, 90]
Мы можем разделить последовательность на несколько шаблонов входа/выхода, называемых выборкой.
В нашем примере мы будем использовать три временных этапа, которые используются в качестве входных данных, и один временной шаг, который используется для изучаемого прогноза.
X, y
10, 20, 30 40
20, 30, 40 50
30, 40, 50 60
…
Далее, мы создаем функцию split_sequence(), которая реализует это поведение и разделит одномерный набор на несколько выборок, каждая из которых имеет определенное количество временных шагов, и выход — это единичный временной шаг.
Мы можем протестировать нашу функцию на небольшом наборе данных, таких как уже придуманные в вышеуказанном примере.
# univariate data preparation from numpy import array # split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): # find the end of this pattern end_ix = i + n_steps # check if we are beyond the sequence if end_ix > len(sequence)-1: break # gather input and output parts of the pattern seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return array(X), array(y) # define input sequence raw_seq = [10, 20, 30, 40, 50, 60, 70, 80, 90] # choose a number of time steps n_steps = 3 # split into samples X, y = split_sequence(raw_seq, n_steps) # summarize the data for i in range(len(X)): print(X[i], y[i])
При выполнении примера одномерная серия делится на шесть выборок, каждая из которых имеет три временных шага входа и один временной шаг выхода.
[10 20 30] 40
[20 30 40] 50
[30 40 50] 60
[40 50 60] 70
[50 60 70] 80
[60 70 80] 90
Чтобы продолжить, нам нужно разделить выборку на X (feature) и y (target), чтобы мы могли обучить сеть. Для этого мы будем использовать функцию split_sequence(), которую мы создали ранее.
X_train, y_train = split_sequence(train, 3) X_test, y_test = split_sequence(test, 3)
Теперь, когда мы подготовили наши образцы данных, мы можем создать сеть MLP.
Простая модель MLP имеет единственный скрытый слой узлов (нейронов) и выходной слой, который используется для прогнозирования.
Мы можем определить MLP для прогнозирования одномерных временных рядов следующим образом.
# define model model = Sequential() model.add(Dense(100, activation='relu', input_dim=n_steps)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse')
Важным моментом в определении является форма входных данных, это то, что модель ожидает в качестве входных данных для каждой выборки с точки зрения количества временных шагов.
Количество временных шагов в качестве входных данных — это число, которое мы выбираем при подготовке нашего набора данных как аргумент функции split_sequence().
Размер входных данных для каждой выборки указывается в аргументе input_dim в определении первого скрытого слоя. Технически модель будет показывать каждый временной шаг как отдельный ресурс, а не как отдельные временные шаги.
У нас почти всегда есть несколько образцов, поэтому модель ожидает, что входной обучающий компонент данных будет иметь размеры или форму:
[samples, features]
Функция split_sequence() генерирует X в форме [образцы, характеристики], готовой к использованию.
Модель обучается с использованием эффективного алгоритма под названием Adam для стохастического градиентного спуска и он оптимизируется с использованием функции потерь среднеквадратичной ошибки, или ‘mse’.
Как только модель определена, мы можем обучить ее с помощью набора данных.
model.fit(X_train, y_train, epochs=100, verbose=2)
После обучения модели мы можем предсказать будущее значение; модель ожидает, что входная форма будет двумерной с [образцы, характеристики], поэтому нам нужно изменить форму единственной входной выборки до того, как сделать прогноз, например, с помощью формы [1, 3] для 1 выборки и 3 временных шагов, используемых в качестве входных характеристик.
Например, мы выберем последнюю запись тестовой выборки «X_test» и после предсказания сравним ее с реальным значением, содержащимся в последней выборке «y_test».
# demonstrate prediction x_input = X_test[-1] x_input = x_input.reshape((1, n_steps)) yhat = model.predict(x_input, verbose=0) print("Valor previsto: ", yhat) print("Valor real: ", y_test[-1])
4. Как интегрировать MQL5 в Python.
Чтобы использовать модель в торговом счете, у нас есть несколько вариантов, один из них — использовать встроенные функции в Python, которые открывают и закрывают позиции, но для этого сценария у нас не будет многих возможностей, которые предлагает нам MQL; по этой причине я выбрал одну интеграцию между Python и средой MQL, что даст нам больше автономии в управлении нашими позициями/ордерами.
Основываясь на статье MQL5 Соединение MetaTrader 5 и Python: получение и отправка данных, написанной Максимом Дмитриевским, я реализовал этот класс, используя шаблон разработки под названием Singleton, который будет отвечать за создание Socket-клиента для соединения. Этот шаблон гарантирует, что существует только одна копия объекта определенного типа, потому что если программа использует два указателя, относящиеся к одному и тому же объекту, они будут указывать на один и тот же объект.
class CClientSocket { private: static CClientSocket* m_socket; int m_handler_socket; int m_port; string m_host; int m_time_out; CClientSocket(void); ~CClientSocket(void); public: static bool DeleteSocket(void); bool SocketSend(string payload); string SocketReceive(void); bool IsConnected(void); static CClientSocket *Socket(void); bool Config(string host, int port); bool Close(void); };
Класс CClienteSocke хранит статический указатель как частный член; у класса есть только конструктор, который является частным и не может быть вызван, вместо вызова конструктора можно использовать метод Socket, этим мы гарантируем, что используется только один объект.
static CClientSocket *CClientSocket::Socket(void) { if(CheckPointer(m_socket)==POINTER_INVALID) m_socket=new CClientSocket(); return m_socket; }
Этот метод проверяет, указывает ли статический указатель на объект CClienteSocket, и если это правда, то он возвращает ссылку; в противном случае создается новый объект и связывается с указателем, тем самым гарантируя исключительность этого объекта в нашей системе.
Чтобы установить соединение с сервером, необходимо запустить соединение, поэтому мы создали метод IsConnected, чтобы установить соединение и мы можем начать передачу/получение данных.
bool CClientSocket::IsConnected(void) { ResetLastError(); bool res=true; m_handler_socket=SocketCreate(); if(m_handler_socket==INVALID_HANDLE) res=false; if(!::SocketConnect(m_handler_socket,m_host,m_port,m_time_out)) res=false; return res; }
После успешного подключения и успешной передачи сообщений, необходимо закрыть это соединение, для этого мы воспользуемся методом Close, чтобы закрыть ранее открытое соединение.
bool CClientSocket::Close(void) { bool res=false; if(SocketClose(m_handler_socket)) { res=true; m_handler_socket=INVALID_HANDLE; } return res; }
Теперь нам нужно прописать наш сервер, который будет получать новые MQL-соединения и отправлять прогнозы нашей модели.
import socket class socketserver(object): def __init__(self, address, port): self.sock = socket.socket(socket.AF_INET, socket.SOCK_STREAM) self.address = address self.port = port self.sock.bind((self.address, self.port)) def socket_receive(self): self.sock.listen(1) self.conn, self.addr = self.sock.accept() self.cummdata = '' while True: data = self.conn.recv(10000) self.cummdata+=data.decode("utf-8") if not data: self.conn.close() break return self.cummdata def socket_send(self, message): self.sock.listen(1) self.conn, self.addr = self.sock.accept() self.conn.send(bytes(message, "utf-8")) def __del__(self): self.conn.close()
Наш объект простой, в его конструкторе мы получаем адрес и порт, с которым будем создавать свой сервер. Метод socket_received отвечает за принятие нового соединения и проверку наличия отправленных сообщений; если есть сообщения, которые нужно получить, мы запускаем цикл, пока не получим все части сообщения, затем мы закрываем соединение с клиентом и выходим из цикла. С другой стороны, метод socket_send отвечает за отправку сообщений нашему клиенту, но имейте в виду, что эта предлагаемая модель не только позволяет нам отправлять прогнозы нашей модели, а также открывает возможности для нескольких других вещей — всё будет зависеть от вашей креативности и потребности.
Теперь, когда у нас есть готовая коммуникация, мы должны подумать о двух вещах:
- Обучить модель и сохранить ее.
- Использовать обученную модель, чтобы делать прогнозы.
Я говорю так, потому что было бы непрактично и неправильно получать данные и проводить обучение каждый раз, когда мы хотим сделать прогноз. По этой причине я всегда провожу обучение, нахожу лучшие гиперпараметры и сохраняю свою модель для её дальнейшего использования.
Я создам файл с именем model_train, который будет содержать обучающий код сети, в нем мы будем использовать процентную разницу между ценами закрытия и попытаемся предсказать эту разницу. Обратите внимание, что меня не интересует модель, я хочу продемонстрировать, как использовать модель, интегрируя ее со средой MQL.
import MetaTrader5 as mt5 from numpy.lib.financial import rate from pandas import to_datetime, DataFrame from datetime import datetime, timezone from matplotlib import pyplot from sklearn.metrics import mean_squared_error from math import sqrt import numpy as np from tensorflow.keras import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras.callbacks import * symbol = "EURUSD" date_ini = datetime(2020, 1, 1, tzinfo=timezone.utc) date_end = datetime(2021, 7, 1, tzinfo=timezone.utc) period = mt5.TIMEFRAME_D1 def train_test_split(values, fator): train_size = int(len(values) * fator) return np.array(values[0:train_size]), np.array(values[train_size:len(values)]) # split a univariate sequence into samples def split_sequence(sequence, n_steps): X, y = list(), list() for i in range(len(sequence)): end_ix = i + n_steps if end_ix > len(sequence)-1: break seq_x, seq_y = sequence[i:end_ix], sequence[end_ix] X.append(seq_x) y.append(seq_y) return np.array(X), np.array(y) if not mt5.initialize(): print("initialize() failed") mt5.shutdown() raise Exception("Error Getting Data") rates = mt5.copy_rates_range(symbol, period, date_ini, date_end) mt5.shutdown() rates = DataFrame(rates) if rates.empty: raise Exception("Error Getting Data") rates['time'] = to_datetime(rates['time'], unit='s') rates.set_index(['time'], inplace=True) rates = rates.close.pct_change(1) rates = rates.dropna() X, y = train_test_split(rates, 0.70) X = X.reshape(X.shape[0]) y = y.reshape(y.shape[0]) train, test = train_test_split(X, 0.7) n_steps = 60 verbose = 1 epochs = 50 X_train, y_train = split_sequence(train, n_steps) X_test, y_test = split_sequence(test, n_steps) X_val, y_val = split_sequence(y, n_steps) # define model model = Sequential() model.add(Dense(200, activation='relu', input_dim=n_steps)) model.add(Dense(1)) model.compile(optimizer='adam', loss='mse') history = model.fit(X_train ,y_train ,epochs=epochs ,verbose=verbose ,validation_data=(X_test, y_test)) model.save(r'C:YOUR_PATHMQL5ExpertsYOUR_PATHmodel_train_'+symbol+'.h5') pyplot.title('Loss') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() history = list() yhat = list() for i in range(0, len(X_val)): pred = X_val[i] pred = pred.reshape((1, n_steps)) history.append(y_val[i]) yhat.append(model.predict(pred).flatten()[0]) pyplot.figure(figsize=(10, 5)) pyplot.plot(history,"*") pyplot.plot(yhat,"+") pyplot.plot(history, label='real') pyplot.plot(yhat, label='prediction') pyplot.ylabel('Price Close', size=10) pyplot.xlabel('time', size=10) pyplot.legend(fontsize=10) pyplot.show() rmse = sqrt(mean_squared_error(history, yhat)) mse = mean_squared_error(history, yhat) print('Test RMSE: %.3f' % rmse) print('Test MSE: %.3f' % mse)
Теперь, когда у нас есть обученная и сохраненная в нашей папке модель с расширением .h5, мы можем использовать ее для прогнозов, поэтому я создам объект, который создаст экземпляр этой модели для использования в соединении.
from tensorflow.keras.models import * class Model(object): def __init__(self, n_steps:int, symbol:str, period:int) -> None: super().__init__() self.n_steps = n_steps self.model = load_model(r'C:YOUR_PATHMQL5ExpertsYOUR_PATHmodel_train_'+symbol+'.h5') def predict(self, data): return(self.model.predict(data.reshape((1, self.n_steps))).flatten()[0])
Наш объект прост, его конструктор создает экземпляр атрибута, называемого моделью, который будет содержать сохраненную модель, а метод прогнозирования отвечает за осуществление прогнозирования.
Теперь нам нужен основной метод, который будет работать и взаимодействовать с клиентами, получая функции и отправляя прогнозы.
import ast import pandas as pd from model import Model from server_socket import socketserver host = 'localhost' port = 9091 n_steps = 60 TIMEFRAME = 24 | 0x4000 model = Model(n_steps, "EURUSD", TIMEFRAME) if __name__ == "__main__": serv = socketserver(host, port) while True: print("<<--Waiting Prices to Predict-->>") rates = pd.DataFrame(ast.literal_eval(serv.socket_receive())) rates = rates.rates.pct_change(1) rates.dropna(inplace=True) rates = rates.values.reshape((1, n_steps)) serv.socket_send(str(model.predict(rates).flatten()[0]))
На стороне нашего MQL-клиента нам нужно создать робота, который будет собирать данные и отправлять их на наш сервер, а затем получать прогнозы. Поскольку наша модель была обучена с данными от закрытых свечей, мы создадим проверку для сбора и отправки этих данных только после закрытия свечи, поэтому у нас будут полные данные для прогнозирования процентной разницы от закрытия только что начавшегося бара, для этого воспользуемся функцией, которая проверяет появление нового бара.
bool NewBar(void) { datetime time[]; if(CopyTime(Symbol(), Period(), 0, 1, time) < 1) return false; if(time[0] == m_last_time) return false; return bool(m_last_time = time[0]); }
Переменная m_last_time объявлена в глобальной области видимости и будет хранить дату и время открытия бара, поэтому мы проводим тест, проверяя, отличается ли переменная time от m_last_time, потому что если это true, это означает, что начал формироваться новый бар. Тут надо заменить значение m_last_time значением time.
Советник не должен открывать позиций, не закрыв предыдущую, поэтому проверяем наличие открытых позиций — для этого используем метод CheckPosition, который задаст значения true или false переменным покупки и продажи, объявленные в глобальной области видимости.
void CheckPosition(void) { buy = false; sell = false; if(PositionSelect(Symbol())) { if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_BUY&&PositionGetInteger(POSITION_MAGIC) == InpMagicEA) { buy = true; sell = false; } if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL&&PositionGetInteger(POSITION_MAGIC) == InpMagicEA) { sell = true; buy = false; } } }
После появления нового бара мы проверяем наличие открытых позиций, и если есть открытые, то будем ждать закрытия. Если открытой позиции нет, мы запустим процесс соединения, вызвав метод IsConnected класса CClienteSocket.
if(NewBar()) { if(!Socket.IsConnected()) Print("Error : ", GetLastError(), " Line: ", __LINE__); ... }
если возвращается true, это потому, что мы можем установить соединение с нашим сервером, мы соберем данные и отправим их.
string payload = "{'rates':["; for(int i=InpSteps; i>=0; i--) { if(i>=1) payload += string(iClose(Symbol(), Period(), i))+","; else payload += string(iClose(Symbol(), Period(), i))+"]}"; }
Я решил отправить данные в формате {‘rates’:[1,2,3,4]}, потому что таким образом мы просто преобразуем их в pandas-датафрейм, и мы не будем тратить время на конверсии.
Как только данные собраны, мы отправляем их и ждем получения прогноза, чтобы мы могли потом принять решение. В этом случае, я буду использовать скользящую среднюю, чтобы проверить направление цены; и в зависимости от стороны и ценности прогноза мы будем покупать или продавать.
void OnTick(void) { .... bool send = Socket.SocketSend(payload); if(send) { if(!Socket.IsConnected()) Print("Error : ", GetLastError(), " Line: ", __LINE__); double yhat = StringToDouble(Socket.SocketReceive()); Print("Value of Prediction: ", yhat); if(CopyBuffer(handle, 0, 0, 4, m_fast_ma)==-1) Print("Error in CopyBuffer"); if(m_fast_ma[1]>m_fast_ma[2]&&m_fast_ma[2]>m_fast_ma[3]) { if((iClose(Symbol(), Period(), 2)>iOpen(Symbol(), Period(), 2)&&iClose(Symbol(), Period(), 1)>iOpen(Symbol(), Period(), 1))&&yhat<0) { m_trade.Sell(mim_vol); } } if(m_fast_ma[1]<m_fast_ma[2]&&m_fast_ma[2]<m_fast_ma[3]) { if((iClose(Symbol(), Period(), 2)<iOpen(Symbol(), Period(), 2)&&iClose(Symbol(), Period(), 1)<iOpen(Symbol(), Period(), 1))&&yhat>0) { m_trade.Buy(mim_vol); } } } Socket.Close(); } }
Последний шаг — закрыть ранее установленное соединение и дождаться появления нового бара, и таким образом запустить процесс отправки и получения прогноза.
Эта архитектура оказалась очень практичная и с низкой задержкой, поскольку ее можно протестировать. В некоторых личных проектах я решил использовать эту архитектуру в коммерческих учетных записях, потому что она позволяет мне пользоваться всей мощью MQL и всеми ресурсами, доступными для машинного обучения, имеющимся в Python.
Что будет дальше?
В следующей статье я хочу разработать немного более гибкую архитектуру, которая позволяет использовать модели в тестере стратегий, поэтому мы преодолеем единственный барьер, который может помешать нам использовать предложенную архитектуру.
Заключение:
Надеюсь, я дал небольшое руководство о том, как мы можем использовать и разрабатывать различные модели Python и передавать их в среду MQL.
Вы научились:
- Настраивать среду разработки Python.
- Мы вспоминали и реализовали нейрон перцептрона и сеть MLP в Python.
- Мы приготовили одномерные данные для изучения простой сети.
- Мы настраивали архитектуру связи между Python и MQL.
Расширения:
В этом разделе перечислены некоторые идеи, которые, возможно, помогут вам расширить руководство, если у вас есть желание их изучать.
- Размер входных данных. Примерно изучите количество дней, используемых в качестве входных данных для модели, например три дня, 21 день, 30 дней и т.д.
- Настройка модели. Изучите различные структуры и гиперпараметры модели и получите среднюю производительность модели.
- Масштабирование данных. Узнайте, можно ли использовать размер данных, например стандартизацию и нормализацию, для повышения производительности модели.
- Диагностика обучения. Используйте такую диагностику, как кривые обучения для потери обучения и валидации, и среднеквадратичную ошибку, чтобы помочь настроить структурy и гиперпараметры модели.
Если вы изучите какое-либо из этих расширений, я был бы рад узнать об этом.
Все курсы > Вводный курс > Занятие 21
В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.
Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).
Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.
Смысл, структура и принцип работы
Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).
Отличие нейросети от других алгоритмов заключается в ее структуре.
Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.
Функционирует нейросеть следующим образом.
На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w1, w2, w3, w4). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b1 и b2).
$$ w_{1}cdot x + w_{3}cdot y + b_{1} $$
$$ w_{2}cdot x + w_{4}cdot y + b_{2} $$
Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h1 и h2).
$$ h_{1} = actfun(w_{1}cdot x + w_{3}cdot y + b_{1}) $$
$$ h_{2} = actfun(w_{2}cdot x + w_{4}cdot y + b_{2}) $$
На втором этапе процесс повторяется для нейронов скрытого слоя (h1 и h2), весов (w5 и w6) и смещения (b3) до получения конечного результата (r).
$$ r = actfun(w_{5}cdot h_{1} + w_{6}cdot h_{2} + b_{3}) $$
Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:
- Восприятие информации через сенсоры (входной слой)
- Создание ассоциаций (скрытый слой)
- Реакцию (выходной слой)
Основы нейронных сетей на простом примере
Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.
В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.
$$ f(x) = frac{mathrm{1} }{mathrm{1} + e^{-x}} $$
График сигмоиды выглядит следующим образом.
Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.
Общее уравнение нейросети выглядит следующим образом.
$$ r = sigmoid(w_{1}cdot weight + w_{2}cdot height + bias) $$
Теперь предположим, что у нас есть следующие данные и параметры нейросети.
Откроем ноутбук к этому занятию⧉
|
# даны вес и рост трех человек # единицей мы обозначим мужской пол, а нулем — женский. data = { ‘Иван’: [84, 180, 1], ‘Мария’: [57, 165, 0], ‘Анна’: [62, 170, 0] } |
|
# и даны следующие веса и смещение w1, w2, b = 0.3, 0.1, —39 |
Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.
|
r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b |
Теперь к полученному результату (r) применим сигмоиду.
|
np.round(1 / (1 + np.exp(—r)), 3) |
Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.
|
# пройдемся по ключам и значениям нашего словаря с помощью метода .items() for k, v in data.items(): # вначале умножим каждую строчку данных на веса и прибавим смещение r1 = w1 * v[0] + w2 * v[1] + b # затем применим сигмоиду r2 = 1 / (1 + np.exp(—r1)) # если результат больше 0,5, модель предскажет мужской пол if r2 > 0.5: print(k, np.round(r2, 3), ‘male’) # в противном случае, женский else: print(k, np.round(r2, 3), ‘female’) |
|
Иван 0.985 male Мария 0.004 female Анна 0.032 female |
Как мы видим, модель отработала верно.
Обучение нейронной сети
В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).
И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.
В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.
Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).
В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.
Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).
Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.
Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.
Создание нейросети в библиотеке Keras
Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.
|
# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist !pip install tensorflow mnist |
И импортируем их.
|
# импортируем рукописные цифры import mnist # и библиотеку keras from tensorflow import keras |
1. Подготовка данных
Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).
В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).
Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.
|
# сохраним обучающую выборку и соответсвующую целевую переменную X_train = mnist.train_images() y_train = mnist.train_labels() # посмотрим на размерность print(X_train.shape) print(y_train.shape) |
Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.
|
# сделаем то же самое с тестовыми данными X_test = mnist.test_images() y_test = mnist.test_labels() # и также посмотрим на размерность print(X_test.shape) print(y_test.shape) |
Таких изображений и целевых значений 10000.
Посмотрим на сами изображения.
|
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, X_train, y_train): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = ‘gray’) # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f‘Target: {label}’) |
Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.
$$ x’ = 2 frac {x-min(x)}{max(x)-min(x)}-1 $$
Применим эту формулу к нашим данным.
|
# функция np.min() возвращает минимальное значение, # np.ptp() — разницу между максимальным и минимальным значениями (от англ. peak to peak) X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 |
Посмотрим на новый диапазон.
|
# снова воспользуемся функцией np.ptp() np.ptp(X_train) |
Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.
Применим этот метод к нашим данным.
|
# «вытянем» (flatten) наши изображения, с помощью метода reshape # у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1) X_train = X_train.reshape((—1, 784)) X_test = X_test.reshape((—1, 784)) # посмотрим на результат print(X_train.shape) print(X_test.shape) |
Посмотрим на получившиеся значения пикселей.
|
# выведем первое изображение [0], пиксели с 200 по 209 X_train[0][200:210] |
|
array([—1. , —1. , —1. , —0.61568627, 0.86666667, 0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373]) |
Наши данные готовы. Теперь нужно задать конфигурацию модели.
2. Конфигурация нейронной сети
Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.
Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).
В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.
|
# импортируем класс Sequential from tensorflow.keras.models import Sequential # и создадим объект этого класса model = Sequential() |
Далее нам нужно прописать сами слои и связи между нейронами.
Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.
|
# импортируем класс Dense from tensorflow.keras.layers import Dense # и создадим первый скрытый слой (с указанием функции активации и размера входного слоя) model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,))) # затем второй скрытый слой model.add(Dense(64, activation = ‘sigmoid’)) # и наконец выходной слой model.add(Dense(10, activation = ‘softmax’)) |
Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).
Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.
$$ text{softmax}(vec{z})_{i} = frac{e^{z_i}}{sum_{j=1}^K e^{z_i}} $$
Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов zi экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.
На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.
Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.
Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.
|
z = ([1, 2, 0.5]) np.exp(z) / sum(np.exp(z)) |
|
array([0.2312239 , 0.62853172, 0.14024438]) |
Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.
3. Настройки
Настроек будет три:
- тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
- способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
- метрика (metric) покажет, насколько точна наша модель
Функция потерь
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.
Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.
Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.
Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.
В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).
Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.
Алгоритм оптимизации
Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.
Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w1 и w2, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.
Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.
Метрика
Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.
Посмотрим на используемый код.
|
model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘sgd’, metrics = [‘accuracy’] ) |
4. Обучение модели
Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.
- Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
- Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
- На выходе из функции softmax мы получаем вероятности для каждой из цифр
- После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
- На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
- После этого процесс повторяется, но уже с новыми весами.
Давайте выполним все эти операции в библиотеке Keras.
|
# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding from tensorflow.keras.utils import to_categorical |
|
# обучаем модель model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 2.0324 — accuracy: 0.4785 Epoch 2/10 1875/1875 [==============================] — 3s 2ms/step — loss: 1.2322 — accuracy: 0.7494 Epoch 3/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.7617 — accuracy: 0.8326 Epoch 4/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.5651 — accuracy: 0.8663 Epoch 5/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4681 — accuracy: 0.8827 Epoch 6/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4121 — accuracy: 0.8923 Epoch 7/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3751 — accuracy: 0.8995 Epoch 8/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3487 — accuracy: 0.9045 Epoch 9/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3285 — accuracy: 0.9090 Epoch 10/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3118 — accuracy: 0.9129 <keras.callbacks.History at 0x7f36c3f09490> |
На обучающей выборке мы добились неплохого результата, 91.29%.
5. Оценка качества модели
На этом шаге нам нужно оценить качество модели на тестовых данных.
|
# для оценки модели воспользуемся методом .evaluate() model.evaluate( X_test, # который применим к тестовым данным to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.2972 — accuracy: 0.9173 [0.29716429114341736, 0.9172999858856201] |
Результат «на тесте» оказался даже чуть выше, 91,73%.
6. Прогноз
Теперь давайте в качестве упражнения сделаем прогноз.
|
# передадим модели последние 10 изображений тестовой выборки pred = model.predict(X_test[—10:]) # посмотрим на результат для первого изображения из десяти pred[0] |
|
array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03, 6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01, 5.3100550e-04, 1.9325638e-02], dtype=float32) |
Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.
Теперь применим к нашим данным.
|
# для кажого изображения (то есть строки, axis = 1) # выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем print(np.argmax(pred, axis = 1)) # остается сравнить с целевой переменной print(y_test[—10:]) |
|
[7 8 9 0 1 2 3 4 5 6] [7 8 9 0 1 2 3 4 5 6] |
Для первых десяти цифр модель сделала верный прогноз.
7. Пример улучшения алгоритма
Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).
Посмотрим на результат на обучающей и тестовой выборке.
|
# снова укажем настройки модели model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘adam’, # однако заменим алгоритм оптимизации metrics = [‘accuracy’] ) # обучаем модель методом .fit() model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # прописываем количество эпох ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.2572 — accuracy: 0.9252 Epoch 2/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1738 — accuracy: 0.9497 Epoch 3/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1392 — accuracy: 0.9588 Epoch 4/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1196 — accuracy: 0.9647 Epoch 5/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1062 — accuracy: 0.9685 Epoch 6/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0960 — accuracy: 0.9708 Epoch 7/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0883 — accuracy: 0.9732 Epoch 8/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0826 — accuracy: 0.9747 Epoch 9/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0766 — accuracy: 0.9766 Epoch 10/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0699 — accuracy: 0.9780 <keras.callbacks.History at 0x7f36c3d74590> |
|
# и оцениваем результат «на тесте» model.evaluate( X_test, to_categorical(y_test) ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.1160 — accuracy: 0.9647 [0.11602973937988281, 0.9646999835968018] |
Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.
Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.
Подведем итог
На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.
При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.
Вопросы для закрепления
Перечислите типы слоев нейронной сети
Посмотреть правильный ответ
Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.
Из каких двух этапов состоит обучение нейронной сети?
Посмотреть правильный ответ
Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.
Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?
Посмотреть правильный ответ
Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.
Ответы на вопросы
Вопрос. Что означает число 1875 в результате работы модели?
Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).
- в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
- во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
- и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1
В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.
Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.
В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.
Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.
Как подготовить прогноз последовательности для усеченного обратного распространения во времени в Керасе
Перевод
Ссылка на автора
Рекуррентные нейронные сети способны изучать временную зависимость на нескольких временных шагах в задачах прогнозирования последовательности.
Современные рекуррентные нейронные сети, такие как длинная кратковременная память или сеть LSTM, обучаются с помощью варианта алгоритма обратного распространения, называемого обратным распространением во времени. Этот алгоритм был дополнительно модифицирован для повышения эффективности задач прогнозирования последовательностей с очень длинными последовательностями и называется усеченным обратным распространением во времени.
Важным параметром конфигурации при обучении повторяющихся нейронных сетей, таких как LSTM, с использованием усеченного обратного распространения через время является решение, сколько временных шагов использовать в качестве входных данных. То есть, как именно разбить ваши очень длинные входные последовательности на подпоследовательности, чтобы получить наилучшую производительность.
В этом посте вы откроете для себя 6 различных способов разделения очень длинных входных последовательностей, чтобы эффективно обучать повторяющиеся нейронные сети, используя усеченное обратное распространение в Python с Keras.
Прочитав этот пост, вы узнаете:
- Что такое усеченное обратное распространение во времени и как оно реализовано в библиотеке глубокого обучения Python Keras.
- Как именно выбор количества входных временных шагов влияет на обучение в периодических нейронных сетях.
- 6 различных техник, которые вы можете использовать, чтобы разделить свои проблемы с предсказанием очень длинной последовательности, чтобы наилучшим образом использовать алгоритм обучения Усеченное обратное распространение через время.
Давайте начнем.
Усеченное обратное распространение во времени
Обратное распространение — это обучающий алгоритм, используемый для обновления весов в нейронной сети, чтобы минимизировать ошибку между ожидаемым выходным сигналом и прогнозируемым выходным сигналом для данного входа.
Для задач прогнозирования последовательности, где существует зависимость порядка между наблюдениями, вместо классических нейронных сетей прямой связи используются рекуррентные нейронные сети. Рекуррентные нейронные сети обучаются с использованием варианта алгоритма Backpropagation, называемого Backpropagation Through Time, или сокращенно BPTT.
Фактически, BPTT развертывает рекуррентную нейронную сеть и распространяет ошибку в обратном направлении по всей входной последовательности, по одному шагу за раз. Веса затем обновляются с учетом накопленных градиентов.
BPTT может медленно обучать рекуррентные нейронные сети на проблемах с очень длинными входными последовательностями. В дополнение к скорости, накопление градиентов в течение стольких временных шагов может привести к уменьшению значений до нуля или росту значений, которые в конечном итоге переполняются или взрываются.
Модификация BPTT состоит в том, чтобы ограничить количество временных шагов, используемых на обратном проходе, и фактически оценить градиент, используемый для обновления весов, а не рассчитать его полностью.
Этот вариант называется усеченным обратным распространением во времени, или TBPTT.
Алгоритм обучения TBPTT имеет два параметра:
- k1: Определяет количество временных шагов, отображаемых в сети на прямом проходе.
- k2: Определяет количество временных шагов, чтобы посмотреть при оценке градиента на обратном проходе.
Таким образом, мы можем использовать обозначение TBPTT (k1, k2) при рассмотрении вопроса о том, как настроить алгоритм обучения, где k1 = k2 = n, где n — длина входной последовательности для классического неусеченного BPTT.
Влияние конфигурации TBPTT на модель последовательности RNN
Современные рекуррентные нейронные сети, такие как LSTM, могут использовать свое внутреннее состояние для запоминания очень длинных входных последовательностей. Например, более тысячи шагов.
Это означает, что конфигурация TBPTT не обязательно определяет память сети, которую вы оптимизируете, с выбором количества временных шагов. Вы можете выбрать, когда внутреннее состояние сети сбрасывается отдельно от режима, используемого для обновления весов сети.
Вместо этого выбор параметров TBPTT влияет на то, как сеть оценивает градиент ошибки, используемый для обновления весов. В более общем смысле конфигурация определяет количество временных шагов, с которых может рассматриваться сеть для моделирования проблемы последовательности.
Мы можем сформулировать это формально как что-то вроде:
yhat(t) = f(X(t), X(t-1), X(t-2), ... X(t-n))Где yhat — это выход для определенного временного шага, f (…) — это отношение, которое аппроксимирует рекуррентная нейронная сеть, а X (t) — наблюдения на определенных временных шагах.
Он концептуально аналогичен (но практически отличается на практике) размеру окна на многослойных персептронах, обученных на задачах временных рядов, или параметрам p и q моделей линейных временных рядов, таких как ARIMA. TBPTT определяет объем входной последовательности для модели во время обучения.
Нужна помощь с LSTM для прогнозирования последовательности?
Пройдите мой бесплатный 7-дневный курс по электронной почте и откройте для себя 6 различных архитектур LSTM (с кодом).
Нажмите, чтобы зарегистрироваться, а также получить бесплатную PDF-версию курса Ebook
Начни свой БЕСПЛАТНЫЙ мини-курс сейчас!
Keras Внедрение TBPTT
Библиотека глубокого обучения Keras обеспечивает реализацию TBPTT для обучения периодических нейронных сетей.
Реализация более ограничена, чем общая версия, указанная выше.
В частности, значения k1 и k2 равны друг другу и являются фиксированными.
- TBPTT (k1, k2), где k1 = k2
Это реализуется с помощью трехмерного ввода фиксированного размера, необходимого для обучения повторяющихся нейронных сетей, таких как сеть с короткой кратковременной памятью или LSTM.
LSTM ожидает, что входные данные будут иметь размеры: выборки, временные шаги и особенности.
Это второе измерение этого входного формата, временные шаги, которые определяют количество временных шагов, используемых для прямого и обратного проходов в задаче прогнозирования последовательности.
Поэтому необходимо тщательно выбирать количество временных шагов, указанное при подготовке ваших входных данных для задач прогнозирования последовательности в Keras.
Выбор временных шагов повлияет на оба:
- Внутреннее состояние накапливается во время прямого прохода.
- Оценка градиента, используемая для обновления весов на обратном проходе.
Обратите внимание, что по умолчанию внутреннее состояние сети сбрасывается после каждого пакета, но более явный контроль за сбросом внутреннего состояния может быть достигнут с помощью так называемого LSTM с состоянием и вызова операции сброса вручную.
Для получения дополнительной информации о сохранении состояния LSTM в Керасе см. Сообщения:
- Как заполнить состояние для LSTM для прогнозирования временных рядов в Python
- LSTM с отслеживанием состояния и сохранением состояния для прогнозирования временных рядов с помощью Python
- Понимание Stateful LSTM рекуррентных нейронных сетей в Python с Keras
Подготовьте данные последовательности для TBPTT в Керасе
То, как вы разбиваете данные вашей последовательности, будет определять количество временных шагов, используемых в прямом и обратном проходах BPTT.
Таким образом, вы должны тщательно продумать, как вы будете готовить данные для тренировок.
В этом разделе перечислены 6 методов, которые вы можете рассмотреть.
1. Используйте данные как есть
Вы можете использовать свои входные последовательности как есть, если число временных шагов в каждой последовательности является скромным, например, десятки или несколько сотен временных шагов.
Практические пределы были предложены для TBPTT приблизительно от 200 до 400 временных шагов.
Если данные вашей последовательности меньше или равны этому диапазону, вы можете изменить наблюдения за последовательностями как временные шаги для входных данных.
Например, если у вас была коллекция из 100 одномерных последовательностей по 25 временных шагов, это можно изменить как 100 выборок, 25 временных шагов и 1 элемент или [100, 25, 1].
2. Наивный разделение данных
Если у вас длинные входные последовательности, такие как тысячи временных шагов, вам может потребоваться разбить длинные входные последовательности на несколько смежных подпоследовательностей.
Это потребует использования LSTM с сохранением состояния в Keras, чтобы внутреннее состояние сохранялось на входе подпоследовательностей и сбрасывалось только в конце действительно более полной входной последовательности.
Например, если у вас было 100 входных последовательностей по 50 000 временных шагов, то каждую входную последовательность можно разделить на 100 подпоследовательностей по 500 временных шагов. Одна входная последовательность станет 100 выборками, поэтому 100 исходных выборок станут 10000. Размерность входных данных для Keras будет составлять 10 000 выборок, 500 временных шагов и 1 элемент или [10000, 500, 1]. Необходимо соблюдать осторожность, чтобы сохранить состояние через каждые 100 подпоследовательностей и сбросить внутреннее состояние после каждых 100 выборок либо явным образом, либо используя размер пакета 100.
Разделение, которое аккуратно делит полную последовательность на подпоследовательности фиксированного размера, является предпочтительным. Выбор множителя полной последовательности (длины подпоследовательности) является произвольным, отсюда и название «наивное разделение данных».
Разбиение последовательности на подпоследовательности не учитывает информацию домена о подходящем количестве временных шагов для оценки градиента ошибки, используемого для обновления весов.
3. Специфичное для домена разделение данных
Может быть трудно узнать правильное количество временных шагов, необходимых для получения полезной оценки градиента ошибки.
Мы можем использовать наивный подход (см. Выше), чтобы быстро получить модель, но модель может быть далека от оптимизации.
Кроме того, мы можем использовать информацию, специфичную для предметной области, чтобы оценить количество временных шагов, которые будут иметь отношение к модели при изучении проблемы.
Например, если проблема последовательности представляет собой временной ряд регрессии, возможно, обзор графиков автокорреляции и частичной автокорреляции может дать информацию о выборе количества временных шагов.
Если проблема последовательности является проблемой обработки естественного языка, возможно, входная последовательность может быть разделена на предложение и затем дополнена до фиксированной длины или разделена в соответствии со средней длиной предложения в домене.
Подумайте широко и подумайте, какие знания, специфичные для вашей области, вы можете использовать, чтобы разбить последовательность на осмысленные куски.
4. Систематическое разделение данных (например, поиск по сетке)
Вместо того, чтобы угадывать подходящее количество временных шагов, вы можете систематически оценивать набор различных длин подпоследовательности для вашей задачи прогнозирования последовательности.
Вы можете выполнить поиск по сетке по каждой длине подпоследовательности и принять конфигурацию, которая в среднем дает наиболее эффективную модель.
Некоторые замечания предостережения, если вы рассматриваете этот подход:
- Начните с длины подпоследовательности, которая является фактором полной длины последовательности.
- Используйте заполнение и, возможно, маскировку, если исследует длину подпоследовательности, которая не является фактором полной длины последовательности.
- Подумайте об использовании сети с небольшим переопределением (больше ячеек памяти и больше периодов обучения), чем необходимо для решения проблемы, чтобы исключить пропускную способность сети в качестве ограничения вашего эксперимента.
- Возьмите среднюю производительность за несколько прогонов (например, 30) для каждой отдельной конфигурации.
Если вычислительные ресурсы не являются ограничением, рекомендуется систематическое исследование различного количества временных шагов.
5. Тяжело полагаться на внутреннее состояние с TBPTT (1, 1)
Вы можете переформулировать свою задачу прогнозирования последовательности, имея один вход и один выход за каждый шаг.
Например, если у вас было 100 последовательностей по 50 временных шагов, каждый временной шаг стал бы новым образцом. 100 образцов станут 5000. Трехмерный ввод станет 5000 выборок, 1 временной шаг и 1 элемент или [5000, 1, 1].
Опять же, это потребует сохранения внутреннего состояния на каждом временном шаге последовательности и сброса в конце каждой фактической последовательности (50 выборок).
Это возложило бы бремя изучения проблемы предсказания последовательности на внутреннее состояние рекуррентной нейронной сети. В зависимости от типа проблемы, это может быть больше, чем может обработать сеть, и проблема прогнозирования может быть недоступна для изучения.
Личный опыт подсказывает, что эта формулировка может хорошо работать для задач прогнозирования, которые требуют памяти поверх последовательности, но неэффективны, когда результат является сложной функцией прошлых наблюдений.
6. Разделите длину последовательности вперед и назад
Библиотека глубокого обучения Keras, используемая для поддержки несвязанного количества временных шагов для прямого и обратного прохода усеченного обратного распространения во времени.
По сути, параметр k1 может быть задан числом временных шагов во входных последовательностях, а параметр k2 может быть задан аргументом «truncate_gradient» на уровне LSTM.
Это больше не поддерживается, но есть желание повторно добавить эту функцию в библиотеку. это неясно, почему именно он был удален хотя данные свидетельствуют о том, что это было сделано из соображений эффективности,
Вы можете изучить этот подход в Керасе. Некоторые идеи включают в себя:
- Установите и используйте более старую версию библиотеки Keras, которая поддерживает аргумент «truncate_gradient» (около 2015 г.).
- Расширьте реализацию уровня LSTM в Keras для поддержки поведения типа «truncate_gradient».
Возможно, есть сторонние расширения, доступные для Keras, которые поддерживают это поведение.
Если вы найдете, дайте мне знать в комментариях ниже.
Резюме
В этой статье вы узнали, как подготовить данные о проблеме прогнозирования последовательности для эффективного использования алгоритма обучения усеченному обратному распространению во времени в библиотеке глубокого обучения Python Keras.
В частности, вы узнали:
- Как работает усеченное обратное распространение через время и как это реализовано в Keras.
- Как переформулировать или разделить ваши данные с помощью очень длинных входных последовательностей в контексте TBPTT.
- Как систематически исследовать различные конфигурации TBPTT в Керасе.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):
То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:
Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:
В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 O_4 = 0.86 O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288
O_6 = f(I_6) = 0.54
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965
w_{68 medspace new} = 0.75+ 0.014 = 0.764
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998
w_{15 medspace new} = 1 + 0.00018 = 1.00018
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Время на прочтение
5 мин
Количество просмотров 5.9K
Салют, Хабр! Построение нейронной сети ― весьма актуальная задача для самых разных направлений: от классификации продуктов на категории до распознавания лиц на видео. Однако для получения качественного результата необходимо грамотно настроить её параметры. Как это сделать? В этом может помочь Keras ― открытая библиотека, написанная на языке Python и обеспечивающая взаимодействие с искусственными нейронными сетями. Просим под кат, где подробно рассказываем о нюансах работы с этой библиотекой.
Зачем эта статья?
Наша команда решила поделиться опытом построения нейронной сети и регулирования её гиперпараметров с помощью Keras. Рассказываем и показываем практически.
Анализ, о котором говорится ниже, мы провели на примере открытого датасета из Kaggle Otto group product classification challenge. Количество строк в нём составляет примерно 62 тысячи. Каждая строка соответствует одному продукту. Необходимо классифицировать продукты компании по девяти категориям, основываясь на 93 характеристиках. Каждая категория ― это тип продукта, например мода, электроника и т. д. Классы не сбалансированы, что можно увидеть на графике.
Описательные статистики для переменных:
В статье шаг за шагом разбираем логические блоки для построения модели: входные данные, слои, количество нейронов, функция активации, процедура обучения.
Как это сделано?
Что же, приступим. Для начала импортируем необходимые библиотеки:
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Activation, Flatten
from tensorflow.keras.optimizers import Adam,SGD,Adagrad
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from tensorflow.keras.initializers import glorot_uniformНа вход нейронной сети подаются тензоры. Это общая форма векторов в виде n-мерной матрицы. Если данные табличные (как в данном случае), то тензор будет двумерный, где каждый столбец этой матрицы ― это одно наблюдение из таблицы (одна строка табличных данных).
y = x.target.values
x.drop('target', axis=1, inplace=True)
x = np.log(1+x.values)Общая структура сети разрабатывается с помощью объекта модели keras Sequential(), который создаёт последовательную модель с пошаговым добавлением слоёв в неё. Dense-слой является самым необходимым и базовым. Он отвечает за соединение нейронов из предыдущего и следующего слоя. Например, если первый слой имеет 5 нейронов, а второй 3, то общее количество соединений между слоями будет равно 15. Dense-слой отвечает за эти соединения, и у него есть настраиваемые гиперпараметры: количество нейронов, тип активации, инициализация типа ядра. Dropout Layer помогает избавиться от переобучения модели. Таким образом, некоторые нейроны становятся равными 0, и это сокращает вычисления в процессе обучения. Базовая модель представлена ниже:
def getModel(dropout=0.00, neurons_first=500, neurons_second=250, learningRate=0.1):
model = Sequential()
model.add(Dense(neurons_first, activation='relu', input_dim=num_features,
kernel_initializer=glorot_uniform(),
name='Dense_first'))
model.add(Dropout(dropout, name='Dropout_first'))
model.add(Dense(neurons_second, activation='relu', kernel_initializer=glorot_uniform(),
name='Dense_second'))
model.add(Dropout(dropout, name='Dropout_second'))
model.add(Dense(num_classes, activation='softmax',
kernel_initializer=glorot_uniform(),
name='Result'))
model.compile(loss='sparse_categorical_crossentropy',
optimizer=Adagrad(lr=learningRate), metrics=['accuracy'])
return modelТеперь давайте разберёмся с тем, что собой представляет функция активации. Так вот, каждый нейрон сети получает один или несколько входных сигналов от нейронов предыдущего слоя. Если речь идёт про первый скрытый слой, то он получает данные из входного потока. Начиная со второго скрытого слоя, на вход каждому нейрону подаётся взвешенная сумма нейронов из предыдущего слоя. На втором скрытом слое происходит активация входных данных за счёт функции активации. С помощью функции активации становится доступной реализация обратного распространения ошибки, которая помогает скорректировать веса нейронов. Таким образом происходит обучение модели. Важный момент ― существует несколько вариантов функции активации.
Для текущей задачи использовались функции активации ReLu и Softmax. Функция ReLu выглядит следующим образом:
Функция Softmax выглядит следующим образом:
Функция потерь ― показатель, который помогает понять, движется ли сеть в правильном направлении. Так как задача решается для многоклассовой классификации, то использовалась функция потерь sparse categorical crossentropy:
Посмотрим теперь на качество модели с параметрами, заданными ранее. Ниже ― график, на котором изображена функция потерь и точность нашего классификатора. Видим, что наилучший результат наблюдается около 13-й эпохи, однако видно переобучение модели из-за большой флуктуации функции потерь.
Что ещё?
Наиболее важной частью обучения модели является оптимизатор. Ранее был упомянут термин обратного распространения ошибки ― это как раз и есть процесс оптимизации. Структура, которая ранее была описана, инициализируется случайными весами между нейронами слоёв. Процесс обучения нужен для того, чтобы обновить эти случайные веса для получения высокой предсказательной способности.
Сеть берёт одну обучающую выборку и использует её значения в качестве входных данных слоя, далее происходит активация этих данных, и на вход следующему слою подаются уже новые взвешенные данные после активации. Аналогичный процесс происходит и на последующих слоях. Результат последнего слоя будет прогнозом для обучающей выборки. Далее применяется функция потерь, которая показывает, насколько сильно ошибается модель. Чтобы эту ошибку уменьшить, применяется ещё одна функция ― оптимизатора. Она использует производные для ответа на вопрос ― насколько сильно изменится функция потерь при небольшом изменении весов между нейронами?
Вычисление одной обучающей выборки из входного слоя называется проходом. Обычно обучение происходит батчами из-за ограничений системы. Батч ― набор обучающих выборок из входных данных. Сеть обновляет свои веса после обработки всех выборок из батча. Это называется итерацией (то есть успешная обработка всех обучающих выборок из батча с последующим обновлением весов в сети). А вычисление всех обучающих выборок, которые были во входных данных, с периодическими обновлениями весов называется эпохой. На каждой итерации сеть использует функцию оптимизации, чтобы внести изменения в веса между нейронами. Шаг за шагом, с помощью нескольких итераций, а затем нескольких эпох, сеть обновляет свои веса и учится делать корректный прогноз. Существует много разных функций оптимизации. В нашем случае была использована Adagrad.
Оптимизируем всё!
Ну а теперь давайте попробуем улучшить качество модели. Здесь пригодится увеличение dropout rate. То есть теперь больше нейронов будут выходить из процесса обучения.
increasedDropout = 0.5
model = getModel(increasedDropout)
net = model.fit(X, y, epochs=15, batch_size=515,
verbose=1, validation_split=0.2)На графике видно, что проблемы переобучения больше нет, так как функция потерь стала более гладкой.
Увеличение количества эпох.
model = getModel(increasedDropout)
net = model.fit(X, y, epochs=25, batch_size=515, verbose=1, validation_split=0.2)Заметно, что качество улучшилось. Задача выполнена, и сделали мы это весьма неплохо, правда?
Увеличение количества нейронов.
increasedNeurons1 = 800
model = getModel(increasedDropout, neurons_first=increasedNeurons1)
net = model.fit(X, y, epochs=25, batch_size=515, verbose=1, validation_split=0.2)Качество модели стало ещё лучше.
Был взят небольшой объём данных, чтобы показать прогноз модели. Из результатов видно, что ошибка модели невелика.
Как и говорилось выше, чаще всего встречаются классы 2 и 6. Соответственно, модель меньше всего ошибается именно в них.
В сухом остатке
Мы смогли избавить модель от переобучения путём увеличения dropout, после чего более высокие результаты были достигнуты за счёт увеличения количества нейронов и эпох. В конечном счёте общая точность предсказания модели по всем классам продуктов составляет чуть больше 0,81, что характеризует её качество. Соответственно, теперь эту модель можно использовать для решения задачи многоклассовой классификации. Плюс в том, что структура является универсальной, так что её можно использовать при решении задач с применением нейронных сетей.
Deep Learning with Keras — Introduction
Deep Learning has become a buzzword in recent days in the field of Artificial Intelligence (AI). For many years, we used Machine Learning (ML) for imparting intelligence to machines. In recent days, deep learning has become more popular due to its supremacy in predictions as compared to traditional ML techniques.
Deep Learning essentially means training an Artificial Neural Network (ANN) with a huge amount of data. In deep learning, the network learns by itself and thus requires humongous data for learning. While traditional machine learning is essentially a set of algorithms that parse data and learn from it. They then used this learning for making intelligent decisions.
Now, coming to Keras, it is a high-level neural networks API that runs on top of TensorFlow — an end-to-end open source machine learning platform. Using Keras, you easily define complex ANN architectures to experiment on your big data. Keras also supports GPU, which becomes essential for processing huge amount of data and developing machine learning models.
In this tutorial, you will learn the use of Keras in building deep neural networks. We shall look at the practical examples for teaching. The problem at hand is recognizing handwritten digits using a neural network that is trained with deep learning.
Just to get you more excited in deep learning, below is a screenshot of Google trends on deep learning here −
As you can see from the diagram, the interest in deep learning is steadily growing over the last several years. There are many areas such as computer vision, natural language processing, speech recognition, bioinformatics, drug design, and so on, where the deep learning has been successfully applied. This tutorial will get you quickly started on deep learning.
So keep reading!
Deep Learning with Keras — Deep Learning
As said in the introduction, deep learning is a process of training an artificial neural network with a huge amount of data. Once trained, the network will be able to give us the predictions on unseen data. Before I go further in explaining what deep learning is, let us quickly go through some terms used in training a neural network.
Neural Networks
The idea of artificial neural network was derived from neural networks in our brain. A typical neural network consists of three layers — input, output and hidden layer as shown in the picture below.
This is also called a shallow neural network, as it contains only one hidden layer. You add more hidden layers in the above architecture to create a more complex architecture.
Deep Networks
The following diagram shows a deep network consisting of four hidden layers, an input layer and an output layer.
As the number of hidden layers are added to the network, its training becomes more complex in terms of required resources and the time it takes to fully train the network.
Network Training
After you define the network architecture, you train it for doing certain kinds of predictions. Training a network is a process of finding the proper weights for each link in the network. During training, the data flows from Input to Output layers through various hidden layers. As the data always moves in one direction from input to output, we call this network as Feed-forward Network and we call the data propagation as Forward Propagation.
Activation Function
At each layer, we calculate the weighted sum of inputs and feed it to an Activation function. The activation function brings nonlinearity to the network. It is simply some mathematical function that discretizes the output. Some of the most commonly used activations functions are sigmoid, hyperbolic, tangent (tanh), ReLU and Softmax.
Backpropagation
Backpropagation is an algorithm for supervised learning. In Backpropagation, the errors propagate backwards from the output to the input layer. Given an error function, we calculate the gradient of the error function with respect to the weights assigned at each connection. The calculation of the gradient proceeds backwards through the network. The gradient of the final layer of weights is calculated first and the gradient of the first layer of weights is calculated last.
At each layer, the partial computations of the gradient are reused in the computation of the gradient for the previous layer. This is called Gradient Descent.
In this project-based tutorial you will define a feed-forward deep neural network and train it with backpropagation and gradient descent techniques. Luckily, Keras provides us all high level APIs for defining network architecture and training it using gradient descent. Next, you will learn how to do this in Keras.
Handwritten Digit Recognition System
In this mini project, you will apply the techniques described earlier. You will create a deep learning neural network that will be trained for recognizing handwritten digits. In any machine learning project, the first challenge is collecting the data. Especially, for deep learning networks, you need humongous data. Fortunately, for the problem that we are trying to solve, somebody has already created a dataset for training. This is called mnist, which is available as a part of Keras libraries. The dataset consists of several 28×28 pixel images of handwritten digits. You will train your model on the major portion of this dataset and the rest of the data would be used for validating your trained model.
Project Description
The mnist dataset consists of 70000 images of handwritten digits. A few sample images are reproduced here for your reference
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Clearly, you can see that the distribution of the pixels (especially those tending towards white tone) differ, this distinguishes the digits they represent. We will feed this distribution of 784 pixels to our network as its input. The output of the network will consist of 10 categories representing a digit between 0 and 9.
Our network will consist of 4 layers — one input layer, one output layer and two hidden layers. Each hidden layer will contain 512 nodes. Each layer is fully connected to the next layer. When we train the network, we will be computing the weights for each connection. We train the network by applying backpropagation and gradient descent that we discussed earlier.
Deep Learning with Keras — Setting up Project
With this background, let us now start creating the project.
Setting Up Project
We will use Jupyter through Anaconda navigator for our project. As our project uses TensorFlow and Keras, you will need to install those in Anaconda setup. To install Tensorflow, run the following command in your console window:
>conda install -c anaconda tensorflow
To install Keras, use the following command −
>conda install -c anaconda keras
You are now ready to start Jupyter.
Starting Jupyter
When you start the Anaconda navigator, you would see the following opening screen.
Click ‘Jupyter’ to start it. The screen will show up the existing projects, if any, on your drive.
Starting a New Project
Start a new Python 3 project in Anaconda by selecting the following menu option −
File | New Notebook | Python 3
The screenshot of the menu selection is shown for your quick reference −
A new blank project will show up on your screen as shown below −
Change the project name to DeepLearningDigitRecognition by clicking and editing on the default name “UntitledXX”.
Deep Learning with Keras — Importing Libraries
We first import the various libraries required by the code in our project.
Array Handling and Plotting
As typical, we use numpy for array handling and matplotlib for plotting. These libraries are imported in our project using the following import statements
import numpy as np import matplotlib import matplotlib.pyplot as plot
Suppressing Warnings
As both Tensorflow and Keras keep on revising, if you do not sync their appropriate versions in the project, at runtime you would see plenty of warning errors. As they distract your attention from learning, we shall be suppressing all the warnings in this project. This is done with the following lines of code −
# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False
Keras
We use Keras libraries to import dataset. We will use the mnist dataset for handwritten digits. We import the required package using the following statement
from keras.datasets import mnist
We will be defining our deep learning neural network using Keras packages. We import the Sequential, Dense, Dropout and Activation packages for defining the network architecture. We use load_model package for saving and retrieving our model. We also use np_utils for a few utilities that we need in our project. These imports are done with the following program statements −
from keras.models import Sequential, load_model from keras.layers.core import Dense, Dropout, Activation from keras.utils import np_utils
When you run this code, you will see a message on the console that says that Keras uses TensorFlow at the backend. The screenshot at this stage is shown here −
Now, as we have all the imports required by our project, we will proceed to define the architecture for our Deep Learning network.
Creating Deep Learning Model
Our neural network model will consist of a linear stack of layers. To define such a model, we call the Sequential function −
model = Sequential()
Input Layer
We define the input layer, which is the first layer in our network using the following program statement −
model.add(Dense(512, input_shape=(784,)))
This creates a layer with 512 nodes (neurons) with 784 input nodes. This is depicted in the figure below −
Note that all the input nodes are fully connected to the Layer 1, that is each input node is connected to all 512 nodes of Layer 1.
Next, we need to add the activation function for the output of Layer 1. We will use ReLU as our activation. The activation function is added using the following program statement −
model.add(Activation('relu'))
Next, we add Dropout of 20% using the statement below. Dropout is a technique used to prevent model from overfitting.
model.add(Dropout(0.2))
At this point, our input layer is fully defined. Next, we will add a hidden layer.
Hidden Layer
Our hidden layer will consist of 512 nodes. The input to the hidden layer comes from our previously defined input layer. All the nodes are fully connected as in the earlier case. The output of the hidden layer will go to the next layer in the network, which is going to be our final and output layer. We will use the same ReLU activation as for the previous layer and a dropout of 20%. The code for adding this layer is given here −
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
The network at this stage can be visualized as follows −
Next, we will add the final layer to our network, which is the output layer. Note that you may add any number of hidden layers using the code similar to the one which you have used here. Adding more layers would make the network complex for training; however, giving a definite advantage of better results in many cases though not all.
Output Layer
The output layer consists of just 10 nodes as we want to classify the given images in 10 distinct digits. We add this layer, using the following statement −
model.add(Dense(10))
As we want to classify the output in 10 distinct units, we use the softmax activation. In case of ReLU, the output is binary. We add the activation using the following statement −
model.add(Activation('softmax'))
At this point, our network can be visualized as shown in the below diagram −
At this point, our network model is fully defined in the software. Run the code cell and if there are no errors, you will get a confirmation message on the screen as shown in the screenshot below −
Next, we need to compile the model.
Deep Learning with Keras — Compiling the Model
The compilation is performed using one single method call called compile.
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
The compile method requires several parameters. The loss parameter is specified to have type ‘categorical_crossentropy’. The metrics parameter is set to ‘accuracy’ and finally we use the adam optimizer for training the network. The output at this stage is shown below −
Now, we are ready to feed in the data to our network.
Loading Data
As said earlier, we will use the mnist dataset provided by Keras. When we load the data into our system, we will split it in the training and test data. The data is loaded by calling the load_data method as follows −
(X_train, y_train), (X_test, y_test) = mnist.load_data()
The output at this stage looks like the following −
Now, we shall learn the structure of the loaded dataset.
The data that is provided to us are the graphic images of size 28 x 28 pixels, each containing a single digit between 0 and 9. We will display the first ten images on the console. The code for doing so is given below −
# printing first 10 images
for i in range(10):
plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])
In an iterative loop of 10 counts, we create a subplot on each iteration and show an image from X_train vector in it. We title each image from the corresponding y_train vector. Note that the y_train vector contains the actual values for the corresponding image in X_train vector. We remove the x and y axes markings by calling the two methods xticks and yticks with null argument. When you run the code, you would see the following output −
Next, we will prepare data for feeding it into our network.
Deep Learning with Keras — Preparing Data
Before we feed the data to our network, it must be converted into the format required by the network. This is called preparing data for the network. It generally consists of converting a multi-dimensional input to a single-dimension vector and normalizing the data points.
Reshaping Input Vector
The images in our dataset consist of 28 x 28 pixels. This must be converted into a single dimensional vector of size 28 * 28 = 784 for feeding it into our network. We do so by calling the reshape method on the vector.
X_train = X_train.reshape(60000, 784) X_test = X_test.reshape(10000, 784)
Now, our training vector will consist of 60000 data points, each consisting of a single dimension vector of size 784. Similarly, our test vector will consist of 10000 data points of a single-dimension vector of size 784.
Normalizing Data
The data that the input vector contains currently has a discrete value between 0 and 255 — the gray scale levels. Normalizing these pixel values between 0 and 1 helps in speeding up the training. As we are going to use stochastic gradient descent, normalizing data will also help in reducing the chance of getting stuck in local optima.
To normalize the data, we represent it as float type and divide it by 255 as shown in the following code snippet −
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Let us now look at how the normalized data looks like.
Examining Normalized Data
To view the normalized data, we will call the histogram function as shown here −
plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))
Here, we plot the histogram of the first element of the X_train vector. We also print the digit represented by this data point. The output of running the above code is shown here −
You will notice a thick density of points having value close to zero. These are the black dot points in the image, which obviously is the major portion of the image. The rest of the gray scale points, which are close to white color, represent the digit. You may check out the distribution of pixels for another digit. The code below prints the histogram of a digit at index of 2 in the training dataset.
plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])
The output of running the above code is shown below −
Comparing the above two figures, you will notice that the distribution of the white pixels in two images differ indicating a representation of a different digit — “5” and “4” in the above two pictures.
Next, we will examine the distribution of data in our full training dataset.
Examining Data Distribution
Before we train our machine learning model on our dataset, we should know the distribution of unique digits in our dataset. Our images represent 10 distinct digits ranging from 0 to 9. We would like to know the number of digits 0, 1, etc., in our dataset. We can get this information by using the unique method of Numpy.
Use the following command to print the number of unique values and the number of occurrences of each one
print(np.unique(y_train, return_counts=True))
When you run the above command, you will see the following output −
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))
It shows that there are 10 distinct values — 0 through 9. There are 5923 occurrences of digit 0, 6742 occurrences of digit 1, and so on. The screenshot of the output is shown here −
As a final step in data preparation, we need to encode our data.
Encoding Data
We have ten categories in our dataset. We will thus encode our output in these ten categories using one-hot encoding. We use to_categorial method of Numpy utilities to perform encoding. After the output data is encoded, each data point would be converted into a single dimensional vector of size 10. For example, digit 5 will now be represented as [0,0,0,0,0,1,0,0,0,0].
Encode the data using the following piece of code −
n_classes = 10 Y_train = np_utils.to_categorical(y_train, n_classes)
You may check out the result of encoding by printing the first 5 elements of the categorized Y_train vector.
Use the following code to print the first 5 vectors −
for i in range(5): print (Y_train[i])
You will see the following output −
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
The first element represents digit 5, the second represents digit 0, and so on.
Finally, you will have to categorize the test data too, which is done using the following statement −
Y_test = np_utils.to_categorical(y_test, n_classes)
At this stage, your data is fully prepared for feeding into the network.
Next, comes the most important part and that is training our network model.
Deep Learning with Keras — Training the Model
The model training is done in one single method call called fit that takes few parameters as seen in the code below −
history = model.fit(X_train, Y_train, batch_size=128, epochs=20, verbose=2, validation_data=(X_test, Y_test)))
The first two parameters to the fit method specify the features and the output of the training dataset.
The epochs is set to 20; we assume that the training will converge in max 20 epochs — the iterations. The trained model is validated on the test data as specified in the last parameter.
The partial output of running the above command is shown here −
Train on 60000 samples, validate on 10000 samples Epoch 1/20 - 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665 Epoch 2/20 - 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715 Epoch 3/20 - 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765 Epoch 4/20 - 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795 Epoch 5/20 - 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792
The screenshot of the output is given below for your quick reference −
Now, as the model is trained on our training data, we will evaluate its performance.
Evaluating Model Performance
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
We will print the loss and accuracy using the following two statements −
print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])
When you run the above statements, you would see the following output −
Test Loss 0.08041584826191042 Test Accuracy 0.9837
This shows a test accuracy of 98%, which should be acceptable to us. What it means to us that in 2% of the cases, the handwritten digits would not be classified correctly. We will also plot accuracy and loss metrics to see how the model performs on the test data.
Plotting Accuracy Metrics
We use the recorded history during our training to get a plot of accuracy metrics. The following code will plot the accuracy on each epoch. We pick up the training data accuracy (“acc”) and the validation data accuracy (“val_acc”) for plotting.
plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')
The output plot is shown below −
As you can see in the diagram, the accuracy increases rapidly in the first two epochs, indicating that the network is learning fast. Afterwards, the curve flattens indicating that not too many epochs are required to train the model further. Generally, if the training data accuracy (“acc”) keeps improving while the validation data accuracy (“val_acc”) gets worse, you are encountering overfitting. It indicates that the model is starting to memorize the data.
We will also plot the loss metrics to check our model’s performance.
Plotting Loss Metrics
Again, we plot the loss on both the training (“loss”) and test (“val_loss”) data. This is done using the following code −
plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')
The output of this code is shown below −
As you can see in the diagram, the loss on the training set decreases rapidly for the first two epochs. For the test set, the loss does not decrease at the same rate as the training set, but remains almost flat for multiple epochs. This means our model is generalizing well to unseen data.
Now, we will use our trained model to predict the digits in our test data.
Predicting on Test Data
To predict the digits in an unseen data is very easy. You simply need to call the predict_classes method of the model by passing it to a vector consisting of your unknown data points.
predictions = model.predict_classes(X_test)
The method call returns the predictions in a vector that can be tested for 0’s and 1’s against the actual values. This is done using the following two statements −
correct_predictions = np.nonzero(predictions == y_test)[0] incorrect_predictions = np.nonzero(predictions != y_test)[0]
Finally, we will print the count of correct and incorrect predictions using the following two program statements −
print(len(correct_predictions)," classified correctly") print(len(incorrect_predictions)," classified incorrectly")
When you run the code, you will get the following output −
9837 classified correctly 163 classified incorrectly
Now, as you have satisfactorily trained the model, we will save it for future use.
Deep Learning with Keras — Saving Model
We will save the trained model in our local drive in the models folder in our current working directory. To save the model, run the following code −
directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)
The output after running the code is shown below −
Now, as you have saved a trained model, you may use it later on for processing your unknown data.
Loading Model for Predictions
To predict the unseen data, you first need to load the trained model into the memory. This is done using the following command −
model = load_model ('./models/handwrittendigitrecognition.h5')
Note that we are simply loading the .h5 file into memory. This sets up the entire neural network in memory along with the weights assigned to each layer.
Now, to do your predictions on unseen data, load the data, let it be one or more items, into the memory. Preprocess the data to meet the input requirements of our model as what you did on your training and test data above. After preprocessing, feed it to your network. The model will output its prediction.
Deep Learning with Keras — Conclusion
Keras provides a high level API for creating deep neural network. In this tutorial, you learned to create a deep neural network that was trained for finding the digits in handwritten text. A multi-layer network was created for this purpose. Keras allows you to define an activation function of your choice at each layer. Using gradient descent, the network was trained on the training data. The accuracy of the trained network in predicting the unseen data was tested on the test data. You learned to plot the accuracy and error metrics. After the network is fully trained, you saved the network model for future use.
Kickstart Your Career
Get certified by completing the course
Get Started

Время на прочтение
5 мин
Количество просмотров 6.8K
Салют, Хабр! Построение нейронной сети ― весьма актуальная задача для самых разных направлений: от классификации продуктов на категории до распознавания лиц на видео. Однако для получения качественного результата необходимо грамотно настроить её параметры. Как это сделать? В этом может помочь Keras ― открытая библиотека, написанная на языке Python и обеспечивающая взаимодействие с искусственными нейронными сетями. Просим под кат, где подробно рассказываем о нюансах работы с этой библиотекой.
Зачем эта статья?
Наша команда решила поделиться опытом построения нейронной сети и регулирования её гиперпараметров с помощью Keras. Рассказываем и показываем практически.
Анализ, о котором говорится ниже, мы провели на примере открытого датасета из Kaggle Otto group product classification challenge. Количество строк в нём составляет примерно 62 тысячи. Каждая строка соответствует одному продукту. Необходимо классифицировать продукты компании по девяти категориям, основываясь на 93 характеристиках. Каждая категория ― это тип продукта, например мода, электроника и т. д. Классы не сбалансированы, что можно увидеть на графике.
Описательные статистики для переменных:
В статье шаг за шагом разбираем логические блоки для построения модели: входные данные, слои, количество нейронов, функция активации, процедура обучения.
Как это сделано?
Что же, приступим. Для начала импортируем необходимые библиотеки:
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout, Activation, Flatten
from tensorflow.keras.optimizers import Adam,SGD,Adagrad
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
from tensorflow.keras.initializers import glorot_uniformНа вход нейронной сети подаются тензоры. Это общая форма векторов в виде n-мерной матрицы. Если данные табличные (как в данном случае), то тензор будет двумерный, где каждый столбец этой матрицы ― это одно наблюдение из таблицы (одна строка табличных данных).
y = x.target.values
x.drop('target', axis=1, inplace=True)
x = np.log(1+x.values)Общая структура сети разрабатывается с помощью объекта модели keras Sequential(), который создаёт последовательную модель с пошаговым добавлением слоёв в неё. Dense-слой является самым необходимым и базовым. Он отвечает за соединение нейронов из предыдущего и следующего слоя. Например, если первый слой имеет 5 нейронов, а второй 3, то общее количество соединений между слоями будет равно 15. Dense-слой отвечает за эти соединения, и у него есть настраиваемые гиперпараметры: количество нейронов, тип активации, инициализация типа ядра. Dropout Layer помогает избавиться от переобучения модели. Таким образом, некоторые нейроны становятся равными 0, и это сокращает вычисления в процессе обучения. Базовая модель представлена ниже:
def getModel(dropout=0.00, neurons_first=500, neurons_second=250, learningRate=0.1):
model = Sequential()
model.add(Dense(neurons_first, activation='relu', input_dim=num_features,
kernel_initializer=glorot_uniform(),
name='Dense_first'))
model.add(Dropout(dropout, name='Dropout_first'))
model.add(Dense(neurons_second, activation='relu', kernel_initializer=glorot_uniform(),
name='Dense_second'))
model.add(Dropout(dropout, name='Dropout_second'))
model.add(Dense(num_classes, activation='softmax',
kernel_initializer=glorot_uniform(),
name='Result'))
model.compile(loss='sparse_categorical_crossentropy',
optimizer=Adagrad(lr=learningRate), metrics=['accuracy'])
return modelТеперь давайте разберёмся с тем, что собой представляет функция активации. Так вот, каждый нейрон сети получает один или несколько входных сигналов от нейронов предыдущего слоя. Если речь идёт про первый скрытый слой, то он получает данные из входного потока. Начиная со второго скрытого слоя, на вход каждому нейрону подаётся взвешенная сумма нейронов из предыдущего слоя. На втором скрытом слое происходит активация входных данных за счёт функции активации. С помощью функции активации становится доступной реализация обратного распространения ошибки, которая помогает скорректировать веса нейронов. Таким образом происходит обучение модели. Важный момент ― существует несколько вариантов функции активации.
Для текущей задачи использовались функции активации ReLu и Softmax. Функция ReLu выглядит следующим образом:
Функция Softmax выглядит следующим образом:
Функция потерь ― показатель, который помогает понять, движется ли сеть в правильном направлении. Так как задача решается для многоклассовой классификации, то использовалась функция потерь sparse categorical crossentropy:
Посмотрим теперь на качество модели с параметрами, заданными ранее. Ниже ― график, на котором изображена функция потерь и точность нашего классификатора. Видим, что наилучший результат наблюдается около 13-й эпохи, однако видно переобучение модели из-за большой флуктуации функции потерь.
Что ещё?
Наиболее важной частью обучения модели является оптимизатор. Ранее был упомянут термин обратного распространения ошибки ― это как раз и есть процесс оптимизации. Структура, которая ранее была описана, инициализируется случайными весами между нейронами слоёв. Процесс обучения нужен для того, чтобы обновить эти случайные веса для получения высокой предсказательной способности.
Сеть берёт одну обучающую выборку и использует её значения в качестве входных данных слоя, далее происходит активация этих данных, и на вход следующему слою подаются уже новые взвешенные данные после активации. Аналогичный процесс происходит и на последующих слоях. Результат последнего слоя будет прогнозом для обучающей выборки. Далее применяется функция потерь, которая показывает, насколько сильно ошибается модель. Чтобы эту ошибку уменьшить, применяется ещё одна функция ― оптимизатора. Она использует производные для ответа на вопрос ― насколько сильно изменится функция потерь при небольшом изменении весов между нейронами?
Вычисление одной обучающей выборки из входного слоя называется проходом. Обычно обучение происходит батчами из-за ограничений системы. Батч ― набор обучающих выборок из входных данных. Сеть обновляет свои веса после обработки всех выборок из батча. Это называется итерацией (то есть успешная обработка всех обучающих выборок из батча с последующим обновлением весов в сети). А вычисление всех обучающих выборок, которые были во входных данных, с периодическими обновлениями весов называется эпохой. На каждой итерации сеть использует функцию оптимизации, чтобы внести изменения в веса между нейронами. Шаг за шагом, с помощью нескольких итераций, а затем нескольких эпох, сеть обновляет свои веса и учится делать корректный прогноз. Существует много разных функций оптимизации. В нашем случае была использована Adagrad.
Оптимизируем всё!
Ну а теперь давайте попробуем улучшить качество модели. Здесь пригодится увеличение dropout rate. То есть теперь больше нейронов будут выходить из процесса обучения.
increasedDropout = 0.5
model = getModel(increasedDropout)
net = model.fit(X, y, epochs=15, batch_size=515,
verbose=1, validation_split=0.2)На графике видно, что проблемы переобучения больше нет, так как функция потерь стала более гладкой.
Увеличение количества эпох.
model = getModel(increasedDropout)
net = model.fit(X, y, epochs=25, batch_size=515, verbose=1, validation_split=0.2)Заметно, что качество улучшилось. Задача выполнена, и сделали мы это весьма неплохо, правда?
Увеличение количества нейронов.
increasedNeurons1 = 800
model = getModel(increasedDropout, neurons_first=increasedNeurons1)
net = model.fit(X, y, epochs=25, batch_size=515, verbose=1, validation_split=0.2)Качество модели стало ещё лучше.
Был взят небольшой объём данных, чтобы показать прогноз модели. Из результатов видно, что ошибка модели невелика.
Как и говорилось выше, чаще всего встречаются классы 2 и 6. Соответственно, модель меньше всего ошибается именно в них.
В сухом остатке
Мы смогли избавить модель от переобучения путём увеличения dropout, после чего более высокие результаты были достигнуты за счёт увеличения количества нейронов и эпох. В конечном счёте общая точность предсказания модели по всем классам продуктов составляет чуть больше 0,81, что характеризует её качество. Соответственно, теперь эту модель можно использовать для решения задачи многоклассовой классификации. Плюс в том, что структура является универсальной, так что её можно использовать при решении задач с применением нейронных сетей.
Джеймс Лой, Технологический университет штата Джорджия. Руководство для новичков, после которого вы сможете создать собственную нейронную сеть на Python.
Мотивация: ориентируясь на личный опыт в изучении глубокого обучения, я решил создать нейронную сеть с нуля без сложной учебной библиотеки, такой как, например, TensorFlow. Я считаю, что для начинающего Data Scientist-а важно понимание внутренней структуры нейронной сети.
Эта статья содержит то, что я усвоил, и, надеюсь, она будет полезна и для вас! Другие полезные статьи по теме:
- Обучение с подкреплением на Python с библиотекой Keras
- Пример решения задачи по машинному обучению на Python
Что такое нейронная сеть?
Большинство статей по нейронным сетям при их описании проводят параллели с мозгом. Мне проще описать нейронные сети как математическую функцию, которая отображает заданный вход в желаемый результат, не вникая в подробности.
Нейронные сети состоят из следующих компонентов:
- входной слой, x
- произвольное количество скрытых слоев
- выходной слой, ŷ
- набор весов и смещений между каждым слоем W и b
- выбор функции активации для каждого скрытого слоя σ; в этой работе мы будем использовать функцию активации Sigmoid
На приведенной ниже диаграмме показана архитектура двухслойной нейронной сети (обратите внимание, что входной уровень обычно исключается при подсчете количества слоев в нейронной сети).
Создание класса Neural Network на Python выглядит просто:
Обучение нейронной сети
Выход ŷ простой двухслойной нейронной сети:
В приведенном выше уравнении, веса W и смещения b являются единственными переменными, которые влияют на выход ŷ.
Естественно, правильные значения для весов и смещений определяют точность предсказаний. Процесс тонкой настройки весов и смещений из входных данных известен как обучение нейронной сети.
Каждая итерация обучающего процесса состоит из следующих шагов
- вычисление прогнозируемого выхода ŷ, называемого прямым распространением
- обновление весов и смещений, называемых обратным распространением
Последовательный график ниже иллюстрирует процесс:
Прямое распространение
Как мы видели на графике выше, прямое распространение — это просто несложное вычисление, а для базовой 2-слойной нейронной сети вывод нейронной сети дается формулой:
Давайте добавим функцию прямого распространения в наш код на Python-е, чтобы сделать это. Заметим, что для простоты, мы предположили, что смещения равны 0.
Однако нужен способ оценить «добротность» наших прогнозов, то есть насколько далеки наши прогнозы). Функция потери как раз позволяет нам сделать это.
Функция потери
Есть много доступных функций потерь, и характер нашей проблемы должен диктовать нам выбор функции потери. В этой работе мы будем использовать сумму квадратов ошибок в качестве функции потери.
Сумма квадратов ошибок — это среднее значение разницы между каждым прогнозируемым и фактическим значением.
Цель обучения — найти набор весов и смещений, который минимизирует функцию потери.
Обратное распространение
Теперь, когда мы измерили ошибку нашего прогноза (потери), нам нужно найти способ распространения ошибки обратно и обновить наши веса и смещения.
Чтобы узнать подходящую сумму для корректировки весов и смещений, нам нужно знать производную функции потери по отношению к весам и смещениям.
Напомним из анализа, что производная функции — это тангенс угла наклона функции.
Если у нас есть производная, то мы можем просто обновить веса и смещения, увеличив/уменьшив их (см. диаграмму выше). Это называется градиентным спуском.
Однако мы не можем непосредственно вычислить производную функции потерь по отношению к весам и смещениям, так как уравнение функции потерь не содержит весов и смещений. Поэтому нам нужно правило цепи для помощи в вычислении.
Фух! Это было громоздко, но позволило получить то, что нам нужно — производную (наклон) функции потерь по отношению к весам. Теперь мы можем соответствующим образом регулировать веса.
Добавим функцию backpropagation (обратного распространения) в наш код на Python-е:
Проверка работы нейросети
Теперь, когда у нас есть наш полный код на Python-е для выполнения прямого и обратного распространения, давайте рассмотрим нашу нейронную сеть на примере и посмотрим, как это работает.
Наша нейронная сеть должна изучить идеальный набор весов для представления этой функции.
Давайте тренируем нейронную сеть на 1500 итераций и посмотрим, что произойдет. Рассматривая график потерь на итерации ниже, мы можем ясно видеть, что потеря монотонно уменьшается до минимума. Это согласуется с алгоритмом спуска градиента, о котором мы говорили ранее.
Посмотрим на окончательное предсказание (вывод) из нейронной сети после 1500 итераций.
Мы сделали это! Наш алгоритм прямого и обратного распространения показал успешную работу нейронной сети, а предсказания сходятся на истинных значениях.
Заметим, что есть небольшая разница между предсказаниями и фактическими значениями. Это желательно, поскольку предотвращает переобучение и позволяет нейронной сети лучше обобщать невидимые данные.
Финальные размышления
Я многому научился в процессе написания с нуля своей собственной нейронной сети. Хотя библиотеки глубинного обучения, такие как TensorFlow и Keras, допускают создание глубоких сетей без полного понимания внутренней работы нейронной сети, я нахожу, что начинающим Data Scientist-ам полезно получить более глубокое их понимание.
Я инвестировал много своего личного времени в данную работу, и я надеюсь, что она будет полезной для вас!
Все курсы > Вводный курс > Занятие 21
В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.
Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).
Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.
Смысл, структура и принцип работы
Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).
Отличие нейросети от других алгоритмов заключается в ее структуре.
Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.
Функционирует нейросеть следующим образом.
На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w1, w2, w3, w4). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b1 и b2).
$$ w_{1}\cdot x + w_{3}\cdot y + b_{1} $$
$$ w_{2}\cdot x + w_{4}\cdot y + b_{2} $$
Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h1 и h2).
$$ h_{1} = actfun(w_{1}\cdot x + w_{3}\cdot y + b_{1}) $$
$$ h_{2} = actfun(w_{2}\cdot x + w_{4}\cdot y + b_{2}) $$
На втором этапе процесс повторяется для нейронов скрытого слоя (h1 и h2), весов (w5 и w6) и смещения (b3) до получения конечного результата (r).
$$ r = actfun(w_{5}\cdot h_{1} + w_{6}\cdot h_{2} + b_{3}) $$
Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:
- Восприятие информации через сенсоры (входной слой)
- Создание ассоциаций (скрытый слой)
- Реакцию (выходной слой)
Основы нейронных сетей на простом примере
Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.
В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.
$$ f(x) = \frac{\mathrm{1} }{\mathrm{1} + e^{-x}} $$
График сигмоиды выглядит следующим образом.
Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.
Общее уравнение нейросети выглядит следующим образом.
$$ r = sigmoid(w_{1}\cdot weight + w_{2}\cdot height + bias) $$
Теперь предположим, что у нас есть следующие данные и параметры нейросети.
Откроем ноутбук к этому занятию⧉
|
# даны вес и рост трех человек # единицей мы обозначим мужской пол, а нулем — женский. data = { ‘Иван’: [84, 180, 1], ‘Мария’: [57, 165, 0], ‘Анна’: [62, 170, 0] } |
|
# и даны следующие веса и смещение w1, w2, b = 0.3, 0.1, —39 |
Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.
|
r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b |
Теперь к полученному результату (r) применим сигмоиду.
|
np.round(1 / (1 + np.exp(—r)), 3) |
Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.
|
# пройдемся по ключам и значениям нашего словаря с помощью метода .items() for k, v in data.items(): # вначале умножим каждую строчку данных на веса и прибавим смещение r1 = w1 * v[0] + w2 * v[1] + b # затем применим сигмоиду r2 = 1 / (1 + np.exp(—r1)) # если результат больше 0,5, модель предскажет мужской пол if r2 > 0.5: print(k, np.round(r2, 3), ‘male’) # в противном случае, женский else: print(k, np.round(r2, 3), ‘female’) |
|
Иван 0.985 male Мария 0.004 female Анна 0.032 female |
Как мы видим, модель отработала верно.
Обучение нейронной сети
В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).
И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.
В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.
Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).
В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.
Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).
Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.
Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.
Создание нейросети в библиотеке Keras
Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.
|
# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist !pip install tensorflow mnist |
И импортируем их.
|
# импортируем рукописные цифры import mnist # и библиотеку keras from tensorflow import keras |
1. Подготовка данных
Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).
В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).
Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.
|
# сохраним обучающую выборку и соответсвующую целевую переменную X_train = mnist.train_images() y_train = mnist.train_labels() # посмотрим на размерность print(X_train.shape) print(y_train.shape) |
Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.
|
# сделаем то же самое с тестовыми данными X_test = mnist.test_images() y_test = mnist.test_labels() # и также посмотрим на размерность print(X_test.shape) print(y_test.shape) |
Таких изображений и целевых значений 10000.
Посмотрим на сами изображения.
|
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, X_train, y_train): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = ‘gray’) # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f‘Target: {label}’) |
Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.
$$ x’ = 2 \frac {x-min(x)}{max(x)-min(x)}-1 $$
Применим эту формулу к нашим данным.
|
# функция np.min() возвращает минимальное значение, # np.ptp() — разницу между максимальным и минимальным значениями (от англ. peak to peak) X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 |
Посмотрим на новый диапазон.
|
# снова воспользуемся функцией np.ptp() np.ptp(X_train) |
Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.
Применим этот метод к нашим данным.
|
# «вытянем» (flatten) наши изображения, с помощью метода reshape # у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1) X_train = X_train.reshape((—1, 784)) X_test = X_test.reshape((—1, 784)) # посмотрим на результат print(X_train.shape) print(X_test.shape) |
Посмотрим на получившиеся значения пикселей.
|
# выведем первое изображение [0], пиксели с 200 по 209 X_train[0][200:210] |
|
array([—1. , —1. , —1. , —0.61568627, 0.86666667, 0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373]) |
Наши данные готовы. Теперь нужно задать конфигурацию модели.
2. Конфигурация нейронной сети
Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.
Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).
В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.
|
# импортируем класс Sequential from tensorflow.keras.models import Sequential # и создадим объект этого класса model = Sequential() |
Далее нам нужно прописать сами слои и связи между нейронами.
Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.
|
# импортируем класс Dense from tensorflow.keras.layers import Dense # и создадим первый скрытый слой (с указанием функции активации и размера входного слоя) model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,))) # затем второй скрытый слой model.add(Dense(64, activation = ‘sigmoid’)) # и наконец выходной слой model.add(Dense(10, activation = ‘softmax’)) |
Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).
Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.
$$ \text{softmax}(\vec{z})_{i} = \frac{e^{z_i}}{\sum_{j=1}^K e^{z_i}} $$
Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов zi экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.
На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.
Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.
Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.
|
z = ([1, 2, 0.5]) np.exp(z) / sum(np.exp(z)) |
|
array([0.2312239 , 0.62853172, 0.14024438]) |
Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.
3. Настройки
Настроек будет три:
- тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
- способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
- метрика (metric) покажет, насколько точна наша модель
Функция потерь
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.
Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.
Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.
Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.
В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).
Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.
Алгоритм оптимизации
Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.
Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w1 и w2, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.
Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.
Метрика
Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.
Посмотрим на используемый код.
|
model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘sgd’, metrics = [‘accuracy’] ) |
4. Обучение модели
Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.
- Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
- Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
- На выходе из функции softmax мы получаем вероятности для каждой из цифр
- После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
- На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
- После этого процесс повторяется, но уже с новыми весами.
Давайте выполним все эти операции в библиотеке Keras.
|
# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding from tensorflow.keras.utils import to_categorical |
|
# обучаем модель model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 2.0324 — accuracy: 0.4785 Epoch 2/10 1875/1875 [==============================] — 3s 2ms/step — loss: 1.2322 — accuracy: 0.7494 Epoch 3/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.7617 — accuracy: 0.8326 Epoch 4/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.5651 — accuracy: 0.8663 Epoch 5/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4681 — accuracy: 0.8827 Epoch 6/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4121 — accuracy: 0.8923 Epoch 7/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3751 — accuracy: 0.8995 Epoch 8/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3487 — accuracy: 0.9045 Epoch 9/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3285 — accuracy: 0.9090 Epoch 10/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3118 — accuracy: 0.9129 <keras.callbacks.History at 0x7f36c3f09490> |
На обучающей выборке мы добились неплохого результата, 91.29%.
5. Оценка качества модели
На этом шаге нам нужно оценить качество модели на тестовых данных.
|
# для оценки модели воспользуемся методом .evaluate() model.evaluate( X_test, # который применим к тестовым данным to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.2972 — accuracy: 0.9173 [0.29716429114341736, 0.9172999858856201] |
Результат «на тесте» оказался даже чуть выше, 91,73%.
6. Прогноз
Теперь давайте в качестве упражнения сделаем прогноз.
|
# передадим модели последние 10 изображений тестовой выборки pred = model.predict(X_test[—10:]) # посмотрим на результат для первого изображения из десяти pred[0] |
|
array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03, 6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01, 5.3100550e-04, 1.9325638e-02], dtype=float32) |
Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.
Теперь применим к нашим данным.
|
# для кажого изображения (то есть строки, axis = 1) # выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем print(np.argmax(pred, axis = 1)) # остается сравнить с целевой переменной print(y_test[—10:]) |
|
[7 8 9 0 1 2 3 4 5 6] [7 8 9 0 1 2 3 4 5 6] |
Для первых десяти цифр модель сделала верный прогноз.
7. Пример улучшения алгоритма
Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).
Посмотрим на результат на обучающей и тестовой выборке.
|
# снова укажем настройки модели model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘adam’, # однако заменим алгоритм оптимизации metrics = [‘accuracy’] ) # обучаем модель методом .fit() model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # прописываем количество эпох ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.2572 — accuracy: 0.9252 Epoch 2/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1738 — accuracy: 0.9497 Epoch 3/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1392 — accuracy: 0.9588 Epoch 4/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1196 — accuracy: 0.9647 Epoch 5/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1062 — accuracy: 0.9685 Epoch 6/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0960 — accuracy: 0.9708 Epoch 7/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0883 — accuracy: 0.9732 Epoch 8/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0826 — accuracy: 0.9747 Epoch 9/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0766 — accuracy: 0.9766 Epoch 10/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0699 — accuracy: 0.9780 <keras.callbacks.History at 0x7f36c3d74590> |
|
# и оцениваем результат «на тесте» model.evaluate( X_test, to_categorical(y_test) ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.1160 — accuracy: 0.9647 [0.11602973937988281, 0.9646999835968018] |
Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.
Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.
Подведем итог
На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.
При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.
Вопросы для закрепления
Перечислите типы слоев нейронной сети
Посмотреть правильный ответ
Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.
Из каких двух этапов состоит обучение нейронной сети?
Посмотреть правильный ответ
Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.
Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?
Посмотреть правильный ответ
Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.
Ответы на вопросы
Вопрос. Что означает число 1875 в результате работы модели?
Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).
- в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
- во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
- и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1
В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.
Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.
В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.
Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.