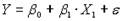Тесты
по дисциплине:
Эконометрика
(ОПД)
Для
специальности(ей):
080100.62
— Экономика
Перечень
тем (в скобках указан условный номер
Дидактической Единицы, к которой
относится тема) :
1
Линейная модель множественной регрессии
[1]
1. Спецификация эконометрической модели
[1]
2. Отбор факторов, включаемых в модель
множественной регрессии
[1]
3. Фиктивные переменные
[1]
4. Линейное уравнение множественной
регрессии
2
Метод наименьших квадратов (МНК)
[2]
5. Оценка параметров линейных уравнений
регрессии
[2]
6. Предпосылки МНК, методы их проверки
[2]
7. Свойства оценок параметров
эконометрической модели, получаемых
при помощи МНК
[2]
8. Обобщенный метод наименьших квадратов
(ОМНК)
3
Оценка качества эконометрической модели
[3]
9. Оценка тесноты связи
[3]
10. Оценка качества подбора уравнения
[3]
11. Проверка статистической значимости
эконометрической модели
[3]
12. Оценка значимости параметров
эконометрической модели
4
Нелинейные модели регрессии
[4]
13. Нелинейные зависимости в экономике
[4]
14. Виды нелинейных уравнений регрессии
[4]
15. Линеаризация нелинейных моделей
регрессии
[4]
16. Оценка качества нелинейных уравнений
регрессии
5
Характеристики временных рядов
[5]
17. Временные ряды данных: характеристики
и общие понятия
[5]
18. Структура временного ряда
[5]
19. Аддитивная и мультипликативная модели
временных рядов
[5]
20. Модели стационарных и нестационарных
временных рядов и их идентификация
6
Система линейных одновременных уравнений
[6]
21. Общие понятия о системах уравнений,
используемых в эконометрике
[6]
22. Классификация систем уравнений
[6]
23. Идентификация систем эконометрических
уравнений
[6]
24. Методы оценки параметров систем
одновременных уравнений: косвенный
метод наименьших квадратов (КМНК) и
двухшаговый метод наименьших квадратов
(ДМНК)
Тема
№ 1. Спецификация эконометрической
модели
(Задание
с выбором одного правильного ответа из
предложенных)
Оригинальное
кол-во заданий: 59, в базе представлено:
5
Вопрос
№ 1.1. Оригинальный порядковый номер: 10
Выбор
формы зависимости экономических
показателей и определение количества
факторов в модели называется _____________
эконометрической модели.
Варианты
ответов. Кол-во правильных ответов — 1
1.
идентификацией
2.
апробацией
3.
спецификацией
4.
линеаризацией
Вопрос
№ 1.2. Оригинальный порядковый номер: 25
При
построении эконометрических моделей
множественная регрессия используется
в случае, если число ______ в модели больше
или равно двум.
Варианты
ответов. Кол-во правильных ответов — 1
1.
случайных факторов
2.
зависимых и независимых переменных
3.
независимых переменных
4.
зависимых переменных
Вопрос
№ 1.3. Оригинальный порядковый номер: 27
Линейные
эконометрические модели описывают
линейные взаимосвязи между …
Варианты
ответов. Кол-во правильных ответов — 1
1.
зависимой переменной и случайными
факторами
2.
независимыми переменными и случайными
факторами
3.
зависимой и независимыми переменными
4.
независимой и зависимыми переменными
Вопрос
№ 1.4. Оригинальный порядковый номер: 44
Спецификация
модели множественной линейной регрессии
в матричной форме имеет вид
…
Варианты
ответов. Кол-во правильных ответов — 1
1.
2.
3.
4.
Вопрос
№ 1.5. Оригинальный порядковый номер: 56
Для
линейного уравнения множественной
регрессии проблема спецификации модели
связана …
Варианты
ответов. Кол-во правильных ответов — 1
1.
анализом качества уравнения регрессии
2.
переходом к стандартизации переменных
3.
с отбором факторов, включаемых в модель
4.
расчетом оценок параметров регрессии
Вопрос
№ 1.1. Оригинальный порядковый номер: 17
Неправильный
выбор вида эконометрической модели
называют ошибкой…
Варианты
ответов. Кол-во правильных ответов — 1
1.
измерения переменных
2.
агрегирования переменных
3.
спецификации модели
4.
параметризации модели
Вопрос
№ 1.3. Оригинальный порядковый номер: 37
Включение
случайных возмущений в уравнения
эконометрической модели является одним
из принципов …
Варианты
ответов. Кол-во правильных ответов — 1
1.
верификации
2.
линеаризации
3.
спецификации
4.
идентификации
Вопрос
№ 1.4. Оригинальный порядковый номер: 40
Отбрасывание
значимой переменной в уравнении
множественной регрессии является
ошибкой …
Варианты
ответов. Кол-во правильных ответов — 1
1.
верификации
2.
идентификации
3.
спецификации
4.
параметризации
Вопрос
№ 1.5. Оригинальный порядковый номер: 57
Регрессионная
модель с одним факторным признаком
называется …
Варианты
ответов. Кол-во правильных ответов — 1
1.
рекурсивной
2.
стандартизированной
3.
парной
4.
множественной
Вопрос
№ 1.1. Оригинальный порядковый номер: 14
Этап
параметризации модели включает в себя…
Варианты
ответов. Кол-во правильных ответов — 1
1.
проверку качества уравнения в целом
2.
прогноз экономических показателей
3.
проверку качества параметров модели
4.
оценку параметров модели
Вопрос
№ 1.2. Оригинальный порядковый номер: 19
Эконометрическая
модель предполагает _______ характер связи
между переменными
Варианты
ответов. Кол-во правильных ответов — 1
1.
стохастический (вероятностный)
2.
строго случайный
3.
несущественный
4.
строго детерминированный
Вопрос
№ 1.3. Оригинальный порядковый номер: 43
Спецификация
модели множественной линейной регрессии
имеет вид …
Варианты
ответов. Кол-во правильных ответов — 1
1.
2.
3.
4.
Вопрос
№ 1.4. Оригинальный порядковый номер: 65
Объясняемые,
зависимые переменные в моделях любого
типа называются …
Варианты
ответов. Кол-во правильных ответов — 1
1.
лаговыми
2.
предопределенными
3.
эндогенными
4.
экзогенными
Вопрос
№ 1.5. Оригинальный порядковый номер: 88
Эконометрические
модели относятся к классу ______
экономико–математических моделей.
Варианты
ответов. Кол-во правильных ответов — 1
1.
оптимизационных
2.
описательных
3.
стохастических
4.
детерминированных
Тема
№ 2. Отбор факторов, включаемых в модель
множественной регрессии
(Задание
с выбором одного правильного ответа из
предложенных)
Оригинальное
кол-во заданий: 56, в базе представлено:
5
Вопрос
№ 2.1. Оригинальный порядковый номер: 20
Проверка
тесноты связи между факторами может
быть осуществлена на основе …
Варианты
ответов. Кол-во правильных ответов — 1
1.
значений стандартизованных коэффициентов
2.
частных уравнений регрессии
3.
матрицы парных коэффициентов корреляции
4.
вектора значений коэффициентов регрессии
Вопрос
№ 2.2. Оригинальный порядковый номер: 22
При
отборе факторов в модель множественной
регрессии проводят анализ значений
межфакторной …
Варианты
ответов. Кол-во правильных ответов — 1
1.
регрессии
2.
автокорреляции
3.
корреляции
4.
детерминации
Вопрос
№ 2.3. Оригинальный порядковый номер: 29
Количественная
измеримость значений экономического
признака (фактора), включаемого в
эконометрическую модель, является …
Варианты
ответов. Кол-во правильных ответов — 1
1.
принципом спецификации
2.
предпосылкой линеаризации
3.
общим требованием к факторам, включаемым
в линейную множественную регрессию
4.
условием гомоскедастичности
эконометрической модели
Вопрос
№ 2.4. Оригинальный порядковый номер: 31
Отсутствие
сильной корреляции факторов друг с
другом является …
Варианты
ответов. Кол-во правильных ответов — 1
1.
условием отсутствия автокорреляции
остатков
2.
предпосылкой линеаризации
3.
требованием к факторам, включаемым в
линейную модель множественной регрессии
4.
условием гомоскедастичности
эконометрической модели
Вопрос
№ 2.5. Оригинальный порядковый номер: 34
Если
в линейной множественной регрессии
более, чем две независимые переменные
связаны между собой достаточно тесной
линейной зависимостью, тогда имеет
место ____ факторов.
Варианты
ответов. Кол-во правильных ответов — 1
1.
гомоскедастичность
2.
автокорреляция
3.
мультиколлинеарность
4.
коллинеарность
Вопрос
№ 2.1. Оригинальный порядковый номер: 2
Взаимодействие
факторов эконометрической модели
означает, что …
Варианты
ответов. Кол-во правильных ответов — 1
1.
влияние факторов на результирующий
признак усиливается, начиная с
определенного уровня значений факторов
2.
факторы не дублируют влияние друг друга
на результат
3.
факторы дублируют влияние друг друга
на результат
4.
влияние одного из факторов на результирующий
признак не зависит от значений
другого фактора
Вопрос
№ 2.2. Оригинальный порядковый номер: 7
Факторы
эконометрической модели являются
коллинеарными, если коэффициент ____
между ними по модулю ____ 0,7.
Варианты
ответов. Кол-во правильных ответов — 1
1.
корреляции … меньше
2.
детерминации … меньше
3.
корреляции … больше
4.
детерминации … больше
Вопрос
№ 2.3. Оригинальный порядковый номер: 11
Матрица
парных линейных коэффициентов корреляции
отображает…
Варианты
ответов. Кол-во правильных ответов — 1
1.
значения стандартизированных коэффициентов
линейной регрессии
2.
вероятность значимости каждой объясняющей
переменной
3.
тесноту линейной связи между переменными
4.
величину вклада каждой объясняющей
переменной в общую дисперсию зависимой
переменной
Вопрос
№ 2.4. Оригинальный порядковый номер: 26
В
эконометрическую модель множественной
регрессии включаются ____ факторы.
Варианты
ответов. Кол-во правильных ответов — 1
1.
мультиколлинеарные
2.
коллинеарные
3.
существенные
4.
несущественные
Вопрос
№ 2.5. Оригинальный порядковый номер: 35
Отсутствие
коллинеарности и мультиколлинеарности
является обязательным требованием для
факторов, включаемых в уравнение ______
регрессии.
Варианты
ответов. Кол-во правильных ответов — 1
1.
нелинейной показательной
2.
нелинейной полулогарифмической
3.
множественной линейной
4.
нелинейной степенной
Вопрос
№ 2.1. Оригинальный порядковый номер: 15
Мультиколлинеарность
– это линейная связь между…
Варианты
ответов. Кол-во правильных ответов — 1
1.
объясняющими и зависимой переменными
2.
одной объясняющей и зависимой переменными
3.
соседними случайными отклонениями
4.
объясняющими переменными
Вопрос
№ 2.2. Оригинальный порядковый номер: 45
Для
отбора факторов множественной линейной
модели регрессии рассматривается вопрос
о взаимосвязи фактора и результата при
неизменности прочих факторов, которые
фиксируются, как правило, на среднем
уровне. В этом случае используется …
Варианты
ответов. Кол-во правильных ответов — 1
1.
автокорреляционная функция
2.
матрица частных коэффициентов корреляции
3.
матрица множественных коэффициентов
корреляции
4.
коррелограмма для факторов модели
Вопрос
№ 2.3. Оригинальный порядковый номер: 54
Оценка
удельного веса влияния каждой из
объясняющих переменных на результирующий
показатель является задачей …
Варианты
ответов. Кол-во правильных ответов — 1
1.
кластерного анализа
2.
метода наименьших квадратов
3.
регрессионного анализа
4.
математического анализа
Вопрос
№ 2.4. Оригинальный порядковый номер: 80
Функциональная
(строгая) или достаточно тесная (нестрогая)
линейная зависимость между объясняющими
переменными называется…
Варианты
ответов. Кол-во правильных ответов — 1
1.
несмещенностью
2.
мультиколлинеарностью
3.
гетероскедастичностью
4.
автокорреляцией
Вопрос
№ 2.5. Оригинальный порядковый номер: 82
Пусть
в результате оценки модели множественной
регрессии каждый из оцененных параметров
является незначимым на 5%-ном уровне, а
уравнение в целом (коэффициент
детерминации) является значимым на том
же уровне. Тогда можно предположить,
что…
Варианты
ответов. Кол-во правильных ответов — 1
1.
в остатках модели присутствует
автокорреляция
2.
в остатках модели присутствует
гетероскедастичность
3.
среди объясняющих переменных есть
мультиколлинеарные
4.
связь между зависимой переменной и
независимыми отсутствует
Тема
№ 3. Фиктивные переменные
(Задание
с выбором одного правильного ответа из
предложенных)
Оригинальное
кол-во заданий: 58, в базе представлено:
5
Вопрос
№ 3.1. Оригинальный порядковый номер: 3
Исходные
значения фиктивных переменных предполагают
_____ значения.
Варианты
ответов. Кол-во правильных ответов — 1
1.
одинаковые
2.
количественно измеримые
3.
качественные
4.
нулевые
Вопрос
№ 3.2. Оригинальный порядковый номер: 5
Строится
модель зависимости спроса от ряда
факторов. Фиктивной переменной в данном
уравнении множественной регрессии не
является
__________ потребителя.
Варианты
ответов. Кол-во правильных ответов — 1
1.
уровень образования
2.
семейное положение
3.
доход
4.
пол
Вопрос
№ 3.3. Оригинальный порядковый номер: 7
Фиктивные
переменные включаются в уравнение
множественной регрессии для учета
действия на результат признаков ______
характера .
Варианты
ответов. Кол-во правильных ответов — 1
1.
случайного
2.
несущественного
3.
качественного
4.
количественного
Вопрос
№ 3.4. Оригинальный порядковый номер: 15
Фиктивными
переменными могут быть…
Варианты
ответов. Кол-во правильных ответов — 1
1.
только зависимые переменные
2.
только случайные факторы
3.
как зависимая, так и объясняющие
переменные
4.
как объясняющие переменные, так и
случайные факторы
Вопрос
№ 3.5. Оригинальный порядковый номер: 23
В
качестве фиктивной переменной в
эконометрическую модель могут быть
включены переменные, отражающие ____
наблюдаемого признака
Варианты
ответов. Кол-во правильных ответов — 1
1.
случайный характер
2.
нулевые значения
3.
качественные характеристики
4.
количественные значения
Вопрос
№ 3.1. Оригинальный порядковый номер: 6
Факторные
переменные уравнения множественной
регрессии, преобразованные из качественных
в количественные называются …
Варианты
ответов. Кол-во правильных ответов — 1
1.
аномальными
2.
парными
3.
фиктивными
4.
множественными
Вопрос
№ 3.2. Оригинальный порядковый номер: 13
Модель,
содержащая фиктивную переменную,
относится к ______ модели .
Варианты
ответов. Кол-во правильных ответов — 1
1.
оптимизационной
2.
сетевой
3.
регрессионной
4.
фиктивной
Вопрос
№ 3.3. Оригинальный порядковый номер: 18
Фиктивная
переменная является ____________ величиной.
Варианты
ответов. Кол-во правильных ответов — 1
1.
кусочно-непрерывной
2.
случайной
3.
дискретной
4.
непрерывной
Вопрос
№ 3.4. Оригинальный порядковый номер: 43
Влияние
фиктивной переменной наклона на
регрессионную модель состоит в …
Варианты
ответов. Кол-во правильных ответов — 1
1.
устранении гетероскедастичности
остатков
2.
увеличении дисперсии оценок параметров
3.
изменении коэффициента перед факторным
признаком, взаимодействующим с
качественной переменной
4.
изменении величины свободного слагаемого
Вопрос
№ 3.5. Оригинальный порядковый номер: 55
Фиктивные
переменные заменяют …
Варианты
ответов. Кол-во правильных ответов — 1
1.
случайные ошибки
2.
количественные данные
3.
качественные переменные
4.
прогнозируемые значения
Вопрос
№ 3.1. Оригинальный порядковый номер: 0
Примерами
фиктивных переменных могут служить:
Варианты
ответов. Кол-во правильных ответов — 2
1.
возраст
2.
пол
3.
образование
4.
доход
Вопрос
№ 3.2. Оригинальный порядковый номер: 6
Фиктивными
переменными в уравнении множественной
регрессии могут быть …
Варианты
ответов. Кол-во правильных ответов — 2
1.
экономические показатели, выраженные
в стоимостном измерении
2.
качественные переменные, преобразованные
в количественные
3.
переменные, исходные значения которых
не имеют количественного значения
4.
количественные переменные
Вопрос
№ 3.3. Оригинальный порядковый номер: 7
Для
учета действия на зависимую переменную
факторов качественного характера (так
называемых фиктивных переменных)
последним могут присваиваться …
Варианты
ответов. Кол-во правильных ответов — 2
1.
цифровые метки
2.
значения 0 и 1
3.
несущественные значения
4.
стоимостные значения
Вопрос
№ 3.4. Оригинальный порядковый номер: 8
Исследуется
зависимость цены квартиры от ряда
факторов: х1
— жилой площади, х2
— стоимости квадратного метра жилья, х3
— расположения квартиры относительно
углов дома (угловая или не угловая), х4
– расположения квартиры на этаже (первый
этаж, последний этаж, не первый и не
последний этаж). Фиктивными переменными
в модели являются …
Варианты
ответов. Кол-во правильных ответов — 2
1.
х3
2.
х1
3.
х4
4.
х2
Вопрос
№ 3.5. Оригинальный порядковый номер: 11
Проводится
эконометрическое моделирование
зависимости объема продаж компании от
ряда факторов: х1
– цены на товар, х2
– степени известности торговой марки
фирмы, х3
– дохода потребителя, х4
– уровня интенсивности рекламной
деятельности (высокий уровень –
массированная реклама; средний уровень
– регулярно повторяющаяся; низкий
уровень – время от времени повторяющаяся).
Фиктивными переменными в модели не
являются
…
Варианты
ответов. Кол-во правильных ответов — 2
1.
х1
2.
х2
3.
х3
4.
х4
Тема
№ 4. Линейное уравнение множественной
регрессии
(Задание
с выбором одного правильного ответа из
предложенных)
Оригинальное
кол-во заданий: 61, в базе представлено:
5
Вопрос
№ 4.1. Оригинальный порядковый номер: 13
Укажите
правильный вариант ответа относительно
числа зависимых переменных, включаемых
в уравнение регрессии:
Варианты
ответов. Кол-во правильных ответов — 1
1.
несколько переменных
2.
количество зависимых переменных равно
количеству независимых
3.
только одна переменная
4.
в парной регрессии одна зависимая
переменная, во множественной – несколько
зависимых переменных
Вопрос
№ 4.2. Оригинальный порядковый номер: 17
Частное
уравнение регрессии характеризует…
Варианты
ответов. Кол-во правильных ответов — 1
1.
силу воздействия фактора на результат
при положительных значениях других
факторов
2.
наличие или отсутствие мультиколлинеарности
факторов
3.
изолированное влияние фактора на
результат при средних значениях других
факторов
4.
изолированное влияние фактора на
результат при нулевых значениях других
факторов
Вопрос
№ 4.3. Оригинальный порядковый номер: 19
В
эконометрическую модель множественной
регрессии необходимо включить факторы,
оказывающие ________ влияние на исследуемый
показатель.
Варианты
ответов. Кол-во правильных ответов — 1
1.
случайное
2.
детерминированное
3.
существенное
4.
несущественное
Вопрос
№ 4.4. Оригинальный порядковый номер: 21
В
эконометрической модели среднее
изменение результата при изменении
фактора на 1 ед. измерения характеризуется
с помощью коэффициента …
Варианты
ответов. Кол-во правильных ответов — 1
1.
детерминации
2.
автокорреляции
3.
регрессии
4.
корреляции
Вопрос
№ 4.5. Оригинальный порядковый номер: 53
В
случае включения в модель переменной,
которая не должна присутствовать в
уравнении, как правило, происходит
увеличение …
Варианты
ответов. Кол-во правильных ответов — 1
1.
F-критерия Фишера
2.
коэффициента множественной корреляции
3.
стандартных ошибок
4.
коэффициента детерминации
Вопрос
№ 4.1. Оригинальный порядковый номер: 7
Для
модели зависимости среднедушевого (в
расчете на одного человека) месячного
дохода населения (р.) от объема производства
(млн. р.) получено уравнение у
= 0,003х + 1200 + е.
При изменении объема производства на
1 млн. р. доход в среднем изменится на …
Варианты
ответов. Кол-во правильных ответов — 1
1.
1200 р.
2.
1200 млн. р.
3.
0,003 р.
4.
0,003 млн. р.
Вопрос
№ 4.2. Оригинальный порядковый номер: 10
В
стандартизованном уравнении свободный
член …
Варианты
ответов. Кол-во правильных ответов — 1
1.
равен коэффициенту множественной
корреляции
2.
равен коэффициенту множественной
детерминации
3.
отсутствует
4.
равен 1
Вопрос
№ 4.3. Оригинальный порядковый номер: 11
В
уравнении регрессии Y
= a+bx+е зависимая
переменная обозначается буквой …
Варианты
ответов. Кол-во правильных ответов — 1
1.
a
2.
b
3.
Y
4.
x
Вопрос
№ 4.4. Оригинальный порядковый номер: 12
В
уравнении регрессии Y
= a+bx+е независимая
переменная обозначается буквой …
Варианты
ответов. Кол-во правильных ответов — 1
1.
a
2.
b
3.
x
4.
Y
Вопрос
№ 4.5. Оригинальный порядковый номер: 26
В
линейном уравнении множественной
регрессии
величина
у
является
Варианты
ответов. Кол-во правильных ответов — 1
1.
постоянной величиной
2.
случайной величиной
3.
зависимой переменной
4.
независимой переменной
Вопрос
№ 4.1. Оригинальный порядковый номер: 3
В
линейном уравнении парной регрессии
коэффициентом
регрессии является значение…
Варианты
ответов. Кол-во правильных ответов — 1
1.
параметра a
2.
параметра b
3.
переменной х
4.
величины
Вопрос
№ 4.2. Оригинальный порядковый номер: 8
В
стандартизованном уравнении множественной
регрессии
переменными
являются …
Варианты
ответов. Кол-во правильных ответов — 1
1.
стандартизованные параметры
2.
исходные переменные y,
x1,
x2,…,xp
3.
средние значения исходных переменных
4.
стандартизованные переменные
Вопрос
№ 4.3. Оригинальный порядковый номер: 32
В
стандартизованном уравнении
стандартизованным
коэффициентом является …
Варианты
ответов. Кол-во правильных ответов — 1
1.
2.
Другие вопросы по предмету Эконометрика
Вопрос № 56222
Отсутствие сильной корреляции факторов друг с другом является …
условием отсутствия автокорреляции остатков
условием гомоскедастичности эконометрической модели
предпосылкой линеаризации
требованием к факторам, включаемым в линейную множественную регрессию
Вопрос № 56233
Регрессионная модель с одним факторным признаком называется …
рекурсивной
стандартизированной
множественной
парной
Вопрос № 56235
Следствием мультиколлинеарности является…
статистическая незначимость коэффициента детерминации
статистическая незначимость коэффициента корреляции
достоверная оценка коэффициентов регрессии
невозможность достоверной оценки коэффициентов регрессии
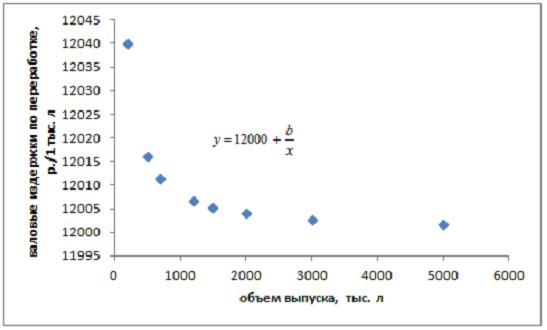
Вопрос № 56261
Для предприятий, осуществляющих переработку молока, анализ зависимости валовых издержек на единицу продукции (на 1 тыс. л) от объема выпуска позволил выявить закономерность, представленную на графике.
Переменные издержки на единицу продукции (на 1 тыс. л) для таких предприятий составят ______ руб.
4.
Использование
предварительной информации о значениях некоторых параметров. Иногда значения некоторых неизвестных параметров
модели могут быть определены по пробным выборочным наблюдениям, тогда
мультиколлинеарность может быть устранена путем установления значений параметра
у одной коррелирующих переменных. Ограниченность метода – в сложности получения
предварительных значений параметров с высокой точностью.
5.
Преобразование переменных. Для устранения мультиколлинеарности можно
преобразовать переменные, например, путем линеаризации или получения
относительных показателей, а также перехода от номинальных к реальным
показателям (особенно в макроэкономических исследованиях).
При построении модели множественной регрессии с точки
зрения обеспечения ее высокого качества возникают следующие вопросы:
1.
Каковы признаки качественной
модели?
2.
Какие ошибки спецификации могут
быть?
3.
Каковы последствия ошибок
спецификации?
4.
Какие существуют методы
обнаружения и устранения ошибок спецификации?
Рассмотрим основные признаки качественной модели
множественной регрессии:
1.
Простота. Из двух моделей примерно одинаковых статистических
свойств более качественной является та, которая содержит меньше переменных, или
же более простая по аналитической форме.
2.
Однозначность. Метод вычисления коэффициентов должен быть одинаков
для любых наборов данных.
3.
Максимальное соответствие. Этот признак говорит о том, что основным критерием
качества модели является коэффициент детерминации, отражающий объясненную
моделью вариацию зависимой переменной. Для практического использования выбирают
модель, для которой расчетное значение F-критерия для
коэффициента детерминации б четыре раза больше табличного.
4.
Согласованность с теорией. Получаемые значения коэффициентов должны быть
интерпретируемы с точки зрения экономических явлений и процессов. К примеру,
если строится линейная регрессионная модель спроса на товар, то соответствующий
коэффициент при цене товара должен быть отрицательным.
5.
Хорошие прогнозные качества.
Обязательным условием построения
качественной модели является возможность ее использования для прогнозирования.
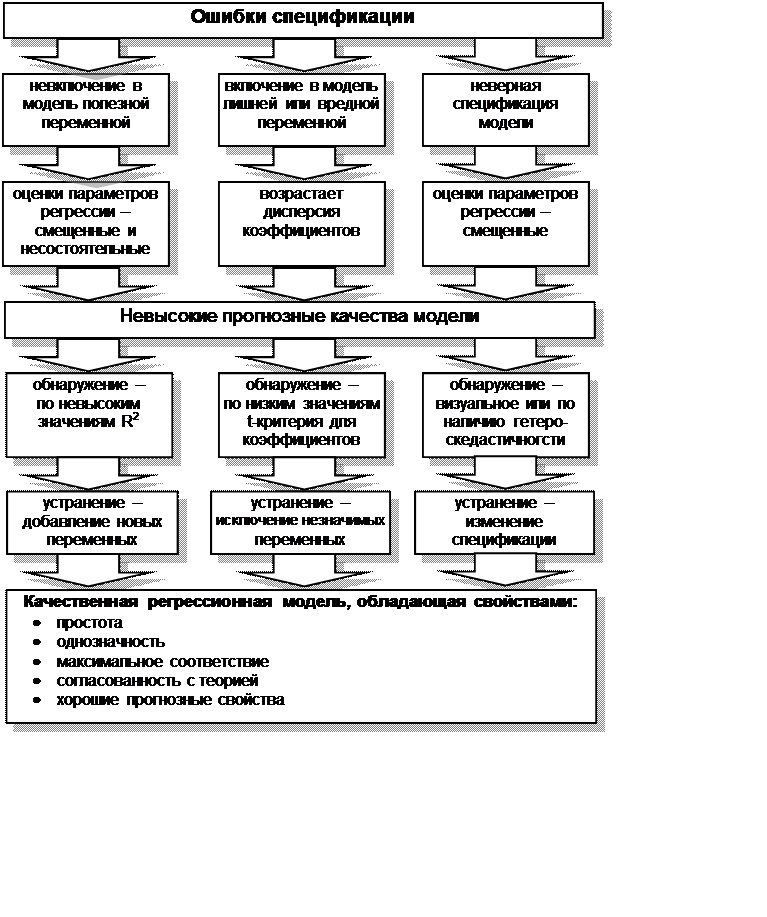
Одной из основных ошибок, допускаемых при построении
регрессионной модели, является ошибка спецификации (рис. 4.3).
Под ошибкой спецификации понимается неправильный выбор функциональной формы
модели или набора объясняющих переменных.
Различают следующие виды ошибок спецификации:
1.
Невключение в модель полезной
(значимой) переменной.
2.
Добавление в модель лишней
(незначимой) переменной
3.
Выбор неправильной функциональной
формы модели
Последствия ошибки первого вида (невключение в
модель значимой переменной) заключаются в том, что полученные по МНК оценки
параметров являются смещенными и несостоятельными, а значение коэффициента
детерминации значительно снижаются.
При добавлении в модель лишней переменной
(ошибка второго вида) ухудшаются статистические свойства оценок
коэффициентов, возрастают их дисперсии, что ухудшает прогнозные качества модели
и затрудняет содержательную интерпретацию параметров, однако по сравнению с
другими ошибками ее последствия менее серьезны.
Если же осуществлен неверный выбор
функциональной формы модели, то есть допущена ошибка третьего вида, то
получаемые оценки будут смещенными, качество модели в целом и отдельных
коэффициентов будет невысоким. Это может существенно сказаться на прогнозных
качествах модели.
Ошибки спецификации первого вида можно обнаружить только
по невысокому качеству модели, низким значениям R2.
Обнаружение ошибок спецификации второго вида, если лишней
является только одна переменная, осуществляется на основе расчета t — статистики для коэффициентов. При лишней переменной коэффициент
будет статистически незначим.
Рис. 4.3 Ошибки спецификации и свойства качественной
регрессионной модели
Хубулава Ное Михайлович
«ЭКОНОМЕТРИКА»
Учебник для студентов экономического профиля
всех специальностей и всех форм обучения, а также
на специалистов, занимающихся проблемами
экономического измерения, прогнозирования
Подписано в печать 10.05.2005. Формат 60×84 1/14.
Бумага офсетная. Печать офсетная. Уч. изд.
Лист 8,1. Тираж 5000.

Москва, Енисеевская 36.
Издательский комплекс
1.1. Эконометрика как наука. Эконометрика — это наука, которая на базе статистических данных строит и анализирует модели, отражающие реальные экономические явления. Модели позволяют:
— изучать реальное состояние объектов или процессов, выявлять и оценивать наиболее существенные факторы, определяющие поведение объекта исследования;
— прогнозировать изменение состояния объекта моделирования во времени.
Эконометрика как наука сформировалась и получила развитие на стыке экономической теории, математической и экономической статистики.
Экономическая теория предоставляет для эконометрики научное обоснование наличия и формы связи между явлениями и процессами. При этом, в отличие от экономической теории, эконометрику интересует не качественный анализ, а количественная оценка связей.
Эта оценка основывается на использовании методов математической статистики, и, прежде всего, корреляционно-регрессионного анализа. Информационной базой для построения моделей являются статистические данные. При построении эконометрической модели крайне важно знать способы получения и методики расчета показателей, поскольку в противном случае полученные на базе моделей выводы могут оказаться неточными. Вместе с тем, наличие статистической информации определяет конкретный состав используемых в модели показателей.
Процесс построения эконометрической модели можно представить следующим образом:
1.2. Эконометрическая модель: основные понятия.
Эконометрическая модель — это уравнение (или система уравнений) ĸᴏᴛᴏᴩᴏᴇ в математической форме описывает основные количественные зависимости между анализируемыми экономическими явлениями и процессами. Несущественные взаимосвязи в модели игнорируются.
Эконометрическая модель включает два вида переменных.
1. Переменные, характеризующие те экономические явления и процессы, которые требуется объяснить. Такие переменные принято называть зависимыми или объясняемыми и обозначать Y.
2. Переменные, характеризующие те процессы и явления, которые влияют на значение объясняемой переменной. Οʜᴎ называются независимыми или объясняющими и обозначаются Х1, Х2, Х3 и т.д.
К примеру, при изучении цен на жилье зависимой переменной Y должна быть цена одного квадратного метра, а независимыми — этаж, на котором расположена квартира (Х1), количество комнат (Х2), год постройки дома (Х3), наличие телефона (Х4) и пр.
Математически связь между зависимой и независимой переменными записывается в виде функции:
Y=f(Х1 , Х2 ,. . . , Хm, ε ). (1)
Поскольку эконометрическая модель не включает абсолютно все связи (это невозможно), а акцентирует внимание только на базовых, построенное уравнение не может абсолютно точно предсказать поведение зависимой переменной. Всегда будут существовать большие или меньшие отклонения фактических значений от тех, которые будут получены в процессе расчетов по модели. Эти случайные отклонения обозначаются символом ε, а сама модель, включающая вероятностные а не жестко и однозначно заданные связи — регрессионной.
При наличии линейной связи между зависимой и независимой переменными, модель приобретает следующий вид:
Y=β0+ β 1X1+ β 2X2+. . . β mXm+ ε (2)
В процессе эконометрического моделирования оценивается ожидаемое теоретическое значение зависимой переменной уt на базе выборочных данных:
уt=b0+b1х1+ b1х1+. . . bmхm. +е (3)
или

Переменные уt, x1, x2 и т.д. оцениваются на базе включаемых в модель статистических данных. Величина е — это остатки.
К примеру, при анализе стоимости жилья собрана информация по двум сотням различных квартир.
По каждой их них определена цена квадратного метра, этаж, количество комнат и пр.
Значение yt1будет представлять собой цену квадратного метра в первой квартире, yt2— во второй квартире так далее вплоть до yt200.
Аналогично определяются значения независимых переменных. Так, значение x11будет представлять собой порядковый номер этажа в первой квартире, x12— во второй квартире, значение x21— количество комнат в первой квартире, x22— во второй и т.д.
По результатам эконометрического анализа определяется усредненное влияние каждой из независимых переменных на зависимую посредством расчета величин b0, b1, b2 и т.д. Οʜᴎ называются параметрами модели.
В нашем случае b1 — усредненное влияние этажа на цену квадратного метра, b2 — усредненное влияние количества комнат и т.д.
Процедура оценивания эконометрических моделей, интерпретация и применение полученных результатов будут рассмотрены в последующих темах курса.
(Задание с выбором одного правильного ответа из предложенных)
Оригинальное кол-во заданий: 59, в базе представлено: 5
Вопрос № 1.1. Оригинальный порядковый номер: 10
Выбор формы зависимости экономических показателей и определение количества факторов в модели называется _____________ эконометрической модели.
Варианты ответов. Кол-во правильных ответов — 1
1. идентификацией
2. апробацией
3. спецификацией
4. линеаризацией
Вопрос № 1.2. Оригинальный порядковый номер: 25
При построении эконометрических моделей множественная регрессия используется в случае, если число ______ в модели больше или равно двум.
Варианты ответов. Кол-во правильных ответов — 1
1. случайных факторов
2. зависимых и независимых переменных
3. независимых переменных
4. зависимых переменных
Вопрос № 1.3. Оригинальный порядковый номер: 27
Линейные эконометрические модели описывают линейные взаимосвязи между …
Варианты ответов. Кол-во правильных ответов — 1
1. зависимой переменной и случайными факторами
2. независимыми переменными и случайными факторами
3. зависимой и независимыми переменными
4. независимой и зависимыми переменными
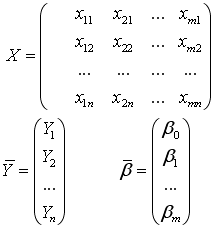
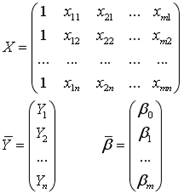
Вопрос № 1.4. Оригинальный порядковый номер: 44
Спецификация модели множественной линейной регрессии в матричной форме имеет вид 
Варианты ответов. Кол-во правильных ответов — 1
1.
2.
3.
4.
Вопрос № 1.5. Оригинальный порядковый номер: 56
Для линейного уравнения множественной регрессии проблема спецификации модели связана …
Варианты ответов. Кол-во правильных ответов — 1
1. анализом качества уравнения регрессии
2. переходом к стандартизации переменных
3. с отбором факторов, включаемых в модель
4. расчетом оценок параметров регрессии
Вопрос № 1.1. Оригинальный порядковый номер: 17
Неправильный выбор вида эконометрической модели называют ошибкой…
Варианты ответов. Кол-во правильных ответов — 1
1. измерения переменных
2. агрегирования переменных
3. спецификации модели
4. параметризации модели
Вопрос № 1.3. Оригинальный порядковый номер: 37
Включение случайных возмущений в уравнения эконометрической модели является одним из принципов …
Варианты ответов. Кол-во правильных ответов — 1
1. верификации
2.
Содержание
- 1. Эконометрическая модель и проблемы эконометрического моделирования
- Эконометрическая модель
- Эконометрическая модель
- 1. роль і місце економетричних моделей в управлінні економічними системами
- Типы эконометрических моделей, их краткая характеристика.
- 2. економетрична модель і проблеми економетричного моделювання
- 3. формування сукупності спостережень
- Вопрос № 1 Сущность эконометрической модели, порядок её построения.
- Больше информации по теме
1. Эконометрическая модель и проблемы эконометрического моделирования
линеаризации
3. спецификации
4. идентификации
Вопрос № 1.4. Оригинальный порядковый номер: 40
Отбрасывание значимой переменной в уравнении множественной регрессии является ошибкой …
Варианты ответов. Кол-во правильных ответов — 1
1. верификации
2. идентификации
3. спецификации
4. параметризации
Вопрос № 1.5. Оригинальный порядковый номер: 57
Регрессионная модель с одним факторным признаком называется …
Варианты ответов. Кол-во правильных ответов — 1
1. рекурсивной
2. стандартизированной
3. парной
4. множественной
Вопрос № 1.1. Оригинальный порядковый номер: 14
Этап параметризации модели включает в себя…
Варианты ответов. Кол-во правильных ответов — 1
1. проверку качества уравнения в целом
2. прогноз экономических показателей
3. проверку качества параметров модели
4. оценку параметров модели
Вопрос № 1.2. Оригинальный порядковый номер: 19
Эконометрическая модель предполагает _______ характер связи между переменными
Варианты ответов. Кол-во правильных ответов — 1
1. стохастический (вероятностный)
2. строго случайный
3. несущественный
4. строго детерминированный
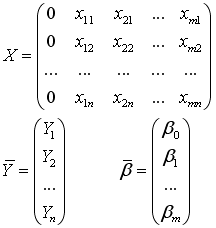
Вопрос № 1.3. Оригинальный порядковый номер: 43
Спецификация модели множественной линейной регрессии имеет вид …
Варианты ответов. Кол-во правильных ответов — 1
1.
2.
3.
4.
Вопрос № 1.4. Оригинальный порядковый номер: 65
Объясняемые, зависимые переменные в моделях любого типа называются …
Варианты ответов. Кол-во правильных ответов — 1
1. лаговыми
2. предопределенными
3. эндогенными
4. экзогенными
Вопрос № 1.5. Оригинальный порядковый номер: 88
Эконометрические модели относятся к классу ______ экономико–математических моделей.
Варианты ответов. Кол-во правильных ответов — 1
1. оптимизационных
2. описательных
3. стохастических
4. детерминированных
⇐ Предыдущая12345678910Следующая ⇒
Дата публикования: 2015-10-09; Прочитано: 694 | Нарушение авторского права страницы
studopedia.org — Студопедия.Орг — 2014-2018 год.(0.003 с)…
Эконометрическая модель
Предыдущая12345678Следующая
Основным понятием в эконометрики является эконометрическая модель.
Эконометрические модели– это модели, количественно описывающие взаимосвязи между экономическими показателями.
В частности, эконометрическая модель – это математическое описание того, что (исходя из предварительного анализа) экономическая теория считает наиболее важным при исследовании данной проблемы.
Эконометрическая модель (в отличие от модели математической экономики) носит конкретный характер и представляет параметры (коэффициенты) в численном виде.
Следовательно, задача эконометрики – на основе имеющихся наблюдений (реальной статистической базы) оценить эти параметры (коэффициенты).
Состав эконометрической модели
Основу эконометрической модели составляет система регрессионных уравнений, каждое из которых отображает одну из зависимостей, одну из закономерностей изменения, одно из свойств изучаемых экономических процессов. Помимо регрессий в модель могут быть включены:
— выражения, описывающие тренды развития отдельных явлений;
— тождества, характеризующие балансовые увязки между переменными;
— уравнения, увязывающие между собой отдельные характеристики модели во времени (динамический вариант модели).
Модель содержит также различного рода параметры (коэффициенты), которые определяются в ходе статистического оценивания путем обработки имеющихся данных наблюдения.
Уравнения-тождества – это соотношения, которые должны выполняться во всех случаях (тождества не содержат подлежащие оценке параметры и случайные составляющие).
Эконометрическая модель
Например, модель спроса и предложения (см. пример 2.6) содержит тождество 
Таким образом, эконометрическая модель представляет собой результат статистического оценивания параметров системы математических выражений, которые характеризуют некоторую экономическую концепцию о взаимосвязи явлений.
Классификация переменных эконометрической модели
Эконометрическая модель содержит так называемые эндогенные и экзогенные переменные. Приставки «эндо» и «экзо» означают соответственно внутренние и внешние.
Эндогенными переменными являются те, значения которых выясняются на основе (внутри) модели. Это зависимые переменные.
Экзогенные переменные – это переменные, значения которых определяются вне модели. Это переменные, влияющие на эндогенные переменные, но не зависящие от них.
Эндогенные и экзогенные переменные могут быть как обычными, так и лаговыми.
Значения обычной переменной соответствуют рассматриваемому периоду времени. Под лаговой переменной понимают переменную, значения которой отстают на один или несколько периодов (если 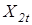

Совместно зависимыми переменными называются обычные эндогенные переменные, которые объясняются эконометрической моделью в момент времени t.
Классификация переменных представлена на рис.2.6.
Пояснения на примере модели «спрос-предложение»: равновесная цена товара 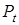
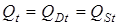
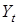

 |
Рис. 2.6. Классификация переменных эконометрической модели
Структурная и приведенная формы эконометрической модели
Взаимозависимые (одновременные) модели имеют две формы: структурную и приведенную.
Структурной формой модели (системой одновременных уравнений) называется система уравнений, в каждом из которых помимо объясняющих переменных могут содержаться объясняемые переменные из других уравнений.
Структурная форма модели создается в процессе формирования самой модели при стремлении отразить причинно-следственный механизм, существующий в реальности.
Параметры (коэффициенты) уравнений модели в структурной форме называются структурными коэффициентами. Использование обычного метода наименьших квадратов для оценивания параметров структурных уравнений, каждого в отдельности, приведет в общем случае к получению смещенных и несостоятельных оценок.
Метод наименьших квадратов (МНК)– построение аппроксимирующей функции из условия минимизации суммы квадратов отклонений значений этой функции от полученных (наблюдаемых) значений при заданном аргументе.
Аппроксимация функций – это приближенное выражение одних функций другими. Например, 
По предположению система уравнений структурной формы модели должна быть совместной и, следовательно, она может быть решена относительно обычных эндогенных переменных. Результат решения представляет собой приведенную форму модели.
Приведенной формой модели называется система уравнений, в каждом из которых обычные эндогенные переменные выражены только через предопределенные переменные и случайные составляющие.
Пример 2.7. Приведенная форма модели спроса и предложения:


Уравнения приведенной формы позволяют получить значения обычных эндогенных переменных, однако они объясняют эти значения только через экзогенные (в общем случае – предопределенные) переменные, т.е. с существенно меньшей детализацией, чем структурная форма, – здесь отсутствуют взаимосвязи зависимых переменных между собой. Параметры приведенной формы модели называются коэффициентами приведенной формы. Коэффициенты приведенной формы могут быть оценены обычным МНК, причем к каждому уравнению этот метод применяется раздельно.
Предыдущая12345678Следующая
1. роль і місце економетричних моделей в управлінні економічними системами
Сучасні методи управління економічними системами та процесами базуються на широкому використанні математичних методів та ЕОМ. Застосовувати математику для розв’язування певних економічних задач почали дуже давно, сотні років тому. Але протягом останніх 50-60 років, коли економічна наука сягнула певних рубежів у своєму розвитку i в ній постали задачі, які не вдається розв’язати за допомогою традиційних економічних методів, математика посіла в цій науці одне з основних місць.
Сформувався напрям теоретично-практичних досліджень – економiко-математичне моделювання. Математичне моделювання є вираженням процесу матем5атизації наукового економічного знання. Математика, проникаючи в сутність економічної науки, приносить із собою точність та унiверсальнiсть розв’язків, строгість i довершеність наукових концепцій. З розвитком математики, електронно-обчислювальної техніки, загальнометодологічних та економічних наук дедалі ширше використовують математичні моделі.
Математична модель об’єкта (процесу, явища) містить три групи елементів:
1) характеристику об’єкта, яку потрібно визначити (невiдомi величини), – вектор Y = (yi);
2) характеристики зовнiшнiх (щодо модельованого об’єкта) умов, які змінюються, – X (xi);
3) сукупність внутрiшнiх параметрів об’єкта – А.
Множини параметрів X і A можуть розглядатись як екзогенні величини (тобто такі, які визначаються поза рамками моделі), а величини, що належать вектору Y, — як ендогенні (тобто такі, які визначаються за допомогою моделі).
Математичну модель можна тлумачити як особливий перетворювач зовнiшнiх умов об’єкта Х (входу) на характеристики об’єкта Y(виходу), які мають бути знайдені.
Залежно від способу вираження спiввiдношень між зовнішніми умовами, внутрiшнiми параметрами та характеристиками, які мають бути знайдені, математичні моделі поділяються на дві групи: структурні та функцiональнi.
Структурні моделі відбивають внутрішню органiзацiю об’єкта: його складові, внутрiшнi параметри, їх зв’язок із «входом» i «виходом» i т. ін. Розрізняють три види структурних моделей:
1) Yi = fj(A, X) (j Î J); (1.1)
2) Yi(A, X, Y) = 0(i Î I); (1.2)
З) iмiтацiйнi моделі.
У моделях першого виду всі невiдомi величини подаються у вигляді явних функцій від зовнiшнiх умов i внутрiшнiх параметрів об’єкта.
У моделях другого виду невiдомi визначаються одночасно із системи I рівнянь, нерівностей i т.
Типы эконометрических моделей, их краткая характеристика.
ін.
В iмiтацiйних моделях невiдомi величини визначаються також одночасно із вхідними параметрами, але конкретний вигляд спiввiдношень невідомий.
Моделі типу (1.1), (1.2) можна розв’язати за допомогою чисельних алгоритмів. Можливості побудови моделей (1.1) практично необмежені. Для розв’язування задачі (1.2), яка не зводиться до задачі (1.1), необхідно мати спеціальний алгоритм, за яким не тільки знаходять розв’язки, а й виявляють загальні властивості розв’язків, що не залежать від конкретних параметрів задачі.
Імiтацiйнi моделі не зводяться до чітко визначених математичних задач, а тому потрібно знаходити особливі способи для відшукання розв’язків. Такі моделі виникають у разі спроб дати математичний опис особливо складних об’єктів (складних систем). Для дослідження цих об’єктів (систем) використовуються порівняно нові математичні методи: теорія випадкових процесів, теорія ігор та статистичних рішень, теорія автоматів і т. ін. Активну роль у процесі такого моделювання відіграють ЕОМ.
Імітаційні моделі не мають чіткого зображення внутрішньої організації (структури) об’єкта, i тому їм належить проміжне місце між структурними та функціональними моделями.
Основна ідея функціональних моделей – пізнання сутності об’єкта через найважливiшi прояви цієї сутності: дiяльнiсть, функціонування, поводження. Внутрішня структура об’єкта при цьому вивчається, а тому iнформацiя про структуру не використовується. Функціональна модель описує поводження об’єкта так, що, задаючи значення «входу» Х, можна дістати значення «виходу» Y (без участі інформації про параметри):
Y = A (X). (1.3)
Побудувати функціональну модель — означає знайти оператор А, який пов’язує Х i Y.
Вiдмiнностi між структурними та функціональними моделями мають відносний характер. Вивчення структурних моделей дає одночасно цінну iнформацiю про поводження об’єкта. Водночас вивчення функціональних моделей супроводжується формулюванням гіпотез про внутрішню структуру об’єкта.
Економетричнi моделі належать до функціональних моделей. Вони кiлькiсно описують зв’язок між вихідними показниками Х економічної системи та результативним показником Y. У загальному вигляді економетричну модель можна записати так:
Y = f (X, u) (1.4)
де Х – вихiднi економiчнi показники;
u – випадкова, або стохастична, складова.
Показники Х бувають детермінованими i стохастичними. Адитивна складова u — це випадкова змінна, а отже, з огляду на те, що залежна змінна Y залежить від u, вона також стохастична. Звідси випливає висновок: економетрична модель є стохастичною.
Побудова i дослідження економетричних моделей мають певні особливості. Ці особливості пов’язані з тим, що економетричнi моделі є стохастичними. Вони описують кореляційно-регресiйний зв’язок між економічними показниками. Цей зв’язок кiлькiсно характеризує наявні закономiрностi економічних процесів та явищ. Отже, щоб побудувати економетричну модель, необхідно:
1) мати достатньо велику сукупність спостережень даних;
2) забезпечити однорiднiсть сукупності спостережень;
3) забезпечити точність вихідних даних.
2. економетрична модель і проблеми економетричного моделювання
Економетричне моделювання реальних соцiально-економiчних процесів i систем, як правило, спрямоване на досягнення двох типів кінцевих прикладних результатів:
отримання прогнозу економічних показників, що характеризують стан та розвиток економічної системи;
iмiтування різних можливих сценаріїв соцiально-економiчного розвитку економічної системи (багатоваріантний сценарій, розрахунки, ситуаційне моделювання).
У постановці задач економетричного моделювання доцільно визначати їхній iєрархiчний рівень i тип. Поставлені задачі можуть належати до макрорівня (країна, міждержавний аналіз), мезорiвня (регіони всередині країни) i мiкрорiвня (підприємства, фірми, сім’я) i бути спрямованими на розв’язок питань iнвестицiйної, фінансової або соціальної політики, ціноутворення, розподільних відносин i т. ін.
Економетрична модель містить набір регресійних рівнянь, що описують стохастичні зв’язки між досліджуваними економічними показниками, а також певні тотожності, які характеризують спiввiдношення між економічними показниками.
Найпоширеніший математичний вид досліджуваних взаємозв’язків лiнiйний (відносно параметрів) i адитивний за формою. При цьому можливі ситуації, коли одні й ті самі показники в одних рівняннях вiдiграють роль пояснюваних змінних, а в інших – пояснювальних (такі моделі називають системами одночасних рівнянь).
До основних проблем економетричного моделювання належать:
iдентифiкацiя змінних та висування гіпотези про специфiкацiю моделі;
специфiкацiя економетричної моделі;
методи оцінювання параметрів моделі;
верифiкацiя моделі;
прогноз пояснюваних змінних на основі моделі.
Розв’язання цих проблем значною мірою базується на математично-статистичному iнструментарiї.
Велика увага приділяється методам багатовимірного аналізу i, передусім, методам розпізнавання соцiально-економiчних образів, їх типологiзацiї.
3. формування сукупності спостережень
Поняття сукупності спостережень є основою економетричного моделювання. Потрібно розрізняти одиницю спостереження – джерело даних і одиницю сукупності – носія ознак, що підлягають спостереженню. Ці поняття найбільш чітко розрізняються в соцiально-економiчнiй статистиці. Наприклад, під час перепису населення одиницею спостереження буде сім’я, а одиницею сукупності – окрема людина. У разі статистичних досліджень із застосуванням методів багатовимірного статистичного аналізу ці поняття часто збігаються. Тому в економетричному моделюванні здебільшого йтиметься про одиницю сукупності.
Сукупність спостережень можна подати у вигляді впорядкованого набору (матриці) даних параметрами n, m, T, де n – кiлькiсть одиниць сукупності (i =



За одиницю сукупності спостережень часто беруть певний економічний об’єкт, що функціонує. Вибрати одиницю сукупності – означає визначити рівень об’єкта моделювання (наприклад, великий технологічний агрегат, цех, підприємство, галузь i т. ін).
Розрізняють три способи формування вибірки: часову, просторову i просторово-часову.
Якщо сукупність спостережень вивчається у статиці (просторова вибірка), то всі дані можна зобразити у вигляді матриці розміром n × m, в якій кожний рядок несе iнформацiю про одиницю вибіркової сукупності, а стовпець характеризує певну ознаку.
Часова вибірка містить набір значень ознак функціонування окремого об’єкта в динамiцi m × T, тобто по суті складається з двовимірного чи багатовимірного часового ряду.
Просторово-часова вибірка являє собою комбiнацiю просторової i часової вибірок n × m × T.
Проблема формування сукупності спостережень та її однорiдностi досить важлива в економетричному моделюванні, бо економетрична модель кiлькiсно описує закономiрнiсть формування економічних процесів та явищ. А ця закономiрнiсть доволі повно може проявитись лише тоді, коли сукупність спостережень достатньо велика.
Вопрос № 1 Сущность эконометрической модели, порядок её построения.
Эконометрика как научная дисциплина получила свое развитие с середины 20 века. Экономические законы, процессы и явления все в большей степени описывают языком математики, и экономику все чаще называют одной из наиболее математизированных наук.
В условиях рыночной экономики невозможно без знания эконометрических методов исследовать и теоретически обобщить эмпирические зависимости экономических переменных, построить прогнозы в банковском деле, финансах или бизнесе.
Единое общепринятое определение эконометрики в настоящее время отсутствует. Сам термин «эконометрика» был введен в 1926 г. норвежским ученым Фришем и в дословном переводе означает «эконометрические измерения». В узкой трактовке эконометрика – это набор математико-статистических методов, используемых в приложениях математики в экономике.
Эконометрика – это наука, изучающая количественные закономерности и взаимозависимости в экономике методами математической статистики.
Эконометрика – это раздел экономики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными.
Цель эконометрики – эмпирический вывод экономических законов.
Задачи – построение экономических моделей и оценивание их параметров, проверка гипотез о свойствах экономических показателей и формах их связи.
Эконометрический анализ служит основой для экономического анализа и прогнозирования, создавая возможность для принятия обоснованных экономических решений.
Благодаря своему предмету исследования: экономические процессы и явления, эконометрика объединяет в себе экономическую теорию, экономическую статистику и математико-статистический инструментарий. С помощью эконометрики происходит проверка экономических законов, которые выражены в виде математических соотношений.
Рассмотрим ситуацию. Предположим, что нам необходимо продать автомобиль. Для этого нужно дать объявление, в котором указывается цена продажи. Как определить эту цену? Предварительно продавец изучит рынок, т.е. проанализирует данные о предложении продажи подобных автомобилей. Что значит подобных автомобилей? То есть тех, которые обладают примерно такими же характеристиками или факторами: год выпуска, пробег, мощность двигателя.
На основании этого будет сформировано представление о ситуации на рынке и назначена цена.
В данном случае цена зависит от нескольких факторов: год выпуска, пробег, мощность двигателя. Цена будет выступать как зависимая от факторов переменная (объясняемая переменная), а факторы – как объясняющие переменные.
Формируя общее мнение о состоянии рынка, мы обращаемся к интересующему нас объекту и получаем ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных. Указанная конкретная цена – наблюдаемое значение зависимой переменной зависит также и от случайных явлений – таких, например, как сроки продажи автомобиля, потребность в конкретной денежной сумме.
Конечно, продавец-одиночка вряд ли будет строить какую-либо математическую модель, а вот менеджер крупного автосалона, специализирующийся на реализации подержанных автомобилей, скорее всего, захочет иметь представление об ожидаемой цене и о возможном поведении случайной составляющей. Поэтому следующий шаг это и есть собственно эконометрическое моделирование.
Общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части – объясненную и случайную. Сформулируем задачу моделирования неформальным образом: на основании экспериментальных данных определить объясненную часть и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.
Таким образом, эконометрическая модель имеет вид:

где у – наблюдаемое значение зависимой переменной;
f(x) – объясненная часть, зависящая от значений объясняющих переменных,


,
где 
х1– срок эксплуатации автомобиля (в годах);
х2– пробег (в тыс. км).
Каково практическое применение полученного результата?
Во-первых, можно понять, как именно формируется рассматриваемая экономическая переменная – цена на автомобиль.
Во-вторых, выражение дает возможность выявить влияние каждой из объясняющих переменных на цену автомобиля. Так при х1= 0, х2 = 0 цена нового автомобиля будет составлять 18000 усл. д. ед., при этом только за счет увеличения срока эксплуатации на 1 год цена автомобиля уменьшится в среднем на 1000 есл. д. ед, а только за счет увеличения пробега на 1 тыс. км – на 0,5 усл. д. ед.
В-третьих, с помощью полученного выражения можно прогнозировать цену на автомобиль, если известны его основные параметры. Менеджеру не составит большого труда определить ожидаемую цену вновь поступившего для продажи автомобиля, даже если его год выпуска и пробег не встречались ранее в данном салоне.

ЭКОНОМЕТРИКА Лекция 14 Последствия ошибок в спецификации моделей Замещающие переменные

Последствия ошибок спецификации модели Возможные ошибки спецификации модели: 1. Неправильный выбор вида уравнения регрессии 2. В уравнение регрессии включена лишняя (незначимая) переменная 3. В уравнении регрессии пропущена значимая переменная

Последствия ошибок спецификации модели 1. Неправильный выбор вида функции в уравнении Пусть на первом этапе была сделана спецификация модели в виде: (1. 1) в которой функция f. F(x, a 0, a 1) выбрана не верно Предположим, что y. T=f. T(x, a 0, a 1)+v – правильный вид функции регрессии Тогда справедливо выражение: (1. 2)

Последствия ошибок спецификации модели Из выражения (1. 2) следует: (1, 3) Иными словами, математические ожидания эндогенной переменной, полученные с помощью функций f. T и f. F не совпадают, т. е. первая предпосылка теоремы Гаусса. Маркова M(ulx)=0 не выполняется Следовательно, в результате оценивания такой модели параметры а 0 и а 1 будут смещенными

Последствия ошибок спецификации модели Симптомы наличия ошибки спецификации первого типа: 1. Несоответствие диаграммы рассеяния, построенной по имеющейся выборке виду функции, принятой в спецификации 2. В динамических моделях длительно сохраняется знак значений оценок случайных возмущений у смежных (по номеру t ) уравнений наблюдений Именно этот симптом и улавливается статистикой DW Дарбина–Уотсона! В силу данного обстоятельства тесту Дарбина– Уотсона в эконометрике придается большое значение.
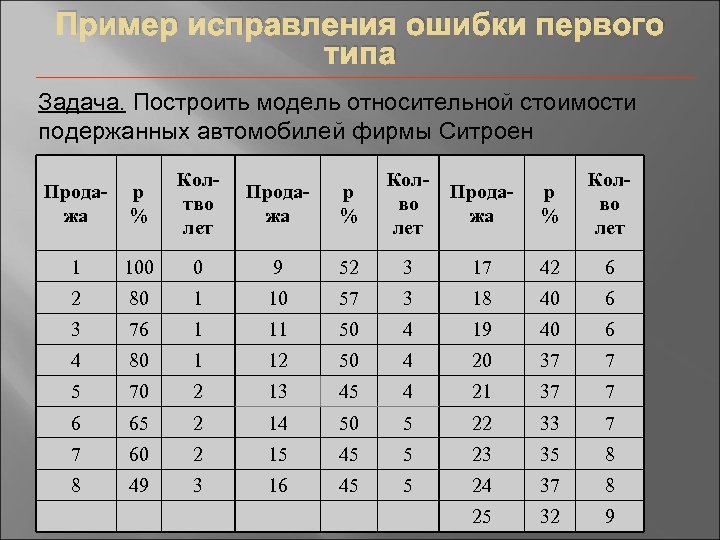
Пример исправления ошибки первого типа Задача. Построить модель относительной стоимости подержанных автомобилей фирмы Ситроен Продажа p % Колтво лет Продажа p % Колво лет 1 100 0 9 52 3 17 42 6 2 80 1 10 57 3 18 40 6 3 76 1 11 50 4 19 40 6 4 80 1 12 50 4 20 37 7 5 70 2 13 45 4 21 37 7 6 65 2 14 50 5 22 33 7 7 60 2 15 45 5 23 35 8 8 49 3 16 45 5 24 37 8 25 32 9
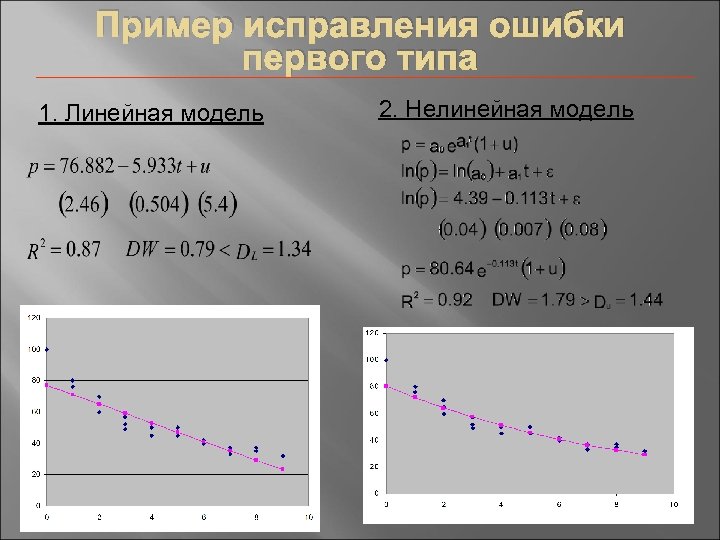
Пример исправления ошибки первого типа 1. Линейная модель 2. Нелинейная модель

Последствия ошибок спецификации модели 2. В уравнение регрессии включена лишняя переменная Пусть на этапе спецификации в модель включена «лишняя» переменная, например, X 2 (2. 1) «Правильная» спецификация должна иметь вид: (2. 2)

Последствия ошибок спецификации модели Последствия: 1. Оценки параметров а 0, а 1, а 2 останутся несмещенными, но потеряют свою эффективность (точность) 2. Увеличивается ошибка прогноза по модели как за счет ошибок оценок коэффициентов и σu, так и за счет последнего слагаемого Это особенно опасно при больших абсолютных значениях регрессора

Последствия ошибок спецификации модели Диагностика: В моделях множественной регрессии необходимо для каждого коэффициента уравнения проверять статистическую гипотезу H 0: ai=0 Вспомним, что для этого достаточно оценить дробь Стьюдента и сравнить ее значение с критическим значением распределения Стьюдента, которое вычисляется по значению доверительной вероятности и значению степени свободы 2 = n – (k+1)

Последствия ошибок спецификации модели 3. В модели не достает важной переменной Последствия такие же, как и в первом случае: получаем смещенные оценки параметров модели Для устранения необходимо вернуться к изучению особенностей поведения экономического объекта, выявить опущенные переменные и дополнить ими модель Вот тут и возникают неприятности!

Замещающие переменные Проблемы в использовании переменных: 1. Не возможно получение данных по переменной 2. Не возможно измерить количественно переменную Такие ситуации характерны для переменных социально-экономического характера (качество образования и т. п. ) Выход из ситуации – подбор переменной заместителя

Замещающие переменные Определение. Переменные, которые вводятся в эконометрические модели вместо тех переменных, которые не поддаются измерению, называются замещающими Требование. Замещающая переменная должна коррелировать с переменной, которую она замещает Если Cor(x, xpr)=1, то xpr – называют совершенным регрессором В качестве замещающей переменной часто используется время и лаговые переменные

Замещающие переменные Пример. Рассмотрим модель связывающую расходы потребителей на питание (y) с личным располагаемым доходом (х) и относительной ценой продовольствия (р) (4. 1) Предположим, что нет доступа к данным о располагаемом личном доходе (х) Если эту переменную не учитывать, то оценки оставшихся параметров будут смещенными, а соответствующие тесты не корректны Предположим, что log(x) имеет временной тренд

Замещающие переменные Тогда уравнение (4. 1) можно записать в виде: Регрес Оценки коэффициентов соры b 1 b 2 b 3 Log(x), 0. 64 log(p) (0. 03) Log(p), t Log(p) -0. 48 (0. 12) -0. 47 (0. 13) 2. 04 (0. 33) R 2 0. 99 0. 023 (0. 001) 0. 98 0. 63

Замещающие переменные В общем случае, пусть «правильная» модель: (4. 2) Предположим, что х1 не доступна для наблюдений Введем переменную z, которая связана с х1 (4. 3) где: λ и μ неизвестные коэффициенты (4. 4) После оценки модели (4. 4) нет формальной возможности получить значения λ, μ, а 1

Проблемы с использованием замещающих переменных Пример построения производственной функции Кобба-Дугласа Индексы реального объема производства, Спецификация модели в промышленности США в 1899 -1922 гг. Год Y K L 1899 100 100 1911 153 216 145 1900 101 107 105 1912 177 226 152 1901 112 114 110 1913 184 236 154 1902 122 118 1914 169 244 149 1903 124 131 123 1915 189 266 154 1904 122 138 116 1916 225 298 182 1905 143 149 125 1917 227 335 196 1906 152 163 133 1918 223 366 200 1907 151 176 138 1919 218 387 193 1908 126 185 121 1920 231 407 193 1909 155 198 140 1921 179 417 147 1910 159 208 144 1922 240 431 161 Оценка модели [d. L; d. U] = [1, 26; 1, 44]

Проблемы с использованием замещающих переменных Проверка адекватности модели Для проверки адекватности взяты данные за 1922 г (Y 1922 = 240; K 1922 = 431; L 1922 = 161). Для этого вычисляем величины и делаем точечный прогноз значения y 0 = ln(Y 1922 /L 1922) = 0, 399: Критическое значение критерия Стьюдента tкрит(0. 99, 21)=2. 8 Тогда доверительный интервал:

Построение функции Кобба-Дугласа Модель оказалась не адекватной Дальнейшие возможности: — проверить возможность исключения незначимых параметров -попытаться изменить вид модели — исследовать возможность включения дополнительной переменной Делаем все по порядку

Построение функции Кобба-Дугласа 1. Проверка возможности исключения параметров Проверяем статистическую гипотезу Н 0: bi=0, tкрит(0. 95, 21)=2. 1 Вывод: b 0=ln(a 0)=0, следовательно, a 0=1

Построение функции Кобба-Дугласа Исследуется спецификация модели вида: (5. 2) Оценка модели (5. 2) по тем же данным есть:

Построение функции Кобба-Дугласа Проверка адекватности модели (5. 2) Вновь вычисляются необходимые величины: Сделаем точечную проверку адекватности для доверительных вероятностей 0. 99 и 0. 95 tкрит(0. 99, 21)=2. 8, tкрит(0. 95, 21)=2. 1

Построение функции Кобба-Дугласа 2. Введем дополнительную переменную Модели (5. 1) и (5. 2) не учитывают влияние технического прогресса на уровень выпуска продукции Учтем это влияние с помощью замещающей переменной t – время следующим образом Введем переменную Et –эффективность единицы труда Et зависит от квалификации, образования и др. личных качеств работников Простейшая модель технологического процесса (5. 3)

Построение функции Кобба-Дугласа С учетом технологического процесса спецификация модели принимает вид: (5. 4) где: a 3 = (1 -a 1) · ln(1+g) 0 В логарифмическом виде модель (5. 4) имеет вид: (5. 5)

Построение функции Кобба-Дугласа Оценка модели (5. 5) по тем же данным приняла вид: (5. 6) Из (5. 6) легко видеть, что оценки коэффициентов b 0=ln(a 0) и а 1 оказались незначимыми (гипотезы Н 0: b 0=0 и H 0: a 1=0 не отвергаются исходными данными) Но это приводит к абсурду: можно не затрачивая ни капитал ни труд производить продукцию

Построение функции Кобба-Дугласа Вопрос. Почему статистические данные «не пустили» в модель время как заместитель технического прогресса? Ответ. Переменная К (капитальные затраты) так же являются функцией времени В результате введения в модель еще переменной времени привело к мультиколинеарности матрицы коэффициентов наблюдения (матрица Х) Выражение стало не устойчивым из-за неустойчивости обратной матрицы

Построение функции Кобба-Дугласа Вывод. Последствием не аккуратного использования замещающих переменных приводит к нарушению обязательного условия МНК о не вырожденности матрицы коэффициентов уравнений наблюдений При использовании замещающих переменных необходим предварительный анализ степени корреляции между экзогенными переменными

Построение функции Кобба-Дугласа 3. Проверка возможности изменить вид модели Откажемся от жесткого условия линейной однородности (а 1+а 2=1) производственной функции Тогда модель примет вид: (5. 7) Оценка модели (5. 7) в конечном итоге получилась следующей:

Замещающие переменные Выводы: 1. Ошибки в спецификации модели могут приводить к нарушению условий теоремы Гаусса-Маркова и потере адекватности 2. Замещающие переменные – эффективный инструмент учета в модели качественных факторов 3. При введении в спецификацию замещающих переменных необходимо исследовать регрессоры на возможность мультиколлинеарности