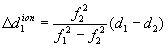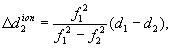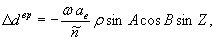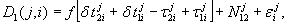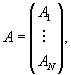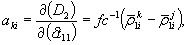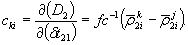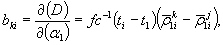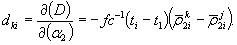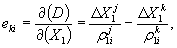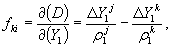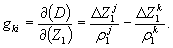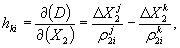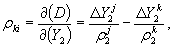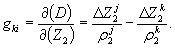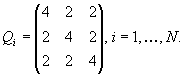Геодезия
Спутниковые системы и технологии позиционирования
Вопрос №1 При кодовых измерениях используются
При кодовых измерениях используются:
- Вариант №1: немодулированные колебания;
- Вариант №2: модулированные колебания;
Формат файла — JPG
Ответ на вопрос №1
Вопрос №2 Допплеровский сдвиг частоты радиоволн, излучаемых спутником, позволяет определять:
Допплеровский сдвиг частоты радиоволн, излучаемых спутником, позволяет определять:
- Вариант №1: скорость электромагнитных волн;
- Вариант №2: радиальную скорость спутника;
- Вариант №3: время распространения спутникового сигнала;
Формат файла — JPG
Ответ на вопрос №2
Вопрос №3 Дифференциальные поправки передаются на подвижной приемник:
Дифференциальные поправки передаются на подвижной приемник:
- Вариант №1: со спутников;
- Вариант №2: с базовой станции;
- Вариант №3: с центральной станции наземного управляющего комплекса;
Формат файла — JPG
Ответ на вопрос №3
Вопрос №4 При использовании в спутниковых измерениях разностно-дальномерного метода сколько требуется последовательных положений спутника для определения местоположения приемника? Отметьте необходимое число.
При использовании в спутниковых измерениях разностно-дальномерного метода сколько требуется последовательных положений спутника для определения местоположения приемника? Отметьте необходимое число.
- Вариант №1: 2;
- Вариант №2: 3;
- Вариант №3: 4;
- Вариант №4: 5;
- Вариант №5: 6;
Формат файла — JPG
Ответ на вопрос №4
Вопрос №5 Неопределенность фазового центра антенны характеризуется ошибкой порядка:
Неопределенность фазового центра антенны характеризуется ошибкой порядка:
- Вариант №1: нескольких дециметров;
- Вариант №2: нескольких сантиметров;
- Вариант №3: нескольких миллиметров;
Формат файла — JPG
Ответ на вопрос №5
Вопрос №6 Интегральный допплеровский счет — это:
Интегральный допплеровский счет — это:
- Вариант №1: счет периодов допплеровской частоты за интервал времени, в течение которого спутник переместился по орбите из одной точки в другую;
- Вариант №2: счет периодов допплеровской частоты за интервал в 1 час;
- Вариант №3: счет периодов допплеровской частоты за время, в течение которого расстояние между спутником и приемником изменилось на 10 км;
Формат файла — JPG
Ответ на вопрос №6
Вопрос №7 Когда началась разработка глобальных систем?
Когда началась разработка глобальных систем?
- Вариант №1: в 70-х годах ХХ столетия;
- Вариант №2: после 1985 года;
- Вариант №3: примерно 5-6 лет назад;
Формат файла — JPG
Ответ на вопрос №7
Вопрос №8 Навигационным сообщением модулируется:
Навигационным сообщением модулируется:
- Вариант №1: только несущая L1;
- Вариант №2: только несущая L2;
- Вариант №3: обе несущих L1 и L2;
Формат файла — JPG
Ответ на вопрос №8
Вопрос №9 Период вращения Земли (сутки) определяется более точно:
Период вращения Земли (сутки) определяется более точно:
- Вариант №1: из наблюдений Солнца;
- Вариант №2: из наблюдений звезд;
Формат файла — JPG
Ответ на вопрос №9
Вопрос №10 Точность фазового светодальномера увеличивается:
Точность фазового светодальномера увеличивается:
- Вариант №1: с увеличением интенсивности излучения;
- Вариант №2: с увеличением длины волны излучения;
- Вариант №3: с увеличением частоты модуляции;
Формат файла — JPG
Ответ на вопрос №10
Вопрос №11 Фазовая скорость — это скорость распространения:
Фазовая скорость — это скорость распространения:
- Вариант №1: фазы огибающей при модуляции колебания;
- Вариант №2: фазы волны строго одной частоты;
Формат файла — JPG
Ответ на вопрос №11
Вопрос №12 Дифференциальный способ абсолютных определений относится:
Дифференциальный способ абсолютных определений относится:
- Вариант №1: к геодезическому режиму работы;
- Вариант №2: к навигационному режиму работы;
Формат файла — JPG
Ответ на вопрос №12
Вопрос №13 Всемирным временем называется:
Всемирным временем называется:
- Вариант №1: местное среднее время на Пулковском меридиане;
- Вариант №2: местное среднее время на Гринвичском меридиане;
Формат файла — JPG
Ответ на вопрос №13
Вопрос №14 Инициализация — это:
Инициализация — это:
- Вариант №1: определение целого числа N о во вторых (двойных) фазовых разностях;
- Вариант №2: исключение числа N о из третьих (тройных) фазовых разностей;-
Формат файла — JPG
Ответ на вопрос №14
Вопрос №15 В последнем поколении лазерных спутниковых дальномеров используются:
В последнем поколении лазерных спутниковых дальномеров используются:
- Вариант №1: наносекундные лазеры;
- Вариант №2: пикосекундные лазеры;
- Вариант №3:фемтосекундные лазеры;
Формат файла — JPG
Ответ на вопрос №15
Назад к списку тестов по предмету — Геодезия
Ответы на тесты по спутниковой геодезии
Так же выполняем любые контрольные и курсовые в МИИГАиК
Введение
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Какое название больше подходит для глобальных спутниковых систем? | получить ответ |
| 2 | Что является главным недостатком допплеровских спутниковых систем? | получить ответ |
| 3 | Когда началась разработка глобальных систем? | получить ответ |
| 4 | Какие геометрические величины, используемые для вычисления координат приемника, получают из измерений допплеровского сдвига частоты? | получить ответ |
| 5 | Что понимается под термином «спутниковое позиционирование»? | получить ответ |
| 6 | Какое направление в спутниковой геодезии получило наибольшее практическое применение? | получить ответ |
| 7 | Глобальные спутниковые системы называются так потому, что они: | получить ответ |
| 8 | Какова высота орбит спутников в системе «Транзит»? | получить ответ |
| 9 | Какой режим работы глобальных спутниковых систем требует санкционированного доступа? | получить ответ |
| 10 | Какая из перечисленных ниже систем является допплеровской? | получить ответ |
Физические основы электронной дальнометрии
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | В чем принципиальное различие между фазовым светодальномером и оптическим интерферометром? | получить ответ |
| 2 | Опорный импульс в импульсном дальномере: | получить ответ |
| 3 | Чем принципиально отличается светодальномер от радиодальномера? | получить ответ |
| 4 | Временной метод реализуется: | получить ответ |
| 5 | Точность импульсного дальномера: | получить ответ |
| 6 | В наземных фазовых дальномерах измеряется | получить ответ |
| 7 | В геодезических наземных дальномерах применяется: | получить ответ |
| 8 | Точность фазового светодальномера увеличивается: | получить ответ |
| 9 | В лазерном интерферометре для выполнения измерений необходимо: | получить ответ |
| 10 | Для определения скорости электромагнитных волн в воздухе надо знать: | получить ответ |
| 11 | В последнем поколении лазерных спутниковых дальномеров используются: | получить ответ |
| 12 | Разрешение многозначности — это: | получить ответ |
| 13 | Электронный дальномер определяет: | получить ответ |
| 14 | Какой из методов линейных измерений дает наибольшую точность? | получить ответ |
Некоторые результаты пройденных тестов
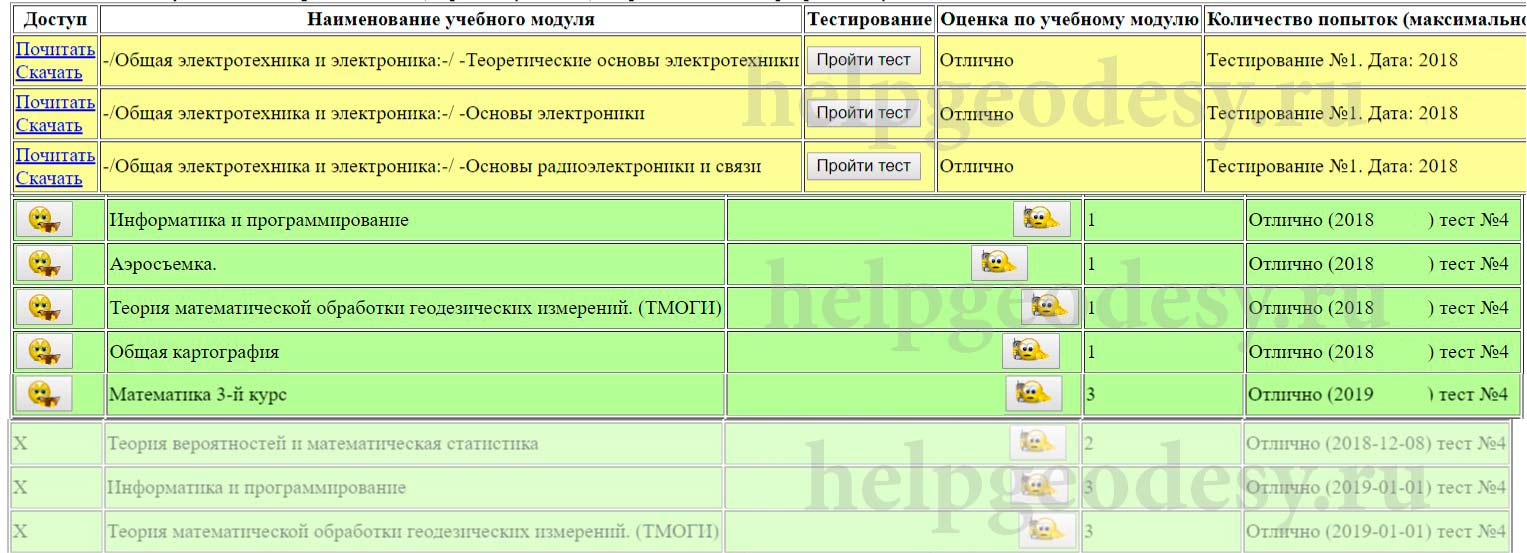
Геометрические принципы позиционирования и системы
координат
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | При определении пространственного положения точки дальномерным методом она получается: | получить ответ |
| 2 | В геоцентрической прямоугольной системе координат: | получить ответ |
| 3 | В какой системе координат работают спутниковые системы GPS и ГЛОНАСС: | получить ответ |
| 4 | Чем отличаются координатные системы WGS-84 и ПЗ-90? (укажите неверный ответ) | получить ответ |
Геометрические принципы позиционирования и системы координат
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Эфемеридами спутника называют: | получить ответ |
| 2 | Широта, долгота и высота используются (укажите неверный ответ): | получить ответ |
| 3 | Местоположение точки в пространстве, определяемое электронными методами, получают: | получить ответ |
| 4 | Какие координаты наиболее удобны для спутниковой геодезии? | получить ответ |
| 5 | Измерение расстояний от двух твердых точек А и В до определяемой неподвижной точки Р на плоскости позволяет построить: | получить ответ |
| 6 | Гипербола — это геометрическое место точек, для которых постоянна: | получить ответ |
| 7 | На плоскости имеются две твердые точки А и В и неподвижная определяемая точка Р. Исключите ненужную операцию из нижеследующих: | получить ответ |
| 8 | Особенности спутникового позиционирования дальномерным методом заключаются в том, что (отметьте неверные утверждения): | получить ответ |
| 9 | На плоскости с трех твердых точек А, В и С, не находящихся на одной линии, измерены расстояния до определяемой точки Р, оказавшиеся равными: АР = 320 м, ВР = 305 м, СР = 270 м. Найдите гиперболические координаты точки Р. | получить ответ |
| 10 | При определении пространственного положения точки разностно-дальномерным методом она получается: | получить ответ |
| 11 | При использовании в спутниковых измерениях разностно-дальномерного метода сколько требуется последовательных положений спутника для определения местоположения приемника? Отметьте необходимое число. | получить ответ |
Отзывы студентов МИИГАиК
Спасибо больше, Илье! Очень быстро и качественно помог в решении тестов??
Всем советую, кому нужна помощь по геодезии)Алина, студентка МИИГАиК
профиль вконтакте
Спасибо большое за помощь, все качественно и быстро!
Екатерина Заворуева, студентка МИИГАиК
профиль вконтакте
Спасибо Илье за качественно оказанную помощь по тестам — сдал на 5!
Виктор Крутиков
профиль вконтакте
Большое спасибо Илье за оказанную помощь! Хороший человек)
Павел, студент МИИГАиК
профиль вконтакте
Беззапросный метод. Шкалы времени и стандарты частоты
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Чем определяется исключительная равномерность шкалы атомного времени? | получить ответ |
| 2 | Обеспечивает ли всемирное время UT создание равномерных шкал времени? | получить ответ |
| 3 | Какой из стандартов частоты имеет наивысшую стабильность? | получить ответ |
| 4 | Является ли всемирное координированное время UTC атомным временем? | получить ответ |
| 5 | При беззапросном методе сигнал проходит: | получить ответ |
| 6 | Выберите формулу для расстояния ρ лежащее в основе беззапросного метода. | получить ответ |
| 7 | Приемник фиксирует момент прихода сигнала со спутника по своим часам. Как приемник «узнаёт» о том, когда был отправлен сигнал со спутника? | получить ответ |
| 8 | Псевдодальность P отличается от геометрической дальности ρ вследствие: | получить ответ |
| 9 | Электромагнитная длина трассы — это (отметьте неверное утверждение): | получить ответ |
| 10 | Период вращения Земли (сутки) определяется более точно: | получить ответ |
| 11 | Всемирным временем называется: | получить ответ |
| 12 | Какая из перечисленных ниже шкал всемирного времени наиболее равномерна? | получить ответ |
| 13 | При определении элементов орбиты (эфемерид) спутников используют: | получить ответ |
| 14 | Системное время GPS: | получить ответ |
| 15 | Системное время ГЛОНАСС: | получить ответ |
Структура глобальных спутниковых систем
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Чему равно типичное значение маски (в градусах)? | получить ответ |
| 2 | Режим кодовых измерений является (указать верные ответы): | получить ответ |
| 3 | Более точными являются: | получить ответ |
| 4 | Режим фазовых измерений является (указать верные ответы): | получить ответ |
| 5 | При фазовых измерениях используются: | получить ответ |
| 6 | Режим интегрального допплеровского счета осуществляется одновременно: | получить ответ |
| 7 | При работе со спутниковыми системами получают: | получить ответ |
| 8 | При кодовых измерениях используются: | получить ответ |
| 9 | Чему равно примерное значение (в тыс. км) ширины полосы радиовидимости? | получить ответ |
| 10 | Какой режим работы системы является вспомогательным? | получить ответ |
| 11 | Зависит ли зона радиовидимости от высоты орбиты спутника? | получить ответ |
| 12 | В чем состоит основная функция станций слежения? | получить ответ |
| 13 | Какова средняя высота орбит спутников в GPS и ГЛОНАСС? | получить ответ |
Оставить заявку на прохождение теста
Работаем без предоплаты!
Спутниковый сигнал
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Дальномерные коды представляют собой: | получить ответ |
| 2 | Что такое фазовая манипуляция? | получить ответ |
| 3 | На скольких частотах излучаются несущие колебания каждым спутником? | получить ответ |
| 4 | В какие моменты происходит фазовая манипуляция ? | получить ответ |
| 5 | Грубым кодом модулируется: | получить ответ |
| 6 | Точным кодом модулируется: | получить ответ |
| 7 | Какой вид модуляции несущих колебаний используется в спутниковом сигнале? | получить ответ |
| 8 | В каком субкадре передается метка времени? | получить ответ |
| 9 | Навигационным сообщением модулируется: | получить ответ |
| 10 | Отметьте номера субкадров, содержащих эфемериды спутника. | получить ответ |
| 11 | Сколько времени затрачивается на передачу альманаха? | получить ответ |
| 12 | Для чего со спутника излучается вторая несущая частота L2? | получить ответ |
Кодовые измерения
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Как определяется временная задержка при кодовых измерениях? | получить ответ |
| 2 | При дифференциальном методе кодовых измерений базовая станция должна устанавливаться: | получить ответ |
| 3 | Сколько неизвестных величин в уравнении для псевдодальности? | получить ответ |
| 4 | Что является неизвестными величинами в уравнении для псевдодальности? | получить ответ |
| 5 | Псевдодальность равна: | получить ответ |
| 6 | Чтобы определить все три координаты приемника, необходимо выполнить одновременные измерения псевдодальностей как минимум до: | получить ответ |
| 7 | Чем наиболее важна одновременность измерения псевдодальностей до спутников? | получить ответ |
| 8 | В каком диапазоне лежит точность кодовых измерений с одним приемником? | получить ответ |
| 9 | Что является измеряемой величиной при кодовых измерениях? | получить ответ |
| 10 | При работе на каком коде отсутствует неоднозначность? | получить ответ |
| 11 | Дифференциальные поправки — это: | получить ответ |
| 12 | Дифференциальные поправки передаются на подвижной приемник: | получить ответ |
| 13 | Дифференциальный способ повышает точность кодовых измерений: | получить ответ |
Оставить заявку на прохождение теста
Работаем без предоплаты!
Фазовые измерения
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Инициализация — это: | получить ответ |
| 2 | Чем обусловлена неоднозначность фазовых измерений? | получить ответ |
| 3 | Фазовые измерения относятся (отметьте правильные ответы): | получить ответ |
| 4 | На какой частоте производятся фазовые измерения? | получить ответ |
| 5 | Что является основной проблемой при фазовых измерениях? | получить ответ |
| 6 | Что является измеряемой величиной при фазовых измерениях? | получить ответ |
| 7 | Чем отличается фазовая псевдодальность от кодовой псевдодальности? (отметьте верные ответы) | получить ответ |
| 8 | Окончательные значения разностей координат двух пунктов при фазовых измерениях получают: | получить ответ |
| 9 | Координаты спутников при фазовых измерениях вычисляют: | получить ответ |
| 10 | Интегральный допплеровский счет — это: | получить ответ |
| 11 | Допплеровский сдвиг частоты радиоволн, излучаемых спутником, позволяет определять: | получить ответ |
| 12 | Эффект Допплера — это: | получить ответ |
| 13 | Фазовые измерения выполняются на несущей частоте. Что требуется для снятия кодовой модуляции с целью восстановления несущей? (Укажите неверный ответ) | получить ответ |
| 14 | Число периодов при интегральном допплеровском счете позволяет определить: | получить ответ |
Факторы, влияющие на точность
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | Ошибка в координатах спутника сильнее влияет на результаты: | получить ответ |
| 2 | Ниже перечислены основные источники ошибок при спутниковых измерениях. Укажите, какие ошибки принадлежат к ошибкам исходных данных. | получить ответ |
| 3 | Рефракционное удлинение траектории максимально, когда спутник находится: | получить ответ |
| 4 | Ошибки из-за отражения радиоволн изменяются во времени: | получить ответ |
| 5 | Влияние отраженных сигналов приводит : | получить ответ |
| 6 | В чем состоит явление многопутности? | получить ответ |
| 7 | Граундплэйн используется для защиты антенны от лучей, отраженных: | получить ответ |
| 8 | Типичная ошибка координат спутника из-за неточности эфемерид составляет: | получить ответ |
| 9 | Какой слой атмосферы является для радиоволн диспергирующей средой? | получить ответ |
| 10 | Ниже перечислены основные источники ошибок при спутниковых измерениях. Укажите, какие ошибки принадлежат к ошибкам, связанным с влиянием внешней среды. | получить ответ |
| 11 | Неопределенность фазового центра антенны характеризуется ошибкой порядка: | получить ответ |
| 12 | Ниже перечислены основные источники ошибок при спутниковых измерениях. Укажите, какие ошибки принадлежат к аппаратурным ошибкам. | получить ответ |
| 13 | Может ли DOP быть меньше единицы? | получить ответ |
| 14 | Геометрический фактор — это коэффициент, зависящий: | получить ответ |
Задержка сигнала в атмосфере
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | В каком случае тропосферная задержка учитывается наиболее полно? | получить ответ |
| 2 | Остаточная погрешность двухчастотного метода составляет: | получить ответ |
| 3 | При распространении спутникового сигнала в ионосфере несущее колебание распространяется: | получить ответ |
| 4 | При кодовых и фазовых измерениях задержки в ионосфере: | получить ответ |
| 5 | В ионосфере фазовый и групповой показатели преломления: | получить ответ |
| 6 | Учет задержек в ионосфере по моделям дает ошибку, доходящую до: | получить ответ |
| 7 | При распространении спутникового сигнала в ионосфере кодовая модуляция распространяется: | получить ответ |
| 8 | Дисперсия — это: | получить ответ |
| 9 | Введение понятия групповой скорости обусловлено: | получить ответ |
| 10 | Двухчастотный метод учета влияния ионосферы основан на составлении разностей результатов измерений на двух несущих частотах, которая оказывается свободной от ионосферного члена. При этом в случае кодовых измерений перед составлением разностей нужно умножить псевдодальность, измеренную на второй частоте: | получить ответ |
| 11 | Двухчастотный метод учета влияния ионосферы основан на составлении разностей результатов измерений на двух несущих частотах, которая оказывается свободной от ионосферного члена. При этом в случае фазовых измерений перед составлением разностей нужно умножить сдвиг фаз, измеренный на второй частоте: | получить ответ |
| 12 | Как определяется значение индекса преломления на поверхности Земли для радиоволн? | получить ответ |
| 13 | Фазовая скорость — это скорость распространения: | получить ответ |
| 14 | Что понимают под моделью тропосферы? | получить ответ |
| 15 | Во сколько раз индекс преломления больше, чем показатель преломления минус 1? | получить ответ |
| 16 | Известен ли закон распределения показателя (индекса) преломления вдоль наклонной трассы? | получить ответ |
| 17 | Чем определяется задержка электромагнитной волны в атмосфере? | получить ответ |
| 18 | тест спутниковые системы и технологии позиционирования | получить ответ |
| 19 | тестирование студентов по спутниковым системам навигации | получить ответ |
| 20 | геодезия тесты онлайнЧ | получить ответ |
Аппаратура пользователя и режимы наблюдений
| # | Текст вопроса | Ответ |
|---|---|---|
| 1 | В чем заключается специфика планирования спутниковых измерений? | получить ответ |
| 2 | Основная особенность кинематических режимов заключается в том, что: | получить ответ |
| 3 | Кинематический режим «в полете»: | получить ответ |
| 4 | Отметьте новые перспективные направления в развитии спутниковых приемников: | получить ответ |
| 5 | В чем заключается преимущество режима кинематики в реальном времени (RTK)? | получить ответ |
| 6 | Производится ли в приемнике генерирование несущих частот и дальномерных кодов, или это делается только в аппаратуре спутника? | получить ответ |
| 7 | Что обеспечивает работу в реальном масштабе времени при режиме RTK? | получить ответ |
| 8 | Кинематический режим «стой и иди»: | получить ответ |
| 9 | Работа спутникового приемника в целом управляется: | получить ответ |
| 10 | Дифференциальный способ абсолютных определений относится: | получить ответ |
| 11 | Необходим ли для работы приемника альманах созвездия спутников? | получить ответ |
| 12 | Основная особенность статического режима заключается в том, что: | получить ответ |
| 13 | Наиболее точным режимом наблюдений является: | получить ответ |
| 14 | Статический и кинематический режимы наблюдений относятся: | получить ответ |
| 15 | Какие приемники обеспечивают наибольшую точность? | получить ответ |
Оставить заявку на прохождение теста
Работаем без предоплаты!
Что такое фазовая неопределённость, фазовая неоднозначность?
Расстояния от спутников до приёмников можно вычислить с помощью фаз несущих частот. В этом случае расстояние от спутника до приёмника равно сумме целых и дробных длин волн, умноженной на длину несущей волны. Точность расстояний, полученных данным способом (фазовым), больше, чем точность расстояний, полученного кодовым способом. Длина волны (пространственное разрешение) фазы несущей частоты составляет 19 сантиметров для частоты L1, что гораздо меньше, чем пространственное разрешение в кодовом способе.
Однако есть одна проблема. Несущие волны являются синусоидальными, что означает, что все длины волн одинаковые. В связи с этим приёмник не может отличить одну длину волны от другой. Другими словами, приёмник не может посчитать количество длин волн на расстоянии от приёмника до спутника. Приёмник лишь может с точностью до 2 миллиметров определить дробную часть длины волны, в то время как число целых волн остаётся неизвестным или неопределённым. Это явление известно под названием «фазовая неопределённость». К счастью, приёмник может отслеживать изменения фазы, когда приёмник включён. Это значит, что по величине фазовая неоднозначность не изменяется с течением времени до тех пор, пока сигнал не будет потерян.
Очевидно, что если фазовая неопределённость разрешена (известно количества целых длин волн от спутника до приёмника) то в результате получается точное значение расстояния от спутника до приёмника. Столь высокая точность может быть достигнута так называемым относительным методом измерений в реальном времени или с постобработкой. К сожалению, данный метод требует использовать 2 приёмника, которые одновременно принимают сигналы от одних и тех же спутников.
Измерения, выполненные с помощью системы GPS отягощены ошибками и задержками, которые трудно предугадать. Именно эти ошибки ограничивают точность абсолютных измерений. К счастью, если 2 приёмника находятся близко друг к другу, то величины ошибок и задержек у них практически одинаковые. Вследствие этого большинство ошибок и задержек может быть исключено из результатов измерений при комбинировании результатов измерений, которые были получены близкорасположенными приёмниками.
Существует 3 вида ошибок и задержек: ошибки, связанные со спутником, ошибки, связанные с приёмником и задержки сигнала в атмосфере. Измерения, выполненные приёмниками одновременно с использованием одних и тех же спутников, содержат более или менее одинаковые ошибки, связанные со спутниками, и атмосферные задержки. Чем ближе приёмники находятся друг к другу, тем меньше рознятся ошибки, связанные со спутниками и атмосферные задержки у этих приёмников. Если рассматривать разницу в измерениях этими двумя приёмниками, то ошибки, связанные со спутниками и атмосферные задержки, будут сведены к минимуму. Ошибки часов спутников могут быть исключены из измерений вследствие применения линейной комбинации.
К тому же две группы измерений, выполненные одним и тем же приёмником, содержат одинаковые ошибки приёмника. В связи с этим, в разнице между этими двумя измерениями отсутствуют ошибки часов приёмника.
В результате одновременных измерений двумя приёмниками, которые используют одни и те же 2 спутника, можно получит две разницы в координатах, известные как двойные разности координат. Данная линейная комбинация исключает из измерений ошибку часов приёмника, а величины остальных ошибок уменьшаются. Стоит отметить, что при этом сохраняется эффект фазовой неоднозначности.
Поэтому эти данные являются только основой для точного позиционирования фазовым методом.
Ещё одна важная линейная комбинация, известная как «тройное дифференцирование», которая получается вследствие обработки двух дважды дифференцированных разностей, относящихся к двум эпохам. Как говорилось ранее, фазовая неоднозначность является постоянной величиной, если нет проскальзываний цикла. При составлении тройной разности проскальзывание цикла исчезает. Однако влияние, оказанное проскальзыванием цикла, остаётся в составе данных, с помощью которых составляются тройные разности, но при построении графика эти данные легко заметить, их изображение похоже на шип. Так как влияние, оказанное проскальзыванием цикла, выявляется на графике, то для обнаружения проскальзываний цикла используются графики результатов тройного дифференцирования.
Все представленные ранее линейные комбинации могут быть составлены по результатам измерений как одночастотными, так и двухчастотными приёмниками, как при использовании фазового, так и при использовании кодового метода измерений. Однако при использовании двухчастотного приёмника могут быть составлены и другие линейные комбинации. Одна из них известна как линейная комбинация свободной ионосферы. Ионосферные задержки прямо-пропорциональны квадрату несущей частоты. Основываясь на этом, линейные комбинации свободной ионосферы включают в себя измерения на частоте L1 и L2 для снижения влияния ионосферы на результаты измерений. Измерения фазы несущей частоты на частотах L1 и L2 могут быть так же использованы для модулирования частоты, длина волны которой составляет примерно 86 сантиметров. Данная величина длинны волны упрощает процесс решения фазовой неопределённости.
Размещено: 23.03.2017
Подстановка соотношения (2.28) в соотношение (2.27) дает:
|
= ( / , „ „ — т г — О — Д о ^ — г , ) , |
(2.29) |
|
откуда |
|
|
^ ~г1 = 7 Ч ( / „ „ о — m — о — * * » ] |
( 1 3 0 ) |
|
JпрО |
|
|
или, переходя к приращениям расстояний |
|
|
Ар = (г2 — г, )с = Япр0 [(.fnp0 — fc)(/, — /2) •- AtfI2 J, |
(2.31) |
где Ял/Ю — длина волны характерных для приемника опорных колебаний.
Первое слагаемое в квадратных скобках формулы (2.31) не связано с доплеровским эффектом и обусловлено неравенством частот несущих колебаний, генерируемых в приемнике и на спутнике. Для устранения влияния такого смещения необходимо или иметь информацию о точных значениях упомянутых частот (или показаний соответствующих часов) на спутнике и в приемнике, или использовать дифференциальный метод вторых разностей.
Второе слагаемое ANn отображает регистрируемые фазовые циклы, рассматриваемые как следствие эффекта Доплера. Оно позволяет определить интересующую нас величину Ар (после соответствующей корректировки, связанной с расхождением частот несущих колебаний на спутнике и в приемнике).
Позитивной стороной доплеровских измерений является то, что при их использовании не возникает необходимость разрешения неоднозначностей (в этом отношении данный метод имеет много общего с методом третьих разностей). Поскольку в системе GPS длина волны несущих колебаний равна примерно 20 см, то целочисленный счет таких длин волн обеспечивает дециметровый уровень точности, т. е. доплеровский метод по своей точности занимает промежуточное положение между фазовыми и кодовыми измерениями.
Рассматриваемый метод используется на геодезических работах пониженной точности или в качестве вспомогательного для определений приближенных значений расстояний при решении проблемы неоднозначности фазовых измерений.
Как уже отмечалось ранее, при определении расстояний до спутников фазовыми методами возникает достаточно сложная проблема разрешения неоднозначности, т. е. нахождения целого числа длин волн N, укладывающихся в измеряемом расстоянии от спутника до приемника. Эта сложность обусловлена, прежде всего, тем, что определяемые дальности оцениваются величинами около 20 ООО км, в то
93
время как длина волны несущих колебаний в системе GPS составляет всего 0,2 м. При таких исходных предпосылках параметр Охарактеризуется числами порядка 108. Следовательно, для того, чтобы не вносить грубых ошибок в результаты измерений, т. е. уверенно определять величину N с точностью до одной целой единицы, необходимо обеспечить надежное нахождение этой величины с относительной погрешностью менее, чем МО’8. При этом приходится учитывать и такие факторы, как непрерывное изменение величины N из-за орбитального движения спутника, а также необходимость нахождения серии таких величин для нескольких одновременно наблюдаемых спутников, поскольку для каждого конкретного спутника величина N имеет свое индивидуальное значение.
При отработке подходов к выбору эффективных методов разрешения неоднозначности наблюдается стремление выполнить следующие основные предпосылки:
1)перед процедурой, связанной с определением параметра N, целесообразно исключить все основные источники систематических ошибок, которые обусловливают смещение результатов измерений и искажают истинное значение N, не позволяя рассматривать ее как целочисленную величину;
2)для исключения необходимости многократного определения величины TVдля каждого спутника по мере его орбитального движения целесообразно ограничиться нахождением этой величины только в начальной точке наблюдения конкретного спутника, а затем отслеживать ее изменения по показаниям фазоизмерительного устройства;
3)выбираемые методы должны обеспечивать точность предварительных определений значений измеряемых расстояний, связанных с процедурой разрешения неоднозначности, не хуже половинного значения длины волны несущих колебаний, т. е. применительно к GPS на уровне около 10 см;
4)желательно, чтобы предлагаемые методы были достаточно универсальными с тем, чтобы можно было их использовать при работе как с двухчастотными, так и с одночастотными приемниками, в которых исключается возможность использования двух несущих частот с целью разрешения неоднозначности.
При выполнении перечисленных выше предпосылок открывается возможность ограничиться нахождением величины Столько в начальной точке отслеживаемой траектории наблюдаемого спутника, т. е. осуществить разрешение так называемой начальной неоднозначности. Применительно к такой постановке задачи рассмотрим несколько наиболее распространенных методов разрешения неоднозначностей, характерных для спутниковых GPS измерений. К ним относятся:
94
—геометрический метод;
—метод, базирующийся на комбинации кодовых и фазовых изме-
рений;
—метод поиска наиболее вероятных значений величины N;
—нетривиальные методы разрешения неоднозначности.
2.8.1.Геометрический метод
Сущность данного метода состоит в том, что после захвата радиосигнала и начала фазовых измерений непрерывно отслеживаются целочисленные изменения фазы, т. е. циклы. Неизвестная начальная величина N считается при этом неизменной при выполнении измерений во всех последующих точках траектории движения наблюдаемого спутника. Измерения моделируются на основе использования уравнения (2.13):
АФ = — f £ + N + AN + f(Stnp -<*,) + , (2.32)
где АN — отсчитываемые с помощью фазометра целочисленные изменения фазовых циклов, обусловленные движением спутника по орбите. Пояснения обозначений остальных входящих в данную формулу величин было дано ранее.
Интересующее нас значение N включается в число неизвестных. Оно определяется в процессе решения системы уравнений, относящихся к отсчетам при нахождении спутника в различных точках траектории. При этом используются первые и вторые разности дифференциальных измерений, а также доплеровские решения.
Надежность нахождения величины N зависит от длительности наблюдения спутника (чем больше эта длительность, тем надежнее определяется величина N). При этом не допускается пропуск отсчитываемых фазовых циклов, который может возникать в случае временных пропаданий радиосигналов от наблюдаемого спутника (например, изза экранировки этих сигналов окружающими объектами).
К положительным сторонам данного метода следует отнести простоту и четкость постановки задачи при моделировании такой процедуры, возможность его применения при работе на одной несущей частоте, а также сравнительно быстрое достижение поставленной цели.
Негативными сторонами рассматриваемой процедуры разрешения неоднозначности являются такие факторы, как рекомендации, связанные с увеличением длительности сеанса наблюдений, влияние недостаточно полно исключенных систематических погрешностей, обусловленных атмосферой (в частности, ионосферой), положением спутника на орбите и другими факторами, а также необходимость предварительного выявления и последующего устранения пропуска фазовых циклов.
95
2.8.2.Метод комбинированного использования кодовых
ифазовых измерений
Реализация данного метода базируется, как правило, на совместном применении двухчастотных фазовых и кодовых измерений. С учетом этого рассмотрим основные особенности двухчастотных фазовых измерений применительно к решению проблемы неоднозначности.
При выполнении фазовых измерений на двух передаваемых со спутника несущих частотах L1 и L2 представляется возможным образовать различные комбинации этих измерений и, в частности, их разность:
где ДФ£1 и ДФ12 — измеряемые GPS-приемником фазовые сдвиги, относящиеся к несущим колебаниям с частотами L1 и L2.
Получаемая при этом разность АФДЬ эквивалентна фазовому сдвигу, характерному для разностной частоты AL, номинальное значе-
|
ние которой равно: |
= 1575,42-1227,6=347,82 Мгц. |
|
/ a l L = / l i — / l 2 |
Длина волны таких разностных колебаний равна 86,2 см. Это значение существенно превышает длины волн основных несущих колебаний, которые соответственно равны 19,0 и 24,4 см.
Отмеченный метод перехода к более низкочастотным колебаниям получил название метода широкой дорожки, при использовании которого существенно облегчается нахождение целочисленных значений N на ранней стадии их вычислений.
Для решения поставленной задачи установим взаимосвязь между значениями N, характерными как для основных несущих частот L1 и L2 , так и для их разностей.
|
В соответствии с формулой (2.13) имеем: |
|
|
ДФц = -Л, ~ + NLl + fLl (&пр -<*,) + Л А,™,, |
(2.34) |
|
с |
Дф.2 = — /i2 — +tfi2 +/«(<*„-stc)+fL1aamML2
В этих формулах атмосферные задержки обусловлены, главным образом, влиянием ионосферы. Модельное представление такого влияния описывается следующим приближенным соотношением:
<«»‘ / 2 ‘ (2.35) где к — коэффициент, зависящий от концентрации электронов в ионосфере, от длины пути прохождения радиосигнала через ионизированную среду и от скорости электромагнитных волн в вакууме;/— частота несущих колебаний.
96
Знак «минус» в формуле (2.35) свидетельствует о том, что отдельные спектральные составляющие излучаемых колебаний при прохождении через ионосферу с фазовой скоростью испытывают не торможение, а, наоборот, ускорение.
С учетом приведенных выше предпосылок формулы (2.34) приобретают вид:
(2.36)
СИ Al
причем для разности величин ДФ£1 и ЛФ12 можно записать:
АФ^ =ЛФ„ -ДФ, 2 =
|
=-г*. — + ^ + и (к -ю- |
— — ! — ) , |
( 1 3 7 ) |
|
|
С |
fu fl.2 |
||
|
Ж Nal= |
Nu-NL2. |
Из совместного решения первого уравнения в системе (2.36) и уравнения (2.37) может быть получено следующее соотношение:
|
Nu =АФи |
— А Ф ^ l ^ |
+ k1» |
. |
(2.38) |
|
JM |
J L\ |
J LI |
Соотношение (2.38) позволяет по найденному для разностной ча- с т о т ы ^ целому количеству фазовых циклов NAL вычислить интересующее нас значение NL]9 а следовательно, и NL2.
Как уже отмечалось ранее, из-за увеличения длины волны для колебаний разностной частоты существенно упрощается процедура разрешения неоднозначности, т.е. нахождение величины N^ .
В частности, эта проблема может быть решена на основе знания приближенного значения определяемого расстояния до спутника, получаемого с использованием кодовых сигналов, третьих разностей или доплеровских методов.
С целью нахождения значения Nal на базе совместного применения кодовых и фазовых методов представим формулу (2.37) в следующем виде:
|
= — + А ф Д 1 -fbL (К -«*,) + |
Л, |
— |
4-У |
(2.39) |
|
С |
fu |
В формуле (2.39) основной неизвестной величиной является приближенное расстояние до спутника р’, которое может быть определено с помощью кодовых (псевдодальномерных) измерений на основе использования формулы (2.6):
р’-R-(а -ас)с-аитмс. (2—40)
97
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- 1 Область применения
- 2 Обозначения и сокращения
- 3 Общие положения
- 4 Алгоритм разрешения неоднозначности
- 4.1 Предварительная обработка фазовых измерений
- 4.2 Определение первых разностей фаз
- 4.3 Определение вторых разностей фаз
- 4.4 Учет корреляции вторых разностей фаз
- 4.5 Получение целочисленных параметров вторых разностей фаз
- 2.8. Принципы разрешения неоднозначностей при фазовых измерениях
- 2.8.1. Геометрический метод
1 Область применения
Настоящий стандарт распространяется на методы и технологии выполнения геодезических и землеустроительных работ с использованием аппаратуры потребителей глобальной навигационной спутниковой системы.
Настоящий стандарт устанавливает методы определения целочисленных параметров измеренных фазовых псевдодальностей до космических аппаратов спутниковых систем типа GPS , выполняемую при высокоточных определениях относительных координат пунктов с использованием наблюдений космических аппаратов этих систем, при выполнении геодезических и землеустроительных работ.
2 Обозначения и сокращения
В настоящем стандарте применяют следующие сокращения:
ГЛОНАСС — глобальная навигационная спутниковая система Российской Федерации;
КА — космический аппарат;
МНК — метод наименьших квадратов;
СКП — среднее квадратическое отклонение;
GPS — глобальная навигационная спутниковая система Соединенных Штатов Америки.
3 Общие положения
3.1 Величина фазовой псевдодальности выражается в виде целого числа длин волн и дробной части длины волны. Дробная часть фазы может быть получена с высокой точностью, характеризуемой СКП на уровне первых единиц миллиметров. Прямое измерение целочисленной части фазы не представляется возможным, вследствие чего возникает неоднозначность фазовых измерений, требующая разрешения.
3.2 Разрешение неоднозначности фазовых измерений псевдодальности представляет собой процесс нахождения целого числа циклов (волн), укладывающихся в расстоянии между навигационным спутником и приемником при обработке фазовых измерений.
3.3 Для решения этой задачи с точностью, требуемой для выполнения геодезических и землеустроительных работ, применяют специальные методы математической обработки фазовых измерений, использующие при обработке не сами измерения, а их разности: первые, вторые и третьи. Это позволяет существенно уменьшить число определяемых параметров без ущерба для точности координатных определений. Основными методами разрешения неоднозначности фазовых измерений псевдодальности являются методы, базирующиеся на использовании вторых разностей фаз. Вторые разности вычисляются с использованием первых разностей фаз.
3.4 Решения, получаемые по вторым разностям фаз, как правило, позволяют при нормальных условиях наблюдений вычислить значения целочисленных параметров комбинаций измеренных фаз и на этой основе определять относительные координаты определяемых пунктов с точностью порядка первых единиц миллиметров.
3.5 Исходными данными, необходимыми для разрешения неоднозначности фазовых измерений, являются:
— фазовые измерения на двух несущих частотах для всех наблюдаемых навигационных спутников ГЛОНАСС и GPS на интервале непрерывного слежения за фазой;
— абсолютные геоцентрические координаты исходного пункта;
— предварительные координаты определяемого пункта.
4 Алгоритм разрешения неоднозначности
4.1 Предварительная обработка фазовых измерений
В измеренные значения фаз несущих вводятся поправки за влияние тропосферы, ионосферы и вращения Земли вокруг своей оси.
Поправки за влияние тропосферы вычисляются одним из существующих методов (например, методы Саастомойнена и Хопфилда). При длине измеряемого базиса не более 5 км введение поправок за тропосферу может быть пропущено.
Поправки за влияние ионосферы могут вычисляться с использованием двухчастотных синхронных измерений кодовых и фазовых псевдодальностей. Поправки за влияние ионосферы для фазовых ПД численно равны поправкам, полученным для кодовых ПД, но знаки их противоположны (поправки к кодовым ПД отрицательны, а поправки к фазовым ПД положительны). В случае измерений кодовых ПД формулы для вычисления этих поправок соответственно на первой и второй частотах имеют вид:
где f 1 f 2 — значения первой и второй несущих частот;
d 1 , d 2 — значения измеренных кодовых ПД соответственно на первой и второй частотах. Поправка на вращение Земли вокруг своей оси за время распространения сигнала от КА до пункта наблюдения (в метрах) вычисляется по формуле:
где ω — угловая скорость вращения Земли вокруг своей оси;
ае — большая полуось общеземного эллипсоида;
ρ — расстояние до КА (в метрах);
с — скорость света, равная 299792498 м/с;
В — широта пункта наблюдения;
A , Z — соответственно азимут и зенитное расстояние КА.
4.2 Определение первых разностей фаз
Исходным соотношением служит формула:
где j — номер спутника;
i — номер момента времени измерения ti ;
1, 2 — номера исходного и определяемого пунктов;
С использованием ряда допущений, практически не влияющих на точность решения, величину S ( j , i ) представляют в виде
где f — несущая частота;
δ tni и τ j ni — поправка к шкале времени и интервал времени прохождения сигналов j -го спутника до n -го пункта в момент ti ( n = 1, 2);
N j 12 — целочисленный параметр ПРФ при i = 1;
ε j i — случайная погрешность измерения первой разности фаз.
Формула (5) нелинейна относительно поправки δ ti в том смысле, что параметр τ j ( i ) должен быть получен на истинный момент приема сигнала ( ti + δ ti ).
Для существенного сокращения числа искомых параметров и повышения точности относительных определений поправки к временным шкалам пунктов представляют в виде:
где δ İ ti — поправка к временной шкале М-г o пункта в момент первого измерения;
α İ — коэффициент линейного ухода временной шкалы М-го пункта;
М — номер пункта (М = 1,2);
Δti — промежуток времени между текущим и начальным моментом измерений.
4.3 Определение вторых разностей фаз
Исходным соотношением служит формула
где D 2 ( j , k , i ) — вторая разность фаз на момент ti .
С учетом полученных первых разностей фаз вторые разности фаз определяют по формуле
D 2 (j, k, I) = f ( δ t k 2i — δ t k 2i ) – fc -1 [ρ k 2i + 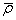
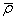
(δt k 1i – ρ k 1i c -1 )] – f (δt j 2i — δt j 1i) + fc -1 [ρ j 2i + 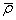
+ fc -1 [ρ j 1i + 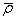
где N kj 12 — целочисленный параметр ВРФ;
ρ j n i и ρ k n i — мгновенные дальности j -го и k -го спутников от n -го пункта в момент ti ;
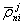
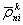
f — частота несущей;
с — скорость света;
ε i jk — случайная погрешность вторых разностей фаз в момент t i .
Линеаризация позволяет получить уравнение погрешностей ВРФ, в котором неизвестными являются следующие параметры:
— поправки к предварительным координатам двух пунктов (шесть параметров);
— временные параметры двух пунктов (четыре неизвестных);
— целочисленные параметры, число которых на единицу меньше числа наблюденных спутников.
Систему уравнений погрешностей ВРФ на моменты t 1 , . , tN Дописывают матрицей коэффициентов и вектором свободных членов.
Матрица коэффициентов представляют в виде
где N — число моментов измерений ВРФ;
A 1 , . , AN — блоки идентичной структуры, зависящие от момента измерений и числа наблюдаемых спутников.
Например, для четырех спутников каждый из блоков A 1 , . , AN определяется по формуле
где akj и cki — коэффициенты при поправках к начальным моментам измерений первого и второго пунктов;
bkj и dkj — коэффициенты при скоростях ухода шкал времени первого и второго пунктов;
eki , fki , gki и hki , ρ ki , qki — коэффициенты при поправках к предварительным координатам первого и второго пунктов.
Коэффициенты akj и cki вычисляются по формулам
Коэффициенты bkj и dkj вычисляются по формулам:
Коэффициенты eki , fki , gki вычисляются по формулам:
Коэффициенты hki , ρ ki , qki вычисляются по формулам:
Коэффициенты при целочисленных параметрах ВРФ образуют единичную матрицу.
Вектор свободных членов системы уравнений погрешностей ВРФ определяется как вектор, элементы которого представляют собой разности ВРФ, вычисляемых по предварительным значениям определяемых параметров, и измеренных значений ВРФ на моменты t 1 , . , tN .
Полученную систему уравнений поправок решают по МНК с учетом корреляции ВРФ.
4.4 Учет корреляции вторых разностей фаз
Корреляцию ВРФ учитывают путем использования в решении ковариационной матрицы ВРФ Q . Данная матрица имеет блочно-диагональную структуру. Диагональные блоки являются квадратными матрицами. Их число равно числу N моментов измерений. Размер блока выражается числом, на единицу меньшим числа М наблюдаемых спутников. Например, при М = 4 каждый из указанных блоков имеет вид
4.5 Получение целочисленных параметров вторых разностей фаз
Определяемые параметры ВРФ получают из решения системы нормальных уравнений. Матрицу системы нормальных уравнений формируют в соответствии с формулой
где А Т — матрица, транспонированная по отношению к матрице А;
Р — весовая матрица, обратная по отношению к ковариационной матрице Q .
Вектор свободных членов системы нормальных уравнений формируют по формуле:
где L — вектор свободных членов уравнений погрешностей ВРФ. Из решения системы нормальных уравнений получают:
— поправки к координатам исходного и определяемого пунктов;
— целочисленные параметры ВРФ.
Вследствие погрешностей измерений, плохих условий наблюдений навигационных спутников (многолучевость, искусственные и естественные препятствия наблюдений и т.д.) фактические значения целочисленных параметров, как правило, не являются целыми числами. Поэтому полученные значения этих параметров должны быть округлены до целого в ближайшую сторону. С этими новыми значениями необходимо перевычислить вектор свободных членов уравнений погрешностей и получить новое решение с учетом поправок к шкалам времени пунктов и скоростям их изменения, а также поправок к координатам пунктов.
Ключевые слова: глобальные навигационные спутниковые системы, геодезические и землеустроительные работы, неоднозначность, фазовая псевдодальность
Источник
2.8. Принципы разрешения неоднозначностей при фазовых измерениях
Как уже отмечалось ранее, при определении расстояний до спутников фазовыми методами возникает достаточно сложная проблема разрешения неоднозначности, т. е. нахождения целого числа длин волн N, укладывающихся в измеряемом расстоянии от спутника до приемника. Эта сложность обусловлена, прежде всего, тем, что определяемые дальности оцениваются величинами около 20 ООО км, в то
время как длина волны несущих колебаний в системе GPS составляет всего 0,2 м. При таких исходных предпосылках параметр Охарактеризуется числами порядка 10 8 . Следовательно, для того, чтобы не вносить грубых ошибок в результаты измерений, т. е. уверенно определять величину N с точностью до одной целой единицы, необходимо обеспечить надежное нахождение этой величины с относительной погрешностью менее, чем МО’ 8 . При этом приходится учитывать и такие факторы, как непрерывное изменение величины N из-за орбитального движения спутника, а также необходимость нахождения серии таких величин для нескольких одновременно наблюдаемых спутников, поскольку для каждого конкретного спутника величина N имеет свое индивидуальное значение.
При отработке подходов к выбору эффективных методов разрешения неоднозначности наблюдается стремление выполнить следующие основные предпосылки:
1) перед процедурой, связанной с определением параметра N, целесообразно исключить все основные источники систематических ошибок, которые обусловливают смещение результатов измерений и искажают истинное значение N, не позволяя рассматривать ее как целочисленную величину;
2) для исключения необходимости многократного определения величины TVдля каждого спутника по мере его орбитального движения целесообразно ограничиться нахождением этой величины только в начальной точке наблюдения конкретного спутника, а затем отслеживать ее изменения по показаниям фазоизмерительного устройства;
3) выбираемые методы должны обеспечивать точность предварительных определений значений измеряемых расстояний, связанных с процедурой разрешения неоднозначности, не хуже половинного значения длины волны несущих колебаний, т. е. применительно к GPS на уровне около 10 см;
4) желательно, чтобы предлагаемые методы были достаточно универсальными с тем, чтобы можно было их использовать при работе как с двухчастотными, так и с одночастотными приемниками, в которых исключается возможность использования двух несущих частот с целью разрешения неоднозначности.
При выполнении перечисленных выше предпосылок открывается возможность ограничиться нахождением величины Столько в начальной точке отслеживаемой траектории наблюдаемого спутника, т. е. осуществить разрешение так называемой начальной неоднозначности. Применительно к такой постановке задачи рассмотрим несколько наиболее распространенных методов разрешения неоднозначностей, характерных для спутниковых GPS измерений. К ним относятся:
— метод, базирующийся на комбинации кодовых и фазовых изме-
— метод поиска наиболее вероятных значений величины N;
— нетривиальные методы разрешения неоднозначности.
2.8.1. Геометрический метод
Сущность данного метода состоит в том, что после захвата радиосигнала и начала фазовых измерений непрерывно отслеживаются целочисленные изменения фазы, т. е. циклы. Неизвестная начальная величина N считается при этом неизменной при выполнении измерений во всех последующих точках траектории движения наблюдаемого спутника. Измерения моделируются на основе использования уравнения (2.13):
АФ = — f £ + N + AN + f(St np — + , (2.32)
где А N — отсчитываемые с помощью фазометра целочисленные изменения фазовых циклов, обусловленные движением спутника по орбите. Пояснения обозначений остальных входящих в данную формулу величин было дано ранее.
Интересующее нас значение N включается в число неизвестных. Оно определяется в процессе решения системы уравнений, относящихся к отсчетам при нахождении спутника в различных точках траектории. При этом используются первые и вторые разности дифференциальных измерений, а также доплеровские решения.
Надежность нахождения величины N зависит от длительности наблюдения спутника (чем больше эта длительность, тем надежнее определяется величина N). При этом не допускается пропуск отсчитываемых фазовых циклов, который может возникать в случае временных пропаданий радиосигналов от наблюдаемого спутника (например, изза экранировки этих сигналов окружающими объектами).
К положительным сторонам данного метода следует отнести простоту и четкость постановки задачи при моделировании такой процедуры, возможность его применения при работе на одной несущей частоте, а также сравнительно быстрое достижение поставленной цели.
Негативными сторонами рассматриваемой процедуры разрешения неоднозначности являются такие факторы, как рекомендации, связанные с увеличением длительности сеанса наблюдений, влияние недостаточно полно исключенных систематических погрешностей, обусловленных атмосферой (в частности, ионосферой), положением спутника на орбите и другими факторами, а также необходимость предварительного выявления и последующего устранения пропуска фазовых циклов.
2.8.2. Метод комбинированного использования кодовых
и фазовых измерений
Реализация данного метода базируется, как правило, на совместном применении двухчастотных фазовых и кодовых измерений. С учетом этого рассмотрим основные особенности двухчастотных фазовых измерений применительно к решению проблемы неоднозначности.
При выполнении фазовых измерений на двух передаваемых со спутника несущих частотах L1 и L2 представляется возможным образовать различные комбинации этих измерений и, в частности, их разность:
где ДФ £1 и ДФ 12 — измеряемые GPS-приемником фазовые сдвиги, относящиеся к несущим колебаниям с частотами L1 и L2.
Получаемая при этом разность АФ ДЬ эквивалентна фазовому сдвигу, характерному для разностной частоты AL, номинальное значе-
ние которой равно:
/ a l L = / l i — / l 2
Длина волны таких разностных колебаний равна 86,2 см. Это значение существенно превышает длины волн основных несущих колебаний, которые соответственно равны 19,0 и 24,4 см.
Отмеченный метод перехода к более низкочастотным колебаниям получил название метода широкой дорожки, при использовании которого существенно облегчается нахождение целочисленных значений N на ранней стадии их вычислений.
Для решения поставленной задачи установим взаимосвязь между значениями N, характерными как для основных несущих частот L1 и L2 , так и для их разностей.
В соответствии с формулой (2.13) имеем:
+ N Ll + f Ll (& пр — + Л А,™,,
Дф.2 = — /i2 — +tfi2 +/«( -st c )+f L1 a amML2
В этих формулах атмосферные задержки обусловлены, главным образом, влиянием ионосферы. Модельное представление такого влияния описывается следующим приближенным соотношением:
2 ‘ (2.35) где к — коэффициент, зависящий от концентрации электронов в ионосфере, от длины пути прохождения радиосигнала через ионизированную среду и от скорости электромагнитных волн в вакууме;/— частота несущих колебаний.
Знак «минус» в формуле (2.35) свидетельствует о том, что отдельные спектральные составляющие излучаемых колебаний при прохождении через ионосферу с фазовой скоростью испытывают не торможение, а, наоборот, ускорение.
С учетом приведенных выше предпосылок формулы (2.34) приобретают вид:
причем для разности величин ДФ £1 и ЛФ 12 можно записать:
Источник