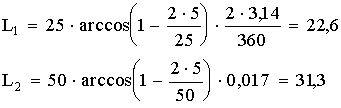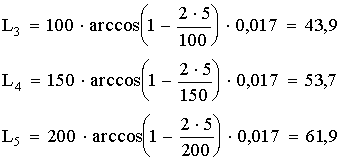1 тест
1. К методам, используемым как на эмпирическом, так и на теоретическом уровне исследования, относятся: 
2. Научный документ, содержащий систематизированные научные данные по какой-либо теме, полученные в итоге анализа первоисточников, — это … 
3. Соединение полученных при анализе частей в нечто целое – это синтез
4. Одним из наиболее распространенных методов познания, позволяющим установить сходство и различие предметов и явлений действительности является сравнение
5. Вторичная информация различной степени свертывания, выполняющая функцию предварительного оповещения, — это информация …
6. Все то, что находится в границах объекта исследования в определенном аспекте рассмотрения, — это … 
7. К методам эмпирического исследования относятся: 
8. Вторичная информация, представляющая собой систематизированные краткие сведения в какой-либо области знаний, — это информация …
9. Вид умозаключения от частных фактов, положений к общим выводам —
10. Мысль, с помощью которой что-либо утверждается или отрицается, — это…
11. Установите соответствие между видом информации и ее содержанием:
12. Вид умозаключения от общего к частному, когда из массы частных случаев делается обобщенный вывод о всей совокупности таких случаев, — …
13. Метод научного исследования путем разложения предмета на составные части – это анализ
14. Информация, заключенная в описании прототипа научной задачи:
15. Процесс или явление, которое содержит противоречие и порождает проблемную ситуацию и избранные для изучения, — это …
16. Вторичная информация, содержащаяся в первичных научных документах, -это информация …
17. Угол зрения, под которым рассматривается объект исследования, — это …
18. Научное предположение, выдвигаемой для объяснения каких-либо явлений и требующее верификации, — это …
19. Частным случаем наблюдения является эксперимент
2 тест
1. Достоверность научных фактов в значительной степени зависит от достоверности первоисточников , от их целевого назначения и характера их информации.
2. Рабочий план имеет произвольную форму и состоит из перечня расположенных в столбик рубрик, связанных внутренней Логикой исследования данной темы и позволяющих по их месту судить об их уместности и значимости.
3. Укажите название реферативных изданий:
4. Научные факты характеризуются следующими свойствами:
5. Публикации рефератов, включающих сокращенное изложение содержания первичных документов (или их частей) с основными фактическими сведениями и выводами, содержат издания Реферативные
6. Укажите последовательность изучения научных публикаций:
7. Библиографические издания разделяются на следующие виды:
3 тест
1. К периодическим изданиям относятся:
2. Совокупность документов, содержащих сведения об открытиях, изобретениях и других видах промышленной собственности, а также сведения об охране прав изобретателей, — это …
3. Установите соответствие между периодичностью выпуска и видом издания:
4. Универсальная иерархическая классификация областей общественных знаний, принятая для систематизации сфер научно-технической информации, представлена в …
5. Укажите названия различных форм информационных изданий:
6. Квалифицированная научная работа в определенной области науки, имеющая внутреннее единство, содержащая совокупность научных результатов, научных положений, выдвигаемых автором для публичной защиты и свидетельствующих о личном вкладе автора в науку и его качествах ученого:
7. К продолжающимся изданиям относятся:
8. В зависимости от периодичности выпуска издания подразделяют на:
9. Информационные издания, содержащие библиографическую запись и реферат, — это … 
10. Патентная документация обладает высокой степенью достоверности , так как подвергается тщательной экспертизе на новизну и полезность.
11. Издания, публикуемые от имени государственных или общественных организаций, учреждений и ведомств, содержащие материалы законодательного, нормативного или директивного характера, называются …
12. Сведения о книгах и брошюрах по всем отраслям знания и практической деятельности и первичная библиографическая регистрация всех новых книг, издаваемых на территории Российской Федерации, а также книг, издаваемых в иностранных государствах по заказу российских издателей, содержатся в …
13. Порядок изложения материала в научных документах диктуется логикой самого научного исследования.
14. В логическом порядке по отдельным отраслям знаний карточки сгруппированы в каталоге:
15. К вторичным опубликованным научным документам относятся:
16. К специальному виду технических изданий относят:
17. Нормативно-технический документ, устанавливающий комплекс норм, правил, требований к объекту и утвержденный компетентным органом, — это …
18. К первичным опубликованным научным документам относятся:
19. Научное издание в виде брошюры, содержащее составленный автором реферат проведенного им исследования, — это …
20. Как расшифровывается аббревиатура УДК:
21. Информационные издания, содержащие расширенные рефераты статей, описания изобретений и другие публикации, позволяющие не обращаться к первоисточнику, — это …
22. Перечень всех материалов, выявленных по какой-то определенной тематике, — это …
23. Индексы УДК приводятся на обороте титульного листа в книгах по наукам:
24. С помощью какого каталога можно выяснить, какие именно произведения и по каким отраслям знаний имеются в библиотеке, подобрать нужную литературу, а также установить автора и название книги, если известно ее содержание?
25. Вторичные научные документы содержат результаты аналитико-синтетической и логической переработки одного или нескольких первичных документов или сведения о них.
26. Информационные издания, содержащие в себе полное библиографическое описание источника информации, — это …
27. В библиотеке применяются следующие виды каталогов:
28. С помощью систематического каталога можно выяснить, какие именно произведения и по каким отраслям знаний имеются в библиотеке, подобрать нужную литературу, а также установить автора и название книги, если известно ее содержание.
29. Все научные документы подразделяются на первичные , содержащие непосредственные результаты научных исследований и разработок, новые научные сведения или новое осмысление известных идей и фактов.
30. Информационные издания, включающие в себя библиографические описания литературы, выходящей по определенным отраслям знаний, основной задачей которых является оперативное информирование обо всех научных и технических новинках, — это …
31. Информационные издания, дающие представление о состоянии и тенденциях развития определенной области (раздела, проблемы) науки или техники, — это …
32. Издания книжного или журнального типа, содержащие библиографические описания вышедших изданий, — это …
33. Наиболее оперативным источником научно-технической информации являются …
34. К непериодическим изданиям относятся:
35. Научное издание, содержащее полное и всестороннее исследование одной проблемы или темы, принадлежащее одному или нескольким авторам, — это …
36. Перечень документальных источников информации, имеющихся в фонде данной библиотеки или бюро НТИ, — это …
37. Укажите примерную последовательность поиска научно-технической информации:
38. Укажите, какие работы относятся к:
4 тест
1. При поиске в Интернете можно расширить запрос до всех слов, содержащих введенную часть слова, используя значок …
2. электронная форма представления информации — способ фиксации информации, допускающий хранение, обработку, распространение и предъявление пользователю информации с помощью средств вычислительной техники.
3. В зависимости от масштабов формирования и использования различают информационные ресурсы:
4. Информационные ресурсы обладают рядом специфических особенностей:
5. Самая популярная в настоящее время отечественная информационно-поисковая система -это …
6. Вся совокупность сведений, получаемых и накапливаемых в процессе развития науки и практической деятельности людей, для их многоцелевого использования в общественном производстве и управлении — это …
7. Самостоятельный законченный продукт, содержащий информацию, представленную в электронной форме, и предназначенный для длительного хранения и многократного использования неопределенным кругом пользователей, все копии которого соответствуют оригиналу, — это …
8. Единственная российская поисковая система, индексирующая документы в форматах PDF, DOC, RTF, SWF, PPT и XLS:
9. В Яндекс можно запрашивать конкретную форму слова при поиске (исключив другие словоформы), поставив перед ним знак:
10. Одна из самых полных зарубежных информационно-поисковых систем — это …
5 тест
1. Укажите вид измерений:
2. Приборы классифицируют по следующим признакам:
3. Простейшим средством измерения является мера , предназначенная для воспроизведения физической величины заданного размера.
4. По характеру внешних воздействий на объект исследования выделяют эксперименты:
5. При проектировании продукции применяют, в основном, методы …
6. По способу формирования условий различают эксперименты:
7. Одновременные измерения неодноименных величин для нахождения зависимости между ними проводят при измерениях …
8. Чем больше случайных факторов, влияющих на опыт, тем больше расхождения значений, получаемых при измерениях.
9. По контролируемым величинам эксперименты разделяют на:
10. Наименьшее значение измеренной величины, вызывающее изменение показания прибора, которое можно зафиксировать, — это …
11. Для определения пищевой и биологической ценности продукции используют методы:
12. Средство измерения, предназначенное для получения определенной информации об изучаемой величине в удобной для экспериментатора форме, — это …
13. Для определения состава и количества входящих в продукцию веществ используют методы:
14. На изучение элементов технологического процесса (продукции, оборудования, деятельности работников и т.п.) или процесса в целом направлен эксперимент …
15. Совокупность мысленных и физических операций, размещённых в определённой последовательности, в соответствии с которой достигается цель исследования, — это …
16. Химические методы исследования пищевых продуктов относятся к методам …
17. По целям исследования различают эксперименты:
18. По организации проведения эксперименты бывают:
19. Разность между максимальным и минимальным показаниями прибора называют:
20. Все приборы, используемые для измерения в научных исследованиях, проходят периодическую поверку на точность …
6 тест
1. Чем больше значение σ, следовательно, тем Больше изменчивость признака исследуемого объекта.
3. Из-за небрежности или некомпетентности исследователя, невнимательности его в работе или плохого знания метода анализа в эксперименте появляются ошибки:
4. Для выбора доверительной вероятности (Р) можно воспользоваться эмпирическим правилом:
6. В большинстве исследований (для решения практических задач) измерения и вычисления ведут с предельной относительной ошибкой порядка:
7. Известными, постоянными причинами, которые можно установить при детальном рассмотрении процедуры анализа, обусловлены ошибки:
9. Ошибка измерения не должна содержать значащих цифр более …
10. В отличие от систематических ошибок Случайные ошибки не имеют видимой причины.
11. В точных аналитических исследованиях ошибка возможна не более:
12. Укажите обозначения статистических величин:
13. Не имеют видимой причины при проведении эксперимента ошибки …
14. По характеру причин в эксперименте различают ошибки:
15. Если содержание влаги в продукте составляет 85,473%, а вычисленная ошибка 0,3425%, то результат следует записать:
7 тест
1. Обязательным элементом введения является формулировка объекта и предмета исследования.
2. Укажите особенности методических приемов изложения научных материалов:
3. Укажите методические приемы изложения научных материалов:
4. Первой страницей научной работы считается:
5. С обоснования значимости выбранной темы начинается актуальность
6. Ошибочное определение, в котором определяющее понятие повторяет определяемое, называется тавтология
7. В заголовки отдельных частей текста не включают:
8. В оглавлении заголовки каждой последующей ступени рекомендуется смещать по отношению к заголовкам предыдущей ступени на:
9. В нижнем поле титульного листа указываются:
10. Введение научной работы пишут:
8 тест
1. Выберите правильные записи порядковых числительных:
2. Выберите правильное обозначение надписи под рисунком:
3. Наиболее наглядное представление о результатах экспериментов, позволяет лучше понять физическую сущность исследуемого процесса, дает Графическое изображение.
4. Выберите правильную запись тематического заголовка таблицы:
5. Выберите правильную запись ссылки на формулу:
6. Части перечисления в тексте чаще всего пишутся с новой строки и отделяются друг от друга …
7. Выберите правильную запись при оформлении порядкового номера таблицы:
8. Выберите правильные записи однозначных количественных числительных:
9. Выберите правильную запись ссылки на приложение:
10. Выберите правильную запись при оформлении ссылки на таблицу в тексте:
Изучение
всех влияющих на исследуемый объект
факторов одновременно провести
невозможно, поэтому в эксперименте
рассматривается их ограниченное число.
Остальные активные факторы стабилизируются,
т.е. устанавливаются на каких-то одинаковых
для всех опытов уровнях.
Некоторые
факторы не могут быть обеспечены
системами стабилизации (например,
погодные условия, самочувствие оператора
и т.д.), другие же стабилизируются с
какой-то погрешностью (например,
содержание какого-либо компонента в
среде зависит от ошибки при взятии
навески и приготовления раствора).
Учитывая также, что измерение
параметра у осуществляется
прибором, обладающим какой-то погрешностью,
зависящей от класса точности прибора,
можно прийти к выводу, что результаты
повторностей одного и того же опыта ук будут
приближенными и должны отличаться один
от другого и от истинного значения
выхода процесса. Неконтролируемое,
случайное изменение и множества других
влияющих на процесс факторов
вызывает случайныеотклонения
измеряемой величины ук от
ее истинного значения — ошибку опыта.
Каждый
эксперимент содержит элемент
неопределенности вследствие ограниченности
экспериментального материала. Постановка
повторных (или параллельных) опытов не
дает полностью совпадающих результатов,
потому что всегда существует ошибка
опыта (ошибка воспроизводимости). Эту
ошибку и нужно оценить по параллельным
опытам. Для этого опыт воспроизводится
по возможности в одинаковых условиях
несколько раз и затем берется среднее
арифметическое всех результатов. Среднее
арифметическое у равно сумме всех n
отдельных результатов, деленной на
количество параллельных опытов n:
Отклонение
результата любого опыта от среднего
арифметического можно представить как
разность y2— ,
где y2 —
результат отдельного опыта. Наличие
отклонения свидетельствует об
изменчивости, вариации значений повторных
опытов. Для измерения этой изменчивости
чаще всего используют дисперсию.
Дисперсией
называется среднее значение квадрата
отклонений величины от ее среднего
значения. Дисперсия обозначается s2 и
выражается формулой:
где
(n-1) — число степеней свободы, равное
количеству опытов минус единица. Одна
степень свободы использована для
вычисления среднего.
Корень
квадратный из дисперсии, взятый с
положительным знаком, называется средним
квадратическим отклонением, стандартом
или квадратичной ошибкой:
Ошибка
опыта является суммарной величиной,
результатом многих ошибок: ошибок
измерений факторов, ошибок измерений
параметра оптимизации и др. Каждую из
этих ошибок можно, в свою очередь,
разделить на составляющие.
Все
ошибки принято разделять на два класса:
систематические и случайные (рисунок
1).
Систематические
ошибки порождаются причинами, действующими
регулярно, в определенном направлении.
Чаще всего эти ошибки можно изучить и
определить количественно. Систематическая
ошибка —
это ошибка, которая остаётся постоянно
или закономерно изменяется при повторных
измерениях одной и той же величины. Эти
ошибки появляются вследствие неисправности
приборов, неточности метода измерения,
какого либо упущения экспериментатора,
либо использования для вычисления
неточных данных. Обнаружить систематические
ошибки, а также устранить их во многих
случаях нелегко. Требуется тщательный
разбор методов анализа, строгая проверка
всех измерительных приборов и безусловное
выполнение выработанных практикой
правил экспериментальных работ. Если
систематические ошибки вызваны известными
причинами, то их можно определить.
Подобные погрешности можно устранить
введением поправок.
Систематические
ошибки находят, калибруя измерительные
приборы и сопоставляя опытные данные
с изменяющимися внешними условиями
(например, при градуировке термопары
по реперным точкам, при сравнении с
эталонным прибором). Если систематические
ошибки вызываются внешними условиями
(переменной температуры, сырья и т.д.),
следует компенсировать их влияние.
Случайными ошибками
называются те, которые появляются
нерегулярно, причины, возникновения
которых неизвестны и которые невозможно
учесть заранее. Случайные ошибки
вызываются и объективными причинами и
субъективными. Например, несовершенством
приборов, их освещением, расположением,
изменением температуры в процессе
измерений, загрязнением реактивов,
изменением электрического тока в цепи.
Когда случайная ошибка больше величины
погрешности прибора, необходимо
многократно повторить одно и тоже
измерение. Это позволяет сделать
случайную ошибку сравнимой с погрешностью
вносимой прибором. Если же она меньше
погрешности прибора, то уменьшать её
нет смысла. Такие ошибки имеют значение,
которое отличается в отдельных измерениях.
Т.е. их значения могут быть неодинаковыми
для измерений сделанных даже в одинаковых
условиях. Поскольку причины, приводящие
к случайным ошибкам неодинаковы в каждом
эксперименте, и не могут быть учтены,
поэтому исключить случайные ошибки
нельзя, можно лишь оценить их значения.
При многократном определении какого-либо
показателя могут встречаться результаты,
которые значительно отличаются от
других результатов той же серии. Они
могут быть следствием грубой ошибки,
которая вызвана невнимательностью
экспериментатора.
Систематические
и случайные ошибки состоят из множества
элементарных ошибок. Для того чтобы
исключать инструментальные ошибки,
следует проверять приборы перед опытом,
иногда в течение опыта и обязательно
после опыта. Ошибки при проведении
самого опыта возникают вследствие
неравномерного нагрева реакционной
среды, разного способа перемешивания
и т.п.
При
повторении опытов такие ошибки могут
вызвать большой разброс экспериментальных
результатов.
Очень
важно исключить из экспериментальных
данных грубые ошибки, так называемый
брак при повторных опытах. Грубые
ошибки легко
обнаружить. Для выявления ошибок
необходимо произвести измерения в
других условиях или повторить измерения
через некоторое время. Для предотвращения
грубых ошибок нужно соблюдать аккуратность
в записях, тщательность в работе и записи
результатов эксперимента. Грубая ошибка
должна быть исключена из экспериментальных
данных. Для отброса ошибочных данных
существуют определённые правила.
Например,
используют критерий Стьюдента t (Р; f):
Опыт считается бракованным, если
экспериментальное значение критерия
t по модулю больше табличного значения
t (Р; f).
Если
в распоряжении исследователя имеется
экспериментальная оценка дисперсии
S2(yk)
с небольшим конечным числом степеней
свободы, то доверительные ошибки
рассчитываются с помощью критерий
Стьюдента t (Р; f):
?()
= t (Р; f)* S(yk)/=
t (Р; f)* S()
?(yk)
= t (Р; f)* S(yk)
6.
Результат прямого измерения — случайная
величина, подчиняющаяся нормальному
закону распределения
Результаты,
которые получаются при экспериментальном
исследовании какого-либо технологического
процесса, зависят от целого ряда факторов.
Поэтому результат исследования является
случайной величиной, распределённой
по нормальному закону распределения.
Оно названо нормальным, т. к. именно
это распределение для случайной величины
является обычным и
называется гаусовским или лапласским. Под распределением
случайной величиныпонимают
совокупность всех возможных значений
случайной величины и соответствующих
им вероятностей.
Законом
распределения случайной величины называется
всякое соотношение, устанавливающее
связь между возможными значениями
случайной величины и соответствующим
им вероятностям.
При
экспериментальном исследовании
какого-либо технологического процесса
измеряемый результат последнего является
случайной величиной, на которую оказывает
влияние огромное число факторов
(изменение погодных условий, самочувствие
оператора, неоднородность сырья, влияние
износа измерительной и стабилизирующей
аппаратуры и т.д. и т.п.). Именно поэтому
результат исследования является
случайной величиной, распределенной
по нормальному закону. Однако если
исследователь какой-либо активный
фактор не заметил или отнес его к
неактивным, а неконтролируемое изменение
этого фактора может вызвать несоразмерно
большое изменение эффективности процесса
и параметра, характеризующего эту
эффективность, то распределение
вероятности последнего может нормальному
закону не подчиниться.
Точно
так же приведет к нарушению нормальности
закона распределения наличие в массиве
экспериментальных данных грубых ошибок.
Именно поэтому в первую очередь проводят
анализ на наличие в экспериментальных
данных грубых ошибок с принятой
доверительной вероятностью.
Случайная
величина будет распределена по нормальному
закону, если она представляет собой
сумму очень большого числа взаимно
зависимых случайных величин, влияния
каждой из которых ничтожно мало. Если
измерения искомой величины y проведены
много раз, то результат можно наглядно
представить, построив диаграмму, которая
показывала бы, как часто получались те
или иные значения. Такая диаграмма
называется гистограммой. Что
бы построить гистограмму нужно разбить
весь диапазон измеренных значений на
равные интервалы. И посчитать сколько
раз каждая величина попадает в каждый
интервал.
Если
измерения продолжать до тех пор, пока
число измеренных значений n не станет
очень большим, то ширину интервала можно
сделать очень малой. Гистограмма перейдёт
в непрерывную прямую, которая
называется кривой
распределения.
В
основе теории случайных ошибок лежат
два предположения:
1.
при большом числе измерений случайные
погрешности одинаково велики, но с
разными знаками встречаются одинаково
часто;
2.
большие (по абсолютной величине)
погрешности встречаются реже, чем малые.
Т. е. вероятность появления погрешности
уменьшается с ростом её величины.
Согласно
закону больших чисел при бесконечно
большом числе измерений n, истинное
значение измеряемой величины y равно
среднеарифметическому значению всех
результатов измерений ?
Для
всех m-повторностей можно записать:
Разделив
это уравнение на число повторностей m,
получим после подстановки:
За
экспериментальную оценку истинного
значения (математического ожидания)
критерия оптимальности у принимается среднеарифметическая
оценкарезультатов
всех т повторностей:
Если
число m велико (m>?), то будет справедливо
равенство:
Таким
образом, при бесконечно большом числе
измерений истинное значение измеряемой
величины y равно среднеарифметическому
значению ? всех результатов произведённых
измерений: y=?, при m>?.
При
ограниченном числе измерений (m??)
среднеарифметическое значение y будет
отличаться от истинного значения, т.е.
равенство y=? будет неточным, а приближённым:
y?? и величину этого расхождения необходимо
оценить.
Если
в распоряжении исследователя имеется
только единичный результат измерения
yk,
то оценка истинного значения измеряемой
величины будет менее точной. чем
среднеарифметическая оценка при любом
числе повторностей: |y-?|<|y-yk|.
Появление
того или иного значения yk в процессе
измерения является случайным событием.
Функция плотности нормального
распределения случайной величины
характеризуется двумя параметрами:
·
истинным значением y;
·
среднеквадратичным отклонением ?.
а)
б)
Рисунок
— 1а — кривая плотности нормального
распределения; 1б — кривая плотности
вероятности нормально распределенной
случайной величины при различных
дисперсиях
Плотность
нормального распределения (рис. 1а)
симметрична относительно y и достигает
максимального значения при yk= y, стремится
к 0 при увеличении.
Квадрат
среднеквадратичного отклонения
называется дисперсией случайной величины
и является количественной характеристикой
разброса результатов вокруг истинного
значения y. Мера рассеяния результатов
отдельных измерений yk от среднего
значения ? должна выражаться в тех же
единицах, то и значения измеряемой
величины. В связи с этим в качестве
показателя разброса гораздо чаще
используют величину ?:
Значения
этой величины определяют форму кривой
распределения py. Площади под тремя
кривыми одинаковы, но при малых значения
? кривые идут более круто и имеют большее
значение py. С увеличением ? значение py
уменьшается и кривая распределения
растягивается вдоль оси y. Т.о. кривая 1
характеризует плотность распределения
случайной величины, воспроизводимость
которой в повторных измерениях лучше,
чем воспроизводимость случайных величин
имеющих плотность распределения 2, 4. На
практике не возможно произвести слишком
много замеров. Поэтому нельзя построить
нормальное распределение, чтобы точно
определить истинное значение y. В этом
случае хорошим приближением к истинному
значению можно считать ?, а достаточно
точной оценкой ошибки выборочную
дисперсию ??n, вытекающую из закона
распределения, но относящуюся к конечному
числу измерения. Такое название величины
??n объясняется тем, что из всего множества
возможных значений yk, т.е. из генеральной
совокупности выбирают лишь конечное
число значений равное m, называемых
выборкой, которая характеризуется
выборочным средним значением и выборочной
дисперсией.
Соседние файлы в папке planirovanie
- #
- #
- #
- #
- #
- #
Погрешности измерений
Под погрешностью
измерения будем понимать совокупность
всех ошибок измерения.
Ошибки измерений
можно классифицировать на следующие
виды:
— абсолютные и
относительные,
— положительные и
отрицательные,
— постоянные и
пропорциональные,
— грубые,
— случайные и
систематические,
— прочие.
Абсолютная
ошибкаединичного результата
измерения (Аy)
определяется как разность следующих
величин:
Аy
= yi
— yист.
yi
-y,
где: yi– единичный результат измерения;yист.– истинный результат измерения;y– среднее арифметическое значение
результата измерения (далее среднее).
Постоянной
называется абсолютная ошибка,
которая не зависит от значения измеряемой
величины (y y
).
Ошибка пропорциональная,
если названная зависимость существует.
Характер ошибки измерения (постоянная
или пропорциональная) определяется
после проведения специальных исследований.
Относительная
ошибкаединичного результата
измерения (Вy)
рассчитывается как отношение следующих
величин:
.
Из этой формулы
следует, что величина относительной
ошибки зависит не только от величины
абсолютной ошибки, но и от значения
измеряемой величины. При неизменности
измеряемой величины (y)
относительную ошибку измерения можно
уменьшить только за счет снижения
величины абсолютной ошибки (Аy).
При постоянстве абсолютной ошибки
измерения для уменьшения относительной
ошибки измерения можно использовать
прием увеличения значения измеряемой
величины.
Знак ошибки
(положительный или отрицательный)
определяется разницей между единичным
и полученным (средним арифметическим)
результатом измерения:
yi-y> 0 (ошибка
положительная);
yi-y< 0 (ошибка
отрицательная).
Грубая ошибкаизмерения (промах) возникает при нарушении
методики измерения. Результат измерения,
содержащий грубую ошибку, обычно
значительно отличается по величине от
других результатов. Наличие грубых
ошибок измерения в выборке устанавливается
только методамиматематической
статистики (при числе повторений
измерения n>2).
С методами обнаружения грубых ошибок
познакомьтесь самостоятельно в [3-6].
К случайным
ошибкамотносят ошибки, которые не
имеют постоянной величины и знака. Такие
ошибки возникают под действием следующих
факторов: не известных исследователю;
известных, но нерегулируемых; постоянно
изменяющихся.
Случайные
ошибки можно оценить только после
проведения измерений.
Количественной
оценкой модуля величины случайной
ошибки измерения могут являться следующие
параметры: выборочная дисперсия
единичных значений и среднего значения;
выборочные абсолютные стандартные
отклонения единичных значений и среднего
значения; выборочные относительные
стандартные отклонения единичных
значений и среднего значения; генеральная
дисперсия единичных значений
),
соответственно, и др.
Случайные ошибки
измерения невозможно исключить, их
можно только уменьшить. Один из основных
способов уменьшения величины случайной
ошибки измерения – это увеличение числа
(объема выборки) единичных измерений
(увеличение величины n).
Объясняется это тем, что величина
случайных ошибок обратно пропорциональна
величинеn, например:
.
Систематические
ошибки– это ошибки с неизменными
величиной и знаком или изменяющиеся по
известному закону. Эти ошибки вызываются
постоянными факторами. Систематические
ошибки можно количественно оценивать,
уменьшать и даже исключать.
Систематические
ошибки классифицируют на ошибки I,IIиIIIтипов.
К систематическим
ошибкам I типаотносят ошибки известного происхождения,
которые могут быть до проведения
измерения оценены путем расчета. Эти
ошибки можно исключить, вводя их в
результат измерения в виде поправок.
Примером ошибки такого типа является
ошибка при титрометрическом определении
объемной концентрации раствора, если
титрант был приготовлен при одной
температуре, а измерение концентрации
проводилось при другой. Зная зависимость
плотности титранта от температуры,
можно до проведения измерения рассчитать
изменение объемной концентрации
титранта, связанное с изменением его
температуры, и эту разницу учесть в виде
поправки в результате измерения.
Систематическиеошибки II типа– это ошибки известного происхождения,
которые можно оценить только в ходе
эксперимента или в результате проведения
специальных исследований. К этому типу
ошибок относят инструментальные
(приборные), реактивные, эталонные и др.
ошибки. Познакомьтесь с особенностями
таких ошибок самостоятельно в [5].
Любой прибор при
его применении в процедуре измерения
вносит в результат измерения свои
приборные ошибки. При этом часть этих
ошибок случайная, а другая часть –
систематическая. Случайные ошибки
приборов отдельно не оценивают, их
оценивают в общей совокупности со всеми
другими случайными ошибками измерения.
Каждый экземпляр
любого прибора имеет свою персональную
систематическую ошибку. Для того чтобы
оценить эту ошибку, необходимо проводить
специальные исследования.
Наиболее надежный
способ оценки приборной систематической
ошибки IIтипа – это сверка
работы приборов по эталонам. Для мерной
посуды (пипетка, бюретка, цилиндры и
др.) проводят специальную процедуру –
калибровку.
На практике наиболее
часто требуется не оценить, а уменьшить
или исключить систематическую ошибку
IIтипа. Самыми распространенными
методами уменьшения систематических
ошибок являютсяметоды релятивизации
и рандомизации. Познакомьтесь с
этими методами самостоятельно в [5].
К ошибкам III
типаотносят ошибки неизвестного
происхождения. Эти ошибки можно обнаружить
только после устранения всех систематических
ошибокIиIIтипов.
К прочим ошибкамотнесем все другие виды ошибок, не
рассмотренные выше (допускаемые,
возможные предельные ошибки и др.).
Понятие возможных предельных ошибок
применяется в случаях использования
средств измерения и предполагает
максимально возможную по величине
инструментальную ошибку измерения
(реальное же значение ошибки может быть
меньше величины возможной предельной
ошибки).
При использовании
средств измерения можно рассчитать
возможную предельную абсолютную ()
или относительную ()
погрешность измерения. Так, например,
возможная предельная абсолютная
погрешность измерения находится как
сумма возможных предельных случайных
()
и неисключенных систематических ()
ошибок:
=
+
При выборках малого
объема (n20)
неизвестной генеральной совокупности,
подчиняющейся нормальному закону
распределения, случайные возможные
предельные ошибки измерений можно
оценить следующим образом:
=
=
,
где:
– доверительный интервал для
соответствующей вероятностиР;
–квантиль
распределения Стьюдента для вероятности
Ри выборки объемомn или при
числе степеней свободыf
= n – 1.
Абсолютная возможная
предельная погрешность измерения в
этом случае будет равна:
=
+
.
Если результаты
измерений не подчиняются нормальному
закону распределения, то оценка
погрешностей проводится по другим
формулам.
Определение
величины
зависит от наличия у средства
измерения класса точности. Если средство
измерения не имеет класса точности, тоза величину
можно принять минимальную цену
деления шкалы(или ее половину) средства
измерения [5]. Для средства измерения с
известным классом точности за величинуможно принять абсолютнуюдопускаемуюсистематическую ошибку средства
измерения ():
.
Величина
рассчитывается исходя из формул,
приведенных в табл. 2.
Для многих средств
измерения класс точности указывается
в виде чисел а10n, гдеаравно 1; 1,5; 2; 2,5; 4; 5; 6 иnравно 1; 0; -1; -2 и т.д., которые показывают
величину возможной предельной допускаемой
систематической ошибки (Еy,
доп.) и специальных знаков,
свидетельствующих о ее типе (относительная,
приведенная, постоянная, пропорциональная).
Если известны
составляющие абсолютной систематической
ошибки среднего арифметического
результата измерения (например, приборная
ошибка, ошибка метода и др.), то ее можно
оценить по формуле
,
где: m– число
составляющих систематическую ошибку
среднего результата измерения;
k– коэффициент,
определяемый вероятностьюРи числомm;
–абсолютная
систематическая ошибка отдельной
составляющей.
Отдельными
составляющими погрешности можно
пренебрегать при выполнении соответствующих
условий.
Таблица 2
Примеры обозначения
классов точности средств измерения
|
Обозначение точности |
Формула |
Характеристика |
|
|
в |
на |
||
|
1,5 |
1,5 |
|
Приведенная |
|
|
1 |
|
Приведенная |
|
|
0,5 |
|
Постоянная |
|
0,02/ 0,01 |
0,02/ 0,01 |
c |
Пропорциональная |
Систематическими
ошибками можно пренебрегать, если
выполняется неравенство
0,8.
В этом случае
принимают
.
Случайными ошибками
можно пренебречь при условии
8.
Для этого случая
.
Чтобы общая
погрешность измерения определялась
только систематическими ошибками,
увеличивают число повторных измерений.
Минимально необходимое для этого число
повторных измерений (nmin) можно
рассчитать только при известном значении
генеральной совокупности единичных
результатов по формуле

Оценка погрешностей
измерения зависит не только от условий
измерения, но и от типа измерения (прямое
или косвенное).
Деление измерений
на прямые и косвенные достаточно условно.
В дальнейшем под прямыми измерениямибудем понимать измерения значения
которых берут непосредственно из опытных
данных, например, считывают
со шкалы прибора (широко известный
пример прямого измерения –измерение
температуры термометром). Ккосвенным
измерениям будем относить
такие, результат которых получают на
основании известной зависимости между
искомой величиной и величинами,
определяемыми в результате прямых
измерений. При этомрезультаткосвенного измеренияполучают расчетным
путемкак значение функции,аргументами которой являются результаты
прямых измерений (x1,x2,
…,xj,.…,xk).
Необходимо знать,
что ошибки косвенных измерений всегда
больше, чем ошибки отдельных прямых
измерений.
Ошибки косвенных
измеренийоцениваются по
соответствующим законам накопления
ошибок (приk2).
Закон накопления
случайных ошибоккосвенных измерений
выглядит следующим образом:
.
Закон накопления
возможных предельных абсолютных
систематических ошибок косвенных
измерений представляется следующими
зависимостями:
;
.
Закон накопления
возможных предельных относительных
систематических ошибоккосвенных
измерений имеет следующий вид:
;
.
В случаях, когда
искомая величина (y) рассчитывается
как функция результатов нескольких
независимых прямых измерений вида,
закон накопления предельных относительных
систематических ошибок косвенных
измерений принимает более простой вид:
;
.
Ошибки и погрешности
измерений определяют их точность,
воспроизводимость и правильность.
Точностьтем
выше, чем меньше величина погрешности
измерения.
Воспроизводимостьрезультатов измерений улучшается при
уменьшении случайных ошибок измерений.
Правильность
результата измерений увеличивается
с уменьшением остаточных систематических
ошибок измерений.
Более
подробно с теорией ошибок измерений и
их особенностями познакомьтесь
самостоятельно [4,5]. Обращаю ваше внимание
на то, что современные формы представления
конечных результатов измерений
обязательно требуют приведения ошибок
или погрешностей измерения (вторичных
данных). При этом погрешности и ошибки
измерений должны представляться числами,
которые содержат не более двух
значащих цифр
[3].
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ УНИТАРНОЕ ПРЕДПРИЯТИЕ
ВСЕРОССИЙСКИЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ МЕТРОЛОГИЧЕСКОЙ СЛУЖБЫ (ВНИИМС)
РЕКОМЕНДАЦИИ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ.
РЕЗУЛЬТАТЫ И ХАРАКТЕРИСТИКИ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ.
ФОРМЫ ПРЕДСТАВЛЕНИЯ. СПОСОБЫ ИСПОЛЬЗОВАНИЯ ПРИ ИСПЫТАНИЯХ ОБРАЗЦОВ ПРОДУКЦИИ И КОНТРОЛЕ ИХ ПАРАМЕТРОВ
МИ 1317-2004
Разработана Федеральным государственным унитарным предприятием Всероссийский научно-исследовательский институт метрологической службы (ФГУП ВНИИМС)
Исполнители
М.А. Земельман, канд. техн. наук (руководитель темы); В.Г. Цейтлин, канд. техн. наук; В.М. Кашлаков, канд. техн. наук; В.П. Кузнецов, канд. техн. наук; Н.П. Миф, канд. техн. наук; В.А. Брюханов, канд. техн. наук; В.И. Гронский, канд. техн. наук; И.М. Тронова
Утверждена ФГУП ВНИИМС 20 декабря 2004 г.
Зарегистрирована ФГУП ВНИИМС 28 декабря 2004 г.
Взамен МИ 1317-86
Настоящая рекомендация распространяется на нормативные, методические и технические документы (проектно-конструкторскую и технологическую документацию, стандарты, технические условия, технические задания, отчеты, протоколы, программы, документы на методики испытаний и контроля образцов продукции, руководящие документы, руководящие технические материалы, документы на методики выполнения измерений), техническую литературу, в которых указывают требования к измерениям или описывают измерения, проводимые в научных исследованиях; при разработке, производстве, эксплуатации продукции; при охране окружающей природной среды; в здравоохранении и др.
Рекомендация устанавливает формы представления результатов измерений, характеристики погрешности измерений и формы их представления для всех возможных случаев применения, а также способы использования характеристик погрешности измерений для определения характеристик погрешности таких испытаний и достоверности такого контроля параметров образцов (проб) продукции, которые проводят с помощью измерений.
В рекомендации использованы ссылки на следующие нормативные документы:
ГОСТ 8.009-84 Государственная система обеспечения единства измерений. Нормируемые метрологические характеристики средств измерений;
ГОСТ Р 8.563-96 Государственная система обеспечения единства измерений. Методики выполнения измерений;
В связи с утратой силы ГОСТ Р 8.563-96, следует руководствоваться принятым взамен ГОСТ Р 8.563-2009
РД 50-453-84 Государственная система обеспечения единства измерений. Характеристики погрешности средств измерений в реальных условиях эксплуатации. Методы расчета;
РМГ 29-99 Государственная система обеспечения единства измерений. Метрология. Основные термины и определения.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1 Непосредственной целью измерений является определение истинных значений постоянной или изменяющейся измеряемой величины. Результат измерений является реализацией случайной величины, равной сумме истинного значения измеряемой величины и погрешности измерений.
Примечание — В качестве измеряемых величин принимают параметры модели объекта измерений. Общие рекомендации по выбору измеряемых величин даны в приложении А.
1.2 Термины «результат измерений» и «погрешность измерений» — в соответствии с РМГ 29.
1.3 Наименьшие разряды числовых значений результатов измерений принимают такими же, как и наименьшие разряды числовых значений среднего квадратического отклонения абсолютной погрешности измерений или числовых значений границ, в которых находится абсолютная погрешность измерений (или статистических оценок этих характеристик погрешности).
близкий к нормальному усеченному, если имеются основания предполагать, что реальная функция плотности распределения функция симметричная, одномодальная, отличная от нуля на конечном интервале значений аргумента, и другая информация о плотности распределения отсутствует.
1.4.1 Если имеется информация о том, что хотя бы одно из указанных в 1.4 условий не выполнено, принимают другую аппроксимацию функции плотности распределения вероятностей погрешности измерений, более соответствующую решаемой измерительной задаче.
1.4.2 В качестве функции плотности распределения вероятностей составляющих погрешности измерений, для которых известны только пределы допускаемых значений, т.е. границы интервала, в пределах которых находится соответствующая составляющая погрешности измерений с вероятностью 1, при расчетах характеристик погрешности измерений принимают закон равномерной плотности, если отсутствует информация об ином виде распределения.
1.5 Для расчета характеристик погрешности измерений при проектировании или аттестации методик выполнения измерений (далее — МВИ) по ГОСТ Р 8.563 в общем случае используют:
— метрологические характеристики средств измерений, нормированные по ГОСТ 8.009;
— характеристики влияющих величин, определяющие условия измерений, в частности, условия применения средств измерений;
— характеристики объекта измерений, влияющие на погрешность измерений.
1.6 Наряду с указанными в настоящей рекомендации можно использовать характеристики погрешности измерений, которые являются функциями характеристик, приведенных в разделе 2.
2. ХАРАКТЕРИСТИКИ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
1.7 Основные обозначения, принятые в настоящей рекомендации, приведены в приложении В.
2.1 Настоящая рекомендация устанавливает следующие группы характеристик погрешности измерений:
выполняемых по одной и той же аттестованной МВИ — приписанные характеристики погрешности измерений.
2.1.3 Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений).
2.2 При массовых технических измерениях, выполняемых при технологической подготовке производства, в процессах разработки, испытаний, производства, контроля и эксплуатации (потребления) продукции, при товарообмене, торговле и др., преимущественно применяют нормы погрешности измерений, а также приписанные характеристики погрешности измерений (по 2.1.1 и 2.1.2). Они представляют собой вероятностные характеристики (характеристики генеральной совокупности) случайной величины — погрешности измерений.
2.3 При измерениях, выполняемых при проведении научных исследований и метрологических работ (определение физических констант, свойств и состава стандартных образцов, индивидуальном исследовании средств измерений и т. п.), преимущественно применяют статистические оценки погрешности измерений (по 2.1.3.). Они представляют собой статистические (выборочные) характеристики случайной величины — погрешности измерений.
2.4 Рекомендация устанавливает следующие альтернативные вероятностные и статистические характеристики погрешности измерений:
среднее квадратическое отклонение погрешности измерений;
границы, в пределах которых погрешность измерений находится с заданной вероятностью;
характеристики случайной и систематической составляющих погрешности измерений.
Примечание:
1. Возможны случаи, когда границам погрешности измерений приписывают вероятность, равную единице.
2. Математическое ожидание погрешности измерений не рассматривают в качестве характеристики погрешности измерений, так как оно представляет собой систематическую погрешность, и если ее значение известно, то на нее в результат измерений вводят поправку.
2.4.1 В качестве характеристик случайной составляющей погрешности измерений используют: среднее квадратическое отклонение случайной составляющей погрешности измерений и (при необходимости) нормализованную автокорреляционную функцию случайной составляющей погрешности измерений или характеристики этой функции.
2.4.2 В качестве характеристик систематической составляющей погрешности измерений используют: среднее квадратическое отклонение неисключенной систематической составляющей погрешности измерений или границы, в которых неисключенная систематическая составляющая погрешности измерений находится с заданной вероятностью (в частности, с вероятностью, равной единице).
2.5 Характеристики погрешности измерений по 2.1.1, 2.1.2,2.1.3. приведены в таблице 1.
2.6 При необходимости средние квадратические отклонения случайной и (или) неисключенной систематической составляющих погрешности измерений сопровождают указанием принятой аппроксимации закона распределения вероятностей погрешности или его качественным описанием (например, симметричный, одномодальный и т.п.).
2.7 В случаях, когда результаты измерений (испытаний) используют (могут быть использованы) совместно с другими результатами измерений, а также при расчетах погрешностей величин, функционально связанных с результатами измерений (например, критериев эффективности, функций потерь, результатов косвенных измерений и др.), в качестве характеристик погрешности измерений применяют, в основном, точечные характеристики погрешности — средние квадратические отклонения погрешности.
В случаях, когда результаты измерений являются окончательными, пригодными для решения определенной технической задачи и не предназначены для совместного использования с другими результатами измерений и для расчетов, применяют, в основном, интервальные характеристики погрешности — границы, в пределах которых погрешность находится с известной (заданной) вероятностью.
Примеры к 2.7:
Пример 1 — Требования к погрешности измерений задают с целью ограничения потерь, вызываемых этой погрешностью. Функция потерь, вызванных погрешностью измерений, имеет квадратичный или V-образный вид. В этом случае погрешность измерений целесообразно задавать допускаемым значением среднего квадратического отклонения, т. к. именно эта характеристика однозначно связана с потерями (с математическим ожиданием потерь) независимо от вида распределения погрешности измерений.
Пример 2 — Оцениваемую погрешность измерений текущих (мгновенных) значений изменяющейся измеряемой величины используют для расчета погрешности средних величин или технико-экономических показателей за различные интервалы времени. В этом случае целесообразно оценивать следующие характеристики погрешности измерений текущих значений: среднее квадратическое отклонение случайной составляющей и интервал корреляции автокорреляционной функции этой составляющей, а также среднее квадратическое отклонение неисключенной систематической составляющей. Оценки таких характеристик дают возможность учесть влияние интервала времени усреднения и числа наблюдений на случайную составляющую погрешности средних значений.
Таблица 1
| Характеристики погрешности измерений | Нормы (по 2.1.1) | Приписанные (по 2.1.2) | Статистические оценки (по 2.1.3.) |
| 1 | 2 | 3 | 4 |
| Среднее квадратическое отклонение погрешности измерений | Предел допускаемых значений |
Наибольшее возможное значение |
Оценка |
| Границы, в которых погрешность измерений находится с заданной вероятностью | Нижняя |
Нижняя |
Оценка нижней |
| Характеристики случайной составляющей погрешности измерений: среднее квадратическое отклонение | Предел допускаемых значений |
Наибольшее возможное значение |
Оценка |
| Нормализованная автокорреляционная функция | Нормализованная функция |
Приписанная функция |
Оценка функции |
| Характеристики нормализованной автокорреляционной функции (например, интервал корреляции) | Нижний и (или) верхний пределы допускаемых значений характеристики | Наибольшее и (или) наименьшее возможные значения характеристики | Оценка характеристики |
| Характеристики неисключенной систематической составляющей погрешности измерений: | |||
| среднее квадратическое отклонение неисключенной систематической составляющей | Предел допускаемых значений |
Наибольшее возможное значение |
Оценка |
| границы, в которых неисключенная систематическая составляющая находится с заданной вероятностью | Нижняя |
Нижняя |
Оценка нижней |
Примечания к таблице 1
1. При одинаковых числовых значениях (без учета знаков) нижних и верхних границ характеристик погрешности указывают одно числовое значение, ставя перед ним знаки ±. В противном случае границы указывают отдельно каждую со своим знаком.
2. В таблице приведены обозначения для характеристик абсолютной погрешности измерений. Для обозначения характеристик относительной погрешности измерений букву заменяют на
(в том числе в индексах).
3. Рекомендуемое значение вероятности (доверительной вероятности) Р=0,95.
4. Пределы допускаемых значений характеристик погрешности определяют интервал, в котором находится данная характеристика, т.е. они соответствуют вероятности нахождения характеристики в данном интервале, равной единице.
5. Если вероятность, для которой нормированы границы допускаемого интервала погрешности измерений (графа 2), равна единице (Р=1), т.е. ни одна из реализаций погрешности измерений не должна выходить за эти границы, то их можно называть пределами допускаемых значений и при этом вероятность Р=1 не указывать.
Пример 3 — Определяют уставки технологической защиты, срабатывающей, когда результат однократного измерения превышает значение уставки. В этом случае для представления о возможности неблагоприятных последствий ограниченной точности измерений (ложного срабатывания или несрабатывания в аварийной ситуации) учитывают границы погрешности измерений. Для подобного учета погрешность измерений целесообразно задавать границами допускаемых значений с заданной вероятностью.
2.8. При условиях, приведенных в 1.4, расчет интервальных характеристик погрешности измерений для заданных вероятностей, меньших единицы, по среднему квадратическому отклонению погрешности может быть проведен в соответствии с приложением Б.
Методика, изложенная в приложении Б, основана на использовании вместо неизвестного реального закона распределения вероятностей погрешности (удовлетворяющего условиям 1.4) такого закона, который дает средние (для класса симметричных одномодальных усеченных законов распределений) значения определяемых характеристик. При этом погрешности получаемых характеристик — наименьшие среди получаемых для всех других возможных видов симметричных одномодальных усеченных распределений. Эти погрешности также приведены в приложении Б.
2.9. При оформлении результатов измерений, связанных с международными работами (международные сличения эталонов, поверка или калибровка средств измерений для зарубежных стран), а также с исследованиями первичных государственных эталонов, вместо характеристик погрешности измерений может быть использована неопределенность измерений (приложение Г) в соответствии с международной рекомендацией «Guide to the expression of uncertainty in measurement». В этом случае среднее квадратическое отклонение погрешности измерений (п.2.4) эквивалентно стандартной неопределенности (standard uncertainty 2.3.1 «Guide») или суммарной стандартной неопределенности (combined standard uncertainty 2.3.4 «Guide»); границы, в которых погрешность измерений находится с заданной вероятностью (п.2.4) эквивалентны расширенной неопределенности (expanded uncertainty 2.3.5 «Guide»).
3. ФОРМЫ ПРЕДСТАВЛЕНИЯ ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИИ
3.1. Погрешность измерений по 2.1.1 и 2.1.2 представляют характеристиками из числа приведенных в графах 2, 3 таблицы 1 с указанием совокупности условий, для которых принятые характеристики действительны. В состав этих условий могут входить: диапазон значений измеряемой величины; частотные спектры измеряемой величины, или диапазон скоростей ее изменений, или частотные спектры, диапазоны скоростей изменений параметров, функционалом которых является измеряемая величина; диапазоны значений всех величин, существенно влияющих на погрешность измерений (средств измерений), а также при необходимости и другие факторы.
3.1.1 Характеристики погрешности измерений указывают в единицах измеряемой величины (абсолютные) или процентах (долях) от результатов измерений (относительные).
Примеры к 3.1:
Пример 1 — Запись в техническом задании на разработку МВИ расхода жидкости (норма).
Норма на абсолютную погрешность измерений расхода жидкости: Условия, при которых погрешность измерений должна находиться в заданных границах: диапазон значений измеряемого расхода
температура жидкости от 15 до 30°С, кинематическая вязкость жидкости от
Пример 2 — Запись в аттестате МВИ добротности катушки индуктивности (приписанная погрешность).
Наибольшее возможное значение среднего квадратического отклонения случайной составляющей абсолютной погрешности измерений наибольшее возможное значение среднего квадратического отклонения неисключенной систематической составляющей абсолютной погрешности измерений
Условия, для которых определены характеристики погрешности измерений: диапазон значений измеряемой добротности от 50 до 80; диапазон частот тока, протекающего через катушку, от 50 до 300 Гц; диапазон температур среды, окружающей катушку и применяемые средства измерений, от 15 до 25 °С; коэффициент нелинейных искажений тока не более 1 %.
Примечание
При практических записях характеристик погрешностей измерений необязательно каждый раз записывать словами название характеристики и условия, которым они соответствуют. Целесообразно записывать их условными обозначениями, приложив отдельный список обозначений.
При регистрации характеристик погрешности измерений с помощью автоматических устройств рекомендуется обозначать характеристики словами и не использовать условные обозначения.
3.2. Статистические оценки характеристик погрешности измерений по 2.1.3. представляют одной или при необходимости несколькими характеристиками из числа приведенных в графе 4 таблицы 1. Дополнительно могут быть указаны частотный спектр или скорость изменения измеряемой величины, или частотный спектр, скорость изменения параметров, функционалом которых является измеряемая величина; значения или диапазоны значений существенно влияющих величин, а также при необходимости и другие факторы, характеризующие проведенные измерения.
Примечание
Каждую статистическую оценку характеристики погрешности измерений относят к определенному результату измерений.
3.2.1. Статистические оценки характеристик погрешности измерений указывают в единицах измеряемой (абсолютные) или в процентах (долях) от результата измерений (относительные).
3.3. Характеристики погрешности измерений и их статистические оценки могут быть указаны в виде постоянных величин или как функции времени, измеряемой или другой величины в виде формулы, таблицы, графика.
3.4. Характеристики погрешности и их статистические оценки выражают числом, содержащим не более двух значащих цифр. При этом для статистических оценок характеристик третий разряд (неуказываемый младший) округляют в большую сторону. Допускается характеристики погрешности и их статистические оценки выражать числом, содержащим одну значащую цифру. В этом случае для статистических оценок характеристик число получают округлением в большую сторону, если цифра последующего неуказываемого младшего разряда равна или больше пяти, или в меньшую сторону, если эта цифра меньше пяти.
3.5. Характеристики погрешности измерений и условия, для которых они действительны, указывают совместно с результатом измерений, к которому их относят, или совместно с группой результатов измерений, к которым их относят, или в свидетельстве о аттестации МВИ, по которой получены данные результаты измерений.
4. ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
4.1. Результат измерений представляют именованным или неименованным числом.
| Пример | — 100 кВт; 20 °С — именованные числа; |
| 0,44; 2,765 — неименованные числа. |
4.2. Совместно с результатом измерений представляют характеристики его погрешности или их статистические оценки. Если результат измерений или определенная группа результатов измерений получены по аттестованной МВИ, то их можно сопровождать вместо характеристик погрешности измерений ссылкой на свидетельство об аттестации МВИ, удостоверяющее характеристики погрешности получаемых при использовании данной МВИ результатов измерений и условия ее применимости.
4.2.1. Если результат измерений получен по такой МВИ, когда характеристики погрешности измерений оценены в процессе самих измерений или непосредственно после или перед ними, результат сопровождают статистическими оценками характеристик погрешности измерений.
4.3. Допускается представление результата измерений доверительным интервалом, покрывающим с известной (указываемой) доверительной вероятностью истинное значение измеряемой величины. В этом случае статистические оценки характеристик погрешности измерений отдельно не указывают.
Примечание — Такая форма представления результатов измерений допускается в случаях, когда характеристики погрешности измерений заранее не установлены и погрешность измерений оценивают в процессе самих измерений или непосредственно после или перед ними.
4.4. Совместно с результатом измерений при необходимости приводят дополнительные к указанным в 3.1 данные.
4.4.1. Представление результатов измерений изменяющейся во времени измеряемой величины при необходимости сопровождают указаниями моментов времени, соответствующих каждому из представленных результатов измерений. При этом началом шкалы времени может служить любой момент времени, принятый для данного эксперимента в качестве начального.
4.4.2. Представление результатов измерений, полученных как среднее арифметическое значение результатов многократных наблюдений, сопровождают указанием числа наблюдений и интервала времени, в течение которого они проведены. Если измерения, при которых получены данные результаты, проводят по МВИ, установленной в каком-либо документе, вместо указания числа наблюдений и интервала, допускается ссылка на этот документ.
4.4.3 При необходимости для правильной интерпретации результатов и погрешности измерений указывают, для данной МВИ модель объекта измерений и ее параметры, принятые в качестве измеряемых величин. Если измеряемую величину выражают функционалом, последний также указывают.
4.4.4 При необходимости результат измерений и характеристики погрешности измерений сопровождают указанием соответствия (или несоответствия) характеристик погрешности нормам точности измерений, если они заданы.
Примеры к 4.4:
Пример 1 — Запись в протоколе результата измерений расхода жидкости, полученного по аттестованной МВИ:
а) Результат измерений Условия измерений: температура жидкости 20 °С, кинематическая вязкость
б) Результат измерений Характеристики погрешности и условия измерений — в соответствии со свидетельством об аттестации МВИ N 17 от 05.07.2003 г.
Пример 2 — Запись в протоколе результата измерений расхода жидкости, полученного по неаттестованной МВИ. Статистические оценки характеристик погрешности измерений определены в процессе измерений:
а) Результат измерений Условия измерений: температура жидкости 20°С, кинематическая вязкость
б)Значение измеряемого расхода — в интервале с доверительной вероятностью 0,95. Условия измерений: температура жидкости 20°С, кинематическая вязкость
Пример 3 — Запись в протоколе результатов измерений изменяющегося электрического напряжения u(t), полученных по аттестованной МВИ:
| U(t), В | 7,55 | 3,15 | -0,35 | -0,50 | -4,70 | -1,57 |
| t, с | 0 | 1 | 2 | 3 | 4 | 5 |
Характеристики погрешности и условия измерений — в соответствии со свидетельством об аттестации МВИ N 5 от 17.01.2003 г.
Пример 4 — Запись в протоколе результата измерений, полученного как среднее арифметическое результатов наблюдений температуры по аттестованной МВИ:
Результат измерений 263,7 °С. Число наблюдений — 50, в течение 49 мин. Характеристики погрешности и условия измерений — в соответствии со свидетельством об аттестации МВИ N 13 от 23.01.2003 г.
5. ИСПОЛЬЗОВАНИЕ РЕЗУЛЬТАТОВ И ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ПРИ ИСПЫТАНИЯХ И КОНТРОЛЕ ПАРАМЕТРОВ ОБРАЗЦОВ (ПРОБ) ПРОДУКЦИИ
5.1 В настоящей рекомендации рассматриваются следующие области использования измерений.
далее — параметров условий испытаний); данную экспериментальную операцию в настоящей рекомендации называют испытаниями образца объекта (далее — образца).
5.1.2 Контроль параметра образца (пробы) на соответствие требованию, заданному в виде где х — истинное значение контролируемого параметра образца;xh, и xl- верхняя и нижняя границы допускаемых значений параметра х, соответственно;
— параметры условий контроля;
— номинальные значения параметров условий контроля; m — количество существенно влияющих и, следовательно, учитываемых условий контроля.
Примечание — Рассматриваются только однопараметровые испытания и контроль.
5.2 За результат испытаний образца принимают результат измерений параметра, определяемого при испытаниях, при фактически установленных значениях параметров условий испытаний. Результат испытаний сопровождают указанием характеристик погрешности испытаний (или статистических оценок характеристик), а также номинальных значений параметров условий испытаний и действительных или допускаемых характеристик погрешности задания этих параметров (или статистических оценок характеристик) или ссылкой на документ, где они указаны.
5.3 За погрешность испытаний образца принимают разность между результатом измерений параметра, определяемого при испытаниях образца продукции, полученным при фактических условиях испытаний, и истинным значением определяемого параметра, которое он имеет при параметрах условий испытаний, точно равных своим номинальным значениям или тем значениям, при которых требуется определять параметр образца. Определенная таким образом погрешность испытаний характеризует степень достижения цели испытаний по 5.1.1.
5.4 Результатом контроля параметра образца (или контроля образца) является суждение о том, находится или не находится значение контролируемого параметра образца в заданных границах. Результат контроля сопровождают указанием показателей достоверности контроля, а также номинальных значений параметров условий контроля и характеристик погрешности задания этих параметров (или статистических оценок характеристик), или ссылкой на документ, где они указаны.
5.5 В качестве характеристик погрешности испытаний образцов используют характеристики, аналогичные приведенным в таблице 1 для погрешности измерений.
5.6 Математическое определение погрешности испытаний образцов продукции приведено в приложении Д.
5.7 В настоящей рекомендации рассматриваются две группы показателей достоверности контроля образцов:
или наибольшая для отдельного образца) вероятность ошибочного отнесения к дефектным в действительности годных образцов; наибольшее отклонение контролируемого параметра от номинального значения у образцов, ошибочно признанных годными.
5.7.2 Вероятность неправильности суждения о годности образца, признанного по результатам контроля годным; вероятность неправильности суждения о дефектности образца, признанного по результатам контроля дефектным.
Примечание — Показатели по 5.7.1 относят к методикам измерительного контроля, предусматривающим фиксацию только результата контроля («годен» — «не годен»), и к устройствам допускового контроля. Показатели по 5.7.2 относят к методикам измерительного контроля, предусматривающим фиксацию результата измерений контролируемого параметра образца.
5.8 Математические определения показателей достоверности измерительного контроля образцов продукции приведены в приложении Д.
5.9 Функциональные взаимосвязи показателей достоверности контроля параметра образца продукции с погрешностью измерений при контроле приведены в приложении Е.
5.10 Инженерные способы расчета характеристик погрешности испытаний образца продукции по известным характеристикам погрешности измерений параметра, определяемого при испытаниях, характеристикам функций влияния условий испытаний на определяемый параметр, характеристикам погрешностей воспроизведения номинальных условий испытаний приведены в приложении Ж.
5.11 Инженерные способы определения основных показателей достоверности методик контроля образцов продукции по известным характеристикам погрешности измерений при контроле и параметрам методик контроля приведены в приложении И.
ПРИЛОЖЕНИЕ А
КОНЕЧНЫЕ ЦЕЛИ ИЗМЕРЕНИЙ И РЕКОМЕНДАЦИИ ПО ВЫБОРУ ИЗМЕРЯЕМЫХ ВЕЛИЧИН
А.1 Измерения не являются самоцелью, а имеют определенную область использования, т.е. их проводят для достижения некоторого конечного результата. Конечный результат не обязательно представляет собой оценку истинного значения измеряемой величины. В зависимости от назначения измерений (для контроля параметров продукции, для испытаний образцов продукции с целью установления ее технического уровня, для учета материальных и энергетических ресурсов, для диагностики технического состояния машин и др.) конечный результат в том или ином виде отражает требуемую информацию о количественных свойствах явлений, процессов (в том числе, технологических), материальных объектов (материалов, полуфабрикатов, изделий и т.п.). В данном случае речь идет только о той информации, которая может быть получена путем измерений. Вследствие этого результат измерений следует рассматривать как промежуточный результат, и номенклатуру характеристик погрешности измерений выбирают, исходя из требуемого конечного результата (результат испытаний или контроля, результат оценки эффективности управления технологическим процессом и др.), методики его расчета, формы представления показателей достоверности конечного результата.
Для этого устанавливают функциональную взаимосвязь результата измерений и характеристик погрешности измерений с требуемым конечным результатом и характеристиками (показателями) его погрешности (достоверности). Например, для планирования процессов испытаний и измерительного контроля параметров продукции, проводимых путем измерений, устанавливают функциональную взаимосвязь результатов и характеристик погрешности измерений с результатами испытаний и измерительного контроля параметров образца продукции, а также с характеристиками погрешности испытаний и показателями достоверности измерительного контроля.
А.2 Для обоснованного планирования измерений и правильной интерпретации результатов и погрешности измерений на начальном этапе решения задачи измерений (например, при разработке МВИ) принимают определенную модель объекта измерений, достаточно адекватную (для решения данной технической задачи) свойствам объекта измерений. В качестве измеряемой величины выбирают такой параметр модели, который также наиболее близко соответствует данной цели измерений. Значение параметра модели, т.е. значение измеряемой величины, может быть выражено числом, функцией или функционалом. Это учитывают при разработке МВИ и при выборе средств измерений.
Пример А.1 — Объект измерений — вал. В соответствии с конечной задачей, решаемой путем измерений, и с априорной информацией о свойствах объекта в качестве модели вала принимают прямой круговой цилиндр. Параметр модели — измеряемая величина — диаметр окружности цилиндра в любом его поперечном сечении; его значение выражают числом.
Пример А.2 — Объект измерений — поршень грузопоршневого манометра. Цель измерений — определение эффективной площади поршня. В соответствии с априорной информацией о том, что поперечное сечение поршня может незначительно отличаться от круга, в качестве модели поршня принимают прямой цилиндр, поперечное сечение которого близко к кругу. Эффективную площадь поршня в некоторых случаях определяют по среднему диаметру его поперечного сечения. Соответственно цели измерений в качестве параметра модели — измеряемой величины — принимают средний диаметр поперечного сечения поршня. Значение измеряемой величины в данном случае можно выразить, например, функционалом вида , где
— диаметр имеющий угловую координату
т.е. функция аргумента a1 в угловых градусах.
Пример А.3 — Объект измерений — изменяющееся электрическое напряжение. Цель измерений — оценка мощности, которая может быть выделена в нагрузку. В соответствии с априорной информацией о том, что форма кривой напряжения близка к синусоидальной, в качестве модели напряжения принимают синусоидальное напряжение. Соответственно цели измерений в качестве параметра модели — измеряемой величины — принимают эффективное (действующее) значение напряжения.
Значение измеряемой величины выражают функционалом
где — амплитуда и круговая частота синусоидального напряжения. Если информация о форме кривой напряжения отсутствует, то в качестве модели напряжения, например, может быть принято случайно изменяющееся электрическое напряжение. Тогда значение измеряемой величины может быть выражено функционалом
где:
T — время интегрирования;
u(t) — реализация случайного процесса — функция времени t.
ПРИЛОЖЕНИЕ Б
МЕТОДИКА РАСЧЕТА ГРАНИЦ ИНТЕРВАЛА, В КОТОРОМ НАХОДИТСЯ ПОГРЕШНОСТЬ ИЗМЕРЕНИЙ С ЗАДАННОЙ ВЕРОЯТНОСТЬЮ, МЕНЬШЕЙ ЕДИНИЦЫ, ПО СРЕДНЕМУ КВАДРАТИЧЕСКОМУ ОТКЛОНЕНИЮ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Нижняя и верхняя
границы интервала, в котором погрешность измерений находится с заданной вероятностью Р, могут быть определены по формуле
(Б.1)
где:
К(Р) — коэффициент, зависящий от вероятности Р;
— среднее квадратическое отклонение погрешности измерений.
Если границы интервала рассчитывают по нормированному среднему квадратическому отклонению, то в формулу подставляют значение предела допускаемого среднего квадратического отклонения; при этом в результате расчета по формуле получают оценку сверху границ интервала.
При соблюдении условий 1.4 коэффициент К(Р) может быть определен по графику (рисунок Б.1)
Рисунок Б.1
При этом модуль наибольшей возможной относительной погрешности || коэффициента К(Р) также определяют по соответствующему графику(рисунок Б.1).
Графики дают результаты, идентичные получаемым по графику РД 50-453.
Если функция плотности распределения вероятностей погрешности измерений не удовлетворяет хотя бы одному из условий 1.4настоящей рекомендации, то границы интервала, в котором погрешность измерений находится с заданной вероятностью Р, могут быть рассчитаны по формуле (Б.1) (предварительно определяют функцию К(Р), соответствующую действительной функции плотности).
Для приближенных расчетов границ интервала в качестве оценок сверху коэффициента К(Р) в диапазоне значений вероятности Р от 0,9 до 0,98 может быть использована формула
(Б.2)
ПРИЛОЖЕНИЕ В
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
— абсолютная погрешность измерений;
— относительная погрешность измерений;
s — абсолютная систематическая составляющая погрешности измерений;
— абсолютная случайная составляющая погрешности измерений;
Р — вероятность;
— среднее квадратическое отклонение абсолютной погрешности измерений (ее составляющих);
х — контролируемый параметр
— отклонение контролируемого параметра от номинального значения;
— номинальное значение параметра;
— нижняя и верхняя границы допускаемых значений параметра х;
— оперативная характеристика;
— наибольшая вероятность ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца (для отдельного образца);
— наибольшее по абсолютному значению возможное отклонение контролируемого параметра любого образца, который при реализации данной методики контроля может быть ошибочно признан годным;
— наибольшая средняя по совокупности годных образцов вероятность ошибочного признания (при реализации данной методики контроля) дефектным в действительности годных образцов;
— средняя на совокупности всех контролируемых образцов вероятность ошибочного признания (при реализации данной методики контроля) дефектными в действительности годных образцов;
— наибольшая вероятность ошибочного признания (при реализации данной методики контроля) дефектным любого в действительности годного образца (для отдельного образца);
— вероятность ошибочности суждения о годности данного образца, признанного по результатам контроля годным (при уже полученном результате контроля);
— вероятность ошибочности суждения о дефектности данного образца, признанного по результатам контроля дефектным (при уже полученном результате контроля);
G — граница поля допуска для отклонения ;
— граница поля контрольного допуска, с которой сравнивают оценку
с целью принятия решения о годности или дефектности образца;
— граница такой области значений
для которой отрицательные результаты контроля (образец признают дефектным) принято считать ошибочным;
— вероятность того, что при полученной в результате измерений (при контроле) оценке
отклонения контролируемого параметра образца истинное значение
отклонения параметра находится в границах поля допуска;
— наибольшая возможная погрешность вероятности
обусловленная отличием реального вида функции плотности распределения вероятностей погрешности измерений от того вида функции плотности , которому соответствует график
на рисунке И 1;
— то же для графика Рbam на рисунке И.2;
— наибольшая возможная погрешность вероятности
обусловленная отличием реального вида функции плотности распределения вероятностей погрешности измерений от того вида функции плотности, которому соответствует график на рисунке И.3;
— то же для графика на рисунке И.4;
— плотность распределения вероятностей отклонения
на совокупности контролируемых образцов;
— плотность распределения вероятностей погрешности измерений при контроле.
Индексы
1 — нижняя (low),
h — верхняя (high),
g — годный (good),
b — дефектный (bad),
a — признанный годным (accepted),
г — признанный дефектным (rejected),
I — контролируемый (inspected),
ex — испытание (examination),
N — номинальное (nomina).
ПРИЛОЖЕНИЕ Г
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЙ
В 2.2.3 «Guide to the expression of uncertainty in measurement» (Первое издание ISO 1993, русский перевод «Руководство по выражению неопределенности измерений», С.-Петербург, ВНИИМ им. Д.И. Менделеева, 1993, далее Руководство) неопределенность измерений определена как «параметр, связанный с результатом измерения, который характеризует рассеяние значений, которые могли быть обоснованно приписаны измеряемой величине». В Руководстве рассматриваются измеряемые величины, характеризуемые единственным значением (1.2 Руководства).
Различие между погрешностью и неопределенностью измерений сводится к различию систем координат, относительно которых рассматривают истинное значение измеряемой величины и результат измерений. При рассмотрении погрешности измерений систему координат привязывают к истинному значению измеряемой величины, наблюдая рассеяние результата измерений (рисунок Г.1); при рассмотрении неопределенности измерений — к результату измерений, что и создает эффект рассеяния единственного значения измеряемой величины (рисунок Г.2)
Рисунок Г. 1
Рисунок Г.2
Обозначения на рисунках:
— результат измерений (
— реализации результата измерений — по 1.1 настоящей рекомендации);
— истинное значение измеряемой величины (
— реализация истинного значения измеряемой величины в системе координат, привязанной к результату измерений);
— погрешность измерений;
— плотность распределения вероятности результата измерений;
— плотность распределения вероятностей погрешности измерений;
— плотность распределения вероятностей единственного истинного значения измеряемой величины, наблюдаемая в системе координат, привязанной к результату измерений.
Таким образом, неопределенность измерений в соответствии с 2.2.3 Руководства может быть определена как параметр центрированной случайной величины, представляющей собой разность между истинным значением измеряемой величины и результатом измерений, т.е. величины, совпадающей по модулю с погрешностью измерений, но противоположной ей по знаку. Закон распределения вероятностей этой случайной величины представляет собой зеркальное отражение закона распределения вероятностей погрешности измерений. Количественно характеристики погрешности измерений и соответствующие виды неопределенности измерений совпадают (п.п. Е.5.3 и Е.5.4 Руководства).
ПРИЛОЖЕНИЕ Д
МАТЕМАТИЧЕСКИЕ ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ ИСПЫТАНИЙ И ПОКАЗАТЕЛЕЙ ДОСТОВЕРНОСТИ ИЗМЕРИТЕЛЬНОГО КОНТРОЛЯ ОБРАЗЦОВ ПРОДУКЦИИ
Д.1 Погрешность испытаний образца определяют по формуле
(Д.1)
где
— погрешность измерений параметра, определяемого при испытаниях;
i — погрешность воспроизведения или измерений i-гo параметра
условий испытаний;
— производная функции зависимости параметра, определяемого при испытаниях, от параметра
в точке
— номинальное значение параметра
;
* — символ объединения (суммирования) случайных величин (процессов);
m — количество учитываемых условий испытаний.
Д.2 Наибольшую вероятность ошибочного признания (при реализации данной методики измерительного контроля) годным любого в действительности дефектного образца определяют по формуле
(Д.2)
где — отклонение контролируемого параметра х образца от номинального значения хм, выраженное в единицах контролируемого параметра;
G — граница поля допуска для отклонения , определяющая годность или дефектность образца продукции по контролируемому параметру;
— оперативная характеристика — зависимость вероятности признания годным образца при его контроле от значения
Д.2.1 Отклонение определяют путем вычитания номинального значения
параметра контролируемого образца из действительного значения х параметра; нижнюю и верхнюю границы поля допуска (G1, Gh) для отклонений
определяют путем вычитания номинального значения
из границ (x1,xh) поля допускаемых значений параметра. Принято:
следовательно, Gh = -Gi = G.
Д.2.2 Вероятность Рbam — наибольшая из тех, которые могут иметь место при
Д.2.3 Оперативная характеристика ( отражает свойства методики контроля.
Д.3 Наибольшее по абсолютному значению возможное отклонение контролируемого параметра образца, который (при реализации данной методики измерительного контроля) может быть ошибочно признан годным, определяют по формуле
(Д.3)
где — условная (при условии, что
плотность распределения вероятностей оценки
отклонения
получаемой путем измерений при измерительном контроле;
Gr — граница поля контрольного допуска, с которой сравнивают оценку с целью принятия решения о годности или дефектности образца
Д.4 Наибольшая средняя для совокупности годных образцов вероятность ошибочного признания (при реализации данной методики измерительного контроля) дефектными в действительности годных образцов определяют по формуле
(Д.4)
где — граница такой области
значений
для которой отрицательные результаты измерительного контроля (образец признают дефектным) рекомендуется считать ошибочными
Д.4.1 Вероятность характеризует долю неверно забракованных в области с границами
образцов
в общем количестве (Ng) годных образцов:
(Д.4а)
Д.4.2 Формула (Д-4)»>Д.4) справедлива при равномерном законе распределения вероятностей отклонений по совокупности годных образцов и может быть использована для расчетов
— в тех случаях, когда закон распределения вероятностей отклонений по всем контролируемым образцам неизвестен. В случаях, когда закон распределения вероятностей отклонений
по всем контролируемым образцам задан (известен), более предпочтительным (по сравнению с
показателем достоверности контроля является средняя по совокупности всех контролируемых образцов вероятность (Pgr) ошибочного признания дефектными в действительности годных образцов, определяемая формулой
(Д.5)
где — плотность распределения вероятностей отклонений
по совокупности контролируемых образцов.
Д.4.3 Вероятность характеризует долю неверно забракованных в области с границами
образцов в общем количестве (NI) контролируемых образцов:
(Д.5а)
Д. 4.4 Выделение области т.е. введение в расчеты границы
имеет смысл в тех случаях, когда контролируемый параметр образца может после контроля измениться настолько, что вскоре после осуществления контроля возможен его выход за границы поля допуска. Ведение
учитывает заинтересованность заказчика в признании дефектными таких образцов, параметры которых, хотя и находятся в границах поля допуска, но близки к этим границам, и, следовательно, образцы вскоре могут потребовать ремонта. Если границу
не вводят, то в формуле (Д-4)»>Д.4) принимают
и формула (Д.4) принимает вид
(Д.6)
Д.4.5 Для отдельного образца наибольшую вероятность ошибочного признания (при реализации данной методики измерительного контроля) дефектным любого в действительности годного образца определяют по формуле
(Д.7)
при если вводится граница
если граница
не вводится
и считают наибольшей из тех, которые могут иметь место при
Д.5 Вероятность неправильности суждения о годности данного образца, признанного по результатам измерительного контроля годным, определяют по формуле
(Д.8)
а вероятность неправильности суждения о дефектности данного образца, признанного по результатам измерительного контроля дефектным, — по формуле
(Д.9)
где — вероятность того, что при полученной в результате измерений (при контроле) оценке
отклонения контролируемого параметра образца истинное значение
отклонения параметра находится в границах поля допуска, т.е.
Характеристика
отражает свойства методики измерительного контроля. Вероятности
могут быть использованы при оценке правильности уже полученного результата контроля параметра образца продукции.
ПРИЛОЖЕНИЕ Е
ФУНКЦИОНАЛЬНЫЕ СВЯЗИ ПОКАЗАТЕЛЕЙ ДОСТОВЕРНОСТИ КОНТРОЛЯ ПАРАМЕТРА ОБРАЗЦА ПРОДУКЦИИ С ПОГРЕШНОСТЬЮ ИЗМЕРЕНИЙ ПРИ КОНТРОЛЕ
Е.1 Функциональная связь наибольшей вероятности Рbam ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца (по Д.2) с погрешностью измерений при контроле определяется формулой
или
где — плотность распределения вероятностей погрешности измерений при контроле.
Е.2.Функциональная связь наибольшего возможного отклонения контролируемого параметра образца, который (при реализации данной методики измерительного контроля) может быть ошибочно признан годным, с погрешностью измерений при контроле (по Д.3) определяется формулой
Е.3 Функциональная связь наибольшей средней для совокупности годных образцов вероятности ошибочного признания (при реализации данной методики измерительного контроля) дефектными в действительности годных образцов (по Д.4) с погрешностью измерений при контроле определяется формулой
Если известен закон распределения вероятностей отклонений контролируемого параметра образца по всей совокупности контролируемых образцов, то целесообразно усреднить вероятность ошибочного признания дефектными в действительности годных образцов не по совокупности годных образцов, а по совокупности всех контролируемых образцов. Связь такой средней вероятности с погрешностью измерений при контроле определяется формулой
Если область не выделяют и границу
не вводят, то в формулах (Е.3) и (Е.4)
заменяют на G. При этом (Е.3) принимает вид
Связь наибольшей вероятности ошибочного признания (при реализации данной методики измерительного контроля) дефектным любого отдельного в действительности годного образца с погрешностью измерений при контроле определяют формулой
Е.4 Функциональную связь вероятности ошибочности суждения о годности данного образца, признанного по результатам измерительного контроля годным (при известной оценке
отклонения контролируемого параметра) (по Д.5), с погрешностью измерений при контроле определяется формулой
Связь вероятности ошибочности суждения о дефектности данного образца, признанного по результатам измерительного контроля дефектным (при известной оценке
отклонения контролируемого параметра), с погрешностью измерений при контроле определяется формулой
Е.5 В случаях, когда контроль проводят при одностороннем ограничении контролируемого параметра образца (xh — верхняя граница допускаемых значений параметра х; xl — нижняя граница значения параметра х) связь показателей достоверности контроля с погрешностью измерений определяется следующими формулами:
Е.5.1 Наибольшая вероятность PbaM ошибочного признания (при реализации данной методики измерительного контроля) годным любого в действительности дефектного образца:
а) при заданной области годности образцов х<= xh:
(E.9)
б) при заданной области годности образцов х >= хl:
(Е.10)
где — заданные границы результатов
измерений параметра х при контроле, при которых образец признают годным: для а) образец признают годным, если
для б) образец признают годным, если
Е.5.2 Наибольшее (хmax)ba или наименьшее (хmin)ba значения контролируемого параметра образца, который (при реализации данной методики измерительного контроля) может быть ошибочно признан годным:
а) при заданной области годности образцов х <= хh:
(Е.11)
б) при заданной области годности образцов х >= хl:
(Е.12)
Е.5.3 Средняя для совокупности контролируемых образцов вероятность ошибочного признания (при реализации данной методики измерительного контроля) дефектными в действительности годных образцов:
а) при заданной области годности образцов х <= хh:
(Е.13)
б) при заданной области годности образцов х >= xl:
Здесь — заданные границы областей таких значений параметров контролируемых образцов, для которых отрицательные результаты контроля (образец признают дефектным) принято считать ошибочными: для а) отрицательный результат контроля признают ошибочным, если х < хbh; для б) отрицательный результат контроля признают ошибочным, если х > xbl
когда при контроле не проводят измерений контролируемого параметра, т.е. результат и погрешность измерений контролируемого параметра отсутствуют, показатели достоверности контроля, характеризующие устройства допускового контроля, определяют приведенными выше формулами при замене в них погрешности k измерений при контроле на эквивалентную погрешность
устройства допускового контроля, определяемую формулой
(Е.15)
где — погрешность задания (индикации) границ поля контрольного допуска Gy (или, если контрольный допуск не вводят, то границ допуска G) на отклонение контролируемого параметра;
_c — погрешность сравнения контролируемого параметра (или его отклонения) с границами поля контрольного допуска (или допуска G).
Е.7 Для определения показателей достоверности уже полученного результата допускового контроля применяют формулы (Е.7) и (Е.8). При подстановке в них и
вместо
_k результаты расчета представляют собой наибольшие возможные вероятности ошибочности отдельного полученного результата допускового контроля.
Е.8 Формулы, определяющие связь других показателей достоверности контроля при одностороннем ограничении контролируемого параметра с погрешностью измерений, могут быть получены аналогично формулам (Е.3) — (Е.8) с учетом при необходимости условия по Е.6.
ПРИЛОЖЕНИЕ Ж
ИНЖЕНЕРНЫЕ СПОСОБЫ РАСЧЕТА ХАРАКТЕРИСТИК ПОГРЕШНОСТИ ИСПЫТАНИЙ ОБРАЗЦА ПРОДУКЦИИ ПО ИЗВЕСТНЫМ ХАРАКТЕРИСТИКАМ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ПАРАМЕТРА, ОПРЕДЕЛЯЕМОГО ПРИ ИСПЫТАНИЯХ, ХАРАКТЕРИСТИКАМ ФУНКЦИЙ ВЛИЯНИЯ УСЛОВИЙ ИСПЫТАНИЙ НА ОПРЕДЕЛЯЕМЫЙ ПАРАМЕТР, ХАРАКТЕРИСТИКАМ ПОГРЕШНОСТИ ВОСПРОИЗВЕДЕНИЯ НОМИНАЛЬНЫХ УСЛОВИЙ ИСПЫТАНИЙ
Ж.1 К определяемым характеристикам погрешности испытаний (по 5.1.1 настоящей рекомендации) отнесены:
наибольшее по абсолютной величине возможное значение , равное половине интервала, в котором погрешность испытаний находится с вероятностью, равной единице;
наибольшее возможное среднее квадратическое отклонение погрешности испытаний.
Ж.2 В соответствии с определением погрешности испытаний по Д.1 для расчета характеристик погрешности испытания могут быть применены следующие формулы:
Ж.2.1 Если в качестве исходных данных известны:
предел допускаемой погрешности измерений параметра, определяемого при испытаниях;
пределы допускаемой погрешности воспроизведения условий испытаний;
линейные аппроксимации функций влияния условий испытаний на параметр, определяемый при испытаниях, в точках номинальных значений условий испытаний,
то наибольшее по абсолютной величине возможное значение погрешности испытаний равно
(Ж.1)
где m — число учитываемых условий испытаний;
— малое отклонение 1-го условия
испытания от номинального значения
— малое изменение параметрах, определяемого при испытаниях, вызванное отклонением
Ж.2.2 Если в качестве исходных данных известны: предел допускаемого среднего квадратического отклонения погрешности измерений параметра, определяемого при испытаниях;
наибольшие возможные средние квадратические отклонения (или пределы допускаемых средних квадратических отклонений
) погрешности воспроизведения условий испытаний;
линейные аппроксимации функций вляния условий испытаний на параметр, определяемый при испытании, в точках номинальных значений условий испытаний,
то квадрат среднего квадратического отклонения погрешности испытаний равен
(Ж.2)
Примечание — Если погрешность испытаний, определение которой дано в Д.1, удовлетворяет условиям 1.4 настоящей рекомендации, то границы интервала, в котором погрешность испытаний находится с любой вероятностью, меньшей единицы, могут быть рассчитаны по известному в соответствии с приложением Б.
ПРИЛОЖЕНИЕ И
ИНЖЕНЕРНЫЕ СПОСОБЫ ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОКАЗАТЕЛЕЙ ДОСТОВЕРНОСТИ МЕТОДИК КОНТРОЛЯ ОБРАЗЦОВ ПРОДУКЦИИ ПО ИЗВЕСТНЫМ ХАРАКТЕРИСТИКАМ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ПРИ КОНТРОЛЕ И ПАРАМЕТРАМ МЕТОДИК КОНТРОЛЯ
И.1 Инженерные способы, рассматриваемые в данном приложении, применимы при соблюдении условий по 1.4 настоящей рекомендации.
И.2 К основным показателям достоверности контроля (по 5.7.1 настоящей рекомендации) образцов продукции отнесены:
И.2.1 Наибольшая вероятность РbaM ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца (по Е.1).
И.2.2 Наибольшее по абсолютному значению возможное отклонение контролируемого параметра любого образца продукции, который (при реализации данной методики контроля) может быть ошибочно признан годным (по Е.2).
И.2.3 Наибольшая средняя для совокупности годных образцов вероятность ошибочного признания (при реализации данной методики контроля) дефектными в действительности годных образцов (по Е.3).
И.3 К параметрам методик контроля образцов продукции отнесены:
И.3.1 Граница G поля допуска для отклонения контролируемого параметра х от номинального значения хN.
И.3.2 Граница поля контрольного допуска для отклонения
И.3.3 Граница такой области отклонений
, для которой отрицательные результаты контроля (образец признают дефектным) принято считать ошибочными.
Примечание — Взаимосвязь параметров методик контроля с показателями достоверности контроля определена в Д.3 и Д.4.
И.4 В качестве известных характеристик погрешности измерений принимают:
а) среднее квадратическое отклонение (его наибольшее возможное значение или предел допускаемого значения
),
б)интервал, в котором с вероятностью, равной единице, находится погрешность измерений, или пределы допускаемых погрешностей измерений
И.5 Наибольшую вероятность РbaM ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца определяют с помощью графика (рисунок И.1 или рисунок И.2 в зависимости от того, какая характеристика погрешности измерений задана или
p).
И.6 Наибольшую возможную погрешность вероятности РbaM обусловленную тем, что вид реальной функции плотности распределения вероятностей погрешности измерений неизвестен, определяют по графику (рисунок И.1) или графику
(рисунок И.2).
И.7 Наибольшее по абсолютному значению возможное отклонение контролируемого параметра любого образца, который (при реализации данной методики контроля) может быть ошибочно признан годным, определяют по формуле
(И.1)
или
(И.2)
в зависимости от того, какая характеристика погрешности измерений задана
Принимают К=3,5; тогда формула (И.1) дает при принятых условиях наибольшее возможное значение данного показателя.
Примечание — Если предполагают, что функция плотности распределения вероятностей погрешности измерений при контроле не только удовлетворяет условиям по 1.4 настоящей рекомендации, но отнесена к достаточно «тупым» функциям, лежащим в области между функцией плотности равномерного распределения и косинусоидальной функцией плотности распределения, то принимают К=2,5.
Рисунок И.1
Рисунок И.2
И.8 Наибольшую среднюю для совокупности годных образцов вероятность ошибочного признания (при реализации данной методики контроля) дефектными в действительности годных образцов определяют графо-аналитическим способом с помощью графика
(рисунок И.3) или графика
(рисунок И.4) в зависимости от того, какая характеристика погрешности измерений задана
Рисунок И.3
Рисунок И.4
Наибольшую возможную погрешность вероятности обусловленную тем, что вид реальной функции плотности распределения вероятностей погрешности измерений неизвестен, определяют графо-аналитическим способом по графику
(рисунок И.3) или по графику
(рисунок И.4).
И.10 Данные инженерные способы могут быть применены при допусковом контроле (результаты измерений и погрешности измерений отсутствуют). При этом, вместо характеристик погрешности измерений используют соответствующую характеристику величины (по Е.6), которую предварительно рассчитывают по техническим характеристикам средства контроля.
И.11 Показатели достоверности контроля образцов продукции, приведенные в приложении Е (кроме рассмотренных в данном приложении) могут быть определены по формулам приложения Е при известной функции (или принятой аппроксимации) плотности распределения вероятностей погрешности измерений при контроле (или величины ) и известных параметрах методики контроля. Также поступают, если погрешности определения показателей достоверности методик контроля образцов продукции по данному приложению для каких-либо случаев недопустимо велики.
И.12 Используя графики и формулы данного приложения, возможно подбирать необходимые параметры методик контроля и метрологические характеристики средств измерений и МВИ для контроля образцов продукции, а также необходимые параметры методик и технические характеристики средств допускового контроля образцов продукция по заданным наибольшим допускаемым показателям если соблюдены условия по 1.4 настоящей рекомендации.
Пример 1 — Заданы следующие параметры методики измерительного контроля и характеристики погрешности измерений: Требуется определить:
а) наибольшую вероятность РbaM ошибочного признания (при реализации данной методики контроля) годным любого в действительности дефектного образца;
б) наибольшее по абсолютному значению возможное отклонение контролируемого параметра любого образца, который (при реализации данной методики контроля) может быть ошибочно признан годным
в) наибольшую среднюю для совокупности годных образцов вероятность ошибочного признания (при реализации данной методики контроля) дефектными в действительности годных образцов
Решение
Вероятность РbaM и погрешность ее определения находят по графикам (рисунок И.1). Параметр равен 1,33. По графику РbaM находят, что приближенно
Для того же значения аргумента по другому графику находят, что погрешность
определения данной вероятности приближенно находится в интервале ± 0,02. Следовательно,
По формуле (И.1) находят
Вероятность и погрешность ее определения находят по графикам (рисунок И.3). Параметр
равен минус 0,67. По графику
находят, что приближенно эта величина равна 0,9.
Тогда = 0,14. Для того же значения аргумента по другому графику на том же рисунке находят, что приближенно величина
равна 0,01. Тогда погрешность, обусловленная отличием реальной функции плотности распределения от принятой средней, лежит в пределах
т.е. считают пренебрежимо мала.
Пример 2 — Заданы следующие параметры методики измерительного контроля и характеристики погрешности измерений: Требуется определить те же показатели достоверности контроля, что и в примере 1.
Решение
Вероятность РbaM и погрешность ее определения находят по рисунку И.2. Параметрравен 0,4. По графику РbaM приближенно находят РbaM = 0,13. Для того же значения аргумента по другому графику на том же рисунке находят, что погрешность (
Р)22 определения данной вероятности находится в интервале от — 0,13 до + 0,17 (так как вероятность отрицательной быть не может). Следовательно, 0<= РbaM .= 0,3.
По формуле (И.2) находят
Вероятность — и погрешность ее определения находят на основании графиков (рисунок И.4). Параметр
равен минус 0,2. По графику
находят, что приближенно эта величина равна 0,26. Тогда
=0,13. Для того же значения аргумента по другому графику на том же рисунке находят, что приближенно величина
Тогда погрешность определения находится в интервале ± 0,05, а сама вероятность лежит в интервале 0,08<=
>= 0,18.
Статьи
Главная страница

видно, что существует вероятность, пусть и очень маленькая, что наше единичное
измерение покажет результат, сколь угодно далеко отстоящий от истинного
значения. Выходом из положения является проведение серии измерений. Если на
разброс данных действительно влияет случай, то в результате нескольких
измерений мы скорее всего получим следующее (рис 2):
Будет ли
рассчитанное среднее значение нескольких измерений совпадать с истинным? Как
правило – нет. Но по теории вероятности, чем больше сделано измерений, тем
ближе найденное среднее значение к истинному. На языке математики это можно
записать так:
Но с бесконечностью у всех дело обстоит неважно. Поэтому на практике мы имеем дело
не со всеми возможными результатами измерений, а с некоторой выборкой из этого
бесконечного множества. Сколько же реально следует делать измерений? Наверное,
до тех пор, пока полученное среднее значение не будет отличаться от истинного
меньше чем точность отдельного измерения.
Следовательно,
когда наше среднее значение (рис. 2) отличается от истинного меньше чем
погрешность измерений, дальнейшее увеличение числа опытов бессмысленно. Однако
на практике мы не знаем истинного значения! Значит, получив среднее по
результатам серии опытов, мы должны определить, какова вероятность того, что
истинное значение находится внутри заданного интервала ошибки. Или каков тот
доверительный интервал, в который с заданной надежностью попадет истинное
значение (рис 3).
Рассмотрим
некоторый условный эксперимент, где в серии измерений получены некоторые
значения величины Х (см. табл. 1). Рассчитаем среднее значение и, чтобы оценить
разброс данных найдем величины DХ = Х –
Хср
|
Таблица |
||||||
|
№ |
Х |
Х ср |
DХ |
DХ2 |
s2 |
s |
|
1 |
130 |
143,5 » 144 |
-13,5 |
182,3 |
420 |
20,5 |
|
2 |
162 |
18,5 |
342,3 |
|||
|
3 |
160 |
16,5 |
272,3 |
s2ср |
sср |
|
|
4 |
122 |
-21,5 |
462,3 |
105 |
10,2 |
Ясно, что
величины DХ как-то характеризуют
разброс данных. На практике для усредненной характеристики разброса серии измерений используется
дисперсия выборки:
и среднеквадратичное или стандартное отклонение выборки:
Последнее
показывает, что каждое измерение в данной серии (в данной выборке) отличается
от другого в среднем на ± s.
Понятно, что каждое отдельное
значение оказывает влияние на средний результат. Но это влияние тем меньше, чем
больше измерений в нашей выборке. Поэтому дисперсия и стандартное отклонение
среднего значения, будет определяться по формулам:
Можем ли мы теперь определить вероятность того, что
истинное значение попадет в указанный интервал среднего? Или наоборот,
рассчитать тот доверительный интервал в который истинное значение
попадет с заданной вероятностью (95%)? Поскольку кривая на наших графиках это
распределение вероятностей, то площадь под кривой, попадающая в указанный
интервал и будет равна этой вероятности (доля площади, в процентах). А площади
математики научились рассчитывать хорошо, знать бы только уравнение этой
кривой.
И здесь мы сталкиваемся еще с одной сложностью. Кривая, которая описывает распределение
вероятности для выборки, для ограниченного числа измерений, уже не будет кривой нормального
распределения. Ее форма будет зависеть
не только от дисперсии (разброса данных) но и от степени свободы для выборки
(от числа независимых измерений) (рис 4):
Уравнения этих кривых впервые были предложены в 1908
году английским математиком и химиком Госсетом, который опубликовал их под
псевдонимом Student (студент), откуда пошло хорошо известные термины
«коэффициент Стьюдента» и аналогичные. Коэффициенты Стьюдента получены на
основе обсчета этих кривых для разных степеней свободы (f = n-1) и уровней
надежности (Р) и сведены в специальные таблицы. Для получения доверительного интервала необходимо
умножить уже найденное стандартное отклонение среднего на соответствующий
коэффициент Стьюдента. ДИ = sср*tf, P
Проанализируем, как меняется доверительный интервал
при изменении требований к надежности результата и числа измерений в серии.
Данные в таблице 2 показывают, что чем больше требование к надежности, тем
больше будет коэффициент Стьюдента и, следовательно, доверительный интервал. В большинстве случаев, приемлемым считают значение Р=95%
|
Таблица |
||||
|
P |
0,9 |
0,95 |
0,99 |
0,999 |
|
t5, |
2,02 |
2,57 |
4,03 |
6,87 |
|
Таблица |
|||||||
|
f= |
1 |
2 |
3 |
4 |
5 |
16 |
30 |
|
tf, |
12,7 |
4,3 |
3,18 |
2,78 |
2,57 |
2,23 |
2,04 |
Из таблицы 3 и графика
видно, что чем больше число измерений, тем меньше коэффициент и доверительный
интервал для данного уровня надежности. Особенно значительное падение
происходит при переходе от степени свободы 1 (два измерения) к 2 (три
измерения). Отсюда следует, что имеет смысл ставить не менее трех параллельных
опытов, проводить не менее трех измерений.
Окончательно
для измеряемой величины Х получаем значение Хсред±sср*tf,P. В
нашем случае получаем: f=3; t=3,18;
ДИ = 3,18*10,2 = 32,6; X = 143,5 ±32,6
Как правило,
значение доверительного интервала округляется до одной значащей цифры, а
значение измеряемой величины – в соответствии с округлением доверительного
интервала. Поэтому для нашей серии окончательно имеем: X = 140 ±30
Найденная
нами погрешность является абсолютной погрешностью и ничего не говорит еще о
точности измерений. Она свидетельствует о точности измерений только в сравнении
с измеряемой величиной. Отсюда представление об относительной ошибке:
Косвенные определения.
Исследуемая величина рассчитывается в этом случае с помощью
математических формул по другим величинам, которые были измерены
непосредственно. В этом случае для расчета ошибок можно использовать
соотношения, приведенные в таблице 4.
|
Таблица |
||
|
Формула |
Абсолютная |
Относительная |
|
x = a ± b |
Dx = Da+Db |
e = |
|
x = a* b; x = a* k |
Dx = bDa+aDb; Dx = kDa |
e = Da/a+Db/b = ea + e b |
|
x = a / b |
Dx = (bDa+aDb) / b2 |
e = Da/a+Db/b = ea + e b |
|
x = a*k; (x = a / k) |
Dx = Da*k; (Dx = Da/k ) |
e = ea |
|
x = a2 |
Dx = 2aDa |
e = 2Da/a = 2ea |
|
x = Öa |
Dx = Da/(2Öa) |
e = Da/2a = ea/2 |
Из таблицы видно, что относительная ошибка и точность определения не изменяются при умножении (делении) на некоторый постоянный коэффициент. Особенно сильно относительная ошибка может возрасти при вычитании
близких величин, так как при этом абсолютные ошибки суммируются, а значение Х
может уменьшиться на порядки.
Пусть например, нам необходимо определить
объем проволочки.
Если диаметр проволочки измерен с погрешностью 0,01 мм (микрометром) и равен 4 мм, то относительная погрешность составит 0,25% (приборная). Если
длину проволочки (200 мм) мы измерим линейкой с погрешностью 0,5 мм, то относительная погрешность также составит 0,25%. Объем можно рассчитать по формуле: V=(pd2/4)*L. Посмотрим, как будут меняться ошибки
по мере проведения расчетов (табл. 5):
|
Таблица 5. Расчет абсолютных и относительных ошибок. |
|||
|
Величина |
Значение |
Абсолютная |
Относительная |
|
d2 |
16 |
Dx = 2*4*0,01=0,08 |
e = 0,5% |
|
pd2 *) |
50,27 |
Dx = 0,08*3,14+0,0016*16 |
e = 0,55% |
|
pd2/4 |
12,57 |
Dx = 0,28/4 = 0,07 |
e = 0,55% |
|
(pd2/4)*L |
2513 |
Dx = 12,57*0,5+200*0,07=20 |
e = 0,8% |
|
*) Если мы возьмем привычное p=3,14, то Dp=0,0016 |
Окончательный
результат V=2510±20 (мм3) e
=0,8%. Чтобы повысить точность косвенного определения, нужно в первую очередь
повышать точность измерения той величины, которая вносит больший вклад в ошибку
(в данном случае – точность измерения диаметра проволочки).
План проведения измерений:
[1]
1. Знакомство
с методикой, подготовка прибора, оценка приборной погрешности d. Оценка возможных причин
систематических ошибок, их исключение.
2.
Проведение серии измерений. Если получены совпадающие результаты, можно
считать что случайная ошибка равна 0, DХ
= d. Переходим к пункту 7.
3.
Исключение промахов – результатов значительно отличающихся по своей
величине от остальных.
4.
Расчет
среднего значения Хср, и стандартного отклонение среднего
значения scp
5.
Задание значения уровня надежности P,
определение коэффициента Стьюдента t и
нахождение доверительного интервала ДИ= t*scp
6.
Сравнение случайной и приборной погрешности, при этом возможны варианты:
—
ДИ << d, можно
считать, что DХ = d, повысить точность измерения
можно, применив более точный прибор
—
ДИ >> d, можно
считать, что DХ = ДИ,
повысить точность можно, уменьшая случайную ошибку, повышая число измерений в
серии, снижая требования к надежности.
—
ДИ » d, в этом
случае расчитываем ошибку по формуле DХ
=
7.
Записывается окончательный результат Х = Хср ± DХ.
Оценивается относительная ошибка
измерения e = DХ/Хср
Если
проводится несколько однотипных измерений (один прибор, исследователь, порядок
измеряемой величины, условия) то подобную работу можно проводить один раз. В
дальнейшем можно считать DХ
постоянной и ограничиться минимальным числом измерений (два-три измерения
должны отличаться не более, чем на DХ)
Для косвенных
измерений необходимо провести обработку данных измерения каждой величины. При
этом желательно использовать приборы, имеющие близкие относительные погрешности
и задавать одинаковую надежность для расчета доверительного интервала. На
основании полученных значений Da, Db, определяется DХ
для результирующей величины (см табл. 4). Для повышения точности надо
совершенствовать измерение той величины, вклад ошибки которой в DХ наиболее существенен.
Изучение зависимостей.
Частым вариантом экспериментальной работы является
измерение различных величин с целью установления зависимостей. Характер этих
зависимостей может быть различен: линейный, квадратичный, экспоненциальный,
логарифмический, гиперболический. Для выявления зависимостей широко
используется построение графиков.
При построении графиков вручную важно правильно
выбрать оси, величины, масштаб, шкалы. Следует предупредить школьников, что
шкалы должны иметь равномерный характер, нежелательна как слишком детальная,
так и слишком грубая их разметка. Точки должны заполнять всю площадь графика,
их расположение в одном углу, или «прижатыми» к одной из осей, говорит о
неправильно выбранном масштабе и затрудняет определение характера зависимости.
При проведении линии по точкам надо использовать теоретические представление о
характере зависимости: является она непрерывной или прерывистой, возможно ли ее
прохождение через начало координат, отрицательные значения, максимумы и
минимумы.
Наиболее легко проводится и анализируется прямая
линия. Поэтому часто при изучении более сложных зависимостей часто используется
линеаризация зависимостей, которая достигается подходящей заменой переменных.
Например:
Зависимость . Вводя новую переменную
, получаем уравнение
a = bx, которое
будет изображаться на графике прямой линией. Наклон этой прямой позволяет
рассчитать константу диссоциации.
Разумеется и в этом случае полученные в эксперименте данные включают в себя различные ошибки, и точки редко лежат строго на прямой. Возникает
вопрос, как с наибольшей точностью провести прямую по экспериментальным точкам, каковы ошибки в определении
параметров.
Математическая статистика показывает, что наилучшим
приближением будет такая линия, для которой дисперсия (разброс) точек
относительно ее будет минимальным. А дисперсия определяется как средний квадрат
отклонений наблюдаемого положения точки от расчитанного:
Отсюда название этого метода – метод наименьших
квадратов. Задавая условие, чтобы величина s2
принимала минимальное значение, получают формулы для коэффициентов а и b в уравнении прямой у = а + bx:

и формулы для расчета соответствующих ошибок
[2].
Если
делать расчеты, используя калькулятор, то лучше оформлять их в виде таблицы:
|
x |
x2 |
y |
y2 |
xy |
|
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
|
Sx = |
Sx2 |
Sy = |
Sy2 |
Sxy = |
Подводя
итог, следует сказать, что обработка данных эксперимента достаточно сложный
этап работы ученого. Необходимость проведения большого числа измерений требует
большой затраты времени и материальных ресурсов. Громоздкость формул, необходимость
использования большого числа значащих цифр затрудняют вычисления. Поэтому, возможно,
не все рекомендации этой статьи применимы в рамках школьного исследования. Но
понимать их сущность, значимость, необходимость, и в соответствии с этим
адекватно оценивать свои результаты, должен любой исследователь.
В настоящее время обработку экспериментальных данных
существенно облегчают современные компьютерные технологии, современное
программное обеспечение. Об том, как их можно использовать – в следующей
статье.
Литература:
[1]
Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений, М., «Наука»,
1970, 194 с.
[2]
Петерс Д., Хайес Дж., Хифтье Г. Химическое разделение и измерение – М.,: Химия,
1978, 816 с.
Обработка результатов эксперимента
Обработка результатов эксперимента
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
1. ОШИБКИ ИЗМЕРЕНИЙ
1.1. Цели математической обработки результатов эксперимента
1.2. Виды измерений и причины ошибок
1.3. Типы ошибок измерения
1.4. Свойства случайных ошибок
1.5. Наиболее вероятное значение измеряемой величины
1.6. Оценка точности измерений
1.7. Понятие доверительного интервала и доверительной вероятности
1.8. Обнаружение промахов
1.9. Ошибки косвенных измерений
1.10. Правила округления чисел
1.11. Порядок обработки результатов измерений
1.12. Обработка результатов измерений диаметра цилиндра
Контрольные вопросы
2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
2.1. Виды случайных величин и законы их распределения
2.2. Числовые характеристики случайных величин, заданных своими распределениями
2.3. Основные дискретные и непрерывные законы распределения
2.4. Понятие статистической гипотезы и статистического критерия
2.5. Вероятность ошибок первого и второго рода
2.6. Проверка гипотезы вида закона распределения вероятностей
Контрольные вопросы
3. НАХОЖДЕНИЕ ИНТЕРПОЛИРУЮЩИХ КРИВЫХ
3.1. Графический метод обработки результатов
3.2. Функциональные шкалы и их применение
3.3. Аналитические методы обработки результатов
3.3.1. Способ средней
3.3.2. Метод наименьших квадратов
3.3.3. Интерполирование функций
3.3.4. Параболическое интерполирование
Контрольные вопросы
4. ОСНОВЫ НОМОГРАФИИ
4.1. Номограммы в декартовой системе координат
4.2. Составные номограммы с помеченными линиями
Контрольные вопросы
5. ТИПОВЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
ЛИТЕРАТУРА
Изложены некоторые разделы математической обработки результатов наблюдений и экспериментов о действиях со случайными величинами, определения и оценки законов их распределения, аналитического и графического отображения результатов.
ВВЕДЕНИЕ
При исследовании технических систем могут использоваться теоретические и эмпирические методы познания. Каждое из этих направлений обладает относительной самостоятельностью, имеет свои достоинства и недостатки. В общем случае, теоретические методы в виде математических моделей позволяют описывать и объяснять взаимосвязи элементов изучаемой системы или объекта в относительно широких диапазонах изменения переменных величин. Однако при построении теоретических моделей неизбежно введение каких-либо ограничений, допущений, гипотез и т.п. Поэтому возникает задача оценки достоверности ( адекватности ) полученной модели реальному процессу или объекту. Для этого проводится экспериментальная проверка разработанных теоретических моделей. Практика является решающей основой научного познания. В ряде случаев именно результаты экспериментальных исследований дают толчок к теоретическому обобщению изучаемого явления. Экспериментальное исследование дает более точное соответствие между изучаемыми параметрами. Но не следует и преувеличивать результаты экспериментальных исследований, которые справедливы только в пределах условий проведенного эксперимента.
Таким образом, теоретические и экспериментальные исследования дополняют друг друга и являются составными элементами процесса познания окружающего нас мира.
Как правило, результаты экспериментальных исследований нуждаются в определенной математической обработке. В настоящее время процедура обработки экспериментальных данных достаточно хорошо формализована и исследователю необходимо только ее правильно использовать. Круг вопросов, решаемых при обработке результатов эксперимента, не так уж велик. Это —
вопросы подбора эмпирических формул и оценка их параметров, вопросы оценки истинных значений измеряемых величин и точности измерений, вопросы исследования корреляционных зависимостей и некоторые другие.
Настоящее учебное пособие не претендует на оригинальность. Оно содержит некоторые результаты фундаментальных и прикладных работ в области обработки результатов экспериментальных исследований [1…13]. Пособие может служить практическим руководством по обработке результатов эксперимента как студентам, так и научным сотрудникам и инженерам.
1. ОШИБКИ ИЗМЕРЕНИЙ
Основой всего естествознания является наблюдение и эксперимент.
Наблюдение —
это систематическое, целенаправленное восприятие того или иного объекта или явления без воздействия на изучаемый объект или явление. Наблюдение позволяет получить первоначальную информацию по изучаемому объекту или явлению.
Эксперимент —
метод изучения объекта, когда исследователь активно и целенаправленно воздействует на него путем создания искусственных условий или использует естественные условия, необходимые для выявления соответствующих свойств. Достоинствами эксперимента по сравнению с наблюдением реального явления или объекта является:
1. Возможность изучения в “чистом виде”, без влияния побочных факторов, затемняющих основной процесс;
2. В экспериментальных условиях можно получить результат более быстро и точно;
3. При эксперименте можно проводить испытания столько раз, сколько это необходимо.
Результат эксперимента или измерения всегда содержит некоторую погрешность. Если погрешность мала, то ею можно пренебречь. Однако при этом неизбежно возникают два вопроса: во—
первых, что понимать под малой погрешностью, и, во—
вторых, как оценить величину погрешности. То есть, и результаты эксперимента нуждаются в определенном теоретическом осмыслении.
1.1. Цели математической обработки результатов эксперимента
Целью любого эксперимента является определение качественной и количественной связи между исследуемыми параметрами, либо оценка численного значения какого-либо параметра.
В некоторых случаях вид зависимости между переменными величинами известен по результатам теоретических исследований. Как правило, формулы, выражающие эти зависимости, содержат некоторые постоянные, значения которых и необходимо определить из опыта.
Другим типом задачи является определение неизвестной функциональной связи между переменными величинами на основе данных эксперимента. Такие зависимости называют эмпирическими.
Однозначно определить неизвестную функциональную зависимость между переменными невозможно даже в том случае, если бы результаты эксперимента не имели ошибок. Тем более не следует этого ожидать, имея результаты эксперимента, содержащие различные ошибки измерения.
Поэтому следует четко понимать, что целью математической обработки результатов эксперимента является не нахождение истинного характера зависимости между переменными или абсолютной величины какой-либо константы, а представление результатов наблюдений в виде наиболее простой формулы с оценкой возможной погрешности ее использования.
1.2. Виды измерений и причины ошибок
Под измерением понимают сравнение измеряемой величины с другой величиной, принятой за единицу измерения.
Различают два типа измерений: прямые и косвенные. При прямом измерении измеряемая величина сравнивается непосредственно со своей единицей меры. Например, измерение микрометром линейного размера, промежутка времени при помощи часовых механизмов, температуры —
термометром, силы тока —
амперметром и т.п. Значение измеряемой величины отсчитывается при этом по соответствующей шкале прибора.
При косвенном измерении измеряемая величина определяется (вычисляется) по результатам измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. Например, измерение скорости по пройденному пути и затраченному времени, измерение плотности тела по измерению массы и объема, температуры при резании по электродвижущей силе, величины силы —
по упругим деформациям и т.п.
При измерении любой физической величины производят проверку и установку соответствующего прибора, наблюдение их показаний и отсчет. При этом никогда истинного значения измеряемой величины не получить. Это объясняется тем, что измерительные средства основаны на определенном методе измерения, точность которого конечна. При изготовлении прибора задается класс точности. Его погрешность определяется точностью делений шкалы прибора. Если шкала линейки нанесена через 1 мм , то точность отсчета 
Кроме приборной погрешности на результат измерения влияет еще ряд объективных и субъективных причин, обуславливающих появление ошибки измерения —
разности между результатом измерения и истинным значением измеряемой величины. Ошибка измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Исключение составляют измерения известных величин при определении точности измерительных приборов или их тарировке. Поэтому одной из важнейших задач математической обработки результатов эксперимента и является оценка истинного значения измеряемой величины по данным эксперимента с возможно меньшей ошибкой.
1.3. Типы ошибок измерения
Кроме приборной погрешности измерения (определяемой методом измерения) существуют и другие, которые можно разделить на три типа:
1. Систематические погрешности обуславливаются постоянно действующими факторами. Например, смещение начальной точки отсчета, влияние нагревания тел на их удлинение, износ режущего лезвия и т.п. Систематические ошибки выявляют при соответствующей тарировке приборов и потому они могут быть учтены при обработке результатов измерений.
2. Случайные ошибки содержат в своей основе много различных причин, каждая из которых не проявляет себя отчетливо. Случайную ошибку можно рассматривать как суммарный эффект действия многих факторов. Поэтому случайные ошибки при многократных измерениях получаются различными как по величине, так и по знаку. Их невозможно учесть как систематические, но можно учесть их влияние на оценку истинного значения измеряемой величины. Анализ случайных ошибок является важнейшим разделом математической обработки экспериментальных данных.
3. Грубые ошибки (промахи) появляются вследствие неправильного отсчета по шкале, неправильной записи, неверной установки условий эксперимента и т.п. Они легко выявляются при повторном проведении опытов.
В дальнейшем будем считать, что систематические и грубые ошибки из результатов эксперимента исключены.
1.4. Свойства случайных ошибок
Случайные ошибки бывают как положительные, так и отрицательные разной величины, не превосходящей определенного предела. Если обозначить через Х истинное значение измеряемой величины, а результат первого измерения —
а1, то разность
Х — а1 = х1 или а1
— Х = х1
называют истинной абсолютной ошибкой одного измерения. Одновременно она является случайной (при исключении систематических и грубых ошибок).
Если измерения провести многократно в одних и тех же условиях, то результаты отдельных измерений одинаково надежны. Такую совокупность измерений а1, а2 …аn называют равноточными измерениями. Если проанализировать достаточно большую серию равноточных измерений и соответствующих случайных ошибок измерений, то можно выделить 4 свойства случайных ошибок:
1. Число положительных ошибок почти равно числу отрицательных;
2. Мелкие ошибки встречаются чаще, чем крупные;
- Величина наиболее крупных ошибок не превосходит некоторого определенного предела, зависящего от точности измерения. Самую большую ошибку в ряду равноточных измерений называют предельной ошибкой;
4. Частные от деления алгебраической суммы всех случайных ошибок на их общее близко к нулю, т.е.
На основе указанных свойств при учете некоторых допущений математически достаточно строго выводится закон распределения ошибок, описываемый следующей функцией:
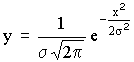
где s
— дисперсия измерений (см. ниже);
е —
основание натуральных логарифмов;
х —
истинная абсолютная ошибка измерений.
Закон распределения случайных ошибок является основным в математической теории погрешностей. Иначе его называют нормальным законом распределения. Особое значение в пользу широкого использования закона Гаусса имеет следующее обстоятельство: если суммарная ошибка измерения появляется в результате совместного действия ряда причин, каждая их которых вносит малую долю в общую ошибку (т.е. нет доминирующих причин), то по какому бы закону не были распределены ошибки, вызываемые каждой из причин, результат их совместного действия приведет
к нормальному распределению ошибок. Эта закономерность является следствием так называемой центральной предельной теоремы Ляпунова и хорошо соотносится с введенным понятием случайной ошибки.
Наряду с нормальным законом распределения ошибок могут встречаться и другие.
1.5. Наиболее вероятное значение измеряемой величины
Допустим, что для определения истинного значения Х измеряемой величины было сделано n равноточных измерений с результатами а1, а2 .. .аn. Естественно, что ряд этих чисел будет больше Х, другие меньше Х и неясно, какое из этих чисел ближе всего подходит к Х.
Представим результаты измерений в виде очевидных равенств:
а1 = Х — Dх1;
а2 = Х — Dх2;
… ; аn = Х — Dхn.
Естественно, что истинные абсолютные ошибки D
хi могут принимать как положительные, так и отрицательные значения.
Суммируя левые и правые стороны равенств получим
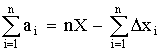
Поделим обе части равенства на число измерений n и получим
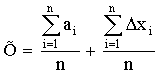
Величина 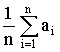
¥), то согласно четвертому свойству случайных ошибок
Это же видно и по кривой Гаусса (рис. 1), где всякой положительной погрешности соответствует равная ей отрицательная.
Из изложенного следует, что
Х = а при n ® ¥
,
т.е. при бесконечном числе измерений истинное значение измеряемой величины равно среднеарифметическому значению результатов всех измерений. При ограниченном числе измерений истинное значение будет отличаться от среднеарифметического и необходимо оценить величину этого расхождения: Х = а ±
Dх.
Следует еще раз подчеркнуть, что среднеарифметическое значение, принимаемое за истинное значение измеряемой величины, является наиболее вероятным значением. Среди значений аi могут оказаться значения, которые в действительности ближе к истинному значению.
Отклонение D
х вероятнейшего значения а от его истинного значения Х называют истинной абсолютной ошибкой.
1.6. Оценка точности измерений
Для ряда равноточных измерений а1, а2 …аn определим его среднеарифметическое значение а и составим разности (а —
а1), (а —
а2), …, (а —
аn).
Каждую из этих разностей называют вероятнейшей ошибкой отдельного измерения
(Vi). Вероятнейшие ошибки, как и истинные ошибки D
хi = (Х — аi), бывают положительные
и отрицательные, нулевые. Рассмотрим
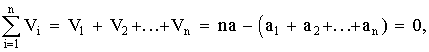
т.е. алгебраическая сумма вероятнейших ошибок равна нулю при любом числе измерений.
Истинные случайные ошибки таким свойством не обладают.
Вероятнейшие ошибки Vi лежат в основе математической обработки результатов измерений: именно по ним вычисляют предельную абсолютную ошибку D
аi среднеарифметического а и тем самым оценивают точность результата измерений.
Средняя истинная случайная ошибка (иначе —
среднее отклонение отдельного измерения) определяется выражением (D
х1+Dх2+…+Dхn)/
n.
Величина [
(Dх1)2+(Dх2)2+…+(Dхn)2]
/
n представляет средний квадрат случайной ошибки или дисперсию S2 выборки (при ограниченном n) или генеральной совокупности s
2 (при бесконечном n). Средняя квадратичная ошибка отдельного измерения S = 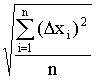
хi и сильнее учитывается действие крупных ошибок.
Поскольку истинное значение Х измеряемой величины неизвестно, то неизвестны и истинные случайные ошибки 
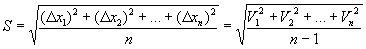
Различный знаменатель объясняется тем, что величины 
Важно, что не зная самих истинных случайных ошибок удается вычислить среднюю квадратичную ошибку определенного измерения:
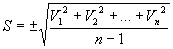
Оценим теперь погрешность результата всей серии эксперимента, т.е. определим величину D
х = Х —
а.
Для этого проведем преобразование выражения
Sn2 = 
= 
= 
 .
.
Если повторить серии по n измерений в каждой N ðàç, ìîæíî ïîëó÷ить средние значения а1, а2, … , аN и погрешности результатов измерений
(Dх)1 = (Х —
а1); (Dх)2 = (Х —
а2); … ; (Dх)N = (Х —
аN)
и среднюю среднеквадратичную погрешность серии
Sa2 =  .
.
При большом числе N S2a ®
s
2a
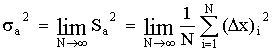
Усредняя выражение S2n по числу серий N, получаем
Sa2 = (D x)2
= Sn2 —  .
.
Учитывая что при большом n S2n ®
s
2 и S2 ®
s
2 получаем искомую
связь между дисперсиями всего опыта s
2a и отдельного эксперимента s
2
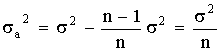
т.е. дисперсия s
2a результата серии из n измерений в n раз меньше дисперсии отдельного измерения. При ограниченном числе n измерений приближенным выражением s
2a будет S2a
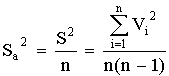
Выражения s 2a и S2a
отражают фундаментальный закон возрастания точности при росте числа наблюдений.
Из него следует, что желая повысить точность измерений в 2 раза мы должны сделать
вместо одного — четыре измерения; чтобы повысить
точность в 3 раза, нужно увеличить число измерений в 9 раз и т.д.
1.7. Понятие доверительного интервала и доверительной вероятности
Как установлено ранее, истинное значение измеряемой величины Х отличается от среднеарифметического a на некоторую величину D
x. На рис. 2 представлено расположение истинного значения Х и а, полученного из некоторых измерений а1, а2, а3.
Ясно, что случайные величины а1, а2, а3 обусловят случайный характер абсолютной погрешности D
x результата серии измерений, которая будет распределена по закону Гаусса:
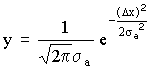
Тогда вместо выражения Х = а ±
Dх можно записать а —
Dх £
Х £
а + D
.
Интервал (а —
Dх; а + D
х), в который по определению попадает истинное значение X называют доверительным интервалом. Надежностью (
уровнем значимости)
результата серии измерений называется вероятность a
того, что истинное значение X измеряемой величины попадет в доверительный интервал. Вероятность a
выражается в долях единицы или процентах. Графически надежность отражается площадью под кривой нормального распределения в пределах доверительного интервала, отнесенной к общей площади. Выбор надежности определяется характером производимых измерений. Например, к деталям самолета предъявляются более жесткие требования, чем к лодочному мотору, а к последнему значительно больше, чем к ручной тачке. При обычных измерениях ограничиваются доверительной вероятностью 0,90 или 0,95. Для любой величины доверительного интервала (
выраженного в долях s
) по формуле Гаусса может быть просчитана соответствующая доверительная вероятность. Эти вычисления проделаны и сведены в таблицу, имеющуюся практически во всей литературе по теории вероятности. На рис. 3 представлены значения надежности a
при величине доверительного интервала ±
s
, ±
2s
, ±
3s. Эти значения доверительной вероятности рекомендуется запомнить.
По рис. 3 видно, что величина абсолютной погрешности D
x может быть представлена в виде К×
s
а, где К некоторый численный коэффициент, зависящий от надежности a
. Однако это справедливо лишь для большого (
бесконечного)
числа n. При малых n этим коэффициентом пользоваться нельзя, т.к. величина s
а неизвестна. Для того, чтобы получить оценки границ доверительного интервала при малом n вводится новый коэффициент t
a
. Этот коэффициент предложен английским математиком и химиком В.С. Госсетом, публиковавшим свои работы под псевдонимом ²
Стьюдент ²
.
И коэффициент t
a
назвали коэффициентом Стьюдента. Коэффициент Стьюдента отражает распределение случайной величины t = 
¥
( практически при n ³
20 )
распределение Стьюдента переходит в нормальное распределение. Значения коэффициента Стьюдента также приводятся практически во всей литературе по теории вероятности.
Зная величину t a можно определить величину
абсолютной погрешности D х = t×
Sa . Следует отметить, что величина абсолютной погрешности еще не
определяет точность измерений. Точность измерений характеризует относительная
погрешность, равная отношению абсолютной погрешности D
x результата измерений к результату измерений а: e
= ± Dх /
а. .
1.8. Обнаружение промахов
Если в ряду измерений встречаются результаты, резко отличающиеся от большей части ряда, то возникает вопрос принадлежности ²
выскакивающих ²
значений этому ряду измерений. Большие ошибки имеют малую вероятность возникновения. Поэтому следует объективно оценить, является ли данное измерение промахом (
тогда его исключают из ряда )
или же это результат случайного, но совершенно закономерного отклонения. Можно считать каждое измерение промахом, если вероятность случайного появления такого значения является достаточно малой.
Если известно точное значение s
, то вероятность появления значения, отличающегося от среднеарифметического а более чем на 3s
£ 0,003 и все измерения, отличающиеся от а на 3s
( и больше )
могут быть отброшены, как маловероятные.
Следует иметь в виду, что для совокупности измерений вероятность появления измерения ³
3s от а всегда больше 0,003. Действительно, вероятность того, что результат каждого измерения не будет отличаться от истинного более чем 3s
составляет 1—
0,003 = 0,997. Вероятность того, что все n измерений не будут отличаться от среднего более чем на 3s
по правилу умножения вероятностей составит (
1 —
0,003 )
n. Для не слишком большого n
(1 —
0,003)n »
1 —
0,003×
n.
Это значит, что вероятность того, что из 10 измерений хотя бы одно будет случайно отличаться от среднего более чем на 3s
будет уже не 0,003, а 0,03 или 3%. А при 100 измерениях вероятность такого события составит уже около 30%.
Обычно число измерений не очень велико. При этом точное значение s
не известно, следовательно, отбрасывать измерения, отличающиеся от среднего более чем на 3s
, нельзя.
Для оценки вероятности b
случайного появления ²
выскакивающих²
значений в ряду n измерений составлены соответствующие таблицы.
Для применения таблицы вычисляется среднее арифметическое а и средняя квадратичная погрешность S
n из всех измерений, включая и подозреваемое значение аk
. Затем вычисляется уклонение подозреваемого значения аk
от среднего арифметического в долях среднеквадратичной ошибки
Vмакс =  .
.
По таблице определяется какой вероятности b
соответствует полученное значение Vмакс.
Если вероятность появления данного измерения в ряду лежит в диапазоне 0,1 >
b
> 0,01, то представляется одинаково правильным —
оставить это измерение или отбросить. В случае же, когда b
выходит за указанные пределы, вопрос об отбрасывании решается практически однозначно. Решая вопрос об отбрасывании полезно посмотреть, как сильно оно меняет окончательный результат по а и S
n.
1.9. Ошибки косвенных измерений
Часто измеряется не непосредственно интересующая нас величина, а другая, зависящая от нее некоторым образом. Например, при резании металлов часто непосредственно измеряются деформации, ЭДС, по которым судят о возникающих силах и температурах. При этом также необходимо оценить ошибку измерения.
При косвенных измерениях значение y измеряемой величины находят по некоторой формуле
y = ¦ (х1, х2, …
, хm),
где x1, x2, … xm — средние арифметические измеряемые (
непосредственно)
величины. Рассмотрим функцию общего вида
y = ¦ (х1, х2, …
, хm)
где x1, x2, … , xm — независимые переменные, для определения которых производятся n прямых независимых измерений по каждой xi.
Обозначим значения переменных через среднее значение и отклонения
y ± D y =
¦ (x1 ±
D x1, x2 ±
D x2, … , xm ±
D xm).
Эту функцию представим рядом Тейлора, ограничив его первыми членами ряда ( принимая D
xi <
<
xi )
y ± D y =
¦ (х1, х2, … , хn)
±  ,
,
где
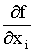
Учитывая, что y = ¦
(x1, x2, … , xm) получаем
D y =  .
.
Чтобы учесть погрешности D
xi всех n опытов целесообразно использовать средние квадратические оценки ( D
xi )2, так как D
xi =
0.
Возведем в квадрат левую и правую части уравнения и разделим на n
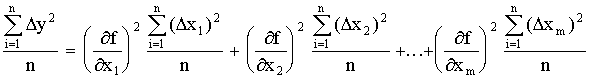
Здесь суммы удвоенных произведений типа
согласно четвертому свойству случайных ошибок ( D
xi =
0 ).
Тогда в левой и правой частях имеем среднеквадратические погрешности функции и аргументов
S .
.
Пример. При тарировке динамометра было получено уравнение зависимости силы от отклонения l луча осциллографа вида P =
25 l. Точность измерения отклонения D
l = 1 мм. Тогда
D P =  .
.
В качестве меры точности лучше выступает не абсолютная, а относительная погрешность.
e  .
.
Рассмотрим ее определение на примере. Пусть
y = cx1a ×
x2b ×
x3g .
Тогда
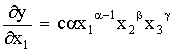
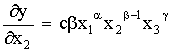
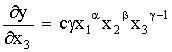
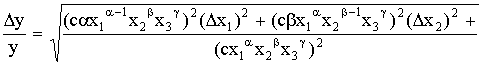
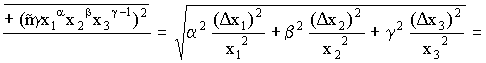
= 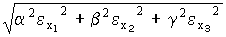
Аналогично можно определить относительную погрешность и при других зависимостях. Зная относительную погрешность, можно определить и абсолютное ее значение:
D y = y× e
y.
1.10. Правила округления чисел
Величина погрешности результата измерений физической величины дает представление о том, какие цифры в числовом значении измеряемой величины сомнительны. Поэтому результаты измерений следует округлять перед тем, как производить с ними дальнейшие вычисления.
Округлять числовое значение результата измерений следует в соответствии с числовым разрядом значащей цифры погрешности. При этом выполняют общие правила округления.
Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются ( как и лишние нули ). Например, если погрешность измерения ±
0,001 мм, то результат 1,07005 округляется до 1,070.
Если первая из изменяемых нулями и отбрасываемых цифр меньше 5, остающиеся цифры не изменяются. Например, число 148935, точность измерения ±
50, округление:
148900.
Если первая из заменяемых нулями или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или идут нули, то округление производится до ближайшего четного числа. Например, число 123,50 округляется до 124.
Если первая из заменяемых нулями или отбрасываемых цифр больше 5 или равна
5, но за ней следует значащая цифра, то последняя остающаяся цифра увеличивается
на единицу. Например, число 6783,6 округляется до 6784.
1.11.Порядок обработки результатов измерений
При практической обработке результатов измерений можно последовательно выполнить следующие операции:
- Записать результаты измерений;
- Вычислить среднее значение из n измерений
а = 
- Определить погрешности отдельных измерений Vi =
а — аi; -
Вычислить квадраты погрешностей отдельных измерений Vi
2; - Если несколько измерений резко отличаются по своим значениям от остальных
измерений, то следует проверить не являются ли они промахом. При исключении
одного или нескольких измерений п.п.1…4 повторить; - Определяется средняя квадратичная погрешность результата серии измерений
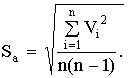
- Задается значение надежности a
; - Определяется коэффициент Стьюдента t
a
(n) для выбранной надежности a
и числа проведенных измерений n; - Находятся границы доверительного интервала
Dх = t a
(n)× Sa
- Если величина погрешности результата измерений (п.9) окажется сравнимой с величиной d
погрешности прибора, то в качестве границы доверительного интервала следует взять величину
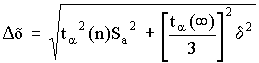
- Записать окончательный результат
X = a ± D
x ;
Оценить относительную погрешность результата серии измерений
e =  .
.
1.12.Обработка результатов измерений диаметра цилиндра
Микрометром было сделано десять замеров диаметра цилиндра. Цена деления микрометра 0,01 мм. Определить диаметр цилиндра с надежностью a
= 0,95 и a
= 0,99. Оценить влияние числа замеров на точность получаемого результата.
аi:
14,85; 14,80; 14,84; 14,81; 14,79;
14,81; 14,80; 14,85; 14,84; 14,80.
- Для первых пяти измерений определим среднеарифметическое значение и границы доверительного интервала. Для удобства расчетов выберем произвольное число ао удобное для расчетов (ао =
14,80 мм) и определим разности (аi — ао) и квадраты этих разностей. Результаты сведены в таблицу.
|
i |
аi, мм |
аi — ао, мм |
(аi — ао)2, мм2 |
|
1 |
14, 85 |
0, 05 |
0, 0025 |
|
2 |
14, 80 |
0, 00 |
0, 0000 |
|
3 |
14, 84 |
0, 04 |
0, 0016 |
|
4 |
14, 81 |
0, 01 |
0, 0001 |
|
5 |
14, 79 |
— |
0, 0001 |
|
|
0, 09 |
0, 0043 |
Найдем среднее значение а и среднеквадратичное отклонение S
а:
а — ао = 0, 018 мм;
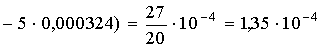
);
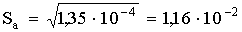
Для надежности a
= 0,95 и n =
5 t
a
=
2,78. Абсолютная погрешность измерения D
х:
Dх = t
a × Sа
= 2,78 × 0,0116
= 0,0322 мм.
Результат измерения можно представить в виде
(14,818 — 0,032)
мм £ а £ (
14,818 + 0,032)
мм
или сохраняя в величине погрешности одну значащую цифру
(14,82 — 0,03)
мм £ а £ (
14,82 + 0,03)
мм,
т.е. 14,79 мм £
а £
14,85 мм или а =
(
14,82 ±
0,03) мм.
Относительная погрешность
e а =  .
.
Теперь найдем абсолютную и относительную погрешность этих измерений при a
=
0,99.
В этом случае t
a
= 4,60. Тогда
Dх = t a
× Sa = 4,60×
1,16× 10-2 = 5,34×
10-2 ( мм ).
Следовательно а =
(
14,82 ±
0,05) мм
e а =  .
.
Видно, что с увеличением надежности границы доверительного интервала возросли, а точность результата уменьшилась.
- Проведем расчет погрешностей для этих же пяти измерений, незаконно полагая, что s
2 =
S
2n (что при n = 5 ошибочно). Для этого используем распределение Гаусса (а не Стюарта). При a
=
0,95 ka
=
Это дает возможность определить
Dх = ka ×
Sa = 1,96× 1,16×
10-2 » 2×
10-2 ( мм ),
т.е. погрешность получилась меньше примерно на 30%. Если по этой величине погрешности определить величину надежности при t
a
=
ka, то из таблицы коэффициентов Стьюдента получим a
< 0,90 вместо заданной a
= 0,95. Следовательно при малом числе измерений n применение закона нормального распределения с s
2 =
S2n вместо распределения Стьюдента приводит к уменьшению надежности результата измерений.
- Найдем средние значения и погрешности следующих пяти измерений
|
i |
аi, мм |
аi — ао, мм |
(аi — ао)2, мм2 |
|
1 |
14, 81 |
0, 01 |
0, 0001 |
|
2 |
14, 80 |
0, 00 |
0 |
|
3 |
14, 85 |
0, 05 |
0, 0025 |
|
4 |
14, 84 |
0, 04 |
0, 0016 |
|
5 |
14, 80 |
0, 00 |
0 |
|
|
0, 10 |
0, 0042 |
ао = 14, 80 мм;
а = ао +  ( мм );
( мм );
а — ао = 0, 02 мм;

 ( мм2 );
( мм2 );
Sa = 1, 05
× 10-2 мм.
При a
=
0,95:
Dх = t a
× Sa = ±
2,78× 1,05×
10-2 = 2,92× 10-2 ( мм
);
e а =  ;
;
Х = 14, 82 ± 0, 03 мм.
При a
=
0,99:
Dх = ± 4,60×
1,05× 10-2 »
5× 10-2 ( мм );
e а = ±

Х = 14, 82 ± 0,05 мм.
Результаты практически не отличаются, от результатов полученных из первой серии.
- Найдем теперь погрешность результата всей серии из десяти измерений. В этом
случае(мм);
(мм2).
Эти величины получаются суммированием последних строк из таблиц частных серий.
ао = 14, 80 мм;
а = ао +  ( мм );
( мм );
а — ао = 0, 019 мм.
Sa2 = 
= ( мм2 );
( мм2 );
Sa = 7, 35× 10-3 мм.
При a
= 0,95 имеем
Dх = ta ×
Sa = ± 2,26×
7,35× 10-3 = ±
1,7× 10-2 ( мм );
e а =  ;
;
а = 14, 819 ± 0, 017 мм.
При a
= 0,99 получаем
Dх = ta ×
Sa = ± 3,25×
7,35× 10-2 = ±
2,4× 10-2 ( мм );
e а =  ;
;
а = 14, 819 ± 0, 024 мм.
Видно, что абсолютная и относительная погрешность результата десяти измерений стали почти в два раза меньше погрешностей пяти измерений.
Применение нормального распределения с s
2 =
S2n дает в случае a
=
0,95 ka
= 1,96 и D
х =
1,4 ×
10—
2 мм, а величина надежности понижается до 0,91; в случае a
= 0,99 получаем ka
= 2,58 и D
х =
1,9 ×
10—
2 мм, а величина надежности понижается до a
=
0,97.
Как видно, с ростом числа измерений различие между результатами, вычислениями по распределению Стьюдента и по нормальному распределению уменьшается.
Контрольные вопросы
- Цель математической обработки результатов эксперимента;
- Виды измерений;
- Типы ошибок измерения;
- Свойства случайных ошибок;
- Почему среднеарифметическое значение случайной величины при нормальном законе ее распределения является вероятнейшим значением?
- Что такое истинная абсолютная и вероятнейшая ошибки отдельного измерения?
- Что такое доверительный интервал случайной величины?
- Что такое уровень значимости (надежности) серии измерений?
- Геометрический смысл уровня значимости;
- Почему при малом числе опытов нельзя погрешность измерений представить в виде D
х =
±
Ks
а? - Что является критерием “
случайности”
большого отклонения измеряемой величины? - Чем определяется величина случайной ошибки косвенных измерений?
- Чем определяется точность числовой записи случайной величины?
2. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
При характеристике случайных величин недостаточно указать их возможные значения. Необходимо еще знать насколько часто возникают различные значения этой величины. Это характеризуется вероятностью p отдельных ее значений.
Соотношение, устанавливающее связь между значениями случайной величины и вероятностями этих значений, называют законом распределения случайной величины. Различают интегральный и дифференциальный законы распределения.
2.1. Виды случайных величин и законы их распределения
Под случайной величиной понимается величина, принимающая в результате опыта какое либо числовое или качественное значение.
Случайная величина, принимающая конечное число или последовательность различных значений, называется дискретной случайной величиной. Случайная величина, принимающая все значения из некоторого интервала, называется непрерывной случайной величиной.
Под интегральным законом распределения (или функцией распределения) F (х) случайной величины Х понимают вероятность p того, что случайная величина Х не превысит некоторого ее значения х
F (х) = p (Х < х).
Основным свойством интегрального распределения является монотонное не убывание в ограниченном диапазоне [
0;
1 ]
.
Действительно, если х1 и х2 некоторые значения случайной величины Х. Причем х2 > х1, то очевидно, что событие p (Х <
х2) ³ p (Х <
х1), т.к. между значениями х1 и х2 могут быть и промежуточные. Из определения интегрального закона следует, что F (х2) ³
F (х1), что говорит о монотонном не убывании функции. Очевидно также, что
F (— ¥ ) =
p (Х < — ¥
) = 0;
Þ F (¥ )
— F (— ¥
) = 1,
F (+ ¥ ) =
p (Х < ¥ ) =
1;
т.е. F (х) изменяется в диапазоне от 0 до 1.
Для дискретной случайной величины
F (x) = P (X < x) = P (—
¥ < X <
x) =  ,
,

хi).
Рассмотрим p (х1 £ Х <
х2). Если х2 > х1, то очевидно, что
p (Х < х2) =
p (Х < х1) +
p (х1 £ Х <
х2).
Тогда
p (х1 £ Х <
х2) = p (Х <
х2) — p (Х <
х1) = F (х2) —
F (х1),
т.е. вероятность попадания случайной величины в интервал [
х1;
х2) равен разности значений интегральной функции граничных точек.
Последнее условие можно использовать для нахождения вероятности p (Х =
х1) для непрерывной случайной величины. Для этого рассмотрим предел
p (X = x1) =  ,
,
т.е. если закон распределения случайной величины есть функция непрерывная, то вероятность того, что случайная величина примет заранее заданное значение, равна нулю.
Здесь видно различие между дискретными и непрерывными случайными величинами. Для дискретных случайных величин, для каждого значения случайной величины существует своя вероятность. И для него справедливо утверждение: событие, вероятность которого равна нулю, невозможно. Для непрерывной случайной величины это утверждение неверно. Как показано, вероятность того, что Х =
х1 ( где х1—
заранее выбранное число) равна нулю, это событие не является невозможным.
Рассмотрим непрерывную случайную величину Х, интегральный закон которой предполагается непрерывным и дифференцируемым. Функцию
¦ (х) = F¢
(х)
называют дифференциальным законом распределения или плотностью вероятности случайной величины Х. Из определения производной можно записать
¦ (x) = F¢
(x) =  ,
,
т.е. плотность вероятности случайной величины Х в точке х равна пределу отношения вероятности попадания величины Х в интервал (х; х +
Dх) к D
х, когда D
х стремится к нулю.
Используя понятия интегральной функции распределения и определенного интеграла можно записать
¦ (x) = F¢
(x) или F (x) = p (x1 < X < x2) =  .
.
Это соотношение имеет простое геометрическое толкование (рис. 5).
Если 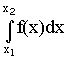
p (х < Х <
х + Dх) »
¦ (х) D х.
Из свойств интегрального распределения следует
 .
.
Зная дифференциальный закон распределения можно определить интегральный закон распределения
F (x) =  .
.
2.2. Числовые характеристики случайных величин, заданных своими распределениями
Основными характеристиками случайной величины, заданной своими распределениями, является математическое ожидание ( или среднее значение ) и дисперсия.
Математическое ожидание случайной величины является центром ее распределения. Дисперсия характеризует отклонение случайной величины от ее среднего значения.
Если Х дискретная случайная величина, значения хi которой принимают с вероятностью pi, так, что 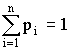
M (X) =  ,
,
т.е. суммой произведений всех ее возможных значений на соответствующие вероятности.
Математическим ожиданием непрерывной случайной величины является аналог его дискретного выражения
M (X) =  .
.
Действительно, все значения в интервале (х; х +
Dх) можно считать примерно равными х, а вероятность таких значений равна ¦
(х) dx (см. ранее). Поэтому значения хi дискретного распределения заменяются х, а вероятности pi — на ¦
(х) dx, а сумма заменяется интегралом.
Дисперсией или рассеянием случайной величины Х называется математическое ожидание квадрата разности случайной величины и ее математического ожидания.
D (Х) = М [
Х — М (Х)] 2
= М (Х — х)2
= s 2
(х)
Если случайная величина Х дискретна и принимает значения хi с вероятностями pi, то случайная величина (Х —
х)2 принимает значения (хi — х)2 с вероятностями Рi. Поэтому для дискретной случайной величины имеем
D (X) = 
Аналогично для непрерывной случайной величины получаем
D (X) =  .
.
Чем меньше величина дисперсии, тем лучше значения случайной величины характеризуются ее математическим ожиданием.
2.3. Основные дискретные и непрерывные законы распределения
Как отмечалось ранее, очень часто случайная величина распределена по нормальному закону. Но существуют и другие распределения, имеющие практическое значение. Рассмотрим некоторые из них по условиям возникновения и основным параметрам их характеризующим.
- Равномерное распределение вероятностей.
Пусть плотность вероятности А равна нулю всюду, кроме интервала (a; b), на котором она постоянна (рис. 6). Тогда можно записать
p (a < X < b) = 
 A =
A =
 .
.
Тогда дифференциальный закон равномерного распределения определяется
¦ (x) = 

Интегральный закон распределения
F (x) =  .
.
При х ³
b имеем
F (x) = 
Таким образом интегральный закон равномерного распределения задается (рис. 6)
F (x) = 
Основные характеристики распределения
М (X) =  ;
;
D(X) = 
= 
= 
 .
.
- Биноминальное распределение
Пусть при некотором испытании событие А может наступить или не произойти (А). Обозначим вероятность А через р, а А через q =
1 —р ( других итогов испытания нет ). Тогда исходами двух последовательных независимых испытаний и их вероятностью будут:
АА — р2; АА —
рq; АА — qр; АА —
q2.
Отсюда видно, что двукратное появление события А равно р2, вероятность однократного появления — 2 рq, а вероятность того, что А не наступит ни разу —
q2. Эти результаты единственно возможные и поэтому
 .
.
Это рассуждение можно перенести на любое число испытаний.
Например, при трех испытаниях получим
 .
.
Подсчитаем вероятность того, что при n испытаниях событие А появится m раз. Это может произойти, например, в последовательности
Ясно, что вероятность равна рmqn—
m. Но m событий А может быть и в другом сочетании. Число всех возможных сочетаний из n элементов по m (количество событий А) равно числу сочетаний 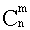
Pm,n = 
=  .
.
Из этой формулы видно, что вероятности Рm,n для различного исхода испытаний (появление или не появление определенного результата А) определяется
pn + npn-1q +  .
.
Коэффициенты перед вероятностями р, q являются биноминальными коэффициентами, а общая вероятность представляет слагаемые в разложении бинома ( р +
q )n. Поэтому закон распределения случайной величины Х, в котором вероятность наступления событий А определяется коэффициентами бинома, называется биноминальным распределением дискретной случайной величины. Этот закон может быть задан в виде таблицы 1.
Таблица 1
Биноминальный закон распределения
|
хi |
0 |
1 |
2 |
… |
m |
… |
n |
|
pi |
qn |
npqn-1 |
|
… |
|
… |
pn |
Биномиальные коэффициенты удобно получать с помощью треугольника Паскаля.
1 n =
0
1 1 n =
1
1 2 1 n = 2
1 3 3 1 n = 3
1 4 6 4 1 n = 4
1 5 10 10 5 1 n = 5
Все строки треугольника ( начинающегося с единицы ) начинаются и заканчиваются единицей. Промежуточные числа получаются сложением соседних чисел вышестоящей строки. Числа, стоящие в одной строке, являются биноминальными коэффициентами соответствующей степени.
Из описания биномиального распределения становится ясно, что область его действия там, где возможно многократное проведение испытаний с известной вероятностью.
Определим основные характеристики этого распределения.
Математическое ожидание
М (Х) = 
+ 
+ 
= np (q + p)n-1 = np.
Дисперсия распределения может быть определена из общего выражения
 ,
,
но это приводит к громоздким вычислениям. В то же время случайная величина Х принимает в каждом опыте только два значения: 1, если событие А произошло и 0, если оно не произошло с вероятностями, соответственно, р или q. Тогда математическое ожидание одного опыта определится
М (Х1) = 0× q +
1×р = р =
х
и соответственно дисперсия одного опыта
D (Х1) = (0 — р)2×
q + (1 —
р)2× р =
р2q + q2р =
рq (р + q) = рq.
Тогда дисперсия всех n опытов составит
D (X) = n×
p× q.
- Закон Пуассона
В случае малых р ( или, наоборот, близких к 1 ) биноминальный закон распределения можно преобразовать следующим образом

 ,
,
где 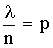
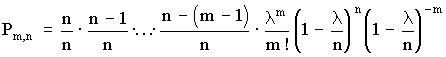
Определим предел Рm,n при n ®
¥ и постоянном m. Тогда пределы
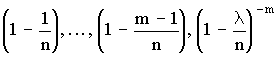
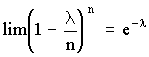
Окончательно имеем
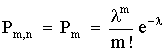
Это распределение называется законом Пуассона, где l
— интенсивность распределения. Используется в задачах с редкими событиями.
Определим его основные характеристики и смысл величины l
.
Запишем закон распределения в виде таблицы.
|
хi |
0 |
1 |
2 |
… |
m |
… |
|
pi |
e—l |
|
|
… |
|
… |
M (X) = 
+  .
.
Выражение в скобках есть разложение функции еl
в ряд Маклорена.
Поэтому
М (Х) = lе—
l еl =
l .
Не рассматривая вывод отметим, что
D (Х) = l
,
т.е. дисперсия равна математическому ожиданию.
Рассмотренные виды распределений случайной величины, конечно, не исчерпывают всех существующих распределений. Можно назвать еще несколько: распределение Бернулли, экспоненциальное распределение, гамма —
распределение, распределение Вейбула, гипергеометрические распределения и др. При определенных условиях и параметрах один вид распределения может переходить в другой. Поэтому при решении практических задач по законам распределения случайных величин следует обращаться к специальной литературе.
2.4. Понятие статистической гипотезы и статистического критерия
Статистической гипотезой называют любое утверждение о виде или свойствах распределения наблюдаемых в эксперименте случайных величин. Такие утверждения можно делать на основе теоретических соображений или статистических исследований других наблюдений. Например, при многократном измерении некоторой физической величины, точное значение Х которой не известно, но в процессе измерений оно меняется. На результат измерений влияют многие случайные факторы, поэтому результат i — го измерения можно записать в виде аi = Х + e
i, где e
i — случайная погрешность измерения. Если e
i складывается из большого числа ошибок, каждая из которых не велика, то на основании центральной предельной теоремы можно предположить, что случайные величины аi имеют нормальное распределение. Такое предположение является статистической гипотезой о виде распределения наблюдаемой случайной величины.
Если для исследуемого явления сформулирована та или иная гипотеза ( обычно ее называют основной или нулевой гипотезой и обозначают символом Но ), то задача состоит в том, чтобы сформулировать правило, которое позволяло бы по результатам наблюдений принять или отклонить эту гипотезу. Правило, согласно которому проверяемая гипотеза Но принимается или отвергается, называется статистическим критерием проверки гипотезы Но .
Наиболее распространены такие статистические гипотезы, как:
а) вида распределения;
б) однородности нескольких серий независимых результатов;
в) случайности результатов эксперимента и т.п.
Статистический критерий проверки гипотезы Но служит для определения возможного отклонения от основной гипотезы. Характер отклонений может быть различным. Если критерий ²
улавливает²
любые отклонения от Но, то такой критерий называют универсальным или критерием согласия. Существуют критерии, которые выявляют отклонения от заданного вида, это узко направленные критерии.
Выбор правила проверки гипотезы Но эквивалентен заданию критической области х1, при попадании в которую переменной х гипотеза Но отвергается. Критерий, определяемый критической областью х1 называют критерием х1.
В процессе проверки гипотезы Но можно прийти к правильному решению или совершить ошибку первого рода —
отклонить Но когда она верна, или ошибку второго рода —
принять Но, когда она ложна. Иными словами, ошибка первого рода имеет место, если точка х попадает в критическую область х1, в то время как верна нулевая гипотеза Но, а ошибка второго рода —
когда х Î
хо, но гипотеза Но ложна.
Желательно провести проверку гипотезы так, чтобы свести к минимуму вероятности обоих ошибок. Однако при данном числе испытаний n в общем случае невозможно одновременно обе эти вероятности сделать как угодно малыми. Поэтому наиболее рационально выбирать критическую область следующим образом: при заданном числе испытаний n устанавливается граница для вероятности ошибки первого рода и при этом выбирается та критическая область х1, для которой вероятность ошибки второго рода минимальна.
2.5. Вероятности ошибок первого и второго рода
Рассмотрим станок, который может работать только в одном из двух состояний. Если он работает в налаженном режиме, то для интересующего нас признака качества, например, длины или диаметра заготовки, имеет место нормальное распределение при работе как в налаженном так и в разлаженном режиме. Оба режима отличаются только уровнем настройки процесса по математическому ожиданию ( М(х) = 10 и 11, соответственно в налаженном и разлаженном режиме ), в то время как дисперсии в обоих случаях составляют s
2 = 4.
Проверить нужно нулевую гипотезу, в соответствии с которой М(х) = 10, против альтернативы ( в данном случае единственной ) М(х) = 11. Конкурирующую гипотезу обозначим Н1. Тогда Но: М(х) = 10; Н1: М(х) = 11.
Необходимо по результатам выборки определить в каком из состояний работает станок. Примем объем выборки n из потенциально бесконечной генеральной совокупности. В качестве контрольной величины возьмем выборочное среднее Хn. На рис. 9 изображены плотности распределения Хn для n = 25 и n = 4.
Для формулировки критерия необходимо разделить область изменения контрольной величины (х) на критическую область отклонения гипотезы Но ( принятия Н1 ) и область принятия гипотезы Но. Для этого необходимо выбрать число К, такое, что 10 <
К <
11, и интервал (
—
¥; К ]
рассматривать как область принятия гипотезы Но, а интервал [
К; ¥
) — как область отклонения гипотезы Но. По рис. 9 видно, что каждая реализация Х25 или Х4 возможна при верности любой из двух гипотез, но с различной вероятностью.
рода a
( отклонения верной гипотезы Но ) и второго рода b
( принятие гипотезы Но, когда она не верна ). Также видно, что увеличение n ведет к уменьшению дисперсии распределения х и тем самым —
к одновременному уменьшению вероятностей a
и b
. В соответствии с рис. 9 можно записать:
 ;
;
 .
.
Эти два уравнения содержат четыре величины a
, b, К, n. Задав две из четырех величин, можно определить две другие.
Например, при n = 25 и К = 10,4 определим:
 ;
;
 .
.
Если задаться величинами a
и b
, то можно определить величины К, n.
2.6. Проверка гипотезы вида закона распределения вероятностей
При проверке эксперимента закон распределения вероятностей случайных величин неизвестен и можно лишь предположительно судить о его виде . Выборочные оценки параметров распределения несут в себе случайные ошибки, искажающие истинный характер распределения. Поэтому после получения эмпирического распределения производится подбор теоретического закона распределения, пригодного для описания вероятностных свойств изучаемой случайной величины. Критерии подбора ( проверки гипотезы соответствия ) называют в статистике критериями согласия. Все они основаны на выборе допустимой меры расхождения между теоретическим распределением и выборочными данными.
Общую процедуру проверки гипотезы закона распределения можно представить в следующей последовательности:
- По опытным данным строится эмпирическая кривая распределения вероятностей;
- Определяются параметры эмпирического распределения ( в соответствии с его видом );
- Выдвигается одна или несколько гипотез о функции плотности исследуемой случайной величины, исходя из внешнего вида эмпирической кривой, значений ее параметров, технических факторов, влияющих на ее вид;
- Эмпирическая кривая выравнивается по одной или нескольким теоретическим кривым;
- Проводится сравнение по одному или нескольким критериям согласия;
- Выбирается теоретическая функция, дающая наилучшее согласование.
Поясним п. 4; 5. Определив по эмпирическим данным параметры распределения, подставляют их в теоретическую кривую закона распределения и рассчитывают вероятность середин интервалов эмпирического распределения. Умножив значение полученной вероятности на общее число опытов, получают теоретическое значение частот случайной величины, которые и определяют ²
выровненную²
кривую. Теперь можно найти вероятность того, что эмпирическая кривая соответствует выбранной теоретической, выбрав вероятность согласия ( уровень значимости ). Если результат расхождения не выйдет за принятый уровень значимости, то считают, что эмпирическое распределение согласуется с теоретическим. Если сравнение осуществляется с несколькими теоретическими законами, то окончательно принимать тот, который дает лучшее соответствие.
Чаще всего в качестве критериев согласия принимают критерий Пирсона ( c
2 ) и критерий Колмогорова —
Смирнова ( К —
С —
критерий ).
Критерий c
2 является наиболее состоятельным при большом числе наблюдений. Он почти всегда опровергает неверную гипотезу, обеспечивает минимальную ошибку в принятии неверной гипотезы по сравнению
с другими критериями.
c 2 =  ,
,
где mj —
наблюдаемая частота случайного события;
m*
j — ожидаемая по принятому теоретическому закону распределения;
К —
число интервалов случайной величины.
Затем определяется число степеней свободы l:
l = К — r —
1;
где К —
число интервалов случайной величины;
r — число параметров теоретической функции распределения.
К —
С —
критерий лучше всего использовать в случае, если теоретические значения параметров распределения известны. При неизвестных параметрах его можно использовать, но он дает несколько завышенные результаты. При использовании этого критерия определяется величина
 ,
,
где
mнj, m*нj — соответственно, накопленные наблюдаемые и ожидаемые
(теоретические) частоты;
n — число проведенных опытов.
То есть, в данном случае оценивается только максимальное отклонение накопленной частоты случайного события, возникающее в одном из диапазонов изменения случайной величины. Полученное значение коэффициента сравнивается с табличным для числа степеней свободы опыта и принятого уровня значимости результата. Если табличное значение коэффициента больше, то гипотеза о принятом законе распределения не отвергается.
Контрольные вопросы
- Сущность непрерывной и дискретной случайной величины;
- Сущность интегрального закона распределения случайной величины;
- Сущность дифференциального закона распределения случайной величины;
- Связь интегрального и дифференциального законов распределения;
- Основные характеристики случайной величины, заданной своим распределением;
- Назовите примеры законов распределения непрерывной и дискретной случайной величины;
- Понятие статистической гипотезы и статистического критерия;
- Назовите примеры статистических гипотез;
- Сущность ошибок первого и второго рода;
- Сущность проверки гипотезы вида закона распределения;
- Принципиальное различие в критериях Пирсона и Колмогорова —
Смирнова.
3. НАХОЖДЕНИЕ ИНТЕРПОЛИРУЮЩИХ КРИВЫХ
В первой части пособия рассматривались измерения той или иной физической величины, находящейся при проведении серии измерений в неизменном состоянии. Очень часто исследуемая величина меняется в соответствии с изменением условий опыта или времени. Цель эксперимента в этом случае состоит в нахождении функциональной зависимости, которая наилучшим образом описывает изменение интересующего нас параметра.
Следует понимать, что однозначно восстановить ( большей частью неизвестную ) функциональную зависимость между переменными невозможно даже в том случае, если бы переменные величины, полученные из опыта, не имели бы ошибки измерения. Тем более не следует ожидать, что это удастся сделать, имея экспериментальные данные, содержащие, по крайней мере, случайные ошибки измерений.
Поэтому математическая обработка результатов наблюдений не может ставить перед собой задачу разгадать истинный характер зависимости между переменными. Она позволяет лишь представить результаты опыта в виде наиболее простой формулы.
В зависимости от назначения этих формул существуют различные методы их получения, отличающиеся сложностью расчетных процедур и точностью получаемых решений.
3.1. Графический метод обработки результатов
Графический метод заключается в построении графика зависимости между исследуемыми величинами с последующим определением уравнения зависимости между ними.
Графики строят прежде всего в равномерных шкалах. Если характер связи между исследуемыми величинами неизвестен, то сначала проверяют совпадение экспериментальных точек с заданной кривой. Если предварительные сведения о характере уравнения отсутствуют, то первым этапом обработки данных является нахождение кривой, совпадающей с опытными точками. Эта задача решается методом подбора. Можно использовать эталон —
кальку с предварительно вычерченным на ней семейством кривых с различными параметрами. Естественно, что масштаб кальки и эмпирической кривой должен быть одинаков.
Построенный по опытным данным отрезок кривой может совпадать с большим количеством различных кривых, проходящих достаточно близко к опытным точкам. В этом случае выбирают кривую с наиболее простым и удобным в использовании уравнением. Иногда эмпирическая кривая может иметь перегибы или состоять из отдельных ярко выраженных участков. Однако при этом необходимо определить координаты точек перехода от одной кривой к другой.
Уравнение зависимости между исследуемыми величинами при графическом методе просто определяется тогда, когда эмпирические точки достаточно хорошо совпадают с прямой линией, т.е. описываются уравнением y = ax + b, где a, b — коэффициенты, подлежащие определению.
Определение коэффициентов при графическом методе основано на ²
способе натянутой нити²
. Нанеся результаты эксперимента на график (лучше, если он выполнен на миллиметровке), подбираем графическую прямую, ближе всего подходящую к нанесенным точкам. Выбрав положение прямой, определяем две произвольные точки на этой прямой (не обязательно являющиеся точками эксперимента), определяем их координаты (x1; y1), (х2; y2). И для определения коэффициентов а и b получаем два простых уравнения
ах1 + b = y1;
ах2 + b = y2.
На рис. 10 приведена иллюстрация этого метода. Точки —
результаты, полученные в эксперименте. Прямая проведена на глаз как можно ближе к экспериментальным точкам. На прямой выбраны точки М (2; 4) и N (13; 10). Коэффициент а характеризует угол наклона прямой.
Поэтому
 .
.
Таким образом y = 0,55х + 2,9.
В случае, если экспериментальная зависимость имеет нелинейный характер, то графическим способом в системе координат с равномерными шкалами определить коэффициенты кривой затруднительно. Но достаточно большой класс нелинейных зависимостей путем замены переменных и графического изображения в функциональных шкалах можно привести к линейным и далее использовать способ натянутой нити.
3.2. Функциональные шкалы и их применение
Пусть функция y = ¦
(х) непрерывна и монотонна на некотором промежутке [
a; b ]. Возьмем ось ОМ, на которой будет строиться шкала, выберем на ней точку начала отсчета О и установим масштаб m
. Функциональная шкала строится следующим образом.
Разбив интервал [
а; b ] на равные части, вычисляем значение функции ¦
(х) в каждой из точек деления и отложим на оси ОМ для каждой точки отрезок m
¦
(х). Получающаяся при этом точка снабжается отметкой х, т.е. откладывается в выбранном масштабе значение функции, а надписывается значение аргумента.
Иногда начало шкалы помещают в первую точку отсчета, т.е. точку с надписью а совмещают с 0. Тогда точка х будет находиться в конце отрезка m
[
¦(х) —
¦(а) ]
. Полученная шкала позволяет судить о поведении функции на рассматриваемом участке: большие промежутки между отметками укажут, что функция изменяется быстрее, чем там, где эти промежутки малы.
Выбор масштаба m
определяет длину шкалы. Чаще поступают наоборот: задаются длиной шкалы l и определяют масштаб.
 Þ m
Þ m
=  .
.
Пример. Построим функциональную шкалу для функции y = x2 на участке [
1; 2 ]. Зададимся длиной шкалы l = 12 см. Тогда m
= 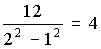
1; 2 ] на десять равных частей и вычислим значения функции во всех точках деления. Совместим начало шкалы с точкой отсчета х = 1. Результаты расчета сведены в табл. 2, а функциональная шкала приведена на рис. 11.
Таблица 2
Расчет функциональной шкалы y = x2
|
х |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2,0 |
|
х2 |
1,0 |
1,21 |
1,44 |
1,69 |
1,96 |
2,25 |
2,56 |
2,89 |
3,24 |
3,61 |
4,00 |
|
х2— 1 |
0 |
0,21 |
0,44 |
0,69 |
0,96 |
1,25 |
1,56 |
1,89 |
2,24 |
2,26 |
3,00 |
|
4(х2— 1) |
0 |
0,84 |
1,76 |
2,76 |
3,84 |
5,00 |
6,24 |
7,56 |
8,94 |
10,44 |
12,0 |
1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0
Рис. 11. Функциональная шкала y = x2
С помощью функциональных шкал графики многих функций могут быть преобразованы к прямолинейному виду.
Например, уравнение параболы y = x2. Если на оси OY нанести равномерную шкалу, а на оси OX1 шкалу квадратов х1 = х2, то получится сетка, где уравнение параболы имеет изображение прямой линии ( y = x1 ),
проходящей через начало координат.
Особенно часто используются различные логарифмические функции, с помощью которых можно ²
выпрямлять²
графики степенных и показательных функций. Например, y = aebx; lg y = (b lg е) х + lg a. Полагая lg y = y1, lg a = A, b lg e = B запишем исходное уравнение в виде y1 = А + Вх, откуда видно, что оставив равномерной шкалу х и построив логарифмическую шкалу y1, можно изобразить исходное уравнение прямой линией. Полученная координатная сетка называется полулогарифмической.
Очевидно, что такого рода преобразования возможны и в более общем случае. Всякая неявная функция, заданная соотношением вида
аj (х) + by
(y) + с = 0,
где a, b, с —
постоянные, будет изображаться прямой линией на функциональной сетке, где на оси ОХ построена шкала j
(х), а на оси OY — шкала функции y
(y). Естественно, что функции j
(х) и y
(y) должны удовлетворять условиям непрерывности и монотонности. В табл. 3 приведены преобразования для некоторых функций.
Таблица 3
Линеаризация некоторых функций
|
Исходная формула |
Преобразованная формула |
Замена переменных |
Линеаризованная формула |
|
y=axb |
lg y=b× |
lg y=y1 lg x=x1 lg a=a1 |
y1=bx1+a1 |
|
y=a× |
¾ |
lg x=x1 |
y=ax1+b |
|
y=ebx+k |
lg y=b× |
lg y=y1 b× k× |
y1=ax+k1 |
|
y=aebx |
lg y=bx× |
lg y=y1 b× lg a=a1 |
y1=b1x+a1 |
|
y= |
¾ |
|
y=ax1+b |
|
y= |
|
|
y1=ax+b |
|
y= |
|
|
y1=bx1+a |
Из сказанного ясна роль функциональных сеток при обработке результатов эксперимента. Если результаты эксперимента располагаются вблизи кривой, то по имеющемуся ограниченному участку кривой трудно судить, какого типа функцией ее лучше всего приближать. Переведя полученные экспериментальные данные на функциональные сетки можно оценить на какой из них эти данные ближе всего подходят к прямой и, следовательно, какой функцией лучше всего описываются.
3.3. Аналитические методы обработки результатов
Графический метод обработки результатов обладает наглядностью, относительной простотой, однако его результаты содержат определенную субъективность и относительно низкую точность.
Аналитические методы лишены в какой —
то степени указанных недостатков и позволяют получить результат для более широкого класса функций с большей точностью, чем графический метод.
Существуют различные аналитические методы получения параметров эмпирических
кривых в зависимости от критерия, принятого при их получении. Рассмотрим некоторые
из существующих способов.
3.3.1.Способ средней
Допустим, что имеется n сочетаний xi, yi, полученных при эксперименте. Даже в том случае, если между х и y теоретически установлена функциональная связь ( в данном случае предположим, что линейная ), то наблюдаемые значения yi будут отличаться от ахi + b вследствие наличия экспериментальных ошибок. Обозначим через D
i соответствующую ошибку
D i = yi —
axi — b (i = 1, 2, …, n)
Если выбирать параметры а и b так, чтобы для всех n наблюдений ошибки уравновешивались, т.е. 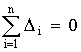
В этом случае можно прийти к системе уравнений
 ,
,
где m — число наблюдений в первой группе.
Данную систему уравнений запишем теперь в виде
 .
.
Изложенное показывает, что метод средних ²
уравновешивает²
положительные и отрицательные отклонения теоретической кривой от экспериментальных значений.
Пример.Используя данные рис. 10 определим коэффициенты а, b методом средней. Для этого семь измерений разделим на две группы m = 3 первых значений, n —
m = 4 последующих
 ;
;  ;
;
 ;
;  .
.
Получаем систему
Решая систему находим
 ;
;
b = 
Таким образом способ средней дает прямую
y = 0,55х + 3,11.
В сравнении с графическим способом коэффициенты а совпадают и имеется различие в коэффициенте b.
3.3.2. Метод наименьших квадратов
В методе средних при определении коэффициентов уравнения использовалось условие равенства нулю алгебраической суммы отклонений результатов эксперимента от теоретической кривой ( в частном случае прямой ). Очевидно, что при этом D
i могут быть значительной величины. Имеет значение только ²
уравновешивание²
положительных и отрицательных отклонений.
Поставим теперь задачу нахождения по результатам наблюдений наиболее вероятные значения неизвестных коэффициентов.
Предположим, что искомая зависимость y = ¦(х) существует. Тогда параметры этой линии необходимо выбрать таким образом, чтобы точки yi располагались по обе стороны кривой y = ¦(х) как можно ближе к последней. Предположим, что разброс точек yi относительно y = ¦(х) подчиняется закону нормального распределения. Тогда мерой разброса является дисперсия s
2 или ее приближенное выражение —
средний квадрат отклонений.
 .
.
И требование минимального разброса будет удовлетворено, если минимизировать выражение ( D
yi )2. Как известно, необходимым условием того, что функция приобретает минимальное значение, является то, что ее первая производная ( или частные производные для функции многих переменных ) равна нулю. Применение метода наименьших квадратов имеет смысл, если число экспериментальных точек n больше числа определяемых коэффициентов.
Рассмотрим реализацию метода наименьших квадратов применительно к уравнению вида y = ax + b.
Для нахождения коэффициентов а, b искомой прямой необходимо минимизировать сумму квадратов расстояний D
yi по ординате от точки (хi; yi) до прямой ( см. рис. 12 ). Расстояния D
yi определятся
D yi = yi —
axi — b.
Для минимизации 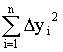
 ;
;
 .
.
Преобразуем эту систему
Получим систему нормальных уравнений метода наименьших квадратов.
Решая ее относительно а, b получаем:
 ;
;  .
.
Вычисляя из n опытов необходимые суммы и производя указанные действия, получаем величину коэффициентов а, b.
Как видно, способ наименьших квадратов достаточно громоздок и при его применении широко используется вычислительная техника. Метод наименьших квадратов может использоваться и в случае нелинейных функций. Например, если определяются параметры квадратичной зависимости:
y = ах2 + bx + с,
то
 .
.
Дифференцируя это соотношение по а, b, с получаем систему нормальных уравнений:
Из этой системы можно определить параметры а, b, с.
При использовании метода наименьших квадратов при других нелинейностях, удобнее будет линеаризовать исходные зависимости.
В табл. 4 приведены системы нормальных уравнений для некоторых исходных уравнений.
Таблица 4
Системы нормальных уравнений
|
Исходное уравнение |
Система нормальных уравнений |
|
y=axb |
|
|
y=a× |
|
|
y=eax+b |
|
|
y=aebx |
|
|
y= |
|
|
y= |
|
|
y= |
|
Примечания: 1. Величины х, y обозначают значения величин хi, yi
в i—ом опыте;
- Знак S обозначают сумму величин от i = 1
до i = n, где n — число равноточных измерений.
- Интерполирование функций
Известно, что под интерполированием понимают отыскание значений функции, соответствующих промежуточным значениям аргумента, отсутствующим в таблице логарифмов, тригонометрических и др. функций.
В общем смысле можно сказать, что задача интерполирования обратна задаче табулирования функций. При интерполировании по таблице значений функции строится ее аналитическое выражение, т.е. по значениям функции yo, y1, …, yn при значениях аргумента хо, х1, …, хn определяется выражение неизвестной функции.
Понятно, что через данные точки ( даже большого числа ) можно провести множество различных кривых. Поэтому существует интерполирование в различных функциях F (х). Чаще всего требуют, чтобы функция F(х) была многочленом степени на единицу меньшей, чем число известных значений.
Таким образом, задачу интерполирования функций можно сформулировать следующим образом.
Для данных значений х º
хо, х1, …, хn и y º
yo, y1, …, yn найти многочлен y = F (х) степени n, удовлетворяющий условиям F (хо) =
yo, F (х1) =
y1, …, F (хn) =
yn. Точки хо, х1, …, хn называют узлами интерполяции. Многочлен F (х) —
интерполяционным многочленом , а формулы его построения —
интерполяционными формулами.
Как видно из описания сущности интерполирования, в отличии от описанных ранее способов получения функций ( графического, метода средних, метода наименьших квадратов ), интерполяционный многочлен опишет кривую, проходящую точно через заданные точки.
- Параболическое интерполирование
При параболическом интерполировании в качестве интерполяционного многочлена F (х) принимают многочлен n — ой степени вида
F (х) = ао + а1х + а2х2
+ … + аnxn.
Используя свойство прохождения функции F (х) через заданные точки для неизвестных коэффициентов аi можно составить n + 1 уравнений с n + 1 неизвестным:
ао + а1хо + а2хо2
+ … + аnхоn =
yo;
ао + а1х1 + а2х12
+ … + аnх12 =
y1;
…………………………………………….
ао + а1хn + а2хn2
+ … + аnхn2 =
yn.
Эта система имеет единственное решение, если значения хi отличны друг от друга. Понятно, что при большом n возникает сложность решения этой системы. Перед рассмотрением общего способа решения, рассмотрим простой пример.
Дано: хо = 0, х1 = 1, х2 = 2, yо = 1, y1 = 1, y2 = 3. Определить многочлен F (х).
Записывая многочлен F (х) в виде
F (х) = ао + а1х + а2х2
составим систему уравнений
 или
или 
откуда ао = 1, а1 = — 1, а2 = 1 и интерполирующий многочлен имеет вид
F (х) = 1 — х + х2.
Теперь рассмотрим общий подход к отысканию интерполяционного многочлена F (х), не решением системы, а непосредственной записью.
Определим выражение для многочлена, принимающего в точке х = хо значение yо = 1, а в точках х = х1, х2, …, хn — значения y1 = y2 = … = yn = 0. Очевидно, что многочлен будет иметь вид
 .
.
Здесь при х = хо числитель и знаменатель равны, а при х = х1, х2, …, хn — числитель равен нулю.
Теперь построим многочлен Fо (х), принимающий в точке хо значение yо и обращающийся в нуль для значений х = х1, х2, …, хn. Учитывая предыдущее построение можно записать
 .
.
Теперь можно записать многочлен F (х) для произвольного значения хi ( i = 0, 1, 2, …, n ) принимающего значения F (хi) = yi, а во всех остальных точках х ¹
хi значение, равное нулю
 .
.
Как видно из записи, числитель не будет содержать выражения (х —
хi), а знаменатель —
(хi — хi), т.е. выражений, обращающих числитель и знаменатель в нуль.
Искомый многочлен будет равен сумме
 ,
,
т.е. снова в каждой точке хi одно из слагаемых принимает нужное значение yi, а все остальные обращаются в нуль.
В развернутом виде
=
… +  .
.
Полученная формула называется интерполяционной формулой Лагранжа.
Используя формулу Лагранжа запишем многочлен F (х) для разобранного выше примера.
= 
= .
.
Получили тоже самое выражение, что и ранее.
Контрольные вопросы
- Назначение графического метода обработки результатов;
- Сущность графического метода обработки результатов;
- Понятие и назначение функциональной шкалы;
- Выбор масштаба функциональной шкалы;
- Сущность аппроксимации методом средних;
- Сущность аппроксимации методом наименьших квадратов;
- Принципиальное отличие метода интерполирования от метода наименьших квадратов.
4.ОСНОВЫ НОМОГРАФИИ
Номография —
слово греческое. Номос —
закон, графо —
пишу, черчу. В буквальном переводе это слово означает ²
черчение закона²
.
Своей задачей номография ставит построение специальных графиков —
номограмм, служащих для решения различных уравнений. Номограммы дают возможность компактно представлять функции многих переменных и таблицы с несколькими входами. На номограммах можно решать некоторые трансцендентные уравнения и системы таких уравнений. Номограммы можно применять не только для вычислительных целей, но и для исследования положенных в их основу функциональных зависимостей.
Наглядность представления различных закономерностей и простота использования номограмм при достаточно высокой точности результата обеспечивают широкое использование номограмм в различных областях техники.
В основе номограмм лежит понятие функциональной шкалы ( см. выше ). На основе функциональных шкал создаются не только номограммы, но и различные вычислительные средства: универсальные вычислительные номограммы, логарифмические линейки и т.п.
В данной главе излагается один из возможных видов номограмм —
номограммы в декартовой системе координат, имеющие достаточно широкое использование в машиностроении.
4.1. Номограммы в декартовой системе координат
В разделах 3.1., 3.2. описана процедура построения графиков для функции одного переменного. При этом на графике получается одна линия ( прямая или кривая ).
Если же изучаемая функция зависит от двух переменных
Z = ¦ (х, y),
то придавая в этом уравнении, например, параметру y ряд частных ( постоянных ) значений y1, y2, …, yn можно, как и для функции одного переменного, построить зависимости
Z = ¦ (х, y1);
Z = ¦ (х, y2);
……………….
Z = ¦ (х, yn).
Получим систему кривых ( в частном случае прямых ), называемых номограммой из ²
помеченных²
линий, т.к. каждая линия помечается соответствующим значением yi.
Пример. При исследовании процесса фрезерования было установлено, что наиболее целесообразно величину радиального биения смежных зубьев фрезы назначать по условию обеспечения участия в процессе резания всех зубьев фрезы. Аналитически это условие выражается уравнением
 ,
,
где Sz —
расчетная величина подачи на зуб, мм/
зуб;
k = 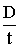
параметр операции;
D — диаметр фрезы, мм;
t — глубина резания, мм;
D
— величина биения смежных зубьев фрезы, мм.
Как видно, Sz = ¦
(k, D
) является функцией двух параметров. Здесь можно отметить, что, фактически Sz = ¦
(D, t, D
), т.е. функцией трех параметров, но два параметра (D, t) заменены одним —
k = 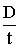
Теперь необходимо определиться с осями и помеченным параметром. В качестве оси ординат, в соответствии с функциональной зависимостью, рационально принять Sz. В качестве же оси абсцисс можно принять либо k, либо D
. Если в качестве оси ординат принять k ( а помеченным параметром D
i ), то зависимость
Sz = ¦ (k, D
i)
будет получаться криволинейной, в соответствии с закономерностью 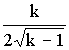
Sz = ¦ (D
, Ki),
где 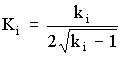
Теперь выбираем масштаб построения и диапазоны изменения переменных. С учетом условий процесса фрезерования принимаем D
£ 0,08 мм; Sz £ 0,20 мм/
зуб. Параметр k изменяем дискретно k = 2; 5; 10; 20; 30; 40; 50. Так как зависимость Sz = ¦
(D
, Ki) является прямой линией, проходящей через начало координат, то для построения графиков достаточно вычислить только одно значение Sz при каком —
либо значении D
. Например, для k = 2, при D
= 0,06 мм имеем
 ( мм/зуб ).
( мм/зуб ).
Теперь через точки ( 0; 0 ) и ( 0,06; 0,06 ) можно провести прямую линию и пометить ее параметр k = 2. Аналогично проводятся и другие линии. На номограмме наносится линия, показывающая порядок ее использования.
4.2. Составные номограммы с помеченными линиями
Номограмму в одной четверти можно построить для функции двух переменных. При большем числе переменных это сделать уже нельзя. В этом случае используют составные номограммы. Идею построения рассмотрим сначала в общем виде.
Пусть нам дано уравнение в неявном виде с четырьмя переменными
¦ (х, y, z, h
) = 0.
Допустим, что его можно привести к виду
¦ 1(х, y) = ¦
2 (z, h ),
т.е. можно разделить переменные. Положим
¦ 1 (х, y) = g
;
¦ 2 (z, h
) = g .
Мы получим два уравнения, зависящих от двух переменных. Каждое из этих уравнений можно номографировать, как описано выше. Обеспечив отсчет величины g
на одинаковой функциональной шкале, можно обойтись и без численных значений g
( если они нас не интересуют по условиям решаемой задачи ).
Аналогично поступают и с уравнениями с большим числом переменных, которое будет приводить к увеличению числа общих шкал и большему числу четвертей построения номограммы. Нужно только иметь в виду, что не всякое уравнение допускает разложение на несколько уравнений с двумя переменными и, следовательно, не всякое уравнение удается таким образом номографировать.
Рассмотрим реальный пример построения составной номограммы.
При исследовании процесса фрезерования было установлено, что сила резания при фрезеровании узких поверхностей приобретает характер повторяющихся импульсов не гармонической формы. И возмущение технологической системы осуществляется не на одной, а в бесконечном диапазоне частот. Наиболее опасно воздействие первых трех гармоник, несущих значительно больше энергии возмущения, чем все другие. Распределение энергии по этим трем гармоникам осуществляется в зависимости от отношения фронтов нарастания и спада силы в импульсе. Это отношение можно характеризовать отношением углов контакта фрезы (j
) и зуба фрезы (y
) с заготовкой. Причем всегда j
³
y
.
Для наглядного представления и определения характера распределения энергии по трем гармоникам в зависимости от условий операции построим номограмму.
В одной из четвертей первоначально отражается характер распределения энергии по гармоникам возмущения в зависимости от j
/
y
(рис. 15). Эти зависимости построены из результатов исследований, которые здесь не отражаются. Коэффициент Х2 характеризует ²
удельный вес²
энергии данной гармоники в общем силовом возмущении. Диапазон j
/
y
=
1…9.
Теперь отношение j
/
y
раскрываем в параметрах инструмента и операции
 .
.
Видно, что здесь четыре переменных величины: D, t, B, w
.
Введем промежуточную ось С и построим номограмму из помеченных линий для одной из переменных величин, а именно Вi
 .
.
Видно, что это уравнения прямых линий, проходящих через начало координат. Задаваясь одним значением j
/
y
и Вi можно провести ее график. Например, при j
/
y
= 5, Вi = 5 получим С = 2×
5×5 = 50. Аналогично поступаем для Вi = 10; 15; 20.
Далее вводим следующую промежуточную ось ( и соответственно переменную ) L = C ×
tg w
i. Задаваясь величинами угла w
i и С можно определить положение помеченных линий. Например, при w
= 45°, С = 50
L = 50×
tg 45°
=50. Àíàëîãè÷íî ïîñòóïàåì и äëÿ äðóãèõ óãëîâ w
i = 15°
; 30°
; 60°
; 75°. Проводим прямые линии через начало системы координат и помечаем значение угла w
i каждой линии.
Таким образом осталась одна взаимосвязь параметров
 .
.
Здесь необходимо определиться с параметром, направленном по оси и ²
помеченным²
параметром. В любом случае зависимость нелинейная. Кроме того, глубина резания является задаваемым параметром и его лучше взять в качестве ²
помеченного²
параметра. Для построения помеченных линий нужно определить несколько координат каждой линии.
Рассмотрим ²
помеченную²
линию t = 5 мм. В качестве переменного параметра принимаем диаметр фрезы D. При D = 25; 50; 100; 150; 200 мм соответственно имеем
По найденным точкам строится линия для t = 5 мм. Аналогично поступают и для других значений t.
Указаны промежуточные оси С, L, которые при использовании номограммы не нужны и могут не указываться, указаны и частные зависимости для каждой четверти номограммы.
Полученная номограмма наглядно показывает, что распределение энергии по гармоникам возмущения технологической системы определяется условиями операции, изменяя которые можно воздействовать на возмущение технологической системы.
Для исключения резонансных явлений необходимо знать спектр собственных частот системы и согласовывать условия операции с их значениями, уменьшая количество энергии на ²
резонансной²
частоте. Эти данные, как правило, отсутствуют. Поэтому используя номограмму можно скорректировать условия операции. Для этого по известным параметрам фрезы, которая показала неудовлетворительные результаты, и элементам режима резания необходимо определить распределение энергии по гармоникам возмущения и выбрать другое распределение. Так как глубину резания и ширину фрезерования изменять, как правило, невозможно, а изменение угла наклона режущей кромки часто нецелесообразно по условиям стойкости инструмента, то новое распределение энергии можно получить изменив диаметр фрезы ( в большую или меньшую сторону по сравнению с первоначальным ). При этом необходимо сохранить прежним относительное число зубьев ( z/D) и скорость резания, так как число оборотов и зубьев фрезы играют самостоятельную роль в определении частотного диапазона возмущения (inz).
Как видно из изложенного, номограмма может существенно помогать в управлении процессом резания, на основе заложенных в нее функциональных зависимостей.
Контрольные вопросы
- Сущность и назначение номографии;
- Функцию какого числа переменных можно отразить в одной четверти декартовой системы координат ?
- Понятие номограммы из ²
помеченных²
линий; - Сущность составной номограммы и промежуточной функциональной шкалы.
5. ТИПОВЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
В целях закрепления знаний и получения практических навыков предлагается решить несколько задач, имеющих практическую направленность.
- При измерении твердости по Роквеллу были получены следующие результаты. Для образца А: 97,0; 98,7; 99,9; 99,5; 97,1; 99,5; 92,0; 100,6; 99,7; 98,0; 98,5; 99,5; 99,7; 99,5; 99,0; 98,5; 99,5; 98,8; 98,5; 99,1; 98,4; 96,6; 97,2; 101,7; 97,2; 98,2; 97,5; 97,7; 99,0; 99,0; 97,5. Для образца В, проверяемого на этом же приборе: 85,6; 87,1; 87,9; 86,9; 85,6; 85,2; 85,5; 85,7; 84,7; 86,4; 80,0; 85,0; 82,0; 86,0; 86,0; 87,3; 84,5; 87,0; 87,3; 85,4; 91,0; 90,0; 90,8; 89,2; 91,0; 90,4; 84,1; 81,7; 87,4; 84,0; 85,2.
Для каждой группы данных определить значение измеряемого параметра, наличие промахов в ряду измерений. Для какой группы измерений результат получен точнее? Выбрав в случайном порядке 1, 4, 9, 16, 25 отсчетов проверить справедливость зависимости точности среднего значения от числа измерений. Построить эмпирические законы интегрального и дифференциального распределений. Подобрать теоретический закон распределения и оценить его соответствие.
- Отклонения диаметра вала распределены по нормальному закону. Половина значений
диаметра лежит в интервале 20 ± 0,1 мм. Отклонения
диаметра отверстия также распределены по нормальному закону. Половина всех
отклонений отверстия находится в интервале 20 ±
0,05 мм. Полагая, что сборка соединения производится вручную, определите,
сколько из 50 валов не подойдет по размеру. Какой номинальный диаметр осевого
отверстия ( вместо 20 мм ) следует задать ( при том же законе распределения
), чтобы все 100% деталей подошли друг к другу
при ручной сборке. -
В цехе машиностроительного завода выполняется сложный заказ, с определенной
вероятностью возникновения брака. Для обеспечения плана выпуска 100 изделий
запущено в производство 110 единиц. Какова вероятность, что заказ будет выполнен
если вероятность получения одного изделия 0,9; 0,95 ? - При исследовании обрабатываемости одного из конструкционных материалов были
получены зависимости периода стойкости зуба фрезы от угла наклона w
стружечной канавки.
Результаты приведены в таблице:
|
w |
20 |
30 |
40 |
50 |
60 |
|
T, мин |
30 |
60 |
80 |
70 |
50 |
Используя метод наименьших квадратов и параболического интерполирования получить аналитическую зависимость стойкости от угла наклона .
- С помощью критерия c
2 проверьте соответствие числа бракованных деталей за 51 смену пуассоновскому распределению.
|
Число бракованных изделий за одну смену, m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Число смен с m бракованными изделиями |
3 |
7 |
9 |
12 |
9 |
6 |
3 |
2 |
0 |
- Известно, что количество бракованных инструментов в партии соответствует закону Пуассона с параметром интенсивности l
= 0,5. Определить количество бракованных изделий в партии. - Случайная величина х распределена по закону равной вероятности в интервале [
1; 10 ]. Определите при каком значении х вероятность его нахождения в заданном интервале равна 0,05 и 0,95 ? - Случайная величина х подчиняется нормальному закону распределения с параметрами х = 3, s
2 = 25. Вычислить вероятности Р ( Х ³
10 ), Р ( —
2 £ Х £
8 ), Р ( Х £
—10 ). Дайте графическую иллюстрацию результата. - Станок —
автомат настроен на выполнение размера 100,1 мм. Разброс размеров деталей подчиняется нормальному закону распределения с дисперсией s
2 = 0,25 мм2. Поле допуска на размер детали составляет 100 ±
0,15 мм. Найдите долю брака при проведенной настройке, представьте ее в виде графика от среднеарифметического значения. На какое значение необходимо настроить автомат, чтобы доля брака была минимальной, определите эту долю. Пусть х = 100, s
= 0,5. Что окажет большее влияние на увеличение доли брака —
сдвиг х на ±
0,5 или увеличение s
на 0,5 ? - При исследовании силы резания в зависимости от глубины резания была измерена главная составляющая силы резания Рz при четырех значениях глубины резания
|
t, мм |
1 |
2 |
3 |
4 |
|
Pz, Н |
2300 |
3200 |
4000 |
4600 |
Графическим методом, методом средних и методом наименьших квадратов установить зависимость составляющей силы от глубины резания.
ЛИТЕРАТУРА
- Теория Вероятностей, М. 1998
- Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической
обработки результатов опыта. — М.: Физматгиз,
1962. — 356 с. - Зайдель А.Н. Ошибки измерения физических величин. —
Л.: Наука, 1974. — 108 с. - Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. —
М.: Наука, 1970. — 104 с. - Колесников А.Ф. Основы математической обработки результатов измерений. —
Томск: ТГУ, 1963. — 49 с. - Плескунин В.И., Воронина Е.Д. Теоретические основы организации и анализа
выборочных данных в эксперименте. Учебное пособие. —
Л.: ЛЭУ, 1979. — 232 с. - Румшинский Л.З. Математическая обработка результатов эксперимента. Справочное
руководство. — М.: Наука, 1971. —
192 с. - Рыжов Э.В., Горленко О.А. Математические методы в технологических исследованиях.
— Киев: Наук. думка, 1990. —
184 с. - Сухов А.Н. Математическая обработка результатов измерений. Учебное пособие.
— М.: МИСИ, 1982. —
89 с. - Чкалова О.Н. Основы научных исследований. —
Киев: Вища школа, 1978. — 120 с.
Дата добавления: 29.03.2001






































































































 1
1 0,5
0,5








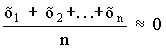
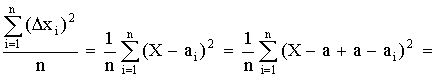
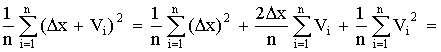
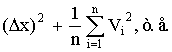
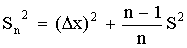 .
. 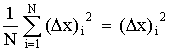 .
.
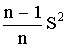 .
.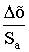
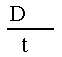 .
.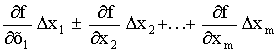 ,
,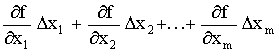 .
.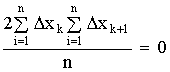
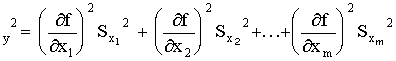 .
.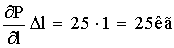 .
.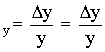 .
.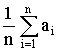
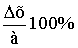 .
.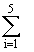
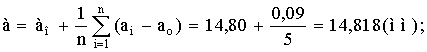
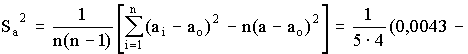
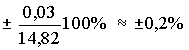 .
.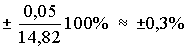 .
.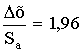
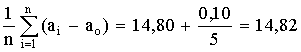 ( мм );
( мм );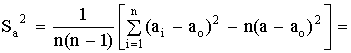
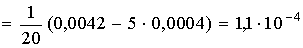 ( мм2 );
( мм2 );
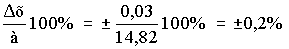 ;
;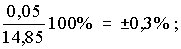
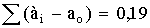 (мм);
(мм); 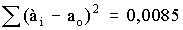 (мм2).
(мм2).
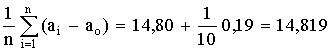 ( мм );
( мм );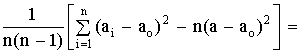
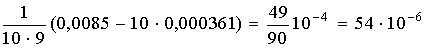 ( мм2 );
( мм2 );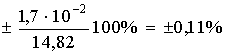 ;
;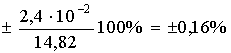 ;
; ,
,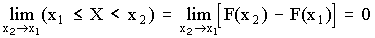 ,
,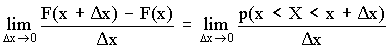 ,
,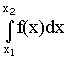 .
.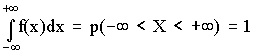 .
.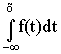 .
.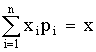 ,
,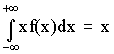 .
.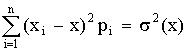
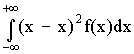 .
.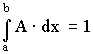
 A =
A = .
.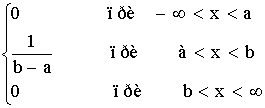
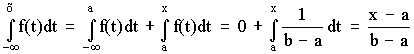 .
.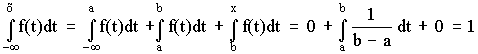
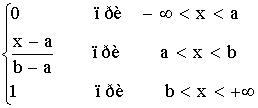
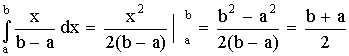 ;
;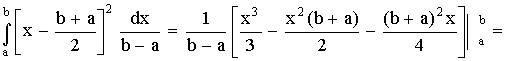
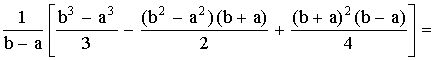
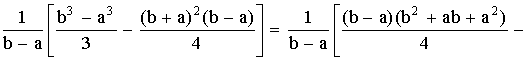
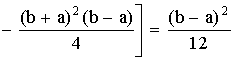 .
.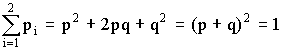 .
.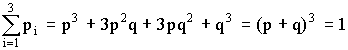 .
.
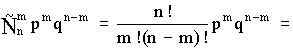
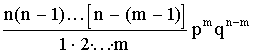 .
.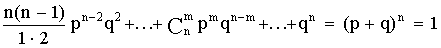 .
.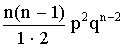
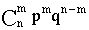
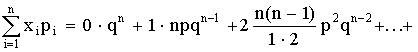
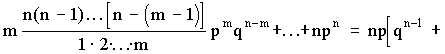
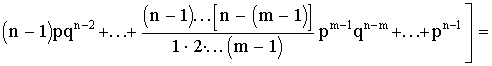
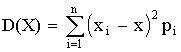 ,
,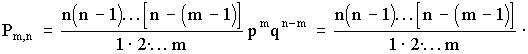
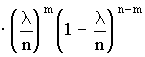 ,
,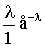
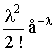
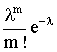
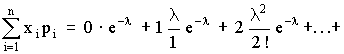
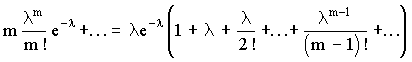 .
.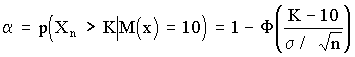 ;
;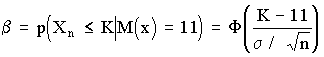 .
.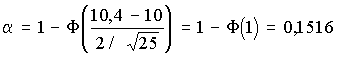 ;
;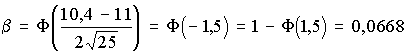 .
.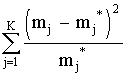 ,
,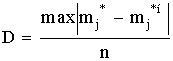 ,
,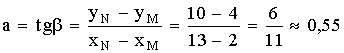
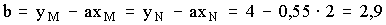 .
.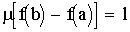
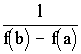 .
.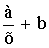
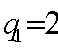
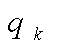
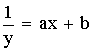
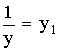
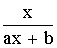
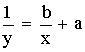
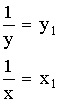
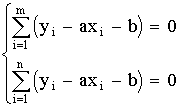 ,
,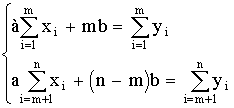 .
.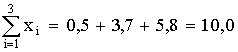 ;
; 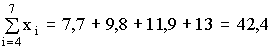 ;
;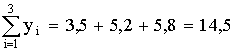 ;
; 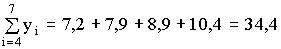 .
.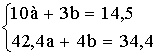
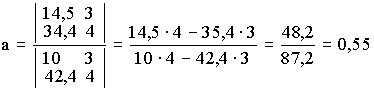 ;
;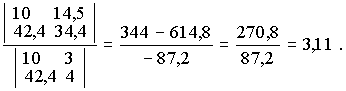
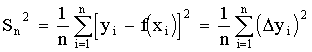 .
.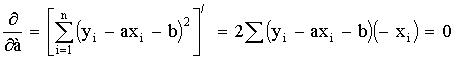 ;
;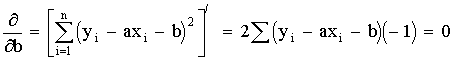 .
.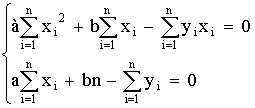
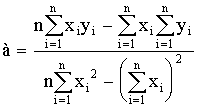 ;
; 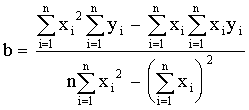 .
.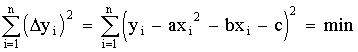 .
.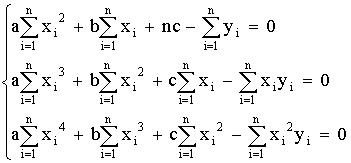
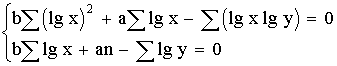
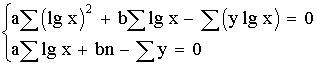
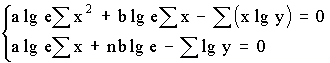
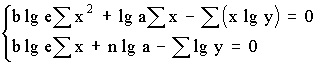
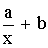
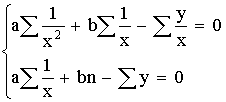
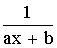
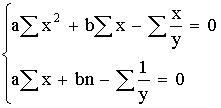
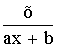
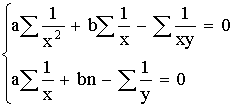
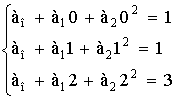 или
или 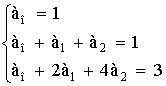
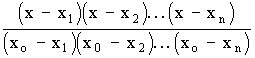 .
.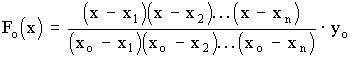 .
.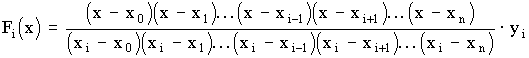 .
.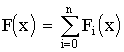 ,
,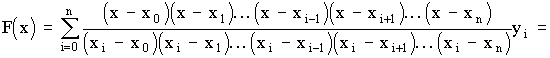
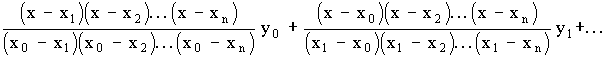
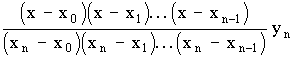 .
.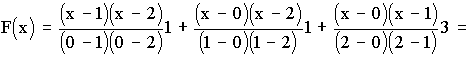
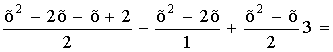
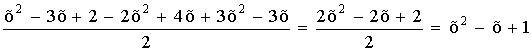 .
.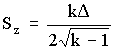 ,
,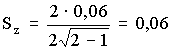 ( мм/зуб ).
( мм/зуб ).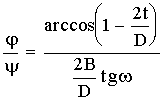 .
.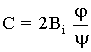 .
.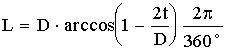 .
.