From Wikipedia, the free encyclopedia
An error correction model (ECM) belongs to a category of multiple time series models most commonly used for data where the underlying variables have a long-run common stochastic trend, also known as cointegration. ECMs are a theoretically-driven approach useful for estimating both short-term and long-term effects of one time series on another. The term error-correction relates to the fact that last-period’s deviation from a long-run equilibrium, the error, influences its short-run dynamics. Thus ECMs directly estimate the speed at which a dependent variable returns to equilibrium after a change in other variables.
History[edit]
Yule (1926) and Granger and Newbold (1974) were the first to draw attention to the problem of spurious correlation and find solutions on how to address it in time series analysis.[1][2] Given two completely unrelated but integrated (non-stationary) time series, the regression analysis of one on the other will tend to produce an apparently statistically significant relationship and thus a researcher might falsely believe to have found evidence of a true relationship between these variables. Ordinary least squares will no longer be consistent and commonly used test-statistics will be non-valid. In particular, Monte Carlo simulations show that one will get a very high R squared, very high individual t-statistic and a low Durbin–Watson statistic. Technically speaking, Phillips (1986) proved that parameter estimates will not converge in probability, the intercept will diverge and the slope will have a non-degenerate distribution as the sample size increases.[3] However, there might be a common stochastic trend to both series that a researcher is genuinely interested in because it reflects a long-run relationship between these variables.
Because of the stochastic nature of the trend it is not possible to break up integrated series into a deterministic (predictable) trend and a stationary series containing deviations from trend. Even in deterministically detrended random walks spurious correlations will eventually emerge. Thus detrending does not solve the estimation problem.
In order to still use the Box–Jenkins approach, one could difference the series and then estimate models such as ARIMA, given that many commonly used time series (e.g. in economics) appear to be stationary in first differences. Forecasts from such a model will still reflect cycles and seasonality that are present in the data. However, any information about long-run adjustments that the data in levels may contain is omitted and longer term forecasts will be unreliable.
This led Sargan (1964) to develop the ECM methodology, which retains the level information.[4][5]
Estimation[edit]
Several methods are known in the literature for estimating a refined dynamic model as described above. Among these are the Engle and Granger 2-step approach, estimating their ECM in one step and the vector-based VECM using Johansen’s method.[6]
Engle and Granger 2-step approach[edit]
The first step of this method is to pretest the individual time series one uses in order to confirm that they are non-stationary in the first place. This can be done by standard unit root DF testing and ADF test (to resolve the problem of serially correlated errors).
Take the case of two different series 

If they are both integrated to the same order (commonly I(1)), we can estimate an ECM model of the form
If both variables are integrated and this ECM exists, they are cointegrated by the Engle–Granger representation theorem.
The second step is then to estimate the model using ordinary least squares:
If the regression is not spurious as determined by test criteria described above, Ordinary least squares will not only be valid, but also consistent (Stock, 1987).
Then the predicted residuals 
One can then test for cointegration using a standard t-statistic on 
While this approach is easy to apply, there are numerous problems:
VECM[edit]
The Engle–Granger approach as described above suffers from a number of weaknesses. Namely it is restricted to only a single equation with one variable designated as the dependent variable, explained by another variable that is assumed to be weakly exogeneous for the parameters of interest. It also relies on pretesting the time series to find out whether variables are I(0) or I(1). These weaknesses can be addressed through the use of Johansen’s procedure. Its advantages include that pretesting is not necessary, there can be numerous cointegrating relationships, all variables are treated as endogenous and tests relating to the long-run parameters are possible. The resulting model is known as a vector error correction model (VECM), as it adds error correction features to a multi-factor model known as vector autoregression (VAR). The procedure is done as follows:
- Step 1: estimate an unrestricted VAR involving potentially non-stationary variables
- Step 2: Test for cointegration using Johansen test
- Step 3: Form and analyse the VECM.
An example of ECM[edit]
The idea of cointegration may be demonstrated in a simple macroeconomic setting. Suppose, consumption 









In this setting a change 











This structure is common to all ECM models. In practice, econometricians often first estimate the cointegration relationship (equation in levels), and then insert it into the main model (equation in differences).
References[edit]
- ^ Yule, Georges Udny (1926). «Why do we sometimes get nonsense correlations between time series? – A study in sampling and the nature of time-series». Journal of the Royal Statistical Society. 89 (1): 1–63. JSTOR 2341482.
- ^ Granger, C.W.J.; Newbold, P. (1978). «Spurious regressions in Econometrics». Journal of Econometrics. 2 (2): 111–120. JSTOR 2231972.
- ^ Phillips, Peter C.B. (1985). «Understanding Spurious Regressions in Econometrics» (PDF). Cowles Foundation Discussion Papers 757. Cowles Foundation for Research in Economics, Yale University.
- ^ Sargan, J. D. (1964). «Wages and Prices in the United Kingdom: A Study in Econometric Methodology», 16, 25–54. in Econometric Analysis for National Economic Planning, ed. by P. E. Hart, G. Mills, and J. N. Whittaker. London: Butterworths
- ^ Davidson, J. E. H.; Hendry, D. F.; Srba, F.; Yeo, J. S. (1978). «Econometric modelling of the aggregate time-series relationship between consumers’ expenditure and income in the United Kingdom». Economic Journal. 88 (352): 661–692. JSTOR 2231972.
- ^ Engle, Robert F.; Granger, Clive W. J. (1987). «Co-integration and error correction: Representation, estimation and testing». Econometrica. 55 (2): 251–276. JSTOR 1913236.
Further reading[edit]
- Dolado, Juan J.; Gonzalo, Jesús; Marmol, Francesc (2001). «Cointegration». In Baltagi, Badi H. (ed.). A Companion to Theoretical Econometrics. Oxford: Blackwell. pp. 634–654. doi:10.1002/9780470996249.ch31. ISBN 0-631-21254-X.
- Enders, Walter (2010). Applied Econometric Time Series (Third ed.). New York: John Wiley & Sons. pp. 272–355. ISBN 978-0-470-50539-7.
- Lütkepohl, Helmut (2006). New Introduction to Multiple Time Series Analysis. Berlin: Springer. pp. 237–352. ISBN 978-3-540-26239-8.
- Martin, Vance; Hurn, Stan; Harris, David (2013). Econometric Modelling with Time Series. New York: Cambridge University Press. pp. 662–711. ISBN 978-0-521-13981-6.
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
15 |
||||||||||||||||
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||||||||
|
C(2) |
1.014411 |
0.020750 |
48.88608 |
0.0000 |
|||||||||||||
|
C(3) |
0.702102 |
0.078268 |
8.970448 |
0.0000 |
|||||||||||||
|
т.е. yt |
= 1.014 yt – 1 + 0.702 (xt – 1.014 xt – 1) + e t , или |
||||||||||||||||
|
yt |
= 1.014 yt – 1 + 0.702 xt |
– 0.712 xt – 1 + e t |
Отметим близость результатов, полученных тремя методами:
|
yt = |
1.005 yt – 1 + 0.695 xt |
– 0.707 xt – 1 + et |
(метод 1), |
|
yt = |
yt – 1 + 0.710 xt |
– 0.710 xt – 1 + et |
(метод 2), |
|
yt = |
1.014 yt – 1 + 0.702 xt |
– 0.712 xt – 1 + e t |
(метод 3). |
Фактически, во всех трех случаях воспроизводится одна и та же линейная модель связи между рядами разностей:
∆yt = 0.7 ∆xt + et .
Эта регрессионная связь между продифференцированными рядами не является ложной (в отличие от регрессионной связи между рядами уровней): статистика Дарбина – Уотсона принимает значение 1.985; P-значение критерия Jarque – Bera равно 0.344.
Замечание
В связи с результатами, полученными при рассмотрении последних примеров, естественно возникает следующий вопрос, который поднимался в свое время различными исследователями. Не будет ли разумным, имея дело с рядами, траектории которых обнаруживают выраженный тренд, сразу приступать к оцениванию связей между рядами разностей (между продифференцированными рядами) ?
Против некритичного использования такого подхода говорят два обстоятельства:
(a)Если ряды в действительности стационарны относительно детерминированного тренда, то тогда дифференцирование приводит к
передифференцированным рядам, имеющим необратимую MA
составляющую.
(b)Если ряды являются интегрированными порядка 1 и при этом коинтегрированы, то при переходе к продифференцированным рядам теряется информация о долговременной связи между уровнями этих рядов.
Дифференцирование рядов оправданно и полезно, если ряды являются интегрированными, но при этом между ними отсутствует коинтеграционная связь.
Пусть yt ~ I(1), xt ~ I(0). Строить регрессию yt на xt в этом случае бессмысленно, т.к. для любых a и b в такой ситуации
yt – a – b xt ~ I(1).
Пусть, наоборот, yt ~ I(0), xt ~ I(1). Для любых a и b ≠ 0 здесь опять yt – a – b xt ~ I(1),
и только при b = 0 получаем yt – a – b xt ~ I(0),
так что и в таком сочетании строить регрессию одного ряда на другой не имеет смысла.
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
16 |
|
|
Пусть теперь yt ~ I(1), |
xt ~ I(1) – два интегрированных ряда. |
|
|
Если для любого b |
||
|
yt – b xt ~ I(1), |
||
|
то регрессия yt на |
xt является фиктивной, и мы уже выяснили, как следует |
действовать в такой ситуации.
Обратимся теперь к случаю, когда при некотором b ≠ 0 yt – b xt ~ I(0) – стационарный ряд.
Если это так, то ряды yt и xt называют коинтегрированными рядами, а вектор (1, – b)T – коинтегрирующим вектором.
Вообще, ряды yt ~ I(1), xt ~ I(1) называют коинтегрированными (в узком смысле – детерминистская коинтеграция), если существует ненулевой (коинтегрирующий)
вектор β = (β1, β2)T ≠ 0 , для которого
β1 xt + β2 yt ~ I(0) – стационарный ряд.
Заметим, что если вектор β = (β1, β2)T является коинтегрирующим вектором для рядов xt и yt , то тогда коинтегрирующим для этих рядов будет и любой вектор вида сβ = (сβ1, сβ2)T , где с ≠ 0 – постоянная величина. Чтобы выделить какой-то определенный вектор, приходится вводить условие нормировки, например, рассматривать только векторы вида (1, – b)T (или только векторы (– a, 1)T ).
Поскольку мы предполагаем сейчас, что xt , yt ~ I(1), то ряды разностей ∆xt , ∆yt стационарны. Будем предполагать в дополнение, что стационарен векторный ряд (∆xt , ∆yt)T , так что для него существует разложение Вольда в виде скользящего среднего
(∆xt , ∆yt)T = µ + B(L) εt ,
где
µ = (µ 1, µ 2 )T , µ 1 = E(∆xt ) , µ 2 = E(∆yt) ;
εt = (ε1t , ε2t )T – векторный белый шум,
т.е.
|
ε 1, ε 2 , … |
– последовательность не коррелированных между собой, одинаково |
||||||||
|
распределенных случайных векторов, для которых |
|||||||||
|
E(εt) = (0, 0)T , |
D(ε1t) = σ12 , D(ε2t) = σ22 , Cov(ε1t , ε2t ) = σ12 – постоянные величины; |
||||||||
|
1 |
0 |
∞ b |
(k ) |
b |
(k ) |
k |
|||
|
11 |
12 |
L |
. |
||||||
|
B(L) = |
0 |
1 |
+∑ |
b |
(k ) |
b |
(k ) |
||
|
k =1 |
|||||||||
|
21 |
22 |
Знаменитый результат Гренджера ([Granger (1983)], см. также [Engle, Granger (1987)])
состоит в том, что в случае коинтегрированности I(1) рядов xt и yt (в узком смысле)
|
(I) |
В разложении Вольда (∆xt , ∆yt)T = µ + B(L) εt матрица B(1) имеет ранг 1. |
|
(II)Система рядов xt и yt допускает векторное ARMA представление |
A(L) (xt, yt )T = c + d(L)εt ,
в котором
εt – тот же векторный белый шум, что и в (I), c = (c1, c2)T , c1 и c2 – постоянные,
A(L) – матричный полином от оператора запаздывания, d(L) – скалярный полином от оператора запаздывания, причем
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
17 |
A(0) = I2 (единичная матрица размера 2×2), rank A(1) = 1 (ранг 2×2-матрицы A(1) равен 1),
значение d(1) конечно.
Всвязи с тем, что в последнем представлении ранг (2×2)-матрицы A(1) меньше двух, об этом представлении часто говорят как о векторной авторегрессии пониженного ранга (reduced rank VAR).
Вразвернутой форме представление (II) имеет вид
|
p |
q |
|||||||||||||||
|
xt =c1 + |
∑(a1j xt − j +b1j yt − j )+ |
∑θkε1,t − k , |
||||||||||||||
|
j =1 |
k = 0 |
|||||||||||||||
|
p |
(a |
)+ |
q θ |
|||||||||||||
|
y |
t |
=c |
2 |
+ |
2 j |
x |
t − j |
+b |
y |
t − j |
ε |
2,t − k |
||||
|
∑ |
2 j |
∑ k |
||||||||||||||
|
j =1 |
k = 0 |
При этом верхние пределы p и q у сумм в правых частях могут быть бесконечными.
Если возможно векторное AR представление, то в нем d(L) ≡ 1 , p < ∞ .
|
(III) |
Система рядов xt и yt допускает представление в форме модели |
||
|
коррекции ошибок (error correction model – ECM) |
|||
|
∆xt =µ1 +α1zt −1 +∑∞ (γ 1j ∆xt − j +δ1j ∆yt − j )+ ∑∞ θkε1,t − k , |
|||
|
j =1 |
k = 0 |
||
|
∆yt = µ2 +α2 zt −1 +∑∞ (γ 2 j ∆xt − j +δ 2 j ∆yt − j )+ ∑∞ θkε2,t − k , |
|||
|
j =1 |
k = 0 |
||
|
где |
|||
|
zt = yt – β xt – E(yt – β xt) |
– стационарный ряд с нулевым |
математическим |
|
|
ожиданием, |
zt ~ I(0),
и
α12 + α22 > 0.
Если в (II) возможно векторное AR(p) представление (p < ∞), то тогда ECM принимает вид
∆xt =µ1 +α1zt −1 +∑p −1(γ 1j ∆xt − j +δ1j ∆yt − j ) +ε1,t , j =1
∆yt = µ2 +α2 zt −1 +∑p −1(γ 2 j ∆xt − j +δ 2 j ∆yt − j )+ε2,t , j =1
Здесь важно отметить следующее:
•Если ряды xt , yt ~ I(1) коинтегрированы, то все составляющие в ECM стационарны.
•Если векторный ряд (xt , yt)T ~ I(1) (так что векторный ряд (∆xt , ∆yt)T стационарен) и порождается ECM моделью, то ряды xt и yt коинтегрированы. (Действительно, в этом случае все составляющие ECM, отличные от zt–1, стационарны; но тогда стационарна и zt – 1.)
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
18 |
• Если ряды xt , yt ~ I(1) коинтегрированы, то тогда VAR в разностях не может иметь конечный порядок. (В отличие от случая, когда ряды xt и yt не коинтегрированы.)
|
Абсолютную величину zt = yt – α – β xt , где α = E(yt – β xt), |
можно рассматривать как |
|
|
расстояние, отделяющее систему в |
момент t от |
равновесия, задаваемого |
|
соотношением yt – α – β xt = 0. |
Величины и направления изменений xt и yt |
принимают во внимание величину и знак предыдущего отклонения от равновесия zt – 1 . Ряд zt , конечно, вовсе не обязательно убывает по абсолютной величине при переходе от одного периода времени к другому, но он является стационарным рядом, и поэтому расположен к движению по направлению к своему среднему.
Замечание 1
Переменная xt не является причиной по Гренджеру для переменной yt , если неучет прошлых значений переменной xt не приводит к ухудшению качества прогноза значения yt по совокупности прошлых значений этих двух переменных. Переменная yt не является причиной по Гренджеру для переменной xt , если неучет прошлых значений переменной yt не приводит к ухудшению качества прогноза значения xt по совокупности прошлых значений этих двух переменных. (Качество прогноза измеряется среднеквадратичной ошибкой прогноза.)
Если xt , yt ~ I(1) и коинтегрированы, то должна иметь место причинность по Гренджеру , по крайней мере, в одном направлении. Этот факт вытекает из представления такой системы рядов в форме ECM, в которой α12 + α22 > 0. Значение xt
– 1 через посредство zt– 1 помогает в прогнозировании значения yt (т.е. переменная xt является причиной по Гренджеру для переменной yt), если α2 ≠ 0. Значение yt – 1 через посредство zt– 1 помогает в прогнозировании значения xt (т.е. переменная yt является причиной по Гренджеру для переменной xt), если α1 ≠ 0.
Замечание 2
Пусть xt , yt ~ I(1) коинтегрированы и wt ~ I(0). Тогда для любого k коинтегрированы ряды xt и γ yt – k + wt , γ ≠ 0. Формально, если xt ~ I(1), то коинтегрированы ряды xt
и xt – k . (Действительно, тогда xt – xt – k = ∆xt + ∆xt – 1 + … + ∆xt – k – сумма I(0)- переменных, которая также является I(0)-переменной.)
Итак, при коинтегрированности рядов xt , yt ~ I(1) мы имеем
|
• |
модель долговременной (равновесной) связи yt = α + β xt ; |
•модель краткосрочной динамики в форме ECM,
иэти модели согласуются друг с другом.
Проблема, однако, состоит в том, что для построения ECM по реальным статистическим данным нам надо знать коинтегрирующий вектор (в данном случае, знать значение β). Хорошо, если этот вектор определяется экономической теорией. К сожалению, чаще его приходится оценивать по имеющимся данным.
Энгл и Гренджер [Engle, Granger (1987)] рассмотрели двухшаговую процедуру, в которой на первом шаге значения α и β оцениваются в рамках модели регрессии yt на xt
yt = α + β xt + ut .
Получив методом наименьших квадратов оценки αˆ и βˆ (НK-оценки), мы тем самым находим оцененные значения отклонений от положения равновесия
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
19 |
zˆt = yt – αˆ – βˆ xt
– это просто остатки от оцененной регрессии.
После этого, на втором шаге, методом наименьших квадратов раздельно (не как система!) оцениваются уравнения
∆xt =µ1 +α1zˆt −1 +∑p −1(γ 1j ∆xt − j +δ1j ∆yt − j ) +ν t , j =1
∆yt = µ2 +α2 zˆt −1 + ∑p −1(γ 2 j ∆xt − j +δ 2 j ∆yt − j ) +wt , j =1
(т.е. предполагается модель VAR(p) для xt , yt).
Определяющим в этой процедуре является то обстоятельство, что получаемая на первом шаге оценка βˆ быстрее обычного приближается (по вероятности) к истинному
значению β – второй компоненте коинтегрирующего вектора (1, β)T . ( βˆ является суперсостоятельной оценкой для β .) Это, в конечном счете, приводит к тому, что оценки в отдельном уравнении ECM, использующие оцененные значения zt−1 , имеют то же самое асимптотическое распределение, что и оценка максимального правдоподобия, использующая истинные значения zt−1 . (Обычно это асимптотически
нормальное распределение.) При этом НК-оценки стандартных ошибок всех коэффициентов являются состоятельными оценками истинных стандартных ошибок.
Заметим, что последние результаты справедливы несмотря на то, что ряд оцененных значений zˆt формально не является стационарным, поскольку βˆ ≠ β.
Отметим также, что если мы хотим использовать другую нормировку коинтегрирующего вектора в виде (β, 1)T , то нам придется оценивать регрессию xt на константу и yt , и это приведет к вектору, не пропорциональному вектору, оцененному в первом случае.
Замечание
|
ˆ |
|
|
Тот факт, что β |
быстрее обычного сходится (по вероятности) к β , вовсе не |
означает,что мы можем пользоваться на первом шаге процедуры Энгла – Гренджера обычными регрессионными критериями. Дело в том, что получаемые на первом шаге оценки и статистики, вообще говоря, имеют нестандартные асимптотические распределения.
Однако первый шаг является в данном контексте вспомогательным, и на этом шаге нет необходимости обращать внимание на сообщаемые в протоколах соответствующих пакетов программ значения статистик.
Напротив, на втором шаге мы можем использовать обычные статистические процедуры (разумеется, если количество наблюдений не мало и если коинтеграция имеется).
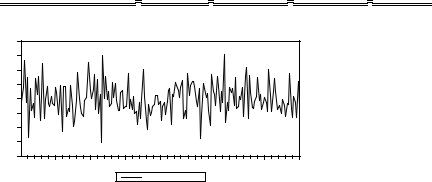
Пример Расмотрим реализацию процесса порождения данных
DGP: xt = xt – 1 + εt , yt = 2 xt + νt ,
где x1 = 0, а εt и νt – порождаемые независимо друг от друга последовательности независимых, одинаково распределенных случайных величин, имеющих стандартное
www.iet.ru/mipt/2/text/curs_econometrics.htm

|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
20 |
|||||||||||
|
нормальное распределение |
N(0, |
1). Графики полученных реализаций рядов |
xt |
и |
yt |
|||||||
|
имеют следующий вид |
||||||||||||
|
10 |
||||||||||||
|
0 |
||||||||||||
|
-10 |
||||||||||||
|
-20 |
||||||||||||
|
-30 |
||||||||||||
|
-40 |
||||||||||||
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
|||
|
Y |
X |
Пара (xt , yt) образует векторный процесс авторегрессии
xt = xt – 1 + εt , yt = 2 xt – 1 + ηt ,
где ηt = νt + 2εt ~ i.i.d. N(0, 5).
В форме ECM пара уравнений принимает вид
∆xt = εt ,
∆yt = – (yt – 1 – 2 xt – 1) + ηt = – zt + где zt = yt – 2 xt ,
или
∆xt = α1 zt – 1 + εt ,
∆yt = α2 zt – 1 + ηt ,
где α1 = 0, α2 = – 1, так что α12
На практике, приступая к анализу статистических данных, исследователь не знает точно, какой порядок имеет VAR в DGP. Имея это в виду, выберем для оценивания в качестве статистической модели ECM в виде
∆xt = α1 zt – 1 + γ11∆xt – 1 + δ11∆yt – 1 + vt ,
∆yt = α2 zt – 1 + γ21∆xt – 1 + δ21∆yt – 1 + wt ,
допуская, что данные порождаются моделью векторной авторегрессии второго порядка (p = 2). Для анализа используем 100 наблюдений.
(I шаг) Исходим из модели yt = α + β xt + ut . Оцененная модель:
|
Dependent Variable: Y |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
-0.006764 |
0.165007 |
-0.040992 |
0.9674 |
|
X |
1.983373 |
0.020852 |
95.11654 |
0.0000 |
|
R-squared |
0.989284 |
Durbin-Watson stat |
2.217786 |
т.е.
yt = – 0.006764 + 1.983373 xt + uˆt ,
так что
zˆt = uˆt = yt + 0.006764 – 1.983373 xt .
www.iet.ru/mipt/2/text/curs_econometrics.htm

|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
21 |
Допустив, что VAR имеет порядок 2, при использовании критерия Дики – Фуллера для проверки рядов yt и xt на коинтегрированность в правую часть уравнения включаем одну запаздывающую разность:
∆zˆt = φ zˆt−1 + θ1∆zˆt−1 + ζt . ,
Оценивая последнее уравнение получаем:
Augmented Dickey-Fuller Test Equation Dependent Variable: D(Z) Sample(adjusted): 3 100
Included observations: 98 after adjusting endpoints
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
Z(-1) |
-1.153515 |
0.151497 |
-7.614088 |
0.0000 |
||||||||
|
D(Z(-1)) |
0.038156 |
0.100190 |
0.380837 |
0.7042 |
||||||||
Полученное значение тестовой статистики tφ = – 7.614 намного ниже 5% критического уровня –3.396 (см. [Patterson (2000), таблица 8.7]). Гипотеза некоинтегрированности рассматриваемых рядов уверенно отвергается. (Ввиду статистической незначимости коэффициента при запаздывающей разности, можно было бы переоценить модель, не включая запаздывающую разность в правую часть уравнения. Это дало бы значение tφ = – 11.423, при котором гипотеза некоинтегрированности отвергается еще более уверенно.)
Таким образом, мы принимаем решение о коинтегрированности рядов yt и xt , и переходим к построению модели коррекции ошибок.
(Шаг II) Сначала отдельно оцениваем уравнение для ∆xt :
|
Dependent Variable: D(X) |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
C |
-0.028016 |
0.100847 |
-0.277810 |
0.7818 |
||||||||
|
Z(-1) |
0.250942 |
0.176613 |
1.420858 |
0.1587 |
||||||||
|
D(X(-1)) |
0.639967 |
0.257823 |
2.482201 |
0.0148 |
||||||||
|
D(Y(-1)) |
-0.258740 |
0.116654 |
-2.218019 |
0.0290 |
||||||||
Поочередное исключение из правой части уравнения переменных со статистически незначимыми коэффициентами и наибольшим P-значением приводит к оцененной модели
|
Dependent Variable: D(X) |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
D(X(-1)) |
0.115141 |
0.100249 |
1.148554 |
0.2536 |
||||||||
и, в конечном счете, к модели
∆xt = νt ,
которая и была использована при порождении ряда xt . Оценивая теперь уравнение для ∆yt , получаем
|
Dependent Variable: D(Y) |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
C |
-0.060101 |
0.211899 |
-0.283630 |
0.7773 |
||||||||
|
Z(-1) |
-0.641060 |
0.371097 |
-1.727472 |
0.0874 |
||||||||
|
D(X(-1)) |
1.313872 |
0.541733 |
2.425311 |
0.0172 |
||||||||
|
D(Y(-1)) |
-0.482981 |
0.245111 |
-1.970459 |
0.0517 |
||||||||
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
22 |
Исключая из правой части оцениваемого уравнения константу, получаем:
|
Dependent Variable: D(Y) |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
Z(-1) |
-0.638888 |
0.369218 |
-1.730381 |
0.0868 |
||||||||
|
D(X(-1)) |
1.317763 |
0.538932 |
2.445138 |
0.0163 |
||||||||
|
D(Y(-1)) |
-0.483722 |
0.243908 |
-1.983217 |
0.0502 |
||||||||
Хотя формально здесь следовало бы начать исключение статистически незначимых переменных с zˆt −1 , мы должны принять во внимание уже принятое решение о
коинтегрированности рядов yt и xt . Но если эти ряды действительно коинтегрированы, то в ECM должно выполняться соотношение α12 + α22 > 0. Поскольку же переменная zt – 1 не вошла в правую часть уравнения для ∆xt , она должна оставаться в правой части уравнения для ∆yt . Если начать исключение с переменной ∆yt – 1 , то в оцененном редуцированном уравнении
|
Dependent Variable: D(Y) |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
Z(-1) |
-1.186411 |
0.248876 |
-4.767072 |
0.0000 |
||||||||
|
D(X(-1)) |
0.331411 |
0.210732 |
1.572671 |
0.1191 |
||||||||
статистически незначим коэффициент при ∆xt – 1 , что приводит нас к уравнению ∆yt = α2 zˆt−1 + wt , оценивая которое, получаем
|
Dependent Variable: D(Y) |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
Z(-1) |
-1.273584 |
0.247887 |
-5.137760 |
0.0000 |
||||||||
Проверка гипотезы H0: α2 = – 1 дает:
|
Null Hypothesis: |
C(1)= -1 |
|||||||||
|
F-statistic |
1.218077 |
Probability |
0.272441 |
|||||||
|
Chi-square |
1.218077 |
Probability |
0.269738 |
|||||||
Поскольку эта гипотеза не отвергается, мы можем остановиться на модели ECM
∆xt = εt , ∆yt = – zˆt−1 + wt ,
где
zˆt−1 = yt – 1 + 0.006764 – 1.983373 xt – 1 .
Подстановка последнего выражения для zˆt−1 в уравнение для ∆yt приводит к соотношению
yt = – 0.0068 + 1.983 xt – 1 + wt ,
которое близко к соотношению yt = 2 xt – 1 + ηt ,
соответствующему использованному DGP.
Заметим, наконец, что последовательность wt = ∆yt + zˆt−1 идентифицируется по
наблюдаемой ее реализации как гауссовский белый шум с оцененной дисперсией 4.62 (использованному DGP соответствует значение 5.00), а последовательность εt = ∆xt идентифицируется как гауссовский белый шум с оцененной дисперсией 1.04 (использованному DGP соответствует значение 1.00).
Оценив ECM и остановившись на модели
∆xt = εt , ∆yt = – zˆt−1 + wt ,
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
23 |
мы тем самым обнаруживаем, что коррекция производится только в отношении ряда yt : при положительных zˆt−1 , т.е. при
yt– 1 – (– 0.0068 + 1.983 xt – 1) > 0,
в правой части уравнения для ∆yt корректирующая составляющая – zˆt−1 отрицательна и действует в сторону уменьшения приращения переменной yt . Напротив, при отрицательных zˆt−1 корректирующая составляющая действует в сторону увеличения приращения переменной yt .
Прошлые значения переменной xt через посредство zˆt−1 помогают в прогнозировании
значения yt , т.е. переменная xt является причиной по Гренджеру для переменной yt . В то же время, прошлые значения переменной yt никак не помогают прогнозированию значения xt , так что yt не является причиной по Гренджеру для xt .
Заметим далее, что даже если в ECM Cov(vt, wt) ≠ 0, оценивание пары уравнений ЕСМ как системы не повышает эффективности оценок, поскольку в правые части обоих уравнений входят одни и те же переменные.
Расмотренный в нашем примере процесс порождения данных
DGP: xt = xt – 1 + εt , yt = 2 xt + νt ,
является частным случаем модели, известной как треугольная система Филлипса. В общем случае (для двух рядов) эта система имеет вид
yt = β xt + νt , xt = xt – 1 + εt ,
где (εt , νt)T ~ i.i.d. N2(0, Σ) – последовательность независимых, одинаково распределенных случайных векторов, имеющих двумерное нормальное распределение с нулевым математическим ожиданием и ковариационной матрицей Σ . (Такая последовательность называется двумерным гауссовским белым шумом.)
Если матрица Σ диагональная, так что Cov(εt , νt) = 0, то тогда xt является экзогенной переменной в первом уравнении, и никаких проблем с оцениванием коэффициента β в этом случае не возникает.
Если же Cov(εt , νt) ≠ 0, то тогда xt уже не является экзогенной переменной в первом уравнении, т.к. при этом Cov(xt , νt) = Cov(xt – 1 + εt , νt) ≠ 0. Поэтому получаемая в первом уравнении оценка наименьших квадратов для β не имеет даже асимптотически нормального распределения.
В дальнейшем мы еще вернемся к проблеме оценивания коинтегрирующего вектора, а сейчас обратимся к вопросу о коинтеграции нескольких временных рядов.
Пусть мы имеем N временных рядов y1t , … , yN t , каждый из которых является интегрированным порядка 1. Если существует такой вектор β = (β1, … , βN)T , отличный от нулевого, для которого
β1 y1t + … + βN yN t ~ I(0) – стационарный ряд,
то говорят, что эти ряды коинтегрированы (в узком смысле); такой вектор β называется коинтегрирующим вектором. Если при этом
c = E(β1 y1t + … + βN yN t),
то тогда можно говорить о долговременном положении равновесия системы в виде
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
24 |
β1 y1t + … + βN yN t = c .
В каждый конкретный момент времени t существует некоторое отклонение системы от этого положения равновесия, характеризующееся величиной
zt = β1 y1t + … + βN yN t – c .
Ряд zt , в силу сделанных предположений, является стационарным рядом, имеющим нулевое математическое ожидание, так что он достаточно часто пересекает нулевой уровень, т.е. система колеблется вокруг указанного выше положения равновесия.
Естественной процедурой для проверки коинтегрированности рядов y1t , … , yN t является построение регрессии одного из этих рядов на остальные N – 1 рядов и проверка гипотезы наличия единичного корня у ряда zt на основании исследования ряда остатков от оцененной регрессии. Иначе говоря, мы оцениваем, например, модель
y1t = θ1 + θ2 y2 t + … + θN yN t + ut ,
и проверяем гипотезу единичного корня на основании исследования ряда остатков uˆt = y1t – (θˆ1+ θˆ2 y2 t + … + θˆN yN t),
опираясь на статистику Дики – Фуллера. Критические значения можно найти, следуя
[MacKinnon (1991)] (см. также [Patterson (2000), таблица A8.1]).
Если гипотеза единичного корня отвергается, то вектор
βˆ = (1, – θˆ2 , … , – θˆN )
берется в качестве оцененного коинтегрирующего вектора. При этом отклонение системы от положения равновесия оценивается величиной
zˆt = uˆt .
Поясним теперь, что мы имели в виду, оговаривая, что приведенные выше определения коинтеграции соответствуют коинтеграции в узком смысле.
В приведенных определениях ненулевой вектор β = (β1, … , βN)T определялся как коинтегрирующий вектор, если β1 y1t + … + βN yN t – стационарный ряд. Это означает, что если ряды y1t , … , yN t (по крайней мере, некоторые из них) содержат, наряду со стохастическим, еще и детерминированные тренды, то тогда коинтегрирующий вектор должен аннулировать оба вида трендов одновременно. И в связи с этим, коинтеграцию в узком смысле называют еще детерминистской коинтеграцией.
7.3. Проверка нескольких рядов на коинтегрированность. Критерии Дики – Фуллера
Здесь надо различать несколько случаев.
(1) Коинтегрирующий вектор определяется экономической теорией.
Тогда надо просто проверить на наличие единичного корня соответствующую линейную комбинацию
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
25 |
β1 y1t + … + βN yN t .
При этом используются те же критические значения, которые рассчитаны на применение к отдельно взятому ряду; эти значения не зависят от количества задействованных рядов N .
Пусть возможный коинтегрирующий вектор не определен заранее.
Тогда отдельно рассматриваются следующие ситуации.
(2) Ряды y1t , … , yN t не имеют детерминированного тренда (точнее, E(∆yk t) = 0).
(2a) В коинтеграционное соотношение (SM) константа не включается.
В этом случае мы оцениваем
SM: y1t = γ2 y2t + … + γN yN t + ut ,
получаем ряд остатков
uˆt = y1t − (γˆ2 y2 t +K+ γˆN yN t ),
оцениваем модель регрессии
∆uˆt = ϕ uˆt −1 +ζ1∆uˆt −1 +K+ζ K ∆uˆt − K + εt
с достаточным количеством запаздывающих разностей и проверяем гипотезу H0: φ
= 0 против альтернативы H0: φ < 0 .
На этот раз критические значения для t-статистики tφ зависят от количества задействованных рядов N . При большом количестве наблюдений можно использовать
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
26 |
критические значения, приведенные в [Hamilton (1994), Table B.9, Case 1]. Однако на практике в правую часть оцениваемого уравнения константа обычно включается.
(2b) В коинтеграционное соотношение (SM) константа включается.
В этом случае мы оцениваем
SM: y1t = α + γ2 y2t + … + γN yN t + ut ,
опять получаем ряд остатков – теперь это будет ряд
uˆt = y1t − (αˆ + γˆ2 y2 t +K+ γˆN yN t ),
оцениваем модель регрессии
∆uˆt = ϕ uˆt −1 +ζ1∆uˆt −1 +K+ζ K ∆uˆt − K + εt
с достаточным количеством запаздывающих разностей и проверяем гипотезу H0: φ
= 0 против альтернативы H0: φ < 0 .
Критические значения в этом случае отличаются от случая (2a). При большом
количестве наблюдений можно использовать критические значения, приведенные в
[Hamilton (1994), Table B.9, Case 2]. При небольших T критические значения
вычисляются по формуле, приведенной в [MacKinnon (1991), таблица 1 (вариант “no
trend”)] и воспроизведенной в [Patterson (2000)].
|
(3) |
Хотя бы один из рядов y2t , … , yN t имеет линейный тренд , так что E(∆yk t) |
|
≠ 0 |
хотя бы для одного из регрессоров. |
(3a) В коинтеграционное соотношение включается константа.
В этом случае оценивается
SM: y1t = α + γ2 y2t + … + γN yN t + ut .
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
27 |
Далее действуем опять как в (2b), только критические значения другие. При
большом количестве наблюдений можно использовать критические значения,
приведенные в [Hamilton (1994), Table B.9, Case 3]. При небольших T критические
значения вычисляются по формуле, приведенной в работе [MacKinnon (1991), Table
1 (вариант “with trend”)] и воспроизведенной в [Patterson (2000)].
(3b) В коинтеграционное соотношение включается линейный тренд.
В этом случае оценивается
SM: y1t = α + δt + γ2 y2t + … + γN yN t + ut .
Действуя так же, как и ранее, используем те же таблицы, что и в (3a), но только не для N , а для N + 1 переменных.
Включение тренда в коинтеграционное соотношение приводит к уменьшению
мощности критерия из-за необходимости оценивания “мешающего” параметра δ .
Однако такой подход вполне уместен в тех случаях, когда нет полной уверенности в
том, имеется ли ненулевой тренд хотя бы у одного из рядов y1t, y2t , … , yN t .
Пример
Смоделируем реализации четырех рядов y1t , y2t , y3t , y4t , следуя процессу порождения данных
DGP: y1t = y2, t + y3, t + y4, t + ε1t ,
y2t = y2, t – 1 + ε2t , y3t = y3, t – 1 + ε3t , y4t = y4, t – 1 + ε4t ,
где ε1t , ε2t , ε3t , ε4t – независимые друг от друга процессы гауссовского белого шума с дисперсиями, равными 1 для ε2t , ε3t , ε4t и 2 для ε1t .
Графики полученных реализаций для T = 200 приведены ниже.
www.iet.ru/mipt/2/text/curs_econometrics.htm

|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
28 |
|||||||||
|
60 |
||||||||||
|
40 |
||||||||||
|
20 |
||||||||||
|
0 |
||||||||||
|
-20 |
||||||||||
|
-40 |
||||||||||
|
-60 |
||||||||||
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
|
Y1 |
Y3 |
|||||||||
|
Y2 |
Y4 |
Не зная точно процесс порождения данных, мы должны были бы начать с исследования отдельных рядов. У всех четырех рядов не обнаруживается детерминированного тренда. Проверка по критерию Дики – Фуллера дает значения t-статистик, равные – 2.18, – 1.78, – 0.57, –1.70, соответственно. Все 4 ряда признаются интегрированными. Продифференцированные ряды идентифицируются как гауссовские белые шумы, так что ряды y1t , y2t , y3t , y4t идентифицируются как AR(1) ряды с единичным корнем, т.е. как интегрированные ряды порядка 1.
Теперь можно приступить к проверке этих четырех рядов на коинтегрированность. (1) Если “экономическая теория” предполагает теоретическое
долговременное соотношение между рассматриваемыми рядами в форме
|
y1t = y2, t + y3, t + y4, t , |
|||||||||
|
то мы просто проверяем на интегрированность ряд |
|||||||||
|
y1t – y2, t – y3, t – y4, t . |
|||||||||
|
График этого ряда |
|||||||||
|
8 |
|||||||||
|
6 |
|||||||||
|
4 |
|||||||||
|
2 |
|||||||||
|
0 |
|||||||||
|
-2 |
|||||||||
|
-4 |
|||||||||
|
-6 |
|||||||||
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
COINT |
вполне похож на график стационарного ряда, что подтверждается проверкой по критерию Дики – Фуллера: вычисленное значение t-статистики критерия равно – 15.07. Гипотеза некоинтегрированности рядов отвергается.
Представим теперь, что теория не предлагает нам готового коинтегрирующего вектора.
(2a) Оценивание статистической модели без включения в нее константы дает:
Dependent Variable: Y1
Method: Least Squares
|
Variable |
Coefficient Std. Error |
t-Statistic |
Prob. |
|||||||||
www.iet.ru/mipt/2/text/curs_econometrics.htm

|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
29 |
||||||||||||||
|
Y2 |
0.996084 |
0.009973 |
99.88161 |
0.0000 |
|||||||||||
|
Y3 |
0.992550 |
0.009578 |
103.6296 |
0.0000 |
|||||||||||
|
Y4 |
1.002305 |
0.012393 |
80.87922 |
0.0000 |
|||||||||||
При оценивании тестового уравнения Дики – Фуллера для ряда остатков получаем
|
Augmented Dickey-Fuller Test Equation |
|||||||||||||
|
Dependent Variable: D(RESID_2A) |
|||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|||||||||
|
RESID_2A(-1) |
-1.075552 |
0.070892 |
-15.17178 |
0.0000 |
|||||||||
Вычисленное значение t-статистики критерия равно – 15.17, что намного ниже 5%
критического значения – 3.74 ([Hamilton (1994), Table B.9, Case 1]). Гипотеза некоинтегрированности отвергается.
(2b) Оценивание статистической модели с включением константы:
|
Dependent Variable: Y1 |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
C |
0.332183 |
0.373542 |
0.889279 |
0.3749 |
||||||||
|
Y2 |
1.002583 |
0.012369 |
81.05843 |
0.0000 |
||||||||
|
Y3 |
0.987369 |
0.011215 |
88.04048 |
0.0000 |
||||||||
|
Y4 |
0.999022 |
0.012937 |
77.22129 |
0.0000 |
||||||||
При оценивании тестового уравнения Дики – Фуллера для ряда остатков получаем
|
Augmented Dickey-Fuller Test Equation |
|||||||||||||
|
Dependent Variable: D(RESID_2B) |
|||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|||||||||
|
RESID_2B(-1) |
-1.079049 |
0.070861 |
-15.22764 |
0.0000 |
|||||||||
Вычисленное значение t-статистики – 15.23 опять намного ниже 5% критического значения, которое здесь равно – 4.11 ([Hamilton (1994), Table B.9, Case 2]). Гипотеза некоинтегрированности отвергается.
|
(3) Модифицируем теперь ряд y1t , переходя к ряду y*1t = y1t + 0.75t , график которого |
|||||||||
|
в сравнении с графиком ряда y1t |
имеет следующий вид: |
||||||||
|
200 |
|||||||||
|
150 |
|||||||||
|
100 |
|||||||||
|
50 |
|||||||||
|
0 |
|||||||||
|
-50 |
|||||||||
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
Y1 |
Y1_STAR |
||||||||
|
Картина изменения всех 4 рядов принимает вид |
www.iet.ru/mipt/2/text/curs_econometrics.htm

|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
30 |
|||||||||
|
200 |
||||||||||
|
150 |
||||||||||
|
100 |
||||||||||
|
50 |
||||||||||
|
0 |
||||||||||
|
-50 |
||||||||||
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
|
Y1_STAR |
Y3 |
|||||||||
|
Y2 |
Y4 |
(3a) Оцениваем статистическую модель с константой в правой части:
|
Dependent Variable: Y1_STAR |
|||
|
Variable |
Coefficient Std. Error |
t-Statistic |
Prob. |
|
C |
11.49053 |
2.704802 |
4.248195 |
0.0000 |
||||||
|
Y2 |
-1.333762 |
0.089561 |
-14.89224 |
0.0000 |
||||||
|
Y3 |
2.856952 |
0.081207 |
35.18115 |
0.0000 |
||||||
|
Y4 |
0.072630 |
0.093677 |
0.775323 |
0.4391 |
||||||
|
В этом случае график остатков имеет несколько отличный вид: |
||||||||||
|
15 |
||||||||||
|
10 |
||||||||||
|
5 |
||||||||||
|
0 |
||||||||||
|
-5 |
||||||||||
|
-10 |
||||||||||
|
-15 |
||||||||||
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
|
|
RESID_3A |
||||||||||
|
Проверка по Дики – Фуллеру дает следующие результаты: |
При оценивании тестового уравнения Дики – Фуллера для ряда остатков получаем
|
Augmented Dickey-Fuller Test Equation |
||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
||||||||
|
RESID_3A(-1) |
-0.119805 |
0.033630 |
-3.562431 |
0.0005 |
||||||||
Вычисленное значение t-статистики – 3.56 выше 5% критического значения, которое здесь равно – 4.16 ([Hamilton (1994), Table B.9, Case 3]). Гипотеза некоинтегрированности не отвергается.
(3b) Включаем в правую часть тренд:
|
Dependent Variable: Y1_STAR |
||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
C |
0.304068 |
0.390739 |
0.778187 |
0.4374 |
www.iet.ru/mipt/2/text/curs_econometrics.htm
|
Эконометрика. Введение в регрессионный анализ временных рядов. В.П.Носко www.iet.ru |
31 |
||||||||||
|
@TREND |
0.751890 |
0.007507 |
100.1621 |
0.0000 |
|||||||
|
Y2 |
1.008470 |
0.026468 |
38.10166 |
0.0000 |
|||||||
|
Y3 |
0.982658 |
0.021830 |
45.01453 |
0.0000 |
|||||||
|
Y4 |
1.001356 |
0.015942 |
62.81247 |
0.0000 |
|||||||
|
График остатков: |
|||||||||||
|
8 |
|||||||||||
|
6 |
|||||||||||
|
4 |
|||||||||||
|
2 |
|||||||||||
|
0 |
|||||||||||
|
-2 |
|||||||||||
|
-4 |
|||||||||||
|
-6 |
|||||||||||
|
-8 |
|||||||||||
|
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
||
|
RESID_3B |
|||||||||||
|
Последний график похож на график стационарного ряда, что подтверждается |
|||||||||||
|
проверкой по Дики – Фуллеру: |
|
Augmented Dickey-Fuller Test Equation |
|||||||||||||
|
Dependent Variable: D(RESID_3B) |
|||||||||||||
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|||||||||
|
RESID_3B(-1) |
-1.079492 |
0.070859 |
-15.23448 |
0.0000 |
|||||||||
Вычисленное значение t-статистики – 15.234 намного ниже 5% критического значения, которое здесь равно –4.49 ([Hamilton (1994), Table B.9, Case 3]). Гипотеза некоинтегрированности отвергается.
Последние два результата весьма важны для уточнения того, что понимается под коинтеграцией в настоящее время.
Фактически, мы обнаружили следующее. Ряды y1t , y2t , y3t , y4t коинтегрированы в том смысле, который был определен выше (коинтегрированы в узком смысле). Именно в таком виде ввели в обиход понятие коинтеграции Энгл и Гренджер. Ряды y*1t , y2t , y3t , y4t не являются коинтегрированными в узком смысле. В то же время, включение в правую часть статистической модели трендовой составляющей приводит к стационарным остаткам.
Вспомним в связи с этим, что при включении тренда в правую часть линейного регрессионного уравнения коэффициенты при объясняющих переменных интерпретируются как коэффициенты линейной связи между переменными, очищенными от детерминированного тренда. Последние же действительно были коинтегрированы по построению.
Наблюдаемая ситуация известна теперь под названием “стохастическая коинтеграция”. Оно указывает на наличие коинтеграционной связи между стохастическими трендами, входящими в состав рассматриваемых рядов, и не требует согласованности детерминированных трендовых составляющих ( если таковые имеются). В этом случае коинтегрирующий вектор аннулирует стохастический тренд, но не обязан одновременно аннулировать и детерминированный тренд. Другими словами, существует линейная комбинация рассматриваемых рядов, которая образует ряд, стационарный относительно детерминированного тренда, но не обязательно стационарный.
В противоположность стохастической коинтеграции, при наличии коинтеграции в узком смысле коинтегрирующий вектор аннулирует и стохастический и
www.iet.ru/mipt/2/text/curs_econometrics.htm
тип модели временного ряда
Модель коррекции ошибок (ECM) принадлежит к Категория нескольких моделей временных рядов , наиболее часто используемых для данных, в которых базовые переменные имеют долгосрочный стохастический тренд, также известный как коинтеграция. ECM — это теоретически обоснованный подход, полезный для оценки как краткосрочного, так и долгосрочного воздействия одного временного ряда на другой. Термин «исправление ошибок» относится к тому факту, что отклонение последнего периода от долгосрочного равновесия, ошибка, влияет на его краткосрочную динамику. Таким образом, ECM напрямую оценивают скорость, с которой зависимая переменная возвращается в состояние равновесия после изменения других переменных.
Содержание
- 1 История ECM
- 2 Оценка
- 2.1 Двухэтапный подход Энгла и Грейнджера
- 2.2 VECM
- 2.3 Пример ECM
- 3 Ссылки
- 4 Далее чтение
История ECM
Юл (1926) и Грейнджер и Ньюболд (1974) первыми привлекли внимание к проблеме ложной корреляции и нашли решения, как ее решить. в анализе временных рядов. Учитывая два совершенно несвязанных, но интегрированных (нестационарных) временных ряда, регрессионный анализ одного из другого будет иметь тенденцию давать явно статистически значимую взаимосвязь, и, таким образом, исследователь может ошибочно полагать, что нашел доказательства существования истинная взаимосвязь между этими переменными. Обычный метод наименьших квадратов больше не будет согласованным, а часто используемая тестовая статистика будет недействительной. В частности, моделирования Монте-Карло показывают, что можно получить очень высокий R в квадрате, очень высокий индивидуальный t-статистический и низкий Дарбина – Ватсона. статистика. С технической точки зрения Филлипс (1986) доказал, что оценки параметров не будут сходиться по вероятности, точка пересечения будет расходиться, а наклон будет иметь невырожденное распределение по мере увеличения размера выборки. Однако может существовать общий стохастический тренд для обоих рядов, который искренне интересует исследователя, поскольку он отражает долгосрочную взаимосвязь между этими переменными.
Из-за стохастического характера тренда невозможно разбить интегрированный ряд на детерминированный (предсказуемый) тренд и стационарный ряд, содержащий отклонения от тренда. Даже при детерминированном удалении тренда случайных блужданий в конечном итоге возникнут ложные корреляции. Таким образом, детрендирование не решает проблему оценки.
Чтобы по-прежнему использовать подход Бокса – Дженкинса, можно было бы различать ряды, а затем оценивать такие модели, как ARIMA, учитывая, что многие часто используемые временные ряды ( например, в экономике) кажутся стационарными в первых разностях. Прогнозы на основе такой модели по-прежнему будут отражать циклы и сезонность, которые присутствуют в данных. Однако любая информация о долгосрочных корректировках, которую могут содержать данные в уровнях, опускается, и долгосрочные прогнозы будут ненадежными.
Это привело Саргана (1964) к разработке методологии ECM, которая сохраняет информацию об уровне.
Оценка
В литературе известно несколько методов. для оценки уточненной динамической модели, как описано выше. Среди них двухэтапный подход Энгла и Грейнджера, оценивающий их ECM за один этап, и векторный VECM с использованием метода Йохансена.
двухэтапного подхода Энгла и Грейнджера
Первый этап этот метод заключается в предварительном тестировании отдельных временных рядов, которые используются, чтобы подтвердить, что они нестационарны в первую очередь. Это можно сделать с помощью стандартного модульного корневого тестирования DF и теста ADF (для решения проблемы серийно коррелированных ошибок). Возьмем случай двух разных серий x t {\ displaystyle x_ {t}}

Если они оба интегрированы в одном порядке (обычно I (1)), мы можем оценить модель ECM в виде
- A (L) Δ yt = γ + B (L) Δ xt + α (yt — 1 — β 0 — β 1 xt — 1) + ν t. {\ Displaystyle A (L) \, \ Delta y_ {t} = \ gamma + B (L) \, \ Delta x_ {t} + \ alpha (y_ {t-1} — \ beta _ {0} — \ beta _ {1} x_ {t-1}) + \ nu _ {t}.}
Если обе переменные интегрированы и этот ECM существует, они коинтегрируются теоремой Энгла – Грейнджера о представлении.
Затем на втором этапе оценивается модель с помощью обычных наименьших квадратов : yt = β 0 + β 1 xt + ε t {\ displaystyle y_ {t} = \ beta _ {0} + \ beta _ {1} x_ {t} + \ varepsilon _ {t}}

- A (L) Δ yt = γ + B (L) Δ xt + α ε ^ t — 1 + ν t. {\ Displaystyle A (L) \, \ Delta y_ {t} = \ gamma + B (L) \, \ Delta x_ {t} + \ alpha {\ hat {\ varepsilon}} _ {t-1} + \ nu _ {t}.}
Затем можно протестировать коинтеграцию, используя стандартную t-статистику на α {\ displaystyle \ alpha}
VECM
Энгл-Грейнджер описанный выше подход имеет ряд недостатков. А именно, он ограничен только одним уравнением с одной переменной, обозначенной как зависимая переменная, объясненной другой переменной, которая, как предполагается, является слабо экзогенной для интересующих параметров. Он также основан на предварительном тестировании временных рядов, чтобы выяснить, являются ли переменные I (0) или I (1). Эти недостатки могут быть устранены с помощью процедуры Йохансена. Его преимущества заключаются в том, что в предварительном тестировании нет необходимости, может быть множество коинтегрирующих взаимосвязей, все переменные рассматриваются как эндогенные, и возможны тесты, относящиеся к долгосрочным параметрам. Полученная модель известна как модель векторной коррекции ошибок (VECM), поскольку она добавляет функции коррекции ошибок в многофакторную модель, известную как векторная авторегрессия (VAR). Процедура выполняется следующим образом:
- Шаг 1: оценка неограниченной VAR, включающей потенциально нестационарные переменные
- Шаг 2: Тест на коинтеграцию с использованием теста Йохансена
- Шаг 3: Сформировать и проанализировать VECM.
Пример ECM
Идея коинтеграции может быть продемонстрирована в простых макроэкономических условиях. Предположим, потребление C t {\ displaystyle C_ {t}}









В этой настройке изменение Δ C t = C t — C t — 1 {\ displaystyle \ Delta C_ {t} = C_ {t} -C_ {t-1}}











Эта структура является общей для всех моделей ECM. На практике эконометристы часто сначала оценивают взаимосвязь коинтеграции (уравнение в уровнях), а затем вставляют его в основную модель (уравнение в разностях).
Ссылки
Дополнительная литература
- Dolado, Juan J.; Гонсало, Хесус; Мармол, Франсеск (2001). «Коинтеграция». В Балтаги, Бади Х. (ред.). Компаньон теоретической эконометрики. Оксфорд: Блэквелл. Стр. 634 –654. doi : 10.1002 / 9780470996249.ch31. ISBN 0-631-21254-X.
- Эндерс, Уолтер (2010). Прикладные эконометрические временные ряды (Третье изд.). Нью-Йорк: Джон Вили и сыновья. С. 272–355. ISBN 978-0-470-50539-7.
- Lütkepohl, Helmut (2006). Новое введение в анализ множественных временных рядов. Берлин: Springer. Стр. 237 –352. ISBN 978-3-540-26239-8.
- Мартин, Вэнс; Херн, Стэн; Харрис, Дэвид (2013). Эконометрическое моделирование с использованием временных рядов. Нью-Йорк: Издательство Кембриджского университета. С. 662–711. ISBN 978-0-521-13981-6.
№32006 *
Векторные модели авторегрессии и коррекции регрессионных остатков (EViews)
Предлагаемая публикация продолжает консультации по сравнительно новым разделам эконометрического инструментария, которые недостаточно представлены в русскоязычной специальной литературе. Речь пойдет о весьма актуальных в прикладном плане векторных авторегрессионных моделях (Vector Autoregression Models или VAR-моделях) и векторных моделях коррекции регрессионных остатков (Vector Error Correction Models или VEC-моделях)’, а точнее — о том, как использовать возможности пакета «E-VIEWS» (версия 5) при анализе таких моделей. Более развернутое описание самих моделей читатель найдет, например, в книгах Вербика [Вербик,
2006)] и Грина [Green, 2003)].
Публикация подготовлена В.А. Банниковым по материалам руководства пользователя пакета «E-Views» (гл. 24).
При структурном подходе к анализу временных рядов для моделирования соотношений между интересующими нас переменными применяется экономическая теория. К сожалению, экономическая теория часто недостаточно богата, чтобы предоставить динамическую спецификацию, которая приводит к идентифицируемости всех таких соотношений. Кроме того, оценивание и вывод усложняются тем фактом, что эндогенные переменные могут появиться в обеих, левой и правой, частях уравнений.
При моделировании соотношения между несколькими переменными эти проблемы приводят к альтернативным, неструктурным подходам. В этой главе дается оценивание и анализ векторной модели авторегрессии (VAR-модели) и векторной модели коррекции регрессионных остатков (VEC-модели). А также будут описаны инструменты программы EViews для тестирования наличия коинтегрирующих соотношений между несколькими нестационарными переменными.
Векторная модель авторегрессии (УАВ-модель) обычно применяется для систем прогнозирования взаимосвязанных временных рядов и для анализа динамического влияния случайных возмущений на систему переменных. Подход к построению УАВ-моделей обходит потребность в структурном моделировании, рассматривая каждую эндогенную переменную в системе как функцию от лагированных значений всех эндогенных переменных.
1 Отталкиваясь от смысла УЕС-модели, ее правильнее было бы называть «векторная модель коррекции регрессионными остатками», однако приведенное в тексте название более распространено в русскоязычной литературе.
Векторные модели авторегрессии (VAR-модели)
№32006
Математическое представление векторной модели авторегрессии имеет вид:
yt = A1 yt-1 +•••+Apyt-p + Bxt +Ef, (1)
гдеyt — ^-мерный вектор эндогенных переменных, xt — d-мерный вектор экзогенных переменных,
Ab…, Ap и B — матрицы коэффициентов, которые подлежат оцениванию, а st — вектор возмущений остатков.
Возмущения могут быть «одновременно коррелированными», но не с их собственными лаги-рованными значениями и переменными в правой части уравнения2.
Так как в правых частях уравнений появляются только лагированные значения эндогенных переменных, то одновременность не является проблемой, и обычный метод наименьших квадратов (OLS-метод) приводит к состоятельным оценкам. Кроме того, даже при том,
что возмущения st могут быть одновременно коррелированными, OLS-метод эффективен и эквивалентен обобщенному методу наименьших квадратов (GLS-методу), поскольку все уравнения имеют идентичные регрессоры.
В качестве примера предположим, что промышленное производство (IP) и денежная масса (M1) совместно описываются VAR-моделью, и пусть константа будет единственной экзогенной переменной. Предполагая, что VAR-модель содержит два лагированных значения эндогенных переменных, векторную модель авторегрессии можно написать в виде:
IPt = a iiIPt-i + a 12 M1t -i + b „¡Pt-2 + b 12 M1t-2 + Ci +su, (2)
M1t = a 21IPt-1 + a 22 M1t -1 + b 21IPt — 2 + b 22 M1t — 2 + c 2 +s 2t,
где a,, bi, Ci — параметры, подлежащие оцениванию.
Оценивание VAR-модели в программе EViews
В программе EViews для спецификации VAR-модели сначала следует создать VAR-объект. Выберите опцию Quick/Estimate VAR… или в окне команд напечатайте var. В диалоге VAR Specification на странице Basics вы должны определить структуру вашей VAR-модели (рис. 1). Вам следует заполнить диалог со следующей информацией:
• Выберите тип VAR-модели: опцию Unrestricted VAR или Vector Error Correction (VEC).
То, что мы называем VAR-моделью — фактически, это неограниченная VAR-модель.
• Установите выборку оценивания (в окне редактирования Estimation Sample).
• В соответствующее окно редактирования (Lag intervals for Endogenous) введите спецификацию лагов. Эта информация вводится попарно: каждая пара чисел определяет диапазон лагов. Например, показанная на рис. 1 лаговая пара:
1 4
говорит программе EViews: использовать в правых частях уравнений системы в качестве переменных все эндогенные переменные с лагами от первого до четвертого порядка.
2 «Одновременная коррелированность» компонент вектора остатков е( = (е1г, е2(,..ей) означает возможность отличия от нуля ковариаций cov (е*, е^) для некоторых / и] (/Ф]), но при одном и том же Г. — Прим. переводчика.
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
Рис. 1. Диалоговое окно для определения структуры VAR-модели
Вы можете добавить любое число интервалов лагирования, притом все интервалы лаги-рования вводите попарно. При лаговой спецификации:
2 4 6 9 12 12
применяются лаги 2-4, 6-9 и 12.
• В соответствующие окна редактирования (Endogenous Variablies и Exogenous Variablies) введите имена эндогенных и экзогенных рядов. На рис. 1 в качестве эндогенных рядов мы ввели IP, M1 и TB3, а в качестве постоянного экзогенного члена применили специальный ряд C. Если бы список рядов был длиннее, то мы могли бы создать объект группы с именем, содержащим этот список, а затем ввести имя этой группы.
Остальные страницы диалога VAR Specification (страницы Cointegration и VEC Restrictions) уместны только для VEC-моделей, что объясняется ниже.
Вывод результатов оценивания VAR-модели
Как только вы специфицировали VAR-модель, щелкните OK. Программа EViews отобразит результаты оценивания в окне VAR (рис. 2).
Каждый столбец в таблице соответствует уравнению в VAR-модели. Для каждой переменной в правой части соответствующего уравнения программа EViews сообщает оцененные коэффициенты, их стандартные ошибки и f-статистики. Например, коэффициент при переменной IP(-1) в уравнении TB3 равен 0,095984.
Программа EViews отображает дополнительную информацию под резюме коэффициентов (рис. 3). Первая часть дополнительного вывода представляет стандартные статистики
№32006
Ж Var: VAFI1 Workfile: VARUVarl m ISJiÜ
View |Prac| Object | Print| Name| Freeze| EstimatE| 5tats| Impulse! Resids|
Vector Autoregression Estimates
VectorAutoregression Estimates Date: 01/15/04 Time: 11:31 Sample (adjusted): 1 959:05 1989:12 included obser>ations: 368 after adjusting endpoints Standard errors in () &. t-statistics in [] A 1
IP M1 TB3
IP(-1) 1.253934 (0.05401) [23.21 47] 0.25321 5 (0.17769) [ 1.42501 ] 0.095984 (0.05021) [1.911 7Ü] «
IP(-2) -0.1 37774 (0.08557) 1-2.19448] -0.230187 (0.28149) [-0.81 7T4] 0.01 5590 (0.07954) [0.19601]
IP(-3) -0.00378D (0.08556) 1 Г-l ni i A .1 -0.15351 5 (0.28146) r n Г i r i ^11 -0.1 73824 (0.07953) Г Л i-,7- “Г .“Л
Рис. 2. Результаты оценивания коэффициентов VAR-модели
IШ Vat VAR1 Workfile: VAR1 Wail НШ
View|Prac|object| Prirtt| Name | Freeze| Estimate Stats| Impulse| Resids| |
Vector Autoregression Estimates |
1 U.i 1 .Г ч U U UJ [■I .ZJi JJJ 1
R-squared 0.999221 0.999915 a.96901 9
Adj. R-squared 0.9991 95 0.999912 a.966937
Sum sq. resids 113.8813 1232.453 98.39849
S.E. equatiDn 0.566385 1.363249 a.526478
F-statistic 37950.20 347533.2 395.4048
Log 1 i ke 1 i h a o d -Э06.Э509 -744.5662 -279.4629
AkaikeAlC 1.735603 4.11 72D8 1.589472
Schwarz SC 1.873660 4.2552Б5 1.727529
Mean dependent 70.9791 9 339.7451 G.333891
S.D. dependent 1 9.95932 198.63D1 2.895381
Determinant resid covariance (düf adj.) 0.289218
Determinant resid covariance 0.259637
Lüg likelihood -1 21 S.2QÜ ±i’.’
Akaike information criterion 7.377118 :j::j::j
Schwanz criterion 7.791200 Tj
Рис. 3. Сводка статистических показателей для VAR-модели
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
N932006
OLS-регрессии для каждого уравнения. При вычислении использовались остатки для каждого уравнения в отдельности. Результаты отображены в соответствующем столбце. Числа в самой нижней части таблицы — итоговые статистики для VAR-системы в целом.
Определитель остаточной ковариационной матрицы (степени свободы скорректированы) вычисляется по формуле:
|Q | = det . (3)
При нескорректированных степенях свободы вформуле (3) число параметров p исключается. При предположении многомерного нормального (гауссовского) распределения значение логарифмической функции правдоподобия вычисляется в виде:
1 = — T {k(1 + log2rn ) + log|Q |}. (4)
Два информационных критерия (Акаике и Шварца) вычисляются по формулам:
A1C =-21/ T + 2n/T,
SC =-21/ T + nlogT/T, (5)
где n = k(d + pk) — общее число оцененных параметров в VAR-модели.
Эти информационные критерии можно использовать для выбора модели, например, для определения длины лагирования в VAR-модели. Здесь предпочтительнее модели с меньшими значениями информационного критерия. Стоит отметить, что в некоторых литературных источниках информационные критерии AIC и SC могут определяться иначе: либо исключением из функции правдоподобия «несущественных» постоянных членов, либо исключением деления на T.
Представления и опции Procs (процедуры) для VAR-модели
Как только вы оценили VAR-модель, программа EViews осуществляет различные представления для работы с оцененной VAR-моделью. В этом параграфе мы обсудим те из них, которые являются специфическими для VAR-модели.
Представления диагностики
В окне VAR для различных представлений диагностики имеются меню View/Lag Structure и View/Residual Tests. Они предназначены для того, чтобы помочь проверить правомерность оцененной VAR-модели.
Меню View/Lag Structure (лаговая структура)
Опции ARRootsTable/Graph (Таблица/график AR-корней). С помощьюэтихопций сообщаются обратные корни характеристического AR-полинома [Lütkepohl (1991)]. Оцененная VAR-модель стационарна, если все обратные корни по модулю меньше единицы и находятся внутри единичного круга. Если VAR-модель не стационарна, то определенные результаты (например, стандартные ошибки отклика на импульс) недопустимы. Существует k • p корней, где k — число эндогенных переменных, а p — наибольший лаг. Если вы оцениваете VEC-модель с r коинтегрирующими соотношениями, то k — r корней должны равняться единице.
100
№32006
Опция Granger Causality/Block Exogeneity Tests (парные тесты причинно-следственной зависимости по Грэнжеру). С помощью этой опции выполняются парные тесты причинно-следственной зависимости по Грэнжеру, посредством которых проверяется, можно ли эндогенную переменную рассматривать как экзогенную. Для каждого уравнения в VAR-модели вывод результатов отображает %2-статистику (Вальда) совместной значимости эндогенной переменной этого уравнения с каждой другой лагированной эндогенной переменной. Статистика в последней строке (All) — %2-статистика совместной значимости эндогенной переменной этого уравнения со всеми другими лагированными эндогенными переменными.
Предупреждение: если вы оценили VEC-модель, то на исключение тестируются только телагированные переменные, которые являются первыми разностями. Лагированныеуров-невые члены в коинтегрирующихуравнениях (члены коррекции регрессионных остатков) не тестируются.
Опция LagExclusion Tests (тесты на исключение лагов). С помощью этой опции для лага каждого порядка в VAR-модели выполняется тестирование на исключение этоголага. Для каждого уравнения в отдельности, для лага каждого порядка сообщается %2-статистика (Вальда) совместной значимости всех лагированных эндогенных переменных с лагом этого порядка в совокупности для всех уравнений (последний столбец).
Опция LagLength Criteria (критерии длины лагирования). С помощью этой опции для неограниченной VAR-модели, чтобы выбрать порядок лагирования, вычисляются различные критерии. Вам будет предложено — специфицировать максимальный порядок лага для «тестирования». Таблица отображает различные информационные критерии для лагов всех порядков, вплоть до лага специфицированного максимального порядка. (Если в VAR-модели нет экзогенных переменных, то лагирование начинается с единицы;в противном случае — с нуля). В таблице для каждого критерия (в столбце) указывается выбранный порядок лагирования, помеченный звездочкой (*). Для столбцов 4-7 это порядок лага с наименьшим значением критерия [Lütkepohl (1991)].
Последовательный модифицированный тест отношения правдоподобия (LR) выполняется следующим образом. Начиная с лага максимального порядка, тестируется нулевая гипотеза, что все коэффициенты при переменных с лагом порядка 1 совместно равны нулю. Для тестирования применяются %2-статистики:
LR = (T — m)log| Q1 -1| — log| Q11 -% 2(k2), (6)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
где m — число параметров на уравнение при альтернативной гипотезе.
Отметим, что используется модификация для малой выборки Симса [Sims (1980)], где применяется множитель T — m, а не T. Мы сравниваем модифицированные LR-статистики с 5%-ми критическими значениями. Начиная с лага максимального порядка, уменьшаем его порядок на единицу — до тех пор, пока не получим первое отклонение нулевой гипотезы. Альтернативный порядок лага при первом отклонении нулевой гипотезы помечается звездочкой (если нулевая гипотеза не отвергается, то минимальный порядок лага будет помечен звездочкой). Стоит подчеркнуть, что, хотя индивидуальный тест имеет размер 0,05, его полный размер не будет соответствовать 5% [Lütkepohl (1991)].
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
N932006
Меню View/Residual Tests (тестирование остатков)
Опция Correlograms (коррелограммы). С помощью этой опции для специфицированного числа лагов отображаются парные перекрестные коррелограммы (выборочные автокорреляции) оцененных остатков VAR-модели. Перекрестные коррелограммы могут отображаться в трех различных форматах. Предоставляются две табличные формы, в одной форме представление упорядочено по переменным (опция Tabulate by Variable), а в другой — по лагам (опция Tabulate by Lag). Форма Graph отображает матрицу парных перекрестных кор-релограмм. Пунктирные линии на каждом графике представляют плюс или минус два, умноженное на асимптотическую стандартную ошибку лагированных корреляций (вычисленную как l/V7).
Опция Portmanteau Autocorrelation Test. С помощью этой опции для остаточной сериальной корреляции до специфицированного порядка вычисляются многомерные Q-статистики Бокса-Пирса/Льюнга-Бокса (Box-Pierce/Ljung-Box) [LUtkepohl (1991)]. Программа EViews предоставляет как обычные Q-статистики, так и скорректированные (с коррекцией для малых выборок). При нулевой гипотезе отсутствия сериальной корреляции вплоть до лага порядка h обе статистики приближенно распределены как %2 со степенями свободы k2(h-p), где p — порядок лага VAR-модели. Асимптотическое распределение приближенно в том смысле, что для него требуется, чтобы MA-коэффициенты (коэффициенты скользящего среднего) равнялись нулю для лагов порядка i > h — p. Поэтому, если корни AR-полинома (полинома авторегрессии) будут близки единице и лаг h мал, то эта аппроксимация некорректна. Фактически, степени свободы для h < p становятся отрицательными.
Опция Autocorrelation LM Test (тест множителей Лагранжа для автокорреляций).
С помощью этой опции сообщаются многомерные статистики LM-теста (теста множителей Лагранжа) остаточной сериальной корреляции вплоть до специфицированного порядка. Критическая статистика для лага порядка h вычисляется построением вспомогательной регрессии остатков ut на исходные регрессоры в правой части уравнения и на лагированные остатки ut-h, для которых недостающие первые h значения заполняются нулями [Johansen (1995)]. При нулевой гипотезе отсутствия сериальной корреляции порядка h, LM-статистика асимптотически распределена как %2 с k2 степенями свободы.
Опция Normality Test (Тестирование на нормальное распределение). С помощью этой опции выполняются многомерные расширения теста Джаркви-Бера (Jarque-Bera) для проверки гипотезы нормального распределения остатков. В процессе тестирования третьи и четвертые моменты остатков сравниваются с соответствующими моментами нормального распределения. Для многомерного теста следует выбрать факторизацию kостатков, которые ортогональны друг другу (дополнительное обсуждение необходимости в ортогонализа-ции — в разделе «Отклики на импульсы»).
Пусть P будет матрицей факторизации, так что:
yf = Put ~ N(0,1k),
(7)
где ut — ведомые остатки.
Определим векторы третьих и четвертых моментов:
т 3 =Хл7 т и т 4 = Х/4/Т. Тогда при нулевой гипотезе нормального распределения:
л/Т
№32006
~ m 3 » ( 61 0 «
^ N 0,
m 4 — 3 V. 0 24/* _
(8)
Так как каждая компонента независима от других, мы можем построить %2-статистику, суммируя квадраты всех третьих и четвертых моментов.
Программа EViews предоставляет нам выбор матрицы факторизации:
• Опция Choleskyof covariance (ковариация Чолески) [Lütkepohl (1991)]: матрица Pявляется обращением нижней треугольной матрицы (фактором Чолески) в разложении Чолески для остаточной ковариационной матрицы. Получающиеся в результате критические статистики зависят от упорядочения переменных в VAR-модели.
• Опция Inverse Square Root of Residual Corrélation Matrix (обратный квадратный корень из остаточной корреляционной матрицы) [Doomik, Hansen (1994)]: матрица P — HA~1/2H’ V, где A — диагональная матрица, содержащая на диагонали собственные значения остаточной корреляционной матрицы, H — матрица, столбцы которой являются соответствующими собственными векторами, а V — диагональная матрица, содержащая на диагонали обратные квадратные корни из остаточных дисперсий. По-существу, эта матрица P является обратным квадратным корнем из остаточной корреляционной матрицы. Тест инвариантен к упорядочению и к масштабу переменных в VAR-модели. Перед вычислением статистики мы выполняем коррекцию для малых выборок для преобразованных остатков vt [Doomik, Hansen (1994)].
• Опция Inverse Square Root of Residual Covariance Matrix (обратный квадратный корень из остаточной ковариационной матрицы) [Urzua (1997)]: матрица P — GD~^2G’, где D — диагональная матрица, содержащая на диагонали собственные значения остаточной ковариационной матрицы, а G — матрица, столбцы которой являются соответствующими собственными векторами. Этот тест имеет специфическую альтернативную гипотезу — биквадратное экспоненциальное распределение. Это распределение — «наиболее вероятная» альтернатива многомерному нормальному распределению с конечными четвертыми моментами, поскольку его можно аппроксимировать многомерным семейством распределений Пирсона «настолько близко, насколько необходимо» [Urzua (1997)]. Перед вычислением статистики мы производим коррекцию преобразованных остатков vt для малых выборок. Эта коррекция для малых выборок отличается от коррекции, используемой в рукописи Хансена [Doornik, Hansen (1994)].
• Опция Factorization from Identified (Structural) VAR (факторизация из идентифицированной (структурной) VAR-модели): матрица P — B_1A, где матрицы A и B оцениваются из структурной VAR-модели. Эта опция доступна, если вы оценили матрицы факторизации A и B, используя структурную VAR-модель.
Критические статистики сообщаются программой EViews для каждой ортогональной компоненты (RESIDI, RESID2 и так далее) и для объединенного теста. Для индивидуальных компонент оцененная асимметрия и эксцесс приводятся в первых двух столбцах вместе
103
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
На32006
с p-значениями из %2-распределения (в квадратных скобках). В столбце Jarque-Bera сообщается:
с р-значениями из %2(2)-распределения.
Замечание. В отличие от статистики Джаркви-Бера (]агцие-8ега), вычисленной в представлении ряда, эта статистика не вычисляется с использованием коррекции степеней свободы.
Для совместных тестов, обычно, сообщается:
Однако, если вы выбираете тестУрзуа [Urzua (1997)], то X будет не только использовать сумму квадратов «чистых» третьих и четвертых моментов, но также будет включать сумму квадратов всех перекрестных третьих и четвертых моментов. В этом случае X асимптотически распределена как %2 с k(k + 1)(k + 2)(k + 7)/24 степенями свободы.
Опция White Heteroskedasticity Test (тест Уайта на наличие гетероскедастичности).
Эти тесты являются расширением теста Уайта [White (1980)] на системы уравнений, что обсуждалось в статье Кележьяна [Kelejian, 1982) и рукописи Дурника [Doornik (1995)]. Тестовая регрессия строится посредством регрессии каждого перекрестного произведения остатков на перекрестные произведения регрессоров и тестируется как совместная значимость регрессии. Опция No CrossTerms используеттолько уровни и квадраты исходных регрессоров, в то время как опция With Cross Terms включает все неизбыточные перекрестные произведения исходных регрессоров в тестовом уравнении. Тестовая регрессия всегда включает в качестве регрессора постоянный член.
Первая часть вывода для каждой тестовой регрессии отображает совместную значимость регрессоров, за исключением постоянного члена. Можно считать, что каждая тестовая регрессия представляет собой тестирование постоянства каждого элемента в остаточной ковариационной матрице в отдельности. При нулевой гипотезе отсутствия гетероскедастичности, или, если нет неправильной спецификации, непостоянные регрессоры не должны быть совместно значимыми.
Последняя строка таблицы вывода результатов показывает LM-статистику для совместной значимости всех регрессоров в системе тестовых уравнений [Doornik (1995)]. LM-статистика системы уравнений распределена как %2 с mn степенями свободы, где m — k (k +1)/2— число перекрестных произведений остатков в системе, а n — общее число переменных в правых частях уравнений в тестовой регрессии.
Замечания относительно сравнимости диагностических тестов
Многие из описанных выше диагностических тестов можно вычислить «вручную», оценив VAR-модель, применив объект системы уравнений и выбрав опцию View/Wald Coefficient
(9)
X3 -Tm’s m3/6 2(k);
X4 — T(m4 -3)'(m4 -3)/24 2(k);
X — X3 +X4 2(2k).
(10)
№32006
Tests…. Мы должны предостеречь, что по разным причинам результаты для этой системы уравнений не будут соответствовать результатам диагностических представлений для VAR-модели:
• В общем, объект системы уравнений будет использовать максимально-возможные наблюдения для каждого уравнения в системе. В отличие от этого, в случае, если имеются пропущенные значения, VAR-объекты порождают сбалансированную выборку.
• Оценки матрицы весов, применяемой при оценивании системы уравнений, не содержат коррекцию степеней свободы (остаточные суммы квадратов делятся на T а не на T — к), вто время какдля оценокVAR-модели эта коррекция выполнима. Даже при применении оцененных сопоставимых спецификаций, приводящих к тождественным коэффициентам, критические статистики для SUR-системы (системы внешне не связанных между собой регрессий) и для VAR-модели приведут к небольшим (асимптотически незначимым) различиям.
Отклики на импульсы
Импульс на i-ую переменную не только непосредственно затрагивает i-ую переменную, нотакже черездинамическую (лаговую) структуру VAR-модели передается всем другим эндогенным переменным. Функция отклика на импульс отслеживает влияние на текущие и будущие значения эндогенных переменных одноразового импульса на одно из возмущений.
Если возмущенияst одновременно некоррелированны, то интерпретация отклика на импульс прямая. i-ое возмущение si,t — просто импульс на i-ую эндогенную переменную yi,t. Однако возмущения обычно коррелированны, и их можно рассматривать как имеющие общую компоненту, которая не может быть связана со специфической переменной. Чтобы интерпретировать импульсы, обычно к возмущениям следует применить такое преобразование P чтобы они стали некоррелированными:
Vt = Pst ~(0, D), (11)
где D — диагональная ковариационная матрица.
Как объясняется ниже, программа EViews предоставляет несколько опций для выбора P.
Чтобы получить функции отклика на импульсы, сначала оцените VAR-модель. Затем на панели инструментов VAR-объекта выберите опцию View/Impulse Response…. Вы увидите диалоговое окно с двумя страницами: Display и Impulse Definition (рис. 4).
Страница диалога Display предоставляет следующие опции:
• Display Format: с помощью этого блока опций отображаются либо табличные, либо графические результаты. Имейте в виду, что, если вы выбираете опцию Combined Graphs, то блок опций Response Standard Errors будет игнорироваться, и стандартные ошибки отображаться не будут. Отметим также, что при выводе в табличном формате проводится упорядочение по переменным отклика, а не по импульсным переменным.
• Display Information: в этом блоке опций следует ввести переменные, для которых вы хотите генерировать возмущения (ввести эти переменные в редактируемое окно Impulses), и переменные, для которых вы хотите наблюдать отклики (ввести эти переменные в редактируемое окно Responses). Вы можете либо ввести имена эндогенных переменных, либо числа,
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
Impulse Responses
Display I In-pulse Definition |
Display Format—————
С Table
(* Mulliple Graphs Combined Graphs
-Response Standard Errors-С None
(* Analytic (asymptotic)
С Monte Carlo
Repetitions: 11 □□
-Display Inlormation-impüses:
ip ml tb3 d
d
Responses:
ip ml tb3 d
d
Periods: |10
I- Accumulated Responses
□I
OK. Cancel
Рис. 4. Диалоговое окно для задания функции отклика на импульсы
соответствующие порядковым номерам переменных. Например, если вы специфицировали VAR-систему с помощью переменных GDP, M1, CPI, то можете напечатать либо:
GDP CPI M1
либо: 1 3 2
Порядок, в котором вводятся эти переменные, влияеттолько на отображение результатов.
Чтобы отследить функцию отклика, следует специфицировать положительное целое для числа периодов. Чтобы отобразить накопленные отклики, сделайте отметку в окошке выбора Accumulate Response. Для стационарных VAR-моделей отклики на импульсы должны затухать на нуле, а накопленные отклики должны асимптотически сходиться к некоторой (отличной от нуля) константе.
• Response Standard Errors: в этом блоке предоставляются опции для вычисления стандартных ошибок откликов. Заметим, что для определенных выборов переменных в редактируемом окне Impulse и для векторных моделей коррекции остатков (VEC-модели) опции Analytic и/или Monte Carlo для выбора стандартных ошибок в настоящее время не доступны. Если для вычисления стандартных ошибок выбирается опция Monte Carlo, то в соответствующем окне редактирования (Repetitions) следует специфицировать число применяемых повторений.
В случае выбора табличного формата, оцененные стандартные ошибки будут представлены в круглых скобках ниже откликов. Если вы захотите отобразить результаты в формате множественных графиков, то график будет содержать полосы (плюс/минус две стандартные
106
№32006
ошибки) около откликов на импульсы. Линии стандартных ошибок на объединенных графиках не отображаются.
Страница Impulse Definition предоставляет следующие опции преобразования импульсов:
• Residual — One Unit: с помощью этой опции на остатки устанавливается воздействие единичных импульсов. Она игнорирует единицы измерения и корреляции в остатках VAR-модели, поскольку никакое преобразование не выполняется. Для этой опции отклики — MA-коэффициенты бесконечного MA-порядка в представлении Вольда (Wold) для VAR-модели.
• Residual — One Std. Dev.: с помощью этой опции устанавливается воздействие импульсов с величинами в одно среднеквадратичное отклонение остатков. Она игнорирует корреляции в остатках VAR-модели.
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
• Cholesky: при выборе этой опции для ортогонализации импульсов применяется обращение нижней треугольной матрицы (фактор Чолески) в разложении Чолески остаточной ковариационной матрицы. С помощью этой опции налагается упорядочение переменных в VAR-модели и весь эффект любой общей компоненты приписывается переменной, которая первой входит в VAR-систему. Отметим, что при изменении упорядочения переменных, отклики могут изменяться разительно. Вы можете специфицировать различное упорядочение вVAR-системе, повторно заказывая переменные вокне редактирования Cholesky Ordering.
Если оценивание остаточной ковариационной матрицы применяется для получения обращения нижней треугольной матрицы (фактора Чолески) в разложении Чолески, то с помощью опции d.f. adjustment (коррекция степеней свободы) проводится коррекция степеней свободы для малых выборок. (i,у)-ый элемент остаточной ковариационной матрицы с коррекцией степеней свободы вычисляется как
Efei,feW(T ~ ^
где p — число параметров на уравнение в VAR-системе.
С помощью опции no d.f. adjustment оценивается (i,у)-ый элемент остаточной ковариационной матрицы как
Ъе«е»1Т.
Замечание. Предшествующие версии программы EViews вычисляли импульсы, используя фактор Чолески из остаточной ковариационной матрицы без коррекции степеней свободы.
• С помощью опции Generalized Impulses (обобщенные импульсы) строится ортогональное множество возмущений, как это описано у Песарана и Шина [Pesaran, Shin (1998)], которое не зависит от упорядочения в VAR-системе. Отклики обобщенного импульса на возмущение j-ой переменной получаются применением переменного специфического фактора Чолески, вычисленного с j-ой переменной вверху упорядочения Чолески.
• При применении опции Structural Decomposition (структурное разложение) используется ортогональное преобразование, оцененное из структурных матриц факторизации. Этот подход не доступен, если вы не оценили структурные матрицы факторизации, как объясняется в разделе «Структурные (идентифицируемые) VAR-модели».
• User Specified (импульсы, специфицированные пользователем) позволяет специфицировать ваши собственные импульсы. Создайте матрицу (или вектор), которая будет содер-
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
На32006
жать импульсы, и напечатайте имя этой матрицы в окне редактирования. Если УДВ-модель имеет к эндогенных переменных, то матрица импульсов должна иметь к строк и один или к столбцов, где каждый столбец — это вектор импульсов.
Например, если в УДВ-системе вы имеете число эндогенных переменных к — 3 и хотите одновременно применить положительный единичный импульс для первой переменной и отрицательный единичный импульс для второй переменной, то следует создать 3 X1 матрицу импульсов, содержащую значения 1, -1 и 0. Вы можете ввести команды:
Несмотря на то, что функции отклика на импульсы отслеживают эффекты воздействия одной эндогенной переменной на другие переменные в VAR-модели, декомпозиция дисперсии разделяет вариацию эндогенной переменной на компоненты воздействия в VAR-модели. Таким образом, декомпозиция дисперсии предоставляет информацию об относительной важности каждого случайного возмущения в воздействии на переменные в VAR-системе.
Чтобы получить декомпозицию дисперсии, на панели инструментов объекта var выберите опцию View/Variance Decomposition… Теперь вам следует предоставить туже самую информацию, что и для откликов на импульсы выше. А поскольку неортогональная факторизация приводит к декомпозициям, которые не удовлетворяют свойству сложения, ваш выбор факторизации ограничивается ортогональными факторизациями.
Формат таблицы отображает декомпозицию на отдельные дисперсии для каждой эндогенной переменной. Второй столбец, помеченный «S.E.», содержит ошибку прогноза переменной в заданном горизонте прогнозирования. Источник этой ошибки прогноза — вариация в текущих и будущих значениях возмущений каждой эндогенной переменной в VAR-модели. Остальные столбцы предоставляют проценты дисперсии прогноза, обусловленные каждым возмущением, и в сумме по каждой строке составляют 100%.
Как и в случае с откликами на импульсы, если изменить упорядочение переменных в VAR-модели, декомпозиция дисперсии, основанная на факторе Чолески, может разительно изменяться. Например, декомпозиция первого периода для первой переменной в упорядочении VAR-модели полностью обусловлена ее собственным возмущением.
Факторизация, основанная на структурной ортогонализации, доступна, если только вы оценили структурные матрицы факторизации, как объясняется в разделе «Структурные (идентифицируемые) VAR-модели». Отметим, что стандартные ошибки прогноза должны быть идентичны стандартным ошибкам из факторизации Чолески, если только структурная VAR-модель идентифицируема. Для сверхидентифицируемых структурных VAR-моделей стандартные ошибки прогноза могут отличаться, чтобы сохранять свойство сложения.
Опции Procs (процедуры) VAR-объекта
Большинство процедур, доступных для VAR-объекта, обычно те же, что и для объекта системы уравнений. Здесь мы обсудим только те, которые уникальны для VAR-объекта.
Matrix (3,1) shock shock.fill (by=c) 1, -1,0
и в окне редактирования напечатать имя матрицы SHOCK.
Декомпозиция (разложение) дисперсии
№32006
Опция Make System (создание системы)
С помощью Make System создается объект системы уравнений, который содержит эквивалентную VAR-спецификацию. Если вы хотите оценить нестандартную VAR-модель, то можете использовать эту опцию как быстрый способ специфицировать VAR-модель в объекте системы уравнений, которую затем можно модифицировать, чтобы удовлетворить своим потребностям. Например, несмотря на то, что VAR-объект требует, чтобы каждое уравнение имело одну и туже структурулагирования, можно ослабить это ограничение. Чтобы оценить VAR-модель с несбалансированной лаговой структурой, используйте процедуру Proc/Make System, создайте VAR-систему со сбалансированной лаговой структурой и отредактируйте ее спецификацию в соответствии с желаемой структурой лагирования.
Применение опции By Variable создает систему, спецификация которой (и порядковые номера коэффициентов) упорядочивается по переменным. Если хотите отредактировать спецификацию, чтобы исключить лаги определенной переменной из некоторых уравнений, примените эту опцию. С помощью опции By Lag создается система, спецификация которой (и порядковые номера коэффициентов) упорядочивается по лагам. Если хотите отредактировать спецификацию, чтобы исключить определенные лаги из некоторых уравнений, используйте эту опцию.
В векторной модели коррекции остатков (в VEC-модели) обработка коэффициентов коин-тегрирующего вектора как дополнительных неизвестных коэффициентов приводит получающуюся в результате систему к неидентифицируемости. В этом случае программа EViews создаст объект системы, коэффициенты которой для коинтегрирующих векторов устанавливаются к оцененным значениям коэффициентов VEC-модели. Если вы хотите оценить коэффициенты коинтегрирующего вектора в системе, то можете отредактировать спецификацию, но прежде удостоверьтесь, что получающаяся система идентифицируема.
Следует также отметить, что, в то время как стандартную VAR-модель можно эффективно оценить с помощью обычного метода наименьших квадратов (OLS-метода), примененного последовательно к каждому уравнению в отдельности, для модифицированной спецификации это не так. Вы можете применить один из методов оценивания всей системы (например, SUR-метод), оценивая нестандартные VAR-модели с использованием объекта системы.
Опция Estimate Structural Factorization (оценивание структурной факторизации)
Эта процедура применяется, чтобы оценить матрицы факторизации для структурной (или идентифицируемой) VAR-модели. Подробное описание деталей этой процедуры приводится в разделе «Структурные (идентифицируемые) VAR-модели». Итак, для начала, вам следует оценить матрицы структурной факторизации, чтобы применить структурные опции Impulse Responses и Variance Decompositions.
Структурные (идентифицируемые) VAR-модели
Главная цель структурногоVAR-оценивания (SVAR-оценивания) состоит втом, чтобы получить нерекурсивную ортогонализацию членов остатков для анализа откликов на импульсы. Эта альтернатива рекурсивной ортогонализации Чолески требует, чтобы пользователь наложил достаточное число ограничений для идентифицируемости ортогональных (структурных) компонент членов остатков.
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
N932006
Пусть у, — ^-элементный вектор эндогенных переменных И пусть 2 = Е[е,, е’ ] будет остаточной ковариационной матрицей. Следуя Амисано и Джанини [АтнБапо, С1апп1п! (1997)], класс БУАВ-моделей, который оценивается программой ЕУ^б, можно написать как:
Ле{ = Виг, (12)
где е, и и, — векторы длины к.
Вектор е, является наблюдаемым остатком (или остатком приведенной формы), тогда как и,является ненаблюдаемым структурным возмущением. Матрицы Л и В — к хк матрицы, которые подлежат оцениванию. Предполагается, что структурные возмущения и, являются орто-нормированными, т. е. их ковариационная матрица — единичная матрица. Предположение ортонормированности возмущений и, налагает следующие идентифицирующие ограничения на матрицы Л и В:
Л2Л’ = В В’. (13)
Отметим, что выражения в обеих частях уравнения (13) являются симметричными, что налагает к (к +1)/2 ограничений на 2к2 неизвестных элементов в матрицах Л и В. Поэтому, чтобы идентифицировать матрицы Л и В Вам следует наложить, по крайней мере, 2к2 — к (к +1)/2 = к (3к -1)/2 дополнительных ограничений.
Спецификация идентифицирующих ограничений
Как объяснялось выше, чтобы оценить ортогональные матрицы факторизации Л и В, следует наложить дополнительные идентифицирующие ограничения. Мы различаем два типа идентифицирующих динамических ограничений: краткосрочные и долгосрочные ограничения. Любой тип идентифицирующих ограничений можно специфицировать либо в виде текста, либо с помощью матриц отображения.
Спецификация краткосрочных динамических идентифицирующих ограничений с помощью матриц отображения
Для многих проблем идентифицирующие ограничения на матрицы Л и В — это простые нулевые ограничения исключения. В этом случае вы можете специфицировать ограничения, создавая матрицы «отображения» с соответствующими присвоенными именами для матриц Л и В. Любые элементы матрицы отображения, которые вы хотите оценить, должны иметь пропущенное значение «МЛ». Все непропущенные значения в матрице отображения будут содержать фиксированные специфицированные значения.
Предположим, что вы хотите представить матрицу Л нижней треугольной матрицей с единицами на главной диагонали, а матрицу В — диагональной матрицей. Тогда матрицы отображения (для к = 3 переменных УАВ-модели) были бы следующими:
(14)
Вы можете создать эти матрицы в интерактивном режиме. Просто примените опцию Object/New Object…, чтобы создать две новые матрицы, A и B, а затем для редактирования
4 0 0^ ‘ NA 0 0 N
A = NA 1 0 , в = 0 NA 0
NA V NA Ъ 0 V 0 NAy
№32006
значений используйте представление крупноформатной таблицы. Альтернативно, можно ввести следующие команды:
Matrix (3,3) pata
‘ fill matrix in row major order
pata.fill (by=r) 1,0,0, na, 1,0, na, na, 1
matrix (3,3) patb = 0
patb (1,1) = na
patb (2,2) = na
patb(3,3) = na
Как только созданы матрицы отображений, из меню окна VAR-объекта выберите опцию Proc/Estimate Structural Factorization…. В диалоге SVAR Options щелкните кнопки Matrix и Short-Run Pattern, и в соответствующих окнах редактирования напечатайте имена матриц отображения.
Спецификация краткосрочных динамических идентифицирующих ограничений
в виде текста
Для более общих ограничений можно специфицировать идентифицирующие ограничения в виде текста. В текстовом виде выписываем соотношение Aet = But как систему уравнений, идентифицируя каждый элемент векторов et и ut с помощью специальных символов. Элементы матриц A и B, которые подлежат оцениванию, должны специфицироваться в виде элементов вектора коэффициентов.
Для примера снова предположим, что вы имеете к = 3 эндогенных переменных в VAR-модели, где хотите ограничить матрицу A нижней треугольной матрицей с единицами на главной диагонали, а матрицу B установить диагональной матрицей. В соответствии с этими ограничениями соотношение Aet = But можно написать в виде:
e i = b „и i,
e 2 = —a 21 e i + Ь jjU 2,
e 3 =— a 3i e 1 — a 32 e 2 + b 33U 3. (15)
Чтобы специфицировать эти ограничения в виде текста, из окна VAR-объекта выберите опцию Proc/Estimate Structural Factorization… и щелкните кнопку Text. В окне редактирования напечатайте следующее:
@e1 =c(1)*@u1
@e2 = -c(2)*@e1 + c(3)*@u2
@e3 = -c(4)*@e1 — c(5)*@e2 + c(6)*@u3
Специальные ключевые символы «@e1», «@e2», «@e3» представляют первый, второй и третий элементы вектора et, в то время как символы «@u1», «@u2», «@u3» представляют
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
N932006
первый, второй и третий элементы вектора ц(. В этом примере все неизвестные элементы матриц Л и В представляются элементами вектора коэффициентов С.
Идентифицируемые ограничения, содержащиеся в равенстве Aet — B ut, обычно называются краткосрочными динамическими ограничениями. Есть альтернативный метод идентифицируемости с помощью ограничений долгосрочных динамических свойств откликов на импульсы [Blanchard, Quah (1989)]. Кумулятивный долгосрочный динамический отклик C на структурные возмущения имеет вид:
где= (I- Д -… — Ар) 1 — оцененные кумулятивные (накопленные) отклики на (наблюдаемые) воздействия приведенной формы.
Долгосрочные динамические идентифицирующие ограничения специфицируются в терми-нахэлементов матрицы С, какправило, ввиде нулевыхограничений. Ограничение С1у- — 0оз-начает, что (накопленный) отклик /-ой переменной нау-ое структурное возмущение в долгосрочной динамике равняется нулю.
Важно отметить, что выражение для долгосрочного динамического отклика (16) включает обращение матрицы А. В настоящее время программа ЕУ^б требует, чтобы все ограничения были линейными по элементам матриц А и В. Поэтому, если вы специфицируете долгосрочное динамическое идентифицирующее ограничение, то матрица А должна быть единичной.
Чтобы специфицировать долгосрочные динамические ограничения с помощью матрицы отображения, создайте матрицу с присвоенным ей именем, содержащую отображение для матрицы долгосрочного динамического отклика С. Неограниченным элементам в матрице С следует присвоить пропущенное значение «МЛ». Предположим, что вы имеете к — 2эндоген-ных переменных в УДВ-модели, в которой хотите ограничить долгосрочный динамический отклик второй эндогенной переменной первым структурным воздействием, равным нулю (С21 — 0). Тогда матрица долгосрочного динамического отклика будет иметь следующее отображение:
Создав матрицу отображения, из меню окна VAR-объекта выберите опцию Proc/Estimate Structural Factorization…. В диалоге SVAR Options щелкните кнопки Matrix и Long-Run Pattern, и в соответствующем окне редактирования напечатайте имя матрицы отображения.
Спецификация долгосрочных динамических идентифицируемых ограничений
С = A-]B,
(16)
(17)
Мы можем создать эту матрицу с помощью следующих команд:
Matrix (2,2) patc = na
Patc (2,1) = 0
№32006
Чтобы специфицировать то же самое долгосрочное динамическое идентифицирующее ограничение в виде текста, из окна VAR-объекта выберите опцию Proc/Estimate Structural Factorization… и щелкните кнопку Text. В окне редактирования следует напечатать следующее:
@LR2(@u1)=0 ‘zero LR response of 2-nd variable to 1-st shock
где после апострофа в строке идет комментарий. Это ограничение начинается со специального ключевого слова « @LR#» с символом «#», представляющим переменную отклика для ограничения. В круглых скобках следует специфицировать ключевое слово «@U» импульса и число возмущений с последующим знаком равенства и значением отклика (как правило, 0). Помните, что, несмотря на то, что вы можете привести список множественных долгосрочных динамических ограничений, вы не можете смешивать краткосрочные динамические и долгосрочные динамические идентифицирующие ограничения.
Отметим, что долгосрочные динамические идентифицирующие ограничения можно специфицировать в виде краткосрочных динамических ограничений (с помощью применения представления MA бесконечного порядка). Несмотря на то, что оцененные матрицы A и B должны быть одинаковыми, стандартные ошибки отклика на импульсы из краткосрочного динамического представления будут некорректными (поскольку неопределенность в оцененных коэффициентах MA бесконечного порядка не принимается в расчет).
Некоторые важные замечания
На данный момент спецификация идентифицирующих ограничений должна подчиняться следующим ограничивающим правилам:
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
• Матрицы A и Bдолжны быть квадратными и невырожденными. Втекстовом видедолжно быть точно столько же уравнений, сколько эндогенных переменных в VAR-модели. Для крат-косрочныхдинамических ограничений в виде отображений следует задать матрицы отображения для обеих матриц A и B.
• Ограничения должны быть линейными по элементам матриц A и B. Кроме того, идентифицирующие ограничения на матрицы A и B должны быть независимыми (не иметь совместных ограничений для элементов матриц A и B).
• Нельзя накладывать краткосрочные динамические и долгосрочные динамические идентифицирующие ограничения.
• В настоящее время структурные разложения для VEC-моделей не доступны.
• Идентифицирующее ограничение предполагает, что структурные возмущения ut имеют единичные дисперсии. Поэтому, почти всегда, будет стремление оценивать диагональные элементы матрицы B так, чтобы получить оценки среднеквадратичных отклонений структурных возмущений.
• Обычно (в соответствующей литературе) предполагается, что структурные возмущения имеют диагональную, а не единичную ковариационную матрицу. Чтобы сравнить ваши результаты с результатами этих исследований, следует разделить элементы каждого столбца матрицы B на соответствующий диагональный элемент этого столбца (так, чтобы получающаяся в результате матрица имела единицы на главной диагонали). Чтобы проиллюстрировать такое преобразование, рассмотрим простую модель к = 2 с переменными A = 1:
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
e u = b „ u u + b Uu 2t,
e 2t = b 2, u 1t + b 22U 2t ,
(18)
где u1,t и u2,t — независимые структурные возмущения с единичными дисперсиями, как предполагается в спецификации программы EViews.
Чтобы переписать эту спецификацию с матрицей B, содержащей единицы на главной диагонали, определите новое множество структурных возмущений с помощью преобразований v 1t = biiUi,t и v2,t = b22U2,t.
Тогда структурное соотношение можно переписать:
e it = v lf + (b 12/ b 22 )v 2t,
e 2t = (b 21 /b 11 )v 1t + v 2t ,
теперь:
B =
b 211 b 1
b 12/ b 2 1
, vf =
«v 1,t » f «0» «b 2 b 11 0»
_v 2,t _ V 0 ‘ 0 b 2 b 22 У
(19)
(20)
Отметим, что преобразование включаетлишь изменение масштаба элементов матрицы В, но не матрицы Л. В случае, если матрица В является диагональной матрицей, элементы на главной диагонали этой матрицы — просто оцененные среднеквадратичные отклонения структурных возмущений.
Условия идентифицируемости
Как было указано выше, предположение ортонормированных структурных возмущений налагает к (к +1)/2 ограничений на 2к2 неизвестных элементов в матрицах Л и В, где к — число эндогенных переменных вУДВ-модели. Чтобы идентифицировать матрицы Л и В, следует предоставить, по крайней мере, к (к +1)/2 — 2к2 = к (3к -1)/2 дополнительных идентифицирующих ограничений. Это необходимое условие порядка для идентифицируемости, и оно проверяется подсчетом числа предоставляемых ограничений.
Так, достаточное условие для локальной идентифицируемости можно проверить обратимостью «пополненной» информационной матрицы [ДтнБапо, С1апп1п1 (1997)]. Это условие локальной идентифицируемости вычисляется в точке начальных значений. Если программа ЕУ^б сообщит об ошибке вырожденности для различных начальных значений, убедитесь, что ваши ограничения идентифицируют матрицы Л и В.
Мы также требуем, чтобы матрицы Л и В были квадратными и невырожденными. Условие невырожденности проверяется численно в точке начальных значений. Если матрицы Л и В в точке начальных значений вырожденны, то в сообщении об ошибке вам будет предложено предоставить другую точку начальных значений.
Неопределенность в знаке
Для некоторых ограничений знаки матриц Л и В не идентифицированы [СЬпбШпо, е! а1. (1999)]. Если знак не определен, мы выбираем такую нормировку, при которой все диагональные элементы матрицы факторизации были бы положительными. Эта нормировка гарантирует, что все структурные импульсы имеют положительные знаки (как это делается при
№32006
факторизации Чолески). «По умолчанию»эти правила нормировки используются всякий раз, когда они применимы. Если вы не хотите изменять знаки, то на странице диалога SVAR Options не выбирайте опцию Normalize Sign.
Оценивание матриц Au B
Как только предоставите идентифицирующие ограничения в любой из описанных выше форм, вы в состоянии оценить матрицы Л и B. Просто в диалоге SVAR Options щелкните кнопку OK. Вам следует оценить эти матрицы, чтобы использовать структурную опцию Impulse Responses и Variance Decompositions.
Матрицы Л и B оцениваются методом максимального правдоподобия, поскольку следует иметь в виду, что возмущения имеют многомерное нормальное распределение. Мы вычисляем правдоподобие втерминах неограниченных параметров с подстановкой ограничений. Логарифмическое правдоподобие максимизируется посредством «metod of scoring» (с диагональной коррекцией типа Маркварта), в котором градиент и математическое ожидание информационной матрицы вычисляется аналитически [Amisano, Giannini (1997)].
Управление оптимизацией
Для управления процессом оптимизации в диалоге SVAR Options на странице Optimization Control предоставляются соответствующие опции. Эти опции предназначаются для того, чтобы специфицировать начальные значения, максимальное число итераций и критерий сходимости.
Начальные значения — это значения для неограниченных параметров после подстановки ограничений. С помощью опции Fixed все свободные параметры устанавливаются относительно значения, специфицированного в окне редактирования. При применении опции User Specified в качестве начальных значений, в векторе коэффициентов используются значения, которые отображаются в виде текста. Для ограничений, специфицированных в виде отображений, начальные значения, специфицированные пользователем, берутся из первых m элементов вектора коэффициентов C«по умолчанию», где m — число свободных параметров. С помощью опций Drawfrom… начальные значения для свободных параметров извлекаются из специфицированных распределений случайным образом.
Вывод результатов оценивания
Как только достигается сходимость, программа EViews отображает вывод результатов оценивания в окне VAR. Приводятся точечные оценки, стандартные ошибки и z-статистики оцененных свободных параметров вместе с максимальным значением логарифмической функции правдоподобия. Оцененные стандартные ошибки основаны на обращении оцененной информационной матрицы (отрицательное математическое ожидание Гессиана), вычисленном в точке сходимости оценок.
Для сверхидентифицируемых моделей также приводятся результаты LR-тестирования (по тесту отношения правдоподобия) для сверхидентифицируемости. Статистика LR-теста вычисляется по формуле:
LR = 2(lu -1r ) = T(tr(P) — log|P| — k), (21)
где P = Л’ B -TB “ME.
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
При нулевой гипотезе, что ограничения справедливы, LR-статистика асимптотически распределена, как %2(q-k), где q — число идентифицирующих ограничений.
Если переключить представление окна VAR с помощью выбора из этого окна опции View/SVAR Output, вы сможете возвратиться к предыдущим результатам (без повторного оценивания). Кроме того, некоторые из результатов SVAR-оценивания можно восстановить как члены данных VAR-модели.
Тест на наличие коинтеграции
Открытие того, что многие макровременные ряды могут содержать единичный корень, стимулировало разработку теории анализа нестационарных временных рядов. Так, Энгель и Грэнжер [Engle, Granger (1987)] показали, что линейная комбинация двух или более нестационарных рядов может быть стационарной. Если такая стационарная линейная комбинация существует, то нестационарные временные ряды называются коинтегрированными. Стационарную линейную комбинацию называют коинтегрирующим уравнением и ее можно интерпретировать как соотношение долгосрочного динамического равновесия между переменными.
Цельтеста на наличие коинтеграции состоит втом, чтобы определить, коинтегрированна или нет группа нестационарных рядов. Как объясняется ниже, присутствие коинтегрирую-щего соотношения формирует основу для VEC-спецификации. Программа EViews выполняет тестирование наличия коинтеграции на основе VAR-модели, используя методологию, разработанную в работах Йохансена [Johansen (1991), (1995)].
Рассмотрим VAR порядка р:
y t = Д yt-1 +… + Apy t — р + Bxt +Et, (22)
гдеyt — k-вектор нестационарных /(1) переменных,
xt — d-вектор детерминированных переменных,
а st — вектор возмущений.
Мы можем переписать эту VAR-модель в виде:
р -1
Ayt =nyt -1 i Ayt — i + Bxt +st, (23)
i =1
где:
рр n=£A, -1, Г, = -£Aj. (24)
i=1 j = i+1
Теорема представления Грэнжера утверждает, что если матрица коэффициентов П име-етуменьшенный рангr < k, то существуютk хr матрицы а и р, имеющие ранг rтак, что П= аР’, а Р’yt — I(0). Число r представляет собой число коинтегрирующих соотношений (коинтег-рирующийранг), а каждый столбец матрицы р — коинтегрирующий вектор. Как объясняется ниже, элементы матрицы а являются параметрами коррекции вVEC-модели. Метод Йохансена применяется для оценивания матрицы П из неограниченной VAR-модели, а также для тестирования того, можно ли отклонить ограничения, подразумеваемые уменьшенным рангом матрицы П.
прикладная эконометрика_______________________________
№32006
Как выполнить тест на наличие коинтеграции
Чтобы выполнить тест на наличие коинтеграции Йохансена, из панели инструментов окна группы или окна VAR выберите опцию View/Cointegration Test…. На странице Cointegration Test Specification будет подсказка: ввести информацию о тесте (рис. 5).
Рис. 5. Диалоговое окно для задания теста на наличие коинтеграции
Поскольку это тест на наличие коинтеграции, он допустим, если только вы работаете с рядами, о которых известно, что они нестационарные. Поэтому сначала вы можете применить тесты единичного корня к каждому ряду в УДВ-модели.
Спецификация детерминированных трендов
Ваш ряд может иметь ненулевые средние значения и детерминированные тренды, а также стохастические тренды. Аналогично коинтегрирующие уравнения могут иметь свободные члены и детерминированные тренды. Асимптотическое распределение _В-статистики (статистики отношения правдоподобия) для коинтеграции не подчиняется обычному X2-распределению, а зависит от предположений, сделанных относительно детерминированных трендов. Поэтому, чтобы выполнить тест, следует сделать предположение относительно тренда, лежащего в основе ваших данных.
Для каждой строки диалога в столбце СО!МТЕО перечисляются детерминированные переменные, которые появляются внутри коинтегрирующих соотношений (члена коррекции регрессионных остатков), в то время как в столбце OUTSIDE перечисляются детерминированные переменные, которые появляются в УЕС-уравнении вне коинтегрирующих соотношений. Случаи 2 и 4 не имеют одного и того же множества (раздел Техническое обсуждение) детерминированных членов в двух столбцах. Для этих двух случаев некоторые детерминиро-
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
ванные члены ограничены принадлежностью только к коинтегрирующему соотношению. Для случаев 3 и 5 детерминированные члены являются общими в двух столбцах и декомпозиция детерминированных эффектов внутри и вне коинтегрирующего пространства однозначно не идентифицирована.
Практически, случаи 1 и 5 используются редко. Применять случай 1 следует, если вы знаете, что все ряды имеют нулевое среднее значение. Случай 5 может предоставить хорошую (внутри выборочной) подгонку, но будет приводить к неправдоподобным вневыбороч-ным прогнозам. В качестве ориентировочного руководства применяйте случай 2, если полагаете, что ни один из рядов не имееттренда. Для трендовых рядов применяется случай 3, когда все тренды являются стохастическими. Если вы полагаете, что некоторые из рядов тренд-стационарны, то воспользуйтесь случаем 4.
Если вы не уверены, какое предположение относительно тренда следует применить, то можете выбрать опцию Summary of all 5 trend assumptions (случай 6), которая поможет вам определить выбор предположения о тренде. Эта опция покажет число коинтегрирующих соотношений для каждого из 5 предположений о тренде, и вы сможете оценить чувствительность результатов к предположению о тренде.
Техническое обсуждение
В программе EViews представлены следующие пять случаевдетерминированноготренда, рассмотренных Йохансеном [Johansen (1995)]:
1. Уровневые данные yt не имеют никаких детерминированных трендов, и в коинтегрирующих уравнениях отсутствуют свободные члены:
2. Уровневые данныеу{ не имеют никакихдетерминированных трендов, и коинтегрирую-щие уравнения содержат свободные члены:
3. Уровневые данные у{ имеют линейные тренды, но коинтегрирующие уравнения имеюттоль-ко свободные члены:
4. Уровневые данные у{ и коинтегрирующие уравнения имеют линейные тренды:
Н*(г): Пуг_ + Бх{ =а(Р’уг_, +ро + р,0 + а±у<,.
5. Уровневые данные у{ имеют квадратные тренды, а коинтегрирующие уравнения — линейные тренды:
Члены, связанные са±, являются детерминированными членами «вне» коинтегрирующих соотношений. Когда детерминированный член появляется внутри и вне коинтегрирующего соотношения, декомпозиция однозначно не идентифицируется. Йохансен [Johansen (1995)] идентифицировал часть, принадлежащую внутренности коррекции регрессионных остат-
H2(r): Пyt_i + Bxt =aP’yt_i.
H*(r): nyt_i + Bxt =a(P’yt_i +po).
Hi(r): nyt_i + Bxt =a(P’yt_i +po) + a±yo.
H(r): nyt_i + Bxt =a(P’yt_i +po +pit) +a±(yo +yit).
№32006
ков, ортогонально проектируя экзогенные члены на пространство a так, что a± является нулевым пространством a (a’a± = o). В программе EViews применяется разностный метод идентифицируемости, при котором член коррекции регрессионных остатков имеет нулевое выборочное среднее значение. Более определенно мы идентифицируем часть внутри члена коррекции регрессионных остатков с помощью регрессии коинтегрирующих соотношений P’yt по константе (и линейному тренду).
Экзогенные переменные
Тестовый диалог позволяет специфицировать дополнительные экзогенные переменные xt, чтобы включить в тестирование VAR-модели. Константа и линейный тренд не должны вносится в список в окне редактирования, поскольку они специфицируются при использовании пяти опций Trend Specification. Если вы хотите включить экзогенные переменные, то знайте, что критические значения, сообщаемые программой EViews, не вычисляются для этих переменных.
Обычно наиболее часто добавляемыми детерминированными членами являются сезонные фиктивные переменные. Однако отметим, что, если при тестировании VAR-модели вы включаете стандартную o-i сезонную фиктивную переменную, то она будет влиять как на среднее значение, так и на тренд уровневого ряда. Для обработки этой проблемы Йохансен [Johansen (i995)] предложил применение центрированных (ортогональных) сезонных фиктивных переменных, которые сдвигают среднее значение, не внося свой вклад в тренд. Центрированные сезонные фиктивные переменные для ежеквартального и ежемесячного ряда можно сгенерировать с помощью команд:
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
series d_q = @seas(q) -1/4 series d_m = @seas(m) -1/12
для квартала q и месяца m соответственно.
Интервалы лагирования
Вам следует специфицировать лаги тестируемой VAR-модели в виде интервальных пар. Отметим, что лаги специфицируются как лаги членов первых разностей, используемых во вспомогательной регрессии, а не втерминахуровней. Например, если в поле редактирования вы печатаете «1 2», то тестируемая VAR-модель регрессирует Ayt по Ayt_,, Ayt_2 и по любым другим экзогенным переменным, которые вы специфицировали. Отметим, что втер-минах уровневого ряда yt наибольший лаг равен 3. Чтобы провести тестирование на наличие коинтеграции с одним лагом в уровневом ряду, в поле редактирования напечатайте «0 0».
Интерпретация результатов теста на наличие коинтеграции
В качестве примера (рис. 6) показана первая часть вывода результатов тестирования на наличие коинтеграции для системы с четырьмя переменными [Johansen, Juselius (i99o)] для данных по Дании.
Как показано в заголовке вывода, тестирование не предполагает никакого тренда в ряду с ограниченным свободным членом в коинтегрирующем соотношении (вторая спецификация тренда в диалоге), включает три ортогональных сезонных фиктивных переменных Di-D3
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
Ns32006
Date: 01/16/04 Time: 11:40 Sample (adjusted): 1974:3 1987:3 Included observations: S3 after adjusting endpoints
Trend assumption: No deterministic trend (restricted constant)
Series: LRM LRY IBO IDE
Lags interval (in first differences): 1 to 1
Unrestricted Cointegration Rank Test (Trace)
Hypothesized No of CE(s) Eigenvalue Trace Statistic 0.05 Critical Value Prob»
None 0.469677 52.71087 54.0790 0.0659
At most 1 0.174241 19.09464 35.1323 0.7814
At most 2 0 118083 8.947661 20.2613 0.7411
At most 3 0.042249 2.287349 9.1645 0.7200
* denotes rejection of the hypothesis at the 0 05 level Trace test indicates no cointegration at the 0.05 level ’■’MacKinnon-Haug-Michelis (1999) p-values
Рис. 6. Результаты теста на наличие коинтеграции
и использует один лаг в разностях (два лага в уровнях), который в поле редактирования специфицирован как «1 1».
Число коинтегрирующих соотношений
Первая часть таблицы сообщает о результатах тестирования числа коинтегрирующих соотношений. Приводится два типа критических статистик. Первый блок дает сведения о так называемых статистиках следа (trace statistics), а второй блок (не показанный выше) — о статистике максимального собственного значения (maximum eigenvalue statistics). Для каждого блока, первый столбец — числа коинтегрирующих соотношений при нулевой гипотезе, второй столбец — упорядоченные собственные значения матрицы П (24), третий столбец — критические статистики, а последние два столбца — 5%-ые и Ш-ые критические значения. Эти критические значения [Osterwald-Lenum (i992)] не намного отличаются от значений в работе Йохансена и Джуселиус [Johansen, Juselius (i99o)].
Чтобы определить число коинтегрирующих соотношений r, зависящее от предположений, сделанных о тренде, мы можем продолжать тестирование последовательно отr = 0до r = k _ i до тех пор, пока не сможем отклонить гипотезу. О результате этой последовательной процедуры сообщается внизу каждого блока таблицы.
Статистика следа, отраженная в первом блоке, проверяет нулевую гипотезу о r коинтегрирующих соотношениях против альтернативной гипотезы относительно k коинтегрирующих соотношений, где k — число эндогенных переменных при r = o,i,…,k _ i. Альтернативная гипотеза для k коинтегрирующих соотношений соответствует случаю, когда ни один из рядов не имеет единичного корня, и стационарную VAR-модель можно специфицировать в терминах уровней всех рядов. Статистика следа для нулевой гипотезы о r коинтегрирующих соотношениях вычисляется как:
№32006
k
LRtr (r| k) = -T^log(1-X,• ),
(25)
i =r +1
где X,• — /-ое наибольшее собственное значение матрицы П (24), которое сообщается во втором столбце таблицы вывода результатов.
Во втором блоке вывода результатов сообщается о статистике максимального собственного значения, которая тестирует нулевую гипотезу о г коинтегрирующих соотношениях против альтернативной гипотезы о г +1 коинтегрирующих соотношений. Эта критическая статистика вычисляется как:
для r = o,i,…,k -1.
Существует несколько других деталей, которые следует иметь в виду:
• Критические значения доступны вплоть до k = io рядов.Также отметим, что критические значения зависят от предположений о тренде и, возможно, не годятся для моделей, которые содержат другие детерминированные регрессоры. Например, фиктивная переменная сдвига в тестируемой VAR-модели подразумевает сдвиговый линейный тренд в уровневом ряду yt.
• Статистики следа и максимального собственного значения могут привести к противоречивым результатам. Для таких случаев мы рекомендуем исследовать оцененный коинтег-рирующий вектор и в своем выборе опираться на интерпретируемость коинтегрирующих соотношений [Johansen, Juselius (199o)].
• В отдельных случаях индивидуальные тесты на наличие единичного корня показывают, что некоторые из рядов являются интегрируемыми, однако тест на наличие коинтеграции выявляет, что матрица П имеет полный ранг (r = k). Это очевидное противоречие может возникнуть в результате малой мощности тестов на наличие коинтеграции и, возможно, из-за малого объема выборки или из-за ошибок спецификации.
Вторая часть вывода результатов содержит оценки коинтегрирующих соотношений р и параметров коррекции а. Как известно, коинтегрирующий вектор р не идентифицируем, если только мы не налагаем некоторую произвольную нормировку. Первый блок дает оценку матрицам р и а, основанную на нормировке Р’, Snp = I, где матрица Sn определена в работе [Johansen (1995)].
Отметим, что транспонированная р сообщается при Unrestricted Cointegrating Coefficients так, что первая строка является первым коинтегрирующим вектором, вторая строка — вторым коинтегрирующим вектором и так далее.
В остальных блоках сообщается об оценках с другой нормировкой для каждого возможного числа коинтегрирующих соотношений r = 0,1,…,k -1. Эта альтернативная нормировка выражает первые r переменные как функции от остальных k — r переменных в системе. В круглых скобках сообщается об асимптотических стандартных ошибках параметров, которые являются идентифицируемыми.
LRmax(r| r +1) = -Tlog(1-Xr+1)
= LRtr ( r| k) — LRtr ( r +11 k)
(26)
Коинтегрирующие соотношения
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
Наложение ограничений
Так как коинтегрирующий вектор р не идентифицируем, вы возможно захотите наложить собственные идентифицирующие ограничения. Ограничения можно наложить на коинтегрирующий вектор (элементы матрицы р) и/или на коэффициенты коррекции (элементы матрицы а). Чтобы наложить ограничения в тесте на наличие коинтеграции, выберите опцию View/ Cointegration Test… и специфицируйте опции на странице Cointegration Test Specification, как объяснялось выше. Затем выберите страницу VEC Restrictions (рис. 7). Введете ваши ограничения в окно редактирования, появляющееся с выбором окна Impose Restrictions.
Рис. 7. Диалоговое окно для наложения ограничений на элементы матрицы а(Р)
Ограничения на коинтегрирующий вектор
Чтобы наложить ограничения на коинтегрирующий вектор р, следует обратиться к(/,у)-му элементу транспонированной матрицы р, обозначенному как В(/, ]). /-ое коинтегрирующее соотношение имеет представление:
В (1,1)*у1 + В (1,2)*у2 + … + В (I, к)*ук
где у1, у2… — (лагированные) эндогенные переменные.
Если вы хотите наложить ограничение — коэффициент во втором коинтегрирующем уравнении при у1 равен единице, тогда в окне редактирования следует напечатать следующее:
Б(2,1) = 1
Вы можете наложить множественные ограничения, отделяя в одной строке каждое ограничение запятой или печатая каждое ограничение в отдельной строке. Например, при наложении ограничения: в первом и втором коинтегрирующем уравнении коэффициенты при у1 равны единице, следует напечатать:
№32006
Б (1,1) = 1
Б(2,1) = 1
На данный момент все ограничения на элементы матрицы Р должны быть линейными (то есть аффинными). Например, применение ограничения:
Б (1,1) * Б (2,1) = 1
вернет сообщение о синтаксической ошибке.
Ограничения на коэффициенты коррекции
Чтобы наложить ограничения на коэффициенты коррекции, вам следует обратиться к(/,у)-му элементу матрицы а, обозначенному как А(/, ]). Члены коррекции регрессионных остатков в /-ом уравнении УБС-модели будут иметь представление:
А (¡,1)*Сот1Ея1 + А (¡,2)*Сот1Ея2 + … + А (¡,г)*Сот1Еяг.
На данный момент ограничения на коэффициенты коррекции определяются гомогенными линейными ограничениями, так что ваше ограничение можно написать как Н уес(а) = 0, где Н — известная qk хг матрица. Это условие подразумевает, что ограничение:
А(1,1)= А(2,1)
является допустимым, но выражение:
А (1,1) = 1
вернет сообщение о синтаксической ошибке ограничения.
Одно особенно интересное ограничение состоит в том, может ли вся /-ая строка матрицы а быть нулевой строкой. Если это так, тогда /-ая эндогенная переменная называется слабоэкзогенной относительно параметров матрицы р. Например, если мы предполагаем, что существует лишь одно коинтегрирующее соотношение в УБС-модели, то для тестирования: является ли вторая эндогенная переменная слабо экзогенной относительно параметров матрицы р — вы можете ввести ограничение:
А (2,1) = 0
Чтобы наложить множественные ограничения, можно либо напечатать ограничения в одной строке, отделяя каждое ограничение запятой, либо разместить каждое ограничение на отдельной строке. Например, чтобы протестировать, является ли слабо экзогенной относительно параметров матрицы р вторая эндогенная переменная в УБС-модели сдвумя коинтег-рирующими соотношениями, вы можете напечатать:
А (2,1) = 0
А (2,2) = 0
Также можно наложить ограничения на обе матрицы, Р и а. Однако ограничения на матрицы р и а должны быть независимыми. Например, ограничения:
А (1,1) = 0
Б (1,1) = 1
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
Ns32006
являются допустимыми, но выражение:
А (1,1) = Б (1,1)
возвратит сообщение о синтаксической ошибке ограничения.
Идентифицирующие ограничения и связывающие ограничения
В программе проверяется, приводят ли к идентифицируемости ограничения, ко-
торые вы предоставили, всех коинтегрирующих векторовдля каждого возможного ранга.Условие идентифируемости проверяется численно с помощью вычисления ранга соответствующей матрицы Якоби [Boswijk (1995)]. Асимптотические стандартные ошибки для оцененных коинтегрирующих параметров будут сообщаться, если только ограничения приводят к идентифицируемости коинтегрирующих векторов.
В случае связывающих ограничений программа EViews приведет 1_Р-статистику (статистику отношения правдоподобия) для тестирования. _В-статистика сообщается, если степени свободы асимптотического %2 распределения положительны. Отметим, что ограничения могут быть связанными, даже если они не приводят к идентифицируемости (например, когда вы налагаете ограничения на коэффициенты коррекции, но не на коинтегрирующий вектор).
Оценивание ограниченных коинтегрирующих векторов р и коэффициентов коррекции а, в общем, включает итерационный процесс. Страница VEC Restrictions диалога Johansen Cointegration Test предоставляет управление итерациями — опции для максимального числа итераций и для критерия сходимости. Программа EViews оценивает ограниченные матрицы р и а, применяя алгоритм переключения [Boswijk (1995)]. Каждый шаг алгоритма гарантирует увеличение правдоподобия, и алгоритм, в конечном счете, должен сходиться (хотя сходимость может быть — к локальному, а не глобальному оптимуму). Возможно, придется увеличить число итераций, если возникнут трудности в достижении сходимости при установках значений «по умолчанию».
Если наложить ограничения в представлении Cointegration Test, то вывод сначала отобразит тестовые результаты без ограничений, как описано выше. Вторая часть вывода результатов начинается с отображения результатов LR-теста (теста отношения правдоподобия) для связывающих ограничений.
Если ограничения не будут связывающими для специфического ранга, соответствующие строки будут заполнены значениями NA. Если ограничения будут связывающими, но алгоритм не сходится, то соответствующая строка будет заполнена звездочками (*). В этом случае следует провести тестирование заново, увеличив число итераций или ослабив критерий сходимости. На примере вывода (рис. мы видим, что единственное ограничение а31 = 0 является связывающим только при предположении, что существует одно коинтег-рирующее соотношение. Зависящий от существования только одного коинтегрирующего соотношения, LR-тест не отклоняет наложенное ограничение при обычных уровнях значимости.
Опции для оценивания при наличии ограничений
Результаты тестирования на наличие коинтеграции при ограничениях
№32006
Restrictions:
а(3,1)=0
Tests of cointegration restrictions:
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Hypothesized Restricted LR Degrees of
No. ofCE(s) Log-likehood Statistic Freedom Probability
1 668.6698 0.891088 1 0.345183
2 674.2964 NA NA NA
3 677.4677 NA NA NA
NA indicates restriction not binding.
Рис. 8. Результаты теста на коинтеграцию при наличии ограничений
Вывод результатов также сообщает об оцененных матрицах р и а с наложенными ограничениями. Поскольку тест на наличие коинтеграции не специфицирует число коинтегрирую-щих соотношений, то будут отображены результаты для всех рангов, которые являются совместимыми со специфицированными ограничениями. Например, предположим, что имеется ограничение:
B(2,1) = 1
Так как это ограничение — на второй коинтегрирующий вектор, то программа EViews отобразит результаты для рангов r — 2,3,…,к -1 (если VAR-модель имеет только к — 2 эндогенных переменных, то программа EViews вернет сообщение об ошибке, указывающее, что «implied rankfrom restrictions must be of reduced order» («предполагаемый из ограничений ранг должен иметь меньший порядок»)).
Для каждого ранга сообщается, была ли достигнута сходимость, и приводится число примененных в результате итераций. В выводе также сообщается, идентифицируютли ограничения все коинтегрирующие параметры при предполагаемом ранге. Если коинтегрирующие векторы являются идентифицируемыми, то об асимптотических стандартных ошибках будет сообщено вместе с предоставлением оценок параметров для матрицы р.
Векторные модели коррекции регрессионных остатков (VEC-модели)
Векторная модель коррекции регрессионных остатков (VEC-модель) является ограниченной VAR-моделью, разработанной для применения к нестационарным рядам, для которых известно, что они являются коинтегрированными. VEC-модель имеет соотношения коинтеграции, встроенные в спецификацию таким образом, чтобы при долгосрочном динамическом поведении эндогенные переменные, сходились к их коинтегрирующим соотношениям с учетом краткосрочной динамической коррекции. Член коинтеграции носит название члена коррекции регрессионных остатков, поскольку отклонение от долгосрочного динамического равновесия корректируется постепенно через ряд частных краткосрочных динамических корректировок.
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
N932006
Приведем самый простой пример. Рассмотрим систему двух переменных с одним коин-тегрирующим уравнением и без лагированных разностных членов. Коинтегрирующее уравнение имеет вид:
у 2,t = Ру „. (27)
Соответствующая VEC-модель есть:
Ау i,f = а i( у 2,f _Ру i,t _,) + sv,
Ay 2,f = а 2 ( y 2,t -1 _Ру i,t _i) +s 2,t. (28)
В этой простой модели единственная переменная в правой части является членом коррекции регрессионных остатков. В долгосрочном динамическом равновесии этот член равен нулю. Однако, если у1 и у2 отклоняются от долгосрочного динамического равновесия, то член коррекции регрессионных остатков будет ненулевым, а каждая переменная корректируется, чтобы частично восстановить отношение равновесия. Коэффициент а i измеряет скорость коррекции к равновесию i-ой эндогенной переменной.
Как оценить модель коррекции регрессионных остатков
Поскольку спецификация VEC-модели применяется только к коинтегрированным рядам,
сначала следует провести тестирование Йохансена на наличие коинтеграции, как описано
выше, и определить число коинтегрирующих соотношений. Предоставить эту информацию следует как часть спецификации VEC-модели.
Чтобы задать установку VEC-модель, на панели инструментов VAR-модели щелкните кнопку Estimate и на странице VAR/VEC Specification выберите спецификацию Vector Error Correction. На странице VAR/VEC Specification следует разместить информацию — подобно тому как это делалось для неограниченной модели VAR, за исключением следующего:
• Константа или член линейного тренда не должны задаваться в окне редактирования Exogenous Series. Их следует расположить на странице Cointegration.
• Спецификация интервала лагирования относится к лагам первых разностных членов в VEC-модели. Например, спецификация лагов «1 1» будет включать в правые части уравнений VEC-модели лагированные первые разностные члены. Переписанная вуровневыхзначе-ниях, эта VEC-модель является ограниченной VAR-моделью с двумя лагами. Чтобы оценить VEC-модель без лагированных первых разностных членов, специфицируйте лаги как «0 0».
• Константа и спецификация тренда для VEC-моделей должны быть специфицированы на ярлыке Cointegration. Вам следует выбрать одну из пяти спецификаций тренда, какэто полагалось в разделе «Спецификация детерминированных трендов». Кроме того, в соответствующем поле редактирования нужно специфицировать число коинтегрирующих соотношений. Это число должно быть положительным целым числом, меньше числа эндогенных переменных в VEC-модели.
• Если вы хотите наложить ограничения на коинтегрирующие соотношения и/или коэффициенты коррекции, используйте страницу Restrictions. Более подробно эти ограничения описаны в разделе «Ограничения на коинтегрирующий вектор». Отметим, что эта страница будет недоступной, если вы не щелкнули спецификацию Vector Error Correction на странице VAR/VEC Specification.
№32006
Как только заполнен диалог, чтобы оценить VEC-модель, просто щелкните OK. Оценивание VEC-модели выполняется за два шага. На первом шаге оцениваются коинтегрирующие соотношения с помощью процедуры Йохансена, которая применяется при тестировании на наличие коинтеграции. Затем из оцененных коинтегрирующих соотношений строятся члены коррекции регрессионных остатков и оценивается VAR-модель в первых разностях, включая члены коррекции регрессионных остатков в качестве регрессоров.
Вывод результатов оценивания модели коррекции регрессионных остатков
(VEC-модели)
Вывод результатов оценивания VEC-модели состоит из двух частей. В первой части вывода сообщается о результатах процедуры Йохансена на первом шаге. Если вы не налагали никаких ограничений, то программа EViews будет использовать нормировку «по умолчанию», которая идентифицирует все коинтегрирующие соотношения. Эта нормировка «по умолчанию» выражает первые r переменных в VEC-модели как функции от остальныхk -r переменных, где r — число коинтегрирующих соотношений, а k — число эндогенных переменных. Для параметров, которые идентифицируемы согласно ограничениям, сообщаются асимптотические стандартные ошибки (скорректированные на степени свободы). Если вы предоставляли ваши собственные ограничения, и если ваши ограничения не идентифицируют все коинтегрирующие векторы, то стандартные ошибки сообщаться не будут.
Во второй части вывода сообщается о результатах на втором шаге для VAR-модели в первых разностях, включая члены коррекции регрессионных остатков, оцененных на первом шаге. При выводе результатов члены коррекции регрессионных остатков обозначаются CointEql, CointEq2 и так далее. Эта часть вывода результатов имеет тот же самый формат, что и для неограниченных VAR-моделей, как объяснялось в разделе «Вывод результатов оценивания для VAR-модели», но с одним отличием. Внизу таблицы вывода результатов для VEC-модели вы увидите, что для системы сообщено два значения логарифмического правдоподобия. Первое значение, помеченное Log Likelihood (d.f. adjusted), вычисляется с помощью определителя остаточной ковариационной матрицы (сообщенного как Determinant Residual Covariance), используя коррекцию степеней свободы для малой выборки как в (3). Оно равно значению логарифмического правдоподобия, определенному для неограниченных VAR-моделей. Значение Log Likelihood вычисляется с использованием остаточной ковариационной матрицы без коррекции степеней свободы. Это значение логарифмического правдоподобия сравнивается со значением логарифмического правдоподобия, выведенным в результатах тестирования на наличие коинтеграции.
Представления и процессы для модели коррекции регрессионных остатков
(VEC-модели)
В основном для VEC-моделей доступны те же самые представления и процессы, которые доступны для VAR-моделей, которые объяснялись выше. Здесь мы упомянем только те, которые являются специфическими для VEC-моделей.
Коинтегрирующие соотношения
При выборе опции View/Cointegration Graph отображается график оцененных коинтегрирующих соотношений, которые применяются для VEC-модели. Чтобы сохранить эти оце-
EViews
Векторные модели авторегрессии и коррекции регрессионных остатков
№32006
ненные коинтегрирующие соотношения в рабочем файле как ряды с именами, примените опцию Proc/Make Cointegration Group. Этот процесс создаст и отобразит объект группы без имени, содержащий оцененные коинтегрирующие соотношения, как ряды с именами. Эти ряды называются COINTEQOI, COINTEQ02 и так далее.
Прогнозирование
Прогнозы можно получить с помощью решения модели, созданной на базе оцененной VAR/VEC-модели. На панели инструментов VAR-окна щелкните опцию Proc/Make Model, чтобы создать объект модели из оцененной VAR/VEC-модели. Затем в модельной спецификации вы можете сделать любые изменения, включая модификацию утверждения ASSIGN перед решением модели для получения прогнозов.
Члены данных
Различные результаты из оцененной VAR/VEC-модели можно восстановить через члены данных командной линии. Здесь мы сосредоточимся на восстановлении оцененных коэффициентов VAR/VEC-модели.
Получение коэффициентов VAR-модели
К коэффициентам неограниченных VAR-моделей можно получить доступ, обращаясь к элементам двумерного массива C. Первая размерность массива C относится к числу уравнений VAR-модели, вто время как вторая размерность массива C относится к числу переменных в каждом уравнении. Например, C(2,3) — коэффициенттретьего регрессора во втором уравнении VAR-модели. Тогда к коэффициенту C(2,3) VAR-модели по имени VAR01 можно получить доступ с помощью команды:
varOl.c (2,3)
Чтобы исследовать соответствие между каждым элементом C и оцененными коэффициентами, на панели инструментов VAR выберите опцию View/Representations.
Получение коэффициентов VEC-модели
Для VEC-моделей оцененные коэффициенты сохраняются в трех разных двухмерных массивах: A, B и C. Массив A содержит параметры коррекции а, массив B содержит коинтегрирующие векторы Р’, а массив C содержит краткосрочные динамические параметры (коэффициенты на лагированные первые разностные члены).
• Первый индекс массива A — номер уравнения VEC-модели, в то время как второй индекс — номер коинтегрирующего уравнения. Например, A(2,1) — коэффициент коррекции первого коинтегрирующего уравнения во втором уравнении VEC-модели.
• Первый индекс массива B — номер коинтегрирующего уравнения, в то время как второй индекс — номер переменной в коинтегрирующем уравнении. Например, B(2,1) — коэффициент первой переменной во втором коинтегрирующем уравнении. Отметим, что эта схема индексации соответствует транспонированию р.
• Первый индекс массива C — номер уравнения VEC-модели, в то время как второй индекс — номер переменной первого разностного регрессора VEC-модели. Например, C(2,1) — коэффициент первого разностного регрессора во втором уравнении VEC-модели.
№32006
Вы можете получить доступ к каждому элементу этих коэффициентов, обращаясь к имени VEC-модели с последующей точкой и элементом коэффициента:
var01.a (2,1) var01.b (2,1) var01.c (2,1)
Чтобы увидеть соответствие между каждым элементом массивов A, B и C и оцененными коэффициентами, на панели инструментов VAR выберите опцию View/Representations.
Литература
ВербикМ. Путеводитель по современной эконометрике. М.: Научная книга, 2006.
Amisano Gianni and Giannini Carlo. Topics in Structural VAR Econometrics, 2-nd ed, Berlin: Springer-Verlag. 1997.
Blanchard Olivier and Quah Danny. «The Dynamic Effects of Aggregate Demand and Aggregate Supply Disturbances»//American Economic Review. 1989. № 79. Pp. 655-673.
Boswijk Peter H. «Identifiability of Cointegrated Systems» /Technical Report //Tinbergen Institute. 1995.
Christiano L. J., Eichenbaum M., Evans C. L. «Monetary Policy Shocks: What Have We Learned and to What End?». Chapter 2 in J. B. Taylor and M. Woodford, (eds.), Handbook of Macroeconomics. V. 1A, Amsterdam: Elsevier Science Publishers B.V. 1999.
Doornik Jurgen A. and Hansen Henrik. «An Omnibus Test for Univariate and Multivariate Normality»// Manuscript. 1994.
Engle R.F., Granger C.W.J. Cointegration and Error Correction: Representation, Estimation, and Testing// Econometrica. V. 55.1987. № 2.
Green W.H. Econometric Analysis (Fifth edition). Prentice Hall International, Inc., 2003.
Johansen S0ren. «Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models»//Econometrica. 1991. №59. Pp. 1551-1580.
Johansen Soren. Likelihood-based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press. 1995.
Johansen S$ren and Juselius Katarina. «Maximum Likelihood Estimation and Inferences on Cointegration — with applications to the demand for money»// Oxford Bulletin of Economics and Statistics. 1990. № 52. Pp. 169-210.
KelejianH. H.«An Extension of a Standard Test for Heteroskedasticity to a Systems Framework»// Journalof Econometrics. 1982. №20. Pp. 325-333.
Lutkepohl Helmut. Introduction to Multiple Time Series Analysis. New York: Springer-Verlag. 1991.
Osterwald-Lenum Michael. «A Note with Quantiles of the Asymptotic Distribution of the Maximum Likelihood Cointegration Rank Test Statistics»// Oxford Bulletin ofEconomics and Statistics. 1992. № 54. Pp. 461-472.
Pesaran M. Hashem and Shin Yongcheol. «Impulse Response Analysis in Linear Multivariate Models»// Economics Letters.1998. № 58. Pp. 17-29.
Sims Chris. «Macroeconomics and Reality»//Econometrica. 1980. №48. Pp. 1-48.
Urzua Carlos M.. «Omnibus Tests for Multivariate Normality Based on a Class of Maximum Entropy Distributions»//in Advances in Econometrics. V. 12. Greenwich, Conn.: JAI Press. 1997. Pp. 341-358.
White Halbert. «A Heteroskedasticity-Consistent Covariance Matrix and a Direct Test for Heteroskedasticity»// Econometrica. 1980. №48. Pp. 817-838.
EViews
Векторная модель коррекции ошибок
Рассмотрим модель р-го порядка:
Где:
-
yt.
k-мерный вектор нестационарных
переменных; -
xt.
d-мерный вектор экзогенных
переменных; -
et.
k-мерный вектор случайных
составляющих.
Модель можно представить в виде:
Где:
Ключевая теорема Гранжера гласит, что если матрица П имеет неполный
ранг r<k,
то существуют kxr
матрицы α и β, каждая ранга r,
такие, что П = α · βT,
ряд βT является
стационарным, и каждый столбец матрицы β является коинтеграционным
вектором, r — число коинтеграционных
связей. Элементы матрицы α называют сглаживающими параметрами модели коррекции
ошибок.
Если у вас имеется k эндогенных
переменных (каждая из которых содержит единичный корень), то может существовать
от нуля до k-1 линейно независимой
коинтеграционной связи. Если коинтеграционных
связей нет, к ряду в первых разностях может быть применен стандартный
анализ временных рядов. И наоборот, если в системе имеется одно коинтеграционное
уравнение, в каждое уравнение системы должна быть добавлена одна линейная
комбинация эндогенных переменных βTyt-1.
После умножения на коэффициент уравнения (т.е. на сглаживающий параметр
α) получается результирующая составляющая α · βT · yt-1,
которая и является составляющей коррекции ошибок. Каждое следующее коинтеграционное
уравнение будет вносить дополнительную составляющую коррекции ошибок,
уникальную по линейной комбинации параметров.
Если существует k коинтеграционных
связей, то ни один из рядов не имеет единичного корня и модель может быть
описана без взятия разностей.
Изучаемые ряды могут содержать ненулевое среднее, или тренд. Аналогично
коинтеграционные уравнения могут содержать константу и тренд. На практике
чаще используются следующие виды моделей:
| Ряд y | Коинтеграционные уравнения | Модель |
| Тренда нет | Константы нет | |
| Тренда нет | Константа есть | |
| Линейный тренд | Константа есть | |
| Линейный тренд | Линейный тренд | |
| Квадратичный тренд |
Линейный тренд |
α’ — матрица, рассчитывающаяся из соотношения αT · α, = 0
В рамках такой схемы, при построении модели, можно варьировать два параметра.
Можно фиксировать вид модели и варьировать ранг. Или наоборот, фиксировать
ранг и выбирать наиболее подходящую форму модели. При построении помимо
статистических критериев следует руководствоваться экономической адекватностью
модели. Следует обратить внимание на нормализованные коинтеграционные
уравнения, чтобы убедится в том, что они отвечают вашим ожиданиям о природе
рассматриваемого процесса.
Модель также может быть приведена к более общему виду:
См. также:
Библиотека методов и моделей
| Коинтегрированные процессы |
Модель коррекции ошибок |
Модель «Векторная
модель коррекции ошибок» | ISmErrorCorrectionModel


