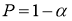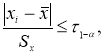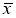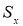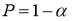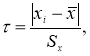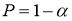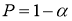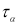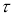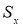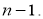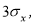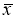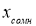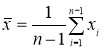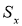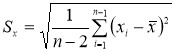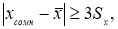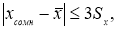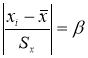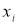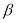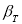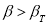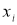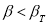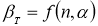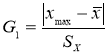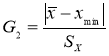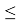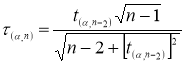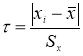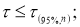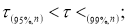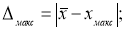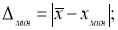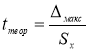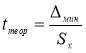Метрология методы исключения ошибок

7.1. Понятие о грубых погрешностях

Грубая
погрешность, или промах, —
это погрешность результата отдельного
измерения, входящего в ряд измерений,
которая для данных условий резко
отличается от остальных результатов
этого ряда. Источником грубых погрешностей
нередко бывают резкие изменения условий
измерения и ошибки, допущенные оператором.
К ним можно отнести:

• неправильный
отсчет по шкале измерительного прибора,
происходящий из-за неверного учета
цены малых делений шкалы;

• неправильная
запись результата наблюдений, значений
отдельных мер использованного набора,
например гирь;

•
хаотические
изменения параметров питающего СИ
напряжения, например его амплитуды или
частоты.

Грубые
погрешности, как правило, возникают
при однократных измерениях и обычно
устраняются путем повторных измерений.
Их причинами могут быть внезапные и
кратковременные изменения условий
измерения или оставшиеся незамеченными
неисправности в аппаратуре.

7.2. Критерии исключения грубых погрешностей

При
однократных измерениях обнаружить
промах не представляется возможным.
Для уменьшения вероятности появления
промахов измерения проводят два-три
раза и за результат принимают среднее
арифметическое полученных отсчетов.
При
многократных измерениях для обнаружения
промахов используют статистические
критерии, предварительно определив,
какому виду распределения соответствует
результат измерений.

Вопрос
о том, содержит ли результат наблюдений
грубую погрешность, решается общими
методами проверки статистических
гипотез. Проверяемая гипотеза состоит
в утверждении, что результат наблюдения
х, не содержит грубой погрешности, т.е.
является одним из значений измеряемой
величины. Пользуясь определенными
статистическими критериями, пытаются
опровергнуть выдвинутую гипотезу. Если
это удается, то результат наблюдений
рассматривают как содержащий грубую
погрешность и его исключают.

Для
выявления грубых погрешностей задаются
вероятностью q
(уровнем значимости) того, что сомнительный
результат действительно мог иметь
место в данной совокупности результатов
измерений.

Критерий
«трех сигм» применяется
для результатов измерений, распределенных
по нормальному закону. По этому критерию
считается, что результат, возникающий
с вероятностью q
< 0,003, маловероятен и его можно считать
промахом, если |х̅
-х_i|
> 3S_x
, где S_x
— оценка СКО измерений. Величины
х и S_x
вычисляют без учета экстремальных
значений x_i.
Данный
критерий надежен при числе измерений
n
>
20…
50.

Критерий
Романовского применяется,
если число измерений n
< 20. При этом вычисляется отношение
|(х̅
— x_i)/S_X|
= 
и сравнивается с критерием _т,
выбранным по табл. 7.1. Если 

_т,
то результат х_i
считается промахом и отбрасывается.

Пример
7.1.
При диагностировании топливной системы
автомобиля результаты пяти измерений
расхода топлива составили: 22, 24, 26, 28, 30
л на 100 км. Последний результат вызывает
сомнение. Проверить по критерию
Романовского, не является ли он промахом.

Найдем
среднее арифметическое значение расхода
топлива и его СКО без учета последнего
результата, т.е. для четырех измерений.
Они соответственно равны 25 и 2,6 л на 100
км.

Поскольку
n
< 20, то по критерию Романовского при
уровне значимости 0,01 и n
= 4 табличный коэффициент _т
= 1,73. Вычисленное для последнего, пятого
измерения 
= |(25 –
30)|/2,6
= 1,92 > 1,73 .

Критерий
Романовского свидетельствует о
необходимости отбрасывания последнего
результата измерения.

Критерий
Шарлье используется,
если число наблюдений в ряду велико
(n>
20).
Тогда по теореме Бернулли [56] число
результатов, превышающих по абсолютному
значению среднее арифметическое
значение на величину К_ШS_x,
будет n[l
— Ф(К_Ш)],
где Ф(К_Ш)
— значение нормированной функции
Лапласа для X
= К_Ш.
Если сомнительным в ряду результатов
наблюдений является один результат,
то n[1-Ф(К_ш)]
= 1. Отсюда Ф(К_Ш)
= (n
-1)/n.

Значения
критерия Шарлье приведены в табл. 7.2.

Таблица
7.1

Значения
критерия
Романовского

Таблица
7.2

Значения
критерия Шарльe

п	5	10	20	30	40	50	100
Кщ	1,3	1,65	1.96	2,13	2,24	2,32	2,58

Таблица
7.3

Значения
критерия Диксона

Пользуясь
критерием Шарлье, отбрасывают результат,
для значения которого в ряду из n
наблюдений выполняется неравенство
|х_i
— х̅|
> К_ШS_x
.

Вариационный
критерий Диксона удобный
и достаточно мощный (с малыми вероятностями
ошибок). При его применении полученные
результаты наблюдений записывают в
вариационный возрастающий ряд х₁,
х₂,
. . ., x_n
(x₁
< х₂
< . . .< х_п).
Критерий Диксона определяется как К_Д
= (х_n
— x_n-1/(x_n
–x₁).
Критическая область для этого критерия
Р(К_Д
> Z_q)
= q.
Значения Z_f(
приведены в табл. 7.3 [56].

Контрольные
вопросы

1.
Что такое грубые погрешности и промахи?
Как определить их присутствие в выборке
по виду закона распределения или
гистограмме?

2.
Расскажите о критерии «трех сигм»
и его модификациях.

3.
Как применить критерий Романовского
для исключения из выборки промахов?

4.
В чем суть критерия Шарлье?

5.
Расскажите об использовании вариационного
критерия Диксона для нахождения
промахов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В статье рассмотрены различные критерии отбрасывания грубых погрешностей измерений, применяемые в практической деятельности, на основе рекомендаций ведущих специалистов-метрологов, а также с учетом действующих в настоящий момент нормативных документов.

Приведен пример использования Excel при оценке грубых погрешностей по критериям Стьюдента и Романовского при обработке реальных результатов измерений.

Ключевые слова:



грубые погрешности, критерии согласия, сомнительные значения, уровень значимости, нормальное распределение, критерий согласия Стьюдента, критерий Романовского, выборка, отклонения, Excel.

Одним из важнейших условий правильного применения статистических оценок является отсутствие грубых ошибок при наблюдениях. Поэтому все грубые ошибки должны быть выявлены и исключены из рассмотрения в самом начале обработки наблюдений.

Единственным достаточно надежным способом выявления грубых ошибок является тщательный анализ условий самих испытаний. При этом наблюдения, проводившиеся в нарушенных условиях, должны отбрасываться, независимо от их результата. Например, если при проведении эксперимента, связанного с электричеством, в лаборатории на некоторое время был выключен ток, то весь эксперимент обязательно нужно проводить заново, хотя результат, быть может, не сильно отличается от предыдущих измерений. Точно так же отбрасываются результаты измерений на фотопластинках с поврежденной эмульсией и вообще на любых образцах с обнаруженным позднее дефектом.

На практике, однако, не всегда удается провести подобный анализ условий испытания. Чаще всего приходится иметь дело с окончательным цифровым материалом, в котором отдельные данные вызывают сомнение лишь своим значительным отклонением от остальных. При этом сама «значительность» отклонения во многом субъективна — зачастую приходится сталкиваться со случаями, когда исследователь отбрасывает наблюдения, которые ему не понравились, как ошибочные исключительно по той причине, что они нарушают уже созданную им в воображении картину изучаемого процесса.

Строгий научный анализ готового ряда наблюдений может быть проведен лишь статистическим путем, причем должен быть достаточно хорошо известен характер распределения наблюдаемой случайной величины. В большинстве случаев исследователи исходят из нормального распределения. Каждая грубая ошибка будет соответствовать нарушению этого распределения, изменению его параметров, иными словами, нарушится однородность испытаний (или, как говорят

,

однородность наблюдений), поэтому выявление грубых ошибок можно трактовать как проверку однородности наблюдений.

Промахи, или грубые погрешности, возникают при единичном измерении и обычно устраняются путем повторных измерений. Причиной их возникновения могут быть:

1. Объективная реальность (наш реальный мир отличается от идеальной модели мира, которую мы принимаем в данной измерительной задаче);
2. Внезапные кратковременные изменения условий измерения (могут быть вызваны неисправностью аппаратуры или источников питания);
3. Ошибка оператора (неправильное снятие показаний, неправильная запись и т. п.).

В третьем случае, если оператор в процессе измерения обнаружит промах, он вправе отбросить этот результат и провести повторные измерения.

В настоящее время определение грубой погрешности приведено в ГОСТ Р 8.736–2011: «Грубая погрешность измерения: Погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей» [1, с. 6].

Общие подходы к методам отсеивания грубых погрешностей, как это уже давно принято в практике измерений, заключаются в следующем.

Задаются вероятностью

Р

или уровнем значимости

α

(

) того, что результат наблюдения содержит промах. Выявление сомнительного результата осуществляют с помощью специальных критериев. Операция отбрасывания удаленных от центра выборки сомнительных значений измеряемой величины называется «цензурированием выборки».

Проверяемая гипотеза состоит в утверждении, что результат наблюдения

x

_i


не содержит грубой погрешности, т. е. является одним из значений случайной величины

x

с законом распределения Fx(x), статистические оценки параметров которого предварительно определены. Сомнительным может быть в первую очередь лишь наибольший x

_max

или наименьший xmin из результатов наблюдений.

Предложим для практического использования наиболее простые методы отсева грубых погрешностей.

Если в распоряжении экспериментатора имеется выборка небольшого объема

n

≤ 25, то можно воспользоваться методом вычисления максимального относительного отклонения [2, с. 149]:

(1)

где

x


_i

— крайний (наибольший или наименьший) элемент выборки, по которой подсчитывались оценки среднего значения

и среднеквадратичного отклонения

;

τ


<sub>1-


p</sub>

— табличное значение статистики

τ

, вычисленной при доверительной вероятности

.

Таким образом, для выделения аномального значения вычисляют значение статистики,

(2)

которое затем сравнивают с табличным значением

τ

_1-α


:

τ


≤


τ

_1-α


. Если неравенство

τ

≤

τ


_1-α

соблюдается, то наблюдение не отсеивают, если не соблюдается, то наблюдение исключают. После исключения того или иного наблюдения или нескольких наблюдений характеристики эмпирического распределения должны быть пересчитаны по данным сокращенной выборки.

Квантили распределения статистики

τ

при уровнях значимости

α

= 0,10; 0,05; 0,025 и 0,01 или доверительной вероятности

=

0,90; 0,95; 0,975 и 0,99 приведены в таблице 1. На практике очень часто используют уровень значимости

α

= 0,05 (результат получается с 95 %-й доверительной вероятностью).

Функции распределения статистики

τ

определяют методами теории вероятностей. По данным таблицы, приведенной в источниках [2, с. 283; 3, с. 184] при заданной доверительной вероятности

или уровне значимости

α

можно для чисел измерения п = 3–25 найти те наибольшие значения

которые случайная величина

может еще принять по чисто случайным причинам.

Процедуру отсева можно повторить и для следующего по абсолютной величине максимального относительного отклонения, но предварительно необходимо пересчитать оценки среднего значения

и среднеквадратичного отклонения

для выборки нового объема

Таблица 1

Квантили распределения максимального относительного отклонения при отсеве грубых погрешностей [2, с. 283]

В литературе можно встретить большое количество методических рекомендаций для проведения отсева грубых погрешностей измерений, подробно рассмотренных в [4, с. 25]. Обратим внимание на некоторые из существующих критериев отсеивания грубых погрешностей.

1. Критерий «трех сигм» применяется для случая, когда измеряемая величина
   
   x
   
   распределена по нормальному закону. По этому критерию считается, что с вероятностью
   
   Р
   
   = 0,9973 и значимостью
   
   α
   
   = 0,0027 появление даже одной случайной погрешности, большей, чем

   

   маловероятное событие и ее можно считать промахом, если

   

   −
   
   x
   
   _i
   
   
   > 3
   
   S
   
   _x
   
   
   , где
   
   S
   
   <sub>x
   
   
   
   
   —</sub>
   
   
   оценка среднеквадратического отклонения (СКО) измерений. Величины

   

   и
   
   S
   
   _x
   
   
   вычисляют без учета экстремальных значений
   
   x
   
   _i
   
   
   . Данный критерий надежен при числе измерений
   
   n
   
   ≥ 20…50 и поэтому он широко применяется. Это правило обычно считается слишком жестким, поэтому рекомендуется назначать границу цензурирования в зависимости от объема выборки: при

6 <

n

≤100 она равна 4

S

_x


; при 100 <

n

≤1000 − 4,5

S

_x


; при 1000 <

n

≤10000–5

Sx

. Данное правило также используется только при нормальном распределении.

Практические вычисления проводят следующим образом [5, с. 65]:

1. Выявляют сомнительное значение измеряемой величины. Сомнительным значением может быть лишь наибольшее, либо наименьшее значение наблюдения измеряемой величины.
2. Вычисляют среднее арифметическое значение выборки

   

   без учета сомнительного значения

   

   измеряемой величины.

(3)

1. Вычисляют оценку СКО выборки

   

   без учета сомнительного значения

   

   измеряемой величины.

(4)

1. Вычисляют разность среднеарифметического и сомнительного значения измеряемой величины и сравнивают.

Если

то сомнительное значение отбрасывают, как промах.

Если

то сомнительное значение оставляют как равноправное в ряду наблюдений.

Данный метод «трех сигм» среди метрологов-практиков является самым популярным, достаточно надежным и удобным, так как при этом иметь под рукой какие-то таблицы нет необходимости.

1. Критерий В. И. Романовского применяется, если число измерений невелико,
   
   n
   
   ≤ 20. При этом вычисляется соотношение

(5)

где

— результат, вызывающий сомнение,

— коэффициент, предельное значение которого

определяют по таблице 2. Если

, сомнительное значение

исключают («отбрасывают») как промах. Если

,

сомнительное значение оставляют как равноправное в ряду наблюдений [5, с. 65].

Таблица 2

Значение критерия Романовского

Несмотря на многообразие существующих и применяемых на практике методов отсеивания грубых погрешностей в настоящее время действует национальный стандарт ГОСТ Р 8.736–2011, который является основным нормативным документом в данной области. В новом стандарте для исключения грубых погрешностей применяется критерий Граббса.

1. Статистический критерий Граббса (Смирнова) исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению [1, с. 8]. Для этого вычисляют критерии Граббса (Смирнова) G1 и G2, предполагая, что наибольший хmax или наименьший xmin результат измерений вызван грубыми погрешностями.

и

(6)

Сравнивают G1 и G2 с теоретическим значением GT критерия Граббса (Смирнова) при выбранном уровне значимости α. Таблица критических значений критерия Граббса (Смирнова) приведена в приложении к стандарту [1, с. 12]. Следует отметить, что критические значения критерия Граббса (Смирнова) GT отличаются от критических значений критериев

t

-статистик или значений критериев Стьюдента при одних и тех же величинах уровней значимости, что может вызывать некоторые трудности у пользователей при выборе конкретного метода отсеивания погрешностей, соответствующего нормативным документам.

Если G1>GТ, то хmax исключают как маловероятное значение. Если G2>GТ, то xmin исключают как маловероятное значение. Далее вновь вычисляют среднее арифметическое и среднее квадратическое отклонение ряда результатов измерений и процедуру проверки наличия грубых погрешностей повторяют.

Если G1

GТ, то хmax не считают промахом и его сохраняют в ряду результатов измерений. Если G2

GТ, то xmin не считают промахом и его сохраняют в ряду результатов измерений.

Отсев грубых погрешностей можно производить и для больших выборок (

n

= 50…100). Для практических целей лучше всего использовать таблицы распределения Стьюдента. Этот метод исключения аномальных значений для выборок большого объема отличается простотой, а таблицы распределения Стьюдента имеются практически в любой книге по математической статистике, кроме того, распределение Стьюдента реализовано в пакете Excel. Распределение Стьюдента относится к категории распределений, связанных с нормальным распределением. Подробно эти распределения рассмотрены в учебниках по математической статистике [3, с. 24].

Известно, что критическое значение

τ


_p

(

p

— процентная точка нормирования выборочного отклонения) выражается через критическое значение распределения Стьюдента

t

_{α, n-2}


[6, с. 26]:

(7)

Учитывая это, можно предложить следующую процедуру отсева грубых погрешностей измерения для больших выборок (

n

= 100):

1) из таблицы наблюдений выбирают наблюдение имеющее наибольшее отклонение;

2)

по формуле

вычисляют значение статистики

τ

;

3)

по таблице (или в программе Excel) находят процентные точки

t

-распределения Стьюдента

t


<sub>(



α,


n


-2



)</sub>

:

t


<sub>(95




%, 98)</sub>

= 1,6602, и

t

<sub>(



99




%, 98)</sub>

= 3,1737;

По предыдущей формуле в программе Excel вычисляют соответствующие точки

t


<sub>(95




%, 100)</sub>

= 1,66023и

t


<sub>(99




%, 100)</sub>

=3,17374.

Сравнивают значение расчетной статистики с табличными критическими значениями и принимают решение по отсеву грубых погрешностей.

Рекомендуемый метод отсева грубых погрешностей удобен еще тем, что максимальные относительные отклонения могут быть разделены на три группы: 1)

2)

3)

.

Наблюдения, попавшие в первую группу, нельзя отсеивать ни в коем случае. Наблюдения второй группы можно отсеять, если в пользу этой процедуры имеются еще и другие соображения экспериментатора (например, заключения, сделанные на основе изучения физических, химических и других свойств изучаемого явления). Наблюдения третьей группы, как правило, отсеивают всегда.

Рассмотрим далее пример с использованием средств программного пакета Excel, который позволяет снизить трудоемкость расчетов при осуществлении данной процедуры. К сожалению, в настоящее время средства Excel не позволяют автоматизировать расчеты по всем известным критериям отсеивания грубых погрешностей, поэтому проиллюстрируем рассмотренные методы с использованием доступных в Excel критериев Стьюдента.

Пример 1.

Имеется выборка из 100 шт. резисторов с номинальным сопротивлением

R


_н

= (150,0 ± 5 %) кОм, которая используется для оценки качества партии резисторов (генеральная совокупность). Используя критерий Стьюдента, отсеем грубые погрешности (промахи) при измерениях.

1. Заносим данные измерений в таблицу Excel в ячейки В2:В101
2. Составляем вариационный ряд — располагаем данные в порядке возрастания с помощью функции «Сортировка по возрастанию» в ячейках С2:С101 (рис. 1)

Рис. 1. Фрагмент диалогового окна с данными измерений и вариационного ряда

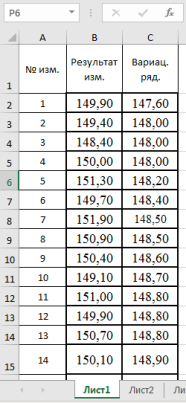
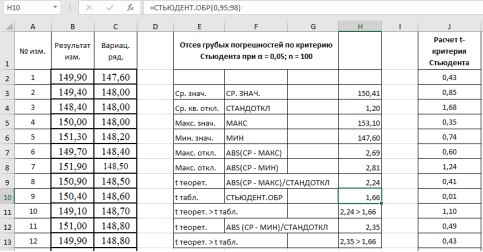
3. Находим среднее значение выборки с помощью мастера функций в категории «Статистические» и функции — СРЗНАЧ, результат в ячейке Н3 (рис. 2).

Рис. 2. Фрагмент диалогового окна при нахождении среднего значения выборки

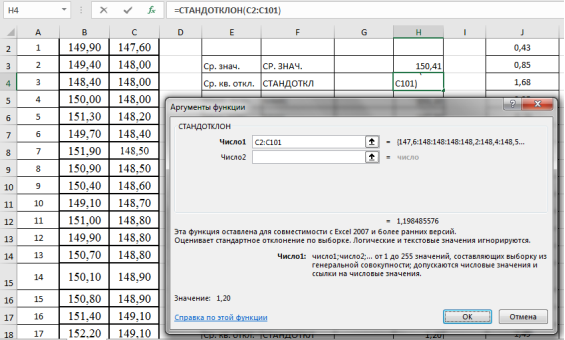
1. Находим среднеквадратическое отклонение —
   
   S
   
   
   _x
   
   . Выделяем ячейку Н4, вызываем «Мастер функций», категория «Статистические», функция — СТАНДОТКЛОН, результат в ячейке Н4–1,20 (рис. 3).

Рис. 3. Фрагмент диалогового окна при нахождении среднего квадратического отклонения

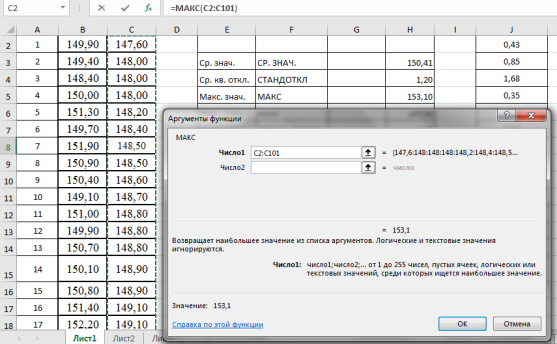
1. Находим максимальное значение в выборке —
   
   x
   
   
   _макс
   
   . Выделяем ячейку Н5, в категории «Статистические», функция — МАКС, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н5–153,10 (рис. 4).

Рис. 4. Фрагмент диалогового окна при нахождении максимального значения

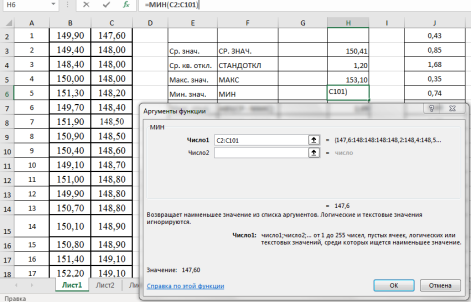
1. Находим минимальное значение в выборке —
   
   x
   
   
   _мин
   
   . Выделяем ячейку Н6, в категории «Статистические», функция — МИН, выделяем мышкой вариационный ряд C2:С101, результат в ячейке Н6–147,6 (рис. 5).

Рис. 5. Фрагмент диалогового окна при нахождении минимального значения

1. Находим максимальное и минимальное отклонения — Δ
   
   _макс
   
   и Δ
   
   _мин
   
   . Вводим в ячейки Н7 и Н8 формулы:

1. Находим теоретическое значение —
   
   t
   
   
   _теор
   
   . для максимального и минимального отклонений. Вводим в ячейки Н9 и Н12 формулу

. и

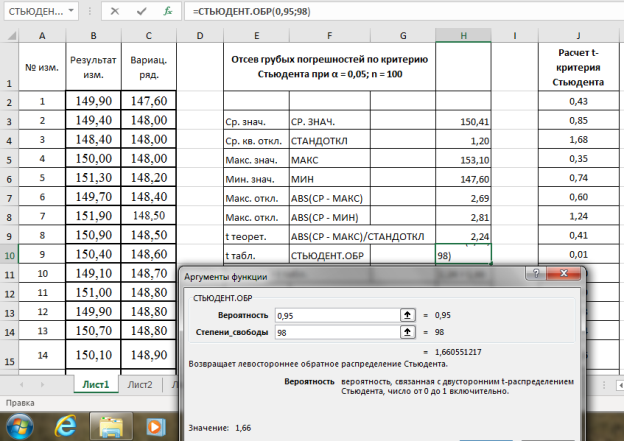
1. Находим табличное значение
   
   t
   
   
   _табл.
   
   Выделяем ячейку Н10, вызываем в категории «Статистические» функцию — СТЬЮДЕНТ.ОБР, «Вероятность» — 0,95, степени свободы (
   
   n
   
   -2) — 98, результат в ячейке Н10–1,66 (рис. 6).

Рис. 6. Фрагмент диалогового окна при нахождении табличного значения критерия Стьюдента

1. Сравниваем теоретическое значение
   
   t
   
   
   _теор
   
   = 2,24 критерия Стьюдента для максимального значения — 153,1 кОм с табличным значением:
   
   t
   
   
   _табл
   
   .= 1,6605.
2. Аналогично п. 9 проверим на наличие грубой погрешности у минимального значения в выборке — 147,6 кОм. Результат в ячейке Н12–2,35 (рис. 7).

Рис. 7. Фрагмент диалогового окна при окончательном анализе данных

1. Делаем вывод о наличии грубых ошибок в данных измерениях. Рассмотренная процедура подтвердила наши сомнения относительно достоверности максимального и минимального значений в данной выборке, т. е., указанные результаты могут быть отброшены из результатов измерений, и проверка может быть повторена снова без этих данных.

Пример расчета теоретического критерия Романовского по аналогичным формулам в Excel и диалоговое окно представлены на рис. 8, при условии α = 0,05, число измерений

n

= 20, β

_табл

= 2,78 (из таблицы 2).

Рис. 8. Фрагмент диалогового окна при расчете критерия Романовского

Выводы

1. Для использования различных критериев отбрасывания грубых погрешностей измерений необходимо учитывать требования действующих нормативных документов.
2. Рассмотренный пример показал, что расчеты погрешностей по критерию Стьюдента с использованием таблиц и формул Excel значительно упрощаются, а процесс отбрасывания грубых погрешностей можно осуществить наиболее качественно и быстро.

Литература:

1. ГОСТ Р 8.736–2011 Государственная система обеспечения единства измерений. Измерения прямые многократные. Методы обработки результатов измерений. Основные положения. — М.: ФГУП Стандартинформ, 2013. — 24 с.

2. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. — М.: Наука, 1968. — 288 с.

3. Львовский Е. Н. Статистические методы построения эмпирических формул: Учеб. пособие. — М.: Высш. школа, 1982. — 224 с.

4. Фаюстов А. А. Ещё раз о критериях отсеивания грубых погрешностей. — Законодательная и прикладная метрология, 2016, № 5, с. 25–30.

5. Сергеев А. Г. Метрология: Учебник. — М.: Логос, 2005. — 272 с.

6. Большев Л. Н., Смирнов Н. В. Таблицы математической статистики. — М.: Наука, Главная редакция физико-математической литературы, 1983. — 416 с.

МОДУЛЬ F. МЕТОДЫ ВЫЯВЛЕНИЯ И ИСКЛЮЧЕНИЯ ПОГРЕШНОСТЕЙ

Выявление и оценка погрешности измерения физической величины («суммарной погрешности») и ее составляющих являются традиционными задачами метрологии. Все методы выявления и оценки погрешностей можно разделить на аналитические (теоретические), экспериментальные и смешанные. Кроме того, в ряде случаев успешно используют оценки погрешностей, взятые из информационных источников. Очевидно, что данные о погрешностях, включенные в эти источники, получены с помощью теоретических расчетов или экспериментов.

Нахождение значения погрешности в информационных источниках применимо как к погрешности измерения в целом, так и к отдельным составляющим. Инструментальные погрешности средств измерений приведены в документации (стандарты, паспорта) и в справочниках. Источниками информации о погрешностях измерений могут быть такие документы, как стандартизованные или аттестованные методики выполнения измерений. Можно использовать в качестве информационных источников также отчеты о научно-исследовательских работах, монографии и другую научно-техническую литературу при достаточной степени доверия к ее авторам.

Базой аналитических методов выявления и оценки погрешностей является функциональный анализ методики выполнения измерений. Для расчетов погрешностей строят специальные аналитические модели. Эти методы применяют для расчета составляющих (инструментальных и методических погрешностей, а также погрешностей из-за несоответствия условий измерений нормальным). Возможно также моделирование некоторых субъективных составляющих погрешности.

Аналитические расчеты на точность средств измерений (расчет инструментальных погрешностей) могут проводиться для оценки теоретических погрешностей преобразования измерительной информации, а также для нахождения допустимых технологических погрешностей изготовления и сборки деталей. При проектировании средств измерений такие расчеты обязательны.

Погрешности из-за отличия условий измерений от номинальных в общем случае должны учитывать воздействие влияющих величин и на средства измерений, и на измеряемые объекты. Рассмотрим, например, температурные погрешности. Для расчета воздействия влияющей величины  на объект измерения, нужно знать функцию f() изменения измеряемой физической величины при изменении аргумента (влияющей величины ) и значение аргумента . Изменение линейного размера (длины, толщины, диаметра, высоты измеряемой детали) под воздействием температуры обычно связывают с так называемой «стержневой моделью» и рассчитывают с использованием элементарной зависимости

_l =  (t_i – t₂₀),

где _l – приращение длины (положительное или отрицательное),

 – температурный коэффициент линейного расширения;

t_i – температура при измерении;

t₂₀ – номинальное значение нормальной температуры при измерении.

Для оценки влияния температуры на возникновение «дополнительной инструментальной погрешности» необходимо проанализировать действие температуры на измерительную цепь средства измерения. Следует выявить те элементы, воздействие на которые приведет к искажению функции измерительного преобразования, и определить характер искажения. Затем, используя измененные аргументы, можно рассчитать изменившееся значение результата измерения. Этот длинный и сложный путь часто оказывается непродуктивным потому, что для построения аналитической модели измерительной цепи прибора приходится задаваться множеством допущений. Результат будет достоверным только при достаточной строгости допущений, что в рассматриваемых случаях не всегда реализуемо. Например, трудно моделировать температурную деформацию точек детали сложной («статически неопределимой») конструкции, а именно к таким можно отнести большинство корпусных и других базовых деталей средств измерений.

Оценку методической погрешности можно рассмотреть на примере измерения массы объекта взвешиванием (метод сравнения с мерой) на двухчашечных весах в воздушной среде. Для этого следует построить модель уравновешивания с учетом архимедовых сил, которые обусловлены вытеснением воздуха и объектом измерения, и гирями.

Для оценки погрешностей отсчитывания результатов с аналоговых приборов (часть субъективной составляющей погрешности измерения) можно построить модель образования погрешности из-за параллакса (если плоскости шкалы и указателя не совпадают), а также модели округления результата или интерполирования дольной части деления. Элементарная модель округления отсчета при положении указателя между отметками шкалы показывает, что в наихудшем случае (положение указателя точно посредине) погрешность округления составит половину цены деления шкалы (j) аналогового прибора. Следовательно, погрешность отсчитывания с округлением составит не более 0,5j, а при интерполировании дольной части деления «на глаз» будет еще меньше. Однако в последнем случае более строгая аналитическая оценка невозможна, поэтому прибегают к экспериментальным методам или к заимствованию данных из информационных источников, которые утверждают, что погрешность интерполирования при хороших эргономических свойствах системы шкала-указатель и хорошем зрении оператора не превышает (0,1…0,2)j.

Уровень полноты информации о составляющих погрешностей может колебаться от оценки по шкале наименований до оценки по шкале отношений. Примерами качественных оценок погрешностей по шкале наименований могут быть утверждение о наличии погрешности, возникающей из-за определенных причин, заключение о характере погрешности (скажем, систематическая постоянная погрешность длины объекта при отличии его температуры от нормальной или прогрессирующая температурная погрешность при монотонном изменении температуры). Использование шкалы порядка может выражаться, например, в оценках значимости составляющих погрешности. Наивысшим уровнем оценок погрешностей будет получение их числовых значений. Возможные уровни полноты оценки погрешностей определяются в ходе исследований на следующих этапах:

• обоснование (фиксация) наличия погрешности от некоторого источника;

• оценка характера погрешности;

• получение оценок порядка и/или числовых значений погрешностей.

Задачей первого (чисто аналитического) этапа является определение составляющих погрешностей, происходящих от любого источника. Анализ проводится с целью констатации наличия или отсутствия погрешностей от конкретных источников, определяемых методикой выполнения измерений. Например, если измерения осуществляются методом сравнения с мерой, в инструментальные погрешности входят не только погрешности прибора, но и погрешности используемых мер или ансамблей (композиций) мер. Возможно ли возникновение значимых инструментальных составляющих погрешности от вспомогательных устройств, таких как стойка или штатив средства линейных измерений, присоединительные провода электрических приборов и др. необходимо выяснить в ходе анализа.

При анализе условий измерения выявляют влияющие величины. Наряду с очевидными воздействиями на объект и/или средства измерений (влияние температуры при линейных измерениях, влияние электромагнитных полей на электрические средства измерений) приходится оценивать более тонкие воздействия, например, влияние атмосферного давления и влажности воздуха на пневматические и емкостные средства измерений.

Обязательными элементами анализа являются также исследование возможности возникновения методических погрешностей из-за идеализации используемого измерительного преобразования и принятой модели объекта измерений, а также выявление составляющих субъективной погрешности.

Второй этап (оценка характера погрешности) может основываться как на аналитическом подходе, так и на экспериментальных данных. Глубина исследований здесь также может быть различной, например, можно только констатировать систематический характер выявленной составляющей погрешности или дополнить описание более конкретными данными, например: «постоянная систематическая погрешность используемой меры«, «прогрессирующая систематическая погрешность из-за повышения температуры в цехе«, «периодическая систематическая погрешность отсчетного устройства прибора из-за эксцентриситета указателя и шкалы«. Для случайной погрешности кроме констатации факта ее стохастического характера важно определить вид распределения (нормальное, равновероятное, трапециевидное и т.д.).

На третьем этапе определяют числовые оценки значения (значений) погрешности. Здесь, как и на втором этапе можно основываться как на аналитическом подходе, так и на экспериментальных данных. При недостаточной информации приходится останавливаться на оценке порядка или значений границ рассматриваемой погрешности. Более полная информация позволяет получать оценки конкретных значений систематической составляющей, функцию ее изменения, необходимые вероятностные характеристики случайной составляющей погрешности.

В метрологии достаточно часто применяют методы оценки комплексной погрешности измерения физической величины. Общие методы, пригодные для выявления и оценки погрешностей измерения независимо от их характера и источников возникновения, базируются на решении уравнения

 = X – Q,

где  – абсолютное значение искомой погрешности,

X – результат измерения,

Q – истинное значение измеряемой величины.

Это уравнение содержит два неизвестных и в строгом математическом смысле неразрешимо, следовательно, для получения удовлетворительного решения необходимо заменить одно из неизвестных его приближенным значением. Получение таких значений и составляет суть общих методов выявления и оценки погрешностей.

Экспериментальные методы оценки погрешностей измерений основаны на замене истинного значения измеряемой величины Q действительным значением Х_д настолько близким к нему, что разность между ними (погрешность _д) может рассматриваться как пренебрежимо малая по сравнению с искомой (исследуемой) погрешностью, то есть

Q  Х_д, или _д  0, что подразумевает _д  .

Экспериментальные методы оценки погрешностей измерений можно разделить на три группы:

• измерение известной физической величины;

• повторное измерение одной и той же физической величины с заведомо более высокой точностью;

• анализ массивов результатов многократных измерений одной и той же физической величины.

Первую группу экспериментальных методов чаще всего реализуют путем измерения физической величины, воспроизводимой «точной» мерой, вторую – с помощью «точных» измерений одной и той же величины с использованием новой методики выполнения измерений. В любом из этих случаев получают количественную оценку погрешности за счет использования заведомо более точной информации об измеряемой физической величине. Различие между методами заключается в том, что первый обеспечивает необходимую точность информации за счет аттестованного размера физической величины, воспроизводимого мерой (предварительная аттестация), а при втором аттестуется сама измеряемая физическая величина (аттестация в ходе исследования).

Метод определения значения погрешности по результатам измерения точной меры применяют для оценки реализуемой погрешности измерений или для оценки инструментальной составляющей, если погрешности от остальных источников удается свести к пренебрежимо малым значениям. Определение значения погрешности измерения или средства измерения возможно только в том случае, когда погрешность измеряемой «точной» меры _м пренебрежимо мала по сравнению с искомой погрешностью .

Искомая погрешность  в этом случае определяется из зависимости:

 = X – Х_м ,

где Х – результат измерения меры,

Х_м – «точное» значение меры (номинальное значение меры или значение меры с поправкой по аттестату), для которого можно записать

_м  .