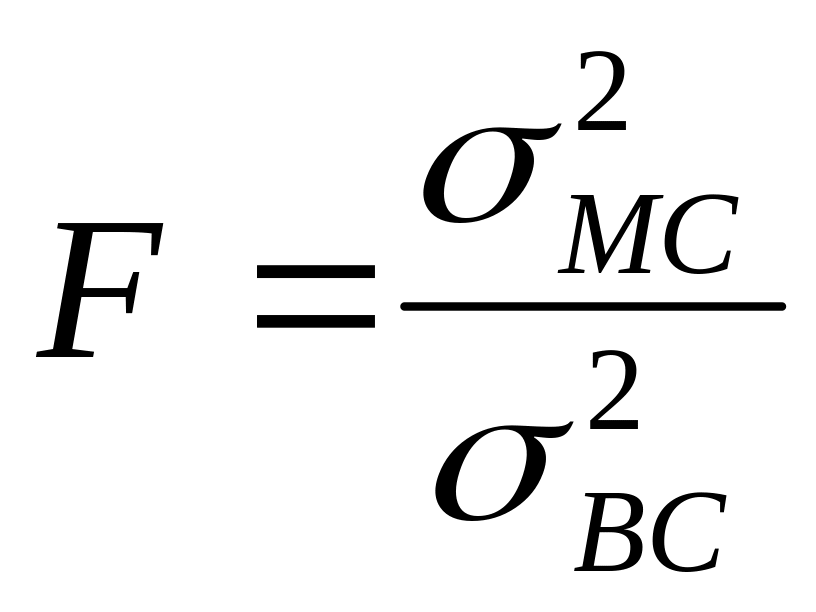Методы устранения систематических ошибок

Результаты наблюдений,
полученные при наличии системати­ческой
погрешности, называются неисправленными.
При проведении
измерений стараются в максимальной
степени исключить или учесть влияние
систематических погрешностей. Это может
быть дос­тигнуто следующими путями:

• устранением источников погрешностей
до начала измерений. В большинстве
областей измерений известны главные
источники систематических погрешностей
и разработаны методы, исключаю­щие
их возникновение или устраняющие их
влияние на результат измерения. В связи
с этим в практике измерений стараются
устра­нить систематические погрешности
не путем обработки экспери­ментальных
данных, а применением СИ, реализующих
соответст­вующие методы измерений;

• определением
поправок и внесением их в результат
измерения;

• оценкой границ неисключенных
систематических погрешностей.

Постоянная систематическая
погрешность не может быть най­дена
методами совместной обработки результатов
измерений. Од­нако она не искажает ни
показатели точности измерений,
характе­ризующие случайную погрешность,
ни результат нахождения переменной
составляющей систематической погрешности.

Дейст­вительно, результат одного
измерения

где х_и
– истинное значение измеряемой величины;
Δ_i
– i-я
случай­ная погрешность; θ_i
– i-я
систематическая погрешность. После
ус­реднения результатов многократных
измерений получаем среднее арифметическое
значение измеряемой величины

Если систематическая
погрешность постоянна во всех измере­ниях,
т.е. θ_i=θ
, то

Таким образом, постоянная систематическая
погрешность не уст­раняется при
многократных измерениях.

Постоянные систематические
погрешности могут быть обнару­жены
лишь путем сравнения
результатов измерений с другими,
по­лученными с помощью более высокоточных
методов и средств. Ино­гда эти
погрешности могут быть устранены
специальными приемами проведения
процесса измерений. Эти методы рассмотрены
ниже.

Наличие существенной переменной
систематической погрешно­сти искажает
оценки характеристик случайной
погрешности и ап­проксимацию ее
распределения. Поэтому она должна
обязательно выявляться и исключаться
из результатов измерений.

Для устранения постоянных систематических
погрешностей при­меняют следующие
методы:

• Метод
замещения,
представляющий собой
разновидность ме­тода сравнения,
когда сравнение осуществляется заменой
измеряе­мой величины известной
величиной, причем так, что при этом в
состоянии и действии всех используемых
средств измерений не про­исходит
никаких изменений. Этот метод дает
наиболее полное ре­шение задачи. Для
его реализации необходимо иметь
регулируе­мую меру, величина которой
однородна измеряемой.

• Метод
противопоставления,
являющийся разновидностью
метода сравнения, при котором измерение
выполняется дважды и проводится так,
чтобы в обоих случаях причина постоянной
по­грешности оказывала разные, но
известные по закономерности воздействия
на результаты наблюдений. Например,
способ взве­шивания Гаусса [3].

Пример 7.1. Измерить
сопротивление с помощью одинарного
моста ме­тодом противопоставления.

Сначала измеряемое
сопротивление R_x
уравновешивают известным со­противлением
R₁
включенным в плечо сравнения моста. При
этом R_х
= R₁·R₃
/R₄,
где R₃,
R₄
– сопротивления плеч моста. Затем
резисторы R_x
и R₁
меняют местами и вновь уравновешивают
мост, регулируя сопро­тивление
резистора R₁.
В этом случае R_x
= R΄₁·R₃/R₄.

Из двух последних уравнений
исключается отношение R₃/R₄.
Тогда

• Метод
компенсации погрешности по знаку
(метод изменения знака
систематической погрешности),
предусматривающий измерение с двумя
наблюдениями, выполняемыми так, чтобы
постоян­ная систематическая погрешность
входила в результат каждого из них с
разными знаками.

Пример 7.2. Измерить ЭДС
потенциометром постоянного тока,
имею­щим паразитную термо–ЭДС.

При выполнении одного
измерения получаем ЭДС Е₁
Затем меняем полярность измеряемой ЭДС
и направление тока в потенциометре.
Вновь проводим его уравновешивание –
получаем значение Е₂.
Если термо–ЭДС дает погрешность ΔЕ
и Е₁=Е_x+ΔЕ,
то Е₂=Е_x–ΔЕ.
Отсюда Е_x
= (Е
₁+
Е₂)/2.
Сле­довательно, систематическая
погрешность, обусловленная действием
термо–ЭДС, устранена.

• Метод
рандомизации –
наиболее универсальный способ ис­ключения
неизвестных постоянных систематических
погрешностей. Суть его состоит в том,
что одна и та же величина измеряется
раз­личными методами (приборами).
Систематические погрешности ка­ждого
из них для всей совокупности являются
разными случайны­ми величинами.
Вследствие этого при увеличении
числа используемых методов (приборов)
систематические погрешности вза­имно
компенсируются.

Для устранения переменных и монотонно
изменяющихся сис­тематических
погрешностей применяют следующие приемы
и ме­тоды.

• Анализ
знаков неисправленных случайных
погрешностей.
Ес­ли знаки
неисправленных случайных погрешностей
чередуются с какой-либо закономерностью,
то наблюдается переменная система­тическая
погрешность. Если последовательность
знаков «+» у слу­чайных погрешностей
сменяется последовательностью знаков
«–» или наоборот, то присутствует
монотонно изменяющаяся система­тическая
погрешность. Если группы знаков «»+ и
«–» у случайных погрешностей чередуются,
то присутствует периодическая
система­тическая погрешность.

• Графический
метод. Он
является одним из наиболее простых
способов обнаружения переменной
систематической погрешности в ряду
результатов наблюдений и заключается
в построении графика последовательности
неисправленных значений результатов
наблю­дений. На графике через построенные
точки проводят плавную кри­вую, которая
выражает тенденцию результата измерения,
если она существует. Если тенденция не
прослеживается, то переменную
сис­тематическую погрешность считают
практически отсутствующей.

• Метод
симметричных наблюдений.
Рассмотрим сущность
этого метода на примере измерительного
преобразователя, передаточная функция
которого имеет вид у = kх
+ у₀,
где х, у – входная и выходная величины
преобразователя; k
– коэффициент, погреш­ность которого
изменяется во времени по линейному
закону; у₀
– постоянная.

Для устранения систематической
погрешности трижды измеря­ется
выходная величина у через равные
промежутки времени Δt.
При первом и третьем измерениях на вход
преобразователя подает­ся сигнал х₀
от образцовой меры. В результате измерений
получа­ется система уравнений:

;

;

Ее решение позволяет получить
значение х, свободное от пере­менной
систематической погрешности, обусловленной
изменением коэффициента k:

Специальные статистические
методы. К
ним относятся спо­соб последовательных
разностей, дисперсионный анализ, и др.
Рас­смотрим подробнее некоторые из
них.

Способ последовательных
разностей (критерий Аббе).
При­меняется для обнаружения
изменяющейся во времени системати­ческой
погрешности и состоит в следующем.
Дисперсию результа­тов наблюдений
можно оценить двумя способами: обычным

и вычислением суммы квадратов
последовательных (в порядке
про­ведения измерений) разностей
(х_i–1
– х_i)²

Если в процессе измерений
происходило смещение центра груп­пирования
результатов наблюдений, т.е. имела место
переменная систематическая погрешность,
то σ²[x]
дает преувеличенную оцен­ку дисперсии
результатов наблюдений. Это объясняется
тем, что на σ²[x]
влияют вариации

.
В то же время изменения центра
груп­пирования

весьма мало сказываются на значениях
последова­тельных разностей d_i
= х_i+1
– х_i
поэтому смещения

почти не отра­зятся на значении Q²[x].

Отношение

является критерием для обнаруже­ния
систематических смещений центра
группирования результа­тов наблюдений.
Критическая область для этого критерия
(крите­рия Аббе) определяется как
Р(v<v_q)=q,
где q=1–Р
– уровень значимости, Р
– доверительная вероятность. Значения
v_ч
для раз­личных
уровней значимости q
и числа наблюдений n
приведены в табл. 7.1. Если полученное
значение критерия Аббе меньше v
при заданных q
и n,
то гипотеза о постоянстве центра
группирования результатов наблюдений
отвергается, т.е. обнаруживается
перемен­ная систематическая погрешность
результатов измерений.

Таблица 7.1

Значения критерия Аббе V_q.

n	Vq при q, равном	n	Vq при q, равном
0,001	0,01	0,05	0,001	0,01	0,05
4 5 6 7 8 9 10 11 12	0,295 0,208 0,182 0,185 0,202 0,221 0,241 0,260 0,278	0,313 0,269 0,281 0,307 0,331 0,354 0,376 0,396 0,414	0,390 0,410 0,445 0,468 0,491 0,512 0,531 0,548 0,564	13 14 15 16 17 18 19 20	0,295 0,311 0,327 0,341 0,355 0,368 0,381 0,393	0,431 0,447 0,461 0,474 0,487 0,499 0,510 0,520	0,578 0,591 0,603 0,614 0,624 0,633 0,642 0,650

Пример 7.3. Используя
способ после до нательных разностей,
определить, присутствует ли систематическая
погрешность в ряду результатов
наблю­дений, приведенных во втором
столбце табл. 7.2.

Таблица 7.2

Результаты наблюдений

n	xi	d1=xi+1–xi	di2		vi2
1	13,4	–	–	–0,6	0,36
2	13,3	–0,1	0,01	–0,7	0,49
3	14,5	+1,2	1,44	+0,5	0,25
4	13,8	–0,7	0,49	–0,2	0,04
5	14,5	+0,7	0,49	+0,5	0,25
6	14,6	+0,1	0,01	+0,6	0,36
7	14,1	–0,5	0,25	+0,1	0,01
8	14,3	+0,2	0,04	+0,3	0,09
9	14,0	+0,3	0,09	0,0	0,0
10	14,3	+0,3	0,09	+0,3	0,09
11	14,2	–1,1	1,21	–0,8	0,64
Σ154,0	–0,2	4,12	0,0	2,58

Для приведенного ряда
результатов вычисляем: среднее
арифмети­ческое

= 154,0/11 = 14; оценку дисперсии σ²[х]
= 2,58/10 = 0,258; зна­чение Q²[х]
= 4,12/(2·10)
= 0,206; критерий Аббе v
= 0,206/0,258 = 0,8.

Как видно из табл. 7.1, для
всех уровней значимости (q
= 0,001; 0,01 и 0,05) при n
= 11 имеем v
>v_q,
т.е. подтверждается
нулевая гипотеза о постоянстве центра
группирования. Следовательно, условия
измерений для приведенного ряда
оставались неизменными и систематических
расхожде­ний между результатами
наблюдений нет.

Дисперсионный анализ
(критерий Фишера). В
практике из­мерений часто бывает
необходимо выяснить наличие систематиче­ской
погрешности результатов наблюдений,
обусловленной влияни­ем какого-либо
постоянно действующего фактора, или
определить, вызывают ли изменения этого
фактора систематическое смещение
результатов измерений. В данном случае
проводят многократные измерения,
состоящие из достаточного числа серий,
каждая из кото­рых соответствует
определенным (пусть неизвестным, но
различным) значениям влияющего фактора.
Влияющими факторами, по кото­рым
производится объединение результатов
наблюдений по сериям, могут быть внешние
условия (температура, давление и т.д.),
временная последовательность проведения
измерений и т.п.

После проведения N
измерений их разбивают на s
серий (s>3)
по n_j
результатов наблюдений (sn_j
= N)
в каждой серии и затем уста­навливают,
имеется или отсутствует систематическое
расхождение между результатами наблюдений
в различных сериях. При этом долж­но
быть установлено, что результаты в
сериях распределены нор­мально.
Рассеяние результатов наблюдений в
пределах каждой се­рии отражает только
случайные влияния, характеризует лишь
случайные погрешности измерений в
пределах этой серии.

Характеристикой совокупности случайных
внутрисерийных по­грешностей будет
средняя сумма дисперсий результатов
наблюде­ний, вычисленных раздельно
для каждой серии, т.е.

,

где

,
x
_ji
– результат i-го
измерения в j-й
серии.

Внутрисерийная дисперсия

,
характеризует случайные по­грешности
измерений, так как только случайные
влияния обуслов­ливают те различия
(отклонения результатов наблюдений),
на ко­торых она основана. В то же время
рассеяние

различных серий обусловливается не
только случайными погрешностями
измерений, но и систематическими
различиями (если они существуют) между
результатами наблюдений, сгруппированными
по сериям. Следова­тельно, усредненная
межсерийная дисперсия

где

–
выражает силу действия фактора,
вызывающего систематические различия
между сериями.

Таким образом,

характеризует долю дисперсии всех
результатов наблюдений, обусловленную
наличием случайных погрешностей
измерений, а

– долю дисперсии, обу­словленную
межсерийными различиями результатов
наблюдений.

Первую из них называют
коэффициентом ошибки,
вторую – пока­зателем
дифференциации.
Чем больше отношение
показателя диф­ференциации к
коэффициенту ошибки, тем сильнее действие
фак­тора, по которому группировались
серии, и тем больше систематическое
различие между ними.

Критерием оценки наличия
систематических погрешностей в данном
случае является дисперсионный критерий
Фишера

.
Критическая область для
критерия Фишера соответ­ствует Р(F>
F_q)
= q.

Значения F_q
для различных уровней значимости q,
числа изме­рений N
и числа серий s
приведены в таблице в конце лекции, где
k₂=
N – s,
k₁
= s
– 1. Если полученное
значение критерия Фишера больше F_q
(при заданных q,
N и s),
то гипотеза об отсутствии систематических
смещения результатов наблюдений по
сериям отвергается, т.е. обна­руживается
систематическая погрешность, вызываемая
тем факто­ром, по которому группировались
результаты наблюдений,

Пример 7.4. Было сделано
38 измерений диаметра детали восемью
различ­ными штангенциркулями. Каждым
из них проводились
по пять измерений. Внутрисерийная
дисперсия равна 0,054 мм²,
межсерийная — 0,2052 мм².
Оп­ределить наличие систематической
погрешности измерения диаметра детали.

Расчетное значение критерия
Фишера F
= 0,2052/0,054 = 3,8. Для s
–1 = 7, N
– s
= 30 по табл. П1.3 приложения 1 имеем при q
= 0,05 F_0,05
= 2,3 и при q
= 0,01 F_0,01
= 3,3. Полученное значение F
больше, чем 2,2 и 2,9. Следовательно, в
результатах наблюдений обнаруживается
наличие систе­матических погрешностей.

Из всех рассмотренных способов обнаружения
систематических погрешностей дисперсионный
анализ является наиболее эффектив­ным
и достоверным, так как позволяет не
только установить факт наличия
погрешности, но и дает возможность
проанализировать источники ее
возникновения.

Критерий Вилкоксона.
Если закон распределения результатов
измерений неизвестен, то для обнаружения
систематической по­грешности применяют
статистический критерий Вилкоксона.

Из двух групп результатов
измерений x₁,
х₂,…,
х_n
и у₁,
у₂,…,
у_m,
где n
m
5
составляется
вариационный ряд, в котором все n+m
значений х₁,
х₂,…,
х_n;
у₁,
у₂,…,
у_m
располагают в порядке их возрастания
и приписывают им ранги – порядковые
номера членов вариационного ряда.
Различие средних значений каждого из
рядов можно считать допустимым, если
выполняется неравенство

где R_i
– ранг (номер) члена x_i
равный его номеру в вариационном ряду;

и

– нижнее и верхнее критические значения
для вы­бранного уровня значимости q.
При m
< 15 эти критические значе­ния
определяются по табл. 7.3. При m>15
они рассчитываются по формулам:

где z_р
– квантиль нор­мированной функции
Лапласа.

Более полная табли­ца
значений критиче­ских значений

и

приведена в реко­мендации МИ 2091-90
«ГСИ. Измерения физи­ческих величин.
Общие требования».

Таблица №7.3

Критические
значения

при q
= 0,05 и 0,01

n	m	q = 0,05	q = 0,01
8	8 10 15	49 53 65	87 99 127	43 47 56	93 105 136
9	9 15	62 79	109 146	56 69	115 156
10	10 15	78 94	132 166	71 84	139 176
12	12 15	115 127	185 209	105 115	195 221
14	14 15	160 164	246 256	147 151	259 268
15	15	184	282	171	294

Если вы устраняете систематическую ошибку модели, то уже слишком поздно

Введение

Машинное обучение — это технологический прорыв, случающийся раз в поколение. Однако с ростом его популярности основной проблемой становятся систематические ошибки алгоритма. Если модели ML не обучаются на репрезентативных данных, у них могут развиться серьёзные систематические ошибки, оказывающие существенный вред недостаточно представленным группам и приводящие к созданию неэффективных продуктов. Мы изучили массив данных CoNLL-2003, являющийся стандартом для создания алгоритмов распознавания именованных сущностей в тексте, и выяснили, что в данных присутствует серьёзный перекос в сторону мужских имён. При помощи наших технологии мы смогли компенсировать эту систематическую ошибку:

1. Мы обогатили данные, чтобы выявить сокрытые систематические ошибки
2. Дополнили массив данных недостаточно представленными примерами, чтобы компенсировать гендерный перекос

Модель, обученная на нашем расширенном массиве данных CoNLL-2003, характеризуется снижением систематической ошибки и повышенной точностью, и это показывает, что систематическую ошибку можно устранить без каких-либо изменений в модели. Мы выложили в open source наши аннотации Named Entity Recognition для исходного массива данных CoNLL-2003, а также его улучшенную версию, скачать их можно здесь.

Систематическая ошибка алгоритма: слабое место ИИ

Сегодня тысячи инженеров и исследователей создают системы, самостоятельно обучающиеся тому, как достигать существенных прорывов — повышать безопасность на дорогах при помощи беспилотных автомобилей, лечить болезни оптимизированными ИИ процедурами, бороться с изменением климата при помощи управления энергопотреблением.

Однако сила самообучающихся систем является и их слабостью. Так как фундаментом всех процессов машинного обучения являются данные, обучение на несовершенных данных может привести к искажённым результатам.

ИИ-системы имеют большие полномочия, поэтому они могут наносить существенный ущерб. Недавние протесты против полицейской жестокости, приведшей к смертям Джорджа Флойда, Бреонны Тейлор, Филандо Кастиле, Сандры Блэнд и многих других, является важным напоминанием о систематическом неравенстве в нашем обществе, которое не должны усугублять ИИ-системы. Но нам известны многочисленные примеры (закрепляющие гендерные стереотипы результаты поиска картинок, дискриминация чёрных подсудимых в системах управления данными нарушителей и ошибочная идентификация цветных людей системами распознавания лиц), показывающие, что предстоит пройти долгий путь, прежде чем проблема систематических ошибок ИИ будет решена.

Распространённость ошибок вызвана лёгкостью их внесения. Например, они проникают в «золотые стандарты» моделей и массивов данных в open source, ставшие фундаментом огромного объёма работы в сфере ML. Массив данных для определения эмоционального настроя текста word2vec, используемый в построении моделей других языков, искажён по этнической принадлежности, а word embeddings — способ сопоставления слов и значений алгоритмом ML — содержит сильно искажённые допущения о занятиях, с которыми ассоциируются женщины.

Проблема (и, как минимум, часть её решения) лежит в данных. Чтобы проиллюстрировать это, мы провели эксперимент с одним из самых популярных массивов данных для построения систем распознавания именованных сущностей в тексте: CoNLL-2003.

Что такое «распознавание именованных сущностей»?

Распознавание именованных сущностей (Named-Entity Recognition, NER) — один из фундаментальных камней моделей естественных языков, без него были бы невозможны онлайн-поиск, извлечение информации и анализ эмоционального настроя текста.

Миссия нашей компании заключается в ускорении разработки ИИ. Естественный язык — одна из основных сфер наших интересов. Наш продукт Scale Text содержит NER, заключающееся в аннотировании текста согласно заданному списку меток. На практике, среди прочего, это может помочь крупным розничным сетям анализировать онлайн-обсуждение их продуктов.

Многие модели NER обучаются и подвергаются бенчмаркам на CoNLL-2003 — массиве данных из примерно 20 тысяч предложений новостных статей Reuters, аннотированных такими атрибутами, как «PERSON», «LOCATION» и «ORGANIZATION».

Нам захотелось изучить эти данные на наличие систематических ошибок. Для этого мы воспользовались своим конвейером разметки, чтобы категоризировать все имена в массиве данных, размечая их как мужские, женские или гендерно-нейтральные, исходя из традиционного использования имён.

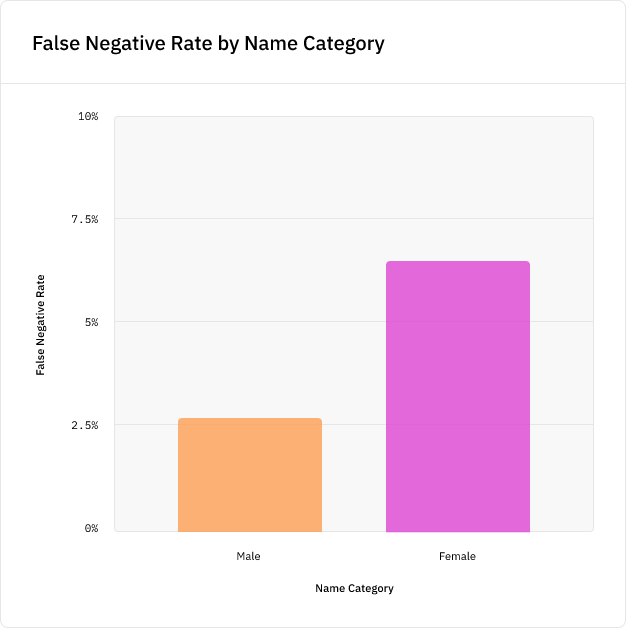
При этом мы выявили существенную разницу. Мужские имена упоминались почти в пять раз чаще женских, и менее 2% имён были гендерно-нейтральными:

Это вызвано тем, что по социальным причинам новостные статьи в основном содержат мужские имена. Однако из-за этого модель NER, обученная на таких данных, лучше будет справляться с выбором мужских имён, чем женских. Например, поисковые движки используют модели NER для классификации имён в поисковых запросах, чтобы выдавать более точные результаты. Но если внедрить модель NER с перекосом, то поисковый движок хуже будет идентифицировать женские имена по сравнению с мужскими, и именно подобная малозаметная распространённая систематическая ошибка может проникнуть во многие системы реального мира.

Новый эксперимент по снижению систематической ошибки

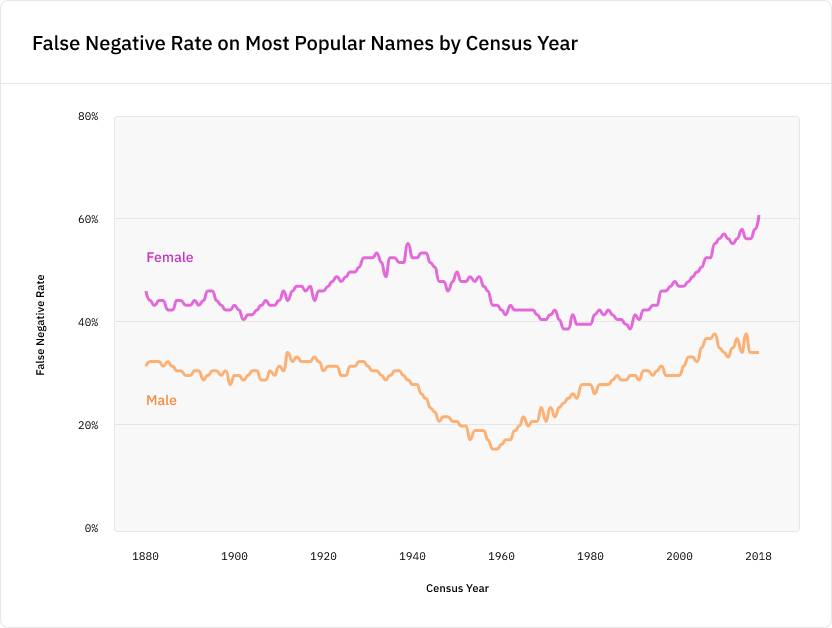
Чтобы проиллюстрировать это, мы обучили модель NER для изучения того, как этот гендерный перекос повлияет на её точность. Был создан алгоритм извлечения имён, выбирающий метки PERSON при помощи популярной NLP-библиотеки spaCy, и на подмножестве данных CoNLL была обучена модель. Затем мы протестировали модель на новых именах из тестовых данных, не присутствовавших в данных обучения, и обнаружили, что модель с вероятностью на 5% больше пропустит новое женское имя, чем новое мужское имя, а это серьёзное расхождение в точности:

Мы наблюдали схожие результаты, когда применили модель к шаблону «NAME is a person», подставив 100 самых популярных мужских и женских имён на каждый год переписи населения США. Результаты работы модели оказались значительно хуже для женских имён во все года переписи:

Критически важно то, что наличие перекоса в данных обучения приводит к смещению ошибок в сторону недостаточно представленных категорий. Эксперимент с переписями демонстрирует это и другим образом: точность модели существенно деградирует после 1997 года (точки отсечения статей Reuters в массиве данных CoNLL), потому что массив данных больше не является репрезентативным отображением популярности имён каждого последующего года.

Модели обучаются соответствовать трендам данных, на которых они обучены. Нельзя ожидать их хорошей точности в случаях, когда они видели лишь малое количество примеров.

Если вы исправляете систематическую ошибку модели, то уже слишком поздно

Как же это исправить?

Один из способов — попробовать устранить систематическую ошибку модели, например, выполнив постобработку модели или добавив целевую функцию для смягчения перекоса, оставив определение подробностей самой модели.

Но это не лучший подход по множеству причин:

1. Справедливость — это очень сложная проблема, и мы не можем ждать, что алгоритм решит её сам. Исследование показало, что обучение алгоритма на одинаковый уровень точности для всех подмножеств населения не обеспечит справедливости и нанесёт вред обучению модели.
2. Добавление новых целевых функций может навредить точности модели, приводя к негативному побочному эффекту. Вместо этого лучше обеспечить простоту алгоритма и сбалансированность данных, что повысит точность модели и позволит избежать негативных эффектов.
3. Неразумно ожидать, что модель покажет хорошие результаты в случаях, примеров которых она видела очень мало. Наилучший способ обеспечения хороших результатов заключается в повышении разнообразия данных.
4. Попытки устранения систематической ошибки при помощи инженерных техник — это дорогой и длительный процесс. Гораздо дешевле и проще изначально обучать модели на данных без перекосов, освободив ресурсы инженеров для работы над реализацией.

Данные — это лишь одна часть проблемы систематических ошибок. Однако эта часть фундаментальна и влияет на всё, что идёт после неё. Именно поэтому мы считаем, что данные содержат ключ к частичному решению, обеспечивая потенциальные систематические улучшения в исходных материалах. Если вы не размечаете критические классы (например, гендер или этническую принадлежность) явным образом, то невозможно сделать так, чтобы эти классы не были источником систематической ошибки.

Такая ситуация контринтуитивна. Кажется, что если нам нужно построить модель, не зависящую от чувствительных характеристик наподобие гендера, возраста или этнической принадлежности, то лучше исключить эти свойства из данных обучения, чтобы модель не могла их учитывать.

Однако принцип «справедливости, реализуемой через неведение» на самом деле усугубляет проблему. Модели ML превосходно справляются с выводом заключений из признаков, они не прекращают делать этого, если мы не разметили эти признаки явным образом. Систематические ошибки просто остаются невыявленными, из-за чего их сложнее устранить.

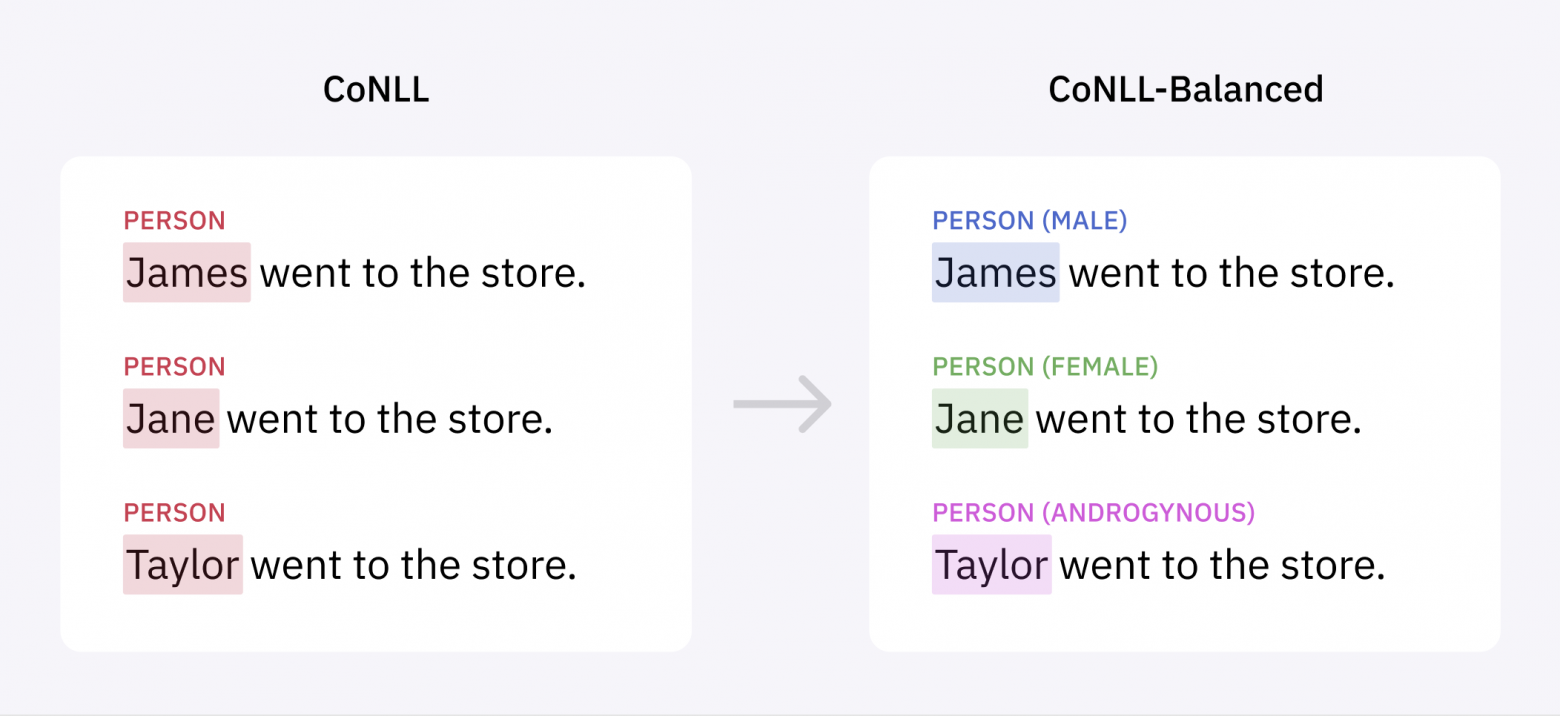
Единственный надёжный способ решения проблемы заключается в разметке большего количества данных, чтобы сбалансировать распределение имён. Мы использовали отдельную модель ML для идентификации предложений в корпусах Reuters и Brown, с большой вероятностью содержащих женские имена, а затем разметили эти предложения в нашем конвейере NER, чтобы дополнить CoNLL.

Получившийся массив данных, который мы назвали CoNLL-Balanced, содержит на 400 с лишним больше женских имён. После повторного обучения на нём модели NER мы обнаружили, что алгоритм больше не имеет систематической ошибки, приводящей к снижению показателей при распознавании женских имён:

Кроме того, модель улучшила показатели и при распознавании мужских имён.

Это стало впечатляющей демонстрацией важности данных. Благодаря устранению перекоса в исходном материале нам не пришлось вносить никаких изменений в нашу модель ML, что позволило сэкономить на времени разработки. И мы достигли этого без негативного влияния на точность модели; на самом деле, она даже слегка увеличилась.

Чтобы позволить сообществу разработчиков развивать нашу работу и устранять гендерный перекос в моделях, построенных на основе CoNLL-2003, мы выложили на наш веб-сайте дополненный массив данных в open source, в том числе и добавив гендерную информацию.

Сообщество разработчиков ИИ/ML имеет проблемы с культурными различиями, но мы испытываем умеренный оптимизм от этих результатов. Они намекают на то, что мы, возможно, сможем предложить техническое решение насущной социальной проблемы, если займёмся проблемой сразу же, выявим сокрытые систематические ошибки и улучшим точность модели для всех.

Сейчас мы изучаем, как этот подход можно применить к ещё одному критичному атрибуту — этнической принадлежности — чтобы придумать, как создать надёжную систему для устранения перекоса в массивах данных, распространяющегося и на другие охраняемые от дискриминации категории населения.

Кроме того, это показывает, почему наша компания уделяет так много внимания качеству данных. Если нельзя доказать, что данные точны, сбалансированы и лишены систематических ошибок, то нет гарантии того, что создаваемые на их основе модели будут безопасными и точными. А без этого мы не сможем создавать качественно новых ИИ-технологий, идущих на пользу всем людям.

Благодарности

Упоминаемый в этом посте массив данных CoNLL 2003 — это тестовый набор Reuters-21578, Distribution 1.0, доступный для скачивания на странице проекта исходного эксперимента 2003 года: https://www.clips.uantwerpen.be/conll2003/ner/.

Анализ причин появления погрешностей измерений, выбор способов их обнаружения и уменьшения являются основными этапами процесса измерений. Погрешности измерений, принято делить на систематические и случайные. В процессе измерений систематические и случайные погрешности проявляются совместно и образуют нестационарный случайный процесс. Деление погрешностей на систематические и случайные является удобным приемом для их анализа и разработки методов уменьшения их влияния на результат измерения.

Рассмотрим способы обнаружения и исключения систематических погрешностей, поскольку они зависят от выбора метода измерений и его осуществелния.

По характеру изменения систематические погрешности делятся:

• постоянные – погрешности, связанные с неточной градуировкой шкалы прибора, отклонением размера меры от номинального значения, неточным выбором моделей объектов.
• переменные
    – периодические – погрешность изменяющаяся по периодическому закону, например погрешность отсчета при определении времени по башенным часам, если смотреть на стрелку снизу, температурная погрешность от изменения температуры в течение суток и т.п.
    – прогрессирующие – погрешности монотонно изменяющиеся (увеличивающиеся или уменьшающиеся) в общем случае по сложному, обычно неизвестному закону. Прогрессирующие погрешности во многих случаях обусловлены старением элементов средств измерений и могут быть скорректированы при его периодической поверке.

По причине возникновения погрешности измерений разделяются на три основные группы:

• методические – погрешности обусловленные неадекватностью принимаемых моделей реальным объектам, несовершенством методов измерений, упрощением зависимостей, положенных в основу измерений, неопределенностью объекта измерения; 
• инструментальные – погрешности обусловленные прежде всего особенностями используемых в средствах измерений принципов и методов измерений, а также схемным, конструктивным и технологическим несовершенством средств измерений.
• взаимодейтствия – обусловлены взаимным влиянием средства измерений, объекта исследования и экспериментатора. Погрешности из-за взаимного влияния средства и объекта измерений обычно принято относить к методическим погрешностям, а погрешности, связанные с действиями экспериментатора, называются личными погрешностями. Однако такая классификация недостаточно полно отражает суть рассматриваемых погрешностей.

Выявление и устранение причин возникновения погрешностей – наиболее распространенный способ уменьшения всех видов систематических погрешностей. Примерами такого способа являются: термостатирование отдельных узлов или прибора в целом, а также проведение измерений в термостатированных помещениях для исключения температурной погрешности, применение экранов, фильтров и специальных цепей (например, эквипотенциальных цепей) для устранения погрешностей из-за влияния электромагнитных полей, наводок и токов утечек, применение стабилизированных источников питания.

Для уменьшения прогрессирующей погрешности из-за старения элементов средств измерений, параметры таких элементов стабилизируют путем искусственного и естественного старения. Кроме этого систематические погрешности можно уменьшить рациональным расположением средств измерений по отношению друг к другу, к источнику влияющих воздействий и к объекту исследования. Например магнитоэлектрические приборы должны быть удалены друг от друга, оси катушек индуктивности, должны быть расположены под углом 90°, выводы термопары должны располагаться по изотермическим линиям объекта.

Многие систематические погрешности, являющиеся не изменяющимися во времени функциями влияющих величин или обусловленные стабильными физическими эффектами, могут быть теоретически рассчитаны и устранены введением поправок или использованием специальных корректирующих цепей.

Другим радикальным способом устранения систематических погрешностей является поверки средств измерений в рабочих условиях с целью определения поправок к результатам измерения. Это дает возможность учесть все систематические погрешности без выяснения причин их возникновения. Степень коррекции систематических погрешностей в этом случае, естественно, зависит от метрологических характеристик используемых эталонных приборов и случайных погрешностей поверяемых приборов.

Фактически поверка средств измерений перед их использованием и введение поправок адекватна применению средств измерений более высоких классов точности при условии, что случайные погрешности средств измерений малы по сравнению с систематическими, а сами систематические погрешности медленно изменяются во времени.

Метод инвертирования широко используется для устранения ряда постоянных и медленно изменяющихся систематических погрешностей. Этот метод и ряд его разновидностей (метод исключения погрешности по знаку, коммутационного инвертирования, структурной модуляции, двукратных измерений, инвертирования функции преобразования и др.) основаны на выделении алгебраической суммы чесного числа сигналов измерительной информации, которые вследствие инвертирования отличаются направлением информативного сигнала, опорного сигнала или знаком погрешности.

Метод модуляции – метод близкий к методу инвертирования, в котором производится периодическое инвертирование входного сигнала и подавление помехи, имеющей однонаправленное действие.

Метод исключения погрешности по знаку — вариант метода инвертирования, который часто применяется для исключения известных по природе погрешностей, источники которых имеют направленное действие, например погрешностей из-за влияния постоянных магнитных полей, ТЭДС и др.

Метод замещения (метод разновременного сравнения) является наиболее универсальным методом, который дает возможность устранить большинство систематических погрешностей. Измерения осуществляются в два приема. Сначала по отсчетному устройству прибора делают отсчет измеряемой величины, затем, сохраняя все условия эксперимента неизменными, вместо измеряемой величины на вход прибора подают известную величину, значение которой с помощью регулируемой меры (калибратором) устанавливают таким образом, чтобы показание прибора было таким же, как при включении измеряемой величины.

Метод равномерного компарирования является разновидностью метода замещения, он используется при измерениях таких величин, которые нельзя с высокой точностью воспроизводить с помощью регулируемых мер или других технических средств. Обычно это величины, изменяющиеся с высокой частотой или по сложному закону. В качестве известных регулируемых величин при этом используются величины такого же рода, как измеряемые, но отличаютщиеся от них спектральным составом (обычно постоянные во времени и в пространстве) и создающие такой же, как и измеряемая величина, сигнал на выходе компарирующего преобразователя.

Метод эталонных сигналов заключается в том, что на вход средств измерений периодически вместо измеряемой величины подаются эталонные сигналы такого же рода, что и измеряемая величина. Разность между реальной градуировочной характеристикой используется для коррекции чувствительности или для автоматического введения поправки в результат измерения. При этом, как и при методе замещения, устраняются все систематические погрешности, но только в тех точках диапазона измерений, которые соответствуют эталонным сигналам. Метод широко используется в современных точных цифровых приборах и в информационно-измерительных системах. Примером использования этого метода является периодическая подстройка рабочего тока в компенсаторах и цифровых вольтметрах постоянного тока при помощи нормального элемента.

Тестовый метод – при использовании данного метода значение измеряемой величины определяется по результатам нескольких наблюдений, при которых в одном случае входным сигналом средства измерений является сама измеряемая величина Х, а в других – так называемые тесты, являющиеся функциями измеряемой величины.

Метод вспомагательных измерений используется для исключения погрешностей из-за влияющих величин и неинформативных параметров входного сигнала. Для реальзации этого метода одновременно с измеряемой величиной Х с помощью вспомогательных измерительных устройств производится измерение каждой из влияющих величин и вычисление с помощью вычислительного устройства, а также формул и алгоритмов поправок к результатам измерения.

Метод симметричных наблюдений заключается в проведении многократных наблюдений через равные промежутки времени и усреднении результатов наблюдений, симметрично расположенных относительно среднего наблюдения. Обычно этот метод применяется для исключения прогрессирующих погрешностей, изменяющихся по линейному закону. Так, при измерении сопротивления резистора путем сравнения напряжения на измеряемом и эталонном резисторах, включенных последовательно и питаемых от общего аккумулятора, может возникнуть погрешность вследствие разряда источника питания. 
Для исключения этой погрешности проводят три измерения падения напряжения:

• на эталонном резисторе U01 = I·R0;
• через равные промежутки времени на измеряемом резисторе UX = (I — ΔI1)·RX;
• снова на эталонном резисторе U02 = (I — ΔI2)·R0.
• Если ток изменяется во времени по линейному закону, то ΔI2 = 2ΔI1; I — ΔI1 = (U01 + U02) / (2R0)  и  RX = R0·2·UX / (U01 + U02).

Метод симметричных наблюдений можно также использовать для устранения других видов погрешностей, например систематических погрешностей из-за влияющих величин, изменяющихся по периодическому закону. В этом случае симметричные наблюдения проводят через половину периода, когда погрешность имеет разные знаки, но одинаковые значения. Таким образом, например, можно исключить погрешность из-за наличия четных гармоник при измерении амплитудного значения напряжения при искаженной форме кривой.