Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).
Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.
Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.
Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.
Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.
Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.
Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.
Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.
Давайте разберемся в матрице ошибок с помощью арифметики.
Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.
Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.
Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.
Отзыв
Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.
$$Отзыв = \frac{TP}{TP + FN} = \frac{2}{2 + 2} = \frac{1}{2}$$
Точность результата измерений (Precision)
В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.
$$Точность\spaceрезультата\spaceизмерений = \frac{TP}{TP + FP} = \frac{2}{2 + 1} = \frac{2}{3}$$
Точность измерений (Accuracy)
Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.
$$Точность\spaceизмерений = \frac{TP + TN}{Всего\spaceзначений} = \frac{2 + 2}{7} = \frac{4}{7}$$
F-мера точности теста
Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.
$$F-мера = \frac{2 * Отзыв * Точность\spaceизмерений}{Отзыв + Точность\spaceизмерений} = \frac{2 * \frac{1}{2} * \frac{2}{3}}{\frac{1}{2} + \frac{2}{3}} = 0,56$$
Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.
SkLearn
С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)Выводом будет ряд, состоящий из трех списков:
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно предсказанных значений.
Фото: @opeleye
From Wikipedia, the free encyclopedia
Sources: Fawcett (2006),[1] Piryonesi and El-Diraby (2020),[2] |
In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as error matrix,[11] is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one; in unsupervised learning it is usually called a matching matrix.
Each row of the matrix represents the instances in an actual class while each column represents the instances in a predicted class, or vice versa – both variants are found in the literature.[12] The name stems from the fact that it makes it easy to see whether the system is confusing two classes (i.e. commonly mislabeling one as another).
It is a special kind of contingency table, with two dimensions («actual» and «predicted»), and identical sets of «classes» in both dimensions (each combination of dimension and class is a variable in the contingency table).
Example[edit]
Given a sample of 12 individuals, 8 that have been diagnosed with cancer and 4 that are cancer-free, where individuals with cancer belong to class 1 (positive) and non-cancer individuals belong to class 0 (negative), we can display that data as follows:
| Individual Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Classification | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Assume that we have a classifier that distinguishes between individuals with and without cancer in some way, we can take the 12 individuals and run them through the classifier. The classifier then makes 9 accurate predictions and misses 3: 2 individuals with cancer wrongly predicted as being cancer-free (sample 1 and 2), and 1 person without cancer that is wrongly predicted to have cancer (sample 9).
| Individual Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Classification | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Predicted Classification | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Notice, that if we compare the actual classification set to the predicted classification set, there are 4 different outcomes that could result in any particular column. One, if the actual classification is positive and the predicted classification is positive (1,1), this is called a true positive result because the positive sample was correctly identified by the classifier. Two, if the actual classification is positive and the predicted classification is negative (1,0), this is called a false negative result because the positive sample is incorrectly identified by the classifier as being negative. Third, if the actual classification is negative and the predicted classification is positive (0,1), this is called a false positive result because the negative sample is incorrectly identified by the classifier as being positive. Fourth, if the actual classification is negative and the predicted classification is negative (0,0), this is called a true negative result because the negative sample gets correctly identified by the classifier.
We can then perform the comparison between actual and predicted classifications and add this information to the table, making correct results appear in green so they are more easily identifiable.
| Individual Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Actual Classification | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Predicted Classification | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Result | FN | FN | TP | TP | TP | TP | TP | TP | FP | TN | TN | TN |
The template for any binary confusion matrix uses the four kinds of results discussed above (true positives, false negatives, false positives, and true negatives) along with the positive and negative classifications. The four outcomes can be formulated in a 2×2 confusion matrix, as follows:
| Predicted condition | |||
| Total population = P + N |
Positive (PP) | Negative (PN) | |
|
Actual condition |
Positive (P) | True positive (TP) |
False negative (FN) |
| Negative (N) | False positive (FP) |
True negative (TN) |
|
| Sources: [13][14][15][16][17][18][19][20] |
The color convention of the three data tables above were picked to match this confusion matrix, in order to easily differentiate the data.
Now, we can simply total up each type of result, substitute into the template, and create a confusion matrix that will concisely summarize the results of testing the classifier:
| Predicted condition | |||
| Total
8 + 4 = 12 |
Cancer 7 |
Non-cancer 5 |
|
|
Actual condition |
Cancer 8 |
6 | 2 |
| Non-cancer 4 |
1 | 3 |
In this confusion matrix, of the 8 samples with cancer, the system judged that 2 were cancer-free, and of the 4 samples without cancer, it predicted that 1 did have cancer. All correct predictions are located in the diagonal of the table (highlighted in green), so it is easy to visually inspect the table for prediction errors, as values outside the diagonal will represent them. By summing up the 2 rows of the confusion matrix, one can also deduce the total number of positive (P) and negative (N) samples in the original dataset, i.e. 

Table of confusion[edit]
In predictive analytics, a table of confusion (sometimes also called a confusion matrix) is a table with two rows and two columns that reports the number of true positives, false negatives, false positives, and true negatives. This allows more detailed analysis than simply observing the proportion of correct classifications (accuracy). Accuracy will yield misleading results if the data set is unbalanced; that is, when the numbers of observations in different classes vary greatly.
For example, if there were 95 cancer samples and only 5 non-cancer samples in the data, a particular classifier might classify all the observations as having cancer. The overall accuracy would be 95%, but in more detail the classifier would have a 100% recognition rate (sensitivity) for the cancer class but a 0% recognition rate for the non-cancer class. F1 score is even more unreliable in such cases, and here would yield over 97.4%, whereas informedness removes such bias and yields 0 as the probability of an informed decision for any form of guessing (here always guessing cancer).
According to Davide Chicco and Giuseppe Jurman, the most informative metric to evaluate a confusion matrix is the Matthews correlation coefficient (MCC).[21]
Other metrics can be included in a confusion matrix, each of them having their significance and use.
| Predicted condition | Sources: [22][23][24][25][26][27][28][29][30]
|
||||
| Total population = P + N |
Positive (PP) | Negative (PN) | Informedness, bookmaker informedness (BM) = TPR + TNR − 1 |
Prevalence threshold (PT) = 
|
|
|
Actual condition |
Positive (P) | True positive (TP), hit |
False negative (FN), type II error, miss, underestimation |
True positive rate (TPR), recall, sensitivity (SEN), probability of detection, hit rate, power = TP/P = 1 − FNR |
False negative rate (FNR), miss rate = FN/P = 1 − TPR |
| Negative (N) | False positive (FP), type I error, false alarm, overestimation |
True negative (TN), correct rejection |
False positive rate (FPR), probability of false alarm, fall-out = FP/N = 1 − TNR |
True negative rate (TNR), specificity (SPC), selectivity = TN/N = 1 − FPR |
|
| Prevalence = P/P + N |
Positive predictive value (PPV), precision = TP/PP = 1 − FDR |
False omission rate (FOR) = FN/PN = 1 − NPV |
Positive likelihood ratio (LR+) = TPR/FPR |
Negative likelihood ratio (LR−) = FNR/TNR |
|
| Accuracy (ACC) = TP + TN/P + N | False discovery rate (FDR) = FP/PP = 1 − PPV |
Negative predictive value (NPV) = TN/PN = 1 − FOR | Markedness (MK), deltaP (Δp) = PPV + NPV − 1 |
Diagnostic odds ratio (DOR) = LR+/LR− | |
| Balanced accuracy (BA) = TPR + TNR/2 | F1 score = 2 PPV × TPR/PPV + TPR = 2 TP/2 TP + FP + FN |
Fowlkes–Mallows index (FM) = 
|
Matthews correlation coefficient (MCC) =  
|
Threat score (TS), critical success index (CSI), Jaccard index = TP/TP + FN + FP |
Confusion matrices with more than two categories[edit]
Confusion matrix is not limited to binary classification and can be used in multi-class classifiers as well.[31] The confusion matrices discussed above have only two conditions: positive and negative. For example, the table below summarizes communication of a whistled language between two speakers, zero values omitted for clarity.[32]
|
Perceived Vowel |
i | e | a | o | u |
|---|---|---|---|---|---|
| i | 15 | 1 | |||
| e | 1 | 1 | |||
| a | 79 | 5 | |||
| o | 4 | 15 | 3 | ||
| u | 2 | 2 |
See also[edit]
- Positive and negative predictive values
References[edit]
- ^ Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512.
- ^ Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
- ^ Chicco D.; Jurman G. (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^ Chicco D.; Toetsch N.; Jurman G. (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
- ^ Chicco D.; Jurman G. (2023). «The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification». BioData Mining. 16 (1). doi:10.1186/s13040-023-00322-4. PMC 9938573.
- ^ Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
- ^ Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215.
- ^ Stehman, Stephen V. (1997). «Selecting and interpreting measures of thematic classification accuracy». Remote Sensing of Environment. 62 (1): 77–89. Bibcode:1997RSEnv..62…77S. doi:10.1016/S0034-4257(97)00083-7.
- ^ Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. S2CID 55767944.
- ^
Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. Bibcode:2006PaReL..27..861F. doi:10.1016/j.patrec.2005.10.010. S2CID 2027090. - ^
Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512. S2CID 213782055. - ^
Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. - ^
Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8. - ^
Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17. - ^
Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477. - ^
Chicco D, Toetsch N, Jurman G (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 13. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410. - ^
Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. 17: 168–192. doi:10.1016/j.aci.2018.08.003. - ^ Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^
Balayla, Jacques (2020). «Prevalence threshold (ϕe) and the geometry of screening curves». PLoS One. 15 (10). doi:10.1371/journal.pone.0240215. - ^
Fawcett, Tom (2006). «An Introduction to ROC Analysis» (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. - ^
Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512. - ^
Powers, David M. W. (2011). «Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation». Journal of Machine Learning Technologies. 2 (1): 37–63. - ^
Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8. - ^
Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). «WWRP/WGNE Joint Working Group on Forecast Verification Research». Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17. - ^
Chicco D, Jurman G (January 2020). «The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation». BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477. - ^
Chicco D, Toetsch N, Jurman G (February 2021). «The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation». BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410. - ^
Tharwat A. (August 2018). «Classification assessment methods». Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003. - ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). «Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index». Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512. S2CID 213782055.
- ^ Rialland, Annie (August 2005). «Phonological and phonetic aspects of whistled languages». Phonology. 22 (2): 237–271. CiteSeerX 10.1.1.484.4384. doi:10.1017/S0952675705000552. S2CID 18615779.
В машинном обучении различают оценки качества для задачи классификации и регрессии. Причем оценка задачи классификации часто значительно сложнее, чем оценка регрессии.
Содержание
- 1 Оценки качества классификации
- 1.1 Матрица ошибок (англ. Сonfusion matrix)
- 1.2 Аккуратность (англ. Accuracy)
- 1.3 Точность (англ. Precision)
- 1.4 Полнота (англ. Recall)
- 1.5 F-мера (англ. F-score)
- 1.6 ROC-кривая
- 1.7 Precison-recall кривая
- 2 Оценки качества регрессии
- 2.1 Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
- 2.2 Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
- 2.3 Коэффициент детерминации
- 2.4 Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
- 2.5 Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
- 2.6 Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
- 2.7 Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
- 3 Кросс-валидация
- 4 Примечания
- 5 См. также
- 6 Источники информации
Оценки качества классификации
Матрица ошибок (англ. Сonfusion matrix)
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов.
Рассмотрим пример. Пусть банк использует систему классификации заёмщиков на кредитоспособных и некредитоспособных. При этом первым кредит выдаётся, а вторые получат отказ. Таким образом, обнаружение некредитоспособного заёмщика () можно рассматривать как «сигнал тревоги», сообщающий о возможных рисках.
Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:
- Кредитоспособный заёмщик распознается моделью как некредитоспособный и ему отказывается в кредите. Данный случай можно трактовать как «ложную тревогу».
- Некредитоспособный заёмщик распознаётся как кредитоспособный и ему ошибочно выдаётся кредит. Данный случай можно рассматривать как «пропуск цели».
Несложно увидеть, что эти ошибки неравноценны по связанным с ними проблемам. В случае «ложной тревоги» потери банка составят только проценты по невыданному кредиту (только упущенная выгода). В случае «пропуска цели» можно потерять всю сумму выданного кредита. Поэтому системе важнее не допустить «пропуск цели», чем «ложную тревогу».
Поскольку с точки зрения логики задачи нам важнее правильно распознать некредитоспособного заёмщика с меткой , чем ошибиться в распознавании кредитоспособного, будем называть соответствующий исход классификации положительным (заёмщик некредитоспособен), а противоположный — отрицательным (заемщик кредитоспособен ). Тогда возможны следующие исходы классификации:
- Некредитоспособный заёмщик классифицирован как некредитоспособный, т.е. положительный класс распознан как положительный. Наблюдения, для которых это имеет место называются истинно-положительными (True Positive — TP).
- Кредитоспособный заёмщик классифицирован как кредитоспособный, т.е. отрицательный класс распознан как отрицательный. Наблюдения, которых это имеет место, называются истинно отрицательными (True Negative — TN).
- Кредитоспособный заёмщик классифицирован как некредитоспособный, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Наблюдения, для которых был получен такой исход классификации, называются ложно-положительными (False Positive — FP), а ошибка классификации называется ошибкой I рода.
- Некредитоспособный заёмщик распознан как кредитоспособный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Наблюдения, для которых был получен такой исход классификации, называются ложно-отрицательными (False Negative — FN), а ошибка классификации называется ошибкой II рода.
Таким образом, ошибка I рода, или ложно-положительный исход классификации, имеет место, когда отрицательное наблюдение распознано моделью как положительное. Ошибкой II рода, или ложно-отрицательным исходом классификации, называют случай, когда положительное наблюдение распознано как отрицательное. Поясним это с помощью матрицы ошибок классификации:
-
Истинно-положительный (True Positive — TP) Ложно-положительный (False Positive — FP) Ложно-отрицательный (False Negative — FN) Истинно-отрицательный (True Negative — TN)
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
P означает что классификатор определяет класс объекта как положительный (N — отрицательный). T значит что класс предсказан правильно (соответственно F — неправильно). Каждая строка в матрице ошибок представляет спрогнозированный класс, а каждый столбец — фактический класс.
# код для матрицы ошибок # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import confusion_matrix from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (англ. Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе # Для расчета матрицы ошибок сначала понадобится иметь набор прогнозов, чтобы их можно было сравнивать с фактическими целями y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687], # [ 1891, 3530]])
Безупречный классификатор имел бы только истинно-положительные и истинно отрицательные классификации, так что его матрица ошибок содержала бы ненулевые значения только на своей главной диагонали (от левого верхнего до правого нижнего угла):
import numpy as np
from sklearn.datasets import fetch_openml
from sklearn.metrics import confusion_matrix
mnist = fetch_openml('mnist_784', version=1)
X, y = mnist["data"], mnist["target"]
y = y.astype(np.uint8)
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки
y_test_5 = (y_test == 5)
y_train_perfect_predictions = y_train_5 # притворись, что мы достигли совершенства
print(confusion_matrix(y_train_5, y_train_perfect_predictions))
# array([[54579, 0],
# [ 0, 5421]])
Аккуратность (англ. Accuracy)
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, что как вариант можно исправить с помощью алгоритмов сэмплирования и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую аккуратность:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
# код для для подсчета аккуратности: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import accuracy_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(accuracy_score(y_train_5, y_train_pred)) # == (53892 + 3530) / (53892 + 3530 + 1891 +687) # 0.9570333333333333
Точность (англ. Precision)
Точностью (precision) называется доля правильных ответов модели в пределах класса — это доля объектов действительно принадлежащих данному классу относительно всех объектов которые система отнесла к этому классу.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive.
Полнота (англ. Recall)
Полнота — это доля истинно положительных классификаций. Полнота показывает, какую долю объектов, реально относящихся к положительному классу, мы предсказали верно.
Полнота (recall) демонстрирует способность алгоритма обнаруживать данный класс вообще.
Имея матрицу ошибок, очень просто можно вычислить точность и полноту для каждого класса. Точность (precision) равняется отношению соответствующего диагонального элемента матрицы и суммы всей строки класса. Полнота (recall) — отношению диагонального элемента матрицы и суммы всего столбца класса. Формально:
Результирующая точность классификатора рассчитывается как арифметическое среднее его точности по всем классам. То же самое с полнотой. Технически этот подход называется macro-averaging.
# код для для подсчета точности и полноты: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.metrics import precision_score, recall_score from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) # print(confusion_matrix(y_train_5, y_train_pred)) # array([[53892, 687] # [ 1891, 3530]]) print(precision_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 687) print(recall_score(y_train_5, y_train_pred)) # == 3530 / (3530 + 1891) # 0.8370879772350012 # 0.6511713705958311
F-мера (англ. F-score)
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Понятно что чем выше точность и полнота, тем лучше. Но в реальной жизни максимальная точность и полнота не достижимы одновременно и приходится искать некий баланс. Поэтому, хотелось бы иметь некую метрику которая объединяла бы в себе информацию о точности и полноте нашего алгоритма. В этом случае нам будет проще принимать решение о том какую реализацию запускать в производство (у кого больше тот и круче). Именно такой метрикой является F-мера.
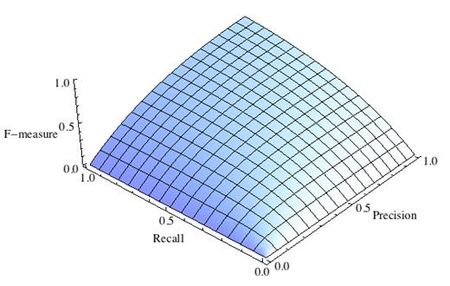
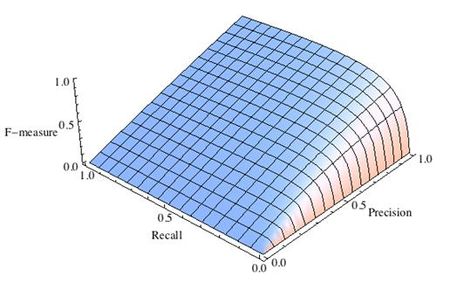
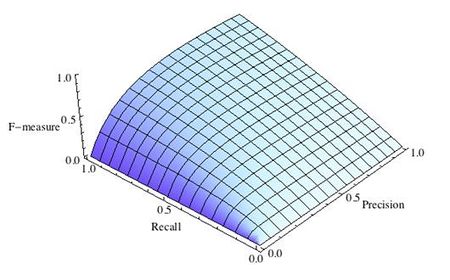
F-мера представляет собой гармоническое среднее между точностью и полнотой. Она стремится к нулю, если точность или полнота стремится к нулю.
Данная формула придает одинаковый вес точности и полноте, поэтому F-мера будет падать одинаково при уменьшении и точности и полноты. Возможно рассчитать F-меру придав различный вес точности и полноте, если вы осознанно отдаете приоритет одной из этих метрик при разработке алгоритма:
где принимает значения в диапазоне если вы хотите отдать приоритет точности, а при приоритет отдается полноте. При формула сводится к предыдущей и вы получаете сбалансированную F-меру (также ее называют ).
-
Рис.1 Сбалансированная F-мера,
-
Рис.2 F-мера c приоритетом точности,
-
Рис.3 F-мера c приоритетом полноты,
F-мера достигает максимума при максимальной полноте и точности, и близка к нулю, если один из аргументов близок к нулю.
F-мера является хорошим кандидатом на формальную метрику оценки качества классификатора. Она сводит к одному числу две других основополагающих метрики: точность и полноту. Имея «F-меру» гораздо проще ответить на вопрос: «поменялся алгоритм в лучшую сторону или нет?»
# код для подсчета метрики F-mera: # Пример классификатора, способного проводить различие между всего лишь двумя # классами, "пятерка" и "не пятерка" из набора рукописных цифр MNIST import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier from sklearn.metrics import f1_score mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распознавать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) print(f1_score(y_train_5, y_train_pred)) # 0.7325171197343846
ROC-кривая
Кривая рабочих характеристик (англ. Receiver Operating Characteristics curve).
Используется для анализа поведения классификаторов при различных пороговых значениях.
Позволяет рассмотреть все пороговые значения для данного классификатора.
Показывает долю ложно положительных примеров (англ. false positive rate, FPR) в сравнении с долей истинно положительных примеров (англ. true positive rate, TPR).
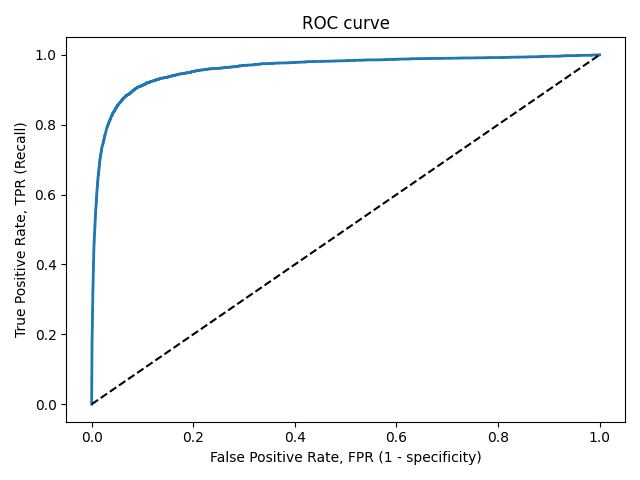
Доля FPR — это пропорция отрицательных образцов, которые были некорректно классифицированы как положительные.
- ,
где TNR — доля истинно отрицательных классификаций (англ. Тrие Negative Rate), представляющая собой пропорцию отрицательных образцов, которые были корректно классифицированы как отрицательные.
Доля TNR также называется специфичностью (англ. specificity). Следовательно, ROC-кривая изображает чувствительность (англ. seпsitivity), т.е. полноту, в сравнении с разностью 1 — specificity.
Прямая линия по диагонали представляет ROC-кривую чисто случайного классификатора. Хороший классификатор держится от указанной линии настолько далеко, насколько это
возможно (стремясь к левому верхнему углу).
Один из способов сравнения классификаторов предусматривает измерение площади под кривой (англ. Area Under the Curve — AUC). Безупречный классификатор будет иметь площадь под ROC-кривой (ROC-AUC), равную 1, тогда как чисто случайный классификатор — площадь 0.5.
# Код отрисовки ROC-кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import roc_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") fpr, tpr, thresholds = roc_curve(y_train_5, y_scores) def plot_roc_curve(fpr, tpr, label=None): plt.plot(fpr, tpr, linewidth=2, label=label) plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal plt.xlabel('False Positive Rate, FPR (1 - specificity)') plt.ylabel('True Positive Rate, TPR (Recall)') plt.title('ROC curve') plt.savefig("ROC.png") plot_roc_curve(fpr, tpr) plt.show()
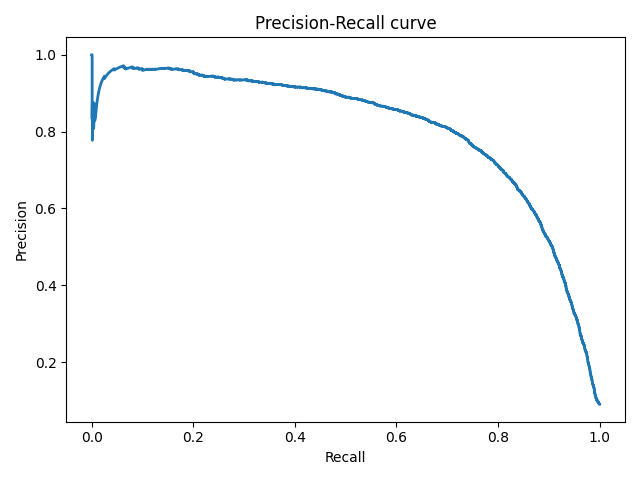
Precison-recall кривая
Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь плохой алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая. Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
# Код отрисовки Precison-recall кривой # На примере классификатора, способного проводить различие между всего лишь двумя классами # "пятерка" и "не пятерка" из набора рукописных цифр MNIST from sklearn.metrics import precision_recall_curve import matplotlib.pyplot as plt import numpy as np from sklearn.datasets import fetch_openml from sklearn.model_selection import cross_val_predict from sklearn.linear_model import SGDClassifier mnist = fetch_openml('mnist_784', version=1) X, y = mnist["data"], mnist["target"] y = y.astype(np.uint8) X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_5 = (y_train == 5) # True для всех пятерок, False для в сех остальных цифр. Задача опознать пятерки y_test_5 = (y_test == 5) sgd_clf = SGDClassifier(random_state=42) # классификатор на основе метода стохастического градиентного спуска (Stochastic Gradient Descent SGD) sgd_clf.fit(X_train, y_train_5) # обучаем классификатор распозновать пятерки на целом обучающем наборе y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3) y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function") precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores) def plot_precision_recall_vs_threshold(precisions, recalls, thresholds): plt.plot(recalls, precisions, linewidth=2) plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall curve') plt.savefig("Precision_Recall_curve.png") plot_precision_recall_vs_threshold(precisions, recalls, thresholds) plt.show()
Оценки качества регрессии
Наиболее типичными мерами качества в задачах регрессии являются
Средняя квадратичная ошибка (англ. Mean Squared Error, MSE)
MSE применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза. Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
- и
Cредняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Среднеквадратичный функционал сильнее штрафует за большие отклонения по сравнению со среднеабсолютным, и поэтому более чувствителен к выбросам. При использовании любого из этих двух функционалов может быть полезно проанализировать, какие объекты вносят наибольший вклад в общую ошибку — не исключено, что на этих объектах была допущена ошибка при вычислении признаков или целевой величины.
Среднеквадратичная ошибка подходит для сравнения двух моделей или для контроля качества во время обучения, но не позволяет сделать выводов о том, на сколько хорошо данная модель решает задачу. Например, MSE = 10 является очень плохим показателем, если целевая переменная принимает значения от 0 до 1, и очень хорошим, если целевая переменная лежит в интервале (10000, 100000). В таких ситуациях вместо среднеквадратичной ошибки полезно использовать коэффициент детерминации —
Коэффициент детерминации
Коэффициент детерминации измеряет долю дисперсии, объясненную моделью, в общей дисперсии целевой переменной. Фактически, данная мера качества — это нормированная среднеквадратичная ошибка. Если она близка к единице, то модель хорошо объясняет данные, если же она близка к нулю, то прогнозы сопоставимы по качеству с константным предсказанием.
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что MAPE=11.4%, то это говорит о том, что ошибка составила 11,4% от фактических значений.
Основная проблема данной ошибки — нестабильность.
Корень из средней квадратичной ошибки (англ. Root Mean Squared Error, RMSE)
Примерно такая же проблема, как и в MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня.
Cимметричная MAPE (англ. Symmetric MAPE, SMAPE)
Средняя абсолютная масштабированная ошибка (англ. Mean absolute scaled error, MASE)
MASE является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.
Обратите внимание, что в MASE мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тенденцию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.
Недостаток MASE в том, что её тяжело интерпретировать. Например, MASE=1.21 ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более.
Кросс-валидация
Хороший способ оценки модели предусматривает применение кросс-валидации (cкользящего контроля или перекрестной проверки).
В этом случае фиксируется некоторое множество разбиений исходной выборки на две подвыборки: обучающую и контрольную. Для каждого разбиения выполняется настройка алгоритма по обучающей подвыборке, затем оценивается его средняя ошибка на объектах контрольной подвыборки. Оценкой скользящего контроля называется средняя по всем разбиениям величина ошибки на контрольных подвыборках.
Примечания
- [1] Лекция «Оценивание качества» на www.coursera.org
- [2] Лекция на www.stepik.org о кросвалидации
- [3] Лекция на www.stepik.org о метриках качества, Precison и Recall
- [4] Лекция на www.stepik.org о метриках качества, F-мера
- [5] Лекция на www.stepik.org о метриках качества, примеры
См. также
- Оценка качества в задаче кластеризации
- Кросс-валидация
Источники информации
- [6] Соколов Е.А. Лекция линейная регрессия
- [7] — Дьяконов А. Функции ошибки / функционалы качества
- [8] — Оценка качества прогнозных моделей
- [9] — HeinzBr Ошибка прогнозирования: виды, формулы, примеры
- [10] — egor_labintcev Метрики в задачах машинного обучения
- [11] — grossu Методы оценки качества прогноза
- [12] — К.В.Воронцов, Классификация
- [13] — К.В.Воронцов, Скользящий контроль
Метрики в задачах машинного обучения
Время на прочтение
9 мин
Количество просмотров 555K
Привет, Хабр!
В задачах машинного обучения для оценки качества моделей и сравнения различных алгоритмов используются метрики, а их выбор и анализ — непременная часть работы датасатаниста.
В этой статье мы рассмотрим некоторые критерии качества в задачах классификации, обсудим, что является важным при выборе метрики и что может пойти не так.
Метрики в задачах классификации
Для демонстрации полезных функций sklearn и наглядного представления метрик мы будем использовать датасет по оттоку клиентов телеком-оператора.
Загрузим необходимые библиотеки и посмотрим на данные
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import rc, plot
import seaborn as sns
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.metrics import precision_recall_curve, classification_report
from sklearn.model_selection import train_test_split
df = pd.read_csv('../../data/telecom_churn.csv')
df.head(5)Предобработка данных
# Сделаем маппинг бинарных колонок
# и закодируем dummy-кодированием штат (для простоты, лучше не делать так для деревянных моделей)
d = {'Yes' : 1, 'No' : 0}
df['International plan'] = df['International plan'].map(d)
df['Voice mail plan'] = df['Voice mail plan'].map(d)
df['Churn'] = df['Churn'].astype('int64')
le = LabelEncoder()
df['State'] = le.fit_transform(df['State'])
ohe = OneHotEncoder(sparse=False)
encoded_state = ohe.fit_transform(df['State'].values.reshape(-1, 1))
tmp = pd.DataFrame(encoded_state,
columns=['state ' + str(i) for i in range(encoded_state.shape[1])])
df = pd.concat([df, tmp], axis=1)Accuracy, precision и recall
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
| True Positive (TP) | False Positive (FP) | |
| False Negative (FN) | True Negative (TN) |
Здесь — это ответ алгоритма на объекте, а
— истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
Обучение алгоритма и построение матрицы ошибок
X = df.drop('Churn', axis=1)
y = df['Churn']
# Делим выборку на train и test, все метрики будем оценивать на тестовом датасете
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.33, random_state=42)
# Обучаем ставшую родной логистическую регрессию
lr = LogisticRegression(random_state=42)
lr.fit(X_train, y_train)
# Воспользуемся функцией построения матрицы ошибок из документации sklearn
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
font = {'size' : 15}
plt.rc('font', **font)
cnf_matrix = confusion_matrix(y_test, lr.predict(X_test))
plt.figure(figsize=(10, 8))
plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'],
title='Confusion matrix')
plt.savefig("conf_matrix.png")
plt.show()
Accuracy
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую accuracy:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Precision, recall и F-мера
Для оценки качества работы алгоритма на каждом из классов по отдельности введем метрики precision (точность) и recall (полнота).
Precision можно интерпретировать как долю объектов, названных классификатором положительными и при этом действительно являющимися положительными, а recall показывает, какую долю объектов положительного класса из всех объектов положительного класса нашел алгоритм.
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive. Recall демонстрирует способность алгоритма обнаруживать данный класс вообще, а precision — способность отличать этот класс от других классов.
Как мы отмечали ранее, ошибки классификации бывают двух видов: False Positive и False Negative. В статистике первый вид ошибок называют ошибкой I-го рода, а второй — ошибкой II-го рода. В нашей задаче по определению оттока абонентов, ошибкой первого рода будет принятие лояльного абонента за уходящего, так как наша нулевая гипотеза состоит в том, что никто из абонентов не уходит, а мы эту гипотезу отвергаем. Соответственно, ошибкой второго рода будет являться «пропуск» уходящего абонента и ошибочное принятие нулевой гипотезы.
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Классическим примером является задача определения оттока клиентов.
Очевидно, что мы не можем находить всех уходящих в отток клиентов и только их. Но, определив стратегию и ресурс для удержания клиентов, мы можем подобрать нужные пороги по precision и recall. Например, можно сосредоточиться на удержании только высокодоходных клиентов или тех, кто уйдет с большей вероятностью, так как мы ограничены в ресурсах колл-центра.
Обычно при оптимизации гиперпараметров алгоритма (например, в случае перебора по сетке GridSearchCV ) используется одна метрика, улучшение которой мы и ожидаем увидеть на тестовой выборке.
Существует несколько различных способов объединить precision и recall в агрегированный критерий качества. F-мера (в общем случае ) — среднее гармоническое precision и recall :
в данном случае определяет вес точности в метрике, и при
это среднее гармоническое (с множителем 2, чтобы в случае precision = 1 и recall = 1 иметь
)
F-мера достигает максимума при полноте и точности, равными единице, и близка к нулю, если один из аргументов близок к нулю.
В sklearn есть удобная функция _metrics.classificationreport, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
report = classification_report(y_test, lr.predict(X_test), target_names=['Non-churned', 'Churned'])
print(report)
| class | precision | recall | f1-score | support |
|---|---|---|---|---|
| Non-churned | 0.88 | 0.97 | 0.93 | 941 |
| Churned | 0.60 | 0.25 | 0.35 | 159 |
| avg / total | 0.84 | 0.87 | 0.84 | 1100 |
Здесь необходимо отметить, что в случае задач с несбалансированными классами, которые превалируют в реальной практике, часто приходится прибегать к техникам искусственной модификации датасета для выравнивания соотношения классов. Их существует много, и мы не будем их касаться, здесь можно посмотреть некоторые методы и выбрать подходящий для вашей задачи.
AUC-ROC и AUC-PR
При конвертации вещественного ответа алгоритма (как правило, вероятности принадлежности к классу, отдельно см. SVM) в бинарную метку, мы должны выбрать какой-либо порог, при котором 0 становится 1. Естественным и близким кажется порог, равный 0.5, но он не всегда оказывается оптимальным, например, при вышеупомянутом отсутствии баланса классов.
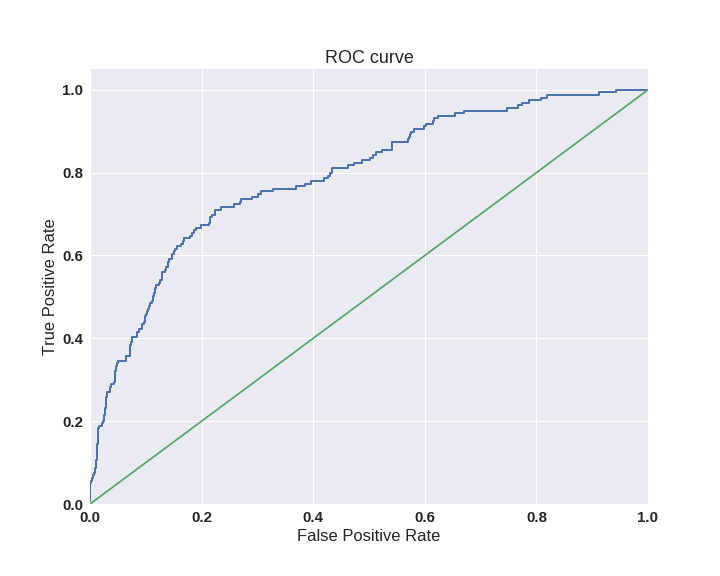
Одним из способов оценить модель в целом, не привязываясь к конкретному порогу, является AUC-ROC (или ROC AUC) — площадь (Area Under Curve) под кривой ошибок (Receiver Operating Characteristic curve ). Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):
TPR нам уже известна, это полнота, а FPR показывает, какую долю из объектов negative класса алгоритм предсказал неверно. В идеальном случае, когда классификатор не делает ошибок (FPR = 0, TPR = 1) мы получим площадь под кривой, равную единице; в противном случае, когда классификатор случайно выдает вероятности классов, AUC-ROC будет стремиться к 0.5, так как классификатор будет выдавать одинаковое количество TP и FP.
Каждая точка на графике соответствует выбору некоторого порога. Площадь под кривой в данном случае показывает качество алгоритма (больше — лучше), кроме этого, важной является крутизна самой кривой — мы хотим максимизировать TPR, минимизируя FPR, а значит, наша кривая в идеале должна стремиться к точке (0,1).
Код отрисовки ROC-кривой
sns.set(font_scale=1.5)
sns.set_color_codes("muted")
plt.figure(figsize=(10, 8))
fpr, tpr, thresholds = roc_curve(y_test, lr.predict_proba(X_test)[:,1], pos_label=1)
lw = 2
plt.plot(fpr, tpr, lw=lw, label='ROC curve ')
plt.plot([0, 1], [0, 1])
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC curve')
plt.savefig("ROC.png")
plt.show()
Критерий AUC-ROC устойчив к несбалансированным классам (спойлер: увы, не всё так однозначно) и может быть интерпретирован как вероятность того, что случайно выбранный positive объект будет проранжирован классификатором выше (будет иметь более высокую вероятность быть positive), чем случайно выбранный negative объект.
Рассмотрим следующую задачу: нам необходимо выбрать 100 релевантных документов из 1 миллиона документов. Мы намашинлернили два алгоритма:
- Алгоритм 1 возвращает 100 документов, 90 из которых релевантны. Таким образом,
- Алгоритм 2 возвращает 2000 документов, 90 из которых релевантны. Таким образом,
Скорее всего, мы бы выбрали первый алгоритм, который выдает очень мало False Positive на фоне своего конкурента. Но разница в False Positive Rate между этими двумя алгоритмами крайне мала — всего 0.0019. Это является следствием того, что AUC-ROC измеряет долю False Positive относительно True Negative и в задачах, где нам не так важен второй (больший) класс, может давать не совсем адекватную картину при сравнении алгоритмов.
Для того чтобы поправить положение, вернемся к полноте и точности :
- Алгоритм 1
- Алгоритм 2
Здесь уже заметна существенная разница между двумя алгоритмами — 0.855 в точности!
Precision и recall также используют для построения кривой и, аналогично AUC-ROC, находят площадь под ней.
Здесь можно отметить, что на маленьких датасетах площадь под PR-кривой может быть чересчур оптимистична, потому как вычисляется по методу трапеций, но обычно в таких задачах данных достаточно. За подробностями о взаимоотношениях AUC-ROC и AUC-PR можно обратиться сюда.
Logistic Loss
Особняком стоит логистическая функция потерь, определяемая как:
здесь — это ответ алгоритма на
-ом объекте,
— истинная метка класса на
-ом объекте, а
размер выборки.
Подробно про математическую интерпретацию логистической функции потерь уже написано в рамках поста про линейные модели.
Данная метрика нечасто выступает в бизнес-требованиях, но часто — в задачах на kaggle.
Интуитивно можно представить минимизацию logloss как задачу максимизации accuracy путем штрафа за неверные предсказания. Однако необходимо отметить, что logloss крайне сильно штрафует за уверенность классификатора в неверном ответе.
Рассмотрим пример:
def logloss_crutch(y_true, y_pred, eps=1e-15):
return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
print('Logloss при неуверенной классификации %f' % logloss_crutch(1, 0.5))
>> Logloss при неуверенной классификации 0.693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2.302585Отметим, как драматически выросла logloss при неверном ответе и уверенной классификации!
Следовательно, ошибка на одном объекте может дать существенное ухудшение общей ошибки на выборке. Такие объекты часто бывают выбросами, которые нужно не забывать фильтровать или рассматривать отдельно.
Всё становится на свои места, если нарисовать график logloss:
Видно, что чем ближе к нулю ответ алгоритма при ground truth = 1, тем выше значение ошибки и круче растёт кривая.
Подытожим:
- В случае многоклассовой классификации нужно внимательно следить за метриками каждого из классов и следовать логике решения задачи, а не оптимизации метрики
- В случае неравных классов нужно подбирать баланс классов для обучения и метрику, которая будет корректно отражать качество классификации
- Выбор метрики нужно делать с фокусом на предметную область, предварительно обрабатывая данные и, возможно, сегментируя (как в случае с делением на богатых и бедных клиентов)
Полезные ссылки
- Курс Евгения Соколова: Семинар по выбору моделей (там есть информация по метрикам задач регрессии)
- Задачки на AUC-ROC от А.Г. Дьяконова
- Дополнительно о других метриках можно почитать на kaggle. К описанию каждой метрики добавлена ссылка на соревнования, где она использовалась
- Презентация Богдана Мельника aka ld86 про обучение на несбалансированных выборках
Благодарности
Спасибо mephistopheies и madrugado за помощь в подготовке статьи.
In machine Learning, Classification is the process of categorizing a given set of data into different categories. In Machine Learning, To measure the performance of the classification model we use the confusion matrix.
Confusion Matrix
A confusion matrix is a matrix that summarizes the performance of a machine learning model on a set of test data. It is often used to measure the performance of classification models, which aim to predict a categorical label for each input instance. The matrix displays the number of true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN) produced by the model on the test data.
For binary classification, the matrix will be of a 2X2 table, For multi-class classification, the matrix shape will be equal to the number of classes i.e for n classes it will be nXn.
A 2X2 Confusion matrix is shown below for the image recognization having a Dog image or Not Dog image.
|
Actual |
|||
|---|---|---|---|
|
Dog |
Not Dog |
||
|
Predicted |
Dog |
True Positive |
False Positive |
|
Not Dog |
False Negative |
True Negative |
- True Positive (TP): It is the total counts having both predicted and actual values are Dog.
- True Negative (TN): It is the total counts having both predicted and actual values are Not Dog.
- False Positive (FP): It is the total counts having prediction is Dog while actually Not Dog.
- False Negative (FN): It is the total counts having prediction is Not Dog while actually, it is Dog.
Example
|
Index |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|---|---|---|---|---|---|---|---|---|---|---|
|
Actual |
Dog |
Dog |
Dog |
Not Dog |
Dog |
Not Dog |
Dog |
Dog |
Not Dog |
Not Dog |
|
Predicted |
Dog |
Not Dog |
Dog |
Not Dog |
Dog |
Dog |
Dog |
Dog |
Not Dog |
Not Dog |
|
Result |
TP |
FN |
TP |
TN |
TP |
FP |
TP |
TP |
TN |
TN |
- Actual Dog Counts = 6
- Actual Not Dog Counts = 4
- True Positive Counts = 5
- False Positive Counts = 1
- True Negative Counts = 3
- False Negative Counts = 1
|
Actual |
|||
|---|---|---|---|
|
Dog |
Not Dog |
||
|
Predicted |
Dog |
True Positive |
False Positive |
|
Not Dog |
False Negative |
True Negative |
Confusion Matrix
Implementations of Confusion Matrix in Python
Steps:
- Import the necessary libraries like Numpy, confusion_matrix from sklearn.metrics, seaborn, and matplotlib.
- Create the NumPy array for actual and predicted labels.
- compute the confusion matrix.
- Plot the confusion matrix with the help of the seaborn heatmap.
Python3
import numpy as np
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
actual = np.array(
['Dog','Dog','Dog','Not Dog','Dog','Not Dog','Dog','Dog','Not Dog','Not Dog'])
predicted = np.array(
['Dog','Not Dog','Dog','Not Dog','Dog','Dog','Dog','Dog','Not Dog','Not Dog'])
cm = confusion_matrix(actual,predicted)
sns.heatmap(cm,
annot=True,
fmt='g',
xticklabels=['Dog','Not Dog'],
yticklabels=['Dog','Not Dog'])
plt.ylabel('Prediction',fontsize=13)
plt.xlabel('Actual',fontsize=13)
plt.title('Confusion Matrix',fontsize=17)
plt.show()
Output:
Confusion Matrix
From the confusion matrix, we can find the following metrics
Accuracy: Accuracy is used to measure the performance of the model. It is the ratio of Total correct instances to the total instances.
For the above case:
Accuracy = (5+3)/(5+3+1+1) = 8/10 = 0.8
Precision: Precision is a measure of how accurate a model’s positive predictions are. It is defined as the ratio of true positive predictions to the total number of positive predictions made by the model
For the above case:
Precision = 5/(5+1) =5/6 = 0.8333
Recall: Recall measures the effectiveness of a classification model in identifying all relevant instances from a dataset. It is the ratio of the number of true positive (TP) instances to the sum of true positive and false negative (FN) instances.
For the above case:
Recall = 5/(5+1) =5/6 = 0.8333
F1-Score: F1-score is used to evaluate the overall performance of a classification model. It is the harmonic mean of precision and recall,
For the above case:
F1-Score: = (2* 0.8333* 0.8333)/( 0.8333+ 0.8333) = 0.8333
Example:2 Binary Classifications for Breast Cancer
Python3
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
X, y= load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.25)
tree = DecisionTreeClassifier(random_state=23)
tree.fit(X_train, y_train)
y_pred = tree.predict(X_test)
cm = confusion_matrix(y_test,y_pred)
sns.heatmap(cm,
annot=True,
fmt='g',
xticklabels=['malignant', 'benign'],
yticklabels=['malignant', 'benign'])
plt.ylabel('Prediction',fontsize=13)
plt.xlabel('Actual',fontsize=13)
plt.title('Confusion Matrix',fontsize=17)
plt.show()
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy :", accuracy)
precision = precision_score(y_test, y_pred)
print("Precision :", precision)
recall = recall_score(y_test, y_pred)
print("Recall :", recall)
F1_score = f1_score(y_test, y_pred)
print("F1-score :", F1_score)
Output:
Confusion Matrix for Breast cancer Classifications
Accuracy : 0.9230769230769231 Precision : 1.0 Recall : 0.8842105263157894 F1-score : 0.9385474860335195
Example 3: Multi-Class Classifications for Handwritten Digit dataset
Python3
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
X, y= load_digits(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.25)
clf = RandomForestClassifier(random_state=23)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test,y_pred)
sns.heatmap(cm,
annot=True,
fmt='g')
plt.ylabel('Prediction',fontsize=13)
plt.xlabel('Actual',fontsize=13)
plt.title('Confusion Matrix',fontsize=17)
plt.show()
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy :", accuracy)
Output:
Confusion Matrix for Handwritten Digit Classifications
Accuracy : 0.9844444444444445
Last Updated :
21 Mar, 2023
Like Article
Save Article































.png)
.png)
.png)