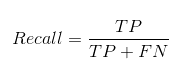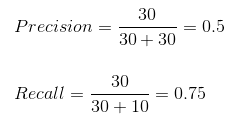В компьютерном зрении обнаружение объекта — это проблема определения местоположения одного или нескольких объектов на изображении. Помимо традиционных методов обнаружения, продвинутые модели глубокого обучения, такие как R-CNN и YOLO, могут обеспечить впечатляющие результаты при различных типах объектов. Эти модели принимают изображение в качестве входных данных и возвращают координаты прямоугольника, ограничивающего пространство вокруг каждого найденного объекта.
В этом руководстве обсуждается матрица ошибок и то, как рассчитываются precision, recall и accuracy метрики.
Здесь мы рассмотрим:
- Матрицу ошибок для двоичной классификации.
- Матрицу ошибок для мультиклассовой классификации.
- Расчет матрицы ошибок с помощью Scikit-learn.
- Accuracy, Precision и Recall.
- Precision или Recall?
Матрица ошибок для бинарной классификации
В бинарной классификации каждая выборка относится к одному из двух классов. Обычно им присваиваются такие метки, как 1 и 0, или положительный и отрицательный (Positive и Negative). Также могут использоваться более конкретные обозначения для классов: злокачественный или доброкачественный (например, если проблема связана с классификацией рака), успех или неудача (если речь идет о классификации результатов тестов учащихся).
Предположим, что существует проблема бинарной классификации с классами positive и negative. Вот пример достоверных или эталонных меток для семи выборок, используемых для обучения модели.
positive, negative, negative, positive, positive, positive, negativeТакие наименования нужны в первую очередь для того, чтобы нам, людям, было проще различать классы. Для модели более важна числовая оценка. Обычно при передаче очередного набора данных на выходе вы получите не метку класса, а числовой результат. Например, когда эти семь семплов вводятся в модель, каждому классу будут назначены следующие значения:
0.6, 0.2, 0.55, 0.9, 0.4, 0.8, 0.5На основании полученных оценок каждой выборке присваивается соответствующий класс. Такое преобразование числовых результатов в метки происходит с помощью порогового значения. Данное граничное условие является гиперпараметром модели и может быть определено пользователем. Например, если порог равен 0.5, тогда любая оценка, которая больше или равна 0.5, получает положительную метку. В противном случае — отрицательную. Вот предсказанные алгоритмом классы:
positive (0.6), negative (0.2), positive (0.55), positive (0.9), negative (0.4), positive (0.8), positive (0.5)Сравните достоверные и полученные метки — мы имеем 4 верных и 3 неверных предсказания. Стоит добавить, что изменение граничного условия отражается на результатах. Например, установка порога, равного 0.6, оставляет только два неверных прогноза.
Реальность: positive, negative, negative, positive, positive, positive, negative
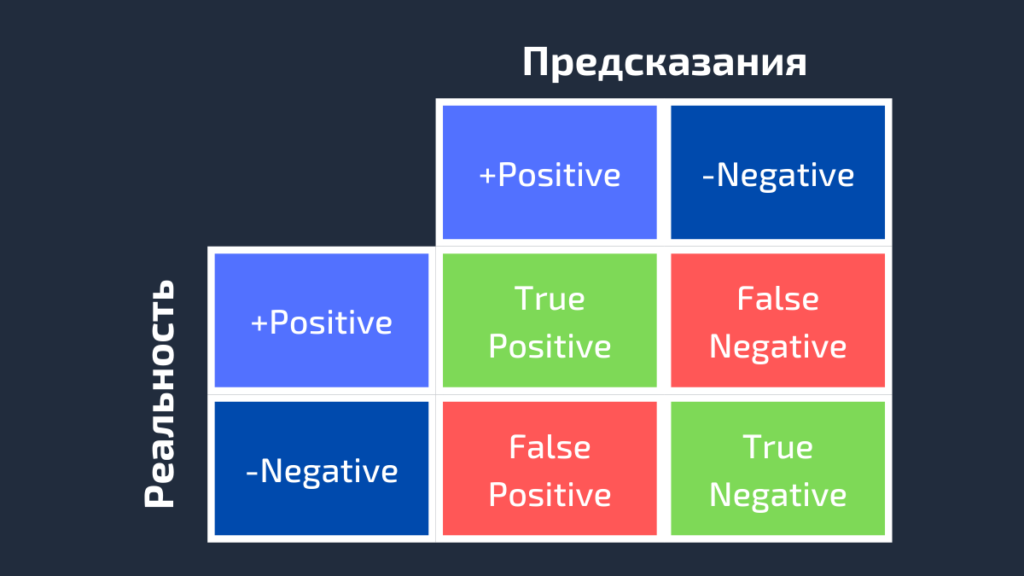
Предсказания: positive, negative, positive, positive, negative, positive, positiveДля получения дополнительной информации о характеристиках модели используется матрица ошибок (confusion matrix). Матрица ошибок помогает нам визуализировать, «ошиблась» ли модель при различении двух классов. Как видно на следующем рисунке, это матрица 2х2. Названия строк представляют собой эталонные метки, а названия столбцов — предсказанные.
Четыре элемента матрицы (клетки красного и зеленого цвета) представляют собой четыре метрики, которые подсчитывают количество правильных и неправильных прогнозов, сделанных моделью. Каждому элементу дается метка, состоящая из двух слов:
- True или False.
- Positive или Negative.
True, если получено верное предсказание, то есть эталонные и предсказанные метки классов совпадают, и False, когда они не совпадают. Positive или Negative — названия предсказанных меток.
Таким образом, всякий раз, когда прогноз неверен, первое слово в ячейке False, когда верен — True. Наша цель состоит в том, чтобы максимизировать показатели со словом «True» (True Positive и True Negative) и минимизировать два других (False Positive и False Negative). Четыре метрики в матрице ошибок представляют собой следующее:
- Верхний левый элемент (True Positive): сколько раз модель правильно классифицировала Positive как Positive?
- Верхний правый (False Negative): сколько раз модель неправильно классифицировала Positive как Negative?
- Нижний левый (False Positive): сколько раз модель неправильно классифицировала Negative как Positive?
- Нижний правый (True Negative): сколько раз модель правильно классифицировала Negative как Negative?
Мы можем рассчитать эти четыре показателя для семи предсказаний, использованных нами ранее. Полученная матрица ошибок представлена на следующем рисунке.
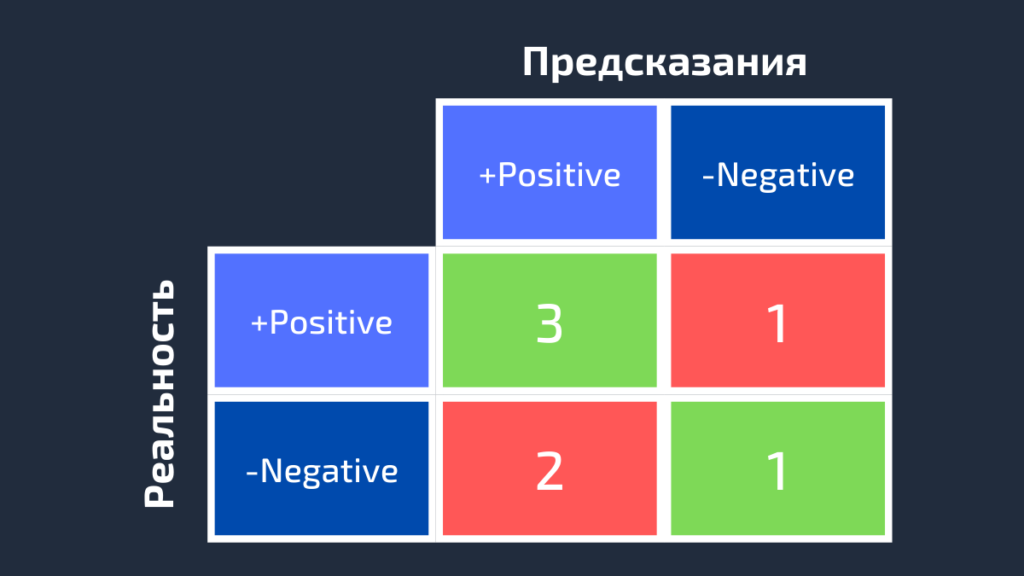
Вот так вычисляется матрица ошибок для задачи двоичной классификации. Теперь посмотрим, как решить данную проблему для большего числа классов.
Матрица ошибок для мультиклассовой классификации
Что, если у нас более двух классов? Как вычислить эти четыре метрики в матрице ошибок для задачи мультиклассовой классификации? Очень просто!
Предположим, имеется 9 семплов, каждый из которых относится к одному из трех классов: White, Black или Red. Вот достоверные метки для 9 выборок:
Red, Black, Red, White, White, Red, Black, Red, WhiteПосле загрузки данных модель делает следующее предсказание:
Red, White, Black, White, Red, Red, Black, White, RedДля удобства сравнения здесь они расположены рядом.
Реальность: Red, Black, Red, White, White, Red, Black, Red, White Предсказания: Red, White, Black, White, Red, Red, Black, White, RedПеред вычислением матрицы ошибок необходимо выбрать целевой класс. Давайте назначим на эту роль класс Red. Он будет отмечен как Positive, а все остальные отмечены как Negative.
Positive, Negative, Positive, Negative, Negative, Positive, Negative, Positive, Negative Positive, Negative, Negative, Negative, Positive, Positive, Negative, Negative, Positive11111111111111111111111После замены остались только два класса (Positive и Negative), что позволяет нам рассчитать матрицу ошибок, как было показано в предыдущем разделе. Стоит заметить, что полученная матрица предназначена только для класса Red.
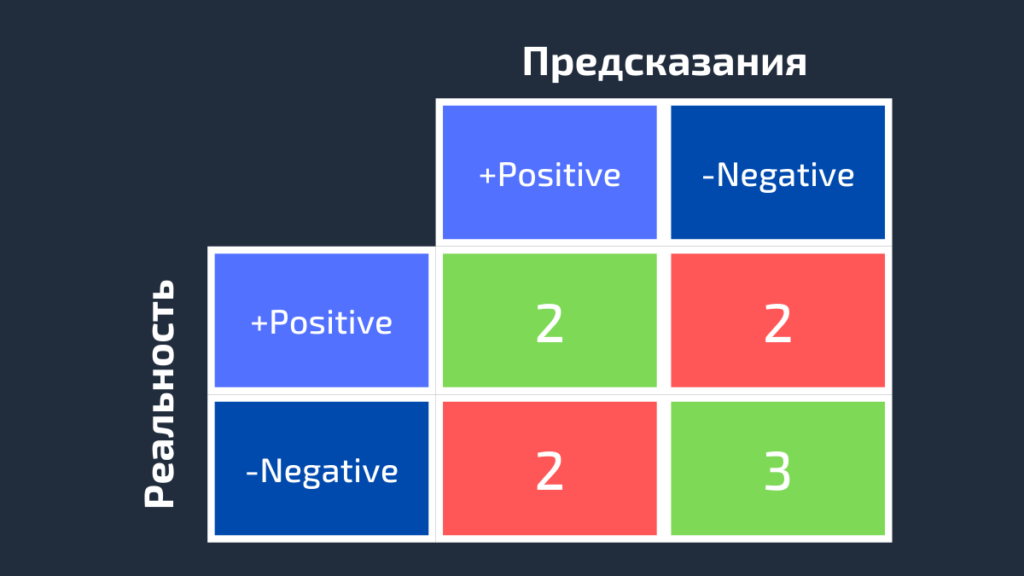
Далее для класса White заменим каждое его вхождение на Positive, а метки всех остальных классов на Negative. Мы получим такие достоверные и предсказанные метки:
Negative, Negative, Negative, Positive, Positive, Negative, Negative, Negative, Positive Negative, Positive, Negative, Positive, Negative, Negative, Negative, Positive, NegativeНа следующей схеме показана матрица ошибок для класса White.
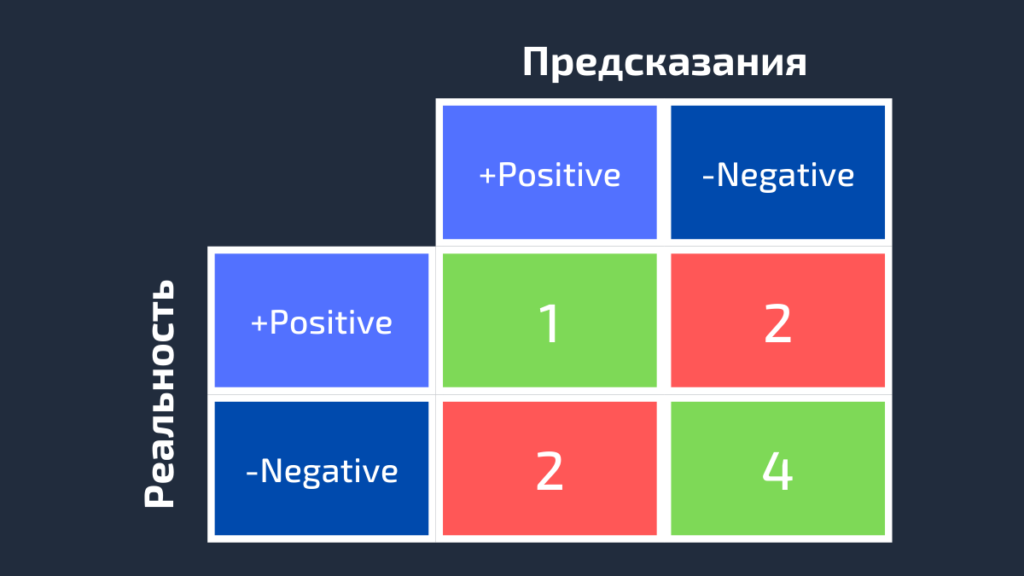
Точно так же может быть получена матрица ошибок для Black.
Расчет матрицы ошибок с помощью Scikit-Learn
В популярной Python-библиотеке Scikit-learn есть модуль metrics, который можно использовать для вычисления метрик в матрице ошибок.
Для задач с двумя классами используется функция confusion_matrix(). Мы передадим в функцию следующие параметры:
y_true: эталонные метки.y_pred: предсказанные метки.
Следующий код вычисляет матрицу ошибок для примера двоичной классификации, который мы обсуждали ранее.
import sklearn.metrics
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative"]
y_pred = ["positive", "negative", "positive", "positive", "negative", "positive", "positive"]
r = sklearn.metrics.confusion_matrix(y_true, y_pred)
print(r)
array([[1, 2],
[1, 3]], dtype=int64)Обратите внимание, что порядок метрик отличается от описанного выше. Например, показатель True Positive находится в правом нижнем углу, а True Negative — в верхнем левом углу. Чтобы исправить это, мы можем перевернуть матрицу.
import numpy
r = numpy.flip(r)
print(r)
array([[3, 1],
[2, 1]], dtype=int64)Чтобы вычислить матрицу ошибок для задачи с большим числом классов, используется функция multilabel_confusion_matrix(), как показано ниже. В дополнение к параметрам y_true и y_pred третий параметр labels принимает список классовых меток.
import sklearn.metrics
import numpy
y_true = ["Red", "Black", "Red", "White", "White", "Red", "Black", "Red", "White"]
y_pred = ["Red", "White", "Black", "White", "Red", "Red", "Black", "White", "Red"]
r = sklearn.metrics.multilabel_confusion_matrix(y_true, y_pred, labels=["White", "Black", "Red"])
print(r)
array([
[[4 2]
[2 1]]
[[6 1]
[1 1]]
[[3 2]
[2 2]]], dtype=int64)Функция вычисляет матрицу ошибок для каждого класса и возвращает все матрицы. Их порядок соответствует порядку меток в параметре labels. Чтобы изменить последовательность метрик в матрицах, мы будем снова использовать функцию numpy.flip().
print(numpy.flip(r[0])) # матрица ошибок для класса White
print(numpy.flip(r[1])) # матрица ошибок для класса Black
print(numpy.flip(r[2])) # матрица ошибок для класса Red
# матрица ошибок для класса White
[[1 2]
[2 4]]
# матрица ошибок для класса Black
[[1 1]
[1 6]]
# матрица ошибок для класса Red
[[2 2]
[2 3]]В оставшейся части этого текста мы сосредоточимся только на двух классах. В следующем разделе обсуждаются три ключевых показателя, которые рассчитываются на основе матрицы ошибок.
Как мы уже видели, матрица ошибок предлагает четыре индивидуальных показателя. На их основе можно рассчитать другие метрики, которые предоставляют дополнительную информацию о поведении модели:
- Accuracy
- Precision
- Recall
В следующих подразделах обсуждается каждый из этих трех показателей.
Метрика Accuracy
Accuracy — это показатель, который описывает общую точность предсказания модели по всем классам. Это особенно полезно, когда каждый класс одинаково важен. Он рассчитывается как отношение количества правильных прогнозов к их общему количеству.
Рассчитаем accuracy с помощью Scikit-learn на основе ранее полученной матрицы ошибок. Переменная acc содержит результат деления суммы True Positive и True Negative метрик на сумму всех значений матрицы. Таким образом, accuracy, равная 0.5714, означает, что модель с точностью 57,14% делает верный прогноз.
import numpy
import sklearn.metrics
y_true = ["positive", "negative", "negative", "positive", "positive", "positive", "negative"]
y_pred = ["positive", "negative", "positive", "positive", "negative", "positive", "positive"]
r = sklearn.metrics.confusion_matrix(y_true, y_pred)
r = numpy.flip(r)
acc = (r[0][0] + r[-1][-1]) / numpy.sum(r)
print(acc)
# вывод будет 0.571
В модуле sklearn.metrics есть функция precision_score(), которая также может вычислять accuracy. Она принимает в качестве аргументов достоверные и предсказанные метки.
acc = sklearn.metrics.accuracy_score(y_true, y_pred)
Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.
Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.
Precision
Precision представляет собой отношение числа семплов, верно классифицированных как Positive, к общему числу выборок с меткой Positive (распознанных правильно и неправильно). Precision измеряет точность модели при определении класса Positive.
Когда модель делает много неверных Positive классификаций, это увеличивает знаменатель и снижает precision. С другой стороны, precision высока, когда:
- Модель делает много корректных предсказаний класса Positive (максимизирует True Positive метрику).
- Модель делает меньше неверных Positive классификаций (минимизирует False Positive).
Представьте себе человека, который пользуется всеобщим доверием; когда он что-то предсказывает, окружающие ему верят. Метрика precision похожа на такого персонажа. Если она высока, вы можете доверять решению модели по определению очередной выборки как Positive. Таким образом, precision помогает узнать, насколько точна модель, когда она говорит, что семпл имеет класс Positive.
Основываясь на предыдущем обсуждении, вот определение precision:
Precision отражает, насколько надежна модель при классификации Positive-меток.
На следующем изображении зеленая метка означает, что зеленый семпл классифицирован как Positive, а красный крест – как Negative. Модель корректно распознала две Positive выборки, но неверно классифицировала один Negative семпл как Positive. Из этого следует, что метрика True Positive равна 2, когда False Positive имеет значение 1, а precision составляет 2 / (2 + 1) = 0.667. Другими словами, процент доверия к решению модели, что выборка относится к классу Positive, составляет 66.7%.
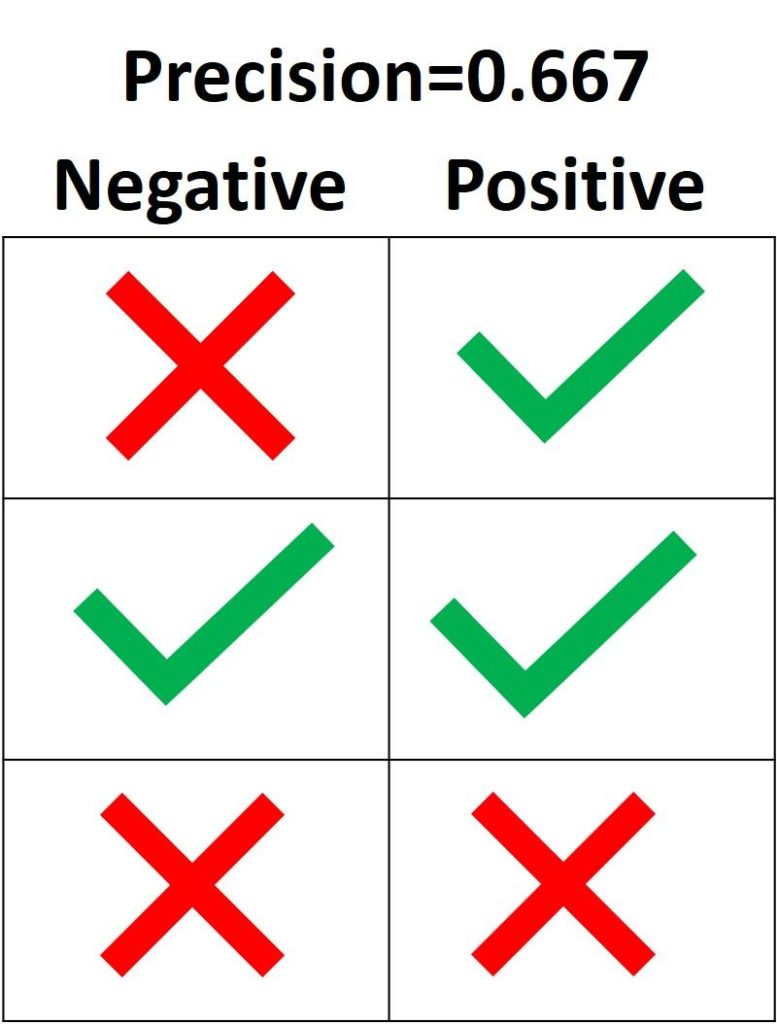
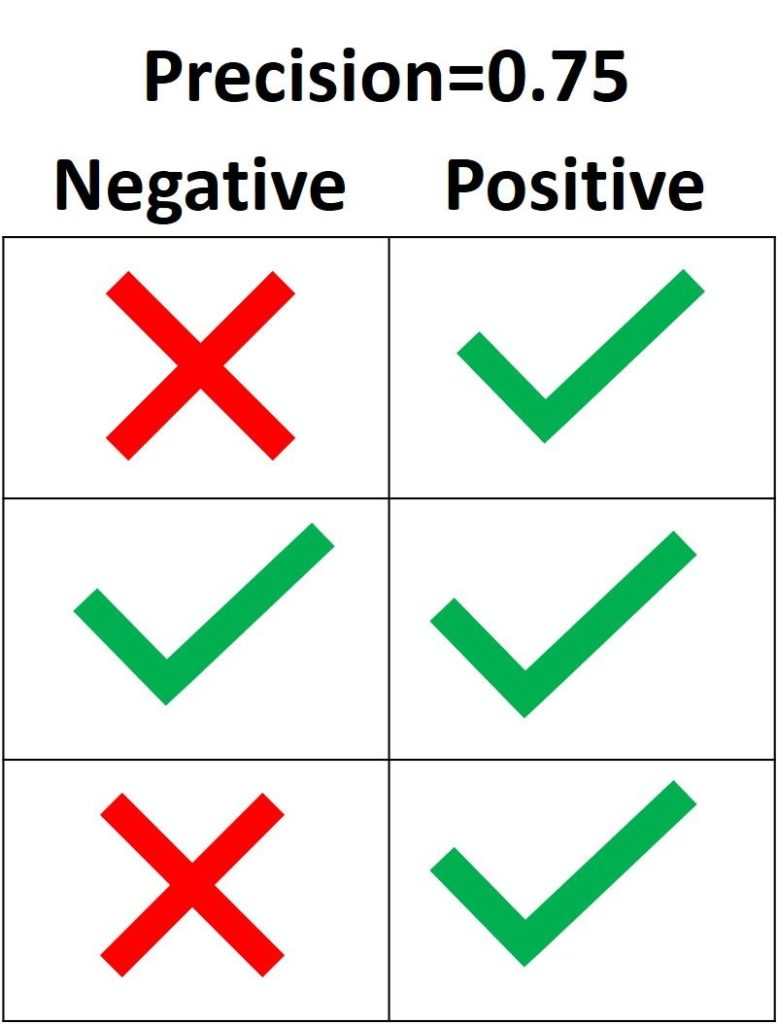
Цель precision – классифицировать все Positive семплы как Positive, не допуская ложных определений Negative как Positive. Согласно следующему рисунку, если все три Positive выборки предсказаны правильно, но один Negative семпл классифицирован неверно, precision составляет 3 / (3 + 1) = 0.75. Таким образом, утверждения модели о том, что выборка относится к классу Positive, корректны с точностью 75%.
Единственный способ получить 100% precision — это классифицировать все Positive выборки как Positive без классификации Negative как Positive.
В Scikit-learn модуль sklearn.metrics имеет функцию precision_score(), которая получает в качестве аргументов эталонные и предсказанные метки и возвращает precision. Параметр pos_label принимает метку класса Positive (по умолчанию 1).
import sklearn.metrics
y_true = ["positive", "positive", "positive", "negative", "negative", "negative"]
y_pred = ["positive", "positive", "negative", "positive", "negative", "negative"]
precision = sklearn.metrics.precision_score(y_true, y_pred, pos_label="positive")
print(precision)
Вывод: 0.6666666666666666.
Recall
Recall рассчитывается как отношение числа Positive выборок, корректно классифицированных как Positive, к общему количеству Positive семплов. Recall измеряет способность модели обнаруживать выборки, относящиеся к классу Positive. Чем выше recall, тем больше Positive семплов было найдено.
Recall заботится только о том, как классифицируются Positive выборки. Эта метрика не зависит от того, как предсказываются Negative семплы, в отличие от precision. Когда модель верно классифицирует все Positive выборки, recall будет 100%, даже если все представители класса Negative были ошибочно определены как Positive. Давайте посмотрим на несколько примеров.
На следующем изображении представлены 4 разных случая (от A до D), и все они имеют одинаковый recall, равный 0.667. Представленные примеры отличаются только тем, как классифицируются Negative семплы. Например, в случае A все Negative выборки корректно определены, а в случае D – наоборот. Независимо от того, как модель предсказывает класс Negative, recall касается только семплов относящихся к Positive.

Из 4 случаев, показанных выше, только 2 Positive выборки определены верно. Таким образом, метрика True Positive равна 2. False Negative имеет значение 1, потому что только один Positive семпл классифицируется как Negative. В результате recall будет равен 2 / (2 + 1) = 2/3 = 0.667.
Поскольку не имеет значения, как предсказываются объекты класса Negative, лучше их просто игнорировать, как показано на следующей схеме. При расчете recall необходимо учитывать только Positive выборки.

Что означает, когда recall высокий или низкий? Если recall имеет большое значение, все Positive семплы классифицируются верно. Следовательно, модели можно доверять в ее способности обнаруживать представителей класса Positive.
На следующем изображении recall равен 1.0, потому что все Positive семплы были правильно классифицированы. Показатель True Positive равен 3, а False Negative – 0. Таким образом, recall вычисляется как 3 / (3 + 0) = 1. Это означает, что модель обнаружила все Positive выборки. Поскольку recall не учитывает, как предсказываются представители класса Negative, могут присутствовать множество неверно определенных Negative семплов (высокая False Positive метрика).

С другой стороны, recall равен 0.0, если не удается обнаружить ни одной Positive выборки. Это означает, что модель обнаружила 0% представителей класса Positive. Показатель True Positive равен 0, а False Negative имеет значение 3. Recall будет равен 0 / (0 + 3) = 0.
Когда recall имеет значение от 0.0 до 1.0, это число отражает процент Positive семплов, которые модель верно классифицировала. Например, если имеется 10 экземпляров Positive и recall равен 0.6, получается, что модель корректно определила 60% объектов класса Positive (т.е. 0.6 * 10 = 6).
Подобно precision_score(), функция repl_score() из модуля sklearn.metrics вычисляет recall. В следующем блоке кода показан пример ее использования.
import sklearn.metrics
y_true = ["positive", "positive", "positive", "negative", "negative", "negative"]
y_pred = ["positive", "positive", "negative", "positive", "negative", "negative"]
recall = sklearn.metrics.recall_score(y_true, y_pred, pos_label="positive")
print(recall)
Вывод: 0.6666666666666666.
После определения precision и recall давайте кратко подведем итоги:
- Precision измеряет надежность модели при классификации Positive семплов, а recall определяет, сколько Positive выборок было корректно предсказано моделью.
- Precision учитывает классификацию как Positive, так и Negative семплов. Recall же использует при расчете только представителей класса Positive. Другими словами, precision зависит как от Negative, так и от Positive-выборок, но recall — только от Positive.
- Precision принимает во внимание, когда семпл определяется как Positive, но не заботится о верной классификации всех объектов класса Positive. Recall в свою очередь учитывает корректность предсказания всех Positive выборок, но не заботится об ошибочной классификации представителей Negative как Positive.
- Когда модель имеет высокий уровень recall метрики, но низкую precision, такая модель правильно определяет большинство Positive семплов, но имеет много ложных срабатываний (классификаций Negative выборок как Positive). Если модель имеет большую precision, но низкий recall, то она делает высокоточные предсказания, определяя класс Positive, но производит всего несколько таких прогнозов.
Некоторые вопросы для проверки понимания:
- Если recall равен 1.0, а в датасете имеются 5 объектов класса Positive, сколько Positive семплов было правильно классифицировано моделью?
- Учитывая, что recall составляет 0.3, когда в наборе данных 30 Positive семплов, сколько представителей класса Positive будет предсказано верно?
- Если recall равен 0.0 и в датасете14 Positive-семплов, сколько корректных предсказаний класса Positive было сделано моделью?
Precision или Recall?
Решение о том, следует ли использовать precision или recall, зависит от типа вашей проблемы. Если цель состоит в том, чтобы обнаружить все positive выборки (не заботясь о том, будут ли negative семплы классифицированы как positive), используйте recall. Используйте precision, если ваша задача связана с комплексным предсказанием класса Positive, то есть учитывая Negative семплы, которые были ошибочно классифицированы как Positive.
Представьте, что вам дали изображение и попросили определить все автомобили внутри него. Какой показатель вы используете? Поскольку цель состоит в том, чтобы обнаружить все автомобили, используйте recall. Такой подход может ошибочно классифицировать некоторые объекты как целевые, но в конечном итоге сработает для предсказания всех автомобилей.
Теперь предположим, что вам дали снимок с результатами маммографии, и вас попросили определить наличие рака. Какой показатель вы используете? Поскольку он обязан быть чувствителен к неверной идентификации изображения как злокачественного, мы должны быть уверены, когда классифицируем снимок как Positive (то есть с раком). Таким образом, предпочтительным показателем в данном случае является precision.
Вывод
В этом руководстве обсуждалась матрица ошибок, вычисление ее 4 метрик (true/false positive/negative) для задач бинарной и мультиклассовой классификации. Используя модуль metrics библиотеки Scikit-learn, мы увидели, как получить матрицу ошибок в Python.
Основываясь на этих 4 показателях, мы перешли к обсуждению accuracy, precision и recall метрик. Каждая из них была определена и использована в нескольких примерах. Модуль sklearn.metrics применяется для расчета каждого вышеперечисленного показателя.
Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу — так где же модель классификации сработала не так? Как это исправить?
Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.
В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок — довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!
Что такое матрица ошибок?
Вопрос на миллион долларов — что такое, в конце концов, матрица ошибок?
Матрица ошибок — это матрица размером N x N, используемая для оценки эффективности модели классификации, где N — количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.
Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:
Расшифруем матрицу:
- Целевая переменная имеет два значения: положительное или отрицательное.
- Столбцы представляют фактические значения целевой переменной.
- Строки представляют собой прогнозируемые значения целевой переменной.
Но подождите — что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.
Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок
True Positive (TP)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было положительным, и модель предсказала положительное значение.
True Negative (TN)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было отрицательным, и модель предсказала отрицательное значение.
False Positive (FP) — ошибка 1-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было отрицательным, но модель предсказала положительное значение.
- Также известна как ошибка 1-го типа.
False Negative (FN) — ошибка 2-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было положительным, но модель предсказала отрицательное значение.
- Также известна как ошибка 2-го типа.
Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:
Различные значения матрицы ошибок будут следующими:
- True Positive (TP) = 560; это означает, что 560 положительных точек данных были правильно классифицированы моделью.
- True Negative (TN) = 330; это означает, что 330 отрицательных точек данных были правильно классифицированы моделью.
- False Positive (FP) = 60; это означает, что 60 отрицательных точек данных были неправильно классифицированы моделью как положительные.
- False Negative (FN) = 50; это означает, что 50 положительных точек данных были неправильно классифицированы моделью как отрицательные.
Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.
Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!
Зачем нам нужна матрица ошибок?
Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.
Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.
Теперь вы, должно быть, задаетесь вопросом — зачем нам матрица ошибок, когда у нас есть наш вечный друг — Точность? Что ж, посмотрим, где точность не работает.
Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:
Посмотрим, как работает наша модель:
Общие значения результатов:
TP = 30, TN = 930, FP = 30, FN = 10
Итак, точность для нашей модели:
96%! Неплохо!
Но это дает неверное представление о результате. Подумайте об этом.
Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!
Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?
Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».
Precision vs. Recall
Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.
Вот как рассчитать точность:
Это определило бы надежность нашей модели.
Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.
А вот как мы можем рассчитать полноту:
Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:
50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!
Точность — полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.
Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.
Полнота — полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.
Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!
В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.
Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!
F1-Score
На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:
F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.
Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор — точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.
Матрица ошибок с использованием scikit-learn в Python
Вы знаете теорию — теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.
# confusion matrix in sklearn
from sklearn.metrics import confusion_matrix
3 from sklearn.metrics import classification_report
# actual values
actual = [1,0,0,1,0,0,1,0,0,1]
# predicted values
predicted = [1,0,0,1,0,0,0,1,0,0]
# confusion matrix
matrix = confusion_matrix(actual,predicted, labels=[1,0])
print(‘Confusion matrix : \n’,matrix)
# outcome values order in sklearn
tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)
print(‘Outcome values : \n’, tp, fn, fp, tn)
# classification report for precision, recall f1-score and accuracy
matrix = classification_report(actual,predicted,labels=[1,0])
print(‘Classification report : \n’,matrix)
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().
возвращает значения матрицы ошибок. Однако результат немного отличается от того, что мы изучили до сих пор. Она принимает строки как фактические значения, а столбцы как прогнозные значения. В остальном концепция осталась прежней.
выводит точность, полноту и f1-score для каждого целевого класса. В дополнение к этому, она также имеет некоторые дополнительные значения: micro avg, macro avg и weighted avg.
Mirco average — это оценка точности/полноты/f1, рассчитанная для всех классов.
Macro average — это среднее значение точности/полноты/f1-score.
Weighted average — это просто средневзвешенное значение точности/полноты/f1-score.
Матрица ошибок для мультиклассовой классификации
Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.
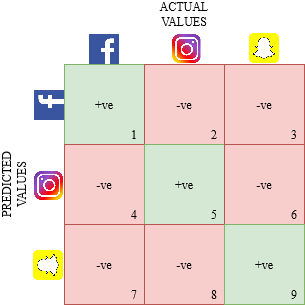
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:
true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:
Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!
Заключение
И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.
Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!
В компьютерном зрении обнаружение объекта — это проблема определения местоположения одного или нескольких объектов на изображении. Помимо традиционных методов обнаружения, продвинутые модели глубокого обучения, такие как R-CNN и YOLO, могут обеспечить впечатляющие результаты при различных типах объектов. Эти модели принимают изображение в качестве входных данных и возвращают координаты прямоугольника, ограничивающего пространство вокруг каждого найденного объекта.
В этом руководстве обсуждается матрица ошибок и то, как рассчитываются precision, recall и accuracy метрики.
Здесь мы рассмотрим:
- Матрицу ошибок для двоичной классификации.
- Матрицу ошибок для мультиклассовой классификации.
- Расчет матрицы ошибок с помощью Scikit-learn.
- Accuracy, Precision и Recall.
- Precision или Recall?
Матрица ошибок для бинарной классификации
В бинарной классификации каждая выборка относится к одному из двух классов. Обычно им присваиваются такие метки, как 1 и 0, или положительный и отрицательный (Positive и Negative). Также могут использоваться более конкретные обозначения для классов: злокачественный или доброкачественный (например, если проблема связана с классификацией рака), успех или неудача (если речь идет о классификации результатов тестов учащихся).
Предположим, что существует проблема бинарной классификации с классами positive и negative. Вот пример достоверных или эталонных меток для семи выборок, используемых для обучения модели.
positive, negative, negative, positive, positive, positive, negativeТакие наименования нужны в первую очередь для того, чтобы нам, людям, было проще различать классы. Для модели более важна числовая оценка. Обычно при передаче очередного набора данных на выходе вы получите не метку класса, а числовой результат. Например, когда эти семь семплов вводятся в модель, каждому классу будут назначены следующие значения:
0.6, 0.2, 0.55, 0.9, 0.4, 0.8, 0.5На основании полученных оценок каждой выборке присваивается соответствующий класс. Такое преобразование числовых результатов в метки происходит с помощью порогового значения. Данное граничное условие является гиперпараметром модели и может быть определено пользователем. Например, если порог равен 0.5, тогда любая оценка, которая больше или равна 0.5, получает положительную метку. В противном случае — отрицательную. Вот предсказанные алгоритмом классы:
positive (0.6), negative (0.2), positive (0.55), positive (0.9), negative (0.4), positive (0.8), positive (0.5)Сравните достоверные и полученные метки — мы имеем 4 верных и 3 неверных предсказания. Стоит добавить, что изменение граничного условия отражается на результатах. Например, установка порога, равного 0.6, оставляет только два неверных прогноза.
Реальность: positive, negative, negative, positive, positive, positive, negative
Предсказания: positive, negative, positive, positive, negative, positive, positiveДля получения дополнительной информации о характеристиках модели используется матрица ошибок (confusion matrix). Матрица ошибок помогает нам визуализировать, «ошиблась» ли модель при различении двух классов. Как видно на следующем рисунке, это матрица 2х2. Названия строк представляют собой эталонные метки, а названия столбцов — предсказанные.
Четыре элемента матрицы (клетки красного и зеленого цвета) представляют собой четыре метрики, которые подсчитывают количество правильных и неправильных прогнозов, сделанных моделью. Каждому элементу дается метка, состоящая из двух слов:
- True или False.
- Positive или Negative.
True, если получено верное предсказание, то есть эталонные и предсказанные метки классов совпадают, и False, когда они не совпадают. Positive или Negative — названия предсказанных меток.
Таким образом, всякий раз, когда прогноз неверен, первое слово в ячейке False, когда верен — True. Наша цель состоит в том, чтобы максимизировать показатели со словом «True» (True Positive и True Negative) и минимизировать два других (False Positive и False Negative). Четыре метрики в матрице ошибок представляют собой следующее:
- Верхний левый элемент (True Positive): сколько раз модель правильно классифицировала Positive как Positive?
- Верхний правый (False Negative): сколько раз модель неправильно классифицировала Positive как Negative?
- Нижний левый (False Positive): сколько раз модель неправильно классифицировала Negative как Positive?
- Нижний правый (True Negative): сколько раз модель правильно классифицировала Negative как Negative?
Мы можем рассчитать эти четыре показателя для семи предсказаний, использованных нами ранее. Полученная матрица ошибок представлена на следующем рисунке.
Вот так вычисляется матрица ошибок для задачи двоичной классификации. Теперь посмотрим, как решить данную проблему для большего числа классов.
Матрица ошибок для мультиклассовой классификации
Что, если у нас более двух классов? Как вычислить эти четыре метрики в матрице ошибок для задачи мультиклассовой классификации? Очень просто!
Предположим, имеется 9 семплов, каждый из которых относится к одному из трех классов: White, Black или Red. Вот достоверные метки для 9 выборок:
Red, Black, Red, White, White, Red, Black, Red, WhiteПосле загрузки данных модель делает следующее предсказание:
Red, White, Black, White, Red, Red, Black, White, RedДля удобства сравнения здесь они расположены рядом.
Реальность: Red, Black, Red, White, White, Red, Black, Red, White Предсказания: Red, White, Black, White, Red, Red, Black, White, RedПеред вычислением матрицы ошибок необходимо выбрать целевой класс. Давайте назначим на эту роль класс Red. Он будет отмечен как Positive, а все остальные отмечены как Negative.
Positive, Negative, Positive, Negative, Negative, Positive, Negative, Positive, Negative Positive, Negative, Negative, Negative, Positive, Positive, Negative, Negative, Positive11111111111111111111111После замены остались только два класса (Positive и Negative), что позволяет нам рассчитать матрицу ошибок, как было показано в предыдущем разделе. Стоит заметить, что полученная матрица предназначена только для класса Red.
Далее для класса White заменим каждое его вхождение на Positive, а метки всех остальных классов на Negative. Мы получим такие достоверные и предсказанные метки:
Negative, Negative, Negative, Positive, Positive, Negative, Negative, Negative, Positive Negative, Positive, Negative, Positive, Negative, Negative, Negative, Positive, NegativeНа следующей схеме показана матрица ошибок для класса White.
Точно так же может быть получена матрица ошибок для Black.
Расчет матрицы ошибок с помощью Scikit-Learn
В популярной Python-библиотеке Scikit-learn есть модуль metrics, который можно использовать для вычисления метрик в матрице ошибок.
Для задач с двумя классами используется функция confusion_matrix(). Мы передадим в функцию следующие параметры:
y_true: эталонные метки.y_pred: предсказанные метки.
Следующий код вычисляет матрицу ошибок для примера двоичной классификации, который мы обсуждали ранее.
array([[1, 2],
[1, 3]], dtype=int64)Обратите внимание, что порядок метрик отличается от описанного выше. Например, показатель True Positive находится в правом нижнем углу, а True Negative — в верхнем левом углу. Чтобы исправить это, мы можем перевернуть матрицу.
array([[3, 1],
[2, 1]], dtype=int64)Чтобы вычислить матрицу ошибок для задачи с большим числом классов, используется функция multilabel_confusion_matrix(), как показано ниже. В дополнение к параметрам y_true и y_pred третий параметр labels принимает список классовых меток.
array([
[[4 2]
[2 1]]
[[6 1]
[1 1]]
[[3 2]
[2 2]]], dtype=int64)Функция вычисляет матрицу ошибок для каждого класса и возвращает все матрицы. Их порядок соответствует порядку меток в параметре labels. Чтобы изменить последовательность метрик в матрицах, мы будем снова использовать функцию numpy.flip().
# матрица ошибок для класса White
[[1 2]
[2 4]]
# матрица ошибок для класса Black
[[1 1]
[1 6]]
# матрица ошибок для класса Red
[[2 2]
[2 3]]В оставшейся части этого текста мы сосредоточимся только на двух классах. В следующем разделе обсуждаются три ключевых показателя, которые рассчитываются на основе матрицы ошибок.
Как мы уже видели, матрица ошибок предлагает четыре индивидуальных показателя. На их основе можно рассчитать другие метрики, которые предоставляют дополнительную информацию о поведении модели:
- Accuracy
- Precision
- Recall
В следующих подразделах обсуждается каждый из этих трех показателей.
Метрика Accuracy
Accuracy — это показатель, который описывает общую точность предсказания модели по всем классам. Это особенно полезно, когда каждый класс одинаково важен. Он рассчитывается как отношение количества правильных прогнозов к их общему количеству.
Рассчитаем accuracy с помощью Scikit-learn на основе ранее полученной матрицы ошибок. Переменная acc содержит результат деления суммы True Positive и True Negative метрик на сумму всех значений матрицы. Таким образом, accuracy, равная 0.5714, означает, что модель с точностью 57,14% делает верный прогноз.
В модуле sklearn.metrics есть функция precision_score(), которая также может вычислять accuracy. Она принимает в качестве аргументов достоверные и предсказанные метки.
Стоит учесть, что метрика accuracy может быть обманчивой. Один из таких случаев — это несбалансированные данные. Предположим, у нас есть всего 600 единиц данных, из которых 550 относятся к классу Positive и только 50 — к Negative. Поскольку большинство семплов принадлежит к одному классу, accuracy для этого класса будет выше, чем для другого.
Если модель сделала 530 правильных прогнозов из 550 для класса Positive, по сравнению с 5 из 50 для Negative, то общая accuracy равна (530 + 5) / 600 = 0.8917. Это означает, что точность модели составляет 89.17%. Полагаясь на это значение, вы можете подумать, что для любой выборки (независимо от ее класса) модель сделает правильный прогноз в 89.17% случаев. Это неверно, так как для класса Negative модель работает очень плохо.
Precision
Precision представляет собой отношение числа семплов, верно классифицированных как Positive, к общему числу выборок с меткой Positive (распознанных правильно и неправильно). Precision измеряет точность модели при определении класса Positive.
Когда модель делает много неверных Positive классификаций, это увеличивает знаменатель и снижает precision. С другой стороны, precision высока, когда:
- Модель делает много корректных предсказаний класса Positive (максимизирует True Positive метрику).
- Модель делает меньше неверных Positive классификаций (минимизирует False Positive).
Представьте себе человека, который пользуется всеобщим доверием; когда он что-то предсказывает, окружающие ему верят. Метрика precision похожа на такого персонажа. Если она высока, вы можете доверять решению модели по определению очередной выборки как Positive. Таким образом, precision помогает узнать, насколько точна модель, когда она говорит, что семпл имеет класс Positive.
Основываясь на предыдущем обсуждении, вот определение precision:
Precision отражает, насколько надежна модель при классификации Positive-меток.
На следующем изображении зеленая метка означает, что зеленый семпл классифицирован как Positive, а красный крест – как Negative. Модель корректно распознала две Positive выборки, но неверно классифицировала один Negative семпл как Positive. Из этого следует, что метрика True Positive равна 2, когда False Positive имеет значение 1, а precision составляет 2 / (2 + 1) = 0.667. Другими словами, процент доверия к решению модели, что выборка относится к классу Positive, составляет 66.7%.
Цель precision – классифицировать все Positive семплы как Positive, не допуская ложных определений Negative как Positive. Согласно следующему рисунку, если все три Positive выборки предсказаны правильно, но один Negative семпл классифицирован неверно, precision составляет 3 / (3 + 1) = 0.75. Таким образом, утверждения модели о том, что выборка относится к классу Positive, корректны с точностью 75%.
Единственный способ получить 100% precision — это классифицировать все Positive выборки как Positive без классификации Negative как Positive.
В Scikit-learn модуль sklearn.metrics имеет функцию precision_score(), которая получает в качестве аргументов эталонные и предсказанные метки и возвращает precision. Параметр pos_label принимает метку класса Positive (по умолчанию 1).
Вывод: 0.6666666666666666.
Recall
Recall рассчитывается как отношение числа Positive выборок, корректно классифицированных как Positive, к общему количеству Positive семплов. Recall измеряет способность модели обнаруживать выборки, относящиеся к классу Positive. Чем выше recall, тем больше Positive семплов было найдено.
Recall заботится только о том, как классифицируются Positive выборки. Эта метрика не зависит от того, как предсказываются Negative семплы, в отличие от precision. Когда модель верно классифицирует все Positive выборки, recall будет 100%, даже если все представители класса Negative были ошибочно определены как Positive. Давайте посмотрим на несколько примеров.
На следующем изображении представлены 4 разных случая (от A до D), и все они имеют одинаковый recall, равный 0.667. Представленные примеры отличаются только тем, как классифицируются Negative семплы. Например, в случае A все Negative выборки корректно определены, а в случае D – наоборот. Независимо от того, как модель предсказывает класс Negative, recall касается только семплов относящихся к Positive.
Из 4 случаев, показанных выше, только 2 Positive выборки определены верно. Таким образом, метрика True Positive равна 2. False Negative имеет значение 1, потому что только один Positive семпл классифицируется как Negative. В результате recall будет равен 2 / (2 + 1) = 2/3 = 0.667.
Поскольку не имеет значения, как предсказываются объекты класса Negative, лучше их просто игнорировать, как показано на следующей схеме. При расчете recall необходимо учитывать только Positive выборки.
Что означает, когда recall высокий или низкий? Если recall имеет большое значение, все Positive семплы классифицируются верно. Следовательно, модели можно доверять в ее способности обнаруживать представителей класса Positive.
На следующем изображении recall равен 1.0, потому что все Positive семплы были правильно классифицированы. Показатель True Positive равен 3, а False Negative – 0. Таким образом, recall вычисляется как 3 / (3 + 0) = 1. Это означает, что модель обнаружила все Positive выборки. Поскольку recall не учитывает, как предсказываются представители класса Negative, могут присутствовать множество неверно определенных Negative семплов (высокая False Positive метрика).
С другой стороны, recall равен 0.0, если не удается обнаружить ни одной Positive выборки. Это означает, что модель обнаружила 0% представителей класса Positive. Показатель True Positive равен 0, а False Negative имеет значение 3. Recall будет равен 0 / (0 + 3) = 0.
Когда recall имеет значение от 0.0 до 1.0, это число отражает процент Positive семплов, которые модель верно классифицировала. Например, если имеется 10 экземпляров Positive и recall равен 0.6, получается, что модель корректно определила 60% объектов класса Positive (т.е. 0.6 * 10 = 6).
Подобно precision_score(), функция repl_score() из модуля sklearn.metrics вычисляет recall. В следующем блоке кода показан пример ее использования.
Вывод: 0.6666666666666666.
После определения precision и recall давайте кратко подведем итоги:
- Precision измеряет надежность модели при классификации Positive семплов, а recall определяет, сколько Positive выборок было корректно предсказано моделью.
- Precision учитывает классификацию как Positive, так и Negative семплов. Recall же использует при расчете только представителей класса Positive. Другими словами, precision зависит как от Negative, так и от Positive-выборок, но recall — только от Positive.
- Precision принимает во внимание, когда семпл определяется как Positive, но не заботится о верной классификации всех объектов класса Positive. Recall в свою очередь учитывает корректность предсказания всех Positive выборок, но не заботится об ошибочной классификации представителей Negative как Positive.
- Когда модель имеет высокий уровень recall метрики, но низкую precision, такая модель правильно определяет большинство Positive семплов, но имеет много ложных срабатываний (классификаций Negative выборок как Positive). Если модель имеет большую precision, но низкий recall, то она делает высокоточные предсказания, определяя класс Positive, но производит всего несколько таких прогнозов.
Некоторые вопросы для проверки понимания:
- Если recall равен 1.0, а в датасете имеются 5 объектов класса Positive, сколько Positive семплов было правильно классифицировано моделью?
- Учитывая, что recall составляет 0.3, когда в наборе данных 30 Positive семплов, сколько представителей класса Positive будет предсказано верно?
- Если recall равен 0.0 и в датасете14 Positive-семплов, сколько корректных предсказаний класса Positive было сделано моделью?
Precision или Recall?
Решение о том, следует ли использовать precision или recall, зависит от типа вашей проблемы. Если цель состоит в том, чтобы обнаружить все positive выборки (не заботясь о том, будут ли negative семплы классифицированы как positive), используйте recall. Используйте precision, если ваша задача связана с комплексным предсказанием класса Positive, то есть учитывая Negative семплы, которые были ошибочно классифицированы как Positive.
Представьте, что вам дали изображение и попросили определить все автомобили внутри него. Какой показатель вы используете? Поскольку цель состоит в том, чтобы обнаружить все автомобили, используйте recall. Такой подход может ошибочно классифицировать некоторые объекты как целевые, но в конечном итоге сработает для предсказания всех автомобилей.
Теперь предположим, что вам дали снимок с результатами маммографии, и вас попросили определить наличие рака. Какой показатель вы используете? Поскольку он обязан быть чувствителен к неверной идентификации изображения как злокачественного, мы должны быть уверены, когда классифицируем снимок как Positive (то есть с раком). Таким образом, предпочтительным показателем в данном случае является precision.
Вывод
В этом руководстве обсуждалась матрица ошибок, вычисление ее 4 метрик (true/false positive/negative) для задач бинарной и мультиклассовой классификации. Используя модуль metrics библиотеки Scikit-learn, мы увидели, как получить матрицу ошибок в Python.
Основываясь на этих 4 показателях, мы перешли к обсуждению accuracy, precision и recall метрик. Каждая из них была определена и использована в нескольких примерах. Модуль sklearn.metrics применяется для расчета каждого вышеперечисленного показателя.
Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу — так где же модель классификации сработала не так? Как это исправить?
Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.
В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок — довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!
Что такое матрица ошибок?
Вопрос на миллион долларов — что такое, в конце концов, матрица ошибок?
Матрица ошибок — это матрица размером N x N, используемая для оценки эффективности модели классификации, где N — количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.
Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:
Расшифруем матрицу:
- Целевая переменная имеет два значения: положительное или отрицательное.
- Столбцы представляют фактические значения целевой переменной.
- Строки представляют собой прогнозируемые значения целевой переменной.
Но подождите — что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.
Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок
True Positive (TP)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было положительным, и модель предсказала положительное значение.
True Negative (TN)
- Прогнозируемое значение соответствует фактическому значению.
- Фактическое значение было отрицательным, и модель предсказала отрицательное значение.
False Positive (FP) — ошибка 1-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было отрицательным, но модель предсказала положительное значение.
- Также известна как ошибка 1-го типа.
False Negative (FN) — ошибка 2-го типа
- Прогнозируемое значение было предсказано неверно.
- Фактическое значение было положительным, но модель предсказала отрицательное значение.
- Также известна как ошибка 2-го типа.
Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:
Различные значения матрицы ошибок будут следующими:
- True Positive (TP) = 560; это означает, что 560 положительных точек данных были правильно классифицированы моделью.
- True Negative (TN) = 330; это означает, что 330 отрицательных точек данных были правильно классифицированы моделью.
- False Positive (FP) = 60; это означает, что 60 отрицательных точек данных были неправильно классифицированы моделью как положительные.
- False Negative (FN) = 50; это означает, что 50 положительных точек данных были неправильно классифицированы моделью как отрицательные.
Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.
Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!
Зачем нам нужна матрица ошибок?
Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.
Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.
Теперь вы, должно быть, задаетесь вопросом — зачем нам матрица ошибок, когда у нас есть наш вечный друг — Точность? Что ж, посмотрим, где точность не работает.
Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:
Посмотрим, как работает наша модель:
Общие значения результатов:
TP = 30, TN = 930, FP = 30, FN = 10
Итак, точность для нашей модели:
96%! Неплохо!
Но это дает неверное представление о результате. Подумайте об этом.
Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!
Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?
Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».
Precision vs. Recall
Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.
Вот как рассчитать точность:
Это определило бы надежность нашей модели.
Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.
А вот как мы можем рассчитать полноту:
Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:
50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!
Точность — полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.
Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.
Полнота — полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.
Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!
В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.
Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!
F1-Score
На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:
F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.
Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор — точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.
Матрица ошибок с использованием scikit-learn в Python
Вы знаете теорию — теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.
# confusion matrix in sklearn
from sklearn.metrics import confusion_matrix
3 from sklearn.metrics import classification_report
# actual values
actual = [1,0,0,1,0,0,1,0,0,1]
# predicted values
predicted = [1,0,0,1,0,0,0,1,0,0]
# confusion matrix
matrix = confusion_matrix(actual,predicted, labels=[1,0])
print(‘Confusion matrix : n’,matrix)
# outcome values order in sklearn
tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)
print(‘Outcome values : n’, tp, fn, fp, tn)
# classification report for precision, recall f1-score and accuracy
matrix = classification_report(actual,predicted,labels=[1,0])
print(‘Classification report : n’,matrix)
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().
возвращает значения матрицы ошибок. Однако результат немного отличается от того, что мы изучили до сих пор. Она принимает строки как фактические значения, а столбцы как прогнозные значения. В остальном концепция осталась прежней.
выводит точность, полноту и f1-score для каждого целевого класса. В дополнение к этому, она также имеет некоторые дополнительные значения: micro avg, macro avg и weighted avg.
Mirco average — это оценка точности/полноты/f1, рассчитанная для всех классов.
Macro average — это среднее значение точности/полноты/f1-score.
Weighted average — это просто средневзвешенное значение точности/полноты/f1-score.
Матрица ошибок для мультиклассовой классификации
Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:
true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:
Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!
Заключение
И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.
Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!
Перевод
Ссылка на автора
Показатели эффективности для точности и отзыва в мультиклассовой классификации (также известной как классификация по нескольким меткам) могут быть немного — или очень — запутанными, поэтому в этом посте я объясню, как используются точность и отзыв и как они рассчитываются. Это на самом деле довольно просто! Но сначала давайте начнем с краткого обзора точности и вспомним бинарную классификацию. (Есть также Часть II: счет F1, но я рекомендую начать с первой части).
В бинарной классификации у нас обычно есть два класса, часто называемые положительными и отрицательными, и мы пытаемся предсказать класс для каждой выборки. Давайте рассмотрим простой пример: наши данные представляют собой набор изображений, некоторые из которых содержат собаку. Мы заинтересованы в обнаружении фотографий с собаками. В этом случае наш Позитивный класс — это класс всех фотографий собак, а Негативный класс включает в себя все остальные фотографии. Другими словами, если образец фотографии содержит собаку, это позитив. Если это не так, это отрицательный. Наш классификатор предсказывает для каждой фотографии, является ли она положительной (P) или отрицательной (N): есть ли собака на фотографии?
Учитывая классификатор, я считаю, что лучший способ думать о производительности классификатора — использовать так называемую «матрицу путаницы». Для двоичной классификации матрица смешения имеет две строки и два столбца и показывает, сколько положительных образцов было предсказано как положительное или отрицательное (первый столбец), а также сколько отрицательных фотографий было предсказано как положительное или отрицательное (второй столбец). Таким образом, он имеет в общей сложности 4 клетки. Каждый раз, когда наш классификатор делает прогноз, одна из ячеек в таблице увеличивается на единицу. К концу процесса мы можем точно увидеть, как работает наш классификатор (конечно, мы можем сделать это, только если наши тестовые данные помечены).
Вот простой пример. Предположим, у нас есть 10 фотографий, и ровно 7 из них имеют собак. Если бы наш классификатор был идеален, матрица путаницы выглядела бы так:
Наш идеальный классификатор не допустил ошибок. Все позитивные фотографии были классифицированы как позитивные, а все негативные фотографии были классифицированы как негативные.
Однако в реальном мире классификаторы допускают ошибки. Бинарный классификатор допускает два вида ошибок: некоторые положительные выборки классифицируются как отрицательные; и некоторые отрицательные образцы классифицируются как положительные. Давайте посмотрим на матрицу путаницы из более реалистичного классификатора:
В этом примере 2 фотографии с собаками были классифицированы как негативные (нет собаки!), А 1 фотография без собаки была классифицирована как позитивные (собака!).
Когда положительный образецложноклассифицируется как отрицательный, мы называем это ложным отрицательным (FN). И аналогично, когда отрицательный образецложноклассифицируется как положительный, он называется ложным положительным. Ниже мы копируем матрицу путаницы, но добавляем TP, FP, FN и TN для обозначения значений True Positive, False Position, False Negative и True Negative:
Теперь, когда мы получили представление о матрице путаницы и различных числах, мы можем начать смотреть на показатели производительности: насколько хорош наш классификатор? (В глубине души мы всегда должны помнить, что «добро» может означать разные вещи, в зависимости от реальной проблемы реального мира, которую нам нужно решить.)
Давайте начнем сточность, который отвечает на следующий вопрос: какая доляпрогнозируемые позитивыдействительно положительно? Нам нужно посмотреть на общее количество прогнозируемых позитивов (истинные позитивы плюс ложные позитивы, TP + FP) и посмотреть, сколько из них являются истинно позитивными (TP). В нашем случае 5 + 1 = 6 фотографий были предсказаны как положительные, но только 5 из них являются настоящими положительными. Таким образом, точность в нашем случае составляет 5 / (5 + 1) =83,3%, В целом, точность равна TP / (TP + FP). Обратите внимание, что TP + FP является суммойПервая строка,
Еще одна очень полезная мераотзыв, который отвечает на другой вопрос: какая доляфактические Позитивыправильно классифицирован? Глядя на таблицу, мы видим, что количество фактических позитивов составляет 2 + 5 = 7 (TP + FN). Из этих 7 фотографий 5 были предсказаны как положительные. Напоминаем, таким образом, 5/7 =71,4%, В общем, вспомним ТП / (ТП + ФН). Обратите внимание, что TP + FN является суммойпервый столбец,
Можно также интересоватьсяточность: какая доля фотографий — как положительных, так и отрицательных — была правильно классифицирована? В нашем случае 5 + 2 = 7 фотографий были правильно классифицированы из общего числа 10. Таким образом, точность составляет 70,0%. Вообще говоря, из фотографий TP + TN + FP + FN есть в общей сложности фотографии TP + TN, и поэтому общая формула точности (TP + TN) / (TP + TN + FP + FN).
Что важнее, точность или отзыв? Это действительно зависит от вашей конкретной проблемы классификации. Представьте, например, что вашему классификатору необходимо выявлять диабет у людей. «Положительный» означает, что у пациента диабет. «Отрицательный» означает, что пациент здоров. (Я знаю, это сбивает с толку. Но это медицинский жаргон!) В этом случае вы, вероятно, захотите убедиться в том, что ваш классификатор имеет высокий уровень отклика, чтобы правильно выявлялось как можно больше диабетиков. Возьмем другой пример — скажем, вы создаете систему рекомендаций по видео, и ваш классификатор прогнозирует «Позитивный» для релевантного видео и «Негативный» для не релевантного видео. Вы хотите убедиться, что почти все рекомендуемые видео относятся к пользователю, поэтому вам нужна высокая точность. Жизнь полна компромиссов, и это также верно для классификаторов. Обычно есть компромисс между хорошей точностью и хорошим отзывом. Вы обычно не можете иметь оба.
Наш пример с собакой был проблемой двоичной классификации. Проблемы бинарной классификации часто сосредоточены на Позитивном классе, который мы хотим обнаружить. Напротив, в типичной многоклассовой проблеме классификации нам нужно классифицировать каждую выборку в 1 из N различных классов. Возвращаясь к нашему примеру с фотографиями, представьте, что у нас есть коллекция фотографий. На каждой фотографии изображено одно животное: либоКот,рыбыиликурицы, Наш классификатор должен предсказать, какое животное показано на каждой фотографии. Это проблема классификации с N = 3 классами.
Давайте посмотрим на образец матрицы путаницы, которая создается после классификации 25 фотографий:
Подобно нашему двоичному случаю, мы можем определить точность и вызвать для каждого из классов. Например,точностьдля класса Cat — количество правильно предсказанных фотографий Cat (4) из всех предсказанных фотографий Cat (4 + 3 + 6 = 13), что составляет 4/13 = 30,8%. Так что только около 1/3 фотографий, которые наш предсказатель классифицирует как кошку, на самом деле являются кошками!
С другой стороны,отзывдля Cat — количество правильно спрогнозированных фотографий Cat (4) из числа действительных фотографий Cat (4 + 1 + 1 = 6), что составляет 4/6 = 66,7%. Это означает, что наш классификатор классифицировал 2/3 фотографий кошек как Cat.
Аналогичным образом мы можем вычислить точность и вспомнить для двух других классов: Рыба и Курица. Для рыбы эти цифры составляют 66,7% и 20,0% соответственно. Для курицы число для точности и отзыва составляет 66,7%. Идите и проверьте эти результаты. Вы можете использовать два изображения ниже, чтобы помочь вам.
В библиотеке Scikit-Learn Python (также известный какsklearn), вы можете легко вычислить точность и вызвать для каждого класса в классификаторе мультикласса. Удобная функция для использования здесьsklearn.metrics.classification_report,
Вот некоторый код, который использует наш пример Cat / Fish / Hen. Сначала я создал список с истинными классами изображений (y_true) и предсказанными классами (y_pred). Обычно y_pred генерируется с использованием классификатора — здесь я устанавливаю его значения вручную, чтобы соответствовать матрице путаницы.
В строке 14 выводится запутанная матрица, а затем в строке 17 выводятся точность и отзыв для трех классов.
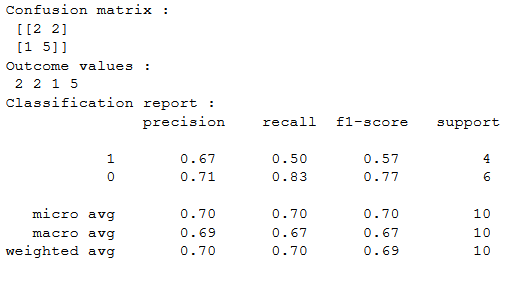
И вот выход. Обратите внимание, что матрица путаницы здесь транспонирована — так работает только sklearn. Обратите внимание наподдержкастолбец: в нем указано количество образцов для каждого класса (6 для кошек, 10 для рыб и т. д.).
classification_reportтакже сообщает о других показателях (например, F1-оценка). В следующем посте я объяснюF1-оценкадля случая мультикласса, и почему вы не должны его использовать
Надеюсь, вы нашли этот пост полезным и легким для понимания!
Продолжите к части II: счет F1
Содержание
- 1 Общие понятия
- 2 Простые оценки
- 3 Различные виды агрегации Precision и Recall
- 4 F-мера
- 5 ROC-кривая
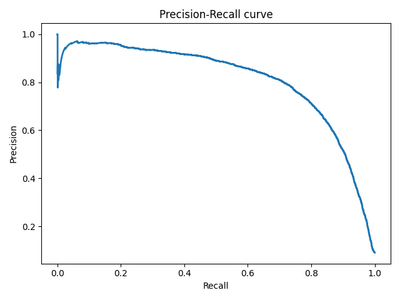
- 6 Precision-Recall кривая
- 7 Источники
Общие понятия
- TP — true positive: классификатор верно отнёс объект к рассматриваемому классу.
- TN — true negative: классификатор верно утверждает, что объект не принадлежит к рассматриваемому классу.
- FP — false positive: классификатор неверно отнёс объект к рассматриваемому классу.
- FN — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу.
Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное число объектов класса 0 (для бинарного случая 0/1) может выражаться как
Confusion matrix (матрица ошибок / несоответствий / потерь, CM)
Вычисление TP, FP, FN по CM
— квадратная матрица размера k × k, где — число объектов класса ,
которые были квалифицированны как класс , а — число классов. Значения ячеек CM могут быть вычислены по формуле:
, где — реальный класс объекта, а — предсказанный.
Для бинарного случая:
| Принадлежит классу (P) | Не принадлежит классу (N) | |
|---|---|---|
| Предсказана принадлежность классу | TP | FP |
| Предсказано отсутствие принадлежности к классу | FN | TN |
Для многоклассовой классификации матрица несоответствий строится по тому же принципу:
| Предсказанный класс | Класс 1 (C₁) | Класс 2 (C₂) | Класс 3 (C₃) |
|---|---|---|---|
| 1 (P₁) | T₁ | F₁₂ | F₁₃ |
| 2 (P₂) | F₂₁ | T₂ | F₂₃ |
| 3 (P₃) | F₃₁ | F₃₂ | T₃ |
В этом случае TP, TN, FP и FN считаются относительно некоторого класса следующим образом:
Простые оценки
- Accuracy — (точность) показывает долю правильных классификаций. Несмотря на очевидность и простоту, является одной из самых малоинформативных оценок классификаторов.
- Recall — (полнота, sensitivity, TPR (true positive rate)) показывает отношение верно классифицированных объектов класса к общему числу элементов этого класса.
- Precision — (точность, перевод совпадает с accuracy)показывает долю верно классифицированных объектов среди всех объектов, которые к этому классу отнес классификатор.
- Specificity — показывает отношение верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря, то, насколько часто классификатор правильно не относит объекты к классу.
- Fall-out — (FPR (false positive rate)) показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу.
Ввиду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), также существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации):
- Precision
- Recall
Различные виды агрегации Precision и Recall
Примеры и картинки взяты из лекций курса «Введение в машинное обучение»[1] К.В. Воронцова
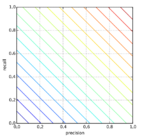
Арифметическое среднее:
Линии уровня для среднего арифметического
- Если precision = 0.05, recall = 1, то A = 0.525
- Если precision = 0.525, recall = 0.525, то A = 0.525.
- Первый классификатор — константный, не имеет смысла.
- Второй классификатор показывает неплохое качество.
Таким образом, взятие среднего арифметического не является показательным.
Минимум:
Линии уровня для минимума
- Если precision = 0.05, recall = 1, то M = 0.05
- Если precision = 0.525, recall = 0.525, то M = 0.525.
То есть, довольно неплохо отражает качество классификатора, не завышая его.
- Если precision = 0.2, recall = 1, то M = 0.2.
- Если precision = 0.2, recall = 0.3, то M = 0.2.
Но не отличает классификаторы с разными неминимальными показателями.
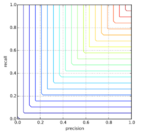
Гармоническое среднее, или F-мера:
- Если precision = 0.05, recall = 1, то F = 0.1.
- Если precision = 0.525, recall = 0.525, то F = 0.525.
- Если precision = 0.2, recall = 1, то F = 0.33.
- Если precision = 0.2, recall = 0.3, то F = 0.24.
Является наиболее точным усреднением, учитывает оба показателя.
Геометрическое среднее, или Индекс Фоулкса–Мэллова (Fowlkes–Mallows index)
Менее строгая мера.
F-мера
Для общей оценки качества классификатора часто используют F₁-меру. Оригинально она вычисляется для позитивного класса случая бинарной классификации, обобщается с помощью приниципа «один против всех» (описан подробнее ниже, для многоклассовой классификации). F₁-мера — среднее гармоническое между precision и recall:
Среднее гармоническое взвешенное Fβ (F1-мера — частный случай Fβ-меры для β = 1).
Fβ измеряет эффективность классификатора учитывая recall в β раз более важным чем precision:
F-мера для многоклассовой классификации. Три вида усреднения
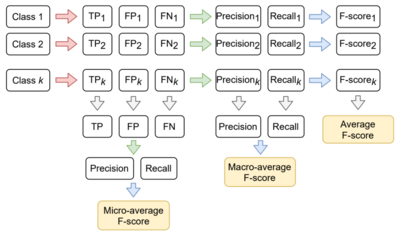
Принцип усреднения различных F-мер для нескольких классов
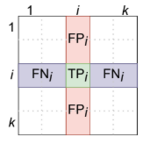
Вычисление TP, FP, FN для многоклассовой классификации
Для вычисления F-меры (и других) метрик в рамках многоклассовой классификации используется подход «один против всех»: каждый класс ровно один раз становится «положительным»,
а остальные — отрицательным (пример вычисления изображён на матрице).
Таким образом, в зависимости от этапа вычисления, на котором производится усреднение, можно вычислить micro-average, macro-average и average F-меры (логика вычисления изображена на схеме справа).
Микро- и макро-:
- ,
где для micro-average precision и recall вычислены из усреднённых TP, FP, FN;
для macro-average precision и recall вычислены из усреднённых precisioni, recalli;
Усреднённая:
- ,
где — индекс класса, а — число классов.
ROC-кривая
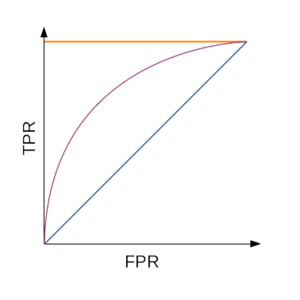
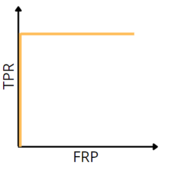
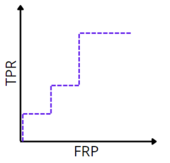
ROC-кривая; оранжевым показан идеальный алгоритм, фиолетовым — типичный, а синим — худший
Для наглядной оценки качества алгоритма применяется ROC-кривая. Кривая строится на плоскости, определённой TPR (по оси ординат) и FPR (по оси абсцисс).
Для построении графика используется мягкая классификация: вместо того, чтобы чётко отнести объект к классу, классификатор возвращает вероятности принадлежности объекта к различным классам. Эта уверенность сравнивается с порогом (какой уверенности «достаточно», чтобы отнести объект к положительному классу). В зависимости от значения этого порога меняются значения TPR и FPR.
Алгоритм построения кривой:
- Запустить классификатор на тестовой выборке
- Отсортировать результаты по уверенности классификатора в принадлежности объекта к классу
- Пока не кончились элементы:
- Взять объект с максимальной уверенностью
- Сравнить метку с реальной
- Пересчитать TPR и FPR на взятых объектах
- Поставить точку, если обе характеристики не NaN / ±∞
- Построить кривую по точкам
Таким образом:
число точек не превосходит число объектов
идеальному алгоритму соответствует ROC-кривая, проходящая через точку
худшему алгоритму (например, монетке) соответствует прямая TPR = FPR.
Для численной оценки алгоритма по ROC-кривой используется значение площади под ней (AUC, area under curve). Идеальный алгоритм имеет AUC, равный 1, худший — 0,5.
С другой стороны, для построения ROC-кривой не обязательно пересчитывать TPR и FPR.
Существует альтернативный алгоритм построения ROC-кривой.
- сортируем объекты по уверенности классификатора в их принадлежности к положительному классу
- начинаем в точке (0, 0)
- последовательно продолжаем кривую вверх:
- для каждого «отрицательного» объекта вверх
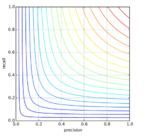
- для каждого «положительного» — вправо.
Корректность алгоритма обосновывается тем, что с изменением предсказания для одного объекта в зависимости от его класса меняется либо TPR, либо FPR (значение второго параметра остаётся прежним). Ниже описана другая логика, подводящая к алгоритму выше.
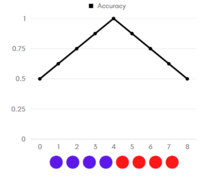
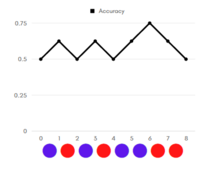
График Accuracy для идеальной классификации
ROC-кривая для идеальной классификации
График Accuracy для неидеальной классификации
ROC-кривая для неидеальной классификации
Напомним, что мы работаем с мягкой классификацией.
Рассмотрим примеры (графики accuracy, цветом указан реальный класс объекта: красный — положительный, синий — отрицательный).
Отсортируем наши объекты по возрастанию уверенности классификатора в принадлежности объекта к положительному классу. Допустим, что объекты находятся на равном (единичном) расстоянии друг от друга.
Начнём перебирать «границу раздела»: если граница в нуле — мы решаем относить все объекты к положительному классу, тогда accuracy = 1/2.
Последовательно сдвигаем границу по единичке вправо:
- если реальный класс объекта, оказавшегося теперь по другую сторону границы — отрицательный, то accuracy увеличивается, так как мы «угадали» класс объекта, решив относить объекты левее границы к отрицательному классу;
- если же реальный класс объекта — положительный, accuracy уменьшается (по той же логике)
Таким образом, на графиках слева, видно, что:
- на графике идеальной классификации точность в 100% достигается, неидеальной — нет;
- площадь под графиком accuracy идеального классификатора больше, чем аналогичная площадь для неидеального.
Заметим, что, повернув график на 45 градусов, мы получим ROC-кривые для соответствующих классификаторов (графикам accuracy слева соответствуют ROC-кривые справа). Так объясняется альтернативный алгоритм построения ROC-кривой.
Precision-Recall кривая
Обоснование: Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь «плохой» алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая.
Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
Источники
- Coursera: https://www.coursera.org/learn/vvedenie-mashinnoe-obuchenie
- Оценка качества в задачах классификации и регрессии
- Лекции А. Забашта
- Лекции Е. А. Соколова
- Оценка классификатора (точность, полнота, F-мера)
Руководство для новичков о том, как рассчитать точность, отзыв и F1-оценку для задачи классификации нескольких классов.
Матрица неточностей — это табличный способ визуализации производительности вашей модели прогнозирования. Каждая запись в матрице неточностей обозначает количество прогнозов, сделанных моделью, в которой классы были правильно или неправильно классифицированы.
Любой, кто уже знаком с матрицей неточностей, знает, что в большинстве случаев это объясняется проблемой двоичной классификации. Что ж, это объяснение не из их числа. Сегодня мы увидим, как матрица путаницы работает в мультиклассовых моделях машинного обучения. Тем не менее, мы начнем с небольшой предыстории, используя двоичную классификацию, чтобы увидеть вещи в перспективе.
Матрица неточностей для двоичной классификации
Как видите, в задаче двоичной классификации нужно классифицировать только два класса, предпочтительно положительный и отрицательный. Теперь давайте посмотрим на показатели Матрицы неточностей.
Истинно положительный (TP): Это относится к количеству прогнозов, при которых классификатор правильно предсказывает положительный класс как положительный.
Истинно отрицательный (TN): Это относится к количеству прогнозов, в которых классификатор правильно предсказывает отрицательный класс как отрицательный.
Ложноположительный (FP): Это относится к количеству прогнозов, в которых классификатор неверно предсказывает отрицательный класс как положительный.
Ложноотрицательный (FN): Это относится к количеству прогнозов, в которых классификатор неверно предсказывает положительный класс как отрицательный.
Всегда лучше использовать матрицу путаницы в качестве критерия оценки модели машинного обучения. Он дает вам очень простые, но эффективные меры производительности для вашей модели. Вот некоторые из наиболее распространенных показателей производительности, которые вы можете использовать из матрицы неточностей.
Точность: показывает общую точность модели, то есть долю от общего числа выборок, которые были правильно классифицированы классификатором. Для расчета точности используйте следующую формулу: (TP + TN) / (TP + TN + FP + FN).
Уровень ошибочной классификации. Он показывает, какая часть прогнозов была неверной. Это также известно как ошибка классификации. Вы можете рассчитать его, используя (FP + FN) / (TP + TN + FP + FN) или (1-точность). .
Точность. Он сообщает вам, какая доля прогнозов в качестве положительного класса была на самом деле положительной. Для расчета точности используйте следующую формулу: TP / (TP + FP).
Напомнить: он сообщает вам, какая доля всех положительных образцов была правильно определена классификатором как положительные. Он также известен как истинно положительный коэффициент (TPR), чувствительность, вероятность обнаружения. Чтобы рассчитать отзыв, используйте следующую формулу: TP / (TP + FN).
Специфичность. Он сообщает вам, какая доля всех отрицательных образцов правильно предсказана классификатором как отрицательная. Он также известен как True Negative Rate (TNR). Для расчета специфичности используйте следующую формулу: TN / (TN + FP).
F1-оценка: он сочетает в себе точность и запоминаемость в одном измерении. Математически это гармоническое среднее значение точности и запоминания. Его можно рассчитать следующим образом:
Теперь, в идеальном мире, нам нужна модель с точностью 1 и отзывом 1. Это означает, что F1-оценка равна 1, то есть 100% точность, которая часто не соответствует модели машинного обучения. . Итак, что мы должны попробовать, так это получить более высокую точность с более высоким значением отзыва. Хорошо, теперь, когда мы знаем о показателях эффективности матрицы путаницы, давайте посмотрим, как мы можем использовать это в модели машинного обучения с несколькими классами.
Матрица неточностей для многоклассовой классификации
Для простоты давайте рассмотрим нашу задачу классификации нескольких классов как задачу классификации трех классов. Скажем, у нас есть набор данных с тремя метками класса, а именно Apple, Orange и Манго. Ниже приводится возможная матрица путаницы для этих классов.
В отличие от бинарной классификации здесь нет положительных или отрицательных классов. Сначала может быть немного сложно найти TP, TN, FP и FN, поскольку нет положительных или отрицательных классов, но на самом деле это довольно просто. Здесь нам нужно найти TP, TN, FP и FN для каждого отдельного класса. Например, если мы возьмем класс Apple, то давайте посмотрим, каковы значения показателей из матрицы неточностей.
- TP = 7
- TN = (2+3+2+1) = 8
- FP = (8+9) = 17
- FN = (1+3) = 4
Поскольку у нас есть все необходимые метрики для класса Apple из матрицы путаницы, теперь мы можем рассчитать показатели производительности для класса Apple. Например, у класса Apple есть
- Точность = 7 / (7 + 17) = 0,29
- Напоминание = 7 / (7 + 4) = 0,64
- F1-оценка = 0,40
Аналогичным образом мы можем рассчитать меры для других классов. Вот таблица, в которой показаны значения каждой меры для каждого класса.
Теперь мы можем сделать больше с помощью этих мер. Мы можем объединить оценку F1 каждого класса, чтобы получить единый показатель для всей модели. Есть несколько способов сделать это, давайте рассмотрим их сейчас.
Микро F1
Это называется микро-усредненным баллом F1. Он рассчитывается с учетом общего TP, общего FP и общего FN модели. Он не рассматривает каждый класс в отдельности, он рассчитывает показатели глобально. Итак, для нашего примера
- Общий TP = (7 + 2 + 1) = 10
- Всего FP = (8 + 9) + (1 + 3) + (3 + 2) = 26
- Итого FN = (1 + 3) + (8 + 2) + (9 + 3) = 26
Следовательно,
- Точность = 10 / (10 + 26) = 0,28
- Напоминание = 10 / (10 + 26) = 0,28
Теперь мы можем использовать обычную формулу для оценки F1 и получить оценку Micro F1, используя указанную выше точность и отзыв.
Micro F1 = 0,28
Как видите, когда мы рассчитываем показатели в глобальном масштабе, все показатели становятся равными. Также, если вы рассчитаете точность, вы увидите, что
Точность = Напоминание = Микро F1 = Точность
Макрос F1
Это макро-средний показатель F1. Он рассчитывает показатели для каждого класса индивидуально, а затем берет невзвешенное среднее значение показателей. Как видно из рисунка «Точность, отзывчивость и F1-оценка для каждого класса»,
- Оценка Apple в классе F1 = 0,40
- Оценка F1 класса Orange = 0,22
- Оценка F1 Class Mango = 0,11
Следовательно,
Макрос F1 = (0,40 + 0,22 + 0,11) / 3 = 0,24
Взвешенный F1
Последний — это средневзвешенный показатель F1. В отличие от макроса F1, он принимает средневзвешенное значение показателей. Веса для каждого класса — это общее количество выборок этого класса. Поскольку у нас было 11 яблок, 12 апельсинов и 13 манго,
Взвешенный F1 = ((0,40 * 11) + (0,22 * 12) + (0,11 * 13)) / (11 + 12 + 13) = 0,24
Наконец, давайте рассмотрим сценарий для вычисления этих показателей с помощью Python Scikit-learn.
Вот результат работы скрипта.
Примечание: Scikit-Learn использует строки как истинный класс, а столбцы — как прогнозируемый класс. Это противоположно нашему рассмотрению для примера Apple, Orange и Mango, но логически схоже. В любом случае вы можете рассматривать истинный и предсказанный класс. Но если вы используете Scikit-Learn, то вам придется играть по их правилам.
Надеюсь, вы нашли то, что искали. Спасибо за прочтение.
Содержание
- 1 Общие понятия
- 2 Простые оценки
- 3 Различные виды агрегации Precision и Recall
- 4 F-мера
- 5 ROC-кривая
- 6 Precision-Recall кривая
- 7 Источники
Общие понятия
- TP — true positive: классификатор верно отнёс объект к рассматриваемому классу.
- TN — true negative: классификатор верно утверждает, что объект не принадлежит к рассматриваемому классу.
- FP — false positive: классификатор неверно отнёс объект к рассматриваемому классу.
- FN — false negative: классификатор неверно утверждает, что объект не принадлежит к рассматриваемому классу.
Здесь про TP, TN, FP, FN и понятия, через них выражающиеся, мы говорим в рамках одного класса бинарной классификации. То есть, в такой системе подразумевается, что реальное число объектов класса 0 (для бинарного случая 0/1) может выражаться как
Confusion matrix (матрица ошибок / несоответствий / потерь, CM)
Вычисление TP, FP, FN по CM
— квадратная матрица размера k × k, где — число объектов класса ,
которые были квалифицированны как класс , а — число классов. Значения ячеек CM могут быть вычислены по формуле:
, где — реальный класс объекта, а — предсказанный.
Для бинарного случая:
| Принадлежит классу (P) | Не принадлежит классу (N) | |
|---|---|---|
| Предсказана принадлежность классу | TP | FP |
| Предсказано отсутствие принадлежности к классу | FN | TN |
Для многоклассовой классификации матрица несоответствий строится по тому же принципу:
| Предсказанный класс | Класс 1 (C₁) | Класс 2 (C₂) | Класс 3 (C₃) |
|---|---|---|---|
| 1 (P₁) | T₁ | F₁₂ | F₁₃ |
| 2 (P₂) | F₂₁ | T₂ | F₂₃ |
| 3 (P₃) | F₃₁ | F₃₂ | T₃ |
В этом случае TP, TN, FP и FN считаются относительно некоторого класса следующим образом:
Простые оценки
- Accuracy — (точность) показывает долю правильных классификаций. Несмотря на очевидность и простоту, является одной из самых малоинформативных оценок классификаторов.
- Recall — (полнота, sensitivity, TPR (true positive rate)) показывает отношение верно классифицированных объектов класса к общему числу элементов этого класса.
- Precision — (точность, перевод совпадает с accuracy)показывает долю верно классифицированных объектов среди всех объектов, которые к этому классу отнес классификатор.
- Specificity — показывает отношение верных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря, то, насколько часто классификатор правильно не относит объекты к классу.
- Fall-out — (FPR (false positive rate)) показывает долю неверных срабатываний классификатора к общему числу объектов за пределами класса. Иначе говоря то, насколько часто классификатор ошибается при отнесении того или иного объекта к классу.
Ввиду того, что такие оценки никак не учитывают изначальное распределение классов в выборке (что может существенно влиять на полученное значение), также существуют взвешенные варианты этих оценок (в терминах многоклассовой классификации):
- Precision
- Recall
Различные виды агрегации Precision и Recall
Примеры и картинки взяты из лекций курса «Введение в машинное обучение»[1] К.В. Воронцова
Арифметическое среднее:
Линии уровня для среднего арифметического
- Если precision = 0.05, recall = 1, то A = 0.525
- Если precision = 0.525, recall = 0.525, то A = 0.525.
- Первый классификатор — константный, не имеет смысла.
- Второй классификатор показывает неплохое качество.
Таким образом, взятие среднего арифметического не является показательным.
Минимум:
Линии уровня для минимума
- Если precision = 0.05, recall = 1, то M = 0.05
- Если precision = 0.525, recall = 0.525, то M = 0.525.
То есть, довольно неплохо отражает качество классификатора, не завышая его.
- Если precision = 0.2, recall = 1, то M = 0.2.
- Если precision = 0.2, recall = 0.3, то M = 0.2.
Но не отличает классификаторы с разными неминимальными показателями.
Гармоническое среднее, или F-мера:
- Если precision = 0.05, recall = 1, то F = 0.1.
- Если precision = 0.525, recall = 0.525, то F = 0.525.
- Если precision = 0.2, recall = 1, то F = 0.33.
- Если precision = 0.2, recall = 0.3, то F = 0.24.
Является наиболее точным усреднением, учитывает оба показателя.
Геометрическое среднее, или Индекс Фоулкса–Мэллова (Fowlkes–Mallows index)
Менее строгая мера.
F-мера
Для общей оценки качества классификатора часто используют F₁-меру. Оригинально она вычисляется для позитивного класса случая бинарной классификации, обобщается с помощью приниципа «один против всех» (описан подробнее ниже, для многоклассовой классификации). F₁-мера — среднее гармоническое между precision и recall:
Среднее гармоническое взвешенное Fβ (F1-мера — частный случай Fβ-меры для β = 1).
Fβ измеряет эффективность классификатора учитывая recall в β раз более важным чем precision:
F-мера для многоклассовой классификации. Три вида усреднения
Принцип усреднения различных F-мер для нескольких классов
Вычисление TP, FP, FN для многоклассовой классификации
Для вычисления F-меры (и других) метрик в рамках многоклассовой классификации используется подход «один против всех»: каждый класс ровно один раз становится «положительным»,
а остальные — отрицательным (пример вычисления изображён на матрице).
Таким образом, в зависимости от этапа вычисления, на котором производится усреднение, можно вычислить micro-average, macro-average и average F-меры (логика вычисления изображена на схеме справа).
Микро- и макро-:
- ,
где для micro-average precision и recall вычислены из усреднённых TP, FP, FN;
для macro-average precision и recall вычислены из усреднённых precisioni, recalli;
Усреднённая:
- ,
где — индекс класса, а — число классов.
ROC-кривая
ROC-кривая; оранжевым показан идеальный алгоритм, фиолетовым — типичный, а синим — худший
Для наглядной оценки качества алгоритма применяется ROC-кривая. Кривая строится на плоскости, определённой TPR (по оси ординат) и FPR (по оси абсцисс).
Для построении графика используется мягкая классификация: вместо того, чтобы чётко отнести объект к классу, классификатор возвращает вероятности принадлежности объекта к различным классам. Эта уверенность сравнивается с порогом (какой уверенности «достаточно», чтобы отнести объект к положительному классу). В зависимости от значения этого порога меняются значения TPR и FPR.
Алгоритм построения кривой:
- Запустить классификатор на тестовой выборке
- Отсортировать результаты по уверенности классификатора в принадлежности объекта к классу
- Пока не кончились элементы:
- Взять объект с максимальной уверенностью
- Сравнить метку с реальной
- Пересчитать TPR и FPR на взятых объектах
- Поставить точку, если обе характеристики не NaN / ±∞
- Построить кривую по точкам
Таким образом:
число точек не превосходит число объектов
идеальному алгоритму соответствует ROC-кривая, проходящая через точку
худшему алгоритму (например, монетке) соответствует прямая TPR = FPR.
Для численной оценки алгоритма по ROC-кривой используется значение площади под ней (AUC, area under curve). Идеальный алгоритм имеет AUC, равный 1, худший — 0,5.
С другой стороны, для построения ROC-кривой не обязательно пересчитывать TPR и FPR.
Существует альтернативный алгоритм построения ROC-кривой.
- сортируем объекты по уверенности классификатора в их принадлежности к положительному классу
- начинаем в точке (0, 0)
- последовательно продолжаем кривую вверх:
- для каждого «отрицательного» объекта вверх
- для каждого «положительного» — вправо.
Корректность алгоритма обосновывается тем, что с изменением предсказания для одного объекта в зависимости от его класса меняется либо TPR, либо FPR (значение второго параметра остаётся прежним). Ниже описана другая логика, подводящая к алгоритму выше.
График Accuracy для идеальной классификации
ROC-кривая для идеальной классификации
График Accuracy для неидеальной классификации
ROC-кривая для неидеальной классификации
Напомним, что мы работаем с мягкой классификацией.
Рассмотрим примеры (графики accuracy, цветом указан реальный класс объекта: красный — положительный, синий — отрицательный).
Отсортируем наши объекты по возрастанию уверенности классификатора в принадлежности объекта к положительному классу. Допустим, что объекты находятся на равном (единичном) расстоянии друг от друга.
Начнём перебирать «границу раздела»: если граница в нуле — мы решаем относить все объекты к положительному классу, тогда accuracy = 1/2.
Последовательно сдвигаем границу по единичке вправо:
- если реальный класс объекта, оказавшегося теперь по другую сторону границы — отрицательный, то accuracy увеличивается, так как мы «угадали» класс объекта, решив относить объекты левее границы к отрицательному классу;
- если же реальный класс объекта — положительный, accuracy уменьшается (по той же логике)
Таким образом, на графиках слева, видно, что:
- на графике идеальной классификации точность в 100% достигается, неидеальной — нет;
- площадь под графиком accuracy идеального классификатора больше, чем аналогичная площадь для неидеального.
Заметим, что, повернув график на 45 градусов, мы получим ROC-кривые для соответствующих классификаторов (графикам accuracy слева соответствуют ROC-кривые справа). Так объясняется альтернативный алгоритм построения ROC-кривой.
Precision-Recall кривая
Обоснование: Чувствительность к соотношению классов.
Рассмотрим задачу выделения математических статей из множества научных статей. Допустим, что всего имеется 1.000.100 статей, из которых лишь 100 относятся к математике. Если нам удастся построить алгоритм , идеально решающий задачу, то его TPR будет равен единице, а FPR — нулю. Рассмотрим теперь «плохой» алгоритм, дающий положительный ответ на 95 математических и 50.000 нематематических статьях. Такой алгоритм совершенно бесполезен, но при этом имеет TPR = 0.95 и FPR = 0.05, что крайне близко к показателям идеального алгоритма.
Таким образом, если положительный класс существенно меньше по размеру, то AUC-ROC может давать неадекватную оценку качества работы алгоритма, поскольку измеряет долю неверно принятых объектов относительно общего числа отрицательных. Так, алгоритм , помещающий 100 релевантных документов на позиции с 50.001-й по 50.101-ю, будет иметь AUC-ROC 0.95.
Precison-recall (PR) кривая.
Избавиться от указанной проблемы с несбалансированными классами можно, перейдя от ROC-кривой к PR-кривой. Она определяется аналогично ROC-кривой, только по осям откладываются не FPR и TPR, а полнота (по оси абсцисс) и точность (по оси ординат). Критерием качества семейства алгоритмов выступает площадь под PR-кривой (англ. Area Under the Curve — AUC-PR)
Источники
- Coursera: https://www.coursera.org/learn/vvedenie-mashinnoe-obuchenie
- Оценка качества в задачах классификации и регрессии
- Лекции А. Забашта
- Лекции Е. А. Соколова
- Оценка классификатора (точность, полнота, F-мера)