Математика учит преодолевать трудности и исправлять собственные ошибки

1


Математика учит преодолевать трудности и исправлять собственные ошибки. (Декарт).

2


К ОД РАЗДЕЛА 3.2 НЕРАВЕНСТВА Код контролируемого элемента Числовые неравенства и их свойства Неравенство с одной переменной. Решение неравенства Линейные неравенства с одной переменной Системы линейных неравенств Квадратные неравенства

3


«Р ЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМ » Учитель математики Соколов В.А.

4


Ц ЕЛИ УРОКА : Образовательная: Повторение и обобщение знаний по теме «Линейные неравенства с одной переменной и их системы.» Продолжить формирование умений работать по алгоритму. Развивающая: Развивать навыки коллективной работы, взаимопомощи, самоконтроля. Воспитывать внимание, математическую зоркость, культуру речи.

5

6


Л ИНЕЙНЫЕ НЕРАВЕНСТВА Линейным неравенством с одной переменной х называется неравенство вида ах + b 0, где а0. Решение неравенства – значение переменной х, которое обращает неравенство в верное числовое неравенство. Два неравенства f(х)

7


Множество чисел, удовлетворяющих неравенству – 4< х 5 изображено на рисунке -45 1) -45 2) -45 4) ) Числовой промежуток ( ; 9] изображен на рисунке 9 1) 3) 9 4) 9 Ответ: 4) Ответ: 3) 7 9 2)

8


Установить соответствие между неравенством и числовым промежутком Х 12 – 4 < Х 0 Х < – 0,3 2,5 Х < 10 3 < Х < 18 4 Х (– ; – 0,3) 2. (3; 18) 3. [12; + ) 4. (– 4; 0] 5. [4; 12] 6. [2,5; 10) 8

9


Т ЕСТИРОВАНИЕ.( ДА — 1, НЕТ — 0 ) 1) Является ли число 12 решением неравенства 2х>10? 2) Является ли число -6 решением неравенства 4х>12? 3) Является ли неравенство 5х-15>4х+14 строгим? 4) Существует ли целое число принадлежащее промежутку [-2,8;-2,6]? 5) При любом ли значении переменной а верно неравенство а² +4 >о? 6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется?

10


Д АВАЙТЕ ПРОВЕРИМ

11


Н АЙДИ ОШИБКУ ! 1. Х 72. y < 2,5 Ответ: (-;7)Ответ: (-;2,5] 3. m x -1,3 Ответ: (-;12)Ответ: [-;-1,3] 7 2, ,3

12


Решаем неравенства. Правила: 1. Решить неравенство – найти значение переменной, которое обращает его в верное числовое неравенство.

13


2.2. :а:а Решаем неравенства. Правила: Решить неравенство – найти значение переменной, которое обращает его в верное числовое неравенство.

14


2.2. :а:а Решаем неравенства. Правила: Решить неравенство – найти значение переменной, которое обращает его в верное числовое неравенство. При делении (умножении) на отрицательное число знак неравенства меняется на противоположный.

15


ПРИМЕР 1)решите неравенство 2(х+3) — 4(х-2) 0 2х х x x -14 :(-2) х 7 Ответ: (-;7) 7

16


2)Решите двойное неравенство: — 4 < х-9 < 5 3) При каких значениях х имеет смысл выражение: 4) Решите двойное неравенство — 6 < 3х < 9 и укажите наибольшее и наименьшее целое число, которое является его решением.

17


*Р ЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ НЕРАВЕНСТВ НАЗЫВАЕТСЯ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ РЕШЕНИЙ ЭТИХ НЕРАВЕНСТВ, Т. Е. ТЕ ЗНАЧЕНИЯ ПЕРЕМЕННОЙ, КОТОРЫЕ ОДНОВРЕМЕННО УДОВЛЕТВОРЯЮТ ВСЕМ НЕРАВЕНСТВАМ СИСТЕМЫ. *Д ЛЯ КАЖДОЙ СИСТЕМЫ НАЙДИТЕ ГРАФИЧЕСКОЕ РЕШЕНИЕ И ЗАПИСЬ РЕШЕНИЯ В ВИДЕ ПРОМЕЖУТКА. О ТВЕТ ЗАПИШИТЕ ТРЕХЗНАЧНЫМ ЧИСЛОМ ( СМОТРИ ОБРАЗЕЦ ). ( СМОТРИ ОБРАЗЕЦ ). Системы линейных неравенств

18

19


П РОВЕРЬ СЕБЯ Самостоятельная работа рассчитана на 10 минут, вы сможете проверить свои знания по теме «Линейные неравенства с одной переменной и их системы». За каждое правильно решенные задания части «А» — поставь себе 1 балл За каждое правильно решенные задания части «В» — поставь себе 2 балл За каждое правильно решенные задания части «С» — поставь себе 3 балл Посчитайте сумму баллов. 6 баллов – «удовлетворительно» 10 баллов – «хорошо» 14 баллов – «отлично»

20


З АДАНИЕ НА ДОМ : Решите неравенства: а) 6 х – 18;в) 0,5( х – 2) + 1,5 х < х + 1. б) – 4 х > 36; 2.Решите систему неравенств: 3.При каких значениях переменной имеют смысл выражения : А) ? Б) ?

21


Всем СПАСИБО ЗА ВНИМАНИЕ !!!

22

Открытый урок по алгебре на тему:

«Неравенства с одной переменной»

8 класс

Цель урока: продолжить формирование умения решать неравенства с одной переменной путем перехода к равносильному неравенству

Планируемые образовательные результаты:

Предметные: знать понятия: «неравенство с переменной», «решение неравенства с переменной», «линейное неравенство», «равносильное неравенство», «равносильное преобразование неравенства», знать правила решения неравенств; уметь решать линейные неравенства и отображать множество его решений на координатной прямой.

Личностные: формирование ответственного отношения к успешной учебной деятельности.

Метапредметные:

регулятивные: уметь ставить цели, планировать свою деятельность, осуществлять самоконтроль и самооценку;

коммуникативные: уметь формулировать свои мысли на математическом уроке, организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками;

познавательные: уметь выполнять упражнения по правилу, алгоритму, формулировать правило по многократно повторенному алгоритму

Тип урока: урок открытия нового знания

Оборудование: компьютер, проектор, интерактивная доска, презентация к уроку, раздаточный материал

Ход урока.

1. Самоопределение к деятельности (организационный момент)

Учитель проверяет готовность класса, приветствует детей, высказывает добрые пожелания детям; предлагает пожелать друг другу удачи, озвучивает эпиграф к уроку:

«Математика учит преодолевать трудности и исправлять собственные ошибки» (Декарт)

Учитель сообщает о раздаточном материале: Оценочный лист, карточки для графического диктанта

Предлагает проверить домашнюю работу с соседом по парте. Обучающиеся проверяют работу, исправляют ошибки (если есть), обращаются к классу, если нет единства в решении.

2. Актуализация знаний и способов действий

Учитель предлагает выполнить графический диктант. До начала диктанта, если необходимо, то на нижней строчке карточки для графического диктанта пронумеровать номера вопросов от 1 до 10 (для удобства)

Графический диктант

Выясните, верны ли утверждения. Если утверждение верное, то заполните клеточку так

, если же утверждение неверное, то так .

Главное требование: каждый следующий ответ должен начинаться в клетке так, чтобы в результате получился именно непрерывный графический рисунок.

1. Верно ли утверждение, что если x 5 и y -3, то x+y 2?

2. Является ли неравенство 2х – 15 4х + 7 строгим?

3. Принадлежит ли отрезку [- 6; — 2] число -6,5?

4. Является ли число -5 решением неравенства 4+2х 0?

5. Верно ли, что решением неравенства 5х – 1 24 является x Î (5; +¥)?

6. Верно ли, что решением неравенства 3х £ 5 является x Î (- ¥; 2]?

7. Изображением решения неравенства 5х 30 служит ?

8. Верно ли, что неравенству x 3,2 соответствует открытый числовой луч

(3,2; +¥) ?

1. Существует ли целое число, принадлежащее отрезку [-3,9; -3,5]?

2. При любом ли значении переменной a верно неравенство а² +2 0?

Один из учеников выходит к доске и изображает получивший графический рисунок

Правильный ответ

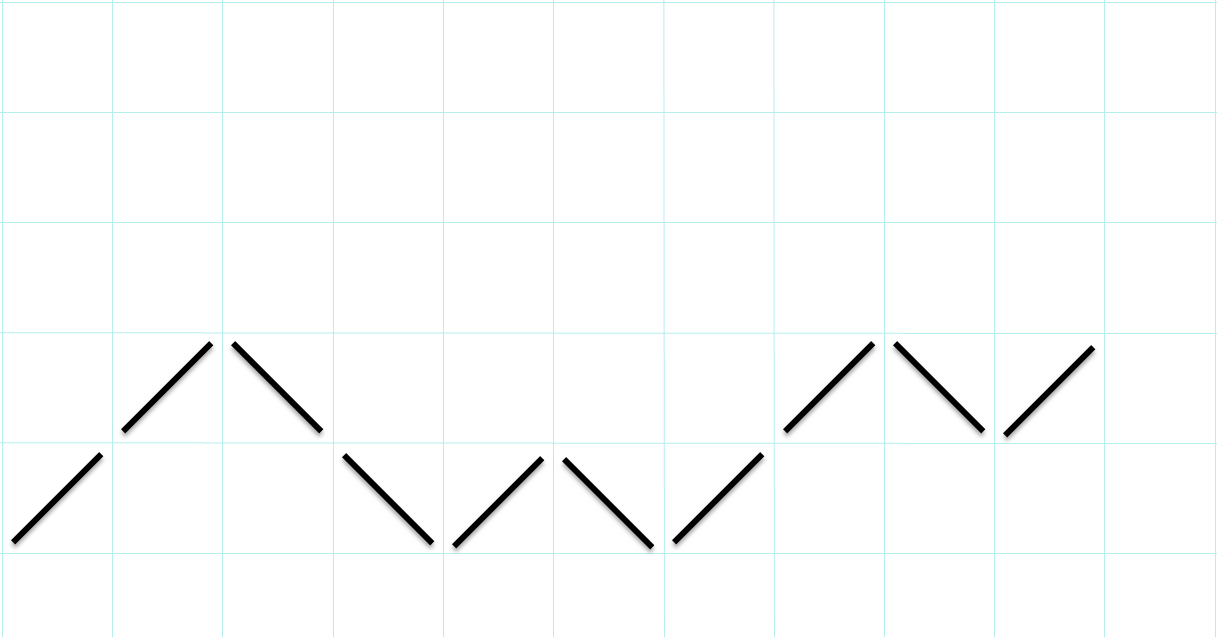
Учитель просит обучающихся посчитать количество верных ответов в выполненном графическом диктанте и занести набранное количество баллов в свой оценочный лист (за каждый правильный ответ – 0,5 балла)

Учитель предлагает выполнить задания устного характера, за каждый правильный ответ обучающиеся получают 1 балл.

Устный счет

• Укажите все целые числа, принадлежащие полуинтервалу [-5; 3) (-5; -4; -3; -2; -1; 0; 1; 2)

• Укажите какое-либо число из интервала (-5,6 ; -5,1)

• Принадлежит ли отрезку [-2; 15] число 14,99? (да)

• Укажите наименьшее целое число, являющееся решением неравенства 8 – 2х (5)

• Является ли число — 5,2 решением неравенства -3х+5 ≤ — 4 ? (нет)

• При каких значениях х выражение 2х – 1 принимает положительные значения? (при x 0,5)

Найди ошибку

1. Х Ответ: (-∞;9]

2. y ≤ 5,5 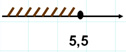Ответ: [-∞;5,5]

3. n -2 Ответ: (-∞;-2]

4. k ≤ -2,1 Ответ: (-∞; -2,1)

3. Определение и поставка учебных задач

В тетрадях записывают дату, классная работа.

На интерактивной доске появляется задание

Решить неравенство

4(2 — 5х) – 3(4 + х) 18 – х

Что это за неравенство?

Чем неравенство отличается от тех, что вы умеете решать?

Учитель предлагает определить тему урока

Озвучивают и записывают тему урока «Решение неравенств с одной переменной»

Предлагает определить цель урока

Цель: продолжить формирование умения решать неравенства с одной переменной путем перехода к равносильному неравенству

4. Усовершенствование знаний, умений

Вопросы

– Дайте определение решения неравенства с одной переменной.
– Что значит «решить неравенство»?
– Какие неравенства называются равносильными?
– Сформулируйте свойства равносильности неравенств, используемые при решении     неравенства с одной переменной.

Учитель возвращает к неравенству, предлагает составить устно алгоритм решения и решить на доске (один ученик у доски, остальные в тетрадях). Ученик у доски и досрочно выполнившие в тетради ученики получают баллы (максимальное 3)

4(2 — 5х) – 3(4 + х) 18 – х

8 — 20х – 12 – 3x 18 – х

— 20х – 3x + x 18 – 8 +12

— 22х 22

х -1

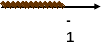
Ответ: х Î (- ¥; -1)

Разминка Игра в домино (на каждую парту выдаются карточки с домино, для удобства проверки учителем карточки цветные)

В парах обучающиеся составляют верную игру, учитель проверяет, выставляет баллы (максимальный 3 балла)

5. Физкультминутка, включающая специальную гимнастику для

глаз.

Цель: снятие зрительного утомления.

1 Вертикальные движения глаз вверх-вниз.

2 Горизонтальное вправо-влево.

3 Вращение глазами по часовой стрелке и против.

4 Закрыть глаза и представить по очереди цвета радуги как можно

отчётливее.

5 Глазами« нарисовать» 8 и знак бесконечности несколько раз, сначала в одном, а затем в другомнаправлении.

Учитель предлагает решить тринадцатое задание ОГЭ (самостоятельно)

Решите неравенство: 6х-2(2х+9) 6x-4x-18x-18 2x 2x x

Варианты (ответа) 1.[-8,5;+∞) 2.[9,5; ∞) 3.(-∞;9,5) 4.(-∞;-8,5] Ответ: 3

За первый правильный ответ обучающийся получает 3 балла

5.Исторические сведения о неравенствах

Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи со счётом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки. Архимед, занимаясь вычислением длины окружности, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых». Иначе говоря, Архимед указал границы числа π:

Ряд неравенств приводит в своём знаменитом трактате «Начала» Евклид. Он, например, доказывает, что среднее геометрическое двух положительных чисел не больше их среднего арифметического, т. е. что верно неравенство

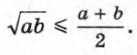
В «Математическом собрании» Паппа Александрийского (III в.) доказывается, что для положительных чисел а, b, с и d

Однако все эти рассуждения проводили словесно, опираясь в большинстве случаев на геометрическую терминологию. Современные знаки неравенств появились лишь в XVII—XVIII вв. Знаки ввёл английский математик Т. Гарриот (1560—1621), знаки ≤ и ≥ — французский математик П. Буге (1698—1758).

6. Подведение итогов урока. Рефлексия

В качестве рефлексии учитель предлагает составить синквейн к уроку (на обратной стороне оценочных листов)

«Синквейн»

 Это способ творческой рефлексии, который позволяет в художественной форме оценить изученное понятие, процесс или явление. В данном случае информация не только более активно воспринимается, но и систематизируется, и оценивается. Слово происходит от французского “5”. Это стихотворение из 5 строк, которое строится по правилам:

1 строка – тема или предмет (одно существительное);
2 строка – описание предмета (два прилагательных);
3 строка – описание действия (три глагола);
4 строка – фраза, выражающая отношение к предмету;
5 строка – синоним, обобщающий или расширяющий смысл темы или предмета (одно слово).

Обучающиеся по желанию могут зачитать свой синквейн классу.

Обучающиеся подсчитывают полученное количество баллов на оценочных листах, переводят в оценки. Сдают оценочные листы учителю для выставления оценок в журнал.

6. Постановка домашнего задания

• Повторить правила решения неравенств

• № 842 (а,б),  № 843 (б),  № 845, № 847 (в, г),

Список использованной литературы:

1. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова «Алгебра. 8 класс». учебник для общеобразовательных учреждений, под ред. С.А. Теляковского. –– М.: Просвещение, 2014 г.

2. Алгебра 8 класс. Задания для обучения и развития учащихся. Учебное пособие / Лебединцева Е.А., Беленкова Е.Ю. – М.: Интеллект-Центр, 2013 г.

3. Брадис В.М., Минковский В.Л., Харчева А.К. Ошибки в математических рассуждениях. Москва: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959.

4. Открытый банк заданий ФИПИ (http://oge.fipi.ru/)

Оценочный лист

Учени _________________________________________

«5» — 15 баллов и выше

«4» — 11 — 14 баллов

«3» — 7-10 баллов

№	Вид работы	Количество баллов
1.	Графический диктант
2.	Устный счет
3.	Домино
4.	Решение упражнений
5.	Работа в группе

«Синквейн»

 Это способ творческой рефлексии, который позволяет в художественной форме оценить изученное понятие, процесс или явление. В данном случае информация не только более активно воспринимается, но и систематизируется, и оценивается. Слово происходит от французского «5”. Это стихотворение из 5 строк, которое строится по правилам:

1 строка – тема или предмет (одно существительное);
2 строка – описание предмета (два прилагательных);
3 строка – описание действия (три глагола);
4 строка – фраза, выражающая отношение к предмету;
5 строка – синоним, обобщающий или расширяющий смысл темы или предмета (одно слово).

Графический диктант

Схема конспекта урока по математике на тему «Решение линейных неравенств с одной переменной
и их систем»

Учитель математики
МБОУ СОШ № 1 Григорьева Татьяна Викторовна.

Предмет: алгебра

Класс: 8 «в»

Цели урока:

Образовательные:

1.Повторить и обобщить знания учащихся по теме «Неравенства с одной
переменной и их системы».

2.Продолжить формирование умений работать по алгоритму.

Развивающие:

1.Развивать математические
мышление и речь.

2.Совершенствовать навыки
в решении линейных неравенств.    

Воспитательные:

1.Воспитывать интерес
к учёбе, дисциплинированность и ответственность в выполнении домашних заданий.

Задачи урока:

1.Закрепить
полученные умения и навыки при решении неравенств с одной переменной и их
систем;

2.Подготовить
учеников к контрольной работе по данной теме.

   «Математика учит преодолевать
трудности и исправлять собственные ошибки»     ( Декарт).

№ п/п	Этапы работы	Цели и задачи этапа	Содержание этапа
1.	Организационный момент: Методы обучения: частично-поисковый. Форма организации работы: фронтальная.	Цель: обеспечить нормальную внешнюю обстановку для работы на уроке, психологически подготовить учащихся к общению и предстоящему занятию. Задачи: Доброжелательный настрой учителя и  учащихся. Готовность класса и оборудования к уроку. Быстрое включение класса в деловой ритм. Определение целей и задач урока.	Взаимное приветствия учителя и учащихся, фиксация отсутствующих, проверка подготовленности учащихся к уроку, организация внимания и внутренней готовности. Слайд 2 Слайд 3
2.	Опрос учащихся по заданному на дом материалу: Методы: словесно- наглядный, самоконтроль, устный контроль. Форма организации работы: фронтальная.	Цель: Глубоко и всесторонне проверить знания учащихся, выявить причины появления обнаруженных пробелов в знаниях и умениях. Задачи: Установление правильности и осознанности выполнения домашнего задания всеми учащимися, устранение в ходе проверки обнаруженных пробелов.	Учитель делает акцент на ключевые моменты домашнего задания, разбирает с учениками наиболее трудный пример на доске, отвечает на вопросы  обучающихся. Обучающиеся осуществляют самопроверку домашнего задания, сверяя решения с образцами на доске, вносят дополнения и исправления. Слайд 4
3.	Обобщения и систематизации изученного материала. а) тестирование; б) дополнительные вопросы; с) устная работа. Методы: частично-поисковый, взаимоконтроль. Форма организации работы: парная, фронтальная.	Цель: Формирование навыка и умения решения неравенств с одной переменной и их систем. Задачи: обеспечить понимание, осмысления и применения свойств, применяемых при решении неравенств с одной переменной и их систем.	Слайд 5 А) Для повторения и понимания темы, проводится тестирование с последующей проверкой. Каждое задание теста предполагает ответ «Да» или «Нет».                      «Да» -1                       «Нет» — 0. В результате выполнения теста получится какое-то число. Слайд 6 №1     Вопросы теста: 1) Является ли число 14 решением неравенства 2х>10? 2) Является ли число -7 решением неравенства 4х>12? 3) Является ли неравенство                    5х-18>4х+11 строгим? 4) Существует ли целое число  принадлежащее промежутку                           [-2,7;-2,4]? 5) При любом ли значении переменной а верно неравенство                                    а² +6>о? 6) Верно ли, что при умножении или делении обеих частей  неравенства на отрицательное число знак неравенства не меняется? Назовите число, которое у вас получилось? Давайте проверим ответ. Слайд 7  1010101. Слайд 8 Б)  Дополнительные вопросы В ходе проверки теста можно задать вопросы по теории темы: 1.Что значит решить неравенство? 2.Что называется решением неравенства? 3.Какие неравенства называются равносильными?  4.Сформулируйте свойства неравенств используемые  при решении и доказательстве неравенств и их систем? 5.Что называется решением системы неравенств? 6.Что значит решить систему неравенств? №2 Устная работа А)  «Найди ошибку!»  Слайд  9 Б) Неравенству х ≥ 15   соответствует числовой промежуток •      1)  (– ¥; 15) •      2)  [15; +¥)    !!!!!! •      3)  (– ¥; 15] •      4)  (15;+¥) Слайд  10 Повторение:    Решение неравенств с одной переменной. Работа у доски.  Слайд  11 1)Решите двойное неравенство: — 3 < х-9 < 5 2) При каких значениях х имеет смысл выражение: 3) Решите двойное неравенство — 6 < 3х < 12 и укажите наибольшее инаименьшее целое число, которое является  его решением. Повторение: Решение систем неравенств с одной переменной. Работа у доски.  Слайд  12 — 13. Решить системы 1.  Варианты ответов: :                             а)  (-∞; ⅓ )      б)   ( ⅓ ; +∞)                                     в)  (-0,6; ⅓ )    г) (-0,6; +∞)             2.      Варианты ответов:                              а)  (-∞;1)      б)  (1; +∞)                                               в)  [-1;  +∞)   г) (-∞;-1] Найдите количество целых чисел, являющихся  решениями систем: 3. Варианты ответов:    а) 7    б) 8   в) 6    г) 9 4.                      Варианты ответов: а) 3   б) 5   в) 4   г) 6
4.	Физкультминутка	Цель: путём несложных физических упражнений снять усталость и напряжение у учеников. Задача: повысить эффективность усвоения учебного материала.
5.	Самостоятельная работа (взаимопроверка)	Цель: проверить качество сформированности навыков в решении линейных неравенств с одной переменной и их систем. Задача: применить знания и умения при решении линейных неравенств с одной переменной и их систем.	Слайд  14 1)Решите неравенство: а) 4 +12х > 7+13х;         б) 7-4х < 6х-23; 2)Решите системы неравенств:   3) Найдите количество целых чисел, являющихся решениями системы                 3-2а ≤ 13,  2.    12a-36 > 0,     1.                 5a < 15             6a  ≤ 48 Взаимопроверка. Слайд 15 Учащиеся сдают работы, предварительно выписав ответы, которые проверяются по окончанию работы или на перемене.
6.	Методы: коммуникативный, рефлексия, и поощрение. Задание на дом. Методы: самостоятельная работа учащихся , проблемно-поисковый. Форма организации работы: индивидуальная.	Цель: подвести итог урока, отметить наиболее активных учеников, выставить оценки. Задачи: провести анализ и дать оценку в достижении поставленных целей. Цели: дать ученикам домашнее задание, разъяснить порядок его выполнения. Задачи: закрепить изученный материал, осуществить контроль уровня его усвоения и полученных навыков  обучающимися по данной теме.	Итог урока. Обобщить теоретические сведения, полученные на уроке. Узнать мнение учеников о трудностях в изучении данной темы. Выставить отметки. Слайд 16 Домашнее задание (задается в виде домашней контрольной работы).

Опубликовано:

• Брук И.И. Высказывания о математике//Математика: учебно-методическая газета.-2007.-16-28 фев (№4)-с.6.
• Брук И.И. Математика. Электронный информационный спутник газеты «Математика», №10 от 1-28 февраля 2007 года, с.6. Скачать можно здесь.

 Десятки лет, а я работаю в школе уже 38 лет, меня спрашивали: зачем нужна математика? Считаю, будет полезна коллегам публикация моих максим о математике.

• Математика начинается с осмысления слов.
• При занятиях математикой человек играет и ум свой развивает.
• Математика учит умению объяснять последовательнее, проще, яснее, доступнее себе и другим.
• Математика делает людей умнее.
• Через математику человек учится умению создавать понятия, создавать новые знания.
• Математика помогает лучше разбираться в жизни.
• Через математику человек учится отличать верное от неверного, ясное от неясного.
• Математика учит преодолевать трудности и исправлять собственные ошибки.
• Многие дети и их родители только для школы занимаются математикой и думают, что математика в дальнейшей жизни нужна только для счета, а не для образования своих умственных способностей.
• Математика учит ориентироваться в пространстве знаний.
• Математика учит умению предвидеть.

Девиз урока

Опубликовано 14 Сентябрь 2013