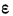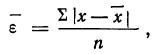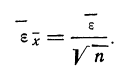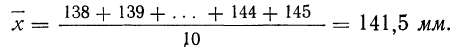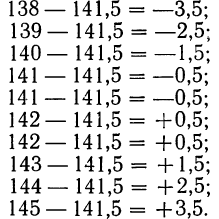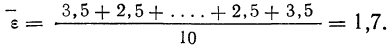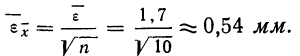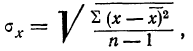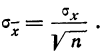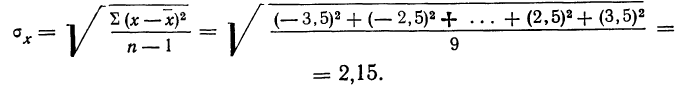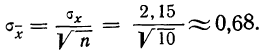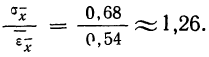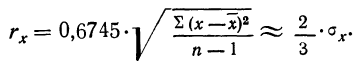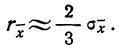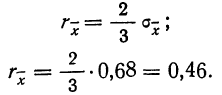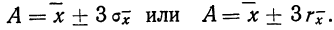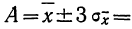Ошибкой результата измерения
называется разность между результатом измерения и точным (истинным) значением измеряемой величины, т.е.
где ∆ – ошибка измерения (иcтинная ошибка); l – результат измерения;
x – точное значение величины.

Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
В соответствии с источниками возникновения различают ошибки:
1)приборов;
2)внешние;
3)личные;
4)объекта;
5)метода измерений.
Приведенная классификация ошибок по источникам возникновения имеет большое значение при изучении приборов и методов

В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и
случайные.
Грубые ошибки (промахи) вызываются невнима-тельностью наблюдателя или неисправностью прибора. Они превосходят по абсолютной величине некоторый предел, установленный для данных условий измерений.
Измерения, содержащие грубые ошибки, бракуются и заменяются новыми. Для выявления грубых ошибок производятся

Систематические ошибки подразделяются на
постоянные, переменные и односторонне
действующие.
Постоянные систематические ошибки при измерении одной и той же величины несколько раз, всякий раз появляются с одним знаком и одинаковые по величине. Например, ошибки за счет неточного центрирования теодолита при измерении углов несколькими приемами будут одинаковыми в каждом приеме.
Переменные систематические ошибки меняются от приема к приему, следуя определённому закону. Например, ошибки в направлениях, обусловленные эксцентриситетом алидады, или ошибками нанесения штрихов лимба теодолита.
Односторонне действующие систематические
ошибки изменяются случайным образом, но сохраняют знак. Например, ошибка в длине

Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.

Случайные ошибки основного типа обладают следующими вероятными свойствами:
1.По абсолютной величине ошибки не превосходят некоторого предела.
2.Положительные и отрицательные ошибки, равные по абсолютной величине, имеют равные вероятности, т.е. встречаются одинаково часто.
З. Чем больше ошибка по абсолютной величине,
тем меньше ее вероятность появления.
4. Среднее арифметическое из значений
случайных ошибок при неограниченном возрастании числа измерений одной и той же величины имеет пределом нуль, т. е.
|
математическое ожидание ошибки равно нулю |
|||||
|
вер . lim |
[ ] |
0 |
. |
||
|
n |
n |

4. Понятие о законах распределения ошибок.
Свойства случайных ошибок являются проявлением закона их распределения.
В общем случае закон распределения ошибок отражает связь между размером ошибки и вероятностью ее появления.
P = f(Δ)d ,
(2)
где Р∆ – вероятность появления ошибки в интервале (∆, ∆+d∆); ∆ – случайная ошибка;
f(∆) – плотность распределения ошибок.

Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Плотность нормального распределения выражается формулой
|
1 |
e |
2 |
||||
|
(3) |
f ( ) |
2 2 |
||||
|
2 |
||||||
где σ – среднее квадратическое отклонение случайной ошибки.
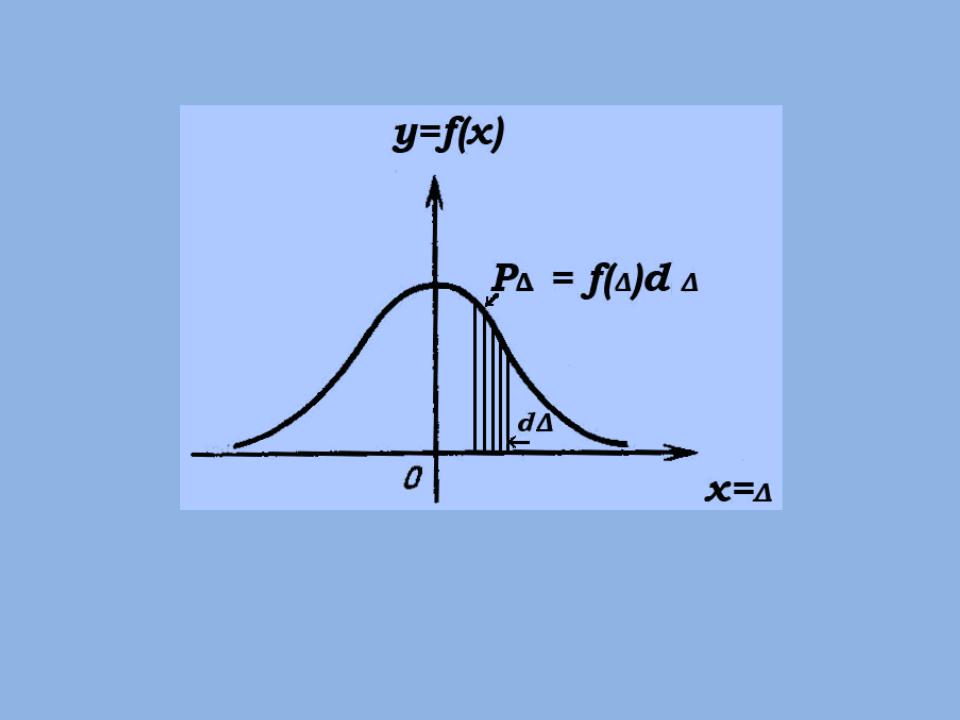
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
Рис. 3. Кривая нормального распределения.
Эта кривая имеет симметричную колоколообразную форму. Заштрихованная площадь представляет собой вероятность
появления ошибки в интервале от ∆ до ∆+d∆.

Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
f ( ) 21 , (4)
где α – наибольшее значение ошибки.
Соседние файлы в папке лекции по геодезии 2 курс
- #
- #
- #
29.02.20162.28 Mб32ЛЕКЦИЯ 13.pptx
- #
- #
- #
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 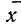
За меру точности соответствия принятой средней арифметической 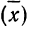
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 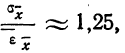
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 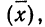
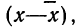
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 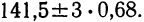
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
Математическое ожидание — ошибка
Cтраница 1
Математическое ожидание ошибки называется систематической ошибкой, ее среднее квадратическое отклонение — среднеквадра-тической ошибкой. Анализ качества систем управления сводится к определению указанных ошибок по вероятностным характеристикам случайных внешних воздействий.
[2]
Математическое ожидание ошибки слежения равно ее среднеарифметическому значению.
[3]
Система имеет математическое ожидание ошибки тст 0 и центрированную составляющую С, подчиненную нормальному закону распределения.
[4]
Известно, что математическое ожидание ошибки уменьшается с увеличением частоты замеров и с уменьшением скорости линейного изменения коэффициентом.
[5]
В этом случае математическое ожидание ошибки равно нулю.
[6]
Учитывая, что при усечении математическое ожидание ошибки квантования отлично от нуля, более целесообразно использовать округление.
[7]
При совпадении ПФ с видом г математическое ожидание ошибки прогноза будет равно нулю.
[9]
Получаемые вероятностные оценки поступают на сумматор 2, который определяет величину математического ожидания ошибок Мп для каждой из сравниваемых кодовых комбинаций.
[10]
Формулы (5.5.12) и (5.5.14) характеризуют собой общие выражения соответственно корреляционной функции и математического ожидания ошибки положения для партии механизмов.
[11]
При приеме в целом принятая кодовая комбинация будет ошибочной, если при математическом ожидании ошибок на ее длине Мл Мп mln и зафиксированное значение кодовой комбинации содержит любые варианты ошибок.
[12]
Согласно соотношению ( 11) каждому из возможных состояний канала связи соответствует случайная величина математического ожидания ошибок Мс, которая через финальные вероятности состояний принятой модели может указать на наличие того или иного состояния с некоторой вероятностью правдоподобия рс.
[13]
Чтобы упростить сравнение указанных методов, будем полагать, что первичные параметры взаимонезависимы, а математическое ожидание ошибок ( допусков) равно нулю.
[14]
Функция потерь) в общем случае является функционалом от выходных сигналов объекта и модели или от математического ожидания ошибок оценок параметров.
[15]
Страницы:
1
2
Содержание ▲
- ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК… - СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В.…
- Задачи теории ошибок измерений.
Задачи теории… - 1. Задачи теории ошибок измерений.…
- Теория ошибок измерений решает
Теория ошибок… - 2. Сущность и виды измерений.
Измерения…
- Непосредственными или прямыми называ-ются…
- Под равноточными понимают измерения, полученные…
- Необходимыми считаются измерения, которые…
- Зависимыми называют измерения, имеющие некоторые…
- 3. Ошибки измерений, их классификация и…
- Причинами возникновения ошибок являются…
- В теории ошибок более важное значение имеет…
- Систематические ошибки подразделяются на…
- Случайными называются ошибки, которые не связаны…
- Случайные ошибки основного типа обладают…
- 4. Понятие о законах распределения ошибок.
4.… - Распределение случайных ошибок измерений наиболее…
- График функции (3) называется кривой нормального…
- Есть ошибки, которые подчиняются закону…
- Основными характеристиками распределения…
- Для непрерывной случайной величины с плотностью…
- Дисперсией случайной величины Х называ-ется…
- Положительное значение квадратного корня из…
- Для случайных ошибок измерений, как уже…
- 5.Числовые характеристики точности измерений.…
- При большом значении n
При большом значении… - Оценку точности измерений характеризуют также…
- Обычно для τ принимают значения 3, 2.5, или 2.…
- При нормальном распределении средняя ошибка v…
-
СПАСИБО ЗА ВНИМАНИЕ.
… - Скачать
- Похожие презентации
Вы можете ознакомиться и скачать презентацию на
тему ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ.
Доклад-сообщение содержит 31 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
ТЕМА ЛЕКЦИИ:
«ОБЩИЕ ПОНЯТИЯ ТЕОРИИ ОШИБОК ИЗМЕРЕНИЙ»
Слайд 2
Описание слайда:
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Маслов А.В. Геодезия: учеб. и уч. пособие для вузов/ А.В. Маслов, А.В. Гордеев, Ю.Г. Батраков: – М.: Колос, 2006. – 598 с.
Маслов А.В. Геодезические работы при землеустройстве: учеб. пособие для вузов / А.В. Маслов, А.Г. Юнусов, Г.И. Горохов 2-е изд., перераб. и доп. — М.: Недра, 1990. – 215 с. .
Неумывакин Ю.К. Геодезическое обеспечение землеустроительных и кадастровых работ: справ. пособие/ Ю.К.Неумывакин, М.И. Перский: – М.: «Картгеоцентр» — «Геодезиздат», 1996. – 344 с.
Геодезия: учеб.-метод. комплекс / БГСХА; сост. С.И. Помелов, Д.А. Чиж. – Горки, 2006. – 256 с.
Практикум по геодезии / Под ред.Бакановой В.В. – М.: Недра, 1989 .
Слайд 3
Описание слайда:
Задачи теории ошибок измерений.
Задачи теории ошибок измерений.
Сущность и виды измерений.
Ошибки измерений, их классификация и свойства.
Понятие о законах распределения ошибок.
Числовые характеристики точности измерений.
Слайд 4
Описание слайда:
1. Задачи теории ошибок измерений.
Геодезические работы связаны с различными методами измерений длин линий, углов, превышений, площадей и пр. Любые измерения, как бы тщательно они не выполнялись, сопровождаются неизбежными ошибками (погрешностями) поэтому измеренные значения величин будут отклоняться от истинных.
На практике измерения выполняют так, чтобы получить результаты с некоторой заданной точностью. Для обоснования необходимой и достаточной точности измерений надо знать причины возникновения ошибок измерений и их свойства. Эти вопросы рассматриваются в теории ошибок измерений, которая в свою очередь основывается на теории вероятностей и математической статистики.
Слайд 5
Описание слайда:
Теория ошибок измерений решает
Теория ошибок измерений решает
четыре основные задачи:
1. Изучение законов возникновения и распределения ошибок измерений и вычислений.
2. Оценка точности результатов измерений и их функций.
З. Отыскание наиболее надёжного значения определяемой величины и характеристики точности.
4. Установление допусков, ограничивающих использование результатов измерений в заданных пределах точности, т. е. критериев указывающих на наличие грубых ошибок.
Слайд 6
Описание слайда:
2. Сущность и виды измерений.
Измерения различают на непосредственные (прямые), посредственные (косвенные), равноточные, неравноточные, необходимые, дополнительные (избыточные), зависимые и независимые.
Под измерением данной физической величины понимается процесс сравнения ее с другой физической величиной того же рода, принятой за единицу измерения.
Полученное именованное число называется результатом измерения.
Слайд 7
Описание слайда:
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Непосредственными или прямыми называ-ются измерения, при которых измеряемая величина непосредственно сравнивается с единицей меры.
Например, измерения линий лентой, углов транспортиром и т.д.
Посредственными или косвенными называются измерения, когда искомая величина находится путем измерения других величин.
Например, определение неприступных расстояний.
Слайд 8
Описание слайда:
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Под равноточными понимают измерения, полученные одним и тем же прибором (или различными приборами одного класса точности), одним и тем же или равноценны-ми методами, одинаковым числом приемов и в одинаковых условиях.
Пример: измерения углов теодолитами одинаковой точности.
Если указанные условия не соблюдаются, то результаты измерений будут неравноточ-ными. Например, измерение углов теодо-литами разной точности или одним теодо-литом, но разным числом приемов.
Слайд 9
Описание слайда:
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Необходимыми считаются измерения, которые позволяют получить искомую величину только один раз.
Если одна величина измерена n-раз, то одно измерение будет необходимым, а остальные n–1 — избыточными.
Например, для определения всех сторон и углов в треугольнике необходимо знать не менее трех его элементов, в т.ч. хотя бы одну сторону. Если измерены все углы и стороны, то три величины будут избыточными.
Избыточные измерения нужны для контроля и повышения точности определения искомых величин, а также оценки точности искомых величин.
Слайд 10
Описание слайда:
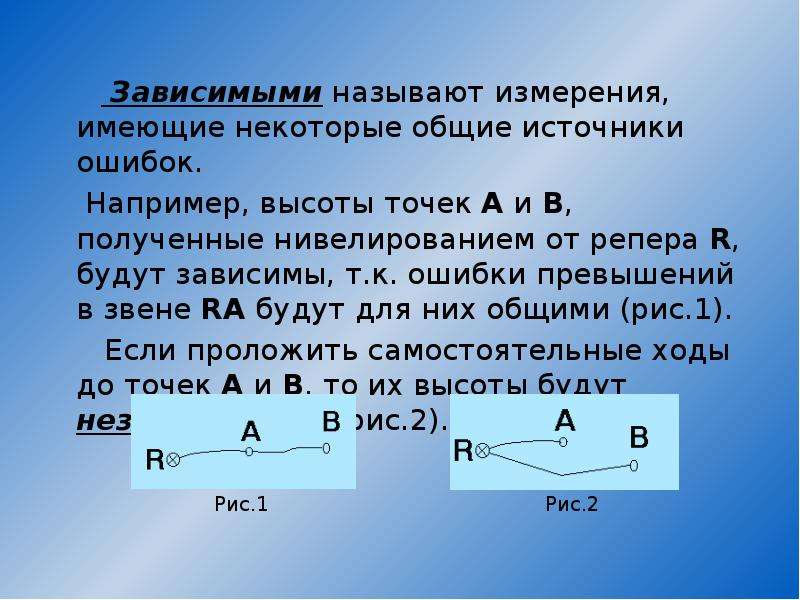
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Зависимыми называют измерения, имеющие некоторые общие источники ошибок.
Например, высоты точек А и В, полученные нивелированием от репера R, будут зависимы, т.к. ошибки превышений в звене RA будут для них общими (рис.1).
Если проложить самостоятельные ходы до точек А и В, то их высоты будут независимыми (рис.2).
Слайд 11
Описание слайда:
3. Ошибки измерений, их классификация и свойства.
Ошибкой результата измерения называется разность между результатом измерения и точным (истинным) значением измеряемой величины, т.е.
∆= l–x, (1)
где ∆ – ошибка измерения (иcтинная ошибка);
l – результат измерения;
x – точное значение величины.
Слайд 12
Описание слайда:
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
Причинами возникновения ошибок являются неточности в изготовлении и юстировке приборов, влияние внешних условий, неточности выполнения операций наблюдателем, изменения самого объекта измерения и несовершенство метода измерений.
В соответствии с источниками возникновения различают ошибки:
1) приборов;
2) внешние;
3) личные;
4) объекта;
5) метода измерений.
Приведенная классификация ошибок по источникам возникновения имеет большое значение при изучении приборов и методов измерений.
Слайд 13
Описание слайда:
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
В теории ошибок более важное значение имеет классификация ошибок по закономерностям их появления. По характеру действия на конечный результат ошибки делятся на грубые, систематические и случайные.
Грубые ошибки (промахи) вызываются невнима-тельностью наблюдателя или неисправностью прибора. Они превосходят по абсолютной величине некоторый предел, установленный для данных условий измерений.
Измерения, содержащие грубые ошибки, бракуются и заменяются новыми. Для выявления грубых ошибок производятся избыточные измерения (линии измеряют дважды, в треугольнике измеряют все три угла и т. п.).
Слайд 14
Описание слайда:
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Систематические ошибки подразделяются на постоянные, переменные и односторонне действующие.
Постоянные систематические ошибки при измерении одной и той же величины несколько раз, всякий раз появляются с одним знаком и одинаковые по величине. Например, ошибки за счет неточного центрирования теодолита при измерении углов несколькими приемами будут одинаковыми в каждом приеме.
Переменные систематические ошибки меняются от приема к приему, следуя определённому закону. Например, ошибки в направлениях, обусловленные эксцентриситетом алидады, или ошибками нанесения штрихов лимба теодолита.
Односторонне действующие систематические ошибки изменяются случайным образом, но сохраняют знак. Например, ошибка в длине линии из-за отклонения мерной ленты от створа.
Слайд 15
Описание слайда:
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Случайными называются ошибки, которые не связаны функциональной зависимостью с какими-либо факторами. Ни величину, ни знак случайной ошибки заранее предсказать нельзя. В последовательности появления ошибок тоже нет никакой закономерности. Однако, если рассматривать их в большом количестве, то выявляются определенные статистические закономерности.
Слайд 16
Описание слайда:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
Случайные ошибки основного типа обладают следующими вероятными свойствами:
1. По абсолютной величине ошибки не превосходят некоторого предела.
2. Положительные и отрицательные ошибки, равные по абсолютной величине, имеют равные вероятности, т.е. встречаются одинаково часто.
З. Чем больше ошибка по абсолютной величине, тем меньше ее вероятность появления.
4. Среднее арифметическое из значений случайных ошибок при неограниченном возрастании числа измерений одной и той же величины имеет пределом нуль, т. е. математическое ожидание ошибки равно нулю
.
Слайд 17
Описание слайда:
4. Понятие о законах распределения ошибок.
4. Понятие о законах распределения ошибок.
Свойства случайных ошибок являются проявлением закона их распределения.
В общем случае закон распределения ошибок отражает связь между размером ошибки и вероятностью ее появления.
PΔ= f(Δ)dΔ, (2)
где Р∆ – вероятность появления ошибки в интервале (∆, ∆+d∆);
∆ – случайная ошибка;
f(∆) – плотность распределения ошибок.
Слайд 18
Описание слайда:
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Распределение случайных ошибок измерений наиболее точно описывается законом нормального распределения.
Плотность нормального распределения выражается формулой
(3)
где σ – среднее квадратическое отклонение случайной ошибки.
Слайд 19
Описание слайда:
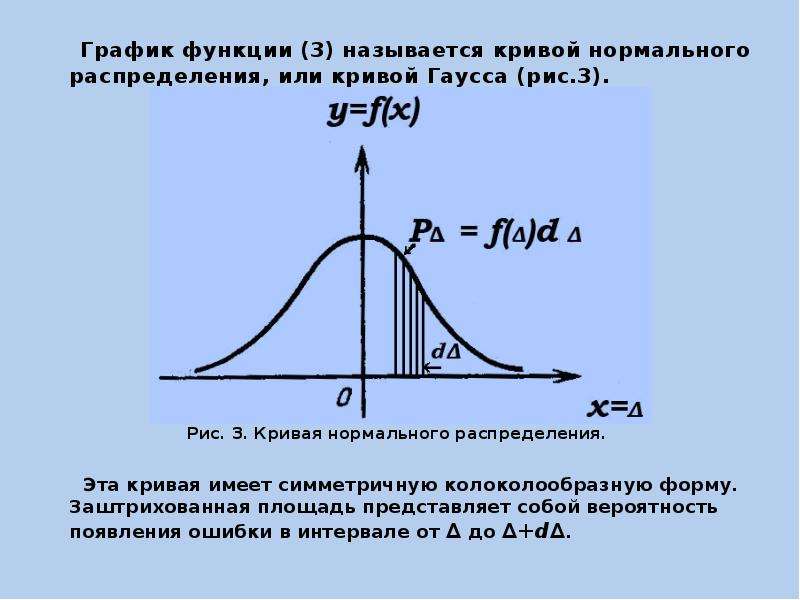
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
График функции (3) называется кривой нормального распределения, или кривой Гаусса (рис.3).
Рис. 3. Кривая нормального распределения.
Эта кривая имеет симметричную колоколообразную форму. Заштрихованная площадь представляет собой вероятность появления ошибки в интервале от ∆ до ∆+d∆.
Слайд 20
Описание слайда:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
Есть ошибки, которые подчиняются закону равномерного или равновероятного распределения, к примеру, ошибки округления. Плотность распределения их выражается формулой:
(4)
где α – наибольшее значение ошибки.
Слайд 21
Описание слайда:
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Основными характеристиками распределения случайной величины являются математическое ожидание и дисперсия.
Математическим ожиданием дискретной случайной величины х называют сумму произведений всех возможных значений случайной величины на соответствующие им вероятности р
. (5)
Слайд 22
Описание слайда:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
Для непрерывной случайной величины с плотностью распределения f(x) матема-тическое ожидание определяется по формуле:
. (6)
Слайд 23
Описание слайда:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
Дисперсией случайной величины Х называ-ется число, определяемое по формуле:
. (7)
Слайд 24
Описание слайда:
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
Положительное значение квадратного корня из дисперсии называют стандартом или средним квадратическим отклонением
. (8)
Слайд 25
Описание слайда:
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
Для случайных ошибок измерений, как уже отмечалось, математическое ожидание равно нулю =0. Поэтому
, (9)
или
(10)
при n стремящемуся к бесконечности.
Слайд 26
Описание слайда:
5.Числовые характеристики точности измерений.
В качестве теоретической характеристики точности измерений обычно пользуются средним квадратическим отклонением σ.
Поскольку величина σ не известна, практически пользуются ее приближенным значением – средней квадратической ошибкой (СКО), определяемой по формуле:
, (11)
где ∆1, ∆2, …, ∆n – истинные ошибки измерений.
Слайд 27
Описание слайда:
При большом значении n
При большом значении n
m ≈ σ. (12)
При ограниченном числе измерений величина m будет характеризовать величину σ с некоторой ошибкой. Для оценки точности определения самой средней квадратической ошибки существует формула:
(13)
Слайд 28
Описание слайда:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
Оценку точности измерений характеризуют также предельной ошибкой, вычисляемой по формуле:
∆пр= τm, (14)
где τ – коэффициент, значение которого прини-мают таким, чтобы была мала вероятность появления ошибки больше вероятной.
Слайд 29
Описание слайда:
Обычно для τ принимают значения 3, 2.5, или 2.
Обычно для τ принимают значения 3, 2.5, или 2.
В дальнейшем при решении задач по оценке точности измерений будем пользоваться формулой
∆пр= 3m.
Для оценки точности иногда пользуются средней ошибкой v и вероятной ошибкой r. Средняя ошибка вычисляется по формуле
(15)
Слайд 30
Описание слайда:
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
При нормальном распределении средняя ошибка v связана со средней квадратичеcкой ошибкой m примерным соотношением
(16)
Если все ошибки расположить в ряд по возрастанию абсолютных значений, то ошибка оказавшаяся в середине ряда будет вероятной. Со средней квадратической ошибкой она связана соотношением
(17)
Ошибка, выраженная в единицах измерения, называется абсолютной. Отношение ее к измеренной величине называется относительной ошибкой.
Слайд 31
Описание слайда:
СПАСИБО ЗА ВНИМАНИЕ.
30 ₽
Количество товара Вопрос №9 Если математическое ожидание ошибки равно нулю, то ее называют
Описание
Если математическое ожидание ошибки равно нулю, то ее называют
- Вариант №1: случайной
- Вариант №2: истинной
- Вариант №3: средней квадратической
- Вариант №4: систематической
- Вариант №5: предельной
Формат файла — JPG
Количество товара Вопрос №9 Если математическое ожидание ошибки равно нулю, то ее называют