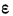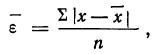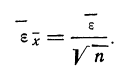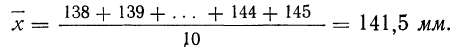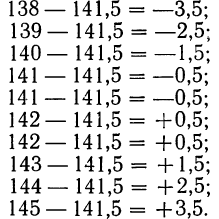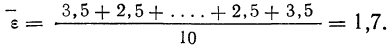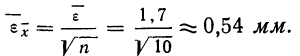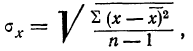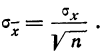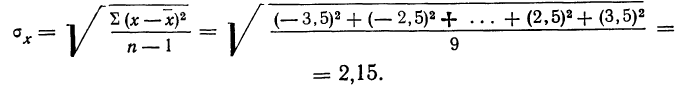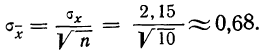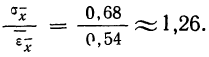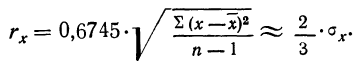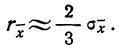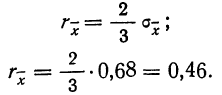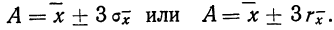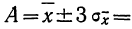11
ЛЕКЦИЯ 4.
Случайные
погрешности измерений и способы их
описания.
При выполнении
повторных измерений одной и той же
величины легко убедиться, что результаты
отдельных измерений отличаются друг
от друга. Это объясняется действием
случайных погрешностей. Случайные
погрешности вызываются большим числом
причин, действующих независимо друг от
друга. Их нельзя исключить опытным
путем, но их влияние на результат
измерения можно оценить, проведя ряд
наблюдений одной и той же величины.
Результат измерения всегда содержит
как систематическую С,
так и случайную погрешности, т.е.
,
поэтому погрешность результата измерения
в общем случае нужно рассматривать как
случайную величину. Тогда систематическая
погрешность есть математическое ожидание
этой величины, а случайная погрешность
– центрированная случайная величина.
Со статистических позиций можно дать
следующие определения составляющих
погрешности.
Систематическая
погрешность
– отклонение математического ожидания
mx
результатов
наблюдений от истинного значения А
измеряемой величины:
.
Случайная
погрешность
— разность между результатом единичного
наблюдения и математическим ожиданием
результатов:
.
Математическое
ожидание погрешности
равно математическому ожиданию
систематической составляющей погрешности,
так как математическое ожидание случайной
погрешности всегда равно нулю:
.
Законы распределения случайных величин
Полным описанием
случайной величины, а, следовательно,
и погрешности является ее закон
распределения. Этим законом распределения
и определяется характер появления
различных результатов отдельных
измерений в ряду наблюдений.
В практике
электрических измерений встречаются
различные законы распределения. Это
равномерное (прямоугольное) распределение,
нормальное распределение Гаусса,
распределение 2
(хи-квадрат), распределение t-Стьюдента
и др. Одним из наиболее распространенных
законов распределения погрешностей
является нормальный закон (Гаусса),
который базируется на центральной
предельной теореме теории вероятностей,
согласно которой нормальное распределение
плотности вероятности имеет сумма
бесконечно большого числа бесконечно
малых случайных возмущений с любыми
распределениями. Применительно к
измерениям это означает, что нормальное
распределение случайных погрешностей
возникает тогда, когда на результат
измерения действует множество случайных
возмущений и ни одно из которых не
является преобладающим. Практически,
суммарное воздействие даже сравнительно
небольшого числа возмущений приводит
к закону распределения результатов и
погрешностей измерений, близкому к
нормальному. Закон нормального
распределения имеет фундаментальное
значение для теории обработки результатов
измерений. Он позволяет вести расчеты
даже тогда, когда действительный закон
неизвестен.
Математически
нормальное распределение случайных
погрешностей может быть представлено
формулой
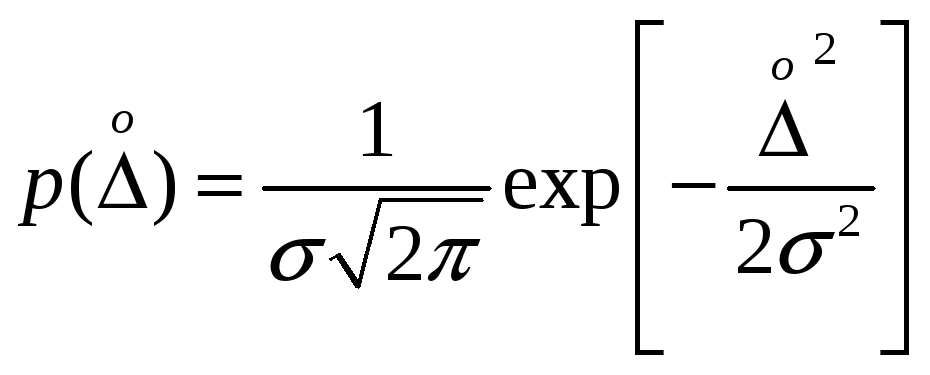
где p()
– плотность вероятности случайной
погрешности
;
s — среднее
квадратическое отклонение.

кривых, описываемых этим уравнением
для двух значений s
(),
показан на рис.4.1.
Из этих кривых
видно, что чем меньше s,
тем чаще встречаются малые случайные
погрешности, т.е. тем точнее выполнены
измерения. Кривые симметричны относительно
оси ординат, так как положительные и
отрицательные погрешности встречаются
одинаково часто.
Основные
характеристики законов распределения.
Основными
характеристиками являются математическое
ожидание и дисперсия.
Математическое
ожидание ряда наблюдений есть
величина, относительно которой
рассеиваются результаты отдельных
измерений. Если систематическая
погрешность отсутствует, и разброс
результатов отдельных измерений
обусловлен только случайной погрешностью,
то математическим ожиданием такого
ряда наблюдений будет истинное значение
измеряемой величины. Если же результаты
отдельных измерений кроме случайной
погрешности содержат постоянную
систематическую погрешность, то
математическое ожидание ряда наблюдений
будет смещено от истинного значения
измеряемой величины на значение
систематической погрешности.
Дисперсия D
ряда наблюдений характеризует степень
рассеивания (разброса) результатов
отдельных наблюдений вокруг математического
ожидания. Чем меньше дисперсия, тем
меньше разброс отдельных результатов,
тем точнее выполнены измерения.
Следовательно, дисперсия может служить
характеристикой точности проведенных
измерений. Однако, дисперсия выражается
в единицах в квадрате измеряемой
величины. Поэтому в качестве характеристики
точности ряда наблюдений наиболее часто
применяют среднее квадратическое
отклонение результата наблюдения (СКО)
s,
равное корню квадратному из дисперсии
с положительным знаком и выражаемое в
единицах измеряемой величины. Среднее
квадратическое отклонение, отнесенное
к значению измеряемой величины, может
быть выражено в относительных единицах
или процентах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Математическое ожидание — погрешность
Cтраница 1
Математическое ожидание погрешности измерения принято называть систематической погрешностью, а ее центрированную случайную составляющую — случайной погрешностью. Такое разделение погрешностей на систематические и случайные обусловлено разным характером их проявления в процессе измерения, а также различием в методах их оценки и учета. Систематическая погрешность при повторных измерениях одной и той же величины остается постоянной или закономерно изменяется. Случайная погрешность при повторных измерениях одной и той же неизменной по значению величины изменяется по значению и знаку случайным образом и зависит от носящих случайный характер изменений условий эксперимента и параметров средств измерений.
[1]
Математическое ожидание погрешности настройки может быть равно нулю. Здесь следует или увеличить число испытаний для получения более надежных результатов, или учесть асимметрию распределения в конструкции устройства.
[2]
Математическое ожидание погрешности ИУ представляет собой систематическую часть общей погрешности, которую для краткости будем называть систематической погрешностью. При выполнении определенных условий систематическая погрешность ИУ в одних случаях может быть полностью скомпенсирована, в других — сведена к минимуму.
[3]
Математическое ожидание погрешности измерения представляет собой некоторую среднюю постоянную погрешность, которая повторяется в каждом t — м наблюдении. Эту погрешность обозначим Лт и будем называть систематической погрешностью. Исследование процессов измерения показывает, что систематическая погрешность в некоторых случаях не остается постоянной, а изменяется плавно по определенному закону.
[4]
Математическое ожидание погрешности измерений есть неслучайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях. Дл: ] Д с — Как числовая характеристика погрешности М [ Ддг ] показывает на смещенность результатов измерения относительно истинного значения измеряемой величины.
[5]
Величина математического ожидания погрешности ( отклонения) отдельного звена размерной цепи характеризует, как правило, систематическую ( динамическую) ошибку системы активного контроля. Однако в реальных ( трассовых) условиях протекания технологических процессов линейного строительства и связанного с ними автоматизированного активного контроля качества может иметь место множество случайных воздействий ( помех), на входе такой системы, что неизбежно будет приводить ее в нестационарный режим функционирования.
[7]
Таким образом, математическое ожидание погрешности каждого коэффициента аппроксимирующего многочлена равно нулю.
[8]
При известной оценке математического ожидания погрешности ее рассматривают как систематическую составляющую погрешности и устраняют изменением коэффициентов преобразования блоков или введением постоянного смещения в зависимости от мультипликативного или аддитивного характера погрешности.
[9]
Для тех же классов функций найдено математическое ожидание погрешности для квадратурных формул со случайно выбираемыми узлами.
[10]
Точность первой операции существенно ниже из-за неравного нулю математического ожидания погрешности, тем не менее отбрасывание заслуживает рассмотрения, так как гораздо проще реализуется.
[11]
Согласно определению, Д / М [ Д у ] — математическое ожидание погрешности по множеству всех возможных результатов анализа / — и пробы.
[12]
Следует заметить, что известны другие, более сложные программные приемы для достижения нулевого математического ожидания погрешности округления.
[13]
Практически этот способ реализуется введением постоянной поправки в X, равной 0 57, которая компенсирует систематическую составляющую или математическое ожидание погрешности от квантования.
[14]
Практически этот способ реализуется введением постоянной поправки в X, равной 0 5 Ахк, которая компенсирует систематическую составляющую или математическое ожидание погрешности от квантования.
[15]
Страницы:
1
2
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений, 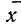
За меру точности соответствия принятой средней арифметической 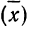
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 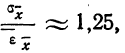
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них 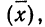
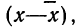
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 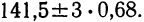
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление