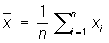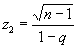Тео́рия оши́бок, раздел математической статистики, посвящённый построению выводов о численных значениях приближённо измеренных величин и об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, т. к. каждое измерение содержит некоторую ошибку. Различают три основных вида ошибок: систематические, грубые и случайные. Систематические ошибки постоянно либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на результаты измерений и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики. Например, в астрономии при измерении величины угла между направлением на светило и плоскостью горизонта систематическая ошибка является суммой двух ошибок: систематической ошибки, которую даёт прибор при отсчёте данного угла (инструментальная ошибка) и систематической ошибки, обусловленной преломлением лучей света в атмосфере (рефракция). Инструментальная ошибка учитывается с помощью таблицы или графика поправок для данного прибора; ошибку, связанную с рефракцией (для углов, меньших 80°), можно достаточно точно вычислить теоретически. Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, как правило, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредсказуемым образом то в сторону уменьшения, то в сторону увеличения результата.
Теория ошибок занимается изучением лишь случайных и грубых ошибок. Основные задачи теории ошибок: определение законов распределения случайных ошибок, построение статистических оценок неизвестных величин по результатам измерений, вычисление погрешностей таких оценок и устранение грубых ошибок.
Пусть в результате nn независимых измерений некоторой неизвестной величины μ\mu получены значения X1,X2,…,XnX_1,X_2,\dots,X_n. Разности
δ1=X1−μ, δ2=X2−μ, …, δn=Xn−μ\delta_1=X_1-\mu,\, \delta_2=X_2-\mu, \,\dots, \, \delta_n=X_n-\muназываются истинными ошибками; в терминах вероятностной теории ошибок все δi\delta_i рассматриваются как случайные величины, независимость измерений понимается как взаимная независимость случайных величин δ1,…,δn\delta_1, \dots, \delta_n. При этом измерения называются равноточными (в широком смысле), если эти величины имеют одно и то же распределение. Т. о., истинные ошибки равноточных измерений суть независимые одинаково распределённые случайные величины. При этом математическое ожидание истинных ошибок b=Eδ1=…=Eδnb=\text{E}\delta_1=\ldots =\text{E}\delta_n называется систематической ошибкой, а разности δ1−b,…,δn−b\delta_1-b,\dots,\delta_n-b – случайными ошибками. Отсутствие систематической ошибки означает, что b=0b=0, в этом случае δ1,…,δn\delta_1,\dots,\delta_n суть случайные ошибки. Величину 1/(2σ)1/(\sqrt{2}\sigma), где σ\sigma – квадратичное отклонение ошибок δ1,…,δn\delta_1,\dots,\delta_n, называют мерой точности (при наличии систематической ошибки мера точности есть 1/2(b2+σ2)1/\sqrt{2(b^2+\sigma^2)}. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений.
В качестве оценки неизвестной величины μ \mu обычно берут арифметическое среднее из результатов измерений X1,…,XnX_1,\dots,X_n:
X‾=1n∑i=1nXi,\displaystyle\overline X=\frac{1}{n}\sum^n_{i=1}X_i,а разности Δ1=X1−X‾,…,Δn−X‾\Delta_1=X_1- \overline X, \dots, \Delta_n — \overline X называются кажущимися ошибками. Выбор X‾\overline X в качестве оценки для μ\mu основан на том, что при достаточно большом числе nn равноточных измерений, лишённых систематической ошибки, оценка X‾\overline X с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины μ\mu (это связано с Законом больших чисел); оценка X‾\overline X лишена систематической ошибки (оценки с таким свойством называются несмещёнными оценками); дисперсия этой оценки есть
DX‾=E(X‾−μ)2=σ2/n.\text D\overline X=\text E(\overline X-\mu)^2=\sigma^2/n.Опыт показывает, что практически очень часто случайные ошибки имеют распределения, близкие к нормальным (это объясняется центральной предельной теоремой). В этом случае распределение величины X‾\overline X мало отличается от нормального распределения с математическим ожиданием μ\mu и дисперсией σ2/n\sigma^2/n. Если распределение величин δ1,…,δn\delta_1,\dots,\delta_n в точности нормально, то дисперсия всякой другой несмещённой оценки для μ\mu, например медианы, не меньше DX‾\text D\overline X. Если же распределение величин δ1,…,δn\delta_1,\dots,\delta_n отлично от нормального, то последнее свойство может не иметь места.
Если дисперсия σ2\sigma^2 отдельных измерений заранее неизвестна, то для её оценки пользуются величиной
s2=1n−1∑i=1nΔi2;\displaystyle s^2=\frac{1}{n-1}\sum^n_{i=1}\Delta^2_i;
s2s^2 – несмещённая оценка для σ2\sigma^2, т. к. Es2=σ2\text E s^2=\sigma^2.
Если случайные ошибки δ1,…,δn\delta_1,\dots,\delta_n имеют нормальное распределение, то отношение
t=(X‾−μ)nst=\dfrac{(\overline X -\mu)\sqrt{n}}{s}имеет распределение Стьюдента с n−1n-1 степенью свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства μ≈X‾\mu \approx \overline X (см. Метод наименьших квадратов). Величина
χ2=(n−1)s2σ2\chi^2=\dfrac{(n-1)s^2}{\sigma^2}при тех же предположениях имеет распределение хи-квадрат с n−1n-1 степенью свободы. Это позволяет оценить погрешность приближённого равенства σ≈s\sigma \approx s. Относительная погрешность ∣s−σ∣/s|s-\sigma|/s не превосходит числа qq с вероятностью
ω=F(z2,n−1)−F(z1,n−1),\omega=F(z^2,n-1)-F(z_1,n-1),
где F(z,n−1)F(z, n-1) – функция распределения хи-квадрат, а
z1=n−11+q,z2=n−11−q.z_1=\dfrac{\sqrt{n-1}}{1+q},\quad z_2 = \dfrac{\sqrt{n-1}}{1-q}.
Опубликовано 1 августа 2022 г. в 13:27 (GMT+3). Последнее обновление 1 августа 2022 г. в 13:27 (GMT+3).
Основные
понятия теории ошибок.
Оценка точности
наблюдений.
Для
последующей ясности, в этой статье, под
наблюдениями будем подразумевать
совокупность одиночных измерений
определенной величины: разница в блеске,
показание шкалы микрометра и прочее.
Это величина называется измеряемой или
наблюдаемой. По особенности проведения,
все наблюдения можно разделить на две
группы: равноточные и неравноточные. К
первой категории относятся такие
наблюдения, которые были выполнены
одним человеком, на одном приборе
(инструменте) в сравнительно короткий
промежуток времени (то есть одинаковое
воздействие внешних факторов). Во вторую
категорию, естественно, попадают те
наблюдения, которые не соответствуют
одному, нескольким или всем условиям
принадлежности к равноточным наблюдениям.
В этой статье не будут описаны точностные
расчеты для наблюдений второй категории,
они более сложны и громоздки, и применяются
чаще в обработке геодезических измерений
и при комплексных астронаблюдениях.
Планируется подробно остановится на
неравноточных измерениях в следующей
статье из этого цикла, которая будет
содержать основные принципы совместного
уравнивания результатов наблюдений по
способу наименьших квадратов.
Типы
погрешностей наблюдений и особенности
их учета
Любое
измерение в реальных условиях производится
с погрешностью, которую можно разделить
на две составляющие — систематическую
и случайную. Систематическая погрешность
возникает в основном из-за ограниченной
точности измерительных приборов,
отчетных механизмов, а так же в связи с
отсутствием учета второстепенных
факторов, влияющих на измерения, или,
если этот учет ведется не корректно.
Систематические погрешности ведут к
одностороннему искажению результатов
наблюдений (постоянное завышение или
занижение значения измеряемой величины).
Их главная особенность — в ходе поверок
инструментов и тестовых измерений
вполне реально выявить такие погрешности
(найти их численные значения и знаки),
и тем самым свести их влияние на результаты
наблюдений к минимуму. Случайные
погрешности появляются из-за
непредсказуемых, хаотичных причин,
искажающих результаты наблюдений. Их
особенность в том, что они приводят к
получению разных значений измерений
при их многократных повторах, проведенных
в одинаковых условиях. Выявить случайные
погрешности из отдельных замеров
практически невозможно, но зато при
достаточном количестве однородных
измерений вполне реально «свести на
нет» их совокупное влияние на результаты
наблюдений. Такое минимизирование
случайных искажений данных основано
на ряде процедур, которые в свою очередь
базируются на выводах и следствиях
теории ошибок. Теория ошибок — математическая
дисциплина, изучающая законы и особенности
«поведения» погрешностей (ошибок)
измерений. Например, нормальное
распределение, эффект взаимной компенсации
по знакам и так далее. Возникла эта
дисциплина, как одно из многочисленных
«ответвлений» от Теории Вероятностей.
Математическая обработка различна для
обоих видов погрешностей. Учет
систематической составляющей есть
процесс почти уникальный для каждого
типа приборов и инструментов, для
различных природных и прочих факторов,
в том числе для каждого отдельного
наблюдателя (так называемая личная
ошибка, которую обычно классифицируют
как подтип систематической составляющей).
Случайные ошибки подчиняются универсальным
законам, которые можно применять не
только при наблюдениях разных объектов
и измерениях разных величин, но и в
разных науках — будь то астрономия,
физика или геодезия. Основные принципы
обработки везде одни и те же. Впрочем
существует еще один класс погрешностей
— грубая ошибка, или ложное измерение.
Точностной
расчет для серии равноточных наблюдений
Рассмотрим
алгоритм первичной обработки серии
равноточных наблюдений. Пусть мы получили
массив замеров измеряемой величины
«Х», который имеет вид: X1, X2, …, Xn,
где n — количество замеров на сеансе.
-
Находим
среднее арифметическое значение «Х»
на сеансе:
Xs
= ( X1 + X2 + … + Xn ) / n
-
Рассчитываем
отклонения среднего значения от
измеренных:
d1
= X1 — Xs, d2 = X2 — Xs, …, dn = Xn — Xs
-
Определяем
среднюю квадратическую погрешность
одного измерения, это параметр, который
характеризует среднюю точность
проведения одного замера:
MX
= SQR ( ( d1 ^ 2 + d2 ^ 2 + … + dn ^ 2 ) / ( n — 1 ) )
-
Находим
среднюю квадратическую ошибку среднего
арифметического, которая определяет
надежность полученного результата:
MXs
= MX / SQR ( n )
-
Рассчитываем
относительную погрешность результата
наблюдений:
U
( в процентах ) = ( MXs * 100% ) / Xs
-
Таким
образом, получаем, что наиболее вероятное
значение измеряемой величины на сеансе
имеет значение:
Xsv
= Xs + MXs
Особенности
точностного расчета для прямых и
косвенных измерений
По
признаку анализирования получаемой
при наблюдении информации, измерения
делятся на прямые и косвенные. При прямых
измерениях значение исследуемой величины
измеряют непосредственно, например
момент или промежуток времени. При
косвенных измерениях, искомую величину
рассчитывают по определенной формуле,
в которую входят величины, измеряемые
непосредственно, а так же заданные
значения вспомогательных величин и
констант, то есть можем записать: Y = F (
X1, X2, …, Xn ), где Y — искомая величина, а X1,
X2, …, Xn — ее аргументы, измеряемые
непосредственно. Пример косвенного
измерения: исходя из снятых отчетов по
окулярному микрометру, впоследствии
переходим к координатам объекта. Важной
задачей при обработке косвенных
наблюдений является определение
погрешности искомой величины по известным
погрешностям величин ее составляющих.
Формула, которая связывает эти параметры,
имеет следующий вид:
MY
= SQR ( ( ( dY / dX1 ) ^ 2 ) * MX1 ^ 2 + ( dY / dX2 ) ^ 2 ) * MX2 ^ 2
+ …
… +
( dY / dXn ) ^ 2 ) * MXn ^ 2 ),
где
( Di / dXi ) — частная производная функции Y
= F ( X1, X2, …, Xn ) по аргументу Xi, вычисленная
в точке Xi.
Пример:
А теперь еще раз «пробежимся» по
описанной выше методики оценки точности
проведенных наблюдений, но уже на базе
конкретного случая. При наблюдениях
деталей на диске Юпитера, на протяжении
ночи были сделаны несколько
зарисовок/фотографий. 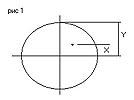
всех рисунках/фотографиях отмечено
точечное образование, находящееся в
южном полушарии и медленно передвигающееся
параллельно экватору за счет суточного
вращения планеты. Задача: определить
широту наблюдаемого образования — по
всей видимости ядра нового мощного
антициклона, на которые богата бурная
юпитерианская атмосфера. С изображения
Юпитера снимем два линейных значения:
расстояние от экватора (его легко
прочертить учитывая значительное сжатие
планеты) до полюса — Y и расстояние от
экватора до зафиксированного образования.
(см. рис 1). Так как масштаб зарисовок/фотографий
может быть разным, вычислим для всех
изображений относительные значения
величины Х ( Y приравняем к единице).
Далее приводится таблица с примером
вычисления средних квадратических
погрешностей одного наблюдения и всего
результата.
Xs
= 2.88 / 8 = 0.360
MX = SQR ( 0.0114 / 8 — 1 ) = 0.040
MXs =
0.040 / SQR ( 8 ) = 0.014
U = ( 0.014 * 100% ) / 0.360 =
3.889%
Xsv = 0.360 + 0.014, или: 0.346 <= Xsv <= 0.374
Но,
результат получен в относительной
линейной мере. Переход к широте в градусах
осуществляется по формуле: B = ARCSIN ( X / Y
), а с учетом того, что Y — единичный
отрезок: Bs = ARCSIN ( X ) = ARCSIN ( 0.360 ) = 21.1002° =
21° 06.01′ Для вычисления средней квадратической
погрешности определения широты объекта
в градусной мере, воспользуемся выражением
описанным в параграфе о прямых и косвенных
наблюдениях, принимая во внимание, что
Y — константа ( Y = 1 ). Находим производную
функции B ( X ): ( dB / dX ) = 1 / SQR ( 1 — X ^ 2 ).
Вычисляем погрешность результата
наблюдений в градусной мере: MBsv = ( r * MXs
) / SQR ( 1 — Xs ^ 2 ), где r — коэффициент перехода
из радианной меры в градусную ( r = 57.2958
). MBsv = (r * 0.014 ) / SQR ( 1 — 0.360 ^ 2 ) = 0.8598° = 51.59′. U
=( 0.8598 * 100% ) / 21.002 = 4.094%
Итог:
Средняя вероятная широта образования,
зафиксированного на диске Юпитера,
составляет: Bsv = 21° 06.01′ + 51.59′, или: 20°14.42′
<= Bsv <= 21°57.60′.
Все
описанные в этой статье этапы обработки
легко программируются (для нахождения
частных производных можно воспользоваться
одним из численных методов, например
Рунге — Кутта), и поэтому впоследствии
не будут отнимать почти никакого времени
— необходимо только создать массив или
файл исходных данных — значений измеренных
величин. Стоит еще добавить, что точностной
расчет проведенных измерений помимо
своего основного назначения (оценка
надежности исследований) имеет еще и
другую немаловажную роль. Проводя изо
дня в день, из месяца в месяц определенный
вид работ, наблюдатель может следить,
как в динамике прогрессирует (или
регрессирует) достоверность и качество
информации, источником которой он
является, то есть проводить своеобразный
самоконтроль. И будет очень неплохо,
если последняя в этой статье фраза в
скобках так и останется «закрытой».
5.
В технических характеристиках приборов
приведены различные данные диапазонов
измерения
и отображения.
В диапазонах
измерения
наших приборов
представлены пределы измерений
с учетом внешних активных сопротивлений
измерительных проводников стандартной
…
Соседние файлы в папке Лабораторные работы
- #
- #
- #
- #
02.05.201416.9 Кб31Расчеты к лабе2.xls
раздел математической статистики (См. Математическая статистика), посвященный построению уточнённых выводов о численных значениях приближённо измеренных величин, а также об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, так как каждое измерение содержит некоторую ошибку. Различают 3 основных вида ошибок: систематические, грубые и случайные. Систематические ошибки всё время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики (см. Наблюдений обработка). Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов.
О. т. занимается изучением лишь грубых и случайных ошибок. Основные задачи О. т.: разыскание законов распределения случайных ошибок, разыскание оценок (см. Статистические оценки) неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и устранение грубых ошибок.
Пусть в результате n независимых равноточных измерений некоторой неизвестной величины а получены значения x1, x2,…, xn. Разности
δ1 = x1 — a,…, δn = xn — a
называются истинными ошибками. В терминах вероятностной О. т. все δi трактуются как случайные величины; независимость измерений понимается как взаимная независимость случайных величин δ1,…, δn. Равноточность измерений в широком смысле истолковывается как одинаковая распределённость: истинные ошибки равноточных измерений суть одинаково распределённые случайные величины. При этом математическое ожидание случайных ошибок b = Eδ1 =...= Еδn называется систематической ошибкой, а разности δ1 — b,…, δn — b — случайными ошибками. Таким образом, отсутствие систематической ошибки означает, что b = 0, и в этой ситуации δ1,…, δn суть случайные ошибки. Величину 

,
а разности Δ1 = x1 — x̅,…, Δn = xn — x̅ называются кажущимися ошибками. Выбор x̅ в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка x̅ с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон); оценка x̅ лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
Dx̅ = E (x̅ — а)2 = σ2/n.
Опыт показывает, что практически очень часто случайные ошибки δi подчиняются распределениям, близким к нормальному (причины этого вскрыты так называемыми предельными теоремами (См. Предельные теоремы) теории вероятностей). В этом случае величина x̅ имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией σ2/n. Если распределения δi в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы (См. Медиана), не меньше Dx̅. Если же распределение δi отлично от нормального, то последнее свойство может не иметь места.
Если дисперсия σ2 отдельных измерений заранее известна, то для её оценки пользуются величиной
(Es2 = σ2, т. е. s2 — несмещенная оценка для σ2), если случайные ошибки δi имеют нормальное распределение, то отношение
подчиняется Стьюдента распределению (См. Стьюдента распределение) с n — 1 степенями свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства а ≈ x̅ (см. Наименьших квадратов метод).
Величина (n — 1) s2/σ2 при тех же предположениях имеет распределение χ2 (см. «Хи-квадрат» (См. Хи-квадрат распределение) распределение) с n — 1 степенями свободы. Это позволяет оценить погрешность приближённого равенства σ ≈ s. Можно показать, что относительная погрешность |s — σ|Is не будет превышать числа q с вероятностью
ω = F (z2, n — 1) — F (z1, n — 1),
где F (z, n — 1) — функция распределения χ2,
,
Лит.: Линник Ю. В., Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962; Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968.
Л. Н. Большев.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Теория ошибок (ошибок теория)
Теория ошибок
–
раздел математической статистики, посвященный построению уточненных выводов о численных значениях приближенно измеренных величин, а также об ошибках (погрешностях) измерений.
Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, так как каждое измерение содержит некоторую ошибку. Различают 3 основных вида ошибок: систематические, грубые и случайные.
Систематические ошибки всё время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики. Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов.
Теория ошибок занимается изучением лишь грубых и случайных ошибок . Основными задачами теории ошибок являются: разыскание законов распределения случайных ошибок, разыскание оценок неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и устранение грубых ошибок .
Алфавитный указатель