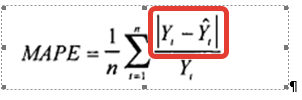From Wikipedia, the free encyclopedia
The mean absolute percentage error (MAPE), also known as mean absolute percentage deviation (MAPD), is a measure of prediction accuracy of a forecasting method in statistics. It usually expresses the accuracy as a ratio defined by the formula:
where At is the actual value and Ft is the forecast value. Their difference is divided by the actual value At. The absolute value of this ratio is summed for every forecasted point in time and divided by the number of fitted points n.
MAPE in regression problems[edit]
Mean absolute percentage error is commonly used as a loss function for regression problems and in model evaluation, because of its very intuitive interpretation in terms of relative error.
Definition[edit]
Consider a standard regression setting in which the data are fully described by a random pair 






In the classical regression setting, the closeness of 


where 
In practice
In practice 
From a practical point of view, the use of the MAPE as a quality function for regression model is equivalent to doing weighted mean absolute error (MAE) regression, also known as quantile regression. This property is trivial since
As a consequence, the use of the MAPE is very easy in practice, for example using existing libraries for quantile regression allowing weights.
Consistency[edit]
The use of the MAPE as a loss function for regression analysis is feasible both on a practical point of view and on a theoretical one, since the existence of an optimal model and the consistency of the empirical risk minimization can be proved.[1]
WMAPE[edit]
WMAPE (sometimes spelled wMAPE) stands for weighted mean absolute percentage error.[2] It is a measure used to evaluate the performance of regression or forecasting models. It is a variant of MAPE in which the mean absolute percent errors is treated as a weighted arithmetic mean. Most commonly the absolute percent errors are weighted by the actuals (e.g. in case of sales forecasting, errors are weighted by sales volume).[3]. Effectively, this overcomes the ‘infinite error’ issue.[4]
Its formula is:[4]
Where 


However, this effectively simplifies to a much simpler formula:
Confusingly, sometimes when people refer to wMAPE they are talking about a different model in which the numerator and denominator of the wMAPE formula above are weighted again by another set of custom weights 
Issues[edit]
Although the concept of MAPE sounds very simple and convincing, it has major drawbacks in practical application,[5] and there are many studies on shortcomings and misleading results from MAPE.[6][7]
To overcome these issues with MAPE, there are some other measures proposed in literature:
- Mean Absolute Scaled Error (MASE)
- Symmetric Mean Absolute Percentage Error (sMAPE)
- Mean Directional Accuracy (MDA)
- Mean Arctangent Absolute Percentage Error (MAAPE): MAAPE can be considered a slope as an angle, while MAPE is a slope as a ratio.[7]
See also[edit]
- Least absolute deviations
- Mean absolute error
- Mean percentage error
- Symmetric mean absolute percentage error
External links[edit]
- Mean Absolute Percentage Error for Regression Models
- Mean Absolute Percentage Error (MAPE)
- Errors on percentage errors — variants of MAPE
- Mean Arctangent Absolute Percentage Error (MAAPE)
References[edit]
- ^ a b de Myttenaere, B Golden, B Le Grand, F Rossi (2015). «Mean absolute percentage error for regression models», Neurocomputing 2016 arXiv:1605.02541
- ^ Forecast Accuracy: MAPE, WAPE, WMAPE https://www.baeldung.com/cs/mape-vs-wape-vs-wmape%7Ctitle=Understanding Forecast Accuracy: MAPE, WAPE, WMAPE. ;
- ^ Weighted Mean Absolute Percentage Error https://ibf.org/knowledge/glossary/weighted-mean-absolute-percentage-error-wmape-299%7Ctitle=WMAPE: Weighted Mean Absolute Percentage Error. ;
- ^ a b «Statistical Forecast Errors».
- ^ a b Tofallis (2015). «A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation», Journal of the Operational Research Society, 66(8):1352-1362. archived preprint
- ^ Hyndman, Rob J., and Anne B. Koehler (2006). «Another look at measures of forecast accuracy.» International Journal of Forecasting, 22(4):679-688 doi:10.1016/j.ijforecast.2006.03.001.
- ^ a b Kim, Sungil and Heeyoung Kim (2016). «A new metric of absolute percentage error for intermittent demand forecasts.» International Journal of Forecasting, 32(3):669-679 doi:10.1016/j.ijforecast.2015.12.003.
- ^ Kim, Sungil; Kim, Heeyoung (1 July 2016). «A new metric of absolute percentage error for intermittent demand forecasts». International Journal of Forecasting. 32 (3): 669–679. doi:10.1016/j.ijforecast.2015.12.003.
- ^ Makridakis, Spyros (1993) «Accuracy measures: theoretical and practical concerns.» International Journal of Forecasting, 9(4):527-529 doi:10.1016/0169-2070(93)90079-3
 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется:
- Для оценки точности прогноза;
- Показывает на сколько велики ошибки в сравнении со значениями ряда;
- Хороша для сравнения 1-й модели для разных рядов;
- Используется для сравнения разных моделей для одного ряда;
- Оценки экономического эффекта, за счет повышения точности прогноза.
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать.
Формула расчета MAPE:
Где:
- Yt – фактический объем продаж за анализируемый период;
- Ŷt — значение прогнозной модели за аналазируемый период;
- n — количество периодов.
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
- Рассчитываем значение модели прогноза — Ŷt;
- Рассчитываем ошибку прогноза;
- Берем ошибку по модулю;
- Определяем абсолютную ошибку;
- Рассчитываем среднюю абсолютную ошибку в процентах — MAPE.
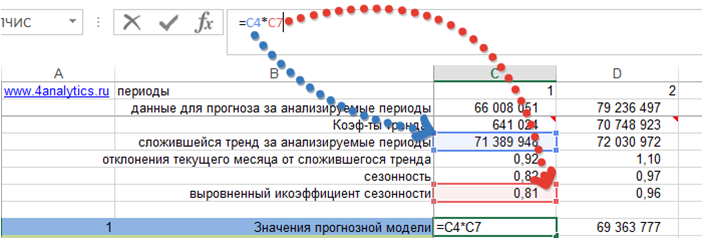
1. Рассчитаем значение модели прогноза — Ŷt
Возьмем модель с трендом и сезонностью. Рассчитаем значение модели для каждого периода, когда нам известны фактические продажи. Для этого сложившийся тренд за анализируемый период умножим на коэффициент сезонности для соответствующего месяца.
Получили значения прогнозной модели для каждого периода времени:
Подробнее о расчете прогноза с помощью тренда и сезонности читайте в статье «Расчет прогноза с помощью тренда и сезонности».
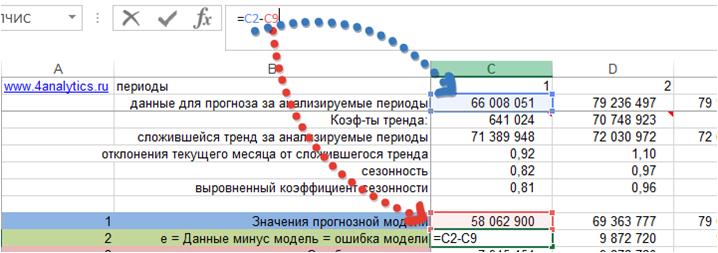
2. Рассчитаем значения ошибки прогноза.
В формуле расчета MAPE – это:
e — Ошибка прогноза — это разность между значениями временного ряда (фактом продаж) и моделью прогноза:
e= Yt — Ŷt
Получили значение ошибки прогноза для каждого момента времени за анализируемый период.
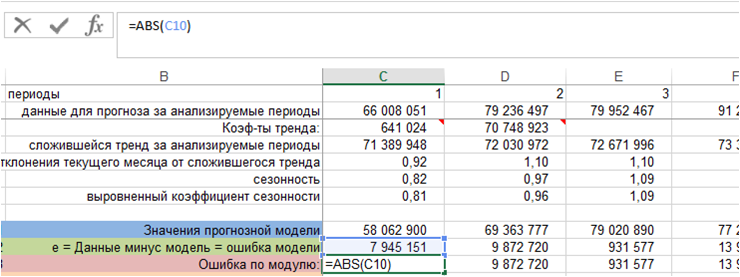
3. Рассчитаем ошибку по модулю.
Для этого воспользуемся функцией Excel =ABC()
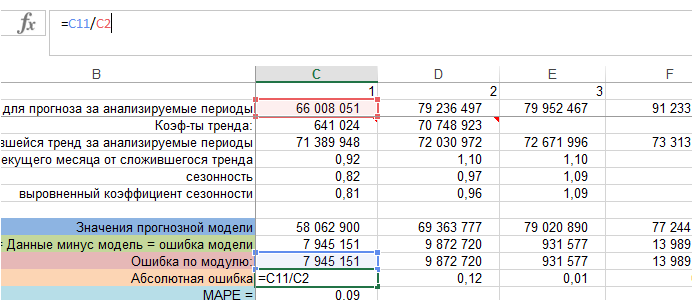
4. Определяем абсолютную ошибку.
Для каждого периода ошибку по модулю делим на фактические значения ряда, т.е. на фактический объем продаж:
Получили абсолютную ошибку для каждого периода фактических продаж. В формуле MAPE — это:
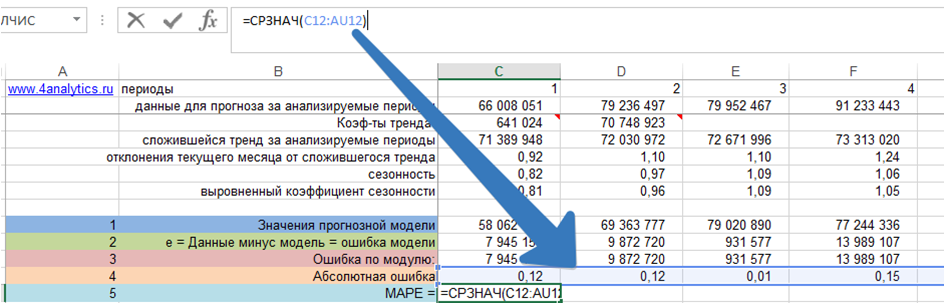
5. Рассчитаем MAPE – среднюю абсолютную ошибку.
Для этого рассчитаем среднее значение абсолютной ошибки за все периоды:
Скачать файл с примером расчета MAPE – средней абсолютной ошибки.
Как рассчитать показатель точность прогноза?
Показатель точность прогноза = 1 –MAPE:
С помощью MAPE вы можете сравнивать различные модели между собой, можете оценивать, как и на сколько модель делает точные прогнозы для разных временных рядов.
А также, что самое главное, можете оценить экономический эффект для компании за счет повышения точности прогноза.
Об этом подробнее можете почитать в нашей статье на сайте http://novoforecast.com/novo-forecast/instruktsiya/item/rost-tochnosti-prognoza-rost-pribyli.html
Если есть вопросы, пожалуйста, пишите в комментариях!
Forecast4AC PRO рассчитает MAPE для каждого временного ряда!
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
читать 2 мин
Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является средняя абсолютная ошибка в процентах , часто обозначаемая аббревиатурой MAPE .
Он рассчитывается как:
MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100
куда:
- Σ — символ, означающий «сумма».
- n – размер выборки
- фактический – фактическое значение данных
- прогноз – прогнозируемое значение данных
MAPE обычно используется, потому что его легко интерпретировать. Например , значение MAPE, равное 14 %, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 14 %.
В следующем примере показано, как рассчитать и интерпретировать значение MAPE для данной модели.
Пример: интерпретация значения MAPE для данной модели
Предположим, сеть продуктовых магазинов строит модель для прогнозирования будущих продаж. На следующей диаграмме показаны фактические продажи и прогнозируемые продажи по модели за 12 последовательных периодов продаж:
Мы можем использовать следующую формулу для расчета абсолютной процентной ошибки каждого прогноза:
- Абсолютная ошибка в процентах = |фактический-прогноз| / |фактическое| * 100
Затем мы можем вычислить среднее значение абсолютных процентных ошибок:
MAPE для этой модели оказывается равным 5,12% .
Это говорит нам о том, что средняя абсолютная процентная ошибка между продажами, предсказанными моделью, и фактическими продажами составляет 5,12% .
Чтобы определить, является ли это хорошим значением для MAPE , необходимо использовать отраслевые стандарты.
Если стандартная модель в продовольственной отрасли дает значение MAPE, равное 2%, то это значение 5,12% можно считать высоким.
И наоборот, если большинство моделей прогнозирования в продуктовой промышленности дают значения MAPE от 10% до 15%, то значение MAPE, равное 5,12%, можно считать низким, и эта модель может считаться отличной для прогнозирования будущих продаж.
Сравнение значений MAPE для разных моделей
MAPE особенно полезен для сравнения соответствия различных моделей.
Например, предположим, что сеть продуктовых магазинов хочет построить модель для прогнозирования будущих продаж и найти наилучшую из возможных моделей.
Предположим, они соответствуют трем различным моделям и находят соответствующие им значения MAPE:
- MAPE модели 1: 14,5%
- MAPE модели 2: 16,7%
- MAPE модели 3: 9,8%
Модель 3 имеет самое низкое значение MAPE, что говорит нам о том, что она способна прогнозировать будущие продажи наиболее точно среди трех потенциальных моделей.
Дополнительные ресурсы
Как рассчитать MAPE в Excel
Как рассчитать MAPE в R
Как рассчитать MAPE в Python
Калькулятор MAPE
Для того чтобы модель линейной регрессии можно было применять на практике необходимо сначала оценить её качество. Для этих целей предложен ряд показателей, каждый из которых предназначен для использования в различных ситуациях и имеет свои особенности применения (линейные и нелинейные, устойчивые к аномалиям, абсолютные и относительные, и т.д.). Корректный выбор меры для оценки качества модели является одним из важных факторов успеха в решении задач анализа данных.
«Хорошая» аналитическая модель должна удовлетворять двум, зачастую противоречивым, требованиям — как можно лучше соответствовать данным и при этом быть удобной для интерпретации пользователем. Действительно, повышение соответствия модели данным как правило связано с её усложнением (в случае регрессии — увеличением числа входных переменных модели). А чем сложнее модель, тем ниже её интерпретируемость.
Поэтому при выборе между простой и сложной моделью последняя должна значимо увеличивать соответствие модели данным чтобы оправдать рост сложности и соответствующее снижение интерпретируемости. Если это условие не выполняется, то следует выбрать более простую модель.
Таким образом, чтобы оценить, насколько повышение сложности модели значимо увеличивает её точность, необходимо использовать аппарат оценки качества регрессионных моделей. Он включает в себя следующие меры:
- Среднеквадратичная ошибка (MSE).
- Корень из среднеквадратичной ошибки (RMSE).
- Среднеквадратичная ошибка в процентах (MSPE).
- Средняя абсолютная ошибка (MAE).
- Средняя абсолютная ошибка в процентах (MAPE).
- Cимметричная средняя абсолютная процентная ошибка (SMAPE).
- Средняя абсолютная масштабированная ошибка (MASE)
- Средняя относительная ошибка (MRE).
- Среднеквадратичная логарифмическая ошибка (RMSLE).
- Коэффициент детерминации R-квадрат.
- Скорректированный коэффициент детеминации.
Прежде чем перейти к изучению метрик качества, введём некоторые базовые понятия, которые нам в этом помогут. Для этого рассмотрим рисунок.
Рисунок 1. Линейная регрессия
Наклонная прямая представляет собой линию регрессии с переменной, на которой расположены точки, соответствующие предсказанным значениям выходной переменной \widehat{y} (кружки синего цвета). Оранжевые кружки представляют фактические (наблюдаемые) значения y . Расстояния между ними и линией регрессии — это ошибка предсказания модели y-\widehat{y} (невязка, остатки). Именно с её использованием вычисляются все приведённые в статье меры качества.
Горизонтальная линия представляет собой модель простого среднего, где коэффициент при независимой переменной x равен нулю, и остаётся только свободный член b, который становится равным среднему арифметическому фактических значений выходной переменной, т.е. b=\overline{y}. Очевидно, что такая модель для любого значения входной переменной будет выдавать одно и то же значение выходной — \overline{y}.
В линейной регрессии такая модель рассматривается как «бесполезная», хуже которой работает только «случайный угадыватель». Однако, она используется для оценки, насколько дисперсия фактических значений y относительно линии среднего, больше, чем относительно линии регрессии с переменной, т.е. насколько модель с переменной лучше «бесполезной».
MSE
Среднеквадратичная ошибка (Mean Squared Error) применяется в случаях, когда требуется подчеркнуть большие ошибки и выбрать модель, которая дает меньше именно больших ошибок. Большие значения ошибок становятся заметнее за счет квадратичной зависимости.
Действительно, допустим модель допустила на двух примерах ошибки 5 и 10. В абсолютном выражении они отличаются в два раза, но если их возвести в квадрат, получив 25 и 100 соответственно, то отличие будет уже в четыре раза. Таким образом модель, которая обеспечивает меньшее значение MSE допускает меньше именно больших ошибок.
MSE рассчитывается по формуле:
MSE=\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{y}_{i})^{2},
где n — количество наблюдений по которым строится модель и количество прогнозов, y_{i} — фактические значение зависимой переменной для i-го наблюдения, \widehat{y}_{i} — значение зависимой переменной, предсказанное моделью.
Таким образом, можно сделать вывод, что MSE настроена на отражение влияния именно больших ошибок на качество модели.
Недостатком использования MSE является то, что если на одном или нескольких неудачных примерах, возможно, содержащих аномальные значения будет допущена значительная ошибка, то возведение в квадрат приведёт к ложному выводу, что вся модель работает плохо. С другой стороны, если модель даст небольшие ошибки на большом числе примеров, то может возникнуть обратный эффект — недооценка слабости модели.
RMSE
Корень из среднеквадратичной ошибки (Root Mean Squared Error) вычисляется просто как квадратный корень из MSE:
RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(y_{i}-\widehat{y_{i}})^{2}}
MSE и RMSE могут минимизироваться с помощью одного и того же функционала, поскольку квадратный корень является неубывающей функцией. Например, если у нас есть два набора результатов работы модели, A и B, и MSE для A больше, чем MSE для B, то мы можем быть уверены, что RMSE для A больше RMSE для B. Справедливо и обратное: если MSE(A)<MSE(B), то и RMSE(A)<RMSE(B).
Следовательно, сравнение моделей с помощью RMSE даст такой же результат, что и для MSE. Однако с MSE работать несколько проще, поэтому она более популярна у аналитиков. Кроме этого, имеется небольшая разница между этими двумя ошибками при оптимизации с использованием градиента:
\frac{\partial RMSE}{\partial \widehat{y}_{i}}=\frac{1}{2\sqrt{MSE}}\frac{\partial MSE}{\partial \widehat{y}_{i}}
Это означает, что перемещение по градиенту MSE эквивалентно перемещению по градиенту RMSE, но с другой скоростью, и скорость зависит от самой оценки MSE. Таким образом, хотя RMSE и MSE близки с точки зрения оценки моделей, они не являются взаимозаменяемыми при использовании градиента для оптимизации.
Влияние каждой ошибки на RMSE пропорционально величине квадрата ошибки. Поэтому большие ошибки оказывают непропорционально большое влияние на RMSE. Следовательно, RMSE можно считать чувствительной к аномальным значениям.
MSPE
Среднеквадратичная ошибка в процентах (Mean Squared Percentage Error) представляет собой относительную ошибку, где разность между наблюдаемым и фактическим значениями делится на наблюдаемое значение и выражается в процентах:
MSPE=\frac{100}{n}\sum\limits_{i=1}^{n}\left ( \frac{y_{i}-\widehat{y}_{i}}{y_{i}} \right )^{2}
Проблемой при использовании MSPE является то, что, если наблюдаемое значение выходной переменной равно 0, значение ошибки становится неопределённым.
MSPE можно рассматривать как взвешенную версию MSE, где вес обратно пропорционален квадрату наблюдаемого значения. Таким образом, при возрастании наблюдаемых значений ошибка имеет тенденцию уменьшаться.
MAE
Cредняя абсолютная ошибка (Mean Absolute Error) вычисляется следующим образом:
MAE=\frac{1}{n}\sum\limits_{i=1}^{n}\left | y_{i}-\widehat{y}_{i} \right |
Т.е. MAE рассчитывается как среднее абсолютных разностей между наблюдаемым и предсказанным значениями. В отличие от MSE и RMSE она является линейной оценкой, а это значит, что все ошибки в среднем взвешены одинаково. Например, разница между 0 и 10 будет вдвое больше разницы между 0 и 5. Для MSE и RMSE, как отмечено выше, это не так.
Поэтому MAE широко используется, например, в финансовой сфере, где ошибка в 10 долларов должна интерпретироваться как в два раза худшая, чем ошибка в 5 долларов.
MAPE
Средняя абсолютная процентная ошибка (Mean Absolute Percentage Error) вычисляется следующим образом:
MAPE=\frac{100}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y_{i}} \right |}{\left | y_{i} \right |}
Эта ошибка не имеет размерности и очень проста в интерпретации. Её можно выражать как в долях, так и в процентах. Если получилось, например, что MAPE=11.4, то это говорит о том, что ошибка составила 11.4% от фактического значения.
SMAPE
Cимметричная средняя абсолютная процентная ошибка (Symmetric Mean Absolute Percentage Error) — это мера точности, основанная на процентных (или относительных) ошибках. Обычно определяется следующим образом:
SMAPE=\frac{100}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y_{i}} \right |}{(\left | y_{i} \right |+\left | \widehat{y}_{i} \right |)/2}
Т.е. абсолютная разность между наблюдаемым и предсказанным значениями делится на полусумму их модулей. В отличие от обычной MAPE, симметричная имеет ограничение на диапазон значений. В приведённой формуле он составляет от 0 до 200%. Однако, поскольку диапазон от 0 до 100% гораздо удобнее интерпретировать, часто используют формулу, где отсутствует деление знаменателя на 2.
Одной из возможных проблем SMAPE является неполная симметрия, поскольку в разных диапазонах ошибка вычисляется неодинаково. Это иллюстрируется следующим примером: если y_{i}=100 и \widehat{y}_{i}=110, то SMAPE=4.76, а если y_{i}=100 и \widehat{y}_{i}=90, то SMAPE=5.26.
Ограничение SMAPE заключается в том, что, если наблюдаемое или предсказанное значение равно 0, ошибка резко возрастет до верхнего предела (200% или 100%).
MASE
Средняя абсолютная масштабированная ошибка (Mean absolute scaled error) — это показатель, который позволяет сравнивать две модели. Если поместить MAE для новой модели в числитель, а MAE для исходной модели в знаменатель, то полученное отношение и будет равно MASE. Если значение MASE меньше 1, то новая модель работает лучше, если MASE равно 1, то модели работают одинаково, а если значение MASE больше 1, то исходная модель работает лучше, чем новая модель. Формула для расчета MASE имеет вид:
MASE=\frac{MAE_{i}}{MAE_{j}}
MASE симметрична и устойчива к выбросам.
MRE
Средняя относительная ошибка (Mean Relative Error) вычисляется по формуле:
MRE=\frac{1}{n}\sum\limits_{i=1}^{n}\frac{\left | y_{i}-\widehat{y}_{i}\right |}{\left | y_{i} \right |}
Несложно увидеть, что данная мера показывает величину абсолютной ошибки относительно фактического значения выходной переменной (поэтому иногда эту ошибку называют также средней относительной абсолютной ошибкой, MRAE). Действительно, если значение абсолютной ошибки, скажем, равно 10, то сложно сказать много это или мало. Например, относительно значения выходной переменной, равного 20, это составляет 50%, что достаточно много. Однако относительно значения выходной переменной, равного 100, это будет уже 10%, что является вполне нормальным результатом.
Очевидно, что при вычислении MRE нельзя применять наблюдения, в которых y_{i}=0.
Таким образом, MRE позволяет более адекватно оценить величину ошибки, чем абсолютные ошибки. Кроме этого она является безразмерной величиной, что упрощает интерпретацию.
RMSLE
Среднеквадратичная логарифмическая ошибка (Root Mean Squared Logarithmic Error) представляет собой RMSE, вычисленную в логарифмическом масштабе:
RMSLE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(log(\widehat{y}_{i}+1)-log{(y_{i}+1}))^{2}}
Константы, равные 1, добавляемые в скобках, необходимы чтобы не допустить обращения в 0 выражения под логарифмом, поскольку логарифм нуля не существует.
Известно, что логарифмирование приводит к сжатию исходного диапазона изменения значений переменной. Поэтому применение RMSLE целесообразно, если предсказанное и фактическое значения выходной переменной различаются на порядок и больше.
R-квадрат
Перечисленные выше ошибки не так просто интерпретировать. Действительно, просто зная значение средней абсолютной ошибки, скажем, равное 10, мы сразу не можем сказать хорошая это ошибка или плохая, и что нужно сделать чтобы улучшить модель.
В этой связи представляет интерес использование для оценки качества регрессионной модели не значения ошибок, а величину показывающую, насколько данная модель работает лучше, чем модель, в которой присутствует только константа, а входные переменные отсутствуют или коэффициенты регрессии при них равны нулю.
Именно такой мерой и является коэффициент детерминации (Coefficient of determination), который показывает долю дисперсии зависимой переменной, объяснённой с помощью регрессионной модели. Наиболее общей формулой для вычисления коэффициента детерминации является следующая:
R^{2}=1-\frac{\sum\limits_{i=1}^{n}(\widehat{y}_{i}-y_{i})^{2}}{\sum\limits_{i=1}^{n}({\overline{y}}_{i}-y_{i})^{2}}
Практически, в числителе данного выражения стоит среднеквадратическая ошибка оцениваемой модели, а в знаменателе — модели, в которой присутствует только константа.
Главным преимуществом коэффициента детерминации перед мерами, основанными на ошибках, является его инвариантность к масштабу данных. Кроме того, он всегда изменяется в диапазоне от −∞ до 1. При этом значения близкие к 1 указывают на высокую степень соответствия модели данным. Очевидно, что это имеет место, когда отношение в формуле стремится к 0, т.е. ошибка модели с переменными намного меньше ошибки модели с константой. R^{2}=0 показывает, что между независимой и зависимой переменными модели имеет место функциональная зависимость.
Когда значение коэффициента близко к 0 (т.е. ошибка модели с переменными примерно равна ошибке модели только с константой), это указывает на низкое соответствие модели данным, когда модель с переменными работает не лучше модели с константой.
Кроме этого, бывают ситуации, когда коэффициент R^{2} принимает отрицательные значения (обычно небольшие). Это произойдёт, если ошибка модели среднего становится меньше ошибки модели с переменной. В этом случае оказывается, что добавление в модель с константой некоторой переменной только ухудшает её (т.е. регрессионная модель с переменной работает хуже, чем предсказание с помощью простой средней).
На практике используют следующую шкалу оценок. Модель, для которой R^{2}>0.5, является удовлетворительной. Если R^{2}>0.8, то модель рассматривается как очень хорошая. Значения, меньшие 0.5 говорят о том, что модель плохая.
Скорректированный R-квадрат
Основной проблемой при использовании коэффициента детерминации является то, что он увеличивается (или, по крайней мере, не уменьшается) при добавлении в модель новых переменных, даже если эти переменные никак не связаны с зависимой переменной.
В связи с этим возникают две проблемы. Первая заключается в том, что не все переменные, добавляемые в модель, могут значимо увеличивать её точность, но при этом всегда увеличивают её сложность. Вторая проблема — с помощью коэффициента детерминации нельзя сравнивать модели с разным числом переменных. Чтобы преодолеть эти проблемы используют альтернативные показатели, одним из которых является скорректированный коэффициент детерминации (Adjasted coefficient of determinftion).
Скорректированный коэффициент детерминации даёт возможность сравнивать модели с разным числом переменных так, чтобы их число не влияло на статистику R^{2}, и накладывает штраф за дополнительно включённые в модель переменные. Вычисляется по формуле:
R_{adj}^{2}=1-\frac{\sum\limits_{i=1}^{n}(\widehat{y}_{i}-y_{i})^{2}/(n-k)}{\sum\limits_{i=1}^{n}({\overline{y}}_{i}-y_{i})^{2}/(n-1)}
где n — число наблюдений, на основе которых строится модель, k — количество переменных в модели.
Скорректированный коэффициент детерминации всегда меньше единицы, но теоретически может принимать значения и меньше нуля только при очень малом значении обычного коэффициента детерминации и большом количестве переменных модели.
Сравнение метрик
Резюмируем преимущества и недостатки каждой приведённой метрики в следующей таблице:
| Мера | Сильные стороны | Слабые стороны |
|---|---|---|
| MSE | Позволяет подчеркнуть большие отклонения, простота вычисления. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. Сложность интерпретации из-за квадратичной зависимости. |
| RMSE | Простота интерпретации, поскольку измеряется в тех же единицах, что и целевая переменная. | Имеет тенденцию занижать качество модели, чувствительна к выбросам. |
| MSPE | Нечувствительна к выбросам. Хорошо интерпретируема, поскольку имеет линейный характер. | Поскольку вклад всех ошибок отдельных наблюдений взвешивается одинаково, не позволяет подчёркивать большие и малые ошибки. |
| MAPE | Является безразмерной величиной, поэтому её интерпретация не зависит от предметной области. | Нельзя использовать для наблюдений, в которых значения выходной переменной равны нулю. |
| SMAPE | Позволяет корректно работать с предсказанными значениями независимо от того больше они фактического, или меньше. | Приближение к нулю фактического или предсказанного значения приводит к резкому росту ошибки, поскольку в знаменателе присутствует как фактическое, так и предсказанное значения. |
| MASE | Не зависит от масштаба данных, является симметричной: положительные и отрицательные отклонения от фактического значения учитываются одинаково. Устойчива к выбросам. Позволяет сравнивать модели. | Сложность интерпретации. |
| MRE | Позволяет оценить величину ошибки относительно значения целевой переменной. | Неприменима для наблюдений с нулевым значением выходной переменной. |
| RMSLE | Логарифмирование позволяет сделать величину ошибки более устойчивой, когда разность между фактическим и предсказанным значениями различается на порядок и выше | Может быть затруднена интерпретация из-за нелинейности. |
| R-квадрат | Универсальность, простота интерпретации. | Возрастает даже при включении в модель бесполезных переменных. Плохо работает когда входные переменные зависимы. |
| R-квадрат скорр. | Корректно отражает вклад каждой переменной в модель. | Плохо работает, когда входные переменные зависимы. |
В данной статье рассмотрены наиболее популярные меры качества регрессионных моделей, которые часто используются в различных аналитических приложениях. Эти меры имеют свои особенности применения, знание которых позволит обоснованно выбирать и корректно применять их на практике.
Однако в литературе можно встретить и другие меры качества моделей регрессии, которые предлагаются различными авторами для решения конкретных задач анализа данных.
Другие материалы по теме:
Отбор переменных в моделях линейной регрессии
Репрезентативность выборочных данных
Логистическая регрессия и ROC-анализ — математический аппарат
Оценка ошибки прогнозирования временного ряда
Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
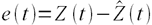
где Z(t) – фактическое значение временного ряда, а 
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.
MAPE – средняя абсолютная ошибка в процентах
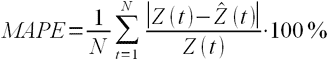
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.
Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.
MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.
После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.
Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.
MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка
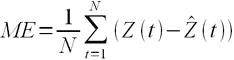
SD – стандартное отклонение
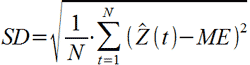
Связь точности и ошибки прогнозирования
Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.
Точность прогноза в % = 100% – MAPE
Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.
При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.


![{\displaystyle g_{\mathrm {MAPE} }(x)=\arg \min _{g\in {\mathcal {G}}}\mathbb {E} {\Biggl [}\left|{\frac {g(X)-Y}{Y}}\right||X=x{\Biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d1d5361807456edf90eb56a90450ac09d5964a2)





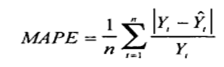 MAPE – средняя абсолютная ошибка в процентах используется:
MAPE – средняя абсолютная ошибка в процентах используется: