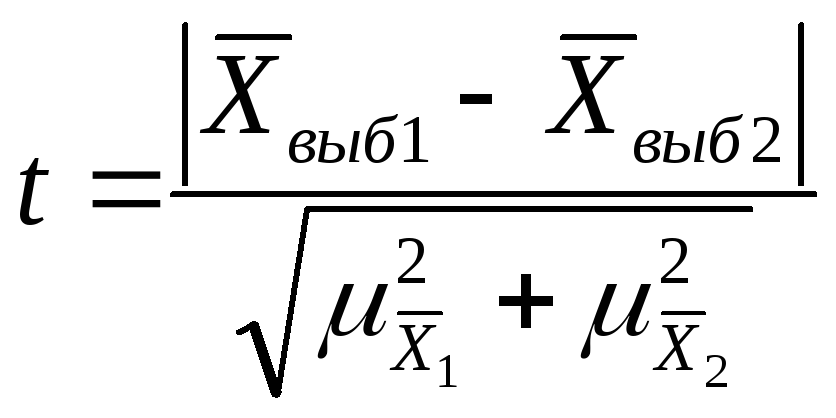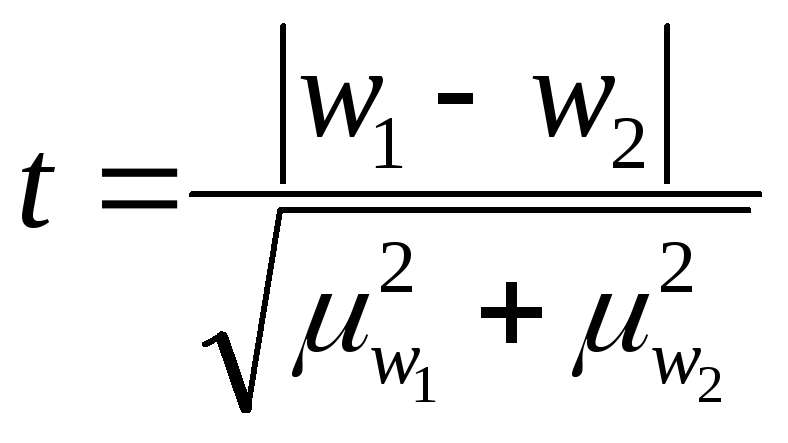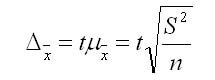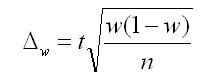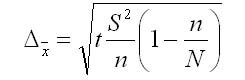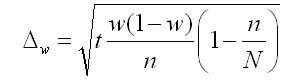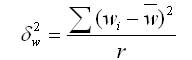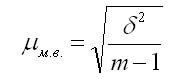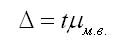Максимальная величина ошибки - Решение и исправление самых разных ошибок на TopOshibok.ru

From Wikipedia, the free encyclopedia

Probability densities of polls of different sizes, each color-coded to its 95% confidence interval (below), margin of error (left), and sample size (right). Each interval reflects the range within which one may have 95% confidence that the true percentage may be found, given a reported percentage of 50%. The margin of error is half the confidence interval (also, the radius of the interval). The larger the sample, the smaller the margin of error. Also, the further from 50% the reported percentage, the smaller the margin of error.

The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, whenever the measure varies.

The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.

Concept[edit]

Consider a simple yes/no poll as a sample of respondents drawn from a population $N{\text{, }}(n\ll N)$ reporting the percentage of yes responses. We would like to know how close is to the true result of a survey of the entire population , without having to conduct one. If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), we would expect those subsequent results $p_{1},p_{2},\ldots$ to be normally distributed about $\overline {p}$ , the true but unknown percentage of the population. The margin of error describes the distance within which a specified percentage of these results is expected to vary from $\overline {p}$ .

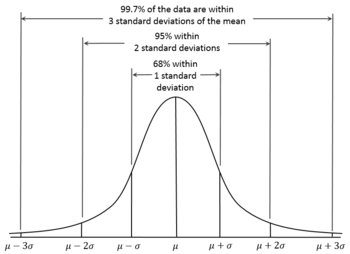
According to the 68-95-99.7 rule, we would expect that 95% of the results $p_{1},p_{2},\ldots$ will fall within about two standard deviations ( $\pm 2\sigma _{P}$ ) either side of the true mean $\overline {p}$ . This interval is called the confidence interval, and the radius (half the interval) is called the margin of error, corresponding to a 95% confidence level.

Generally, at a confidence level $\gamma$ , a sample sized of a population having expected standard deviation $\sigma$ has a margin of error

$MOE_{\gamma }=z_{\gamma }\times {\sqrt {\frac {\sigma ^{2}}{n}}}$

where $z_{\gamma }$ denotes the quantile (also, commonly, a z-score), and ${\sqrt {\frac {\sigma ^{2}}{n}}}$ is the standard error.

Standard deviation and standard error[edit]

We would expect the average of normally distributed values $p_{1},p_{2},\ldots$ to have a standard deviation which somehow varies with . The smaller , the wider the margin. This is called the standard error $\sigma _{\overline {p}}$ .

For the single result from our survey, we assume that $p={\overline {p}}$ , and that all subsequent results $p_{1},p_{2},\ldots$ together would have a variance $\sigma _{P}^{2}=P(1-P)$ .

${\text{Standard error}}=\sigma _{\overline {p}}\approx {\sqrt {\frac {\sigma _{P}^{2}}{n}}}\approx {\sqrt {\frac {p(1-p)}{n}}}$

Note that $p(1-p)$ corresponds to the variance of a Bernoulli distribution.

Maximum margin of error at different confidence levels[edit]

For a confidence level $\gamma$ , there is a corresponding confidence interval about the mean $\mu \pm z_{\gamma }\sigma$ , that is, the interval $[\mu -z_{\gamma }\sigma ,\mu +z_{\gamma }\sigma ]$ within which values of should fall with probability $\gamma$ . Precise values of $z_{\gamma }$ are given by the quantile function of the normal distribution (which the 68-95-99.7 rule approximates).

Note that $z_{\gamma }$ is undefined for $|\gamma |\geq 1$ , that is, $z_{1.00}$ is undefined, as is $z_{1.10}$ .

$\gamma$	$z_{\gamma }$		$\gamma$	$z_{\gamma }$
0.68	0.994457883210	0.999	3.290526731492
0.90	1.644853626951	0.9999	3.890591886413
0.95	1.959963984540	0.99999	4.417173413469
0.98	2.326347874041	0.999999	4.891638475699
0.99	2.575829303549	0.9999999	5.326723886384
0.995	2.807033768344	0.99999999	5.730728868236
0.997	2.967737925342	0.999999999	6.109410204869

Log-log graphs of $MOE_{\gamma }(0.5)$

vs sample size n and confidence level γ. The arrows show that the maximum margin error for a sample size of 1000 is ±3.1% at 95% confidence level, and ±4.1% at 99%.
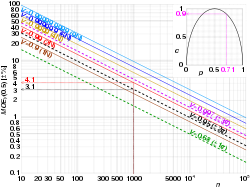
The inset parabola $\sigma _{p}^{2}=p-p^{2}$

illustrates the relationship between $\sigma _{p}^{2}$

at $p=0.71$

and $\sigma _{max}^{2}$

. In the example, MOE₉₅(0.71) ≈ 0.9 × ±3.1% ≈ ±2.8%.

Since $\max \sigma _{P}^{2}=\max P(1-P)=0.25$ at p=0.5 , we can arbitrarily set $p={\overline {p}}=0.5$ , calculate $\sigma _{P}$ , $\sigma _{\overline {p}}$ , and $z_{\gamma }\sigma _{\overline {p}}$ to obtain the maximum margin of error for at a given confidence level $\gamma$ and sample size , even before having actual results. With $p=0.5,n=1013$

$MOE_{95}(0.5)=z_{0.95}\sigma _{\overline {p}}\approx z_{0.95}{\sqrt {\frac {\sigma _{P}^{2}}{n}}}=1.96{\sqrt {\frac {.25}{n}}}=0.98/{\sqrt {n}}=\pm 3.1\%$

$MOE_{99}(0.5)=z_{0.99}\sigma _{\overline {p}}\approx z_{0.99}{\sqrt {\frac {\sigma _{P}^{2}}{n}}}=2.58{\sqrt {\frac {.25}{n}}}=1.29/{\sqrt {n}}=\pm 4.1\%$

Also, usefully, for any reported $MOE_{95}$

$MOE_{99}={\frac {z_{0.99}}{z_{0.95}}}MOE_{95}\approx 1.3\times MOE_{95}$

Specific margins of error[edit]

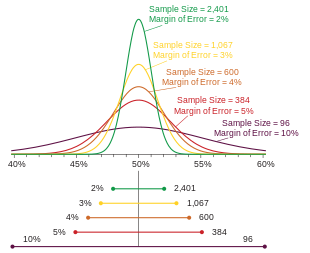
If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll reports $p_{a},p_{b},p_{c}$ as $71\%,27\%,2\%,n=1013$

$MOE_{95}(P_{a})=z_{0.95}\sigma _{\overline {p_{a}}}\approx 1.96{\sqrt {\frac {p_{a}(1-p_{a})}{n}}}=0.89/{\sqrt {n}}=\pm 2.8\%$

(as in the figure above)

$MOE_{95}(P_{b})=z_{0.95}\sigma _{\overline {p_{b}}}\approx 1.96{\sqrt {\frac {p_{b}(1-p_{b})}{n}}}=0.87/{\sqrt {n}}=\pm 2.7\%$

$MOE_{95}(P_{c})=z_{0.95}\sigma _{\overline {p_{c}}}\approx 1.96{\sqrt {\frac {p_{c}(1-p_{c})}{n}}}=0.27/{\sqrt {n}}=\pm 0.8\%$

As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.

Comparing percentages[edit]

Imagine multiple-choice poll reports $p_{a},p_{b},p_{c}$ as $46\%,42\%,12\%,n=1013$ . As described above, the margin of error reported for the poll would typically be $MOE_{95}(P_{a})$ , as $p_{a}$ is closest to 50%. The popular notion of statistical tie or statistical dead heat, however, concerns itself not with the accuracy of the individual results, but with that of the ranking of the results. Which is in first?

If, hypothetically, we were to conduct poll over subsequent samples of respondents (newly drawn from ), and report result $p_{w}=p_{a}-p_{b}$ , we could use the standard error of difference to understand how $p_{w_{1}},p_{w_{2}},p_{w_{3}},\ldots$ is expected to fall about ${\overline {p_{w}}}$ . For this, we need to apply the sum of variances to obtain a new variance, $\sigma _{P_{w}}^{2}$ ,

$\sigma _{P_{w}}^{2}=\sigma _{P_{a}-P_{b}}^{2}=\sigma _{P_{a}}^{2}+\sigma _{P_{b}}^{2}-2\sigma _{P_{a},P_{b}}=p_{a}(1-p_{a})+p_{b}(1-p_{b})+2p_{a}p_{b}$

where $\sigma _{P_{a},P_{b}}=-P_{a}P_{b}$ is the covariance of $P_{a}$ and $P_{b}$ .

Thus (after simplifying),

${\text{Standard error of difference}}=\sigma _{\overline {w}}\approx {\sqrt {\frac {\sigma _{P_{w}}^{2}}{n}}}={\sqrt {\frac {p_{a}+p_{b}-(p_{a}-p_{b})^{2}}{n}}}=0.029,P_{w}=P_{a}-P_{b}$

$MOE_{95}(P_{a})=z_{0.95}\sigma _{\overline {p_{a}}}\approx \pm {3.1\%}$

$MOE_{95}(P_{w})=z_{0.95}\sigma _{\overline {w}}\approx \pm {5.8\%}$

Note that this assumes that $P_{{c}}$ is close to constant, that is, respondents choosing either A or B would almost never chose C (making $P_{a}$ and $P_{b}$ close to perfectly negatively correlated). With three or more choices in closer contention, choosing a correct formula for $\sigma _{P_{w}}^{2}$ becomes more complicated.

Effect of finite population size[edit]

The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population , but only on the sample size . According to sampling theory, this assumption is reasonable when the sampling fraction is small. The margin of error for a particular sampling method is essentially the same regardless of whether the population of interest is the size of a school, city, state, or country, as long as the sampling fraction is small.

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula^[1]

$\operatorname {FPC} ={\sqrt {\frac {N-n}{N-1}}}$

…and so, if poll were conducted over 24% of, say, an electorate of 300,000 voters,

$MOE_{95}(0.5)=z_{0.95}\sigma _{\overline {p}}\approx {\frac {0.98}{\sqrt {72,000}}}=\pm 0.4\%$

$MOE_{95_{FPC}}(0.5)=z_{0.95}\sigma _{\overline {p}}{\sqrt {\frac {N-n}{N-1}}}\approx {\frac {0.98}{\sqrt {72,000}}}{\sqrt {\frac {300,000-72,000}{300,000-1}}}=\pm 0.3\%$

Intuitively, for appropriately large ,

$\lim _{n\to 0}{\sqrt {\frac {N-n}{N-1}}}\approx 1$

$\lim _{n\to N}{\sqrt {\frac {N-n}{N-1}}}=0$

In the former case, is so small as to require no correction. In the latter case, the poll effectively becomes a census and sampling error becomes moot.

References[edit]

^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)

Sources[edit]

Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.

External links[edit]

«Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. «Margin of Error». MathWorld.

Источник

Средняя и предельная ошибки выборки

Средняя ошибка выборкивсегда
присутствует в выборочных исследованиях
и появляется вследствие того, что
обследуются не все единицы статистической
совокупности, а лишь ее часть.

Средняя ошибка выборки превращается в
предельную ошибкуΔ
при умножении ее на коэффициент
доверияt, который задается
предварительно, исходя из требуемой
точности наблюдения. Предельная ошибка
позволяет судить об «истинном» размере
параметра в генеральной совокупности
с определенной степенью вероятности

-предельная
ошибка ,-средняя
ошибка, t – коэффициент доверия

При типическом и серийном
отборе, при расчете ошибки выборки
вместо общей дисперсии (σ²)
следует использовать
среднюю из внутригрупповых дисперсий
и межгрупповую дисперсию,
где—
частная дисперсия i группы,объем i группы

Формулы предельной ошибки случайной
выборки при определении средней

Для повторного отбора

где
средняя
ошибка выборки

Для бесповторного отбора

Формулы предельной ошибки случайной
выборки при определении доли

Для повторного отбора

где
средняя ошибка выборочной доли

Для бесповторного отбора

где
средняя ошибка выборочной доли

Формулы численности случайной
выборки при определении средней величины

Для повторного отбора	Для бесповторного отбора

Формулы численности случайной выборки при определении доли изучаемого признака

Для повторного отбора	Для бесповторного отбора

Предельная разница между генеральной
и выборочной средней соответствует
величине предельной ошибки

для средней	для доли:

Значения вероятности и соответственно
tнаходятся по таблицам
распределения:

Лапласа
Стьюдента (в случае малой выборки)

Формулы случайной выборки подходят и
для механической выборки.

При необходимости округления, при
случайной выборке – округление в большую
сторону, при механической – в меньшую.

Малая выборка

Если численность выборочной совокупности
не более 30 единиц, то средняя ошибка
малой выборки при определении средней
величины рассчитывается по формуле:

	при определении доли по формуле:

Для расчета ошибки малой выборки
применяется уточненная формула дисперсии

где n-1 —
представляет собой «число степеней
свободы», т.е. количество вариантов,
могущих принимать произвольные
значения, не меняющие величины средней.

Типы задач выборочного наблюдения

определение ошибки выборки,
определение численности выборочной
совокупности n
,
определение вероятности того, что
выборочная средняя (или доля) отклонится
от генеральной не более, чем на заданную
величину t=Δ/μ,
оценка случайности расхождений
показателей выборочных наблюдений,
перенос выборочных характеристик на
генеральную совокупность.

Проверка гипотез о средней и доле

Оценка случайности расхождений
показателей выборочных наблюдений

Если при n>30 коэффициент t<3, то делается
вывод о случайности расхождений.
Если n≤ 30 , то полученное
значение t сравнивают с табличным,
определяемым по таблице распределения
Стьюдента
Если,
расхождение считается существенным.
Если
,
расхождение считается случайным.

Методы переноса выборочных данных на
генеральную совокупность

метод взвешивания;
метод перевзвешивания;
метод заполнения случайным подбором
в классах замещения.

Источник

Предельная ошибка выборки

Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.

1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:

где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;

мю х — средняя ошибка выборки.

2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:

3. Предельная ошибка выборки для средней при бесповторном отборе:

4. Предельная ошибка выборки для доли при бесповторном отборе:

Предельная относительная ошибка выборки

Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:

Малая выборка

Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.

Средняя и предельная ошибки для малой выборки

В малой выборке средняя ошибка рассчитывается по формуле:

Предельная ошибка малой выборки рассчитывается по формуле:

где t — отношение Стьюдента

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

Материалы сайта

Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.

Источник

Concept[edit]

Standard deviation and standard error[edit]

Maximum margin of error at different confidence levels[edit]

Specific margins of error[edit]

Comparing percentages[edit]

Effect of finite population size[edit]

See also[edit]

References[edit]

Sources[edit]

External links[edit]

Средняя и предельная ошибки выборки

Формулы численности случайной выборки при определении доли изучаемого признака

Малая выборка

Предельная ошибка выборки

Предельная относительная ошибка выборки

Малая выборка

Средняя и предельная ошибки для малой выборки

Материалы сайта