From Wikipedia, the free encyclopedia
The margin of error is a statistic expressing the amount of random sampling error in the results of a survey. The larger the margin of error, the less confidence one should have that a poll result would reflect the result of a census of the entire population. The margin of error will be positive whenever a population is incompletely sampled and the outcome measure has positive variance, which is to say, whenever the measure varies.
The term margin of error is often used in non-survey contexts to indicate observational error in reporting measured quantities.
Concept[edit]
Consider a simple yes/no poll 











According to the 68-95-99.7 rule, we would expect that 95% of the results 


Generally, at a confidence level 


where 

Standard deviation and standard error[edit]
We would expect the average of normally distributed values 



For the single result from our survey, we assume that 


Note that 
Maximum margin of error at different confidence levels[edit]
For a confidence level 

![{\displaystyle [\mu -z_{\gamma }\sigma ,\mu +z_{\gamma }\sigma ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4568060e0cffbc8dfb793aa2ef4617c89cb9e94)



Note that 




|

|

|

|
|
|---|---|---|---|---|
| 0.68 | 0.994457883210 | 0.999 | 3.290526731492 | |
| 0.90 | 1.644853626951 | 0.9999 | 3.890591886413 | |
| 0.95 | 1.959963984540 | 0.99999 | 4.417173413469 | |
| 0.98 | 2.326347874041 | 0.999999 | 4.891638475699 | |
| 0.99 | 2.575829303549 | 0.9999999 | 5.326723886384 | |
| 0.995 | 2.807033768344 | 0.99999999 | 5.730728868236 | |
| 0.997 | 2.967737925342 | 0.999999999 | 6.109410204869 |

The inset parabola 




Since 









Also, usefully, for any reported 
Specific margins of error[edit]
If a poll has multiple percentage results (for example, a poll measuring a single multiple-choice preference), the result closest to 50% will have the highest margin of error. Typically, it is this number that is reported as the margin of error for the entire poll. Imagine poll 


(as in the figure above)
As a given percentage approaches the extremes of 0% or 100%, its margin of error approaches ±0%.
Comparing percentages[edit]
Imagine multiple-choice poll 




If, hypothetically, we were to conduct poll 






where 


Thus (after simplifying),
Note that this assumes that 



Effect of finite population size[edit]
The formulae above for the margin of error assume that there is an infinitely large population and thus do not depend on the size of population 

In cases where the sampling fraction is larger (in practice, greater than 5%), analysts might adjust the margin of error using a finite population correction to account for the added precision gained by sampling a much larger percentage of the population. FPC can be calculated using the formula[1]
…and so, if poll 
Intuitively, for appropriately large 
In the former case, 
See also[edit]
- Engineering tolerance
- Key relevance
- Measurement uncertainty
- Random error
References[edit]
- ^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. Blackwell Publishing. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
Sources[edit]
- Sudman, Seymour and Bradburn, Norman (1982). Asking Questions: A Practical Guide to Questionnaire Design. San Francisco: Jossey Bass. ISBN 0-87589-546-8
- Wonnacott, T.H.; R.J. Wonnacott (1990). Introductory Statistics (5th ed.). Wiley. ISBN 0-471-61518-8.
External links[edit]
- «Errors, theory of», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. «Margin of Error». MathWorld.
В конкретной выборке действительная
ошибка может быть больше средней, меньше
средней или равна средней. Каждое из
этих расхождений имеет определенную
вероятность.
Предельная
ошибка выборки
– это максимальное различие между
выборочной и генеральной характеристикой,
гарантируемое с определенной вероятностью
(48).
,
,
где
t
– нормированное отклонение, зависящее
от вероятности, определяемое как аргумент
интегральной функции Лапласа. Определение
предельной ошибки выборки основано на
теореме Чебышева –Ляпунова.
Теорема
Чебышева-Ляпунова.
Свероятностью сколь угодно близкой к
единице можно утверждать, что при
достаточно большом объеме выборки и
ограниченной дисперсии выборочная
характеристика будет очень мало
отличаться от генеральной характеристики.
Значение
этой функций находиться по статистической
таблице интегральной функции Лапласа
Ф(t),
поэтому, зная вероятность P
= Ф(t),
можно определить аргумент t.
Наиболее
часто используемые значения Ф (t)
и t
приведем в таблице 20.
Таблица
20
|
Р |
0,683 |
0,95 |
0,954 |
0,99 |
0,997 |
|
t |
1 |
1,96 |
2 |
2,58 |
3 |
Чем
больше вероятность, с которой гарантируются
результаты, тем больше будет предельная
ошибка и менее надежные результаты
выборки. Поэтому
в экономических исследованиях используются
Р = 0,95 и Р = 0,954.
-
Распространение
результатов выборки
на
генеральную совокупность
Конечным
итогом выборочного обследования
является оценка неизвестных генеральных
характеристик на основе данных выборки.
По
этой оценке строится доверительный
интервал для генеральной средней и
генеральной доли.
Ошибка
выборки зависит не только от вероятности,
но и от того, как было организовано
выборочное обследование.
Выделим
основные
этапы
выборочного обследования:
1
определение объекта исследования;
2
постановка цели и задач;
3
определение процедуры отбора, проведение
отбора единиц в выборку;
4
подготовка кадров и инструментария;
5
сбор данных;
6
определение выборочных характеристик,
ошибок выборки;
7
оценка доверительных интервалов;
8
оценка возможностей распространения
результатов на генеральную совокупность.
Для этого определяют относительные
ошибки выборки. Если эти ошибки не
превышают заранее заданной величины,
то результаты можно распространить на
генеральную совокупность, если превышают,
то изменить процедуру отбора или методы
ремонта выборки.
9 распространение результатов. Для
этого применяются следующие способы:
-
прямой
пересчет, т. е. границы доверительного
интервала умножаются на объем генеральной
совокупности; -
способ
поправочных коэффициентов – используется
в тех случаях, когда корректируются
данные сплошного обследования. По
выборке рассчитывается поправочный
коэффициент, и данные сплошного
обследования исправляются на этот
коэффициент.
8.7 Определение необходимой численности
выборки
При
проведении выборочного обследования
возникает вопрос, сколько нужно отобрать
единиц в выборку, чтобы результаты
обследования удовлетворяли заранее
заданным величинам, т.е. предельная
ошибка не превышала определенного
значения. Для определения необходимой
численности выборки применяются формулы,
которые выводятся из предельной ошибки.
Для
собственно-случайного повторного
отбора.
______
∆x
= t∙μx
= t∙√Sx2
/ n
=> n
= t2·
Sx2
/ ∆x2
.
Для
собственно-случайного бесповторного
отбора.
___________
∆x
= t·√Sx
/ n·(1-n/N)
=> n
= t2·N·Sx2
/ (∆x2·N
+ t2·
Sx2).
Для
других способов отбора формулы необходимой
численности выборки аналогичны,
изменяется только дисперсия.
Значение
дисперсии при определении необходимой
численности выборки достаточно часто
бывает неизвестно. В этом случае ее
определяют:
-
из
предыдущего обследования на данную
тему; -
рассчитывают
приближенно Sx2≈(R/6)2
по пробному обследованию малого
количества единиц; -
неизвестную
дисперсию для доли берут равной 0,25.
Области
применения выборочного метода сбора
данных.
В
настоящее время выборочный метод сбора
данных является одним из наиболее часто
используемых. Выборочное наблюдение
используется в следующих случаях:
-
для
статистического оценивания и проверки
различных гипотез; -
при
контроле технологических процессов и
показателей качества продукции; -
при
различных отраслевых обследованиях; -
при
решении задач в сфере предпринимательства.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предельная ошибка выборки
Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.
1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:
где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;
мю х — средняя ошибка выборки.
2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:
3. Предельная ошибка выборки для средней при бесповторном отборе:
4. Предельная ошибка выборки для доли при бесповторном отборе:
Предельная относительная ошибка выборки
Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:
Малая выборка
Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.
Средняя и предельная ошибки для малой выборки
В малой выборке средняя ошибка рассчитывается по формуле:
Предельная ошибка малой выборки рассчитывается по формуле:
где t — отношение Стьюдента
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки (
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки (

Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки (
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки (

Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Ошибкой
выборочного среднего
или ошибкой
выборки
называется абсолютная величина разности
генерального и выборочного средних.
Так как генеральное среднее неизвестно,
ошибку выборки вычислить нельзя, но ее
можно оценить с помощью предельной
ошибки:
,
(1.10.15)
где
предельная
ошибка выборки;
средняя ошибка,
вычисляемая по формуле, зависящей от
вида выборки;
доверительный
коэффициент, значение которого находится
по заданной вероятности р
в специальных таблицах.
Доверительный
интервал, в котором с вероятностью р
находится генеральное среднее, имеет
вид:
.
(1.10.16)
Средняя
ошибка
малой выборки
вычисляется
по формуле
,
(1.10.17)
где
дисперсия
малой выборки, вычисляемая по формуле
.
(1.10.18)
Предельная
ошибка малой выборки
вычисляется по формуле (1.10.15), где
коэффициент
находится по уровню значимости
и числу
в табл. П4.
Пример
1.10.4.
При проверке качества партии колбасы
получены следующие данные о процентном
содержании поваренной соли в 10 пробах:
4,3; 4,2; 3,8; 4,3; 3,7; 3,9; 4,5; 4,4; 4,0; 3,9. Найдем с
вероятностью 0,95 границы, в которых
находится средний процент содержания
поваренной соли в партии колбасы.
Составим
расчётную табл. 1.10.10. По суммам в итоговой
строке табл. 1.10.10 вычислим
выборочную среднюю, выборочную дисперсию
и среднюю ошибку выборки:
,
,
.
Таблица
1.10.10
Расчетные показатели
|
i |
(%) |
|
|
|
1 |
4,3 |
0,2 |
0,04 |
|
2 |
4,2 |
0,1 |
0,01 |
|
3 |
3,8 |
0,3 |
0,09 |
|
4 |
4,3 |
0,2 |
0,04 |
|
5 |
3,7 |
– 0,4 |
0,16 |
|
6 |
3,9 |
– 0,2 |
0,04 |
|
7 |
4,5 |
0,4 |
0,16 |
|
8 |
4,4 |
0,3 |
0,09 |
|
9 |
4,0 |
–0,1 |
0,01 |
|
10 |
3,9 |
– 0,2 |
0,04 |
|
41,0 |
0,68 |
В
табл. П4 по уровню значимости
и числу
находим доверительный коэффициент:
=2,262.
Вычислим предельную ошибку выборки:
.
Найдем доверительный интервал (1.10.16):
или
.
Таким
образом, с вероятностью 0,95 можно
утверждать, что в партии колбасы
содержание поваренной соли находится
в пределах от 3,9%
до 4,3%.
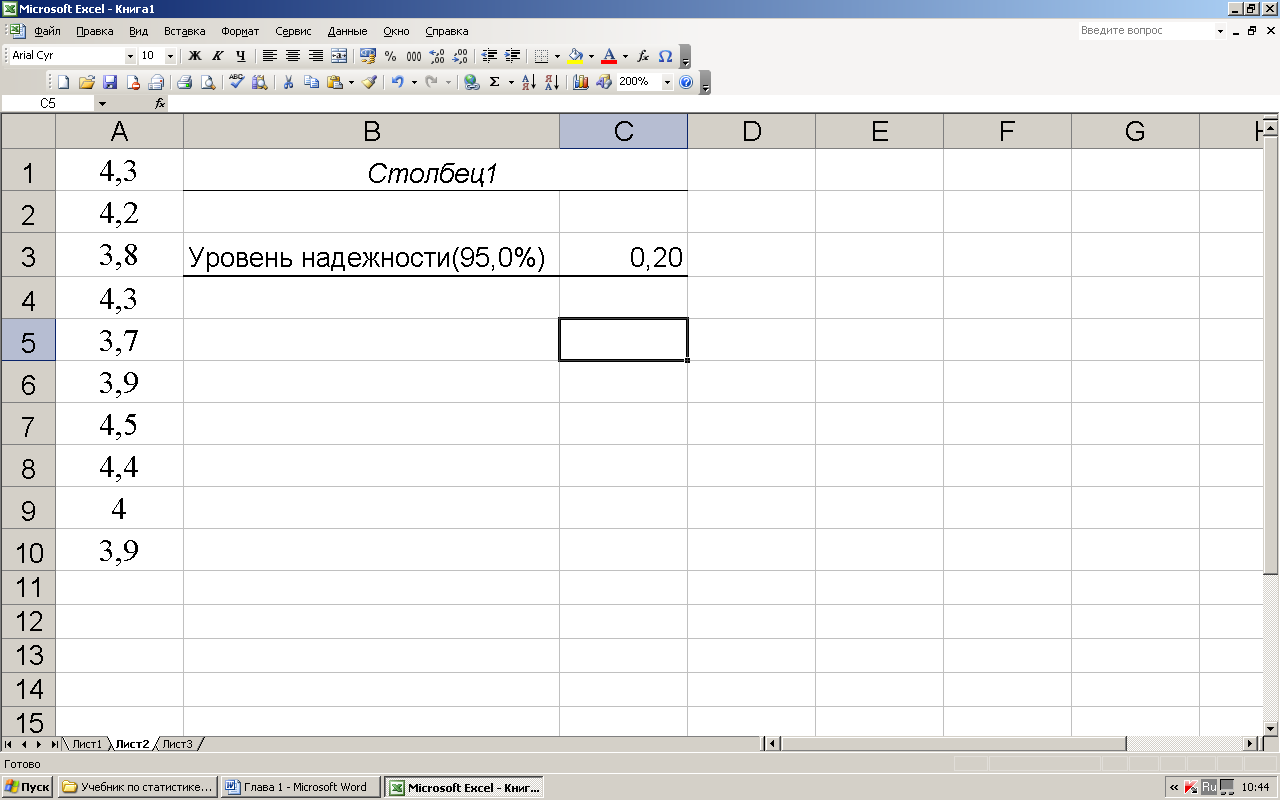
1.10.6. Вычисление предельной ошибки (пример 1.10.4)
Предельную
ошибку малой выборки можно найти,
применяя Excel
(рис. 1.10.6).
Для этого надо:
1)
в столбце
ячеек записать выборку;
2)
в меню
СЕРВИС
выбрать ОПИСАТЕЛЬНАЯ
СТАТИСТИКА;
3)
указать
уровень надежности
(доверительную
вероятность);
4)
снять остальные флажки, указать ячейку
выходного интервала и выбрать ОК.
Упражнение
1.10.7.
Отобрано 10 рабочих цеха для определения
среднего времени выполнения определенной
операции рабочими цеха. Выборочное
среднее время оказалось равным 10,4 мин,
а выборочное среднеквадратическое
отклонение –
2 мин. Найдите границы, в которых с
вероятностью 0,99 находится генеральная
средняя.
Приведем
следующие формулы для вычисления средней
ошибки
большой выборки (
):
1)
средняя ошибка
случайной повторной или бесповторной
выборки вычисляется соответственно
по формуле
или
;
(1.10.19)
2)
средняя ошибка
типической повторной или бесповторной
выборки вычисляется соответственно
по формуле
или
,
(1.10.20)
где
– средняя
генеральных групповых дисперсий;
3)
средняя ошибка
серийной повторной или бесповторной
выборки вычисляется соответственно по
формуле
или
,
(1.10.21)
где
– генеральная
межгрупповая (межсерийная) дисперсия;
r
и
R
число серий
соответственно в выборке и в генеральной
совокупности.
Генеральная
дисперсия
связана с выборочной дисперсией
соотношением
.
(1.10.22)
При
больших значениях n
генеральная
дисперсия приближенно равна выборочной
дисперсии.
Предельная
ошибка
большой выборки
вычисляется по формуле (1.10.15), где
коэффициент
определяется
из соотношения
.
Напомним,
что выборочное среднее значение
альтернативного признака равно выборочной
доле единиц в выборке, обладающих этим
признаком (
),
а выборочная дисперсия равна произведению
.
Пример
1.10.5.
При проверке
качества хлебобулочных изделий проведено
5%-е выборочное обследование партии
нарезных батонов. Из 100 отобранных в
выборку батонов 90 батонов оказались
стандартными. Средний вес одного батона
в выборке составил 500,5 г при
среднеквадратическом отклонении 15,4 г.
Найдем с вероятностью 0,95 доверительные
интервалы для доли стандартных батанов
и среднего веса одного батона во всей
партии.
По
условию выборочная доля:
.
Было
проведено 5%-е
выборочное обследование, следовательно,
во всей партии
2000 батонов. Так как выборка
бесповторная механическая или случайная,
средняя ошибка выборочной доли равна:
.
Из
соотношения
,
используя табл. П2, найдем доверительный
коэффициент:
.
Вычислим
предельную ошибку:
.
Найдем
доверительный интервал (1.10.16):
или
.
Таким
образом, с вероятностью 0,95 можно
утверждать, что доля стандартных батонов
во всей партии батонов находится в
интервале от 0,84 до 0,96.
Вычислим
среднюю и предельную ошибки выборочного
среднего веса одного батона:
1,5
и
.
Найдем
доверительный интервал (1.10.16):
или
.
Таким
образом, с вероятностью 0,95 можно
утверждать, что средний вес одного
батона во всей партии батонов находится
в интервале от 497,6 г до 503,4 г.
Упражнение
1.10.8.
Дано распределение пачек чая по весу в
выборке из партии чая (табл. 1.10.11).
Таблица
1.10.11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Повторный и бесповторный отбор.
Ошибка выборки
Краткая теория
На основании выборочных данных дается оценка статистических
показателей по всей (генеральной) совокупности. Подобное возможно, если выборка
основывается на принципах случайности отбора и репрезентативности
(представительности) выборочных данных. Каждая единица генеральной совокупности
должна иметь равную возможность (вероятность) попасть в выборку.
При формировании выборочной совокупности используются следующие
способы отбора: а) собственно-случайный отбор; б) механическая выборка; в)
типический (районированный) отбор; г) многоступенчатая (комбинированная)
выборка; д) моментно-выборочное наблюдение.
Выборка может осуществляться по схеме повторного и бесповторного
отбора.
В первом случае единицы совокупности, попавшие в выборку, снова
возвращаются в генеральную, а во втором случае – единицы совокупности, попавшие
в выборку, в генеральную совокупность уже не возвращаются.
Выборка может осуществляться отдельными единицами или сериями
(гнездами).
Собственно-случайная выборка
Отбор в этом случае производится либо по жребию, либо по таблицам
случайных чисел.
На основании приемов классической выборки решаются следующие
задачи:
а) определяются границы среднего значения показателя по генеральной
совокупности;
б) определяются границы доли признака по генеральной совокупности.
Предельная ошибка средней при собственно-случайном отборе
исчисляется по формулам:
а) при повторном отборе:
б) при бесповторном отборе:
где
– численность выборочной совокупности;
– численность генеральной совокупности;
– дисперсия признака;
– критерий кратности ошибки: при
;
при
;
при
.
Значения
определяются
по таблице функции Лапласа.
Границы (пределы) среднего значения признака по генеральной
совокупности определяются следующим неравенством:
где
– среднее значение признака по выборочной
совокупности.
Предельная ошибка доли при собственно-случайном отборе определяется
по формулам:
а) при повторном отборе:
при бесповторном отборе:
где
– доля единиц совокупности с заданным
значением признака в обзей численности выборки,
– дисперсия доли признака.
Границы (пределы) доли признака по всей (генеральной) совокупности
определяются неравенством:
где
– доля признака по генеральной совокупности.
Типическая (районированная) выборка
Особенность этого вида
выборки заключается в том, что предварительно генеральная совокупность по
признаку типизации разбивается на частные группы (типы, районы), а затем в
пределах этих групп производится выборка.
Предельная ошибка средней
при типическом бесповторном отборе определяется по формуле:
где
– средняя из внутригрупповых дисперсий
по каждой типичной группе.
При пропорциональном отборе из групп генеральной совокупности
средняя из внутригрупповых дисперсий определяется по формуле:
где
– численности единиц совокупности групп по выборке.
Границы (пределы) средней по генеральной совокупности на основании
данных типической выборки определяются по тому же неравенству, что при
собственно-случайной выборке. Только предварительно необходимо вычислить общую
выборочную среднюю
из частных выборочных средних
.
Для случая пропорционального отбора это определяется по формуле:
При непропорциональном отборе средняя из внутригрупповых дисперсий вычисляется по
формуле:
где
– численность единиц групп по генеральной
совокупности.
Общая выборочная средняя в этом случае определяется по формуле:
Предельная ошибка доли
признака при типическом бесповторном отборе определяется формулой:
Средняя дисперсия доли
признака из групповых дисперсий доли
при
типической пропорциональной выборке вычисляется по формуле:
Средняя доля признака по
выборке из показателей групповых долей рассчитывается формуле:
Средняя дисперсия доли при
непропорциональном типическом отборе определяется следующим образом:
а средняя доля признака:
Формулы ошибок выборки при типическом повторном отборе будут те же,
то и для случая бесповторного отбора. Отличие заключается только в том, что в
них будет отсутствовать по корнем сомножитель
.
Серийная выборка
Серийная ошибка выборки
может применяться в двух вариантах:
а) объем серий различный
б) все серии имеют
одинаковое число единиц (равновеликие серии).
Наиболее распространенной
в практике статистических исследований является серийная выборка с
равновеликими сериями. Генеральная совокупность делится на одинаковые по объему
группы-серии
и
производится отбор не единиц совокупности, а серий
. Группы (серии) для обследования отбирают в
случайном порядке или путем механической выборки как повторным, так и
бесповторными способами. Внутри каждой отобранной серии осуществляется сплошное
наблюдение. Предельные ошибки выборки
при
серийном отборе исчисляются по формулам:
а) при повторном отборе
б) при бесповторном отборе
где
– число
серий в генеральной совокупности;
– число
отобранных серий;
– межсерийная дисперсия, исчисляемая для случая равновеликих
серий по формуле:
где
–
среднее значение признака в каждой из отобранных серий;
– межсерийная
средняя, исчисляемая для случая равновеликих серий по формуле:
Определение численности выборочной совокупности
При проектировании
выборочного наблюдения важно наряду с организационными вопросами решить одну из
основных постановочных задач: какова должна быть необходимая численность
выборки с тем, чтобы с заданной степенью точности (вероятности) заранее
установленная ошибка выборки не была бы превзойдена.
Примеры решения задач
Задача 1
На основании результатов проведенного на заводе 5%
выборочного наблюдения (отбор случайный, бесповторный) получен следующий ряд
распределения рабочих по заработной плате:
| Группы рабочих по размеру заработной платы, тыс.р. | до 200 | 200-240 | 240-280 | 280-320 | 320 и выше | Итого |
| Число рабочих | 33 | 35 | 47 | 45 | 40 | 200 |
На основании приведенных данных определите:
1) с вероятностью 0,954 (t=2) возможные пределы, в которых
ожидается средняя заработная плата рабочего в целом по заводу (по генеральной
совокупности);
2) с вероятностью 0,997 (t=3) предельную ошибку и границы доли
рабочих с заработной платой от 320 тыс.руб. и выше.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
Вычислим среднюю з/п: Для этого просуммируем произведения середин
интервалов и соответствующих частот, и полученную сумму разделим на сумму
частот.
2) Выборочная дисперсия:
Найдем доверительный интервал для средней. Предельная ошибка выборочной
средней считается по формуле:
где
—
аргумент функции Лапласа.
Искомые возможные пределы, в которых ожидается средняя заработная плата
рабочего в целом по заводу:
Найдем доверительный интервал для выборочной доли. Предельная ошибка
выборочной доли считается по формуле:
Доля рабочих с з/п от 320 тыс.р.:
Искомые границы доли рабочих с заработной платой от 320 тыс.руб. и выше:
Задача 2
В
городе 23560 семей. В порядке механической выборки предполагается определить
количество семей в городе с числом детей трое и более. Какова должна быть
численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала
0,02 человека. На основе предыдущих обследований известно, что дисперсия равна
0,3.
Решение
Численность
выборки можно найти по формуле:
В нашем случае:
Вывод к задаче
Таким образом численность
выборки должна составить 2661 чел.
Задача 3
С
целью определения средней месячной заработной платы персонала фирмы было
проведено 25%-ное выборочное обследование с отбором
единиц пропорционально численности типических групп. Для отбора сотрудников
внутри каждого филиала использовался механический отбор. Результаты
обследования представлены в следующей таблице:
| Номер филиала | Средняя месячная заработная плата, руб. |
Среднее квадратическое отклонение, руб. | Число сотрудников, чел. |
| 1 | 870 | 40 | 30 |
| 2 | 1040 | 160 | 80 |
| 3 | 1260 | 190 | 140 |
| 4 | 1530 | 215 | 190 |
С
вероятностью 0,954 определите пределы средней месячной заработной платы всех
сотрудников гостиниц.
Решение
Предельная
ошибка выборочной средней:
Средняя
из внутригрупповых дисперсий:
Получаем:
Средняя
месячная заработная плата по всей совокупности филиалов:
Искомые
пределы средней месячной заработной платы:
Вывод к задаче
Таким
образом с вероятностью 0,954 средняя месячная заработная плата всех сотрудников
гостиниц находится в пределах от 1294,3 руб. до 1325,7 руб.
Предельная ошибка выборки равна t-кратному числу средних ошибок выборки:
μ – средняя ошибка выборки, рассчитанная с учетом поправки, на которую производится корректировка в случае бесповторного отбора;
t – коэффициент доверия, который находят при заданном уровне вероятности. Так для Р=0,997 по таблице значений интегральной функции Лапласа t=3
Величина предельной ошибки выборки может быть установлена с определенной вероятностью. Вероятность появления такой ошибки, равной или больше утроенной средней ошибки выборки, крайне мала и равна 0,003 (1–0,997). Такие маловероятные события считаются практически невозможными, а потому вероятность того, что эта разность превысит трехкратную величину средней ошибки, определяет уровень ошибки и составляет не более 0,3%.
Определение предельной ошибки выборки для доли
Условие:
Из готовой продукции, в порядке собственно-случайного бесповторного отбора, было отобрано 200 ц, из которых 8 ц оказалось испорчено. Можно ли полагать с вероятностью 0,954, что потери продукции не превысят 5%, если выборка составляет 1:20 часть ее размера?
Дано:
- n =200ц – объем выборки (выборочная совокупность)
- m =8ц — кол-во испорченной продукции
- n:N = 1:20 – пропорция отбора, где N- объем совокупности (генеральная совокупность)
- Р = 0,954 – вероятность
Определить: ∆ω< 5% (согласуется ли то, что потери продукции не превысят 5%)
Решение:
1. Определим выборочную долю-такую долю составляет испорченная продукция в выборочной совокупности:
2. Определим объем генеральной совокупности:
N=n*20=200*20=4000(ц) – количество всей продукции.
3. Определим предельную ошибку выборки для доли продукции, обладающей соответствующим признаком, т.е. для доли испорченной продукции: Δ = t*μ, где µ– средняя ошибка доли, обладающей альтернативным признаком, с учетом поправки, на которую производится корректировка в случае бесповторного отбора; t – коэффициент доверия, который находят при заданном уровне вероятности Р=0,954 по таблице значений интегральной функции Лапласа: t=2
4. Определим границы доверительного интервала для доли альтернативного признака в генеральной совокупности, т.е. какую долю испорченная продукция составит в общем объеме: поскольку доля испорченной продукции в выборочном объеме составляет ω = 0,04, то с учетом предельной ошибки ∆ω= 0,027 генеральная доля альтернативного признака (p) примет значения:
ω-∆ω < p < ω+∆ω
0.04-0.027< p < 0.04+0.027
0.013 < p < 0.067
Вывод: с вероятностью Р=0,954 можно утверждать, что доля испорченной продукции при выборке большего объема не выйдет за пределы найденного интервала (не менее 1,3% и не более 6,7%). Но остается вероятность того, что доля испорченной продукции может превысить 5% в пределах до 6,7%, что, в свою очередь, не согласуется с утверждением ∆ω< 5%.
*******
Условие:
Менеджер магазина по опыту знает, что 25% входящих в магазин покупателей, совершают покупки. Предположим, что в магазин вошло 200 покупателей.
Определить:
- долю покупателей, совершивших покупки
- дисперсию выборочной доли
- среднее квадратическое отклонение выборочной доли
- вероятность того, что выборочная доля будет в пределах между 0,25 и 0,30
Решение:
В качестве генеральной доли (p) принимаем выборочную долю (ω) и определяем верхнюю границу доверительного интервала.
Зная критическую точку (по условию: выборочная доля будет в пределах 0,25-0,30), строим одностороннюю критическую область (правостороннюю).
По таблице значений интегральной функции Лапласа находим Z
Этот же вариант можно рассматривать и как повторный отбор при условии, если один и тот же покупатель, не купив в 1-й раз, возвращается и совершает покупку.
В случае, если выборку рассматривать как бесповторную, необходимо среднюю ошибку скорректировать на поправочный коэффициент. Тогда, подставив скоррекированные значения предельной ошибки для выборочной доли, при определении критической области, изменятся Z и P
Определение предельной ошибки выборки для средней
По данным 17 сотрудников фирмы, где работает 260 человек, среднемесячная заработная плата составила 360 у.е., при s=76 у.е. Какая минимальная сумма должна быть положена на счет фирмы, чтобы с вероятностью 0,98 гарантировать выдачу заработной платы всем сотрудникам?
Дано:
- n=17 — объем выборки (выборочная совокупность)
- N=260 — объем совокупности (генеральная совокупность)
- Хср.=360 — выборочная средняя
- S=76 — выборочное среднеквадратическое отклонение
- Р = 0,98 – доверительная вероятность
Определить: минимально допустимое значение генеральной средней (нижнюю границу доверительного интервала).
Решение:
Для определения доверительного интервала для средней, необходимо найти предельную ошибку для средней: при Р=0,98 по таблице значений интегральной функции Лапласа — t=2.33
Из условия определения границ доверительного интервала для средней:
Хср.-Δх≤Х≤ Хср.+Δх определяем нижнюю границу (левосторонняя критическая область): 360-41,52=318,48
Отсюда: 318,48*260=82804,7 у.е. — такова минимальная сумма, которая должна быть положена на счет фирмы.
1.1. Ошибки
выборочного наблюдения
Средняя
ошибка выборки показывает, как генеральная средняя отклоняется в среднем от выборочной средней в ту или другую сторону. Формула
расчета средней ошибки выборки определяется видом исследуемого признака единиц
совокупности (количественный или альтернативный) и
способом отбора (бесповторный или повторный).
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
, где
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный

число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный

доля
·
Если отбор бесповторный, а признак
альтернативный
Предельная ошибка выборки— показывающая с определенной степенью вероятности
отклонения средней от выборочной средней.
Предельная ошибка выборки
, где параметр t зависит
от вероятности
Некоторые значения параметра t приведены
в таблице:
|
Вероятность, p |
0.95 |
0.954 |
0.9876 |
0.9907 |
0.9973 |
0.9999 |
|
Параметр t |
1.96 |
2.0 |
2.5 |
2.6 |
3.0 |
4.0 |
·
Если отбор повторный, а признак количественный
средняя ошибка выборки определяется по формуле
, где
— дисперсия признака в выборочной совокупности
n- число единиц
в выборке
·
Если отбор бесповторный, а признак
количественный

число единиц в генеральной совокупности
·
Если отбор повторный, а признак альтернативный

доля
·
Если отбор бесповторный, а признак
альтернативный
Доверительный интервал для генеральной средней
Доверительный интервал для
генеральной доли
Пример расчета доверительного
интервала:
При выборочном обследовании 5% продукции по методу случайного
бесповторного отбора получены данные о содержании сахара в образцах:
|
Сахарность, % |
Число |
|
16-17 17-18 18-19 19-20 20-21 |
10 158 154 50 28 |
|
На основании этих данных вычислите:
1. Средний процент сахаристости.
2. Дисперсию и среднее квадратическое
отклонение.
3. С вероятностью 0.954 возможные пределы среднего значения
сахаристости продукции для всей партии.
4. С вероятностью 0.997 возможный процент продукции высшего
сорта по всей партии, если известно, что из 400 проб, попавших в выборку , 80
ед. отнесены к продукции высшего сорта.
Решение.
1.
Средний процент сахаристости найдем по формуле средней взвешенной
, где xi–
середина i-го интервала
=18,32 %
2.
Дисперсия
=336,49
D(X)=336.49–
18.322=0.8676
Среднее квадратическое отклонение
=0,93%
5. Предельная ошибка для
среднего процента сахаристости
для вероятности 0,954 параметр t=2.0
Доверительный интервал для среднего значения процента
сахаристости
С вероятностью 0,954 можно утверждать, что в генеральной
совокупности средний процент сахаристости лежит в пределах от 18,23% до 18,41%.
5. Доля продукции высшего сорта в выборочной совокупности
Предельная ошибка для
доли продукции высшего сорта
для вероятности 0,997 параметр t=3.0
Доверительный интервал для доли продукции высшего сорта
С вероятностью 0,997 можно утверждать, что в генеральной
совокупности доля продукции высшего сорта лежит в пределах от 14,0% до 26,0%.
Выборка. Типы выборок. Расчет ошибки выборки
Калькуляторы
Калькулятор расчета ошибки и размера выборки
Калькулятор расчета статистической значимости различий
Генеральная совокупность
Суммарная численность объектов наблюдения (люди, домохозяйства, предприятия, населенные пункты и т.д.), обладающих
определенным набором признаков (пол, возраст, доход, численность, оборот и т.д.), ограниченная в пространстве и
времени. Примеры генеральных совокупностей
- Все жители Москвы (10,6 млн. человек по данным переписи 2002 года)
- Мужчины-Москвичи (4,9 млн. человек по данным переписи 2002 года)
- Юридические лица России (2,2 млн. на начало 2005 года)
- Розничные торговые точки, осуществляющие продажу продуктов питания (20 тысяч на начало 2008 года) и
т.д.
Выборка (Выборочная совокупность)
Часть объектов из генеральной совокупности, отобранных для изучения, с тем чтобы сделать заключение обо всей
генеральной совокупности. Для того чтобы заключение, полученное путем изучения выборки, можно было распространить на
всю генеральную совокупность, выборка должна обладать свойством репрезентативности.
Репрезентативность выборки
Свойство выборки корректно отражать генеральную совокупность. Одна и та же выборка может быть репрезентативной и
нерепрезентативной для разных генеральных совокупностей.
Пример:
- Выборка, целиком состоящая из москвичей, владеющих автомобилем, не репрезентирует все население
Москвы. - Выборка из российских предприятий численностью до 100 человек не репрезентирует все предприятия России.
- Выборка из москвичей, совершающих покупки на рынке, не репрезентирует покупательское поведение всех москвичей.
В то же время, указанные выборки (при соблюдении прочих условий) могут отлично репрезентировать
москвичей-автовладельцев, небольшие и средние российские предприятия и покупателей, совершающих покупки на рынках
соответственно.
Важно понимать, что репрезентативность выборки и ошибка выборки – разные явления. Репрезентативность, в отличие от
ошибки никак не зависит от размера выборки.
Пример:
Как бы мы не увеличивали количество опрошенных москвичей-автовладельцев, мы не сможем репрезентировать этой выборкой
всех москвичей.
Ошибка выборки (доверительный интервал)
Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера
выборки. Чем больше размер выборки, тем она ниже.
Пример:
Для простой случайной выборки размером 400 единиц максимальная статистическая ошибка (с 95% доверительной
вероятностью) составляет 5%, для выборки в 600 единиц – 4%, для выборки в 1100 единиц – 3% Обычно, когда говорят об
ошибке выборки, подразумевают именно статистическую ошибку.
Систематическая ошибка зависит от различных факторов, оказывающих постоянное воздействие на исследование и смещающих
результаты исследования в определенную сторону.
Пример:
- Использование любых вероятностных выборок занижает долю людей с высоким доходом, ведущих активный образ жизни.
Происходит это в силу того, что таких людей гораздо сложней застать в каком-либо определенном месте (например,
дома). - Проблема респондентов, отказывающихся отвечать на вопросы
анкеты (доля «отказников» в Москве, для разных опросов,
колеблется от 50% до 80%)
В некоторых случаях, когда известны истинные распределения, систематическую ошибку можно нивелировать введением квот
или перевзвешиванием данных, но в большинстве реальных исследований даже оценить ее бывает достаточно проблематично.
Типы выборок
Выборки делятся на два типа:
- вероятностные
- невероятностные
1. Вероятностные выборки
1.1 Случайная выборка (простой случайный отбор)
Такая выборка предполагает однородность генеральной совокупности, одинаковую вероятность доступности всех элементов,
наличие полного списка всех элементов. При отборе элементов, как правило, используется таблица случайных чисел.
1.2 Механическая (систематическая) выборка
Разновидность случайной выборки, упорядоченная по какому-либо признаку (алфавитный порядок, номер телефона, дата
рождения и т.д.). Первый элемент отбирается случайно, затем, с шагом ‘n’ отбирается каждый ‘k’-ый элемент. Размер
генеральной совокупности, при этом – N=n*k
1.3 Стратифицированная (районированная)
Применяется в случае неоднородности генеральной совокупности. Генеральная совокупность разбивается на группы
(страты). В каждой страте отбор осуществляется случайным или механическим образом.
1.4 Серийная (гнездовая или кластерная) выборка
При серийной выборке единицами отбора выступают не сами объекты, а группы (кластеры или гнёзда). Группы отбираются
случайным образом. Объекты внутри групп обследуются сплошняком.
2.Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности,
типичности, равного представительства и т.д..
2.1. Квотная выборка
Изначально выделяется некоторое количество групп объектов (например, мужчины в возрасте 20-30 лет, 31-45 лет и 46-60
лет; лица с доходом до 30 тысяч рублей, с доходом от 30 до 60 тысяч рублей и с доходом свыше 60 тысяч рублей) Для
каждой группы задается количество объектов, которые должны быть обследованы. Количество объектов, которые должны
попасть в каждую из групп, задается, чаще всего, либо пропорционально заранее известной доле группы в генеральной
совокупности, либо одинаковым для каждой группы. Внутри групп объекты отбираются произвольно. Квотные выборки
используются в маркетинговых исследованиях достаточно
часто.
2.2. Метод снежного кома
Выборка строится следующим образом. У каждого респондента, начиная с первого, просятся контакты его друзей, коллег,
знакомых, которые подходили бы под условия отбора и могли бы принять участие в исследовании. Таким образом, за
исключением первого шага, выборка формируется с участием самих объектов исследования. Метод часто применяется, когда
необходимо найти и опросить труднодоступные группы респондентов (например, респондентов, имеющих высокий доход,
респондентов, принадлежащих к одной профессиональной группе, респондентов, имеющих какие-либо схожие хобби/увлечения
и т.д.)
2.3 Стихийная выборка
Опрашиваются наиболее доступные респонденты. Типичные примеры стихийных выборок – опросы в газетах/журналах, анкеты, отданные респондентам на самозаполнение, большинство
интернет-опросов. Размер и состав стихийных выборок заранее не известен, и определяется только одним параметром –
активностью респондентов.
2.4 Выборка типичных случаев
Отбираются единицы генеральной совокупности, обладающие средним (типичным) значением признака. При этом возникает
проблема выбора признака и определения его типичного значения.
Курс лекций по теории статистики
Более подробную информацию по выборочным наблюдениям можно получить просмотрев видеокурс по теории статистики:
Выборочное наблюдение Способы формирование выборки
Специальные виды отбора
Калькулятор расчета ошибки и размера выборки (для простой случайной выборки)
Пояснения к полям:
Доверительная вероятность
Вероятность того, что доверительный интервал накроет неизвестное истинное значение параметра, оцениваемого по
выборочным данным. В практике исследований чаще всего используют 95%-ую доверительную вероятность
Ошибка выборки (доверительный интервал)
Интервал, вычисленный по выборочным данным, который с заданной вероятностью (доверительной) накрывает неизвестное
истинное значение оцениваемого параметра распределения.
Доля признака
Ожидаемая доля признака, для которого рассчитывается ошибка. В случае, если данные о доле признака отсутствуют,
необходимо использовать значение равное 50, при котором достигается максимальная ошибка.
Калькулятор расчета статистической значимости различий
Калькулятор позволяет проверить есть ли статистически значимая разница между долями признака, полученными из
независимых выборок.
Например, если до начала рекламной кампании марку знали 55% респондентов, а по окончании – 60% — есть ли между этими
долями статистически значимая разница, или же эта разница укладывается в ошибку выборки?
Примечание. Эта процедура может законно использоваться, только если обе выборки удовлетворяют следующему условию:
произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, должны быть не меньше 5.
Оставить свои комментарии по затронутой теме Вы можете на наших страницах в Facebook и Вконтакте.
При перепечатке материалов ссылка на маркетинговое агентство обязательна
FDF Group © 2023
Разработка сайта — Монохром

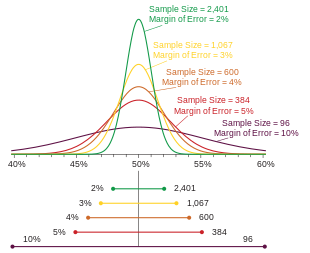


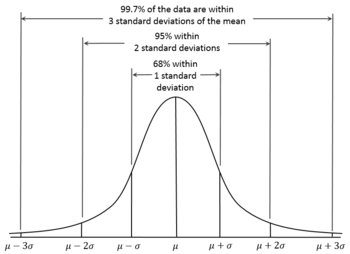















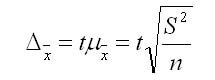
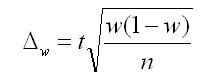
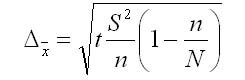
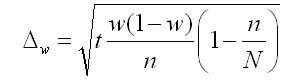

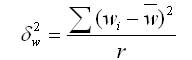
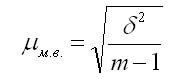
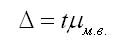
































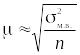
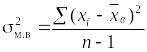
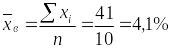
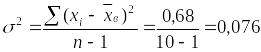
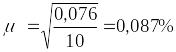
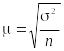
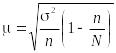
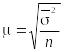
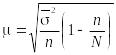

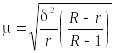
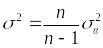
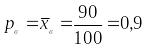
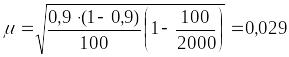
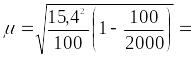
![Rendered by QuickLaTeX.com [mathop Delta nolimits_x = t cdot mu = t cdot sqrt {frac{{sigma _x^2}}{n}left( {1 - frac{n}{N}} right)} ;; to mathop sigma nolimits_x = sqrt {frac{{sum {{{mathop xnolimits_i }^2} cdot {f_i}} }}{{sum {{f_i}} }} - {{bar x}^2}} ]](https://helpstat.ru/wp-content/ql-cache/quicklatex.com-fa201fe3a31654b55abb613dbfce4f62_l3.png)




