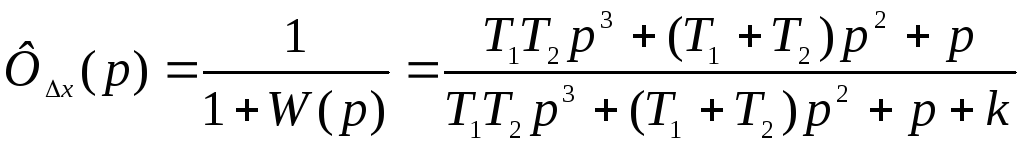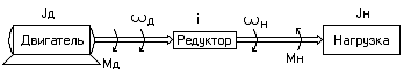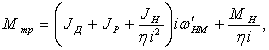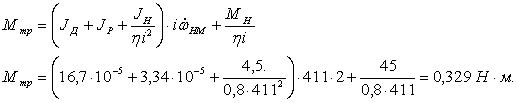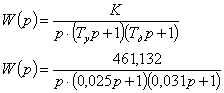Следящие системы обычно являются
астатическими системами с астатизмом
первого порядка, работающими при
переменном управляющем воздействии.
Для таких систем в установившемся режиме
наиболее характерным является изменение
входной величины по линейному закону
с постоянной скоростью
,
чему соответствует операторное
изображение вида
(3.8)
На
основании выражений (3.1),
(3.2),
(3.8)
при
будем иметь
.
(3.9)
Установившуюся
ошибку следящей системы при входном
сигнале, изменяющимся с постоянной
скоростью, называют скоростной
ошибкой. Обозначив скоростную ошибку
,
а отношение
через
,
на основании
(3.9),
окончательно получим
.
(3.10)
Постоянная
величина
(3.11)
называется
добротностью следящей системы по
скорости и имеет размерность с-1
. Она показывает величину установившейся
скорости выходной оси следящей
системы, развиваемой на единицу
скоростной ошибки.
В
следящей системе с астатизмом второго
порядка
()
скоростная ошибка равняется нулю,
вследствие этого установившуюся ошибку
определяют при изменении входной
величины по квадратичному закону с
постоянным ускорением
.
При этом
;
,
(3.12)
где
–
добротность следящий системы по
ускорению, имеющая размерность с—
2.
Величины
и
зависят от параметров
САУ. В одноконтурных системах без местных
обратных связей они определяются как
произведения передаточных коэффициентов
звеньев системы. В более сложных САУ
при определении установившихся
ошибок удобнее пользоваться не готовыми
формулами, а теоремой о предельном
значении функции
(3.1). Применяя
её к операторному изображению ошибки
следящей системы в каждом конкретном
случае.
В
общем случае, если
имеет произвольную форму и имеет
конечное число производных, то ошибку
системы можно определить следующим
образом. Найдём изображение ошибки
,
(3.13)
где
— передаточная функция замкнутой системы
по ошибке;
—
передаточная функция разомкнутой
системы;
—
изображение воздействия (задающего или
возмущающего).
Разложим
передаточную функцию по ошибке в ряд
по возрастающим степеням комплексной
величины
.
(3.14)
Этот
ряд сходится при малых значениях
,
т.е. при достаточно большом
,
что соответствует установившемуся
процессу.
Переходя
от изображения
(3.1) к
оригиналу, получаем формулу для
установившейся ошибки

(3.15)
Величины
,
,…,Сm
называют коэффициентами ошибок. Они
могут определяться согласно общему
правилу разложения функции в ряд Тейлора
по формулам:
;
;
………;

Так
как передаточная функция по ошибке
представляет собой дробно-рациональную
функцию, то коэффициенты ошибок можно
более просто получить делением числителя
на знаменатель и сравнением получающегося
ряда с выражением (3.14).
Коэффициент
отличен от нуля только в статических
системах.
В системах с астатизмом первого порядка
;
.
В системах с астатизмом второго порядка
;
;
.
Если задающее
воздействие имеет ограниченное число
производных, то ряд будет иметь
ограниченное число членов.
Пример.
Определить первые три коэффициента
ошибки по задающему воздействию,
если передаточная функция разомкнутой
системы имеет вид
.
Найдем
передаточную функцию по ошибке
Делим числитель на знаменатель и получаем
ряд
Таким
образом,
;
;
.
Если задающее
воздействие в этой системе меняется по
закону
;
;
,
то установившаяся
ошибка будет равна
.
ЛЕКЦИЯ
7
План лекции:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аналоговая следящая система для ручного управления телекамерой
Содержание
1. Введение
2. Аналоговая следящая система для ручного управления
телекамерой
3. Исходные данные
4. Задание на проектирование
5. Функциональная схема следящей системы
6. Выбор исполнительного двигателя следящей системы и
передаточного отношения редуктора
7. Определение передаточной функции двигателя и ее
параметров
. Выбор датчиков углов поворота и схемы их включения в
измерителе рассогласования
9. Расчет диодной схемы синхронизации
10. Разработка принципиальной схемы устройства
управления исполнительным двигателем
11. Схема гармонического детектирования
амплитудно-модулированного сигнала
12. Электрический расчет принципиальной схемы
13. Расчёт требуемых значений коэффициентов усиления
разомкнутой системы и усилителя
14. Динамический расчет системы
. Выбор корректирующего устройства
16. Поверочный расчёт и построение переходного процесса
17. Заключение
18. Список литературы
1. Введение
Широкий размах автоматизации во всём мире привёл к необходимости
использования во всех производствах разнообразных автоматических систем,
выполняющих те или иные функции по управлению самыми различными физическими
процессами. В этих системах сочетаются весьма разнообразные механические,
электрические и другие устройства, составляя сложный комплекс взаимодействующих
друг с другом звеньев. Одним из классов подобных автоматических систем являются
следящие системы.
Данный курсовой проект посвящён разработке следящей системы и включает в
себя выбор основных элементов замкнутой системы регулирования, разработку
принципиальной схемы управляющего устройства и электрический расчёт основных её
узлов, синтез параметров следящей системы из условия обеспечения заданных
точностных и качественных показателей её работы.
Следящей системой называется такая система регулирования, которая
поддерживает регулируемую величину на заданном значении, причём это значение
изменяется по заранее неизвестному закону. Один из примеров следящей системы —
оптическая телевизионная система сопровождения цели. В телевизионном комплексе
можно выделить четыре следящих привода, которые следует рассматривать как
различные задания на проектирование системы.
В данном курсовом проекте нужно разработать одно из заданий — аналоговую
следящую систему для ручного управления телекамерой.
2. Аналоговая
следящая система для ручного управления телекамерой
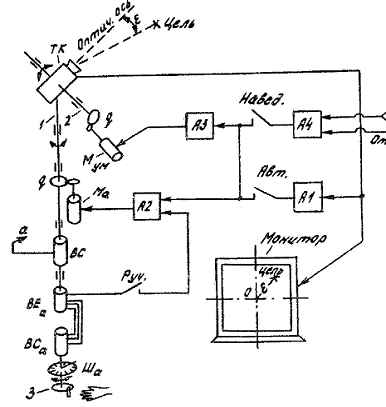
При ручном управлении оператор, наблюдая на экране монитора изображение,
получаемое с телекамеры, с помощью ручки управления 3 (рис.1) задает требуемое
изменение угла поворота телекамеры (рассматривается только управление движением
в азимутальной плоскости). В схеме управления используются два сельсина: BCа , соединенный с ручкой управления
на пульте оператора, и BEа ,
ротор которого вращается по азимуту вместе с осью 1 телекамеры. Если задающий и
принимающий валы и связанные с ними сельсины находятся в согласованном
положении, то напряжение на вторичной обмотке сельсина BEa равно нулю. Двигатель Ma азимутального канала обесточен, и, следовательно, привод
находится в состоянии покоя. При отклонении любого из валов от положения
согласования выходное напряжение сельсина BEa через усилитель A2 обеспечивает включение двигателя Ма и вращение телекамеры через
редуктор q по азимуту. Для зрительного
определения координаты цели по азимуту служит отсчетное устройство Ша. Ручное
управление телекамерой по углу места строится аналогично.
Рис.1. Ручное управление телекамерой.
3.
Исходные данные
Исходные данные для проектирования приведены в таблице 1:
Таблица №1
|
JНМ, Н·м·с2 |
MНМ, Н·м |
ωНМ, рад/с |
ω’НМ, рад/с2 |
εМ, угл. мин. |
σ, |
tр, с |
|
4,5 |
45 |
0,5 |
2 |
8 |
15 |
0,04 |
JНМ — максимальный момент инерции
нагрузки (подвижной платформы с закрепленной на ней телекамерой);
MНМ — максимальный момент
сопротивления на оси нагрузки;
ωНМ, ω’НМ — требуемые максимальные
значения скорости и ускорения вращения оси телекамеры;
eМ — максимально допустимая ошибка
следящей системы, учитывающая влияние момента сопротивления на оси нагрузки,
скоростную ошибку системы при скорости изменения угла задания, равной по
величине wНМ, и
инструментальную погрешность измерителя рассогласования;
σ,
%; tp — максимально
допустимые значения перерегулирования и времени регулирования в следящей
системе.
4. Задание на проектирование
1. Дать описание функциональной схемы следящей системы (по азимуту)
при ручном управлении.
2. Выбрать исполнительный двигатель следящей системы и передаточное
отношение силового редуктора, связывающего исполнительный двигатель с
нагрузкой.
. Определить передаточную функцию двигателя и ее параметры.
. Выбрать датчики углов поворота и схему их включения в измерителе
рассогласования.
. Разработать принципиальную схему устройства управления
исполнительным двигателем.
. Рассчитать требуемые значения коэффициентов усиления разомкнутой
системы и усилителя.
. Произвести динамический расчет системы.
. Дать расчет принципиальной схемы.
. Дать заключение по разработанному проекту системы и привести
список используемой литературы (библиографический список).
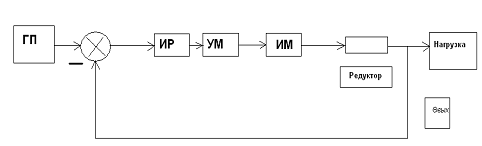
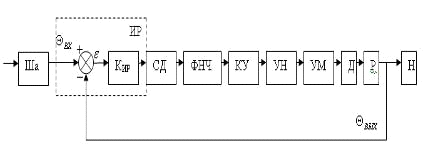
. Функциональная схема следящей системы
Функциональная схема следящей системы (по азимуту) при ручном управлении
представлена на рис.2.
Рис.2. Функциональная схема следящей системы.
Ша — отсчетное
устройство;
ИР — измеритель
рассогласования между и
;
KИР — коэффициент
передачи измерителя рассогласования;
УН — усилитель
напряжения;
УМ — усилитель
мощности;
Д — двигатель;
Р — редуктор;
Н — нагрузка.
6. Выбор
исполнительного двигателя следящей системы и передаточного отношения редуктора
Выбор двигателя системы — одна из основных задач проектирования следящей
системы. Следует отметить, что если выбранный двигатель не может обеспечить
требуемых режимов движения нагрузки, то уже никакими ухищрениями, в том числе
повышением коэффициента усиления разомкнутой системы, использованием
корректирующих устройств и т. п., нельзя добиться требуемого качества работы
системы.
При выборе двигателя следящей системы рассмотрим узел
«двигатель-редуктор-нагрузка», представленный на рис. 3:
Рис. 3. Узел «двигатель-редуктор-нагрузка»
МД , ωД — момент вращения и скорость, развиваемые на валу
двигателя;
Мн , ωн — момент сопротивления со стороны нагрузки и
скорость вращения вала нагрузки;
i=ωД/ωн — передаточное отношение
редуктора, согласующего
двигатель с нагрузкой.
Полагается также, что подвижные части двигателя обладают моментом инерции
JД, а нагрузка — моментом инерции Jн.
Для расчета требуемой мощности двигателя используем методику, приведенную
в [1]. Положим, согласно [1], КПД h=0,8.
Вт.
Нужно
выбрать двигатель, мощность которого больше Ртр. Выберем из таблицы,
приведённой в [1] , двигатель типа СЛ: СЛ-521 со следующими параметрами:
Pном = 77 Вт;
nном = 3000 об/мин => ωном = nном · π / 30 = 314,16 рад/с;
Uном = 110 В;
Iя ном. = 1,2 А;
Rя = 8,5
Ом;
Mном = 0,245 Н·м;
Mп = 0,638
Н·м;
Jд = 16,7·10-5
кг·м2.
Проверим перегрузку двигателя при пуске:
.
Превышения
нет (), следовательно, двигатель допускает прямое включение
на номинальное напряжение.
Момент инерции редуктора:
Jр =
0,2 * Jд=0,2*16,7*10-5=3,34*10-5 кг·м2.
Требуемый вращающий момент на валу двигателя определяется при заданных
характеристиках нагрузки как:
где h — КПД
редуктора,
i — передаточное
отношение редуктора,
JД — момент
инерции якоря двигателя.
Как видим, требуемый от двигателя момент вращения зависит от
передаточного отношения редуктора i. Для нахождения значения i = iопт , при котором требуемый от
двигателя момент был бы минимален, т.е. МТР=МТРmin, вычислим производную от МТР по i и приравняем ее нулю. Имеем:
Решение
данного уравнения дает оптимальное значение передаточного отношения редуктора:
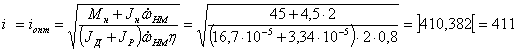
Подставив
вычисленное значение iопт = 411 в выражение для требуемого вращающего
момента на валу двигателя, получим:
Далее произведём проверку выбранного нами двигателя на перегрузку по
требуемым от него максимальному моменту и скорости вращения, которая не должна
превышать допустимую:
—
допустимый коэффициент перегрузки по моменту:;
допустимый
коэффициент перегрузки по скорости:.
—
двигатель недогружен по моменту;
— двигатель недогружен по скорости.
Как видно, ограничения по перегрузкам выполняются, значит выбранный нами
двигатель подходит для использования в системе с заданными характеристиками.
7.
Определение передаточной функции двигателя и ее параметров
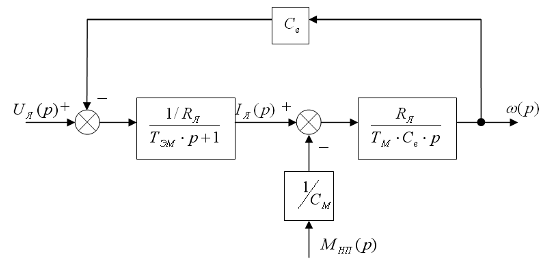
Структурную схему коллекторного двигателя постоянного тока с независимым
возбуждением, который мы используем в системе в качестве исполнительного
устройства, можно представить, как показано на рисунке 3 [7]:
Рис. 3. Структурная схема двигателя.
Мнп — момент нагрузки, приведённый к оси двигателя;
Cе — коэффициент
пропорциональности по противо-ЭДС;
СM — коэффициент пропорциональности
по моменту.
Полагаем, что электромагнитная постоянная времени двигателя много меньше,
чем электромеханическая постоянная, т.е. ТЭ << ТМ = ТД. Тогда
передаточные функции двигателя будут иметь вид [7]:
— передаточная
функция по скорости,
— коэффициент
передачи двигателя;
— передаточная
функция по моменту.
Нашей задачей является определить указанные параметры КД, КМ, ТД. Для их
нахождения рассчитаем сначала коэффициенты Cе , СМ:
;
.
Теперь, используя полученные выше результаты, вычислим искомые параметры
передаточной функции двигателя:
Коэффициент передачи двигателя:
;
Постоянная
времени двигателя:
ручной управление телекамера редуктор
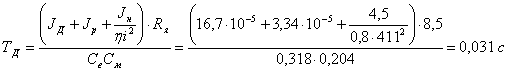
Коэффициент
передачи двигателя по моменту сопротивления:
Теперь, используя полученные выше результаты, вычислим искомые
передаточной функции двигателя:
,
.
8. Выбор
датчиков углов поворота и схемы их включения в измерителе рассогласования
Датчик угла поворота следящей системы предназначен для измерения
рассогласования положений командного и исполнительного валов. В аналоговых следящих
системах используют различные датчики угла: потенциометрические, индуктивные,
ёмкостные, индукционные, фотометрические, сельсины и другие. Среди них
наибольшее практическое распространение в следящих системах нашли индукционные
датчики, которые характеризуются высокой надёжностью, хорошими
эксплуатационными свойствами, высокой стабильностью параметров и характеристик,
возможностью создания бесконтактных схем.
Среди индукционных датчиков, как наиболее дешевые и простые выделяют
сельсины. Сельсины по принципу действия относятся к трансформаторным
индукционным датчикам. Конструктивно они представляют собой электрические
машины, имеющие трёхфазную статорную и однофазную роторную обмотки (бывает
наоборот). В зависимости от величины инструментальной погрешности сельсины
подразделяют на 3 класса точности. Первый класс, наиболее точный, имеет
погрешность до ±0.25 угл. град (сельсины-датчики) и до ±0.75 угл. град
(сельсины-приемники) [8]. Для уменьшения влияния инструментальной погрешности
сельсинов на точность работы системы используют двухканальную схему измерения
рассогласования, включающую в себя канал грубого отсчёта и канал точного
отсчёта.
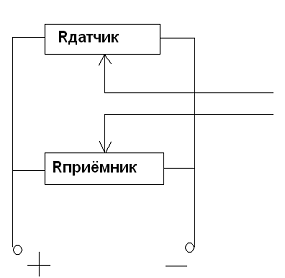
Изобразим функциональную схему следящей системы:
Рис. 4
Где ГП представлен 2-мя потенциометрическими датчиками(резисторами)
В качестве измерителя рассогласования используют трансформаторную схему
включения сельсинов.
Проведем расчет измерителя рассогласования на сельсинах:
tир =1/(2.fпит),
а fпит=50 Гц , тогда получаем tир = 0,01 с.
Длительность переходного процесса в измерителе рассогласования на сельсинах
соизмерима с допустимой длительностью переходного процесса системы (tp=0,04), поэтому частоту питания сельсинов можно
выбрать равной 50 Гц.
Согласно
рекомендациям величину допустимой ошибки измерителя рассогласования следует
принимать равной одной третьей — одной второй от допустимой ошибки работы
следящей системы, и инструментальной погрешностью используемых датчиков угла
[1]: .
.
Класс
точности сельсинов и коэффициент передачи редукторов между точным и грубыми
каналами выбираются с учетом следующего соотношения:
,
где
— коэффициент передачи механического
редуктора между роторами сельсинов;
— ошибка, обусловленная наличием
люфта редуктора между грубым и точным каналами;
— ошибка,
вносимая измерителем рассогласования в общую ошибку следящей системы;
— инструментальная
погрешность пары сельсинов точного канала.
Потребуем,
чтобы , тогда
.
Будем
использовать в дальнейшем сельсины второго класса точности типа БД-501А и
БС-501А с параметрами [8]:
Таблица
№2
|
Параметры сельсина |
БД-501А |
БС-501А |
|
Номинальная частота, Гц |
50 |
50 |
|
Номинальное напряжение, В |
110 |
110 |
|
Максимальное вторичное |
55 |
55 |
|
Номинальный ток |
1,2 |
1,2 |
|
Потребляемая мощность, Вт |
27 |
27 |
|
Момент трения, Н×см |
0,35 |
0,35 |
|
Номинальная частота |
500 |
500 |
Сельсины БД-501А и БС-501А являются бесконтактными. Отсутствие у них
скользящих контактов позволяет получить лучшую устойчивость характеристик и
длительно сохранить высокую точность. [7]
Коэффициент измерителя рассогласования (ИР) находим по максимальному
вторичному напряжению:
.
Для
второго класса точности сельсинов погрешность одного сельсина Δc = ±30’. Для пары сельсинов: , а т.к.
это значение превышает допустимую ошибку ИР , то
необходимо использовать двухканальную схему ИР.
Коэффициент
рассчитаем из соотношения
.
Примем
=29, а т.к. рекомендуется
=(15…75) [2], то коэффициент находится в допустимом
диапазоне.
В
следящей системе с двухканальной схемой ИР должно быть устройство переключения
каналов. Для переключения каналов используют схемы с электромагнитным реле,
неоновыми лампами, но наиболее широко распространена диодная схема переключения
каналов из-за простоты и надежности.
9. Расчет диодной схемы синхронизации
Диодная схема синхронизации представлена ниже рис. 6:
Рис.6. Диодная схема синхронизации
каналов.
Синхронизатор состоит из двух смежных контуров, построенных на базе
выходных обмоток сельсинов трансформаторов точного и грубого каналов и диодов,
включённых встречно-параллельно для обеспечения прохождения тока в течение
обоих полупериодов. В точном канале диоды включены параллельно нагрузке и,
благодаря свойству изменять внутреннее сопротивление в зависимости от
приложенного напряжения, выполняют роль амплитудного ограничителя напряжения
погрешности. При напряжениях рассогласования, меньших напряжения переключения,
сопротивление диодов в прямом направлении велико и всё напряжения в точном
канале падает на этих диодах. В грубом канале в это время выходной сигнал
формируется таким образом, что его амплитуда становится близкой к нулю. Таким
образом, управление осуществляется с помощью напряжения, поступающего с точного
канала.
При напряжениях рассогласования превышающих порог включения ограничителя,
вследствие резкого уменьшения прямого сопротивления диодов и их шунтирующего
действия, напряжение на выходе точного канала перестаёт изменяться и остаётся
равным напряжению, соответствующему углу переключения. Управление переходит к
грубому каналу, т.к. в нём также происходит перераспределение падений
напряжения, и всё напряжение выделится на резисторе грубого канала. В
результате на выходе устройства синхронизации напряжение будет определяться
суммой напряжений точного и грубого каналов, как показано на рис. 7:
Рис. 7. Напряжение на выходе устройства
синхронизации.
На первом этапе расчёта диодной схемы синхронизации определяем угол
переключения каналов:
. Берём
.
Определим
параметры схемы грубого канала.
,
.
Пусть
используются диоды Д2Г со следующими параметрами:
.
Проверим
диоды на перегрузку при e=90о, , при
этом
.
Так
как максимальный ток через диод меньше допустимого, то данный диод можно
использовать в схеме переключения.
Определим
параметры схемы точного канала.
Рекомендация:
при напряжение грубого канала должно быть
;
при КT >> 1.
.
При
выборе коэффициента получим:.
,
где
n — количество последовательно соединенных диодов в
одной цепочке.
.
Возьмём
диода.
Далее
рассчитаем сопротивление точного канала:
.
10.
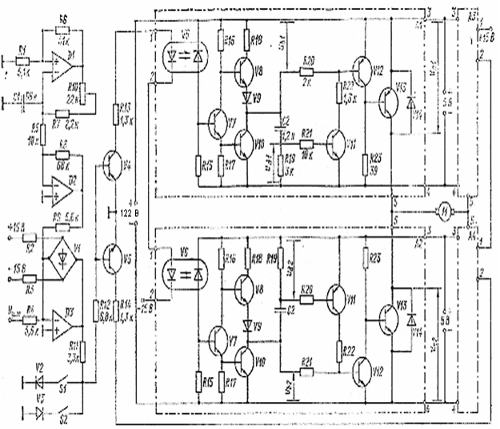
Разработка принципиальной схемы устройства управления исполнительным двигателем
Рис.8. Принципиальная схема усилителя
мощности.
Техническое совершенство привода следящей системы с двигателем
постоянного тока определяется усилителем мощности (УМ). В настоящее время
применяют полупроводниковые — транзисторные УМ. Транзисторные УМ работают в
режиме класса Д с широтно-импульсной модуляцией (ШИМ) силовых транзисторов.
Область применения транзисторных УМ расширяется и они вытесняют тиристорные
преобразователи, что связано с освоением сильноточных транзисторов с
коммутируемым током до 500 А и коллекторным напряжением до 700 В. Схема
усилителя мощности приведена на рис.8. [4]
Устройство состоит из генератора пилообразного напряжения, выполненного
на операционных усилителях D1 и D2; двухпорогового компаратора D3 с диодным ограничителем V1; двухплечевого импульсного
усилителя мощности на транзисторах V4 и V5; четырех плеч мостового усилителя:
двух верхних А1 и А3 и двух нижних А2 и А4.
Верхнее плечо А1 (А3) состоит из оптронного усилителя типа 249ЛП1Б,
выполненного на диодной оптопаре V6 и
транзисторах V7, V8, V10;
дифференцирующей RC-цепи на
конденсаторе C2 и резисторе R19 с усилителем мощности
дифференцирующего сигнала на транзисторе V11; управляющего транзистора V12 и силового транзистора V13.
Нижнее плечо А2 (А4) состоит из тех же элементов, что и верхнее, но
отличается от верхнего местом подключения дифференцирующей RC-цепи и противоположным типом
проводимости транзисторов V11-V13.
Помимо двух основных источников питания ±122В и ±15В, УМ нуждается в двух дополнительных источниках напряжения
5В для схем управления нижними и верхними плечами моста.
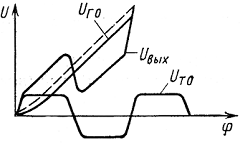
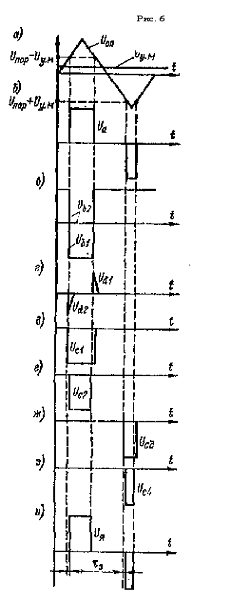
Работу схемы поясняет диаграмма напряжений на рис.9, где показаны:
а) — пилообразное напряжение Uоп, снимаемое с Д2, входное напряжение Uу.м. и пороговое напряжение ±Uпор компаратора Д3;
б) — импульсное напряжение Uа,
снимаемое с выхода компаратора Д3;
в) — выходное напряжение первого Ub1 и второго Ub2
оптронных усилителей;
г) — выходные напряжения первой Ud1 и второй Ud2
дифференцирующих RC-цепей;
д), е), ж), з) — коллекторные напряжения Uc1-Uc4 выходных
транзисторов соответственно первого-четвертого плечей моста; u- выходное напряжение Uя на якоре двигателя.
Период
работы усилителя состоит из отрезков времени, в которые импульс сигнала Ua=0,
Ua>0 и Ua<0. При Ua=0 напряжение . При этом в верхнем плече А1 транзистор V12
закрыт, выходной транзистор V13 открыт током, протекающим через резистор R23.
Выходной транзистор V13 нижнего плеча А2 будет закрыт. Состояние левых плеч
А1 и А2 усилителя не изменится и при Ua>0, так как их оптронные
усилители включаются напряжением Ua отрицательной полярности. При Ua<0
выходные напряжения оптронных усилителей . При
этом транзистор V13 верхнего плеча А1 будет закрыт, а V13
нижнего плеча А2 открыт. Импульс напряжения, открывающий транзисторы V13,
подается с задержкой времени относительно импульса напряжения, снимаемого с
выхода соответствующего оптронного усилителя. Эта задержка обеспечивается
дифференцирующими импульсами напряжений Ud1 и Ud2.
Импульс напряжения Ud1 положительной полярности открывает транзистор V11
верхнего плеча, который в течение времени действия импульса сохраняет открытым
транзистор V12 и закрытым V13.
Аналогично
дифференцирующий импульс Ud2 отрицательной полярности, открывая транзистор V11
нижнего плеча А2, оставляет открытым транзистор V12, задерживая
тем самым включение транзистора V13 нижнего плеча, пока транзистор V13
верхнего плеча не перешел в режим отсечки. Время задержки определяется
постоянной времени дифференцирующей цепи, которая выбирается несколько больше
времени запирания выходных транзисторов. Так как выходные транзисторы V13
при запирании шунтируются управляющими транзисторами V12, то время
запирания и задержки получается минимально возможным. Два других плеча УМ А3 и
А4 работают аналогично при положительной полярности сигнала Uа.
Диаграмма выходного напряжения УМ зависит от соотношения напряжений и амплитуды пилы Uоп. При Uу.м.=0
и c выхода УМ снимаются симметричные разнополярные
импульсы с коэффициентом заполнения . При
этом крутизна статической характеристики на начальном участке будет вдвое выше, а коэффициент усиления равен:
, где
.
Схема
усилителя универсальная, так как она удовлетворяет всем требованиям,
предъявляемым к УМ приводов следящих систем. Отметим ее достоинства:
1. минимальные потери и максимальная частота ШИМ, обеспечиваемые
шунтированием цепи база-эмиттер при запирании силовых транзисторов и
использованием низковольтных источников в цепях управления;
2. симметрия верхнего и нижнего плеч усилителя с использованием
одних и тех же однотипных элементов;
. простая схема защиты от сквозного короткого замыкания,
основанная на формировании импульсного сигнала в слаботочном участке схемы;
4. отсутствие влияния выходных каскадов на входную цепь благодаря
их гальванической развязке;
. простая схема ШИМ входного сигнала, основанная на использовании
двух порогового компаратора;
6. безынерционность цепи управления;
7. наличие схемы ограничения движения привода (V2, V3, SI, S2)
. обеспечение режима динамического торможения двигателя М, так как
при Ua=0 выходные транзисторы V13 верхних плеч А1 и A3 находятся в режиме
насыщения; отлаженная на определенную нагрузку схема не требует настройки
последующих образцов.
Недостатком этой схемы является то, что требуется много источников
питания (122В, 15В, 5В). Параметры схемы на рис.7(а) соответствуют току
нагрузки 10А при минимальном коэффициенте усиления по току транзисторов V13 β = 100.
11. Схема гармонического детектирования амплитудно-модулированного
сигнала
На
выходе датчика угла рассогласования, выполненного на сельсинах, включенных по
трансформаторной схеме, амплитуда напряжения пропорциональна синусу угла
рассогласования . Частота напряжения определяется частотой питания
сельсина, в нашем случае составляет 50 Гц.
Для
работы корректирующей цепочки требуется постоянное напряжение, поэтому для
согласования датчика угла рассогласования с корректирующим устройством,
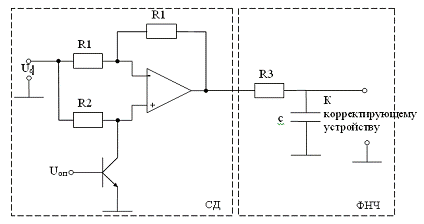
необходимо между ними включить амплитудный детектор. Амплитудный детектор (рис.
10) состоит из синхронного детектора (СД) и фильтра низкой частоты (ФНЧ).
Рис.
10. Амплитудный детектор
Передаточная
функция фильтра определяется выражением:
,
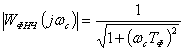
где
— частота опорного напряжения,
—
требуемая постоянная времени фильтра.
Параметры
ФНЧ выбираются таким образом, чтобы подавлялись составляющие частотой и выше.
Полуволны
с выхода СД можно приближенно представить двумя слагаемыми ряда Фурье — это
постоянная составляющая и первая гармоника с частотой . При расчете ФНЧ надо задаться коэффициентом
подавления первой гармоники n.
, где n =
(5…10).
Чем
больше n, тем сильнее подавляется гармоника, но тем более
длительный переходный процесс фильтра.
Можно
считать, что . Тогда,
.
Зададимся
n = 8 с учетом =50 Гц,
получим = 0,025 с.
12. Электрический расчет принципиальной схемы
На
начальном этапе электрического расчёта принципиальной схемы выберем силовые
транзисторы и диоды, используемые в мостовой схеме усилителя [3]. Расчёт
мостовой схемы сводится к выбору величины напряжения источника питания этой схемы, к выбору силовых транзисторов и диодов.
Сначала рассчитаем напряжение питания. Рекомендуется:
.
Выбор
транзистора осуществляем по справочникам из следующих ограничений:
Пусковой
ток якоря . Пусть
, тогда:
(при этом мы ранее предусмотрели ограничение тока якоря в схеме).;
.
Рассеивание мощности в основном имеет место в периоде включения и
запирания транзистора. Для получения простого расчётного предполагается, что в
периоды включения и запирания транзистора ток и напряжение на нём меняются по
линейному закону.
Ррасс = Рвкл + Рзапир;
;
.
Рекомендуемая
частота , возьмём
, тогда с
учетом этого
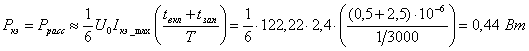
где
для рассмотренной схемы
— время включения,
По полученным выше значениям выбираем транзисторы КТ864А (n-p-n) и КТ865А (p-n-p) со следующими
параметрами:
UКЭ
доп = 200В; IКЭ доп = 10А; РКЭ доп = 100Вт;
b = 40 ¸ 200 =
100 — коэффициент усиления транзистора по току;
UКЭ
нас £ 2В; Iб £ 2А.
Выбор диодов осуществляется при следующих ограничениях:
,
.
Выбираем
диоды Д243Б со следующими параметрами:
= 200 В;
= 10 А.
Далее определяем требуемый ток базы силового транзистора:
,
где
— коэффициент насыщения транзистора (1,5…2).
13. Расчёт требуемых значений коэффициентов усиления разомкнутой системы
и усилителя
Для обеспечения заданной точности работы системы при заданном входном
воздействии необходимо правильно рассчитать коэффициент усиления разомкнутой
системы. Для его расчета используем методику, приведенную ниже. Структурная
схема системы изображена на рис.11 при выполнении условия
ТЭ << ТМ = ТД
где:
ТЭ — электромагнитная постоянная времени якорной цепи двигателя;
ТМ — электромеханическая постоянная времени двигателя;
ТД — постоянная времени двигателя.
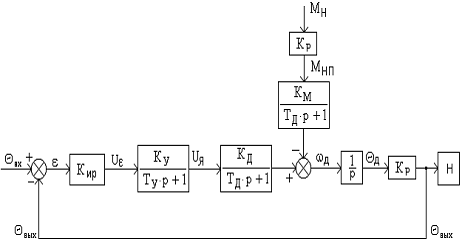
Рис.
11. Структурная схема нескорректированной следящей
системы.
Tу — постоянная
времени, отнесенная к усилителю и обусловленная наличием инерционного силового
преобразователя;
Ку — коэффициент передачи усилителя;
Н — нагрузка;
Мнп — момент нагрузки, приведённый к оси двигателя;
Кир — коэффициент
передачи измерителя рассогласования;
Км — коэффициент передачи двигателя по моменту;
Кр — коэффициент передачи силового редуктора.
Передаточная функция разомкнутой системы будет определяться следующим
выражением:
,
где
— коэффициент передачи разомкнутой системы, который
мы будем определять, исходя из допустимой ошибки отработки задающего воздействия,
.
Воспользуемся
уже готовой формулой для нахождения коэффициента передачи К при меняющимся с
постоянной скоростью входном воздействии и постоянном моменте сопротивления
нагрузки.
Таким
образом, если , где Qвх0=const,
Мн(t)=Мнм=const, то К определяется следующим выражением:
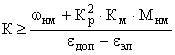
где eдоп — допустимая
ошибка следящей системы, eдоп
= 8’ ;
eэл — элементная составляющая ошибки следящей системы,
вносимая в основном измерителем рассогласования .
С учётом этих данных и начальных условий вычислим К:
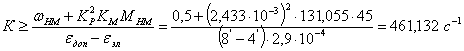
Данное
значение коэффициента усиления разомкнутой системы обеспечим за счет коэффициента
передачи КУ усилителя:
.
Т.к.
усилитель включает в свой состав синхронный детектор для детектирования
амплитудно-модулированного напряжения ошибки, то в качестве будет выступать постоянная времени сглаживающего
фильтра синхронного детектора, которой пренебрегать нельзя:
Тогда
передаточная функция разомкнутой нескорректированной системы определится
следующим выражением:
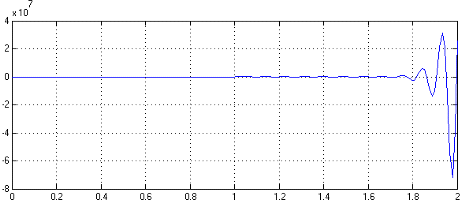
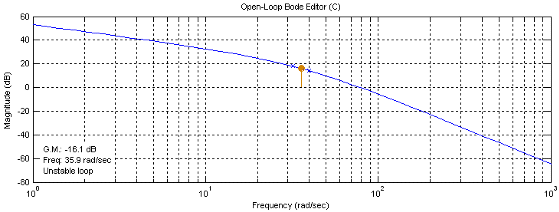
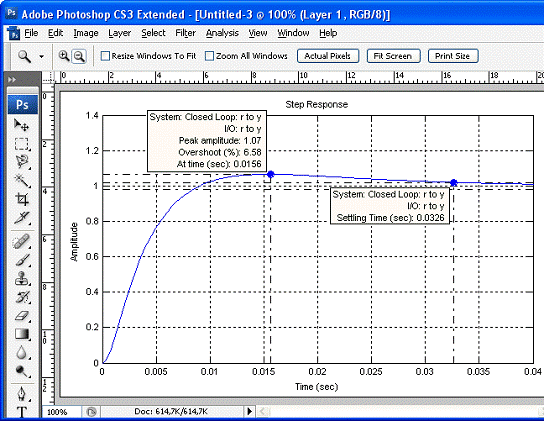
Результаты
моделирования передаточной функции приведены на рис.12 и рис.13:
Рис.
12. Схема замкнутой системы с отрицательной обратной
связью.
Рис.
13. Реакция системы на ступенчатое воздействие.
14. Динамический
расчет системы
Следящая система, которая была исследована нами в предыдущих пунктах, не
удовлетворяет заданному качеству переходного процесса. Необходимо построить
корректирующее устройство, чтобы обеспечить требуемые точностные характеристики
системы: заданные перерегулирование и длительность переходного процесса.
Наиболее широкое применение при синтезе систем автоматического
регулирования получил метод логарифмических амплитудно-частотных характеристик
[6], т.к. построение ЛАЧХ, как правило, может делаться почти без вычислительной
работы. Особенно удобно использовать асимптотические ЛАЧХ.
Процесс синтеза методом ЛАЧХ включает в себя следующие операции:
· построение располагаемой ЛАЧХ;
· построение желаемой ЛАЧХ;
· определение вида и параметров корректирующего устройства;
· техническая реализация корректирующего устройства;
· поверочный расчёт и построение переходного процесса.
Построение желаемой ЛАЧХ — выполняется на основе тех требований, которые
предъявляются к проектируемой системе регулирования [6], а именно на основании
времени переходного процесса и допустимого перерегулирования: tр и σ.
Построение располагаемой ЛАЧХ — построение ЛАЧХ исходной системы,
выполненное исходя из требуемых мощности, скорости, ускорения и т.п. В данном
случае под исходной системой понимается система, состоящая из регулируемого
объекта и регулятора и не снабженная необходимыми корректирующими средствами,
обеспечивающими требуемое качество переходного процесса.
Вид и параметры корректирующего устройства определяются из следующего
условия: если передаточная функция желаемой разомкнутой системы − Wж(p), передаточная функция нескорректированной системы — Wнс(p), а передаточная функция корректирующего звена
последовательного типа — Wк(p), то можно записать равенство:
исходя
из этого для ЛАЧХ корректирующего звена:
Построение располагаемой ЛАЧХ.
Под располагаемой ЛАЧХ понимается характеристика исходной системы
управления, не снабжённая необходимыми корректирующими средствами. ПФ
нескоррективанной системы имеет следующий вид:
,
в
численной форме
ЛАЧХ
LН имеет две сопрягающие частоты:
, lg w2 = 1,602.
Н
пересекает ось ординат в точке равной
От
этой точки до первой сопрягающей частоты асимптотическая LН
имеет наклон с осью частот -20 дБ/дек — это низкочастотный участок ЛАЧХ.
На
среднечастотном участке (от первой сопрягающей частоты до второй) LН
имеет наклон -40 дБ/дек.
На
высокочастотном участке наклон -60 дБ/дек.
ЛАЧХ
непрерывной нескорректированной разомкнутой системы LН изображена на
рис.14.
Рис.14.
ЛАЧХ непрерывной нескорректированной разомкнутой системы.
Построение
желаемой ЛАЧХ.
Построение
желаемой ЛАЧХ делается на основе тех требований, которые предъявляются к
проектируемой системе управления, а именно:
— перерегулирование s % при единичном ступенчатом
воздействии на входе;
время переходного процесса tp .
Используя методику, изложенную в [6], найдём частоту среза wср желаемой ЛАЧХ LЖ .
Для заданного перерегулирования s % = 15 % находим зависимость между длительностью переходного
процесса tp = 0,04 [с] и частотой wп (интервал положительности),
используя номограммы Солодовникова [6]:
.
Теперь
найдём частоту среза wср желаемой ЛАЧХ так, чтобы она удовлетворяла условию:
wср = (0,6 ¸ 0,9)×wп.
wср = 0,9 × wп = 0,9 × 314,159 =282,743 ; lg wср =2,451.
При
синтезе системы необходимо обеспечить не только её устойчивость, но и
определённый запас устойчивости. Для заданного значения перерегулирования s % = 15 % выбираем требуемое значение запаса устойчивости по модулю L1= |
L2 | = 30 дБ.
Построение
желаемой асимптотической ЛАЧХ производится в следующем порядке.
Первая
низкочастотная асимптота проводится так, чтобы она имела наклон -20 дБ/дек,
соответствующий астатизму первого порядка.
Среднечастотный
участок желаемой ЛАЧХ образуется асимптотой с наклоном -20 дБ/дек, проводимой
так, чтобы она пересекала ось частот при wср. Этот участок
проводится влево и вправо до достижения модулей, равных L1 и L2.
Затем
производится сопряжение среднечастотного участка с низкочастотными асимптотами
и высокочастотной частью (рис. 15).
Рис.
15. Желаемая ЛАЧХ
Для
ЛАЧХ можно записать:
LКУ(w) = LЖ(w) — LН(w) .
Таким
образом, ЛАЧХ корректирующего устройства, полученная простым вычитанием ординат
нескорректированной ЛАЧХ из ординат желаемой.
ЛАЧХ
корректирующего устройства представлена на рис. 16.
Рис.
16. ЛАЧХ корректирующего устройства
15. Выбор корректирующего устройства
Корректирующие устройства предназначаются для такого изменения структуры
системы, при котором возможно получение нужных динамических свойств.
Корректирующие устройства представляют собой динамические звенья различной
физической природы со специально выбранными передаточными функциями.
Сначала рассчитаем параметры корректирующего устройства. Система слежения
имеет структуру, представленную на рис. 17:
Рис. 17. Структура системы слежения
,
где WЖ(р) — ПФ желаемой системы;
WНС(р) — ПФ нескорректированной
системы;
WКУ(р) — ПФ корректирующего
устройства последовательного типа.
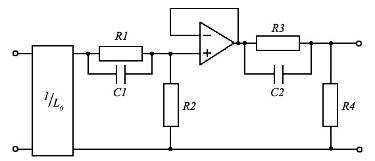
Схема и параметры корректирующего звена подбирается по виду ЛАЧХ. В нашем
случае ПФ корректирующего устройства имеет вид:
.
По графику определяем сопрягающие частоты ПФ КУ:
Таким
же образом определяем коэффициент усиления корректирующего устройства .
Передаточная
функция корректирующего устройства имеет вид:
.
Передаточная
функция корректирующего устройства будет выглядеть следующим образом:
Далее
определяем номиналы элементов корректирующего звена, исходя из следующих
выражений:
Для
расчета корректирующей цепочки зададимся С1 = 10 нФ=10-8Ф.
Зададимся С2 = 100 нФ=10-7Ф.
Тогда
Структурная
схема корректирующего устройства представлена на рис 18:
Рис.
18. Схема корректирующего устройства.
. Поверочный расчёт и построение переходного процесса
Построим переходную характеристику полученной замкнутой системы
управления вместе с корректирующим устройством и проверим, удовлетворяет ли
данная система заданному качеству переходного процесса.
Схема моделирования (рис. 19) и переходная характеристика замкнутой
скорректированной системы (рис. 20), представлены ниже.
Рис. 19 Схема моделирования.
Рис.20. Переходная характеристика скорректированной
системы.
Из графика видно, что для скорректированной системы выполняются требуемые
условия относительно качества переходного процесса:
s % =6,85 % < sЗАД
% = 15 %;
tР
=0,0326 c < tР ЗАД = 0,04 c .
Заключение.
В результате была разработана следящая система, рассчитанная на условия
работы, предусмотренные заданием, обладающая предъявленным к ней требованиям
точности и качества переходного процесса, функциональная схема которой примет
вид (рис. 21):
Рис. 21. Функциональная схема аналоговой
следящей системы.
Ша — отсчетное устройство;
КИР — коэффициент передачи измерителя рассогласования;
СД — синхронный детектор;
ФНЧ — фильтр низких частот;
КУ — корректирующее устройство;
УН — усилитель напряжения;
УМ — усилитель мощности;
Д — двигатель;
Р — редуктор;
Н — нагрузка.
Список литературы
1. Проектирование
систем автоматического управления: Задания и методические указания к курсовому
проекту / РГРТА. Сост. Степашкин А. И. Рязань, 1994 г.
2. Степашкин
А. И., Алпатов Б. А. Проектирование и надежность систем автоматики и
телемеханики: Учебное пособие. Рязань, 1984.
. Руководство
по проектированию систем автоматического управления / Под ред. В. А.
Бесекерского. М.: Высш. школа, 1983.
4. Кочергин
В. В, Следящие системы с двигателем постоянного тока. Л.: Энергоатомиздат.
Ленингр. Отд-ние, 1988.
5. Ахметжанов
А. А., Кочемасов А. В, Следящие системы и регуляторы. М.: Энергоатомиздат,
1986.
. Бесекерский
В. А., Попов Е. П. Теория систем автоматического регулирования. М.: Наука,
1966.
7. Кузнецов
В. П. Промышленные роботы. Проектирование электромеханических приводов: Учебное
пособие. Рязань, 1991.
8. Волков Н.
И., Миловзоров В. П. Электромашинные устройства автоматики. М.: Высшая школа,
1978.
Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
гдепередаточная
функция замкнутой системы по ошибке,изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этоми
.
Тогдаи статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
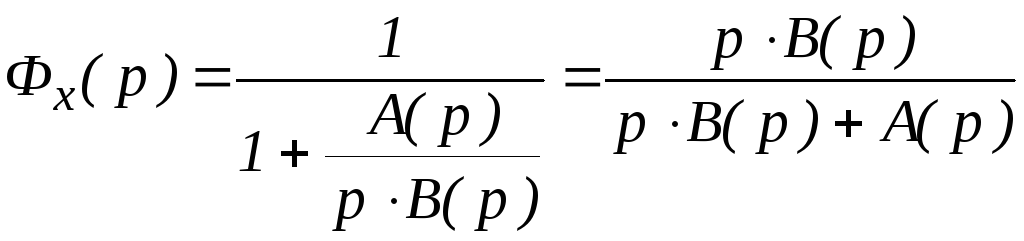
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Щербаков В.С. и др. Элементы автоматики и системы автоматического управления — файл n1.doc
приобрести
Щербаков В.С. и др. Элементы автоматики и системы автоматического управления
скачать (618.5 kb.)
Доступные файлы (1):
- Смотрите также:
- Барышев Г.А., Муромцев Д.Ю. Основы автоматики и системы автоматического управления. Лабораторный практикум (Документ)
- Келим Ю.М. Основы автоматики предприятий почтовой связи (Документ)
- Красовский А.А., Вавилов Ю.А., Сучков А.И. Системы автоматического управления летательных аппаратов (Документ)
- Рубанов В.Г. Линейные системы автоматизированного управления (САУ) (Документ)
- Маругин А.П. Элементы систем автоматики (Документ)
- Маругин А.П. Элементы систем автоматики (Документ)
- Глазырин А.С. Элементы системы автоматики. Практикум (Документ)
- Нетушил А.В. Теория автоматического управления (Документ)
- Кузнецов В.П., Лукьянец С.В., Крупская М.А. Теория автоматического управления. Часть 1: Линейные непрерывные системы (Документ)
- Соломенцев Ю.М. Теория автоматического управления (Документ)
- Теория автоматического управления (Документ)
- Барашко О.Г. Автоматика, автоматизация и автоматизированные системы управления (Документ)
n1.doc
ИССЛЕДОВАНИЕ РАБОТЫ СЛЕДЯЩЕГО ПРИВОДА
Цель работы: изучение принципа действия электрической следящей системы и экспериментальное определение статической ошибки.
- Общие положения
Следящие системы – это устройства автоматического управления, предназначенные для воспроизведения величины, изменяющейся по произвольному закону.
Следящие системы можно разделить на две основные группы:
а) самосинхронизирующиеся следящие системы;
б) следящие системы с искусственной внешней синхронизацией при помощи обратных связей.
К самосинхронизирующимся следящим системам, в которых с определенной степенью точности осуществляется синхронное и синфазное перемещение двух или нескольких не связанных между собой механических валов, относятся следящие приводы. Следящим приводом называется устройство, при помощи которого объект регулирования с определенной точностью воспроизводит движение, задаваемое следящим органом.
Следящий привод, включающий элементы автоматического управления, позволяет воспроизводить требуемые перемещения в широких пределах по произвольному закону от устройства (датчика), задающего этот закон, что обуславливает его широкое применение. Следящий привод может использоваться для автоматического контроля за изменением различных физических величин, для автоматического управления поворотом массивных платформ на заданный угол, например, в экскаваторах, в системе автоматического вождения автомобиля, при автоматизации процессов управления землеройно-планировочными машинами.
В данной работе рассматривается синхронно следящий привод, который состоит из сельсина-датчика (задающий орган, сельсина-трансформатора (датчика угла поворота объекта), фазочувствительного электронного усилителя и исполнительного двигателя, перемещающего какой-либо объект. Структурная схема следящего привода приведена на рис.5.1.
ЭС
Рис. 5.1. Структурная схема следящего привода: ЗО – задающий орган; У – усилитель; ИО – исполнительный орган; О – объект регулирования; Д – датчик; ЭС – элемент сравнения
Элементы следящего привода соединены между собой так, что изменение в положении датчика воздействует через элемент сравнения и усилитель на исполнительный двигатель, который отрабатывает заданную величину перемещения. Процесс работы следящего привода сводится к автоматическому устранению возникающего рассогласования.
Синхронноследящие приводы с электронными усилителями обладают следующими достоинствами:
- быстрое протекание переходных процессов благодаря сравнительно малой инерционности системы управления;
- отсутствие вращающихся и трущихся частей в усилителе.
К недостаткам системы можно отнести:
- ограниченную мощность исполнительного двигателя;
- сравнительно большую ошибку в слежении при установившемся режиме;
- чувствительность работы системы к колебаниям напряжения сети.
Особенности работы системы синхронно следящего привода выявляются при анализе ее статических и динамических характеристик.
Под статическими характеристиками следящего привода понимают зависимость момента, тока и других параметров в схеме от величины угла рассогласования в установившемся режиме, когда отработка угла исполнительным двигателем происходит с неизменной скоростью. Однако только статические характеристики неполно характеризуют работу следящего привода. Необходимо, кроме статических характеристик, знать также и динамические свойства системы, определяющие устойчивость, величину угла рассогласования в переходном режиме, время переходного режима и т.п. Эти свойства системы анализируются на основании уравнений переходного режима. В данной работе изучаются только статические характеристики.
Важной характеристикой следящего привода является статическая ошибка, которая в данном случае представляет собой разность между углом поворота ротора сельсина-датчика (задающий орган) и углом поворота объекта (вала исполнительного двигателя). Статическая ошибка измеряется после прохождения всех переходных процессов, после полной остановки двигателя. Статическая ошибка зависит от состояния вращающихся частей: трения, момента сопротивления повороту двигателя, от колебаний напряжения сети и от инерционности вращаемого объекта.
- Вопросы допуска к лабораторной работе
- Что следует понимать под следящей системой и следящим приводом?
- Область применения следящего привода.
- Элементы следящего привода.
- Достоинства и недостатки синхронно-следящего привода с электронным усилителем.
- Характеристики, применяемые при анализе работы синхронно следящего привода.
- Описание лабораторного стенда
Синхронно следящий привод малой мощности с электронным усилителем смонтирован на лабораторном стенде. Электрическая схема стенда представлена на рис. 5.2. В его схему входят: сельсин-датчик СД со шкалой, сельсин-приемник (сельсин-трансформатор) СТ, электронный фазочувствительный усилитесь, исполнительный двигатель М. Исполнительным двигателем является двухфазный асинхронный двигатель, который обычно применяется для маломощных следящих приводов. На валу исполнительного двигателя находится стрелка, которая в данном случае является объектом регулирования. Стрелка перемещается по круговой шкале.
Принцип работы следящего привода заключается в следующем. При повороте ротора сельсина-датчика СД в однофазной обмотке сельсина-трансформатора СТ наводится ЭДС (напряжение ошибки) и поступает на вход усилителя. На выходе усилителя одна статорная (управляющая) обмотка ?1 исполнительного двигателя. Другая статорная обмотка ?2. включена в переменное напряжение сети через конденсатор, который создает между токами в статорных обмотках сдвиг фаз примерно в 90°.
Исполнительный двигатель М приходит во вращение и перемещает управляемый объект и ротор сельсина-трансформатора CТ. Вращение двигателя происходит до тех пор, пока не произойдет согласование углов поворота входного и выходного валов, при котором напряжение ошибки равно нулю. Для реверсирования исполнительного двигателя в системе необходимо изменить направление рассогласования, что осуществляют изменением направления вращения ротора сельсина-датчика. При этом изменяется фаза напряжения ошибки на 1800 и исполнительный двигатель реверсируется.
Рис. 5.2. Принципиальная схема следящего привода
4. Задание на выполнение работы
1. Сделать отсчет статической ошибки по круговой шкале измерений.
2. Построить график кривой статических ошибок n = ѓ(?).
3. Произвести расчет среднего значения статической ошибки.
- Порядок выполнения работы
- Собрать схему следящего привода (см. рис.5.2).
- Проверить работоспособность следящего привода. Для этого, поворачивая ротор сельсина-датчика по часовой стрелке и против, убедиться, что стрелка, связанная с исполнительным двигателем, поворачивается в ту же сторону.
- Установить ротор сельсина-датчика на нуль по его шкале и убедиться, что стрелка на валу двигателя останавливается в пределах 1. Если этого нет, то расстопорить стрелку и установить в соответствующее положение.
4. Последовательно вращая ротор сельсина-датчика против часовой стрелки и останавливая через 30°, определить установившиеся значения положения стрелки, связанной с двигателем.
5. Выполнить п.4 с поворотом в противоположную сторону.
- Результаты измерений занести в табл. 5.1, где ? – угол поворота задатчика, град; n1 и n2 – угол поворота стрелки исполнительного механизма, град, соответственно по и против часовой стрелки.
- Определить статические ошибки ? n1 и ? n2 по формулам:
?n1 =│? – n1│ , ?n2 = │? – n2│.
Таблица 5.1
| ? | 0 | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 | 360 |
| n1 | |||||||||||||
| n2 | |||||||||||||
| ?n1 | |||||||||||||
| ?n2 |
- Содержание отчета
1. Название и цель работы.
2. Электрическая схема следящего привода.
3. Результаты измерений, представленные в виде таблицы, и расчет
средней статической ошибки.
7.Контрольные вопросы
- Принцип работы синхронно следящего привода.
- Объясните, что следует понимать под статической ошибкой следящей системы?
- Чем объяснить возникновение статической ошибки системы?
- Как определить статическую ошибку следящей системы?
- Каким образом можно изменить направление вращения исполнительного двигателя, не меняя направления вращения сельсина-датчика?
Библиографический список
- Бородин И. Ф. Технические средства автоматики: Учебник для вузов/ И.Ф. Бородин. – М.:Колос, 1982. – 303 с.
- Казаков А. А. Стационарные устройства автоматики и телемеханики: Учебник/А.А. Казаков, В.Д. Бубнов, Е.А. Казаков. – М.: Транспорт, 1990. – 431 с.
- Кузнецов Е.С. Управление техническими системами: Учеб. пособие/Е.С. Кузнецов; МАДИ(ТУ). – 3-е изд., перераб. и доп. М., 2001. – 262 с.
- Курсовое и дипломное проектирование по автоматизации технологических процессов: Учеб. пособие для вузов/Ф.Я. Изаков, В.Р. Казадаев, А.Х. Ройтман, Б.В. Шмаков. – М.:Агропромиздат, 1988.–183 с.
Учебное издание
ЭЛЕМЕНТЫ АВТОМАТИКИ
И СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания к лабораторным работам
Составители:
Виталий Сергеевич Щербаков
Алексей Александрович Руппель
Виталий Алексеевич Глушец
* * *
Редактор Н.И. Косенкова
Лицензия ИД № 00064 от 16.08.99
Подписано к печати 2003
Формат 60х90 1/16. Бумага писчая
Оперативный способ печати
Гарнитура Times New Roman
Усл. п. л. 2,75 , уч. — изд. л. 2,75
Тираж 300 экз. Изд. № 44. Заказ
Цена договорная
Издательство СибАДИ
644099, Омск, ул. П.Некрасова, 10
Отпечатано в ПЦ издательства СибАДИ
644099, Омск, ул. П.Некрасова, 10
ИССЛЕДОВАНИЕ РАБОТЫ СЛЕДЯЩЕГО ПРИВОДА
Лабораторная работа N 1
ИССЛЕДОВАНИЕ СЛЕДЯЩЕЙ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С РЕОСТАТНОЙ ОБРАТНОЙ СВЯЗЬЮ
Цель работы: Ознакомиться с принципом работы и устройством следящей САР с реостатной обратной связью на постоянном токе; исследовать статическую характеристику системы; определить качество процесса регулирования.
Инструмент и принадлежности к работе
1. Лабораторная установка 1 шт.
2. Цифровая измерительная установка Ф-5071/75 1 шт.
Основные положения
Следящей САР называется такая система, алгоритм функционирования которой содержит предписание изменять управляемую величину в зависимости от неизвестного заранее значения переменной величины на входе автоматической системы. Следящие системы являются частью семейства систем, известных как системы регулирования с обратной связью. Широко распространены дистанционные следящие системы воспроизведения угла и линейных перемещений. Дистанционные следящие системы применяются для управления станками, дистанционной передачи информации, управления антеннами, положением орудий, в управлении высотой и курсом самолёта с помощью автопилота, в счётно-решающих устройствах и др.
Функциональная схема следящей САР в общем виде приведена на рис. 1. Специфика работы систем, описанных выше, связана с требованиями получения необходимой точности передачи угловых и линейных перемещений.
Рис. 1. Функциональная схема следящей САР.
Существует большое множество следящих систем, отличающихся принципом действия, структурными элементами, принципом управления, исполнительным устройством, родом источников питания и пр.
По методу сравнения сигналов следящие системы могут быть аналоговыми, в которых сигнал рассогласования выделяется различными методами в аналоговой форме, цифровыми, в которых задающим устройством является ЭВМ, а сигнал рассогласования выделяется в цифровой форме в виде кода, и цифро-аналоговыми.
По структурной схеме следящие системы могут быть одно- и двухканальными, с одним или несколькими принимающими устройствами, с последовательными или параллельными корректирующими устройствами, простыми и взаимосвязанными сложными и т.п.
На практике наиболее распространёнными являются одноканальные следящие системы. Для повышения точности применяются двухканальные следящие системы, известные как системы с грубого и точного отсчётов.
В случае, когда суммарная погрешность исчисляется угловыми секундами при большом передаточном отношении электрической редукции, применяются трёхканальные следящие системы.
По типу измерительных элементов следящие системы могут иметь индуктивные, индукционные, потенциометрические, фотоэлектрические, ёмкостные, генераторные и другие датчики.
По типу исполнительных устройств следящие системы могут быть гидравлическими, пневматическими и комбинированными (с муфтами), с электродвигателями переменного и постоянного токов, шаговыми двигателями, моментными двигателями и т.п.
В зависимости от типа исполнительных устройств в маломощных системах применяются, главным образом, полупроводниковые усилители постоянного и переменного токов. В системах средней мощности возможно применение магнитных и тиристорных усилителей. В мощных системах применяются электромашинные усилители и тиристорные преобразователи.
По принципу управления исполнительным двигателем наибольшее распространение имеют следящие системы непрерывного действия с пропорциональным изменением сигнала. На обмотку управления двигателем подаётся напряжение, пропорциональное углу рассогласования, и, соответственно, частота вращения исполнительного двигателя пропорциональна сигналу рассогласования.
Применяется также управление релейного типа, при котором на обмотку управления двигателя при определённом угле рассогласования или при определённом значении управляющего сигнала подаётся максимальное напряжение. При частотном управлении двигателем на обмотку управления подаются импульсы определённой длительности во времени, но изменяется частота их следования или при постоянной частоте следования импульсов изменяется их длительность. При этом частота вращения двигателя пропорциональна частоте импульсов или соответственно длительности импульсов.
Возможны схемы управления, в которых при малом рассогласовании имеется линейный участок изменения сигнала, а при каком-то заданном угле рассогласования применяется релейное управление.
При создании следящих систем в технических требованиях задаются следующие параметры: точность, диапазон работы, максимальная скорость и ускорение входной оси, величина, и характер нагрузки, род источника, питания, габариты и надежность, а также условия эксплуатации систем – температура, влажность окружающей среды, вибрации и пр. В соответствии с этими требованиями предварительно выбирают измерительные элементы, отвечающие требованиям точности в заданном диапазоне работ.
Исходя из значений нагрузки, скорости и ускорения, а также из режима работы, выбирают исполнительное устройство и передаточное отношение редуктора привода. В маломощных следящих системах в качестве исполнительного элемента получили широкое распространение двухфазные асинхронные двигатели. При проектировании необходимы малые люфты и малый момент инерции редуктора. Момент инерции редуктора должен быть меньше момента инерции ротора двигателя, поэтому необходимо предельно уменьшать момент инерции трибки на валу двигателя. Для уменьшения диаметра шестерни, зацепляющейся с трибкой, передаточное отношение первой пары шестерён редуктора следует выбирать в пределах 2-3, передаточное отношение второй пары должно быть не более 4-6. Приведенный момент инерции последующих пар будет пренебрежимо малым. Тип усилителя и входящие в него преобразовательные элементы выбирают в соответствии с выходными параметрами измерительных элементов (выходным сопротивлением приемника, остаточным и максимальным выходными напряжениями приёмника и т. д.) и исполнительного элемента (сопротивлением нагрузки и максимальной выходной мощностью) с учётом принципа управления двигателем. В маломощных следящих системах используются полупроводниковые усилители. Постоянные времени всех цепей и элементов, коэффициенты усиления преобразователей и усилителей, передаточные отношения и прочие параметры элементов определяются расчётным или экспериментальным путем, а также по справочным данным. Далее выбирается структурная схема и составляются дифференциальные уравнения звеньев системы и передаточные функции звеньев для расчёта системы на устойчивость и выбора корректирующих цепей в целях обеспечения необходимого запаса устойчивости и необходимого качества переходного процесса.
При расчете погрешностей следящих систем учитывают, что суммарная погрешность состоит из статической Δφст динамической Δφдин погрешностей.
Статическая погрешность следящей системы представляет собой разность между угловыми наложениями входной и выходной осей после отработки двигателем системы заданного угла. Эта погрешность складывается из погрешностей измерительных элементов Δφиз датчика и приёмника системы, погрешностей преобразователей аналоговых сигналов в код в цифровых следящих системах Δφак, погрешности зоны нечувствительности Δφ3,.обусловленной моментом нагрузки, погрешности от дрейфа нулевого положения датчика и приемника, усилительно-преобразовательного устройства Δφз погрешности изготовления зубчатых колёс редуктора в системах грубого и точного отсчётов Δφзк погрешности люфта в них Δφл. Часто необходимо учитывать погрешности от температуры окружающей среды Δφt изменения напряжения и частоты питания и от каких-либо других факторов. Так как перечисленные источники погрешностей являются взаимно независимыми, суммарную погрешность можно определить как среднеквадратическую, т. е.:
.
Динамическая погрешность следящей системы Δφдин представляет собой разность между угловыми положениями входной и выходной осей при произвольном законе вращения входной оси. Слежение за положением входной оси осуществляется с определённой точностью в зависимости от выбранных параметров системы. Оценку динамической погрешности, как правило, производят либо при непрерывном вращении, либо при гармонических колебаниях входной оси. При допустимой динамической погрешности требуемый переходной процесс должен обеспечиваться выбором необходимых корректирующих устройств и их параметров. Погрешность в установившемся режиме при вращении входной оси с постоянной скоростью называют кинетической погрешностью. Она зависит от коэффициента усиления усилителя и параметров следящей системы. Отношение частоты вращения входного вала системы к установившемуся значению скоростной погрешности Δφск носит название добротности системы по скорости К: Δφск = Ωвх/К.
Перечисленные динамические погрешности должны быть либо одного порядка со значением основной погрешности – погрешности измерительных элементов, либо меньше её даже в тех случаях, когда погрешность измерительных элементов исчисляется угловыми секундами. Таким образом, суммарная погрешность всей системы ΔφΣ может быть определена как
.
На рисунке 2 представлена следящая система автоматического регулирования (САР), состоящая из потенциометра-датчика ПД и потенциометра-приёмника ПП, включенных параллельно к общему источнику питания Uп. Подвижные контакты потенциометров соответственно соединены механически с задающим и исполнительным рабочими органами. Напряжение Uс, снимаемое с подвижных контактов потенциометров, является напряжением сигнала рассогласования системы. При согласованном положении рабочих органов, когда φд = φп, напряжение сигнала равно нулю. Напряжение сигнала рассогласования Uс поступает на вход электронного усилителя У, а далее на исполнительный асинхронный двигатель Д. Вал двигателя через зубчатую передачу связан с подвижным контактом потенциометра приёмника. Система работает на устранение ошибки рассогласования. Для отсчёта углов поворота задающего и исполнительного органов применена цифровая измерительная установка Ф-5071/75, в качестве датчиков угла поворота используются сельсины СД1 и СД2, кинематически связанные c задающими и исполнительными рабочими органами. Отсчётным устройством служат блоки индикации Х и Z.
Рис. 2. Следящая САР угла поворота.
Порядок выполнения работы
- Включить установку в сеть 220 В.
- Включить питание установки и прогреть в течение 3 минут.
- Установить шкалу потенциометра-датчика на «НОЛЬ».
- Нажать на блоках индикации X, Z кнопку «СБРОС».
- Установить минимальный коэффициент усиления усилителя при помощи ручки регулятора «УСИЛЕНИЕ».
- Поворачивая движок потенциометра-датчика по часовой стрелке на углы кратные 20˚, снять показания значений угла поворота с блоков индикации Х и Z (Х – угол поворота потенциометра-датчика, Z – угол поворота потенциометра-приемника). После поворота на 360˚ измерения повторить, поворачивая рукоятку против часовой стрелки.
- Пункты 3-6 повторить для среднего и максимального значения коэффициента усиления усилителя.
- Полученные данные занести в таблицу.
|
№ |
По часовой стрелке |
Против часовой стрелки |
||||
|
Х |
Z |
σ |
Х |
Z |
σ |
|
- Определить для каждого направления вращения потенциометра-датчика и коэффициента усиления усилителя максимальную погрешность передачи угла в установившемся режиме σ = X – Z.
- Построить график зависимости z = f(x) для поворота по часовой и против часовой стрелки.
Содержание отчёта
- Результаты измерений в виде таблицы.
- Графики зависимости z = f(x) для различных коэффициентов усиления.
- Выводы по работе.
Контрольные вопросы к лабораторной работе
- Принцип действия и классификация следящих САР.
- Основные источники погрешностей следящих САР.
- Потенциометрические следящие САР угла поворота.
- Какие параметры задаются в технических требованиях при создании следящих систем?
- Как определить добротность следящей САР?
ПРОЕКТИРОВАНИЕ ЦИФРОВОЙ СЛЕДЯЩЕЙ СИСТЕМЫ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к курсовой работе
по курсу
“Теория автоматического управления”
для студентов специальности 7.091 401
560 IF S = 2 THEN T(3) = .8 * T(3)
570 IF S > 2 THEN T(3) = .7 * T(3)
580 X3 = LOG(1 / T(3))
590 PRINT «T(1)=»; T(1); «T(2)=»; T(2); «T(3)=»; T(3)
600 PRINT «Cкобка в знаменателе (Т(3)*Р+1) должна возводиться в степень (n-m)»
610 PRINT «n-m=»; S
620 FOR I = 1 TO M
630 K = 3 + M
640 PRINT «T(«; K; «)=»; T(K)
650 NEXT I
660 PRINT «Wc=»; OC; «LgWc=»; XC
670 PRINT «Lg(1/T1)=»; X1; «Lg(1/T2)=»; X2; «Lg(1/T3)=»; X3
680 END
О Г Л А В Л Е Н И Е
1. Введение
2. ЗАДАНИЕ НА ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ
3. ПОРЯДОК РАСЧЕТА СЛЕДЯЩЕЙ СИСТЕМЫ
3.1. Разработка функциональной схемы.
3.2. Выбор исполнительного двигателя.
3.3. Выбор усилителя мощности.
3.4. Составление передаточных функций элементов следящей системы
3.5. Расчет последовательного непрерывного корректирующего звена методом ЛАЧХ
3.6. Моделирование следящей системы с непрерывным последовательным корректирующим звеном
3.7. Определение дискретной передаточной функции корректирующего звена
3.8. Моделирование цифровой следящей системы.
3.9. Получение рекуррентного уравнения цифрового корректирующего звена.
3.10. Разработка принципиальной схемы цифровой следящей системы.
ПРИЛОЖЕНИЯ
1. Введение
Цель курсовой работы — получить навыки расчета линейных систем автоматического управления с цифровым корректирующим звеном, роль которого может выполнять микропроцессор, управляющая вычислительная машина, или любое специализированное цифровое управляющее устройство.
В соответствии с заданием необходимо разработать следящую систему, удовлетворяющую определенным техническим условиям. Система должна обеспечивать синхронное и синфазное вращение двух осей, механически не связанных между собой. Входом системы является угол поворота сельсина-датчика, а выходом — угол поворота выходного вала редуктора, механически связанного с рабочим механизмом и с ротором сельсина-приемника.
Следящие системы рассматриваемого типа широко применяются для дистанционного управления различными механизмами, а также при построении автоматических систем управления в различных отраслях промышленности.
Для обеспечения заданных показателей качества переходного процесса в систему вводится цифровое управляющее (корректирующее) звено. Расчет корректирующего звена проводится методом логарифмических частотных характеристик, разработанным для расчета непрерывных систем управления. Использование данного метода для расчета цифрового корректирующего звена основано на предположении о том, что при малом периоде квантования по времени цифровая система по своим свойствам приближается к непрерывной, а при достаточно большом числе цифровых разрядов вычислительного устройства нелинейностью, вносимой квантованием сигналов по уровню, можно пренебречь. Современный уровень развития цифровой вычислительной техники позволяет применять в управляющем вычислительном устройстве период квантования непрерывных сигналов по времени порядка 0,01-0,001с. , что обычно является вполне достаточным для обеспечения адекватности по динамическим свойствам цифровой и непрерывной систем.
190 PRINT «Введите величину макс. перерегулирования»
200 PRINT «Сигма макс.,% =»
210 INPUT SM
220 IF SM = 10 THEN C = 5: L1 = 18
230 IF SM = 15 THEN C = 4.4: L1 = 15
240 IF SM = 20 THEN C = 4: L1 = 13.5
250 IF SM = 25 THEN C = 3.6: L1 = 12
260 IF SM = 30 THEN C = 3.2: L1 = 11
270 IF SM = 35 THEN C = 3: L1 = 10.5
280 IF SM = 40 THEN C = 2.8: L1 = 10
290 PRINT «Порядок астатизма NU=»
300 INPUT NU
310 PRINT «Коэффициент усиления желаемой системы Кс=»
320 INPUT KC
330 PRINT «Время регулирования TR=»
340 INPUT TR
350 M1 = .434
360 OC = C * 3.14 / TR
370 XC = LOG(OC) * M1
380 B = 20 * XC
390 X2 = (B — L1) / 20
400 T(2) = 1 / (10 ^ X2)
410 A = 20 * LOG(KC) * M1
420 X1 = (L1 + 40 * X2 — A) / 20
430 T(1) = 1 / (10 ^ X1)
440 X3 = (L1 + 20 * XC) / 20
450 T(3) = 1 / 10 ^ X3
460 IF NU = 1 THEN GOTO 490
470 X1 = (40 * X2 + L1 — A) / 40
480 T(1) = 1 / (10 ^ X1)
490 M = 0
510 FOR I = 1 TO N
520 IF T3(I) <= T(3) * .75 THEN M = M + 1: T(3 + M) = T3(I)
540 NEXT I
550 S = N — M
2330 PRINT «T2(«; I; «)=»
2340 INPUT T(I)
2350 NEXT I
2420 GOTO 2120
Приложение 5
Программа LOGHAR. doc
Определение постоянных времени
передаточной функции желаемой системы
10 PRINT «Определение пост. времени передат. функции желаемой системы»
20 PRINT «Искомая перед. ф-ция имеет вид:»
30 PRINT » Kc(T(2)*P+1)/((T(1)*P+1)*(T(3)*P+1)^(n- m)*(T(4)P+1)*..(T(m+3)P+1)*P)»
40 PRINT «n-степень полинома Q(P) — знаменателя перед. ф-ции заданной сист.»
50 PRINT «m-количество пост. времени Q(P), меньших, чем Т(3)»
60 PRINT «Q(P)=(Tз(1)*P+1)*(Tз(2)*P+1)*…*(Tз(N)*P+1)»
70 PRINT «Введите порядок полинома знаменателя Q(P) заданной перед. ф-кции»
80 PRINT «N=»
90 INPUT N
100 DIM T3(5), T(8)
110 FOR I = 1 TO 8
120 T(I) = 0
130 NEXT I
140 PRINT «Введите пост. времени знаменат. заданной перед. ф-ции Q(P)»
150 FOR I = 1 TO N
160 PRINT «Tз(«; I; «)=»
170 INPUT T3(I)
180 NEXT I
2. ЗАДАНИЕ НА ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ
2.1. Цель курсовой работы — проектирование следящей системы, удовлетворяющей заданным техническим условиям.
2.2. Измерительное устройство — сельсинная пара.
2.3. Исполнительный двигатель — двигатель постоянного тока серии МИ.
2.4. Усилитель мощности — электромашинный усилитель с поперечным полем.
2.5. Исходные данные для проектирования системы.
2.5.1. Статический момент нагрузки объекта управления
— Mос, Н.м.
2.5.2. Момент инерции объекта управления — Jо, кг.м2
2.5.3. Максимальная угловая скорость объекта
управления — wо max.
2.5.4. Максимальное угловое ускорение объекта
управления — eо max.
2.5.5. Требования, предъявляемые к качеству процесса управления:
максимальное перерегулирование — s max,;
время регулирования — tр, с;
максимальная кинетическая ошибка — xmax, рад.
Варианты исходных данных приведены в прил. 1.
2.6. Курсовая работа должна содержать следующие разделы.
2.6.1. Разработка функциональной схемы.
2.6.2. Выбор элементов системы — исполнительного двигателя (серии МИ) и электромашинного усилителя мощности (ЭМУ), расчет передаточного числа редуктора.
2.6.3. Составление передаточных функций элементов нескорректированной следящей системы.
2.6.4. Построение логарифмических частотных характеристик (ЛАЧХ ) нескорректированной системы, желаемой системы и последовательного корректирующего звена.
2.6.5. Построение на ЭВМ переходной функции H(t) и определение по ней показателей качества переходного процесса для системы с непрерывным последовательным корректирующим звеном.
2.6.6. Определение дискретной передаточной функции последовательного корректирующего звена по его непрерывной передаточной функции.
2.6.7. Построение на ЭВМ переходной функции H(t) и определение по ней показателей качества переходного процесса для системы с дискретным корректирующим звеном.
2.6.8. Определение рекуррентного уравнения дискретного корректирующего звена.
2.6.9. Разработка принципиальной схемы цифровой следящей системы.
2.7. Расчетно-пояснительная записка должна содержать следующие разделы.
2.7.1. Введение (цель выполнения работы, описание следящей системы, принцип ее работы, описание функциональной схемы системы).
2.7.2. Исходные данные для проектирования системы.
2.7.3. Расчетная часть.
2.7.4. Заключение (основные характеристики спроектированной системы).
2.7.5. Список литературы.
2.8. Расчетно-пояснительная записка должна включать в себя функциональную, структурную и принципиальную электрические схемы следящей системы; ЛАЧХ и ЛФЧХ скорректированной и нескорректированной системы, графики переходных функций системы с непрерывным и с дискретным корректирующим звеном, другие рисунки, таблицы и графики, необходимые для выполнения данной работы.
2.9. Записка должна быть оформлена в соответствии с требованиями ЕСКД (написана черными чернилами или пастой, либо отпечатана на принтере на листах формата 11). Ориентировочный объем записки — 25 — 30 страниц.
620 GOTO 270
630 FOR I = 0 TO N
640 PRINT «S(«; I; «)=»; S1(I); TAB(40); «G(«; I; «)=»; S(I)
650 NEXT I
660 END
2060 L = 1
2070 PRINT «Введите постоянные времени числителя T1(I)»
2080 FOR I = 1 TO N
2090 PRINT «T1(«; I; «)=»
2100 INPUT T(I)
2110 NEXT I
2112 PRINT «Введите коэффициент K»
2114 PRINT «K=»
2116 INPUT K
2120 A(0) = 1
2130 A(1) = T(1) + T(2) + T(3) + T(4) + T(5)
2140 X1 = T(1) * T(2) + T(1) * T(3) + T(1) * T(4) + T(1) * T(5)
2150 X2 = T(2) * T(3) + T(2) * T(4) + T(2) * T(5)
2160 X3 = T(3) * T(4) + T(3) * T(5) + T(4) * T(5)
2170 A(2) = X1 + X2 + X3
2180 X1 = T(1) * T(2) * T(3) + T(1) * T(2) * T(4) + T(1) * T(2) * T(5)
2190 X2 = T(1) * T(3) * T(4) + T(1) * T(3) * T(5) + T(1) * T(4) * T(5)
2200 X3 = T(2) * T(3) * T(4) + T(2) * T(3) * T(5) + T(3) * T(4) * T(5)
2210 A(3) = X1 + X2 + X3 + T(2) * T(4) * T(5)
2220 X1 = T(1) * T(2) * T(3) * T(4) + T(1) * T(2) * T(3) * T(5)
2230 X2 = T(1) * T(2) * T(4) * T(5) + T(1) * T(3) * T(4) * T(5)
2240 A(4) = X1 + X2 + T(2) * T(3) * T(4) * T(5)
2250 A(5) = T(1) * T(2) * T(3) * T(4) * T(5)
2260 IF L = 2 GOTO 240
2270 FOR I = 0 TO N
2280 B(I) = A(I) * K
2290 NEXT I
2300 L = 2
2310 PRINT «Введите постоянные времени знаменателя T2(I)»
2320 FOR I = 1 TO N
280 V2 = 4 * B(2) * T ^ (N — 2)
290 V3 = 8 * B(3) * T ^ (N — 3): V4 = 16 * B(4) * T ^ (N — 4)
300 V5 = 32 * B(5)
310 S(N) = V0 + V1 + V2 + V3 + V4 + V5
320 X1 = V0 * N + V1 * (N — 2) + V2 * (N — 4)
330 X2 = V3 * (N — 6) + V4 * (N — 
340 S(N — 1) = X1 + X2
350 X1 = V0 * N * (N — 1) / 2 + V1 * (N — 1) * (N — 4) / 2
360 X2 = V2 * ((N — 2) * (N — 7) + 2) / 2
370 X3 = V3 * ((N — 3) * (N — 10) + 6) / 2
380 X4 = V4 * (22 — 4 * N) + 10 * V5
390 S(N — 2) = X1 + X2 + X3 + X4
400 X0 = V0 * N * (N — 1) * (N — 2) / 6
410 X1 = V1 * (N — 1) * (N — 2) * (N — 6) / 6
420 X2 = V2 * ((N — 2) * (N — 3) * (N — 10) + 6 * (N — 2)) / 6
430 X3 = V3 * (3 * (N — 3) * (6 — N) — 2) / 2
440 X4 = V4 * (6 * N — 28) — 10 * V5
445 IF N < 3 GOTO 550
450 S(N — 3) = X0 + X1 + X2 + X3 + X4
460 X0 = V0 * N * (N — 1) * (N — 2) * (N — 3) / 24
470 X1 = V1 * (N — 1) * (N — 2) * (N — 3) * (N — 
480 X2 = V2 * (N — 2) * (N — 3) * (3 — 2 * (N — 4)) / 6
490 X3 = V3 * (N — 3) * (3 * (N — 4) — 2) / 2
500 X4 = V4 * (17 — 4 * N) + 5 * V5
510 IF N < 4 GOTO 550
520 S(N — 4) = X0 + X1 + X2 + X3 + X4
530 IF N < 5 GOTO 550
540 S(N — 5) = V0 — V1 + V2 — V3 + V4 — V5
550 IF R = 2 GOTO 630
560 FOR I = 0 TO N
570 B1(I) = B(I)
580 B(I) = A(I)
590 S1(I) = S(I)
600 NEXT I
610 R = 2
3. ПОРЯДОК РАСЧЕТА СЛЕДЯЩЕЙ СИСТЕМЫ
3.1. Разработка функциональной схемы
В проектируемой следящей системе в качестве исполнительного двигателя (Д) должен быть использован двигатель постоянного тока серии МИ, в качестве усилителя мощности — электромашинный усилитель с поперечным полем (ЭМУ). Для измерительного устройства (ИУ) рекомендуется использовать сельсинную пару: сельсин-датчик и сельсин-трансформатор (приемник). Так как измерительное устройство работает на переменном токе, а усилитель мощности и исполнительный двигатель — на постоянном токе, то после измерительного устройства должен быть применен фазовый детектор (ФД). Кроме указанных элементов в функциональную схему входят корректирующее устройство (КУ), усилитель напряжения (У), редуктор (Р), посредством которого исполнительный двигатель соединяется с объектом управления и ротором сельсина-трансформатора, и объект управления (ОУ). Корректирующее устройство представлено тремя блоками: аналого-цифровой преобразователь (АЦП), вычислитель (В) и цифро-аналоговый преобразователь (ЦАП).
Функциональная схема цифровой следящей системы приведена на рис.1.
ОУ
Рис.1. Функциональная схема цифровой следящей системы
3.2. Выбор исполнительного двигателя
Выбор двигателя начинают с расчета требуемой мощности, которая должна быть достаточной для обеспечения заданных скорости и ускорения объекта управления при заданной нагрузке.
Требуемая мощность, Вт:
где hр — КПД редуктора, hр = 0,72 .
По каталогу (прил.2) выбираем ближайший двигатель большей мощности Рн > Ртр и выписываем его паспортные данные:
Рн — номинальная мощность (Вт);
nн — номинальная скорость вращения (об/мин);
Uн — номинальное напряжение (В);
Iн — номинальный ток якоря (А);
Rд— сопротивление цепи обмотки якоря (Ом);
Jд — момент инерции якоря (кг.м2);
hд— КПД двигателя.
Затем последовательно определяем следующие величины:
номинальная угловая скорость двигателя wн (с-1) —
wн = pnн/30 ;
номинальный момент двигателя Мн (Н.м) —
Мн = 9,55Рн/nн ;
оптимальное передаточное число редуктора iр —
Jр = 1.10-4 кг.м2 — момент инерции редуктора.
35 PRINT «R(P)=K*(T1(1)*P+1)*(T1(2)*P+1)*…*(T1(N)*P+1)»
36 PRINT «Q(P)=(T2(1)*P+1)*(T2(2)*P+1)*…*(T2(N)*P+1)»
60 PRINT «Искомая дискретная передаточная функция имеет вид:»
70 PRINT «K(Z)=S(Z)/G(Z), где»
80 PRINT «S(Z)=S(0)+S(1)*Z+S(2)*Z^2+…+S(N)*Z^N»
9 0 PRINT G(Z)=G(0)+G(1)*Z+G(2)*Z^2+…+G(N)*Z^N+G(N+1)*
*Z^(N+1)»
100 DIM A(5), B(5), B1(5), S(5), S1(5), G(6), T1(5), T2(5)
102 FOR I = 0 TO 5
104 A(I) = 0: B(I) = 0: S(I) = 0: G(I) = 0
106 NEXT I
108 R = 1
110 PRINT «Введите порядок полинома Q(P) -N, N<=5»
120 PRINT «N=»
130 INPUT N
131 PRINT «Задайте величину коэффициента F»
132 PRINT «F=»
133 INPUT F
134 IF F = 1 GOTO 140
135 IF F = 2 GOTO 2060
136 GOTO 131
140 PRINT «Введите коэффициенты числителя В(0)…В(N)»
150 FOR I = 0 TO N
160 PRINT «B(«; I; «)=»
170 INPUT B(I)
180 NEXT I
190 PRINT «Введите коэффициенты знаменателя A(0)…A(N)»
200 FOR I = 0 TO N
210 PRINT «A(«; I; «)=»
220 INPUT A(I)
230 NEXT I
240 PRINT «Введите период квантования по времени Т»
250 PRINT «T=»
260 INPUT T
270 V0 = B(0) * T ^ N: V1 = 2 * B(1) * T ^ (N — 1)
Приложение 3 Технические данные ЭМУ
|
Тип ЭМУ |
Мощ- |
Мощн. управ- |
Напря- |
Ток якоря |
Сопрот. обмот- |
Постоянные Ту Ткз |
|
|
кВт |
Вт |
В |
А |
Ом |
с |
с |
|
|
ЭМУ-3А3 |
0,2 |
0,4 |
115 |
1,75 |
1000 |
0,005 |
0,018 |
|
ЭМУ-5А3 |
0,5 |
0,4 |
115 |
4,35 |
1000 |
0,01 |
0,033 |
|
ЭМУ-12А3 |
1,0 |
0,4 |
115 |
8,7 |
2200 |
0,015 |
0,06 |
|
ЭМУ-25А3 |
2,0 |
0,4 |
230 |
9,1 |
1500 |
0,02 |
0,1 |
|
ЭМУ-50А3 |
4,0 |
0,5 |
230 |
17,4 |
2200 |
0,03 |
0,17 |
|
ЭМУ-70А3 |
6,0 |
0,5 |
230 |
26 |
1500 |
0,04 |
0,22 |
|
ЭМУ-100А3 |
8,5 |
0,5 |
230 |
37 |
1000 |
0,06 |
0,28 |
Приложение 4
Программа расчета коэффициентов дискретной передаточной функции по коэффициентам непрерывной передаточной функции
10 REM Определение дискретной передаточной функции по непрерывной
11 REM Используется билинейное преобразование
12 REM P=2*(Z-1)/(T*(Z+1))
20 PRINT «Исходная передаточная функция должна быть представлена в виде»
30 PRINT «K(P)=R(P)/Q(P), возможны две формы представления»
31 PRINT «Форма 1 — F=1:»
32 PRINT «R(P)=B(0)+B(1)*P+B(2)*P^2+…+B(N)*P^N»
33 PRINT «Q(P)=A(0)+A(1)*P+A(2)*P^2+…+A(N)*P^N»
34 PRINT «Форма 2 — F=2:»
Определяем требуемый момент на валу двигателя:
Выбранный двигатель нужно проверить, удовлетворяет ли он по моменту и скорости в соответствии со следующими условиями:
Мтр/Мн l ; wo max iр / wн a ;
где l — коэффициент допустимой перегрузки двигателя по моменту (для двигателя постоянного тока l = 10 ); a — коэффициент допустимого кратковременного увеличения скорости двигателя сверх номинальной, обычно a = 1,2 — 1,5.
Пример. Выбрать исполнительный двигатель следящей системы, если согласно техническому заданию: Jо= 100 кг.м2;
Мос= 120 Нм; wоmax= 0,7 с-1; eomax= 0,44 с-2 ; hр = 0,72.
Требуемая мощность двигателя
Ртр = 2(120 + 100. 0,44). 0,7 /0,72 = 319 Вт .
Выбираем двигатель типа МИ-22 (прил.2) со следующими параметрами: Рн = 370 Вт; Uн = 110 В; nн = 3000 об/мин;
Jд = 0,004 кг.м2.
Зададимся моментом инерции редуктора, приведенного к валу двигателя Jр=1.10-4 кг.м2, найдем передаточное число редуктора
Требуемый момент
Номинальный момент выбранного двигателя равен:
Проведем проверку двигателя:
по моменту — 1,28/1,18< 10 ;
по скорости — 0,7.355/314 = 0,79 < 1,5 .
В результате проверок двигателя по моменту и скорости видно, что он не перегружен. Следовательно, двигатель МИ-22 выбран правильно.
3.3. Выбор усилителя мощности
В качестве усилителя мощности используем ЭМУ с поперечным полем. При выборе усилителя необходимо соблюдать следующие условия.
1. Номинальная мощность усилителя должна удовлетворять неравенству
Рун Рн / hд ,
где hд — КПД двигателя.
2. Номинальное напряжение усилителя должно быть не меньше номинального напряжения исполнительного двигателя.
3. Номинальный ток усилителя должен быть не меньше, чем номинальный ток двигателя.
Учитывая указанные условия выбираем тип ЭМУ (см. прил. 3).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
МИ-32 |
0,76 |
2500 |
110 |
8,2 |
0,368 |
80 |
0,0132 |
|
0,45 |
1500 |
110 |
5,0 |
0,975 |
75 |
0,0132 |
|
|
0,37 |
1000 |
110 |
4,2 |
2,21 |
73 |
0,0132 |
|
|
0,76 |
2500 |
220 |
4,1 |
1,36 |
80 |
0,0132 |
|
|
0,37 |
1000 |
220 |
2,1 |
8,37 |
73 |
0,0132 |
|
|
МИ-41 |
1,6 |
2500 |
110 |
19,5 |
0,249 |
73 |
0,035 |
|
1,1 |
1500 |
110 |
13,0 |
0,67 |
74 |
0,035 |
|
|
0,76 |
1000 |
110 |
9,0 |
1,3 |
72 |
0,035 |
|
|
1,6 |
2500 |
220 |
9,5 |
0,93 |
73 |
0,035 |
|
|
1,1 |
1500 |
220 |
6,4 |
2,63 |
75 |
0,035 |
|
|
0,76 |
1000 |
220 |
4,5 |
5,32 |
72 |
0,035 |
|
|
МИ-42 |
3,2 |
2500 |
110 |
36,3 |
0,1 |
78 |
0,065 |
|
1,6 |
1500 |
110 |
18,2 |
0,32 |
78 |
0,065 |
|
|
1,1 |
1000 |
110 |
12,6 |
0,75 |
75 |
0,065 |
|
|
3,2 |
2500 |
220 |
18,0 |
0,376 |
79 |
0,065 |
|
|
1,6 |
1500 |
220 |
9,1 |
1,28 |
78 |
0,065 |
|
|
1,1 |
1600 |
220 |
6,3 |
2,95 |
75 |
0,065 |
|
|
Ми-51 |
5,5 |
2500 |
220 |
27,2 |
0,164 |
82 |
0,125 |
|
3,2 |
1500 |
220 |
17,1 |
0,46 |
82 |
0,125 |
|
|
1,6 |
1000 |
220 |
8,7 |
1,1 |
79 |
0,125 |
|
|
МИ-52 |
7,0 |
2500 |
220 |
37,0 |
0,088 |
84 |
0,15 |
|
4,5 |
1500 |
220 |
23,3 |
0,26 |
85 |
0,15 |
|
|
2,5 |
1000 |
220 |
13,1 |
0,569 |
82 |
0,15 |
Приложение 2
Технические данные двигателей серии МИ
|
Тип двига- теля |
Мощ- ность |
Ско- рость вращ. |
Напря- жение |
Ток якоря |
Сопрот цепи якоря |
КПД |
Момент инерц. |
|
Рн, кВт |
nн, об/мин |
Uн, В |
Iн, А |
Rд, Ом |
hд, % |
Jд, кгм2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
МИ-11 |
0,12 |
3000 |
60 |
2,87 |
0,46 |
62 |
0,0015 |
|
0,1 |
2000 |
60 |
2,27 |
0,94 |
63 |
0,0015 |
|
|
0,12 |
3000 |
100 |
1,53 |
1,48 |
62 |
0,0015 |
|
|
0,1 |
2000 |
110 |
1,22 |
3,60 |
63 |
0,0015 |
|
|
МИ-12 |
0,2 |
3000 |
60 |
4,57 |
0,23 |
66 |
0,002 |
|
0,12 |
2000 |
60 |
2,72 |
0,52 |
64 |
0,002 |
|
|
0,2 |
3000 |
110 |
2,46 |
0,765 |
66 |
0,002 |
|
|
0,12 |
2000 |
110 |
1,46 |
1,74 |
64 |
0,002 |
|
|
МИ-21 |
0,25 |
3000 |
60 |
5,6 |
0,284 |
67 |
0,0035 |
|
0,2 |
2000 |
60 |
4,3 |
0,645 |
68 |
0,0035 |
|
|
0,25 |
3000 |
110 |
3,05 |
0,945 |
67 |
0,0035 |
|
|
0,2 |
2000 |
110 |
2,33 |
2,20 |
68 |
0,0035 |
|
|
МИ-22 |
0,37 |
3000 |
60 |
8,2 |
0,195 |
71 |
0,04 |
|
0,25 |
2000 |
60 |
5,5 |
0,360 |
75 |
0,004 |
|
|
0,12 |
1000 |
60 |
2,6 |
1,44 |
64 |
0,004 |
|
|
0,37 |
3000 |
110 |
4,4 |
0,546 |
72 |
0,004 |
|
|
0,25 |
2000 |
110 |
2,9 |
1,29 |
70 |
0,004 |
|
|
0,12 |
1000 |
110 |
1,4 |
4,58 |
64 |
0,004 |
|
|
МИ-31 |
0,45 |
3000 |
60 |
10,3 |
0,204 |
68 |
0,009 |
|
0,37 |
2000 |
60 |
8,2 |
0,405 |
70 |
0,009 |
|
|
0,45 |
3000 |
110 |
5,6 |
0,585 |
68 |
0,009 |
|
|
0,2 |
1000 |
60 |
4,4 |
1,32 |
66 |
0,009 |
|
|
0,37 |
2000 |
110 |
4,4 |
1,16 |
70 |
0,009 |
|
|
0,2 |
1000 |
110 |
2,4 |
3,9 |
66 |
0,009 |
3.4. Составление передаточных функций
элементов следящей системы
3.4.1. Исполнительный двигатель
Передаточная функция исполнительного двигателя по углу поворота имеет вид (если пренебречь индуктивностью цепи якоря)
где Кд — коэффициент усиления двигателя, рад/В.с : Кд = wн / Uн ;
Тд — электромеханическая постоянная времени:
В последней формуле a =1,2 — постоянный коэффициент;
Jc — cуммарный момент инерции, приведенный к валу двигателя.
;
3.4.2. Электромашинный усилитель
Передаточная функция ЭМУ
Кэму — коэффициент усиления ЭМУ по напряжению
Uэму — напряжение на выходе ЭМУ ; Uу — напряжение обмотки управления ЭМУ —
Ру, Rу — соответственно мощность и сопротивление обмотки управления ЭМУ,
Ту, Ткз — постоянные времени обмотки управления и короткозамкнутой обмотки якоря ЭМУ.
3.4.3. Усилитель
Усилитель (на функциональной схеме — У) служит для согласования выходного сигнала ЦАП с входным сопротивлением обмотки управления ЭМУ. Его можно считать безинерционным звеном с передаточной функцией Wу(Р) = Ку .
В расчетах принять Ку = 1 .
3.4.4. Фазовый детектор
Передаточная функция фазового детектора Wфд (P) = Кфд,
где Кфд=1 — коэффициент усиления фазового детектора.
3.4.5. Измерительное устройство
Передаточная функция измерительного устройства Wиу(Р)=Киу,
где Киу=1 — коэффициент усиления измерительного устройства.
Приложение 1 (продолжение)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
17 |
250 |
180 |
1,0 |
0,04 |
0,01 |
25 |
|
18 |
300 |
150 |
1,5 |
0,02 |
0,02 |
25 |
|
19 |
350 |
150 |
0,5 |
0,02 |
0,05 |
30 |
|
20 |
50 |
70 |
2,5 |
0,05 |
0,01 |
30 |
|
21 |
100 |
50 |
3,0 |
0,05 |
0,01 |
20 |
|
22 |
150 |
100 |
2,5 |
0,08 |
0,05 |
25 |
|
23 |
200 |
120 |
1,5 |
0,05 |
0,02 |
30 |
|
24 |
70 |
25 |
0,75 |
0,025 |
0,01 |
20 |
|
25 |
120 |
50 |
0,8 |
0,01 |
0,02 |
20 |
|
26 |
110 |
60 |
0,5 |
0,04 |
0,01 |
25 |
|
27 |
300 |
120 |
0,5 |
0,01 |
0,02 |
25 |
|
28 |
150 |
100 |
1,0 |
0,02 |
0,05 |
30 |
|
29 |
100 |
70 |
1.2 |
0,05 |
0,02 |
20 |
|
30 |
75 |
50 |
1,0 |
0,01 |
0,05 |
25 |
Время регулирования tр: для студентов группы АТ-1 tp=2 c.,
АТ-2 tp=2,5 c., АТ-3 tp=3 c.
Приложение 1
Варианты исходных данных для проектирования следящей
системы
|
Вари- |
Статиче- Мос, Нм |
Момент Jо, кгм2 |
Максим. wо max, с-1 |
Максим. eо max, с-2 |
Максим. Xmax, рад. |
Максим. smax, % |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
50 |
20 |
0,5 |
0,02 |
0,01 |
20 |
|
2 |
100 |
70 |
1,0 |
0,06 |
0,02 |
25 |
|
3 |
200 |
100 |
1,5 |
0,06 |
0,01 |
25 |
|
4 |
300 |
90 |
2,0 |
0,08 |
0,02 |
30 |
|
5 |
350 |
120 |
2,5 |
0,08 |
0,02 |
30 |
|
6 |
50 |
30 |
3,0 |
0,05 |
0,03 |
35 |
|
7 |
100 |
60 |
0,5 |
0,02 |
0,01 |
20 |
|
8 |
150 |
90 |
1,0 |
0,06 |
0,02 |
20 |
|
9 |
200 |
80 |
1,5 |
0,05 |
0,02 |
25 |
|
10 |
250 |
120 |
2,0 |
0,08 |
0,03 |
25 |
|
11 |
300 |
100 |
0,5 |
0,02 |
0,01 |
30 |
|
12 |
350 |
100 |
1,0 |
0,04 |
0,02 |
30 |
|
13 |
50 |
50 |
0,5 |
0,05 |
0,01 |
35 |
|
14 |
100 |
100 |
0,2 |
0,08 |
0,02 |
35 |
|
15 |
150 |
120 |
0,5 |
0,02 |
0,05 |
35 |
|
16 |
200 |
150 |
1,0 |
0,03 |
0,02 |
20 |
3.4.6. Редуктор
Передаточная функция редуктора Wред(Р)=Кред=1/iр .
Структурная схема нескорректированной следящей системы представлена на рис.2.

Рис.2. Структурная схема нескорректированной следящей системы
3.5. Расчет последовательного непрерывного
корректирующего звена методом ЛАЧХ
Построение логарифмической амплитудно-частотной характеристики (ЛАЧХ) последовательного корректирующего звена проводится в такой последовательности.
1. Строится ЛАЧХ заданной (нескорректированной) системы.
2. Строится желаемая ЛАЧХ по заданным показателям качества переходного процесса.
3. Строится ЛАЧХ последовательного корректирующего звена путем графического вычитания ЛАЧХ заданной системы из желаемой ЛАЧХ.
4. По виду ЛАЧХ корректирующего звена определяется его передаточная функция (непрерывная).
3.5.1. Построение ЛАЧХ заданной системы
по виду передаточной функции
Передаточную функцию разомкнутой системы нужно представить в виде произведения передаточных функций типовых динамических звеньев (ограничимся случаем, когда в системе отсутствуют
колебательные звенья и звенья с запаздыванием). Например, пусть передаточная функция разомкнутой системы имеет вид:
Построение удобно проводить в такой последовательности.
1. Определить сопрягающие частоты wi=1/Тi и отложить их по оси абсцисс в логарифмическом масштабе (Тi — постоянные времени передаточной функции Кз(Р) ).
2. Отложить точку A1 с координатами wA1=1c-1 и L(wA1)=20lgКз ( см. рис. 3). Через точку A1 провести прямую с наклоном -20 дБ/дек. Построенная таким образом прямая линия совпадает с ЛАЧХ при частотах, меньших первой сопрягающей частоты (по порядку их расположения на оси частот слева направо).
3. На частоте сопряжения wi характеристика меняет свой наклон либо на +20 дБ/дек, если постоянная времени Тi=1/ wi находится в числителе исходной передаточной функции, либо на -20 дБ/дек, если постоянная времени Тi находится в знаменателе передаточной функции.
Для исследования системы на устойчивость по амплитудно-фазовому критерию устойчивости с помощью логарифмических частотных характеристик необходимо кроме ЛАЧХ построить еще логарифмическую фазо-частотную характеристику (ЛФЧХ). По оси абсцисс откладывается частота в логарифмическом масштабе (используют ту же ось частот, что и для построения ЛАЧХ), а по оси ординат откладывают аргумент амплитудно-фазовой характеристики j(w) в градусах или в радианах в линейном масштабе. Для рассматриваемого примера j(w) рассчитывается по формуле
j(w)= — 90 — arctgTу w — arctgTкзw — arctgTдw (гр.) .
такту k моменты времени.
Из последнего уравнения выразим U[k]:
U[k]=(S0X[k-n]+S1X[k-n+1]+…+SmX[k-n+m] — (7)
— G0U[k-n]-G1U[k-n+1]-. . .-Gn-1U[k-1])/Gn
Уравнение (7) является рекуррентным уравнением, описывающим алгоритм работы цифрового корректирующего устройства. По нему должна быть составлена программа работы данного устройства.
3.10. Разработка принципиальной схемы цифровой
следящей системы
На принципиальной схеме должны быть изображены сельсин-датчик и сельсин-трансформатор, фазовый детектор, АЦП, цифровой вычислитель, ЦАП, электронный усилитель мощности, ЭМУ, двигатель, редуктор.
Проводить расчет электронных схем и изображать их развернутые принципиальные схемы не требуется.
Л И Т Е Р А Т У Р А
1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1972. 766 с.
2. Батоврин А.А., Дашевский П.Г. и др. Цифровые следящие системы судовой автоматики. Л. : Судостроение, 1972. 445 с.
Если в результате моделирования дискретной системы качество переходного процесса окажется хуже заданного, то нужно ввести в корректирующее звено изменения. Изменения нужно вносить в непрерывную передаточную функцию, пересчитывая ее затем в дискретную. При высокой колебательности процесса можно попробовать изменить в ту или иную сторону наименьшие постоянные времени знаменателя. В некоторых случаях дает хороший результат отбрасывание наименьших постоянных времени в числителе и знаменателе.
3.9. Получение рекуррентного уравнения
цифрового корректирующего звена
Пусть дискретная передаточная функция имеет вид (3). Уравнение (3) запишем следующим образом:
, (5)
где U(Z) — Z-изображение выходной величины цифрового корректирующего устройства;
X(Z) — Z-изображение входной величины корректирующего устройства.
Перепишем уравнение (5), избавившись от знаменателя в левой и правой частях:
U(Z)(G0+G1Z+…+GnZn)=X(Z)(S0+S1Z+…+SmZm) . (6)
Раскрыв скобки, поделив левую и правую части уравнения на Zn и перейдя от изображений к оригиналам, получим:
G0U[k-n]+G1U[k-n+1]+…+GnU[k]=
=S0X[k-n]+S1X[k-n+1]+…+SmX[k-n+m]
здесь X[k] , U[k] — значения входной и выходной величин в произвольный такт времени k , X[k-1], X[k-2] . . ., U[k-1], U[k-2] . . . — значения входной и выходной величин в предшествующие
3.5.2. Построение желаемой ЛАЧХ
При построении желаемой ЛАЧХ выделяют три области: область низких частот, область средних частот и область высоких частот. Вид ЛАЧХ в каждой из областей по разному влияет на качество системы. В области низких частот вид ЛАЧХ определяет точность работы системы в установившихся режимах. Область средних частот определяет динамические свойства системы (быстродействие, колебательность). Вид ЛАЧХ в области высоких частот практически мало влияет на качество системы.
Построение желаемой ЛАЧХ удобно начинать с области средних частот в такой последовательности.
По заданным величинам smax и tр определяем с помощью табл. 1 частоту среза wс .
Например, пусть задано, что smax=30 % , tр=1,5 с. Из табл.1 для smax =30% определяем tрwс/p=3,2, откуда следует:
wс= 3,2p/1,5=6,7 c-1 .
Таблица 1
|
smax , % |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
tрwс/p |
5 |
4,4 |
4 |
3,6 |
3,2 |
3 |
2,8 |
|
L1, дБ |
18 |
15 |
13,5 |
12 |
11 |
10,5 |
10 |
|
q, гр |
85 |
80 |
65 |
55 |
45 |
40 |
35 |
Наносим на ось абсцисс частоту среза wс и проводим через нее прямую линию с наклоном -20 дБ/дек (рис.3).
Частота w2 , ограничивающая область средних частот желаемой ЛАЧХ слева определяется величиной отрезка L1, которая может быть найдена в зависимости от заданной величины smax из табл.1. Частота w3, ограничивающая область средних частот справа, определяется величиной отрезка L2, при этом .
В области высоких частот желаемую ЛАЧХ нужно строить в виде прямолинейных отрезков с наклоном, кратным -20 дБ/дек. (т.е. -40, — 60, -80 и т.д.) , таким образом, чтобы разность характеристик желаемой и заданной в пределе при w ® ¥ составляла прямую линию, параллельную оси частот.
В области низких частот желаемая ЛАЧХ строится следующим образом. По заданной величине коэффициента усиления системы Кс=wоmax/xmax
определяем величину LA2=20LgKc и отмечаем на чертеже точку A2 c координатами wA2=1 c-1 и LA2 (cм. рис.3). Через точку A2 проводим прямую линию с наклоном -20 дБ/дек.
От точки М, ограничивающей область средних частот слева, проводим прямую линию с наклоном -40дБ/дек до пересечения с низкочастотной частью желаемой ЛАЧХ.
Рис.3. а-а-а . . . — ЛАЧХ заданной (неизменяемой части) системы;
б-б-б . . . — ЛАЧХ желаемая;
с-с-с . . . — ЛАЧХ последовательного корректирующего звена
Порядок полинома знаменателя n должен быть не меньше порядка полинома числителя и не больше 5.
В программу нужно ввести также период квантования по времени Т0. Как уже было сказано ранее, чем меньше Т0 , тем более дискретная система приближается по своим свойствам к непрерывной. Однако при слишком малых значениях Т0 процессор в реальной системе может не успевать выполнять все необходимые вычисления. Кроме того, при уменьшении Т0 увеличивается число шагов переходного процесса. Так как вычисления проводятся по рекуррентным формулам, неизбежные ошибки вычислений накапливаются от шага к шагу и при чрезмерно большом числе шагов ошибка вычислений может превысить допустимую величину (система может оказаться неустойчивой, либо с неудовлетворительным качеством переходного процесса). В силу сказанного, Т0 не должно быть слишком мало. Рекомендуется выбирать Т0 в пределах (0,1 — 0,01)/wc , где wс — частота среза скорректированной системы.
3.8. Моделирование цифровой следящей системы
После того как дискретная передаточная функция определена можно приступить к моделированию цифровой следящей системы. Рекомендуется проводить моделирование, используя специализированные пакеты программ: MATLAB-simulink, либо ДИСПАС.
В пакете MATLAB-simulink дискретное звено, также как и непрерывные звенья, набирается по коэффициентам передаточной функции. Никаких дополнительных элементов, учитывающих преобразование сигналов из непрерывных в дискретные и наоборот, вводить в модель не требуется. Все преобразования в системе производятся автоматически.
В пакете ДИСПАС дискретное звено вводится тремя элементами: преобразователем непрерывный сигнал — код, вычислителем и преобразователем код — непрерывный сигнал.
Вычислитель задается рекуррентным уравнением, которое нужно определить из дискретной передаточной функции (см. п.3.9).
ДИСПАС позволяет моделировать дискретное звено, порядок которого не более 3.
Если окажется , что показатели качества скорректированной системы хуже заданных, то нужно вносить в коррекцию соответствующие изменения. Так, если перерегулирование оказалось больше заданного, то нужно увеличивать отрезки L1 и L2. Если время регулирования оказалось больше заданного, то нужно увеличивать частоту среза желаемой ЛАЧХ.
3.7. Определение дискретной передаточной функции
корректирующего звена
Для получения дискретной передаточной функции звена по его непрерывной передаточной функции рекомендуется воспользоваться билинейным преобразованием. Для этого нужно в непрерывную передаточную функцию корректирующего звена сделать подстановку
Для проведения подобных расчетов можно воспользоваться программой (см. приложение 4), написанной на языке BASIC.
Искомая передаточная функция в общем случае имеет вид:
(3)
C помощью программы определяются коэффициенты Si и Gi передаточной функции (3).
Непрерывная передаточная функция может быть задана либо в форме (2) постоянными времени числителя и знаменателя и коэффициентом усиления звена, либо в форме дробно-рациональной функции коэффициентами полиномов числителя и знаменателя:
(4)
Если в задании на разработку следящей системы указана максимально допустимая ошибка слежения Хmax при условии, что входной сигнал может изменяться с максимальной угловой скоростью womax и с максимальным угловым ускорением eomax , то для выполнения этих требований необходимо, чтобы желаемая ЛАЧХ не попадала бы в запретную область.
Запретная область строится следующим образом. Отмечаем на чертеже точку В с координатами:
.
От точки В вправо проводим прямую линию с наклоном
-40 дБ/дек, а влево — прямую линию с наклоном -20 дБ/дек.
Если ЛАЧХ, построенная по заданному коэффициенту Кс , попадает в запретную область, то это означает, что при данном коэффициенте Кс заданная точность слежения не может быть обеспечена и нужно его увеличить, т.е. поднять желаемую ЛАЧХ так, чтобы она не попадала в запретную область.
По виду ЛАЧХ желаемой можно записать передаточную функцию непрерывной скорректированной (желаемой) системы. Для рассматриваемого примера (кривая б-б-б… рис.3) передаточная функция имеет вид:
(1)
Для определения передаточной функции желаемой системы можно воспользоваться программой , приведенной в приложении 4. Программа написана на языке BASIC и позволяет найти постоянные времени T1, Т2, Т3 желаемой передаточной функции по показателям качества sm и tp. При этом передаточная функция записывается в виде
(2)
Типовая желаемая ЛАЧХ, по которой записана передаточная функция (2), показана на рис. 4.
Показатель степени k определяется наклоном заданной ЛАЧХ в области высоких частот.
Рис 4. Типовая ЛАЧХ желаемой следящей системы
Для обеспечения заданных показателей качества переходного процесса скорректированная система должна обладать определенным запасом устойчивости по фазе. Необходимая величина запаса устойчивости по фазе (q) для заданной величины максимального перерегулирования указана в табл.1. После построения желаемой ЛАЧХ нужно рассчитать и построить ЛФЧХ скорректированной системы и определить q .
3.5.3. Расчет последовательного корректирующего звена
ЛАЧХ последовательного непрерывного корректирующего звена строится путем графического вычитания из ЛАЧХ желаемой ЛАЧХ заданной части системы ( на рис.3 — линия с-с-с…).
По виду ЛАЧХ нужно записать передаточную функцию непрерывного последовательного корректирующего звена. Для ЛАЧХ
с-с-с… на рис.3 передаточная функция имеет вид:
(2)
Коэффициент Ккор определяется из соотношения: 20lgКкор=L3 .
Эту же передаточную функцию можно получить, если передаточную функцию желаемую Кж(Р) поделить на передаточную функцию заданной части системы Кз(Р).
3.6. Моделирование следящей системы с непрерывным
последовательным корректирующим звеном
Для того, чтобы убедиться, что коррекция системы проведена правильно и скорректированная система имеет показатели качества переходного процесса не хуже заданных, нужно провести моделирование. Рекомендуется моделировать скорректированную систему на ПЭВМ, используя специализированные пакеты программ ДИСПАС или
Matlab simulink.
Аналоговая следящая система для ручного управления телекамерой
Содержание
1. Введение
2. Аналоговая следящая система для ручного управления
телекамерой
3. Исходные данные
4. Задание на проектирование
5. Функциональная схема следящей системы
6. Выбор исполнительного двигателя следящей системы и
передаточного отношения редуктора
7. Определение передаточной функции двигателя и ее
параметров
. Выбор датчиков углов поворота и схемы их включения в
измерителе рассогласования
9. Расчет диодной схемы синхронизации
10. Разработка принципиальной схемы устройства
управления исполнительным двигателем
11. Схема гармонического детектирования
амплитудно-модулированного сигнала
12. Электрический расчет принципиальной схемы
13. Расчёт требуемых значений коэффициентов усиления
разомкнутой системы и усилителя
14. Динамический расчет системы
. Выбор корректирующего устройства
16. Поверочный расчёт и построение переходного процесса
17. Заключение
18. Список литературы
1. Введение
Широкий размах автоматизации во всём мире привёл к необходимости
использования во всех производствах разнообразных автоматических систем,
выполняющих те или иные функции по управлению самыми различными физическими
процессами. В этих системах сочетаются весьма разнообразные механические,
электрические и другие устройства, составляя сложный комплекс взаимодействующих
друг с другом звеньев. Одним из классов подобных автоматических систем являются
следящие системы.
Данный курсовой проект посвящён разработке следящей системы и включает в
себя выбор основных элементов замкнутой системы регулирования, разработку
принципиальной схемы управляющего устройства и электрический расчёт основных её
узлов, синтез параметров следящей системы из условия обеспечения заданных
точностных и качественных показателей её работы.
Следящей системой называется такая система регулирования, которая
поддерживает регулируемую величину на заданном значении, причём это значение
изменяется по заранее неизвестному закону. Один из примеров следящей системы —
оптическая телевизионная система сопровождения цели. В телевизионном комплексе
можно выделить четыре следящих привода, которые следует рассматривать как
различные задания на проектирование системы.
В данном курсовом проекте нужно разработать одно из заданий — аналоговую
следящую систему для ручного управления телекамерой.
2. Аналоговая
следящая система для ручного управления телекамерой
При ручном управлении оператор, наблюдая на экране монитора изображение,
получаемое с телекамеры, с помощью ручки управления 3 (рис.1) задает требуемое
изменение угла поворота телекамеры (рассматривается только управление движением
в азимутальной плоскости). В схеме управления используются два сельсина: BCа , соединенный с ручкой управления
на пульте оператора, и BEа ,
ротор которого вращается по азимуту вместе с осью 1 телекамеры. Если задающий и
принимающий валы и связанные с ними сельсины находятся в согласованном
положении, то напряжение на вторичной обмотке сельсина BEa равно нулю. Двигатель Ma азимутального канала обесточен, и, следовательно, привод
находится в состоянии покоя. При отклонении любого из валов от положения
согласования выходное напряжение сельсина BEa через усилитель A2 обеспечивает включение двигателя Ма и вращение телекамеры через
редуктор q по азимуту. Для зрительного
определения координаты цели по азимуту служит отсчетное устройство Ша. Ручное
управление телекамерой по углу места строится аналогично.
Рис.1. Ручное управление телекамерой.
3.
Исходные данные
Исходные данные для проектирования приведены в таблице 1:
Таблица №1
|
JНМ, Н·м·с2 |
MНМ, Н·м |
ωНМ, рад/с |
ω’НМ, рад/с2 |
εМ, угл. мин. |
σ, |
tр, с |
|
4,5 |
45 |
0,5 |
2 |
8 |
15 |
0,04 |
JНМ — максимальный момент инерции
нагрузки (подвижной платформы с закрепленной на ней телекамерой);
MНМ — максимальный момент
сопротивления на оси нагрузки;
ωНМ, ω’НМ — требуемые максимальные
значения скорости и ускорения вращения оси телекамеры;
eМ — максимально допустимая ошибка
следящей системы, учитывающая влияние момента сопротивления на оси нагрузки,
скоростную ошибку системы при скорости изменения угла задания, равной по
величине wНМ, и
инструментальную погрешность измерителя рассогласования;
σ,
%; tp — максимально
допустимые значения перерегулирования и времени регулирования в следящей
системе.
4. Задание на проектирование
1. Дать описание функциональной схемы следящей системы (по азимуту)
при ручном управлении.
2. Выбрать исполнительный двигатель следящей системы и передаточное
отношение силового редуктора, связывающего исполнительный двигатель с
нагрузкой.
. Определить передаточную функцию двигателя и ее параметры.
. Выбрать датчики углов поворота и схему их включения в измерителе
рассогласования.
. Разработать принципиальную схему устройства управления
исполнительным двигателем.
. Рассчитать требуемые значения коэффициентов усиления разомкнутой
системы и усилителя.
. Произвести динамический расчет системы.
. Дать расчет принципиальной схемы.
. Дать заключение по разработанному проекту системы и привести
список используемой литературы (библиографический список).
. Функциональная схема следящей системы
Функциональная схема следящей системы (по азимуту) при ручном управлении
представлена на рис.2.
Рис.2. Функциональная схема следящей системы.
Ша — отсчетное
устройство;
ИР — измеритель
рассогласования между и
;
KИР — коэффициент
передачи измерителя рассогласования;
УН — усилитель
напряжения;
УМ — усилитель
мощности;
Д — двигатель;
Р — редуктор;
Н — нагрузка.
6. Выбор
исполнительного двигателя следящей системы и передаточного отношения редуктора
Выбор двигателя системы — одна из основных задач проектирования следящей
системы. Следует отметить, что если выбранный двигатель не может обеспечить
требуемых режимов движения нагрузки, то уже никакими ухищрениями, в том числе
повышением коэффициента усиления разомкнутой системы, использованием
корректирующих устройств и т. п., нельзя добиться требуемого качества работы
системы.
При выборе двигателя следящей системы рассмотрим узел
«двигатель-редуктор-нагрузка», представленный на рис. 3:
Рис. 3. Узел «двигатель-редуктор-нагрузка»
МД , ωД — момент вращения и скорость, развиваемые на валу
двигателя;
Мн , ωн — момент сопротивления со стороны нагрузки и
скорость вращения вала нагрузки;
i=ωД/ωн — передаточное отношение
редуктора, согласующего
двигатель с нагрузкой.
Полагается также, что подвижные части двигателя обладают моментом инерции
JД, а нагрузка — моментом инерции Jн.
Для расчета требуемой мощности двигателя используем методику, приведенную
в [1]. Положим, согласно [1], КПД h=0,8.
Вт.
Нужно
выбрать двигатель, мощность которого больше Ртр. Выберем из таблицы,
приведённой в [1] , двигатель типа СЛ: СЛ-521 со следующими параметрами:
Pном = 77 Вт;
nном = 3000 об/мин => ωном = nном · π / 30 = 314,16 рад/с;
Uном = 110 В;
Iя ном. = 1,2 А;
Rя = 8,5
Ом;
Mном = 0,245 Н·м;
Mп = 0,638
Н·м;
Jд = 16,7·10-5
кг·м2.
Проверим перегрузку двигателя при пуске:
.
Превышения
нет (), следовательно, двигатель допускает прямое включение
на номинальное напряжение.
Момент инерции редуктора:
Jр =
0,2 * Jд=0,2*16,7*10-5=3,34*10-5 кг·м2.
Требуемый вращающий момент на валу двигателя определяется при заданных
характеристиках нагрузки как:
где h — КПД
редуктора,
i — передаточное
отношение редуктора,
JД — момент
инерции якоря двигателя.
Как видим, требуемый от двигателя момент вращения зависит от
передаточного отношения редуктора i. Для нахождения значения i = iопт , при котором требуемый от
двигателя момент был бы минимален, т.е. МТР=МТРmin, вычислим производную от МТР по i и приравняем ее нулю. Имеем:
Решение
данного уравнения дает оптимальное значение передаточного отношения редуктора:
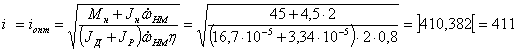
Подставив
вычисленное значение iопт = 411 в выражение для требуемого вращающего
момента на валу двигателя, получим:
Далее произведём проверку выбранного нами двигателя на перегрузку по
требуемым от него максимальному моменту и скорости вращения, которая не должна
превышать допустимую:
—
допустимый коэффициент перегрузки по моменту:;
допустимый
коэффициент перегрузки по скорости:.
—
двигатель недогружен по моменту;
— двигатель недогружен по скорости.
Как видно, ограничения по перегрузкам выполняются, значит выбранный нами
двигатель подходит для использования в системе с заданными характеристиками.
7.
Определение передаточной функции двигателя и ее параметров
Структурную схему коллекторного двигателя постоянного тока с независимым
возбуждением, который мы используем в системе в качестве исполнительного
устройства, можно представить, как показано на рисунке 3 [7]:
Рис. 3. Структурная схема двигателя.
Мнп — момент нагрузки, приведённый к оси двигателя;
Cе — коэффициент
пропорциональности по противо-ЭДС;
СM — коэффициент пропорциональности
по моменту.
Полагаем, что электромагнитная постоянная времени двигателя много меньше,
чем электромеханическая постоянная, т.е. ТЭ << ТМ = ТД. Тогда
передаточные функции двигателя будут иметь вид [7]:
— передаточная
функция по скорости,
— коэффициент
передачи двигателя;
— передаточная
функция по моменту.
Нашей задачей является определить указанные параметры КД, КМ, ТД. Для их
нахождения рассчитаем сначала коэффициенты Cе , СМ:
;
.
Теперь, используя полученные выше результаты, вычислим искомые параметры
передаточной функции двигателя:
Коэффициент передачи двигателя:
;
Постоянная
времени двигателя:
ручной управление телекамера редуктор
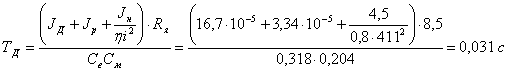
Коэффициент
передачи двигателя по моменту сопротивления:
Теперь, используя полученные выше результаты, вычислим искомые
передаточной функции двигателя:
,
.
8. Выбор
датчиков углов поворота и схемы их включения в измерителе рассогласования
Датчик угла поворота следящей системы предназначен для измерения
рассогласования положений командного и исполнительного валов. В аналоговых следящих
системах используют различные датчики угла: потенциометрические, индуктивные,
ёмкостные, индукционные, фотометрические, сельсины и другие. Среди них
наибольшее практическое распространение в следящих системах нашли индукционные
датчики, которые характеризуются высокой надёжностью, хорошими
эксплуатационными свойствами, высокой стабильностью параметров и характеристик,
возможностью создания бесконтактных схем.
Среди индукционных датчиков, как наиболее дешевые и простые выделяют
сельсины. Сельсины по принципу действия относятся к трансформаторным
индукционным датчикам. Конструктивно они представляют собой электрические
машины, имеющие трёхфазную статорную и однофазную роторную обмотки (бывает
наоборот). В зависимости от величины инструментальной погрешности сельсины
подразделяют на 3 класса точности. Первый класс, наиболее точный, имеет
погрешность до ±0.25 угл. град (сельсины-датчики) и до ±0.75 угл. град
(сельсины-приемники) [8]. Для уменьшения влияния инструментальной погрешности
сельсинов на точность работы системы используют двухканальную схему измерения
рассогласования, включающую в себя канал грубого отсчёта и канал точного
отсчёта.
Изобразим функциональную схему следящей системы:
Рис. 4
Где ГП представлен 2-мя потенциометрическими датчиками(резисторами)
В качестве измерителя рассогласования используют трансформаторную схему
включения сельсинов.
Проведем расчет измерителя рассогласования на сельсинах:
tир =1/(2.fпит),
а fпит=50 Гц , тогда получаем tир = 0,01 с.
Длительность переходного процесса в измерителе рассогласования на сельсинах
соизмерима с допустимой длительностью переходного процесса системы (tp=0,04), поэтому частоту питания сельсинов можно
выбрать равной 50 Гц.
Согласно
рекомендациям величину допустимой ошибки измерителя рассогласования следует
принимать равной одной третьей — одной второй от допустимой ошибки работы
следящей системы, и инструментальной погрешностью используемых датчиков угла
[1]: .
.
Класс
точности сельсинов и коэффициент передачи редукторов между точным и грубыми
каналами выбираются с учетом следующего соотношения:
,
где
— коэффициент передачи механического
редуктора между роторами сельсинов;
— ошибка, обусловленная наличием
люфта редуктора между грубым и точным каналами;
— ошибка,
вносимая измерителем рассогласования в общую ошибку следящей системы;
— инструментальная
погрешность пары сельсинов точного канала.
Потребуем,
чтобы , тогда
.
Будем
использовать в дальнейшем сельсины второго класса точности типа БД-501А и
БС-501А с параметрами [8]:
Таблица
№2
|
Параметры сельсина |
БД-501А |
БС-501А |
|
Номинальная частота, Гц |
50 |
50 |
|
Номинальное напряжение, В |
110 |
110 |
|
Максимальное вторичное |
55 |
55 |
|
Номинальный ток |
1,2 |
1,2 |
|
Потребляемая мощность, Вт |
27 |
27 |
|
Момент трения, Н×см |
0,35 |
0,35 |
|
Номинальная частота |
500 |
500 |
Сельсины БД-501А и БС-501А являются бесконтактными. Отсутствие у них
скользящих контактов позволяет получить лучшую устойчивость характеристик и
длительно сохранить высокую точность. [7]
Коэффициент измерителя рассогласования (ИР) находим по максимальному
вторичному напряжению:
.
Для
второго класса точности сельсинов погрешность одного сельсина Δc = ±30’. Для пары сельсинов: , а т.к.
это значение превышает допустимую ошибку ИР , то
необходимо использовать двухканальную схему ИР.
Коэффициент
рассчитаем из соотношения
.
Примем
=29, а т.к. рекомендуется
=(15…75) [2], то коэффициент находится в допустимом
диапазоне.
В
следящей системе с двухканальной схемой ИР должно быть устройство переключения
каналов. Для переключения каналов используют схемы с электромагнитным реле,
неоновыми лампами, но наиболее широко распространена диодная схема переключения
каналов из-за простоты и надежности.
9. Расчет диодной схемы синхронизации
Диодная схема синхронизации представлена ниже рис. 6:
Рис.6. Диодная схема синхронизации
каналов.
Синхронизатор состоит из двух смежных контуров, построенных на базе
выходных обмоток сельсинов трансформаторов точного и грубого каналов и диодов,
включённых встречно-параллельно для обеспечения прохождения тока в течение
обоих полупериодов. В точном канале диоды включены параллельно нагрузке и,
благодаря свойству изменять внутреннее сопротивление в зависимости от
приложенного напряжения, выполняют роль амплитудного ограничителя напряжения
погрешности. При напряжениях рассогласования, меньших напряжения переключения,
сопротивление диодов в прямом направлении велико и всё напряжения в точном
канале падает на этих диодах. В грубом канале в это время выходной сигнал
формируется таким образом, что его амплитуда становится близкой к нулю. Таким
образом, управление осуществляется с помощью напряжения, поступающего с точного
канала.
При напряжениях рассогласования превышающих порог включения ограничителя,
вследствие резкого уменьшения прямого сопротивления диодов и их шунтирующего
действия, напряжение на выходе точного канала перестаёт изменяться и остаётся
равным напряжению, соответствующему углу переключения. Управление переходит к
грубому каналу, т.к. в нём также происходит перераспределение падений
напряжения, и всё напряжение выделится на резисторе грубого канала. В
результате на выходе устройства синхронизации напряжение будет определяться
суммой напряжений точного и грубого каналов, как показано на рис. 7:
Рис. 7. Напряжение на выходе устройства
синхронизации.
На первом этапе расчёта диодной схемы синхронизации определяем угол
переключения каналов:
. Берём
.
Определим
параметры схемы грубого канала.
,
.
Пусть
используются диоды Д2Г со следующими параметрами:
.
Проверим
диоды на перегрузку при e=90о, , при
этом
.
Так
как максимальный ток через диод меньше допустимого, то данный диод можно
использовать в схеме переключения.
Определим
параметры схемы точного канала.
Рекомендация:
при напряжение грубого канала должно быть
;
при КT >> 1.
.
При
выборе коэффициента получим:.
,
где
n — количество последовательно соединенных диодов в
одной цепочке.
.
Возьмём
диода.
Далее
рассчитаем сопротивление точного канала:
.
10.
Разработка принципиальной схемы устройства управления исполнительным двигателем
Рис.8. Принципиальная схема усилителя
мощности.
Техническое совершенство привода следящей системы с двигателем
постоянного тока определяется усилителем мощности (УМ). В настоящее время
применяют полупроводниковые — транзисторные УМ. Транзисторные УМ работают в
режиме класса Д с широтно-импульсной модуляцией (ШИМ) силовых транзисторов.
Область применения транзисторных УМ расширяется и они вытесняют тиристорные
преобразователи, что связано с освоением сильноточных транзисторов с
коммутируемым током до 500 А и коллекторным напряжением до 700 В. Схема
усилителя мощности приведена на рис.8. [4]
Устройство состоит из генератора пилообразного напряжения, выполненного
на операционных усилителях D1 и D2; двухпорогового компаратора D3 с диодным ограничителем V1; двухплечевого импульсного
усилителя мощности на транзисторах V4 и V5; четырех плеч мостового усилителя:
двух верхних А1 и А3 и двух нижних А2 и А4.
Верхнее плечо А1 (А3) состоит из оптронного усилителя типа 249ЛП1Б,
выполненного на диодной оптопаре V6 и
транзисторах V7, V8, V10;
дифференцирующей RC-цепи на
конденсаторе C2 и резисторе R19 с усилителем мощности
дифференцирующего сигнала на транзисторе V11; управляющего транзистора V12 и силового транзистора V13.
Нижнее плечо А2 (А4) состоит из тех же элементов, что и верхнее, но
отличается от верхнего местом подключения дифференцирующей RC-цепи и противоположным типом
проводимости транзисторов V11-V13.
Помимо двух основных источников питания ±122В и ±15В, УМ нуждается в двух дополнительных источниках напряжения
5В для схем управления нижними и верхними плечами моста.
Работу схемы поясняет диаграмма напряжений на рис.9, где показаны:
а) — пилообразное напряжение Uоп, снимаемое с Д2, входное напряжение Uу.м. и пороговое напряжение ±Uпор компаратора Д3;
б) — импульсное напряжение Uа,
снимаемое с выхода компаратора Д3;
в) — выходное напряжение первого Ub1 и второго Ub2
оптронных усилителей;
г) — выходные напряжения первой Ud1 и второй Ud2
дифференцирующих RC-цепей;
д), е), ж), з) — коллекторные напряжения Uc1-Uc4 выходных
транзисторов соответственно первого-четвертого плечей моста; u- выходное напряжение Uя на якоре двигателя.
Период
работы усилителя состоит из отрезков времени, в которые импульс сигнала Ua=0,
Ua>0 и Ua<0. При Ua=0 напряжение . При этом в верхнем плече А1 транзистор V12
закрыт, выходной транзистор V13 открыт током, протекающим через резистор R23.
Выходной транзистор V13 нижнего плеча А2 будет закрыт. Состояние левых плеч
А1 и А2 усилителя не изменится и при Ua>0, так как их оптронные
усилители включаются напряжением Ua отрицательной полярности. При Ua<0
выходные напряжения оптронных усилителей . При
этом транзистор V13 верхнего плеча А1 будет закрыт, а V13
нижнего плеча А2 открыт. Импульс напряжения, открывающий транзисторы V13,
подается с задержкой времени относительно импульса напряжения, снимаемого с
выхода соответствующего оптронного усилителя. Эта задержка обеспечивается
дифференцирующими импульсами напряжений Ud1 и Ud2.
Импульс напряжения Ud1 положительной полярности открывает транзистор V11
верхнего плеча, который в течение времени действия импульса сохраняет открытым
транзистор V12 и закрытым V13.
Аналогично
дифференцирующий импульс Ud2 отрицательной полярности, открывая транзистор V11
нижнего плеча А2, оставляет открытым транзистор V12, задерживая
тем самым включение транзистора V13 нижнего плеча, пока транзистор V13
верхнего плеча не перешел в режим отсечки. Время задержки определяется
постоянной времени дифференцирующей цепи, которая выбирается несколько больше
времени запирания выходных транзисторов. Так как выходные транзисторы V13
при запирании шунтируются управляющими транзисторами V12, то время
запирания и задержки получается минимально возможным. Два других плеча УМ А3 и
А4 работают аналогично при положительной полярности сигнала Uа.
Диаграмма выходного напряжения УМ зависит от соотношения напряжений и амплитуды пилы Uоп. При Uу.м.=0
и c выхода УМ снимаются симметричные разнополярные
импульсы с коэффициентом заполнения . При
этом крутизна статической характеристики на начальном участке будет вдвое выше, а коэффициент усиления равен:
, где
.
Схема
усилителя универсальная, так как она удовлетворяет всем требованиям,
предъявляемым к УМ приводов следящих систем. Отметим ее достоинства:
1. минимальные потери и максимальная частота ШИМ, обеспечиваемые
шунтированием цепи база-эмиттер при запирании силовых транзисторов и
использованием низковольтных источников в цепях управления;
2. симметрия верхнего и нижнего плеч усилителя с использованием
одних и тех же однотипных элементов;
. простая схема защиты от сквозного короткого замыкания,
основанная на формировании импульсного сигнала в слаботочном участке схемы;
4. отсутствие влияния выходных каскадов на входную цепь благодаря
их гальванической развязке;
. простая схема ШИМ входного сигнала, основанная на использовании
двух порогового компаратора;
6. безынерционность цепи управления;
7. наличие схемы ограничения движения привода (V2, V3, SI, S2)
. обеспечение режима динамического торможения двигателя М, так как
при Ua=0 выходные транзисторы V13 верхних плеч А1 и A3 находятся в режиме
насыщения; отлаженная на определенную нагрузку схема не требует настройки
последующих образцов.
Недостатком этой схемы является то, что требуется много источников
питания (122В, 15В, 5В). Параметры схемы на рис.7(а) соответствуют току
нагрузки 10А при минимальном коэффициенте усиления по току транзисторов V13 β = 100.
11. Схема гармонического детектирования амплитудно-модулированного
сигнала
На
выходе датчика угла рассогласования, выполненного на сельсинах, включенных по
трансформаторной схеме, амплитуда напряжения пропорциональна синусу угла
рассогласования . Частота напряжения определяется частотой питания
сельсина, в нашем случае составляет 50 Гц.
Для
работы корректирующей цепочки требуется постоянное напряжение, поэтому для
согласования датчика угла рассогласования с корректирующим устройством,
необходимо между ними включить амплитудный детектор. Амплитудный детектор (рис.
10) состоит из синхронного детектора (СД) и фильтра низкой частоты (ФНЧ).
Рис.
10. Амплитудный детектор
Передаточная
функция фильтра определяется выражением:
,
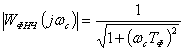
где
— частота опорного напряжения,
—
требуемая постоянная времени фильтра.
Параметры
ФНЧ выбираются таким образом, чтобы подавлялись составляющие частотой и выше.
Полуволны
с выхода СД можно приближенно представить двумя слагаемыми ряда Фурье — это
постоянная составляющая и первая гармоника с частотой . При расчете ФНЧ надо задаться коэффициентом
подавления первой гармоники n.
, где n =
(5…10).
Чем
больше n, тем сильнее подавляется гармоника, но тем более
длительный переходный процесс фильтра.
Можно
считать, что . Тогда,
.
Зададимся
n = 8 с учетом =50 Гц,
получим = 0,025 с.
12. Электрический расчет принципиальной схемы
На
начальном этапе электрического расчёта принципиальной схемы выберем силовые
транзисторы и диоды, используемые в мостовой схеме усилителя [3]. Расчёт
мостовой схемы сводится к выбору величины напряжения источника питания этой схемы, к выбору силовых транзисторов и диодов.
Сначала рассчитаем напряжение питания. Рекомендуется:
.
Выбор
транзистора осуществляем по справочникам из следующих ограничений:
Пусковой
ток якоря . Пусть
, тогда:
(при этом мы ранее предусмотрели ограничение тока якоря в схеме).;
.
Рассеивание мощности в основном имеет место в периоде включения и
запирания транзистора. Для получения простого расчётного предполагается, что в
периоды включения и запирания транзистора ток и напряжение на нём меняются по
линейному закону.
Ррасс = Рвкл + Рзапир;
;
.
Рекомендуемая
частота , возьмём
, тогда с
учетом этого
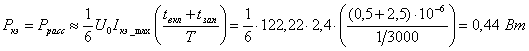
где
для рассмотренной схемы
— время включения,
По полученным выше значениям выбираем транзисторы КТ864А (n-p-n) и КТ865А (p-n-p) со следующими
параметрами:
UКЭ
доп = 200В; IКЭ доп = 10А; РКЭ доп = 100Вт;
b = 40 ¸ 200 =
100 — коэффициент усиления транзистора по току;
UКЭ
нас £ 2В; Iб £ 2А.
Выбор диодов осуществляется при следующих ограничениях:
,
.
Выбираем
диоды Д243Б со следующими параметрами:
= 200 В;
= 10 А.
Далее определяем требуемый ток базы силового транзистора:
,
где
— коэффициент насыщения транзистора (1,5…2).
13. Расчёт требуемых значений коэффициентов усиления разомкнутой системы
и усилителя
Для обеспечения заданной точности работы системы при заданном входном
воздействии необходимо правильно рассчитать коэффициент усиления разомкнутой
системы. Для его расчета используем методику, приведенную ниже. Структурная
схема системы изображена на рис.11 при выполнении условия
ТЭ << ТМ = ТД
где:
ТЭ — электромагнитная постоянная времени якорной цепи двигателя;
ТМ — электромеханическая постоянная времени двигателя;
ТД — постоянная времени двигателя.
Рис.
11. Структурная схема нескорректированной следящей
системы.
Tу — постоянная
времени, отнесенная к усилителю и обусловленная наличием инерционного силового
преобразователя;
Ку — коэффициент передачи усилителя;
Н — нагрузка;
Мнп — момент нагрузки, приведённый к оси двигателя;
Кир — коэффициент
передачи измерителя рассогласования;
Км — коэффициент передачи двигателя по моменту;
Кр — коэффициент передачи силового редуктора.
Передаточная функция разомкнутой системы будет определяться следующим
выражением:
,
где
— коэффициент передачи разомкнутой системы, который
мы будем определять, исходя из допустимой ошибки отработки задающего воздействия,
.
Воспользуемся
уже готовой формулой для нахождения коэффициента передачи К при меняющимся с
постоянной скоростью входном воздействии и постоянном моменте сопротивления
нагрузки.
Таким
образом, если , где Qвх0=const,
Мн(t)=Мнм=const, то К определяется следующим выражением:
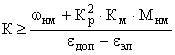
где eдоп — допустимая
ошибка следящей системы, eдоп
= 8’ ;
eэл — элементная составляющая ошибки следящей системы,
вносимая в основном измерителем рассогласования .
С учётом этих данных и начальных условий вычислим К:
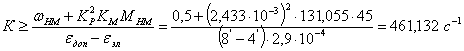
Данное
значение коэффициента усиления разомкнутой системы обеспечим за счет коэффициента
передачи КУ усилителя:
.
Т.к.
усилитель включает в свой состав синхронный детектор для детектирования
амплитудно-модулированного напряжения ошибки, то в качестве будет выступать постоянная времени сглаживающего
фильтра синхронного детектора, которой пренебрегать нельзя:
Тогда
передаточная функция разомкнутой нескорректированной системы определится
следующим выражением:
Результаты
моделирования передаточной функции приведены на рис.12 и рис.13:
Рис.
12. Схема замкнутой системы с отрицательной обратной
связью.
Рис.
13. Реакция системы на ступенчатое воздействие.
14. Динамический
расчет системы
Следящая система, которая была исследована нами в предыдущих пунктах, не
удовлетворяет заданному качеству переходного процесса. Необходимо построить
корректирующее устройство, чтобы обеспечить требуемые точностные характеристики
системы: заданные перерегулирование и длительность переходного процесса.
Наиболее широкое применение при синтезе систем автоматического
регулирования получил метод логарифмических амплитудно-частотных характеристик
[6], т.к. построение ЛАЧХ, как правило, может делаться почти без вычислительной
работы. Особенно удобно использовать асимптотические ЛАЧХ.
Процесс синтеза методом ЛАЧХ включает в себя следующие операции:
· построение располагаемой ЛАЧХ;
· построение желаемой ЛАЧХ;
· определение вида и параметров корректирующего устройства;
· техническая реализация корректирующего устройства;
· поверочный расчёт и построение переходного процесса.
Построение желаемой ЛАЧХ — выполняется на основе тех требований, которые
предъявляются к проектируемой системе регулирования [6], а именно на основании
времени переходного процесса и допустимого перерегулирования: tр и σ.
Построение располагаемой ЛАЧХ — построение ЛАЧХ исходной системы,
выполненное исходя из требуемых мощности, скорости, ускорения и т.п. В данном
случае под исходной системой понимается система, состоящая из регулируемого
объекта и регулятора и не снабженная необходимыми корректирующими средствами,
обеспечивающими требуемое качество переходного процесса.
Вид и параметры корректирующего устройства определяются из следующего
условия: если передаточная функция желаемой разомкнутой системы − Wж(p), передаточная функция нескорректированной системы — Wнс(p), а передаточная функция корректирующего звена
последовательного типа — Wк(p), то можно записать равенство:
исходя
из этого для ЛАЧХ корректирующего звена:
Построение располагаемой ЛАЧХ.
Под располагаемой ЛАЧХ понимается характеристика исходной системы
управления, не снабжённая необходимыми корректирующими средствами. ПФ
нескоррективанной системы имеет следующий вид:
,
в
численной форме
ЛАЧХ
LН имеет две сопрягающие частоты:
, lg w2 = 1,602.
Н
пересекает ось ординат в точке равной
От
этой точки до первой сопрягающей частоты асимптотическая LН
имеет наклон с осью частот -20 дБ/дек — это низкочастотный участок ЛАЧХ.
На
среднечастотном участке (от первой сопрягающей частоты до второй) LН
имеет наклон -40 дБ/дек.
На
высокочастотном участке наклон -60 дБ/дек.
ЛАЧХ
непрерывной нескорректированной разомкнутой системы LН изображена на
рис.14.
Рис.14.
ЛАЧХ непрерывной нескорректированной разомкнутой системы.
Построение
желаемой ЛАЧХ.
Построение
желаемой ЛАЧХ делается на основе тех требований, которые предъявляются к
проектируемой системе управления, а именно:
— перерегулирование s % при единичном ступенчатом
воздействии на входе;
время переходного процесса tp .
Используя методику, изложенную в [6], найдём частоту среза wср желаемой ЛАЧХ LЖ .
Для заданного перерегулирования s % = 15 % находим зависимость между длительностью переходного
процесса tp = 0,04 [с] и частотой wп (интервал положительности),
используя номограммы Солодовникова [6]:
.
Теперь
найдём частоту среза wср желаемой ЛАЧХ так, чтобы она удовлетворяла условию:
wср = (0,6 ¸ 0,9)×wп.
wср = 0,9 × wп = 0,9 × 314,159 =282,743 ; lg wср =2,451.
При
синтезе системы необходимо обеспечить не только её устойчивость, но и
определённый запас устойчивости. Для заданного значения перерегулирования s % = 15 % выбираем требуемое значение запаса устойчивости по модулю L1= |
L2 | = 30 дБ.
Построение
желаемой асимптотической ЛАЧХ производится в следующем порядке.
Первая
низкочастотная асимптота проводится так, чтобы она имела наклон -20 дБ/дек,
соответствующий астатизму первого порядка.
Среднечастотный
участок желаемой ЛАЧХ образуется асимптотой с наклоном -20 дБ/дек, проводимой
так, чтобы она пересекала ось частот при wср. Этот участок
проводится влево и вправо до достижения модулей, равных L1 и L2.
Затем
производится сопряжение среднечастотного участка с низкочастотными асимптотами
и высокочастотной частью (рис. 15).
Рис.
15. Желаемая ЛАЧХ
Для
ЛАЧХ можно записать:
LКУ(w) = LЖ(w) — LН(w) .
Таким
образом, ЛАЧХ корректирующего устройства, полученная простым вычитанием ординат
нескорректированной ЛАЧХ из ординат желаемой.
ЛАЧХ
корректирующего устройства представлена на рис. 16.
Рис.
16. ЛАЧХ корректирующего устройства
15. Выбор корректирующего устройства
Корректирующие устройства предназначаются для такого изменения структуры
системы, при котором возможно получение нужных динамических свойств.
Корректирующие устройства представляют собой динамические звенья различной
физической природы со специально выбранными передаточными функциями.
Сначала рассчитаем параметры корректирующего устройства. Система слежения
имеет структуру, представленную на рис. 17:
Рис. 17. Структура системы слежения
,
где WЖ(р) — ПФ желаемой системы;
WНС(р) — ПФ нескорректированной
системы;
WКУ(р) — ПФ корректирующего
устройства последовательного типа.
Схема и параметры корректирующего звена подбирается по виду ЛАЧХ. В нашем
случае ПФ корректирующего устройства имеет вид:
.
По графику определяем сопрягающие частоты ПФ КУ:
Таким
же образом определяем коэффициент усиления корректирующего устройства .
Передаточная
функция корректирующего устройства имеет вид:
.
Передаточная
функция корректирующего устройства будет выглядеть следующим образом:
Далее
определяем номиналы элементов корректирующего звена, исходя из следующих
выражений:
Для
расчета корректирующей цепочки зададимся С1 = 10 нФ=10-8Ф.
Зададимся С2 = 100 нФ=10-7Ф.
Тогда
Структурная
схема корректирующего устройства представлена на рис 18:
Рис.
18. Схема корректирующего устройства.
. Поверочный расчёт и построение переходного процесса
Построим переходную характеристику полученной замкнутой системы
управления вместе с корректирующим устройством и проверим, удовлетворяет ли
данная система заданному качеству переходного процесса.
Схема моделирования (рис. 19) и переходная характеристика замкнутой
скорректированной системы (рис. 20), представлены ниже.
Рис. 19 Схема моделирования.
Рис.20. Переходная характеристика скорректированной
системы.
Из графика видно, что для скорректированной системы выполняются требуемые
условия относительно качества переходного процесса:
s % =6,85 % < sЗАД
% = 15 %;
tР
=0,0326 c < tР ЗАД = 0,04 c .
Заключение.
В результате была разработана следящая система, рассчитанная на условия
работы, предусмотренные заданием, обладающая предъявленным к ней требованиям
точности и качества переходного процесса, функциональная схема которой примет
вид (рис. 21):
Рис. 21. Функциональная схема аналоговой
следящей системы.
Ша — отсчетное устройство;
КИР — коэффициент передачи измерителя рассогласования;
СД — синхронный детектор;
ФНЧ — фильтр низких частот;
КУ — корректирующее устройство;
УН — усилитель напряжения;
УМ — усилитель мощности;
Д — двигатель;
Р — редуктор;
Н — нагрузка.
Список литературы
1. Проектирование
систем автоматического управления: Задания и методические указания к курсовому
проекту / РГРТА. Сост. Степашкин А. И. Рязань, 1994 г.
2. Степашкин
А. И., Алпатов Б. А. Проектирование и надежность систем автоматики и
телемеханики: Учебное пособие. Рязань, 1984.
. Руководство
по проектированию систем автоматического управления / Под ред. В. А.
Бесекерского. М.: Высш. школа, 1983.
4. Кочергин
В. В, Следящие системы с двигателем постоянного тока. Л.: Энергоатомиздат.
Ленингр. Отд-ние, 1988.
5. Ахметжанов
А. А., Кочемасов А. В, Следящие системы и регуляторы. М.: Энергоатомиздат,
1986.
. Бесекерский
В. А., Попов Е. П. Теория систем автоматического регулирования. М.: Наука,
1966.
7. Кузнецов
В. П. Промышленные роботы. Проектирование электромеханических приводов: Учебное
пособие. Рязань, 1991.
8. Волков Н.
И., Миловзоров В. П. Электромашинные устройства автоматики. М.: Высшая школа,
1978.