Максимальная абсолютная ошибка формула - Решение и исправление самых разных ошибок на TopOshibok.ru

Загрузить PDF

Абсолютная ошибка – это разность между измеренным значением и фактическим значением.^[1] Эта ошибка характеризует точность измерений. Если вам известны фактическое и измеренное значения, можно с легкостью вычислить абсолютную ошибку. Но иногда фактическое значение не дано, поэтому в качестве абсолютной ошибки пользуются максимально возможной ошибкой.^[2] Если даны фактическое значение и относительная ошибка, можно вычислить абсолютную ошибку.

1

Запишите формулу для вычисления абсолютной ошибки. Формула: $\Delta x=x_{{0}}-x$ , где $\Delta x$ – абсолютная ошибка (разность между измеренным и фактическим значениями), $x_{{0}}$ – измеренное значение, – фактическое значение.^[3]
2
Подставьте в формулу фактическое значение. Фактическое значение должно быть дано; в противном случае используйте принятое опорное значение. Фактическое значение подставьте вместо .
- Например, нужно измерить длину футбольного поля. Фактическая длина (принятая опорная длина) футбольного поля равна 105 м (именно такое значение рекомендуется FIFA). Таким образом, фактическое значение равно 105 м: $\Delta x=x_{{0}}-105$ .
3
Подставьте в формулу измеренное значение. Оно будет дано; в противном случае измерьте величину (длину или ширину и так далее). Измеренное значение подставьте вместо $x_{0}$ .
- Например, вы измерили длину футбольного поля и получили значение 104 м. Таким образом, измеренное значение равно 104 м: $\Delta x=104-105$ .
4
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[4] Так вы вычислите абсолютную ошибку.
- В нашем примере: $\Delta x=104-105=-1$ , то есть абсолютная ошибка измерения равна 1 м.
Реклама

1

Запишите формулу для вычисления относительной ошибки. Формула: $\delta x={\frac {x_{{0}}-x}{x}}$ , где $\delta x$ – относительная ошибка (отношение абсолютной ошибки к фактическому значению), $x_{{0}}$ – измеренное значение, – фактическое значение.^[5]
2
Подставьте в формулу относительную ошибку. Скорее всего, она будет дана в виде десятичной дроби. Относительную ошибку подставьте вместо $\delta x$ .
- Например, если относительная ошибка равна 0,02, формула запишется так: $0,02={\frac {x_{{0}}-x}{x}}$ .
3
Подставьте в формулу фактическое значение. Оно будет дано. Фактическое значение подставьте вместо .
- Например, если фактическое значение равно 105 м, формула запишется так: $0,02={\frac {x_{{0}}-105}{105}}$ .
4

Умножьте обе стороны уравнения на фактическое значение. Так вы избавитесь от дроби.
5

Прибавьте фактическое значение к каждой стороне уравнения. Так вы найдете $x_{{0}}$ , то есть измеренное значение.
6
Вычтите фактическое значение из измеренного значения. Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[6] Так вы вычислите абсолютную ошибку.
- Например, если измеренное значение равно 107,1 м, а фактическое значение равно 105 м, вычисления запишутся так: . Таким образом, абсолютная ошибка равна 2,1 м.
Реклама

1
Определите единицу измерения. То есть выясните, было ли значение измерено с точностью до сантиметра, метра и так далее. Возможно, эта информация будет дана (например, «длина поля измерена с точностью до метра»). Чтобы определить единицу измерения, посмотрите на то, как округлено данное значение.^[7]
- Например, если измеренная длина поля равна 106 м, значение было округлено до метров. Таким образом, единица измерения равна 1 м.
2
3
Используйте максимально возможную ошибку в качестве абсолютной ошибки.^[9] Так как абсолютная ошибка всегда положительна, возьмите абсолютное значение этой разницы, то есть не учитывайте знак «минус».^[10] Так вы вычислите абсолютную ошибку.
- Например, если измеренная длина поля равна $106\pm 0,5$ м, то есть абсолютная ошибка равна 0,5 м.
Реклама

Советы

Если фактическое значение не указано, найдите принятое опорное или теоретическое значение.

Об этой статье

Эту страницу просматривали 26 271 раз.

Была ли эта статья полезной?

Источник

Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».

Сначала надо вспомнить основные понятия теории погрешности.

Абсолютная погрешность физической величины ΔА — это
разница между точным значением физической величины и ее приближенным значением и измеряется в тех же единицах, что и сама величина:

ΔА = А — А_пр .

Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной
погрешности мы можем определить лишь приблизительно. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.

Относительная погрешность измерения
ε_Аравна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из
множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.

Зная относительную погрешность, найти абсолютную погрешность измерений можно так:

ΔА = ε_A· А.

«Правило ничтожных погрешностей»

при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟4 от другого.

Запись результата с указанием погрешности.

Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.

Пример:

Результат записывается в виде:

А = А_изм ± ΔА, например: ℓ = (13 ± 2) мм.

При этом в измеренном значении следует оставлять столько десятичных знаков, сколько их в значении
погрешности (последняя цифра погрешности «поправляет» последнюю цифру измеренного значения). Значение величины и погрешность следует
выражать в одних и тех же единицах!

Пример:

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения

Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?

Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за
топливо?

Источник

Абсолютная и относительная погрешность

4.2

Средняя оценка: 4.2

Всего получено оценок: 2248.

4.2

Средняя оценка: 4.2

Всего получено оценок: 2248.

Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.

Опыт работы учителем математики — более 33 лет.

Абсолютная погрешность

Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.

Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.

Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:

Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.

На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.

Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.

Относительная погрешность

Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.

Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.

Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.

Правила подсчета погрешностей

Для номинальной оценки погрешностей существует несколько правил:

при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
при делении и умножении чисел требуется сложить относительные погрешности;
при возведении в степень относительную погрешность умножают на показатель степени.

Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.

Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.

Что мы узнали?

Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Светлана Лобанова-Асямолова

10/10
Валерий Соломин

10/10
Анастасия Юшкова

10/10
Ксюша Пономарева

7/10
Паша Кривов

10/10
Евгений Холопик

9/10
Guzel Murtazina

10/10
Максим Аполонов

10/10
Olga Bimbirene

9/10
Света Колодий

10/10

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 2248.

А какая ваша оценка?

Источник

Максимальное значение погрешности равно при этом

ΔА
=
ΔX
+ ΔY. (13)

Такова
ие будет максимальная абсолютная
погрешность при

А
=
X
– Y.
Таким
образом, относительные погрешности
величин, являющихся суммой или разностью
двут! параметров, равны соответственно
:

(14)

Пусть
теперь A
= X^.Y
—
тогда

Пренебрегая
слагаемым второго порядка малости |ΔX^.
ΔY|
имеем
:

(15)

или(16)

Если
,
то

Максимальное
значение погрешности ΔА
получится
в случае, если погрешности в числителе
и в знаменателе данного выражения взять
с разными знаками. Тогда можно записать
:

Здесь мы
пренебрегли членами (ΔY)²и ΔX^.ΔY.Максимальная абсолютная
погрешность равна в этом случае

, (17)

а
относитедьная погрешностс, как и в
(16), равна

Полученные
результаты легко обобщаются на
произвольное количество сомножителей.
Если в самом общем случае

где
С — постоянный коэффициент, а α, β, γ,
… — любые целые или дробные числа,
то относительную погрешность косвенного
измерения величины А можно эаплеать
в виде :

(18)

Простота
последнего выражения указывает на то,
что в большинстве случаев удобно оценить
сначала относительную погрешность
косвенного измерения, а потом уже найти
его абсолютную погрешность. Следует,
однако, обратить внимание на то
обстоятельство, что приведенные формулы
применимы только в том случае, если
параметры X
,
Y
, Z , ….
не зависят друг от друга. Если же, к
примеру,

, где Z
= X
+ Y
расчет
по формуле
(18)
приведет к неправильному результату,
т.к. погрешности одной и той же величины
Y
будут приписаны различные знаки,
поскольку указанная величина фигурирует
как в числителе, так и в знаменателе
исходного выражения.

Более
общие правила вычисления погрешностей,
позволяющие избежать подобных ошибок,
можно получить, используя дифференциальное
исчисление.

Пусть
по-прежнему A
= ƒ(X,
Y,
Z,
…) .
Тогда относительную погрешность
косвенного измерения
можно записать в виде.
С другой стороны,

Таким образом, относительая погрешность
величины А равна полному дифференциалу
натурального логарифма функции,
определяющей зависимость данной величины
от измеряемых, т.е.

Таким
образом, для нахождения
необходимо:

прологарифмирэвать
исходную формулу
ln
A
= ln
ƒ(X,
Y,
Z,
…)

2)
продифференцировать полученное
уравнение, заменив затем дифференциалы
dA
,
dX
,
dY
…
погрешностями ΔA , ΔX
, ΔY
, …
;

3)
сгруппировать члены, содержащие одни
и те же погрешности, вынести эти
погрешности за скобки, а выражения в
скобках взять по модулю;

4)
заменить знаки
“-”
перед коэффициентами при погрешностях
на знак “+”
(для
нахождения максимального значения Е).

Общая
формула для расчета относительной
погрешности будет при этом выглядеть
следующим образом:

, (19)

В
качества примера приведем оценку
относительной погрешности величины γ,
вычисляемой по формуле
,
где средние значения параметров,
полученные после проведения серии
измерений
(отсчеты
по шкале манометра в работе
1.65 ).

Надо сказать,
что расчет по формуле (20)приводит, как правило, к завышению
погрешности результата косвенных
измерений. Причем это завышение
зависит от числа параметров Х
, Y, Z , …Если, например, имеется пять таких
параметров, то вероятность того, что
все ошибки будут иметь заданный знак
равна.
При большем их числе указанная вероятность
будет еще меньше. Таким образом, понятно,
что максимально возможное значение
относительной погрешности, даваемое
выражением (20),во многих
случаях значительно больше реальной
погрешности результата.

Теория
вероятностей дает более правильные
формулы для оценки погрешностей косвенных
измерений. Если при прямых измерениях
параметров X
,
Y
, Z
…
доминирующей является случайная
погрешность, то погрешность косвенного
измерения также является случайной
величиной. Это означает, что следует
искать среднюю квадратичную погрешность
результата. Так, если A
= X + У
,
то вместо выражений (13) и
(14)
будем иметь
:

и
(21)

Общая
формула для расчета относительной
погрешности будет в этом случае иметь
следующий вид
:

(22)

или

(23)

В
частности, при
имеем:

(24)

Следует
подчеркнуть, что расчет погрешностей
по формулах
(22) — (24)
желательно производить в тех случаях,
когда погрешности измеряемых
параметров имеют, в основном, случайный
характер. В условиях же, например, учебной
лаборатории. ввиду несовершенства
измерительных приборов приходится
главным образом иметь дело с приборными
погрешностями. При этом большинство
величин, входящих в расчетную формулу,
измеряются только один раз. К тому
же общее число параметров обычно
невелико. Поэтому можно рекомендовать
для оценки погрешностей косвенных
измерений более простые формулы (13) –
(20).

Очень
часто в выражении, используемом для
определения искомой величины, встречаются
параметры, которые в данном эксперименте
непосредственно не измеряются. Это
могут быть табличные величины
(π ,
g
, и т.п.), либо величины, определенные
кем-либо заранее и представленные в
виде готового результата
(например,
масса гири или диаметр катушки,
заключенной внутри установки).
Поскольку указанное величины не являются
абсолютно точным, следует учесть вклад
соответствующих погрешностей в
погрешность вычисляемого результата
(см.
работы
1.01, 1.25).,

Для
оценки погрешности в этих случаях (если,
конечно, последняя не задана в явном
виде)
может быть рекомендовано следующее
общее правило:
абсолютная погрешность берется равной
половине единицы наименьшего разряда,
представленного в числе. Так, если задана
плотность жидкости

ρ
=
4,0380·10³
кг/м³,
то погрешность следует взять равной
0,00003 кг/м³

Указанный
способ оценки погрешностей вытекает
из того факта, что последняя цифра в
числе уже не является в большинстве
случаев точной
(смотри
ниже правила округления). Что касается
табличных величин, то они при необходимости
могут быть взяты с очень большой
точностью. Тогда связанными с ними
ошибками пренебрегают. При значительном
же округлении этих величин погрешности
возрастают и, в принципе, должны быть
учтены. Их расчет обычно ведется по
общему правилу, т.е. если используется
значение π
= 3,14,
то Δπ = 0,005.

Рассчитав
окончательно относительную погрешность
Е , находят затем абсолютную погрешность
косвенного измерения ΔА = Е·А.
(25)

Обработка
результатов измерений

Все
экспериментальные данные, получаемые
в результате прямых измерений, должны
быть занесены в специальную таблицу
(
или таблицы). Для величин, значения
которых измерялись по нескольку раз,
необходимо подсчитать среднее
арифметическое серии измерений. При
этом следует пенить, что точность
обработки числового материала должна
быть согласована с точностью самих
измерений. Обычно при вычислении средних
значений рекомендуется оставлять на
одну значащую цифру больше, чем содержится
в непосредственно измеренных значениях.

Затем
необходимо произвести оценку случайной
погрешности. Используемые для расчетов
средней квадратичной ошибки значения
ΔX_i
и (ΔХ_i)²
удобно поместить в ту же таблицу, где
находятся результаты опытов
(т.е.
значения X_i).
Для сравнения там же обычно указывают
и погрешности использовавшихся приборов.

Расчет
конечного результата измерений, которые
являются в большинстве случаев
косвенными, производится один раз. При
этом в расчетную формулу подставляются
средние значения измеренных параметров.
Дальнейшая обработка сводится к
вычислению относительной и абсолютной
погрешностей по изложенной методике.

Для
правильной записи конечного результата
в виде (12) необходимо округлить значение
абсолютной погрешности и сам результат
измерений. Как правило, точность оценки
погрешности оказывается очень небольшой,
особенно в тех случаях, когда число
входящих в расчетную формулу параметров
велико. Поэтому абсолютная погрешность
округляется, как правило, до одной
значащей цифры. Если, однако, эта цифра
оказалась единицей, следует оставить
две значащие цифры.

Округление
самой измеренной величины следует
проводить, учитывая ее абсолютную
погрешность. При этом последняя значащая
цифра в приводимом результате должна
быть того же порядка величины
(находиться
в той же десятичной позиции),
что
и погрешность. Все более мелкие разряды
не несут никакой информации и должны
быть отброшены
(или
заменены нулями).
Особенно строго следует придерживаться
этого правила в тех случаях, когда
погрешность не указывается в явном
виде, так как именно последний разряд
числа, дающего значение физической
величины, показывает точность ее
определения. Или, например, в результате
расчетов получено, что
J
=
0,1428 кг·м³,
ΔJ
= 0,00791 кг·м³,
то правильная запись конечного
результата будет выглядеть так
:

J
= 0,014
±
0,008
кг·м³.

В
некоторых случаях при обработке
результатов измерений удобно
пользоваться графическим методом. Этот
метод позволяет проследить зависимость
одной физической величины от другой
(например,
зависимость периода колебаний физического
маятника от расстояния между его центром
масс и осью вращения
).
Иногда построение графиков необходимо
для определения усредненных значений
тех или иных параметров. (
Можно,
к примеру, найти ускорение тела по
графику зависимости пути от квадрата
времени).

При
построении графиков обычно используется
прямоугольная систем координат с
равномерным масштабом по осям Х и Y.
Значения аргумента следует откладывать
по оси X
,
а значение функции
—
по оси Y.
Масштаб может быть произвольным, но
при его выборе рекомендуем руководствоваться
следующими указаниями.

Проводимая
кривая должна занимать весь лист
используемой миллиметровой бумаги.
При этом следует иметь в виду, что
пересечение координатных осей совсем
необязательно должно совпадать с
нулевыми значениями аргумента и функции.
Важную роль играет также удобство
построения и использования графиком.
Надо поэтому выбирать такой масштаб,
чтобы координаты любой точки графика
могли быть быстро и легко определены.
Это условие всегда выполняется, если в
единице масштаба (например,
в 1см)заключается 10ⁿ
,2·10ⁿили5·10ⁿединиц измерения физических величин,
откладываемых по осям координат
(n -любое
целое число).

После
того, как масштаб выбран, следует
начертить координатные оси, отметив
на них деления масштаба. и указать
буквенные обозначения и размерность
откладываемых величин. Если эти величины
очень малы
(или
очень велики) при нанесении масштаба
удобно использовать рационализированную
форму записи, указывая порядок
величины рядом с ее буквенным обозначением.
При этом допускается два вида записи.
Пусть, например, индукция магнитного
поля катушки с током меняется в пределах
(2÷8) 10^-5
Тл. На графике зависимости В(I)
около
делений масштаба надо проставить числа
2, 3, 4
и т.д., а сверху написать либо В,
10^-5
Тл, либо Вx10^-5,
Тл.

Полученные
экспериментальные данные наносятся в
виде графика Y
= Y(Х),
где точки имеют координаты Х_n
,
Y_n
, окруженные
эллипсами с главными полуосями ΔX_n
,
ΔY_n
. Эллипсы
отражают погрешности измерения. Часто
вместо эллипсов рисуют крестики,
точки, кружочки и пр. Затем строится
кривая, демонстрирующая вид изучаемой
функции. Кривая должна быть плавной и
может проходить как через экспериментальные
точки, так и в непосредственной близости
от них. Желательно, чтобы указанные
точки оказались па обе стороны кривой,
приблизительно на одинаковых от нее
расстояниях.

Для
наиболее точного построения искомой
кривой используют так называемый
метод наименьших квадратов
(см.
Дополнение). Следует подчеркнуть, что
указанный метод не дает ответа на
вопрос, какого вида функция наилучшие
образом аппроксимирует данные точки,
а позволяет лишь выбрать наиболее
подходящую кривую определенного вида
(параболу,
прямую, экспоненту и т.д.).

Как
правило, отклонение точек от кривой не
должно превышать абсолютную погрешность
проведенных измерений. Эти погрешности,
как уже говорилось, могут быть указаны
на графике в виде эллипсов или
отрезков, отложенных от каждой точки
(рис.
2).
Сильное отклонение отдельных точек от
аппроксимирующей кривой связано в
основном с ошибками, допущенными при
восполнении опытов. Поэтов желательно
строите графики в процессе измерений
или сразу же после них, чтобы иметь
возможность выявить подобные ошибки,
называемые промахами, и при
необходимости, провести дополнительные
измерения.

П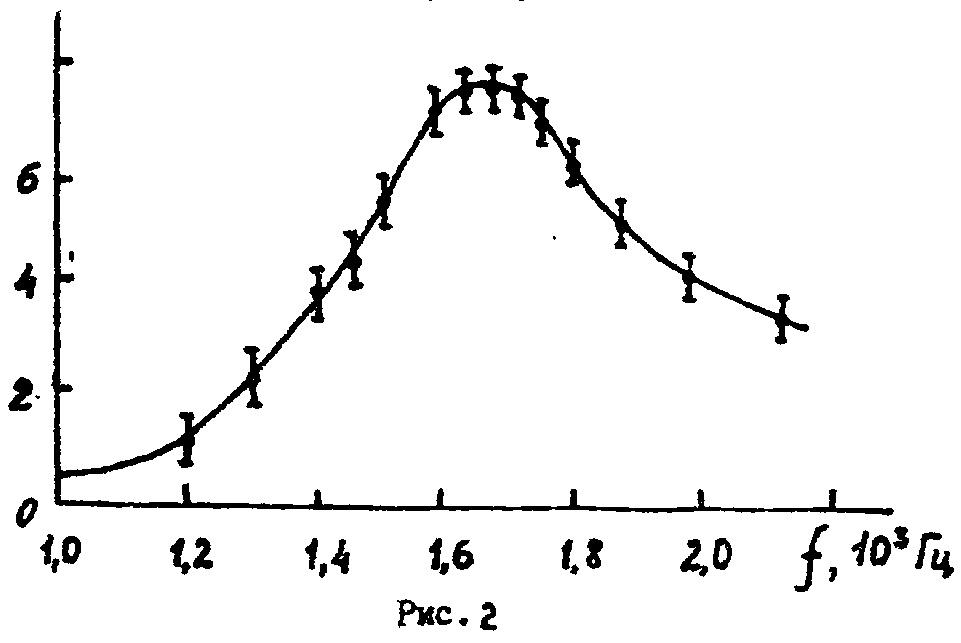остроение
графика в ходе эксперимента позволяет
также осуществить наиболее рациональное
количество измерений. В тех областях,
где ход кривой монотонный, можно
ограничиться небольшим числом измерений.
Вблизи максимумов, минимумов и точек
перегибов кривой измерения надо
производить значительно чаще.

Пользуясь
полученной кривой, можно оценить значения
изучаемой функции для тех значений
аргумента, которые непосредственно
не наблюдались
(интерполяция).
Для этого из любой точки на оси абсцисс
(в
пределах диапазона изменения аргумента)
надо провести перпендикуляр до пересечения
с кривой. Его длина с учетом масштаба
даст значение искомой функции,
соответствующее выбранному значению
аргумента. Примерный вид графика,
построенного по экспериментально
полученной зависимости напряжения
на конденсаторе колебательного контура
от частоты генератора
(вынужденные
колебания), показан на рисунке
2 (см.
работу
2.39).

Электронная версия
лабораторных работ по физике

Сканировал (очень плохо
– лучше бы не сканировал) Комаров Н.,
распознавали и редактировали Смирнов
К. и Молоков В.

Источник

Статья обновлена 10.07.2022

Что такое погрешность измерения

Любой расчет состоит из истинного и вычисляемого значения. При этом всегда должны учитываться значения ошибки или погрешности. Погрешность — это расхождение между истинным значением и вычисляемым. В маркетинге выделяют следующие виды погрешностей.

Математическая погрешность. Она описывается алгебраической формулой и бывает абсолютной, относительной и приведенной. Абсолютная погрешность измерения — это разница между вычисляемым и истинным значением. Относительная погрешность вычисляется в процентном соотношении истинного значения и полученного. Вычисление погрешности приведенной схоже с относительной, указывается она также в процентах, но дает разницу между нормирующей шкалой и полученными данными, то есть между эталонными и полученными значениями.
Оценочная погрешность. В маркетинге она бывает случайной и систематической. Случайная погрешность возникает из-за любых факторов, которые случайным образом влияют на измерение переменной в выборке. Систематическая погрешность вызывается факторами, которые систематически влияют на измерение переменной в выборке.

Математическая погрешность: формула для каждого типа

Если определение погрешности можно провести точным путем, она считается математической. Зачем нужно вычисление этого значения в маркетинге?

Погрешности возникают настолько часто, что популярной практикой в исследованиях является включение значения погрешности в окончательные результаты. Для этого используются формулы. Математическая погрешность — это значение, которое отражает разницу между выборкой и фактическим результатом. Если при расчетах учитывалась погрешность, в тексте исследования указывается что-то вроде: «Абсолютная погрешность для этих данных составляет 3,25%». Погрешность можно вычислить с любыми цифрами: количество человек, участвующих в опросе, погрешность суммы, затраченной на маркетинговый бюджет, и так далее.

Формулы погрешностей вычисляются следующим образом.

Абсолютная погрешность измерений: формула

Формула дает разницу между измеренным и реальным значением.

Формула абсолютной погрешности

Относительная погрешность: формула

Формула использует значение абсолютной погрешности и вычисляется в процентах по отношению к фактическому значению.

Формула относительной погрешности

Приведенная погрешность: формула

Формула также использует значение абсолютной погрешности. В чем измеряется приведенная погрешность? Тоже в процентах, но в качестве «эталона» используется не реальное значение, а единица измерения любой нормирующей шкалы. Например, для обычной линейки это значение равно 1 мм.

Формула приведенной погрешности

Классификация оценочной погрешности

Определение погрешности в оценках — это всегда методическая погрешность, то есть допустимое значение ошибки, основанное на методах проведения исследования. Погрешность метода вызывает два типа погрешностей — случайные и систематические. Таблица погрешностей в графической форме покажет все возможные типы.

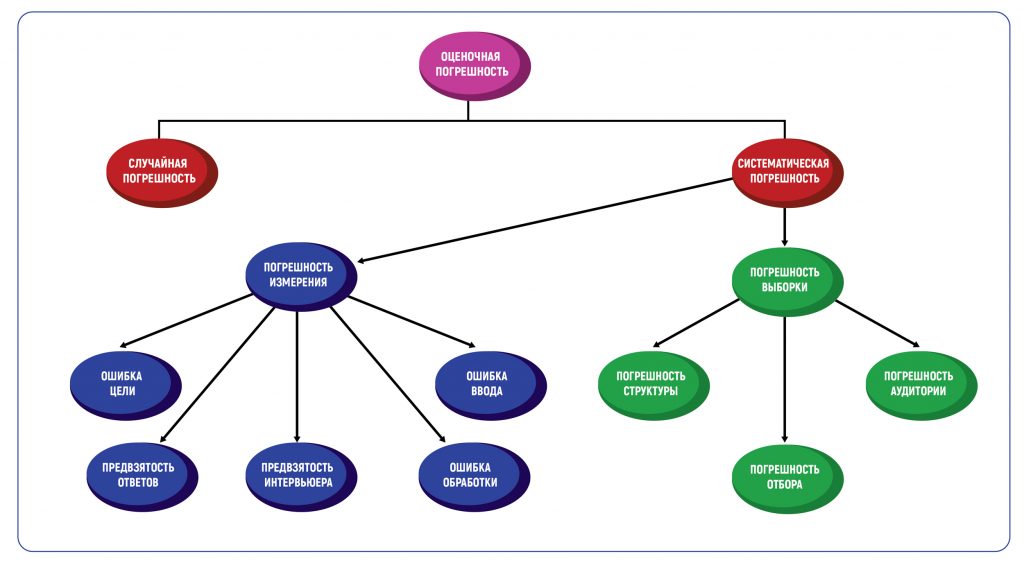
Классификация оценочной погрешности

Что такое случайная погрешность

Случайная погрешность бывает статической и динамической. Динамическая погрешность возникает, когда мы имеем дело с меняющимися значениями — например, количество человек в выборке при маркетинговом исследовании. Статическая погрешность описывает ошибки при вычислении неизменных величин — вроде количества вопросов в вопроснике. Все они относятся к случайным погрешностям.

Типичный пример возникновения случайной погрешности — настроение участников маркетингового опроса. Как известно, эмоциональный настрой человека всегда влияет на его производительность. В ходе тестирования одни люди могут быть в хорошем расположении духа, а другие — в «миноре». Если настроение влияет на их ответы по заданному критерию выборки, это может искусственно завышать или занижать наблюдаемые оценки. Например, в случае с истинным значением 1 случайная погрешность может дать как -0,8, так и +0,5 к этому числу. Очень часто это случается при оценке времени ответа, например.

Случайная погрешность добавляет изменчивости данным, но не оказывает постоянного влияния на всю выборку. Вместо этого она произвольно изменяет измеряемые значения в диапазоне. В маркетинговой практике считается, что все случайные погрешности в распределении перекрывают друг друга и практически не влияют на конечный результат. Поэтому случайная погрешность считается «шумом» и в расчет не принимается. Эту погрешность нельзя устранить совсем, но можно уменьшить, просто увеличив размер выборки.

Что такое систематическая погрешность

Систематическая погрешность существует в результатах исследования, если эти результаты показывают устойчивую тенденцию к отклонению от истинных значений. Иными словами, если полученные цифры постоянно выше или ниже расчетных, речь идет о том, что в данных имеется систематическая погрешность.

В маркетинговых исследованиях есть два основных типа систематической погрешности: погрешность выборки и погрешность измерения.

Погрешность выборки

Погрешность выборки возникает, когда выборка, используемая в исследовании, не репрезентативна для всей совокупности данных. Типы такой погрешности включают погрешность структуры, погрешность аудитории и погрешность отбора.

Погрешность структуры

Погрешность структуры возникает из-за использования неполной или неточной основы для выборки. Распространенным источником такой погрешности в рамках маркетинговых исследований является проведение какого-либо опроса по телефону на основе существующего телефонного справочника или базы данных абонентов. Многие данные там указаны неполно или неточно — например, если люди недавно переехали или изменили свой номер телефона. Также такие данные часто указывают неполную или неверную демографию.

Если в качестве основы для исследования взят телефонный справочник, оно подвержено погрешности структуры, так как не учитывает всех возможных респондентов.

Погрешность аудитории

Погрешность аудитории возникает, если исследователь не знает, как определить аудиторию для исследования. Пример — оценка результатов исследования, проведенного среди клиентов крупного банка. Доля ответов на анкету составила чуть менее 1%. Анализ профессий всех опрошенных показал, что процент пенсионеров среди них в 20 раз выше, чем в целом по городу. Если эта группа значительно различается по интересующим переменным, то результаты будут неверными из-за погрешности аудитории.

Погрешность отбора

Даже если маркетологи правильно определили структуру и аудиторию, они не застрахованы от погрешности отбора. Она возникает, когда процедуры отбора являются неполными, неправильными или не соблюдаются должным образом. Например, интервьюеры при полевом исследовании могут избегать людей, которые живут в муниципальных домах. Потому что, по их мнению, жители вряд ли согласятся пройти такой опрос. Если жители муниципальных домов отличаются от тех, кто проживает в домах бизнес-класса, в результаты опроса будет внесена погрешность отбора.

Как минимизировать погрешность выборки

Знайте свою аудиторию.
Знайте, кто покупает ваш продукт, использует его, работает с вами и так далее. Имея базовую социально-экономическую информацию, можно составить стабильную выборку целевой аудитории. Маркетинговые исследования часто касаются одной конкретной группы населения — например, пользователей Facebook или молодых мам.
Разделите аудиторию на группы.
Вместо случайной выборки разбейте аудиторию на группы в соответствии с их численностью в общей совокупности данных. Например, если люди с определенной демографией составляют 35% населения, убедитесь, что 35% респондентов исследования отвечают этому условию.
Увеличьте размер выборки.
Больший размер выборки приводит к более точному результату.

Погрешность измерения

Погрешность измерения представляет собой серьезную угрозу точности исследования. Она возникает, когда существует разница между искомой информацией — то есть истинным значением, и информацией, фактически полученной в процессе измерения. К таким погрешностям приводят различные недостатки процесса исследования. Погрешность измерения, в основном, вызывается человеческим фактором — например, формулировкой вопросника, ошибками ввода данных и необъективными выводами.

К погрешностям измерения приводят следующие виды ошибок.

Ошибка цели

Ошибка цели возникает, когда существует несоответствие между информацией, фактически необходимой для решения проблемы, и данными , которые собирает исследование. Например, компания Kellogg впустую потратила миллионы на разработку завтраков для снижения уровня холестерина. Реальный вопрос, который нужно было бы задать в исследовании, заключался в том, купят ли люди овсяные хлопья для решения своей проблемы. Ответ «Нет» обошелся бы компании дешевле.

Предвзятость ответов

Некоторые люди склонны отвечать на конкретный вопрос определенным образом. Тогда возникает предвзятость ответа. Предвзятость ответа может быть результатом умышленной фальсификации или неосознанного искажения фактов.

Умышленная фальсификация происходит, когда респонденты целенаправленно дают неверные ответы на вопросы. Есть много причин, по которым люди могут сознательно искажать информацию. Например, они хотят скрыть или хотят казаться лучше, чем есть на самом деле.

Бессознательное искажение информации происходит, когда респондент пытается быть правдивым, но дает неточный ответ. Этот тип предвзятости может возникать из-за формата вопроса, его содержания или по другим причинам.

Предвзятость интервьюера

Интервьюер оказывает влияние на респондента — сознательно или бессознательно. Одежда, возраст, пол, выражение лица, язык тела или тон голоса могут повлиять на ответы некоторых или всех респондентов.

Ошибка обработки

Примеры включают наводящие вопросы или элементы дизайна анкеты, которые затрудняют запись ответов или приводят к ошибкам в них.

Ошибка ввода

Это ошибки, возникающие при вводе информации. Например, документ может быть отсканирован неправильно, и его данные по ошибке перенесутся неверно. Или люди, заполняющие опросы на смартфоне или ноутбуке, могут нажимать не те клавиши.

Виды проводимых маркетинговых исследований различны, поэтому универсальных рецептов не существует. Мы дадим несколько общих советов, используемых для минимизации систематических погрешностей разного типа.

Как минимизировать погрешность измерения

Предварительно протестируйте.
Погрешностей обработки и предвзятости можно избежать, если проводить предварительные тесты вопросника до начала основных интервью.
Проводите выборку случайным образом.
Чтобы устранить предвзятость, при выборке респондентов можно включать каждого четвертого человека из общего списка.
Тренируйте команду интервьюеров и наблюдателей.
Отбор и обучение тех, кто проводит исследования, должен быть тщательным. Особое внимание нужно уделять соблюдению инструкций в ходе каждого исследования.
Всегда выполняйте проверку сделанных записей.
Чтобы исключить ошибки ввода, все данные, вводимые для компьютерного анализа, должны быть перепроверены как минимум дважды.

Мир без ошибок не может существовать. Но понимание факторов, влияющих на маркетинговые исследования и измеряемые погрешности, имеет важное значение для сбора качественных данных.

Источник