Локальные минимумы мешают всем алгоритмам обучения, основанным на поиске минимума функции ошибки, включая сети обратного распространения, и представляют серьезную и широко распространенную проблему. Стохастические методы позволяют решить эту проблему. Стратегия коррекции весов, вынуждающая веса принимать значение глобального оптимума, возможна.
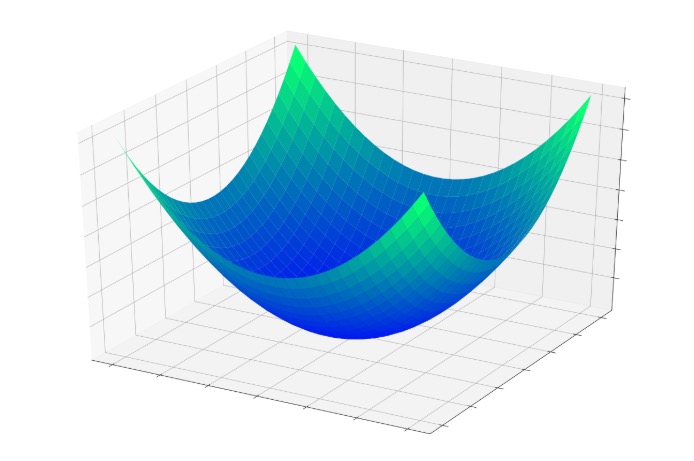
Рис. 22. Проблема локальных минимумов
В качестве объясняющей аналогии предположим, что на рис. 22 изображен шарик на поверхности в коробке. Если коробку сильно потрясти в горизонтальном направлении, то шарик будет быстро перекатываться от одного края к другому. Нигде не задерживаясь, в каждый момент шарик будет с равной вероятностью находиться в любой точке поверхности. Если постепенно уменьшать силу встряхивания, то будет достигнуто условие, при котором шарик будет на короткое время «застревать» в точке В. При еще более слабом встряхивании шарик будет на короткое время останавливаться как в точке А, так и в точке В. При непрерывном уменьшении силы встряхивания будет достигнута критическая точка, когда сила встряхивания достаточна для перемещения шарика из точки А в точку В, но недостаточна для того, чтобы шарик мог выбраться из В в А. Таким образом, окончательно шарик остановится в точке глобального минимума, когда амплитуда встряхивания уменьшится до нуля.
6.1. Обучение Больцмана
Искусственные нейронные сети могут обучаться по существу тем же самым образом посредством случайной коррекции весов. Вначале делаются большие случайные коррекции с сохранением только тех изменений весов, которые уменьшают целевую функцию. Затем средний размер шага постепенно уменьшается, и глобальный минимум в конце концов достигается.
Это сильно напоминает отжиг металла, поэтому для ее описания часто используют термин «имитация отжига». В металле, нагретом до температуры, превышающей его точку плавления, атомы находятся в сильном беспорядочном движении. Как и во всех физических системах, атомы
41
стремятся к состоянию минимума энергии, но при высоких температурах энергия атомных движений препятствует этому. В процессе постепенного охлаждения металла возникают все более низкоэнергетические состояния, пока в конце концов не будет достигнуто наиболее низкое из возможных состояний – глобальный минимум. В процессе отжига распределение энер-
−E
гетических уровней описывается следующим соотношением: P(E) = e kT ,
где Р(E) – вероятность того, что система находится в состоянии с энергией E; k – постоянная Больцмана; Т – температура по шкале Кельвина.
При высоких температурах Р(E) приближается к единице для всех энергетических состояний. Таким образом, высокоэнергетическое состояние почти столь же вероятно, как и низкоэнергетическое. По мере уменьшения температуры вероятность высокоэнергетических состояний уменьшается по сравнению с низкоэнергетическими. При приближении температуры к нулю становится весьма маловероятным, чтобы система находилась в высокоэнергетическом состоянии.
Этот стохастический метод непосредственно применим к обучению искусственных нейронных сетей и относится к классу алгоритмов обуче-
ния с учителем.
Алгоритм обучения Больцмана Шаг 1. Определить переменную Т, представляющую искусственную температуру. Придать Т большое начальное значение.
Шаг 2. Подать на вход сети один из входных образов обучающей выборки и вычислить реальный выход и значение функции ошибки сети (как в алгоритме обратного распространения).
Шаг 3. Придать случайное изменение wij выбранному весу wij и пере-
считать выход сети и изменение функции ошибки в соответствии со сделанным изменением веса.
Шаг 4. Если функция ошибки уменьшилась, то сохранить изменение веса. Если изменение веса приводит к увеличению функции ошибки, то вероятность сохранения этого изменения вычисляется с помощью распределения
|
− |
wij |
||
|
Больцмана: P( w ) = e |
T |
. Выбирается случайное число r из равномерно- |
|
|
ij |
го распределения от нуля до единицы. Если P( wij ) больше, чем r, то из-
менение сохраняется, в противном случае величина веса возвращается к предыдущему значению.
Шаг 5. Повторять шаги 3 и 4 для каждого из весов сети, постепенно уменьшая температуру Т, пока не будет достигнуто допустимо низкое значение целевой функции.
42
Шаг 6. Повторять шаги 2–5 для всех векторов обучающей выборки, (возможно неоднократно), пока функция ошибки не станет допустимой для каждого из них.
Замечание 1. На шаге 4 система может делать случайный шаг в направлении, портящем функцию ошибки, позволяя ей тем самым вырываться из локальных минимумов, где любой малый шаг увеличивает целевую функцию.
Замечание 2. В работах, посвященных больцмановскому обучению, показано, что для достижения сходимости к глобальному минимуму скорость уменьшения искусственной температуры должна подчиняться закону:
|
TN = |
T0 |
где N – номер итерации обучения. Этот результат предска- |
|
|
ln(1 |
+ N ) |
||
зывает очень медленную сходимость процесса обучения, что является существенным недостатком данного метода.
6.2.Обучение Коши
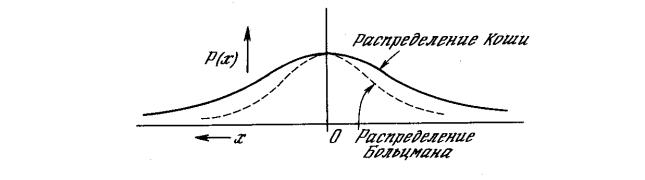
Вэтом методе распределение Больцмана заменяется на распределение Коши. Распределение Коши имеет, как показано на рис. 15, более высокую вероятность больших шагов. В действительности распределение Коши имеет бесконечную (неопределенную) дисперсию. С помощью такого простого изменения максимальная скорость уменьшения температуры становится обратно пропорциональной линейной величине, а не логарифму, как для алгоритма обучения Больцмана. Это резко уменьшает время
|
обучения. Эта |
связь может быть выражена следующим |
образом: |
|||||||
|
T = |
T0 |
. |
Распределение Коши имеет вид: |
P( w ) = |
TN |
, |
|||
|
N |
1+ N |
ij |
T 2 |
+ |
w2 |
||||
|
N |
ij |
||||||||
|
где P( wij ) есть вероятность принять изменение веса |
wij . |
||||||||
Рис. 23. Распределение Коши и распределение Больцмана
Несмотря на улучшение скорости обучения, даваемое распределением Коши по сравнению с распределением Больцмана, время сходимости все еще может в 100 раз превышать время для алгоритма обратного распространения.
43
Комбинирование обратного распространения с обучением Коши
Коррекция весов в комбинированном алгоритме, использующем обратное распространение и обучение Коши, состоит из двух компонент: компоненты, вычисляемой с использованием алгоритма обратного распространения, и случайной компоненты, определяемой распределением Коши. Эти компоненты вычисляются для каждого веса, и их сумма является величиной, на которую изменяется вес. Как и в алгоритме Коши, после вычисления изменения веса вычисляется целевая функция. Если имеет место улучшение, изменение сохраняется. В противном случае оно сохраняется с вероятностью, определяемой распределением Коши.
Коррекция веса вычисляется с использованием представленных ранее
|
уравнений для каждого из алгоритмов: wN +1 |
= wN −ηα |
∂E |
+(1−η) |
wN , |
|
ij |
ij |
∂wij |
ij |
|
где η – коэффициент, управляющий относительными величинами обучения Коши и обратного распространения в компонентах весового шага. Если η приравнивается нулю, метод становится полностью обучением Коши. Если η приравнивается единице, метод становится алгоритмом обратного распространения.
Комбинированная сеть, использующая обратное распространение и обучение Коши, обучается быстрее, чем каждый из алгоритмов в отдельности. Сходимость к глобальному минимуму гарантируется алгоритмом Коши, и во многих экспериментах по обучению сеть практически не попадала в локальные минимумы.
УПРАЖНЕНИЯ
1. Стохастические нейронные сети можно использовать для поиска глобального минимума в невыпуклых или не имеющих строгой математической формализации задачах оптимизации. На первом этапе обучения (например, по методу Коши) подстраиваются весовые коэффициенты сети так, чтобы она аппроксимировала данную функцию (в качестве обучающей выборки используются наборы значений переменных, для которых известно значение функции). На втором этапе весовые коэффициенты сети остаются без изменения, а определению подлежат входные значения сети, которые пересчитываются по тому же закону, что и весовые коэффициенты, но в качестве функции ошибки используется оптимизируемая функция, аппроксимируемая данной сетью (за ее уменьшением или увеличением должен следить алгоритм обучения). Напишите программу, опреде-
ляющую с помощью обучения Коши глобальный минимум функции F(x) = 3х3 + 6х2 – 2х + 3.
2. Напишите программу, обучающую стохастическую сеть распознаванию цифр. На вход сети подаются графические изображения цифр, разби-
44

тые на квадраты (или пиксели) аналогично, как для однослойного персептрона или сети обратного распространения. Используйте не менее 15–20 различных написаний цифр. Выходом сети служит двоичное представление входной цифры.
§ 7. СЕТИ С ОБРАТНЫМИ СВЯЗЯМИ
Рассмотренные ранее нейросетевые архитектуры относятся к классу сетей с направленным потоком распространения информации и не содержат обратных связей. После обучения на этапе функционирования сети каждый нейрон выполняет свою функцию – передачу выходного сигнала – ровно один раз. В общем случае может быть рассмотрена нейронная сеть, содержащая произвольные обратные связи, то есть пути, передающие сигналы от выходов к входам. Отклик таких сетей является динамическим, т. е. после подачи нового входа вычисляется выход и, передаваясь по обратной связи, модифицирует вход. Затем выход повторно вычисляется, и процесс повторяется снова и снова. Для устойчивой сети последовательные итерации приводят к все меньшим изменениям выхода, и в результате выход становится постоянным. Для многих сетей процесс никогда не заканчивается, такие сети называют неустойчивыми. Неустойчивые сети обладают интересными свойствами и могут рассматриваться в качестве примера хаотических систем, но для большинства практических приложений используются сети, которые дают постоянный выход.
7.1. Сеть Хопфилда
Рассмотрим однослойную сеть с обратными связями, состоящую из n входов и n нейронов (рис. 24). Каждый вход связан со всеми нейронами. Так как выходы сети заново подаются на входы, то yi – это значение i-го
выхода, который на следующем этапе функционирования сети становится i-м входом.
Рис. 24. Модель сети Хопфилда
45
Совокупность выходных значений всех нейронов yi на некотором этапе N образует вектор состояния сети Y N . Нейродинамика приводит к
изменению вектора состояния на Y N +1 .
Обозначим силу синапсической связи от i-го входа к j-му нейрону как wij. Каждый j-й нейрон сети реализует пороговую активационную функцию следующего вида:
|
−1, s |
< Θ |
; |
||||||||||||
|
j |
j |
|||||||||||||
|
N +1 |
||||||||||||||
|
y |
= f (s |
> Θ |
; |
|||||||||||
|
j |
) = 1, s |
j |
j |
|||||||||||
|
j |
||||||||||||||
|
yN |
, s |
j |
=Θ |
j |
. |
|||||||||
|
j |
||||||||||||||
|
n |
||||||||||||||
|
Здесь s j = ∑yiN wij , yNj |
– значение выхода j-го нейрона на предыдущем |
|||||||||||||
|
i =1 |
– пороговое значение j-го нейрона. |
|||||||||||||
|
этапе функционирования сети, Θj |
В модели Хопфилда предполагается условие симметричности связей wij=wji, с нулевыми диагональными элементами wii=0. Устойчивость такой сети может быть доказана следующим образом. Ведем в рассмотрение функцию, зависящую от состояния сети Y и называемую функцией энергии сети Хопфилда:
|
n n |
yi y j |
n |
y j . |
|
|
E(Y ) = − |
1∑∑wij |
+∑Θj |
||
|
2 i=1 j=1 |
j=1 |
|||
|
Вычислим изменение функции энергии |
Е, вызванное изменением |
состояния j-нейрона y j :
E = (−∑wij yi +Θj ) y j = −(s j −Θj ) y j i≠ j
(здесь мы воспользовались симметричностью связей и тем, что wii = 0). Допустим, что величина s j больше порога Θj . Тогда выражение в скобках
будет положительным, а из вида активационной функции следует, что новый выход нейрона j должен быть 1, то есть измениться в положительную сторону (или остаться без изменения). Это значит, что y j ≥ 0 и тогда
E ≤ 0 . Следовательно, энергия сети либо уменьшится, либо останется без изменения. Далее, допустим, что величина s j меньше порога. Тогда новое
значение y j = –1 и величина y j может быть только отрицательной или
нулем. Следовательно, опять энергия должна уменьшиться или остаться без изменения. Если величина s j равна порогу Θj , y j равна нулю и энер-
гия остается без изменения.
46

Эти рассуждения показывают, что любое изменение состояния нейрона либо уменьшит функцию энергии, либо оставит ее без изменения. Так как функция энергии задана на конечном множестве ( yi {−1,1}), то она
ограничена снизу и вследствие непрерывного стремления к уменьшению в конце концов должна достигнуть минимума и прекратить изменение. По определению такая сеть является устойчивой.
Поверхность функции энергии E в пространстве состояний имеет весьма сложную форму с большим количеством локальных минимумов. Стационарные состояния, отвечающие минимумам, могут интерпретироваться, как образы памяти нейронной сети. Сходимость к такому образу соответствует процессу извлечения из памяти. При произвольной матрице связей W образы также произвольны. Для записи в память сети какой-либо конкретной информации требуется определенное значение весов W, которое может получаться в процессе обучения.
Правило обучения Хебба
Метод обучения для сети Хопфилда опирается на исследования Дональда Хебба, реализовавшего простой механизм обучения, названный правилом Хебба. Рассмотрим его подробно.
Пусть задана обучающая выборка образов X k , k =1, K . Требуется
построить такую матрицу связей W, что соответствующая нейронная сеть будет иметь в качестве стационарных состояний образы обучающей выборки (значения порогов нейронов Θj положим равными нулю). В случае
одного обучающего образа X = (x1,…, xn ), xi {−1,1}, правило Хебба приводит к матрице: wij = xi x j ,i ≠ j, wii =0. Покажем, что состояние Y=X явля-
ется стационарным для сети Хопфилда с данной матрицей W. Действительно, значение функции энергии в состоянии X является для нее глобальным минимумом:
|
n n |
n n |
n n |
= −1 n2 |
|||||
|
E(X ) = − |
1 ∑∑wij xi x j = −1 ∑∑xi x j xi x j = −1 ∑∑xi2 x2j |
, |
||||||
|
2 i =1 j =1 |
2 i =1 j =1 |
2 i =1 j =1 |
2 |
|||||
|
то есть сеть прекратит изменения, достигнув состояния X. |
||||||||
|
Для запоминания K образов применяется итерационный процесс: |
||||||||
|
wk |
= wk −1 |
+ xk xk , k = |
(считаем, что |
w0 = 0). Этот процесс приводит к |
||||
|
1, K |
||||||||
|
ij |
ij |
i |
j |
ij |
||||
|
K |
||||||||
|
полной матрице связей: |
wij = ∑xik xkj . |
k =1
Сеть Хопфилда нашла широкое применение в системах ассоциативной памяти, позволяющих восстанавливать идеальный образ по имеющейся неполной или зашумленной его версии.
Пример. В качестве примера рассмотрим сеть, состоящую из 70 нейронов, упорядоченных в матрицу 10 × 7.
47

Рис. 25. Идеальные образы обучающей выборки
Сеть обучалась по правилу Хебба на трех идеальных образах – шрифтовых начертаниях латинских букв А, B и C (рис. 25). Темные ячейки соответствуют нейронам в состоянии +1, светлые –1. После обучения нейросети в качестве начальных состояний нейронов предъявлялись различные искаженные версии образов, которые в процессе функционирования сети сходились к стационарным состояниям. Для каждой пары изображений на рисунках 26, 27 и 28 левый образ является начальным состоянием, а правый – результатом работы сети – достигнутым стационарным состоянием.
Рис. 26. Сеть Хопфилда распознает образ с информационным шумом
Рис. 27. Сеть Хопфилда распознает образ по его небольшому фрагменту
Рис. 28. Сеть Хопфилда генерирует ложный образ
Опыт практического применения сетей Хопфилда показывает, что эти нейросетевые системы способны распознавать практически полностью
48

зашумленные образы и могут ассоциативно узнавать образ по его небольшому фрагменту. Однако особенностью работы данной сети является возможная генерация ложных образов. Ложный образ является устойчивым локальным минимумом функции энергии, но не соответствует никакому идеальному образу. На рис. 21 показано, что сеть не смогла различить, какому из идеальных образов (B или C) соответствует поданное на вход зашумленное изображение, и выдала в качестве результата нечто собирательное.
Ложные образы являются «неверными» решениями, и поэтому для исключения их из памяти сети на этапе ее тестирования применяется механизм «разобучения». Суть их заключается в следующем. Если обученная сеть на этапе тестирования сошлась к ложному образу Z = (z1,…, zn ), т.о. ее
весовые коэффициенты пересчитываются по формуле: wij ‘= wij −εzi z j , где
ε −малое число ( 0 <ε < 0.1), что гарантирует незначительное ухудшение полезной памяти. После нескольких процедур разобучения свойства сети улучшаются. Это объясняется тем, что состояниям ложной памяти соответствуют гораздо более «мелкие» энергетические минимумы, чем состояниям, соответствующим запоминаемым образом.
Другим существенным недостатком сетей Хопфилда является небольшая емкость памяти. Многочисленные исследования показывают, что нейронная сеть, обученная по правилу Хебба, может в среднем, при размерах сети n , хранить не более чем 0.14 n различных образов. Для некоторого увеличения емкости памяти сети используется специальный алгоритм ортогонализации образов.
Процедура ортогонализации образов
Два различных запоминаемых векторных образа сети X k , X l (k ≠ l) называются ортогональными, если их скалярное произведение равно нулю:
n
∑xkj xlj = 0 . Если все запоминаемые образы сети X k , k =1, K попарно ор-
j =1
тогональны, емкость памяти сети Хопфилда увеличивается до n , то есть сеть может запомнить количество образов, не превосходящее число нейронов в ней. На этом свойстве основано улучшение правила Хебба: перед запоминанием в нейронной сети исходные образы следует ортогонализовать. Процедура расчета весовых коэффициентов в этом случае имеет следующий вид:
Шаг 1. Вычисляются элементы матрицы B = (bkl ), k,l =1, K :
n
bkl = ∑xkj xlj . j =1
Шаг 2. Определяется матрица C , обратная к матрице B : C = B−1.
49
Шаг 3. Задаются весовые коэффициенты сети Хопфилда:
K K
wij =∑∑xik xljckl . k =1 l=1
Cущественным недостатком метода ортогонализации является его нелокальность: прежде чем начать обучение, необходимо наперед знать все обучающие образы. Добавление нового образа требует полного переобучения сети.
7.2. Сеть Хэмминга
Основным недостатком сети Хопфилда является ее большая ресурсоемкость. Сеть Хэмминга характеризуется, по сравнению с сетью Хопфилда, меньшими затратами памяти и меньшим объемом вычислений. Эта сеть состоит из двух слоев. Каждый слой имеет по m нейронов, где m – число запоминаемых образов. Сеть имеет n входов, соединенных со всеми нейронами первого слоя (W – матрица весовых коэффициентов связей). Значения входов сети – биполярные (из множества {–1,1}). Нейроны второго слоя связаны между собой отрицательными обратными (ингибиторными) связями. Единственный вес с положительной обратной связью для каждого нейрона соединен с его же выходом.
Идея работы сети состоит в оценке величины, обратной расстоянию Хэмминга, от тестируемого образа до всех эталонных образцов (расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах). Сеть должна выбрать образец с минимальным расстоянием
|
Хэмминга до неизвестного входного |
сигнала – и активизировать только |
|||||
|
один выход сети, соответствующий этому образцу. |
||||||
|
Активационная функция нейронов первого слоя – линейная: |
||||||
|
n |
n |
|||||
|
f (s) = s + |
= ∑wij xi + |
n |
, где n – это число входов сети. Активационная |
|||
|
2 |
2 |
|||||
|
i =1 |
||||||
|
функция нейронов второго слоя имеет вид линейного порога: |
||||||
|
0, |
s <0 |
|||||
|
0 |
≤ s <T , где |
|||||
|
y= f (s) = s, |
||||||
|
≥T |
||||||
|
T , s |
y – значение активационой функции;
s – аргумент активационой функции (взвешенная сумма входов); T – величина порога.
Величина T должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению за одну итерацию работы сети.
50
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь \Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
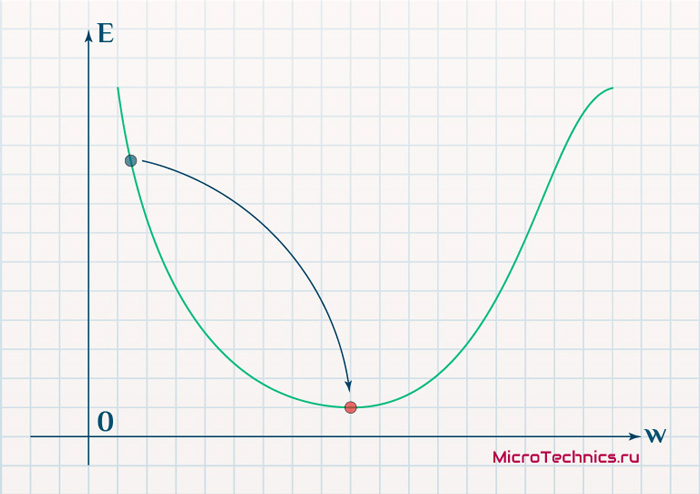
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
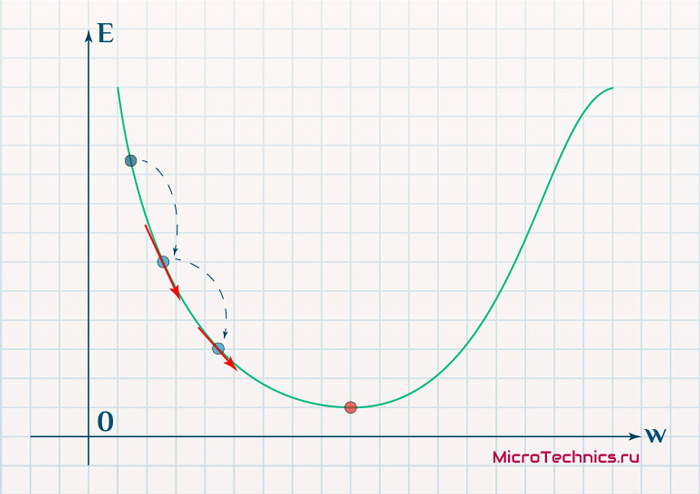
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
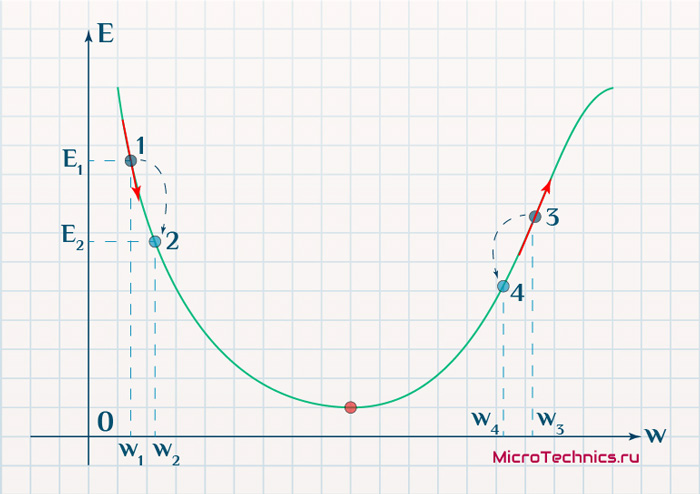
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение \Delta w (\Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: \Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | \bold{\Delta w} | Знак \bold{\Delta w} | Градиент |
|---|---|---|---|
| 1 \rArr 2 | w_2 — w_1 | + | — |
| 3 \rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
\Delta w = -\alpha \cdot \frac{dE}{dw}
Имеем в наличии:
- \Delta w — величина, на которую необходимо изменить значение w.
- \frac{dE}{dw} — градиент в этой точке.
- \alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина \frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
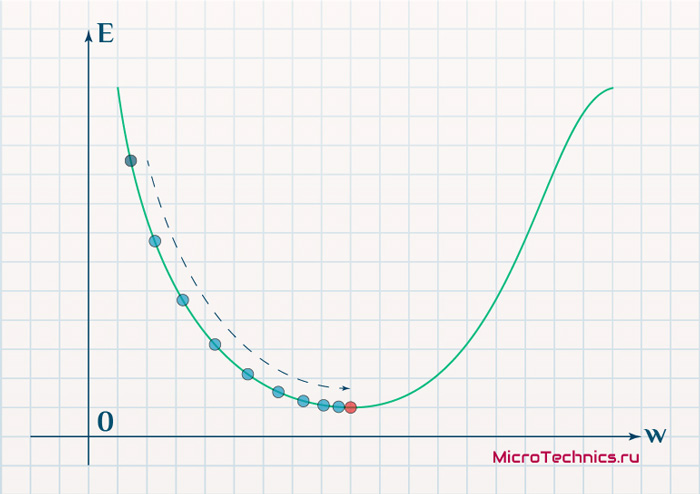
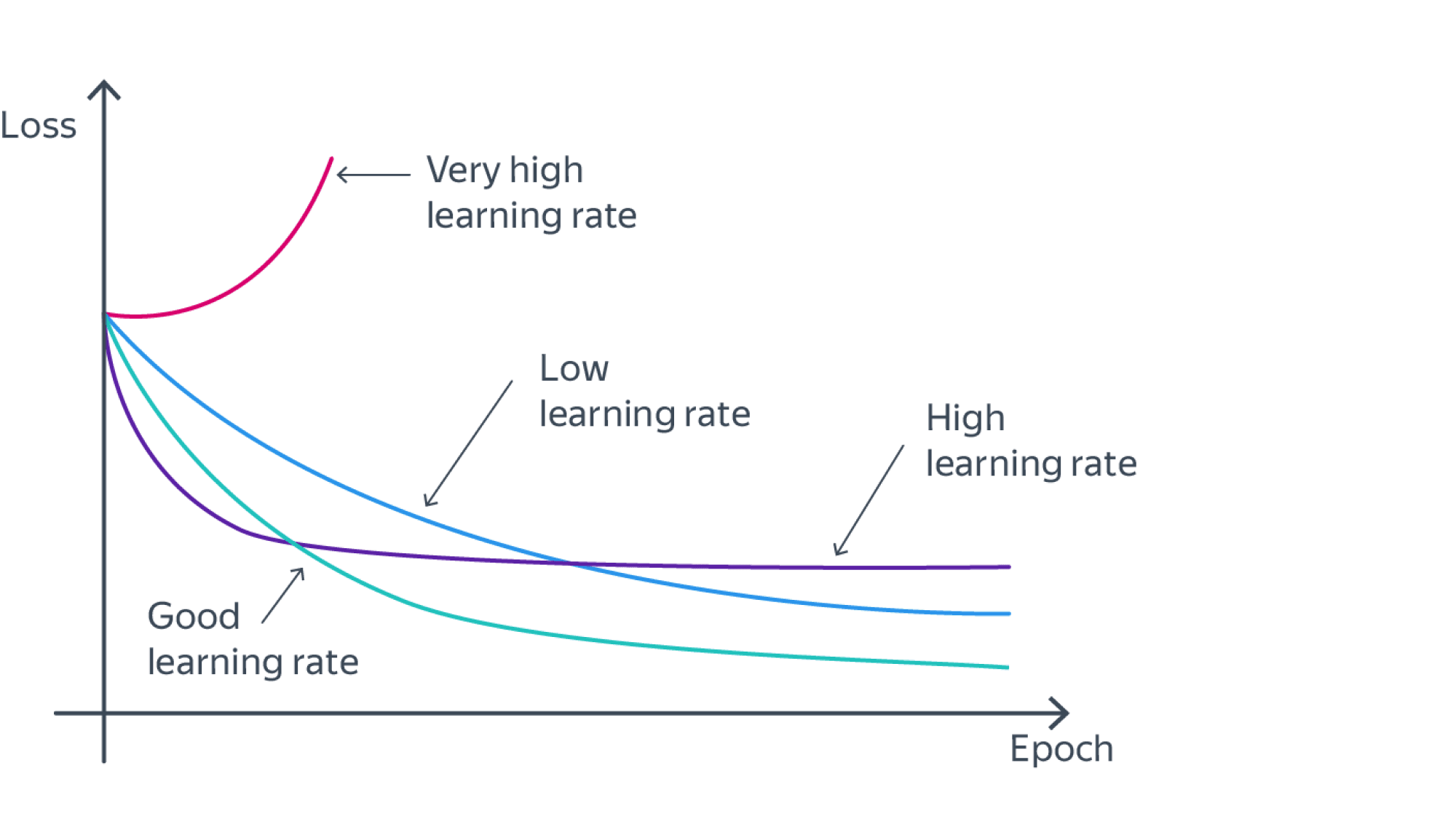
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
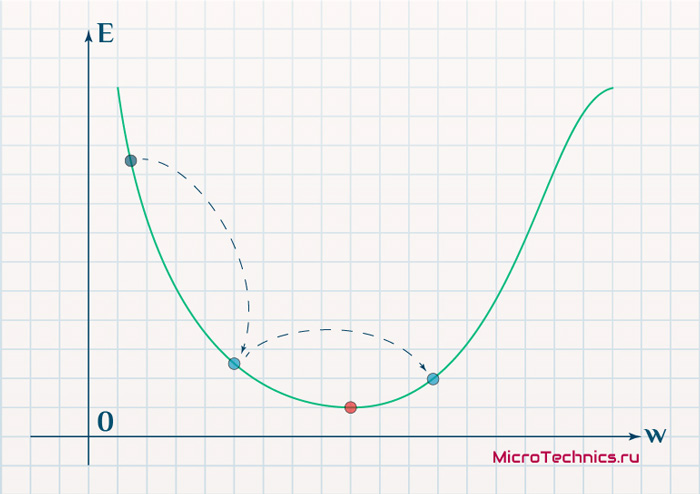
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
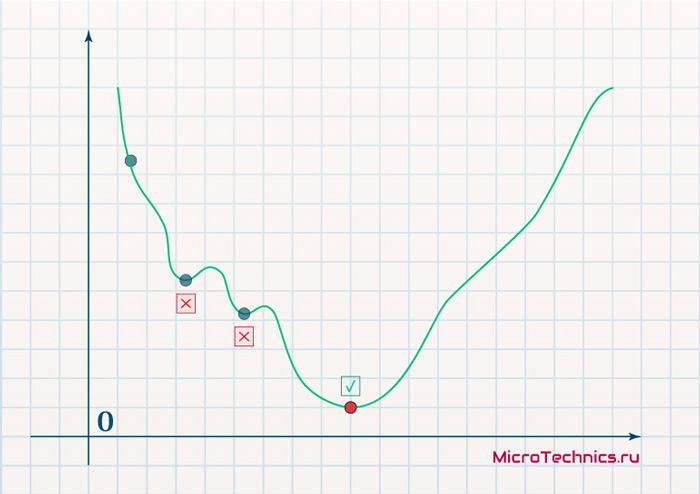
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
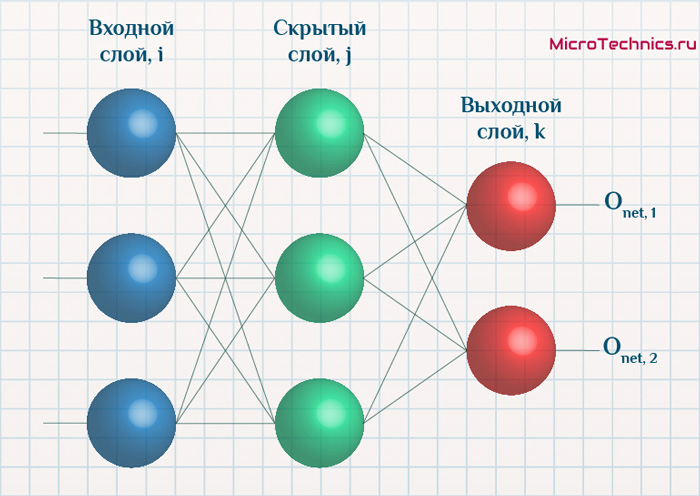
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины \Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (\frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | \bold{O_{net}} | \bold{O_{correct}} | \bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
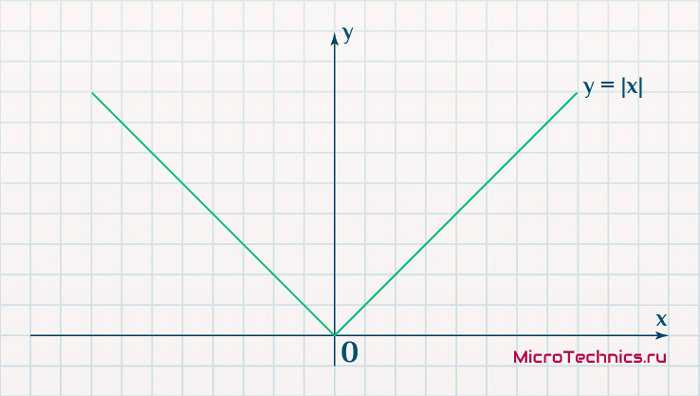
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: \frac{dE}{dw_{jk}} = \frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: \Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
\frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) \cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
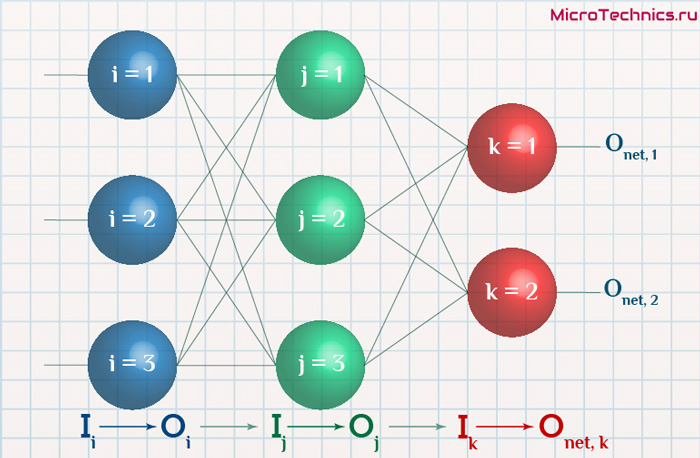
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{\Large{\prime}}(\sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что \sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k).
Итог: \frac{dE}{d w_{jk}} = -\delta_k \cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
\frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
Который примет следующий вид:
\delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
\frac{dE}{d w_{ij}} = -(\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j) \cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- скрытые слои: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Градиент: \frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
- Корректировка весовых коэффициентов: \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
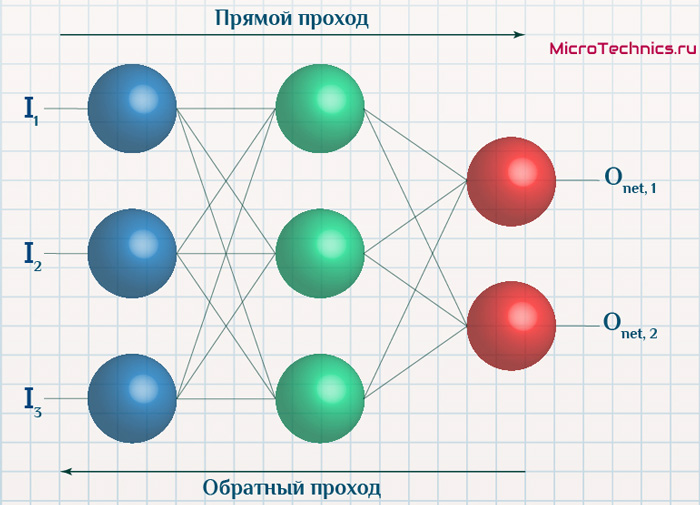
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: \delta_k = (O_{correct, k} — O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- для скрытых: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Далее используем полученные значения для расчета \Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij \medspace new} = w_{ij} + \Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
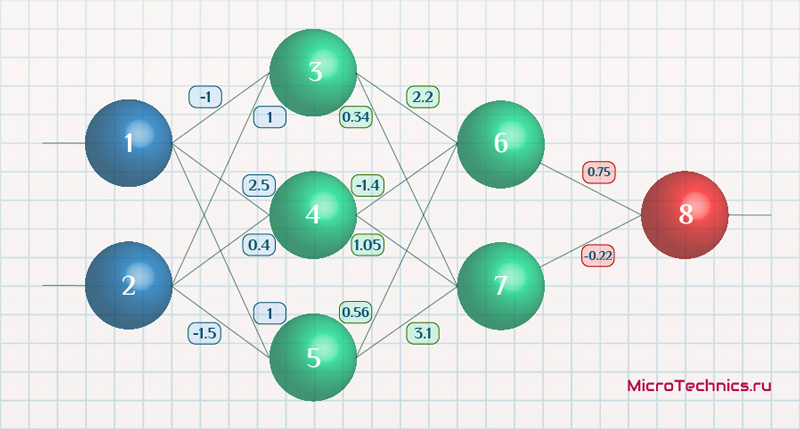
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = \frac{1}{1 + e^{-x}}
И ее производная:
f{\Large{\prime}}(x) = f(x)\medspace (1\medspace-\medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения \alpha пусть будет равна 0.3, момент — \gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \\ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 \cdot w_{13} + O_2 \cdot w_{23} = 0.6 \cdot (-1\medspace) + 0.7 \cdot 1 = 0.1 \\
I_4 = 0.6 \cdot 2.5 + 0.7 \cdot 0.4 = 1.78 \\
I_5 = 0.6 \cdot 1 + 0.7 \cdot (-1.5\medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3\medspace) = 0.52 \\ O_4 = 0.86\\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 \cdot w_{36} + O_4 \cdot w_{46} + O_5 \cdot w_{56} = 0.52 \cdot 2.2 + 0.86 \cdot (-1.4\medspace) + 0.39 \cdot 0.56 = 0.158 \\
I_7 = 0.52 \cdot 0.34 + 0.86 \cdot 1.05 + 0.39 \cdot 3.1 = 2.288 \\
O_6 = f(I_6) = 0.54 \\
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 \cdot w_{68} + O_7 \cdot w_{78} = 0.54 \cdot 0.75 + 0.908 \cdot (-0.22\medspace) = 0.205 \\
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
\delta_8 = (O_{correct} - O_{net}) \cdot f{\Large{\prime}}(I_8) = (O_{correct} - O_{net}) \cdot f(I_8) \cdot (1-f(I_8)) = (0.9 - 0.551\medspace) \cdot 0.551 \cdot (1-0.551\medspace) = 0.0863 \\
\delta_7 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_7) = (\delta_8 \cdot w_{78}) \cdot f{\Large{\prime}}(I_7) = 0.0863 \cdot (-0.22\medspace) \cdot 0.908 \cdot (1 - 0.908\medspace) = -0.0016 \\
\delta_6 = 0.086 \cdot 0.75 \cdot 0.54 \cdot (1 - 0.54\medspace) = 0.016 \\
\delta_5 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_5) = (\delta_7 \cdot w_{57} + \delta_6 \cdot w_{56}) \cdot f{\Large{\prime}}(I_7) = (-0.0016 \cdot 3.1 + 0.016 \cdot 0.56) \cdot 0.39 \cdot (1 - 0.39\medspace) = 0.001 \\
\delta_4 = (-0.0016 \cdot 1.05 + 0.016 \cdot (-1.4)) \cdot 0.86 \cdot (1 - 0.86\medspace) = -0.003 \\
\delta_3 = (-0.0016 \cdot 0.34 + 0.016 \cdot 2.2) \cdot 0.52 \cdot (1 - 0.52\medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
Как вы помните, \Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
\Delta w_{78} = \alpha \cdot \delta_8 \cdot O_7 = 0.3 \cdot 0.0863 \cdot 0.908 = 0.0235 \\
\Delta w_{68} = 0.3 \cdot 0.0863 \cdot 0.54= 0.014 \\
\Delta w_{57} = \alpha \cdot \delta_7 \cdot O_5 = 0.3 \cdot (−0.0016\medspace) \cdot 0.39= -0.00019 \\
\Delta w_{47} = 0.3 \cdot (−0.0016\medspace) \cdot 0.86= -0.0004 \\
\Delta w_{37} = 0.3 \cdot (−0.0016\medspace) \cdot 0.52= -0.00025 \\
\Delta w_{56} = \alpha \cdot \delta_6 \cdot O_5 = 0.3 \cdot 0.016 \cdot 0.39= 0.0019 \\
\Delta w_{46} = 0.3 \cdot 0.016 \cdot 0.86= 0.0041 \\
\Delta w_{36} = 0.3 \cdot 0.016 \cdot 0.52= 0.0025 \\
\Delta w_{25} = \alpha \cdot \delta_5 \cdot O_2 = 0.3 \cdot 0.001 \cdot 0.7= 0.00021 \\
\Delta w_{15} = 0.3 \cdot 0.001 \cdot 0.6= 0.00018 \\
\Delta w_{24} = \alpha \cdot \delta_4 \cdot O_2 = 0.3 \cdot (-0.003\medspace) \cdot 0.7= -0.00063 \\
\Delta w_{14} = 0.3 \cdot (-0.003\medspace) \cdot 0.6= -0.00054 \\
\Delta w_{23} = \alpha \cdot \delta_3 \cdot O_2 = 0.3 \cdot (−0.0087\medspace) \cdot 0.7= -0.00183 \\
\Delta w_{13} = 0.3 \cdot (−0.0087\medspace) \cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 \medspace new} = w_{78} + \Delta w_{78} = -0.22 + 0.0235 = -0.1965 \\
w_{68 \medspace new} = 0.75+ 0.014 = 0.764 \\
w_{57 \medspace new} = 3.1 + (−0.00019\medspace) = 3.0998\\
w_{47 \medspace new} = 1.05 + (−0.0004\medspace) = 1.0496\\
w_{37 \medspace new} = 0.34 + (−0.00025\medspace) = 0.3398\\
w_{56 \medspace new} = 0.56 + 0.0019 = 0.5619 \\
w_{46 \medspace new} = -1.4 + 0.0041 = -1.3959 \\
w_{36 \medspace new} = 2.2 + 0.0025 = 2.2025 \\
w_{25 \medspace new} = -1.5 + 0.00021 = -1.4998 \\
w_{15 \medspace new} = 1 + 0.00018 = 1.00018 \\
w_{24 \medspace new} = 0.4 + (−0.00063\medspace) = 0.39937 \\
w_{14 \medspace new} = 2.5 + (−0.00054\medspace) = 2.49946 \\
w_{23 \medspace new} = 1 + (−0.00183\medspace) = 0.99817 \\
w_{13 \medspace new} = -1 + (−0.00157\medspace) = -1.00157\\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Понятие локальных минимумов в обучении нейронных сетей
Добавлено 15 февраля 2020 в 19:38
В данной статье обсуждается сложность, которая может помешать нашему перцептрону достичь адекватной точности классификации.
В серии статей о нейронных сетях мы охватили широкий круг вопросов, связанных с пониманием и разработкой нейронных сетей многослойный перцептрон. Прежде чем читать эту статью о локальных минимумах, ознакомьтесь с остальными статьями выше, в меню с содержанием.
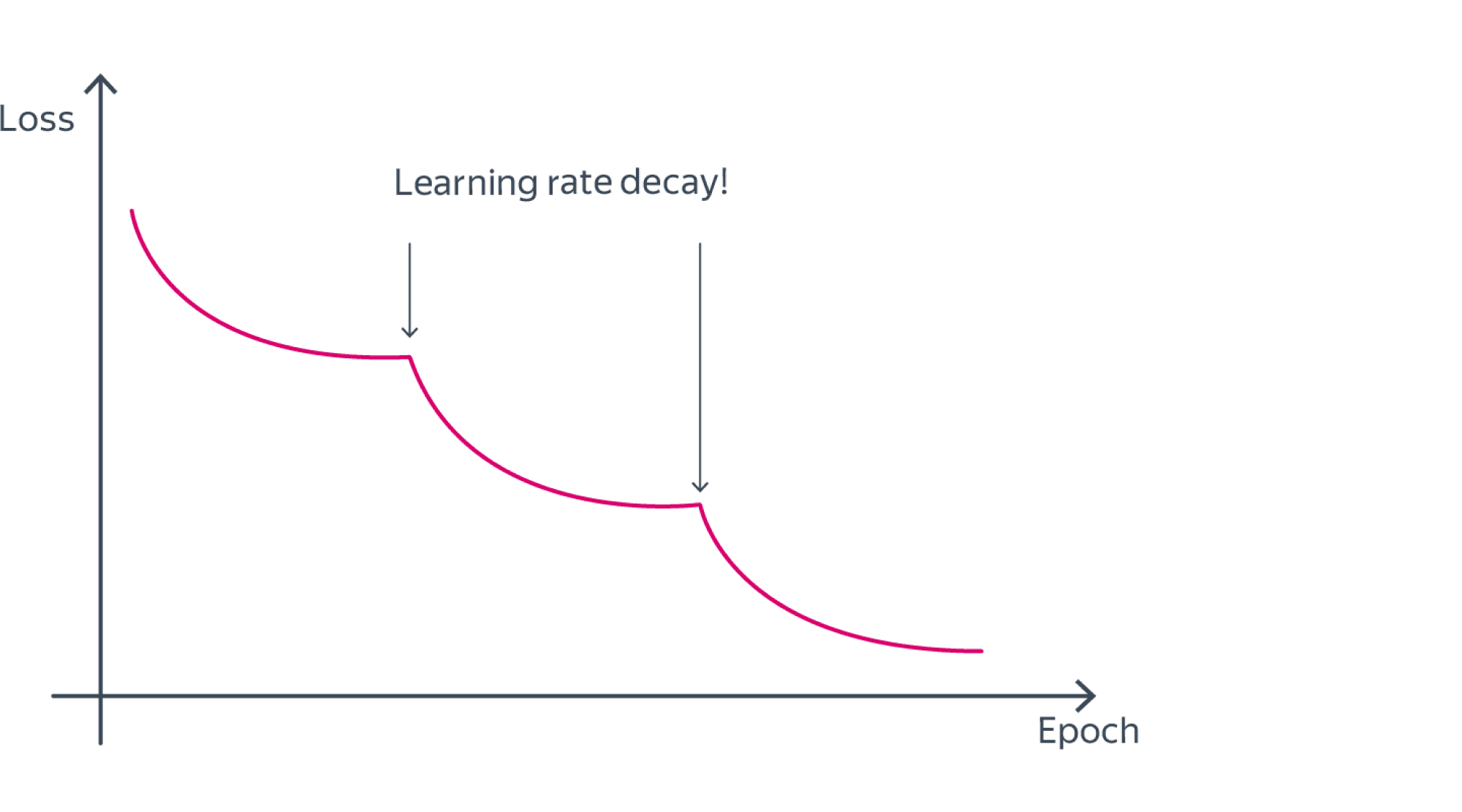
Обучение нейронной сети – сложный процесс. К счастью, нам не нужно понимать его идеально, чтобы извлечь пользу: архитектуры нейросетей и процедуры обучения, которые мы используем, действительно приводят к работоспособным системам, которые достигают очень высокой точности классификации. Тем не менее, есть один теоретический аспект обучения, который, хотя и несколько труден для понимания, но заслуживает нашего внимания.
Мы назовем это «проблемой локальных минимумов».
Почему локальные минимумы заслуживают нашего внимания?
Ну… я не уверен. Когда я впервые узнал о нейронных сетях, у меня сложилось впечатление, что локальные минимумы действительно являются серьезным препятствием для успешного обучения, по крайней мере, когда мы имеем дело со сложными связями вход-выход. Тем не менее, я считаю, что недавние исследования преуменьшают важность локальных минимумов. Возможно, новые структуры нейросетей и методы обработки позволили смягчить остроту проблемы, или, возможно, мы просто стали лучше понимать, как нейронные сети на самом деле переходят к необходимому решению.
Мы вернемся к текущему состоянию локальных минимумов в конце этой статьи. А пока я отвечу на свой вопрос следующим образом: локальные минимумы заслуживают нашего внимания, потому что:
- во-первых, они помогают нам глубже задуматься о том, что действительно происходит, когда мы обучаем нейросеть с помощью градиентного спуска;
- и, во-вторых, потому что локальные минимумы считаются (или, по крайней мере, считались) серьезным препятствием для успешного внедрения нейронных сетей в реальных системах.
Что такое локальный минимум?
В части 5 мы рассмотрели «чашу ошибки», показанную ниже, и я описал обучение как, по сути, стремление к самой нижней точке в этой чаше.
Примечание: в данной статье мои изображения и объяснения будут опираться на наше интуитивное понимание трехмерных структур, но следует помнить, что общие понятия не ограничиваются трехмерными отношениями. На самом деле мы часто используем нейронные сети, размерность которых намного превышает две входных переменных и одну выходную переменную.
Если бы вы прыгали в эту чашу, вы бы каждый раз скользили вниз. Независимо от того, откуда вы начнете, вы окажетесь в самой нижней точке всей функции ошибки. Эта самая низкая точка является глобальным минимумом. Когда нейросеть приблизилась к этому глобальному минимуму, она оптимизировала свою способность классифицировать обучающие данные, и теоретически это является основной целью обучения: продолжать изменять веса до тех пор, пока не будет достигнут глобальный минимум.
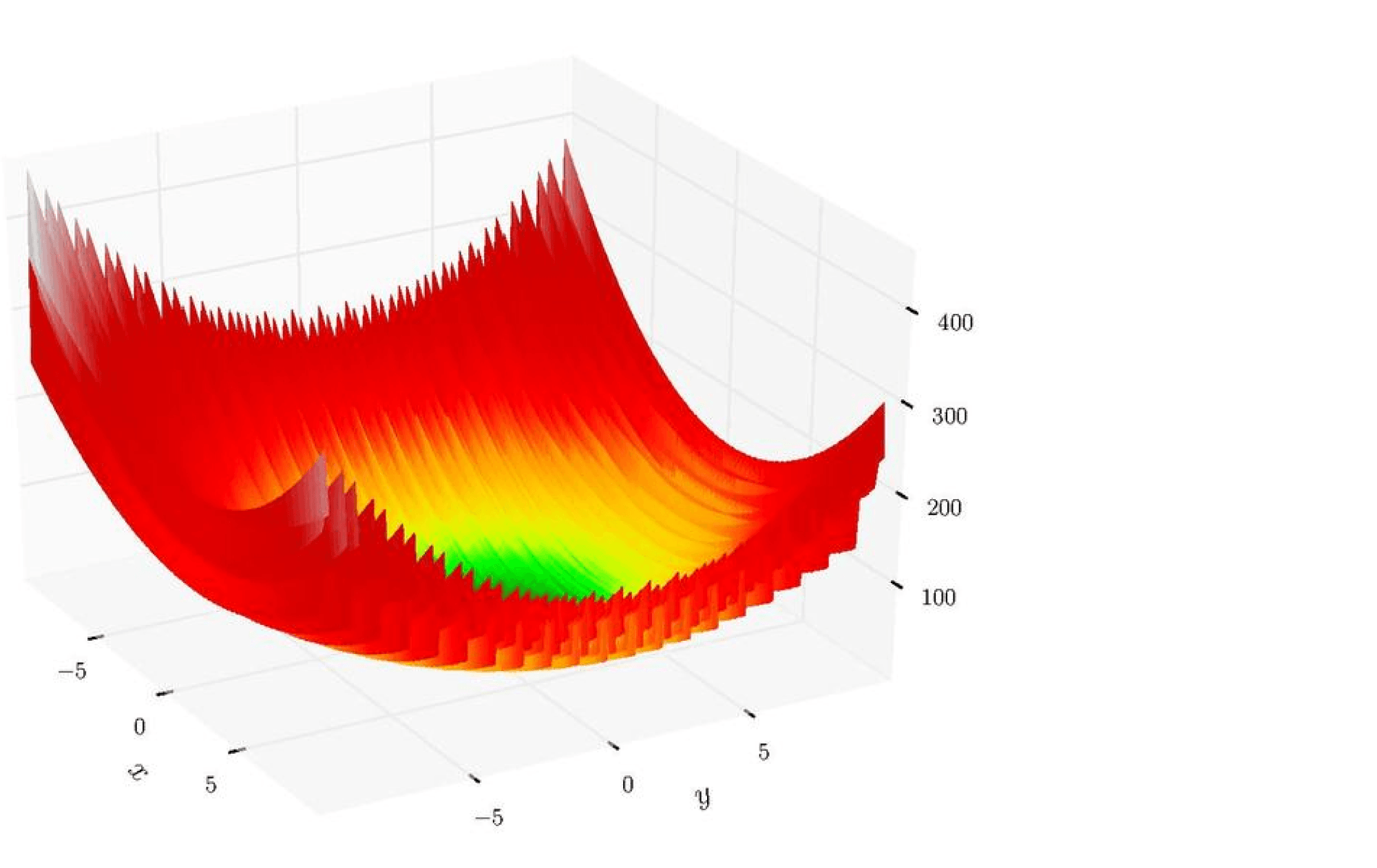
Однако мы знаем, что нейронные сети способны аппроксимировать чрезвычайно сложные связи вход-выход. Показанная выше чаша ошибки не совсем подходит под категорию «чрезвычайно сложных». Это просто график функции \(f(x,y) = x^2 + y^2\)
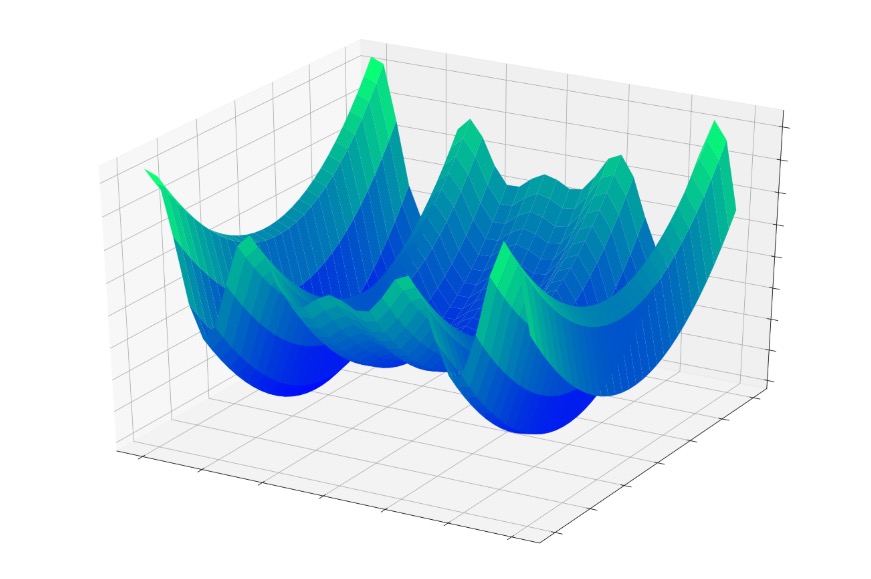
Но теперь представьте, что функция ошибки выглядит примерно так:
Или так:
Или так:
Если вы прыгали в одну из этих функций случайным образом, вы часто скатывались бы к локальному минимуму. Вы бы находились в самой низкой точке локализованной части графика, но, возможно, вы не приблизились бы к глобальному минимуму.
То же самое может случиться с нейронной сетью. Градиентный спуск зависит от локальной информации, которая, как мы надеемся, приведет нейросеть к глобальному минимуму. У нейросети нет предварительных знаний о характеристиках всей поверхности ошибки, и, следовательно, когда она достигает точки, которая кажется нижней частью поверхности ошибки на основе локальной информации, она не может вытащить топографическую карту и определить, что ей нужно подняться в гору и перейти ее, чтобы найти точку, которая на самом деле ниже, чем все остальные.
Когда мы реализуем базовый градиентный спуск, мы говорим нейросети: «Найди дно поверхности ошибки и оставайся там». Мы не говорим: «Найди дно поверхности ошибки, запиши свои координаты, а затем продолжай идти вверх и вниз, пока не найдешь следующее дно. Дай мне знать, когда закончишь».
Действительно ли мы хотим найти глобальный минимум?
Разумно предположить, что глобальный минимум представляет собой оптимальное решение, и сделать вывод о том, что локальные минимумы создают проблемы, поскольку обучение может «затормозиться» локальным минимумом, а не продолжать поиск глобального минимума.
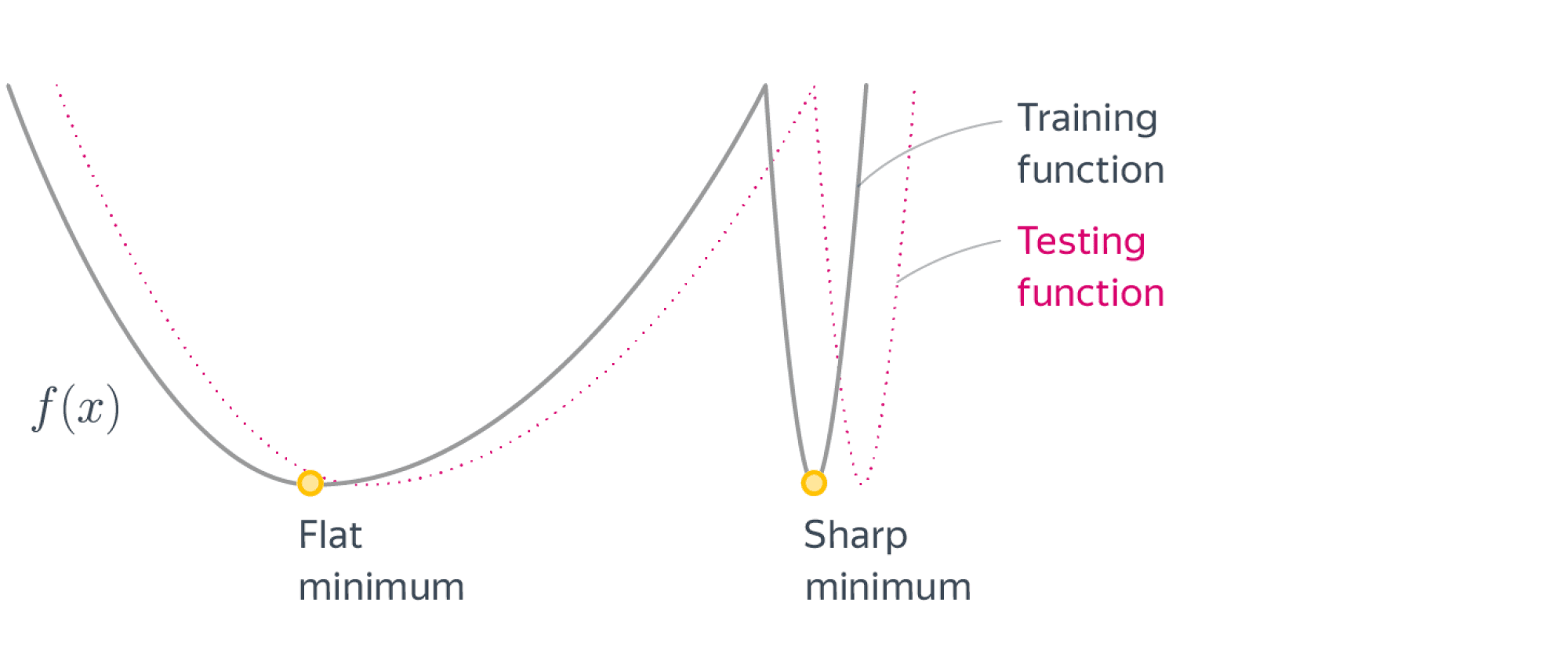
Я думаю, что это предположение справедливо во многих случаях, но сравнительно недавнее исследование поверхностей потерь нейронных сетей предполагает, что сети высокой сложности могут на самом деле извлечь выгоду из локальных минимумов, потому что сеть, которая находит глобальный минимум, будет перетренирована и, следовательно, будет менее эффективна при обработке новых входных выборок.
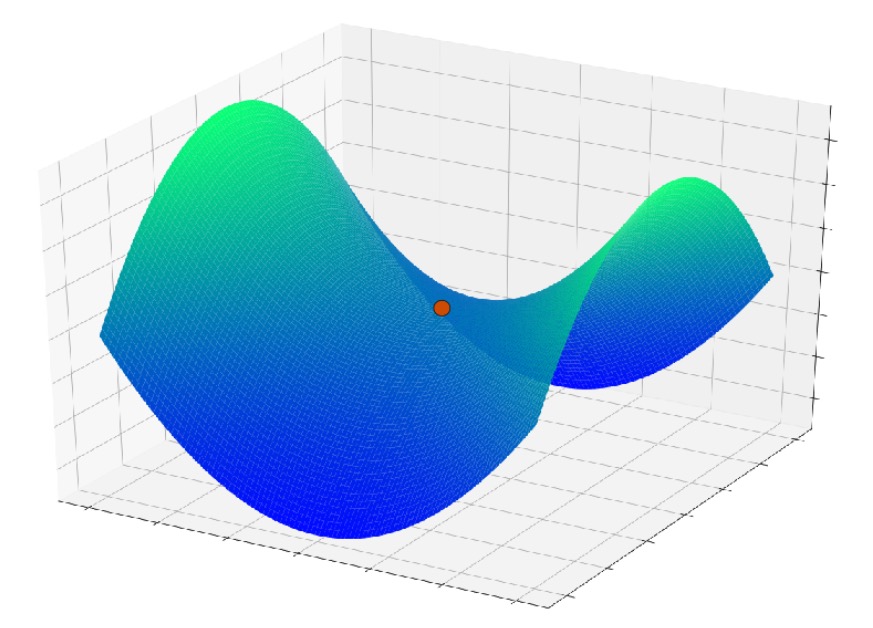
Еще одна проблема, которая здесь возникает, – это особенность поверхности, называемая точкой перевала; вы можете увидеть пример на графике ниже. Вполне возможно, что в контексте реальных приложений на нейронных сетях точки перевала на поверхности функции ошибки на самом деле являются более серьезной проблемой, чем локальные минимумы.
Заключение
Я надеюсь, что вам понравилось это обсуждение локальных минимумов. В следующей статье мы обсудим некоторые методы, которые помогают нейронной сети достичь глобального минимума (если мы действительно этого хотим).
Теги
Локальный минимумМашинное обучение / Machine LearningНейросеть / Нейронная сетьПерцептрон / PerceptronЧаша ошибки
Введение
Зачастую задачи машинного обучения формулируются таким образом, что «веса» модели, которую мы строим, возникают, как решение оптимизационной задачи. В качестве VIP-примера рассмотрим задачу линейной регрессии:
$$
\Vert y — Xw \Vert_2^2 \to \min_w,
$$
По сути, мы получили чистейшую задачу квадратичной оптимизации. В чем особенность конкретно этой задачи? Она выпуклая.
Для интересующихся определением.
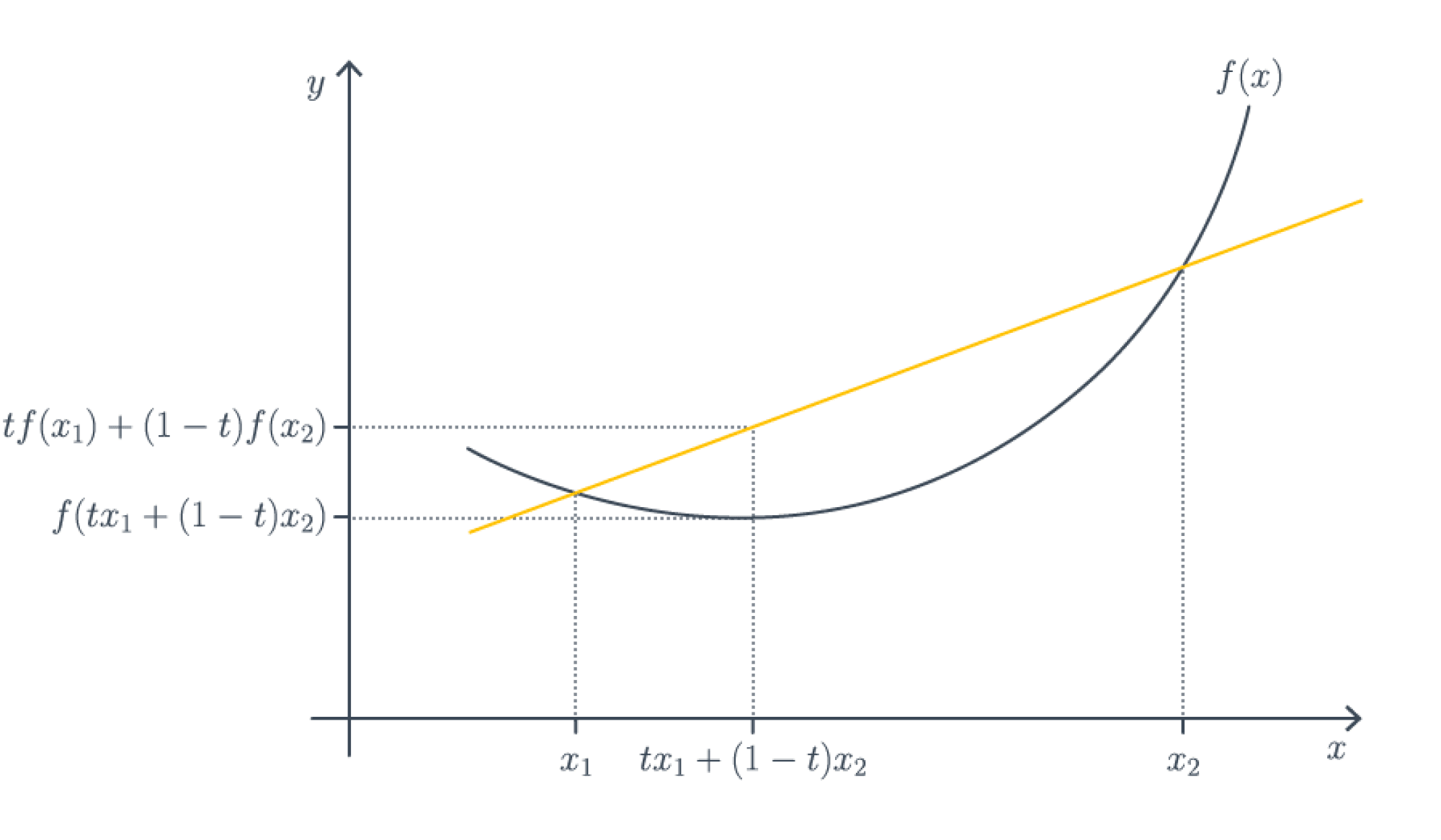
Функция $f \colon \mathbb{R}^d \to \mathbb{R}$ является (нестрого) выпуклой (вниз), если для любых $x_1,x_2 \in \mathbb{R}^d$ верно, что
$$
\forall t \in [0,1] : f(tx_1 + (1-t)x_2) \leq t f(x_1) + (1-t) f(x_2).
$$
Чтобы запомнить, в какую сторону неравенство, всегда полезно рисовать следующую картинку с графическим определением выпуклой функции.
Эквивалентное определение, если функция достаточно гладкая – гессиан неотрицательно определен в любой точке, то есть в каждой точке функция хорошо приближается параболоидом ветвями вверх. Отсюда по критерию минимальности второго порядка автоматически следует, что всякая точка локального оптимума является точкой локального минимума, то есть локальных максимумов и сёдел в выпуклом мире попросту не существует.
Важное свойство выпуклых функций – локальный минимум автоматически является глобальным (но не обязательно единственным!). Это позволяет избегать уродливых ситуаций, которые с теоретической точки зрения могут встретиться в невыпуклом случае, например, вот такой:
Теорема (No free lunch theorem) Пусть $A$ – алгоритм оптимизации, использующий локальную информацию (все производные в точке). Тогда существует такая невыпуклая функция $f \colon [0,1]^d \to [0,1]$, что для нахождения глобального минимума на квадрате $[0,1]^d$ с точностью $\frac{1}{m}$ требуется совершить хотя бы $m^d$ шагов.
Для интересующихся доказательствами.
Будем строить наш контрпример, пользуясь принципом сопротивляющегося оракула (или рассуждениями с противником, кому как привычнее называть).
Разделим нашу область на подкубики размера $1/m \times \ldots \times 1/m$. Зададим функцию следующим образом – она будет тождественно равна $1$ на всех кубиках, кроме одного, в середине которого будет точка с значением $0$ (мы не специфицируем, как значение будет гладко «снижаться» до $0$; можно построить кусочно-линейную функцию, а потом сгладить её).
А именно поставим ноль в тот кубик, который наш алгоритм оптимизации $A$ посетит последним. Так как кубиков у нас $m^d$, то алгоритм должен всегда совершить как минимум $m^d$ шагов, попробовав все кубики. Итого у нас следующая картинка ($m=3, d=2$):
Отметим дополнительно, что полученный контрпример можно сделать какой угодно гладкости (но не аналитическим).
Мы видим, что в общем случае без выпуклости нас ожидает полное разочарование. Ничего лучше перебора по сетке придумать в принципе невозможно. В выпуклом случае же существуют алгоритмы, которые находят глобальный минимум за разумное время.
Встречаются ли в жизни функции невыпуклые? Повсеместно! Например, функция потерь при обучении нейронных сетей, как правило, не является выпуклой. Но отсюда не следует, что любой алгоритм их оптимизации будет обязательно неэффективным: ведь «контрпример» из теоремы довольно специфичен. И, как мы увидим, оптимизировать невыпуклые функции очень даже возможно.
Найти глобальный минимум невыпуклой функции – очень трудная задача, но зачастую нам хватает локального, который является, в частности, стационарной точкой: такой, в которой производная равна нулю. Все теоретические результаты в случае невыпуклых задач, как правило, касаются поиска таких точек, и алгоритмы тоже направлены на их отыскание.
Этим объясняется и то, что большинство алгоритмов оптимизации, придуманных для выпуклого случая, дословно перешли в невыпуклый. Теоретическая причина в следующем: в выпуклом случае поиск стационарной точки и поиск минимума – буквально одна и та же задача, поэтому то, что хорошо ищет минимум в выпуклом случае, ожидаемо будет хорошо искать стационарные точки в невыпуклом. Практическая же причина в том, что оптимизаторы в библиотеках никогда не спрашивают, выпуклую ли им функцию подают на вход, а просто работают и работают хорошо.
Внимательный читатель мог возразить на моменте подмены задачи: подождите-ка, мы ведь хотим сделать функцию как можно меньше, а не стационарную точку искать какую-то непонятную. Доказать в невыпуклом случае тут, к сожалению, ничего невозможно, но на практике мы снова используем алгоритмы изначально для выпуклой оптимизации. Почему?
Причина номер 1: сойтись в локальный минимум лучше, чем никуда. Об этом речь уже шла.
Причина номер 2: в окрестности локального минимума функция становится выпуклой, и там мы сможем быстро сойтись.
Причина номер 3: иногда невыпуклая функция является в некотором смысле «зашумленной» версией выпуклой или похожей на выпуклую. Например, посмотрите на эту картинку (функция Леви):
У этой функции огромное количество локальных минимумов, но «глобально» она кажется выпуклой. Что-то отдаленно похожее наблюдается и в случае нейронных сетей. Нашей задачей становится не скатиться в маленький локальный минимум, который всегда рядом с нами, а в большую-большую ложбину, где значение функции минимально и в некотором смысле стабильно.
Причина номер 4: оказывается, что градиентные методы весьма часто сходятся именно к локальным минимумам.
Сразу отметим важную разницу между выпуклой и невыпуклой задачами: в выпуклом случае работа алгоритма оптимизации не очень существенно зависит от начальной точки, поскольку мы всегда скатимся в точку оптимума. В невыпуклом же случае правильно выбранная точка старта – это уже половина успеха.
Теперь перейдём к разбору важнейших алгоритмов оптимизации.
Градиентный спуск (GD)
Опишем самый простой метод, который только можно придумать – градиентный спуск. Для того, чтобы его определить, вспомним заклинание из любого курса матанализа: «градиент – это направление наискорейшего локального возрастания функции», тогда антиградиент – это направление наискорейшего локального убывания.
Для интересующихся формализмом.
Воспользуемся формулой Тейлора для $\Vert h \Vert = 1$ (направления спуска):
$$
f(x + \alpha h) = f(x) + \alpha \langle \nabla f(x), h \rangle + o(\alpha).
$$
Мы хотим уменьшить значение функции, то есть
$$
f(x) + \alpha \langle \nabla f(x), h \rangle + o(\alpha) < f(x).
$$
При $\alpha \to 0$ имеем $\langle \nabla f(x), \Delta x \rangle \leq 0$. Более того, мы хотим наискорешйшего убывания, поэтому это скалярное произведение хочется минимизировать. Сделаем это при помощи неравенства Коши-Буняковского:
$$
\langle \nabla f(x), h \rangle \geq — \Vert \nabla f(x) \Vert_2 \Vert h \Vert_2 = \Vert \nabla f(x) \Vert_2.
$$
Равенство в неравенстве Коши-Буняковского достигается при пропорциональности аргументов, то есть
$$
h = — \frac{\nabla f(x)}{\Vert \nabla f(x) \Vert_2}.
$$
$$\tag*{$\blacksquare$}$$
Тогда пусть $x_0$ – начальная точка градиентного спуска. Тогда каждую следующую точку мы выбираем следующим образом:
$$
x_{k+1} = x_k — \alpha \nabla f(x_k),
$$
где $\alpha$ – это размер шага (он же learning rate). Общий алгоритм градиентного спуска пишется крайне просто и элегантно:
x = normal(0, 1) # можно пробовать и другие виды инициализации
repeat S times: # другой вариант: while abs(err) > tolerance
h = grad_f(x) # вычисляем направление спуска
x -= alpha * h # обновляем значение в точке
Эту схему в приложении к линейной регрессии можно найти в главе про линейные модели.
После всего этого начинаются тонкости:
- А как вычислять градиент?
- А как выбрать размер шага?
- А есть ли какие-то теоретические оценки сходимости?
Начнем разбирать вопросы постепенно. Для вычисления градиентов современный человек может использовать инструменты автоматического дифференцирования. Идейно, это вариация на тему алгоритма обратного распространения ошибки (backpropagation), ведь как правило человек задает функции, составленные из элементарных при помощи умножений/делений/сложений/композиций. Такой метод реализован во всех общих фреймворках для нейронных сетей (Tensorflow, PyTorch, Jax).
Но, вообще говоря, возникает некоторая тонкость. Например, расмотрим задачу линейной регрессии. Запишем её следующим образом:
$$
f(w) = \frac{1}{N} \sum_{i=1}^N (w^\top x_i — y_i)^2.
$$
Видим, что слагаемых суммарно $N$ – размер выборки. При $N$ порядка $10^6$ и $d$ (это количество признаков) порядка $10^4$ вычисление градиента за $O(Nd)$ становится жутким мучением. Но если от $d$ избавиться без дополнительных предположений (например, о разреженности) нельзя, то с зависимостью от $N$ в каком-то смысле удастся разделаться при помощи метода стохастического градиентного спуска.
Хранение градиентов тоже доставит нам проблемы. У градиента столько же компонент, сколько параметров у модели, и если мы имеем дело с глубокой нейросетью, это даст значительные затраты дополнительной памяти. Хуже того, метод обратного распространения ошибки устроен так, что нам приходится помнить все промежуточные представления для вычисления градиентов. Поэтому вычислить градиент целиком невозможно ни для какой нормальной нейросети, и от этой беды тоже приходится спасаться с помощью стохастического градиентного спуска.
Теперь перейдем к размеру шага. Теория говорит о том, что если функция гладкая, то можно брать достаточно маленький размер шага, где под достаточно маленьким подразумевается $\alpha \leq \frac1L$, где $L$ – некоторая константа, которая зависит от гладкости задачи (так называемая константа Липшица). Вычисление этой константы может быть задачей сложнее, чем изначальная задача оптимизации, поэтому этот вариант нам не годится. Более того, эта оценка крайне пессимистична – мы ведь хотим размер шага как можно больше, чтобы уменьшить функцию как можно больше, а тут мы будем изменять все очень мало.
Существует так называемый метод наискорейшего спуска: выбираем размер шага так, чтобы как можно сильнее уменьшить функцию:
$$
\alpha_k = \arg\min_{\alpha \geq 0} f(x_k — \alpha \nabla f(x_k)).
$$
Одномерная оптимизация является не сильно сложной задачей, поэтому теоретически мы можем её совершать (например, методом бинарного/тернарного поиска или золотого сечения), можно этот шаг также совершать неточно. Но сразу стоит заметить, что это можно делать, только если функция $f$ вычислима более-менее точно за разумное время, в случае линейной регрессии это уже не так (не говоря уже о нейронных сетях).
Также есть всевозможные правила Армихо/Гольдштейна/Вульфа и прочее и прочее, разработанные в давние 60-е, и для их проверки требуется снова вычислять значения функции в точке. Желающие могут посмотреть на эти условия на википедии. Про более хитрые вариации выбора шагов мы поговорим позже, но сразу стоит сказать, что эта задача довольно сложная.
По поводу теории: сначала скажем что-то про выпуклый случай.
В максимально общем выпуклом случае без дополнительных предположений оценки для градиентного спуска крайне и крайне пессимистичные: чтобы достичь качества $\varepsilon$, то есть
$$\vert f(x_k) — f(x^*) \vert\leq \varepsilon $$
достаточно сделаеть $O(R^2/\varepsilon^2)$ шагов, где $R^2$ — это расстояние от $x_0$ до $x^*$. Выглядит очень плохо: ведь чтобы достичь точности $10^{-2}$, необходимо сделать порядка $10^4$ шагов градиентного спуска. Но на практике такого не происходит, потому что на самом деле верны разные предположения, дающие более приятные свойства. Для контраста, укажем оценку в случае гладкой и сильно выпуклой в точке оптимума функции: за $k$ шагов будет достигнута точность
$$
O\left( \min\left\{R^2 \exp
\left(-\frac{k}{4\kappa}\right), \frac{R^2}{k} \right\}\right),
$$
где $\kappa$ – это так называемое число обусловленности задачи. По сути, это число измеряет, насколько линии уровня функции вытянуты в окрестности оптимума.
Морали две:
- Скорость сходимости градиентного спуска сильно зависит от обусловленности задачи;
- Также она зависит от выбора хорошей точки старта, ведь везде входит расстояние от точки старта до оптимума.
В качестве ссылки на доказательство укажем на работу Себастиана Стича, где оно довольно простое и общее.
В невыпуклом же случае все куда хуже с точки зрения теории: требуется порядка $O(1/\varepsilon^2)$ шагов в худшем случае даже для гладкой функции, где $\varepsilon$ – желаемая точность уменьшения нормы градиента.
Стохастический градиентный спуск (SGD)
Теперь мы попробуем сэкономить в случае регрессии и подобных ей задач. Будем рассматривать функционалы вида
$$
f(x) = \sum_{i=1}^N \mathcal{L}(x, y_i),
$$
где сумма проходится по всем объектам выборки (которых может быть очень много). Теперь сделаем следующий трюк: заметим, что это усреднение – это по сути взятие матожидания. Таким образом, мы говорим, что наша функция выглядит как
$$
f(x) = \mathbb{E}[\mathcal{L}(x, \xi)],
$$
где $\xi$ равномерно распределена по обучающей выборке. Задачи такого вида возникают не только в машинном обучении; иногда встречаются и просто задачи стохастического программирования, где происходит минимизация матожидания по неизвестному (или слишком сложному) распределению.
Для функционалов такого вида мы также можем посчитать градиент, он будет выглядеть довольно ожидаемо:
$$
\nabla f(x) = \mathbb{E} \nabla \mathcal{L}(x, \xi).
$$
Будем считать, что вычисление матожидания напрямую невозможно.
Новый взгляд из статистики дает возможность воспользоваться классическим трюком: давайте подменим матожидание на его несмещенную Монте-Карло оценку. Получается то, что можно назвать стохастическим градиентом:
$$
\tilde \nabla f(x) = \frac{1}{B} \sum_{i=1}^B \nabla \mathcal{L}(x, \xi_i).
$$
Говоря инженерным языком, мы подменили вычисление градиента по всей выборке вычислением по случайной подвыборке. Подвыборку $\xi_1,\ldots,\xi_B$ часто называют (мини)батчем, а число $B$ – размерном батча.
По-хорошему, наука предписывает нам каждый раз независимо генерировать батчи, но это трудно с вычислительной точки зрения. Вместо этого воспользуемся следующим приёмом: сначала перемешаем нашу выборку (чтобы внести дополнительную случайность), а затем будем рассматривать последовательно блоки по $B$ элементов выборки. Когда мы просмотрели всю выборку – перемешиваем еще раз и повторяем проход. Очередной прогон по обучающей выборке называется эпохой. И, хотя, казалось бы, независимо генерировать батчи лучше, чем перемешивать лишь между эпохами, есть несколько результатов, демонстрирующих обратное: одна работа и вторая (более новая); главное условие успеха – правильно изменяющийся размер шага.
Получаем следующий алгоритм, называемый стохастическим градиентным спуском (stochastic gradient descent, SGD):
x = normal(0, 1) # инициализация
repeat E times: # цикл по количеству эпох
for i = 0; i <= N; i += B:
batch = data[i:i+B]
h = grad_loss(batch).mean() # вычисляем оценку градиента как среднее по батчу
x -= alpha * h
Дополнительное удобство такого подхода – возможность работы с внешней памятью, ведь выборка может быть настолько большой, что она помещается только на жёсткий диск. Сразу отметим, что в таком случае $B$ стоит выбирать достаточно большим: обращение к данным с диска всегда медленнее, чем к данным из оперативной памяти, так что лучше бы сразу забирать оттуда побольше.
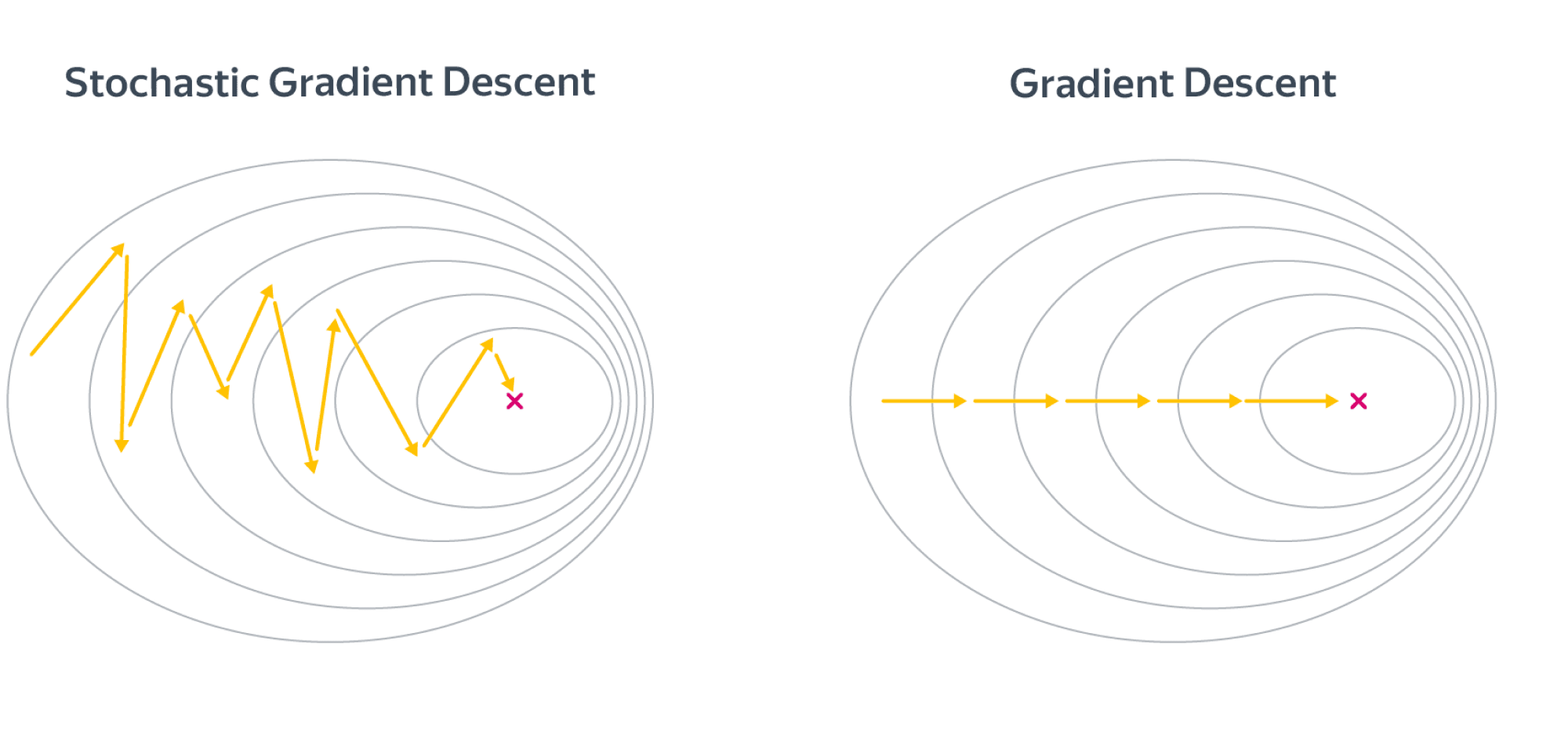
Поскольку стохастические градиенты являются лишь оценками истинных градиентов, SGD может быть довольно шумным:
Поэтому если вы обучаете глубокую нейросеть и у вас в память влезает лишь батч размером с 2-4 картинки, модель, возможно, ничего хорошего не сможет выучить. Аппроксимация градиента и поведение SGD может стать лучше с ростом размера батча $B$ – и обычно его действительно хочется подрастить, но парадоксальным образом слишком большие батчи могут порой испортить дело (об этом дальше в этой главе!).
Теоретический анализ
Теперь перейдем к теоретической стороне вопроса. Сходимость SGD обеспечивается несмещенностью стохастического градиента. Несмотря на то, что во время итераций копится шум, суммарно он зачастую оказывается довольно мал.
Теперь приведем оценки. Сначала, по традиции, в выпуклом случае. Для выпуклой функции потерь за $k$ шагов будет достигнута точность порядка
$$
O\left( \min\left\{R^2 \exp
\left(-\frac{k}{4\kappa} \right)+ \frac{\sigma^2}{\mu k}, \frac{R^2}{k} + \frac{\sigma^2 R}{\sqrt{k}} \right\}\right),
$$
где $\sigma^2$ – это дисперсия стохградиента, а $\mu$ – константа сильной выпуклости, показывающая, насколько функция является «не плоской» в окрестности точки оптимума. Доказательство в том же препринте С. Стича.
Мораль в следующем: дисперсия стохастического градиента, вычисленного по батчу размера $B$ равна $\sigma_0^2/B$, где $\sigma_0^2$ – это дисперсия одного градиента. То есть увеличение размера батча помогает и с теоретической точки зрения.
В невыпуклом случае оценка сходимости SGD просто катастрофически плохая: требуется $O(1/\varepsilon^4)$ шагов для того, чтобы сделать норму градиента меньше $\varepsilon$. В теории есть всевозможные дополнительные способы снижения дисперсии с лучшими теоретическими оценками (Stochastic Variance Reduced Gradient (SVRGD), Spider, etc), но на практике они активно не используются.
Использование дополнительной информации о функции
Методы второго порядка
Основной раздел.
Постараемся усовершенствовать метод стохастического градиентного спуска. Сначала заметим, что мы используем явно не всю информацию об оптимизируемой функции.
Вернемся к нашему VIP-примеру линейной регресии с $\ell_2$ регуляризацией:
$$
\Vert y — Xw \Vert_2^2 + \lambda \Vert w \Vert_2^2 \to \min_w.
$$
Эта функция достаточно гладкая, и может быть неплохой идеей использовать её старшие производные для ускорения сходимости алгоритма. В наиболее чистом виде этой философии следует метод Ньютона и подобные ему; о них вы можете прочитать в соответствующем разделе. Отметим, что все такие методы, как правило, довольно дорогие (исключая L-BFGS), и при большом размере задачи и выборки ничего лучше вариаций SGD не придумали.
Проксимальные методы
Основной раздел.
К сожалению, не всегда функции такие красивые и гладкие. Для примера рассмотрим Lasso-регресию:
$$
\Vert y — Xw \Vert_2^2 + \lambda \Vert w \Vert_1 \to \min_w.
$$
Второе, не гладкое слагаемое резко ломает все свойства этой задачи: теоретически оценки для градиентного спуска становятся гораздо хуже (и на практике тоже). С другой стороны, регуляризационное слагаемое устроено очень просто, и эту дополнительную структурную особенность можно и нужно эксплуатировать. Методы решения задачи вида
$$
f(x) + h(x) \to \min_x,
$$
где $h$ – простая функция (в некотором смысле), а $f$ – гладкая, называются методами композитной оптимизации. Глубже погрузиться в них можно в соответствующем разделе, посвященном проксимальным методам.
Использование информации о предыдущих шагах
Следующая претензия к методу градиентного спуска – мы не используем информацию о предыдущих шагах, хотя, кажется, там может храниться что-то полезное.
Метод инерции, momentum
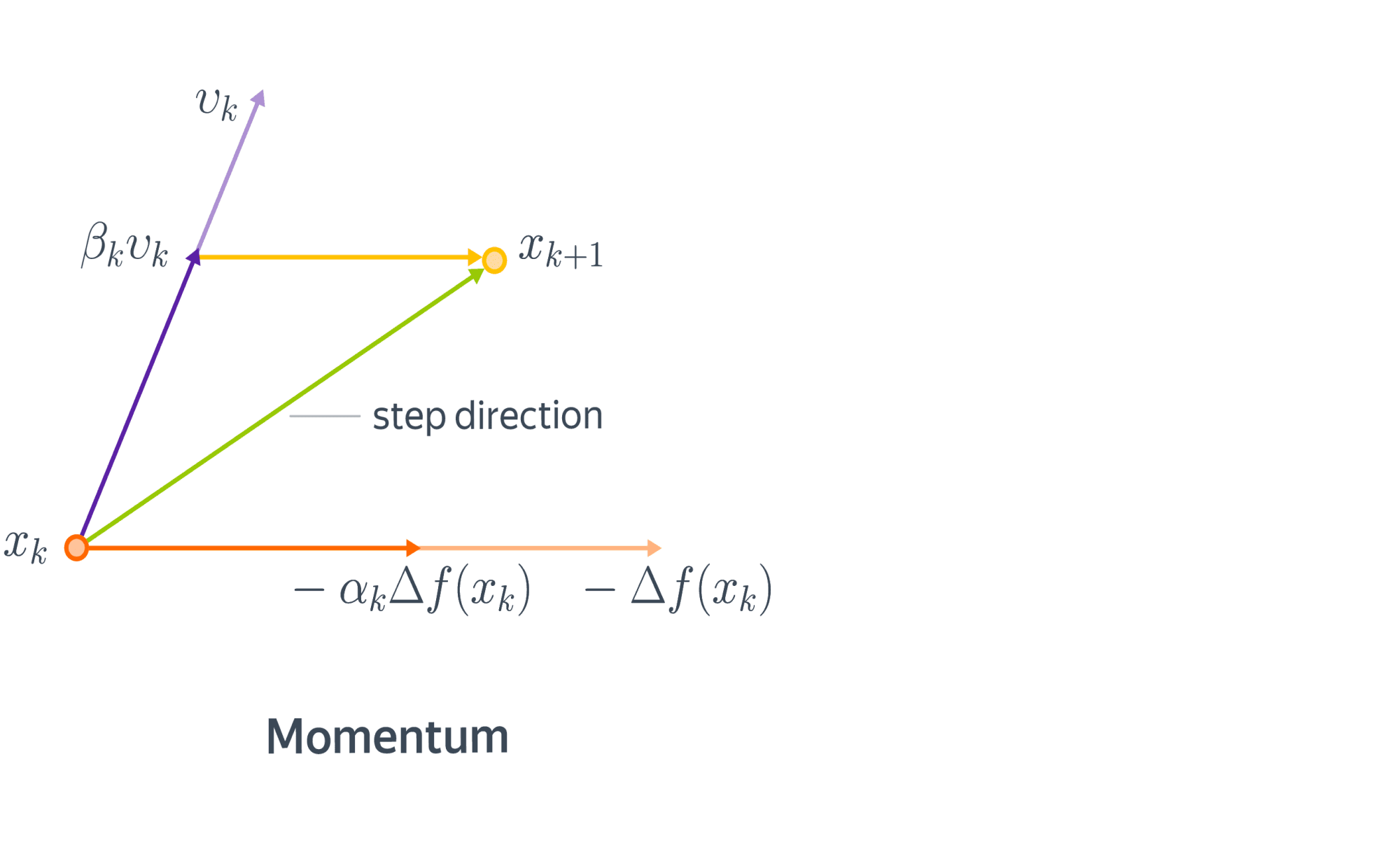
Начнем с физической аналогии. Представим себе мячик, который катится с горы. В данном случае гора – это график функции потерь в пространстве параметров нашей модели, а мячик – её текущее значение. Реальный мячик не застрянет перед небольшой кочкой, так как у него есть некоторая масса и уже накопленный импульс – некоторое время он способен двигаться даже вверх по склону. Аналогичный прием может быть использован и в градиентной оптимизации. В англоязычной литературе он называется Momentum.
С математической точки зрения, мы добавляем к градиентному шагу еще одно слагаемое:
$$
x_{k+1} = x_k — \alpha_k \nabla f(x_k) + \color{red}{\beta_k (x_k — x_{k-1})}.
$$
Сразу заметим, что мы немного усугубили ситуацию с подбором шага, ведь теперь нужно подбирать не только $\alpha_k$, но и $\beta_k$. Для обычного, не стохастического градиентного спуска мы можем адаптировать метод наискорейшего и получить метод тяжелого шарика:
$$
(\alpha_k, \beta_k) = \arg\min_{\alpha,\beta} f(x_k — \alpha \nabla f(x_k) + \beta (x_k — x_{k-1})).
$$
Но, увы, для SGD это работать не будет.
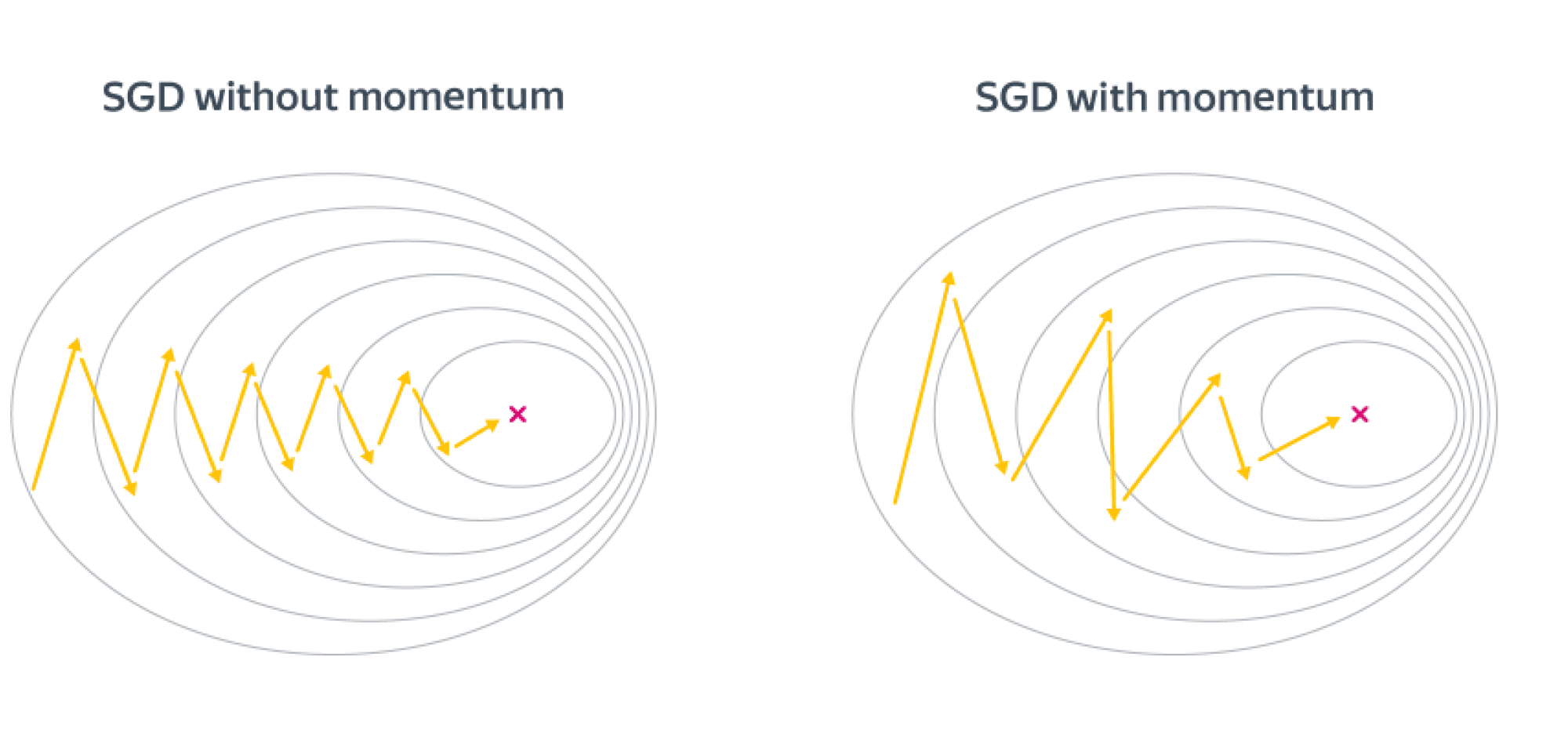
Выгода в невыпуклом случае от метода инерции довольно понятна – мы будем пропускать паразитные локальные минимумы и седла и продолжать движение вниз. Но выгода есть также и в выпуклом случае. Рассмотрим плохо обусловленную квадратичную задачу, для которой линии уровня оптимизируемой функции будут очень вытянутыми эллипсами, и запустим на SGD с инерционным слагаемым и без него. Направление градиента будет иметь существенную вертикальную компоненту, а добавление инерции как раз «погасит» паразитное направление. Получаем следующую картинку:
Также удобно бывает представить метод моментума в виде двух параллельных итерационных процессов:
$$\begin{align}
v_{k+1} &= \beta_k v_k — \alpha_k \nabla f(x_k)\
x_{k+1} &= x_k + v_{k+1}.
\end{align}
$$
Accelerated Gradient Descent (Nesterov Momentum)
Рассмотрим некоторую дополнительную модификацию, которая была предложена в качестве оптимального метода первого порядка для решения выпуклых оптимизационных задач.
Можно доказать, что в сильно выпуклом и гладком случае найти минимум с точностью $\varepsilon$ нельзя быстрее, чем за
$$
\Omega\left( R^2\exp\left(-\frac{k}{\sqrt{\kappa}}\right) \right)
$$
итераций, где $\kappa$ – число обусловленности задачи. Напомним, что для обычного градиентного спуска в экспоненте у нас был не корень из $\kappa$, а просто $\kappa$, то есть, градиентный спуск справляется с плохой обусловленностью задачи хуже, чем мог бы.
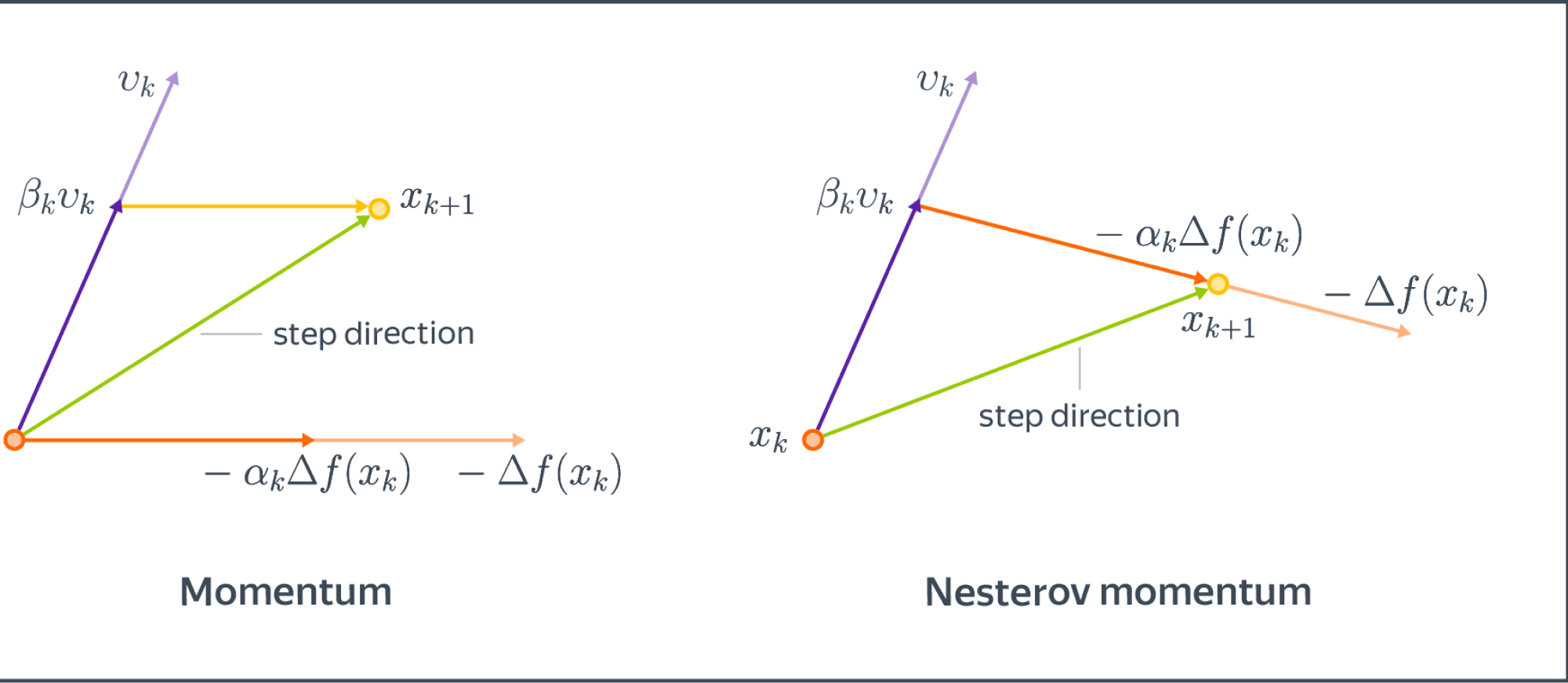
В 1983 году Ю.Нестеровым был предложен алгоритм, имеющий оптимальную по порядку оценку. Для этого модифицируем немного моментум и будем считать градиент не в текущей точке, а как бы в точке, в которую мы бы пошли, следуя импульсу:
$$\begin{align}
v_{k+1} &= \beta_k v_k — \alpha_k \nabla f(\color{red}{x_k + \beta_k v_k})\
x_{k+1} &= x_k + v_{k+1}
\end{align}
$$
Сравним с обычным momentum:
Комментарий: иногда упоминается, что Nesterov Momentum «заглядывает в будущее» и исправляет ошибки на данном шаге оптимизации. Конечно, никто не заглядывает в будущее в буквальном смысле.
В работе Нестерова были предложены конкретные (и довольно магические) константы для импульса, которые получаются из некоторой еще более магической последовательности. Мы приводить их не будем, поскольку мы в первую очередь заинтересованы невыпуклым случаем.
Nesterov Momentum позволяет значительно повысить устойчивость и скорость сходимости в некоторых случаях. Но, конечно, он не является серебряной пулей в задачах оптимизации, хотя в выпуклом мире и является теоретически неулучшаемым.
Также отметим, что ускоренный метод может напрямую примениться к проксимальному градиентному спуску. В частности, применение ускоренного метода к проксимальному алгоритму решения $\ell_1$ регрессии (ISTA) называется FISTA (Fast ISTA).
Общие выводы:
- Добавление momentum к градиентному спуску позволяет повысить его устойчивость и избегать маленьких локальных минимумов/максимумов;
- В выпуклом случае добавление моментного слагаемого позволяет доказуемо улучшить асимптотику и уменьшить зависимость от плохой обусловленности задачи.
- Идея ускорения применяется к любым около-градиентным методам, в том числе и к проксимальным, позволяя получить, например, ускоренный метод для $\ell_1$-регрессии.
Адаптивный подбор размера шага
Выше мы попытались эксплуатировать свойства градиентного спуска. Теперь же пришел момент взяться за больной вопрос: как подбирать размер шага? Он максимально остро встаёт в случае SGD: ведь посчитать значение функции потерь в точке очень дорого, так что методы в духе наискорейшего спуска нам не помогут!
Нужно действовать несколько хитрее.
Adagrad
Рассмотрим первый алгоритм, который является адаптацией стохастического градиентного спуска. Впервые он предложен в статье в JMLR 2011 года, но она написана в очень широкой общности, так что читать её достаточно сложно.
Зафиксируем $\alpha$ – исходный learning rate. Затем напишем следующую формулу обновления:
$$\begin{align}
G_{k+1} &= G_k + (\nabla f(x_k))^2 \
x_{k+1} &= x_k — \frac{\alpha}{\sqrt{G_{k+1} + \varepsilon}} \nabla f(x_k).
\end{align}
$$
Возведение в квадрат и деления векторов покомпонентные. По сути, мы добавляем некоторую квазиньютоновость и начинаем динамически подбирать размер шага для каждой координаты по отдельности. Наш размера шага для фиксированной координаты – это какая-то изначальная константа $\alpha$ (learning rate), деленная на корень из суммы квадратов координат градиентов плюс дополнительный параметр сглаживания $\varepsilon$, предотвращающий деление на ноль. Добавка $\varepsilon$ на практике оставляется дефолтными 1e-8 и не изменяется.
Идея следующая: если мы вышли на плато по какой-то координате и соответствующая компонента градиента начала затухать, то нам нельзя уменьшать размер шага слишком сильно, поскольку мы рискуем на этом плато остаться, но в то же время уменьшать надо, потому что это плато может содержать оптимум. Если же градиент долгое время довольно большой, то это может быть знаком, что нам нужно уменьшить размер шага, чтобы не пропустить оптимум. Поэтому мы стараемся компенсировать слишком большие или слишком маленькие координаты градиента.
Но довольно часто получается так, что размер шага уменьшается слишком быстро и для решения этой проблемы придумали другой алгоритм.
RMSProp
Модифицируем слегка предыдущую идею: будем не просто складывать нормы градиентов, а усреднять их в скользящем режиме:
$$\begin{align}
G_{k+1} &= \gamma G_k + (1 — \gamma)(\nabla f(x_k))^2 \
\end{align}
$$
$$\begin{align}
x_{k+1} &= x_k — \frac{\alpha}{\sqrt{G_{k+1} + \varepsilon}} \nabla f(x_k).
\end{align}
$$
Такой выбор позволяет все еще учитывать историю градиентов, но при этом размер шага уменьшается не так быстро.
Общие выводы:
- Благодаря адаптивному подбору шага в современных оптимизаторах не нужно подбирать последовательность $\alpha_k$ размеров всех шагов, а достаточно выбрать всего одно число – learning rate $\alpha$, всё остальное сделает за вас сам алгоритм. Но learning rate все еще нужно выбирать крайне аккуратно: алгоритм может либо преждевременно выйти на плато, либо вовсе разойтись. Пример приведен на иллюстрации ниже.
Объединяем все вместе…
Adam
Теперь покажем гвоздь нашей программы: алгоритм Adam, который считается решением по умолчанию и практически серебряной пулей в задачах стохастической оптимизации.
Название Adam = ADAptive Momentum намекает на то, что мы объединим идеи двух последних разделов в один алгоритм. Приведем его алгоритм, он будет немного отличаться от оригинальной статьи отсутствием коррекций смещения (bias correction), но идея останется той же самой:
$$\begin{align}
v_{k+1} &= \beta_1 v_k + (1 — \beta_1) \nabla f(x_k) \
\end{align}
$$
$$\begin{align}
G_{k+1} &= \beta_2 G_k + (1 — \beta_2)(\nabla f(x_k))^2 \
\end{align}
$$
$$\begin{align}
x_{k+1} &= x_k — \frac{\alpha}{\sqrt{G_{k+1} + \varepsilon}} v_{k+1}.
\end{align}
$$
Как правило, в этом алгоритме подбирают лишь один гиперпараметр $\alpha$ – learning rate. Остальные же: $\beta_1$, $\beta_2$ и $\varepsilon$ – оставляют стандартными и равными 0.9, 0.99 и 1e-8 соответственно. Подбор $\alpha$ составляет главное искусство.
Зачастую, при начале работы с реальными данными начинают со значения learning rate равного 3e-4. История данного значения достаточно забавна: в 2016 году Андрей Карпатый (Andrej Karpathy) опубликовал шутливый пост в Twitter.
После чего сообщество подхватило эту идею (до такой степени, что иногда число 3e-4 называют Karpathy constant).
Обращаем ваше внимание, что при работе с учебными данными зачастую полезно выбирать более высокий (на 1-2 порядка) начальный learning rate (например, при классификации MNIST, Fashion MNIST, CIFAR или при обучении языковой модели на примере поэзии выбранного поэта).
Также стоит помнить, что Adam требует хранения как параметров модели, так и градиентов, накопленного импульса и нормировочных констант (cache). Т.е. достижение более быстрой (с точки зрения количества итераций/объема рассмотренных данных) сходимости требует больших объемов памяти. Кроме того, если вы решите продолжить обучение модели, остановленное на некоторой точке, необходимо восстановить из чекпоинта не только веса модели, но и накопленные параметры Adam. В противном случае оптимизатор начнёт сбор всех своих статистик с нуля, что может сильно сказаться на качестве дообучения. То же самое касается вообще всех описанных выше методов, так как каждый из них накапливает какие-то статистики во время обучения.
Интересный факт: Adam расходится на одномерном контрпримере, что совершенно не мешает использовать его для обучения нейронных сетей. Этот факт отлично демонстрирует, насколько расходятся теория и практика в машинном обучении. В той же работе предложено исправление этого недоразумения, но его активно не применяют и продолжают пользоваться «неправильным» Adamом потому что он быстрее сходится на практике.
AdamW
А теперь давайте добавим $\ell_2$-регуляризацию неявным образом, напрямую в оптимизатор и минуя адаптивный размер шага:
$$\begin{align}
v_{k+1} &= \beta_1 v_k + (1 — \beta_1) \nabla f(x_k) \
\end{align}
$$
$$\begin{align}
G_{k+1} &= \beta_2 G_k + (1 — \beta_2)(\nabla f(x_k))^2 \
\end{align}
$$
$$\begin{align}
x_{k+1} &= x_k — \left( \frac{\alpha}{\sqrt{G_{k+1} + \varepsilon}} v_{k+1} \color{red}{ + \lambda x_{k}} \right).
\end{align}
$$
Это сделано для того, чтобы эффект $\ell_2$-регуляризации не затухал со временем и обобщающая способность модели была выше. Оставим ссылку на одну заметку про этот эффект. Отметим, впрочем, что этот алгоритм особо не используется.
Практические аспекты
Расписания
Часто learning rate понижают итеративно: каждые условные 5 эпох (LRScheduler в Pytorch) или же при выходе функции потерь на плато. При этом лосс нередко ведет себя следующим схематичным образом:
Помимо этого используют другие варианты «расписаний» для learning rate. Из часто применяемых неочевидных лайфхаков: сначала сделать warmup, то есть увеличивать learning rate, а затем начать постепенно понижать. Использовалось в известной статье про трансформеры. В ней предложили следующую формулу:
$$
lr = d^{-0.5}_{\rm{model}} \cdot \min(step_ num^{-0.5}, step_ num \cdot warmup_ steps^{-1.5}).
$$
По сути, первые $warmup_ steps$ шагов происходит линейный рост размера шага, а затем он начинает уменьшаться как $1/\sqrt{t}$, где $t$ — число итераций.
Есть и вариант с косинусом из отдельной библиотеки для трансформеров.
В этой же библиотеке можно также почерпнуть идею рестартов: с какого-то момента мы снова включаем warmup, увеличивая размер шага.
Большие батчи
Представим ситуацию, что мы хотим обучить свою нейронную на нескольких GPU. Одно из решений выглядит следующим образом: загружаем на каждую видеокарту нейронную сеть и свой отдельный батч, вычисляем стохастические градиенты, а затем усредняем их по всем видеокартам и делаем шаг. Что плохого может быть в этом?
По факту, эта схема в некотором смысле эквивалентна работе с одним очень большим батчем. Хорошо же, нет разве?
На самом деле существует так называемый generalization gap: использование большого размера батча может приводить к худшей обобщающей способности итоговой модели. О причине этого эффекта можно поспекулировать, базируясь на текущих знаниях о ландшафтах функций потерь при обучении нейронных сетей.
Больший размер батча приводит к тому, что оптимизатор лучше «видит» ландшафт функции потерь для конкретной выборки и может скатиться в маленькие «узкие» паразитные локальные минимумы, которые не имеют обобщающий способности — при небольшом шевелении этого ландшафта (distributional shift c тренировочной на тестовую выборку) значение функции потерь резко подскакивает. В свою очередь, широкие локальные минимумы дают модель с лучшей обобщающей способностью. Эту идею можно увидеть на следующей картинке:
Иными словами, большие батчи могут приводить к переобучению, но это можно исправить правильным динамическим подбором learning rate, как будет продемонстрировано далее. Сразу отметим, что совсем маленькие батчи – это тоже плохо, с ними ничего не получится выучить, так как каждая итерация SGD знает слишком мало о ландшафте функции потерь.
LARS
Мы рассмотрим нестандартный оптимизатор для обучения нейронных сетей, которого нет в Pytorch по умолчанию, но который много где используется: Layer-wise Adaptive Rate Scaling (LARS). Он позволяет эффективно использовать большие размеры батчей, что очень важно при вычислении на нескольких GPU.
Основная идея заключена в названии – нужно подбирать размер шага не один для всей сети или каждого нейрона, а отдельный для каждого слоя по правилу, похожему на RMSProp. По сравнению с оригинальным RMSProp подбор learning rate для каждого слоя дает большую стабильность обучения.
Теперь рассмотрим формулу пересчета: пусть $w_l$ – это веса слоя $l$, $l < L$. Параметры алгоритма: базовый learning rate $\eta$ (на который запускается расписание), коэффициент инерции $m$, коэффециент затухания весов $\beta$ (как в AdamW).
for l in range(L): # Цикл по слоям
g_l = stochgrad(w_prev)[l] # Вычисляем стохградиент из батча для текущего слоя
lr = eta * norm(w[l]) / (norm(g_l) + beta * norm(w[l])) # Вычислеяем learning rate для текущего слоя
v[l] = m * v[l] + lr * (g_l + beta * w[l]) # Обновляем momentum
w[l] -= v[l] # Делаем градиентный шаг по всему слою сразу
w_prev = w # Обновляем веса
LAMB
Этот оптимизатор введен в статье Large Batch Optimization For Deep Learning и является идейным продолжателем LARS, более приближенным к Adam, чем к обычному RMSProp. Его параметры – это параметры Adam $\eta, \beta_1, \beta_2, \varepsilon$, которые беруется как в Adam, а также параметр $\lambda$, который отвечает за затухание весов ($\beta$ в LARS).
for l in range(L): # Цикл по слоям
g_l = stochgrad(w_prev)[l] # Вычисляем стохградиент из батча для текущего слоя
m[l] = beta_1 * m[l] + (1 - beta_1) * g_l # Вычисляем моментум
v[l] = beta_2 * v[l] + (1 - beta_2) * g_l # Вычисляем новый размер шага
m[l] /= (1 - beta_1**t) # Шаг для уменьшения смещения из Adam
v[l] /= (1 - beta_2**t)
r[l] = m[l] / sqrt(v[l] + eps) # Нормируем моментум как предписывает Adam
lr = eta * norm(w[l]) / norm(r[l] + llambda * w[l]) # Как в LARS
w[l] = w[l] - lr * (r[l] + llambda * w[l]) # Делаем шаг по моментуму
w_prev = w # Обновляем веса
Усреднение
Теперь снова заглянем в теорию: на самом деле, все хорошие теоретические оценки для SGD проявляются, когда берётся усреднение по точкам.
Этот эффект при обучении нейронных сетей был исследован в статье про алгоритм SWA. Суть очень проста: давайте усреднять веса модели по каждой $c$-й итерации; можно считать, что по эпохам. В итоге, веса финальной модели являются усреднением весов моделей, имевщих место в конце каждой эпохи.
В результате такого усреднения сильно повышается обобщающая способность модели: мы чаще попадаем в те самые широкие локальные минимумы, о которых мы говорили в разделе про большие батчи. Вдохновляющая картинка из статьи прилагается:
На второй и третьей картинке изображено сравнение SGD и SWA при обучении нейронной сети (Preactivation ResNet-164 on CIFAR-100) при одной и той же инициализации.
На первой же картинке изображено, как идеологически должен работать SWA. Также мы видим тут демонстрацию эффекта концентрации меры: после обучения стохастический градиентный спуск становится случайным блужданием по области в окрестности локального минимума. Если, например, предположить, что итоговая точка – это нормальное распределение с центром в реальном минимуме в размерности $d > 10^6$, то все эти точки с большой вероятности будут находиться в окрестности сферы радиуса $\sqrt{d}$. Интуитивную демонстрацию многомерного нормального распределения можно увидеть на следующей картинке из книги Р.Вершинина «High-Dimensional Probability» (слева в размерности 2, справа в большой размерности):
Поэтому, чтобы вычислить центральную точку этой гауссианы, усреднение просто необходимо, по такому же принципу работает и SWA.
Предобуславливание
Теперь мы снова обратимся к теории: скорость сходимости градиентного спуска (даже ускоренного) очень сильно зависит от числа обусловленности задачи. Разумной идеей будет попытаться использовать какие-то сведения о задаче и улучшить этот показатель, тем самым ускорив сходимость.
В теории, здесь могут помочь техники предобуславливания. Но, к сожалению, попытки наивно воплотить эту идею приводят к чему-то, похожему на метод Ньютона, в котором нужно хранить большую-большую матрицу для обучения больших моделей. Способ обойти эту проблему рассмотрели в статье о методе Shampoo, который использует то, что веса нейронной сети зачастую удобно представлять как матрицу или даже многомерный тензор. Таким образом, Shampoo можно рассматривать как многомерный аналог AdaGrad.
В серии нейронных сетей AAC мы охватили широкий круг тем, связанных с пониманием и развитием многослойных нейронных сетей Perceptron. Прежде чем читать эту статью о локальных минимумах, ознакомьтесь с остальными статьями ниже:
- Как выполнить классификацию с помощью нейронной сети: каково восприятие?
- Как использовать простой пример нейронной сети Perceptron для классификации данных
- Как тренировать базовую нейронную сеть восприятия
- Понимание простого обучения нейронной сети
- Введение в теорию обучения для нейронных сетей
- Понять скорость обучения в нейронных сетях
- Продвинутое машинное обучение с многослойным восприятием
- Функция активации сигмоида: активация в нейронных сетях многослойного восприятия
- Как обучить многослойную перцепционную нейронную сеть
- Понимать обучающие формулы и обратное распространение для многослойных персептронов
- Архитектура нейронной сети для реализации Python
- Как создать многослойную perceptrn нейронную сеть в Python
- Обработка сигналов с использованием нейронных сетей: валидация при проектировании нейронных сетей
- Обучающие наборы данных для нейронных сетей: как обучить и проверить нейронную сеть Python
- Сколько слоев и скрытых узлов вам нужна нейронная сеть?
- Как повысить точность скрытого слоя нейронной сети
- Включение смещенных узлов в вашу нейронную сеть
- Понять локальные минимумы в обучении нейронных сетей
Обучение нейронной сети – сложный процесс. К счастью, нам не нужно понимать это полностью, чтобы извлечь из этого пользу: сетевые архитектуры и процедуры обучения, которые мы используем, фактически приводят к функциональным системам, которые достигают очень высокой точности классификации. Тем не менее, есть теоретический аспект обучения, который, несмотря на некоторую абсурдность, заслуживает нашего внимания.
Мы назовем это «проблемой локальных минимумов».
Почему местные минимумы заслуживают нашего внимания?
Ну, я не уверен. Когда я впервые узнал о нейронных сетях, у меня сложилось впечатление, что локальные минимумы действительно являются серьезным препятствием для успешного обучения, по крайней мере, когда речь идет о сложных отношениях ввода-вывода. Однако я считаю, что недавние исследования сводят к минимуму важность местных минимумов. Возможно, новые сетевые структуры и методы обработки уменьшили серьезность проблемы, или, возможно, мы просто лучше понимаем, как нейронные сети действительно переходят к желаемому решению.
Мы рассмотрим текущее состояние минимального локального в конце этой статьи. А пока ответьте на мой вопрос следующим образом: локальные минимумы заслуживают нашего внимания, потому что, во-первых, они помогают нам глубже задуматься о том, что действительно происходит, когда мы обучаем сеть посредством градиентного спуска, и, во-вторых, потому что местные минимумы: или, по крайней мере, они былиРассмотрим существенное препятствие для успешного внедрения нейронных сетей в реальных системах.
Что такое минимум местный?
В части 5 мы рассмотрим «чашу с ошибками», показанную ниже, и описываем обучение как поиск самой нижней точки в этой чаше.
(примечаниеВ этой статье мои изображения и объяснения будут основаны на нашем интуитивном понимании трехмерных структур, но следует помнить, что общие понятия не ограничиваются трехмерными отношениями. Фактически, мы часто используем нейронные сети, размерность которых намного превышает две входные переменные и одну выходную переменную).
Если бы я прыгнул в эту чашу, она каждый раз будет скользить вниз. Неважно, с чего начать, конец в самой низкой точке всей функции ошибки. Эта самая низкая точка глобальный минимум, Когда сеть приблизилась к глобальному минимуму, она оптимизировала свою способность классифицировать данные обучения и В теорииЭто основная цель тренинга: продолжать изменять вес до достижения глобального минимума.
Однако мы знаем, что нейронные сети способны аппроксимировать чрезвычайно сложные отношения ввода-вывода. Показанная выше ошибка не совсем подходит под категорию «чрезвычайно сложная». Это просто график функции (f (x, y) = x ^ 2 + y ^ 2).
Но теперь представьте, что функция ошибки выглядит так:

Или это:
Или это:
Если вы случайно перепрыгиваете на одну из этих функций, вы часто будете скользить к локальному минимуму. Это будет в самой низкой точке локализованной части графика, но это может не быть рядом с глобальной минимум.
То же самое может случиться с нейронной сетью. Градиентный спуск зависит от местный информация, которую мы надеемся вести сеть глобальной минимум. Сеть не имеет предварительных знаний о характеристиках общей поверхности ошибки и, следовательно, когда она достигает точки, которая кажется нижней частью поверхности ошибки на основании местной информации, вы не можете извлечь топографическую карту и определить, что вам нужно обратно в гору чтобы найти точку, которая действительно ниже, чем все остальные.
Когда мы реализуем базовый градиентный спуск, мы говорим сети: «Найдите дно поверхности ошибки и оставайтесь там». Мы не говорим: «Найдите дно поверхности ошибки, запишите ее координаты и продолжайте идти. Вверх и вниз по склону, пока не найдете следующий. Дайте мне знать, когда закончите».
Действительно ли мы хотим найти глобальный минимум?
Разумно предположить, что глобальный минимум представляет собой оптимальное решение, и сделать вывод, что локальные минимумы проблематичны, потому что обучение может «застопориться» в локальном минимуме вместо продолжения к глобальному минимуму.
Я полагаю, что это предположение справедливо во многих случаях, но сравнительно недавнее исследование поверхностей потерь нейронных сетей предполагает, что сети высокой сложности могут фактически извлечь выгоду из локальных минимумов, потому что сеть, которая находит глобальный минимум, должна быть перегружена и, следовательно, быть менее эффективным при обработке новых входных выборок.
Другая проблема, которая возникает здесь, – это поверхностная особенность, называемая седловой точкой; Вы можете увидеть пример на следующем графике. Возможно, что в контексте реальных приложений нейронных сетей седловые точки на поверхности ошибок, на самом деле, являются более серьезной проблемой, чем локальные минимумы.
заключение
Надеюсь, вам понравилась эта дискуссия о локальных минимумах. В следующей статье мы обсудим некоторые методы, которые помогают нейронной сети достичь глобального минимума (если мы хотим именно этого).
Post Views: 164